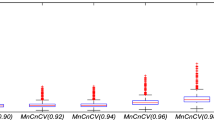
Appendix
Proof of Proposition 3 is given below.
Proof
Following are known integrals with normal pdfs:
$$\begin{aligned} \int z\phi (z) \, d z&= -\phi (z) + C , \\ \int z^2\phi (z) \, d z&= \varPhi (z) - z\phi (z) + C . \end{aligned}$$
We will write \(f\) instead od \(f_Z\) and \(g\) instead of \(g_Z\) for simplicity and expand the basic formula for variance:
$$\begin{aligned} \mathrm{var }_{g}\left[ \mathsf {Q}^i_Z\right]&= \mathbf{E}_{g}\left[ \left( \mathsf {Q}^i_Z\right) ^2\right] - \left( \mathbf{E}_{g}\left[ \mathsf {Q}^i_Z\right] \right) ^2 , \nonumber \\ \mathbf{E}_{g}\left[ \left( \mathsf {Q}^i_Z\right) ^2\right]&= \underbrace{\mathbf{E}_{g}\left[ \frac{f^2}{g^2} \left( 1 - \lambda \right) ^2 Z^2\right] }_{(1)} + \underbrace{\mathbf{E}_{g}\left[ \frac{f^2}{g^2} \frac{\lambda ^2}{\alpha ^2} \left[ Z - u_{Z}\right] _+^2 \right] }_{(2)} + \underbrace{\mathbf{E}_{g}\left[ \frac{f^2}{g^2} \lambda ^2 u_{Z}^2 \right] }_{(3)} \nonumber \\&\quad + \underbrace{2 \mathbf{E}_{g}\left[ \frac{f^2}{g^2} \left( 1 - \lambda \right) \frac{\lambda }{\alpha } Z \left[ Z - u_{Z}\right] _+\right] }_{(4)}\nonumber \\&\quad + \underbrace{2 \mathbf{E}_{g}\left[ \frac{f^2}{g^2} \left( 1 - \lambda \right) \lambda u_{Z}Z \right] }_{(5)} + \underbrace{2 \mathbf{E}_{g}\left[ \frac{f^2}{g^2} \frac{\lambda }{\alpha } \lambda u_{Z}\left[ Z - u_{Z}\right] _+\right] }_{(6)} . \end{aligned}$$
(25)
Next, we calculate all terms from the previous equations:
$$\begin{aligned} \mathbf{E}_{g}\left[ \left( \mathsf {Q}^i_Z\right) \right]&= \int _{ u_{Z}}^{\infty } (z- u_{Z}) \frac{\alpha }{\beta } \frac{\lambda }{\alpha } \frac{\beta }{\alpha } \phi (z) \, d z+ \lambda u_{Z}\\&= \frac{\lambda }{\alpha } \left( \int _{ u_{Z}}^{\infty } z\phi (z) \, d z- u_{Z}\int _{ u_{Z}}^{\infty } \phi (z) \, d z\right) + \lambda u_{Z}\\&= \frac{\lambda }{\alpha } \left( \phi (u_{Z}) - u_{Z}(1 - \varPhi (u_{Z}) \right) + \lambda u_{Z}= \frac{\lambda }{\alpha } \phi (u_{Z}) . \end{aligned}$$
$$\begin{aligned} (1)\quad \mathbf{E}_{g}\left[ \frac{f^2}{g^2} \left( 1 - \lambda \right) ^2 Z^2\right]&= \int _{-\infty }^{ u_{Z}} z^2 \frac{(1-\alpha )^2}{(1-\beta )^2} \left( 1 - \lambda \right) ^2 \frac{1-\beta }{1-\alpha } \phi (z) \, d z\\&\quad + \int _{ u_{Z}}^{\infty } z^2 \frac{\alpha ^2}{\beta ^2}\left( 1 - \lambda \right) ^2 \frac{\beta }{\alpha }\phi (z) \, d z\\&= \frac{1-\alpha }{1-\beta } \left( 1 - \lambda \right) ^2 \left( \varPhi ( u_{Z}) - u_{Z}\phi (u_{Z})\right) \\&\quad + \frac{\alpha }{\beta }\left( 1 - \lambda \right) ^2 \left( 1 - \varPhi ( u_{Z}) +u_{Z}\phi (u_{Z})\right) \\&= \frac{1-\alpha }{1-\beta } \left( 1 - \lambda \right) ^2 \left( 1 - \alpha - u_{Z}\phi (u_{Z})\right) \\&\quad + \frac{\alpha }{\beta }\left( 1 - \lambda \right) ^2 \left( \alpha + u_{Z}\phi (u_{Z})\right) , \end{aligned}$$
$$\begin{aligned} (2)\quad \mathbf{E}_{g}\left[ \frac{f^2}{g^2} \frac{\lambda ^2}{\alpha ^2} \left[ Z - u_{Z}\right] _+^2 \right]&= \int _{ u_{Z}}^{\infty } (z- u_{Z})^2 \frac{\alpha ^2}{\beta ^2} \frac{\lambda ^2}{\alpha ^2}\phi (z) \frac{\beta }{\alpha }\, d z\\&= \frac{\alpha }{\beta } \frac{\lambda ^2}{\alpha ^2} \int _{ u_{Z}}^{\infty } (z^2 - 2 u_{Z}z+ u_{Z}^2) \phi (z) \, d z\\&= \frac{1}{\beta }\frac{\lambda ^2}{\alpha } \left( 1 - \varPhi (u_{Z}) + u_{Z}\phi (u_{Z})\right. \\&\quad \left. - 2 u_{Z}\phi (u_{Z}) + u_{Z}^2 - u_{Z}^2\varPhi (u_{Z}) \right) \\&= \frac{\lambda ^2}{\alpha \beta } \left( \alpha - u_{Z}\phi (u_{Z}) + u_{Z}^2 \alpha \right) , \end{aligned}$$
$$\begin{aligned} (3)\quad \mathbf{E}_{g}\left[ \frac{f^2}{g^2} \lambda ^2 u_{Z}^2 \right]&= \int _{-\infty }^{ u_{Z}} \frac{(1-\alpha )^2}{(1-\beta )^2} \lambda ^2 u_{Z}^2 \frac{1-\beta }{1-\alpha } \phi (z) \, d z+ \int _{ u_{Z}}^{\infty } \frac{\alpha ^2}{\beta ^2} \lambda ^2 u_{Z}^2 \frac{\beta }{\alpha }\phi (z) \, d z\\&= \frac{1-\alpha }{1-\beta } (1-\alpha ) \lambda ^2 u_{Z}^2 + \frac{\alpha }{\beta } \alpha \lambda ^2 u_{Z}^2\\&= \lambda ^2 u_{Z}^2 \left( \frac{(1-\alpha )^2}{1-\beta } +\frac{\alpha ^2}{\beta } \right) , \end{aligned}$$
$$\begin{aligned} (4)\quad 2 \mathbf{E}_{g}\left[ \frac{f^2}{g^2} \left( 1 - \lambda \right) \frac{\lambda }{\alpha } Z \left[ Z - u_{Z}\right] _+\right]&= 2 \int _{ u_{Z}}^{\infty } z(z- u_{Z}) \frac{\alpha ^2}{\beta ^2} \left( 1 - \lambda \right) \frac{\lambda }{\alpha } \frac{\beta }{\alpha } \phi (z) d z\\&= 2\frac{\alpha }{\beta } \left( 1 - \lambda \right) \frac{\lambda }{\alpha } \left( \int _{ u_{Z}}^{\infty } \!z^2 \phi (z) d z- u_{Z}\int _{ u_{Z}}^{\infty } z\phi (z) d z\!\right) \\&= 2 \frac{\lambda (1-\lambda )}{\beta } \left( 1 - \varPhi (u_{Z}) + u_{Z}\phi (u_{Z}) - u_{Z}\phi (u_{Z}) \right) \\&= 2 \frac{\lambda (1-\lambda )\alpha }{\beta } ,\end{aligned}$$
$$\begin{aligned} (5)\quad 2 \mathbf{E}_{g}\left[ \frac{f^2}{g^2} \left( 1 - \lambda \right) \lambda u_{Z}Z \right]&= 2\int _{-\infty }^{ u_{Z}} \frac{(1-\alpha )^2}{(1-\beta )^2} \lambda u_{Z}\left( 1 - \lambda \right) \frac{1-\beta }{1-\alpha } z\phi (z) d z\\&+ 2\int _{ u_{Z}}^{\infty } \frac{\alpha ^2}{\beta ^2} \lambda u_{Z}\left( 1 - \lambda \right) \frac{\beta }{\alpha } z\phi (z) d z\\&= 2\lambda u_{Z}\left( 1 - \lambda \right) \phi (u_{Z}) \left( \frac{\alpha }{\beta } - \frac{1-\alpha }{1-\beta } \right) , \end{aligned}$$
$$\begin{aligned} (6)\quad 2 \mathbf{E}_{g}\left[ \frac{f^2}{g^2} \frac{\lambda }{\alpha } \lambda u_{Z}\left[ Z - u_{Z}\right] _+\right]&= 2 \int _{ u_{Z}}^{\infty } \frac{\alpha ^2}{\beta ^2} \frac{\lambda }{\alpha } \lambda u_{Z}\frac{\beta }{\alpha } (z- u_{Z}) \phi (z) d z\\&= 2 \frac{\alpha }{\beta } \frac{\lambda }{\alpha } \lambda u_{Z}\left( \phi (u_{Z}) - \alpha u_{Z}\right) \\&= 2 \frac{\lambda ^2}{\beta } u_{Z}\left( \phi (u_{Z}) - \alpha u_{Z}\right) , \end{aligned}$$
Substituting all above terms into (25):
$$\begin{aligned} \mathrm{var }_{g}\left[ \mathsf {Q}^i_Z\right]&= \frac{1-\alpha }{1-\beta } \left( 1 - \lambda \right) ^2 \left( 1 - \alpha - u_{Z}\phi (u_{Z})\right) + \frac{\alpha }{\beta }\left( 1 - \lambda \right) ^2 \left( \alpha + u_{Z}\phi (u_{Z})\right) \nonumber \\&\quad + \frac{\lambda ^2}{\alpha \beta } \left( \alpha - u_{Z}\phi (u_{Z}) + u_{Z}^2 \alpha \right) + \lambda ^2 u_{Z}^2 \left( \frac{(1-\alpha )^2}{1-\beta } +\frac{\alpha ^2}{\beta } \right) \nonumber \\&\quad + 2 \frac{\lambda (1-\lambda )\alpha }{\beta }\nonumber \\&\quad + 2\lambda u_{Z}\left( 1 - \lambda \right) \phi (u_{Z}) \left( \frac{\alpha }{\beta } - \frac{1-\alpha }{1-\beta } \right) \nonumber \\&\quad + 2 \frac{\lambda ^2}{\beta } u_{Z}\left( \phi (u_{Z}) - \alpha u_{Z}\right) - \left( \frac{\lambda }{\alpha } \phi (u_{Z}) \right) ^2 . \end{aligned}$$
(26)
Consider a random variable \(X = Z+ \frac{\mu }{\sigma }\). Then by using Proposition 1:
$$\begin{aligned} \mathrm{var }_{g_X}\left[ \mathsf {Q}^i_X\right] = \mathrm{var }_{g_Z}\left[ \mathsf {Q}^i_Z\right] + 2\frac{\mu }{\sigma } \mathbf{E}_{}\left[ \left( \frac{f_Z}{g_Z} - 1 \right) \mathsf {Q}^s_Z\right] + \frac{\mu ^2}{\sigma ^2} \frac{(\alpha -\beta )^2}{\beta (1-\beta )} \end{aligned}$$
(27)
Since \(\mathbf{E}_{}\left[ Z\right] = 0\):
$$\begin{aligned}&\!\!\!\mathbf{E}_{}\left[ \left( \frac{f_Z}{g_Z} - 1 \right) \mathsf {Q}^s_Z\right] = \mathbf{E}_{}\left[ \left( \frac{f_Z}{g_Z} - 1 \right) \left( \left( 1 - \lambda \right) Z+ \lambda \left( u_{Z}+ \frac{1}{\alpha } \left[ Z- u_{Z}\right] _+ \right) \right) \right] \nonumber \\&\quad = \left( 1 - \lambda \right) \underbrace{\mathbf{E}_{}\left[ \frac{f_Z}{g_Z}Z\right] }_{(1)} + \lambda u_{Z}\underbrace{\mathbf{E}_{}\left[ \left( \frac{f_Z}{g_Z} -1\right) \right] }_{(2)} + \frac{\lambda }{\alpha } \underbrace{\mathbf{E}_{}\left[ \left( \frac{f_Z}{g_Z} -1\right) \left[ Z- u_{Z}\right] _+ \right] }_{(3)}\qquad \\&\quad (1) \qquad \mathbf{E}_{}\left[ \frac{f_Z}{g_Z}Z\right] = \int _{-\infty }^{ u_Z} \frac{1-\alpha }{1-\beta } z\phi (z) d z+ \int _{ u_Z}^{\infty } \frac{\alpha }{\beta } z\phi (z) d z= \phi (u_Z)\left( \frac{\alpha }{\beta } - \frac{1-\alpha }{1-\beta } \right) ,\nonumber \\&\quad (2) \qquad \mathbf{E}_{}\left[ \left( \frac{f_Z}{g_Z} -1\right) \right] = \frac{(1-\alpha )^2}{1-\beta } + \frac{\alpha ^2}{\beta } - 1 = \frac{(\alpha -\beta )^2}{\beta (1-\beta )} ,\nonumber \\&\quad (3) \qquad \mathbf{E}_{}\left[ \left( \frac{f_Z}{g_Z} -1\right) \left[ Z- u_{Z}\right] _+ \right] =\int _{ u_Z}^{\infty } \left( \frac{\alpha }{\beta } -1 \right) \left( z- u_Z\right) \phi (z) d z\nonumber \\&\quad \qquad \qquad \qquad \quad \qquad \qquad \qquad \quad \qquad \qquad \, =\left( \frac{\alpha }{\beta } -1 \right) \left( \phi (u_Z) - \alpha u_Z\right) ,\nonumber \end{aligned}$$
(28)
Substituting all above terms into (28):
$$\begin{aligned} \mathbf{E}_{}\left[ \left( \frac{f_Z}{g_Z} - 1 \right) \mathsf {Q}^s_Z\right]&= \left( 1 - \lambda \right) \phi (u_Z)\left( \frac{\alpha }{\beta } - \frac{1-\alpha }{1-\beta } \right) \nonumber \\&\quad + \lambda u_{Z}\frac{(\alpha -\beta )^2}{\beta (1-\beta )} + \frac{\lambda }{\alpha } \left( \frac{\alpha }{\beta } -1 \right) \left( \phi (u_Z) - \alpha u_Z\right) \end{aligned}$$
(29)
Combining (26), (27) and (29):
$$\begin{aligned} \mathrm{var }_{g_X}\left[ \mathsf {Q}^i_X\right]&= \frac{1-\alpha }{1-\beta } \left( 1 - \lambda \right) ^2 \left( 1 - \alpha - u_{Z}\phi (u_{Z})\right) + \frac{\alpha }{\beta }\left( 1 - \lambda \right) ^2 \left( \alpha + u_{Z}\phi (u_{Z})\right) \nonumber \\&\quad + \frac{\lambda ^2}{\alpha \beta } \left( \alpha - u_{Z}\phi (u_{Z}) + u_{Z}^2 \alpha \right) \nonumber \\&\quad + \lambda ^2 u_{Z}^2 \left( \frac{(1-\alpha )^2}{1-\beta } +\frac{\alpha ^2}{\beta } \right) + 2 \frac{\lambda (1-\lambda )\alpha }{\beta }\nonumber \\&\quad + 2\lambda u_{Z}\left( 1 - \lambda \right) \phi (u_{Z}) \left( \frac{\alpha }{\beta } - \frac{1-\alpha }{1-\beta } \right) \nonumber \\&\quad + 2 \frac{\lambda ^2}{\beta } u_{Z}\left( \phi (u_{Z}) - \alpha u_{Z}\right) - \left( \frac{\lambda }{\alpha } \phi (u_{Z}) \right) ^2 \nonumber \\&\quad + 2\frac{\mu }{\sigma } \left( 1 - \lambda \right) \phi (u_Z)\left( \frac{\alpha }{\beta } - \frac{1-\alpha }{1-\beta } \right) \nonumber \\&\quad + 2\frac{\mu }{\sigma } \frac{\lambda }{\alpha } \left( \frac{\alpha }{\beta } -1 \right) \left( \phi (u_Z) - \alpha u_Z\right) \nonumber \\&\quad + \frac{(\alpha -\beta )^2}{\beta (1-\beta )} \left( 2\frac{\mu }{\sigma } \lambda u_{Z}+ \frac{\mu ^2}{\sigma ^2} \right) . \end{aligned}$$
(30)
We want to find a minimum with respect to the parameter \(\beta \) and therefore we differentiate:
$$\begin{aligned} \frac{\partial }{\partial \beta } \left( \mathrm{var }_{g_X}\left[ \mathsf {Q}^i_X\right] \right)&= \frac{1-\alpha }{(1-\beta )^2} \left( 1 - \lambda \right) ^2 \left( 1 - \alpha - u_{Z}\phi (u_{Z})\right) \nonumber \\&\quad - \frac{\alpha }{\beta ^2}\left( 1 - \lambda \right) ^2 \left( \alpha + u_{Z}\phi (u_{Z})\right) \\&\quad - \frac{\lambda ^2}{\alpha \beta ^2} \left( \alpha - u_{Z}\phi (u_{Z}) + u_{Z}^2 \alpha \right) + \lambda ^2 u_{Z}^2 \left( \frac{(1-\alpha )^2}{(1-\beta )^2} -\frac{\alpha ^2}{\beta ^2} \right) \\&\quad - 2 \frac{\lambda (1-\lambda )\alpha }{\beta ^2} + 2\lambda u_{Z}\left( 1 - \lambda \right) \phi (u_{Z}) \left( - \frac{\alpha }{\beta ^2} - \frac{1-\alpha }{(1-\beta )^2} \right) \\&\quad - 2 \frac{\lambda ^2}{\beta ^2} u_{Z}\left( \phi (u_{Z}) - \alpha u_{Z}\right) \\&\quad + 2\frac{\mu }{\sigma } \left( 1 - \lambda \right) \phi (u_Z) \left( - \frac{\alpha }{\beta ^2} - \frac{1-\alpha }{(1-\beta )^2} \right) \nonumber \\&\quad - 2\frac{\mu }{\sigma } \frac{\lambda }{\beta ^2} \left( \phi (u_Z) - \alpha u_Z\right) \\&\quad + \frac{2\alpha ^2\beta -2\alpha \beta ^2-\alpha ^2+\beta ^2}{\beta ^2(1-\beta )^2} \left( 2\frac{\mu }{\sigma } \lambda u_{Z}+ \frac{\mu ^2}{\sigma ^2} \right) . \end{aligned}$$
By Proposition 2 we have that for \(Y = \sigma X\): \(Y \sim \mathbf{N}(\mu ,\sigma ^2)\) & \(\mathrm{var }_{g_Y}\left[ \mathsf {Q}^i_Y\right] = \sigma ^2 \mathrm{var }_{g_X}\left[ \mathsf {Q}^i_X\right] \). Therefore by solving the quadratic equation
$$\begin{aligned} \frac{\partial }{\partial \beta } \left( \mathrm{var }_{g_X}\left[ \mathsf {Q}^i_X\right] \right) = 0 , \end{aligned}$$
we obtain the optimal selection of \(\beta \) with respect to the choice of parameters \(\alpha \) and \(\lambda \) under the assumption of normal distribution. \(\square \)