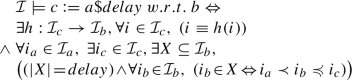Abstract
Distributed, software-intensive systems (e.g., in the automotive sector) must fulfill communication requirements under hard real-time constraints. The requirements have to be documented and validated carefully using a systematic requirements engineering (RE) approach, for example, by applying scenario-based requirements notations. The resources of the execution platforms and their properties (e.g., CPU frequency or bus throughput) induce effects on the timing behavior, which may lead to violations of the real-time requirements. Nowadays, the platform properties and their induced timing effects are verified against the real-time requirements by means of timing analysis techniques mostly implemented in commercial-off-the-shelf tools. However, such timing analyses are conducted in late development phases since they rely on artifacts produced during these phases (e.g., the platform-specific code). In order to enable early timing analyses already during RE, we extend a scenario-based requirements notation with allocation means to platform models and define operational semantics for the purpose of simulation-based, platform-aware timing analyses. We illustrate and evaluate the approach with an automotive software-intensive system.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Distributed, software-intensive systems are becoming more and more complex. For instance, in the automotive domain, the growing number of functionalities has led to thousands of software operations distributed across hundreds of electronic control units (ECUs) that communicate via multiple bus systems [104]. Cyber-physical systems additionally communicate among themselves via wireless ad hoc networks (e.g., automotive vehicle-to-X communication) to provide more advanced functionalities. More generally, these systems increasingly rely on message-based communications. Additionally, the correctness of such systems does not only rely on the functional correctness but also on the time at which actions are performed: They are real-time systems. Since a timing error can lead to human life threat, these systems have to fulfill hard real-time requirements.
For example, the so-called Emergency Braking & Evasion Assistance System (EBEAS) [64, Chapter 4] is an automotive vehicle-to-vehicle driver assistance system, which coordinates with other vehicles (and other in-vehicle ECUs) to autonomously perform actions like emergency braking or evasion of obstacles. Performing emergency braking or evasion only milliseconds too late can harm the life of the passengers and other lives in the environment. Usually, such functionality is subject to end-to-end real-time requirements (e.g., the EBEAS has to perform emergency braking within 50 time units after it detected an obstacle).
Violations of such real-time requirements can occur for various reasons: The ECUs executing the software have restricted resources (e.g., processing power, memory) that increase execution times; the buses and wireless communication media have restricted resources (e.g., throughput, latency) increasing transmission times; the preemption induced by scheduling policies increase response times, etc. More generally, the various properties of the particular resources of the execution platform (resource properties) impact the timing behavior by inducing timing effects (i.e., delays) during the provision of the actual functionality.
Hence, safety standards for the development of software-intensive systems like the automotive-specific ISO 26262 [67] require the estimation of execution times and needed communication resources. Additionally, to make sure that real-time requirements are fulfilled, timing analyses particularly for the highly safety-critical parts of the system under development shall be performed.
Most of the state-of-the-art approaches for timing analyses taking into account the execution platform apply simulative techniques typically implemented in commercial-off-the-shelf tools (e.g., [102, 113]). However, such approaches are applied late in the development process, mostly because they rely on the existence of the execution platform or the compiled platform-specific code [29, 90, 91] (e.g., to compute or measure a worst-case execution time [107]). The detection and fixing of such problems in later engineering phases causes costly development iterations [13, 103]. Consequently, there is a need to apply platform-aware timing analyses earlier in the development process, ideally in the requirements engineering (RE) phase. Particularly, the timing-relevant platform resource properties are typically known or well estimated in such early engineering phases due to the knowledge from prior development projects [60, 91].
For enabling timing analyses already in the early RE phase, related work provides means to specify and analyze timed behavioral models (typically relying on scenario- or automata-based notations), thereby abstracting from the final platform-specific artifacts. However, approaches analyzing timed scenario-based models require to pre-calculate the timing effects induced by the resource properties and to specify them as part of the time-constrained scenarios [45, 55, 56, 119] or as part of design models that are verified against the scenarios [77, 78, 81, 82]. Approaches analyzing automata-based models likewise require specifying the pre-calculated timing effects as part of the automata [2, 11, 70, 71, 79, 98], require detailed task models like the state-of-the-art approaches mentioned above [4, 5], or provide neither simulation nor visualization means to reveal the causes of real-time requirement violations [40]. Summarizing, most of the related work on analyzing timed models requires reenacting, pre-calculating, and explicitly specifying the timing effects induced by the resource properties (e.g., CPU processing power, bus throughput) in a low-level manner as part of the behavioral models. Thus, timing analysts cannot pragmatically (re-)use platform models with specified resource properties stemming from other sources in the development process (e.g., for documentation and design review purposes) and verify them against the real-time requirements, thereby hindering a broad acceptance of such approaches.
In order to relieve the timing analysts from the burden to pre-calculate and to specify the timing effects induced by the platform resource properties as part of behavioral models, we propose an approach to enable early and platform-aware timing analyses already during the RE phase. Since the targeted real-time software-intensive systems strongly rely on message-based communication, we base the real-time requirements on our timed and component-based dialect [17, 64, 65] of the scenario-based notation of Modal Sequence Diagrams (MSDs) [48]. Like the related work, the modeling and analysis means provided by our dialect enable specifying and validating real-time requirements but incorporate platform-specific aspects only insufficiently. Thus, to provide both an abstract specification of the execution platform with its particular resource properties and the allocation of MSD specifications to the execution platform, we furthermore extend platform modeling concepts of the real-time modeling UML profile Marte [93]. Based on the modeling languages mentioned above, we mainly introduce a new operational semantics for platform-aware MSDs dedicated to timing analyses. This semantics encompasses an extended MSD message event handling semantics as inspired by Tindell et al. [115] and particularly encapsulates the computation of the resource properties into platform-induced timing effects. This enables verifying the timing effects w.r.t. the real-time requirements specified by timed MSDs in timing analyses through applying simulation and model checking in our tool suite TimeSquare [28]. To operationalize the semantics, we apply our Gemoc approach [22, 80] for the specification of executable modeling languages. We illustrate and evaluate the approach with the automotive software-intensive system EBEAS.
In terms of related work, our previous works, and article contributions, we reformulate as follows:
-
In contrast to related work, our approach enables that the timing effects do not have to be pre-calculated and explicitly specified as part of the behavioral models, so that scenario- and component-based models with real-time requirements and platform models with resource properties can be independently conceived and (re-)used.
-
In terms of our previous works, we employ our timed [17, 64] and component-based [65] dialect of MSDs [48] for the specification of time-constrained scenario requirements and software architectures. Furthermore, we apply different languages and the tooling of our Gemoc approach [22, 80] for the specification of our platform-aware MSD semantics. Based on our semantics and taking the platform models and the allocated time-constrained scenario requirements and software architectures as input, Gemoc generates timed models based on our Clock Constraint Specification Language [24]. These models are executable in our timing analysis tool suite TimeSquare [28].
-
As the main contribution, we introduce our new operational semantics for platform-aware MSDs through the application of Gemoc, which computes and thereby separates the timing effects from their inducing platform resource properties, and which extends the abstract MSD message event handling semantics as inspired by Tindell et al. [115]. Furthermore, we introduce a new modeling language for enabling the specification of execution platforms with their resource properties and the allocation of MSD specifications to them through extending the platform modeling concepts of the real-time modeling UML profile MARTE [93].
In Sect. 2, we introduce the foundations that our approach relies on. Section 3 outlines an overview of the approach. Subsequently, we present it in more detail by first presenting our modeling language for execution platforms and the allocation from requirement scenarios to them (cf. Sect. 4). In Sect. 5, we provide conceptual extensions and definitions for message event semantics and timing effects to be considered by timing analyses. Based on these ingredients, Sect. 6 presents our operational semantics for timing analyses. Section 7 illustrates the results through an exemplary timing analysis and model checking. We describe the evaluation in Sect. 8 and related work in Sect. 9. Finally, we conclude and sketch future work in Sect. 10.
2 Foundations
In the following, we present the foundations for the comprehension of the particular ingredients that our approach relies on. Section 2.1 introduces general foundations on the kind of timing analysis we focus on. In Sect. 2.2, we present the basics of MSDs. Section 2.3 outlines the Marte profile, and Sect. 2.4 introduces the basics of a language for the specification of executable time models. Finally, Sect. 2.5 outlines the Gemoc approach.
2.1 Timing analysis for hard real-time systems
We focus on hard real-time systems, for which the violation of a hard real-time requirement may cause catastrophic consequences (e.g., people are harmed) [18]. Hard real-time systems must be designed to tolerate worst-case conditions [72]. Typically, a schedulability analysis (e.g., [18]) for hard real-time systems investigates whether jobs with each an activation time, a processing time, and a deadline w.r.t. the activation time can be scheduled on resources so that always all deadlines are met. As motivated in the introduction, such schedulability analyses are demanded by standards for the development of safety-critical systems.
Response time analysis [8, 112] is a well-established a priori analysis technique to check the timing properties of hard real-time systems, which is implemented in many commercial-off-the-shelf tools (e.g., [102, 113]). It computes upper bounds on the response times of all jobs and checks whether all response times fulfill the corresponding timing requirements. In simplified terms, the response time of a job is defined as its activation time plus its processing time plus the sum of potential preemption times by other jobs. A job can be a task to be executed on a processing unit or a message to be transmitted via a communication medium. In the case of tasks, the job processing time is the execution time that a processing unit needs to execute the task. The worst-case execution times of the tasks are inputs to task response time analyses [105], and their computation requires the final platform-specific code or a very detailed model of the system [107].’
In the case of messages, the job processing time is the transmission time that the communication medium needs to transmit the message. Its computation relies on the properties of the physical medium which influence the transmission time (e.g., technology or protocol). Additionally, the activation time also encompasses a queuing jitter that is inherited from the worst-case response time of the sending task [117]. Thus, the results of message response time analyses also depend on the final platform-specific code.
Beyond the timing properties of individual tasks and messages, determining the overall timing properties of distributed real-time systems requires a more holistic view of the system [75]. These timing properties are usually based on event chains starting with an initial system stimulus; involving multiple software components that may be deployed on different ECUs; until the production of an externally observable response event. The timing behavior of event chains converges from the occurrence of task start and completion events, as well as of different events involved in the message transmission. The most used event chain timing property is the end-to-end response time, which is defined as the amount of time elapsed between the arrival of an event at the first task and the production of the response by the last task in the chain [90].
This is of specific importance in our approach, because high-level real-time requirements are usually formulated w.r.t. such end-to-end response times of the event chains. That is, such requirements impose timing constraints between an initial system stimulus and an externally observable response of event chains.
To verify such high-level real-time requirements, existing approaches for end-to-end response time analysis like [29, 36, 88,89,90, 116] still rely ultimately on the response times of the individual jobs and consequently require the final platform-specific implementation. Thus, they can be applied only in late development phases, like the techniques and tools for the analysis of the individual response times.
Here, we rely on the fact that coarse-grained information about the timing-relevant resource properties is mostly known in the early RE phase from prior projects or expert knowledge [60, 91]. Also, we propose to express the real-time requirements based on Modal Sequence Diagrams introduced in the next section.
2.2 Modal Sequence Diagrams (MSDs)
Scenario-based notations enable the intuitive specification and comprehension of message-based interaction requirements, and UML Interactions [96, Clause 17] provide such a notation as a visual modeling language by means of sequence diagrams.
To make UML Interactions more suitable regarding universal/existential properties, the Modal profile [48] syntactically extends UML Interactions with modeling constructs as known from Live Sequence Charts (LSCs) [23]. Therefore, this profile introduces a UML-compliant form of LSCs, called Modal Sequence Diagrams (MSDs). In previous works, based on the Play-out algorithm [50], we extended MSDs with modeling constructs and operational semantics for component-based software architectures [65] and for high-level real-time requirements [17, 64]. The resulting Real-time Play-out approach [17] defined the operational semantics of such timed MSD requirements and thereby enables their simulative validation.
In this paper, we focus on providing modeling constructs and an operational semantics for the early consideration of execution platform impacts on the timing requirements. However, in order to ease the reading of the proposition, we introduce MSD constructs and semantics (and later our approach) based on the EBEAS example (see Fig. 1). The proposed excerpts of the EBEAS example in Fig. 1 highlight a real-time requirement on the automatic emergency braking maneuver in the case of an obstacle detection.
Figure 1 represents a component-based MSD specification (in the middle) together with involved types (in the top) and one of the MSDs (in the bottom).
The next sections describe more in detail the structure of component-based MSD specifications (Sect. 2.2.1) as well as their basic and timed semantics (Sect. 2.2.2).
2.2.1 Structure of MSD specifications
A component-based MSD specification is structured by means of MSD use cases. Each MSD use case encapsulates for a specific functionality several interrelated scenarios, which specify requirements on the message-based interaction behavior to be provided by the system under development.
An MSD use case encompasses the participants involved in providing the functionality, as well as a set of MSDs describing the requirements on the interactions between these participants. Such an MSD specification is subdivided into three parts: Types, collaborations, and interaction behaviors, explained in the following.
UML interfaces and components provide reusable types for all MSD use cases of the specification. The interfaces encompass operations that are used as message signatures in the MSDs. For example, the class diagram for the UML package ObstacleDetection::Interfaces in the top of Fig. 1 contains an interface Decisions, which contains an operation enableBraking. This interface is used as required and provided interface in each one port of the components SituationAnalysis and VehicleControl, respectively (see package ObstacleDetection::Types in Fig. 1). For any MSD use case, the actual component-based software architecture is defined by roles of the components. More precisely, we specify component roles and their interconnections by using an UML collaboration (dashed ellipse symbol) [96, Clause 11.7] (ObstacleDetection in Fig. 1). We distinguish between system component roles that are controlled by the system under development (component symbols) and environment component roles that are controlled by the environment (cloud symbols).
For example, the system components sa: SituationAnalysis and vc: VehicleControl communicate with each other via the connector sa2vc. The interface Decisions typing the ports of the corresponding component types determine which messages can be exchanged through this connector. Additionally, both system component roles in turn interact with the environment component role esc: ElectronicStabilityControl via dedicated connectors.
The MSDs define the behavior of the collaboration (cf. abstract syntax links ownedBehavior). We distinguish MSDs into requirement MSDs (no stereotype applied) and assumption MSDs (an MSD with the stereotype «EnvironmentAssumption» applied). The former ones specify requirements on the interaction behavior of the system under development, whereas the latter ones specify assumptions on the behavior of the environment. For example, the MSD EmcyBraking in the bottom of Fig. 1 is a requirement MSD specifying the emergency braking behavior of the EBEAS in the case the adaptive cruise control detects an obstacle, whereas an assumption MSD is only indicated.
An MSD itself encompasses MSD messages, which are associated with a sending and a receiving lifeline, an operation signature, and a connector.
For example, the lifeline vc: VehicleControl (receiving the enableBraking message) represents the equally named role in the collaboration. Consequently, the enableBraking message is associated with the operation signature from the Decisions interface and is specified to be sent via the connector sa2vc in the software architecture.
Based on the kind of the sender role, MSD messages are further distinguished into environment messages and system messages. The former ones are messages sent by the environment to the system (e.g., obstacle and standstill), whereas the latter ones are messages sent by the system internally (e.g., enableBraking) or to the environment (e.g., emcyBraking).
After this short introduction about the structure of component-based MSD specifications, we explain the basic and timed MSD semantics in the following.
2.2.2 MSD semantics
An MSD progresses as message events corresponding to the specified MSD messages occur in the system at runtime (i.e., during Play-out or an actual system execution). Each MSD message is of two different kinds, where both kinds determine for the corresponding message events their safety and liveness properties, respectively. In this article, we focus on MSD messages that allow no occurrences of message events that the scenario specifies to occur earlier or later (safety) and whose corresponding message events must occur eventually (liveness). Message events that do not correspond to any MSD messages are ignored, that is, they do not influence the progress of the MSDs and the MSDs do not impose requirements on them.
As message events occur that can be correlated by the Play-out algorithm with MSD messages, the MSDs progress. This progress is captured by the cut, which marks for every lifeline the locations of the MSD messages that were correlated with the message events.
For example, Fig. 1 shows for the depicted MSD in the bottom its particular cuts c0–c4.
Timed MSDs allow defining real-time requirements by referring to clock variables, which are adopted from Timed Automata [2] and represent real-value variables that increase synchronously and linearly with time. We distinguish clock resets and time conditions. Clock resets are visualized as rectangles with an hour-glass icon, containing an expression of the form \(c = 0\) over a clock variable c. Time conditions are visualized as hexagons with an hour-glass icon and define assertions w.r.t. clock variables. To this end, each time condition defines an expression of the form \(c \bowtie value\), with a clock c, an operator \(\bowtie \,\in \lbrace <,\le ,>,\ge \rbrace \), and an Integer value value. We distinguish minimal delays (\(\bowtie \,\in \lbrace >,\ge \rbrace \)) and maximal delays (\(\bowtie \,\in \lbrace <,\le ,\rbrace \)).
For example, the MSD in Fig. 1 contains a clock reset and a maximal delay defining that the message events corresponding to all enclosed MSD messages must occur within 50 time units after the message event occurrence corresponding to the MSD message obstacle prior to the clock reset. Such a combination of a clock reset and a time condition forms a real-time requirement. More complex real-time requirements can be formed by specifying multiple MSDs with constraints on overlapping message events (see also our MSD requirement pattern catalog [38] for details).
We opt for applying these existing timed MSD modeling constructs and semantics, instead of ignoring them and adding real-time requirements to the scenarios by means of the Marte profile (cf. next section). By doing so, we do not introduce a further variant of the MSD language and thereby can use the timed MSDs both in Real-time Play-out and in the approach presented in this article.
2.3 Platform modeling and allocation with MARTE
The UML profile Modeling and Analysis of Real-Time Embedded Systems (Marte) [93, 111] provides modeling means for design and analysis aspects for the embedded software part of software-intensive systems. Marte consists of several subprofiles; and we have sought to reuse as much as possible existing suitable concepts from these subprofiles. In the following, we introduce the subprofiles we use and/or extend: Non-functional properties; generic resource modeling; generic quantitative analysis; and allocations.
-
From the Marte subprofile Non-functional Properties Modeling (NFPs) [93, Chapter 7/Annex F.2] and its model library Marte_Library [93, Annex D] we used pre-defined measurement units. We mostly reused measurement units for the time. We also reused intervals for numeric data types, percentages, durations, data sizes, and transmission rates.
-
The Marte subprofile Generic Resource Modeling (GRM) [93, Chapter 10/Annex F.4] provides modeling means for the specification of generic resources of execution platforms. From this subprofile, we reuse modeling concepts for memory resources, processing resources (with a relative speed factor), communication media (with a transmission rate and blocking time), schedulers (with a scheduling policy), and resource usages (with operation execution times and message sizes).
-
The Marte subprofile Generic Quantitative Analysis Modeling (GQAM) [93, Chapter 15/Annex F.10] provides modeling means for the specification of generic and quantitative aspects relevant to automatic analysis techniques. From this subprofile, we reused so-called analysis contexts, which encompass workload behaviors based on the distribution of stimulus events.
-
The Marte subprofile Allocation Modeling (Alloc) [93, Chapter 11/Annex F.5] provides modeling means for the specification of allocations of logical elements (i.e., application software) to physical and technical elements (i.e., execution platform). From this subprofile, we reused the «allocate» stereotype, which enable the specification of a directed allocation link between software and execution platform components, which are part of an MSD specifications (cf. Sect. 2.2.1).
2.4 Clock Constraint Specification Language (CCSL)
Associated with the Marte profile, we proposed in previous work [24, 28] the Clock Constraint Specification Language (CCSL) dedicated to timing specifications. This language is formally defined and tooled to enable the analysis of resulting specifications. CCSL is a formal declarative language for the modeling and manipulation of time in real-time embedded systems [7], initially and informally introduced in Marte [93, Chapter 9/Annex C.3]. The formalism bases on the notion of logical time [37, 76], which was originally designed for distributed and concurrent systems, but which was also used in synchronous languages. CCSL generalizes different descriptions of time, based on the notion of clocks, a clock being an ordered set of instants (or ticks) named \(\mathcal {I}\). The notion provides a sound way to mix synchronous and asynchronous constraints between clocks. Such a mix enables the symbolic specification of partial order sets on the instants of clocks, which are well suited for the description of a large set of model control flow (e.g., [41, 42, 73, 85, 101]).
Solving a CCSL model (i.e., doing a run) results in a schedule. A schedule \(\sigma \) over a set of clocks C is a possibly infinite sequence of steps, where a step is a set of ticking clocks \(\sigma : \mathbb {N}\rightarrow 2^C\). For each step, one or several clock(s) can tick depending on the constraints.
The operational semantics of CCSL models [6] specifies how to construct the acceptable schedules step by step and is given as a mapping to a Boolean expression on \(\mathscr {C}\), where \(\mathscr {C}\) is a set of Boolean variables in bijection with C. For any \(c \in \mathscr {C}\), if c is valued to true, then the corresponding clock ticks; if valued to false, then it does not tick. Note that if no constraints are defined, each Boolean variable can be either true or false and, consequently, there are \(2^n\) possible futures for all steps, where n is the number of clocks.
Each time a constraint is added to the specification, it adds Boolean constraints on \(\mathscr {C}\). The Boolean constraints depend on the definition of the constraint and its internal state. When several constraints are defined, their Boolean expressions are put in conjunction so that each added constraint reduces the set of acceptable schedules. (It is a trace refinement according to [3].)
CCSL models are inputs to our tool suite TimeSquare [28], which supports their simulation with the generation of timing diagrams, the animation of UML models, etc. It also supports the exhaustive simulation (when the state space is bounded), enabling the model checking of CCSL models. TimeSquare has been applied for the timing analysis (cf. Sect. 2.1) of software-intensive systems (e.g., [20, 41, 42, 84, 85, 101]).
For a CCSL model, the actual constraints can be specified by means of two ways explained in the following sections. On the one hand, CCSL provides pre-defined constraints on language level (metamodel level M2) that the engineer can call and pass arguments to at model level (metamodel level M1) (cf. Sect. 2.4.1). On the other hand, a CCSL extension enables the engineer to specify user-defined constraints that can be used like the pre-defined ones afterward (cf. Sect. 2.4.2). Finally, a CCSL model, either based on pre- or user-defined constraints, can be used to perform an exhaustive state space exploration (if the state space is finite) and model checking (cf. Sect. 2.4.3).
2.4.1 Pre-defined CCSL constraints
CCSL defines the two constraint kinds clock expressions and clock relations. André [6] formalizes a set of pre-defined CCSL constraints, which TimeSquare provides as a model library so that these constraints can be conveniently used during the specification and the TimeSquare-based simulation of CCSL models. In the following, we explain the pre-defined clock expressions and relations that we apply in this article.
Clock relations impose (synchronous or asynchronous) orderings between the instants of participating clocks.
-
\(\boxed {\subset }\): SubClock (subClock: Clock, superClock: Clock ) This relation constrains all ticks of subClock to coincide with a tick of superClock but not vice versa. That is, subClock can only tick when superClock ticks, but it does not have to.
 (1)
(1)where the coincidence relation \(\equiv \) is an equivalence relation (reflexive, symmetric and transitive). It reflects the fact that two instants have the exactly same logical time.
-
\(\boxed {=}\): Coincides (clock1: Clock, clock2: Clock )
This relation constrains all instants of clock1 and clock2 to coincide. That is, the events represented by clock1 and clock2 must occur simultaneously.
 (2)
(2) -
\(\boxed {\prec }\): Precedes (leftClock: Clock, rightClock: Clock )
This relation constrains the \(k^{th}\) instant of leftClock to precede the \(k^{th}\) instant of rightClock \(\forall k \in \mathbb {N}\). That is, the event represented by leftClock always occurs before rightClock.
 (3)
(3)where the precedence relation \(\mathrel {\prec }\) is a strict order relation (irreflexive, asymmetric, and transitive) between two instants. Figure 2 depicts an exemplary TimeSquare simulation run of this clock relation. In this example, the relation enforces that clock1 always ticks before clock2 ticks.
-
\(\boxed {\preccurlyeq }\): NonStrictPrecedes (leftClock: Clock, rightClock: Clock) This non-strict version of the Precedes relation constrains the \(k^{th}\) instant of leftClock to coincide with or precede the \(k^{th}\) instant of rightClock \(\forall k \in \mathbb {N}\). That is, the events can also occur simultaneously.
 (4)
(4)where the non-strict precedence relation \(\mathrel {\preccurlyeq }\) is defined by \(\mathrel {\prec }\vee \equiv \).
Clock expressions define a new clock based on other clocks and possibly extra parameters. In the following, we describe the expressions used in this article.
-
\(\mathrel {+}\): Union ( clocks: Set(Clock) ) The clock specified by this expression ticks whenever one of the clocks in its parameter set clocks ticks. Consequently, the instant set of the resulting clock (named c here) is such that:
 (5)
(5)where \(\equiv \) means coincides with. Intuitively, for all instants of the clocks a and b, there exists an instant of the clock c and there is no instant of c that does not coincide with an instant of a, or b, or both. Figure 3 depicts an exemplary TimeSquare simulation run of this clock expression. In this example, a new clock unionOfCl1Cl2 is specified that ticks whenever one or both of the argument clocks clock1 and clock2 tick.
-
$: DelayFor (clockForCounting: Clock, clockToDelay: Clock, delay: Integer) This expression delays any tick of the clock clockToDelay by delay ticks w.r.t. a reference clock clockForCounting. Note that we apply in this article an always ticking clock globalTime as argument for the reference clock parameter clockForCounting, so that the clock defined by this expression simply ticks delay instants after clockToDelay (named a below).
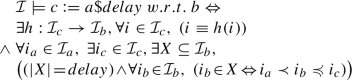 (6)
(6)meaning that it exists X instants of b between instants of a and the delayed instant of c, and instants of c coincide with some instants of b.
-
\(every ... on\): PeriodicOffsetP (baseClock: Clock, period: Integer) The clock specified by this expression ticks any periodth tick of the baseClock. Note that we apply in this article an always ticking clock globalTime as argument for baseClock so that the clock defined by this expression simply ticks any periodth tick.
 (7)
(7)where \(idx(i_{bc})\) is the index of the \(i_{bc}\) instant in \(\mathcal {I}_{bc}\).
-
\(\mathrel {\vee }\): Sup ( clocks: Set(Clock) ) The clock specified by this expression ticks with a clock in the parameter set that does not precede the other clocks; that is, it specifies the supremum of the particular instant sets.
 (8)
(8)meaning that there is no clock d being slower than a or b or being faster than c.
We provide the whole formal semantics definition in [24]. These clock constraints are integrated in our tool suite TimeSquare. Additionally, to ease the application of constraints to specific domains, it is possible to specify user-defined constraints, as introduced in the next subsection.
2.4.2 User-defined constraints
To ease the specification of domain-specific CCSL constraints, we extended CCSL in prior work with the Model of Concurrency and Communication Modeling Language (MoCCML) [25, 26]. MoCCML is a specific form of automata that integrates seamlessly with the semantics of CCSL. The automata are a way to specify clock relations, which can be simulated in TimeSquare and stored in user-defined model libraries.
Exemplary TimeSquare simulation run of the MoCCML relation depicted in Fig. 4
For example, Fig. 4 depicts the MoCCML relation MyUser-definedRelation, which has three clock parameters and a local Integer variable counter initialized with zero. Figure 5 depicts a corresponding exemplary TimeSquare simulation run that initializes three clocks and applies the clock relation myRelation typed by the MoCCML relation on them. The automaton specifies two states A and B with a transition from one state to the other for each of the states. Such transitions specify possibly coincident parameter clock triggers, guards, and effects. For example, the transition from A to B fires when both the clock parameters cl1 and cl2 (i.e., the clock arguments clock1 and clock2 in the simulation run) tick simultaneously and additionally the guard [counter < 1] holds. When the transition fires, its effect counter++ increments the counter. The transition from state B to A fires on the tick of the clock parameter cl3 (i.e., the clock clock3 in the simulation run) and sets the counter to zero.
The triggers of a transition that leave a state specify which clocks are allowed to tick in this state. For example, the clock parameter cl3 is not allowed to tick in state A, and the clock parameters cl1 and cl2 are not allowed to tick in state B. Furthermore, when in state A, the clocks cl1 and cl2 are forced to tick simultaneously to fire the transition. We provide all the details on the formal semantics in [25].
2.4.3 Model checking CCSL models
TimeSquare is a direct implementation of the formal operational semantics as specified in our previous work [25]. As such, the state of each constraint during the simulation is clearly defined, so that it is also for a CCSL model. Consequently, it is possible based on a CCSL model to exhaustively explore its acceptable simulations. Each time a new state is reached, it is compared to already visited states. If it does not exist, it is added to the visited states, otherwise, a new transition to an existing visited state is created, and it creates a loop representing an acceptable periodic behavior of the CCSL model. In case the set of possible simulations is computed completely, it means that the whole state space is also computed completely and can be serialized. In TimeSquare, such state spaces are typically serialized in the dot language [30] as well as in the Aldebaran format [1]. The resulting files (and consequently the CCSL model) can be verified against properties written in the Model Checking Language [86].
2.5 Specifying operational semantics with GEMOC
According to Harel and Rumpe [51], a modeling language consists of an abstract syntax specifying the language concepts and their relations, a semantic domain describing the language meaning, and a semantic mapping relating the language concepts to the semantic domain elements. Our Gemoc approach [22, 80] enables to flexibly specify operational semantics for a modeling language following these definitions.
Specifically, the semantic domain is specified by means of a Model of Concurrency and Communication (MoCC). This MoCC is defined by semantic constraints in the form of pre-defined CCSL constraints (cf. Sect. 2.4.1) as well as user-defined MoCCML constraints (cf. Sect. 2.4.2). The MoCC defines the concurrency, the synchronizations, and the possibly timed way the elements of a program interact during an execution. The semantic mapping is specified by the declaration of Domain-Specific Events (DSEs), which associate the abstract syntax and the MoCC. The DSEs are specified by means of our declarative Event Constraint Language (ECL) [27]. ECL is an extension of the Object Constraint Language [94], augmented with the notions of DSEs as well as behavioral invariants, which use CCSL and MoCCML constraints.
The approach is implemented in our modeling language workbench Gemoc Studio [16] for building and composing executable modeling languages. Gemoc Studio takes a language metamodel, an ECL mapping specification, and semantic constraints specified through a MoCC as inputs and automatically derives a modeling workbench with simulation and debugging facilities. Specifically, it automatically derives a dedicated QVTo model transformation [95]. This derived model transformation takes an instance of the language metamodel as input and generates a CCSL model that parameterizes an execution engine based on TimeSquare. The model transformation maps the associated DSEs to CCSL clocks based on the ECL mapping specification and applies the semantic constraints from the behavioral invariants on these clocks.
3 Approach overview
As outlined in the introduction, our approach encompasses three main ingredients:
-
1.
We propose a Marte-based (cf. Sect. 2.3) UML profile to augment the timed and component-based version of the scenario notation Modal Sequence Diagrams (MSDs) (cf. Sect. 2.2) with platform aspects. This encompasses specification means for a) an execution platform model together with timing-relevant resource properties, b) the allocation of MSD specifications onto these platform models, and c) analysis contexts to be considered during the timing analyses. We call the resulting models platform-specific MSD specifications and describe them in Sect. 4.
-
2.
We conceptually extend the message event semantics for scenario notations in general and MSDs in particular by introducing additional event kinds that occur during the execution of the software on its target platforms. This enables time to elapse between such events during our end-to-end response time analyses, and consequently to introduce platform-specific delays (cf. Sect. 2.1). We also provide means to compute these different delays based on the resource properties defined in platform-specific MSD specifications, which we describe in Sect. 5.
-
3.
The main contribution is the specification of platform-aware MSD operational semantics dedicated to timing analyses. We apply the Gemoc approach (cf. Sect. 2.5) to declaratively specify these operational semantics, which formalizes and spawns the platform-induced timing behavior of MSD specifications. Based on the semantics specification, Gemoc automatically derives CCSL models that are input to the timing simulation and model checking tool TimeSquare (cf. Sect. 2.4). We present the semantics specification in Sect. 6 and an illustrating timing analysis in Sect. 7.
Figure 6 gives an overview of our application of the Gemoc approach. The Abstract Syntax of conventional (i.e., component-based and timed) MSD specifications is defined at the language level (metamodel level M2) by several parts of the UML metamodel and the Modal profile (cf. Sect. 2.2). We extended this Abstract Syntax by introducing platform and timing analysis aspects through our Marte-based TAM profile. The Mapping Specification declares Domain-Specific Events (DSEs) in the context of Abstract Syntax concepts and constrains their behavior through Semantic Constraints applied by using the Event Constraint Language (ECL) (cf. Sect. 2.5). The set of Semantic Constraints defines the Model of Concurrency and Communication (MoCC) by means of Pre-defined CCSL Constraints (cf. Sect. 2.4.1) as well as User-defined MoCCML Constraints (cf. Sect. 2.4.2).
At the model level (metamodel level M1), we provide a Preprocessing QVTo [95] model transformation that takes a Platform-specific MSD Specification as input and computes derived properties. That is, based on the resource properties, this transformation computes delays, which we conceptually present in Sect. 5. The output is a Platform-specific MSD Specification with Computed Static Delays, which is input to another QVTo model transformation MSD-to-CCSL Transformation. This model transformation is automatically derived by Gemoc Studio from our declared DSEs and their MoCC. It encodes the functional and real-time requirements as well as the pre-computed delays and further timing-relevant resource properties into constrained timing effects as part of a CCSL Model. At runtime level (M0), a timing analyst can simulate such CCSL models in TimeSquare to reveal potential real-time requirement violations.
4 The TAM profile for platform-specific interactions
Conventional component-based and timed MSD specifications as introduced in Sect. 2.2 define platform-independent requirement specifications with real-time constraints; i.e., the software architecture and the MSD specifications have no correlation to any concrete target execution platform. In this paper, we propose to consider the timing behavior emerging from the allocation of component-based MSD specifications to concrete target execution platforms, which we together call platform-specific MSD specifications.
In order to support the modeling of platform-specific MSD specifications, we present in this section the most important concepts of our Timing Analysis Modeling (TAM) UML profile: Execution platforms including the specification of the resource properties that have to be considered in the timing analysis (and consequently in the proposed platform-specific MSD semantics), allocations of logical software components to the platform elements, and analysis contexts. All these concepts extend existing concepts from the Marte UML profile [93] (cf. Sect. 2.3). The overall profile (as fully presented in [61, Section 4.6.1]) encompasses 5 subprofiles containing 29 stereotypes with 54 tagged values (including tagged values inherited from Marte) and stems from a literature review on resource properties that impact the timing behavior [12, Chapter 3]. We do not present the full TAM profile here but illustrate its use through a platform-specific MSD specification for the EBEAS example, which will also be used as basis to explain the extension of the MSD semantics amenable to timing analysis (cf. Sect. 6).
In the following, we explain the most important stereotypes by illustrating their application to an EBEAS execution platform model depicted in Fig. 7. Therefore, we add platform-specific information to the platform-independent MSD specification introduced in Fig. 1. In Sect. 4.1, we explain how we specify execution platforms with our TAM profile. Subsequently, we explain the allocation of the software components to the resulting execution platform elements in Sect. 4.2. Finally, we present the specification of application software timing properties in Sect. 4.3 and the definition of analysis contexts in Sect. 4.4.
4.1 Specifying execution platforms
We provide three subprofiles for the specification of concrete execution platforms together with the properties that impact the timing behavior of the system. For instance, the bottom of Fig. 7 (Platform Model package) illustrates the use of the subprofiles to define the EBEAS execution platform model. In the following subsections, we use this package to illustrate the application of the three subprofiles: The hardware execution platform (Sect. 4.1.1), the real-time operating system (Sect. 4.1.2), and the communication infrastructure (Sect. 4.1.3).
4.1.1 Specifying the hardware processing
In this section, we illustrate means for the specification of hardware elements and processing units. The TamECU is an extension of the Marte stereotype GRM::Resource, which serves as a container for other elements of the hardware platform (e.g., the memory units, the communication media, the peripherals, the processing units or the operating system). The stereotype TamProcessingUnit, contained by the TamECU, extends the Marte stereotype GRM::ProcessingResource. It describes the properties of the processing unit of an ECU or of a microcontroller. Among further properties, it inherits the tagged value speedFactor, which describes the relative speed w.r.t. to the normalized speed of a reference processing unit [93, Section 10.3.2.10]. Furthermore, it adds the tagged value numCores, which specifies the amount of cores that the processing unit provides and consequently the number of tasks that can be handled concurrently.
For example, the EBEAS execution platform (Platform Model package of Fig. 7) contains two microcontrollers («TamECU») :\(\mu \) C1 and :\(\mu \) C2. Both of them specify each 1 processing unit («TamProcessingUnit»), respectively :PU\(\mu \) C1 and :PU\(\mu \) C2; and both of them are single-core. However, according to their speed factor value, the :PU\(\mu \) C2 processing unit is two times faster than :PU\(\mu \) C1.
4.1.2 Specifying the real-time operating system
In this section, we illustrate means to specify timing-related properties of real-time operating systems, which run on ECUs or microcontrollers and provide services for the application software. The stereotype TamRTOS describes properties of such real-time operating systems. Among others, it enables the specification of shared resources, operating system services, and communication channels on operating system level for ECU-internal communication. In the following, we focus on the specification of the operating system’s scheduler since the scheduling strategy strongly impacts the timing behavior of the system. For this purpose, we provide the stereotype TamScheduler, which extends the Marte stereotype GRM::Scheduler. Besides specifications means of properties like the overhead introduced by the scheduler, it inherits two tagged values: the scheduling policy (schedPolicy, e.g., fixed priority or round-robin), and the preemption capability (isPreemptible).
For example, in the execution platform of the EBEAS, the schedulers of both :PU\(\mu \) C1 and :PU\(\mu \) C2 processing units depicted in Fig. 7 implement the most prominent [92, 112] real-time operating system scheduling policy FixedPriority and are specified to be non-preemptible. In this policy, all tasks have fixed priorities so that the scheduler dispatches the highest priority task among the ready tasks again and again after the task that is executing has finished. This scheduling strategy is supported by the widespread real-time operating systems of AUTOSAR [9] and OSEK/VDX [66], for example.
4.1.3 Specifying the communication infrastructure
In this section, we illustrate means for the specification of the infrastructure for the communication between distributed components. We provide the stereotype TamComConnection, which extends the Marte stereotype GRM::CommunicationMedia. It provides additional properties compared to the communication media stereotype, but we focus here on the most important ones that are inherited from Marte. The first important property of a communication medium is its latency, which is specified through the inherited blockT tagged value. The second important property of a communication medium is its throughput, specified through the inherited capacity tagged value.
Furthermore, the network interfaces between a TamECU and a TamComConnection need time to encode messages from the software representation to a representation suitable for the transport via a communication medium and vice versa. Such properties are captured as part of the TamComInterface stereotype for ports of TamECUs, inter alia. The TamComInterface stereotype extends the Marte stereotype GQAM::GaExecHost and inherits two tagged values representing the overhead duration implied by the encoding/decoding of the information to and from a communication media: commTxOvh and commRcvOvh.
For example, in the execution platform of the EBEAS, one bus ( Can Bus) is used to communicate between the two ECUs. The throughput of the «TamComConnection» Can Bus connector is set to 100kbit/s and its latency is set to 1ms. Additionally, the communication interface of :\(\mu \) C1’s port («TamComInterface») specifies a message encoding overhead of 1ms (commTxOvh=1ms), and the communication interface of :\(\mu \) C2’s port specifies a message decoding overhead of 1ms (commRcvOvh=1ms).
4.2 Specifying allocations
The Marte subprofile Alloc provides means to allocate software elements to resources of execution platforms (cf. Section 2.3). We reuse the Alloc::Allocate stereotype to specify allocations of MSD application elements onto TAM execution platform elements. This stereotype defines a link that can be used to allocate software components onto processing units, as well as logical connectors onto communication media.
For instance, in the platform-specific EBEAS example, the software components sa: SituationAnalysis and vc: VehicleControl are, respectively, allocated to the :\(\mu \) C1 and :\(\mu \) C2 microcontrollers. This is illustrated in Fig. 7 by the «allocate» links from the logical software components as part of the collaboration to the «TamECU» microcontrollers as part of the execution platform. Analogously, logical connectors between the software components in the collaboration are allocated to «TamComConnection» links in the Platform Model. For instance, the logical connector sa2vc between sa: SituationAnalysis and vc: VehicleControl is allocated to the Can Bus connecting :\(\mu \) C1 and :\(\mu \) C2.
4.3 Defining the software timing properties
In this section, we illustrate means to specify information about the estimated resource consumption of the application software. Its most important element is the TamOperation stereotype, which inherits tagged values from the Marte stereotype GRM::ResourceUsage [93, Section 10.3.2.13]. It is used to specify the platform-specific timing-related aspects of the operations used as MSD message signatures. We consider here only the two most important tagged values: execTime and msgSize. The tagged value execTime specifies the best-/worst-case execution time of an operation with respect to a processing unit with a speed factor of 1. The msgSize specifies the size of the message associated with the operation.
For instance, in the EBEAS example, both the «TamOperation»s obstacle and trajectoryBeacon on the right-hand side of Fig. 7 have a worst-case execution time of 5ms (i.e., the worst-case execution time is specified through one value). In contrast, the operation enableBraking has, specified by the interval value, a best-case execution time of 6ms and a worst-case execution time of 9ms. Note that since the enableBraking operation is part of the vc: VehicleControl, which is allocated to the :\(\mu \) C2 processing unit; and that :\(\mu \) C2 has a speed factor of 2, then the actual best-/worst-case execution time of enableBraking spans an interval of \([3\mathrel {..}4.5]ms\). Additionally, the enableBraking operation is associated with a message whose size is 500bit, and its actual message transmission time has to be calculated based on this size w.r.t. the throughput of the Can Bus. These are concrete examples of timing effects (i.e., concrete delay times in an execution context) that are induced by the specified resource properties.
4.4 Specifying analysis contexts
In this section, we illustrate means to specify the timing behavior of the system environment. More precisely, it defines a set of timed scenarios that make explicit the hypothesis under which the timing behavior of the system is realized. Such simulation scenarios are called analysis contexts [111, Chapter 9] (cf. Section 2.3).
The main stereotype of the corresponding TAM subprofile is the TamAnalysisContext, which extends the Marte stereotype GQAM::GaAnalysisContext. This stereotype references the platform under analysis and the concrete workload that defines the timed scenarios. The workload is specified through the TamWorkloadBehavior stereotype, which extends the GQAM::GaWorkloadBehavior stereotype. From the extension, it inherits the tagged values demand and behavior that, respectively, define the analysis (timing) assumptions on the environment on the one hand and the system expected (timing) requirements on the other hand. In our context, the behaviors are the requirement MSDs as presented earlier while the demands are assumption MSDs (cf. Section 2.2) triggering the system behavior, where the timing of the environment message is constrained by an arrival pattern. For this purpose, we provide the TAM stereotype TamAssumptionMSD that refines the Modal stereotype EnvironmentAssumption and references an arrival pattern.
We support periodic and sporadic arrival patterns. A periodic arrival pattern, specified by the stereotype TamPeriodicPattern, constrains the environment message to occur periodically every period time units. We currently do not support explicit jitter deviations from the periodical occurrences, as this timing information would be very detailed in the early RE phase. However, if a jitter is known and as large that a requirements engineer wants to specify it, sporadic arrival patterns can be applied. These are specified by the stereotype TamSporadicPattern and constrain an environment message to occur with a uniform distribution between a minArrivalRate and/or a maxArrivalRate.
For example, Fig. 8 depicts an analysis context for the EBEAS. The entry point is the «TamAnalysisContext» Ebeas AnalysisContext. It references the Ebeas Platform container depicted in the bottom of Fig. 7 as well as the «TamWorkloadBehavior» Ebeas Workload. The Ebeas Workload references the behavior MSDs depicted or indicated in Fig. 1. Furthermore, the workload references demand assumption MSDs. These specify that the trajectoryBeacon message occurs periodically every 25ms and that the obstacle message occurs sporadically with a rate ranging from 50ms to 55ms, respectively.
5 Definition of interaction events and delays required for timing analyses
The existing operational semantics for platform-independent MSD specifications as defined by Real-time Play-out [17] only considers synchronous messages, where the events of sending and receiving a message at runtime coincides and no notion of tasks exists. This abstraction is well suited to analyze idealized systems but is not adequate for platform-aware analyses. Such analyses require considering different delays introduced by the actual execution on a platform. In order to define these delays, we introduce in this section additional message event kinds, in between which the delays are defined. We associate each message event kind with an equally named lifeline location for MSD messages. To ease readability, we refer to the event kinds and the associated lifeline locations in an undifferentiated way.
According to Tindell et al. [115], four kinds of delays are required for the analysis of distributed real-time systems: the message dispatch delay, the message transmission delay, the message consumption delay and the task execution delay (see Fig. 9). These delays are based on locations allowing a more fine-grain cut progression. In case the execution platform does not introduce some of the delays, then the associated events occur immediately one after the other (i.e., at the next instant). In the other case, these delays usually contain two parts, a so-called static part, which can be computed statically according to the properties of the system; and a so-called dynamic part which dynamically emerges from certain workload situation at runtime due to mutual resource exclusion. The static part of the delays and their computation are defined in the remainder of the section and technically implemented as part of the preprocessing transformation mentioned in Sect. 3, whereas the handling of the dynamic part is presented in Sect. 6.2.2.
Figure 9 illustrates the location kinds, the fine-grained cuts, and the delays for the enableBraking and emcyBraking MSD messages.
In the definitions of the delays, instead of considering only the worst case (execution/transmission) delays, we also consider their best cases, which are likewise of high interest since they potentially modify the access orders to mutually exclusive resources [10, 19, 100]. Thus, we compute both lower and upper bounds for all delays and define them as intervals (cf. the specification of best-/worst-case execution times in Sect. 4.3). For space reasons, we only show hereafter the formulas for each upper bound, where the corresponding lower bounds are computed analogously.
The delay definitions presented in the following encompass derived properties (prefixed with a / as in UML). These derived properties are calculated based on a variety of detailed property values as part of the TAM platform models. Furthermore, we encapsulate behind the derived properties the distinct delay computations regarding message exchange between software components allocated to different ECUs (i.e., distributed communication) or to the same ECU (i.e., ECU-internal communication). We only outline the particular ingredients of the derived properties in the following and present the full computations behind them in detail in [61, Section 4.6.1.2].
5.1 Message transmission delays
The use of communication media and communication protocols (e.g., the properties of the connector Can Bus in Fig. 7) causes a message transmission delay, which must be taken into account by a timing analysis [115]. In order to consider this delay, we encompass the concept of synchronous and asynchronous messages introduced by Harel’s original Play-out semantics [50] for Live Sequence Charts (LSCs) [23]. In other words, we distinguish between message send events and message reception events. In case the platform is not defined, such events coincide and correspond to synchronous messages as in Real-time Play-out [17]. However, once the platform is defined, these events are not synchronously correlated with a whole MSD message. In contrast, a causality is defined between the message send and the message reception location of the corresponding MSD message, respectively. See, for instance, the enableBraking message in Fig. 9, where the cut c1.2 marks that the message is sent but not yet received, whereas the cut c1.3 marks that the message is received but not yet consumed.
The message transmission delays encompass the overall propagation latency (i.e., net latency plus potential overheads) of the communication channel as well as the time to transmit the message. This transmission time depends on the overall message size (i.e., net message size plus control overheads like check sums) in relation to the overall throughput (i.e., media throughput minus potential overhead deductions) of the communication channel. In case of a distributed communication, this overall throughput encompasses its net throughput minus the percentage transmission overhead of the applied transmission protocol and of the applied middleware communication services. Thus, we compute the upper bound of the message transmission delay for an MSD message m as
where m.connector is a UML::Connector associated with m, m.connector.supplier is a TamComConnection (distributed communication) or a TamOSComChannel (ECU-internal communication) that the connector is allocated to, and m.signature is a TamOperation associated with m.
5.2 Message dispatch and consumption delays
The notion of message reception in scenario-based formalisms is ambiguous, because it is not clear whether a message reception is the instant when the message arrives at the receiver communication interface or the instant when the receiver application software consumes the message [59]. The distinction between message reception and message consumption is necessary in order to take the message consumption delays into account [115]. Such delays occur due to the decoding of network messages from a representation suitable for the transport via a network to a logical representation suitable to be processed by the application software. Similarly, there is a message dispatch delay between the instant when a message is created by the sending software component and the instant when it is actually dispatched to the network by its network interface [115]. Such delays occur due to the encoding of a logical representation into a representation suitable for the transport via a communication medium.
To distinguish between message creation and message sending as well as between message reception and message consumption, we introduced two additional message event kinds message creation event and message consumption event. These event kinds capture the instant when a message is created by the sending software component and consumed by the receiving software component, respectively. Figure 9 illustrates these event kinds and locations. We define the message creation location to be positioned on the sending lifeline directly before the message sending location (cf. cut c1.1). Similarly, the message consumption location is positioned on the receiving lifeline directly after the message reception location (cf. cut c1.4).
The message dispatch delays encompass the overhead to gain write access to a communication channel (in case of distributed communication, an arbitration time for gaining access to the overall communication system is added) as well as the time to encode a message from its logical representation to a format suitable for the transfer via the communication channel. This encoding time depends on the overall message size (i.e., net size plus potential overheads) in relation to the encoding rate of the communication channel. In case of distributed communication, this encoding rate further depends on the encoding rate of the applied transmission protocol and of the applied middleware communication services. Thus, we compute the upper message dispatch delay for an MSD message m as
where m.connector is a UML::Connector associated with m, m.connector.supplier is a TamComConnection (distributed communication) or a TamOSComChannel (ECU-internal communication) that the connector is allocated to, and m.signature is a TamOperation associated with m.
Analogously to message dispatch delays, message consumption delays encompass the time to gain read access to a communication channel as well as the time to decode a message from the communication channel format to its logical representation. The decoding time depends on the overall message size in relation to the decoding rate of the communication channel. Thus, we compute the upper bound of the message consumption delay for an MSD message m as
where m.connector is a UML::Connector associated with m, m.connector.supplier is a TamComConnection (distributed communication) or a TamOSComChannel (ECU-internal communication) that the connector is allocated to, and m.signature is a TamOperation associated with m.
5.3 Task execution delays
The semantics for platform-independent MSD specifications focuses on the message exchange between software components. However, it neglects internal procedures (i.e., tasks) that are executed by the software components to process consumed messages and to create the messages to be sent. This message processing by tasks leads to task execution delays that affect the timing behavior of the system [115] (cf. the execution times of the particular software operations in Fig. 7).
In order to consider such effects, we do not specify explicit task models but rather define that each message is associated with exactly one task that is executed upon the consumption of the message by the receiving software component. That is, we introduce the two new event kinds task start event and task completion event, which, respectively, represent the start and the end of a task execution. Figure 9 illustrates the new event and location for the enableBraking MSD message. We define the task start to be positioned on the receiving lifeline directly after the message consumption (cf. cut c1.5). Similarly, the task completion is positioned on the receiving lifeline directly after the task start, representing also the cut for the next MSD message (cf. cut c2). The next location is the message creation location (cf. cut 2.1), and so on.
Task execution delays encompass the normalized overall execution time (i.e., net execution time plus potential overheads) required to process a message in relation to the relative speed factor of the executing processing unit (cf. Sect. 4.1) as well as the overall times for accessing memory and resources (i.e., net access times plus overheads). Omitting the access times for comprehensibility reasons, we hence compute the upper task execution delay for an MSD message m as
where m.signature is a TamOperation associated with m, m.connector[receiver] is the receiving software component, m.connector[receiver].supplier is a TamECU that the receiving software component is allocated to, and m.con[receiver].supplier.procUnit is the TamProcessingUnit of the ECU.
We define a task to start immediately (i.e., at the next instant) after it has consumed its corresponding message if the scheduler can dispatch it (cf. cuts c1.4 and c1.5 in Fig. 9). If the scheduler cannot dispatch it immediately, a dynamic delay occurs (cf. Sect. 6.2.2). When a software component completed a task, it creates a potential subsequent message at the next instant afterward (cf. c2 and c2.1 in Fig. 9).
6 Specifying operational semantics for the timing analysis of platform-specific interaction models
In Sect. 4, we introduced the TAM profile to enable the modeling of platform-specific MSD specifications. Furthermore, we introduced additional message event kinds to support platform-specific timing analyses as well as the computations for the static delays in between these events (see Sect. 5). In this section, we overview the proposed platform-specific MSD operational semantics dedicated to timing analyses.
This section consequently details the semantics-related parts of Fig. 6 from the approach overview section (Sect. 3). The section elaborates on the EBEAS model to illustrate the most important concepts of the semantics, and the reader can refer to [61, Appendix B] for the illustrations of further concepts as well as the complete operational semantics of the TAM profile. Furthermore, our supplementary material [63] and our companion webpage [62] provide the actual technical artifacts as well as additional information.
For each of the following subsections, we start by describing the semantic mapping between the element of the abstract syntax and the CCSL constraints, realized at the language level (metamodel level M2). At this level, Domain-Specific Events (DSEs) are specified with the Event Constraint Language (ECL) in the context of concepts from the abstract syntax, and constrained by behavioral invariants (cf. Section 2.5). This generates a transformation of TAM models into CCSL specifications. Then, we illustrate the CCSL models generated for some TAM models (metamodel level M1). Finally, at the runtime level (metamodel level M0) we describe the corresponding CCSL simulation runs.Section 6.1 describes our encoding of the extended message event handling semantics for MSDs in terms of CCSL. Section 6.2 describes how we encode timing effects induced by the resource properties, and Sect. 6.3 describes our encoding of real-time requirements on these effects and of timing analysis contexts.
6.1 Encoding of message event kinds and their order
In order to enable simulative timing analyses of platform-specific MSD requirements, we encoded the semantics of MSDs in terms of CCSL. This encompasses the general occurrences of message events corresponding to the specified MSD messages (cf. Section 2.2.2) as well as the additional message event kinds introduced in Sect. 5.
Language level At the language level, we explicitly define DSEs and constraints that define the acceptable orders between the occurrences (at runtime) of the DSE instances (at the model level). The order of the occurrences represents the fine-grained cut progression w.r.t. the MSD message locations (cf. Fig. 9).
The upper part of Fig. 10 depicts an excerpt from the semantics specification of MSD message event occurrences. It depicts part of the Abstract Syntax, of the Mapping Specification, and of the applied Semantic Constraints.
Applying ECL, the Mapping Specification in the middle upper part of Fig. 10 defines the DSEs identified in Sect. 5 in the context of a TamModalMessage, like msgCreateEvt (1) and msgSendEvt (2). Each instance of a TamModalMessage will then be equipped with an instance of each DSE. The Mapping Specification also specifies an invariant eventOrder in the context of a TamModalMessage. Each instance of the DSEs will then be constrained according to this invariant, which specifies the allowed order of the message event occurrences. This order is specified by the user-defined MoCCML relation EventOrderRelation, whose parameters are DSEs.
Consequently, the DSE definition together with the invariants define the mapping between the concepts from the abstract syntax and the semantic constraints.
Looking at the constraint EventOrderRelation, it is specified by a constraint automaton, which defines the allowed order of the DSE parameters. Here, it specifies that the events shall only occur in the following order msgCreateEvt, msgSendEvt, msgReceiveEvt, msgConsumeEvt, taskStartEvt, and taskCompleteEvt; possibly infinitely. Note that there is no notion of time in this constraint, meaning that an arbitrary time can elapse between two occurrences.
From this specification, a transformation is automatically generated, to be used at the model level.
Model level At the model level, a timing analyst creates a platform-specific MSD specification and uses the previously generated transformation to generate a CCSL model, which acts as a symbolic representation of all acceptable schedules of the MSD specification; as defined by the semantics specification. The lower part of Fig. 10 depicts an excerpt from the Platform-specific MSD Specification and the corresponding CCSL Model, generated through the MSD-to-CCSL Transformation.
The MSD in the left lower part specifies the enableBraking MSD message and its event kinds (1–6) as part of the EmcyBraking MSD (cf. Section 5).
As indicated in the generated CCSL Model in the right lower part of Fig. 10, the derived transformation translates any MSD message to six clocks.
For instance, the enableBraking MSD message is translated to the six clocks (1–6) of the CCSL model of Fig. 10.
Furthermore, for any MSD message, the transformation generates a clock relation typed by the MoCCML relation associated by the ECL invariant (defined at the language level).
For example, for the enableBraking MSD message, the transformation generates the enableBraking_eventOrder clock relation typed by the MoCCML relation EventOrderRelation. This relation gets the argument enableBraking_msgCreateEvt for the parameter msgCreateEvt, the argument enableBraking_msgSendEvt for the parameter msgSendEvt, etc.
Runtime level The CCSL models generated at the model level are simulated in TimeSquare at the runtime level. Figure 11 depicts a CCSL run resulting from the CCSL model depicted in the right lower part of Fig. 10. This CCSL run represents the occurrence order of the particular message event kinds for the MSD message enableBraking.
Example: Simulated order of message event occurrences, enforced by the CCSL model clock relation enableBraking_eventOrder (cf. CCSL Model in the lower right of Fig. 10)
The rows depict ticks of the clocks, which themselves represent the particular message event occurrences. They are ordered from the top to the bottom, where the topmost row represents the occurrence of a message creation event and the bottommost row represents the occurrence of a task completion event. The ticks correspond to the transitions in the MoCCML relation EventOrderRelation. We assume that at instant 0 the MoCCML relation is in state 1, so that due to the tick of the clock \(\textsf {enableBraking}_{\textsf {msgCreateEvt}}\) at instant 1 the state is changed to 2. After the subsequent tick of the clock representing the message send event occurrence at the instant 2, the relation is in state 3 for the next 3 instants, and so on. The arrows visualize the causal dependencies between the clock ticks.
6.2 Encoding of platform-induced timing effects
In this section, we present how we encoded the semantics of the timing effects that are induced by the properties of the execution platform. We support two general classes of timing behavior effects. The first class encompasses the different kinds of static delays between the particular message event kinds as discussed in Sect. 5. The second class encompasses delays that dynamically emerge from mutual exclusion of resources when different software components try to access the same resource (e.g., the processor for the task execution, peripheral hardware, or an operating system service) at the same time.
6.2.1 Static delays between message event kinds
As discussed in Sect. 5, message-based communication and task processing involves multiple events during the actual execution on a target platform, and static delays occur between such events. In this section, we present how we encoded these static delays, based on the example of task execution time. Besides the different static delay kinds presented in Sect. 5, the complete semantics also distinguishes between distributed and ECU-internal communication.
As outlined in Sect. 3, we apply a preprocessing step for the computation of the static delays. The lower part of Fig. 12 exemplifies this Preprocessing transformation at model level by illustrating how some delays are computed based on the information in the MSD model. The computed lower and upper bound values are then stored in derived properties specified by tagged values defined as part of the TamModalMessage stereotype at the language level. In the following, we present how we specified the operational semantics based on these pre-computed static delays.
Language level In order to consider timing behaviors, we have to keep track of the global time progress. For this purpose, we introduced the globalTime DSE defined in the context of a Model (see Mapping Specification in the middle upper part of Fig. 12). The occurrence of the globalTime instance represents the discretization of the time. This discretization is usually set to the greatest common divisor of all timing requirements; however, to simplify, here it is set to 1ms in the remainder of this paper.
Consequently, we used the globalTime DSE as a reference for counting time, that is, to determine the occurrence of the different delayed DSE instances that are introduced in the following.
Besides the two taskStartEvt (1) and taskCompleteEvt (2) DSEs defined in the context of a TamModalMessage (cf. Sect. 6.1), the Mapping Specification defines two invariants to encode the task execution delay interval. The minExecutionDelay invariant defines the timing behavior for the lower bound of this interval.
To this end, a new DSE taskStartAfterMinExecDelay (3) is defined through the CCSL expression DelayFor (cf. Equation 6). According to the provided parameter arguments (i.e., globalTime, taskStartEvt, minTaskExecutionDelay), this clock expression delays the DSE taskStartEvt by the minimum task execution delay. Then, we specified that the DSE taskCompleteEvt must not occur earlier than this delayed event through the CCSL relation NonStrictPrecedes (cf. Equation 4). Analogously, the invariant maxExecutionDelay defines the timing behavior for the upper bound of task execution delay intervals and restricts the DSE taskCompleteEvt to occur not later than the maximum execution delay (4).
Model level The excerpt from the MSD in the left lower part shows the MSD message enableBraking with the focus on its Task Start (1) and Task Completion (2) events. The MSD message references the equally named «TamOperation» with a minimum execution time of 6ms and a maximum execution time of 9ms. The lifeline vc: VehicleControl represents the equally named component role allocated to the «TamECU» :µC2. This ECU contains a «TamProcessingUnit» with the speed factor 2.
Our Preprocessing model transformation takes these resource properties as input and computes the static delay intervals from it as defined in Sect. 5, resulting in the Platform-specific MSD Specification with Computed Static Delays. The transformation stores the computed lower and upper bounds in the corresponding tagged values of «TamModalMessage».
For example, the minimum and maximum task execution delay values of the MSD message are stored in the tagged values minTaskExecutionDelay and maxTaskExecutionDelay with the values \(\frac{trajectoryBeacon.minExecTime}{PU\mu C2.speedFactor} = \frac{6ms}{2} = 3ms\) and \(\frac{trajectoryBeacon.maxExecTime}{PU\mu C2.speedFactor} = \frac{9ms}{2} \approx 5ms\), respectively (cf. Equation 12).
As indicated by the excerpt from the generated CCSL Model in the right lower part of Fig. 12, the automatically derived transformation generates a globalTime clock for any MSD specification. Besides the clocks representing the particular message event kinds (1/2, cf. Sect. 6.1), the transformation also generates, for any MSD message, two clock expressions delaying the task start clock by the minimum and maximum execution time, respectively. For instance, the MSD message enableBraking is translated into two CCSL clock expressions DelayFor, defining the new enableBraking_taskStartAfterMinExecDelay (3) and enableBraking_taskStartAfterMaxExecDelay (4) clocks, respectively. These expressions delay the task start event clock enableBraking_taskStartEvt by the corresponding minimum and maximum task execution delays w.r.t. the globalTime clock.
Finally, the transformation generates two clock relations, which restrict the task completion event clock to tick in between the minimum task execution delay clock and the maximum task execution delay clock. For instance, the transformation generates the CCSL relations enableBraking_minExecutionDelay and enableBraking_ maxExecutionDelay typed by the CCSL relation NonStrictPrecedes. Both relations enforce the enableBraking_taskCompleteEvt clock to tick in between the occurrences of the clocks enableBraking_taskStartAfterMinExecDelay and enableBraking_taskStartAfterMaxExecDelay.
Runtime level Figure 13 depicts a CCSL run resulting from the CCSL model depicted in the right lower part of Fig. 12. This CCSL run represents the task execution time interval of the MSD message enableBraking.
The topmost row depicts the ticks of the globalTime reference clock (which always ticks in this run). The row below depicts the tick of the \(\textsf {enableBraking}_{\textsf {taskStartEvt}}\) clock at instant 1. This clock tick is delayed by 3 and 5 ticks of the globalTime clock and results in the \(\textsf {enableBraking}_{\textsf {taskStartAfterMinExecDelay}}\) and \(\textsf {enableBraking}_{\textsf {taskStartAfterMaxExecDelay}}\) clocks, respectively. The two NonStrictPrecedes clock relations enforce the clock \(\textsf {enableBraking}_{\textsf {taskCompleteEvt}}\) to tick at some instant between 4 and 6, and it actually ticks at instant 5 in this run.
6.2.2 Dynamic delays due to mutual resource exclusion
Target execution platforms of software-intensive systems have restricted resources, which may not be simultaneously used by different parts of the application.
Middleware and operating system services manage the access of the competing software parts to these restricted resources. Typically, such services provide mechanisms ensuring that the resources are accessed in a mutually exclusive manner.
Thus, our proposed operational semantics supports delays that dynamically emerge from the mutual exclusion of processing unit cores, communication media, peripherals, and operating system resources. In the following, we illustrate this with the scheduling of two tasks (each associated with a message processing) that belong to different software components allocated to a same ECU.
Language level The Mapping Specification in the middle upper part of Fig. 14 defines the taskStartEvt and taskCompleteEvt DSEs in the context of a TamModalMessage as defined in Sect. 6.2.1. Additionally, the DSE dispatch defined in the context of a TamScheduler represents the instants when the scheduler selects a task for the execution on a processing unit (i.e., the scheduler dispatches the task).
Furthermore, we define two behavioral invariants. The first one, named claimCoreOnTaskStart, is defined in the context of a TamModalMessage. It expresses the relation between the taskStartEvt and the DSE dispatch of the corresponding scheduler (determined via the simplifying pseudocode function “getRelevantScheduler()”) by using the CCSL relation SubClock (cf. Equation 1). The relation allows the subClock argument taskStartEvt to tick only when the superClock argument dispatch ticks. We specified whether the dispatch clock can tick through the invariant occupyCoreOnTaskStart defined in the context of a TamScheduler, which we explain below. By doing so, we prevent a scheduler from dispatching a task when the corresponding processing unit is busy with the execution of another task.
To this end, we first determine all MSD messages that can be sent to one of the software components allocated to the TamECU containing the TamScheduler. From these messages, we define two DSEs through the CCSL expression Union (cf. Equation 5): The DSEs anyTaskStart (1) and anyTaskComplete (2), which represent the union of all task start and task completion events, respectively. These DSEs determine whether any task is started or any task gets completed.
The actual behavior of the occupyCoreOnTaskStart invariant is specified by using the MoCCML relation NonPreemptiveTaskExecution. Its arguments are the DSE dispatch for the parameter clock occupy, the clocks representing the union of all relevant taskStartEvt and taskCompleteEvt DSEs for the newTask and the taskFinish clock, respectively, and the amount of cores of the corresponding processing unit for the Integer parameter numCores. Furthermore, we define a local Integer variable runningTasks that captures the amount of tasks currently running on the processing unit.
The initial state of the MoCCML relation is Cores Available, which defines that the scheduler is able to dispatch new tasks because the processing unit is not busy with processing other tasks. When a new task is ready to be dispatched in this state and hence the occupy parameter clock as well as the newTask parameter clock tick simultaneously, the variable runningTasks is incremented if the guard [runningTasks + 1 < numCores] holds. Analogously, when any task running on the processing unit is finished in this state and hence the parameter clock taskFinish ticks, the variable runningTasks is decremented. If the amount of currently running tasks equals the amount of cores in this state, the transition to the state All Cores Busy is fired. In this state, dispatching new tasks is not allowed. When any task running on the processing unit gets completed in this state and hence the parameter clock taskFinish ticks, the variable runningTasks is decremented and the transition to the initial state is fired.
Our semantics supports multiple software components allocated to one processing unit, multiple cores per processing unit, and different task priorities, which we do not further discuss here.
Model level The MSD specification excerpt in the left lower part of Fig. 14 shows the MSD message obstacle focusing on its Task Start (1) and Task Completion (2) events. The lifeline represents the software component sa: SituationAnalysis, which is allocated to the «TamECU» :\(\upmu \) C1. This ECU contains a «TamProcessingUnit» :PU\(\upmu \) C1 with one core as well as a «TamRTOS» with a «TamScheduler» :OSEK/VDX-Scheduler.
The right lower part of Fig. 14 depicts an excerpt from the generated CCSL Model. Besides the clocks representing the particular MSD message events (cf. Section 6.1), the derived transformation generates for any «TamScheduler» each a scheduler dispatch clock. For example, the transformation generates the clock variable OSEK/VDX-Scheduler_dispatch for the :OSEK/VDX-Scheduler.
Furthermore, the transformation creates for any MSD message each a SubClock clock relation that restricts the related task start clock to tick only when the scheduler’s dispatch clock can tick simultaneously. For instance, the transformation generates for the MSD message obstacle the clock relation obstacle_claimCoreOnTaskStart using the SubClock relation.
For any «TamScheduler», the transformation generates two clocks defined by Union clock expressions that determine the union of ticks of all task start and completion clocks. For example, the scheduler :OSEK/VDX-Scheduler is translated to the clocks OSEK/VDX-Scheduler_anyTaskStart (1) and OSEK/VDX-Scheduler_anyTaskComplete (2). The clock expressions get the obstacle_taskStartEvt and obstacle_taskCompleteEvt clocks as a set argument, along with other task start and completion clocks.
Finally, the transformation generates for any «TamScheduler» a clock relation that uses the user-defined MoCCML relation NonPreemptiveTaskExecution. For example, the transformation translates the scheduler :OSEK/VDX-Scheduler into the clock relation OSEK/VDX-Scheduler_occupyCoreOnTaskStart. This relation gets the argument OSEK/VDX-Scheduler_dispatch for the parameter occupy, OSEK/VDX-Scheduler_anyTaskStart for newTask, OSEK/VDX-Scheduler_anyTaskComplete for taskFinish, and 1 for numCores.
Runtime level Figure 15 depicts a CCSL run resulting from the CCSL model in the right lower part of Fig. 14. This CCSL run represents a situation in which two different messages request to be processed concurrently by the «TamECU» :µC1.
More precisely, let us assume that the MSD BeaconAcknowledgement indicated in Fig. 1 specifies that sa: SituationAnalysis is responsible for processing information about the trajectories of other vehicles via a message trajectoryBeacon, additionally to processing the obstacle messages as specified by the MSD EmcyBraking. The three topmost rows in Fig. 15 depict the ticks of the clocks representing the consumption, task start, and task completion of the trajectoryBeacon message. The processing unit of :µC1 is not busy with another task at instant 1 when the trajectoryBeacon message is consumed. Consequently, the MoCCML relation NonPreemptiveTaskExecution that types the CCSL relation OSEK/VDX-Scheduler_occupyCoreOnTaskStart is in the state Cores Available (cf. Fig. 14). Thus, the clock \(\textsf {OSEK/VDX-Scheduler}_{\textsf {dispatch}}\) is allowed to tick, meaning that the scheduler of :µC1 is able to dispatch the corresponding task. Hence, the clock \(\textsf {trajectoryBeacon}_{\textsf {taskStartEvent}}\) ticks simultaneously with the clock \(\textsf {OSEK/VDX-Scheduler}_{\textsf {dispatch}}\) at instant 2. Consequently, the clock \(\textsf {OSEK/}\textsf {VDX-Scheduler}_{\textsf {anyTaskStart}}\) ticks at this instant as defined by the clock expression Union. Analogously, the clock \(\textsf {OSEK/VDX-Scheduler}_{\textsf {anyTaskComplete}}\) ticks at instant 5 due to the tick of \(\textsf {trajectoryBeacon}_{\textsf {taskStartComplete}}\).
The obstacle message is consumed at instant 2, resulting in the tick of the clock \(\textsf {obstacle}_{\textsf {msgConsumeEvt}}\) at this instant. Due to the fact that :PUµC1 has only one core and due to the dispatching of the trajectoryBeacon processing task at the same instant, the MoCCML relation NonPreemptiveTaskExecution is in the state All Cores Busy from instant 2 to instant 4. Thus, :PUµC1 is blocked from instant 2 to 4 so that the task processing of the obstacle message can be dispatched not earlier than instant 6, at which the \(\textsf {obstacle}_{\textsf {taskStartEvt}}\) clock actually ticks. This causes a dynamic delay of 3 time units between the consumption and the actual processing of the message obstacle.
6.3 Encoding of real-time requirements and timing analysis contexts
In this section, we present the crucial aspects of the semantics encoding for both the timing analysis results and the timing analysis setup. In Sect. 6.3.1, we explain how we encode the MSD clock resets and time conditions (i.e., the real-time requirements) in CCSL, which the timing analysis in TimeSquare determines as fulfilled or violated by the timing behavior of the system. In Sect. 6.3.2, we explain how we encode analysis contexts defined by timing analysts to investigate the simulation scenarios that interest them.
6.3.1 Clock resets and time conditions
The combination of a clock reset and a time condition in an MSD represents a real-time requirement (cf. Sect. 2.2.2). A violation of such real-time requirements can lead to hazards in the case of safety-critical systems, and our timing analysis approach aims at revealing such violations in the early RE phase.
In this section, we present how our proposed semantics encodes combinations of clock resets and time conditions. We illustrate the semantics for delays with a strict upper bound, representing a maximum message treatment response time. In the complete semantics specification, we also support minimal delays and non-strict bounds.
Language level The Mapping Specification in the middle upper part of Fig. 16 shows the invariant rtReqStrictUpperBound defined in the context of the Modal stereotype ClockReset. The invariant initially determines the time condition associated with the clock reset. If the operator of the time condition defines a strict upper bound (i.e., the operator equals “<”), the implication becomes true so that the invariant is relevant to the context clock reset.
Remember that we do not extend the MSD modeling language but refine its semantics for the purpose of timing analysis. For example, we conceptually introduce more fine-grained event kinds in Sect. 5 and describe their realization in the Gemoc mapping specification in Sect. 6.1. That also implies that we have to define in the following for the semantics of real-time requirements which of the new fine-grained event kinds they constrain, as the clock resets and time conditions can only be specified between messages.
Thus, for strict upper bound maximal delays, we define that the real-time requirement constrains the time elapsed between the message reception (prior to the clock reset) and the task completion (prior to the maximal delay). For this purpose, we first determine the last message reception DSE precedingMessageReceptionEvent (1) directly preceding the clock reset. We illustrate this in a simplifying manner with a pseudocode function, which applies the clock expression Sup (reference not depicted in the figure, cf. Equation 8). Analogously, we determine the last task completion DSE constrainedTaskCompletionEvent (2), that is, the completion DSE of the task that precedes the associated time condition. Then, we define a new clock upperBoundEvent (3) representing the upper bound of the time condition by using the clock expression DelayFor, which delays precedingMessageReceptionEvent by the upper bound value. Finally, we constrain the ticks of constrainedTaskCompletionEvent to occur before the ticks of upperBoundEvent by using the clock relation Precedes (cf. Equation 3).
Model level The left lower part of the figure shows an excerpt from the MSD EmcyBraking, which encompasses the MSD message obstacle prior to the clock reset clockReset1 and the MSD message standstill prior to the time condition \(\textsf {c}\,<\,\textsf {t}_{\textsf {brake}}\), parameterized by the tbrake variable. The focus is on the message reception event for obstacle (1), the task completion event for standstill (2), and the time condition defining an upper bound w.r.t. the clock reset (3).
The derived transformation generates the CCSL Model whose excerpt is represented in the right lower part of Fig. 16. It contains the globalTime clock keeping track of the overall time progress, as well as the clocks for the occurrences of the message reception and task completion events for both the obstacle and standstill MSD messages, respectively (cf. Sect. 6.1).
Furthermore, the transformation generates for any clock reset each three CCSL expressions. The first expression defines a new clock clockReset1_precedingMessage ReceptionEvent (1) that represents the slowest occurrence of the message reception event among the MSD messages that precede the clock reset. In the specific case of the MSD EmcyBraking, this clock captures the ticks of the clock obstacle_msgReceiveEvt.
The second Sup expression defines a new clock clockReset1_constrainedTaskCompletionEvent (2) that represents the occurrence of the task completion event of the last MSD message prior to the time condition, that is, the clock standstill_taskCompleteEvt. Third, the transformation generates a clock expression DelayFor defining the clock clockReset1_upperBoundEvent (3). This expression delays the message reception event clock stemming from the last MSD message prior to the clock reset by the value of the time condition. In the case of the MSD model in Fig. 16, it delays clockReset1_precedingMessageReceptionEvent by t_brake time units w.r.t. globalTime.
Finally, the transformation generates for any clock reset each a CCSL relation Precedes, which enforces the task completion event clock stemming from the last MSD message prior to the time condition to tick before the delayed clock representing the upper bound value of the time condition. In our example, the relation clockReset1_rtReqStrict UpperBound applies the clock clockReset1_constrained TaskCompletionEvent as argument for leftClock and the clock clockReset1_upperBoundEvent as argument for rightClock.
Runtime level Figure 17 depicts a CCSL run resulting from the CCSL model depicted in the right lower part of Fig. 16. This CCSL run represents a fictional situation, where the time condition value placeholder \(\textsf {t}_{\textsf {brake}}\) has two distinct concrete values, leading one time to the fulfillment and another time to the violation of the real-time requirement.
The ticks of the clocks \(\textsf {obstacle}_{\textsf {msgReceiveEvt}}\) and \(\textsf {standstill}_{\textsf {taskCompleteEvt}}\) (row 2 and 7) represent the occurrences of the message reception and task completion events of the MSD messages obstacle and standstill, respectively. For both, the clock expression Sup is used to define the new clocks \(\textsf {clockReset1}_{\textsf {precedingMessageReceptionEvent}}\) (row 3) and \(\textsf {clockReset1}_{\textsf {constrainedTaskCompletionEvent}}\) (row 6). Furthermore, the CCSL expression DelayFor delays the clock \(\textsf {clockReset1}_{\textsf {precedingMessageReceptionEvent}}\) by \(\textsf {t}_{\textsf {brake}}\) time units, defining the new clock \(\textsf {clockReset1}_{\textsf {upperBoundEvent}}\). This clock is depicted in both the rows 4 and 5 for the two distinct concrete values of \(\textsf {t}_{\textsf {brake}}\). The relation Precedes enforces the tick of \(\textsf {clockReset1}_{\textsf {constrainedTaskCompletionEvent}}\) to occur before the tick of \(\textsf {clockReset1}_{\textsf {upperBoundEvent}}\).
In the example situation, \(\textsf {clockReset1}_{\textsf {constrainedTaskCompletionEvent}}\) ticks at the instant 7. This clock tick fulfills the Precedes relation if the value \(\textsf {t}_{\textsf {brake}}\) is 8 so that \(\textsf {clockReset1}_{\textsf {upperBoundEvent}}\) ticks at the instant 9 (row 4). This means that the software execution on the specified platform fulfills the real-time requirement for the given analysis context.
However, if the value of \(\textsf {t}_{\textsf {brake}}\) is 4 (row 5), the tick of \(\textsf {clockReset1}_{\textsf {constrainedTaskCompletionEvent}}\) does not fulfill the Precedes relation because the real-time requirement is too tight. More precisely, TimeSquare cannot solve the underlying Boolean expression (cf. Sect. 2.4), and the simulation stops with a deadlock in case \(\textsf {t}_{\textsf {brake}}=4\). This situation represents a real-time requirement violation. Note that instead of classically defining the clockReset1_rtReqStrictUpperBound as a relation, it is possible to define it as an assertion in which case TimeSquare stipulates where the assertion is violated instead of producing a deadlock.
6.3.2 Timing analysis contexts
To conduct a particular timing analysis, the engineers have to specify the concrete simulation scenario that they want to investigate. Such an analysis scenario is known as an analysis context [93, 111].
The analysis context defines how often and at which instants the environment events triggering the system behavior can occur. Like in Marte, we refer to them as arrival patterns.
We support periodic as well as sporadic arrival patterns in our semantics (cf. Sect. 4.4). Whereas periodic arrival patterns specify the triggering of environment events that occur repeatedly with a fix period and without jitter, sporadic arrival patterns specify the triggering of environment events that occur sporadically with certain restrictions. These restrictions encompass a minimum arrival rate before an event may occur, a maximum arrival rate until an event has to occur, and combinations of both that can also be applied to represent jitters. In this section, we exemplify the semantics of analysis context scenarios with a periodic arrival rate, whereas we define the semantics of sporadic arrival patterns by combining the semantics of periodic ones and of delay intervals (cf. Sect. 6.2.1).
Language level The Mapping Specification in the middle upper part of Fig. 18 shows the invariant periodicPattern defined in the TamAssumptionMSD context. This invariant enforces MSD message creation events defined as part of a «TamAssumptionMSD» with a periodic arrival pattern to occur periodically.
In the invariant periodicPattern, we first determine whether the associated arrival pattern of the context TamAssumptionMSD is a periodic one. If this implication holds, we define a new DSE periodicActivation (1) that ticks every period ticks due to the CCSL expression PeriodicOffsetP (cf. Equation 7). Its arguments are the globalTime DSE and the tagged value period of the TamPeriodicPattern. Subsequently, we determine the initial MSD message of the TamAssumptionMSD. Finally, we enforce the msgCreateEvt DSE of this MSD message to tick simultaneously with the periodicActivation DSE by using the CCSL relation Coincides (cf. Equation 2).
Model level The excerpt from the MSD in the left lower part shows the «TamAssumptionMSD» BeaconFrequency. It specifies the trajectoryBeacon environment message to be sent from the environment role v2x: V2XCommunication to the sa: SituationAnalysis. The «TamPeriodicPattern» associated with the «TamAssumptionMSD» defines that the creation event of this environment message occurs periodically every 3ms (1).
As indicated in the excerpt from the generated CCSL Model in the right lower part of Fig. 18, the derived transformation generates for any «TamAssumptionMSD» with a periodic pattern each a CCSL expression PeriodicOffsetP. This CCSL expression gets the globalTime as argument for the baseClock parameter and the tagged value period of the «TamPeriodicPattern» as argument for the equally named clock parameter. In our example, the transformation generates the PeriodicOffsetP expression with the value 3 applied as argument for period, defining the new clock trajectoryBeacon_periodicActivation (1).
Finally, the transformation generates for any «TamAssumptionMSD» with a periodic pattern each a CCSL relation Coincides. This clock relation gets two clocks as arguments: The clock representing the message creation event of the initial MSD message, and the newly defined clock representing the periodic activation. In our example, the transformation generates the Coincides relation trajectoryBeacon_periodicPattern with the clocks trajectoryBeacon_msgCreateEvt and trajectoryBeacon_periodic Activation as arguments. This relation forces the clock trajectoryBeacon_msgCreateEvt to tick every 3 ticks of the globalTime, meaning that the message creation event of the initial MSD message trajectoryBeacon occurs every 3ms.
Runtime level Figure 19 depicts a CCSL run resulting from the CCSL model depicted in the right lower part of Fig. 18. This CCSL run represents the periodic occurrence of the message creation event of the initial MSD message trajectoryBeacon defined in the MSD BeaconAcknowledgement.
The topmost row depicts the ticks of the globalTime reference clock. The middle row depicts the ticks of the \(\textsf {trajectoryBeacon}_{\textsf {periodicActivation}}\) clock, which ticks every 3rd tick of the globalTime clock. The bottommost row depicts the ticks of the \(\textsf {trajectoryBeacon}_{\textsf {msgCreateEvt}}\) clock, where the Coincides relation enforces this clock to tick simultaneously with the \(\textsf {trajectoryBeacon}_{\textsf {periodicActivation}}\) clock.
7 Timing analysis example
In this section, we illustrate how the different aspects of the semantics presented in Sect. 6 work together. For this purpose, we first explain a simulation of a CCSL model generated from the whole platform-specific MSD specification example presented in Sect. 4. Afterward, we illustrate the possibility to perform model checking on the CCSL model.
7.1 Simulation of a platform-specific MSD model
As a recapitulation, Fig. 20 depicts the MSD specification parts that are the most relevant for the timing analysis example illustrated in this section. Let us consider the MSD BeaconAcknowlegement, which was in Sect. 2.2 only indicated as part of the MSD specification introduced in Fig. 1. This MSD specifies the exchange of trajectory information between a vehicle and the other vehicles in its environment (through trajectory beacons). More precisely, it specifies the v2x: V2XCommunication to send a trajectoryBeacon message to the sa: SituationAnalysis, which shall acknowledge the reception by sending back an ack message. These interactions have to be executed on the target platform in addition to the MSD EmcyBraking.
In our context, an end-to-end response time analysis has to determine whether such platform-specific MSD specifications fulfill their high-level real-time requirements (cf. Section 2.1). One key question of such timing analyses is whether the resources provided by the platform have a sufficient performance to execute the application software consuming the resources. For example, it can reveal that the processing resource executing the software component sa: SituationAnalysis is not fast enough to process some operations in time; or that the latency of the communication media is too high to deliver some messages in time. Answering such questions is even more important when, at some points in time, the system workload is high. For example, several messages like obstacle and trajectoryBeacon can arrive at sa: SituationAnalysis within a small timeframe so that the receiving software component has to process them concurrently. The very same situation occurs when several messages have to be delivered via a single communication medium at the same time.
Excerpt from the simulation run of the CCSL model automatically generated from the platform-specific MSD specification described in Sect. 4 (only part of the clocks are depicted)
In the following, we illustrate the detection of a real-time requirement violation by means of a simulation in TimeSquare. The violation occurs due to a situation, in which the workload triggered by the environment is too high so that the target platform is not able to fulfill the real-time requirement. Figure 21 depicts an excerpt of the CCSL simulation run, which results from the platform-specific MSD specification excerpt in Fig. 20.
- Row 1:
-
depicts the tick of the clock \(\textsf {trajectoryBeacon}_{\textsf {msgCreateEvt}}\) at instant 50. This tick stems from the environment message trajectoryBeacon defined in the assumption MSD BeaconFrequency, where its arrival pattern specifies this message event to occur periodically every 25ms. As explained in Sect. 6.3.2, our semantics enforces the message creation events to occur exactly at these periodic instants. Thus, \(\textsf {trajectoryBeacon}_{\textsf {msgCreateEvt}}\) occurs any 25ms, and the simulation excerpt depicts its second tick in the overall run.
- Row 2:
-
depicts the \(\textsf {trajectoryBeacon}_{\textsf {taskStartEvt}}\) clock tick at instant 54, which emerges due to two aspects. First, we assume that the (not depicted) clocks representing the preceding trajectoryBeacon send, reception, and consumption events occur with small static delays at the instants 51, 52, and 53. Second, the corresponding task can only start when its scheduler can dispatch it. As described in Sect. 6.2.2, \(\textsf {trajectoryBeacon}_{\textsf {taskStartEvt}}\) depends on its superclock \(\textsf {OSEK/VDX-Scheduler-}\upmu \textsf {C1}_{\textsf {dispatch}}\) (row 4), which is able to tick at this instant as explained in the description for row 4.
- Row 3:
-
depicts the subsequent tick of the \(\textsf {trajectory}\textsf {Beacon}_{\textsf {taskCompleteEvt}}\) clock at instant 60. This instant results from a task execution delay, which is computed as described in Sects. 5.3 and 6.2.1 as follows. The operation signature of trajectoryBeacon is a «TamOperation» having an execTime with the value 5 ms . The corresponding receiving component role sa: SituationAnalysis is allocated to the «TamECU» :µC1, whose «TamProcessingUnit» :PUµC1 has a speedFactor with the value 1. Thus, the task executing the operation needs \(\frac{5ms}{1}=5ms\) for the processing.
- Row 4:
-
depicts the ticks of the \(\textsf {OSEK/VDX-Scheduler-}\upmu \textsf {C1}_{\textsf {dispatch}}\) clock. As described in Sect. 6.2.2, this clock can only tick if the corresponding processing unit for the execution of a requested task dispatching has a free core. This is the case at instant 54, where the trajectoryBeacon is ready to be processed by its corresponding task. Thus, the \(\textsf {trajectoryBeacon}_{\textsf {taskStartEvt}}\) clock depicted in row 2 is allowed to tick simultaneously. However, \(\textsf {OSEK/VDX-Scheduler-}\upmu \textsf {C1}_{\textsf {dispatch}}\) cannot tick during the 6 following instants because the task for processing trajectoryBeacon is not completed until then and the processing unit has only one and thereby no further free core.
- Row 5:
-
depicts the tick of the \(\textsf {obstacle}_{\textsf {msgCreateEvt}}\) clock. This tick stems from the obstacle environment message defined in the ObstacleArrivalRate assumption MSD. The arrival pattern of this message specifies that the corresponding environment event occurs sporadically between any 50 and 55ms. Our semantics enforces the corresponding message creation event to occur at instants inside this interval. In the proposed run, \(\textsf {obstacle}_{\textsf {msgCreateEvt}}\) occurs within this instant interval, at instant 51.
- Row 6:
-
depicts the tick of the clock \(\textsf {clockReset1}_{\textsf {precedingMessageReceptionEvent}}\) at instant 53. This clock stems from the clock reset (assuming that it has the identifier clockReset1) defined in the EmcyBraking MSD, which is specified directly below the obstacle environment message. As explained in Sect. 6.3.1, the corresponding semantics enforces \(\textsf {clockReset1}_{\textsf {precedingMessageReceptionEvent}}\) to tick on the last message reception event occurrence before the clock reset. Thus, this clock ticks on the tick of \(\textsf {obstacle}_{\textsf {msgReceiveEvt}}\) depicted in row 7.
- Row 7:
-
depicts the tick of \(\textsf {obstacle}_{\textsf {msgReceiveEvt}}\) clock at instant 53. Here, we assume that it ticks immediately after the preceding (not depicted) message send clock, which itself ticks immediately after the tick of \(\textsf {obstacle}_{\textsf {msgCreateEvt}}\) (row 5).
- Row 8:
-
depicts the subsequent \(\textsf {obstacle}_{\textsf {msgConsumeEvt}}\) clock tick at instant 54 without a substantial delay.
- Row 9:
-
depicts the tick of the \(\textsf {obstacle}_{\textsf {taskStartEvt}}\) clock at instant 61. This tick emerges from the fact that its superclock \(\textsf {OSEK/VDX-Scheduler-}\upmu \textsf {C1}_{\textsf {dispatch}}\) (row 4) cannot tick earlier than this instant, because the trajectoryBeacon processing task is completed only one instant before. Thus, a dynamic delay occurs until the scheduler can dispatch the obstacle task.
- Row 10:
-
depicts the \(\textsf {obstacle}_{\textsf {taskCompleteEvt}}\) clock tick at instant 67 after the obstacle processing task is completed. The task execution delay of 5ms is computed analogously as described above for trajectoryBeacon in row 3.
We skip the detailed explanation of the computation and determination of the further static and dynamic delays and focus in the remainder on the clocks generated from the elements specified at the end of the MSD EmcyBraking.
- Row 15:
-
depicts the tick of the \(\textsf {clockReset1}_{\textsf {upperBoundEvent}}\) clock. As explained in Sect. 6.3.1, our semantics uses this clock to represent the maximal delay c < 50 w.r.t. the preceding clock reset in the EmcyBraking MSD. As explained in the description for row 6, this clock reset is represented by the clock \(\textsf {clockReset1}_{\textsf {precedingMessageReceptionEvent}}\). To represent the maximal delay value 50 and span the corresponding real-time requirement, \(\textsf {clockReset1}_{\textsf {upperBoundEvent}}\) ticks at instant 103, that is, 50 instants after the tick of \(\textsf {clockReset1}_{\textsf {precedingMessageReceptionEvent}}\) at instant 53.
- Row 16:
-
depicts the \(\textsf {standstill}_{\textsf {taskCompleteEvt}}\) clock tick, which represents the final task completion event for the message standstill at instant 105 due to the delays between the event occurrences before.
- Row 17:
-
depicts the tick of the clock \(\textsf {clockReset1}_{\textsf {constrainedTaskCompletionEvent}}\). As explained in Sect. 6.3.1, our semantics enforces this clock to tick at the same instant as the last task completion event clock before a clock reset (cf. row 16). Furthermore, this clock tick has to precede the tick of the \(\textsf {clockReset1}_{\textsf {upperBoundEvent}}\) clock at instant 103 (row 15) to fulfill the real-time requirement. However, the clock ticks at instant 105 due to the platform-induced timing effects. Thus, TimeSquare cannot solve the underlying Boolean expression (cf. Sect. 2.4), and the simulation stops with a deadlock (or an assertion is notified, see Sect. 6.3.1) This represents a real-time requirement violation for the analysis context in which the trajectoryBeacon and obstacle messages are almost simultaneously received by the software component sa: SituationAnalysis.
The detection of such a real-time requirement violation typically opens up a variety of potential countermeasures to fix the defect. One possible countermeasure would be to speed up the «TamECU» :µC1 to which the sa: SituationAnalysis software component is allocated to: A speedFactor of 2 would allow to process trajectoryBeacon and obstacle within each 3 instants. This would reduce the end-to-end response time until the task completion of standstill by altogether 4 instants, thereby fulfilling the real-time requirement. Other countermeasures are the addition of a further core to :µC1 enabling the concurrent processing of the two messages, an exchange of the communication medium between the two TamECUs improving the message transmission times, the relaxation of the real-time requirement in communication with all stakeholders, etc.
7.2 Model checking of a platform-specific MSD model
As presented in Sect. 2.4.3, TimeSquare allows constructing the state space representing the set of all possible simulations. The fact that there are different simulations possible from a single CCSL model results from different sources of non-determinism. For example, the clock \(\textsf {obstacle}_{\textsf {msgCreateEvt}}\) in the proposed model is subject to a sporadic arrival pattern so that it can tick between any 50 and 55ms. It is important to verify the status of the requirements for any of these values. This is also true for all the interval delays defined in Sect. 5.
We ran the state space construction on the model generated from the MSD specification in Fig. 20. It contains 9,775 states and 14,865 transitions. More interestingly, it contains a periodic behavior that fulfills the requirements [62]. This happens when the \(\textsf {obstacle}_{\textsf {msgCreateEvt}}\) ticks at time 55, reducing the dynamic delay of the associated task and allowing the standstill task to complete before the deadline.
This shows the known fact that simulation and formal verification complement each other [43]. Typically, there are traces in specification state spaces that fulfill the requirements, whereas other traces violate them. This can be dangerous, because timing analysts who are not aware of the fact that the simulations cover only a subset of the overall state space could be easily satisfied with some conducted simulations yielding only positive results. This can happen despite the debugging environment provided by Gemoc Studio, which allows for a step-by-step investigation of specific executions by discovering the state space dynamically, helping the timing analysts to investigate different simulations [16].
While we prove the possibility to use the generic exhaustive simulation feature to model check a platform-specific MSD specification, it remains very costly. We are currently investigating if it is possible to make it more affordable; even if not totally exhaustive, typically by running parallel simulations as inspired by Monte Carlo techniques.
8 Evaluation: Example application EBEAS
We evaluate our timing analysis approach by means of an example application [121] and organize its description in this section according to the guidelines by Kitchenham et al. [74] and by Runeson et al. [108]. In our example application, we investigate the efficacy of our approach with the running EBEAS example, serving as a representative for software-intensive distributed real-time systems. To answer the evaluation questions, we apply different variants of the platform-specific MSD specification introduced in Sect. 4.
In the example application, we evaluate a software prototype based on the Eclipse Modeling Framework (EMF) [33]. For the modeling language aspects, we rely on the EMF-based UML modeling tool Papyrus [34]. Beyond editors for conventional UML models, Papyrus enables the specification of UML profiles and provides the Marte profile. Furthermore, the Papyrus-based tool suite ScenarioTools MSD [109] provides the Modal profile and corresponding editor and analysis functionality. We extended both profiles by our TAM profile as sketched on the left upper side of Fig. 6 in Sect. 3. For the semantics specification (right upper side of Fig. 6), we rely on the tool suite Gemoc Studio [32]. It provides the timing analysis tool TimeSquare [114] as well as the languages ECL, CCSL (including libraries for the pre-defined constraints), and MoCCML, with their textual editors relying on the EMF-based language development framework Xtext [120]. Finally, it applies the EMF-based QVTo implementation [35] for the model transformations. We provide the application and an evaluation dataset in our supplementary material [63].
8.1 Context
The objective of our example application is to evaluate whether our approach is useful for timing analysts. For this purpose, we examine the following evaluation questions (EQ):
- EQ1::
-
Does our timing analysis approach generate syntactically and semantically correct CCSL models?
- EQ2::
-
Does our timing analysis approach reduce the engineering effort for specifying CCSL models?
Based on the aforementioned example application objective and evaluation questions, we define three evaluation hypotheses H1–H3. Their detailed evaluation is described in Sects. 8.3 to 8.5.
8.2 Subject Specifications
Besides the first author, we employ two different master-level students, student-1 and student-2 to support the evaluation. Student-1 has approximately four-year experience in modeling and simulating MSD specifications, as well as one-year experience with Marte platform modeling and timing analysis in TimeSquare during the evaluation conduct. Furthermore, he conceived and implemented a very early version of our timing analysis approach [12]. Student-2 has approximately one-year experience with modeling MSD and Marte specifications, as well as with TimeSquare during the evaluation conduct.
8.3 Hypothesis H1
We define evaluation hypothesis H1 as follows:
Our MSD semantics for timing analyses correctly encodes the timing effects that are induced by the resource properties provided as modeling means by our TAM profile (cf. evaluation question EQ1).
For evaluating H1, two different students prepare four different platform-specific MSD specifications that jointly cover all resource properties that are provided as modeling means by our TAM profile. Afterward, they generate CCSL models from them and investigate whether any of the platform properties induces each the expected timing effect with the expected delay duration.
We consider H1 fulfilled if the students observe each a timing effect as we expect to be induced by all resource properties specifiable with our TAM profile.
8.3.1 Data collection preparation
As a basis for evaluating H1, the students prepare a set of platform-specific MSD specifications that jointly cover all resource properties that are supported by our semantics. A large part of these resource properties is covered by a platform-specific MSD specification that is presented in [12, Section 7.2] as a proof of concept by student-1, which we call MSD-spec-1. In this proof of concept, typical use cases in the course of a timing analysis are constructed. This encompasses the determination of several real-time requirement violations through the timing analysis and the repeated adaptation of the specification until the real-time requirements are fulfilled.
For any of the remaining resource properties that are not covered by MSD-spec-1, student-2 specifies each a dedicated model (altogether 17 further models) that covers the respective resource property to reproduce the corresponding induced timing effect.
8.3.2 Data collection procedure
For evaluating hypothesis H1 with MSD-spec-1, student-1 conducts the following specification and timing analysis process:
-
1.
He specifies a platform-independent MSD specification as explained in Sect. 2.2.1.
-
2.
He specifies a platform model based on information about real-world platforms, as explained in Sect. 4.
-
3.
He specifies an allocation from the MSD specification to the platform model and annotates software component resource consumption properties.
-
4.
He specifies analysis contexts and iteratively conducts the timing analysis in TimeSquare. In the course of the timing analysis, he iteratively encounters platform-induced real-time requirement violations, determines their respective causes, and adapts the resource properties until all real-time requirements are fulfilled. This procedure enables him to reenact every timing effect induced by a resource property that is both considered by our semantics and specified in the proof of concept model. Particularly, he simulatively determines whether for any specified resource property each the expected timing effect occurs.
To evaluate hypothesis H1 for the remaining resource properties that are not covered by MSD-spec-1, student-2 proceeds for any dedicated model specific to a resource property as follows:
-
1.
He specifies the resource property with one value each so that the expected induced timing effect in one case fulfills a real-time requirement and in the other case violates the same real-time requirement. For this purpose, he reenacts the semantics for the corresponding resource property to conceive a property value such that the induced timing effect leads to each the fulfillment and the violation of a real-time requirement according to his expectations. In the case of static delays, he reenacts the respective delay computation formula (cf. Sect. 5). One example of dynamic delays is the construction of a runtime situation in which two software components concurrently access one resource.
-
2.
He conducts the timing analysis in TimeSquare. For the static delays, he already determines in the preprocessed model (cf. Sect. 6.2.1) whether the corresponding delay changes according to his expectations. For both dynamic and static delays, he simulatively determines whether the corresponding timing effect as well as the real-time requirement fulfillment or violation for the resource property under investigation occurs as expected.
We documented the test results for all resource properties that induce timing effects, as covered by our MSD semantics for timing analyses. This includes how a particular resource property induces a respective timing effect and how this timing effect sums up to which kind of delay. Furthermore, the documentation includes which platform-specific MSD specification covers the resource property and whether the student observed the delay as expected. We omitted this documentation in this paper for space reasons; their details can be found in [61, 63].
8.3.3 Interpreting the results
Our documented test results show that our semantics encodes the timing effects induced by the resource properties as expected. Furthermore, all modeling means as provided by our TAM profile are considered by the semantics. Thus, we consider our hypothesis H1 fulfilled.
8.4 Hypothesis H2
We define evaluation hypothesis H2 as follows:
Manually specifying a platform-specific MSD specification from scratch and automatically generating a CCSL model from it is more efficient than specifying the corresponding CCSL model manually from scratch (cf. evaluation question EQ2).
For evaluating H2, the first author counts the number of model elements for the four platform-specific MSD specifications as well as the CCSL models. He categorizes each model element w.r.t. atomic model operation kinds and measures the durations for conducting each operation kind. Furthermore, one student measures the transformation execution times for generating CCSL models from the four platform-specific MSD specifications.
Finally, on the one hand, the averaged measurement values for each operation kind are multiplied by the corresponding number of model elements in the four MSD specifications and summed. The transformation execution times are also for each model added to the aforementioned sum, yielding variable H2.1. On the other hand, the averaged measurement values for each operation kind are multiplied by the corresponding model elements in the generated CCSL models, yielding variable H2.2.
At the end, the results for the MSD specification and the CCSL models are compared. We consider H2 fulfilled if H2.1 < H2.2.
8.4.1 Data collection preparation
Model preparations As a basis for evaluating H2, student-2 copies MSD-spec-1, extends the platform model to five TamComConnections connecting five TamECUs, and allocates the software architecture to it. We present the resulting model in Fig. 7 and call it MSD-spec-2. Furthermore, student-1 specifies another variant of a platform-independent MSD specification for the EBEAS, which encompasses 24 MSDs and hence is more complex in terms of interaction requirements. He allocates it to the simple platform model of MSD-spec-1, which we call MSD-spec-3. Finally, student-2 copies the variant of the platform-independent MSD specification encompassing 24 MSDs, extends the platform model of MSD-spec-2, and adds the allocation specification. We call the resulting model MSD-spec-4, which is the most complex of all considered MSD specifications in terms of interaction requirements as well as the platform model.
Technical measurement preparations To technically prepare the duration measuring of the different model operation kinds as part of the evaluation of H2, we apply and adapt the Eclipse plugin ModRec [87, 106]. ModRec aims at designing and executing empirical studies on modeling in a Papyrus and EMF context. As a prerequisite for this purpose, it provides a Papyrus model listener to record atomic model operations, which we consider in H2.
For measuring atomic model operation kinds in the Papyrus-based ScenarioTools MSD, we slightly adapt ModRec to simply log timestamps for each of the model operations. In addition, we implement a custom listener for the Xtext-based CCSL editor, because Xtext renders the underlying EMF model on every keystroke in a new model copy. Furthermore, we prepare a dedicated measurement model for both the platform-specific MSD specifications and the CCSL models. We provide the measurement tool suite and models in our supplementary material [63].
Empirical measurement preparations Regarding the design of the evaluation of H2, the first author automatically counts the different model elements for MSD-spec-1 to MSD-spec-4 as well as the different model elements of the corresponding generated CCSL models CCSL-model-1 to CCSL-model-4. Afterward, we categorize the model elements w.r.t. to different atomic model operation kinds that are required to specify each of these model elements. This includes, for example, the initial creation of a model element, specifying its name attribute, specifying further values, or referencing other model elements. This procedure yielded the following amounts of different model operation kinds:
-
34 conventional UML model operation kinds that are required for the platform-independent part of MSD specifications, spanning several kinds of individual UML editors (e.g., class diagrams for component types and interfaces, composite structure diagrams for architectures, sequence diagram editors for interactions, and form editors to set the detailed properties of all elements). The conventional UML model operation kinds strongly depend on the editor capabilities provided by Papyrus for the particular type of the considered UML partial model. Consequently, we measure each of them individually in the data collection (cf. Sect. 8.4.2). For example, MSD-spec-1 contains 5 component types, and for each of them the requirements engineer has to 1) create the component type and 2) specify its name attribute, resulting in 2 atomic model operation kinds for this model element.
-
7 generic stereotype model operation kinds, as the editor capabilities for stereotypes in Papyrus are all the same. That is, we generalized the 69 different operation kinds for specifying the platform-specific information via our TAM profile to these 7 generic stereotype operation kinds. These encompass, for example, 1) creating a UML base model element, 2) applying a stereotype, and 3) specifying a numeric tagged value. In the data collection (cf. Sect. 8.4.2), we use the measurement values of these generic stereotype operation kinds in a representative manner for each of the 69 TAM stereotype operations. For example, MSD-spec-1 contains 2 TamProcessingUnits, and each of them requires creating the UML base element (generic stereotype operation kind 1), applying the stereotype (operation kind 2), and specifying the numerical tagged values numCores and speedFactor (each time operation kind 3).
-
19 CCSL editor operation kinds, which directly emerge from the different kinds of model elements used in our transformation and thereby CCSL models. These CCSL editor operation kinds encompass the declaration of Integer and clock variables, as well as the specification of the clock expressions and clock relations as introduced in Sect. 2.4 and as used by our operational semantics overview in Sect. 6.
8.4.2 Data collection procedure
For any of the 34 UML model operation kinds, the 7 generic stereotype model operation kinds (representative for the 69 TAM stereotype model operations), and the 19 CCSL editor operation kinds (cf. Sect. 8.4.1), the first author measures each 10 times the duration for conducting the operation as fast as possible in the dedicated measurement models. That is, we measure the raw, time-wise effort for conducting the particular operations in the corresponding editors, which also includes typical duration deviations due to wrong mouse clicks or correcting typing errors. We provide all measurement points as well as minimum/maximum times and standard deviations in our dataset [63].
We then multiply the average values of the measurements for the operation kinds with the number of the corresponding modeling elements in MSD-spec-1 to MSD-spec-4 and CCSL-model-1 to CCSL-model-4. The second column of both the left- and right-hand side of Table 1 shows the aggregated amounts of model elements for the MSD specifications and CCSL models, respectively. For both the MSD specifications and CCSL models, the table also includes a breakdown into the particular model element kinds. First, it details for the MSD specifications the amounts of types, architectural elements, and interaction elements for the platform-independent part (cf. Sect. 2.2.1) as well as the amounts of the different element kinds of the platform-specific part (cf. Sect. 4). Second, it details for CCSL models the amounts of the particular model element kinds like variable declarations, clock expressions, and the different clock relation kinds (cf. Sect. 2.4). Then, the third column of both the left- and right-hand side of Table 1 shows the aggregated sums of the average measurement values multiplied by the number of corresponding model elements, where we again provide the detailed multiplication scheme and values in our dataset [63].
To yield H2.1, we add the averaged transformation execution times for deriving the corresponding CCSL model (fourth column on the left-hand side of Table 1) to the sum of the multiplied mean average measurement values for the effort on specifying the platform-specific MSD specification. For measuring the particular times, student-2 instruments the particular QVTo transformations in such a way that timestamps are generated and performs several times the transformation from any platform-specific MSD specification to each the corresponding CCSL model. The fifth column on the left-hand side of Table 1 lists the summarized times of specifying the platform-specific MSD specifications and of executing the transformation, representing the variable H2.1. The third column on the right-hand side of Table 1 yields H2.2 directly.
8.4.3 Interpreting the results
Relating the variables H2.2 and H2.1, we observe that the raw effort on manually specifying CCSL-model-1 (H2.2) is \(\approx \) 353% of the summarized effort on specifying MSD-spec-1 and on generating CCSL-model-1 (H2.1), \(\approx \) 297% for MSD-spec-/CCSL-model-2, \(\approx \) 827% for MSD-spec-/CCSL-model-3, and \(\approx \) 847% for MSD-spec-/CCSL-model-4. Thus, we consider H2 fulfilled as H2.1 < H2.2 always holds.
8.5 Hypothesis H3
We define evaluation hypothesis H3 as follows:
The generated CCSL models are syntactically correct (cf. evaluation question EQ1).
For evaluating H3, all generated CCSL models used for the evaluation of H1 and H2 are opened in the CCSL editor and simulated in TimeSquare.
We consider H3 fulfilled if all CCSL models generated during the evaluation of H1 and H2 can be opened in the CCSL editor and can be simulated in TimeSquare without the occurrence of any error.
8.5.1 Data collection preparation
The model preparations described in Sects. 8.3.2 and 8.4.1 form also the basis for evaluating H3.
8.5.2 Data collection procedure
During the evaluation of H1 and H2, the students open every generated CCSL models in the CCSL model editor and simulate them in TimeSquare. These models encompass CCSL-model-1, CCSL-model-2, CCSL-model-3, CCSL-model-4, and the 17 further CCSL models dedicated to certain resource properties. The students were able to open and simulate all models without the occurrence of any error.
8.5.3 Interpreting the results
We consider hypothesis H3 fulfilled because 100% of the 21 CCSL models generated during the evaluation of H1 and H2 were opened in the CCSL model editor and simulated in TimeSquare without the occurrence of any error.
8.6 Summarizing the results
The fulfilled hypotheses indicate a positive answer to our evaluation questions. That is, our timing analysis approach generates syntactically and semantically correct CCSL models and reduces the engineering effort for specifying them. The effort is even less if we assume that the platform-specific aspects are added to an already existing platform-independent MSD specification as presented in Sect. 2.2.1. Summarizing, the fulfilled hypotheses give rise to the assumption that our timing analysis approach is indeed useful for a timing analyst.
8.7 Threats to validity
The threats to validity in our example application according to the taxonomy of Runeson et al. [108] are:
Construct validity
-
During the evaluation conduct, both students had little knowledge on timing analysis and on the Marte platform modeling, and they had a lot and little knowledge on modeling MSDs, respectively (cf. Sect. 8.2). Thus, the students’ knowledge is not comparable to the knowledge of timing analysis experts, who are versed in applying conventional timing analysis tools for later development phases or TimeSquare. Such experts might tend to apply the commercial-off-the-shelf-tools that they are used to, or might argue that timing analyses are too imprecise in an early development phase with only coarse-grained information.
However, with their limited knowledge, the students managed to specify the particular models, to inject and understand real-time requirement violations, and to reenact the computation of timing effects based on resource properties through our operational semantics. This indicates that the approach is indeed applicable and efficient, especially for timing analysis novices.
-
Student-1 conceived the initial timing analysis approach as well as MSD-spec-1 in the context of [12], and the other platform-specific MSD specifications are variants of MSD-spec-1. Thus, he knew the functional principle of the approach and could have been biased toward it.
However, in addition we employed student-2 for conceiving the other platform-specific MSD specifications as well as evaluating the hypotheses, and the first author had comprehensive discussions with both students.
-
Regarding the evaluation of H1, the resource properties provided as modeling means by our TAM profile might not be extensive enough, might not be useful, or might not be applicable during the early development phase of RE.
However, we argue that the considered resource properties represent typical timing-relevant ones at an adequate abstraction level due to their systematic determination by means of a literature review [12, Chapter 3]. This literature review considered scientific as well as industrial-grade publications and investigated which resource properties influence the timing behavior of software-intensive systems and which concrete effects on the timing behavior they induce. Furthermore, it ensured the applicability during RE by excluding publications describing resource properties that have a too detailed abstraction level for a timing analysis during this early development phase.
-
Regarding the evaluation of H2, conducting a user study on specifying complete particular models might provide more information on the subjective efforts. In contrast, we measure the raw, time-wise efforts on conducting the particular model operation kinds in dedicated measurement models.
Nevertheless, Durisic et al. [31] report that such simple and atomic metrics based on model operations are a good and objective indicator for predicting the overall effort, though having certain threats to validity as every metric. Particularly, we do not measure and thereby depend on any cognitive effort that is very subjective and difficult to measure: Conceiving the models on paper or whiteboards before modeling in the tool, discussions with peers, design and complexity issues of the respective modeling languages, diagram layouting or text indenting, error search and debugging, model evolution, general cognitive abilities or current cognitive state of the engineer, language expertise, etc.
Internal validity Regarding the evaluation of H2, we multiply the amount of model elements of the four complete MSD specifications and CCSL models with the measured raw, time-wise efforts of corresponding atomic model operation kinds, where the measurements stem from dedicated measurement models. Under consideration of the transformation execution times, we then conclude that the effort on specifying platform-specific MSD specifications and generating CCSL models is less than the effort on manually specifying the corresponding CCSL models. These relations might be incorrect. However, comparing the sheer amounts of model elements for both model kinds, it is obvious that manually specifying a CCSL model cannot outperform an automatic CCSL model generation, even under consideration that platform-specific MSD specifications have to be created beforehand.
External validity We only considered one example application, and the platform-specific MSD specifications are variants of the same system. Furthermore, example applications in general cannot ensure external validity. Thus, we cannot generalize the conclusions to all possible platform-independent MSD specifications, other types of software-intensive systems, or software-intensive systems in other industry sectors. Nevertheless, the example application is typical for software-intensive systems, so that we do not expect large deviations for other types of systems.
Reliability
-
Regarding the evaluation of H1, the students could have judged incorrectly whether the platform-induced timing effects occur as expected. However, we mitigate this threat by employing two different students, whose judgments complement each other and are critically scrutinized by the first author. Furthermore, we provide the evaluation data on H1 and the example application in our supplementary material [63] for the sake of replicability.
-
Regarding the evaluation of H2, a different person could have a different modeling scheme or a different setup of hardware and operating system, so that this other person’s measurements would yield different duration values. However, we believe that we applied the most efficient modeling scheme for each of the operation kinds and that the hardware and operating system setup can be neglected on modern systems in a human interaction context. Furthermore, we provide all the data, the measurement software, and the measurement models in our supplementary material [63], so that interested people can replicate the measurements in other settings.
9 Related work
The approaches described in this section analyze timed models. Typically, they specify behavioral models and analyze them for safety and liveness properties in a timed setting. The expressiveness of the underlying notations and the particular model contents influence the purposes and capabilities of the analysis techniques, as explained in the following two paragraphs.
Approaches that only specify application behavior or the requirements on it can only verify that the timed behavior fulfills the checked properties and can be implemented at all. However, such approaches are not platform-aware: They are not intended to verify that an execution platform is sufficient to fulfill the real-time requirements (cf. Sect. 2.1). This is due to the fact that the timing effects induced by the resource properties are not in the scope of the analysis techniques or the analyzed models. Thus, such approaches can be compared to our Real-time Play-out approach [17], which simulatively validates timed MSDs to reveal unintended behavior and is the basis for verifying MSDs for safety/liveness properties [44].
If the models additionally specify the timing effects induced by the execution platform, the analysis techniques can also include (end-to-end) response time analyses as outlined in Sect. 2.1 and addressed by the approach presented in this article. However, this causes much effort, because these low-level timing effects (e.g., ECU, bus, and scheduling behavior) have to be pre-calculated based on the platform resource properties and explicitly specified for this purpose (e.g., through delays in the particular timed notations)—additionally to the (requirements on the) timed application behavior. Furthermore, such models dedicated only to the purpose of timing analyses are typically difficult to reuse for or base on existing models for other purposes in the design process (e.g., discussing the requirements models with stakeholders or conducting design reviews of the platform models).
In contrast, our approach enables to reuse existing timed scenario-based requirements as well as platform models. The application of de facto standard, UML-based modeling languages that are understandable for many stakeholders, and, particularly, the straightforward specification of resource properties instead of their induced timing effects facilitates to (re-)use models also for/from other design process purposes. Our semantics encapsulates the computation of the timing effects induced by the particular resource properties and enables to simulatively verify them against real-time requirements as part of the timed MSDs.
The related approaches can be distinguished into approaches for analyzing timed scenario-based models (Sect. 9.1) and for analyzing timed automata-based models (Sect. 9.2).
9.1 Analysis of timed scenario-based models
Beyond the explanations regarding the analysis of timed models in general above, most approaches described in this section annotate scenario-based requirements formalisms with real-time requirements as well as timing effects induced by the platform resources (cf. [58] for an overview on timed scenario notations). Furthermore, these approaches provide different non-simulative techniques for their respective timing analyses. However, the outputs of these timing analysis techniques are plain yes/no results and partly logged information about the processing times. In contrast, our timing analysis of the generated CCSL time models in TimeSquare enables to comprehensively detect real-time requirement violations straightaway by means of interactive simulation.
Live Sequence Charts (LSCs) [23] extend Message Sequence Charts [68] with modeling constructs and semantics for specifying and analyzing safety and liveness properties. Harel and Maoz [48] transferred these modeling constructs to a UML profile to enable the specification and analysis of LSC models in the widespread UML tools. Extended with time conditions and their semantics [47, 49], they form our timed MSD variant with its operational semantics given by Real-time Play-out [17] (cf. Sect. 2.2). Thus and as explained above, approaches based on timed LSCs/MSDs typically specify and analyze the (requirements on the) general application behavior constrained by real-time requirements but do not consider response time analysis based on platform models.
In contrast, Larsen et al. [77, 78, 82] present an approach to formally verify real-time design behavior specified through Timed Automata (TA) [2] against scenario-based functional and real-time requirements specified by means of time-enriched LSCs. For this purpose, the LSC requirements are translated to observer TA that are composed with the design behavior TA that encompass pre-calculated timing effects induced by the platform. The resulting TA network is verified against reachability properties on the observer TA in a model checking tool. However, the need for detailed intra-component design models encompassing platform timing effects impedes the application of the approach in the early RE phase.
Similarly, Lettrari and Klose [81] simulatively verify real-time design models against scenario-based functional and real-time requirements that are specified by means of time-constrained UML 1.3 Sequence Diagrams augmented with concepts from LSCs. For this purpose, they generate instrumented code from the design models so that timestamps are recorded in the simulative code execution. These timestamps are used to check whether the implementation fulfills the real-time requirements specified in the scenarios. However, the need for executable software code generated from detailed design models again impedes the application of the approach in early RE.
Hassine [55, 56] annotates the scenario notation of Timed Use Case Maps (TUCM) [57] and its underlying architecture with timing-relevant effects. The annotated TUCM model is transformed into an Abstract State Machine model [14] that is simulated in an external tool, similarly to our approach. However, the simulation tool is not capable of interpreting the annotations. Instead, it is instrumented so that execution traces are generated and persisted in a text file. These execution traces potentially contain log messages about real-time requirement violations and have to be inspected manually to reveal the violated requirement and the violating timing effect. In contrast, we generate CCSL specifications that we directly simulate in TimeSquare, enabling to detect and comprehend potential real-time requirement violations straightaway. Furthermore, the approach only allows to specify delays (i.e., timing effects) induced by the platform, but not the causes of these effects (i.e., the resource properties).
Wang and Tsai [119] apply Message Sequence Charts [68] to specify functional requirements and the Specification and Description Language [69] to specify the underlying architecture. They annotate these models with a task model including real-time requirements and with timing-relevant effects, respectively. They use algorithms to first compute an allocation of tasks to processing resources and subsequently perform a schedulability analysis to verify the effects against real-time requirements, yielding a plain yes/no result. In contrast, we explicitly specify the allocation of software components to processing resources in our platform-specific MSD specifications and simulate the resulting CCSL specifications, where the simulation facilitates to comprehend potential real-time requirement violations. Again, the approach does not distinguish between resource properties and the timing effects that they induce.
Han and Youn [45] apply Interval Timed Colored Petri Nets [15] to specify delays for the execution of event sequences and annotate these models with real-time requirements. They present algorithms for the computation of event sequence processing delays and for the verification of the delays w.r.t. the real-time requirements. Similarly to the approaches mentioned above, the outputs of these algorithms are plain yes/no results as well as the logged processing times. Thus, our simulative approach again enables a better comprehension of real-time requirement violations. Furthermore, the approach only allows to specify static delays in terms of timing effects.
9.2 Analysis of timed automata-based models
Automata-based notations are in terms of expressiveness similar to scenario-based notations. However, scenario-based models are quicker to understand than automata-based ones [83, 99]. Due to the focus on the inter- instead of the intra-component behavior, we further argue that a scenario-based notation is the natural choice for the requirements on the message-based interactions of distributed software-intensive systems, which we address in this article. Apart from that, our approach is different from most of the approaches mentioned in this section as explained in the beginning of Sect. 9. That is, it does not require specifying the low-level timed platform behavior with timing effects pre-calculated from the resource properties, but rather enables using the resource properties as part of dedicated platform models in a straightforward manner.
Gerber and Lee [40] present the automata-like process algebra Calculus for Communicating Shared Resources and an accompanying proof system for schedulability analyses. Beyond timing effects and constraints for the behavioral part, it allows the allocation to shared and prioritizable resources like CPUs or communication links. The underlying computational model captures the fact that a resource can only process one action at an instant. Thus, from the approaches described in this section, it comes closest to our approach of allocating behavioral to platform models and encapsulating timing effects in the operational semantics. However, the resources are part of the behavioral model, so that behavioral and platform aspects cannot be conceived independently. From an analysis point of view, the approach is not capable of interactively simulating and visualizing the timed behavior for revealing the causes of real-time requirement violations.
Jahanian et al. [70, 71] introduce the graphical specification language Modechart, which is inspired by Harel’s Statecharts [46] and allows to annotate real-time requirements (i.e., deadlines) and timing effects (i.e., delays) to automata-based behavioral models. Modechart comes with a tool set [21] for the specification, formal verification, and simulation of the corresponding models. Unlike in our approach, neither dedicated platform models specifying the resource properties nor their translation into the induced timing effects are in the scope of Modechart. Thus, the detailed scheduling behavior of the whole system has to be specified and annotated with all possible timing effects to verify it against the real-time requirements.
Ostroff [98] introduces time-augmented automata called Timed Transition Models and an automatic verification approach for this language. The timing behavior is specified by means of lower and upper time bounds for the transitions, and the real-time requirements are specified through properties in real-time temporal logic [97]. Two different algorithms compute reachability graphs from the timed transitions models and analyze them for different temporal properties. Again, every possible timing effect induced by the execution platform has to be calculated and explicitly specified by means of time bounds for the transitions to consider it in the analysis.
Timed Automata (TA) [2] (cf. Sect. 9.1 for an approach applying TA in combination with LSCs) provide modeling means for adding delays and timed conditions to the states and transitions of automata. Particularly, their efficient implementation by means of a simplified TA variant in the model checking tool UPPAAL [11, 79] led to a wide range of approaches using TA as basis for the formal verification of timed behavior (see, e.g., [118] for a list of UPPAAL case studies). As the approaches mentioned before, specifying and analyzing TA either only consider the timed application behavior or requires to know and specify additionally the behavior of the platform and its timing effects. Thus, for applying TA for the purpose of schedulability analysis, the UPPAAL variant TIMES [4, 5] enables to specify and analyze task models based on TA. However, this approach requires as much detailed knowledge of the final implementation or models of it that it can be applied only in later engineering phases, like conventional commercial-off-the-shelf-tools for response time analysis.
10 Conclusion and future work
In this paper, we presented an approach that enables end-to-end response time analyses based on MSD specifications encompassing real-time requirements in the early RE phase of the development process. For this purpose, we introduced the Marte-based TAM profile that provides modeling means for platforms, their timing-relevant resource properties, and the allocation of MSD specifications to the platform models. Furthermore, we conceptually extend the event handling semantics of MSDs by introducing event kinds for the consideration of static and dynamic delays that occur during the software execution on a target platform. Finally, as the main contribution, we specified the operational semantics of platform-specific MSD specifications with extended event handling for the purpose of timing analyses. To this end, we applied the Gemoc approach enabling the automatic derivation of CCSL models from platform-specific MSD specifications based on our semantics specification. These CCSL models are executable in the simulative timing analysis tool TimeSquare, which also provides model checking features. Using an example application, we evaluated the approach with the automotive EBEAS example and outline the timing problems that we are able to identify on this abstraction level.
Our timing analysis approach enables to identify platform-induced real-time requirement violations in MSD requirements specifications that could otherwise be revealed only in late engineering phases through conventional timing analysis techniques. The TAM profile provides comprehensive modeling means to add timing-relevant platform-specific aspects to MSD specifications at an abstraction level suitable for RE. The extended event handling semantics for MSDs enables a more realistic consideration of the particular event occurrences and the delays in between. The specification of the MSD semantics for timing analyses encodes, in terms of CCSL and MoCCML, a subset of the conventional MSD semantics, the extended MSD event handling, and the platform resource properties’ effects on the timing behavior. Particularly, the automatic computation and separation of the timing effects from their inducing resource properties enables the straightforward usage of platform models. Furthermore, the declarative semantics specification with Gemoc allows the flexible encoding of additional resource properties’ timing effects or the adaption to other scenario-based notations. The model transformation generation feature of Gemoc Studio takes this specification as input and thereby reduces the effort of moving from MSDs to the CCSL formalism. The evaluation of the example application indicates the efficacy of the approach.
A promising starting point for future work is the size of the solution space, which arises out of the detection of a real-time requirement (cf. the discussion on the variety of potential fixes to a violation in the end of Sect. 7.1). Such challenges, where a large solution space exists and several constraints have to be considered, are subject to optimization questions and can be boiled down to a search problem in the solution space. Search-based software engineering [52,53,54] is a well-established software engineering field that applies meta-heuristic algorithms [39] to automatically solve such search problems. Similar to our previous work on automatically completing underspecified scenario models [110], the problem of finding real-time-feasible platform-specific MSD specifications could be encoded as input to a meta-heuristic algorithm that has to incorporate the timing analysis results.
References
Aldebaran file format. https://www.mcrl2.org/web/user_manual/language_reference/lts.html#aldebaran-format. Accessed Jan 2022
Alur, R., Dill, D.L.: A theory of timed automata. Theoret. Comput. Sci. 126(2), 183–235 (1994). https://doi.org/10.1016/0304-3975(94)90010-8
Alur, R., Henzinger, T.A., Kupferman, O., Vardi, M.Y.: Alternating refinement relations. In: International Conference on Concurrency Theory, no. 1466 in LNCS, pp. 163–178. Springer (1998). https://doi.org/10.1007/BFb0055622
Amnell, T., Fersman, E., Mokrushin, L., Pettersson, P., Yi, W.: TIMES—a tool for modelling and implementation of embedded systems. In: Tools and Algorithms for the Construction and Analysis of Systems, no. 2280 in LNCS, pp. 460–464. Springer (2002). https://doi.org/10.1007/3-540-46002-0_32
Amnell, T., Fersman, E., Mokrushin, L., Pettersson, P., Yi, W.: TIMES: A tool for schedulability analysis and code generation of real-time systems. In: Revised Papers of the 1st International Workshop on Formal Modeling and Analysis of Timed Systems (FORMATS 2003), no. 2791 in LNCS, pp. 60–72. Springer (2004). https://doi.org/10.1007/978-3-540-40903-8_6
André, C.: Syntax and semantics of the clock constraint specification language (CCSL). Research Report RR-6925, INRIA (2009)
André, C., Mallet, F., de Simone, R.: Modeling time(s). In: ACM/IEEE International Conference on Model Driven Engineering Languages and Systems (MoDELS/UML), no. 4735 in LNCS, pp. 559–573. Springer (2007)
Audsley, N.C., Burns, A., Davis, R.I., Tindell, K.W., Wellings, A.J.: Fixed priority pre-emptive scheduling: an historical perspective. Real-Time Syst. 8(2), 173–198 (1995). https://doi.org/10.1007/BF01094342
AUTOSAR GbR: AUTomotive Open System ARchitecture (AUTOSAR) Standard. https://www.autosar.org. Accessed Jan 2022
Bate, I.J.: Scheduling and timing analysis for safety critical real-time systems (1998)
Bengtsson, J., Yi, W.: Timed Automata: Semantics, Algorithms and Tools, pp. 87–124. No. 3098 in LNCS. Springer (2004). https://doi.org/10.1007/978-3-540-27755-2_3
Bernijazov, R.: Early timing analysis of scenario-based software requirements. Master’s thesis, Paderborn University (2017)
Boehm, B.W.: Software Engineering Economics. Prentice-Hall, Englewood Cliffs (1981)
Börger, E., Stark, R.: Abstract State Machines: A Method for High-Level System Design and Analysis. Springer, New York (2003)
Boucheneb, H.: Interval timed coloured petri net: efficient construction of its state class space preserving linear properties. Formal Asp. Comput. 20(2), 225–238 (2008). https://doi.org/10.1007/s00165-007-0050-7
Bousse, E., Degueule, T., Vojtisek, D., Mayerhofer, T., DeAntoni, J., Combemale, B.: Execution framework of the Gemoc studio (tool demo). In: 9th International Conference on Software Language Engineering. ACM (2016)
Brenner, C., Greenyer, J., Holtmann, J., Liebel, G., Stieglbauer, G., Tichy, M.: ScenarioTools real-time play-out for test sequence validation in an automotive case study. In: 13th International Workshop on Graph Transformation and Visual Modeling Techniques, no. 67 in Electronic Communications of the EASST. EASST (2014). https://doi.org/10.14279/tuj.eceasst.67.948
Buttazzo, G.C.: Hard Real-Time Computing Systems-Predictable Scheduling Algorithms and Applications, 3rd edn. Springer, New York (2011). https://doi.org/10.1007/978-1-4614-0676-1
Byhlin, S., Ermedahl, A., Gustafsson, J., Lisper, B.: Applying static WCET analysis to automotive communication software. In: 17th Euromicro Conference on Real-Time Systems (ECRTS’05), pp. 249–258. IEEE (2005). https://doi.org/10.1109/ECRTS.2005.7
Chen, X., Liu, J., Mallet, F., Jin, Z.: Modeling timing requirements in problem frames using CCSL. In: 18th Asia-Pacific Software Engineering Conference (APSEC), pp. 381–388. IEEE (2011). https://doi.org/10.1109/APSEC.2011.30
Clements, P.C., Heitmeyer, C.L., Labaw, B.G., Rose, A.T.: MT: A toolset for specifying and analyzing real-time systems. In: 1993 Real-Time Systems Symposium, pp. 12–22 (1993). https://doi.org/10.1109/REAL.1993.393519
Combemale, B., DeAntoni, J., Larsen, M.V., Mallet, F., Barais, O., Baudry, B., France, R.: Reifying concurrency for executable metamodeling. In: 6th International Conference on Software Language Engineering, no. 8225 in LNCS, pp. 365–384. Springer (2013). https://doi.org/10.1007/978-3-319-02654-1_20
Damm, W., Harel, D.: LSCs: Breathing life into message sequence charts. Formal Methods Syst. Des. 19(1), 45–80 (2001). https://doi.org/10.1023/A:1011227529550
DeAntoni, J., André, C., Gascon, R.: CCSL denotational semantics. Research Report RR-8628, INRIA (2014)
DeAntoni, J., Diallo, I.P., Champeau, J., Combemale, B., Teodorov, C.: Operational semantics of the model of concurrency and communication language. Research Report RR-8584, INRIA (2014)
DeAntoni, J., Diallo, I.P., Teodorov, C., Champeau, J., Combemale, B.: Towards a meta-language for the concurrency concern in DSLs. In: Design, Automation & Test in Europe, pp. 313–316 (2015). https://doi.org/10.7873/DATE.2015.1052
DeAntoni, J., Mallet, F.: ECL: the event constraint language, an extension of OCL with events. Research Report RR-8031, INRIA (2012)
DeAntoni, J., Mallet, F.: TimeSquare: Treat your models with logical time. In: 50th International Conference on Objects, Models, Components, Patterns, no. 7304 in LNCS, pp. 34–41. Springer (2012). https://doi.org/10.1007/978-3-642-30561-0_4
Dietrich, C., Wägemann, P., Ulbrich, P., Lohmann, D.: SysWCET: Whole-system response-time analysis for fixed-priority real-time systems. In: 2017 IEEE 23rd Real-Time and Embedded Technology and Applications Symposium (RTAS), pp. 37–48. IEEE (2017). https://doi.org/10.1109/RTAS.2017.37
The DOT language. https://graphviz.org/doc/info/lang.html. Accessed Jan 2022
Durisic, D., Staron, M., Tichy, M., Hansson, J.: Assessing the impact of meta-model evolution: a measure and its automotive application. Softw. Syst. Model. (2017). https://doi.org/10.1007/s10270-017-0601-1
Eclipse Gemoc Studio. https://projects.eclipse.org/projects/modeling.gemoc. Accessed Jan 2022
Eclipse Modeling Framework (EMF). https://www.eclipse.org/modeling/emf. Accessed Jan 2022
Eclipse Papyrus™ modeling environment. https://www.eclipse.org/papyrus/. Accessed Jan 2022
Eclipse QVT Operational. https://projects.eclipse.org/projects/modeling.mmt.qvt-oml. Accessed Jan 2022
Feiertag, N., Richter, K., Nordlander, J., Jonsson, J.: A compositional framework for end-to-end path delay calculation of automotive systems under different path semantics. In: 1st International Workshop on Compositional Theory and Technology for Real-Time Embedded Systems (CRTS) (2008)
Fidge, C.: Logical time in distributed computing systems. Computer 24(8), 28–33 (1991)
Fockel, M., Holtmann, J., Koch, T., Schmelter, D.: Formal, model- and scenario-based requirement patterns. In: 6th International Conference on Model-Driven Engineering and Software Development (MODELSWARD). SCITEPRESS (2018). https://doi.org/10.5220/0006554103110318
Gendreau, M., Potvin, J.Y. (eds.): Handbook of Metaheuristics. International Series in Operations Research & Management Science, vol. 272, 3rd edn. Springer, New York (2019). https://doi.org/10.1007/978-3-319-91086-4
Gerber, R., Lee, I.: CCSR: a calculus for communicating shared resources. In: Theories of Concurrency: Unification and Extension (CONCUR’90), no. 458 in LNCS, pp. 263–277. Springer (1990). https://doi.org/10.1007/BFb0039065
Glitia, C., DeAntoni, J., Mallet, F., Millo, J.V., Boulet, P., Gamatié, A.: Progressive and explicit refinement of scheduling for multidimensional data-flow applications using UML Marte. Des. Autom. Embed. Syst. 19(1–2), 1–33 (2015). https://doi.org/10.1007/s10617-014-9140-y
Goknil, A., DeAntoni, J., Peraldi-Frati, M.A., Mallet, F.: Tool support for the analysis of TADL2 timing constraints using TimeSquare. In: 2013 18th International Conference on Engineering of Complex Computer Systems, pp. 145–154. IEEE (2013). https://doi.org/10.1109/ICECCS.2013.28
Goldberg, E.: On bridging simulation and formal verification. In: Verification, Model Checking, and Abstract Interpretation, pp. 127–141 (2008). https://doi.org/10.1007/978-3-540-78163-9_14
Greenyer, J., Brenner, C., Cordy, M., Heymans, P., Gressi, E.: Incrementally synthesizing controllers from scenario-based product line specifications. In: 2013 9th Joint Meeting on Foundations of Software Engineering (ESEC/FSE 2013), pp. 433–443. ACM (2013). https://doi.org/10.1145/2491411.2491445
Han, S., Youn, H.Y.: Modeling and analysis of time-critical context-aware service using extended interval timed colored petri nets. IEEE Trans. Syst. Man Cybern. Part A: Syst. Hum. 42(3), 630–640 (2012). https://doi.org/10.1109/TSMCA.2011.2170064
Harel, D.: Statecharts: a visual formalism for complex systems. Sci. Comput. Program. 8(3), 231–274 (1987). https://doi.org/10.1016/0167-6423(87)90035-9
Harel, D., Kugler, H., Pnueli, A.: Smart play-out extended: time and forbidden elements. In: 4th International Conference on Quality Software (QSIC), pp. 2–10. IEEE (2004). https://doi.org/10.1109/QSIC.2004.1357938
Harel, D., Maoz, S.: Assert and negate revisited: modal semantics for UML sequence diagrams. Softw. Syst. Model. 7(2), 237–252 (2008). https://doi.org/10.1007/s10270-007-0054-z
Harel, D., Marelly, R.: Playing with time: On the specification and execution of time-enriched LSCs. In: 10th IEEE International Symposium on Modeling, Analysis and Simulation of Computer and Telecommunications Systems 2002 (MASCOTS 2002), pp. 193–202. IEEE (2002). https://doi.org/10.1109/MASCOT.2002.1167077
Harel, D., Marelly, R.: Come, Let’s Play: Scenario-Based Programming Using LSCs and the Play-Engine. Springer, New York (2003). https://doi.org/10.1007/978-3-642-19029-2
Harel, D., Rumpe, B.: Meaningful modeling: what’s the semantics of “semantics’’? IEEE Comput. 37(10), 64–72 (2004)
Harman, M.: The current state and future of search based software engineering. In: Future of Software Engineering (FOSE’07), pp. 342–357 (2007). https://doi.org/10.1109/FOSE.2007.29
Harman, M., Jones, B.F.: Search-based software engineering. Inf. Softw. Technol. 43(14), 833–839 (2001). https://doi.org/10.1016/S0950-5849(01)00189-6
Harman, M., Mansouri, S.A., Zhang, Y.: Search-based software engineering: trends, techniques and applications. ACM Comput. Surv. 45(1), 2379787 (2012). https://doi.org/10.1145/2379776.2379787
Hassine, J.: Early schedulability analysis with timed use case maps. In: 14th International SDL Forum, no. 5719 in LNCS, pp. 98–114. Springer (2009). https://doi.org/10.1007/978-3-642-04554-7_7
Hassine, J.: Early modeling and validation of timed system requirements using timed use case maps. Requirem. Eng. 20(2), 181–211 (2015). https://doi.org/10.1007/s00766-013-0200-9
Hassine, J., Rilling, J., Dssouli, R.: Timed use case maps. In: Revised Selected Papers of the 5th International Workshop on System Analysis and Modeling, no. 4320 in LNCS, pp. 99–114. Springer (2006)
Hassine, J., Rilling, J., Dssouli, R.: An evaluation of timed scenario notations. J. Syst. Softw. 83(2), 326–350 (2010). https://doi.org/10.1016/j.jss.2009.09.014
Haugen, Ø., Husa, K.E., Runde, R.K., Stølen, K.: Why timed sequence diagrams require three-event semantics. In: Scenarios: Models, Transformations and Tools, no. 3466 in LNCS, pp. 1–25. Springer (2005). https://doi.org/10.1007/11495628_1
Heumesser, N., Houdek, F.: Experiences in managing an automotive requirements engineering process. In: 12th IEEE International Requirements Engineering Conference, pp. 322–327. IEEE (2004). https://doi.org/10.1109/ICRE.2004.1335690
Holtmann, J.: Improvement of software requirements quality based on systems engineering. Ph.D. thesis, Paderborn University (2019). https://doi.org/10.17619/UNIPB/1-730
Holtmann, J., Deantoni, J., Fockel, M.: Early timing analysis based on scenario-based requirements specifications—description of SoSyM validation artifacts (2020). https://project.inria.fr/platformawaremsd/
Holtmann, J., DeAntoni, J., Fockel, M.: Supplementary material on “Early timing analysis based on scenario requirements and platform models” (2022). https://doi.org/10.5281/zenodo.4769781
Holtmann, J., Fockel, M., Koch, T., Schmelter, D., Brenner, C., Bernijazov, R., Sander, M.: The MechatronicUML requirements engineering method: Process and language. Tech. Rep. tr-ri-16-351, Fraunhofer IEM / Heinz Nixdorf Institute (2016). https://doi.org/10.13140/RG.2.2.33223.29606
Holtmann, J., Meyer, M.: Play-out for hierarchical component architectures. In: 11th Workshop on Automotive Software Engineering, GI-Edition—Lecture Notes in Informatics, vol. P-220, pp. 2458–2472. Koellen (2013)
International Organization for Standardization (ISO): Road vehicles—open interface for embedded automotive applications—part 3: OSEK/VDX operating system (OS). ISO 17356-3:2005 (2005)
International Organization for Standardization (ISO): ISO 26262-6:2018(E): Road vehicles – Functional safety. Part 6: Product development at the software level (2018)
ITU Telecommunication Standardization Sector: ITU-T Recommendation Z.120 (02/2011): Message Sequence Chart (MSC) (2011)
ITU Telecommunication Standardization Sector: ITU-T Recommendation Z.101 (04/2016): Specification and Description Language—Basic SDL-2010 (2016)
Jahanian, F., Lee, R., Mok, A.K.: Semantics of Modechart in real time logic. In: 21st Annual Hawaii International Conference on System Sciences (HICSS), pp. 479–489. IEEE (1988). https://doi.org/10.1109/HICSS.1988.11840
Jahanian, F., Mok, A.K.: Modechart: a specification language for real-time systems. IEEE Trans. Softw. Eng. 20(12), 933–947 (1994). https://doi.org/10.1109/32.368134
Joseph, M., Pandya, P.: Finding response times in a real-time system. Comput. J. 29(5), 390–395 (1986). https://doi.org/10.1093/comjnl/29.5.390
Khecharem, A., Gomez, C., DeAntoni, J., Mallet, F., De Simone, R.: Execution of heterogeneous models for thermal analysis with a multi-view approach. In: Forum on specification and Design Languages (FDL 2014). IEEE (2014)
Kitchenham, B., Pickard, L., Pfleeger, S.L.: Case studies for method and tool evaluation. IEEE Softw. 12(4), 52–62 (1995). https://doi.org/10.1109/52.391832
Kopetz, H.: Real-Time Systems-Design Principles for Distributed Embedded Applications, 2nd edn. Springer, New York (2011). https://doi.org/10.1007/978-1-4419-8237-7
Lamport, L.: Time, clocks, and the ordering of events in a distributed system. Commun. ACM 21(7), 558–565 (1978)
Larsen, K.G., Li, S., Nielsen, B., Pusinskas, S.: Verifying real-time systems against scenario-based requirements. In: 2nd World Congress on Formal Methods, no. 5850 in LNCS, pp. 676–691. Springer (2009). https://doi.org/10.1007/978-3-642-05089-3_43
Larsen, K.G., Li, S., Nielsen, B., Pusinskas, S.: Scenario-based analysis and synthesis of real-time systems using Uppaal. In: Design, Automation & Test in Europe Conference & Exhibition (DATE 2010), pp. 447–452. EDAA/IEEE (2010). https://doi.org/10.1109/DATE.2010.5457164
Larsen, K.G., Pettersson, P., Yi, W.: UPPAAL in a nutshell. Int. J. Softw. Tools Technol. Transf. 1, 134–152 (1997). https://doi.org/10.1007/s100090050010
Latombe, F., Crégut, X., Combemale, B., DeAntoni, J., Pantel, M.: Weaving concurrency in executable domain-specific modeling languages. In: 8th International Conference on Software Language Engineering. ACM (2015)
Lettrari, M., Klose, J.: Scenario-based monitoring and testing of real-time UML models. In: 4th International Conference on the Unified Modeling Language (\(\ll \)UML\(\gg \) 2001—The Unified Modeling Language: Modeling Languages, Concepts, and Tools), no. 2185 in LNCS, pp. 317–328. Springer (2001). https://doi.org/10.1007/3-540-45441-1_24
Li, S., Balaguer, S., David, A., Larsen, K.G., Nielsen, B., Pusinskas, S.: Scenario-based verification of real-time systems using Uppaal. Formal Methods Syst. Des. 37(2), 200–264 (2010). https://doi.org/10.1007/s10703-010-0103-z
Liebel, G., Tichy, M.: Comparing comprehensibility of modelling languages for specifying behavioural requirements. In: 1st International Workshop on Human Factors in Modeling (HuFaMo), pp. 17–24 (2015)
Mallet, F., André, C.: On the semantics of uml/Marte clock constraints. In: International Symposium on Object/Component/Service-Oriented Real-Time Distributed Computing (ISORC’09), pp. 301–312. IEEE (2009). https://doi.org/10.1109/ISORC.2009.27
Mallet, F., André, C., DeAntoni, J.: Executing AADL models with UML/Marte. In: International Conference on Engineering of Complex Computer Systems, pp. 371–376 (2009)
Mateescu, R., Thivolle, D.: A model checking language for concurrent value-passing systems. In: International Symposium on Formal Methods, pp. 148–164. Springer (2008)
ModRec. https://gitlab.com/grischal/is.ru.cs.papyrusactivitylogger. Accessed Jan 2022
Mubeen, S., Mäki-Turja, J., Sjödin, M.: Support for end-to-end response-time and delay analysis in the industrial tool suite-issues, experiences and a case study. Comput. Sci. Inf. Syst. 10(1), 453–482 (2013). https://doi.org/10.2298/CSIS120614011M
Mubeen, S., Mäki-Turja, J., Sjödin, M.: Communications-oriented development of component-based vehicular distributed real-time embedded systems. J. Syst. Architect. 60(2), 207–220 (2014). https://doi.org/10.1016/j.sysarc.2013.10.008
Mubeen, S., Nolte, T., Sjödin, M., Lundbäck, J., Lundbäck, K.L.: Supporting timing analysis of vehicular embedded systems through the refinement of timing constraints. Softw. Syst. Model. (2017). https://doi.org/10.1007/s10270-017-0579-8
Mubeen, S., Sjödin, M., Nolte, T., Lundbäck, J., Gålnander, M., Lundbäck, K.L.: End-to-end timing analysis of black-box models in legacy vehicular distributed embedded systems. In: 21st International Conference on Embedded and Real-Time Computing Systems and Applications, pp. 149–158. IEEE (2015). https://doi.org/10.1109/RTCSA.2015.24
Nolin, M., Mäki-Turja, J., Hänninen, K.: Achieving industrial strength timing predictions of embedded system behavior. In: 2008 International Conference on Embedded Systems & Applications (ESA), pp. 173–178. CSREA Press (2008)
Object Management Group (OMG): UML Profile for Marte: Modeling and Analysis of Real-Time Embedded Systems—Version 1.1. OMG Specification formal/2011-06-02 (2011)
Object Management Group (OMG): OMG Object Constraint Language (OCL)—Version 2.4. OMG Specification formal/2014-02-03 (2014)
Object Management Group (OMG): Meta object facility (MOF) 2.0 query/view/transformation specification—version 1.3. OMG Specification formal/2016-06-03 (2016)
Object Management Group (OMG): OMG Unified Modeling Language (OMG UML)—Version 2.5.1. OMG Specification formal/2017-12-05 (2017)
Ostroff, J.S.: Temporal Logic for Real Time Systems. Wiley, New York (1989)
Ostroff, J.S.: Automated verification of timed transition models. In: International Workshop on Automatic Verification Methods for Finite State Systems, no. 407 in LNCS, pp. 247–256. Springer (1990). https://doi.org/10.1007/3-540-52148-8_20
Otero, M.C., Dolado, J.J.: Evaluation of the comprehension of the dynamic modeling in UML. Inf. Softw. Technol. 46(1), 35–53 (2004). https://doi.org/10.1016/S0950-5849(03)00108-3
Palencia Gutierrez, J.C., Gutierrez Garcia, J.J., Gonzalez Harbour, M.: Best-case analysis for improving the worst-case schedulability test for distributed hard real-time systems. In: 10th EUROMICRO Workshop on Real-Time Systems, pp. 35–44 (1998). https://doi.org/10.1109/EMWRTS.1998.684945
Peraldi-Frati, M.A., DeAntoni, J.: Scheduling multi clock real time systems: from requirements to implementation. In: 14th International Symposium on Object/Component/Service-oriented Real-time Distributed Computing, pp. 50–57. IEEE (2011). https://doi.org/10.1109/ISORC.2011.16
Platform Architect. https://www.synopsys.com/verification/virtual-prototyping/platform-architect.html. Accessed Jan 2022
Pohl, K., Rupp, C.: Requirements Engineering Fundamentals, 2nd edn. Rocky Nook, San Rafael (2016)
Prasad, K.V., Broy, M., Krüger, I.: Scanning advances in aerospace & automobile software technology. Proc. IEEE 98(4), 510–514 (2010)
Puschner, P., Burns, A.: Guest editorial: a review of worst-case execution-time analysis. Real-Time Syst. 18(2), 115–128 (2000). https://doi.org/10.1023/A:1008119029962
Ragnarsson, A., Chakraborty, S., Liebel, G.: ModRec: a tool to support empirical study design for Papyrus and the Eclipse Modeling Framework. In: 5th International Workshop on Human Factors in Modeling/Modeling of Human Factors (HuFaMo). IEEE (2021). https://doi.org/10.1109/MODELS-C53483.2021.00059
Wilhelm, R., et al.: The worst-case execution-time problem—overview of methods and survey of tools. ACM Trans. Embedd. Comput. Syst. 7(3), 36:1-36:53 (2008). https://doi.org/10.1145/1347375.1347389
Runeson, P., Höst, M., Austen, R., Regnell, B.: Case Study Research in Software Engineering—Guidelines and Examples, 1st edn. Wiley, New York (2012)
ScenarioTools MSD tool suite. https://bitbucket.org/jgreenyer/scenariotools. Accessed Jan 2022
Schmelter, D., Greenyer, J., Holtmann, J.: Toward learning realizable scenario-based, formal requirements specifications. In: 4th International Workshop on Artificial Intelligence for Requirements Engineering (AIRE). IEEE (2017). https://doi.org/10.1109/REW.2017.14
Selic, B., Gérard, S.: Modeling and Analysis of Real-Time and Embedded systems with UML and Marte: Developing Cyber-Physical Systems. Elsevier, Amsterdam (2014)
Sha, L., Abdelzaher, T., Årzén, K.E., Cervin, A., Baker, T., Burns, A., Buttazzo, G., Caccamo, M., Lehoczky, J., Mok, A.K.: Real time scheduling theory: a historical perspective. Real-Time Syst. 28(2–3), 101–155 (2004). https://doi.org/10.1023/B:TIME.0000045315.61234.1e
TA tool suite. https://www.vector.com/int/en/products/products-a-z/software/ta-tool-suite/. Accessed Jan 2022
TimeSquare. http://timesquare.inria.fr/. Accessed Jan 2022
Tindell, K., Burns, A., Wellings, A.J.: Analysis of hard real-time communications. Real-Time Syst. 9(2), 147–171 (1995). https://doi.org/10.1007/BF01088855
Tindell, K., Clark, J.: Holistic schedulability analysis for distributed hard real-time systems. Microprocess. Microprogram. 40(2), 117–134 (1994). https://doi.org/10.1016/0165-6074(94)90080-9
Tindell, K.W., Hansson, H., Wellings, A.J.: Analysing real-time communications: controller area network (CAN). In: 1994 Real-Time Systems Symposium (RTTS), pp. 259–263. IEEE (1994). https://doi.org/10.1109/REAL.1994.342710
UPPAAL case studies. https://uppaal.org/casestudies/. Accessed Jan 2022
Wang, S., Tsai, G.: Specification and timing analysis of real-time systems. Real-Time Syst. 28(1), 69–90 (2004). https://doi.org/10.1023/B:TIME.0000033379.78994.1a
Xtext language development framework. https://www.eclipse.org/Xtext/. Accessed Jan 2022
Zannier, C., Melnik, G., Maurer, F.: On the success of empirical studies in the international conference on software engineering. In: 28th International Conference on Software Engineering, pp. 341–350. ACM (2006). https://doi.org/10.1145/1134285.1134333
Acknowledgements
We particularly thank Ruslan Bernijazov (aka student-1) for conceiving and implementing a very early version [12] of our approach. Furthermore, we thank Kai Biermeier (aka student-2) for supporting us in early stages of the evaluation as well as Grischa Liebel for pointing us to ModRec. Parts of this research were sponsored by Vinnova under grant agreement nr. 2018-02228 as part of the ITEA4 project BUMBLE.
Funding
Open access funding provided by University of Gothenburg.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by J. Araujo, A. Moreira, G. Mussbacher, and P. Sánchez.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work is an improved and condensed version of a part of the first author’s Ph.D. thesis [61, Chapter 4], with the main work conducted at his former affiliation at Fraunhofer IEM.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Holtmann, J., Deantoni, J. & Fockel, M. Early timing analysis based on scenario requirements and platform models. Softw Syst Model 21, 2171–2211 (2022). https://doi.org/10.1007/s10270-022-01002-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10270-022-01002-3