Abstract
Automatically synthesizing consistent models is a key prerequisite for many testing scenarios in autonomous driving to ensure a designated coverage of critical corner cases. An inconsistent model is irrelevant as a test case (e.g., false positive); thus, each synthetic model needs to simultaneously satisfy various structural and attribute constraints, which includes complex geometric constraints for traffic scenarios. While different logic solvers or dedicated graph solvers have recently been developed, they fail to handle either structural or attribute constraints in a scalable way. In the current paper, we combine a structural graph solver that uses partial models with an SMT-solver and a quadratic solver to automatically derive models which simultaneously fulfill structural and numeric constraints, while key theoretical properties of model generation like completeness or diversity are still ensured. This necessitates a sophisticated bidirectional interaction between different solvers which carry out consistency checks, decision, unit propagation, concretization steps. Additionally, we introduce custom exploration strategies to speed up model generation. We evaluate the scalability and diversity of our approach, as well as the influence of customizations, in the context of four complex case studies.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Motivation. The recent increase in popularity of cyber-physical systems (CPSs) such as autonomous vehicles has resulted in a rising interest in their safety assurance. Since existing tools and approaches commonly represent CPSs as (typed and attributed) graph models [43], automated generation of test models has become a core challenge for their effective testing. Recent testing approaches [9] use simulators to place the CPS under test in challenging traffic scenarios defined by (generated) test configurations. In such approaches, the CPS is considered as a black box and its safety is evaluated at the system level, without direct handling of internal components and their interactions. In order to synthesize adequate (realistic) test data for safety assurance of CPSs, data generation approaches must handle complex structural and numeric constraints.
Problem statement. Unfortunately, the automated synthesis of consistent graph-based models that satisfy (or deliberately violate) a set of well-formedness constraints is a very challenging task. While various underlying logic solvers like SAT, SMT (Satisfiability Modulo Theories) or CSP (Constraint Satisfaction Problem) solvers have been repeatedly used for such purposes in tools, like in USE [26, 27], UML2CSP [15], Formula [38], various theorem provers [5], or Alloy [35] thanks to many favorable theoretical properties (e.g., soundness or completeness) such solvers primarily excel in detecting inconsistencies and not in deriving models used as test cases. Rather than being used to address the model generation task as a whole, such specialized solvers (e.g., dReal [23]) may be more useful for handling only specific aspects (e.g., numeric constraints) of model generation. In fact, although there does exist research [4, 75, 76] that uses such solvers for testing purposes, the use of such solvers as a stand-alone model generation tools is frequently hindered by the lack of scalability [71, 82] (i.e., the size of generated models is limited) and diversity [37, 70] (i.e., generated models often have similar or identical structure).
Recent model generators [71, 81, 82] have successfully improved on scalability by lifting the model synthesis problem on the level of graph models by using meta-heuristic search [81], possibly within a hybrid approach alongside an SMT-solver [82]. Alternatively, partial model refinement [71] can be used as search strategy, while efficient query/constraint evaluation engines [83, 86] validate the constraints during state space exploration. However, there are also important restrictions imposed by these tools such as lack of completeness [81, 82] or lack of attribute handling [71] in constraints.
Contributions. In this paper, we propose a model generation technique which can automatically derive consistent graph models that satisfy both structural and attribute constraints. For that purpose, the structural constraints are satisfied along partial model refinement [71], while attribute constraints are satisfied by repeatedly calling the Z3 SMT-solver [17] or the dReal quadratic solver (like [82]). We define refinement units (in analogy with an abstract DPLL procedure modulo theories (Davis–Putnam–Logemann–Loveland) [51] or SMT-solvers [50]) with consistency checking, decision, unit propagation and concretization steps to enable a bidirectional interaction between a graph solver and a numeric solver where a decision in one solver can be propagated to the other solver and vice versa.
Specific contributions of the paper include:
-
Precise semantics: We define 3-valued logic semantics for evaluating structural and attribute constraints over partial models.
-
Qualitative abstractions: We propose qualitative abstractions to uniformly represent attribute constraints as (structural) relations in a model.
-
Mapping for numeric constraints: We define a mapping from attribute constraints to a numerical problem interpreted by a numeric solver.
-
Model generation approach: We propose a generic model generation strategy with bidirectional interaction between a structural solver and two numeric solvers to handle int or double constraints.
-
Custom exploration strategy: We propose a technique to define custom explorations for model generation to exploit domain-specific hints.
-
Evaluation: We evaluate a prototype implementation of the approach on four case studies to assess scalability and diversity properties of model generation, as well as the influence of customizations.
This paper extends our earlier work in [67] by
-
1.
introducing a new motivating example for traffic scenario generation with nonlinear constraints;
-
2.
integrating an approximate numeric solver dReal [23] to handle non-linear geometric constraints;
-
3.
providing a detailed mapping from attribute constraints to numerical problems;
-
4.
introducing custom exploration strategies;
-
5.
extending experimental evaluation with a complex case study (traffic scenario) and research question.
Added value. Our approach provides good scalability for automatically generating consistent models with structural and attribute constraints while still providing completeness and diversity. We also successfully generate models of traffic scenarios operating in physical space, which is a promising result toward complex simulation analysis for safety assurance of CPSs.
Structure of the paper. The rest of the paper is structured as follows: Sect. 2 describes the motivating case study related to traffic scenario generation. Section 3 presents a running example and summarizes core concepts pertaining to partial models and their refinements. Sections 4 and 5 detail our model generation approach that combines structural and numeric reasoning. Section 6 provides evaluation results of our proposed approach for four case studies. Section 7 overviews related approaches available in the literature. Finally, Sect. 8 concludes the paper.
2 Motivating example
2.1 The Crossing Scenario domain
We illustrate various challenges of model generation and state space exploration in the context of critical traffic scenarios for autonomous driving. Specifically, we aim at generating instances of traffic scenarios where the vision of the vehicle-under-test (referred to as the ego-vehicle [25, 60]) is obstructed by the presence of other actors. Such scenarios have been identified as key challenges for the development of autonomous vehicle safetyFootnote 1. A sample scenario is shown in Fig. 1, where the actors are placed in such a way that the ego-vehicle (blue) is unable to see the pedestrian that is crossing the road due to the presence of the orange vehicle. As a result, there is a risk of collision between the ego-vehicle and the pedestrian if both of these actors decide to cross the intersection simultaneously.
By using the novel model generation techniques proposed in this paper, we aim to automatically synthesize traffic scenarios where actors are positioned in such a way that the ego-vehicle and the target pedestrian cannot see each other initially. Furthermore, these actors are given velocities such that they will collide with each other within a certain time limit to enforce reaction. These requirements correspond to complex geometric (numeric) constraints that must be handled during model generation.
To precisely capture this modeling domain, we use a metamodel (Sect. 2.2) and complex well-formedness (WF) constraints defined by graph patterns (in the VQL language [85, 86]) in Sect. 2.3.
2.2 Metamodel
A  is composed
is composed  s,
s,  s and
s and  s between actors. It also contains numerical attribute that act as bounds for actor positions (
s between actors. It also contains numerical attribute that act as bounds for actor positions ( and
and  ), actor speeds (
), actor speeds ( and
and  ) and collision time (
) and collision time ( ) between actors.
) between actors.
 objects are static elements in the scenario which are provided as input for model generation. In our metamodel, we include abstractions for vertical and horizontal
objects are static elements in the scenario which are provided as input for model generation. In our metamodel, we include abstractions for vertical and horizontal  s, which refers to their orientation when seen from a bird’s-eye view (see Fig. 12e for an example). This ensures that the respective lanes in a scenario intersect with each other. Each
s, which refers to their orientation when seen from a bird’s-eye view (see Fig. 12e for an example). This ensures that the respective lanes in a scenario intersect with each other. Each  contains a
contains a  attribute which designates the left boundary for vertical lanes, and the bottom boundary for the horizontal lanes. Lanes have a predefined width, which is identical for all lanes.
attribute which designates the left boundary for vertical lanes, and the bottom boundary for the horizontal lanes. Lanes have a predefined width, which is identical for all lanes.
Scenario specifications, such as the existence of certain  s or certain
s or certain  s between actors, are also included as inputs for model generation. For example, in the scenario shown in Fig. 1b, model generation inputs would enforce the existence of two actors (the ego-vehicle and the target pedestrian) which have their vision blocked and which will eventually collide (if there is no change in their behavior). It is the task of the model generator to create a new actor, place all actors appropriately and set their speeds such that the scenario specifications are satisfied.
s between actors, are also included as inputs for model generation. For example, in the scenario shown in Fig. 1b, model generation inputs would enforce the existence of two actors (the ego-vehicle and the target pedestrian) which have their vision blocked and which will eventually collide (if there is no change in their behavior). It is the task of the model generator to create a new actor, place all actors appropriately and set their speeds such that the scenario specifications are satisfied.
Actors are placed on a lane and have a concrete numeric position ( ,
,  ), size (
), size ( ,
,  ) and speed (
) and speed ( ,
,  ).
).
 objects defined over two actors (
objects defined over two actors ( and
and  ) represent qualitative abstractions of certain sequences of events or trajectories. For the sake of brevity, we only include two different types of
) represent qualitative abstractions of certain sequences of events or trajectories. For the sake of brevity, we only include two different types of  s, namely
s, namely  and
and  . Relation
. Relation  signifies that the
signifies that the  and
and  actors are unable to see each other because their line of sight (vision) is blocked by another actor which is physically placed between them. Relation
actors are unable to see each other because their line of sight (vision) is blocked by another actor which is physically placed between them. Relation  denotes that the two actors involved are given velocities such that they will collide at a time
denotes that the two actors involved are given velocities such that they will collide at a time  . The metamodel can be extended to incorporate further
. The metamodel can be extended to incorporate further  types.
types.
Such qualitative abstractions help enforce complex trajectories and behaviors without the need for continuously handling the exact attribute values. For example, if a relation  (A1, A2) exists between actors A1 and A2, then the numerical attributes of those actors are set up in a way that they would surely collide along the default behavior (without further control intervention like braking), but not vice versa.
(A1, A2) exists between actors A1 and A2, then the numerical attributes of those actors are set up in a way that they would surely collide along the default behavior (without further control intervention like braking), but not vice versa.
2.3 Well-formedness constraints
Our motivating example includes 32 constraints to restrict various parts of the metamodel. Actors have bounded positions, sizes and speeds, which are further constrained by the orientation and  of the lane on which they are placed. A minimum Euclidean distance is also enforced between any pair of actor to avoid overlaps. Qualitative relations (see Sect. 2.2) enforce custom constraints on attribute values.
of the lane on which they are placed. A minimum Euclidean distance is also enforced between any pair of actor to avoid overlaps. Qualitative relations (see Sect. 2.2) enforce custom constraints on attribute values.
This case study includes complex geometric constraints, quadratic inequalities, non-constant divisions and numeric if-then-else blocks. The violating cases of three representative constraints, implemented as VQL graph patterns ([85, 86]), are shown in Fig. 3.
-
 : checks if any actor in a
: checks if any actor in a  relation is not the blocking actor;
relation is not the blocking actor; -
 : checks (using slopes) that the blocking actor of a
: checks (using slopes) that the blocking actor of a  relation is physically placed between the
relation is physically placed between the  and
and 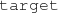 actors;
actors; -
 : enforces a minimum Euclidean distance of 5 between any pair of distinct actors.
: enforces a minimum Euclidean distance of 5 between any pair of distinct actors.
In this paper, we use color coding to separate  and
and  reasoning. The first constraint is a
reasoning. The first constraint is a  (i.e., only navigation along object references). The second constraint is a
(i.e., only navigation along object references). The second constraint is a  which accesses the
which accesses the  and
and  attributes of actors a1 and a2 to check the Euclidean distance between them. The third constraint contains both
attributes of actors a1 and a2 to check the Euclidean distance between them. The third constraint contains both  and
and  which mutually depend on each other. (A) If the vision between a1 and a2 is blocked by a new actor aB, then a new numeric constraint needs to be enforced between their positions and sizes (
which mutually depend on each other. (A) If the vision between a1 and a2 is blocked by a new actor aB, then a new numeric constraint needs to be enforced between their positions and sizes ( \(\rightarrow \)
\(\rightarrow \)
 dependency). (B) If the positions and sizes of actors a1, a2 and aB are already determined, then a new
dependency). (B) If the positions and sizes of actors a1, a2 and aB are already determined, then a new  reference pointing to one of the actors may (or must not) be added (
reference pointing to one of the actors may (or must not) be added ( \(\rightarrow \)
\(\rightarrow \)
 dependency).
dependency).
The Crossing Scenario domain extends [67] by showcasing complex, nonlinear numeric constraints over real numbers. These constraints can only be handled efficiently by specialized numeric solvers, such as dReal [23], which are limited in scalability and diversity when reasoning over structural constraints.
Consistent model generation is further complicated by the existence of mutual dependencies between structural and numeric constraints. Thus, generating models that conform to the Crossing Scenario domain requires an intelligent integration and bidirectional interaction between underlying numeric and structural (graph) solvers. In the paper, the bidirectional interaction is exemplified for numerical attributes, but the conceptual framework is applicable to attributes of other domains (e.g., strings, bitvectors) assuming the existence of an underlying solver (e.g., SMT-solver) for the background theory of the respective attribute.
3 Preliminaries
3.1 Running example
To succinctly present the formal background of our model generation approach, we present a simple running example of family trees with a metamodel (Fig. 4) and WF constraints defined by graph patterns (Fig. 5). This domain is intentionally chosen to contain only few concepts, while it can demonstrate all key technical challenges of constraint evaluation.
A  contains
contains  s with an integer
s with an integer  attribute.
attribute.  are related to each other by
are related to each other by  relations. The violating cases of the three WF constraints are defined by VQL graph patterns that all consistent family tree models need to respect:
relations. The violating cases of the three WF constraints are defined by VQL graph patterns that all consistent family tree models need to respect:
-
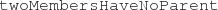 : There is at most one member in a family tree without a parent;
: There is at most one member in a family tree without a parent; -
 : All age attributes of family members are non-negative numbers;
: All age attributes of family members are non-negative numbers; -
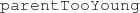 : There must be more than 12 years of difference between the
: There must be more than 12 years of difference between the  of a parent and a child.
of a parent and a child.
3.2 Domain-specific partial models
Domain specification We formalize the concepts in a target domain \(\langle \Sigma ,\alpha \rangle \) using an algebraic representation with signature \(\Sigma \) and arity function \(\alpha :\Sigma \rightarrow {\mathbb {N}}\). Such a signature  can be easily derived from EMF-like formalisms [84].
can be easily derived from EMF-like formalisms [84].
-
Unary predicate symbols
 (
( ) are defined for each EClass and EEnum in the domain,
) are defined for each EClass and EEnum in the domain,  denotes the EBoolean type,
denotes the EBoolean type, 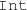 denotes integer numbers types like EInt or EShort, etc.
denotes integer numbers types like EInt or EShort, etc. -
Binary predicate symbols
 (
( 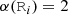 ) are defined for each EReference and EAttribute in the metamodel. For example,
) are defined for each EReference and EAttribute in the metamodel. For example, 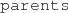 represent the parent reference between two Members, and
represent the parent reference between two Members, and 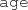 represents the age attribute relation between a Member and an EInt.
represents the age attribute relation between a Member and an EInt. -
Structural predicate symbols
 are n-ary predicates derived from graph queries (
are n-ary predicates derived from graph queries ( , the number of formal parameters of a graph query); e.g.,
, the number of formal parameters of a graph query); e.g., 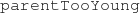 is a binary predicate symbol.
is a binary predicate symbol. -
Attribute predicate symbols
 represent n-ary predicates derived from attribute (check) expressions of queries (
represent n-ary predicates derived from attribute (check) expressions of queries ( ); e.g.,
); e.g., 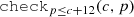 is a binary attribute predicate with parameters c and p.
is a binary attribute predicate with parameters c and p. -
The unary symbol
 denotes the existence of objects.
denotes the existence of objects. -
The binary symbol
 explicitly represents the equivalence relation between two objects.
explicitly represents the equivalence relation between two objects.
Partial models Partial models can explicitly represent uncertainty in models [18, 64], which is particularly relevant for intermediate steps of a model generation process. We use 3-valued partial models where the traditional 
 (
( ) and
) and  (
( ) are extended with a third truth value
) are extended with a third truth value  to denote
to denote  structural parts of the model [29, 61, 72]. Similarly, we extend the domain of traditional
structural parts of the model [29, 61, 72]. Similarly, we extend the domain of traditional  (e.g.,
(e.g.,  or
or  ) with
) with  to denote an
to denote an  .
.
Definition 1
(Numerical partial model) For a signature \(\langle \Sigma ,\alpha \rangle \), a numerical partial model is a logic structure  where:
where:
-
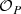 is the finite set of objects in the model,
is the finite set of objects in the model, -
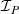 gives a 3-valued logic interpretation for each symbol
gives a 3-valued logic interpretation for each symbol  as
as 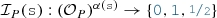 ,
, -
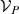 gives a numeric value interpretation for each object in the model:
gives a numeric value interpretation for each object in the model: 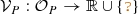 .
.
Note that this definition uniformly handles domain objects (e.g.,  ) and data objects (e.g.,
) and data objects (e.g.,  ), which is frequently the case in object-oriented languages. Next, we capture some regularity restrictions to exclude irrelevant (irregular) partial models:
), which is frequently the case in object-oriented languages. Next, we capture some regularity restrictions to exclude irrelevant (irregular) partial models:
Definition 2
(Regular partial models) A partial model  is regular, if it satisfies the following conditions:
is regular, if it satisfies the following conditions:
-
R1
 (non-existing objects are omitted)
(non-existing objects are omitted) -
R2
 (
( is reflexive)
is reflexive) -
R3
 (
( is symmetric)
is symmetric) -
R4
 (two different objects cannot be equivalent)
(two different objects cannot be equivalent) -
R5
 (domain objects have no values)
(domain objects have no values) -
R6
 (objects with values are numbers)
(objects with values are numbers) -
R7
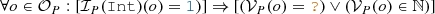 (only natural numbers are bound to
(only natural numbers are bound to  objects)
objects)
Example 1
Figure 9 illustrates partial models. In State 1, we have three concrete objects (where  and
and  are
are  ):
):  f1 and a
f1 and a  m1, and an unbound
m1, and an unbound  data object a1 (with
data object a1 (with  value). The partial model also contains an abstract “new objects” node that represents multiple potential new nodes (using
value). The partial model also contains an abstract “new objects” node that represents multiple potential new nodes (using  values for
values for  and dashed borders for
and dashed borders for  ), and a “new integers” node representing the potential new integers. In Fig. 9, predicates with value
), and a “new integers” node representing the potential new integers. In Fig. 9, predicates with value  are denoted by solid lines (as for the
are denoted by solid lines (as for the  edge between f1 and m1 in State 1) and predicates with value
edge between f1 and m1 in State 1) and predicates with value  are denoted by dashed lines (like the potential
are denoted by dashed lines (like the potential  edge in State 1).
edge in State 1).
3.3 Refinement and concretization
During model generation, the level of uncertainty in partial models will be gradually reduced by refinements. In a refinement step, uncertain  values can be refined to either
values can be refined to either  or
or  , or unbound values
, or unbound values  are refined to concrete numeric values. This is captured by an information ordering relation
are refined to concrete numeric values. This is captured by an information ordering relation  where an
where an  is either refined to another value Y, or \(X=Y\) remains equal. An information ordering can be defined between numeric values x and y similarly
is either refined to another value Y, or \(X=Y\) remains equal. An information ordering can be defined between numeric values x and y similarly 
A refinement from partial model P to partial model Q is a mapping that respects both information ordering relations ( ).
).
Definition 3
(Partial model refinements) A refinement  from regular partial model P to regular partial model Q is defined by a refinement function between the objects of the partial model
from regular partial model P to regular partial model Q is defined by a refinement function between the objects of the partial model  which respects information ordering:
which respects information ordering:
-
For each n-ary symbol \(s\in \Sigma \), each object
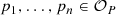 , and for each refinement \(q_1\in ref (p_1),\ldots ,q_n\in ref (p_n)\):
, and for each refinement \(q_1\in ref (p_1),\ldots ,q_n\in ref (p_n)\): 
-
For each object \(p\in {\mathcal {O}}_{P}\) and its refinement \(q\in ref (p)\):

-
All objects in Q are refined from an object in P, and existing objects
 must have a non-empty refinement.
must have a non-empty refinement.
Model generation along refinements eventually resolves all uncertainties to obtain a concrete model.
Definition 4
(Concrete partial model) A regular (see Definition 2) partial model P is concrete, if (a) \({\mathcal {I}}_P\) does not contain  values, and (b) \({\mathcal {V}}_P\) does not contain
values, and (b) \({\mathcal {V}}_P\) does not contain  values for integer and real data objects (for object o where
values for integer and real data objects (for object o where  or
or  ).
).
Example 2
Figure 9 illustrates several refinement steps. Between State 0 and State 1, new object is split into two objects by refining  to
to  between new object and m1, creating one concrete object m1 by refining
between new object and m1, creating one concrete object m1 by refining  on m1 to
on m1 to  . Moreover, type
. Moreover, type  is refined to
is refined to  ,
,  refined to
refined to  , and reference
, and reference  from f1 to m1 is refined to
from f1 to m1 is refined to  . Eventually, the value of data object a1 is refined from
. Eventually, the value of data object a1 is refined from  to
to  in State 4.2.
in State 4.2.
3.4 Constraints over partial models
Syntax Both structural (logical) and numeric constraints can be evaluated on partial models. For each graph pattern we derive a logic predicate (LP) defined as  , where \(\varphi \) is a logic expression (LE) constructed inductively from the pattern body as follows (assuming the standard precedence for operators).
, where \(\varphi \) is a logic expression (LE) constructed inductively from the pattern body as follows (assuming the standard precedence for operators).
-
if \(s \in \Sigma \) is an n-ary predicate symbol (i.e.,
 ,
, 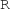 ,
,  ,
,  ,
,  or
or  ) then \(s(v_1,\ldots ,v_n)\) is a logic expression;
) then \(s(v_1,\ldots ,v_n)\) is a logic expression; -
if \(\varphi _1\) and \(\varphi _2\) are logic expressions, then \(\varphi _1\vee \varphi _2\), \(\varphi _1\wedge \varphi _2\), and \(\lnot \varphi _1\) are logic expressions;
-
if \(\varphi \) is a logic expression, and v is a variable, then \(\exists v:\varphi \) and \(\forall v:\varphi \) are logic expressions.
For each attribute constraint, we derive attribute predicates (as helpers) by reification to enable seamless interaction between structural and attribute solvers along a compatibility (if and only if) operator \(\Leftrightarrow \) (see Fig. 6). In case of numbers, such an attribute predicate is tied to a numerical predicate defined as  where \(\psi \) is constructed from numerical expressions. The expressiveness of those expressions is limited by the background theories of the underlying backend numeric solver. Here we define a core language of basic arithmetical expressions, which is supported by a wide range of numeric solvers:
where \(\psi \) is constructed from numerical expressions. The expressiveness of those expressions is limited by the background theories of the underlying backend numeric solver. Here we define a core language of basic arithmetical expressions, which is supported by a wide range of numeric solvers:
-
each variable v, constant symbol and literal (concrete number) c is a numerical expression,
-
if \(\psi _1\) and \(\psi _2\) are numerical expressions, then \(\psi _1 + \psi _2\), \(\psi _1 - \psi _2\), \(\psi _1 \times \psi _2\) and \(\psi _1 \div \psi _2\) are numerical expressions.
-
if \(\psi _1\) and \(\psi _2\) are numerical expressions, then \(\psi _1 < \psi _2\), \(\psi _1 > \psi _2\), \(\psi _1 \ge \psi _2\), \(\psi _1 \le \psi _2\), \(\psi _1 = \psi _2\), \(\psi _1 \ne \psi _2\) are numerical predicates.
-
if \(\varphi \) is a logic expression, and \(\psi _1\) and \(\psi _2\) are numerical expressions, then
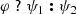 is a numerical expression (standing for “if \(\varphi \) then \(\psi _1\) else \(\psi _2\)”, commonly used in programming languages).
is a numerical expression (standing for “if \(\varphi \) then \(\psi _1\) else \(\psi _2\)”, commonly used in programming languages).
Example 3
Pattern parentTooYoung(child, parent) of Fig. 5 is formalized as the following logic predicate:

 is a numerical predicate.
is a numerical predicate.
Later such predicates will help communicate between different solvers, e.g., if  is found to be
is found to be  by the graph solver for some members \(c_1\) and \(p_1\), then the numerical predicate \(p_1\le c_1+12\) needs to be enforced by a numeric solver for the respective data objects and vice versa.
by the graph solver for some members \(c_1\) and \(p_1\), then the numerical predicate \(p_1\le c_1+12\) needs to be enforced by a numeric solver for the respective data objects and vice versa.
Semantics
A logic predicate  can be evaluated on a partial model P along a variable binding
can be evaluated on a partial model P along a variable binding  (denoted as
(denoted as  ), which can result in three truth values:
), which can result in three truth values:  ,
,  or
or  . The inductive semantic rules of evaluating a logic expression are listed in Fig. 6. Note that \(\mathop {min}\) and \(\mathop {max}\) take the numeric minimum and maximum values of
. The inductive semantic rules of evaluating a logic expression are listed in Fig. 6. Note that \(\mathop {min}\) and \(\mathop {max}\) take the numeric minimum and maximum values of  ,
,  and
and  .
.
A numerical predicate  can be evaluated on a partial model P along variable binding
can be evaluated on a partial model P along variable binding  (denoted as
(denoted as  ) with a result of
) with a result of  ,
,  or
or  . The inductive semantic rules of logic expressions are listed in Fig. 6. Note that
. The inductive semantic rules of logic expressions are listed in Fig. 6. Note that  means the truth value of numerical comparison
means the truth value of numerical comparison  (e.g., \(3<5\) is
(e.g., \(3<5\) is  ), while
), while  means the numeric value of the result of an operation \(\langle {\textit{op}}\rangle \) (e.g., \(3+5\) is
means the numeric value of the result of an operation \(\langle {\textit{op}}\rangle \) (e.g., \(3+5\) is  ).
).
Constraint approximation When a predicate is evaluated on a partial model, the 3-valued semantics of constraint evaluation guarantees that certain (over- and under-approximation) properties hold for all potential refinements or concretizations of the partial model. For all logic and numerical predicates \(\varphi \) and \(\psi \),  , thus:
, thus:
-
Logic under-approximation: If
 in a partial model P, then
in a partial model P, then  in any partial model Q where
in any partial model Q where  .
. -
Numeric under-approximation: If
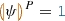 in a partial model P, then
in a partial model P, then  in any partial model Q where
in any partial model Q where  .
. -
Logic over-approximation: If
 in a partial model Q, then
in a partial model Q, then  in a partial model P where
in a partial model P where  .
. -
Numeric under-approximation: If
 in a partial model Q, then
in a partial model Q, then 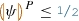 in a partial model P where
in a partial model P where 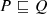 .
.
These properties ensure that model generation is a monotonous derivation sequence of partial models which starts from the most abstract partial model where all predicate constraints are evaluated to  . As the partial model is refined, more and more predicate values are evaluated to either
. As the partial model is refined, more and more predicate values are evaluated to either  or
or  . The under-approximation lemmas ensure that when an error predicate is evaluated to
. The under-approximation lemmas ensure that when an error predicate is evaluated to  , it will remain
, it will remain  ; thus, exploration branch can be terminated without loss of completeness [87]. The over-approximation lemmas assure that if a partial model can be refined to a concrete model where error predicate is
; thus, exploration branch can be terminated without loss of completeness [87]. The over-approximation lemmas assure that if a partial model can be refined to a concrete model where error predicate is  , then it will not be dropped.
, then it will not be dropped.
4 Model generation with refinement
4.1 Functional overview
Our framework takes the following inputs:
-
1.
the signature of a domain \(\langle \Sigma ,\alpha \rangle \) (derived from a metamodel or ontology) with structural logic symbols
 and numerical attribute symbols
and numerical attribute symbols  ,
, -
2.
a logic theory consisting of the negation of the error predicates and the compatibility of the predicate symbols with their definition (i.e., the axioms):

-
3.
some search parameters (e.g., the required size, or the required number of models).
The output of the generator is a sequence of models \(M_1, \ldots , M_m\), where each \(M_i\) is consistent, which means
-
1.
a regular concrete model of \(\langle \Sigma ,\alpha \rangle \);
-
2.
consistent with \({\mathcal {T}}\) (
 ), i.e., for any i, j, no error predicates have a match
), i.e., for any i, j, no error predicates have a match 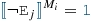 , and all predicates
, and all predicates  and
and 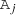 are compatible with their definition
are compatible with their definition 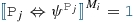 and
and  ;
; -
3.
adheres to search parameters (e.g.,
 ).
).
The model generator combines individual refinement units to solve structural and numerical problems. Each refinement unit analyzes a partial model (which is an intermediate state of the model generation), and it collaborates with other units by refining it. This is in conceptual analogy with the interaction of background theories in SMT-solvers [50, 51]. A refinement unit provides four main functionalities (see Fig. 7):
-
Consistency check: The refinement unit evaluates whether a partial model may satisfy the target theory (thus it can be potentially completed to a consistent model), or it surely violates it (thus no refinement is ever consistent).
-
Decision: The unit makes an atomic decision by a single refinement in the partial model (e.g., adding an edge by setting a
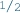 value to
value to 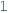 ) which is consistent with the target theory. This new information makes the model more concrete, thus reducing the number of potential solutions.
) which is consistent with the target theory. This new information makes the model more concrete, thus reducing the number of potential solutions. -
Unit propagation: After a decision, the unit executes further refinements necessitated by the consequences of previous refinements wrt. the target theory without introducing new information or excluding potential solutions. This step automatically does necessary refinements on the partial model without making any decisions.
-
Concretization: Finally, the unit attempts to complete the partial model by setting all uncertain
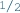 edges to
edges to 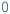 , and checks if the concrete model is consistent with the target theory or not.
, and checks if the concrete model is consistent with the target theory or not.
In this paper, we combine two of such refinements units: We reuse a graph solver [71] as  to efficiently generate the structural part of models to reason about
to efficiently generate the structural part of models to reason about  . Moreover, we propose a novel
. Moreover, we propose a novel
 that uses two efficient backend SMT-solvers (Z3 [17] and dReal [23]) to solve the numerical problems reasoning about
that uses two efficient backend SMT-solvers (Z3 [17] and dReal [23]) to solve the numerical problems reasoning about  . The refinement units interact with each other bidirectionally via the refinement of partial models: The
. The refinement units interact with each other bidirectionally via the refinement of partial models: The
 refines truth values on attribute predicates (based on the structural part of the error predicates), which need to be respected by the
refines truth values on attribute predicates (based on the structural part of the error predicates), which need to be respected by the
 . Symmetrically, the
. Symmetrically, the
 can refine attribute predicates (based on the numerical part of the error predicates), which need to be respected by the
can refine attribute predicates (based on the numerical part of the error predicates), which need to be respected by the
 in turn.
in turn.
In case of circular dependencies between structural and numeric constraints, the
 first enumerates all possible non-isomorphic structures, then the
first enumerates all possible non-isomorphic structures, then the
 attempts to resolve the attribute values, given the graph structure. Potential conflicts between refinement units are handled during consistency checks in subsequent exploration steps, as described in Sect. 4.2. Nevertheless, more complex decision procedures may be implemented to handle such circular constraints.
attempts to resolve the attribute values, given the graph structure. Potential conflicts between refinement units are handled during consistency checks in subsequent exploration steps, as described in Sect. 4.2. Nevertheless, more complex decision procedures may be implemented to handle such circular constraints.
4.2 Default exploration strategy by refinements
Our model generation framework derives models by exploring the search space of partial models along refinements carried out by refinement units. Thus, the size of the partial models is continuously growing up to a designated size, while the default exploration strategy aims to intelligently minimize the search space. The detailed steps of this default strategy are shown in Fig. 8.
Our framework takes as input a domain metamodel provided by an engineer. Optionally, engineers may also provide as input additional logic constraints and an initial partial model, as well as some search parameters.
0. Initialization: First, we initialize our search space with an initial partial model. This is derived either from an existing initial model provided as input (thus each solution will contain this seed model as a submodel), or it can be the most general partial model  where
where  has a single element,
has a single element,  is
is  for every symbol, and
for every symbol, and  .
.
1. Decision: Next, we select an unexplored decision candidate proposed by a refinement unit, and execute it to refine the partial model by adding new nodes and edges, or by populating a data object with a concrete value. In the default strategy, this decision step is executed mainly by the structural refinement unit which has more impact on model generation. If no decision candidates are left unexplored, the search concludes with an UNSAT result and returns the models that have been saved during previous iterations, if any.
2. Unit propagation: After a decision, the framework executes unit propagation in all refinement units until a fixpoint is reached in order to propagate all consequences of the decision.
3. State coding: The search can reach isomorphic partial models along multiple trajectories. To prevent the repeated exploration of the same state, a state code is calculated and stored for a new partial model by using shape-based graph isomorphism checking [55, 56]. If exploration detects that a partial model has already been explored, it drops the partial model and continues search from another state. Otherwise, the framework calculates the state code of the newly explored partial model and continues with its evaluation.
4. Consistency check: Next, each refinement unit checks whether the partial model contains any inconsistencies that cannot be repaired.
 evaluates the (logic) under-approximation of the error predicates (see Sect. 3.4), which can detect irreparable structural errors. The
evaluates the (logic) under-approximation of the error predicates (see Sect. 3.4), which can detect irreparable structural errors. The
 carries out a satisfiability check of the numeric constraint determined by a call to the numeric solver.
carries out a satisfiability check of the numeric constraint determined by a call to the numeric solver.
5. Concretization: Then, the framework tries to concretize the partial model to a fully defined solution candidate by resolving all uncertainties, and checks its compliance with the target theory and model size. If no violations are found and the model reaches the target size, then the instance model is saved as a solution. (Thus, consistency is ensured for all solutions.) If this concretization fails, it indicates that something is missing from the model, so the refinement process continues.
6.1. Approximate distance & Add to state space: When a partial model is refined, our framework estimates its distance from a solution [44]. This heuristic is based on the number of missing objects and the number of violations in its concretization. Then, the new partial model is added to the search space of unexplored decisions where the exploration continues at 1. Decision.
Further heuristics: For selecting the next unexplored decision to refine, we use a combined exploration strategy with best-first search heuristic, backtracking, backjumping and random restarts with an advanced design space exploration framework [31, 71].
6.2. Save Model: If concretization is successful, the instance model is saved as a solution. At this stage, if the required number of models has been reached, the search concludes with a SAT result and returns all the models that have been saved. Otherwise, the refinement process continues.
7. Prevent identical attributes: After finding a concrete instance model, we avoid finding duplicates during future iterations by adding constraints to the logic theory. These constraints ensure that the numeric attribute assignments are not identical to assignments provided for a previous model. Exploration then continues at 1. Decision.
Diversity in attributes: The feedback loop provided by the 7. Prevent identical attributes step may also be used to increase diversity in attribute values. For example, instead of just preventing duplicate numeric solutions, one may enforce certain domain-specific coverage criteria during numeric concretization (e.g., solutions must be generated such that they are evenly distributed over an interval). One may also implement equivalence classes for attribute values through qualitative abstractions to further improve both structural and numeric diversity. We plan to address these enhancements as part of our future work.
Example 4
Figure 9 illustrates a model generation run to derive a family tree. Search is initialized with a
 \( f1 \) as root and two (abstract) objects to represent new objects and new integers.
\( f1 \) as root and two (abstract) objects to represent new objects and new integers.
State 1 highlights the execution of a decision that splits the new object and the new integer, creating a new
 m1 with its undefined
m1 with its undefined
 attribute.
attribute.
In State 2.1, a loop  edge is added as a decision. When investigating error predicate
edge is added as a decision. When investigating error predicate  , the search reveals that all conditions of the error predicate are surely satisfied on objects m1 and a1 except for attribute predicate
, the search reveals that all conditions of the error predicate are surely satisfied on objects m1 and a1 except for attribute predicate  . Therefore, the
. Therefore, the
 can refine the partial model by setting
can refine the partial model by setting  to
to  without excluding any valid refinements, which implies that
without excluding any valid refinements, which implies that  . The
. The
 (with the help of an underlying numeric solver) can detect that no value \({\mathcal {V}}_{S2.1}(a1)\) can be bound to object a1 such that \({\mathcal {V}}_{S2.1}(a1)\le {\mathcal {V}}_{S2.1}(a1)+12\) is false; therefore, the model cannot be finished to a consistent model; thus, it can be safely dropped.
(with the help of an underlying numeric solver) can detect that no value \({\mathcal {V}}_{S2.1}(a1)\) can be bound to object a1 such that \({\mathcal {V}}_{S2.1}(a1)\le {\mathcal {V}}_{S2.1}(a1)+12\) is false; therefore, the model cannot be finished to a consistent model; thus, it can be safely dropped.
In State 2.2, a new
 m2 is added to the
m2 is added to the
 , and the framework attempts to concretize the model by resolving all uncertainty in State 3.1. First, the
, and the framework attempts to concretize the model by resolving all uncertainty in State 3.1. First, the
 concretizes in the structural part of the model, all
concretizes in the structural part of the model, all  values are set to
values are set to  (e.g., all the potential
(e.g., all the potential
 edges disappear). Then, sample valid values are generated for the attributes by the
edges disappear). Then, sample valid values are generated for the attributes by the
 . When the concretization is checked, error pattern \((m1,m2)\) indicates that there are missing
. When the concretization is checked, error pattern \((m1,m2)\) indicates that there are missing
 edges, so the framework drops the concretization but continues to explore State 2.2.
edges, so the framework drops the concretization but continues to explore State 2.2.
Eventually, after adding a
 edge in State 3.2, the framework is able to concretize a (consistent) model in State 4.2 that satisfies the target theory. In this case, we only require a single output instance model; thus, the search terminates.
edge in State 3.2, the framework is able to concretize a (consistent) model in State 4.2 that satisfies the target theory. In this case, we only require a single output instance model; thus, the search terminates.
4.3 Custom exploration strategies
The default exploration strategy in Sect. 4.2 handles model generation domain-independently. As such, it cannot exploit the specificities of a modeling domain to accelerate state space exploration. Furthermore, the default approach handles the constantly growing partial model representation as a whole during refinements. Although this does simplify the process, it also poses a scalability challenge for complex model generation tasks like in the Crossing Scenario domain.
To address these issues, typical theorem proving practices expose the internal decision processes and enable users to define custom search space exploration strategies. The approach proposed in [24] explicitly provides preferred states as hints to guide exploration towards preferred search space regions. The authors of [59] place domain-independent conditions to restrict the instantiation of quantifiers during search. The Z3 SMT solver [17] provides tactics and probes, as well as combinators to allow significant customization of underlying decision processes. In all cases, the proposed customizations allow users to strategically restrict the search space, thus guiding exploration.
Here, we adapt similar concepts to model generation and propose an approach to define domain-specific, custom exploration strategies. These strategies are used to restrict the search space and guide exploration towards desired search space regions. Users may specify strategies (based on domain knowledge and requirements), which can split the modeling domain into fragmentsFootnote 2 that are handled consecutively in accordance with the divide-and-conquer principle. An example of such a strategy is proposed in [53] and is applied to the context of test generation for Software Product Lines.
Syntax: A custom strategy is composed of phases, where each phase is responsible for the creation of a concrete fragment of the partial model. A phase may contain one
 (pertaining to structural decisions), followed potentially by a
(pertaining to structural decisions), followed potentially by a
 (pertaining to numeric decisions). Additionally, a strategy may include a final subphase that is not associated with any phase and that marks the end of the strategy. Furthermore, each phase contains a set of relaxed constraints (not checked) which are excluded, while the exploration is at the corresponding phase. Finally, phases may also contain a set of preferred numeric solver, only one of which may be used at each phase.
(pertaining to numeric decisions). Additionally, a strategy may include a final subphase that is not associated with any phase and that marks the end of the strategy. Furthermore, each phase contains a set of relaxed constraints (not checked) which are excluded, while the exploration is at the corresponding phase. Finally, phases may also contain a set of preferred numeric solver, only one of which may be used at each phase.
Definition 5
(Custom strategy) For a set D of decisions, a set C of constraints and a set N of numeric solvers, a custom strategy is defined by a deterministic control flow graph \( CFG = \langle S,s, T\rangle \), where
-
S represents a finite set of subphases,
-
\(s\in S\) is the initial subphase,
-
\(T\subseteq S \times 2^{D} \times 2^{C} \times 2^{N} \times S\) represents the set of transitions where a tuple \(( src , dec , rel , num , trg )\in T\) is composed of the source subphase \( src \), the set of allowed decisions \( dec \), the set of relaxed constraints \( rel \), the set of preferred numeric solvers \( num \), and the target subphase \( trg \).
Additionally, given a subphase \(c \in S\) and the set of all its outgoing transitions \(\{x_0, \ldots , x_m\} \subset T\), where \(x_i = (c,d_i,r_i,n_i,t_i)\), deterministic execution is enforced by \(\{ d_j \cap d_k = \emptyset : 0 \le j \le k \le m\}\).
Example 5
Figure 10 defines a 3-phase custom strategy for the domain of critical traffic scenarios. Subphases are named according to their corresponding phase, and colored according to the nature of the decisions in their outgoing transitions (
 or
or
 ). The control flow graph also contains a final subphase F. Transitions are labeled with corresponding decisions (Dec), relaxed constraints (Rel) and preferred numeric solver (Numeric Solver), where applicable.
). The control flow graph also contains a final subphase F. Transitions are labeled with corresponding decisions (Dec), relaxed constraints (Rel) and preferred numeric solver (Numeric Solver), where applicable.
Figure 10 illustrates a sample strategy designed specifically for the domain of traffic scenarios. A different strategy could be defined for the family tree domain (see Sect. 3.1), which refer to concepts and attributes of that domain (e.g., family members or parenthood instead of vehicle speed and visibility). As such, the main structural constituents of an exploration strategy (i.e., decisions, relaxed constraints and preferred number solver) will always refer to domain-specific concepts.
Semantics: A model generation run using a custom strategy corresponds to a traversal of the associated control flow graph which is defined by a sequence of transitions traversals. Semantically, a transition traversal corresponds to an iteration of the default exploration strategy. Thus, a traversal potentially involves all four refinement unit functionalities of Fig. 8.
A custom strategy can restrict the default strategy, but cannot extend it: relaxed constraints are excluded, allowed decisions are restricted and a preferred numeric solver is used for numeric decisions. As a result, each transition traversal addresses only a specific fragment of the modeling domain. Therefore, a sequence of transition traversals may address the entire modeling domain through a divide-and-conquer approach.
Definition 6
(Execution of custom strategies) Let  be a custom strategy over a set of decisions
be a custom strategy over a set of decisions  , constraints
, constraints  , and numeric solvers
, and numeric solvers  . Iteration i from state \( src \) to state \( trg \) conforms with \( CFG \), if there is a transition
. Iteration i from state \( src \) to state \( trg \) conforms with \( CFG \), if there is a transition  , where:
, where:
-
the refinement applies a decision \(d\in dec \),
-
the refinement excludes constraints in \( rel \) during consistency check
-
the refinement uses a numeric solver \(n\in num \)
An iteration sequence \(i_1,\ldots ,i_n\) conforms with \( CFG \), if:
-
iteration \(i_1\) from initial state s conforms with \( CFG \),
-
for each pair \((i_j, i_{j+1}) : 1 \le j \le {n-1}\) iteration \(i_j\) to state x conforms with \( CFG \), and \(i_{j+1}\) from state x conforms with \( CFG \).
Sample traversal of the control flow graph defined shown in Fig. 10
Object diagrams and visualizations for selected nodes in the CFG traversal shown in Fig. 11
Example 6
Figure 11 illustrates a traversal of the CFG for the 3-phase custom strategy of Crossing Scenario in Fig. 10. Each column corresponds to a phase and includes the associated subphases and transitions.
Key subphases are accompanied by corresponding object diagrams (concretized from the underlying partial model) and visualizations in Fig. 12. The objects diagrams show existing (filled) attributes and structural components in black. Unknown partial model elements, such as attribute values and relations, are highlighted in dark gray. Elements that have been defined as a result of decisions executed during the previous phase are colored according to their type (
 or
or
 ). These elements are also explicitly indicated in the corresponding phase blocks of Fig. 11.
). These elements are also explicitly indicated in the corresponding phase blocks of Fig. 11.
P1.0 is the initial subphase, where the underlying partial model (in Fig. 12e) contains an empty road map with 3 vertical lanes and 3 horizontal lanes. Figure 12a shows two unplaced actors a1 and a2 that have their vision blocked and that must eventually collide. At this stage, actor a1 is placed on horizontal lane hl3, then assigned concrete numeric position and size values.
At P2.0, the strategy moves to P2.1 by setting a1 as the vision blocking actor between itself and a2. After a structural consistency check, this partial model is dropped, and the exploration backtracks.
P2.0 is reached for a second time. At this stage, a new actor a3 is created and the exploration moves to P2.2. It sets a3 as the vision-blocking actor and places actors a2 and a3 on horizontal lanes. Once the structural consistency checks succeed, the exploration moves to P2.3 and assigns concrete numeric position and size values to a2 and a3. The exploration reaches P3.1, where a3 is clearly blocking the vision between a1 and a2, as seen in Fig. 12g. However, we notice that since all actors can only move in a horizontal direction, there is no chance for any of them to collide. As a result, when the exploration tries to enforce the collision between actors a1 and a2 in P3.1, the consistency check fails and the exploration backtracks.
P2.0 is reached for a third time. As in the previous traversal, a new actor a3 is created, set as the blocking actor and placed on a horizontal lane. However, actor a2 is placed on a vertical lane. Once concrete position and size values are provided to a2 and a3, the exploration moves to P3.2. At this stage, a possible collision does exist between actors a1 and a2, as seen in Fig. 12h. The corresponding numeric decisions are made and the exploration moves to state F, which outputs the concrete model shown in Fig. 12d.
4.4 Summary
Our framework constructs models by applying partial model refinements proposed by refinement units. This paper uses a combination of three refinement units:
The framework combines the refinement units to explore the search space of potential refinements using different strategies.
-
Default strategy follows a general purpose execution plan detailed in Sect. 4.2.
-
A custom strategy restricts the exploration with domain-specific hints to improve performance as illustrated on generating traffic layouts in Sect. 4.3.
-
Finally, a combined strategy applies a custom strategy first, and if it fails, the exploration backs of to the default exploration strategy. Therefore, the custom strategy is used only as a heuristic to select the preferred refinements, if possible.
5 Structural and numerical refinement units
In this section, we summarize the
 and
and
 used in this paper. We also detail a mapping from a partial model to a numerical problem handled by an underlying numeric solver.
used in this paper. We also detail a mapping from a partial model to a numerical problem handled by an underlying numeric solver.
5.1 Structural refinements by a graph solver
The structural consistency of a partial model can be verified by checking the compatibility of all predicates
 as
as  . If a predicate is incompatible with its definition, or an error predicate is satisfied, the partial model is inconsistent (see Sect. 3.4).
. If a predicate is incompatible with its definition, or an error predicate is satisfied, the partial model is inconsistent (see Sect. 3.4).
Our framework operates on a graph representation of partial models (without a mapping to a logic solver); thus, structural predicates are evaluated directly on this graph representation. The query rewriting technique [72] enables to efficiently evaluate the 3-valued semantics of logic predicates  by a high-performance incremental model query engine [85, 86], which caches and maintains the truth values of logic predicates during exploration.
by a high-performance incremental model query engine [85, 86], which caches and maintains the truth values of logic predicates during exploration.
Structural refinements are implemented by graph transformations [71, 87]. Decisions are simple transformation rules that rewrite a single  value to a
value to a  in the partial model, or an equivalence predicate
in the partial model, or an equivalence predicate  to
to  to split an object to two (like \( m1 \) is separated from new object in State 1). On the other hand, concretization rewrites all
to split an object to two (like \( m1 \) is separated from new object in State 1). On the other hand, concretization rewrites all  values to
values to  , and self-equivalences to
, and self-equivalences to  .
.
The compatibility of predicate symbols is checked by structural unit propagation rules, which are derived from error predicates to refine a partial model when needed to avoid a match of an error predicate. We rely on two kinds of unit propagation rules:
-
We derive unit propagation rules from the structural constraints imposed by the metamodel to enforce type hierarchy, multiplicities, inverse references, and containment hierarchy [71]. For example, when a new
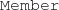 is created, a new
is created, a new
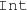 is also created with an
is also created with an  predicate between them.
predicate between them. -
Unit propagation rules are derived from each error predicate
 to check if a
to check if a  (or
(or 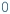 ) value would satisfy the error predicate
) value would satisfy the error predicate 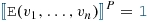 . In such cases, the value is refined to the opposite
. In such cases, the value is refined to the opposite  (or
(or 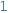 ). Such unit propagation rules may add numerical implications of error predicates.
). Such unit propagation rules may add numerical implications of error predicates.
5.2 Numerical refinements by numeric solvers
The
 is responsible for maintaining the compatibility of numeric constraints and attribute predicates, checking consistency of numeric constraints, and deriving concrete numeric values.
is responsible for maintaining the compatibility of numeric constraints and attribute predicates, checking consistency of numeric constraints, and deriving concrete numeric values.
Numerical refinement is based on a purely numerical interface of a partial model. Let P be a partial model with attribute predicates  . Let
. Let  denote the set of data objects where
denote the set of data objects where  . The numerical interface
. The numerical interface  consists of the objects in
consists of the objects in  , and of the numerical predicate values of the logic interpretations
, and of the numerical predicate values of the logic interpretations  .
.
Numerical interfaces for two states in Fig. 9
Example 7
We extract numerical interfaces of the partial models for State 3.2 and for State 4.1 in Fig. 9. These numerical interfaces are shown in Fig. 13, which contains edges, representing attribute predicates, labeled with the negations of the corresponding numeric constraint. Constraint negations are more common within partial models as their violating cases are included in the modeling domain. For both interfaces, the numeric objects are  . The numeric values for interpretations
. The numeric values for interpretations  and
and  of predicates
of predicates  and
and  are:
are:


A numeric solver is called on the numerical interface  of a partial model P. The solver call returns a truth value for the satisfiability of
of a partial model P. The solver call returns a truth value for the satisfiability of  . For satisfiable numerical interfaces, the solver also returns a numeric value assignment for each object in
. For satisfiable numerical interfaces, the solver also returns a numeric value assignment for each object in  .
.
A consistency check for partial models involves a numeric solver call where only the satisfiability of the numerical interface is verified without any value assignments. An unsatisfiable numerical interface  implies that the partial model P cannot be completed with consistent numeric values; thus, it can be dropped.
implies that the partial model P cannot be completed with consistent numeric values; thus, it can be dropped.
If the interface is satisfiable, numeric value assignments for elements in  are used to complete partial models by providing an interpretation for all unbounded data objects during concretization. Moreover, fixing potential values for certain data objects can be used as a decision. Numerical interfaces formulated on real numbers need special attention. A numeric solver may provide either exact or approximated solutions.
are used to complete partial models by providing an interpretation for all unbounded data objects during concretization. Moreover, fixing potential values for certain data objects can be used as a decision. Numerical interfaces formulated on real numbers need special attention. A numeric solver may provide either exact or approximated solutions.
-
An exact solution is a mathematically precise solution to a given numerical interface.
-
An approximated solution is a numeric solution that satisfies a \(\delta \)-perturbed form of the input formula (as defined in [22]), where the preciseness is controlled with a \(\delta \) approximation parameter.
The numerical consequences of the constructed  can be used to refine a partial model during unit propagation. In our framework, three kinds of unit propagation operations are supported:
can be used to refine a partial model during unit propagation. In our framework, three kinds of unit propagation operations are supported:
-
Values\(\rightarrow \)Predicate. When the values of numeric objects \(o_1,...,o_n\) are known in a partial model (i.e.,
 ), then the truth value of a predicate
), then the truth value of a predicate  can be evaluated and updated in the model. This step can be done without calling the numeric solver, as the numerical expression can be evaluated pragmatically (e.g.,
can be evaluated and updated in the model. This step can be done without calling the numeric solver, as the numerical expression can be evaluated pragmatically (e.g.,  for
for 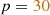 and
and  is
is
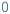 ).
). -
Predicate\(\rightarrow \)Predicate. If an attribute predicate
 has an unknown value
has an unknown value  , and
, and 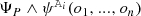 is numerically inconsistent, then
is numerically inconsistent, then 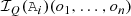 can be refined to
can be refined to  . Similarly, if
. Similarly, if  is inconsistent, the attribute can be refined to
is inconsistent, the attribute can be refined to 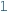 . For example, in partial model S3.2, a value
. For example, in partial model S3.2, a value
 for predicate
for predicate  on \(i_1, i_1\) would cause numerical inconsistency, so the framework can refine it to
on \(i_1, i_1\) would cause numerical inconsistency, so the framework can refine it to
 . (In our case studies, this step was impractical thus this feature was not used.)
. (In our case studies, this step was impractical thus this feature was not used.) -
Predicate\(\rightarrow \)Values. If there is only a single solution x for a numeric object o, then the unique value of can be set in an unit propagation step \({\mathcal {V}}_P(o)=x\). For example, if
 , then
, then 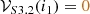 would be the only solution, and it can be refined in the partial model as a unit propagation.
would be the only solution, and it can be refined in the partial model as a unit propagation.
5.3 Mapping of numerical interfaces
In this section, we describe how a numerical interface  of a partial model P is mapped to a numerical problem that is handled by an underlying numeric solver. As discussed in Sect. 5.2,
of a partial model P is mapped to a numerical problem that is handled by an underlying numeric solver. As discussed in Sect. 5.2,  is defined over the set of data objects
is defined over the set of data objects  . It also contains the numerical predicate values of the logic interpretations
. It also contains the numerical predicate values of the logic interpretations  where
where  are attribute predicates contained in P and defined by
are attribute predicates contained in P and defined by  .
.
Each data object  is mapped to a numeric variable
is mapped to a numeric variable  denoting its potential value. If
denoting its potential value. If  , then the type of this variable is integer, while if
, then the type of this variable is integer, while if  , then it is real. The numerical problem derived from
, then it is real. The numerical problem derived from  is defined over those variables.
is defined over those variables.
A numerical problem is constructed as the conjunction of numerical assertions as follows. If the value of o is already known in the partial model ( ), then we assert its value as a numerical equation:
), then we assert its value as a numerical equation:  . Additionally, for each attribute constraint
. Additionally, for each attribute constraint  in P, we assert its definition
in P, we assert its definition  for all data objects:
for all data objects:
-
If
 , then
, then 
-
If
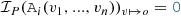 , then
, then 
-
If
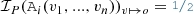 , then nothing is asserted.
, then nothing is asserted.
This mapping extends our previous work [69], where we provide a complete mapping from structural constraints to FOL.
Example 8
We illustrate this mapping for the numerical interface shown in Fig. 13b, which corresponds to the partial model for State 4.1 of Fig. 9. The values for the interpretation  of relevant attribute predicates are indicated in Sect. 7.
of relevant attribute predicates are indicated in Sect. 7.
Mapping outputs are shown in Fig. 14. We include the logic formulation of the numerical interface as a Numerical Problem. Furthermore, we provide a translation of the numerical problem into the concrete SMT2 syntax that is handled by numeric solvers such as Z3. We may notice that we only include (negated) assertions for attribute constraints  with logic interpretation
with logic interpretation  , while predicates with interpretation
, while predicates with interpretation  are disregarded.
are disregarded.
Mapping outputs for the numerical interface shown in Fig. 13b
5.4 Soundness and completeness
With the combination of the
 and
and
 , our proposed approach generates models with numerical attributes using partial model refinement. For an input domain \({\langle \Sigma ,\alpha \rangle }\), theory (constraints) \({\mathcal {T}}\) and the required number and size of models, it generates a sequence of models \(M_1,\ldots ,M_n\).
, our proposed approach generates models with numerical attributes using partial model refinement. For an input domain \({\langle \Sigma ,\alpha \rangle }\), theory (constraints) \({\mathcal {T}}\) and the required number and size of models, it generates a sequence of models \(M_1,\ldots ,M_n\).
In this section, we evaluate the theoretical properties and guarantees of our approach in different configurations. The model generator can be executed using one of the three following strategies:
-
Default strategy (detailed in Sect. 4.2)
-
Custom strategy (detailed in Sect. 4.3)
-
Combined strategy (detailed in Sect. 4.4)
For
 , the model generator has two options:
, the model generator has two options:
-
use exact numeric solvers only (like Z3).
-
use approximate numeric solvers (like dReal).
With respect to decidability of the numerical problem:
-
If the numerical fragment is decidable, then the
 always terminates.
always terminates. -
If the numerical fragment is undecidable, then the
 may not terminate for certain numerical problems.
may not terminate for certain numerical problems.
Definition 7
(Consistency) A model generation approach is (approximately) consistent, if every model in the generated sequence \(M_i\in \{M_1,\ldots ,M_n\}\) is consistent (approximately) satisfies the theory \({\mathcal {T}}\) ( ) and adheres to the search parameters.
) and adheres to the search parameters.
According to this definition, our model generation is consistent if it uses exact numeric solvers, and it is approximately consistent, if it uses approximate numeric solvers. This is guaranteed by the direct evaluation of the error predicates and compatibility predicates on the final stage of model refinement with the underlying refinement units (see 5. Concretization in Sect. 4.2). Consistency is not influenced by the decidability of the numerical problem, or the strategy.
To discuss completeness, model equivalence is defined first.
Definition 8
(Model isomorphism) Two partial models P and Q are structurally isomorphic, if there is a bijective function  , where for each n-ary symbol \(s\in \Sigma \) and for all objects
, where for each n-ary symbol \(s\in \Sigma \) and for all objects  :
:

Partial models P and Q are isomorphic, if for each object  : \({\mathcal {V}}_{P}(o) = {\mathcal {V}}_{P}(m(o))\) is also satisfied. Two models P and Q are (structurally) different, if they are not (structurally) isomorphic.
: \({\mathcal {V}}_{P}(o) = {\mathcal {V}}_{P}(m(o))\) is also satisfied. Two models P and Q are (structurally) different, if they are not (structurally) isomorphic.
Therefore, we can define completeness properties for the model generator.
Definition 9
(Structural completeness) A model generation approach is structurally complete, if for the given theory \({\mathcal {T}}\) and a search parameters, it can generate a sequence \(M_I\in \{M_1,\ldots ,M_n\}\) that contains all structurally different and consistent models.
Our default exploration strategy approach is structurally complete on decidable numerical refinement unit: For a given scope (size), it is able to generate all models with different graph structures, which is ensured by the approximation lemmas in Sect. 3.4 and in [71, 87]. We intentionally avoid fulfilling numerical completeness, since even simple models could have potentially infinite number of attribute bindings. A custom strategy restricts the search space to improve the performance of model generation at the cost of completeness guarantees. As the combined strategy eventually terminates, and continues with the default exploration strategy, it has the same completeness guarantee as default exploration strategy. If the numerical fragment is not decidable, then we cannot ensure that the numeric solver is able to provide numeric solutions for each structure, and we cannot guarantee completeness.
6 Evaluation
We conducted various measurements to address the following research questions:
- RQ1::
-
How do the different exploration steps contribute to the execution time for generating models?
- RQ2::
-
How does model generation scale to derive large models with structural and attribute constraints?
- RQ3::
-
How do various exploration strategies influence the efficiency of model generation?
- RQ4::
-
How structurally diverse are synthetic models?
6.1 Target domains
We perform model generation campaigns in four complex case studies. The target domain artifacts, output models and measurement results are available on GitHubFootnote 3.
 : The FamilyTree domain is presented in Sect. 3.1 as our running example. We use the metamodel shown in Fig. 4 which captures parenthood relations and the age of family tree members (with 2 classes, 3 references and 1 numerical attribute). Furthermore, 3 constraints are defined as graph predicates that place structural and numerical restrictions on family tree members. The initial model used for model generation contains a single
: The FamilyTree domain is presented in Sect. 3.1 as our running example. We use the metamodel shown in Fig. 4 which captures parenthood relations and the age of family tree members (with 2 classes, 3 references and 1 numerical attribute). Furthermore, 3 constraints are defined as graph predicates that place structural and numerical restrictions on family tree members. The initial model used for model generation contains a single
 node. While this domain looks simple, there is a subtle mutual dependency between structural and attribute constraints, which provides extra challenges for the interaction of different solvers.
node. While this domain looks simple, there is a subtle mutual dependency between structural and attribute constraints, which provides extra challenges for the interaction of different solvers.
 : The Satellite domain (introduced in [32]) represents interferometry mission architectures used for space mission planning at NASA. Such an architecture consists of collaborating satellites and radio communication between them, which are captured by a metamodel with 15 classes, 5 references and 2 numerical attributes. Additionally, 18 constraints are defined as graph predicates to capture restrictions on collaborating satellites. The initial model contains a single root node as the starting point for model generation.
: The Satellite domain (introduced in [32]) represents interferometry mission architectures used for space mission planning at NASA. Such an architecture consists of collaborating satellites and radio communication between them, which are captured by a metamodel with 15 classes, 5 references and 2 numerical attributes. Additionally, 18 constraints are defined as graph predicates to capture restrictions on collaborating satellites. The initial model contains a single root node as the starting point for model generation.
 : The Taxation domain (used in [81, 82]) represents the personal income tax management application used by the Government of Luxembourg. We reused the original metamodel which contains 54 classes (including 15 Enum classes), 52 relations and 92 attributes, 44 of which are numerical. Additionally, we replicated the OCL constraints used in [82] as graph predicates.
: The Taxation domain (used in [81, 82]) represents the personal income tax management application used by the Government of Luxembourg. We reused the original metamodel which contains 54 classes (including 15 Enum classes), 52 relations and 92 attributes, 44 of which are numerical. Additionally, we replicated the OCL constraints used in [82] as graph predicates.
To independently replicate the case study of [82] in a pure EMF context with strict containment hierarchy (instead of UML), we include a
 class in the metamodel that contains instances of the
class in the metamodel that contains instances of the
 class, which was the root class of the original Taxation metamodel. This allows the instantiation of multiple
class, which was the root class of the original Taxation metamodel. This allows the instantiation of multiple
 instances within the same model generation task. To enforce the same number of objects, we include an initial model containing a predefined number of
instances within the same model generation task. To enforce the same number of objects, we include an initial model containing a predefined number of
 instances and we prevent the generation of further instances of that class as in [82].
instances and we prevent the generation of further instances of that class as in [82].
 : The CrossingScenario domain is presented in Sect. 2 as our motivating example. We identify two variants of this domain for our experimental evaluation:
: The CrossingScenario domain is presented in Sect. 2 as our motivating example. We identify two variants of this domain for our experimental evaluation:
 is used for RQ1 and
is used for RQ1 and
 used for RQ3. Both variants use the metamodel in Fig. 2 to capture the actors and lanes of a traffic scenario, as well as certain spatial and temporal relations between actors (with 10 classes, 7 references and 13 numerical attributes).
used for RQ3. Both variants use the metamodel in Fig. 2 to capture the actors and lanes of a traffic scenario, as well as certain spatial and temporal relations between actors (with 10 classes, 7 references and 13 numerical attributes).
 includes 10 constraints defined as graph predicates that place structural and numerical restrictions on the positioning and size of actors with respect to their corresponding lanes. Additionally, we include a (quadratic) constraint to set a minimum Euclidean distance between any pair of actors in the model. The initial model for this variant includes 5 vertical lanes and 5 horizontal lanes. The model generation challenge is to populate the existing lanes by placing new
includes 10 constraints defined as graph predicates that place structural and numerical restrictions on the positioning and size of actors with respect to their corresponding lanes. Additionally, we include a (quadratic) constraint to set a minimum Euclidean distance between any pair of actors in the model. The initial model for this variant includes 5 vertical lanes and 5 horizontal lanes. The model generation challenge is to populate the existing lanes by placing new
 objects (but without extra lanes or relations).
objects (but without extra lanes or relations).
 includes 32 constraints defined as graph predicates that place restrictions on all components of the metamodel. We incorporate complex numeric constraints such as quadratic inequalities, non-constant divisions and numeric if-then-else blocks. The initial model for this variant includes 4 vertical lanes and 4 horizontal lanes, as well as two black actors (with empty attributes) which are connected by a
includes 32 constraints defined as graph predicates that place restrictions on all components of the metamodel. We incorporate complex numeric constraints such as quadratic inequalities, non-constant divisions and numeric if-then-else blocks. The initial model for this variant includes 4 vertical lanes and 4 horizontal lanes, as well as two black actors (with empty attributes) which are connected by a
 relation and a
relation and a
 relation. The model generation task consists of placing the actors on specific lanes and filling their attribute values such that the constraints are satisfied. Additional actors may be generated if required. This variation provides a significant model generation challenge not only due to the complexity of the included numeric constraints, but also due to their mutual dependencies with structural constraints, which necessitates a bidirectional interaction between the underlying solvers.
relation. The model generation task consists of placing the actors on specific lanes and filling their attribute values such that the constraints are satisfied. Additional actors may be generated if required. This variation provides a significant model generation challenge not only due to the complexity of the included numeric constraints, but also due to their mutual dependencies with structural constraints, which necessitates a bidirectional interaction between the underlying solvers.
General setup: To account for warm-up effects and memory handling of the Java 8 VM, an initial model generation task is performed before the actual measurements and the garbage collector is called explicitly between runs. We performed the measurements on an enterprise serverFootnote 4.
6.2 RQ1: cost of exploration phases
Measurement setup: We perform measurements in all four domains to compare runtimes and their distribution between the different phases of model generation. For each domain, we run measurements twice, with different underlying numeric solvers (Z3 and dReal). Note that the numeric solvers are only used to assess the numeric constraints of the model generation task and not the structural constraint as poor scalability was reported in [5, 69] for the latter.
We generate models with an increasing minimum model size of 20, 40, 60, 80 and 100. The range for numeric values was not bounded a priori. We exclude larger model sizes to ensure high success rates and to enable cross-domain comparison of execution phases. For the
 domain, the initial model contains one instance of the
domain, the initial model contains one instance of the
 class for every 20 generated nodes (which is the typical size of a household in the models generated in [82]) to balance the difficulty of model generation regardless of the target model size.
class for every 20 generated nodes (which is the typical size of a household in the models generated in [82]) to balance the difficulty of model generation regardless of the target model size.
Initial measurements showed that the complexity of numeric constraints in
 causes low success rates even for small models. Thus, we generate models containing only up to 21 nodes (with a step size of 3).
causes low success rates even for small models. Thus, we generate models containing only up to 21 nodes (with a step size of 3).
We execute 10 runs per target model size and take the median runtime values. For each model generator run, we aim to produce the first 10 models within a timeout of 5 minutes. For the
 domain, we excluded the generation of additional models due to the low success rates.
domain, we excluded the generation of additional models due to the low success rates.
Analysis of results: The decomposition of runtime measurements for all four domains is shown in Fig. 15. Each phase of model generation is represented by a different color. The initialization phase (0.9 seconds for
 , 3.5 seconds for
, 3.5 seconds for
 , 150 seconds for
, 150 seconds for
 , 0.4 seconds for
, 0.4 seconds for
 ) is a one-time penalty which is proportional to the size of the metamodel and to the number of additional WF constraints.
) is a one-time penalty which is proportional to the size of the metamodel and to the number of additional WF constraints.
In the
 domain, the runtime is dominated by numeric solver calls. This is attributed to the fact that this domain needs to enforce a global structural constraint (families must have an acyclic graph structure with respect to the parenthood relation) by solving numeric constraints, while the numeric constraints of other domains are dominantly local (e.g., to fill attribute values). However, extra cost of generating subsequent models is low.
domain, the runtime is dominated by numeric solver calls. This is attributed to the fact that this domain needs to enforce a global structural constraint (families must have an acyclic graph structure with respect to the parenthood relation) by solving numeric constraints, while the numeric constraints of other domains are dominantly local (e.g., to fill attribute values). However, extra cost of generating subsequent models is low.
In the
 case study, generating the first model takes less than 30 seconds (dominated by the time required for state encoding), but the cost of incrementally generating the next model is relatively larger. For the target model sizes, execution times in the
case study, generating the first model takes less than 30 seconds (dominated by the time required for state encoding), but the cost of incrementally generating the next model is relatively larger. For the target model sizes, execution times in the
 case study are still mostly dominated by the initialization phase due to the large metamodel and numerous constraints of the domain. However, we do notice that a significant portion of the execution time is dedicated to numeric solver calls, due to the large quantity of numeric constraints.
case study are still mostly dominated by the initialization phase due to the large metamodel and numerous constraints of the domain. However, we do notice that a significant portion of the execution time is dedicated to numeric solver calls, due to the large quantity of numeric constraints.
In all of the above cases, we notice that dReal requires more time than Z3 (by an order of magnitude for
 and
and
 ) to handle the numeric constraints. Thus, we conclude that for simple numeric constraints, Z3 is the more performant underlying numeric solver.
) to handle the numeric constraints. Thus, we conclude that for simple numeric constraints, Z3 is the more performant underlying numeric solver.
However, we notice that dReal is the better performing numeric solver for the
 domain. Figure 15g and 15h shows that the runtime is significantly dominated by numeric solver calls, as expected. The figures also show the decreasing success rate for model generation runs for both numeric solvers. We notice that although runtimes for Z3 are slightly faster than for dReal, we can see that success rates of Z3 decrease more rapidly. This is attributed to the underlying background theories used in dReal, which make it more suitable for complex, nonlinear constraints such as those in
domain. Figure 15g and 15h shows that the runtime is significantly dominated by numeric solver calls, as expected. The figures also show the decreasing success rate for model generation runs for both numeric solvers. We notice that although runtimes for Z3 are slightly faster than for dReal, we can see that success rates of Z3 decrease more rapidly. This is attributed to the underlying background theories used in dReal, which make it more suitable for complex, nonlinear constraints such as those in
 .
.

6.3 RQ2: scalability of model generation
Measurement setup: We perform measurements in the
 ,
,
 and
and
 domains with increasing model sizes starting from 100 objects with a step size of 50/100 objects and timeout of 1 hour. We exclude the
domains with increasing model sizes starting from 100 objects with a step size of 50/100 objects and timeout of 1 hour. We exclude the
 domain from this experiment considering its low success rates for small models reported in RQ1. A single model is generated in each run. A campaign of 10 runs is executed for each measurement point and the median of successful execution times is taken (i.e., that provide a finite model as result within the given time). Additionally, we only gather measurement data for model sizes where 100% of runs are successful. In other words, we terminate the scalability measurements for a domain if any of the 10 runs at a particular size fails to output a finite model. For the
domain from this experiment considering its low success rates for small models reported in RQ1. A single model is generated in each run. A campaign of 10 runs is executed for each measurement point and the median of successful execution times is taken (i.e., that provide a finite model as result within the given time). Additionally, we only gather measurement data for model sizes where 100% of runs are successful. In other words, we terminate the scalability measurements for a domain if any of the 10 runs at a particular size fails to output a finite model. For the
 domain, we provide
domain, we provide
 instances as part of the initial model following the 1-to-20 ratio discussed in Sect. 6.2.
instances as part of the initial model following the 1-to-20 ratio discussed in Sect. 6.2.
Analysis of results: Measurement results for RQ2 are shown in Fig. 16. Interestingly, the proposed approach scaled best for the largest metamodel of the
 case deriving models with 1100 objects within an hour. Furthermore, we were able to generate models with 1200 objects within the same time limit with a success rate of 80%. Model generation with 100% success rate scaled up to 300 objects for the
case deriving models with 1100 objects within an hour. Furthermore, we were able to generate models with 1200 objects within the same time limit with a success rate of 80%. Model generation with 100% success rate scaled up to 300 objects for the
 and
and
 domains. However, root cause of scalability limits was very different (the numeric solver in
domains. However, root cause of scalability limits was very different (the numeric solver in
 and graph solver in
and graph solver in
 ). Interestingly,
). Interestingly,
 turned out to be the most complex case study for assessing the use of numeric solvers.
turned out to be the most complex case study for assessing the use of numeric solvers.

6.4 RQ3: influence of exploration strategy
Measurement setup: We compare five state space exploration strategies:
-
Def (used as a baseline) calls a numeric solver at every model generation step to repeatedly evaluate numeric constraints using the default strategy;
-
Qual includes manually added qualitative abstractions of numeric constraints, which are assessed at every model generation step;
-
LowB explicitly sets a lower bound of one for the number of newly created actors, which is the minimum requirement for
 (this new actor will block the vision between the two actors included in the initial model);
(this new actor will block the vision between the two actors included in the initial model); -
Qual-LowB incorporates the additional constraints used in Qual and in LowB;
-
Cust uses the custom exploration strategy presented in Sect. 4.3 without additional qualitative abstractions or scope constraints.
The default exploration strategy Cont is used as our baseline. Qual, LowB and Qual-LowB also follow the default strategy with additional constraints which implicitly enforce particular decisions at each iteration. Due to the poor results reported in [67], we exclude measurements for a strategy that only makes numeric solver calls as a postprocessing step.
For RQ3, we perform measurements exclusively in the
 domain, which has complex dependencies between structural and numeric constraints as well as complex numeric constraints. In fact, the complexity of the underlying numerical problem is shown in RQ1 to pose a significant challenge when used with Def, which makes
domain, which has complex dependencies between structural and numeric constraints as well as complex numeric constraints. In fact, the complexity of the underlying numerical problem is shown in RQ1 to pose a significant challenge when used with Def, which makes
 an adequate case study for testing the influence of different exploration strategies. For the variations of the default strategy, we only use dReal as it is the more successful numeric solver which performed better for this domain (as shown in Sect. 6.2).
an adequate case study for testing the influence of different exploration strategies. For the variations of the default strategy, we only use dReal as it is the more successful numeric solver which performed better for this domain (as shown in Sect. 6.2).
We aim to generate a single model that satisfies the constraints of
 . Ten runs are executed for each approach with a timeout of 5 minutes. Since the runtime of model generation is dominated by numeric solver calls (see RQ1), we calculate only the runtime of numeric solver calls and the success rates.
. Ten runs are executed for each approach with a timeout of 5 minutes. Since the runtime of model generation is dominated by numeric solver calls (see RQ1), we calculate only the runtime of numeric solver calls and the success rates.
Analysis of results: Results are shown in Fig. 17. When using the default strategy without any additional hints (Def), we indicate a numeric solver call time of 12.601 s, with a 90% success rate. Adding qualitative abstractions of numeric constraints (Qual and Qual-LowB) does significantly reduce the numeric solver call time, as expected, given our result in [67], but also reduces the success rate. However, when qualitative abstractions are not included, we notice that when adding scope constraints (LowB) is detrimental to numeric solver call time. This is due to the heuristic used in the default strategy that is negatively affected by the additional scope constraint for this case study.
Despite achieving impressive runtime reductions by manually adding different constraints to the modeling domain, we notice that the most significant improvement is provided by the custom exploration strategy (cust). The latter reduces numeric solver call time by a factor of 40 without decreasing success rate.

6.5 RQ4: diversity
Measurement setup: To evaluate the structural diversity of the generated models, we used a neighborhood-based [57] internal diversity metric [70, 73], which correlates with mutation score in mutation testing scenarios. This metric calculates the proportion of different local neighborhoods of nodes included in a graph model. For this research question, we checked the structural diversity of models only.
We used a neighborhood range=4, which classifies two objects to be identical, if they cannot be distinguished with at most 4 links (hops). To measure structural diversity, the values of data objects are not taken into account (but data objects count as objects). We measured the diversity of 10\(\times \)10 models (we execute 10 runs, where each run produces 10 models) for case studies
 ,
,
 and
and
 with 100 objects, and measured the diversity of
with 100 objects, and measured the diversity of
 with 18 objects. We compared the diversity of models generated with dReal and Z3.
with 18 objects. We compared the diversity of models generated with dReal and Z3.
Analysis of Results: The distribution of internal diversity is illustrated in Fig. 18. The proportion of different object neighborhoods with respect to the number of objects is measured in percentage.
 , and
, and
 showed high internal diversity (between 65 and 80%), and
showed high internal diversity (between 65 and 80%), and
 provided even higher diversity (around 90% median).
provided even higher diversity (around 90% median).
 provided the lowest internal diversity (44%), which can be partially explained by the large number of similar attributes of the domain. Numeric solvers Z3 and dReal provided similar diversity.
provided the lowest internal diversity (44%), which can be partially explained by the large number of similar attributes of the domain. Numeric solvers Z3 and dReal provided similar diversity.

6.6 Threats to validity
Construct validity. We have selected the
 domain as a representative case study for the generation of critical traffic scenarios. In fact, it has been identified by IntelFootnote 5 as a fundamental safety principle for autonomous vehicles. However, we do use various approximations (i.e., actors are modeled as rectangles, lanes have a fixed width) when implementing the case study to simplify the model generation task. We intend use the
domain as a representative case study for the generation of critical traffic scenarios. In fact, it has been identified by IntelFootnote 5 as a fundamental safety principle for autonomous vehicles. However, we do use various approximations (i.e., actors are modeled as rectangles, lanes have a fixed width) when implementing the case study to simplify the model generation task. We intend use the
 domain as a proof of concept for generating critical traffic scenarios using our proposed approach.
domain as a proof of concept for generating critical traffic scenarios using our proposed approach.
We replicated the
 case study [82] in a new technological context, which involved (1) to create an Ecore metamodel from an equivalent UML diagram and (2) to manually transform the OCL constraints into equivalent VQL graph patterns. The Ecore metamodel was kindly provided to us by the authors of [82], while we validated each replicated OCL constraint by performing manual equivalence checks. We used similar number of Household objects as in [82] and investigated the output models by graph visualization tools to ensure that similar model generation outputs are obtained, but we refrain from direct numerical comparison of execution times due to those technological differences.
case study [82] in a new technological context, which involved (1) to create an Ecore metamodel from an equivalent UML diagram and (2) to manually transform the OCL constraints into equivalent VQL graph patterns. The Ecore metamodel was kindly provided to us by the authors of [82], while we validated each replicated OCL constraint by performing manual equivalence checks. We used similar number of Household objects as in [82] and investigated the output models by graph visualization tools to ensure that similar model generation outputs are obtained, but we refrain from direct numerical comparison of execution times due to those technological differences.
Internal Validity. To strengthen internal validity, our experiments include a warm-up run executed prior to the actual measurements to decrease the fluctuation of runtimes caused by the Java VM instead of the natural fluctuation of solver runtimes. As the exploration strategy relies on some randomness, our scalability measurements only report cases with over 90% success rate—except for the
 domain, where all success rates are reported explicitly.
domain, where all success rates are reported explicitly.
External Validity. We mitigate threats to external validity by including a diverse set of case studies which involve calls to both a structural and a numeric solver. Furthermore, we incorporate and compare two distinct numeric solvers. We focused on numerical attributes as they are the most frequent data types. Handling models containing different kinds of attributes (e.g., string or bitvectors) can be a challenge in terms of performance (although Z3 does promise efficient background theorems for both [17, 89]). Additionally, the numeric values derived by the underlying numeric solver may not be diverse.
7 Related work
We provide an overview of graph generation approaches that derive consistent graphs. We also discuss some key numerical abstractions and decision procedures, as well as traffic scenario generation approaches.
Logic solver approaches. These approaches translate graphs and WF constraints into a logic formulae and use underlying solvers to generate graphs that satisfy them. Back-end technologies used for this purpose include SMT solver such as Z3 [36, 66, 88], SAT-based model finders (like Alloy [35]) [3, 6, 13, 33, 40, 46, 49, 69, 74, 77, 78, 80], CSP-solvers [12, 14, 15, 28], theorem provers [5], first-order logic [8], constructive query containment [54], higher-order logic [30] and an incremental query engine [71].
For most of these approaches, scalability is limited to small models/counter-examples. These approaches are either a priori bounded (where the search space needs to be restricted explicitly) or they have decidability issues. Furthermore, handling of numeric constraints is not available for some of these approaches, particularly ones based on SAT-solvers and first-order logic formulations.
Uncertain models. Partial models are similar to uncertain models, which offer a rich specification language [18, 62] amenable to analysis. They provide a more intuitive, user-friendly language compared to 3-valued interpretations, but without handling additional WF constraints. Potential concrete models compliant with an uncertain model can be synthesized by the Alloy Analyzer [64], or refined by graph transformation rules [63].
Strategies. Iterative approaches generate models by multiple solver calls. An iterative approach is proposed specifically for allocation problems in [39] based on Formula. In [74], models are generated by calling Alloy in multiple steps, where each step extends the instance model by a few elements. Finally, an iterative, counterexample-guided synthesis is proposed for higher-order logic formulae in [47]. For these approaches, when scalability evaluation is included, it is limited to 50 nodes.
Some logic and numeric solvers provide an interface to configure the background theories and the strategy of the solving process. For example, the Z3 SMT solver [17] provides tactics and probes, and combinators to guide the solver. Similarly, portfolio solvers like [10] provide options to split reasoning tasks between a set of independent theorem provers.
Symbolic model generation techniques. Certain techniques use abstract (or symbolic) graphs for analysis purposes. A tableau-based reasoning method is proposed for graph properties [1, 52, 65], which automatically refines solutions based on WF constraints, and handles the state space in the form of a resolution tree as opposed to a partial model. When scalability evaluation is included, these techniques demonstrated to derive only small graphs (\(<10\) objects).
Different approaches use abstract interpretation [57], or predicate abstraction [19, 29, 58] for partial modeling. In those approaches, concretization is used to materialize (typically small) counterexamples for designated safety properties in a graph transformation system. However, their focus is to support model checking of abstract graph transformation systems, which can evaluate complex trajectories, but do not scale in the size of the models.
Hybrid approaches. These approaches divide the model generation task into multiple sub-tasks and use a different underlying techniques to resolve each one. The PLEDGE model generation tool [82] provides such a scalable implementation by combining metaheuristic search for model structure generation with an SMT-solver based approach for attribute handling. The Evacon tool [34] implements a search-based evolutionary testing approach, followed by symbolic execution to generate tests for object-oriented programs. Autograph [66] sequentially combines a tableau-based approach for model structure generation with an SMT-solver-based approach for attribute handling. Such approaches combine multiple techniques in a sequential manner, which is a conceptual restriction for mutually dependent structural and numeric constraints. Moreover, none of these techniques assure completeness of model generation.
Another category of hybrid approaches involves assessing multiple components of the model generation task in parallel. This requires the implementation of a certain decision procedure such as DPLL(T) [21, 51] to iterate between underlying techniques, or combine them by sharing variables in their proofs [50]. Such decision procedures are presented alongside their associated properties (e.g., soundness and completeness) at an abstract level in [11, 51], which allows for formal reasoning about their implementations. However, those approaches handle graph-based models inefficiently [74, 87]; thus, the scalability of those techniques is limited.
Numerical abstractions. Handling numeric (integer or real) variables and constraints in model generation scenarios requires their abstract interpretation through numerical abstract domains [48, 79]. Numerical abstract domains may be used to summarize object attributes in value analysis of heap programs [19, 41, 45]. Summarized dimensions [29] were introduced to succinctly represent attributes of a potentially unbounded set of objects via multi-objects. This approach enables attribute handling in 3-valued partial models, and allows checking for refinements by abstract subsumption [2]. But these approaches do not generate graph models.
The uniqueness of our approach lies in combining numerical abstractions with partial models to guarantee soundness and completeness, while generating models with favorable scalability.
Generating traffic scenarios. Recently, testing autonomous vehicles with synthetic traffic scenarios has become a popular target for model generation. AsFault [20] proposes an approach using metaheuristic search and procedural content generation to derive challenging world maps for testing autonomous vehicles. This tool only generates static parts of a scenario: it provides no reasoning for dynamic components such as vehicles or pedestrians. A more complete scenario generation approach is proposed in [9], which uses a learnable evolutionary algorithm to guide exploration toward critical regions of the search space, and ultimately toward critical scenarios. Despite being able to generate both static and dynamic components, this approach lacks numeric reasoning, since numeric attributes are taken from a predefined finite set.
Other approaches use an underlying parametrized representation of scenarios. Paracosm [42] applies Halton sampling on the parameter space to generate scenarios according to coverage criteria. The approach proposed in [60] combines combinatorial interaction testing, backtracking and motion planning to generate test cases for regression testing of autonomous vehicles. The authors of [16] propose a weighted search-based approach to find test scenarios with avoidable collisions. In these cases, key information of the generated scenarios (e.g., the road map) must be provided as input, and only certain parameters (e.g., weather condition) are varied. This provides limited expressivity compared to our approach where we generate the entire underlying graph structure of the scenario from scratch.
8 Conclusions
In this paper, we proposed an automated model generation approach to derive consistent models that satisfy structural and complex numeric constraints, which necessitates a bidirectional interaction between a graph solver and a numeric (SMT or quadratic) solver. As a conceptual novelty, we proposed refinement units that carry out consistency checking, decision, unit propagation and concretization steps in conceptual analogy with background theories used in SMT-solvers as part of an abstract DPLL procedure [51]. Therefore, refinement units can seamlessly incorporate different kinds of solvers (similarly to [50]) for handling attribute constraints in the presence of a graph solver that handles partial models. Additionally, the interactions between refinement units can be customized as domain-specific strategies. We implemented our approach in the Viatra Solver framework [68]. The source code of our approach is publicly available (https://github.com/viatra/VIATRA-Generator).
We carried out a detailed experimental evaluation of our approach in four complex case studies to assess scalability, diversity and the influence of custom strategies. We obtained favorable scalability results by consistently deriving models with over 250 objects in two cases within an hour, and models with over 1000 objects in a third case with same time limits. These model sizes are substantially larger than logic solver-based model generation approaches (e.g., Alloy or Z3) could derive in the presence of structural constraints (see [5, 71, 82]). In the fourth case study, which contains complex numeric constraints, we show the significant positive impact on runtime of custom exploration strategies. Moreover, our approach maintains other favorable quality attributes such as diversity and completeness investigated in depth in [70, 87].
Notes
A fragment here refers to a subset of domain components, such as metamodel classes or selected WF constraints unlike in [7] where it refers to a part of the search space.
12 \(\times \) 2.2 GHz CPU, 64 GiB RAM, CentOS 7, Java 1.8, 12 GiB Heap.
References
Al-Sibahi, A.S., Dimovski, A.S., Wasowski, A.: Symbolic execution of high-level transformations. In: SLE 2016, pp. 207–220. Springer (2016)
Anand, S., Păsăreanu, C.S., Visser, W.: Symbolic execution with abstraction. Int. J. Softw. Tools Technol. Transf. 11(1), 53–67 (2009)
Anastasakis, K., Bordbar, B., Georg, G., Ray, I.: On challenges of model transformation from UML to Alloy. Softw. Syst. Model. 9(1), 69–86 (2010)
Aydal, E.G., Paige, R.F., Utting, M., Woodcock, J.: Putting formal specifications under the magnifying glass: Model-based testing for validation. In: Proceedings - 2nd International Conference on Software Testing, Verification, and Validation, ICST 2009, pp. 131–140 (2009)
Babikian, A.A., Semeráth, O., Varró, D.: Automated generation of consistent graph models with first-order logic theorem provers. In: International Conference on Fundamental Approaches to Software Engineering, pp. 441-461. Springer (2020)
Bak, K., Diskin, Z., Antkiewicz, M., Czarnecki, K., Wasowski, A.: Clafer: unifying class and feature modeling. Softw. Syst. Model. 1–35, (2013)
Baudry, B.: Testing Model Transformations: A case for Test Generation from Input Domain Models. In: Babau, J.-P., Blay-Fornarino, M., Champeau, J., Gèrard, S., Robert, S., Sabetta, A. (eds.) Model Driven Engineering for Distributed Real-time Embedded Systems. ISTE (2009)
Beckert, B., Keller, U., Schmitt, P.H.: Translating the Object Constraint Language into First-order Predicate Logic. Proc. VERIFY, Workshop at FLoC (2002)
Ben Abdessalem, R., Nejati, S., C. Briand, L., Stifter, T.: Testing vision-based control systems using learnable evolutionary algorithms. In: ICSE, pp. 1016–1026 (2018)
Bobot, F., Filliâtre, J.C., Marché, C., Paskevich, A.: Why3: Shepherd your herd of provers. In: Boogie 2011: First International Workshop on Intermediate Verification Languages, pp. 53–64. , Wrocław, Poland (2011)
Brain, M., DSilva, V., Haller, L., Griggio, A., Kroening, D.: An abstract interpretation of DPLL(T). In: Giacobazzi, R., Berdine, J., Mastroeni, I. (eds.) Verification, Model Checking, and Abstract Interpretation, pp. 455–475. Springer, Berlin (2013)
Büttner, F., Cabot, J.: Lightweight string reasoning for OCL. In: A. Vallecillo, J.P. Tolvanen, E. Kindler, H. Störrle, D.S. Kolovos (eds.) ECMFA 2012, LNCS, vol. 7349, pp. 244–258. Springer (2012)
Büttner, F., Egea, M., Cabot, J., Gogolla, M.: Verification of ATL transformations using transformation models and model finders. In: ICFEM, pp. 198–213. Springer (2012)
Cabot, J., Clarisó, R., Riera, D.: UMLtoCSP: a tool for the formal verification of UML/OCL models using constraint programming. In: ASE 2017, pp. 547–548. ACM (2007)
Cabot, J., Clarisó, R., Riera, D.: On the verification of UML/OCL class diagrams using constraint programming. J. Syst. Softw. (2014)
Calò, A., Arcaini, P., Ali, S., Hauer, F., Ishikawa, F.: Generating avoidable collision scenarios for testing autonomous driving systems. In: 2020 IEEE 13th International Conference on Software Testing, Validation and Verification (ICST), pp. 375-386 (2020)
de Moura, L., Bjørner, N.: Z3: An efficient SMT solver. In: Tools and Algorithms for the Construction and Analysis of Systems, 14th International Conference (TACAS 2008), LNCS, vol. 4963, pp. 337–340. Springer (2008)
Famelis, M., Salay, R., Chechik, M.: In: In: ICSE, (ed.) Partial models: Towards modeling and reasoning with uncertainty, pp. 573–583. IEEE Computer Society (2012)
Ferrara, P., Fuchs, R., Juhasz, U.: TVAL+: TVLA and value analyses together. In: SEFM 2012, LNCS, vol. 7504, pp. 63–77. Springer (2012)
Gambi, A., Mueller, M., Fraser, G.: Automatically testing self-driving cars with search-based procedural content generation. In: Proceedings of the 28th ACM SIGSOFT International Symposium on Software Testing and Analysis, ISSTA 2019, p. 318–328. Association for Computing Machinery, New York, NY, USA (2019)
Ganzinger, H., Hagen, G., Nieuwenhuis, R., Oliveras, A., Tinelli, C.: DPLL(T): Fast decision procedures. In: R. Alur, D.A. Peled (eds.) Computer Aided Verification, pp. 175–188 (2004)
Gao, S., Avigad, J., Clarke, E.M.: \(\delta \)-complete decision procedures for satisfiability over the reals. In: Gramlich, B., Miller, D., Sattler, U. (eds.) Automated Reasoning, pp. 286–300. Springer, Berlin (2012)
Gao, S., Kong, S., Clarke, E.M.: dReal: An SMT solver for nonlinear theories over the reals. In: Bonacina, M.P. (ed.) Automated Deduction - CADE-24, pp. 208–214. Springer, Berlin (2013)
Ge, Y., de Moura, L.: Complete instantiation for quantified formulas in satisfiabiliby modulo theories. In: Bouajjani, A., Maler, O. (eds.) Computer Aided Verification, pp. 306–320. Springer, Berlin (2009)
Geyer, S., Baltzer, M., Franz, B., Hakuli, S., Kauer, M., Kienle, M., Meier, S., Weigerber, T., Bengler, K., Bruder, R., Flemisch, F., Winner, H.: Concept and development of a unified ontology for generating test and use-case catalogues for assisted and automated vehicle guidance. IET Intell. Transp. Syst. 8(3), 183–189 (2014)
Gogolla, M., Büttner, F., Richters, M.: USE: A UML-based specification environment for validating UML and OCL. Sci. Comput. Programm. 69(1), 27–34 (2007)
Gogolla, M., Hilken, F., Doan, K.: Achieving model quality through model validation, verification and exploration. Comput. Lang. Syst. Struct. 54, 474–511 (2018)
González, C.A., Büttner, F., Clarisó, R., Cabot, J.: EMFtoCSP: a tool for the lightweight verification of EMF models. FormSERA 2012, 44–50 (2012)
Gopan, D., DiMaio, F., Dor, N., Reps, T., Sagiv, M.: Numeric domains with summarized dimensions. In: TACAS 2004, LNCS, vol. 2988, pp. 512–529. Springer (2004)
Grönniger, H., Ringert, J.O., Rumpe, B.: System model-based definition of modeling language semantics. In: FORTE, LNCS, vol. 5522, pp. 152–166. Springer (2009)
Hegedüs, Á., Horváth, Á., Varró, D.: A model-driven framework for guided design space exploration. Autom. Softw. Eng. 22(3), 399–436 (2015)
Herzig, S.J.I., Mandutianu, S., Kim, H., Hernandez, S., Imken, T.: Model-transformation-based computational design synthesis for mission architecture optimization. IEEE Aerospace Conference. IEEE (2017)
Hilken, F., Gogolla, M., Burgueño, L., Vallecillo, A.: Testing models and model transformations using classifying terms. Softw. Syst. Model. 17(3), 885–912 (2018)
Inkumsah, K., Xie, T.: Improving structural testing of object-oriented programs via integrating evolutionary testing and symbolic execution. In: 2008 23rd IEEE/ACM International Conference on Automated Software Engineering, pp. 297-306 (2008)
Jackson, D.: Alloy: a lightweight object modelling notation. Trans. Softw. Eng. Methodol. 11(2), 256–290 (2002)
Jackson, E.K., Levendovszky, T., Balasubramanian, D.: Reasoning about metamodeling with formal specifications and automatic proofs. In: Model Driven Engineering Languages and Systems, pp. 653–667. Springer (2011)
Jackson, E.K., Simko, G., Sztipanovits, J.: In: Diversely enumerating system-level architectures, p. 11. IEEE Press (2013)
Jackson, E.K., Sztipanovits, J.: In: In: EMSOFT, (ed.) Towards a formal foundation for domain specific modeling languages, pp. 53–62. , ACM, New York, NY, USA (2006)
Kang, E., Jackson, E., Schulte, W.: An approach for effective design space exploration. In: Monterey Workshop, LNCS, vol. 6662, pp. 33–54. Springer (2010)
Kuhlmann, M., Hamann, L., Gogolla, M.: Extensive validation of OCL models by integrating SAT solving into USE. TOOLS ’11, LNCS 6705, 290–306 (2011)
Magill, S., Berdine, J., Clarke, E., Cook, B.: Arithmetic strengthening for shape analysis. In: SAS 2007, LNCS, vol. 4634, pp. 419–436. Springer (2007)
Majumdar, R., Mathur, A., Pirron, M., Stegner, L., Zufferey, D.: Paracosm: A Test Framework for Autonomous Driving Simulations, pp. 172–195. Springer, Cham (2021)
Majzik, I., Semeráth, O., Hajdu, C., Marussy, K., Szatmári, Z., Micskei, Z., Vörös, A., Babikian, A.A., Varró, D.: In: Towards system-level testing with coverage guarantees for autonomous vehicles, pp. 89–94. IEEE (2019)
Marussy, K., Semeráth, O., Varró, D.: Automated generation of consistent graph models with multiplicity reasoning. Submitted to the IEEE for possible publication. (2020)
McCloskey, B., Reps, T., Sagiv, M.: Statically inferring complex heap, array, and numeric invariants. In: SAS 2010, LNCS, vol. 6337, pp. 71–99. Springer (2010)
Meng, B., Reynolds, A., Tinelli, C., Barrett, C.: Relational constraint solving in SMT. In: CADE 2017, LNCS, vol. 10395, pp. 148–165. Springer (2017)
Milicevic, A., Near, J.P., Kang, E., Jackson, D.: Alloy*: A general-purpose higher-order relational constraint solver. In: ICSE 2015, pp. 609–619. IEEE (2015)
Miné, A.: Weakly relational numerical abstract domains. Ph.D. thesis (2004)
Mottu, J.M., Sen, S., Tisi, M., Cabot, J.: Static analysis of model transformations for eective test generation. In: Proceedings - International Symposium on Software Reliability Engineering, ISSRE, pp. 291-300 (2012)
Nelson, G., Oppen, D.C.: Simplification by cooperating decision procedures. ACM Trans. Programm. Languag. Syst. (TOPLAS) 1(2), 245–257 (1979)
Nieuwenhuis, R., Oliveras, A., Tinelli, C.: Solving SAT and SAT modulo theories: From an abstract Davis-Putnam-Logemann-Loveland procedure to DPLL(T). J. ACM 53(6), 937–977 (2006)
Pennemann, K.H.: Resolution-like theorem proving for high-level conditions. In: ICGT 2008, LNCS, vol. 5214, pp. 289–304. Springer (2008)
Perrouin, G., Sen, S., Klein, J., Baudry, B., Le Traon, Y.: Automated and scalable T-wise test case generation strategies for Software Product Lines. In: ICST 2010 - 3rd International Conference on Software Testing, Verification and Validation, pp. 459-468 (2010)
Queralt, A., Artale, A., Calvanese, D., Teniente, E.: OCL-Lite: Finite reasoning on UML/OCL conceptual schemas. Data Knowl. Eng. 73, 1–22 (2012)
Rensink, A.: Canonical graph shapes. In: ESOP, pp. 401–415. Springer (2004)
Rensink, A.: Isomorphism checking in groove. Electronic Communications of the EASST 1 (2007)
Rensink, A., Distefano, D.: Abstract graph transformation. Electron Notes Theor. Comput. Sci. 157(1), 39–59 (2006)
Reps, T.W., Sagiv, M., Wilhelm, R.: Static program analysis via 3-valued logic. In: International Conference on Computer Aided Verification, pp. 15-30 (2004)
Reynolds, A., Tinelli, C., Goel, A., Krstić, S.: Finite model finding in SMT. In: Sharygina, N., Veith, H. (eds.) Computer Aided Verification, pp. 640–655. Springer, Berlin (2013)
Rocklage, E., Kraft, H., Karatas, A., Seewig, J.: Automated scenario generation for regression testing of autonomous vehicles. In: 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), pp. 476-483 (2017)
Sagiv, M., Reps, T., Wilhelm, R.: Parametric shape analysis via 3-valued logic. ACM Trans. Programm. Languages Syst. (TOPLAS) 24(3), 217–298 (2002)
Salay, R., Chechik, M.: A generalized formal framework for partial modeling. In: Egyed, A., Schaefer, I. (eds.) Fundamental Approaches to Software Engineering, LNCS, vol. 9033, pp. 133–148. Springer, Berlin (2015)
Salay, R., Chechik, M., Famelis, M., Gorzny, J.: A methodology for verifying refinements of partial models. J. Object Technol. 14(3), 3:1-31 (2015)
Salay, R., Famelis, M., Chechik, M.: In: In: FASE, (ed.) Language independent refinement using partial modeling, pp. 224–239. Springer (2012)
Schneider, S., Lambers, L., Orejas, F.: Symbolic model generation for graph properties. In: FASE 2017, LNCS, vol. 10202, pp. 226–243. Springer (2017)
Schneider, S., Lambers, L., Orejas, F.: Automated reasoning for attributed graph properties. STTT 20(6), 705–737 (2018)
Semeráth, O., Babikian, A.A., Li, A., Marussy, K., Varró, D.: Automated generation of consistent models with structural and attribute constraints. In: Proceedings of the 23rd ACM/IEEE International Conference on Model Driven Engineering Languages and Systems, pp. 187-199 (2020)
Semeráth, O., Babikian, A.A., Pilarski, S., Varró, D.: In: VIATRA Solver: A framework for the automated generation of consistent domain-specific models, pp. 43–46. IEEE (2019)
Semeráth, O., Barta, Á., Horváth, Á., Szatmári, Z., Varró, D.: Formal validation of domain-specific languages with derived features and well-formedness constraints. Softw. Syst. Model 16(2), 357–392 (2017)
Semeráth, O., Farkas, R., Bergmann, G., Varró, D.: Diversity of graph models and graph generators in mutation testing. Int. J. Softw. Tools Technol. Transf. 22(1), 57–78 (2020)
Semeráth, O., Nagy, A.S., Varró, D.: A graph solver for the automated generation of consistent domain-specific models. In: ICSE, pp. 969–980. ACM (2018)
Semeráth, O., Varró, D.: Graph Constraint Evaluation over Partial Models by Constraint Rewriting. In: ICMT, pp. 138–154 (2017)
Semeráth, O., Varró, D.: Iterative generation of diverse models for testing specifications of DSL tools. In: FASE, pp. 227–245. Springer (2018)
Semeráth, O., Vörös, A., Varró, D.: Iterative and incremental model generation by logic solvers. In: FASE, pp. 87–103. Springer (2016)
Sen, S.: Découverte automatique de modèles effectifs (Automatic Effective Model Discovery). University of Rennes 1, France (2010).. (Ph.D. thesis)
Sen, S., Baudry, B., Mottu, J.M.: On combining multiformalism knowledge to select models for model transformation testing. In: Proceedings of the 1st International Conference on Software Testing, Verification and Validation, ICST 2008, pp. 328-337 (2008)
Sen, S., Baudry, B., Mottu, J.M.: Automatic model generation strategies for model transformation testing. Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), vol. 5563 LNCS, pp. 148–164. Springer, Berlin, Heidelberg (2009)
Shah, S.M.A., Anastasakis, K., Bordbar, B.: From UML to Alloy and back again. In: MoDeVVa ’09: Proceedings of the 6th International Workshop on Model-Driven Engineering, Verication and Validation, pp. 1-10. ACM (2009)
Singh, G., Püschel, M., Vechev, M.: A practical construction for decomposing numerical abstract domains. Proc. ACM Program. Lang. 2(POPL) (2018). Article no. 2
Soeken, M., Wille, R., Kuhlmann, M., Gogolla, M., Drechsler, R.: Verifying UML/OCL models using boolean satisfiability. In: DATE’10, pp. 1341–1344. IEEE (2010)
Soltana, G., Sabetzadeh, M., Briand, L.C.: Synthetic data generation for statistical testing. In: ASE, pp. 872–882 (2017)
Soltana, G., Sabetzadeh, M., Briand, L.C.: Practical constraint solving for generating system test data. ACM Trans. Softw. Eng. Methodol. 29(2) (2020)
The Object Management Group: Object Constraint Language, p. v2.4. (2014)
The Eclipse Project: Eclipse Modeling Framework. (2019). http://www.eclipse.org/emf
Ujhelyi, Z., Bergmann, G., Hegedüs, Á., Horváth, Á., Izsó, B., Ráth, I., Szatmári, Z., Varró, D.: EMF-IncQuery: An integrated development environment for live model queries. Sci. Comput. Program. 98, 80–99 (2015)
Varró, D., Bergmann, G., Hegedüs, Á., Horváth, Á., Ráth, I., Ujhelyi, Z.: Road to a reactive and incremental model transformation platform: three generations of the VIATRA framework. Softw. Syst. Model. 15(3), 609–629 (2016)
Varró, D., Semeráth, O., Szárnyas, G., Horváth, Á.: Towards the automated generation of consistent, diverse, scalable and realistic graph models. In: Graph Transformation, Specifications, and Nets - In Memory of Hartmut Ehrig, LNCS, vol. 10800, pp. 285–312. Springer (2018)
Wu, H., Monahan, R., Power, J.F.: Exploiting attributed type graphs to generate metamodel instances using an SMT solver. In: TASE, pp. 175–182 (2013)
Zheng, Y., Zhang, X., Ganesh, V.:ACM, : Z3-str: a Z3-based string solver for web application analysis. In: Joint Meeting of the European Software Engineering Conference and the ACM SIGSOFT Symposium on the Foundations of Software Engineering, pp. 114-124. ACM (2013)
Acknowledgements
We would like to thank Ghanem Soltana and Lionel C. Briand for their help in running the Taxation case study. This paper is partially supported by the NSERC RGPIN-04573-16 project, the Natural Sciences and Engineering Research Council of Canada (NSERC) PGSD3-546810-2020, the NRDI Fund based on the charter of bolster issued by the NRDI Office under the auspices of the Ministry for Innovation and Technology, and by the ÚNKP-20-4 New National Excellence Program of the Ministry for Innovation and Technology from the source of the National Research, Development and Innovation Fund. During the development of the achievements, we took into consideration the goals set by the Balatonfüred System Science Innovation Cluster and the plans of the “BME Balatonfüred Knowledge Center,” supported by EFOP 4.2.1-16-2017-00021.
Funding
Open access funding provided by Budapest University of Technology and Economics.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by S. Abrahão, E. Syriani, H. Sahraoui, and J. de Lara.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Babikian, A.A., Semeráth, O., Li, A. et al. Automated generation of consistent models using qualitative abstractions and exploration strategies. Softw Syst Model 21, 1763–1787 (2022). https://doi.org/10.1007/s10270-021-00918-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10270-021-00918-6








 : checks if any actor in a
: checks if any actor in a  relation is not the blocking actor;
relation is not the blocking actor; : checks (using slopes) that the blocking actor of a
: checks (using slopes) that the blocking actor of a  relation is physically placed between the
relation is physically placed between the  and
and 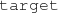 actors;
actors; : enforces a minimum Euclidean distance of 5 between any pair of distinct actors.
: enforces a minimum Euclidean distance of 5 between any pair of distinct actors.
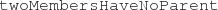 : There is at most one member in a family tree without a parent;
: There is at most one member in a family tree without a parent; : All age attributes of family members are non-negative numbers;
: All age attributes of family members are non-negative numbers;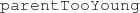 : There must be more than 12 years of difference between the
: There must be more than 12 years of difference between the  of a parent and a child.
of a parent and a child.
 (
( ) are defined for each EClass and EEnum in the domain,
) are defined for each EClass and EEnum in the domain,  denotes the EBoolean type,
denotes the EBoolean type, 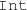 denotes integer numbers types like EInt or EShort, etc.
denotes integer numbers types like EInt or EShort, etc. (
( 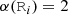 ) are defined for each EReference and EAttribute in the metamodel. For example,
) are defined for each EReference and EAttribute in the metamodel. For example,  represent the parent reference between two Members, and
represent the parent reference between two Members, and  represents the age attribute relation between a Member and an EInt.
represents the age attribute relation between a Member and an EInt. are n-ary predicates derived from graph queries (
are n-ary predicates derived from graph queries ( , the number of formal parameters of a graph query); e.g.,
, the number of formal parameters of a graph query); e.g., 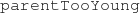 is a binary predicate symbol.
is a binary predicate symbol. represent n-ary predicates derived from attribute (check) expressions of queries (
represent n-ary predicates derived from attribute (check) expressions of queries ( ); e.g.,
); e.g., 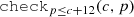 is a binary attribute predicate with parameters c and p.
is a binary attribute predicate with parameters c and p. denotes the existence of objects.
denotes the existence of objects. explicitly represents the equivalence relation between two objects.
explicitly represents the equivalence relation between two objects. is the finite set of objects in the model,
is the finite set of objects in the model, gives a 3-valued logic interpretation for each symbol
gives a 3-valued logic interpretation for each symbol  as
as 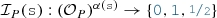 ,
,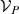 gives a numeric value interpretation for each object in the model:
gives a numeric value interpretation for each object in the model: 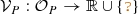 .
. (non-existing objects are omitted)
(non-existing objects are omitted) (
( is reflexive)
is reflexive) (
( is symmetric)
is symmetric) (two different objects cannot be equivalent)
(two different objects cannot be equivalent) (domain objects have no values)
(domain objects have no values) (objects with values are numbers)
(objects with values are numbers)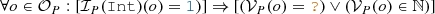 (only natural numbers are bound to
(only natural numbers are bound to  objects)
objects)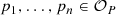 , and for each refinement
, and for each refinement 

 must have a non-empty refinement.
must have a non-empty refinement. ,
, 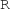 ,
,  ,
,  ,
,  or
or  ) then
) then 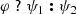 is a numerical expression (standing for “if
is a numerical expression (standing for “if 
 in a partial model P, then
in a partial model P, then  in any partial model Q where
in any partial model Q where  .
.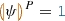 in a partial model P, then
in a partial model P, then  in any partial model Q where
in any partial model Q where  .
. in a partial model Q, then
in a partial model Q, then  in a partial model P where
in a partial model P where  .
. in a partial model Q, then
in a partial model Q, then 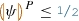 in a partial model P where
in a partial model P where 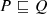 .
. and numerical attribute symbols
and numerical attribute symbols  ,
,
 ), i.e., for any i, j, no error predicates have a match
), i.e., for any i, j, no error predicates have a match 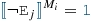 , and all predicates
, and all predicates  and
and 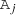 are compatible with their definition
are compatible with their definition 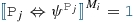 and
and  ;
; ).
).

 value to
value to  ) which is consistent with the target theory. This new information makes the model more concrete, thus reducing the number of potential solutions.
) which is consistent with the target theory. This new information makes the model more concrete, thus reducing the number of potential solutions. edges to
edges to  , and checks if the concrete model is consistent with the target theory or not.
, and checks if the concrete model is consistent with the target theory or not.



 ;
; ;
; .
. is created, a new
is created, a new
 is also created with an
is also created with an  predicate between them.
predicate between them. to check if a
to check if a  (or
(or  ) value would satisfy the error predicate
) value would satisfy the error predicate 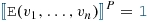 . In such cases, the value is refined to the opposite
. In such cases, the value is refined to the opposite  (or
(or  ). Such unit propagation rules may add numerical implications of error predicates.
). Such unit propagation rules may add numerical implications of error predicates.
 ), then the truth value of a predicate
), then the truth value of a predicate  can be evaluated and updated in the model. This step can be done without calling the numeric solver, as the numerical expression can be evaluated pragmatically (e.g.,
can be evaluated and updated in the model. This step can be done without calling the numeric solver, as the numerical expression can be evaluated pragmatically (e.g.,  for
for  and
and  is
is
 ).
). has an unknown value
has an unknown value  , and
, and 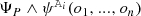 is numerically inconsistent, then
is numerically inconsistent, then 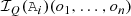 can be refined to
can be refined to  . Similarly, if
. Similarly, if  is inconsistent, the attribute can be refined to
is inconsistent, the attribute can be refined to  . For example, in partial model S3.2, a value
. For example, in partial model S3.2, a value
 for predicate
for predicate  on
on  . (In our case studies, this step was impractical thus this feature was not used.)
. (In our case studies, this step was impractical thus this feature was not used.) , then
, then 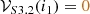 would be the only solution, and it can be refined in the partial model as a unit propagation.
would be the only solution, and it can be refined in the partial model as a unit propagation. , then
, then 
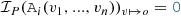 , then
, then 
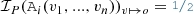 , then nothing is asserted.
, then nothing is asserted.
 always terminates.
always terminates. may not terminate for certain numerical problems.
may not terminate for certain numerical problems.

 (this new actor will block the vision between the two actors included in the initial model);
(this new actor will block the vision between the two actors included in the initial model);
