Abstract
RoboChart is a timed domain-specific language for robotics, distinctive in its support for automated verification by model checking and theorem proving. Since uncertainty is an essential part of robotic systems, we present here an extension to RoboChart to model uncertainty using probabilism. The extension enriches RoboChart state machines with probability through a new construct: probabilistic junctions as the source of transitions with a probability value. RoboChart has an accompanying tool, called RoboTool, for modelling and verification of functional and real-time behaviour. We present here also an automatic technique, implemented in RoboTool, to transform a RoboChart model into a PRISM model for verification. We have extended the property language of RoboTool so that probabilistic properties expressed in temporal logic can be written using controlled natural language.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Autonomous robots must carry out their missions without human intervention. Uncertainty in real-world environments, including the physical robotic platform, presents major challenges for these robots. To address these challenges and deal with unknown aspects of the environment, robots often use probabilistic control algorithms. For example, a robot without a detailed map of its environment might resort to using a random walk to carry out its mission, overcoming the uncertainty about its position. This paper addresses modelling and formal verification of robotic controllers that use probabilistic algorithms to deal with uncertainty.
Robotic applications are often designed using state machines that have no formal semantics or even precise syntax. These machines can involve advanced features, including probability, real-time, and shared-variable concurrency. To model and analyse such complex systems, roboticists require knowledge of formal languages and probability theory. Our approach is to use a domain-specific notation, RoboChart [1], and model transformation to support probabilistic reasoning using a notation familiar to roboticists. Usability and automation are key considerations for RoboChart.
Previous work [2] presents the RoboChart, metamodel and semantics, and an Eclipse-based tool, RoboTool, for modelling, verification, and code generation using RoboChart. This paper covers its extension to cater for probabilistic modelling and verification: we have (1) extended RoboChart’s state machines to enrich them with a construct for probabilistic choice (with our extension, RoboChart allows four forms of choice between behaviour: conditional, external or guarded by events, nondeterministic, and probabilistic), and (2) developed an automatic technique for verification by model checking using PRISM [3]. Our results are illustrated via several case studies.
The core of RoboChart is a subset of UML state machines that allows modelling of robotic applications, and has a constrained semantics for automated reasoning. RoboChart can be regarded as a profile of UML, enriched with time constructs. In a RoboChart model, physical robots are abstracted into robotic platforms defined by variables, events, and operations. RoboChart also has a component model with notions of controller and module to foster reuse. A state machine is the basic element to model behaviour. A controller includes one or more parallel state machines. Communication between state machines in the same controller is synchronous, while communication between controllers can also be asynchronous. A module defines the boundaries of the robotic application and is composed of one robotic platform and one or more controllers.
RoboChart has a semantics for formal reasoning based on Hoare and He’s Unifying Theories of Programming (UTP) [4], with the process algebra CSP [5,6,7], which has a UTP semantics [4, 7], used as a front-end. RoboTool generates models written in CSP and tock-CSP [6, 8], an encoding that uses an event tock to mark the passage of time, from RoboChart models [2] to enable use of the refinement model checker FDR [9, 10] to verify properties, such as deadlock and livelock freedom. We can also verify specific behavioural properties, including time budgets and deadlines. We cannot, however, verify probabilistic properties.
Standard CSP and tock-CSP do not support probabilistic choice. An experimental extension of CSP included a probabilistic choice construct, and a specific version of FDR was developed to translate refinement checks in CSP to the PRISM language [3] through the WatchDog Transformation [11]. This approach, however, only supports CSP traces refinement reasoning [6] (so limited to reachability properties) and is not supported by recent FDR versions.
RoboChart also has support for semiautomated verification by theorem proving using Isabelle/UTP [12, 13]. Both FDR and Isabelle/UTP verification target only proof of reactive and timed behaviours of RoboChart models, not probabilistic, as we do here.
RoboChart differs from the PRISM language in several aspects: abstraction level, data types, variable sharing, and event synchronisation. Our technique to generate PRISM scripts addresses all these issues. The technique is formalised by transformation rules that we present here, and automated in RoboTool.
A property language facilitates the writing of properties for verification in PRISM using a controlled natural language. It can express probabilistic properties that are based on temporal logic. This also improves performance, by enabling the running of multiple PRISM instances in parallel when several properties are stated.
In [2], we have described a CSP semantics for a version of RoboChart that supports standard features of statecharts and time constructs, but not probabilistic choice. In [14], we have studied the imperative, sequential action language for RoboChart, and explicated the weakest completion approach [15] to give UTP semantics to a nondeterministic probabilistic programming language. This work shows how informal proofs can be turned into formal proofs for implementation in Isabelle/UTP, which enables future application of theorem proving to verify RoboChart models. Here we cover most features of RoboChart, not only its imperative and sequential action language, and pursue support for model checking, not theorem proving.
A recent work by Conserva Filho et al. [16] interprets the probabilistic choice in RoboChart using the probabilistic CSP operator \(_{p}\boxplus _{1-p}\) [11]. This preserves semantics for all other constructors in RoboChart, because RoboChart’s semantics is given in CSP. Verification uses refinement model checking: \(S \sqsubseteq _{T} I\). Here, S is the property to be verified and described by a nonprobabilistic CSP process, and I is a probabilistic CSP process under analysis, generated from a probabilistic model in RoboChart. An extended version of FDR supports probabilistic choice in CSP and translation of the refinement check to a PRISM model. Our work is different from that in [16] in several aspects. Verification in [16] covers only trace refinement and so is limited to reachability properties. Our work supports all the temporal logics in PRISM. CSP processes are used in [16] to specify properties. Consequently, users need to have knowledge of CSP. In contrast, in our work, we use a customised property language, RoboCert. Finally, their approach is only supported by one version of FDR and not by the more recent versions being used with RoboTool.
Our novel contributions here are as follows: (1) the introduction of a new construct for probabilistic choice in RoboChart’s state machines for probabilistic modelling; (2) a metamodel for PRISM; (3) RoboChart’s probabilistic semantics in PRISM (for a subset of RoboChart constructs), including not only the new probabilistic construct but state machines and the component model in a context where probabilities are captured; (4) the implementation of the semantics in RoboTool for automated generation of PRISM models; and (5) a property language for verification of qualitative and quantitative properties.
The remainder of this paper is organised as follows. We review related work in Sect. 2. Section 3 examines core features of RoboChart, introduces our new probabilistic choice construct through an internal mail delivery robot example, and presents extra well-formedness conditions. In Sect. 4, we describe the PRISM language and its semantics, and present a PRISM metamodel that we have developed for transformation. Section 5 formalises our technique to transform RoboChart into PRISM models, and illustrates it using the mail delivery robot. Section 6 describes how RoboTool supports probabilistic modelling and the application of the transformations to automatically generate PRISM models. The property language for probabilistic properties is described in Sect. 7. Finally, we conclude and discuss future work in Sect. 8.
2 Related work
In this section, we set RoboChart in context by discussing its relation to fundamental probabilistic frameworks or models in Sect. 2.1, notations for probabilistic modelling with rich expressions and high abstraction in Sect. 2.2, and model-based domain-specific languages for robotics in Sect. 2.3.
2.1 Fundamental probabilistic frameworks
This section describes notations and formalisms that are at the same level of abstraction as PRISM, but at a different level of abstraction as RoboChart. Some of their features, however, have inspired the design of RoboChart as acknowledged below.
Segala and Lynch [17] introduce probabilistic automata as a specialised form of labelled transition system. A transition is labelled with probability values, so that they map a source state to probability distributions over (action, target state) pairs. Actions can be external, modelling interactions with the environment through events, or internal, modelling computation steps through internal events \(\tau \). If, in each probability distribution, the action is always the same for every target state, the probabilistic automaton is called simple. Two simple probabilistic automata can be composed in parallel; this is a kind of combination that is also available in RoboChart, via use of multiple machines and controllers in a model.
The probabilistic semantics of RoboChart that is embedded in PRISM, as presented later on, can be regarded as corresponding to a simple probabilistic automaton in that the actions in a probability distribution for every target state are the same. Transitions map states and actions to probability distributions over states. RoboChart also distinguishes nondeterministic choice and probabilistic choice. RoboChart, however, has more modelling constructs and is more expressive, when compared to probabilistic automata.
Hansson [18] presents an alternating model that distinguishes between nondeterministic and probabilistic choice. Either a nondeterministic choice or a probabilistic choice can be made in each state of this model, and the order of availability of these choices is strictly alternating between a nondeterministic and a probabilistic choice. For the target state of a transition originating from a nondeterministic state (that is the state where only a nondeterministic choice can be made), only a probabilistic choice can be made. Conversely, for the target state of a transition originating from a probabilistic state (that is the state where only a probabilistic choice can be made), only a nondeterministic choice can be made. RoboChart adopts the same alternation between nondeterministic and probabilistic choice, but the point where a probabilistic choice is made in RoboChart is not a state. Instead, a probabilistic choice is made within a transition originating from a nondeterministic state. RoboChart is similar to a simple probabilistic automaton in this aspect. The alternating model and the simple probabilistic automata model with respect to probabilistic bisimulation (strong bisimulation) [19] are isomorphic [20]: one model can be translated to another, and vice versa.
Van Glabbeek et al.’s reactive model [21] partially corresponds to the simple probabilistic automaton model as it allows external nondeterministic choice between different actions (that is, multiple transitions with different external actions from the same state), but without internal nondeterministic choice involving the same actions. In RoboChart, on the contrary, we can model internal nondeterministic choice via transitions that have no trigger, or transitions from the same state with the same trigger.
A variety of Markov models are used for discrete probability modelling. Discrete-time Markov chains (DTMCs) [22, 23], in which each state leads to a probabilistic choice directly, are purely probabilistic without nondeterminism. A DTMC is equivalent to a fully probabilistic automaton in discrete time.
Markov decision processes (MDPs) [24, 25], which extend DTMCs, can be regarded as simple probabilistic automata without internal nondeterministic choices. From each state, an action is associated with a probability distribution. Transitions from the same state with the same actions are, therefore, not allowed. Similar to MDPs, RoboChart models exhibit both probabilistic and nondeterministic choice.
A variety of DTMCs and MDP-based languages have been designed to facilitate systems modelling and analysis. Additionally, labelling functions for states (called atomic propositions) and cost or reward functions for states and transitions are also introduced. The PRISM language, which is supported by the widely used probabilistic model checker PRISM and other model checking tools such as Storm [26], is one such language. It is based on reactive modules [27] and is a low-level guarded-command language.
MODEST [28, 29], a modelling and analysis framework for stochastic hybrid systems, uses a comparatively higher-level language that is inspired by process algebras. It is supported by the MODEST Toolset.Footnote 1 PRISM, Storm, and MODEST all support DTMC and MDP models for discrete probabilities.
These languages often are textual and support only basic types of variables: boolean, integer numbers, and real numbers. To use the tools, knowledge of underlying probability models, formal methods, and temporal logic is often required. On the contrary, RoboChart is a diagrammatic notation, in line with current practice of developing robotic control software often using diagrammatic state machines [30,31,32,33]. RoboChart offers more facilities for abstraction. This includes a component model to define services of a platforms, and an architecture of controllers and parallel threads, and their connections. In addition, RoboChart offers a richer set of data types, including many mathematical data types such as relations and functions, in addition to basic data types, to facilitate reasoning. The comprehensive expression language of RoboChart is that of the Z notation (see the ISO Z StandardFootnote 2), albeit with a more roboticist-friendly syntax and a few syntactic-sugaring constructs.
Table 1 shows a comparison between these probabilistic frameworks and RoboChart according to their support of nondeterministic choice and probabilistic choice, abstraction, and expressiveness. Those frameworks provide different mathematical accounts of probabilistic behaviour, and have a role similar to that of PRISM, rather than RoboChart, in our work.
2.2 Improved modelling languages
A probabilistic finite state machine (PFSM) [33] extends state machines with probability and real-time behaviour. It is used to describe the behaviour of an individual foraging robot in a swarm. Both simulation [33] and formal verification [34] are used to understand and analyse the behaviour of the controller. A PFSM guides the development of a simulation and a formal model, but only loose connections between the machine and the simulation or the model are claimed. RoboChart also extends state machines with probability and real-time behaviour, but it has a formal semantics that can be automatically generated for given models.
Probabilistic timed Behaviour Trees (ptBTs) [35] extend Behaviour Trees [36], a formal and graphical notation to construct a design out of a set of functional requirements in a stepwise and traceable way, with probabilistic behaviour. The meaning of a ptBT is given using probabilistic timed automata (PTAs) [37]. Verification of a ptBT model is realised through translation to a DTMC or MDP model, which is analysed using PRISM. Notations based on behaviour trees treat an individual functional requirement as a behaviour tree, and integrate all these trees into an integrated design behaviour tree that allows defect detection and is traceable to the requirements. Compared to the notations based on state machines, those based on behaviour trees are not well developed and studied. One reason is the lack of sophisticated tool support.
Among the modelling notations extended to accommodate probability, UML state machines [38] are the most popular. DAMRTS (Dependability Analysis Models for Real-Time Systems) [39, 40] is an UML profile that extends UML Statecharts with time and probability. Discrete probabilities are associated with events and a discrete probability distribution is defined over (event, state) pairs. We need a construct to group all transitions that are from the same state and form a probability distribution, but it is not clear what method, if any, is used for that in DAMRTS. From an example in [39], transitions with probabilities do not form a complete cover. So it can be the case that a transition is labelled with an event and a probability p, but there are no other transitions with the same event and the complementary probability \(1-p\). The semantics in this case is not clear. DAMRTS models can be automatically translated to probabilistic timed automata and analysed by PRISM. This translation is, however, not formalised. In contrast, in RoboChart, a probability distribution is associated with a single transition, which defines the target states like in a probabilistic automaton. Moreover, the probabilities in such a transition add up to 1. So, there is no ambiguity. Our translation to PRISM is formalised in this paper.
Jansen et al. [41] describe a probabilistic conservative extension of UML’s Statechart notation, called P-statecharts. Since the extension is conservative, we know that all the behaviours of the original semantics are behaviours of the probabilistic semantics. A transition can lead to one of several states depending on a specified probability distribution. Each probability distribution is guarded by a trigger, either an event or no event, which corresponds to an external action or an internal action \(\tau \) in a probabilistic automaton. Discrete probabilities are associated with actions and a discrete probability distribution is defined over (action, state) pairs. A P-statechart alternates between nondeterministic choices and probabilistic choices using the strictly alternating model [18, 42]. Transitions that exit nondeterministic choices enter only probabilistic choices. A P-statechart deals not only with nondeterminism and probabilism, but also with priorities within Statecharts. The semantic models of P-statechart are based on MDPs. Properties of a P-statechart written in the probabilistic branching time logic (PCTL) can, therefore, be automatically checked using PRISM.
Probabilistic modelling and verification using RoboChart are inspired by Jansen et al.’s P-statecharts. Similar to P-statecharts, RoboChart also deals with nondeterminism and probabilistic choices in the same strictly alternating way: transitions that exit nondeterministic choices enter only probabilistic choices. In the probabilistic model, even if two states are connected by a transition directly, therefore without an explicit probabilistic choice, it is treated as having an implicit probabilistic choice with the probability of the outgoing transition as 1. So, since every transition is probabilistic, after a nondeterministic choice selects an enabled transition, there is a probabilistic choice.
A conflict arises when a transition from a composite state and a transition from a substate are both enabled. A P-statechart assumes a given priority scheme to resolve the conflict. RoboChart has a simpler semantics, which leaves the choice nondeterministically. In this way, we treat them as another level of nondeterminism in order to avoid dealing with the complexity of priorities in the semantics. Differently from P-statecharts, RoboChart does not support AND-states within a state machine (but supports parallelism between state machines) to simplify the semantics, and, therefore, make reasoning more tractable and improve automation of verification. Regarding triggers, RoboChart supports input and output triggers in addition to simple triggers just for synchronisation.
Richer action constructs are available in RoboChart, including assignments, communications, sequential composition, and conditionals. P-statecharts only support assignments and communications. Functions and operations can be specified using preconditions and postconditions described in the rich language of Z predicates.
Table 2 summarises the comparison of RoboChart with the modelling languages above.
2.3 Domain-specific languages for robotics
Model-driven software development in robotics has been studied [43] and several domain specific languages are available [44]. SmartSoftFootnote 3 [45], V3CMM [46], BRICS Component Model (BCM) [47], RobotML [48], SafeRobots [49], and the work in [50] all employ component models like in RoboChart. Although some of them, such as BCM, have a degree of formal modelling, they usually do not have a formal semantics (and, therefore, cannot support formal reasoning and verification) or have a formal semantics only for part of their constructs. RoboChart, however, has a formal semantics defined for all its constructs, including its component model.
GenoM3 [51, 52] is a model-based engineering framework for robotics software. It supports verification using model checking via translation to Petri Nets [53] and deadlock checking using BIP [54]. It is also an executable language. RoboChart, nevertheless, provides various levels of abstraction, and also supports theorem proving in addition to model checking.
As far as we know, none of these notations support probabilistic modelling and reasoning, as we propose here for RoboChart. Extending these notations, however, may benefit from the results we present here.
Thrun et al. [55] uses MDPs as the underlying mathematical framework to model uncertainty in robot action selection for probabilistic planning and control, and introduces the value iteration algorithm to find control policies for these models. They use partially observable Markov decision processes (POMDPs) to model uncertainty in perception because the environment is usually only partially observable through sensors. Probabilistic modelling in RoboChart, as discussed in this paper, covers uncertainty in robot action selection. Our probabilistic semantics is also based on MDPs. RoboChart, however, supports different levels of abstraction through a component model, abstract data types, and a rich action languages (see Table 2).
In summary, the probabilistic modelling of RoboChart is based on existing notations, but provides abstraction and improved modelling practice for the robotics domain. The analysis of probabilistic behaviour in RoboChart models is fully automated, and the transformation from RoboChart to PRISM is formalised.
Next, we describe and illustrate RoboChart.
3 RoboChart
This section gives an overview of our approach to probabilistic modelling using an example. Part of the novelty of our work is related to the component model of RoboChart, not only the novel state machine constructs. For this reason, we present an example that illustrates the use of probabilistic choices, challenging constructs of machines, such as composite states, and the core elements of the RoboChart component model: controllers, robotic platforms, and modules. In Sect. 3.1, we present our probabilistic choice operator and an informal account of its effect on the RoboChart semantics. We refer to the RoboChart reference manual [1] for a complete account of the notation. Sections 3.2 and 3.3 present the metamodel and well-formedness conditions for the probabilistic constructors.
3.1 Notation
Map of the workplace from [56]
We describe our facilities for modelling probabilistic controllers using as an example a mail delivery robot from [56]. It delivers mail to eight offices arranged in the configuration in Fig. 1. An office 0 is the station to charge its battery. A worker in an office can send mail to another, but not to the charging station.
The robot can deal with only one delivery at a time. Upon receipt of a delivery request, the robot starts to fetch the mail by moving to the sending office. Upon arrival, it fetches the mail and then moves to its destination to deliver it. After delivering the mail to its destination, it is ready for the next request.
The robot is not equipped with particular cameras or sensors for dynamic route allocation. Instead, it uses a random algorithm, similar to those of vacuum cleaning robots, to choose its moves. With equal probability, it either stays where it is or moves to adjacent offices. For example, if its current location is at office 1, it remains at office 1, moves to office 2, or moves to office 4. Each choice has probability 1/3.
Module and Robotic Platform. The module of our RoboChart model for this example is shown in Fig. 2. The module deliverMOD is composed of one robotic platform deliverRP and a controller deliverCTRL.
The notion of robotic platform is a crucial element in the definition of a module (and so, of a model). It captures the services that need to be offered by a robotic platform to enable the use of the control software. For abstraction, these services are not specified in a module. This ensures that a module is platform-independent. The robotic platform, however, is the link to connect a module to a model for a physical robot, for example. This is described in detail in [57].
A platform includes variables, events, and operations that represent sensors and actuators. It may also define constants that characterise parameters of the model. In our example, we collect in an interface ctrlVarInf variables and constants of deliverRP. The current location and battery level of the robot are recorded as variables  p and c. The battery capacity batteryCapacity and the battery charged per update chargeStep are design parameters and treated as constants
p and c. The battery capacity batteryCapacity and the battery charged per update chargeStep are design parameters and treated as constants  .
.
We use interfaces to group elements for reuse and to describe dependencies. The interface ctrlVarInf in Fig. 2 is provided  by the robotic platform. The variables and constants defined in ctrlVarInf are used in the controller and all its state machines, which require
by the robotic platform. The variables and constants defined in ctrlVarInf are used in the controller and all its state machines, which require  the interface (see Figs. 3, 4, 5, and 6).
the interface (see Figs. 3, 4, 5, and 6).
In addition to variables and constants, the robotic platform can communicate with controllers via connected events  .
.
The controller deliverCTRL in Fig. 2 gets a mail delivery request including an office number that locates the mail to be delivered and a destination office number from the platform via the typed events request and dest. After delivery, the controller notifies the robotic platform via the delivered event.
Controllers. The definition of the deliverCTRL controller is given in Fig. 3. It has three state machines  : movingSTM, batterySTM, and taskSTM, which correspond to three separate functionalities: movement control, battery management, and task management. The machines are defined in Figs. 4, 5, and 6.
: movingSTM, batterySTM, and taskSTM, which correspond to three separate functionalities: movement control, battery management, and task management. The machines are defined in Figs. 4, 5, and 6.
A controller  in RoboChart encapsulates one or more (parallel) state machines. Connections between a controller and its state machines are used to relay information through the events of the controller. The connections on the events request and dest of the controller in Fig. 3 pass information from the platform to the machine taskSTM. The machine taskSTM acknowledges delivery via the delivered event relayed through the event delivered of the controller.
in RoboChart encapsulates one or more (parallel) state machines. Connections between a controller and its state machines are used to relay information through the events of the controller. The connections on the events request and dest of the controller in Fig. 3 pass information from the platform to the machine taskSTM. The machine taskSTM acknowledges delivery via the delivered event relayed through the event delivered of the controller.
Connections between machines represent synchronisations and interactions. The machines movingSTM and taskSTM shown in Fig. 3 synchronise with each other on a move event used to trigger movement when the current position of the robot is different from the goal (either the mail request office or mail destination office), while movingSTM and batterySTM synchronise on the upstart and upend events to trigger start and end of an update of the current battery level after a move.
State machines. Behaviour descriptions are given by state machines in RoboChart. They may require interfaces and declare local constants, variables, and events, like controllers. For example, the taskSTM machine (Fig. 4) declares two variables g and fd. The variable g is a natural number: an office number where mail needs to be fetched or delivered; g is initialised to 0. We call g the goal of the robot. The variable fd is an element of the enumeration FD defined in Fig. 4. It represents three stages of a delivery task: idle, fetching, and delivering mail. The variable fd is initialised to NoTask. These variables are local to taskSTM. All declared events appear on the border of machines.
A state machine comprises states, junctions, and transitions. States may be simple or composite. A composite state itself contains a state machine. A state may also have entry, exit, and during actions, executed when the state is entered, exited, and active.
Transitions connect states and junctions. A self-transition has the same source and target states. Transitions have a label with the following optional features:
-
A trigger event;
-
A guard, specifying the conditions that need to hold for the transition to be enabled;
-
A probability value, defining the probability of occurrence of this transition; and
-
An action that is executed if the transition is taken.
Actions are statements. The action constructs are skip, an action that terminates immediately, assignment (=), sequential composition (;), conditional (if), input events (of the form evt?v where evt is an event and v is a variable that records the input value), output events (of the form evt!e where e is an expression whose value is output), or synchronisations (of the form evt or evt.e).
A junction is different from a state in that the control flow of a machine cannot stop at a junction. With a junction, we can break the flow of a transition by creating points of decision in between states. Junction is a concept of UML state machines and other Statechart notations. Junctions represent decision points that must be made immediately. As a consequence, a junction must always have at least one outgoing transition enabled in order to leave the junction. RoboChart has three types of junctions: initial junctions  , normal junctions
, normal junctions  , and probabilistic junctions
, and probabilistic junctions  defined here. An initial junction indicates the starting point of execution of a state machine, and cannot have incoming transitions. Normal junctions have both incoming and outgoing transitions, but these transitions cannot be labelled with probability values.
defined here. An initial junction indicates the starting point of execution of a state machine, and cannot have incoming transitions. Normal junctions have both incoming and outgoing transitions, but these transitions cannot be labelled with probability values.
Probabilistic junctions, also used in other techniques [58, 59], are a special form of junction introduced to capture probabilistic choices. Only transitions from a probabilistic junction can be labelled with probability values, which must add up to 1. This imposes a proof obligation, since probabilities can be given by expressions involving variables.
The taskSTM machine in Fig. 4 has just one state taskState with four self-transitions. The top-right transition is taken when there is a mail delivery request (trigger request?g) and the robot is idle (guard fd=FD::NoTask where FD::NoTask is a constant of the enumeration FD). If that transition is taken, its action establishes that if the goal g is an office number from 1 to 8, the robot moves to the fetching mail stage (FetchMail); otherwise, it ignores the request (skip). The bottom-right transition is taken if the robot is not idle and its current position is not the goal. If so, the machine waits for a synchronisation on the move event, as specified by the transition action move (a synchronisation action). The top-left transition is enabled if the robot arrives at the office to fetch mail (g==p) when it is fetching mail. If that transition is taken, the machine waits for an input dest?g from the platform giving the delivery destination g. If the destination office is valid (between 1 and 8), the robot switches to the delivering stage. Otherwise, it discards the request. The bottom-left transition is enabled if the robot reaches the destination when it is delivering. If so, it returns to the idle stage and sends a delivered acknowledgement.
The batterySTM machine in Fig. 5 manages the battery. It has only the state batteryState. The transition from the initial junction sets the battery level c to its capacity batteryCapacity to record that initially the battery is full. Two self-transitions of batteryState can be taken when the event upstart occurs. One is taken when the robot is at the charging station (p==0 , where p is provided by deliverRP shown in Fig. 2 and required here through an interface ctrlVarInf), and another when the robot is not there and the battery is not empty. In the first scenario, the battery is charged and its level is increased by the constant chargeStep per update till it is full. In the second scenario, one unit of the battery is consumed. In both scenarios, the upend event is used to signal that the battery state has been updated. Both upstart and upend are synchronisations with events in the movingSTM machine to allow the battery to be updated when the robot is moving.
The movingSTM machine in Fig. 6 controls movement of the robot. The machine has two states: Stuck and Move. The transition from the initial junction sets the current position p of the robot to the charging station. The Move state is composite. Its machine has nine states (from s0 to s8). Each such state corresponds to one office and has an entry action such as p=2 that sets p to 2 upon entering of the state s2 to record in p the office in which the robot is located. The transitions from such states are connected to probabilistic junctions and are labelled with a trigger move and a guard condition (c>0). So, these transitions are taken only when movement is triggered by the taskSTM machine and the battery is not empty. All transitions leaving one of the probabilistic junctions are labelled with the same probability value, and so the robot randomly chooses its next position based on the map in Fig. 1. No matter which outgoing transition is taken, the machine updates the battery by synchronising with the batterySTM machine using upstart and upend events.
When the robot is not at the charging station and its battery is empty, the transition from the Move state with guard c==0 is taken. A junction in this transition defines a decision based on the current robot position. If it is at the charging station, the battery is charged by synchronising with the batterySTM machine and movingSTM reenters Move. Otherwise, the machine movingSTM enters the Stuck state because the robot has no battery and cannot charge. Stuck has no outgoing transitions. So the robot cannot move again.
Next, we describe the RoboChart metamodel, and return to this example later in Sect. 5.2.
3.2 Metamodel
Here, we describe the RoboChart metamodel [1] and the changes needed to include probabilistic choice.
A RoboChart model is defined by a module, whose metamodel is shown in Fig. 7. A Module comprises a collection of nodes (ConnectionNode) and connections (Connection). A ConnectionNode can be a RoboticPlatform, a Controller, or a StateMachine. A RoboticPlatform is either given by a definition (RoboticPlatformDef) or by a reference to a definition (RoboticPlatformRef). A RoboticPlatformRef refers to exactly one RoboticPlatformDef. The metamodel for controllers and state machines is similar. A node in a module can be a definition or a reference to a definition of a robotic platform or a controller, but not a state machine as specified by well-formedness conditions discussed later.
A StateMachineDef is a StateMachineBody that can be used as a ConnectionNode (in a ControllerDef). So, StateMachineDef needs to inherit from both StateMachineBody and ConnectionNode. We, however, have an intermediate concept of a StateMachine that inherits from ConnectionNode. StateMachineDef inherits from ConnectionNode via StateMachine, which allows different forms of definition. In particular, a StateMachine may be defined by reference to a StateMachineDef.
Robotic platform and controller definitions may provide and require interfaces through extending Context. The class Context contains variables (VariableList), operations (OperationSig), and events (Event), and refers to three kinds of interfaces: provided interfaces (pInterfaces), required interfaces (rInterfaces), and defined interfaces (interfaces). Connection links one node to another by their events. A connection can be asynchronous or synchronous, and unidirectional or bidirectional. The metamodel permits connections between any two nodes, but not every connection is valid. For example, a robotic platform cannot connect to a state machine. We connect them through a controller. Well-formedness conditions enforce such restrictions.
ControllerDefinitions, are composed of a collection of state machines and connections. The structure of a state machine is detailed in Fig. 8. A state machine is a NodeContainer that includes a collection of nodes (Node) and transitions (Transition). States (State), junctions (Junction), and probabilistic junctions (ProbabilisticJunction) are possible nodes. State is also a NodeContainer, so a state can include nodes and transitions. This supports hierarchical state machines. State contains entry, exit, and during Actions. Initial is a junction and Final is a state. Transitions are directional and connect one source node to a target node. A transition may have a trigger (Communication), a guard (Expression), a probability value (Expression), and an action (Statement).
The metamodel of variables, communications, events, and operations is shown in Fig. 9. A Variable, an OperationSig, and an Event all have a Name. A Variable also has a Type and an optional initial value, given by an Expression. A VariableList contains one or more variables and has a modifier (VariableModifier) from which the counterpart in a Variable derives. An operation signature (OperationSig) contains zero or more parameters (Parameter). A Communication has a type (CommunicationType), and may have a parameter (Variable), a value (Expression), and refer to an Event. An Action contains exactly one Statement. A CommunicationStmt is a Statement that contains exactly one communication: that uses an Event.
The changes we have made to the original RoboChart metamodel presented in [1] to cater for probability are minor: addition of ProbabilisticJunction, and a probability value to Transition. Next, we define healthiness conditions associated with these constructs.
3.3 Well-formedness conditions
Well-formedness conditions define restrictions on models to make them meaningful. It includes typing and scope rules for expressions and actions, and imposes various conditions, such as uniqueness of names in all components. The RoboChart reference manual [1] gives a full account of these conditions.
We now present the extra well-formedness conditions imposed on transitions (Sect. 3.3.1) and on the new probabilistic junction (Sect. 3.3.2).
3.3.1
 Transitions
Transitions
-
PT1
The source of a transition with a probability value must be a probabilistic junction, that is, states, initial junctions, and normal junctions cannot be the sources of these transitions.
-
PT2
The probability value of a transition must be between 0 and 1.
We introduce PT1 because RoboChart implements an alternating model between nondeterministic choice and probabilistic choice. (This is in line with other authors to simplify the semantic model, and in particular the interaction between nondeterministic choice and probabilistic choice—see references [18, 41]. This follows, for example, the reactive modules formalism of PRISM.) Therefore, it would be awkward at best to have arbitrary probabilistic transitions in state machines. The probabilistic junctions provide a syntactic mechanism to isolate the probabilistic choices. Probabilistic choice is only made and resolved at probabilistic junctions.
3.3.2
 Probabilistic junctions
Probabilistic junctions
Probabilistic junctions are also junctions, but with extra well-formedness conditions.
-
PJ1
There must be a probability value on every outgoing transition from a probabilistic junction.
-
PJ2
There must not be a guard on an outgoing transition from a probabilistic junction.
-
PJ3
The probability values of all outgoing transitions from a probabilistic junction must sum to 1.
PJ2 enforces construction of simple models by separating concerns. If a guard is needed, then it can be added with a preceding transition, so there is no loss of expressiveness. PJ2 is also helpful in simplifying the process of counting transitions and choice resolution; these counts are used in the notion of time in the Markov semantics and probabilistic temporal property language.
Before defining our model transformation, the next section describes the target language, the notation adopted by PRISM, its semantics, and its metamodel.
4 The PRISM notation
In the previous section, we have described how to use RoboChart to model discrete-time probabilistic systems. Another question follows: how do we verify these systems? As mentioned, this work enables model checking using probabilistic model checkers, specifically PRISM [3], but potentially also Storm [26] and MRMC [60], which adopt the same input notation.
Section 4.1 describes the notation that supports. We then present a metamodel that we have defined for that notation in Sect. 4.2.
4.1 PRISM
PRISMFootnote 4 is a model checker for verifying probabilistic behaviour. It allows us to analyse various probabilistic models, including DTMCs and MDPs.
The PRISM language is similar to Alur’s Reactive Modules formalism [27], but with a different variable model. In a reactive module, variables fall into three groups: private, interface, and external. A module M can read every other modules’ interface and external variables, but not their private variables. M can write to its own private and interface variables, but not to other modules’ external variables. PRISM does not have private variables: all local variables in a module are interface variables. PRISM also has global variables shared by all modules for reading or writing. Interleaving global-variable updates avoids race conditions.
PRISM employs a closed-world assumption, that is, systems are not subjected to inputs from the environment. In order to take specific environmental inputs into account, another module can be added to the model to encode generation of desired inputs.
PRISM’s semantics is not compositional: parallel modules are flattened into a single system module [61]. Module combinators are similar to CSP process algebraic operators, including parallel composition, action (event) hiding, and action renaming. The parallel composition operators are as follows:
-
\(M_1 \llbracket A \rrbracket M_2\), requiring both modules to synchronise on the actions in the set A.
-
\(M_1 \parallel M_2\), which is equal to \(M_1 \llbracket A_1 \cap A_2 \rrbracket M_2\), where \(A_1\) and \(A_2\) are the sets of actions used in the modules \(M_1\) and \(M_2\), respectively.
-
\(M_1 |||M_2\), which is equal to \(M_1 \llbracket \emptyset \rrbracket M_2\).
Communication between modules in PRISM, however, is not based on actions. These have only names and cannot carry messages (or data). So actions are used only for synchronisation. Exchange of messages is through variables: both global and local variables.
An important feature of PRISM is statistical model checking (SMC) [62, 63]. This is a Monte Carlo discrete-event simulation technique based on randomised sampling of simulations of a PRISM model. It approximates numerical and symbolic results for property checking that economises on computation. Although approximate, SMC is effective in dealing with state-space explosion. (For the robotics domain, it is also an important technique for design-space exploration.)
To support SMC, however, the PRISM model cannot have multiple initial states and process algebraic operators in the construction of the system module. So no parallel composition can be specified. PRISM implicitly uses \(\parallel \) to define a system \(M_1 \parallel M_2 \parallel \cdots \parallel M_n\) from all modules \(M_1, M_2, ... , M_n\) in the model.
The structure of a PRISM model is illustrated in Fig. 10. There are six sections in a PRISM model:
- S1:
-
is mandatory and gives the model type. In Fig. 10, S1 is given on line
 , which defines DTMC as the type for this example. Other available model types are MDP, continuous-time Markov chain (CTMC), and probabilistic timed automata (PTA).
, which defines DTMC as the type for this example. Other available model types are MDP, continuous-time Markov chain (CTMC), and probabilistic timed automata (PTA). - S2:
-
declares constants used in the model. In Fig. 10, S2 is given on line
 , which declares one constant pi that is of type double and set to a real number.
, which declares one constant pi that is of type double and set to a real number. - S3:
-
declares global variables. In Fig. 10, S3 is given on lines
 -
- , which declare an integer variable i and a variable j with range [0..10]. Both initialised to 0.
, which declare an integer variable i and a variable j with range [0..10]. Both initialised to 0. - S4:
-
defines formulas that give names to expressions. In Fig. 10, S4 is given on line
 , which defines a formula f1 associated with expression pi*2.
, which defines a formula f1 associated with expression pi*2. - S5:
-
defines the individual modules. Each module has two subsections: S5_1 for local variable declarations and S5_2 for commands described in the sequel. S5 is given on lines
 -
- , which indicate the definition of modules M1, M2, and Mn. S5_1 is on line
, which indicate the definition of modules M1, M2, and Mn. S5_1 is on line  , which declares a local boolean variable l initialised to false, and S5_2 has a single command given on line
, which declares a local boolean variable l initialised to false, and S5_2 has a single command given on line  . The command has an action e1, a guard condition g1, and a set of updates separated by +. An update is composed of an optional probability value, such as p1 in the example, and an assignment, such as u1.
. The command has an action e1, a guard condition g1, and a set of updates separated by +. An update is composed of an optional probability value, such as p1 in the example, and an assignment, such as u1. - S6:
-
defines rewards associated with models. In Fig. 10, S6 is given on lines
 -
- , which define two rewards: a reward on line
, which define two rewards: a reward on line  associated with states, and another on
associated with states, and another on  associated with transitions. Rewards, which are used in properties (but defined within models) to allow reasoning about a wide range of quantitative measures, assign particular values to certain states or transitions. If a reward has an action, then this applies to all transitions labelled by that action.
associated with transitions. Rewards, which are used in properties (but defined within models) to allow reasoning about a wide range of quantitative measures, assign particular values to certain states or transitions. If a reward has an action, then this applies to all transitions labelled by that action.
A state is a valuation of all variables (global and local) in the model. The state space S of the model is all valuations of variables. A command

defines a transition augmented with probabilities. The optional action e is available for synchronisation with other modules. The guard condition g ranges over the state space S. In other words, g characterises a subset of the state space, denoted by \(S_g\), that satisfies the condition. The collection of state updates pi : ui, where \(\sum \nolimits _{1\le i \le n}^{} pi=1\), comprises a probability pi and a collection of assignments ui. Each pair defines the probability pi of the transition going from a source state s in \(S_g\) to a target state \(s'\) specified by the set of assignments ui. A command cannot update a global variable if it has an action. This avoids two commands synchronising with different updates for a global variable.
Example 1
We present below the PRISM model for a simple robot that moves along a corridor following a random walk. It randomly chooses its moving direction: either to the left or to the right with probability p or \((1-p)\) respectively. If, however, the robot reaches an end of the corridor, it can only move to one direction: turn around and move away from the end. Initially, the robot is at the center of the corridor.
The PRISM script, as shown in Fig. 11, defines a DTMC model (line  ). A constant p represents the probability described above (line
). A constant p represents the probability described above (line  ). A constant N records half of the length of the corridor (line
). A constant N records half of the length of the corridor (line  ). The only module random_walker (lines
). The only module random_walker (lines  -
- ) has one local variable: x for the current location of the robot, defined over a range from -N to N, and initialised to 0 for the centre of the corridor (line
) has one local variable: x for the current location of the robot, defined over a range from -N to N, and initialised to 0 for the centre of the corridor (line  ). The commands on lines
). The commands on lines  -
- define the transition system of the module. In the commands, we use x’ to represent the after-transition value of x. Every move event represents one step of the robot. In the left end, the robot can move only to the right (line
define the transition system of the module. In the commands, we use x’ to represent the after-transition value of x. Every move event represents one step of the robot. In the left end, the robot can move only to the right (line  ), while in the right end, it can move only to the left (line
), while in the right end, it can move only to the left (line  ). In locations other than the ends (
). In locations other than the ends ( on line
on line  , where
, where  denotes conjunction), it can move to the left (line
denotes conjunction), it can move to the left (line  ) or to the right (line
) or to the right (line  ) with probability p and (1-p).
) with probability p and (1-p).
The rewards on lines  -
- assign a reward of 1 to every state in which the robot reaches the location N/2 (line
assign a reward of 1 to every state in which the robot reaches the location N/2 (line  ) or the location -N/2 (line
) or the location -N/2 (line  ). This enables us to specify reward-based properties [64] (the properties of DTMCs or MDPs augmented with rewards) that allow quantitative measures of the model at the two locations. For example, the quantitative property
). This enables us to specify reward-based properties [64] (the properties of DTMCs or MDPs augmented with rewards) that allow quantitative measures of the model at the two locations. For example, the quantitative property  , where R=? denotes reward-based operator [64], and F and X stand for the eventually and next operators in PCTL, specifies a property of the expected cumulated reward that the robot receives when it passes through the two locations before it returns to the centre of the corridor.
, where R=? denotes reward-based operator [64], and F and X stand for the eventually and next operators in PCTL, specifies a property of the expected cumulated reward that the robot receives when it passes through the two locations before it returns to the centre of the corridor.
Next, we describe the PRISM metamodel.
4.2 PRISM metamodel
We show the metamodel we have defined for the structure of a PRISM model in Fig. 12. A Model contains one or more modules (Module), and zero or more constants (Constant), global variables (VarDecl), formulas (Formula), labels (Label), and rewards (Rewards).
A Constant associates a name (Name) with a type (Type) and an optional value (Expr). A VarDecl declares a variable with a name, a type, and an initial value (Expr). Formula and Label are similar but do not have a type. Both associate a (formula or label) name with an expression. A Label requires a boolean expression (BoolExpr), but a Formula can have any expression (Expr). The complete metamodel is in [1].
Figure 13 depicts the metamodel for PRISM modules. There are two ways to specify a module: either with a ModuleDefinition; or by renaming (ModuleRename, omitted in the diagram for simplicity). ModuleDef defines a module by its name, local variables (VarDecl), and commands (Command).
A command contains an optional action (Action), an optional guard (BoolExpr), and one or more updates (Update). An update has an optional probability (Expr) and a collection of assignments (AbsAssignment). There are two types of assignments: Assignment associates a variable with a value (Expr); and Skip is an empty assignment, in which no variable is updated.
There are four primitive Types, as shown in Fig. 14: boolean (BoolType), integer (IntType), range (RangeType), and double (DoubleType).
Figure 15 displays the reward metamodel. An action is optional. Without an action, the reward item assigns a reward (Expr) for all states satisfying the guard condition (BoolExpr). If there is no trigger event for these transitions, we assign the silent action "tau".
The next section defines our model transformation.
5 Model transformation
RoboChart is different from PRISM in various aspects. To deal with these differences, we structure the translation in two steps: normalisation of the RoboChart model and transformation of normalised RoboChart models to PRISM. Section 5.2 gives an overview of the translation. In Sect. 5.2.1, we define our normal form, namely restrictions on RoboChart models that ensure all transitions between two states are probabilistic, and define a strategy for normalisation. We describe a strategy to transform from a RoboChart model in normal form to a PRISM model in Sect. 5.2.2. We present formal rules used to normalise RoboChart models in Sect. 5.3 and to transform normalised models in Sect. 5.4. Extra rules are presented in “Appendix A”. The complete set of rules can be found in [1]. Not all features of RoboChart are currently supported. Section 5.1 presents our assumptions.
5.1 Translation requirements
We list the conditions that need to be satisfied by a RoboChart model for our technique to be applicable.
In DTMCs and MDPs, transitions occur in discrete-time steps. Every transition takes one unit of time. Time primitives [2] in RoboChart, however, capture budgets and deadlines using clocks and constructs like wait(n), which defines a waiting period of n units of time, and read?x\(\textsf {<}\) {2}, in which reading a value x through an event read is given a deadline of 2 units of time. DTMCs and MDPs do not intrinsically support clocks, time budgets and deadlines. Our first translation requirement, TR-TP1 below, therefore, rules out translation of time constructs for now.
-
TR-TP1
Time primitives are not used.
In addition to DTMCs and MDPs, the PRISM notation also supports probabilistic timed automata (PTAs) [65, 66], which extend MDPs with the ability to model real-time behaviour through real-valued clocks [67]. The timed semantics of RoboChart, however, are based on time units [2], instead of real-valued time. The default verification method (quantitative abstraction refinement [68]) for PTAs in PRISM, therefore, cannot be used. Instead, we can use the digital clocks [69] method which uses an integral time model. We will extend our transformation to support PTAs to deal with time primitives in RoboChart, which is part of our future work, as discussed in Sect. 8.
-
TR-CN1
Connections between controllers are not asynchronous.
-
TR-OP1
Operations cannot be defined in controllers.
-
TR-ST1
States cannot have during actions.
To cater for these constructs, the PRISM model needs to include extra modules to deal with shared variables, buffers for asynchronous communication, operation calls, and interruptions of during actions by outgoing transitions. Dealing with these extra constructs is part of our agenda for future work.
-
TR-TY1
Only primitive types and enumerations, sequences of these types, or sequences of sequences of these types are used.
-
TR-EX1
Quantification, lambda, and definite description expressions cannot be used since the PRISM notation is concrete.
PRISM supports only integer, boolean, and real numbers. Refinement techniques [70, 71] are a possible solution to deal with abstract data types and constructs in RoboChart. For example, we can refine a variable of the type \({\mathbb {P}}~T\), where T is an enumeration, in RoboChart to a variable over an integer range in PRISM, and use it as a bitmap. Support of more abstract data types and expressions is part of our plans for future work.
In the next section, we give an overview of our translation strategy, which is formalised later in Sects. 5.3 and 5.4. We deal with a rich set of features: parallel controllers, with parallel hierarchical machines, nondeterminism, junctions, probabilistic junctions, synchronous connections, input and output triggers, and functions.
5.2 Overview
In this section, we first present the normal form that we define for RoboChart models and the strategy for normalisation in Sect. 5.2.1, and then we describe the strategy for their transformation to PRISM models in Sect. 5.2.2.
5.2.1 Normalisation
A normalised RoboChart model satisfies the following extra conditions on transitions and junctions.
-
NFM-1
A state has at least one outgoing transition.
-
NFM-2
A transition that is from a state or a normal junction to a normal junction has an action.
-
NFM-3
A transition can have a trigger or an action, but not both together.
NFM-1 is needed due to the fact that DTMCs and MDPs are stochastic. Any state in a PRISM model has to have at least one outgoing transition.
If an incoming transition to a normal junction has no actions, this transition can be combined with outgoing transitions of the junction, which can be removed. The combination of transitions and the removal of junctions reduce the translated PRISM models.
For transitions with a trigger and an action, the action may a) update global variables, and b) have input and output events, or synchronisations, such as the action in the label close[g]/collect. Such transition cannot be translated to a PRISM command directly because a command a) cannot have an action and an update to global variables together, and b) cannot have more than one action. So we impose NFM-3.
To illustrate normalisation, we use the taskSTM machine in Fig. 4 and the movingSTM machine in Fig. 6 as examples. We present their normal forms, and describe how to get a normalised machine.
The taskSTM machine is not in normal form because the transition with a trigger request?g has an action as well, which does not satisfy the condition NFM-3.
A normalised version of taskSTM is shown in Fig. 16 where the changed parts are highlighted in a dashed box. The original transition is replaced by a transition to a new probabilistic junction, and a transition from the probabilistic junction to the original target. The condition of the original transition is used in the transition to the new probabilistic junction, ensuring that a transition is not taken unless the guard holds. The single transition from the probabilistic junction has probability 1 and the action of the original transition. So this new transition is always taken, and the action is executed, as in the original model.
The movingSTM machine has an initial junction, a normal junction, and two states: a simple state Stuck and a composite state Move. The machine movingSTM is not in normal form because a) the incoming transition of the junction in the machine has no action, which does not satisfy the condition NFM-2, and b) Stuck has no outgoing transitions, which does not satisfy NFM-1.
A normalised version of movingSTM is shown in Fig. 17 where the changes are highlighted in a dashed box. The junction and its corresponding incoming and outgoing transitions in the original machine are replaced by two transitions: one from Move to Stuck, and another from Move to itself. They are guarded by the conjunction of the guards of the transitions to and from the junction. The target states are the same.
In the normalised machine, the Stuck state has a new outgoing transition to a new state loop. In general, we add a state loop for each state machine or composite state that has at least one state with no outgoing transition. The new transition (from Stuck in our example) has no trigger, guard, or action. So this transition introduces no new visible behaviour. From loop, a similar transition leads back to loop itself. Overall, where the original machine deadlocked, the normalised machine livelocks. As already mentioned, this is what is required for a probabilistic analysis using DTMCs and MDPs. In the example, there is no loop state in Move because all its substates have outgoing transitions.
In Sect. 5.3, we present the rule that can be used to normalise the original model if applied exhaustively (to all its state machines). Before presenting that rule, however, we give an overview of the normalisation process, explaining how each of the transitions and junctions of movingSTM are affected by it.
Each state machine is normalised by a) adding the loop state and corresponding transitions, if needed; b) combining incoming and outgoing transitions of normal junctions as illustrated for the transition out of Move in movingSTM; c) splitting each transition that has a trigger and an action together into two transitions connected via a new probabilistic junction as illustrated for a self transition of taskState in taskSTM; and d) normalising machines of composite states.
As illustrated above, the combination of transitions to satisfy NFM-2 may lead to the introduction of multiple outgoing transitions from the original source junction with stronger guards. Because there can be only one outgoing transition from an initial junction, we cannot combine outgoing transitions of initial junctions in this way. For probabilistic junctions, PJ2 forbids the presence of guards on outgoing transitions. We cannot, therefore, consider the optimisation enabled by NFM-2 for transitions from initial or probabilistic junctions.
The use of normalisation deals with all the complexity of a RoboChart model to produce a module in a form that is convenient for a direct translation to PRISM.
5.2.2 Transformation to PRISM
The structure of our translation is sketched in Fig. 18. The structure of a RoboChart model is illustrated at the top, and the structure of its corresponding PRISM model is given at the bottom on the left.
The RoboChart module, M, contains a robotic platform RP and multiple controllers (C1, ..., Cj, ...). Each controller contains various state machines (STM1, ..., STMi or STMk, ...). The robotic platform, controllers, and state machines all have a declaration part, which includes variables, constants, and events. We distinguish events in four groups, we use: a) a blank box for independent events that are not connected; b) a box with a C inside for the events that are connected from or to a controller; c) a box with an R inside for the events that are connected from or to the robotic platform; and d) a box with an S inside for the events that are connected from or to a state machine. Additionally, boxes drawn with the same sort of lines (solid, dashed, and so on) indicate events that are connected (either directly or indirectly). For example, the machine STM1 in C1 has a dotted box (C), a dashed box (S), and a blank box. The dotted box denotes the events of the machine that are connected to the events of its controller C1 that are represented by a dotted box too. The dotted box of C1, however, has an R, so these events are further connected to those of the robotic platform (represented by the same dotted box). The dashed box (S) of STM1 represents the events that are connected to other machines in C1, specifically STMi. Particularly, STMi of C1 contains events represented by the bold box (C) that are connected to C1, then to Cj, and finally to the events of STM1 in Cj represented also by a bold box (C).
Generally, the resulting PRISM model (see bottom left of Fig. 18) contains three parts: (a) constants that correspond to the constants of the robotic platform, denoted M.RP.C in Fig. 18, where we use qualified names for all components (see id in Table 3), the controllers (M.C1.C), and the state machines (M.C1.STM1.C) in the RoboChart model; (b) global variables that correspond to the variables of the robotic platform (M.RP.V) and the controllers (M.C1.STM1.V); and (c) a variety of modules that are in parallel (denoted as parallel lines): one (M.RP) corresponding to the robotic platform and others corresponding to state machines. The local variables of a state machine become local variables of the corresponding module, such as M.C1.STM1.V in the M.C.STM1 module.
Renaming plays an important role in the translation of a RoboChart model to PRISM because the variable model of RoboChart is different from that of PRISM. Each element in RoboChart has a given scope. For example, a variable defined in a controller is visible to its inner state machines, but not to the state machines in other controllers. Two variables of the same name in different controllers or state machines are permitted. In contrast, the PRISM language has a flat structure. If two variables in different modules have the same name, then this results in a name conflict. To address this problem, we rename all elements, with the exception of events, used in a RoboChart model to ensure that they all have unique names before translation.
In RoboChart, connections can associate events of different names. This means that a component (machine, controller, or robotic platform) can be used in any context, irrespective of the names that they use for their events. In PRISM, however, connections are realised via synchronisation based on the names of the actions. So, we must make sure that actions in different PRISM modules that need to synchronise have the same name. In our translation, we represent RoboChart events using PRISM actions and connections using synchronisation. Therefore, we ensure, before translation, that events are renamed so that all connections associate events of the same name.
For example, the independent events (represented by the blank box) in STM1 of C1 become independent actions represented in the same style in the M.C1.STM1 module. The actions represented by the dotted box in the module have the same names as the actions represented by the same type box in the robotic platform module. So the modules M.C1.STM1 and M.RP synchronise on these actions, which reflects the connection of their corresponding events in the RoboChart model. Other actions represented by a dashed box, or a bold box, or a bold dashed box are handled similarly.
To illustrate the overall structure of the translation, we use the mail delivery robot model introduced in Sect. 3. We present the structure of its PRISM script, and describe how to get it from the RoboChart model.
The PRISM script is sketched in Fig. 19, where elements not relevant to the structure are omitted, such as the naming, constant declarations, and command details. The model type is on line  ; we use the type DTMC so that we can obtain probabilities of the robot running out of power at different offices. The model type is a parameter to the translation.
; we use the type DTMC so that we can obtain probabilities of the robot running out of power at different offices. The model type is a parameter to the translation.
A translated PRISM model can also use another model type: MDP. The selection of the model type depends on the properties to be analysed using PRISM. For DTMC, PRISM randomises nondeterministic choice and regards them as uniformly probabilistic choices. So PRISM can check quantitative properties such as “what is the probability of the robot running out of power and stay stuck at office 2”. For MDP models, PRISM does not treat nondeterministic choice probabilistically, and aims for establishing minimum and maximum probabilities, not exact probabilities.
Constants and global variables are declared on lines  -
- , and four modules are defined on lines
, and four modules are defined on lines  -
- . The module deliverRP on lines
. The module deliverRP on lines  -
- corresponds to the robotic platform, and the other three modules on lines
corresponds to the robotic platform, and the other three modules on lines  -
- ,
,  -
- , and
, and  -
- correspond to three state machines in the RoboChart model.
correspond to three state machines in the RoboChart model.
Constants and variables provided by the robotic platform are translated to constants and global variables, as shown on lines  -
- . MININT and MAXINT are placeholders for the smallest and largest integer to be included in the set to represent the integer numbers. Their values are parameters for the translation.
. MININT and MAXINT are placeholders for the smallest and largest integer to be included in the set to represent the integer numbers. Their values are parameters for the translation.
The robotic platform module deliverRP in PRISM represents the environment of the system modelled, and generates inputs (using a nondeterministic choice over possible input values) to the software. Two local variables on lines  -
- correspond to the output events request and dest of the robotic platform (see Fig. 2), that is, the inputs to the controller. They have the same type as the request and dest events. MAXNAT is similar to MAXINT but represents the largest natural number. When a synchronisation on either action (request or dest) occurs, the corresponding local variable (either EVT__request or EVT__dest) is assigned a value nondeterministically chosen. The commands on lines
correspond to the output events request and dest of the robotic platform (see Fig. 2), that is, the inputs to the controller. They have the same type as the request and dest events. MAXNAT is similar to MAXINT but represents the largest natural number. When a synchronisation on either action (request or dest) occurs, the corresponding local variable (either EVT__request or EVT__dest) is assigned a value nondeterministically chosen. The commands on lines  -
- define the choice for EVT__request. The other module involved in the synchronisation (in this case, taskSTM) copies the value to a local variable (as illustrated by the command on line
define the choice for EVT__request. The other module involved in the synchronisation (in this case, taskSTM) copies the value to a local variable (as illustrated by the command on line  ) to simulate the acceptance of input values from the environment.
) to simulate the acceptance of input values from the environment.
The actions move, upstart, upend, request, dest, and delivered in four modules correspond to the events in the RoboChart model. Since in this example only events of the same name are connected, there is no need to rename events. The actions of the same name such as move on line  in movingSTM and line
in movingSTM and line  in taskSTM allow synchronisation of the two modules, as specified by the connection in Fig. 3.
in taskSTM allow synchronisation of the two modules, as specified by the connection in Fig. 3.
The events upstart and upend are used for synchronisation between two state machines. They are not events of the robotic platform; therefore, the visible behaviour of the RoboChart module does not include occurrences of these events. In PRISM, it is possible to use a hiding operator (similar to that of CSP) to make synchronisations on given actions internal (not visible). The use of such operator, however, makes statistic model checking infeasible. So, we keep these actions visible.
Two local variables (g and fd) of the taskSTM module on lines  -
- are translated from the corresponding local variables in taskSTM (see Fig. 4). The type of fd is a range that relates to the number of literals in the enumeration FD (see Fig. 4). The initial value of fd is NoTask that is represented by 0 (line
are translated from the corresponding local variables in taskSTM (see Fig. 4). The type of fd is a range that relates to the number of literals in the enumeration FD (see Fig. 4). The initial value of fd is NoTask that is represented by 0 (line  ).
).
We illustrate our approach to modelling state machines in PRISM in Fig. 20, where we present the module for the normalised taskSTM machine in Fig. 16 on lines  -
- . We use three (sets of) variables: program counter scpc, lock, and exit variables, in addition to the local variables of the state machine. In this simple example, we have local variables fd and g, and just two variables scpc and lock. Later in this section, we consider examples with extra variables including exit variables. The required variables c and p, and the required constants batteryCapacity and chargeStep are declared globally, as shown in Fig. 19.
. We use three (sets of) variables: program counter scpc, lock, and exit variables, in addition to the local variables of the state machine. In this simple example, we have local variables fd and g, and just two variables scpc and lock. Later in this section, we consider examples with extra variables including exit variables. The required variables c and p, and the required constants batteryCapacity and chargeStep are declared globally, as shown in Fig. 19.
A program counter variable scpc records the current state of the machine. In our example, we have just the initial state and the taskState. We name the initial state i0 and declare two constants i0 and taskState to associate these states with the numbers 1 (line  ) and 2 (line
) and 2 (line  ). Extra constants declared on lines
). Extra constants declared on lines  -
- , associated with the numbers from 3 to 12, are needed because the notion of state in RoboChart does not match that of PRISM (see Sect. 4.1), which is based on valuation of variables. So, we have constants for each action of RoboChart whose encoding in PRISM may lead to a change of the value of the variables in the scope of the machine module taskSTM.
, associated with the numbers from 3 to 12, are needed because the notion of state in RoboChart does not match that of PRISM (see Sect. 4.1), which is based on valuation of variables. So, we have constants for each action of RoboChart whose encoding in PRISM may lead to a change of the value of the variables in the scope of the machine module taskSTM.
We associate these constants with a sequence of integer numbers starting from 0 and increasing in increments of one. For convenience, we refer to these numbers as state numbers because they are used to index states in machine modules. In principle, all that is required is that the constants uniquely identify a module state. The definition of the type of the program counter variable, scpc, which needs to range over the values of these constants, however, imposes an extra challenge. In PRISM, the type of a variable must be finite, which means integer numbers (int) cannot be the type of scpc. MININT and MAXINT, previously described, are used to define the set of integer numbers in RoboChart models. The state numbers, however, might be larger than MAXINT. We, therefore, number the states sequentially, and use specifically a contiguous range of integers, starting at 0, such as  shown on line
shown on line  , to specify all values that scpc can take. The upper limit 12 of the interval is the maximum number associated with these state constants in the module. Any finite set would be appropriate for the translation, but that set needs to be identified to define the constants and the type of scpc. Our particular approach is based on an integer interval starting at 0.
, to specify all values that scpc can take. The upper limit 12 of the interval is the maximum number associated with these state constants in the module. Any finite set would be appropriate for the translation, but that set needs to be identified to define the constants and the type of scpc. Our particular approach is based on an integer interval starting at 0.
In principle, the execution of the commands for each transition of the machine can lead to a change of state of the PRISM module, because a transition can have an action. So, each transition is given a set of numbers used to record the states of the PRISM module that are reached when the encoding of the transition is executed. Figure 21 presents an annotated version of the normalised taskSTM where the transitions are associated with the numbers used in the PRISM module in Fig. 20 to encode the transitions.
For example, the transition labelled  in Fig. 21 is associated with the state
in Fig. 21 is associated with the state  , for taskState, and also, with an extra state
, for taskState, and also, with an extra state  , due to the action move. The transition
, due to the action move. The transition  is associated with states
is associated with states  ,
,  ,
,  , and
, and  ; similarly,
; similarly,  and
and  are associated with other states. The names of the constants representing the extra states are based on the name of the source state of the transition. In the example, we have
are associated with other states. The names of the constants representing the extra states are based on the name of the source state of the transition. In the example, we have  ,
,  , and so on. When the source is the probabilistic junction, we use
, and so on. When the source is the probabilistic junction, we use  and
and  . What is essential is a mechanism to give unique names to the extra-states constants.
. What is essential is a mechanism to give unique names to the extra-states constants.
Since the execution of a RoboChart transition may take the PRISM module through several states, we need a mechanism to prevent the interference from other transitions when the machine module is in one of these intermediary states. For instance, if  is taken, and the module is in the state
is taken, and the module is in the state  , other transitions should not be taken until
, other transitions should not be taken until  is completed by returning to taskState. For this reason, we introduce a lock variable (line
is completed by returning to taskState. For this reason, we introduce a lock variable (line  ) for the machine module. This variable initially takes the value 0, represented by a constant
) for the machine module. This variable initially takes the value 0, represented by a constant  (declared on line
(declared on line  ). It records that there is no transition in execution, and, therefore, other transitions can be taken. In addition to 0, lock can also take other values in the range 1 to 5 (line
). It records that there is no transition in execution, and, therefore, other transitions can be taken. In addition to 0, lock can also take other values in the range 1 to 5 (line  -
- ). Each number represents a transition. For example, 5 (represented by T4 on line
). Each number represents a transition. For example, 5 (represented by T4 on line  ) denotes the transition
) denotes the transition  . For convenience, we call these numbers transition numbers because they are used to index transitions in machine modules. The need to record in lock a transition number is not illustrated in this example, but it is explained later when the example for movingSTM is presented.
. For convenience, we call these numbers transition numbers because they are used to index transitions in machine modules. The need to record in lock a transition number is not illustrated in this example, but it is explained later when the example for movingSTM is presented.
In the initial state of the PRISM module, the values of the local variables scpc and lock are i0 and  . The PRISM transition system simulates the behaviour of the machine. In the initial state, the single transition
. The PRISM transition system simulates the behaviour of the machine. In the initial state, the single transition  is available and can be taken. So, when the value of scpc is i0, it can be changed to taskState as shown by the command on line
is available and can be taken. So, when the value of scpc is i0, it can be changed to taskState as shown by the command on line  .
.
When scpc records that the current state is taskState, there are four transitions available, captured by the commands on lines  ,
,  ,
,  , and
, and  . They all have guard conditions to ensure scpc is taskState and lock is free. Other guard conditions in these commands are from the guards of the corresponding transitions. Particularly, the transition
. They all have guard conditions to ensure scpc is taskState and lock is free. Other guard conditions in these commands are from the guards of the corresponding transitions. Particularly, the transition  has a trigger request?g, which is recorded in the command on line
has a trigger request?g, which is recorded in the command on line  with an action request and an update to the local variable g from the value of the variable
with an action request and an update to the local variable g from the value of the variable  to simulate a communication between the machine and the robotic platform. If these transitions are enabled and taken, the updates of these commands change the value of lock to the corresponding transition number and the value of scpc to the first state number corresponding to the transition. For example, the command on line
to simulate a communication between the machine and the robotic platform. If these transitions are enabled and taken, the updates of these commands change the value of lock to the corresponding transition number and the value of scpc to the first state number corresponding to the transition. For example, the command on line  updates lock to T1 and scpc to
updates lock to T1 and scpc to  (
( ). After one of these commands is executed, the value of lock is not
). After one of these commands is executed, the value of lock is not  any more, therefore, none of these commands are no longer enabled to avoid interrupting the taken transition.
any more, therefore, none of these commands are no longer enabled to avoid interrupting the taken transition.
Each transition corresponds to several commands in the PRISM module. The transition  is encoded by two commands on lines
is encoded by two commands on lines  and
and  . The first command deals with scpc and lock as just explained. When the current state of the machine is
. The first command deals with scpc and lock as just explained. When the current state of the machine is  , only the second command on line
, only the second command on line  is enabled. The action move of the command corresponds to the action move of the transition. After the synchronisation of the move action, the command changes the values of scpc and lock to taskState and
is enabled. The action move of the command corresponds to the action move of the transition. After the synchronisation of the move action, the command changes the values of scpc and lock to taskState and  to encode that the transition is completed and its target state is entered.
to encode that the transition is completed and its target state is entered.
The transition  is implemented by six commands on lines
is implemented by six commands on lines  -
- . After it is taken, scpc and lock are updated to
. After it is taken, scpc and lock are updated to  and T2 on line
and T2 on line  . As shown in Fig. 21, a sequential composition of actions is encountered at
. As shown in Fig. 21, a sequential composition of actions is encountered at  . The first action
. The first action  is encoded by the command on line
is encoded by the command on line  , while the second conditional action corresponds to the subsequent commands on lines
, while the second conditional action corresponds to the subsequent commands on lines  -
- , of which two are for the if branch and two for the else branch. In each pair, the first command is related to the branch condition and the second to its action. When the module is at the state
, of which two are for the if branch and two for the else branch. In each pair, the first command is related to the branch condition and the second to its action. When the module is at the state  because of the synchronisation on dest, if the value of g is valid (between 1 and 8), the command on line
because of the synchronisation on dest, if the value of g is valid (between 1 and 8), the command on line  is executed next, which takes the module to
is executed next, which takes the module to  . At this state, only one command on line
. At this state, only one command on line  is enabled. Upon its execution, fd becomes DeliverMail. If the value of g is not valid, fd is set back to idle (NoTask) on lines
is enabled. Upon its execution, fd becomes DeliverMail. If the value of g is not valid, fd is set back to idle (NoTask) on lines  and
and  .
.
The transition  is enabled if the destination of the delivery is reached (g is equal to p) and the robot is delivering as shown by the command on line
is enabled if the destination of the delivery is reached (g is equal to p) and the robot is delivering as shown by the command on line  . After the transition is taken, the module passes through states
. After the transition is taken, the module passes through states  and
and  . Finally, the task returns to NoTask and a delivered event is signalled, shown by the commands on lines
. Finally, the task returns to NoTask and a delivered event is signalled, shown by the commands on lines  and
and  .
.
The transition  has an input trigger (request?g) and its target is a probabilistic junction represented by the constant p0 on line
has an input trigger (request?g) and its target is a probabilistic junction represented by the constant p0 on line  . The command on lines
. The command on lines  and
and  corresponds to
corresponds to  ; it updates scpc to p0. The probabilistic junction has one outgoing transition to taskState with probability 1. The action of this transition is a conditional that involves two states
; it updates scpc to p0. The probabilistic junction has one outgoing transition to taskState with probability 1. The action of this transition is a conditional that involves two states  and
and  . From p0, the next state is
. From p0, the next state is  , as shown on line
, as shown on line  . The conditional action is encoded by the commands on lines
. The conditional action is encoded by the commands on lines  -
- . The encoding is similar to that for the transition
. The encoding is similar to that for the transition  , but since the action of the else branch is skip, there is no additional state, and, therefore, only one command encodes that branch.
, but since the action of the else branch is skip, there is no additional state, and, therefore, only one command encodes that branch.
Since none of the states in the taskSTM machine has an exit action, its PRISM module in Fig. 20 has no exit variable. If a state has an exit action, such as the state s0 in Fig. 22, an exit variable is used in PRISM, as shown in Fig. 23. Constants  ,
,  , and
, and  , declared on lines
, declared on lines  -
- , represent three extra states in PRISM as annotated
, represent three extra states in PRISM as annotated  ,
,  , and
, and  in Fig. 22. Intuitively, we can think of the exit action as being part of the action of every transition out of the state. So, we deal with exit actions much in the same way as we deal with transition actions.
in Fig. 22. Intuitively, we can think of the exit action as being part of the action of every transition out of the state. So, we deal with exit actions much in the same way as we deal with transition actions.
The PRISM snippet of the simple s0 in Fig. 22
The snippet in Fig. 23 encodes the exit of the transitions  and
and  in Fig. 22 from their source state s0. The commands on lines
in Fig. 22 from their source state s0. The commands on lines  and
and  are specific to
are specific to  , and those on lines
, and those on lines  and
and  are for
are for  . Both transitions share an exit from s0, as encoded on lines
. Both transitions share an exit from s0, as encoded on lines  -
- , using an exit variable declared on line
, using an exit variable declared on line  . This variable records the exit states that arise by the execution of the exit action and takes three possible values in this simple example. They represent the states in which the execution of the exit action has not started (
. This variable records the exit states that arise by the execution of the exit action and takes three possible values in this simple example. They represent the states in which the execution of the exit action has not started ( ), has started (
), has started ( ), and has completed (
), and has completed ( ). These values are represented by three constants declared on lines
). These values are represented by three constants declared on lines  -
- .
.
If  is taken, lock is set to T1 and an exit request is triggered by updating exit to
is taken, lock is set to T1 and an exit request is triggered by updating exit to  , as shown on line
, as shown on line  . The next command on line
. The next command on line  for
for  checks the exit completion indicated when the value of exit is
checks the exit completion indicated when the value of exit is  . The value
. The value  indicates an exit request to the current state of the module. Since
indicates an exit request to the current state of the module. Since  is taken, the current state is s0 (that is,
is taken, the current state is s0 (that is,  ). So the guard on line
). So the guard on line  is satisfied, and s0 receives the request and updates the counter to
is satisfied, and s0 receives the request and updates the counter to  to deal with its exit action in the commands on lines
to deal with its exit action in the commands on lines  -
- . In the end of its exit action, s0 marks that it has exited by setting exit to
. In the end of its exit action, s0 marks that it has exited by setting exit to  (on line
(on line  ). The command on line
). The command on line  , therefore, is enabled. So after exiting from its source state,
, therefore, is enabled. So after exiting from its source state,  continues to deal with its transition action and targets, omitted in Fig. 23. The way we encode
continues to deal with its transition action and targets, omitted in Fig. 23. The way we encode  is very similar.
is very similar.
We use this simple state s0 with an exit action to demonstrate how an exit variable is used in our PRISM models to deal with the exit of states. The extra exit variable, however, is not needed to deal with state exit. We could use the counters; in this example, we could set the value of scpc to the extra state numbers, such as  , in the first command corresponding to a transition: the command on line
, in the first command corresponding to a transition: the command on line  or
or  , for example. The last command, such as that on line
, for example. The last command, such as that on line  , then would set the counter to the state just after the exit from the source state, such as
, then would set the counter to the state just after the exit from the source state, such as  . The exit variables are, however, necessary to deal with composite states.
. The exit variables are, however, necessary to deal with composite states.
In the next example, in Fig. 24, we consider a transition t0 whose source state S0 is composite. The execution sequence of the transition starts with a request for S0 to exit. That state then passes the request into its inner states recursively. Upon receipt of an exit request, the innermost (simple) substate executes its exit action (if any). Afterwards, each enclosing state repeats this process up to the source state.
In Fig. 24, all states have an exit action and at least one outgoing transition. In exiting S0, the exit actions of its substates are executed sequentially: the exit action of S2, the exit action of S1, and the exit action of S0, if the current substate of S1 is S2, or the exit action of S3, the exit action of S1, and the exit action of S0, if the current substate of S1 is S3. One possible approach to encode this uses sets of PRISM commands for each of the exiting paths, with corresponding guards to determine the current substates. This leads to duplication of extra states introduced by exit actions. In this example, the exit action of S1 is shared by both paths to exit. We could encode this by introducing an extra state in the beginning of the exit action, such as  , and then the end of the encodings of the exit actions of S2 and S3 leads to
, and then the end of the encodings of the exit actions of S2 and S3 leads to  . To use this approach, however, the encoding of the transition t0 needs to take into account the internal structure of S0. This is neither straightforward nor compositional.
. To use this approach, however, the encoding of the transition t0 needs to take into account the internal structure of S0. This is neither straightforward nor compositional.
Instead, we use a staged approach, in which the encoding of a transition (like t0) triggers an exit request to its source state (S0), and waits for it to exit. It is the encoding of the source state that reflects its internal structure. For this example, the commands for S0 deal with an exit request, relay the request to its current substate S1, and wait for S1 to exit. The commands for S1 are similar. The commands for S2 deal with the exit request from S1, execute its exit action, and exit S2 using the approach in Fig. 23 because S2 is simple. Afterwards, the command for S1 that waits for S2 to exit becomes enabled. After it is taken, the encodings for its exit action are executed, and so exit S1. In a similar way, the encoding for S0 controls its exit.
To control this exit flow in PRISM, we introduce an extra exit variable for each composite state, and define the exit of a composite state in six stages:
-
EX-S1
it is not in an exit flow;
-
EX-S2
it gets an exit request either from a transition or from its parent;
-
EX-S3
it passes the exit request to its substates;
-
EX-S4
it waits for its substates to exit;
-
EX-S5
its substates have exited (at this point, its exit action is executed); and
-
EX-S6
it is exited (after execution of its exit action).
To illustrate our approach to translating state machines with composite states, we present in Fig. 25 the module for the normalised machine movingSTM in Fig. 17, lines  -
- . That module has two program counter variables: scpc and
. That module has two program counter variables: scpc and  , one lock variable lock, and two exit variables: exit and
, one lock variable lock, and two exit variables: exit and  .
.
The counter scpc encodes the current state of the machine, while  encodes the current state of the composite state Move. In the normalised machine movingSTM, we have one initial junction named i0 and three states (Move, Stuck, and loop). Four constants are declared for these states (lines
encodes the current state of the composite state Move. In the normalised machine movingSTM, we have one initial junction named i0 and three states (Move, Stuck, and loop). Four constants are declared for these states (lines  -
- ). Extra constants declared on lines
). Extra constants declared on lines  -
- are needed for the actions in transitions or states. Since Move is composite, there are additional nodes within it: one initial junction named i0 in PRISM, nine states s0 to s8, and nine probabilistic junctions named p0 to p8 in PRISM. A set of constants is declared to associate them with numbers, as illustrated in Fig. 26. We name these constants with a prefix
are needed for the actions in transitions or states. Since Move is composite, there are additional nodes within it: one initial junction named i0 in PRISM, nine states s0 to s8, and nine probabilistic junctions named p0 to p8 in PRISM. A set of constants is declared to associate them with numbers, as illustrated in Fig. 26. We name these constants with a prefix  (see lines
(see lines  -
- ). Like in the previous example, extra constants are also needed for the actions. Finally, we have a value,
). Like in the previous example, extra constants are also needed for the actions. Finally, we have a value,  , for the counter of Move, when this state is not active.
, for the counter of Move, when this state is not active.
The full state of the machine is given by the combination of both counter values. For example, if the state machine movingSTM is in the state Stuck, then scpc and  have values Stuck and
have values Stuck and  . If the machine is in the state s1, then scpc and
. If the machine is in the state s1, then scpc and  have values Move and
have values Move and  .
.
In addition to the states, we also number the transitions in movingSTM, as shown in Fig. 26, with associated constants on lines  -
- . We also name the transitions in Move with a prefix
. We also name the transitions in Move with a prefix  . Besides
. Besides  on line
on line  , these are all the possible values that the variable lock can take as shown on line
, these are all the possible values that the variable lock can take as shown on line  .
.
In addition, two exit variables exit and  are declared on lines
are declared on lines  and
and  . Both can take the values 0 to 6 of the constants:
. Both can take the values 0 to 6 of the constants:
-
 corresponds to EX-S1 above,
corresponds to EX-S1 above, -
 corresponds to EX-S2 for the request from the parent state, if any,
corresponds to EX-S2 for the request from the parent state, if any, -
 corresponds to EX-S2 for the request from a transition,
corresponds to EX-S2 for the request from a transition, -
 corresponds to EX-S3,
corresponds to EX-S3, -
 corresponds to EX-S4,
corresponds to EX-S4, -
 corresponds to EX-S5,
corresponds to EX-S5, -
 corresponds to EX-S6.
corresponds to EX-S6.
In the initial state of the module movingSTM, the values of the local variables scpc and  are
are  and
and  , which indicates the machine starts from its initial junction and the composite state Move is initially inactive. The initial value of lock is
, which indicates the machine starts from its initial junction and the composite state Move is initially inactive. The initial value of lock is  . The values of both exit variables are
. The values of both exit variables are  , so no states are being exited. In the initial state, the single transition encoded on line
, so no states are being exited. In the initial state, the single transition encoded on line  is available. So when the value of scpc is i0, it is changed to
is available. So when the value of scpc is i0, it is changed to  and the value of lock is changed to T0. Since the value of lock is not
and the value of lock is changed to T0. Since the value of lock is not  , other transitions in the module that correspond to the transitions from a state in the machine are not available because they have a guard condition
, other transitions in the module that correspond to the transitions from a state in the machine are not available because they have a guard condition  .
.
When scpc is  , the single transition encoded on line
, the single transition encoded on line  is taken. The update changes the value of p, the position of the robot, to 0, which is the effect of the transition action in RoboChart, and the values of scpc and
is taken. The update changes the value of p, the position of the robot, to 0, which is the effect of the transition action in RoboChart, and the values of scpc and  to Move and
to Move and  .
.
According to the normalised machine in Fig. 17, if the current state is Move and the battery level is 0 when the robot is not in the charging station, the transition  from Move to Stuck in Fig. 26 is enabled. The encoding of this transition is shown on line
from Move to Stuck in Fig. 26 is enabled. The encoding of this transition is shown on line  . When it is taken, the module is locked in T1 and the exit stage of Move is set to an exit request from a transition (
. When it is taken, the module is locked in T1 and the exit stage of Move is set to an exit request from a transition ( ) to source state Move. The command on line
) to source state Move. The command on line  waits for Move to exit and is enabled only if the module is locked in T1 and Move has been exited (
waits for Move to exit and is enabled only if the module is locked in T1 and Move has been exited ( ). When an exit request is recorded in
). When an exit request is recorded in  , the next available command is on lines
, the next available command is on lines  -
- . Since Move is composite, the update changes
. Since Move is composite, the update changes  to
to  to request its substates to exit first. Depending on the current state of Move, different commands are available. If the current state of Move is s0 (that is,
to request its substates to exit first. Depending on the current state of Move, different commands are available. If the current state of Move is s0 (that is,  is
is  ), the command on line
), the command on line  is enabled. Since s0 has no exit action, the update simply sets the exit procedure to the next stage: the substate of Move has been exited (
is enabled. Since s0 has no exit action, the update simply sets the exit procedure to the next stage: the substate of Move has been exited ( ). Similarly, if the current state of Move is s1, the command on line
). Similarly, if the current state of Move is s1, the command on line  is available. We omit similar commands for other states in Move.
is available. We omit similar commands for other states in Move.
After the substate is exited, the next available command is on line  . Since Move has no exit action, the update records that the exit procedure of Move finished (
. Since Move has no exit action, the update records that the exit procedure of Move finished ( ), and at the same time, the counter of Move becomes
), and at the same time, the counter of Move becomes  . Afterwards, the command on line
. Afterwards, the command on line  is available. The update changes the counter scpc to
is available. The update changes the counter scpc to  , which records the start state of the entry action of Stuck. The next command on line
, which records the start state of the entry action of Stuck. The next command on line  encodes the effect of the entry action (p is set to 9), the entering of the target state (the counter is at Stuck), and the completion of the transition
encodes the effect of the entry action (p is set to 9), the entering of the target state (the counter is at Stuck), and the completion of the transition  (the lock becomes
(the lock becomes  ).
).
Other transitions are encoded in a similar way, and therefore omitted in Fig. 25.
In Figs. 20, 23 and 25, we illustrate the encodings of transitions from initial junctions, states, and probabilistic junctions that have one single outgoing transition. We illustrate our approach when there are multiple transitions in Fig. 27, where we present the encodings of the incoming and outgoing transitions of the probabilistic junction  in Fig. 26.
in Fig. 26.
The junction  is a node in the state Move with one incoming transition
is a node in the state Move with one incoming transition  from the state s1, and three outgoing transitions to the states s1, s2, and s4. Each of these outgoing transitions has an action that requires two extra states (because they are sequences of two basic actions). Along with the state for
from the state s1, and three outgoing transitions to the states s1, s2, and s4. Each of these outgoing transitions has an action that requires two extra states (because they are sequences of two basic actions). Along with the state for  , there are seven states represented by the constants on lines
, there are seven states represented by the constants on lines  -
- .
.
The command on lines  -
- encodes the transition from s1 to
encodes the transition from s1 to  . The command on lines
. The command on lines  -
- encodes the probabilistic choice and has three updates with equal probability
encodes the probabilistic choice and has three updates with equal probability  . Each update changes the counter of Move (
. Each update changes the counter of Move ( ) to a state representing the start of one of the outgoing transition action. For example, the assignment in the first update changes
) to a state representing the start of one of the outgoing transition action. For example, the assignment in the first update changes  to
to  , which represents the start of the action of the transition from
, which represents the start of the action of the transition from  to s2 and is also annotated in Fig. 26. The commands on lines
to s2 and is also annotated in Fig. 26. The commands on lines  -
- ,
,  -
- , and
, and  -
- are the encodings of the three transition actions in PRISM. In the end of each transition action, the counter is set to an extra state representing the start of the entry action of the target state, such as
are the encodings of the three transition actions in PRISM. In the end of each transition action, the counter is set to an extra state representing the start of the entry action of the target state, such as  for s1. The entry action of s1 is encoded by the command on line
for s1. The entry action of s1 is encoded by the command on line  .
.
Next, we present the normalisation rules.
5.3 Normalisation rules
In terms of model transformations, normalisation is characterised as a rule-based, homogeneous, and declarative transformation. We present here a set of functions from a RoboChart model that satisfies our translation requirements to a RoboChart model in normal form. These functions are defined via rules.
To normalise a RoboChart model, we apply Rule 1 to each state machine. This is the rule applied exhaustively to all state machines in the normalisation process discussed previously. In the definition of all rules, we use the constructs from Z [70, 72] as a meta-notation. Their syntax is summarised in Table 3.
Generally, a rule characterises a function on elements of the RoboChart metamodel. A rule definition is composed of a declaration, a body, and a  clause. The declaration gives the function name, its parameters (names and types), and its return type. In Rule 1, the function is
clause. The declaration gives the function name, its parameters (names and types), and its return type. In Rule 1, the function is  . It has one parameter
. It has one parameter  of type
of type  , that is, a state machine, and also returns a state machine: an element of the same type.
, that is, a state machine, and also returns a state machine: an element of the same type.
The body of a rule defines an object of the return type. For example, the body of Rule 1 is an object of the class StateMachineDef of the metamodel.
The variables used in the body may be parameters or may be defined in the  clause. The order of these definitions is not relevant.
clause. The order of these definitions is not relevant.
The body of Rule 1 defines a state machine whose name, variable list, operations, events, and interfaces are the same as those of the parameter  . The nodes and transitions, however, are different and are specified using the definitions from the
. The nodes and transitions, however, are different and are specified using the definitions from the  clause. The first four definitions are related to the four steps of the state machine normalisation process presented above.
clause. The first four definitions are related to the four steps of the state machine normalisation process presented above.
-
 is a pair characterised by applying
is a pair characterised by applying  to
to  (see Rule 9 in “Appendix A”). This function is concerned with the possible need to introduce loop states. The result of
(see Rule 9 in “Appendix A”). This function is concerned with the possible need to introduce loop states. The result of  is a pair, whose first element
is a pair, whose first element  is a set either empty or containing a new loop state for
is a set either empty or containing a new loop state for  , and whose second element
, and whose second element  is a set of the new transitions to and from loop.
is a set of the new transitions to and from loop. -
 is a triple of sets: a set of junctions, and two sets of transitions defined by an application of the function
is a triple of sets: a set of junctions, and two sets of transitions defined by an application of the function  . This function is concerned with the combination of incoming and outgoing transitions of normal junctions, if needed. The first argument of the application is a set of normal junctions, characterised by a function
. This function is concerned with the combination of incoming and outgoing transitions of normal junctions, if needed. The first argument of the application is a set of normal junctions, characterised by a function  (see Rule 10 in “Appendix A”). These are the normal junctions that have incoming and outgoing transitions that need to be combined. The second argument of the application is the set of transitions of
(see Rule 10 in “Appendix A”). These are the normal junctions that have incoming and outgoing transitions that need to be combined. The second argument of the application is the set of transitions of  that are to or from junctions in the first argument; this is characterised by a generalised union of a relational image. The function application
that are to or from junctions in the first argument; this is characterised by a generalised union of a relational image. The function application  identifies the set of incoming and outgoing transitions of a given node
identifies the set of incoming and outgoing transitions of a given node  that are in the set of transitions
that are in the set of transitions  . So the relational image of
. So the relational image of  under
under  is the set of sets of all incoming and outgoing transitions of the normal junctions. A generalised union
is the set of sets of all incoming and outgoing transitions of the normal junctions. A generalised union  combines all these sets. The first and seconds elements
combines all these sets. The first and seconds elements  and
and  of the result of the application of
of the result of the application of  contain the junctions in the first argument and the transitions in the second argument removed by normalisation, and the third element
contain the junctions in the first argument and the transitions in the second argument removed by normalisation, and the third element  contains the new transitions arising from the normalisation.
contains the new transitions arising from the normalisation. -
 is a set of pairs defined by applying
is a set of pairs defined by applying  (Rule 13 in “Appendix A”) to each transition in
(Rule 13 in “Appendix A”) to each transition in  (
( ), to the new transitions identified by
), to the new transitions identified by  (that is, in
(that is, in  ), and to the transitions from the new loop states (identified by
), and to the transitions from the new loop states (identified by  ), but not to the transitions removed by the normalisation (that is, in
), but not to the transitions removed by the normalisation (that is, in  ).
). -
 is a set of normalised composite states resulting from the application of a normalisation function
is a set of normalised composite states resulting from the application of a normalisation function  for states to each node
for states to each node  of the machine that is a state (
of the machine that is a state ( ) and has nodes itself (
) and has nodes itself ( ). These are the composite states. Normalisation of composite states by
). These are the composite states. Normalisation of composite states by  is similar to that of state machines except that composite states do not declare variables, operations, and events. So the formalisation is simpler and omitted here; it can be found in the RoboChart reference manual [1].
is similar to that of state machines except that composite states do not declare variables, operations, and events. So the formalisation is simpler and omitted here; it can be found in the RoboChart reference manual [1]. -
 is the set of nodes
is the set of nodes  of
of  that are neither the normal junctions removed by the normalisation in
that are neither the normal junctions removed by the normalisation in  (that is,
(that is,  ) nor composite states. They are unaffected by normalisation.
) nor composite states. They are unaffected by normalisation.
The nodes of the normalised machine, as defined in the body of Rule 1, include the loop states in  , the new probabilistic junctions in the second element of each pair in
, the new probabilistic junctions in the second element of each pair in  (obtained using generalised union \(\bigcup \)), the normalised composite states, and all other nodes as identified in
(obtained using generalised union \(\bigcup \)), the normalised composite states, and all other nodes as identified in  . The transitions of the normalised machine are just those in the first element of each pair in
. The transitions of the normalised machine are just those in the first element of each pair in  .
.
Next, we present the second stage of translation from a RoboChart model in normal form to PRISM.
5.4 Transformation to PRISM
In this section, we present the translation rules used in our approach in Sects. 5.4.1 to 5.4.4.

5.4.1 Module, robotic platform, and controllers

The main translation function  (defined in Rule 2) is for a RoboChart module. It has a parameter
(defined in Rule 2) is for a RoboChart module. It has a parameter  of type Module, and characterises a PRISM model of type Model constructed from
of type Module, and characterises a PRISM model of type Model constructed from  , global variables
, global variables  , and
, and  from the translation of the controllers and the robotic platform of
from the translation of the controllers and the robotic platform of  .
.
In this section, we use the following conventions for function definitions in rules: the types of the arguments are assumed to be classes of the RoboChart metamodel and the types of the results are assumed to be classes of the PRISM metamodel if no subscripts are specified. For example, the type of  in the definition of the function
in the definition of the function  ,
,  , is the class in the RoboChart. Particularly, if a class in the PRISM metamodel is used as a type for arguments, or a class in the RoboChart metamodel is used as a type for results, we use an explicit subscript to indicate it.
, is the class in the RoboChart. Particularly, if a class in the PRISM metamodel is used as a type for arguments, or a class in the RoboChart metamodel is used as a type for results, we use an explicit subscript to indicate it.
The result of the translation of the controllers is recorded in a set of quadruples  , while that of the robotic platform is in a triple
, while that of the robotic platform is in a triple  . Each quadruple in
. Each quadruple in  records information about the translation of a controller. The first element of each quadruple
records information about the translation of a controller. The first element of each quadruple  in
in  ,
,  , is a set of constants resulting from the translation of a controller. So the constants for the all controllers of
, is a set of constants resulting from the translation of a controller. So the constants for the all controllers of  are combined using generalised union
are combined using generalised union  and contributed to
and contributed to  . The second and third elements of
. The second and third elements of  ,
,  and
and  , are sets of global variables and modules. They are combined using generalised union and contributed to
, are sets of global variables and modules. They are combined using generalised union and contributed to  and
and  . Accordingly,
. Accordingly,  ,
,  , and
, and  are a set of constants, a set of variables, and a module, contributed to
are a set of constants, a set of variables, and a module, contributed to  ,
,  , and
, and  .
.
Additionally, a set of constants  is used to specify the control flow of execution of a state machine with composite states; in particular, the constants are useful to define the flow when exiting a composite state. This is discussed later on in Sect. 5.4.2.
is used to specify the control flow of execution of a state machine with composite states; in particular, the constants are useful to define the flow when exiting a composite state. This is discussed later on in Sect. 5.4.2.
The variables  ,
,  ,
,  ,
,  , and
, and  are defined in the
are defined in the  clause of Rule 2.
clause of Rule 2.
-
 is a set of quadruples: sets of constants, variables, and modules, and a relation defined by an application of
is a set of quadruples: sets of constants, variables, and modules, and a relation defined by an application of  (Rule 4) to a controller in the set
(Rule 4) to a controller in the set  of nodes of
of nodes of  . The relation establishes a mapping from operations provided by the platform and required by the controller, to PRISM actions corresponding to these operations.
. The relation establishes a mapping from operations provided by the platform and required by the controller, to PRISM actions corresponding to these operations. -
 is used in the translation of the robotic platform. It is the set of events of the robotic platform used to communicate data to a controller. These are the events
is used in the translation of the robotic platform. It is the set of events of the robotic platform used to communicate data to a controller. These are the events  that are the source of a connection
that are the source of a connection  in the set
in the set  of connections of
of connections of  whose source
whose source  is a platform and whose type
is a platform and whose type  is not
is not  . So, data (of type
. So, data (of type  ) is communicated.
) is communicated. -
 is a triple: a set of constants, a set of variables, and a module defined by an application of
is a triple: a set of constants, a set of variables, and a module defined by an application of  (Rule 3) for robotic platforms. This function is applied to the platform of
(Rule 3) for robotic platforms. This function is applied to the platform of  , identified by a unique (
, identified by a unique ( ) node
) node  that is in the set
that is in the set  of nodes of
of nodes of  and is a robotic platform. Extra arguments are the set of events
and is a robotic platform. Extra arguments are the set of events  and the relation from the translation of controllers, formed by generalised union of the relation
and the relation from the translation of controllers, formed by generalised union of the relation  for each controller. As said, the events used to send data to a controller are represented by a shared variable in the platform module. (Its value is nondeterministically chosen and copied in modules for state machines upon synchronisation.) So, the definition of the module for a platform requires the identification of these events, which are in the set
for each controller. As said, the events used to send data to a controller are represented by a shared variable in the platform module. (Its value is nondeterministically chosen and copied in modules for state machines upon synchronisation.) So, the definition of the module for a platform requires the identification of these events, which are in the set  . The relation identifies how the translation of the controllers (or, more specifically, of their state machines) have mapped their required operations to PRISM actions. The module for the platform synchronises on these actions.
. The relation identifies how the translation of the controllers (or, more specifically, of their state machines) have mapped their required operations to PRISM actions. The module for the platform synchronises on these actions. -
 is a set of constants resulting from the function
is a set of constants resulting from the function  , omitted here.
, omitted here.
In Fig. 19, the result of the translation of the unique controller of our example gives rise to the declaration of NoTask in the  section and all
section and all  except
except  . The declarations of two constants and two global variables in the
. The declarations of two constants and two global variables in the  and
and  sections and the module deliverRP are the result of the translation of the robotic platform. The constant NoTask is the result of the translation of the enumerated type FD in Fig. 4. More constants result from the translation of the controller, but are omitted in Fig. 19. The details are presented in Sects. 5.4.2 and 5.4.3.
sections and the module deliverRP are the result of the translation of the robotic platform. The constant NoTask is the result of the translation of the enumerated type FD in Fig. 4. More constants result from the translation of the controller, but are omitted in Fig. 19. The details are presented in Sects. 5.4.2 and 5.4.3.
Figure 19 gives the module for deliverRP, and corresponding constants and global variables provided by it. As shown in Fig. 2, deliverRP provides two constants and two variables. Their counterparts in PRISM are two constants and two global variables, shown on lines  -
- , of type int. The platform has two output events request and dest as identified from connections in deliverMOD in Fig. 2. Both events are of type nat, natural numbers. For each output event, we add an extra local variable of a corresponding type, such as EVT__request (on line
, of type int. The platform has two output events request and dest as identified from connections in deliverMOD in Fig. 2. Both events are of type nat, natural numbers. For each output event, we add an extra local variable of a corresponding type, such as EVT__request (on line  in Fig. 19) for request, and a set of commands with a corresponding action for the event name such as the commands indicated on lines
in Fig. 19) for request, and a set of commands with a corresponding action for the event name such as the commands indicated on lines  -
- , to the module. Together, the commands characterise a nondeterministic choice of the value of the variable. Other events used for output are handled in a similar way.
, to the module. Together, the commands characterise a nondeterministic choice of the value of the variable. Other events used for output are handled in a similar way.

As mentioned,  defines a module like deliverRP; it has three parameters: a robotic platform
defines a module like deliverRP; it has three parameters: a robotic platform  , a set
, a set  of events of
of events of  used for output, and a relation
used for output, and a relation  that maps operations provided by
that maps operations provided by  to PRISM actions. In Rule 3, we note the type of
to PRISM actions. In Rule 3, we note the type of  is
is  , not
, not  used in Rule 2. The class RoboticPlatform is inherited by both RoboticPlatformDef and RoboticPlatformRef. So the robotic platform identified in Rule 2 is either a RoboticPlatformDef or a RoboticPlatformRef object. For a RoboticPlatformRef
used in Rule 2. The class RoboticPlatform is inherited by both RoboticPlatformDef and RoboticPlatformRef. So the robotic platform identified in Rule 2 is either a RoboticPlatformDef or a RoboticPlatformRef object. For a RoboticPlatformRef  , another rule specifies its result just as the function application
, another rule specifies its result just as the function application  (the unique identifiers defined by
(the unique identifiers defined by  - see Table 3 - take references into account). Rules for ControllerRef and StateMachineRef are similar and omitted here.
- see Table 3 - take references into account). Rules for ControllerRef and StateMachineRef are similar and omitted here.
The result of  is a triple, whose first and second elements are a set of constants (
is a triple, whose first and second elements are a set of constants ( where
where  is a pair of sets of constants and variables) and a set of variables (
is a pair of sets of constants and variables) and a set of variables ( ) defined by the constants and variables
) defined by the constants and variables  (a set of pairs) provided by
(a set of pairs) provided by  , and whose third element is the PRISM
, and whose third element is the PRISM  corresponding to
corresponding to  . The variables
. The variables  and
and  are defined in the
are defined in the  clause of Rule 3 and described below.
clause of Rule 3 and described below.
-
 is a set of pairs of sets. The first and second elements of each pair are a set of constants and a set of variables, translated from each variable list
is a set of pairs of sets. The first and second elements of each pair are a set of constants and a set of variables, translated from each variable list  in
in  by the function
by the function  (omitted here). The lists of variables provided by
(omitted here). The lists of variables provided by  are identified using the function
are identified using the function  whose definition is omitted here. A variable list consists of a set of constant and variable declarations. The translation of variable declarations maps the RoboChart types to the PRISM types, and translates the initial value given, if any, accordingly.
whose definition is omitted here. A variable list consists of a set of constant and variable declarations. The translation of variable declarations maps the RoboChart types to the PRISM types, and translates the initial value given, if any, accordingly. -
 is a set of PRISM declarations of variables like EVT__request corresponding to the events
is a set of PRISM declarations of variables like EVT__request corresponding to the events  from
from  . In the rules, we use black typewriter font, like in \(\texttt {{true}}\), for PRISM terms. They are abbreviations for instances of the classes of the PRISM metamodel presented in Sect. 4.2. For clarity, however, we use the PRISM concrete syntax to represent them. Each declaration in
. In the rules, we use black typewriter font, like in \(\texttt {{true}}\), for PRISM terms. They are abbreviations for instances of the classes of the PRISM metamodel presented in Sect. 4.2. For clarity, however, we use the PRISM concrete syntax to represent them. Each declaration in  is for a variable, whose name is based on the name of
is for a variable, whose name is based on the name of  in PRISM (
in PRISM ( ) with a prefix (\(\texttt {{EVT\_\_}}\)), and whose type
) with a prefix (\(\texttt {{EVT\_\_}}\)), and whose type  is obtained by translating the type
is obtained by translating the type  of
of  using
using  .
. -
 is a set of sets of commands for each event
is a set of sets of commands for each event  of
of  , that are identified using the function
, that are identified using the function  whose definition is omitted here. If
whose definition is omitted here. If  is an output event (that is,
is an output event (that is,  ), a set of commands is included in
), a set of commands is included in  to define a nondeterministic choice of the values for the corresponding variable
to define a nondeterministic choice of the values for the corresponding variable  . Each command corresponds to one possible value
. Each command corresponds to one possible value  in the event type
in the event type  . The action of the command (inside square brackets) is the name
. The action of the command (inside square brackets) is the name  of the event
of the event  , the guard is \(\texttt {{true}}\), and the only update (between \({\rightarrow }\) and \(\texttt {{;}}\)) assigns
, the guard is \(\texttt {{true}}\), and the only update (between \({\rightarrow }\) and \(\texttt {{;}}\)) assigns  to
to  . The commands on lines
. The commands on lines  -
- in Fig. 19 are obtained in this way. If
in Fig. 19 are obtained in this way. If  is not an event for output, a set containing one command is included in
is not an event for output, a set containing one command is included in  . It has
. It has  for its action and \(\texttt {{true}}\) for both its guard and its updates, which means the command is always ready for synchronisation on the action and no variable is changed upon synchronisation. The command on line
for its action and \(\texttt {{true}}\) for both its guard and its updates, which means the command is always ready for synchronisation on the action and no variable is changed upon synchronisation. The command on line  is obtained in this way.
is obtained in this way. -
 is a set of PRISM commands. Each command corresponds to one PRISM action
is a set of PRISM commands. Each command corresponds to one PRISM action  in the range
in the range  of the relation
of the relation  . As previously mentioned,
. As previously mentioned,  records a mapping from operations provided by the robotic platform (and possibly called in state machines) to PRISM actions corresponding to these operations. We use this relation to translate calls to the operations in state machines into communications with the environment (modelled by the module for the robotic platform) that provides the operations. Our PRISM models, as explained in Sect. 4, rely on the name of actions for synchronisation. This imposes extra challenges on modelling of operations in PRISM because the calls to a same operation from different state machines must not be synchronised. We consider, for instance, an example in which an operation moveSteps with a parameter of type int is provided by the robotic platform, and required and called using an action moveSteps(1) in a state machine stm1 and moveStep(2) in another state machine stm2. The operation calls are translated to communications in PRISM through synchronisation on actions with assistance of variables. If two calls were mapped into an action of the same name such as moveSteps_act, then both state machines and the robotic platform would synchronise on this action, which is not the right semantics of operation calls. For this reason, we allocate a unique action name for an operation in each state machine, such as stm1_moveSteps_act for stm1 and stm2_moveSteps_act for stm2. So in the platform, an operation is mapped to several actions: one for each machine that requires the operation. For this example,
records a mapping from operations provided by the robotic platform (and possibly called in state machines) to PRISM actions corresponding to these operations. We use this relation to translate calls to the operations in state machines into communications with the environment (modelled by the module for the robotic platform) that provides the operations. Our PRISM models, as explained in Sect. 4, rely on the name of actions for synchronisation. This imposes extra challenges on modelling of operations in PRISM because the calls to a same operation from different state machines must not be synchronised. We consider, for instance, an example in which an operation moveSteps with a parameter of type int is provided by the robotic platform, and required and called using an action moveSteps(1) in a state machine stm1 and moveStep(2) in another state machine stm2. The operation calls are translated to communications in PRISM through synchronisation on actions with assistance of variables. If two calls were mapped into an action of the same name such as moveSteps_act, then both state machines and the robotic platform would synchronise on this action, which is not the right semantics of operation calls. For this reason, we allocate a unique action name for an operation in each state machine, such as stm1_moveSteps_act for stm1 and stm2_moveSteps_act for stm2. So in the platform, an operation is mapped to several actions: one for each machine that requires the operation. For this example,  is given below. $$\begin{aligned} \quad \left\{ \begin{array}{lll} \left( moveSteps, {stm1\_moveSteps\_act}\right) , \\ \left( moveSteps, {stm2\_moveSteps\_act}\right) \end{array} \right\} \end{aligned}$$(1)
is given below. $$\begin{aligned} \quad \left\{ \begin{array}{lll} \left( moveSteps, {stm1\_moveSteps\_act}\right) , \\ \left( moveSteps, {stm2\_moveSteps\_act}\right) \end{array} \right\} \end{aligned}$$(1)Since the mapping is established in the state machines, the relation is a result of the translation of controllers (which involves translating their machines) and passed to
 . For each action
. For each action  in the range of
in the range of  (for our example, \(\left\{ stm1\_moveSteps\_act, stm2\_moveSteps\_act \right\} \)), one command, whose action is
(for our example, \(\left\{ stm1\_moveSteps\_act, stm2\_moveSteps\_act \right\} \)), one command, whose action is  , is included in
, is included in  . This command in the platform module synchronises with the commands in a machine module whose action is also
. This command in the platform module synchronises with the commands in a machine module whose action is also  , to allow the environment to record the calls to the operation. The arguments of these calls are recorded in local variables of the machine modules. The details of the declaration and use of these variables are presented in Rule 5. Both the guard and the updates of the command are \(\texttt {{true}}\), so the platform module cannot refuse synchronisation on
, to allow the environment to record the calls to the operation. The arguments of these calls are recorded in local variables of the machine modules. The details of the declaration and use of these variables are presented in Rule 5. Both the guard and the updates of the command are \(\texttt {{true}}\), so the platform module cannot refuse synchronisation on  and no variable is changed upon synchronisation. For our example,
and no variable is changed upon synchronisation. For our example,  contains the commands in Fig. 28. They allow the platform module to record the call to moveSteps from both stm1 and stm2, though in different actions.
contains the commands in Fig. 28. They allow the platform module to record the call to moveSteps from both stm1 and stm2, though in different actions. -
 is a PRISM module with the name
is a PRISM module with the name  of
of  ,
,  , and commands obtained by the generalised union of the commands in
, and commands obtained by the generalised union of the commands in  and
and  .
.

The modules in Fig. 19 other than  are defined by the function
are defined by the function  for a controller
for a controller  Rule 4. The result is a quadruple: a set of constant declarations, a set of variable declarations, a set of modules, and a relation from the operations provided by the platform and required by the machines in the controller to corresponding PRISM actions. For the moveSteps example, if both stm1 and stm2 are in
Rule 4. The result is a quadruple: a set of constant declarations, a set of variable declarations, a set of modules, and a relation from the operations provided by the platform and required by the machines in the controller to corresponding PRISM actions. For the moveSteps example, if both stm1 and stm2 are in  , then the resulting relation is the one shown in (1). Analogous to Rule 3, we define
, then the resulting relation is the one shown in (1). Analogous to Rule 3, we define  in the
in the  clause to record the constants and variables provided by
clause to record the constants and variables provided by  .
.
The results of the translation of all state machines of  are recorded in a set of pairs
are recorded in a set of pairs  , also defined in the
, also defined in the  clause. Each pair corresponds to one state machine and includes a set of constants and a module. The constants in these pairs are combined using generalised union and are also contributed to the result of
clause. Each pair corresponds to one state machine and includes a set of constants and a module. The constants in these pairs are combined using generalised union and are also contributed to the result of  . Additionally, the relation is recorded in
. Additionally, the relation is recorded in  .
.
Each pair in  is the result of the translation of one state machine
is the result of the translation of one state machine  in the set of machines
in the set of machines  of
of  by the function
by the function  (Rule 5), as defined in the
(Rule 5), as defined in the  clause. The function application takes two arguments: the state machine
clause. The function application takes two arguments: the state machine  and a set
and a set  of events of
of events of  used for output. The set
used for output. The set  includes events of the state machine used to communicate data to the controller or to another state machine in the controller. These are the events
includes events of the state machine used to communicate data to the controller or to another state machine in the controller. These are the events  that are the source of a connection
that are the source of a connection  in the set
in the set  of connections of
of connections of  whose source
whose source  is
is  and whose type
and whose type  is not
is not  . So data (of type
. So data (of type  ) is communicated. These events are used in the definition of
) is communicated. These events are used in the definition of  to identify variables that need to be included in the module for
to identify variables that need to be included in the module for  to assist communications. We consider, for instance, a state machine stm1 with one event out used for output. So
to assist communications. We consider, for instance, a state machine stm1 with one event out used for output. So  , in this case, has one element out. The module for stm1, translated by
, in this case, has one element out. The module for stm1, translated by  , therefore has a local variable \(\texttt {{EVT\_\_out}}\) of the same type as out for the purpose of communications.
, therefore has a local variable \(\texttt {{EVT\_\_out}}\) of the same type as out for the purpose of communications.
The relation  is also defined in the
is also defined in the  clause. It is the result of combining the relations established for state machines by the function
clause. It is the result of combining the relations established for state machines by the function  (Rule 14 in “Appendix A”), using generalised union. The function
(Rule 14 in “Appendix A”), using generalised union. The function  takes one argument: a state machine
takes one argument: a state machine  in the set of machines
in the set of machines  of
of  .
.
Next, we describe how to translate state machines.
5.4.2 State machines and composite states
Here, we present the rule that can be used to translate a RoboChart state machine to PRISM.

Each machine module in Fig. 19, such as taskSTM and movingSTM in Figs. 20 and 25, is defined by the function  in Rule 5. As mentioned previously, this function is concerned with the translation of a state machine
in Rule 5. As mentioned previously, this function is concerned with the translation of a state machine  , having a set
, having a set  of events of
of events of  used for output as an extra parameter. Its result is a pair: a set of constants and a module.
used for output as an extra parameter. Its result is a pair: a set of constants and a module.
Analogous to Rule 3, we define  as a set of pairs to record the constants and variables required by or defined in
as a set of pairs to record the constants and variables required by or defined in  . The first element
. The first element  of each pair
of each pair  in
in  is a set of constant declarations and the second element
is a set of constant declarations and the second element  is a set of variable declarations. Generalised union
is a set of variable declarations. Generalised union  combines all these sets. A constant, named
combines all these sets. A constant, named  , such as
, such as  on line
on line  in Fig. 20, is associated with 0 and results from the translation of
in Fig. 20, is associated with 0 and results from the translation of  . Rule 5 uses
. Rule 5 uses  as a prefix for the constant or variable names to ensure unicity. Other constants, such as those on lines
as a prefix for the constant or variable names to ensure unicity. Other constants, such as those on lines  -
- , for the values that lock can take, and on lines
, for the values that lock can take, and on lines  -
- , for the states in taskSTM, are recorded in
, for the states in taskSTM, are recorded in  .
.
The machine module is named  and contains variable declarations and commands. The variables include lock, whose type is an interval with upper limit
and contains variable declarations and commands. The variables include lock, whose type is an interval with upper limit  , such as that on line
, such as that on line  in Fig. 20; the local variables of
in Fig. 20; the local variables of  , like fd and g on lines
, like fd and g on lines  -
- , as recorded in the second element
, as recorded in the second element  of pairs
of pairs  in
in  , and combined using generalised union; the variables to encode communication through the events in
, and combined using generalised union; the variables to encode communication through the events in  , in
, in  ; the scpc and exit variables, like those on lines
; the scpc and exit variables, like those on lines  -
- in Fig. 25, as recorded in
in Fig. 25, as recorded in  ; and the variables to encode the arguments of calls to the operations required by
; and the variables to encode the arguments of calls to the operations required by  , in
, in  . The set of commands is recorded in
. The set of commands is recorded in  .
.
The  clause in the rule gives more details.
clause in the rule gives more details.
-
 is a set of PRISM declarations of variables (similar to EVT__request for the robotic platform) corresponding to the events
is a set of PRISM declarations of variables (similar to EVT__request for the robotic platform) corresponding to the events  from
from  . Each declaration in
. Each declaration in  is for a variable whose name is based on the name of
is for a variable whose name is based on the name of  in PRISM (
in PRISM ( ) with a prefix (\(\texttt {{EVT\_\_}}\)), and whose type
) with a prefix (\(\texttt {{EVT\_\_}}\)), and whose type  is obtained by translating the type
is obtained by translating the type  of
of  using the function
using the function  .
. -
 is a quadruple of an integer, and sets of constants, variables, and commands, resulting from the application of
is a quadruple of an integer, and sets of constants, variables, and commands, resulting from the application of  (Rule 6) to
(Rule 6) to  to translate its nodes and transitions. This function is concerned with the translation of a NodeContainer (a state machine or composite state) given as its first argument, with the machine that owns the NodeContainer as its second argument. An extra third argument is a set of boolean expressions that records the containers for the node and defines the guard for the commands that encode the node. The guard is the conjunction of these expressions, which are equalities involving the counter variables that, together, indicate that the control flow has reached the node. For example, to translate Move in movingSTM using this function, the right argument is
to translate its nodes and transitions. This function is concerned with the translation of a NodeContainer (a state machine or composite state) given as its first argument, with the machine that owns the NodeContainer as its second argument. An extra third argument is a set of boolean expressions that records the containers for the node and defines the guard for the commands that encode the node. The guard is the conjunction of these expressions, which are equalities involving the counter variables that, together, indicate that the control flow has reached the node. For example, to translate Move in movingSTM using this function, the right argument is  to indicate the control flow has reached Move. If Move has another composite substate S, then the right argument to translate S is
to indicate the control flow has reached Move. If Move has another composite substate S, then the right argument to translate S is  to indicate the control flow has reached both Move and S. The corresponding guard is \( \texttt {{scpc=Move \& Move\_scpc=}}\) \(\texttt {{Move\_S}}\), the conjunction of both expressions. A final argument for
to indicate the control flow has reached both Move and S. The corresponding guard is \( \texttt {{scpc=Move \& Move\_scpc=}}\) \(\texttt {{Move\_S}}\), the conjunction of both expressions. A final argument for  indicates the first integer not yet used to declare a constant for a lock value. In Rule 5,
indicates the first integer not yet used to declare a constant for a lock value. In Rule 5,  is applied to the whole machine
is applied to the whole machine  , which, by convention, is owned by itself. The third argument is just
, which, by convention, is owned by itself. The third argument is just  , because the control flow is always in the machine. Finally, the final argument indicates that declarations of lock variables can use integers from
, because the control flow is always in the machine. Finally, the final argument indicates that declarations of lock variables can use integers from  . (We recall that
. (We recall that  is used for the \(\texttt {{LOCK\_FREE}}\) constant.) As a result of this function application,
is used for the \(\texttt {{LOCK\_FREE}}\) constant.) As a result of this function application,  is the next available number that can be used to number a transition. So the maximum transition number is
is the next available number that can be used to number a transition. So the maximum transition number is  , which is used for the upper limit of the interval type of the lock variable. For the taskSTM module in Fig. 20, the next available transition number is 6 because the numbers 1 to 5 are used in the declarations on lines
, which is used for the upper limit of the interval type of the lock variable. For the taskSTM module in Fig. 20, the next available transition number is 6 because the numbers 1 to 5 are used in the declarations on lines  -
- . The second and third elements identify sets of constant and variable declarations, like those on lines
. The second and third elements identify sets of constant and variable declarations, like those on lines  -
- and the scpc declaration on line
and the scpc declaration on line  . These are the constants and variables used in the encoding of the control flow of the node. The fourth element is the set of all commands in the module.
. These are the constants and variables used in the encoding of the control flow of the node. The fourth element is the set of all commands in the module. -
 is a set of variable declarations for each parameter
is a set of variable declarations for each parameter  of an operation
of an operation  required by
required by  . The variable has a fresh name
. The variable has a fresh name  and is of type
and is of type  obtained by translating the type
obtained by translating the type  of
of  using the function
using the function  . For the operation moveSteps with parameter steps of type int, the value of
. For the operation moveSteps with parameter steps of type int, the value of  is
is  .
.

In Rule 6, the parameters for  are a NodeContainer
are a NodeContainer  , the state machine
, the state machine  containing
containing  , a set of PRISM expressions
, a set of PRISM expressions  recording constraints on the program counters, and the next number
recording constraints on the program counters, and the next number  that can be used to define a constant for a transition.
that can be used to define a constant for a transition.
As illustrated in Fig. 25, the translation of a NodeContainer  such as Move introduces a) one program counter variable and one exit variable; b) the encoding for exiting
such as Move introduces a) one program counter variable and one exit variable; b) the encoding for exiting  , such as the commands on lines
, such as the commands on lines  -
- ; c) the encoding for exiting the substates of
; c) the encoding for exiting the substates of  , such as the commands on lines
, such as the commands on lines  -
- ,
,  , and
, and  ; d) the encoding for entering the substates of
; d) the encoding for entering the substates of  that have entry actions, such as the command on line
that have entry actions, such as the command on line  ; e) the encoding for the transitions of
; e) the encoding for the transitions of  , such as the commands on lines
, such as the commands on lines  ; and f) the encoding for the composite substates of
; and f) the encoding for the composite substates of  . There may also be constant declarations, such as those on lines
. There may also be constant declarations, such as those on lines  -
- .
.
In the definition of  , the declarations of the program counter and the exit variable are recorded in
, the declarations of the program counter and the exit variable are recorded in  and
and  . The encoding for exiting
. The encoding for exiting  , and exiting and entering the substates of
, and exiting and entering the substates of  are recorded in triples
are recorded in triples 
 ,
, 
 , and
, and 
 . The first element of each of these triples is the next available number for the states of the resulting module, such as the numbers associated with the states on lines
. The first element of each of these triples is the next available number for the states of the resulting module, such as the numbers associated with the states on lines  -
- in Fig. 25. The second element is a set of constants associated with the states introduced. The third element is a set of commands. The translation of the transitions in
in Fig. 25. The second element is a set of constants associated with the states introduced. The third element is a set of commands. The translation of the transitions in  is recorded in a quadruple
is recorded in a quadruple  . Finally, the encodings for the composite substates of
. Finally, the encodings for the composite substates of  are, as defined by recursion, recorded in a quadruple
are, as defined by recursion, recorded in a quadruple  .
.
The result of  is a quadruple, whose first element is the next available transition number after the translation of
is a quadruple, whose first element is the next available transition number after the translation of  and recorded in
and recorded in  . The second element of the quadruple is a set of constant declarations including the constant
. The second element of the quadruple is a set of constant declarations including the constant  denoting an inactive state, such as the one on line
denoting an inactive state, such as the one on line  in Fig. 25, the constants in
in Fig. 25, the constants in  ,
,  ,
,  ,
,  , and
, and  , and the constants in
, and the constants in  . The third element of the quadruple is a set of variable declarations including
. The third element of the quadruple is a set of variable declarations including  ,
,  , and the variable declarations in the third element of
, and the variable declarations in the third element of  . The fourth element of the quadruple is a set of commands including the commands in
. The fourth element of the quadruple is a set of commands including the commands in  ,
,  ,
,  ,
,  and
and  .
.
The  clause in Rule 6 gives more details about the variables in these definitions.
clause in Rule 6 gives more details about the variables in these definitions.
-
 declares a PRISM constant associated with number 0 and representing the inactive status of
declares a PRISM constant associated with number 0 and representing the inactive status of  .
. -
 declares the program counter variable for
declares the program counter variable for  ; its type is a range from 0 to the maximum state number (that is,
; its type is a range from 0 to the maximum state number (that is,  ). If
). If  is a machine, the counter is set to a state in PRISM corresponding to the initial junction
is a machine, the counter is set to a state in PRISM corresponding to the initial junction  (that is, a node
(that is, a node  of
of  that is initial,
that is initial,  ) identified by
) identified by  , the name of
, the name of  in PRISM. Otherwise,
in PRISM. Otherwise,  is a composite state and inactive initially. So the counter is set to
is a composite state and inactive initially. So the counter is set to  .
. -
 is the declaration of the exit variable for
is the declaration of the exit variable for  .
. -
 is a triple containing a state number, a set of constants, and a set of commands to record the exit of
is a triple containing a state number, a set of constants, and a set of commands to record the exit of  . The first element
. The first element  is the first state number available. Examples include the numbers on lines
is the first state number available. Examples include the numbers on lines  -
-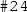 in Fig. 25, for the state machine, and on lines
in Fig. 25, for the state machine, and on lines  -
-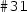 , for Move. If
, for Move. If  is a state machine (
is a state machine ( ), there is no need for it to exit, and, therefore, the state number is
), there is no need for it to exit, and, therefore, the state number is  to record the use of
to record the use of  for
for  , making
, making  the next available number for states, and the sets of constants and commands are empty (
the next available number for states, and the sets of constants and commands are empty ( ). Otherwise, the triple is defined by an application of the function
). Otherwise, the triple is defined by an application of the function  (omitted here) , which is used to generate the two commands of the module on lines
(omitted here) , which is used to generate the two commands of the module on lines  -
- of Fig. 25. More constants and commands might result if
of Fig. 25. More constants and commands might result if  has an exit action. Its third argument is the name of
has an exit action. Its third argument is the name of  (that is,
(that is,  ). Its last argument
). Its last argument  is the next available state number.
is the next available state number. -
 is also a triple defined by the application of the function
is also a triple defined by the application of the function  (whose definition is omitted here). This function is concerned with the encoding of the exit of all substates (that is, all the subnodes
(whose definition is omitted here). This function is concerned with the encoding of the exit of all substates (that is, all the subnodes  of
of  of
of  that are
that are  ). The fifth argument of the application is the next available state number as recorded in
). The fifth argument of the application is the next available state number as recorded in  . The first element
. The first element  is the new available number. The second element
is the new available number. The second element  and the third element
and the third element  are sets of constants and commands encoding the exit of these substates. This function is used to generate the commands on lines
are sets of constants and commands encoding the exit of these substates. This function is used to generate the commands on lines  -
- and the related constants on lines
and the related constants on lines  -
- in Fig. 23 for exiting the state s0 in Fig. 22, and the commands on lines
in Fig. 23 for exiting the state s0 in Fig. 22, and the commands on lines  -
- in Fig. 25 for exiting the state Move in Fig. 17.
in Fig. 25 for exiting the state Move in Fig. 17. -
 is a triple defined by applying
is a triple defined by applying  (omitted) to a set of states that have an entry action (that is, whose action
(omitted) to a set of states that have an entry action (that is, whose action  is not
is not  ). The fourth argument of the application is the next available state number,
). The fourth argument of the application is the next available state number,  . The first element
. The first element  is the new state number, and
is the new state number, and  and
and  are sets of constants and commands used to encode the entering of these substates. This function is used for example, to generate the command on line
are sets of constants and commands used to encode the entering of these substates. This function is used for example, to generate the command on line  in Fig. 25 for entering the simple state Stuck in Fig. 17.
in Fig. 25 for entering the simple state Stuck in Fig. 17. -
 is a pair defined by the application of
is a pair defined by the application of  to all subnodes
to all subnodes  of
of  and to the current available state number (
and to the current available state number ( ). This function characterises a set of constants (in
). This function characterises a set of constants (in  ) representing states in PRISM that correspond to subnodes of
) representing states in PRISM that correspond to subnodes of  like i0, taskState, and p0 in the module in Fig. 20. The first element
like i0, taskState, and p0 in the module in Fig. 20. The first element  is the new state number.
is the new state number. -
 is a quadruple of the next available state and transition numbers, a set of constants, and a set of commands resulting from the translation of the transitions from the nodes
is a quadruple of the next available state and transition numbers, a set of constants, and a set of commands resulting from the translation of the transitions from the nodes  of
of  by the application of
by the application of  (see Sect. 5.4.3). All commands of taskSTM in Fig. 20 are generated by this function.
(see Sect. 5.4.3). All commands of taskSTM in Fig. 20 are generated by this function. -
 is a quadruple resulting from applying the function
is a quadruple resulting from applying the function  (omitted) to the set of composite states of
(omitted) to the set of composite states of  , that is, each node
, that is, each node  that is a
that is a  and is composite (
and is composite ( ). The fifth argument representing the available transition number is from
). The fifth argument representing the available transition number is from  . The function
. The function  applies
applies  to each composite state recursively.
to each composite state recursively.
Next, we discuss how to translate transitions from RoboChart to PRISM and present the rule to do that.
5.4.3 Transitions
As mentioned previously, transitions are translated by  , whose definition is omitted here. This simple function takes a set of nodes and defines the cumulative result of the application of a function
, whose definition is omitted here. This simple function takes a set of nodes and defines the cumulative result of the application of a function  , which applies to a node
, which applies to a node  and translates the transitions from this node. We present Rule 7, defining
and translates the transitions from this node. We present Rule 7, defining  if
if  is a probabilistic junction (
is a probabilistic junction ( ), and omit the definition of defining
), and omit the definition of defining  for other node types. The result of translating the transitions from
for other node types. The result of translating the transitions from  in Fig. 26 using
in Fig. 26 using  gives rise to the constant declarations and commands on lines
gives rise to the constant declarations and commands on lines  -
- and
and  -
- in Fig. 27.
in Fig. 27.

The function  has eight parameters:
has eight parameters:  is the node that identifies the transitions to be translated, namely, those with
is the node that identifies the transitions to be translated, namely, those with  as a source;
as a source;  is the parent of
is the parent of  , either a state machine or a state, of class
, either a state machine or a state, of class  ;
;  is the state machine containing
is the state machine containing  ;
;  is the declaration of the exit variable for
is the declaration of the exit variable for  ;
;  is the name of the program counter variable for
is the name of the program counter variable for  ;
;  is a set of PRISM boolean expressions on the counter variables to identify the control of
is a set of PRISM boolean expressions on the counter variables to identify the control of  at
at  ;
;  is the next available number for a state; and
is the next available number for a state; and  is the next available number for a transition.
is the next available number for a transition.
In Rule 7, the result of translating transitions from  is defined in the
is defined in the  clause as a quadruple
clause as a quadruple  . The first element
. The first element  is the new next available state number;
is the new next available state number;  is a set of constants corresponding to the extra states for the actions of the transitions, such as those on lines
is a set of constants corresponding to the extra states for the actions of the transitions, such as those on lines  -
- in Fig. 27;
in Fig. 27;  is a set of updates that capture the probabilities of the outgoing transitions, such as the three updates on line
is a set of updates that capture the probabilities of the outgoing transitions, such as the three updates on line  ; and
; and  is a set of commands for the actions of the outgoing transitions, such as the six commands on lines
is a set of commands for the actions of the outgoing transitions, such as the six commands on lines  -
- . The first and third elements of the result of
. The first and third elements of the result of  are just
are just  and
and  . The second element is the argument
. The second element is the argument  , relevant for other forms of nodes, not the probabilistic junctions considered in Rule 7. The fourth element of the result includes those in
, relevant for other forms of nodes, not the probabilistic junctions considered in Rule 7. The fourth element of the result includes those in  and a command
and a command  encoding the probabilistic choice, such as that on lines
encoding the probabilistic choice, such as that on lines  -
- in Fig. 27. The definitions of
in Fig. 27. The definitions of  ,
,  ,
,  ,
,  and
and  are in the
are in the  clause and explained below.
clause and explained below.
-
 results from applying
results from applying  to the actual set
to the actual set  of transitions of
of transitions of  that are from
that are from  . This function defines the cumulative result of applying
. This function defines the cumulative result of applying  (Rule 8), which translates each transition in
(Rule 8), which translates each transition in  . The commands on lines
. The commands on lines  -
- and the constants on lines
and the constants on lines  -
- in Fig. 27 are specified by
in Fig. 27 are specified by  when applied to the transition from
when applied to the transition from  to s2 in Fig. 26. Similarly, the commands on lines
to s2 in Fig. 26. Similarly, the commands on lines  -
- and
and  -
- , and the constants on lines
, and the constants on lines  -
- are the result of applying
are the result of applying  to the transitions from
to the transitions from  to s4 and s1. The function
to s4 and s1. The function  also gives rise to an update: for our example, the three updates on line
also gives rise to an update: for our example, the three updates on line  for the three transitions from
for the three transitions from 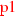 to s1, s2, and s4.
to s1, s2, and s4. -
 is a command in PRISM encoding the choice made at
is a command in PRISM encoding the choice made at  probabilistically. Its guard ensures that the counter variables indicate that the current state is that identified by the node
probabilistically. Its guard ensures that the counter variables indicate that the current state is that identified by the node  . We have a conjunction of two terms. The first,
. We have a conjunction of two terms. The first,  , is itself a conjunction of the boolean expressions in the argument
, is itself a conjunction of the boolean expressions in the argument  , which are equalities regarding the counter variables for all states and machine containing
, which are equalities regarding the counter variables for all states and machine containing  . The second conjunct requires that the counter variable for the state or machine containing
. The second conjunct requires that the counter variable for the state or machine containing  , whose name is given by the argument
, whose name is given by the argument  , has the value
, has the value  for the probabilistic junction identified by
for the probabilistic junction identified by  . The updates of
. The updates of  are those in the set
are those in the set  .
.

Rule 8 defines  , which is concerned with the translation of a transition
, which is concerned with the translation of a transition  , when its source
, when its source  is a probabilistic junction. Since
is a probabilistic junction. Since  has no trigger or guard, its translation is the result
has no trigger or guard, its translation is the result  of encoding its action
of encoding its action  and the entering in its target
and the entering in its target  .
.
Precisely, the result of  is a quintuple, whose first element is the next available state number after the translation of
is a quintuple, whose first element is the next available state number after the translation of  as recorded in
as recorded in  . The second element is the next available transition number: the argument
. The second element is the next available transition number: the argument  . The third and fifth elements are sets of constants and commands resulting from the translation of
. The third and fifth elements are sets of constants and commands resulting from the translation of  . The fourth element is a set containing only one update whose probability is the translation of the probability
. The fourth element is a set containing only one update whose probability is the translation of the probability  of
of  by
by  , and whose assignments are the set of assignments resulting from the translation of
, and whose assignments are the set of assignments resulting from the translation of  that updates the counter to the start state for the encoding of the action.
that updates the counter to the start state for the encoding of the action.
The quadruple  is defined in the
is defined in the  clause described below.
clause described below.
-
 is the name of the constant representing the final state in PRISM for the encoding of the action
is the name of the constant representing the final state in PRISM for the encoding of the action  . If the target
. If the target  of
of  is a state with an entry action, the encoding of
is a state with an entry action, the encoding of  leads to the start state of that entry action, represented by the constant named
leads to the start state of that entry action, represented by the constant named  , such as
, such as  in Fig. 27. Otherwise,
in Fig. 27. Otherwise,  is just the identifier
is just the identifier  of
of  in PRISM.
in PRISM. -
 is a set of assignments to encode entering the target of
is a set of assignments to encode entering the target of  when it is a state without entry action. If it is a composite state, we need to update the counter variable
when it is a state without entry action. If it is a composite state, we need to update the counter variable  of that state to the constant representing its initial junction
of that state to the constant representing its initial junction  . If the target is a simple state,
. If the target is a simple state,  is completed by entering its target, and so the lock variable
is completed by entering its target, and so the lock variable  is set to be free
is set to be free  .
. -
 is a quadruple defined by application of
is a quadruple defined by application of  to the action
to the action  of
of  . The fifth argument
. The fifth argument  of this function application means the start state of the encoding of
of this function application means the start state of the encoding of  is not specified, and so its translation generates a fresh name for the constant for that state. For the action of the transition from
is not specified, and so its translation generates a fresh name for the constant for that state. For the action of the transition from  to s2 in Fig. 26, the constant to encode its start state in PRISM is
to s2 in Fig. 26, the constant to encode its start state in PRISM is  . The sixth argument is a set of PRISM assignments containing an update of the counter
. The sixth argument is a set of PRISM assignments containing an update of the counter  for the state or machine of the action to
for the state or machine of the action to  and
and  .
.
Next, we discuss how to translate actions in RoboChart to PRISM and the definition of  .
.
5.4.4 Actions
Previously in Fig. 20, we show that the action of  in Fig. 21 is modelled by five commands shown on lines
in Fig. 21 is modelled by five commands shown on lines  -
- , and the action of
, and the action of  is modelled by two commands shown on lines
is modelled by two commands shown on lines  -
- . Generally, an action in RoboChart is modelled by a set of commands with a set of corresponding constants to represent extra states required to encode state change in PRISM.
. Generally, an action in RoboChart is modelled by a set of commands with a set of corresponding constants to represent extra states required to encode state change in PRISM.
We define  to translate a RoboChart action to PRISM. An action
to translate a RoboChart action to PRISM. An action  contains a single statement
contains a single statement  , and so
, and so  is defined by its translation by
is defined by its translation by  . We define
. We define  for synchronisation and input or output events in Rule 15 in “Appendix A”.
for synchronisation and input or output events in Rule 15 in “Appendix A”.
The complete set of translation rules, covering all forms of action, is available in [1]. Next, we present RoboTool, which implements our translation.
6 Automatic model generation
RoboToolFootnote 5 supports modelling, validation, and automatic generation of mathematical definitions of RoboChart models written in CSP for use of FDR. We describe here our work extending RoboTool to generate PRISM models automatically: a set of Eclipse pluginsFootnote 6 that provide textual and graphical modelling tools using the Eclipse Modeling framework (EMF).Footnote 7
We have extended RoboTool’s validation facilities with checks of the well-formedness conditions in Sect. 3.3. Fig. 29 shows as an example the implementation for the condition PJ3. The code uses Xtend,Footnote 8 a dialect of Java. The method junctionWFC_PJ3 has a probabilistic junction  as parameter. It iterates over all transitions in the
as parameter. It iterates over all transitions in the  (machine or composite state) of
(machine or composite state) of  , whose source node is
, whose source node is  . These are all outgoing transitions of
. These are all outgoing transitions of  . The loop adds the probabilities of these transitions into an array. Afterwards, the method
. The loop adds the probabilities of these transitions into an array. Afterwards, the method  is called to evaluate whether the sum is 1. If not (
is called to evaluate whether the sum is 1. If not ( returns false), RoboTool displays a warning. This check works for probabilities defined by a number, but not more general expressions. In general, checking PJ3 requires theorem proving.
returns false), RoboTool displays a warning. This check works for probabilities defined by a number, but not more general expressions. In general, checking PJ3 requires theorem proving.
The RoboChart PRISM Generator plugin implements the rules from Sect. 5. The implementation of the rules is the way in which models are generated automatically. The implementation uses Epsilon,Footnote 9 which provides a collection of languages and tools to support tool development. The first stage of the translation, normalisation, uses the Epsilon Object Language (EOL)Footnote 10 for an in-place modification of the RoboChart model. The second stage, transformation, is based on the Epsilon Transformation Language (ETL),Footnote 11 a rule-based model-to-model transformation notation.
The transformation of a RoboChart model produces a model in the PRISM metamodel. To generate the textual model accepted by PRISM from the metamodel, we use the Epsilon Generation Language (EGL),Footnote 12 a template-based language tailored for model-to-text transformation. In the next section, we describe RoboTool facilities for verification using the PRISM model generated automatically.
7 Verification support
PRISM verifies properties defined in probabilistic temporal logics. To improve usability, especially for those without experience with PRISM, we have defined and implemented a property language, called RoboCert. We can specify both properties in CSP (then verify these properties against the standard RoboChart model using FDR) and probabilistic properties in temporal logics (LTL, CTL and PCTL), then verify them against the generated PRISM model using PRISM. In Sect. 7.1, we present examples for the mail delivery robot. The syntax of constructs for the probabilistic properties is summarised in Sect. 7.2. The RoboTool implementation is described in Sect. 7.3.
7.1 Constructs and examples
We present below examples of RoboCert statements, in the context of the module deliverMOD in Fig. 2.
A probabilistic property contains a probabilistic formula with an optional constant configuration to assign the constants that are either declared in the property file or from the RoboChart model with specific values.
Example 2
(Deadlock)

Example 2 defines a constants configuration  that sets the constants
that sets the constants  and
and  of the robotic platform (reference)
of the robotic platform (reference)  in
in  to 20 and 4. Qualified names uniquely identify an element in the RoboChart model. The property
to 20 and 4. Qualified names uniquely identify an element in the RoboChart model. The property  specifies that there does not exist a path along which the system deadlocks if the constants are set using
specifies that there does not exist a path along which the system deadlocks if the constants are set using  .
.
We can also define multiple constant configurations for a property, illustrated by Example 3. This feature is useful for design-space exploration (DSE) by analysing multiple designs simultaneously.
Example 3
(Stuck)

In Example 3, we declare an integer constant  and then use it in the property
and then use it in the property  , which quantitatively measures the probability (
, which quantitatively measures the probability ( ) for the robot to run out of power (
) for the robot to run out of power ( ) in
) in  identified by
identified by  , when
, when  and
and  are set to 20 and 4, and
are set to 20 and 4, and  ranges from 1 to 8 (where
ranges from 1 to 8 (where  denotes a set of integers that is between 1 to 8 inclusive).
denotes a set of integers that is between 1 to 8 inclusive).
RoboCert also supports labels and formulas. A label is a boolean expression, while a formula can be any expression. Example 4 illustrates the usage of labels.
Example 4
(Always get stuck?)

This property states that the robot always finally gets stuck. Here we define a label named  , which is a boolean expression that asserts that movingSTM referenced by
, which is a boolean expression that asserts that movingSTM referenced by  is at the Stuck state.
is at the Stuck state.
Probabilistic properties can also use a reward operator ( ). Example 5 demonstrates its usage.
). Example 5 demonstrates its usage.
Example 5
(Average number of moves before running out of power)

The reward  assigns 1 to each synchronisation over the
assigns 1 to each synchronisation over the  event from the machine referenced by
event from the machine referenced by  . In the property, the reward operator uses
. In the property, the reward operator uses  to state the average number of synchronisations over
to state the average number of synchronisations over  when the robot runs out of power.
when the robot runs out of power.
Both probability and reward properties support statistical model checking in addition to probabilistic model checking. Statistical model checking uses sample-based discrete-event simulation as in Example 6.
Example 6
(Simulation)

This example applies statistic model checking ( ) to verify the property using the
) to verify the property using the  (Confidence Interval) method with supplied parameters. Other methods are
(Confidence Interval) method with supplied parameters. Other methods are  (Asymptotic Confidence Interval),
(Asymptotic Confidence Interval),  (Approximate Probabilistic Model Checking), and
(Approximate Probabilistic Model Checking), and  (Sequential Probability Ratio Test). Information about these methods can be found online.Footnote 13
(Sequential Probability Ratio Test). Information about these methods can be found online.Footnote 13
BNF syntax of the probabilistic constructs in the property language ( - a metasymbol and interpreted as ‘is defined as’;
- a metasymbol and interpreted as ‘is defined as’;  - separation of alternatives;
- separation of alternatives;  - a terminal or non-terminal symbol ‘Name’;
- a terminal or non-terminal symbol ‘Name’;  - appear zero or one time;
- appear zero or one time;  - repeat one or more times;
- repeat one or more times;  - repeat any number of times;
- repeat any number of times;  - keyword ‘const’;
- keyword ‘const’;  - group one or more symbols;
- group one or more symbols;  - a special terminal
- a special terminal  for identifiers;)
for identifiers;)
7.2 Syntax
The BNF syntax of the probabilistic constructs of RoboCert is sketched in Fig. 30.
There are six types of statements ( ) to specify probabilistic properties: constant declarations (
) to specify probabilistic properties: constant declarations ( ), and configurations (
), and configurations ( ), label (
), label ( ), formula (
), formula ( ), and reward definitions (
), and reward definitions ( ), and probabilistic properties (
), and probabilistic properties ( ).
).
A  associates a constant name (
associates a constant name ( ) to a RoboChart type (
) to a RoboChart type ( ). We reuse
). We reuse  in RoboChart and omit its rule here. The constants that are either declared in the property file or from the RoboChart model are configured via constructs defined on lines #4-#9 in Fig. 30. A configuration name is given and various constants (identified by
in RoboChart and omit its rule here. The constants that are either declared in the property file or from the RoboChart model are configured via constructs defined on lines #4-#9 in Fig. 30. A configuration name is given and various constants (identified by  ) are set to specified values (
) are set to specified values ( ).
).  on line #40 uniquely identifies a RoboChart model element through fully qualified names. In the configuration rule on line #8, the value of a constant can be chosen from a set (
on line #40 uniquely identifies a RoboChart model element through fully qualified names. In the configuration rule on line #8, the value of a constant can be chosen from a set ( ) that are defined by either an extension such as {1,2} or an integer interval such as
) that are defined by either an extension such as {1,2} or an integer interval such as  for integers ranging from
for integers ranging from  to
to  by step
by step  .
.
The production rules for labels, formulas, and rewards as shown on lines #10-#13 are straightforward.
A probabilistic property has a name ( ), and a probability formula (
), and a probability formula ( ) under specific constant configurations (defined by a
) under specific constant configurations (defined by a  or a reference to an existing configuration by
or a reference to an existing configuration by  ). A property may also have associated command options (
). A property may also have associated command options ( ), which are passed to the PRISM tool directly.
), which are passed to the PRISM tool directly.
A probability formula can be a boolean expression ( ), or a state formula (
), or a state formula ( ), or a composition of two state formulas by logic conjunction, disjunction, implication, or biconditional. A state formula can refer to a defined label name enclosed within a string (at line #22), or could be a negation of another state formula, or a probability measure with a bound (
), or a composition of two state formulas by logic conjunction, disjunction, implication, or biconditional. A state formula can refer to a defined label name enclosed within a string (at line #22), or could be a negation of another state formula, or a probability measure with a bound ( ) or a quantitative measure (
) or a quantitative measure ( ), or a reward measure, or a CTL universal or existential quantifier over paths. A probability measure is over a path formula (
), or a reward measure, or a CTL universal or existential quantifier over paths. A probability measure is over a path formula ( ), while a reward measure is over a reward path formula (
), while a reward measure is over a reward path formula ( ). Path formulas include general LTL operators, but with optional bounded variants, where an additional time bound is imposed on the property being satisfied. Reward path formulas specify different types of reward properties: reachability rewards, cumulative rewards, total rewards, or instantaneous rewards.
). Path formulas include general LTL operators, but with optional bounded variants, where an additional time bound is imposed on the property being satisfied. Reward path formulas specify different types of reward properties: reachability rewards, cumulative rewards, total rewards, or instantaneous rewards.
Both probability and reward measures support statistical as well as probabilistic model checking. Statistical model checking uses sample-based discrete-event simulation. A state formula can specify the simulation methods to be used ( ), and a simulation method is configured using
), and a simulation method is configured using  .
.
7.3 A RoboCert plugin in RoboTool
A plugin is available in RoboTool to generate PRISM properties from RoboCert properties. The plugin accepts a property file, parses it, translates constructors in the file to their counterparts in the PRISM property specification language or the PRISM model language, and finally generates a PRISM property file. The plugin provides a modelling environment to edit properties with syntax and error highlighting. It also has content assist through scoping for qualified names.
Translated formulas and rewards are part of PRISM models, instead of property files. Therefore, we need to update the translated PRISM model. The plugin adds the formula and reward definitions from the properties to the PRISM model, and generates the corresponding PRISM properties. RoboTool then runs multiple instances of the PRISM command line tool to verify the generated properties in parallel.
Upon a successful verification, results are shown in a report. Otherwise, error messages indicate problems in the model or properties. The plugin translates the elements in error messages from PRISM back to RoboChart. This improves traceability of errors and results. Counterexamples found by PRISM can be linked back to the original RoboChart model.
RoboTool has been used in the verification of several examplesFootnote 14 using both probabilistic and statistical model checking. They show that the translation time does not add burden to the verification: a couple of seconds, for verifications that take minutes.
8 Conclusions and future work
Previous work [2] has shown modelling and verification of functional behaviour using RoboChart and RoboTool. This work covers its extension for probabilistic modelling and verification. We have introduced a new construct, probabilistic junctions, for modelling of probabilistic software systems. This new construct impose extra well-formedness conditions. We have extended RoboTool to support modelling of probabilistic systems, including checking of these conditions.
We have derived a metamodel for PRISM and developed and formalised a probabilistic semantics of RoboChart in PRISM. It covers the most challenging constructs of hierarchical state machines and the component model of RoboChart covering parallel controllers.
We have developed support for automatic verification of probabilistic RoboChart models by translating them to the PRISM notation, and then using the PRISM model checker. The translation is in two steps, normalisation of RoboChart models and transformation of normalised models to PRISM. We have formalised and presented here both steps. The translation is automated in RoboTool, and so PRISM models can be generated from RoboChart models automatically.
We have also extended the standard property language [1, Section 5.1] in RoboTool and developed probabilistic property constructs. We have based this on the PRISM property language, but favour a controlled natural language syntax. We use qualified names for references to RoboChart elements. These names are also used in error logs from model checking. This makes model checking tools transparent to RoboTool users. The property language allows RoboTool to verify each property using one instance of PRISM. For instance, RoboTool uses 10 PRISM instances to verify 10 properties in parallel. This reduces model checking time (to the longest checking time of a property).
The translation presented in this paper cannot deal with all features in RoboChart, and our immediate future work is to extend it in order to overcome current limitations. The extension includes support of time primitives, asynchronous connections, operations defined in controllers, during actions, and richer abstract data types to relax TR-TY1 and corresponding expressions. The most significant restriction is the handling of time primitives. The other restrictions just require an additional encoding. Regarding time, our translation is restricted to models that correspond to the Markov models we use (DTMCs and MDPs). RoboChart has a more sophisticated model of time that complements this basic model, and translation of this richer time model is our future work. Many robotic models, however, do not require the super-dense model of time that results from combining the two time-models. So our work caters for many robotic applications.
For the examples we have considered so far, the transformations take a couple of seconds. We do not expect that it raises issues of scalability. Larger case studies and physical modelling are our future work.
The translation defined in this paper is unidirectional from RoboChart to PRISM. It is also feasible to define a translation from PRISM to RoboChart; this is actually not very challenging when compared to the translation defined here. This is also part of our future work to form a bidirectional translation.
It is possible to verify generated PRISM models using other model checkers that accept the same notation, such as Storm and MRMC. Use of other tools that accept different languages, such as the MODEST Toolset, requires different translations. They can, however, capitalise on the normalisation defined here, since it simplifies the structure of models.
RoboChart supports verification of robotic systems by model checking, but the long-term plan is combined use of model checking and theorem proving to deal with larger models and collections. Our immediate future work is to establish a link between model checking and theorem proving in order to verify probabilistic systems in RoboChart complementary. One scenario is to verify a RoboChart model using both model checking and theorem proving, and then compare their results. Another scenario is to use theorem proving as a guaranteed simplifier to simplify part of a RoboChart model (such as state machines, transitions, and states) in order to reduce the complexity for model checking. This could improve model checking performance dramatically.
To support theorem proving, and to connect RoboChart’s CSP and PRISM semantics, we are pursuing a unifying theory of CSP and PRISM. This is based on Hoare and He’s Unifying Theories of Programming [4]. In [14], we define the probabilistic semantics of the RoboChart action language in a new theory, and use the weakest completion technique [15] to embed the theory of designs [4, 73] (for total correctness) in the probabilistic semantic domain. We call this new theory this theory of probabilistic designs. We are mechanising the theory in Isabelle/UTP. This allows us to analyse non-reactive RoboChart models. Our next step is to develop a reactive probabilistic design semantics. Our proof technique is to use reactive relations and Kleene algebra-based verification of reactive programs [74] to calculate contracts for RoboChart models.
With mechanised reactive probabilistic designs semantics, we have a UTP semantics for DTMCs and MDPs (then for PRISM). With that, given that CSP also has a theory of reactive designs, RoboChart and PRISM will then have the same semantic foundation, and we can establish soundness of our transformation with respect to the CSP work.
Using reactive probabilistic designs, we can calculate contracts for RoboChart. Those cut unnecessary internal states and variables generated during transformation. This reduces the state space size of transformed models and will improve model checking performance.
In addition to RoboChart, we are also developing tools and techniques that make use of RoboChart to generate robotic simulations and tests automatically. After these lines of future work are complete, formal studies on usability of these tools and techniques in the robotics domain can be conducted.
Notes
http://standards.iso.org/ittf/PubliclyAvailableStandards/c021573_ISO_IEC_13568_2002(E).zip.), albeit with a more roboticist-friendly syntax and a few syntactic-sugaring constructs.
References
Miyazawa, A., Cavalcanti, A., Ribeiro, P., Li, W., Woodcock, J., Timmis, J.: RoboChart Reference Manual. University of York, Tech. rep. (2018) www.cs.york.ac.uk/circus/publications/techreports/reports/robochart-reference.pdf
Miyazawa, A., Ribeiro, P., Li, W., Cavalcanti, A., Timmis, J., Woodcock, J.: RoboChart: modelling and verification of the functional behaviour of robotic applications. Softw. Syst. Model. (2019). https://doi.org/10.1007/s10270-018-00710-z
Kwiatkowska, M.Z., Norman, G., Parker, D.: PRISM 4.0: Verification of probabilistic real-time systems. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV, Lecture Notes in Computer Science, vol. 6806, pp. 585–591. Springer (2011) dblp.uni-trier.de/db/conf/cav/cav2011.html#KwiatkowskaNP11
Hoare, C.A.R., He, J.: Unifying Theories of Programming. Prentice-Hall (1998)
Hoare, C.A.R.: Communicating Sequential Processes. Prentice-Hall Int. (1985)
Roscoe, A.W.: Understanding Concurrent Systems. Texts in Computer Science. Springer (2011)
Cavalcanti, A.L.C., Woodcock, J.C.P.: A Tutorial Introduction to CSP in Unifying Theories of Programming. In: Refinement Techniques in Software Engineering. Lecture Notes in Computer Science, vol. 3167, pp. 220–268. Springer-Verlag (2006). https://doi.org/10.1007/11889229_6www-users.cs.york.ac.uk/~alcc/publications/papers/CW06.pdf
Baxter, J., Ribeiro, P., Cavalcanti, A.: Sound reasoning in tock-csp. Acta Informatica (in press)
FDR: Failures-Divergences Refinement https://www.cs.ox.ac.uk/projects/fdr/
Gibson-Robinson, T., Armstrong, P., Boulgakov, A., Roscoe, A.W.: FDR3: A modern refinement checker for CSP. In: Tools and Algorithms for the Construction and Analysis of Systems, pp. 187–201 (2014)
Goldsmith, M., East, I., Duce, D., Green, M., Martin, J., Welch, P.: CSP: The best concurrent-system description language in the world—probably! Communicating Process Architectures, pp. 227–232 (2004)
Foster, S., Zeyda, F., Woodcock, J.C.P.: Isabelle/UTP: A mechanised theory engineering framework. In: UTP 2015, LNCS, vol. 8963, pp. 21–41. Springer (2015)
Nipkow, T., Wenzel, M., Paulson, L.C.: Isabelle/HOL: A Proof Assistant for Higher-Order Logic. Springer (2002)
Woodcock, J.C.P., Cavalcanti, A.L.C., Foster, S., Mota, A., Ye, K.: Probabilistic semantics for RoboChart: A weakest completion approach. In: Unifying Theories of Programming. Lecture Notes in Computer Science, p. to appear, Springer (2019)
He, J., Morgan, C., McIver, A.: Deriving probabilistic semantics via the ‘weakest completion’. In: Davies, J., Schulte, W., Barnett, M. (eds.) Formal Methods and Software Engineering, pp. 131–145. Springer, Berlin Heidelberg, Berlin, Heidelberg (2004)
Conserva Filho, M.S., Marinho, R., Mota, A., Woodcock, J.: Analysing RoboChart with probabilities. Formal Methods: Foundations and Applications (2018). https://doi.org/10.1007/978-3-030-03044-5_13
Segala, R., Lynch, N.A.: Probabilistic simulations for probabilistic processes. Nord. J. Comput. 2(2), 250–273 (1995)
Hansson, H.: Time and probabilities in formal design of distributed systems. Department of Computer Systems, Uppsala University, Phd thesis (1991)
Larsen, K.G., Skou, A.: Bisimulation through probabilistic testing. Inf. Comput. 94(1), 1–28 (1991). https://doi.org/10.1016/0890-5401(91)90030-6
Stoelinga, M.: An introduction to probabilistic automata. Bull. EATCS 78, 176–198 (2002)
van Glabbeek, R.J., Smolka, S.A., Steffen, B., Tofts, C.M.N.: Reactive, generative, and stratified models of probabilistic processes. In: Proceedings of the Fifth Annual Symposium on Logic in Computer Science (LICS ’90), Philadelphia, Pennsylvania, USA, June 4–7, 1990, pp. 130–141. IEEE Computer Society (1990). https://doi.org/10.1109/LICS.1990.113740
Kemeny, J.G., Snell, J.L.: Finite Markov Chains: With a New Appendix “Generalization of a Fundamental Matrix” (Undergraduate Texts in Mathematics). Springer (1983)
Kemeny, J.G., Snell, J.L., Knapp, A.W.: Denumerable Markov Chains (1976). https://doi.org/10.1007/978-1-4684-9455-6
Howard, R.: Dynamic Probabilistic Systems: Semi-Markov and decision processes. Series in Decision and Control. Wiley (1971) https://books.google.co.uk/books?id=vuZQAAAAMAAJ
Puterman, M.L.: Markov Decision Processes: Discrete Stochastic Dynamic Programming, 1st edn. Wiley (1994)
Dehnert, C., Junges, S., Katoen, J.P., Volk, M.: A storm is coming: A modern probabilistic model checker. In: Majumdar, R., Kunčak, V. (eds.) Computer Aided Verification, pp. 592–600. Springer, Cham (2017)
Alur, R., Henzinger, T.A.: Reactive modules. Formal Methods Syst. Design 15(1), 7–48 (1999)
Bohnenkamp, H., d’Argenio, P.R., Hermanns, H., Katoen, J.P.: Modest: A compositional modeling formalism for hard and softly timed systems. IEEE Trans. Softw. Eng. 32(10), 812–830 (2006)
Hahn, E.M., Hartmanns, A., Hermanns, H., Katoen, J.P.: A compositional modelling and analysis framework for stochastic hybrid systems. Formal Methods Syst. Design 43(2), 191–232 (2013)
Park, H.W., Ramezani, A., Grizzle, J.W.: A finite-state machine for accommodating unexpected large ground-height variations in bipedal robot walking. IEEE Trans. Robot. 29(2), 331–345 (2013)
Rabbath, C.A.: A finite-state machine for collaborative airlift with a formation of unmanned air vehicles. J. Intell. Robot. Syst. 70(1), 233–253 (2013)
Tomic, T., Schmid, K., Lutz, P., Domel, A., Kassecker, M., Mair, E., Grixa, I.L., Ruess, F., Suppa, M., Burschka, D.: Toward a fully autonomous UAV: research platform for indoor and outdoor urban search and rescue. IEEE Robot. Autom. Mag. 19(3), 46–56 (2012)
Liu, W., Winfield, A.F., Sa, J.: Modelling swarm robotic systems: a case study in collective foraging. Towards Auton. Robot. Syst. 25–32 (2007)
Konur, S., Dixon, C., Fisher, M.: Analysing robot swarm behaviour via probabilistic model checking. Robot. Auton. Syst. 60(2), 199–213 (2012)
Colvin, R., Grunske, L., Winter, K.: Probabilistic timed behavior trees. In: International Conference on Integrated Formal Methods, pp. 156–175. Springer (2007)
Dromey, R.G.: From requirements to design: Formalizing the key steps. In: First International Conference onSoftware Engineering and Formal Methods, 2003. Proceedings., pp. 2–11. IEEE (2003)
Beauquier, D.: On probabilistic timed automata. Theor. Comput. Sci. 292(1), 65–84 (2003)
Object Management Group: OMG Unified Modeling Language (OMG UML), Superstructure, Version 2.4.1 (2011) www.omg.org/spec/UML/2.4.1
Addouche, N., Antoine, C., Montmain, J.: Uml models for dependability analysis of real-time systems. In: 2004 IEEE International Conference on Systems, Man and Cybernetics (IEEE Cat. No. 04CH37583), vol. 6, pp. 5209–5214. IEEE (2004)
Addouche, N., Antoine, C., Montmain, J.: Combining extended UML models and formal methods to analyze real-time systems. In: International Conference on Computer Safety, Reliability, and Security, pp. 24–36. Springer (2005)
Jansen, D.N., Hermanns, H., Katoen, J.: A probabilistic extension of UML statecharts. In: Damm, W., Olderog, E. (eds.) FTRTFT 2002: 7th International Symposium on Formal Techniques in Real-Time and Fault-Tolerant Systems, Co-sponsored by IFIP WG 2.2, Oldenburg, 9–12 September 2002, Lecture Notes in Computer Science, vol. 2469, pp. 355–374. Springer (2002)
Hansson, H., Jonsson, B.: A logic for reasoning about time and reliability. Formal Asp. Comput. 6(5), 512–535 (1994). https://doi.org/10.1007/BF01211866
Schlegel, C., Hassler, T., Lotz, A., Steck, A.: Robotic soft. systems: from code-driven to model-driven designs. In: ICAR 2009, pp. 1–8. IEEE (2009)
Nordmann, A., Hochgeschwender, N., Wigand, D., Wrede, S.: A survey on domain-specific modeling and languages in robotics. In: FTRTFT 2002: 7th International Symposium on Formal Techniques in Real-Time and Fault-Tolerant Systems, Co-sponsored by IFIP WG 2.2, Oldenburg, 9–12 September 2002, vol. 7, pp. 75–99 (2016)
Schlegel, C., Worz, R.: The software framework smartsoft for implementing sensorimotor systems. In: Proceedings 1999 IEEE/RSJ International Conference on Intelligent Robots and Systems. Human and Environment Friendly Robots with High Intelligence and Emotional Quotients (Cat. No. 99CH36289), vol. 3, pp. 1610–1616. IEEE (1999)
Alonso, D., Vicente-Chicote, C., Ortiz, F., Pastorfranco, J.: V3cmm: a 3-view component meta-model for model-driven robotic software development. J. Softw. Eng. Robot. 1, 3–17 (2010)
Bruyninckx, H., Klotzbücher, M., Hochgeschwender, N., Kraetzschmar, G., Gherardi, L., Brugali, D.: The brics component model: a model-based development paradigm for complex robotics software systems. In: Proceedings of the 28th Annual ACM Symposium on Applied Computing, pp. 1758–1764 (2013)
Dhouib, S., Kchir, S., Stinckwich, S., Ziadi, T., Ziane, M.: RobotML, a Domain-Specific Language to Design, Simulate and Deploy Robotic Applications. In: SIMPAR 2012, pp. 149–160. Springer (2012)
Ramaswamy, A., Monsuez, B., Tapus, A.: Saferobots: A model-driven framework for developing robotic systems. In: Proc. IEEE/RSJ Int. Conf. Intelligent Robots and Systems, pp. 1517–1524 (2014). https://doi.org/10.1109/IROS.2014.6942757
Hochgeschwender, N., Gherardi, L., Shakhirmardanov, A., Kraetzschmar, G.K., Brugali, D., Bruyninckx, H.: A model-based approach to software deployment in robotics. In: IEEE/RSJ Int. Conf. on Intelligent Robots and Systems, pp. 3907–3914 (2013)
Mallet, A., Pasteur, C., Herrb, M., Lemaignan, S., Ingrand, F.: Genom3: Building middleware-independent robotic components. IEEE Int. Conf. Robot. Automat. , 4627–4632 (2010)
Foughali, M., Berthomieu, B., Zilio, S.D., Ingrand, F., Mallet, A.: Model Checking Real-Time Properties on the Functional Layer of Autonomous Robots. In: Formal Methods and Soft. Eng., pp. 383–399. Springer (2016)
Berthomieu, B., Vernadat, F.: Time petri nets analysis with TINA. In: Third International Conference on the Quantitative Evaluation of Systems, pp. 123–124. IEEE Computer Society, Riverside, California, USA (2006). https://doi.org/10.1109/QEST.2006.56
Basu, A., Bozga, M., Sifakis, J.: Modeling heterogeneous real-time components in BIP. In: Fourth IEEE International Conference on Software Engineering and Formal Methods (SEFM 2006), 11-15 September 2006, Pune, India, pp. 3–12. IEEE Computer Society (2006). https://doi.org/10.1109/SEFM.2006.27
Thrun, S., Burgard, W., Fox, D.: Probabilistic Robotics (Intelligent Robotics and Autonomous Agents). The MIT Press (2005)
PRISM Lab Session, Part B: Mail Delivery Robot http://www.prismmodelchecker.org/courses/aims1617/deliveryRobot.php
Cavalcanti, A., Barnett, W., Baxter, J., Carvalho, G., Conserva Filho, M., Miyazawa, A., Ribeiro, P., Sampaio, A.: In: Cavalcanti, A., Dongol, B., Hierons, R., Timmis, J., Woodcock, J. (eds.) RoboStar technology: a roboticist’s toolbox for combined proof, simulation, and testing. Software Engineering for Robotics. Springer International Publishing (2021)
Jansen, D.N., Hermanns, H., Katoen, J.P.: A Probabilistic Extension of UML Statecharts. In: Formal Tec. in Real-Time and Fault-Tolerant Syst., LNCS, vol. 2469, pp. 355–374. Springer (2002)
Nokovic, B., Sekerinski, E.: Verification and code generation for timed transitions in pcharts. In: Proceedings of the 2014 International C* Conference on Computer Science & Software Engineering, p. 3. ACM (2014)
Katoen, J.P., Khattri, M., Zapreevt, I.: A Markov reward model checker. In: Second International Conference on the Quantitative Evaluation of Systems (QEST’05), pp. 243–244. IEEE (2005)
PRISM Team: The PRISM Language: Semantics (2008) www.prismmodelchecker.org/doc/semantics.pdf
Younes, H.L.S., Kwiatkowska, M.Z., Norman, G., Parker, D.: Numerical vs. statistical probabilistic model checking. STTT 8(3), 216–228 (2006). https://doi.org/10.1007/s10009-005-0187-8
Sen, K., Marinov, D., Agha, G.: CUTE: a concolic unit testing engine for C. In: 10th Joint Meeting of the European Soft. Eng. Conf. and the ACM SIGSOFT Symp. on the Foundations of Soft. Eng., pp. 263–272. ACM (2005)
PRISM Team: The PRISM Language: Reward-based Properties www.prismmodelchecker.org/manual/PropertySpecification/Reward-basedProperties
Jensen, H.: Model checking probabilistic real time systems. In: Proc. 7th Nordic Workshop on Programming Theory, pp. 247–261. Citeseer (1996)
Kwiatkowska, M., Norman, G., Segala, R., Sproston, J.: Automatic verification of real-time systems with discrete probability distributions. Theor. Comput. Sci. 282(1), 101–150 (2002)
Kwiatkowska, M.Z., Norman, G., Parker, D.: Prism 4.0: Verification of probabilistic real-time systems. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV. Lecture Notes in Computer Science, vol. 6806, pp. 585–591. Springer (2011). https://doi.org/10.1007/978-3-642-22110-1_47 dblp.uni-trier.de/db/conf/cav/cav2011.html#KwiatkowskaNP11
Kattenbelt, M., Kwiatkowska, M., Norman, G., Parker, D.: A game-based abstraction-refinement framework for markov decision processes. Formal Methods Syst. Design 36(3), 246–280 (2010)
Kwiatkowska, M., Norman, G., Parker, D., Sproston, J.: Performance analysis of probabilistic timed automata using digital clocks. Formal Methods Syst. Design 29(1), 33–78 (2006)
Woodcock, J.C.P., Davies, J.: Using Z-Specification, Refinement, and Proof. Prentice-Hall (1996)
Cavalcanti, A.L.C., Sampaio, A.C.A., Woodcock, J.C.P.: A Refinement Strategy for Circus. Formal Aspects Comput. 15(2–3), 146–181 (2003)
Spivey, J.M.: The Z Notation: A Reference Manual, 2nd. Prentice-Hall (1992)
Woodcock, J.C.P., Cavalcanti, A.L.C.: A tutorial introduction to designs in Unifying Theories of Programming. In: Boiten, E.A., Derrick, J., Smith, G. (eds.) IFM 2004: Integrated Formal Methods, LNCS, vol. 2999, pp. 40–66. Springer-Verlag (2004). Invited tutorial
Foster, S., Ye, K., Cavalcanti, A., Woodcock, J.: Calculational verification of reactive programs with reactive relations and Kleene Algebra. In: International Conference on Relational and Algebraic Methods in Computer Science, pp. 205–224. Springer (2018)
Acknowledgements
This work is funded by the EPSRC grants EP/M025756/1 and EP/R025479/1, and by the Royal Academy of Engineering grant CiET1718/45. The icons used in RoboChart have been made by Sarfraz Shoukat, Freepik, Google, Icomoon and Madebyoliver from www.flaticon.com, and are licensed under CC 3.0 BY.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Jeff Gray.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Translation rules
Translation rules
1.1 Normalisation
The function  defined in Rule 9 deals with a machine in which there are states having no outgoing transitions. So that the model does not satisfy NFM-1. This function specifies a new loop state and corresponding transitions from the original states to the loop state.
defined in Rule 9 deals with a machine in which there are states having no outgoing transitions. So that the model does not satisfy NFM-1. This function specifies a new loop state and corresponding transitions from the original states to the loop state.

The first parameter of the function is a  , the parent class of both StateMachineDef and State. So this function is applicable to both state machine definitions such as
, the parent class of both StateMachineDef and State. So this function is applicable to both state machine definitions such as  in Rule 1, and composite states. If the
in Rule 1, and composite states. If the  has one or more nodes
has one or more nodes  that have no outgoing transitions (
that have no outgoing transitions ( ) , then the result is a pair formed by the set
) , then the result is a pair formed by the set  containing a new state
containing a new state  , and a set of transitions (
, and a set of transitions ( ) including a self-transition
) including a self-transition  for
for  and transitions in
and transitions in  from the states without outgoing transitions to
from the states without outgoing transitions to  . Otherwise, there is no need to introduce loop, and the result is a pair of empty sets. The
. Otherwise, there is no need to introduce loop, and the result is a pair of empty sets. The  clause of the rule has three definitions explained below.
clause of the rule has three definitions explained below.
-
 is a new state specified by a function
is a new state specified by a function  with a fresh name specified by
with a fresh name specified by 
 . The function
. The function  characterises a State whose name takes the value
characterises a State whose name takes the value  , but whose nodes, transitions, and actions are empty. So, it is a simple state without transitions or actions. We note that it is possible to directly define what
, but whose nodes, transitions, and actions are empty. So, it is a simple state without transitions or actions. We note that it is possible to directly define what  specifies using a class instantiation
specifies using a class instantiation 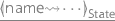 . We define
. We define  , however, to facilitate reuse and hide other fields of the class State that are set to empty or
, however, to facilitate reuse and hide other fields of the class State that are set to empty or  for simplicity. The introduction of the function
for simplicity. The introduction of the function  is similar.
is similar. -
 is a new self-transition for
is a new self-transition for  , defined by a function
, defined by a function  with three parameters: the name, the source, and the target of the new transition. Other components of the transitions are null: it has no label.
with three parameters: the name, the source, and the target of the new transition. Other components of the transitions are null: it has no label. -
 is a set of new transitions. For each state
is a set of new transitions. For each state  without any outgoing transitions, this set includes one transition from
without any outgoing transitions, this set includes one transition from  to the new state
to the new state  .
.
If a transition from a state or a normal junction to a normal junction has no action, the model does not satisfy NFM-2. Such a transition, however, can be combined with outgoing transitions from its target normal junction. We identify these transitions as combinable transitions through a function  defined by Rule 11. In a state machine, all normal junctions that have at least one combinable incoming transition are identified by a function
defined by Rule 11. In a state machine, all normal junctions that have at least one combinable incoming transition are identified by a function  defined in Rule 10. Such a normal junction and its incoming and outgoing transitions are
defined in Rule 10. Such a normal junction and its incoming and outgoing transitions are

then combined by a function  defined in Rule 12. Details of these rules are explained next.
defined in Rule 12. Details of these rules are explained next.
The function  takes a state machine as argument, and identifies a subset of its nodes
takes a state machine as argument, and identifies a subset of its nodes  . They are normal junctions, that is, junctions (
. They are normal junctions, that is, junctions ( ), but not initial (
), but not initial ( ) and not probabilistic (
) and not probabilistic ( ), and at least one transition
), and at least one transition  among their incoming transitions (
among their incoming transitions ( ) needs to be combined.
) needs to be combined.

As already mentioned, the need to combine a transition  is characterised by
is characterised by  defined by Rule 11. Such transition has no action (
defined by Rule 11. Such transition has no action ( ) and its source node
) and its source node  is not an initial or probabilistic junction.
is not an initial or probabilistic junction.
The function  has two parameters:
has two parameters:  is a set of normal junctions whose incoming transitions can be combined with outgoing transitions, and
is a set of normal junctions whose incoming transitions can be combined with outgoing transitions, and  is a set of incoming and outgoing transitions of these normal junctions. If
is a set of incoming and outgoing transitions of these normal junctions. If  is empty, then the result is just a triple of empty sets, because there are no transitions to be combined, and so no junctions or transitions to be removed, and no new transitions. Otherwise, the result is basically the cumulative result of applying the function
is empty, then the result is just a triple of empty sets, because there are no transitions to be combined, and so no junctions or transitions to be removed, and no new transitions. Otherwise, the result is basically the cumulative result of applying the function  to each junction. We omit the definition of
to each junction. We omit the definition of  here, but the complete set of rules can be found in [1].
here, but the complete set of rules can be found in [1].
The function  defined in Rule 12 has two parameters: a normal junction
defined in Rule 12 has two parameters: a normal junction  and the set of its incoming and outgoing transitions
and the set of its incoming and outgoing transitions  . If the set
. If the set  of incoming transitions of
of incoming transitions of  that cannot be combined is not empty, then the result is a triple containing the empty set, because
that cannot be combined is not empty, then the result is a triple containing the empty set, because  is not removed, the set
is not removed, the set  of the incoming transitions that can be combined, and do need to be removed, and the set
of the incoming transitions that can be combined, and do need to be removed, and the set  of the transitions resulting from the combination. Otherwise, the resulting triple includes
of the transitions resulting from the combination. Otherwise, the resulting triple includes  , so that
, so that  is removed, the set
is removed, the set  , so that all transitions to and from
, so that all transitions to and from  are removed, and the set of new transitions
are removed, and the set of new transitions  . All the sets are defined in the
. All the sets are defined in the  clause.
clause.

-
 is a set of incoming transitions
is a set of incoming transitions  of
of  that can be combined (and so removed). This is characterised by
that can be combined (and so removed). This is characterised by  .
. -
 has all other incoming transitions of
has all other incoming transitions of  .
. -
 is the set of outgoing transitions from
is the set of outgoing transitions from  .
. -
 is a set of new transitions that combine each incoming transition
is a set of new transitions that combine each incoming transition  from
from  and each outgoing transition
and each outgoing transition  from
from  . The new transition has a unique name
. The new transition has a unique name  , the same source as
, the same source as  , the same target of
, the same target of  , the trigger of
, the trigger of  , and the action of
, and the action of  . The condition is the conjunction of that of
. The condition is the conjunction of that of  and that of
and that of  .
.

If a transition has a trigger and an action, the model does not satisfy NFM-3. We, therefore, define  in Rule 13 to define the result of splitting such a transition into two transitions connected via a new probabilistic junction.
in Rule 13 to define the result of splitting such a transition into two transitions connected via a new probabilistic junction.
The function  defines the normalisation of a transition
defines the normalisation of a transition  with a trigger and an action. In this case, the transition is split into two transitions connected via a new probabilistic junction
with a trigger and an action. In this case, the transition is split into two transitions connected via a new probabilistic junction  , defined in the
, defined in the  clause to have a unique name
clause to have a unique name  . The result of
. The result of  is a pair including the two new transitions, and the new junction
is a pair including the two new transitions, and the new junction  . In the set of transitions, we have a transition to
. In the set of transitions, we have a transition to  , and a transition from
, and a transition from  . The transition to
. The transition to  has the trigger and the condition of
has the trigger and the condition of  , and the outgoing transition has the action of
, and the outgoing transition has the action of  and a probability value 1. If
and a probability value 1. If  does not have both a trigger and an action, the result is the set containing
does not have both a trigger and an action, the result is the set containing  itself, and the empty set, since no new junction is needed.
itself, and the empty set, since no new junction is needed.


1.2 Transformation to PRISM
Rule 14 defines the function  used in Rule 4. It has one parameter:
used in Rule 4. It has one parameter:  of type
of type  , and characterises a relation from operations to PRISM actions. This relation establishes a mapping from each operation
, and characterises a relation from operations to PRISM actions. This relation establishes a mapping from each operation  in the operations
in the operations  required by
required by  to a PRISM action with a fresh name specified by
to a PRISM action with a fresh name specified by  . (We recall that this is used to collect information about how operations are used in each machine, so that they can be encoded in the platform module.) For the previously discussed operation moveSteps in Sect. 5.4.1, the result is
. (We recall that this is used to collect information about how operations are used in each machine, so that they can be encoded in the platform module.) For the previously discussed operation moveSteps in Sect. 5.4.1, the result is  .
.
Rule 15 defines the function  that translates a statement. The parameter
that translates a statement. The parameter  is a CommunicationStmt, which contains a Communication encapsulating a synchronisation, an input or an output event. The function
is a CommunicationStmt, which contains a Communication encapsulating a synchronisation, an input or an output event. The function  also has the following parameters:
also has the following parameters:  records constraints on the counters that identify the state in which
records constraints on the counters that identify the state in which  is executed;
is executed;  is the next available number for states;
is the next available number for states;  is the name of the current counter;
is the name of the current counter;  is the optional declaration of a PRISM constant representing the state at the start of
is the optional declaration of a PRISM constant representing the state at the start of  ; and
; and  is a set of PRISM assignments that encode the change to the state after the execution of
is a set of PRISM assignments that encode the change to the state after the execution of  . The constant
. The constant  , if present (not
, if present (not  ), indicates that
), indicates that  is an entry action. In this case, it is used by all transitions to the state with that entry action.
is an entry action. In this case, it is used by all transitions to the state with that entry action.
The result of  is a quadruple. The first element is the new available state number. The second is a set of new constants to identify extra states, of which there may be several if the action is compound. The third element
is a quadruple. The first element is the new available state number. The second is a set of new constants to identify extra states, of which there may be several if the action is compound. The third element  is a set
is a set  of assignments to update the state of the module to the start state for the encoding of
of assignments to update the state of the module to the start state for the encoding of  . Finally, the fourth element is a set containing one command
. Finally, the fourth element is a set containing one command  to encode
to encode  . If
. If  is not
is not  , the supplied
, the supplied  encodes the start of
encodes the start of  , and so no new constant is needed: the new available state number is still
, and so no new constant is needed: the new available state number is still  and the result has an empty set of constants. Otherwise, a fresh constant, such as
and the result has an empty set of constants. Otherwise, a fresh constant, such as  , is declared and associated with
, is declared and associated with  as shown by the definition of
as shown by the definition of  in the
in the  clause. In this case, the new available state number is
clause. In this case, the new available state number is  , and the set of constants includes a single element
, and the set of constants includes a single element  . For the application of
. For the application of  to translate the statement in the action of
to translate the statement in the action of  in Fig. 21, the first element of the result is
in Fig. 21, the first element of the result is  because
because  identifies
identifies  on line
on line  in Fig. 20, the second is the declaration of
in Fig. 20, the second is the declaration of  on line
on line  , the third is the set containing
, the third is the set containing  on line
on line  , and the fourth element is the command on line
, and the fourth element is the command on line  . The variables used in Rule 15 are defined in the
. The variables used in Rule 15 are defined in the  clause explained below.
clause explained below.
-
 is the constant encoding the start of the statement
is the constant encoding the start of the statement  . If the argument
. If the argument  is not
is not  , the constant is just
, the constant is just  . Otherwise, it is a constant with a fresh name given by
. Otherwise, it is a constant with a fresh name given by  and associated with
and associated with  .
. -
 is a set of assignments. If
is a set of assignments. If  is an output event (its communication is of type
is an output event (its communication is of type  ) or a synchronisation (its communication is of type
) or a synchronisation (its communication is of type  ), it contains an assignment to update the event related variable
), it contains an assignment to update the event related variable  from the value
from the value  carried by the event, to encode communication. Otherwise, it is empty.
carried by the event, to encode communication. Otherwise, it is empty. -
 contains an assignment to update the counter variable to the start state for the encoding of
contains an assignment to update the counter variable to the start state for the encoding of  and assignments in
and assignments in  explained above.
explained above. -
 is also a set of assignments. If
is also a set of assignments. If  is an input event (that is, its communication is of type
is an input event (that is, its communication is of type  ), this set contains an assignment to update the input variable
), this set contains an assignment to update the input variable  to the value of the variable used for output, to encode the input communication. Otherwise,
to the value of the variable used for output, to encode the input communication. Otherwise,  is empty since there is no data exchange.
is empty since there is no data exchange. -
 is a command. Its action is the name of the event of
is a command. Its action is the name of the event of  given by
given by  . Its guard ensures that the counter variables indicate that the current state is that identified by
. Its guard ensures that the counter variables indicate that the current state is that identified by  . We have a conjunction of two terms. The first,
. We have a conjunction of two terms. The first,  , is itself a conjunction of the boolean expressions in the argument
, is itself a conjunction of the boolean expressions in the argument  , which are equalities regarding the counter variables for all states and state machine containing
, which are equalities regarding the counter variables for all states and state machine containing  . The second conjunct requires that the counter variable for the state or machine containing
. The second conjunct requires that the counter variable for the state or machine containing  , whose name is given by the argument
, whose name is given by the argument  , has the value
, has the value  for the encoding of
for the encoding of  . The update of
. The update of  has probability 1 and assignments containing the argument
has probability 1 and assignments containing the argument  to update the counters to the final state of the encoding of
to update the counters to the final state of the encoding of  and
and  explained above.
explained above.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ye, K., Cavalcanti, A., Foster, S. et al. Probabilistic modelling and verification using RoboChart and PRISM. Softw Syst Model 21, 667–716 (2022). https://doi.org/10.1007/s10270-021-00916-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10270-021-00916-8














 Transitions
Transitions Probabilistic junctions
Probabilistic junctions
 , which defines DTMC as the type for this example. Other available model types are MDP, continuous-time Markov chain (CTMC), and probabilistic timed automata (PTA).
, which defines DTMC as the type for this example. Other available model types are MDP, continuous-time Markov chain (CTMC), and probabilistic timed automata (PTA). , which declares one constant
, which declares one constant  -
- , which declare an integer variable
, which declare an integer variable  , which defines a formula
, which defines a formula  -
- , which indicate the definition of modules
, which indicate the definition of modules  , which declares a local boolean variable
, which declares a local boolean variable  . The command has an action
. The command has an action  -
- , which define two rewards: a reward on line
, which define two rewards: a reward on line  associated with states, and another on
associated with states, and another on  associated with transitions. Rewards, which are used in properties (but defined within models) to allow reasoning about a wide range of quantitative measures, assign particular values to certain states or transitions. If a reward has an action, then this applies to all transitions labelled by that action.
associated with transitions. Rewards, which are used in properties (but defined within models) to allow reasoning about a wide range of quantitative measures, assign particular values to certain states or transitions. If a reward has an action, then this applies to all transitions labelled by that action.















 corresponds to EX-S1 above,
corresponds to EX-S1 above, corresponds to EX-S2 for the request from the parent state, if any,
corresponds to EX-S2 for the request from the parent state, if any, corresponds to EX-S2 for the request from a transition,
corresponds to EX-S2 for the request from a transition, corresponds to EX-S3,
corresponds to EX-S3, corresponds to EX-S4,
corresponds to EX-S4, corresponds to EX-S5,
corresponds to EX-S5, corresponds to EX-S6.
corresponds to EX-S6.
 is a pair characterised by applying
is a pair characterised by applying  to
to  (see Rule 9 in “Appendix
(see Rule 9 in “Appendix  is a pair, whose first element
is a pair, whose first element  is a set either empty or containing a new
is a set either empty or containing a new  , and whose second element
, and whose second element  is a set of the new transitions to and from
is a set of the new transitions to and from  is a triple of sets: a set of junctions, and two sets of transitions defined by an application of the function
is a triple of sets: a set of junctions, and two sets of transitions defined by an application of the function  . This function is concerned with the combination of incoming and outgoing transitions of normal junctions, if needed. The first argument of the application is a set of normal junctions, characterised by a function
. This function is concerned with the combination of incoming and outgoing transitions of normal junctions, if needed. The first argument of the application is a set of normal junctions, characterised by a function  (see Rule 10 in “Appendix
(see Rule 10 in “Appendix  that are to or from junctions in the first argument; this is characterised by a generalised union of a relational image. The function application
that are to or from junctions in the first argument; this is characterised by a generalised union of a relational image. The function application  identifies the set of incoming and outgoing transitions of a given node
identifies the set of incoming and outgoing transitions of a given node  that are in the set of transitions
that are in the set of transitions  . So the relational image of
. So the relational image of  under
under  is the set of sets of all incoming and outgoing transitions of the normal junctions. A generalised union
is the set of sets of all incoming and outgoing transitions of the normal junctions. A generalised union  combines all these sets. The first and seconds elements
combines all these sets. The first and seconds elements  and
and  of the result of the application of
of the result of the application of  contain the junctions in the first argument and the transitions in the second argument removed by normalisation, and the third element
contain the junctions in the first argument and the transitions in the second argument removed by normalisation, and the third element  contains the new transitions arising from the normalisation.
contains the new transitions arising from the normalisation. is a set of pairs defined by applying
is a set of pairs defined by applying  (Rule 13 in “Appendix
(Rule 13 in “Appendix  (
( ), to the new transitions identified by
), to the new transitions identified by  (that is, in
(that is, in  ), and to the transitions from the new loop states (identified by
), and to the transitions from the new loop states (identified by  ), but not to the transitions removed by the normalisation (that is, in
), but not to the transitions removed by the normalisation (that is, in  ).
). is a set of normalised composite states resulting from the application of a normalisation function
is a set of normalised composite states resulting from the application of a normalisation function  for states to each node
for states to each node  of the machine that is a state (
of the machine that is a state ( ) and has nodes itself (
) and has nodes itself ( ). These are the composite states. Normalisation of composite states by
). These are the composite states. Normalisation of composite states by  is similar to that of state machines except that composite states do not declare variables, operations, and events. So the formalisation is simpler and omitted here; it can be found in the RoboChart reference manual [
is similar to that of state machines except that composite states do not declare variables, operations, and events. So the formalisation is simpler and omitted here; it can be found in the RoboChart reference manual [ is the set of nodes
is the set of nodes  of
of  that are neither the normal junctions removed by the normalisation in
that are neither the normal junctions removed by the normalisation in  (that is,
(that is,  ) nor composite states. They are unaffected by normalisation.
) nor composite states. They are unaffected by normalisation. is a set of quadruples: sets of constants, variables, and modules, and a relation defined by an application of
is a set of quadruples: sets of constants, variables, and modules, and a relation defined by an application of  (Rule 4) to a controller in the set
(Rule 4) to a controller in the set  of nodes of
of nodes of  . The relation establishes a mapping from operations provided by the platform and required by the controller, to PRISM actions corresponding to these operations.
. The relation establishes a mapping from operations provided by the platform and required by the controller, to PRISM actions corresponding to these operations. is used in the translation of the robotic platform. It is the set of events of the robotic platform used to communicate data to a controller. These are the events
is used in the translation of the robotic platform. It is the set of events of the robotic platform used to communicate data to a controller. These are the events  that are the source of a connection
that are the source of a connection  in the set
in the set  of connections of
of connections of  whose source
whose source  is a platform and whose type
is a platform and whose type  is not
is not  . So, data (of type
. So, data (of type  ) is communicated.
) is communicated. is a triple: a set of constants, a set of variables, and a module defined by an application of
is a triple: a set of constants, a set of variables, and a module defined by an application of  (Rule 3) for robotic platforms. This function is applied to the platform of
(Rule 3) for robotic platforms. This function is applied to the platform of  , identified by a unique (
, identified by a unique ( ) node
) node  that is in the set
that is in the set  of nodes of
of nodes of  and is a robotic platform. Extra arguments are the set of events
and is a robotic platform. Extra arguments are the set of events  and the relation from the translation of controllers, formed by generalised union of the relation
and the relation from the translation of controllers, formed by generalised union of the relation  for each controller. As said, the events used to send data to a controller are represented by a shared variable in the platform module. (Its value is nondeterministically chosen and copied in modules for state machines upon synchronisation.) So, the definition of the module for a platform requires the identification of these events, which are in the set
for each controller. As said, the events used to send data to a controller are represented by a shared variable in the platform module. (Its value is nondeterministically chosen and copied in modules for state machines upon synchronisation.) So, the definition of the module for a platform requires the identification of these events, which are in the set  . The relation identifies how the translation of the controllers (or, more specifically, of their state machines) have mapped their required operations to PRISM actions. The module for the platform synchronises on these actions.
. The relation identifies how the translation of the controllers (or, more specifically, of their state machines) have mapped their required operations to PRISM actions. The module for the platform synchronises on these actions. is a set of constants resulting from the function
is a set of constants resulting from the function  , omitted here.
, omitted here. is a set of pairs of sets. The first and second elements of each pair are a set of constants and a set of variables, translated from each variable list
is a set of pairs of sets. The first and second elements of each pair are a set of constants and a set of variables, translated from each variable list  in
in  by the function
by the function  (omitted here). The lists of variables provided by
(omitted here). The lists of variables provided by  are identified using the function
are identified using the function  whose definition is omitted here. A variable list consists of a set of constant and variable declarations. The translation of variable declarations maps the RoboChart types to the PRISM types, and translates the initial value given, if any, accordingly.
whose definition is omitted here. A variable list consists of a set of constant and variable declarations. The translation of variable declarations maps the RoboChart types to the PRISM types, and translates the initial value given, if any, accordingly. is a set of PRISM declarations of variables like
is a set of PRISM declarations of variables like  from
from  . In the rules, we use black typewriter font, like in
. In the rules, we use black typewriter font, like in  is for a variable, whose name is based on the name of
is for a variable, whose name is based on the name of  in PRISM (
in PRISM ( ) with a prefix (
) with a prefix ( is obtained by translating the type
is obtained by translating the type  of
of  using
using  .
. is a set of sets of commands for each event
is a set of sets of commands for each event  of
of  , that are identified using the function
, that are identified using the function  whose definition is omitted here. If
whose definition is omitted here. If  is an output event (that is,
is an output event (that is,  ), a set of commands is included in
), a set of commands is included in  to define a nondeterministic choice of the values for the corresponding variable
to define a nondeterministic choice of the values for the corresponding variable  . Each command corresponds to one possible value
. Each command corresponds to one possible value  in the event type
in the event type  . The action of the command (inside square brackets) is the name
. The action of the command (inside square brackets) is the name  of the event
of the event  , the guard is
, the guard is  to
to  . The commands on lines
. The commands on lines  -
- in Fig.
in Fig.  is not an event for output, a set containing one command is included in
is not an event for output, a set containing one command is included in  . It has
. It has  for its action and
for its action and  is obtained in this way.
is obtained in this way. is a set of PRISM commands. Each command corresponds to one PRISM action
is a set of PRISM commands. Each command corresponds to one PRISM action  in the range
in the range  of the relation
of the relation  . As previously mentioned,
. As previously mentioned,  records a mapping from operations provided by the robotic platform (and possibly called in state machines) to PRISM actions corresponding to these operations. We use this relation to translate calls to the operations in state machines into communications with the environment (modelled by the module for the robotic platform) that provides the operations. Our PRISM models, as explained in Sect.
records a mapping from operations provided by the robotic platform (and possibly called in state machines) to PRISM actions corresponding to these operations. We use this relation to translate calls to the operations in state machines into communications with the environment (modelled by the module for the robotic platform) that provides the operations. Our PRISM models, as explained in Sect.  is given below.
is given below.  . For each action
. For each action  in the range of
in the range of  (for our example,
(for our example,  , is included in
, is included in  . This command in the platform module synchronises with the commands in a machine module whose action is also
. This command in the platform module synchronises with the commands in a machine module whose action is also  , to allow the environment to record the calls to the operation. The arguments of these calls are recorded in local variables of the machine modules. The details of the declaration and use of these variables are presented in Rule 5. Both the guard and the updates of the command are
, to allow the environment to record the calls to the operation. The arguments of these calls are recorded in local variables of the machine modules. The details of the declaration and use of these variables are presented in Rule 5. Both the guard and the updates of the command are  and no variable is changed upon synchronisation. For our example,
and no variable is changed upon synchronisation. For our example,  contains the commands in Fig.
contains the commands in Fig.  is a PRISM module with the name
is a PRISM module with the name  of
of  ,
,  , and commands obtained by the generalised union of the commands in
, and commands obtained by the generalised union of the commands in  and
and  .
.

 is a set of PRISM declarations of variables (similar to
is a set of PRISM declarations of variables (similar to  from
from  . Each declaration in
. Each declaration in  is for a variable whose name is based on the name of
is for a variable whose name is based on the name of  in PRISM (
in PRISM ( ) with a prefix (
) with a prefix ( is obtained by translating the type
is obtained by translating the type  of
of  using the function
using the function  .
. is a quadruple of an integer, and sets of constants, variables, and commands, resulting from the application of
is a quadruple of an integer, and sets of constants, variables, and commands, resulting from the application of  (Rule 6) to
(Rule 6) to  to translate its nodes and transitions. This function is concerned with the translation of a
to translate its nodes and transitions. This function is concerned with the translation of a  to indicate the control flow has reached
to indicate the control flow has reached  to indicate the control flow has reached both
to indicate the control flow has reached both  indicates the first integer not yet used to declare a constant for a lock value. In Rule 5,
indicates the first integer not yet used to declare a constant for a lock value. In Rule 5,  is applied to the whole machine
is applied to the whole machine  , which, by convention, is owned by itself. The third argument is just
, which, by convention, is owned by itself. The third argument is just  , because the control flow is always in the machine. Finally, the final argument indicates that declarations of lock variables can use integers from
, because the control flow is always in the machine. Finally, the final argument indicates that declarations of lock variables can use integers from  . (We recall that
. (We recall that  is used for the
is used for the  is the next available number that can be used to number a transition. So the maximum transition number is
is the next available number that can be used to number a transition. So the maximum transition number is  , which is used for the upper limit of the interval type of the
, which is used for the upper limit of the interval type of the  -
- . The second and third elements identify sets of constant and variable declarations, like those on lines
. The second and third elements identify sets of constant and variable declarations, like those on lines  -
- and the
and the  . These are the constants and variables used in the encoding of the control flow of the node. The fourth element is the set of all commands in the module.
. These are the constants and variables used in the encoding of the control flow of the node. The fourth element is the set of all commands in the module. is a set of variable declarations for each parameter
is a set of variable declarations for each parameter  of an operation
of an operation  required by
required by  . The variable has a fresh name
. The variable has a fresh name  and is of type
and is of type  obtained by translating the type
obtained by translating the type  of
of  using the function
using the function  . For the operation
. For the operation  is
is  .
. declares a PRISM constant associated with number 0 and representing the inactive status of
declares a PRISM constant associated with number 0 and representing the inactive status of  .
. declares the program counter variable for
declares the program counter variable for  ; its type is a range from 0 to the maximum state number (that is,
; its type is a range from 0 to the maximum state number (that is,  ). If
). If  is a machine, the counter is set to a state in PRISM corresponding to the initial junction
is a machine, the counter is set to a state in PRISM corresponding to the initial junction  (that is, a node
(that is, a node  of
of  that is initial,
that is initial,  ) identified by
) identified by  , the name of
, the name of  in PRISM. Otherwise,
in PRISM. Otherwise,  is a composite state and inactive initially. So the counter is set to
is a composite state and inactive initially. So the counter is set to  .
. is the declaration of the exit variable for
is the declaration of the exit variable for  .
. is a triple containing a state number, a set of constants, and a set of commands to record the exit of
is a triple containing a state number, a set of constants, and a set of commands to record the exit of  . The first element
. The first element  is the first state number available. Examples include the numbers on lines
is the first state number available. Examples include the numbers on lines  -
- in Fig.
in Fig.  -
- , for
, for  is a state machine (
is a state machine ( ), there is no need for it to exit, and, therefore, the state number is
), there is no need for it to exit, and, therefore, the state number is  to record the use of
to record the use of  for
for  , making
, making  the next available number for states, and the sets of constants and commands are empty (
the next available number for states, and the sets of constants and commands are empty ( ). Otherwise, the triple is defined by an application of the function
). Otherwise, the triple is defined by an application of the function  (omitted here) , which is used to generate the two commands of the module on lines
(omitted here) , which is used to generate the two commands of the module on lines  -
- of Fig.
of Fig.  has an exit action. Its third argument is the name of
has an exit action. Its third argument is the name of  (that is,
(that is,  ). Its last argument
). Its last argument  is the next available state number.
is the next available state number. is also a triple defined by the application of the function
is also a triple defined by the application of the function  (whose definition is omitted here). This function is concerned with the encoding of the exit of all substates (that is, all the subnodes
(whose definition is omitted here). This function is concerned with the encoding of the exit of all substates (that is, all the subnodes  of
of  of
of  that are
that are  ). The fifth argument of the application is the next available state number as recorded in
). The fifth argument of the application is the next available state number as recorded in  . The first element
. The first element  is the new available number. The second element
is the new available number. The second element  and the third element
and the third element  are sets of constants and commands encoding the exit of these substates. This function is used to generate the commands on lines
are sets of constants and commands encoding the exit of these substates. This function is used to generate the commands on lines  -
- and the related constants on lines
and the related constants on lines  -
- in Fig.
in Fig.  -
- in Fig.
in Fig.  is a triple defined by applying
is a triple defined by applying  (omitted) to a set of states that have an entry action (that is, whose action
(omitted) to a set of states that have an entry action (that is, whose action  is not
is not  ). The fourth argument of the application is the next available state number,
). The fourth argument of the application is the next available state number,  . The first element
. The first element  is the new state number, and
is the new state number, and  and
and  are sets of constants and commands used to encode the entering of these substates. This function is used for example, to generate the command on line
are sets of constants and commands used to encode the entering of these substates. This function is used for example, to generate the command on line  in Fig.
in Fig.  is a pair defined by the application of
is a pair defined by the application of  to all subnodes
to all subnodes  of
of  and to the current available state number (
and to the current available state number ( ). This function characterises a set of constants (in
). This function characterises a set of constants (in  ) representing states in PRISM that correspond to subnodes of
) representing states in PRISM that correspond to subnodes of  like
like  is the new state number.
is the new state number. is a quadruple of the next available state and transition numbers, a set of constants, and a set of commands resulting from the translation of the transitions from the nodes
is a quadruple of the next available state and transition numbers, a set of constants, and a set of commands resulting from the translation of the transitions from the nodes  of
of  by the application of
by the application of  (see Sect.
(see Sect.  is a quadruple resulting from applying the function
is a quadruple resulting from applying the function  (omitted) to the set of composite states of
(omitted) to the set of composite states of  , that is, each node
, that is, each node  that is a
that is a  and is composite (
and is composite ( ). The fifth argument representing the available transition number is from
). The fifth argument representing the available transition number is from  . The function
. The function  applies
applies  to each composite state recursively.
to each composite state recursively. results from applying
results from applying  to the actual set
to the actual set  of transitions of
of transitions of  that are from
that are from  . This function defines the cumulative result of applying
. This function defines the cumulative result of applying  (Rule 8), which translates each transition in
(Rule 8), which translates each transition in  . The commands on lines
. The commands on lines  -
- and the constants on lines
and the constants on lines  -
- in Fig.
in Fig.  when applied to the transition from
when applied to the transition from  to
to  -
- and
and  -
- , and the constants on lines
, and the constants on lines  -
- are the result of applying
are the result of applying  to the transitions from
to the transitions from  to
to  also gives rise to an update: for our example, the three updates on line
also gives rise to an update: for our example, the three updates on line  for the three transitions from
for the three transitions from 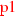 to
to  is a command in PRISM encoding the choice made at
is a command in PRISM encoding the choice made at  probabilistically. Its guard ensures that the counter variables indicate that the current state is that identified by the node
probabilistically. Its guard ensures that the counter variables indicate that the current state is that identified by the node  . We have a conjunction of two terms. The first,
. We have a conjunction of two terms. The first,  , is itself a conjunction of the boolean expressions in the argument
, is itself a conjunction of the boolean expressions in the argument  , which are equalities regarding the counter variables for all states and machine containing
, which are equalities regarding the counter variables for all states and machine containing  . The second conjunct requires that the counter variable for the state or machine containing
. The second conjunct requires that the counter variable for the state or machine containing  , whose name is given by the argument
, whose name is given by the argument  , has the value
, has the value  for the probabilistic junction identified by
for the probabilistic junction identified by  . The updates of
. The updates of  are those in the set
are those in the set  .
. is the name of the constant representing the final state in PRISM for the encoding of the action
is the name of the constant representing the final state in PRISM for the encoding of the action  . If the target
. If the target  of
of  is a state with an entry action, the encoding of
is a state with an entry action, the encoding of  leads to the start state of that entry action, represented by the constant named
leads to the start state of that entry action, represented by the constant named  , such as
, such as  in Fig.
in Fig.  is just the identifier
is just the identifier  of
of  in PRISM.
in PRISM. is a set of assignments to encode entering the target of
is a set of assignments to encode entering the target of  when it is a state without entry action. If it is a composite state, we need to update the counter variable
when it is a state without entry action. If it is a composite state, we need to update the counter variable  of that state to the constant representing its initial junction
of that state to the constant representing its initial junction  . If the target is a simple state,
. If the target is a simple state,  is completed by entering its target, and so the lock variable
is completed by entering its target, and so the lock variable  is set to be free
is set to be free  .
. is a quadruple defined by application of
is a quadruple defined by application of  to the action
to the action  of
of  . The fifth argument
. The fifth argument  of this function application means the start state of the encoding of
of this function application means the start state of the encoding of  is not specified, and so its translation generates a fresh name for the constant for that state. For the action of the transition from
is not specified, and so its translation generates a fresh name for the constant for that state. For the action of the transition from  to
to  . The sixth argument is a set of PRISM assignments containing an update of the counter
. The sixth argument is a set of PRISM assignments containing an update of the counter  for the state or machine of the action to
for the state or machine of the action to  and
and  .
.

 is a new state specified by a function
is a new state specified by a function  with a fresh name specified by
with a fresh name specified by 
 . The function
. The function  characterises a
characterises a  , but whose nodes, transitions, and actions are empty. So, it is a simple state without transitions or actions. We note that it is possible to directly define what
, but whose nodes, transitions, and actions are empty. So, it is a simple state without transitions or actions. We note that it is possible to directly define what  specifies using a class instantiation
specifies using a class instantiation  . We define
. We define  , however, to facilitate reuse and hide other fields of the class
, however, to facilitate reuse and hide other fields of the class  for simplicity. The introduction of the function
for simplicity. The introduction of the function  is similar.
is similar. is a new self-transition for
is a new self-transition for  , defined by a function
, defined by a function  with three parameters: the name, the source, and the target of the new transition. Other components of the transitions are
with three parameters: the name, the source, and the target of the new transition. Other components of the transitions are  is a set of new transitions. For each state
is a set of new transitions. For each state  without any outgoing transitions, this set includes one transition from
without any outgoing transitions, this set includes one transition from  to the new state
to the new state  .
. is a set of incoming transitions
is a set of incoming transitions  of
of  that can be combined (and so removed). This is characterised by
that can be combined (and so removed). This is characterised by  .
. has all other incoming transitions of
has all other incoming transitions of  .
. is the set of outgoing transitions from
is the set of outgoing transitions from  .
. is a set of new transitions that combine each incoming transition
is a set of new transitions that combine each incoming transition  from
from  and each outgoing transition
and each outgoing transition  from
from  . The new transition has a unique name
. The new transition has a unique name  , the same source as
, the same source as  , the same target of
, the same target of  , the trigger of
, the trigger of  , and the action of
, and the action of  . The condition is the conjunction of that of
. The condition is the conjunction of that of  and that of
and that of  .
. is the constant encoding the start of the statement
is the constant encoding the start of the statement  . If the argument
. If the argument  is not
is not  , the constant is just
, the constant is just  . Otherwise, it is a constant with a fresh name given by
. Otherwise, it is a constant with a fresh name given by  and associated with
and associated with  .
. is a set of assignments. If
is a set of assignments. If  is an output event (its communication is of type
is an output event (its communication is of type  ) or a synchronisation (its communication is of type
) or a synchronisation (its communication is of type  ), it contains an assignment to update the event related variable
), it contains an assignment to update the event related variable  from the value
from the value  carried by the event, to encode communication. Otherwise, it is empty.
carried by the event, to encode communication. Otherwise, it is empty. contains an assignment to update the counter variable to the start state for the encoding of
contains an assignment to update the counter variable to the start state for the encoding of  and assignments in
and assignments in  explained above.
explained above. is also a set of assignments. If
is also a set of assignments. If  is an input event (that is, its communication is of type
is an input event (that is, its communication is of type  ), this set contains an assignment to update the input variable
), this set contains an assignment to update the input variable  to the value of the variable used for output, to encode the input communication. Otherwise,
to the value of the variable used for output, to encode the input communication. Otherwise,  is empty since there is no data exchange.
is empty since there is no data exchange. is a command. Its action is the name of the event of
is a command. Its action is the name of the event of  given by
given by  . Its guard ensures that the counter variables indicate that the current state is that identified by
. Its guard ensures that the counter variables indicate that the current state is that identified by  . We have a conjunction of two terms. The first,
. We have a conjunction of two terms. The first,  , is itself a conjunction of the boolean expressions in the argument
, is itself a conjunction of the boolean expressions in the argument  , which are equalities regarding the counter variables for all states and state machine containing
, which are equalities regarding the counter variables for all states and state machine containing  . The second conjunct requires that the counter variable for the state or machine containing
. The second conjunct requires that the counter variable for the state or machine containing  , whose name is given by the argument
, whose name is given by the argument  , has the value
, has the value  for the encoding of
for the encoding of  . The update of
. The update of  has probability
has probability  to update the counters to the final state of the encoding of
to update the counters to the final state of the encoding of  and
and  explained above.
explained above.