Abstract
In this paper, we present a novel technique to automatically synthesize consistent, diverse and structurally realistic domain-specific graph models. A graph model is (1) consistent if it is metamodel-compliant and it satisfies the well-formedness constraints of the domain; (2) it is diverse if local neighborhoods of nodes are highly different; and (1) it is structurally realistic if a synthetic graph is at a close distance to a representative real model according to various graph metrics used in network science, databases or software engineering. Our approach grows models by model extension operators using a hill-climbing strategy in a way that (A) ensures that there are no constraint violation in the models (for consistency reasons), while (B) more realistic candidates are selected to minimize a target metric value (wrt. the representative real model). We evaluate the effectiveness of the approach for generating realistic models using multiple metrics for guidance heuristics and compared to other model generators in the context of three case studies with a large set of real human models. We also highlight that our technique is able to generate a diverse set of models, which is a requirement in many testing scenarios.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Motivation
Automated graph model generation has recently become a key research component in many areas of software and systems engineering. As object-oriented programs are frequently represented as graphs (with objects as nodes and pointers as edges), automatically generated models may serve as complex test stubs [38, 48]. In the assurance of smart cyber-physical systems (CPS), prototypical test contexts are synthesized in the form of graph models [1, 30, 47]. Auto-generated graphs can also help the testing of graph databases [10].
In testing scenarios, synthetic graph models frequently need to be consistent to satisfy the complex constraints of the target domain (captured by OCL constraints [55] or graph patterns [81, 82]). Consistent model generators like Alloy [32, 80], Formula [33, 36], SDG [75, 76] and Viatra Solver [65, 67] are able to automatically derive well-formed models for a given domain specification. These generators either use an underlying logic solver (like SAT solvers [19, 42] or SMT solvers [51]), or use logic reasoning or search-based techniques directly on the level of graphs [69, 75, 76].
The diversity of a synthetic graph model is also of high importance in testing. Unfortunately, real models created by domain experts fail to provide sufficient diversity for testing purposes [70]. Furthermore, only very recent consistent model generation approaches [68] managed to successfully demonstrate the diversity of automatically derived set of models. In fact, past research [35] has shown that diversity is very problematic for logic solver-based approaches.
1.2 Problem statement
Realistic synthetic models have been used in testing software-intensive cyber-physical systems in [1, 3, 18, 30, 75, 76] as well as testing software tools (e.g., design or analysis tools) used for engineering safety-critical systems [14, 22, 33, 37, 56, 74, 90]. For example, realistic test models used for autonomous cars represent test environments [1, 30] where unrealistic test cases (e.g., obscure traffic situations) are considered false positives. Failures caused by realistic models are more severe, as they have more chance to happen on real workload. Moreover, it is easier for a test engineer to evaluate the outcome of test on a realistic model. Furthermore, real engineering models may not be available for testing purposes due to the protection of intellectual property rights.
The key challenge addressed in the paper is to automatically synthesize domain-specific graph models that are simultaneously consistent, diverse and realistic.
However, there is no guarantee that consistent or diverse synthetic models are also realistic at the same time. In fact, as measured in [3, 35, 70], solver-based test generators tend to generate simple, highly symmetric models (e.g. isolated nodes with the same type). Advanced search-based approaches [75, 76] can incorporate the realistic distribution of node types, but the distribution of node types or attribute values is still only one factor of the realistic nature for a graph model.
1.3 Characterization of structurally realistic graph models
Realistic models are domain-specific, i.e., graphs of biomedical systems can be very different from graphs of social networks or software models. An engineer can easily distinguish an auto-generated model from a manually designed model by inspecting key attributes (e.g. names), but the same task becomes more challenging if one can only inspect the (typed) graph structure but none of the attributes. In fact, the problem of providing realistic attribute values in a model is orthogonal to ensuring that a model is structurally realistic.
The characterization of structurally realistic graphs has been studied in different domains (including network science, databases, or software engineering [11, 12, 31, 54]), and it is frequently based on the use of various graph metrics, many of which were systematically collected in [78]. Informally, a graph model is considered to be structurally realistic if the values of various graph metrics are at close distance to the values of the same metrics for a representative real (human) model in a given domain.
1.4 Contributions
In this paper, we propose a novel technique to generate consistent, diverse and structurally realistic domain-specific graph models. In particular:
-
We measure various structural graph metrics used in [75, 76, 78] for a large set of real graph models in three domains of industrial relevance.
-
We use statistical distance metrics to domain-independently measure the similarity between the values of graph metrics for a pair of models.
-
We precisely characterize and differentiate the consistent, diverse and realistic nature of graph models.
-
We propose a consistent, diverse and realistic graph generator by extending an open-source graph solver to guide the generation toward more realistic models along various graph metrics.
-
We conduct experimental evaluation in three domains with real data to evaluate various guidance strategies.
-
We also compare the realistic nature and the diversity of graphs derived by using our approach with other model generators.
1.5 Added value
In each application domain, the realistic nature of models can possibly be characterized by different graph metrics, or the judgment of domain experts. To make our approach domain-customizable, we only assume that (relevant statistics of) a representative real model is provided to the generator (e.g., elected by domain experts or obtained by some combination of statistical and clustering techniques). Then, the realistic nature of synthetic models is evaluated by measuring statistical distance from this representative model by using generic or domain-specific graph metrics.
Our paper is the first approach to generate complex (connected) graphs that are simultaneously consistent (i.e., satisfy first-order logic constraints), diverse (wrt. various diversity metrics) and structurally realistic (i.e., similar to representative real models wrt. some target graph metrics).
In order to achieve this, our approach builds on and extends [67, 84] (where a consistent graph solver was presented) and [68] (where the diversity of the generated models were evaluated in various testing scenarios). Thanks to the mathematical proofs of consistency and diversity in those papers (which are not repeated here), we can still enforce that the derived models are consistent and structurally diverse, while the current paper also ensures reasonably high statistical resemblance to real models. In fact, our experimental evaluation investigates to what extent the derived models are consistent, realistic and diverse.
2 Preliminaries
First, we provide an overview of some core concepts, such as metamodels and (graph) models, graph predicates, graph shapes and various distance metrics.
2.1 Models and metamodels
In domain-specific modeling tools, like Capella, Artop, Yakindu, or Papyrus, a domain specification (DS) typically contains a metamodel and a set of well-formedness (WF) constraints. A metamodel defines the main concepts and relations in a domain and specifies the underlying graph structure of the models. This paper uses Eclipse Modeling Framework (EMF) [79] for metamodeling, which is widely used in the industrial modeling tools above. In EMF, concepts of the metamodels are defined with a set of EClasses (or simply classes, denoted with  ) and EReferences (references, denoted with
) and EReferences (references, denoted with  ).
).
Example 1
Core domain modeling concepts will be illustrated in the context of Yakindu Statecharts [88], which is an industrial DSL for developing reactive, event-driven systems. A simplified metamodel for Yakindu state machines is illustrated in Fig. 1. A
 consists of
consists of
 s, which in turn contain states (called
s, which in turn contain states (called
 es) and
es) and
 s. The abstract state
s. The abstract state
 is further refined into
is further refined into
 s (like
s (like
 or
or
 ) and
) and
 s (like
s (like
 ,
,
 or
or
 ).
).
An instance model can be represented as a logic structure \(M = \langle {{\mathcal {O}}_{M}}, {{\mathcal {I}}_{M}} \rangle \) of a metamodel  , where \({\mathcal {O}}_{M}\) is the finite set of individuals in the model (i.e., the objects) and
, where \({\mathcal {O}}_{M}\) is the finite set of individuals in the model (i.e., the objects) and  provides an interpretation for all
provides an interpretation for all  classes and
classes and  references. In the context of a model M, we use
references. In the context of a model M, we use  to denote the truth value of whether an object o is an instance of a class
to denote the truth value of whether an object o is an instance of a class  , and
, and  to denote the truth value of whether there is a reference
to denote the truth value of whether there is a reference  from \(o_1\) to \(o_2\) (\(o,o_1,o_2\in {\mathcal {O}}_{M}\)). Let \({\mathcal {M}}_ MM \) denote the set of all (instance) models of a metamodel \( MM \).
from \(o_1\) to \(o_2\) (\(o,o_1,o_2\in {\mathcal {O}}_{M}\)). Let \({\mathcal {M}}_ MM \) denote the set of all (instance) models of a metamodel \( MM \).
Example 2
Figure 2 illustrates two example (partial) statecharts \(M_1\) and \(M_2\). First, \(M_1\) contains a simple model with a single
 s1 in a
s1 in a
 r with a loop
r with a loop
 t1 where
t1 where  and
and  . For the sake of clarity, references
. For the sake of clarity, references
 - and
- and
 are omitted from Fig. 2. Model \(M_2\) extends \(M_1\) with an additional
are omitted from Fig. 2. Model \(M_2\) extends \(M_1\) with an additional
 ,
,
 , and two
, and two
 s.
s.
2.2 Graph predicates
Graph predicates are widely used to query different properties of a model [83]. In many industrial modeling tools, WF constraints are captured either by OCL constraints [55] or graph patterns (GP) [81] where the latter captures errors as structural conditions over an instance model as paths in a graph. To have a unified and precise handling of evaluating WF constraints, we use a tool-independent logic representation (which was influenced by [61, 66, 69]) that covers the key features of concrete graph pattern languages and a first-order fragment of OCL. In our current implementation, we used the graph pattern language of Viatra [81, 82], where error patterns describe malformedness of the model, and derived logic predicates in accordance with [66].
2.2.1 Syntax
A first-order logic (FOL) graph predicate \(\varphi (v_1, \ldots , v_n)\) over (object) variables \(v_1, \ldots , v_n\) (called formal parameters, abbreviated as \({\bar{v}}\)) can be inductively constructed by using class and relation predicates  and
and  (as literals), equality check \(=\), standard FOL connectives \(\lnot \), \(\vee \), \(\wedge \), and quantifiers \(\exists \) and \(\forall \).
(as literals), equality check \(=\), standard FOL connectives \(\lnot \), \(\vee \), \(\wedge \), and quantifiers \(\exists \) and \(\forall \).
2.2.2 Semantics
A graph predicate \(\varphi (v_1,\ldots ,v_n)\) with formal parameters \(v_1,\ldots ,v_n\) can be evaluated on model M along a variable binding \(Z:\{v_1,\ldots ,v_n\} \rightarrow {\mathcal {O}}_{M}\) from variables to objects in M. The truth value of \(\varphi \) can be evaluated over model M along the mapping Z (denoted by \({[\![ \varphi (v_1,\ldots ,v_n) ]\!]}^{M}_Z\)) in accordance with the semantic rules defined in Fig. 3.
A variable binding Z where the predicate \(\varphi \) is evaluated to  over M (i.e.,
over M (i.e.,  ) is called a \(match \). Otherwise, if there are no bindings Z to satisfy a predicate, i.e.,
) is called a \(match \). Otherwise, if there are no bindings Z to satisfy a predicate, i.e.,  for all Z, then the predicate \(\varphi \) is evaluated to
for all Z, then the predicate \(\varphi \) is evaluated to  over M. Graph query engines like [81] can retrieve (one or all) matches of a graph predicate over a model. In our current work, such graph predicates will be used uniformly when capturing consistency constraints as well as diversity and realistic metrics.
over M. Graph query engines like [81] can retrieve (one or all) matches of a graph predicate over a model. In our current work, such graph predicates will be used uniformly when capturing consistency constraints as well as diversity and realistic metrics.
2.3 Graph shapes for diversity
Graph shaping [60, 61] is an abstraction technique that extracts structural properties of graphs. As such, shaping techniques can be used to measure structural similarity between graphs [65, 68, 70]: if two graphs have the same shape, then they are considered structurally similar; otherwise, they are considered different.
In this paper, we use neighborhood shapes [60] to characterize local structural properties of objects for a range of size r. More precisely, the neighborhood of an object describes all unary (class) and binary (reference) relations of objects within the given range r. Neighborhood shapes can also be interpreted as refined types where the original classes are split into multiple subclasses based on the difference in the incoming and outgoing references.
In neighborhood shapes, each node is characterized with a predicate \(S^{r}(v)\) (for a range r), which has three components: (i) the shape of v for one less range \(S^{r-1}(v)\), (ii) the neighborhoods of objects \(o_1,\ldots ,o_n\) via outgoing references  , and (iii) the neighborhoods of objects \(i_1,\ldots ,i_m\) via incoming references
, and (iii) the neighborhoods of objects \(i_1,\ldots ,i_m\) via incoming references  .
.
Formally, a neighborhood shape for range r is defined as a node predicate \(N^{r}(v)\) in the following format:

Semantically, neighborhood predicates entail (imply) a wide range of literals (elementary predicates):
and the negation of some other literals:
Therefore, we can estimate the number of predicates that can differentiate two models by using neighborhood predicates. In this paper, we will use neighborhood shapes to evaluate the diversity of models, which is shown to be a good diversity metric in mutation testing scenarios [68, 70].
2.4 Metric distances over distributions
A generic graph metric takes a graph model and calculates a value (either a single numeric value or a complex distribution).
Definition 1
A graph metric with range of set V is a function \(\mathop {m}:{\mathcal {M}}_ MM \rightarrow V\).
The most simple form of metric is a scalar metric function, which maps graphs to real numbers:
Definition 2
A scalar metric is a model function \(m_s:{\mathcal {M}}_ MM \rightarrow {\mathbb {R}}\).
Next, a categorical distribution maps each node in the graph a value from a given category for each object.
Definition 3
A categorical distribution metric of a function \(f:{\mathcal {O}}_{M} \rightarrow C\) over the objects of a model M with categories \(C=\{c_1,...,c_n\}\) is a graph metric:
And finally, a cumulative distribution maps a numerical value to each node.
Definition 4
A cumulative distribution function of an object function \(f:{\mathcal {O}}_{M} \rightarrow {\mathbb {R}}\) over the objects of a model M is a graph metric:
In this paper, a graph model is considered to be more realistic if it is closer to real graph models with respect to some distance function, which measures how significant the difference is between two graphs [5]. Note that we require the use of pseudo-distance functions; otherwise, a model at zero distance would reveal the original graph model. Moreover, we further require that the distance function should also be continuous.
Definition 5
(Metric distance) A metric distance between two distributions over a domain V is a function \(d:V\times V \rightarrow {\mathbb {R}}\) that satisfies the following properties:
-
1.
\(d(v_1,v_2)\ge 0\),
-
2.
\(d(v,v)=0\),
-
3.
\(d(v_1,v_2)=0 \Rightarrow v_1 = v_2\),
-
4.
\(d(v_1,v_2)=d(v_2,v_1)\), and
-
5.
\(d(v_1,v_2)+d(v_2,v_3)\ge d(v_1,v_3)\).
Without 3. d is a pseudo-distance.
As a mathematical consequence, a distance d over a graph metric m with values in range V also serves as a pseudo-distance for models, and it is calculated as \(d(m(M_1),m(M_2))\). In the paper, we use (a) the Kolmogorov–Smirnov (KS) distance (as proposed in [78]) between continuous metrics defined as cumulative distribution functions, (b) the Manhattan distance for categorical distributions, and (c) absolute deviation for scalar metrics.
Definition 6
The Kolmogorov–Smirnov (KS) distance measures the maximal difference between two cumulative distributions. Formally, the KS distance between two functions \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\) and \(g:{\mathbb {R}}\rightarrow {\mathbb {R}}\) is
We compare cumulative distributions \( cdf _{f}^M(x)\) and \( cdf _{f}^N(x)\) of a graph property f between models M and N. Those functions are monotonically increasing step functions, and they can change value only between 0 and 1, and only between steps of \(1/|{\mathcal {O}}_{M}|\) and \(1/|{\mathcal {O}}_{N}|\). Therefore, the KS distance can be calculated by comparing the values of \( cdf _{f}^M(x)\) and \( cdf _{f}^N(x)\) at every step.
Example 3
The left part of Fig. 4 compares the models \(M_1\) and \(M_2\) to a representative human model using their KS distances. Since \(KS(OD(Hum), OD(M_1)) = 0.2904\) while \(KS(OD(Hum), OD(M_2)) = 0.2211\), we will consider \(M_2\) to be structurally more realistic (wrt. the human model) than \(M_1\).
The right side of Fig. 4 illustrates the cumulative distributions of the out-degree metric of three models: Hum is a human statechart of an engineer, while \(M_1\) and \(M_2\) are the models from Fig. 2. The horizontal axis lists the out-degree of nodes (from 0 to 14), and the vertical axis shows the proportion of nodes that have less or equal out degree (measured from 0 to 1). To compare \(M_1\) and \(M_2\), one can say that the distribution of \(M_2\) follows the distribution of Hum more closely than \(M_1\), so it is considered to be more realistic. Note that the (single) median of out-degree is 2 for Hum, \(M_1\) and \(M_2\); thus, it cannot distinguish those models.
Definition 7
Manhattan distance (MD) between two categorical distributions is measured as the sum of differences between the proportions for each category. Formally, for categories \(C=\{c_1,...,c_n\}\), categorical distributions \( pmf _{f}^M\) and \( pmf _{f}^N\) of a graph property f the Manhattan distance between models M and N is \( MD (M,N,f) = \sum _{c \in C}| pmf _{f}^M(c) - pmf _{f}^N(c)|\).
Definition 8
Absolute deviation (AD) of a scalar metric \(m_s:{\mathcal {M}}_ MM \rightarrow {\mathbb {R}}\) between two models M and N is calculated as the difference between the metric values: \( AD (M,N,m_s)=|m_s(M)-m_s(N)|\).
3 Model metrics by graph predicates
We assume that various metrics for structural properties (i.e., consistency, diversity, realistic nature) of graph models can be expressed by using graph predicates. Table 1 collects some graph metrics found to be relevant in [75, 76, 78] that we use in the paper. In general, we make the following assumptions about graph metrics:
-
Structural-only: Metrics should only use structural properties of graph elements, but not their actual values, e.g., the equality of attributes can be checked, but the actual values should be hidden.
-
Confidentiality: Metrics should not reveal any confidential information stored in actual graph models. This implies that model generation cannot use values stored in a real model, only some statistics computed from a real model, so no one should be able to reconstruct the real model from the metrics.
-
Domain-agnostic: As a specific graph metric is not equally relevant in different domains [78], we only assume that graph metrics can be computed in a domain-independent way when evaluating the realistic nature of a graph model. However, the actual distribution of the metric value may differ very much from domain to domain.
-
Continuous: Metrics should be continuous in the sense that changing a single graph element should result in a small change in the metric’s value as the size of a model grows. Thus, one can use the continuity assumption to guide the search. Most graph metrics in [62] are continuous by default, i.e., adding a new node or edge to a large graph only does not have a major impact on the value of the metric.
3.1 Consistency metrics as graph predicates
A domain specification contains well-formedness (WF) constraints to restrict the range of consistent models. Without loss of generality, we assume that WF constraints are formalized as error predicates. Let \(\varphi ({\bar{v}})\) be a first-order logic (error) predicate with formal parameters \({\bar{v}}\). When \(\varphi ({\bar{v}})\) has a match in model M, i.e.,  along some objects \({\bar{o}}\), then it represents a violation of the WF constraint. The goal of consistent graph generation is to generate models where all error predicates evaluate to
along some objects \({\bar{o}}\), then it represents a violation of the WF constraint. The goal of consistent graph generation is to generate models where all error predicates evaluate to  (i.e., there are no violations).
(i.e., there are no violations).
However, consistency can also be handled as a soft constraint when model generation aims to minimize the number of violating matches, as discussed in [41]. To evaluate the level of consistency in real models, we define two consistency metrics (see Table 1). Under closed world assumption, we count the total number of violations (\(\textit{VIO}\)) and the number of repairable violations (\(\textit{MVIO}\)), which is currently a violation but it can potentially be repaired by extending the graph with new elements. Both \(\textit{VIO}\) and \(\textit{MVIO}\) are scalar metrics, and distances between two models wrt. these metrics are measured as absolute deviation (AD).
Example 4
A WF constraint for statecharts prescribes that each region needs to have an entry state:

This error predicate has a match in \(M_1\) (in Fig. 2) for
 r, so \(M_1\) is inconsistent. But in the extended model \(M_2\), the match of the constraint disappears after adding the missing
r, so \(M_1\) is inconsistent. But in the extended model \(M_2\), the match of the constraint disappears after adding the missing
 e. This illustrates the concept of a repairable violation.
e. This illustrates the concept of a repairable violation.
3.2 Characterization of realistic models
To objectively measure and compare the realistic nature of graph models, we use a generalized formalization of various graph metrics proposed in [75, 76, 78] in the form of (cumulative or regular) distribution functions. As noted in [84], the cumulative distribution function of an object property contains more representative information than simply the mean or the average. Moreover, [45, 57, 62, 90] also use cumulative distributions for comparing various graph properties.
Table 1 contains various graph metrics to capture the realistic nature of models, such as out-degree, node activity, dimensional degree, multiplex participation coefficient (all widely used in network science). The realistic nature of models was measured by various node type distributions (\(\textit{NTD}\)) in [76] (see also in Table 1), which is a specific kind of categorical distribution metric that counts the number of objects for each type (f(o)).
Given a set of human real models \(\{M_1, \ldots , M_k\}\) and a set of synthetic models \(\{S_1, \ldots S_l \} \) derived by a model generator Gen, we aim at characterizing the realistic nature of a single synthetic model or a set of synthetic models. Informally, one synthetic model is considered to be realistic wrt. a given graph metric m, if one cannot distinguish it from a real human model by evaluating that metric. In other terms, a realistic model is as close to some human model as another human model.
We calculate the minimum distance \(d_{min}(M_i) = min_{1\le j\le k, i\ne j}d(M_i, M_j)\) between each human model \(M_i\) and its nearest neighbor \(M_j\) from the set of real models (so called 1-nearest neighbor [28]). Note that distance calculation can be different for each metrics of interest, e.g., MD is used for node type distribution, KS is used for all cumulative metrics. As human models may have outliers, we consider only the first t percentile of such distances (i.e., we exclude \(1-t\) percentage of human models), and define a threshold of realisticness T as the largest distance within the first t-percentile.
Definition 9
A synthetic model \(S_i\) is defined as realistic if it is closer to the human models than threshold T, i.e., if \(d_{min}(S_i) = min_{1\le j \le k}(d(S_i, M_j)) < T\).
To characterize the quality of an auto-generated set of models, we calculate the percentage of realistic synthetic models. Furthermore, we calculate the average minimal distance of a synthetic models from its closest human model, i.e., \(d_{avg} = mean_{1\le i \le l}(d_{min}(S_i))\).
3.3 Characterization of diverse models
Model diversity has been studied extensively in [68]. Here, we revisit two metrics defined for model diversity based upon neighborhood shapes. Internal diversity captures the diversity of a single model, i.e., it can be evaluated individually for each generated model. As neighborhood shapes introduce extra subtypes for objects, this model diversity metric measures the number of neighborhood types used in the model with wrt. the size of the model. External diversity captures the distance between pairs of models. Informally, this diversity distance between two models is proportional to the number of different neighborhoods covered in one model but not the other.
Definition 10
For a range i of neighborhood shapes for model M, internal diversity of M is the number of different shapes wrt. the size of the model: \(d_{i}^{int}(M) = | S^{i}(M) | / | M |\).
The range of this internal diversity metric \(d_{i}^{int}(M)\) is [0..1], and a model M with \(d_{1}^{int}(M) = 1\) (and \(| M | \ge | MM |\)) guarantees full metamodel coverage [85], i.e., it surely contains all elements from a metamodel as types. As such, it is an appropriate diversity metric for a model in the sense of [84]. Furthermore, given a specific range i, the number of potential neighborhood shapes within that range is finite, but it grows superexponentially. Therefore, for a small range i, one can derive a model \(M_j\) with \(d_{i}^{int}(M_j) = 1\), but for larger models \(M_k\) (with \(| M_k | > | M_j |\)) we will likely have \(d_{i}^{int}(M_j) \ge d_{i}^{int}(M_k)\). However, due to the rapid growth of the number of shapes for increasing range i, for most practical cases, \(d_{i}^{int}(M_j)\) will converge to 1 if \(M_j\) is sufficiently diverse.
Definition 11
Given a range i of neighborhood shapes, the external diversity of models \(M_j\) and \(M_k\) is the sum of differences between the number of shapes contained in \(M_j\) or \(M_k\) but not in the other, formally, \(d_{i}^{ext}(M_j, M_k) = | MD (S^{i}(M_j),S^{i}(M_k)) |\) where \( MD \) denotes the Manhattan distance of the categorical distribution of shapes.
External model diversity metrics allows to compare two models. One can show that this metric is a (pseudo)-distance in the mathematical sense, and thus, it can serve as a diversity metric for a model generator in accordance with [84].
3.4 Relation between consistency, realistic nature and diversity
In our approach, graph predicates are uniformly used to capture the consistent, realistic and diverse nature of models. Next, we summarize these concepts and highlight the fundamental differences between them.
-
Consistency metrics (like VIO and MVIO) measure the matches of a predefined set of selected predicates (i.e., the WF constraints) \(P^{WF}_1,\ldots ,P^{WF}_w\) on the models. In a consistent model, the number of such matches is strictly zero.
-
For a set of graph predicates \(P_1,\ldots ,P_r\), realistic metrics are some functions of the number of matches of the predicates. In general, a model is considered realistic, if the number of matches is statistically close to the number of matches in a real model.
-
For a set of graph predicates \(P_1,\ldots ,P_d\), diversity metrics are derived by counting the number of predicates with non-zero matches. In general, a model is considered diverse if many different predicates have at least one match.
Using this interpretation, consistency can be also considered as a special subclass of realistic metric, which has a constant zero value on real models. Note that this is also in line with one of our major empirical findings that real models are dominantly consistent, or equivalently, inconsistent models cannot be realistic.
Example 5
Table 2 illustrates four models (\(M_1\),...,\(M_4\)) with different realistic and diversity metrics in a simplified setting. Each model consists of only four objects with different ratios of
 and
and
 objects.
objects.
For the sake of this example, let us assume that the realistic ratio of
 s and
s and
 s is 7:1, so 12.5% of
s is 7:1, so 12.5% of
 s should be
s should be
 in a realistic model. Therefore, models \(M_3\) and \(M_4\) could be considered the most realistic models, as both of them are equally close to a realistic ratio of 12.5%.
in a realistic model. Therefore, models \(M_3\) and \(M_4\) could be considered the most realistic models, as both of them are equally close to a realistic ratio of 12.5%.
Additionally, we calculated the internal diversity of the models for range \(r=1\), which is presented in the third line of the table. Informally, models containing both
 and
and
 objects are more diverse than those that contain only one type of object. According to this, models \(M_2\) and \(M_3\) are the most diverse.
objects are more diverse than those that contain only one type of object. According to this, models \(M_2\) and \(M_3\) are the most diverse.
Therefore, Table 2 illustrates all four potential combinations for diverse and realistic nature.
4 Generation of consistent, realistic and diverse graph models
4.1 Black-box view of model generation
We propose a model generation approach to derive graphs which are simultaneously realistic, consistent and diverse. As input (see Fig. 5), our approach takes
-
1.
a designated graph metric m with a metric distance d to measure the realistic nature of models;
-
2.
a target metric value \(v_R=m(R)\) calculated from some representative real model R;
-
3.
a set of error predicates \(\varphi _1,\ldots ,\varphi _k\) of the domain derived from the metamodel MM and the WF constraints.
The output of a generator is a set of synthetic models \(S_1,\ldots ,S_n\) which are
-
consistent: each \(S_i\) is an instance of the metamodel \(S_i\in {\mathcal {M}}_ MM \) and no error predicate \(\varphi _j\) is violated
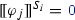 ,
, -
diverse: there is a minimal difference between any pair of models, i.e., for each generated model \(M_j\) and \(M_k\) \(d_{i}^{ext}(M_j, M_k)>1\).
-
realistic: the distance \(d(m(S_i),v_r)\) from the target metric is minimized.
Conceptually, our model generation approach is separated into two phases:
-
I.
Selection of representative models: First, we select or derive one or more representative models from the available set of real models, and we calculate the target metric values for those representative models.
-
II.
Generation of realistic models: Next, we generate models with respect to the target metric and the domain specification to obtain realistic consistent, and diverse synthetic models.
4.2 Selection of representative models
To guide the generation toward realistic models, our approach relies upon the selection of one or more representative real models as a first step. Model synthesis will then be guided toward the values of various graph metrics measured on the representative model by disregarding the actual contents of the representative model. Naturally, there are various ways to identify a representative model.
-
1.
Manual selection. A domain expert can select a model, and evaluate the relevant graph metrics on it. If there are multiple groups of models (i.e., along different modeling styles or conventions), the domain expert needs to select a representative from each group. This approach requires the most amount of human interaction, but it exposes the least amount of undesired information about the model.
-
2.
Deriving representatives with mutations. Model mutations can be applied on models to derive models with small differences [25, 26, 50]. This could be used to automatically derive models similar to selected representative, but the provider of the mutation operators need to ensure that the mutation operators do not hinder the realistic nature or the consistency of the model. It is rarely the case though since mutations may insert model changes that violate consistency, for instance. On the other hand, model mutations can be potentially used to enrich the set of available models (as a data augmentation technique frequently used in few shot learning techniques [86]) as a post-processing step.
-
3.
Statistical selection. Finally, standard statistical methods can be applied to automatically select representative models from a group of real models. In this paper, we used an automated selection of representative models using medoids for evaluation, which is detailed in the sequel.
For a sufficiently large set of real models, a representative model can be selected automatically (illustrated in Fig. 6). First, we calculate the metric values on each real model. The metric distance can be used to detect clusters of models, and some central elements can be used as representatives. In this paper, we use the statistical concepts of medoids as a potential way to select a central element (with maximum likelihood decision) to demonstrate the feasibility of automated selection. But identifying the best statistical selection technique is outside the scope of the paper; hence, medoids are only one of the possible techniques that could be used.
Definition 12
(Medoid) A medoid of a model set \(S=\{M_1,\ldots ,M_n\}\) wrt. a distance d is a model \(M_i\in S\) which minimizes \(\sum _{M_j\in S}d(M_i,M_j)\).
Based on the triangle inequality of distance metrics, if a real model M is at a certain distance d(M, R) from the selected representative R, and a generated synthetic model S is at a distance d(S, R) to R, then the distance \(d(M,S) \le d(M,R) + d(S,R)\). Thus, a synthetic model S that is close to the representative R cannot be far from the set of real models M (if the set of real models is clustered).
4.3 Model generation as state space exploration
Our model generation approach is implemented as a state space exploration technique implemented in the Viatra Solver framework [67] (see Fig. 7), where states are partial graph models, transitions between states are triggered by executing model extension operations (which add new objects and references as decision and unit propagation rules implemented by graph transformation rules). As such, the size of partial models is continuously growing up to the designated model size, while the consistency of the model and the designated graph metric are continuously evaluated. The generation follows a customized hill-climbing strategy (with potential back-jumps) guided by the selected graph metric m and target metric value \(v_R = m(R)\) of the representative model.
A synthetic model S is accepted as a (consistent) solution if it reaches a designated size and it satisfies all WF constraints. One could introduce some acceptance criteria for the realistic nature of models (e.g., \(d(m(R),m(S)) < \varepsilon \)), but we rather treat the target metric m as a soft constraint for optimization.
The steps of model generation are the following:
- (0):
-
By default, the model generation is initialized with an empty model (model without any objects). Optionally, the generation can be with a partial snapshots, which can serve as the seed for model generation. In that case, each generated model will be the extension of the partial model, i.e., each generated model will contain the partial model as a submodel.
- (1):
-
An unexplored partial model P closest to the target metric value \(v_R\) is selected from the search space for exploration.
- (2):
-
Next, all potential applications of the model extension operations are applied on the selected partial model P. This results in a set of extended partial solutions for the graph generation \( Front =\{P_1, \ldots ,P_n\}\).
- (3):
-
To prevent traversing the same state (graph) twice, a state code is calculated and stored for the new partial models \(P_1, \ldots ,P_n\) by using graph isomorphism checks over graph shapes [58]. Graph shapes abstract from node identities, but they efficiently identify whether two graphs can be distinguished by the neighborhood (i.e., incoming and outgoing edges) of a node. Had the new state been already explored, the partial model is dropped from \( Front \).
- (4):
-
For all models in \( Front =\{P_1, \ldots ,P_n\}\), we check if \(P_i\) satisfies all under-approximated (must) constraints by partial evaluation of these constraints [69] using an incremental graph query engine [81]. If an under-approximated constraint is violated by the partial model then an inconsistency is detected, thus the partial model can never be refined into a consistent instance model, so it can be dropped from \( Front \).
- (5):
-
If \( Front \) still has consistent model candidates, the designated graph metric m and distance d is evaluated on each model in \( Front \), and the best model \(P_i\) is selected wrt. to its distance \(d(m(P_i),v_R)\) to the target metric value \(v_R\) of the representative model. Otherwise, if \( Front \) is empty, the generation process continues to explore a new partial solution in 1.
- (6):
-
Finally, the consistency of the selected partial model \(P_i\) is checked. If the model is consistent as no violation of error predicates is found (for each
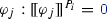 ) and a designated model size is reached, \(P_i\) is accepted as a solution. Note that checking the original WF constraints on the final solution candidates guarantees the correctness of our approach. Otherwise, if the model has some violations, or the requested size is not reached, exploration continues from 2 with \(P_i\) as the selected model. If more than one realistic model is requested, the exploration continues at 1.
) and a designated model size is reached, \(P_i\) is accepted as a solution. Note that checking the original WF constraints on the final solution candidates guarantees the correctness of our approach. Otherwise, if the model has some violations, or the requested size is not reached, exploration continues from 2 with \(P_i\) as the selected model. If more than one realistic model is requested, the exploration continues at 1.
When the exploration process stops as the requested number of models has been reached, the unfinished models of the search space are dropped, and the search restarts from scratch. However, if the generator fails to derive sufficient number of consistent models (e.g. due to performance limitations), the intermediate solutions in the search space could be used as best-effort partial solutions. This way, the solver provides graceful degradation [84]. Moreover, in theory, the solver can reuse the search space between model generations, but based on our experience, this can dramatically decrease model diversity since the solver tends to select the same partial solutions for subsequent exploration [68].
4.4 Guidance heuristic for model metrics
In practice, a combination of multiple graph metrics \(m_1,\ldots ,m_n\) and distances \(d_1,\ldots ,d_n\) can be used to characterize the realistic models in a domain and to guide model generation. In this combination, a distance between a partial model P and the representative model \(M_r\) is measured as a linear combination of some distances:
We used the following principles to combine metrics at Step 5:
-
Since our approach operates on strongly typed models [79], node type distribution (\(\textit{NTD}\)) is a critical metric. Without realistic \(\textit{NTD}\) distributions, different edge-based distributions cannot be enforced, as reference multiplicities and reference type compliance strictly control the potential references added to the model during generation. Thus, we prioritized the NTD metric in combination with other metrics.
-
The number of may-violations (MVIO) is very important for consistency reasons. This metric guides the search toward models where the number of violations is relatively low (thus, the model can be easily finished). This also increased the realistic nature of models, as during the manual construction of real models, modelers keep the number of violations low (in order to commit intermediate solutions, or to test partially finished features).
-
To guide the generation more efficiently, we maintain a linear regression model to extrapolate the effect of each model extension operation on the final solution. A regression coefficient is trained and maintained for each model extension operation (i.e., adding an object of class
 or a reference
or a reference 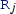 ) based on observed changes in the distances upon the previous applications of the same operation. When guiding the generation, the metric values extrapolated to the final size of the model are used.
) based on observed changes in the distances upon the previous applications of the same operation. When guiding the generation, the metric values extrapolated to the final size of the model are used. -
In early stages of generation, a weight function w is further applied to the results of the linear regression to ensure that graph generation is correctly guided toward a realistic model. This step is necessary because the regression model is not yet properly trained at an early stage.
4.5 Semantic guarantees and limitations
This model generation is compliant with the refinement calculus of [84] to provide theoretical guarantees for the correctness and completeness of the generation (i.e., all consistent models can be derived). However, if no consistent solution can be found, no unsatisfiable cores are provided.
As a practical limitation of our approach, we focused on the realistic nature of the underlying graph structure and excluded the handling of realistic attribute values ( [64] elaborates the handling of attribute values in our framework.). In fact, we intentionally exclude to use specific values to comply with confidentiality of real models. Thus, our approach is complementary to [75] which provides support for attributes, but derives very simple graphs.
As a further limitation, while each synthetic model is realistic wrt. a representative human model (on a best-effort basis), the set of synthetic models does not necessarily follow the statistical properties of the set of human models. However, this limitation can be mitigated by using several representative models.
5 Evaluation
5.1 Research questions
We conducted several measurements to address the following research questions:
- RQ 1::
-
What graph metrics are effective for guiding model generators toward realistic graph models?
- RQ 2::
-
How realistic are the models generated by our approach compared to other generators?
- RQ 3::
-
How diverse are the models derived by our approach compared to other model generators?
- RQ 4::
-
How does our approach scale when generating models with increasing size?
5.2 Target domains
To answer these questions, we executed model generation campaigns in three complex case studies with a large set of real models.
Stc: Yakindu Statecharts [88] is an industrial modeling environment. We used the metamodel extract of Figure 1 which captures the state hierarchy and transitions of statecharts (with 12 classes and 6 references). Moreover, we formalized 10 constraints as graph predicates that restrict the transitions based on the built-in validation of Yakindu. For real human models, we collected 304 statechart models with a size ranging from 90 to 110 objects. The models were created by undergraduate students as solutions for similar (but not identical) statechart modeling homework assignments.
Met: Eclipse Modeling Framework [79] is a widely used DSL environment. We used an effective metamodel of EMF (which consisted of 13 classes excluding
 s and 45 references), and formalized 3 additional constraints. For realistic models, we gathered the recently updated EMF models from GitHub by querying code using GitHub API (as of 31/07/2019). We selected models ranging from 30 to 500 objects in size, and filtered out models that are not manually created (e.g., derived from an XML schema) resulting in 198 human models.
s and 45 references), and formalized 3 additional constraints. For realistic models, we gathered the recently updated EMF models from GitHub by querying code using GitHub API (as of 31/07/2019). We selected models ranging from 30 to 500 objects in size, and filtered out models that are not manually created (e.g., derived from an XML schema) resulting in 198 human models.
Scm: Finally, we gathered and generated software configuration models of GitHub projects [24] representing the connection between the developers, commits and issues of a project within a time window. The metamodel is derived from the data model of [24] consisting of 6 relevant classes and 10 references. We also formalized 4 constraints regulating the commits. The human data is collected from GHTorrent [24], from repositories created between 1/1/2017 and 1/1/2018. We gathered the commits and issues and active users created within 8 months from the day of repository creation. Finally, we kept 70 models ranging from 30 to 200 objects.
5.3 Compared approaches and metrics
We compared different model generation approaches to evaluate how realistic are the generated models.
-
1.
As a reference, a large set of real models were collected for each domain (denoted as Hum).
-
2.
We generated consistent models with Alloy Analyzer [32, 80] (All), a well-known SAT solver-based model finder by using known mappings [13, 66]. We used the latest stable version of Alloy (v4.2) with the default background solver configuration [42]. For enabling statistical analysis, we added a random amount of extra true statements (as used in [70]) to prevent the solver from running deterministically.
-
3.
We implemented a simple black-box search-based model generator, which (1) repeatedly calls a back-end model generator until a time limit (1h), and (2) it continuously maintains a population of the best \(N = 100\) models with respect to a target metric of interest (Comb). We instantiated this framework with two existing model generators:
-
(a)
We generated random models for each domain using EMF random instantiator [9] (Rand), which does not support WF constraints; thus, the models are not guaranteed to be consistent. To provide a fair comparison with other approaches, we implemented a feature in Rand to specify the root element of the model.
-
(b)
We generated consistent models with the Viatra Solver [65, 67] (GS) using the latest version of the graph solver algorithm. Model generation was restarted from scratch when deriving a new model (i.e., the search space was not preserved).
-
(a)
-
4.
We evaluated our realistic graph generator (Real) guided with the graph metrics \(\textit{OD}\), \(\textit{NA}\), \(\textit{MPC}\), \(\textit{NTD}\) and \(\textit{VIO}\) (see Table 1) using the appropriate distances (KS, MD, AD). Moreover, we used a combined metric \(\textit{Comb}\) that measures all these metrics simultaneously, with or without the number of violations (\(Comb+V\) vs. \(Comb-V\)).
The generated and collected models are available on a publication pageFootnote 1 dedicated to this paper.
5.4 RQ 1: Effectiveness of metrics in guidance
Setup To compare the effectiveness of various metrics used for guiding our approach (Real) in realistic model synthesis, we generated models using metrics \(\textit{OD}\), \(\textit{NA}\), \(\textit{MPC}\), \(\textit{NTD}\) and \(\textit{VIO}\) and the combined metric \(\textit{Comb}\) (subsection 4.4) with and without \(\textit{VIO}\) (\(Comb+V\) and \(Comb-V\)). In this measurement setup, we used \(\textit{VIO}\) only as a guidance metric for the hill-climbing approach (i.e., a soft constraint subject to optimization); thus, the consistency of models is not guaranteed.
For each domain (Stc, Met and Scm), we generated 100 models with 100 objects using each metric separately. As a representative model, we selected the medoid of the human models (Hum) in each domain. Then, we measured the distance of each model from the representative model by evaluating all metrics (i.e. one metric to guide, all metrics to evaluate). If the distance between a synthetic graph and the representative model is close to zero, then the metric is better at guiding the synthetic model generator toward a representative model wrt. the given metric.
Analysis of results Table 3 presents the metric values measured on the graphs generated using different guidance metric in a \(5 \times 3\) layout. Each column represents a target domain, while each row corresponds to a graph metric from Table 1. For any cell in Table 3, we consider the graphs produced using the seven different guiding strategies for a given target domain. We measure the metric values corresponding to the row of the cell on the seven sets of generated graphs and on the real graphs. As a result, in each cell, we obtain eight distributions, which are represented as box plots. The median value in each box plot is highlighted in orange.
We performed statistical analysis to find the dominating guidance metric in each case, i.e., the one where the median of respective measurements is closest to zero. We conclude that the combined guidance metric \(Comb+V\) produced the most realistic set of models, by dominating all other approaches in 6/15 cases, and producing similar results as the best one in 3/15 other cases. Interestingly, the combined metric strategy \(Comb+V\) often produced more realistic results than using the target metric as a guidance strategy. This means that the combined metric can help avoid local optima by considering many different aspects of the model. For example, in a combined metric, node-type distribution (NTD) can guide the exploration process to place the right amount of objects by type (e.g., a large number of
 s in a
s in a
 ), which can enable the satisfaction of Out Degree (OD) metric (e.g., with the addition of
), which can enable the satisfaction of Out Degree (OD) metric (e.g., with the addition of
 ). On the other hand, if the exploration process focuses only on the Out Degree metric, it may fail to place the right amount
). On the other hand, if the exploration process focuses only on the Out Degree metric, it may fail to place the right amount
 s early on.
s early on.
Another key observation is that all human models have a very low number of constraint violations, i.e., they are dominantly consistent. This provides empirical evidence that a realistic model also needs to be consistent. As such, addressing the generation of models which are simultaneously consistent and realistic is a relevant challenge.

We use \(Comb+V\) for guidance in the subsequent measurements as this strategy was the most efficient.
5.5 RQ 2: Realistic nature of models
Setup We compared the realistic nature of models generated with various approaches. Consistent model generators included our approach Real (using \(Comb+V\) as guidance metric toward the medoid), the Viatra Solver (GS), and Alloy (All). Moreover, we used the best 100 random models (Rand) as a baseline (which may violate WF constraints). We also included all the human models in the comparison (Hum) as a reference.
For this measurement, we generated the first 100 models with Real and All and the best 100 models with Rand and GS with a timeout of 1 hour. This timeout was determined by the approximate generation time of the first 100 models using Real. Target model size was limited to 30 objects using each approach (as All failed to generate larger models). We measured the distance between each pair with metrics \(\textit{OD}\), \(\textit{NA}\), \(\textit{MPC}\) and \(\textit{NTD}\). Moreover, we evaluated the percentage of consistent models for Hum and Rand models to measure \(\textit{VIO}\).
Analysis of results The measured distances between any pair of graphs are depicted in Table 4 in a \(5 \times 3\) layout. Each column corresponds to a target domain, while each row is associated with a metric. For any cell in the first four rows of Table 4, we consider the graphs generated using the different approaches for a target domain. We measure the pairwise distance between the generated graphs wrt. the metric in the row of the cell.
The distances between models are depicted as scatter-plots in Table 4 using multidimensional scaling [23]. According to this technique, the distance between two points in the scatter-plot is proportional to the distance between the two graphs (i.e., metric values measured on the graphs). For instance, if two points are close to each other in the scatter-plot, then the distance between the metric values measured on the corresponding graphs is small. The axes represent the scaling unit for interpreting the geometric distance. For instance, if the distance between two dots is 2 unit long, then the metric distance between the models is 2. However, the exact values on the x and y-axis are irrelevant.
To identify the best model generation approach for each case, visual data analytics can be used: a synthetic model can be considered to be realistic if it lies within the cluster of human models, i.e., it cannot be distinguished from human models by the given metric. For a more formal treatment, we calculated the average minimal distance (of a generated model from the closest human model) for each generator. We underline the best performing generator in each case. Moreover, we calculated the percentage of realistic models using the \(t = 97\%\) percentile of the nearest neighbor distances between human models as the threshold of realisticness \(T\) (Definition 9).
Concerning the average minimal distance, Real provided the most realistic models for all 8/12 cases (once in a tie with All and GS for \(\textit{MPC}\) in Stc). Moreover, Real derived the largest percentage of realistic models in 10 out of 12 cases (twice in tie with Rand in Stc with 100%). In general, Rand performed better than All and GS wrt. the realistic nature of models. As an outlier in Scm, all 100 models derived by All were isomorphic so they are plotted as a single model.

5.6 RQ 3: Diversity of models
To evaluate the diversity [70, 84] of the generated models, we measured structural distance between the models using the internal and external diversity metrics. Moreover, we also adopted the exploration process of [70] as a baseline technique to ensure the diversity of models. As such, we expect that our realistic models are structurally different from each other.
Setup
We compared diversity of models generated with various approaches for each domain (Stc, Met and Scm). We used the same set of models and model generators (All, All, GS, Real) as in RQ 2, and we also human models in the comparison (Hum).
In separate measurements, we calculated the internal and external diversity metrics for each approach to evaluate how symmetric the derived models are (see [68, 70] and subsection 3.3 for technical details).
-
High internal diversity of a model shows that the model contains a large number of different structures (wrt. to its size), and a low internal diversity implies that the models are highly symmetric.
-
High external diversity between two models denotes a high number of structural differences, and low external diversity means that the models are structurally similar.
In this paper, we measured the distribution of both internal and external diversities using range 5, and used Manhattan distance to measure external diversity [68].
Analysis of results Table 5 illustrates the distribution of internal diversity of models for each approach in each domain.
-
In all domains, human models Hum showed low diversity (from 0.45 to 0.8) but with high variance.
-
Real generated models with highest diversity in Met and Scm, and the second highest diversity in Stc.
-
GS showed high internal diversity in Stc and Met, but provided highly symmetric models in with low internal diversity values in Scm. Since the same solver previously provided consistently high diversity in [68], this result must be a side-effect of maintaining the 100 most realistic models, which may negatively influence diversity.
-
Rand provided reasonably high internal diversity in Stc and Scm domains but not in Met.
-
All only provided high internal diversity in Stc.
Table 6 illustrates the distribution of external diversity between each model pair of the same approaches. In each domain, the external diversity of Hum was high, compared to the other approaches, and varied greatly. Real outperformed all other generators in Met and Scm, and became close second behind GS in Stc. Rand consistently achieved better diversity than All, but worse diversity than graph solver-based approaches. There were two notable outliers in the Scm case: GS showed low diversity, while all models derived by All were isomorphic (thus zero diversity).

Note that the realistic nature and the diversity of models may differ drastically. For example, in domain Met, models generated with Real were statistically similar, but the external diversity was one of the highest (in contrast to All, which provided models with different realistic metric values but low external diversity). These differences provide empirical evidence that diversity and realistic nature are two different properties of models, which is also a key finding.
5.7 RQ 4: Scalability evaluation
Setup We measured the runtime of model generation to derive consistent and realistic graphs with increasing size. We set up a timeout of 1 hour for each generation run. To account for the variability of execution times due to randomized exploration, model generation was executed 10 times for each measurement point and the median of the runs was taken. Warm-up effects and memory handling of the Java 11 VM were accounted for by calling the garbage collector explicitly between runs. We measured the runtime of the main components of the approach separately on a virtual serverFootnote 2.
Analysis of results Execution times for the Stc, Met and Scm domains for measurements with 100% success rate, i.e., all 10 runs managing to generate a model within an hour, are shown in Table 8. The largest models had 600, 150, and 600 objects, respectively. We managed to generate even larger models, albeit with a lower success rate: 1000 objects for Stc (10% success rate), 300 for Met (30% success rate) and 900 for Scm (40% success rate). As a comparison, [70] reported models for Met with 2000 objects for GS, and 28 objects for All within 5 minutes.
Notice that most generation time is spent in state coding, i.e., testing for graph isomorphism between the states being traversed [59]. This implies that the hill-climbing strategy traverses a large number of states (which is significantly more than best-first search traversed in consistent model generation [67]).
For Met, the runtime jumps after \(125\) model element, and it has very high variance for larger cases, which is due to the handling of constraints regarding
 references as WF constraints instead of metamodel constraints. This reduced the ability of the generator to apply propagation rules and caused it to spuriously explore a significant fraction of the state space which contained no consistent solutions.
references as WF constraints instead of metamodel constraints. This reduced the ability of the generator to apply propagation rules and caused it to spuriously explore a significant fraction of the state space which contained no consistent solutions.

Similar scalability has been reported when generating realistic models with machine learning [89].
5.8 Threats to validity and limitations
Internal validity To increase internal validity for measuring graph metrics (for realisticness), we considered human and synthetic models of similar size. As a data cleansing step for human models, we removed corrupt model instances or instances with too few objects. Moreover, we manually checked that medoids are not outliers in the given domain. In case of the scalability measurements, we mitigated warm-up effects and garbage collection. We selected graph metrics based on [78] to distinguish real models from synthetic ones.
External validity To identify representative models, we used the medoid of a domain, which is a standard statistical approach, but its usefulness to characterize realistic models is not yet empirically justified. However, our approach does not depend on the use of medoids, only the existence of a selected representative model in a domain; thus, the use of other selection techniques can be easily incorporated. Otherwise, the medoid of a set of real models is a typical technique to select a statistically well-founded representative. If there are multiple representatives in a set of models (i.e., there are a cluster of models), we can generate models similar to a representative of each cluster separately. The statistical properties of the selected graph metrics ensure that the size of the representative model does not affect the respective metric. Moreover, since our model generator performed well for all graph metrics we used to characterize realistic models, we expect advantageous behavior for other graph metrics of similar complexity. Finally, while we used three case studies of different size and complexity, we might obtain different results for other domains, e.g., when real models are not human-made but reverse-engineered.
Construct validity We used the 97% as t to calculate the threshold of realistic nature (considering 3% of Hum models unrealistic), which roughly followed the number of outliers in the distances. Selecting other t value would change the number (and percentage) of real models for each approach, but without changing the average minimal distance or the ranking of the approaches. Thus, our approach remains superior to the compared approaches. To measure diversity, we used a neighborhood range of 5 to compare the number of structures in the models (based on [68]). For greater ranges, the diversity values changed only slightly.
6 Related work
First, we overview graph metrics that could have potentially included in our experiments to characterize the realistic nature of graph models. Then, we overview various graph generation approaches that claim to derive realistic graphs, summarized in Table 8. We evaluate whether the generated models are (a) consistent wrt. WF constraints and metamodel constraints, (b) realistic, i.e., similar to real models and (e) multidimensional if multiple types exist in the generated nodes. We also check whether the generation approach is (c) scalable whether very large graphs can be generated and (d) domain-customizable, i.e., if they can be used for various domains.
Graph metrics A wide range of graph metrics have been used to characterize real graphs. Unidimensional metrics also include joint degree distribution [18], orbit counting [29, 89] and eigenvalues of adjacency matrices [2, 18, 40, 43, 44, 71]. These metrics have been measured on domains such as grid graphs, proteins, social networks, actors in movies and links between web pages.
Some studies use other multidimensional graph metrics to characterize realistic nature. For example, [12] proposes a method to extend unidimensional metrics to handle multiple dimensions. Nevertheless, purely multidimensional metrics do exist, such as node and edge dimension connectivity [12], node and pair D-Correlation [12], layer activity [54], edge overlap and overlapping degree [11]. These metrics have been measured on real-life networks, e.g., transportation, social (Flickr), co-authorship (DBLP), utility, terrorists.
Other research suggests the use of global metrics such as graph diameter [43, 44], number of connected components and K-Core decomposition [18] for checking the realistic nature of graphs. The realistic nature of graph models can be checked wrt. domain-specific criteria (ex. if a generated molecule is chemically valid [46, 74]) or domain-specific metrics (ex. the PageRank distribution for web pages [18]). Those metrics, in general, cannot be directly applied on custom domains.
Learning-based graph generation Learning-based model generation approaches require a training set of models to derive new models with similar features as the training set. Approaches like GraphVAE [74] and VGAE [39] may use variational autoencoders, which are based on the adjacency matrix representation of graphs, for learning and generating graphs. Another approach [46] considers the graph generation process as a sequence of node or edge addition operations where decisions on which elements to add are made according to training models. GraphRNN [89] is a framework that uses deep autoregressive models for graph generation.
As a common limitation, the scalability of learning-based graph generation approaches is limited. Moreover, the generation process can be only partially controlled by the input data provided by users. As a result, consistency of WF constraints or metamodel compliance is not guaranteed for these approaches. While learning-based approaches are domain-customizable, they are typically limited to unidimensional (untyped) graphs.
Some of these limitations are avoided by an approach based on learning from the editing histories of models proposed in [72, 73]. This approach generates models using realistic editing sequences and performs consistency checks after every edit operation. However, the proposed papers do not assess the structural realisticness of the models themselves and do not provide any scalability analysis.
Matrix-based generators. Graphs can be represented by their adjacency matrices, and matrix operations can be used for graph generation. For example, authors of [37, 43, 44] use Kronecker graphs (i.e., adjacency matrices obtained by Kronecker operations). Furthermore, a matrix-based recursive approach is used in [15] to distribute edges in within graph partitions. Random typing is used in a matrix-based algorithm to generate realistic graphs in [2].
Matrix-based graph generation provides good scalability and they are domain-customizable, but the realistic nature of graphs is restricted to unidimensional graph metrics. Moreover, there is no evidence of consistency or multidimensional support in the papers.
Template-based generators. Other graph generation approaches may use custom graph representations and a template or iteration-based algorithm. gMark [10] uses a schema-based representation and algorithm to generate multidimensional graphs and queries, but only with schema-level consistency guarantees and the realistic nature of generated graphs is limited. GSCALER [90] and ReCoN [77] focus purely on graph scalability: given an input graph, these tools generate a similar graph with a certain number of nodes and edges. Similarly, [53] proposes a rule-based approach for scalable model generation which evaluates diversity and ensures adherence to metamodel constraints, but it does not handle extra additional WF constraints and excludes analysis of realistic nature. S3G2 [56] uses a MapReduce-based iterative algorithm to generate realistic and scalable multidimensional graphs, but it is demonstrated for a single domain (social networks) without consistency constraints.
Results proposed in [18, 40, 71] involve building up realistic and scalable graphs by interconnecting smaller Erdős-Rényi models [20]. [62] uses a property graph model to generate scalable multidimensional graphs and compares the degree distribution of the generated graph with that of the ground truth to ensure realistic nature, but it lacks consistency guarantees. Authors of [6] propose a custom methodology for generating realistic and large social graphs within the context of a Facebook database benchmark, but the approach is domain-specific and unidimensional.
Logic solver-based generators. Logic solver-based approaches translate graphs and WF constraints into logic formulas and using a logic solver to generate graphs that satisfy the formulas. EMF2CSP/UML2CSP [14, 22] translates model generation to a constraint programing problem, and solves it by an underlying CSP solver. [27] reports class-diagram generation with EMF2CSP, where model generation is guided by class diagram-specific metrics (like LCOM and Class Cohesion [16]). ASMIG [87] uses the Z3 SMT solver [52] to generate typed and attributed graphs with inheritance. An advanced model generation approach was presented in the Formula Framework [34] also using the Z3 SMT solver. Paper [35] applies stochastic random sampling to increase the diversity of models generated by Formula, but it is not aimed to generate realistic models. [17] extends the Kodkod relational model finder [80] to generate models that are similar to a provided target model. Finally, AutoGraph [63] generates consistent attributed multidimensional graphs by separating the generation of the graph structure and the attributes. Graph generation is driven by a tableau approach, while attribute handling uses the Z3 SMT-solver.
Logic-solver based generators are domain-customizable and multidimensional, and ensure consistency. But their scalability is limited and there is no guarantee for the realistic nature of models.
Search-based generators. SDG [75] proposes an approach that uses a search-based custom OCL solver to generate synthetic data for statistical testing. Generated models are multidimensional, consistent (for local constraints) and realistic. The study demonstrates scalability by generating a large set of small (unconnected) models. Since the search-based approach handles WF constraints as soft constraints, the chance of deriving consistent models decreases with model size. Our paper significantly improves on handling the core aspects of graph structure, but it does not provide the same guarantees for attributes. Thus, approaches of [75] and our paper are complementary.
Research in [76] proposes a hybrid approach that uses both a meta-heuristic search-based OCL solver [4] for structural constraints and an SMT solver for attribute constraints, based on the snapshot generator of the USE framework [21]. Generated models are multidimensional, (locally) consistent and large. The realistic nature of the models is limited to type and attribute distributions.
Cartesian genetic programming (CGP) [49] encodes graphs with linear or grid-based genotypes and produces new ones by evolving the initial graph, originally used produce electronic circuits. A recent line of work [7, 8] introduced evolving graphs by graph programming, CGP’s generalization to arbitrary graphs.
7 Conclusion and future work
In this paper, we addressed to characterize structurally realistic nature of synthetic graph models by using a variety of graph metrics proposed in various branches of science. Given a set of real (human) models, and using appropriate distance functions for a specific metric, we can statistically measure in a domain-independent way how far a given synthetic model is from a (representative) real model, or what is the minimal distance from the closest real model. We also proposed an approach based on a hill-climbing strategy to automatically generate synthetic graph models that are simultaneously consistent, realistic and more diverse than other approaches, which was justified in a series of experiments carried out in the context of three case studiesFootnote 3.
As future work, we aim to extend our experiments by incorporating more complex graph metrics (e.g., triangle counts, subgraph-based metrics).
Notes
\(12 \times 2.2\) GHz CPU, 64 GiB RAM, Java 11.0.7, 12 GiB heap
The domain specification of the case studies, the human and synthetic models as XMI documents, and the measured metrics and distances are made available for the reviewers in the supplementary material uploaded with the paper.
References
Abdessalem, R.B., Nejati, S., Briand, L.C., Stifter, T.: Testing vision-based control systems using learnable evolutionary algorithms. In: ICSE, pp. 1016–1026. ACM (2018). https://doi.org/10.1145/3180155.3180160
Akoglu, L., Faloutsos, C.: RTG: a recursive realistic graph generator using random typing. Data Min. Knowl. Discov. 19(2), 194–209 (2009). https://doi.org/10.1007/s10618-009-0140-7
Al-Refai, M., Cazzola, W., Ghosh, S.: A fuzzy logic based approach for model-based regression test selection. In: MoDELS, pp. 55–62. IEEE (2017)
Ali, S., Iqbal, M.Z., Khalid, M., Arcuri, A.: Improving the performance of OCL constraint solving with novel heuristics for logical operations: a search-based approach. Empir. Softw. Eng. 21(6), 2459–2502 (2016). https://doi.org/10.1007/s10664-015-9392-6
Arkhangel’skii, A., Fedorchuk, V.: General topology I: basic concepts and constructions dimension theory, vol. 17. Springer (2012)
Armstrong, T.G., Ponnekanti, V., Borthakur, D., Callaghan, M.: Linkbench: a database benchmark based on the Facebook social graph. In: SIGMOD, pp. 1185–1196 (2013). https://doi.org/10.1145/2463676.2465296
Atkinson, T., Plump, D., Stepney, S.: Evolving graphs by graph programming. In: EuroGP, pp. 35–51. Springer (2018). https://doi.org/10.1007/978-3-319-77553-1_3
Atkinson, T., Plump, D., Stepney, S.: Evolving graphs with horizontal gene transfer. In: GECCO, pp. 968–976. ACM (2019). https://doi.org/10.1145/3321707.3321788
AtlanMod Team (Inria, Mines-Nantes, Lina): EMF random instantiator (2019). https://github.com/atlanmod/mondo-atlzoo-benchmark/tree/master/fr.inria.atlanmod.instantiator
Bagan, G., Bonifati, A., Ciucanu, R., Fletcher, G.H.L., Lemay, A., Advokaat, N.: gMark: schema-driven generation of graphs and queries. IEEE Trans. Knowl. Data Eng. 29(4), 856–869 (2017). https://doi.org/10.1109/TKDE.2016.2633993
Battiston, F., Nicosia, V., Latora, V.: Structural measures for multiplex networks. Phys. Rev. E 89, 032,804 (2014). https://doi.org/10.1103/PhysRevE.89.032804
Berlingerio, M., Coscia, M., Giannotti, F., Monreale, A., Pedreschi, D.: Multidimensional networks: foundations of structural analysis. World Wide Web 16(5–6), 567–593 (2013). https://doi.org/10.1007/s11280-012-0190-4
Büttner, F., Egea, M., Cabot, J., Gogolla, M.: Verification of ATL transformations using transformation models and model finders. In: ICFEM, pp. 198–213. Springer (2012). https://doi.org/10.1007/978-3-642-34281-3_16
Cabot, J., Clarisó, R., Riera, D.: On the verification of UML/OCL class diagrams using constraint programming. J. Syst. Softw. (2014). https://doi.org/10.1016/j.jss.2014.03.023
Chakrabarti, D., Zhan, Y., Faloutsos, C.: R-MAT: A recursive model for graph mining. In: SDM, pp. 442–446. SIAM (2004). https://doi.org/10.1137/1.9781611972740.43
Chidamber, S.R., Kemerer, C.F.: A metrics suite for object oriented design. IEEE Trans. Softw. Eng. 20(6), 476–493 (1994)
Cunha, A., Macedo, N., Guimarães, T.: Target oriented relational model finding. In: Proceedings of the 17th international conference on fundamental approaches to software engineering - Volume 8411, p. 1731. Springer-Verlag, Berlin, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54804-8_2
Edunov, S., Logothetis, D., Wang, C., Ching, A., Kabiljo, M.: Generating synthetic social graphs with darwini. In: ICDCS, pp. 567–577. IEEE Computer Society (2018). https://doi.org/10.1109/ICDCS.2018.00062
Eén, N., Sörensson, N.: An extensible SAT-solver. In: SAT, pp. 502–518. Springer (2003)
Erdős, P., Rényi, A.: On the evolution of random graphs. In: Publication of the Mathematical Institute of the Hungarian Academy of Sciences, pp. 17–61 (1960)
Gogolla, M., Bttner, F., Richters, M.: USE: A UML-based specification environment for validating UML and OCL. Science of Computer Programming 69(1), 27 – 34 (2007). https://doi.org/10.1016/j.scico.2007.01.013. Special issue on Experimental Software and Toolkits
González Pérez, C.A., Buettner, F., Clarisó, R., Cabot, J.: EMFtoCSP: A tool for the lightweight verification of emf models. In: Formal methods in software engineering: rigorous and agile approaches (FormSERA). Zurich, Switzerland (2012). https://hal.inria.fr/hal-00688039
Gordon, A.: The user’s guide to multidimensional scaling, with special reference to the Mds (X) library of computer programs. J. Royal Stat. Soc. Series D (The Statistician) 32(3), 355–356 (1983)
Gousios, G.: The GHTorrent dataset and tool suite. In: Proceedings of the 10th working conference on mining software repositories, MSR ’13, pp. 233–236. IEEE Press, Piscataway, NJ, USA (2013). http://dl.acm.org/citation.cfm?id=2487085.2487132
Guerra, E., Cuadrado, J.S., de Lara, J.: Towards effective mutation testing for atl. In: 2019 ACM/IEEE 22nd International conference on model driven engineering languages and systems (MODELS), pp. 78–88. IEEE (2019)
Gmez-Abajo, P., Guerra, E., Lara, J., Merayo, M.: A tool for domain-independent model mutation. Sci. Comput. Program. (2018). https://doi.org/10.1016/j.scico.2018.01.008
Hao, W.: Automated metamodel instance generation satisfying quantitative constraints. Ph.D. thesis, National University of Ireland Maynooth (2013)
Hautamaki, V., Karkkainen, I., Franti, P.: Outlier detection using k-nearest neighbour graph. In: Proceedings of the 17th International conference on pattern recognition, 2004. ICPR 2004., vol. 3, pp. 430–433 Vol.3 (2004). https://doi.org/10.1109/ICPR.2004.1334558
Hocevar, T., Demsar, J.: A combinatorial approach to graphlet counting. Bioinformatics 30(4), 559–565 (2014). https://doi.org/10.1093/bioinformatics/btt717
Iqbal, M.Z.Z., Arcuri, A., Briand, L.C.: Environment modeling and simulation for automated testing of soft real-time embedded software. Softw. Syst. Model. 14(1), 483–524 (2015). https://doi.org/10.1007/s10270-013-0328-6
Izsó, B., Szatmári, Z., Bergmann, G., Horváth, Á., Ráth, I.: Towards precise metrics for predicting graph query performance. In: ASE, pp. 421–431 (2013). https://doi.org/10.1109/ASE.2013.6693100
Jackson, D.: Alloy: a lightweight object modelling notation. Trans. Softw. Eng. Methodol. 11(2), 256–290 (2002). https://doi.org/10.1145/505145.505149
Jackson, E.K., Levendovszky, T., Balasubramanian, D.: Reasoning about metamodeling with formal specifications and automatic proofs. In: MODELS, pp. 653–667. Springer (2011). https://doi.org/10.1007/978-3-642-24485-8_48
Jackson, E.K., Levendovszky, T., Balasubramanian, D.: Reasoning about metamodeling with formal specifications and automatic proofs. In: Model driven engineering languages and systems, pp. 653–667. Springer (2011)
Jackson, E.K., Simko, G., Sztipanovits, J.: Diversely enumerating system-level architectures. In: Proceedings of the 11th ACM Int. Conf. on Embedded Software, p. 11. IEEE Press (2013)
Jackson, E.K., Sztipanovits, J.: Towards a formal foundation for domain specific modeling languages. In: EMSOFT, pp. 53–62. ACM, New York, NY, USA (2006)
Kepner, J., et al.: Design, generation, and validation of extreme scale power-law graphs. In: GABB at IPDPS, pp. 279–286 (2018). https://doi.org/10.1109/IPDPSW.2018.00055
Khurshid, S., Marinov, D.: TestEra: specification-based testing of java programs using SAT. Autom. Softw. Eng. 11(4), 403–434 (2004). https://doi.org/10.1023/B:AUSE.0000038938.10589.b9
Kipf, T.N., Welling, M.: Variational graph auto-encoders. CoRR arXiv:1611.07308 (2016)
Kolda, T.G., Pinar, A., Plantenga, T.D., Seshadhri, C.: A scalable generative graph model with community structure. SIAM J. Sci. Comput. (2014). https://doi.org/10.1137/130914218
Kosiol, J., Strüber, D., Taentzer, G., Zschaler, S.: Graph consistency as a graduated property. In: Gadducci, F., Kehrer, T. (eds.) Graph Transormation, pp. 239–256. Springer International Publishing, Cham (2020)
Le Berre, D., Parrain, A.: The Sat4j library, release 2.2. Journal on Satisfiability, Boolean Modeling and Computation (2-3), 59–64 (2010)
Leskovec, J., Chakrabarti, D., Kleinberg, J.M., Faloutsos, C.: Realistic, mathematically tractable graph generation and evolution, using kronecker multiplication. In: KDD, pp. 133–145 (2005). https://doi.org/10.1007/11564126_17
Leskovec, J., Chakrabarti, D., Kleinberg, J.M., Faloutsos, C., Ghahramani, Z.: Kronecker graphs: an approach to modeling networks. J. Mach. Learn. Res. 11, 985–1042 (2010)
Leskovec, J., Faloutsos, C.: Sampling from large graphs. In: T. Eliassi-Rad, L.H. Ungar, M. Craven, D. Gunopulos (eds.) Proceedings of the Twelfth ACM SIGKDD International conference on knowledge discovery and data mining, pp. 631–636. ACM (2006). https://doi.org/10.1145/1150402.1150479
Li, Y., Vinyals, O., Dyer, C., Pascanu, R., Battaglia, P.W.: Learning deep generative models of graphs. CoRR arXiv:1803.03324 (2018)
Micskei, Z., Szatmári, Z., Oláh, J., Majzik, I.: A concept for testing robustness and safety of the context-aware behaviour of autonomous systems. In: KES-AMSTA, pp. 504–513. Springer (2012). https://doi.org/10.1007/978-3-642-30947-2_55
Milicevic, A., Misailovic, S., Marinov, D., Khurshid, S.: Korat: A tool for generating structurally complex test inputs. In: ICSE, pp. 771–774. IEEE Computer Society (2007). https://doi.org/10.1109/ICSE.2007.48
Miller, J.F.: Cartesian genetic programming: its status and future. Genet. Program. Evol. Mach. (2019). https://doi.org/10.1007/s10710-019-09360-6
Mottu, J.M., Baudry, B., Le Traon, Y.: Mutation analysis testing for model transformations. In: Rensink, A., Warmer, J. (eds.) Model driven architecture - foundations and applications, pp. 376–390. Springer, Berlin Heidelberg, Berlin, Heidelberg (2006)
de Moura, L., Bjørner, N.: Z3: An efficient SMT solver. In: TACAS, pp. 337–340. Springer (2008)
de Moura, L.M., Bjørner, N.: Z3: an efficient SMT solver. In: TACAS, pp. 337–340 (2008). https://doi.org/10.1007/978-3-540-78800-3_24
Nassar, N., Kosiol, J., Kehrer, T., Taentzer, G.: Generating large EMF models efficiently: A rule-based, configurable approach. In: Lecture notes in computer science (including subseries Lecture Notes in artificial intelligence and lecture notes in bioinformatics), vol. 12076 LNCS, pp. 224–244. Springer (2020). https://doi.org/10.1007/978-3-030-45234-6_11
Nicosia, V., Latora, V.: Measuring and modeling correlations in multiplex networks. Phys. Rev. E (2015). https://doi.org/10.1103/PhysRevE.92.032805
The object management group: object constraint language, v2.4 (2014)
Pham, M., Boncz, P.A., Erling, O.: S3G2: A scalable structure-correlated social graph generator. In: TPCTC, pp. 156–172. Springer (2012). https://doi.org/10.1007/978-3-642-36727-4_11
Prat-Pérez, A., Guisado-Gámez, J., Salas, X.F., Koupy, P., Depner, S., Bartolini, D.B.: Towards a property graph generator for benchmarking. In: GRADES at SIGMOD, pp. 6:1–6:6 (2017). https://doi.org/10.1145/3078447.3078453
Rensink, A.: Canonical graph shapes. In: ESOP, pp. 401–415. Springer (2004). https://doi.org/10.1007/978-3-540-24725-8_28
Rensink, A.: Isomorphism checking in GROOVE. Electron. Commun. Eur. Assoc. Softw. Sci. Technol. (2006). https://doi.org/10.14279/tuj.eceasst.1.77
Rensink, A., Distefano, D.: Abstract graph transformation. Electr. Notes Theor. Comput. Sci. 157(1), 39–59 (2006)
Reps, T.W., Sagiv, M., Wilhelm, R.: Static program analysis via 3-valued logic. In: International Conference on Computer Aided Verification, pp. 15–30 (2004)
Sathanur, A.V., Choudhury, S., Joslyn, C., Purohit, S.: When labels fall short: Property graph simulation via blending of network structure and vertex attributes. CoRR arXiv:1709.02339 (2017)
Schneider, S., Lambers, L., Orejas, F.: Automated reasoning for attributed graph properties. STTT 20(6), 705–737 (2018). https://doi.org/10.1007/s10009-018-0496-3
Semeráth, O., Babikian, A.A., Li, A., Marussy, K., Varró, D.: Automated generation of consistent models with structural and attribute constraints. In: Proceedings of the 23rd ACM/IEEE International conference on model driven engineering languages and systems, pp. 187–199 (2020)
Semeráth, O., Babikian, A.A., Pilarski, S., Varró, D.: VIATRA Solver: a framework for the automated generation of consistent domain-specific models. In: ICSE, pp. 43–46 (2019)
Semeráth, O., Barta, Á., Horváth, Á., Szatmári, Z., Varró, D.: Formal validation of domain-specific languages with derived features and well-formedness constraints. Software and systems modeling pp. 357–392 (2017). https://doi.org/10.1016/j.entcs.2008.04.038
Semeráth, O., Nagy, A.S., Varró, D.: A graph solver for the automated generation of consistent domain-specific models. In: ICSE, pp. 969–980. ACM (2018). https://doi.org/10.1145/3180155.3180186
Semeráth, O., Rebeka, F., Bergmann, G., Varró, D.: Diversity of graph models and graph generators in mutation testing. Int. J. Softw. Tools Technol. Trans. (2019). https://doi.org/10.1007/s10009-019-00530-6
Semeráth, O., Varró, D.: Graph Constraint Evaluation over Partial Models by Constraint Rewriting. In: ICMT, pp. 138–154 (2017). https://doi.org/10.1007/978-3-319-61473-1_10
Semeráth, O., Varró, D.: Iterative generation of diverse models for testing specifications of DSL tools. In: FASE, pp. 227–245. Springer (2018). https://doi.org/10.1007/978-3-319-89363-1_13
Seshadhri, C., Kolda, T.G., Pinar, A.: Community structure and scale-free collections of Erdős-Rényi graphs. CoRR arXiv:1112.3644 (2011)
Shariat Yazdi, H., Angelis, L., Kehrer, T., Kelter, U.: A framework for capturing, statistically modeling and analyzing the evolution of software models. J. Syst. Softw. 118, 176–207 (2016). https://doi.org/10.1016/j.jss.2016.05.010
Shariat Yazdi, H., Pietsch, P., Kehrer, T., Kelter, U.: Synthesizing realistic test models. Comput. Sci. Res. Dev. 30(3–4), 231–253 (2015). https://doi.org/10.1007/s00450-014-0255-y
Simonovsky, M., Komodakis, N.: GraphVAE: Towards generation of small graphs using variational autoencoders. In: ICANN, pp. 412–422. Springer (2018). https://doi.org/10.1007/978-3-030-01418-6_41
Soltana, G., Sabetzadeh, M., Briand, L.C.: Synthetic data generation for statistical testing. In: ASE, pp. 872–882 (2017). https://doi.org/10.1109/ASE.2017.8115698
Soltana, G., Sabetzadeh, M., Briand, L.C.: Practical model-driven data generation for system testing. CoRR arXiv:1902.00397 (2019)
Staudt, C.L., Hamann, M., Gutfraind, A., Safro, I., Meyerhenke, H.: Generating realistic scaled complex networks. Appl. Netw. Sci. 2(1), 1–29 (2017). https://doi.org/10.1007/s41109-017-0054-z
Szárnyas, G., Kővári, Z., Salánki, Á., Varró, D.: Towards the characterization of realistic models: evaluation of multidisciplinary graph metrics. In: MODELS, pp. 87–94. ACM (2016)
The Eclipse Project: Eclipse Modeling Framework (2019). http://www.eclipse.org/emf
Torlak, E., Jackson, D.: Kodkod: A relational model finder. In: TACAS, pp. 632–647. Springer (2007). https://doi.org/10.1007/978-3-540-71209-1_49
Ujhelyi, Z., Bergmann, G., Hegedüs, Á., Horváth, Á., Izsó, B., Ráth, I., Szatmári, Z., Varró, D.: EMF-IncQuery: an integrated development environment for live model queries. Sci. Comput. Program. 98, 80–99 (2015). https://doi.org/10.1016/j.scico.2014.01.004
Varró, D., Balogh, A.: The model transformation language of the VIATRA2 framework. Sci. Comput. Program. 68(3), 214–234 (2007). https://doi.org/10.1016/j.scico.2007.05.004
Varró, D., Bergmann, G., Hegedüs, Á., Horváth, Á., Ráth, I., Ujhelyi, Z.: Road to a reactive and incremental model transformation platform: three generations of the viatra framework. Softw. Syst. Model. 15(3), 609–629 (2016)
Varró, D., Semeráth, O., Szárnyas, G., Horváth, Á.: Towards the automated generation of consistent, diverse, scalable and realistic graph models. In: Graph transformation, specifications, and nets - In Memory of Hartmut Ehrig, pp. 285–312. Springer (2018). https://doi.org/10.1007/978-3-319-75396-6_16
Wang, J., Kim, S., Carrington, D.A.: Verifying metamodel coverage of model transformations. In: ASWEC, pp. 270–282. IEEE (2006)
Wang, Y., Yao, Q., Kwok, J.T., Ni, L.M.: Generalizing from a few examples: a survey on few-shot learning. ACM Comput. Surv. (CSUR) 53(3), 1–34 (2020)
Wu, H., Monahan, R., Power, J.F.: Exploiting attributed type graphs to generate metamodel instances using an SMT solver. In: TASE, pp. 175–182 (2013). https://doi.org/10.1109/TASE.2013.31
Yakindu Statechart Tools: Yakindu (2019). http://statecharts.org/
You, J., Ying, R., Ren, X., Hamilton, W.L., Leskovec, J.: GraphRNN: Generating realistic graphs with deep auto-regressive models. In: ICML, pp. 5694–5703 (2018)
Zhang, J.W., Tay, Y.C.: GSCALER: synthetically scaling a given graph. In: EDBT, pp. 53–64 (2016). https://doi.org/10.5441/002/edbt.2016.08
Acknowledgements
We would like to thank all three reviewers for their detailed and insightful feedback. This paper was partially supported by the NSERC RGPIN-04573-16 project, the NSERC PGSD3-546810-2020 scholarship, the McGill Grad Excellence Award-90025, the Fonds de recherche du Québec - Nature et technologies (FRQNT) B1X scholarship (file number: 272709), the ÚNKP-20-4 New National Excellence Program of the Ministry for Innovation and Technology from the source of the National Research, Development and Innovation Fund, and by the NRDI Fund based on the charter of bolster issued by the NRDI Office under the auspices of the Ministry for Innovation and Technology. We would like to thank the Department of Electrical and Computer Engineering, and the School of Computer Science of McGill University for providing resources to run our measurements. During the development of the achievements, we took into consideration the goals set by the Balatonfüred System Science Innovation Cluster and the plans of the “BME Balatonfüred Knowledge Center,” supported by EFOP 4.2.1-16-2017-00021.
Funding
Open access funding provided by Budapest University of Technology and Economics.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Andy Schürr.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Semeráth, O., Babikian, A.A., Chen, B. et al. Automated generation of consistent, diverse and structurally realistic graph models. Softw Syst Model 20, 1713–1734 (2021). https://doi.org/10.1007/s10270-021-00884-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10270-021-00884-z









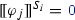 ,
,


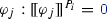 ) and a designated model size is reached,
) and a designated model size is reached,  or a reference
or a reference 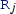 ) based on observed changes in the distances upon the previous applications of the same operation. When guiding the generation, the metric values extrapolated to the final size of the model are used.
) based on observed changes in the distances upon the previous applications of the same operation. When guiding the generation, the metric values extrapolated to the final size of the model are used.