ChronoSphere: a graph-based EMF model repository for IT landscape models

2.1 Deriving requirements from the context

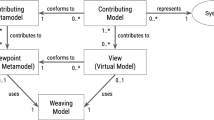
IT architectures and their terminology (e.g., the exact definition of general terms like Service or Application) vary by company. Therefore, the structure of the resulting IT Landscape models also differs. One solution to these Heterogeneous Architectures [C1] is to unify them under a common, fixed metamodel (e.g., ArchiMate [43]). However, this can lead to poor acceptance in practice due to its rigidity and the additional complexity introduced by its generality. From our past surveys and case studies [17, 18, 19, 20, 73], we inferred the requirement that the metamodel should be configurable by the user [R1]. The companies which utilize IT Landscape models the most are usually large companies [C2], or companies with a strong focus on IT (such as data centers). This entails that the corresponding models will grow to considerable sizes, and a repository must offer the necessary scalability [R5].

Documenting the IT Landscape of a company is a continuous effort. In the industrial context, we are therefore faced with long-running endeavors [C4] that span several years. In situations where responsible persons change and team members leave while new ones join, the ability to comprehend and reflect upon past decisions becomes crucial. Versioning the model content [R2] meets these demands, and also enables use cases that involve auditing, as well as use cases where versioning is required for legal compliance [C6]. The underlying requirement for these use cases is to not only store the version history, but also to analyze history traces [R8]. During a long-term documentation project, the metamodel sometimes also needs to be adapted [R3], for example due to technological shifts [C3] that introduce new types of assets. Examples for technological shifts include the introduction of virtualization technologies in data centers, and the advent of cloud computing. Another direct consequence of long-running projects is that the change history of individual model elements can grow to large sizes [R5] which must be considered in the technical realization of a repository.

In industrial contexts, several different stakeholders collaborate in documenting the IT Landscape. Depending on the scope of the project, stakeholders can involve a wide variety of roles, ranging from IT operations experts to database managers and enterprise architects [C5]. This entails that the repository must support concurrent access [R6] for multiple users. Another requirement that follows directly from concurrent access is that the structural consistency of the model contents must be ensured by the repository [R6, R9] (e.g., conformance to the metamodel and referential integrity). From the analysis perspective, concurrent access is also a threat to the consistency and reproducibility of query results, which is required for reliable model analysis [R9]. Apart from analyzing the current and past states of the model, IT Landscape models are also used to plan for future transformations [C7]. The general workflow involves the creation of “to-be” scenarios based on the current state which are then compared against each other in order to select the best candidate. In order to cope with such use cases, the repository must support branching [R4]. Branches allow the plans to be based on the actual model and to change it independently without affecting the as-is state. Since the comparison of two model states is an important part of planning (as well as a number of other use cases), the repository needs to be able to evaluate an analysis query on any model version and on any branch [R7] without altering the query.

2.2 Deriving features from requirements

From the set of requirements, we inferred the technical features which our model repository has to support. As we want our users to be able to provide their own metamodels, we employ the standard Eclipse Modeling Framework (EMF [70]) as our modeling language of choice [F1]. The fact that the data managed by our repository consists of a large and densely connected model which has to be put under version control lead to the decision to employ a per-element versioning strategy [F2], as a coarse-grained whole-model versioning strategy would cause performance issues for such models.

Supporting a user-defined metamodel, element versioning and metamodel evolution at the same time is a challenging task. The combination of these requirements entails that our repository must support metamodel versioning, metamodel evolution and instance co-adaptation [F3]. From a technical perspective, it is also inadvisable to create a full copy of a model version each time a branch is created due to the potential size of the model. We therefore require a branching mechanism that is lightweight [F4] in that it reuses the data from the origin branch rather than copying it when a new branch is created. Since IT Landscape models can grow to large sizes and will potentially not fit into the main memory of the machine which runs our repository, we require a mechanism for dynamic on-demand loading and unloading of model elements [F5].

A technical feature which is crucial for efficient querying of the entire model is indexing [F6]. The primary index allows to locate a model element by its unique ID without linear iteration over all elements. Secondary indices can be defined by the user for a given metamodel and can be used to efficiently find all elements in the model where a property is set to a specified value (e.g., finding all servers where the name contains “Production”). In addition, indexing has to consider the versioned nature of our repository, as we want our indices to be usable for all queries, regardless of the chosen version or branch. In other words, even a query on a model version that is one year old should be able to utilize our indices. In order for queries to be executable on any branch and timestamp, we require a framework that allows for the creation of queries that are agnostic to the chosen branch and version [F9].

All queries and modifications in our repository are subject to concurrent access. We meet this requirement by providing full ACID [38] end-to-end transaction support in our repository [F8]. Finally, in order to support long histories, we implement a feature called Temporal Rollover which enables the archiving of historical entries [F7]. This feature allows for indefinite growth of element histories and will be explained in detail in later sections.

4.1 Formal foundation

The key concept behind our formalism is based on the observation that temporal information always adds an additional dimension to a dataset. A key-value format has only one dimension, which is the key. By adding temporal information, the two resulting dimensions are the key, and the time at which the value was inserted. Therefore, a matrix is a very natural fit for formalizing the versioning problem, offering the additional advantage of being easy to visualize. The remainder of this section consists of definitions which provide the formal semantics of our solution, interleaved with figures and (less formal) textual explanations.

In Definition 1, we define a Temporal Data Matrix, which is a key-value mapping enhanced with temporal information [R2, R3]. Note that the number of rows and columns in this matrix is infinite. In order to retrieve a value from this matrix, a key string and a timestamp are required. We refer to such a pair as a Temporal Key. The matrix can contain an array of binary values in every cell, which can be interpreted as the serialized representation of an arbitrary object. The formalism is therefore not restricted to any particular value type. The dedicated null value (which is different from all other bit-strings and also different from the \(\epsilon \) values used to initialize the matrix) will be used as a marker that indicates the deletion of an element later in Definition 3.

In order to guarantee the traceability of changes [R8], entries in the past must not be modified, and new entries may only be appended to the end of the history, not inserted at an arbitrary position. We use the notion of a dedicated now timestamp for this purpose.

Definition 2 introduces the concept of the now timestamp, which is the largest (i.e., latest) timestamp at which data has been inserted into the store so far, initialized at zero for empty matrices. This particular timestamp will serve as a safeguard against temporal inconsistencies in several operations. We continue by defining the temporal counterparts of the put and get operations of a key-value store.

The write operation put replaces a single entry in a Temporal Data Matrix by specifying the exact coordinates and a new value for that entry. All other entries remain the same as before. Please note that, while v must not be \(\epsilon \) in the context of a put operation (i.e., a cell cannot be “cleared”), v can be null to indicate a deletion of the key k from the matrix. Also, we require that an entry must not be overwritten. This is given implicitly by the fact that each put advances the result of now(D), and further insertions are only allowed after that timestamp. Furthermore, write operations are not permitted to modify the past in order to preserve consistency and traceability, which is also asserted by the condition on the now timestamp. This operation is limited in that it allows to modify only one key at a time. In the implementation, we generalize it to allow simultaneous insertions in several keys via transactions.

The function get first attempts to return the value at the coordinates specified by the key and timestamp (\(u = t\)). If that position is empty, we scan for the entry in the same row with the highest timestamp and a non-empty value, considering only entries with lower timestamps than the request timestamp. In the formula, we have to add \(-~1\) to the set from which u is chosen to cover the case where there is no other entry in the row. If there is no such entry (i.e., \(u = -~1\)) or the entry is null, we return the empty binary string, otherwise we return the entry with the largest encountered timestamp.

This process is visualized in Fig. 4. In this figure, each row corresponds to a key, and each column to a timestamp. The depicted get operation is working on timestamp 5 and key ‘d’. As \(D_{5,d}\) is empty, we attempt to find the largest timestamp smaller than 5 where the value for the key is not empty, i.e., we move left until we find a non-empty cell. We find the result in \(D_{1, d}\) and return v1. This is an important part of the versioning concept: a value for a given key is assumed to remain unchanged until a new value is assigned to it at a later timestamp. This allows any implementation to conserve memory on disk, as writes only occur if the value for a key has changed (i.e., no data duplication is required between identical revisions). Also note that we do not need to update existing entries when new key-value pairs are being inserted, which allows for pure append-only storage. In Fig. 4, the value v1 is valid for the key ‘d’ for all timestamps between 1 and 5 (inclusive). For timestamp 0, the key ‘d’ has value v0. Following this line of argumentation, we can generalize and state that a row in the matrix, identified by a key \(k \in K\), contains the history of k. This is formalized in Definition 5. A column, identified by a timestamp \(t \in T\), contains the state of all keys at that timestamp, with the additional consideration that value duplicates are not stored as they can be looked up in earlier timestamps. This is formalized in Definition 6.

Open image in new window

In Definition 5, we define the history of a key k up to a given timestamp t in a Temporal Data Matrix D as the set of timestamps less than or equal to t that have a non-empty entry for key k in D. Note that the resulting set will also include deletions, as null is a legal value for \(D_{x,k}\) in the formula. The result is the set of timestamps where the value for the given key changed. Consequently, performing a get operation for these timestamps with the same key will yield different results, producing the full history of the temporal key.

As shown in Definition 6, the keyset in a Temporal Data Matrix changes over time. We can retrieve the keyset at any desired time by providing the appropriate timestamp t. Note that this works for any timestamp in the past, in particular we do not require that a write operation has taken place precisely at t in order for the corresponding key(s) to be contained in the keyset. In other words, the precise column of t may consist only of \(\epsilon \) entries, but the key set operation will also consider earlier entries which are still valid at t. The version operation introduced in Definition 7 operates in a very similar way, but returns tuples containing keys and values, rather than just keys.

Figure 5 illustrates the key set and version operations by example. In this scenario, the key set (or version) is requested at timestamp \(t = 5\). We scan each row for the latest non-\(\epsilon \) entry and add the corresponding key of the row to the key set, provided that a non-\(\epsilon \) right-most entry exists (i.e., the row is not empty) and is not null (the value was not removed). In this example, keyset(D, 5) would return \(\{a,c,d\}\), assuming that all non-depicted rows are empty. b and f are not in the key set, because their rows are empty (up to and including timestamp 5), and e is not in the set because its value was removed at timestamp 4. If we would request the key set at timestamp 3 instead, e would be in the key set. The operation version(D, 5) returns \(\{ \langle a,v0\rangle , \langle c, v2\rangle , \langle d, v4\rangle \}\) in the example depicted in Fig. 5. The key e is not represented in the version because it did not appear in the key set.

Open image in new window

Table 2

Mapping capabilities to operations [25]

Capability	Realization in formalism
Pure-Timeslice	Equivalent to keyset operation
Range-Timeslice	One get operation per given key
Pure-Key	One history operation per given key

With the given set of operations, we are able to answer all three kinds of temporal queries identified by Salzberg and Tsotras [62], as indicated in Table 2. Due to the restrictions imposed onto the put operation (see Definition 3), data cannot be inserted before the now timestamp (i.e., the history of an entry cannot be modified). Since the validity range of an entry is determined implicitly by the empty cells between changes, existing entries never need to be modified when new ones are being added. The formalization therefore fulfills all requirements stated at the beginning of this section.

4.2 Implementation

ChronoDB is our implementation of the concepts presented in the previous section. It is a fully ACID compliant, process-embedded, temporal key-value store written in Java. The intended use of ChronoDB is to act as the storage backend for a graph database, which is the main driver behind numerous design and optimization choices. The full source code is freely available on GitHub under an open-source license.

4.2.1 Implementing the matrix

As the formal foundation includes the concept of a matrix with infinite dimensions, a direct implementation is not feasible. However, a Temporal Data Matrix is typically very sparse. Instead of storing a rigid, infinite matrix structure, we focus exclusively on the non-empty entries and expand the underlying data structure as more entries are being added.

There are various approaches for storing versioned data on disk [15, 46, 50]. We reuse existing, well-known and well-tested technology for our prototype instead of designing custom disk-level data structures. The temporal store is based on a regular B\(^{+}\)-Tree [61]. We make use of the implementation of B\(^{+}\)-Trees provided by the TUPL⁸ library. In order to form an actual index key from a Temporal Key, we concatenate the actual key string with the timestamp (left-padded with zeros to achieve equal length), separated by an ‘@’ character. Using the standard lexicographic ordering of strings, we receive an ordering as shown in Table 3. This implies that our B\(^{+}\)-Tree is ordered first by key, and then by timestamp. The advantage of this approach is that we can quickly determine the value of a given key for a given timestamp (i.e., get is reasonably fast), but the keyset (see Definition 6) is more expensive to compute.

Table 3

Ascending Temporal Key ordering by example [25]

Order	Temporal key	Key string	Timestamp
0	a@0123	a	123
1	a@0124	a	124
2	a@1000	a	1000
3	aa@0100	aa	100
4	b@0001	b	1
5	ba@0001	ba	1

The put operation appends the timestamp to the user key and then performs a regular B\(^{+}\)-Tree insertion. The temporal get operation requires retrieving the next lower entry with the given key and timestamp.

This is similar to regular B\(^{+}\)-Tree search, except that the acceptance criterion for the search in the leaf nodes is “less than or equal to” instead of “equal to”, provided that nodes are checked in descending key order. TUPL natively supports this functionality. After finding the next lower entry, we need to apply a post-processing step in order to ensure correctness of the get operation. Using Table 3 as an example, if we requested aa@0050 (which is not contained in the data), searching for the next-lower key produces a@1000. The key string in this temporal key (a) is different from the one which was requested (aa). In this case, we can conclude that the key aa did not exist up to the requested timestamp (50), and we return null instead of the retrieved result.

Due to the way we set up the B\(^{+}\)-Tree, adding a new revision to a key (or adding an entirely new key) has the same runtime complexity as inserting an entry into a regular B\(^{+}\)-Tree. Temporal search also has the same complexity as regular B-Tree search, which is \(\mathcal {O}(\hbox {log}(n))\), where n is the number of entries in the tree. From the formal foundations onward, we assert by construction that our implementation will scale equally well when faced with one key and many versions, many keys with one revision each, or any distribution in between [R5]. An important property of our data structure setup is that, regardless of the versions-per-key distribution, the data structure never degenerates into a list, maintaining an access complexity of \(\mathcal {O}(\hbox {log}(n))\) by means of regular B\(^{+}\)-Tree balancing without any need for additional algorithms.

Open image in new window

4.2.2 Branching

Figure 6 shows how the branching mechanism works in ChronoDB [R4]. Based on our matrix formalization, we can create branches of our history at arbitrary timestamps. To do so, we generate a new, empty matrix that will hold all changes applied to the branch it represents. We would like to emphasize that existing entries are not duplicated. We therefore create lightweight branches. When a get request arrives at the first column of a branch matrix during the search, we redirect the request to the matrix of the parent branch, at the branching timestamp, and continue from there. In this way, the data from the original branch (up to the branching timestamp) is still fully accessible in the child branch.

Open image in new window

For example, as depicted in Fig. 7, if we want to answer a get request for key c on branch branchA and timestamp 4, we scan the row with key c to the left, starting at column 4. We find no entry, so we redirect the call to the origin branch (which in this case is master), at timestamp 3. Here, we continue left and find the value \(c_{1}\) on timestamp 1. Indeed, at timestamp 4 and branch branchA, \(c_{1}\) is still valid. However, if we issue the same original query on master, we would get \(c_{4}\) as our result. This approach to branching can also be employed recursively in a nested fashion, i.e., branches can in turn have sub-branches. The primary drawback of this solution is related to the recursive “backstepping” to the origin branch during queries. For deeply nested branches, this process will introduce a considerable performance overhead, as multiple B\(^{+}\)-Trees (one per branch) need to be opened and queried in order to answer this request. This happens more often for branches which are very thinly populated with changes, as this increases the chances of our get request scan ending up at the initial column of the matrix without encountering an occupied cell. The operation which is affected most by branching with respect to performance is the keySet operation (and all other operations that rely on it), as this requires a scan on every row, leading to potentially many backstepping calls.

4.2.3 Caching

A disk access is always slow compared to an in-memory operation, even on a modern solid state drive (SSD). For that reason, nearly all database systems include some way of caching the most recent query results in main memory for later reuse. ChronoDB is no exception, but the temporal aspects demand a different approach to the caching algorithm than in regular database systems, because multiple transactions can simultaneously query the state of the stored data at different timestamps. Due to the way we constructed the Temporal Data Matrix, the chance that a given key does not change at every timestamp is very high. Therefore, we can potentially serve queries at many different timestamps from the same cached information by exploiting the periods in which a given key does not change its value. For the caching algorithm, we apply some of the ideas found in the work of Ramaswamy [57] in a slightly different way, adapted to in-memory processing and caching idioms.

Open image in new window

Figure 8 displays an example for our temporal caching approach which we call Mosaic. When the value for a temporal key is requested and a cache miss occurs, we retrieve the value together with the validity range (indicated by gray background in the figure) from the persistent store, and add the range together with its value to the cache. Validity ranges start at the timestamp in which a key-value pair was modified (inclusive) and end at the timestamp where the next modification on that pair occurred (exclusive). For each key, the cache manages a list of time ranges called a cache row, and each range is associated with the value for the key in this period. As these periods never overlap, we can sort them in descending order for faster search, assuming that more recent entries are used more frequently. A cache look-up is performed by first identifying the row by the key string, followed by a linear search through the cached periods.⁹ We have a cache hit if a period containing the requested timestamp is found. When data is written to the underlying store, we need to perform a write-through in our cache, because validity ranges that have open-ended upper bounds potentially need to be shortened due to the insertion of a new value for a given key. The write-through operation is fast, because it only needs to check if the first validity range in the cache row of a given key is open-ended, as all other entries are always closed ranges. All entries in our cache (regardless of the row they belong to) share a common least recently used registry which allows for fast cache eviction of the least recently read entries.

In the example shown in Fig. 8, retrieving the value of key d at timestamp 0 would result in adding the validity range [0; 1) with value v0 to the cache row. This is the worst-case scenario, as the validity range only contains a single timestamp, and can consequently be used to answer queries only on that particular timestamp. Retrieving the same key at timestamps 1 through 4 yields a cache entry with a validity range of [1; 5) and value v1. All requests on key d from timestamp 1 through 4 can be answered by this cache entry. Finally, retrieving key d on a timestamp greater than or equal to 5 produces an open-ended validity period of \([5;\infty )\) with value v2, which can answer all requests on key d with a timestamp larger than 4, assuming that non-depicted columns are empty. If we would insert a key-value pair of \(\langle d, v3\rangle \) at timestamp 10, the write-through operation would need to shorten the last validity period to [5; 10) and add a cache entry containing the period \([10;\infty )\) with value v3.

4.2.4 Incremental commits

Database vendors often provide specialized ways to batch-insert large amounts of data into their databases that allow for higher performance than the usage of regular transactions. ChronoDB provides a similar mechanism, with the additional challenge of keeping versioning considerations in mind along the way. Even when inserting large amounts of data into ChronoDB, we want the history to remain clean, i.e., it should not contain intermediate states where only a portion of the overall data was inserted. We therefore need to find a way to conserve RAM by writing incoming data to disk while maintaining a clean history. For this purpose, the concept of incremental commits was introduced in ChronoDB. This mechanism allows to mass-insert (or mass-update) data in ChronoDB by splitting it up into smaller batches while maintaining a clean history and all ACID properties for the executing transaction.

Open image in new window

Figure 9 shows how incremental commits work in ChronoDB. The process starts with a regular transaction inserting data into the database before calling commitIncremental(). This writes the first batch (timestamp 2 in Fig. 9) into the database and releases it from RAM. However, the now timestamp is not advanced yet. We do not allow other transactions to read these new entries, because there is still data left to insert. We proceed with the next batches of data, calling commitIncremental() after each one. After the last batch was inserted, we conclude the process with a call to commit(). This will merge all of our changes into one timestamp on disk. In this process, the last change to a single key is the one we keep. In the end, the timestamps between the first initial incremental commit (exclusive) to the timestamp of the final commit (inclusive) will have no changes (as shown in timestamps 3 and 4 in Fig. 9). With the final commit, we also advance the now timestamp of the matrix and allow all other transactions to access the newly inserted data. By delaying this step until the end of our operation, we keep the possibility to roll back our changes on disk (for example in case that the process fails) without violating the ACID properties for all other transactions. Also, if data generated by a partially complete incremental commit process is present on disk at database start-up (which occurs when the database is unexpectedly shut down during an incremental commit process), these changes can be rolled back as well, which allows incremental commit processes to have “all or nothing” semantics.

A disadvantage of this solution is that there can be only one concurrent incremental commit process on any data matrix. This process requires exclusive write access to the matrix, blocking all other (regular and incremental) commits until it is complete. However, since we only modify the head revisions and now does not change until the process ends, we can safely perform read operations in concurrent transactions, while an incremental commit process is taking place. Overall, incremental commits offer a way to insert large quantities of data into a single timestamp while conserving RAM without compromising ACID safety at the cost of requiring exclusive write access to the database for the entire duration of the process. These properties make them very suitable for data imports from external sources, or large scale changes that affect most of the key-value pairs stored in a matrix. This will become an important factor when we consider global model evolutions in the model repository layer [R3]. We envision incremental commits to be employed for administrative tasks which do not recur regularly, or for the initial filling of an empty database.

4.2.5 Supporting long histories

In order to create a sustainable versioning mechanism, we need to ensure that our system can support a virtually unlimited number of versions [R2, R5]. Ideally, we also should not store all data in a single file, and old files should remain untouched when new data is inserted (which is important for file-based backups). For these reasons, we must not constrain our solution to a single B-Tree. The fact that past revisions are immutable in our approach led to the decision to split the data along the time axis, resulting in a series of B-Trees. Each tree is contained in one file, which we refer to as a chunk file. An accompanying meta file specifies the time range which is covered by the chunk file. The usual policy of ChronoDB is to maximize sharing of unchanged data as much as possible. Here, we deliberately introduce data duplication in order to ensure that the initial version in each chunk is complete. This allows us to answer get queries within the boundaries of a single chunk, without having to navigate to the previous one. As each access to another chunk has CPU and I/O overhead, we should avoid accesses on more than one chunk to answer a basic query. Without duplication, accessing a key that has not changed for a long time could potentially lead to a linear search through the chunk chain which contradicts the requirement for scalability [R5].

Open image in new window

The algorithm for the “rollover” procedure outlined in Fig. 10 works as follows.

Open image in new window

In Line 1 of Algorithm 1, we fetch the latest timestamp where a commit has occurred in our current head revision chunk. Next, we calculate the full head version of the data in Line 2. With the preparation steps complete, we set the end of the validity time range to the last commit timestamp in Line 3. This only affects the metadata, not the chunk itself. We now create a new, empty chunk in Line 4, and set the start of its validity range to the split timestamp plus one (as chunk validity ranges must not overlap). The upper bound of the new validity range is infinity. In Line 5 we copy the head version of the data into the new chunk. Finally, we update our internal look-up table in Line 6. This entire procedure only modifies the last chunk and does not touch older chunks, as indicated by the grayed-out boxes in Fig. 10.

The look-up table that is being updated in Algorithm 1 is a basic tree map which is created at start-up by reading the metadata files. For each encountered chunk, it contains an entry that maps its validity period to its chunk file. The periods are sorted in ascending order by their lower bounds, which is sufficient because overlaps in the validity ranges are not permitted. For example, after the rollover depicted in Fig. 10, the time range look-up would contain the entries shown in Table 4.

Table 4

Time range look-up [26]

Time range	Chunk number
\([0 \ldots 300]\)	0
\([301 \ldots 1000]\)	1
\([1001 \ldots \infty ]\)	2

We employ a tree map specifically in our implementation for Table 4, because the purpose of this look-up is to quickly identify the correct chunk to address for an incoming request. Incoming requests have a timestamp attached, and this timestamp may occur exactly at a split, or anywhere between split timestamps. As this process is triggered very often in practice and the time range look-up map may grow quite large over time, we are considering to implement a cache based on the least-recently-used principle that contains the concrete resolved timestamp-to-chunk mappings in order to cover the common case where one particular timestamp is requested more than once in quick succession.

With this algorithm, we can support a virtually unlimited number of versions [R6] because new chunks always only contain the head revision of the previous ones, and we are always free to roll over once more should the history within the chunk become too large. We furthermore do not perform writes on old chunk files anymore, because our history is immutable. Regardless, thanks to our time range look-up, we have close to \(O(\log {}n)\) access complexity to any chunk, where n is the number of chunks.

This algorithm is a trade-off between disk space and scalability. We introduce data duplication on disk in order to provide support for large histories. The key question that remains is when this process happens. We require a metric that indicates the amount of data in the current chunk that belongs to the history (as opposed to the head revision) and thus can be archived if necessary by performing a rollover. We introduce the Head–History–Ratio (HHR) as the primary metric for this task, which we defined as follows:

$$\begin{aligned} HHR(e, h) = {\left\{ \begin{array}{ll} e, &{} \text {if } e = h\\ \frac{h}{e-h}, &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

...where e is the total number of entries in the chunk, and h is the size of the subset of entries that belong to the head revision (excluding entries that represent deletions). By dividing the number of entries in the head revision by the number of entries that belong to the history, we get a proportional notion of how much history is contained in the chunk that works for datasets of any size. It expresses how many entries we will “archive” when a rollover is executed. When new commits add new elements to the head revision, this value increases. When a commit updates existing elements in the head revision or deletes them, this value decreases. We can employ a threshold as a lower bound on this value to determine when a rollover is necessary. For example, we may choose to perform a rollover when a chunk has an HHR value of 0.2 or less. This threshold will work independently of the absolute size of the head revision. The only case where the HHR threshold is never reached is when exclusively new (i.e., never seen before) keys are added, steadily increasing the size of the head revision. However, in this case, we would not gain anything by performing a rollover, as we would have to duplicate all of those entries into the new chunk to produce a complete initial version. Therefore, the HHR metric is properly capturing this case by never reaching the threshold, thus never indicating the need for a rollover.

4.2.6 Secondary indexing

There are two kinds of secondary indices in ChronoDB. On the one hand, there are indices which are managed by ChronoDB itself (“system indices”) and on the other hand there are user-defined indices. As indicated in Table 3, the primary index for each matrix in ChronoDB has its keys ordered first by user key and then by version. In order to allow for efficient time range queries, we maintain a secondary index that is first ordered by timestamp and then by user key. Further system indices include an index for commit metadata (e.g., commit messages) that maps from timestamp to metadata, as well as auxiliary indices for branching (branch name to metadata). User-defined indices [R5] help to speed up queries that request entries based on their contents (rather than their primary key). An example for such a query is find all persons where the first name is ’Eva’. Since ChronoDB stores arbitrary Java objects, we require a method to extract the desired property value to index from the object. This is accomplished by defining a ChronoIndexer interface. It defines the index(Object) method that, given an input object, returns the value that should be put on the secondary index. Each indexer is associated with a name. That name is later used in a query to refer to this index. The associated query language provides support for a number of string matching techniques (equals, contains, starts with, regular expression...), numeric matching (greater than, less than or equal to...) as well as Boolean operators (and, or, not). The query engine also performs optimizations such as double negation elimination. Overall, this query language is certainly less expressive than other languages such as SQL. Since ChronoDB is intended to be used as a storage engine and embedded in a database frontend (e.g., a graph database), these queries will only be used internally for index scans while more sophisticated expressions are managed by the database frontend. Therefore, this minimalistic Java-embedded DSL has proven to be sufficient. An essential drawback of this query mechanism is that the number of properties available for querying is determined by the available secondary indices. In other words, if there is no secondary index for a property, that property cannot be used for filtering. This is due to ChronoDB being agnostic to the Java objects it is storing. In absence of a ChronoIndexer, it has no way of extracting a value for an arbitrary request property from the object. This is a common approach in database systems: without a matching secondary index, queries require a linear scan of the entire data store. When using a database frontend, this distinction is blurred, and the difference between an index query and a non-index query is only noticeable in how long it takes to produce the result set.

In contrast to the primary index, entries in the secondary index are allowed to have non-unique keys. For example, if we index the “name” attribute, then there may be more than one entry where the name is set to “John”. We therefore require a different approach than the temporal data matrices employed for the primary index. Inspired by the work of Ramaswamy et al. [57], we make use of explicit time windows. Non-unique indices in versioned contexts are special cases of the general interval stabbing problem [31].

Table 5

Secondary indexing in ChronoDB

#	Index	Branch	Keyspace	Key	Value	From	To
1	name	master	default	e1	“john”	1234	\(\infty \)
2	name	master	default	e2	“john”	1234	5678
3	name	master	default	e3	“john”	1234	7890
4	name	master	default	e2	“jack”	5678	\(\infty \)

Table 5 shows an example of a secondary index. As such a table can hold all entries for all indices, we store the index for a particular entry in the “index” column. The branch, keyspace and key columns describe the location of the entry in the primary index. The “value” column contains the value that was extracted by the ChronoIndexer. “From” and “To” express the time window in which a given row is valid. Any entry that is newly inserted into this table initially has its “To” value set to infinity (i.e., it is valid for an unlimited amount of time). When the corresponding entry in the primary index changes, the “To” value is updated accordingly. All other columns are effectively immutable.

In the concrete example shown in Table 5, we insert three key-value pairs (with keys e1, e2 and e3) at timestamp 1234. Our indexer extracts the value for the “name” index, which is “john” for all three values. The “To” column is set to infinity for all three entries. Querying the secondary index at that timestamp for all entries where “name” is equal to “john” would therefore return the set containing e1, e2 and e3. At timestamp 5678, we update the value associated with key e2 such that the indexer now yields the value “jack”. We therefore need to terminate the previous entry (row #2) by setting the “To” value to 5678 (upper bounds are exclusive), and inserting a new entry that starts at 5678, has the value “jack” and an initial “To” value of infinity. Finally, we delete the key e3 in our primary index at timestamp 7890. In our secondary index, this means that we have to limit the “To” value of row #3 to 7890. Since we have no new value due to the deletion, no additional entries need to be added.

This tabular structure can now be queried using well-known techniques also employed by SQL. For usual queries, the branch and index is fixed, the value is specified as a search string and a condition (e.g., “starts with [jo]”) and we know the timestamp for which the query should be evaluated. We process the timestamp by searching only for entries where

$$\begin{aligned} From \le timestamp < To \end{aligned}$$

...in addition to the conditions specified for the other columns. Selecting only the documents for a given branch is more challenging, as we need to traverse the origin branches upwards until we arrive at the master branch, performing one subquery for each branch along the way and merging the intermediate results accordingly.

Open image in new window

5.1 Apache TinkerPop

The TinkerPop framework is the de-facto standard interface between applications and graph databases. Its main purpose is to allow application developers to exchange a graph database implementation with another one without altering the application source code that accesses the database. The TinkerPop standard is designed in a modular fashion. The core module is the property graph API [58] which specifies the Java interfaces for vertices, edges, properties and other structural elements.

In a property graph, each vertex and edge can have properties which are expressed as key–value pairs. According to the standard, each vertex must have an identifier which is unique among all vertices, and the same is true for edges. In practice, database vendors often recommend to use identifiers which are globally unique in the database. Furthermore, in addition to the unique ID and the user-defined properties, each vertex and edge has a label, which is defined to be a single-valued string that is intended to be used for categorization purposes. All user-defined properties are untyped by definition, i.e., no restriction is imposed on which values a user-defined property may have. However, some graph database vendors such as Titan DB¹⁰ and OrientDB¹¹ offer the possibility to define a schema which is evaluated at runtime. The only unsupported value for any user-defined property is the null value. Instead of assigning null to a property, it is recommended to delete the property on the target graph element entirely.

Another module in the TinkerPop standard is the graph query language Gremlin. In contrast to the property graph API, which is only a specification, Gremlin comes with a default implementation that is built upon the property graph API interfaces. This implementation also includes a number of built-in query optimization strategies. Other modules include a standard test suite for TinkerPop vendors, and a generic server framework for graph databases called Gremlin Server.

5.2 ChronoGraph architecture

Our open-source project ChronoGraph provides a fully TinkerPop-compliant graph database implementation with additional versioning capabilities. In order to achieve this goal, we employ a layered architecture as outlined in Fig. 12a. In the remainder of this section, we provide an overview of this architecture in a bottom-up fashion.

The bottom layer of the architecture is a versioned key-value store, i.e., a system capable of working with time–key–value tuples as opposed to plain key–value pairs in regular key-value stores. For the implementation of ChronoGraph, we use ChronoDB, as introduced in Sect. 4.

ChronoGraph itself consists of three major components. The first component is the graph structure management. It is responsible for managing the individual vertices and edges that form the graph, as well as their referential integrity [R9]. As the underlying storage mechanism is a key-value store, the graph structure management layer also performs the partitioning of the graph into key-value pairs and the conversion between the two formats. We present the technical details of this format in Sect. 5.3. The second component is the transaction management. The key concept here is that each graph transaction is associated with a timestamp on which it operates. Inside a transaction, any read request for graph content will be executed on the underlying storage with the transaction timestamp. ChronoGraph supports full ACID transactions [R6] with the highest possible isolation level (“serializable”, also known as “snapshot isolation”, as defined in the SQL Standard [38]). The underlying versioning system acts as an enabling technology for this highest level of transaction isolation, because any given version of the graph, once written to disk, is effectively immutable. All mutating operations are stored in the transaction until it is committed, which in turn produces a new version of the graph, with a new timestamp associated with it. Due to this mode of operation, we do not only achieve repeatable reads, but also provide effective protection from phantom reads, which are a common problem in concurrent graph computing. The third and final component is the query processor itself which accepts and executes Gremlin queries on the graph system. As each graph transaction is bound to a branch and timestamp, the query language (Gremlin) remains agnostic of both the branch and the timestamp, which allows the execution of any query on any desired timestamp and branch [R8].

The application communicates with ChronoGraph by using the regular TinkerPop API, with additional extensions specific to versioning. The versioning itself is entirely transparent to the application to the extent where ChronoGraph can be used as a drop-in replacement for any other TinkerPop 3.x compliant implementation. The application is able to make use of the versioning capabilities via additional methods, but their usage is entirely optional and not required during regular operation that does not involve history analysis.

5.3 Data layout

In order to store graph data in our Temporal Key–Value Store, we first need to disassemble the graph into partitions that can be serialized as values and be addressed by keys. Then, we need to persist these pairs in the store. We will first discuss how we disassemble the graph, followed by an overview of the concrete key–value format and how versioning affects this process.

5.3.1 Partitioning: the star graph format

Like many other popular graph databases, e.g., Titan DB, we rely on the Star Graph partitioning in order to disassemble the graph into manageable pieces.

Open image in new window

Figure 13 shows an example of a star graph. A star graph is a subset of the elements of a full graph that is calculated given an origin vertex, in this case v0. The star graph contains all properties of the vertex, including the id and the label, as well as all incoming and outgoing edges (including their label, id and properties). All adjacent vertices of the origin vertex are represented in the star graph by their ids. Their attributes and remaining edges (indicated by dashed lines in Fig. 13) are not contained in the star graph of v0. This partitioning was chosen due to its ability to reconstruct the entire graph from disk without duplicating entire vertices or attribute values. Furthermore, it is suitable for lazy loading of individual vertices, as only the immediate neighborhood of a vertex needs to be loaded to reconstruct it from disk.

5.3.2 Key–value layout

Starting from a star graph partitioning, we design our key–value layout. Since all graph elements in TinkerPop are mutable by definition and our persistent graph versions have to be immutable, we perform a bijective mapping step before persisting an element. We refer to the persistent, immutable version as a Record, and there is one type of record for each structural element in the TinkerPop API. For example, the mutable Vertex element is mapped to an immutable VertexRecord. A beneficial side-effect of this approach is that we hereby gain control over the persistent format, and can evolve and adapt each side of the mapping individually if needed. Table 6 shows the contents of the most important record types.

Table 6

TinkerPop API to Record Mapping [27]

TinkerPop	Record	Record contents
Vertex	VertexRecord	id, label,
		PropertyKey \(\rightarrow \) PropertyRecord
		In: EdgeLabel \(\rightarrow \) EdgeTargetRecord
		Out: EdgeLabel \(\rightarrow \) EdgeTargetRecord
Edge	EdgeRecord	id, label,
		PropertyKey \(\rightarrow \) PropertyRecord
		id of InVertex, id of OutVertex
Property	PropertyRecord	PropertyKey, PropertyValue
—	EdgeTargetRecord	id of edge, id of other-end Vertex

In Table 6, all id and label elements, as well as all PropertyKeys, are of type String. The PropertyValue in the PropertyRecord is assumed to be in byte array form. An arrow in the table indicates that the record contains a mapping, usually implemented with a regular hash map. An element that deserves special attention is the EdgeTargetRecord that does not exist in the TinkerPop API. Traversing from one vertex to another via an edge label is a very common task in a graph query. In a naive mapping, we would traverse from a vertex to an adjacent edge and load it, find the id of the vertex at the other end, and then resolve the target vertex. This involves two steps where we need to resolve an element by ID from disk. However, we cannot store all edge information directly in a VertexRecord, because this would involve duplication of all edge properties on the other-end vertex. We overcome this issue by introducing an additional record type. The EdgeTargetRecord stores the id of the edge and the id of the vertex that resides at the “other end” of the edge. In this way, we can achieve basic vertex-to-vertex traversal in one step. At the same time, we minimize data duplication and can support edge queries (e.g., g.traversal().E() in TinkerPop), since we have the full EdgeRecords as standalone elements. A disadvantage of this solution is the fact that we still need to do two resolution steps for any query that steps from vertex to vertex and has a condition on a property of the edge in between. This trade-off is common for graph databases, and we share it with many others, e.g., Neo4j. We will discuss this with a concrete example in Sect. 5.4.

For each record type, we create a keyspace in the underlying key–value store. We serialize the record elements into a binary sequence. This binary sequence serves as the value for the key–value pairs and the id of the element is used as the corresponding key. The type of record indicates which keyspace to use, completing the mapping to the key–value format. The inverse mapping involves the same steps: given an element ID and type, we resolve the key–value pair from the appropriate keyspace by performing a key look-up using the ID. Then, we deserialize the binary sequence, and apply our bijective element-to-record mapping in the inverse direction. When loading a vertex, the properties of the incoming and outgoing edges will be loaded lazily, because the EdgeTargetRecord does not contain this information and loading edge properties immediately would therefore require an additional look-up. The same logic applies to resolving the other-end vertices of EdgeTargetRecords, allowing for a lazy (and therefore efficient and RAM-conserving) solution.

Open image in new window

Figure 14 shows an example for the translation process between the Graph format and the Key-Value-Store format. In this example, we express the fact “John Doe knows Jane Doe since 1999” in a property graph format. Each graph element is transformed into an entry in the key–value store. In the example, we use a JSON-like syntax; our actual implementation employs a binary serialization format. Please note that the presented value structures correspond to the schema for records presented in Table 6.

5.4 Versioning concept

When discussing the mapping from the TinkerPop structure to the underlying key–value store in Sect. 5.3, we did not touch the topic of versioning. This is due to the fact that our key–value store ChronoDB is performing the versioning on its own. The graph structure does not need to be aware of this process. We still achieve a fully versioned graph, an immutable history and a very high degree of sharing of common (unchanged) data between revisions. This is accomplished by attaching a fixed timestamp to every graph transaction. This timestamp is always the same as in the underlying ChronoDB transaction. When reading graph data, at some point in the resolution process we perform a get(...) call in the underlying key–value store, resolving an element (e.g., a vertex) by ID. At this point, ChronoDB uses the timestamp attached to the transaction to perform the temporal resolution. This will return the value of the given key, at the specified timestamp.

Open image in new window

Note that this final navigation step starts at an element that was reused from the commit at timestamp 1065 and ends at the state of v2 that was produced by the commit at timestamp 1203. This is possible because graph elements refer to each other by ID, but these references do not include the branch or timestamp. This information is injected from the transaction at hand, allowing for this kind of navigation and data reuse. This is a major step toward fulfilling requirement [R8]. As ChronoDB offers logarithmic access time to any key-value pair on any version, this is also in line with requirement [R5].

5.5 TinkerPop compatibility and extensions

The Apache TinkerPop API is the de-facto standard interface between graph databases and applications built on top of them. We therefore want ChronoGraph to implement and be fully compliant to this interface as well. However, in order to provide our additional functionality, we need to extend the default API at several points. There are two parts to this challenge. The first part is compliance with the existing TinkerPop API, the second part is the extension of this API in order to allow access to new functionality. In the following sections, we will discuss these points in more detail.

5.6 Transaction semantics

The Apache TinkerPop API is currently available in its third version. It evolved alongside its implementations, which range from local graphs (e.g., the in-memory reference implementation TinkerGraph) to highly distributed systems (e.g., Titan DB). Due to this diversity, the requirements toward transaction semantics, in particular behavior under concurrent access [R6], are specified very loosely in TinkerPop itself. For example, when iterating over the outgoing edges of a vertex, TinkerPop only specifies that the iteration itself should never return a null value and should never throw a ConcurrentModificationException, but details regarding the visibility of changes made by other, concurrent transactions are unspecified.

Since the reference implementation TinkerGraph, which is provided alongside the API, does not support transactions,¹⁵ we had to design the transaction semantics by ourselves. When we implemented ChronoDB, we envisioned it to be a system suitable for storing data for analysis purposes, therefore the consistency of a view and the contained data is paramount. As all stored versions are effectively immutable, we chose to implement a full ACID transaction model in ChronoDB with the highest possible isolation level (“Serializable” [38]). As ChronoGraph is based on ChronoDB, it follows the same transaction model. To the best of our knowledge, ChronoGraph is currently the only implementation of the TinkerPop API v3.x that is full ACID in the strict sense, as many others opt for repeatable reads isolation (e.g., OrientDB), while ChronoGraph supports snapshot isolation. A proposal for snapshot isolation for Neo4j was published recently [55], but it is not part of the official version. Graph databases without ACID transactions and snapshot isolation often suffer from issues like Ghost Vertices¹⁶ or Half Edges¹⁷ which can cause inconsistent query results and are very difficult to deal with as an application developer. These artifacts are negative side-effects of improper transaction isolation, and application developers have to employ techniques such as soft deletes (i.e., the addition of “deleted” flags instead of true element deletions) in order to avoid them. As ChronoGraph adheres to the ACID properties, these inconsistencies can not appear by design.

5.7 Functionality and usage implications

Our implementation is a stark contrast to existing solutions. We implement the versioning process at a lower level, in the generic temporal key–value store ChronoDB. This store is aware of the semantics of the versioning process, and is capable of solving the problem of long histories [26] (c.f. Sect. 4.2), unlike the previously mentioned solutions. There are no additional mapping steps required in order to achieve graph versioning, in fact our graph to key-value mapping is very similar to the algorithm employed by Titan DB. In particular, no additional auxiliary graph elements are introduced for the purpose of versioning. To the end user, the versioning process is completely transparent, as our implementation is fully compliant with the standard TinkerPop API for non-versioned graphs. There is no need for translating one graph query into another in order to run it on a different version of the graph. A developer familiar with the TinkerPop API can start using ChronoGraph without any particular knowledge about its versioned nature. By offering additional methods, which are very much in line with the intentions of the TinkerPop API, we grant access to the versioning-related features. Additionally, ChronoGraph is fully ACID compliant with snapshot isolation for concurrent transactions, preventing common artifacts that arise in other, non-ACID graph databases, such as ghost vertices and half edges. Our solution is strongly based on immutability of existing versions, which aids in preserving traceability of changes and allows extensive sharing of data that remained unchanged between revisions.

5.8 Conflict resolution

In case of concurrent write transactions, the versioning engine is sometimes faced with conflicting commits. This situation occurs when two transactions simultaneously intend to modify the very same graph element. In this section, we describe our current conflict resolution approach.

The conflict resolution algorithm implemented in ChronoGraph differentiates between addition and removal of entire graph elements on the one hand and property value changes on the other hand. Additions of graph elements can never cause a true conflict: even if two concurrent transactions add a vertex or edge with the same new identifier (which is highly unlikely, since we employ universally unique identifiers), then the resulting state in both transactions is identical: the new vertex or edge exists. They may still differ in their properties, which we consider at a later stage.

When either side of the conflict is a graph element deletion, we are faced with two options: either we undo the deletion to apply the changes from the other side of the conflict, or we retain the deletion and discard the other changes. In our current implementation, the removal of a graph element always takes precedence over any other conflicting modification on this element. This may cause the loss of property changes on the deleted element in the concurrent transaction. However, the alternative of “undeleting” the graph element is even more undesirable. In particular if the deleted element was a vertex, then its adjacent edges have also been deleted, which would result in a completely isolated vertex if we chose to undelete it. Isolated vertices are no problem for the storage engine, but they don’t add much value to the semantics of the graph, as they will never contribute to the results of traversal queries (since they are not connected to any other element).

In case of a conflict on property values, it is important to know that ChronoGraph tracks all modifications on vertex and edge properties individually. This means that the conflict resolution algorithm has access to the information whether or not any given vertex property or edge property has been modified within the transaction. For example, if two concurrent transactions perform a commit on the same vertex, and one of them sets the firstname property to John, while the other sets the lastname property to Doe, then the conflict is resolved by accepting both changes (the resulting vertex will have a firstname of John and a lastname of Doe). Only if both transactions modify the same property on the same graph element, then a true conflict occurs. Here, we employ the same strategy as for graph elements: if either side of the conflict is a deletion, the deletion wins. If neither side is a deletion, then the last writer wins. For example, if one transaction sets firstname to John and a concurrent transaction sets firstname to Jack on the same graph element, then the conflict is resolved by using the firstname value from the transaction which was committed later in time.

5.9 Limitations and drawbacks

Our approach is tailored toward the use case of having a versioned graph (as opposed to a temporal graph), which entails that queries on a single timestamp are the prevalent form of read access. Even though we support additional auxiliary methods for traversing the history of a single vertex or edge, and listing all changes within a given time range, our approach is far less suitable for use cases with an emphasis on temporal analysis that require time range queries, or detection of patterns on the time axis (as in graph stream analysis [47, 56]). For example, answering the question “Which elements often change together?”, while possible in our solution, can not be implemented in an efficient way that does not require linear scanning through the commit logs. Another example would be the query “List all vertices that have ever been adjacent to a given one”, which would again involve linear iteration in our solution. In general, our graph is a TinkerPop implementation and therefore optimized with the traversal language Gremlin in mind. As such, it does not lend itself as well to declarative, pattern-driven search approaches like Cypher as a dedicated Cypher graph implementation (e.g., Neo4j) would do.

Open image in new window

We are currently also not offering any means for distributing the graph among multiple machines (see Sect. 10 for details). This limits the scale of our graph to sizes manageable within the physical memory and computing resource restrictions of a single machine. An essential drawback of our solution is that, due to the versioned nature of our data, we cannot rely as much on dictionaries with \(\mathcal {O}(1)\) access times (e.g., Hash Maps) as regular general-purpose graph databases, because of the temporal resolution steps that happen on every navigation. Those steps have a complexity of \(\mathcal {O}(\log {}(n))\), which also limits the scalability of our graph.

Finally, we have to acknowledge the fact that ChronoGraph is an ongoing work-in-progress research project, therefore numerous optimization possibilities have not been exploited yet. For a detailed evaluation of ChronoGraph, we refer the interested reader to our previous work [27].

6.1 Graph layout

In order to store EMF metamodels and their corresponding instance models in our graph database, we need to define a bijective transformation for each element between its EMF (in-memory) representation and its (persistent) graph representation. Our approach to this task is inspired by Neo4EMF [4] which uses a similar mapping.

Open image in new window

Figure 17 shows a small example for our model-to-graph mapping. Please note that this example is not complete; several properties were omitted for visual clarity. As outlined earlier, we store the Ecore metamodel (EPackages, EClasses, ...) together with the actual instance model (EObjects) in the same graph in order to support metamodel evolution and model versioning at the same time. The two vertices at the top represent two EPackages, with “MySubPackage” being owned by “MyPackage”. The metamodel also contains two EClasses, one of which has an EAttribute and an EReference attached. Note that, in contrast to regular Ecore, we attach unique identifiers to every element in the meta- and instance model. This allows for easier object comparison in cases where an element was loaded more than once from the graph.

The two vertices with box icons represent actual EObjects. Each EObject vertex is connected with an edge labeled as “eClass” to the vertex in the metamodel that represents the EClass of the EObject. References are represented as edges as well. They use the unique ID of the EReference to which they belong as the edge label, prefixed with “eRef_”. This allows for efficient identification during the mapping process and eliminates the possibility of unintentional name clashes on edges. A similar pattern is applied for attribute values. The left EObject vertex has a property prefixed with “eAttr_”, followed by the unique identifier of the “name” EAttribute. Again, this schema prevents name clashes and allows for fast identification of the corresponding meta-element. By following this schema, we can efficiently and unambiguously map each EMF model into its graph representation, and vice versa.

There are several additional details to be considered which are not represented in this figure. For example, Ecore allows to define an EReference which is many-valued and has a fixed ordering for its targets. By definition, edges on a vertex are unordered. Hence, we need to assign explicit numeric “order” attributes to these edges to retain this information. Even though such corner cases do exist and require special attention during the design of the mapping algorithm, the overall graph format is very concise, especially when compared to the large number of tables required in equivalent SQL representations.

6.2 EQuery

Storing and retrieving models are basic capabilities that are offered by all model repositories. However, only very few tools allow for queries that operate on model content, such as CDO. Often, languages like OCL [53], EOL [42] or the Hibernate Query Language (HQL²⁰) are employed for this purpose. HQL translates directly into SQL queries, utilizing the object-relational mapping information. From the modeling perspective, HQL is therefore a rather low-level language that is furthermore bound specifically to stores implemented in SQL. It operates on storage level, as opposed to working on the model level. OCL allows for model-level queries, but the execution of these statements often suffers from poor performance on larger instance models. Both OCL and HQL require that their statements are written as plain strings in an application, effectively circumventing any validation by compilers.

In the context of ChronoSphere, we introduce a new query language called EQuery. It uses familiar syntax and is implemented as an internal domain-specific language (DSL) embedded in Java itself. EQuery is based on traversals rather than declarative statements. Queries form an integral part of an application’s business logic, and embedding them directly into the Java source code has many benefits. Application developers can make full use of the Java compiler for validation, and benefit from their Java IDEs when it comes to editor support features, such as code completion and syntax highlighting. Queries will never go out of sync with the code that operates on them, and Java-level type safety is also preserved at compile time, which cannot be achieved with string-based query formats. Finally, EQuery also defines generic traversal steps that accept Java Lambda Expressions, which greatly enhances the flexibility and expressivity of queries.

EQuery works by first stating a starting element, then navigating the model from there to arrive at the desired result element(s). In between, EQuery allows for a wide range of operations, including filters, loops and subqueries. Before execution, the traversals are scanned and optimized to make best use of the indices maintained by ChronoSphere [R5]. Internally, those queries are translated to graph traversal queries on the underlying ChronoGraph structure. Those queries allow for highly efficient, stream-based lazy evaluation. The entire EQuery framework is also easily extensible with new operations, such as the evaluation of OCL statements [53] or expressions in the Epsilon Object Language [42]. There is also an ongoing research project for translating OCL statements directly into graph traversals called Mogwaï [11], which might also be incorporated into our framework in the future.

The remainder of this section is dedicated to examples on how to use EQuery. We use the IT Landscape metamodel for this purpose, as shown in Fig. 20.

Open image in new window

Listing 1 shows a basic example of the EQuery syntax. Here, we start our traversal from the set of all EObjects in our model. We then narrow the search space by restricting the elements to have an EClass named “Application”. We then filter the EAttributes of the EObjects and look for Applications with a “name” equal to “Mail Server”. Then, we navigate along the “runsOn” EReference using the familiar eGet(...) syntax. The result is a stream of arbitrary objects²¹ which needs to be filtered to include only EObjects. Finally, we convert the stream into a Set for further processing. All of this is expressed within regular Java code.

Open image in new window

Listing 2 shows a query that retrieves all clusters which are mixed, i.e., run on physical as well as virtualized hardware. The query starts from the set of all clusters and then specifies an and(...) step. This step will filter out all EObjects where at least one of the provided subqueries does not produce any object. Each subquery starts at the same object, which is the one which was passed into the and step. In our example, we pass in a cluster object into the and step, and check if it runs on at least one physical and at least one virtual machine.

Open image in new window

Our final query example in Listing 3 involves the retrieval of all Applications which run on virtualized hardware. To do so, we start from all applications in our model, and create a name for this traversal step (“apps”). This name can be arbitrary and is not connected to the model in any way; it merely acts as a marker in our query. From the applications, we navigate along the “runsOn” EReference to the virtual machines. For every application where this navigation step produced a valid result (i.e., application.eGet("runsOn") is non-empty), we check if at least one of the resulting EObjects is of type Virtual Machine. If there is such an instance, we navigate back to the previously marked “apps” position. This produces a stream that only contains EObjects that have at least one target for the “runsOn” EReference which is a Virtual Machine. It is important to note here that the back step will only be performed if at least one element passed the previous step. This style of backtracking works in arbitrary distances between query steps, and the programmer can define an arbitrary number of (uniquely) named steps to jump back to. They are useful in cases where the required filter condition is not on an element itself but on its neighbors, or in order to avoid long backtracking navigation. A final detail worth mentioning in Listing 3 is that we first retrieve the EClasses from the EPackage. In most places, the EQuery API allows the programmer to choose between passing a name (EClass name, EAttribute name...) or a variable of the appropriate type. Generally speaking, passing in the metamodel element directly is more efficient than specifying it by name. In all further listings, we will not include the variable definitions.

6.3 Metamodel evolution

One of the major benefits of employing model repositories is the freedom of defining a custom, domain-specific metamodel for any given use case. In practice, users often cannot take full advantage of this benefit because they are hampered by the lack of proper tool support, in particular in cases where the metamodel evolves over the duration of a project [37]. These cases are very common in industrial contexts with long-running endeavors. In traditional enterprise software engineering scenarios, developers create database scripts that migrate the database schema (and contained data) from one version to the next. There is a wide variety of tools for this purpose (e.g., Flyway²² and LiquiBase²³). In a model-based environment, this translates to the concept of metamodel evolution [R3], sometimes also referred to as metamodel adaptation [74]. The key challenge of metamodel evolution is to keep the instance model consistent with the metamodel, i.e., the instances need to be co-adapted such that they conform to the new metamodel [9].

Open image in new window

As shown in Fig. 18, every version in every branch of the model can have its own metamodel to which it corresponds. A direct consequence of this approach is that the application developer needs to be aware of those (potentially) multiple metamodels, and create queries dynamically based on that metamodel. While this will entail additional efforts in development, it is the only fully consistent way of managing versioned models with evolving metamodels.

The alternative would be to retroactively adapt every stored version of the model to a single new metamodel. However, since this adaptation process is not guaranteed to conserve all information (e.g., consider a new metamodel where an EAttribute has been deleted), we would not be able to guarantee traceability anymore. Consequently, we would introduce a considerable threat to the validity of audits. By storing a new metamodel alongside the co-adapted instance model, we restrict the impact of a metamodel evolution to a single version (e.g., the version that simultaneously introduces \(m_{4}\) and \({mm_{2}}\) in Fig. 18) and can still guarantee traceability in the remaining sections of our data. As we will discuss in the remainder of this section, in our approach, we can guarantee traceability even across metamodel evolutions.

Open image in new window

Algorithm 2 shows how metamodel evolution works in ChronoSphere when using an Incubator. In the beginning of the metamodel evolution algorithm, we open two transactions on the repository, and we refer to them as txOld and txNew. We will use txOld in order to read the repository state before the evolution has occurred, and txNew to perform our modifications. We assume that txOld contains a metamodel and a corresponding instance model (otherwise the evolution is a regular insertion). It is crucial at this point that these two transactions are able to work in parallel, and are furthermore completely isolated from each other. Our first actual modification is to override the previous metamodel in txNew. We can safely do so because the original is still stored in txOld. There is no metamodel differencing taking place in this phase, we perform a plain overwrite. We initially delete all elements in txNew (lines 4 to 5) and start with an empty instance model. Afterward, we begin our first instance evolution phase (lines 6 to 9). We iterate over all EObjects stored in the old repository state, and ask our Incubator for a new EClass for this particular EObject. If there is a corresponding EClass in the new metamodel, we recreate the EObject with the same ID, preserving the historical traceability link. Otherwise, we discard the EObject. In lines 10 through 12, we iterate over the elements that received a new EClass previously and look for their counterparts in txOld. We ask the Incubator to transfer any desired EAttribute values from the old version to the new one, which may also involve a value transformation step. For the fulfillment of all of its tasks, the Incubator has access to the Ecore API as well as the ChronoSphere API, allowing for very clean and expressive implementations. Finally, we construct the EReference instances by iterating over the EObjects again (lines 13 to 15). Once more, the Incubator is responsible for the actual semantics. In the last phase, we perform the commit that persists our changes to disk (and creates a new entry in the version history), and roll back the historical transaction.

Overall, we have maintained our traceability links (by retaining the IDs of EObjects) and performed a metamodel evolution with instance adaptation that is ACID safe and creates a clean history without partially evolved intermediate states. The evolution process with a full-fledged Evolution Controller works in much the same way. The primary difference is that the lines 6 through 15 are replaced by a call to the controller, allowing for a maximum of flexibility in the controller implementation. This algorithm requires efficient management of RAM in practice, in particular when working with larger models. Since txNew needs to manage all changes applied to all model elements, the change set can grow to very large sizes. By utilizing incremental commits, we can mitigate the problem by flushing batches to disk while providing the same level of ACID safety and equivalent histories.

6.4 Advantages and limitations of the incubator approach

Using the incubator algorithm as described in section reduces the amount of manual coding required to perform a metamodel evolution with instance adaptation. The incubator assists the programmer in the common case that an EObject before the metamodel evolution conforms to at most one EObject after the metamodel evolution. This covers a lot of cases, including:

• Removal of classes

• Addition of new classes

• Renaming of any metamodel element

• Any changes to EAttributes and EReferences

• Any combination of changes listed above

In all of these cases, the incubator provides utilities such as a fixed migration process and a fixed element iteration order. The goal of the incubator approach is to drastically reduce the required amount of manual coding for common cases. However, it is not applicable in all scenarios. For example, when a single class C is split into two classes (\(C_{1}\) and \(C_{2}\)), then each EObject E conforming to C must be split into two EObjects \(E_{1}\) and \(E_{2}\), where \(E_{1}\) becomes an instance of \(C_{1}\), and \(E_{2}\) an instance of \(C_{2}\). Cases such as this (which are less common and often fairly complex) are not covered by the incubator. In such cases, the programmer needs to implement the migration code manually. We consider the current features to be a baseline that provides the necessary raw functionality. We aim to build more sophisticated and user-friendly evolution mechanisms on top in the future, gradually reducing the amount of required manual coding (see Sect. 10).

Open image in new window

6.5 Transaction and versioning concepts

Transactional safety [R6] is the foundation of all features in ChronoSphere which are related to collaboration and evolution. Originally coined by the database community, this concept has since been adopted by other domains as well. In the context of modeling and model repositories, transactional safety implies that several clients can work in parallel on a model without interfering with each other.

In ChronoSphere, a client²⁴ requests a transaction, then operates on it by executing queries and applying changes locally in this transaction. Afterward, the transaction can either be committed (local changes will be made available globally by creating a new version) or rolled back (reverting all local changes). The isolation property defined in the SQL Standard [38] states that any operation executed within a transaction must not be affected by other, concurrent transactions [R6]. In order to achieve the highest possible isolation level (serializable [38], also known as snapshot isolation), databases traditionally either need to perform excessive pessimistic locking, or allocate considerable amounts of RAM to open transactions in order to retain duplicates of concurrently modified entries. Thanks to its versioning capabilities, ChronoSphere can provide snapshot isolation with minimal locking, no additional memory overhead and without sacrificing performance. This is a direct consequence of our design: once a model version is committed, it is effectively immutable. Further changes will create new versions. Therefore, as long as a client is working on any given version (i.e., the used transaction timestamp does not change), the model content will not change, thus guaranteeing snapshot isolation.

8.1 Model insertion

The first benchmark scenario consists of loading the 200000 EObjects into the system and persisting them to disk.

Open image in new window

As Fig. 21 shows, there are significant performance differences during model insertion when using different database back-ends for CDO. The embedded H2 database offers faster insertion speed compared to PostGreSQL. ChronoSphere is the middle ground between the two. The primary factor which is slowing ChronoSphere down in this comparison is the fact that both H2 and PostGreSQL have access to fixed schemas, which allows for a very compact binary representation of each EObject. ChronoSphere uses a more flexible approach, resulting in less densely packed data structures and consecutively lower insertion speed. CDO accomplishes this performance also by deliberately working without foreign key constraints in the database itself, thus forfeiting one of the biggest advantages of relational storage systems.

8.2 Assets By Name

A very common task for any repository is to allow a user to find an element by its name. In this scenario, we are searching for a Physical Machine by name. We use the following queries:

Open image in new window

Open image in new window

We repeat each query 100 times, using a different replacement for the \({\texttt {<name\_placeholder>}}\) in every iteration. Using the same name in every execution would entail the possibility that the tool under test is simply returning a cached query result which contradicts our measurement goals (Fig. 22).

Open image in new window

Given the fact that relational databases have been designed especially for this kind of query, it might lead to the assumption that CDO is capable of answering this query very efficiently. However, it turns out that the CDO query evaluation engine for OCL does not inspect the provided OCL statement for optimization possibilities. Instead of creating a suitable SQL statement and forwarding it to the underlying database, the OCL statement is evaluated simply by iterating over the EObjects in memory. Another shortcoming of CDO is the fact that it does not create secondary indices on model data, and also does not offer such an option through its API. While it is possible to manually create secondary indices in the underlying database, they will not be utilized by CDO. ChronoSphere analyzes and optimizes the passed query and utilizes a secondary index on the element name, allowing for greatly reduced query response times in this scenario.

8.3 Root cause analysis

After retrieving a particular element by name, a common task in the IT Landscape context is to perform a Root Cause Analysis. Such an analysis attempts to track down the root cause for a failing asset. For example, an application might fail to operate properly because the underlying virtual machine fails. The query therefore needs to retrieve the transitive dependencies of a given asset. For this particular scenario, we consider the transitive dependencies of a Service asset down to the PhysicalMachine level. This is commonly referred to as the deployment stack. We measure the accumulated time for 1000 executions of this query on different initial start objects. The queries in OCL and EQuery are formulated as follows:

Open image in new window

Open image in new window

In this benchmark, we utilize the closure statement in both languages to navigate the transitive paths. We require this statement because the path length is unknown—a Virtual Machine may run on a Cluster which in turn is deployed on Virtual Machines. Such a query is very difficult to express in SQL and would require recursive JOIN operations. However, since CDO resolves OCL queries via in-memory iteration, it circumvents this issue.

Open image in new window

Figure 23 shows that CDO provides acceptable performance in this scenario; however, ChronoSphere outperforms it by a factor of 2. The reason for this speedup lies within the architecture of ChronoSphere: after consolidating the EQuery steps, it transforms them into a Gremlin graph traversal. This highly optimized traversal engine is then executing the query on the data structures provided by ChronoGraph. We avoid the overhead of the reflective EObject API completely, granting ChronoSphere faster query execution.

8.4 Impact analysis

Root Cause Analysis, as introduced in the previous section, finds the cause of failure of a particular asset. The inverse question is also relevant in IT Landscape management: given an asset, we need to determine which higher-level assets are affected in case that this asset fails. For our model-level query, this means that we need to find the incoming transitive dependencies of a model element. For our benchmark, we perform the impact analysis from a Physical Machine all the way up to the Services. We formulated the corresponding queries as follows:

Open image in new window

Open image in new window

In this particular scenario, we encounter a shortcoming of OCL: it does not allow to formulate query steps across the incoming references of an object. This issue has been perceived by tool authors and there are extensions to OCL which allow for an eInverse step, e.g., in the Acceleo framework.³⁰ However, as CDO only supports the official OCL standard, our options for formulating this query (without having to modify our metamodel) are very limited. We iterate over all services, build the deployment stack for each service, and then check if our Physical Machine in question is contained in the resulting set of elements.

Open image in new window

As Fig. 24 clearly shows, the limitations of OCL severely impact the performance of the query in CDO. In contrast, the EQuery expression in ChronoSphere has approximately the same performance as the forward-navigating Root Cause Analysis query. Please note that we reduced the number of input elements from 1000 to 10 in this scenario in order to get results from CDO within a reasonable time frame. Multiplying the result of ChronoSphere by 100 yields the same results as in the Root Cause Analysis scenario. This demonstrates that ChronoSphere queries can navigate along outgoing and incoming references without any performance penalty.

8.5 Threats to validity

8.6 Benchmark summary

In this comparative evaluation (which is summarized in Table 7), we demonstrated that ChronoSphere offers competitive performance, even though it does not require a metamodel to be constant over time. The underlying graph database allows for schema-free model storage without sacrificing query execution speed. This benchmark also demonstrates that avoiding O/R-mapping techniques has a positive influence on the overall performance. We also showcased the expressiveness of our query framework, which allows for more flexible navigation than OCL. This advantage is crucial in the IT Landscape domain and generally beneficial in model analysis. Our results are also in line with the extensive comparative benchmark by Barmpis et. al [1] which demonstrates the advantages of graph-based storage over relational solutions for model persistence.

Please note that we focused exclusively on ChronoSphere in this evaluation. For an evaluation on ChronoDB [25] and ChronoGraph [27], we refer the interested reader to the respective publications.

9.1 Related Key-Value-Store versioning solutions

Database content versioning is a well-known topic. Early work in this area dates back to the 1986 when Richard Snodgrass published his article on Temporal Databases [69]. Adding a time dimension to the data stored in a database considerably increases the complexity of the data management, because the additional dimension introduces new demands regarding data consistency and several tried-and-true solutions are no longer applicable to the same extent as with non-versioned data (e.g., hash tables for caching). Key-value stores have become attractive formats for versioned data due to their simple nature when compared to relations, graphs or documents.

Sridhar Ramaswamy published a paper in 1997 on indexing for temporal databases [57]. He proposes an approach based on validity ranges for each entry to which he refers as windows. Each entry is valid from its insertion until its validity is explicitly terminated by an update or deletion. This transforms the problem of a search in a versioned database into an instance of the well-known interval stabbing problem [65]: given a set of intervals and a number, find all intervals containing this number. This approach strongly inspired our efforts. The major difference between the algorithms we employ in ChronoDB (c.f. Sect. 4.1) and Ramaswamy’s approach is that in our case, the upper limit of each validity window is given implicitly by the matrix structure. We therefore do not need to update a previously stored validity range in our database when a new version is added. This allows our data store to operate in a strictly append-only fashion, which entails a number of technical advantages in the implementation. Also, deletions of entries do not impact our data structure in any different way than inserts or modifications, which was an issue in Ramasway’s solution.

Felber et. al [21] propose a different solution. For every key, the store manages a list of values, each value corresponding to one version. This is a simple and effective system for managing elements with independent histories (e.g., wiki pages). However, this solution does not preserve the historical correlation between elements. For example, given a key \(k_{1}\) with values \(a_{1}\) and \(a_{2}\), and a key \(k_{2}\) with values \(b_{1}\) and \(b_{2}\), there is no way to tell if the entry \((k_{1},a_{1})\) existed at the same time as \((k_{1},b_{1})\), or \((k_{1},b_{2})\) or neither of them. This temporal correlation is crucial when individual values can contain references to one another, as it is the case with ChronoGraph.

Commercial database vendors also explored the possibilities for database content versioning. Lomet et.al [44, 45] developed an approach named ImmortalDB which was later integrated into Microsoft SQL Server. This solution is based on history chains: each entry refers to its predecessor via a pointer (alongside timestamp metadata). This approach allows for high performance of queries on the latest version of the data. However, as the request timestamps are moved further back in time, the query performance degrades linearly, as the history chains need to be traversed. ChronoDB avoids this problem and offers logarithmic access time to any entry, regardless of its age. Further commercial projects in this area include Temporal Tables in IBM DB2 [63] or Oracle’s Flashback technology [32]. The choice between history chains and time-indexing (as shown in Sect. 4) depends on the use case. History chains offer almost the same performance for queries on the latest version as an unversioned system, but when previous versions are requested, the performance decreases linearly with the age of the requested version, as all intermediate chain links need to be traversed. Time-indexed solutions are engineered to offer nearly identical query performance on any requested version, but the overall query performance decreases in a logarithmic fashion as new versions are being added. We mitigate this issue by splitting the data along the time axis, thus limiting the search space of each request (see Algorithm 1). For systems which primarily serve the latest version, history chains are a viable choice. However, in particular for the use case of IT Landscapes, the performance of historical queries matters to the end users, as the repository is used for audits and history analysis.

9.2 Related graph versioning solutions

In comparison with Key-Value stores and SQL databases, graph databases as we know them today are a relatively new technology. Consequently, there are fewer approaches regarding content versioning.

Considering the large amount of development and quality assurance efforts that has been invested into existing graph databases (e.g., Neo4J or TitanDB), it is a tempting idea to integrate versioning in these systems rather than developing new ones. Castelltort and Laurent published one of the first papers [8] that seek to integrate versioning into general-purpose graph databases. This is achieved by creating a layout for a “meta-graph” that can contain and manage multiple versions of itself. The graph database contains this meta-graph, and incoming queries need to be aware of this structure in order to extract the information they require. As Castelltort and Laurent clearly show in their paper, the complexity of queries sharply increases in such a scenario. Due to the increased number of checks that need to be performed by each query, the performance inevitably degrades as well. Perhaps the largest drawback of this approach is that the application needs to be aware of and manage this additional layer of complexity. There are several different approaches for creating a layout for the meta-graph, e.g., the solution proposed by Taentzer et al. [71] which is based on modeling differences between versions as graphs. There is one central issue which is shared by all layouts: Given a suitable set of graph changes, they introduce vertices in the graph which have a very high degree of incoming and/or outgoing edges for the purpose of version control. Such super vertices represent a problematic corner case in any graph database and may lead to poor performance and storage space utilization. As ChronoGraph manages version control on a lower level, there is no need to introduce any additional graph elements in order to achieve versioning. The disadvantage of our solution in that regard is that a completely new implementation was required and existing graph databases could not be reused.

Other related approaches, e.g., by Semertzidis and Pitoura [66, 67] or by Han et al. [29], assume the existence of a series of graph snapshots as input to their solutions. These approaches do not aim for online transaction processing (OLTP) capabilities and focus on the analysis of a series of static graphs. A direct comparison with our approach is therefore not feasible. However, the data managed by ChronoGraph may serve as an input to those tools, as each graph revision can be extracted individually and consequently be treated as a series of snapshots.

9.3 Related repository solutions

Table 8 shows a comparison of related model repositories based on the required features we established in Sect. 2. The table can be divided into two sections, which are cloud (Software-as-a-Service) solutions and on premise solutions. While cloud-based solutions for EAM models exist (e.g., Iteraplan³¹), more fine-grained IT Landscape models are widely considered to be very sensitive data in industry. Unauthorized access to such models could guide a potential attacker to the servers where the impact of the attack is maximized. Most companies therefore require an on premise deployment of the software that manages their IT Landscapes. This eliminates cloud-based tools such as MDEForge [3] and GenMyModel [14] from the list of possible repository candidates for IT Landscape models.

Connected Data Objects (CDO)³² is widely considered to be the gold standard of model repositories. This repository uses SQL databases to store model data in a versioned fashion. CDO handles the versioning process internally, it does not make use of versioning features in the underlying database. With respect to features, CDO is the most complete competitor to ChronoSphere. However, CDO exhibits several weaknesses when employed in practice [68]. In particular, the lack of any support for metamodel evolution motivated our decision to implement a novel model repository. ChronoSphere also avoids the Object-Relational Mapping (O/R-Mapping) process which is employed by CDO in order to transfer model data into and out of the underlying database. As we have shown in Sect. 6.1, there is a natural pattern for transforming model elements into graph elements (and vice versa), whereas O/R-Mapping is a fairly involved process [39], both conceptionally as well as with respect to resource usage (e.g., CPU and RAM). We also performed a comparative benchmark between CDO and ChronoSphere in Sect. 8.

Neo4EMF [4] was the first storage solution for EMF models that is based on graph database technology. This work has inspired and guided our efforts. ChronoSphere utilizes a similar model-to-graph mapping as Neo4EMF, albeit a different implementation for technical reasons. Neo4EMF showed the advantages of graph-based persistence, however it is a persistence framework rather than a model repository. Central features, such as versioning, branching and ACID transaction support, remain unaddressed by this technology.

Hawk Model Indexer [2] is another solution in the realm of model engineering that seeks to utilize graph-based persistence for models. As the name implies, Hawk is primarily an indexer. It is therefore not responsible for the actual model persistence, but rather for creating a secondary structure to speed up incoming queries. Hawk is intended to be used as an assistive technology and does not qualify as a standalone model repository. Just as with Neo4EMF, features like versioning and branching are not considered by this approach.

MORSA [54] was one of the first NoSQL model repositories. It stores models in a document-based backend (MongoDB³³). The main features of MORSA include model versioning and persistence. However, in contrast to ChronoSphere, MORSA treats a model as a single atomic artifact. Queries on the model content are therefore not supported. Also, the versioning process takes place on the granularity of the entire model (rather than per-element as in ChronoSphere). MORSA is suitable for storing and retrieving hand-crafted models of smaller sizes. The large models generated by automated processes in IT Landscapes would introduce a prohibitive amount of overhead for whole-model versioning approaches.

EMFStore [41] is a model repository that operates on model differences, which are stored in files in an XML-based format. This allows EMFStore to support per-element versioning and branching as well as efficient storage utilization for long history chains. However, EMFStore does not offer support for model content indexing and/or querying. Retrieving a model version requires a checkout operation as seen in traditional version control systems, e.g., Git or SVN. The commercial tool MagicDraw Teamwork Server³⁴ follows a similar approach as EMFStore. Teamwork Server internally stores the XMI [52] representation of a model in a folder controlled by SVN, which introduces similar scalability issues as discussed about MORSA. ChronoSphere follows a different approach: each version of each model element is accessible in logarithmic time without requiring a checkout procedure of the entire model. Also, ChronoShpere allows for indexing and querying of the model content in contrast to the other mentioned solutions in this category. Teamwork Server has been superseded by MagicDraw Teamwork Cloud³⁵ which employs a per-element versioning approach and is based on Apache Cassandra. Even though this approach allows for a higher scalability, due to the nature of Cassandra, this solution cannot support ACID transactions. As of the current version (19.0), according to the official API documentation³⁶ Teamwork Cloud does not offer any extended querying capabilities beyond retrieving a model as a whole and picking individual elements by ID. It does however utilize the same retrieval model as ChronoSphere, where elements are retrieved by stating their ID as well as their branch and timestamp.

An approach that is conceptually close to ChronoSphere, but does not declare itself as a model repository, is GreyCat³⁷ [33, 34]. GreyCat stores models in versioned graphs. It is based on the Kevoree Modeling Framework [23] (KMF), which is an alternative to EMF that focuses on models-at-runtime scenarios. KMF metamodels can be automatically derived from Ecore definitions (hence we consider the metamodeling process to be Ecore compliant in Table 8). Much like ChronoGraph, GreyCat implements its own graph layer on top of a NoSQL storage. In its storage layer, GreyCat uses history chains (traces in GreyCat terminology) which consist of change operations. Thus, GreyCat utilizes difference-based versioning, whereas ChronoGraph employs state-based versioning. While GreyCat also implements a property graph, it does not support the TinkerPop API. A major difference that sets ChronoSphere and GreyCat apart is the fact that GreyCat is heavily relying on code generation. This entails that the metamodel for GreyCat is fixed for all versions and branches, and metamodel evolution cannot be supported in the same way as it is possible in ChronoSphere. GreyCat (and its predecessors) and ChronoSphere have been developed during the same time periods as independent projects, which is the reason why neither of them is built on top of the other. The existence of two independent solutions also highlights both the importance of versioned model storage as well as the suitability of property graphs for this task.

Table 8 shows two important facts. On the one hand all of the features we implemented in ChronoSphere (except for historical archiving) are present in at least one related tool. This emphasizes the importance of the chosen feature set. On the other hand, this table shows that ChronoSphere also fulfills all requirements of a general-purpose model repository and is therefore not restricted to IT Landscape modeling in any way.

9.4 ChronoSphere as a generic model repository

ChronoSphere has been created specifically for the use case of IT Landscape documentation. However, the resulting concepts and software are generic and have no dependencies to this particular domain. As a general-purpose EMF model repository with a rich feature set, ChronoSphere can be applied in a wide range of use cases, in particular in models-at-runtime scenarios. In the context of this paper, we decided to focus on the domain for which the tool was originally created. While the features of ChronoSphere are generic, it is optimized for the workloads expected in the IT Landscape domain (model sizes, frequency of insertions and queries, number of concurrent users...). We will conduct further studies in the future where we apply ChronoSphere in different domains.