Small area prediction of proportions and counts under a spatial Poisson mixed model

Abstract

This paper introduces an area-level Poisson mixed model with SAR(1) spatially correlated random effects. Small area predictors of proportions and counts are derived from the new model and the corresponding mean squared errors are estimated by parametric bootstrap. The behaviour of the introduced predictors is empirically investigated by running model-based simulation experiments. An application to real data from the Spanish living conditions survey of Galicia (Spain) is given. The target is the estimation of domain proportions of women under the poverty line.

1 Introduction

This paper introduces statistical methodology for estimating proportions and counts, with applications to poverty mapping in areas of Galicia. This is an autonomous community in the northwest of Spain with an economic activity strongly related to natural resources. The beginning of the 21th century has been characterized by the increase in the differences between the areas of the inner zone, which are poorer, and the coastal areas, which present greater development. One of the Spanish statistical sources to monitor poverty indicators is the living conditions survey. Unfortunately, the sample sizes of this survey do not allow obtaining precise direct estimators for the counties of Galicia. Small area estimation (SAE) deals with this problem by introducing indirect predictors based on statistical models. The monographs of Rao and Molina (2015); Pratesi (2016) and Morales et al. (2021) are introductory texts to SAE. Recent methodology for SAE is described in the review papers of Jiang and Lahiri (2006); Rao (2008); Pfeffermann (2013) and Sugasawa and Kubokawa (2020).

Developing statistical methodologies to model counting data and to predict domain counts and proportions in small areas is important to understand the phenomena studied (like poverty) and, consequently, to make decisions about public policies. This manuscript introduces a spatial extensions of the basic area-level Poisson mixed model, for better fitting the needs of real data and giving rise to increasingly complex and realistic models. The main contribution is the introduction of small area predictors that incorporates information from other domains, auxiliary variables and spatial correlation.

Without taking into account the spatial correlation at the domain level, the statistical literature on area-level mixed models for count data has interesting contributions to SAE. We can find univariate and multivariate models for count data. In the first case, regression models with Poisson distribution have been widely used. Some contributions in this field are Ghosh et al. (1998), Trevisani and Torelli (2017), Boubeta et al. (2016, 2017) or Reluga et al. (2021). In the second case, the multivariate models for the count data additionally borrow the strength of the correlation between the target variables to introduce new predictors. This was done by Ferrante and Trivisano (2010), López-Vizcaíno et al. (2013, 2015), Esteban et al. (2020) or Burgard et al. (2022), among others. These models link all the domains to enhance the estimation at a particular area, that is, they borrow strength from other areas. The models have random effects taking into account the between-domain variability that is not explained by the auxiliary variables, but they assume that the domain random effects are independent. However, in socioeconomic, environmental and epidemiological applications, estimates for areas that are spatially close may be more alike than estimates for areas that are further apart. In fact, Cressie (93) shows that not employing spatial models may lead to inefficient inferences when the auxiliary variables does not explain the spatial correlation of the study variable.

In other fields of statistics than SAE, such as econometrics or epidemiology, spatial models for count data have wide applicability. See for example the papers of Anselin (2001), Wakefield (2007), Mohebbi et al. (2011) or Glaser (2017) and references therein, or the books of LeSage and Pace (2009), Dubé and Legros (2014) and Banerjee et al. (2015). Among those models are the “spatial autocorrelation” or “simultaneous autoregressive” (SAR) Poisson regression models. However, SAR Poisson models do not play the most relevant role in those areas, unlike normal models, because there is no direct functional relationship between the dependent and the explanatory variables. On the other hand, the area-level approach to SAE looks for the relation between the intensity parameter (conditional expectation of the dependent variable) and the regressors. The reason is that the dependent variable is an estimator obtained from unit-level survey data and not the area-level population parameter of interest. In the SAE setup, population parameters (such as poverty proportions) are directly related to the conditional expectation of the dependent variable.

In SAE, modelling the spatial correlation between data from different areas allows to borrow even more strength from the areas. This recommendation was applied to the basic Fay–Herriot model by Singh et al. (2005). Later, several authors have proposed new spatial area-level linear mixed models. Petrucci and Salvati (2006); Pratesi and Salvati (2008); Molina et al. (2009); Marhuenda et al. (2013) and Chandra et al. (2015) consider linear mixed models (LMM) that extend the Fay–Herriot model. Most of these papers assume that area effects follow a simultaneously autoregressive process of order 1 or SAR(1).

In the Bayesian framework, Moura and Migon (2002) and You and Zhou (2011) consider spatial stationary mixed models, Sugasawa et al. (2020) study an empirical Bayesian estimation method with spatially non-stationary hyperparameters for area-level discrete and continuous data having a natural exponential family distribution. Arima et al. (2012) propose a full Bayesian separable spatio-temporal hierarchical Bayesian model, which allows the integration of missing data imputation and pollutant concentration prediction. Choi et al. (2011) apply the spatio temporal models to study chronic obstructive pulmonary disease at county level in Georgia.

Concerning nonparametric and robust methods, Opsomer et al. (2008) give a small area estimation procedure using penalized spline regression with applications to spatially correlated data. Ugarte et al. (2006) and Ugarte et al. (2010) study the geographical distribution of mortality risk using small area techniques and penalized splines. Chandra et al. (2012) introduce a geographical weighted empirical best linear unbiased predictor for small area averages. Baldermann et al. (2016) describe robust SAE methods under spatial non-stationarity linear mixed models. Chandra et al. (2017) introduce small area predictors of counts under a non-stationary spatial model. Chandra et al. (2018) develop a geographically weighted regression extension of the logistic-normal and the Poisson-normal generalized linear mixed models (GLMM) allowing for spatial nonstationarity.

The above cited papers introduce SAE procedures that borrow strength from spatial correlations. Assuming the frequentist parametric inference setup, they mainly apply spatial LMMs to small area estimation. However, few of them deal with empirical best predictors (EBP) under spatial GLMMs. This work partially fills that gap and studies an area-level Poisson mixed model containing SAR(1) spatially correlated domain effects. The final target is the estimation of domain counts and proportions.

This paper has a double starting point. On the one hand, it modifies the spatial LMM of Pratesi and Salvati (2008) by changing the conditional distribution of the target variable from normal to Poisson. On the other hand, it extends the model of Boubeta et al. (2016) by including random effects with SAR(1) distribution. The proposed model and the predictors derived from it are new. There is also no statistical software that allows estimating the parameters of the new model. For this reason, we adapt and implement the method of simulated moments (MSM) studied by Jiang (1998). Further, we give approximate EBPs to avoid the problem of approximating multiple integrals and we empirically investigate their behavior.

The manuscript is organized as follows. Section 2 introduces the model and a fitting algorithm based on the MSM method. Section 3 gives empirical best and plug-in predictors of domain proportions and counts, provides approximations to the integrals that appear in the predictor formulas and proposes a parametric bootstrap method for estimating their mean squared errors (MSE). Section 4 empirically investigates the introduced predictors by means of simulation experiments. Section 5 gives a relevant application to real data in the socio-economic field. The target is the estimation of women poverty proportion in counties of Galicia. Section 6 collects the main conclusions. Finally, the paper contains a supplementary material with some appendixes. Appendix A provides the nonlinear system of MSM equations that must be solved to estimate the model parameters. Appendixes B and C describe algorithms to calculate the penalized maximum likelihood (PQL) and the maximum likelihood (ML) estimators of the model parameters. Appendix D shows two bootstrap algorithms to test hypotheses about the variance and correlation parameters. Appendix E gives some additional simulation results by considering deviations from normality in the data generating processes. Appendix F presents complementary results to the application to real data, including the analysis of the goodness-of-fit of alternative Poisson regression models and the use of EBLUPs based on a spatial Fay–Herriot model.

2 The model

This section introduces an area-level Poisson mixed model in the context of spatial correlation. Specifically, it assumes a SAR(1) process on the random effects. Let us consider a population partitioned into D domains and let us denote each particular domain by d, $d=1,\ldots , D$. Let $\varvec{v}= (v_1, \ldots , v_D)^{\prime }$ be a vector of spatially correlated random effects following a SAR(1) process with unknown autoregression parameter $\rho$ and known proximity matrix $\varvec{W}$. This means that the vector of random effects $\varvec{v}$ fulfills the linear combination

$$\begin{aligned} \varvec{v}=\rho \varvec{W}\varvec{v}+\varvec{u}, \end{aligned}$$

(2.1)

where $\varvec{u}\sim N_D(\varvec{0},\varvec{I}_D)$, $\varvec{0}$ is the $D\times 1$ zero vector and $\varvec{I}_D$ denotes the $D \times D$ identity matrix. Assuming that $(\varvec{I}_D-\rho \varvec{W})$ is non-singular, the equation (2.1) can be expressed as

$$\begin{aligned} \varvec{v}=(\varvec{I}_D-\rho \varvec{W})^{-1}\varvec{u}. \end{aligned}$$

(2.2)

For the proximity matrix $\varvec{W}$, we assume that it is row stochastic, i.e. the elements of each row are positive and add up to 1. Then, the autoregression parameter $\rho$ is a correlation and is called spatial autocorrelation parameter. Some of the most used proximity matrices are based on: (i) common borders, (ii) distances and (iii) k-nearest neighbours. In all cases, the proximity matrix $\varvec{W}$ is obtained from an original proximity matrix $\varvec{W}^0$ with diagonal elements equal to zero and remaining entries depending on the employed option. In option (i), the non diagonal elements of $\varvec{W}^0$ are equal to 1 when the two domains corresponding to the row and the column indices are regarded as neighbours and zero otherwise. In option (ii), the nondiagonal elements of the proximity matrix $\varvec{W}^0$ are defined by applying a monotonically decreasing function to the domain distances; for example, by using the inverse function. Finally, the non diagonal elements of $\varvec{W}^0$ in option (iii) are 1 if they correspond to the k-nearest neighbours of a given domain and zero otherwise. For each option, the row standardization is carried out by dividing each entry of $\varvec{W}^0$ by the sum of the elements in its row. Consequently, $\varvec{W}$ is row stochastic. Spatial weights are usually standardized by row, especially in binary weights strategies (i) and (ii). Row standardization is used to create proportional weights in cases where domains have an unequal number of neighbours. Row standardization involves dividing the weight of each neighbour of a domain by the sum of the weights of all neighbours of that domain. For area-level models, the row standardization is recommended when the distribution of the target variable is potentially influenced due to the sampling design or to the aggregation scheme. More information on row standardization can be found in the monograph Viton 2010.

Equation (2.2) implies that $\varvec{v}\sim N_D(\varvec{0},\varvec{\Gamma }(\rho ))$, where

$$\begin{aligned} \varvec{\Gamma }(\rho )=\big (\gamma _{d_1d_2}(\rho )\big )_{d_1,d_2=1,\ldots ,D}=\varvec{C}^{-1}(\rho ) \end{aligned}$$

(2.3)

and $\varvec{C}(\rho )=(\varvec{I}_D-\rho \varvec{W})^{\prime }(\varvec{I}_D-\rho \varvec{W})$. Therefore, the density function of the random effects is

$$\begin{aligned} f_v(\varvec{v})=(2\pi )^{-D/2}|\varvec{\Gamma }(\rho )|^{-1/2}\exp \left\{ -\frac{1}{2}\varvec{v}^\prime \varvec{\Gamma }^{-1}(\rho )\varvec{v}\right\} . \end{aligned}$$

The vector of response variables $\varvec{y}= (y_1,\ldots , y_D)^\prime$ follows an area-level Poisson mixed model with a SAR(1) vector of domain random effects $\varvec{v}$ if its components $y_1,\ldots ,y_D$ are independent conditionally on $\varvec{v}$ and the conditioned distribution of $y_{d}$, given $\varvec{v}$, is

$$\begin{aligned} y_{d} \vert \varvec{v}\sim y_{d} \vert v_{d}\sim \text{ Poiss }(\mu _{d}), \quad d=1,\ldots , D, \end{aligned}$$

where $\mu _{d}$ denotes the mean of the Poisson distribution. We assume that $\mu _{d}$ can be expressed as $\nu _d p_d$, where $\nu _d$ and $p_d$ are size and probability parameters respectively. We find two advantages of using a Poisson mixed model instead of a binomial mixed model. The first is that we can avoid calculating combinatorial numbers with values outside the range of the computer. The second is that we can explicitly compute some integrals and this avoids the need to use approximation methods. This is particularly important when applying the MSM method. Besides, by the nature of our problem, $\nu _d$ takes large values and $p_d$ small values. Then, everything points to a good behavior of the Poisson model in addition to its computational advantages. As $\nu _d$ is assumed to be known, the Poisson parameter, $\mu _d$, is determined if and only if one knows the parameter $p_d$. In what follows, we will refer to $p_d$ as target parameter. To finish the definition of the area-level Poisson mixed model with SAR(1) random effects (Model S1), we express the natural parameter $\log \mu _d$ in terms of a set of q covariates $\varvec{x}_{d}=(x_{d1},\ldots , x_{dq})$ and the random effect $v_d$, i.e.

$$\begin{aligned} \log \mu _{d}=\log \nu _{d}+\log p_{d}=\log \nu _{d}+ \varvec{x}_{d}\varvec{\beta }+\phi v_{d},\quad d=1,\ldots ,D,\, \end{aligned}$$

where $\varvec{\beta }=(\beta _1,\ldots ,\beta _q)^\prime$ and $\phi$ are the regression and standard deviation parameters respectively. We denote the vector of all model parameters by $\varvec{\theta }=(\varvec{\beta }^\prime ,\phi ,\rho )^\prime$.

Under Model S1, it holds that

$$\begin{aligned} \mathbb {P}(y_{d}|\varvec{v}) = \mathbb {P}(y_{d}|v_d)=\frac{1}{y_{d}!}\exp \{-\nu _{d}p_{d}\} \nu _{d}^{y_{d}} p_{d}^{y_{d}}, \end{aligned}$$

where the target parameter is $p_{d}=\exp \left\{ \varvec{x}_{d}\varvec{\beta }+\phi v_{d}\right\}$. The probability function (likelihood) of the response variable $\varvec{y}$ is

$$\begin{aligned} \mathbb {P}(\varvec{y})=\int _{\mathbb {R}^{D}} \mathbb {P}(\varvec{y}|\varvec{v}) f_{v}(\varvec{v})\,d\varvec{v}= \int _{\mathbb {R}^{D}} \prod _{d=1}^D \mathbb {P}(y_{d}|v_d)f_{v}(\varvec{v})\,d\varvec{v}= \int _{\mathbb {R}^{D}} \psi (\varvec{y},\varvec{v})\,d\varvec{v}, \end{aligned}$$

(2.4)

where

$$\begin{aligned} \psi (\varvec{y},\varvec{v})&= f_v(\varvec{v})\prod _{d=1}^D\frac{\exp \{-\nu _{d}p_{d}\} \nu _{d}^{y_{d}} \exp \left\{ y_{d}(\varvec{x}_{d}\varvec{\beta }+\phi v_{d})\right\} }{y_{d}!}\\&= f_v(\varvec{v})\left( \prod _{d=1}^Dy_{d}!\right) ^{-1} \exp \left\{ \sum _{d=1}^D\Big \{-\nu _{d}\exp \{\varvec{x}_{d}\varvec{\beta }+\phi v_{d}\}+y_{d}\log \nu _{d}\Big \}\right\} \\&\quad \cdot \exp \left\{ \sum _{k=1}^p\left( \sum _{d=1}^Dy_{d}x_{dk}\right) \beta _k+\phi \sum _{d=1}^Dy_{d}v_{d}\right\} . \end{aligned}$$

To estimate the parameters of Model S1, the natural procedure would be to calculate the ML estimators. However, the likelihood (2.4) is a multiple integral over $\mathbb {R}^{D}$, which makes it necessary to combine an integral approximation procedure with another for maximization of multivariate functions. Since the size of the integral to be approximated coincides with the number of domains (sample size in the aggregated data set on which the area models are fitted), the optimization algorithms are inefficient in terms of stability (convergence) and computation time. For the sake of completeness of exposition, Appendix C of the supplementary material presents a likelihood optimization algorithm that combines the Laplace approximation of the multiple integral with the Newton–Raphson optimization algorithm. For the reasons stated, this ML-Laplace algorithm has not been selected to estimate the parameters of Model S1.

The scientific literature on GLMMs presents alternative procedures to the ML method. One of these methods consists of maximizing the joint likelihood of the fixed and random effects of the model, for each optimal selection of the variance and correlation parameters. This procedure, which we call PQL, alternately combines two optimization algorithms, the first on $\varvec{\beta }$ and $\varvec{u}$ and the second on $\phi$ and $\rho$, such that the output of one algorithm feeds the input from the other and vice versa. It is a procedure that calculates ML estimators in the case of LMMs but does not guarantee consistent estimators for GLMMs. The method has a lower computational cost than the ML-Laplace algorithm, but it presents instability problems (lack of convergence) in complex models, such as those of spatial correlation. Appendix B of the supplementary material describes the PQL method. Due to the mentioned drawbacks, we have not selected the PQL algorithm to estimate the parameters of the S1 model.

Jiang (1998) proposed the MSM method as a computationally efficient alternative to procedures based on maximizing likelihood. Under regularity conditions, Jiang (1998) proved that the MSM method gives consistent estimators of GLMM parameters. In addition, it is a computational stable and economic method that only requires solving a non linear system of $p+2$ equations. This is why, we have decided to apply the MSM method to estimate the parameters of Model S1. In what follows, we describe how the MSM method estimates the vector of parameters, $\varvec{\theta }$, of Model S1.

A natural set of equations for applying the MSM algorithm is

$$\begin{aligned} 0&=f_k(\varvec{\theta })=M_k(\varvec{\theta })-{\hat{M}}_k= \frac{1}{D}\sum _{d=1}^D \mathbb {E}_{\varvec{\theta }}[y_{d}]x_{dk} -\frac{1}{D}\sum _{d=1}^Dy_{d}x_{dk},\quad k=1,\ldots , p, \nonumber \\ 0&=f_{p+1}(\varvec{\theta }) = M_{p+1}(\varvec{\theta })-{\hat{M}}_{p+1} =\frac{1}{D}\sum _{d=1}^D \mathbb {E}_{\varvec{\theta }}[y_{d}^2]-\frac{1}{D}\sum _{d=1}^Dy_{d}^2,\nonumber \\ 0&=f_{p+2}(\varvec{\theta })=M_{p+2}(\varvec{\theta })-{\hat{M}}_{p+2}=\frac{1}{D(D-1)}\sum _{d_1\ne d_2}^{D} \mathbb {E}_{\varvec{\theta }}[y_{d_1}y_{d_2}] -\frac{1}{D(D-1)}\sum _{d_1\ne d_2}^{D}y_{d_1}y_{d_2}, \end{aligned}$$

(2.5)

where $\sum _{d_1\ne d_2}^{D}$ is a double sum with $d_1,d_2=1,\ldots ,D$, $d_1\ne d_2$, in the $(p+2)$th equation. The MSM estimator of $\varvec{\theta }$ is the solution of the system of nonlinear equations (2.5). For solving this system, we may apply the Newton–Raphson algorithm with updating formula

$$\begin{aligned} \varvec{\theta }^{(m+1)}=\varvec{\theta }^{(m)}- \varvec{H}^{-1}(\varvec{\theta }^{(m)})\varvec{f}(\varvec{\theta }^{(m)}), \end{aligned}$$

(2.6)

where

$$\begin{aligned} \varvec{\theta }=\underset{1\le k \le p+2}{\hbox {col}}(\theta _k),\quad \varvec{f}(\varvec{\theta })=\underset{1\le k \le p+2}{\hbox {col}}(f_k(\varvec{\theta })),\quad \varvec{H}(\varvec{\theta })=\left( \frac{\partial f_k(\varvec{\theta })}{\partial \theta _r}\right) _{k,r=1,\ldots ,p+2}, \end{aligned}$$

(2.7)

and the components of the vector $\varvec{\theta }$ are $\theta _1=\beta _1,\ldots ,\theta _p=\beta _p$, $\theta _{p+1}=\phi$, $\theta _{p+2}=\rho$. Appendix A contains the calculations of the expectations appearing in $\varvec{f}(\varvec{\theta })$ and $\varvec{H}(\varvec{\theta })$. Appendixes B and C describe the PQL and the ML methods, and discuss the pros and cons of the three fitting algorithms.

As algorithm starting points for $\varvec{\beta }$ and $\phi$, we can take maximum likelihood estimates under Model S1 with $\rho =0$ (denoted by Model 1). In the case of independent random effects ($\rho =0$), we have functions to fit the model in different programming languages. For example, we can employ the glmer function of R. Concerning the parameter $\rho$, we take the Moran’s I measure of spatial autocorrelation based on the Pearson residuals obtained under Model 1, i.e.

$$\begin{aligned} I=\frac{D}{\sum _{d_1=1}^D\sum _{d_2=1}^Dw_{d_1d_2}} \frac{\sum _{d_1=1}^D\sum _{d_2=1}^D w_{d_1d_2}({\tilde{e}}_{d_1}-{\bar{e}})({\tilde{e}}_{d_2}-{\bar{e}})}{\sum _{d=1}^D({\tilde{e}}_{d}-{\bar{e}})^2}, \end{aligned}$$

(2.8)

where ${\tilde{e}}_d$, $d=1,\ldots , D$, denote the Pearson residuals under Model 1, ${\bar{e}}=\frac{1}{D}\sum _{d=1}^D {\tilde{e}}_{d}$ and $w_{d_1d_2}$, $d_1, d_2 = 1, \ldots , D$, are the elements of the proximity matrix $\varvec{W}$. Moran’s I measures spatial autocorrelation based on the locations and values of the target variable simultaneously. Given a set of domains and a target variable, it evaluates whether that variable has a clustered, dispersed, or random pattern. Moran’s I is also a statistic that allows testing the null hypothesis of no spatial correlation. The null hypothesis establishes that the variable being analysed is randomly distributed among the entities in the study area; that is, the spatial processes that promote the observed pattern of values is a random mechanism.

3 The predictors

This section gives the empirical best and plug-in predictors of $p_d$ under Model S1. We focus on the calculation of the EBP of $p_d$, given its relationship with $\mu _d$, and assuming that the size parameter $\nu _d$ is known. The corresponding prediction of the expected count $\mu _d$ is straightforward. The EBP of $p_d$ is obtained from the best predictor (BP) by replacing the vector of model parameters $\varvec{\theta }$ by an estimator ${\hat{\varvec{\theta }}}$. The BP of $p_d$ is the unbiased predictor that minimizes the MSE and it is given by

$$\begin{aligned} {\hat{p}}_{d}(\varvec{\theta })=\mathbb {E}_{\varvec{\theta }}[p_{d}|\varvec{y}]= \frac{ \int _{\mathbb {R}^D}\exp \{\varvec{x}_{d}\varvec{\beta }+\phi v_{d}\}\prod _{i=1}^D \mathbb {P}(y_i|v_i)f_v(\varvec{v})\,d\varvec{v}}{\int _{\mathbb {R}^D}\prod _{i=1}^D \mathbb {P}(y_i|v_i)f_v(\varvec{v})\,d\varvec{v}} =\frac{N_{d}(\varvec{y},\varvec{\theta })}{D_{d}(\varvec{y},\varvec{\theta })}, \end{aligned}$$

(3.1)

where

$$\begin{aligned} N_{d}(\varvec{y},\varvec{\theta })&=\int _{\mathbb {R}^D}\exp \left\{ \sum _{i=1}^D\Big [(y_{i}+\delta _{id})(\varvec{x}_{i}\varvec{\beta }+\phi v_{i}) - \nu _{i}\exp \big \{\varvec{x}_{i}\varvec{\beta }+\phi v_{i}\big \}\Big ]\right\} f_v(\varvec{v})\,d\varvec{v}, \\ D_{d}(\varvec{y},\varvec{\theta })&=\int _{\mathbb {R}^D}\exp \left\{ \sum _{i=1}^D\Big [y_{i}(\varvec{x}_{i}\varvec{\beta }+\phi v_{i}) - \nu _{i}\exp \big \{\varvec{x}_{i}\varvec{\beta }+\phi v_{i}\big \}\Big ]\right\} f_v(\varvec{v})\,d\varvec{v}, \end{aligned}$$

and $\delta _{ij}$ is the Kronecker’s delta; i.e. $\delta _{ij}=1$ if $i=j$ and $\delta _{ij}=0$ otherwise. The EBP of $p_{d}$ is ${\hat{p}}_{d}({\hat{\varvec{\theta }}})$ and it can be approximated by using an antithetic Monte Carlo algorithm. The steps are:

• 1. Generate $\varvec{v}^{(\ell )}$ i.i.d. $N_D(\varvec{0},\varvec{\Gamma }(\hat{\rho }))$ and calculate their antithetics $\varvec{v}^{(L+\ell )}=-\varvec{v}^{(\ell )}$, $\ell =1,\ldots ,L$.

• 2. Calculate

  $$\begin{aligned} {} {\hat{p}}_{d}({\hat{\varvec{\theta }}})={\hat{N}}_{d}/{\hat{D}}_{d}, \end{aligned}$$

  (3.2)

  where

  $$\begin{aligned} {\hat{N}}_{d}&=\frac{1}{2L}\sum _{\ell =1}^{2L}\exp \left\{ \sum _{i=1}^D\Big [(y_{i}+\delta _{id})(\varvec{x}_{i}\hat{\varvec{\beta }}+\hat{\phi } v_{i}^{(\ell )}) - \nu _{i}\exp \big \{\varvec{x}_{i}\hat{\varvec{\beta }}+\hat{\phi } v_{i}^{(\ell )}\big \}\Big ]\right\} , \\ {\hat{D}}_{d}&=\frac{1}{2L}\sum _{\ell =1}^{2L}\exp \left\{ \sum _{i=1}^D\Big [y_{i}(\varvec{x}_{i}\hat{\varvec{\beta }}+\hat{\phi } v_{i}^{(\ell )}) - \nu _{i}\exp \big \{\varvec{x}_{i}\hat{\varvec{\beta }}+\hat{\phi } v_{i}^{(\ell )}\big \}\Big ]\right\} . \end{aligned}$$

As the BP of $p_d$ involves high-dimensional integrals on $\mathbb {R}^D$, we propose a computationally less demanding approximation. For that, let us divide the response variable $\varvec{y}$ and the vector of random effects $\varvec{v}$ into two parts $(y_d,\varvec{y}_{d-})$ and $(v_d,\varvec{v}_{d-})$, where $\varvec{y}_{d-}=\underset{1\le i\le D,\, i\ne d}{\hbox {col}}(y_{i})$ and $\varvec{v}_{d-} = \underset{1\le i \le D,\, i\ne d}{\hbox {col}}(v_{i})$. The conditional distribution of $\varvec{y}$, given $\varvec{v}$, is

$$\begin{aligned} \mathbb {P}(\varvec{y}|\varvec{v})=\prod _{i=1}^D \mathbb {P}(y_i|v_i)=\mathbb {P}(y_{d}|v_{d})\prod _{i=1, i\ne d}^D \mathbb {P}(y_{i}|v_{i})= \mathbb {P}(y_{d}|v_{d})\mathbb {P}(\varvec{y}_{d-}|\varvec{v}_{d-}). \end{aligned}$$

(3.3)

Using (3.3), the component $D_{d}(\varvec{y},\varvec{\theta })$ in (3.1) can be rewritten as

$$\begin{aligned} D_{d}(\varvec{y},\varvec{\theta })=\int _{\mathbb {R}} \Big [\int _{\mathbb {R}^{D-1}}\mathbb {P}(\varvec{y}_{d-}|\varvec{v}_{d-})f(\varvec{v}_{d-}|v_d)\,d\varvec{v}_{d-}\Big ]\mathbb {P}(y_d|v_d)f(v_d)\,dv_d, \end{aligned}$$

and since $\mathbb {P}(\varvec{y}_{d-}|\varvec{v}_{d-})f(\varvec{v}_{d-}|v_d)=\mathbb {P}(\varvec{y}_{d-}|\varvec{v}_{d-},v_d)f(\varvec{v}_{d-}|v_d)$, the inner integral is

$$\begin{aligned} \int _{\mathbb {R}^{D-1}}\mathbb {P}(\varvec{y}_{d-}|\varvec{v}_{d-},v_d)f(\varvec{v}_{d-}|v_d)\,d\varvec{v}_{d-}=\mathbb {P}(\varvec{y}_{d-}|v_d). \end{aligned}$$

Therefore

$$\begin{aligned} D_{d}(\varvec{y},\varvec{\theta })=\int _{\mathbb {R}}\mathbb {P}(\varvec{y}_{d-}|v_d)\mathbb {P}(y_d|v_d)f(v_d)\,dv_d. \end{aligned}$$

Taking into account the relationship given in equation (3.3) and reasoning analogously with the component $N_{d}(\varvec{y},\varvec{\theta })$, we have that

$$\begin{aligned} N_{d}(\varvec{y},\varvec{\theta })=\int _{\mathbb {R}}\exp \{\varvec{x}_{d}\varvec{\beta }+\phi v_{d}\} \mathbb {P}(\varvec{y}_{d-}|v_d)\mathbb {P}(y_d|v_d)f(v_d)\,dv_d. \end{aligned}$$

Under the assumption that $\mathbb {P}(\varvec{y}_{d-}|v_d)\approx \mathbb {P}(\varvec{y}_{d-})$, $d=1,\ldots ,D$, the BP of $p_{d}$, ${\hat{p}}_{d}(\varvec{\theta })$, can be approximated by

$$\begin{aligned} {\hat{p}}_d^a (\varvec{\theta })= N_{d}^a(\varvec{y},\varvec{\theta })/D_{d}^a(\varvec{y},\varvec{\theta }), \end{aligned}$$

(3.4)

where

$$\begin{aligned} N_{d}^a (\varvec{y},\varvec{\theta })&=\int _{\mathbb {R}}\exp \left\{ (y_{d}+1)(\varvec{x}_{d}\varvec{\beta }+\phi v_{d}) - \nu _{d}\exp \big \{\varvec{x}_{d}\varvec{\beta }+\phi v_{d}\big \}\right\} f(v_d)\, dv_d,\\ D_{d}^a (\varvec{y},\varvec{\theta })&=\int _{\mathbb {R}}\exp \left\{ y_{d}(\varvec{x}_{d}\varvec{\beta }+ \phi v_{d}) - \nu _{d}\exp \big \{\varvec{x}_{d}\varvec{\beta }+ \phi v_{d} \big \}\right\} f(v_d)\, dv_d. \end{aligned}$$

Equating $\mathbb {P}(\varvec{y}_{d-}|v_d)$ to $\mathbb {P}(\varvec{y}_{d-})$ in the derivation of ${\hat{p}}_d^a (\varvec{\theta })$ implies violating the dependency of the components of $\varvec{v}=(v_1,\ldots ,v_D)^\prime$ for each $d=1,\ldots ,D$. This is to say, the approximate BP of $p_d$ treats $\varvec{y}_{d-}$ as independent of $y_d$. However, this predictor maintains the inner dependency structure of $\varvec{y}_{d-}$. On the other hand, the integrals involved in the calculation of the approximate BP, ${\hat{p}}_d^a (\varvec{\theta })$, are on $\mathbb {R}$ and not on $\mathbb {R}^D$. This is a great computational advantage. As before, the integrals on $\mathbb {R}$ have a complex analytical solution. Therefore, they are approximated by using an antithetic Monte Carlo algorithm analogous to the previous case, but running the new Step 2’.

• 2’. Approximate the EBP of $p_d$ as

  $$\begin{aligned} {} {\hat{p}}_{d}^a({\hat{\varvec{\theta }}})={\hat{N}}_{d}^a/{\hat{D}}_{d}^a\quad (d=1,\ldots ,D), \end{aligned}$$

  (3.5)

  where

  $$\begin{aligned} {\hat{N}}_{d}^a&=\frac{1}{2L}\sum _{\ell =1}^{2L}\exp \left\{ (y_{d}+1)(\varvec{x}_{d}\hat{\varvec{\beta }}+\hat{\phi } v_{d}^{(\ell )}) - \nu _{d}\exp \big \{\varvec{x}_{d}\hat{\varvec{\beta }}+\hat{\phi } v_{d}^{(\ell )}\big \}\right\} ,\\ {\hat{D}}_{d}^a&=\frac{1}{2L}\sum _{\ell =1}^{2L}\exp \left\{ y_{d}(\varvec{x}_{d}\hat{\varvec{\beta }}+\hat{\phi } v_{d}^{(\ell )}) - \nu _{d}\exp \big \{\varvec{x}_{d}\hat{\varvec{\beta }}+\hat{\phi } v_{d}^{(\ell )}\big \}\right\} . \end{aligned}$$

The approximate EBP of $p_d$ depends on the predictor ${\hat{v}}_d$ of the random effect $v_d$ and of the estimator ${\hat{\varvec{\theta }}}$ of the model parameters $\varvec{\theta }$, under the assumed Model S1. This is to say, the spatial correlation plays an active role in the construction of ${\hat{p}}_{d}^a({\hat{\varvec{\theta }}})$ by the approximation the conditional distribution of $\varvec{v}$ given $\varvec{y}$ and by the incorporation of ${\hat{v}}_d$ and ${\hat{\varvec{\theta }}}$.

Another estimator of $p_d$, commonly used in this context, is the plug-in predictor. It is obtained by replacing, in the theoretical expression of $p_d$, the unknown parameters and random effects by their estimators and predictors, i.e.

$$\begin{aligned} {} {\hat{p}}_d^{P}({\hat{\varvec{\theta }}})= \exp \left\{ \varvec{x}_{d}\hat{\varvec{\beta }} + \hat{\phi } {{\hat{v}}}_{d} \right\} . \end{aligned}$$

(3.6)

Unlikely to the approximate EBP, the plug-in predictor takes advantage of the spatial correlation structure only through the predictors ${\hat{v}}_d$ and the estimator ${\hat{\theta }}$, but it does not incorporate information by means of the conditional distribution of $\varvec{v}$ given $\varvec{y}$.

It is important to note that the MSM algorithm only provides estimates for the fixed effects $\varvec{\beta }$, the standard deviation $\phi$ and the autocorrelation parameter $\rho$. However, for obtaining ${\hat{p}}_d^P$ it is necessary to predict the vector of random effects $\varvec{v}= (v_1, \ldots , v_D)$. For this sake, we propose to use their EBPs that are obtained from the corresponding BPs. The BP of $v_d$ is

$$\begin{aligned} {\hat{v}}_d(\varvec{\theta })= \mathbb {E}_{\varvec{\theta }}[v_{d}|\varvec{y}]= \frac{ \int _{\mathbb {R}^D}v_{d}\prod _{i=1}^D \mathbb {P}(y_i|v_i)f_v(\varvec{v})\,d\varvec{v}}{\int _{\mathbb {R}^D}\prod _{i=1}^D\mathbb {P}(y_i|v_i)f_v(\varvec{v})\,d\varvec{v}} =\frac{N_{v,d}(\varvec{y},\varvec{\theta })}{D_{d}(\varvec{y},\varvec{\theta })}, \end{aligned}$$

where

$$\begin{aligned} N_{v,d}(\varvec{y},\varvec{\theta })=\int _{\mathbb {R}^D}v_d\exp \left\{ \sum _{i=1}^Dy_{i}(\varvec{x}_{i}\varvec{\beta }+\phi v_{i}) - \nu _{i}\exp \{\varvec{x}_{i}\varvec{\beta }+\phi v_{i}\}\right\} f_v(\varvec{v})\,d\varvec{v}. \end{aligned}$$

If the assumption $\mathbb {P}(\varvec{y}_{d-}|v_d)\approx \mathbb {P}(\varvec{y}_{d-})$, holds for $d=1,\ldots ,D$, similar mathematical developments as those presented above yield to an approximation to ${\hat{v}}_d(\varvec{\theta })$ equivalent to that obtained for the target parameter $p_d$. The approximate BP of $v_d$ is ${\hat{v}}_d^a(\varvec{\theta })= N_{v, d}^a (\varvec{y}, \varvec{\theta }) / D_{d}^a (\varvec{y}, \varvec{\theta })$, where

$$\begin{aligned} N_{v,d}^a(\varvec{y},\varvec{\theta })=\int _{\mathbb {R}}v_d\exp \big \{y_d(\varvec{x}_d\varvec{\beta }+\phi v_d) - \nu _d\exp \{\varvec{x}_d\varvec{\beta }+\phi v_d\}\big \}f(v_d)\,dv_d. \end{aligned}$$

By plugging ${\hat{v}}_d^a(\varvec{\theta })$ in the formula of $p_d$, we get a non calculable plug-in predictor. The approximate plug-in-BP predictor of $p_d$ is

$$\begin{aligned} {} {\hat{p}}_d^{P^{a}}(\varvec{\theta }) = \exp \left\{ \varvec{x}_{d}\varvec{\beta }+ \phi {\hat{v}}_d^a(\varvec{\theta }) \right\} . \end{aligned}$$

(3.7)

The EBP of $v_{d}$ is ${\hat{v}}_{d}={\hat{v}}_{d}({\hat{\varvec{\theta }}})$ and it can be approximated by ${\hat{v}}_{d}^a={\hat{v}}_{d}^a({\hat{\varvec{\theta }}})$. We propose approximating the analytical integrals by using the same described antithetic Monte Carlo algorithm, but with the new Step 2”.

• 2”. Calculate ${\hat{v}}_{d}^a={\hat{v}}_{d}^a({\hat{\varvec{\theta }}})={\hat{N}}_{v,d}^a/{\hat{D}}_{d}^a$ ($d=1,\ldots ,D$), where

  $$\begin{aligned} {\hat{N}}_{v,d}^a =\frac{1}{2L}\sum _{\ell =1}^{2L}v_d^{(\ell )}\exp \left\{ y_{d}(\varvec{x}_{d}\hat{\varvec{\beta }}+\hat{\phi } v_{d}^{(\ell )}) - \nu _{d}\exp \big \{\varvec{x}_{d}\hat{\varvec{\beta }}+\hat{\phi } v_{d}^{(\ell )}\big \}\right\} . \end{aligned}$$

The approximate plug-in predictor of $p_d$, which is the fully empirical version of (3.7) calculated from ${\hat{v}}_{d}^a$, is

$$\begin{aligned} {} {\hat{p}}_d^{P^{a}}({\hat{\varvec{\theta }}}) = \exp \left\{ \varvec{x}_{d}\hat{\varvec{\beta }} + \hat{\phi } {{\hat{v}}}_{d}^{a} \right\} . \end{aligned}$$

(3.8)

Concerning the prediction of the Poisson parameter $\mu _d=\nu _d p_d$ (expected count), the EBP is ${\hat{\mu }}_{d}({\hat{\varvec{\theta }}})=\nu _d {\hat{p}}_{d} ({\hat{\varvec{\theta }}})$, the approximate EBP is $\hat{\mu }_{d}^a({\hat{\varvec{\theta }}}) = \nu _d {\hat{p}}_{d}^a ({\hat{\varvec{\theta }}})$, the plug-in predictor is $\hat{\mu }_{d}^P({\hat{\varvec{\theta }}}) = \nu _d {\hat{p}}_{d}^P ({\hat{\varvec{\theta }}})$, and the approximate plug-in predictor is $\hat{\mu }_{d}^{P^{a}}({\hat{\varvec{\theta }}}) = \nu _d {\hat{p}}_{d}^{P^{a}} ({\hat{\varvec{\theta }}})$.

The MSE is a measure of the accuracy of the predictors of $p_d$. Boubeta et al. (2016) showed that the analytical approach is computationally demanding in Model 1. This is why we recommend estimating the MSE of ${\hat{p}}_d$ under Model S1 by using a parametric bootstrap procedure based on the ones given in González-Manteiga et al. (2008, 2010). The steps are

• 1. Fit Model S1 to the sample and calculate the estimator ${\hat{\varvec{\theta }}}=(\hat{\varvec{\beta }}^\prime ,\hat{\phi },\hat{\rho })$.

• 2. For each domain d, $d=1,\ldots , D$, repeat B times ($b=1,\ldots , B$):

  • i) Generate the bootstrap random effects $\varvec{v}^{*(b)}=(v_1^{*(b)},\ldots ,v_D^{*(b)})^\prime \sim N_D(\varvec{0},\varvec{\Gamma }(\hat{\rho }))$, where $\varvec{\Gamma }(\hat{\rho })$ is the plug-in version of the covariance matrix (2.3).

  • ii) Calculate the theoretical bootstrap parameter $p_d^{*(b)}=\text {exp}\{\varvec{x}_d{\hat{\varvec{\beta }}}+{\hat{\phi }} v_d^{*(b)}\}$.

  • iii) Generate the response variables $y_d^{*(b)}\sim \text{ Poiss }(\nu _{d}p_{d}^{*(b)})$.

  • iv) Calculate the estimator ${\hat{\varvec{\theta }}}^{*(b)}$ and the EBP $\hat{p}_d^{*(b)}=\hat{p}_d^{*(b)}({\hat{\varvec{\theta }}}^{*(b)})$.

• 3. Output:    $\displaystyle mse^*({\hat{p}}_d)=\frac{1}{B}\sum _{b=1}^B\big ({\hat{p}}_d^{*(b)}-p_d^{*(b)}\big )^2$.

4 Simulation experiment

This section presents a simulation experiment for investigating the performance of the proposed predictors (EBP, approximate EBP and plug-in) based on Model S1, with SAR(1)-correlated random effects. It also studies the performance of the proposed predictors when model parameters are known (BP and approximate BP and plug-in-BP). In addition, we also consider the corresponding predictors based on Model 1, with independent random effects, to analyse the loss of efficiency when the spatial autocorrelation is not taken into account.

The simulations are based on the application to real data of poverty in Galicia during 2013 (see Sect. 5 for more details). We use the same explanatory variables as those used in the real case, i.e. proportions of unemployed (lab2) and of people with university level completed (edu3) by counties. We generate independent response variables $y_d|v_d \sim \text{ Poiss }(\nu _d p_d)$, where $\nu _d$ and $p_d = \exp \{\beta _0 + lab_2\beta _1 + edu_3\beta _2 + \phi v_d\}$ are the sample size and target parameter, $d=1,\ldots , D$. The domain sample sizes and the model parameters $\beta _0, \, \beta _1, \, \beta _2, \phi$ and $\rho$ are taken from the real data case. That is, we simulate the target variable from the Model S1 selected in the application to Galician data.

The domain random effects, $v_d$, $d=1,\ldots , D$, are generated according to a SAR(1) process with autocorrelation parameter $\rho$ and the proximity matrix $\varvec{W}$ given in Sect. 5. The number of domains (counties of Galicia) is $D=49$. As the estimation of the autocorrelation parameter in the application to real data was $\hat{\rho }=0.324$, we take $\rho =0.1, 0.3, 0.5$. The number of Monte Carlo iterations (simulated data sets) is $K=500$.

Tables 1 and 2 present the average across domains of the biases (BIAS) and the root-MSEs (RMSE), both multiplied by $10^2$, of the theoretical predictors BP (3.1), approximate BP (3.4) and approximate plug-in-BP (3.7) based on Model S1. They are labelled as BP, BP$^{a}$ and P$_{BP}^{a}$ respectively. These tables also present the same performance measures for the empirical predictors EBP (3.2), approximate EBP (3.5) and approximate plug-in (3.8). They are labelled as EBP, EBP$^{a}$ and P$_{EBP}^{a}$ respectively. The plug-in predictors P$_{BP}^{a}$ and P$_{EBP}^{a}$ are obtained by predicting the vector of random effects $\varvec{v}$ by its approximate BP $\hat{\varvec{v}}^a(\varvec{\theta })$ and EBP $\hat{\varvec{v}}^a({\hat{\varvec{\theta }}})$ respectively. We implement the Monte Carlo algorithms for approximating integrals with $L=5000$ iterations. For the sake of comparisons, Tables 1 and 2 also present the BIAS and the RMSE, both multiplied by $10^2$, of the theoretical predictors BP, and plug-in-BP based on Model 1. They are labelled as BP and P$_{BP}$ respectively. These tables present the same performance measures for the EBP and plug-in predictors based on Model 1. They are labelled as EBP and P$_{EBP}$ respectively. Again, the Monte Carlo algorithms for approximating integrals is carried out with $L=5000$ iterations.

Table 1 BIAS ($\times 10^2$) of predictors of $p_d$ based on Models 1 and S1

Table 1 shows an increase in bias when we consider empirical predictors. Regarding the comparison between Model 1 and Model S1, there are no substantial differences between the two models, although in general the approximate predictors based on Model S1 have slightly lower biases than the corresponding predictors of Model 1. Because of the approximation of multiple integrals, the BP and EBP based on Model S1 do not outperforms the BP and EBP based on Model 1. If the average across domains is ignored, the behaviour of the domain biases, $B_d$’s, shows that predictors of Model 1 are not centered in many domains (see Fig. 1 for more details). For low values of the correlation parameter $\rho$ the predictors have lower biases than for high values. The plug-in predictors based on Model 1 have greater bias than the corresponding BP and EBP. When the variance components are known, the difference between the predictors BP, BP$^{a}$ and P$_{BP}^{a}$ based on Model S1 have the theoretical expected good behaviour with low biases. However, when we substitute the variance components by the their MSM estimators, the corresponding predictors EBP, EBP$^{a}$ and P$_{EBP}^{a}$ based on Model S1 have larger biases.

Table 2 presents the average across domains of the RMSEs ($\times 10^2$) of the BP, EBP and plug-in for both area-level Poisson mixed models: Model 1 and Model S1. It reveals an increase in the RMSE as the parameter $\rho$ increases and also when one uses empirical versions instead of theoretical ones. Regarding the comparisons between predictors, the plug-in predictor P$_{BP}^{a}$ has, in general, a slight lower RMSE than the best predictors BP and BP$^{a}$ based on Model S1. On the other hand, approximate predictors BP$^a$ and EBP$^a$ reduce the RMSE with respect to BP and EBP respectively. Then, in terms of RMSE, it is preferable to use the approximate predictors based on Model S1. For any estimator, the variance is the most important term of the MSE since the bias is much smaller than the RMSE.

In summary, the biases of predictors EBP and P$_{EBP}$ based on Model S1 are greater than the corresponding biases s (simulated data sets) of EBP$^{a}$ and P$_{EBP}^{a}$ based on Model S1. The same happens with root-MSEs if $\rho \le 0.5$. For the cases $\rho \ge 0.6$, the fitting algorithm becomes more unstable and produces an increase in the variance of predictors. Therefore, some improvement is achieved when using predictors based on model S1 that take advantage of the spatial correlation structure. In the application to real data it is worthwhile to apply predictors based on the Model S1, as ${\hat{\rho }}=0.324$.

Table 2 RMSE ($\times 10^2$) of predictors of $p_d$ based on Models 1 and S1

Figure 1 shows the boxplots of the domain biases, $B_d$’s, (first column) and the domain root-MSEs, $RE_d$’s, (second column) for the predictors and the values of $\rho$ appearing in Tables 1 and 2. In each graph, the first four boxplots refer to the predictors based on Model 1 and the remaining six to the predictors based on Model S1. The BP’s and EBP’s (${\hat{p}}_d (\varvec{\theta })$ and ${\hat{p}}_d (\hat{\varvec{\theta }})$) are represented in blue, their approximations based on the Model S1 (${\hat{p}}_d^a (\varvec{\theta })$ and ${\hat{p}}_d^a (\hat{\varvec{\theta }})$) are plotted in green and the plug-in predictors (${\hat{p}}_d^P (\varvec{\theta })$ and ${\hat{p}}_d^P (\hat{\varvec{\theta }})$) are colored in orange.

The boxplots show an increase of the variability in both $B_d$’s and $RE_d$’s when one uses the empirical predictors. The bias of the predictors based on Model 1 has less variability, but these predictors are clearly biased (except the BP). This fact was not shown in Table 1. The predictors based on Model S1 are unbiased except the P$_{BP}^{a}$ plug-in predictor. The behaviour of the $RE_d$’s for the predictors based on Model 1 is similar to the one based on Model S1, although for $\rho =0.3$, the $RE_d$’s of the plug-in estimator are slightly lower. For predictors based on Model S1, the $RE_d$’s of the approximate BP ${\hat{p}}_d^a (\varvec{\theta })$ and EBP ${\hat{p}}_d^a (\hat{\varvec{\theta }})$ are similar to those of P$_{BP}$ (${\hat{p}}_d^P (\varvec{\theta })$) and P$_{EBP}$ (${\hat{p}}_d^P (\hat{\varvec{\theta }})$) respectively, while the $RE_d$’s of the BP ${\hat{p}}_d (\varvec{\theta })$ and EBP ${\hat{p}}_d (\hat{\varvec{\theta }})$ are generally bigger.

Fig. 1

Boxplots of $B_d$’s (first column) and $RE_d$’s (second column) for the predictors of $p_d$ and values of $\rho$ shown in Tables 1 and 2

From Tables 1 and 2 and Fig. 1, we conclude that the approximate EBP ${\hat{p}}_d^a({\hat{\varvec{\theta }}})$ (EBP$^a$) shows a competitive performance when there is an underlying spatial correlation structure in the data, since it is unbiased and its $RE_d$’s behave similarly to those of ${\hat{p}}_d^{P^{a}}({\hat{\varvec{\theta }}})$ (P$^a_{EBP}$).

Appendix E of supplementary material extends the above simulation experiments to other data generating processes. Instead of generating $u_1,\ldots ,u_D$ i.i.d. N(0, 1), before applying the transformation $\varvec{v}=(\varvec{I}_D-\rho \varvec{W})^{-1}\varvec{u}$, with $\varvec{u}=(u_1,\ldots ,u_D)^\prime$, we generate $u_1,\ldots ,u_D$ i.i.d from the distributions t-Student, Gumbel and skew normal. Appendix E shows some increase of bias and RMSE when deviating from the hypothesis of normality.

The system of MSM nonlinear equations (2.5) is solved by using the nleqslv package of R. We have also used the mvtnorm package to generate samples following a SAR(1) process and the package spdep to construct the proximity matrix $\varvec{W}$ and to test the null hypothesis of no spatial autocorrelation. For $\rho =0.3$, the average runtime of the MSM fitting algorithm was 0.51 seconds. The computational average runtime of the approximate EBP, ${\hat{p}}_d^a({\hat{\varvec{\theta }}})$, is 0.41 seconds. On the other hand, the EBP ${\hat{p}}_d({\hat{\varvec{\theta }}})$ has a high computational burden compared to its competitors. Its average runtime was 48.73 seconds. The employed computer has a processor Intel$\copyright$ Core$^{\textrm{TM}}$ i7-8750 H CPU @ 2.20GHz $\times$ 6, and 16 GBs of RAM memory.

5 Applications to real data

This section applies the developed methodology to the estimation of poverty proportions, $p_d$, in Galicia. The data are taken from the 2013 Spanish living conditions survey (SLCS). The Galician counties are the study territories. The domains of interest are constructed by crossing the variables county and sex = women. In Galicia there are 53 counties, but in four of them there are no available data. Therefore, the number of considered domains is $D=49$. The performance of Model S1 depends on the choice of the proximity matrix $\varvec{W}$. To the best of our knowledge, there is no a priori procedure to determine or estimate the proximity matrix in GLMM with random effects having SAR(1) spatial correlation. Therefore, the way to proceed is to propose several intuitively reasonable alternatives, based on knowledge of the socioeconomic situation of Galicia and on similar applications of SAR models to real data, and carry out the pertinent studies for the selection of explanatory variables, applying goodness-of-fit tools and performing a complete diagnosis of the model. Based on this statistical analysis, the most appropriate proximity matrix is chosen. Following this strategy, three different options are tested: common-borders, distances and k-nearest neighbours. In the first option (common-borders), two domains are neighbours if they have a common delimitation. The second option considers the Euclidean distance between the centroids of the counties and sets up a proximity measure by taking the inverse of the distance between domains. The last option applies k-nearest neighbours with $k=3$. After analyzing the three possibilities in Appendix F of the supplementary material, we selected the first option because the common-borders proximity matrix makes Model S1 have a good fit to the data and present better diagnostics.

Figure 2 shows the proximity map that determines the proximity matrix $\varvec{W}^0$, i.e. it provides for each domain, which are its neighbours. See Sect. 2 for more details on the construction of the proximity matrix $\varvec{W}^0$ and $\varvec{W}$.

Fig. 2

Proximity map for each domain d ($d=1,\ldots , D$)

The target variable, $y_d$, counts the number of women under the poverty line in the domain d and $\nu _d$ is the corresponding women sample size. The minimum, median and maximum values of $\nu _d$ are 19, 152 and 1384, respectively. The minimum has been reached in the south east of the region, while the median and maximum belong to the south west. The auxiliary variables $\varvec{x}_d$ are given in Table 4. We first fit Model 1 to the data $(y_d,\nu _d,\varvec{x}_d)$, $d=1,\ldots ,D$ and we apply Moran’s I test for spatial autocorrelation. As the obtained p-value is lower than 0.001, we assume that $y_d$, $d=1,\ldots , D$, follows Model S1 and we fit this model to the data.

Table 3 provides a descriptive analysis for the logarithm of the response variable, log(y), and the considered covariates (lab2 and edu3). Specifically, it presents their mean, standard deviation (sd), median, minimum and maximum values (min and max) and the correlation (cor) between the covariates and log(y).

Table 3 Descriptive analysis

Table 4 presents the significant estimates (p-value $<0.05$) of the fixed effect coefficients under Model S1 and their standard errors, z-values and p-values.

Table 4 MSM estimates of regression parameters under Model S1

Taking into account the signs of the estimates, the auxiliary variable lab2 (proportion of unemployed women), is directly related to the response variable while edu3 (proportion of women with university level of education), helps to decrease the counts of women under the poverty line. Each domain d, $d=1,\ldots ,D$, has a random intercept with distribution $N(0, \phi ^2)$, where $\hat{\phi }=0.130$. The 95% percentile bootstrap confidence interval for the standard deviation parameter is (0.001, 0.331). The estimated autocorrelation parameter is $\hat{\rho } = 0.324$. To test the null hypothesis $H_0: \phi ^2=0$, Algorithm 1 of Appendix B is applied. The obtained p-value is 0.018. Then, taking $\alpha =0.05$, the null hypothesis is rejected. The Algorithm 2 of Appendix B is applied to test $H_0: \rho =0$. The obtained bootstrap p-value is 0.001. Taking $\alpha =0.05$, the bootstrap test concludes that the autocorrelation parameter $\rho$ is significantly different from 0. Therefore, this test recommends fitting Model S1 to the data, instead of Model 1.

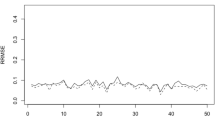
Figure 3 plots the Pearson residuals of the EBP approximation under Model S1, i.e.

$$\begin{aligned} r_d^P=\frac{y_d-\nu _d{\hat{p}}_d^{a}(\hat{\varvec{\theta }})}{\sqrt{\nu _d{\hat{p}}_d^{a}(\hat{\varvec{\theta }})}},\quad d=1,\ldots ,D. \end{aligned}$$

The distribution of the Pearson residuals is symmetrical around 0 and takes values in the interval $(-2,2)$. In addition the tested hypotheses on $\rho$ and $\phi$, the conclusion is again that Model S1 is appropriate to fit the women poverty data in Galicia by counties in 2013. This is to say, the incorporation of the underlying spatial correlation structure to the inference process seems to be beneficial.

Fig. 3

Pearson residuals of the EBP approximation under Model S1

Concerning the prediction of the poverty proportions $p_d$, $d=1,\ldots ,D$, the plug-in predictor based on Model S1 had a good performance in the simulations and lower computational cost than the approximate EBP. Therefore, it is a good candidate to be employed in this application to real data. On the other side, the plug-in predictor takes less amount of information from the spatial correlation structure than the approximate EBP. This is why we prefer to apply the approximate EBP.

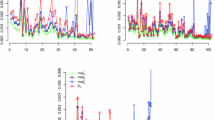
Figure 4 (left) compares the behaviour of the approximate EBP (3.5) and direct estimations. The direct estimators are calculated by using the Hájeck formula with the officially calibrated sampling weights. The domains are sorted by the sample sizes $\nu _d$’s. The direct estimators present oscillations of large amplitude, while the approximate EBPs have a smoother behaviour, which is something preferred by the statistical offices when publishing estimations. As the sample size increases, both sets of estimates tend to overlap.

Figure 4 (right) plots the relative root-MSEs (RRMSE) of the approximate EBPs based on Model S1 and the relative root-variances of the direct estimators. The direct estimates have high variability, specially for small sample sizes. As above, when the sample size $\nu _d$ increases, both accuracy measures follow the same pattern. The RRMSEs of the approximate EBPs are estimated by using the bootstrap procedure of Sect. 3 with $B=500$ replicates. The averages of the relative root-variances of the direct estimator and of the RRMSEs of the approximate EBP are 0.2595 and 0.1323, respectively. According to these results, we conclude that the approximate EBP performs better.

Fig. 4

Direct estimates and approximate EBPs of poverty proportions $p_d$ (left) and relative root-MSEs (right) for women in 2013

Figure 5 (left) maps the approximate EBP estimation of $p_d$ for women in 2013. The regions where there is no data, are in white. Model S1 gives the following predictions of women poverty proportions: 1 county with poverty proportion $p_d \le 0.12$, 12 counties with $0.12 < p_d \le 0.15$, 24 counties with $0.15 < p_d \le 0.18$ and 12 counties with $p_d > 0.18$. Highest levels of poverty are found in the south and west of the community. On the other hand, the counties with the lowest estimated poverty proportion are located in the north-east of the region.

Fig. 5

Poverty proportion approximate EBPs for women based on Model S1 (left) and RRMSEs (right) in Galicia during 2013

Figure 5 (right) maps the RRMSE estimates of the approximate EBP of $p_d$ by counties in 2013. There are 8 counties with RRMSE $\le 10$%, 8 counties with $10\%<$ RRMSE $\le 13$%, 19 counties with $13\%<$ RRMSE $\le 16$% and 14 counties with RRMSE $> 16$%. The highest values are found in the north-east of the region. Their minimum and maximum are 8.82 and 18.49%, respectively. As the highest RRMSE is lower than 20%, these estimates could be accepted for publication by statistical offices.

6 Concluding remarks

This paper introduces an area-level Poisson mixed model with SAR(1) domain effects. The new model is a GLMM counterpart of the LMM considered by Pratesi and Salvati (2008) and generalises the area-level Poisson mixed model studied in Boubeta et al. (2016) to the context of spatial correlation. The MSM algorithm of Jiang (1998) is employed for estimating the model parameters. The empirical best predictor and a plug-in predictor of the target parameter $p_d$ are given. As these predictors involve integrals in $R^D$, approximate predictors requiring the calculation of integrals in R are derived. As accuracy measure of the predictors, the MSE is considered and it is estimated by a parametric bootstrap approach.

For scenarios that mimic the application to real data, a simulation experiment studies the bias and the MSE of the new predictors. Specifically, this simulation investigates: (1) the behaviour of the EBPs and the plug-in predictors, (2) the performance of the suggested approximations to the multiple integrals, and (3) the loss of efficiency of BPs and plug-in predictors when model parameters are not known and estimated by the MSM method.

From the simulation experiment, we may give the following conclusions. First, the approximate EBPs and plug-in predictors have similar computational cost and behavior. They also have better performance than their theoretical counterparts. Second, the approximation of integrals in $R^D$ introduces a source of error that can only be reduced with high computational cost; that is, by greatly increasing the number of Monte Carlo iterations. Third, the good properties of BPs do not necessarily carry over to EBPs, especially when the number of domains is not large.

We use the approximate EBP for estimating women poverty proportions in Galician counties. The data are taken from the 2013 SLCS. As the the Moran’s I test indicates spatial correlation, we fit Model S1 to the data. In addition, the proposed predictions are compared against the direct estimates. The approximate EBPs of the women poverty proportion are smoother. As the RRMSE of the direct estimator is too high when the sample size $\nu _d$ is small, it is preferable to use the approximate EBP. The predictions based on Model S1 suggests that the highest levels of women poverty are found in the south and west of the region. The average percentage of women poverty is 16.89% and its average error is 13.23%.

It is worth mentioning the programming problems of the predictors constructed under the introduced spatial model, which leads us to use numerical approaches that introduce an additional source of error. However, we have observed in the simulations that the suggested approximate predictors (EBP and plug-in) have a lower computational cost and behave as well as their corresponding non approximate predictors.

The computations in this article have been performed entirely in the R programming language. The developed codes are available upon request.