1 Introduction

A neighborhood effect is the independent causal effect of a neighborhood (i.e., residential community) on any number of health and/or social outcomes (Mayer and Jencks 1989). In epidemiology and public health, the identification of neighborhood effects must be taken into account to acknowledge the existence and causes of health differences in the territory. Understanding the role of the environment in cities is very complex since many interrelated aspects must be considered.

Health outcomes are primarily influenced by individual characteristics, which at the same time lead to a mechanism of self-selection and possible aggregation of individuals in neighborhoods (Oakes 2004). For example, more wealthy people will be inclined to seek housing in areas that are more attractive, accessible, with prestigious accommodation, while less wealthy people will settle in areas where housing is more affordable. Literature points out that a higher socio-economic level corresponds to better health. However, studies on health in cities show how this effect may be mitigated, for example, by the concentration of immigrant workers—typically carriers of good health capital—in more disadvantaged socio-economic areas. Thus, the geography of health is not easily interpretable, because of the different mechanisms of residential mobility, which are not random but selective, both by social and migration history and by health history (Duncan et al 2018).

At the same time, health outcomes can be influenced by characteristics of the surrounding environment, such as the presence of green areas, socialization spaces, walkability, and security (Michael and Yen 2014; Blackwood et al 2022). Therefore, we look at observational studies in which individual variables act as determinants of health and generate self-selection in the choice of the area in which to live, and contextual variables may also act on health outcomes.

The goal of this work is to identify and represent clusters of neighborhoods with greater health risks within a city, after balancing the distribution of individual confounders among the neighborhoods. Our aim is also to evaluate the presence of clusters before and after considering the characteristics of neighborhoods in the analysis.

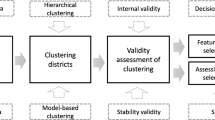
The present study considers a large number of zones (72), so the balancing problem is complex and is addressed by an approach based on the partially ordered theory (poset). The approach, originally proposed by Silan et al (2021b) and named MARMoT (Matching on Poset-based Average Rank for Multiple Treatments), allows balancing even in a very large number of “treatments”, in our case represented by neighborhoods. Moreover, as a comparison, we used another alternative technique to solve the balancing problem, called template matching (Silber et al 2014; Cannas et al 2018), to check the effectiveness of MARMoT in improving the balance of covariates and the robustness of its results.

After balancing according to the distribution of individual confounding variables, the work proceeds with the identification of clusters of areas at higher risk through a spatial scan that allows the identification of geographical clusters. This scan also takes into account area-level covariates. The reliability of the clustering procedure has been monitored by comparing the results produced by the spatial scan with a Ward hierarchical cluster, as implemented by Weaver et al (2022).

The health outcome considered in this analysis consists of hospitalized fractures, most of which are femur fractures. This outcome is a serious problem, as it can result in permanent disability, dependence on others, and increased mortality (Burge et al 2007). It is estimated that about half of all fractures occur outdoors, and several studies show that neighborhood environments can facilitate health practices that protect against falls and fractures (Li et al 2006).

The geographical area considered is the city of Turin, located in north-western Italy and capital of the Piedmont region. Turin has approximately 850,000 inhabitants. The study was made possible thanks to the wealth of information available on the city of Turin from the Turin Longitudinal Study (Costa et al 2017).

The article is then structured as follows: Sect. 2 tackles the data used in this study, Sect. 3 describes the methods, specifically the MARMoT method for balancing in 72 neighborhoods and the method for defining spatial clusters, Sect. 4 reports the results in terms of effectiveness of balancing and definition of clusters. Section 3 and Sect. 4 contain benchmark methods to which obtained results are compared. Finally, there are some concluding remarks and directions for future research.

2 Data

In this work we use both individual data coming from the Turin Longitudinal Study, and areal data that are used to describe neighborhoods. The analysed population has been selected from the Turin 2001 census, considering individuals aged 60 or more in December, 2001. Moreover, we limited the analysis to those individuals who have been living in Turin between January 1, 1997 and December 31, 2002, since we observed individual health characteristics in the four years preceding the census and the occurrence of the health outcome during 2002. Individual characteristics were drawn from the Turin Longitudinal Study (thanks to the formal agreement between the Epidemiology service of the Piedmont Region and the Department of Statistical Sciences of the University of Padova).

The Turin Longitudinal Study (SLT) comprises several data sources linked together that give rise to an integrated database. In SLT, censuses from 1971 to 2011 and several administrative health care data sources, such as hospital discharge records, prescription charges and exemptions, and territorial drug prescriptions, are pooled over time. In particular, the health outcome we considered, i.e. hospitalized bone fracture, may be observed through the analysis of hospital discharge records. This healthcare data source contains a record for each hospitalization and a list of the patient’s diagnoses that contributed to admission, together with information about when and how patients were admitted and discharged.

As confounders, we assembled the following socio-economic variables from census:

  • Gender;

  • Age, considering five-year-age brackets: 60–64; 65–69; 70–74; 75–79; 80 and more;

  • Region of birth, that distinguishes between individuals born: in regions of Northern Italy; in the rest of Italy (Centre, South, or islands); or outside Italy;

  • Family composition, combining marital status and the number of family components. It distinguishes: individuals living alone; married and living only with a partner (family of two); unmarried and not living alone (family of two or more); married and living in a family of more than two people;

  • Educational attainment, a dummy variable that assumes value 1 for individuals with primary or lower education and 0 for those with a secondary degree or higher;

  • The last known occupational status, a variable obtained from the census data from 1971 to 2001. It aims to capture the last type of occupation prior to retirement; However, it was not available for some individuals who were either already retired in 1971 (or in all censuses concerning them), or not working for other reasons. Thus, this variable distinguishes between the above-mentioned cases and homemakers, entrepreneurs, and employees (white-collar and manual workers);

  • Homeownership, a dummy variable that highlights individuals who own the house in which they live.

The study of neighborhoods strictly depends on the definition adopted to describe neighborhoods, as dealt with by a large body of literature. Turin, in particular, can be divided into 10 districts, 23 areas, or 94 zones. As already shown in Silan et al (2021b), if we consider a partition with few large neighborhoods, the estimated neighborhood effects are smoother than in partitions consisting of many small neighborhoods. In this work, we considered smaller areas to identify neighborhood effects at a higher level of geographical detail. However, 94 zones are difficult to balance because some of them are scarcely populated, so it was necessary to perform some aggregations that ultimately led to 72 zones. Following aggregation, the less populated zone counts 672 individuals, while the one with the highest number of inhabitants counts 7758 individuals. The average number of individuals living across partitions is 3136.5.

Furthermore, we considered some variables at the neighborhood level to describe the characteristics of the zones: deprivation, availability of green and pedestrian areas, walkability, and the rate of violent crimes (Costa et al 2017).

Deprivation is measured by a composite indicator derived from the combination of five dimensions: the percentage of residents with low education (standardised by age), low social class, unemployment, living in deprived housing, and living in overcrowded housing (Caranci et al 2010).

The availability of green and pedestrian areas indicates the presence of parks, gardens, and green areas (excluding sports areas) combined with pedestrian areas.

Walkability is particularly important when focusing on fractures. The set of environmental characteristics that are considered useful to encourage walking (availability and accessibility to services, shops, green areas, public transport, sports facilities, urban and road safety) is defined as walkability. Attributing different weights to men and women for these aspects, two walkability indicators are calculated (Stroscia 2018). In this work, we considered the mean of the two.

The last indicator (rate of violent crimes) examines the impact of public order problems on urban safety and civil coexistence in terms of personal injury. Crimes against individuals reported by the police are taken into account, including assault, murder, fights, kidnapping, and sexual assault (Melis et al 2015).

3 Methods

One of the most relevant methodological problems to face when estimating neighborhood effects is selection bias. In fact, dealing with observational data, it is difficult to establish whether differences with respect to the outcome between treatment groups can be attributed to the treatment itself, rather than differences between subjects’ characteristics in the groups (Austin 2011). Thus, in order to solve this issue, the focus is on balancing the distribution of confounders among the treatment groups. To reach this goal, the techniques usually exploited are based on the propensity score, that is, the probability to be treated conditional on a set of confounders. In this peculiar application, the treatment is represented by neighborhoods, thus the number of groups to handle is very large, since we are dealing with 72 zones.

In this framework, propensity score methods are unpractical and unfeasible (Silan et al 2021a), having some important assumptions, i.e., the overlap assumption, which is difficult to satisfy, and the computational cost of the propensity score calculation. In a multiple-treatment framework, a promising technique to balance the distribution of covariates among several treatment groups is MARMoT (Silan et al 2021b). An alternative approach, found in literature, is template matching, which is based on the comparison of treatment groups to a selected subset of the whole population, called template (Silber et al 2014).

3.1 MARMoT

The Matching on Poset based Average Rank for Multiple Treatments (MARMoT) proposal summarizes individual characteristics that need to be balanced among treatment groups with the help of partially ordered set (poset) theory. Exploiting poset theory, instead of propensity score techniques, is useful because it allows to estimate a balancing score only based on individual characteristics, with no need for a dependent variable. Another advantage of poset theory with respect to propensity score techniques is that no additional assumptions about the functional form or specification of the model regarding the treatment allocation assignment are needed.

Each analysed subject is identified by the profile corresponding to the set of its own characteristics (Brüggemann and Patil 2011; Davey and Priestley 2002). An approximation of the average rank is associated with each profile (De Loof 2009), a value that summarizes individual characteristics that are important for treatment allocation, and that can be normalized between 0 and 1 to have a more readable number. In this case, the average rank is used as a balancing tool and it does not have a substantial interpretation.

Once the average rank is computed using the R package deloof (Caperna 2019), it is involved in the matching procedure that produces a synthetic population with a similar composition in all treatment groups. As a scheme for matching, a frequency table is created (Table 1) with as many rows as the different values the average rank (\(AR_j\)) assumes (J) and K columns, where K is the number of treatment groups considered in the analysis. Since the goal is to obtain a comparable population with respect to observable variables, in every treatment group, each average rank value needs to be equally represented among all treatment groups. The translation of this concept in the frequency table is to get, for every row j, \(f_{j,1}=\dots =f_{j,K}=f_j^*\), \(\forall k=1,\dots ,K\), where \(f_j^*\) is a frequency reference fixed by the researcher.

Table 1 An example of the frequency table involved in the matching of the MARMoT approach
Full size table

The frequency reference \(f_j^*\) is defined as

$$\begin{aligned} f_j^*= {\left\{ \begin{array}{ll} 1 &{} \text{ if } \text{ median } (f_{j,1}, f_{j,2}, \dots , f_{j,K})=0\\ \text{ median }(f_{j,1}, f_{j,2}, \dots , f_{j,K}) &{} \text{ otherwise }\\ \end{array}\right. }. \end{aligned}$$
(1)

Starting from the frequency table and the reciprocal dimensions of \(f_{j,k}\) and \(f_j^*\), the matching algorithm proceeds in three different ways, for every j and every k:

  1. 1.

    if \(f_{j,k}=f_j^*\): all individuals with \(AR_j\) (the AR value in row j) in the treatment group \(t_k\) are copied in the final dataset.

  2. 2.

    if \(f_{j,k}\ne f_j^*\) and \(f_{j,k}\ne 0\): a random sample with replacement of size \(f_j^*\) is selected from among the individuals with \(AR_j\) in the treatment group \(t_k\), and included in the final dataset.

  3. 3.

    if \(f_{j,k}=0\): a random sample with replacement of size \(f_j^*\) is selected among the individuals with an AR close enough (with a given tolerance interval) to \(AR_j\) in treatment group \(t_k\), and included in the final dataset. If there are no individuals close enough, then all individuals with an AR equal to \(AR_j\) must be deleted from the final dataset.

The tolerance interval to select subjects that need to be discarded to comply with the overlap assumption is defined as \(\left[ AR_r-\frac{S_{AR}}{4}; AR_r+\frac{S_{AR}}{4}\right]\), considering as a caliper the value \(\frac{S_{AR}}{4}\), where \(S_{AR}\) is the AR’s sample standard deviation.

At the end of the MARMoT procedure, all treatment groups are comparable with respect to observable confounders and, under the unconfoundedness assumption, it is possible to estimate the treatment effect. The unconfoundedness assumption implies that the set of observed pretreatment confounders includes all variables directly influencing both treatment assignment and the outcome (Hu et al 2020).

All in all, the MARMoT procedure is useful to balance the distribution of individual observable characteristics among treatment groups, thus, to check if the balance is reached after the algorithm, we rely on the most commonly employed measure of comparability of treatment groups, the absolute standardized bias (ASB). The ASB has also been found to be superior to other measures in its ability to predict the bias of causal effects estimators (Cannas and Arpino 2019) and is defined as:

$$\begin{aligned} ASB=\frac{|{\bar{X}}_{t}-{\bar{X}}|}{\sqrt{\frac{S^2_{t}}{2}+\frac{S^2}{2}}} \end{aligned}$$
(2)

where \({\bar{X}}\) and \({\bar{X}}_{t}\) are the means of the variable X of individuals living respectively in the whole city, and in the neighborhood t; and S and \(S_{t}\) are the standard deviations of the variable X of individuals living respectively in the whole city, and in the neighborhood t. Additional details about the MARMoT procedure can be found in Silan et al (2021b).

In order to validate MARMoT results with another balancing approach, we also performed a template matching on our data (Silber et al 2014; Cannas et al 2018). This method is based on the selection of a template that resembles the mean of the whole population. Once the template is selected, all treatment groups are matched with it. Thus, the final balanced population, that will be used for the estimation of the treatment effect, will consist of the repetition of a set of observations similar to the template in every treatment group and will have a structure similar to the whole population average with respect to observable variables. Choosing the template and its size is extremely important in performing this procedure, because they largely affect the structure and the size of the final population, thus the estimation of treatment effects on the outcome.

3.2 Disease clustering using a spatial scan

A further step after estimating the neighborhood effects is to check whether the risk of fracture for the subjects analyzed is constant across the territory or is significantly higher in some contiguous areas (known as geographical clusters). To do this, we resort to using a spatial scan capable of identifying the presence of clusters and quantifying the increased risk.

Spatial scans were first discussed during the 1960 s (Naus 1965) and later formalized by Kulldorff in a general format (Kulldorff 1999). The idea behind a spatial scan is to conduct the test

$$\begin{aligned} H_0:&\quad \gamma _i = \gamma _{{\bar{i}}} \nonumber \\ H_1:&\quad \gamma _i > \gamma _{{\bar{i}}} \end{aligned}$$
(3)

where i is a candidate cluster part of the geographical space, \(\gamma _i\) is the risk within the cluster and \(\gamma _{{\bar{i}}}\) is the risk outside the cluster. The test formalized by Kulldorff is based on the likelihood ratio statistic, with p-values computed via randomization testing. Later on, many authors have proposed different versions of the spatial scan (i.e., Jung (2009); Zhang and Lin (2009)) with applications in different fields, such as ordinal data (Jung et al 2007), survival data (Huang et al 2007), or moving into the Bayesian framework (Neill et al 2005; Bilancia and Demarinis 2014). Our analysis relies on the spatial scan introduced by Gómez-Rubio et al (2019); the reason why we have chosen this particular spatial scan over the others is the importance of considering the covariates at the area level and the availability of a fast and accurate algorithm available in the R package DClusterm developed by the same authors.

DClusterm is based on a Poisson GLM and uses a distinct dummy variable for each cluster to perform the likelihood test shown in (3). First, the baseline Poisson regression (null model) has been fitted with intercept only and the number of observed cases per area as the dependent variable. Having that, the baseline represents the average risk in the whole population. The expected number of cases per area has been used as an offset, doing so the actual output of the model turns out to be the standardized mortality ratio (SMR) of the disease.

Then, many models have been fitted one-by-one adding different cluster dummy variables of the type

$$\begin{aligned} d_i^{(j)} = {\left\{ \begin{array}{ll} 1 &{} \text{ if } \text{ area } i \text{ belongs } \text{ to } \text{ cluster } j\\ 0 &{} \text{ if } \text{ area } i \text{ does } \text{ not } \text{ belong } \text{ to } \text{ cluster } j \end{array}\right. }. \end{aligned}$$
(4)

The parameter associated with \(d_i^{(j)}\), denoted by \(\gamma _j\), is a measure of the risk within the clusters: if \(\gamma _j\) is significantly higher than 0, the cluster has a risk greater than the baseline. Since multiple tests have been carried out, the significance level used to determine whether an area belongs to a cluster, originally set to 5%, has been corrected using the Bonferroni procedure. Every area has been taken as a candidate center for a cluster and dummy cluster variables are iteratively created for the areas close to it. There is no maximum radius for the the geographical clusters growth, but the maximum fraction of the total population inside a single cluster has been set to 15%. Finally, duplicated clusters have been removed as well as clusters too small to be considered (made of less than 3 areas).

The entire process can be repeated adding one or more area-level covariates to the Poisson model to evaluate if their effects modify the shape of the clusters. Once again, the resulting estimate of the increased risk is obtained from the coefficient associated with the dummy cluster variable.

The mathematical and computational details of the statistics scan used, both with and without covariates, are addressed in Section 2.1 of Gómez-Rubio et al (2019). The entire analysis has been run in R—4.1.2 “Bird Hippie” (R Core Team 2021).

We compared the spatial clustering algorithm with a Ward’s hierarchical clustering, as implemented by Weaver et al (2022). This procedure, however, does not consider the spatial proximity of areas in the clustering procedure, thus it may produce a more spotted outcome that the spatial scan. The hierarchical clustering procedure included, in addition to the risk of fracture, the area deprivation index, the availability of green and pedestrian areas, the walkability index, and the rate of violent crimes. We selected three different clusters using the optimal height of the dendrogram.

4 Results

The occurrence of the analysed outcome, which is hospitalized fracture, is \(0.90\%\) among the elderly in the whole city, with some differences in the distribution among neighborhoods (Fig. 1). The zone with the lowest fracture ratio, \(0.18\%\), is in the North-West part of Turin, while the neighborhood where fractures are more common (with a fracture ratio equal to \(1.64\%\)) is in the South-East part of Turin, close to the city center. In general, the fracture distribution in Turin seems to follow a concentric pattern starting from the city center, where the concentration is higher, to the suburban area where the outcome ratio is lower.

However, the crude distribution of fractures in the territory is affected by the unbalanced distribution of individual characteristics. Indeed, subjects freely chose the neighborhoods to live in according to their own resources and preferences. For instance, a family with low income, unable to afford a house in a neighborhood with better characteristics, will have to settle in an average or impoverished zone. On the other hand, it is necessary to discern whether the differences observed between neighborhoods depend on population composition and, simultaneously, how much they depend on the neighborhood itself. To do so, the observable covariates are balanced among neighborhoods using MARMoT procedure and making different treatment groups comparable.

Fig. 1
figure 1

Fractures ratio before the MARMoT adjustment (Map obtained by QGIS 3.16 software)

Full size image

4.1 Evaluation of the balance before and after MARMoT procedure

As mentioned before, the distribution of confounders among neighborhoods before the balancing procedure is highly unbalanced. For every variable level and every treatment group, a value of absolute standardized bias is computed, both on real data and on balanced data. Among those, almost a third of the values was higher than \(10\%\) before the MARMoT adjustment and more than half of them were higher than \(5\%\) (Table 2). The most unbalanced variables are educational attainment (with a mean ABS equal to \(25.88\%\)), region of birth (with mean ASB \(16.13\%\)) and home ownership (with mean ASB \(13.48\%\)), as shown in Fig. 2.

Fig. 2
figure 2

Mean ASBs for every balanced variable before and after MARMoT adjustment

Full size image

In the balanced population, the values of ASBs are reduced (Table 2) with the median ASB equal to \(2.87\%\). Some ASBs remain quite high, as the maximum equal to \(46.39\%\), but there is only a small portion of them, indeed only 100 values are higher than \(10\%\), which corresponds to less than one-tenth of the total ASB computed values. The most problematic variables are educational attainment, region of birth, and home ownership, even after the balancing procedure, but with a well-reduced mean ASB lower than \(10\%\) for all of them (the mean ASBs of the three variables are \(7.76\%\), \(5.85\%\) and \(7.05\%\), respectively). The mean ASBs referred to the other four variables after the MARMoT procedure is lower than \(5\%\) (Fig. 2).

Table 2 Distribution of ASBs before and after MARMoT adjustment
Full size table

Neighborhoods that are more difficult to balance are scarcely populated ones. Indeed, an inversely proportional relation may be found between the size of the neighborhood population before the adjustment of MARMoT and the mean of all ASBs computed for each neighborhood (Fig. 3). The median size of the population before the adjustment is 2548 inhabitants, neighborhoods with a higher population size have a mean ASB lower than \(5\%\) (except for 2 of them), while almost half of the neighborhoods less populated than the median have a mean ASB higher than \(5\%\).

Fig. 3
figure 3

Mean ASBs for every balanced neighborhood and neighborhood dimension before MARMoT adjustment

Full size image

Performing the MARMoT procedure, a table is created that has as many rows as the different values the average rank assumes in the pooled population. In this application, the table counts 1708 rows. Considering this threshold, half of the neighborhoods with a population lower than 1708 have a mean ASB higher than \(5\%\), as about one-tenth of the neighborhoods above this threshold. In other words, neighborhoods with at least one subject (on average) for each average rank value are well balanced by the MARMoT procedure, while other groups may present a more critical situation (in this application less than \(30\%\) of neighborhoods).

After the MARMoT balancing procedure, the differences observed in the distribution of hospitalized fractures among neighborhoods should no longer depend on individual confounders, under the unconfoundedness assumption. Even if the ranking of neighborhoods according to the risk of hospitalized fracture is not completely altered, there are some substantial changes (Fig. 4). First, the ratios of fractures are smoother, the range of values goes from \(0.30\%\) in the most virtuous neighborhood to \(1.60\%\) in the more risky neighborhood. In the general ranking of neighborhoods, some of them acquire quite a different position. For instance, the neighborhood that before the adjustment was the one with the highest ratio of fractures becomes lower in the ranking with a balanced hospitalized fracture ratio equal to \(1.24\%\); while the neighborhood that before the balancing procedure was the second best in terms of fractures ratio (\(0.24\%\)), after the adjustment is in the middle of the ranking (with a fractures ratio of \(0.95\%\)).

Fig. 4
figure 4

Fractures ratio after the MARMoT adjustment (Map obtained by QGIS 3.16 software)

Full size image

4.1.1 Validation of MARMoT procedure through template matching

According to literature (Silber et al 2014; Cannas et al 2018), the size of the template corresponds to the minimum efficient number of observations, the choice is a trade off between the difficulty to match observations in smaller treatment groups and the need to consider a large portion of the whole population. Usually the template size is close to half the size of the less common treatment group; in this case, the template size is equal to 400.

After extracting 1000 samples of 400 units from the entire population, the template was chosen as the one with the most similar mean characteristics to the average of the entire population (measuring the distance with the Mahalanobis metric).

Once the template was selected, it was matched with all treatment groups following an exact match (with a small tolerance) on the covariates. The final population counts 28800 units.

Having a small template that resembles the average of the population simplifies the matching procedure, but it implies that several observations are discarded: only 11.15% of the original population is included in the final balanced sample.

Table 3 Performance of MARMoT and template matching with respect to ASBs and percentage of inclusion
Full size table

In Table 3 the ASBs are shown after MARMoT and after template matching. The performance in terms of ASBs after adjustment of the two techniques is comparable, except for some extreme values in the MARMoT ASBs distribution. These values may be explained by some treatment groups that are more difficult to balance due to their small size.

As a general consideration, even if MARMoT extreme ASBs could still be improved, especially for less frequent treatments, larger sample sizes allow a better representation of the original population. Indeed, the common support considered in the MARMoT procedure considers a portion of the population as large as possible, while the template matching treats a simplified version of the total population. However, the treatment estimates produced by the two balanced procedures are highly correlated (correlation equal to 0.51).

4.2 Disease clustering results

The percentage of hospitalized fractures in the whole population, after MARMoT adjustment, is \(0.90\%\) with a \(95\%\) confidence interval (C.I.) between \(0.86\%\) and \(0.94\%\). First, the disease clustering procedure described in Sect. 3.2 has been run without neighborhood covariates, with the aim of identifying the actual presence of clusters at higher risk. Two clusters have been detected (Fig. 5): the first consists of six areas and presents a hospitalized fractures percentage equal to \(1.16\%\) (C.I. 1.01–\(1.30\%\)). This cluster involves three macro-areas in the city of Turin: Santa Rita (entirely included), and parts of Lingotto and Mirafiori. The second cluster consists of seven areas, has an outcome percentage equal to \(1.12\%\) (C.I. 0.99–\(1.26\%\)), and mainly comprises the city center.

Fig. 5
figure 5

Cluster obtained without considering territorial covariates in the model (Map obtained by QGIS 3.16 software)

Full size image

Then, the clustering procedure has been run including 4 area-level covariates: deprivation, availability of green and pedestrian areas, walkability, and rate of violent crimes. Once again, two clusters have been detected (Fig. 6): the first consists of 10 areas and presents a percentage of fractures equal to \(1.08\%\) (C.I. 0.97–\(1.19\%\)). This cluster is similar to the first one obtained without covariates, but it includes the whole Mirafiori macro-area, which is historically the most industrialized area in Turin, where most manual workers live, half of Santa Rita, and the majority of Lingotto. The second cluster consists of five areas and has a percentage of fractures equal to \(1.12\%\) (C.I. 0.96–\(1.28\%\)), including the entire Aurora macro-area and a small part of the city center.

Fig. 6
figure 6

Clusters obtained by adding territorial covariates in the model (Map obtained by QGIS 3.16 software)

Full size image
Table 4 Details of the clusters, showing percentages of hospitalized fractures and odds-ratios (having as reference the not-clustered area) with corresponding \(95\%\) confidence interval in brackets
Full size table

The reason given for these differences is that the effect of the covariates is capable of explaining part of the clusters and, at the same time, their presence brings out new areas of high risk that were previously masked. All details of the clusters are summarized in Table 4.

Fig. 7
figure 7

Clusters obtained excluding one variable at a time, percentages of hospitalized fractures and odds-ratios (having as reference the not-clustered area) with corresponding \(95\%\) confidence interval in brackets (Maps obtained by QGIS 3.16 software)

Full size image

With the aim of better understanding the role that each variable has on the clustering procedure, we excluded one of them at a time observing four new clusters and comparing them with the complete one. The results of the analysis are shown in Fig. 7.

Even changing the covariates involved in the clustering procedure, the cluster that includes the City center remains unchanged. On the other hand, the other cluster, involving South of Turin, is reduced if we exclude the variable that represents the availability of green and pedestrian areas and changes significantly with the elimination of the area deprivation index. When we exclude the rate of violent crimes from the clustering procedure, the two clusters shown in Fig. 6 are unchanged, but a new cluster is created with a lower risk of incurring a hospitalized fracture compared to the other two clusters (odds ratio equal to 1.23, having as reference the not-clustered area). The variable that seems to have the greatest influence on the clustering procedure is the one representing the availability of green and pedestrian areas because its absence modifies clusters deeply, making them more similar to the model without covariates also in the outcome percentages.

4.2.1 Validation of disease clustering results through hierarchical clustering

To validate the disease clustering performed with the spatial scan as described in the previous section, we also clustered neighborhoods using a Ward hierarchical cluster that included the same covariates as in the spatial scan. Following the dendrogram, the first partition of neighborhoods distinguished between cluster 1 and clusters 2 and 3 (considered jointly). Then, clusters 2 and 3 are separated (Fig. 8).

Fig. 8
figure 8

Clusters obtained by hierarchical clustering (Map obtained by QGIS 3.16 software)

Full size image

Comparing the clusters produced by the two methods (Figs. 6 and 8), some similarities can be discerned between cluster 1 (Fig. 8) and the cluster representing the South of Turin (Mirafiori, Lingotto, Santa Rita in Fig. 6); cluster 2 (Fig. 8) and the cluster representing the city center (Fig. 6); and, cluster 3 (Fig. 8) and the unclustered area in Fig. 6. However, since the hierarchical clustering does not consider the spatial correlation, these similarities are not so clear-cut, but are somewhat confused by the spotty classification produced by this method.

Table 5 Comparison of clusters produced by the spatial scan with covariates and the hierarchical clustering, showing percentages of hospitalized fractures and odds-ratios (having as reference the not-clustered area for the spatial scan clustering and the remaining part of the city for the hierarchical clustering) with corresponding 95% confidence interval in brackets
Full size table

In Table 5 the percentages and odds ratios of the clusters obtained by the two methods are compared. The risk of hospitalized fractures is smoother among the three clusters defined by the hierarchical clustering procedure. The reason for this result is probably due to the clustering procedure, which is more focused on the classification of neighborhoods according to five variables (risk of fractures and the four covariates), while the spatial scan has the goal of identifying spatial clusters with an increased outcome risk.

5 Conclusion

The study of neighborhood effects is an important topic of social epidemiology, with repercussions in public health strategies. This study constitutes a complex challenge, as health events are influenced both by individual and environmental/contextual characteristics, with the former influencing the latter (for example, the socio-economic characteristics of individuals define the level of deprivation of an area) and at the same time determining a self-selection effect, i.e., the residence in certain areas.

This work aimed to identify spatial clusters at higher risk of adverse health outcomes, by aggregating neighborhoods defined as administrative territorial units. These clusters were identified after balancing the individual confounding variables in each neighbourhood, in order to equalize neighborhoods in terms of individual characteristics and define clusters whose differences in terms of health risk are attributable to characteristics of the area (assuming that all confounding variables have been considered at the individual level). The inclusion of neighborhood-level variables in the cluster definition allows to gain insight into the role of these variables by comparing the clusters with and without them. The health outcome considered is given by hopitalized fractures, which constitute an outcome that is affected by both individual factors and environmental characteristics, an aspect that affects many other health outcomes.

The objective of the study was pursued in two phases: the first consisted in balancing individual characteristics, the second in identifying clusters of neighborhoods with higher health risk.

The balancing of the individual characteristics was performed using a recent original procedure, called MARMoT, and proposed by the authors themselves in a previous paper.

This procedure allows to handle the balance of several treatment groups considering at the same time a consistent number of variables. With respect to competing methods based on propensity score, MARMoT allows to examine a higher number of treatment groups and guarantees extremely smaller computational times (a few hours instead of a few days). Moreover, no hypotheses about the functional form of the treatment allocation mechanism are needed thanks to the involvement of poset theory in the computation of the balancing score. Furthermore, once the population is balanced, it is possible to deepen the analysis using other techniques, such as the spatial scan to observe clusters among neighborhoods.

The main contributions of the work are multiple: first, the proposal to identify spatial clusters after balancing according to individual confounders; second, the overcoming of the logic of neighborhoods understood as administrative units through the identification of neighborhoods sharing similar levels of increased risk; third, the application of an original and effective proposal for the balancing of individual confounders in complex situations from a computational point of view due to the high number of treatments.

Although MARMoT represents an effective original proposition, its comparison with template matching reveals points for improvement.

The balance produced by the two techniques is comparable with only a few more difficulties for MARMoT with regard to treatments with a small sample size. This difference is due to the fact that the MARMoT goal is to represent the widest possible part of the population in the final balanced population, seeking the largest possible common support. Thus, balance in smaller treatment groups is more difficult to obtain. On the other hand, template matching only selects the minimum common support (template) which simplifies the matching procedure, but it may distance the balanced population from the complexity of the original one. Although there is still room for improvement in the management of small treatment groups that produce ASBs higher than \(10\%\), we acknowledge the potential of the MARMoT method. Therefore, we will also conduct further research on the adjustment of this promising technique for small treatment groups.

Given its ability to handle area-level covariates together with spatial correlation, the spatial scan DClusterm has been chosen. Moreover, we have also found some consistency in the comparison of clusters distinguished by Ward’s hierarchical clustering.

Thanks to the combination of the MARMoT procedure and a spatial scan, it was possible to highlight two clusters of neighborhoods in Turin where there is an increased risk of hospitalized fractures for the elderly.

In addition to the margins for improvement mentioned above, the limitations of this study can typically be found in social epidemiology studies, characterized in particular by an availability of data that will never effectively cover all the possible variables that come into play in complicated causal mechanisms (for a detailed review of the methodological problems related to the estimation of neighborhood effects, see, for example, Roux (2004)).

The results obtained here are a useful indication for policymakers, who can insert this piece into a wider set of information, also of a qualitative nature, to address the complicated issue of health inequalities in cities and, more generally, in the territory.