Automatic robust Box–Cox and extended Yeo–Johnson transformations in regression

Abstract

The paper introduces an automatic procedure for the parametric transformation of the response in regression models to approximate normality. We consider the Box–Cox transformation and its generalization to the extended Yeo–Johnson transformation which allows for both positive and negative responses. A simulation study illuminates the superior comparative properties of our automatic procedure for the Box–Cox transformation. The usefulness of our procedure is demonstrated on four sets of data, two including negative observations. An important theoretical development is an extension of the Bayesian Information Criterion (BIC) to the comparison of models following the deletion of observations, the number deleted here depending on the transformation parameter.

1 Introduction

In the final sentence of Hinkley (1975), David Hinkley wrote ‘Data transformation in the presence of outliers is a risky business’. The risk arises particularly in robust fitting of transformations. If a symmetrical model is fitted to a skewed distribution, the observations in the longer tail may be spuriously treated as outliers and downweighted. The need for a non-symmetric transformation of the data is then obscured. In this paper we present an automatic method, including robustness, for the Box–Cox transformation and also for the extended Yeo–Johnson transformation which allows for both positive and negative observations. Atkinson et al. (2021) give a review of these transformations and exemplify the lack of robustness of the appealing non-parametric transformations ACE and AVAS (Breiman and Friedman 1985; Tibshirani 1988). Our inferences about transformations and outliers use a new extension of the BIC (Schwarz 1978) in combination with the mean shift outlier model. This allows the automatic comparison of fitted models in which, due to outlier deletion, the number of observations differs. The emphasis in our paper is on automatic determination of robust parametric response transformations in regression. We analyse four sets of data and describe the programs used to generate the analyses.

The Box–Cox transformation is recalled in Sect. 2.1 as, in Sect. 2.2, is the approximate score test for the transformation parameter $\lambda$, which we call $T_A$ for the Box–Cox transformation. This is found by Taylor series expansion of the expression for the transformed response, leading to the inclusion of a constructed variable in the regression model. Robustness is introduced in Sect. 2.3 where the forward search (Atkinson et al. 2010), ordering the data by the use of residuals (Riani and Atkinson 2000), leads to the fan plot for assessing transformations over a grid of values of $\lambda$. The aim of all transformations is to find a model for which the error variance is constant, the distribution of residuals is approximately normal and the linear model is simple and, ideally, additive.

The paper proceeds by direct use of the numerical information in the fan plot; automatic assessment of this information replaces visual inspection of plots and subsequent manual adjustment of parameter values leading to further calculations and plots (Atkinson et al. 2020). Section 3 provides the necessary inferential tools. The stages in choice of the transformation parameter are:

• 1. The forward search (FS) orders the data by closeness to the fitted model and leads to the trimming of outliers in the transformation model (Sect. 2.3).

• 2. Use of the mean shift outlier model (Sect. 3.1) provides a likelihood adjusted for the trimming of observations.

• 3. This likelihood is used in Sect. 3.1 to calculate the extended BIC, used for comparing different transformations with varying numbers of trimmed observations. In Sect. 3.2 we adjust this BIC for consistent estimation of the error variance.

The agreement index (AGI), a diagnostic tool supplementing the use of BIC, is introduced in Sect. 3.3. A second diagnostic tool is the extension of the coefficient of determination ($R^2$) to allow for the deletion of outliers. These tools are used in Sect. 4 to build the automatic procedure for the Box–Cox transformation, illustrated in Sect. 5 by the automatic analysis of data on hospital stays and on loyalty cards. In Sect. 6 we conclude our investigation of automatic procedures for the Box–Cox transformation with a simulation study comparing our work with that of Marazzi et al. (2009). For simple regression, the procedures provide estimates with similar bias, but the computation time for that of Marazzi et al. increases rapidly with the sample size. For multiple regression our procedure has the lower bias.

Section 7 introduces the extended Yeo–Johnson transformation of Atkinson et al. (2020) which develops the transformation of Yeo and Johnson (2000) to allow differing values of the transformation parameter for positive and negative observations. The subject of Sect. 8 is the adaptation of the automatic procedure to the extended Yeo–Johnson transformation. Because there are two score statistics, for the transformation parameters for positive and negative observations, a more complicated form of the agreement index is required. Examples of the use of this automatic procedure are in Sect. 9. In the larger example we analyse 1405 observations on the profitability of firms, 407 of which make a loss. In the concluding Sect. 10 we discuss potential further extensions to the Yeo–Johnson transformation and relate our results to the remark of Hinkley quoted at the beginning of this paper.

The Appendix contains algebraic details of the normalized version of the extended Yeo–Johnson transformation and of the constructed variables used in our automatic procedure. Links to our programs for automatically determining transformations are at the end of Sect. 10.

2 The Box–Cox transformation

2.1 Aggregate statistics

The Box–Cox transformation for non-negative responses is a function of the parameter $\lambda$. The transformed response is

$$\begin{aligned} \begin{array}{cccc} y(\lambda ) = ({y^{\lambda } - 1})/{\lambda } \quad&(\lambda \ne 0); \quad&\log y \quad&(\lambda = 0), \end{array} \end{aligned}$$

(1)

where y is $n \times 1$. In (1) $\lambda = 1$ corresponds to no transformation, $\lambda = 1/2$ to the square root transformation, $\lambda = 0$ to the logarithmic transformation and $\lambda = -1$ to the reciprocal transformation, thus avoiding a discontinuity at zero.

The development in Box and Cox (1964) is for the normal theory linear model

$$\begin{aligned} y(\lambda ) = X\beta + \epsilon , \end{aligned}$$

(2)

where X is $n \times p$, $\beta$ is a $p \times 1$ vector of unknown parameters and the variance of the independent errors $\epsilon _i\quad (i = 1,...,n)$ is $\sigma ^2$. For given $\lambda$ the parameters can be estimated by least squares. To estimate $\lambda$ it is necessary to allow for the change of scale of $y(\lambda )$ with $\lambda$. The likelihood of the transformed observations relative to the original observations y is

$$\begin{aligned} (2\pi \sigma ^2)^{-n/2}\exp \{-S(\lambda )/2\sigma ^2\}J^n_{{\mathrm{BC}}}, \end{aligned}$$

(3)

where $S(\lambda ) = \{y(\lambda )-X\beta \}^T\{y(\lambda )-X\beta \}$ and the Jacobian

$$\begin{aligned} J^n_{{\mathrm{BC}}} = \prod _{i=1}^n \left| \partial y_i(\lambda )/\partial y_i \right| . \end{aligned}$$

(4)

For the power transformation (1), $\partial y_i(\lambda )/\partial y_i = y_i^{\lambda -1},$ so that

$$\begin{aligned} \log J^n_{{\mathrm{BC}}} = (\lambda - 1)\sum \log y_i = n (\lambda - 1) \log {\dot{y}}, \end{aligned}$$

where ${\dot{y}}$ is the geometric mean of the observations. Box and Cox (1964) show that a simple form for the likelihood is found by working with the normalized transformation

$$\begin{aligned} z(\lambda ) = y(\lambda )/J^{1/n}_{{\mathrm{BC}}} =( y^{\lambda }-1)/\lambda {\dot{y}}^{\lambda - 1}. \end{aligned}$$

(5)

If an additive constant is ignored, the profile loglikelihood, maximized over $\beta$ and $\sigma ^2$, is

$$\begin{aligned} L_{\max }(\lambda )&= -(n/2)\log \{S(\lambda )/n\} + \log J^n_{{\mathrm{BC}}} \\ &= -(n/2)\log \{R(\lambda )/n)\}, \end{aligned}$$

(6)

with $R(\lambda )$ the residual sum of squares of $z(\lambda )$. Thus ${\hat{\lambda }}$ minimizes $R(\lambda )$.

For inference about plausible values of the transformation parameter $\lambda$, Box and Cox suggest the likelihood ratio test that $\lambda = \lambda _0$ using (6), that is the statistic

$$\begin{aligned} T_{LR} = 2\{L_{\max }({\hat{\lambda }}) - L_{\max }(\lambda _0)\} = n\log \{R(\lambda _0) / R({\hat{\lambda }})\}. \end{aligned}$$

(7)

Although Box and Cox (1964) find the estimate ${\hat{\lambda }}$ that maximizes the profile loglikelihood, they select the estimate from those values of $\lambda$ from the grid ${\mathcal {G}}$ that lie within the confidence interval generated by (7). In their examples where $n = 27$ and 48, ${\mathcal {G}} = [-1, -0.5, 0, 0.5, 1].$ Carroll (1982) argues that the grid needs to become denser as n increases. An example is in Sect. 5.2.

This formulation has led to some controversy in the statistical literature. Bickel and Doksum (1981) and Chen et al. (2002) ignore the suggested procedure. The variability of the estimated parameters in the linear model can be greatly increased when $\lambda$ is estimated by ${\hat{\lambda }}$, particularly for regression models with response $y(\lambda )$. McCullagh (2002) is very clear that the Box–Cox procedure does not lead to ${\hat{\lambda }}$. Box and Cox (1982), Hinkley and Runger (1984), Cox and Reid (1987) and Proietti and Riani (2009) provide further discussion.

The practical procedure indicated by Box and Cox is analysis in terms of $z(\lambda )$ leading to ${\hat{\lambda }}$ with an associated confidence interval and hence to a, hopefully, physically interpretable estimate ${\hat{\lambda }}_G$. To avoid dependence on ${\dot{y}}$ in comparisons across sets of data, parameter estimates need to be calculated using $y({\hat{\lambda }}_G)$ rather than $z({\hat{\lambda }}_G)$.

In the later sections of this paper we are concerned with power transformations of responses that may be both positive and negative. One procedure, analysed by Box and Cox, is the shifted power transformation in which the transformation is of $(y + \mu )^\lambda$, with the value $\mu$ greater than the minimum value of y. If $\mu$ is a known offset, such as 273.15 in converting from Celsius temperatures to Kelvin, the transformation is unproblematic. But if $\mu$ is a parameter to be estimated from the data, inferential difficulties arise because the range of the observations depends on $\mu$ (Atkinson et al. 1991). In addition the shifted power transformation is not sufficiently flexible to model data such as the examples presented in Sect. 9.

2.2 Constructed variables

The robust transformation of regression data is complicated by the inter-relationship of outliers and the value of $\lambda$. Examples are in Atkinson and Riani (2000, Chapter 4). To determine the effect of individual observations on the estimate of $\lambda$ we use the approximate score statistic $T_{A}(\lambda )$, (Atkinson 1973) derived by Taylor series expansion of $z(\lambda )$ (5) about $\lambda _0$. For a general one-parameter transformation this leads to the approximate regression model

$$\begin{aligned} z(\lambda _0)&= x^T\beta - (\lambda - \lambda _0) w(\lambda _0) + \epsilon \\ &= x^T\beta + \gamma \ w(\lambda _0) + \epsilon , \end{aligned}$$

(8)

where $\gamma =- (\lambda -\lambda _0)$ and the constructed variable $w(\lambda _0) = \left. \partial z(\lambda )/\partial \lambda \right| _{\lambda =\lambda _0}$, which only requires calculations at the hypothesized value $\lambda _0$.

The approximate score statistic for testing the transformation is the t statistic for regression on $- w(\lambda _0)$ , that is the test for $\gamma = 0$ in the presence of all components of ${\beta }$. Because $T_A(\lambda _0)$ is the t test for regression on $- w(\lambda _0)$, large positive values of the statistic mean that $\lambda _0$ is too low and that a higher value should be considered.

2.3 The fan plot

We use the forward search to provide a robust plot of the approximate score statistic $T_A(\lambda )$ over a grid ${\mathcal {G}}$ of values of $\lambda$. For each $\lambda$ we start with a fit to $m_0= p+1$ observations. These are robustly chosen to be the subset providing the Least Median of Squares estimates of the parameters of the linear regression model, allowing for the additional presence of the parameter $\lambda$ (Atkinson and Riani 2000, p. 31). We then successively fit to larger subsets. For the subset of size m we order all observations by closeness to the fitted model; the residuals determine closeness. The subset size is increased by one to consist of the subset with the $m+1$ smallest squared residuals and the model is refitted to this new subset. Observations may both leave and join the subset in going from size m to size $m+1$. The process continues with increasing subset sizes until, finally, all the data are fitted. The process moves from a very robust fit to non-robust least squares. Any outliers will enter the subset towards the end of the search. We thus obtain a series of fits of the model to subsets of the data of size $m, m_0 \le m \le n$ for each of which we refit the model and calculate the value of the score statistics for selected values of $\lambda _0 \in {\mathcal {G}}$. These are then plotted against the number of observations m used for estimation to give the “fan plot". The ordering of the observations in a fan plot, which reflects the presence of outliers, may depend on the value of $\lambda _0$. Because we are calculating score statistics we avoid the estimation of $\lambda$ and its confidence interval which is required in the original Box–Cox procedure.

2.4 Hospital data 1

Neter et al. (1996, pp. 334, 438) analyse 108 observations on the times of survival of patients who had a particular kind of liver surgery. There are four explanatory variables, with response taken as the logarithm of survival time. To check whether this is the best transformation in the Box–Cox family requires the constructed variables

$$\begin{aligned} w_{{\mathrm{A}}}(\lambda ) = \left\{ \begin{array}{ll} [ y^{\lambda }\{\log (y/{\dot{y}}) - 1/\lambda \}]/ ( \lambda {\dot{y}}^{\lambda -1}) &{} \lambda \ne 0 \\ {\dot{y}} \log y (0.5\log y - \log {\dot{y}}) &{} \lambda = 0, \end{array} \right. \end{aligned}$$

(9)

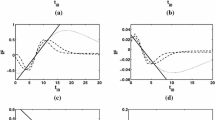
regression on which for the null value $\lambda _0$ of $\lambda$ gives the statistic $T_{{\mathrm{A}}}(\lambda _0)$. The fan plot of Fig. 1 for the five most commonly used values of $\lambda _0 \; (-1, -0.5, 0, 0.5, 1)$ confirms that the logarithmic transformation is suitable for these survival data, as it is for the survival times in the poison data analysed by Box and Cox (1964). The trajectory of the score statistic for $\lambda _0 = 0$ lies within the central pointwise 99% band throughout, whereas those for the other four values of $\lambda _0$ are outside the bands by the end of the search.

Fig. 1

Hospital data. Fan plot for five commonly used values of $\lambda$. The horizontal bands are the 99% and 99.99% pointwise intervals for normal random variables. The vertical line at $m = 65$, the rounded value of 0.6n, indicates the point at which automatic monitoring starts

Since the constructed variables are functions of the response, the statistics cannot exactly follow the t distribution. Atkinson and Riani (2002) provide some numerical results on the distribution in the fan plot of the score statistic for the Box–Cox transformation; increasingly strong regression relationships lead to null distributions that are closer to t.

3 Inference and outlier deletion

This section introduces the novel extension of BIC for choice of transformation parameters and supplements it with two further diagnostic tools, the Agreement Index AGI, and an extended form of $R^2$. Section 4 describes the combination of these tools to provide the automatic procedure for the Box–Cox transformation.

3.1 BIC and the mean shift outlier model

As our main tool in assessing numerical information from score statistics calculated during the FS, we use the extended Bayesian Information Criterion (BIC). The original version (Schwarz 1978) can be used to choose the value of $\lambda$ for complete data with n observations. Then, from (6)

$$\begin{aligned} \text {BIC}(\lambda ) = - n \log \{S(\lambda )/n\} + 2 \log J^n_{{\mathrm{BC}}} -(p+n_{\lambda })\log (n), \end{aligned}$$

(10)

where there are p parameters in the linear model and, for the Box–Cox transformation, the single transformation parameter $\lambda$, so that $n_{\lambda } =1.$ Written in this form, large values of the index are to be preferred, corresponding to small values of $R(\lambda )$, that is to maximizing the likelihood.

Use of the forward search to provide robustness against outliers and incorrect transformations leads to the comparison of fitted models with different numbers of observations. We render outlier deletion compatible with BIC through use of the mean shift outlier model in which deleted observations are each fitted with an individual parameter, so having a zero residual.

Let the forward search terminate with h observations. Then $n-h$ observations will have been deleted. This can be expressed by writing the regression model as

$$\begin{aligned} z(\lambda ) = X\beta + D \phi + \epsilon , \end{aligned}$$

(11)

where D is an $n \times (n-h)$ matrix with a single one in each of its columns and $n-h$ rows, all other entries being zero. These entries specify the observations that are to have individual parameters or, equivalently, are to be deleted (Cook and Weisberg 1982, p. 21).

To incorporate deletion of observations in BIC (10) for values of $\lambda \in {\mathcal {G}}$, let the value of $S(\lambda )$ when $n-h(\lambda )$ observations are deleted be $S(\lambda ,h)$. Then BIC$(\lambda )$ is replaced by

$$\begin{aligned} \text {BIC}(\lambda ,h) = - n \log \{S(\lambda ,h)/h\} + 2 \log J^n_{{\mathrm{BC}}} -\{p+n_{\lambda }+n-h(\lambda )\}\log (n), \end{aligned}$$

(12)

in which $S(\lambda ,h)$ is divided by h. A full treatment is in Riani et al. (2022).

3.2 The Tallis correction

To find the $n-h$ outlying observations we have used the FS which orders the observations from those closest to the fitted model to those most remote. If there are no outliers and the value of $\lambda$ is correct, the value of $S(\lambda )$ at the end of the search will lead to an unbiased estimate of $\sigma ^2$. The deletion of the $n-h$ most remote observations yields the residual sum of squares $S(\lambda ,h)$ and to a too small estimate of $\sigma ^2$ based on the central h observations. The variance of the truncated normal distribution containing the central h/n portion of the full distribution is

$$\begin{aligned} \sigma ^2(h)=1- \frac{2n}{h} \varPhi ^{-1} \left( \frac{n+h}{2n}\right) \phi \left\{ \varPhi ^{-1}\left( \frac{n+h}{2n} \right) \right\} , \end{aligned}$$

(13)

where $\phi (\cdot )$ and $\varPhi (\cdot )$ are respectively the standard normal density and c.d.f. See, for example, Johnson et al. (1994, pp. 156–162). We scale up the value of $S(\lambda ,h)$ in (12) to obtain the extended BIC

$$\begin{aligned} \text {BIC}_{\mathrm{EXT}}(\lambda , h) = - n \log [S(\lambda ,h)/\{h \sigma ^2(h)\} ] + 2 \log J^n_{{\mathrm{BC}}} -\{p+n_{\lambda }+n - h(\lambda )\}\log (n). \end{aligned}$$

(14)

This consistency correction is standard in robust regression (Rousseeuw and Leroy 1987, p. 130). The correction $\sigma ^2(h)$ in (13) is the one-dimensional case of the general result in Tallis (1963) on elliptical truncation in the multivariate normal distribution. This result is useful in determining correction factors for variance estimation in robust methods for multivariate normal data. An example is Riani and Atkinson (2007).

Neykov et al. (2007) use a related form of extended BIC for model choice in clustering when estimation is by trimmed likelihood.Their procedure differs from ours in two important ways:

• i Because they do not have a regression model they do not use the mean shift outlier model to add parameters as observations are trimmed. In consequence, their procedure differs from ours in the penalty function applied to the trimmed likelihood. In our notation their penalty term is $-p \log {h}$ whereas, if we ignore the effect of varying $\lambda$, our penalty term is $- (p + n - h)\log {n}$, a stronger penalty;

• ii We do not directly use the likelihood estimate of $\sigma ^2$ based on the trimmed residual sum of squares $S(\lambda )$, but apply the consistency factor (13) in the estimation.

Similar comments apply to the extended BIC used by Greco and Agostinelli (2020) for weighted likelihood estimation, again in clustering.

3.3 The agreement index AGI

The value of $\text {BIC}_{\mathrm{EXT}}(\lambda ,h)$ presents the information on the transformation for the subset of size $h(\lambda )$. It can be helpful also to consider the history of the evidence for the transformation as a function of the subset size m. A correct transformation leads to identification of the outliers and to a normalizing transformation of the genuine data. The most satisfactory transformation will be one which is stable over the range of m for which no outliers are detected and will lead to small values of $T_{\mathrm{A}}(\lambda _0,m)$, indicating that the value of ${\hat{\lambda }}$ is consistent with $\lambda _0$ over a set of subset sizes. The trajectory of $T_{\mathrm{A}}(0,m)$ in Fig. 1 is an example.

We introduce an empirical diagnostic quantity, the agreement index, AGI, which leads to a graphical representation of this idea. The forward search procedure for testing the transformation monitors absolute values of the statistic from M to $m = h(\lambda )$. The default is to take the integer part of $M = 0.6n$. For ease of comparison with $\text {BIC}_{\mathrm{EXT}}(\lambda ,h)$ we take the reciprocal of the mean of the absolute values of $T_{\mathrm{A}}(\lambda _0,m)$ so that large values are again desired. In order to give more weight to searches with a larger value of $h(\lambda )$, we rescale the value of the index by the variance of the truncated normal distribution. Let ${\mathcal {M}} = m \in [M,h(\lambda )].$ Then the agreement index

$$\begin{aligned} \text{ AGI } = \{h(\lambda )-M+1\} / \left\{ \sigma ^2(h)\sum _{m \in {\mathcal {M}}} |T_{\mathrm{A}}(\lambda ,m)| \right\} , \end{aligned}$$

(15)

calculated for $\lambda \in {\mathcal {G}}$.

3.4 The coefficient of determination R$^{\mathbf {2}}$

The main tools for determining the correct transformation are plots of $h(\lambda )$ and $\text {BIC}_{\mathrm{EXT}}$ with the agreement index as a further diagnostic. In addition, we calculate values of a form of $R^2$, extended to allow for the value of the size $h(\lambda )$ of the final cleaned sample:

$$\begin{aligned} R^2_{\mathrm{EXT}} = R^2/\{{\sigma ^{2}}h(\lambda )\}. \end{aligned}$$

(16)

4 The automatic procedure for the Box–Cox transformation

The automatic procedure for robust selection of the transformation parameter and the identification of outliers requires the use of two functions. Section 5 provides data analyses for the Box–Cox transformation computed with these functions. Links to the functions and to full documentation are at the end of Sect. 10.

• 1. Fan Plot. Subroutine FSRfan. This Forward Search Regression function takes as input the data and the grid ${\mathcal {G}}$ of $\lambda$ values to be evaluated as transformation parameters.

  • (a) There are two automatic choices of ${\mathcal {G}}$. When $n < 200, \lambda _0 = -1. -0.5, 0, 0.5$ and 1. For $n \ge 200$ the default grid is ${\mathcal {G}} = -1,-0.9,\ldots ,1$. Alternatively, specific grids of $\lambda$ values can be provided.

  • (b) Each value of $\lambda$ has a separate forward search. Output structure outFSR contains numerical information to build fan plots such as Fig. 1. Optionally, the fan plot can be produced.

• 2. Outlier Detection, BIC and Model Selection. Subroutine fanBIC(outFSR).

  • (a) Outlier detection. The forward search uses residuals to order the observations in such away that outliers, if any, enter the subset used in fitting towards the end of the search. In fan plots, such as that of Fig. 1, we use this ordering, but monitor the value of score statistics. In the automatic procedure, for each $\lambda \in {\mathcal {G}}$, the values during the forward search of the score statistic $T_A(\lambda )$ of Sect. 2.2 are assessed against the standard normal distribution to estimate the maximum number $m^*(\lambda )$ of observations in agreement with that transformation. This procedure for testing the transformation monitors absolute values of the statistic from M to $m = h(\lambda )$. The default is $M = 0.6n$.

    Simulations not reported here show that the size of this simultaneous procedure when testing at 1% is close to the nominal value. For a regression model with two variables the size is 0.75% when $n = 100$, 0.95% when $n = 1000$ and 1.11% when $n = 10{,}000$, a sample size well in excess of that of the largest example we analyse.

  • (b) The presence of any remaining outliers in the $m^*(\lambda )$ transformed observations is checked using the forward search procedure now monitoring deletion residuals. If any outliers are found in the transformed data the sample size of the cleaned data is $h(\lambda ) < m^*(\lambda )$. Otherwise $h(\lambda ) = m^*(\lambda )$.

  • (c) The extended BIC (14) allows comparisons of results from models with differing numbers of non-deleted observations $h(\lambda )$. The maximal value determines the preferred parameter value ${\tilde{\lambda }}$. The agreement index (15) is also calculated over ${\mathcal {G}}$.

  • (d) The results are summarised in a single plot with three panels, for example, Fig. 2. The main panel is that of BIC. Also included are a diagnostic plot of the agreement index and a combined plot of $h(\lambda )$ and $m^*(\lambda )$.

  • (e) The procedure suggests the value of $\lambda$ for further data analysis and indicates a set of outliers in that scale. Further analyses using robust techniques, including model selection, could follow these suggestions and are certainly indicated if the three panels of plots like Fig. 2 disagree on the best transformation. Figures 2 and 4 show analyses in which all three panels agree.

5 Two examples of the automatic Box–Cox transformation

5.1 Hospital data 2

The conclusion from the analysis of the hospital data following from the fan plot of Fig. 1 was that the logarithmic transformation was appropriate; for other values of $\lambda$ several observations appeared outlying. The results from the automatic method of Sect. 4 for finding the cleaned sample size $h(\lambda )$, when $\lambda = -1, -0.5, 0, 0.5$ and 1, are given in Table 1. There are no deletions of outliers in the searches on residuals, so $h(\lambda ) = m^*(\lambda )$ for all $\lambda$. No observations are deleted when $\lambda = 0$ so, in line with the earlier results, $h(0) = n$.

Table 1 Hospital data $(n = 108)$. Size of cleaned samples, $h(\lambda ),$ as a function of $\lambda$ when ${\mathcal {G}} = -1, -0.5, 0, 0.5$ and 1. For all $\lambda \in {\mathcal {G}}, h(\lambda ) = m^*(\lambda )$

The results from the automatic analysis are summarised in the single plot with three panels of Fig. 2. The automatic analysis has faithfully extracted all features of Fig. 1 in which the trajectory of $T_{{\mathrm{A}}}(0)$ oscillates around zero, without large divergences and remains inside the 99% bounds over the whole search. This figure is a typical example of the results of a seemingly straightforward analysis. The upper left panel of the figure shows the plot of extended BIC for the five values of $\lambda$. There is a clear peak at $\lambda = 0$ and the log transformation is indicated. The upper right-hand panel shows the plot for the agreement index, again with a peak at zero, and the lower panel shows the proportion of observations included in the final transformed analyses.

Fig. 2

Hospital data. Output from automatic analysis with ${\mathcal {G}} = -1, -0.5, 0, 0.5$ and 1. Upper left panel, extended BIC; upper right panel agrement index AGI; lower panel, proportions $h(\lambda )/n$

5.2 Loyalty cards data

We now analyse data from Atkinson and Riani (2006) on the behaviour of customers with loyalty cards from a supermarket chain in Northern Italy. The data are a random sample from a larger database. There are 509 observations: the response is the amount, in euros, spent at the shop over 6 months and the explanatory variables are: the number of visits to the supermarket in the 6 month period; the age of the customer and the number of members of the customer’s family.

Fig. 3

Loyalty cards data. Top panel: fan plot for 11 values of $\lambda ;(0,0.1,\ldots ,1)$. Lower 3 panels: output from automatic analysis with ${\mathcal {G}} = -1, -0.5, 0, 0.5$ and 1. Left mid-panel, extended BIC; right mid-panel agrement index AGI; Bottom panel, proportions $h(\lambda )/n$

The upper top panel of Fig. 3 is a fan plot for 11 values of $\lambda \;(0,0.1,\ldots , 1)$ with $\lambda = 1$ at the bottom and $\lambda = 0$ providing the top trajectory. It is clear that the trajectories for two of the five standard values of $\lambda$ (0 and 0.5) steadily leave the central band in opposite directions. For the best of the five values, $\lambda = 0.5$, the automatic procedure (mid and bottom panels of Fig. 3) deletes 37 observations as not agreeing with the transformation. The indication is that a finer grid of values of $\lambda$ is required, in line with the argument of Carroll (1982).

Fig. 4

Loyalty cards data. Output from automatic analysis with finer grid; ${\mathcal {G}} = -1, (0.1), 1.$ Upper left panel, extended BIC; upper right panel agreement index AGI; lower panel $h(\lambda )/n$ as red bars (in the on line version); if $m^*(\lambda )/n \ne 0$, the value is plotted in white within $h(\lambda )/n$

We now consider analysis with the finer grid ${\mathcal {G}} = -1,-0.9,\ldots ,1.$ Trajectories of the values of $T_{\text {A}}(\lambda )$ for positive values of $\lambda$ are given in the upper top panel of Fig. 3. The upper left-hand panel of Fig. 4 shows the extended BIC plot which is complemented by the plot in the lower panel of the proportion of clean observations $h(\lambda )/n$. For $\lambda$ in the range $-1$ to 0.2, $h(\lambda ) = 0.6n$, the point at which monitoring starts. The plot of the extended BIC shows that ${\hat{\lambda }}_G = 0.4$ with 0.3 and 0.5 giving slightly smaller values. An important feature in the lower panel is that, when $\lambda = 0.4$, checking residuals for the presence of outliers, leads to the deletion of 16 observations from the $m^*(\lambda )$ found by checking the score statistic. These deleted observations are shown as the unfilled part of the bar in the plot. The plot of the agreement index in the right-hand panel also indicates a value of 0.4 for the transformation, a value which Perrotta et al. (2009) show provides a significantly better fit to the data than the value of 1/3 suggested by Atkinson and Riani (2006). Figure 6 of Perrotta et al. (2009) reveals that the outlying observations form a group lying on a distinct regression line with consumers of varying age and family size spending much less than would be expected given their high number of visits to the supermarket.

6 Comparison with the procedure of Yohai and Marazzi

The purpose of our paper is to provide a practical method of automatic transformation of data in the presence of outliers; robust methods are necessary. It is instructive to compare our approach to that of Marazzi et al. (2009) who have the same goal. They however chose MM estimation (Yohai 1987) and only considered the Box–Cox transformation. Different values of $\lambda$ are compared using a robust prediction error.

We start our comparisons with simulations. To enhance comparability, we based the structure of the simulations on those in §5 of Marazzi et al., initially for simple regression with homoscedastic errors. The comparisons were over the series of, mostly long-tailed, error distributions used by Marazzi et al. In the list below we give, in italics, the names of the distributions used in the tables of this section.

• Unif.  Uniform:  $U(-0.5,0.5)$

• Gauss.  Normal:  ${\mathcal {N}}(0,1)$

• t6, t3.  Student’s t on 6 and 3 degrees of freedom

• CntG.  Contaminated Gaussian:  $0.9{\mathcal {N}}(0,1) + 0.1{\mathcal {N}}(0,5^2)$

• MxtG.  Symmetric bimodal normal mixture:  $0.5{\mathcal {N}}(-1.5,1) + 0.5{\mathcal {N}}(1.5,1)$

• Exp.  Exponential, mean 1.

Let the unscaled simulated errors from the listed distributions be $e_i^u$. These do not have the same variance. To remove this effect from the comparisons, Marazzi et al. used a robust estimator of standard deviation to standardize the additive errors for the homoscedastic simulations as $e_i = e_i^u/\text {MAD}(e_i^u)$, where MAD is the median absolute deviation. The $e_i$ therefore have MAD one.

All simulations were for $n = 100$ observations with $\lambda _0 = 0.5$. The simulated responses are $y_i^{\lambda _0} = \eta _i + e_i = x_i^T\beta + e_i$. The results in Table 2 are for simple regression, that is $\eta _i = \beta _0+ \beta _1x_i.$ The parameter values were chosen to avoid negative responses (intercept $\beta _0 = 10$ and slope $\beta _1 = 2).$ The 100 values of the explanatory variable are given by the uniform grid $x_i = 0.2i, i = 1, \ldots , 100.$ There were 1000 replicates of each simulation, interest being in the estimated value of $\lambda$. In order to provide easily readable values of the results, Marazzi et al. multiplied the values of bias and, in their case, root mean squared error, by 1000, a procedure we follow in our tables for the bias and standard error of ${\hat{\lambda }}$. The average bias of the simulated estimates given in the tables is therefore calculated as BIAS = $1000\, \text {mean}({\hat{\lambda }} - \lambda _0)$ with the standard deviation of the estimate similarly scaled.

The results of Table 2 suggest that there is little difference between the bias of the two methods; our method had the smaller bias for four of the seven error distributions. However, the method of our paper performed better for six out of the seven error distributions when the comparison was based on the estimated standard deviation of ${\hat{\lambda }}$. Although some of the differences in performance are not large, that for uniform errors is appreciable. In interpreting these results we recall the reference to McCullagh (2002). The purpose of the transformation method is to find a transformation which, hopefully, has a physical interpretation, rather than establishing a precise value of ${\hat{\lambda }}$ for use in data analysis. Here $\lambda = 0.5$ is the often easily interpreted square root transformation.

Table 2 Properties of estimated values of $\lambda$ for homoscedastic simple regression

We now extend our comparison to multiple regression with outliers at leverage points. We remain with homoscedastic regression, but now $p = 5$. The 100 values of the four explanatory variables were drawn independently from uniform distributions on [0.2, 20], one set of values beng used for all simulations. We considered only two error distributions: Gauss and CntG. In this we again follow Marazzi et al. The parameters of the linear model were (20, 1, 1, 1, 1). We performed two simulations. In the first, “without leverage points", all simulations were drawn from this model. In the second, “with leverage points”, 90 of the simulated observations followed the preceding model. There were, in addition, 10 outliers at $x_i^T = (1,40,40,40,40)$ with 150 subtracted from each response value. The results are in Table 3. They show that, for all combinations studied, our automatic procedure produces estimates with lower biases than those for Marazzi et al.; the difference is largest for Gauss without leverage points. However, this is the only combination for which our method had the smaller standard deviation. The differences are not great, with the root mean squared errors (not given in the table) for all comparisons being smaller for RAC than those for MY.

Table 3 Properties of estimated values of $\lambda$ for homoscedastic multiple regression ($p=5$) without and with outliers at leverage points

The simulations for our method were performed using a Matlab program. For the method of Marazzi et al. we used their R package strfmce embedded in Matlab. That is the data, simulated in Matlab, were passed to the R package for estimation of ${\hat{\lambda }}$, the resulting estimate beng returned to Matlab for the analyses of bias.

We now compare timings of the two methods, calculated just for the time each program took to find the best estimate of $\lambda$; thus the relevant part of our Matlab procedure is compared directly with the times for the R code. The results in Table 4 are for homoscedastic simple regression with uniform and normal error distributions as the number of observations n increases from 100 to 1000. The results are very clear. For a sample size of 100 MY is faster than RAC, although only statistically significantly so for the normal distribution. But for $n = 200$ or more RAC is faster, becoming increasingly so as n increases. For MY the timings as n increases seem not to depend on the error distribution, whereas for RAC, the times for the normal distribution are close to twice those for the uniform distribution. When $n = 1000$ MY takes almost 6 min for either error distribution, whereas RAC takes 6 or 12 s. This difference would become of greater practical significance if model building required the fitting of several models, or if simulation were needed to determine the properties of the procedures for a specific application.

Table 4 Comparison of number of seconds to compute estimated values of $\lambda$ for homoscedastic simple regression with uniform and normal distributions for the errors as a function of sample size n

We now turn to the comparative analysis of data. We first analysed the data on 78 patients given by Marazzi et al. and recovered their solution with our version of MY. We then used their algorithm to analyse our two examples of the Box–Cox transformation. For the hospital data we obtained a value of 0.134 for ${\hat{\lambda }}$ which is in agreement with the log transformation indicated by our robust analysis. However, the hospital data do not contain any outliers and the data are small. We next analysed the 509 observations on loyalty cards in Sect. 5.2. The R-code returned three possible values for the estimate of $\lambda :$ 0.534, 0.699 and 0.777. None is close to the value of 0.4 that we recommend. However, the fan plot in the top panel of Fig. 3 gives some explanation. Particularly for the trajectory for $\lambda = 0.7,$ there is a local maximum in the trajectory around $m = 450$. This suggests that a local minimum of the robust prediction error used in estimation of $\lambda$ has been identified. The trajectory for $\lambda = 0.4$, on the other hand, has the desired shape of being reasonably stable until the end of the search when outliers enter and a different transformation starts to be indicated.

The conclusions from these comparisons are that our automatic procedure is to be preferred, both in terms of performance and, especially, for time. We also would like to stress that the procedure of Marazzi et al. has so far only been implemented for the Box–Cox transformation, whereas our automatic procedure is also available for the transformation of responses that can be both positive and negative, a topic covered in the remainder of our paper.

7 The extended Yeo–Johnson transformation

Yeo and Johnson (2000) generalised the Box–Cox transformation to observations that can be positive or negative. Their extension used the same value of the transformation parameter $\lambda$ for positive and negative responses. Examples in Atkinson et al. (2020) show that the two classes of response may require transformation with different values of $\lambda$. The Box–Cox transformation (1) has two regimes, that for $\lambda \ne 0$ and the other for $\lambda = 0$. Both the Yeo–Johnson transformation and its extended version require four regimes. The two unnormalised transformations for these regions are in Table 5.

Table 5 Yeo–Johnson transformation and its extension. Form and range of unnormalised transformations

For $y \ge 0$ the Yeo–Johnson transformation is the generalized Box–Cox transformation of $y+1$. For negative y the transformation is of $-y +1$ to the power $2 - \lambda$. For the extended Yeo–Johnson transformation the transformation parameter for positive y is $\lambda _P$, with that for negative y being $2 - \lambda _N$.

Inference about the values of the transformation parameters needs to take account of the Jacobians of these transformations. As in Sect. 2.1, the maximum likelihood estimates can be found either through minimization of the sum of squares $S(\lambda )J$ or of the sum of squares $R(\lambda )$ of the normalized transformed variables z. Score tests for the parameters use constructed variables that are derivatives of z. We denote the score test for the overall parameter $\lambda$ in the Yeo–Johnson transformation as $T_O$. In the extended Yeo–Johnson transformation there are in addition approximate score tests $T_P$ for $\lambda _P$ and $T_N$ for $\lambda _N$. These include separate Jacobians for the positive and negative observations. Full details of the constructed variables for these models are in the Appendix.

8 The automatic procedure for the extended Yeo–Johnson transformation

The procedure introduced by Atkinson et al. (2020) for the analysis of data with the extended Yeo–Johnson transformation again depends heavily on the numerical identification of patterns in a series of trajectories of score tests. The analysis starts with the Yeo–Johnson transformation of Sect. 7 in which negative and positive observations are subject to transformation with the same value of $\lambda$. The next stage is to determine whether this transformation parameter should be used for both positive and negative observations.

The general procedure is to test whether $\lambda _0 = (\lambda _{P0}, \lambda _{N0})$ is the appropriate transformation by transforming the data using $\lambda _0$ and then checking an “extended" fan plot to test the hypotheses for the transformed data that no further transformation is required. The three score tests in the extended fan plot are listed in (25) in the Appendix. They check the individual values of $\lambda _{P0}$ and $\lambda _{N0}$ as well as of the overall transformation $\lambda _0$. This information is incorporated in the extended agreement index defined in Point 3(d) below.

The automatic numerical procedure can be divided into three parts. The first provides information from the fan plots for the one-parameter Yeo–Johnson transformation which is used by the BIC in the second part to determine ${\tilde{\lambda }}$, the best overall parameter for this transformation. The third uses the value of ${\tilde{\lambda }}$ to calculate an appropriate grid of parameter values for the extended transformation, which is used, in conjunction with the BIC, to find the best parameters for the extended transformation. Developments in output conclude the section.

• 1. Fan Plot. Function FSRfan(‘family’,‘YJ’)

  • (a) Since $\lambda$ is a scalar, this problem has the same structure as that of the Box–Cox transformation in Sect. 4. Choice of the family YJ fits the one-parameter Yeo–Johnson transformation of Table 5 using the FS over a grid of values of $\lambda$.

  • (b) The output structure outFSRfan contains numerical information to select the best transformation value. Optionally the fan plot can be generated.

• 2. Estimation of parameter${\tilde{\varvec{\lambda }}}$ for the YJ transformation. Function fanBIC(‘family’,‘YJ’)

  • (a) Function fanBIC inputs outFSRfan to calculate provisional clean subsets $m^*(\lambda )$, followed by a forward search on residuals to detect outliers. The final outlier-free subsets are $h(\lambda )$.

  • (b) Once $h(\lambda )$ is established for $\lambda \in {\mathcal {G}},$ the BIC (14) is used to select ${\tilde{\lambda }}$, the estimate of the best transformation for the Yeo–Johnson family.

  • (c) Optionally a plot like Fig. 4 can be produced.

• 3. The Extended Yeo–Johnson Transformation. A call is made to function FSRfan(‘family’, ‘YJpn’), followed by one to function fanBICpn to first establish the grid ${\mathcal {G}}$ of pairs of $(\lambda _P, \lambda _N)$ to be searched and then to choose the best pair.

  • (a) FSRfan calculates the three score statistics from the extended fan plot at ${\tilde{\lambda }}$. The output is outFSRfanpn.

  • (b) Function fanBICpn(outFSRfanpn) calculates the grid ${\mathcal {G}}$ for pairs of parameter values, which depends on both the values of ${\tilde{\lambda }}$ and on the values of the score statistics $T_P({\tilde{\lambda }})$ and $T_N({\tilde{\lambda }})$ at $h({\tilde{\lambda }})$. The procedure calculates the grid ${\mathcal {G}}$ which is part of the grid of values of $\lambda _P$ and $\lambda _N$ bounded by $-1$ and 1.5 in steps of 0.25. For example, if ${\tilde{\lambda }}$ is 0.25 and $T_P \ge T_N,$ one possibility is $\lambda _P = 0.25, 0.5, \ldots , 1.5 \, \text{ and } \, \lambda _N = -1, -0.75 \ldots , 0.25.$ User provided grids are another possibility.

  • (c) The numerical values of the three score statistics are calculated over ${\mathcal {G}}$.

  • (d) The BIC, now with $n_\lambda = 2$, is calculated for the cleaned samples of observations for each combination of values of $\lambda _P$ and $\lambda _N$. This information is supplemented by the diagnostic use of an extended agreement index, which measures agreement between the values of $T_P$ and $T_N$ and checks that no further overall transformation is needed. Agreement between the values of $T_P$ and $T_N$ is measured by the absolute value of the difference. We also require a small value of $T_O$. Then the index depends on the sums

    $$\begin{aligned} S_{O}= \sum _{m=M}^{h} |T_O(\lambda _0,m)|/ (h-M+1) \end{aligned}$$

    (17)
    $$\begin{aligned} S_{PN}= \sum _{m=M}^{h} |T_P(\lambda _0,m) -T_N(\lambda _0,m) |/(h-M+1) . \end{aligned}$$

    (18)

    As in (15) the sums are adjusted to give weight to searches with a larger value of h. Then

    $$\begin{aligned} \text{ Agreement } \text{ Index } = \{(\sigma ^2_T)^2S_{O}S_{PN}\}^{-1}. \end{aligned}$$

    (19)

    As before, larger values are desired.

• 4. Output

  • (a) The extended BIC (23) in the Appendix, calculated using the Jacobian $J^n_{{\mathrm{EYJ}}}$, the agreement index AGI and the values of $h(\lambda _P, \lambda _N)$ are presented as heat maps over the grid of values of $\lambda _P$ and $\lambda _N$. These three plots summarize the properties of the best transformation and those close to it.

  • (b) We also produce a heat map of the extended coefficient of determination, $R^2_{{\mathrm{EXT}}}$, defined in (16), where the extension allows for the number of observations $h(\lambda _P, \lambda _N)$.

9 Two examples of the automatic extended Yeo–Johnson transformation

This section presents the results of the automatic analysis of two sets of data, both of which include negative responses, so that the extended Yeo–Johnson transformation, Sect. 7, may be appropriate. We follow the procedure of Sect. 8.

9.1 Investment funds

We start with a straightforward example, without outliers once the correct transformation has been determined. The regression data concern the relationship of the medium term performance of 309 investment funds to two indicators. The data come from the Italian financial newspaper   Il Sole - 24 Ore. An analysis of the data based on conclusions from fan plots is presented by Atkinson et al. (2020).

Of the funds, 99 have negative performance. Scatterplots of y against the two explanatory variables show a strong, roughly linear, relationship between the response and both explanatory variables. It is also clear that the negative responses have a different behaviour from the positive ones: the variance is less and the slope of the relationship with both explanatory variables appears to be smaller. The purpose of using the extended Yeo–Johnson transformation is to find a transformation in which the transformed response, as for the Box–Cox transformation, satisfies the three requirements of homogeneity, additivity and approximate normality of errors.

The automatic analysis of Sect. 8 starts with the Yeo–Johnson transformation in which positive and negative observations are subject to transformation with the same value of $\lambda$. Use of the standard five values of $\lambda$ leads to searches all of which immediately terminate at $m^*(\lambda ) = 0.6n$. A series of searches over a finer grid of values suggests ${\tilde{\lambda }} = 0.75$. The three-panel plot summarising the results is shown as Fig. 5. The values of $\lambda$ belong to the large grid ${\mathcal {G}} = [-1,-0.9,\ldots ,1].$ The lower plot of values of $h(\lambda )$ shows that when $\lambda$ is less than 0.2, $m^*(\lambda ) = 0.6n$ and that $h(\lambda )$ is mostly appreciably less. The interpretation is that inappropriate values of the transformation parameter are indicating a large number of spurious outliers; the values of statistics in the upper plots are then based on an unrepresentative subset of the data, so that we exclude them from consideration. The two upper plots, excluding values of $\lambda < 0.2,$ show that both the extended BIC and the agreement index indicate a value of 0.8 for ${\tilde{\lambda }}$. In calculating the extended BIC we have replaced $J^n_{{\mathrm{BC}}}$ by the Jacobian $J^n_{{\mathrm{YJ}}}$ given in (20).

Fig. 5

Investment funds data. Output from automatic analysis of the Yeo–Johnson transformation with finer grid; ${\mathcal {G}} = -1, (0.1), 1.$ Upper left panel, extended BIC; upper right panel agrement index; lower panel $h(\lambda )/n$ as red bars in the on line version; when $m^*(\lambda )/n \ne 0$, the value is plotted in white within $h(\lambda )/n$. There are numerous spurious outliers. For $\lambda < 0.2, m^*(\lambda ) = 0.6n$ and the values in the upper panels are not plotted

The next stage is to determine whether this transformation parameter should be used for both positive and negative observations. The general procedure is to test whether $\lambda _0 = (\lambda _{P0}, \lambda _{N0})$ is the appropriate transformation by transforming the data using $\lambda _0$ and then testing the hypotheses for the transformed data that no further transformation is required.

Fig. 6

Investment funds data. Heat maps as functions of $\lambda _P$ and $\lambda _N$. Left-hand panel $h(\lambda )$; right-hand panel extended BIC. Cell left blank if $h(\lambda ) \le 0.6n$

The left-hand panel of Fig. 6 shows the heat map for the values of $h(\lambda )$. For $\lambda _P = 1$ and $\lambda _N = 0$ this is 309, that is, all the data are in agreement with this transformation model. For any other pair of parameter values, at least two observations are deleted and, in some cases, many more. The right-hand panel of the figure shows the heat map for the extended BIC, which has a sharp maximum at the same parameter value. In both panels the performance of ${\tilde{\lambda }}$ is so poor that the values for (0.75, 0.75) are not plotted.

Fig. 7

Investment funds data. Heat maps as functions of $\lambda _P$ and $\lambda _N$. Left-hand panel, Agreement Index AGI; right-hand panel, extended coefficient of determination $R^2_{{\mathrm{EXT}}}$. Cell left blank if $h(\lambda ) \le 0.6n$

Two further heat maps are in Fig. 7. That in the left-hand panel, for AGI, has a much sharper peak than that for $R^2_{{\mathrm{EXT}}}$ in the right-hand panel, but both again support the transformation indicated in Fig. 6. The automatic method for this example has used numerical information to provide a firm decision on the best transformation within the extended Yeo–Johnson family.

9.2 Balance sheet data

The data come from balance sheet information on limited liability companies. The response is profitability of individual firms in Italy. There are 998 observations with positive response and 407 with negative response, making 1,405 observations in all. Details of the response and the five explanatory variables are in Atkinson et al. (2020, §9), together with the results of a series of data analyses involving visual inspection of fan plots.

Fig. 8

Balance sheet data. Output from automatic analysis of the Yeo–Johnson transformation $(\lambda _P = \lambda _N)$ with ${\mathcal {G}} = -1, (0.25), 1.5$. Upper left panel, extended BIC; upper right panel AGI; lower panel $h(\lambda )/n$ as red bars in the on line version; if $m^*(\lambda )/n \ne 0$, the value is plotted in white within $h(\lambda )/n$

The automatic procedure starts with the Yeo–Johnson transformation of the data leading to the parameter estimate ${\tilde{\lambda }}$ (Point 2 of Sect. 8). The three resulting plots form Fig. 8. The plot of extended BIC indicates a value of 0.75 for ${\tilde{\lambda }}$, whereas the agreement index suggest a value of 1. The lower panel of the number of cleaned observations shows that $h(\lambda )$ is greatest for ${\tilde{\lambda }}$ and is equal to 1,279. The forward search on values of $T_O(\lambda )$ finds more observations that are in agreement with the transformation when $\lambda = 1$. But 169 of these are rejected as outliers by the outlier detection procedure, ending up with a final value of $h(1)=1,206.$

Fig. 9

Balance sheet data. Heat maps as functions of $\lambda _P$ and $\lambda _N$. Left-hand panel $h(\lambda )$; right-hand panel extended BIC. Cell left blank if $h(\lambda ) \le 0.6n$

The analysis then moves to the extended Yeo–Johnson transformation. The left-hand panel of Fig. 9 shows the heat map of $h(\lambda )$, the number of cleaned observations (Point 4 of Sect. 8). The values of the extended BIC (Point 3 of Sect. 8) are in the right-hand panel. Both support the transformation $\lambda _P = 0.5$ and $\lambda _N = 1.5$. Figure 10 shows further support for this transformation from the plots of Point 4 of Sect. 8); the left-hand panel is of the agreement index AGI (19) and the right-hand panel is of the values of $R^2_{{\mathrm{EXT}}}$ (16). In ambiguous cases the heat maps could be extended so that the highest values of the properties are not at an edge of the display.

Fig. 10

Balance sheet data. Heat maps as functions of $\lambda _P$ and $\lambda _N$. Left-hand panel, Agreement Index; right-hand panel, extended coefficient of determination $R^2_{{\mathrm{EXT}}}$. Cell left blank if $h(\lambda ) \le 0.6n$

The automatic procedure leads to the same result as the analysis based on the adjustment of fan plots presented by Atkinson et al. (2020, §9) who also discuss the economic interpretation of the regression model fitted to the transformed responses.

10 Comparison and developments

The purpose of our paper is to provide a practical method of automatic transformation of data in the presence of outliers, robust methods being necessary. Here we consider a few further points.

The assumption in the Yeo–Johnson transformation and its extension is that there is something special about zero. In some examples it may however be that the change from one transformation to the other occurs at some other threshold, which may perhaps need to be estimated. Atkinson et al. (2020) and Atkinson et al. (2021) compare the extended Yeo–Johnson transformation with the nonparametric methods ACE (Breiman and Friedman 1985) and AVAS (Tibshirani 1988) which do not divide the transformation into regions. The results from ACE for the investment funds data show a slight increase in the value of $R^2$ compared with the extended Yeo–Johnson transformation and a change in the transformation at $y = 4$ rather than zero. Since the non-parametric transformations are not robust, our recommendation is to use them on cleaned data to check on the assumptions in the parametric transformation.

The largest timings of Sect. 6 for the Box and Cox method of Marazzi et al. are for simple regression and 1000 observations. We have not explored timings for multiple regression with samples of this size. However, it is clear that the use of simulation to obtain results about the behaviour of this method will be problematic. The results of Table 2 were for 1000 replications of the simulation. For simple regression with $n = 1000$, the results of Table 4 suggest a time of about 100 h.

Our data analytical results show that we have developed a useful new tool for the automatic determination of power transformations of data contaminated by outliers. We have based this on the development of an extended BIC, the theory behind which incorporates inferences about the effect of the trimming of observations into the more customary use of BIC for model choice for data with a fixed number of observations.

The calculations in this paper used Matlab routines from the FSDA toolbox, available as a Matlab add-on from the Mathworks file exchange https://www.mathworks.com/matlabcentral/fileexchange/ or from github at the web address https://github.com/UniprJRC/FSDA.

The data, the code used to reproduce all results including plots, and links to FSDA routines are available at http://www.riani.it/RAC2021.

Appendix: Constructed variables and the extended Yeo–Johnson transformation

The normalized form of the Yeo–Johnson transformation is given in Table 5. The Jacobian for this transformation (Yeo and Johnson 2000) is

$$\begin{aligned} \log J^n_{{\mathrm{YJ}}} = (\lambda - 1)\sum \text{ sgn }(y_i) \log (|y_i| + 1). \end{aligned}$$

(20)

The four unnormalised forms of the extended Yeo–Johnson transformation, corresponding to different regions of values of $\lambda _P$ and $\lambda _N$ are also given in Table 5. Two Jacobians are required for the normalised transformation; one for positive observations and the other for the negative ones. For $y \ge 0$ let $v_P = y+1$ with $v_N = -y +1$ when $y < 0$. For the negative observations

$$\begin{aligned} S_N = \sum _{y_i< 0} -\log (-y_i +1) = \sum _{y_i < 0} -\log v_{i,N} \quad \text{ and }\quad {\dot{y}}_N = \exp (S_N/n). \end{aligned}$$

(21)

Division is by n, not $n_N$ (the number of negative $y_i$), as the Jacobian is spread over all observations.

Similarly, for the non-negative observations

$$\begin{aligned} S_P = \sum _{y_i \ge 0}\log (y_i +1) = \sum _{y_i \ge 0}\log v_{i,P} \quad \text{ and }\quad {\dot{y}}_P = \exp (S_P/n). \end{aligned}$$

(22)

The Jacobian of the sample is then

$$\begin{aligned} \log J^n_{{\mathrm{EYJ}}} = (\lambda _N - 1)S_N + (\lambda _P - 1)S_P = n \{(\lambda _N - 1) \log \dot{y_N} + (\lambda _P - 1) \log \dot{y_P}\}. \end{aligned}$$

(23)

The normalised form of the extended Yeo–Johnson transformation is

$$\begin{aligned} z_{{\mathrm{EYJ}}}(\lambda _N,\lambda _P) = \left\{ \begin{array}{ccc} \dfrac{v_p^{\lambda _P} - 1}{\lambda _P {{\dot{y}}_N}^{\lambda _N -1}{\dot{y}}_P^{\lambda _P -1}} &{} y \ge 0 &{} \lambda _P \ne 0 \\ ({\dot{y}}_P /{\dot{y}}_N^{\lambda _N-1})\log v_P &{} y \ge 0 &{} \lambda _P = 0 \\ - \dfrac{v_N^{2 - \lambda _N} - 1}{(2 - \lambda _N) {{\dot{y}}_N}^{\lambda _N -1}{\dot{y}}_P^{\lambda _P -1}} &{} y< 0 &{} \lambda _N \ne 2 \\ - \log v_N /{\dot{y}}_N{\dot{y}}_P^{\lambda _P -1} &{} y < 0 &{} \lambda _N = 2. \end{array} \right. \end{aligned}$$

(24)

This extended transformation reduces to the standard Yeo–Johnson transformation when $\lambda _N = \lambda _P$.

The three score tests test three different departures from $\lambda = (\lambda _P, \lambda _N$). The alternatives are

$$\begin{aligned} T_O: \lambda _P +\alpha , \lambda _N +\alpha ; \quad T_P: \lambda _P +\alpha , \lambda _N; \quad T_N: \lambda _P, \lambda _N +\alpha , \end{aligned}$$

(25)

tested as $\alpha \rightarrow 0$. General expressions for the constructed variables used to calculate these test statistics are in Atkinson et al. (2020).

In the automatic procedure of this paper we first transform the data using the null values of $\lambda _P$ and $\lambda _N$ and then test the hypothesis that no further transformation is needed, that is that, for the transformed data, one or both of $\lambda _P$ and $\lambda _N =1$. There is then a simplification of the constructed variables.

For the overall test $T_O$:

$$\begin{aligned} w_O(1,1) = \left\{ \begin{array}{cc} v_P(\log v_P -k_P) + k_P, &{} y \ge 0 \\ v_N(\log v_N + k_N) - k_N &{} y < 0 \\ \end{array} \right. \end{aligned}$$

(26)

In (26) $k_P = 1 + \log {\dot{y}}_O$ and $k_N = \log {\dot{y}}_O - 1$ and, from (21) and (22) ${\dot{y}}_O = \exp \{(S_P + S_N)/n\}$.

For $T_P$, the test of the value of $\lambda _P$:

$$\begin{aligned} w_P(1,1) = \left\{ \begin{array}{cc} v_P(\log v_P -k_P^*) + k_P^* &{} y \ge 0 \\ -y \log {\dot{y}}_P &{} y < 0, \end{array} \right. \end{aligned}$$

(27)

where $k_P^* = 1 + \log {\dot{y}}_P$. The structure is similar to that of the constructed variables $w_O$ in (26). The result for $y < 0$ arises because the transformation for $y < 0$ only depends on $\lambda _P$ through the Jacobian.

Similarly for $T_N$, the test of the value of $\lambda _N$:

$$\begin{aligned} w_N(1,1) = \left\{ \begin{array}{cc} -y\log {\dot{y}}_N &{} y \ge 0 \\ v_N(\log v_N + k_N^*) - k_N^* &{} y < 0 \\ \end{array} \right. \end{aligned}$$

(28)

where $k_N^* = \log {\dot{y}}_N - 1$.