Abstract
The use of network analysis to investigate social structures has recently seen a rise due to the high availability of data and the numerous insights it can provide into different fields. Most analyses focus on the topological characteristics of networks and the estimation of relationships between the nodes. We adopt a different perspective by considering the whole network as a random variable conveying the effect of an exposure on a response. This point of view represents a classical mediation setting, where the interest lies in estimating the indirect effect, that is, the effect propagated through the mediating variable. We introduce a latent space model mapping the network into a space of smaller dimension by considering the hidden positions of the units in the network. The coordinates of each node are used as mediators in the relationship between the exposure and the response. We further extend mediation analysis in the latent space framework by using Generalised Linear Models instead of linear ones, as previously done in the literature, adopting an approach based on derivatives to obtain the effects of interest. A Bayesian approach allows us to get the entire distribution of the indirect effect, generally unknown, and compute the corresponding highest density interval, which gives accurate and interpretable bounds for the mediated effect. Finally, an application to social interactions among a group of adolescents and their attitude toward substance use is presented.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Past decades have witnessed an explosion of network data in all corners of science (Kolaczyk and Csárdi 2014). The increasing availability of interactions data, where by interaction we indicate any relation between actors, and the wide range of fields where networks find applications, have contributed to developing several techniques for analysing network data. Most analyses focus on the topological characteristics of networks and the estimation of relationships between the nodes. Graph theory is used to examine the network structure. Fast and efficient algorithms are used to detect network communities, and a number of statistical models are adopted to understand the formation of connections between units. A review of statistical networks models, algorithms and software can be found in Salter-Townshend et al. (2012). See also Newman (2010) for a general introduction to networks and Ni et al. (2021) for a recent review on the applications of Bayesian graphical models in biology.
In this work, we address the network as a random variable M having a role in the mechanism through which an explanatory variable X affects a response Y. The aim is to decompose the total effect of X on Y into a direct and an indirect effect. Mediation analysis is a statistical technique widely used for this purpose (VanderWeele 2009). The intermediate variable conveying the indirect effect is called mediator. As an example, we consider an empirical analysis in which the social network of a sample of adolescents is regarded as a mediator in the relationship between gender and substance use, and between the amount of pocket money each participant had per month and substance use. The goal is to understand how social interactions can represent the intermediate variable in the mechanism through which gender or pocket money availability can affect the adolescent propensity to smoke (tobacco or cannabis) and drink alcohol.
A major issue is related to the mismatch of dimensions between the network and the other variables. Following Liu et al. (2021), to deal with this evident mismatch, we do not use the network directly. Instead, we reduce its dimension through the latent space model proposed by Hoff et al. (2002). This model projects the network into a space of smaller dimension, where each unit in the network is assumed to have an unknown position. These latent positions are estimated by modelling the link between two units in the network as dependent on their distance and possibly on additional covariates, which may explain the relationship. The coordinates of each node in the latent space become the mediators of the relationship between the exposure and the outcome of interest.
When variables are linked via linear relationships, the mediated effect can be obtained as a product of two coefficients (MacKinnon 2008). However, when relationships are nonlinear, the computation of the indirect effect is not straightforward. We use an approach based on derivatives, as proposed by Stolzenberg (1980) and Geldhof et al. (2018), which allows us to obtain several indirect effects, conditional on the different values taken by the exposure.
Inference on confidence intervals of the mediated effect is complex even in the linear case since the distribution of the product of two coefficients is generally unknown and challenging to obtain in closed form. Bayesian methods are particularly suited to overcome the latter problem: using Monte-Carlo Markov Chains (MCMC), one can get the entire posterior distribution of the indirect effects, making it easy to compute the highest density credibility intervals (HDIs).
Liu et al. (2021) analyse network data with a binary response, but they use the latent response approach. They assume the existence of a latent normally distributed response \(Y^*\), such that when it exceeds a certain threshold the observed response is one, zero otherwise. This approach allows them to estimate the indirect effect as a product of regression coefficients and avoid the difficulties related to a link function different from identity.
However, in some cases, this approach may not be the most appropriate. As an example, imagine to make a survey on a group of adolescents between 13 and 17 years and ask them if they have ever experienced bullying. It is diffcult to imagine an underlying latent variable which, adequately categorised, may give rise to the binary variable ‘ having experienced bullying’. In addition, even leaving aside binary variables, many other distributions are hard to cope with in a mediational context and for some of them it is challenging to conceive a corresponding normal latent variable.
In this paper, we extend and generalise Liu et al. (2021) approach by integrating it with that of Hayes and Preacher (2010), and Geldhof et al. (2018). This union allows researchers to handle different kinds of mediators and outcomes without resorting to the latent response formulation. The indirect effect is no more a unique value constant over units. It still is a product but involving nonlinear terms dependent on the values taken by the exposure and possibly other covariates, as will be explained in the following sections.
The remainder of the paper is organised as follows: in Sect. 2, the latent space model approach is introduced; Sect. 3 is devoted to a brief description of mediation analysis and the Geldhof et al. (2018) method; Sect. 4 illustrates how to combine the two techniques, to include a network in the mediation model, and provides an overview of Bayesian inference; Sect. 5 is devoted to the data analysis and is followed by some conclusions.
2 Latent space model
Network data consist of a set of n units and a relation tie \(a_{ij}\), measured on each ordered pair of units \(i, j = 1, \ldots , n\). The latent space approach assumes the existence of a latent space where each unit in the network has a hidden position and relative distances predict the formation of a tie among units. The main contributions to this theory can be found in Hoff et al. (2002); Hoff (2003); Handcock et al. (2007) and Krivitsky et al. (2009).
Formally, a network with n nodes can be represented by an \(n\times n\) matrix \(\varvec{A}\), where each entry \(a_{ij}\) denotes a relationship between the units i and j. We focus on Boolean relationships and, as a consequence, on adjacency matrices, but other kinds of relationships can be modelled as well. The probability that a link between nodes i and j exists, denoted by \(p_{ij}\), is assumed independent of all other ties in the network conditionally on the latent positions \(\mathbf {z}\), and possibly on other covariates, and is modeled via a logistic regression
where \(\mathbf {z}_{i} = (z_{i1}, \ldots , z_{iD})^\intercal\) and \(\mathbf {z}_{j} = (z_{j1}, \ldots , z_{jD})^\intercal\) are the latent positions of units i and j, \(\mathbf {v}_{ij}\) is a set of covariates characterising the dyad, and \(\Vert \cdot \Vert\) is the Euclidean distance.
In other words, the more similar and closer are two units, the higher is the probability of a tie between them. The likelihood of this model is relatively simple, so likelihood-based methods of estimation are feasible. Unfortunately, Euclidean distances are preserved under isometric transformations, i.e. rotations, reflections and translations. This characteristic implies that, for any matrix of latent positions \(\mathbf {Z}\) associated with a certain likelihood, there exist infinite other matrices having the same likelihood as \(\mathbf {Z}\). In other words, the latent positions held by the actors of a network are not unique. To overcome the issue of identifiability, we change the object of inference. Denoting by \([\mathbf {Z}]\) the class of positions equivalent to \(\mathbf {Z}\) under isometric transformations, each equivalence class, called configuration, is characterised by a unique set of distances. Thus, configurations give us unique positions according to an appropriate summary statistic. This approach was adopted by Hoff et al. (2002), who propose a ‘ Procrustean’ statistic for uniquely representing each configuration and provide a Bayesian algorithm to obtain it. We explore the inferential problem in Sect. 4.1.
The main advantage of the latent space approach is that most networks can be represented in a space of dimension \(D \ll n\); moreover, the coordinates are orthogonal. Having established the setting, similarly to Liu et al. (2021), the idea is to use the components of the D-dimensional vector representing the position of each unit in the network as mediators in the relationship between an exposure and a response to estimate the indirect effect.
3 Mediation analysis
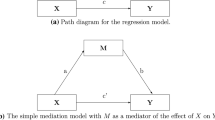
In the most straightforward setting, a mediation model includes three variables, as shown in Fig. 1. Let X be an explanatory variable, which, from now on, we will call exposure. If the mediator M and the outcome Y are assumed to be Normally distributed and to have linear relationships, the regression equations can be specified by:
Equation (2) is the marginal model for the outcome; therefore, \(\tau _1\) represents the total effect of X on Y. Equation (3) shows the mediator model, while in the last equation, the outcome model conditional on both the mediator and the exposure is specified. In the general associational framework, \(\gamma _1\) represents the direct effect of the exposure on the outcome. The indirect effect can be computed via the product method by multiplying \(\beta _1\) and \(\gamma _2\), that is, the coefficients corresponding to the arrows lying on the path connecting X to Y through the mediator M (Baron and Kenny 1986; MacKinnon 2008). More generally, consider a graphical model \(\mathcal {G}\) expressing the relationships among a set of variables, and a related set of equations which formalise such relationships. The product method simply consists of multiplying the coefficients corresponding to arrows along the path of interest in \(\mathcal {G}\). The product method relies on the assumption of linear relationships among variables, and has its roots in the path analytic framework conceptualised by Wright (1934) and further developed by Duncan (1966); Alwin and Hauser (1975) and Bollen (1987).
When the assumption of linearity does not hold, either for the mediator or the response, the product method is not appropriate to estimate the indirect effect. Researchers have mainly focused on binary or count outcome variables, for which indirect effects are obtained by appropriately standardising the coefficients or by asymptotic approximations (MacKinnon 2008; Mascha et al. 2013; Cheng et al. 2018; Gaynor et al. 2019; Vanderweele 2015). Very little has been done to extend mediation analysis to Generalised Linear Models (Schluchter 2008; Wagner et al. 2018).
In this work we use an approach dating back to the ’80s (Stolzenberg 1980) and revived by Hayes and Preacher (2010) and Geldhof et al. (2018). Stolzenberg (1980) noticed that indirect effect can be seen as the rate at which a change in the exposure produces a change in the response indirectly through the mediator. In a more formal way, this can be expressed as the derivative of Y with respect to X taking into account the dependence from M, that is, writing the response as a composite function, since Y depends on M, which in turns depends on X. Using the chain rule, the indirect effect can then be written as a product of derivatives, the one with respect to the exposure in the mediator model and the one with respect to the mediator in the outcome model. For example, differentiating Eqs. (3) and (4) with respect to X and M, respectively, yields \(\beta _1\) and \(\gamma _2\), whose product is exactly the indirect effect in the classical Normal linear case.
Formulas for the indirect effect when at least one between the mediator and the outcome model is nonlinear are more complex and depend on the values of X and/or M (see Table 1). Hayes and Preacher (2010) remark that the value of M cannot be chosen at random, but relies on the value of X. This is the reason why Geldhof et al. (2018) suggest to call these effects conditional, in contrast to Hayes and Preacher (2010), who proposed the term instantaneous. Geldhof et al. (2018) also point out that interpreting these effects as the increment in Y due to a unitary increment in X, mediated by M, is incorrect and that they should rather be commented in terms of increments of standard deviation, i.e. taking their magnitude into account.
In the presence of multiple mediators, the computation of indirect effects becomes trickier. One can distinguish mediator-specific indirect effects, that is, indirect effects conveyed by each mediator, and total indirect effect. Except for the unlikely case of perfectly uncorrelated mediators, when the total indirect effect can be obtained by simply summing up the mediator-specific indirect effects, the magnitude of the correlation between mediators may affect the estimate of the total indirect effect (Preacher and Hayes 2008).
In the current setting, since we consider as mediators the latent coordinates corresponding to each subject in the network, the assumption of uncorrelated mediators sounds plausible, as will be discussed in Sect. 5. In this case, the extension of Hayes and Preacher (2010) and Geldhof et al. (2018) approach is straightforward. The response variable can be seen as a composite vector function \(y(m_1(x), m_2(x), \dots ,\) \(m_D(x))\). Scalar derivatives become vector derivatives and the chain rule leads to
i.e. the dot product between the gradient \(\nabla y(\mathbf {m}) = \partial y/\partial \mathbf {m}\), the vector of derivatives of Y with respect to the mediators, and \(\mathbf {m}^\prime (x) = d\mathbf {m}/dx\), the vector of derivatives of the mediators with respect to X.
When both the mediator and the outcome models are linear, this yields the sum of mediator-specific indirect effects, i.e. \(\sum _{k =1}^D \beta _{1k}\, \gamma _{2k}\) . In this simple case the total indirect effect does not differ across subjects. On the contrary, if at least one between the mediators and the outcome model is not linear, the total indirect effect is still a sum of products, but it varies according to the values of the exposure, so that each subject has his/her own total indirect effect.
4 Combining latent space and mediation models: model specification and estimation
To date, there have been very few attempts to include networks in mediation models. To the best of the authors’ knowledge, there are only two works proposing approaches to address the issue: Liu et al. (2021) propose the use of latent space models to reduce the dimensionality of the network, while Sweet (2019) method is based on a stochastic blockmodel. While the latter approach can be defined network-oriented, since it entails a number of networks to be summarised through a relevant parameter, the former, on which our work partly relies, is actor-oriented, since a unique network is summarised by the latent positions of its nodes.
We extend Liu et al. (2021) proposal by using a multiple-mediator approach which allows the outcome distribution to belong to the exponential family, and to depend non linearly on its predictors. Mediational effects are obtained through the Geldhof et al. (2018) approach based on derivatives and extended to multiple mediators, as described in the previous section.
4.1 Bayesian models and inference
Making inference on the indirect effect is not straightforward even in the linear case, since, even assuming that the two regression coefficients estimators are Normally distributed, generally their product, i.e. the indirect effect in linear models, has an unknown, possibly highly skewed distribution. This complicates the estimation of confidence intervals for the mediated effect (MacKinnon et al. 2004).
Bayesian MCMC methods provide a flexible way to deal with the above mentioned inferential problem, since they allow researchers to obtain the distribution of the effect and a highest density credibility interval (HDI). In the context of mediation analysis, HDIs are easier to obtain than their frequentist counterpart and less computationally demanding than other non-parametric methods used to compute confidence intervals, such as bootstrap. Therefore, in this paper, inference is carried out within a Bayesian framework via an MCMC approach (Hoff 2009; Spade 2020).
To make inference on the indirect effect, we proceed with a two-step approach. First, we select the dimension D of the latent space and estimate the latent positions held by each subject in the network. Second, we estimate the parameters of the mediation model and the mediational effects.
In the first step we fit the latent space model shown in Eq. (1) using the method proposed in Hoff et al. (2002) and Handcock et al. (2007). Their procedure makes inference on the configuration corresponding to the network using a Procrustean transformation
where T ranges over the set of rotations, translations and reflections and \(Z_0\) is a set of fixed starting positions, generally the maximum-likelihood estimates of the latent positions centered at the origin. \(Z^*\) is ‘ the element of the configuration [Z] closest to \(Z_0\) in terms of the sum of squared positional difference’ (Hoff et al. 2002) and can be obtained through a Metropolis-Hastings algorithm. The prior distributions for the model parameters and the latent positions are
where the \(\mu\)’s represent expectations, with \(\varvec{\mu }_z = (\mu _{z1}, \mu _{z2}, \dots , \mu _{zD})\), and \(\tau _{\alpha _0},\, \varvec{T}_{\alpha _1}, \, \varvec{T}_z\) are precision matrices (\(\tau _{\alpha _0}\) is a \(1\times 1\) matrix, i.e. a scalar). In particular, \(\varvec{T}_z\) is assumed to be diagonal, with elements \(\tau _{zk}, \, k = 1, \dots , D\). The posterior distribution of \(Z^*\) can be summarised either with the posterior mean or median. A detailed description of the estimation procedure can be found in Hoff et al. (2002) and Handcock et al. (2007).
A crucial part of the inferential process is the choice of the latent space dimension. This can be done in different ways, and one of the most common entails the estimation of a number of models, using different values of D, and the choice of the dimension corresponding to the model showing the best fit, on the basis of a measure like the Bayesian Information Criterion or the F1-score. The latter is used to evaluate the accuracy of a test, taking into account the precision and the recall. In a diagnostic test with a binary response, say positive or negative, the precision indicates the proportion of elements correctly classified as positive among all those classified as positive, i.e. the ratio of true positive over the sum of true and false positive, while the recall indicates the proportion of positive correctly classified over all actual positive, i.e. the ratio of true positive over the sum of true positive and false negative
The F1-score is the harmonic mean of precision and recall
and ranges between 0, when the test performs poorly, and 1 when the test is extremely accurate.
In the context of networks, one can compare the actual network with that predicted by the latent space model, and examine if the presence of a tie between two nodes is correctly detected by the predicted network. Then, the true positive are the links present in the observed network which are correctly predicted by the model, while the false negative are those links present in the observed network but not detected by the predicted network. Definitions of false positive and true negative can be obtained analogously. The higher the F1-score, the better the prediction made by the latent space model.
The second step of the estimation procedure involves the mediation model. Let X and Y denote the exposure and the outcome of interest, respectively. Recall that, for every subject \(i = 1, \dots , n\), each coordinate \(Z_{ik}\) of his/her position in the latent space is regarded as a mediator of the X-Y relationship. The Bayesian mediation model is made up of two parts: a generalisation of models (3)–(4) and the prior distributions of the models’ parameters. The former can be specified as
for \(i = 1, \dots , n\), and \(k = 1, \dots , D\), with \(Z_{ik}\sim \text {N}(\mu _{z_{ik}}, \tau _{zk})\), \(Y_i\) belonging to the natural exponential class (NEC) and having expectation \(\mu _{yi}\), and \(g_1\) and \(g_2\) being two link functions.
The second part, i.e. the prior distributions are assumed to be
Except for the random variable Y, which can belong to the natural exponential family, and the parameters \(\tau _{zk}\), all the remaining variables and parameters have a (univariate or multivariate) Normal distribution. Notice that the second parameter in the specification of the Normal distribution is not the variance, but its inverse, that is, the precision. It is also worth noting that the mediators are not correlated. This assumption is quite reasonable considering the nature of the variable, since they are coordinates in a Euclidean space.
Figure 2 shows the steps of the proposed approach. If \(D = 1\) we have a single mediator model, as in Fig. 1. If \(D >1\) we have a multiple-mediator model, as shown in Fig. 2c for the simple case \(D=2\).
The indirect effect can be estimated as the scalar product of two vector derivatives (Sect. 3). If the mediators and outcome models are as in Eqs. (6)–(7), denoting by \(\eta _{zk}\) and \(\eta _y\) the linear predictors of the mediator and the outcome, respectively, the total mediated effect can then be estimated as
where \(h_r = g_r^{-1}, r = 1,2.\) In the MCMC Bayesian framework, we can easily get a chain of total indirect effects for each subject, from which to estimate the posterior mean or median and the HDI.
5 Data analysis
The data used in the analysis are a subsample of the 160 adolescents enrolled in the Teenage Friends and Lifestyle Study, a cohort study carried out in a secondary school of Glasgow between 1995 and 1997 intending to investigate how smoking behaviours and substance use change over time, and the extent to which social interactions influence them.
5.1 Dataset description
Except for participants’ sex and age, which were recorded at baseline, other variables were collected at three different time occasions. Information on substance use (tobacco, alcohol, cannabis), leisure time activities, music taste, romantic relationships and several others are available. Moreover, social matrices representing friendship relationships among participants are included in the dataset. The subsample of subjects selected for the analysis consists of the 129 students present at all three measurement times. We conducted a cross-sectional analysis for each time point. Our interest lies on the way two exposures, Sex, participant’s gender, and Money, the amount of pocket money each participant had per month, affect substance use through the relationship network. Sex is a binary variable, 0 denotes male and 1 female, Money is a continuous variable ranging from 0 to 40 pounds at the first time, from 0 to 50 pounds at the second time and from 0 to 70 pounds at the third. As it will be explained in the next section, we used the variable as it is, when it plays the role of exposure in the mediation model, and a categorical version obtained through the quartiles of Money at time 3, when it needs to be included in the latent space model as covariate. The categorisation choice is clearly arbitrary, but generates meaningful categories with acceptable ranges. Figure 3 represents the network at time 3, where nodes are coloured according to Sex (a) and categories of Money (b).
The social networks representing relationships among students are defined by non-symmetric matrices, since in the data collection phase students were asked to name up to six friends. The lists thus obtained are partially overlapping, but in some cases the relationship of friendship is not reciprocal. Each cell \(a_{ij}\) can take three values: 0 if subjects \(i-j\) are not friends, 1 if subject i considers j as a friend and 2 if i considers j as a best friend. We transformed these matrices into adjacency matrices by merging the last two categories and coding them with 1, to simply indicate friendship.
The three response variables, Smoke, Cannabis and Alcohol, are measured at each time point and are categorical. Smoke has three categories: 0 indicates non-smoker, 1 occasional and 2 regular smoker (i.e. more than once a week). Cannabis has four levels: 1-never used, 2-tried once, 3 occasional and 4 regular user. Finally, Alcohol is a five-category variable coded as follows: 1 non user, 2 once or twice a year, 3 once a month, 4 once a week and 5 more than once a week. This variable presents some missing values: we excluded subjects lacking two or three values and, for subjects presenting only a missing, we imputed it on the basis of the other two collected. This led to the exclusion of 12 students. We converted all variables into binary ones by appropriately merging categories: 2 and 3 for Smoke, to distinguish between smokers (occasional and regular) and non smokers, 1–2 versus 3–4 for Cannabis and 1–2 versus 3–4–5 for Alcohol, respectively, to denote no or sporadic consumption versus regular consumption. In fact, nothing would have prevented us from using categorical responses. However, this would have entailed fitting multinomial models and deriving expressions for the indirect effect involving more complex derivatives. For the sake of simplicity, and to make our application easier to understand, we preferred to convert response variables into binary and to estimate logistic models.
5.2 Model implementation
All analyses were carried out in R, using the latentnet and rjags packages. We implemented the Bayesian model described in Sect. 4.1 in the software JAGS.
As previously discussed, our analysis consisted of a two-step procedure: first, for each network, we obtained the coordinates of each subject in a latent space of appropriate dimension; second, we used these positions as mediators in the mediation model described by (6)–(7). The model parameters and the effects of interest were estimated through MCMC.
In the first step, we fitted two versions of model in Eq. 1: one without covariates and one including covariates. As regards the latter, the covariates have to be dyadic: if Sex takes the role of covariate in the latent space model, it assumes value one if two subjects have the same gender and zero otherwise. Money becomes a dyadic variable assuming value one if two subjects fall in the same category of pocket money received by parents, zero otherwise. This is the reason why we categorised Money as detailed in the previous section. Clearly, results may change according to categorisation; then, to overcome the arbitrariness of the choice, one can use a continuous dyadic variable, for example the difference between two subjects’ pocket money. We carried out analyses also with this continuous dyadic variable as covariate in the latent model, but, since results were not different from those obtained with the categorical version of Money, we discuss only the latter.
As already mentioned in Sect. 2, inference is not carried out on positions, which are not identifiable, but on configurations. The latentnet package uses an MCMC algorithm to estimate the posterior distribution of the configuration which maximizes the model likelihood, as described in Hoff et al. (2002). We did not specify the hyperparameters characterising the prior distributions of the latent space model parameters in Eq. (5). The latentnet package selects the priors through a heuristic rule which performs well on the great majority of networks. See Sect. 2.4 of Krivitsky and Handcock (2008) for further details.
To assess model fit and, as a consequence, the most appropriate latent space dimension to represent the networks, we fitted the latent models discussed above, with and without covariates, for D ranging from 1 to 10. We specified 100,000 iterations, adaptation = 50,000 and thinning = 50. Graphical inspection of the chains revealed convergence and absence of autocorrelation. The chains of the latent dimensions were summarised through their posterior means, which uniquely characterise the distribution of the configuration. We compared the adjacency matrices corresponding to the actual networks to the matrices obtained from the relative distances between the estimated latent positions in terms of F1-score, as described in Sect. 4.1.
The optimal dimension of the latent space varies for each network and model. The short period covered by the data made us think that networks should be characterised by a structural invariance over time, so, given the model, they can be represented by the same number of dimensions, selected through the F1-score, as discussed in Sect. 4.1. For the latent model without covariates and the latent model with Sex as covariate we selected seven dimensions. For the latent model with Money as covariate, both four and seven dimensions could have been chosen, but we selected seven to be consistent with the dimensions of the other models.
Before fitting mediation models, we checked for correlation between mediators. We inspected the chains used to estimate the latent positions and derived the posterior distribution of their correlation matrices. For each extra-diagonal element we derived the correspondent HDI and checked if it contained 0. For each model, all \(\frac{D(D-1)}{2} = \frac{7\times 6}{2} = 21\) correlations resulted non-significant.
Then, in the second step, we fitted the mediation model. Specifically, for each variable selected as exposure in the mediation model, the mediators derive either from the latent space model without covariates or the latent model including the non selected exposure as a covariate. Thus, if Money is selected as exposure in the mediation model, the mediators, i.e. the latent positions, are from the model where Sex takes the role of covariate. Vice versa, if Sex is the exposure, mediators are from the latent space model including Money as a covariate.
We fitted linear models for the mediators (i.e. the coordinates) and logistic models for the binary outcomes
With reference to Eq. (8), we specified the following non-informative priors
where \(\varvec{T_{\beta _1}} = \varvec{T}_{\gamma _2} = \text {diag}(0.01)\) are \(7 \times 7\) diagonal matrices with diagonal elements equal to 0.01.
Using these priors, we obtained posteriors of the direct effect \(\gamma _1\) and the total indirect effect. The formula for the latter can be derived combining Eq. (9) with results in Table 1 as
where \(h_1\) is the identity and \(h_2\) is the antilogit, i.e. \(h_2(\eta _y) = \frac{\exp (\eta _y)}{1+\exp (\eta _y)}\). The selected MCMC algorithm was Gibbs sampling: we used a unique chain of length 100,000, adaptation 50,000 and 50 thinning. Finally, we computed 95% HDI for both the effects. The trace plot and the autocorrelation plot of the indirect effect at the first time occasion for both exposures and outcome Smoke are represented in Fig. 4. It can be noticed that the chains converged and they do not show any sign of autocorrelation. The graphs for the other outcomes and the other time occasions show very similar patterns and are not reported.
5.3 Results
Before commenting the results, it is worth remarking that reasoning in terms of unit increase or decrease of latent positions, as traditionally done in regression, is pointless. Latent positions do not have substantive meaning, they are just the result of a dimensionality reduction technique, used to summarise the network and include it in the mediation analysis. Therefore, although the exposure can positively or negatively affect latent positions, this is not interpretable. What we can say is just that the exposure influences the structure of the network, or, in other words, the relationships linking actors. Latent positions help us to incorporate the network into regression models, making it tractable as a set of different variables which play the role of mediators. Thus, if a total indirect effect turns out to be significant, the latent positions convey the effect of the exposure on the outcome, and this means that the friendship ties between subjects mediate the effect of X on Y.
In the following, we will denote by \(\mathcal {LM}(\textit{Covariate})\) the latent space model including Covariate as predictor, and by \(\mathcal {LM}(\cdot )\) the latent space model without any additional covariate.
Let us start from models having Sex as exposure, whose results are shown in Tables 2, 3, 4. Since it is a binary variable, the total mediated effect can assume only two values according to subjects’ gender. For Smoke (Table 2), the direct effect is significant only at time 1, like the indirect effect, but the latter only for females and for mediators estimated through \(\mathcal {LM}(\cdot )\). The direct effect is positive, then the probability of smoking tobacco regularly is higher for 13-year-old girls than for boys. In contrast, the total indirect effect for girls is negative, then the effect of gender on the chance of smoking reduces through friendship relationships.
Gender seems to have no effects on the probability of smoking cannabis neither direct nor indirect (Table 3). Thus, the attitude towards the use of cannabis does not vary across boys and girls and is not influenced by friendship ties. It is interesting, though, to notice that, for both \(\mathcal {LM}(\cdot )\) and \(\mathcal {LM}(Money )\), the direct effect is positive at time 1 and tends to decrease over time, becoming negative. In addition, total indirect effects are always a bit larger for males, and they show a slight increase over time.
As regards Alcohol (see Table 4), the direct effect results significant only at time 1 for \(\mathcal {LM}(\cdot )\) and it is positive, thus 15-year-old girls seem more prone to drink than boys. Indirect effects are also significant, but again, only at time 1 for \(\mathcal {LM}(\cdot )\), and they are negative. Then, gender negatively affects the probability of drinking through the relationships among students. The difference in mediational effects between models including latent positions estimated in \(\mathcal {LM}(\cdot )\) as mediators and models including positions estimated through \(\mathcal {LM}(Sex)\) shows that including a covariate in the latent space model (1) may affect results substantively.
Moving to mediation models including Money as exposure, direct effects differ between models with mediators from \(\mathcal {LM}(\cdot )\) or \(\mathcal {LM}(Sex )\). Specifically, in models where the mediators were obtained using \(\mathcal {LM}(Sex)\), Money does not affect directly any of the outcomes, at any time occasions. In contrast, in models where the latent positions were estimated through \(\mathcal {LM}(\cdot )\), Money has a significant positive direct effect on the probability of smoking cannabis and drinking alcohol at time 1. In other words, wealthier pupils are more likely to make use of substances when they are 13, while at other subsequent time occasions Money seems not to play a role in the students’ attitude towards substance use. For Cannabis the direct effect results significant and positive also at time 2.
Indirect effects are significant only at time 3 for Smoke and Cannabis in models where the mediators derive from \(\mathcal {LM}(\cdot )\), while they are significant only at time 2 for Cannabis and Alcohol when mediators derive from \(\mathcal {LM}(Sex).\) Notice how, also in this case, mediational effects differ between models, according to whether the mediators are from \(\mathcal {LM}(\cdot )\) or \(\mathcal {LM}(Sex)\).
Since Money is continuous, total indirect effects do not assume only a finite set of values, but are continuous functions of the exposure. Figure 5 shows total indirect effects on each response and for each measurement time.
For all outcome variables, indirect effects at time 2 assume the highest values, followed by indirect effects at time 1 and finally effects at time 3, which tend to be small and to vary little. Indirect effects on Smoke and Cannabis are not monotonic, showing a peak and then a decrease. For Smoke, the peak seems to remain stable over time, at around 35£. At time 1 the total indirect effect shows greater variability and becomes flatter at successive time occasions. This may indicate that friendship relationships have a major role in making adolescents start smoking when they are younger, while they become less important on the decision to continue smoking as youngsters get older. As regards Cannabis, the total indirect effect is higher at time 2. Again, the peak is approximately the same at all occasions, and at time 3 the indirect effect does not vary much among different values of Money.
The indirect effects on Alcohol are decreasing at all time occasions and, at the first and the last measurement occasion, they approach 0. Thus, the more pocket money a student gets the smaller is the odds he/she drinks very much due to the mediation of friendships.
6 Conclusions
In this work, we have addressed the issue of estimating the indirect effect in a mediational setting where the mediator is a network. We have used a latent space approach to reduce the dimensionality of the network, mapping each actor into his/her latent coordinates, which were then used as mediators in mediation models of interest. In order to estimate the indirect effect when at least one between the mediator and the outcome model is non-linear, we resorted to the concept of conditional indirect effect based on derivatives, and we extended it to the case of multiple uncorrelated mediators.
A Bayesian MCMC provides inferential results on the indirect effect. In particular, we computed HDIs to test for its significance, a task generally very difficult in a non-Bayesian context, due to the fact that the distribution of the indirect effect is hardly ever known or obtainable in closed form.
Finally, we analysed a dataset regarding substance use of a group of adolescents, in order to understand how friendship relationships can mediate the effect of two explanatory variables on it. Although friendship relationships do not generally seem to have a mediating role, since indirect effects result non significant in most of the analyses, it was possible to notice some interesting patterns. Gender has a significant positive direct effect on smoking attitudes and alcohol consumption at time 1. Thus, girls have a larger odds of smoking tobacco and regularly drinking alcohol than males. The total indirect effects are significant and negative for Smoke and Alcohol, but only in models where the latent positions were estimated through \(\mathcal {LM}(\cdot )\). Money has a positive direct effect on the odds of smoking tobacco and drinking alcohol. Indirect effects reach a peak in models for Smoke and Cannabis, while are always decreasing in models for Alcohol.
Although the method proposed has the unquestionable advantage of reducing the dimensionality of the network, allowing us to include it in regression models, the method has also some drawbacks which are worth mentioning. First, as pointed out in Sect. 5.3, the latent dimensions have not substantive meaning per se, and this makes the interpretation of the results not straightforward. Second, the two-step estimation procedure introduces uncertainty in the estimates, since the latent positions are themselves estimated. We treated the latent positions as deterministic, but the use of methods to address their uncertainty could be an interesting direction for future research.
There are several directions this work can be developed on. It is necessary to carry out more research on how to extend latent space models for accommodating different types of dyadic relationships. Extending mediation models to GLMs is still a hot research topic: the definition of indirect effects through derivatives may be a promising way to tackle the issue of estimation. Moreover, dealing with multiple mediators taking into account correlations among them is still an open problem in the literature. We are confident that the method we adopted in the easier case of uncorrelated mediators can be extended to incorporate correlations.
It is worth noting that we could have included additional covariates in our mediation models, but this does not add conceptual difficulties to the method described and can be easily addressed by implementing more complex formulas, as described in Hayes and Preacher (2010).
Although we used longitudinal data, analyses were cross-sectional and we limited our analyses to the comparison of the results among different time occasions. More efforts need to be devoted to capturing the dynamics of networks change and incorporating such information in latent space models.
Finally, we did not draw any causal conclusion from our analyses. The concepts of direct and indirect effects are widely employed in the structural equation modeling framework and have been used in associational terms since the late ’80s (Baron and Kenny 1986). In our analysis, the indirect effect simply expresses how the effect of a change in the exposure on the outcome propagates through the mediators. This differs from the counterfactual reasoning traditionally employed to address causality (Rubin 1974, 1978), where the causal mediational effects are defined in terms of nested counterfactuals, which entail interventions on both the exposure and the mediator (Pearl 2001; Vanderweele 2015). The identifiability of these effects, i.e. the possibility to express them in terms of observed variables, relies on strong assumptions which a researcher may be willing to make or not, and which are still subject of debate among scholars, see Robins and Richardson (2011). How these assumptions could be integrated within a latent space mediational modeling framework leaves room for future work.
Availability of data and material.
Data from the “Teenage Friends and Lifestyle Study” are publicly available at http://www.stats.ox.ac.uk/ snijders/siena/.
Code availability
Available upon request.
References
Alwin DF, Hauser RM (1975) The Decomposition of Effects in Path Analysis. Am Sociol Rev 40(1):37–47
Baron RM, Kenny DA (1986) The moderator-mediator variable distinction in social psychological research: conceptual, strategic and statistical considerations. J Personal Soc Psychol 51(6):1173–1182
Bollen KA (1987) Total, direct, and indirect effects in structural equation models. Sociol Methodol 17:37–69
Cheng J, Cheng NF, Guo Z, Gregorich S, Ismail AI, Gansky SA (2018) Mediation analysis for count and zero-inflated count data. Stat Methods Med Res 27(9):2756–2774
Duncan OD (1966) Path analysis: sociological examples. Am J Sociol 72(1):1–16
Gaynor SM, Schwartz J, Lin X (2019) Mediation analysis for common binary outcomes. Stat Med 38:512–529
Geldhof GJ, Anthony KP, Selig JP, Mendez-Luck CA (2018) Accommodating binary and count variables in mediation: a case for conditional indirect effects. Int J Behav Develop 42(2):300–308
Handcock MS, Raftery AE, Tantrum JM (2007) Model-based clustering for social networks. J R Stat Soc A 170(2):301–354
Hayes AF, Preacher KJ (2010) Quantifying and testing indirect effects in simple mediation models when the constituent paths are nonlinear. Multivar Behav Res 45:627–660
Hoff PD (2003) Random effects models for network data. In: Dynamic social network modeling and analysis: workshop summary and papers, Citeseer
Hoff PD (2009) A first course in Bayesian statistical methods. Springer, New York, NY
Hoff PD, Raftery AE, Handcock MS (2002) Latent space approaches to social network analysis. J Am Stat Assoc 97(460):1090–1098
Kolaczyk ED, Csárdi G (2014) Statistical analysis of network data with R. Springer, New York, NY
Krivitsky PN, Handcock MS (2008) Fitting position latent cluster models for social networks with latentnet. J Stat Softw 24(5):1–23
Krivitsky PN, Handcock MS, Raftery AE, Hoff PD (2009) Representing degree distributions, clustering, and homophily in social networks with latent cluster random effects models. Soc Netw 31(3):3204–3213
Liu H, Jin I, Zhang Z, Yuan YS (2021) Social network mediation analysis: a latent space approach. Psychom 86(1):272–298
MacKinnon DP (2008) Introduction to statistical mediation analysis. Taylor and Francis Group, New York, NY
MacKinnon DP, Lockwood CM, Williams J (2004) Confidence limits for the indirect effect: distribution of the product and resampling methods. Multivar Behav Res 39(1):99–128
Mascha EJ, Dalton JE, Kurz A, Saager L (2013) Understanding the mechanism: mediation analysis in randomized and nonrandomized studies. Anesth Analg 117(4):980–994
Newman MEJ (2010) Networks. An introduction. Oxford University Press, New York, NY
Ni Y, Baladandayuthapani V, Vannucci M, Stingo FC (2021) Bayesian graphical models for modern biological applications. Stat Methods Appl. https://doi.org/10.1007/s10260-021-00572-8
Pearl J (2001) Direct and indirect effects. In: Breese JS, Koller D (eds) Proceedings of 7th conference on uncertainty in artificial intelligence, Morgan Kaufmann, San Francisco, CA, pp 411–420
Preacher KJ, Hayes AF (2008) Asymptotic and resampling strategies for assessing and comparing indirect effects in multiple mediator models. Behav Res Methods 40(3):879–891
Robins JM, Richardson TS (2011) Alternative graphical causal models and the identification of direct effects. In: Shrout P, Keyes K, Ornstein K (eds) Causality and psychopathology: finding the determinants of disorders and their cures. Oxford University Press, Oxford, pp 103–158
Rubin DB (1974) Estimating causal effects of treatments in randomized and nonrandomized studies. J Educ Psychol 66(5):688–701
Rubin DB (1978) Bayesian inference for causal effects: the role of randomization. Ann Stat 6(1):34–58
Salter-Townshend M, White A, Gollini I, Murphy TB (2012) Review of statistical network analysis: models, algorithms, and software. Stat Anal Data Min 5:243–264
Schluchter MD (2008) Flexible approaches to computing mediated effects in generalized linear models: generalized estimating equations and bootstrapping. Multivar Behav Res 43(2):268–288
Spade DA (2020) Markov chain Monte Carlo methods: theory and practice. In: Srinivasa Rao AS, Rao C (eds) Principles and methods for data science. Handbook of statistics, vol 43. Elsevier, pp 1–66
Stolzenberg RM (1980) The measurement and decomposition of causal effects in nonlinear and nonadditive models. Sociol Methodol 11:459–488
Sweet TM (2019) Modeling social networks as mediators: a mixed membership stochastic blockmodel for mediation. J Educ Behav Res Methods 44(2):210–240
VanderWeele TJ (2009) Mediation and mechanism. Eur J Epidemiol 24:217–224
Vanderweele TJ (2015) Explanation in causal inference. Oxford University Press, New York, NY
Wagner BD, Kroehl M, Gan R, Mikulich-Gilbertson SK, Sagel SD, Riggs PD, Brown T, Snell-Bergeon J, Zerbe GO (2018) A multivariate generalized linear model approach to mediation analysis and application of confidence ellipses. Stat Biosci 10:139–159
Wright S (1934) The method of path coefficients. Ann Math Stat 5(3):161–215
Funding
Not applicable.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest.
The author declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Di Maria, C., Abbruzzo, A. & Lovison, G. Networks as mediating variables: a Bayesian latent space approach. Stat Methods Appl 31, 1015–1035 (2022). https://doi.org/10.1007/s10260-022-00621-w
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10260-022-00621-w


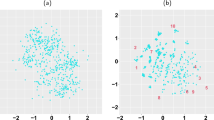



 = male and
= male and  = female, on the right panel (b)
= female, on the right panel (b)  = 1 (0–7£),
= 1 (0–7£),  = 2 (7–12£),
= 2 (7–12£),  = 3 (12–20£),
= 3 (12–20£),  = 4 (20–70£)
= 4 (20–70£)
