Bridge closure in the road network of Lombardy: a spatio-temporal analysis of the socio-economic impacts

Abstract

This paper introduces a methodology to evaluate the socio-economic impacts of closure for maintenance of one or more infrastructures of a large and complex road network. Motivated by a collaboration with Regione Lombardia, we focus on a subset of bridges in the region, although we aim at developing a method scalable to all road infrastructures of the regional network, consisting of more than 10,000 tunnels, bridges and overpasses. The final aim of the endeavor is to help decision-makers in prioritizing their interventions for maintaining and repairing infrastructure segments. We develop two different levels of impact assessment, both providing a unique global score for each bridge closure and investigating its spatio-temporal effects on mobility. We take advantage of a functional data analysis approach enhanced by a complex network theory perspective, thus modelling the roads of Lombardy as a network in which weights attributed to the edges are functional data. Results reveal the most critical bridges of Lombardy; moreover, for each bridge closure, the most impactful hours of the day and the most impacted municipalities of the region are identified. The proposed approach develops a flexible and scalable method for monitoring infrastructures of large and complex road networks.

1 Introduction

Civil structures and infrastructure facilities play a pivotal role in the modern society and are generally considered one of the main drivers of socio-economic development. However, these structures are naturally subject to both obsolescence and deterioration caused by the effects of natural hazards, operational and environmental conditions (Wang et al. 2017). As a result, many countries are currently facing the problem of the progressive aging of their civil structure and infrastructure facilities (Ellingwood 2005). In the U.S. a relevant portion of the civil infrastructure has exceeded its useful life, and a quarter of U.S. highway bridges has been classified by the ASCE as either structurally deficient or functionally obsolete (Sabatino et al. 2016). The situation is not much different in Europe. According to a report published by the German Institute for Economic Research (DIW), about 46% of bridges, 41% of streets, and 20% of highways in Germany were in need of repair (Llana 2015; Caspeele et al. 2018). More recently, the collapse of the Morandi bridge in Italy and the Vigo oceanside boardwalk in Spain sounded the alarm on the conditions of infrastructures in Europe.

In order to allow these infrastructures to be safe and to continue creating value over their entire life, monitoring and maintenance activities are necessary. Still these activities require considerable resources, in terms of both time and cost for visiting the structures, evaluating their conditions, and then performing the needed repairs. In a situation where resources are shrinking, it is clear the importance of planning maintenance interventions based on some priorities, for defining which facilities should be visited, when and how maintenance should be carried out, respecting budget and other resource constraints, like manpower and equipment (e.g. Frangopol and Liu 2007; Shah et al. 2014). The evaluation of the priority of intervention and the development of an adequate maintenance planning is a complex task, because it requires to take into considerations many different variables, concerning the life-cycle and the characteristics of the infrastructure, its operating and environmental conditions, and also the consequences of the unavailability of the infrastructure itself (Furuta et al. 2006). The complexity of such a heterogeneous set of information is further amplified when dealing with an infrastructure system that consists of numerous and dispersed facilities (Pantha et al. 2010).

This paper addresses the issue of prioritization of maintenance activities, with reference to a particular type of infrastructure—the system of road bridges in Lombardy—and focusing on one specific dimension, unavoidable when defining such prioritization—the effects of a bridge closure to the movement of people. Specifically, we asses the impact of a bridge closure according to its importance for maintaining a proper connectivity between all areas of the region, allowing users to move from one point to another and reach their destinations (Berdica and Mattsson 2007; Sullivan et al. 2009; Rupi et al. 2015). This aspect is particularly relevant because it provides a measure of the socio-economic impact of a bridge closure. The collapse or, more in general, the unavailability for maintenance of a bridge, in fact, can cause long deviations and traffic congestion, and result in a damage for its users (Stein et al. 1999; Taylor et al. 2006).

Evaluating the impact of the closure of road infrastructures is not a new problem in the literature on transportation networks. Several measures of impact assessment have been introduced in the past, looking at different indicators based on generalized costs, user costs, efficiency measures, network topological features and congestion effects (e.g. Taylor et al. 2006; Jenelius et al. 2006; Scott et al. 2006; Sullivan et al. 2009, 2010; Qiang and Nagurney 2012; Balijepalli and Oppong 2014; Xiaofei et al. 2015; Rupi et al. 2015; Cantillo et al. 2019). In Taylor et al. (2006), generalized costs - a measure of disutility of travel, such as distance, time or money - are used to estimate the impacts of network degradation for a very simplified model of the Australian road network. In Xiaofei et al. (2015) user costs, in terms of extra vehicle-miles traveled, are used to find optimal maintenance plans for deteriorating bridges in large-scale networks. In Rupi et al. (2015), the level of usage of a link and the impact of the closure of that link on the general functionality of the network are used to obtain a ranking of importance for the links of a real-scale network in the province of Bolzano in Italy. In Cantillo et al. (2019), a novel evaluation model for correctly taking into account the social costs, which includes both logistic and deprivation costs (Holguín-Veras et al. 2013), is presented and it is applied to assess the Colombian Coffee Zone road network. However, all these works, even if they are key to help decision makers for planning the maintenance of a road infrastructure, do not address two issues which we deem to be important for the correct management of human mobility in a damaged network: the temporal and the spatial aspects. To fill this gap, this paper proposes a novel two-way approach which investigates the impacts of a bridge closure from a spatio-temporal perspective: from the temporal point of view, we analyze how the impact of a bridge closure varies according to the hour of the day, addressing the problem of the traffic variability in time and allowing to better organize the road works during the day; from the spatial point of view, we identify the areas most affected by the closure, obtaining useful information that can be passed on to the affected travelers. The proposed approach is designed to be scalable and appropriate for large scale analysis at a regional network level: in particular, it has been conceived for being applicable to any road infrastructure of Lombardy—meaning any of its more than 10,000 tunnels, bridges and overpasses - while it has been tested on a sample of 290 bridges of the region. The final aim of the endeavor is to help the regional government in prioritizing its interventions for maintaining and repairing road infrastructures.

Specifically, for each bridge, we provide different levels of impact assessment, investigating the spatio-temporal effects of the closure of the bridge and providing a unique global score which could be used for ranking. For this purpose, beside a graph model of the regional road infrastructure of Lombardy, we leverage the information on travel demand captured by the origin-destination matrices (OD) publicly provided by Regione Lombardia. An OD matrix can be viewed as a weighted directed graph where nodes are origins and destinations, while edges allow for the representation of the number of trips between nodes (Saberi et al. 2017, 2018). OD matrices are provided by Regione Lombardia for each of the 24 h of a representative working day in 2016. We include in the analysis this temporal information since it is well known that daily traffic profiles are characterized by a large within-day variability (Weijermars and Van Berkum 2005). Indeed, since mobility is continuously dependent on time, a natural way to analyze mobility between an origin and a destination during the 24 h, is to represent it by means of a point belonging to a space of continuous functions defined on the time domain (0,24). The basic idea is that OD mobility data, even if they are recorded at a discretized level (hourly level), are actually a representation of a continuous phenomenon. The analysis will then make use of methods and algorithms of Functional Data Analysis (FDA), the branch of statistics dealing with object data which are curves or surfaces (Ramsay and Silverman 2005). In this way, we are able to explicitly model the functional nature of the data (Bouveyron et al. 2015) that would be lost with a simpler approach. Previous works on mobility data have already used FDA to model, for instance, the number of vehicles passing through a specific location (Chiou 2012; Guardiola et al. 2014; Crawford et al. 2017), or the bike sharing demand at different bike stations (Bouveyron et al. 2015; Gervini and Khanal 2019); Torti et al. 2021). Differently from other works, however, we mix motifs from FDA and network theory and we represent the road network of Lombardy as a graph evolving over time. The topology of the graph is fixed, but the weights attributed to the edges are functional data, representing the time varying mobility over the edge.

The rest of the paper is organized as follows. In Sect. 2 we present the data and we construct our continuous time dependent network. In Sect. 3 we describe the methodology used to evaluate the impacts of a bridge closure. In Sect. 4 results of the analysis of a sample of 290 bridges in Lombardy are reported. In Sect. 5 the case of the simultaneous closure of more bridges is discussed. In Sect. 6 we investigate the robustness of the obtained results under a perturbation of the origin-destination trips. Conclusions are presented in Sect. 7.

2 The mobility network of Lombardy: a time varying weighted directed graph

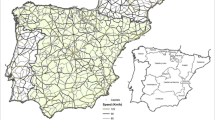
Lombardy is one of the twenty administrative regions of Italy with an area of 23,844 square kilometres and a resident population of about 10 million people, forming one-sixth of Italy’s population. Every day Lombardy witnesses 17 million trips across the region, with different means of transport—e.g. by car, by train, by bus, on foot etc.. This makes Lombardy the region of Italy with the highest number of daily trips (https://www.dati.lombardia.it). Moreover, almost 75% of all the trips involve a motor vehicle on the road. The road network of Lombardy counts 70,000 km of roads: 560 km are highways, 900 km are state roads, 11,000 are provincial roads and 58000 km are municipal roads, one-third of which are suburban. On this road network there are almost 10,000 infrastructures, e.g. bridges, tunnels, overpasses etc.. In this paper, we will focus on a small sample of road infrastructures, made of 290 bridges (Fig. 1). The selection of this sample is a milestone of a collaborative project between Politecnico di Milano and Regione Lombardia. The sample includes the most relevant bridges for each of the twelve provinces the region is divided into: Bergamo (BG), Brescia (BS), Milano (CMM), Como (CO), Cremona (CR), Lecco (LC), Lodi (LO), Monza Brianza (MB), Mantova (MN), Pavia (PV), Sondrio (SO) and Varese (VA). For each bridge an identification code of the road section, the province it belongs to and the GPS position are available. Moreover, we have access to two main complementary information sources: a road network data model and OD matrices, both provided by the regional government of Lombardy.

The road network data model is a spatial network made of about 37,000 nodes and 82,000 directional links, i.e. segments of road between two intersections, which model all types of roads of the real network with a major simplification for the municipal roads. For each directed edge of the network, an identification code of the road section, the length (km), the typical velocity without traffic (km/hour), and therefore the typical travel time (hour), are known. The road network data model is in a geospatial polyline vector format (Shapefile ESRI) where spatial entities are recorded as lists collecting 2D geospatial coordinates. This file has been converted into a igraph object in R through R package shp2graph (Binbin et al. 2018). Moreover, each bridge has been assigned to an edge of the network by matching its identification code with those of the road sections. Notice that, all the analysed bridges of our sample belong to different edges of the network. Figure 1 shows both the road network and the 290 bridges under examination.

Fig. 1

The road network of Lombardy highlighting in blue the position of the 290 bridges and the provincial borders in grey (color figure online)

The OD matrices of Lombardy contain the number of trips between 1450 internal mobility areas, during a typical working day observed in the time span between February and May 2016. A mobility area usually corresponds to the geographical area occupied by a municipality of the region; very small municipalities have been aggregated into a single area, whereas big municipalities have been split into districts, each one represented by a mobility area. For example Milan, the main city of Lombardy, is split into 16 mobility areas. For each area, the centroid’s GPS position is known. Each OD matrix reports the number of trips departing from one area to another in a given hour of the day (00:00–00:59, 01:00–01:59, ..., 23:00–23:59). Trips are classified according to eight modalities (car driver, car passenger, motorbike, bus, train, bike, foot and others) and five purposes (work, study, business, occasional and return home). For the scope of our analyses, we aggregated all trips with respect to their purpose and we considered only those of people moving with a motor vehicle on the road, hence aggregating the modalities car driver, car passenger, motorbike and bus, while disregarding the trips related to the other modalities. We obtain a total of almost 12.4 million of trips distributed over the day. On average, a trip - which is equivalent to a person’s travel - has a length of 10 km and lasts about 13 min.

For every couple of mobility zones $O$ and $D$, we estimate a flow function $f_{(O,D)}$ representing over time the departure rate of people leaving from origin $O$ to destination $D,$ in the working day reported in the OD matrices. The basic idea is that the OD mobility data, even if recorded at the hourly level, are a representation of a continuous phenomenon. Indeed, given a couple $(O,D),$ we model the time of the day when a person leaves $O$ for $D$ as a continuous random variable $X_{(O,D)} \in [0,24],$ taking the hour as the unit of measure for time. The data relative to $(O,D)$ and recorded in the OD matrices are the counts of people departing from O towards D at each time interval of length one hour along the day (e.g. 00:00–00:59; 01:00–01:59;...; 07:00–07:59; ...). We interpret these count data as empirical absolute frequencies, relative to the 24 time intervals of length one hour forming the day, of the realizations of $X_{(O,D)}$ observed on the sample of people traveling from $O$ to $D$ during the day and recorded in the OD matrix. This empirical frequency distribution is then smoothed to obtain the flow function $f_{(O,D)}$ representing over time the departure rate of people leaving from origin $O$ to destination $D,$ at each instant of the day. More precisely, for $t \in [0,24],$ $f_{(O,D)}(t)dt$ estimates the number of people leaving $O$ for $D$ during the infinitesimal time interval $dt$ centered at t. The flow function $f_{(O,D)}$ is obtained by considering the input hourly count data as an histogram and by applying a kernel density estimation technique (Weglarczyk 2018) to move from a discrete representation to a continuous smooth estimate of the density of $X_{(O,D)}.$ Smoothing is obtained by means of a kernel density estimation method with a tri-cube kernel function and a bandwidth equal to 0.5 hour (see, for instance, Hastie et al. 2001), constraining the function to be non negative, to be daily periodic (since each function is defined on a periodic circular domain [0,24] representing the time of a typical working day, the first and the last element of the estimated function must be equal) and such that the integral of the smoothed function is equal to the total number of daily trips from $O$ to $D$, obtained by summing the hourly numbers of trips reported in the OD matrices. The daily smoothed function is estimated on a numerical grid of 1440 points, equal to the minutes of a day. Applying this smoothing procedure to every couple of $O$ and $D$ belonging to the 1450 mobility areas of Lombardy, we obtain $1450^2= 21,02,500$ flow functions. As an example, in Fig. 2 we depict the two flow functions between Milano 3 (a central district of Milan) and Abbiategrasso (a municipality of 30,000 inhabitants 25 km distant to Milan). It is immediate to observe that the two functions representing opposite flows do not have the same shape: the flow function on the right, the one from Abbiategrasso to Milano 3, has only one peak in the morning between 6:00–8:00, indicating a large number of commuters leaving Abbiategrasso for Milano in the early morning; the opposite flow, instead, has two main peaks, one in the morning between 6:00–8:00 and an higher one in the afternoon between 17:00–19:00, indicating the return to Abbiategrasso of the commuters who left in the morning.

Fig. 2

The two flow functions from Abbiategrasso to Milano 3 (on the right) and viceversa (on the left)

2.1 A data fusion step

For the scope of our analyses, we pass through a data fusion step which aggregates our two sources of information, the road network data model and the OD matrices. As explained below, the road network is weighted by travelling time in the first part, and successively these weights are substitute by trips contained in the OD matrices. First, for each mobility area of the OD matrices, its centroid, whose GPS coordinate is known, is associated to the closest node of the road network data model, in which gps coordinate for each node are also known, by observing the euclidean distance in kilometers between the two. Next, for every couple of mobility areas $O$ and $D$ the shortest time path $O \rightarrow D$ on the road network data model connecting $O$ and $D$ is found by means of the Dijkstra’s algorithm (Newman 2018), using traveling time as weight for each edge of the network. We are thus in the position to associate each edge $e$ of the network to an attribute related to the number of trips which pass through that edge; this is obtained by summing over all couples of origin $O$ and destination $D$ whose shortest connecting path $O \rightarrow D$ goes through $e.$ The relevant attribute can be, for instance, the flow function describing the number of trips passing from $e$ at any time $t$ of the day,

$$\begin{aligned} f_e(t)=\sum _{(O,D): e \in O\rightarrow D} f_{(O,D)} (t-t_{(O,e)}), \end{aligned}$$

(1)

or the total number of trips in the day over the edge $e,$

$$\begin{aligned} F_e = \sum _{(O,D): e \in O\rightarrow D} \int f_{(O,D)} (t-t_{(O,e)}) dt=\int f_e(t) dt \end{aligned}$$

(2)

where $t_{(O,e)}$ indicates the travel time necessary for reaching the midpoint of edge $e$ starting from $O$, computed over the the shortest time path $O \rightarrow D$. Notice that, as a result of the daily periodicity of the functional flow data over the domain [0, 24], $\int f_{(O,D)} (t-t_{(O,e)})dt =\int f_{(O,D)}(t)dt$. Analogously to $F_e$, we could estimate the number of trips over the edge e during a particular time interval $\tau$, e.g. $\tau =(7,9)$, by calculating the integral $\int _{\tau } f_e(t) dt$. In each case, we obtain a weighted directed graph, where weights are represented by trips contained in the OD matrices, i.e. by functions (1) or by numbers (2), respectively. This is illustrated in Fig. 3. Note that, while

Fig. 3

A simplified weighted directed network whose edge attributes can be both scalars (left), obtained with Eq. (2), and functions (right), obtained with Eq. (1)

3 Measuring the impact of a bridge closure

To measure the impact of a bridge closure, we define an index focusing on the importance of that bridge in maintaining a proper connectivity between all origin and destination couples of the OD matrices (Berdica and Mattsson 2007; Sullivan et al. 2009; Rupi et al. 2015). We evaluate the effects of a bridge closure on the movement of people, by estimating an index expressed in terms of extra person-hours traveled. Note that the level of usage of a bridge - i.e. the number of travelers passing on that bridge - is represented by the number of trips, expressed by the function in Eq. (1) or the scalar in Eq. (2). However, these edge attributes relay information only about the "local" importance of the bridge, disregarding the global functionality of the network that is the object of our analyses.

3.1 A global index

Assume we want to measure the impact of the closure of a bridge belonging to the edge $e$ of the road network data model; for us, this is tantamount to the removal of the edge $e$ from the network. For every couple of mobility zones $O$ and $D,$ we measure the increase in travel time of the shortest time path connecting $O$ and $D$ after the removal of the edge e; this is the time

$$\begin{aligned} t^{-e}_{(O,D)} - t_{(O,D)}, \end{aligned}$$

(3)

where $t_{(O,D)}$ is the travel time of the shortest time path $O \rightarrow D$ connecting $O$ to $D$ on the full network, while $t^{-e}_{(O,D)}$ is the travel time of the shortest time path $O \xrightarrow {-e} D$ connecting $O$ to $D$ after the removal of the edge $e$ from the road network data model. The time computed in (3) represents the cost (measured as extra traveled time) each trip from $O$ to $D$ must incur due to the removal of the edge $e$ from the network, which is equivalent to the closure of a bridge belonging to $e$. Hence, to obtain a global index of impact for the closure of a bridge belonging to $e,$ it is natural to multiply this cost by the number of trips it affects:

$$\begin{aligned} I_e= \sum _{(O,D): e \in O \rightarrow D} [t^{-e}_{(O,D)} - t_{(O,D)}] \int f_{(O,D)}(t) dt . \end{aligned}$$

(4)

$I_e$ is measured in person-hours and indicates the cumulative extra-time, spent on road in the typical working day by people traveling within the region, due to the closure of a bridge belonging to the edge $e.$ Giving an economic value to the person-hour, one obtains the socio-economic impact of a bridge closure. Indeed the analysis could be further refined, by disaggregating $I_e$ according to the purpose of the trips affected by the time increase due to the removal of the edge $e$ from the network (trip purposes are reported in the OD matrices), and by attributing different economic values to the person-hour associated with different purposes for a trip. In our analyses, however, we decided to give the same value to the person-hour of every trip, its purpose notwithstanding.

A possible problem with the computation of $I_e$ occurs if the removal of $e$ from the network isolates some centroids of the OD matrices; the network becomes thus disconnected and its topology does not cover the paths between all origins and destinations. In this case, the value of $I_e$ becomes infinite, due to the infinite increase of travel time incurred by those paths connecting origins and destinations lying in parts of the network which are disconnected after the removal of the edge $e,$ that is those couples of origins $O$ and destinations $D$ such that $O \xrightarrow {-e} D$ is empty, although $\int f_{(O,D)}(t) dt >0.$ Edges causing this problem are called "isolating-links", and they are analyzed aside. One popular approach to address the problems associated with isolating-links is to use a high percentage-based link capacity-disruption level instead of completely removing the link from the network, using for example a 99% capacity-reduction (Sullivan et al. 2010). A different approach consists in measuring the importance of the isolating link proportionally to the amount of unsatisfied trips (Jenelius et al. 2006). In the present study, we assume that isolating-links are more important than edges for which $I_e$ is finite, due to the fact that they are qualitatively different from the other ones since they necessarily require infrastructural interventions to create alternative paths. We analyze them aside in a spatio-temporal prospective, highlighting both the unsatisfied mobility functional flows and the isolated centroids.

3.2 Spatial-temporal indexes

The global index $I_e$ has the benefit of providing an estimate of the total impact of a bridge closure, but is not able to explain how this impact spreads during the day and across the region. To fill this gap, we provide a novel two-way approach exploring both the temporal and the spatial dimensions.

From a temporal perspective, we estimate how the impact of a bridge closure changes along time. To this end, we follow the argument used above to build the global impact index $I_e$, but instead of multiplying the travel time increments by the total number of trips affected, we use the flow functions representing the number of trips affected at time $t \in [0,24].$ Hence, to measure along time the impact of the closure of a bridge belonging to the edge $e,$ we measure the temporal impact function

$$\begin{aligned} i_e(t)= \sum _{(O,D): e \in O \rightarrow D} [t^{-e}_{(O,D)} - t_{(O,D)}] f_{(O,D)}(t-t_{(O,e)}). \end{aligned}$$

(5)

Obviously,

$$\begin{aligned} I_e = \int i_e(t) dt. \end{aligned}$$

From a spatial perspective, we want to estimate how the impact of a bridge closure is distributed across the region, namely the most impacted areas of Lombardy. Hence, we apply again the same argument used above for the construction of $I_e,$ but now we fix the origins or the destinations. For each origin $O$ we measure the cumulated impact of the closure of a bridge belonging to the edge $e$ as

$$\begin{aligned} I_e(O\rightarrow )= \sum _{D: e \in O\rightarrow D}[t^{-e}_{(O,D)} - t_{(O,D)}] \int f_{(O,D)}(t) dt \end{aligned}$$

(6)

whereas, for each destination $D$ the cumulated impact of the closure of a bridge belonging to the edge $e$ is

$$\begin{aligned} I_e(\rightarrow D)= \sum _{O: e \in O\rightarrow D}[t^{-e}_{(O,D)} - t_{(O,D)}] \int f_{(O,D)}(t) dt. \end{aligned}$$

(7)

Obviously,

$$\begin{aligned} I_e= \sum _O I_e(O\rightarrow ) = \sum _D I_e(\rightarrow D). \end{aligned}$$

Analogously, for each origin $O,$ we could define the temporal impact function at time t due to the closure of a bridge belonging to the edge $e,$

$$\begin{aligned} i_e(O\rightarrow ) (t)= \sum _{D: e \in O\rightarrow D}[t^{-e}_{(O,D)} - t_{(O,D)}] f_{(O,D)}(t) \end{aligned}$$

(8)

and the same for each destination $D,$

$$\begin{aligned} i_e(\rightarrow D) (t) = \sum _{O: e \in O\rightarrow D}[t^{-e}_{(O,D)} - t_{(O,D)}] f_{(O,D)}(t-t^{-e}_{(O,D)}). \end{aligned}$$

(9)

It should be noticed that the temporal impact on origins is estimated according to the value of the flow functions at time $t,$ the time at which people are starting their trips, while the temporal impact on the destinations is estimated according to the value of the flow functions at time $t-t^{-e}_{(O,D)}$, the time at which people are finishing their trips. Obviously, thanks to the daily periodicity of the functional flow data, $I_e(A\rightarrow )$ and $I_e(\rightarrow B)$ are the integrals of $i_e(A\rightarrow )$(t) and of $i_e(\rightarrow B)$(t), respectively.

4 Results

In this section we report the main results of the analysis of the sample of 290 bridges under investigation in Lombardy.

4.1 Results: the global index

Figures 4 and 5 show the value of $I_e$ for each bridge, computed using Eq. (4). Each bridge is coloured according to its global impact in terms of person-hours per day going from a minimum value of zero to a maximum of almost 10,000. There is one isolating bridge, coloured in blue, which is characterised by an infinite value due to the isolation of a centroid of the OD matrices. Comments related to this bridge will be reported in Sect. 4.3 and it will not be further analysed in Sects. 4.1 and 4.2.

Looking at the Figs. 4 and 5, it appears that the most critical bridges are located in the north side of the region in the provinces of Bergamo and Brescia, which are mainly in a mountain area with a sparse road network made of few main roads mostly located at the valley bottom with very time-consuming alternative paths. It is also possible to notice two bridges with an elevate impact, around 2000, in the south-west (province of Pavia) and in the south-est (province of Mantova) of the region, respectively. Both of them are over the river Po, the main river of Italy, which is flowing in a large flatland (i.e. the Po Valley) and characterized by a reduced number of crossing bridges. Moreover, the values of $I_e$ in the different provinces follow a strongly right-skewed distribution characterised by few bridges with high values and many bridges with low values. More precisely, there are only four bridges with an impact higher than 6000 and there are 27 bridges with a null impact. These null impact bridges are distinguished by the fact that our analysis of the OD of Regione Lombardia does not assign to them any trip during the day, presumably because these bridges are mostly located on the border areas of the region. In fact, even for the other bridges next to the regional borders the estimates of $I_e$ are not likely to be accurate, due to a lack of data in the OD matrices we are analyzing related to the road network and traffic flows outside Lombardy.

The ranking of the bridges according to $I_e$ is of great importance to the regional government since it allows to prioritize maintenance investments and the correct allocation of available resources.

Fig. 4

Map of Lombardy highlighting the 290 analysed bridges according to their global impact in terms of person-hours. The only isolating bridge is coloured in blue (color figure online)

Fig. 5

Distribution of the global impact (person-hours) of the 290 bridges for each province

4.2 Results: the spatio-temporal effects

We now characterize each bridge closure by its temporal impact during the day using the functions $i_e(t)$ defined in Eq. (5). Figure 6 depicts the daily person-hours impact functions for each bridge. The curves seem to follow a clear pattern with two peaks, respectively, one in the morning between 07:00 and 08:00 and another one in the afternoon between 18:00 and 19:00. The first peak appears more concentrated in time than the second one; this is the typical pattern in mobility data due to commuters mobility flows.

To better explore the behaviour of these curves, we observe their derivatives and, for each curve, we estimate when the maximum value is reached. Of the analysed 289 bridges, it appears that, excluding the 27 bridges which have a null impact during the entire day, there are 234 bridges having the highest peak in the interval between 07:27 and 08:03 (morning-peak) and 28 bridges in the interval between 18:32 and 18:55 (afternoon-peak). Results are reported in Fig. 6, bottom image, splitting the bridges in the three highlighted groups and showing their positions on the road network. These analyses turn out to be, for instance, useful to best handle the road works along the day by choosing accurately the time-slots in which do the maintenance for each bridge.

Fig. 6

Top Figure: the curves representing the temporal impact function for each bridge closure. Bottom Figure: the curves representing the temporal impact function for each bridge closure divided in three groups and their geographical disposition on the map of Lombardy

The next step is to show the spatial effects due to the closure of each bridge. Illustrative examples are those reported in Figs. 7 and 9, related to two specific bridges: the first one is the most impacting one among the 234 morning-peak bridges, while the second bridge is the most impacting among the 28 afternoon-peak bridges. Results are obtained using the indicators $I_e(O\rightarrow )$ and $I_e(\rightarrow D),$ introduced in Eqs. (6) and (7) respectively.

Figure 7 shows the spatio-temporal effects due to the closure of the most critical morning-peak bridge: on top, the selected bridge is highlighted together with the function $i_e$ quantifying the temporal impact of its closure; at the bottom, the spatial impacts $I_e(O\rightarrow )$ and $I_e(\rightarrow D)$ for all origins and destinations are reported. The range of values goes from no impact to a maximum of 1824 person-hours per day. Results reveal a symmetry between origins and destinations, which in fact appear to be interchangeable. This is likely due to the fact that the selected bridge is on a double way road on which people are used to pass both in the morning going to work and in the afternoon coming back home. Indeed, $i_e$ follows the typical commuting signature, with a sharp peak in the morning and a gentler hill in the late afternoon. Focusing on the spatial effects, it is evident that the most affected areas are close to the bridge, whereas the impact decreases moving away from the bridge. However, some of the impacted origins and destinations are very far from the selected bridge revealing an impact which is geographically spread over the region. It is also possible to explore how the spatial effects vary within the day. For instance, Fig. 8 shows the spatial effects on both origins and destinations in the time intervals 7:00–8:00, 12:00–13:00 and 18:00–19:00. These are obtained by integrating the functions $i_e(O \rightarrow )$ and $i_e(\rightarrow D)$ defined in (8) and (9), on the time intervals $\tau _1=(7,8)$, $\tau _2=(12,13)$ and $\tau _3=(18,19)$. Each area is coloured according to its spatial impact going from no impact to a maximum value of 370 person-hours. It can be observed that the impacts during the lunch break are lower than in the rush hours for all origins and destinations. Moreover, focusing on the rush hours it is evident a loss of symmetry between origins and destinations. For example, at 7:00–8:00 one might notice that the origins on the north of the bridge have an higher impact than the destinations while the origins on the south have a lower one. At 18:00–19:00, instead, the situation seems just the opposite.

Figure 9 shows the spatio-temporal effects due to the closure of the most critical afternoon-peak bridge: on top, the selected bridge is highlighted together with the temporal impact function of its closure; at the bottom, the spatial impacts on both origins and destinations are reported. The range of values goes from no impact to a maximum of 476 person-hours per day. Results reveal a clear difference between the impacted origins, all on the west of the bridge, and the impacted destinations, all on the east of the bridge. This is due to the fact that the selected bridge is on a one way road going from west to east. Looking at the temporal impact function, the afternoon peak appears to be higher than the morning peak, probably due to the fact that people moving on this road are mostly commuters coming back home after going west to work in the morning. Moreover, even in this case, results reveal that the most affected areas are close to the bridge, whereas the impact decreases moving away from the bridge.

These valuable information on the spatio-temporal effects of a bridge closure can be passed—before the bridge closure—to the stakeholders of the affected origins and destinations. Moreover the same information can be instrumental in optimizing the road maintenance schedule. For example, knowing the most impacting hours of the day for each bridge closure, road works can be planned accurately by choosing the time-slots in which to do the maintenance work or by opening and closing the lanes of the road accordingly to mitigate the effects of its closure.

Fig. 7

Top: the selected bridge on the road network of Lombardy and its temporal impact function. Bottom: the spatial impacts of the bridge closure, highlighted with a blue point, on both origins and destinations (color figure online)

Fig. 8

The spatial impacts (in terms of person-hours) of the bridge closure on both origins and destinations are reported in the time intervals 7:00–8:00, 12:00–13:00 and 18:00–19:00

Fig. 9

Top: the selected bridge on the road network of Lombardy and its temporal impact function. Bottom: the spatial impacts of the bridge closure, highlighted with a blue point, on both origins and destinations (color figure online)

4.3 The isolating bridge

Among the 290 analysed bridges there is one isolating link causing a disconnection of the road network and the consequent impossibility to travel between all origin-destination pairs. This bridge has therefore an infinite global index $I_e$ and turns out to be the most critical bridge of the road network belonging to our sample. Specifically, this bridge closure causes the isolation of one mobility area, preventing the travels of 1200 people unable to leave that origin or reach that destination. Figure 10, on the left, depicts the position of the isolating bridge, the isolated area and its centroid.

To go deeper in this issue, we look at this isolating bridge from a spatio-temporal perspective by displaying both the two flow functions accounting for the unsatisfied mobility demand, in and out, along time and the affected mobility areas. For the trips flowing out of the isolated centroid $IC$, we sum the flow functions $f_{(IC,D)}(t)$ with respect to all destinations $D$ different from $IC,$ thus obtaining an estimate over time of the unsatisfied mobility demand from $IC$ equal to $\sum _{D \not = IC} f_{(IC,D)}(t)$. The total number of trips over the day flowing out of $IC$ and made impossible by the bridge closure is naturally $\sum _{D \not = IC} \int f_{(IC,D)}(t) dt,$ while, for any $D,$ the integral $\int f_{(IC,D)}(t) dt$ estimates the total number of trips from $IC$ to destination $D.$ Analogous estimates are obtained for the unsatisfied mobility demand flowing in $IC.$ Figure 10, on the right, depicts the two flow functions estimating the unsatisfied in and out mobility demands for $IC.$ Outgoing flows reveal a morning peak at 7:00, while incoming flows reveal an afternoon peak at 18:00. Figure 11 shows both the impacted origins and the impacted destinations. In details, the mobility areas are coloured according to the number of people leaving from or going to the isolated centroid over the entire day. In addition to a perfect symmetry among origins and destinations, the figure reveals that the affected areas are all close to $IC$ with the exception of two zones in the south of Lombardy.

Fig. 10

Left: the isolating-bridge, blue point, the isolated area, in dark red, and its centroid in black. Right: the flow functions describing the unsatisfied in and out mobility demands for the isolated centroid (color figure online)

Fig. 11

The impacted origins, on the left, and the impacted destinations, on the right. The isolated area is coloured in blue (color figure online)

5 Simultaneous closure of two or more bridges

The results reported in Sect. 4 show the socio-economic impacts of the closure of a single bridge. However, the methodology developed in Sect. 3 is flexible and ready to be applied to the evaluation of the impact due to the simultaneous closure of more than one bridge.

Assume that a specified set of $N \ge 1$ bridges are simultaneously closed; each of them singles out an edge belonging to the set $E=\{e_1, ..., e_K\}, \; 1\le K \le N$. Then, any couple of mobility zones $O$ and $D$ is affected by an increase in travel time equal to $t^{-E}_{(O,D)} - t_{(O,D)}$, where $t^{-E}_{(O,D)}$ is the travel time of the shortest time path connecting $O$ to $D$ after the removal of the edges in the set $E$ from the road network data model. To measure the impact of the simultaneous closure of the N bridges, we weight each time delay by the number of trips it affects and we define a global index generalizing that defined in Eq. (4) as follows:

$$\begin{aligned} I_E= \sum _{(O,D)} [t^{-E}_{(O,D)} - t_{(O,D)}] \int f_{(O,D)}(t) dt . \end{aligned}$$

(10)

A natural issue is to compare the index $I_E,$ quantifying the total impact due to the simultaneous closure of the N bridges, with the sum of the global indexes quantifying the impact of the single closure of each of the edges in the set $E$, i.e. $\sum _{k=1}^{K}I_{e_k}$ (we are assuming that if two or more bridges belong to the same edge, they will be closed together). Depending on the the location of the $N$ bridges on the road network three cases may occur:

• super-additive effect: $I_E>\sum _{k=1}^{K}I_{e_k};$

• sub-additive effect: $I_E<\sum _{k=1}^{K}I_{e_k};$

• additive effect: $I_E=\sum _{k=1}^{K}I_{e_k}.$

The last scenario is the less interesting and it happens when the selected bridges are far away one from the other and they do not interact in the shortest path trips computed over the road network and connecting origins with destinations. More interesting are the first and the second scenario: the super-additive effect identifies set of bridges that should not be simultaneously closed, while the sub-additive effect indicates set of bridges which is advisable to close together. Illustrative examples are the two different couples of bridges reported in Figs. 12 and 13 for which we observe a super-additive effect and a sub-additive effect respectively. Figure 12 shows both the single global indexes $I_{e_1}$ and $I_{e_2}$ defined by Eq. (4) and quantifying the impacts due to the closure of the two bridges one-at-the-time, and the global index $I_{E=\{e_1,e_2\}}$ quantifying the impact due to their simultaneous closure, as defined in Eq. (10). The super-additive effect is evident and it warns against the simultaneous closure of the two bridges. Figure 13 shows $I_{e_1}, I_{e_2}$ and $I_{E=\{e_1,e_2\}}$ for a different couple of bridges. In this case a sub-additive effect is evident, suggesting their simultaneous closure, due to the fact that the two bridges lie on consecutive segments of a road.

These analyses may be relevant to assist decision makers in managing their interventions for the maintenance of the road infrastructures: comparing the impact scenario resulting from the simultaneous closure of more bridges with that occurring when the same bridges are closed one-at-the-time might be relevant for scheduling the road works. However, designing the optimal schedule for the sequential closure of set of bridges is beyond the scope of this paper and will be the object of future work.

Fig. 12

Example of a super-addictive effect

Fig. 13

Example of a sub-addictive effect

6 Uncertainty quantification analysis

The results reported in Sect. 4 measure for each bridge the impact of its closure to the movement of people by means of a global index which can be used for ranking. However, these results lack of a quantification of uncertainty and a robustness analysis which may be relevant to assist decision makers in prioritizing their interventions and correctly allocate the available resources. Therefore, in this section, we make a first attempt at uncertainty quantification, a topic that has yet to be addressed in the literature related to the closure of road infrastructures. We leverage on an iterative simulation which we now summarily describe.

For 1000 iterations:

• 1. we perturb the OD input data;

• 2. we estimate the global index for each bridge closure using Eq. (4) (whose unit of measure is person-hours);

• 3. we compute the ranking of the bridges (from the most impactful to the lowest one) according their global indexes.

Hence, as output of this procedure, for each bridge we obtain 1000 values of the global index measuring the impact of its closure—i.e. the distribution of the global index for the bridge under perturbation of the input data—and, correspondingly, 1000 different rankings.

In detail, to perturb the input OD count data, at each iteration of the simulation, for each couple $(O,D)$ we randomly and independently increase or decrease the total daily number of trip from O to D of a percentage between 0 and 5%, multiplying the total by ($1+p$) with $p$ uniformly distributed in $[-.05,+.05].$ Notice that the expected total number of daily trips in the perturbed OD matrices is the same as the total number recorded in the original and non perturbed OD matrices.

To investigate uncertainty w.r.t. the global index associated to each bridge and estimate the variabiality of the estimator, in Fig. 14 we display the distributions of the global indexes obtained after perturbation, each box-plot representing a bridge. Bridges are ordered, from left (the less impactful) to right (the most impactful) using the ranking obtained when the input data are the original non perturbed OD matrices. In detail, on the left of the figure we display the results for all the analysed bridges, while on the right we focus on the most impactful 10 bridges. It is immediate to observe that the variability expressed by all box-plots is negligible, and the index numbers reflecting the impact of bridge closure are not highly affected by a moderate perturbation of the OD input data, as the one we are implementing. Moreover, the final ranking of the most impactful bridges is only slightly affected. To test robustness of the final ranking for the most impactful bridges, we compute the number of times each of the first 10 most impactful bridges undergoes a change of position with respect to the ranking obtained with the original non perturbed OD input data. In fact, a change of position happens less than 1% of the times, and this is always due to bridges ranked as 7th and 8th swapping their positions. More in general, focusing on the entire sample of bridges, we observe that less than one-third of the bridges undergoes a change of position and that almost 99% of the bridges that change position do not move of more than two positions. These results indicate that the final ranking obtained with the original non perturbed OD matrices has a low degree of uncertainty and is very robust with respect to a moderate perturbation of the OD input data.

Fig. 14

Distribution of the global indexes for each bridge closure

7 Conclusions

This paper discusses methodologies to assess critical infrastructures in a road network, stimulated by the analysis of a sample of bridges in the region of Lombardy, Italy. Specifically, we defined and estimated the socio-economic impacts of bridge closures to the movement of people with the purpose of helping decision-makers in prioritizing their interventions for maintaining and repairing infrastructure segments.

From a methodological point of view, we provided different levels of impact assessments, evaluating the impact of a bridge closure by means of a global index (which can be used for ranking) and focusing on its spatio-temporal effects. From a temporal point of view, we evaluated how the impact of a bridge closure varies according to the time of the day; from a spatial point of view, we identified the areas most affected by the closure of the bridge. This has been obtained by modeling a road network as a time-varying graph with fixed nodes and with functions as weight of the edges.

The methodology has been tested on the real-scale network of the road system of Lombardy in Italy, analysing the impact of the closure of 290 different bridges. Results have revealed the most critical bridges of the region, highlighting for each bridge both the most impacting hours of the day and the most impacted mobility areas of the region. These results should be useful for risk management, if the goal is to anticipate the damage on the users caused by maintenance interventions on road infrastructures. Moreover, in a world where financial resources are limited, knowing the most critical road infrastructures is essential to prioritise maintenance investments and for the correct allocation of available resources.

Finally, the proposed approach has been applied to evaluate the impacts of the simultaneous closure of more than one bridge. Indeed, the developed methodology has proved to be flexible, scalable and repeatable, thus ready to be applied to other realities in other countries.