A multivariate test for detecting fraud based on Benford’s law, with application to music streaming data

Abstract

Benford’s law became a prevalent concept for fraud and anomaly detection. It examines the frequencies of the leading digits of numbers in a collection of data and states that the leading digit is most often 1, with diminishing frequencies up to 9. In this paper we propose a multivariate approach to test whether the observed frequencies follow the theoretical Benford distribution. Our approach is based on the concept of compositional data, which examines the relative information between the frequencies of the leading digits. As a result, we introduce a multivariate test for Benford distribution. In simulation studies and examples we compare the multivariate test performance to the conventional chi-square and Kolmogorov-Smirnov test, where the multivariate test turns out to be more sensitive in many cases. A diagnostics plot based on relative information allows to reveal and interpret the possible deviations from the Benford distribution.

1 Introduction

Nowadays, Benford’s law is a well established concept for detecting fraudulent activities in economics, politics and natural sciences. Its application ranges from forensic accounting to auditing or investigating election and insurance fraud (Nigrini and Wells 2012; Nigrini and Miller 2007; Deckert et al. 2011; Maher and Akers 2002). In the underlying paper, we examine the frequencies of the first as well as the first two digits of a number. The resulting Benford distribution is defined as follows, see Benford (1938):

$$\begin{aligned} b_j = \log \left( 1+\frac{1}{j} \right) , \end{aligned}$$

(1)

where “log” refers to the base 10 logarithm, for $j=1,\ldots ,9$ in case of analyzing the first digits, or $j=10,\ldots ,99$ if the first two digits are analyzed. In either case, the sum of $b_j$ over all j is 1, and thus $b_j$ represents the theoretical probability of occurrence of the j-th digit.

The empirical distribution is obtained from a sample with N numbers, and by recording the frequencies $x_j$ of the first (two) digits of these numbers. If the frequencies follow Benford’s law, they should be close to the theoretical frequencies $N b_j$. A test for determining whether there is a significant difference between the theoretical and observed frequencies in one or more categories is the chi-square ($\chi ^2$-) test. The test statistic is defined as

$$\begin{aligned} \chi ^2 = \sum _j \frac{(x_j-N b_j)^2}{N b_j} , \end{aligned}$$

(2)

where the sum is over all j in $\{1,\ldots ,9\}$ in case of a first-digit test, or over j in $\{10,\ldots ,99\}$ for the first-2-digit test. The critical value is the quantile $1-\alpha$ of a chi-square distribution with $D-1$ degrees of freedom, where $D=9$ for 1-digit, and $D=90$ for 2-digit tests, and $\alpha$ is the significance level. Another popular test with a higher power in this context is the Kolmogorov-Smirnov (KS-) test, with the test statistic

$$\begin{aligned} D = \sup _j \left| \sum _{i=1}^j \left( \frac{x_i}{N} - b_i\right) \right| . \end{aligned}$$

(3)

The p-value can be obtained by simulating under the null hypothesis. In more detail, N numbers are generated from a Benford distribution, and the resulting digit frequencies are used in the KS-test test to result in a value of the test statistic. This is replicated many times (in our applications 10.000 times), and the p-value is obtained by comparing with the value of the test statistic from the original digit distribution. We refer to Cinelli (2018) for more details and alternative tests.

In this paper we propose a multivariate approach to test whether observed digit frequencies correspond to Benford’s law or not. This approach makes use of the concepts of compositional data analysis, a methodology that has been developed mainly in the context of geochemistry, but is widely used nowadays also in other disciplines, such as economics, ecology, bioinformatics, official statistics, etc. (Aitchison 1986; Baxter 1999; Quinn et al. 2018; Fry et al. 2000; Larrosa 2003). Sect. 2 provides a brief introduction into these concepts, broken down to the problem at hand. Based on these ideas, Sect. 3 introduces a multivariate test for Benford distribution. Up to the best of our knowledge, this is the first multivariate treatment of the Benford problem. Section 4 investigates the performance of the new test on simulated data, and compares with the results from a $\chi ^2$-test and a KS-test. Since the practitioner also wants to know in which digits the data at hand might deviate from a Benford distribution, we introduce a diagnostic plot in Sect. 5. Section 6 demonstrates the developed tools at some real data examples from the literature and from digital music streaming, and the final Sect. 7 summarizes and concludes.

2 Compositional data analysis

In contrast to traditional ways of data analysis, compositional data analysis focuses on analyzing relative rather than absolute information. The most established approach for this purpose is called log-ratio methodology for compositions (Aitchison 1986; Pawlowsky-Glahn et al. 2015), and it is based on logarithms of ratios between the variables $x_1,\ldots ,x_D$ forming the composition. The variables – in this context usually called compositional parts – are in our case the frequencies of the first (two) digits, and the interest is in analyzing log-ratios of the digit frequencies, thus values $\ln (x_j/x_k)$ for two compositional parts $x_j$ and $x_k$. Here, “ln” refers to the natural logarithm, but a base 10 logarithm could be used as well.

Log-ratios do not depend on the number of values underlying the digit distribution, if we assume that the relative frequencies $x_j/N$ do not change with different N. This principle is also called scale invariance, and it is one of the main principles of the log-ratio approach (Aitchison 1986). However, it is clear that with increasing N, the relative frequencies get closer to the theoretical Benford values $b_j$, and thus it will be important that N enters a test on Benford distribution somehow. We will come back to this issue in Sect. 3.

It turns out that all possible pairwise log-ratios $\ln (x_j/x_k)$, for $j,k \in \{1,\ldots ,D\}$ can be represented in a $D-1$-dimensional real Euclidean space (Filzmoser et al. 2018). It has been shown that there is a convenient way to construct $D-1$ coordinates in this space by making use of the log-ratio information (Egozcue et al. 2003), and the resulting coordinates are called isometric log-ratio (ilr) coordinates. One out of infinitely many possibilities for such a coordinate system are so-called pivot coordinates (Filzmoser et al. 2018), defined as ${\mathbf {z}}=(z_1,\ldots ,z_{D-1})'$, with

$$\begin{aligned} z_{j}=\sqrt{\frac{D-j}{D-j+1}}\,\ln \frac{x_{j}}{\root D-j \of {\prod _{k=j+1}^D x_{k}}} \quad \text{ for } \quad j=1,\ldots ,D-1 , \end{aligned}$$

(4)

forming an orthonormal coordinate system. A closer look at $z_1$, for instance, shows that

$$\begin{aligned} z_1=\sqrt{\frac{1}{D(D-1)}} \left( \ln \frac{x_1}{x_2}+\ln \frac{x_1}{x_3} + \ldots + \ln \frac{x_1}{x_D} \right) , \end{aligned}$$

which indeed involves relative information, here in terms of an aggregation of all (different and relevant) pairwise log-ratios with the first part $x_1$. One can also see that information about $x_1$ is only contained in coordinate $z_1$, but in none of the other coordinates. Thus, $z_1$ can be interpreted in terms of $x_1$, but it is not so straightforward to find an interpretation for the other coordinates.

The orthonormal basis vectors corresponding to pivot coordinates are

$$\begin{aligned} {\mathbf {v}}_{j}=\sqrt{\frac{D-j}{D-j+1}}\left( 0,\ldots ,0,1, -\frac{1}{D-j},\dots ,-\frac{1}{D-j}\right) ' \end{aligned}$$

(5)

for $j=1,\dots ,D-1$, with $j-1$ zero entries. Collecting these basis vectors as columns in the matrix ${\mathbf {V}}=({\mathbf {v}}_{1},\ldots ,{\mathbf {v}}_{D-1})$ of dimension $D\times (D-1)$ allows to represent pivot coordinates as so-called centered log-ratio (clr) coefficients ${\mathbf {y}}=(y_1,\ldots ,y_D)' ={{\mathbf {V}}}{{\mathbf {z}}}$, where

$$\begin{aligned} y_j=\ln \frac{x_j}{\root D \of {\prod _{k=1}^Dx_k}} \end{aligned}$$

(6)

for $j=1,\ldots D$. The denominator in Equation (6) is the geometric mean, and it is the same for all j. Note again that $y_j$ can be represented by aggregated pairwise log-ratios, and it is not difficult to see that $y_1=\sqrt{(D-1)/D}~z_1$ (Filzmoser et al. 2018). This link, however, only exists to the first pivot coordinate $z_1$, and thus $y_1$ has an equivalent interpretation, containing all relative information about $x_1$. Since $x_1$ is involved in the geometric mean, also the remaining clr coefficients contain information of $x_1$ (in fact also of every other clr coefficient), and thus it is no longer possible to extract all relative information about one compositional part in only one clr coefficient. The clr coefficients are not even forming a basis system, because $y_1+ \ldots +y_D=0$, and this singularity may cause difficulties for methods where full rank is required (Filzmoser et al. 2018).

In the next section we will introduce a multivariate test which makes use of relative information, and also requires the inverse of the correlation matrix. Thus, we will represent the compositions in ilr coordinates, and our choice for this purpose are pivot coordinates. In Sect. 5 we will introduce diagnostics plots, focusing on the interpretability of the results, and thus we will present the results by clr coefficients.

3 Multivariate Benford test

A representation of the digit distribution in isometric logratio coordinates leads to multivariate information, and thus a multivariate statistical test for Benford distribution needs to be developed. According to Equation (1), the Benford distribution results in probabilities for each digit, which are collected in the D-dimensional vector ${\mathbf {b}}$, for the digits 1 to 9 (or 10 to 99). Denote the pivot coordinate representation of ${\mathbf {b}}$ by ${\mathbf {z}}_{{\mathbf {b}}}$, with length $D-1$.

Consider a new data set which needs to be tested according to Benford’s law. The data set consists of N numbers, and tabulating the data into the leading digits 1 to 9 (or 10 to 99) results in the frequencies collected in the D-dimensional vector ${\mathbf {x}}$. After using the same ilr coordinate representation as before, we obtain a vector ${\mathbf {z}}$ of length $D-1$, representing the composition in the real Euclidean space. The task is to compare ${\mathbf {z}}$ and ${\mathbf {z}}_{{\mathbf {b}}}$ within a multivariate statistical test.

A conventional test for this purpose would be Hotelling’s $T^2$-test, which assumes an underlying multivariate normal distribution with a certain mean ${\varvec{\mu }}$ and covariance $\mathbf {\Sigma }$, testing the hypothesis if ${\varvec{\mu }}={\varvec{\mu }}_0$, for some ${\varvec{\mu }}_0$ under consideration (Anderson 2003). In our case, ${\varvec{\mu }}_0$ would be equal to ${\mathbf {z}}_{{\mathbf {b}}}$, and ${\varvec{\mu }}$ would correspond to the random vector which we observe as realization ${\mathbf {z}}$. However, it is unclear how $\mathbf {\Sigma }$ could be determined. A theoretical derivation of the covariance of the Benford distribution expressed in coordinates seems infeasible. A further difficulty is that the test statistic of Hotelling’s $T^2$-test includes the sample size, since usually ${\varvec{\mu }}$ is estimated as the arithmetic mean from a sample. Here, we only know that the underlying number of data values is N, leading to only one “sample” with the digit distributions. Of course, N should play an important role in a test, because more underlying data values will yield less uncertainty.

We thus will consider a sampling-based test procedure, which is made up of two steps. In Step 1 we estimate the covariance matrix $\mathbf {\Sigma }$ out of a large number of simulated digits sampled from a Benford distribution. The corresponding correlation matrix is decomposed and used as an input for the test proposed in Step 2. Thus, Step 1 results in the following procedure:

• 1a. Simulate observations ${\mathbf {b}}_i$, for $i=1,\ldots ,100.000$, following a Benford distribution. This is done by taking the frequency distributions of the first (or first two) digits of the values $10^{u_l}$, where $u_l$ are random numbers from a uniform distribution on [0, 1], and $l=1,\ldots ,100.000$ (Hill 1995; Berger and Hill 2011).

• 1b. Represent ${\mathbf {b}}_i$ in pivot coordinates, and estimate the sample covariance matrix ${\mathbf {S}}$ from these transformed observations. Denoting ${\mathbf {L}}=\text{ diag }({\mathbf {S}})$ as the diagonal matrix with the sample variances in the diagonal, the sample correlation matrix is ${\mathbf {R}}={\mathbf {L}}^{-1/2}{\mathbf {S}}{\mathbf {L}}^{-1/2}$.

• 1c. Perform a spectral decomposition of ${\mathbf {R}}$ as

  $$\begin{aligned} {\mathbf {R}}=\mathbf {GAG}' \end{aligned}$$

  with the eigenvectors ${\mathbf {G}}=({\mathbf {g}}_1,\ldots ,{\mathbf {g}}_{D-1})$ of ${\mathbf {R}}$, and the diagonal matrix ${\mathbf {A}}$ with the corresponding eigenvalues $a_1,\ldots ,a_{D-1}$. Compute a rank-k approximation of the inverse of ${\mathbf {R}}$ as

  $$\begin{aligned} {\mathbf {R}}_k^{-1}={\mathbf {G}}_k {\mathbf {A}}_k^{-1} {\mathbf {G}}_k' \end{aligned}$$

  with ${\mathbf {G}}_k=({\mathbf {g}}_1,\ldots ,{\mathbf {g}}_k)$ and ${\mathbf {A}}_k^{-1}=\text{ Diag }(1/a_1,\ldots ,1/a_k)$, for $k\in \{1,\ldots ,D-1\}$.

Step 1 is only carried out once, and it is not yet related to a frequency distribution under investigation. This step provides the multivariate relationships between the digit frequencies if they originate from a Benford distribution.

The actual test consists of the following procedure, formulated as Step 2:

• 2. For testing the null hypothesis using the realization ${\mathbf {z}}$, where ${\mathbf {z}}$ is based on N numbers, simulate $n=1.000$ observations ${\mathbf {b}}_i$ as in Step 1a, based on N random numbers. Express these values in pivot coordinates, yielding observations ${\mathbf {z}}_{{\mathbf {b}}_i}$, and compute the values

  $$\begin{aligned} T_i=({\mathbf {z}}_{{\mathbf {b}}_i}-{\mathbf {z}}_{{\mathbf {b}}})'{\mathbf {L}}^{-1/2}{\mathbf {R}}_k^{-1} {\mathbf {L}}^{-1/2}({\mathbf {z}}_{{\mathbf {b}}_i}-{\mathbf {z}}_{{\mathbf {b}}}) \end{aligned}$$

  (7)

  for $i=1,\ldots ,n$, and

  $$\begin{aligned} T=({\mathbf {z}}-{\mathbf {z}}_{{\mathbf {b}}})'{\mathbf {L}}^{-1/2} {\mathbf {R}}_k^{-1}{\mathbf {L}}^{-1/2}({\mathbf {z}}-{\mathbf {z}}_{{\mathbf {b}}}). \end{aligned}$$

  (8)

  The p-value is defined as the relative frequency of values $T_i$ exceeding T, thus as

  $$\begin{aligned} \# \{T_i> T,~ i=1,\ldots ,n\} / n \end{aligned}$$

  (9)

If ${\mathbf {z}}={\mathbf {z}}_{{\mathbf {b}}}$ in Equation (8), the resulting p-value is 1 and the null hypothesis will never be rejected. For a manipulated frequency distribution, T is supposed to be larger than $T_i$ in Equation (7) for many or most observations, yielding a small p-value. It is important for the accuracy of the test that the estimated correlation matrix ${\mathbf {R}}$ is close to the theoretical one, and thus the numbers used in Step 1 to generate the observations and to estimate the covariance matrix should be chosen sufficiently high.

This test does not depend on distributional assumptions, and it accounts for the number of values N used for constructing the digit distribution. Since only relative information is used in the log-ratio approach, ${\mathbf {z}}$ and ${\mathbf {z}}_{{\mathbf {b}}_i}$, both constructed with N observations, can be directly compared to ${\mathbf {z}}_{{\mathbf {b}}}$ which is based on the probabilities for the Benford distribution. The scaling in Equations (7) and (8) by the square-root of the diagonal elements of ${\mathbf {L}}$ gives the same importance to each pivot coordinate. Using a reduced rank for the inverse correlation matrix allows to focus on differences in a sub-space rather than in the full $D-1$-dimensional space, which may lead to higher accuracy in case of only small deviations from the Benford distribution.

As a final remark we emphasize that the principle of permutation invariance of the log-ratio approach is not of importance in this context. This principle states that any permutation of the compositional parts should give the same results (Aitchison 1986). Here we assume that the digit distribution is available in the natural order of the digits. Moreover, it is important that for the coordinate representations of the simulated, the empirical and the theoretical digit distributions always the same ilr coordinates are used. In all our numerical experiments we used pivot coordinates for this purpose, but another choice is also possible. When sticking to pivot coordinates, it is not necessary to repeat the simulations in Step 1a-c for carrying out a new test, but one can simply use the obtained sample correlation matrix ${\mathbf {R}}$, with the decomposition from Step 1c. Thus, for the hypothesis test of a new digit distribution, only Step 2 needs to be performed.

4 Numerical experiments

In the following experiments we consider different scenarios of digit manipulations. In all scenarios, we start from a frequency distribution according to the Benford distribution, and then manipulate the frequencies. We compare the performance of the $\chi ^2$-test and the KS-test with the multivariate test introduced in Sect. 3, which is called M-test in the following.

Figure 1 shows an example of two modifications of data values. In both examples, the number of underlying data values was $N=500$, which leads to Benford frequencies of 151, 88, 62, 48, 40, 33, 29, 26 and 23 for the digits 1 to 9. In the left plot of Fig. 1, the Benford frequencies have been modified by reducing the frequencies of digit 1 and adding frequencies to digit 9, in steps of one. In total, 29 such modifications are done, one after the other, and after the 29th modification, the Benford frequencies are 122, 88, 62, 48, 40, 33, 29, 26 and 52. The horizontal axis represents the single steps of the modifications. In each step, the $\chi ^2$-test, the KS-test, and the M-test with rank $k=1,\ldots ,8$ are carried out, and the corresponding p-values are shown, together with a horizontal line, representing the significance level of 5%. It can be seen that the $\chi ^2$-test rejects after 18 modifications, and the KS-test after 26 modifications. The performance of the M-test depends on the rank k used to compute the inverse of the correlation matrix. For $k=1$, the M-test rejects after 15 steps, while for $k=8$ it rejects after 26 steps.

The right plot of Fig. 1 follows the same idea, but the modifications are done from digit 9 to digit 1, starting again from the Benford frequencies 151, 88, 62, 48, 40, 33, 29, 26 and 23. Obviously, after the 23rd modification, the frequency for digit 9 is zero. In the subsequent steps, we keep this frequency at zero, but continue increasing the frequency for digit 1, until 180. Since the M-test cannot work with frequencies of zero, we replace these values by random uniformly distributed values in the interval [0.5, 1]. Depending on k, the M-test rejects after the 11th-13th modification, so even before zeros had to be replaced, while the $\chi ^2$-test rejects only after step 18, and the KS-test after step 27.

Fig. 1

Starting from the Benford frequency distributions, frequencies are modified by moving step-by-step (horizontal axes) one count from digit 1 to 9 (left plot) and from 9 to 1 (right plot), respectively. The plots show the corresponding p-values of the M-test using different rank k (denoted by $M\_k$), the $\chi ^2$-test, and the KS-test, together with a horizontal line for the significance level 0.05

The above experiments are extended in the following by modifying the number N of values underlying the Benford frequency distribution. As before, the frequencies are modified step-by-step by one count. Moreover, additional scenarios are considered to modify the frequencies of Benford, such as moving frequencies from digit 1 to 9, from 9 to 1, from 1, 2, 3, 4 to 6, 7, 8, 9, etc., see Table 1, top two rows. The results of these experiments are shown in the rows of Table 1. The row blocks represent different numbers N, and the values in the table show at which manipulation step the tests lead to significance according to a level of 0.05. For the M-test we report the range of values obtained for all ranks from $k=1,\ldots ,8$. In all experiments, $k=1$ or $k=2$ led to the smallest numbers, and $k=8$ to the biggest values.

The table shows that in almost all experiments, the M-test with small k leads to earlier detection of the manipulation than the $\chi ^2$-test and the KS-test. Bigger k usually leads to worse performance. For $N=100$ and manipulation from digit 9 to 1 we do not report results because of the low digit-9 frequencies. The bigger N, the more pronounced is the performance difference between the M-test (using small k) and the two alternative tests. The performance difference also depends on the type of manipulation. The most common type might be manipulations to digits 9, thus column 3 or 7 of the results. Note that a manipulation from digits 1 to 4 to digit 9 means that in each step the frequencies of digits 1-4 are reduced by one, and that of digit 9 is increased by four.

Table 1 Step-wise modifications of the Benford frequencies for different numbers of underlying values N, and different types of modifications of the digit frequencies (rows refer to these digits). Shown are the steps where the M-test, the $\chi ^2$-test, and the KS-test reach significance for the first time

Figure 2 shows two examples of manipulations in case of a two-digit Benford distribution. The left plot is based on a frequency distribution with $N=500$ numbers, and the Benford distribution has been modified by reducing step-by-step one count in the digits 90-99, and adding one count in the digits 10-19. The M-test results are computed for the ranks $k \in \{2,3,5,10,20,50,80,89\}$, referring to the abbreviations $M\_1$ to $M\_8$ in the plot legend. After the 2nd manipulation, the frequencies of digits 90-99 are already zero, and we keep them at zero also in the next manipulations, but add counts to digits 10-19. Thus, the total number of counts changes, and the manipulation only gets more extreme in the first digits. This is also the reason of the big variability in the results for the M-test, depending on k. However, for small k, this test already rejects after the second manipulation, the KS-test after 4 steps, and the $\chi ^2$-test rejects only after 15 steps. Table 2 also shows this particular case, and the symbol “*” refers to this problem with zero frequencies.

The right plot of Fig. 2 is for $N=50.000$ and a manipulation from the digit range 10-54 (reduction) to 55-99 (increase). Again, with a small rank k one can obtain significance much earlier, already after 7 manipulations; the same happens for the KS-test, while the $\chi ^2$-test rejects only after 23 steps.

Fig. 2

Starting from the Benford frequency distributions for the first 2 digits, frequencies are modified by moving step-by-step (horizontal axes) one count from digits 90:99 to 10:19 (left plot) and from 10:54 to 55:99 (right plot), respectively. The plots show the corresponding p-values of the M-test with different values of k, the $\chi ^2$-test, and the KS-test, together with a horizontal line for the significance level 0.05

Similar as in Fig. 2, Table 2 shows results also for other values of N, and for other types of manipulations (top two rows). There are no results reported if the frequencies were too low for the manipulation, and the symbol “*” indicates that frequencies already reached zero with this reported number. The numbers in the table refer to the number of manipulation steps where significance was obtained for the first time. In case of the M-test, the indicated range refers to the rank k, taken in the interval 2-89. Here, $k=2$ always gave the smallest value, and $k=89$ the largest. The only cases where the $\chi ^2$-test is competitive to the M-test or sometimes even gave better results are manipulations where frequencies from a range of digits are reduced, and the frequency of one particular digit is increased, here from 10-39 to 89, and from 80:99 to 19. In all other cases, the M-test is superior, especially with small k. The KS-test gives comparable results to the M-test in case of large ranges of manipulations (last two columns of the table), and for smaller N. For bigger N, the M-test usually outperforms the KS-test.

Table 2 Step-wise modifications of the Benford 2-digit frequencies for different numbers of underlying values N, and different types of modifications of the digit frequencies. Shown are the steps where the tests reach significance for the first time. For the M-test we report the range for the first significance depending on the rank k. In some situations, indicated by *, the digit frequency goes down to zero

In a final simulation study we simulate N digit frequencies from a Benford distribution, and replace a fraction of the N frequencies by digit frequencies derived from random uniformly distributed data. We call this fraction “contamination”, and the interest is again in comparing the test outcomes for different N and different levels of contamination. Every simulation setting is replicated 1,000 times, and we count for each test the proportion of rejections at a significance level of 0.05. For the M-test, only the results for the smallest rank ($k=1$ for 1-digit, $k-2$ for 2-digit) are reported.

Figure 3 shows the results of this study. The top row refers to experiments with the first digit, the bottom row to those with the first two digits. The different plots are for different N, and the horizontal axes show the level of contamination, starting from zero, thus from uncontaminated Benford data, up to a level of 0.5. The lines in the plots refer to the different tests, and the horizontal lines show the significance level 0.05. It can be seen that with zero contamination, all tests result in the correct size 0.05. Exceptions are for the M-test if N is small, which is due to the need to replace zero frequencies by positive values. The KS-test generally has a higher power than the $\chi ^2$-test, and with increasing N, the power of the M-test is very comparable to that of the KS-test.

Fig. 3

Simulation for the size and power of the tests, by adding contamination to the Benford distribution with uniform numbers. For the M-test, the smallest ranks have been taken: $k=1$ for first digit on top row, $k=2$ for first two digits on bottom row

5 Diagnostics

In Sect. 2 we have argued that clr coefficients are convenient for the interpretation, because they represent all relative information about a particular compositional part. Using the same notation as in Sect. 3, we consider a composition ${\mathbf {x}}$ and express it in pivot coordinates to obtain ${\mathbf {z}}$. This coordinate is centered and scaled in the same way as in Sect. 2, see Equations (7) and (8), and expressed in clr coefficients, i.e.

$$\begin{aligned} {\mathbf {y}}={\mathbf {V}}{\mathbf {L}}^{-1/2}({\mathbf {z}}-{\mathbf {z}}_b). \end{aligned}$$

(10)

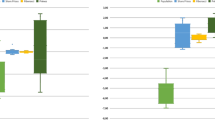
In the diagnostics plots in Figs. 4–7 we visualize the clr coefficients of the simulated Benford numbers ${\mathbf {b}}_i$, see Step 4 in Sect. 3, by connected gray lines. Further, we show the clr coefficients of those modified Benford distributions, where significance was first obtained by the M-test with $k=2$ (green solid line), the $\chi ^2$-test (blue dashed line), and by the KS-test (brown dot-dashed line). In particular, Fig. 4 shows the same scenario as in Fig. 1 left, with $N=500$ and modification of frequencies from digit 1 to 9. The $\chi ^2$-test was significant after 18 manipulations, the KS-test after 26, and the M-test with $k=2$ after 15. The corresponding frequency distributions are shown as clr coefficients in the left plot, and in terms of absolute frequencies in the right plot. The dashed lines correspond to the exact Benford distribution. The plots with clr coefficients show more clearly (and normed) the reduction in the 1st digit and the addition to the 9th digit.

Fig. 4

Diagnostics plots referring to the setting of Figure 1 (left). The gray lines show the simulated Benford data, and the green solid, blue dashed, and brown dot-dashed lines the modified data where the M-test with $k=2$, the $\chi ^2$-test and the KS-test, respectively, indicated significance for the first time. Left for clr coefficients, right for absolute frequencies

Figure 5 presents the diagnostics plots for the situation shown in Fig. 1 (right). Here, indeed the $\chi ^2$-test and the KS-test yielded significance only after much more pronounced modifications, compared to the M-test.

Fig. 5

Diagnostics plots referring to the setting of Fig. 1 (right). The gray lines show the simulated Benford data, and the green solid, blue dashed, and brown dot-dashed lines the modified data where the M-test with $k=2$, the $\chi ^2$-test and the KS-test, respectively, indicated significance for the first time. Left for clr coefficients, right for absolute frequencies

Even clearer differences between the three tests are seen in the diagnostics plots of Figs. 6 and 7, which correspond to the situations shown in Fig. 2 (left and right, respectively). In the first situation, the M-test with $k=2$ already gave significance after 2 manipulations, which is almost indistinguishable from the Benford distribution in the diagnostic plots. Also for the second situation (Fig. 7), the different performance of the tests gets clearly visible in the clr coefficients, where the $\chi ^2$-test required many more manipulations before yielding significance.

Fig. 6

Diagnostics plots referring to the setting of Fig. 2 (left). The gray lines show the simulated Benford data, and the green solid, blue dashed, and brown dot-dashed lines the modified data where the M-test with $k=2$, the $\chi ^2$-test and the KS-test, respectively, indicated significance for the first time. Left for clr coefficients, right for absolute frequencies

Fig. 7

Diagnostic plots referring to the setting of Fig. 2 (right). The gray lines show the simulated Benford data, and the green solid, blue dashed, and brown dot-dashed lines the modified data where the M-test with $k=2$, the $\chi ^2$-test and the KS-test, respectively, indicated significance for the first time. Left for clr coefficients, right for absolute frequencies

6 Examples

Fig. 8

Data set sino.forest ($N=772$) with financial statement numbers of Sino-Forest Corporation’s 2010 Report. Several irregularities have been identified in these statements. The p-value for the $\chi ^2$-test is zero, th KS-test gives a p-value of 0.48. The M-test yields 0.761 ($k=2$), 0.870 ($k=3$), 0.952 ($k=5$), 0.776 ($k=10$), 0.371 ($k=20$), 0.165 ($k=50$), 0.037 ($k=80$), 0.069 ($k=89$)

Fig. 9

Data set corporate.payment ($N=185.083$) with data of invoices from 2010 processed by a publicly traded utility company. Manipulations are clearly visible by a spike at 50, but also at 10, 11, 98, and 99. All p-values are zero

6.1 Examples from the literature

The R package benford.analysis (Cinelli 2018) contains several data sets with digit frequency distributions, where the underlying data have either been manipulated, or the frequency distributions are spoiled by considering only specific data subsets. All these data are explained in detail in Nigrini and Wells (2012). Here we just refer to the data files in the R package, present diagnostic plots, and report the test results, see Figs 8–14.

Fig. 10

Data set taxable.incomes.1978 ($N=150.760$) from 1978 with individual tax income reports in the US. A reduction of the taxable income leads to an increase of the digits 47, 48, 49, 97, and 98. All p-values are zero

Fig. 11

Data set lakes.perimeter ($N=248.607$) from a database reporting the perimeter of lakes with an area of at least 1 hectare. The perimeter range from 3 to 5 km dominates. All p-values are zero

Fig. 12

Data set census.2000_2010$pop.2000 ($N=3.137$) with population numbers in the US from 2000. The p-value for the $\chi ^2$-test is 0.521, for the KS-test it is 0.147. The M-test yields 0.125 ($k=2$), 0.202 ($k=3$), 0.424 ($k=5$), 0.348 ($k=10$), 0.146 ($k=20$), 0.568 ($k=50$), 0.317 ($k=80$), 0.395 ($k=89$)

The results from Fig. 8 refer to quite complex irregularities. Here, the $\chi ^2$-test clearly rejects Benford distribution, but the M-test only rejects with $k=80$ components – otherwise the p-value is even quite high. The KS-test does not reject. Figures 9–11 in contrast show very pronounced irregularities, partly also caused by constraints in the data selection, and all tests deliver p-values of zero. According to Nigrini and Wells (2012), the population data used in Figures 12–14 conforms to Benford’s law. Indeed, for the $\chi ^2$-test the p-values are exceeding 0.05. Also the M-test does not indicate significance, although it seems more sensitive than the $\chi ^2$-test. The KS-test rejects in the last example.

Fig. 13

Data set census.2000_2010$pop.2010 ($N=3.143$) with population numbers in the US from 2010. The p-value for the $\chi ^2$-test is 0.665, for the KS-test it is 0.258. The M-test yields 0.106 ($k=2$), 0.178 ($k=3$), 0.267 ($k=5$), 0.552 ($k=10$), 0.754 ($k=20$), 0.504 ($k=50$), 0.587 ($k=80$), 0.694 ($k=89$)

Fig. 14

Data set census.2009 ($N=19.509$) with population numbers in the US from 2009. The p-value for the $\chi ^2$-test is 0.092, for the KS-test it is 0.044. The M-test yields 0.177 ($k=2$), 0.108 ($k=3$), 0.213 ($k=5$), 0.220 ($k=10$), 0.273 ($k=20$), 0.505 ($k=50$), 0.365 ($k=80$), 0.165 ($k=89$)

6.2 Application for music streaming auditing

Music streaming has been increasing tremendously over the past few years. According to IFPI (International Federation of the Phonographic Industry), the digital music market covered a volume of 11.1bn US Dollars in 2018, which makes up 59$\%$ of the total music market (IFPI 2018). With the increasing amount of data related to music streaming and downloading, a strong urge arises for control and transparency, as “data provided to artists with royalty payments is often opaque and artists often do not understand the payments and accountings they receive.” (Rethink Music 2015)

The Recording Industry Accounting Practices Act was a response to the continuing outcry against royalty accounting practices in the music business and granted artists a statutory right to audit their record labels (Sorensen 2005). When it comes to auditing and forensic accounting, Benford’s law is an established tool and even accepted by courts of law (Nigrini 2019; Pomykacz et al. 2017).

In this section we illustrate a possible use case for music streaming auditing. Therefore, we examine real streaming accounting data provided by Rebeat Digital GmbH, an Austria based music distribution company.

For this purpose we analyze the download revenues of a sample of 300 music titles that are featured on different DSPs (Digital Service Providers). The data base goes back to the year 2013, but most titles existed only for a shorter period. Each observation represents multivariate information containing the music title, DSP, date, units and revenue. As an example, we focus on one particular DSP, and consider the monthly aggregated revenues for each of the 300 music titles. In total, this gives 2.683 monthly revenue numbers. Figure 15 (left) shows the resulting frequency distribution of the first two digits for the monthly revenues of this DSP. It is obvious that the frequencies deviate strongly from the Benford distribution (dashed line). The largest peak is visible at digit 61, but there are very pronounced peaks also at digits 12, 18, 24, 30, 36, 42, 48, 49, 54, 55, 67, 68, 73, 79, 85, 91, and 97.

Since the frequencies are aggregated over 300 titles, it is unclear if the peaks are caused by single titles, or if this is structural in all titles. Figure 15 (right) shows line plots with the frequencies of each individual title (300 lines), and the peaks discovered in the left plot are indicated by vertical dashed lines. It can be seen that many of the titles have high frequencies at these indicated digits, and thus this is a structural phenomenon. Looking more closely into the data, we found that there seems to be a “revenue unit” of 0.61 Euros, referring to one download per month. Multiples of 0.61 are 1.22, 1.83, 2.44, 3.05, 3.66, 4.27, 4.88, 5.49, 6.10, 6.71, 7.32, 7.93, 8.54, 9.15, 9.76, etc. This exactly corresponds to the previously identified peaks.

We conclude from this experiment that revenues may lead to particular discretizations of the digit distributions, especially in case of small frequencies, and if single DSPs are investigated (which usually is of major interest), because they have “normed” unit prices. For the purpose of fraud detection it might thus be better to directly investigate the original frequencies rather than revenues, and to look at the first-digit distributions, especially in case of small frequencies.

Fig. 15

Digit distribution of revenues of a particular Digital Service Provider, aggregated for 300 titles (left), and frequencies for each title as line plot (right)

The next example refers to the number of 300 monthly aggregated streams of different titles, separately investigated for six different DSPs. We select only titles where the total frequency per DSP exceeds 100, ending up with 15 titles, and compare the first-digit distribution with the Benford distribution. Figure 16 compares the p-values from the three tests for all 90 experiments. The upper plots compare the results of the $\chi ^2$-test with the M-test, and the bottom plots compare the KS-test with the M-test. The plots on the right-hand side zoom into the interesting part with small p-values. For the M-test we report the results for $k=1$ (pink $+$ symbols) and $k=8$ (light blue $\times$ symbols), and they are connected by dotted lines. It can be seen that the M-test yields significance in many more cases than the $\chi ^2$-test, and if not significant, it is usually more strict, mostly for the choice $k=1$. The KS-test and the M-test lead to quite comparable results. Only in few cases, the KS-test yields significance, while the M-test does not, but there are also cases where the M test is weakly significant, while the KS-test is not.

Fig. 16

Pairwise comparisons of the p-values for the $\chi ^2$-test (p-chi2) and the KS-test (p-KS) with the M-test (p-M) for the digit distributions of the number of streams per month for 15 selected titles and 6 DSPs. For the M-test, the results for $k=1$ are shown by pink $+$ symbols, and for $k=8$ by light blue $\times$ symbols, which are connected by dotted lines. The right plots zoom into the left plot for small p-values

Finally, Fig. 17 shows a selection of the 90 results reported in Fig. 16 with visual comparisons of the digit distributions with the Benford distribution. In the upper plots, all three tests agree in their outcome: left not significant, right weakly significant. In the remaining plots they disagree, and often this happens in case of small numbers N.

Fig. 17

Selection of some test results from Fig. 16, with visual comparisons to the Benford distribution (dashed line)

7 Discussion and summary

A multivariate version of a test for Benford distribution has been introduced. This test is based on the ideas of compositional data analysis, investigating relative information between the digit frequencies. To the best of our knowledge, this is the first proposal of a multivariate test, called M-test, in this context. In simulated data experiments, but also in applications to data sets from the literature and to data from digital music streaming it turned out that the M-test is usually more sensitive compared to a $\chi ^2$-test, and in many cases also more sensitive than the KS-test, which are standard tests used for this purpose.

Since standard approaches for compositional data analysis do not account for the “total”, i.e. for the sum N of all digit frequencies, the M-test is constructed as a sampling-based test, where the frequency distribution under investigation is compared to frequency distributions sampled from a Benford distribution with N observations. The test works according to the principle of Mahalanobis distances, and the involved covariance matrix is estimated through simulation. This only needs to be done once, and the computational task is thus only to simulate from the Benford distribution, and to compare the distance-outcome with the result from the investigated data, yielding the p-value of the test. The M-test is thus nonparametric and does not rely on distributional assumptions.

An important issue in fraud detection is the false positive rate (FPR), which is the proportion of rejections of the null hypothesis that turn out to be wrong, see also discussion in Cerioli et al. (2019) in this context. The size and power comparisons in Fig. 3 have shown that if we can assume that the model holds, and thus the frequency distribution follows Benford’s law in the case when no fraud happens, the M-test still delivers the correct size – with slight deviations if the underlying number N of observations is very low. The higher N gets, the closer is the power of the M-test to the KS-test, which itself is generally higher than that of the $\chi ^2$-test.

A critical point for compositional data analysis is the occurrence of zeros. Here, zeros occur typically if the number N of observations is low, resulting in zero counts in the digit distribution. We have replaced zero frequencies by small numbers, simulated from a uniform distribution. The simulation experiments have shown that the test is still reliable, but the size and power can be lower (Fig. 3). In case of many zero frequencies it can thus be advisable to double-check with the results an alternative test.

The $\chi ^2$-test seems to have slight advantages if the manipulation is done in a specific digit, such as changing data values to the leading digit 9, for instance. However, potential fraudsters would probably apply a more clever scheme, and manipulate the numbers in order to modify multiple (leading) digits. This is the situation where the M-test shows its strength, and where fraud is detected already when the manipulated frequencies only slightly deviate from a Benford distribution, as the simulation experiments have shown. In general, the numerical experiments revealed that the M-test is more sensitive than the $\chi ^2$-test to small deviations from the Benford distributions, and it works for a wide range N of underlying values. The simulations have also shown that the M-test is preferable to the KS-test if the number of underlying values is high – in particular for the first-digit testing problem. If testing is done with the first two digits, the performance of the tests depends on the type of manipulation.

We have also developed a diagnostics plot for the M-test, which can provide deeper insight into the type of manipulation. The diagnostics based on clr coefficients seem to make possible deviations much clearer visible than diagnostics based on absolute frequencies.