Estimation and computations for Gaussian mixtures with uniform noise under separation constraints

Abstract

In this paper we study a finite Gaussian mixture model with an additional uniform component that has the role to catch points in the tails of the data distribution. An adaptive constraint enforces a certain level of separation between the Gaussian mixture components and the uniform component representing noise and outliers in the tail of the distribution. The latter makes the proposed tool particularly useful for robust estimation and outlier identification. A constrained ML estimator is introduced for which existence and consistency is shown. One of the attractive features of the methodology is that the noise level is estimated from data. We also develop an EM-type algorithm with proven convergence. Based on numerical evidence we show how the methods developed in this paper are useful for several fundamental data analysis tasks: outlier identification, robust location-scale estimation, clustering, and density estimation.

1 Introduction

We study a class of mixture models for univariate data sets that can be used for several distinct goals: outlier identification, robust location-scale estimation, robust clustering, and density estimation.

Atypical outlying samples can break down most routine procedures such as location-scale estimation, visualization, density approximation, etc. There may be different reasons why one would flag an observation as an outlier. However, a universal definition for outliers does not exist. In homogenous populations, they are thought of as points lying at some distance from the distribution center. However, extreme points may well be non-atypical when they reflect the heavy tail structure of the underlying generating mechanism. In clustered populations, the distinction between outlying vs. non-outlying points is even more problematic; what we would qualify as a subset of atypical points could constitute a special cluster instead. Following Banfield and Raftery (1993) and Coretto and Hennig (2011, 2016) among the others, in this paper we consider a model strategy that accommodates the presence of “noise”. By noise, we mean a mechanism that: (i) generates outlying points that arise in low-density regions of the data space; (ii) generates observations that have an unstructured behavior compared with the majority of the data set so that they are considered outside the scope of the modeling. To motivate the methods proposed in this paper, we introduce three data sets that will be analyzed in Sect. 6.

• TiO2 concentration: the data set was introduced in Reimann et al. (2000). A total of n = 768 measurements of elements in soil samples around the Baltic Sea were taken. Extensive details about how these concentration measures are constructed are given in the aforementioned paper. We focus on TiO2 (Titanium dioxide) concentration.

• pH of blood: the data set is obtained from Hartigan (1975) and contains n=40 samples of various compounds in cerebrospinal fluid and blood for acidosis patients. A total of 6 variables are sampled, in this paper, we focus on pH of blood.

• Realized volatility: the data set has been studied in Coretto et al. (2020), it contains a cross-sectional measurement of realized volatility for n = 123 traded on the New York Stock Exchange (NYSE) market between years 1998–2008. Here we consider a cross-section taken on 25/Aug/1998.

In Fig. 1 we report kernel density estimates of the distributions of the three data sets. Kernel estimates are computed using the Epanechnikov kernel function and the adaptive optimal bandwidth estimator of Sheather and Jones (1991). Other data-driven bandwidth selectors have been tried, but the method of Sheather and Jones (1991) provided the most credible results. The common characteristics of these data distributions are that: (i) they have an elongated right tail with few scattered points that sometimes appear far from the main bulk of the data; (ii) for all of them the tail behavior affects the optimal bandwidth estimate, which introduces undersmoothing so that these extreme points are fitted essentially alone by the kernel function. This is particularly evident in Panel (c) of Fig. 1; (iii) in all panels there is evidence of multimodality which may indicate the existence of groups. However, this multimodality may well be introduced by the undersmoothing issue, and therefore, the existence of groups in the data is not clear. The discovery of clusters in the presence of noise is a challenging issue, for an in-depth discussion consider Hennig (2004) and Ritter (2014), and references given therein.

Fig. 1

Kernel density estimates for the three real data sets introduced in Sect. 1. Each panel shows the stripchart of the observed data points on the horizontal axis. Panel a TiO2 (Titanium dioxide) concentration data set. Panel b pH of blood data set Panel c realized volatility data set.

In this paper, we study estimation methods and algorithms for a model consisting of a mixture of Gaussian distributions with the addition of a uniform component that has the role to capture the noise, and that is constrained to overlap with the main location-scale components in a user-controlled way. The model was introduced in Coretto et al. (2020) as an extension of a general class of models of this kind proposed in Coretto and Hennig (2011), which in turn generalized an original proposal of Banfield and Raftery (1993). We introduce a model restriction that ensures that the overlap between the noise and non-noise components can be controlled by the user. The model restriction is embodied in the formulation of a constrained ML estimator for which existence and consistency are studied. A feasible EM algorithm is shown to approximate the constrained ML estimator. A detailed treatment of the computational properties of the algorithm is given.

Other robust approaches can handle groups in the data. Coretto and Hennig (2016) and Coretto and Hennig (2017) propose the addition of a noise component with an improper distribution. But there exists another approach where outliers are represented as points arising from the tail regions of the mixture components. In this direction, McLachlan and Peel (2000a) proposed to achieve robustness with ML estimation for mixtures of Student-t distributions. Punzo and McNicholas (2016) and Farcomeni and Punzo (2020) recently proposed ML methods for mixtures of contaminated Gaussian distributions. Another body of work defines the outliers as points drawn from a “spurious” distribution not specified at the modeling stage. Within the previous framework, robustness is typically achieved through trimming methods. Gallegos and Ritter (2005), and García-Escudero et al. (2008) introduced ML-type procedures for partition models with trimming that discards a fixed proportion of observations treated as outliers. For an review of the main ideas in robust model-based clustering see Ritter (2014), Farcomeni and Greco (2015), and Hennig et al. (2016).

Most well established robust methods treat the tails of the distribution symmetrically. The model presented here is particularly useful when contamination processes affect the data distribution asymmetrically, in the sense that noise affects one of the two tails only. This is a specific situation, but it occurs often in practice as shown in the examples of Fig. 1. An additional advantage of the proposed methodology is that it estimates the noise level from the data so that the method decides whether or not contamination affects the data (see Sect. 6). The latter is important when expert supervision is not possible, for example when thousands of features are machine scanned for outlier identification (e.g. this is routinely done in genomic studies, see) Marshall 2004. The methodology can be also used to investigate group structures in the data by applying model-based clustering techniques. In Sects. 5 and 6 we show how the method under study applies to fundamental tasks in data analysis: density approximation, robust estimation, outlier identification, and clustering.

The present paper is organized as follows: in Sect. 2 we introduce and discuss the model and its possible applications; in Sect. 3 we analyze the ML estimation method, and we propose a feasible EM algorithm; in Sect. 5 an extensive Monte Carlo experiments are performed to assess the finite sample properties of the proposed methods; in Sect. 6 we analyze the three data-set discussed above. Finally, in Sect. 7 we conclude the paper with some final remarks.

2 Gaussian mixtures with tail uniform noise

Let us fix some notation first. For $g=1,2,\ldots , G$ define a collection of normal densities $\phi (x; \theta _g)$. $\phi (x; \theta _g)$ is the density at a point $x \in \mathbb {R}$, where $\theta _g = (\mu _g, \sigma _g)\in \mathbb {R}\times (0,+\infty )$ is the mean and standard deviation parameter vector. Let $I_A(x)$ be the usual indicator function, that is $I_A(x) = 1$ if $x \in A$, and $I_A(x) =0$ otherwise. Let $(\pi _0, \pi _1, \ldots , \pi _G)$ be a vector of mixing proportions such that $\pi _g \in (0,1)$ for all $g=0,1,\ldots , G$ and $\pi _0+\pi _1+,\ldots ,+\pi _G=1.$ The density function

$$\begin{aligned} f(x ; \theta ):= \pi _0 \frac{I_{[\beta _1, \beta _2]}(x)}{\beta _2-\beta _1} + \sum _{g=1}^{G} \pi _g \phi (x; \theta _g), \end{aligned}$$

(1)

is a finite mixture model of G Gaussian densities with uniform noise. The parameter vector $\theta _0 = (\beta _1, \beta _2)$, with $\beta _1<\beta _2$, contains the limits of the support of the uniform distribution. The mixing proportions have the usual sampling interpretation McLachlan and Peel (2000a) in an iid sample from a distribution having density (1) a proportion $\pi _g$ of points is expected to be sampled under the g-th component density $\phi (\cdot ; \theta _g)$, while a proportion $\pi _0$ of points is expected to be generated under the uniform component. The model parameter vector is defined as $\theta = (\pi _0, \beta _1, \beta _2, \pi _1, \mu _1, \sigma _1, \ldots , \pi _G, \mu _G, \sigma _G)$, or in more compact form $\theta = (\pi _0, \theta _0, \pi _1, \theta _1, \ldots , \pi _G,\theta _G)$.

Originally, this class of models was introduced in Banfield and Raftery (1993) with the main goal of performing robust model-based clustering. The uniform component had the role of catching outliers. Banfield and Raftery (1993) proposed to fix $[\beta _1, \beta _2]$ to be equal to the data range. Coretto and Hennig (2011) generalized to the case of mixtures of general location-scale densities with an arbitrary finite number of uniform distributions having disjoint supports.

It is well known that mixtures of normal distributions can fit almost any distribution in a semiparametric way. Here the uniform distribution in (1) is called the “noise component”. Such a model can be used so that the Gaussian mixture part represents most of the data structure, while the uniform noise component is meant to represent regions of the data that do not have a clear shape or structure. Moreover, we want to use model (1) so that the uniform distribution is specifically designed to catch “atypical” points when these arise from one of the two tails of the distribution.

Although the estimator and algorithms developed in Coretto and Hennig (2011) should be able to cope with the situations described above, in some situations, their method is not able to distinguish the tails of the normal mixture part of the model from the uniform component as noted in Coretto and Hennig (2010). The latter would result in estimates where both the location and the variance of the normal components are seriously biased. For these reasons, Coretto et al. (2020) used model (1) to cluster financial data, and they modified the algorithm of Coretto and Hennig (2011) to ensure a certain separation between the tails of the normal components and the uniform component. In order to achieve the previous goal, we introduce three “model-constraints”. By “model-constraints”, we mean constraints on the parameters that translate the interpretation of the model that needs to be addressed by the fitting procedure. Consider the following constraints

Since $\phi (\cdot )$ is symmetric about $\mu _g$, the constraints (RS) and (LR) imply that the support of the uniform component has a bounded amount of overlap with the region where the location-scale components put most of their mass. The degree of overlap is controlled by $\gamma$. For example, assume $G=2$ with $\sigma _1=\sigma _2$ and $\mu _1 < \mu _2$. Take $\gamma =z_{0.98}$, i.e. $\gamma$ is the 98% quantile of standard Gaussian distribution. Now, if (RS) holds, the second Gaussian component (the component with the right-most peak) can only overlap with the uniform noise component in the region corresponding to its $2\%$ tail probability. Moreover, since (RS) has to hold for all other g, the first component cannot overlap with the uniform support more than the second one. The constraints (RS) and (LS) are mutually exclusive, in fact, only one of them can hold.

The third constraint is called the “noise proportion constraint” (NPR). It bounds the noise level, i.e. the expected fraction of points generated from the uniform distribution under (1). The NPR rules out the possibility that the noise becomes the majority if $\pi _{\max }< 50\%$. The latter corresponds to the robust statistic’s classical assumption that one cannot distinguish outliers if they are a majority. However, in clustering applications one would set $\pi _{\max }$ not smaller than the smallest fraction of points that would be genuinely considered as a “cluster”.

A model like (1) can be used with different aims: density approximation, robust estimation, robust model-based clustering, etc. Some of the applications will be seen in Sect. 5. The use of the word robust here does not mean formal robustness. Hennig (2004) showed that MLE corresponding to the model (1) could break-down in the presence of arbitrarily large observations. In practice, this is not common, and in fact, we will show that the proposed MLE can adapt to heavy tails and strong skewness showing good resistance to outliers.

2.1 Clustering

Insights into the clusters generating ability of (1) are central for the subsequent developments. Consider an iid sample $\{X_1, X_2, \ldots , X_n \}$, where $X_i \in \mathbb {R},$ for all $i=1,2,\ldots ,n$, and $X_i$ has a distribution having density $f(\cdot , \theta )$. Let $\varvec{x}_n:=\{x_1, x_2, \ldots , x_n \}$ be the observed sample. If the component densities of (1) are sufficiently separated one would observe G distinct clusters of points, and if $\pi _0 >0$ an additional group of more “unstructured points” would appear in the sample depending on the size of the interval $[\beta _1,\beta _2]$. Define the following quantities

$$\begin{aligned} \tau _0(x; \theta ) = \frac{\pi _0\frac{I_{[\beta _1, \beta _2]}(x)}{\beta _2-\beta _1}}{f(x;\theta )}, \quad \text {and} \quad \tau _g(x; \theta ) = \frac{\pi _g \phi (x;\theta _g)}{f(x;\theta )}, \quad \text {for~} g=1,2,\ldots , G \end{aligned}$$

(2)

(2) will have a crucial role. These ratios are called “posterior membership probabilities”, because in the iid sampling case $\tau _g(x_i;\theta )$ is the posterior probability that a point $x_i$ has been generated by the g-th component of (1) at $\theta$ conditional on the observed sample. Assuming that $\theta$ is known, the optimal assignment rule minimizing the misclassification rate is the following Bayes assignment

$$\begin{aligned} A(x_i; \theta ) := \; {\arg \max }_{g=0,1,\ldots ,G} \; \tau _g(x_i; \theta ), \end{aligned}$$

(3)

In reality $\theta$ is not known, and typically the assignment is based on its estimate, usually an ML estimate.

3 Estimation

This section gives a detailed account of the ML estimation and computation for fitting $\theta$. First, we consider G fixed and known. Data-driven choice of G will be considered in 1 and Sect. 5. ML estimation for finite Gaussian mixtures has been a fascinating problem studied for a long time. A framework that allows for simple existence and consistency proofs does not exist. Chen (2017) is the most recent comprehensive account of this subject’s main theoretical contributions.

The log-likelihood function associated with an observed data set $\varvec{x}_n$ from an iid sample from (1) is given by

$$\begin{aligned} L_n(\theta )= \sum _{i=1}^{n} \log f(x_i;\theta ). \end{aligned}$$

(4)

Day (1969) noted a fundamental issue connected to the unboundedness of $L_n(\theta )$. In fact, fix $\mu _g = x_i$ for arbitrary i and g, and it happens that taking $\sigma _g \rightarrow 0$ implies $L_n(\theta ) \rightarrow +\infty$. The same happens if we fix an arbitrary $\beta _1 < x_i$ for some i, and then taking $\beta _2 \rightarrow \beta _1$ the variance of the uniform component $(\beta _2 - \beta _1)^2/12 \rightarrow 0$ and $L_n(\theta ) \rightarrow +\infty$. Therefore, the ML estimation needs to take into account constraints that bound scale parameters from below. One can simply require for example that $\sigma _g>= \sigma _0 >0$, but: (i) these constraints will not produce a scale-equivariant ML; (ii) the choice of an effective $\sigma _0$ is not trivial and it is shown to affect the fitting. There are several alternative approaches, although none of them translates into simple numerical approximating algorithms. The ML theory developed in Coretto and Hennig (2011) is based on scale constraints proposed by Dennis (1981) and Hathaway (1985) that are scale-equivariant. In the multivariate setting these constraints where rediscovered later due to Ingrassia (2004). However, these are not feasible here. In fact, the (RS) and (LS) constraints are an additional complication in the numerical optimization of (4). Define scale parameters

$$ s_{g} : = \left\{ {\begin{array}{*{20}l} {\sigma _{g} } \hfill & {{\text{if}}~{\text{g = 1}},{\text{2}}, \ldots ,{\text{G}},} \hfill \\ {\frac{{\beta _{2} - \beta _{1} }}{{\sqrt {12} }}} \hfill & {{\text{if}}~{\text{g = 0}}.} \hfill \\ \end{array} } \right. $$

Fix $0<d<1$, and consider the constraint $s_g \ge s_{\min }=\exp (-n^d)$ studied in Tanaka and Takemura (2006). Although these constraints are not scale-equivariant at fixed n, they are asymptotically scale-equivariant since $s_{\min } \rightarrow 0$ as $n \rightarrow +\infty$. Suppose that $n=1300$ and that we fix $d=0.5$, the resulting constraint would be $s_g \ge s_{\min } = 2.22{\times }{10}^{-16}$, where $s_{\min }$ is equal to the so called machine epsilon. The latter means that for any $n>1300$, in practical computations, we would treat $s_{\min }$ as it was a positive number that numerically cannot be distinguished from zero. (RS) and (LS) are mutually exclusive, hence it is simpler to treat them separately, and finally, we will give some ideas on how to choose between them. We treat estimation with (RS) in mind because positively skewed data are more common in applications. The second constraint for model-interpretation is the (NPR) constraint. While the previous scale constraint is the method’s regulation tool for obtaining a well-defined and consistent ML estimator, the (RS), (LS), and (NPR) constraints restrict the domain of the parameters to gain a certain interpretation of the model.

We look for the maximizer of $L_n(\theta )$ over the following constrained parameter space

$$\begin{aligned} \Theta _n := \left\{ \theta \in \Theta \; | \; s_g \ge \exp (-n^{d}) , \; \mu _g + \gamma \sigma _g \le \beta _1, \; \pi _0 \le \pi _{\max }\;\; (g=0,1\ldots , G) \right\} , \end{aligned}$$

(5)

for fixed $0<d<1$ and $\gamma >0$ constants. The constrained sample ML estimator is defined as

$$\begin{aligned} \hat{\theta }_n:= {\arg \max }_{\theta \in \Theta _n} \; L_n(\theta ). \end{aligned}$$

(6)

For simplicity we defined the ML estimator in the (RS) case, for the (LS) case one replaces $\mu _g + \gamma \sigma _g \le \beta _1$ in (5) with $\beta _2 \le \mu _g + \gamma \sigma _g$. Note from (5) that, contrary to the classical case, here the parameter space changes with n. Moreover, because of the uniform component, the objective function of the ML problem is not continuous. Therefore, the existence of the ML in both finite and infinite samples is not obvious. The next 1 state the finite sample existence of the sample ML estimator.

Proposition 1

$L_n(\theta )$ achieves its maximum over $\Theta _n$.

The proof of the statement above is given in the final Appendix. The next 2 states the consistency of the ML estimator. Finite mixture can only be identifiable up to component label switching, in fact, in this case any permutation of the indexes $g=1,\ldots ,G$, leads to the same mixture model (1). As in Teicher (1963) we state consistency on a quotient space of the original parameter space. In practice we look for the consistency with respect to one of such permutation of the Gaussian components’ indexes. Define

$$\begin{aligned} h(\theta ):=\{\theta ' \in \Theta \;|\; f(x;\theta ) = f(x;\theta ') \; \forall x\}, \end{aligned}$$

For $A,B \subset \Theta$, define ${{\,\mathrm{dist}\,}}(A,B):= \inf _{\theta \in A} \inf _{\theta ' \in B} {{\,\mathrm{dist}\,}}(\theta , \theta ')$, where ${{\,\mathrm{dist}\,}}(\theta , \theta ')$ is the ordinary Euclidean distance.

Proposition 2

Let $\theta _0 \in \Theta$, and suppose that (RS) holds for $\theta _0$. Let $\theta _0$ be the generating parameter vector, in the sense that the sample $\{X_1, \ldots , X_n\}$ is an iid sequence from a distribution having density $f(\cdot ; \theta _0)$. Then

$$\begin{aligned} \Pr \left\{ \lim _{n \rightarrow \infty } {{\,\mathrm{dist}\,}}(h(\hat{\theta }_n), h(\theta _0)) \right\} = 1. \end{aligned}$$

(7)

The proof of the statement above is given in the final Appendix. We treated G as fixed and known. However, in density estimation, G controls the number of peaks in the final density estimate. In clustering applications, often G coincides with the number of clusters. There are several approaches to select an appropriate G. The most popular approach is to rely on information-theoretic quantities discussed in more detail in Sect. 5.

Remark 1

For univariate samples, the choice of the appropriate constrained model, i.e. deciding about (RS) vs. (LS), could be based on subject-matter considerations and visual inspection of the data. However, in cases where data are processed in an unsupervised way, it may be possible to choose the model version that fits that data better in terms of expected log-likelihood. This appears as an approach technically correct because, for a given G, both (RS) and (LS) have the same number of parameters. The joint tuning of constraints’ hyperparameters and G is more problematic here. In the mixture context, the most popular approach for choosing the number of mixture components G is to use information criteria such as the AIC and the BIC. Classical approximate estimators of the information criteria have the form: (fitted likelihood - penalty), where the penalty term increases with the number of parameters. The number of parameters is generally interpreted as a proxy for model complexity and degrees of freedom. Observe that for a given G different specifications of $(\gamma , \pi _{\max }, d)$ modify the ability of the model to adapt to the data distribution, which in practice means that constraints will change the “effective degrees of freedom” of the model. A “more constrained parameter space” allows the fitting of the model to adapt less to the data, and therefore it will lead to a “simpler” model. Thus, the well-known bias-variance trade-off arising from the model selection is certainly affected by changing the parameter constraints. However, classical estimators of the AIC and the BIC will not reflect the effects of the constraints. Model selection frameworks that account for these effects exist only for specific cases (for instance see)Kuiper et al. 2011. In practice, we suggest that whenever G needs to be selected, classical information criteria are used for a fixed set of model’s hyperparameters $(\gamma , \pi _{\max }, d)$.

4 MEMR algorithm

It is well known that, even in the one-dimensional case, computation of the sample ML estimator in the finite mixture context is not an easy task due to the highly complex likelihood function surface (see) McLachlan and Krishnan 1997. Moreover, the uniform distribution here adds some more difficulties due to its discontinuities and the fact that it introduces many local maxima in $L_n(\cdot )$ (see the proof of 1). The Expectation-Maximization (EM) algorithm of Dempster et al. (1977) is a popular choice for approximating the MLE of finite mixture models. We exploit the discontinuities of $L_n(\cdot )$, and we propose the “multiple EM runs” (MEMR) Algorithm 1. We show that the MEMR algorithm is monotonic and converges to a stationary point of the likelihood surface.

Let $s=0,1,\ldots$ be the iteration index. Let $a^{(s)}$ be the quantity a computed at the s-th step of the algorithm. Define

$$\begin{aligned} Q(\theta , \theta ^{(s)}) =&\sum _{i=1}^{n} \sum _{g=0}^{G} \tau _{g}(x_i, \theta ^{(s)}) \log \pi _g + \; \sum _{i=1}^n \tau _0(x_i, \theta ^{(s)})\log \left( \frac{I_{[\beta _1, \beta _2]}(x_i)}{\beta _2-\beta _1} \right) + \nonumber \\ +&\sum _{i=1}^{n} \sum _{g=1}^{G} \tau _{g}(x_i, \theta ^{(s)}) \log \phi (x_i; \mu _g,\sigma _g). \end{aligned}$$

(8)

By applying Theorem 4.1 in Redner and Walker (1984) it can be established that if there exists $\theta '$ such that $Q(\theta ', \theta ^{(s)}) \ge Q( \theta ^{(s)}, \theta ^{(s)})$, then $L_n(\theta ') \ge L_n(\theta ^{(s)})$. Therefore, iteratively increasing (8) with an appropriate choice of a sequence $\{\theta ^{(s)}\}$, one obtains a monotonically increasing sequence $\{ L_n(\theta ^{(s)})\}$. This is the a standard EM algorithm that is not feasible in our case. Rewrite (8) according to the following decomposition

$$\begin{aligned} Q(\theta , \theta ^{(s)})= Q_u(\theta _u, \theta ^{(s)}) + Q_\phi (\theta _\phi , \theta ^{(s)}) + Q_\pi (\theta _\pi , \theta ^{(s)}), \end{aligned}$$

(9)

where

$$\begin{aligned} Q_u(\theta _u, \theta ^{(s)})={}&\sum _{i=1}^n \tau _0(x_i, \theta ^{(s)})\log \left( \frac{I_{[\beta _1, \beta _2]}(x_i)}{\beta _2-\beta _1} \right) , \nonumber \\ Q_\phi (\theta _\phi , \theta ^{(s)})={}&\sum _{i=1}^{n} \sum _{g=1}^{G} \tau _{g}(x_i, \theta ^{(s)}) \log \phi (x_i; \mu _g,\sigma _g), \nonumber \\ Q_\pi (\theta _\pi , \theta ^{(s)})={}&\sum _{i=1}^{n} \sum _{g=0}^{G} \tau _{g}(x_i, \theta ^{(s)}) \log (\pi _g). \nonumber \end{aligned}$$

The sequential maximization of $Q(\cdot )$ is separable in its three components above.

Remark 2

The usual M-step for Gaussian parameters does not work here, and the optimal solution for $Q_\phi (\cdot )$ cannot be calculated with a closed-form formula as in the case of the unconstrained Gaussian mixture model. Because of the scale and the (RS) constraint, the optimization concerning $\theta _\phi$ requires numerical optimization. In our implementation (see Sections 5 and 6), we perform the M1-step using the gradient-based algorithm of Svanberg (2001) included in the NLOpt library of Johnson (2020). Although solving the M1-step requires iterative numerical optimization, both the gradient and the Jacobian of the objective function are computed in closed form.

$Q_u(\cdot )$ is not differentiable, and it introduces many stationary points into $Q(\cdot )$. The latter is related to the multiple local maxima behavior of $L_n(\cdot )$ seen in the proof of 1. The next 3 characterizes this behavior that is rather central in developing the MEMR algorithm.

Proposition 3

Assume $\theta ^{(0)} \in \Theta _n$ such that $[\beta _1^{(0)}, \beta _2^{(0)}]$ contains at least a data point. Consider an “improving” sequence $\{ \theta ^{(s)}_* \}$ in the sense that $Q(\theta ^{(s+1)}_*, \theta ^{(s)}_*) \ge Q(\theta ^{(s)}_*, \theta ^{(s)}_*)$ for all $s=0,1,\ldots$. Assume $\theta ^{(0)}_* \in \Theta _n$. Then, the uniform parameters change at most in the first step, that is $\beta _{1*}^{(s)} = \min \{x_i \in \varvec{x}_n \;|\; x_i \ge \beta _{1*}^{(0)}\}$ $\beta _{2*}^{(s)} = \max \{x_i \in \varvec{x}_n \;|\; x_i \le \beta _{2*}^{(0)}\}$ for any $s=1,2,\ldots$

Proof of 3 is given in the Appendix. The previous statement is crucial because it handles the likelihood’s discontinuities caused by the uniform component. The local maxima of $Q_u(\cdot )$, and therefore the local maxima of $Q(\cdot )$ and $L_n(\cdot )$, are such that the corresponding $\theta _u$ coincides with a pair of distinct data points. In the Algorithm 1, the previous argument is exploited to decompose the optimization of $L_n(\cdot )$ into multiple local searches where for each pair of distinct data points (that are local optimal for $(\beta _1,\beta _2)$), the optimization is performed on the remaining parameters $(\theta _{\phi }, \theta _{\pi })$.

Remark 3

3 does not depend on whether we implement (RS) or (LS) constraint. The Algorithm 1 can be adapted to find a solution with (LS) constraints rather easily. In particular two modifications are required: (i) the trimmed set into the initialization step $\{x_i \in \varvec{x}_n \;|\; x_i < \beta _1^{(0)} \}$ is replaced with the trimmed set $\{x_i \in \varvec{x}_n \;|\; x_i > \beta _2^{(0)} \}$; (ii) the second inequality constraint in M1 is replaced with $\beta _2^{(0)}-\mu _g+\gamma \sigma _g \le 0$ for all $g=1,2,\ldots ,G$.

The proportion parameters belong to the compact set $P=[0, \pi _{\max }]\times [0,1]^{G}$. The M2-step in the Algorithm 1 takes care of the noise proportion constraint. The next proposition states that at any step s, the updating given in M2a-M2b maximizes $Q_\pi (\cdot )$ fulfilling the noise proportion constraint.

Proposition 4

Assume that Algorithm 1 is performed for steps $1, 2, \ldots , S$. M2a-M2b solve the following optimization program

$$\begin{aligned}&\underset{\theta _\pi \in P}{{{\,\mathrm{maximize}\,}}} Q_\pi (\theta _\pi , \theta ^{(s)}), \\ & \text {subject to}&\pi _0+\pi _1+,\ldots , \pi _g = 1, \\& \pi _0-\pi _{\max }\le 0, \\& \pi _g \in [0,1] \quad \text {for all}\;\; g=1,2,\ldots , G. \end{aligned} $$

(10)

Proof of the previous 4 is given in the Appendix. 4 establishes that the updates in M2a and M2b of the Algorithm 1 implement the closed-form solutions for the constrained M-step with respect to the proportion parameters. Although the implementation of the noise proportion constraint into the MEMR algorithm is similar to the RIMLE algorithm of Coretto and Hennig (2017), there are substantial differences. Here the M-step is unconditional, and it is based on closed formula calculations, whereas the RIMLE relies on conditional optimization and the noise proportion update requires solving nonlinear equations iteratively.

Proposition 5

(Convergence of MEMR algorithm) For every r-th pair of distinct data points $\{x^{(r)}_i, x^{(r)}_j\} \in \varvec{x}_n$ such that $x^{(r)}_i< x^{(r)}_j$ and $x^{(r)}_j - x^{(r)}_i \ge \sqrt{12}\exp (-n^d)$, the following holds

• 1. $L_{n}(\theta ^{(s)})$ is increased in every step $s=1,2,\ldots$;

• 2. the sequence $\{\theta ^{(s)}\}$ produced by Algorithm 1 converges to a stationary point $\theta ^{(r)} \in \Theta _n$.

The proof of the previous Proposition is given in the Appendix. 5 ensures that for an appropriate small $\varepsilon$ (stopping criterion), $\theta ^{(r)}$ approximates a local optimum of the log-likelihood function, or unfortunately, a stationary point of the likelihood surface. The initialization strategy forms all possible candidates for ML estimates of the uniform parameter, each of which will qualify a local maximum of $L_n(\cdot )$. Therefore the last step of the algorithm selects the best of such local maxima, $\theta ^{(r*)}$, for a candidate global solution of the sample ML problem.

Remark 4

The algorithm requires several iterations, one for each pair of distinct data points that initialize the uniform parameter. The latter requires too many EM runs if n is large. In both (RS) and (LS) cases, we seek models where the uniform component captures noise in the tails. Therefore a possible strategy is not to run the EM iteration for all pairs $\{x^{(r)}_i, x^{(r)}_j\}$ of 5 but for a subsample of the data. Random subsampling is a possibility, although, in experiments, it introduced additional variability. For $n>500$, our software implementation allows switching to faster options that work as follows.

• Option A Compute ˜xn = fQn(ak); k = 1;2; : : : ;Kg, where Qn(a) is the empirical quantile function at a, fakg is an appropriate sequence of probabilities (e.g. ˜xn are empirical percentiles), and K <n. Note that an empirical quantile is always an observed data point. Form all pairs fx(r) i ;x(r) j g of Proposition 5 from the data subset ˜xn. In this case the number of pairs used to initialize the uniform parameters depend on K and not n.

• Option B This is similar to option A but it excludes further non-tail points from .....depending on.....If the (RS) version is fitted, set minfak; k = 1;2; : : : ;Kg = (1pmax). Otherwise, if (LS) version is fitted, set maxfak; k = 1;2; : : : ;Kg = pmax: This shortcut strategy exploits the fact that the noise level is bounded by pmax, and since the separation constraints pushes the uniform component in the tails, it is not necessary to look for (b1;b2) everywhere on the data range.

We experimented extensively with samples of size $n>250$ using both A and B, and we never experimented with significantly detrimental effects. On the other hand, we obtained significant gains in computational efficiency.

5 Numerical experiments

5.1 Experimental settings

In this section, we assess the proposed ML estimator’s finite sample performance, and we provide comparisons with existing methods in the literature. We consider three different data-generating mechanisms to show possible different uses of the proposal in the context of semiparametric density estimation, mixture parameters estimation, clustering, outlier identification, and robust location-scale estimation. We want to assess the methodology under three different circumstances embodied in the following three sampling designs.

MIXs. Data are generated from the following Gaussian mixture model with the uniform noise acting on the right tail:

$$\begin{aligned} \pi _0 \; \mathcal {U}(50, 123) + (1-\pi _0)\; \{ 0.6 \; \mathcal {N}(0,50) + 0.4 \; \mathcal {N}(27.5,50) \} , \end{aligned}$$

(11)

where $\mathcal {U}(\beta _1,\beta _2)$ denotes the uniform distribution on the interval $[\beta _1, \beta _2]$, and $\mathcal {N}(\mu _j,\sigma ^2_j)$ is the Gaussian distribution with mean $\mu _j$ and variance $\sigma ^2_j$ for $j=\{1,2\}$. Three values of the expected proportion for the uniform component are considered: $\pi _0 \in \{0.05, 0.1, 0.25\}$. The choice of the parameters is based on the following arguments. The three values of $\pi _0$ will produce increasing level of uniform noise. The separation ratio between Gaussian components is $|\mu _1-\mu _2|/\sigma = 4.5$, which is sufficient enough to produce a multimodal density McLachlan and Peel (2000a). The variance is set equal for both components to calibrate the separation ratio easily. $\Pr \{\mathcal {N}(\mu _2,\sigma ^2_2) \le \beta _1\} = 0.9993$, therefore, there is a small overlap between the right-most Gaussian component and the uniform component. Given $\beta _1=50$, the value $\beta _2=123$ is fixed so that, when $\pi _0=10\%$, the density contribution of the second Gaussian component in (11) at its 99%-quantile matches the density contribution of the uniform noise. This setting is challenging because it makes difficult to distinguish the normal tails from the uniform component. The MIXs data generating process fulfills the model assumption of the proposed method producing points that are “clearly” clustered, plus an elongated right tail.

MIXo. This is a variation of MIXs that changes the separation between the Gaussian components by reducing $\mu _2$. The data generating model is

$$\begin{aligned} \pi _0 \; \mathcal {U}(50, 123) + (1-\pi _0)\; \{ 0.6 \; \mathcal {N}(0,50) + 0.6 \; \mathcal {N}(17.5,50) \}. \end{aligned}$$

(12)

Now the separation $|\mu _1-\mu _2|/\sigma$ is roughly about 2.5 producing a strong overlap that leads to unimodality. Note that now $\Pr \{\mathcal {N}(\mu _2,\sigma ^2_2) \le \beta _1\} \approx 1$, and in practice the uniform component and the right-most Gaussian distribution do not overlap. With the MIXo sampling design, we again have a data generating process fulfilling the model assumptions, but it does not have a multimodal distribution and it does not produce well-clustered points.

ASY. Points are sampled from the following non-Gaussian mixture distribution

$$\begin{aligned} \pi _0 \; \mathcal {U}(20, 50) + (1-\pi _0) \; \mathcal {\chi }^2(3), \end{aligned}$$

(13)

where $\mathcal {\chi }^2(\nu )$ denotes the $\mathcal {\chi }^2$ distribution with $\nu$ degrees of freedom. The aim of the ASY experiments is different from that of the previous MIX cases. ASY model has skewed density, and its right-tail is much heavier from what we would expect under a $\mathcal {\chi }^2(3)$. Model assumptions for the proposed method are not fulfilled here. The core of the non-tail part of the sampling mechanism is not Gaussian, and it is not symmetric. For the ASY model we also consider $\pi _0 \in \{0.05, 0.1, 0.25\}$.

For each of the three sampling designs, we experiment with sample size $n \in \{50,100,1000\}$. The proposed method is compared against alternative methods depending on the investigated aspect. In order to ease the presentation, each method is labeled as follows.

GM:

EM approximation of the MLE for Gaussian mixture models.

SGM:

EM approximation of the MLE for skew Gaussian mixture models proposed by Lin et al. (2007). Software implementation: EMMIXskew package of Wang et al. (2018) available via the “Comprehensive R Archive Network” (CRAN).

GUM:

EM approximation of the MLE for Gaussian mixture models with uniform component proposed in Coretto and Hennig 2011.

GRUM:

The method proposed in this paper, that is, the EM approximation (Algorithm 1) of the MLE for Gaussian mixture models with the uniform component under separation constraints.

KEM:

Kernel density estimator computed with Epanechnikov’s kernel function, and optimal bandwidth estimator developed by Sheather and Jones 1991. Software implementation: KernSmooth package of Wand (2020) available on (CRAN).

AO:

“Adjusted Outlyingness” method for outlier detection developed by Brys et al. (2005) and Hubert and Vandervieren (2008). Software implementation: mrfDepth package of Segaert et al. (2020) available on (CRAN).

TRIMADSE:

Location-scale estimation based on Trimean and Mad estimators. Location-scale estimation based on the sampling mean and the standard deviation

Software for GM, GUM, and GRUM methods have been specifically implemented to manage all their common elements exactly in the same way. For example, in Coretto and Hennig (2011), the GUM is implemented with a different class of scale constraints. Here it is implemented with the same scale constraints proposed for the GRUM method. Moreover, the work of Coretto and Hennig (2011) did not consider the noise proportion constraint that here we implemented as for the GRUM method. Initialization for all mixture-based methods is performed in the same manner as for the GRUM method, eventually ignoring the uniform component’s initialization. Throughout the experiments, hyperparameter settings are: $d=0.5$, $\gamma = z_{0.975}$ (the 97.5%-quantile of standard normal distribution), $\pi _{\max }=50\%$. For sample size $n>500$, we perform GRUM computations using the fast option B explained in the 4. For the GUM computations, we consider option A because the method does not constraint the uniform component to catch the data distribution tails. For each combination of the sample design, n, and $\pi _0$, we perform 1000 Monte Carlo replicates.

5.2 Experimental results

This study investigates parameter estimation, model selection and density fit, outlier identification, clustering, and robust location-scale estimation.

Parameter estimation. The comparison only involves MIXs and MIXo designs and GUM and GRUM methods whose parameters are consistent with the ground truth. The number of Gaussian mixture components is fixed at $G=2$, and true parameters are compared with estimated parameters in terms of Mean Squared Error (MSE). Since the three classes of parameters (proportions, locations, scales) play a different role, the MSE is given for sub-vectors of parameters $\varvec{\pi }=(\pi _0, \pi _1, \pi _2)$, $\varvec{\mu }=(\mu _1, \mu _2)$, $\varvec{\sigma }=(\sigma _1, \sigma _2)$, $\varvec{\beta }=(\beta _1, \beta _2)$. Results are shown in Fig. 2. The estimation of the mean parameters is satisfactory for both methods. However, GRUM outperforms GUM in terms of estimation of scales and uniform parameters. The latter is because the GRUM method often fails to identify $\beta _1$, and it tempts to confuse the tail of the right-most Gaussian with the uniform component. The GUM bias is larger for the case when $\pi _0=10\%$ because, as explained before, this is the case where, by construction, it’s harder for a method to distinguish between tails of non-uniform components and uniform component.

Fig. 2

Barplots representing Monte Carlo estimates of the MSE for parameter sub-vectors. Error bars are “1-standard-error intervals” for the corresponding Monte Carlo average.

Model Selection and density estimation. With a non-fixed G, the model can fit the data distribution in a semiparametric fashion. The information criteria are popular methods for performing model selection in the mixture framework McLachlan and Peel (2000a). The Akaike Information Criterion (AIC), and the Bayesin Information Criterion (BIC) are not specific to the mixture context (see) Konishi and Kitagawa 2008. In this work, we also consider the Integrated Completed Likelihood criterion (ICL) of Biernacki et al. (2000), which is specifically designed for selecting G when the mixture model is fitted to recover clusters. Whenever the AIC is reported in this work, it is corrected for small sample bias. In other words, we computed what in the literature is known as AICc (see) Konishi and Kitagawa 2008. All the mixture-based methods under comparison have been fitted for $G \in \{1,2,\ldots , 10\}$, and the three information criteria are used to select G. We then compared the fitted density against the true underlying density in terms of Mean Integrated Squared Error (MISE). The MISE’s computation requires numerical integration, which has been performed using stratified Monte Carlo integration with the strata adaptively chosen to achieve an integration error never larger than $10^{-4}$.

Fig. 3

Barplots of the Monte Carlo estimates of the MISE obtained from models selected by the AIC. Each panel a–c displays a sampling design. Colors represent methods according to the bottom legend. Error bars are “1-standard-error intervals” for the corresponding Monte Carlo estimate.

Fig. 4

Monte Carlo estimates of the proportion of times that the AIC selects a given G. Each panel a–c) displays refers to a sampling design. Colors represent methods according to the bottom legend.

In terms of density estimation, the AIC selection performed the best, although the BIC was fairly close. The latter was expected since it is known that the AIC is not generally consistent in model-selection, but provides better fits of the data distribution in a non-parametric sense Burnham and Anderson (2002). In Fig. 3 we report the MISE performance, while Fig. 4 we report results about the AIC selection. For both MIX and ASY designs, all mixture methods outperformed nonparametric kernel density with asymptotically optimal bandwidth selection (KERN). For large n, all mixture-based methods perform remarkably well. For smaller n SGM does overall marginally better. It is interesting to note that AIC selects the model so adaptively that the noise level does not affect the performance. The sample size drives the MISE. As expected for the ASY case, SGM does particularly better than the other mixture model-based competitors, although the gap almost disappears for $n=1000$. Figure 4 shows that SGM, GUM, and GRUM need fewer components to fit the data than GM. The latter is because the elongated tails can be captured by the uniform component in GUM and GRUM and the skewness parameters in the SGM method.

Outlier identification. True outliers are defined as points sampled under the uniform distribution. Both GUM and GRUM can be used to detect outliers applying the assignment rule (3) and using the estimated $\theta$ with G selected based on one of the three information criteria. Points assigned to the uniform noise component are flagged as “positives”, i.e., outliers. While there are many effective methods to identify outliers in the elliptical-symmetric family framework, the world of asymmetrical contamination is less explored due to the intrinsic difficulty to define outliers in such circumstances. We compare GUM and GRUM with the “adjusted outlyingness” (AO) method developed by Brys et al. (2005) and Hubert and Vandervieren (2008) that extends Stahel-Donoho outlyingness towards skewed distributions (see) Stahel 1981. For both GUM and GRUM, G needs to be fixed. The idea is that the method should be able to distinguish between a majority of points having a more compact shape, and a minority points (the outliers) not consistent with the main mass of the data. Because AIC showed better behavior in recovering the underlying density, in this case, we fix G based on the AIC.

Fig. 5

Barplots of the Monte Carlo estimates for outlier detection performance measures. Panel a–c refer to sampling designs. Colors represent methods according to the bottom legend. Error bars are “1-standard-error intervals” for the corresponding Monte Carlo estimate of TNR, TPR and Precision. Each method classifies outliers (positives) based on the AIC selection.

Fig. 6

Barplots of Monte Carlo estimates of misclassfication rates (%). Cluster is obtained fitting the mixture model with the true $G=2$. Each panel (a)–(c) refers to a sampling design. Colors represent methods according to the bottom legend. Error bars are “1-standard-error intervals” for the corresponding Monte Carlo estimate.

In Fig. 5 we report the true negative rate (TNR, also known as specificity); the True Positive Rate (TPR, also known as sensitivity); and the Precision. Recall that Precision = 1-FDR, where the FDR is the False Discovery Rate. The proposed method outperforms its competitors in all situations for each of the three metrics. AO is the second best, although its performance is far from that of GRUM, even in the ASY case, where it is expected to be at its best. For different reasons, both AO and GUM cannot detect the location where the uniform component takes over. Again, comparing the performance metrics in each case, the GRUM tends to confuse the Gaussian tails with the uniform contribution.

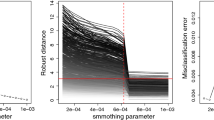
Clustering. We assess clustering on MIXs and MIXo designs. The ASY sampling does not produce clustered points. Evaluation of the clustering performance requires the definition of a “true” partition. The true cluster label of a point is defined as the mixture component from which the point is drawn. To compute misclassification rates (expected 0–1 loss), for mixture-based methods, we only consider the fitting with G fixed at the true $G=2$. Only GUM and GRUM are considered because the other mixture-based methods do not have a noise component. In Fig. 6 we report Misclassification Rates [%] of GRUM and GUM compared to the Bayes Optimal Classifier (OBC). OBC is the classifier that one would build if one knew the true model parameters. In other words, the OBC is obtained using the assignment rule 3 with the true generating mixture parameters. The latter implies that the MCR obtained for OBC in Fig. 6 represents the optimal Bayes risk. Under the usual 0–1 loss, the Bayes risk gives the best possible MCR. Comparing with the OBC is particularly convenient in situations with strong overlap as for the MIXo. GRUM outperforms GUM for smaller sample size, and its performance is closer to the optimal error rate corresponding to the OBC’s error. The performance gap between GUM And GRUM is clearer in the case of overlapped clusters (MIXo).

If one wants to estimate the number of clusters as the number of non-noise mixture component G, probably the ICL and the BIC do the best job. ICL performed slightly better, and for brevity, we only report its performance in Fig. 7. In the separated case (MIXs), $G=2$ clusters have a clear intuition because of the separation. In the latter case, GRUM and GUM often pick $G=2$. GRUM shows an overall advantage over its competitor. In the MIXo case, the clustering is not obvious, and in fact, the ICL tempts to choose $G=1$ for GRUM and GUM, and it chooses $G=2$ for the remaining methods. In the clustering perspective, probably $G=1$ is a more sensible choice for MIXo.

Fig. 7

Monte Carlo estimates of the proportion of times that the ICL selects a given G. Each panel a–c refers to a sampling design. Colors represent methods according to the bottom legend.

Robust location–scale estimation. In a non-clustered population like the ASY model, one could be interested in estimating the location and the scale of the uncontaminated data robustly. For the ASY model, true location and scale are defined as the mean and the standard deviation of the $\mathcal {\chi }^2(3)$ component. Here we compare the mixture-based methods GUM and GRUM with AO, TRIMAD, and SE. In Fig. 8 we report MSE for location and scale parameters.

Fig. 8

For the ASY design, we report barplots of the Monte Carlo estimates of the MSE for location and scale estimators. The fitted model is selected based on the AIC. Error bars are “1-standard-error intervals” for the corresponding Monte Carlo estimate. Competing methods are represented by colors given in the bottom legend.

For GUM, GRUM, and AO, we define robust location–scale estimates as the weighted average and standard deviations pairs:

$$\begin{aligned} \text {location} = \frac{1}{W}\sum _{i=1}^n w(x_i)x_i, \quad \text {scale} = \sqrt{\frac{1}{W}\sum _{i=1}^n w(x_i)(x_i-\text {location})^2}, \end{aligned}$$

where $W=\sum _{i=1}^{n} w(x_i)$. For GUM and GRUM, $x_i$ is weighted by the estimated posterior probability that $x_i$ does not belong to the uniform noise component, i.e. $w(x_i; \theta ) = 1-\tau _0(x_i; \theta )$. These weights are smooth. For the AO methods $w(x_i) = 1$ if the $x_i$ is not flagged as outlier, and $w(x_i) = 0$ otherwise. GRUM and GUM require, again, a decision about how to select G. In this case, the underlying model is used to fit the data distribution and not for finding the groups in the data. Therefore, the GRUM and GUM parameters are fitted based on the AIC selection. TRIMAD consists of the Tukey’s Trimean and the MAD from the Trimean. Tukey’s Trimean is a particularly effective measure of location in situations deviating from symmetry. The Trimean and the MAD are very easy to compute, and they are robust routine alternatives to the sampling estimators (SE). SE estimates are included as non-robust benchmarks. There is a huge catalog of robust location-scale estimators for one–dimensional data, and considering all of them is outside the scope of this paper. GRUM and TRIMAD report the best performance, although, for larger contamination rates, GRUM does better. Note that the nominal breakdown point of the TRIMEAN is 25%. Therefore, in finite samples, we would expect a deterioration of the performance even before $\pi _0$ hits 25%. The GUM and AO’s problematic performance was expected based on the outlier detection performance documented in Fig. 5.

6 Applications to real data sets

This section presents an application of the GRUM method to the three data sets introduced in Sect. 1. We considered $G=1,2,\ldots ,10$, and the corresponding AIC and BIC values are shown in Fig. 9. GRUM’s hyperparameters are set as in the numerical experiments of Sect. 9. In Fig. 9, the information criteria have been individually rescaled onto the interval [0,100] in order to ease the comparison. Overall the ordering of the fitted models provided by the AIC and the BIC agrees with some exceptions. ICL behaves differently, pursuing a more parsimonious representation of the data distribution. The latter confirms the tendency of the ICL in detecting clustered regions rather than the distribution fit pursued by the AIC and the BIC. The BIC has the most monotonic behavior, whereas the ICL is on the opposite side.

Fig. 9

AIC, BIC and ICL information criteria for the GRUM method fitted on the real data sets introduced in Sect. 1. The tree information criteria are individually rescaled onto the interval [0,100] in order to ease the comparison. Panel a TiO2 (Titanium dioxide) concentration data set. Panel b pH of blood data set Panel c realized volatility data set.

TiO2 concentration data. Both AIC and BIC choose $G=2$ Gaussian components, while the estimated noise proportion $\pi _0=1.526\%$ The corresponding density estimate is shown in Panel (a) of Fig. 10. With $G=2$ the GRUM fits two overlapped Gaussian components with means $(\mu _1, \mu _2) = ( 0.309 0.606)$, variances $(\sigma ^2_1, \sigma ^2_2) = (0.016, 0.032)$, and proportions $(\pi _2, \pi _2)=(50.125\%, 48.350\%)$. In the non-uniform part of the data distribution there seems to be some skewness rather then a clustering structure.

Fig. 10

Density fitted with the GRUM method on the real data sets introduced in Sect. 1. G is selected based on the AIC. Cluster=0 denotes points assigned to the uniform component. The remaining cluster labels denote points assigned to the Gaussian components of the fitted model. Panel a TiO2 (Titanium dioxide) concentration data set. Panel b pH of blood data set Panel c realized volatility data set.

The fact that GRUM fits a $\pi _0>0$ is an indication that the tail behavior of the data distribution can be distinguished from the shape of the main part of the distribution. ICL selects $G=1$, completely merging the previous two Gaussian components fitted by both AIC and BIC. The interesting thing here is that the set of points assigned to the uniform component remain unchanged under all three information criteria.

The density fitted by both AIC and BIC is not dramatically different from that produced by the kernel method shown in Panel (a) of Fig. 1. However, GRUM provides a smoother approximation, although carefully looking at the density plot, there is a discontinuity at the estimated $\beta _1$.

PH of blood data. In Fig. 9 all three information criteria select $G=1$. GRUM assigns 15.114% of the observed data to the uniform noise component. The latter can be seen form the density estimate in Panel (b) of Fig. 10.

The GRUM’s mean estimate of the pH of Blood concentration is 38.71, while the sample mean is 41.55. The GRUM estimates a pH of blood variance of 9.3, while the sample variance is 74.54.

Further checks showed that the GRUM method does not agree with some of the best performing robust univariate location-scale estimators. For example the optimal M-estimator computed at 95% efficiency (implemented in the RobStatTM package of Yohai et al. (2020)) estimates the distribution’s center at 39.96 and a squared dispersion (proxy for variance) of 14.29. Overall the density fit shown in Panel (b) of Fig. 10 looks rather credible compared with Panel (b) of Fig. 1.

Realized volatility data. The AIC and the BIC both agree on $G=2$ plus a uniform noise component representing a small group of 3 data points (estimated $\pi _0=2.329\%$). See Panel (c) in Fig. 10. The effect of these 3 data points on the optimal bandwidth estimation for kernel density is enormous. To see the latter, Panel (c) in Fig. 10 is compared with Panel (c) in Fig. 1. With the $G=2$ selected by AIC and BIC, the GRUM method fits two normal components of almost equal size $(\pi _1,\pi _2) =(57.309\%, 40.362\%)$, with means $(\mu _1, \mu _2) = (0.00092, 0.00255)$, and variances $(\sigma ^2_1, \sigma ^2_2) = (1.13{\times }10^{-7}, 1.04{\times }10^{-6})$.

As explained before, the GRUM’s d hyperparameter is always set to $d=0.5$ for all computations in this paper. For this data set, the scale lower bound in terms of the minimum variance would be $5.4{\times }10^{-20}$. Hence, none of the fitted mixture components hits the border of the parameter space. With $G=2$, we obtain a multimodal density that may correspond to the low-vs-high volatility clusters of stocks in the data sets. In this case, the two identified volatility clusters may be conveniently used to transform a continuous notion (volatility) into two easy to interpret categories that are particularly useful for risk analysts. In fact, in risk analysis is not essential the absolute level of volatility but how the volatility of an asset compares with the cross-sectional distribution at some time point. The three outliers correspond to three exceptional risky assets traded on 28/Aug/1998, and these are “Nationstar Mortgage HO”, “Micron Technology” and “Intuit Inc”.

The ICL chooses $G=1$, merging the two Gaussian components found by both AIC and BIC. The set of identified outlying data remains almost unchanged except that for one data point. We note that the ICL has a more “unstable” behavior (Fig. 11).

Fig. 11

Density fitted with the GRUM method on the real data sets introduced in Sect. 1. Here G is selected based on the ICL. Cluster=0 denotes points assigned to the uniform component. The remaining cluster labels denote points assigned to the Gaussian components of the fitted model. Panel a TiO2 (Titanium dioxide) concentration data set. Panel b pH of blood data set Panel c realized volatility data set.

7 Conclusions and final remarks

In this paper, we study a model that is a mixture where atypical observations on one of the two tails are represented by a uniform noise component whose separation from the main Gaussian components is controlled by the user. The proposed method can be used for several purposes: cluster analysis, outlier identification, robust-location scale estimation in unclustered populations, semiparametric density estimation. As most flexible tools (e.g. robust estimators, nonparametric density estimators, etc.), the GRUM method requires hyperparameters’ settings, and these hyperparameters can be easily interpreted.

We showed theoretical results, and we supported the analysis with both artificial data experiments and real data applications. The extension of the methods studied here to the multidimensional setting is difficult both theoretically and computationally. High-dimensional analysis plays a crucial role in modern applications, but the proposed method is a valid tool for the many one-dimensional analysis that we continue to perform routinely.

Appendix: Poofs of statements

Proof

Proof of 1.  The argument is organized in three steps. The idea of the proof is as follows: first, we show that the mean, scale, and uniform parameters maximizing $L_n(\cdot )$ are bounded (steps 1–3); the parameter space is compactified (step 4); the discontinuity introduced by ($\beta _1, \beta _2$) is treated in step 5 where we show that the set of all local maxima of $L_n(\cdot )$ is finite (step 5); the proof is concluded selecting the best local maxima.

Step 1.   Take $\theta ' \in \Theta _n$ with $\mu '_g \le m_n$ for some $g=1,\ldots ,G$. Consider the vector $\theta '' \in \Theta _c$ that is equal to $\theta '$ except that now $\mu ''_g = \min ({\varvec{x}_n})$. This implies that $L_n(\theta ') \le L_n(\theta '')$. By analogy, $\mu '_g > \max ({\varvec{x}_n})$ can be ruled out.

Let $\theta '$ be such that $\beta '_1 = \min ({\varvec{x}_n})- \varepsilon$ for some $\varepsilon >0$, take also $\theta ''$ be such that $\theta ''$ is the same as $\theta '$ except that ${\beta ''}_1 = \min ({\varvec{x}_n})$. This implies that $L_n(\theta ') \le L_n(\theta '')$ for every $\varepsilon >0$ such that the scale constraint is still satisfied. If the constraint cannot be satisfied at ${\beta ''}_1 = \min ({\varvec{x}_n})$, take ${\beta ''}_1 = \min ({\varvec{x}_n})-\alpha$ with the smallest $\alpha >0$ such that the scale constraint is satisfied at ${\beta ''}_1$, and note that $L_n(\theta ') \le L_n(\theta '')$ for any choice $\varepsilon >\alpha$. By the same arguments we can show that, in order to improve $L_n(\theta )$, either one chooses $\beta _2=\max ({\varvec{x}_n})$, or if the scale constraints binds one chooses $\beta _2=\max ({\varvec{x}_n})+ \alpha$ with the smallest $\alpha >0$ such that the scale constraint is satisfied.

Because of the scale constraint all standard deviations, including that of the uniform component, are such that $s_g\ge s_{\min }>0$, where $s_{\min }=\exp (-n^d)$. Step 1 and 2 imply that the optimal choice of $\theta \in \Theta _n$ is such that all means and uniform parameters will be finite. Because of the (RS) constraint $\sigma _g \le s_{\max }=\min _g \{ (\beta _1 -\mu _g)/\gamma \} < +\infty$.

Also note that for all $\theta \in \Theta _n$, the proportion parameters must belong to the compact set $P=[0, \pi _{\max }]\times [0,1]^{G}$.

Step 2.   Fix $s_{\max } < +\infty$, $-\infty< a< b < +\infty$, and define the compact set $\dot{\Theta }_n \subset \Theta _n$ as

$$\begin{aligned} \dot{\Theta }_n:= \left\{ \theta \in \Theta _n \;|\; \min ({\varvec{x}_n})\le \mu _g \le \max ({\varvec{x}_n}), \; a \le \beta _1<\beta _2 \le b, \; s_{\min } \le s_g \le s_{\max }, \; , \pi _g \in P \right\} . \end{aligned}$$

Based on Step 1, we conclude that $\sup _{\theta \in {\Theta }_n} L_n(\theta ) = \sup _{\theta \in \dot{\Theta }_n} L_n(\theta )$ for some suitable choice of $s_{\max }, a, b$. The latter means that the optimal solution to (6) belongs to a compact subset of the parameter space.

Step 3.   By applying Lemma 2 in Coretto and Hennig (2011), and taking into consideration the additional (RS) constraint, we note that if $\tilde{\theta }\in \dot{\Theta }_n$ is a local maximum of $L_n(\theta )$, then $(\tilde{\beta }_1, \tilde{\beta }_2)$ either coincides with a pair of distinct points in $\varvec{x}_n$, or $(\tilde{\beta }_1, \tilde{\beta }_2)$ is such that $\tilde{\beta }_2 - \tilde{\beta }_1 = \sqrt{12}\; s_{\min }$ (the scale constraint binds) and $[\tilde{\beta }_1, \tilde{\beta }_2]$ contains at least one data point.

All possible values of the uniform parameters for which the corresponding $\theta$ is a candidate for a local maximum can be obtained from the previous argument. The latter leads to only finitely many possible values for $L_n(\theta )$. Consider the vector $t(\tilde{\beta }_1, \tilde{\beta }_2)$ are fixed to be one of the many local maxima described in Step 3. Note that $t(\tilde{\beta }_1, \tilde{\beta }_2)$ will be contained in a compact set because of previous Steps 1. $L_n(t(\tilde{\beta }_1, \tilde{\beta }_2))$ is continuous with respect to $t(\tilde{\beta }_1, \tilde{\beta }_2)$ for every choice $(\tilde{\beta }_1, \tilde{\beta }_2)$, moreover since such $t(\tilde{\beta }_1, \tilde{\beta }_2)$ is contained in a compact set, then $L_n(t(\tilde{\beta }_1, \tilde{\beta }_2))$ has a well defined maximum. Applying this argument for all finitely many possible choice of $(\tilde{\beta }_1,\tilde{\beta }_2)$, we can find all possible local maxima of $L_n(\theta )$ on $\dot{\Theta }_n$, and hence among these we get the global maximum.

Proof

Proof of 2.  The present framework is consistent with the setup of Tanaka and Takemura (2006). For brevity we refer to Assumptions 1–4 in Tanaka and Takemura (2006) as TT1–TT4. It suffices to show that TT1–TT4 are satisfied in the case considered in this paper. First notice that both the Gaussian density and the uniform density have tails that that are of order smaller than $o(|x|^{-q})$ for $q>1$, therefore TT1 is satisfied. Also the Gaussian density and uniform density can be bounded above in $\Theta$, therefore TT2 is fulfilled. TT4 is also trivially satisfied because it can be easily seen that $\int | \log (f(x;\theta _0))| f(x;\theta _0) dx < \infty$. TT3 requires some specific care. First TT3 is fulfilled if for any sequence $\{\theta _{(m)}\}$ taken in a compact subset $A \subset \Theta$ and $\theta ' \in A$ such that $\theta _{(m)} \rightarrow \theta '$, the limit $f(x ; \theta _{(m)}) \rightarrow f(x ; \theta ')$ holds except perhaps on a set E which may depend on $\theta '$ and of which the Lebesgue measure is zero. Since $f(\cdot )$ is a linear combination, it suffice to check the condition on the summands on of $f(\cdot )$. $\phi (\cdot )$ is continuous with respect to both x and parameter, however the uniform distribution is discontinuous with respect the parameters for a given x.If $x \ne \beta '_1$ and $x \ne \beta '_2$ TT3 holds because $I_{[\beta _{1,(m)}, \beta _{2,(m)}]}(x) \rightarrow I_{[\beta '_{1}, \beta '_{2}]}(x)$. However, the latter is not true for the set $E=\{x_1=\beta '_{1}, x_2=\beta '_{2}\}$. Hence, TT3 holds except that for $x \in E$ that has zero Lebesgue measure. Since TT1–TT4 are fulfilled, Theorem 2 in Tanaka and Takemura (2006) holds which proves the result.

Proof

Proof of 3. The proof just follows proof of Theorem 4 in Coretto and Hennig (2011) by taking their $q=1$ and their $g(\cdot )=\phi (\cdot )$.

Proof

Proof of 4. For now, we ignore the third constraint. We will show that any solution to (10) without the third constraint will automatically fulfill it. The objective function in (10) is strictly concave and the equality constraint is linear. The Karush–Kuhn–Tucker (KKT) conditions are necessary for a globally optimal solution (see) Bertsekas 1999. Such a solution will be a stationary point of the Lagrangian function

$$\begin{aligned} \Lambda (\theta _\pi ,l_1,l_2):= Q_\pi (\theta _\pi , \theta ^{(s)}) + l_1 \left( 1-\sum _{j=0}^G \pi _j \right) + l_2 (\pi _{\max }- \pi _0) , \end{aligned}$$

where $l_1$ and $l_2$ are the KKT dual variables. Let $\nabla _g$ denote the gradient of $\Lambda (\cdot )$ with respect to the g-th component of $\theta _\pi$. Let $\theta _\pi ^*$ the optimal solution. KKT conditions establish that there exist $(l_1^*,h_2^*)$ such that the first order conditions are fulfilled for all g, i.e.

$$\begin{aligned} \nabla _g \; Q_\pi (\theta _\pi ^*, \theta ^{(s)}) - l_1^* - l_2^* \pi _0^* = 0, \qquad \text {for all} \quad {g \ge 0}, \end{aligned}$$

(14)

and also the KKT’s complementary conditions are satisfied, that is

$$\begin{aligned} l_2^*(\pi _0^* - \pi _{\max })=0, \quad l_2^* \ge 0. \end{aligned}$$

(15)

Recall the notation $T_g^{(s)}= \sum _{i=1}^n\tau _g(x_i; \theta ^{(s)})$. Consider now an optimal solution that does not hit the border of the parameter space, and label this solution $(\tilde{\theta }_\pi , \tilde{l}_1, \tilde{l}_2)$. For an interior solution $\tilde{l}_2 = 0$. Therefore, from (14) it holds true that $T_g^{(s)}/\tilde{\pi }_g - \tilde{l}_1 = 0$ for all $g\ge 0$. Solve the latter for $\tilde{\pi }_g$, use the equality constraint $\tilde{\pi }_0+ \tilde{\pi }_1+\ldots ,+\tilde{\pi }_G = 1$, and also use the fact that $\sum _{g=0}^G T_g^{(s)}= n$, and obtain $\tilde{l}_1 = n$ and

$$\begin{aligned} \tilde{\pi }_g = \frac{T_g^{(s)}}{n} \quad \text {for all}\;\; g \ge 0. \end{aligned}$$

(16)

Consider the second case when the optimal solution hits the border of the parameter space, denote the border solution with $(\bar{\theta }_\pi , \bar{l}_1, \bar{l}_2)$. For a border solution $\bar{l}_2 > 0$. The condition (14) implies again that $T_g^{(s)}/ \bar{\pi }_g - \bar{l}_1 = 0$ for all $g\ge 1$. As before, solve the previous equation for $\bar{\pi }_g$, use the equality constraint $\bar{\pi }_1+ \bar{\pi _2}+, \ldots , + \bar{\pi }_G = 1- \bar{\pi }_0$, and obtain $\bar{l}_1 = \sum _{g=1}^G T_g^{(s)}/ (1- \bar{\pi }_0)$. Since $\sum _{g=1}^G T_g^{(s)}= n - T_0^{(s)}$, then

$$\begin{aligned} \bar{\pi }_g = \frac{1-\bar{\pi }_0}{n-T_0^{(s)}}T_g^{(s)}\quad \text {for all~~} g \ge 1, \quad \text {and} \quad \bar{\pi }_0 = \pi _{\max }. \end{aligned}$$

(17)

Plug both the interior and the border solution, (16) and (17) respectively, into the objective function $Q_\pi (\cdot )$ and obtain

$$\begin{aligned} \frac{T_0^{(s)}}{n}\log \left( \bar{\pi }_0\right) + \sum _{g=1}^G \frac{T_g^{(s)}}{n} \log \left( \frac{1-\bar{\pi }_0}{n-T_0^{(s)}}T_g^{(s)}\right) \;\le \; \sum _{j=0}^G \frac{T_g^{(s)}}{n} \log \left( \frac{T_g^{(s)}}{n}\right) , \end{aligned}$$

which holds with equality if and only if $\bar{\pi }_0 = \tilde{\pi }_0 = T_0^{(s)}/n$. Therefore, if the interior solution is feasible, that is if $\bar{\pi }_0 = T_0^{(s)}/n \le \pi _{\max }$, the objective function is globally maximized by (16). If this is not the case, i.e. $T_0^{(s)}> n\pi _{\max }$, the optimal solution is (17). The proof is completed by noting that the selection between (16) and (17), corresponds to the updating rules (M2a) and (M2b).

Proof

Proof of 5. First we need to show that for every pair $\{x^{(r)}_i, x^{(r)}_j\} \in \varvec{x}_n$ such that $x^{(r)}_i< x^{(r)}_j$ and $x^{(r)}_j - x^{(r)}_i \ge \sqrt{12}\exp (-n^d)$, it happens that $L_{n}(\theta ^{(s+1)}) > L_{n}(\theta ^{(s)})$ for every $s=1,2,\ldots$. Using Theorem 4.1 in Redner and Walker (1984) it suffices to show that $Q(\theta ^{(s+1)}, \theta ^{(s)}) \ge Q(\theta ^{(s)}, \theta ^{(s)})$.

Consider the decomposition of $Q(\cdot )$ in equation (9). For every pair $\{x^{(r)}_i, x^{(r)}_j\}$, $\theta _u^{0} = (x^{(r)}_i, x^{(r)}_j) \in \Theta _n$ because the initialization step is constructed so that the initial uniform parameters are contained in $\Theta _n$. Moreover, because of 3 the algorithm does not update the uniform parameters and $Q_u(\theta _u^{(s+1)}, \theta ^{(s)})=Q_u(\theta _u^{(s)}, \theta ^{(s)}) = Q_u(\theta _u^{^{(0)}}, \theta ^{(s)})$ for any $s=1,2,\ldots$.

Now consider the optimization program M1. By construction $\theta _\phi ^{(s+1)}\in \Omega _n$. Observe that the objective function is concave and the inequality constraints are linear, therefore a global optimal solution exists (see) Bertsekas 1999. This implies that for all $s=1,2,\ldots$, $Q_\phi (\theta _\phi ^{(s+1)}, \theta _\phi ^{(s)}) \ge Q(\theta _\phi ^{(s)}, \theta _\phi ^{(s)})$.

By 4, the M2-steps, i.e. M2a and M2b, solve the optimization program (10). Therefore $Q_\pi (\theta _\pi ^{(s+1)}, \theta _\pi ^{(s)}) \ge Q(\theta _\pi ^{(s)}, \theta _\pi ^{(s)})$. Hence, each component of $Q(\theta , \theta ^{(s)})$ is increased or let constant in each step, therefore $Q(\theta ^{(s+1)}, \theta ^{(s)}) \ge Q(\theta ^{(s)}, \theta ^{(s)})$ which, by Theorem 4.1 in Redner and Walker (1984) implies that $\{L_n(\theta ^{(s)}\}$ is a monotonically increasing sequence. And this proves part 1 of the statement.

Because of the compactness of $\Theta _n$, and since 1 guarantees that a maximum of $L_n(\cdot )$ exists, the sequence $\{\theta ^{(s)}\}$ converges to a stationary point in $\Theta _n$ by Theorem 4.1 in Redner and Walker (1984). The latter proves the second part of the statement.