Abstract
Applying quantile regression to count data presents logical and practical complications which are usually solved by artificially smoothing the discrete response variable through jittering. In this paper, we present an alternative approach in which the quantile regression coefficients are modeled by means of (flexible) parametric functions. The proposed method avoids jittering and presents numerous advantages over standard quantile regression in terms of computation, smoothness, efficiency, and ease of interpretation. Estimation is carried out by minimizing a “simultaneous” version of the loss function of ordinary quantile regression. Simulation results show that the described estimators are similar to those obtained with jittering, but are often preferable in terms of bias and efficiency. To exemplify our approach and provide guidelines for model building, we analyze data from the US National Medical Expenditure Survey. All the necessary software is implemented in the existing R package qrcm.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The analysis of count data represents an important topic in the statistic literature and numerous textbooks (e.g., Cameron and Trivedi 1998; McCullagh and Nelder 1989; Hastie and Tibshirani 1990; Winkelmann 2005) have been partially or entirely dedicated to the subject. The most well-established approach is to utilize parametric or semiparametric regression models that are typically based on the Poisson distribution and its generalizations, and maximize a pseudo-likelihood to estimate conditional means (Gourieroux et al. 1984).
Machado and Santos Silva (2005) proposed analyzing count data using quantile regression (\(\textsc {qr}\); Koenker and Bassett 1978; Koenker 2005). Their approach permits avoiding strong parametric assumptions and enables investigating every aspect of the conditional distribution, and not just its mean. This idea, however, comes with some complications. The fact that the conditional density of the data is not absolutely continuous, in combination with the non-smoothness of the objective function, causes a non-standard rate of convergence (Manski 1975, 1985) and may as well generate identifiability issues and computational problems.
The solution proposed in Machado and Santos Silva’s paper is to artificially smooth the data by applying jittering (Stevens 1950). A continuous outcome is generated by adding a random quantity in [0, 1) to the original counts, and estimation and inference are carried out by applying standard \(\textsc {qr}\). A one-to-one correspondence between the quantiles of the counts and those of the artificial data can be established. This method has been applied in various fields including analysis of fertility (Miranda 2008; Booth and Kee 2009), frequency of doctor visits (Moreira and Barros 2010; Winkelmann 2006), car accidents (Qin and Reyes 2011), and capacity of pre-enrollment test to predict students’ performance (Grilli et al. 2016). A Bayesian version of jittering has been proposed by Lee and Neocleous (2010). Jittering has been advocated as a computational trick to avoid degenerated solutions (e.g., Koenker 2017), which commonly occur in presence of discrete responses.
Other recent approaches include that of Congdon (2017), in which the asymmetric Laplace distribution is combined with a Poisson model in a Bayesian framework, and the model-based quantile regression of Padellini and Rue (2018), in which quantiles are mapped to the parameters of a generalized linear model identified by a continuous version of a valid count distribution. Tzavidis et al. (2015) proposed a semiparametric M-quantile approach for counts that extends the ideas of Cantoni and Ronchetti (2001) and Breckling and Chambers (2001). These methods avoid jittering, but depend on a limited choice of predefined parametric models.
The idea presented in this paper is to describe the quantile regression coefficients, say \(\varvec{\beta }(p)\), by parametric, smooth functions of p, say \(\varvec{\beta }(p \mid \varvec{\theta })\), using the quantile regression coefficients modeling (qrcm) framework described in Frumento and Bottai (2016, 2017). With this approach, the conditional quantile function is modeled parametrically as if the response variable was continuous. The goal is to utilize a “working model” that does not reflect the actual data distribution, but permits estimating a smooth quantile function by minimizing a smooth loss function, in the same spirit of Efron (1992).
The proposed method bears some similarities with Padellini and Rue’s (2018) approach, in which a statistical model describes a hypothetical continuous counterpart of an originally discrete response. Our modeling framework, however, does not utilize known families of distributions such as Poisson or Negative Binomial, and allows to estimate quantile functions with an arbitrary parametric structure. As shown in the paper, this approach not only permits to avoid jittering, but also generates more efficient estimators, simplifies estimation and inference, and facilitates the interpretation of the results.
The paper is structured as follows. In Sect. 2 we describe the \(\textsc {qrcm}\) framework in a general quantile regression situation. In Sect. 3 we show how \(\textsc {qrcm}\) can be applied to count data. We describe computation and inference in Sect. 4, and report simulation results in Sect. 5. In Sect. 6 we show the usefulness of the proposed method by analyzing a dataset relating the frequency of doctor’s visits to a set of demographic and socio-economic predictors. The R package qrcm implements the described estimator and includes all the necessary functions for inference, prediction, and plotting.
2 Quantile regression coefficients modeling
We denote by \(Y_i\) a response variable of interest, and by \(\varvec{x}_i\) a q-dimensional vector of observed covariates, \(i = 1, \ldots , n\). The standard quantile regression (qr) model assumes that
is the conditional quantile function of some known, monotone transformation \(T(\cdot )\) of Y. Working with a transformed response is common in practice and may be convenient with non-negative or bounded outcomes. Note that, in a general \(\textsc {qr}\) framework, the response variable is assumed to be sampled from an absolutely continuous population, which is not true if Y is a count. Estimation of \(\varvec{\beta }(p)\) is carried out by minimizing the objective function
in which \(y_i\) is a realization of \(Y_i\), and \(\omega _{p,i} = I(T(y_i) \le \varvec{x}^{\mathrm {\scriptscriptstyle T} }_i\varvec{\beta }(p))\).
Quantile regression does not require distributional assumptions and permits investigating every aspect of possibly asymmetric, heavy-tailed, or multimodal response variables, showing the effect of covariates at different quantiles. Although the distribution-free nature of \(\textsc {qr}\) is generally seen as an advantage, it also represents its main weakness. Quantiles are estimated one at a time and no parametric structure is assigned to the coefficient functions \(\varvec{\beta }(p)\). This makes estimation inefficient, generates a large amount of random variability, and causes both the loss function, \(L(\varvec{\beta }(p))\), and the estimated coefficients, \({\hat{\varvec{\beta }}}(p)\), to be non-smooth functions of their arguments.
Joint estimation of multiple quantiles has been discussed by numerous authors (e.g., Tokdar and Kadane 2012; Reich 2012; Reich and Smith 2013; Yang and Tokdar 2017; Das and Ghosal 2017, 2018; Fabrizi et al. 2020), and is implemented in the R packages BSquare (Smith and Reich 2013) and qrjoint (Tokdar and Cunningham 2018). The idea of simultaneous quantile regression is recurrent in the literature on quantile crossing (e.g., He 1997; Bondell et al. 2010; Liu and Wu 2011), and can be used to improve estimation of individual fixed effects (Koenker 2004).
Frumento and Bottai (2016, 2017) suggested using a fully parametric approach and reformulated model (1) as
where \(\varvec{\theta }\) is a vector of model parameters that describe the functional form of the coefficient functions, \(\varvec{\beta }(p) = \varvec{\beta }(p \mid \varvec{\theta })\). This approach is referred to as quantile regression coefficients modeling (qrcm) and is implemented in the qrcm R package (Frumento 2020). An estimate of \(\varvec{\theta }\) can be obtained by minimizing
which is the integral, with respect to the order of the quantile, of the loss function of standard quantile regression displayed in (2). Unlike \(L(\varvec{\beta }(p))\), the loss defined in Eq. (4) is a smooth function of its arguments, which permits using Newton-type algorithms to carry out minimization, and applying the standard theory of M-estimator (e.g., Newey and McFadden 1994) to derive and implement asymptotics.
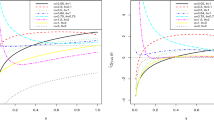
An illustration of the parametric approach described in model (3) is given in Fig. 1, which is constructed using simulated data. On the left, we report the estimated \(\textsc {qr}\) coefficients of order \(p = 0.01,0.02, \ldots , 0.99\). On the right, we show a parametric fit based on a cubic function, \(\beta (p \mid \varvec{\theta }) = \theta _0 + \theta _1p + \theta _2p^2 + \theta _3p^3\). Describing coefficients by smooth functions with closed-form mathematical expressions comes with an obvious gain in efficiency, especially in the tails, and makes it simpler to report and interpret the results.
Comparison between \(\textsc {qr}\) and \(\textsc {qrcm}\). Left: coefficient function estimated by standard quantile regression. Right: the coefficient is modeled by a cubic function, \(\beta (p \mid \theta ) = \theta _0 + \theta _1p + \theta _2p^2 + \theta _3p^3\), and estimation is carried out by minimizing \(L(\varvec{\theta })\) (Eq. 4). Shaded areas represent pointwise confidence intervals
3 Quantile regression coefficients modeling with counts
When \(\textsc {qr}\) is applied to count data, a non-standard rate of convergence is obtained as a result of the non-smoothness of the objective function in conjunction with the discreteness of the response variable. The problem was undertaken, among others, by Manski (1975, 1985) and Huber (1981). In their paper, Machado and Santos Silva (2005) suggested generating an artificial continuous variable \(Y^* = Y + U\) by adding a quantity \(U \in [0,1)\) to the original counts Y, a procedure that was referred to as jittering (Stevens 1950). The most common choice is to define U to be a uniform random variable, independent of Y and \(\varvec{x}\). A quantile regression model of the form
is assumed to hold for some known monotone transformation \(T(\cdot )\) of \(Y^*\). Because \(Y^*\) is continuous, ordinary quantile regression can be applied to \(T(Y^*)\) and standard asymptotic theory holds. Given an estimate \({\hat{\varvec{\beta }}}(p)\) of \(\varvec{\beta }(p)\), quantiles of the original count Y are consistently estimated by
where \(\lceil a \rceil\) denotes the ceiling operator. Because the value of \({\hat{\varvec{\beta }}}(p)\) depends on the specific realization \(\{u\}_{i = 1}^n\) of U, it is preferable to compute \({\hat{\varvec{\beta }}}(p)\) as the average estimate across m jittered samples (average-jittering). Another solution is to adopt the Bayesian framework described by Lee and Neocleous (2010), in which new values of U are simulated at each iteration of the Monte Carlo Markov Chain algorithm.
Alternative approaches, that are briefly discussed in Machado and Santos Silva’s paper, aim to replace \(L(\varvec{\beta }(p))\) with a smooth objective function. This can be obtained by replacing the indicator functions \(\omega _{p,i} = I(T(y_i^*) \le \varvec{x}^{\mathrm {\scriptscriptstyle T} }_i\varvec{\beta }(p))\) (Eq. 2) with a smooth counterpart (e.g., an integrated kernel), or by directly using a different loss, such as the asymmetric maximum likelihood proposed by Efron (1992).
In this paper, we suggest applying the \(\textsc {qrcm}\) framework to model a discrete response, using a parametric quantile function as if the data were generated from an absolutely continuous population. The objective is that of imposing some degree of smoothing to the assumed distribution, without altering the response itself.
Our proposal is based on the empirical evidence that almost identical estimators are obtained by applying \(\textsc {qrcm}\) to the jittered response, \(Y^*= Y + U\), and directly to \(Y^\circ = Y + E[U]\). Such equivalence results from the parametric structure that is imposed to the quantile function, which permits “smoothing away” the points of mass in the empirical distribution of the data.
Without loss of generality, we assume \(E[U] = 0.5\) and apply model (3) to some transformation \(T(\cdot )\) of \(Y^\circ = Y + 0.5\),
Here, \(\varvec{\beta }(p \mid \varvec{\theta })\) is a vector of parametric coefficient functions that are assumed to be continuous and differentiable functions of p. The resulting quantile function is itself continuous, and depends on the covariates according to the same modeling structure used in standard quantile regression. The function to be minimized, \(L(\varvec{\theta })\), is given in Eq. (4) and, unlike \(L(\varvec{\beta }(p))\), is also continuous and continuously differentiable.
After an estimate \({\hat{\varvec{\theta }}}\) of \(\varvec{\theta }\) has been computed, quantile regression coefficients are obtained as \({\hat{\varvec{\beta }}}(p) = \varvec{\beta }(p \mid {\hat{\varvec{\theta }}})\), and Eq. (6) can be used to estimate the quantiles of Y,
By definition, model (7) cannot be the true data-generating process and should be thought of as a “working model”. Although an interpretation in terms of a latent continuous variable is possible, the idea of fitting a continuous quantile function to a discrete outcome should be regarded as a computational expedient and can be seen as an implicit way of performing jittering.
3.1 A toy example
Suppose that a discrete response variable Y is uniformly distributed on the support \(\{0,1,2, \ldots 9\}\). Assuming \(U \sim U[0,1)\), the jittered response \(Y^*= Y + U\) has a continuous U[0, 10) distribution, with quantile function \(Q_{Y^*}(p) = 10p\). To implement \(\textsc {qrcm}\), define a parametric model \(Q(p \mid \theta ) = \theta p\), in which the true value of the parameter is \(\theta = 10\). Simple algebra permits showing that the minimizer of \(L(\theta )\) under this model solves \(n^{-1}\sum _i \min (y_i/\theta ,1)^2 = 1/3\) and is a function of the quadratic mean of the data. It can be easily shown that, asymptotically, the same estimators of quantiles are obtained with the following three methods: (1) standard \(\textsc {qr}\) applied to \(Y^*\); (2) \(\textsc {qrcm}\) estimator applied to \(Y^*\); and (3) \(\textsc {qrcm}\) estimator applied to \(Y^\circ = Y + \sqrt{903}/6 - 4.5 \approx Y + 0.508\). To prove this result, just note that \((3E[(Y^*)^2])^{1/2} = (3E[(Y^\circ )^2])^{1/2} = 10\). While the equivalence between (1) and (2) is straightforward, point (3) shows that the same estimator can be obtained without jittering.
3.2 Model building
As shown in simulations in Sect. 5, a “good” parametric model may outperform standard \(\textsc {qr}\) with uniform jittering in terms of bias and standard error. Defining a parametric model for a quantile function, however, is not trivial. Numerous alternative strategies to model \(\varvec{\beta }(p \mid \varvec{\theta })\) parametrically are presented in Frumento and Bottai’s (2016; 2017) papers, and the excellent book by Gilchrist (2000) can also be used for inspiration. The coefficient functions are usually simple, often monotone, and can sometimes be well approximated by linear or even constant functions. On the other hand, when flexibility is needed, polynomials or spline functions can be used. Some sensible options for model building are reported in Table 1.
Note that standard \(\textsc {qr}\) estimators can be obtained as a special case of \(\textsc {qrcm}\) by allowing \(\varvec{\beta }(p \mid \varvec{\theta })\) to be an arbitrarily flexible function of p. The linear regression model, in which \(Y \sim N(\beta _0 + \beta _1x_1 + \beta _2x_2 + \cdots , \sigma ^2)\), is also a special case of model (3) and corresponds to the parametric quantile function defined by \(Q_Y(p \mid x) = \beta _0 + \sigma z(p) + \beta _1x_1 + \beta _2x_2 + \cdots\), where z(p) is the quantile function of a standard Normal distribution.
In this section, we describe a general strategy to formulate parametric quantile regression models that can be applied to count data. We assume to fit the working model defined by (7),
where \(Y^\circ = Y + 0.5\).
In their 2005 paper, Machado and Santos Silva suggested modeling the following quantity: \(T(Y^*, p) = \log (Y^*- p)I(Y^*> p) + \log (\epsilon )I(Y^*\le p)\), where \(Y^*= Y + U\) is the jittered variable, and \(\epsilon\) some small positive number. This transformation is justified by the fact of using uniform jittering and, being a function of p, is only convenient when quantiles are estimated one at a time.
Here we suggest two alternative options: (i) to directly model \(Y^\circ\), letting \(T(\cdot ) = I(\cdot )\); and (ii) to use a \(\log\) transformation, \(T(Y^\circ ) = \log (Y^\circ )\), by analogy with the standard link function of log-linear models. The choice is mainly determined by whether the association with the covariates is assumed to be linear or \(\log\)-linear. Note, however, that a \(\log\)-linear association could be well approximated by a linear model in which the covariates have been suitably transformed, e.g., by replacing them by the corresponding spline basis.
To formulate a parametric model for the coefficient functions, \(\varvec{\beta }(p \mid \varvec{\theta })\), we suggest using the following linear parametrization:
where \(\varvec{b}(p) = \left[ b_1(p), \ldots , b_k(p)\right] ^{{\mathrm {\scriptscriptstyle T} }}\) is a set of k known functions of p, and \(\varvec{\theta }\) is a \(q\times k\) matrix with entries \(\theta _{jh}\), \(j = 1, \ldots , q\), \(h = 1, \ldots , k\). The j-th regression coefficient is given by \(\beta _j(p \mid \varvec{\theta }) = \theta _{j1}b_1(p) + \cdots + \theta _{j_k}b_k(p)\), and the quantile function is rewritten as
This parametrization can prove flexible and computationally convenient (Frumento and Bottai 2016, 2017).
Consider, for example, a regression model with a single covariate x:
Some distributional assumptions can be directly translated into a parametric model for \(\beta _0(p \mid \varvec{\theta })\) and \(\beta _1(p \mid \varvec{\theta })\). For instance, if the working model assumes \((Y^\circ - \theta _1x) \sim \text {Exp}(1/\theta _0)\), the quantile function is \(Q_{Y^\circ }(p \mid x, \varvec{\theta }) = -\theta _{00}\log (1 - p) + \theta _{11}x\), which can be written as
identifying \(\varvec{b}(p) = \left[ 1, -\log (1 - p)\right] ^{{\mathrm {\scriptscriptstyle T} }}\) as the “basis” to be used for model building.
To avoid strong parametric assumptions, it may be preferable to formulate a more flexible working model:
In this model, the intercept is described by the quantile function of an Exponential distribution, \(-\log (1 - p)\), that determines the shape of the right tail, and a combination of trigonometric functions; while the coefficient associated with x is assumed to be linear. In matrix form, the model is defined by
Note that this quantile function does not correspond to any known, closed-form family of probability distribution.
An alternative flexible parametrization is given by
Here, the intercept is modeled by a quantile function that includes as special cases that of the (shifted) Exponential (\(\theta _{01} = \theta _{03} = 0\)), the asymmetric Logistic (\(\theta _{01} = 0\)), the standard Logistic (\(\theta _{01} = 0, \theta _{02} = \theta _{03}\)), and the Uniform (\(\theta _{02} = \theta _{03} = 0\)). The slope of x is a combination of linear and cubic functions. If \(x \ge 0\), then \(\varvec{\theta }\ge \varvec{0}\) is a sufficient condition for \(Q_{T(Y^\circ )}(p \mid x, \varvec{\theta })\) to be monotonically increasing. This makes it simple to control for quantile crossing, that represents a common issue in standard quantile regression.
Possible choices of \(\varvec{b}(p)\) include polynomials \(\left[ p, p^2, p^3, \ldots \right]\), splines, piecewise linear functions, roots \([p^{1/2}\), \((1 - p)^{1/2}\), \(p^{1/3}\), \((1 - p)^{1/3}, \ldots ]\), logarithms \(\left[ \log (p), -\log (1 - p)\right]\), trigonometric functions \(\left[ \cos (\pi p), \sin (\pi p)\right]\), quantile functions of known distribution (e.g., that of a Beta or Gamma distribution), and combinations of the above. The intercept, \(\beta _0(p \mid \varvec{\theta })\), is more frequently modeled using unbounded functions, while the coefficients associated with \(\varvec{x}\) are usually assumed to be bounded and, in some situations, can be described by linear or even constant functions. A variety of modeling options will be used in the application described in Sect. 6.
As shown in the above examples, a common feature of parametric quantile functions is that the support of the response, which is identified by quantiles of order \(p = 0\) and \(p = 1\), may depend on estimated parameters. This is always the case, for example, if \(\varvec{\beta }(p \mid \varvec{\theta })\) is assumed to be polynomial. In this situation, maximum likelihood estimators do not meet regularity conditions and cannot be computed by standard algorithms, which explains why most methods involving some sort of parametric modeling (e.g., Reich and Smith 2013) use Bayesian inference. This does not represent an issue in the current framework, where the likelihood function is not used. The minimizer of the simultaneous loss function \(L(\varvec{\theta })\) defined in (4) always corresponds to an interior point.
4 Computation and inference
Define the model as in (7),
where \(Y^\circ = Y + 0.5\), and denote by \(y_i^\circ = y_i + 0.5\), \(i = 1, \ldots , n\), a vector of observed responses. We remark that, since Y is a count while \(Q_{T(Y^\circ )}(p \mid \varvec{x}, \varvec{\theta })\) describes a continuous response, the model does not directly reflect the true data-generating process. If an underlying continuous variable Z is invoked such that \(Y = \lfloor Z \rfloor\), where \(\lfloor a \rfloor\) denotes the floor operator, then the model may be assumed to correctly describe the quantile function of Z. In this case, however, \(Y^\circ = Y + 0.5\) should be considered interval-censored between \(Y^\circ - 0.5\) and \(Y^\circ + 0.5\). Here we avoid questioning whether \({\hat{\varvec{\theta }}}\) consistently estimates a true parameter \(\varvec{\theta }_0\), and treat \(Q_{T(Y^\circ )}\) as a working model.
As shown in (4), an estimate \({\hat{\varvec{\theta }}}\) of \(\varvec{\theta }\) is computed as the minimizer of
Numerical integration can be used to evaluate \(L(\varvec{\theta })\), and Newton-type algorithms can be applied to perform optimization. When \(\varvec{\beta }(p \mid \varvec{\theta }) = \varvec{\theta }\varvec{b}(p)\) as in model (9), the following expression can be obtained (Frumento and Bottai 2016):
where
In the above formulas, \(p_i = F(T(y_i^\circ ) \mid \varvec{x}_i, \varvec{\theta })\) corresponds to the cumulative distribution function of \(y^\circ _i\) evaluated at \(\varvec{\theta }\), and can be obtained as the inverse of \(Q_{T(Y^\circ )}\). In the implementation of the qrcm R package, \(\varvec{B}(p)\) and \({\bar{\varvec{B}}}\) are evaluated numerically, and a bisection algorithm is used to compute \(p_i\) at the current estimate of \(\varvec{\theta }\).
Following the standard theory of M-estimators (e.g., Newey and McFadden 1994), an estimate of \(\text {cov}({\hat{\varvec{\theta }}})\) can be obtained as
where \({\hat{\varvec{H}}}\) is the matrix of second derivatives of \(L(\varvec{\theta })\), evaluated at \({\hat{\varvec{\theta }}}\), and \({\hat{\varvec{\Omega }}}\) is the outer product of the summands of the gradient. The exact expressions for \(\varvec{H}\) and \(\varvec{\Omega }\), of which \({\hat{\varvec{H}}}\) and \({\hat{\varvec{\Omega }}}\) are the sample counterparts, are provided in Frumento and Bottai (2016). Note that, unlike standard \(\textsc {qr}\), the asymptotic covariance matrix of \(\textsc {qrcm}\) estimator does not involve nuisance parameters, which makes it unnecessary to estimate the sparsity function (e.g., Koenker and Machado 1999) or to use bootstrap to perform inference.
If \(\varvec{\beta }(p \mid \varvec{\theta }) = \varvec{\theta }\varvec{b}(p)\) as in model (9), an estimate of \(\text {cov}({\hat{\varvec{\beta }}}(p \mid \varvec{\theta }))\) is easily obtained from \({\widehat{\text{cov}}}({\hat{\varvec{\theta }}})\) by using quadratic forms. Obviously, the described inferential procedures are imperfect, as they ignore the fact that \(Q_{T(Y^\circ )}\) is not the true quantile function. However, simulation results show that reliable estimates of the standard errors are obtained even with a relatively small sample size.
5 Simulation results
We considered a model of the form
where \(x_1\) was uniform between 0 and 3, and \(x_2\) was binary with \(P(x_2 = 1) = 0.5\). To generate discrete data, we first simulated a continuous variable Z from model (12); then, we defined \(Y = \lfloor Z \rfloor\). We considered two scenarios. In scenario 1 we defined
In scenario 2 we defined
These scenarios were regarded as “true” models, although they describe the conditional quantile function of the unobserved response Z, and not that of the observed count Y. Both scenarios generate relatively small counts, rarely exceeding \(Y = 15\).
For each scenario, we simulated \(R = 1000\) datasets of size \(n = 300\). For each simulated dataset we computed: (1) the \(\textsc {qr}\) estimators of \(\varvec{\beta }(p)\), using average jittering with \(m = 100\) replicates; (2) the \(\textsc {qrcm}\) estimators, defining \(\varvec{\beta }(p \mid \varvec{\theta })\) as for the “true” model; and (3) the \(\textsc {qrcm}\) estimators, defining \(\varvec{\beta }(p \mid \varvec{\theta })\) to be a third-degree shifted Legendre’s polynomial (e.g., El Attar 2009), an orthogonal polynomial in (0, 1) that can be used to formulate flexible models for the coefficient functions. \(\textsc {qr}\) estimators were applied to the response variable \(Y^*= Y + U\) with \(U \sim U[0,1)\), while \(\textsc {qrcm}\) were applied to \(Y^\circ = Y + 0.5\).
In Tables 2 and 3, we report the average estimates of \(\varvec{\beta }(p)\) at different values of p, and the corresponding standard errors. When the “true” model was fitted, \(\textsc {qrcm}\) estimators were much more efficient than standard \(\textsc {qr}\), and their average was closer to the “true” parameters. When a flexible model was used instead, the performance of \(\textsc {qrcm}\) estimators was more similar to that of average-jittering \(\textsc {qr}\), although some relevant efficiency gains were observed in the right tails where the data were more sparse. This suggests that describing \(\varvec{\beta }(p \mid \varvec{\theta })\) by a parsimonious model can substantially improve on standard \(\textsc {qr}\) estimators, while overfitting tends to nullify the gain.
In the last two columns of each table, only for \(\textsc {qrcm}\) estimators, we report the average estimated standard errors computed using the asymptotic covariance matrix defined by Eq. (11). Results suggest that inferential procedures are reliable, although the working model is only an approximation of the true data-generating process.
6 Analysis of NMES data
To illustrate the usefulness of the proposed method, we analyzed data from the US National Medical Expenditure Survey (nmes) conducted in 1987 and 1988 (Deb and Trivedi 1997; Kleiber and Zeileis 2008). The dataset includes a representative sample of \(n = 4406\) US civilians aged \(\ge 66\), for which numerous socio-economic indicators (age, gender, marital status, education, income) and indicators of health condition are available.
The goal of our analysis was to predict the number of doctor’s visits during a one-year period. The response variable had a skewed distribution with a very long right tail (Fig. 2). Higher-order quantiles, which correspond to very frequent doctor’s visits, were considered particularly important. We formulated the following quantile regression model:
where “Health” is a self-perceived health status, with levels “poor”, “average”, and “excellent”; “Nchronic” is the number of chronic diseases; “Male” is an indicator of male gender; the age was expressed in decades, and centered at its median; “School” is the number of years of education, and was centered at its modal value of 12 years; “Married” is an indicator of marital status; “Employed” is an indicator of employment (about \(90\%\) of subjects were retired); the household income (in tens of thousands US dollars) was centered at its median. All individuals in the sample were covered by Medicare, a public insurance program that offers protection against health-related costs. “Insurance” is an indicator of whether the subject was also covered by a private insurance; and “Medicaid” indicates whether he or she was covered by MedicAid, a federal program complementary to Medicare.
Considering that most predictors were binary, and that the association between the number of doctor’s visits and the non-binary covariates appeared to be well approximated by a straight line, we decided not to transform the response variable.
We first estimated a grid of percentiles, \(p = \{0.01, 0.02, \ldots , 0.99\}\), by using ordinary quantile regression with average-jittering (\(m = 100\)). We used bootstrap (\(R = 100\)) to estimate the standard errors. Note that this procedure is very time-consuming, as it requires to estimate \(99 \times 100 \times 100 = 990,000\) quantile regression models. In Figs. 3 and 4, the estimated coefficient functions are represented by broken dashed lines.
We then formulated a variety of parametric models to be applied to \(Y^\circ = Y + 0.5\). We considered the following alternative parametrizations:
\(j = 0, \ldots , 11\). All models were formed by the combination of a 2nd-degree polynomial, and a function that could be used to describe a long right tail. Other flexible models could be defined using splines, trigonometric functions, or piecewise-linear functions. We considered a variety of \(\delta\), namely \(\delta = \{0.5,1,2\}\) in model (i), \(\delta = \{0.05,0.10,0.25\}\) in model (ii), and \(\delta = \{1,5,10\}\) in model (iii). We allowed the parametric form of \(\beta _0(p \mid \varvec{\theta })\) to differ from that of the other coefficients. For example, we could use model (i) for \(\beta _0(p \mid \varvec{\theta })\), and model (ii) for \(\beta _1(p \mid \varvec{\theta }), \beta _2(p \mid \varvec{\theta }), \ldots\).
Since all models had the same number of parameters, we selected the “best” model based on the minimized loss function. Note, however, that information criteria such as aic and bic can also be used for model selection. For general results on information criteria for M-estimators, see Machado (1993); a discussion of criteria for quantile regression models can be found in Lee et al. (2014).
The optimal model had all coefficients parametrized as in (i), with \(\delta = 2\):
The estimated coefficient functions are represented by continuous lines in Figs. 3 and 4. The model parameters are summarized in Table 4, while selected percentiles are reported in Table 5.
Result showed that more frequent doctor’s visits were associated with poorer health conditions, female gender (at least at quantiles below 0.75), higher education, and having additional private or public insurances. Age, marital status, and economic indicators did not appear to have a clear association with the response. Importantly, predictors affected the large quantiles much more than the low quantiles of the distribution. For example, the regression coefficient associated with poor health was less than 2 at the median, greater than 3 at the 75th percentile, and greater than 6 at the 95th percentile. The quantile function of two representative individuals, computed using Eqs. (6) and (8), is exemplified in Fig. 5.
The estimates obtained using the described \(\textsc {qrcm}\) approach were very close to those of ordinary quantile regression with average-jittering, showing that the two methods are virtually equivalent. Using \(\textsc {qrcm}\), however, resulted in a much faster computation and did not require using bootstrap to compute standard errors. Additionally, using a parametric model allowed to describe the coefficient functions by means of simple mathematical equations, improving the efficiency of the estimators and making it easier to summarize and interpret the results.
Estimated quantile regression coefficient functions. The dashed lines are obtained using standard quantile regression with average-jittering. The continuous lines (with pointwise confidence intervals represented by shaded areas) are based on the parametric model summarized in Table 4. For a better readability, all figures are truncated at \(p = 0.97\)
Estimated quantile regression coefficient functions (continued from Fig. 3)
Estimated quantile function of the number of doctor’s visits, obtained using quantile regression with average-jittering (qr) and quantile regression coefficients modeling (qrcm). Left: quantile function of the “typical” individual: average perceived health, one chronic condition, male, median age, 12 school years, married, not employed, median income, with a private insurance, no MedicAid. Right: quantile function of a “disadvantaged” individual: poor health, three chronic conditions, male, age = 80, 6 school years, not married, not employed, 1st decile of income, no private insurance, no MedicAid
7 Conclusions
We showed how the \(\textsc {qrcm}\) paradigm can be applied to count data, using a working model in which the assumed quantile function describes a continuous response. This, in combination with the smoothness of the objective function, avoids using jittering, generates efficient estimators, and simplifies inference.
Unlike other forms of model-based quantile regression, in which estimation is carried out in a Bayesian framework, the proposed approach adopts the frequentist paradigm. This is only possible because the minimizers of the objective function \(L(\varvec{\theta })\), unlike those of the likelihood function, correspond to interior points whether or not the model parameters affect the support of the response. This not only avoids the problem of selecting prior distributions, but may be considered an advantage in fields, like Medicine and Epidemiology, where Bayesian techniques are only used sparely.
In the paper, we only considered a linear quantile regression model of the form \(Q_{T(Y)}(p \mid \varvec{x}, \varvec{\theta }) = \varvec{x}^{\mathrm {\scriptscriptstyle T} }\varvec{\beta }(p \mid \varvec{\theta })\), and we used a linear parametrization \(\varvec{\beta }(p \mid \varvec{\theta }) = \varvec{\theta }\varvec{b}(p)\) to describe the regression coefficients. These assumptions could be relaxed, for example by allowing \(Q_{T(Y)}(p \mid \varvec{x}, \varvec{\theta })\) to be a nonlinear function of \(\varvec{x}\) or \(\varvec{\beta }\), or by assuming that \(\varvec{\beta }(p \mid \varvec{\theta })\) is a nonlinear function of \(\varvec{\theta }\). This would not affect the estimation method, but would make computation much more complicated without necessarily representing an advantage in terms of model flexibility. Describing a variety of meaningful parametric quantile functions can be the subject of future research.
Although empirical evidence suggests that parametric models are relatively immune to quantile crossing, the monotonicity of the estimated quantile function is not generally guaranteed. Some special parametrization (e.g., Reich and Smith 2013; Yang and Tokdar 2017; Das and Ghosal 2017) can be used to avoid crossing. Alternatively, \(L(\varvec{\theta })\) could be minimized subject to monotonicity constraints. This represent an important subject for future work, and a challenge from a computational standpoint.
Quantiles are often more interesting than simple measures of location and scale, such as the mean and the variance. For example, many applications aim to describe the tail behavior and the impact of extreme observations. Our proposal may promote the widespread adoption of quantile regression methods in the analysis of count data. Possible applications are found in medicine, epidemiology, life sciences in general, sociology, psychology, and economics.
Providing a user-friendly implementation of the described estimator is an important part of our work. All software used in this paper is implemented in the qrcm R package. The package includes a main function iqr that carries out model fitting, and a variety of auxiliary functions that permit extracting information from the fitted model, performing prediction and extrapolation, plotting the estimated regression coefficients, and obtaining goodness-of-fit measures. The R package is available at http://CRAN.R-project.org/package=qrcm, and upon request to the authors.
Availability of data and material
The data are public.
References
Amemiya T (1985) Advanced econometrics. Harvard University Press, Cambridge
Barrodale I, Roberts FDK (1973) An improved algorithm for discrete \(L_1\) linear approximation. SIAM J Numer Anal 10:839–848
Bondell HD, Reich BJ, Wang H (2010) Non-crossing quantile regression curve estimation. Biometrika 97(4):825–838
Booth AL, Kee HJ (2009) Intergenerational transmission of fertility patterns. Bull Econ Stat 71:183–208
Breckling J, Chambers R (1988) M-quantiles. Biometrika 75:761–771
Cameron AC, Trivedi PK (1998) Regression analysis of count data. Cambridge University Press, Cambridge
Cantoni E, Ronchetti E (2001) Robust inference for generalized linear models. J Am Stat Assoc 96:1022–1033
Congdon P (2017) Quantile regression for area disease counts: Bayesian estimation using generalized Poisson regression. Int J Stat Med Res 6:92–103
Das P, Ghosal S (2017) Bayesian quantile regression using random B-spline series prior. Comput Stat Data Anal 109:121–143
Das P, Ghosal S (2018) Bayesian non-parametric simultaneous quantile regression for complete and grid data. Comput Stat Data Anal 127:172–186
Deb P, Trivedi PK (1997) Demand for medical care by the elderly: a finite mixture approach. J Appl Econom 12:313–336
Efron B (1992) Poisson overdispersion estimates based on the method of asymmetric maximum likelihood. J Am Stat Assoc 87:98–107
El Attar R (2009) Legendre polynomials and functions. CreateSpace ISBN: 978-1-4414-9012-4
Fabrizi E, Salvati N, Trivisano C (2020) Robust Bayesian small area estimation based on quantile regression. Comput Stat Data Anal 145:12. https://doi.org/10.1016/j.csda.2019.106900
Frumento P (2020) qrcm: quantile regression coefficients modeling. R package version 2.2. http://CRAN.R-project.org/package=qrcm
Frumento P, Bottai M (2016) Parametric modeling of quantile regression coefficient functions. Biometrics 72(1):74–84 [Epub ahead of print]
Frumento P, Bottai M (2017) Parametric modeling of quantile regression coefficient functions with censored and truncated data. Biometrics 73(4):1179–1188
Gilchrist W (2000) Statistical modeling with quantile functions. Chapman & Hall, London
Gourieroux C, Monfort A, Trognon A (1984) Pseudo maximum likelihood methods: applications to Poisson models. Econometrica 52:702–720
Grilli L, Rampichini C, Varriale R (2016) Statistical modelling of gained university credits to evaluate the role of pre-enrolment assessment tests: an approach based on quantile regression for counts. Stat Model 16(1):47–66
Hastie TJ, Tibshirani RJ (1990) Generalized additive models. Chapman and Hall/CRC, London
He X (1997) Quantile curves without crossing. Am Stat 51(2):186–192
Huber PJ (1967) The behavior of maximum likelihood estimates under nonstandard conditions. In: LeCam LM, Neyman J (eds) Proceedings of the fifth Berkeley symposium on mathematical statistics and probability, vol 1. University of California Press, Berkeley, pp 221–233
Huber PJ (1981) Robust statistics. Wiley, New York
Kleiber C, Zeileis A (2008) Applied econometrics with R. Springer, New York
Koenker R (2004) Quantile regression for longitudinal data. J Multivar Anal 91(1):74–89
Koenker R (2005) Quantile regression. Econometric Society Monograph Series. Cambridge University Press, Cambridge
Koenker R (2017) quantreg: quantile regression. R package version 5:33. https://CRAN.R-project.org/package=quantreg
Koenker R, Bassett G Jr (1978) Regression quantiles. Econometrica 46:33–50
Koenker R, Machado JAF (1999) Goodness of fit and related inference processes for quantile regression. J Am Stat Assoc 94(448):1296–1310
Lee D, Neocleous T (2010) Bayesian quantile regression for count data with application to environmental epidemiology. J R Stat Soc Ser C (Appl Stat) 59(5):905–920
Lee ER, Noh H, Park BU (2014) Model selection via Bayesian information criterion for quantile regression models. J Am Stat Assoc 109(505):216–229
Liu Y, Wu Y (2011) Simultaneous multiple non-crossing quantile regression estimation using kernel constraints. J Nonparametric Stat 23(2):415–437
Machado JAF (1993) Robust model selection and M-estimation. Econom Theory 9(3):478–493
Machado JAF, Santos Silva JMC (2005) Quantiles for counts. J Am Stat Assoc 100(472):1226–1237
Manski CF (1975) Maximum score estimation of the stochastic utility model of choice. J Econom 3:205–228
Manski CF (1985) Semiparametric analysis of discrete response: asymptotic properties of the maximum score estimator. J Econom 27:313–333
McCullagh P, Nelder J (1989) Generalized linear models, 2nd edn. Chapman and Hall/CRC, Boca Raton
Miranda A (1985) Planned fertility and family background: a quantile regression for counts analysis. J Popul Econ 21:67–81
Moreira S, Barros PP (2010) Double health insurance coverage and health care utilisation: evidence from quantile regression. Health Econ 19:1075–1092
Newey WK, McFadden D (1994) Large sample estimation and hypothesis testing. In: RF. Engle, DL. McFadden (eds.), Handbook of econometrics ,vol 4, No. 2. pp 2111–2245. North-Holland, Amsterdam
Padellini T, Rue H (2018) Model-based quantile regression for discrete data. arXiv:1804.03714
Qin X, Reyes P (2011) Conditional quantile analysis for crash count data. Transp Eng 137:601–607
Reich BJ (2012) Spatiotemporal quantile regression for detecting distributional changes in environmental processes. J R Stat Soc Ser C (Appl Stat) 61(4):535–553
Reich BJ, Smith LB (2013) Bayesian quantile regression for censored data. Biometrics 69(3):651–660
Smith LB, Reich BJ (2013) Bsquare: Bayesian simultaneous quantile regression. R package version 1.1. http://CRAN.R-project.org/package=BSquare
Stevens WL (1950) Fiducial limits of the parameter of a discontinuous distribution. Biometrika 37:117–129
Tokdar S, Cunningham E (2018) qrjoint: joint estimation in linear quantile regression. R package version 2.0-2. http://CRAN.R-project.org/package=qrjoint
Tokdar S, Kadane JB (2012) Simultaneous linear quantile regression: a semiparametric Bayesian approach. Bayesian Anal 7(1):51–72
Tzavidis N, Ranalli M, Salvati N, Dreassi E, Chambers R (2015) Robust small area prediction for counts. Stat Methods Med Res 24(3):373–395
Winkelmann R (2003) Econometric analysis of count data, 4th edn. Springer, Berlin
Winkelmann R (2006) Reforming health care: evidence from quantile regressions for counts. J Health Econ 25:131–145
Yang Y, Tokdar S (2017) Joint estimation of quantile planes over arbitrary predictor spaces. J Am Stat Assoc 112(519):1107–1120
Funding
Open Access funding provided by Università di Pisa.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authour declares that they have no conflict of interest statement.
Code availability
The R code is public.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Frumento, P., Salvati, N. Parametric modeling of quantile regression coefficient functions with count data. Stat Methods Appl 30, 1237–1258 (2021). https://doi.org/10.1007/s10260-021-00557-7
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10260-021-00557-7