Including covariates in a space-time point process with application to seismicity

Abstract

The paper proposes a spatio-temporal process that improves the assessment of events in space and time, considering a contagion model (branching process) within a regression-like framework to take covariates into account. The proposed approach develops the forward likelihood for prediction method for estimating the ETAS model, including covariates in the model specification of the epidemic component. A simulation study is carried out for analysing the misspecification model effect under several scenarios. Also an application to the Italian seismic catalogue is reported, together with the reference to the developed R package.

1 Introduction

Contagious phenomena are well described in space and time by self-exciting point processes, such that the conditional intensity function is obtained as the sum of the long-term variation component (the so-called endemic) and the short-term variation one (the epidemic part). This kind of models have been widely used in the literature: infectious disease (Paul et al. 2008; Paul and Held 2011; Meyer et al. 2012, 2017), crime (Mohler et al. 2011), quakes (Ogata 1998; Adelfio and Chiodi 2009; Adelfio and Ogata 2010; Adelfio and Chiodi 2015a; Zhuang et al. 2002). To model earthquake activity in space and time accounting both for the endemic (background activity) and epidemic (aftershocks) effect, the Epidemic-Type Aftershock Sequences (ETAS) model (Ogata 1988, 1998) is widely used, describing events starting from their space-time coordinates (and magnitude as mark) and incorporating seismological laws in a mechanistic approach, as a natural approach in the context of earthquake data.

In this paper, we aim at providing an improved framework for further computational and theoretical development of the study and the description of epidemic phenomena. In particular, extending the model formulation proposed by Meyer et al. (2012) in the context of infectious disease transmission, we suggest the use of a specific branching-type model for earthquake description (the ETAS model) in a regression-oriented version modelling, accounting also for external covariates, expected to explain some of the overall variability of the studied phenomenon and lead to a decrease in the unpredictable variability. We apply the Forward Likelihood for prediction (FLP) method (Chiodi and Adelfio 2011) for estimating the ETAS model components, also introducing a covariate vector for the epidemic part, crucial for a more realistic description of the observed activity. Indeed from previous studies (e.g., Adelfio and Chiodi 2015b) on the basis of the diagnostic results, the need of a more flexible model for the triggered component of the ETAS model revealed, noticing that even if the background seismicity is well described by the FLP estimated intensity, at least if compared with existing methods, something is still missing in the description of the space-time triggered part. In our opinion, considering external information (such as geological information related to faults distribution) for the description of spatio-temporal earthquakes could be a promising direction of study for this field of research.

Previous studies tried to incorporate the external information in the self-exciting model: Meyer et al. (2012) proposes a model for the epidemic forecast with a linear predictor, where background function is composed of a function of population density and of a vector of covariates; Schoenberg (2016) proposed an application to southern California earthquake forecasting using weather data as an additive component; Reinhart and Greenhouse (2018) incorporate piecewise constant covariates only for the background component of the model.

In the survival analysis, an example of such two-component temporal point process regression modelling for independent individuals is the additive-multiplicative model (Lin and Ying 1995; Sasieni 1996), such that the conditional intensity consist of additive endemic (the risk of infection from external sources, independent of the past) and epidemic components (individual-to-individual transmission of the disease and thus depends on the internal history of the process). In these models, the endemic risk can be expressed as a function of external covariates, introduced as a multiplicative function (Höhle 2009; Martinussen and Scheike 2002).

In this paper, using the terminology of the survival analysis, we propose a more general additive-multiplicative model for the conditional intensity function of a space-time self-exciting point process with covariates which may vary also continuously in space, incorporating their effect in the triggering effect, using the FLP approach as in Chiodi and Adelfio (2017b) for the estimation of the background intensity. The methodology here proposed can be extended in any context, different from the original seismic one, e.g., the credit risk one, where there is a contagious effect of the previous history in space and time, together with specific covariates, such as macroeconomic characteristics of the considered countries, as in Adelfio et al. (2018).

This paper is organized as follows. In Sect. 2 the theoretical background is defined, recalling some basic theory of space-time point processes and the ETAS model. In Sect. 3, the proposed extension of the ETAS model with the inclusion of covariates is provided. A simulation study with several scenarios is carried out to assess the performance of the proposed method (see Sect. 4). Finally, we present a seismic application, where external variables with respect to the usual event’s coordinates may provide information for the description of the seismic activity of the defined area. Section 6 is devoted to conclusive remarks.

2 Point processes and ETAS model

A spatial-temporal point process is a random collection of points, whose realisations consists of a finite or a countably infinite set of points in a space-time domain. We consider a spatio-temporal point process with no multiple points as a random countable subset X of ${\mathbb{R}}^{d-1}\times {\mathbb{R}}$, where a point $({\mathbf{s}},t)\in X$ corresponds to an event at ${\mathbf{s}}\in {\mathbb{R}}^{d-1}$ occurring at time $t\in {\mathbb{R}}$. We observe n events $\{({\mathbf{s}}_i,t_i)\}_{i=1}^{n}$ of distinct points of X occurring in n distinct times $\{t_i\}_{i=1}^{n}$ within a bounded spatio-temporal region $W\times T\subset {\mathbb{R}}^{d-1}\times {\mathbb{R}}$, with volume $|W|>0$, and with length $|T|>0$ where $n\ge 0$ is not fixed in advance (for more details see Diggle 2013).

A spatial-temporal point process is uniquely characterized by its associated conditional intensity function (CIF), $\lambda _{\varvec{\theta }}(t,{{\mathbf{s}}}|{\mathscr{H}}_t)$, (Daley and Vere-Jones 2003) i.e., the instantaneous rate or hazard for events at time t and location ${{\mathbf{s}}}$ given all the observations up to time t, conditioning on the random past history of the process. Let N(B) denote the number of events of the process falling in a bounded region $B \subset W \times T$. A completely stationary spatio-temporal point process has a constant intensity $\lambda$, defined as $\lambda =E[N(B)]$, i.e., $\lambda$ is the mean number of points per unit volume and unit time (Illian et al. 2008).

To model events that are clustered together, self-exciting point processes are often used. These models are used mainly to describe earthquakes characteristics, assuming that the occurrence of an event increases the probability of occurrence of other events in time and space. The Hawkes model (Hawkes and Adamopoulos 1973) and the ETAS model (Ogata 1988) are examples of self-exciting point processes.

The self-exciting process can be interpreted as a generalized Poisson cluster process associating to centres, of rate $\lambda$, a branching process of descendants. This kind of models are used to model reproduction phenomena and have been recently considered for the description of different applicative fields: biology (Caron-Lormier et al. 2006), demography (Johnson and Taylor 2008), epidemiology (Becker 1977; Balderama et al. 2012). According to a branching structure, the conditional intensity function of the self-exciting model is defined as the sum of a term describing the large-time scale variation (spontaneous activity or background, generally assumed homogeneous in time but not in space) and one relative to the small-time scale variation due to the interaction with the events in the past (induced or triggered activity):

$$\begin{aligned} \lambda _{\varvec{\theta }}(t,{{\mathbf{s}}}|{\mathscr{H}}_t )= \mu f({{\mathbf{s}}})+ \sum _{t_j<t}\nu _{\varvec{\phi }}(t-t_j,{\mathbf{s}}-{\mathbf{s}}_j) \end{aligned}$$

(1)

with ${\mathscr{H}}_t$ the past history of the process, $\varvec{\theta }=(\varvec{\phi },\mu )'$, the vector of parameters of the induced intensity ($\varvec{\phi }$) together with the parameter of the background general intensity ($\mu$), $f({{\mathbf{s}}})$ the spatial density and $\nu _{\varvec{\phi }}(\cdot )$ the spatial-temporal triggered density.

The triggering component of the model essentially provides a description of the intensity at a space-time location $(t,{{\mathbf{s}}})$ induced by each previous event, as a function of the spatial distances ${\mathbf{s}}-{\mathbf{s}}_j$ and temporal lags $t-t_j$, $\forall j$. In a clustered process, $\nu _{\varvec{\phi }}$ is a decreasing function of ${\mathbf{s}}-{\mathbf{s}}_j$ and $t-t_j$.

Simultaneously estimating the different components of the intensity function (large-time scale and small-time scale) in (1) is a main issue. If the large-time scale component $\mu f({{\mathbf{s}}})$ is known, the parameters ${\varvec{\phi }}$ can be usually estimated by the Maximum Likelihood method. In applications, the large-time scale component $\mu f({{\mathbf{s}}})$ is usually estimated through nonparametric techniques, like kernel estimators.

As introduced above, a branching process for earthquake description, widely used in seismological context, is the Epidemic Type Aftershocks-Sequences (ETAS) model (Ogata 1988, 1998). The ETAS conditional intensity function can be written, starting from model (1), as follows:

$$\begin{aligned} { \lambda _{\varvec{\theta }}(t,{\mathbf{s}}|{\mathscr{H}}_t )= \mu f({\mathbf{s}})+ \sum _{t_j<t} \frac{\kappa _0\ \exp { (\alpha (m_j-m_0)) }}{(t-t_j +c)^p}\left\{ ({\mathbf{s}}-{\mathbf{s}}_j)^2+d \right\} ^{-q} } \end{aligned}$$

(2)

The aftershock/induced component is the product of the density of aftershocks in time, i.e., the Omori law, representing the occurrence rate of aftershocks at time t, following the earthquake of time $t_j$ and magnitude $m_j$, and the density of aftershocks in space. In particular, $m_j$ is the magnitude of the j-th event and $m_0$ the threshold magnitude, that is, the lower bound for which earthquakes with higher values of magnitude are surely recorded in the catalogue, $\kappa _0$ is a normalizing constant, $c \text{ and } p$ are characteristic parameters of the seismic activity of the given region; p is useful for characterizing the pattern of seismicity, indicating the decay rate of aftershocks in time; d and q are two parameters related to the spatial influence of the mainshock. $\alpha$ is related to the expected number of offsprings generated by a single event, which is proportional to $\kappa _0 \exp \{\alpha (m_j-m_0)\}$.

For providing a simultaneous estimation of the background intensity and the triggered intensity components of an Epidemic-type model, in a previous paper, we developed the FLP approach (Adelfio and Chiodi 2015a). It is a nonparametric estimation procedure based on the subsequent increments of the log-likelihood obtained adding an observation one at a time, to account for the information of the observations until $t_k$ on the next one. This approach allows the estimation of smoothing constants to get a reliable kernel estimate of the background intensity. The simultaneous estimation of the two parametric components of a branching-type model alternating the standard parametric likelihood method with the FLP approach is here denoted by ETAS-FLP. Given the lack of specific open-source tools, the package etasFLP (Chiodi and Adelfio 2017a, b) provides tools to implement this mixed approach for a wide class of ETAS models for the description of seismic events, developed in a R environment.

In the provided methodology, the kernel background estimation is improved by weighting observations according to weights $\rho _i$, given by the ratio between the background and total intensity, for each observed event occurred at time $t_i$ in location ${\mathbf{s}}_i$, according to the following relationship:

$$\begin{aligned} { {\hat{\rho }}_i = \frac{{\hat{\mu }} {\hat{f}}({\mathbf{s}}_i)}{\lambda _{\hat{\varvec{\theta }}}(t_i,{\mathbf{s}}_i|{\mathscr{H}}_t )} } \end{aligned}$$

(3)

The quantity in Eq. (3) also gives an estimate of the probability that the i-th event $E_i$ has been generated by the background component of the process.

3 The ETAS model with covariates

In this paper, we propose an additive-multiplicative model for the conditional intensity function of a space-time point process defined in $[0,T] \times W\subset {\mathbb{R}}^3, T>0$, in the classical ETAS model framework.

In the ETAS model defined in (2), the expected number of offsprings generated by a single event is related to the magnitude of generating events, i.e., $\kappa _0 \exp \{\alpha (m_j-m_0)\}$. In this paper, we make it possible to include other covariates, besides the magnitude, related to every single event. Starting from the definition provided in Eq. (1), we propose to modify its additive formulation (sum of the “endemic” and “epidemic” parts), considering the offspring component in a novel regression view, that is, accounting for a vector of covariates. For interpretation convenience, in our proposal, we model covariates of the ETAS model as in a GLM framework, such that $\eta _j$ is a classical linear predictor given by $\eta _j = \varvec{\beta }'\textit{\textbf{z}}_j$, where $\textit{\textbf{z}}_j$ is the vector of covariates observed for the j-th event and $\varvec{\beta }$ is a vector of unknown parameters. This choice makes the methodology simple and easily extensible for any general linear predictor $\eta$.

As proposed by Meyer et al. (2012) in a context of infection occurrences, we incorporate the space-time phenomenological laws of the triggering part of ETAS model with the effects of covariates.

This triggering function is factorized into separate effects of marks, time, and relative location:

$$\begin{aligned} {\lambda _{\varvec{\tilde{\theta }}}(t,{\mathbf{s}}|{\mathscr{H}}_t )= \mu f({\mathbf{s}})+\sum _{t_j<t}\frac{\kappa _0\ exp{(\eta _j)} }{(t-t_j +c)^p}\left\{ ({\mathbf{s}}-{\mathbf{s}}_j)^2+d \right\} ^{-q}} \end{aligned}$$

(4)

where $(t_j , {\mathbf{s}}_j )$ is the time and location of individual occurrence j, $\eta _j = \varvec{\beta }'\textit{\textbf{Z}}_j$ is a linear predictor, with $\textit{\textbf{Z}}_j$ the external known covariate vector, including the magnitude (usually coinciding with the first covariate), acting in a multiplicative fashion on the base risk and $\tilde{\theta }=(\mu , \kappa _0, c, p, d, q, \varvec{\beta })'$, with $\varvec{\beta }$ a k-components vector, to be estimated.

More in details, in the usual ETAS model, $k=1$, $\textit{\textbf{Z}}_{j1}=m_j-m_0,$ and $\beta _1=\alpha$. In this model formulation, for an easier correspondence with the ETAS parametrization, in the $\varvec{\beta }$ vector an intercept term is not included, because of the presence of the parameter $\kappa _0$ in the model.

In the seismic context, this extension would provide a more general formalism for the earthquake occurrence in space and time. Indeed, the main idea is that the effect on the future activity depends not only on the closeness of the previous events, but also on other characteristics of the main event, like magnitude, as usual, and also quadratic components like $(m_j-m_0)^2$, or the geometric distance from the generating faults, or other geological sources.

The extended version of the package etasFLP v. 2.0 for generalized offspring component is going to appear into the CRAN (Chiodi and Adelfio 2020). Indeed, the introduction of a general linear predictor did not introduce serious computational or theoretical difficulties, since $\varvec{\beta }$ has been estimated with the parametric component in the etasFLP algorithm using the semi-parametric FLP approach.

4 Simulation study

The accuracy of the ETAS-FLP model with covariates can be evaluated under various conditions using simulations. In particular, we aim to assess the misspecification model effect, that is the properties of estimators of an ETAS model when the estimated linear predictor $\eta _j$ is different from the real one.

Specifically, we consider the case where an ETAS model is simulated in the presence of some covariate (as in Eq. 4) and then for each simulation the model is estimated by the proposed approach as though the covariates were completely ignored and compared with the estimation under the correct model. The issue is whether the parameters of the ETAS model can be accurately estimated though the model is misspecified.

Indeed, inferential theoretical results for the proposed model are quite difficult to perform, since properties of the sampling distribution of the estimated quantities in the ETAS model are not known, but asymptotic general results are known (Ogata 1978; Rathbun 1996). Furthermore, in observed seismic catalogues, the presence of the nonparametric estimation of the background seismicity represents a further complication for the study of the parametric component properties.

In this section, we provide results of a simulation study for describing the properties of the estimators of the ETAS model parameters. However, this study holds under some assumptions, and a reasonable set of true values of the parameters. For example, the choice of the values of the parameters $\mu , \kappa _0, c, p, d, q$ for the model with intensity in (4) could be an issue, since their influence is not separable from the one of $\eta$; specifically the choice of $\mu , \kappa _0$ influences the ratio between the background events (i.e., Poisson-like) and the triggered ones (i.e the clustered events).

Concerning the background intensity, in our simulations we assume a constant intensity, proportional to $\mu$, such that in our parametrization, the expected number of events in a given region is $E(N)=\mu \Delta t$, avoiding the influence of the estimation of the spatial background intensity. For the choice of $\mu , \kappa _0, c, p, d, q$, we use values close to those estimated for the Italian catalogue of the seismic events of magnitude greater than 2.5 (used in Sect. 5), assuming a constant background intensity, although this hypothesis may be unrealistic for the given area. However, different values of $\kappa _0$ are used to assess the effect of different weights of the aftershock component.

In the linear predictor $\eta$ we consider two covariates: the first covariate is always the magnitude, while the second covariate is an artificial variable generated in two different ways:

• (a) a geometrical choice, in which the covariate associated to each event is the distance of the event from the main diagonal of the space region, as it were a seismic fault;

• (b) a random choice, in which the covariate is the square of a standard normal random number.

In all considered scenarios, magnitudes are obtained generating random numbers from a Gutenberg-Richter distribution with a parameter $b=1.0789$, which is the estimated value for the used Italian catalogue. Moreover, a rectangular space region approximately equivalent to the rectangle embedding Italy is considered.

Therefore, we developed the following algorithm to simulate one catalogue from an ETAS process with conditional intensity function as in (4), which strictly depends on the branching nature of the generating process:

• 1. Input the true parameters values: $\mu , \kappa _0, c, p, d, q$, the parameters $\beta _1$ and $\beta _2$ related to covariates, and some other control parameters, that are the boundaries of the space-time region and the parameter b of the Gutenberg-Richter distribution;

• 2. generate a random number $n_0$ from a Poisson distribution with parameter $E(N)=\mu \Delta t$;

• 3. generate $n_0$ triples of space-time uniform coordinates in the spatial-temporal region together with $n_0$ random magnitudes and $n_0$ covariates, according to method (a) or (b);

• 4. for each point $P_j$ generate a random number $n_j$ from a Poisson distribution with parameter proportional to $\exp {\eta _j}$;

• 5. generate $n_j$ triples of space-time coordinates of aftershocks in the spatial-temporal region together with $n_j$ random magnitudes and $n_j$ covariates, according to methods (a) or (b), reported above;

• 6. add the $n_j$ new points to the set of events. Proceed with step (2) until all the events inside the region are involved in the simulation process as possible generators of further events.

Details of the method to generate random sequences from a branching process are in Zhuang and Touat (2015).

For simulating the triggered component, we consider 36 different scenarios:

• two different values of $\kappa _0$: 0.003, 0.006;

• three different values of p: 1.05, 1.10, 1.15;

• three different values of q: 1.2, 1.3, 1.4;

• two different methods to generate the second covariate, that is (a) and (b) mentioned above.

Moreover, for the r-th simulated sample($r=1,\ldots , N$, with N the number of the simulated samples for each scenario, fixed to 100 in this paper), two different ETAS models are fitted: the first one (Model1) is a misspecified model considering the magnitude as the only covariate, and the second one (Model2) is the right model, including both the magnitude and the further covariate, really used.

Let $I_{ir}$ be the indicator variable assigned to each simulated event, that is 1 if the i-th event of the r-th simulated sample belongs to the Poisson generated set, 0 if it belongs to the aftershocks set. For the r-th sample, the following quantities are computed: the estimates of the parameters $\varvec{\theta }$ under Model1, $\hat{\varvec{\theta }}_{r(1)}$, and under Model2, $\hat{\varvec{\theta }}_{r(2)}$; the length of the simulated sample $n_r$, the number of events generated according to the Poisson background process $n_{r0}$ and the number of aftershock events $n_{r1}$, such that $n_{r0}+n_{r1}=n_r$.

Therefore, for the r-th sample and for the model M ($M=1,2$), we compute the area under the ROC curve, denoted by $AUC_{r(M)}$, as a measure of the properness of ${\hat{\rho }}_{ir(M)}$ to classify induced and background events ($I_{ir}=0,1$).

Furthermore, for each event of the r-th sample and for each model $M=1,2$, the intensities $\lambda _{ir}$ according to the true values of the parameters are computed, and compared with the intensities ${\hat{\lambda }}_{ir(M)}$ estimated under the model M for $M=1,2$, computing the following mean absolute difference:

$$\begin{aligned} \Delta _{r(M)}(\lambda )=\frac{\sum _{i=1}^{n_r}|{\hat{\lambda }}_{ir(M)}-\lambda _{ir}|}{n_r} \end{aligned}$$

Eventually, for each scenario we get $N=100$ simulations, summarized in Tables 1, 2, 3 and 4. In particular, in these tables we report the following quantities:

• average of the simulated background events, $n_{r0}$,

• average of the simulated induced events, $n_{r1}$,

• relative ratios between the averages values of the two models of $\Delta _{r(M)}(\lambda )$, that is:

  $$\begin{aligned} RR_{\Delta (\lambda )}=\frac{\sum _{r=1}^{N}\Delta _{r(1)}(\lambda )-\sum _{r=1}^{N}\Delta _{r(2)}(\lambda )}{\sum _{r=1}^{N}\Delta _{r(2)}(\lambda )} \end{aligned}$$

• relative ratios between the averages values of the $AUC_{r(M)}$:

  $$\begin{aligned} RR_{AUC}=\frac{\sum _{r=1}^{N}AUC_{r(2)}-\sum _{r=1}^{N}AUC_{r(1)}}{\sum _{r=1}^{N}AUC_{r(1)}} \end{aligned}$$

• relative ratios between the simulated mean square errors of the two models for each parameter estimate ${\hat{\phi }}$, where $\phi$ is any of the parameter $\mu , \kappa _0, c, p,d, q, \beta _1$

  $$\begin{aligned} RR_{{\hat{\phi }}}= \frac{\sum _{r=1}^{N}({\hat{\phi }}_{r(1)}-{\phi })^2 - \sum _{r=1}^{N}({\hat{\phi }}_{r(2)}-{\phi })^2}{\sum _{r=1}^{N}({\hat{\phi }}_{r(2)}-{\phi })^2} \end{aligned}$$

For more details, the tables reporting the simulated mean square errors (MSE) of the parameter estimates, estimated under the wrong model (Model1) and the right model (Model2) are reported in section “Appendix” (see Tables 8, 9, 10, 11, 12, 13, 14, 15).

The simulations results using a geometrical covariate, as described in the point (a) above, for $\kappa _0=0.003$, are reported in Table 1. The corresponding results using a simulated covariate, as described in the point (b) above, are reported in Table 2.

Table 1 Average of $n_0, n_1$, $RR_{AUC}, RR_{\Delta (\lambda )}$ and $RR_{{\hat{\phi }}}$ between the mean square errors for the parameters of models Model1 and Model2, with the other parameters true values $\mu =0.079, \kappa _0= 0.003, c=0.013, d=0.5, \beta _1=0.39, \beta _2=-0.03$, using a geometrical covariate

Table 2 Average of $n_0, n_1$, $RR_{AUC}, RR_{\Delta (\lambda )}$ and $RR_{{\hat{\phi }}}$ between the mean square errors for the parameters of models Model1 and Model2, with the other parameters true values $\mu =0.079, \kappa _0= 0.003, c=0.013, d=0.5, \beta _1=0.39$, using a simulated covariate

The tables reporting the same comparisons for a greater value of $\kappa _0$ are reported in Table 3, using the geometric covariate, and in Table 4, for the case including a simulated covariate.

It could be noticed that all the AUC values used for the $RR_{AUC}$ values (see Tables 1, 2, 3 and 4) are however in the range 0.8881–0.9999.

Table 3 Average of $n_0, n_1$, $RR_{AUC}, RR_{\Delta (\lambda )}$ and $RR_{{\hat{\phi }}}$ between the mean square errors for the parameters of models Model1 and Model2, with the other parameters true values $\mu =0.079, \kappa _0= 0.006, c=0.013, d=0.5, \beta _1=0.39, \beta _2=-0.03$, using a geometrical covariate.

Table 4 Average of $n_0, n_1$, $RR_{AUC}, RR_{\Delta (\lambda )}$, $RR_{{\hat{\phi }}}$ between the mean square errors for the parameters of models Model1 and Model2, with the other parameters true values $\mu =0.079, \kappa _0= 0.006, c=0.013, d=0.5, \beta _1=0.39, \beta _2=-0.4$, using a simulated covariate.

The results reported in the Tables 1 and 2 show that, in general, the estimation of the parameters can still be performed in the absence of data on covariates, since it does not greatly affect the conditional intensity of the process, confirming results reported in Schoenberg (2016) for different formulations of self-exciting models including covariates. Conversely, the misspecification has a peculiar effect on the parameter $\kappa _0$ behaviour, comparing to the other parameters of the model. In particular, for a lower value of $\kappa _0=0.003$, the averages of the MSE estimating the Model1 are generally lower than the corresponding ones estimating the Model2 (see the negative sign of the RR reported in the Table 1). This effect is less evident if we use a random covariate in the simulation procedure (see the Table 2). Moreover, as described above, similar simulations are carried out accounting for a higher value of $\kappa _0=0.006$, that is with a greater influence of the aftershock component (Tables 3 and 4).

Here we observe that the $\kappa _0$ estimation provides higher MSE when the wrong model Model1 is estimated than estimating the true model Model2. We also note that this effect, though of minor size, seems to be opposite for the parameter $\mu$. In particular, the smaller the true value $\kappa _0$ is (that is, the more Poissonian the generating process is), the more variable its estimator is (see the Tables 8, 9, 10, 11, 12, 13, 14, 15 in the Appendix). In general, the misspecification model effect on the estimation of $\kappa _0$ can be explained as the consequence of the different number of simulated events ($n_0$) and induced events ($n_1$), depending on the true value of $\kappa _0$. Indeed, for $\kappa _0=0.003$ the simulated catalogues are mostly composed by background events, and therefore the estimation of the $\kappa _0$ parameter appears to be more unstable. Otherwise, increasing $\kappa _0$ the simulated catalogues have more aftershock events, providing more information for the triggered component estimation and more evidence in favour of Model2.

Actually, this last result can be also affected by our assumption related to the use of a constant background density in space and therefore, could require deeper analyses.

5 Application to the Italian earthquakes and comments

In this section, we report some of the results of the proposed ETAS-FLP approach with covariates, starting from the Italian catalogue of the space-time Italian seismicity, from May 5th, 2012 to May 7th, 2016, with 2.5 as the threshold magnitude (i.e. the lower bound for which earthquakes with higher values of magnitude are surely recorded in the catalogue). The catalogue reports 2226 events with the usual hypocentral coordinates (longitude, latitude, depth, time) together with the events magnitude, and also some additional information, such as: the hypocentral uncertainty, the distance from the nearest station (for shallow earthquakes, this distance should be sufficiently small), a measure of the quality of the location (named rms), the number of stations that recorded the event (this number is heavily influenced by the magnitude of the event and strongly influences the accuracy of the location) and the distance from the nearest fault (i.e., the identified earthquakes sources in that area).

The ETAS-FLP estimating results of Model1, as in Eq. (2), accounting both for the epicentral coordinates (longitude, latitude and time) and the magnitude of the inducing event, are not completely satisfying, suggesting, as usual, some lack of fitting mostly due to the triggered component (see Table 5). However, adding also the available covariates (Model2, reported in Fig. 1), that is considering the model in Eq. (4) with covariates, starting from the complete model, including all the available covariates, the best selected one includes, together with the magnitude m, also the depth z, the number of stations $n^{st}$, the distance from the nearest station $\delta ^{st}$ and the distance from the nearest fault $\delta$, such that we have a model with $k=5$ covariates and a total of 11 parameters. In particular, the last four covariates have both a negative effect on the space-time reproducing activity (see Table 6).

Table 5 Estimates, and standard errors within brackets, of the parameters of models Model1. In Eq. (2) $\alpha$ corresponds to $\beta _1$ of the linear predictor in Eq. (4)

Table 6 Estimates, and standard errors within brackets, of the parameters of models Model2

Looking at Tables 5 and 6, as already observed from our simulation study, the estimation of the parameters $\mu , \ c,\ p,\ d,$ and q is not strongly affected by the introduction of the covariates; conversely, the estimation of $\kappa _0$ is more sensitive to the choice of the model, since it is strictly related to the linear predictor value, that affects in turn the triggered component. Indeed, coherently with results observed in Sect. 4, the relative standard error of $\hat{\kappa _0}$ (w.r.t. its estimated value) is much higher than the relative standard errors of the other estimators.

For the temporal domain diagnostics of the fitted model, the marginal time process is obtained by integrating the estimated intensity function with respect to the observed space region (see Adelfio and Chiodi 2015b). As in Adelfio and Chiodi (2015b), let $\{t_i\}$ be data of a temporal point process identified by the conditional intensity function $\lambda (t)$. Therefore, the residual temporal process can be obtained moving each point $(t_i) \ \forall \ i$ on the real half-line to the point:

$$\begin{aligned} \tau _i=\Lambda (t_i)=\int _0^{t_i} \lambda (t)dt \end{aligned}$$

(5)

(Meyer 1971; Cox and Isham 1980; Ogata 1988). The process $\{\tau _i\}$ in (5) is a homogeneous Poisson process with unit intensity. Then, a plot of $\tau _i$ versus i can inform about bad fitting in time. In particular, this plot, together with a plot of the estimated time intensities, informs on the time at which departures from model assumptions are more evident.

Now, let N be a spatial process ${\textit{\textbf{S}}}$, with ${\textit{\textbf{s}}}=\{s_1,\ldots ,s_n\}$ the vector of its observed locations in a bounded region W of the plane ${\mathbb{R}}^2$. For a spatial point process, a useful definition of residuals has been introduced by Baddeley et al. (2005), based on the innovation process, extended by the Georgii–Nguyen–Zessin identity:

$$\begin{aligned} E\Big [\sum _{i=1}^n b(u_{i},{\textit{\textbf{s}}})\Big ]=E\int _{W} b(u,{\textit{\textbf{s}}})\lambda (u,{\textit{\textbf{s}}})du \end{aligned}$$

(6)

where $b(u,{\textit{\textbf{s}}})$ is a non-negative integrable function. For an exploratory data analysis, Pearson residuals are obtained considering in (6) the integrand function defined by: ${\hat{b}}(u,{\textit{\textbf{x}}})=1/\sqrt{{\hat{\lambda }}(u,{\textit{\textbf{x}}})}$ (Baddeley et al. 2005).

In this paper, as described in Adelfio and Chiodi (2015b), due to their interpretative simplicity, the above defined Pearson spatial residuals are computed in a space-time region Q, which extends over the whole time interval and on a rectangular space area. These tools have been also implemented in the version 2.0 of the package etasFLP. This area is determined by an equally spaced grid of q intervals for each dimension, such that the observed space area is divided in $q \times q$ rectangular cells. According to this approach, the classical comparison between observed and theoretical frequencies is considered and a $\chi ^2$-measure, based on the computed Pearson residuals, can be easily computed.

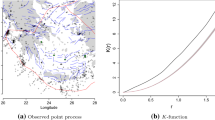
As further investigation, we also perform a spatio-temporal diagnostics based on the second-order statistics coming from weighted measures (Adelfio and Schoenberg 2009; Adelfio et al. 2020). The used method assesses goodness-of-fit of spatio-temporal models by using weighted second-order statistics, computed after weighting the contribution of each observed point by the inverse of the conditional intensity function that identifies the process. Weighted second-order statistics directly apply to data without assuming homogeneity nor transforming the data into residuals, eliminating thus the variability due to transforming procedures, such as a random thinning procedure (Baddeley et al. 2006). In particular, in this paper we use the weighted K-function, obtained by weighting the process by the inverse of the conditional intensity function of the estimated model. Indeed, if departures from a such a behaviour were observed, then the data would be supposed to come from a model identified by a conditional intensity function different from the one used in the weighting procedure.

For other relevant diagnostics methods for self-exciting point process models see also Schoenberg (2003), Ogata and Tanemura (2003), Bray et al. (2014).

In our application, diagnostic results suggest a more satisfying fitting for Model2 than Model1, as shown in the Figs. 2 (see the better time residuals using Model2), 3 and 4, and summarized in Table 7. This result is more evident from the total intensity diagnostic plots than the background ones, suggesting that the real fit improvement is due to the introduction of covariates in the induced component of the model, since the observed data are characterised by the presence of big sequences, affecting the estimation procedure.

Therefore, the omission of influential external variables may be relevant on the characterisation of the conditional rate of seismicity, mostly when the analysed area is characterised by severe seismicity, with characteristics of evident dependence both in space and time, like Italy.

Moreover, Fig. 5 reports the difference between the observed values of the global weighted spatio-temporal K-function and the expected ones, weighting by the MLE intensity under Model1 and Model2, respectively. As a $\chi ^2$-type statistic, we evaluate this distance computed over a fixed grid that covers the region of interest, and obtain $\chi ^2= 120.58$ (under the Model1), $\chi ^2= 11.35$ (under the Model2). It is evident that this difference is significantly larger in the first case corresponding to the model without covariates, providing further evidence about the necessity of a more complex model for the description of the observed data.

Fig. 1

Output of the estimated ETAS-FLP model with covariates: estimated total intensity together with the observed points (old in blue and recent in red) and available line-faults

Fig. 2

Temporal residuals for Model1 (on the left); Temporal residuals for Model2 (on the right)

Fig. 3

Spatial residuals for the total intensity Model1 (on the left); Spatial residuals for the total intensity Model2 (on the right)

Fig. 4

Spatial residuals for the background intensity Model1 (on the left); Spatial residuals for the background intensity Model2 (on the right)

Table 7 AIC and $\chi ^2$-statistic ($20\times 20$ grid), for the two estimated models

Fig. 5

Difference between the global weighted spatio-temporal K-function and the expected ones, weighting by the MLE intensity of the Model1 (left) and of the Model2 (right), respectively.

6 Conclusive remarks

In this paper, we have proposed a novel contagion risk measurement model, aimed at improving earthquake risk measurement taking both space and time dependence into account, by means of the ETAS space-time point process, estimated by the ETAS-FLP approach.

The simulation study confirms the importance of well specifying the model, properly accounting for further variables, mostly in case of catalogues with several sequences and many events and, in particular, for parameters describing the size of the clustered component. Indeed, the misspecification effect is more evident for the estimation of the parameters $\kappa _0$, and slightly for $\mu$, that characterize, respectively, the induced and the background components of the conditional intensity function of the ETAS model. When the catalogue is compounded by several sequences, then the estimation of $\kappa _0$ is more sensitive to the misspecification of the model. Comments invert in case of a lower number of induced events. However, we have to stress that in our simulation study we assume just a constant background, and therefore the real model misspecification effect on $\mu$ should require deeper reflections.

The importance of the proposed method is also confirmed by the reported application, related to the Italian area. Indeed, Italy is characterized by a strong clustered seismicity (Adelfio and Chiodi 2009; Giunta et al. 2009), for which further information related to the spatial-temporal characterization can be relevant for a better description of the seismic activity. Indeed, in the seismic context, the proposed approach would provide a more general formalism for the earthquake occurrence in space and time, since the main idea is that the effect on the future activity does not depend only on the closeness of the previous events, but also on specific characteristics of the main event, like magnitude, as usual, and also further information, such as geological features.

The reported results, though partial and provisional, confirm our intuition reported in previous studies (e.g., Adelfio and Chiodi 2015b). Indeed, the need of a more flexible model for the space-time triggered component of the ETAS model is often revealed, although the background seismicity is well described by the FLP estimated intensity. In our opinion, considering external information (such as geological information related to faults distribution) for the description of spatio-temporal earthquakes is an innovative and promising perspective of study, even relevant in different fields of research.

Future research developments include evaluating the robustness of the results with respect to different spatial regions (that is to extend the proposed study also to areas with different characteristics) and to the inclusion of other specific covariates, to study the dependence of observed intensity in space and time from other external factors (e.g., GPS information, external marks, etc).

Appendix

See the Tables 8, 9, 10, 11, 12, 13, 14 and 15.

Table 8 Simulated MSE of parameters estimates on the 100 simulated catalogues under the wrong Model1 and the parameters true values $\mu =0.079, \kappa _0= 0.003, c=0.013, d=0.5, \beta _1=0.39$, using a geometrical covariate

Table 9 Simulated MSE of parameters estimates on the 100 simulated catalogues under the true Model2 and the parameters true values $\mu =0.079, \kappa _0= 0.003, c=0.013, d=0.5, \beta _1=0.39, \beta _2=-0.03$, using a geometrical covariate

Table 10 Simulated MSE of parameters estimates on the 100 simulated catalogues under the wrong Model1 and the parameters true values $\mu =0.079, \kappa _0= 0.003, c=0.013, d=0.5, \beta _1=0.39$, using a simulated covariate

Table 11 Simulated MSE of parameters estimates on the 100 simulated catalogues under the true Model2 and the parameters true values $\mu =0.079, \kappa _0= 0.003, c=0.013, d=0.5, \beta _1=0.39, \beta _2=-0.4$, using a simulated covariate

Table 12 Simulated MSE of parameters estimates on the 100 simulated catalogues under the wrong Model1 and the other parameters true values $\mu =0.079, \kappa _0= 0.006, c=0.013, d=0.5, \beta _1=0.39$, using a geometrical covariate

Table 13 Simulated MSE of parameters estimates on the 100 simulated catalogues under the true Model2 and the other parameters true values $\mu =0.079, \kappa _0= 0.006, c=0.013, d=0.5, \beta _1=0.39, \beta _2=-0.03$, using a geometrical covariate

Table 14 Simulated MSE of parameters estimates on the 100 simulated catalogues under the wrong Model1 and the other parameters true values $\mu =0.079, \kappa _0= 0.006, c=0.013, d=0.5, \beta _1=0.39$, using a simulated covariate

Table 15 Simulated MSE of parameters estimates on the 100 simulated catalogues under the true Model2 and the other parameters true values $\mu =0.079, \kappa _0= 0.006, c=0.013, d=0.5, \beta _1=0.39, \beta _2=-0.4$, using a simulated covariate