Abstract
In this article we estimate health transition probabilities using longitudinal data collected in France for the survey on handicaps, disabilities and dependencies from 1998 to 2001. Life expectancies with and without disabilities are estimated using a Markov-based multi-state life table approach with two non-absorbing states: able to perform all activities of daily living (ADLs) and unable or in need of help to perform one or more ADLs, and the absorbing state of death. The loss of follow-up between the two waves induces biases in the probabilities estimates: mortality estimates were biased upwards; also the incidence of recovery and the onset of disability seemed to be biased. Since individuals were not missing completely at random, we correct this bias by estimating health status for drop-outs using a non parametric model. After imputation, we found that at the age of 70 disability-free life expectancy decreases by 0.5 years, whereas the total life expectancy increases by 1 year. The slope of the stable prevalence increases, but it remains lower than the slope of the cross sectional prevalence. The gender differences on life expectancy did not change significantly after imputation. Globally, there is no evidence of a general reduction in ADL disability, as defined in our study. The added value of the study is the reduction of the bias induced by sample attrition.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The debate on aging in Europe is currently paying considerable attention on healthy life expectancy (HLE) of the elderly. Following the approach of the World Health Organization (WHO), health should be considered as having a dynamic nature,Footnote 1 and should be taken into consideration in the context of life, as the ability to fulfill actions or to carry out a certain role in society. This is the so-called functional approach, taken by the WHO in the elaboration of the international frame of reference on the matter.
The most suitable indicator to measure the state of health of a population is health expectancy, which measures the length of life spent in different states of health. The term is often used in a general sense for all indicators of health expressed in terms of expectancy, but the definition most frequently used in Europe is that of disability-free life expectancy (Perenboom 2003), where disability is defined as the impact of disease or injury on the functioning of individuals. In other words, a disability is the inability of accomplishing tasks of daily living which someone of the same age is able to perform (Freedman 2006; Verbrugge 1989).
To better clarify our work, we distinguish between the model used to estimate the parameters of the so called health process (i.e. the probability of becoming impaired, the probability of recovery, and the probability of dying from either healthy or unhealthy state) and the methods that use these parameters to estimate health expectancies.
Health expectancy’s estimation method. There are several methods to estimate health expectancies. Among them the most commonly used are the Sullivan and the multi-state, respectively based on classical life table and longitudinal data.
The first method was pioneered by Wolfbein on the length of “working life” (Wolfbein 1949) and is described in details in Sullivan (1971); it combines prevalence of disability obtained through a cross-sectional survey and a period life table. The incidence of incapacity in the period of reference is not taken into account; the prevalence observed at a given moment derives from past health transitions, and therefore depends on the history of the cohorts which make up the sample group. Age-specific cross-sectional prevalences are analogous to age-specific proportions of survivors from the corresponding cohorts (Brouard 1986; Guillot 2003) in the sense that they are not subject to current mortality trends, but to delayed trends.
The combination of a cross-sectional prevalence, with a period life table yields to the so called Sullivan index, which is often and improperly called health expectancy. As stressed in the literature, such an health expectancy is not satisfactory in order to monitor the evolution of the current health conditions of a population and to forecast its future development.
The second method, named multi-state tables, was pioneered by Rogers (1975) and Willekens for migration and marital status (Willekens 1979; Hoem and Fong 1976) for the multi-state table of working life and Brouard for the introduction of the period prevalence of labor participation (Brouard 1980; Cambois et al. 1999). Multi-state models are based on the analysis of the transitions between states in competition with the probabilities of dying from each state.
The information necessary for this type of analysis derives from longitudinal surveys. The result, in this case, is the so called period (or stable) prevalence and can be interpreted analogously to the stationary population of a period life table, as the proportion of the disabled amongst the survivors of successive fictitious cohorts, subject to the flows of entry on disability, recovery and death observed in the period under examination.
Thus, the period health expectancy is the expected number of years to be spent in the healthy state by this fictitious cohort. The analogy with the period life expectancy or simply “life expectancy”, which is the expectancy of the distribution of deaths by age, is obvious.
In the classical life table analysis, the survivors of any age are supposed to be at the same risk of dying. When taking heterogeneity into account, the simplest model consists in considering two states (healthy vs unhealthy, enabled vs disabled), but assuming that the population in each state is homogeneous over time, i.e at each age they are at the same risks of changing their status. This corresponds to the common Markov hypothesis.
Estimation of health transition probabilities. Almost all health expectancy research implicitly assumes that age-related health transitions are governed by a Markov process. Thus, the parameters of the health process are generally estimated by recovering the parameters of the embedded Markov process (Laditka and Hayward 2003).
Computational issues concerning estimation of health expectancies from longitudinal surveys have been developed by Bonneuil and Brouard (1992) while Lièvre et al. (2003) provided a complete solution with standard errors. The authors developed the embedded Markov chain maximum likelihood procedures pioneered by Laditka and Wolf (1998). They estimate parameterized transition probabilities following the Interpolation of Markov Chain approach (IMaCh).Footnote 2
The IMaCh approach has been recently applied in several analyses dealing with health (Lièvre et al. 2007; Crimmins et al. 2009; Andrade 2010), including studies based on the French HID survey (Cambois and Lièvre 2004; Giudici and Arezzo 2009). In these studies, information on health status is given by the interviews at different time, but non random loss of follow-up “within” successive waves can induce biases in the statistical results. It’s not uncommon that demographers treat this problem by omitting data having missing values (listwise deletion). Unfortunately this approach has many inconveniences: even in the most favorable case, i.e. if the data are missing completely at random (MCAR), estimates suffer a loss of precision. In case data are missing non at random (MNAR), estimates are also biased. Very good treatment of the issue of missing data can be found in Little and Rubin (2002), Howell (2007) and Allison (2001).
Modern approaches, for example maximum likelihood via EM algorithm and multiple imputation, impute missing values using statistical models. For more details on imputation via EM algorithm see Schafer (1997) and on multiple imputation see Scheuren (2005), Rubin (1987).
A popular model choice for implementing imputation is multiple imputation by chained equation (MICE) (Raghunathan et al. 2002; Van Buuren and Oudshoorn 1999). When having many variables or when relations among variables are likely to be non linear and interactions among regressors have a non negligible effect, this method can be a very laborious task with no guarantee of success. Another problem is that variables often have distributions that are not easily captured by parametric models (Burgette and Reiter 2010). For all these reasons we preferred to use a non parametric approach that can easily manage many different regressors, both categorical and numerical, and that naturally takes into account variables interactions and non linear structures.
In our study we estimate the probability of transition between different states of health for the population of 70 years old or older in France, during the period 1998–2001, following the multi-state table approach and using the IMaCh program. We based the analysis on the French HID survey, taking into account the loss of follow-up within the two survey waves, and imputing an health state through a non-parametric model named Classification and regression tree (CART), firstly introduced by Breiman in 1984.
Taking into account the heterogeneity of mortality due to health states, we compute life expectancy in different states of health and the period prevalence of disability implied by the estimated health transitions. We examine how health transitions are influenced by demographic variables, in order to estimate differences in health expectancy. The added value of the study is the reduction of the bias induced by the loss of follow-up within the two waves of the HID survey.
The rest of the paper is organized as follows: Sect. 2.1 describes the HID survey and the drop-out mechanism, Sect. 2.2 describes the model, gives some relevant characteristics of the imputation procedure and outlines the method used for estimating the transition probabilities, Sect. 3 shows results and Sect. 4 concludes.
2 Data and methods
2.1 Data
Our study is based on the national survey on handicaps, disabilities and dependency (HID), carried out in France by INSEE, between 1998 and 2001, in collaboration with several research institutes including Institut National d’Etudes Démographiques (INED) and Institut National de Recherches Médicales (INSERM).
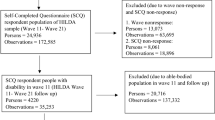
The survey was carried out both in medico-social institutions and private dwellings,Footnote 3 and aimed at describing disability and handicaps for the whole French population. Briefly, a first wave of the HID survey was carried out in late 1998; 14,611 people living in institutions were interviewed. The same persons have been surveyed again in late 2000.
In addition, between 300,000 and 400,000 people living in private dwellings filled out a brief questionnaire on “daily life and health” during the 1999 population census. After this filtering operation,Footnote 4 16,924 respondents have been interviewed, once in late 1999 and again in late 2001. Table 1 summarize some relevant characteristics of the survey whereas a detailed explanation of it can be found in Mormiche (1998).
Two types of weights are available in HID: the first are representative of the total population living in France in late 1998 and late 1999, in institutional and ordinary settings respectevely; the second are representative of the evolution (between the two waves) of the individuals interviewed at the baseline. For imputation, we used the latter whereas for health estimation we used the first.
To carry out our analysis, we selected only the population aged 55 and over at the baseline.
On the basis of the HID survey, health is measured through a functional approach: disability refers to the activities needed for independent living and personal care and has been operationalized as the difficulty or inability to perform one of the five activities of daily living (ADL): bathing, dressing, eating, getting in/out of a bed or chair and toileting. Three states are used in the analysis: 1-able to perform all ADLs, 2-unable or in need of help to perform one or more ADLs, and 3-deceased.
It’s worth stressing that, after the second wave was completed, an in-depth analysis was performed by mean of government records (vital statistics) so that the information on an individual’s death was recorded. This imply that, if someone was not re-interviewed in the second wave and therefore the health status is not known, he or she is for sure not dead. As can be easily noticed from Table 1, there is a total of 2,356 people (477 in institutions and 1,879 in ordinary settings) whose health state at the second wave is missing. They couldn’t be included in the estimation model without imputation: missing data at the second wave are automatically dropped out by IMaCh, and this induces an upwards bias in the probability of dying.
In the following we will discuss the drop-out mechanism and give some characteristics of the missing group which help evaluate the nature of this mechanism. We start with people in ordinary settings. At the second wave INSEE decided to leave aside a large part (572 individuals of 55 and over years old) of the department of Hérault in the region of Languedoc–Roussillon in the south of France. We haven’t found any official documentation explaining the reasons of this choice, but our guess is budget constraint. The remaining individuals were not re-interviewed either because they refused to answer or because they have changed address and were not found. On behalf of the institutionalized individuals, the reasons for not re-interviewing lies on a change of address (i.e. they moved to another institution or to the household of origin). We were concerned that the refuse to answer or the address change could depend on a worsening of health state and therefore decided to proceed with imputation, using a model which controlled for some relevant variables (i.e. age and health status at baseline).
Table 2 shows the distibution of ADL in the second wave conditional on those categorical covariates that we found to be relevant in the model. In the right most column, there are the p-values for 2-samples proportion tests. They clearly show that the probability that an observation is missing is related to the value of some covariates and therefore the drop-outs are not random.
In order to reduce the bias due to the attrition, missing data for individual known to be alive in the second wave, but not interviewed, were assigned through CART as explained in detail in Sect. 2.2.1.
2.2 Methods
2.2.1 Sample correction
Let \(I(ADL2w)\) be an indicator function taking value 1 if ADL at the second wave is missing and 0 otherwise. As stated in 2.1, once we found the non randomness of drop-outs we decided to input the ADL at the second wave using a model which exploits the influence of the covariates. This simply means to build a model for ADL at the second wave using only the individuals with a known health status.
The dependent variable (i.e. ADL at second wave) is binary: disability or disability free. Model building can be done in many different ways, for example using a logit or a probit model. We decided to use a non-parametric model for reasons that were partly disclosed in Sect. 1 and that will be further discussed at the end of the paragraph.
CART is a supervised classification algorithm, introduced by Breiman in 1984. A supervised classification problem can be summarized as follows: for \(n\) objects, characterized by a set of \(k\) features \(X = (X_1, X_2,\ldots , X_k)\), is known a priori the class \(j = 1, 2 , 3\ldots J\) to which they belong. Classes are generally indicated with variable \(Y\). The scope is to predict which is the class a new object belong to, given its characteristics.
A supervised classification algorithm is a mathematical rule which assign a new object to a class \(j\). A function \(d(X)\), called classifier, is built in a way that it generates a partition of the feature space \(X\) into \(J\) non overlapping subsets. CART is a binary recursive partitioning procedure capable of handling both continuous and nominal characteristics.
Starting with the entire sample (parent node), it divides it into two children nodes; any of them are then divided into two grandchildren. To split a node into two child nodes, CART always asks questions that have a “yes” or “no” answer. For example, the question “Is age \(\le \) 72?” splits the tree’s root, or parent node, into two branches with “yes”cases going to the left child node and “no” cases to the right. A node is said to be final if it cannot be divided. The procedure stops when the tree reaches its maximum size. The full grown tree is then pruned back in order to look for the best final tree. This is the one that minimize the so called cost-complexity function, which is a function that takes into account at the same time the misclassification rate of individuals and the total number of final nodes. Note that the ensemble of the splitting questions form a rule which allows to assign any individual (also new ones) to a specific final node.
The original data has a certain level of heterogeneity: if all individuals belong to the same class, there is no heterogeneity in the data. Conversely, if individuals are uniformly distributed among the \(J\) classes, heterogeneity reaches its maximum level. Heterogeneity can be measured according to different method; one of the most common is the Gini index which is the one we used.
Any split is done according to a variable \(X_i\): the algorithm searches over all feature space looking for the optimal division that is for the binary split that reduces data heterogeneity most. Impurity reduction can be measured and it gives variables ranking based on their capability to separate objects. This is called variable importance.
An important issue is the capability of a tree to correctly classify a new individual. A measure of this generalization power is the misclassification rate which is simply the number of misclassified individuals out of all observed individuals. If the original sample is big enough, a good estimate of the true misclassification rate is obtained by randomly splitting the sample in two sub samples and using the first part of the data (normally 70 % of it) to grow the tree and the second to test it.
As we briefly mentioned, we used CART for two reasons: the first one is that it generally classifies more accurately than other models (Breiman et al. 1984) and the second is that it naturally takes into account interactions among variables and we believed this is important when dealing with a complex task such as health transitions determinants. To confirm the first statement we tried several logistic models and found that the best rate of correct classification was 77.8 % whereas for CART was 86 %.
Table 3 shows the variable importance in predicting the health status at the second wave: CART shows that ADL at the baseline is by far the most important variable. Once we estimated the model, we proceed to imputation for the 2,356 people whose health status was unknown (1,879 for menage group and 477 for institution). Imputation was done using the optimal splitting rules found. Since the values of variables \(X\) are known for each new individual, an unique assignment to a final node can be done and the imputed ADL is the mode of the node.
Table 4 shows the predictive ability of CART and tells how reliable the performed imputation is: results are good because the global error rate is about 19 %. In order to provide an indication of state changes in the study, Table 5 shows the sample distribution by status in both waves, before and after imputation: most people began and ended disability-free; recovery percentages changes slightly after imputation, whereas the percentage of those who remained disable increases.
2.2.2 Transition probabilities estimation method
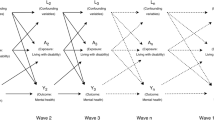
We estimate the age-specific flows of entry into and exit from disability, and the matrix of the transition probabilities between good health (coded 1), disability (coded 2) and deceased (coded 3) employing the IMaCh program.
The probability for an individual aged \(x\), observed in the state \(i\) during the first wave, to find him/herself in state \(j\) at the second wave is indicated by \(p_{ij}^x\), and the transition probabilities are estimated based on a series of 3\(\times \)3 matrices:
The first and the second rows represent transitions for individuals who begin the interval respectively non disabled and ADL disabled. The third row represents the absorbing state of death. The probabilities of transition are then parameterized using the following logistic multinomial logit:
The software IMaCh is able to provide standard errors for the estimated parameters, which are then used to derive standard errors for the life expectancies implied in the transition probabilities. This is an important characteristic which allows for the assessment of whether results are statistically meaningful.
On the basis of transition probabilities estimates, IMaCh provide the so-called period (or stable) prevalence, which can be interpreted, analogously to the stationary population of a life table, as the proportion of the disabled amongst the survivors of successive fictitious cohorts, subject to the flows of entry on disability and recovery observed in the period under examination. In other words, the stable prevalence is implied in the health transitions observed during the survey, whereas the observed prevalence synthesize the history of disability onset, recovery and mortality of the population. Thus, the comparison between the stable and observed prevalence allows to make hypothesis on the future trend of health prevalence for cohorts under examination (Lièvre et al. 2003).
3 Results
3.1 Probabilities of transition
For each age we estimate the probability of death within a year from each initial health status and compare the results with the 1998–2000 national age-specific mortality, as shown in Fig. 1. Total mortality rate is obtained by weighting each status-based probability of death with the proportion of people in each health status, given by the observed HID prevalence. Before CART imputation, mortality seems to be overestimated: the reason is that, since IMaCh automatically excludes individuals with missing ADL, the denominator of mortality rate is biased downward. The bias is reduced after the imputation. Figure 2 shows the transition probabilities from different initial state of health. As expected, the probability of dying is higher among the disabled. Regardless of the initial health state, the slope decreases after imputation, but the reduction is larger for those who were disabled at the baseline. The imputation modifies mainly the transition rates in older ages, except for recovery; in this case the intercept is reduced, and the slope did not change significantly.
3.2 Health Expectancies
As shown in Fig. 3, at all ages, our estimates of LE perfectly overlap those based on national statistics: at age 70, our estimates after CART correction are 15.21 years (95 % CI [14.67–15.75]) compared to the 1998–2000 French life table of 15.17 years. Estimation before imputation was lower, due to the overestimation of mortality. According to our model, people aged 70 can expect to live 9.37 years in disability-free state, given that they were in that state initially, but the expectation is reduced to 5.53 years if they were in the disabled state at age 70. The corresponding health expectancies for the disabled state are 6.10 and 8.64 years respectively (Table 6).
3.3 Implied prevalence
The impact of continuing the rates of disability onset, recovery and death on ADL prevalence is shown in Figs. 4 and 5: as expected, the transition probabilities from both initial states (disability free and disabled) to a final state of disability at age x+h (and h=12 months), converge to the so called period, or stable, prevalence of disability. The period prevalence is obtained by simulating cohorts aged 70 years and over which experience over time the observed transitions of health. As widely stressed in the literature, the comparison of the stable with the observed prevalence provides an indication on the evolution of age-specific prevalence of disability, if current transition rates of disability onset and recovery continue indefinitely (Lièvre et al. 2003; Jagger et al. 2003; Laditka and Laditka 2006; Manton and Land 2000; Minicuci et al. 2004; Reynolds et al. 2005; Crimmins et al. 2009).
Figure 4 compares the observed and stable prevalence of disability before and after correction. Our imputation of a health state for lost individuals modifies the slope of the curves, but the effect on the stable prevalence is stronger than the effect on observed prevalence. Figure 5 focuses on results after the estimation of missing health status: the slope of the stable prevalence seems to be always lower than slope of the cross sectional prevalence, and globally there is no evidence of a generalreduction in ADL.
3.4 Gender disparities
As stressed by Giudici (2006), Giudici and Arezzo (2009), holding all the other independent variables constant, disability is lower for men, and our analysis shows that the gender differences on expected life free of disability did not change significantly after imputation: Fig. 6 shows the transition probabilities for each sex from different initial states of health before and after imputation.
Before imputation, the probability of death for disabled men at age 70 is close to that of women at age 78. But, if men are disability free, their probability of dying at 70 is close to that of women at the same age. After imputation, mortality decreases for both sexes, but the gender gap at different ages is almost the same (Fig. 6). Globally, for both sexes the probability of dying is higher among the disabled than among the non-disabled. In both cases women show higher onset of disability and lower recovery incidences than men. These results are reflected on the estimation of health expectancies and stable prevalence implied in the computed probabilities: Table 7 shows gender differences in health expectancies before and after imputation.
It’s clear that in both cases the extra years lived by women (about 3.6 years at age of 70) are spent in disability.
4 Summary and conclusions
The HID survey, as other surveys dealing with health, is characterized by quite a relevant loss of individuals between waves. This attrition biases the transition probability estimates and, consequently, health expectancies in different states of health are also biased. In this work, health is measured through a functional approach, and people are considered disabled if they are unable or in need of help to perform one or more ADLs. In order to reduce the bias due to the attrition, we assigned a state of health to individuals known to be alive in the second wave, whose state of health was unknown, through CART. The correction allows to reduce the bias due to the overestimation of mortality and recovery on the one hand, and to the underestimation of onset of disability on the other hand. According to our model, people aged 70 can expect to live 9.37 years in disability-free state, given that they were in that state initially, but the expectation is reduced to 5.53 years if they were in the disabled state at age 70. The corresponding health expectancies for the disabled state are 6.10 and 8.64 years respectively. Regardless of the initial state of health, people aged 70 can expect to live 15.2 years, of which 6.6 in disability. The main effect of CART imputation on health expectancies is related to the increase of life expectancy of 0.62 years, due to the increase of disabled life expectancy of almost 1.2 years, associated to the reduction of disability free life expectancy of 0.5 of a year. After the imputation, the slope of the stable prevalence seems to be always lower than the slope of the cross sectional prevalence, and globally there is no evidence of a general reduction in ADL. The gender differences on expected life free of disability did not change significantly after imputation. Nevertheless, women show higher onset of disability and lower recovery; and these results are reflected on the estimates of health expectancies and stable prevalence.
Notes
Social, economic and environmental consequences of illness can be summarized in the sequence: illness or disorder—impairment or invalidity—disability—handicap. According to this sequence, handicap has its origins in a disease (including accidents or other causes of moral or physical traumas) which, as a consequence, causes problems in body functions or structure such as significant deviation or loss (impairment or invalidity). Invalidity constitutes in turn greater or lesser difficulty in performing daily activities (disability). Every dimension of handicap is effectively defined in relation to a norm: for example a disability consists in the reduction of the ability to carry out determined tasks in the way considered normal for a human being.
IMaCh is a publicly available computer program introduced by Brouard and Lièvre (2002) and mostly used for the estimation of Health Expectancy from longitudinal surveys. It allows to estimate transition probabilities using a discrete time embedded Markov chain approach. Transitions are supposed to occur at any time and death is always an additional competing risk. See for example (Andrade 2010; Crimmins et al. 2009; Molla and Madans 2008; Yong and Saito 2012) for some interesting applications.
In the following we will refer at the two groups as istitution and ménage respectively.
The brief questionnaire was administered with the intent of quantifying the disabled population and correctly sampling it.
References
Allison PD (2001) Missing data. Sage Publications, Thousand Oaks
Andrade FCD (2010) Measuring the impact of diabetes on life expectancy and disability-free life expectancy among older adults in Mexico. J Gerontol Ser B: Psychol Sci Soc Sci 65B(3):381–389
Bonneuil N, Brouard N (1992) Methods of calculation of health expectancy: application to the LSOA surveys (1984–86-88). In: 5th meeting of the international network on health expectancy (REVES-5): future uses of health expectancy indices, Ottawa
Breiman L, Friedman JH, Olshen RA, Stone CJ (1984) Classification and regression trees. Wadsworth International Group, Belmont
Brouard N (1980) Espérance de vie active, reprises d’activité féminine: un modèle. Revue économique 31:1260–1287
Brouard N (1986) Structure et dynamique des populations. La pyramide des années à vivre, aspect nationaux et exemples regionaux. Espace Popul Soc 2:157–168
Brouard N, Lièvre A (2002) Computing health expectancies using IMaCh (A maximum likelyhood computer program using interpolation of Markov chains), version 0.71a. Paris, France. INED and EUROREVES
Burgette LF, Reiter JP (2010) Multiple imputation for missing data via sequential regression trees. Am J Epidemiol 172(9):1070–1076
Cambois E, Robine JM, Brouard N (1999) Life expectancies applied to specific statuses. A history of the indicators and methods of calculation. Popul Engl Sel 11:7–34
Cambois E, Lièvre A (2004) Risques de perte d’autonomie et chances de récupération chez les personnes âgées de 55 ans ou plus: une évaluation à partir de l’enquête Handicaps, incapacité, dépendance. Etudes et Résultats, 349:1–11 Paris, DRESS
Crimmins EM, Hayward MD, Hagedorn A, Saito Y, Brouard N (2009) Change in disability-free life expectancy for americans 70 years old and over. Demography 46(3):627–646
Freedman VA (2006) Late-life disability trends: an overview of current evidence. In: Field MJ, Jette AM, Martin L (eds) Workshop on disability in America: a new look—summary and background papers. National Academies Press: Washington. url: http://www.nap.edu/catalog/11579.html
Giudici C (2006) Les déterminants socio-démographiques de la santé aux grands âges. Paris, Working paper Les Lundis de l’INED
Giudici C, Arezzo MF (2009) Social inequalities in health expectancy of elderly: evidence from the HID Survey. In: IUSSP-UIESP, XXXVI international population conference; Marrakech, IUSSP-UIESP
Guillot M (2003) The cross-sectional average length of life (cal): a cross-sectional mortality measure that reflects the experience of cohorts. Popul Stud 57(1):41–54
Hoem J, Fong M (1976) A Markov chain model of working life tables. Working paper 2 Laboratory of Actuarial Mathematics, University of Copenhagen
Howell DC (2007) The analysis of missing data. In: Outhwaite W, Turner S (eds) Handbook of social science methodology. Sage: London
Jagger C, Goyder E, Clarke M, Brouard N, Arthur A (2003) Active life expectancy in people with and without diabetes. J Publ Heal Med 25:42–46
Laditka SB, Wolf D (1998) New method for analyzing active life expectancy. J Aging Heal 10(2):214–241
Laditka SB, Hayward MD (2003) The evolution of demographic methods to calculate health expectancies. In: Robine JM, Jagger C, Mathers CD, Crimmins EM, Suzman RM (eds) Determining health expectancies. Wiley, London
Laditka SB, Laditka JN (2006) Effects of diabetes on healthy life expectancy: shorter lives with more disability for both women and men. In: Yi Z, Crimmins EM, Carriere Y, Robine J-M (eds) Longer life and healthy ageing. Springer, Dordrecht, pp 71–90
Lièvre A, Brouard N, Heathcote CR (2003) The estimation of health expectancies from cross-longitudinal surveys. Math Popul Stud 10:211–248
Lièvre A, Jusot F, Barnay T, Sermet C, Brouard N, Robine JM, Brieu MA, Forette F (2007) Healthy working life expectancies at age 50 in Europe: a new indicator. J Nutr Heal Aging 11(6):508–514
Little RJA, Rubin DB (2002) Statistical analysis with missing data, 2nd edn. Wiley, New York
Manton KG, Land K (2000) Active life expectancy estimates for the U.S. elderly population: a multidimensional continuous mixture model of funtional change applied to completed cohorts, 1982–1996. Demography 37:253–65
Minicuci N, Noale M, Pluijm SMF, Zunzunegui MV, Blumstein T, Deeg DJH, Bardage C, Jylha M (2004) Disability free life expectancy: a cross national comparison of six longitudinal studies on ageing. The CLESA project. Eur J Ageing 1:37–44
Molla MT, Madans JH (2008) Estimating healthy life expectancies using longitudinal survey data: methods and techniques in population health measures. National Center for Health Statistics. Vital Health Stat 2(146). URL:http://www.cdc.gov/nchs/data/series/sr02/sr02146.pdf
Mormiche P (1998) L’enquête HID de l’INSEE. Objectifs et schéma organisationnel. Courrier des Statistiques. 87–88:7–18
Perenboom RJM (2003) Health expectancies in european countries. In: Robin JM, Jagger C, Mathers CD (eds) Determining health expectancies. Wiley, Chichester
Raghunathan T, Solenberger P, Van Hoewyk J (2002) A multivariate technique for multiply imputing missing values using a sequence of regression models. Surv Methodol 27(1):85–96
Reynolds SL, Saito Y, Crimmins EM (2005) The impact of obesity on active life expectancy in older american men and women. Gerontol 45:438–444
Rogers A (1975) Introduction to multi regional mathematical demography. Wiley, England
Rubin DB (1987) Multiple imputation for nonresponse in surveys. Wiley New Jersey, Hoboken
Schafer JL (1997) Analisys on incomplete multivariate data. Chapman and Hall, London
Scheuren F (2005) Multiple imputation: how it began and continues. Am Stat 59:315–319
Sullivan D (1971) A single index of mortality and morbidity. HSMHA Heal Rep 86(4):347–354
Van Buuren S, Oudshoorn K (1999) Flexible multivariate imputation by MICE. Leiden, Netherlands
Verbrugge LM (1989) Recent, present, and future health of american adults. Annu Rev Publ Heal 10: 333–361
Willekens F (1979) Computer program for increment-decrement (multistate) life table analysis: a user’s manual to lifeindec. Working papers of the international institute for applied systems analysis
Wolfbein S (1949) The length of working life. Popul Stud 3:286–294
Yong V, Saito Y (2012) Are there education differentials in disability and mortality transitions and active life expectancy among japanese older adults? Findings from a 10-year prospective cohort study. J Gerontol Ser B: Psychol Sci Soc Sci 67(3):343–353
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Giudici, C., Arezzo, M.F. & Brouard, N. Estimating health expectancy in presence of missing data: an application using HID survey. Stat Methods Appl 22, 517–534 (2013). https://doi.org/10.1007/s10260-013-0233-8
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10260-013-0233-8