Abstract
This paper revisits the Dutch disease by analyzing the general equilibrium effects of a resource shock on a dependent economy, both in a static and dynamic setting. The novel aspect of this study is to incorporate in one coherent framework two distinct features of the Dutch disease literature that have previously been analyzed in isolation: capital accumulation with absorption constraint, and productivity growth induced by learning-by-doing. The result of long run exchange rate appreciation is maintained in line with part of the Dutch Disease literature. In addition, a permanent change in the employment shares occurs after the resource windfall, in favor of the non-traded sector and away from the traded sector growth engine of the economy. In other words, in the long run both of the classic symptoms of the Dutch Disease remain in place.





Similar content being viewed by others
Notes
This formulation of technical progress implies balanced growth by definition since relative productivity is exogenous to the model.
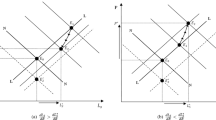
It is relevant to point out that a downward sloping NN curve (due to the assumption of weak reaction of the investment) is not necessary for the resource windfall R to determine positive changes in P and η. Even an upward sloping NN curve (although less steep than the LL) would ensure the presence of the two classic symptoms of the Dutch Disease.
This happens to be the case as long as \(\frac {\partial I_{N}}{\partial K_{N}} <0\) which is analytically verified as long as \(\varphi ^{\prime }(\cdot )> \frac {\varphi (\cdot )}{\alpha (1-\alpha )}\left (\frac {K_{N}}{A\eta } \right )^{1-\alpha }\). It is important to notice that this assumption does not necessarily need to hold for the total effect of capital stock on the exchange rate to be negative, since in any case the excess supply from production is likely to overcome the demand generated by the positive investment effect.
Looking exclusively at the derivation in Eqs. 35 and 36, I cannot infer which of the two isoclines has higher slope. In case (35) has higher slope than (36), the dynamic equilibrium would be a saddle point. In the opposite case, the dynamic equilibrium is locally stable. The results obtained from the stability analysis in A3 of the Appendix with negative trace and non-negative determinant allows me to disregard the former case and to plot the dynamic system as it appears in Fig. 3.
The general equilibrium derivation of [∂ P t /∂ R t ] in the present dynamic setting gives a derivative with undefined overall sign, due to production and investment effects pointing in different directions. The analytical formulation is of course available on request. I have carefully verified that, by imposing for instance an overall positive sign for [∂ P t /∂ R t ], no inconsistency is found with respect to each and one of the analytical conditions assumed to hold for the derivative of the investment function, as given in (16,42).
References
Alberola E, Benigno G (2017) Revisiting the commodity curse: a financial perspective. J Int Econ, forthcoming. https://doi.org/10.1016/j.jinteco.2017.02.001
Blanchard O, Fischer S (1989) Lectures on macroeconomics. MIT Press
Corden MW, Neary JP (1982) Booming sector and de-industrialization in a small open economy. Econ J 923:825–848
Harding T, Stefanski R, Toews G (2016) Boom goes the price: giant resource discoveries and real exchange rate appreciation. OxCarre Working Papers 174, Oxford Centre for the Analysis of Resource Rich Economies, University of Oxford
Krugman P (1987) The narrow moving band, the dutch disease, and the competitive consequences of Mrs. Thatcher. J Dev Econ 27:41–55. North-Holland. https://doi.org/10.1016/0304-3878(87)90005-8
Matsuyama K (1992) Agricultural productivity, comparative advantage, and economic growth. J Econ Theory 58:317–334. https://doi.org/10.1016/0022-0531(92)90057-O
Sachs JD, Warner AM (1995) Natural resource abundance and economic growth. NBER working paper 5398. https://doi.org/10.3386/w5398
Salter WEG (1959) Internal and external balance: the role of price and expenditure effects. Economic Record 35:226–238
Torvik R (2001) Learning by doing and the dutch disease. Eur Econ Rev 45:285–306. https://doi.org/10.1016/S0014-2921(99)00071-9
van der Ploeg F (2011) Fiscal policy and dutch disease. International Economics and Economic Policy, Springer 8(2):121–138. https://doi.org/10.1007/s10368-011-0191-2
van der Ploeg F (2012) Bottlenecks in ramping up public investment. Int Tax Public Financ 19(4):509–538. https://doi.org/10.1007/s10797-012-9225-0
van Der Ploeg F, Poelhekke S (2016) The impact of natural resources: survey of recent quantitative evidence. J Dev Stud 1–12
van der Ploeg F, Venables AJ (2013) Absorbing a windfall of foreign exchange: Dutch disease dynamics. J Dev Econ, Elsevier 103(C):229–243. https://doi.org/10.1016/j.jdeveco.2013.03.001
van Wijnbergen S (1984) The Dutch disease: a disease after all?. Econ J 94:41–55
Vaz PH (2017) Discovery of natural resources: a class of general equilibrium models. Energy Econ 61:174–178. https://doi.org/10.1016/j.eneco.2016.11.005
Acknowledgements
I am grateful for comments and suggestions from Egil Matsen, Ragnar Torvik and from seminar participants at the NTNU Department of Economics.
Author information
Authors and Affiliations
Corresponding author
Appendix: A
Appendix: A
1.1 A1
The representative household endowed with Cobb-Douglas utility function maximizes the static utility \(u(C_{N},C_{T})=C_{T}^{\delta }C_{N}^{1-\delta }\) subject to the static version of the aggregate income constraint given in (7):
Setting the Lagrangian Γ and computing the first order conditions, the solution to this static problem is:
1.2 A2
Let us give a closer look at the overall sign of the derivatives in (20, 23):
The common denominator of both derivatives is always positive since:
which is always true since by definition φ ′ > 0. As regards the numerator, we observe that as long as the following condition holds:
we can determine the overall signs of both derivatives and conclude that \( \frac {\partial \eta }{\partial A}>0\) and \(\frac {\partial \eta }{\partial K_{N}}<0\). Notice that this condition is not inconsistent with the condition given in Eq. 16.
1.3 A3
Dynamic stability analysis. At first, by totally differentiating (33, 34) and exploiting the convenient result that (∂ g t /∂ R t ) = 0, the dynamic system can be rewritten as:
Let us then insert these derivatives into the Jacobian J and evaluate it at the dynamic steady-state (26) (for any given g t ):
By recalling from the static model and from the Section A2 of the Appendix that \(\frac {\partial \eta }{\partial A}>0\) and \(\frac {\partial \eta }{ \partial K_{N}}<0\) we can immediately evaluate that:
The trace is unambiguously negative. The determinant is instead given by:
Let us now substitute for the analytical expression of the two derivatives (20, 23). Redefine for convenience the positive common denominator as \({\Psi } =1+\frac {\left (1-\alpha \right ) \left (1-\delta \right ) }{\delta }-\alpha \left [ \varphi \left (\cdot \right ) \left (\frac {K_{N}}{A\eta }\right )^{1-\alpha }+\varphi ^{\prime }(\cdot )(1-\alpha )\right ] \) and rewrite det(J) as:
1.4 A4
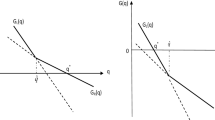
Let us analyze closely the change in the ratio of the productivity level with respect to the non-traded capital stock level Φ t , after the resource shock. As it can be seen from Fig. 4 in the paper and the Fig. 6 below, the information at our disposal is that the new dynamic equilibrium F will in any case lay in the area down to the right of the two initial isoclines. The border of this area is marked by thicker isoclines:
Let us redefine for convenience, in the most general case, the two isoclines as such (with A > 0,K N > 0):
This allows me to start computing the ratio at the initial dynamic equilibrium in E:
In order to cover all the possible outcomes for the new ratio between productivity and the capital level, let us consider the two following “corner solutions”, in which all the possible new equilibriums lay to the right of (but infinitely close to) the thicker parts of the isoclines:
where ε > 0 is infinitely small. It is easy to show that, for both of these cases:
which completes the proof. The ratio between productivity and capital stock in the new dynamic equilibrium has in any case decreased after the resource shock, with respect to the initial dynamic equilibrium [Φ F <Φ E ].
About this article
Cite this article
Iacono, R. The Dutch disease revisited: absorption constraint and learning by doing. Port Econ J 17, 61–85 (2018). https://doi.org/10.1007/s10258-017-0137-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10258-017-0137-x