The economic effects of improving investor rights in Portugal

Abstract

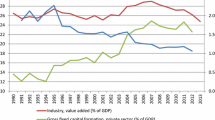
The Portuguese economy has performed remarkably well since joining the EU in 1986. Output per worker grew at an annual rate of 2.25%. The relative price of investment has declined. Real investment has increased compared to output, in part fuelled by an increase in capital inflows. At the same time, resource allocation seems to have improved as well: firm-level data shows a significant decline in the dispersion of labor productivity and size across firms. This paper argues that improvements in outside investor rights that have taken place since Portugal joined the EU is a prime candidate to explain this set of facts.

Appendices

Appendix A: Data

All macro-level data used in this paper was obtained from the Bank of Portugal’s Boletim Económico, and spans the 1978–2006 period. The data on the relative price of investment is from Heston-Summers-Aten-06 version 6.2 of the Penn World Tables, and it only spans the 1978–2004 period.

The micro-level data set is the Quadros do Pessoal, an annual survey conducted by the Portuguese Ministry of Employment which is mandatory for all Portuguese firms. We focus on the maximum available period length of data collection, 1982–2005, except for 2001 because no data is available for this year.²³ The Quadros do Pessoal contains a wealth of information on Portuguese firms (and workers). In this paper we focus on nominal sales, number of employees, and 2 and 3-digit sector of activity.

1.1 A.1 Sales

Ideally one would like to have information on value-added per firm. Unfortunately, Quadros do Pessoal does not have data on the cost of intermediate inputs. To circumvent this problem, we’ll make some assumptions and we’ll use some economic theory. Suppose firm i in sector j at time t produces according to

$$y_{ijt}=z_{ijt}k_{ijt}^{\alpha_j} x_{ijt}^{\gamma_j} \ell_{ijt}^{1-\alpha_j -\gamma_j}, $$

where y _ijt is gross output (total sales), z _ijt is total factor productivity, k _ijt is capital services, ℓ _ijt are labor services, and x _ijt are the intermediate inputs. The parameters α _j ,γ _j  ∈ (0,1) , the shares of capital and intermediate goods in production, are potentially sector-specific. Value-added (net output) is given by

$$va_{ijt}=p^y_{ijt} y_{ijt}-p^x_t x_{ijt}, $$

where $p^y_{ijt}$ is the price of firm i’s output and $p^x_t$ is the price of the intermediate input. If the market for intermediate goods is perfectly competitive, then

$$p^y_{ijt}\gamma_j \frac{y_{ijt}}{x_{ijt}}=p^x_t. $$

Replacing in the definition of value-added

$$va_{ijt}=\left(1-\gamma _j\right)p^y_{ijt}y_{ijt}. $$

In other words, value-added is proportional to nominal sales, and the constant of proportionality is sector-specific. Up to this constant, one can measure (real) value added by (real) sales. In most scenarios considered in this paper, this turns out to be very convenient—for sufficiently low levels of sectoral disaggregation, the results do not hinge upon knowing γ _j . Due to the absence of comprehensive data on firm or even sectoral level price deflators, nominal sales were deflated by the GDP deflator.

One issue in Quadros do Pessoal, relevant for computing labor productivity, is that sales and the number of employees measure in a given year do not refer to the same time period. For the following discussion, it’s important to distinguish between the data collection year (the year attached to the variables in Quadros do Pessoal), and the observation year (the year the variable corresponds to). In any given data collection year, Quadros do Pessoal gathers information in the month of October. The information collected on nominal sales is always for the whole previous year. The observation year for sales is thus the year before the data collection year. Until 1993, the number of employees is for the month of March of that data collection year. However, since 1994, the number of employees is for the month of October of that data collection year—implying a 1-year observation lag between sales and the number of employees since 1994. We’ll assume that, until 1993, the information on the number of employees is coincidental with the information on sales. In this case, the observation year for both variables is the one before the data collection. After 1994, we need to lag the number of employees one year, so that sales collected in a given year coincides with the number of employees collected the year before. In this case, after 1994, sales and lagged employees refer both to the observation year prior to the data collection year. This procedure implies a missing observation for employees in the observation year 1993. we compute the number of employees in this year as the average between the number of employees in March 1993 (collected in 1993) and the number of employees in October 1994 (collected in 1994). It follows that there is no missing observation, due to this procedure, for the number of employees from observation year 1981 until 2005.

1.2 A.2 Sectoral codes

The sectoral codes are CAE codes (Portuguese Classification of Economic Activities), Revision 2 (REV2). The challenge is to obtain codes that are consistent through time. The codes were revised twice since 1982, in 1995 and again in 2003. The 2003 change (from REV2 to REV2.1) is minimal, and affects only a couple of 3-digit codes (516 and 519, which can be easily recoded back to their REV2 values). The 1995 change (from REV1 to REV2) is more comprehensive, and sometimes there is not a one-to-one mapping between REV1 and REV2 codes at the 3-digit level, and more often at the 2-digit level. Another issue is that there is a non-negligible fraction of firms that change sectoral code for reasons unrelated to the official revision. We assigned REV2 codes to REV1 codes using the following rule. From 1994 to 1995, we assumed that every code change was due to the official revision. For each REV1 code in 1994, we computed the modal REV2 code, to which the largest number of firms switched in 1995. We attributed this code to firms that exited the sample before 1994.

1.3 A.3 Sample selection

We eliminated observations with missing number of employees. We also eliminated firms with a share of public capital larger than 50% at any point in the sample. Finally, we eliminated firms in sectors that either tend to be highly-regulated, or are not primarily engaged in market activities: utilities (2-digit codes 40 and 41), public mail (3-digit sector 641), financial (2-digit codes 65, 66 and 67), public administration (2-digit code 75), education (2-digit code 80), health (2-digit code 85), public cleaning (2-digit code 90), individual’s associations (2-digit code 90), and international organizations (2-digit code 99). We also eliminated firms with sector code 000000.

Table 3 contains the subset of sector codes that are used in this study, after applying the sample selection criteria.

Table 3 Two-digit sector codes (CAE, rev. 2)

Appendix B: Transitional dynamics

We consider the economy with exogenous TFP growth, as described in Section 4.1. For any variable x _t , let its detrended value be $\widehat{x}_t=\gamma^{-\frac{1}{1-\alpha}t}x_t$.

The price level p and the relative size Q are constant in a balanced-growth path. Also, detrended transfers depend on the time-invariant g _j (z) functions. Since these objects are time-invariant, they may be computed independently from initial conditions. Given an initial level of capital supply $\hat{K}^S_0$, the economy’s transition path is then fully characterized by sequences $\{\hat{K}^S_{t+1}\}_{t=0}^\infty$, $\{\hat{K}^D_{t}\}_{t=0}^\infty$, $\{\hat{k}_{It}\}_{t=0}^\infty$, $\{N_t\}_{t=0}^\infty$, $\{r_t\}_{t=0}^\infty$ which solve:

$$\begin{array}{rll} p\hat{K}_{t+1}^{S}\gamma ^{\frac{1}{1-\alpha }}& =&\kappa (r_{t+1})\hat{k} _{It}^{\alpha }\left[ pN_{t}\textrm{E}\left(g_{I}(z)\right)+(1-N_{t})Q^{\alpha }\textrm{E}\left({g}_{C}(z)\right)\right] \\ (1-N_{t})\bar{z}_{C}Q^{\alpha }& =& N_{t}p\textrm{E}\left(g_{I}(z)\right)+(1-N_{t})\textrm{E}\left({g}_{C}(z)\right)Q^{\alpha } \\ &&-\hat{k}_{It}^{-\alpha }p\left[ \gamma ^{\frac{1}{1-\alpha }}\hat{K}_{t+1}^{S}-(1+r_{t})\hat{K}_{t}^{S}\right] \\ \hat{K}_{t}^{D}& =&\hat{k}_{It}\left[ N_{t}+(1-N_{t})Q\right] \\ r_{t}+\delta & =&\alpha \hat{k}_{It}^{\alpha -1}\left( \bar{z}_{I}-\xi \omega _{I}\right) \\ (r^{\ast }-r_{t})\hat{B}_{t}& =&\varphi \left( \frac{\hat{B}_{t}}{\hat{Y}_{t}} \right) ^{2}\hat{Y}_{t} \end{array}$$

where

$$\begin{array}{rll} \kappa\left( r_{t+1}\right)& \equiv & \frac{1}{1+\beta^{-\frac{1}{\sigma} }\left(1+r_{t+1}\right)^{\frac{\sigma-1}{\sigma}}}\\ \hat{Y}_{t} & = & \hat{k}_{It}^{\alpha }\left[ N_{t}p\bar{z}_{I}+(1-N_{t})\bar{z}_{C}Q^{\alpha } \right]\\ \hat{B}_{t}&=&p(\hat{K}_{t}^{S}-\hat{K}_{t}^{D}). \end{array}$$

The above system of equations defines the economy’s transition mapping, from $\left(N_t,\hat{K}_t^S\right)$ into $\left(N_{t+1},\hat{K}_{t+1}^S\right)$. Given $\hat{K}^S_0>0$, one needs to compute the unique value of N ₀ that puts the economy on the saddle path. In practice, N ₀ is computed as the value such that the economy converges to the steady-state starting from $\left(N_0,\hat{K}_0^S\right)$. The full solution sequences are obtained in the process of solving for N ₀, by iterating forward on the economy’s transition function.