Application of Data-Driven computing to patient-specific prediction of the viscoelastic response of human brain under transcranial ultrasound stimulation

Abstract

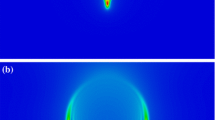
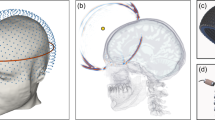
We present a class of model-free Data-Driven solvers that effectively enable the utilization of in situ and in vivo imaging data directly in full-scale calculations of the mechanical response of the human brain to sonic and ultrasonic stimulation, entirely bypassing the need for analytical modeling or regression of the data. The well-posedness of the approach and its convergence with respect to data are proven analytically. We demonstrate the approach, including its ability to make detailed spatially resolved patient-specific predictions of wave patterns, using public-domain MRI images, MRE data and commercially available solid-mechanics software.

A Proofs of theorems

Proof of Proposition 1

Suppose there is $U \in \mathbb {C}^n$ such that

$$\begin{aligned} B^T W \mathbb {E}(\Omega ) B U - \Omega ^2 M U = 0. \end{aligned}$$

(33)

Testing this equation with U, we obtain

$$\begin{aligned} (W \mathbb {E}(\Omega )) (B U) \cdot (B U^*) - M \Omega ^2 U \cdot U^* = 0, \end{aligned}$$

(34)

and taking the imaginary part,

$$\begin{aligned} (W \mathbb {E}''(\Omega )) (B U) \cdot (B U^*) = 0. \end{aligned}$$

(35)

By assumptions (i) and (ii),

$$\begin{aligned}&(W \mathbb {E}''(\Omega )) (B U) \cdot (B U^*) \ge \\ {}&c \Vert B U \Vert ^2 \ge c \, C^{-2} \, \Vert U \Vert ^2, \end{aligned}$$

(36)

which, together with (35) implies $U=0$, as required. $\square$

Lemma 3

Let $\omega _0 > 0$; $\alpha$, $\beta \in \mathbb {R}$, $|\beta -\alpha | \le 2 \omega _0$; $\mathbb {E}(\alpha )$, $\mathbb {E}(\beta ) \in \mathbb {C}$. Let E, $S\in \mathbb {C}^N$, $S = \mathbb {E}(\beta ) E$, $Z=(E,S)$, ${\hat{z}} = 2\pi Z \delta _\beta$. Let

$$\begin{aligned}&\mathcal {S} = \{ {\hat{y}} = 2\pi Y \delta _\alpha \,: \, \\ {}&\quad Y = (A,B), \; A,\; B \in \mathbb {C}^N, \; B = \mathbb {E}(\alpha ) A \}. \end{aligned}$$

(37)

Assume:

• (i) The complex modulus $\mathbb {E}(\omega )$ is Lipschitz continuous with Lipschitz constant $\mathbb {L} > 0$, i.e.,

  $$\begin{aligned} |\mathbb {E}(\omega ') - \mathbb {E}(\omega '')| \le \mathbb {L} \, |\omega '-\omega ''|, \end{aligned}$$

  (38)

  for all $\omega '$, $\omega '' \in \mathbb {R}$.

• (ii) The complex modulus is bounded above and below, i.e., there are $0< \mathbb {C}_{\text{min}} < \mathbb {C}_{\text{max}}$ such that

  $$\begin{aligned} \mathbb {C}_{\text{min}} \le |\mathbb {E}(\omega )| \le \mathbb {C}_\text{max}, \end{aligned}$$

  (39)

  for all $\omega \in \mathbb {R}$.

Then, there is $C>0$ such that

$$\begin{aligned} \text{dist}(z,{\mathcal {S}}) \le C \, |\beta -\alpha |. \end{aligned}$$

(40)

Proof

Let $Y=(A,B)$ be the closest-point projection of Z on the linear subspace $\{ B = \mathbb {E}(\alpha ) A \}$. A straightforward calculation gives

$$\begin{aligned} \Vert Y-Z\Vert = \frac{ \Vert S - \mathbb {E}(\alpha ) E \Vert }{ (\mathbb {C} + \mathbb {C}^{-1} |\mathbb {E}(\alpha )|^2)^{1/2} }, \end{aligned}$$

(41)

and

$$\begin{aligned} \Vert Y\Vert = \frac{ \Vert \mathbb {C}\, E + \mathbb {E}^*(\alpha ) \mathbb {C}^{-1} S\Vert }{ (\mathbb {C} + \mathbb {C}^{-1} |\mathbb {E}(\alpha )|^2)^{1/2} }. \end{aligned}$$

(42)

By orthogonality, $\Vert Y\Vert \le \Vert Z\Vert$ and, from (24),

$$\begin{aligned}&\Vert {\hat{y}} - {\hat{z}} \Vert _{\text{FN}} &=\Vert Y - Z\Vert + \Vert Y\Vert \, \frac{|\alpha -\beta |}{\omega _0} &= \frac{ \Vert S - \mathbb {E}(\alpha ) E \Vert }{ (\mathbb {C} + \mathbb {C}^{-1} |\mathbb {E}(\alpha )|^2)^{1/2} } &\quad + \frac{ \Vert \mathbb {C}\, E + \mathbb {E}^*(\alpha ) \mathbb {C}^{-1} S\Vert }{ (\mathbb {C} + \mathbb {C}^{-1} |\mathbb {E}(\alpha )|^2)^{1/2} } \, \frac{|\alpha -\beta |}{\omega _0} \end{aligned}$$

(43)

Assume $S = \mathbb {E}(\beta ) E$. Then,

$$\begin{aligned}&\Vert {\hat{y}} - {\hat{z}} \Vert _{\text{FN}} &= \frac{ | \mathbb {E}(\beta ) - \mathbb {E}(\alpha ) | \, \Vert E \Vert }{ (\mathbb {C} + \mathbb {C}^{-1} |\mathbb {E}(\alpha )|^2)^{1/2} } &\quad+ \frac{ | \mathbb {C} + \mathbb {E}^*(\alpha ) \mathbb {C}^{-1} \mathbb {E}(\beta )| \, \Vert E\Vert }{ (\mathbb {C} + \mathbb {C}^{-1} |\mathbb {E}(\alpha )|^2)^{1/2} } \, \frac{|\alpha -\beta |}{\omega _0} &= \frac{ | \mathbb {E}(\beta ) - \mathbb {E}(\alpha ) | + | \mathbb {C} + \mathbb {E}^*(\alpha ) \mathbb {C}^{-1} \mathbb {E}(\beta )| \, |\alpha -\beta |/\omega _0 }{ (\mathbb {C} + \mathbb {C}^{-1} |\mathbb {E}(\alpha )|^2)^{1/2} (\mathbb {C} + \mathbb {C}^{-1} |\mathbb {E}(\beta )|^2)^{1/2} } \, \Vert Z \Vert , \end{aligned}$$

(44)

By (i),

$$\begin{aligned}&\Vert {\hat{y}} - {\hat{z}} \Vert _{\text{FN}} \le \\ {}&\frac{ \mathbb {L} \, | \beta - \alpha | + | \mathbb {C} + \mathbb {E}^*(\alpha ) \mathbb {C}^{-1} \mathbb {E}(\beta )| \, |\alpha -\beta |/\omega _0 }{ (\mathbb {C} + \mathbb {C}^{-1} |\mathbb {E}(\alpha )|^2)^{1/2} (\mathbb {C} + \mathbb {C}^{-1} |\mathbb {E}(\beta )|^2)^{1/2} } \, \Vert Z \Vert , \end{aligned}$$

(45)

and by (ii),

$$\begin{aligned}&\Vert {\hat{y}} - {\hat{z}} \Vert _{\text{FN}} \le \\ {}&\frac{ \mathbb {L} \omega _0 + \mathbb {C} + \mathbb {C}^{-1} \mathbb {C}_{\text{max}}^2 }{ \mathbb {C} + \mathbb {C}^{-1} \mathbb {C}_{\text{min}}^2 } \, \Vert Z \Vert \, \frac{| \beta - \alpha |}{\omega _0} \end{aligned}$$

(46)

and (40) follows with

$$\begin{aligned} C = \frac{ \mathbb {L} \omega _0 + \mathbb {C} + \mathbb {C}^{-1} \mathbb {C}_{\text{max}}^2 }{ \mathbb {C} + \mathbb {C}^{-1} \mathbb {C}_{\text{min}}^2 } \, \frac{\Vert Z \Vert }{\omega _0}, \end{aligned}$$

(47)

as advertised. $\square$

Lemma 4

(Transversality) Suppose that the matrix $B^T W \mathbb {E}(\Omega ) B$ is non-singular and the viscoelasticity problem (10) has a unique solution for every $\Omega \in \mathbb {R}$, $F\in \mathbb {R}^n$ and $G\in \mathbb {R}^N$. Let $\mathcal {D}$ be as in (17) and $\mathcal {E}$ as in (16). Assume assumption (ii) of Lemma 3 holds and choose the constant $\mathbb {C}$ in (27) such that $\mathbb {C}_{\text{min}} \le \mathbb {C} \le \mathbb {C}_{\text{max}}$. Then, there are $c>0$, $b\ge 0$ such that

$$\begin{aligned} \text{dist}(y, z) \ge c \, ( \Vert y \Vert + \Vert z \Vert ) - b, \end{aligned}$$

(48)

for all $y \in \mathcal {D}$ and $z \in \mathcal {E}$.

Proof

The intersection of $\mathcal {D}$ and $\mathcal {E}$ consists of one single point $z_0$ corresponding to the unique solution of the linear viscoelasticity problem (10). Let $\mathcal {E}_0$ be the constraint set for zero forcing, i.e., (16) with $F=0$ and $G=0$. Then, by linearity, we have $\mathcal {E} = z_0 + \mathcal {E}_0$. We claim that there is $c > 0$ such that

$$\begin{aligned} \text{dist}(y', z') \ge c \, ( \Vert Y' \Vert + \Vert Z' \Vert ), \end{aligned}$$

(49)

for every $y' = Y' \text{e}^{i\alpha t} \in \mathcal {D}$ and $z' = Z' \text{e}^{i\beta t} \in \mathcal {E}_0$. Write $Z' = (E',F') \in \mathbb {C}^N \times \mathbb {C}^N$. Then,

$$\begin{aligned}&\text{dist}(y', z') \ge \text{dist}(z',{\mathcal {D}}) \ge &\inf \big \{ \Vert (A,B) - Z'\Vert :\, \\ {}&\qquad A,B \in \mathbb {C}^N, \; B = \mathbb {E}(\gamma ) A, \; \gamma \in \mathbb {R} \big \} =&\inf _{\gamma \in \mathbb {R}} \frac{ \Vert \mathbb {C}^2 E' + \mathbb {E}(\gamma ) S'\Vert ^2 }{ \mathbb {C}(\mathbb {C}^2 + |\mathbb {E}(\gamma )|^2) }. \end{aligned}$$

(50)

Expanding the square with $z' \in \mathcal {E}_0$, we obtain

$$\begin{aligned} \Vert \mathbb {C}^2 E' + \mathbb {E}(\gamma ) S'\Vert ^2 = \Vert \mathbb {C}^2 E'\Vert ^2 + \Vert \mathbb {E}(\gamma ) S'\Vert ^2, \end{aligned}$$

(51)

whence

$$\begin{aligned}&\text{dist}(y', z') \ge \\ {}&\inf _{\gamma \in \mathbb {R}} \frac{ \mathbb {C}^4 \Vert E'\Vert ^2 + |\mathbb {E}(\gamma ) |^2 \, \Vert S'\Vert ^2 }{ \mathbb {C}(\mathbb {C}^2 + |\mathbb {E}(\gamma )|^2) } \ge \\ {}&\frac{ \mathbb {C}^4 \Vert E'\Vert ^2 + \mathbb {C}_{\text{min}}^2 \, \Vert S'\Vert ^2 }{ \mathbb {C}(\mathbb {C}^2 + \mathbb {C}_{\text{max}}^2) }. \end{aligned}$$

(52)

With $\mathbb {C}_{\text{min}} \le \mathbb {C} \le \mathbb {C}_\text{max}$, we further have

$$\begin{aligned} \text{dist}(y', z')&\ge \frac{ \mathbb {C} \Vert E'\Vert ^2 + \mathbb {C}^{-1} \, \Vert S'\Vert ^2 }{ 1 + \mathbb {C}_\text{max}^2/\mathbb {C}_{\text{min}}^2 } \\ {}&= \frac{ \Vert Z'\Vert ^2 }{ 1 + \mathbb {C}_{\text{max}}^2/\mathbb {C}_\text{min}^2 }. \end{aligned}$$

(53)

Finally, the estimates

$$\begin{aligned}&\text{dist}(y', z') \ge \frac{1}{2} \text{dist}(y', z') + \\ {}&\frac{1}{2} \frac{ \Vert Z'\Vert ^2 }{ 1 + \mathbb {C}_{\text{max}}^2/\mathbb {C}_\text{min}^2 } \ge c \, ( \Vert Y'\Vert +\Vert Z'\Vert ), \end{aligned}$$

(54)

yield (49), as surmised. Let now $y\in \mathcal {D}$, $z\in \mathcal {E}$, and define $z'=z-z_0\in \mathcal {E}_0$. Then, a triangular inequality gives $\Vert Z' \Vert \ge \Vert Z \Vert - \Vert Z_0 \Vert$ and we obtain

$$\begin{aligned} \text{dist}(y, z) \ge c \, ( \Vert Y \Vert + \Vert Z \Vert ) - c \, \Vert Z_0 \Vert , \end{aligned}$$

(55)

which gives (48) with $b = c \, \Vert Z_0 \Vert$. $\square$

Proof of Prop. 2

Let $y_*=z_*$ be the unique solution of the $\mathbb {E}(\Omega )$–problem. Set $z'_h=z_*$ and let $y'_h$ the closest point to $z_*$ on the subspace

$$\begin{aligned}&\mathcal {S} = \{ {\hat{y}} = Y \delta _\omega \,: \, \\ {}&\quad Y = (A,B), \; A,\; B \in \mathbb {C}^N, \; B = \mathbb {E} A \}. \end{aligned}$$

(56)

with $(\omega ,\mathbb {E})$ $\in$ $\mathcal {P}_{h}$ such that $|\omega - \Omega | \le \delta _h$. Then, by optimality,

$$\begin{aligned} \text{dist} (y_h, z_h) \le \text{dist} (y'_h, z'_h), \end{aligned}$$

(57)

where $(y_h,z_h)$ is the solution of the $\mathcal {P}_{h}$–Data-Driven problem. By Lemma 3,

$$\begin{aligned} \text{dist} (y_h,z_h) \le C \, \delta _h, \end{aligned}$$

(58)

whence in follows that $\text{dist} (y_h,z_h) \rightarrow 0$. By Lemma 4, it follows that, possibly up to subsequences, there exist Y, $Z \in \mathbb {C}^N$ such that $Y_h \rightarrow Y$ and $Z_h \rightarrow Z$. By the continuity of the distance, it follows that $\text{dist} (y,z) = 0$, hence $y=z$ is classical solution. By the uniqueness of the classical solution, Prop. 1, it follows that $y=y_*$ and $z=z_*$. $\square$