Three-dimensional flows in a hyperelastic vessel under external pressure

Abstract

We study the collapsible behaviour of a vessel conveying viscous flows subject to external pressure, a scenario that could occur in many physiological applications. The vessel is modelled as a three-dimensional cylindrical tube of nonlinear hyperelastic material. To solve the fully coupled fluid–structure interaction, we have developed a novel approach based on the Arbitrary Lagrangian–Eulerian (ALE) method and the frontal solver. The method of rotating spines is used to enable an automatic mesh adaptation. The numerical code is verified extensively with published results and those obtained using the commercial packages in simpler cases, e.g. ANSYS for the structure with the prescribed flow, and FLUENT for the fluid flow with prescribed structure deformation. We examine three different hyperelastic material models for the tube for the first time in this context and show that at the small strain, all three material models give similar results. However, for the large strain, results differ depending on the material model used. We further study the behaviour of the tube under a mode-3 buckling and reveal its complex flow patterns under various external pressures. To understand these flow patterns, we show how energy dissipation is associated with the boundary layers created at the narrowest collapsed section of the tube, and how the transverse flow forms a virtual sink to feed a strong axial jet. We found that the energy dissipation associated with the recirculation does not coincide with the flow separation zone itself, but overlaps with the streamlines that divide the three recirculation zones. Finally, we examine the bifurcation diagrams for both mode-3 and mode-2 collapses and reveal that multiple solutions exist for a range of the Reynolds number. Our work is a step towards modelling more realistic physiological flows in collapsible arteries and veins.

1 Introduction

Fluid–structure interaction (FSI) between flow and biological vessel walls is intrinsic to the circulatory and respiratory systems. For example, in cardiovascular diseases, wall shear stress, blood flow patterns, and pressure can all impact the vessel integrity, leading to endothelial cell damage, thickness change of the endarterium, hyperplasia of intimal smooth muscle cells and proliferating intimal connective tissue (Nerem 1992). The abnormal tissue stress on the vascular wall is the key cause of atherosclerosis (Ku et al. 1985; Giddens et al. 1993; Papaioannou et al. 2006). Pressure increase against the vascular wall can affect oxygen transmission through the wall (Moore and Ethier 1997). In an vessel aneurysm, a high mortality cardiovascular disease, FSI-induced mechanical forces regulate its growth and rupture (Liepsch 2002; Hoi et al. 2004). Experimental observation shows that flow circulation regions exist in an arterial aneurysm and sluggish flow of blood in the circulation regions accelerates the formation of thrombus and the coagulation of blood (Gobin et al. 1994). Flows in collapsible vessels, in particular, are associated with some interesting physiological and pathological problems. For example, airflow in the lungs can be limited due to the large-airway collapse, despite a strongly forced expiration. Wheezing is a manifestation of collapsible vessel-induced self-excited oscillations. In jugular veins of giraffe, the return of blood to the heart from the head must be accompanied by a partial venous collapse (Pedley et al. 1996). Measurement of blood pressure is based on the collapsible behaviour of the elastic artery (Korotkov sounds) when compressed by a blood-pressure cuff (Pedley and Pihler-Puzović 2015). These provide motivations for studying flows in a collapsible vessel.

Many experimental studies of flows in a collapsible vessel are based on a Starling Resistor set-up, which consists of a collapsible rubber tube whose two ends are clamped onto rigid tubes and placed inside a chamber, so that the pressure external to the tube can be adjusted. Fluid flow is then driven through the collapsible tube, and resistors are in place to control pressure and flow at the entrance and exit of the collapsible segment. As the transmural (internal minus external) pressure becomes negative, the tube is buckled (collapsed) into a shape of two-lobed (mode-2) or higher circumferential modes, and rich dynamic phenomena signatured by self-excited oscillations prevail (Truong and Bertram 2009; Bertram and Elliott 2003; Bertram and Tscherry 2006). Bertram et al. studied the conditions, in terms of the upstream transmural (internal minus external) pressure and the Reynolds number, for the onset of flow limitation (Bertram and Elliott 2003). Barclay et al. identified various self-excited oscillations by changing parameters such as the tube length-to-diameter ratios, Reynolds numbers, and the ratio of the transmural pressure to pressure drop (Barclay and Thalayasingam 1986). Bertram found that self-excited oscillations in the tubes are highly nonlinear and in four frequency bands (Bertram 1986).

Conrad was the first to investigate the relationship between flow and external pressure in collapsible tubes (Conrad 1969). Many theoretical and numerical studies have since been carried out. The simplest approach used lumped-parameter models in which the system’s characteristics are described by a small number of scalar variables, such as the cross-sectional area, the transmural pressure and the fluid velocity at the point of strongest collapse (Bertram and Pedley 1982). The next level of modelling is the one-dimensional approach (Cancelli and Pedley 1985; Jensen 1990, 1992; Shapiro 1977), which enabled wave propagation to be included in the system, leading to the “choking” mechanism. Indeed, some of these one-dimensional models are extremely useful in explaining some system mechanisms (Stewart et al. 2010; Stewart 2017). A more rational two-dimensional fluid-membrane model was developed by Pedley and coworkers, in which the collapsible tube is represented by a channel with part of the upper wall replaced by a thin and inextensible membrane (Pedley and Luo 1998; Lowe and Pedley 1995; Luo and Pedley 1996, 2000). To reflect the fact that physiological vascular walls often experience elastic stretching and bending, Cai and Luo proposed a fluid-beam model and incorporated bending and extensional stiffness into a geometrically nonlinear Lagrangian representation of the wall (Cai and Luo 2003).

Ultimately, it is necessary to develop full three-dimensional (3D) models to more accurately explain experimental observations and physiological problems. Heil and coworkers used finite element methods to couple geometrically nonlinear Kirchoff–Love shell theory to an internal 3D Navier–Stokes flow (Heil 1997; Heil and Pedley 1996). Restricting attention initially to Stokes flows, they showed how non-axisymmetric buckling of the tube contributes to nonlinear pressure-flow relations that can exhibit flow limitation through purely viscous mechanisms. These computations were then extended to describe steady 3D flows in nonuniformly buckled tubes at Re of a few hundred (Hazel and Heil 2003) for a mode-2, or two-lobed, buckling tube, which revealed twin jets downstream, consistent with the experimental observations (Bertram and Godbole 1997). These jets were also found by  (Marzo et al. 2005), whose work included the effects of thick-walled tubes. Using a prescribed oscillations of the tube wall, work by (Heil and Waters 2008; Whittaker et al. 2010a, b) suggested that the essential elements of the sloshing instability mechanism identified in two-dimensional flows (Jensen and Heil 2003) are also present in the three-dimensional flow. The theoretical work was extended to a tube of an initially elliptical cross section (Whittaker et al. 2010c).

As three-dimensional approaches require extensive computation, many model simplifications were made in previous studies. For example, only a quarter of the tube was modelled, and the focus was mostly on mode-2 collapse (Heil 1997; Heil and Pedley 1996; Marzo et al. 2005), the solid mechanics was represented using a thin-shell theory or even a tube-law (Whittaker et al. 2010d; Whittaker 2015). On the other extreme, Zhu et al. (Zhu et al. 2008, 2010, 2012) adopted a purely solid mechanics approach to study a three-dimensional nonlinear thick-walled tube under external pressure and axial loading. Despite the absence of fluid, their model offered some important insights on the collapsible behaviour of the tube. Using infinitesimal deformations superimposed on a deformed circular cylindrical configuration, Zhu et al. (Zhu et al. 2008) found that the critical bifurcation pressure deviates from the thin shell prediction in both the very thin and thick-walled regimes. For very short and sufficiently thick tubes, transition from lower to higher circumferential modes occurs in the range of axial compression. Contrary to thin-shell theory, in thick-walled tubes, mode 2 bifurcation becomes the dominant mode, as shown in Fig. 1. The same authors (Zhu et al. 2010) also carried out numerical simulations for large nonlinear deformation of thick-walled tubes with the initial configuration constrained to a circular cylindrical shape. The work was later extended to a fully 3D and nonlinear thick-walled tube model, which showed that the axisymmetric analysis provides a good approximation for the critical bifurcation pressure in short tubes (Zhu et al. 2012). However, the critical bifurcation pressure for longer tubes is smaller in the non-axisymmetric three-dimensional model, and the post-buckling solution is no longer unique. In particular, they found many different intriguing mode-3 and higher mode bifurcations at the same critical transmural pressure. Mixed modes collapse and mode transitions were also observed (Zhu et al. 2012).

Fig. 1

Reproduced with permission from  (Zhu et al. 2008)

Non-dimensional critical pressure plotted against the tube length L / B, for different values of thinness B / H, where B is the external radius of the tube, L is the tube length, and H is the tube thickness. When tube wall is thicker, e.g. $B/H=1.58$, mode-2 buckling dominants except the very short tubes. However, when tube wall is thinner, e.g. $B/H=50$, and $L/B<10$, higher modes collapse first under the critical pressure

Compared to the mode-2 collapse, flows in a collapsible tube that has three-lobed mode received much less attention. This is because in many experiments using the Starling resistor, the elastic tubes used are usually too long or too thick for the mode-3 buckling to appear. However, in many physiological applications, vessels are neither very long or thick-walled, and thus, higher mode collapses can occur. For example, the collapsed airways are often in mode-3 with a shorter collapsed section (Gaver et al. 1996; Hell 1999). In aortic dissection, flow going through the false lumen often induces collapses of the true lumen in mode-3 or higher, sometimes mixed modes (Sun et al. 2014; Wang et al. 2017, 2016). To date, detailed 3D flow patterns in an elastic vessel under a higher-mode buckling, say, a three-lobed collapse, have not been studied.

We develop a new three-dimensional model of a nonlinear incompressible hyperelastic tube that is fully coupled with the fluid flow governed by the Navier–Stokes equations. A monolithic finite element solver that combines the Arbitrary Lagrangian–Eulerian (ALE) and frontal approach is developed for the coupled fluid-structure system equations. The method of spines with three-dimensional rotating spines is used to update the adaptive mesh deformation. We perform extensive verification of the solver against the commercial software (ANSYS, on solid solver, and FLUENT, on fluid solver), and compare the results using different nonlinear constitutive laws for the tube. We show, for the first time, detailed 3D flow patterns following a mode-3 or mixed-mode buckling of an elastic tube, and where the energy is dissipated in the system. We also study the bifurcation diagrams for both mode-2 and mode-3 buckling and show how the system yields multiple solutions at certain ranges of the Reynolds number.

2 The mathematical model

2.1 The model

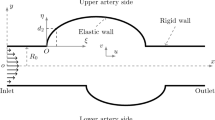
We consider fluid flow through a three-dimensional tube as shown in Fig. 2, where the elastic section is initially cylindrical. The tube is divided into three sections; an elastic section in the middle and the two rigid upstream and downstream sections. The tube is made of an incompressible hyperelastic material. The fluid is assumed to be incompressible Newtonian fluid. The system is flux-driven, and the tube deforms under an applied external pressure and the fluid stresses due to the fluid-structure interaction.

Fig. 2

Geometry of the collapsible tube, where $L_{u}$, $L_{m}$ and $L_{d}$ are the lengths of the upstream, collapsible, and downstream sections, respectively. The middle section is collapsible with wall thickness h and subjected to an external pressure of $P_\mathrm{ext}$

In our ALE model, the fluid field is described by the Eulerian coordinate system with the position vector $\mathbf{x}$ and the tube is described by two Lagrangian coordinate systems, using $\mathbf{x}_\mathbf{e}$ and $\mathbf{X}_\mathbf{e}$, respectively. $\mathbf{x}_\mathbf{e}$ is the position vector in the current configuration and $\mathbf{X}_\mathbf{e}$ is the position vector in the reference configuration. In the following, we denote the variables in the reference configurations using capital letters, and the variables in the current configuration using lower case.

Let $U^*_0$ be the average flow velocity at the entrance of the tube, $D^*$ be the inner diameter of the tube, $\rho ^*$ and $\mu ^*$ be the fluid density and viscosity, respectively. Unless otherwise stated, we adopt the dimensionless variables and parameters defined as follows,

$$\begin{aligned} x_i= & {} x_i^*/D^*, x_{ei} = x_{ei}^*/D^*, {X_{ei} = X_{ei}^*/D^*,} v_i=v_i^*/U_0^*, \nonumber \\ u_i= & {} u_i^*/D^*, \quad \ i=1,2,3, \nonumber \\ \ p= & {} p^*/\rho ^* U_0^{*2}, \,\ L=L^*/D^*, \,\ h=h^*/D^*, \,\ \nonumber \\ Re= & {} U_0^* D^*\rho ^* /\mu ^*, \,\ P_\mathrm{ext} = P_{ext}^*/\rho ^* U_0^{*2} , \nonumber \\ \,\ c_1= & {} c_1^*/\rho ^* U_0^{*2}, \,\ c_2 = c_2^*/\rho ^* U_0^{*2}, \,\ \nonumber \\ \mu _e= & {} \mu _e^*/\rho ^* U_0^{*2}, \,\ \rho _e=\rho _e^*/D^*\rho ^*, \end{aligned}$$

(2.1)

where the quantities with a star are the dimensional ones. $v_i$, $x_i$ ($i=1,2,3$) are the velocity and coordinate components of the fluid, $u_i$ are the displacement components of the structure, and $x_{ei}$, $X_{ei}$ are the coordinate components of the structure in the current and reference configuration, respectively. p is the fluid pressure, Re is the Reynolds number, $P_\mathrm{ext}$ is the external pressure, h and L are the thickness and length of the tube, $\rho _e$ is the density of the tube wall. $\mu _e$, $c_0$ and $c_1$ are material constants of the tube wall; each has the unit Pa.

2.2 The governing equations

We first consider the governing equations of the tube wall. In the absence of body force, the momentum equations in the reference (undeformed and stress-free) configuration are given by

$$\begin{aligned} \mathbf{S} _{Ai,A} = \rho _e u_{i,tt} \end{aligned}$$

(2.2)

where $\mathbf{S}$ is the nominal stress tensor (which is the transpose of the first Piola–Kirchoff stress tensor), i, $A \in \{1,2,3\}$ refer to the Cartesian indices in the current and reference configurations, respectively, $u_i$ are the displacement components of the elastic wall. For a given strain-energy function (per unit volume) W, the constitutive relation can be written as

$$\begin{aligned} \mathbf{S}_{Ai} = \left( \frac{{\partial W}}{{\partial {\mathbb {F}}}}\right) _{Ai} - p_e({\mathbb {F}}^{ - 1})_{Ai}, \end{aligned}$$

(2.3)

where $\mathbb {F}$ is the deformation gradient, and $p_e$ is the Lagrange multiplier to ensure the material incompressibility (Cai and Fu 1999),

$$\begin{aligned} \det {\mathbb {F}} = 1. \end{aligned}$$

(2.4)

The Cauchy stress tensor can be computed from

$$\begin{aligned} {{\varvec{\sigma }}} = \frac{1}{\det {\mathbb {F}}} {\mathbb {F}}{} \mathbf{S}. \end{aligned}$$

(2.5)

We consider three types of nonlinear materials: Neo–Hookean, Mooney–Rivlin and Gent, for which the strain-energy functions are given, respectively, by  (Holzapfel 2002)

$$\begin{aligned} W= & {} \frac{{\mu _e}}{2}(I - 3), \end{aligned}$$

(2.6)

$$\begin{aligned} W= & {} \frac{{c_0 }}{2}(I - 3) + \frac{{c_1 }}{2}(II - 3), \,\ c_0+c_1 = \mu _e, \end{aligned}$$

(2.7)

$$\begin{aligned} W= & {} - \frac{1}{2}\mu _e J_m \ln \left( 1 - \frac{I-3}{{J_m }}\right) , \end{aligned}$$

(2.8)

where I, II are the first and second invariants of the right Cauchy–Green deformation tensor, respectively. $\mu _e$, $c_0$, $c_1$ and $J_m$ are material constants. $\mu _e$ is the shear modulus, and $J_\mathrm{m}$ is a non-dimensional parameter to indicate the material hardening. However, although the sum of $c_0$ and $c_1$ represents the shear modulus, individually, $c_0$ or $c_1$ does not have a clear physical explanation. In the following, we will use the Neo–Hookean material model as an example to establish the governing equations. Substituting (2.3), (2.6) into (2.2), we have

$$\begin{aligned} \mu _e F_{iA,A} - p_eF_{Ai,A}^{-1} = \rho _e u_{i,tt}. \end{aligned}$$

(2.9)

Equations (2.4) and (2.9) are the governing equations of the hyperelastic tube.

The motion of the flow field is governed by the Navier–Stokes equations and the continuity equation. The governing equations for the coupled fluid-structure interaction system are, thus:

$$\begin{aligned} \frac{{\partial v_i }}{{\partial t}} + v_j \frac{{\partial v_i }}{{\partial x_j }}= & {} -\frac{{\partial p}}{{\partial x_i }} + \frac{1}{Re}\nabla ^2 v_i \nonumber , \\ \frac{{\partial v_i }}{{\partial x_i }}= & {} 0,\quad \det {\mathbb {F}}=1, \nonumber \\ \mu _e F_{iA,A}-p_e F_{Ai,A}^{-1}= & {} \rho _e u_{i,tt}, \,\ i,j,A= 1,2,3. \end{aligned}$$

(2.10)

In the following, we may also use (x, y, z), (u, v, w), and $(u_e, v_e, w_e)$ as surrogates for $x_i$, $v_i$, and $u_i$, $i=1,2,3$, respectively.

2.3 The boundary conditions

We impose the following boundary conditions:

• Parabolic inlet flow: ($z=0$): $v_1=v_2=0, v_3=2-8(x_1^2+x_2^2)$.

• Zero velocity at the rigid walls: $v_i=0$,   $i=1,2,3$,   at $r = R$, $0\le z \le L_u$, and $L_u + L_m \le z\le L$, where $r=\sqrt{x^2+y^2}$.

• Stress free at the outflow: $\sigma _t = 0,\sigma _n =0$, at $z=L$.

• Clamped ends of the elastic tube: $u_i=0$,   $i=1,2,3$,   at $z = L_u$, and $L_u + L_m$.

• No slip condition at the interface: $v_i(t) = \dot{u}_i(t)$, $x_i= x_{ei}$, $L_u \le z\le L_u + L_m$, $i=1,2,3.$

• External pressure on the outer wall of the tube: ${{\varvec{\sigma }}} \mathbf{n} = - P_\mathrm{ext}{} \mathbf{n}$, $L_u \le z\le L_u + L_m$, where $\mathbf{n}$ is the outward normal vector of the tube.

3 The numerical method

3.1 Mesh generation

In the finite element analysis, the elements for the fluid are isoparametric triangular prism elements with 15 nodes, and the elements for the elastic tube are isoparametric hexahedron elements with 20 nodes. At the interface, the elements are made to conform to each other. We first obtain the grids on a circular cross section as shown in Fig. 3, which is extruded to the three-dimensional domain using a mesh mapping method.

Fig. 3

The schematic mesh structure of the circular cross section of the tube—the grids used in the simulations are much denser. The thicker (purple) lines are the rotating spines. The mesh points within the concentric circle are fixed, and these outside the circle are movable. The nodes on the FSI interface are also called the public nodes. The ratio of the concentric circle and the tube radii is denoted by $b_r$, the region within the concentric circle is divided into $n_{r2}$ layers, and immediate layer outside the circle, has $n_b+n_b(n_{r2}-1)$ divisions. For description of the other symbols, see text

To resolve the boundary layer near the tube wall, we increase the density of the mesh towards the wall. The cross section of the fluid field is divided into the internal and external regions by a concentric circle. The ratio of the concentric circle and the tube radii is denoted by $b_r$. We divide the internal region into $n_{r2}$ layers. We use $n_b$ to indicate the number of divisions of the most inner layer along the ring direction. The number of divisions of the subsequent layers are $n_b+n_b(j-1)$, $j=1, \ldots n_{r2}$.

In the external region, the most inner layer, which overlaps with the most outer layer of the internal region, has $n_b+n_b(n_{r2}-1)$ divisions, and the other layers have $(i+1)[n_b+n_b(n_{r2}-1)], i=1, \ldots n_r$ divisions. The external region is divided into equal sections by the rotating spines as shown in Fig. 3. (Details are given in the following section.) Mesh quality of the circular cross section can be controlled by adjusting the numbers $n_r$, $n_{r2}$ and $n_b$. To get the coordinates of the nodes of the external region, the coordinates of the two ends of the rotating spines, such as $A_0 (x_0 ,y_0 ,z_0 )$, $A_1 (x_1 ,y_1 ,z_1)$ are determined first. The coordinates of all other nodes on the rotating spines, say $A(x_a ,y_a ,z_a )$, are interpolated using

$$\begin{aligned} x_a= & {} x_0+\omega _A(x_1-x_0), \,\ y_a = y_0+\omega _A(y_1-y_0), \nonumber \\ z_a= & {} z_0+ \omega _A (z_1- z_0), \end{aligned}$$

(3.1)

where $\omega _A$ is a scaling factor between 0 and 1. The coordinates of the nodes that are not on the rotating lines are linearly interpolated from those on the rotating spines. For instance, the coordinates of the node $C(x_c ,y_c ,z_c)$ in Fig. 3 are calculated from:

$$\begin{aligned} x_c =\frac{1}{2}x_a+\frac{1}{2}x_b,y_c = \frac{1}{2}y_a+\frac{1}{2}y_b,z_c = \frac{1}{2}z_a+\frac{1}{2}z_b \end{aligned}$$

(3.2)

where ($x_a, y_a, z_a$) and ($x_b, y_b, z_b$) are the coordinates of points A and B, respectively, both are on the rotating lines. The collapsible tube wall is divided into $n_{r1}$ layers, each layer has the same number of divisions in the radial direction determined by $n_r$, $n_{r2}$ and $n_b$. The numbers of divisions of the upstream, elastic and downstream sections are denoted by $n_{u}$, $n_{m}$ and $n_{d}$, respectively. The upstream section is divided equally along the tube, the downstream section is divided sparser towards the outlet of the tube and the grids of the elastic section are denser towards the two ends. Figure 4 shows an example grid of the whole model.

Fig. 4

The finite element mesh of the whole model

Fig. 5

Selected cross-sectional slices of the finite element mesh for the fluid in the elastic section of the domain after large deformation

To see the mesh quality after deformation, two selected cross sections for the fluid in the elastic section of the domain (for a simulated case where the large deformation occurs) are shown in Fig. 5. It can be seen that there is controlled mesh distortion even at the most collapsed section. The largest ratio between the maximum and the minimum sizes of any single element is $<\,4.0$. Almost all the pentahedron elements at these cross sections remain acute triangles after deformation.

3.2 Mesh adaptation and rotating spines

The elastic boundary of the fluid field moves according to the wall deformation. To ensure the mesh can cope with the moving boundary, the fluid mesh is made adaptive by adopting the method of rotating spines initially developed for two-dimensional problems (Cai and Luo 2003). This method is illustrated on a circular cross section as shown in Fig. 6. A set of spines originating from the fixed concentric circle are connected to the tube wall. These spines remain straight, but can rotate around the fixed points as the tube wall deforms. For example, in the reference configuration, the spine k connects a fixed node $(x_b^k ,y_b^k ,z_b^k )$ on the concentric circle to a material point $(X_e^k ,Y_e^k, Z_e^k )$ on the tube wall. After the deformation, $(X_e^k, Y_e^k, Z_e^k)$ moves to $(x_e^k(t) ,y_e^k(t) ,z_e^k(t))$ according to:

$$\begin{aligned} x_e^k(t) =\! X_e^k + u_e(t), \,\ y_e^k(t)=\! Y_e^k+v_e(t), \,\ z_e^k(t)=\!Z_e^k+w_e(t), \end{aligned}$$

(3.3)

where ($u_e$, $v_e$, $w_e$) are the corresponding displacements. The mesh nodes of spine k move along it according to

$$\begin{aligned} x_{j}^k(t)= & {} x_b^k+\omega _j^k(x_e^k(t)-x_b^k), \,\, \nonumber \\ y_j^k(t)= & {} y_b^k+ \omega _j^k (y_e^k(t)-y_b^k), \,\, \nonumber \\ z_j^k(t)= & {} z_b^k+ \omega _j^k (z_e^k(t)-z_b^k), \end{aligned}$$

(3.4)

where ($j=1,2,3,\ldots n_k$), $n_k$ is the total number of nodes on spine k, and $\omega _j^k$ are the fixed scaling factors defined by

$$\begin{aligned} \omega _j^k= {\frac{\sqrt{(x_j^k(0)-x_b^k)^2+(y_j^k(0)-y_b^k)^2+(z_j^k(0)-z_b^k)^2}}{\sqrt{(X_e^k-x_b^k)^2+(Y_e^k-y_b^k)^2+(Z_e^k-z_b^k)^2}}},\,\ \end{aligned}$$

(3.5)

with $x_j^k(0), y_j^k(0), z_j^k(0)$ being the initial coordinates of the (fluid) node j on spine k. This spine-based mesh adaptation is automatic as no new meshing and interpolations are needed. Our previous studies on a 2D model showed that this was not only computationally efficient, but also numerically accurate (Liu et al. 2012).

Fig. 6

A sketch of two rotating spines

3.3 The ALE finite element approach

The time derivatives appearing in the Navier–Stokes equations are the Eulerian time derivatives $\partial /\partial t$ which are defined in the fixed space. However, as the grid is moving, we need to define the time derivatives with respect to the moving grid, say $\delta /\delta t$. Using the chain rule, we write the relation between $\delta /\delta t$ and $\partial /\partial t$ as

$$\begin{aligned} \frac{{\delta v_i }}{{\delta t}} = \frac{{\partial v_i }}{{\partial t}} + {\mathbf{w}} \cdot \nabla v_i, \quad \ i=1,2,3, \end{aligned}$$

(3.6)

where $\mathbf{w}$ is the velocity of the moving grid. The ALE Navier–Stokes equations become,

$$\begin{aligned} \frac{{\delta v_i }}{{\delta t}}- {\mathbf{w}} \cdot \nabla v_i + v_j \frac{{\partial v_i }}{{\partial x_j }}= & {} -\frac{{\partial p}}{{\partial x_i }} + \frac{1}{Re}\nabla ^2 v_i. \end{aligned}$$

(3.7)

We employ the Petrov–Galerkin method to improve the numerical convergence, the velocities and displacements are interpolated using the quadratic shape functions $\psi$, and $\psi ^{(e)}$, respectively, and the fluid pressure and solid’s ‘pressure’ are interpolated using the linear shape functions $\phi$, and $\phi ^{e}$, respectively:

$$\begin{aligned} v_j= & {} \sum \limits _{i=1}^{15}{v_{ji}\psi _i}(L_1,L_2,L_3,L_z), \nonumber \\ \,u_j= & {} \sum \limits _{i=1}^{20}{u_{ji}\psi ^e_i }(\xi ,\eta ,\zeta ),\,\ j=1,2,3 \nonumber \\ p= & {} \sum \limits _{i=1}^6 {p_i\phi _i } (L_1 ,L_2 ,L_3,L_z ), \, \nonumber \\ p_e= & {} \sum \limits _{i = 1}^8 {p_{ei} \phi _i^e}(\xi ,\eta ,\zeta ), \end{aligned}$$

(3.8)

where $(L_1,L_2, L_3, L_z)$, and $(\xi ,\eta ,\zeta )$ are the local coordinates of the isoparametric fluid triangular and solid hexahedron elements, respectively. All the fifteen nodes of the fluid elements have degrees of freedom of velocity, only the six vertices have the degree of freedom of pressure. Likewise, all the 20 nodes of the solid elements have degrees of freedom of displacement and only the eight vertices have degree of freedom of ‘pressure’. On the public nodes of the fluid and solid’s elements, both the fluid’s and solid’s degrees of freedom exist.

The finite element formulation of the ALE and continuity equations, after integration by parts, can be written as

$$\begin{aligned}&\int _\Omega \left[ \left( \frac{\delta v_i}{\delta t} - {\mathbf{w}} \cdot \nabla v_i+ v_j \frac{\partial v_i }{\partial x_j }\right) \psi \right. \nonumber \\&\left. \quad -p\frac{\partial \psi }{\partial x_i} + \frac{1}{Re}\frac{\partial v_i }{\partial x_j }\frac{\partial \psi }{\partial x_j} \right] \,\mathrm{d}\omega \nonumber \\&\quad + \int _A \left( pn_i-\frac{1}{Re}\frac{\partial v_i}{\partial x_j }n_j\right) \psi \, \mathrm{d}a=0, \end{aligned}$$

(3.9)

$$\begin{aligned}&\int _\Omega \frac{\partial v_i }{\partial x_i }\phi \,\mathrm{d}\omega =0. \end{aligned}$$

(3.10)

where $n_i$ are the components of the outwards unit normal vector of the fluid boundary, and $\Omega$ and A denote the total volume and area of the fluid in the current configuration, respectively.

The finite element form of the solid governing equations in the current configuration is:

$$\begin{aligned}&-\int _v {\left( {\sigma _{ij,j}- \rho _e u_{i,tt} } \right) } \psi ^{(e)} \mathrm{d}v \nonumber \\&\quad + \int _{s_\sigma } {\left( {\sigma _{ij} m_j - {f}_{ij} m_j } \right) } \psi ^{(e)}\mathrm{d}s=0 \end{aligned}$$

(3.11)

$$\begin{aligned}&\int _v {\left( {\det ({\mathbb {F}}) - 1} \right) } \phi ^{e} \mathrm{d}v=0 \end{aligned}$$

(3.12)

where ${\sigma _{ij}}$ are the Cauchy stress components, v and $s_{\sigma }$ are the volume and the stress boundary of the solid in the current configuration, respectively, $m_j$ are the outward normal unit vector components of the structure boundary, and $f_{ij}m_j$ are the components of the force vector acting on the elastic tube,

$$\begin{aligned} f_{ij} m_j= {\left\{ \begin{array}{ll} \left\{ -p\delta _{ij}+ \frac{1}{{{{Re}} }}\left( \frac{{\partial v_i }}{{\partial x_j }} + \frac{{\partial v_j }}{{\partial x_i }}\right) \right\} m_j, &{} \text{ on } \text{ the } \text{ inner } \text{ wall } \text{ of } \text{ the } \text{ tube, } \\ -P_{ext}\delta _{ij}m_j, \,\ &{} \text{ on } \text{ the } \text{ outer } \text{ wall } \text{ of } \text{ the } \text{ tube. } \end{array}\right. } \end{aligned}$$

(3.13)

We may also push back the solid governing equations to the reference configuration,

$$\begin{aligned}&\!-\!\int _V( \mathbf{S}_{Ai} \frac{{\partial \psi ^e }}{{\partial X_A }} \!+\!\rho _e u_{i,tt}\psi ^e )\mathrm{d}V \!+\! \int _{S_\sigma }f_{ik}F_{Pk}^{-1} N_P\psi ^e \mathrm{d}S \!=\! 0,\nonumber \\ \end{aligned}$$

(3.14)

$$\begin{aligned}&\int _V {\left( {\det ({\mathbb {F}}) - 1} \right) } \phi ^{e} \mathrm{d}V = 0, \end{aligned}$$

(3.15)

where use of

$$\begin{aligned} \sigma _{ij}=\frac{1}{{\det ({\mathbb {F}})}}F_{iA}{} \mathbf{S}_{Aj}, \quad m_j \mathrm{d}s = F_{Pj}^{-1} N_P \det ({\mathbb {F}})\mathrm{d}S, \end{aligned}$$

(3.16)

has been made in deriving (3.14) and (3.15), V and $S_{\sigma }$ are the volume of the solid and the stress boundary of the solid in the reference configuration, respectively, and $N_P$ are the unit outward normal vector components of $S_\sigma$.

3.4 Numerical implementation

We now limit ourselves to consider quasi-static wall and steady flows only, hence, the coupled system equations (3.9), (3.10), (3.14) and (3.15), when discretised and assembled, can be written in a matrix form

$$\begin{aligned} {\mathbf{K(U)U}} - \mathbf{F} = \mathbf{R} = \mathbf{0}. \end{aligned}$$

(3.17)

where ${\mathbf{U}}$ is the global vector of unknowns $(u,v,w,p,u_e,v_e,w_e,p_e)$, ${\mathbf{M}}$ is the mass matrix, ${\mathbf{K}(\mathbf{U})}$ represents the nonlinear stiffness matrix, ${\mathbf{F}}$ is a force vector, and ${\mathbf{R}}$ is the overall residual vector. (3.17) is solved using a second order Newton–Raphson method.

3.4.1 Numerical solvers and the frontal approach

We use the frontal scheme to solve the algebraic matrix equation during each iteration to avoid forming the large sparse global matrices, $\mathbf{K}$ and $\mathbf{M}$. The frontal method was initially developed by (Irons 1970) and has been successful used in numerical simulations of two dimensional collapsible channel flows (Rast 1994; Cai and Luo 2003; Luo et al. 2008; Liu et al. 2012; Hao et al. 2016). Building on a LU or Cholesky decomposition, the frontal solver assembles and eliminates the equations only on a subset of elements at a time. This subset is the so-called front, and it is essentially the transitional region between the part of the system already solved and the part unsolved. In essence, we make use of the frontal solver by storing the element matrices together with a steering matrix which points to the location of the element entries in the global matrices. The full sparse global matrices are never assembled. Processing the front involves operations on dense but much smaller matrices, which uses the CPU efficiently (Hao et al. 2016).

3.4.2 Continuation techniques and initial perturbations

The strong nonlinearity of the system often presents multiple solutions of different post-buckling modes (Zhu et al. 2008). To ensure that simulations converge to the required solutions, one must use an efficient continuation technique. Inspired by the arc-length continuation proposed by (Keller 1977), here we follow a simplified version of the idea by either controlling the external pressure, or the displacement (Heil 2004), with a simple switch between the pressure and displacement-control as appropriate. The pressure-control solves a fully displacement-based problem, while the displacement-control method specifies a displacement of the tube at one specific point and regards the external pressure $P_\mathrm{ext}$ as an unknown. We choose the control point on a solid element (say, at $x=R+h, y=0, z = L_u+0.75L_m$) and prescribe the displacement in the x direction which is typically varied between 0 and $0.5-br$.

All variables are set to zero in the initial guess for the Newton iterations. In order to ensure convergence, the displacement-control starts with a small value at the first iteration. Since the axisymmetric solution is remarkably robust, it is necessary to add an asymmetric perturbation to the pressure to follow the non-axisymmetric solution branch. This is done using the perturbation $P_c \cos (N\theta )$, where N indicates the buckling mode or lobe number of the tube in the azimuthal direction, and $P_c$ regulates the magnitude of the perturbation. The numerical perturbation is removed once the tube is buckled.

3.4.3 Parallel computations

We adopt parallel computations based on the substructure method and implement this using the Open Multi-Processing (https://en.wikipedia.org/wiki/OpenMP). The computational domain is divided into several sections along the tube, as shown in Fig. 7. Every segment is a substructure which can be regarded as a “big element”, with the links to other substructures through the nodes of the cross sections (interfaces). The variables of the internal nodes of each substructure are eliminated using the frontal method to obtain a large element stiffness matrix which is only related to the nodal variables of the interfaces. The elimination of each substructure is performed by one core. Once the variables of the interfacial nodes are obtained, all the internal nodal variables can then be recovered from the frontal method.

Fig. 7

The whole model is divided into several substructures for parallel computations

To test the parallel efficiency of the program, we compare the computations using two different grids. Both have the same discretizing parameters along the tube, but the discretization of the cross sections differ. The two grids have the interfacial nodes of 289 and 385, and the total nodal number of 40,469 and 53,885, respectively. Figure 8 shows the speedup (the ratio of the running time between a single processor and parallel processors for the same task) in latency of the execution of a task at a fixed workload. We can see that the parallel efficiency is good in both cases, though it is better for the grid with less number of nodes on the collapsible cross section. This is because added nodes on the collapsible cross sections increase the maximum matrix width of the frontal solver. Obviously, computational efficiency needs to be balanced with the numerical accuracy. All simulations are performed on a 3.2 GHz Linux computer. Extensive model validation and grid independence tests are provided in the Appendix.

Fig. 8

The speedup ratio (Sp) versus number of cores, n, for two different meshes

4 Results

4.1 Different material models

To study the impact of three different hyperelastic tube materials, we choose the same value of $\mu _e$ in all three models, and the additional parameters are $J_m = 3.5$ for the Gent material model and $c_0=0.7\mu _e, c_1= 0.3\mu _e$ for the Mooney–Rivlin material model. These parameters are chosen so that all three models have the same linear elastic response when strain is small. In the first case, case A, we compare the results with that of (Marzo et al. 2005), who verified their results against a case by (Hazel and Heil 2003). We set all the parameters to be the same as in (Marzo et al. 2005) ($Re=128$, $P^*_\mathrm{ext}=1.4\,\hbox {Pa}$, $D=4\,\hbox {mm}$, $L_u=0.5$, $L_m=L_d=5$, and $d=1/40$), except we use nonlinear models with $\mu _e^*=1530$ Pa and they used a linear material model with the Poisson ratio of $\mu =0.49$, and Young’s modulus of 4559.4 Pa. The result, in terms of pressure drop along the tube axis, is shown in Fig. 9a. Notice that all the three material models yield the similar results. This is because the maximum strain in the deformed tube is small (about 0.066 in this case), and the different nonlinear material models have the same response in this case.

In the second case, case B, we change the parameters to be $\mu _e^*=23.75\,\hbox {Pa}$, $Re=64$, and $P^*_\mathrm{ext}= - 0.7488\,\hbox {Pa}$ and the others are kept to be the same as in the previous case. The pressure drops are plotted in Fig. 9b. In this case, a greater difference in the results of different models exists. The maximum xy shear strains from the three material models are 1.21 (Neo–Hookean), 0.95 (Mooney–Rivlin) and 0.69 (Gent) models, respectively. For a finite strain problems as in this case, the nonlinear characteristic, represented differently in each model, becomes prominent. These simulations show that it is important to choose a suitable constitutive law that can describe the tissue material in a nonlinear range. For example, flows in arteries with an aneurysm could operate in such a parameter range.

Fig. 9

The axial pressure drop along the elastic section of three different material models in the situation of a small strain, case A, and b finite strain, case B

Fig. 10

a The collapsed tube, showing a circumferential waves (buckling mode of three) towards downstream. As the tube is very long, only the segment between $z=0$ and $z=13$ is shown, where the elastic section lies between $z=3$ and $z=8$. The flow is from left to right. The contours show the pressure dropping along the tube, the downstream end is subject to the strongest compressive load. The corresponding flow field is shown in Fig. 11. b the grey lines are the stream lines of the fluid field, showing three flow separation zones downstream the collapsed section. The coloured contours show the distribution of energy dissipation

Fig. 11

Flow patterns at twelve different cross sections along the tube from z equals 3–14, where the elastic section lies between $z=3$ and $z=8$. The contours indicate the magnitude of the axial velocity, the black curves are the transverse streamlines of the cross sections. a $z=3.1$, b $z=4.0$, c $z=5.5$ (A), d $z=6.0$ (B), e $z=6.6$ (C), f $z=6.8$ g $z=7.04$ (D), h $z=7.46$ (E), i $z=7.98$ (F), j $z=8.3$ (G), k $z=11.0$, k $z=14.0$

4.2 Flows and energy dissipation in a mode-3 buckling tube

Under external pressure, the cross section of the tube may buckle into multiple lobes. Since mode-2 post-buckling flow patterns have been extensively studied (Hazel and Heil 2003; Marzo et al. 2005), here we concentrate on the buckling mode-3, which becomes dominant when either when for thinner or shorter vessels, as shown in Fig. 1. Consider a small strain bucking case, we use the Neo–Hookean material model with the dimensionless parameters:

$$\begin{aligned} L_u= & {} 3.0, \quad L_m = 5.0, \quad L_d = 30.0, \quad d = 0.0102,\nonumber \\ \mu _e= & {} 15370.62, \quad P_\mathrm{ext}= 3.0789, \quad Re= 450, \quad P_d=0.\nonumber \\ \end{aligned}$$

(4.1)

The corresponding dimensional values are in the range for human arteries (Horgan and Saccomandi 2003; Prendergast et al. 2003).

Fig. 12

The contours of the energy dissipation at different cross sections along the collapsed tube where the flow separation zones are shown. The contours are plotted between 0.5 and 7.5 with a equal space of 0.5. The cross sections A–G are located at ${A}=5.5$, ${B}=6.0$, ${C}=6.6$, ${D}=7.04$, ${E}=7.46$, ${F}=7.98$ and ${G}=8.3$, respectively

Fig. 13

Flow patterns at nine different cross sections along the tube from z equals 3.5 to 10, where the elastic section lies between $z=3$ and $z=8$. The contours indicate the magnitude of the axial velocity, the black curves are the transverse streamlines of the cross sections. a $z = 3.5$, b $z = 4.7$, c $z = 4.85$, d $z = 5.5$, e $z = 6.5$, f $z = 7.0$, g $z = 7.25$, h $z = 8.0$, i $z = 10.0$

The pressure distribution and flow streamlines overlapped with viscous energy dissipation along the bucked mode-3 tube are shown in Fig. 10a, b. We can see that immediately after the tube collapses, there are three strong flow separation zone associated with the three concave sides, and a higher viscous dissipation appears at the most inward wall—we will come back to this later. The flow features are better viewed from the cross-sectional views shown in Fig. 11. At locations upstream of the elastic tube, the flow is more or less Poiseuille flow with only negligible transverse flow. Then just before the collapsed section at $z=4.0$ the transverse flow moves away from the centre, forming a six regional patterns. As we move into the collapsed section at location A ($z=5.5$), some fluid from the side walls moves towards the centre some moves while towards the lobes. The central flow is intensified as the collapse becomes more severe at location B ($z=6.0$). Further downstream at location C ($z=6.6$), the narrowest cross section, there is clearly defined tri-diagonal lines join at the centre, fluid moving towards the centre to form a 2D sink, which feeds into the axial jet. The sink becomes slightly weaker at $z=6.8$ as indicated by the transverse velocity values and the tri-diagonal lines started to disappear. At location D ($z=7.04$), flow continues to be drawn from the lobes but in the centre it starts to move towards the sides. The tube starts to recover at $\hbox {E}\,({z}=7.46)$ and F ($z=7.98$), the jet weakens, and the secondary flow pattern becomes complex, with all six streams of flows moving away from the walls but moving towards what were the concave sides to form three forks, totally avoiding the centre. Indeed, these fork-like streamlines are associated with the three flow separations in the axial direction, as indicated by the negative value (in blue). This pattern persists until location G ($z=8.3$) when the flow starts to reattach. Further downstream at $z=11.0$ the transverse flow forms six beautiful vortices, which slowly merge into three pairs at $z=14.0$. The vortices gradually disappear as z increases, and the flow eventually recovers to its Poiseuille profile (not shown).

We remark that the mode-3 flow patterns are very different to those of mode-2 buckling reported previously, where often there are two central axial jets and the transverse flow is typically signatured by four regional patterns (Marzo et al. 2005; Hazel and Heil 2003).

The viscous energy dissipation in the flow domain, computed from ${\mathbf{D}}=\frac{1}{Re}(u_{i,j}+u_{j,i})u_{i,j}$, is deemed important in the onset of instability in collapsible tubes. It is shown in Fig. 10b on the tube outer surface. More details can be seen in Fig. 12. We note that most of the energy dissipation sites are in the boundary layers of the domain where the tube is most collapsed, similar to what was found in a two-dimensional model (Luo and Pedley 1996; Liu et al. 2012; Luo et al. 2008). There are also some small dissipations distributed in the domain where the flow separations exist. Interestingly, the energy dissipation does not appear directly at the sites of the flow separations but occurs at the transverse streamlines that separate the flow separation zones, as shown in cross sections E–G in Fig. 12. Interestingly, the maximum dissipations occur at the concave sides, but the there appear to be two maximum points within each side, as is shown in Fig. 10b. We also note that the energy dissipation associated with the transverse vortices downstream is almost negligible.

4.3 The mixed-mode bifurcation

When the tube is softer and thinner, e.g. $d = 0.0102$, $\mu _e =2161.49$, then mixed buckling modes can also occur. One such an example is shown in Fig. 13 for $P_\mathrm{ext}=3.408$, $Re=300$. Despite a mode-2 or mode-3 perturbation, the solution converges to a buckling state that is a mixed-mode. In this case, the flow patterns are qualitatively different to the mode-3 case shown in Fig. 11. There is a shift of the symmetry in the transverse flows, and no sink is formed at the centre. At the beginning of the elastic section, although the cross section is still circular, we can see the changes in the transverse flow, reflecting the tube deformation downstream. However, these appear to be either four (e.g. $z=4.7$) or six regional flows (e.g. $z=4.85$ and 5.5), which are usually associated with of mode-2 or mode-3 buckling. As the tube starts to deform, these patterns disappear at $z=6.5$. At the most collapsed section ($z=7$), the flow is pushed to left by the wall deformation and then scatters in all directions ($z=7.25$), before moving back to right as the tube is reopened ($z=8$). As the total collapse is small, no flow separations are observed, although there are complex transverse flow patterns with two large vortices forming downstream of the elastic section $(z=10)$.

Fig. 14

Mode-3 buckling solutions at different values of $P^*_\mathrm{ext}$: a two cuts that cross the most bludged and collapsed wall sides, b The pressure drop $dp^*$ against Reynolds number, c shapes of the cross sections at $z-L_u=4$, for $P^*_{ext}=21.141\,\hbox {Pa}$ and $Re = 500$ (one solution), 400 (two solutions), and 437 (three solutions), and d the bifurcation diagrams of the radial displacement at fixed axial position $z-L_u=4$ plotted against Re

4.4 The bifurcation diagrams

We now study the changes of the system buckling behaviour due changes in flow rate or the Reynolds number. We use the same model as in the previous section, except that we will present results in terms of the dimensional shear modulus and pressure, i.e. $\mu _e^*\,(= 124502.016\,\hbox {Pa})$, $P^*_\mathrm{ext}$, and the pressure drop, $dp^*$, across the tube between $z=0$ and 15. This is to enable us to interpret the results more easily, since the corresponding non-dimensional quantities are scaled with $Re^2$.

Fig. 15

Same as in Fig. 14, but for buckling mode-2 and cuts 3 and 4, and shapes of cross sections are for $P^*_\mathrm{ext}= 159.744\,\hbox {Pa}$ and $Re=405$ (one solution), 25 (two solutions), and 275 (three solutions)

We vary the Reynolds numbers from 25 to 600 and study the results at three different values of external pressure: $P_\mathrm{ext}^*=15.911$, 21.141, and $24.939\,\hbox {Pa}$, respectively as shown in Fig. 14. The relationship between the Reynolds number and the pressure drop $dp^*$ is shown in Fig. 14b for different values of the external pressure. The straight lines are obtained for axisymmetric deformation, and these remain almost the same under the different external pressures. At $P^*_\mathrm{ext}=15.911\,\hbox {Pa}$, two solutions exit, one axisymmetric and one buckling. As Re increases, to $302< Re < 315$, there are three solutions, one symmetric and two different buckled configurations, and the tube recovers to its axisymmetric solution for Re $>315$ This trend is more obvious when external pressure is increased. For $P^*_\mathrm{ext}=21.141\,\hbox {Pa}$, there are two solutions exist for Re $<430$, and three solutions at $\hbox {Re}=430{-}450$, as shown in Fig. 14b. Again, the tube recovers to its axisymmetric solution for $\hbox {Re} >450$. Similar behaviour is seen for $P^*_\mathrm{ext}=24.939\,\hbox {Pa}$, except that the deformation is greater, and the critical values of Re are shifted higher, to 522 for two solutions to occur, and 522–548 for three solutions, before the buckling solutions disappear at $Re > 548$. Notice that the axisymmetric solutions (non-buckling) are independent of the external pressure.

The multiple solutions, in terms of shapes of the cross sections at $z-L_u=4$, for $P^*_\mathrm{ext}=21.141\,\hbox {Pa}$ and $Re=500, 400, 437$ are shown in Fig. 14c. Choosing the points with the same axial location ($z-L_u=4.0$), we can also plot a bifurcation diagram in terms of tube deformation and Re as shown in Fig. 14d. The positive values indicate the wall bulged out, and the negative ones showing the opposite wall collapse at the same axial location. The straight line at $r-r_0=0$ stands for the axisymmetric pre-bucking deformation, which is independent of the external pressure.

For comparison, we also obtain the corresponding results of mode-2 by setting $N=2$ in the pressure perturbation. All the parameters are the same as in the model-3 case except the tube wall is twice as thick: $d=0.05$. This is because a thicker tube loses stability to mode-2 first, as suggested by Fig. 1. A thicker tube will also buckle under a greater external pressure. The results are shown in Fig. 15 for three different external pressure. The bifurcation diagrams for mode-2 buckling in Fig. 1 are quite different to the mode-3 case. In particular, we found that the ranges of Re where three buckling solutions occur are much greater, namely, $\hbox {Re}=44-200$, $170-300$, and $267-402$, for $P^*_\mathrm{ext}=152.258$, 156.060, $159.744\,\hbox {Pa}$, respectively. The range of $\hbox {Re}$ with multiple solutions increases with the external pressure.

Finally, we confirm that the bifurcation diagrams from the Gent or Mooney–Rivlin material models are similar to that of the Neo–Hookean model, with critical points shifted slightly towards left ($\approx 3\%$ difference in $\hbox {Re}$). This is because the strains are small (around $5\%$) in these simulations.

4.5 Discussion and conclusion

We have carried out a extensive study on three-dimensional flows in a hyperelastic collapsible tube. Novel finite element approaches such as rotating spines, frontal solver and substructure-based parallel computing are adopted for the strongly coupled fluid-structure interaction problem. The incompressibility of the tube material is solved explicitly. To induce the asymmetrical deformation, both pressure- and displacement-control techniques are implemented to obtain various circumferential buckling modes of the tube. Our model is extensively verified against the previous publications for a simpler material model, and against two commercial software (ANSYS and FLUENT), for the solid and fluid solvers, separately.

New results in this study include detailed flow patterns of flows in a circumferential mode-3 buckling tube. Our results show a rich pattern of flow separations and transverse vortex formation. It is interesting to see that the transverse flow forms a virtual sink in the centre of the tube at the most collapsed section, which then feeds into a single axial jet. An energy analysis reveals that the maximum energy dissipation occurs at the narrowest section of the collapsible tube as shown in Fig. 11, which is consistent with the findings of previous 2D models (Luo and Pedley 1996). However, this 3D model reveals that the energy at the flow separation is dissipated via the streamlines that separate the three flow separations zones. This is because dissipation always occurs at higher shears. We also show that despite the complex transverse vortices downstream, these consume very little energy. When the tube is thinner and softer, mixed mode bifurcation also occurs. These mixed modes are qualitatively similar to some of the CT images reported for true lumen in aortic dissection (Sun et al. 2014; Wang et al. 2017, 2016). The flow patterns within these tubes are very different from mode-3 or mode-2 collapsed tube flows, and these can only be simulated using a whole tube model.

For the mode-3 buckling case, we found there exists a range of Reynolds numbers when two or three solutions exist at a same external pressure, with one non-buckling and one or two different buckling scenarios (Fig. 14 c). This type of bifurcation diagrams for the mode-3 buckling has not been reported before.

By way of comparison, bifurcation diagram of the mode-2 buckling is also shown. The bifurcation diagrams are very different to that of mode-3. In particular, the range of Re for which three solutions can occur is much greater than that of mode-3 case. These results are also different from those by (Heil and Pedley 1996), who studied the bifurcation diagram of the mode-2 buckling for a pressure-driven system, in which the upstream transmural pressure is kept as zero (Heil and Pedley 1996). This is different to our flux-driven case, where we impose stress-free condition at the flow outlet, so the tube is always compressed under a positive external pressure.

It is worth pointing out that not all the solutions identified here are physically stable. To study the stability of the solutions requires dynamic simulations or an eigenvalue study (Luo and Pedley 1996; Luo et al. 2008), which is beyond the scope of this paper.

The success of a mathematical modelling relies on rationally reduced mathematical models given the highly complex physiological systems. These models can provide insight on the most important factors or can be experimentally tested. Our model is based on the Starling resistor set-up, and hence, is a simplified geometric representation of arteries and veins. However, compared to many published papers on flows in collapsible vessels (Heil and Pedley 1996; Luo and Pedley 1996; Luo et al. 2008; Hazel and Heil 2003; Whittaker 2015), the new model is sophisticated (realistic) in terms of taking account of the fully coupled FSI, while representing the vessel wall using large deformation nonlinear strain energy functions (i.e. Neo–Hookean, Mooney–Rivlin, and Gent). Indeed, the development of the hyperelastic wall model enables us to study the impact of different nonlinear material models on the collapsible vessel flows, and the FSI allows us to assess the critical buckling load more accurately. Importantly, our results show that for small strain problems, all the nonlinear models yield very similar solutions as linear material models used in previous studies. However, in the finite strain case, the characteristics of individual nonlinearity of each model differ. Furthermore, when the tube is bulged out, the strain tends to be greater than when it is collapsed. As a result, the differences in both the mode-2 and mode-3 bifurcation diagrams are small ($<\,3\%$) between the different material models. However, when the arteries are diseased, and the material stiffness decreases, the strain will increase, and the system behaviour will be different. It is, therefore, important to choose a suitable model with parameters determined from experiments for a particular problem at hand. We are aware that biological vessels such as arteries and veins also consist of more than two families of collagen fibres and obey anisotropic hyperelastic constitutive laws (Holzapfel et al. 2000; Gasser et al. 2006). In addition, physiological vessels present residual stress even without loading. Both of these aspects were studied in our previous work on an arterial model (Wang et al. 2016, 2017), albeit without FSI. Results from those models (Wang et al. 2016, 2017) suggest that the wall anisotropy and residual stress will potentially increase the critical pressure of the buckling in our present model. Taking the fibre distribution into consideration, our Neo–Hookean model can be readily extended to the HGO model (Holzapfel et al. 2000), which is the state-of-the-art constitutive law for realistic arteries. Research is underway to quantify the effects of the material anisotropy and residual stress on biological flows in healthy and diseased collapsible vessels.

Appendix: Model validation

1.1 A1: Grid independence test

To ensure numerical convergence, grid independence tests are carried out, particularly under the condition of large deformation. We choose the test case to be the same as used by (Marzo et al. 2005), who reproduced the results by (Hazel and Heil 2003) for a three-dimensional steady collapsible tube flow with the maximum degree of collapse of 80%. We choose the Neo–Hookean material model and the same parameters as they used, i.e. $D^*=8\,\hbox {mm}$ , $L_u=0.5$ , $L_m=L_d=5$, $d=0.025$, $\rho ^*=1000\,\hbox {Kg}/\hbox {m}^3$, $\mu ^*=0.001\,\hbox {Pa}\,\hbox {s}$, $\mu _e^*=1530\,\hbox {Pa}$, $Re=128$, and $P^*_\mathrm{ext}=1.4\,\hbox {Pa}$. Two different meshes are used. The coarser model is discretized to 16,200 finite elements and 50,507 nodes, and the finer one is discretized to 33,888 finite elements and 105,313 nodes. The wall shapes along the tube in the symmetry planes $x =0$ and $y =0$, respectively, are compared in Fig. 16. It can be seen that the two different grids predict identical elastic wall shapes along the tube.

Fig. 16

Shapes of the tube projected to the two symmetry planes ($x=0$: above, and $y=0$: below) for the testing case using two different grids. The results from the two grids are identical

Fig. 17

a Pressure drop along the tube axis $(z-L_u)/R$, b the elastic wall shape in the symmetry plane $y=0$ as a function of the axial distance, compared with the results by (Marzo et al. 2005) for the same model problem. Note in order to compare the fluid pressure, we rescaled the pressure in the same way as by (Marzo et al. 2005) (i.e. our results are multiplied by $\rho U_0^2$ to get the dimensional values first, and then divide by the bending stiffness $K ={Ed^{*3} }/[3(1 - \upsilon ^2 )D^{*3}]$, to obtain the dimensionless values)

Fig. 18

Comparison of the flow fields computed using FLUENT and our code. a FLUENT—velocity. b Our fluid velocity. c FLUENT—pressure. d Our fluid pressure

Fig. 19

Comparison of the tube displacements between ANSYS and our code. a ANSYS—$u_e$, b Our $u_e$, c ANSYS—$v_e$, d Our $v_e$, e ANSYS—$w_e$, f Our $w_e$

1.2 A2: Comparison with published results by Marzo et al. (Marzo et al. 2005)

The fluid pressures along the tube axis are compared with the results by  (Marzo et al. 2005) in Fig. 17a. The agreement is generally very good, except for a small discrepancy at the upstream. We think this may be caused by the fact that the incompressibility was not strictly satisfied in their model; we use the Poisson’s ratio of 0.5, but 0.49 was used in (Marzo et al. 2005). We also compare the displacements of the internal wall of the tube at the intersection of the symmetry plane in Fig. 17b. Again, excellent agreement is obtained.

1.3 A3: Comparison with the results of ANSYS and FLUENT

There are very few commercial softwares that can simulate nonlinear large deformation FSI problems directly. Thus, to verify our coupled solver, we use the commercial solid software ANSYS and fluid software FlUENT, to verify our solid and fluid solvers separately. The parameters are chosen to be:

$$\begin{aligned} D^*= & {} 0.02\,\hbox {m}, \quad L_u =2.5, L_m = 2.5, \\ L_d= & {} 5, \quad d = 0.05,\quad \mu _e= 151.98, \\ \rho ^*= & {} 10^3\, \hbox {kg}/\hbox {m}^3, \quad \mu ^* = 4 \times 10^{-3} \hbox {Pa}\,\hbox {s}, \\ P^*_\mathrm{ext}= & {} 0.47968\,\hbox {Pa}, \quad Re = 50. \end{aligned}$$

The Neo–Hookean material model is used for the validation purpose. All the parameters are non-dimensionalized as in (2.1). For the flow simulations, we import the final configuration of the tube into FLUENT as the boundary of the flow field. Comparing the Navier–Stokes equations before and after nondimensionalization, we set $\rho ^* = 1\,\hbox {kg}/\hbox {m}^3, \mu ^* =\frac{1}{Re}= 0.02\,\hbox {Pa}\,\hbox {s}$ to make the parameters consistent for the fluid simulation. The results of the flow field are compared in Fig. 18. It can be seen that both the velocity and pressure fields calculated using our code agree well with those calculated using FLUENT. The maximum relative error in the maximum velocity and pressure between the two simulations is $<\,0.6\%$.

The solid modelling is verified using ANSYS. We first build a model of the deformation section of the tube for ANSYS and select the Neo–Hookean material with the shear modulus $\mu _e= 151.98$ and incompressibility parameter $d_e = 0$ (The incompressibility parameter in ANSYS is defined by $d_e=2/K=6\times (1-2\mu )/E$, where K is the bulk modulus. Here we use $\mu =0.5$, so $d_e=0.$). To ensure that we use the same boundary conditions, we impose the viscous fluid forces from our coupled model as the loading condition for the ANSYS model. The comparison is shown in Fig. 19. Again, almost identical results are obtained; the maximum relative error of the displacement between the two solvers is $<\,0.5\%$.