A validated patient-specific FSI model for vascular access in haemodialysis

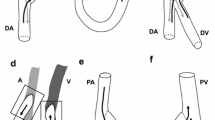
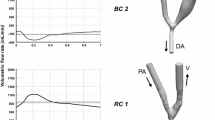
Abstract

The flow rate inside arteriovenous fistulas is many times higher than physiological flow and is accompanied by high wall shear stress resulting in low patency rates. A fluid–structure interaction finite element model is developed to analyse the blood flow and vessel mechanics to elucidate the mechanisms that can lead to failure. The simulations are validated against flow measurements obtained from magnetic resonance imaging data.

Appendices

Appendix 1

1.1 Linearized Navier–Stokes equations

Three-directional derivatives of the momentum balance equation of the fluid in the reference configuration are required. The directional derivative with respect to a incremental velocity field $\varDelta {\mathbf {v}}$ is given by

$$\begin{aligned} D_{\varDelta \varvec{v}}(R_{\mathrm{f}},\delta {{\mathbf {v}}}) =&\int _{\varOmega _{\mathrm{f}}} \delta {{\mathbf {v}}}\cdot J\rho _{\mathrm{f}}\frac{\partial \varDelta {\mathbf {v}}}{\partial t}d\mathrm{V} \nonumber \\&+\int _{\varOmega _{\mathrm{f}}}\delta {{\mathbf {v}}} \cdot J\rho _{\mathrm{f}}\,\mathrm{Grad}\,(\varDelta {\mathbf {v}}){\mathbf {F}}^{-1}{\mathbf {v}}\,d\mathrm{V} \nonumber \\&+ \int _{\varOmega _{\mathrm{f}}}\delta {{\mathbf {v}}}\cdot J\rho _{\mathrm{f}}\mathrm{Grad}\,{{\mathbf {v}}}{\mathbf {F}}^{-1}\varDelta {\mathbf {v}}\,d\mathrm{V} \nonumber \\&+\int _{\varOmega _{\mathrm{f}}} \nabla \delta {{\mathbf {v}}}:{J}\rho _{\mathrm{f}}\nu _{\mathrm{f}}\,(\mathrm{Grad}\,(\varDelta {\mathbf {v}})\mathbf {F}^{-1} \nonumber \\&+\mathbf {F}^{-T}\mathrm{Grad}(\varDelta {\mathbf {v}})^{\mathrm{T}})\mathbf {F}^{-T}\,d\mathrm{V}. \end{aligned}$$

(41)

Next the directional derivative resulting from a incremental displacement field in the mesh motion $\varDelta \mathbf {u}$ is

$$\begin{aligned} D_{\varDelta \varvec{u}}(R_{\mathrm{f}},\delta {{\mathbf {v}}}) =&\int _{\varOmega _{\mathrm{f}}} \delta {{\mathbf {v}}}\cdot D_{\varDelta \varvec{u}}(J)\rho _{\mathrm{f}}\Big (\varDelta {\mathbf {v}}-\mathrm{Grad}\,{\mathbf {v}} f\frac{\partial \mathbf {u}_{\mathrm{f}}}{\partial t}\Big )\,d\mathrm{V}\nonumber \\&-\int _{{\varOmega }_{\mathrm{f}}} \delta {{\mathbf {v}}} \cdot J\rho _{\mathrm{f}}\,\mathrm{Grad}\,{{\mathbf {v}}}{D_{\varDelta \varvec{u}}\mathbf {F}^{-1}}\frac{\partial \mathbf {u}_{\mathrm{f}}}{\partial t}\,d\mathrm{V} \nonumber \\&-\int _{{\varOmega }_{\mathrm{f}}} \delta {{\mathbf {v}}} \cdot J\rho _{\mathrm{f}}\,\mathrm{Grad}\,{{\mathbf {v}}}\mathbf {F}^{-1}\frac{\partial \varDelta \mathbf {u}_{\mathrm{f}}}{\partial t}\,d\mathrm{V} \nonumber \\&+ \int _{{\varOmega }_{\mathrm{f}}} \nabla \delta {{\mathbf {v}}}: D_{\varDelta \varvec{u}}(J)\varvec{\sigma }_{\mathrm{f}}\mathbf {F}^{-T}\,d\mathrm{V} \nonumber \\&+ \int _{{\varOmega }_{\mathrm{f}}} \nabla \delta {{\mathbf {v}}}: J\varvec{\sigma }_f D_{\varDelta \varvec{u}}\mathbf {F}^{-T}\,d\mathrm{V} \nonumber \\&+ \int _{{\varOmega }_{\mathrm{f}}}\nabla \delta {{\mathbf {v}}}: J\rho _{\mathrm{f}}\nu _{\mathrm{f}}\,(\mathrm{Grad}\,{\mathbf {v}}{D_{\varDelta \varvec{u}}\mathbf {F}^{-1}} \nonumber \\&+D_{\varDelta \varvec{u}}\mathbf {F}^{-T}\,\mathrm{Grad}\,{\mathbf {v}}^T)\mathbf {F}^{-T}\,d\mathrm{V} , \end{aligned}$$

(42)

with

$$\begin{aligned} D_{\varDelta \varvec{u}}(J)&=\frac{\partial J}{\partial \mathbf {F}}:\nabla (\varDelta \mathbf {u}) \nonumber \\&= J\mathbf {F}^{-1}:\nabla (\varDelta \mathbf {u}) \nonumber \\&= J\mathbf {I}:\mathbf {F}^{-1}\nabla (\varDelta \mathbf {u}), \end{aligned}$$

(43)

$$\begin{aligned} D_{\varDelta \varvec{u}}(\varvec{F}^{-1})&= \frac{\partial (\mathbf {F})}{\partial \mathbf {F}}:\nabla (\varDelta \mathbf {u}) \nonumber \\&= -\mathbf {F}^{-1}\nabla (\varDelta \mathbf {u})\mathbf {F}^{-1}, \end{aligned}$$

(44)

and

$$\begin{aligned} D_{\varDelta \varvec{u}}(\mathbf {F}^{-T})&= \frac{\partial (\mathbf {F}^{-T})}{\partial \mathbf {F}}:\nabla (\varDelta \mathbf {u}) \nonumber \\&= -\mathbf {F}^{-T}\nabla (\varDelta \mathbf {u})^T\mathbf {F}^{-T}. \end{aligned}$$

(45)

Lastly the directional derivative of the momentum equation with respect to an incremental change in the pressure field $\varDelta p$ is shown:

$$\begin{aligned} D_{\varDelta p}(R_{\mathrm{f}},\delta {{\mathbf {v}}}) = \int _{\varOmega _{\mathrm{f}}}\nabla ^{{\mathbf {v}}}: J\rho _{\mathrm{f}}\nu _{\mathrm{f}}\varDelta p\mathbf {F}^{-T}\,d\mathrm{V}. \end{aligned}$$

(46)

Directional derivatives for the incompressibility constraint are found with respect to the incremental changes in the velocity and displacement fields. Note that the directional derivative with respect to pressure is zero in the fluid domain. This results in zeroes on the diagonal of the Jacobian matrix on the fluid domain. The directional derivative for the incompressibility constraint with respect to $\varDelta v$ is given by

$$\begin{aligned} D_{\varDelta \varvec{v}}(R_{\mathrm{f}},\delta p)=\int _{\varOmega _{\mathrm{f}}}\delta p\big (\mathrm {Div}\,\big (J\mathbf {F}^{-1}\varDelta {\mathbf {v}}\big ),\delta p\big )\,d\mathrm{V}, \end{aligned}$$

(47)

and with respect to $\varDelta u$ by

$$\begin{aligned} D_{\varDelta \varvec{u}}(R_{\mathrm{f}},\delta p)=&\int _{\varOmega _{\mathrm{f}}}\delta p \Big ( \mathrm{Div}\, \big (D_{\varDelta \varvec{u}}(J)\varvec{F}^{-1}{\mathbf {v}}\big )\Big )\,d\mathrm{V} \nonumber \\&+\int _{\varOmega _{\mathrm{f}}}\delta p\Big (\mathrm{Div}\, \big ({J D_{\varDelta \varvec{u}}(\varvec{F}^{-1})}{\mathbf {v}}\big ) \Big )\,d\mathrm{V}. \end{aligned}$$

(48)

1.2 Linearized mesh motion equations

The mesh motion equation is only a function of $\mathbf {u}$ and there is only one nonzero directional derivative:

$$\begin{aligned} D_{\varDelta \varvec{u}}(R_{\mathrm{f}}, \delta {\mathbf {u}}) =\int _{\varOmega _{\mathrm{f}}}\nabla \delta {\mathbf {u}} :\alpha \nabla (\varDelta {\mathbf {u}})\,d\mathrm{V}. \end{aligned}$$

(49)

1.3 Linearized structure equations

The linearized equations associated with the structure are as follows. The directional derivatives for (25)$_1$ are

$$\begin{aligned} D_{\varDelta \varvec{v}}(R_{\mathrm{s}},\delta {{\mathbf {v}}})&= \int _{\varOmega _{\mathrm{s}}}\delta {{\mathbf {v}}}\cdot \rho _{\mathrm{s}}\frac{\partial \varDelta {\mathbf {v}}}{\partial t}\,d\mathrm{V}, \end{aligned}$$

(50)

$$\begin{aligned} D_{\varDelta \varvec{u}}(R_{\mathrm{s}},\delta {{\mathbf {v}}})&= \int _{\varOmega _{\mathrm{s}}}\nabla \delta {{\mathbf {v}}} \cdot \big (\frac{\partial \mathbf {P}}{\partial \mathbf {F}}:\nabla (\varDelta \mathbf {u})\big )\,d\mathrm{V} , \end{aligned}$$

(51)

$$\begin{aligned} D_{\varDelta p}(R_{\mathrm{s}},\delta {{\mathbf {v}}})&= \int _{\varOmega _{\mathrm{s}}}\nabla \delta {{\mathbf {v}}} \cdot \varDelta pJ\mathbf {F}^{-T} \,d\mathrm{V} . \end{aligned}$$

(52)

The directional derivatives for (25)$_2$ are

$$\begin{aligned} D_{\varDelta \varvec{v}}(R_{\mathrm{s}},\delta {\mathbf {u}})&=-\int _{\varOmega _{\mathrm{s}}}\delta {\mathbf {u}}\cdot \varDelta {{\mathbf {v}}}\,d\mathrm{V}, \end{aligned}$$

(53)

$$\begin{aligned} D_{\varDelta \varvec{u}}(R_{\mathrm{s}},\delta {\mathbf {u}})&= \int _{{\varOmega }_s}\delta {\mathbf {u}} \cdot \rho _{\mathrm{s}}\varDelta {\mathbf {u}}\,d\mathrm{V}. \end{aligned}$$

(54)

The directional derivatives for (25)$_3$ are

$$\begin{aligned} D_{\varDelta \varvec{u}}(R_{\mathrm{s}},\delta p) =\int _{{\varOmega }_s} \delta p \big (D_{\varDelta \varvec{u}}(J)\big )\,d\mathrm{V}. \end{aligned}$$

(55)

The tangent $\mathscr {A}={\partial \mathbf {P}}/{\partial \mathbf {F}}$ can be split additively into an isotropic part and a part associated with anisotropic deformations,

$$\begin{aligned} \mathscr {A}=\mathscr {A}_{\mathrm{g}}+\mathscr {A}_{\mathrm{fib}}. \end{aligned}$$

(56)

The calculations for the tangent make use of the chain rule. Before the tangent is computed, partial derivatives of (21) and the Cauchy–Green tensor are shown:

$$\begin{aligned} \Big [\frac{\partial {S}_{\mathrm{g}}}{\partial {C}}\Big ]_{mjop} =\,&\mu \frac{\partial J^{-\frac{2}{3}}}{\partial C_{op}}I_{mj} -\left( \frac{\mu I_{1}}{3}\frac{\partial J^{-\frac{2}{3}}}{\partial C_{op}}\right) C^{-1}_{mj}\nonumber \\&- \left( \frac{\mu J^{-\frac{2}{3}}}{3}\frac{\partial I_{1}}{\partial C_{op}}\right) C^{-1}_{mj} -\left( \frac{\mu J^{-\frac{2}{3}}I_{1}}{3}\right) \frac{\partial C^{-1}_{mj}}{\partial C_{op}}\nonumber \\&+ p\left( \frac{\partial J}{\partial C_{op}}C^{-1}_{mj} + J \frac{\partial C^{-1}_{mj}}{\partial C_{op}} \right) \nonumber \\ =&-\frac{1}{3}\mu J^{-\frac{2}{3}}{I}_{mj}{C}_{op}^{-1}+ \nonumber \\&\left( pJ{C}_{op}^{-1}-\frac{\mu }{3}\left( J^{-\frac{2}{3}}{I}_{op}-\frac{{I}_{1}}{3}J^{-\frac{2}{3}}{C}_{op}^{-1}\right) \right) {C}_{mj}^{-1}\nonumber \\&+\frac{1}{2}\left( -pJ+\frac{\mu J^{-\frac{2}{3}}{I}_{1}}{3}\right) \left( {C}_{mo}^{-1}{C}_{jp}^{-1}+{C}_{mp}^{-1}{C}_{jo}^{-1}\right) , \end{aligned}$$

(57)

and

$$\begin{aligned} \Big [\frac{\partial {C}}{\partial {F}}\Big ]_{ijkl}&= \frac{[\partial {F^{T}F}]_{ij}}{\partial {F_{kl}}}=\frac{\partial (F_{im}^{T}F_{mj})}{\partial F_{kl}} \nonumber \\&= \frac{\partial F_{mi}}{\partial F_{kl}}F_{mj}+F_{mi}\frac{\partial F_{mj}}{\partial F_{kl}}\nonumber \\&= \delta _{mk}\delta _{il}F_{mj}+F_{mi}\delta _{mk}\delta _{jl} \nonumber \\&= \delta _{il}F_{kj}+F_{ki}\delta _{jl}. \end{aligned}$$

(58)

Using (57–58), the tangent associated with the ground matrix is calculated as

$$\begin{aligned} \mathscr {A}_{{\mathrm{g}}, ijkl} =&\left[ {\frac{\partial \mathbf {P}}{\partial \mathbf {F}}}\right] _{ijkl}\\ = \,&\frac{\partial (F_{im}S_{mj})}{\partial F_{kl}}\\ = \,&\frac{\partial F_{im}}{\partial F_{kl}}S_{mj}+F_{im}\frac{\partial S_{mj}}{\partial C_{op}}\frac{\partial C_{op}}{\partial F_{kl}}\\ = \,&\delta _{ik}\delta _{ml}\bigg (\mu J^{-\frac{2}{3}}I+\left( pJ-\frac{\mu J^{-\frac{2}{3}}I_{1}}{3}\right) C^{-1}\bigg )_{mj}\\&+ F_{im}\bigg [\left( pJC_{op}^{-1} -\frac{\mu }{3}\left( J^{-\frac{2}{3}}I_{op}-\frac{I_{1}}{3}J^{-\frac{2}{3}}C_{op}^{-1}\right) \right) C_{mj}^{-1}\\&-\frac{1}{2} \left( pJ-\frac{\mu J^{-\frac{2}{3}}I_{1}}{3}\right) \left( C_{mo}^{-1}C_{jp}^{-1}+C_{mp}^{-1}C_{jo}^{-1}\right) \bigg ]\\&\left( \delta _{ol}F_{kp}+F_{ko}\delta _{pl}\right) \\&+F_{im}\big [-\frac{1}{3}\mu J^{-\frac{2}{3}}C_{op}^{-1}I_{mj}\big ]\left( \delta _{ol}F_{kp}+F_{ko}\delta _{pl}\right) \\ =&\ \delta _{ik}(\mu J^{-\frac{2}{3}}I_{lj}+\bigg (pJ-\frac{\mu J^{-\frac{2}{3}}I_{1}}{3}\bigg )C_{lj}^{-1})\\&+F_{im}\bigg [\left( pJC_{lp}^{-1}-\frac{\mu }{3}\left( J^{-\frac{2}{3}}I_{lp}-\frac{I_{1}}{3}J^{-\frac{2}{3}}C_{lp}^{-1}\right) \right) C_{mj}^{-1} \\&+ \frac{1}{2} \left( -pJ+\frac{\mu J^{-\frac{2}{3}}I_{1}}{3}\right) \left( C_{ml}^{-1}C_{jp}^{-1}+C_{mp}^{-1}C_{jl}^{-1}\right) \bigg ]F_{kp}\\&+ F_{im}\bigg [\bigg (pJC_{ol}^{-1}-\frac{\mu }{3}\left( J^{-\frac{2}{3}}I_{ol}-\frac{I_{1}}{3}J^{-\frac{2}{3}}C_{ol}^{-1}\right) \bigg )C_{mj}^{-1} \\&+\frac{1}{2} \left( -pJ+\frac{\mu J^{-\frac{2}{3}}I_{1}}{3}\right) \left( C_{mo}^{-1}C_{jl}^{-1}+C_{ml}^{-1}C_{jo}^{-1}\right) \bigg ]F_{ko}\\&+ F_{im}\bigg [\!\!-\frac{1}{3}\mu J^{-\frac{2}{3}}C_{lp}^{-1}I_{mj}\bigg ]F_{kp}+F_{im}\bigg [\!\!-\frac{1}{3}\mu J^{-\frac{2}{3}}C_{ol}^{-1}I_{mj}\bigg ]F_{ko} . \end{aligned}$$

The tangent associated with the fibres can be calculated using (23), (24) and (58) as:

$$\begin{aligned} \mathscr {A}_{{\mathrm{fib}},ijkl} =\,&\left[ {\frac{\partial \mathbf {P}}{\partial \mathbf {F}}}\right] _{ijkl}\nonumber \\ =&\ \frac{\partial (F_{im}S_{mj})}{\partial F_{kl}}\nonumber \\ =&\ \frac{\partial F_{im}}{\partial F_{kl}}S_{{\mathrm{fib}},mj}+F_{im}\frac{\partial S_{{\mathrm{fib}},mj}}{\partial C_{op}}\frac{\partial C_{op}}{\partial F_{kl}}\nonumber \\ =&\ \Big [\delta _{ik}S_{\mathrm{fib}, lj} \nonumber \\&+F_{im}\Big [\frac{\partial S_{\mathrm{fib}}}{\partial C}\Big ]_{mjop}\left( \delta _{ol}F_{kp}+F_{ko}\delta _{pl}\right) \Big ]\nonumber \\ =&\ \Big [\delta _{ik}\big [(2k_{1} G_i)\mathrm {exp}\left( k_{2}G_i^{2}\right) \frac{\partial G_i}{\partial C}\big ]_{lj}\nonumber \\&+F_{im}\left( 2\frac{\partial S_{f,mj}}{\partial I_{1}}F_{ko}I_{ol}+\frac{\partial S_{f,mj}}{\partial I_{4}}F_{kp}A_{pl}^{T} \nonumber \right. \\&\left. +\frac{\partial S_{f,mj}}{\partial I_{4}}F_{ko}A_{ol}\right) \Big ], \end{aligned}$$

(59)

with

$$\begin{aligned} \Big [\frac{\partial S_{\mathrm{fib}}}{\partial C}\Big ]_{mjop} =\,&\frac{\partial S_{{\mathrm{fib}},mj}}{\partial I_{1}}\frac{\partial I_{1}}{\partial C_{op}}+\frac{\partial S_{{\mathrm{fib}},mj}}{\partial I_{i}}\frac{\partial I_{i}}{\partial C_{op}} \end{aligned}$$

(60)

$$\begin{aligned} \frac{\partial S_{{\mathrm{fib}},mj}}{\partial I_{1}}\frac{\partial I_{1}}{\partial C_{op}} =&\,2k_1\bigg [\frac{\partial G}{\partial I_1}\mathrm {exp}\left( k_{2}G_i^{2}\right) \frac{\partial G_i}{\partial C} \nonumber \\&+ G\frac{\partial \left( \mathrm {exp}\left( k_{2}G_i^{2}\right) \right) }{\partial I_1}\frac{\partial G_i}{\partial C} \nonumber \\&+ G\mathrm {exp}\left( k_{2}G_i^{2}\right) \frac{\partial }{\partial I_1}\left( \frac{\partial G_i}{\partial C}\right) \bigg ]_{mj} I_{op}\nonumber \\ =&\ 2k_1\bigg [\kappa J^{-\frac{2}{3}} \mathrm {exp}\left( k_{2}G_i^{2}\right) \frac{\partial G_i}{\partial C} \nonumber \\&+2k_2\kappa G^2J^{-\frac{2}{3}}\mathrm {exp}\left( k_{2}G_i^{2}\right) \frac{\partial G_i}{\partial C} \nonumber \\&+ \frac{1}{3}\kappa J^{-\frac{2}{3}}G\mathrm {exp}\left( k_{2}G_i^{2}\right) C^{-1}\bigg ]_{mj} I_{op} \end{aligned}$$

(61)

$$\begin{aligned} \frac{\partial S_{{\mathrm{fib}},mj}}{\partial I_{i}}\frac{\partial I_{i}}{\partial C_{op}} =&\,2k_1\bigg [\frac{\partial G}{\partial I_i}\mathrm {exp}\left( k_{2}G_i^{2}\right) \frac{\partial G_i}{\partial C} \nonumber \\& +G\frac{\partial (\mathrm {exp}\left( k_{2}G_i^{2}\right) )}{\partial I_i}\frac{\partial G_i}{\partial C} \nonumber \\& + G\mathrm {exp}\left( k_{2}G_i^{2}\right) \frac{\partial }{\partial I_i}\left( \frac{\partial G_i}{\partial C}\right) \bigg ]_{mj}A_{op} \nonumber \\ =&\ 2k_1\bigg [(1-3\kappa )J^{-\frac{2}{3}}\mathrm {exp}\left( k_{2}G_i^{2}\right) \frac{\partial G_i}{\partial C} \nonumber \\&+2k_2G^2(1-3\kappa )J^{-\frac{2}{3}}\mathrm {exp}\left( k_{2}G_i^{2}\right) \frac{\partial G_i}{\partial C} \nonumber \\&+ \frac{1}{3}(1-3\kappa )J^{-\frac{2}{3}}G\mathrm {exp}\left( k_{2}G_i^{2}\right) C^{-1}\bigg ]_{mj} A_{op}. \end{aligned}$$

(62)

Appendix 2

1.1 Linearization of backflow stabilization

The linearization of the boundary condition requires a precomputed global vector which contains the linearization of the flow terms

$$\begin{aligned} D_{\varDelta {\mathbf {v}}} Q_{\mathrm{out}} = \int _{\varGamma _{\mathrm{out}}} \varDelta {\mathbf {v}} \cdot J\mathbf {F}^{-T}\mathbf {N} \, d\mathrm{S}. \end{aligned}$$

(63)

$D_{\varDelta {\mathbf {v}}} Q_{\mathrm{out}}$ is the directional derivative of $Q_{\mathrm{out}}$ at a given velocity ${\mathbf {v}}$ in the direction of the incremental velocity field $\varDelta {\mathbf {v}}$. The linearization of the second term in (30) using the generalized resistive boundary condition is given by

$$\begin{aligned} D_{\varDelta \varvec{v}} f(Q_{\mathrm{out}}) {=}&\left( \int _{\varGamma _{\mathrm{out}}} \delta {\mathbf {v}} \cdot J\mathbf {F}^{-T}\mathbf {N} \, {d\mathrm{S}} \right) \left( { f }'(Q_{\mathrm{out}}\right) )D_{\varDelta \varvec{v}} Q_{\mathrm{out}}. \end{aligned}$$

(64)

For the particular case of a purely resistive boundary, such as present in (30), $f(Q_{\mathrm{out}})=R_RQ_{\mathrm{out}}$ and the derivative to be used in (64) is $f'(Q_{\mathrm{out}}))=R_R$.

Appendix 3

1.1 Weak form of Windkessel model

To prescribe the relationship between the flow and pressure, $f(Q_{\mathrm{out}})$ is given by

$$\begin{aligned} f(Q_{\mathrm{out}}) {=} R_R\int _{\varGamma _{\mathrm{out}}} {\mathbf {v}} \cdot J\mathbf {F}^{-T}\mathbf {N} \, d\mathrm{S} +\int _0^{t_{n+1-\alpha _{\mathrm{f}}}} \frac{e^{-\frac{t-s}{\tau }}}{C} Q_{\mathrm{out}} \, \mathrm{ds} \end{aligned}$$

(65)

where C is the capacitance, $R_R$ the resistance at the outlet, $\tau =R_{\mathrm{d}}C$ the relaxation parameter, and $R_d$ the resistance downstream. The velocity evaluated at some time s during the timestep $t^l$ to $t^{l+1}$ is given by

$$\begin{aligned} {\mathbf {v}}(s)&={\mathbf {v}}^l+({\mathbf {v}}^{l+1}-{\mathbf {v}}^l)\left( \frac{s-t_l}{t_{l+1}-t_l}\right) \nonumber \\&={\mathbf {v}}^l\left( \frac{t_{l+1}-s}{\triangle t}\right) +{\mathbf {v}}^{l+1}\left( \frac{s-t_{l}}{\triangle t}\right) . \end{aligned}$$

(66)

Here $\triangle t$ is the size of the timestep. After time discretization $f(Q_{\mathrm{out}}^{n+1-\alpha _{\mathrm{f}}})$ can be evaluated by

$$\begin{aligned} f(Q_{\mathrm{out}}^{n+1-\alpha _f})= R_R\left( (1-\alpha _{\mathrm{f}})Q^{n+1}+\alpha _{\mathrm{f}}Q^{n}\right) +h^{n+1}, \end{aligned}$$

(67)

where $h^{n+1}$ is given by

$$\begin{aligned} h^{n+1}=&\left( e^{-\frac{\bigtriangleup t}{\tau }}\right) h^{n}+ \int _{t_n}^{t_{n+1-\alpha _{\mathrm{f}}}} \frac{e^{-\frac{t-s}{\tau }}}{C}\left( Q_{\mathrm{out}}^n\left( \frac{t_{n+1}-s}{\triangle t}\right) \right. \nonumber \\&\left. + \,Q_{\mathrm{out}}^{n+1}\left( \frac{s-t_{n}}{\triangle t}\right) \right) \, \mathrm{ds}. \end{aligned}$$

(68)

Finally, after integrating over time,

$$\begin{aligned}&h^{n+1}= \left( e^{-\frac{\bigtriangleup t}{\tau }}\right) h^{n}\nonumber \\&+ R_d\Big [ Q^n\left( \frac{t_{n+1}-t_{n+1-\alpha _{\mathrm{f}}}}{\triangle t}-e^{-\frac{t-s}{\tau }} +\frac{\tau }{\triangle t}\left( 1-e^{-\frac{t-s}{\tau }}\right) \right) \nonumber \\&+Q^{n+1}\left( \frac{t_{n+1-\alpha _{\mathrm{f}}}-t_n}{\triangle t}-\frac{\tau }{\triangle t}\left( 1-e^{-\frac{t-s}{\tau }}\right) \right) \Big ]. \end{aligned}$$

(69)