Cellular blebs: pressure-driven, axisymmetric, membrane protrusions

Abstract

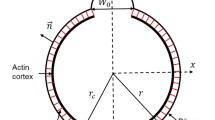
Blebs are cellular protrusions that are used by cells for multiple purposes including locomotion. A mechanical model for the problem of pressure-driven blebs based on force and moment balances of an axisymmetric shell model is proposed. The formation of a bleb is initiated by weakening the shell over a small region, and the deformation of the cellular membrane from the cortex is obtained during inflation. However, simply weakening the shell leads to an area increase of more than 4 %, which is physically unrealistic. Thus, the model is extended to include a reconfiguration process that allows large blebs to form with small increases in area. It is observed that both geometric and biomechanical constraints are important in this process. In particular, it is shown that although blebs are driven by a pressure difference across the cellular membrane, it is not the limiting factor in determining bleb size.

Appendix: Geometric model

In this appendix, we summarise the equations that relate the radius, R, of an initial sphere to the radii, $r_b$ and $r_c$, of an equivalent volume system of two spheres connected through a pinned neck region, see Fig. 17. We follow the geometric construction of a blebbing cell as derived by Hu (2009).

Fig. 17

Geometric model of blebbing

From Fig. 17, we see that the equality

$$\begin{aligned} R\sin (\varTheta )=r_c\sin (\theta _c)=r_b\sin (\theta _b), \end{aligned}$$

(39)

must always hold. Further, we demand that the cell volume be constant,

$$\begin{aligned} V&= \frac{4}{3}\pi R^3=v_c+v_b\nonumber \\&= \pi r_c^3\left( \frac{2}{3}+\cos (\theta _c)-\frac{1}{3}\cos ^3(\theta _c)\right) \nonumber \\&+\,\pi r_b^3\left( \frac{2}{3}-\cos (\theta _b)+\frac{1}{3}\cos ^3(\theta _b)\right) . \end{aligned}$$

(40)

Finally, we define the bleb volume fraction, x, as $v_b=xV$, and hence, the cell volume fraction is $v_c=(1-x)V$. This parameter $x$ is an input to the problem.

From Eqs. (39) and (40), we can derive equations satisfied by the radii and connection angles:

$$\begin{aligned}&16(1-x)\left( \frac{r_c}{R}\right) ^3-3\left( \frac{r_c}{R}\right) ^2\sin ^4(\varTheta )\nonumber \\&\quad -\left( 16(1-x)^2+\sin ^6(\varTheta )\right) =0,\end{aligned}$$

(41)

$$\begin{aligned}&\cos (\theta _c)=\frac{4(1-x)-2\left( \frac{r_c}{R}\right) ^3}{2\left( \frac{r_c}{R}\right) ^3+\left( \frac{r_c}{R}\right) \sin ^2(\varTheta )},\end{aligned}$$

(42)

$$\begin{aligned}&16x\left( \frac{r_b}{R}\right) ^3-3\left( \frac{r_b}{R}\right) ^2\sin ^4(\varTheta )\nonumber \\&\quad -\left( 16x^2+\sin ^6(\varTheta )\right) =0,\end{aligned}$$

(43)

$$\begin{aligned}&\cos (\theta _b)=\frac{-4x+2\left( \frac{r_b}{R}\right) ^3}{2\left( \frac{r_b}{R}\right) ^3+\left( \frac{r_b}{R}\right) \sin ^2(\varTheta )}, \end{aligned}$$

(44)

where $R,\,\varTheta$ and x all input parameters. Observe that x is varied from the initial bleb volume ratio,

$$\begin{aligned} x_0=\frac{v_b}{V}=\frac{2-3\cos (\varTheta )+\cos ^3(\varTheta )}{4}, \end{aligned}$$

(45)

to the maximal bleb ratio, $1-x_0$.

Originally, R was taken as a free variable (Hu 2009). However, using Eqs. (19)–(25) and assuming spherical symmetry of the solution, we can derive the initial radius of the unweakened cell, R. The unique solution can be seen to be:

$$\begin{aligned} y&= R\sin (\theta ), \end{aligned}$$

(46)

$$\begin{aligned} z&= R\cos (\theta ),\end{aligned}$$

(47)

$$\begin{aligned} s&= R\theta ,\end{aligned}$$

(48)

$$\begin{aligned} \theta&= \frac{\sigma }{\rho },\end{aligned}$$

(49)

$$\begin{aligned} t_s&= \frac{\varDelta \,\textit{PR}}{2},\end{aligned}$$

(50)

$$\begin{aligned} \kappa _s&= \kappa _\psi =\frac{1}{R},\end{aligned}$$

(51)

$$\begin{aligned} q_s&= 0. \end{aligned}$$

(52)

Substituting these back into the constitutive Eq. (16), we find

$$\begin{aligned} \frac{\varDelta \,\textit{PR}}{2}=A\left( \left( \frac{R}{\rho }\right) ^2-1\right) \left( 1+\mu \right) . \end{aligned}$$

(53)

The positive root of this quadratic, which depends on $\varDelta P,\,\rho ,\,A$ and $\mu$, then provides the desired radius.