1 Introduction

Over the past decade, major efforts have been made by the Government of Canada, under the Canadian Operational Networks of Environmental Prediction Systems (CONCEPTS) initiative, to develop ocean-sea-ice models based on the Nucleus of European Modelling of the Ocean (NEMO; http://www.nemo-ocean.eu), for operational ocean, sea ice and coupled atmosphere-ocean-ice forecasting. For short- to medium-term forecasts, CONCEPTS has now developed the Global Ice-Ocean Prediction System (GIOPS; Smith et al. 2015), a North Atlantic-Arctic Regional Ice-Ocean Prediction System (RIOPS; Dupont et al. 2015) and two Coastal Ice-Ocean Prediction Systems (CIOPS) which are currently under development for the East and West Coasts of Canada. The horizontal grids of GIOPS, RIOPS and CIOPS all follow the tri-polar ORCA configuration produced by the DRAKKAR group (2007), with nominal horizontal resolutions of 1/4°, 1/12° and 1/36° in longitude/latitude, respectively. These systems are linked using a one-way nesting approach and form the backbone for further downscaling to nearshore areas (including harbours) through efforts such as reported in the present work.

Recently, the Government of Canada has announced a new strategy to increase marine safety and environmental emergency response capability through the Oceans Protection Plan (OPP). The present work aims to evaluate the capability of the NEMO modelling framework to provide very-high-resolution modelling at port-scale. Although NEMO was initially developed with climate and global-scale modelling in mind, the development work described in this manuscript would allow the ocean and coastal areas to be modelled using the same modelling framework, simplifying the model development and maintenance of the operational systems.

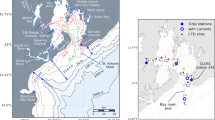
The port selection took into account the various challenges that would be encountered as such systems are developed for several major Canadian ports. The port of Saint John, located in the Bay of Fundy (Fig. 1), was selected due to its significant marine traffic, including tankers, containers and cruise ships and complex oceanographic conditions, including the presence of large tides, dynamic river input, strong currents, complex bathymetry and narrow passages, and the existence of sufficient observations to support a high-resolution model evaluation.

Fig. 1
figure 1

(left) Location of Saint John Harbour (red star). (right) Location of various types of observations in the Bay of Fundy used for model evaluation. Inset shows detailed map of the Saint John Harbour Area. Historical harmonic constants are available at locations throughout the Bay of Fundy (black dots), while CTD (blue squares) and ADCPs (orange triangles) were selected specifically for the area around the Harbour. The Atlantic Smart buoy is represented by the red star on the inset and the tide gauge at Saint John is denoted with a purple triangle. The green lines delimits the inner harbour, approach and outer harbour areas used in the model evaluation. MH marks the location of Musquash Harbour

Full size image

The tidal range in the Bay of Fundy is among the largest in the world, reaching a maximum of around 16 m in the upper bay and about 8 m in Saint John harbour. The harbour receives freshwater input from the Saint John River, with the maximum runoff reaching up to 5000 m3 s−1 during the spring freshet. The combination of tidal flow and river runoff leads to sharp fronts being generated in the vicinity of the harbour. The harbour is connected to the Saint John River through a large lake system. Between the harbour and the lake, there exists a narrow meandering strait named the ‘Reversing Falls’ (see inset on Fig. 1). These geometric constraints lead to a substantial reduction of tidal amplitude and higher mean water level upstream of Reversing Falls relative to that in the harbour. The flow condition in Reversing Falls drastically changes over the course of a tidal cycle. During the flood tide, the sea level in the harbour rises at a much higher rate than it does upstream of the Falls and sea water flows into the channel. During the ebb tide, sea level in the harbour rapidly drops to much lower levels than that upstream of the Falls, creating a series of rapids running from the lake system into the harbour. Due to the large tidal amplitudes in Saint John harbour and throughout the Bay of Fundy, significant inter-tidal zones (tidal flats) are found in the area of interest.

There has been a significant body of ocean modelling studies for the region with a focus on the Bay of Fundy, using both structured and unstructured grid models. These include studies considering only barotropic processes (e.g. Lynch et al. 1996; Aretxabaleta et al. 2008, 2009; Hannah et al. 2001; Dupont et al. 2005; He et al. 2005; Greenberg et al. 2012), as well as systems that include baroclinic processes (Katavouta et al. 2016; Katavouta and Thompson 2016). Barotropic models are generally considered sufficient to adequately simulate the tidal and wind-induced variations of sea levels and currents in this region. On the other hand, baroclinic models can additionally simulate the variations of temperature and salinity caused by surface and lateral heat and freshwater fluxes (e.g. coastal runoff and river discharge), as well as their influences on tidal currents (e.g. Katavouta et al. 2016) and coastal processes (e.g. Chegini et al. 2018). In the context of OPP where there is a focus on improving numerical products for emergency response (e.g. oil spill), the development of very-high-resolution baroclinic models is necessary to include the evolution of ocean variables (temperature, salinity, density and three-dimensional currents) that would affect the fate and behaviour of hazardous chemicals.

There have been significant recent developments in modelling regional ocean domains with high resolutions. Graham et al. (2018) demonstrated the overall better performance achieved by increasing the horizontal grid resolution from 7 to 1.5 km for the Northwest European Shelf Seas, with the presence of strong tides and the long-term changes of the circulation in the Norwegian Trench and the Baltic Sea channels. Maraldi et al. (2013) developed a 2.0–3.0-km resolution NEMO configuration for the Iberia-Biscay-Ireland region of the North Atlantic, and showed the system’s capacity to reproduce accurately the tidal features (e.g. elevation and currents, tidal fronts and residual elevation). Using the Regional Ocean Modeling System (ROMS) in the Gulf of Mexico, Bracco et al. (2016) demonstrated the increased complexity of simulated sub-mesoscale eddies and vorticity filaments near the shelf break when increasing the horizontal resolution from mesoscale resolving (5 km) to ‘sub-mesoscale permitting’ (1.6 km). Using a structured grid model developed by Barron et al. (2006), Jacobs et al. (2016) applied a three-level nesting approach to evaluate the impact of downscaling from a 3-km resolution to 1-km, 250-m and finally 50-m grid on surface numerical drifter trajectories and clustering. They show that increases in material density over time were a result of increasingly resolved small-scale divergence features. For the Gulf of Taranto in the Mediterranean Sea, Trotta et al. (2017) developed a three-level nested model based on the Structured and Unstructured grid Relocatable ocean platform for Forecasting (SURF; Trotta et al. 2016) with horizontal resolutions of 2 km, 680 m and 227 m. This work demonstrated for the first time in a forecasting context that a resolution of 200 m is required to reproduce an observed sub-mesoscale eddy. On the east coast of Canada, Shan et al. (2011) proposed a multi-nested coastal prediction system using five structured grid domains to downscale from a Northwest Atlantic model (at a horizontal resolution of 1/12°) to a model covering Halifax harbour in Nova Scotia at 200-m resolution. They showed the capacity of their approach to represent accurately the tidal and non-tidal water levels, seasonal variations of temperature and salinity including the two-level estuarine circulation.

In addition to nested approaches with structured grid models, unstructured grid models are widely used for coastal and near-shore modelling and forecasting. For example, recently, Lin and Fissel (2018) applied the Finite Volume Coastal Ocean Model (FVCOM; Chen et al. 2006) at 210-m horizontal resolution to simulate circulation and hydrography variations in Chatham Sound, near Prince Rupert, British Columbia. The model realistically simulated the baroclinic tidal flow, the seasonal variations of the circulation due to the contributions of river runoff and surface winds in this complicated channel system. In the Saint John harbour and adjacent waters, a high-resolution model based on FVCOM has also been developed (O’Flaherty-Sproul and Haigh, pers. comm.), extending the work of Wu et al. (2016). This model can simulate the tidal flats effects using a wetting-drying scheme in FVCOM. Clearly, the absence of a wetting-drying scheme is a limiting factor in the current version of NEMO. We plan to test the new version of NEMO with such a scheme included, and perform a detailed comparison with the aforementioned FVCOM model in a future project.

The present work aims at exploring and demonstrating the capability of very-high-resolution models based on NEMO with successively increasing resolutions down to 100 m for simulating the variations of water levels, currents and hydrography for the challenging oceanography characterizing the Bay of Fundy and Saint John harbour. The evaluation focuses on near-surface ocean variables to evaluate the model’s capability to provide a more accurate representation of surface drift trajectories to provide numerical guidance for marine emergency response. Section 2 describes the details of the three-level model configuration, the one-way nesting method, modification of the model boundary condition code to include the freshwater forcing from the Saint John River and the drift modelling and evaluation methods. Section 3 presents the model evaluation against a large set of observational data of sea levels, temperature, salinity and currents. Section 4 presents the results of drifter analysis and evaluation. Section 5 provides a summary of the conclusions.

2 Model description

In the present work, we develop three configurations of NEMO, downscaling from the 1/12° Regional Ice Ocean Prediction System version 1 (RIOPS). The three configurations have horizontal grid spacing of 2.5 km, 500 m and 100 m respectively. RIOPS covers the North Atlantic (from 27° N) and the Arctic Ocean (up to Bering Strait) and is used to provide the initial and boundary conditions for the 2.5 km (1/36°) configuration. The 2.5-km model output is used to provide the initial and boundary conditions for the next nested domain at 500 m and, similarly, the 500-m model provides initial and boundary information for the 100-m resolution nested grid. The following sub-sections provide details of the model configuration, a description of the model parameters for each nested grid, followed by strategy adopted for the boundary forcing and the freshwater flux from the Saint John River.

2.1 Model configurations

The ocean model used in this study is based on NEMO version 3.6 (Madec et al. 2015). The ocean core of NEMO solves the three-dimensional hydrostatic equations of motion for an incompressible fluid under the Boussinesq approximation on a structured computational grid. Although a sea-ice component is available within the NEMO framework, it is not used in the present study as ice is only marginally present along the Bay of Fundy coast in winter. Rather, the minimum water temperature is simply set to freezing temperature. Z-level grids are used in the vertical, with bottom partial cells used for an accurate representation of the varying bathymetry. The ‘variable volume level’ scheme (Levier et al. 2007) is applied to allow for the stretching and compression of the thickness of the vertical levels according to the changes of sea surface height.

The domains of the three model components are shown in Fig. 2. The horizontal grids of all three components are aligned with the tri-polar ORCA grids created by the DRAKKAR group (2007) to simplify the downscaling from RIOPS. The coarsest domain, Bay of Fundy-Scotian Shelf (hereafter BoFSS1/36), with a horizontal resolution of about 2.5 km (nominally 1/36° in longitude/latitude), does not include the Saint John lake system as the relatively coarse resolution severely limits the representation of the small channels and lakes. In a future operational context, the BoFSS1/36 would be replaced by the 1/36° resolution Coastal Ice Ocean Prediction System for the East Coast of Canada (CIOPS-E) currently under development. The second nested grid covers the Bay of Fundy with a 500-m horizontal resolution (hereafter BoF500). The third nested grid covers Saint John harbour and the approach at 100-m resolution (SJAP100). Both BoF500 and SJAP100 domains include a substantial portion of the lake and river system, including Reversing Falls. The location of the boundary condition for Saint John River (star on Fig. 2c) is located upstream of Reversing Falls where the tidal amplitudes are small and salinity approaches zero. This allows us to treat the boundary condition as a freshwater boundary condition (see Section 2.4 for details).

Fig. 2
figure 2

Bathymetry (colour shading, in m) and domain configurations. a Bathymetry of RIOPS and the outlines of BoFSS1/36 (solid line), BoF500 (dot-dash line) and SJAP100 (dashed line). b, c Bathymetry and domain details for BoF500 and SJAP100. Note the differences in colour scale between panels. In a, the triangle denotes the location of tide gauge at Yarmouth. In c, markers identify the location of the Saint John tide gauge (star), the Oak point water level station (square) and the model river boundary location (circle). The river boundary in BoF500 is located at the same geographical location. d Distribution of the model vertical levels for RIOPS and BoFSS1/36 (blue) and refined vertical grid used for BoF500 and SJAP100 (red)

Full size image

A high-resolution coastline dataset provided by the Canadian Hydrographic Service (CHS) is used to define each model component’s coastline. This coastline data is referred to as the Canadian Continuous Vertical Datum Hydrographic Vertical Separation (HyVSEP) solution (CANEAST2015v1CL). For the model bathymetry within the Bay of Fundy and part of the Gulf of Maine, high-resolution bathymetry data from CHS is interpolated to an ORCA grid at 100-m resolution. This data provides bathymetry directly to the inner model domain (SJAP100) and is spatially averaged to generate bathymetry for BoF500. Over a small area at the southwest corner of the BoF500 domain, not covered in the CHS database, we interpolate the bathymetry from the global high-resolution SRTM30 product (Becker et al. 2009). In the absence of a wetting-drying scheme in the NEMO version used for this study, the bathymetry of the upper Bay of Fundy was adjusted to ensure numerical stability required because of the large tidal range. The modification included shortening the length of Minas Basin while increasing the mean depth of the water points to avoid drying, while conserving the volume of the basin. As described in Section 3.1, that modification locally decreased the maximum tidal amplitude in the upper Bay of Fundy. The model bathymetry and coastline were tuned to have a good representation of the M2 tides in the area of interest near Saint John harbour. The BoFSS1/36 domain extends onto the shelf, and its bathymetry is interpolated from the refined bathymetry used in the 1/36° grid from the Gulf of Maine–Scotian Shelf model (GOMSS; Katavouta et al. 2016). For all three model components, the minimum water depth is set to 7.5 m for most of the domain, and 9.5 m where the tidal amplitude exceeds 6 m.

Figure 2 d shows the vertical grids of the three components. BoFSS1/36 uses the same 50-level vertical grid as RIOPS, with the full cell sizes varying from 1 m at the surface to 450 m at 5000 m. However, since the maximum water depth within the BoFSS1/36 domain is about 275 m, only the upper 28 levels are active. To improve the representation of the near-surface layer for currents, temperature and salinity in BoF500 and SJAP100, the vertical grid was refined to 1 m for the top 20 m of the water column, gradually decreasing to reach 18.5 m at 400 m. There are 41 and 35 active levels in BoF500 and SJAP100, respectively.

2.2 Model parameters and surface forcing

The momentum advection follows the standard 2nd-order vector form (Madec et al. 2015). Along the lateral boundary (coastline), a partial slip boundary condition was used for all three model components. Partial slip is an approximation to a no-slip condition, and allows the frictional effects of lateral boundaries to be included without the restrictive resolution required to represent the lateral boundary layer under no slip conditions. Tracers are advected using the Total Variance Dissipation (TVD) scheme in both horizontal and vertical directions (Madec et al. 2015). The lateral diffusion on momentum uses 3D time-varying viscosity following Smagorinsky (1993) where the viscosity coefficient is proportional to a local deformation rate based on horizontal shear and tension, with an effective lower bound of 20 (5) m2 s−1 for stability in BoFSS1/36 (BoF500 and SJAP100). A time-splitting scheme is applied for the internal (baroclinic) and external (barotropic) modes. The time steps for the internal (external) mode is set to be 180 s (6 s), 30 s (1 s) and 10 s (1 s), for BoFSS1/36, BoF500 and SJAP100, respectively. To ensure stability in SJAP100, a vertical split-explicit time stepping is used, with five sub-time steps. Vertical turbulence and mixing was calculated through the k − ε configuration of the generic length scale (GLS) turbulence closure (Umlauf and Burchard 2003) with background vertical eddy viscosity and diffusivity set to 1 × 10−4 m2 s−1 and 1 × 10−5 m2 s−1, respectively. Quadratic bottom drag is applied to all three model components, with the drag coefficient for each component tuned to ensure that (a) the model remains stable, and (b) the discrepancy in the M2 tidal elevation (for both amplitude and phase) is acceptably small. For BoFSS1/36, BoF500 and SJAP100, the background bottom drag coefficients are set to 2.5 × 10−3, 4 × 10−3 and 5 × 10−3, respectively. In the presence of the strong tidal currents in the upper Bay of Fundy and within the narrow Reversing Falls, we locally increased the bottom drag coefficient as well as making the bathymetry adjustments listed in Section 2.1. In BoF500, the coefficient was increased linearly up to a factor of 3 in Reversing Falls and in the upper Bay of Fundy, respectively, in Minas Passage, Minas Basin and Chignecto Bay (see Fig. 1). For SJAP100, the bottom drag coefficient was increased up to a factor of 5 locally over Reversing Falls.

The model’s sea surface is forced with hourly 10-m winds, 2-m air temperature and specific humidity, precipitation and surface incoming longwave and shortwave radiation from the 2.5-km High-Resolution Deterministic Prediction System (HRDPS; Milbrandt et al. 2016) running operationally at the Canadian Centre for Meteorological and Environmental Prediction (CCMEP). The sea surface momentum flux, sensible and latent heat fluxes and the rate of evaporation are computed using the bulk formulae of the Coordinated Ocean-ice Reference Experiments (CORE; Large and Yeager 2004).

2.3 Model simulation sequence, initialization and lateral open boundary conditions

Forcing variables for the lateral open boundary conditions (OBCs) for all nested grids include the sea surface height, and the three-dimensional fields of the horizontal velocities, temperature and salinity. A flow relaxation scheme (Engedahl 1995) is used for temperature, salinity and baroclinic velocities within a ten-grid-point-wide relaxation zone inside the lateral boundary. For better consistency between model domains, the bathymetry within the relaxation zone in the higher resolution nested grid is identical to the lower resolution model providing boundary information. The restoring strength decreases linearly from 1 day−1 at the outer boundary point to zero at the 10th grid point inside. The radiation scheme of Flather (1976) is applied for the barotropic current normal to the lateral open boundary and sea surface height. The barotropic velocity tangential to the open boundary is set to the values from the outer domain.

The lateral boundary forcing for BoFSS1/36 is provided by RIOPS. This includes the de-tided sea surface height and depth-averaged velocities, as well as daily averaged 3-dimensional temperature, salinity and baroclinic velocities. Due to the insufficient resolution and a lack of specific tuning for this region, the tidal elevation and velocities from RIOPS are not sufficiently accurate in the Bay of Fundy for use as lateral boundary forcing. Hence, BoFSS1/36 takes barotropic tidal elevation and velocities from the solution of an unstructured tidal model, WebTide, highly tuned for the Bay of Fundy (Dupont et al. 2005). In the present development stage, the five main tidal constituents (M2, N2, S2, K1 and O1) are imposed at the BoFSS1/36 lateral boundary. These constituents have tidal amplitudes of 306 cm, 61 cm, 48 cm, 15 cm and 12 cm respectively at the Saint John harbour tide gauge. We note that the minor semi-diurnal tidal constituents, L2, NU2, K2 and 2N2, have non-negligible contributions to the total water level variations in the Bay of Fundy, with amplitudes of 19 cm, 15 cm, 13 cm and 5.5 cm respectively at the tide gauge. Including only five constituents enables a shorter (27 days) simulation duration to perform tidal analysis, compare to 206 days required for 9 constituents. This shorter duration facilitated the tuning process of the tides. For a future operational implementation, the minor semi-diurnal constituents (L2, K2, NU2 and 2N2) would be included in the tidal boundary forcing.

The tidal evaluation (in Section 3) shows that BoFSS1/36 produces water levels sufficiently accurate for providing the tidal boundary conditions for BoF500. Thus, half-hourly instantaneous 3D fields for temperature, salinity, sea surface height and horizontal velocities from BoFSS1/36 are used to force the 500-m configuration at its (ocean) boundaries. Similarly, the same variables from BoF500 are used to force SJAP100. Therefore, the tidal signal for elevation and velocities are resolved in the high-frequency boundary conditions and propagates from the shelf model to the port-scale model, with external tidal forcing applied only at the BoFSS1/36 boundaries.

As part of the one-way nesting approach, the three models are required to run sequentially to provide boundary conditions for the next higher resolution model. Staggered start dates are required to allow the different systems to spin-up sufficiently before beginning the next level. The evaluation period is defined from May 2015 to mid-June 2016, based on the availability of a significant number of high-quality observational datasets within Saint John harbour and the surrounding area (Fig. 1). As such, the BoFSS1/36 model is initialized on February 1, 2015, from the RIOPS 1/12° solution and is allowed to spin up for 2 months before providing the initial conditions for the Bay of Fundy on April 1, 2015. Because stratification is weak in the Bay of Fundy in winter, we expect that the 2-month spin-up is sufficient for BoFSS1/36. The lake system introduced in BoF500 requires a longer spin-up to develop the two-layer system generated by the interaction between the river freshwater flux and the inflow of salt water through Reversing Falls over each tidal cycle. In the absence of adequate observations, the temperature and salinity in the lake system are initialized from the solution of a previous BoF500 1-year simulation using realistic atmospheric and Saint John River forcing. Finally, SJAP100 is initialized on April 10, 2015, from the BoF500 solution, allowing a 20-day spin-up of fine-scale features before the beginning of the evaluation period. Evaluation results suggests that the above simulation sequence does not introduce significant errors in the model results.

2.4 Including the influence of runoff from the Saint John River

The Saint John River watershed covers over 55,000 km2 and represents the dominant contributor of freshwater into the Bay of Fundy with an annual average discharge of around 1100 m3 s−1 (Cunjak and Newbury 2005). As such, freshwater input from the river dominates the salinity structure and may also have a significant influence on temperature in Saint John harbour and adjacent waters. While a climatological river discharge is included in RIOPS, it is not included in the BoFSS1/36 in the present development stage as this component is mainly used to provide boundary conditions for BoF500. Evaluation in Section 3 suggests that excluding the river forcing in BoFSS1/36 does not introduce significant errors in the solutions of the inner two models. In future development, CIOPS-E will replace BoFSS1/36 and will include a representation of all major rivers on the east coast of North America, including the Saint John River.

The location of the Saint John River boundary in the 500-m and 100-m models (Fig. 2) is chosen far enough upstream so the tidal amplitude is small and salinity is close to zero, therefore allowing us to define a freshwater boundary. Observed river discharge data is not available near the entrance to the lake system, but is available at Grand Falls, New Brunswick (position shown in Fig. 3). As the Grand Falls station only catches about 40% of the total watershed of the Saint John River, a crude estimate of the total river discharge could be obtained by multiplying the observed values at the station by a factor of 1.9, representing the ratio of the total area of the watershed to the area represented by the station. However, the Mactaquac Dam is located between Grand Falls and our model domains, and there is no publicly available information regarding its regulation of discharge. As such, there is no reliable river discharge data available to force the model.

Fig. 3
figure 3

Grand Falls discharge data and Oak Point water level. Left panel: the Saint John River watershed (green shaded area), Grands Falls station (black star), Oak Point (blue star) and Mactaquac Dam (purple circle). Right panel: time series of adjusted Grand Falls discharge (black), the discharge rate diagnosed from the SJAP100 solution (red) and the Oak Point water level (blue)

Full size image

However, there are several stations with measurements of water levels along the lake system, and the station at Oak Point (position shown in Figs. 2c and 3) is located fairly close to the entrance of the lake system and within the domains of SJAP100 and BoF500. Therefore, we take an alternative approach of using the observed water levels at Oak Point to introduce the river forcing. To achieve this, we modified the barotropic OBC at this location to specify the water level as the input data.

The reference level used to report the Oak Point water level is referenced to the Canadian Geodetic Vertical datum of 1928 (CGVD28) and may not be the same as the reference level in our model. Therefore, it was necessary to adjust the Oak Point data to ensure we use a consistent reference level. At three representative tide gauges in the region (Saint John, Yarmouth and Halifax), the observed mean water level (MWL) relative to CGVD28 is 0.314, 0.299 and 0.277 m, respectively. The water levels of the different NEMO model components share the same reference level through the setting up of the barotropic OBC, but their reference to the CGVD28 is unknown. To determine this, we first computed the MWL based on the solution from RIOPS. At the above three locations, the modelled estimated MWL are − 0.373, − 0.382 and − 0.415 m. These estimates are lower than the MWL in the observational data by 0.687, 0.681 and 0.693 m, respectively. This gives 0.69 m as a good estimate of the offset between the reference levels used for the observed Oak Point water level and by the model.

Therefore, we subtract 0.69 m from the time series of the observed water level at Oak Point before applying it as the model’s river OBC. One may argue that the reverse approach would also work, i.e. adding 0.69 m to the sea surface height of the RIOPS solution before providing it to the OBC of BoFSS1/36. However, this implies adding 0.69 m to the bathymetry of SJAP100, BoF500 and BoFSS1/36, creating a discrepancy with the bathymetry of RIOPS. In effect, this would change the total water volume of the system and hence affect the model’s tidal solutions.

Figure 3 (right panel) presents three times series: (a) the adjusted Grand Falls runoff, (b) the diagnosed volume transport at a cross-section downstream of Oak Point and (c) the observed Oak Point water level after the reference level adjustment (− 0.69 m). The broad features of the time series of (a) and (b) are similar, notably the timing, duration and intensity of the spring freshet. However, there are also significant differences, particularly during the fall and winter months. There is good correspondence between time series of (b) and (c): both show a fall freshet in October 2015, and a series of short freshwater events throughout the winter. These events are totally absent in the time series of (a), suggesting that a reliable runoff input cannot be obtained by simply adjusting the Grand Falls runoff to account for the ungauged area of the watershed. Lastly, the water temperature at the model boundary uses the only available observed time series from the Tracey Mills station (01AJ004), located on a tributary of the Saint John River.

2.5 Drift modelling and evaluation

One key objective of this study is to improve the accuracy of modelling and prediction of the trajectories of drifting objects and substances in the water. To do this, we will compare the observed surface drifter trajectories and the virtual trajectories simulated using the Canadian Oil Spill Modelling Suite (COSMoS; Marcotte et al. 2016). COSMoS uses meteorological and oceanographic forecasts from the HRDPS and NEMO solutions to calculate Lagrangian trajectories in dispersion kernels. It was initially developed by adapting the atmospheric dispersion kernel (Modèle Lagrangien de Dispersion des Particules d’ordre n (MLDPn); D’Amours et al. 2015) to forecast marine oil spills, and was recently extended for drifter verification in a drift-specific kernel (MLDPn-DRIFTER). This simplified offline particle-tracking model linearly interpolates the surface winds and currents at the specified depth to calculate the Lagrangian trajectories using a 4th-order Runge-Kutta integration algorithm. In drift mode, a particle (object) is launched in accordance with each drifter observation, and is then advected using surface currents and a user-defined windage (i.e. a small fraction of the wind speed, applied in the direction of the wind). While the drift kernel is able to include stochastic displacements, here we only carry out direct advection using 1-min outputs of surface currents from NEMO and hourly 10-m wind from HRDPS. The drift model integration time step is 5 s and the modelled drifter coordinates are written every 2 min.

3 Evaluation of water levels, currents and water properties

This section aims to evaluate the system’s capacity to reproduce the dominant oceanographic conditions and variability with a focus on Saint John harbour and the adjacent waters. Figure 1 presents the distribution of high-quality observations used to evaluate the model. The evaluation focuses on the representation of (1) the tidal and (2) the non-tidal (residual) water levels and currents, and (3) variations of the water mass properties (temperature and salinity).

3.1 Tidal water level and currents

3.1.1 Tidal water level

The tide gauge located in Saint John harbour (Fig. 1) provides observations of the water level over the complete period of the model evaluation. As the harbour is represented in all nested grids, to different levels of accuracy, a harmonic analysis of observed and simulated water levels is performed on hourly data using the t-tide tool (Pawlowicz et al. 2002). The principal lunar semi-diurnal component (M2) is the dominant tidal constituent in the Bay of Fundy, with an amplitude of 306 cm. Table 1 compares the amplitude and phase of the M2 constituent from the observation with the three nested-grid solutions, RIOPS and WebTide.

Table 1 Comparison of the tidal amplitude and phase of water level for M2 tidal constituent at the Saint John tide gauge, derived from a 1-year hourly time series (May 2015–June 2016) for observations, the solutions of the three NEMO model components, RIOPS and WebTide
Full size table

Table 1 shows gradual improvement of the M2 amplitude with increased resolution, with the largest errors in the BoFSS1/36, of 9.8 cm (3.2% error), decreasing in the BoF500 to 5.9 cm (1.9% error), reaching a minimum of 4.6 cm (1.5% error) in the SJAP100. The error reduction is likely related to the inclusion an explicit Reversing Falls and lake system, allowing propagation and dissipation of the tidal energy upstream of the tide gauge. The M2 phase is generally overestimated, with errors of the order of 3° representing about a 6-min delay. The nested-grid models show a significant improvement over RIOPS, which shows much larger errors in magnitude (> 25 cm) and phase (> 50°). WebTide underestimates the amplitude by 6 cm, but overestimates the phase by only 1.6° (a 3-min delay). The three models show skill comparable to WebTide for the M2 amplitude and are only slightly less accurate than it for the phase.

Table 2 compares the observed and modelled amplitudes and phases of the next two largest tidal constituents at Saint John harbour, N2 and S2, with amplitudes of 60 cm and 49 cm respectively. For N2, an improvement with increased resolution is also noticeable with SJAP100 showing an error of 1.7 cm (2.8% error). The three model components overestimate the observed phase by about 5° (a 10-min delay). The model accuracy for S2 is similar to that for N2, with amplitude and phases errors of 5.6% and a 14-min delay respectively.

Table 2 Comparison of the tidal amplitude and phase of water level for N2 and S2 tidal constituents at the Saint John tide gauge, derived from 1-year hourly time series (May 2015–June 2016) for observations, the three NEMO model components, RIOPS and WebTide
Full size table

For all the three tidal constituents, the model tends to consistently overestimate the amplitudes and phases. As the model resolution increases, the amplitude error decreases while the phase error remains similar. Note also that the accuracy (or error) of SJAP100 depends on that of BoF500 and BoFSS1/36, due to the use of one-way nesting approach of the current model setup. Hence, any further improvements of the innermost SJAP100 component will require the improvements of the outer BoF500 and BoFSS1/36 components, in particular for the phases of the tides. Nevertheless, the quality of the simulated tides in the three nested grids represent a significant improvement over RIOPS, which is currently used operationally. Although the errors are slightly larger than those from the barotropic tidal model WebTide, these results are encouraging for the use of a NEMO baroclinic solution for emergency response to spills, where information on stratification will be required.

There are a few dozen locations around the Bay of Fundy for which the CHS has historical tidal constituent data (black dots on Fig. 1). Historical stations are mostly concentrated in the upper Bay of Fundy and Passamaquoddy Bay. Passamaquoddy Bay opens on the Bay of Fundy through several narrow channels that are poorly resolved even in the BoF500 grid, limiting the representation of the tidal propagation. Additionally, the geometry of the upper Bay of Fundy has been adjusted to ensure numerical stability as described in Section 2, which may have negatively impacted the representation of tides. Despite these limitations, the mean absolute differences for the M2 amplitude and phase between the historical observations and the model are 11 cm and 3.7°, with standard deviations of 13 cm and 3.1°. The M2 amplitudes are generally overestimated in Passamoquoddy Bay and underestimated in the Chignecto Bay and Minas Basin. We conclude that our model performs acceptably well outside of the Saint John harbour, even though most of the gauges with historical records are located in regions with the presence of tidal flats.

In addition to an evaluation using observations at tide gauges, we also compared the BoF500 tidal constituents over the entire domain with WebTide (Dupont et al. 2005), which provides tidal forcing at the lateral open boundary of BoFSS1/36. Figure 4 shows the comparison of amplitude and phase for M2. In the open parts of the Bay of Fundy, the differences in amplitude and phase are small, within 12 cm and 3° respectively. Larger differences in amplitude, up to 45 cm, are found in Chignecto Bay and Minas Basin, where the M2 tidal amplitude reaches up to 6 m. This is expected from the modification of the model bathymetry and coastline, and by the absence of a wetting-drying module in this version of NEMO. The addition of a wetting-drying scheme may provide improvements to the representation of tides in the upper Bay of Fundy and reduce some of these errors.

Fig. 4
figure 4

The amplitude (colour shading, in m) and phase (contours, in degrees, relative to UTC) of sea levels of the principal lunar semi-diurnal tidal constituent (M2): a BoF500 solution, and b difference BoF500 minus WebTide. The difference in land/sea masks between a and b is due to the lack of coverage by WebTide in certain areas (e.g. Saint John River and Annapolis Basin)

Full size image

3.1.2 Tidal currents

Currents were observed by a series of acoustic Doppler current profilers (ADCPs) deployed in the inner harbour and its approach (see inset in Fig. 1). Figure 5 presents the tidal ellipses calculated from the hourly near-surface currents from the ADCPs and the SJAP100 solution for the three principal tidal constituents (M2, N2 and S2) at three locations. Tidal ellipses from WebTide are also presented in Fig. 5. First, the observations and model results show good agreement in the phases of the tidal currents for the three constituents, as indicated by the co-location of the black and red dots (marking the beginning of the tidal cycle, see the caption of Fig. 5). Station 585 shows the best agreement in terms of the magnitude of the current and the inclination angle of the major axis for all the three constituents. As this station is close to the shore, the tidal flow is constrained by the coastline and oscillates rectilinearly. At station 576 near the head of the inner harbour, the observed and modelled tidal currents are still close to rectilinear oscillations. The agreement in terms of the magnitude and inclination of the major axis is the best for M2, while for N2 and S2 the model underestimates the magnitudes. Close to the edge of the inner harbour (station 573), both observations and model show that the currents are no longer rectilinear, except for the observed ellipse of M2. The model reproduces well the magnitude of currents along the major axis for all the three components, and the magnitude along the minor axis for N2 and S2. The observed and modelled N2 and S2 ellipses show a 10–30° difference in the inclination angle of the major axis.

Fig. 5
figure 5

Ellipses of tidal currents for the M2, N2 and S2 constituents at three locations (marked by the orange solid triangles on the maps) for observations (black), the SJAP100 model (red) and WebTide (blue). Number in each panel denotes depth (in m) below surface. Grey crosses indicate currents of ± 0.1 m s−1. The coloured dots mark the location of a particle at the end of a tidal cycle, i.e. when each horizontal component of the tidal flow equals its magnitude multiplied by the cosine of its phase. The first 15° of the tidal cycle is not plotted to deduce the sense of rotation

Full size image

Next, we assess the skill of the model in simulating the vertical structure of tidal currents. Figure 6 shows the M2 tidal ellipses at two depths below the surface for each of the three locations. At both depths, the model generally reproduces the M2 ellipses to a high degree of accuracy. More interesting is the model’s capacity to also reproduce the vertical variations of the tidal ellipses. These variations are likely due to the presence of a dredged channel (for navigation) close to the location of the ADCPs, having a direct influence on the propagation of the tidal currents at depth, while the vertical density gradient resulting from the freshwater outflow through Reversing Falls tends to decouple the surface layer. It is very encouraging to see that the SJAP100 model reproduces the characteristics of the vertical variation, in particular the changes in the inclination angle of the major axis, at all the three sites.

Fig. 6
figure 6

Tidal ellipses of the M2 tidal constituent at three locations (orange triangles on the maps), and at two depths at each location. The definitions of colour and symbols are the same as in Fig. 5

Full size image

Finally, the SJAP100 shows a significant improvement compared to WebTide, which lacks the resolution to accurately represent the complex geometry of Saint John harbour or the dredged channel. Moreover, WebTide does not take into account the effect of the Saint John River on currents as it neither takes into account the volume flux from any rivers nor resolves the lake and river system upstream. As a result, the near-surface drift due to tidal motion is expected to be relatively well captured by the SJAP100 model with some discrepancies in the approach to Saint John harbour.

3.2 Residual water level and currents

In this study, the residual water level is found by subtracting both the mean water level and the tidal elevation from the total time series; currents are treated similarly. These time series are filtered with Butterworth band-stop filters to remove energy around M2 and its harmonics, as tidal energy can leak into adjacent frequencies that are then not captured in harmonic analysis. A low-pass filter removes energy at frequencies higher than 6.0 cycles per day (cpd), as this band is poorly resolved in our (hourly) data, is generally noisy and obscures the lower frequency signal in the time series. A three-bin-wide running median filter is used to smooth the variance-conserving power spectra without drastically altering the shape of the spectra.

3.2.1 Water level

Figure 7 (top panel) shows the observed and modelled time series of the residual water level at the Saint John tide gauge during May 2015–April 2016. The residual time series have a correlation coefficient of 0.63 and their differences have a standard deviation of 8.3 cm. Both time series also show seasonal characteristics in the intensity of high-frequency variations: weak variability from May to September 2015 and again in April 2016, with large spikes from October 2015 to March 2016 due largely to more intense atmospheric synoptic systems over the winter period. The model generally underestimates the magnitude of the residuals compared to observations. This underestimation may likely be related to errors in the HRDPS winds, limited by the 2.5-km resolution in the representation of local effects. The bottom panel of Fig. 7 show the spectra (in the variance-conserving form) of the residual water level. The spectra are normalized such that the largest value in the two spectra is set to 1.0. The model is able to reproduce the shape of the observed spectrum at most frequencies, capturing peaks at higher frequencies and matching the relatively flat shape at frequencies below 0.1 cpd. However, the model does not consistently match the energy in the observed spectra, underestimating peaks and features at most frequencies. The peak at 0.1–0.3 cpd corresponds to the atmospheric synoptic (i.e. weather) band, and the significant peak indicates that the weather variability is a key driver of residual water level.

Fig. 7
figure 7

Residual (non-tidal) water level at the Saint John tide gauge from May 2015 to April 2016 from observations (black) and the SJAP100 model (red): (top panel, a) hourly time series with the time mean values removed, and b spectra in variance-preserving form. Narrow band-stop filters are applied to remove spikes near tidal frequencies, and at all frequencies higher than 6 cycles per day (cpd). The spectra are also smoothed with a median filter with a width of three bins

Full size image

3.2.2 Currents

Figure 8 compares the residual near-surface currents from observations and the SJAP100 model during August 12–November 3, 2015, at stations 576 and 573. Note that the tidal ellipses from these stations are shown in Figs. 5 and 6. The (removed) mean currents are consistently southeastward, with observed (eastward, northward) speeds of (0.15, − 0.37) m/s 3 m below the surface at station 576, and (0.23, − 0.35) m/s 2 m below the surface at station 573. SJAP100 accurately reproduces the direction of the mean current to within 1° but underestimates the speed by roughly 25%, with mean currents of (0.11, − 0.28) m/s and (0.17, − 0.27) m/s at the same two locations and depths respectively. The model reproduces the variability of the observations, including a very strong southeastward flow event in early October 2015. This event is related to the fall freshet and is evident in both the Oak Point water level record and the model diagnosed river runoff (Fig. 3). Note that the model captures the observed timing, direction and (at station 576) speed of this event accurately. As with the residual water level, SJAP100 reproduces the variation on daily-to-weekly time scales at both stations, but it only reproduces the speed of the flow accurately at the station closer to the head of the harbour (station 576). The currents at station 573, in the middle of the harbour and analysed at a shallower depth than at station 576, are somewhat underestimated relative to observations at all frequencies. This may be due to a discrepancy between the modelled and the physical river plume, which is constrained to the near surface.

Fig. 8
figure 8

Residual (non-tidal) currents from observations (black) and the SJAP100 model (red) from August 12 to November 3, 2015, at two ADCP stations (orange triangle on maps): (left column) station 576 at 3 m below surface, and (right column) station 573 at 2 m below surface. Top row: eastward flow. Middle row: northward flow. Bottom row: the sum of the spectra for the two flow components in variance-conserving form. Narrow band-stop filters are applied as with the residual water level, and the spectra are then smoothed with a three-bin-wide median filter. All spectra are normalized such that the largest value present is set to 1.0

Full size image

3.3 Temperature and salinity

A set of 81 CTD casts taken at 35 locations were obtained in the study area within the 1-year evaluation period, with most casts being taken in the summer and fall months (see blue squares in Fig. 1). Up to four casts were gathered throughout the year at 18 locations, and a further 17 cases were taken at unique locations. In the inset of Fig. 1, green lines define three regions that we use for aggregating statistics of the temperature and salinity data: the inner harbour (including two stations in between the harbour and Reversing Falls), the approach and the outer harbour.

The top three rows of Fig. 9 show a representative set of temperature, salinity and density profiles for each region from CTD casts and SJAP100. In each panel, the pale red–shaded area denotes the maximum extent of the modelled profiles within 3 h before and after observation, representing the variability of the profiles within a 6-h tidal half-cycle. SJAP100 reproduces the shape and magnitude of all three variables well even when unusual features are present, like the warm maximum seen around 10–15 m below the surface in cast 3893. At any given point in the harbour near the river outflow, the depth of the interface between the fresher near-surface layer water and the salty water below it changes over the tidal cycle, as the salt wedge propagates through the river system raising the interface towards the surface as the tide floods. As the tide ebbs and the wedge recedes, the interface sinks deeper in the water column. Cast 3897 has the transition from fresher to saltier at 5–7 m below the surface, but in cast 3922 (which is further from the fresh water outflow), the transition is at only 2–4 m below the surface. In the outer harbour (e.g. station 3893), the vertical gradients in temperature, salinity and density are generally much smaller than those in the inner harbour and approach due to mixing of the freshwater plume and seawater.

Fig. 9
figure 9

Temperature, salinity and density profiles from observations (black) and SJAP100 (red), at locations shown by solid blue squares on maps. Top three rows: the second, third and fourth columns in each row show vertical profiles of temperature (in °C), salinity (in psu) and density (in kg m−3), respectively. The shading in pale red denotes the maximum extent of the modelled profiles within 3 h before and after the CTD casts. Bottom row: time series of daily averaged sea surface temperature from Smart Atlantic buoy (black) and SJAP100 (red) during May–December 2015

Full size image

To make an aggregate comparison, Fig. 10 shows scatter plots of the SJAP100 model solution against observations from all 81 CTD casts. The same data is plotted in both rows, with data grouped by cast location in the top row and by depth below the surface in the bottom row. For temperature, tight agreement is found in the outer harbour and at depths greater than 20 m below the surface. In the river (defined here between Reversing Falls and the harbour) and the inner harbour, the model shows warm biases related to well-mixed warmer water existing from the lake system. Similarly, salinities at depth and in the outer harbour are well reproduced by SJAP100. The largest discrepancies are found in the river stations and near the surface, where the freshwater plume dominates. Consistent with the residual currents and water level, the model does not precisely reproduce the fresh water plume. The scatter in the inner harbour may be related to errors in the vertical mixing in SJAP100 at Reversing Falls. Scatter of results in the approach and outer harbour may be due to small errors in the generation of sharp tidal fronts found throughout the domain. Considering the complexity of the conditions, the average biases in the model data are small: only 0.56 °C for temperature and 0.07 psu for salinity. When only the data in the approach and outer harbour (at all depths) are considered, the biases decrease to 0.47 °C and − 0.02 psu.

Fig. 10
figure 10

Scatter plots of CTD observations (horizontal axes) against SJAP100 model (vertical axes): temperature (left panels) and salinity (right panels); with data grouped by depth below surface (top row) and by geographic areas (bottom row) (see fig. 1 for definition of areas). The straight line in each panel show the 1:1 ratio

Full size image

3.4 Sea surface temperature

In situ sea surface temperature (SST) data was taken from the Smart Atlantic buoy moored in the approach (see the red star in Fig. 1). Daily averages from the buoy and SJAP100 are shown in the bottom row of Fig. 9. SJAP100 reproduces both the seasonal and sub-seasonal variations well, with a correlation of 0.95. The model has a small warm bias of 0.45 °C on average, with a standard deviation of the difference of 1.1 °C. The warm bias is most evident from May to September when there are more high-frequency variations in the time series; in October to January, both time series are less variable and they match very closely.

We also compare the SST over the domain of BoF500 to both RIOPS and a 0.1 degree resolution analysis produced by the CCMEP. The latter is based on an optimal interpolation scheme that assimilates multiple sources of satellite remote sensing and observational data (Brasnett and Surcel Colan 2016; Brasnett 2008). Figure 11 shows the three datasets for four representative days during May 2015–April 2016: the summer and winter solstices, and the vernal and autumnal equinoxes.

Fig. 11
figure 11

Daily averaged sea surface temperature (in °C) for (rows from top to bottom): summer solstice (June 21, 2015), fall equinox (September 23, 2015), winter solstice (December 22, 2015) and spring equinox (March 20, 2016), for BoF500 (left column), CMC SST analysis (middle column) and RIOPS (right column). Note that the colour bars are the same for each row, but vary between rows

Full size image

The model shows good agreement with the analysis in terms of the seasonal evolution and the large-scale patterns. On the summer solstice (June 21, 2015), the model reproduces well the temperature structures of the Bay of Fundy. Near the head of the bay, the solar radiation increases temperature up to 12–14 °C, warmer by 1 to 2 °C compared to the analysis. In the upper Bay of Fundy, tidal mixing is strong enough to overcome the summer stratification caused mainly by increased solar radiation (Garrett et al. 1978; Loder and Greenberg 1986). The model reproduces accurately the extent of the tidally mixed region, with colder temperatures with SSTs of 7–8 °C. Further south, a cyclonic gyre circulation, between Grand Manan Island and the coast of Nova Scotia (Aretxabaleta et al. 2008, 2009; He et al. 2005), is directly influenced by the freshwater input from the Saint John River, resulting in increased near-surface stratification visible by the locally higher SST. The gyre position and extent are well reproduced in the model, with temperatures between 9 and 11 °C. Loder and Greenberg (1986) identified a second tidally mixed region west of Grand Manan Island. This area is noticeable in the analysis by its low SST signature (< 7 °C), and is well represented in the model, albeit with a slightly warmer SST of 8 to 9 °C.

On the autumnal equinox (September 23, 2015), the head of the bay shows important warming, with temperatures exceeding 18 °C in both the analysis and model. Warm temperatures of around 15 °C extend into the tidally mixed region in both the model and the analysis. Colder water is constrained to the Nova Scotian coast and south of Grand Manan Island. On the day of winter solstice (December 22, 2015), the whole bay can be divided into two areas: the colder shallow waters with the lowest SST (< 6 °C) near the head of the bay, and the rest of the bay with relatively uniform SST values. In this second region, the analysis has values around 8.5 °C, while the model is slightly colder with values around 8 °C. Similarly, on the vernal equinox (March 20, 2016), the bay can be divided into two areas: the colder area expanding from shallow waters into the upper part of the Bay with the lowest SST falling below 1 °C, and the rest of the bay with temperatures of 4–5 °C. The pattern of the temperature gradient in the upper Bay of Fundy in the model agrees with the analysis.

BoF500 is consistently more accurate than RIOPS at reproducing the satellite analysis; RIOPS is typically several degrees warmer than the analysis during the summer and fall months. This may be due to weaker tidal mixing or weaker tidal residual circulation, as RIOPS has weaker tidal amplitudes and nonlinear effects than BoF500.

In the context of an oil spill, accurate modelling of the SST would have a significant impact on the prediction of the fate and behaviour of the oil, particularly with respect to its evaporation, viscosity and density dependence on temperature. Likewise, the representation of areas of enhanced tidal mixing would also have an impact of the vertical distribution of the oil product in the water column. As such, the improved SST and mixing provided by the BoF500 model relative to RIOPS (currently used at CCMEP for emergency response) might prove critical in supporting the fate and behaviour and dispersion modelling efforts in OPP, eventually improving the numerical guidance to emergency responders mitigating the impacts of oil spills.

4 Drifter analysis and evaluation

In addition to the evaluation using the Eulerian types of observations presented in Section 3, we evaluate the model’s skill in drift prediction against the observed trajectories of 129 surface drifters released near the Canaport terminal (see Fig. 1). Three types of drifters were used: (1) the barrel-shaped Seimac AST drifters (with a draft of 0.8 m); (2) the spherical MetOcean iSphere drifters (with a diameter of 0.4 m, and a ratio of 1:1 for exposed vs submerged cross-sectional areas); and (3) the MetOcean CODE/Davis drifters with cross-shaped vanes following the design of Davis (1985) (with a draft of 1 m, and a ratio of 1:40 for exposed vs submerged cross-sectional areas). These drifters were released in 10 deployments during July–October 2015 and a single deployment in January 2016. Each deployment included multiple types of drifters, though the CODE/Davis drifters were included in only 6 of the 11 deployments. All drifters reported their position approximately every 30 min. Virtual trajectories were simulated offline using the drift-specific kernel MLDPn–DRIFTER of COSMoS described in Section 2.5, driven with currents from the SJAP100 and BoF500 models and winds from the HRDPS atmospheric model. A new virtual trajectory is launched from every observed drifter location.

Wind has both direct and indirect impacts on drifter trajectories, and these effects vary with drifter geometry and experimental setup. Spherical drifters have a significant cross-sectional area exposed to wind, while the CODE/Davis drifters have minimal wind effects and are considered ‘good water followers’ (Niiler et al. 1995; Novelli et al. 2017). Describing and assessing the effects of wind on drift is an area of active research (Niiler et al. 1995; Novelli et al. 2017; Röhrs et al. 2012; Röhrs and Christensen 2015). When calculating the virtual drifter tracks, the effect of wind is often parameterized by adding a fraction of the wind speed (i.e. windage) to the ocean currents (Breivik and Allen 2008; Röhrs et al. 2012). The windage values are empirical adjustments, and a value of 1% has been suggested for spherical drifters, when wind effects were assumed to be a combination of wind drag and the wave-induced Stokes drift (Röhrs et al. 2012). In our simulations, we test windage values between 0 and 1% in 0.1% increments, as well as a value of 3%. The latter value corresponds to the analytically derived estimate that total currents are between 3.1 and 3.4% of the wind speed (Weber 1983), which is often used to parameterize drift where no information about currents is available.

Figure 12 compares the observed tracks from one deployment with all three types of surface drifters in early October 2015 (shortly after the fall freshet) starting from a location near the Canaport terminal, and the modelled tracks using the surface currents from the BoF500 and SJAP100 models. Modelled tracks with zero and 1% windage are shown. The observed tracks from the three types of drifters and the modelled tracks from the two models with different horizontal resolutions show generally good agreement in terms of the direction and distance of the drift. Some notable differences are present: for example, some of the iSphere drifters show an initial northward movement, and this is reproduced only by the virtual drifters based on the BoF500 model with 1% windage included. Including 1% windage has more impact on the modelled tracks based on BoF500 than on those based on SJAP100.

Fig. 12
figure 12

Drifter trajectories from a single deployment in early October 2015. The deployment location near the Canaport terminal is shown with an orange circle. Thin grey solid lines: trajectories of a set of three types of surface drifters. Thick coloured lines: trajectories calculated using surface currents from BoF500 (in blue) and SJAP100 (in red), without windage (dashed lines) or including 1% windage (solid lines)

Full size image

We now evaluate the model skill using two scores, namely an instantaneous skill score defined as (Molcard et al. 2009):

$$ {SS}_1=1-\mathit{\min}\left(\frac{d_j}{S_j},1\right) $$

and a cumulative skill score defined as (Liu and Weisberg 2011):

$$ {SS}_C=1-\mathit{\min}\left(\frac{\sum_{i=1}^j{d}_i}{\sum_{i=1}^j{D}_i},1\right) $$

In the above equations, Sj and Dj are measured on the observed drifter track, with Sj being the linear distance between the deployment location and the observed location at an evaluation point (location or time segment) j, and Dj being the distance that the drifter travels between evaluation locations j and j-1; and, finally, dj is the separation distance between the virtual and observed trajectories at the evaluation point j.

The two scores evaluate two aspects of the model’s ability to reproduce an observed drifter trajectory: the cumulative score evaluates how the well model reproduces the entire path of a drifting object up to a specified time, while the instantaneous score evaluates how closely the model reproduces an observed drifter’s location at a specified time. The cumulative score is a more demanding metric, as in order to reach a value closer to 1, it requires accurate prediction of the direction and magnitude of the drift at all times throughout the observed drifter’s path. On the other hand, the instantaneous score is of practical value in use in, for example, marine search and rescue and oil spill response, as it evaluates the distance between the virtual and real (observed) drift locations at a specified evaluation point, scaled by the linear distance between the present and initial positions of the drifting object. Knowledge of the model’s instantaneous skill along with the last observed position of a search target therefore allows a practical search radius around the predicted model position to be deduced.

Figure 13 presents the skill scores of the virtual drift evaluated against the 129 observed drift trajectories. First, we identify a drastic difference between the two types of scores in terms of their variations with the progression in time relative to the initial deployment time. The mean cumulative score decreases rapidly with time, with typical values of 0.2–0.3 after 0.5 h, and negligibly small values after 1.5 h. The instantaneous scores show much slower changes with time, with non-negligible values 24 h after the initial deployment.

Fig. 13
figure 13

The instantaneous (left column) and cumulative skill scores (right column) for the virtual trajectories as a function of time (in hours), evaluated against the observed trajectories by (top row) AST (‘Barrel’), (middle row) iSphere (‘Sphere’) and (bottom row) CODE/Davis (‘Davis’) drifters. In each group, 8 coloured bars are 8 grouped into 4 pairs according to colour: (from left to right) red, blue, green and yellow denoting the inclusion of 0, 0.5%, 1% and 3% windage in virtual drifter calculation. In each pair, the solid (cross-hatched) coloured bar on left (right) corresponds to calculation using SJAP100 (BoF500) model results

Full size image

Next, we assess the impacts of windage values on the skill scores. For both the instantaneous and cumulative scores, adding 3% windage obtains the overall lowest score values. For windage values of 0, 0.5% and 1%, the cumulative score does not show obvious differences. For the evaluation with the AST and iSphere drifters, adding 1% windage obtains the overall highest instantaneous scores. This is consistent with the ‘Eulerian Leeway’ model (Röhrs et al. 2012), in which both the direct wind effects and wave-induced circulation are parameterized as a function of wind speed. Without adding windage, the instantaneous score evaluated with the iSphere drifters decreases significantly with time, in fact lower than the score of adding 3% windage. This indicates the strong influence of winds on this type of drifter, which can be related to the large (1:1) ratio of the exposed versus submerged cross-section area in their configuration. Finally, regarding the differences in scores computed using currents from models with different horizontal resolutions, we found that for evaluations with the CODE/Davis drifters, the instantaneous score is generally higher based on the SJAP100 model, but the cumulative score is slightly higher based on the BoF500 model at 0.5 h after the initial deployment. For evaluations with the AST and iSphere drifters, the cumulative scores are slightly higher based on SJAP100 at 0.5 h after the initial deployment, while the instantaneous scores are higher based on BoF500 using 0.5% or 1% windage after 12, 18 and 24 h after the initial deployment.

5 Summary

In this work, a three-level one-way nested model for the Saint John harbour is developed based on version 3.6 of the structured grid NEMO framework. The model includes fully baroclinic processes forced by surface momentum and buoyancy fluxes, lateral forcing of strong tides and the large-scale ocean variations on the adjacent shelf and deep ocean, and the significant river runoff connected to the harbour through a complicated river-lake system. The following main technical challenges were solved during the development: (1) The barotropic component of the lateral open conditions is modified to include the river forcing by using the observed water levels near the river mouth, due to the absence of observed river runoff. (2) The offset in the reference levels for sea levels of the model and tidal gauge observations is determined, and a correction (offset) is applied to the observed water level time series before providing it to force the model. (3) The bottom drag coefficient in areas with strong tidal flow is adjusted to keep the model stable and to improve the accuracy of tidal solutions. (4) A mixed treatment of lateral open boundary conditions for different physical variables is designed, and, in particular, the barotropic tidal signal is removed from the large-scale model (RIOPS) solution, and the solution of a more accurate barotropic tidal model (WebTide) is used to force the outermost nested grid.

The accuracy of the model solution is assessed using a variety of observational data, including sea level, current, temperature, salinity and surface drifter trajectories. The model solution has a good accuracy for tidal elevations in the Saint John harbour area, overestimating the observed amplitudes and phases by no more than 5 cm and 7° for any of the three largest constituents. Comparing BoF500 with historical stations around the bay, the average error for M2 is only 11 cm and 3.7°. The largest M2 error is found near the head of the bay where the M2 amplitude reaches 6 m. In these areas, we expect that including a wetting/drying scheme will help to improve the model accuracy. In terms of tidal currents, the model reproduces well the main properties of the tidal ellipses derived from ADCP observations in the Saint John harbour, as well as the variations of these properties in the horizontal and vertical spaces.

The model reproduces the observed variability of the residual water level at the Saint John tide gauge well at all time scales, including stronger (weaker) high-frequency fluctuations in fall-winter (spring-summer), with a correlation of 0.63 between the observed and SJAP100 time series. The model also captures the observed variability of the residual current, including the distribution of spectral energy according to frequencies. In particular, the model accurately captures the direction and magnitude of the flow variations associated with the fall freshet in October 2015. However, the model underestimates the magnitude of the southeastward time-mean current in Saint John harbour, which may be related to nonlinear interaction processes that are not fully resolved.

The density structure in the study area is dominated by changes in salinity. The model reproduces the observed salinity variations accurately, in terms of both the vertical structure and the horizontal variations from the inner to the outer harbour. Averaged over all 81 CTD casts, the salinity bias in SJAP100 is only 0.07 psu. The best agreement is found in the outer harbour, where the range of the salinity variations is small. In the inner harbour and approach, the model reproduces the large ranges of the salinity variations associated with the presence of a freshwater plume. The modelled temperature also shows good agreement with CTD observations in the outer harbour, but there is a warm bias in the inner harbour leading to an overall warm bias of 0.56 °C. The modelled SST agrees well with that from a Smart Atlantic buoy in the harbour approach area, in terms of both the seasonal and sub-seasonal variations. The model has a small warm bias of 0.45 °C at the buoy, and this bias is obvious in spring (May, June) but not in fall (September to December). The seasonal evolution of the large-scale SST variations in BoF500 matches well with the satellite-based CMC analysis product, and is a marked improvement from the coarser resolution RIOPS solution, most likely due to RIOPS’s weaker tidal residual circulation associated with the weaker nonlinear dynamics. Hence, enabling the simulation of the detailed variations in the nearshore area is a significant additional benefit of the high-resolution models which would be the better representation of the nonlinear dynamics.

The modelled surface currents are combined with wind fields to compute ‘virtual trajectories’ for comparison with the observed tracks of three different types of surface drifters. The observed and modelled trajectories are both complicated but overall show good agreement in terms of the direction and distances of drift. We apply two different skill scores to assess the dependence of calculation of virtual tracks on (a) the specification of windage, and (2) the use of surface currents from models with different horizontal resolutions. The values of the cumulative score rapidly decrease with time, possibly related to the high turbulent nature of the flow variations in the region. The instantaneous score decreases much more slowly with time, suggesting that the virtual tracks can be used to constrain the potential search area for a drift object. The evaluation suggests overall that 1% is an optimal value for windage for this setting. Regarding the dependence on the model’s resolutions, the evaluation results are mixed. Higher instantaneous scores for CODE/Davis drifters are obtained using the modelled currents from SJAP100. For AST and iSphere drifters, currents from the coarser resolution BoF500 performed best.

Additional work is needed to improve the drifter analysis and evaluation. For example, both the observed and virtual tracks show distinct characteristics between the area near the Saint John harbour, and the southern area further away from the harbour (Fig. 12). The differences may be related to the differences in tidal flow, residual flow forced by wind or river runoff and the mean flow or transient eddies due to the nonlinear dynamics. Separating these different components, analysing the spatial patterns of their variation characteristics, and assessing their relative contributions to the virtual tracks, will all help to refine the quantification on the influences of windage and model resolution on the skill scores. Furthermore, we also expect that the scores may vary in different seasons, as we have noted the distinct seasonal variations in terms of the magnitudes of high-frequency residual currents. The 129 drifters used for providing observed tracks were mostly deployed during the summer and in fair weather conditions, with only one set deployed in the winter months. As marine accidents or oil spills are more likely to occur under poor weather conditions, further deployments in a broader range of meteorological conditions are needed for more comprehensive evaluation of the drifter prediction.

Aside from improving the robustness of the drifter analysis, we are pursuing several avenues of future work. First, we are conducting sensitivity tests to better understand how model parameters change the flow throughout the model. Secondly, we anticipate that including wetting/drying in the model will improve the accuracy of the tidal solutions, particularly in the upper Bay of Fundy, and the residual currents in the Saint John harbour area. Thirdly, we plan to add the minor semi-diurnal tidal constituents that make non-negligible contributions to water level and currents. Finally, we plan to carry out more in depth studies on the complicated physical processes in the region, including oscillating tidal fronts, non-stationary tidal eddies and movement and mixing of ‘double salt wedges’ in the estuary that are qualitatively reproduced by the model.

This study demonstrates a successful application of the NEMO model to a coastal region with the presence of strong tides, significant river runoff and complicated geometry. This enables the Government of Canada to achieve a nearly ‘seamless’ operational ocean forecasting system covering the global, basins, shelf and coastal seas and nearshore waters, based on NEMO. Clearly, more work is needed to improve the system and enhance this capacity, and develop applications with the forecasting results in order to improve the numerical guidance in the event of an oil spill and to support the oil spill modelling effort within Canada’s Oceans Protection Plan.