Analysis of one-dimensional models for exchange flows under strong stratification

Abstract

One-dimensional models of exchange flows driven by horizontal density gradients are well known for performing poorly in situations with weak turbulent mixing. The main issue with these models is that the horizontal density gradient is usually imposed as a constant, leading to non-physically high stratification known as runaway stratification. Here, we propose two new parametrizations of the horizontal density gradient leading to one-dimensional models able to tackle strongly stratified exchange flows at high and low Schmidt number values. The models are extensively tested against results from laminar two-dimensional simulations and are shown to outperform the models using the classical constant parametrization for the horizontal density gradients. Four different flow regimes are found by exploring the parameter space defined by the gravitational Reynolds number Re_g, the Schmidt number Sc, and the aspect ratio of the channel Γ. For small values of Re_gΓ, when diffusion dominates, all models perform well. However, as Re_gΓ increases, two clearly distinct regimes emerge depending on the Sc value, with an equally clear distinction of the performance of the one-dimensional models.

1 Introduction

Gravity-driven exchange flows due to horizontal density differences occur in many natural environmental situations, for example, at the junction between two water bodies with different densities, such as the ocean and a river. A gravity-driven exchange flow or gravitational current, broadly defined, is a flow in which denser water flows over the bottom from the dense water body towards the less dense water body, and lighter water flows at the surface in the opposite direction. This type of exchange flows can take various forms, such as lock-exchange type of gravity currents with an initial horizontal density step (Benjamin 1968; Shin et al. 2004), the gravitational circulation in estuaries (Hansen and Rattray 1965; MacCready 2004; Burchard and Hetland 2010; Burchard et al. 2011; Geyer and MacCready 2014), natural convection in a closed cavity with heated end walls (Cormack et al. 1974), exchange flows in straits (Gregg et al. 1999; Gu and Lawrence 2005), or exchange flows that are not confined to channels such as the ones occurring in coastal areas close to river plumes (Simpson et al. 1990).

Very often, these exchange flows strongly impact the hydrodynamics of a large surrounding area due to the density stratification they generate. Additionally, strong (vertical) stratification limits vertical mixing in the water column, and these exchange flows are known for driving disproportionately large horizontal transport of different substances such as pollutants, sediment, and microorganisms (Geyer and MacCready 2014). These properties make the understanding of exchange flows of the utmost importance in coastal oceanography.

As a result, models have been developed to estimate their properties, ranging from one-dimensional (1D) water column models (Hansen and Rattray 1965; Blaise and Deleersnijder 2008; Burchard and Hetland 2010), to two-layer models (Gu and Lawrence 2005; Shin et al. 2004) or idealized three-dimensional models with periodic horizontal forcing (Li et al. 2008, 2010), called from now on three-dimensional horizontally periodic models, abbreviated as 3D-HP models. A common challenge of all these models is to parametrize the driving force due to the horizontal difference in density. In 1D or 3D-HP models, the horizontal density differences are often parametrized using an imposed, constant horizontal density gradient. This choice allows to reformulate the governing equations (i.e., those for momentum and transport of salinity or density) in such a way that the mean velocity variable and the mean density variable are independent of the horizontal coordinate (an example of a reformulation is given in Appendix A). This feature is crucial, particularly in the 3D-HP models, for the consistency with periodic boundary conditions and needs to be upheld throughout a simulation. However, an inconvenience of imposing a constant horizontal density gradient is that the steady state is determined by the equilibrium between the imposed gradient and diffusion of both momentum and density. This equilibrium causes the stratification to grow out of bounds, a phenomenon usually called “runaway stratification.”

The extent to which 1D models and 3D-HP models are affected by runaway stratification differs. For example, in early 1D models of the gravitational circulation (Hansen and Rattray 1965; Chatwin 1976), the stratification generated by the density gradients was limited by turbulent mixing due to tides, via the eddy viscosity and eddy diffusivity constants. The magnitude of the exchange flow was assumed to be proportional to the horizontal density gradient and the mean eddy viscosity. The eddy viscosity coefficient was then tuned to fit the measurements (Hansen and Rattray 1965; Chatwin 1976; MacCready and Geyer 2010). If chosen sufficiently high, it was able to counterbalance the increasing stratification. However, in estuaries characterized by very weak tides, the magnitude of the required eddy viscosity turned out to become unrealistically large (Simpson et al. 1990). In 3D-HP models, adjusting the eddy viscosity is not an option, since (a large part of) it is directly resolved in the numerical computations (e.g., in an LES) and can, therefore, not be imposed. Accordingly, the value of the horizontal density gradient should be kept low to avoid runaway stratification. This constraint implies that only exchange flows driven by very weak density gradients can be investigated with existing 3D-HP models. An improved parametrization of the horizontal density gradient is required to allow application of 3D-HP models, and even 1D models, to zones of the parameter space currently out of reach due to runaway stratification. Application of new and improved parametrizations in these 3D-HP models requires conservation of the linearity of the horizontal density gradient to properly satisfy the periodic boundary conditions in the horizontal direction.

In the present study, we isolated the ingredients generating environmental exchange flows (i.e., an initial horizontal density gradient and a quasi-infinite source of potential energy), and analyzed and modelled the resulting flow. We first propose a two-dimensional (2D) numerical setup to simulate idealized exchange flows inside a channel for both the transient and the steady-state flow. This setup is similar to those used in previous numerical and experimental studies on idealized gravity-driven exchange flow (see, e.g., Anati et al. 1977; Maderich et al. 1998; Hogg et al. 2001). Subsequently, numerical simulations using this setup are performed to characterize the stratification process associated with horizontal density gradients as a function of the parameters of the problem. The results of the 2D model are then used to develop improved 1D models for the cross-sectional velocity profile along the channel and for the density profile at the center of the channel (with respect to the inlet and outlet). The performance of the models is discussed as a function of their suitability to be incorporated in water column models and their suitability as homogeneous forcing in 3D-HP models.

2 Two-dimensional asymptotic model for exchange flows

2.1 Numerical setup

The numerical setup for the 2D simulations is displayed in Fig. 1. The flow is described in a Cartesian reference frame (x,z), in which x represents the along-channel direction and z represents the vertical direction, with velocity vector u = (u,w). Gravity acts in the negative z-direction. The setup, which is inspired by different experimental configurations (see, for example, Simpson and Linden1989; Meyer and Linden 2014; Lefauve et al. 2018), consists of two reservoirs connected by a channel of height h and length L, with L ≫ h (implicitly assuming that end effects at x = ±L/2 can be ignored). Each reservoir contains water with a different initial salt concentration, denoted by the salinities s₁ and s₂ in the left and right reservoirs, respectively. Initially, the salinity s(x,z) in the channel is uniform in the vertical, and the salinity gradient in the along-channel direction is constant: ∂s/∂x = (s₂ − s₁)/L. The salt concentration is the only physical quantity altering the fluid density in the present setup.

Fig. 1

Side view of the 2D computational domain, with the initial distribution of salt. This sketch is not to scale as L ≫ h and we assume very large salt reservoirs. The salt concentration in the left reservoir is denoted by the salinity s₁ and will be kept constant (as we assume an infinitely large reservoir). Similarly, the salt concentration in the right reservoir is denoted s₂ > s₁ (and also kept constant). The acceleration of the gravity g is in the negative z-direction

The inhomogeneous initial horizontal salt distribution leads to an unstable horizontal density gradient driving an exchange flow and generating vertical stratification. The steady state is reached once the driving mechanism (due to the density difference between the two reservoirs) is balanced by diffusion of both momentum and salt. Since this setup represents environmental situations where the availability of the fresher and saltier water can be considered infinite, the reservoirs are much larger than the channel. In this way, the salinity of each reservoir can be considered constant and will not be influenced by the inflow of water from the other reservoir. In our 2D computational model, the size of a reservoir is equal to 6400h², which is basically a trade-off between available computational resources and keeping the salinity in both reservoirs within an accepted margin of their initial values.

The 2D numerical setup is implemented in COMSOL, using the “laminar flow” and the “transport of diluted species” modules (for details, see COMSOL multiphysics reference manual, version 5.3.). The flow is governed by the 2D continuity and Navier-Stokes equations in Boussinesq approximation for an incompressible fluid:

$$ \begin{array}{@{}rcl@{}} \frac{\partial u}{\partial x}+\frac{\partial w}{\partial z} & = & 0~, \end{array} $$

(1)

$$ \begin{array}{@{}rcl@{}} \frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+w\frac{\partial u}{\partial z} & = & -\frac{1}{\rho_{\text{ref}}}\frac{\partial p}{\partial x}+\nu \left( \frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial z^{2}} \right) , \end{array} $$

(2)

$$ \begin{array}{@{}rcl@{}} \frac{\partial w}{\partial t}+u\frac{\partial w}{\partial x}+w\frac{\partial w}{\partial z} & = & -\frac{1}{\rho_{\text{ref}}}\frac{\partial p}{\partial z}+\nu \left( \frac{\partial^{2} w}{\partial x^{2}}+\frac{\partial^{2} w}{\partial z^{2}} \right)\\ && - \frac{1}{\rho_{\text{ref}}}\tilde{\rho}g~, \end{array} $$

(3)

where p denotes the pressure, and $\tilde {\rho }$ denotes the variable part of the total density. The constant ν represents the kinematic viscosity of the fluid (which is assumed to be independent of the salinity). The density ρ_ref is a reference density, related to the total density ρ and to $\tilde {\rho }$ by $\rho = \rho _{\text {ref}}+\tilde {\rho }$, with $\rho _{\text {ref}} \gg \tilde {\rho }$. The salinity s is governed by the advection-diffusion equation:

$$ \frac{\partial s}{\partial t}+ u\frac{\partial s}{\partial x}+ w\frac{\partial s}{\partial z} = \kappa \left( \frac{\partial^{2} s}{\partial x^{2}} + \frac{\partial^{2} s}{\partial z^{2}} \right) , $$

(4)

in which κ is the diffusivity of salt. The density ρ depends on the salinity s, via the equation of state $\rho = \rho _{0}\left (1+\beta s \right )$, in which ρ₀ is the density of fresh water and β≅ 7.7 × 10^− 4 (MacCready 2004; Geyer and MacCready 2014). The salinity is expressed in the practical salinity scale (PSS). The reference density is defined as $\rho _{\text {ref}}=\rho _{0}[1+\frac {1}{2}\beta (s_{1}+s_{2})] = \rho _{0}(1+\beta s_{\text {av}})$, with $s_{\text {av}}=\frac {1}{2}(s_{1}+s_{2})$ the average salinity of both reservoirs. The equation of state for the variable part of the density is then

$$ \tilde{\rho} = \rho_{0}\beta [s-\frac{1}{2}(s_{1}+s_{2})] = \rho_{0}\beta (s-s_{\text{av}})~. $$

(5)

For simplicity, only exchange flows with constant viscosity ν and salt diffusivity κ are considered, i.e., no turbulence model is used. Furthermore, simulations are stopped and results rejected for further analysis, once shear instabilities start to develop at the quasi-horizontal density interface, during the flow evolution for simulations for high Reynolds number values. This justifies the use of a 2D numerical setup instead of a 3D one, saving computational time and allowing for a thorough exploration of the parameter space. The use of a constant kinematic viscosity and salt diffusivity for application to coastal flows can be regarded as considering a constant effective turbulent (or eddy) viscosity and diffusivity. This simplification is common in classical studies of exchange flows (see, e.g., Geyer and MacCready 2014), and it is used here because it allows for analytical solutions that further our understanding of the system.

Initially, the fluid is at rest and the salinity in each reservoir is uniform. In the channel, the salinity at initial time t₀ is given by

$$ s(x,z;t_{0}) = \frac{\Delta s}{L}x + s_{\text{av}}~~~{\text{for}}~~~-\frac{1}{2}L\le x\le \frac{1}{2}L~, $$

(6)

where the initial salinity difference Δs = s₂ − s₁ has been introduced. As a result, the isopycnals at t = t₀ are vertical and equidistant. The horizontal density gradient in the center of the channel (x = 0) is given by

$$ \frac{\partial \tilde{\rho}}{\partial x}(x=0,z;t_{0}) = \frac{\Delta \rho}{L} , $$

(7)

with Δρ = ρ₀βΔs the initial density difference. Subsequently, $\tilde {\rho }$ at x = 0 is equal to zero at t = t₀ over the whole depth.

At the solid walls of both reservoirs and the channel, no-slip boundary conditions are applied for the fluid velocity and no-flux boundary conditions for the salinity. This choice of boundary conditions in the channel results in an antisymmetric horizontal velocity profile with respect to z = 0 at x = 0. Additionally, the profile of the variable density ${\tilde {\rho }}$ and salinity ${\tilde {s}}$ are also antisymmetric with respect to z = 0 at x = 0. The case with a no-slip boundary condition for the fluid velocity at the bottom and a no-stress boundary condition at the top of the channel is discussed in Section 3.4.

The equations are solved in their non-dimensional form. To make them dimensionless, the buoyancy velocity scale U_g is introduced and linked to the previously defined Δs:

$$ U_{g} = \sqrt{\frac{\rho_{0}\beta{\Delta} s}{\rho_{\text{ref}}}gh} = \sqrt{\frac{\beta{\Delta} s}{1+\beta s_{\text{av}}}gh}~. $$

(8)

The spatial coordinates are scaled with h, time with a buoyancy time scale h/U_g, the fluid velocities with U_g, the pressure with $\rho _{\text {ref}}{U_{g}^{2}}$, the density with Δρ, and the salinity with Δs. By eliminating the density in Eqs. 3 using 5, the set of Eqs. 1–4 are rewritten in non-dimensional form yielding

$$ \begin{array}{@{}rcl@{}} \frac{\partial u^{*}}{\partial x^{*}}+\frac{\partial w^{*}}{\partial z^{*}} & = & 0~, \end{array} $$

(9)

$$ \begin{array}{@{}rcl@{}} \frac{\partial u^{*}}{\partial t^{*}}+u^{*}\frac{\partial u^{*}}{\partial x^{*}}+w^{*}\frac{\partial u^{*}}{\partial z^{*}} & = & -\frac{\partial \tilde{p}^{*}}{\partial x^{*}}+\frac{1}{\textsf{Re}}_{\text{g}} \left( \frac{\partial^{2} u^{*}}{\partial x^{*2}}+\frac{\partial^{2} u^{*}}{\partial z^{*2}} \right) , \end{array} $$

(10)

$$ \begin{array}{@{}rcl@{}} \frac{\partial w^{*}}{\partial t^{*}}+u^{*}\frac{\partial w^{*}}{\partial x^{*}}+w^{*}\frac{\partial w^{*}}{\partial z^{*}} & = & -\frac{\partial \tilde{p}^{*}}{\partial z^{*}}+\frac{1}{\textsf{Re}}_{\text{g}} \left( \frac{\partial^{2} w^{*}}{\partial x^{*2}}+\frac{\partial^{2} w^{*}}{\partial z^{*2}} \right)\\ &&- \left( s^{*}-\frac{1}{2}s^{*}_{\text{av}}\right) , \end{array} $$

(11)

$$ \begin{array}{@{}rcl@{}} \frac{\partial s^{*}}{\partial t^{*}}+ u^{*}\frac{\partial s^{*}}{\partial x^{*}}+ w^{*}\frac{\partial s^{*}}{\partial z^{*}} & = & \frac{1}{\textsf{Re}_{\text{g}}\textsf{Sc}} \left( \frac{\partial^{2} s^{*}}{\partial x^{*2}} + \frac{\partial^{2} s^{*}}{\partial z^{*2}} \right) , \end{array} $$

(12)

where the asterisk (^∗) denotes a non-dimensional variable. In the case that the left reservoir contains fresh water, thus with s₁ = 0, $s^{*}_{\text {av}}=s_{2}/2$ and $U_{g} = \sqrt {\beta gh s_{2}/(1+\frac {1} {2}\beta s_{2})}$. In these equations, there are two non-dimensional parameters: the gravitational Reynolds number Re_g = U_gh/ν and the Schmidt number Sc = ν/κ. The last non-dimensional number that we need to introduce is the aspect ratio Γ = h/L, that does not appear explicitly in Eqs. 9–12 but plays a role via the computational domain. Note that the Grashof number Gr, which quantifies the ratio of the buoyancy to viscous force, is related to the Reynolds number such that $\textsf {Gr}=\textsf {Re}_{\text {g}}^{2}$. Both Gr and Re_g are commonly used to characterize density-driven flows governed by Eq. 12 (see, e.g., Ottolenghi et al. 2016; Härtel et al.2000). Here, we will use the Reynolds number throughout.

The momentum equations are discretized using a first-order finite-element method for the pressure and the velocity. The equation for the transport of salt is discretized using a quadratic method. The computational domain is meshed with a triangular grid, using 62 elements over the depth of the channel. The time-integration is performed with an implicit backward-difference scheme (more details about spatial discretization, grids, and time integration can be found in COMSOL multiphysics reference manual, version 5.3). The grid in the reservoirs is coarser since these reservoirs act just as a supply of water and salt, and the details of the hydrodynamics in these reservoirs are not of interest to us in the present investigation.

2.2 Salinity distribution in the channel: flow regime identification

Depending on the values of the parameters Re_g, Sc, and Γ, the initial situation evolves towards a steady state governed by the competition between diffusive and advective processes. In this section, we describe the steady-state conditions of four distinct flow regimes: the diffusion-dominated regime, the transition regime, the high-advection/high-diffusion regime, and the high-advection/low-diffusion regime. We show results for three simulations with Sc = 300 and Γ = 1/60 for which we varied the value of the gravitational Reynolds number, and one simulation with Sc = 1, Γ = 1/60 and Re_g = 5000. For these four simulations in the steady state, Fig. 2 shows the density field and the isopycnals, and Fig. 3 shows the vertical profiles of density, of the horizontal density gradient, and of the mean horizontal velocity for x = 0. The results of a thorough exploration of the parameter space are presented in Section 3.3.

Fig. 2

The density distribution in the channel (not to scale as h ≪ L) for four simulations in the four different regimes: a the diffusion-dominated regime (here with Re_g = 50, Sc = 300 and Γ = 1/60), b the transition regime (Re_g = 200, Sc = 300 and Γ = 1/60), c the high-advection/high-diffusion regime (Re_g = 5000, Sc = 1 and Γ = 1/60), and d the high-advection/low-diffusion regime (Re_g = 1000, Sc = 300 and Γ = 1/60). Note that ${\tilde {\rho }}/{\Delta } \rho = s^{*} - s^{*}_{\text {av}}$. With s₁ = 0 this implies $s^{*}_{\text {av}}=\frac {1}{2}$ and 0 ≤ s^∗≤ 1 and thus $-0.5\le {\tilde {\rho }}/{\Delta } \rho \le 0.5$

Fig. 3

The profiles at x = 0 of the resolved density (a), the horizontal density gradient (b) , and the mean horizontal velocity (c) in the steady state for the same four simulations used to describe the four regimes in Fig. 2. The solid black line represents the initial condition

In the diffusion-dominated regime, a steady state is reached once the mechanism driving the exchange flow due to the horizontal density gradient is balanced by momentum diffusion, and when the vertical stratification process is balanced by salt diffusion. Effectively, the advective transport of salt from the saltier to the fresher reservoir is fully counteracted. The isopycnals in the steady state of the diffusion-dominated regime are no longer vertical but are sigmoid functions of the depth and resemble the typical lines of equal density observed in some estuaries (MacCready and Geyer 2010), as can be seen in Fig. 2a. The isopycnals are still equidistant close to the center of the channel (around x = 0), suggesting a conservation of the linearity of the initial horizontal density gradient. Additionally, $\tilde {\rho }$ at x = 0 is no longer constant and equal to zero over the height of the channel, as seen in Fig. 3a. The water column is now stratified close to z = 0, and very weakly stratified close to the top and bottom boundaries due to the no-flux boundary condition applied there. Finally, the value of the horizontal density gradient at x = 0 has slightly decreased with respect to its original value, but remains in good approximation constant over the depth of the channel, as seen in Fig. 3b.

In the transition regime, momentum and salt diffusion are no longer strong enough to balance the force driving the exchange flow and the formation of the stratification. This means that net transport of salt from the saltier to the fresher reservoir will occur. In the steady state, water with salinity s₁, flowing along the top wall of the channel, reaches the saltier water reservoir, and water with salinity s₂, flowing over the bottom of the channel, reaches the fresh water reservoir. This process can be observed in Fig. 2b, where the lines of equal density for $\tilde {\rho }/{\Delta } \rho =0$ and $\tilde {\rho }/{\Delta } \rho =\pm 0.2$ span over the entire channel in the horizontal direction between − L/2 ≤ x ≤ L/2. The lines of equal density for $\tilde {\rho }/{\Delta } \rho =\pm 0.4$ do not span the whole channel, suggesting that diffusion of momentum and salt still plays a role in the steady-state balance. The vertical density profile ${\tilde {\rho }}/{\Delta } \rho$ at x = 0 in the transition regime has a similar shape to the density profile in the diffusion-dominated regime, but clearly, with a larger amplitude (Fig. 3a). A clear stratification is present close to z = 0, and a very weak stratification close to the top and bottom boundaries. In comparison with the diffusion-dominated regime, the amplitude of the density profile has increased and $\tilde {\rho }/{\Delta } \rho$ at z = ±h/2 has reached its possible extreme values: ± 1/2 at z = ∓h/2.

In practice, this steady state is achieved already in a finite time denoted by t_s. The profiles of the horizontal density gradient at x = 0 in the steady state (i.e., for t > t_s) are significantly different to those of the diffusion-dominated regime, as seen in Fig. 3b. The horizontal density gradient is no longer constant over the depth. Instead, it has decreased towards zero at the top and bottom boundaries, and it has increased around z = 0, taking the shape of a Gaussian function.

In the high-advection/high-diffusion regime, the density distribution in the steady state is similar to the distribution in the transition regime (see Fig. 2). In both cases, fluid from each reservoir reaches the opposing reservoir, but there is a diffuse interface separating them. Some differences between these two regimes are mainly observed at the ends of the channel. In fact, Fig. 3a shows that the density profile at x = 0 for the simulations in these two regimes are almost indistinguishable. However, the flow velocity (Fig. 3c) is clearly much stronger for the simulation within the high-advection/high-diffusion regime. This implies that in spite of the strong advection by the flow, the interface is spread out due to the high diffusion.

In the high-advection/low-diffusion regime, the steady state is characterized by water from each reservoir being able to reach unmixed the opposite reservoir. Diffusion of both momentum and salt plays hardly a role in balancing the force driving the exchange flow and the stratification. This can be seen in Fig. 2d, where all the isopycnals span over the entire channel length from x = −L/2 to x = L/2 and nearly collapse onto each other: diffusion is too small to smoothen the sharp interface generated by the exchange flow, an advective process. In Fig. 3a, it can be seen that the thickness of the pycnocline decreases drastically and that any vertical stratification is absent close to the channel boundaries. The density in the upper layer is equal to −Δρ/2 while the density in the lower layer is equal to Δρ/2. The horizontal density gradient still takes the shape of a Gaussian function but with a much narrower and much higher peak (Fig. 3b). This observation suggests that as advection becomes increasingly important while diffusion is weak, the steady-state system converges towards a two-layer system. At x = 0, each layer has a constant density equal to Δρ/2 for z < 0 and −Δρ/2 for z > 0. As a result, the density at the top and bottom boundaries in the steady state is given by

$$ \tilde{\rho} \left( x=0,z=\mp \frac{1}{2}h; t\rightarrow \infty \right) = \pm \frac{1}{2}{\Delta} \rho. $$

(13)

It is relevant to mention that, although this relationship must be satisfied in the high-advection/low-diffusion regime, it already emerges in the transition regime and might also occur in the high-advection/high-diffusion regime. Similarly, the horizontal density gradient at those boundaries is given by

$$ \frac{\partial \tilde{\rho}}{\partial x} \left( x=0,z=\mp \frac{1}{2}h; t>{t_{s}} \right) = 0. $$

(14)

3 Proposals for one-dimensional models

Based on the characteristics of the different regimes and the initial condition, it is possible to develop a parametrization of the horizontal density gradient at the center of the channel, x = 0. In this way, the time evolution of the horizontal velocity profile at x = 0 is governed by a 1D diffusion equation supplemented with a specific source term containing information on the horizontal density gradient, and the time evolution of the density profile at this location is governed by a classical 1D advection-diffusion equation.

3.1 Mathematical formulation

The equations governing the 1D model at x = 0 are

$$ \begin{array}{@{}rcl@{}} \frac{\partial u}{\partial t} & = & \nu \frac{\partial^{2} u}{\partial z^{2}}+\frac{g}{\rho_{\text{ref}}}{{\int}_{0}^{z}}\frac{\partial {\tilde{\rho}}}{\partial x}d{\hat{z}}~, \end{array} $$

(15)

$$ \begin{array}{@{}rcl@{}} \frac{\partial \tilde{\rho}}{\partial t} & = & \kappa \frac{\partial^{2} \tilde{\rho}}{\partial z^{2}} - u\frac{\partial \tilde{\rho}}{\partial x}~, \end{array} $$

(16)

in which $\partial \tilde {\rho }/\partial x$ is the term that needs to be parametrized. For a derivation of the momentum equation, the reader is referred to Appendix A. Based on the steady-state horizontal density gradient profiles obtained in Section 2.2, the parametrized horizontal density gradient needs to satisfy three conditions. First, it should be constant over the vertical in the absence of stratification. Second, it should decrease at the boundaries with the onset of stratification. Third, it should increase in the center of the channel once the flow converges towards a two-layer system. We expect then that the parametrized horizontal density gradient $\partial \tilde {\rho }/\partial x$ depends on both $\tilde {\rho }$ and $\partial \tilde {\rho }/\partial z$. A parametrization satisfying these conditions is

$$ \frac{\partial \tilde{\rho}}{\partial x} = a_{0}+a_{1}\left| \tilde{\rho} \right| + a_{2} \left| \frac{\partial \tilde{\rho}}{\partial z} \right|, $$

(17)

where a₀, a₁, and a₂ are constants to be determined. Note that, in the case a₂ = 0, the parametrization resembles the one proposed by Blaise and Deleersnijder (2008), while in the case a₁ = 0 and a₂ = 0, the classical constant horizontal density gradient parametrization is recovered.

To find a₀, the initial condition at t = t₀ in the channel is used: $\tilde {\rho }=0$, $\partial \tilde {\rho }/\partial z=0$ and $\partial \tilde {\rho }/\partial x$ is given by Eq. 7. Substituting these values in the density parametrization given by Eq. 17 yields

$$ a_{0}=\frac{\Delta \rho}{L}. $$

(18)

To find a₁, Eqs. 13 and 14, which are valid from the transition regime, are used in combination with the no-flux boundary condition at the top boundary of the channel, i.e., $\partial \tilde {\rho }/\partial z=0$ at z = h/2 to obtain

$$ a_{1}=-\frac{2}{L}. $$

(19)

Finding a₂ is more challenging and, to our current knowledge, it cannot be obtained from the steady-state conditions in the advection-dominated regime (Section 2.2). We will see in Section 3.2 that its value can be chosen equal to Γ/3 for high Sc values, but we leave a₂ for now.

Equations 15–17 are scaled as in Section 2, i.e., with h for the spatial coordinates, h/U_g for the time, U_g for the velocities, $\rho _{\text {ref}}{U_{g}^{2}}$ for the pressure, and Δρ for the density. This scaling results in

$$ \begin{array}{@{}rcl@{}} \frac{\partial u^{*}}{\partial t^{*}} & = & \frac{1}{\textsf{Re}_{\text{g}}} \frac{\partial^{2} u^{*}}{\partial z^{*2}}+{\int}_{0}^{z^{*}}\frac{\partial \tilde{\rho}^{*}}{\partial x^{*}}d\hat{z}^{*}, \end{array} $$

(20)

$$ \begin{array}{@{}rcl@{}} \frac{\partial \tilde{\rho}^{*}}{\partial t^{*}} & = & \frac{1}{\textsf{Re}_{\text{g}}\textsf{Sc}}\frac{\partial^{2} \tilde{\rho}^{*}}{\partial z^{*2}}-u^{*}\frac{\partial \tilde{\rho}^{*}}{\partial x^{*}}, \end{array} $$

(21)

$$ \begin{array}{@{}rcl@{}} \frac{\partial \tilde{\rho}^{*}}{\partial x^{*}} & = & {\Gamma}\left( 1-2 \left| \tilde{\rho}^{*} \right|\right)+a_{2} \left| \frac{\partial \tilde{\rho}^{*}}{\partial z^{*}} \right|, \end{array} $$

(22)

where the asterisk (^∗) denotes a non-dimensional variable. The aspect ratio Γ was previously a parameter tunable through the computational domain, but in the present 1D model, it appears directly in the equations.

3.2 Limiting cases

The set of Eqs. 20–22 is a priori not integrable analytically. However, by simplifying the equations, it is possible to have an exact solution of the approximated problem, which can in turn provide some scaling properties for the amplitudes of the exchange flow and the stratification.

In the diffusion-dominated regime, the horizontal density gradient is in good approximation constant over the depth, i.e., $\partial \tilde {\rho }^{*}/\partial x^{*}={\Gamma }$, such that the equations governing the flow and the density distribution in a steady state become

$$ \begin{array}{@{}rcl@{}} 0 & = & \frac{1}{\textsf{Re}_{\text{g}}} \frac{\partial^{2} u^{*}}{\partial z^{*2}}+{\Gamma} z^{*}, \end{array} $$

(23a)

$$ \begin{array}{@{}rcl@{}} 0 & = & \frac{1}{\textsf{Re}_{\text{g}}\textsf{Sc}}\frac{\partial^{2} \tilde{\rho}^{*}}{\partial z^{*2}}-{\Gamma} u^{*}. \end{array} $$

(23b)

Using no-slip boundary conditions for the velocity and no-flux boundary conditions for the density at the top and at the bottom wall of the channel, we obtain $u_{d,\infty }$ and $\tilde {\rho }_{d,\infty }$, the steady-state solutions for the velocity and the density in the diffusion-dominated regime

$$ \begin{array}{@{}rcl@{}} \frac{u_{d,\infty}(z)}{U_{g}} & = & \frac{\textsf{Re}_{\text{g}}{\Gamma}}{24}\left( \frac{z}{h}-4\left( \frac{z}{h}\right)^{3} \right), \end{array} $$

(24a)

$$ \begin{array}{@{}rcl@{}} \frac{\tilde{\rho}_{d,\infty}(z)}{\Delta \rho} & = & \frac{\textsf{Re}_{\text{g}}^{2}{\Gamma}^{2}\textsf{Sc}}{24}\left( -\frac{1}{16}\left( \frac{z}{h}\right)+ \frac{1}{6}\left( \frac{z}{h}\right)^{3} - \frac{1}{5}\left( \frac{z}{h} \right)^{5} \right).\\ \end{array} $$

(24b)

It is clear that $u_{d, \infty }$ depends on Re_gΓ (this combination of parameters is also known as the Simpson number) while $\tilde {\rho }_{d,\infty }$ depends on $\textsf {Re}_{\text {g}}^{2}{\Gamma }^{2}\textsf {Sc}$ so that only two parameters govern the steady-state solutions. This solution is commonly known as the viscous-advective-diffusive (VAD) solution (Cormack et al. 1974; Hogg et al. 2001). Notice, however, that it is valid for both low and high Sc values.

As the value of Re_gΓ increases, two distinct possibilities emerge. For small Sc values, the flow will tend towards the hydraulic limit (Hogg et al. 2001). In this limit, mixing, viscosity, and friction are neglected, and the density and velocity both have a two-layer configuration. In each of these layers, the density and velocity can be considered as uniform, and the non-dimensional volume flux becomes independent of Re_gΓ.

For large Sc values, the flow tends towards the high-advection/low-diffusion regime and the density in the channel also converges towards a two-layer system. In this case, the horizontal density gradient reduces to $\partial \tilde {\rho }^{*}/\partial x^{*} = a_{2} \left | \partial \tilde {\rho }^{*}/\partial z^{*} \right | = -a_{2} \partial \tilde {\rho }^{*}/\partial z^{*}$ (as $\partial \tilde {\rho }^{*}/\partial z^{*}\le 0$ for $-\frac {1}{2}\le z^{*}\le \frac {1}{2}$) such that the equations governing the flow and the density distribution become

$$ \begin{array}{@{}rcl@{}} 0 & = & \frac{1}{\textsf{Re}_{\text{g}}} \frac{\partial^{2} u^{*}}{\partial z^{*2}}-a_{2}{\int}_{0}^{z^{*}}\frac{\partial \tilde{\rho}^{*}}{\partial {\hat{z}}^{*}}d\hat{z}^{*}~, \end{array} $$

(25a)

$$ \begin{array}{@{}rcl@{}} 0 & = & \frac{1}{\textsf{Re}_{\text{g}}\textsf{Sc}}\frac{\partial^{2} \tilde{\rho}^{*}}{\partial z^{*2}}+a_{2} u^{*}\frac{\partial \tilde{\rho}^{*}}{\partial z^{*}}. \end{array} $$

(25b)

The last term in the first equation can be integrated, and in the limit $\textsf {Sc} \to \infty$, the system of Eq. 25a, b can be rewritten as

$$ \begin{array}{@{}rcl@{}} \frac{\partial^{2} u^{*}}{\partial z^{*2}} &=& {\textsf{Re}_{\text{g}}}a_{2} {\tilde{\rho}}^{*}~, \end{array} $$

(26a)

$$ \begin{array}{@{}rcl@{}} a_{2} u^{*}\frac{\partial \tilde{\rho}^{*}}{\partial z^{*}} &=& 0. \end{array} $$

(26b)

The non-trivial solution (i.e., with u^∗≠ 0) for Eq. 26b is the steady-state solution for the density in the high-advection/low-diffusion regime where $\tilde {\rho }^{*}$ is a constant. However, this solution can have a jump at z = 0 since u^∗(z = 0) = 0 due to symmetry. This can be seen by integrating (26b) from z = −𝜖 to z = +𝜖 (with 𝜖 a positive real number) yielding

$$ \lim_{\epsilon \downarrow 0} u^{*}(z=0)[\tilde{\rho}^{*}(z=+\epsilon)-\tilde{\rho}^{*}(z=-\epsilon)]=0. $$

Since u^∗(z = 0) = 0, $[\tilde {\rho }^{*}(z=+\epsilon )-\tilde {\rho }^{*}(z=-\epsilon )]$ can take any value. This means that the solution to Eq. 26b is a piecewise constant function, and in agreement with Eq. 13, we take

$$ \displaystyle \frac{\tilde{\rho}_{a,\infty}(z)}{\Delta \rho} = \frac{1}{2} - H(z)~, $$

(27)

where H(z) is the Heavyside function which is defined as: H(z > 0) = 1, H(z < 0) = 0, and H(z = 0) = 1/2. Moreover, dH(z)/dz = δ(z) with δ(z) the Dirac delta function (which also satisfies ${\int \limits }_{-\infty }^{+\infty } \delta (z)=1$ and ${{\int \limits }_{0}^{z}} \delta (z)=\frac {1}{2}$). The steady-state solution for the velocity in the high-advection/low-diffusion regime, $u_{a,\infty }$, follows:

$$ \frac{u(z)_{a,\infty}}{U_{g}}= \left\lbrace \begin{array}{ll} \displaystyle \textsf{Re}_{\text{g}} a_{2} \left[\frac{1}{8}\frac{z}{h}+\frac{1}{4}\left( \frac{z}{h}\right)^{2}\right] & \text{ for }z\leq 0, \\ &\\ \displaystyle \textsf{Re}_{\text{g}} a_{2} \left[\frac{1}{8}\frac{z}{h}-\frac{1}{4}\left( \frac{z}{h}\right)^{2} \right] & \text{ for }z\geq 0. \end{array} \right. $$

(28)

From this solution, the constant a₂ can be determined by assuming that the shear at z = 0 is conserved from the diffusion-dominated (obtained from Eq. 24a) regime to the advection-dominated regime, which gives

$$ a_{2} = \frac{1}{3}{\Gamma}~. $$

(29)

This also means that the magnitude of the velocity and the volume flux still depend exclusively on Re_gΓ as long as the Sc value is large. We use the 2D simulations to test this assumption. The resulting shear at z = 0 is displayed as a function of Re_gΓ in Fig. 4. Despite some small deviations, there is a good agreement between our assumption and the 2D numerical data for high Schmidt number values where the flow is dominated by the shear at the interface. Clearly, this agreement is not as good for low Schmidt number values and large values of Re_gΓ (i.e., towards the high-advection/high-diffusion regime and the hydraulic limit). The difference between these two limiting cases is that in the high-advection/low-diffusion regime, viscosity and friction play a role close to the top and bottom boundaries and at the interface so that the velocity is not uniform in each of the layers.

Fig. 4

Shear at mid-depth as a function of Re_gΓ spanning all different flow regimes, from the diffusion-dominated to the high-advection/low-diffusion. Low Schmidt number values correspond to Sc = 1, and high Schmidt number values correspond to Sc = 50, 300, and 1000

The ability of the 1D model to reproduce correctly the steady-state velocity profiles and density profiles in the different regimes determines its validity. This ability is investigated in the next section by comparing the results of the new 1D model to results of the 2D model, and to results from 1D models using more classical parametrizations of the horizontal density gradient.

3.3 Numerical results: model comparison

The 1D set of non-dimensional Eqs. (20)–(22) is integrated numerically using a centred finite-difference scheme for the spatial derivatives, a trapezoidal numerical method for the integral and an explicit upwind time integration scheme. The numerical algorithm is, therefore, globally first-order accurate in time and second-order accurate in space. The steady-state results of the 1D model are compared with the steady-state results (evaluated for t > t_s) of the 2D model in terms of four different quantities: (i) the amplitude of the stratification ${\Delta } \tilde {\rho }=\tilde {\rho }(-\frac {1}{2}h)-\tilde {\rho }(\frac {1}{2}h)$, (ii) the integral over the channel cross section of the absolute value of the density, (iii) the amplitude of the exchange flow ${\Delta } u_{\max \limits }=u_{\max \limits }-u_{{\min \limits } }$, and (iv) the integral of the absolute value of the velocity profile over the channel cross section.

We consider three versions of the 1D model: the 1D0 model, where a₀ = Δρ/L and a₁ = a₂ = 0, which corresponds to the classical parametrization with a constant, uniform horizontal density gradient; the 1D1 model, where a₀ = Δρ/L, a₁ = − 2/L and a₂ = 0, which is similar to the parametrization suggested by Blaise and Deleersnijder (2008); and the new 1D2 model, where a₀ = Δρ/L, a₁ = − 2/L, and a₂ = Γ/3. In the present study, four different values of the Schmidt number Sc are considered: 1, 50, 300, and 1000, and three different values of the aspect ratio, Γ = 1/30, 1/60, and 1/120. The value of the Reynolds number Re_g is varied between 2 and 4000. For certain combinations of Re_g, Γ and Sc, the simulations show the emergence of shear instabilities, such as the appearance of Kelvin-Helmholtz billows. These simulations are not considered in the analysis as they are outside the scope of the present investigation.

In Fig. 5, the magnitude of the steady-state stratification ${\Delta } \tilde {\rho } / {\Delta } \rho$ and the steady-state exchange flow are first analyzed only for the 2D model. The main objective of this figure is to provide a first impression of the different trends that the 1D models should be able to reproduce. When plotting the magnitude of the steady-state stratification ${\Delta } \tilde {\rho }/{\Delta } \rho$ as a function of $\textsf {Re}_{\text {g}} {\Gamma } \textsf {Sc}^{1/2}$ (Fig. 5a), there is a clear collapse of the data. This collapse indicates that $\textsf {Re}_{\text {g}} {\Gamma } \textsf {Sc}^{1/2}$ is the governing parameter for the stratification. For small values of $\textsf {Re}_{\text {g}}{\Gamma }\textsf {Sc}^{1/2}$, ${\Delta } \tilde {\rho }/{\Delta } \rho$ follows the theoretical curve of the diffusion-dominated regime. For intermediate values of $\textsf {Re}_{\text {g}}{\Gamma }\textsf {Sc}^{1/2}$, ${\Delta } \tilde {\rho }/{\Delta } \rho$ deviates from this theoretical curve as the increase in stratification slows down. In this transition, the data points for Sc = 1 lie slightly under the data points for other Sc values. For high values of $\textsf {Re}_{\text {g}}{\Gamma }\textsf {Sc}^{1/2}$, ${\Delta } \tilde {\rho }/{\Delta } \rho$ reaches its maximum possible value when ${\Delta } \tilde {\rho }={\Delta } \rho$. This value corresponds to the initial density difference between the reservoirs. It is possible to define a transition point indicating the intersection between the theoretical line of the diffusion-dominated regime and the line given by ${\Delta } \tilde {\rho }/{\Delta } \rho =1$. This transition occurs at $\textsf {Re}_{\text {g}}{\Gamma }\textsf {Sc}^{1/2}=12\sqrt {5}\approx 26.8$.

Fig. 5

Magnitude of the steady-state stratification (a) and the steady-state exchange flow scaled with Sc^1/2 (b) as a function of $\textsf {Re}_{\text {g}} {\Gamma } \textsf {Sc}^{1/2}$ as obtained from the 2D simulations. Different Schmidt number values are displayed with different colors. The gray solid line represents the analytical solution in the diffusion-dominated regime (i.e., the solution to Eqs. 24b and 24a), and the gray dashed line represents the analytical solution for the high-advection/low-diffusion regime (i.e., the solution to Eqs. 27 and 28). Both of these solutions are derived in Appendix B. The black vertical dashed line at $\textsf {Re}_{\text {g}}{\Gamma }\textsf {Sc}^{1/2}=12\sqrt {5}$ represents the transition at which the two analytical solutions for ${\Delta } \tilde {\rho }/{\Delta } \rho$ intersect

The magnitude of the exchange flow obtained from the reference 2D model shows a clearly distinct behavior between high and low Schmidt number values (Fig. 5b). This magnitude follows the theoretical line of the diffusion-dominated regime for relatively small values of Re_gΓ for both low and high values of the Schmidt number. Slightly before the transition point at $\textsf {Re}_{\text {g}}{\Gamma }\textsf {Sc}^{1/2}=12\sqrt {5}$, it deviates (in a rather subtle way) towards the theoretical prediction for the high-advection/low-diffusion regime (high Schmidt number values). However, for low Schmidt number values, the deviation is more pronounced since the solution tends towards the hydraulic limit, where the velocity becomes independent of Re_gΓ. Note, however, that our simulations do not reach this limit since the simulations with Sc = 1 go up to a value of Re_gΓ ≈ 10², while the hydraulic limit is reached for Re_gΓ ≈ 10³ (Hogg et al. 2001).

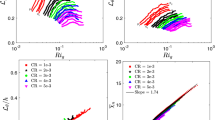
The performance of the 1D models is tested through an analysis of the magnitude of the steady-state stratification in Fig. 6. A distinction is made between the results for high Schmidt number values, Sc = 50,300,1000, shown in Fig. 6a, b, and for low Schmidt number value, Sc = 1, shown in Fig. 6c, d. The different 1D models reproduce the results from the 2D model with different levels of accuracy. The stratification predicted by the 1D0 model grows linearly with $(\textsf {Re}_{\text {g}}{\Gamma }\textsf {Sc}^{1/2})^{2}$, as given by Eq. 24b, even beyond the transition point between the diffusion regime and the high-advection regimes. This is a perfect illustration of runaway stratification. Naturally, $\textsf {Re}_{\text {g}}{\Gamma }\textsf {Sc}^{1/2}=12\sqrt {5}$ is the limit of applicability of the 1D0 model. In contrast, the 1D1 model and the 1D2 model reproduce the trend of the 2D model for all the values of $\textsf {Re}_{\text {g}}{\Gamma }\textsf {Sc}^{1/2}$ that were investigated, with the data points of the 1D2 model being almost superimposed on the data points of the 2D model. The relative errors shown in Fig. 6b, d quantify the performances previously observed. The relative error of the 1D0 model grows indefinitely beyond the transition point, while the error of the 1D1 model and the 1D2 model is maximum around this transition point, before decreasing again. Globally, the 1D2 model performs better than the 1D1 model: their respective maximum relative errors are approximately 10% and 30% for high Schmidt number values and approximately 10% and 20% for low Schmidt number values.

Fig. 6

The magnitude of the steady-state stratification for the different models for high Sc values (a) and for Sc = 1 (c), and the corresponding errors between the 2D model and the 1D models for high Sc values (b) and for Sc = 1 (d). The gray solid line represents the analytical solution in the diffusion-dominated regime (i.e., the solution to Eqs. 24b and 24a), and the gray dashed line represents the analytical solution for the high-advection/low-diffusion regime (i.e., the solution to Eqs. 27 and 28). Both of these solutions are derived in Appendix B. The black vertical dashed line at $\textsf {Re}_{\text {g}}{\Gamma }\textsf {Sc}^{1/2}=12\sqrt {5}$ represents the transition at which the two analytical solutions intersect; see panels (a) and (c)

We have also evaluated the integral of $\left | \tilde {\rho }/{\Delta } \rho \right |$ over the channel height, which is a measure of the stratification in the channel. The dependence of this integral quantity on the value of $\textsf {Re}_{\text {g}}{\Gamma }\textsf {Sc}^{1/2}$ (not shown) is similar to that of ${\Delta } \tilde {\rho }/{\Delta } \rho$. In addition, the comparisons between the 2D model and the three 1D models give similar results, with the trends in the errors being comparable with those shown in Fig. 6. This proves that not only the steady-state stratification is well predicted, but that the entire density profile is well approximated over the channel height (around x = 0) by the 1D1 and the 1D2 models.

The magnitude of the velocity in the exchange flow from the 1D models and the 2D model is displayed in Fig. 7. For this quantity, there is a strong Schmidt number dependence that contrasts with the weak Schmidt-number dependence of the reference stratification, discussed in the previous paragraphs. This has a significant impact on the accuracy of the 1D models in modeling the flow velocity. As expected from the analytical derivation in Section 3.2, all 1D models agree well with the theoretical prediction and the 2D model within the diffusion-dominated regime independently of the Schmidt number value. Also independently of the Schmidt number values, the relative error of the 1D0 model increases drastically as the value of $\textsf {Re}_{\text {g}}{\Gamma }\textsf {Sc}^{1/2}$ approaches the transition value of $12\sqrt {5}$ and the runaway stratification appears. The 1D1 and 1D2 models perform significantly differently for high Schmidt number values and low Schmidt number values. For high Schmidt number values, the relative error of the 1D2 model peaks approximately at a value of 25% around the transition point $\textsf {Re}_{\text {g}}{\Gamma }\textsf {Sc}^{1/2}=12\sqrt {5}$ and decreases for larger values of $\textsf {Re}_{\text {g}}{\Gamma }\textsf {Sc}^{1/2}$. The relative error in the 1D1 model continues increasing with increasing values of $\textsf {Re}_{\text {g}}{\Gamma }\textsf {Sc}^{1/2}$. Clearly, the 1D2 model gives the closest results to the 2D model in terms of exchange flow magnitude for high Schmidt numbers. For low Schmidt number values, the trend in the magnitude of the exchange flow predicted by the 2D model is, in contrast, very well reproduced by the 1D1 model (Fig. 7c) resulting in almost no relative error (Fig. 7d). On the other hand, the 1D2 model strongly deviates from the results of the 2D model as $\textsf {Re}_{\text {g}}{\Gamma }\textsf {Sc}^{1/2}$ approaches the transition values (Fig. 7c, d). The error of the 1D2 model is, in fact, comparable with the error of the 1D0 model (Fig. 7d). The 1D1 model outperforms the 1D2 model in predicting the exchange flow magnitude, for the high-advection/high-diffusion regime, because the 1D2 model results in a large horizontal density gradient at the interface that is not present in that regime; see Fig. 3b.

Fig. 7

Magnitude of the steady-state exchange flow for the different models for high Sc in (a) and Sc = 1 in (c), and the corresponding errors between the 2D model and the 1D models in (b) for high Sc and in (d) for Sc = 1. The gray solid and dashed lines display the trends resulting from the analytical solutions for Δu/U_g, based on Eqs. 24a and 28, and explicitly written in Appendix B. The black vertical dashed line represents the transition point at $\textsf {Re}_{\text {g}}{\Gamma }\textsf {Sc}^{1/2}=12\sqrt {5}$

In analogy with the height-integrated density, the results for the integral over the channel height of $\left | u/U_{g} \right |$ and the associated relative error are almost identical to the results for Δu/U_g (not shown). The ability to reproduce the magnitude of the exchange flow from the 2D model—or the incapability to reproduce it—extends to the entire velocity profile.

3.4 Extension to flows with a no-stress top boundary condition

The previous results correspond to an exchange flow in the plane channel flow configuration. This configuration, with a no-slip boundary condition for the velocity at the lower and upper walls of the channel, preserves the symmetry of the flow. Although this symmetry was convenient for estimating steady-state conditions, it is not realistic for environmental exchange flows. An open-channel flow configuration, with a no-stress boundary condition at the top wall of the channel (or a free surface), would be a better approximation. In such a case, the non-dimensional momentum equation for the horizontal velocity (20) is slightly modified yielding

$$ \frac{\partial u^{*}}{\partial t^{*}} = \frac{1}{\textsf{Re}_{\text{g}}} \frac{\partial^{2} u^{*}}{\partial z^{*2}}+\tau_{w}^{*}- {\int}_{z^{*}}^{\frac{1}{2}}\frac{\partial \tilde{\rho}^{*}}{\partial x^{*}}d\hat{z}^{*} +{\int}_{-\frac{1}{2}}^{\frac{1}{2}}({\hat{z}^{*}}+\frac{1}{2})\frac{\partial \tilde{\rho}^{*}}{\partial x^{*}}d\hat{z}^{*}, $$

(30)

with the appearance of a new term:

$$ \tau_{w}^{*}=\frac{1}{\textsf{Re}_{\text{g}}}\left.\frac{\partial u^{*}}{\partial z^{*}}\right|_{z^{*}=-\frac{1}{2}}, $$

(31)

which represents the non-dimensional wall shear stress.

Results for the stratification in the open-channel flow configuration are similar to those in the plane-channel flow configuration. The magnitude of the stratification ${\Delta } \tilde {\rho }/{\Delta } \rho$ in the 2D model follows the theoretical solution in the diffusion-dominated regime before the stratification saturates at ${\Delta } \tilde {\rho }/{\Delta } \rho =1$ (Fig. 8a, c). The 1D0 model reproduces the 2D results within the diffusion-dominated regime, but the error increases drastically towards the transition to the advection-dominated regimes (Fig. 8b, d). The 1D1 model and the 1D2 model reproduce the stratification very well, with a maximum error near the transition point of around 25% and 10% for the models 1D1 and 1D2, respectively. The results of the integral over the channel height of $\left | \tilde {\rho }/{\Delta } \rho \right |$ confirm that the trends observed in ${\Delta } \tilde {\rho }/{\Delta } \rho$ are representative for the entire profile. However, a major difference with respect to the plane-channel configuration is the increase of the magnitude of stratification as a function of $\textsf {Re}^{2}_{\text {g}}{\Gamma }^{2}\textsf {Sc}$. For the plane-channel configuration, it increases as $\textsf {Re}^{2}_{\text {g}}{\Gamma }^{2}\textsf {Sc}/720$ while for the open channel configuration, it increases much faster as $\textsf {Re}^{2}_{\text {g}}{\Gamma }^{2}\textsf {Sc}/320$ due to the absence of friction at the top boundary. As a result, the transition $\textsf {Re}_{\text {g}}{\Gamma }\textsf {Sc}^{1/2}=8\sqrt {5}\approx 17.9$ occurs sooner in the open-channel configuration.

Fig. 8

Magnitude of the steady-state stratification for the different models in the open-channel configuration for high Sc values (a) and Sc = 1 (c). The corresponding errors between the 2D model and the 1D models are also shown for high Sc values (b) and for Sc = 1 (d). The gray solid and dashed lines display the trends resulting from the analytical solutions for ${\Delta }{\tilde {\rho }}/{\Delta } \rho$, based on Eqs. 49 and 27 for the diffusion dominated and high-advection/low-diffusion flows, respectively, and explicitly written in Appendix C. The black vertical dashed line represents the transition where the two analytical solutions intersect at $\textsf {Re}_{\text {g}}{\Gamma }\textsf {Sc}^{1/2}=8\sqrt {5}$

Again, the results of the 2D model show a clear difference in the magnitude of the velocities between the high Schmidt number values (Fig. 9a), where Δu/U_g deviates only slightly from the theoretical line, and the low Schmidt number value (Fig. 9c), where this deviation is much more pronounced as it tends towards the hydraulic limit. The 1D2 reproduces the 2D results better in the high Schmidt number regime, while the 1D1 model performs better for low Schmidt number values. The analysis of the integral over the channel height of $\left | u/U_{g} \right |$ confirms that the trend observed for Δu/U_g is representative for the entire profile.

Fig. 9

Magnitude of the steady-state exchange flow velocities for the different models in the open-channel configuration for high Sc values (a) and for Sc = 1 (c). The corresponding errors between the 2D model and the 1D model are given for high Sc values (b) and for Sc = 1 (d). The gray solid lines in panels (a) and (c) represent the trend resulting from the analytical solution for Δu/U_g, based on Eq. 46 for the diffusion-dominated flows and derived in Appendix C. The black vertical dashed line represents the critical value $\textsf {Re}_{\text {g}}{\Gamma }\textsf {Sc}^{1/2}=8\sqrt {5}$ for transition between the diffusion and advection-dominated regimes

4 Discussion

In laminar flows, the diffusion of salt is governed at a molecular level with the Schmidt number of order 700. In turbulent flows, the diffusion of salt at large scales is governed by turbulent diffusion that can be represented using a turbulent Schmidt number, which is usually of order 1. The results presented in the current paper imply then that the choice of 1D model should be based on the regime of the flow, i.e. the 1D2 model for laminar flows and the 1D1 for turbulent flows. In addition, if 3D-HP models are implemented using direct numerical simulation (DNS) or large-eddy simulation (LES) techniques, turbulent diffusion is solved for rather than imposed or parametrized. From a numerical point of view, such flows have high Schmidt number values, but from a physical point of view, such flows are governed by low Schmidt number values at the large scales. These differences in Schmidt number values can lead to inconsistencies when a 1D model is used as a body force in 3D-HP models, such that the choice will have to be carefully motivated.

Up to now, the results show that the new parametrization of the density gradient leads to a significant improvement in the ability of 1D models to reproduce the density profiles obtained from numerical simulations of a 2D reference model. However, despite this agreement, there are still discrepancies between the 1D models in their ability to reproduce the velocity profiles. To better analyze the differences between the 1D1 and 1D2 models, the steady-state vertical profiles of the horizontal density gradient are displayed in Fig. 10 for different parameter values covering the four distinct regimes (i.e., diffusion-dominated, transition, high-advection/high-diffusion, and high-advection/low-diffusion). Globally, the 1D models reproduce the general evolution of the horizontal density gradient of the 2D model quite well. For example, it is seen that for the diffusion-dominated regime (Fig. 10a), the nearly constant profile of the horizontal density gradients is reproduced by all the models.

Fig. 10

Vertical profiles of the horizontal density gradient for the four cases representative of the four regimes. The cases correspond to the those in Fig. 2. a Diffusion-dominated regime (Re_g = 50, Sc = 300), b transition regime (Re_g = 200, Sc = 300), c high-advection/high-diffusion regime (Re_g = 5000, Sc = 1), and d high-advection/low-diffusion regime (Re_g = 1000, Sc = 300. Γ = 60 for all four cases)

However, some features are not well reproduced by the 1D models. For all cases, the horizontal density gradient resulting from the 1D1 model is limited to a maximum value of unity, while the horizontal density gradient resulting from the 2D simulation can reach values higher than unity (see, e.g., Fig. 10a, b, d). On the other hand, the 1D2 model tends to overestimate the value of the horizontal density gradient around mid-depth. This is mostly observed in the high-advection/high-diffusion regime (Fig. 10c), which explains the large discrepancies between the 1D2 model and the 2D model for low Sc values. Nonetheless, in the high-advection/low-diffusion regime, where the density profile tends towards a two-layer configuration but the velocity profile does not, there is a good agreement between the 2D and the 1D2 models, as expected from the analytical solution in this limit (see Section 3.2).

The results of this study have implications for the range of applicability of 1D water column models in environmental exchange flows with external turbulent mixing. In the case of the gravitational circulation, for example, the traditional version of the 1D model (i.e., with the constant density gradient or 1D0 model) can still be used for well-mixed estuaries, in which the tidal turbulence is strong enough to (partly) destroy the stratification in agreement with Hansen and Rattray (1965) and Chatwin (1976). However, with the new parametrization of the horizontal density gradient, the estuarine circulation can also be simulated in cases of week tidal flows, for which runaway stratification would occur (Burchard et al. 2011) or for which the eddy-viscosity was set to high (Simpson et al. 1990). However, knowledge about the turbulent nature of the flow is crucial to justify the choice between the 1D1 and 1D2 models. In turbulent estuaries, the flow is likely to be governed by the turbulent Schmidt number rather than the molecular Schmidt number such that the use of the 1D1 model should be preferred (see Fig. 7c, d). On the other hand, high-resolution numerical simulations of the mixing processes in an exchange flow subjected to instabilities (e.g., Salehipour et al. 2016) or relatively small-scale experiments of exchange flows (e.g., Lefauve et al. 2018) have to be performed in three-dimensional domains. Note, however, that in earlier experimental work on exchange flows through straits (Anati et al. 1977; Maderich et al. 1998), temperature was used to generate the density differences. In such a case, the Prandtl number (the equivalent to the Schmidt number for heat) is approximately equal to 7, which facilitated reaching the hydraulic limit.

Considering the turbulent viscosity and diffusivity as constant and homogeneous is a first approximation for the exchange flows in estuaries. Nonetheless, spatial and temporal variability of the eddy viscosity can give rise to more complex dynamics (see, e.g., Geyer and MacCready 2014). Of particular relevance here is the generation of a more complex vertical flow structure in strongly stratified situations due to eddy viscosity-shear covariance circulation (ESCO circulation) (Cheng et al. 2013; Chen and de Swart 2018; Dijkstra et al. 2017). However, this dynamics should emerge naturally when an appropriate one-dimensional model for the horizontal density gradient is used to force the flow.

5 Conclusion

In the present study, we introduce two new parametrizations for the horizontal density gradient driving environmental exchange flows that can be incorporated in one-dimensional water column models. These one-dimensional models incorporate a feedback of the stratification on the driving horizontal density gradient to limit the effect of runaway stratification. The parametrizations have been extensively tested by comparing their results of the 1D models with the results of 2D numerical simulations of laminar exchange flows, and with those of previous parametrizations. Depending on the values of the gravitational Reynolds number and the Schmidt number, four different regimes are identified: (i) diffusion dominated, (ii) transition, (iii) high-advection/high-diffusion, and (iv) high-advection/low-diffusion. The classical model, which considers a constant horizontal density gradient, only performs well in the diffusion-dominated regime, where the stratification is weak. The new 1D models outperform the classical model in all other regimes, but they perform differently depending on the Schmidt number. For low Schmidt number values, the so-called 1D1 model should be preferred, for example for models of turbulent gravitational flows in estuaries. For high Schmidt number values, the so-called 1D2 model should be preferred, for example for the simulation of laminar exchange flows at laboratory scale. Both the 1D1 model and the 1D2 model predict the steady-state stratification very well. The new parametrizations were able to reproduce the density profiles obtained with the 2D model within 10% of accuracy, resolving the problem of runaway stratification. They are also able to predict a reduction of the magnitude of the exchange flow velocities observed in strongly stratified situations.

The improvements in 1D models of exchange flow can have a significant impact in the future research of these types of flows. For example, it unlocks the possibility to explore regions of the estuarine-circulation parameter space characterized by strong stratification. Additionally, the formulation of the model, which is independent of the horizontal coordinates, also opens the traditional direct numerical simulation setups with horizontally periodic domains to the simulation of density-driven exchange flows. The simulation of turbulent flows with lateral induced stratification is now possible.

Appendices

Appendix A: Determination of the barotropic pressure gradient

The equations of motion for a 1D water column model located at x = 0 are obtained by assuming w(z) = 0. Substitution of this assumption in Eq. 1 for mass conservation immediately implies ∂u/∂x = 0. Using both expressions to simplify Eqs. 2 and 3 results in

$$ \begin{array}{@{}rcl@{}} \frac{\partial u}{\partial t} & = & -\frac{1}{\rho_{\text{ref}}}\frac{\partial \tilde{p}}{\partial x}+\nu \frac{\partial^{2} u}{\partial z^{2}}~, \end{array} $$

(32)

$$ \begin{array}{@{}rcl@{}} 0 & = & -\frac{\partial \tilde{p}}{\partial z} - \tilde{\rho}g~. \end{array} $$

(33)

To determine the barotropic pressure gradient, Eq. 33 is integrated between z and $\frac {1}{2}h$, which gives

$$ \tilde{p}(z) = g{\int}_{z}^{\frac{1}{2}h}\tilde{\rho}d\hat{z}+\tilde{P}_{\frac{h}{2}}, $$

(34)

where $\tilde {P}_{\frac {h}{2}}$ is the pressure at $z=\frac {1}{2}h$. Then, Eq. 34 is substituted into in Eq. 32 which results in

$$ \frac{\partial u}{\partial t} = \nu \frac{\partial^{2} u}{\partial z^{2}}-\frac{g}{\rho_{\text{ref}}}{\int}_{z}^{\frac{1}{2}h}\frac{\partial \tilde{\rho}}{\partial x}d\hat{z}-\frac{1}{\rho_{\text{ref}}}\frac{\partial \tilde{P}_{\frac{h}{2}}}{\partial x}. $$

(35)

The unknown quantity $\partial {\tilde {P}}_{\frac {h}{2}}/\partial x$ can be evaluated by imposing the no net-flow condition over the vertical:

$$ {\int}_{-\frac{1}{2}h}^{\frac{1}{2}h}u(z;t)dz = 0, $$

(36)

such that integrating (35) over z between $-\frac {1}{2}h$ and $\frac {1}{2}h$ gives

$$ h\frac{\partial \tilde{P}_{\frac{h}{2}}}{\partial x} = \rho_{\text{ref}}\nu \left( \left.\frac{\partial u}{\partial z} \right|_{\frac{1}{2}h} - \left.\frac{\partial u}{\partial z} \right|_{-\frac{1}{2}h} \right) - g{\int}_{-\frac{1}{2}h}^{\frac{1}{2}h}{\int}_{z}^{\frac{1}{2}h}\frac{\partial \tilde{\rho}}{\partial x}d\hat{z}dz. $$

(37)

The pressure gradient $\partial \tilde {P}_{\frac {h}{2}}/\partial x$ then depends on the boundary conditions for the velocity. If a no-slip boundary condition is used both at the bottom wall and at the top wall, the solution for the horizontal velocity u(z) is antisymmetric with respect to z = 0, and one can easily show that ∂u/∂z|_−h/2 = ∂u/∂z|_+h/2. By partial integration and employing the fact that $\partial {\tilde {\rho }}/\partial x$ is an even function of z (at x = 0) (see Fig. 3b), we finally obtain

$$ h\frac{\partial \tilde{P}_{\frac{h}{2}}}{\partial x} = -g{\int}_{-\frac{1}{2}h}^{\frac{1}{2}h}{\int}_{z}^{\frac{1}{2}h}\frac{\partial \tilde{\rho}}{\partial x}d\hat{z}dz = -gh{\int}_{0}^{\frac{1}{2}h}\frac{\partial{\tilde{\rho}}}{\partial x}d{\hat{z}}. $$

(38)

Substitution of this expression in Eq. 35 gives

$$ \frac{\partial u}{\partial t} = \nu \frac{\partial^{2} u}{\partial z^{2}}+\frac{g}{\rho_{\text{ref}}}{{\int}_{0}^{z}}\frac{\partial \tilde{\rho}}{\partial x}d\hat{z}, $$

(39)

which is the expression for the momentum (15).

Appendix B: Maximum velocities and density differences

In the diffusion-dominated regime, $\left |u_{d,\infty }/U_{g}\right |$ is maximum at $\frac {z}{h}=\pm \frac {1}{6}\sqrt {3}$ and

$$ \begin{array}{@{}rcl@{}} \frac{({\Delta} u_{d, \infty})_{\max}}{U_{g}} & =& \frac{\sqrt{3}}{108}\textsf{Re}_{\text{g}}{\Gamma}~, \end{array} $$

(40a)

$$ \begin{array}{@{}rcl@{}} \frac{({\Delta} \rho_{d,\infty})_{\max}}{\Delta \rho} & =& \frac{1}{720}\textsf{Re}_{\text{g}}^{2}{\Gamma}^{2}\textsf{Sc}, \end{array} $$

(40b)

$$ \begin{array}{@{}rcl@{}} {\int}_{-\frac{1}{2}}^{\frac{1}{2}}\left| \frac{\Delta u_{d, \infty}}{U_{g}} \right|dz^{*} & =& \frac{\textsf{Re}_{\text{g}}{\Gamma}}{192}, \end{array} $$

(40c)

$$ \begin{array}{@{}rcl@{}} {\int}_{-\frac{1}{2}}^{\frac{1}{2}}\left| \frac{\Delta \tilde{\rho}_{d, \infty}}{\Delta \rho} \right|dz^{*} & =& \frac{11}{23040}\textsf{Re}_{\text{g}}^{2}{\Gamma}^{2}\textsf{Sc}. \end{array} $$

(40d)

In the high-advection/low-diffusion regime, $\left |u_{a,\infty }/U_{g}\right |$ is maximum for $\frac {z}{h}=\pm \frac {1}{4}$, and the magnitude of the velocity and density profiles is then

$$ \begin{array}{@{}rcl@{}} \frac{({\Delta} u_{a, \infty})_{\max}}{U_{g}} & = &\frac{1}{96}\textsf{Re}_{\text{g}}{\Gamma}, \end{array} $$

(41a)

$$ \begin{array}{@{}rcl@{}} \frac{({\Delta} \rho_{d,\infty})_{\max}}{\Delta \rho} & =& 1~, \end{array} $$

(41b)

$$ \begin{array}{@{}rcl@{}} {\int}_{-\frac{1}{2}}^{\frac{1}{2}}\left| \frac{\Delta u_{a, \infty}}{U_{g}} \right|dz^{*} & =& \frac{\textsf{Re}_{\text{g}}{\Gamma}}{288}~, \end{array} $$

(41c)

$$ \begin{array}{@{}rcl@{}} {\int}_{-\frac{1}{2}}^{\frac{1}{2}}\left| \frac{\Delta \tilde{\rho}_{d, \infty}}{\Delta \rho} \right|dz^{*} & = &\frac{1}{2}. \end{array} $$

(41d)

Appendix C: Open-channel flow in the diffusion-dominated regime

In environmental flows, the pressure at the upper boundary is obviously constant and equal to the atmospheric pressure. In addition, one key assumption for the exchange flow is that the there is no net flow over the vertical. In other words, the integral of the velocity is zero over the vertical. However, the pressure induced by the horizontal density gradient varies linearly with distance from the surface, but does not change sign over the depth. Therefore, a small slope in the water surface is required, in order to generate a constant pressure gradient with opposite sign to the baroclinic pressure gradient. The sum of the two pressure gradients leads to a pressure gradient that depends linearly on the depth and changes sign, driving the typical exchange flow.

In our numerical setup, this slope in the surface is not possible, since we have a rigid lid and just apply a no-stress condition. However, conservation of mass still applies and the integral of the velocity over the channel height should be zero. The only way to realize this is to have a non-constant pressure at the top boundary:

$$ \frac{\partial{\tilde{P}}_{\frac{1}{2}h}}{\partial x} \ne 0~. $$

(42)

The derivation of Eq. 30 is similar as outlined in Appendix A but with a stress-free boundary condition for the flow at the top of the channel. Additionally, we need to take into account that for the open-channel flow $\partial {\tilde {\rho }}/\partial x$ is not an even function with respect to z = 0, in contrast to the derivation in Appendix A.

In the diffusion-dominated regime, Eq. 30 reduces to

$$ \frac{\partial u^{*}}{\partial t^{*}} = \frac{1}{\textsf{Re}_{\text{g}}} \frac{\partial^{2} u^{*}}{\partial z^{*2}}+{\Gamma}~z+\tau_{w}^{*}. $$

(43)

After integration, using a no-slip boundary condition at $z^{*}=-\frac {1}{2}$ and a no-stress condition at $z^{*}=\frac {1}{2}$, the steady-state solution $u_{d,\infty }$ is

$$ \begin{array}{@{}rcl@{}} \frac{u_{d,\infty}(z)}{U_{g}} &=& \frac{\textsf{Re}_{\text{g}}{\Gamma}}{24}\left[3\frac{z}{h}-4\left( \frac{z}{h}\right)^{3}+1 \right]\\ &&+\frac{\textsf{Re}_{\text{g}}\tau_{w}^{*}}{24}\left[12 \frac{z}{h}-12\left( \frac{z}{h}\right)^{2}+9 \right]. \end{array} $$

(44)

By setting the integral over the depth of Eq. 44 equal to zero, the unknown $\tau _{w}^{*}$ can be determined and is found to be equal to $-\frac {1}{8}{\Gamma }$. Thus, finally

$$ \frac{u_{d,\infty}(z)}{U_{g}} = \frac{\textsf{Re}_{\text{g}}{\Gamma}}{192}\left[12\frac{z}{h}+12\left( \frac{z}{h} \right)^{2}-32\left( \frac{z}{h} \right)^{3}-1 \right]. $$

(45)

In the diffusion-dominated regime, $u_{d,\infty }/U_{g}$ is maximum at $z/h=\frac {1}{2}$ and minimum $z/h=-\frac {1}{4}$, thus

$$ \frac{\left( {\Delta} u_{d,\infty}\right)_{\max}}{U_{g}}=\frac{27}{768}\textsf{Re}_{\text{g}}{\Gamma}. $$

(46)

In the diffusion-dominated regime, $u_{d, \infty }/U_{g}$ is negative for $-1/2 \leq z^{*} \leq (7-\sqrt {33})/16$, and positive for $(7-\sqrt {33})/16 \leq z^{*} \leq 1/2$ (with $(7-\sqrt {33})/16\approx 0.078$). As a result, the magnitude of the exchange flow is

$$ {\int}_{-\frac{1}{2}}^{\frac{1}{2}}\left| \frac{\Delta u_{d, \infty}}{U_{g}} \right|dz^{*} = \frac{39 + 55\sqrt{33}}{32768}\textsf{Re}_{\text{g}}{\Gamma} \approx 0.011 \textsf{Re}_{\text{g}}{\Gamma}~. $$

(47)

The evolution of the density in the diffusion-dominated regime still satisfies

$$ \frac{\partial \tilde{\rho}^{*}}{\partial t} = \frac{1}{\textsf{Re}_{\text{g}}\textsf{Sc}}\frac{\partial^{2} \tilde{\rho}^{*}}{\partial z^{*2}}-{\Gamma}~u^{*}. $$

(48)

The steady-state solution of this equation, using to no-flux conditions at $z=\pm \frac {1}{2}h$,

$$ \begin{array}{@{}rcl@{}} \frac{\Delta \tilde{\rho}}{\Delta \rho} &=& \frac{\textsf{Re}_{\text{g}}^{2}{\Gamma}^{2}\textsf{Sc}}{1920}\left[ -10\frac{z}{h} - 5\left( \frac{z}{h}\right)^{2} + 20\left( \frac{z}{h}\right)^{3}+10\left( \frac{z}{h}\right)^{4}\right.\\ &&\left.{\kern6pc}-16\left( \frac{z}{h}\right)^{5}+A_{1} \right]. \end{array} $$

(49)

If one of the two no-flux boundary conditions is satisfied, the polynomial given by Eq. 49 automatically satisfies the other no-flux boundary condition, such that one integration constant, A₁, remains undetermined. This constant can be found by integrating (48) between $z=-\frac {1}{2}h$ and $z=\frac {1}{2}h$ and using

$$ \frac{\partial}{\partial t}{\int}_{-\frac{1}{2}}^{\frac{1}{2}}\tilde{\rho}dz^{*} = 0. $$

(50)

Since initially $\tilde {\rho }=0$, it follows that A₁ = 7/24. The steady-state stratification will become

$$ \frac{({\Delta} \rho_{d,\infty})_{\max}}{\Delta \rho} = \frac{1}{320}\textsf{Re}_{\text{g}}^{2}{\Gamma}^{2}\textsf{Sc}. $$

(51)

Since the solution ${\Delta } \tilde {\rho }/{\Delta } \rho$ is a fifth-order polynomial, there is no general solution to find its roots analytically. Numerically, it is found that the only root, ${\Delta } \tilde {\rho }/{\Delta } \rho =0$, for − 0.5 ≤ z ≤ 0.5 is z = 2.88 × 10^− 2, such that

$$ {\int}_{-\frac{1}{2}}^{\frac{1}{2}}\left| \frac{\Delta \tilde{\rho}_{d, \infty}}{\Delta \rho} \right|dz^{*} \approx 1.02\times 10^{-3}\textsf{Re}_{\text{g}}^{2}{\Gamma}^{2}\textsf{Sc}. $$

(52)