Weakly compressible SPH simulation of cnoidal waves with strong plunging breakers

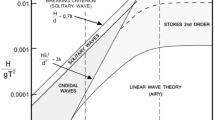
Abstract

Hydrodynamics of highly nonlinear cnoidal waves and their subsequent strong plunging breakers are among the least understood and most significant issues in coastal engineering. In this work, a weakly compressible smoothed particle hydrodynamics (SPH) formulation is used for the study of the generation and propagation of cnoidal waves and investigation of the characteristics of the induced strong plunging breakers. Numerical results show the capability of the SPH scheme for properly simulating the cnoidal waves. For the case of strong plunging breakers, dynamic and kinematic features of the flow are computed and compared with certain implementations of other numerical techniques. SPH is shown to be more accurate compared with other numerical techniques. Power spectral density of both horizontal and vertical dynamic velocities at still water level demonstrates existing of 2D isotropy of dynamics for a typical beach profile with cross-section of slowly varying bottom.

Appendix (fifth-order cnoidal wave theory and its generation)

Cnoidal wave theory by Fenton (1990) makes no approximation based on the wave height. The solution displays that the free surface elevation contains cn(X, m), which is a Jacobian elliptic function of argument X and modulus m. m can be computed using the following equation:

$$ \frac{4K(m)}{\sqrt{\frac{3H}{d}}}\left\{\begin{array}{l}1+\frac{H}{d}\left(\frac{5}{8}-\frac{3}{2}\varDelta \right)+{\left(\frac{H}{d}\right)}^2\left(-\frac{21}{128}+\frac{1}{16}\varDelta +\frac{3}{8}{\varDelta}^2\right)\\ {}-{\left(\frac{H}{d}\right)}^3\left(\frac{20127}{179200}-\frac{409}{6400}\varDelta +\frac{7}{64}{\varDelta}^2+\frac{1}{16}{\varDelta}^3\right)\\ {}-{\left(\frac{H}{d}\right)}^4\left(\frac{1575087}{28672000}+\frac{1086367}{1792000}\varDelta -\frac{2679}{25600}{\varDelta}^2+\frac{13}{128}{\varDelta}^3+\frac{3}{128}{\varDelta}^4\right)\end{array}\right\}=\frac{L}{d} $$

(15)

where, K(m) is the complete elliptic integral of the first kind, H is the wave height, d is the still water depth, L is the wavelength (Fig. 15), $\varDelta =\frac{E(m)}{K(m)}$, and E(m) is the complete elliptic integral of the second kind.

Fig. 15

Spatial definition of a cnoidal wave

The free surface elevation (η) can be specified by:

$$ {\displaystyle \begin{array}{l}\frac{\eta }{h_t}=1+\frac{H}{h_t}{\mathrm{cn}}^2\left(\alpha \frac{\left(x- ct\right)}{h_t},m\right)+{\left(\frac{H}{h_t}\right)}^2\left(-\frac{3}{4}{\mathrm{cn}}^2+\frac{3}{4}{\mathrm{cn}}^4\right)\\ {}+{\left(\frac{H}{h_t}\right)}^3\left(\frac{5}{8}{\mathrm{cn}}^2-\frac{151}{80}{\mathrm{cn}}^4+\frac{101}{80}{\mathrm{cn}}^6\right)\\ {}+{\left(\frac{H}{h_t}\right)}^4\left(-\frac{8209}{6000}{\mathrm{cn}}^2+\frac{11641}{3000}{\mathrm{cn}}^4-\frac{112393}{24000}{\mathrm{cn}}^6+\frac{17367}{8000}{\mathrm{cn}}^8\right)\\ {}+{\left(\frac{H}{h_t}\right)}^5\left(\frac{364671}{196000}{\mathrm{cn}}^2-\frac{2920931}{392000}{\mathrm{cn}}^4+\frac{2001361}{156800}{\mathrm{cn}}^6-\frac{17906339}{1568000}{\mathrm{cn}}^8+\frac{1331817}{313600}{\mathrm{cn}}^{10}\right)\end{array}} $$

(16)

where, c is the wave celerity, h_t is the distance between the bottom to the wave trough (Fig. 15), and α is given by:

$$ \alpha ={\left(\frac{3}{4}\frac{H}{h_t}\right)}^{\frac{1}{2}}\left(1-\frac{5}{8}\frac{H}{h_t}+\frac{71}{128}{\left(\frac{H}{h_t}\right)}^2-\frac{100627}{179200}{\left(\frac{H}{h_t}\right)}^3+\frac{16259737}{28672000}{\left(\frac{H}{h_t}\right)}^4\right) $$

(17)

Horizontal fluid velocity (u) is calculated by:

$$ \frac{u}{\sqrt{g{h}_t}}=\frac{c}{\sqrt{g{h}_t}}-1+\sum \limits_{i=1}^5{\delta}^i\sum \limits_{j=0}^{i-1}{\left(\frac{z}{h_t}\right)}^{2j}\sum \limits_{l=0}^i{\mathrm{cn}}^{2l}\left(\alpha \frac{\left(x- ct\right)}{h_t},m\right){\varPhi}_{ijl} $$

(18)

where, $\delta =\frac{4}{3}{\alpha}^2$. Φ_ijl depends on i, j, and k, and can be found in Table 3 of Fenton (1990).

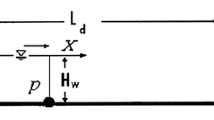
To generate cnoidal waves in a flume, Goring (1978) equated the velocity of the wave-maker plate (dξ/dt), with the corresponding velocity of the water particles. So, on the face of the wave-maker:

$$ \frac{d\xi}{d t}=\overline{u}\left(\xi, t\right)=\frac{c\eta \left(\xi, t\right)}{d+\eta \left(\xi, t\right)} $$

(19)

Goring (1978) assumed that η(ξ, t) can be written as:

(20)

where, k is the wave number. Based on this, the following implicit equation can be written as:

$$ \xi (t)=\frac{H}{kd}\underset{0}{\overset{\theta }{\int }}f\left(\chi \right) d\chi $$

(21)

Now, ξ(t) can be computed by numerical method, such as Newton’s rule. The function F is defined as:

$$ F=\theta - kct+\frac{H}{d}\underset{0}{\overset{\theta }{\int }}f\left(\chi \right) d\chi =0 $$

(22)

By solving the above equation using the Newton’s rule, one can compute θ, that is used to solve for $\xi (t)= ct-\frac{\theta }{k}$.

Application of the Goring’s method to generate the cnoidal theory is limited to 10 ≤ U_r ≤ 1230 (Steven 1993).