1 Introduction

Inlet processes can define several types of barrier island terminus-shapes (Fitzgerald et al. 1984; van Heteren et al. 2006; Mulhern et al. 2017). For barrier islands at the Dutch Wadden sea region, terminus-shapes are typically developed as wide sand flats. Those sand flats are large (scale of km) flat accumulations of sand built by inlet processes that face both the sea and the inland basin. Due to their overall setting, such areas have great potential for dune growth and development due to their beach width size, wind velocity, and climate (Bauer et al. 2009; Houser and Ellis 2013). However, not all sand flats promote dune growth or show similar dune development patterns. Spatial variation of dune development across a single sand flat is not uncommon, as various dune types and growth rates can be seen onto the same sand flat.

Sand supply, surface moisture, vegetation characteristics, and wind velocity are, among others, characteristics that can drive spatial variations in coastal dune development, although just a few studies have been published on sand flat environments (Hesp 2002; van Heteren et al. 2006; Poortinga et al. 2015; Engelstad et al. 2017; van Puijenbroek et al. 2017). Zarnetske et al. (2015) argue that, for a straight beach, vegetation and sand supply are important factors that control foredune morphology, depending on the time-scale considered and coastline position variability. Regarding sediment supply, some authors have suggested that water table depth and consequently surface moisture are important determinants for sediment supply and, consequently, for dune development (Hesp 2002; Bauer et al. 2009; Poortinga et al. 2015).

Surface moisture is known to affect aeolian sediment transport, which on natural beaches can be related to groundwater levels (Arens 1996; Yang and Davidson-Arnott 2005; Oblinger and Anthony 2008; Bauer et al. 2009; Houser and Ellis 2013). Water table fluctuations, which are related to several atmospheric (e.g., pressure, precipitation) and oceanographic (e.g., tidal cycle, wave run-up) variables, influence the variability of surface moisture and hence the potential for aeolian transport (Yang and Davidson-Arnott 2005; Darke and Neuman 2008; Houser and Ellis 2013; Poortinga et al. 2015). In a study on the Dutch island of Ameland, Poortinga et al. (2015) suggest that high groundwater levels can be supply limiting in an event scale (i.e., length of days), and therefore limit the amount of sand available for aeolian transport. Water table levels are often higher than the tidal elevation, and this effect (termed overheight) behaves in inverse proportion to beach face slope and sediment size but is directly proportional to tidal range and wave infiltration (Turner et al. 1997; Horn 2006). On sand flats where the slope is close to zero, amplitude fluctuations of the water table tend to be at a minimum, whereas lag between water table and tide tends to increase landward (Horn 2002; Zhou et al. 2013).

Considering that the behavior of the water table levels and the seepage exit point along the sand flat coastline can vary along the flat due to spatial morphological variations, spatial variations in groundwater levels could potentially lead to variations in the amount of sediment available for aeolian transport. Thus, it can lead to spatially different types and rates of dune development along the same stretch of coast. However, no studies so far have related variations on dune development with potential spatial variations of groundwater levels on a sand flat setting. Therefore, the aim of this study is to improve current understanding of the spatial variability of dune development on sand flats, based on the hypothesis that spatial variability of dune development is affected by groundwater levels and consequently by sediment supply spatial variations. Given the focus of the present study on understanding trends emerging from local conditions and feedbacks, a cellular automata approach is chosen to test this hypothesis. Cellular automata models have been considered as a primary choice of simplified modeling in geomorphology due to the balance between flexibility and range of modeling possibilities with a relatively low computer effort (Fonstad 2006; 2013). Thus, the cellular automata model DUBEVEG (Keijsers et al. 2016) has been used to analyze dune development on both idealized and realistic case scenarios.

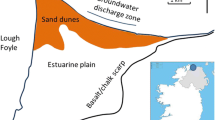
This paper is organized as follows. In Section 2, the model is described. In Section 3, chosen cases are described. In Section 4, idealized cases are tested under a range of conditions involving groundwater levels and initial topographic scenarios to evaluate the effects of groundwater level in a controlled environment. Further, the acquired insights are tested on a real case study on a real sand flat (Fig. 1), where patterns, similarities, and mismatches found on real datasets are evaluated and discussed.

Fig. 1
figure 1

Study area. Upper panel shows the overall setting for the inlet and the sand flat. Lower panel shows a satellite photography from Google Earth, highlighting differences on height and moisture, as well as a picture taken from the Coppice-shaped dune field (highlighted by the black rectangle)

Full size image

2 The DUBEVEG model

The DUBEVEG model (DUne, BEach and VEGetation, Keijsers et al. 2016), based on previous models proposed by Werner (1995) and Baas (2002), simulates beach dune development considering aeolian sand transport, groundwater influence, biotic processes related to vegetation, and hydrodynamic sediment input and erosion in a probabilistic rule-based approach (Fig. 2). Rules control the probability of discrete sand slabs being eroded, transported, and deposited over a cellular grid domain. A “sand slab” is the model representation of a standard volume of sand, which can be visualized as a square flat box. All the rules are intended to represent complex processes by capturing the essential interaction between factors and variables that are important for dune development in coastal areas. Small-scale interactions and feedback processes tend to result in emergent large-scale patterns and trends (Baas 2002; Nield and Baas 2007).

Fig. 2
figure 2

Model outline, highlighting the Aeolian module (a), the hydrodynamic module (b), and the vegetation module (c), with the main processes and possible interaction scenarios

Full size image

Individual slabs displaced over the domain are picked stochastically, based on a probability of erosion P e and transported downwind by a hop distance D. Based on a deposition probability P d , the individual slabs can either be deposited or transported a hop further. The iteration finishes once all moving slabs have been deposited. Both P e and P d values depend on the state of the cell on each iteration (e.g., vegetation cover or bare sand) and the surrounding cells (e.g., situated on a shadow zone). The model also accounts for avalanching due to angle of repose.

The height and width of each square slab are predefined and can be related to a real-world scenario based on a potential aeolian transport per meter alongshore Q (m3/m/y):

$$ Q = H_{s} \times L \times (P_{e} / P_{d}) \times n $$
(1)

where H s is the slab height (m), L is the cell width (m), P e is the erosion probability, P d is the deposition probability, and n is the number of iterations over one year (Nield and Baas 2007; Keijsers et al. 2016).

Table 1 Summary of the standard values used on the simulations
Full size table

Vertically, the amount of sand available to be transported depends on a pre-defined mean sea level and a groundwater level. In the model, the groundwater level represents the depth on which the degree of water saturation is sufficiently high to cancel any aeolian sediment transport. In reality, this level may vary to somewhere in between the vadose (or intermediate) zone and upper capillary fringe. Hence, the groundwater level is defined as an elevation proportional to a pre-defined reference surface, ranging from 0 (groundwater at mean sea level, thus farther from the surface) to 1 (groundwater level equals the reference surface) (Fig. 3). Values are dimensionless and refer to the proportion relative to the surface rather than groundwater depth and are used throughout the text to avoid misinterpretations relative to elevation/depth of the groundwater.

Fig. 3
figure 3

Groundwater concept applied in the DUBEVEG model

Full size image

The hydrodynamics module represents the re-arrangement of the beach topography due to the action of the sea. For each inundated cell, a probability to return to its reference level is given

$$ P_{hydro}=(1-R_{v})\times ((W_{E} - W_{diss}) + P_{inun}) \times S $$
(2)

where R v is the resistance to erosion due to the vegetation V, W E is the maximum erosive strength of the waves, W d i s s is a cumulative dissipation factor based on an inverse function of the remaining water depth in the cross-shore direction, P i n u n is the probability of bed level change due to the inundation regardless of the presence of waves, and S is the stochasticity term representing unaccounted or unpredictable conditions (e.g., grain size variability, wave/current interactions). Cell inundation and wave action also depend on the position relative to the surrounding topography (i.e., wave sheltering). The hydrodynamic module accounts for both sand erosion and accretion by the sea. For the inundated grid cells selected to change, the topography Z t o p o returns to its reference level Z e q . If Z t o p o < Z e q , sediment input from the sea occurs (i.e., addition of sand slabs), whereas hydrodynamic erosion occurs (i.e., removal of sand slabs) when Z t o p o > Z e q . The amount of sand slabs introduced and removed is summed and represents the net sea input per iteration. This module runs after a number of iterations that represents 2 weeks in order to mimic a full neap-spring tide cycle. It uses a cumulative probability curve of daily maximum water levels to define a water level at each hydrodynamic iteration, whereas wave run-up estimates are based on empirical relations described in Stockdon et al. (2006). The empirical relation is chosen for consistency with the rule-based approach used in the model, since the model does not account for wave transformation equations to solve and estimate run-up. Combined, these determine the maximum water level that occurred in a 2-week period, hence the topographic area subject to be affected by marine processes.

The vegetation module mimics the growth and decay of species that are common on dune systems by means of growth curves. The curves describe the growth rate or decay as a function of bed level change. The vegetation is incorporated as a dimensionless value named vegetation effectiveness (Nield and Baas 2007), which represents the effect of vegetation on the aeolian sand transport and can be related conceptually to vegetation cover. In the model, two vegetation types are defined: a pioneer species (e.g., Ammophila sp.) and a conservative species (e.g. ,Hippophae rhamnoides). Pioneer species show optimal growth when buried to some extent, but have less capacity to survive erosion events. The conservative species are more resistant to losses of sand and present optimal growth in neutral conditions (i.e., no bed level change). Establishment of new vegetation on bare cells and lateral expansion is included in the model, following (Keijsers et al. 2016). The vegetation component not only adds a determinant factor for dune development, but also establishes a direct scale in time and space for the model due to the physiological characteristics incorporated indirectly on the growth curves, thus making comparisons to real cases possible (Nield and Baas 2007). Values used for all the simulations can be found in Table 1.

3 Case studies

3.1 Idealized cases

For the idealized cases, three domains are built and used to represent distinct situations that are present on the sand flat of De Hors. Case 1 represents the more wave-sheltered situation on the tidal basin side of the sand flat (East). Case 2 and 3 represent the sea side of the sand flat which is more exposed to wave attack and differ in their initial topography by the presence/absence of a foredune. A summary of the scenarios can be seen in Table 2.

Table 2 Summary of the simulated scenarios
Full size table

Case 1 has a domain size of 200 × 200 m and is defined as a horizontal surface at 1.3 m above MSL with a small vegetated dune in the middle. The reference surface used is a plain domain of 1.3 m above MSL, without any dune. Since the eastern section is sheltered from waves, the wave energy is initially settled at its minimum to account only for small erosive effects that can happen during storms. The wind is considered to be unidirectional, from west to east (left to right, in the model).

For cases 2 and 3 (without and with a foredune), the initial elevation is based on two cross-shore profiles (400 m long) derived from the 1997-LIDAR survey (a northern profile, with a foredune, and a profile located on the sand flat, without dunes), which were repeated over a distance of 200 m alongshore. The reference surface is based on the initial topography without any dunes for both cases. The wave forcing is present and is directed from west to east, with wave dissipation starting at a water depth of 2 m. For all idealized cases, initial values of vegetation effectiveness are assigned randomly with values between 0 and 0.5 at slabs higher than 2 m above MSL and 0 at slabs less than 2 m above MSL. All simulations have a time span of 15 years. Water level input series were based on a tide gauge available at the harbor of Den Helder, on the opposite side of the inlet, and used for all cases.

For all cases, runs with groundwater levels ranging from 0 to 0.9 were carried out, and the final topographies after 15-year simulation were analyzed and compared with respect to the type of dune morphology, dune volume, average crest height, crest spacing, 75 and 95% elevation percentiles, and extent of dune area. For dune volume and dune area calculations, the 3-m elevation contour is used to define the dune foot. Tests using different contours have been done, resulting in trends similar to those for 3-m contour. Elevation percentiles are another statistic method to characterize the size of the aeolian topography that develops, e.g., a 75% elevation percentile value of 3 m means that 75% of the elevation nodes are smaller than 3 m.

3.2 De Hors

The island of Texel, the westernmost island in a chain of barrier islands in the North of the Netherlands, was chosen for the realistic case. On its southern side, bordering the inlet, there is a sand flat (de Hors) of roughly 3 km2, where coastal dunes have been forming over the last decades. The inlet is a mixed energy wave-dominated inlet called the Texel inlet, with a predominant wind direction from southwest (Fig. 1). Large parts of the plain are above the mean spring high tide level, being flooded only during energetic events. Morphologically, the sand flat can be divided into three sections: one particularly exposed to waves, a central region, and an inner part facing the basin (Fig. 4a). In general, coppice-like dunes are found in the central part, whereas a continuous dune row with several small incipient dunes can be seen on the exposed and inner parts. Regarding grain size, recent surface sampling showed grain sizes ranging between fine and medium sand, with D50 values ranging from 210 to 395 μ m.

Fig. 4
figure 4

a 2017 LIDAR-derived topographic map, highlighting the different dune areas: West (1), center (2), east (3), and big dune (4). Red letters show three distinct parts of the flat as mentioned throughout the text (W, west; C, center; E, east). b Variance map of the elevation, based on the topographic time series from 1997 to 2015. c Borehole survey locations used for the capillary fringe measurements. d Annual rate of change, based on the topographic time series. Cold colors mean erosive trend, whereas warm colors relate to accretionary trends

Full size image

For the realistic case, the initial elevation is based on the 1997-LIDAR survey at 5-m grid resolution. Since the flat has shown low inter-annual variability in its height throughout the previous 18 years (Fig. 4b), the reference surface was based on a smoothed version of the 1997-LIDAR survey using a Gaussian low-pass filter to remove any dune feature. The wind is considered unidirectional, from south to north (bottom to upper side in the model), to approximate the dominant wind direction. Like the idealized cases, initial values of vegetation effectiveness are assigned randomly with values between 0 and 0.5 for slabs more than 2 m above MSL and 0 at slabs less than 2 m above MSL. All simulations have a time span of 15 years. Water level input series were based on a tide gauges available at the harbor of Den Helder, close to the sand flat. Like the idealized cases, groundwater scenarios ranging from 0 to 0.9 have been tested and the results compared to the actual data in terms of dune morphology, dune volume, and dune area.

Detailed topographic data (5 × 5 m grid) from 1997 to 2015 was used to evaluate the morphological evolution of both the sand flat and the dune area and compared with the model outputs. The data has been acquired annually by the Dutch authorities (Rijkswaterstaat) using LIDAR technology. Data were interpolated on a 5 × 5 grid (inverse distance weighting, power 2) and the resulting digital elevation models were used to compute elevation statistics (average, variance, annual rate of change), as well as dune volume estimates. Dune volumes are defined using the 3-m contour as the hypothetical dunefoot, whereas the waterline limit is defined by the mean water level retrieved from tide gauge available at the harbor of Den Helder, on the other side of the inlet. The area was separated into four different sectors based on a visual assessment of morphological differences: west, central, east and “big dune,” which is a big sand body forming in front of the dunes located at the east and central areas (Fig. 4a).

For estimates of the spatial variation in capillary fringe depth, a field survey was carried out on which approximately 70 holes were bored along the sand flat until water started to emerge within the hole (Fig. 4c). Next, the elevation of both the surface and the hole depth to slack sand was measured using a RTK-GPS system. Although not ideal due to local changes on pore water pressure (thus changing variations on the local balance between pore pressure and atmospheric pressure), this method was considered sufficiently robust to address qualitatively the spatial variability within the sand flat and of sufficient accuracy for comparison to the schematized results of the cellular automata model.

4 Results

4.1 Idealized cases

Results from the idealized cases suggest that there is a threshold level on which groundwater start to affect dune development. For case 1 (Fig. 5a), deep groundwater levels (0 to 0.6) resulted in a topography of continuous dune rows, exhibiting a downwind decrease in dune height and width (from west to east) due to a sediment supply decrease induced by vegetation. For groundwater levels closer to the surface (0.7 to 0.9), dunes tend to become smaller in width and height, and for groundwater level greater than 0.9, dunes develop as just small Nebkah/Coppice shaped dunes. Regarding vegetation development, most of vegetation growth occurs on the first dune, which is related to larger sand supply compared to the dunes behind it. The amount of vegetation decreases in the presence of small waves due to wave-induced erosion. Most of the vegetation present after 15 years consists of pioneer species rather than the conservative species, and its coverage area is small compared to the dune area.

Fig. 5
figure 5

a Simulation output after 15-year period for case 1 (east side). Upper panels display topography for different groundwater settings. Vegetation is displayed in the lower panels, where gray lines represent 3-m topographic contours. Pioneer vegetation displayed in green, whereas conservative species are displayed in blue. b Topographic patterns after 15-year simulation for case 2 (west side, with no initial foredune). Numbers represent the groundwater level applied. c Topographic patterns after 15-year simulation for case 3 (west side, with initial foredune). Numbers represent the groundwater level applied. For all panels, wind is from west (left of the figure)

Full size image

The threshold level can also be seen on other morphological parameters such as volume growth and average crest height (Fig. 6). Regarding volume growth, groundwater values from 0 to 0.4 resulted in a total volume of approximately 200 m3/m (± 4.5). Between 0.4 and 0.6, volume growth decreased an average of 3% per 0.1 step of groundwater level increase. From groundwater level of 0.7 to 1, the influence of groundwater level increased by an order of magnitude, with a reduction in the order of 20% per 0.1 step of groundwater level increase. In the average crest height results, values from 4.6 m (± 1.2) to 4 m (± 0.7) emerge between groundwater levels of 0 to 0.6, and values of 3.7 m (± 0.5) to 3.2 m (± 0.1) from 0.7 to 0.9 (reduction of 0.17 m per 0.1 step of groundwater level increase). Values of average distance between crests are of the same order of magnitude between groundwater levels of 0 to 0.8, with a large deviation at the shallowest groundwater level due to the low number of dunes present under these conditions. Regarding percentile distributions of elevation, groundwater level from 0 to 0.6 had its 75% elevation percentile above the height of 3 m (3.4 at 0 groundwater level to 3.1 at groundwater level at 0.6), whereas from groundwater levels between 0.7 and 0.9, values range from 2.4 to 1.7.

Fig. 6
figure 6

Topographic characteristics for cases 1 (east) and 2 (west, no initial foredune)

Full size image

For case 2, the results for groundwater levels ranging from 0 to 0.6 are very similar (Fig. 5b). However, in this case, discontinuous dune rows appear at this location, with this time increasingly larger dunes from left (water line) to the right (inland), the opposite trend of case 1. Once the groundwater level reaches levels higher than 0.7, it affects the overall size of any of the dunes that develop, with no elevation contour higher than 3 m if the groundwater levels is at 0.9. Furthermore, although the amount of sand at the dunes reduces inversely with the groundwater level, the cross-shore location of the first dune does not change significantly.

Regarding vegetation development, despite small patches growing sparsely, especially under deep groundwater conditions, almost no growth occurred in most of groundwater conditions tested. The calculated dune volume growth for groundwater levels between 0 and 0.5 was of 67 m3/m (± 3.8), with values ranging from 72 to 60 m3/m. From 0.6 to 1, the average change in volume growth reduces at an average rate of 19% of the highest volume, in contrast to the 4% growth rate between 0 and 0.5. The average crest height reduces from 3.4 m (± 0.36) at groundwater level of 0 to 3.2 m (± 0.12) at 0.9. Although on average similar, the spatial average standard deviation of elevation between 0 and 0.5 is 0.33 m (± 0.02), whereas it reduces to approximately half of that between 0.6 and 0.8. Maximum dune height ranges from 5 to 4.5 between 0 and 0.5 (a reduction of 0.08 per scenario, in average), whereas it goes from 4.2 to 3.4 m between 0.6 and 0.8 (an average reduction of 0.27 per groundwater level). Regarding values for elevation percentiles, case 2 presented less prominent trends than case 1, although drops on its values can be seen for groundwater levels higher than 0.6 (Fig. 6).

For case 3, like cases 1 and 2, topographic developments for groundwater levels between 0 and 0.6 are similar, with a reduction of dune development for groundwater levels above 0.7 (Fig. 5c). The dune type is similar throughout most of the scenarios, with this time a first dune row appearing in front of the initial dune, combined with small dune rows developing more seaward for groundwater levels of 0 to 0.6. For higher groundwater levels, small dunes appear in the upper beach region, until no dune is formed when groundwater is at 0.9.

In terms of volume growth, the same pattern observed for cases 1 and 2 can be seen, with similar values between groundwater levels of 0 and 0.6 (volume change in order of 1% between groundwater levels), with an increase in the volume change rate between 0.7 and 0.9 (of the order of 8%).

Since case 3 represents a commonly occurring situation (beach with a well-developed foredune), an interesting aspect to analyze is the amount of sand transported by aeolian transport and imported/eroded by marine processes. Figure 7 shows boxplot distributions of both the net amount of sand being imported and eroded by the sea throughout the year (referred to as sea input) and the annual amount of wind transport across the full domain during the year (total amount of sand slabs that have been in transport). During the simulation, the volume in transport by the wind remains fairly constant between groundwater levels of 0 to 0.4. However, this amount starts to decrease constantly from 0.5 onward up to 0.9. Regarding sea input, an import trend can be seen in most conditions simulated, with a decrease in its median and spreading values. The decrease in its spreading is due to the decrease of available sand to be transported in each groundwater scenario. Deep groundwater levels require more sand to maintain the reference profile, whereas high groundwater levels require less sand to compensate the aeolian transport.

Fig. 7
figure 7

a Variation in annual sediment input from the sea for case 3. Values are defined by the total of sand slabs introduced/removed by the sea. N= 15. b Annual amount of sand that have been in transport by the wind. N= 15

Full size image

4.2 Real case - De Hors

4.2.1 Observed development

The 18-year topographic dataset shows a steady dune growth in the area, with a total net accretion of 1.2 × 106 m3, at an average accretion rate of 6.6 × 104 (± 2.4 × 104) m3/year. The west region accounted for 60.3% of the total amount of volume increase, at an average of 4.104 (± 1.6 × 104) m3/year, followed by the central region at 29.6% of the total accretion, at an average of 2.104 (± 9.6 × 103) m3/year. The east part accounted for only 5% of the total accretion, at an average rate of 3.2 × 103 (± 3.7 × 103) m3/year, being the only region where years with net erosion trends were observed (between 1998–1999 and 2004–2005). The remaining volume increase is related to the sand body that developed in front of the eastern and central regions, which is treated separately due to its unique size and form.

Regarding the area covered by dunes, all sectors present an overall trend of dune area increase throughout the period (Fig. 8). West and central areas present a faster rate of area expansion as the east and big dune areas. The central area presented an increase of more than 15 times of the initial dune area, whereas the west presented an increase of approximately two times over the initial dune area in the west. The western sector also presented two distinct periods of dune area expansion: one between 1997 and 2004 and another between 2005 and 2015. The increase in dune area expansion rate in 2005 is related to a sudden dune expansion in the south of the western sector, which might be related to a coastline change at the same period.

Fig. 8
figure 8

Left: temporal evolution of dune area, separated by its respective regions of analyze. Right: evolution of dune volume throughout the time series. Data for 2000 and 2002 has been linearly interpolated in time

Full size image

Regarding the sand flat, the topographic data shows a lower average flat elevation on the east side than in the central and west areas (Table 3). The central area presented the highest average sand flat elevation among the areas. For the average temporal variance of the flat elevation, the west side showed the highest values, at an average of 0.26 (± 0.28) m2, compared with 0.08 (± 0.17) m2 for the east side and 0.06 (± 0.11) m2 for the central area. Regarding the elevation rate of change, values for the sand flat are close to 0 (between 0.005 and − 0.005 m/year). Locally, values can be higher or lower than 0.1 and − 0.1 m/year, respectively, being regarded as locations dominated by hydrodynamics processes. On the other hand, higher values can be seen at the dune area, with higher values in the west part than in the other regions (Fig. 4d).

Table 3 Statistics for topographic dataset
Full size table

The spatial pattern in the depth of the top of the capillary fringe, as approximated from the boreholes, shows values of 0.4 to 0.6 m on the east side, with higher values of around 0.7 to 0.8 m in the central and western parts (Fig. 9).

Fig. 9
figure 9

a Approximate depth of capillary fringe estimated level. b Groundwater level for 0.8 in model simulation

Full size image

4.2.2 Simulated development

The simulation over De Hors area shows that dune development varies with imposed groundwater levels (Fig. 10). Deep groundwater levels (between 0 and 0.6) resulted in dunes developing over most of the plain, with an average crest height of 1.5 m in the central part of the flat. In the western part, only small morphological features of a half meter order developed. On the eastern part of the flat, morphological features in the order of 1-m height developed. For a high groundwater level (above 0.7), a much more pronounced spatial variability on the dune development over the flat occurred. The east side of the plain does not show any new dune development on the area, whereas on the central part, dunes higher than 2-m height emerge only in the upper zone of the plain (i.e., farthest from the water line).

Fig. 10
figure 10

Topographic results of evolution of dune evolution for two groundwater levels (a and b), as well as one with a different probability of deposition of a bare cell (c). Real topographic data is displayed for comparison (d)

Full size image

Comparing to observed patterns, some similarities appear. The spatial variability in dune development is similar to patterns found on the measured data. On the west side, the results are similar to those under low groundwater level conditions. Results with high groundwater level tend to represent three distinct areas as seen in the actual flat, especially the expanding dune field on the central area. The overall volume increase is well simulated, with values being around 81–91% of the measured dune volume increase between groundwater levels of 0.6 and 0.8. The same aspect can be seen in the dune area, with values ranging from 85–91% of the measured dune area for groundwater levels of 0.6 to 0.8. Trends on sediment input by marine processes are similar to those shown on Fig. 6 for case 3, with a predominance of accretive trends rather than erosive trends, especially on deep groundwater levels.

Comparing the simulations to the actual state after 15 years, three main differences can also be identified: (1) no development of a foredune on the east side; (2) the position, size and form of the dunes on the central part differs; and (3) the absence of a new dune ridge on the west side. Regarding 1, simulations show that when the probability of deposition of the cells is increased, the foredune on the east side emerges, although this also affected the size and distribution of dunes emerging in the central area (Fig. 10). Regarding 2, dunes tend to form in bigger slabs on the simulation than in the real data, although the overall region is similar, whereas the development of the new dune ridge on the simulation might be related to the absence of any shoreline variability within the model.

Regarding aeolian fluxes (amount of sand that crossed a given longshore shore transect), deep groundwater levels returned similar values for the three regions, resulting in values in the order of 30–40% of the total flux, with the western part showing the highest value (38%), followed by the east (32%) and central with the lowest value of about 30% (Fig. 11). High groundwater levels lead to different and more pronounced variations in regional fluxes, with a decrease on the flux related to the east area (5%) in comparison to the fluxes on the west (55%) and central areas (40%).

Fig. 11
figure 11

a Percentage of total flux for each region, representative for a deep groundwater level (0.2). b Percentage of total flux for each region, representative for a high groundwater level (0.8)

Full size image

5 Discussion

Our findings suggest that groundwater level induces spatial variability in sediment supply and dune development in sand flat environments near inlets. Sand flats, such as De Hors, present large areas in which aeolian sand transport and dunes can develop. The groundwater level can raise surface moisture, thus limiting the aeolian transport and dune formation regardless of the available space (de M. Luna et al. 2011; Poortinga et al. 2015).

Conceptually, over a long time scale, average deep groundwater levels imply that more sediment is available to be transported than at higher groundwater levels. Considering the relation between groundwater depth and sediment supply, the sand flat topography and groundwater level gradients across the area can determine which regions will have the highest potential for aeolian transport and dune development by spatially controlling the sediment supply. That effect can be exemplified by comparing the eastern and western parts of the plain. The eastern part is, on average, lower than the western and central parts. The lower elevation results in relatively higher groundwater levels and, therefore, a reduction in the available sand compared to the other areas. At De Hors, dune growth and sediment transport are much higher in the western, less moist side than it is in the inner, more humid eastern part.

An important part of this concept is the low height variability of the sand flat, which can be related to an import of sand by marine processes that compensates for the aeolian transport. To maintain the sand flat at a fairly constant height, a net input of sediment has to be achieved. Two hypotheses are proposed for this scheme: either the flat itself does not act as a primary source, being all the sand introduced solely by the intertidal area; or there is an input of sand from the sea onto the flat which compensates for the aeolian transport. Our results show a positive balance on the sea input, suggesting that more sediment has been introduced by the sea than has been eroded, and that deeper groundwater levels tend to require more sand input from the subtidal area. Considering the whole flat as a potential sediment source, energetic events that inundates the flat might have an accretive component to replenish the flat rather than an erosive component only (Wijnberg et al. 2017).

Variations in sediment supply can also lead to different dune types. All scenarios presented seem to have a threshold at which the groundwater level starts to influence the dune development. Our simulations show that this occurs between values of 0.5 and 0.7, depending on other characteristics such as the hydrodynamic conditions and initial topography. Therefore, the value of the groundwater parameter cannot be translated to a in situ groundwater depth in meter that would lead to sufficient sand saturation to affect dune development using the current modelling approach.

Previous studies have suggested that dune type and sediment supply are closely related (Hesp 2002; Martínez and Psuty 2004; Nield and Baas 2008). Nield and Baas (2007) found that sediment supply is a key part of the types of dunes that are predicted within a similar model when paired together with the vegetation. Nebkah dunes, for example, were only predicted on limited supply situations, whereas an increase of sediment supply leads to an evolution from barchan dunes to transverse dunes. Since groundwater essentially limits sediment availability, the same effect could be seen in our simulations, with variations in dune formation from medium to high groundwater levels.

Recent studies have addressed the importance of vegetation on dune-building processes (Durán and Moore 2013; Durán Vinent and Moore 2014; Keijsers et al. 2015; Zarnetske et al. 2015; Goldstein et al. 2017). Durán and Moore (2013) argue that maximum foredune heights are mainly controlled by vegetation zonation rather than sediment supply. Furthermore, they argue that the foredune formation time is controlled by the sediment supply (i.e., places with abundant vegetation and low sediment supply will tend to see the dunes build over a longer time period than at sites with abundant sediment supply). Vegetation in the present model is represented simply by a relation between erosion/deposition sediment rates and evolves as direct interactions with sediment supply and net vertical topographic evolution. Changes on specific vegetation parameters may allow changes on dune position and maximum dune height as suggested by Durán and Moore (2013). External influences on vegetation development such as salt spray and soil salinity are accounted within the stochasticity of the model, thus no tests varying specific vegetation parameters have been done. The overall trend regarding spatial variation in sediment supply due to groundwater levels tend to remain present even though including spatial variability in terms of vegetation characteristics might also affect dune growth and spatial distribution of dune morphology.

Intriguingly, the appearance of a new foredune on the east side is highly sensitive to the model setting for the probability of deposition. Increasing slightly the value to 0.3 leads to the appearance of this dune. Considering that a new foredune has evolved in the actual site in the inner part, our results suggest that there is a spatial dependence on probability of deposition which can lead to the appearance of the inner dune. One characteristic that can induce spatial variations on deposition probabilities is grain characteristics such as grain size. Another characteristic capable of inducing spatial changes on deposition probability is the surface moisture, which theoretically could explain the spatial variability in the probability of deposition necessary for the inner foredune growth. However, the current model does not account for any direct spatial dependency on P d , explaining the no-appearance of all characteristics on just one simulation.

It is important to note that spatial variability in sediment supply can be related to other parameters than moisture, such as grain size distribution and beach armoring (Hesp 2002; Hoonhout and de Vries 2017). Temporal variability of these properties is assumed to be introduced stochastically and accounted for in the probability of erosion of a sandy cell. The probability of bare soil erosion and deposition is not imposed to be spatially dependent. Hence, any spatially coherent trends in these properties are not accounted for in the simulation. It is unknown, however, whether such spatial trends do exist.

6 Conclusion

A cellular automata model was used to understand the relation between groundwater level and aeolian dune development on sand flats close to inlets. Increasing groundwater levels lead to a decrease in sediment supply which affected the types of dunes that emerge in the tested scenarios. Coppice/Nebkah-like dunes only appear in scenarios where the groundwater is high enough to limit the sediment supply, whereas long dune rows appear when groundwater levels do not limit supply. Qualitatively, there is a threshold level at which the effect of groundwater reduction on sediment supply starts to affect dune growth and dune type. The threshold can vary spatially due to variations in the groundwater depth relative to the topography. Thus, groundwater level is capable of inducing spatial variability in sediment supply and, therefore, influencing dune growth and distribution on a sand flat. This is consistent with volume change estimated from the data, where the eastern side presents much less dune growth than the rest of the flat due to its lower average elevation and, consequently, higher groundwater levels. The model is sufficiently robust to simulate specific characteristics found on the flat such as zonation related to dune morphology and trends on dune growth.