1 Introduction

Predicting the drift of substances and objects on the surface of the sea is an important practical task. The true drift in the ocean surface layer results from a complex combination of various forcing factors and the properties of the drifter. Surface winds, currents induced by wind stress, wind waves and general circulation all affect the path of a drifter. In seasonally ice-covered seas, the effects of ice need to be considered, too. Traditionally, the drift models account for drift induced by wind forcing, mean wind shear surface currents and general circulation. The Stokes drift (Stokes 1847) that the surface gravity waves induce is often neglected or taken into account using parameterisations.

The importance of the Stokes drift as a component of the surface layer transport has been noted in several studies. Jenkins (1989) combined data from a wave prediction model and a hydrodynamic model to forecast the surface drift more accurately. Spaulding (1999) showed that the performance of oil drift models could be improved by using both wind-induced and wave-induced drift. In a study involving the effect of waves on surface currents, Perrie et al. (2003) found that drifter displacement was most accurately produced when wave-induced currents were included. They also discussed that waves have the greatest impact on the magnitude of surface currents during a rapidly developing storm. Recently, Röhrs et al. (2012) showed that if the drifting object is surface following (resembling, e.g. the behaviour of oil), the Stokes drift can have a high impact on its drift trajectory. They also assert that the predictability of drift trajectories improves if wave information is added to the calculations. Rixen et al. (2008), too, have shown that taking the combined effect of wind, currents and waves into account leads to more accurate predictions of the surface drift. In our study area, the Baltic Sea, taking into account wave conditions, has been found to improve the modelled drift of objects in some cases (Gästgifvars et al. 2004).

The Stokes drift can be calculated from the two-dimensional (2D) wave spectrum, as presented by Kenyon (1969). The 2D wave spectra can be obtained from directional wave observations or from a wave model. In drift forecasting, a third-generation wave model is thus an appropriate tool. However, in practice, not all forecasting centres store wave spectra or Stokes drift profiles, and thus, these data might not be available for users. There is therefore a need for simpler methods to estimate the Stokes drift from, e.g. wind speed and integrated wave parameters, as presented by Ardhuin et al. (2009). In some oil drift forecast models, such as SeaTrackWeb (STW; Liungman and Mattson 2011) and MEDSLIK (De Dominicis et al. 2013), the wave information estimate is based only on the fetch and the wind speed—an approach that is generally limited in accuracy. It has been shown, e.g. by Webb and Fox-Kemper (2011) and Tamura et al. (2014), that estimates based on parameterised wave spectrum or bulk formulations may considerably differ from estimates calculated with a spectral wave model. Furthermore, when using parameterisations, there is a question of what the best estimate for Stokes drift direction is, especially in cases and areas where the wave direction may considerably differ from the wind direction.

Our aim here is to evaluate the magnitude of the Stokes drift in the Baltic Sea and assess its importance and relative contribution to the surface drift in comparison to mean wind shear currents. The Baltic Sea is a relatively small sea consisting of several even smaller sub-basins. The significant wave height is typically considerably smaller than in the oceans. The mean significant wave height in the largest sub-basin, the Baltic Proper, has been estimated to be 1–1.5 m (e.g. Räämet and Soomere 2010; Tuomi et al. 2011). However, observations indicate and model studies have shown that significant wave height can exceed 8 or even 9 m during the most severe storms (Soomere et al. 2008; Tuomi et al. 2011; Björkqvist et al. 2017). In addition, the geometry of the Baltic Sea steers the wave direction, especially in narrow sub-basins such as the Gulf of Finland (GoF) (Pettersson et al. 2010). The difference between the wind and the wave directions in the GoF can be up to 50° (Pettersson 2004), and thus, the direction of the wave-induced surface drift may also differ from the wind direction.

To our knowledge, this is the first paper where statistics of the surface Stokes drift, based on modelled 2D wave spectra, are presented for the Baltic Sea. Previously, Alari et al. (2016) have evaluated the importance of surface wave effects in the sea surface layer and identified that even in moderate storms, the surface Stokes drift can reach up to 0.35 ms−1.

Here, we calculated the surface Stokes drift for the entire Baltic Sea with the wave model WAM and gave mean values and percentiles of the Stokes drift speed from a 10-year model simulation (2006–2015). The accuracy of the simulation was evaluated by comparing the modelled significant wave height, peak wave period and mean direction at the spectral peak with measurements from two wave buoys. Furthermore, we used measured wave spectra from 2012 to evaluate the surface Stokes drift and compared those values to the ones calculated from WAM spectra. Our aim was to study how the Stokes drift calculated in WAM affects the drift trajectories of an object and compare the results with data from a drifter experiment that was done in the Gulf of Finland in September 2012. The Stokes drift calculated with WAM from the 2D wave spectrum was compared with drift data calculated using a method that uses a parameterised one-dimensional wave spectrum.

2 Modelling

2.1 Wave model WAM

We used the third-generation wave model WAM cycle 4.5.4, which is an upgraded version of the WAM cycle 4 with the same physics for the most part. There are enhancements in near-coastal areas to benefit high-resolution coastal modelling, as suggested by Monbaliu et al. (2000). WAM solves the spectral action balance, which without currents can be written in the following form (Komen et al. 1994):

$$ \frac{\partial }{\partial t}\left(\frac{F}{\sigma}\right)+{\overrightarrow{c}}_g\cdotp \frac{\partial }{\partial \overrightarrow{x}}\left(\frac{F}{\sigma}\right)-\left({\nabla}_x\sigma \right)\cdotp \frac{\partial }{\partial \overrightarrow{k}}\left(\frac{F}{\sigma}\right)=\frac{S_{tot}}{\sigma } $$
(1)

Here, F(k, x, t) is the wave energy spectrum, k is the wave number, h is the water depth, σ(k, h) is the intrinsic frequency, c g is the group velocity and S tot is the sum of the source terms. The shallow water source terms are the depth-induced wave breaking (Battjes and Janssen 1978) and bottom friction (Hasselmann et al. 1973). The deep water source terms cover the energy input from the wind, the dissipation of energy caused by white capping and the energy transfer between different frequencies by weak non-linear wave-wave interactions. Because calculating the wave-wave interactions exactly is computationally very heavy, WAM uses the discrete interactions (DIA) of Hasselmann et al. (1985).

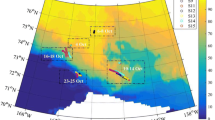
The modelling area covered the Baltic Sea with 2 nmi horizontal resolution (bathymetry shown in Fig. 1). For the frequency band of the wave spectrum, we used the range 0.04177–1.0672 Hz, comprising 35 logarithmically spaced frequencies, and the directional resolution was set to 10°.

Fig. 1
figure 1

Bathymetry of the Baltic Sea used in the WAM model. Locations of the Northern Baltic Proper (NBP) and Gulf of Finland (GoF) wave buoys are shown with black circles and the location of the Kalbådagrund weather station with a red triangle

Full size image

2.2 Stokes drift

The Stokes drift,\( \overrightarrow{v_s} \), is calculated in WAM using the equation

$$ \overrightarrow{v_s}=\frac{16{\pi}^3}{g}{\int}_0^{2\pi }{\int}_0^{\infty }{f}^3\widehat{k}{e}^{2 kz}F\left(f,\theta \right) dfd\theta $$
(2)

where F(f, θ) is the energy spectrum of the surface waves (cf. Sect. 2), f is the frequency, k is the wave number, \( \widehat{k}=\overrightarrow{k}/k \) is the unit vector into the direction of the wave component, θ is the propagation direction of the waves, z is the water depth and g is the acceleration due to gravity. WAM also adds the contribution from the spectral tail to the surface Stokes drift to account for the energy beyond the cut-off frequency.

We computed the Stokes drift both by using WAM and by the method presently used in the SeaTrackWeb (STW) drift model. In the latter, the calculation is based on a parameterised wave spectrum using the fetch and wind speed. STW uses a Donelan-Banner spectrum (Donelan et al. 1985), which in non-directional form reads

$$ F(f)=\frac{\alpha {g}^2}{{\left(2\uppi \right)}^4{f}^4{f}_p}\exp \left\{-{\left(\frac{f_p}{f}\right)}^4\right\}{\gamma}^{\varGamma } $$
(3)

where

$$ \varGamma =\exp \left\{\frac{-{\left(f-{f}_p\right)}^2}{2{\sigma}^2{f}_p^2}\right\} $$
(4)

The shape parameters defined by the wind speed U; the peak frequency f p , following Kahma and Calkoen (1992) and the peak phase speed c p , estimated from deep water linear wave theory, are

$$ \alpha =0.006{\left(\frac{U}{c_p}\right)}^{0.55} $$
(5)
$$ \sigma =0.08\left(1+\frac{4}{{\left(\frac{U}{c_p}\right)}^3}\right) $$
(6)
$$ \gamma =\Big\{{\displaystyle \begin{array}{ccc}1.7,& \mathrm{for}& 0.83<\frac{U}{c_p}\le 1\\ {}1.7+6.0{\log}_{10}\left(\frac{U}{c_p}\right),& \mathrm{for}& 1\le \frac{U}{c_p}<5\end{array}} $$
(7)

The directional spread of the spectrum is added by multiplying Eq. 4 with term

$$ H\left(\omega, \theta \right)=\frac{1}{2}\beta \sec {h}^2\left(\beta \left(\theta -{\theta}_w\right)\right) $$
(8)

where θ w is the wind direction and β is an empirically fitted coefficient that depends on the dimensionless peak frequency f/f p . The symmetry of this spreading function aligns the Stokes drift with the wind. STW uses a frequency band comprising 52 frequencies (0.04–5.17 Hz) and 24 directions to calculate the spectrum. The fetch in the present STW is calculated for eight directions and is capped to 270 nmi (for a more in-depth description, the reader is referred to Liungman and Mattson (2011)).

2.3 Ice concentration

The Baltic Sea has, at least partly, a seasonal ice cover. That should be taken into account when modelling the wave conditions. The ice season typically starts at the end of October/beginning of November, when the coastal areas of the Bothnian Bay start to freeze. The ice season typically lasts until mid-May. On an average ice winter, there is at least some ice in the Bothnian Bay, Bothnian Sea, Gulf of Finland, Northern Baltic Proper and Gulf of Riga. Even during a mild winter, the Bothnian Bay and eastern part of Gulf of Finland have ice. Within our study period, the Baltic Sea ice season was average in winters 2006, 2007, 2010, 2012 and 2013; mild in winters 2008, 2009, 2014 and 2015 and severe in winter 2011.

We used the ice charts produced by the Finnish Meteorological Institute’s (FMI’s) Ice Service to provide ice information to the wave model. Grid cells with an ice concentration of over 30% were excluded from calculations by setting the energy of wave spectrum to zero before each propagation time step.

2.4 Wind forcing

The wind forcing for the years 2006–2015 that we used for WAM comes from the FMI’s numerical weather prediction (NWP) system, HIRLAM (HIRLAM-B, 2017). This system produces a 54-h-long weather forecast every 6 h (at 00, 06, 12 and 18 h UTC). The wind forcing was gathered from these forecasts by utilising every third and sixth hour forecast lengths of every forecast cycle. From 2006 to 2015, the NWP system changed several times. During the period from January 2006 to October 2007, the wind field was extracted from the meso-beta-scale HIRLAM, version 6.2.1, with a horizontal resolution of c. 9 km. During the period from November 2007 to February 2012, version 7.1 of the FMI’s meso-beta-scale HIRLAM was used with a horizontal resolution of c. 7.4 km. After February 2012, data from the RCR HIRLAM version 7.4 with a horizontal resolution of c. 7.4 km was used till December 2015. The changes in the NWP system have affected the quality of the forecast wind field. The effect of the heterogeneous quality of the forcing wind field on the quality of wave hindcast has been previously discussed and analysed by, e.g. Tuomi et al. (2011). They concluded that, even though the heterogeneity affects the quality of the resulting wave field, the simulated parameters can still be used to compile statistics if verification of the wave model results is carefully done.

3 Measurements

3.1 Wave measurements

We used data from two wave buoys to evaluate the accuracy of the wave hindcast. The wave buoys are Datawell Directional Waveriders, and the significant wave height \( {H}_s={H}_{m_0}=4\sqrt{m_0} \) is solved from a time series lasting 1600 s, following Longuet-Higgins et al. (1963). The mean direction and directional spreading are calculated following Kuik et al. (1988). The highest frequency in the wave buoy spectrum is 0.58 Hz. A more detailed description of the data processing is available in Datawell BV (2017).

The wave buoys are located in the Northern Baltic Proper (NBP, 59° 15′ N, 21° 00′ E, bottom depth at the site 100 m) and in the Gulf of Finland (GoF, 59° 57′ 54″ N, 25° 14′ 06″ E; depth 64 m). The data from both wave buoys cover the whole simulation period, excluding the ice seasons. In the winter, the wave buoys are recovered from the sea when there is a risk of freezing in the area. They are deployed again in the spring, when the ice season is over. The ice-free season in the GoF lasts from May/June till December. In the Northern Baltic Proper, the measurement period varies; during mild winters, the buoy is usually there throughout the year, and during average and severe winters, the measurement period is typically from May till December.

3.2 Drifter data

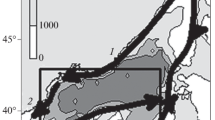
The FMI conducted a research cruise with R/V Aranda to measure and study surface drift in the Gulf of Finland during the period 19–27 September 2012. During the cruise, several drifters of different types were released and followed from a distance. In this paper, we use data from only one of the drifters, MetOcean iSPHERE,Footnote 1 to study if and how the drift of an object at the sea surface was affected by the Stokes drift. This data was chosen, because the drifter’s trajectory was long, and another drifter of the same type, released at the same location and same time, had a similar drift trajectory. Both devices also ended up in almost the same location. Thus, the drift can be considered reliable and representative of the conditions.

The buoy was released on 19 September 2012 at 19:00 UTC at 59° 49.3476′ N, 24° 16.4448′ E. The buoy ended up on the shore on 22 September 2012 at 12:30 UTC at 60° 08.6796′ N, 24° 57.6144′ E. Half of the buoy remained above and half below the surface during its drift. The buoy sent its position and sea surface temperature every half-hour via Iridium satellite.

4 Wave model verification

It is difficult to evaluate the accuracy of the Stokes drift calculations, because direct field measurements of the Stokes drift are practically impossible to obtain. Smith (2006) has estimated the Stokes drift indirectly using velocity and acoustic backscatter intensity data from long-range phased-array Doppler sonar. Ardhuin et al. (2009) estimated the Stokes drift from coastal HF radar data by combining wave model results and radar measurements, and Liu et al. (2014) used scatterometer data and empirical models in estimating the Stokes drift. To our knowledge, such estimates have not been done in the Baltic Sea. Further, Ardhuin et al. (2009) and Rascle and Ardhuin (2013) calculated the surface Stokes drift based on measured wave spectra and evaluated the accuracy of the modelled values against them.

4.1 Bulk parameters

Some indication of the general accuracy of the wave model hindcast can be gained by comparing the model results against wave buoy measurements. We evaluated the accuracy of the wave model hindcast against measurements from the two wave buoys. The model seemed to slightly underestimate the significant wave height (Fig. 2, upper panel) for the Northern Baltic Proper (bias = − 0.03 m) and overestimate it for the Gulf of Finland (bias = 0.02 m). In the Gulf of Finland, the overestimation is larger for higher significant wave heights (those of over 3 m). The model underestimates the wave peak period at both locations (Fig. 2, middle panel). The bias is slightly larger for the GoF (− 0.33 s) than for the NBP (− 0.11 s).

Fig. 2
figure 2

Measured significant wave height (upper panel), peak period (middle panel) and mean wave direction at spectral peak (lower panel) at the NBP (on the left) and GoF (on the right) wave buoys, compared to modelled values. Locations of the buoys shown in Fig. 1

Full size image

The accuracy of the modelled wave direction at both locations is reasonable for most of the propagation directions (Fig. 2, lower panel). However, in the GoF, there is a large scatter in model direction when the measured direction is between 240 and 260° and a slightly smaller scatter for measured directions between 90 and 110°. This behaviour has previously been reported by Tuomi (2008) and Pettersson et al. (2010), for example, and is most likely related to the wave model’s tendency of underestimating the swell energy in the wave spectrum and also to deficiencies in its capability of describing the steering effect of the GoF geometry. In the NBP, there was also a larger scatter in the modelled values from 180 to 210°.

4.2 Evaluation of the accuracy of the surface Stokes drift

We used measured wave buoy spectra from the Northern Baltic Proper and the Gulf of Finland wave buoys to gauge the accuracy of the simulated Stokes drift. We chose to use data from the year 2012, since it is the year when drifter data is also available (cf. Sect. 3.2). In November 2012, there was also a record high value of significant wave height, 5.2 m, measured for the second time within the wave buoy’s measurement history. This gives an opportunity for interesting insights into more extreme conditions. From the GoF, spectra were available for the whole year excluding the ice season (3 February–24 April). The wave spectra from the NBP covered the period of 17 April–14 August.

We estimated the directional wave buoy spectra from the mean wave direction and directional spreading by assuming the directional distribution of Donelan et al. (1985) (Eq. 8). The Stokes drift was then calculated in Eq. 2 up to a cut-off frequency 0.58 Hz. Also, the surface Stokes drift from the wave model was recalculated from the stored wave spectra for the buoy locations using the same cut-off frequency as for the buoy data.

The comparison shows that the wave model is able to fairly well represent the surface Stokes drift values up to 0.15 ms−1 (Fig. 3). The bias at both locations is c. − 0.003 ms−1. At the GoF site, it is evident that the higher values of the surface Stokes drift are overestimated. This is consistent with the overestimation of the higher values of modelled significant wave height at the GoF location (cf. Fig. 2). At the NBP site, the estimates of the surface Stokes drift are from the summer season, which typically has a milder wave climate and thus smaller values of the surface Stokes drift.

Fig. 3
figure 3

Surface Stokes drift estimated from the wave buoy spectra from NBP (on the left) and GoF (on the right) compared to the surface Stokes drift calculated from WAM spectra using the same cut-off frequency (f c = 0.58 Hz) as in the buoy spectra

Full size image

The surface Stokes drift values calculated from the WAM spectra for 2012, with the cut-off frequency of 0.58 Hz, were, for the NBP, c. 74% and, for the GoF, c. 66% of the values calculated for the whole spectral range used in WAM and c. 67% (NBP) and 57% (GoF) of the values calculated internally by WAM (including the added energy from the spectra tail). These comparisons indicate that the contribution of the high-frequency part of the spectrum to the magnitude of the Stokes drift is quite large. This has also been shown by Breivik et al. (2014), for example, who estimated that the contribution from the spectral tail is about one third and can even exceed 75%. Further studies are needed to more comprehensively evaluate the accuracy of the modelled Stokes drift in the Baltic Sea.

5 Stokes drift statistics

We compiled annual and seasonal statistics of the surface Stokes drift for the Baltic Sea by using values calculated in WAM according to Eq. 2. Periods of ice coverage were excluded from the statistics (statistics type F, Tuomi et al. (2011)).

5.1 Annual Stokes drift statistics

The annual mean speed of the Stokes drift is smaller than 0.1 ms−1 everywhere in the Baltic Sea (Fig. 4). The values are the largest in the Baltic Proper, between 0.08 and 0.10 ms−1, and smallest in the coastal areas (c. 0.04 ms−1). The mean values of the surface Stokes drift produced by WAM can be assumed quite accurate when considering the verification of the modelled wave parameters, and the comparison to the Stokes drift estimated from the buoy spectra. The mean speed of wind shear surface current is typically considered to be from a few centimetres per second up to 0.1 ms−1 in the Baltic Sea, on the basis of both measurement campaigns (e.g. Witting 1912; Palmén 1930) and modelling studies (e.g. Andrejev et al. 2004; Myrberg and Andrejev 2006). The annual mean value of the Stokes drift speed is thus of the same order of magnitude as the mean wind shear surface current. However, the definition of surface layer is not necessarily the same for surface currents and Stokes drift. For example, the models typically calculate the surface current in a layer that is 1–3 m thick, whereas the surface Stokes drift calculated by WAM is at the surface (z = 0 m).

Fig. 4
figure 4

Annual mean values of surface Stokes drift in the Baltic Sea (ice-free time statistics, type F)

Full size image

The 99th percentile of the surface Stokes drift magnitude was between 0.2 and 0.3 ms−1. The values were slightly higher in the eastern parts of the Gulf of Bothnia and the Baltic Proper than they were in the western parts (Fig. 5, on the left). The 99.9th percentile had larger spatial variability than the mean values or the 99th percentile (Fig. 5, on the right). The largest values, 0.35–0.4 ms−1, were in the southern Baltic Proper, close to the Bornholm basin. In the Gulf of Finland and in the Northern Baltic Proper, the 99.9th percentiles were mainly between 0.3 and 0.35 ms−1. The 99.9th percentiles were of the same magnitude reported by Alari et al. (2016) in moderate storms. The maximum speed of the surface Stokes drift had large spatial variability (not shown). Generally, the largest values were in the southern Baltic Proper, being between 0.5 and 0.6 ms−1 and even over 0.6 ms−1 in some places. According to the verification presented in Sect. 4.2, the 99th and 99.9th percentile values are most likely slightly overestimated. However, more detailed studies are needed to verify this.

Fig. 5
figure 5

Ninety-ninth (on the left) and 99.9th (on the right) percentiles of surface Stokes drift in the Baltic Sea (ice-free time statistics, type F)

Full size image

5.2 Seasonal Stokes drift statistics

The seasonal mean values of the surface Stokes drift speed were largest in the winter and smallest in the summer (Fig. 6). In the winter, they were generally between 0.1 and 0.125 ms−1 in the open sea areas. The mean values were under 0.1 ms−1 only close to the shoreline. In the summer, the values were smaller than 0.075 ms−1 in the whole Baltic Sea. In the autumn, the largest mean values were in the Baltic Proper (between 0.1 and 0.125 ms−1), while they were only between 0.025 and 0.075 ms−1 in the spring.

Fig. 6
figure 6

Seasonal mean values of the surface Stokes drift in the Baltic Sea for spring (MAM, upper left), summer (JJA, upper right), autumn (SON, lower left) and winter (DJF, lower right) (ice-free time statistics, type F)

Full size image

The seasonal cycle is typical in the Baltic Sea following the prevailing wind conditions. The wind speed in the ice-free area during the autumn and the winter is generally higher than in the spring and the summer. In the Gulf of Bothnia, the Gulf of Finland and the Gulf of Riga, the ice cover also affects the mean values and percentiles (Tuomi et al. 2011). In the northernmost part of the Bothnian Bay and the easternmost part of the Gulf of Finland, there were on average over 100 days in a year that the sea area was ice covered during the period presented in this paper.

The 99th percentiles of the seasonal Stokes drift speed were the largest in the winter and smallest in the summer, similar to the seasonal mean values. In the winter, the largest values were in the Baltic Proper, 0.30–0.35 ms−1 (Fig. 7). In the Gulf of Finland and the Gulf of Bothnia, the seasonal ice cover affected the percentiles. The values in winter were between 0.25 and 0.30 ms−1, being of the same order of magnitude as in autumn. In the spring and in the summer, the 99th percentiles of the Stokes drift speed were between 0.20 and 0.25 ms−1 in the southern Baltic Proper. In the northern part of the Baltic Sea, the values were smaller in the summer than in the spring, being between 0.15 and 0.20 ms−1.

Fig. 7
figure 7

Ninety-ninth percentile of seasonal surface Stokes drift in the Baltic Sea for spring (MAM, upper left), summer (JJA, upper right), autumn (SON, lower left) and winter (DJF, lower right). Ice-free time statistics, type F

Full size image

6 Directionality of the Stokes drift

Webb and Fox-Kemper (2015) present that the direction of the Stokes drift matches the wind direction relatively well at the surface, since it is more sensitive to the high-frequency part of the wave spectra. We wanted to examine this more closely in the Baltic Sea, where there are narrow gulfs in which the wave direction may differ considerably from the wind direction. We evaluated the directional distribution of the Stokes drift over our study period (2006–2015) at the two wave buoy locations. The directional distribution of the Stokes drift is much wider in the Northern Baltic Proper than in the Gulf of Finland (Fig. 8, upper panel). The narrowness of the Gulf of Finland channels the directions, resulting in the largest proportion of the propagation being towards ENE. The directional distribution of the Stokes drift (current roses) in both the NBP and the GoF is quite similar to the wind roses from the forcing wind for the same locations (Fig. 8, lower panel). Indeed, in the GoF, the Stokes drift direction matches the wind direction better than the mean direction at the spectral peak (Fig. 9).

Fig. 8
figure 8

Surface Stokes drift roses for the NBP (on the left) and GoF (on the right) buoy locations. The upper panel is based on the surface Stokes drift calculated by WAM according to Eq. 2. The lower panel presents the wind roses based on the HIRLAM wind speed and direction at the buoy locations. All directions are given as direction to

Full size image
Fig. 9
figure 9

Surface Stokes drift direction compared to the wind direction (on the left) and to the mean wave direction at the spectral peak (on the right) at the GoF wave buoy location

Full size image

Pettersson et al. (2010) have shown that even though the mean direction at the spectral peak tends to align with the axis of the gulf in the GoF, the high-frequency part of the wave spectrum follows the wind direction. Therefore, the wind direction may be a good estimate for the surface Stokes drift direction, even in areas where the basin geometry strongly affects the wave directions.

As presented in Sect. 4, WAM had some difficulties in simulating the mean wave direction at the spectral peak at both locations from certain wave directions. However, when the surface Stokes drift direction is considered, it seems to be more important to have the forcing wind direction accurately represented. This is in accordance with findings by Webb and Fox-Kemper (2015), who showed that the direction of the surface Stokes drift mostly follows the wind direction. However, they also showed that sub-surface Stokes drift directions turn more towards the mean wave direction. This is due to the exponential function in Eq. 2, which diminishes the effect of the third frequency moment with depth, thus turning the direction more towards the mean wave direction. The sub-surface behaviour of the Stokes drift direction should therefore be further studied in the GoF and other similar areas.

7 Case study

To study how the Stokes drift calculated by WAM affects the drift of objects in the Gulf of Finland, we made manual calculations for a drifter that was deployed during a drifter experiment in 2012 (cf. Sect. 3.2). During the drift, the buoy travelled over 71 km with an average speed of 30.5 cm s−1.

The surface drift was evaluated separately for the Stokes drift calculated by the wave model by using the calculated speed and direction at the nearest grid point to the drifter location. Similarly, the drift based on surface currents was evaluated using the forcing wind speed and direction by multiplying the wind velocity by 0.015; the wind drift direction is the direction of the wind plus 15° (clockwise). This estimate is based on the analysis of Palmén (1930), who, based on wind and current measurements in the Gulf of Finland, evaluated that for SW, WSW and W winds, the magnitude of the surface current is c. 1.2–1.5% of the wind speed, and the turning angle is between 8 and 21°. The total drift of the object was evaluated by summing these two terms.

Neither drift induced by wind stress nor waves could solely describe the drift speed or direction of the object (Fig. 10, left panel). When combined, the drift speed and direction of the object are fairly well predicted, although this simple method cannot account for all small-scale dynamics.

Fig. 10
figure 10

Drifter experiment in the Gulf of Finland (on the left, blue line). Calculated drift based on Stokes (brown line) and wind shear drifts (orange line) and the total drift (red line). The measured (solid line) and modelled (dashed line) wind speed and direction at the Kalbådagrund weather station and the measured (solid line) and modelled (dashed line) significant wave height and wave direction at GoF wave buoy from 19 to 22 September, during the drift experiment

Full size image

The wind speed and the significant wave height were slightly overestimated compared to the wind measurements at the Kalbådagrund weather station and wave measurements taken at the GoF wave buoy during this period (Fig. 10, right panel). The turning of the wind and wave direction at the end of the period were simulated with good accuracy.

8 Parameterised Stokes drift estimate

Even though the Stokes drift calculated by the wave model from the directional wave spectra is considered to be the best approximation, when considering modelled values, it is sometimes beneficial to have a less computationally demanding way to account for the Stokes drift. Therefore, we evaluated the magnitude of Stokes drift calculated using parameterised wave spectrum (Donelan-Banner), wind speed and fetch, according to Eq. 3. This method is used, for example, in the STW model and is based on parameters that are often more easily available for a drift forecaster than those calculated with a wave model.

The Stokes drift estimate based on the Donelan-Banner spectrum underestimated the larger values of the Stokes drift by over 0.3 ms−1, when compared to the WAM (Fig. 11). Smaller values (of under 0.2 ms−1) tended to be overestimated especially at the NBP location (Fig. 11, right panel) and showed quite high scatter. Compared to WAM, the Donelan-Banner spectrum underestimates the wave energy in high wind situations, which causes the underestimation of the higher Stokes drift values. The overestimation of lower values is related to the cut-off frequency, which for STW is 5.17 Hz (compared to 1.07 Hz in WAM). When the Donelan-Banner spectra determined in STW are integrated to approximately the same cut-off frequency as in WAM, the positive bias in smaller Stokes drift values is reduced (not shown). However, this approach reduces the higher values of the STW Stokes drift, increasing their negative bias compared to WAM and also compared to buoy data (not shown).

Fig. 11
figure 11

Magnitude of surface Stokes drift calculated with WAM compared to values determined based on Donelan-Banner spectra at the NBP (on the left) and GoF (on the right) wave buoy locations. Locations of the wave buoys are shown in Fig. 1

Full size image

The direction estimate agrees fairly well with the directions calculated by WAM (Fig. 12). As discussed in Sect. 6, the surface Stokes drift tends to align more with the wind direction than with the peak wave direction. Therefore, the estimate based on wind direction is a good estimate for the direction of the surface Stokes drift. However, there are occasions when the estimated Stokes drift direction differs from the direction calculated by WAM. In most of the cases where there is significant difference between the wind and the Stokes drift directions, the magnitude of Stokes drift is relatively small, usually under 0.02 ms−1. The large differences in directions were mostly in situations when the wind speed was low and the wind was turning (not shown). For the higher values of Stokes drift, of over 0.25 ms−1, there was at most a 20° difference between the Stokes drift direction and the wind direction, and in most of the cases, the difference was smaller than 10°.

Fig. 12
figure 12

Direction of the surface Stokes drift calculated with WAM, compared to the direction estimated with Donelan-Banner spectra based on wind direction at the NBP location (on the left) and GoF location (on the right). Locations of the wave buoys are shown in Fig. 1

Full size image

9 Summary and conclusions

Our aim was to estimate the importance of the Stokes drift as a component of the total surface drift of substances and objects in the Baltic Sea. We found that the Stokes drift is an important component with annual mean values between 0.04 and 0.10 ms−1 in the studied area. As the direction of the Stokes drift may differ from the direction of the surface current, it is important to include both directions when evaluating drift trajectories.

The accuracy of the modelled Stokes drift is relatively difficult to evaluate, since there are no direct measurements available. The accuracy of the modelled significant wave height, peak wave period and mean direction at the spectral peak was evaluated against two wave buoys. The significant wave height was fairly well simulated in both locations, but the comparison of the peak wave period and the peak wave direction indicated that the distribution of energy in frequency and direction bands of the wave spectra is not reproduced well in all cases, especially in the Gulf of Finland. Furthermore, the comparison of the modelled surface Stokes drift to the ones calculated from measured spectra for 2012 showed that the lower values of Stokes drift (up to 0.15 ms−1) were fairly well reproduced by the model, but the higher values were overestimated, at least in the Gulf of Finland. In the future, a more detailed analysis of the accuracy of the modelled Stokes drift in the various sub-basins of the Baltic Sea is needed.

In our analysis based on the modelled 2D wave spectrum, the direction of the surface Stokes drift was usually close to that of the wind direction. This indicates that when the directional wave spectrum is lacking, wind direction is a good estimate for the surface Stokes drift direction in the Baltic Sea. This was also the case in the Gulf of Finland, where the mean wave direction at the spectral peak does not always follow the wind direction due to the steering effect of the geometry of the gulf. Our results showed that the largest differences in the Stokes drift direction calculated by WAM and the direction evaluated based on wind direction were generally small. Mostly, the differences occurred during low wind speeds when the wind was turning. Further studies are needed to estimate how well WAM can represent the wave spectrum compared to measurements and how the possible inaccuracies affect the magnitude and direction of the Stokes drift and to evaluate how the direction of the surface Stokes drift differs from the direction of the sub-surface drift.

Although calculating the Stokes drift from the 2D wave spectrum is considered to be the most accurate estimate, it is also the most time-consuming and space-consuming. It is not always possible, or even necessary, to have an operational wave forecasting system if one needs an estimate for the Stokes drift. Thus, it is important to know the limitations of the parameterised estimates of the Stokes drift. The magnitude of the Stokes drift, estimated using the Donelan-Banner spectra (a method used, e.g. in the STW drift model), tended to overestimate the smaller values of Stokes drift compared to the ones calculated by WAM and from the buoy spectra. The higher values of Stokes drift were underestimated by the STW method compared to the ones calculated by WAM. However, the comparison of Stokes drift values calculated by WAM against the ones calculated from the wave spectra showed that WAM slightly overestimated the larger values of Stokes drift in the Gulf of Finland. The direction of the Stokes drift was better estimated, since it was based on the wind direction. Implementing the Stokes drift calculated by a wave model as a forcing to STW will be the next step in evaluating to what extent the differences between these two methods affects the drift trajectories.

In the accuracy of the modelled surface Stokes drift, the accuracy of the forcing wind field is an important factor. The wind forcing is also the main reason for errors in the significant wave height in the open sea areas. Although, the accuracy of the HIRLAM forcing has been shown to be relatively good in the Baltic Sea (e.g. Tuomi et al. 2012), the possible biases in the modelled wind speed and direction will affect both the surface Stokes drift values calculated by WAM and the values calculated using parameterized methods.

Our findings can be summarised in the following conclusions:

  • Our analysis confirmed that the Stokes drift is an important component in the surface drift in the Baltic Sea. Our simulations with the wave model WAM showed that the annual mean values of Stokes drift were 0.08–0.1 ms−1 in most of the areas of the Baltic Sea, which is of a similar magnitude compared to estimated mean values of the surface currents.

  • The direction of the modelled surface Stokes drift mostly followed the forecast wind direction. The largest differences occurred when the wind speed was low and the wind was turning. Therefore, in the absence of directional information of the Stokes drift, the wind direction is a relatively good proxy for the direction of the surface Stokes drift.

  • There were quite large differences in the magnitude of the Stokes drift calculated by WAM and estimated with a parameterized method. The smaller value (up to 0.2 ms−1) WAM was able to simulate with better accuracy than the parameterized method. For evaluating the accuracy of the higher values, further studies with a more comprehensive measured dataset are needed.

The case study with the drifter in the Gulf of Finland further verified that the Stokes drift is an important component in the surface drift, in both magnitude and direction. The next step is to introduce the Stokes drift calculated by a wave model to a drift forecast model and more extensively analyse the effect of the Stokes drift on forecasts in different conditions.