1 Introduction

Worldwide, river plumes are formed due to a large freshwater outflow of rivers into coastal seas and oceans. As a result of the Earth’s rotation, the freshwater discharge deflects towards the coast, forming a downstream plume along the coast (Chao and Boicourt 1986; Fong 1998; Garvine 1999). River plumes are also referred to as Regions of Freshwater Influence (ROFI), a term introduced by Simpson et al. (1993) to demarcate this distinctive region in coastal seas and oceans. The freshwater outflow leads to stratification, while other forces (tide, wind and waves) result in mixing the water column over the vertical. River plumes affect the structure of currents in coastal seas, and thus affect the transport and fate of suspended particulate matter (SPM) in coastal seas. The influence of ROFI’s on the distribution of SPM has been investigated for many years. Geyer (1993) showed with numerical modelling that stratification shuts down turbulence at the pycnocline. De Nijs et al (2010, 2011) were some of the first to use in situ data to show this mechanism. More studies showed that the development of a halocline causes a drop in surface SPM concentrations and an increase in bottom concentrations (Pietrzak et al. 2011; Souza et al. 2007; Burchard and Baumert 1998; McCandliss et al. 2002; Joordens et al. 2001). In addition, understanding the behaviour of SPM is important with respect to the effects of dredging activities, especially for the maintenance and protection of the coast, on coastal ecosystems. Understanding the current structure and mixing is important for the biotic environment as SPM influences the light penetration which has an effect on the primary growth of algae (phytoplankton) (Los et al. 2008). It is therefore of great importance to gain a better understanding of the processes influencing the currents along the Dutch coast.

Off the Dutch coast, a complex hydrodynamic system is generated by the freshwater discharge of the Rhine River and Meuse River (Fig. 1). These rivers discharge a yearly average of 2300 m3/s fresh water into the southern north sea creating the Rhine ROFI. This ROFI can be split into a near-field bulge region, around the river mouth, and a downstream plume. The downstream plume can extend 100 km northwards of the river mouth and has a width of 20 to 40 km (de Ruijter et al. 1997). The Rhine ROFI is dominated by friction and tides in contrast to classic river plumes (Horner-Devine et al. 2015). In the Rhine ROFI, the tides also determine the release of the freshwater lenses at the river mouth (de Ruijter et al. 1997), which influence the evolution of the entire system. There is a strong interaction between the tides, wind, waves and buoyancy input. As a result, the Rhine ROFI switches between a well-mixed and a stratified state at multiple timescales.

Fig. 1
figure 1

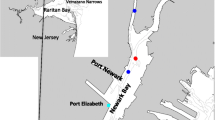
The measured transects at the 13th of October 2011. The northern transect is measured by PoR, NIOZ measured the southern transect. The four measuring stations per transect are located at 1, 2, 4 and 8 km from the coast and are each measured eight times. The triangles represent the measurement stations for the tidal elevations. The square represents the measurement station for the wave data. A circle represents a meteorological measurement station and stars represent stations for discharge data. The bottomtopography is shown in the right panel (in meters)

Full size image

The competition between stratifying and destratifying processes determines the state of the ROFI in time and space (Simpson 1997; Simpson et al. 1990; Souza and Simpson 1997; de Boer et al. 2008). The processes causing stratification and mixing can be classified into reversible and irreversible processes (see Table 1). Advection and straining (differential advection) are reversible (sometimes called ”elastic”) and can act both to increase and to decrease stratification. Decrease of stratification can also be caused by irreversible mixing due to wind, wave and tidal energy. Stratification can also be increased by irreversible processes due to the supply of lower density water, such as heating of the surface and freshwater discharges.

Table 1 Overview of the reversible and irreversible stratifying and stirring processes
Full size table

The interaction between the tide and stratification in the Rhine ROFI acts on two time scales, the fortnightly and the semi-diurnal tidal cycle. First, the fortnightly spring-neap tidal cycle causes the Rhine ROFI to switch between a well-mixed and a stratified system. During spring tide, the high kinetic energy enhances mixing and was found to result in a well-mixed ROFI at a location about 30 km downstream of the river mouth (Simpson et al. 1993). In contrast, Simpson et al. (1993) showed that the ROFI is stratified during neap tide because of low kinetic energy. During these stratified conditions, Visser et al. (1994) found tidal currents in the Rhine ROFI, which rotate anti-cyclonically at the surface and cyclonically near the bed.

Second, during low kinetic energy events such as neap tide, Simpson and Souza (1995) showed that a semi-diurnal signal of stratification and destratification is present in the Rhine ROFI as well. The aforementioned cross-shore currents interact with the cross-shore horizontal density gradient. This interaction between the tidal velocity shear and the horizontal density gradient is defined as tidal straining (Simpson et al. 1990), which simply can be explained as differential advection and is also referred to as strain induced periodic stratification (SIPS). Tidal straining enhances stratification from low to high water and enhances destratification from high to low water. Besides SIPS and the release of freshwater lenses, also the depth mean along-shore advection has been shown to induce periodic stratification (Van Alphen et al. 1988).

From a numerical model study, where both processes SIPS and (along-shore) depth mean advection were investigated, it follows that both cross-shore straining and depth mean along-shore advection play a significant role in the bulge region and in the downstream plume (de Boer et al. 2008). According to this study, one should refer to the sum of the processes as ASIPS (advection and strain induced periodic stratification).

In this study, we use field data to investigate the contribution of advection and strain-induced periodic stratification (ASIPS) in the along- and cross-shore direction. The novel field data presented here contributes to ROFI knowledge in two ways. First, the study area is located at 80 km downstream of the Rotterdam Waterway, which is in the far-field plume of the Rhine ROFI. Previous studies were performed in the area up to 40 km from the river mouth. Second, the novelty of the data lies in the fourth dimension. The existing knowledge on straining and advection in the Rhine ROFI is based on limited in situ data only, such as sparse time-series, cross-shore transects and synoptic remote sensing images. Here, we present observations where two vessels sailed simultaneously along two cross-shore parallel transects during one semi-diurnal tidal cycle, while measuring over the water column. This resulted in a four-dimensional dataset which contains information in cross-shore, along-shore, depth and time. This dataset allows us to apply the 3D potential energy anomaly (φ, J/m3) equation to analyse two parallel transects. Becherer et al. (2015) used a similar approach in a curved tidal inlet in the German Wadden Sea. Their study demonstrated the importance of lateral circulation, in addition to classic estuarine circulation. Here, the potential energy anomaly equation is used to study the contribution of the stratifying and destratifying processes on the evolution of periodic stratification in the Rhine ROFI (Simpson et al. 1990). Both, de Boer et al. (2008) and Burchard and Hofmeister (2008), derived a (φ) equation for 3D flows in numerical models. We apply the 3D φ equation from de Boer et al. (2008) to the field data. The equation needs to be simplified to apply it to the space and time domain of the field data. In addition, not all processes can be calculated. Section 2 describes the method and gives an overview of the dataset used. The most important processes such as straining and depth mean advection will be calculated and presented in the results section, Section 3. The relative importance of these processes will be analysed in the discussion, Section 4.

2 Methodology

2.1 Location and instrumentation

Two parallel transects were simultaneously measured with the BRA-7 hired by the Port of Rotterdam Authority (PoR) and the Navicula from NIOZ (the Royal Netherlands Institute for Sea Research). On the 13th of October 2011, they sailed simultaneously on two parallel cross-shore transects off the Dutch coast for thirteen hours (Fig. 1). PoR collected the data of the northern transect located near Egmond aan Zee, 82 km from the New Waterway. The southern transect near Wijk aan Zee, 70 km from the river source, was sailed by NIOZ. Each transect consists of four measurement stations located 1, 2, 4 and 8 km, respectively, offshore.

The bathymetry in Fig. 1 shows that at the Northern transect the depth is typically 20 m offshore decreasing to about 9.5 m onshore. At the Southern transect, there is a depression between station 1 and 2 (respectively 8 and 4 km offshore). The depth at station 1, most offshore, is about 15–16 m, this is shallower than the depth at station 2. The depression has a depth of about 17 m. The bathymetry data is measured at 20-m intervals.

Both PoR and NIOZ used a CTD (conductivity, temperature and depth sensors), an OBS (optical backscatter sensor) and an ADCP (acoustic doppler current profiler) to measure vertical profiles of conductivity, temperature, turbidity and velocities at each station. The OBS and CTD were mounted on the same frame. The ADCP is mounted alongside both ships at a depth between 1 and 2 m below the water surface. The data is processed following a standard procedure where spikes are removed and the data is averaged over vertical bins. The ADCP data has vertical bins of 0.5 m and the CTD data bins of 0.05 m. Therefore, a general grid is made with steps of 0.5 m. The CTD data is averaged over 0.5 m. Then the CTD and ADCP data are displayed on the same grid.

The sensors of PoR and NIOZ needed intercalibration to be able to interpret the difference between the two transects. Therefore, calibration measurements were carried out at the 14th of October 2011. The two vessels sailed, next to each other, on both transects. The data were used to compare the sensors used by PoR and NIOZ, here we are only interested in the salinity and temperature data. The salinity data are in agreement. The temperature sensors showed a small consistent difference that was corrected. More detailed information on the used instrumentation and procedures can be found in Rijnsburger (2014).

2.2 Environmental conditions

The meteorological data consists of wind, wave, discharge and sea surface data. Wind velocities and direction are measured by the Royal Dutch Meteorological Office (KNMI) at a station near IJmuiden. The sea surface, wave and discharge data are retrieved from the database of Rijkswaterstaat (2015). Figure 1 shows the location of the measurement stations.

2.3 Potential energy anomaly analysis

The potential energy anomaly, φ, is used to identify the different processes which are involved in the change of the vertical density profile at a given location (Simpson et al. 1990). The potential energy anomaly is defined as the required depth averaged energy which would be needed to mix the entire watercolumn and can be written as

$$ \varphi = \frac{1}{H} {\int}_{-h}^{\eta} (\overline{\rho} - \rho)gz\mathrm{d}z $$
(1)

The change of φ over time [W/m3], also called the potential energy anomaly equation, is used to get information of the influence of the stratifying, destratifying and stirring processes.

$$ \frac{\partial \varphi}{\partial t} = \frac{g}{H} {\int}_{-h}^{\eta} \frac{\partial (\overline{\rho} - \rho)}{\partial t} z \mathrm{d}z $$
(2)

where H = h + η is the total water depth [m], η is the free surface relative to mean sea level (MSL) [m], h is the distance between the bed and the mean water level [m], g is the gravitational acceleration (9,81 m2/s), z is the vertical coordinate relative to MSL defined positively upwards [m], ρ is the water density [kg/m3] and \(\overline {\rho }\) is the depth averaged density. φ defines the actual state of the water column. ∂ φ/ ∂ t defines whether the water column is stratifying or destratifying. When ∂ φ/ ∂ t is positive, the water column is stratifying and when it is negative the water column destratifies or is being mixed.

This study uses the 3D potential energy anomaly equation derived for numerical modelling (de Boer et al. 2008) and applies it to field data. The equation is given by

$$\begin{array}{@{}rcl@{}} &&\frac{\partial \varphi}{\partial t} = \frac{g}{H}\int\limits_{- h}^{\eta} \left( \begin{array}{l} \overbrace {\tilde u\frac{{\partial \bar \rho} }{{\partial x}}}^{{S_{x}}}\overbrace {+ \bar u\frac{{\partial \tilde \rho} }{{\partial x}}}^{{A_{x}}}\overbrace { + \tilde u\frac{{\partial \tilde \rho}}{{\partial x}}}^{{N_{x}}}\overbrace{ - \frac{1}{H}\frac{{\partial \overline {\tilde u\tilde \rho} H}}{{\partial x}}}^{{C_{x}}}\overbrace{+ w\frac{{\partial \rho} }{{\partial z}}}^{{W_{z}}} + ...\\ \underbrace {\tilde v\frac{{\partial \bar \rho} }{{\partial y}}}_{{S_{y}}}\underbrace {+ \bar v\frac{{\partial \tilde \rho} }{{\partial y}}}_{{A_{y}}}\underbrace { + \tilde v\frac{{\partial \tilde \rho}}{{\partial y}}}_{{N_{y}}}\underbrace {- \frac{1}{H}\frac{{\partial \overline {\tilde v\tilde \rho} H}}{{\partial y}}}_{{C_{y}}}\underbrace {+ \frac{\partial \left\langle {\rho^{\prime}w^{\prime}} \right\rangle}{\partial z}}_{{M_{z}}} \end{array}\right) zdz + ...\\ &&\int\limits_{- h}^{\eta} \left( \begin{array}{l} \underbrace {\frac{{\partial \left\langle {\rho^{\prime}u^{\prime}} \right\rangle} }{{\partial x}}}_{{D_{x}}} + \underbrace {\frac{{\partial \left\langle {\rho^{\prime}v^{\prime}} \right\rangle} }{{\partial y}}}_{{D_{y}}} - \frac{1}{H}\left( {\underbrace {\left\langle {\rho^{\prime}w^{\prime}} \right\rangle \left| {{~}_{s}} \right.}_{{D_{s}}}\underbrace { - \left\langle {\rho^{\prime} w^{\prime}} \right\rangle \left| {{~}_{b}} \right.}_{{D_{b}}}} \right)zdz \end{array}\right) \end{array} $$
(3)

where \(\tilde {\rho } = \rho - \bar {\rho }\) ,\(\tilde {u} = u - \bar {u}\) and \(\tilde {v} = v - \bar {v}\) are the deviations from the depth mean values, u is the cross-shore component of the velocity and v is the along-shore component. Straining in along- and cross-shore direction is presented by the terms S x and S y . The terms A x and A y are advection in cross- and along-shore direction. The nonlinear interaction between the deviation from both vertical density and velocity are described by N x and N y , in other words, they represent non-linear straining. Dispersion is described by C x and C y . M z represents the vertical mixing due to turbulence on the vertical density profile. W z is the vertical advection term (up- and downwelling). The horizontal depth averaged dispersion terms are described by D x and D y . The surface and bed density fluxes are presented by the terms D s and D b . The changes in surface elevation and water depth are small and have been neglected.

However, any observational study is limited in spatial extent and time. Therefore, assumptions have to be made and the full 3D equation needs to be simplified in order to apply it to the data. As a result of the availability of the data, the following terms from Eq. 3 could be calculated: reversible cross-shore straining S x , along-shore straining S y , cross-shore depth mean advection A x , along-shore depth mean advection A y , cross-shore non-linear straining N x , along-shore non-linear straining N y , dispersion in cross- and along-shore direction C x, y and irreversible mixing M z (see Eq. 4). de Boer et al. (2008) demonstrated that these are the main terms that give an acceptable representation of the total change of φ in time at a location near the river mouth. The simplified equation becomes:

$$\begin{array}{@{}rcl@{}} \frac{\partial \varphi_{t}}{\partial t} \approx \frac{g}{H} {\int}_{-h}^{\eta} \left( \overbrace{\underbrace{ \tilde{u} \frac{\partial \bar{\rho}}{\partial x}}_{{S_{x}}}}^{{C_{x}}} + \overbrace{\underbrace{ \bar{u} \frac{\partial \tilde{\rho}}{\partial x}}_{{A_{x}}}}^{{C_{y}}} + \overbrace{\underbrace{\tilde{v} \frac{\partial \bar{\rho}}{\partial y}}_{{S_{y}}}}^{{N_{x}}} + \overbrace{\underbrace{\bar{v} \frac{\partial \tilde{\rho}}{\partial y}}_{{A_{y}}}}^{{N_{y}}}\right) z \mathrm{d}z\\ -\underbrace{\epsilon k \rho \left( \frac{\vert\overline{u}^{3}\vert}{h}\right)}_{M} -\underbrace{\delta k_{s} \rho_{a} \left( \frac{W^{3}}{h}\right)}_{M_{\text{wind}}} -\underbrace{\eta \rho \frac{\pi^{2}}{h} \left( \frac{SWH}{T}\right)^{3}}_{M_{\text{wave}}} \end{array} $$
(4)

Vertical mixing, M z , is difficult to determine. Turbulent quantities are necessary, which are difficult to measure in the field. One way of determining this term is using the eddy viscosity principle (Becherer et al. 2015) . However, the collected dataset does not contain enough information to use this method. Therefore, M z is calculated analytically following Simpson et al. (1990). They determine vertical mixing by dividing it into the components tidal stirring, M tide, and wind stirring M wind. Their study was in the Liverpool Bay area. The area of our transects is much shallower, therefore, waves could play a role in mixing the water column as well. Therefore, wave energy is added here according Wiles et al. (2006) . Within these mixing terms, \(\overline {u}\) is the depth mean tidal current, W is the wind velocity and ρ a is the air density (kg/m3).SWH is the significant wave height, T the wave period and η is the wave mixing efficiency. A wave mixing efficiency of 4 × 10−6 is used based on Wiles et al. (2006). The mixing coefficients for tide and wind energy are based on Simpson et al. (1991). The effective drag coefficient for bottom stresses, k, is 0.0025, the effective drag coefficient for surface stresses, k s , is 6.4 × 10−5, the efficiency for mixing, δ, is 0.039 and the efficiency for mixing, 𝜖, is 0.0038. Equation 4 will show some difference from the original equation (Eq. 2) as a result of the omission of the neglected terms of Eq. 3, due to the limitation of the dataset. In addition, the parameterization of the mixing term, M z , will cause a deviation as well.

Before applying the simplified equation on the data, the missing surface values needed to be extrapolated. Otherwise, the PEA terms will be underestimated. Subsequently, the simplified equation (Eq. 4) is applied to the study area. To discretize Eq. 4, a grid is introduced. As gradients have to be defined, a staggered grid is proposed in the alongshore direction. Figure 2 shows the spatial grid used based on the two parallel transects. The grid has n by m grid points, where m are the points in along-shore direction and n in cross-shore direction. The outer grid points (m = 0 and m = 2) represent all the stations where the vessels collected data.

Fig. 2
figure 2

A grid of the two transects used for calculating the spatial gradients. Density (ρ) and velocity data (v and u) are available at four points at each transect. These black points represents the measurement stations. The change in density in along- and cross-shore direction is determined at the grey points, in between the two transects. Therefore, the terms of Eq. 4 are determined at the grey points as well

Full size image

The along-shore terms were calculated in the y-direction with the use of the two transects. The partial derivatives of ρ were estimated at (n = 1) between the two transects (at m = 1). Due to the limited resolution, the estimation of the cross-shore terms was more complicated. The partial derivatives of ρ in the x-direction for the most outer stations (n = 1,4) were calculated using a first-order up- and downwind scheme. For the two inner points (n = 2,3), a central scheme was used to calculate the cross-shore derivative.

For calculating the cross-shore derivatives, the time was assumed to be instantaneous. This was based on two criteria. First, the maximum time difference between two points was 45 min. This is much smaller than the duration of one tidal cycle. Secondly, the change of the density in time is small compared to the change in cross-shore direction. Therefore, the assumption of quasi-instantaneous transect measurements is considered a reasonable approximation.

The accuracy of the equation was checked by comparing it to Eq. 2, which was calculated based on the measured salinity, temperature and pressure data. If one examines the difference between Eqs. 2 and 4, this will act as a measure for the missing terms needed for the closure of Eq. 3 and the errors introduced due to the different assumptions made for the calculation of the terms. Although we cannot calculate all the terms of Eq. 3, the difference allows us to assess what percentage of ∂ φ/ ∂ t is accounted for by Eq. 4.

3 Results

Figure 3 highlights the background conditions. Figure 4 shows the along-shore velocity, temperature and salinity data in three dimensions, while Figs. 5 and 6 show cross-sections of velocity, salinity, temperature, density difference and the potential energy anomaly per transect. In the following, we first consider the background conditions in Section 3.1. Secondly, the velocity distribution is considered in Section 3.2, then the salinity distribution in Section 3.3 and in the end we show the potential energy anomaly analysis in Section 3.4.

Fig. 3
figure 3

The conditions from the 5th of October to the 14th of October 2011. The upper panel shows the tidal elevations at IJmuiden and Petten Zuid. The second panel shows the wind speed and direction collected at a measuring station near IJmuiden. The significant wave height and direction is presented in the third panel. The data is collected from a measuring station near IJmuiden. The last panel gives the discharges from the Haringvliet, the Maasmond and the North Sea Channel IJmuiden. The tidal, wave and discharge information is obtained from the database of Rijkswaterstaat (2015). The wind data is retrieved from the KNMI database (www.knmi.nl)

Full size image
Fig. 4
figure 4

The salinity, temperature and along-shore velocity profiles in three-dimensions for both transects. On the left, the profiles for the southern transect are shown and on the right for the northern transect. The vertical axis represents the depth and the horizontal axis represents the time and the distance to the shore. The along-shore tidal velocity is displayed at the back of the figure to indicate the time within the tidal cycle. The measurements started offshore and sailed onshore, this is called a track. From top to bottom, the following information is presented: (1) salinity (psu), (2) temperature (∘C) and (3) along-shore velocity (m/s), where positive is northwards

Full size image
Fig. 5
figure 5

Data from the northern transect on the 13th of October 2013. The vertical dotted lines represent the measurement stations with corresponding measurement time. For easy interpretation, the long sailing interval at the end of each track is not interpolated but left blank, unlike Fig. 4. From top to bottom the following information is presented: (1) the blue line is the tidal elevation in m, in black the sailed traject (top is offshore, station 1). Each transect is sailed from offshore to nearshore. The red dotted line represents the depth mean along-shore velocity in m/s, where positive is northwards, (2) cross-sections of the along-shore velocity in m/s, where positive is northwards, (3) cross-sections of the cross-shore velocity in m/s, where positive is onshore, (4) cross-sections of salinity (psu), (5) cross-sections of temperature (∘C), (6) cross-sections of the salinity difference between bottom and location in water column and (7) the potential energy anomaly (φ) in J/m3

Full size image
Fig. 6
figure 6

Data from the southern transect at the 13th of October 2013. For further explanation see Fig. 5

Full size image

3.1 Background conditions

During the 13th of October, the weather was quite calm, wind velocity varied between 3.75 and 4.5 m/s and the wind came from north easterly to easterly direction. The days before were windy, with wind velocity peaking around 12 m/s and blowing from south-west to north-west (Fig. 3, second panel).

Significant wave heights of 2.5 meter occurred the days before due to the stormy weather. During the measurement campaign, the waves were coming from the north and had a significant wave height of ∼1 m and a wave period varying between 5.5 and 6.5 s (Fig. 3, third panel).

Figure 3 (upper panel) shows the tidal levels during the campaign and the week before. The measuring stations at IJmuiden and Petten Zuid are used to get an impression of the tidal level at both transects. The campaign was carried out 1 day before spring tide. The campaign lasted for 13 h starting just after high water and ending after the next high water. Therefore, an entire semi-diurnal tidal cycle was captured.

At two locations along the Dutch coast, fresh river water is discharged into the north sea. The Meuse and Rhine river discharge via the Maasmond and the Haringvliet into the southern north sea. Figure 3 (lower panel) shows the discharges of both rivers, before and during the measurement period. South of the transect locations the north sea channel at IJmuiden releases fresh water at irregular time intervals into the north sea. The days before the campaign, the channel discharged an amount of about 120 m 3/s.

3.2 Velocity distribution

Distinct southward ebb and northward flood velocities are observed in the Figs. 4, 5 and 6. The first panel of Figs. 5 and 6 shows that the tidal elevation is asymmetrical and out of phase with the depth mean along-shore velocity. The alongshore velocity is almost symmetrical though: six and a half hours between the two slack waters is observed. The figures show that the velocity leads the tidal elevation. During high water, the velocity leads by 1 h and during low water by 3 h. The data also shows that the reversal from flood to ebb at the southern transect is about 20 min before the switch at the northern transect. No delay is observed when the velocity switches from ebb to flood.

The third panel in Figs. 5 and 6 shows the presence of cross-shore components in the velocities. These velocities have a magnitude between 0 and ± 0.3 m/s. They are 50 % smaller than the along-shore velocity. The data shows periods where the bottom and surface currents are in opposite directions. In particular during the reversal from ebb to flood (track 5 and 6) offshore surface currents and onshore bottom currents are observed. During the reversal from flood to ebb mainly onshore currents are observed over depth. Conceptually, a picture of the plume emerges based on these velocities. During ebb the water flows southwards, the depth mean along-shore advection dominates. During the reversal from ebb to flood cross-shore differential advection is evident. The surface offshore directed and the near bed onshore directed advection of the flow will likely increase stratification during this phase of the tide. During flood, the water flows northwards mainly due to depth mean advection and during the reversal from flood to ebb the cross-shore currents advect the fresher water shoreward throughout the watercolumn.

3.3 Salinity distribution

Figure 4 shows the 3D salinity and temperature distribution of both transects. Figures 5 and 6 also present the salinity and temperature profiles for both transects. They show a minimum salinity of 29.5 psu at the southern transect and 30 psu at the northern transect, which indicates the presence of fresh riverine water (based on, e.g., de Ruijter et al. 1997; van der Giessen et al. 1990). Maximum salinity is 32.7 psu for the northern transect and 31.8 psu for the southern transect. Therefore, the southern transect contains fresher water than the northern transect. The northern salinity values are higher than those close to the river mouth. This can be explained by the mixing of the river plume with the surrounding seawater when the plume moves farther northwards. This results in higher salinity values further away from the river mouth. This is shown in the data as well. An along-shore salinity gradient is observed. The northern transect is more saline than the southern transect, with a maximum difference of about 1 psu. The along-shore differences are larger offshore (at 8 km) than closer to the shore. Offshore, a minimum and maximum depth mean along-shore salinity gradient of respectively 3.855 × 10−5 and 8.353 × 10−5 psu/m is observed, where positive is defined northwards. Near shore (at 1 km from the shore), the minimum depth mean salinity gradient is in the order of 1.383 × 10−5 psu/m and the maximum depth mean salinity gradient is about 4.116 × 10−5 psu/m. These depth mean salinity gradients indicate that the north is more saline.

In addition to the along-shore salinity gradient, a cross-shore salinity gradient is observed. Figure 4 shows more saline water offshore and fresher water onshore. These horizontal differences are an order of magnitude larger than the along-shore gradients. They are in the order of 1.5 and 2 psu, resulting in cross-shore salinity gradients of 2.5 × 10−4 psu/m for the northern transect and 2.0 × 10−4 psu/m for the southern transect. A positive gradient is defined offshore. The cross-shore gradient is slightly higher for the northern transect. At the start of the measurements the water column is well-mixed at both transects. During the day fresher water is flowing on top of more saline water, which results in maximum stratification at track 6 (ca. 10–1.5 h before maximum flood velocities). This results in vertical salinity differences (see Figs. 5 and 6, sixth panel). Both transects show this trend. The maximum vertical salinity difference for both transects is in the order of 1.3 psu. Figures 5 and 6 indicate a difference in stratification between the northern and southern transect. The northern transect is stratified for a much longer period than the southern transect. The southern transect shows a (very) weak stratification at high water slack (between track 1 and 2). The water column returns immediately into a well-mixed state during ebb. Around 1–1.5 h before maximum flood velocities, the water column is stratified again. The northern transect starts to stratify after maximum ebb velocities, also reaching maximum stratification 1–1.5 h before maximum flood velocities. From these observations, follow that the stratification at the northern transect is larger than at the southern transect (see Figs. 5 and 6). So, the southern transect is less stratified over the vertical despite the fact that it is fresher, while it would be expected that the southern transect is fresher and more stratified (de Ruijter et al. 1997). Therefore, this will affect ASIPS, because the along-shore depth mean advection A y will advect a less stratified water column northwards during flood enhancing destratification instead of the other way around.

3.4 Potential energy anomaly analysis

The change of φ in time (∂ φ/ ∂ t) is used to identify the competition between the stratifying and stirring processes. When ∂ φ/ ∂ t is larger than zero, the water column is stratifying while a negative ∂ φ/ ∂ t means that the water column is destratifying or mixing. Figure 7 shows the components of the simplified 3D equation (Eq. 4) and ∂ φ/ ∂ t calculated from Eq. 2. It is evident from Fig. 7 that there is a difference between the simplified equation (Eq. 4) and ∂ φ/ ∂ t (Eq. 2). However, in general, both equations do show the same trend.

Fig. 7
figure 7

The upper panel represents the along-shore velocity (grey dotted line), cross-shore velocity (black dotted line) and the transect sailed (top is offshore, station 1). Each transect is sailed from offshore to nearshore. The second till fifth panels show the contribution of the ASIPS and mixing terms separately, which are determined between the two transects. The local time rate of change of φ in time is also drawn in black (Eq. 2). The graph shows for each gridpoint, as in Fig. 2, in blue the total of all the terms in Eq. 4, in grey with a dotted line ASIPS+N+C, with a small dotted black line ASIPS and in red with a dotted line the mixing part. The terms are expressed in W/m 3

Full size image

The total response of the water column is interpreted as follows. The total value estimated from the simplified equation (Eq. 4) is slightly negative from 1 h after maximum flood velocities till maximum ebb velocities, it works in a destratifying manner. At maximum ebb velocities, the estimated value becomes increasingly positive, the water column is stratifying till it reaches maximum stratification 1–1.5 h before maximum flood velocities. Then ∂ φ/ ∂ t computed from Eq. 4 decreases again, and the water column goes slowly back to a well-mixed state.

In addition, Fig. 7 shows that each station behaves differently regarding the various terms of the simplified equation Eq. 4. Nearshore (at 1 km) depth mean advection and straining are hardly present, almost zero and the mixing processes dominate and determine the state of the water column. In the offshore direction, the depth mean advection and straining processes become increasingly larger. At 2 km offshore, the mixing and ASIPS + N x,y + C x,y terms are all of the same order. The water column is only stratifying just before maximum flood velocities (track 6). More offshore (4 and 8 km) ASIPS + N x,y + C x,y dominates. The water depth increases and therefore the contribution of mixing processes becomes less important.

Figure 7 shows that the total decrease or increase of ∂ φ/ ∂ t is mostly dependent on ASIPS, except close to the shore. This is inline with de Boer et al. (2008) , who concluded that although C x, y and N x, y are large, their sum largely cancels out. Figure 8 gives insight into the influence of these individual terms, for each station. This figure shows that the sum of all nonlinear terms (C x, y and N x, y ) is small. Mainly ASIPS dominates at all the stations, except at track 5 and 6 (about one and an half hour till half an hour before maximum flood velocities). At that moment, cross-shore dispersion (C x ) comes into play and slightly results in mixing. This is at the moment when the cross-shore surface velocity is directed offshore.

Fig. 8
figure 8

The upper panel represents the along-shore velocity (grey dotted line), cross-shore velocity (black dotted line) and the transect sailed (top is offshore, station 1). Each transect is sailed from offshore to nearshore. The second till fifth panels represent the change of φ over time for each measuring station, based on the straining and advection terms (i.e. ASIPS). The terms are determined between the two transects. In black, the behaviour of all the terms together (Eq. 4) is presented, the dotted black line is ASIPS, in blue the straining term is presented, in grey advection, in red nonlinear straining and in light blue dispersion. Where a line represents the cross-shore direction and the dotted line the along-shore direction. The terms are expressed in W/m 3

Full size image

Onshore (1 km) all processes, except for cross-shore dispersion, are hardly present. At the other stations, cross-shore straining (S x ) is generally dominant. At 2km offshore (station 3) cross-shore straining (S x ) is the main contributor, only at track 4, 5 and 6 (about half an hour before till one hour after maximum flood velocities) cross-shore dispersion (C x ) comes into play. The cross-shore straining term, S x , is in favour of stratification from high water slack till half an hour before maximum flood velocities (after track 2 till track 6). After track 6 (about half an hour before maximum flood velocities) cross-shore straining, S x , becomes negative and works in favour of destraining the water column.

At the offshore stations (4 and 8 km), all the reversible ASIPS terms and C x , except A x , are contributing significantly. Especially from track 4 to 7, all the terms influence the state of the water column. Cross-shore depth mean advection (A x ) only occurs during flood (track 6 and 8). During ebb, from track 2 to track 5, the along-shore straining (S y ) is negative and works in favour of mixing. During ebb, the along-shore velocity is headed southwards, as a result the fresh water is advected southwards by the higher surface velocity. During flood (after track 5), the freshwater at the surface is advected northward and act in a stratifying manner. Figure 8 shows that the along-shore depth mean advection (A y ) works in the opposite direction of S y at all the stations. The along-shore depth mean advection (A y ) is positive during ebb and negative during flood, instead of negative during ebb and positive during flood. Based on de Boer et al. (2008), both were expected to work in the same direction.

4 Discussion

This paper presents measurements off the Dutch coast that are novel in two ways. First, the dataset is collected in the far downstream plume (80 km) instead of close to the mouth of the Rotterdam Waterway as done for the historical cruises. Second, the data consists of two cross-shore parallel transects sailed simultaneously. The three-dimensional Potential Energy Anomaly equation is applied to this dataset to investigate the influence of straining and depth mean advection on stratification. In addition, the equation is used to see whether nonlinear straining and dispersion are very small. These two items are discussed below.

4.1 Stratified 80 km downstream

The field data presented here suggests that the Rhine ROFI extends over 80 km downstream, whereas previous studies focused on the area near the river mouth, and only treated the far downstream area as a secondary feature. The observations show periodic stratification at both transects over one tidal cycle. We also found that the southern transect—closer to the river mouth—has fresher waters than the northern transect, while the southern transect is vertically more homogeneous than the northern transect. This has consequences for the stratifying and destratifying processes, as we will discuss later on. Most studies analysing stratification in the ROFI have focused on the bulge region and the near field plume (Simpson and Souza 1995; Souza and Simpson 1997). However, stratification has been observed in the far plume region as well by van der Giessen et al. (1990). de Ruijter et al. (1992) found weak stratification at Callantsoog, 100 km downstream the river mouth. An analysis of satellite images (de Boer et al. 2009; Pietrzak et al. 2011) found that the plume is expected to extend even further downstream.

Previous studies indicated a stratified state only during neap tides (periods of low energy) and a mixed state during spring tide (Simpson et al. 1990; de Boer et al. 2006). Here, we find that 1 day before spring tide stratification still occurs. The stratification is weak though with maximum vertical salinity difference between surface and bottom of 1.3 psu at both transects. The weak easterly wind could play a role, because it acts in the direction to enhance stratification (Munchow and Garvine 1993; Fong et al. 1997; Wiechen 2011). The wind ageostrophically pushes the surface water in the direction of the wind. In addition wind driven Ekman dynamics advects the water towards the right, in this case northwards. Therefore, fresher surface water will flow over more saline water enhancing stratification.

4.2 Two parallel transects

This study, in addition to Becherer et al. (2015), shows that a simplified φ equation such as Eq. 4 is a useful tool to capture the influence of processes such as straining, depth mean advection, nonlinear processes and stirring. However, the change of φ as determined by the ASIPS, nonlinear straining, dispersion and mixing terms does not fully describe the local time rate of change calculated with Eq. 2. These differences can be ascribed to the simplification of the formula, the parameterization of vertical mixing, interpolation artefacts between ADCP and CTD data, the chosen discretization method and the assumption that the transect measurements are instantaneously. Despite describing 50 % of the signals variance, Figure 7 shows that the result of Eq. 4 follows the same trend. Therefore, this approach can be used qualitatively on in situ data to investigate the competing processes responsible for changing the stratification.

Korotenko (2012) and Korotenko et al. (2014) show that vertical mixing due to tide, wind, waves and bottom topography is important for the vertical density structure. They show that bottom topography (a 5 m deep plateau) can play an important role for producing turbulence. In this study, the bathymetry is gently sloping with no shallow plateaus. We do not have bathymetry that will create turbulence throughout the water column (Fig. 1). In addition, their studies indicate that a bulk mixing parameterization, such as we applied here, is a rough approximation. However, de Boer et al. (2008) used a second-order turbulence model (k-epsilon) in a similar fashion to Korotenko et al. (2014) (Mellor-Yamada) to calculate vertical turbulent mixing. In this study, de Boer et al. (2008) found that the influence of vertical mixing is much smaller than the influence of tidal straining on the evolution of stratification during a tidal cycle. This is in agreement with our findings for low wind speeds. The bulk parameterization was used here because of the limitations of the dataset and for a better closure of the equation.

The φ analysis shows that depth mean advection and straining are dominant at the offshore stations (4 and 8 km) and determine the periodic stratification. Therefore, this analysis shows that along-shore straining and depth mean advection not only contribute to (de)stratification in the bulge region but also in the river plume far downstream. Van Alphen et al. (1988) suggested that the periodic stratification in the Rhine ROFI is caused by along-shore depth mean advection. In contrast, Simpson and Souza (1995) stated that cross-shore tidal straining dominates the ROFI in the downstream plume near Noordwijk (40 km downstream river mouth). Additionally, de Boer et al. (2008) showed the importance of both along-shore depth mean advection and cross-shore straining within the bulge and in the downstream plume close to the river mouth. Our data shows that all previous authors were partially right, in the sense that in the ROFI a complex interplay between all depth mean advection and straining modes occurs. Yet, here we find that cross-shore straining is still the largest contributor of ASIPS. It enhances stratification, from maximum ebb till maximum flood velocities, in line with the findings of Simpson and Souza (1995).

The nonlinear straining terms and along-shore disperion are very small at all locations. However, some cross-shore dispersion is present between maximum ebb and maximum flood velocities. This is when cross-shore surface velocities are offshore directed. This process works in a mixing manner at the onshore and offshore stations. In general, the nonlinear straining and dispersion terms are small at locations downstream of the river mouth, as found for the case of no wind forcing byde Boer et al. (2008).

Onshore (1 km from the shore), the mixing processes are dominant. Thus, at the onshore stations, no stratification has been observed. This is in line with de Ruijter et al. (1997), who observed maximum mixing energy within 3 km from the shore. Closer to the coast, it is shallower (the most offshore station is 16–20 m deep, the onshore station is 8–10 m deep) resulting in higher mixing energy due to tides, waves and wind. During the measurements, the wind conditions were mild though (3.5–4 m/s), which resulted in a small contribution of wind and wave stirring.

In this study, we find that the along-shore depth mean advection works in favour of stratification during ebb (from north to south) and in favour of de stratification during flood. This means that exactly the opposite behaviour is observed than expected. According to de Boer et al. (2008), along-shore depth mean advection works in the same direction as along-shore straining. The unexpected working of the along-shore depth mean advection is a direct consequence of the more homogeneous waters observed at the southern transect compared to the northern transect. This effect is sketched at items 6 and 8 in Fig. 9, where an increasing along-shore density gradient in northern direction is visible between the southern and northern transect. During flood, the depth mean along-shore current advects a more homogeneous water column northwards, enhancing destratification. This is visible at the end of the flood period (Fig. 9, item 8). During ebb, a more stratified water column is advected southwards inducing stratification, this is visible at the end of the ebb period (Fig. 9, item 6). The fact that the northern transect is more stratified than the southern transect is not in line with plume theory. Generally, plume theory assumes that on average further away from the river mouth the river plume gradually mixes up, leading to higher salinity and lower stratification (de Ruijter et al. 1997). The field data captures an event that is not in line with this theory. This event might be due to a pulse of fresher water traversing the area during the campaign.

Fig. 9
figure 9

A sketch of the downstream plume of the Rhine ROFI in four dimensions, respectively time (with T the tidal period), depth, cross- and along-shore locations. The combined effect of along-shore depth mean advection A y , along-shore straining S y (in y direction) and cross-shore straining S x (in x-direction) is sketched at two different locations in the plume, respectively, 30–40 km and 70–82 km from the river mouth. For one tidal cycle, from t= 0 to t = T, the influence of the different processes in cross- and along-shore direction is shown. The hashed grey area indicates the period in which minimum and maximum stratification could occur based on the direction and magnitude of all the processes in normal conditions (pattern //) where the north is more saline and less stratified and this campaign (pattern ∖∖) where the northern transect is saltier and more stratified. The numbers 2 and 4 show the maximum influence of only the along-shore advection and straining at slack tide at 30–40 km downstream the river mouth (Van Alphen et al. 1988; de Boer et al. 2008). The numbers 6 and 8 show the influence of the along-shore processes 70–82 km downstream that we found in this study. The numbers 1 and 3 show the maximum influence of cross-shore straining at maximum and minimum tidal velocities (Simpson and Souza 1995). The influence of cross-shore straining at two parallel transects 70–82 km downstream is shown by the numbers 5, 6, 7 and 8

Full size image

We found that the exact timing of maximum stratification differs from previous studies (Simpson and Souza 1995; Van Alphen et al. 1988; de Boer et al. 2008). Maximum stratification occurs between 1 and 1.5 h before maximum flood velocities (Fig. 9, between items 6 and 7). Simpson and Souza (1995) concluded that minimum stratification occurs at maximum ebb velocities under influence of only cross-shore tidal straining (Fig. 9, item 1). And maximum stratification occurs at maximum flood velocities (Fig. 9, item 3). In the situation of only along-shore depth mean advection and straining, minimum stratification was thought to occur at LW slack and maximum stratification at HW slack (Van Alphen et al. 1988)(Fig. 9, items 2 and 4). de Boer et al. (2008) pointed out that when the sum of both cross- and along-shore straining and depth mean advection are equal (i.e., ASIPS) maximum stratification occurs at maximum flood velocities plus 1/8 of a tidal cycle.

The difference in timing observed in our campaign of 1–1.5 h is close to this 1/8 of a tidal cycle. However, it is 1/8 before HW instead of after HW. This can be explained by the unexpected ”reverse” behaviour of the along-shore depth mean advection. First, along-shore depth mean advection works in a stratifying manner during ebb velocities, enhancing stratification instead of destratification. Second, it cancels the mechanism of the along-shore straining, therefore the cross-shore processes have a larger contribution in determining the timing of maximum stratification. In normal conditions, where the northern transect is saltier and less stratified, maximum stratification is expected somewhere between t = 3T/4 and t = T and minimum stratification between t = T/4 and t = T/2 (Fig. 9, pattern //). When the northern transect is more stratified and more saline than the southern transect maximum stratification is expected between t = T/2 and t = 3T/4 and minimum stratification between 0 and t = T/4 (Fig. 9, pattern ∖∖). It can be concluded that the timing of maximum and minimum stratification depends on the proportion and the direction of ASIPS.

5 Conclusion

Within this study, it is shown that the 3D potential energy anomaly equation can be applied on field data. It showed that the different terms can be estimated giving a picture of the processes that lead to stratification and destratification. As Simpson and Souza (1995) showed classic cross-shore straining S x , de Boer et al. (2008) found that depth mean along-shore advection A y plays a role near the mouth as well. Here, we show that both straining S x, y and depth mean along-shore advection A y are important even in more well-mixed waters 80 km downstream the river mouth. In addition, it is shown here that the sum of nonlinear straining N x, y and dispersion C x, y are small compared to ASIPS. The importance of cross-shore dispersion increases towards the coast. The question remains about the terms we cannot calculate from Eq. 3 and the assumptions made which are needed for the closure of this equation. The difference between Eqs. 2 and 4 suggests that these terms could play a role in this area, but this needs further investigation.

A ROFI is a complex interplay between the tidal velocity field and the history of the 3D density structure. This history includes phenomena of various origins at various time scales, such as meteo-driven advection and mixing, and river discharge variations ranging from seasonal to formation of tidal lenses in estuaries and sluices. It is of importance for ROFI knowledge to understand the influence of along and cross-shore processes on stratification and the dispersion of the freshwater lenses. These processes are of a direct relevance for the transport of pollutants, SPM and nutrients. In addition, it helps to understand the influence of human interferences and the protection of coasts. The presence of stratification changes the tidal currents and therefore influences the distribution of SPM. As a result of the difference in stratification between the two transects, which are only 12 km apart, it is expected that the local response of SPM could be different. Numerical models such as those by de Boer (2008) are an important factor to understand the ROFI systems. They can help interpret the entire area. Field data can help improve these models to reproduce accurately the physics in these systems. This study shows that when companies and institutions strengthen together it can lead to new datasets and extending our knowledge of ROFIs.