Three-dimensional semi-idealized model for tidal motion in tidal estuaries

Abstract

In this paper, a three-dimensional semi-idealized model for tidal motion in a tidal estuary of arbitrary shape and bathymetry is presented. This model aims at bridging the gap between idealized and complex models. The vertical profiles of the velocities are obtained analytically in terms of the first-order and the second-order partial derivatives of surface elevation, which itself follows from an elliptic partial differential equation. The surface elevation is computed numerically using the finite element method and its partial derivatives are obtained using various methods. The newly developed semi-idealized model allows for a systematic investigation of the influence of geometry and bathymetry on the tidal motion which was not possible in previously developed idealized models. The new model also retains the flexibility and computational efficiency of previous idealized models, essential for sensitivity analysis. As a first step, the accuracy of the semi-idealized model is investigated. To this end, an extensive comparison is made between the model results of the semi-idealized model and two other idealized models: a width-averaged model and a three-dimensional idealized model. Finally, the semi-idealized model is used to understand the influence of local geometrical effects on the tidal motion in the Ems estuary. The model shows that local convergence and meandering effects can have a significant influence on the tidal motion. Finally, the model is applied to the Ems estuary. The model results agree well with observations and results from a complex numerical model.

1 Introduction

Estuaries are regions of large economical (navigation channels, sand and gas mining, recreation, etc.) and ecological importance. Recently, various contributions (e.g., Chernetsky et al. (2010), de Jonge et al. (2012), Winterwerp et al. (2013), Winterwerp and Wang (2013)) have indicated that tidal characteristics can change significantly due to anthropogenic measures. These changes can endanger safety, i.e., changes in the surface elevation may cause flooding in the surrounding area, and transport (related to the changes in the three-dimensional velocity field) or accumulation of sediments and pollutants which leads to poor quality of water. It is therefore essential to accurately describe and understand the tidal water motion including its response to natural changes and anthropogenic disturbances.

Different types of process-based models can be used to gain understanding of tidal motion (Murray 2003; de Vriend 1992; 1991). These models can be broadly divided into two categories: complex simulation models and idealized models. A complex simulation model aims at resolving all known physical processes, using state-of-the-art parameterizations of unresolved processes. Concerning complex model simulations of the Ems estuary, one can find the studies by Van de Kreeke and Robaczewska (1993), Pein et al. (2014), and van Maren et al. (2015). An idealized model on the other hand considers only those physical processes which are dominant for the phenomenon under investigation. Idealized models use simplified geometric and bathymetric profiles. The schematizations of idealized models allow for quick solution techniques, often analytic, which makes these type of models suitable for extensive parameter sensitivity analysis.

Idealized models, used to study the tidal motion in estuaries, can be further divided into different categories. Averaging the governing equations over the cross-section results in one-dimensional models, see Lanzoni and Seminara (1998) and Valle-levinson (2010) for an overview. Ianniello (1977) and Chernetsky et al. (2010) developed width-averaged (2DV) models to gain insight in the vertical flow structure in the longitudinal direction. The geometry was assumed to be exponentially converging, while the depth was assumed constant in Ianniello (1977) and varying in the longitudinal direction in Chernetsky et al. (2010). Assuming along-estuary uniform conditions, Huijts et al. (2009) developed an idealized model to study the water motion in an estuarine cross-section, allowing for an arbitrary bathymetry in the lateral direction. To study the interaction of lateral and longitudinal flows, Li and Valle-levinson (1999) used a depth-averaged (2DH) model that allowed for an arbitrary bathymetric and geometric profile, but ignored Coriolis effects. Winant (2007) developed a three-dimensional idealized model for tidal motion on a rotating (Coriolis effects included) elongated (width is much smaller than the length) rectangular domain with a parabolic bathymetric profile in the lateral direction together with constant physical parameters and constant density. Winant’s three-dimensional idealized model is limited to an estuary with elongated rectangular domain and constant physical parameters.

In light of the above, it is clear that currently there is no idealized model that allows for a systematic investigation of the influence of arbitrary geometry and bathymetry on three-dimensional water motion. Therefore, the aim of this paper is to develop a three-dimensional idealized model for tidal water motion in an estuary with arbitrary geometry and bathymetry. The physical parameters are allowed to vary in the horizontal direction as well. The surface elevation is obtained from a two-dimensional elliptic partial differential equation, which is solved numerically using the finite element method. The vertical profile of the three-dimensional velocity can be explicitly calculated in terms of the first and second-order partial derivatives of the surface elevation, i.e., the three-dimensional velocity profile is analytic in the vertical direction.

This model is a first step in bridging the gap between idealized models and complex models: the model can still be systematically analyzed to gain understanding of important physical mechanisms, but allows for more complex geometries and bathymetries.

Our three-dimensional semi-idealized model is first tested by comparing its results with the results of the width-averaged model of Chernetsky et al. (2010) and the three-dimensional idealized model of Winant (2007). Extensive error and convergence analyses are performed to evaluate the finite element method and various methods to compute its partial derivatives. Next, the model is applied to complex geometry of the Ems estuary and the influence of local geometrical effects on the tidal motion is investigated.

The structure of the paper is as follows. The governing equations of the three-dimensional semi-idealized model are described in Section 2. These equations are solved in Section 3. The comparison of the three-dimensional semi-idealized model with the width-averaged model is presented in Section 4 and with the three-dimensional idealized model in Section 5. Using this novel three-dimensional semi-idealized model, the influence of local geometrical effects on the tidal motion of the Ems estuary are investigated in Section 6. Finally, conclusions are presented in section 7.

2 Model formulation

We consider a tidal estuary of arbitrary shape and bathymetry (Fig. 1), with x and y denoting the horizontal coordinates and z the vertical coordinate pointing upwards. The two-dimensional surface of the estuary is denoted by Ω. Note that, since the shape of the estuary is arbitrary, x (y) need not represent the along-channel (cross-channel) coordinate. The bathymetric profile is denoted by h(x, y), with the mean depth at the seaward side given by H.

Fig. 1

Three-dimensional sketch of an estuary with arbitrary geometric and bathymetric profiles. The bathymetric profile is shown on a grayscale. The seaward side (denoted by ∂ _D Ω) is shown in magenta color ( ) and the river side (denoted by ∂ _R Ω) is shown in cyan color (). The other boundaries (denoted by ∂ _N Ω) are assumed to be closed walls. The surface of the estuary is discretized using linear triangles in order to compute the surface elevation with the finite element method. The constrained nodes (nodes where the surface elevation is known) are indicated by blue diamonds () and unconstrained nodes (nodes where the surface elevation has to be computed) by red diamonds (). All the interior nodes are by default unconstrained. At each node in the triangulization of the surface, the vertical profile of the velocity field can be computed analytically using partial derivatives of the surface elevation as shown by yellow dashed lines (). The velocity at the surface is depicted by green arrows () and, in the rest of the water column, by yellow arrows ()

The water motion is governed by the three-dimensional shallow water equations, including the Coriolis effect. The estuary is assumed to be partially-mixed or well-mixed. Following Winant (2007), the equations are scaled and the physical variables are asymptotically expanded in powers of a small parameter $\epsilon = \tilde {A}/H$, where $\tilde {A}$ is the mean amplitude of the semi-diurnal lunar (M ₂) tidal wave at the seaward side. In leading order, i.e., at $\mathcal {O}$(𝜖 ⁰), the dimensional system of equations is given by

$$\begin{array}{@{}rcl@{}} &&u_{x}+v_{y}+w_{z}=0, \end{array} $$

(1a)

$$\begin{array}{@{}rcl@{}} &&u_{t} - f v = -g \eta_{x} + ({A}_{\mathrm{v}} u_{z})_{z}, \end{array} $$

(1b)

$$\begin{array}{@{}rcl@{}} &&v_{t} + f u = -g \eta_{y} + ({A}_{\mathrm{v}} v_{z})_{z}, \end{array} $$

(1c)

where f = 2Ω^∗sinθ is the Coriolis parameter, Ω^∗ = 7.292×10⁻⁵ rad s ⁻¹, the angular frequency of the Earth’s rotation, θ latitude, g is the gravitational acceleration, and A _v (m ² s ⁻¹) is the eddy viscosity. At the seaward side (denoted by ∂ _D Ω), the system is forced with a prescribed M ₂ tide,

$$ \eta = A(x,y) \cos \omega t, \quad \forall \quad (x,y) \in \partial_{D} {\Omega}, $$

(2a)

where A(x, y) is the spatially varying elevation amplitude along this boundary and ω = 2π/T is the tidal frequency of the M ₂ tide with tidal period T = 12.42 h. Also “ ∀(x, y)∈∂ _D Ω” means for all points (x, y) on the seaward boundary (∂ _D Ω). At the other boundaries, either a no-flux condition (for boundaries denoted by ∂ _N Ω) or a river discharge (for boundaries denoted by ∂ _R Ω) is prescribed. Assuming that the river outflow gives a minor contribution (only occurring at first order rather than zeroth order in 𝜖), the normal component of the volume transport is required to vanish at the remaining boundaries,

$$ \left( \int \limits_{-h}^{0} \! (u,v) \ \mathrm{d} z \right)\cdot \hat{\mathbf{n}} = 0, \quad \forall \quad (x,y) \in \partial_{N} {\Omega} \cup \partial_{R} {\Omega}, $$

(2b)

where $\hat {\mathbf {n}}$ is the local unit normal pointing outwards. As dynamic boundary conditions, a no-stress condition at the surface z = 0 and a partial slip condition at the bottom z = −h are prescribed, i.e.,

$$\begin{array}{@{}rcl@{}} {A}_{\mathrm{v}} (u_{z},v_{z}) = (0,0), \qquad&&\text{at}\,\,z=0, \end{array} $$

(2c)

$$\begin{array}{@{}rcl@{}} {A}_{\mathrm{v}} (u_{z},v_{z}) = s (u,v), \qquad &&\text{at}\,\,z=-h, \end{array} $$

(2d)

where s (m s ⁻¹) is the stress parameter which follows from the linearization of the quadratic friction law (for details, see Schramkowski et al. (2002) and Zimmerman (1992)). In the present model, the eddy viscosity A _v and the stress parameter s are assumed to be constant in the vertical direction and in time. As kinematic boundary conditions, the linearized boundary condition is applied at z = 0, and the impermeability of the bottom is imposed at z = −h, i.e.,

$$\begin{array}{@{}rcl@{}} &&w = \eta_{t}, \qquad\qquad\qquad\text{at} \quad z=0, \end{array} $$

(2e)

$$\begin{array}{@{}rcl@{}} &&w = -u h_{x}-v h_{y}, {} \quad\quad\text{at} \quad z=-h. \end{array} $$

(2f)

3 Solution method

The system of Eq. 1, together with the boundary conditions (2), constitute a closed set of equations that can be solved for the surface elevation η and velocity components (u, v, w). Usually, this problem is solved numerically by spatial and temporal discretization. In the approach presented below, the tidal motion is solved in terms of tidal constituents, i.e., without discretizing in time. Furthermore, the vertical structure of the velocity components is obtained analytically resulting in a two-dimensional elliptic partial differential equation (Section 3.1) for the surface elevation that, in general, has to be solved numerically (Section 3.2).

3.1 Analytical part of the solution method

Since the water motion is forced by an oscillating water level (2a) and the system of equations is linear, solutions of the system of equations are of the form

$$ (\eta,u,v,w) = \Re\{(N,U,V,W)e^{i \omega t}\}, $$

(3)

where ℜ stands for the real part of a complex variable, and $i =\sqrt {-1}$ is the unit imaginary number. Furthermore, N(x, y), U(x, y, z), V(x, y, z), and W(x, y, z) are the complex amplitudes of the surface elevation and the three velocity components, respectively. Substituting (3) into Eq. 1 gives

$$\begin{array}{@{}rcl@{}} &&U_{x} + V_{y} + W_{z} = 0, \end{array} $$

(4a)

$$\begin{array}{@{}rcl@{}} &&i \omega U - f V = -g N_{x} + {A}_{\mathrm{v}} U_{zz}, \end{array} $$

(4b)

$$\begin{array}{@{}rcl@{}} &&i \omega V + f U = -g N_{y} + {A}_{\mathrm{v}} V_{zz}. \end{array} $$

(4c)

To solve this coupled set of equations, we introduce rotating flow variables R ₁ and R ₂ with

$$\begin{array}{@{}rcl@{}} R_{1} = U+i V \quad \text{and} \quad R_{2}= U-i V, \end{array} $$

(5)

such that

$$\begin{array}{@{}rcl@{}} U = \frac{R_{1} + R_{2}}{2} \quad \text{and} \quad V = \frac{R_{1}-R_{2}}{2i}. \end{array} $$

(6)

We add Eq. 4c multiplied by i to Eq. 4b and Eq. 4c multiplied by -i to Eq. 4b. These give differential equations for the rotating flow variables:

$$ R_{j,zz} - {\alpha_{j}^{2}} R_{j} = \frac{g}{{A}_{\mathrm{v}}} \mathcal{L}_{j}N, \quad j=1,2, $$

(7a)

with differential operators $\mathcal {L}_{1}$ = ∂ _x + i ∂ _y , $\mathcal {L}_{2}$ = ∂ _x −i ∂ _y , and coefficients $\alpha _{1} = \sqrt {i\frac {\omega + f}{{A}_{\mathrm {v}}}}$, and $\alpha _{2} = \sqrt {i \frac {\omega - f}{{A}_{\mathrm {v}}}}$. Following the same procedure for the boundary conditions, we get,

$$\begin{array}{@{}rcl@{}} &&{A}_{\mathrm{v}} R_{j,z} = 0, \quad \text{at} \quad z=0, \end{array} $$

(7b)

$$\begin{array}{@{}rcl@{}} &&{A}_{\mathrm{v}} R_{j,z} = s R_{j}, \quad \text{at} \quad z=-h, \end{array} $$

(7c)

Here, ∂ _x and ∂ _y are the first-order partial derivatives with respect to x and y, respectively. For each j = 1,2, Eq. 7a is a linear, second-order ordinary differential equation in the vertical coordinate z, which can be solved analytically in terms of the unknown pressure gradients N _x and N _y . The resulting rotating flow variables read

$$ R_{j} = c_{\alpha_{j}}(z) \mathcal{L}_{j} N, \quad j = 1,2, $$

(8)

with vertical structure $c_{\alpha _{j}}$ given by

$$\begin{array}{@{}rcl@{}} c_{\alpha_{j}}(z) =\frac{g}{{\alpha_{j}^{2}} {A}_{\mathrm{v}}}\left[ \frac{s \cosh(\alpha_{j} z)}{\alpha_{j} {A}_{\mathrm{v}} \sinh(\alpha_{j} h) + s \cosh(\alpha_{j} h)} -1 \right]. \end{array} $$

Note that through the (x, y) dependency of the depth h, the stress parameter s and the eddy viscosity A _v, the function $c_{\alpha _{j}}$ also depends on the horizontal coordinates x and y. Integrating the continuity Eq. 4a from z = −h to z = 0, using the kinematic boundary conditions Eqs. 2e and 2f, we find that

$$ \partial_{x} \int \limits_{-h}^{0} \! U \ \mathrm{d} z + \partial_{y} \int \limits_{-h}^{0} \! V \ \mathrm{d} z + i \omega N = 0. $$

(9)

To express the depth-integrated horizontal velocity in terms of the surface elevation, define $C_{\alpha _{j}}(z)$ as

$$\begin{array}{@{}rcl@{}} &&C_{\alpha_{j}}(z) = \int \limits_{-h}^{z} \! c_{\alpha_{j}}(z^{\prime}) \ \mathrm{d} z^{\prime} \\ &&= \frac{g}{{\alpha_{j}^{3}} {A}_{\mathrm{v}}} \left[ \frac{ s (\sinh(\alpha_{j} z) + \sinh(\alpha_{j} h) )} { \alpha_{j} {A}_{\mathrm{v}} \sinh(\alpha_{j} h) + s \cosh(\alpha_{j} h)} - \alpha_{j} (z+h) \right]. \end{array} $$

Integrating (8) over the water column from z ^′ = −h to z ^′ = z, results in

$$ \int \limits_{-h}^{z} \! R_{j} \ \mathrm{d} z^{\prime} = C_{\alpha_{j}}(z)\mathcal{L}_{j} N, \quad j = 1,2. $$

(10)

Combining (6), (8), and (10), the depth-integrated horizontal velocities can be expressed as

$$\begin{array}{@{}rcl@{}} \int \limits_{-h}^{z} \! U \ \mathrm{d} z^{\prime} &=& \int \limits_{-h}^{z} \! \frac{R_{1}+R_{2}}{2} \ \mathrm{d} z^{\prime} \\ & =& \underbrace{\frac{ C_{\alpha_{1}}(z) + C_{\alpha_{2}}(z)}{2}}_{C_{1}(z)} N_{x} + \underbrace{i \frac{C_{\alpha_{1}}(z) - C_{\alpha_{2}}(z)}{2}}_{C_{2}(z)} N_{y} \\ & =& C_{1}(z) N_{x} + C_{2}(z) N_{y}, \end{array} $$

(11a)

and,

$$\begin{array}{@{}rcl@{}} \int \limits_{-h}^{z} \! V \ \mathrm{d} z^{\prime} &= \int \limits_{-h}^{z} \! \frac{R_{1}-R_{2}}{2i} \ \mathrm{d} z^{\prime} \\ & \,=\, -\! \underbrace{ i \frac{ C_{\alpha_{1}}(z) - C_{\alpha_{2}}(z)}{2}}_{C_{2}(z)} N_{x} \,+\, \underbrace{ \frac{C_{\alpha_{1}}(z) + C_{\alpha_{2}}(z)}{2}}_{C_{1}(z)} N_{y} \\ & = -C_{2}(z) N_{x} + C_{1}(z) N_{y}. \end{array} $$

(11b)

Substituting (11a) and (11b) in Eq. 9, results in an equation for the surface elevation:

$$ \nabla \cdot [\mathbf{D}(0) \nabla N] + i \omega N = 0, $$

(12a)

with ∇=(∂ _x , ∂ _y )^T, where the superscript T denotes the transpose operator, and

$$ \mathbf{D}(z)= \left[ {\begin{array}{rr} C_{1}(z) & C_{2}(z) \\ -C_{2}(z) & C_{1}(z) \end{array}} \right]. $$

(12b)

The corresponding boundary conditions read

$$\begin{array}{@{}rcl@{}} N &=& A, \quad \text{on} \quad \partial_{D} {\Omega}, \end{array} $$

(12c)

$$\begin{array}{@{}rcl@{}} \left[\mathbf{D}(0) \nabla N\right] \cdot \hat{\mathbf{n}}&=&0, \quad \text{on} \quad \partial_{N} {\Omega} \cup \partial_{R} {\Omega}. \end{array} $$

(12d)

Equation (12a) is a two-dimensional linear elliptic partial differential equation with complex coefficient matrix D(0). This matrix depends on the bathymetric profile h, the eddy viscosity A _v, the stress parameter s, and Coriolis parameter f, all of which can be arbitrary functions of the horizontal coordinates x and y. Therefore, an analytic solution of Eq. 12 cannot be obtained in general, and a numerical approach will be pursued. In Section 3.2, the numerical solution procedure will be discussed in detail.

Once the surface elevation N(x, y) is known, we have to calculate its gradients N _x and N _y to obtain the vertical profiles of the horizontal flow components. The vertical velocity W is obtained by integrating the continuity equation (4a) from z ^′ = −h to z ^′ = z, together with the aid of Leibniz integral rule and the kinematic boundary conditions ((2e) and (2f)), resulting in

$$\begin{array}{@{}rcl@{}} W &=& -\partial_{x} \int \limits_{-h}^{z} \! U(x,y,z^{\prime}) \ \mathrm{d} z^{\prime} - \partial_{y} \int \limits_{-h}^{z} \! V(x,y,z^{\prime}) \ {\mathrm{d}} z^{\prime} \\ &=& -\nabla \cdot [\mathbf{D}(z) \nabla N], \end{array} $$

(13)

with D(z) given by Eq. 12b. This completes the derivation of the three-dimensional flow profile expressed in terms of the first-order partial derivatives (for horizontal velocities) and the second-order partial derivatives (for vertical velocity) of the surface elevation.

3.2 Numerical part of the solution method

In general, for an arbitrary domain, bathymetry and spatially varying parameters, Eq. 12 cannot be solved analytically. Therefore, a numerical approach, the finite element method (Gockenbach 2006), is adopted. As a first step, Eq. 12 is written in its weak form,

$$\begin{array}{@{}rcl@{}} &- &\iint \limits_{\Omega} [\mathbf{D}(0) \nabla \tilde{N}]\cdot \nabla \phi \hspace{3 pt} \mathrm{d} {\Omega} + i \omega \iint \limits_{\Omega} \tilde{N} \phi \hspace{3 pt} {\mathrm{d}} {\Omega} \\ &=&\! \iint \limits_{\Omega} [\mathbf{D}(0) \nabla N_{D}]\cdot \nabla \phi \hspace{3 pt} \mathrm{d} {\Omega} \,-\, i \omega \iint \limits_{\Omega} N_{D} \phi \hspace{3 pt} {\mathrm{d}} {\Omega} \quad \!\forall \hspace{2pt} \phi \in {\Sigma},\\ \end{array} $$

(14)

where $N = \tilde {N} + N_{D}$, N _D = A on ∂ _D Ω and ϕ is a test function belonging to the space of test functions Σ. Equation (14) implies that since N _D is known, the problem of finding N now reduces to finding $\tilde {N}$. Details concerning the derivation of the weak form can be found in Appendix B.

Next, the software package Triangle (Shewchuk 1996) is used to discretize the domain Ω using triangles (Fig. 1). The discretized domain is denoted by ${\Omega }_{\tilde {h}}$, where $\tilde {h}$ is the mean step size (defined as the mean of the length of all the edges in the discretization of the domain). The total number of nodes equals n + m with the first n nodes located in the interior or on the no-flux boundary (unconstrained or free nodes, denoted by red diamonds in Fig. 1 together with all the interior nodes) and the last m nodes located on the seaward boundary (constrained nodes, denoted by blue diamonds in Fig. 1). Next, the unknown complex surface elevation amplitude $\tilde {N}$ is approximated by

$$ \tilde{N}_{\tilde{h}}(x,y) = \sum\limits_{l=1}^{n} N_{l} \phi_{l} (x,y), $$

(15)

where ϕ _l ’s are so-called Lagrange basis functions that equal one at node l and zero at all other nodes. The coefficients N _l , l = 1,…, n are unknown complex amplitudes. In this study, we will consider linear and quadratic polynomials as basis functions.

Next, we substitute the finite element approximation of $\tilde {N}_{\tilde {h}}$ (15) in the weak form (14) and choose test functions ϕ equal to basis functions ϕ _k , k = 1,…, n. This results in a linear system of equations for the unknown N _l ’s that can be solved numerically (see Appendix B for a detailed explanation). Once $\tilde {N}_{\tilde {h}}$ is known, we can write down the finite element approximation $N_{\tilde {h}}$ of N over the whole domain as,

$$\begin{array}{@{}rcl@{}} N_{\tilde{h}}(x,y) &=& \tilde{N}_{\tilde{h}}(x,y) + N_{D}(x,y) \\ &=& \sum\limits_{l=1}^{n} {N}_{l} \phi_{l}(x,y) + \sum\limits_{l=n+1}^{n+m} A(x_{l},y_{l}) \phi_{l}(x,y). \end{array} $$

(16)

Once we have computed the numerical solution $N_{\tilde {h}}$, its accuracy is assessed by performing error and convergence analyses. Denoting the exact solution of Eq. 12a by N, the error function $E_{\tilde {h}}$ is defined as

$$\begin{array}{@{}rcl@{}} E_{\tilde{h}} = N - N_{\tilde{h}}. \end{array} $$

The numerical solution $N_{\tilde {h}}$ converges to the exact solution N if

$$\begin{array}{@{}rcl@{}} {||E_{\tilde{h}}||}_{2} \to 0 \quad \text{as} \quad { \tilde{h}} \to 0, \end{array} $$

where ||⋅||₂ is the L ² norm defined in Appendix B. To make our error measure independent of the size of the domain and the range of the solution, we define the relative error as

$$\begin{array}{@{}rcl@{}} r({ \tilde{h}}) = \frac{||E_{\tilde{h}}||_{2}}{||N||_{2}}. \end{array} $$

(17)

The order of convergence p is the rate at which the numerical solution $N_{\tilde {h}}$ converges to the exact solution N, given by

$$\begin{array}{@{}rcl@{}} p = \frac{\log({||E_{\tilde{h}_{1}}||}_{2}/{||E_{\tilde{h}_{2}}||}_{2})}{\log(\tilde{h}_{1}/ \tilde{h}_{2})}. \end{array} $$

(18)

In general, if polynomial basis functions of order q are used, the numerical solution $N_{\tilde {h}}$ converges to the exact solution N with rate q+1, provided numerical integrals are computed accurately enough (Gockenbach 2006). For linear (quadratic) basis functions, we thus expect second (third) order convergence of the numerical solution.

To compute the three-dimensional flow components, the first-order and the second-order partial derivatives of N have to be computed. Since the surface elevation itself is obtained numerically using the finite element method, its partial derivatives have to be obtained numerically as well. It is therefore essential to determine these derivatives as accurately as possible to get accurate velocity fields.

The most straightforward way to compute the partial derivatives is the direct derivative method (from now on denoted by DD-method) in which the numerical approximation given by Eq. 16 is differentiated directly, i.e.,

$$\begin{array}{@{}rcl@{}} \frac{\partial^{a+b} N_{\tilde{h}}} {\partial x^{a} \partial y^{b}} = \sum\limits_{l=1}^{n} {N}_{l} \frac{\partial^{a+b} \phi_{l}} {\partial x^{a} \partial y^{b}} + \sum\limits_{l=n+1}^{n+m} A(x_{l},y_{l}) \frac{\partial^{a+b} \phi_{l}} {\partial x^{a} \partial y^{b}} , \end{array} $$

where a and b are the order of differentiation in the x and y directions, respectively. When linear basis functions are used, it is only possible to calculate the first-order partial derivatives. Hence, the vertical velocity W can not be reconstructed. For this reason, we use quadratic basis functions. The quadratic basis functions allow both the first-order and the second-order partial derivatives to be computed at minimum computational cost. Hence, the three components of the velocity can be computed.

A main drawback of the DD-method is that for each order of differentiation, the order of convergence of the resulting derivative decreases by one. For quadratic basis functions, the numerical solution for N is expected to converge with rate three. The first-order and the second-order partial derivatives calculated using the DD-method are then expected to converge with rates two and one, respectively.

In the literature, various methods (Carey (1982), Zienkiewicz and Zhu (1992a), Zienkiewicz and Zhu (1992b), Ilinca and Pelletier (2007)) are proposed to recover partial derivatives more accurately than with the DD-method. For the problem under consideration, the method proposed by Carey (1982) only resulted in superconverging (converging faster than expected) partial derivatives on a structured grid. For unstructured grids, the method failed to converge. The method proposed by Ilinca and Pelletier (2007) did not produce superconverging results even for a structured grid.

The method proposed by Zienkiewicz and Zhu (1992a) (from now on denoted by ZZ-method) was shown to produce superconverging results for the first-order partial derivatives of a numerical solution calculated using linear basis functions. Here, we will apply the ZZ-method twice to compute the first-order and the second-order partial derivatives of a numerical solution calculated using quadratic basis functions. In the literature, no proof exists that using the ZZ-method recursively gives accurate results.

Apart from the two approaches discussed above, the DD-method and the ZZ-method, we combine these two methods to compute the second-order partial derivatives of the numerical solution obtained using quadratic basis functions. This new method works as follows. First, the DD-method is used to calculate the first-order partial derivatives. The ZZ-method is then used on these first-order partial derivatives to obtain the second-order partial derivatives. By doing so, the recursive use of the ZZ-method is avoided. We refer to this method as the mixed-method.

In summary, the surface elevation in our model is computed using either linear or quadratic basis functions. When linear basis functions are used, it is only possible to compute the first-order partial derivatives either by the DD-method or the ZZ-method. For quadratic basis functions, it is possible to compute both the first-order and the second-order partial derivatives. The first-order partial derivatives can be computed either by the DD-method or the ZZ-method. For the second-order partial derivatives, either of the DD-method, the ZZ-method, or the mixed-method can be used. The order of convergence of the surface elevation and its partial derivatives calculated using various methods will be assessed in Section 4.

4 Comparison with a width-averaged model

4.1 Introduction and geometry

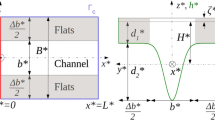
Chernetsky et al. (2010) developed a width-averaged (2DV) model for an exponentially converging estuary (Fig. 2). The width is given by $B(x) = B_{0}e^{-x\left /{\phantom {{3}^{L_{b}}}}\right .\!\!\!\!\!\!\!\!\!\!\!L_{b}}$ $2B(x) = B_{0}e^{-x/L_{b}}$, with 2B ₀ the width at the entrance and L _b the e-folding length scale. The along-channel coordinate x varies from x = 0 at the seaward side to x = L at the landward side, with L being the length of the estuary. The lateral boundaries are located at y = −B(x) and y = B(x). If L _b →∞, the exponentially converging domain becomes a rectangular domain with a constant width of 2B ₀.

Fig. 2

Sketch of the idealized geometry used by Chernetsky et al. (2010). The width B varies exponentially as $\protect B(x)= B_{0} e^{-x/L_{b}}$, where 2B ₀ the total width at the entrance and L _b the e-folding length (blue solid line, ). If $L_{b} \to \infty$, the exponential domain becomes a rectangular domain (blue dashed line, ). The bed profile varies parabolically in the transverse direction (maintaining a constant lateral depths of ${H_{o}^{y}}$ at y = ±B) and linearly in the longitudinal direction, with a depth of H at the entrance (x = 0, y = 0) and ${H_{o}^{x}}$ at the end (x = L, y = 0)

The governing equations for the 2DV model are obtained by averaging the three-dimensional continuity and momentum equations (given by Eq. 1a) over the width, using the appropriate boundary conditions. Similar to the approach in Section 3.1, the vertical profile of the velocities is calculated analytically. The velocities themselves are proportional to the first and second order derivatives of the surface elevation.

If the bed profile h and physical parameters are allowed to vary in the along-channel direction, the surface elevation has to be obtained numerically (which is done using standard numerical techniques). For a uniform bed profile and spatially uniform physical parameters, an analytical solution of the 2DV model can be obtained.

To reproduce the results of a 2DV model by our 3D semi-idealized model, the Coriolis parameter f in our model is set to zero. In addition to that, the bathymetry and physical parameters are only allowed to vary in the along-channel direction. The results of the 3D semi-idealized model are averaged over the width for a fixed longitudinal coordinate to allow for a comparison of the results obtained with the 2DV model. The one-dimensional width-averaged surface elevation is calculated from the two-dimensional surface elevation N(x, y) obtained from the 3D semi-idealized model as

$$\begin{array}{@{}rcl@{}} \bar{N}(x) = \int\limits_{-B(x)}^{B(x)} \! \! \! N(x,y) \ \mathrm{d} y, \end{array} $$

(19)

with $\bar {N}$ the one-dimensional width-averaged surface elevation.

4.2 Validation and convergence analysis

In this section, the results of the 2DV and 3D semi-idealized models are compared. The convergence properties of the numerical scheme are also investigated. A channel of uniform width (L _b →∞ limit of exponentially converging domain) of length L = 50 km and total width 2B = 1000 m, together with a uniform bed profile of constant depth of 10 m, is considered. The eddy viscosity A _v is set to 0.01 m ² s ⁻¹.

4.2.1 Surface elevation

In Fig. 3, the surface elevation is compared for different values of the stress parameter s ranging from a no-slip condition (s≫1), to a moderate value (s = 0.01 m s ⁻¹), to a free-slip condition (s = 0 m s ⁻¹). The domain is discretized using right-angled triangles with 24 nodal points in the along-channel direction and 20 nodal points in the cross-channel direction. For all three values of the stress parameter, the results obtained with the 3D semi-idealized model for both the amplitude and the phase of the surface elevation agree well with those obtained with the 2DV model.

Fig. 3

Comparison of 3D semi-idealized and 2DV model results for the amplitude (left panel) and the phase (right panel) of the surface elevation for different values of the stress parameter. The 3D semi-idealized model result is shown using black asterisks and the 2DV model result is denoted by the solid black line (-)

To investigate the convergence properties of the numerical solution, we systematically increase the number of nodes using an unstructured grid, i.e., the triangles need not be right-angled. Results are compared for s = 0.01 m s ⁻¹. With both linear and quadratic basis functions, the relative error defined in Eq. 17 decreases for an increasing number of nodes (Fig. 4). For approximately 10^4.2 nodes, using quadratic basis functions, the relative error approaches computer accuracy and decreases only slowly afterwards. Note that for the same number of nodes, the relative error using quadratic basis functions is at least 100 times smaller than the relative error found with linear basis functions. The order of convergence for linear basis functions converges to 2 (Fig. 4b, red line), and for quadratic basis functions, the order of convergence converges to 3 (Fig. 4b, blue line). For the number of nodes larger than 10^4.2, the order of convergence for quadratic basis functions decreases due to the slow decrease in the relative error related to computer accuracy. To conclude, the numerical solution for the surface elevation converges with the expected order of convergence for both linear and quadratic basis functions.

Fig. 4

Relative error (left panel) and order of convergence (right panel) for the surface elevation of the 3D semi-idealized model. The red line shows the results for linear basis functions (P1 elements) and blue line for quadratic basis functions (P2 elements). The golden line over the blue line for P2 elements depicts the behavior of relative error and order of convergence after the solution has reached the computer accuracy. The values p = 2 and p = 3 (right panel) indicate the order of convergence of the finite element method for linear and quadratic basis functions, respectively

4.2.2 Flow field

In Fig. 5, the absolute values of the horizontal and vertical velocities from the 2DV and 3D semi-idealized models are plotted. The domain is discretized using right-angled triangles with 2000 nodes in the along-channel direction and 40 nodes in the cross-channel direction. Quadratic basis functions together with the mixed-method are used to calculate the surface elevation and its first-order and second-order partial derivatives. Figure 5 shows that the 3D semi-idealized model is able to reproduce the amplitudes of the horizontal and vertical velocities of the 2DV model.

Fig. 5

Amplitudes of the horizontal (left panel) and vertical velocities (right panel) computed using 3D semi-idealized (lower panel) and 2DV (upper panel) models. The units for the colorbars are m s ⁻¹

To assess the accuracy of these velocities, the convergence properties of the first-order and the second-order partial derivatives will be examined. As explained in Section 3.2, only the first-order partial derivatives of the surface elevation can be obtained when linear basis functions are used. With quadratic basis functions, both the first-order and the second-order partial derivatives can be computed.

We first consider linear basis functions to compute the surface elevation. Both the DD-method and the ZZ-method are used to compute the first-order partial derivative of the surface elevation in the along-channel direction.

Figure 6a shows that the relative error for the first-order partial derivative of the surface elevation decreases with increasing number of nodes for both the DD-method and the ZZ-method. The relative error for the ZZ-method is approximately ten times smaller than that of the DD-method. Concerning the order of convergence, the ZZ-method converges at a faster rate than the DD-method. Increasing the number of nodes shows that the order of convergence for both methods approaches 1 (Fig. 6b). There is a loss of one order of accuracy compared to the second-order convergence of the surface elevation for linear basis functions. Clearly, the ZZ-method is more accurate than the DD-method both in terms of the relative error and the order of convergence of the first-order partial derivatives of the surface elevation.

Fig. 6

Relative error (left panel) and order of convergence (right panel) for the first-order partial derivative of the surface elevation in the along-channel direction for linear basis functions. The red line shows the results for the DD-method and blue line for the ZZ-method. The middle brown line in the right panel shows that both the methods converge to p = 1

Considering the quadratic basis functions, the convergence of both the first-order and the second-order partial derivatives can be assessed. The ZZ-method and DD-method are applied to compute the relative error for the first-order partial derivatives of the surface elevation.

Figure 6a shows that the relative error for the DD-method decreases with an increasing number of nodes. However, when using the ZZ-method, the relative error decreases up to approximately 10^4.2 nodes and then starts to increase. Ignoring the last two entries of the ZZ-method, both methods converge with order 2 (Fig. 6b). Unlike linear basis functions (Fig. 6), there is only a small gain in using the ZZ-method over the DD-method for calculating the first-order partial derivatives with quadratic basis functions.

As discussed in Section 3.2, the second-order partial derivatives can be computed in three ways: (1) DD-method, (2) ZZ-method, and (3) mixed-method. Figure 7c shows that the relative error for the DD-method and the mixed-method decrease monotonically with increasing number of nodes. The relative error for the mixed-method is approximately a factor 10 smaller than the relative error found with the DD-method. Furthermore, the mixed-method converges faster than the DD-method. Up to 10^4.2 nodes, i.e., as long as the relative error of the ZZ-method decreases, the ZZ-method gives the most accurate results both in terms of the relative error and the order of convergence. However, the relative error of the ZZ-method starts to increase when further increasing the number of nodes, which makes it unreliable for use. All three methods ultimately appear to converge with order 1.

Fig. 7

Relative error (left panel) and order of convergence (right panel) for the first-order (upper panel) and the second-order (lower panel) partial derivatives of the surface elevation in the along-channel direction for quadratic basis functions. The red line shows the results for the DD-method, blue line for the ZZ-method, and green line for the mixed-method (only for second-order partial derivatives)

At this point, it is important to mention that for quadratic basis functions, the unreliable behavior of the ZZ-method for computing the first-order and the second-order partial derivatives with sufficiently large number of nodes is independent of the choice of the bed profile. Similar convergence tests for the ZZ-method were carried out using non-uniform bathymetric profiles with quadratic basis functions, resulting in a similar behavior of the ZZ-method.

To conclude, when using the linear basis functions, the ZZ-method is recommended to compute the first-order partial derivatives. For quadratic basis functions, the DD-method for the first-order partial derivatives and the mixed-method for the second-order partial derivatives are recommended.

4.3 Parameter sensitivity

To investigate the influence of the geometry, the width at the entrance B ₀ will be varied in Section 4.3.1, keeping the e-folding length L _b constant. The influence of the variations in the bathymetry will be studied in Section 4.3.2. To compute the numerical solution of the 3D semi-idealized model, the domain under consideration is discretized using an unstructured triangular mesh with approximately 400,000 nodal points. Choosing such a fine mesh minimizes the numerical error in the 3D semi-idealized model. The eddy viscosity A _v and stress parameter s are set to 0.01 m ² s ⁻¹ and 0.01 m s ⁻¹, respectively.

4.3.1 Influence of width at the entrance

To study the influence of the width at the entrance B ₀ on the surface elevation in isolation, an exponential domain of length L = 50 km and an e-folding length L _b = 10 km together with a flat bed profile of 10-m depth is considered. The width at the entrance B ₀ is varied and the width-averaged surface elevations obtained with the 2DV and 3D semi-idealized models are compared.

In Fig. 8a, the width-averaged surface elevation (given by Eq. 19) is shown for different values of the width B ₀ at the entrance. For B ₀ = 2.5 km, both the 2DV and 3D semi-idealized models produce similar results for the amplitude of the surface elevation. It is important to note that the one-dimensional surface elevation from the 2DV model is independent of the width at the entrance (B ₀). Because of this, the amplitude of the surface elevation for any value of B ₀ will be the same for a 2DV model. As B ₀ increases, the width-averaged amplitude of the surface elevation obtained with the 3D semi-idealized model starts to deviate from the results obtained from the 2DV model. This deviation increases with increasing value of B ₀. For a width B ₀ = 40 km, a deviation of approximately 10 % is observed.

Fig. 8

(Top left panel) Amplitude of the width-averaged surface elevation for different values of B ₀. The solid black line shows the results for the 2DV model. The lines with markers show the width-averaged results for the 3D semi-idealized model for different values of B ₀. (Top right and bottom panel) Two-dimensional amplitude of the surface elevation plotted in the horizontal space for different values of B ₀. The unit in the colorbar is m

To understand the cause of this deviation, the amplitude of the surface elevation obtained with the 3D semi-idealized model is plotted in the horizontal space for different values of B ₀. It is clear from Fig. 8b–d that the solution is radially constant away from the entrance. At the entrance, a constant surface elevation has been prescribed, which as it breaches the radial symmetry, results in the non-uniformity close to the entrance.

4.3.2 Influence of varying bathymetry

A rectangular channel of length L = 50 km and width 2B ₀ = 1000 m is considered. A parabolic bed profile is adopted,

$$\begin{array}{@{}rcl@{}} h = {H_{o}^{y}} + (H-{H_{o}^{y}})(1-y^{2}/B^{2}), \end{array} $$

(20)

where ${H_{o}^{y}}$ is the constant depth at the lateral sides (y = ±B) and H is the maximum depth which is attained at the center line (y = 0) of the channel. To use the 2DV model, this bathymetric profile is averaged over the width, resulting in

$$\begin{array}{@{}rcl@{}} \bar{h} = \frac{1}{2 B}\int \limits_{-B}^{B} \! \! h \ \mathrm{d} y = \frac{1}{3} \left[ {H_{o}^{y}} + 2 H \right]. \end{array} $$

(21)

In Fig. 9, the water depth at the sides is varied from 1 to 10 m (which is a channel with uniform bed again), and the difference between the amplitude of the width averaged surface elevation obtained with the 2DV and 3D semi-idealized models is shown. For ${H_{o}^{y}}$ = 1 m, a difference of approximately 8 cm in amplitude of the surface elevation towards the landward side is found. For each value of ${H_{o}^{y}}$, the difference in the amplitude increases along the channel. As ${H_{o}^{y}}$ increases, the difference in the amplitude decreases. The positive value for the difference of amplitudes show that the amplitude of the surface elevation from the 3D semi-idealized model is always larger than that of the 2DV model.

Fig. 9

Difference in the amplitude of the surface elevation between the 3D semi-idealized and 2DV models. The unit in the colorbar is m

5 Comparison with three-dimensional asymptotic model

5.1 Introduction and geometry

Winant (2007) developed a three-dimensional idealized model for an elongated rectangular basin of length L and width 2B. The along-channel coordinate x varies from x = 0 at the seaward side to x = L at the landward side. The cross-channel coordinate y varies from y = −B at the lower boundary to y = B at the upper boundary. The term elongated implies that the horizontal aspect ratio α = B/L has to be small. A no-slip condition is imposed at the bottom z = −h. This limit is found by taking s→∞ in our 3D semi-idealized model. The eddy viscosity A _v is assumed to be spatially uniform. The bed profile given by Eq. 20 is used (see Fig. 2).

The surface elevation N follows from Eq. 12, but Winant (2007) uses a different solution method. Assuming that α≪ 1, an asymptotic expansion of N in α is made;

$$\begin{array}{@{}rcl@{}} N = N_{0} + \alpha N_{1} + \mathcal{O}(\alpha^{2}), \end{array} $$

(22)

and substituted in Eq. 12. This results in a system of equations for various orders of α, such that the leading order (N ₀) and the first order (N ₁) solutions can be calculated analytically. The surface elevation is approximated by

$$\begin{array}{@{}rcl@{}} N \approx N_{0} + \alpha N_{1} = N_{\text{Winant}}. \end{array} $$

(23)

It is important to realize that the solution N _Winant given in Eq. 23 is not an exact solution of system (12) as $\mathcal {O}$(α ²) and higher order terms are ignored. Therefore, in this paper, we refer to this model as the 3D asymptotic model.

5.2 Validation

In this section, the 3D asymptotic and 3D semi-idealized model results for the surface elevation (Section 5.2.1) and the velocity (Section 5.2.2) are compared. An elongated rectangular basin of length L = 50 km and total width 2B = 200 m such that α (=0.002)≪ 1, is considered. The default parameter values from Table 1 are used.

Table 1 Default parameter values used for the comparison of the 3D asymptotic model and 3D semi-idealized model. A no slip condition ($s \to \infty$) is imposed at the bottom

5.2.1 Surface elevation

First, the surface elevations for different values of the eddy viscosities are compared, A _v = 10⁻³, 10⁻², and 10⁻¹ m ² s ⁻¹. The rectangular basin is discretized using right-angled triangles with 24 nodes in the along-channel direction and 20 nodes in the cross-channel direction. Figure 10 shows that the amplitudes of the width-averaged surface elevations obtained from the 3D asymptotic model and 3D semi-idealized model appear to agree well.

Fig. 10

Width averaged amplitude of the surface elevation for f = Ω^∗/2 and different values of the eddy viscosity. The black solid line depicts the 3D asymptotic model solution and black asterisk depict the 3D semi-idealized model solution

Note that for the parameter settings considered here, the Coriolis effects only influence the amplitude of the surface elevation marginally. This is because the width of the channel 2B = 200 m is much smaller than the Rossby radius of deformation $R^{*}=\sqrt {g H}/f \approx 71$ km, which is the length scale of the cross-channel variations for the surface elevation.

5.2.2 Flow field

The rectangular domain is discretized using right-angled triangles with 200 nodes each in both the along-channel and cross-channel directions. This relatively large number of nodes is used to avoid numerical inaccuracies in the computation of the velocity components.

Quadratic basis functions together with the mixed-method are used to compute the surface elevation and its first-order and second-order partial derivatives. Three velocity components are compared in the cross-channel direction at a distance x = 25 km from the entrance. It is evident from Fig. 11 that our 3D semi-idealized model is able to reproduce all three velocity profiles of the 3D asymptotic model, even small details in the vertical velocity W have been reproduced accurately. It is important to mention that the comparison of the velocity field at other locations is as good as at x = 25 km.

Fig. 11

Comparison of the amplitude of three flow components (in m s ⁻¹). The velocities have been plotted in the cross-section at a distance 25 km from the entrance. The upper panel shows the velocities from the 3D asymptotic model and the lower panel from the 3D semi-idealized model. Left, central, and right panels show the along-channel, cross-channel and vertical velocities, respectively

5.3 Parameter sensitivity

In Section 5.2, the results for the surface elevation and three flow components from 3D asymptotic and 3D semi-idealized models were compared for a rectangular channel whose horizontal aspect ratio α was small (2.0×10⁻³). In this section, α will be systematically increased and the difference between the two models will be discussed.

From Eqs. 22 and 23, it follows that

$$\begin{array}{@{}rcl@{}} |N-N_{\text{Winant}}| = |\mathcal{O}(\alpha^{2})|. \end{array} $$

Assuming that the solution of the 3D semi-idealized model $N_{\tilde {h}}$ converges to the exact solution N, it follows that

$$\begin{array}{@{}rcl@{}} |N_{\tilde{h}}-N_{\text{Winant}}| \approx |\mathcal{O}(\alpha^{2})|, \end{array} $$

(24)

which implies that for a channel geometry with horizontal aspect ratio α, an error of $\mathcal {O}(\alpha ^{2})$ is expected provided the 3D semi-idealized solution has been calculated with high enough accuracy.

To verify Eq. 24, a rectangular channel of length L = 50 km with different widths at the entrance is considered, B = [250,500,1000,2000,4000,8000,16000], all in meters. For each value of B, the rectangular domain is discretized by refining a coarse grid with approximately 10² nodes to the finest grid with approximately 10⁶ nodes. Linear basis functions are used to compute the finite element approximation of the surface elevation. For each value of B (hence α), the relative error of the surface elevation between the 3D asymptotic and 3D semi-idealized models is computed for different numbers of nodes.

Figure 12 shows the influence of α on the accuracy of the 3D asymptotic model. For each α, the relative error becomes constant after a large enough number of nodes. This constant relative error is proportional to $\mathcal {O}(\alpha ^{2})$, thus suggesting that Eq. 24 is indeed correct. As α increases, the relative error between the 3D semi-idealized and 3D asymptotic models increases. For the largest number of nodal points used in the experiments, the relative error for different values of α appear to be equispaced. More precisely, there is approximately a difference of a factor 4 between the error for each α, coinciding with the fact that the size of the domain is doubled each time. This clearly demonstrates the sensitivity of the 3D asymptotic model to the horizontal aspect ratio.

Fig. 12

Relative error for the surface elevation as a function of the number of nodes for different values of the horizontal aspect ratio α plotted on log-log scale

6 Application to the Ems estuary

Our 3D semi-idealized model allows us to study the tidal motion in an estuary with arbitrary shape and bathymetry. As an example, we apply this model to the Ems estuary, situated on the border of the Netherlands and Germany (Fig. 13). In Section 6.1, the surface elevation of the M ₂ tide obtained with the 3D semi-idealized model will be calibrated for the Ems estuary. The results for the amplitude and the phase of the surface elevation are compared with the results of a complex numerical model (Delft3D) setup by van Maren et al. (2015). Next, the influence of the local width convergence on the tidal motion will be investigated in Section 6.2.

Fig. 13

Map of the Ems estuary (from Chernetsky et al. (2010))

6.1 Calibration

The observational data for the water level in the Ems estuary for the year 2005 are used from six locations in the estuary, namely Emden, Pogum, Terborg, Leerort, Weener, and Papenburg (shown in magenta color in Fig. 14). The objective is to find the parameter values for the 3D semi-idealized model such that the model results fit the observations for the water level at these locations best. To this end, the geometric and bathymetric profiles of the year 2005 of the Ems estuary is used in the 3D semi-idealized model (Fig. 14). The Coriolis parameter f is assumed to be constant throughout the estuary i.e., f = 1.166×10⁻⁴ rad s ⁻¹ (latitude = 53.32 ^∘).

Fig. 14

The geometry and bathymetry of the Ems estuary for the year 2005 (left panel). The data for the surface elevation of the M ₂ tide is available at six locations (shown in the magenta color). The right panel describes how the realistic domain is transformed into a symmetric domain. Red asterisks show the boundary points of the transects. The green dashed line passes through the mid points of these transects shown by green squares . The width B of the each transect is divided into −B/2 and B/2 with respect to the middle green line as shown by blue lines

The physical parameters such as the eddy viscosity A _v and the stress parameter s are also assumed to be constant in space. The 3D semi-idealized model is forced with a semi-diurnal (M ₂) tide of constant amplitude at the seaward side (North sea side, see Fig. 14). The domain is discretized with approximately 200,000 nodes using an unstructured grid. The amplitude and the phase of the surface elevation obtained with the 3D semi-idealized model is then scaled in such a way that they match the observations at Emden. Next, the optimal values of A _v and s are found such that the mean squared error between the model results and the observations is minimum, i.e.,

$$\begin{array}{@{}rcl@{}} \min \limits_{{A}_{\mathrm{v}},s} \left\{ \frac{1}{2}\underset{i}{\sum} \left\{ (N_{o,i} - N_{m,i})^{2} + 2 N_{o,i} N_{m,i} \right.\right. \\ \left.\left. [ 1-\cos(\phi_{o,i} - \phi_{m,i})] \right\} \right\}, \end{array} $$

where N _{o, i} and ϕ _{o, i} are the amplitude and the phase of the surface elevation observed at location i, whereas N _{m, i} and ϕ _{m, i} are the amplitude and the phase of the surface elevation obtained with the 3D semi-idealized model. The optimal values of A _v and s are 0.0036 m ² s ⁻¹ and 0.0588 m s ⁻¹, respectively.

van Maren et al. (2015) set up a Delft3D model to understand the role of deepening of the channel on the sediment concentration in the Ems estuary. The authors calibrated their model using the same data as used in this paper. Figure 15 shows the observations, results from the 3D semi-idealized model and results from the Delft3D model of van Maren. It is evident from Fig. 15 that the 3D semi-idealized model is able to reproduce the amplitude and the phase of the surface elevation at six different locations fairly well. It is interesting to see that for the amplitude of the surface elevation, the 3D semi-idealized model fits the observations at least as accurately as the Delft3D model at all locations except Pogum. For the phase of the surface elevation, both the 3D semi-idealized and the Delft3D models fit the observations equally well.

Fig. 15

Amplitude (left panel) and phase (right panel) of the surface elevation from observations, 3D semi-idealized model and Delft3D model. The observations are shown in black asterisks , results from 3D semi-idealized model in red squares and results from Delft3D model in blue circles

6.2 Influence of local convergence

We focus on the upper part of the Ems estuary, starting from Knock up to the weir at Herbrum. This part of the estuary consists of a narrow, meandering channel with decreasing width towards the landward side. In this section, the effects of channel convergence and meandering are investigated.

To study the influence of the local convergence on the water motion, the channel from Knock to Herbrum is transformed into a symmetric domain bounded by y = −B(x)/2 at the lower boundary to y = B(x)/2 at the upper boundary. For this, the widths B along many transects in the channel (red asterisks, Fig. 14, right panel) are mapped to a new domain bounded by y = −B/2 to y = B/2 (blue lines, Fig. 14, right panel), with the central line y = 0 passing through the middle of the channel (green dashed line, Fig. 14, right panel). The resulting data set is shown in Fig. 16 (red asterisks). We call this domain the scattered domain. It is important to note that the scattered domain is similar to the realistic domain except that the meandering effects in the scattered domain have been ignored.

Fig. 16

Approximation of the geometry of the Ems estuary. See Fig. 14 (right panel) for meaning of various colors

First, this data set is fit with an exponential function given by

$$\begin{array}{@{}rcl@{}} B = B_{0} \exp(-x/L_{b}), \end{array} $$

where 2B ₀ is the total width at the entrance and L _b is the e-folding length.

The optimal values of B ₀ and L _b fitting the data are calculated using the least square method and are given as B ₀ = 543.9 m, L _b = 24.5 km. The corresponding domain is shown in Fig. 16. It is also possible to fit the data with a polynomial function. From Fig. 16, it is evident that a 9th degree polynomial function fits the width data more accurately than the exponential function.

The values of the eddy viscosity A _v and the stress parameter s, found during the calibration process in the previous section, are used. To understand the influence of geometrical effects in isolation, a uniform bed profile is considered. Water depth of 15 m is chosen such that the amplitude of the surface elevation exhibits a similar trend as shown in Fig. 15a. The system is forced with a semi-diurnal (M ₂) tide with an amplitude of 1.42 m at Knock. The domain is discretized using an unstructured grid with approximately 200,000 nodes. Linear basis functions together with the ZZ-method are used to compute the surface elevation and the horizontal velocities.

Figure 17a shows the amplitude of the surface elevation along the middle line (shown in green color in Figs. 16 and 14) for different schematization of the domain. It is evident that with the exponential domain, the amplitude of the surface elevation throughout the domain is underestimated. Using the polynomial function of 9th degree to approximate the width compares well in the first 30 km, further upstream, the amplitude is slightly underestimated. The results with the scattered domain shows the same behavior. This deviation between the realistic and scattered domains is probably due to the meandering effects. Similar behavior is observed for the phase of the surface elevation.

Fig. 17

Left panel shows the amplitude of the surface elevation and right panel the depth-averaged horizontal velocity along the middle of the channel for different types of channel domains

Next, we look at the amplitude of the depth-averaged horizontal velocity which is defined as $\sqrt {\bar {|U|}^{2} + \bar {|V|}^{2}}$, where $\bar {U}$ and $\bar {V}$ are the depth-averaged along-channel and cross-channel velocities, respectively and |⋅| denotes the absolute value. Figure 17b shows that the results for the depth-averaged horizontal velocity with exponential domain deviates significantly from the results with the realistic domain. The domain constructed with a 9th degree polynomial captures the overall behavior of the depth-averaged horizontal velocity profile throughout the domain. It is interesting to see the agreement between the results obtained with the scattered domain and the realistic domain. The scattered domain is able to accurately reproduce the depth-averaged horizontal velocity at the entrance and the end of the channel.

To understand the influence of different channel domains on the vertical structure of the flow, the absolute value of the horizontal velocity, which is defined as $\sqrt {|U|^{2} + |V|^{2}}$, where U and V are the along-channel and cross-channel velocities, respectively, is plotted along the middle of the channel. Figure 18 shows that the scattered and polynomial domains are able to reproduce the overall behavior of the horizontal velocity of the realistic domain. It is interesting to see that smoothing the scattered domain with a polynomial function also smoothes the contour lines of the velocity in the vertical direction, capturing the main features. The exponential domain on the other hand clearly seems to miss the information throughout the domain, especially at the entrance. This is also observed in Fig. 17b.

Fig. 18

Absolute value of the horizontal velocity along the middle of the channel for different types of channel domains. The axes are same in all the plots. The units in the colorbars are m s ⁻¹

7 Conclusions

A three-dimensional semi-idealized model for the tidal motion in an estuary with arbitrary geometric and bathymetric profiles has been developed. This model is intended to bridge the gap between idealized and complex simulation models by retaining the advantages of the idealized models (developed to obtain insight in physical mechanisms, well suited to perform quick sensitivity analysis), but removing one of its weak points (namely the requirement of idealized geometry and bathymetry). In this model, the three-dimensional velocity field is expressed in terms of the first- and second-order partial derivatives of the surface elevation. The surface elevation itself follows from a two-dimensional linear elliptic partial differential equation which is solved numerically using the finite element method. Linear and quadratic polynomials are considered as basis functions for the finite element approximation of the surface elevation. Concerning the accuracy and convergence properties of the newly developed model, we found a second-order convergence with linear basis functions and a third order convergence with quadratic basis functions. With linear basis functions, ZZ-method proposed by Zienkiewicz and Zhu (1992a) gives the most accurate results for the first-order partial derivatives of the surface elevation. With quadratic basis functions, direct differentiation (DD-method) of the finite element approximation of the surface elevation is recommended for the first-order partial derivatives. For the second-order partial derivatives, a new method known as the mixed-method, which is a combination of DD-method and ZZ-method, is shown to work the best.

To investigate the influence of geometry and bathymetry on the tidal characteristics, the results obtained with the three-dimensional semi-idealized model are compared to those obtained with a width-averaged model developed by Chernetsky et al. (2010). For an exponentially converging estuary with a flat bed, the deviation for the surface elevation between the width-averaged model and the three-dimensional semi-idealized model increases with increasing width at the entrance. For an estuary with constant width and parabolic bed profile in the lateral direction, the width-averaged model underestimates the amplitude of the surface elevation for all values of the lateral water depths. The comparison between the three-dimensional semi-idealized model and the three-dimensional asymptotic model developed by Winant (2007) for an elongated rectangular channel shows that the absolute difference in the surface elevation obtained with these two models increases for increasing horizontal aspect ratio, and is proportional to the square of the horizontal aspect ratio.

To assess the influence of a more complex geometry on tidal propagation, the Ems estuary is considered. First, the three-dimensional semi-idealized model is calibrated using the observed geometry and bathymetry of the Ems estuary for the year 2005. Concerning the amplitude and the phase of the surface elevation of the M ₂ tide, a good agreement is found between the observations, the model results of three-dimensional semi-idealized model, and the model results of a complex numerical model (Delft3D) setup by van Maren et al. (2015). The model suggests that approximating the geometry of the Ems estuary with an exponential function gives unsatisfactory results for the surface elevation and the horizontal velocity compared to the results with the realistic geometric profile. When approximated with a function that captures the local convergence effects (in this case, a 9th degree polynomial) of the Ems estuary, a good agreement with the results obtained with realistic geometry was found. It is therefore recommended to consider local geometrical effects when using simplified geometry to model tidal motion.

Appendices

Appendix A: Scaling analysis

The water motion is described by the three-dimensional shallow water equations. Using the Boussinesq approximation and hydrostatic balance, the system of equations can be written as,

$$\begin{array}{@{}rcl@{}} && u_{x} + v_{y} + w_{z} = 0, \end{array} $$

(25a)

$$\begin{array}{@{}rcl@{}} && u_{t}+uu_{x}+vu_{y}+wu_{z} - fv = -g \eta_{x} - \frac{g}{\rho_{o}} (\eta-z)\rho_{x} \\ && + ({A}_{\mathrm{h}} u_{x})_{x} + ({A}_{\mathrm{h}} u_{y})_{y} + ({A}_{\mathrm{v}} u_{z})_{z}, \end{array} $$

(25b)

$$\begin{array}{@{}rcl@{}} && v_{t} + u v_{x} +vv_{y}+wv_{z}+ fu = -g\eta_{y} - \frac{g}{\rho_{o}} (\eta-z)\rho_{y} \\ &&+ ({A}_{\mathrm{h}} v_{x})_{x} + ({A}_{\mathrm{h}} v_{y})_{y} +({A}_{\mathrm{v}} v_{z})_{z}. \end{array} $$

(25c)

It is assumed that the estuary is partially to well mixed such that the density can be approximated as ρ: = ρ(x, y, t). A _h is the coefficient of horizontal mixing. To scale the equations, the following dimensionless variables are introduced;

$$\begin{array}{@{}rcl@{}} &&t^{*} =\omega t,\quad f^{*}=f/\omega,\quad (x^{*},y^{*})=(x,y)/L, \\ && \!(z^{*},h^{*})\,=\,(z,h)/H, \,\,\,\, \!u^{*}\,=\,u/U, \,\,\,\, \!v^{*}\,=\,v/V,\,\,\,\, \!w^{*}\,=\,w/W, \\ && \eta^{*}=\eta/A, \quad \rho_{x}^{*}= \rho_{x}/|\rho_{x}|, \quad \rho_{y}^{*}= \rho_{y}/|\rho_{y}|, \end{array} $$

where asterisk (∗) denotes the dimensionless variables and 𝜖 = A/H≪1, where A is the amplitude of the surface elevation and H is the mean depth at the seaward side, L is the typical length scale, U = V = 𝜖 ω L, and W = 𝜖 ω H are the typical scales of tidal velocities. In the above scaling, gradients of the density are scaled instead of the density itself. This is because it is the variation in density that drives density-driven currents. The primitive equations in dimensionless form reduce to:

$$\begin{array}{@{}rcl@{}} &&u^{*}_{x^{*}} + v^{*}_{y^{*}}+ w^{*}_{z^{*}}=0, \\ &&u^{*}_{t^{*}} + \epsilon(u^{*}u^{*}_{x^{*}} + v^{*}u^{*}_{y^{*}} +w^{*}u^{*}_{z^{*}} ) - f^{*} v^{*} \\ &&= -\frac{g H}{\omega^{2}L^{2}} \eta^{*}_{x^{*}} - \frac{g H |\rho_{x}|} {\rho_{o} U \omega} (\epsilon \eta^{*}-z^{*}) {\rho}^{*}_{x} \\ && + \frac{1}{\omega L^{2}} \left[ ({A}_{\mathrm{h}} \upsilon^{*}_{x^{*}})_{x^{*}} + ({A}_{\mathrm{h}} u^{*}_{y^{*}})_{y^{*}} \right] + \frac{1}{\omega H^{2}}(A_{\mathrm{v}} u^{*}_{z^{*}})_{z^{*}}, \\ &&v^{*}_{t^{*}} + \epsilon(u^{*}v^{*}_{x^{*}} + v^{*}v^{*}_{y^{*}} +w^{*}v^{*}_{z^{*}} ) + f^{*} u^{*} \\ && = -\frac{g H}{\omega^{2}L^{2}} \eta^{*}_{y^{*}} - \frac{g H |\rho_{y}|}{\rho_{o} V \omega}(\epsilon \eta^{*}-z^{*}) {\rho}^{*}_{y} \\ && + \frac{1}{\omega L^{2}} \left[ ({A}_{\mathrm{h}} v^{*}_{x^{*}})_{x^{*}} + ({A}_{\mathrm{h}} v^{*}_{y^{*}})_{y^{*}} \right] + \frac{1}{\omega H^{2}}(A_{\mathrm{v}} \upsilon^{*}_{z^{*}})_{z^{*}}. \end{array} $$

We also assume that the horizontal mixing is much smaller compared to the vertical mixing (Winant 2007), i.e., A _h H ²/A _v L ²≪1. With this assumption, x and y momentum equations further reduce to,

$$\begin{array}{@{}rcl@{}} &&u^{*}_{t^{*}} + \epsilon(u^{*}u^{*}_{x^{*}} + v^{*}u^{*}_{y^{*}} +w^{*}u^{*}_{z^{*}} ) - f^{*} v^{*} \\ && = -\frac{g H}{\omega^{2}L^{2}} \eta^{*}_{x^{*}} - \frac{g H |\rho_{x}|} {\rho_{o} U \omega} (\epsilon \eta^{*}-z^{*}) {\rho}^{*}_{x} \\ && + \frac{1}{\omega H^{2}}({A}_{\mathrm{v}} u^{*}_{z^{*}})_{z^{*}}, \\ &&v^{*}_{t^{*}} + \epsilon(u^{*}v^{*}_{x^{*}} + v^{*}v^{*}_{y^{*}} +w^{*}v^{*}_{z^{*}} ) + f^{*} u^{*} \\ && = -\frac{g H}{\omega^{2}L^{2}} \eta^{*}_{y^{*}} - \frac{g H |\rho_{y}|}{\rho_{o} V \omega}(\epsilon \eta^{*}-z^{*}) {\rho}^{*}_{y} \\ && + \frac{1}{\omega H^{2}}({A}_{\mathrm{v}} v^{*}_{z^{*}})_{z^{*}}. \end{array} $$

Using typical scales for the density gradients in partially to well mixed estuaries, we find that $\frac {g H}{\rho _{0} U \omega } \nabla \rho$ is of order 𝜖. Next, we expand the unknown variables. u ^∗, v ^∗, w ^∗, and η ^∗ in the small parameter 𝜖,

$$\begin{array}{@{}rcl@{}} u^{*} &=&u^{*}_{0} + \epsilon^{1} u^{*}_{1} + \mathcal{O}(\epsilon^{2}), \\ v^{*} &=&v^{*}_{0} + \epsilon^{1} v^{*}_{1} + \mathcal{O}(\epsilon^{2}), \\ w^{*} &=&w^{*}_{0} + \epsilon^{1} w^{*}_{1} + \mathcal{O}(\epsilon^{2}), \\ \eta^{*} &=&\eta^{*}_{0} + \epsilon \eta^{*}_{1} + \mathcal{O}(\epsilon^{2}). \\ \end{array} $$

Substituting the asymptotic expansions in the dimensionless equations results in the following leading-order system of equations,

$$\begin{array}{@{}rcl@{}} &&u^{*}_{0,x^{*}} + v^{*}_{0,y^{*}} + w^{*}_{0,z^{*}} =0, \\ && u^{*}_{0,t^{*}} - f^{*}v^{*}_{0} = -\frac{g H}{\omega^{2} L^{2}} \eta^{*}_{0,x^{*}} + \frac{1}{\omega H^{2}}({A}_{\mathrm{v}} u^{*}_{0,z^{*}})_{z^{*}}, \\ && v^{*}_{0,t^{*}} + f^{*}u^{*}_{0} = -\frac{g H}{\omega^{2} L^{2}} \eta^{*}_{0,y^{*}} + \frac{1}{\omega H^{2}} ({A}_{\mathrm{v}} v^{*}_{0,z^{*}})_{z^{*}}. \end{array} $$

In the dimensional form, the system reads

$$\begin{array}{@{}rcl@{}} &&u_{0,x}+v_{0,y}+w_{0,z}=0, \\ &&u_{0,t} - f v_{0} = -g \eta_{0,x} + ({A}_{\mathrm{v}} u_{0,z})_{z}, \\ &&v_{0,t} + f u_{0} = -g \eta_{0,y} + ({A}_{\mathrm{v}} v_{0,z})_{z}. \end{array} $$

For the sake of simplicity, we remove the subscript 0 from the variables, i.e., (η ₀, u ₀, v ₀, w ₀)=(η, u, v, w). Similar treatment can be given to the boundary conditions.

B weak formulation

To solve the system (12) to obtain the surface elevation, the finite element method is adopted (Gockenbach 2006). As a first step towards the finite element method, a weak form of system (12) has to be derived. To this end, define L ²(Ω) and H ¹(Ω) function spaces as

$$\begin{array}{@{}rcl@{}} L^{2}({\Omega}) &=& \{ \phi \text{ such that} ||\phi||_{2} = \left( \iint \limits_{\Omega} |\phi|^{2} \right)^{1/2} < \infty \}, \\ H^{1}({\Omega}) &=& \{ \phi \in L^{2}({\Omega}) \text{ such that} \phi_{x}, \phi_{y} \in L^{2}({\Omega})\}. \end{array} $$

Assume that there exists a function N _D in H ¹(Ω) such that N _D = A on ∂ _D Ω. Then, the function $\tilde {N}=N-N_{D}$ vanishes over ∂ _D Ω and $N = \tilde {N} + N_{D}$. Define a function space Σ for test functions as

$$\begin{array}{@{}rcl@{}} {\Sigma} = \{ \phi \in H^{1}({\Omega}) \text{ such that} \phi = 0 \text{ on} \partial_{D} {\Omega} \}. \end{array} $$

Multiplying Eq. (12a) by ϕ∈Σ and integrating over the domain Ω gives,

$$\begin{array}{@{}rcl@{}} &\iint \limits_{\Omega} \left\{ \nabla \cdot [\mathbf{D}(0) \nabla N] + i \omega N \right\} \ \phi \hspace{3 pt}\mathrm{d} {\Omega} = 0, \\ \Rightarrow \quad &\int \limits_{\partial_{D} {\Omega}} [\mathbf{D}(0)\nabla N] \cdot \hat{\mathbf{n}} \underbrace{\phi}_{=0} \mathrm{d} {\Omega} + \int \limits_{\partial_{N} {\Omega} \cup \partial_{R} {\Omega}} \underbrace{[D(0)\nabla N] \cdot }_{=0} \phi \hspace{3 pt} d {\Omega} \\ &- \iint \limits_{\Omega} [\mathbf{D}(0) \nabla N] \cdot \nabla \phi \hspace{3 pt} \mathrm{d} {\Omega} + i \omega \iint \limits_{\Omega} N \phi \hspace{3 pt} d {\Omega} = 0, \\ \Rightarrow \quad &- \iint \limits_{\Omega} [\mathbf{D}(0) \nabla N] \cdot \nabla \phi \hspace{3 pt} \mathrm{d} {\Omega} + i \omega \iint \limits_{\Omega} N \phi \hspace{3 pt} d {\Omega} = 0, \\ \Rightarrow \quad& - \iint \limits_{\Omega} [\mathbf{D}(0) \nabla (\tilde{N} +N_{D})]\cdot \nabla \phi \hspace{3 pt} \mathrm{d} {\Omega} + i \omega \iint \limits_{\Omega} (\tilde{N} +N_{D}) \phi \hspace{3 pt} d {\Omega} = 0, \\ \Rightarrow \quad& - \iint \limits_{\Omega} [\mathbf{D}(0) \nabla \tilde{N}]\cdot \nabla \phi \hspace{3 pt} \mathrm{d} {\Omega} + i \omega \iint \limits_{\Omega} \tilde{N} \phi \hspace{3 pt} d {\Omega} \\ &= \iint \limits_{\Omega} [\mathbf{D}(0) \nabla N_{D}]\cdot \nabla \phi \hspace{3 pt} \mathrm{d} {\Omega} - i \omega \iint \limits_{\Omega} N_{D} \phi \hspace{3 pt} d {\Omega}.\\ \end{array} $$

(27)

Equation 27 is the weak formulation of system (12). The solution $N=\tilde {N} + N_{D}$ obtained after solving the Eq. 27 is called the weak solution of system (12). This equation is solved numerically.

Let $\tilde {N}_{\tilde {h}}$ denote the finite element approximation of $\tilde {N}$ defined on the discretized domain ${\Omega }_{\widetilde {h}}$ (see main text) as

$$ \tilde{N} \approx \tilde{N}_{\tilde{h}} = \sum\limits_{l=1}^{n} {N}_{l} \phi_{l}, $$

(28)

where N _l ^′ s are unknown complex coefficients, ϕ _l ^′ s are so-called Lagrange basis functions. Now, substituting Eq. 28 in Eq. 27 and choosing ϕ = ϕ _k , k = 1,…, n gives

$$\begin{array}{@{}rcl@{}} &&\sum\limits_{l=1}^{n} {N}_{l} \underbrace{\iint \limits_{\Omega} [-\mathbf{D}(0) \nabla \phi_{l}] \cdot \nabla \phi_{k}}_{[\mathbf{S}]_{k,l}} + \sum \limits_{l=1}^{n} {N}_{l} \underbrace{\ i \omega \! \! \iint \limits_{\Omega} \phi_{l} \ \phi_{k}}_{[\mathbf{M}]_{k,l}} \\ && \,=\, \underbrace{\iint \limits_{\Omega} [\mathbf{D}(0) \nabla N_{D}] \cdot \nabla \phi_{k} \,-\, i \omega \iint \limits_{\Omega} N_{D} \ \phi_{k}}_{[\mathbf{F}]_{k}}, \hspace{3 pt} \,\,\, \!\forall k \,=\, 1,\ldots,n. \end{array} $$

which can be compactly written as

$$\begin{array}{@{}rcl@{}} (\mathbf{S} + \mathbf{M}) {\mathbf{N}} = \mathbf{F}, \end{array} $$

where S, $\mathbf {M} \in \mathbb {C}^{n\times n}$ are called the stiffness and mass matrices, respectively. $\mathbf {F} \in \mathbb {C}^{n\times 1}$ is the forcing vector and N = $\{{N}_{1}, {N}_{2},\ldots , {N}_{n} \}^{\text {T}} \in \mathbb {C}^{n\times 1}$ is the unknown vector consisting of complex surface elevation amplitudes at unconstrained nodes. Once N is known, we can write the numerical approximation of N over the whole domain as

$$\begin{array}{@{}rcl@{}} N(x,y) \approx N_{\tilde{h}}(x,y) &=& \sum\limits_{l=1}^{n} {N}_{l} \phi_{l}(x,y)\\ &&+ \sum\limits_{l=n+1}^{n+m} A(x_{l},y_{l}) \phi_{l}(x,y). \end{array} $$