1 Introduction

Storm surges in the North Sea present a continuous threat to its coastal areas. During storm surges, detailed and timely water level forecasts provided by an operational storm surge forecasting system are necessary to issue warnings in case of high water threats. This can only lead to effective precautions if done with at least a few hours lead time. The importance of providing precise and reliable warnings is only enhanced by the presence of movable barriers such as the Thames Barrier, the Eastern Scheldt Barrier and the Maeslant Barrier in the Rotterdam Waterway, which require the decision to close to be taken in advance and only when strictly necessary.

The countries around the North Sea have their own national storm surge forecasting service with numerical models that come in a range of resolutions and spatial extents. In the Netherlands, the development of numerical tide-surge models for the northwest European shelf started in the 1980s. In Verlaan et al. (2005), the main phases of the development and operational set-up of the Dutch Continental Shelf Model (DCSM) are described, starting with the emergence of the first numerical hydrodynamic models for surge forecasting at the beginning of the 1980s. Since the mid-1980s, these forecasts are based on a numerical hydrodynamic model called the DCSM version 5. For the development of DCSM version 5, see Verboom et al. (1992), Philippart et al. (1998), Flather (2000) and Verlaan et al. (2005). This model uses forecasts of the meteorological high-resolution limited area model (HiRLAM) as input. Since the 1980s, DCSM has been the main hydrodynamic model for storm surge forecasting in the Netherlands. The model has been through many rounds of improvements since. In the early 1990s, a Kalman filter was added to this system to improve the accuracy of the forecasts further by assimilating measurements from a network of tide gauges along the UK and Dutch coast (Verlaan et al. 2005; Philippart et al. 1998; Heemink 1986, 1990; Heemink and Kloosterhuis 1990).

After the November 2006 All Saints storm, it was decided that further improvements to the then operational version of the DCSM model were required. However, with a limited spatial resolution of 1°/12° by 1°/8° and with doubts about the quality of the model bathymetry at the time, further calibration based on the existing schematization was assumed not to be worthwhile (Verlaan et al. 2005). Instead, a decision was made to develop a completely redesigned operational model, DCSM version 6, as part of a more comprehensive development to upgrade the operational forecasting framework for the North Sea. In 2012, the new generation model (Zijl et al. 2013) became the preferred operational model for Dutch coastal water level forecasting.

Despite the huge improvements in water level representation achieved with the new model, forecast will always be subject to uncertainty, caused by errors in the boundary or surface forcing, uncertainty in model parameters and poorly described or neglected physical processes in the system equations as well as mathematical approximations (Canizares et al. 2001). Many of these potential sources of error can be and have been addressed during development of the DCSM version 6 model, aided by the use of parameter estimation techniques to decrease uncertainty in time-independent parameters (Zijl et al. 2013). Since this has substantially improved the accuracy of the tide representation and, through non-linear tide-surge interaction, also the surge representation, the main remaining source of errors is the inaccuracy in the meteorological forcing, especially during storm surge conditions. This is due to errors in the parameters forecasted by the meteorological model as well as uncertainty in the parameterization of the complex processes governing the exchange of momentum between atmosphere and water (WMO 2011). Without a suitable real-time data assimilation procedure, errors in the meteorological forcing will inevitably be propagated to the surge prediction. This can be prevented by integrating observational data, e.g. tide gauge observations, into the hydrodynamic forecast model by means of real-time data assimilation. Since the North Sea is one of the most intensively monitored seas in the world, water level observations describing the state of the system are readily available, also in near real time.

The assimilation of available observations into a real-time operational numerical model leads to a more realistic estimate of the initial state of the system at the start of the forecast. By updating the system state in the model, the errors are prevented from propagating further, leading to more accurate forecast as the forecasted surge wave is, to some extent, dependent on its initial state. Likewise, the meteorological models used to drive storm surge models usually incorporate observations through data assimilations. Still, by the time the assimilated meteorological forecasts are available, which may take a couple of hours, many new measurements describing the system state have been obtained, which can then be used to assimilate the storm surge model.

This paper aims to show the improved forecasting skill of a dynamical model, by adopting an adequate data assimilation procedure based on a tide gauge observational network around the North Sea basin. While data assimilation of observed water levels is commonly applied in storm surge modelling (Verboom et al. 1992; Mouthaan et al. 1994; Gerritsen et al. 1995; Philippart et al. 1998; Canizares et al. 2001) and, as a result, it is known that the assimilation of observational data into real-time operational models is a successful approach to improving forecasts, a key addition to the existing literature is the completeness of the development presented here, characterized by the following aspects.

1.1 Use of accurate, operational models

Most published material on real-time data assimilation applied to storm surge forecasting systems concern prototypes (e.g. Lionello et al. 2006; Canizares et al. 2001; Yu 2012; Karri et al. 2014) instead of real-life (pre-) operational systems. In Yu (2012), the applied process models have a resolution that is modest compared to other models proposed for the same area. Presumably, this affects the accuracy of the model, giving more scope for the data assimilation to enhance the results. In contrast, the process model applied here has a high resolution compared to other applications of this scale. In addition, the non-assimilated model has been through rounds of rigorous parameter optimization to reduce uncertainty in time-independent parameters (Zijl et al. 2013). While this has yielded superior accuracy of the non-assimilated model, it raises the question whether further improvements with real-time data assimilation are still possible.

In many publications (e.g. Canizares et al. 2001; Lionello et al. 2006), the impact of the data assimilation scheme is assessed in hindcast mode only, with observations feeding into the assimilation scheme available throughout the computation. In the present paper, we supplement the impact on hindcast quality by an assessment of the impact on the forecasting skill, for various lead times.

1.2 Thorough assessment of effectiveness and applicability in a real-life situation

To assess the effectiveness of a data assimilation scheme, we use actual tide gauge observations to assimilate and compare against, instead applying the commonly used twin experiment method (Karri et al. 2014; Butler et al. 2012; Peng and Xie 2006), where real observations are replaced with synthetic observations generated by running a perturbed non-assimilated model. Our approach gives an essentially more realistic picture of the effectiveness and applicability of the data assimilation approach in a real-life situation.

1.3 Complete set-up

Our set-up is complete in the sense that the system uses many techniques of practical significance such as regionalization or localization (identified as a first direction of improvement in Karri et al. 2014), where the spatial influence of assimilated observations is gradually limited, in order to avoid spurious oscillations far away from an observation location. Finally, WMO (2011) notes that the main challenge for local and regional applications is to be accurate while practicable, ensuring that useful forecasts reach the public in a timely fashion. Besides using a time-efficient data assimilation scheme, our set-up includes parallelization of the code to enhance the speed with which forecasts become available.

The data assimilation schemes used in this study are described in Section 2, while the study domain and the set-up of the hydrodynamic model and monitoring network are described in Section 3. The assessment of the effectiveness of the real-time data assimilation is described in Section 4. This includes the model validation against shelf-wide tide gauge measurements, addressing the improvements in water level representation both in space (away from the assimilation stations) and in time (i.e. the forecast accuracy). The results are summarized and discussed in Section 5.

2 Data assimilation schemes

2.1 The data assimilation methods

The data assimilation method used in this work is based on the Kalman filter (Kalman 1960). It provides optimal state estimates by sequentially combining model and observations and also by taking into account the uncertainties of the model and observations. A complete description of the Kalman filter can be found in Jazwinski (1970) and Maybeck (1979). For linear systems, the Kalman filter provides optimal solution in various senses. Difficulties in implementing a Kalman filter are the linearity assumption and the dimensionality problem. The ensemble Kalman filter (EnKF) provides a solution for these difficulties and can be implemented relatively easily.

2.1.1 Ensemble Kalman filter

EnKF (Evensen 2003) approximates the Kalman filter equations using a Monte Carlo approach in representing the uncertainties. In the forecast step, a forecast state x f i of ensemble member i is generated by propagating the model state in time while being perturbed by a realization of the model error ω i (t k ).

$$ {\boldsymbol{x}}_i^f\left({t}_k\right)=\boldsymbol{M}\left({t}_k\right){\boldsymbol{x}}_i^a\left({t}_{k-1}\right)+{\boldsymbol{\omega}}_i\left({t}_k\right), $$
(1)

and the forecast mean x f(t k ) is approximated by the ensemble mean \( {\overline{\boldsymbol{x}}}^f\left({t}_k\right) \)

$$ {\overline{\boldsymbol{x}}}^f\left({t}_k\right)=\frac{1}{N}{\displaystyle \sum_{i=1}^N{\boldsymbol{x}}_i^f\left({t}_k\right)} $$
(2)

where N is the ensemble size. The covariance is approximated by

$$ {\boldsymbol{P}}^f\left({t}_k\right)\cong {\boldsymbol{L}}^f\left({t}_k\right){\boldsymbol{L}}^f\hbox{'}\left({t}_k\right) $$
(3)

where L f(t k ) is defined as

$$ {\boldsymbol{L}}^f\left({t}_k\right)=\frac{1}{\sqrt{N-1}}\left[{\boldsymbol{x}}_1^f\left({t}_k\right)-{\overline{\boldsymbol{x}}}^f\left({t}_k\right),\dots, {\boldsymbol{x}}_N^f\left({t}_k\right)-{\overline{\boldsymbol{x}}}^f\left({t}_k\right)\right] $$
(4)

Here, it should be noted that model operator M(t k ) in Eq. (1) can be non-linear and it is not necessary in practice to compute P f(t k ).

In the analysis step, each ensemble member is updated by

$$ {\boldsymbol{x}}_i^a\left({t}_k\right)={\boldsymbol{x}}_i^f\left({t}_k\right)+{\boldsymbol{K}}_e\left({t}_k\right)\left({\boldsymbol{y}}^0\left({t}_k\right)-\boldsymbol{H}\left({t}_k\right){\boldsymbol{x}}_i^f\left({t}_k\right)+{\boldsymbol{\upsilon}}_i\left({t}_k\right)\right) $$
(5)

where υ i (t k ) is a realization of the observational error. The analysis state is approximated by the analysis ensemble mean

$$ {\overline{\boldsymbol{x}}}^a\left({t}_k\right)=\frac{1}{N}{\displaystyle \sum_{i=1}^N{\boldsymbol{x}}_i^a\left({t}_k\right)} $$
(6)

and the Kalman gain K e (t k ) is computed by

$$ {\boldsymbol{K}}_e\left({t}_k\right)={\boldsymbol{L}}^f\left({t}_k\right){\boldsymbol{L}}^f\hbox{'}\left({t}_k\right)\boldsymbol{H}\hbox{'}\left({t}_k\right){\left(\boldsymbol{H}\left({t}_k\right){\boldsymbol{L}}^f\left({t}_k\right){\boldsymbol{L}}^f\hbox{'}\left({t}_k\right)\boldsymbol{H}\hbox{'}\left({t}_k\right)+\boldsymbol{R}\left({t}_k\right)\right)}^{-1} $$
(7)

Inherent in any ensemble-based method is the problem of spurious correlation due to a limited ensemble size. This problem may lead to filter divergence. A common way to reduce this problem in EnKF is the use of a distance-dependent covariance localization (Houtekamer and Mitchell 2001; Hamill et al. 2001). Covariance localization cuts off longer-range correlation in the error covariance at a specified distance and is formally performed by applying a Schur product between the forecast error covariance and the correlation function with a local support. Local support here means that the function is non-zero only in a small local region and zero elsewhere. In this study, however, the localization is performed directly on the Kalman gain (e.g. Zhang and Oliver 2011)

$$ \boldsymbol{K}\left({t}_k\right)=\boldsymbol{\rho} o\left({\boldsymbol{L}}^f\left({t}_k\right){\boldsymbol{L}}^f\hbox{'}\left({t}_k\right)\boldsymbol{H}\hbox{'}\left({t}_k\right){\left(\boldsymbol{H}\left({t}_k\right){\boldsymbol{L}}^f\left({t}_k\right){\boldsymbol{L}}^f\hbox{'}\left({t}_k\right)\boldsymbol{H}\hbox{'}\left({t}_k\right)+\boldsymbol{R}\left({t}_k\right)\right)}^{-1}\right) $$
(8)

where each column of ρ is the compactly supported fifth order piecewise rational function of Gaspari and Cohn (1999) and (A o B) denotes the Schur product of two matrices, A and B, of identical dimension, i.e. (A o B) i,j  = (A) i,j (B) i,j .

EnKF is simple to implement and can be used for non-linear models but requires a considerable amount of computational time. For illustration, with 100 ensemble members on our operational machines (a CPU with 12 cores), a 2-week simulation time costs about 2 weeks of actual time.

It should be noted here that in our work, the model state vector x f consists of water levels and flow velocities in all model grid cells. Moreover, the observational error is assumed to be independent in time and space. The observational error covariance matrix R(t k ) is therefore diagonal.

2.1.2 Steady-state Kalman filter

It is known that for a stable and time-invariant system, that is, a system with constant model parameters and error statistics and fixed observing network, the Kalman gain K(t k ) will converge to a limiting value K (Anderson and Moore 1979)

$$ \underset{k\to \infty }{ \lim}\boldsymbol{K}\left({t}_k\right)=\boldsymbol{K} $$
(9)

In this situation, it is not necessary anymore to propagate the forecast covariance nor to recompute the Kalman gain. The forecast step is identical with the original Kalman filter, which is actually the state propagation by the original deterministic model. The analysis step now simply reads

$$ {\boldsymbol{x}}^a\left({t}_k\right)={\boldsymbol{x}}^f\left({t}_k\right)+\boldsymbol{K}\left({\boldsymbol{y}}^o\left({t}_k\right)-\boldsymbol{H}{\boldsymbol{x}}^f\left({t}_k\right)\right) $$
(10)

Once the steady-state Kalman gain is obtained, one only needs to implement the analysis in Eq. (10). A steady-state Kalman filter (SSKF) adds, therefore, only a little extra computational cost to the cost of the state propagation by the original deterministic model. Hence, it is computationally attractive for operational purposes. SSKF has also been proven efficient in many applications (e.g. Heemink 1990; Canizares et al. 2001; Verlaan et al. 2005; Sørensen et al. 2006; El Serafy and Mynett 2008; Karri et al. 2014). Successful application of SSKF requires (i) a stationary observational network, (ii) a nearly linear process model and (iii) a stationary system error covariance.

Various techniques have been proposed for computing a steady-state Kalman gain (Mehra 1970; Mehra 1972; Kailath 1973; Rogers 1988; Sumihar et al. 2008). In this study, we use the one introduced by El Serafy and Mynett (2008), which computes a steady-state Kalman gain by averaging a series of Kalman gains computed using an EnKF (EnSSKF).

In short, the procedure for computing the steady-state Kalman gain is as follows:

  1. a)

    Run an EnKF over a certain period, complete with the forecast-analysis cycles, where all observations are assimilated sequentially in time.

  2. b)

    Store the Kalman gains with a certain time interval.

  3. c)

    Average the Kalman gains over time. In principle, for stable time-invariant systems, the Kalman gain will become constant if the ensemble is infinitely large. However, in practice, the ensemble size is always limited and the estimate of the error covariance, hence the Kalman gain, suffers from sampling error. Averaging the Kalman gain over time is necessary to reduce the sampling error.

  4. d)

    Use the averaged gain as a steady-state Kalman gain.

Note that in our case, it is necessary to use covariance localization in running the EnKF. Without localization, the filter became divergent and so the model became unstable.

2.2 OpenDA data assimilation toolbox

Data assimilation experiments in this study are performed using the open source data assimilation toolbox OpenDA. OpenDA is a generic framework for parameter calibration and data assimilation applications (El Serafy et al. 2007; van Velzen and Segers 2010). It makes use of the fact that it is possible, and convenient, to separate the code of data assimilation methods from that of the forecast models. Within this framework, it is possible to try out various algorithms for a given model, without any extensive programming. Various data assimilation methods have been available in OpenDA. It has been successfully applied, for example, for data assimilation of currents and salinity profiles (El Serafy et al. 2007), flood forecasting (Weerts et al. 2010), and forecasting of non-tidal water level and residual currents (Babovic et al. 2011; Wang et al. 2011; Karri et al. 2014; Zijl et al. 2013). Both steady-state KF and EnKF, with localizations, are available in OpenDA and used in this study.

To use the data assimilation methods available in OpenDA, one only needs to program a coupling between OpenDA and the process model. Various types of coupling are possible ranging from in-memory coupling to a black box wrapper where communication is achieved through model input and output files. In this study, the in-memory coupling with the fast native routines of OpenDA is used in combination with parallel computing to speed up the computation.

3 Experiment set-up

3.1 The Dutch Continental Shelf Model (version 6)

The tide-surge model we use in our data assimilation experiments is the Dutch Continental Shelf Model version 6, which was developed by Zijl et al. (2013) as part of a comprehensive study to improve water level forecasting in Dutch coastal waters. This hydrodynamic model covers the northwest European continental shelf, specifically the area between 15° W to 13° E and 43° N to 64° N (Fig. 1). The spherical grid, specified in geographical coordinates (WGS84), has a uniform cell size of 1°/40° in east–west direction and 1°/60° in north–south direction, which corresponds to a grid cell size of about 1 × 1 nautical miles and yields ∼106 computational cells.

Fig. 1
figure 1

DCSM version 6 model bathymetry (depths relative to Mean Sea Level).The blue dots represent boundary support points

Full size image

At the northern, western and southern sides of the model domain, open water level boundaries are defined. The tidal water levels at the open boundaries are specified in the frequency domain; i.e. the amplitudes and phases of 22 harmonic constituents are specified.

While wind set-up at the open boundary can safely be neglected because of the deep water locally (except near the shoreline), the (non-tidal) effect of local pressure will be significant. The impact of this is approximated with an inverse barometer correction (IBC; Wunsch and Stammer 1997), which is added to the tidal water levels prescribed at the open boundaries.

For meteorological surface forcing of the model, the KNMI provided time- and space-varying wind speed (at 10 m in height) and air pressure at Mean Sea Level (MSL) from the numerical weather prediction (NWP) high-resolution limited area model (HiRLAM). The wind stress at the surface, associated with the air-sea momentum flux, depends on the square of the local U10 wind speed and the wind drag coefficient, which is a measure of the surface roughness.

To translate wind speed to surface stresses, the local wind speed-dependent wind drag coefficient is calculated using the Charnock formulation (Charnock 1955). The empirically derived dimensionless Charnock coefficient has been set to a constant value of 0.025, which corresponds to the value used in the HiRLAM meteorological model.

3.1.1 Software framework

The non-linear forecast model is developed as an application of the WAQUA software package, which solves the depth-integrated shallow water equations for hydrodynamic modelling of free-surface flows (Leendertse 1967; Stelling 1984). As required to model non-linear surge-tide interaction, WAQUA includes the non-linear bottom friction and advection terms as well as a robust drying and flooding algorithm. With approximately 106 computational cells and a numerical time step of 120 s, it takes about 2 min to compute 1 day on five Intel Core i7 (quad core) 3.4 MHz CPUs. This computational efficiency makes the model well applicable to operational forecasting, where timely delivery of forecasts is vital.

3.1.2 Parameter optimization

Even though Zijl et al. (2013) show excellent agreement between predicted water levels and shelf-wide in situ and space-borne measurements, the version of the model used here has undergone additional parameter optimization to reduce uncertainty in model parameters governing (tidal) wave propagation and dissipation (bottom friction coefficient and bathymetry). The experiment set-up was similar to that of Zijl et al. (2013), but now covering the entire calendar year 2007, instead of 4 months within this period. The additional length is significant as tidal amplitudes and phases cannot be assumed stationary in shallow waters due to non-linear interactions between the tide and surge.

With the tide representation optimized, our strategy is to subsequently focus on improving the surge representation by reducing errors in the wind forcing through a real-time data assimilation approach.

3.2 Observation network

The improvement in water level forecasting skill that can be obtained with a Kalman filter is, to a large extent, dependent on the observational network applied. A careful selection of observation locations is important as in past applications (Verlaan et al. 2005), and not all observations contributed to an improved forecast quality. For this application, the first consideration in the selection of observation stations was the continued, real-time availability of tide gauge measurements. In the past, this significantly restricted the choice of stations (Verlaan et al. 2005), but nowadays, many more tide gauge observations have become available for real-time use.

A second consideration had to do with an understanding of the North Sea system behaviour as, in general, the dynamics of the wave propagation within a basin determine the potential benefit of data assimilation for a certain location. It is well known that as the main M 2 tide from the deep Atlantic Ocean enters the northwest European shelf, it propagates around the north of Scotland, entering the semi-enclosed North Sea proper. From there, it travels in anti-clockwise direction down the eastern British coast, towards the Netherlands and further (Otto et al. 1990; Huthnance 1991).

While storm surges are not freely propagating waves, since they react to local wind stress and atmospheric pressure gradients, at least part of the storm surge can be considered a Kelvin wave, travelling in roughly the same direction as the tide (Huthnance 1991). By having a good real-time observational coverage of the progressing surge wave in the upstream part of its trajectory, data assimilation can improve storm surge forecasting with sufficient lead time.

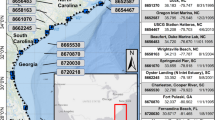
Similar to other applications for the Dutch coast (Verlaan et al. 2005), this led to a selection of tide gauge stations along the Dutch coast, Belgian and eastern UK coast (cf. Fig. 2, Table 1).

Fig. 2
figure 2

Spatial distribution of the tide gauge stations included in the Kalman filter observational network. The numbers refer to the station names listed in Table 1

Full size image
Table 1 Names of the tide gauge stations included in the Kalman filter observational network
Full size table

The time it takes a surge wave to travel from an assimilation location to a forecast location (i.e. dependent on distance and propagation speed) would then define the lead time an observation location could provide. The further away a station, the more potential is the lead time to increase but also the more the surge is generated between the observation location and the area of interest. Along the same lines, while stations close to the areas of interest have great potential to improve the surge representation, the short travel time would reduce the lead time within which the beneficial impact of these stations would be felt. At some point, the lead time becomes shorter than the processing time required to produce and disseminate a forecast, or shorter than the time between successive runs. For these reasons, stations inside estuaries have been excluded from the observational network. Furthermore, to prevent a negative impact on forecasting skill, stations in areas dominated by local processes not well resolved on the grid have also been excluded. Examples of these are tide gauge stations such as Immingham, Sheerness and Delfzijl, which are located in or close to shallow areas with a relatively variable bathymetry and geometry in relation to the model resolution. In the deterministic model, this results in the difficulty of reproducing higher harmonics properly, which have large amplitudes there, and consequently affects the representation of the non-linear interaction with the surge (Zijl et al. 2013).

Based on the above considerations, a total of 32 assimilation stations have eventually been selected. This is much more than the eight stations that were used in the previous generation Kalman filter for Dutch storm surge forecasting (Verlaan et al. 2005) and creates enhanced redundancy. Consequently, the dependency on specific assimilation stations is reduced, especially since the new Kalman filter is less sensitive to gaps in the observational data.

3.2.1 Ensemble-based observation sensitivity

In principle, it is possible to optimize the observational network with data denial experiments. In these experiments, the impact of an observation location on forecast quality can be obtained by comparing the forecast skill of two assimilation computations, one including and the other excluding this station. The drawback of this is that it requires a lot of time, since with the potential availability of many tide gauge observations, many time-consuming experiments have to be performed. Another possibility is to use an ensemble-based observation sensitivity (Liu and Kalnay 2008; Li et al. 2010), a technique to estimate the impact of assimilated observations to the forecast accuracy. In this study, a variant of this technique is used for estimating the observation impact. This technique requires time series of observations and, crucially, only unassimilated hindcast model residuals (Sumihar and Verlaan 2010). In this technique, forecast accuracy J is defined as a quadratic function of the observation minus the model differences

$$ \boldsymbol{J}\left({t}_k\right)=\left({\boldsymbol{y}}^o\left({t}_k\right)-\boldsymbol{H}{\boldsymbol{x}}^f\left({t}_k\right)\right){\boldsymbol{R}}^{-1}\left({\boldsymbol{y}}^o\left({t}_k\right)-\boldsymbol{H}{\boldsymbol{x}}^f\left({t}_k\right)\right) $$

The technique estimates observation impact ΔJ that is defined as the difference between model accuracy with and without assimilating individual or group of stations. Hence, negative ΔJ means that data assimilation is expected to improve the model accuracy. In this work, since the main goal is to have accurate water level forecasts along the Dutch coasts, the observation impact is evaluated over ten validation stations that cover approximately the entire Dutch coasts.

In Fig. 3, an example of the impact of observations on the accuracy at a selection of stations along the Dutch coast is presented. As expected from the Kelvin wave behaviour of the surge wave discussed above, results show that assimilating nearby stations gives immediate impact on the forecast accuracy while assimilating stations further upstream improves the accuracy at larger forecast lead times. This analysis strengthens the assumption that the Kelvin wave behaviour of the surge and the time it takes to travel towards a forecast location determine the lead time with which the impact of the assimilation can be expected to occur.

Fig. 3
figure 3

Assimilation station impact (as a function of lead time) on the model accuracy at a selection of ten validation stations along the Dutch coast. The cost is computed over locations Cadzand, Hoek van Holland, Scheveningen, Ijmuiden Buitenhaven, Terschelling Noordzee, Huibertgat, Vlissingen, Roompot Buiten, Den Helder and Eemshaven

Full size image

3.2.2 Pre-processing of Kalman filter observations

The aim of the Kalman filter is primarily to improve surge forecasts. The assumption is that the errors in the modelled surge are meanly caused by errors in the wind stress and pressure gradients applied to the numerical model. However, the modelled water levels that are assimilated also contain tide errors, which in most applications for the northwest European shelf are much larger than the surge error. Therefore, in conventional operational systems, the surge component from numerical model simulations is used while the harmonically predicted tide, accurately known from harmonic analysis of tide gauge measurements, is then added to predict the full water level signal at the tide gauge locations (Flather 2000). To prevent the Kalman filter mainly correcting errors in the modelled astronomical tide, which due to the astronomical correction is not used anyway, before feeding the observations to the Kalman filter, the tide can be adjusted by subtracting the harmonically analyzed tide and adding the astronomical tide as calculated by the model without meteorological forcing. This pre-processing step is applied to the observations fed to the Kalman filter of the previous generation DCSM version 5 Kalman filter (Gerritsen et al. 1995).

Zijl et al. (2013) claim that the deterministic model used here is the first application on this scale in which the tidal representation is such that astronomical correction no longer improves the accuracy of the total water level representation and where, consequently, the straightforward direct forecasting and assimilation of total water levels (instead of surge elevation) is better. For the Kalman filter application presented here that implies that the use of ‘harmonically adjusted observations’ as described above is no longer necessary. This reduces the complexity of the operational process, removes the need for a tide only simulation and eases the interpretation of results.

The only correction that is still made to the assimilated observations is a bias correction. Since baroclinic pressure gradients inside the model domain as well as steric effects affecting the open boundary are not taken into account, the model cannot be expected to accurately represent the long-term mean water level. To prevent the Kalman filter from correcting for this, the bias between measured and computed water levels determined over a multi-year period is first removed by adjusting the Kalman filter observations and, after the assimilation step, by adjusting the model predictions.

3.3 Kalman filter settings

Here, we have taken a pragmatic approach in setting up the Kalman filter by adopting as much as possible the Kalman filter setting of the existing operational DCSM version 5 model (Heemink and Kloosterhuis 1990). The idea is to start with this setting and recalibrate it if necessary. Like with DCSM version 5, here, the uncertainty of DCSM version 6 is assumed to come from the wind input forcing. The wind error is modelled by an additive error term on the water flow velocities. The error is represented as an autoregressive model of order 1 (AR1) with decorrelation time of 95 min to represent a temporally correlated noise process. The error term is augmented in the state vector and, hence, also being updated in the analysis step. This term ensures a smooth transition to the predictive mode and avoids inconsistency between wind forcing and initial condition at the start of forecast. Also, it contributes to the persistence of the update as the model propagates. The error is assumed to be spatially uniform, isotropic, and normally distributed with a spatial correlation length of 165 km. To reduce computational cost, the error is defined on a coarser grid with a grid size of 240 km.

In the EnKF, a characteristic distance of 300 km is used for the localization of the Kalman gain. This length is obtained by trial and error. The idea is that the length should be as large as possible to let the Kalman gain structure be determined mostly by the forecast ensemble. However, it should not be too large to let the EnKF run without any divergence problem. With this characteristic length, the Kalman gain structure of the previous generation model DCSM version 5 can be reproduced.

For the observations, we assume uncorrelated errors with a standard deviation of 0.05 m.

3.3.1 Deriving the steady-state Kalman gain

The SSKF uses a constant Kalman gain generated by running an offline ensemble Kalman filter computation with 100 ensemble members. The EnKF assimilates the observations sequentially in time from all assimilation stations, i.e. every 10 min. After allowing for 1 week of spin-up, the Kalman gains were averaged over an additional period of about 1 week, from 20 June 2007 at 0400 hours to 25 June 2007 at 2200 hours, with an output interval of 3 h. This is a sufficiently long period as, according to Canizares et al. (2001), tests for barotropic, depth-averaged North Sea models have shown that the error covariance matrix becomes nearly invariant after 1–2 days of simulation. This period was chosen because it covers the longest period among the data available for our work, where observations from all the 32 assimilation stations are complete. Note that we have performed also some experiments where the Kalman gain is averaged over a period longer than 1 week. However, the results are similar (not shown).

For illustration, Fig. 4 shows the Kalman gain component of water level for assimilation stations Wick and Scheveningen.

Fig. 4
figure 4

Kalman gain component of water level for assimilation stations Wick and Scheveningen. The assimilation stations are indicated with red dots

Full size image

4 Results

4.1 Quantitative evaluation measures

4.1.1 Time series

To assess the effectiveness of the data assimilation scheme, the root-mean-square error (RMSE) is computed based on total water levels obtained from the assimilated model predictions as well as the reference simulation with no assimilation applied. In addition to assessing the quality of the full water level signal, it can be insightful to make a distinction between the tide and surge component of the signal by means of harmonic analysis. For this, the program T_TIDE (Pawlowicz et al. 2002) was used. Analyses were undertaken on series of an entire calendar year, with a set of 118 tidal constituents including many user-specified shallow water constituents. The (practical) surge, or non-tidal residual, is then computed by subtracting the predicted tide from the total water level signal.

Since, operationally, the simulated water levels are corrected to reflect the fact that they cannot be expected to accurately represent the long-term mean (cf. Section 3.2), the bias between measured and computed water levels determined over a full year will be disregarded in all evaluation criteria used here.

4.1.2 High waters

For water level predictions, the quality of the prediction during peak water levels is especially important. Minor differences in timing between the computed and measured high waters are less critical. Therefore, the quality of the representation of high waters (approximately twice a day) is determined by computing the root-mean-square (RMS) of differences between measured and observed high waters.

4.2 Hindcast effectiveness of SSKF

The evaluation of the effectiveness of the Kalman filter in hindcast mode is based on the entire calendar year 2007. The solutions were generated from initial conditions of zero elevation and motion, with an additional period of 7 days allowed for spin-up. The most significant North Sea storm surge event within this period occurred on 8 and 9 November. To enable the assessment of the effectiveness of the Kalman filter, the hindcast model simulation is performed both with and without data assimilation.

4.2.1 Shelf-wide effectiveness

In Table 2, a summary of the shelf-wide water level representation quality for the year 2007 is shown. This is done for the results with and without Kalman filtering. Considering all the stations, the results show an excellent agreement between the simulated and observed water levels. Moreover, the application of the Kalman filter has a positive impact on the overall goodness-of-fit measures presented here, with e.g. the RMSE of total water levels decreasing from 9.5 to 8.5 cm. However, the reduction of GoF values considering all the stations understates the impact in specific regions. In the North Sea proper, a larger reduction, from 9.4 to 7.3 cm, is obtained. The limited impact of assimilation in e.g. the Skaggerak and Kattegat area and the English Channel area is most likely caused by the lack of assimilated observations in the neighbourhood.

Table 2 Summary of the water level representation quality, in terms of RMSE of tide, surge, total water level, high waters and low waters over the entire calendar year of 2007
Full size table

The only regions where results, in terms of total water levels, deteriorate are the Irish and Celtic seas. Although no assimilation stations from these regions have been included in the Kalman filter set-up, the deterioration there is still noteworthy. Apparently, some of the mainly tidal errors originating elsewhere in the model are compensated in the local parameter settings. Decreasing these errors with help the Kalman filter leads the model to overcompensate locally.

4.2.2 Effectiveness at assimilation stations

As the observational network of assimilation stations was specifically designed to improve forecasting skill in Dutch coastal waters, further evaluation of the Kalman filter impact will focus on this area. The improvements obtained at the Dutch assimilation stations using SSKF are shown in Table 3. It can be seen that the errors in the assimilated model are significantly smaller than those in the deterministic model, by around 50 %. An already excellent total water level RMSE of 7.2 cm in the deterministic results is reduced to only 3.5 cm in the analysis by adding the assimilation of measurements. The improvement is apparent in both the tide and surge component of the water level signal as well as in all stations, with the relative total water level improvement ranging from 29 to 69 %.

Table 3 Comparison of water level representation (RMSE) for the entire calendar year of 2007 at the Dutch assimilation locations between the deterministic (det.) and assimilated model (ass.), for tide, surge total water level signal, high waters and low waters
Full size table

4.3 Spatial distribution of skill improvement

4.3.1 Dutch non-assimilated stations

While it is good to see that improvements are obtained at the assimilation stations, it is especially important to study the spatial extent of the skill improvement. This is first done by assessing the impact at non-assimilated, independent, tide gauge locations (cf. Table 4). Like at the assimilation locations, improvements are evident at all locations, regardless the evaluation criterion considered. Although still substantial, the relative magnitude of the improvement is less, on average 18 % compared to 51 % at the assimilated stations, while the range over the stations considered is much larger, from just 5 % at Schiermonnikoog to 52 % at Haringvliet 10.

Table 4 Comparison of water level representation (RMSE) for the entire calendar year of 2007 at the Dutch non-assimilated locations between the deterministic (det.) and assimilated model (ass.), for tide, surge and total water level signal
Full size table

In addition, it is striking that improvement is larger in the surge than in the tide, unlike in the assimilation stations. Note that the noise model we use in the Kalman filter was designed for wind errors, which implies that the surge errors are more consistent with the assumptions in the Kalman filter.

Furthermore, the stations with the least relative surge improvement are those with a relatively poor tide representation in the non-assimilated simulation. At these locations, mainly in the eastern Wadden Sea, the representation of higher harmonics presumably suffers from lack of grid resolution and, consequently, a poor representation of local bathymetric features, such as narrow tidal channels, on the computational grid. This also shows up in the (practical) surge representation, since also the non-linear tide-surge interaction suffers from the same lack of resolution. Both higher harmonics and non-linear tide-surge interaction have smaller spatial scales than the surge and are therefore less susceptible to improvement with a nearby assimilation location.

Note that tide gauge stations with the best tide representation have been selected as assimilation locations, which leaves the ones with a poorer representation as validation locations. The exceptions are Haringvliet 10 and Petten Zuid, which have a good tide representation and are less affected by nearby shallow seas and estuaries. Indeed, the assimilation impact there (52 and 46 %, respectively) is better than average for the validation locations (18 %) and similar to the average impact at the Dutch assimilation locations (50 %).

4.4 Skill improvement during storm surge events

From Table 1, it appears that the impact of the Kalman filter is limited to the reduction of the RMSE by a few centimetres. Note, however, that these skill statistics are determined over the entire calendar year 2007. One can expect the impact of the Kalman filter to be non-homogeneous in time. During storm surge conditions, subsequent meteorological forecasts can be expected to differ more from one another, and reality, than under calm weather conditions. During the former conditions, the impact of the Kalman filter is consequently expected to be much larger.

To test this, the RMSEs of high waters are presented in Table 5, comparing the assimilated with the deterministic simulation results. This is done for all high waters of 2007 as well as the high waters with the 1 % highest measured skew surges in that period, which includes the extreme North Sea storm surge event on 8 and 9 November 2007. As expected, the results show that the high water error is significantly larger during storm surges. Moreover, comparison of the deterministic and assimilated results shows that the absolute impact of the Kalman filter is indeed larger during storm conditions (with a RMSE reduction of 2.8 vs. 4.4 cm).

Table 5 Comparison of high water representation (RMSE) at the Dutch assimilation locations between the deterministic (det.) and assimilated model (ass.)
Full size table

Figure 5 shows the impact of the Kalman filter for the tide gauge station Hoek van Holland, which is one of the main forecasting locations during storm surge conditions. The under prediction of the first high water on 9 November is clearly much smaller in the assimilated model (−12 cm against −36 cm in the unassimilated model). Remaining errors, especially during the most extreme storm surges, can partially be explained by higher frequency variability in measurements that is not being picked up by both process model and Kalman filter. As the frequency of some of these phenomena is much smaller than the time scale of the surge event, neglecting these processes in the model will, on average, lead to an under prediction of the peak water levels, also in the assimilated results. This is also evident in the under prediction of the 9 November high water (with a measured skew surge height of 1.9 m above MSL in Hoek van Holland).

Fig. 5
figure 5

Water level elevation at tide gauge station Hoek van Holland for the deterministic (upper plot) and assimilated model (lower plot) (black simulation; red measurement; blue residual)

Full size image

To check whether errors in the high water predictions are systematic or correlate with the skew surge, the high water errors are plotted in Fig. 6, both for the unassimilated and assimilated results. Further analysis of the results in this figure shows that when the entire year is considered, the bias in both model runs does not exceed 1 cm. Although it only concerns a limited number of events, the results suggest that for the 1 % highest skew surges, there is a systematic under prediction of high waters of 7 cm in the unassimilated computation. With assimilation, this reduces to just 3 cm.

Fig. 6
figure 6

High water error for the year 2007 as a function of measured skew surge height, for tide gauge station Hoek van Holland (upper plot unassimilated; lower plot assimilated)

Full size image

4.4.1 An example of spatial improvements in the Western Scheldt

Another example shows the impact of the Kalman filter in the Western Scheldt during the November 2007 storm. The only assimilation station in the Western Scheldt is at the entrance (tide gauge station Vlissingen), while further upstream independent stations are assessed (Bath and Antwerp). Since the Western Scheldt is poorly represented in DCSM version 6, with the upstream part missing since its width is less than the cell size of ∼1 nm × 1 nm, for this example, a locally refined model is used.

Figure 7 shows that during the November 2007 storm, an under prediction occurs throughout the Western Scheldt. In the assimilated model, this under prediction is absent at assimilation station Vlissingen and, crucially, also further upstream. This demonstrates the positive impact of the Kalman filter away from the assimilation stations.

Fig. 7
figure 7

Surge elevation at tide gauge station Vlissingen (top), Bath (middle) and Antwerp (bottom) for the deterministic (left) and assimilated model (right) (black simulation; red measurement; blue residual)

Full size image

4.5 Assessment of forecasting skill

While good hindcast quality can be valuable for many studies, e.g. through the provision of accurate boundary conditions for local impact studies, for an operational storm surge forecasting system, the critical importance of real-time data assimilation lies in improved forecast accuracy with sufficient lead time.

To assess the impact on the forecasting skill, we made a sequence of historical forecasts for the entire calendar year 2007, a forecast horizon of 48 h and a forecast cycle every 6 h. The frequency of the forecast cycle coincides with the operational availability of new meteorological forecasts (which is related to the data assimilation cycle of the meteorological model). Observations are made available to the Kalman filter for 3 h after the start of the meteorological model forecast (T0), which more or less reflects the situation under actual operational conditions. The resulting ∼1500 forecasts enable us to compute the quantitative performance measures as a function of the lead time interval.

In Fig. 8, the RMSE of water levels at the Dutch assimilations stations is presented for the assimilated and deterministic model results, as a function of the lead time interval. In Fig. 9, this is done for a set of independent Dutch stations (cf. Section 4.4). This shows that in the deterministic results, error growth is generally small. One reason for this is that the surge is determined by the wind stress and atmospheric pressure gradients integrated over a large area and a considerable time. Errors in the meteorological forecasts can therefore average out.

Fig. 8
figure 8

Water level RMSE of the assimilated (red) and deterministic (blue) water levels at Dutch assimilation stations as a function of the lead time interval for the year 2007

Full size image
Fig. 9
figure 9

RMSE of the assimilated (red) and unassimilated (blue) water levels at independent Dutch tide gauge stations for a range of lead time intervals

Full size image

A positive impact of the Kalman filter is evident for lead time intervals up to 12 to 18 h after T0, which corresponds to 9–15 h after the last assimilated water level measurements. While Gerritsen et al. (1995) report a significant decrease in the performance of the Kalman filter for lead times larger than 18 h, here, the assimilated model has a quality that is similar to the unassimilated results. This reduces the need to run the deterministic model alongside the assimilated model.

4.5.1 Xaver storm surge

The capability of the forecasting system, including the performance of its Kalman filter, was critically tested during the Xaver storm and accompanying storm surge on 5 and 6 December 2013. This enables us to assess the added value of the data assimilations scheme during a real-life event. A difference with the previously presented results for the year 2007 is the meteorological forcing, which is now obtained from the more recent HiRLAM 7.2, with a higher spatial resolution and an hourly instead of 3-h output.

The deterministic results for tide gauge station Hoek van Holland, from a hindcast simulation for the year 2013, show an under prediction during the 5 and 6 December 2013 event (Fig. 10a). While the results for the entire year in Fig. 10b indicate that, in general, the surge error does not correlate with the observed surge level (as results follows the diagonal), the most extreme event is under predicted as indicated by a tilt upward with respect to the diagonal. This under prediction is absent in the assimilated results.

Fig. 10
figure 10

Time series of simulated and observed surge elevation during the 5–6 December 2013 storm surge event (black simulation; red measurement; blue residual) and scatter plots of observed surge as a function of simulated surge during the year 2013. The upper plots show the deterministic model results, while the lower plots present the assimilated results

Full size image

More importantly, with results available from the actual operational system, in which the model with and without Kalman filter was running pre-operationally, we can also assess the lead time with which the positive impact of the Kalman filter is evident. Again, tide gauge station Hoek van Holland is taken as an example in Fig. 11, where the observed and predicted water level of the first and most extreme water level peak is shown as a function of the time at which a water level forecast became operationally available (i.e. approximately 4 h later than T0 of the meteorological model). These results show that, with the Kalman filter, an under prediction of 35 cm is reduced to just 10 cm in the hindcast. Crucially, while a small positive impact is evident in the predictions operationally available 12 h before the peak water level, also the results available 6 h before the peak water level show a large improvement, from 29 to 9 cm under prediction.

Fig. 11
figure 11

Predicted extreme water level of the first peak during the 5 and 6 December storm surge event at tide gauge station Hoek van Holland, as a function of the time at which the forecast became available, relative to the occurrence of the peak water level

Full size image

5 Summary, discussion and conclusions

5.1 Summary

We have presented an application of real-time operational data assimilation where measurements from a tide gauge observational network around the North Sea basin are integrated into a hydrodynamic tide-surge forecast model. We have demonstrated that even though we apply a state-of-the-art, highly accurate deterministic model for the northwest European shelf, substantial improvements in forecasting skill, aided by a computationally efficient steady-state Kalman filter, are still possible.

This is evident from a ∼50 % improved hindcast accuracy in a selection of 18 assimilation stations, reducing an already excellent total water level RMSE of 7.2 cm in the deterministic results to only 3.5 cm. The positive contribution away from the assimilation stations is demonstrated by a ∼20 % average skill improvement in a selection of non-assimilated, independent tide gauge locations. In addition, the positive impact of the Kalman filter away from assimilation stations is demonstrated by an example where during the extreme North Sea storm surge event on 8 and 9 November 2007, the deterministic model under predicts throughout the Western Scheldt. In the assimilated results, this under prediction is absent at assimilation station Vlissingen and, crucially, also further upstream up to Antwerp, which is ∼80 km further upstream.

Furthermore, the impact on skew surge is assessed, for the year 2007 and during the 1 % highest skew surges. This shows that during storm surge conditions, the absolute impact of the Kalman filter is larger than average with a RMSE reduction of 2.8 vs. 4.4 cm throughout the year. We supplement these hindcast assessments with an assessment of the impact on forecasting skill as a function of lead time by producing a sequence of ∼1500 historical forecasts for the entire calendar year 2007. By making use of the Kelvin wave nature of the surge in the selection of assimilation stations, a positive impact of the Kalman filter is evident for lead time up to 9–15 h after the last assimilated water level measurements. Thereafter, the forecast skill of the deterministic and assimilated model converges.

Finally, the capability of the forecasting system, including the performance of its Kalman filter, was critically tested during the Xaver storm and accompanying storm surge on 5 and 6 December 2013. This enabled us to get a realistic picture of the effectiveness and applicability of the data assimilation approach in a real-life situation. Crucially, at the important forecast location Hoek van Holland, the results available 6 h before the peak water level show a large improvement, from 29 to just 9 cm under prediction.

5.2 Discussion

The results indicate that the improvements using the Kalman filter are larger for errors in the wind forcing than for errors in the tides. This is, for instance, seen in the increased impact of the filter during storms. Although the errors in the wind forcing increase during storms, so does the impact of the filter. One must keep in mind that the errors in the tidal reproduction of the model were already reduced by the automated calibration of the model (Zijl et al. 2013). Although a theoretical framework is still lacking, it seems that our strategy of first improving the tidal representation offline and subsequently reducing wind errors in real-time seems to work. However, it should be noted that it is no longer useful to calibrate the model against tidal predictions, as was common before. The errors introduced in the harmonic analysis combined with the effects of non-linear interaction between tide and surge now introduce non-negligible differences during the calibration. With today’s accuracies, the model needs to simulate the combined effects of tides and wind when comparing with observations. The use of tidal analysis is now reduced to analysis of the results and is no longer part of the forecasting system itself, except for the model boundary conditions on deep water, where we still neglect interaction effects and assume an inverse barometer response to meteorological forcing.

The results seem to indicate that sufficient resolution to represent the local bathymetry around the tide gauge, which is necessary to reproduce the tides accurately in the hydrodynamic model, is also necessary to make the tide gauge data useful for assimilation. In this study, we have selected locations that were well represented at the 1 nautical mile resolution for assimilation. One could make better use of more tide gauges if the resolution was locally refined.

Moreover, in the present configuration, the selection of tide gauges for data assimilation was mainly restricted by several practical requirements. At the moment, the exchange within NOOS (www.noos.cc) makes a much larger set of tide gauges available for assimilation. The limited impact of assimilation in some areas of the model is most likely caused by the lack of assimilated observations in the neighbourhood. It is therefore likely that extending the set of assimilated locations will further improve the performance in those regions for the analysis. This, in turn, may improve the accuracy of the forecast in other regions as well as we have shown that the improvements due to assimilation are propagated by the model into other regions during the forecast computations.

In addition, the observations that we received mostly used a national vertical reference system or one based on LAT, which is not convenient for use of the data at a larger scale. It would be very helpful if the tide gauges would all be linked to an ellipsoid vertical reference system. This, together with the development of accurate geoid models and inclusion of density effects in the hydrodynamic model, would remove the need for bias correction of the sea level observations (Slobbe et al. 2013). Moreover, it would facilitate the combined use of tide gauges and satellite altimeter for validation and assimilation of the model.

5.3 Future work

Future work in improving the forecasting capabilities will concentrate on (i) improving water level representation inside the shallow seas and estuaries throughout the model domain, aided by increased grid resolution, and (ii) reducing uncertainty in the parameterization of the complex processes governing the exchange of momentum between atmosphere and water. While we have shown that the use of real-time data assimilation in the form of SSKF is a successful and practicable approach to improving water level forecasts, preventing errors from occurring in the deterministic model is essentially better.