Abstract
Sea-level and current measurements have been performed in the Mok Bay, a tidal embayment in the Dutch Wadden Sea, situated on the island of Texel, the Netherlands. Characteristic for this estuary is its nonuniform hypsometry. Oscillations in both water level and inflow of the estuary were observed, with characteristic frequencies of 31 and 48 cycles per day. The significant change in basin shape between low and high water is the cause for the existence of these two frequencies of resonance. Due to its semi-enclosed nature, the basin could at both tidal phases be characterized as a Helmholtz resonator, albeit of different dimensions. Depth measurements were performed to find these characteristic dimensions of the estuary, allowing the determination of its theoretical Helmholtz frequencies. These estimates match to within 10% with the observed frequencies, and this deviation can partly be explained. Although sea level oscillations at these frequencies have small amplitude (of order 1 cm), the accompanying oscillatory flow at the entrance is of similar magnitude as the tidal flow. The water level measurements (spanning only 8 days of data) were therefore modeled using a piecewise-uniform hypsometry that approximates the real hypsometric curve well. The simplified semi-analytical piecewise-linear viscous Helmholtz model captures the observed combination of tidal and eigenoscillations well. However, despite its simplicity, this model is able to display nonlinear behavior for certain parameter values. This is because of the intrinsic nonlinearity that accompanies the matching of the low and high water phases. In the setting studied here, bifurcations up to period 13 were found. This nonlinear type of response may be of importance in facilitating an extra exchange of sediments and nutrients between the Bay and the sea.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Coastal communities have been familiar with the tides for many centuries; already Aristotle (320 B.C.) was aware of the strong Greek tidal currents (Pugh 1987). This periodic motion of coastal waters was of great interest to fishermen, navigators, and pirates. During medieval times, simple observations resulted in the first mappings of the periodic relation between spring tide and the lunar phase (Cartwright 2001).
More recently, interest in coastal tides has shifted toward coastal engineering (Kim 2009), harbor management (Gonzalez-Marco et al. 2008; Rabinovich 2009), oceanography (Maas 1997), biology (Sanford 1985), and even mathematics (Frison 2000; Maas and Doelman 2002). Apart from local amplification of the tide (by resonance), also high-frequency oscillations have been observed in coastal embayments. Even a chaotic response of the tide can be present, both kinematically, in the form of chaotic tidal mixing (Ridderinkhof and Zimmerman 1992; Beerens et al. 1994), as well as dynamically (Maas 1997; Maas and Doelman 2002). Since the mixing and flushing of estuaries is of great importance for the functioning of the local ecosystem, fundamental understanding is necessary. It is especially of importance to consider the impact of a possibly chaotic response as compared to a purely periodic tidal motion because of its potential implication for enhancing sediment and nutrient fluxes.
Tsunami is Japanese for “harbor wave,” after the observed irregular sea level motion in Japanese harbors caused by underwater earthquakes. Already since the beginning of the twentieth century, these high-frequency oscillations have been studied intensively (Honda et al. 1908). For about 50 Japanese bays, so-called secondary undulations were found: oscillations with periods varying from minutes to hours. Apart from their appearance after underwater earthquakes, as in Carbajal and Galicia-Perez (2002), similar frequencies were excited by atmospheric forcing, showing that the local behavior is related to the bay itself. Furthermore, the basin-related frequency (eigenfrequency) turned out to match satisfactorily with those predicted by a model used for acoustic oscillators—a Helmholtz model (Honda et al. 1908). In addition to the appearance of eigenfrequencies per se, Nakano (1932) investigated the structure and regularity of the observed amplitudes.
More recently, Golmen et al. (1994) observed secondary undulations (“super-tidal oscillations”) in the Norwegian Moldefjord. By measuring not only water level but also flow velocities at the bay’s entrance, coherence between water level and inflow was found at certain spectral frequencies. However, no existing mathematical model could relate the observed periods of oscillation to the fjord’s dimensions.
By contrast, part of the Estonian coast of the Baltic Sea did seem to be modeled well as a set of five Helmholtz resonators interacting with each other. Since tides play no significant role in the Baltic Sea, it is the wind that forces the basins to resonance, according to numerical simulations (Otsmann et al. 2001).
The most recent and interesting measurements of tidal resonance deals with the coupled system of a tidal bay (quarter-wave resonator) and a connected cove (acting as a Helmholtz resonator). The Helmholtz frequency of the cove comes close to the quarter-wavelength frequency of the bay, but due to the cove’s sloping bottom, its eigenfrequency changes slightly. This makes the response in the cove explicitly transient, and the flow in the connecting channel is modulated significantly. Numerical simulations show that a (modulated) standing wave is present in the connecting channel (Mullarney et al. 2008).
Coastal resonances have been investigated numerically very often, including the buildup of the resonant Helmholtz mode (Bellotti 2007), the influence of increasing water surface area for a Helmholtz oscillator due to a sloping bottom (Green 1992), the influence of oscillations on tidal mixing (Geyer and Signell 1992), and the consequences of tidal resonance to harbor operation (Gonzalez-Marco et al. 2008).
Apart from observations to find the underlying mechanism, recently quite some attention is put on characterizing the measured oscillations themselves rather than the Helmholtz or quarter-wave resonator that “drives” them. Frison (2000) showed that the linear decomposition of water level measurements (obtained at various stations along the US coast) into a “tidal” and “residual” part is inappropriate since (nonlinear) low-dimensional chaos is present in the residual part. The traditional elimination of the residual prior to modeling, although widely used, is thus not correct.
As an extension of the theory described in Maas (1997) and Maas and Doelman (2002) and the laboratory observations of Terra (2005) on tidal Helmholtz resonators, this study focuses on the tidal behavior of an actual tidal basin which under certain circumstances may continuously excite eigenoscillations. In this paper, first a description of the measurement site and setup will be presented, together with the methods used to chart the Mok Bay’s depth. Then, a short description of the theoretical background of a Helmholtz resonator and the consequences of a nonuniform bathymetry are introduced. After this, the obtained measurements are presented and discussed. This is followed by an analytic model that possibly explains the observed oscillations. Finally, the consequences of both the observations and properties of the analytic model are discussed.
2 Measurements
The tidal basin of concern in this study is the Mok Bay, a shallow natural tidal basin with sloping bottom situated in the northwest of the Netherlands at the southeastern part of the island of Texel, see Fig. 1. Inside the Mok Bay, a navy harbor (Mok Harbor) is located, which at low water (LW) can only be reached through the ship route. At high water (HW), the large tidal flats increase the surface area of the bay significantly, as can be seen in Fig. 2. Because of its shape (a basin with narrow entrance), Mok Bay was expected to behave like a Helmholtz oscillator: that is, to show equal surface elevation throughout the basin and a pumping motion at the entrance.
Location of Marsdiep inlet (main panel) in the Dutch coast (bottom right panel), connecting the North Sea to the Wadden Sea. The Mok Bay, on the southern part of the island of Texel, is in turn connected to Marsdiep Inlet. The Marsdiep bathymetry is shown with 10-m contour lines, relative to mean sea level. Positions of measurements: H at Mok Harbor (triangle), E at the Mok Bay entrance (cross), and NIOZ Jetty (asterisk)
Depth chart of the Mok Bay, containing depth contours (colorbar in meters) estimated from all depth measurements, relative to NAP (Amsterdam reference level). Broken lines indicate the location of the Mok Bay’s entrance (E) and the length of the channel during low (L − ) and high water (L + ). All wet area northwest of such L ± contributes to A ± as listed in Table 1. Symbols indicate the location of the depth meters at Mok Harbor H (triangle) and the MK-2 beacon at Mok Bay entrance E (cross); the bird reserve (B) and oyster beds (O) resulted in uncertainties regarding depth charting. Black broken line near the Harbor indicates the contour of the Mok (Navy) Harbor, whose surface area is taken into account in Table 1
To investigate the dynamic properties of the Mok Bay, measurements were performed at two different locations (Fig. 2): the head of the bay (Mok Harbor, location H) and Mok Bay entrance (MK-2 beacon, location E). A frame was situated at the bottom of the entrance (next to the MK-2 beacon) of the ship route that leads into the Mok Bay. This frame was equipped with an acoustic Doppler current profiler (Workhorse Rio Grande 1,200-kHz ADCP). A depth meter (Keller PR-46X/8935) was mounted to the beacon. Based on the Doppler-shifted acoustic reflection of suspended matter and sediment, the ADCP measures the current profile from the ADCP transducer to the water surface. Table 2 lists the data of employment for the separate instruments.
Mok Harbor is situated at the head of the Mok Bay, see Fig. 2. At HW, this is, however, not the farthest point inside the bay (at LW it is), but it is the end of the ship route into the Mok Bay. This ship route is relatively deep and expected to be dominant for wave propagation over the shallow tidal flats (when flooded at HW). Consequently, an identical pressure sensor was mounted inside Mok Harbor to find any difference in water level over the Mok Bay. Continuous water level measurements were also available from the NIOZ Jetty outside the Mok Bay (asterisk), separated less than 500 m from the MK-2 beacon (cross), see Fig. 1.
2.1 Bathymetry Mok Bay
Accurate depth charts of the Mok Bay (Fig. 2) were not available, neither from land nor from water maps. So the relatively deep ship route in the Mok Bay was charted using a jetski equipped with GPS and echosounder; the tidal flats were charted using hand-held GPS and NIOZ Jetty water level measurements for vertical reference. Since tidal banks flood in a short amount of time, the spatial density of the waterline-tracked paths is not constant throughout the bay. The bird reserve (B, Fig. 2) in the most northwestern part of the Mok bay could not be entered, resulting in lack of accurate depth measurements (depths were interpolated); also the oyster beds (O) could not be walked around just northwest of the center of the bay.
2.2 Mok Bay dimensions
Estimates of the relevant length scales of the Mok Bay are obtained from the depth measurements. A simplified basin is characterized by the basin’s water surface area A and the narrow channel (width B, length L, depth H) that connects it to the tidal sea. The jetski depth measurements yield estimates for H, B, L (all for both LW and HW) and A = A − at LW; the charted tidal banks give an estimate for (and the transition to) its area, A + , at HW, see Table 1. The channel’s ends are defined as the locations where the channel suddenly increases its width, see Fig. 2, which occurs much more rapidly at LW. At HW, no distinct channel connects the Mok Bay to the Wadden Sea since the tidal flats are flooded as well. The ship route, however, remains about five times deeper than the flooded tidal flats and thus is still defined as being the “connecting channel” between basin and tidal sea, albeit of significantly decreased length (L + ≪ L −). Uncertainties regarding length scales are also shown in Table 1.
3 Theoretical background
A harbor or bay can respond significantly to an external forcing, i.e., a passing (long) wave, at a remarkably low frequency, well below the lowest quarter wave resonance frequency. Such harbor or Helmholtz resonances occur in basins that are separated from a tidal sea by a narrow channel and that are relatively short (so that an entering tidal wave can cross it almost instantaneously). For such a Helmholtz bay, the Helmholtz frequency is described in terms of the parameters characterizing basin and narrow channel by
where g denotes the acceleration of gravity. For Long Beach Harbor, the Helmholtz model approximates the frequency of tidal resonance to within 1% (Miles and Lee 1975). The frequency of resonance is approximated well for not too extreme dimension ratios, as investigated by Kela (2009).
For Helmholtz resonator basins whose hypsometry, i.e., its available (“wetted”) surface area A, varies as a function of depth z, (Maas 1997) derived the following nonlinear oscillator equation in terms of excess volume V(t) as a function of time t
Here the restoring term, ζ(V), representing water level overshoot, is the inverse of the relation coupling excess volume V to sea surface elevation ζ:
This relation can be made explicit for some simple hypsometric shapes A(z), such as, for example, a linearly sloping basin. The main approximations in this model are: (1) a uniform sea level rise within the basin and (2) a negligible sea level rise (and plug flow) in the connecting channel.
Excess volume, V(t), in the basin is driven by tidal forcing (first term on the right hand side), which represents the tidal sea level in the connecting sea oscillating at tidal frequency σ. The last two terms on the right-hand side (RHS) represent dissipation. This is due to radiation of waves back into the tidal sea (linear, second term on RHS) and the combination of bottom friction and form drag, the pressure difference over the channel (quadratic, nonlinear third term on RHS). Here r = σB/2L is the radiation damping coefficient and μ = (δ/L + k/H)A/B, with k the bottom friction coefficient and δ = O(1) an empirical proportionality constant (Maas 1997).
For vertical side walls, the restoring term is linear. However, if the basin has sloping sides, the basin’s surface area, and hence its restoring pressure gradient, changes with water level. The Helmholtz resonator now has a nonlinear restoring force (second term on LHS in Eq. 2), as investigated by Maas (1997). A linear Helmholtz resonator has a simple resonance curve, which is bent into a “resonance horn” for a nonlinear system. Such a resonance horn shows that under certain conditions, over a finite forcing frequency interval, multiple equilibria are possible for identical system parameter values. Depending on initial conditions, an amplified or choked response can be found for single-frequency forcing of the nonlinear Helmholtz resonator (Maas 1997).
When another frequency is added to the forcing—creating a slowly modulating “beat”—the system can even experience a chaotic response (Maas and Doelman 2002). A chaotic response means broadening of spectral peaks, noisiness of tidal “constants,” and irregular subsequent elevation maxima (Doelman et al. 2002). This is in stark contrast to the notion, persisting for many centuries, that tides are always precisely linked to the astronomical phase and are therefore thought to be highly periodic and predictable. Doelman et al. (2002) investigated the influence of various hypsometries, ranging from linear to hyperbolic, and found them leading to different types of chaotic responses. Especially shallow tidal basins, which are partly dry at ebb tide, seem to be well-described by such hyperbolic hypsometric curves. Such basins, having rapidly changing surface areas, motivate us to take this consideration here one step further and consider a step-function hypsometry. This results, as will be discussed later in this paper, in a piecewise-linear system, whose coupling at the transition from low to high water, still contains the remnant of the original nonlinearity, yet is piecewise integrable in the LW and HW phases, respectively.
4 Results
Similar to observations in the Moldefjord (Golmen et al. 1994), measurements of the water level in Mok Bay reveal oscillations at a frequency much higher than those of the tides. The magnitude of these high-frequency sea level oscillations is rather small: about 1 cm. But if a 20-min running mean is subtracted and the resulting oscillation magnified by a factor 10, it becomes clear that it is almost continuously present (see Fig. 3), much like the observation in Honda et al. (1908). In the case of a Helmholtz resonator, the sea surface height within the sea strait does not vary as much as inside the basin (Fig. 3). In the strait, oscillations can be visible in the form of a rapidly oscillating flow superimposed on the gradual tidal flow.
For the three sites of water level measurements (Fig. 1; Table 2), a power spectral density is calculated. Using this, a spatial variation of the oscillations is found: at approximately 31 and 48 cycles per day, clearly most energy is present inside the Mok Bay (as measured at H), see Fig. 4. Also, due to its sheltered location, the measurements performed at H show a damped response for frequencies above 60 cycles per day.
Power spectral density for band-pass filtered water level measurements at the NIOZ Jetty (thin dashed line), Mok Harbor H (solid line), and Mok Bay entrance E (bold, dashed line). At H, less energy is present for frequencies above 60 cycles per day due to its sheltered location. Resonance peaks at 31.1 and 48.4 cycles per day (indicated by arrows) were used to determine the Mok Bay’s Q-factor
More specific information can be obtained by splitting the period of measurements into a LW and a HW part. The LW part is defined as the period during which the water level is below mean sea level (and HW when above). The measured water level does not consist purely of (constant) sinusoids, so a linear spectrum is not the proper way to visualize results on ground of energy conservation (Bodén et al. 2009). But only the linear method of harmonic analysis allows for gaps in input time series, so a linear spectrum is used to show an important distinction between low and high water moments.
The least squares harmonic analysis according to Emery and Thomson (2001) is performed over the selected intervals that are flagged as LW or HW, and the resulting (band-passed) frequency content is shown in Fig. 5. Again, amplitudes should be interpreted relative to each other, and this linear spectrum is not meant for absolute interpretation. Two things are visible here: (1) During LW periods, resonances occur with 48 cycles per day (31 cycles per day during HW) and (2) during LW the water level residual has larger amplitudes (for all frequencies f < 85 cycles per day) as compared to HW periods. The flooded tidal flats at HW allow water to enter and leave the bay without flowing strictly through the ship route, which might explain the lower amplitudes (as measured in the ship route) for this HW spectrum. A shared peak in both spectra at 72 cycles per day (20-min period) approximately coincides with the frequency of arrival and departure of the ferry to the mainland, whose harbor on Texel is situated nearby, between Mok Bay entrance E (cross) and NIOZ Jetty (asterisk), see Fig. 1.
Frequency content of the least squares harmonic fit to the water level residuals (as measured at H) at LW and HW periods between 26 February and 6 March 2010. Frequency of resonance during LW is f − ≈ 48 cycles per day and during HW f + ≈ 32 cycles per day. The common peak at f = 72 cycles per day (20-min period) is approximately the frequency of the ferry leaving and entering its harbor (close to E)
As can be seen in Fig. 6, there is a clear relation between the oscillations in water level as measured at H and the measured current in the sea strait at E. This figure also gives an indication of the significance of the oscillating flow: With O(0.1 m/s), it is of the order of magnitude of the tidal current! When the tidal flats are flooded, the flushing occurs no longer through the channel only. This reduces the amplitude of the oscillating current. The increased exchange rate is especially of importance for understanding estuarine flushing (of nutrients, sediment, and silt). The calculated coherence spectrum between the low-pass filtered water level (H) and flow (E) oscillations is shown in Fig. 7. Coherence of water level and flow velocity fluctuations is again visible at both 31 and 48 cycles per day.
Six-hour detail of alongstream velocity magnitude (black) and water level residual (blue). Water level residual is obtained by subtracting a 20-min running mean (the tidal elevation) from the low-passed water level measurements (location H, cutoff period: 5 min). Flow velocity magnitude is low-pass filtered with a cutoff period of 10 min (location E). Close-up (red rectangle) shows a coherent event of oscillating inflow and water level rise, at which the flow magnitude reaches 0.1 ms − 1
Coherence between current measurement (E) and water level measurements (H) of the 7.7-day water level record. Increased coherence at 31 and 48 cycles per day is clearly present, as indicated by the arrows. Low-frequency content (f < 15 cycles per day) is due to tidal motion. Cutoff frequency for low-pass filter: 288 cycles per day (T = 5 min)
A measure of the amount of damping in a harbor (or similar coastal system) can be expressed by means of a so-called quality of resonance, or “Q-factor,” given by the width of the resonance peak. A highly resonant tuning fork, e.g., has typically a Q = 1,000, whereas a damper on a door is typically Q = 0.5 (highly damped). According to Rabinovich (2009), the expression of the Q-factor is
where \(\Delta f=f_{1/2}^+-f_{1/2}^-\) and the resonant frequency \(f_0 = T_0^{-1}\). Here \(f_{1/2}^{\pm}\) indicate the half-power frequency, below ( − ) and above ( + ) the frequency of resonance, respectively. It can easily be found from water level power spectra, see Fig. 4. For the Malokurilsk Bay (Japan), depending on the site of measurement within the bay, Q-factors of 9 and 10 (side) and 12–14 (center) were found (Rabinovich 2009).
Similar to the Japanese Malokurilsk Bay, the Mok Bay has distinct peaks in the power spectrum of water level measurements. One difference is that here only 10 days of measurements are available, compared to multiple months for the Malokurilsk Bay. Probably more important is that the power spectrum of the Mok Bay represents two states: HW and LW. According to Fig. 5, the main difference between these two states is a change of eigenfrequency from 31.1 to 48.4 cycles per day (roughly no other major changes in the spectra happen), which partly justifies the use of one figure representing two states.
From Fig. 4, two Q-factors can be estimated for the resonances at 31.1 and 48.4 cycles per day: Q 48 = 5.6 and Q 31 = 3.0. The latter is lower due to the larger side lobes. These values of Q are comparable to those found for example in the Bay of Fundy and Gulf of Maine (Q = 5.25), the North coast of British Columbia (Q = 9.5), and, as mentioned, the Malokurilsk Bay (Q = 12–14). Super-tidal oscillations are found over large parts of the time series, and thus, the Q-factor was not expected to be small. The Chesapeake Bay is considered highly dissipative, having a Q-factor of 0.9 (Rabinovich 2009). The Mok Bay’s characteristic is quite average compared to other bays, but slightly more dissipative at flood tide. Physically, the HW quality of Mok Bay is reduced relative to that at LW because its configuration as a resonator is less pure, and having water draining over the tidal flats, frictional effects increase. The growing importance of friction may also be reflected in the amount of tidal distortion, the development of time asymmetries in the evolution of sea surface and tidal currents, as reflected in the nonlinear growth of harmonics and compound tides.
5 Modeling
To determine if the Mok Bay can actually be described as a Helmholtz oscillator, the period of oscillation has to be linked to the basin’s physical dimensions, according to Eq. 1. We can rule out the ferry to the mainland as source of the observed oscillations since oscillations are also present at night, when the ferry has stopped sailing. Also, Merian’s formula for natural periods in a (rectangular) coastal basin does not come close to the observed periods (Rabinovich 2009). Assuming uniform depth and an open entrance, the periods of oscillation (quarter wave length resonator model) are described by
Even the lowest mode (n = 0) yields a period of 12.8 min (L = 1200 m, H = 4 m) which is much too short. For larger depths (at HW), the wave propagation is even faster, opposite to the observations at HW. Wilson’s change of Eq. 5 to take into account different basin shapes—the Mok Bay is far from rectangular—still does not approximate the observations (Rabinovich 2009).
In Golmen et al. (1994), a Helmholtz resonator is ruled out as the driving mechanism for the oscillations, since the period, T H = 50 min, demands an effective strait length being four times the actual entrance length. An effective length includes mass outside the strait that oscillates as well during part of the eigenoscillation and so increases the real channel length to an “effective length” (Maas 1997). For the Mok Bay, however, the Helmholtz model describes the measured frequencies of oscillation quite well. Table 3 lists theoretical eigenfrequencies, obtained from measured dimensions and using Eq. 1. The maximal deviation of 10% (HW) can be explained by the fact that the effective entrance area is smaller than (HB) due to wall friction and the aforementioned increased effective entrance length. Both effects yield a lower estimate of the theoretical frequency, approximating the observations.
Oscillations in enclosed waters (lakes) are usually caused by direct external forcing on the surface, for example, by atmospheric pressure changes or wind. A basin with a connection to (a tidal) sea can be forced to resonance by, for example, long ocean waves that span a wide frequency range when reaching the coastal basin. Such ocean waves can originate from atmospheric pressure differences, underwater earthquakes (tsunamis), and internal waves (Rabinovich 2009).
Apart from ocean waves, a tidal current can also play an important role. Flow around a large obstacle or between islands can trigger regular (von Karman-like) vortices. Resonant amplification is possible if the basin’s eigenfrequency matches the frequency of vortex shedding. A shear flow (Kelvin–Helmholtz instabilities) is shown to be capable of having a reflection coefficient larger than 1 for a certain frequency band. Resonant amplification occurs in this case if the eigenfrequency of the basin is within the specific frequency band (Fabrikant 1995).
Most of the above-described mechanisms can, however, be ruled out for the Mok Bay. In the 10-day period of water level measurements in the Mok Bay, at almost every slack (of flood and ebb), oscillations in water level and currents were measured. This excludes causes like (atmospherically induced) wind setup, tsunamis, and nonlinear wind–wave interactions on the ground of their occasional character. As described, a certain frequency band can be amplified by a shear flow. For the Marsdiep channel (2 m/s) and the connecting Mok Bay (\(f = \text{31--48}\) cycles per day), a typical length of 500 m is necessary between shear flow and basin entrance for amplification to occur. From maps and satellite images, this is approximately the observed distance, but no Kelvin–Helmholtz instabilities were observed. Instead, the tides in the nearby Marsdiep can possibly be directly related to these basin oscillations as we will now argue.
5.1 Self-oscillations
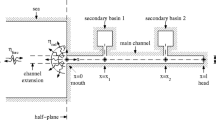
A very interesting and possible cause for the oscillations to be continuously present is the principle of self-oscillation. At high water, the Helmholtz frequency is different from that at low water; it is a function of the water surface area. The sudden change in surface area between high and low water is mathematically equivalent to a sudden change in system parameters. If the bathymetry of the Mok Bay is simplified to a step function (see Fig. 8), a piecewise-linear Helmholtz oscillator is obtained. For such systems, oscillations can be present continuously without the need for reflectional amplification and/or external disturbances.
For a linear oscillator, the response to periodic forcing is exactly known, for both its amplitude and phase. A piecewise-linear single degree-of-freedom oscillator behaves, however, like a nonlinear oscillator (Shaw and Holmes 1983; Kang and Chang 1998; Schulman 1983; van Horssen et al. 2006). A simple and practical example of this is the harmonic oscillator, in which the piecewise linearity can be implemented as an excitation-related spring stiffness or mass. Examples in nature of such systems are the human eardrum (Schulman 1983), swinging electricity wires (van Horssen et al. 2006), and, as we will discuss here, possibly also shallow tidal estuaries.
A nonlinear response can manifest itself in the presence of multiple equilibria (Nayfeh and Mook 1979), transitions to higher-period motion, chaotic regimes, higher-period intermittent regimes, jump-phenomena, hysteresis, and multiple stable attractors (Cvitanovich 1984; Kang and Chang 1998). An example of higher-period motion can be found in Schulman (1983), where the harmonic oscillator experienced period-9 motion for certain parameter combinations. This means that after each ninth period, the system is back at its original state. For slightly different parameter combinations, period-10 and even period-13 motion is found. Shaw and Holmes (1983) also reported period-doubling bifurcations for certain settings of the harmonic oscillator up to period-32 motion. Although the general idea is that periodic motion undergoes bifurcations until finally chaotic motion is found (Cvitanovich 1984), this is not necessarily always the case. Apart from different types of bifurcations, a Chay neuron model can experience bifurcations without a final transition to chaos (Yang and Lu 2004).
5.2 Analytic piecewise-linear Helmholtz oscillator
A Helmholtz oscillator can be compared with a damped mass-spring system (harmonic oscillator), in which the spring is gravity trying to equal the water level difference over the channel (between bay and sea). The mass in the system is the amount of water in the connecting channel and adjacent parts that contribute to the filling and draining of the basin (extending the channel’s effective length). Neglecting the quadratic friction in Eq. 2 and rewriting volume V as a piecewise linear function of vertical elevation ζ, the remaining viscous oscillator is similar to that of a driven, damped (damping constant c) mass-spring (mass m and stiffness k) system, also known as the harmonic oscillator:
Here x is the mass’ displacement from equilibrium and Z e (σt) the system’s forcing function. Equation 6 is equal to the linearized version of Eq. 2 when one substitutes V = ζA, k = 1 (so that x = ζ), m = A, and c = A r (where A = A − for ζ < 0 and A = A + for ζ > 0).
This simple damped and driven harmonic oscillator has a widely documented solution, consisting of a particular part, matching the forcing, and a (decaying) homogeneous part that accommodates for differences in initial conditions. Because of this decay of the homogeneous part, memory of its initial conditions is usually rapidly lost. It is the unique property of the piecewise linear nature of our tidal system that the transient solution is here triggered at each switching of system parameters (water surface area).
Note that for simplicity, in the present analytic model, this parameter switching is assumed to occur at mean sea level, whereas Fig. 8 shows that for the Mok Bay this actually occurs at about − 0.3 m NAP. Since we feel that our measured time series is too short to make a careful comparison to the observations, we present this analytical model here as sketching how to obtain the continuous presence of eigenoscillations in purely tidally forced Helmholtz basins. For the simplified model thus holds:
For high damping rates, the homogeneous part is a significant part of the solution. Furthermore, the analytic solution allows solving the system response stepwise, rather than via (numerical) time integration. As soon as the “initial” condition, at the switch from LW to HW and vice versa, i.e., the vertical velocity dζ/dt at transit, is known, the solution in the remaining “half-cycle” is completely determined analytically. It thus does not need to be computed numerically. These LW and HW parts of the cycle are referred to as “half-cycles” because their precise duration is one of the unknowns that needs to be determined (together with, again, the vertical velocity at transition). The eigenfrequencies of the harmonic oscillator, \(\omega^2_{\pm} = k/m_{\pm}\), are related to the Helmholtz frequencies (and are also scaled by the frequency of forcing). Here subscripts − and + refer to the LW and HW phases, respectively. Since both c ± and m ± are proportional to area A ±, \(\gamma_{\pm}= c_{\pm}/2m_{\pm}=(2r)^{-1}\) is a constant, and we will drop its subscript.
Although the exact solution to Eq. 6 is known, the exact instant at which the system passes ζ = 0 is not. So the instant at which the system changes parameters (or, changes sign, since the water surface area suddenly increases or decreases at ζ = 0) is determined numerically. The time instant of the change of sign is determined easily and interpolated back using the local derivative to the instant of actually crossing. The local derivative is in turn used as an initial condition for the system evolution in the following half-cycle. Subsequent crossings of the ζ = 0-plane are determined this way, and every second intersection of this plane yields the intersections with the Poincaré plane that we define to be ζ = 0 and \(\dot{\zeta}>0\) . Identical crossings of this Poincaré plane after one cycle indicate a steady state (a period-1 motion): identical crossings after two cycles, a period-2 motion, etc. Using \(\dot{\zeta}=\dot{x}=v\), one can find a function F + that relates \(v_0\equiv \dot{\zeta}(t_0)\) to the vertical velocity at the next crossing of ζ = 0,
and similarly a function F −, describing the same for the second half-cycle, i.e. linking v 1 to v 1/2:,
whose functional forms can be determined but are not shown explicitly here. To assure continuity of the rate with which the bay’s excess volume V = A ζ changes at each i-th mid-plane crossing, we required \(A_{i}\dot{\zeta_{i}}=A_{i-1}\dot{\zeta}_{i-1}\). As can be expected, F + and F − are functions of the system parameters: the different spring “masses” and “spring constants” that cause the distinction between the two states. These functions can, however, not be determined exactly since the instant of switching between the states has to be determined numerically. Similarly, linking two passings of the Poincaré plane (being separated by one cycle), this corresponds to
Equation 11 describes the composite function F(v) ≡ F − (F + (v)) that can be used as a return map, v 1 = F(v 0), relating the subsequent intersection of the Poincaré surface, v 1, to the previous crossing, v 0. It displays cyclic behavior as function of the initial conditions, at least for some initial conditions. Figure 9 shows such a return map for one set of parameters (ω − , ω + , γ). The behavior converges to a steady period-3 motion just a few cycles after startup. The period-3 regime for the parameter values in Fig. 9 can be found in the bifurcation diagram in Fig. 10 for γ = 0.1, but a slight decrease of friction parameter γ will yield even higher-period motion. At approximately γ = 0.05, the highest periodic motion is found: period-13 motion. As can also be seen in Fig. 10, no intermitting regimes of chaos are present in this bifurcation diagram. They are not necessarily present (Yang and Lu 2004) but might appear for different settings of the other parameters.
Discontinuous return map, v 1 = F(v 0), denoted by crosses of subsequent crossings of the Poincaré plane ζ = 0, \(\dot{\zeta}>0\), in response to an initial condition \(\dot{\zeta}_0 = v_0 = 2\) (red line). After a few periods, the stable period-3 motion (marked by red circles) is reached. Here, ω − = 12.12, ω + = 8.06 (close to a 3:2 resonance) and γ = 0.1 are taken. The bisectrix (green line) is helpful in graphical use of the map
6 Discussion
Further investigation of the presented piecewise-linear Helmholtz oscillator can give insight whether its behavior in parameter space is described by period-doubling bifurcations with (possibly) intermediate regimes of chaos, as described by Coombes and Osbaldestin (2000), Duarte et al. (2006), and Yang and Lu (2004), or by tangent bifurcations. Localizing the shallow Mok Bay in parameter space can in turn show the theoretical presence (or absence) of such behavior for this bay.
Both the presented model and its implementation are thus topic of further research since hardly anything is documented on dynamics of driven, viscous, piecewise-linear Helmholtz oscillators. A linearization can be used to find a simplified analytic expression, from which directly specific parameters can be found that lead to bifurcations. The corresponding reduced number of parameters (that span the parameter space) will yield a more efficient calculation of system behavior (return map or Poincaré plane and bifurcation diagram).
The analytic model for the piecewise linear Helmholtz oscillator, derived here, has too many parameters to map its behavior properly, but certain sets of parameters already show period-adding bifurcations. These are indications of nonlinear behavior that possibly leads to a chaotic response, in contrast to the general belief that coastal resonances are regular. After mapping the complete range of interest using one nonlinearity parameter, placing of the Mok Bay in this regime will show whether chaotic behavior could be present. Extended measurements can in turn show the actual presence (or absence) of this behavior, of which especially the oscillating flow is of importance for the estuarine flushing and consequently for the local ecosystem.
To conclude, we find that a model using a deterministic tidal forcing of a natural estuary of nonuniform hypsometry suggests that the basin response may be chaotic. Our field observations of relatively short duration (7.7 days) confirm the continuous presence of two distinct eigenoscillations, both of Helmholtz type, and suggest that the basin may be in a state of “continuous adjustment.” Thus, nonharmonic aspects may appear for dynamical reasons, adding to those due to changes in the phase of the moon and in the declination and parallax of the moon and sun. Longer observations have to clarify whether the oscillations are of quasi-periodic or chaotic type. The permanent participation of eigenoscillations in the Mok Bay, driven by the tide, gives rise to the question whether other tidal estuaries behave in a similar unexpected nonlinear fashion and what the precise consequences for basin exchange are. Likely these short-term, strong velocity variations are of importance for mixing, fluxes, and shipping on many other locations as well, where they may have been overlooked or filtered out. In the face of climate change, the investigation of how the resonance properties of tidal basins, as discussed here, may depend on an induced slow rise in mean sea level becomes opportune in the near future.
References
Beerens SP, Ridderinkhof H, Zimmerman JTF (1994) An analytical study of chaotic stirring in tidal areas. Chaos Solitons Fractals 4:1011–1029
Bellotti G (2007) Transient response of harbours to long waves under resonance conditions. Coast Eng 54:680–693
Bodén H, Ahlin K, Carlsson U (2009) Signaler och mekaniska system. World Scientific, Stockholm
Carbajal N, Galicia-Perez MA (2002) Earthquake-induced Helmholtz resonance in Manzanillor lagoon, Mexico. Rev Mex Fis 48:192–196
Cartwright DE (1999) Tides: a scientific history. Cambridge University Press, Cambridge
Coombes S, Osbaldestin A (2000) Period-adding bifurcations and chaos in a periodically stimulated excitable neural relaxation oscillator. Phys Rev E 62:4057–4066
Cvitanovich P (1984) Universality in chaos. Adam Hilger, Bristol
Doelman A, Koenderink AF, Maas LRM (2002) Quasi-periodically forced nonlinear Helmholtz oscillators. Physica D 164:1–27
Duarte J, Silva L, Ramos J (2006) Types of bifurcations of Fitzhugh–Nagumo maps. Nonlinear Dyn 44:231–242
Emery WJ, Thomson RE (2001) Data analysis methods in physical oceanography. Elsevier, Amsterdam, pp 392–404
Fabrikant AL (1995) Harbour oscillations generated by shear flow. J Fluid Mech 282:203–217
Frison TW (2000) Dynamics of the residuals in estuary water levels. Phys Chem Earth Part B Hydrol Oceans Atmos 25(4):359–364
Geyer W, Signell R (1992) A reassessment of the role of tidal dispersion in estuaries and bays. Estuar Coast 15:97–108
Golmen LG, Molvaer J, Magnusson J (1994) Sea level oscillations with super-tidal frequency in a coastal embayment of western Norway. Cont Shelf Res 14(13–14):1439–1454
Gonzalez-Marco D, Sierra JP, Fernandez de Ybarra O, Sanchez-Arcilla A (2008) Implications of long waves on harbor management: the Gijon port case study. Ocean Coast Manag 51:180–201
Green T (1992) Liquid oscillations in a basin with varying surface area. Phys Fluids A Fluid Dyn 4(3):630–632
Honda K, Terada T, Yoshida Y, Isitani D (1908) An investigation on the secondary undulations of oceanic tides. J Coll Sci Imp Univ Tokyo 24:1–113
Kang Y, Chang YP (1998) Strongly non-linear oscillations of winding machines, part I: mode-locking motion and routes to chaos. J Sound Vib 209:473–492
Kela L (2009) Resonant frequency of an adjustable Helmholtz resonator in a hydraulic system. Arch Appl Mech 79:1115–1125
Kim YC (2009) Handbook of coastal and ocean engineering. World Scientific, Singapore
Maas LRM (1997) On the nonlinear Helmholtz response of almost-enclosed tidal basins with sloping bottoms. J Fluid Mech 349:361–380
Maas LRM, Doelman A (2002) Chaotic tides. J Phys Oceanogr 32(3):870–890
Miles JW, Lee YK (1975) Helmholtz resonance of harbours. J Fluid Mech 67:445–464
Mullarney JC, Hay AE, Bowen AJ (2008) Resonant modulation of the flow in a tidal channel. J Geophys Res 113:4057–4066
Nakano M (1932) Preliminary note on the accumulation and dissipation of energy of the secondary oscillations in a bay. Proc Phys Math Soc Jpn 3(14):44–56
Nayfeh A, Mook D (1979) Nonlinear oscillations. Wiley, New York
Otsmann M, Suursaar U, Kullas T (2001) The oscillatory nature of the flows in the system of straits and small semienclosed basins of the Baltic Sea. Cont Shelf Res 21:1577–1603
Pugh DT (1987) Tides, surges, and mean sea-level/a handbook for engineers and scientists. Wiley, New York
Rabinovich A (2009) Seiches and harbor oscillations. In: Kim YC (ed) Handbook of coastal engineering. World Scientific, Singapore
Ridderinkhof H, Zimmerman JTF (1992) Chaotic stirring in a tidal system. Science 258:1107–1111
Sanford L (1985) Turbulent mixing in experimental ecosystem studies. Mar Ecol Prog Ser 161:265–293
Schulman JN (1983) Chaos in piecewise-linear systems. Phys Rev A 28:477–479
Shaw SW, Holmes PJ (1983) A periodically forced piecewise linear oscillator. J Sound Vib 90:129–155
Terra G (2005) Nonlinear tidal resonance. Ph.D. thesis, Utrecht University
van Horssen WT, Abramian AK, Hartono (2006) On the free vibrations of an oscillator with a periodically time-varying mass. J Sound Vib 298:1166–1172
Yang Z, Lu Q (2004) Characteristics of period-adding bursting bifurcation without chaos in the Chay neuron model. Chin Phys Lett 21(11):2124–2127
Acknowledgements
We thank Janine Nauw and Sjoerd Groeskamp for help with the data acquisition.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible Editor: Alejandro Jose Souza
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
de Boer, J.P., Maas, L.R.M. Amplified exchange rate by tidal forcing of a piecewise-linear Helmholtz bay. Ocean Dynamics 61, 2061–2072 (2011). https://doi.org/10.1007/s10236-011-0479-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10236-011-0479-3