1 Introduction

Ocean models have reached a high level of complexity, and eddy resolving simulations are now much more affordable than in the past. However, mainstream models still fit into the same framework as the pioneering model published by Bryan (1969). This approach, which uses conservative finite differences on structured grids, approximates the coastlines as staircases and prevents flexible implementation of variable resolution. Yet, during the last 40 years, numerical methods have dramatically evolved. It is now time for ocean modeling to benefit from all those advances by developing ocean models using state-of-the-art numerical methods on unstructured grids (Griffies et al. 2009).

Unstructured grid methods are mainly of two kinds: finite volumes and finite elements. In short, finite volumes were first developed for problems predominantly hyperbolic (i.e., dominated by waves or advective transport), while finite element methods were first developed for problems dominated by elliptic terms. The two research communities have evolved toward solutions that manage to treat efficiently both hyperbolic and elliptic problems. Unstructured grid marine modeling is an active area of research for coastal applications (Deleersnijder and Lermusiaux 2008). Indeed, the coastlines must be accurately represented, as they have a much stronger influence at the regional scale than at the global scale. Finite volume methods are now widely used, and models like FVCOM (Finite Volume Community Ocean Model) (Chen et al. 2003) have a large community of users. Many other groups are developing finite volume codes for ocean, coastal, and estuarine areas, such as Fringer et al. (2006), Ham et al. (2005), Stuhne and Peltier (2006), and Casulli and Walters (2000). Nonhydrostatic finite element methods are found in Labeur and Wells (2009) for small-scale problems. For large-scale ocean modeling, continuous finite element methods are used in FEOM (Finite Element Ocean Model) (Wang et al. 2008a, b; Timmermann et al. 2009), and Imperial College Ocean Model (Ford et al. 2004a) relies on mesh adaptivity to capture the multiscale aspects of the flow (Piggott et al. 2008).

In the realm of finite difference methods, Arakawa’s C grid allows for a stable and relatively noise-free discretization of the shallow water equations and is now very popular for ocean modeling (Arakawa and Lamb 1977; Griffies et al. 2000). However, the search for an equivalent optimal finite element pair for the shallow water equations is still an open issue. Le Roux et al. (1998) gave the first review of available choices. More recent mathematical and numerical analysis of finite element pairs for gravity and Rossby waves are provided in Le Roux et al. (2007, 2008), Rostand and Le Roux (2008), and Rostand et al. (2008). Hanert et al. (2005) proposed to use the \(P_1^{\rm NC}\)–P 1 pair, following Hua and Thomasset (1984). It appears that the \(P_1^{\rm NC}\)–P 1 pair is a stable discretization, but its rate of convergence is suboptimal on unstructured grids (Bernard et al. 2008b). Following the same philosophy, the \(P_1^{\rm DG}\)–P 2 pair was proposed by Cotter et al. (2009a). Such an element exhibits both stability and optimal rates of convergence for the Stokes problem and the wave equation (Cotter et al. 2009b). A review of the numerical properties of those pairs stabilized by interface terms can be found in Comblen et al. (2010b).

This paper focuses on the development of a marine model, called Second-generation Louvain-la-Neuve Ice–ocean Model (SLIMFootnote 1) that should be able to deal with problems ranging from local and regional scales to global scales. In this model, we choose equal-order discontinuous interpolations for the elevation and velocity fields, as it allows us an efficient and easier implementation. Such an equal-order mixed formulation is stable as the interface stabilizing terms allows us to circumvent the Ladyzhenskaya–Babŭska–Brezzi conditions and to take advantage of the inherent good numerical properties of the discontinuous Galerkin (DG) methods for advection dominated processes. It also allows us to decouple horizontal and vertical dynamics, thanks to the block-diagonal nature of the corresponding mass matrix. DG methods can be viewed as a kind of hybrid between finite elements and finite volumes. They enjoy most the strengths of both schemes while avoiding most of their weaknesses: Advection schemes take into account the characteristic structure of the equations, as for finite volume methods, and the polynomial interpolation used inside each element allows for a high-order representation of the solution. Moreover, no degree of freedom is shared between two geometric entities, and this high level of locality considerably simplifies the implementation of the method. Finally, the mass matrix is block diagonal, and for explicit computations, no linear solver is needed. We also observe a growing interest for the discontinuous Galerkin methods in coastal and estuarine modeling (Aizinger and Dawson 2002; Dawson and Aizinger 2005; Kubatko et al. 2006; Aizinger and Dawson 2007; Bernard et al. 2008a; Blaise et al. 2010). For atmosphere modeling, the high-order capabilities of this scheme are really attractive (Nair et al. 2005; Giraldo 2006), and the increasing use of DG follows the trend to replace spectral transform methods with local ones.

Herein, we provide the detailed description of the spatial discretization used in our discontinuous Galerkin finite element marine model SLIM, as well as an illustrative example of the ability of the model to represent complex baroclinic flows. Section 2 describes the partial differential equations considered. Sections 3 and 4 provide the numerical tools needed to derive an efficient stable and accurate discrete formulation. Section 5 details the discrete discontinuous formulation. Finally, in Section 6, we study the internal waves generated in the lee of an isolated seamount as computed with our model. In a companion paper, the time integration procedure will be discussed.

2 Governing equations

Large-scale ocean models usually solve the hydrostatic Boussinesq equations for the ocean. As a result of the hydrostatic approximation, the vertical momentum equation is reduced to a balance between the pressure gradient force and the weight of the fluid. The conservation of mass degenerates into volume conservation, and the density variations are taken into account in the buoyancy term only. This set of equations is defined on a moving domain, as the sea-surface evolves according to the flow.

Using the notations given in Table 1, the governing equations read:

  • Horizontal momentum equation:

    $$ \begin{array}{rll} &&{\kern-6pt}\frac{\partial \boldsymbol{u}}{\partial t} + \boldsymbol{\nabla}_h \cdot {\left(\boldsymbol{u}\boldsymbol{u}\right)} + \frac{\partial (w\boldsymbol{u})}{\partial z} \! + \! f\mathbf{e}_z\wedge\boldsymbol{u} \! + \! \frac{1}{\rho_0}\boldsymbol{\nabla}_h p \! + \! g\boldsymbol{\nabla}_h \eta \\ && {\kern1pc} = \boldsymbol{\nabla}_h\cdot \left(\nu_h \boldsymbol{\nabla}_h \boldsymbol{u}\right) +\frac{\partial }{\partial z}\left( \nu_v \frac{\partial \boldsymbol{u}}{\partial z}\right), \end{array} $$
    (1)

  • Vertical momentum equation:

    $$ \frac{\partial p}{\partial z}=-g\rho(T,S)\qquad \mathrm{with}\qquad \rho=\rho_0+\rho^{\prime}(T,S). $$
    (2)

  • Continuity equation:

    $$ \boldsymbol{\nabla}_h\cdot{\boldsymbol{u}}+\frac{\partial w}{\partial z}=0, $$
    (3)

  • Free-surface equation:

    $$ \frac{\partial \eta}{\partial t}+\boldsymbol{u}^{\eta}\cdot\nabla_h \eta-w^{\eta} = 0. $$
    (4)

  • Tracer equation:

    $$ \begin{array}{rll} \frac{\partial c}{\partial t}+\boldsymbol{\nabla}_h\cdot{\left(\boldsymbol{u} c\right)}+\frac{\partial (wc)}{\partial z}&=&\boldsymbol{\nabla}_h\cdot{\left(\kappa_h\boldsymbol{\nabla}_h{c}\right)} \\ &&+\frac{\partial }{\partial z}\left(\kappa_v\frac{\partial c}{\partial z }\right), \end{array} $$
    (5)
Table 1 Notations for the governing equations of the three-dimensional baroclinic marine model
Full size table

This set of equations defines the mathematical three-dimensional baroclinic marine model and must be solved simultaneously with the suitable initial and boundary conditions. However, no models solve the primitive equations simultaneously. In practice, dynamic and thermodynamic equations are always decoupled.

In order to build a numerical discrete spatial scheme, it is usual to associate the unknown field with a given equation. The horizontal velocity \(\boldsymbol{u}(x,y,z,t)\) is obtained from the horizontal momentum equation (Eq. 1), while the vertical velocity w(x, y, z, t) is deduced from the continuity equation (Eq. 3). The three-dimensional tracers c(x, y, z, t), which can be T or S, are associated with the tracer equation (Eq. 5). The density deviation ρ′(x, y, z, t) is then deduced from temperature and salinity using an appropriate equation of state ρ′(T, S). As we only need the pressure gradient and not the pressure itself, we follow Wang et al. (2008b) and only calculate the pressure gradient \(\boldsymbol{p}(x,y,z,t) = \boldsymbol{\nabla}_h p(x,y,z,t)\) from

$$ \frac{\partial \boldsymbol{p}}{\partial z}=-g\boldsymbol{\nabla}_h{\rho'(T,S)}, $$
(6)

which is the horizontal gradient of equation (Eq. 2), as ρ 0 is constant. Such an approach allows us to partly circumvent the numerical inaccuracies observed in the calculation of the baroclinic pressure gradient term in the momentum equation with a transformed vertical coordinate (e.g., sigma coordinates; Deleersnijder and Beckers 1992; Haney 1991). Finally, the sea elevation η(x, y, t) can be deduced from a modified form of the free-surface equation (Eq. 4) which specifies the associated impermeability condition at the sea surface. Integrating the continuity equation (Eq. 3) along the vertical direction yields

$$ \displaystyle w^\eta-w^{-h}+\int_{-h}^{\eta} \boldsymbol{\nabla}_h\cdot \boldsymbol{u} dz = 0, $$

which may be transformed to:

$$ \displaystyle \underbrace{\frac{\partial \eta}{\partial t}+\boldsymbol{u}^\eta\cdot \boldsymbol{\nabla}_h\eta }_{\displaystyle w^\eta}-\underbrace{\boldsymbol{u}^{-h}\cdot \boldsymbol{\nabla}_h(-h)}_{\displaystyle w^{-h}}+\int_{-h}^{\eta} \boldsymbol{\nabla}_h\cdot \boldsymbol{u} dz = 0 , $$

where we substitute the vertical velocities by using both associated impermeability conditions at the sea surface and the sea bottom. Applying the Leibniz integral rule leads to

$$ \frac{\partial \eta}{\partial t}+ \boldsymbol{\nabla}_h\cdot\int_{-h}^{\eta}\boldsymbol{u} dz=0. $$
(7)

The integral free-surface equation (Eq. 7) exactly corresponds to the mass conservation of the shallow water equations. This prompts us to use this form rather than the local form. Mode-splitting procedures, where three-dimensional baroclinic and two-dimensional barotropic modes are time-stepped separately, are often resorted to. Therefore, it is very useful to have the same free-surface equation for the three-dimensional and two-dimensional formulations. The three-dimensional equations are designed so that the discretely depth-integrated equations are as close as possible to an accurate discretization of the shallow water equations. To achieve this, most ocean models rely on the integral form of the free-surface equation for the baroclinic three-dimensional model.

Finally, a very common approximation consists in substituting Eq. 7 by the linear free surface equation defined by :

$$ \frac{\partial \eta}{\partial t}+\nabla_h\cdot\int_{-h}^{0}\boldsymbol{u} dz=0., $$
(8)

This equation simply corresponds to the mass conservation equation of the linear shallow water problem and describes the surface height of the flow with a linear free surface approximation. Such an approximation cannot be used in coastal flows but is very convenient in large-scale applications.

3 Geometrical numerical tools

Before deriving the discrete formulation, we first present the geometrical tools that are valid for all finite element (continuous or discontinuous) discretizations.

  • The computational domain evolves with time, and it is required to take into account the evolution of the domain in the discrete model. In Section 3.1, the standard ALE technique (arbitrary Lagrangian–Eulerian) implemented in the model is described.

  • Moreover, the computational domain lies on a sphere. In Section 3.2, we recall the algorithm that renders the model able to operate on any manifold including a sphere or a planar surface.

3.1 Arbitrary Lagrangian–Eulerian methods

As the variation of the sea surface elevation modifies the domain of integration, the position of the nodes at the sea surface will move in the vertical direction as prescribed by the elevation field η. Moving the free surface nodes without changing the position of interior nodes will lead to unacceptable element distortions along the sea surface. Then, we must propagate the motion of the boundary nodes into the domain by means of a moving mesh algorithm. Its purpose is to avoid mesh distortion due to the sea surface motion and to maintain the original element density in the deformed mesh. In the model, the computational domain is stretched uniformly in the vertical direction. If we denote z * the original vertical coordinate of the nodes in the initial reference fixed domain Ω* (the computational domain with the sea surface at rest), the vertical position z(x, y, z *, t) and the vertical velocity \(w_z(x,y,z^*,t)\) of the nodes in the moving domain Ω(t) are prescribed by

$$ z(x,y,z^*,t) = z^* + \eta(x,y,t) \ \displaystyle\frac{h(x,y)+z^*}{h(x,y)}, $$
(9)
$$ \underbrace{ \frac{\partial z}{\partial t}(x,y,z^*,t)}_{\displaystyle w_z}=\frac{\partial \eta}{\partial t}(x,y,t) \ \displaystyle\frac{h(x,y)+z^*}{h(x,y)} $$
(10)

The mesh velocity w z is relative to the motion of the mesh that is stretched uniformly only to maintain the original aspect ratio in the deformed mesh. Such a velocity is fully independent of the Lagrangian velocity of the fluid particle. This velocity can be chosen in order to maintain the mesh quality and, in this sense, can be viewed as arbitrary with respect to the motion of the fluid. This is why such an approach is usually called an arbitrary Lagrangian–Eulerian method. Dealing with a moving domain requires the modification of the material derivative of a field c

$$ \displaystyle\frac{Dc}{Dt} = \frac{\partial c}{\partial t} + \boldsymbol{u} \cdot \boldsymbol{\nabla}_h{c} + (w-w_z) \frac{\partial c}{\partial z}. $$
(11)

Therefore, the tracer equation (Eq. 5) has to be modified to take into account the moving mesh algorithm

$$ \begin{array}{rll} &&{\kern-6pt}\frac{\partial c}{\partial t}+\boldsymbol{\nabla}_h\cdot{\left(\boldsymbol{u} c\right)}+\frac{\partial (wc-w_zc)}{\partial z} + c\frac{\partial w_z}{\partial z} \\ &&{\kern1pc} =\boldsymbol{\nabla}_h\cdot{\left(\kappa_h\boldsymbol{\nabla}_h{c}\right)}+\frac{\partial }{\partial z}\left(\kappa_v\frac{\partial c}{\partial z }\right), \end{array} $$
(12)

where the mesh velocity is subtracted from the vertical fluid velocity in the vertical advection term. The second additional term can be viewed as a correction to the volume modification introduced by the displacement of the moving mesh. The vertical derivative of the mesh velocity can be directly deduced from Eq. 10

$$ \frac{\partial w_z}{\partial z}=\frac{\partial \eta}{\partial t} \ \frac{1}{h}. $$
(13)

A similar adaptation must be applied for the horizontal momentum equation (Eq. 1). In other words, all new terms involving the vertical velocity in Eq. 12 have to be included for all material derivatives appearing in discrete equations which are calculated on a moving domain. For sake of brevity, we will not add these terms in the later sections, even if they are really included in the model.

3.2 Dealing with flows on the sphere

The model operates on arbitrarily shaped surfaces, including the sphere or plane surfaces, following Comblen et al. (2009). The basic idea of the procedure is that each local geometrical entity supporting vectorial degrees of freedom has its own Cartesian coordinate system. There are also coordinate systems associated with each vector test and shape functions for the horizontal velocity field. To supply a vectorial degree of freedom from a frame of reference to another, we only need to build local rotation operators.

The global linear system of discrete equations is then formulated in terms of the vector degrees of freedom expressed in their own frame of reference. To build and assemble the local matrix corresponding to an element, we first fetch all the needed vectorial degrees of freedom into the coordinate system of this element, and then we compute the local matrix or vector. We then apply rotation matrices to this matrix so that its lines and columns are expressed in the frame of reference of the corresponding test and shape functions, respectively. The transformation of the local linear system can be expressed in terms of x P ξ and ξ P x , the rotation matrices from and to the frame of reference in which the integration is performed, respectively (Comblen et al. 2009).

All the transfer matrices operators are computed once at the initialization of the algorithm. The local system of discrete equations in the basis of the element can be written as:

$$ {_{\xi}}\mathbf{A}_{\xi} \ {_\xi}\mathbf{\mathbf{U}}\quad~~=~ {_\xi}\mathbf{B} $$

where ξ A ξ and ξ B are the local discrete matrix and right hand in the basis of the element. The local vector of unknowns is denoted ξ U in this local basis. Once this system is computed, the system can be rewritten with velocities and test functions expressed in the basis of the degrees of freedom:

$$\begin{array}{rll} _{\xi}\mathbf{A}_{\xi} \quad _{\xi}\mathbf{U} &=&\quad _{\xi}\mathbf{B} \\ _{\xi}\mathbf{A}_{\xi}\,\,\overbrace{ _{\xi}\mathbf{P}_{x}\, _{x}\mathbf{U}}^{\downarrow} &=&\quad _{\xi}\mathbf{B} \\ \underbrace{ _{x}\mathbf{P}_{\xi}\, _{\xi}\mathbf{A}_{\xi}\, _{\xi}\mathbf{P}_{x}}_{\downarrow}\,\, _{x}\mathbf{U} &=& \underbrace{ _{x}\mathbf{P}_{\xi}\, _{\xi}\mathbf{B}}_{\downarrow} \\ _{x}\mathbf{A}_{x} \quad _{x}\mathbf{U} &=&\quad _{x}\mathbf{B}.\end{array} $$

Similarly, to assemble local matrices and vectors corresponding to the integral over an interface between two elements with different coordinate systems, we first fetch all the information in the frame of reference of the interface, then compute the integral, and fetch back the lines and columns of the matrices in the frame of reference of the corresponding test and shape functions. All the curvature treatment is embedded in the rotation matrices, and the discrete equations are expressed exactly as if the domain was planar.

With such a procedure, it is possible to solve the equations on the sphere, circumventing completely any possible singularity problem. For notational convenience, the full discrete formulation will be presented within a Cartesian framework, but it is important to note that the model is fully implemented to operate on the sphere.

4 Discontinuous Galerkin methods

Now, let us introduce the finite element mesh and the discrete discontinuous approximations of the field variables of the model (η, \(\boldsymbol{u}\), w, c, ρ′, \(\boldsymbol{p}\)). The three-dimensional mesh is made up of prismatic elements, as illustrated in Fig. 1, and is obtained from the extrusion of triangular two-dimensional elements. The vertical length scale is typically much smaller than the horizontal length scale. In other words, the prisms are thin. We choose prismatic elements to obtain a mesh unstructured in the horizontal direction and structured in the vertical direction. On the sphere, these columns of prisms are obtained by extruding the surface triangles in the direction normal to these triangles. As the extrusion is parallel, the prisms have the same width at the sea surface and at the sea bottom. This alignment of the elements along the vertical axis allows natural treatment of the continuity equation (Eq. 3) and the pressure gradient equation (Eq. 6) that can be integrated along the vertical direction.

Fig. 1
figure 1

Sketch of prismatic elements. The vertical length scale is typically much smaller than the horizontal length scale, i.e., the prisms are thin

Full size image

The three-dimensional fields (\(\boldsymbol{u}\), w, c, ρ′, \(\boldsymbol{p}\)) are discretized on the mesh of prisms. The two-dimensional elevation field η is discretized onto the two-dimensional mesh of triangles. The shape functions for \(\boldsymbol{u}\), w, c are obtained as the tensorial product of the linear discontinuous triangle \(P_1^{\rm DG}\) and the linear discontinuous one-dimensional element \(L_1^{\rm DG}\). The shape functions of the density deviation and the baroclinic pressure gradient are \(P_1^{\rm DG}\times L_1\). The use of different discrete vertical spaces for ρ′ and the baroclinic pressure gradient \(\boldsymbol{p}\) can be viewed as an appropriate way to average the vertical variation of the tracers in the calculation of the baroclinic pressure gradient. The summary of the finite element spaces is given in Table 2. For the procedure to simulate flow on the sphere, each column of prisms defines the basic geometrical entity to assemble. It has its own coordinate system, as the degrees of freedom for a discontinuous approximation are all associated with elements and not with interfaces or vertices. Finally, we will describe in details the two most important aspects of the spatial discretization :

  • Choosing the way to compute the discrete values at the inter-element interfaces is the critical ingredient to obtain a stable and accurate discrete formulation in the framework of the DG methods. The discrete fields are dual-valued at the inter-element interfaces. For the advective fluxes at these interfaces, the values of the variables are obtained on Riemann solvers applied to the hyperbolic terms of the model. Details about the Riemann solvers are given in Section 4.1.

  • Incorporating the diffusion operators inside a DG formulation also requires special care. We use the Symmetric Interior Penalty Galerkin (SIPG) technique to accommodate diffusion operators. Moreover, the mathematical formulation exhibits anisotropic diffusion and the algorithm is adapted by computing the interior penalty coefficients on a virtual stretched geometry. The methodology used is summarized in Section 4.2.

Table 2 Summary of the finite element spaces used for each field. Triangular linear elements are noted P 1 while vertical linear elements are noted L 1. The superscript DG stands for Discontinuous Galerkin
Full size table

4.1 Riemann solvers

A two-dimensional set of barotropic discrete equations can be obtained by the vertical depth integration (or the algebraic stacking of the resulting lines and columns of the global system) of the three-dimensional set of baroclinic discrete equations. The basic idea of this procedure is to define the lateral interface in the discrete three-dimensional baroclinic equations in such a way that the corresponding two-dimensional discretization by depth integration is a robust stable formulation. In particular, the use of the integral free-surface equation (Eq. 7) and the selection of the discrete spaces should lead to a stable and accurate corresponding two-dimensional discrete problem. Here, the resulting corresponding discrete problem is close to the discretization of the shallow water equations with \(P_1^{\rm DG}\) shape functions for the two-dimensional velocities and elevation. A robust formulation can be derived for this problem, following Comblen et al. (2010b).

The key ingredient of a stable and accurate DG formulation is the choice of the definition for a common value for the variables along the interfaces. It is necessary to define adequately these common values with a Riemann solver. For nonlinear problems, it can be quite complicated to compute the exact Riemann solver, and approximate Riemann solvers are usually resorted to. For the shallow water equations, approximate Riemann solvers are deduced from the conservative form of the equations (LeVeque 2002; Toro 1997; Comblen et al. 2010b).

For the linear shallow water equations, the exact solver yields the following interfacial values:

$$ \boldsymbol{u}^\text{riemann} \cdot \mathbf{n} = \left\{\boldsymbol{u}\right\} \cdot \mathbf{n} +\sqrt{\frac{g}{h}}[\eta], $$
(14)
$$ \eta^\text{riemann} = \left\{\eta\right\}+\sqrt{\frac{h}{g}}[\boldsymbol{u}]\cdot\mathbf{n}, $$
(15)

where \(\left\{\ \right\}\) and [ ] denote the mean and the jump operators, respectively. The jump is defined by [ a] = (a L  − a R )/2 and the mean by { a } = (a L  + a R )/2 where a L and a R are the left and right values of the field a. The vector n is the rightward normal corresponding to the jump operator. The linear shallow water equations are simple wave equations, and those interfacial values correspond only to the terms generating the surface gravity waves and are not valid for the non-linear two-dimensional barotropic problem. However, as oceanic flows usually exhibit small Froude numbers, the linear Riemann solver can be viewed as a very good approximation of the nonlinear solver.

The three-dimensional equations allow several hyperbolic phenomena to take place. Surface gravity waves are the fastest phenomena, with phase speed \(\sqrt{gh}\). The second fastest phenomena are the internal gravity waves. Their propagation speed depends on the stratification. It can be as large as a few meters per second. As the set of the three-dimensional baroclinic marine flow equations cannot be cast into a conservative form, it is not possible to deduce an approximate Riemann solver such as the Roe solver by simply linearizing the problem. Therefore, we selected a Lax–Friedrichs flux. This flux is commonly used due to its simplicity. The flux is simply defined as the sum of the mean flux and the jump of the variables multiplied by an upper bound γ on the phase speed of the fastest internal wave (the maximum eigenvalue of the Jacobian matrix):

$$ \text{flux}^{\text{lax--friedrichs}}=\left\{\text{flux}\right\}+\gamma \left[\text{variable}\right] $$
(16)

In this work, we use the Riemann solver of the linear shallow-water equations (Eqs. 14 and 15) for the terms corresponding to surface gravity waves (i.e., elevation gradient in the two-dimensional, depth-averaged momentum equation and velocity divergence in the continuity equation (Comblen et al. 2010a)). In the three-dimensional problem, i.e., in the momentum equation and in the active tracers equations (typically temperature and salinity), we add to the mean flux the jump of the variables multiplied by an upper bound on the second fastest wave, which is the sum of the fastest internal wave phase speed and the advection velocity. Determining the phase speed of the fastest internal wave is not easy for a complicated stratification profile.

In our examples, we simply use values of γ deduced from some numerical experiments, by a trial and error procedure. The selection of the coefficient γ is a key ingredient of the numerical technique. In fact, in our computations, we select an ad hoc coefficient that is selected with some physical intuition. However, it is not a robust procedure and this can prevent the model from being used if there are no general solutions for it. In other words, this problem is not fully solved but the importance of Riemann solvers in shallow water models were discussed in Comblen et al. (2010b).

4.2 Symmetric interior penalty Galerkin methods

In the realm of discontinuous Galerkin methods, various discretizations of the Laplacian operator are reviewed in, e.g., Arnold et al. (2002). Two of them are especially popular: the interior penalty methods (Riviere 2008) and the local DG method (Cockburn and Shu 1998).

To accurately handle the diffusion terms, we use the SIPG technique. Basically, the weak form of the Laplace equation \(\nabla^2 c = 0\) can be obtained by multiplying this equation with a test function and by integrating this product on the whole domain. Integrating by parts and choosing the mean values at the interfaces yields:

$$ \sum\limits_{e=1}^{N_e}\Big[\ll\hat{c}\left\{ \boldsymbol{\nabla} c\right\} \cdot \boldsymbol{n}\gg_{e}-< \boldsymbol{\nabla} \hat{c} \cdot \boldsymbol{\nabla} c>_{e}\Big]=0, $$
(17)

where < >  e and ≪ ≫  e denote respectively the integral over the element Ω e and its boundary. The number of elements is N e . Choosing the mean values at the interface seems natural for an elliptic operator where the information propagates along all directions. However, such a simple and intuitive treatment of the Laplacian operator is incomplete. Indeed, the discrete solution is not unique, as at the boundary of each element, only Neumann boundary conditions are prescribed. In order to partly complete the discrete formulation, the Incomplete Interior Penalty Galerkin method (IIPG) consists in adding a penalty term on the discontinuities of the field at the inter-element interfaces

$$ \sum\limits_{e=1}^{N_e} \Big[\ll \hat{c}\left\{ \boldsymbol{\nabla} c\right\}\cdot \boldsymbol{n}\gg_{e} +\sigma \ll\hat{c}\left[c\right]\gg_{e} -<\boldsymbol{\nabla} \hat{c} \cdot \boldsymbol{\nabla} c >_{e} \Big] = 0, $$
(18)

where σ is a penalty parameter scaled in such a way that \(\sigma\left[c\right]\) is a term similar to a gradient, at the interface level. In other words, 1/σ has to be an suitable length scale. It is shown in Riviere (2008) that this formulation provides optimal results when shape functions of odd polynomial order are used (i.e., P 1, P 3, ...) but lacks convergence for even polynomial orders. Further, the resulting discrete matrix is not symmetric, while the continuous operator is symmetric. The SIPG solves both of these issues (Riviere 2008), by adding a symmetrizing term to the IIPG formulation (Eq. 18).

$$ \begin{array}{rll} && \sum\limits_{e=1}^{N_e} \Big[\ll\hat{c}\left\{ \boldsymbol{\nabla} c\right\}\cdot \boldsymbol{n}\gg_{e} +\ll \boldsymbol{\nabla}\hat{c}\cdot \boldsymbol{n} \left[c\right]\gg_{e} \\ &&{\kern24pt}+\sigma \ll\hat{c}\left[c\right]\gg_{e} -<\boldsymbol{\nabla} \hat{c} \cdot \boldsymbol{\nabla} c>_{e} \Big]=0. \end{array} $$
(19)

There is a lower bound on σ that ensures optimal convergence. This bound must be as tight as possible, as the larger the value of σ, the worse the conditioning of the operator. Shahbazi (2005) suggests to use the following formula:

$$ \sigma=\bigg[\frac{2(k+1)(k+3)}{3}\frac{A(\Gamma_k)}{V(\Omega_e,\Omega_f)}\bigg], $$
(20)

where k is the order of the interpolation, A(Γ k ) is the area of the interface Γ k between the two considered elements, and V(Ω e ,Ω f ) is the mean volume of the two neighboring elements Ω e and Ω f .

Finally, the diffusion terms are split into a horizontal part and a vertical part, preventing the implementation of rotated diffusion tensors as described for instance by Redi (1982). Such rotated diffusion is not implemented in the current SLIM model. Distinct viscosity and diffusivity coefficients are chosen to represent the different effects of each of the many unresolved physical processes. Both the diffusion operator and the mesh can be anisotropic. A simple procedure consists in virtually stretching the mesh in the vertical direction so that we recover an isotropic diffusion in the deformed geometry. The mesh is not really modified, but the local interior penalty coefficients are chosen in such a way that they correspond to an isotropic diffusion on the modified mesh.

5 Discrete DG finite element formulations

For the sake of completeness, we provide here the full weak DG finite element formulations for each equation of the SLIM model (Eqs. 1, 3, 5, 6, and 7) using the numerical tools described in both previous sections. The discrete formulations can be then derived by replacing the test functions and the solution by the corresponding DG polynomial approximation.

5.1 Horizontal momentum equation

The discrete formulation of the horizontal momentum equation is obtained by multiplying Eq. 1 by a test function \(\widehat{\boldsymbol{u}}\) and integrating over the whole domain Ω:

$$ \begin{array}{lll} && <\widehat{\boldsymbol{u}} \cdot \frac{\partial \boldsymbol{u}}{\partial t} > + <\widehat{\boldsymbol{u}} \cdot \left( \boldsymbol{\nabla}_h \cdot \left( \boldsymbol{u} \boldsymbol{u} \right) \right) > + <\widehat{\boldsymbol{u}} \cdot \frac{\partial (w - w_z) \boldsymbol{u}}{\partial z} > \\ &&{\kern12pt}+<\widehat{\boldsymbol{u}} \cdot f\mathbf{e}_z\wedge\boldsymbol{u}> + <\widehat{\boldsymbol{u}} \cdot \frac{\boldsymbol{p}}{\rho_0}> + <\widehat{\boldsymbol{u}} \cdot g\boldsymbol{\nabla}_h \eta> \\ &&{\kern12pt} -<\widehat{\boldsymbol{u}} \cdot \left(\boldsymbol{\nabla}_h \cdot \left(\nu_h \boldsymbol{\nabla}_h \boldsymbol{u}\right)\right)> - <\widehat{\boldsymbol{u}} \cdot \frac{\partial}{\partial z}\left(\nu_v \frac{\partial \boldsymbol{u}}{\partial z} \right)> = 0, \end{array} $$
(21)

where <   > denotes the volume integral over the domain Ω. In order to be able to introduce discontinuous approximations, this integral is split into N e integrals on each element Ω e .

$$ \begin{array}{lll} && \sum\limits_{e=1}^{N_e} \left[ <\widehat{\boldsymbol{u}} \cdot \frac{\partial \boldsymbol{u}}{\partial t}>_{e} + \underbrace{<\widehat{\boldsymbol{u}} \cdot \vphantom{\frac{\boldsymbol{p}}{\rho_0}} \left( \boldsymbol{\nabla}_h \cdot \left( \boldsymbol{u} \boldsymbol{u} \right) \right)>_{e}}_{\text{horizontal advection}} \right. +\underbrace{\widehat{\boldsymbol{u}} \cdot \vphantom{\frac{\boldsymbol{p}}{\rho_0}} \frac{\partial (w-w_z) \boldsymbol{u}}{\partial z}}_{\text{vertical advection}} +\underbrace{<\widehat{\boldsymbol{u}} \cdot \vphantom{\frac{\boldsymbol{p}}{\rho_0}} f\mathbf{e}_z\wedge\boldsymbol{u}>_{e}}_{\text{Coriolis}} \\ &&{\kern18pt}+\underbrace{<\widehat{\boldsymbol{u}} \cdot \frac{\boldsymbol{p}}{\rho_0}>_{e}}_{\text{baroclinic pressure gradient}} +\underbrace{<\widehat{\boldsymbol{u}} \cdot \vphantom{\frac{\boldsymbol{p}}{\rho_0}} g\boldsymbol{\nabla}_h \eta>_{e}}_{\text{elevation gradient}} \left. -\underbrace{<\widehat{\boldsymbol{u}} \cdot \vphantom{\frac{\boldsymbol{p}}{\rho_0}} \left(\boldsymbol{\nabla}_h \cdot \left(\nu_h \boldsymbol{\nabla}_h \boldsymbol{u}\right)\right)>_{e}}_{\text{horizontal dif\/fusion}} -\underbrace{< \widehat{\boldsymbol{u}} \cdot \frac{\partial}{\partial z}\left( \nu_v \frac{\partial \boldsymbol{u}}{\partial z}\right)>_{e}}_{\text{vertical dif\/fusion}} \right] =0. \end{array} $$
(22)

Apart from the baroclinic pressure terms, all terms containing spatial derivatives are integrated by parts on each element. Therefore, boundary fluxes appear along the interfaces between the elements. If we use discontinuous approximations, the key ingredient of the weak formulation is the way to define those fluxes as the variables are not uniquely defined on those interfaces. Each term of Eq. 22 is then derived as follows:

  • Horizontal advection:

    $$ \begin{array}{rll} \sum\limits_{e=1}^{N_e} \bigg[&-& <\boldsymbol{\nabla}_h \widehat{\boldsymbol{u}} : \boldsymbol{u} \boldsymbol{u}>_{e} + \ll \widehat{\boldsymbol{u}} \cdot \left\{\boldsymbol{u}\right\} \left\{\boldsymbol{u}\right\} \cdot \boldsymbol{n}_h\gg_{e} \\ &+& \ll \gamma \left[\boldsymbol{u}\right]\cdot \widehat{\boldsymbol{u}} \gg_{e}\bigg] \end{array} $$

  • Vertical advection:

    $$ \begin{array}{rll} \sum\limits_{e=1}^{N_e} \bigg[&-& < \frac{\partial \widehat{\boldsymbol{u}}}{\partial z}\cdot (w-w_z)\boldsymbol{u}>_{e} \\ &+& \ll\widehat{\boldsymbol{u}} \cdot (w-w_z)^\text{down} \ \boldsymbol{u}^\text{upwind} \ n_z\gg_{e}\bigg] \end{array} $$

  • Elevation gradient:

    $$ \sum\limits_{e=1}^{N_e} \bigg[ - <\boldsymbol{\nabla}_h \cdot \widehat{\boldsymbol{u}} \ g \eta>_{e} + \ll g \eta^\text{riemann} \ \widehat{\boldsymbol{u}} \cdot \boldsymbol{n}_h\gg_{e} \bigg] $$

  • Horizontal diffusion:

    $$ \begin{array}{rll} \sum\limits_{e=1}^{N_e} \bigg[&-& <\nu_h \left(\boldsymbol{\nabla}_h \widehat{\boldsymbol{u}}\right) : \left( \boldsymbol{\nabla}_h \boldsymbol{u}\right)^T>_{e} \\ &+& \ll\nu_h \widehat{\boldsymbol{u}} \cdot \left\{\boldsymbol{\nabla}_h \boldsymbol{u}\right\}\cdot \boldsymbol{n}\gg_{e}\\ &+& \ll \nu_h \boldsymbol{\nabla}_h\widehat{\boldsymbol{u}}\cdot \boldsymbol{n} \cdot \left[\boldsymbol{u}\right]\gg_{e} +\sigma \ll \nu_h \widehat{\boldsymbol{u}} \cdot \left[\boldsymbol{u}\right]\gg_{e} \bigg] \end{array} $$

  • Vertical diffusion:

    $$ \begin{array}{rll} \sum\limits_{e=1}^{N_e} \bigg[ &-& < \nu_v\frac{\partial \widehat{\boldsymbol{u}}}{\partial z} \cdot \frac{\partial \boldsymbol{u}}{\partial z}>_{e} + \ll \nu_v \widehat{\boldsymbol{u}} \cdot \left\{\frac{\partial \boldsymbol{u}}{\partial z}\right\}n_z\gg_{e}\\&+&\ll \nu_v \frac{\partial \widehat{\boldsymbol{u}}}{\partial z}n_z \cdot \left[\boldsymbol{u}\right]\gg_{e} +\,\sigma \ll \nu_v \widehat{\boldsymbol{u}} \cdot \left[\boldsymbol{u}\right]\gg_{e} \bigg] \end{array} $$

  • Baroclinic pressure gradient and Coriolis:

    $$ \sum\limits_{e=1}^{N_e} \bigg[ <\widehat{\boldsymbol{u}} \cdot \frac{\boldsymbol{p}}{\rho_0}>_{e} + f\mathbf{e}_z\wedge\boldsymbol{u} \ \bigg] $$

where \(\boldsymbol{n}_h = (n_x, n_y)\) and n z are respectively the horizontal and the vertical components of the outgoing normal of the boundary of the element. In the interface term for vertical advection, we perform upwinding of the advected variable \(\boldsymbol{u}\), and we use the vertical velocity of the prism below the interface, so that the discrete vertical advection term is as close as possible to the corresponding term in the continuity equation. As we use the Riemann solver associated to the non-conservative \(P_1^{\rm DG} - P_1^{\rm DG}\) discrete formulation of the two-dimensional shallow water equations for the gravity waves, it is critical that the resulting two-dimensional discrete equations obtained by integrating the momentum equation along the vertical axis approximately degenerate to this discrete formulation of the two-dimensional shallow water equations. To achieve this, the test function \(\widehat{\boldsymbol{u}}\) is now the shape function divided by the depth at rest. Finally, the Lax–Friedrichs flux for the internal waves requires the additional boundary term \( \ll\gamma \left[\boldsymbol{u}\right]\cdot\widehat{\boldsymbol{u}} \gg_{e}\) where γ is an upper bound of the fastest propagation speed of a three-dimensional phenomena, namely the sum of the phase speed of the fastest internal wave and the advection velocity. The interface terms for horizontal and vertical diffusion are directly derived from the SIPG procedure described by Eq. 19.

5.2 Vertical momentum equation

As the discrete variable associated with the vertical momentum equation is the vector field \(\boldsymbol{p}\) that stands for the numerically computed baroclinic pressure horizontal gradient, we discretize the gradient of the balance of the vertical momentum (Eq. 6) as follows:

$$ \begin{array}{lll} && \sum\limits_{e=1}^{N_e}\bigg[<\widehat{\boldsymbol{p}}^\text{up} \cdot \frac{\partial \boldsymbol{p}}{\partial z}>_{e}\bigg] \\ &&{\kern18pt} =\sum\limits_{e=1}^{N_e}\bigg[-<\widehat{\boldsymbol{p}}^\text{up} \cdot (g \boldsymbol{\nabla}_h{\rho'(T,S)})>_{e}\bigg]. \end{array} $$
(23)

To take into account that the integration is performed from top to bottom with a constant pressure at the sea surface (and therefore a vanishing pressure gradient), we use some fully upwinded test functions derived as the tensorial product between the usual \(P_1^{\rm DG}\) triangle and the upwinded linear unidimensional element, whose values are 1 for the degree of freedom above the element and 0 for the degree of freedom below the element.

5.3 Continuity equation

The continuity equation can be viewed as a steady transport equation along the vertical direction where the divergence of the horizontal velocity acts as a source term. The continuity equation is used to deduce the vertical velocity by integrating the horizontal velocity divergence from bottom to top. The discrete formulation of the continuity equation is obtained by multiplying Eq. 3 by a test function \(\hat{w}\) and integrating over the whole domain Ω:

$$ \sum\limits_{e=1}^{N_e} \bigg[<\hat{w}\frac{\partial w}{\partial z}>_{e}+<\hat{w}\boldsymbol{\nabla}_h\cdot{\boldsymbol{u}}>_{e}\bigg]=0. $$
(24)

where the integral on the domain Ω is split into N e integrals on Ω e . Integrating by parts all terms containing spatial derivatives yields:

$$ \begin{array}{lll} && \sum\limits_{e=1}^{N_e} \bigg[\ll\hat{w} w^\text{down} n_z\gg_{e}-<\frac{\partial \hat{w}}{\partial z}w>_{e}\bigg. \\ &&{\kern26pt} \bigg.+\ll\hat{w} \boldsymbol{u}^\text{riemann}\cdot \boldsymbol{n}_h\gg_{e}-<\boldsymbol{\nabla}_h{\hat{w}}\cdot\boldsymbol{u}>_{e}\bigg]=0. \end{array} $$
(25)

where we use \(w^\text{down}\) the value from the bottom element at the interfaces between layers of prisms, as the information goes from bottom to top in this pure transport equation. Moreover, a impermeability condition has to be prescribed at the sea bed, namely:

$$ w^{-h} + \boldsymbol{u}^{-h} \cdot \boldsymbol{\nabla}_h h = 0, $$
(26)

This boundary condition is weakly imposed by using \(-\boldsymbol{u}^{-h} \cdot \boldsymbol{\nabla}_h h\) for \(w^\text{down}\) in the first term of Eq. 25 at the sea bed. This only occurs on the first layer of prisms.

In the lateral interface, we use \(\boldsymbol{u}^\text{riemann}\) because the discrete two-dimensional integral free surface equations will be obtained by aggregating the three-dimensional discrete continuity equations. In fact, the discrete procedure mimics the algebra performed to obtain the integral free-surface equation (Eq. 7) by integrating the equation of continuity (Eq. 3) and substituting the impermeability conditions at both the sea bed and the sea surface. The sea bed impermeability is already included in the discrete formulation of the continuity equation, and the sea-surface condition will be incorporated by the motion of the free surface. Finally, let us recall that when we deduce \(\boldsymbol{u}^\text{riemann}\) and \(\eta^\text{riemann}\) with the exact Riemann solver of the linear shallow water equations, we use the fact that the depth integration of the momentum equation coupled with the free surface equation has to degenerate into a stable and an accurate \(P_1^{\rm DG}-P_1^{\rm DG}\) discretization of the two-dimensional shallow water equations. Therefore, as the discrete free-surface equation will be obtained by aggregating the discrete continuity equation, it is mandatory to use \(\boldsymbol{u}^\text{riemann}\) here, to have it in the resulting free-surface equation. As a last remark, it is also important to emphasize that the vertical velocity is not a prognostic field. It is a by-product used to deduce the vertical advection terms in the momentum and tracer equations. Elevation, velocities, and tracer are prognostic fields. An accurate DG discretization of our set of equation should be such that these fields are computed with an optimal accuracy, i.e., p + 1 convergence rate if order p shape functions are used. It is not the case for vertical velocity. Vertical velocity is not smooth because it results from the integration of the divergence of the horizontal velocity. It behaves similarly to the volume term from an advection term integrated by parts: It is not smooth, but it does not impair the optimal convergence of the other fields. Indeed, at the discrete level, it is easily seen that, if the prisms are straight, the vertical velocity lives in a discrete space that is piecewise constant in the horizontal direction rather than linear. The smoothness of tracer and horizontal velocity field is recovered as usual in DG, using the interface term, acting as a penalty term.

5.4 Free-surface equation

Formally, the discrete formulation of the free-surface equation is obtained by multiplying Eq. 7 by a test function \(\hat{\eta}\) and integrating over the two-dimensional basement of the three-dimensional computational domain Ω. This basement is paved of N f triangles Δ f that are the elements of the initial two-dimensional mesh that was extruded to produce the three-dimensional mesh of prisms. This discrete formulation reads:

$$ \begin{array}{lll} &&{\kern-8pt} \sum\limits_{f=1}^{N_f} \bigg[\ll\hat{\eta}\frac{\partial \eta}{\partial t}\gg_{\Delta f}+ \ll\hat{\eta} \ \boldsymbol{u}^{\eta} \cdot \boldsymbol{\nabla}_h \eta \gg_{\Delta f} \\ &&{\kern2pt}+ \!\underbrace{\ll\hat{\eta} \ \boldsymbol{u}^{-h} \cdot \boldsymbol{\nabla}_h h \gg_{\Delta f} + \ll\hat{\eta} \int_{-h}^{\eta}\nabla_h \cdot \boldsymbol{u} dz \gg_{\Delta f} }_{\displaystyle \mbox{aggregated discrete continuity equations}} \bigg]=0. \end{array} $$
(27)

where ≪ ≫ Δf denotes the integral over the triangle Δ f of the two-dimensional mesh of N f triangles.

The last two terms can be obtained by the aggregation of the discrete continuity equation (Eq. 25). It can be shown that the aggregation of unconstrained discrete continuity equation corresponds to the discrete form of the depth-integrated continuity equation :

$$ \sum\limits_{f=1}^{N_f} \bigg[\ \ll\hat{\eta} \ \int_{-h}^{\eta}\nabla_h\cdot \boldsymbol{u} dz \gg_{\Delta f} \bigg]. $$

Moreover, imposing the impermeability at the sea bed on the bottom interface will add an additional contribution that corresponds to :

$$ \sum\limits_{f=1}^{N_f} \bigg[\ll\hat{\eta} \ \boldsymbol{u}^{-h} \cdot \boldsymbol{\nabla}_h h \gg_{\Delta f} \bigg]. $$

The opposite sign and the difference between the areas of integration are counterbalanced by the vertical component of the outgoing normal n z . It is only necessary to add the missing term in order to obtain the full linear free surface equation.

At this stage, the linear free surface approximation consists in omitting this additional term or in substituting Eq. 27 by:

$$ \begin{array}{lll} &&{\kern-8pt} \sum\limits_{f=1}^{N_f} \bigg[ \ll\hat{\eta}\frac{\partial \eta}{\partial t}\gg_{\Delta f} \\ &&{\kern2pt} + \underbrace{\ll \hat{\eta} \ \boldsymbol{u}^{-h} \cdot \boldsymbol{\nabla}_h h \gg_{\Delta f} + \ll \hat{\eta} \ \int_{-h}^{0}\nabla_h \cdot \boldsymbol{u} dz \gg_{\Delta f} }_{\displaystyle \mbox{aggregated discrete continuity equation}} \bigg]=0. \end{array} $$
(28)

Again, such an approximation may be convenient in some large-scale application but must be avoided in coastal problems. Equation 28 can also be viewed as the discretization of Eq. 8 which is the mass conservation equation of the linear shallow water problem.

5.5 Tracer equation

As for the momentum equation, the weak formulation for the tracer equation can be written on each element as follows:

$$\begin{array}{lll} && \sum\limits_{e=1}^{N_e} \left[ <\hat{c}\frac{\partial c}{\partial t}>_{e} + \underbrace{<\hat{c} \vphantom{\frac{\boldsymbol{p}}{\rho_0}}\ \left( \boldsymbol{\nabla}_h \cdot \left( \boldsymbol{u} c \right) \right)>_{e}}_{\text{horizontal advection}} \right. \\ && {\kern26pt}+\underbrace{<\hat{c} \frac{\partial (w-w_z) c}{\partial z}>_{e}}_{\text{vertical advection}} -\underbrace{<\hat{c} \vphantom{\frac{\boldsymbol{p}}{\rho_0}}\ \left(\boldsymbol{\nabla}_h \cdot \left(\kappa_h \boldsymbol{\nabla}_h c \right)\right)>_{e}}_{\text{horizontal dif\/fusion}} \\ && {\kern26pt}\left. -\underbrace{<\hat{c} \ \frac{\partial}{\partial z}\left( \kappa_v \frac{\partial c }{\partial z}\right)>_{e}}_{\text{vertical dif\/fusion}} \right] =0. \end{array} $$
(29)

We integrate by parts the transport and diffusion terms and choose the suitable values for the interface terms. As for the momentum equation, we add the interface term \(\ll \hat{c} \gamma \left[c\right] \gg_{e}\) that is deduced from the Lax–Friedrichs solver for internal waves. It is a very important term for the numerical properties of the model as internal waves are a phenomenon that couples momentum and tracers. Each term of Eq. 29 is then derived as follows:

  • Horizontal advection:

    $$ \begin{array}{rll} \sum\limits_{e=1}^{N_e} \bigg[ &-&<\boldsymbol{\nabla}_h{\hat{c}}\cdot\boldsymbol{u} c>_{e} + \ll \hat{c} \left\{c\right\} \boldsymbol{u}^\text{riemann}\cdot \boldsymbol{n}_h\gg_{e} \\&+& \ll \hat{c} \gamma \left[c\right] \gg_{e}\bigg] \end{array} $$

  • Vertical advection:

    $$ \begin{array}{rll} \sum\limits_{e=1}^{N_e} \bigg[ &-& < \frac{\partial \hat{c}}{\partial z} \ (w-w_z)c>_{e} \\ &+& \ll\left(\hat{c} \ (w-w_z)^\text{down} c^\text{upwind}\right) n_z\gg_{e}\bigg] \end{array} $$

  • Horizontal diffusion:

    $$ \begin{array}{rll} \sum\limits_{e=1}^{N_e} \bigg[&-& <\kappa_h \left(\boldsymbol{\nabla}_h \hat{c}\right) \cdot \left( \boldsymbol{\nabla}_h c \right)>_{e} + \ll\kappa_h \hat{c} \left\{\boldsymbol{\nabla}_h c\right\} \cdot \boldsymbol{n}\gg_{e} \\ &+&\ll \kappa_h \boldsymbol{\nabla}_h\hat{c}\cdot \boldsymbol{n} \cdot \left[c\right]\gg_{e} +\sigma \ll \kappa_h \hat{c} \left[c\right]\gg_{e} \bigg] \end{array} $$

  • Vertical diffusion:

    $$ \begin{array}{rll} \sum\limits_{e=1}^{N_e} \bigg[ &-& < \kappa_v\frac{\partial \hat{c}}{\partial z} \frac{\partial c}{\partial z}>_{e} + \ll \kappa_v \hat{c} \left\{\frac{\partial c}{\partial z}\right\} n_z\gg_{e}\\ &+&\ll \kappa_v \frac{\partial \hat{c}}{\partial z} n_z \left[c\right]\gg_{e} +\sigma \ll \kappa_v \hat{c} \left[c\right]\gg_{e} \bigg] \end{array} $$

To ensure consistency, it is mandatory that the discrete advection term degenerates to the continuity equation when a unit tracer concentration is considered (White et al. 2008). Therefore, the same discrete space must be used for both c and w. Moreover, we must use the same velocity approximations in the interface terms \(\boldsymbol{u}^\text{riemann}\) for the horizontal advection and \(w^\text{down}\) for the vertical advection. But the interface value for the tracer concentration c at the interface is not constrained by consistency considerations: Upwind or centered values can be used. The additional term from the Lax–Friedrichs solver does not impair consistency as it is exactly nil for a constant tracer. The bottom boundary conditions must also be compatible, this being ensured by suppressing the boundary terms for advection at the sea bottom.

5.6 Validation and mesh refinement analysis

As a first numerical check, we consider a simple gravity waves problem. The domain is an rectangular cuboid ocean of [0, L] × [0, L] × [0, H]. The length and depth are respectively 103 and 1 km. An analytical solution can be derived for the initial elevation given by:

$$ \eta(x,y,t=0) = \sin^2 \left(\frac{x \pi}{L} \right) \sin^2 \left(\frac{y \pi}{L} \right). $$

The maximal value reached at the center of the square is 1 m. Even if this problem is two-dimensional, it can be a quite efficient test for a three-dimensional if we use several layers with nonconstant depths as illustrated in Fig. 2. If the fluxes through horizontal and vertical faces are not accurately computed, the behavior will be strongly affected and the theoretical rates of convergence cannot be achieved. We deliberately select highly unstructured pattern in order to check that the code converges for both regular and irregular grids. The same convergence test is also obtained for uniformly refined graded mesh. In Fig. 3, we observe the theoretical quadratic rate of convergence for a time step of 250 s and four meshes with following characteristic lengths h = 200, 100, 50, and 25 km. The time step was selected in such a way that the temporal error is negligible with respect to the spatial error.

Fig. 2
figure 2

Gravity waves for a cuboid ocean of \(\text{1,000} \times \text{1,000} \times 1\) km: mesh refinement analysis with four meshes exhibiting three layers of different depths. Initial elevation (top) and two-dimensional traces of the used meshes (bottom). The characteristic lengths are h = 200, 100, 50, and 25 km, respectively

Full size image
Fig. 3
figure 3

Gravity waves test case: mesh refinement analysis

Full size image

6 Numerical results

We simulate the internal waves in the lee of a moderately tall seamount. The simulation of such a complex flow can be considered as a relevant test case. Complicated phenomena can be observed in the wake of mountains, such as internal wave structures and vortex streets (Chapman and Haidvogel 1992, 1993; Ford et al. 2004b). Such a problem was simulated with three-dimensional baroclinic finite difference (Huppert and Bryan 1976; Chapman and Haidvogel 1992, 1993), finite volume (Adcroft et al. 1997), and finite element models (Ford et al. 2004b; Wang et al. 2008a, b). If the seamount is small enough, a complicated structure of standing internal waves can develop in the wake of the seamount. Chapman and Haidvogel (1993) provide a detailed numerical study of internal lee waves trapped over isolated Gaussian-shaped seamounts. Such a testcase is also used by Ford et al. (2004b) to assess the qualities and drawbacks of their model. With our three-dimensional baroclinic marine model SLIM, we simulate the internal lee waves for a seamount whose height is 30% of the total depth.

The setup of the problem can be summarized as follows: A Gaussian seamount is located at a latitude of 45° N with a bathymetry given by:

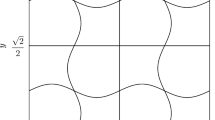
$$ 1 - \displaystyle\frac{h(x,y)}{H} = \delta \exp\left(\frac{\left(x - \frac{R}{2}\right)^2 + \left(y - \frac{R}{2}\right)^2 + \left(z -\frac{R}{\sqrt{2}}\right)^2}{-L^2}\right), $$
(30)

where H = 4.5 km is the maximum depth, δ = 0.3 is the relative height of the seamount, \(R = \text{6,372}\) km is Earth radius, and L = 25 km is the length scale of the seamount. The coordinates x, y, and z are relative to the global Cartesian frame of reference. The flow simulation is initiated with a global zonal geostrophic equilibrium ignoring the seamount. In other words, the initial guess of the calculation is selected as in the testcase #5 of Williamson et al. (1992) where the velocity field only exhibits a nonvanishing east component u e . In this testcase, the elevation and velocity fields are shown in Fig. 4 and are respectively given by

$$ \displaystyle\frac{\eta}{U^2 / g}=- \frac{z^2}{R^2} \left(1 + \sqrt{2} \ \frac{ R\Omega}{U} \right),$$
(31)
$$ \displaystyle\frac{u_e}{U}=\sqrt{\frac{x^2+y^2}{R^2}}, $$
(32)

where U = 0.516 m s − 1 is the velocity scale at a latitude of 45° N, Ω = 7.292 × 10 − 5 s − 1 is Earth rotation rate, and g = 9.81 m s − 2 is the gravitational acceleration. We consider the density deviation ρ′ as the unique tracer of the model, and the initial value of the density deviation is a linear function of the vertical coordinate, with vanishing mean. The derivative of the density with respect to the vertical coordinate is given by \(\partial \rho / \partial z = -3.43\times 10^{-5}\) kg m − 4, and the reference density is selected as \(\rho_0 = \text{1,025}\) kg m − 3. The turbulent viscosities and diffusivities are given by: ν h  = κ h  = 12.9 m2 s − 1, ν v  = 0.0001 m2 s − 1, and κ v  = 0. With those parameters, the flow is characterized by the same four dimensionless numbers as that of the Section 3d of Ford et al. (2004b). These dimensionless numbers are defined as follows:

Seamount ratio:

δ = 0.3

Rossby number:

\(\displaystyle Ro=\frac{U}{fL} = 0.2\)

Reynolds number:

\(\displaystyle Re=\frac{UL}{\nu_h} = \text{1,000}\)

Burger number:

\(\displaystyle Bu = \frac{NH}{fL} = \sqrt{\frac{-g}{\rho_0}\frac{\partial \rho}{\partial z}}\frac{H}{fL} = 1\)

where N is the Brunt–Väisälä frequency.

Fig. 4
figure 4

Initial condition for sea-surface elevation and velocities. The mesh is refined in the lee of the seamount

Full size image

The computational domain is the whole sphere, as we can take advantage of a highly variable mesh density. It allows us to avoid open boundary conditions, while previous publications use rectangular domains, with imposed inflow, sponge layer as outflow condition, and lateral walls (Chapman and Haidvogel 1992). Figure 5 shows a close-up view of the mesh and the bathymetry near the seamount. The mesh resolution is refined in the lee of the seamount to capture accurately the flow structure. Indeed, we know a priori that the structures generated in the lee of the seamount are deviated to the right, due to the mean transverse flow generated between the two vortices that are generated. In this zone, we refined the mesh so that the element size is sufficiently small compared to the wave length of the generated internal waves. The edge length in this refined zone is 2 km. This mesh is made up of 23,562 triangles extruded into 25 σ layers. Basically, it can also be viewed as a trial and error procedure where a preliminary calculation allows us to a fine tuning of the mesh refinement. Obviously, the automatic adaptive refinement procedure will be a more general approach.

Fig. 5
figure 5

Close-up view on the mesh and the bathymetry around the seamount. The mesh is refined in the lee of the seamount

Full size image

The only numerical parameter that has to be selected in the three-dimensional baroclinic model is the jump penalty parameter γ in the Lax–Friedrichs solver. For this problem, we select γ = 4 m s − 1. This parameter must be an upper bound of the phase speed of the fastest wave. From the linear theory, we know that with the prescribed stratification, the maximum phase speed of an internal wave is about c = 1 m s − 1, so that the fastest three-dimensional phenomenon propagates at c + U ≈ 1.5 m s − 1. For discontinuous linear elements combined with the second-order explicit Runge–Kutta time-stepper (Chevaugeon et al. 2007) used in this simulation, the relevant CFL conditions leads us to select a time step of 30 s.

The two-dimensional mesh on the sea bottom and the time evolution for the isosurfaces of the density perturbations are shown in Fig. 6. The density perturbation is defined as the density deviation field ρ′ from which the initial density deviation has been removed. The density perturbation can be considered as a good diagnostics: As the flow is dominated by geostrophy, it is directly an image of the vorticity induced by the fact that the flow is impulsively started. The free surface is raised upstream of the seamount and lowered downstream, leading thanks to geostrophic adjustment to an upstream clockwise vortex, and a downstream counterclockwise vortex, which are both visible in Fig. 6. The flow is strong enough to directly shed the counterclockwise eddy away from the seamount. The mean flow is deviated rightward downstream of the seamount. The clockwise eddy is trapped over the seamount. In the zone between the two eddies, internal waves are generated. Rather than being radiated away from the seamount, they are trapped in the lee of the seamount.

Fig. 6
figure 6

Time evolution of the isosurfaces of the density perturbation. Isovalues for the density perturbation of − 0.001 kg m − 3 are in green. Isovalues for the density perturbation of 0.001 kg m − 3 are in orange. The two-dimensional mesh is given on the sea bottom

Full size image

In Fig. 7, we also see that these waves have a particular structure. In the plots of the time evolution of the density perturbation at a 400-m depth, we observe that the waves are generated by the shedded eddy, propagate westward, and stack in the lee of the seamount. Again, the upstream clockwise vortex and the downstream counterclockwise vortex are both clearly visible in Fig. 7.

Fig. 7
figure 7

Time evolution of the density perturbation field at a 400-m depth. The internal waves lying between the two vortices are clearly visible

Full size image

At the seventh day, two well-separated modes in the density perturbation field are clearly visible as shown in Fig. 8. In the left side of the lee, looking downstream, an internal mode with two extrema appears. In the right side of the lee, an internal wave mode with three extrema appears. These numerical results can be compared with the theoretical analysis of the internal waves given in Lecture 17 of the book of Pedlosky (2003). The theory of the internal waves in a flat bottom ocean with uniform stratification implies the occurrence of eigenmodes. The vertical wave number is:

$$ m=\frac{i\pi}{H}, $$
(33)

with the integer i being the number of extrema of the vertical wave profile. In a linear analysis, these modes are independent and each of these modes behaves as a shallow water layer, with an equivalent depth defined as:

$$ h_i=\frac{N^2H^2}{i^2\pi^2 g}. $$
(34)
Fig. 8
figure 8

Illustration of the two well-separated modes at day 7. The top panel shows a view of the isocontours of the density perturbation. Two cuts are defined and are given on the two lower panels. Isocontours values range from − 0.02 to 0.02 kg m − 3 with an interval of 0.002. Isovalues of − 0.005 and 0.005 are added, while the zero isovalue is removed

Full size image

As for the usual shallow water equations, Kelvin waves along coastlines, Poincaré waves, and Rossby waves can be observed. However, as we are interested in a flow over a relatively short period of time on a aquaplanet without coastlines, only the Poincaré waves are relevant here. The phase speed of the Poincaré waves is given by:

$$ c_i=\sqrt{gh_i+\frac{f^2}{k^2}}=\sqrt{\frac{N^2H^2}{i^2\pi^2}+\frac{f^2}{k^2}}, $$
(35)

where k is the horizontal wavenumber. For the flow to support standing waves, the propagation speed of internal waves in the opposite direction of the mean flow must be equal to the mean flow speed:

$$ c_i=U \cos(\alpha),\label{eq:c_u_cos_a} $$
(36)

where α is the angle between the mean flow speed and the direction of the wave propagation. The direction of wave propagation is normal to the wave crests.

In Fig. 9, we represent the wave modes and propagation speeds. The mean velocity vector is not aligned because the mean flow is deviated to the right by the seamount. The phase speed vector for mode 2 and mode 3 internal waves are also given, with the amplitude of the phase speed vectors selected for stationary waves. From such a picture, the angle α between the mean flow speed and the propagation of the wave propagation can be deduced. For mode 2 waves, the observed angle between the mean flow velocity and the wave propagation direction is about \(\alpha \approx 35\ensuremath{^\circ}\) in Fig. 9. Taking advantage of the theoretical linear analysis, we use Eqs. 35 and 36 to estimate the horizontal wavenumber of the waves from the observed angle α and the vertical wavenumber (i.e., the number of modes)

$$ \begin{array}{rll} c &=& 0.42 \ {\rm m~s}^{-1},\\ k&=&1.03\ 10^{-3} \ {\rm m}^{-1}. \end{array} $$

This speed is close to the threshold value 0.410 m s − 1, under which the flow is subcritical for mode 2, and stationary lee waves cannot exist. From the calculated horizontal wavenumber, the wave length is estimated to be 2π/ k = 6.1 km and should correspond to the crest to crest distance. However, in Fig. 9, we observe a crest to crest distance of 18.75 km for mode 2. Such a discrepancy between those two results can be explained by the fact that the phase speed is very close to the threshold value for which no wave can exist. Therefore, the phase speed does not depend so strongly on the wavenumber. Moreover, if we perform a vertical slice in the density deviation field ρ′, we observe that the amplitude of the waves is significant compared to the total depth in Fig. 10. Therefore, considering the linear regime for the theoretical computation of the dispersion relation is probably a bad assumption and can induce significant errors.

Fig. 9
figure 9

Sketch of the wave modes and propagation speeds. \(\vec{U}\) denotes the mean velocity vector. It is not horizontal because the mean flow is deviated to the right by the seamount. \(\vec{c_2}\) and \(\vec{c_3}\) denote the phase speed vector for mode 2 and mode 3 internal waves, respectively. The amplitude of the phase speed vectors is taken for the waves to be stationary

Full size image
Fig. 10
figure 10

Density field at day 7, along the plane for mode 2 defined in Fig. 8

Full size image

7 Conclusions

The spatial discretization of a three-dimensional baroclinic free-surface marine model is introduced. This model relies on a discontinuous Galerkin method with a mesh of prisms extruded in several layers from an unstructured two-dimensional mesh of triangles. As the prisms are vertically aligned, the calculation of the vertical velocity and the baroclinic pressure gradient can be implemented in an efficient and accurate way. All discrete fields are defined in discontinuous finite element spaces, to take advantage of the good numerical properties of the discontinuous Galerkin methods for advection dominated problems and for wave problems. To be able to use the Riemann solver of the shallow water equations, the discretization of the three-dimensional horizontal momentum and the continuity equations are defined in such a way that their discrete integration along the vertical axis provides a stable \(P_1^{\rm DG}-P_1^{\rm DG}\) formulation of the shallow water equations. Therefore, we can stabilize the discrete equations by using the exact Riemann solver of the linear shallow water for the gravity waves. For internal waves, an additional stabilizing term is derived from a Lax–Friedrichs solver. In the baroclinic dynamics, the vertical velocity acts as a source term, while the role of the approximate Riemann solver is to penalize inter-element jumps to recover optimal accuracy. Consistency is ensured. The model is able to advect exactly a tracer with a constant concentration, meaning that the discrete transport term is compatible with the continuity equation.

A key advantage of discontinuous Galerkin finite elements is their ability to naturally handle higher order discretizations. The discrete formulation with the same approximate Riemann solvers can be used for high-order shape functions. As an illustrative example, we simulate the same problem as in Section 6 with second-order shape functions and a mesh two times coarser involving 12 layers. The triangles are twice larger than in the previous calculation. A comparison of the density perturbation field after 2 days is shown in Fig. 11. We observe the same behavior, as both simulations are performed on a sufficiently fine mesh. However, some small oscillations are induced by the subparametric representation of the bottom topography. They appear above the seamount for the quadratic shape functions computation. Indeed, the bathymetry is still represented using piecewise linear polynomials, while the fields are represented using piecewise quadratic polynomials. But we think that such a discretization of a three-dimensional baroclinic finite element marine model is an effective way for higher-order elements, paving the way for high-order ocean models based on discontinuous Galerkin methods. Finally, even if this contribution can be viewed as important effort to the development of unstructured mesh ocean models, our model has only a dynamic core and is not ready for realistic applications in this sense.

Fig. 11
figure 11

Density perturbation isocontours after 2 days. Linear (left) and quadratic (right) discretizations for the 30% height case

Full size image

In conclusion, we use a three-dimensional finite element baroclinic free-surface model to represent accurately the complex structure of the internal waves in the lee of an isolated seamount, using either linear or quadratic shape functions. The model does not yet handle internally supercritical flows that occur for instance when internal waves break or in steed gravity currents. Including a limiting strategy to handle shockwaves would be the next required step. Finally, the second key ingredient for an efficient three-dimensional marine model is the definition of a good time integration procedure. This will be the topic of the second part of this contribution.