1 Introduction

Shoreface-connected sand ridges (hereafter abbreviated as sfcr) are rhythmic bottom patterns that are found on sandy, storm-dominated inner shelves in water depths of 5–30 m. During storms, the water motion is characterized by high waves (wave heights of 2–4 m) and a mean storm-driven alongshore flow of up to 0.5 m s − 1. Field observations (Swift et al. 1978; Antia 1996; Van de Meene and Van Rijn 2000; Schwab et al. 2000, and references therein) reveal that crests of sfcr have a length between 10 and 25 km, their heights are 1–6 m, and distances between successive crests are 2–6 km. Sfcr are attached to the shoreface and their seaward ends are located further upstream (with respect to the direction of the storm-driven flow). Angles between the crests and the coastline are in the range 20–50°. Sfcr evolve on a time scale of centuries, and they migrate in the direction of the storm-driven flow with 1–50 m year − 1, depending on the measuring period. Furthermore, field data indicate a persistent pattern of grain sorting over sfcr. In many cases, the sediment at the seabed is coarsest on the landward flanks and finest on the seaward flanks. This phase shift between the mean grain size and topography variations is documented for sfcr on the Mid Atlantic shelf (e.g., Swift et al. 1972; Schwab et al. 2000), the inner shelf of Argentina (Parker et al. 1982), and the German Bight (Antia 1996).

Both observations (Swift and Field 1981) and model studies (Trowbridge 1995; Calvete et al. 2001) have indicated that sfcr can grow due to positive feedbacks between the water motion and the erodible sandy bed. During storms, bottom stresses exerted by the waves are strong enough to entrain the sediment, which is subsequently transported by the storm-driven flow. The ridges induce spatial variations in the flow and in the sediment transport. This results in net deposition of sediment over the crests, whilst net erosion occurs in the troughs. As a result, the ridges grow. Their migration is due to the fact that the maximum deposition occurs slightly downstream of their crests. The models investigate the formation of sfcr by calculating the growth of arbitrary bottom perturbations with small amplitudes. Calvete et al. (2001) demonstrated that their fastest growing bottom perturbations have characteristics that agree quite well with those of observed sfcr.

One limitation of these models is that they consider sediment with a uniform grain size, which is not in accordance with field data. Walgreen et al. (2003) analyzed a model that considers the effect of sediment sorting on the formation of sfcr. Results of this model indicate that the phase shift between bed topography and mean grain size is due to the selective transport via suspended load of grains with different sizes. Furthermore, sediment sorting has a net stabilizing effect on the growth of sfcr, whereas their migration speed becomes larger and their wavelength is only slightly affected. Process-based models have also been developed to investigate grain sorting over other coastal bedforms, such as ripples (Foti and Blondeaux 1995), sorted bedforms on the inner shelf (Murray and Thieler 2004; Coco et al. 2007a, b; Huntley et al. 2008), tidal sand banks (Walgreen et al. 2004; Roos et al. 2007), and tidal sand waves (Roos et al. 2008; Van Oyen and Blondeaux 2009); see also the review by Holland and Elmore (2008).

The models on sfcr discussed above employ a strongly simplified description of waves in calculating stirring of sediment. In two recent studies by Lane and Restrepo (2007) and Vis-Star et al. (2007), a more sophisticated description of waves is applied, based on linear wave theory, which enables to include explicit feedbacks between waves and sfcr. The latter results in additional transport (by the storm-driven flow) of sediment being entrained by the wave orbital motion, which is generated by the bedforms. In the latter study, it is demonstrated that the spatial variations in this sediment transport are such that both the growth and downstream migration of sfcr are enhanced. Lane and Restrepo (2007), on the other hand, report that they do not obtain growth of bedforms if they include wave–bedform interactions. This seems to be a consequence of their assumption that sediment transport is proportional to the mass transport velocity (which accounts for currents and wave-induced Stokes drift), rather than being proportional to the near-bed current.

In this paper, the model of Vis-Star et al. (2007) is extended such that it enables the exploration of wave–bedform feedbacks in a model for bimodal sediment mixtures. This is done by adopting and extending the sediment sorting module for a bimodal sediment mixture of Walgreen et al. (2003). The first aim of this work is to investigate whether wave–bedform interactions play an important role in the initial growth of sfcr, as well as in the initial onset of grain sorting over sfcr. Secondly, the influence of sediment sorting on the characteristics of sfcr is explored. Several new aspects are included in the sediment module. First, the longshore-averaged value of the mean grain size is allowed to vary in the cross-shore direction. Second, motivated by the work of Murray and Thieler (2004), Coco et al. (2007a, b), and Huntley et al. (2008), settling lag and roughness-induced turbulence are accounted for when computing suspended load sediment transport.

In Section 2, a detailed discussion of the process-based model is given, followed by a description of the solution method in Section 3. Section 4 presents the results, which are discussed in Section 5. Finally, the conclusions are drawn in Section 6.

2 Model formulation

2.1 Shelf geometry

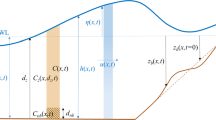
The geometry is shown in Fig. 1 and represents a semi-infinite domain, bounded on the landward side by the transition from shoreface to inner shelf. In the seaward direction, the water depth increases up to the transition to the outer shelf, where the latter is characterized by a flat bottom. In the absence of bedforms, the geometry is assumed to be longshore uniform. The x-, y-, and z-axes of the orthogonal coordinate system point in the cross-shore, alongshore, and vertical directions, respectively. The water depth on the landward side of the inner shelf (x = 0) is H 0, L s is the inner shelf width, and the depth of the outer shelf is indicated by H s.

Fig. 1
figure 1

Side view of a typical longshore- and time-averaged bottom topography of the continental shelf, representing the inner and outer shelves, in the shore-normal direction. Symbols are explained in the text

Full size image

2.2 Hydrodynamics

2.2.1 Waves

Linear wave theory is used to describe the properties of offshore waves approaching the shoreface. For the waves and water depths considered here (the inner shelf region), this approximation is reasonable. The equations used are similar to those in the study by Vis-Star et al. (2007). Rayleigh distributed random waves are considered, characterized by a narrow band of frequencies and orientations. The narrow spectrum is centered around a peak frequency, wavenumber, and wave orientation.

The rigid-lid approximation is used, i.e., the effects of the free surface on the local water depth are neglected. Thus, the local water depth \(\tilde{D}=z_{\rm s}-z_{\rm b}\) is approximated by D = − z b. Here, z s and z b are the free surface elevation and the bottom depth both measured with respect to the undisturbed water level z = 0. Refraction of waves by currents is not taken into account.

Stationary wave conditions are assumed, which is justified by the fact that the time scale of the waves (order of 10 s) is very small compared to the morphodynamic time scale (order of 100 years). Under this assumption, the law of conservation of wave crests implies that the radian wave frequency ω is constant. Subsequently, the dispersion relation

$$\label{4eq:dispersion} \omega\,^2=g \kappa \tanh(\kappa {D}) $$
(1)

determines the wavenumber κ of the waves, with g as the acceleration due to gravity. The angle of wave incidence with respect to the shore-normal, θ (defined positive in clockwise direction), is governed by the wavenumber identity relation

$$\label{4eq:wir} \frac{\partial}{\partial y}\left(\kappa \cos\theta\right)+\frac{\partial}{\partial x}\left(\kappa \sin\theta\right)=0. $$
(2)

The root-mean square wave height H rms follows from

$$ \mathcal{E}=\rho g \mathcal{H}_{\rm rms}^2/8\,, $$
(3)

with ρ the water density and \(\mathcal{E}\) the energy density. The latter is governed by the energy balance

$$\label{4eq:energy} {\boldsymbol{\nabla}} \cdot (\mathbf{c}_g \mathcal{E}) =\mathcal{F}^*-\mathcal{D}. $$
(4)

The group velocity vector of the waves c g has magnitude \(c_g=\partial\omega/\partial\kappa\) and components c gx  = − c g cosθ and c gy  = c g sinθ. Furthermore, \(\mathcal{F}^*\) and \(\mathcal{D}\) are a forcing and a dissipation term, which are modeled as

$$\label{4eq:diss} \mathcal{D}= \frac{2 c_{f*} \kappa\, u_{w}\;\mathcal{E}}{\sinh\left(2 \kappa D\right)}\,,\qquad \mathcal{F}^*=\mathcal{D}|_{x=L_{\rm s}}\,, $$
(5)

where c f* is a constant friction coefficient and

$$\label{5eq:eq1} u_w=\frac{\omega \mathcal{H}_{\rm rms}}{2\sinh(\kappa D)} $$
(6)

is the root-mean-square amplitude of the near-bed wave orbital velocity (hereafter called wave orbital velocity). The choice of the forcing function is such that, on the outer shelf, the waves neither gain nor lose energy. As boundary conditions, offshore wave properties (height, period, and angle of incidence) are imposed.

2.2.2 Currents

The water motion is described by the quasi-steady depth- and wave-averaged (2DH) shallow water equations

$$\label{5eq:eq2} (\mathbf{v} \cdot {\boldsymbol{\nabla}} ) \mathbf{v} + f \,\mathbf{e}_z \times \mathbf{v} = - g {\boldsymbol{\nabla}}z_{{\rm s}} + \frac{ \bf{\tau}_{{\rm s}} - \bf{\tau}_{{\rm b}}}{ \rho {D}}, $$
(7)
$$\label{5eq:eq3} {\boldsymbol {\nabla}} \cdot (D \mathbf{v}) = 0. $$
(8)

Here, v = (u,v) is the depth- and wave-averaged velocity, f is the Coriolis parameter, e z is a unit vector in the vertical direction, and g is the gravitational acceleration. Furthermore, τ s represents the wind stress, τ b represents the bed shear-stress, and \({\boldsymbol{\nabla}}\) is the two-dimensional (horizontal) nabla vector. In the momentum equations (Eq. 7), forcing terms due to wave-induced radiation stresses, horizontal momentum diffusion, density gradients, and tides are not considered. It is assumed that the mean storm-driven flow is in the alongshore direction (cross-shore component is neglected), due to a given wind stress τ sy .

This model only represents stormy weather conditions, during which the wave orbital velocity is much larger than the magnitude of the storm-driven current. It is assumed that, during fair weather conditions, the water motion is not strong enough to erode the sediment from the bottom. In the case of storms, the bed shear-stress is linearly related to the mean flow,

$$\label{5eq:eq3b} \bf{\tau}_{{\rm b}} = \rho r u_w \mathbf{v}, $$
(9)

with r as a dimensionless friction coefficient computed for random waves and u w given in Eq. 6. Boundary conditions are that the cross-shore flow component u vanishes at x = 0 and far offshore and periodic conditions in the longshore direction are assumed.

2.3 Sediment characteristics

The sediment considered in the present study is a mixture of grains of two different sizes, with d 1 and d 2 as the grain diameters of the fine and coarse material, respectively. As the distribution of grain sizes in a mixture appears to be close to log-normal, it is convenient to use a logarithmic scale for the grain diameter, the phi-scale:

$$\label{5eq:phi} d_i=2^{-\phi_i} \qquad \text{or} \qquad \phi_i=-\log_2 d_i \qquad \left(i=1,2\right), $$
(10)

where d i is measured in units of millimeters (Dyer 1986). Note that the larger the phi-value, the smaller the grain size. The weight percentages of the fine and coarse grain size class are given by \(\mathcal{F}_1\) and \(\mathcal{F}_2\), respectively, and

$$\label{5eq:sumf} \sum\limits_{i=1}^{2}\mathcal{F}_i=1. $$
(11)

The probabilities are used to calculate two statistical properties of the sediment mixture, the mean grain diameter d m (or the grain size φ m), and the standard deviation υ s. Their definitions read

$$\label{5eq:pdfprop} d_{\rm m}\!=\!2^{-\phi_{\rm m}}\,, \kern6pt \phi_{\rm m}\!=\!\sum\limits_{i=1}^{2} \phi_i \mathcal{F}_i, \kern6pt \upsilon_{\rm s}^2\!=\!\sum\limits_{i=1}^{2} \left( \phi_i \!-\!\phi_{\rm m}\right)^2 \mathcal{F}_i. $$
(12)

The standard deviation of the distribution gives a measure of the sorting of the sediment mixture. A poorly sorted mixture of sediment has large values of υ s, whereas a well-sorted, almost uniform sample corresponds to small υ s values.

2.4 Sediment dynamics

The bottom evolution is determined by divergence of the sediment transport. The latter depends on the sediment composition. In the case of a sediment mixture, the grain size distribution itself will also change. A simple model, originally proposed by Hirano (1971), is used to describe the bottom sediment as consisting of a well-mixed active layer (probabilities \(\mathcal{F}_i\) are independent of depth), and a substrate underneath where the probabilities \(\mathcal{F}_{{\rm s}i}\) do not vary in time. A sketch is given in Fig. 2, where z b = − H + h′ denotes the bottom location, H denotes the undisturbed water depth, and h′ is the bed elevation with respect to this reference level. The thickness of the active layer L a is in the order of (2 − 3)d 90, where d 90 is the sediment size for which 90% of the grains are finer.

Fig. 2
figure 2

Definition of the sediment layer as used in the model. The thickness of the active layer is denoted by L a and h′ is the elevation of the bottom with respect to the reference level z = − H

Full size image

Mass conservation for each size class is given by

$$ (1\!-\!p) \left( \mathcal{F}_{\eta,i} \frac{\partial z_{\rm b}}{\partial t} \! +\! L_{\rm a} \frac{\partial \mathcal{F}_i}{\partial t}\! +\! \left(\mathcal{F}_i\!-\!\mathcal{F}_{\eta,i}\right) \frac{\partial L_{\rm a}}{\partial t} \right) \!=\! - {\boldsymbol{\nabla}} \cdot \mathbf{q}_i \label{5eq:eq7} $$
(13)
$$ \begin{array}{lcl} {\kern-2pt}\mbox{Sedimentation: \quad}& \displaystyle\frac{\partial z_{\eta}}{\partial t}=\displaystyle\frac{\partial }{\partial t}\big(z_{\rm b}-L_{\rm a}\big) > 0 : & \displaystyle\mathcal{F}_{\eta,i} = \mathcal{F}_i \\[8pt] {\kern-2pt}\mbox{Erosion: \quad} & \displaystyle\frac{\partial z_{\eta}}{\partial t}=\displaystyle\frac{\partial }{\partial t}\big(z_{\rm b}-L_{\rm a}\big) < 0 : & \mathcal{F}_{\eta,i} = \mathcal{F}_{{\rm s}i} \end{array} $$

Here, p is the bed porosity, t is time, and q i is the wave-averaged total volumetric transport of sediment per unit width of grains with size d i .

Sediment in each grain size class is transported both as bedload (q bi ) and suspended load (q si ); thus,

$$\label{5eq:sedtot} \mathbf{q}_i=\mathbf{q}_{{\rm b}i}+\mathbf{q}_{{\rm s}i}. $$
(14)

Expressions for q bi and q si are derived from expressions for a single grain size. Corrections for the availability of sediment in a size class and for dynamic hiding effects (fine grains hide between the coarser grains and, hence, experience a smaller fluid drag) are needed to calculate the sediment transport of grains of a specific size. Static hiding effects due to the presence of a critical shear-stress for erosion are neglected.

The bedload sediment transport is calculated as

$$\label{5eq:eq9} \begin{array}{lcl} &&\mathbf{q}_{{\rm b}i} = \mathcal{F}_i \mathcal{G}_{{\rm b}i}\mathbf{q}_{{\rm b}}, \qquad \mathbf{q}_{{\rm b}}=\frac{3}{2} \nu_{\rm b} u_w^2 \left(\mathbf{v}-\lambda_{\rm b} u_w {\boldsymbol{\nabla}}z_{\rm b}\right), \\ &&\mathcal{G}_{{\rm b}i}=\left(\frac{d_i}{d_{\rm m}}\right)^{c_{\rm b}}. \end{array} $$
(15)

Here, the strength of hiding is indicated by exponent c b in the transport capacity function \(\mathcal{G}_{{\rm b}i}\) for bedload. Note that, in the absence of hiding, c b = 0, whereas for typical sand mixtures, c b ∼0.75 (Egiazaroff 1965). Thus, the bedload transport for grains with a diameter d i  > d m (d i  < d m) is enhanced (reduced) compared to the bedload transport for grains with a diameter d m due to dynamic hiding. The expression for q b originates from Bailard (1981), where the first contribution represents the net sediment transport due to stirring of sediment by waves and the subsequent transport by the net current. Coefficient ν b depends on sediment properties (but not on d i , which is already included in \(\mathcal{G}_{{\rm b}i}\)). The second contribution to q b accounts for the effect of bottom slopes, with λ b the bed slope parameter, which is assumed to be constant.

Suspended load transport plays a significant role during storms (Green et al. 1995) and is formulated as

$$\label{5eq:eq10} \mathbf{q}_{{\rm s}i}= \mathcal{C}_i \left( \mathbf{v}-{\lambda}_{\rm s} u_w^2 {\boldsymbol{\nabla}}z_{\rm b} \right). $$
(16)

Here, all grain size dependence is included in \(\mathcal{C}_i\), which is the depth-integrated volumetric concentration of available grains in class i. Furthermore, λ s is the bed slope coefficient for suspended load transport. The contribution in Eq. 16 related to bed slopes is subject to discussion, but in this study, its effect is not important (see Section 4). The depth-integrated volumetric concentration of suspended grains of class i, \(\mathcal{C}_i\), is governed by

$$ {\boldsymbol{\nabla}} \cdot(\mathbf{v} \mathcal{C}_i) =w_{{\rm s}i} \big(\mathcal{F}_i E_{i} - c_{{\rm b}i}\big). \label{5eq:conc} $$
(17)

The term on the left-hand side accounts for settling lag effects, i.e., it takes time for sediment to reach the bottom when the decreasing current cannot maintain it in suspension. Thus, settling occurs at some distance from the location where sediment has been entrained. The first term on the right-hand side accounts for the entrainment of sediment into suspension, the second term for deposition of sediment. Furthermore, w si is the settling velocity of grains of diameter d i , E i is the dimensionless entrainment of these grains, and c bi is their actual volume concentration near the bed. The entrainment of a size fraction is multiplied by the probability \(\mathcal{F}_i\) that sediment of this grain size is actually present. In this paper, the entrainment formulation of Garcia and Parker (1991) is used because it is based on laboratory experiments with sediment mixtures, thereby accounting for possible hiding effects. This formulation reads

$$\begin{array}{rcl} &&E_{i} = A \lambda_{\mbox{\scriptsize{E}}}^5 Z_{i}^5 u_w^5, \qquad Z_{i} = \frac{\sqrt{c_{{\rm f}i}}}{w_{{\rm s}i}} R_{{\rm p}i}^{0.6}\left(\frac{d_i}{d_{{\rm m}}}\right)^{e_h},\\ &&\lambda_{\mbox{\scriptsize{E}}}=1-0.288\,\upsilon_{\rm s}\,, \label{5eq:entrain} \end{array}$$
(18)

with A = 1.3×10 − 7 as a constant and \(\lambda_{\mbox{\scriptsize{E}}}\) as a sorting-dependent straining parameter. Furthermore, c fi is a friction coefficient of grains in size class i and \(R_{{\rm p}i}~=~(g'd_i^3)^{1/2}/\nu\) is the particle Reynolds number of these grains, with g′ the reduced acceleration due to gravity and ν ∼ 1.36×10 − 6 m2 s − 1 the kinematic viscosity coefficient of water. Hiding effects are described by the last factor in the expression for Z i and involves the exponent e h .

The actual near-bed volume concentration c bi in Eq. 17 can be expressed in terms of the depth-integrated volumetric concentration \(\mathcal{C}_i\) by using that the dominant balance in the full 3D concentration equation is between the settling flux and the vertical turbulent diffusive flux and employing a standard formulation for the vertical eddy diffusivity. The result is

$$ c_{{\rm b}i}=\frac{\mathcal{C}_i}{\delta_i D}\,,\label{5eq:cbi} $$
(19)

with δ i the ratio of the thickness of the suspended load layer for grains of diameter d i and depth D. Parameter δ i is inversely proportional to the settling velocity, and it has typical values of order 0.2.

In the present model, it is assumed that

$$ \frac{c_{{\rm f}i}}{c_{f*}}=\left(\frac{d_i}{d_*}\right)^{e_f}, \qquad \frac{w_{{\rm s}*}}{w_{{\rm s}i}}=\left(\frac{d_i}{d_*}\right)^{-e_w},\label{5eq:rel1} $$
(20)

with d * as a constant reference grain size and c f*, w s* as the friction coefficient and settling velocity for that specific grain size. Likewise, using the definition for R pi and δ i , it follows

$$ \frac{R_{{\rm p}i}}{R_{p*}}=\left(\frac{d_i}{d_*}\right)^{3/2}, \qquad \frac{\delta_i}{\delta_*}=\frac{w_{{\rm s}*}}{w_{{\rm s}i}}.\label{5eq:rel2} $$
(21)

The entrainment of grains with size d i , as described by Eq. 18, involves four different effects. The factor \(\lambda_E^5 (d_i/d_{\rm m})^{5e_h}\) describes hiding effects. It accounts for the fact that (1) the entrainment of fine grains is tempered with respect to that of coarse grains and (2) a reduced entrainment of grains from both size classes for a poorly sorted sediment mixture compared to grains in uniform sediment due to a more efficient packing of the bottom sediment. Typically, e h  = 0.2 (Garcia and Parker 1991). The entrainment also depends on the particle Reynolds number and the settling velocity. As the settling velocity decreases with increasing grain size, both factors favor the entrainment of fine sediment over coarser sediment (which is opposite to the hiding effect). The formulation of Hallermeier (see Soulsby 1997) for fine to coarse sand yields e w  = 1.1. The final effect, which has not been considered in the context of sfcr, represents the dependence of the friction coefficient on the grain size. Following work on sorted bedforms by Murray and Thieler (2004), Coco et al. (2007a), and Huntley et al. (2008), it accounts for more vigorous turbulent motions and related increase of entrainment of sediment, above a rough (coarse) surface compared to a fine sediment surface. According to Murray and Thieler (2004), e f should be in the order of 1.

The boundary conditions for Eqs. 13 and 17 are that the bed level is fixed at x = 0 and far offshore and that \(\mathcal{C}_i\) is bounded far offshore.

3 Solution method

The initial growth of morphodynamic features is investigated by applying a linear stability analysis. It is a similar analysis to that employed in the early study by Trowbridge (1995), and it is based on the hypothesis that sfcr form as free morphodynamic instabilities of a basic state. As the initial growth is considered, equations are linearized. The basic state is discussed in Section 3.1 and the linearization procedure is outlined in Section 3.2.

3.1 Basic state

For a longshore uniform bottom profile z b = − H(x) without bedforms, the model allows for a basic state, which is steady and alongshore uniform (variables only depend on x). The solution for the waves and currents in this state is identical to that discussed in Vis-Star et al. (2007); hence, only the essential aspects are discussed here. The dispersion relation of the waves, Eq. 1, becomes

$$ \omega^2=gK\tanh \left(K H\right). $$
(22)

As ω is constant, the latter relates the basic state wavenumber K to water depth H. Expressions for the angle of wave incidence Θ and wave energy E in the basic state result from substitution of basis state variables in Eqs. 2–4. Likewise, the wave orbital velocity in the basic state follows from Eq. 6 and is given by

$$ U_w=\frac{\omega H_{\rm rms}}{2\sinh(K H)}, \qquad H_{\rm rms}^2=\frac{8 E}{\rho g}, $$
(23)

with H rms as the root-mean-square wave height in the basic state.

The cross-shore and alongshore momentum balance in the basic state describe a longshore current V(x), which is driven by an alongshore wind stress τ sy . Due to Coriolis effects, it induces a mean sea level Z(x). The magnitude of V is inversely related to the local wave orbital velocity due to frictional effects. There is no cross-shore velocity in the basic state, i.e., U = 0.

Next, we specify the basic state probabilities F i and F si of grains of class i in the active layer and in the substrate, respectively. Here, it is assumed that

$$ F_i=F_{{\rm s},i} \qquad (i=1,2) \,, $$
(24)

and F i can have any cross-shore distribution. Note that, for the present two-size sediment mixture, F 2 = 1 − F 1. The corresponding expressions for the mean grain diameter d m0, mean grain size Φm, and the standard deviation Υ s are derived from Eq. 12 and read

$$ \begin{array}{lcl} d_{{\rm m}0}&=&2^{-\Phi_{\rm m}}\,, \quad \Phi_{{\rm m}}= \phi_1 F_1 + \phi_2 F_2, \\ \Upsilon_{\rm s}^2 &=& F_1 F_2(\phi_1-\phi_2)^2. \end{array} $$
(25)

Substitution of the basic state variables in the concentration equations (Eq. 17) results in expressions for the depth-integrated volumetric suspended sediment concentrations C i (x) for the grain sizes i,

$$\label{5eq:basiccm} C_i=F_i \, \delta_i\, H\, E_{0i}\;,\qquad E_{0i}=A\, \Lambda_{\mbox{\scriptsize{E}}}^5\, Z_{0i}^5 \,\, U_w^5\,, $$
(26)

with

$$\label{5eq:rel3} \Lambda_{\mbox{\scriptsize{E}}}=1-0.288\, \Upsilon_{\rm s}\,,\quad Z_{0i}=\frac{\sqrt{c_{{\rm f}i}}}{w_{{\rm s}i}} R_{{\rm p}i}^{0.6}\left(\frac{d_i}{d_{{\rm m}0}}\right)^{e_h}\,. $$
(27)

For later use, it is convenient to rewrite the expressions (Eq. 26) for the sediment concentrations as

$$\label{5eq:cs} C_i=F_i G_{{\rm s}i} C_*\,, \qquad C_*=\delta_* H E_{0*}\,, $$
(28a)
$$ G_{{\rm s}i}= \left(\frac{d_i}{d_*}\right)^{c_{\rm s}}\,, \qquad c_{\rm s}=\frac{5}{2}e_f - 6e_w + \frac{9}{2}+5e_h\,, $$
(28b)

where definitions 20, 21, and 27 have been used and in which E 0* is the entrainment of sediment with grain diameter d *. This result shows that, in the case where F 1 = F 2 and c s < 0, the concentration of fine sediment is larger than that of the coarse sediment. Conversely, if c s > 0, there is more coarse than fine sediment in suspension.

It follows from Eqs. 15 and 16 that the total sediment transport in the basic state, Q i  = Q bi  + Q si , has a longshore component that is independent of y, and a nonconstant offshore-directed cross-shore component (due to the transverse bed slope). Here, the bed slope-induced sediment transport is neglected, as the change in bed level due to divergence of this transport is much slower (∼10 − 5 m year − 1) than the change in bed level of sfcr (∼10 − 2 m year − 1). Thus,

$$\label{5eq:basicq} \begin{array}{rcl} \mathbf{Q}_{{\rm b}i}&=&F_i G_{{\rm b}i} \mathbf{Q}_{\rm b} \simeq F_i G_{{\rm b}i} \frac{3}{2} \nu_{\rm b} U_w^2 V \mathbf{e}_y ,\\ \mathbf{Q}_{{\rm s}i} &\simeq& C_i V \mathbf{e}_y, \end{array} $$
(29)

where e y is a unit vector in the y-direction. Thus, to a good approximation, the basic state defines a morphodynamic equilibrium.

3.2 Linear stability analysis

The dynamics of small perturbations on the basic state is investigated in order to gain knowledge about the stability of these features. Hereafter, perturbed variables are denoted by primes. Hence, solutions are written as

$$ \begin{array}{rcl} &&\kappa\!=\!K(x)\!+\!\kappa' , \qquad \theta=\Theta(x) + \theta' , \qquad \;\;\mathcal{E}\!=\!E(x) \!+\! e',\\ && u_w\!=\!U_w(x)\!+\!u_w', \;\;\;u=u' \qquad \;\;\;\;\;\;\;\;\;\;\;\;\;\;v\!=\!V(x)+ v', \\ && z_{\rm s}\!=\! Z(x) \!+\! \eta', \qquad z_{\rm b}\!=\!-H(x)\!+\!h' , \qquad {\mathcal C}_i\!=\!C_i(x)\!+\!c_i' (i\!=\!1,\!2).\\ \end{array}$$
(30)

As the focus is on the initial growth of bedforms, the equations are linearized with respect to the small perturbations. The perturbed wavenumber κ′, angle of wave incidence θ′, wave energy e′, and wave orbital velocity u w ′ are functions of the bottom perturbation h′ and depend on x, y, and t. The final expressions are given in Appendix A, together with the linearized versions of equations for the perturbed flow.

Considering the sediment characteristics, perturbations are added to the probabilities that characterize the basic state, so that \(\mathcal{F}_i=F_i+f_i'\), the mean grain size ϕ m = Φm + φ m′, and standard deviation υ s = Υ s + υ s′. The constraint on the probabilities (Eq. 11), in its linearized form, reads

$$ f_1' =- f_2'. \label{5eq:constraint3} $$
(31)

The perturbations in the mean grain diameter, mean grain size, and standard deviation are expressed in f 1′ by using expressions 12 and 31,

$$\begin{array}{rcl} d_{\rm m}'&=&-\ln(2)\,d_{{\rm m}0}\,\phi'_{\rm m}, \qquad \phi'_{\rm m} =\frac{\Upsilon_{\rm s}}{\sqrt{ F_2 F_1} }\,f_1', \\ \upsilon_{\rm s}'&=&\frac{ \Upsilon_{\rm s} (F_2 - F_1) }{2 F_2 F_1} f_1'. \label{5eq:sigma1} \end{array} $$
(32)

Finally, the linearized versions of the mass balance equations of sediment of class i are derived. Substitution variables containing a basic state part and perturbations into Eq. 13 yields, after linearization,

$$ (1\!-\!p)\left(F_i\,\frac{\partial h'}{\partial t} \!+\! L_{\rm a}\,\frac{\partial f'_i}{\partial t}\right)\!=\! -{\boldsymbol{\nabla}}\cdot{\mathbf q}'_i \,, \quad i\!=\!1,2 \,. $$
(33)

This equation shows that, during the initial growth stage of bedforms, only rearrangement occurs of material in the active layer, i.e., the interaction between the substrate and the active layer is negligible. From the result above, two equations can be derived which govern the time evolution of the perturbed bed level h′ and the fraction f′1 of fine sediment. The first follows by adding the mass balances for i = 1 and i = 2 and using the constraints F 1 + F 2 = 1, f′2 = − f′1. The second follows by back-substitution of these results into the mass balance for class i. The results are

$$ \left(1-p\right)\frac{\partial h'}{\partial t}=-{\boldsymbol{\nabla}} \cdot \mathbf{q}_1\,'-{\boldsymbol{\nabla}} \cdot \mathbf{q}_2\,',\label{5eq:p1} $$
(34a)
$$\label{5eq} 0=F_1\, {\boldsymbol{\nabla}} \cdot \mathbf{q}_2\,'- F_2\, {\boldsymbol{\nabla}} \cdot \mathbf{q}_1\,'. $$
(34b)

Note that, in the second equation, the term involving the time derivative of f′1 has been neglected, as its magnitude is much smaller than that of the terms on the right-hand side. Expressions for q 1 ′ and q 2 ′ are given in Appendix B.

The system of linear equations can be symbolically written as

$$\label{5eq:linfull} {\bf S}\cdot\frac{\partial}{\partial t}\bf{\Psi} \,=\, \bf{\cal L}\cdot\bf\Psi \,, $$
(35)

where \(\bf\Psi\!=\!(\kappa',\theta',e',u'_w,u',v',\eta',c'_1,c'_2,f'_1,h')^T\) is a vector of state variables, S is an 11×11 matrix of which all elements are zero, except S(11,11) = (1 − p), and \(\bf{\mathcal L}\) is a linear matrix operator. The corresponding boundary conditions are u′, h′ →0 for x → ∞ and u′ = 0, h′ = 0 at x = 0. This system allows for solutions that represent waves that travel along the coast and of which the amplitude may exponentially grow (or damp) in time,

$$\label{5eq:periodic} \bf\Psi\,=\,\Re \mathrm{e} \left\{\bf{\hat{\Psi}}(x)\, e^{iky+\sigma t}\right\}. $$
(36)

Here, \(\Re\mathrm{e}\) denotes the real part of the solution, k denotes the longshore wavenumber (which can be assigned any value), the hat denotes the as yet unknown cross-shore structure of the solutions, and σ denotes the complex frequency. The growth rate and migration speed of the perturbations are given by the complex frequency (σ = σ r  + i σ i ). The real part σ r is the growth rate and the migration speed is given by V m = − σ i /k. If, for specific choices of the model parameters, σ r  < 0 for all k, the basic state is stable. The basic state is unstable if there is a range of wavenumbers k for which σ r  > 0. The mode that has the largest growth rate is called the fastest growing or most preferred mode. The inverse of the growth rate σ r gives a characteristic time scale for the formation in nature (called the e-folding growth time T g ).

To calculate the growth rates, the solutions (Eq. 36) are substituted into system 35, which results in

$$\label{5eq:linred} \sigma\,{\bf S}\cdot\bf{\hat\Psi} \,=\, {\bf L}_k\cdot\bf{\hat\Psi} \,. $$
(37)

Matrix operator L k follows from matrix operator \(\bf{\mathcal L}\) by replacing derivatives \(\partial/\partial y\) by ik. The system (Eq. 37), together with the boundary conditions, defines a generalized eigenvalue problem, with σ as the eigenvalues and \({\bf{\hat\Psi(x)}}\) as the corresponding eigenfunctions.

Solutions of this eigenvalue problem were obtained numerically using a spectral collocation method. This method involves an expansion of variables in Chebyshev polynomials, and it is subsequently imposed that the equations are exactly obeyed at N collocation points (for details, see Boyd 2001).

4 Results

4.1 Parameter values: default case

Parameter values are representative for the Long Island inner shelf and are partly taken from Figueiredo et al. (1982) and Schwab et al. (2000). Long Island is located along the Atlantic coast of North America at a latitude of ∼40° N, for which the Coriolis parameter is f = 1×10 − 4 s − 1. Going seaward, the depth of the inner shelf increases from H 0 = 14 m to H s = 20 m, and the inner shelf width is L s = 5.5 km. Therefore, the transverse bottom slope is \(\beta=(H_{\rm s}-H_0)/L_{\rm s} \sim 1.1\times10^{-3}\). Typical values for the offshore root-mean-square wave height, offshore angle of wave incidence, wave period, and alongshore wind stress are H rms,s = 1.5 m, \(\Theta_{{\rm s}}=-20^\circ\), T = 11 s, and τ sy  = − 0.4 N m − 2 (southward), respectively. In the default experiment, a uniform fraction of fine and coarse sand is used: F 1 = 0.7 and F 2 = 0.3. Furthermore, a mean grain size d m = 0.35 mm (Φm = 1.5) is adopted with a sorting parameter Υ s = 0.5. For the exponent in the transport capacity function for bedload, c b = 0.75 is used. In Eqs. 18–20, e h  = 0.2, e w  = 1.1, and e f  = 0 are chosen, such that in Eq. 28a, for the sediment concentration in the basic state, the exponent c s = − 1.1. Note that roughness-induced turbulence effects are neglected for the moment. Values of the other parameters are: r = 2.0×10 − 3, \(\nu_{\rm b}=5.6\times10^{-5}\) s2 m − 1, λ b = 0.65, λ s = 0.30 s m − 1, w s* = 0.04 m s − 1, \(E_{0*}=1.3\times10^{-4}\), \(\delta_*=0.20, c_{f*}=3.5\cdot 10^{-3}\), and p = 0.4. In the computations, 160 collocation points were used.

4.2 Basic state and linear stability analysis: default case

In this section, solutions of the morphodynamic (eigenvalue) problem are presented for the parameter values specified in the previous section. The characteristics of the basic state were already discussed in Vis-Star et al. (2007). In particular, the wave orbital velocity U w decreases monotonically with increasing depth (U w (x = 0) = 0.54 ms − 1, U w (x = L s) = 0.40 ms − 1). The longshore current V points in the negative y direction and its magnitude increases with increasing depth (V(x = 0) = − 0.36 ms − 1, V(x = L s) = − 0.48 ms − 1) since it experiences less bottom friction for larger depth.

The growth rates and migration velocities for the default case as a function of the longshore wavenumber are shown in Fig. 3a and b, respectively. Sfcr, for which a maximum growth rate is attained, have a wavelength \(\lambda_p=2 \pi k_p^{-1}\sim2.7\) km. The corresponding e-folding time scale for the initial growth is about 180 years. The sfcr migrate with a speed of 48 m year − 1 in the downstream direction.

Fig. 3
figure 3

Growth rates (a) and migration velocities (b) as a function of the longshore wavenumber, default case. The most preferred mode (with wavenumber k = k p ) is indicated by the dashed black lines. c Bottom pattern (grayscale; light: crests, dark: troughs) and perturbations in the distribution of the mean grain size (contours; solid lines: finer; dashed lines: coarser) for the most preferred mode. The dashed white lines indicate the position of normal and longshore cross-sections through the sfcr, which are shown in Fig. 4. The arrow indicates the direction of the basic state longshore velocity

Full size image

In Fig. 3c, the bottom pattern of the initially fastest growing mode is shown. In this figure, the basic state velocity is directed from top to bottom, and thus, sfcr are characterized by an up-current orientation. The sfcr extend approximately 1 km offshore. Furthermore, the contour lines indicate the distribution of the fine and coarse sediment over the sfcr. They reveal that the grain size distribution is approximately 180° out of phase with the ridge topography: the finest sediment is found slightly upstream of the troughs. The latter is confirmed by the normal and longshore cross-sections through the sfcr (see Fig. 4), which show the bottom topography and perturbed fraction of fine grains along the dashed white lines in Fig. 3c.

Fig. 4
figure 4

Normal (a) and longshore (b) cross-section through the sfcr in Fig. 3c at the location of the white dashed lines. Shown are perturbations in bottom h′ and in the fraction of fine grains f 1′ (or similar, in mean grain size ϕ m′). Quantities are scaled by their maximum values

Full size image

The ratio of the maximum variation in the perturbed fraction of fine grains and the maximum variation in the bottom topography is [f 1′]/[h′] ∼0.56 /H 0 . Thus, in the case of a ridge of 2 m in height, the variation in the fraction of fine grains will be ∼0.1. For diameters of the fine and coarse grains of 0.28 and 0.59 mm, respectively (as in the default case), this corresponds to a total variation in the mean grain size of approximately 0.05 mm.

As long as F 1 ≠ F 2, Eq. 32 indicates that υ s′ ≠ 0, and thus, changes in the standard deviation of the sediment mixture occur. Shore-normal and alongshore cross-sections of the bottom topography and perturbed standard deviation are shown in Fig. 5. Clearly, the (finer) sediment, which is located in the troughs, is better sorted (υ s′ < 0) than the (coarser) sediment on the crests. The ratio of the maximum variation in the perturbed sediment sorting and the maximum variation in the bottom topography is [υ s′]/[h′] ∼0.26 /H 0. Thus, in the case of a ridge of 2 m in height, the variation in sediment sorting will be ∼0.05, which is approximately a 10% change with respect to the basic state sediment sorting of 0.5.

Fig. 5
figure 5

Normal (a) and longshore (b) cross-section through the sfcr in Fig. 3c at the location of the white dashed lines. Shown are perturbations in bottom h′ and in the standard deviation υ s′. Quantities are scaled by their maximum values

Full size image

4.3 Sensitivity to settling lag effects

In order to investigate the sensitivity of results to settling lag effects in the concentration equation, the parameter δ * was varied. The importance of settling lag effects is, among other things, dependent on the grain size of the sand that is considered: the smaller the grain size, the stronger the settling lag effects. Results are shown in Fig. 6 for a case in which settling lag effects are not taken into account, a case in which δ * has its default value and a case in which δ * has a value being twice the default one.

Fig. 6
figure 6

Growth rates (a) and migration velocities (b) as a function of the longshore wavenumber to show sensitivity of model results to settling lag effects. The dotted curve is the result in case that settling lag effects are neglected, the straight curve represents the default experiment, and the dashed curve is the result in case of a δ * that is twice as large as in the default experiment

Full size image

Experiments reveal that settling lag effects are crucial for the damping of high wavenumber perturbations. Furthermore, growth rates become considerably smaller when settling effects are included, whereas migration speeds are hardly affected. The mean grain size and sorting pattern is not affected by settling lag effects. On the other hand, the ratio of the maximum variation in the perturbed mean grain size/sediment sorting and the maximum variation in the bottom topography slightly decreases when settling lag effects become more important.

4.4 Sensitivity to sediment characteristics

Experiments were conducted to explore the sensitivity of model results to different values of the standard deviation of the sediment mixture. For a fixed fraction of the fine and coarse sediment in the mixture and for a fixed mean grain size (default values), the standard deviation of the mixture was varied between zero and one. Thus, in the case where Υ s = 0.0, sediment is uniform with a grain size d 1 = d 2 = 0.35 mm, whereas for, e.g., Υ s = 1.0, sediment is nonuniform with d 1 = 0.22 mm and d 2 = 1.0 mm.

Results (shown in Fig. 7) indicate that a poorly sorted sediment mixture (large Υ s) causes sfcr to grow slower compared to sfcr composed of a well-sorted mixture. With an increase in standard deviation, the total transport of the two grain sizes in a mixture is reduced. The latter can be interpreted as the result of a more efficient packing of the bottom material when grains of different sizes are present. Also, a decrease in the migration speed of the most preferred mode is found when Υ s is increased. An interpretation of the results will be given in Section 5.

Fig. 7
figure 7

Contour plots of equal a growth rate (10 − 2 year − 1) and b migration speed (m year − 1) of the initially most preferred mode in the k − Υ s plane. All other parameter values, except those of d 1 and d 2, are as in the default case

Full size image

Figure 8 shows that the longshore spacing of the most preferred mode does not change significantly if the value of Υ s is varied. The change in e-folding growth time (thus, in growth rate) is about a factor 3.5, and the change in migration speed is about a factor 4 over the complete range of standard deviation Υ s. The bottom pattern of the most preferred mode remains unaltered if the standard deviation of the mixture is varied and is similar to that in Fig. 3c. The same holds for the locations of the maxima and minima in the mean grain size: a persistent 180° phase shift between the perturbed topography and the perturbed mean grain size is found.

Fig. 8
figure 8

Longshore spacing (a), e-folding growth time (b), and migration speed (c) of the initially fastest growing mode as a function of the standard deviation Υ s of the sediment mixture. All other parameter values, except for d 1 and d 2, are as in the default case. The uncertainty in longshore spacing is indicated with the error bars. Uncertainties in the e-folding time and migration speed are very small, so no error bars are shown

Full size image

The influence of the relative weight percentage of the grains in the coarse and fine size class on the characteristics of sfcr was investigated. For a fixed mean grain size and standard deviation of the mixture (default values), the fraction of fine grains was varied such that 0.1 ≤ F 1 ≤ 0.9 (if F 1 equals 0 or 1, sediment is uniform). In the case where F 1 = 0.1, this means considering a sediment mixture with d 1 = 0.12 mm and d 2 = 0.39 mm, whereas for, e.g., F 1 = 0.9, the fine particles have a diameter d 1 = 0.31 mm and the coarse particles a diameter d 2 = 0.99 mm. Results (shown in Fig. 9) indicate that a larger fraction of fine grains does not significantly influence the wavelength of the preferred mode, but it has a stabilizing effect on growth rates and migration speeds. The change in e-folding growth time and migration speed is about a factor 1.5 over the entire range of values of probability F 1. The cross-shore extent of the bottom patterns slightly decreases with an increase in F 1. The distribution of the mean grain size is not affected by changing the value of probability F 1. However, the sorting pattern is affected (results not shown): for F 1 > 0.5, the sediment is best sorted in the troughs, whereas for F 1 < 0.5, the best sorted sediment is found on the crests. In the case where F 1 = F 2 = 0.5, the sediment sorting is equal to that of the basic state in the whole domain.

Fig. 9
figure 9

Longshore spacing (a), e-folding growth time (b), and migration speed (c) of the initially fastest growing mode as a function of the fraction of fine grains F 1 of the sediment mixture. The uncertainty in longshore spacing is indicated with the error bars. Uncertainties in the e-folding time and migration speed are very small, so no error bars are shown

Full size image

Also, the mean grain size d m0 was varied. Keeping all the other parameters at their default values, a mean grain size of d m0 = 0.20 mm implies that d 1 = 0.16 mm and d 2 = 0.34 mm. A mixture with a mean grain size of d m0 = 0.60 mm consists of small grains with a diameter d 1 = 0.48 mm and coarse grains of diameter d 2 = 1.02 mm. Results are summarized in Table 1. Within the present parameter setting, the sediment mixture requires a mean grain size d m0 > 0.20 mm to obtain the growth of sfcr. Once this threshold is exceeded, an increase in the mean grain size results in an increase in growth rate and a decrease in migration speed. Furthermore, a reduction in alongshore spacing between successive crests and a decrease in the cross-shore extent of sfcr is obtained for an increase in d m0. Neither the phase shift between sfcr and perturbations in the mean grain size nor the sorting pattern are affected by the mean grain size of the mixture.

Table 1 Bedform characteristics (longshore spacing, cross-shore extent, growth rate, e-folding growth time, migration speed, H 0 [f 1′]/[h′], and H 0 [υ s′]/[h′]) of the initially fastest growing mode as a function of the mean grain diameter d m0 of the sediment mixture
Full size table

In the previous experiments, it was assumed that the basic state properties of the sediment mixture (grain size distribution function, mean grain size, and standard deviation) have a fixed value in space. However, observations indicate that, often, sediment becomes finer as it goes offshore. To investigate the effect of an x-dependent sediment distribution, a run was performed for a grain size fraction, which is linear dependent on x: F 1 = 0.5 at the shoreface to F 1 = 0.8 at the transition to the outer shelf. The grain size of both the coarse and fine fractions are the same as in the default experiment. Thus, the mean grain size and the sorting parameter are also dependent on the cross-shore position. Results (not shown) indicate that bedform characteristics are hardly affected by including x-dependent sediment properties. The sorting pattern will change as soon as F 1 < F 2 in that part of the domain where sfcr are situated: the sediment is finer and more poorly sorted in the troughs, whilst it is coarser and better sorted on the crests.

4.5 Sensitivity to hiding and roughness-induced turbulence

In this section, the effect of including a grain-size-dependent friction coefficient in the sediment transport is investigated. Thus, parameter e h in Eq. 18 was changed from e h  = 0 into e h  = 1.0. Consequently, parameter c s in Eq. 28a changed from a negative value (c s = − 1.1) into a positive value (c s = 1.4). Figure 10 shows the growth rates and migration velocities as a function of the longshore wavenumber.

Fig. 10
figure 10

As Fig. 3, but now, e h  = 1, so that entrainment of sediment depends on bottom roughness. The white dashed lines in c indicate the position of normal and longshore cross-sections through the sfcr, which are shown in Fig. 11. Here, entrainment of sediment depends on bottom roughness such that c s = 1.4

Full size image

A maximum growth rate of about 0.66×10 − 2 year − 1 is found for k = k p ∼2.4 km − 1, which corresponds to a longshore wavelength of the bedforms of ∼2.7 km. This initially most preferred mode migrates with a speed of ∼65 m year − 1 in the downstream (southward) direction. Taking into account roughness-induced turbulence effects thus leads to an increase in growth rates and a slight increase in migration speeds. The bottom pattern of the most preferred mode is shown in Fig. 10c and shows up-current-oriented sfcr that extend approximately 1 km offshore. The contour lines in this figure indicate the perturbations in the distribution of the mean grain size. Clearly, including roughness-induced turbulence effects leads to a change in the phase difference between the ridge topography and grain size distribution: the finest sediment is found slightly up-current of the crests instead of the troughs. The ratio of the maximum variation in f 1′ and the maximum variation in h′ increases to become [f 1′]/[h′] ∼0.84/H 0.

Cross-sections of the bottom perturbations and perturbations in the standard deviation of the sediment mixture are given in Fig. 11. Clearly, the (finer) sediment, which is located on the crests, is better sorted (υ s′ < 0) than the (coarser) sediment in the troughs. The ratio of the maximum variation in the perturbed sediment sorting and the maximum variation in the bottom topography [υ s′]/[h′] ∼0.41 /H 0 and is larger compared to the case where roughness-induced turbulence effects were neglected.

Fig. 11
figure 11

Normal (a) and longshore (b) cross-section through the sfcr in Fig. 10 at the location of the white dashed lines. Shown are perturbations in bottom h′ and in the standard deviation υ s′. Quantities are scaled by their maximum values. Here, entrainment of sediment depends on bottom roughness such that c s = 1.4

Full size image

4.6 Sensitivity to other model parameters

The dependence of results on wave height, wave period, and angle of wave incidence at the offshore boundary was investigated, as well as the dependence on the water depth H s at the outer shelf. The resulting trends in the growth rate, migration speed, and shape of bedforms are similar to those reported by Vis-Star et al. (2007). The phase shift between maxima in f 1′ and h′ is very robust (180°) under changes in offshore wave properties

Finally, the dependence of model results on the bed slope parameter λ s in Eq. 16 was investigated. It turns out that, with decreasing values of λ s→0, the sfcr become shorter and they grow faster. In the limit, λ s→0, i.e., suspended load transport is not affected by the presence of bed slopes, the ridges grow a factor of 2 larger than in the default case, and their wavelengths are 20% smaller.

5 Discussion

5.1 Physical interpretation

A physical interpretation of the results presented so far will be given in this section. The growth of sfcr in the present model is due to three different mechanisms. The first mechanism was already described by Trowbridge (1995), in which the offshore deflection of the storm-driven flow over sfcr for a transversely sloping bottom of the inner shelf is essential. The second is the one described by Calvete et al. (2001), which involves both the offshore deflection of the current over sfcr and cross-shore gradients in the depth-averaged volumetric suspended sediment concentration in the basic state. The third mechanism was found most recently and described by Vis-Star et al. (2007) as the wave–bedform feedback mechanism. The up-current-oriented sfcr affect the wave field in such a way that wave rays converge on the upstream sides of sfcr. As a result, the perturbed wave energy in these areas increases, and stirring of sediment by waves is enhanced. Subsequently, the storm-driven flow transports the additional sediment as suspended load downstream. The third mechanism is more effective than the first two in the case of obliquely incident waves and even active in the absence of a transversely sloping bed. Both growth and migration of sfcr are controlled by suspended load transport of sediment in the case of the wave–bedform feedback mechanism. Below, an explanation is given of (1) the damping of high wavenumber perturbations due to settling lag effects, (2) the distribution of the mean grain size and standard deviation over sfcr, and (3) the sensitivity of model results to changes in characteristics of the sediment mixture.

5.1.1 Damping of high wavenumber perturbations due to settling lag effects

For small-scale (high wavenumber) perturbations, the terms in the concentration equation (Eq. 54) involving y derivatives constitute the major balance; thus,

$$\label{5eq:cmslag} c_i'\simeq -\frac{C_{\rm m}}{H}h'. $$
(38)

As the left-hand side of this equation defines the divergence of suspended load transport of class i, it follows

$$ {\boldsymbol{\nabla}} \cdot \mathbf{q}'_{{\rm s}i}=\frac{w_{{\rm s}i}\, C_i}{\delta_i \,H}\left(M_3\, f'_1 + \frac{5u'_w}{U_w} + \frac{f'_i}{F_i}\right)\,, $$
(39)

with

$$ M_3 =5 \Upsilon_{\rm s}\left(\frac{e_h\ln2}{\sqrt{F_1 F_2}} + \frac{0.288 (F_1-F_2)}{2\Lambda_{\mbox{\scriptsize{E}}} F_1F_2}\right). $$

The divergence of the suspended load transport of both classes thus becomes

$$ {\boldsymbol{\nabla}} \cdot\left( \mathbf{q}'_{{\rm s}1}+\mathbf{q}'_{{\rm s}2}\right)\,=\, \frac{w_{{\rm s}*}\,C_*}{\delta_*\, H}\left(B_1\frac{u'_w}{U_w}+B_2\,f'_1\right)\,, $$
(40)

with

$$\begin{array}{rcl} &&B_1=5\sum\limits_{i=1}^2 \left(\frac{d_i}{d_*}\right)^{2e_w} F_i G_{{\rm s}i},\\ &&B_2=\sum\limits_{i=1}^2 \left(\frac{d_i}{d_*}\right)^{2e_w}G_{{\rm s}i}\left(M_3F_i + (-1)^{i-1}\right)\,. \end{array} $$
(41)

For the default parameter values, B 1 is positive, B 2 is negative, u w ′ ∝ h′, and f′1 ∝ − h′. As a consequence, at the crests (h′ > 0), the suspended load transport is divergent, which explains that high wavenumber perturbations are more effectively damped when settling lag effects are included. This result is consistent with results obtained by Schramkowski et al. (2002) for local bedforms in tidal embayments. They argue that, for long-wave perturbations, the sediment dynamics can be approximated by a balance between erosion and deposition. However, in the case of short-wave perturbations, the advective contributions to the sediment concentration cannot be neglected and have a stabilizing effect.

5.1.2 Distribution of the mean grain size and standard deviation over sfcr

To understand the distribution of the mean grain size and sorting of sediment over the bedforms, the evolution equation (Eq. 34b) for the perturbed fraction of fine sand is analyzed. In the case where only suspended load transport is considered (it dominates over bedload transport), bed slope effects are neglected and F 1 and F 2 are constants, it reduces to

$$\begin{array}{rcl}\label{5eq:fog2} &&M_1\left(H\frac{d}{dx}\left(\frac{C_*}{H}\right)u'+5\frac{V C_*}{U_w}\frac{\partial u_w'}{\partial y}\right)\\ && = V C_* \left(M_2+M_1 M_3\right)\frac{\partial f_1'}{\partial y}, \end{array} $$
(42)

where

$$\begin{array}{rcl} M_1 &=& F_1F_2(G_{{\rm s}1}- G_{{\rm s}2}),\\ M_2 &=& F_2G_{{\rm s}1}+ F_1 G_{{\rm s}2} . \end{array} $$
(43)

To derive this result, expression 28a for the concentrations C i (x) in the basic state has been used. Also, since settling lag effects are ignored, the terms on the left-hand side of Eq. 54 for the perturbed sediment concentrations vanish, so that these equations describe a balance between erosion and deposition of sediment.

In Eq. 42 above, V < 0 (southward) and the cross-shore gradient in the depth-averaged volumetric suspended sediment concentration C */H is negative, i.e., d/dx (C */H) < 0. In the default case, e h  = 0 and c s < 0; hence, in the basic state, the suspended sediment concentration of fine sediment is larger than that of coarse sediment (G s1 > G s2). This implies that parameter M 1 is positive. Furthermore, (M 2 + M 1 M 3) is positive for default parameter values.

The distribution of the mean grain size over the bedforms is dependent on the relative magnitude of the two terms on the left-hand side of Eq. 42. In previous work, only the term related to u′ was present, as interactions between bedforms and waves were ignored. In that case, the distribution of the fraction of fine grains is related to the perturbed cross-shore velocity. Trowbridge (1995) already showed that u′ > 0 if h′ > 0. Hence, \(\partial f_1'/\partial y \propto -u' \propto -h'\). As a consequence, the distribution of the mean grain size for suspended load is 90° out of phase with the topography such that the finer sand is found on the seaward (down-current) flank of sfcr. In this paper, wave–bedform interactions are included and appear to play a dominant role in both the evolution of the bottom and the mean grain size. Thus, the term proportional to \(\partial u_w'/\partial y\) dominates over the term proportional to u′ in Eq. 42. It follows immediately that f 1′ ∝ − u w ′. The study by Vis-Star et al. (2007) revealed that the pattern of the perturbed wave orbital velocity is slightly shifted up-current with respect to that of the bottom. Thus, an approximate 180° phase shift exists between the pattern of the mean grain size for suspended load and the topography. According to Eq. 32, υ s′ ∝ − f 1′ for F 1 > F 2, and thus, the perturbed sorting of sediment is in phase with the topography. This explains the results shown in Section 4.2, where the finer and better-sorted sediment is found in the troughs and the coarser and more poorly sorted sediment on the crests.

As was shown in Section 4.5, including roughness-induced turbulence effects leads to a change in the phase difference between the perturbed mean grain size and the bedforms. Roughness-induced turbulence effects cause c s to become positive, which implies that G s1 < G s2 and, thus, M 1 < 0. The sign of (M 2 + M 1 M 3) does not change and is still positive. Therefore, the balance in Eq. 42 becomes f 1′ ∝ u w ′ ∝ h′ due to the wave–bedform feedback mechanism. This explains the 0° phase shift between the bottom and mean grain size pattern, as obtained in Section 4.5. The finer (coarser) sediment, which is now located on the crests (in the troughs), is still better (more poorly) sorted, as υ s′ ∝ − f 1′ still holds.

5.1.3 Sensitivity results to changes in sediment characteristics

For a bimodal sediment mixture compared to uniform sediment, both the growth rate and migration speed of sfcr decrease if the standard deviation is increased (see Fig. 7). The latter is caused by a reduction of the entrainment of both fine and coarse sediment due to a better packing of the sediment for a more poorly sorted sediment mixture (which is represented by the straining factor \(\lambda_{\mbox{\scriptsize{E}}}\) in the entrainment of sediment). In case that wave–bedform feedbacks are important, both growth and migration are controlled by suspended load transport and, thus, reduce with an increase in the standard deviation of the sediment mixture. Note that the decrease in migration speed with increase in standard deviation of the mixture is in contrast with previous results (Walgreen et al. 2003), which is due to the fact that, in their case, the migration speed was determined by bedload transport due to the neglect of wave–bedform interactions.

Figure 9 reveals that growth rates and migration speeds become smaller if the fraction F 1 of fine sediment is increased. This is because a larger F 1, while keeping the standard deviation of the mixture fixed, implies a larger difference between the grain sizes of the coarse and fine sediment, and thus, hiding effects are more effective. Finally, the finding that growth of sfcr requires a minimum mean grain size of the sediment mixture (Table 1) is due to the fact that a smaller mean grain size causes settling lag effects in the concentration equation to become larger with respect to deposition and erosion terms. Thus, if the mean grain size is decreased, a more effective damping of all bottom perturbations occurs.

5.2 Comparison with observations

Most field data on sfcr, including sfcr on the Long Island shelf, reveal a phase difference of approximately 90° between the mean grain size and the topography: the coarsest sand appears on the landward (up-current) flank and the finest sediment on the seaward (down-current) flank. However, the modeled phase shift between the pattern of the mean grain size and the bottom topography for the default case is 180°: troughs (crests) consist of the finest (coarsest) sediment. The latter is attributed to the importance of wave–bedform interactions. The 180° phase difference between f 1′ and h′ is quite robust. It only changes when the hiding coefficient for suspended load transport c s becomes positive, which is the case when the grain size dependency of the friction coefficient is taken into account. In that case, the mean grain size and topography are approximately in phase, with the finest sediment on the crests and coarsest sediment in the troughs. Notice that, for some of the sfcr, a phase shift between the mean grain size and topography is observed that is different from 90°. According to Hoogendoorn and Dalrymple (1986), the finest sediment is observed at the base of the downstream flanks of the Canadian sfcr, which seems to indicate a phase shift close to 180°. Figueiredo (1980) reports for the ridges on the inner shelf of southern Brazil that the coarse sediment is found in the troughs and the medium to fine sand appears on the ridge crests, thus implying a 0° phase shift. Grain size variations are also observed over other type of bedforms. Miselis and McNinch (2006) report for nearshore oblique bars of North Carolina that the coarser sediment almost always appears in the troughs. Both 0° and 180° phase shifts between mean grain size and topography are observed for tidal sand waves in the southern North Sea (Roos et al. 2007).

A considerable improvement with respect to Walgreen et al. (2003) is that the modeled maximum variation in the fraction of fine and coarse sediment over sfcr has increased. The latter is contributed to the fact that interactions between waves and the topography are included. According to model results in case c s < 0, variations in the mean grain size d m are ∼0.02 [h′] mm. For heights of sfcr h′∼1 − 6 m (observed values), the mean grain size would vary between 0.02 mm and 0.12 mm. These values become slightly higher for simulations with c s > 0: grain size variations are 0.03–0.18 mm. Observations (e.g., Schwab et al. 2000, for the Long Island shelf) suggest that the variation in the mean grain size is in the order of 0.25–0.40 mm. Inspection of grain size variations on other shelves, as presented in Swift et al. (1978) and Stubblefield and Swift (1981), reveals grain size variations in the range of 0.05–0.65 mm. Thus, modeled grain size variations are slightly smaller than observed, but seem to be the right order of magnitude.

In literature, mostly qualitative information is given about variations in the standard deviation of sand over sfcr. For sfcr in general, including the sfcr on the Long Island shelf, sediment is best sorted on the crest and most poorly sorted in the troughs (Swift et al. 1972, 1978; Schwab et al. 2000). Data from sfcr in the German Bight (Antia 1993) indicate a better degree of sorting on the downstream flank. In the model, F 1 > F 2, which implies that υ s′ ∝ − f 1′ (see Eq. 32). Thus, the finer sediment (f 1′ > 0) is better sorted (υ s′ < 0). Therefore, model results for which the friction coefficient is grain-size-dependent (c s > 0) are in best agreement with the data for Long Island.

5.3 Model simplifications

The model used in this paper is based on several simplifying assumptions. First, a linear stability analysis is employed, which only yields information about the initial growth of and grain sorting over sfcr. If wave–bedform feedbacks are taken into account, both growth and migration of sfcr are still controlled by suspended load transport. However, in the case of finite-amplitude bedforms, exchanges of sediment between the active layer and the underlying substrate will occur, and they will probably have profound implications for the dynamics of the ridges.

In recent years, studies by Murray and Thieler (2004), Coco et al. (2007a, b), and Huntley et al. (2008) have focused on investigating so-called “sorted bedforms,” which are particularly found on sediment-starved shoreface and inner shelf environments. The sorted bedforms are found in very poorly sorted sediment mixtures, and a robust phase shift of 90° between f 1′ and h′ is observed. Inspired by their work, the effect of including the term \(L_{a0}\frac{\partial f_1'}{\partial t}\), which was excluded on the left-hand side of Eq. 34b, was investigated. This term defines the adjustment time scale of the grain size distribution to bottom changes, which, in general, will be very small for sfcr. For the default model setting, the thickness of the active layer in the basic state is \(L_{a0}=d_{\rm m} 2^{\Upsilon_{\rm s}}\sim 5\times10^{-4}\) m. In additional simulations, the latter was increased to a value of ∼3 m, which is the value used for sorted bedforms. The distribution of the mean grain size and standard deviation over sfcr was not affected. Only increasing L a0 up to about 10 m would change the phase shift between h′ and f 1′ from 180° to 0°. However, this is certainly not realistic for sfcr.

6 Conclusions

The main objective of the present study was to obtain a better understanding of the initial formation of sfcr and the corresponding grain size distribution. For this, a model was developed and analyzed, which consists of the depth-averaged shallow water equations, a sediment transport formulation, and mass balance of sediment. A new aspect in the hydrodynamic module (with respect to previous studies on sfcr) is that the behavior of waves is described by equations, which follow from physical principles, rather than by parameterizations. The inclusion of feedbacks between the growing bedforms and the waves is important. The sediment is represented by two grain size classes. The important new aspects in the sediment transport module are that the entrainment of suspended sediment depends on bottom roughness, and settling lag effects are included in the sediment concentration equation.

Default model experiments for a setting that resembles the Long Island micro-tidal inner shelf show that the growth and migration of sfcr stabilizes for a bimodal sediment mixture compared to uniform sediment. Furthermore, results reveal the presence of the finer sand approximately in the troughs and the coarser sand slightly up-current of the crests. In the case where roughness-induced turbulence effects are taken into account in the suspended sediment transport, the trend is the opposite: the coarser sand is located in the troughs and the finer sand on the crests. Both results are not in agreement with field data for the Long Island sfcr in which the coarsest sand is found on the landward flank and the finest sand on the seaward flank. However, field data on, e.g., Canadian and Brazilian sfcr, and also on some other types of bedforms, reveal that, often, coarse sediment is observed in the troughs. An interesting model result is that the modeled maximum variation in the probabilities of fine and coarse sediment over the sfcr has the right order of magnitude (10 − 1 mm). The inclusion of wave–bedform interactions is crucial here.

A physical analysis has revealed that the phase shift between the mean grain size and the bottom topography obtained by the model is due to the wave–bedform feedback mechanism. It causes convergence of wave rays at the upstream sides of sfcr and, thus, results in enhanced stirring of sediment by waves at these locations. In the case where roughness-induced turbulence effects are neglected, the additional entrainment of grains is more effective for grains of size smaller than the mean compared to grains of size larger than the mean. Thus, more fine than coarse sand is eroded from the crests, and therefore, the crests become coarser. On the other hand, more fine than coarse sand is deposited in the troughs where wave energy is reduced, which results in troughs consisting of finer sand. In the case where the friction coefficient is dependent on the physical roughness of the seabed, results are fundamentally different. Due to a change in grain size and ripple size from the coarse to fine domains, the physical roughness of the seabed is larger (smaller) in areas where the sediment is relatively coarse (fine). Including this effect, the entrainment of grains of size larger than the mean is enhanced compared to the entrainment of grains of size smaller than the mean: troughs become coarser and crests become finer. Furthermore, the effects of settling lag are crucial to cause damping of small-scale perturbations.