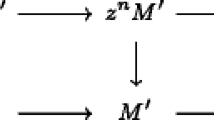Hilbert polynomial of length functions

Abstract

Let $\lambda$ be a general length function for modules over a Noetherian ring R. We use $\lambda$ to introduce Hilbert series and polynomials for R[X]-modules, measuring the growth rate of $\lambda$. We show that the leading term $\mu$ of the Hilbert polynomial is an invariant of the module, which refines both the algebraic entropy and the receptive algebraic entropy; its degree is a suitable notion of dimension for R[X]-modules. Similar to algebraic entropy, $\mu$ in general is not additive for exact sequences of R[X]-modules: we demonstrate how to adapt certain entropy constructions to this new invariant. We also consider multi-variate versions of the Hilbert polynomial.

1 Introduction

Let R be a commutative ring with unity; for this introduction and most of the article R will be Noetherian.

A generalized length function on the category ${{\,\mathrm{ R\mathrm -mod}\,}}$ of R-modules is a function

$$\begin{aligned} \lambda : {{\,\mathrm{ R\mathrm -mod}\,}}\rightarrow \mathbb {R}_{\ge 0} \cup \{\infty \}\end{aligned}$$

satisfying the following conditions:

• (1) $\lambda (0) = 0$;

• (2) $\lambda (M) = \lambda (M')$ when M and $M'$ are isomorphic;

• (3) for every exact sequence $0 \rightarrow A \rightarrow B \rightarrow C \rightarrow 0$,

  $$\begin{aligned} \lambda (B) = \lambda (A) + \lambda (C) \end{aligned}$$

  (with the usual rule that $x + \infty = x$);

• (4) for every $M \in {{\,\mathrm{ R\mathrm -mod}\,}}$,

  $$\begin{aligned} \lambda (M) = \sup \{\lambda (M'): M' \le M\text { finitely generated }R \text {-submodule}\}. \end{aligned}$$

Generalized length functions were introduced in [17] and further studied (among other sources) in [18, 24]: see also Sect. 3 for a brief introduction; we will simply say “length” or “lenght function” in the rest of the paper.

Fix $1 \le k \in \mathbb {N}$ and let $S:= R[x_{1}, \dotsc , x_{k}]$. Let M be an S-module.

We generalize the theory of Hilbert series and Hilbert polynomial for S-modules when R is a field and the linear dimension is the length function (see e.g. [9, 15]), to the case of S-modules with an arbitrary length function $\lambda$. We begin by assuming that M is an $\lambda _{S}$-small module, i.e., there exists a finitely generated R-submodule V of M with finite $\lambda$-length such that $SV = M$ (we say that V witnesses that M is $\lambda _S$-small). We denote by $S_{n}$ the set of polynomials in S of total degree less or equal to n, and consider the formal power series

$$\begin{aligned} \sum _{n = 0}^{\infty } \lambda (S_{n} V) t^{n} \end{aligned}$$

and prove that it is a rational function (of t). We also show that for large enough n, the function $n \mapsto \lambda (S_{n} V)$ is a polynomial, whose leading term $\mu (M)$ is independent of the choice of the witness V (Theorem 6.6): thus, $\mu _{\lambda }(M)$ is an invariant of M that measures the asymptotic growth of $\lambda$ on M, and refines both the algebraic entropy and the receptive algebraic entropy. Moreover, the degree of $\mu (M)$ gives a well-behaved notion of dimension (w.r.t. $\lambda$) for S-modules.

In Sect. 4 we review some basic notions and results about graded and filtered modules over a Noetherian ring. In Sect. 5, we construct the Hilbert series for two classes of modules: graded modules (Theorem 5.1) and upward filtered modules (Corollary 5.2). We choose to work with upward filtered modules instead of the more common downward filtered modules, because they are more suitable for the applications in Sects. 6.2 and 8 (see also [14, §1.3]).

In Sect. 6, we prove the existence of a Hilbert polynomial for $\lambda _S$-small modules, and show that its leading term, denoted by $\mu (M)$, is an invariant of M

In Sect. 7, we extend the definition of $\mu (M)$ to the case when M is not $\lambda _S$-small, and show that $\mu$ is an additive function on the class of modules that are locally $\lambda _R$-finite (see Def. 3.1 and Theorem 8.1).

The coefficient of the k-term of the Hilbert polynomial is (up to a constant factor) the algebraic entropy of the action of $\mathbb {N}^{k}$ on M (see Sect. 3 for the definition of algebraic entropy and its main properties). Therefore, the additivity of $\mu$ is a refinement of the known additivity of algebraic entropy (see Fact 3.7 and [6, 18, 19]). However, the additivity of algebraic entropy has already been proved under weaker assumptions: one of the most general results considers the case when the acting monoid $\mathbb {N}^{k}$ is replaced by a cancellative and amenable monoid (and M is locally $\lambda _{R}$-finite): see [6, 26].

In Sect. 10 we show how the usual construction of Hilbert-Samuel polynomial can be extended to length functions, thus obtaining another invariant of M.

In Sect. 9 we replace S with a finitely generated R-algebra T and define a corresponding Hilbert polynomial for each T-module M: its degree will be an invariant of M (while the leading coefficient will depend on the choice of a set of generators for T).

In Sect. 11 we introduce the d-dimensional entropy as a generalization of the receptive entropy in [2], and relate it to the Hilbert polynomial.

It is well known that the algebraic entropy of modules that are not $\lambda _R$-finite may fail to be additive, which is a desirable property. To overcome this limitation, some alternative notions of algebraic entropy have been introduced in the literature. We will explore how similar adaptations can be applied to $\mu$, the leading term of the Hilbert polynomial.

In Sect. 12, we use a technique from [24] to define ${\hat{\mu }}$, an additive function on all S-modules that extends $\mu$ on locally $\lambda _R$-finite modules. This construction also works for the (d-dimensional) entropy.

In Sect. 13, we define the “intrinsic” Hilbert polynomial, which is related to the intrinsic algebraic entropy introduced in [7]: see Sect. 3.3. We obtain another invariant $\tilde{\mu }$ from the intrinsic Hilbert polynomial. We conjecture that $\tilde{\mu }$ is additive on S-modules, and prove that it is sub-additive. Under this conjecture, we have two additive invariants, ${\hat{\mu }}$ and $\tilde{\mu }$, which may differ in general.

Moreover, in Sect. 14, we consider a finer version of the Hilbert series where the grading is given by a suitable monoid $\Gamma$ instead of $\mathbb {N}$.

We mostly adapt well-known results about Hilbert series and polynomials to our setting, or prove them by simple arguments. Therefore, we omit some proofs for brevity.

In most of the results, we assume that R is Noetherian ring (or at least that the relevant modules are Noetherian).

We conjecture that some of our results can be extended to non-Noetherian rings. However, we lack a satisfactory notion of “Noetherianity with respect to $\lambda$” for rings, which prevents us from pursuing this direction further. We remark that, without any Noetherian assumption, a Hilbert polynomial may not exist (see Sect. 6.3). On the other hand, the algebraic entropy and its intrinsic version have been studied for non-Noetherian rings (see e.g. [19, 21]).

We also leave as an open problem the case when either R or S are non-commutative rings. See [16] for the case when R is not commutative, and [6, 26] for the case when S is not commutative. Some partial results are in Appendix B.

We believe that most results (except possibly Proposition 12.7 and its corollaries) can be generalized to the case when R is non-commutative, but we do not explore this possibility here due to our limited expertise in non-commutative rings.

2 Preliminaries, assumptions, and notation

2.1 Notation

$\mathbb {N}$ denotes the set of natural numbers, including 0.

$\infty$ denotes some element that is greater than any real number.

R is a ring (commutative with 1) and $\lambda$ is a length function on ${{\,\mathrm{ R\mathrm -mod}\,}}$.

We write $I \lhd R$ if I is an ideal of R, and $A \le M$ if A is a submodule of the module M.

We fix $1 \le k \in \mathbb {N}$ and denote ${\bar{x}}{:=}\langle x_{1}, \dotsc , x_{k} \rangle$ and $S {:=}R[{\bar{x}}]$.

Given $n \in \mathbb {N}$, $S^{(n)}$ denotes the set of homogeneous polynomials in S of degree exactly n (plus the 0 polynomial), while $S_{n}$ is the set of polynomials in S of degree at most n (they are both finitely generated R-modules: notice that $S_{0} = R$).

From Sect. 6 to the appendices R will be a Noetherian ring (therefore, S and S[y] will also be Noetherian rings).

2.2 Polynomial coefficients for some rational functions

In this subsection we gather some results: probably they are well known, but we could not find a reference.

We fix some $\ell \in \mathbb {N}$ and denote ${\bar{t}} {:=}\langle t_{1}, \dotsc , t_{\ell } \rangle$.

The case $\ell = 1$ of the next proposition is well-known, and the one we will use for most of the article (see e.g. [1, Ch.11]).

Proposition 2.1

Let K be a ring of characteristic 0, and $p({\bar{t}}) \in K[{\bar{t}}]$. Let $\gamma _{1}, \dotsc , \gamma _{\ell } \in \mathbb {N}$. Define

$$\begin{aligned} f({\bar{t}}):= \frac{p({\bar{t}})}{\prod _{i=1}^{\ell }(1 - t_{i})^{\gamma _{i}}} \in K({\bar{t}}) \end{aligned}$$

and expand f as

$$\begin{aligned} f({\bar{t}}) = \sum _{{\bar{n}} \in \mathbb {N}^{\ell }} a_{{\bar{n}}} {\bar{t}}^{\, {\bar{n}}} \in K[[{\bar{t}}]]. \end{aligned}$$

Then, there exists a polynomial $q({\bar{t}}) \in K[{\bar{t}}]$ such that:

• (1) For every ${\bar{n}} \in \mathbb {N}^{\ell }$ large enough

  $$\begin{aligned} a_{{\bar{n}}} = q({\bar{n}}); \end{aligned}$$

• (2) for every $i= 1, \dotsc , \ell$

  $$\begin{aligned} \deg _{t_{i}}(q) \le \gamma _{i} - 1 \end{aligned}$$

  with $\deg _{t_{i}}(q) = \gamma _{i} - 1$ if K is an integral domain and $p \ne 0$.

Proof

It is clear that it suffices to treat the case when $p=1$. We proceed by induction on $\ell$. If $\ell = 0$, then $f=1$, and $q= 0$. If $\ell = 1$, the result is easy: by further induction on $\gamma _{1}$, one can prove that $a_{n} = \left( {\begin{array}{c}n+\gamma _{1} - 1\\ \gamma _{1} - 1\end{array}}\right)$.

Assume now that we have already proved the result for $\ell -1$: we want to prove it for $\ell$. Denote ${\tilde{t}}:= \langle t_{2}, \dotsc , t_{\ell } \rangle$ and

$$\begin{aligned} g({\tilde{t}}) {:=}\frac{1}{\prod _{i=2}^{\ell }(1 - t_{i})^{\gamma _{i}}} {:=}\sum _{{\tilde{n}} \in \mathbb {N}^{\ell -1}} b_{{\tilde{n}}} {\tilde{t}}^{\, {\tilde{n}}}. \end{aligned}$$

By inductive hypothesis, there exists $r({\tilde{t}}) \in K[{\tilde{t}}]$ satisfying (1) and (2) for g. Moreover,

$$\begin{aligned} f = g \cdot \frac{1}{(1 - t_{1})^{\gamma _{1}}} = \sum _{{\tilde{n}} \in \mathbb {N}^{\ell -1}} b_{{\tilde{n}}} {\tilde{t}}^{\, {\tilde{n}}} \cdot \sum _{m \in \mathbb {N}} c_{m} t_{1}^{m}, \end{aligned}$$

where $\frac{1}{(1 - t_{1})^{\gamma _{1}}} = \sum _{m \in \mathbb {N}} c_{m} t_{1}^{m}$. Thus, denoting by $a_{m, {\tilde{n}}}$ the coefficient of $t_{1}^{m} {\tilde{t}}^{\, {\tilde{n}}}$ in f, we have

$$\begin{aligned} a_{m, {\tilde{n}}} = c_{m}b_{{\tilde{n}}}. \end{aligned}$$

By the case $\ell = 1$ there exists $s(t_{1}) \in K[t_{1}]$ of degree $\gamma _{1}-1$ such that, for every $m \in \mathbb {N}$ large enough,

$$\begin{aligned} c_{m} = s(m). \end{aligned}$$

Thus, taking $m \in \mathbb {N}$ and ${\tilde{n}} \in \mathbb {N}^{\ell - 1}$ large enough, we have

$$\begin{aligned} a_{m,{\tilde{n}}} = s(m)r({\tilde{n}}), \end{aligned}$$

and the polynomial $q(t_{1}, {\tilde{t}}):= s(t_{1})r({\tilde{t}}) \in K[t]$ satisfies the conclusion. $\square$

Definition 2.2

Let $p({\bar{t}}), q({\bar{t}})\in \mathbb {R}[{\bar{t}}]$; we write $p = p_{0} + p_{1} + \cdots + p_{d}$, where each $p_{i} \in \mathbb {R}[{\bar{t}}]$ is homogeneous of degree i, and $p_{d} \ne 0$. We call $p_{d}$ the leading homogeneous component of p (if $p = 0$ then, by convention, the leading homogeneous component of p is 0). As usual, if $\ell = 1$ we call the leading homogeneous component of p the leading term of p.

Definition 2.3

We write

• $p \preceq q$ if there exists ${\bar{c}}\in \mathbb {N}^{\ell }$ such that, for every ${\bar{n}} \in \mathbb {N}^{\ell }$ large enough, $p({\bar{n}}) \le q({\bar{n}} + {\bar{c}})$;

• $p \simeq q$ if $p \preceq q$ and $q \preceq p$;

• $p \succeq 0$ if, for every ${\bar{n}} \in \mathbb {N}^{\ell }$ large enough, $p({\bar{n}}) \ge 0$.

Proposition 2.4

Let $p,q \in \mathbb {R}[{\bar{t}}]$ such that:

• (1) $p \succeq 0$,

• (2) $q \succeq 0$,

• (3) $p \simeq q$.

Then, p and q have the same leading homogeneous component.

Proof

If either p or q is zero, it is clear that the other is also zero (and therefore they have the same leading homogeneous component). Thus, without loss of generality, we may assume that they are both non-zero. Let $p'$ and $q'$ be the leading homogeneous component of p and q respectively, and $h'$ be the leading homogeneous component of $h {:=}p - q$. If, by contradiction, $p' \ne q'$, then $\deg h = \max (\deg p, \deg q)$. Let ${\bar{v}} \in \mathbb {N}^{\ell }$ such that $h'({\bar{v}}) \ne 0$. Then,

$$\begin{aligned} r {:=}\lim _{s \rightarrow + \infty ,\ s \in \mathbb {N}} h(s {\bar{v}}) \in \{\pm \infty \}. \end{aligned}$$

Since $q \preceq p$, we have $r = +\infty$, but since since $p \preceq q$, we have $r = -\infty$, absurd. $\square$

3 Length functions and their entropy

3.1 Length functions

It can happen that $\lambda (R)$ is infinite: the following definition deals with that situation.

Definition 3.1

Let N be an R-module. We say that N is locally $\lambda _R$ -finite¹ if either of the following equivalent conditions hold:

• (1) For every $v \in N$, $\lambda (Rv) < \infty$;

• (2) For every $N_{0} \le N$ finitely generated R-submodule, $\lambda (N_{0}) < \infty$.

Examples 3.2

• (a) If R is a field, then the linear dimension is the unique length $\lambda$ on ${{\,\mathrm{ R\mathrm -mod}\,}}$ such that $\lambda (R) = 1$.

• (b) Let $R = \mathbb {Z}$, and define $\lambda (M)$ to be the logarithm of the cardinality of M. Then, $\lambda (R) = \infty$, and an Abelian group is locally $\lambda _R$-finite iff it is torsion. We call $\lambda$ the standard length on $\mathbb {Z}$-modules, and we will use it often in examples.

• (c) Given any ring R, the (classical) length of an R-module M is the length of a composition series for M (see e.g. [9]).

• (d) The following are two “trivial” lengths:

  • i) $\lambda (M) = 0$ for every M;

  • ii) $\lambda (M) = \infty$ for every $M \ne 0$, and $\lambda (0) = 0$.

• (e) The following function is a length on $\mathbb {Z}$-modules:

  $$\begin{aligned} \lambda (A) {:=}{\left\{ \begin{array}{ll} 0 &{}{} \text{ if } A \text{ is } \text{ torsion }\\ \infty &{}{} \text{ otherwise }. \end{array}\right. } \end{aligned}$$

Exercise 3.3

$\lambda$ is nonzero iff $\lambda (R) > 0$.

Exercise 3.4

Let R be an integral domain. Then, there exists a unique length $\lambda _{0}$ on R-modules satisfying $\lambda _{0}(R) = 1$. Denoting by K the field of fractions of R, $\lambda _{0}$ is defined by:

$$\begin{aligned} \lambda _{0}(M) {:=}\dim _{K} (K \otimes M). \end{aligned}$$

The two trivial lengths in 3.2(d) and the one in 3.2(e) are particular cases of “singular” lengths, i.e. lengths taking values only 0 or $\infty$ (see [23, §6] for a characterization): in the present treatment we will mostly ignore them, since the associated entropies, the invariant $\mu$, and its modifications ${\hat{\mu }}$ and $\tilde{\mu }$ are all 0.

A property we will use often in the rest of the paper is the following:

Definition 3.5

Given an R-algebra T and a T-module M, we say that M is $\lambda _T$ -small if M is finitely generated (as T-module) and locally $\lambda _R$-finite.²

Remark 3.6

Assume that T is a Noetherian R-algebra and let M be a T-module. The following are equivalent:

• (1) M is $\lambda _{T}$-small;

• (2) there exists $V \le M$ R-submodule such that:

  • i) $TV = M$,

  • ii) V is finitely generated (as R-module),

  • iii) $\lambda (V) < \infty$;

• (3) every submodule and every quotient of M is $\lambda _{T}$-small.

Any submodule $V \le M$ satisfying (2) in the above remark is a witness of the $\lambda _{T}$-smallness of M.

[24, Thm.5] characterizes length functions on Noetherian rings: for every prime ideal $P \le R$ there is a canonical length function $l_{P}$ on ${{\,\mathrm{ R\mathrm -mod}\,}}$, and any length function $\lambda$ can be written as

$$\begin{aligned} \lambda = \sum _{P \lhd R \text { prime ideal}} r_{P}^{\lambda } \cdot l_{P} \end{aligned}$$

for some $r_{P}^{\lambda } \in \mathbb {R}_{\ge 0} \cup \{\infty \}$ (we use the convention that $0 \cdot \infty = 0$).

3.2 Algebraic entropy

The content of this and the following subsection can be skipped: it is mostly a motivation for the definitions and results in the paper. We recall the definition of algebraic entropy and its main properties.

Let M be an R-module and $\phi$ be an endomorphism of M. Given an R-submodule $V \le M$, we define

$$\begin{aligned} H_{\lambda }(\phi ; V):= \lim _{n \rightarrow \infty } \frac{\lambda \bigl ( V + \phi (V) + \dots + \phi ^{n-1}(V) \bigr )}{n} \end{aligned}$$

(the limit always exists by Fekete’s Lemma, since the function $n \mapsto \lambda \bigl ( V + \phi (V) + \dots + \phi ^{n-1}(V) \bigr )$ is subadditive: but see also later in this subsection). The entropy of $\phi$ (according to the length $\lambda$) is defined by

$$\begin{aligned} h_{\lambda }(\phi ) = \sup \{H_{\lambda }(\phi ;V): V \le M\ \ R\text {-submodule of finite length}\}. \end{aligned}$$

Equivalently, we can see M as an R[X]-module (with X acting on M as $\phi$), and consider $h_{\lambda }$ as an invariant of M as R[X]-module. For the relationship between algebraic entropy and multiplicity, see [16, 18].

More generally, given an S-module M, and an R-submodule $V \le M$ of finite length, define

$$\begin{aligned} H_{\lambda }(M; V)&{:=}\lim _{n \rightarrow \infty } {\lambda (S_{n}V)}\big /{\genfrac(){0.0pt}1{n+k}{k}} = k! \lim _{n \rightarrow \infty } \lambda (S_{n}V) \big / n^{k} \end{aligned}$$

(1)

$$\begin{aligned} h_{\lambda }(M)&{:=}\sup \{H_{\lambda }(M;V): V \le M\ \ R\text {-submodule of finite length}\}. \end{aligned}$$

(2)

The limit in the definition of $H_{\lambda }(M; V)$ exists, and $h_{\lambda }$ is the algebraic entropy (relative to the length function $\lambda$). We prove the stronger result that $\lambda (S_{n}V)$ is eventually equal to a polynomial as Theorem 6.5, and therefore the limit in (1) exists. However, the existence of the limit was already well-known: e.g., [4, 6] give a more general version. [6] consider the action of a cancellative amenable monoid: in our case, we can identify S with the group ring $R[\mathbb {N}^{k}]$, and therefore an S-module is the same as an R-module M together with an action $*$ of $\mathbb {N}^{k}$ on M by endomorphisms, and $\mathbb {N}^{k}$ is a cancellative amenable monoid. Let $B_{n}$ be the set of tuples ${\bar{m}} \in \mathbb {N}^{k}$ such that $m_{1} + \cdots + m_{k} \le n$. Then $\left( {\begin{array}{c}n+k\\ k\end{array}}\right)$ is the cardinality of $B_{n}$. Moreover, the family $(B_{n})_{n \in \mathbb {N}}$, is a Følner sequence for $\mathbb {N}^{k}$ and therefore, as in [6], we can apply the machinery in [4] to obtain that the following limit exists (and is independent from the choice of the Følner sequence):

$$\begin{aligned} \lim _{n \rightarrow \infty } \frac{\lambda (B_{n} * V) }{|B_{k}|} = \lim _{n \rightarrow \infty } \frac{\lambda (S_{n} V) }{\genfrac(){0.0pt}1{n+k}{k}}. \end{aligned}$$

See also [26] for an proof in the case when the acting monoid is a finitely generated group.

One of the most important properties of algebraic entropy is its additivity:

Fact 3.7

Let $0 \rightarrow A \rightarrow B \rightarrow C \rightarrow 0$ be an exact sequence of S-modules. Assume that B is locally $\lambda _R$-finite. Then,

$$\begin{aligned} h_{\lambda }(B) = h_{\lambda }(A) + h_{\lambda }(C). \end{aligned}$$

We prove a stronger version of the above fact as Theorem 8.1. However, the fact was well-known: see [19] for the case when $k=1$; [6] gives a general version for $\mathbb {Z}$-modules with the action of an amenable cancellative monoid (but the proof generalizes to R-modules), while [26] treats the case of the action of an amenable finitely generated group on R-modules.

Length functions on R-modules were explicitly introduced in [17] and further studied in [24, 25]; however, additive functions on modules is a “classical” topic (see e.g. [1, Chapters 2 and 11]): one of the novelties was allowing values in $\mathbb {R}_{\ge 0} \cup \{\infty \}$. Algebraic entropy was introduced in [8]: it and its variants have been extensively studied, both in particular cases (e.g., $R = \mathbb {Z}$ and $k=1$) and in general (including for non-Noetherian rings): see e.g. [2, 5, 10, 13, 19, 22] and see [12, 18] for surveys.

3.3 Intrinsic algebraic entropy

Let M be an R-module and $\phi$ be an endomorphism of M. Given an R-submodule $V \le M$ such that $\lambda ((V + \phi (V)) / V) < \infty$, define

$$\begin{aligned} {\tilde{H}}_{\lambda }(\phi ; V):= \lim _{n \rightarrow \infty } \frac{\lambda \bigl ( (V + \phi (V) + \dots + \phi ^{n-1}(V)) / V \bigr )}{n} \end{aligned}$$

(the limit always exists, again by Fekete’s Lemma). The intrinsic entropy of $\phi$ (according to the length $\lambda$), introduced in [7], is defined by

$$\begin{aligned} {\tilde{h}}_{\lambda }(\phi ) = \sup \{H_{\lambda }(\phi ;V): V \le M\ \ R\text {-submodule such that } \lambda ((V + \phi (V)) / V) < \infty \}. \end{aligned}$$

There is a corresponding addition theorem

Fact 3.8

Let $0 \rightarrow A \rightarrow B \rightarrow C \rightarrow 0$ be an exact sequence of R[x]-modules. Then,

$$\begin{aligned} {\tilde{h}}_{\lambda }(B) = {\tilde{h}}_{\lambda }(A) + {\tilde{h}}_{\lambda }(C). \end{aligned}$$

For a proof of the above fact, see [7, 20]: we will consider a stronger version in a more general setting in Sect. 13 (however, we were not able to prove additivity but only sub-additivity).

4 Graded and filtered modules

In this section we gather a few definitions and facts about graded and filtered S-modules. The most important ones are: how to construct a graded S[y]-module ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{A}})$ starting from an upward filtered module ${\overline{A}}$ (Definitions 4.5 and 4.6), and a version of Artin-Rees Lemma for upward filtered modules (Proposition 4.9).

4.1 Graded modules

Definition 4.1

Fix ${\bar{\gamma }} = \langle \gamma _{1}, \dotsc , \gamma _{k} \rangle \in \mathbb {N}^{k}$. An $\mathbb {N}$ -graded S-module of degree ${\bar{\gamma }}$ is given by an S-module M and a decomposition

$$\begin{aligned} M = \bigoplus _{n \in \mathbb {N}} M_{n}, \end{aligned}$$

where each $M_{n}$ is an R-module, and, for every $i \le k$ and $n \in \mathbb {N}$,

$$\begin{aligned} x_{i} M_{n} \le M_{n+ \gamma _{i}}. \end{aligned}$$

We denote by ${\overline{M}}$ the module M with the given grading (including the tuple ${\bar{\gamma }}:= \langle \gamma _{1}, \dotsc , \gamma _{k} \rangle$).

Given ${\bar{\jmath }}\in \mathbb {N}^{k}$ and ${\bar{\gamma }} \in \mathbb {N}^{k}$, we denote

$$\begin{aligned}\begin{aligned} |{\bar{\jmath }}|_{{\bar{\gamma }}}&{:=}{\bar{\jmath }}\cdot {\bar{\gamma }} {:=}j_{1} \gamma _{1} + j_{2} \gamma _{2} + \dots + j_{k} \gamma _{k} \\ {\bar{x}}^{{\bar{\jmath }}}&{:=}x_{1}^{j_{1}} x_{2}^{j_{2}} \cdots x_{k}^{j_{k}}. \end{aligned} \end{aligned}$$

Thus, if ${\overline{M}}$ is a graded module of degree ${\bar{\gamma }}$, then, for every ${\bar{\jmath }}\in \mathbb {N}^{k}$ and $m \in M_{n}$,

$$\begin{aligned} {\bar{x}}^{{\bar{\jmath }}} m \in M_{n + |{\bar{\jmath }}|_{{\bar{\gamma }}}} \end{aligned}$$

We will use implicitly the following lemma many times in the remainder of the article.

Lemma 4.2

Let ${\overline{M}}$ be an $\mathbb {N}$-graded S-module of degree ${\bar{\gamma }}$. Assume that:

• (1) $\gamma _{\ell } > 0$ for each $\ell = 1, \dotsc , k$;

• (2) M is finitely generated (as S-module).

Then, each $M_{n}$ is also finitely generated (as R-module).

Proof

Let $m_{1}, \dotsc , m_{p} \in M$ generate M (as S-module). Fix $n \in \mathbb {N}$; we want to show that $M_{n}$ is finitely generated. Without loss of generality, we may assume that each $m_{i}$ is homogeneous of degree $d_{i}$ (i.e., $m_{i} \in M_{d_{i}}$).

Let $a \in M_{n}$. There exist $s_{1}, \dotsc , s_{p} \in S$ such that

$$\begin{aligned} a = \sum _{i=1}^{p} s_{i} m_{i}. \end{aligned}$$

Write

$$\begin{aligned} s_{i} = \sum _{{\bar{\jmath }}\in \mathbb {N}^{k}} r_{i, {\bar{\jmath }}}\, {\bar{x}}^{{\bar{\jmath }}} \end{aligned}$$

for some (unique) $r_{i, {\bar{\jmath }}} \in R$. Let

$$\begin{aligned} c_{i, {\bar{\jmath }}} {:=}x^{{\bar{\jmath }}} m_{i} \in S_{|{\bar{\jmath }}|_{{\bar{\gamma }}}} M_{d_{i}} \subseteq M_{|{\bar{\jmath }}|_{{\bar{\gamma }}} + d_{i}} \end{aligned}$$

Thus,

$$\begin{aligned} a = \sum _{i=1}^{p} \sum _{{\bar{\jmath }}\in \mathbb {N}^{k}} r_{i,{\bar{\jmath }}}\, x^{{\bar{\jmath }}} m_{i} = \sum _{i=1}^{p} \sum _{{\bar{\jmath }}\in \mathbb {N}^{k}} r_{i, {\bar{\jmath }}}\, c_{i,{\bar{\jmath }}}. \end{aligned}$$

(3)

For every ${\bar{\jmath }}\in \mathbb {N}^{k}$, let

$$\begin{aligned} I_{{\bar{\jmath }}} {:=}\{i \le p:\ |{\bar{\jmath }}|_{{\bar{\gamma }}} + d_{i} = n\}; \end{aligned}$$

(4)

notice that $I_{{\bar{\jmath }}}$ is finite (since each $\gamma _{\ell } > 0$) and, for every $i \in I_{{\bar{\jmath }}}$,

$$\begin{aligned} c_{i,{\bar{\jmath }}} \in M_{n}. \end{aligned}$$

Since $a \in M_{n}$, we have that that in (3) only the $c_{i, {\bar{\jmath }}}$ in $M_{n}$ contribute to the sum: that is, only the ones such that $i \in I_{{\bar{\jmath }}}$. Therefore,

$$\begin{aligned} a = \sum _{{\bar{\jmath }}\in \mathbb {N}^{k}}\sum _{i \in I_{{\bar{\jmath }}}} r_{i, {\bar{\jmath }}}\, c_{i,{\bar{\jmath }}}. \end{aligned}$$

Thus, $M_{n}$ is generated (as R-module) by the finite set

$$\begin{aligned} \{c_{i,{\bar{\jmath }}}: {\bar{\jmath }}\in \mathbb {N}^{k},\ |{\bar{\jmath }}|_{{\bar{\gamma }}} \le n, i \in I_{{\bar{\jmath }}}\} \end{aligned}$$

$\square$

Definition 4.3

An $\mathbb {N}$-graded S-module ${\overline{A}}$ is acceptable if:

• (1) A is finitely generated (as S-module);

• (2) each $x_{i}$ has degree 1.

Proposition 4.4

Let ${\overline{A}}$ be an acceptable graded S-module. Then, there exists $d \in \mathbb {N}$ such that, for every $n \in \mathbb {N}$,

$$\begin{aligned} A_{d+n} = S^{(n)} A_{d}. \end{aligned}$$

Proof

It is always true that $S^{(n)} A_{d} \le A_{d+n}$. We want to show the opposite containment.

Let $a_{1}, \dotsc , a_{\ell } \in A$ be generators of A. Without loss of generality, we may assume that each $a_{i}$ is homogeneous of degree $d_{i}$ (i.e., $a_{i} \in A_{d_{i}}$).

Let $d {:=}\max (d_{i}: i = 1, \dotsc , \ell )$. Let $b \in A_{n+d}$. We can write

$$\begin{aligned} b = \sum _{i=1}^{\ell } s_{i} a_{i}, \end{aligned}$$

for some $s_{i} \in S$. For every $i = 1, \dotsc , \ell$, write

$$\begin{aligned} s_{i} = \sum _{{\bar{\jmath }}\in \mathbb {N}^{k}} r_{i,{\bar{\jmath }}}\, {\bar{x}}^{{\bar{\jmath }}} \end{aligned}$$

for some (unique) $r_{i,{\bar{\jmath }}} \in R$. Without loss of generality, as in the proof of Lemma 4.2, we may assume that $r_{i,{\bar{\jmath }}} = 0$ when $d_{i} + |{\bar{\jmath }}| \ne n + d$. For each $i, {\bar{\jmath }}$ such that $d_{i} + |{\bar{\jmath }}| = n+d$, pick ${\bar{\jmath }}[i], {\bar{\jmath }}''[i] \in \mathbb {N}^{k}$ such that:

$$\begin{aligned} {\bar{\jmath }}'[i] + {\bar{\jmath }}''[i]= {\bar{\jmath }}\qquad \text {and} \qquad |{\bar{\jmath }}'[i]| =n. \end{aligned}$$

Let

$$\begin{aligned} \begin{aligned} c_{i,{\bar{\jmath }}}&\,\,{:=}\,\, {\bar{x}}^{{\bar{\jmath }}'[i]} a_{i} \in S^{n-d_{i}} A_{d_{i}} \subseteq A_{n}\\ t_{i,{\bar{\jmath }}}&\,\,{:=}\,\, r_{i,{\bar{\jmath }}}\, {\bar{x}}^{{\bar{\jmath }}''[i]} \in S^{(n)}. \end{aligned}\end{aligned}$$

Thus,

$$\begin{aligned} b = \sum _{i + |{\bar{\jmath }}| =n} t_{i,{\bar{\jmath }}}\,c_{i,{\bar{\jmath }}} \in S^{(n)} A_{n} \end{aligned}$$

$\square$

4.2 Filtered modules

Definition 4.5

Let ${\bar{\gamma }}:= \langle \gamma _{1}, \dotsc , \gamma _{k} \rangle \in \mathbb {N}^{k}$ and N be an S-module.

An increasing filtering on N with degrees ${\bar{\gamma }}$ is an increasing sequence of R-submodules of N

$$\begin{aligned} N_{0} \le N_{1} \le N_{2} \le \cdots \le N \end{aligned}$$

such that $x_{i} N_{j} \le N_{j + \gamma _{i}}$ for every $j \in \mathbb {N}$, $i \le k$. We denote by ${\overline{N}}$ the S-module with the given tuple ${\bar{\gamma }}$ and the filtering $(N_{i})_{i \in \mathbb {N}}$. Such a filtering is exhaustive if $\bigcup _{i\in \mathbb {N}} N_{i} = N$.

From now on, unless explicitly specified, all filterings will be increasing.

Definition 4.6

The blow-up of the filtered S-module ${\overline{N}}$ is the following graded S[y]-module ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{N}})$.³

As a graded R-module,

$$\begin{aligned} {{\,\mathrm{{\mathcal {B}}}\,}}({\overline{N}}):= \bigoplus _{n \in \mathbb {N}} N_{n} y^{n}. \end{aligned}$$

The multiplication by $x_{i}$ on ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{N}})$ is defined as:

$$\begin{aligned} x_{i}(v y^{j}):= (x_{i}v) y^{j + \gamma _{i}}, \end{aligned}$$

for every $i \le k$, $j \in \mathbb {N}$, $v \in N_{j}$, and then extended by R-linearity on all ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{N}})$: notice that the $x_{i}$ has degree $\gamma _{i}$ in ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{N}})$. The multiplication by y on ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{N}})$ is defined as:

$$\begin{aligned} y (v y^{j}):= v y^{j+1}, \end{aligned}$$

for every $j \in \mathbb {N}$, $v \in N_{j}$, and then extended by R-linearity on all ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{N}})$: notice that y has degree 1.

Let M be an S-module and ${\overline{M}} = (M_{n})_{n\in \mathbb {N}}$ be a filtering of M with degrees ${\bar{\gamma }}$. For every $m \in \mathbb {N}$, we define

$$\begin{aligned} M^{m}:= \bigoplus _{n \le m} M_{n} y^{n} \le {{\,\mathrm{{\mathcal {B}}}\,}}(M). \end{aligned}$$

We say that $M_{m}$ tightly generates ${\overline{M}}$ if: for every $n \in \mathbb {N}$ and $v \in M_{n}$,

($\dagger$) There exist $m_{1}, \dotsc , m_{r} \in \mathbb {N}$ with $m_{j} \le m$, and $v_{1}, \dotsc , v_{r} \in M$ such that $v_{j} \in M_{m_{j}}$, and ${\bar{n}}_{1}, \dotsc , {\bar{n}}_{r} \in \mathbb {N}^{k}$ such that:

$$\begin{aligned}\begin{aligned} v&= {\bar{x}}^{{\bar{n}}_{1}} v_{1} + \dots + {\bar{x}}^{{\bar{n}}_{r}} v_{r},\\ n&\ge {\bar{n}}_{j} \cdot {\bar{\gamma }} + m_{j}, \quad j = 1, \dots , r, \end{aligned} \end{aligned}$$

where we are using the notations

$$\begin{aligned} {\bar{n}}_{j} \cdot {\bar{\gamma }}:= n_{j,1} \gamma _{1} + \dots + n_{j,k} \gamma _{k} \qquad \qquad {\bar{x}}^{{\bar{n}}_{j}}:= x_{1}^{n_{j,1}} \cdot \cdots \cdot x_{k}^{n_{j,k}}. \end{aligned}$$

Notice that ($\dagger$) is equivalent to:

($\dagger '$) There exist $m_{1}, \dotsc , m_{r} \in \mathbb {N}$ with $m_{j} \le m$, $v_{1}, \dotsc , v_{r} \in M$ such that $v_{j} \in M_{m_{j}}$, and $p_{1}, \dotsc , p_{r} \in S$ such that:

$$\begin{aligned}\begin{aligned} v&= p_{1} v_{1} + \dots + p_{r}v_{r},\\ n&\ge \deg _{{\bar{\gamma }}}(p_{j}) + m_{j}, \quad j = 1, \dots , r. \end{aligned} \end{aligned}$$

Lemma 4.7

Let $m \in \mathbb {N}$. $M^{m}$ generates ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{M}})$ (as an S[y]-module) iff $M_{m}$ tightly generates ${\overline{M}}$.

Proof

$\Rightarrow$) Let $n \in \mathbb {N}$ and $v \in M_{n}$. Since $M^{m}$ generates ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{M}})$, there exist $v_{1} y^{m_{1}}, \dotsc , v_{r}y^{m_{r}} \in M^{m}$ and $q_{1}({\bar{x}},y), \dotsc , q_{r}({\bar{x}}, y) \in R[{\bar{x}},y]$ (remember that $S = R[{\bar{x}}]$) such that:

$$\begin{aligned} v y^{n} = q_{1}({\bar{x}}, y) v_{1} y^{m_{1}} + \dots + q_{r}({\bar{x}}, y) v_{r}y^{m_{r}}. \end{aligned}$$

Thus, if we define $p_{j}({\bar{x}}):= q_{j}({\bar{x}}, 0) \in S$, $j = 1, \dotsc , r$, we have

$$\begin{aligned} v = p_{1} v_{1} + \dots + p_{r} v_{r}. \end{aligned}$$

Moreover, $\deg _{\gamma }(p_{j}) + m_{j} \le m$, $j = 1, \dotsc , r$, showing that $M_{m}$ tightly generates ${\overline{M}}$.

$\Leftarrow$) Let $n \in \mathbb {N}$ and $v y^{n} \in M_{n} y^{n}$. Let $m_{1}, \dotsc , m_{r} \in \mathbb {N}$, $v_{1}, \dotsc v_{r} \in M$, and ${\bar{n}}_{1}, \dotsc , {\bar{n}}_{r} \in \mathbb {N}^{k}$ as in ($\dagger$). For $j = 1, \dotsc , r$, define

$$\begin{aligned} d_{j}:= n - ({\bar{n}}_{j} \cdot {\bar{\gamma }} + m_{j}) \in \mathbb {N}, \qquad p_{j}:= {\bar{x}}^{{\bar{n}}_{j}} y^{d_{j}} \in S[y]. \end{aligned}$$

We have $v_{j} y^{m_{j}} \in M^{m}$ and

$$\begin{aligned} v y^{n} = \sum _{i=1}^{m} p_{j } \cdot (v_{j} y^{d_{j}}) \in S[y] M^{m}. \end{aligned}$$

$\square$

4.3 Acceptable filterings and upward Artin-Rees Lemma

Definition 4.8

Let M be an S-module. An acceptable filtering of M is given by a filtering ${\overline{M}}:= (M_{n}: {n \in \mathbb {N}})$ such that ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{M}})$ is an acceptable graded module; that is:

• (1) each $x_{i}$ has degree 1;

• (2) ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{M}})$ is finitely generated (as an S[y]-module).

The following is an upward version of Artin-Rees Lemma: however, as it can be easily seen, the proof does not require R to be a commutative ring.

Proposition 4.9

Let M be an S-module. Let ${\overline{M}}$ be an exhaustive acceptable filtering of M. Then, there exists $d \in \mathbb {N}$ such that:

• (i) $M_{d}$ generates M (as S-module);

• (ii) for every $n \in \mathbb {N}$, $M_{n+d} = S_{n} M_{d}$.

Proof

Since ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{M}})$ is finitely generated, Lemma 4.7 implies that there exists $d \in \mathbb {N}$ such that $M_{d}$ tightly generates ${\overline{M}}$: thus, (i) is proven.

Claim 1

(ii) also holds (for the same d).

By assumption, ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{M}})$ is an acceptable graded S[y]-module. Thus, by (the proof of) Proposition 4.4, for every $n \in \mathbb {N}$,

$$\begin{aligned} M_{n+d} y^{n+d} = S[y]^{(n)} M_{d} y^{d} \end{aligned}$$

(as submodules of ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{M}})$) which is equivalent to (ii). $\square$

5 Hilbert series for graded and filtered modules

In this section we define the Hilbert series associated to the length function $\lambda$, following the ideas in [14] and [1, Ch.11]; in Sect. 6 we will define the corresponding Hilbert polynomial.

Theorem 5.1

Let ${\overline{M}}$ be an $\mathbb {N}$-graded S-module of degree ${\bar{\gamma }} \in \mathbb {N}^{k}$. For every $n \in \mathbb {N}$, let $a_{n}:= \lambda (M_{n})$. Define

$$\begin{aligned} F_{{\overline{M}}}(t):= \sum _{n} a_{n} t^{n}. \end{aligned}$$

Assume that:

• (1) $\gamma _{i} > 0$ for $i = 1, \dotsc , k$;

• (2) $\lambda (M_{n}) < \infty$ for every $n \in \mathbb {N}$;

• (3) M is a Noetherian S-module.

Then, there exists a polynomial $p(t) \in \mathbb {R}[t]$ such that

$$\begin{aligned} F_{{\overline{M}}}(t) = \frac{p(t)}{\prod _{i=1}^{k}(1 - t^{\gamma _{i}})}. \end{aligned}$$

Proof

By induction on k.

If $k = 0$, then, since M is Noetherian, only finitely many of the $M_{n}$ are nonzero. Thus, $F_{{\overline{M}}}(t)$ is a sum of finitely many (finite) terms, and hence it is a polynomial.

Assume now that we have proven the conclusion for $k - 1$. Let $y: M \rightarrow M$ be the multiplication by $x_{k}$ and $\alpha := \gamma _{k}$. For every $n \in \mathbb {N}$, let $y_{n}: M^{n} \rightarrow M^{n + \alpha }$ be the restriction of y to $M_{n}$. Let $K:= {{\,\textrm{Ker}\,}}(y)$ and $K_{n}:= K \cap M_{n} = {{\,\textrm{Ker}\,}}(y_{n})$. Let $C_{n}:= {{\,\textrm{Coker}\,}}(y_{n}) = M_{m+ \alpha } / yM_{n}$, and $C:= \bigoplus _{n \in \mathbb {N}} C_{n}$. Notice that both $\lambda (K_{n})$ and $\lambda (C_{n})$ are finite. Therefore, both K and C are $\mathbb {N}$-graded $R[x_{1}, \dotsc , x_{k-1}]$-modules, and satisfy the assumptions of the theorem (that is, they are Noetherian modules, and each $K_{n}$ and each $C_{n}$ has finite $\lambda$).

For every $n \in N$, consider the exact sequence

$$\begin{aligned} 0 \longrightarrow K_{n} \longrightarrow M_{n} \overset{y_{n}}{\longrightarrow }M_{n+ \alpha } \longrightarrow C_{n} \longrightarrow 0. \end{aligned}$$

Since $\lambda$ is additive, we have

$$\begin{aligned} a_{n + \alpha } - a_{n} = - \lambda (K_{n}) + \lambda (C_{n}). \end{aligned}$$

Thus,

$$\begin{aligned} \sum _{n} a_{n} t^{n + \alpha } - \sum _{n} a_{n} t^{n} = - \sum _{n} \lambda (K_{n})t^{n} + \sum _{n} \lambda (C_{n})t^{n}. \end{aligned}$$

Therefore,

$$\begin{aligned} (t^{\alpha }-1) F_{{\overline{M}}}(t) = - F_{{\overline{K}}} (t) + F_{{\overline{C}}}(t) \end{aligned}$$

(where ${\overline{K}}$ is the $R[x_{1}, \dotsc , x_{k-1}]$-module with the given grading, and similarly for ${\overline{C}}$).

Thus, by induction, there exist polynomials $q, q' \in \mathbb {R}[t]$ such that

$$\begin{aligned} F_{{\overline{K}}}(t) = \frac{q(t)}{\prod _{i=1}^{k-1}(1 - t^{\gamma _{i}})}, \qquad F_{{\overline{C}}}(t) = \frac{q'(t)}{\prod _{i=1}^{k-1}(1 - t^{\gamma _{i}})}. \end{aligned}$$

Therefore,

$$\begin{aligned} F_{{\overline{M}}}(t) = \frac{q'(t) - q(t)}{\prod _{i=1}^{k}(1 - t^{\gamma _{i}})}. \end{aligned}$$

$\square$

5.1 Filtered modules

We move now from graded modules to (upward) filtered modules.

Corollary 5.2

Let ${\overline{N}}$ be a filtering on N with degrees ${\bar{\gamma }}$.

Define

$$\begin{aligned} F_{{\overline{N}}}(t):= \sum _{n = 0}^{\infty } \lambda (N_{n}) t^{n}. \end{aligned}$$

Then,

$$\begin{aligned} F_{{\overline{N}}} = F_{{{\,\mathrm{{\mathcal {B}}}\,}}({\overline{N}})}. \end{aligned}$$

Therefore, if we assume that

• (1) $\gamma _{i} > 0$ for $i = 1, \dotsc , k$;

• (2) $\lambda (N_{n}) < \infty$ for every $n \in \mathbb {N}$;

• (3) ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{N}})$ is Noetherian as S[y]-module;

then, there exists a polynomial $p(t) \in \mathbb {R}[t]$ such that

$$\begin{aligned} F_{{\overline{N}}}(t) = \frac{p(t)}{ (1 - t) \prod _{i = 1}^{k} (1 - t^{\gamma _{i}})}. \end{aligned}$$

(5)

Proof

Apply Theorem 5.1 to the graded ring ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{N}})$. The $(1 - t)$-factor in the denominator of (5) is due to the action of y on ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{N}})$ of degree 1. $\square$

6 Hilbert polynomials for small modules

For the remainder of the article, excluding the appendices, we assume that R is a Noetherian ring (commutative with 1).

6.1 Hilbert polynomial for filtered modules

Definition 6.1

Let M be an S-module. A good filtering of M is given by an acceptable filtering ${\overline{M}}:= (M_{n}: {n \in \mathbb {N}})$ (see Definition 4.8) such that:

• (3) $\forall n \in \mathbb {N}$ $\lambda (M_{n}) < \infty$.

Remark 6.2

Let ${\overline{M}}$ be an acceptable filtering of an S-module M. Then, since R is Noetherian, ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{M}})$ is Noetherian.

Theorem 6.3

Let M be an S-module and ${\overline{M}}:= (M_{n})_{n \in \mathbb {N}}$ be a good filtering of M. Then, for $n \in \mathbb {N}$ large enough, $\lambda (M_{n})$ is equal to a polynomial $q_{{\overline{M}}}(n)$ of degree at most k.

If moreover ${\overline{M}}$ is an exhaustive (and good) filtering of M, then the leading monomial of $q_{{\overline{M}}}$ does not depend on the choice of the exhaustive good filtering (but only on M and $\lambda$).

Therefore, we can denote by $\mu (M)$ the leading monomial of the polynomial $q_{{\overline{M}}}$ associated to some exhaustive good filtering of M (if such good filtering exists).

Proof

By Corollary 5.2,

$$\begin{aligned} F_{{\overline{M}}}(t) = \frac{p(t)}{(1-t)^{k+1}}, \end{aligned}$$

for some polynomial $p(t) \in \mathbb {R}[t]$. Thus, by Proposition 2.1, for n large enough the coefficients $\lambda (M_{n})$ of the power series $F_{{\overline{M}}}$ are equal to some polynomial $q(n) \in \mathbb {R}[n]$ of degree at most k.

Assume now ${\overline{M}}$ is exhaustive, and that ${\overline{M}}':= (M'_{n}: n \in \mathbb {N})$ is another exhaustive good filtering of M. By Proposition 4.9, there exists $d_{0} \in \mathbb {N}$ such that, for every $n \in \mathbb {N}$,

$$\begin{aligned} M'_{n + d_{0}} = S_{n} M'_{d_{0}} \end{aligned}$$

Let $d_{1} \in \mathbb {N}$ such that $M'_{d_{0}} \le M_{d_{1}}$ ($d_{1}$ exists because $M'_{d_{0}}$ is finitely generated as R-module). Thus, for every n large enough,

$$\begin{aligned} q_{{\overline{M}}'}(n+d_{0}) = \lambda (M'_{n+d_{0}}) = \lambda (S_{n}M'_{d_{0}}) \le \lambda (S_{n}M_{d_{1}}) = q_{{\overline{M}}}(n + d_{1}). \end{aligned}$$

Similarly,

$$\begin{aligned} q_{{\overline{M}}}(n + d'_{0}) \le q_{{\overline{M}}'}(n + d'_{1}) \end{aligned}$$

for some $d'_{0}, d'_{1} \in \mathbb {N}$ and every n large enough, showing that $q_{{\overline{M}}}$ and $q_{{\overline{M}}'}$ have the same leading monomial. $\square$

6.2 Growth function

Definition 6.4

Let N be an S-module, and $V_{0} \le N$ be an R-submodule. For every $n \in \mathbb {N}$, let $V_{n}:= S_{n} V_{0}$ (notice that $V_{0} = S_{0} V_{0}$, and that $S_{n}$ and $V_n$ are R-modules). We denote by

$$\begin{aligned} {{\,\text {Filt}\,}}(V_{0}; N) := (V_{n})_{n \in \mathbb {N}} \end{aligned}$$

the corresponding filtering of N (as S-module), where each $x_{i}$ has degree 1, and

$$\begin{aligned} {{\,\text {Gr}\,}}(V_{0}; N) := {{\,\mathrm {{\mathcal {B}}}\,}}({{\,\text {Filt}\,}}(V_{0}; N)) = \bigoplus _{n \in \mathbb {N}} S_{n} V_{0}\, y^{n} \end{aligned}$$

be the corresponding graded S[y]-module.

Notice that ${{\,\textrm{Gr}\,}}(V_{0}; N)$ depends not on N but only on $SV_{0} \le N$.

Theorem 6.5

Let N be an S-module. Let $V_{0} \le N$ be an R-submodule. Define

$$\begin{aligned} G_{V_{0}}(t):= \sum _{n \in \mathbb {N}} \lambda (S_{n} V_{0}) t^{n}. \end{aligned}$$

Assume that:

• (1) $\lambda (V_{0}) < \infty$;

• (2) $V_{0}$ is finitely generated as R-module.

Then, each $\lambda (S_{n} V_{0})$ is finite, and there exists a polynomial $p(t) \in \mathbb {R}[t]$ such that

$$\begin{aligned} G_{V_{0}}(t) = \frac{p(t)}{(1 - t)^{k+1}}. \end{aligned}$$

Proof

First, we show that (1) implies that $\lambda (S_{n} V_{0})$ is finite for every $n \in \mathbb {N}$. In fact, $S_{n}V_{0}$ is a quotient of $V_{0}^{\ell }$, where $\ell {:=}\genfrac(){0.0pt}1{n+k}{n} \in \mathbb {N}$ is the number of monic monomials in S of degree less or equal to n, and $\lambda (V_{0}^{\ell })$ is finite.

Notice that ${\overline{V}} {:=}{{\,\textrm{Filt}\,}}(V_{0};N)$ is an filtering of N (as S-module). Moreover, $F_{{\overline{V}}} = G_{V_{0}}$. Thus, by Theorem 6.3, it suffices to show that ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{V}}) = {{\,\textrm{Gr}\,}}(V_{0}; N)$ is Noetherian as an S[y]-module to conclude (since then the filtering ${\overline{V}}$ is good). Since S[y] is a Noetherian ring, it suffices to show that ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{V}})$ is finitely generated (as an S[y]-module). It is easy to see that ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{V}})$ is generated by $V_{0} y^{0}$, and the latter is finitely generated (as R-module) by (2). $\square$

Theorem 6.6

(Hilbert polynomial) Let N and $V_{0}$ be as in Theorem 6.5 and assume that (1), (2) as in there hold. Then, there exists a polynomial $q_{V_{0}}(t) \in \mathbb {R}[t]$ of degree at most k, such that, for every n large enough,

$$\begin{aligned} \lambda (S_{n}V_{0}) = q_{V_{0}}(n). \end{aligned}$$

Assume moreover that $N = SV_{0}$ (that is, $V_{0}$ witnesses that N is $\lambda _S$-small). Let $V_{0}'$ also witness that N is $\lambda _S$-small. Then, $q_{V_{0}}$ and $q_{V_{0}'}$ have the same leading term.

Therefore, if we define $\mu _{\lambda }(N)$ to be the leading term of $q_{V_{0}}$, then $\mu _{\lambda }(N)$ does not depend on the choice of the witness $V_{0}$.

Finally, let $c_{k}$ be the coefficient of $q_{V_{0}}$ of degree k. Then,

$$\begin{aligned} c_{k} = \frac{h_{\lambda }(N)}{k!} \end{aligned}$$

where $h_{\lambda }(N)$ is the algebraic entropy of N according to $\lambda$ (see Sect. 3.2).

Proof

Let ${\overline{V}} {:=}(S_{n} V_{0})_{n \in \mathbb {N}}$.

Notice that ${\overline{V}}$ is a good filtering of N, and that ${\overline{V}}$ is exhaustive iff $SV_{0} = N$. Therefore, Theorem 6.3 implies the existence of the polynomial $q_{V_{0}}$, and that if $V_{0}$ witnesses that N is $\lambda _S$-small, then the leading monomial of $q_{V_{0}}$ is independent of the choice of the witness.

If $V_{0}$ is a witness, then

$$\begin{aligned} c_{k} = \lim _{n \rightarrow \infty } \frac{q(n)}{n^{k}} = \lim _{n \rightarrow \infty } \frac{\lambda (V_{n})}{n^{k}} = \frac{h_{\lambda }(N)}{k!}. \end{aligned}$$

$\square$

Notice that many authors (e.g., [14]) use a slightly different construction: in the situation when R is a field, they consider the function

$$\begin{aligned} H(n) {:=}\dim (V_{n+1}/ V_{n}). \end{aligned}$$

It is easy to see that there exists a polynomial ${\tilde{G}}_{V_{0}}(t) \in \mathbb {N}[t]$ such that, for n large enough, $H(n) = {\tilde{G}}_{V_{0}}(t)$; from the definition it follows that ${\tilde{G}}_{V_{0}}(t) = G_{V_{0}}(t+1) - G_{V_{0}}(t)$. In the present situation, we found it easier to work with the function $\lambda (V_{n})$ (but see Sect. 13).

Definition 6.7

Let M be a $\lambda _S$-small S-module. We define $\mu _{\lambda }(M)$ as in Theorem 6.6 (with $\mu _{\lambda }(M) = 0$ iff $q_{V_{0}} = 0$): then, $\mu _{\lambda }(M)$ does not depend on the choice of a witness. When $\lambda$ is clear from the context, we will write $\mu$ instead of $\mu _{\lambda }$.

Let d be the degree of $\mu (M)$ and m be the coefficient of $\mu (M)$. We define the $\lambda$ -dimension of M (as an S-module) to be equal to d, and its $\lambda$ -degree as

$$\begin{aligned} d!\, m \end{aligned}$$

When $\lambda$ is clear, we will simply say “dimension” and “degree”, respectively.⁴

If $\mu (M) = 0$, by convention we say that M has dimension $-1$ and degree undefined.

One reason of the normalizing coefficient d! is the following:

Example 6.8

Assume that $0< \lambda (R) < \infty$ and fix $d \le k$. Let $M {:=}R[x_{1}, \dotsc , x_{d}]$ as an S-module, by defining the action of $x_{j}$ on M as multiplication by 0 for $j > d$. Let $V_{0} = R$ as a submodule of M. Then,

$$\begin{aligned} q_{V_{0}}(n) = \left( {\begin{array}{c}n+d\\ d\end{array}}\right) \lambda (R) \qquad \mu (M) = \frac{t^{d}}{d!} \lambda (R) \end{aligned}$$

Therefore, the $\lambda$-dimension of M is d, and its $\lambda$-degree is $\lambda (R)$.

Remark 6.9

Let M be an $\lambda _S$-small S-module. Then, $\mu (M) = 0$ iff $\lambda (M) = 0$. Moreover, the dimension of M is 0 iff $0< \lambda (M) < \infty$.

Notice that, if $\lambda (R) = 0$, then $\mu (M) = 0$ for every $\lambda _S$-small S-module: hence we often assume that $\lambda (R) \ne 0$ in the following.

Proposition 6.10

Assume that $\lambda (R) = \ell$ with $0< \ell < \infty$. Let $p({\bar{x}}) \in S$ of degree $e>0$. Assume that $p_{e}$, the leading homogeneous component of p (see Def. 2.2), is not a zero-divisor (in S). Let $M {:=}S/(p)$. Then, the $\lambda$-dimension of M is $k-1$ and it $\lambda$-degree is $\ell e$.

Proof

“Usual” proof. Let $N:= (p) \lhd S$. We choose $M_{0} {:=}R \le M$. We have $S M_{0} = M$. For each $n \in \mathbb {N}$, we denote $M_{n} {:=}S_{n} M_{0} = S_{n} / ((p) \cap S_{n}) \le M$. Notice that, since $p_{e}$ is not a zero-divisor, for every $n \in \mathbb {N}$ we have

$$\begin{aligned} p \cdot S_{n} = (p) \cap S_{n+e} \end{aligned}$$

and therefore $S_{n+e} / p \cdot S_{n}$ and $M_{n+e}$ are isomorphic (as R-modules). Moreover also p is not a zero-divisor, and therefore the multiplication by p is an injective function (on S). Therefore, for every $n \in \mathbb {N}$, the following sequence is exact:

$$\begin{aligned} 0 \longrightarrow S_{n} \overset{\cdot p}{\longrightarrow }S_{n+e} \longrightarrow M_{n+e} \longrightarrow 0 \end{aligned}$$

Therefore, if $q^{(S)}$ and $q^{(M)}$ are the Hilbert polynomials associated to S and M respectively, we have that, for every $n \in \mathbb {N}$ large enough,

$$\begin{aligned} q^{(M)}(n+e) = q^{(S)}(n+e) - q^{(S)}(n). \end{aligned}$$

The conclusion follows. $\square$

Corollary 6.11

Assume that $\lambda (R) = 1$. Let $p \in S$ be as in Proposition 6.10. Then, the $\lambda$-degree of S/(p) is equal to $\deg (p)$, and in particular it is independent from $\lambda$.

The above corollary implies that, if R is an integral domain and $\lambda (R) = 1$, then the $\lambda$-degree of S/(p) does not depend on $\lambda$ (since the leading homogeneous component of p is not a zero divisor). However, this is hardly surprising, since under the above assumption $\lambda$ is unique (see Exercise 3.4).

6.3 Necessity of noetherianity

We give an example of a $\lambda _S$-small module over a non Noetherian ring T with no associated Hilbert polynomial.

Define the following ring

$$\begin{aligned} T {:=}\bigoplus _{p} \mathbb {Z}/p\mathbb {Z}\end{aligned}$$

where p varies among the set of primes. Thus, T is a direct sum of fields and it is not Noetherian (notice that it is also not unitary). Any T-module M can be decomposed uniquely into the direct sum of its p-components:

$$\begin{aligned} M = \bigoplus _{p} M_{p} \end{aligned}$$

where each $M_{p}$ is a $\mathbb {Z}/p\mathbb {Z}$-vector space with a certain dimension $\dim _{p}(M_{p})$. Fix a sequence $\bigl ( \alpha _{p}: p \text { prime} \bigr )$ of real numbers such that, for each prime p, $0< \alpha _{p} < 1$, and $\sum _{p} \alpha _{p} = 1$. Define the followng lenght function on ${{\,\mathrm{ T\mathrm -mod}\,}}$ as

$$\begin{aligned} \lambda (M) = \sum _{p} \alpha _{p} \dim _{p}(M_{p}); \end{aligned}$$

thus, $\lambda (T) = 1$. Let $M {:=}S {:=}T[x]$, where we see S as a ring and M as a T-module. To give to M a structure as S-module, we specify the action of x on M in the following way:

$$\begin{aligned} x \cdot (v_{p} x^{i}) {:=}{\left\{ \begin{array}{ll} v_{p} x^{i+1} &{} \text { if } p > i,\\ 0 &{} \text { otherwise,} \end{array}\right. } \end{aligned}$$

where $v_{p} \in \mathbb {Z}/p\mathbb {Z}$, and extend it by linearity to all M. Let $V_{0} {:=}T \le M$. Thus, $V_{0}$ is a finitely generated T-submodule of M of finite length, but $\lambda (S_{n+1} V_{0}/S_{n} V_{0})$ is a strictly decreasing sequence of real numbers in (0, 1), and therefore $\lambda (S_{n} V_{0})$ is not eventually equal to any polynomial.

Notice that the algebraic entropy, i.e. the limit $\lim _{n \rightarrow \infty } \lambda (S_{n} V_{0}) / n$, still exists.

7 Dimension and degree: the general case

We defined $\mu (M)$ when M is a $\lambda _S$-small S-module. We will extend the definition to the case when M is not necessarily $\lambda _S$-small. We need first to explain what is the range of $\mu$.

7.1 The value monoid

(Remember that we fixed $k \in \mathbb {N}$). We define the following ordered monoids ${\mathcal {V}}$ and $\overline{{\mathcal {V}}}$. An element of $\overline{{\mathcal {V}}}$ is either 0 or a monomial $r t^{d}$, where $r \in \mathbb {R}_{> 0} \cup \{\infty \}$ and $d \in \{0, 1,\dotsc , k\}$. Given a monomial $0 \ne r t^{d} \in \overline{{\mathcal {V}}}$, its degree is d and its coefficient is r; for completeness we define the degree of 0 to be $-1$. ${\mathcal {V}}$ is the subset of $\overline{{\mathcal {V}}}$ given by 0 and the monomials with coefficient which is not $\infty$.

Remember that we follow the convention that $r + \infty = \infty$ for every $r \in \mathbb {R}\cup \{\infty \}$. The sum of two monomials in $\overline{{\mathcal {V}}}$ is defined as

$$\begin{aligned} r t^{n} \oplus s t^{m} = {\left\{ \begin{array}{ll} r t^{n} &{} \text {if } n > m\\ s t^{m} &{} \text {if } n < m \\ (r + s) t^{n} &{} \text {if } n = m \end{array}\right. } \end{aligned}$$

and $0 + \mu = \mu$ for every $\mu \in \overline{{\mathcal {V}}}$. We also define an ordering $\le$ on $\overline{{\mathcal {V}}}$ with the rule that

$$\begin{aligned} r t^{n} \le s t^{m} \end{aligned}$$

iff either $n < m$ or $n = m$ and $r \le s$, and $0 \le \mu$ for every $\mu \in \overline{{\mathcal {V}}}$.

With the above definitions, $\langle \overline{{\mathcal {V}}}; \oplus , 0, \le \rangle$ is a commutative ordered monoid (with 0 the neutral element) and $\le$ is a linear ordering. Moreover, ${\mathcal {V}}$ is a submonoid of $\overline{{\mathcal {V}}}$.

Notice that $\le$ is a complete ordering on $\overline{{\mathcal {V}}}$: given $I \subseteq \overline{{\mathcal {V}}}$, its supremum $\sup (I)$ is 0 if I is empty or $I = \{0\}$; otherwise, $\sup (I)$ is the monomial $r t^{d}$, where

$$\begin{aligned}\begin{aligned} d&:= \max \{d': d' \text { is the degree of some } \mu \in I\} \in \{0, \dotsc , k\} \\ r&:= \sup \{r': r' t^{d} \in I\} \in \mathbb {R}_{> 0} \cup \{\infty \}. \end{aligned}\end{aligned}$$

Moreover, 0 is the minimum of $\overline{{\mathcal {V}}}$ and $\infty t^{k}$ is its maximum, and $\infty t^{k}$ is an absorbing element: as an ordered set, $\overline{{\mathcal {V}}}$ is isomorphic to the real interval [0, 1].

We give now an equivalent description of the value monoid. Let

$$\begin{aligned} P {:=}\{p \in \mathbb {R}[t]: \deg (p) \le k \text { and } p(t) \ge 0 \text { eventually}\}. \end{aligned}$$

We endow P with the (total) quasi-ordering $\preceq$ defined in Def. 2.3, and the binary operation $+$ given by pointwise addition. It is easy to see that $\langle P; +, 0, \preceq \rangle$ is an ordered commutative monoid, and that the equivalence relation $\simeq$ on P in Def. 2.3 is compatible with the structure of ordered monoid. Therefore, $P/\mathord {\simeq }$ is also an ordered monoid (and the induced quasi-ordering on $P/\mathord {\simeq }$ is a linear ordering).

Proposition 2.4 easily implies the following⁵:

Remark 7.1

$P/\mathord {\simeq }$ is isomorphic to ${\mathcal {V}}$ (as an ordered monoid), with the canonical isomorphism given by the function mapping the equivalence class of a polynomial p to the leading term of p.

Remark 7.2

$\overline{{\mathcal {V}}}$ is the completion of ${\mathcal {V}}$ (as an ordered set).

7.2 Non-small modules

Let M be an S-module (which might not be $\lambda _S$-small). Given $M' \le M$ S-submodule which is $\lambda _S$-small (see Definition 3.5), let $\mu (M')$ be as in Definition 6.7: notice that $\mu (M') \in {\mathcal {V}}$.

Thus, we can define $\mu (M) \in \overline{{\mathcal {V}}}$ as the supremum of $\mu (M')$, where $M'$ varies among all the possible S-submodules $M' \le M$ which are $\lambda _S$-small. We can then define as before the $\lambda$-dimension and $\lambda$-degree of M as the coefficient (up to a multiplicative constant) and the degree of $\mu (M)$, respectively: the latter can be infinite.

From Remark 6.9 the following follows immediately.

Remark 7.3

$\mu (M) = 0$ iff all submodules of M of finite length have length 0. In particular, if 0 is the only submodule of M of finite length, then $\mu (M) = 0$.

An analogy from geometry that might help the intuition is the following. A semi-algebraic set $X \subseteq \mathbb {R}^{k}$ has a dimension $d \in \{0, \dotsc , k\}$ and a corresponding d-dimensional (Hausdorff) measure $r:= {\mathcal {H}}_{d}(X) \in \mathbb {R}_{> 0} \cup \{\infty \}$: we could define $\mu (X) {:=}r t^{d} \in \overline{{\mathcal {V}}}$ as the object encapsulating both the dimension and the measure of X (with $\mu (X) = 0$ iff X is empty). The definition of $\oplus$ is such that if X and Y are disjoint manifolds, then $\mu (X \cup Y) = \mu (X) \oplus \mu (Y)$; if X and Y are not necessarily disjoint, then

$$\begin{aligned} \mu (X \cup Y) \oplus \mu (X \cap Y)= \mu (X) + \mu (Y). \end{aligned}$$

(6)

Thus, the $\lambda$-dimension of M is the analogue of the dimension of X, and the $\lambda$-degree of M is the analogue of the measure of X. We will see in Sect. 8 that (6) has an analogue for $\lambda _S$-small modules: the additivity of $\mu$.

8 Addition theorem for exact sequences

In this section we will prove the following Theorem.

Theorem 8.1

Let $0 \longrightarrow A \overset{\iota }{\longrightarrow }B \overset{\pi }{\longrightarrow }C \longrightarrow 0$ be an exact sequence of S-modules. Assume that B is locally $\lambda _R$-finite. Then, $\mu (B) = \mu (A) \oplus \mu (C)$ (see 7.1 for the definition of $\oplus$).

Notice that, under the assumptions of the above theorem, also A and C are locally $\lambda _R$-finite. Notice moreover that $\mu (B)$ might have coefficient $\infty$.

It is well-known that without the assumption that B is locally $\lambda _R$-finite, the theorem may fail.

Example 8.2

Let $R = \mathbb {Z}$ with the standard length $\lambda$ (see Example 3.2b). Let $A {:=}B {:=}\mathbb {Z}[x]$ and $C {:=}\mathbb {Z}/2\mathbb {Z}[X]$. Let $\iota : A \rightarrow B$, $a \mapsto 2 a$ and let $\pi : B \rightarrow C$ be the canonical projection. Then, $0 \longrightarrow A \overset{\iota }{\longrightarrow }B \overset{\pi }{\longrightarrow }C \longrightarrow 0$ is an exact sequence of $\mathbb {Z}[x]$-modules, but $\mu (A) =\mu (B) = 0$ while $\mu (C) = \log 2 \cdot t$.

The main ingredient is the following proposition, which treats the case of $\lambda _S$-smallness (where in particular $\mu (B)$ has finite coefficient).

Proposition 8.3

(Additivity) Let $0 \longrightarrow A \overset{\iota }{\longrightarrow }B \overset{\pi }{\longrightarrow }C \longrightarrow 0$ be an exact sequence of S-modules. Assume that B is $\lambda _S$-small. Then, $\mu (B) = \mu (A) \oplus \mu (C)$.

Notice that, under the assumptions of the above propositions, also A and C are $\lambda _S$-small.

Proof

Let $B_{0}$ be an R-submodule of B such that $B_{0}$ is finitely generated, $\lambda (B_{0}) < \infty$, and $S B_{0} = B$. For every $i \in N$, define

$$\begin{aligned}\begin{aligned} B_{i}&:= S_{i} B_{0}\\ A_{i}&:= \iota ^{-1}(B_{i})\\ C_{i}&:= \pi (B_{i}), \end{aligned} \end{aligned}$$

and define ${\overline{B}}:= (B_{i}: i \in \mathbb {N})$, ${\overline{A}}:= (A_{i}: i \in \mathbb {N})$, and ${\overline{C}}:= (C_{i}: i \in \mathbb {N})$. Notice that ${\overline{A}}$, ${\overline{B}}$, and ${\overline{C}}$ are good filterings of A, B, and C, respectively (see Definiton 6.1). Thus, by Theorem 6.3, for $n \in \mathbb {N}$ large enough, $\lambda (A_{n})= q_{{\overline{A}}}(n)$ and $\mu (A)$ is the leading term of $q_{{\overline{A}}}$, and similarly for B and C. Moreover, for every $n \in \mathbb {N}$, $\lambda (A_{n}) + \lambda (C_{n}) = \lambda (B_{n})$: thus,

$$\begin{aligned} q_{{\overline{A}}} + q_{{\overline{C}}} = q_{{\overline{B}}}, \end{aligned}$$

and therefore $\mu (A) \oplus \mu (C) = \mu (B)$. $\square$

Proof of Thm. 8.1

Since B is locally $\lambda _R$–finite, every submodule of A, B, or C is locally $\lambda _R$-finite. $\square$

Claim 2

$$\begin{aligned} \mu (B) \le \mu (A) \oplus \mu (C). \end{aligned}$$

Let $B' \le B$ be an S-submodule which is finitely generated. Define

$$\begin{aligned} A':= \iota ^{-1}(B'), \qquad C':= \pi (B'). \end{aligned}$$

Notice that the sequence

$$\begin{aligned} 0 \longrightarrow A' \longrightarrow B' \longrightarrow C' \longrightarrow 0 \end{aligned}$$

is exact, and therefore, by Proposition 8.3,

$$\begin{aligned} \mu (B') = \mu (A') \oplus \mu (C') \le \mu (A) \oplus \mu (C). \end{aligned}$$

Taking the supremum among all the $B'$, we get the Claim.

Claim 3

$$\begin{aligned} \mu (B) \ge \mu (A) \oplus \mu (C). \end{aligned}$$

Let $A' \le A$ and $C' \le C$ be finitely generated S-submodules. Since $C'$ is finitely generated and $\pi$ is surjective, there exists $B' \le B$ finitely generated and such that $\pi (B') = C'$. Define

$$\begin{aligned} B'':= B' + \iota (A'), \qquad A'':= \iota ^{-1}(B''). \end{aligned}$$

We have that the sequence

$$\begin{aligned} 0 \longrightarrow A'' \longrightarrow B'' \longrightarrow C' \longrightarrow 0 \end{aligned}$$

is exact, and $B''$ is finitely generated and locally $\lambda _R$-finite. Thus, by Proposition 8.3,

$$\begin{aligned} \mu (A') \oplus \mu (C') \le \mu (A'') \oplus \mu (C') = \mu (B'') \le \mu (B). \end{aligned}$$

Taking the supremum on the left-hand side among all possible $A'$ and $C'$, we get the Claim.$\square$

9 Modules over R-algebrae

Let T be a finitely generated commutative R-algebra (therefore, T is Noetherian). Let M be a T-module. We want to define the $\lambda$-dimension of M as a T-module.

Fix $\gamma _{1}, \dotsc , \gamma _{k}$ generators of T as R-algebra. Equivalently, we fix a surjective homomorphism of R-algebrae

$$\begin{aligned} \phi : S \rightarrow T \end{aligned}$$

and denote $\gamma _{i} {:=}\phi (x_{i})$, $i = 1, \dotsc , k$. We can therefore see M as an S-module, and we denote it either by $\langle M; \phi \rangle$ or by $\langle M; {\bar{\gamma }} \rangle$.

We assume M is $\lambda _T$-small.

Thus, we can use the above data to compute $\mu (M; \phi )$ (which will depend on $\phi$).

We prove now that, while the coefficient of $\mu$ may depend on $\phi$, its degree does not. Thus, we can define the $\lambda$-dimension of M (as a T-module) as the degree of $\mu (M; \phi )$.

Definition 9.1

Spelling out all the assumptions, assume that:

• (1) R is Noetherian;

• (2) T is a finitely generated commutative R-algebra;

• (3) M is a T-module;

• (4) there exists $M_{0} \le M$ finitely generated R-submodule, such that $\lambda (M_{0}) < \infty$ and $T M_{0} = M$.

Then, we can define as before the $\lambda$-dimension of M as a T-module, and this dimension does not depend on the choice of $M_{0}$ or of $\phi$.

Examples 9.2

Fix some length function $\lambda$ on R such that $\lambda (R) = 1$.

• a) Let $M:= T = R[z]$, ${\bar{\gamma }}:= \langle z \rangle$, ${\bar{\delta }}:= \langle z, z^{3} \rangle$. Thus, $\langle M; {\bar{\gamma }} \rangle$ is R[z] seen as R[z]-module with the canonical action, while $\langle M;{\bar{\delta }} \rangle$ is R[z] seen as $R[x_{1}, x_{2}]$-module, with $x_{1}$ acting as multiplication by z and $x_{2}$ as multiplication by $z^{3}$. Then, $\mu (M; {\bar{\gamma }}) = t$, while $\mu (M; {\bar{\delta }}) = 3 t$.

• b) Let $M:= T = R[z, z^{-1}]$, ${\bar{\gamma }}:= \langle z,z^{-1} \rangle$, ${\bar{\delta }}:= \langle z, z^{-3} \rangle$. Thus, $\langle M; {\bar{\gamma }} \rangle$ is T seen as $R[x_{1},x_{2}]$-module with $x_{1}$ acting as multiplication by z, and $x_{2}$ as multiplication by $z^{-1}$, while $\langle M;{\bar{\delta }} \rangle$ is T seen as $R[x_{1}, x_{2}]$-module, with $x_{1}$ acting as multiplication by z and $x_{2}$ as multiplication by $z^{-3}$. Then, $\mu (M; {\bar{\gamma }}) = 2t$, while $\mu (M; {\bar{\delta }}) = 4 t$.

In both examples, we see that the two modules have different degrees, but have the same dimension.

It remains to prove that the dimension of $\langle M; \phi \rangle$ does not depend on the choice of $\phi$. It is clear that it suffices to prove the following:

Theorem 9.3

Let ${\bar{\delta }} \in T^{k'}$ be another tuple of generators of T. Then, $\langle M; {\bar{\gamma }} \rangle$ and $\langle M; {\bar{\delta }} \rangle$ have the same dimension.

Proof

After exchanging the rôles of ${\bar{\gamma }}$ and ${\bar{\delta }}$ if necessary, we may assume that $k \ge k'$. After extending $\delta$ by setting $\delta _{i} = 0$ for $i \ge k'$, we may assume that $k = k'$.

We denote by $\psi : R[x_{1}, \dotsc , x_{k}] \rightarrow M$ the surjective homomorphism of R-algebrae corresponding to ${\bar{\delta }}$ (and by $\phi$ the one corresponding to ${\bar{\gamma }}$).

For every $n \in \mathbb {N}$, define

$$\begin{aligned} \begin{aligned} T_{n}&:= \phi (S_{n}),&T_{n}'&:= \psi (S_{n}),\\ M_{n}&:= T_{n}M_{0},&M_{n}'&:= T_{n}' M_{0}. \end{aligned} \end{aligned}$$

Notice that both $(T_{n})_{n \in \mathbb {N}}$ and $(T_{n}')_{n \in \mathbb {N}}$ are filterings of T as an R-module, that $(M_{n})_{n \in \mathbb {N}}$ and $(M_{n}')_{n \in \mathbb {N}}$ are filterings of M as an R-module, and that each $T_{n}$, $T_{n}'$, $M_n$ and $M_{n}'$ are finitely generated (as R-modules).

Moreover, $M_{0}$ generates both $\langle M; {\bar{\gamma }} \rangle$ and $\langle M; {\bar{\gamma }}' \rangle$ as S-modules. Thus, we can apply Theorem 6.6; we denote by q (resp., $q'$) the Hilbert polynomial of $\langle M; {\bar{\gamma }} \rangle$ (resp., of $\langle M; {\bar{\gamma }}' \rangle$).

Let $c \in \mathbb {N}$ such that $\gamma _{1}, \dotsc , \gamma _{k} \in T_{c}'$. Thus, $T_{1} \le T_{c}'$.$\square$

The following is then clear

Claim 4

For every $n \in \mathbb {N}$, $T_{n} \le (T_{c}')^{n}$

Therefore, for every $n \in \mathbb {N}$

$$\begin{aligned} M_{n} = T_{n} M_{0} \le (T_{c}')^{n} M_{0} \le T_{cn}' M_{0} = M'_{cn} \end{aligned}$$

Therefore, for every $n \in \mathbb {N}$,

$$\begin{aligned} \lambda (M_{n}) \le \lambda (M'_{cn}). \end{aligned}$$

Therefore, for every n large enough,

$$\begin{aligned} q(n) = \lambda (M_{n}) \le \lambda (M'_{cn}) = q'(nc), \end{aligned}$$

proving that $\deg q \le \deg q'$. Exchanging the rôles of $\phi$ and $\phi '$, we see that q and $q'$ have the same degree. $\square$

We end this section with a comparison between $\lambda$-dimension and Krull dimension for affine rings.

Lemma 9.4

Let R be a field and $\lambda$ equal to the linear dimension (as R-vector spaces). Let T be a finitely generated R-algebra. Then, the $\lambda$-dimension and the Krull dimension of T coincide.

Proof

Let d be equal to the Krull dimension of T. By Noether Normalization (see [9, Thm.13.3], there exists an R-subalgebra $A \le T$ such that:

• (1) A, as an R-algebra, is isomorphic to the polynomial ring $R[y_{1}, \dotsc , y_{d}]$;

• (2) T is finitely generated as A-module.

Thus, T and A have the same Krull dimension d. $\square$

Claim 5

For any T finitely generated A-module, $\dim _{\lambda }(T) \le \dim _{\lambda }(A)$ (where $\dim _{\lambda }$ denotes the $\lambda$-dimension).

In fact, T is a quotient of $A^{n}$ (for some $n \in \mathbb {N}$), and Theorem 8.1 implies that

$$\begin{aligned} \dim _{\lambda }(T) \le \dim _{\lambda }(A^{n}) = \dim _{\lambda }(A). \end{aligned}$$

Since moreover $A \le T$, we conclude that $\dim _{\lambda }(T) = \dim _{\lambda }(A) = d$. $\square$

Lemma 9.4 answers positively and extends the conjecture in [2, Remark 5.9].

Here is another example of equality between Krull and $\lambda$ dimensions.

Lemma 9.5

Fix $2 \le n \in \mathbb {N}$. Let $R {:=}\mathbb {Z}/(n)$. Let $\lambda$ be the length on ${{\,\mathrm{ R\mathrm -mod}\,}}$ given by

$$\begin{aligned} \lambda (M) {:=}\log (|M|). \end{aligned}$$

Let A be a finitely generated R-algebra. Then, $\dim _{\lambda }(A)$ is equal to the Krull dimension of A.

Proof

We denote by $\dim _{K}$ the Krull dimension.

Write the factorization of n into primes:

$$\begin{aligned} n = p_{1}^{e_{1}} \cdots p_{\ell }^{e_{\ell }}. \end{aligned}$$

Decompose A into a direct sum of $Z_{p_{i}^{e_{i}}}$-algebrae $A_{i}$. Since $\dim (A) = \max (\dim (A_{i}: i = 1, \dotsc , \ell )$, where $\dim$ is either $\dim _{K}$ or $\dim _{\lambda }$, it suffices to treat the case when $\ell = 1$, i.e. $n = p^{e}$.

Let $B_{i}:= p^{i} A$ as R-submodule of A, for $i = 1, \dotsc , e$. We have $0 = B_{e} \le B_{e-1} \le \dotsc \le B_{0} = A$. Notice that, for every $i < e$, ${\tilde{B}}_{i} {:=}B_{i}/B_{i+1}$ is a Z/(p)-algebra. Moreover, there exists a surjective homomorphism of $\mathbb {Z}$-modules between $\tilde{B}_{0}$ and ${\tilde{B}}_{i}$, mapping $a + pA$ to $p^{i} a + p^{i+1} A$. Thus, $\mu ({\tilde{B}}_{i}) \le \mu ({\tilde{B}}_{0})$ and therefore

$$\begin{aligned} \dim _{\lambda }(A) = \dim _{\lambda }({\tilde{B}}_{0}) = \dim _{\lambda }(A /pA). \end{aligned}$$

Moreover, for $\mathbb {Z}/(p)$-modules, $\lambda$ (up to a constant factor) is equal to the linear dimension, and Lemma 9.4 implies that

$$\begin{aligned} \dim _{\lambda }(A/pA) = \dim _{K}(A/pA). \end{aligned}$$

Finally, pA is the unique minimal prime ideal of A, and therefore

$$\begin{aligned} \dim _{K}(A) = \dim _{K}(A/pA). \end{aligned}$$

$\square$

10 Hilbert-Samuel polynomial for homogeneous modules

Let $I {:=}(x_{1}, \dotsc , x_{k}) \lhd S$. Let M be an S-module. For every $n \in \mathbb {N}$, define $c_{n} {:=}\lambda (M/I^{n+1}M)$.

Theorem 10.1

Assume that:

• (i) M is finitely generated (as S-module);

• (ii) $\lambda (M/IM)$ is finite.

Then, for every $n \in \mathbb {N}$, $c_{n}$ is finite, and there exists a polynomial ${\bar{q}}(t) \in \mathbb {R}[t]$ such that:

• (1) for every $n \in \mathbb {N}$ large enough, $c_{n} = {\bar{q}}(n)$;

• (2) $\deg {\bar{q}} \le k$.

Proof

Usual proof (see e.g. [9, Prop.12.2]). $\square$

Assume moreover, besides the hypothesis in the theorem, that $V \le M$ witnesses that M is $\lambda _S$-small. Notice that

$$\begin{aligned} c_{n} = \lambda (M/I^{n+1}M) = \lambda (S_{n}V/I^{n+1}M) \le \lambda (S_{n }V). \end{aligned}$$

Therefore, denoting by $q_{V}$ the Hilbert polynomial associated to V, we have ${\bar{q}}(t) \le q_{V}(t)$ for every t large enough. If ${\bar{\mu }}(M)$ is the leading term of ${\bar{q}}$, we have therefore ${\bar{\mu }}(M) \le \mu (M)$.

In general, it can happen that ${\bar{\mu }}(M) < \mu (M)$.

Example 10.2

Let K be a field, $\lambda$ be the linear dimension over K, $S {:=}K[x_{1},x_{2}]$, $M {:=}K[x_{1},x_{2}]/(x_{1}x_{2} - 1)$. Then, $\mu (M) = 2t$, while ${\bar{\mu }}(M) = 0$.

It is easy to prove that for homogeneous ideals the situation is different.

Exercise 10.3

Let $J \lhd S$ be a homogeneous ideal, and $M {:=}S/J$. Then,

$$\begin{aligned} \mu (M) = {\bar{\mu }}(M). \end{aligned}$$

More precisely, fix a finite set G generating J, and let $n_{0}$ be the maximum degree of the polynomials in G. Let $V {:=}R$. Then, for every $n > n_{0}$, $S_{n} V$ and $M/I^{n+1}$ are isomorphic (as R-modules), and therefore

$$\begin{aligned} \lambda (S_{n} V) = \lambda (M/I^{n+1}) = c_{n}. \end{aligned}$$

See also [9, Ch.12] and [16, Ch.7] for the “classical” version of the Hilbert-Samuel polynomial.

11 d-dimensional and receptive versions of entropy

Let M be an S-module. Let m be the coefficient of $\mu (M)$. For every $d \le k$, define

$$\begin{aligned} h^{(d)}_{\lambda }(M) {:=}{\left\{ \begin{array}{ll} \infty &{} \text {if } \deg \mu (M) > d\\ 0 &{} \text {if } \deg \mu (M) < d\\ d!\, m &{} \text {if } \deg \mu (M) = d. \end{array}\right. } \end{aligned}$$

The value $h^{(1)}(M)$ is the receptive entropy of M w.r.t. the standard regular system generated by $(x_{1}, \dotsc , x_{k})$ (see [2, 3]); we call each $h^{(d)} (M)$ the d -dimensional entropy of M (and thus the algebraic entropy h is the k-dimensional entropy).

The case $d= 1$ of the following Proposition answers positively (and extends) [2, Question 5.10].

Proposition 11.1

Let $0 \rightarrow A \rightarrow B \rightarrow C \rightarrow 0$ be an exact sequence of S-modules. Assume that B is locally $\lambda _R$-finite. Then, for every $d \le k$

$$\begin{aligned} h^{(d)} (B) = h^{(d)}(A) + h^{(d)}(C). \end{aligned}$$

Proof

Denote by $\dim (A)$ the $\lambda$-dimension of A (that is, the degree of $\mu _{\lambda }(A)$). By Theorem 8.1, $\dim (B) = \max (\dim (A), \dim (C))$. Assume, for simplicity, that $\dim (A) \le \dim (C)$, and therefore $\dim (B) = \dim (C)$ (the other case when $\dim (A) > \dim (C)$ is similar).

If $d < \dim (B)$, then $h^{(d)}(B) = h^{d}(C) = h^{(d)}(A) = 0$.

If $d < \dim (B)$, then $h^{(d)}(B) = h^{d}(C) = \infty$.

If $d = \dim (B) = \dim (A)$, then Theorem 8.1 again implies that $h^{(d)} (B) = h^{(d)}(A) + h^{(d)}(C)$.

If $d = \dim (B) > \dim (A)$, then $h^{(d)}(A) = 0$ and Theorem 8.1 again implies that $h^{(d)}(B) = h^{(d)}(C)$.

In all four cases, the conclusion follows. $\square$

Let T be a finitely generated R-algebra (thus, T is Noetherian). We can give similar definitions of entropies for T-modules. Fix ${\bar{\gamma }} = \langle \gamma _{1}, \dotsc , \gamma _{k} \rangle$ generators of T (as R-algebra). Let $\langle M, {\bar{\gamma }} \rangle$ be the S-algebra defined in Sect. 9. We define

$$\begin{aligned} h^{(d, {\bar{\gamma }})}_{\lambda }(M) {:=}\sup \{ h^{(d)}(M'; {\bar{\gamma }}): M' \le M \lambda _T\text { -small }T\text { -submodule }\}. \end{aligned}$$

$h^{(1, {\bar{\gamma }})}_{\lambda }(M)$ is the receptive entropy of M w.r.t. the standard regular system generated by ${\bar{\gamma }}$ (see [2, 3]); we call each $h^{(d, {\bar{\gamma }})} (M)$ the d -dimensional entropy of M w.r.t. ${\bar{\gamma }}$.

Theorem 11.2

Let $0 \rightarrow A \rightarrow B \rightarrow C \rightarrow 0$ be an exact sequence of T-modules. Assume that B is locally $\lambda _R$-finite. Then, for every $d \le k$,

$$\begin{aligned} h^{(d, {\bar{\gamma }})} (B) = h^{(d, {\bar{\gamma }})}(A) + h^{(d, {\bar{\gamma }})}(C). \end{aligned}$$

In particular, the receptive entropy $h^{(1, {\bar{\gamma }})}$ is additive (under the assumptions of Noetherianity of R and local $\lambda _R$-finiteness!).

12 Totally additive versions of $\mu$ and (receptive) entropy

The definition of $\mu (M)$ reflects the usual definition of algebraic entropy (see Sect. 3.2). Following a construction in [24, Prop.3], we propose an alternative invariant, which is in some ways better behaved.

Definition 12.1

Let A be an S-module. A $\lambda _S$-small chain in A is a sequence of S-submodules

$$\begin{aligned} {\mathfrak {A}}= \bigl ( A_{1} \le A_{2} \le \dots \le A_{2n-1} \le A_{2n} \le A \bigr ), \end{aligned}$$

where, for every $i \le n$,

$$\begin{aligned} {\hat{A}}_{i} {:=}A_{2i}/A_{2i-1} \end{aligned}$$

is $\lambda _S$-small. We call n is the size of ${\mathfrak {A}}$.

Definition 12.2

Let $\theta$ be a partial function from ${{\,\mathrm{ S\mathrm -mod}\,}}$ to $\overline{{\mathcal {V}}}$.

We will be interested only in functions $\theta$ which satisfy the following conditions:

Domain:

the domain of $\theta$ includes all $\lambda _S$-small S-modules;

Additivity:

$\theta (0) = 0$ and, for every exact sequence $0 \rightarrow A \rightarrow B \rightarrow C \rightarrow 0$ of $\lambda _S$-small S-modules, $\theta (B) = \theta (A) \oplus \theta (C)$;

Invariance:

if A and B are isomorphic S-modules in the domain of $\theta$, $\theta (A) = \theta (B)$.

Let A be any S-module. Given a $\lambda _S$-small chain ${\mathfrak {A}}$ in A of size n, we define

$$\begin{aligned} \begin{aligned} \theta ({\mathfrak {A}})&{:=}\sum _{i=1}^{n} \theta (\hat{A}_{i})\\ {\hat{\theta }}(A)&{:=}\sup \{\theta ({\mathfrak {A}}): {\mathfrak {A}}\ \lambda _S \text{-small } \text{ chain } \text{ in } A\}. \end{aligned} \end{aligned}$$

We will see later that ${\hat{\theta }}$ can be defined in a simpler way (Proposition 12.7); see also [24, Prop.3] for an equivalent approach.

For “well-behaved” length functions $\lambda$, we have ${\hat{\lambda }} = \lambda$ (here we take $S = R$). However, the following example shows that it is not always the case.

Example 12.3

Let $\lambda$ be any singular non-zero length (e.g., the length in Example 3.2(e)). Then, $\lambda \ne 0$ but ${\hat{\lambda }} = 0$.

Proposition 12.4

Assume:

• (1) the domain of $\theta$ includes all $\lambda _S$-small S-modules;

• (2) $\theta$ is additive and invariant (on $\lambda _S$-small S-modules).

Then,

• (a) ${\hat{\theta }}$ is also additive and invariant;

• (b) if A is a $\lambda _S$-small S-module, then ${\hat{\theta }}(A) = \theta (A)$;

• (c) For every S-module A,

  $$\begin{aligned} {\hat{\theta }}(A) = \sup \{{\hat{\theta }}(B): B \le A \text{ finitely } \text{ generated } S\text{-submodule } \} \end{aligned}$$

• (d) if A is a locally $\lambda _R$-finite S-module, then

  $$\begin{aligned} {\hat{\theta }}(A) = \sup \{\theta (B): B \le A \text{ finitely } \text{ generated } S\text{-submodule }\} \end{aligned}$$
• (e)
  $$\begin{aligned} \hat{{\hat{\theta }}} = {\hat{\theta }}. \end{aligned}$$

Proof

The proof is quite straightforward; we will prove that ${\hat{\theta }}$ is additive, and leave the remainder as an exercise (see also [24]). Thus, let $0 \longrightarrow A \overset{\iota }{\longrightarrow }B \overset{\pi }{\longrightarrow }C \longrightarrow 0$ be an exact sequence of S-modules. $\square$

Claim 6

$$\begin{aligned} {\hat{\theta }}(B) \le {\hat{\theta }}(A) \oplus {\hat{\theta }}(C). \end{aligned}$$

Let ${\mathfrak {B}}= \bigl ( B_{1} \le B_{2} \le \dots \le B_{2n-1} \le B_{2n} \le B \bigr )$ be a $\lambda _S$-small chain in B. For every $i \le n$, define

$$\begin{aligned} A_{i} {:=}\iota ^{-1}(B_{i}) \qquad C_{i} {:=}\pi (A_{i}). \end{aligned}$$

Then, ${\mathfrak {A}}{:=}\bigl ( A_{1} \le A_{2} \le \dots \le A_{2n-1} \le A_{2n} \le A \bigr )$ and ${\mathfrak {C}}{:=}\bigl ( C_{1} \le C_{2} \le \dots \le C_{2\,m-1} \le C_{2\,m} \le C \bigr )$ are $\lambda _S$-small chains in A and C, respectively. Moreover, for every $i \le n$, we have an exact sequence

$$\begin{aligned} 0 \longrightarrow {\hat{A}}_{i} \longrightarrow {\hat{B}}_{i} \longrightarrow {\hat{C}}_{i} \longrightarrow 0. \end{aligned}$$

Therefore, $\theta ({\mathfrak {B}}) = \theta ({\mathfrak {A}}) \oplus \theta ({\mathfrak {C}})$, and the claim follows.

Claim 7

$$\begin{aligned} {\hat{\theta }}(B) \ge {\hat{\theta }}(A) \oplus {\hat{\theta }}(C) \end{aligned}$$

Let ${\mathfrak {A}}= \bigl ( A_{1} \le A_{2} \le \dots \le A_{2n-1} \le A_{2n} \le A \bigr )$ and ${\mathfrak {C}}= \bigl ( C_{1} \le C_{2} \le \dots \le C_{2\,m-1} \le C_{2\,m} \le C \bigr )$ be $\lambda _S$-small chains in A and C, respectively. For every $i \le 2(m+n)$

$$\begin{aligned} B_{i} {:=}{\left\{ \begin{array}{ll} \iota (A_{i}) &{} \text {if } i \le 2n;\\ \pi ^{-1}(C_{i-2n}) &{}\text {if } 2n < i \le 2(n+m). \end{array}\right. } \end{aligned}$$

Then, ${\mathfrak {B}}{:=}\bigl ( B_{1} \le B_{2} \le \dots \le B_{2n+2\,m-1} \le B_{2n + 2\,m} \le B \bigr )$ is a $\lambda _S$-small chain in B. Moreover, for every $i \le n+m$,

$$\begin{aligned} {\hat{B}}_{i} = {\left\{ \begin{array}{ll} {\hat{A}}_{i} &{} \text {if } i \le n;\\ {\hat{C}}_{i} &{} \text {if } n < i \le n+m. \end{array}\right. } \end{aligned}$$

Therefore, $\theta ({\mathfrak {B}}) = \theta ({\mathfrak {A}}) \oplus \theta ({\mathfrak {C}})$, and the claim follows. $\square$

Definition 12.5

Given an ideal $I \lhd R$, we say that I is $\lambda$-cofinite if $\lambda (R/I) < \infty$.

Remark 12.6

Let $I \lhd R$ be a $\lambda$-cofinite ideal, and A be an R-module. Then, A/IA is locally $\lambda _R$-finite.

Proposition 12.7

Let $\theta$ be as above and total. Assume that, for every S-module A

$$\begin{aligned} \theta (A) = \sup \{\theta (B): B \le A\ \lambda _S\text{-small } S\text{-submodule }\}. \end{aligned}$$

Then,

$$\begin{aligned} {\hat{\theta }}(A) \ge \theta (A) \end{aligned}$$

and, if A is finitely generated,

$$\begin{aligned} {\hat{\theta }}(A) = \sup \{\theta (A/IA): I \lhd R \,\, \lambda \text{-cofinite } \,\, \text{ ideal }\}. \end{aligned}$$

The proof of the above proposition is in the next subsection: for now we will record some consequences.

Corollary 12.8

• (1) ${\hat{\mu }}$ satisfies the conclusions of Propositions 12.4 and 12.7;

• (2) ${\hat{\mu }}(S) = {\hat{\lambda }}(R) t^{k}$;

• (3) ${\hat{\mu }}(A) = \mu (A)$ for every locally $\lambda _R$-finite S-module A;

• (4) if $\lambda (R) < \infty$, then ${\hat{\mu }}= \mu$.

Corollary 12.9

For every $d \le k$,

• (1) the d-dimensional entropy (see Sect. 11) $\hat{h}^{(d)}_{\lambda }$ is a length functions (on all S-modules) and satisfies the conclusion of Proposition 12.7;

• (2) $\hat{h}^{(d)}_{\lambda }(A) = h^{(d)}_{\lambda }(A)$ for every locally $\lambda _R$-finite S-module A;

• (3) if $\lambda (R) < \infty$, then $\hat{h}^{(d)}_{\lambda } = h^{(d)}_{\lambda }$.

Remember that

$$\begin{aligned} {\hat{h}}_{\lambda } = {\hat{h}}^{(k)} \end{aligned}$$

and therefore from the above Corollary we obtain that ${\hat{h}}$ is a length function ${{\,\mathrm{ S\mathrm -mod}\,}}$, that ${\hat{h}}(A) = h(A)$ when A is locally finite, and ${\hat{h}} = h$ when $\lambda (R) < \infty$.

Corollary 12.10

Let T be a finitely generated R-algebra, ${\bar{\gamma }} \in T^{k}$ be a set of generators of T. Given $d \le k$, let $h^{(d, {\bar{\gamma }})}$ be defined as in Sect. 11. Then:

• (1) $\hat{h}^{(d, {\bar{\gamma }})}_{\lambda }$ is a length functions (on all T-modules) and satisfies the conclusion of Proposition 12.7;

• (2) $\hat{h}^{(d, {\bar{\gamma }})}_{\lambda }(A) = h^{(d, {\bar{\gamma }})}_{\lambda }(A)$ for every locally $\lambda _R$-finite S-module A;

• (3) if $\lambda (R) < \infty$, then $\hat{h}^{(d, {\bar{\gamma }})}_{\lambda } = h^{(d, {\bar{\gamma }})}_{\lambda }$.

Proof

Apply Proposition 12.4 to the function $h^{(d, {\bar{\gamma }})}$. $\square$

Corollary 12.11

Let $\lambda$ be the standard length on $\mathbb {Z}$-modules introduced in Example 3.2(b). Then, for every finitely generated $\mathbb {Z}[{\bar{x}}]$-module A,

$$\begin{aligned} {\hat{\mu }}(A) = \sup \{\mu (A/n A): 2 \le n \in \mathbb {N}\} = \lim _{n \rightarrow \infty } \mu (A/n!\, A). \end{aligned}$$

We cannot drop the assumption that A is finitely generated in Proposition 12.7.

Example 12.12

Let $R {:=}\mathbb {Z}$ and $\lambda$ be the standard length. Let $A {:=}\mathbb {Q}[{\bar{x}}]$ (seen as a $\mathbb {Z}[{\bar{x}}]$-module). Then,

$$\begin{aligned}\begin{aligned} {\hat{\mu }}(A)&= \infty \cdot t^{k} \\ \sup \{\mu (A/nA): 2 \le n \in \mathbb {N}\}&= 0. \end{aligned} \end{aligned}$$

12.1 Proof of Proposition 12.7

Lemma 12.13

Let $I, J \lhd R$ be $\lambda$-cofinite ideals. Then, $I \cap J$ is also $\lambda$-cofinite.

Proof

$R/I\cap J$ embeds into $R/I \times R/J$. $\square$

Lemma 12.14

Let $I, J \lhd R$ be $\lambda$-cofinite ideals. Then, IJ is also $\lambda$-cofinite.

Proof

Let ${\bar{a}}= (a_{1}, \dotsc , a_{\ell })$ generate I. Then, I/IJ is a quotient of $(R/J)^{\ell }$ via the map

$$\begin{aligned} (r_{1} + J, \dotsc , r_{\ell } + J) \mapsto r_{1} a_{1} + \dots + r_{\ell } a_{\ell } + IJ. \end{aligned}$$

Therefore, $\lambda (I/IJ) \le \ell \lambda (R/J) < \infty$, and

$$\begin{aligned} \lambda (R/IJ) \le \lambda (R/I) + \lambda (I/IJ) < \infty . \end{aligned}$$

$\square$

Lemma 12.15

Let A be an S-module. Assume that A is $\lambda _S$-small. Then,

$$\begin{aligned} Ann_{R}(A) {:=}\{r \in R: r A = 0\} \end{aligned}$$

is $\lambda$-cofinite

Proof

Let $a_{1},\dotsc , a_{\ell }$ be generators of A (as S-module). For every $i \le \ell$, $\lambda (Ra_{i}) < \infty$. Moreover, $Ra_{i}$ is isomorphic (as R-module) to $R/Ann_{R}(a_{i})$, and therefore $Ann_{R}(a_{i})$ is $\lambda$-cofinite. Finally,

$$\begin{aligned} Ann_{R}(A) = Ann_{R}(a_{1}) \cap \cdots \cap Ann_{R}(a_{\ell }) \end{aligned}$$

and the conclusion follows from Lemma 12.13. $\square$

Proof of Proposition 12.7

Let $B \le A$ be an $\lambda _S$-small S-submodule. By definition, ${\hat{\theta }}(A) \ge \theta (B)$: therefore, by the assumption, ${\hat{\theta }}(A) \ge \theta (A)$.

Define

$$\begin{aligned} \theta '(A) {:=}\sup \{\theta (A/IA): I \lhd R\ \, \,\lambda \text { -cofinite} \,\, \text { ideal }\}. \end{aligned}$$

We want to prove that, when A is finitely generated, ${\hat{\theta }}(A) = \theta '(A)$. It suffices to show that $\theta '$ is additive on finitely generated S-modules. Thus, let

$$\begin{aligned} 0 \longrightarrow A \longrightarrow B \longrightarrow C \longrightarrow 0 \end{aligned}$$

be an exact sequence of finitely generated S-modules. $\square$

Claim 8

${\hat{\theta }}(B) \le {\hat{\theta }}(A) \oplus {\hat{\theta }}(C)$.

Let $I \lhd R$ be a $\lambda$-cofinite ideal. We have the exact sequence of $\lambda _S$-small S-modules

$$\begin{aligned} 0 \longrightarrow A/(A \cap IB) \longrightarrow B/IB \longrightarrow C/IC \longrightarrow 0. \end{aligned}$$

Since $\theta$ is additive on $\lambda _S$-small S-modules, and $IA \le A \cap IB$, we have

$$\begin{aligned} {\hat{\theta }}(A) + {\hat{\theta }}(C) \ge \theta (A/IA) \oplus \theta (C/IC) \ge \theta (A/(A \cap IB)) \oplus \theta (C/IC) = \theta (B/IB), \end{aligned}$$

and the claim follows.

Claim 9

${\hat{\theta }}(B) \ge {\hat{\theta }}(A) \oplus {\hat{\theta }}(C)$.

Let $I, I' \lhd R$ be $\lambda$-cofinite ideals. We want to prove that

$$\begin{aligned} \theta (A/IA) + \theta (C/I'C) \le {\hat{\theta }}(B). \end{aligned}$$

Replacing $I, I'$ with $I \cap I'$, without loss of generality we may assume that $I = I'$. By Artin-Rees Lemma (see e.g. [16, §4.7]), there exists $1 \le n_{0} \in \mathbb {N}$ such that, for every $m \in N$,

$$\begin{aligned} A \cap I^{m + n_{0}} B = I^{m}(A \cap I^{n_{0}} B). \end{aligned}$$

(7)

Let $J {:=}I^{n_{0}}$ and $A' {:=}A \cap JB$: notice that J is also $\lambda$-cofinite. Taking $m {:=}n_{0}$ in (7), we obtain:

$$\begin{aligned} A \cap J^{2} B = J A'. \end{aligned}$$

Thus, we have the exact sequence

$$\begin{aligned} 0 \longrightarrow A/ JA' \longrightarrow B/J^{2}B \longrightarrow C/J^{2}C \longrightarrow 0. \end{aligned}$$

The modules appearing above are all $\lambda _S$-small: therefore,

$$\begin{aligned} \theta (A/IA) \oplus \theta (C/IC) \le \theta (A/JA') \oplus \theta (C/J^{2}C) = \theta (B/J^{2}B) \le {\hat{\theta }}(B), \end{aligned}$$

proving the Claim. $\square$

12.2 Examples

Let $R {:=}\mathbb {Z}$, $\alpha$ be the standard length introduced in Example 3.2(b) and $\beta$ be the length given by the rank (i.e., $\beta (M) = \dim _{\mathbb {Q}}(M \otimes \mathbb {Q})$). Since $\beta (\mathbb {Z}) = 1 < \infty$, $\mu _{\beta } = {\hat{\mu }}_{\beta }$.

1) Let $S {:=}\mathbb {Z}[x]$, I be an ideal of S, and $M:= S/I$. The following table shows the values of $\mu _{\alpha }(M)$, ${\hat{\mu }}_{\alpha }(M)$, and $\mu _{\beta }(M)$ for some values of I:

I	$\mu _{\alpha }(S/I)$	${\hat{\mu }}_{\alpha }(S/I)$	$\mu _{\beta }(S/I)$
0	0	$\infty \cdot t^1$	$t^1$
S	0	0	0
(n) ; $2 \le n \in \mathbb {N}$	$\log (n) \cdot t^1$	$\log (n) \cdot t^1$	0
(p(x)) ; $\deg p \ge 1$	0	$\infty \cdot t^{0}$	$\deg p\cdot t^0$
(p(x), n) ; $2 \le n \in \mathbb {N}$,	$\log (n) \deg p \cdot t^0$	$\log (n) \deg p \cdot t^0$	0
p monic, $\deg p \ge 1\,$

2) Let $S {:=}\mathbb {Z}[x_{1}, x_{2}]$ and $M {:=}S/(x_{1}x_{2})$. Then,

$$\begin{aligned} \mu _{\alpha }(M) = 0, \quad {\hat{\mu }}(M) = \infty \cdot t, \quad \mu _{\beta }(M) = 2 t. \end{aligned}$$

13 Intrinsic Hilbert polynomial

In [7] the authors introduced the “intrinsic” algebraic entropy, a variant of the more usual algebraic entropy: following a similar pattern, we introduce here the intrinsic Hilbert polynomial.

Let A be an S-module. Let ${\overline{A}} {:=}(A_{i})_{i \in \mathbb {N}}$ be a filtering on A. For each $i \in \mathbb {N}$, define ${\tilde{A}}_{i} {:=}A_{i+1}/A_{i}$ (as R-modules). Define

$$\begin{aligned} \tilde{{\mathcal {B}}}({\overline{A}}){:=}\bigoplus _{i \in \mathbb {N}} {\tilde{A}}_{i} \end{aligned}$$

as graded S-module (where all the $x_{i}$ have degree 1). An equivalent description of $\tilde{{\mathcal {B}}}({\overline{A}})$ is the following. Remember that ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{A}})$ is an S[y]-module. Let

$$\begin{aligned} \cdot y: {{\,\mathrm{{\mathcal {B}}}\,}}({\overline{A}}) \rightarrow {{\,\mathrm{{\mathcal {B}}}\,}}({\overline{A}}) \end{aligned}$$

be the multiplication by y. Then,

$$\begin{aligned} \tilde{{\mathcal {B}}}({\overline{A}})= {{\,\textrm{Coker}\,}}(\cdot y); \end{aligned}$$

notice that ${{\,\textrm{Coker}\,}}(\cdot y)$ is an S[y]-module: however, y acts trivially on ${{\,\textrm{Coker}\,}}(\cdot y)$, hence we lose nothing in considering ${{\,\textrm{Coker}\,}}(\cdot y)$ as an S-module; moreover, the above isomorphism is of graded S-modules. In particular, if ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{A}})$ is Noetherian (as S[y]-module), then $\tilde{{\mathcal {B}}}({\overline{A}})$ is also Noetherian (as S-module).

Definition 13.1

We say that ${\overline{A}}$ is a $\lambda$ -inert filtering on A if:

• (1) $\tilde{{\mathcal {B}}}({\overline{A}})$ is Noetherian (as S-module);

• (2) there exists $n_{0} \in \mathbb {N}$ such that, for every $n \ge n_{0}$,

  $$\begin{aligned} \lambda ({\tilde{A}}_{n}) < \infty . \end{aligned}$$

Proposition 13.2

Assume that ${\overline{A}}$ is a $\lambda$-inert filtering on A. Then, there exists a polynomial ${\tilde{q}}_{{\overline{A}}}(t) \in \mathbb {Q}[t]$ of degree at most $k-1$ such that, for every $n \in \mathbb {N}$ large enough,

$$\begin{aligned} \lambda ({\tilde{A}}_{n}) = {\tilde{q}}_{{\overline{A}}}(n). \end{aligned}$$

Proof

Same proof as Theorem 6.6. $\square$

We call ${\tilde{q}}_{{\overline{A}}}$ the intrinsic Hilbert polynomial of ${\overline{A}}$, and denote by $\tilde{\mu }({\overline{A}})$ its leading term.

Remark 13.3

Assume that ${\overline{A}}$ is a $\lambda$-inert filtering on A. Assume moreover that $\lambda (A_{0}) < \infty$. In this situation, we have defined the Hilbert polynomial $q_{{\overline{A}}}$. We have, for every $n \in \mathbb {N}$

$$\begin{aligned} \lambda ({\tilde{A}}_{n}) = \lambda (A_{n+1}) - \lambda (A_{n}), \end{aligned}$$

and therefore

$$\begin{aligned} {\tilde{q}}_{{\overline{A}}} = \Delta q_{{\overline{A}}}, \end{aligned}$$

where $\Delta p$ is the difference of p: the polynomial defined by $\Delta p(t) = p(t+1) - p (t)$.

The intrinsic Hilbert polynomial becomes interesting when $\lambda (A_{0})$ is infinite (and therefore we cannot compute the usual Hilbert polynomial).

Definition 13.4

Let $A_{0} \le A$ be an R-submodule. Denote ${\tilde{A}}_{0} {:=}(S_{1} A_{0})/A_{0}$. We say that $A_{0}$ is $\lambda$ -inert if:

• (1) ${\tilde{A}}_{0}$ is finitely generated (as R-module);

• (2) $\lambda ({\tilde{A}}_{0}) < \infty$.

Assume that $A_{0}$ is $\lambda$-inert. We can define the associated filtering ${{\,\textrm{Filt}\,}}(A_{0};A)$ of A. We denote

$$\begin{aligned} \tilde{{{\,\textrm{Gr}\,}}}(A_0; A){:=}\tilde{{\mathcal {B}}}({{\,\textrm{Filt}\,}}(A_{0};A)) = \bigoplus _{n} (S_{n+1}A_{0})/(S_{n} A_{0})\, t^{n}. \end{aligned}$$

Then, $\tilde{{{\,\textrm{Gr}\,}}}(A_0; A)$ is a Noetherian S-module (since it is generated by ${\tilde{A}}_{0}$), and therefore ${{\,\textrm{Filt}\,}}(A_{0},A)$ is a $\lambda$-inert filtering.

Therefore, ${\tilde{q}}_{\tilde{{{\,\textrm{Gr}\,}}}(A_0; A)}$ exists; we define

$$\begin{aligned} {\tilde{q}}_{A_{0}} {:=}q_{\tilde{{{\,\textrm{Gr}\,}}}(A_0; A)}, \qquad \tilde{\mu }[A_{0}] {:=}\mu (\tilde{{{\,\textrm{Gr}\,}}}(A_0; A)). \end{aligned}$$

Thus, by definition, for n large enough,

$$\begin{aligned} {\tilde{q}}_{A_{0}}(n) = \lambda (S_{n+1} A_{0}/S_{n} A_{0}). \end{aligned}$$

Unlike $\mu$, it can happen that $\tilde{\mu }[A_{0}]$ depends on the choice of $A_{0}$ (even when $S A_{0} = A$), as the following example shows (suggested by S. Virili):

Example 13.5

Let $R {:=}\mathbb {Z}$, $A {:=}S$, $\lambda$ be the standard length. Fix $n \in \mathbb {N}$ and let

$$\begin{aligned} V {:=}\mathbb {Z}+ n S = \mathbb {Z}\oplus n\mathbb {Z}{\bar{x}}\oplus n\mathbb {Z}{\bar{x}}^{2} \oplus \cdots \le A. \end{aligned}$$

Then,

$$\begin{aligned} \widetilde{V} = (V + {\bar{x}}V)/V \simeq {\bar{x}}\mathbb {Z}/n. \end{aligned}$$

Thus, $\lambda ({\tilde{V}}) = k\log n < \infty$; moreover, V is finitely generated and $S V = A$. Moreover,

$$\begin{aligned} V_{i} {:=}S_{i} V = S_{i} \mathbb {Z}+ n S_{i} S = S_{i} + n S, \end{aligned}$$

and therefore

$$\begin{aligned} {\tilde{V}}_{i} = (S_{i+1} + nS)/(S_{i} + nS) \simeq S^{(i + 1)}/(n). \end{aligned}$$

Thus,

$$\begin{aligned} \lambda ({\tilde{V}}_{i}) = \log n \cdot |S^{(i+1)}| = \genfrac(){0.0pt}1{i+k}{k-1} \log n \end{aligned}$$

and therefore

$$\begin{aligned} \tilde{\mu }[V] = \frac{\log n}{(k-1)!} \cdot t^{k-1}. \end{aligned}$$

Therefore,

$$\begin{aligned} \tilde{\mu }(A) = \infty t^{k-1}, \end{aligned}$$

and $\tilde{\mu }[V]$ depends in this case on the choice of V.

Definition 13.6

Define

$$\begin{aligned} \tilde{\mu }(A) {:=}\sup \{ \tilde{\mu }[ V_{0}]:\ V_{0} \le A \text { is }\lambda \text { -inert} \} \in \overline{{\mathcal {V}}}. \end{aligned}$$

Lemma 13.7

Let A be an S-module. Let ${\overline{A}} {:=}(A_{i})_{i \in \mathbb {N}}$ be a $\lambda$-inert filtering on A. Then, $\tilde{{\mathcal {B}}}({\overline{A}})$ is an acceptable graded S-module (see Definition 4.3) and therefore, by Proposition 4.4, there exists $d_{0} \in \mathbb {N}$ such that, for every $n \in \mathbb {N}$,

$$\begin{aligned} {\tilde{A}}_{n+d_{0}} = S^{(n)} {\tilde{A}}_{d_{0}} = S_{n} A_{d_{0}}. \end{aligned}$$

Let $d_{1} \ge d_{0}$ such that $\lambda ({\tilde{A}}_{d_{1}}) < \infty$. Then, $A_{d_{1}}$ is $\lambda$-inert and $S A_{d_{1}} = S A_{d_{0}}$. Moreover,

$$\begin{aligned} \tilde{\mu }({\overline{A}}) = \tilde{\mu }[A_{d_{1}}]. \end{aligned}$$

(8)

Therefore,

$$\begin{aligned} \tilde{\mu }(A) = \sup \{\tilde{\mu }[{\overline{A}}]: \ {\overline{A}} \lambda \text { -inert filtering on } A\}, \end{aligned}$$

and if A is finitely generated, then

$$\begin{aligned} \tilde{\mu }(A) = \sup \{\tilde{\mu }[{\overline{A}}]: \ {\overline{A}} \lambda \text {-inert exhaustive filtering on } A\}. \end{aligned}$$

Proof

It suffices to prove (8): the rest of the lemma is clear. However, we have, for every $n \in \mathbb {N}$

$$\begin{aligned} {\tilde{A}}_{n+d_{1}} = S_{n} \cdot {\tilde{A}}_{d_{1}}; \end{aligned}$$

therefore,

$$\begin{aligned} \lambda ({\tilde{A}}_{n+d_{1}}) = \lambda (S_{n} \cdot {\tilde{A}}_{d_{1}}) \end{aligned}$$

proving that

$$\begin{aligned} {\tilde{q}}_{{\overline{A}}}(n + d_{1}) = {\tilde{q}}_{A_{d_{1}}}(n) \end{aligned}$$

and thus (8) follows. $\square$

Conjecture 13.8

Let $0 \longrightarrow A \longrightarrow B \overset{\pi }{\longrightarrow }C \longrightarrow 0$ be an exact sequence of S-modules. Then,

$$\begin{aligned} \tilde{\mu }(B) = \tilde{\mu }(A) \oplus \tilde{\mu }(C). \end{aligned}$$

A particular case of the above conjecture (when $k = 1$ and $R = \mathbb {Z}$) is known from [7, 20].

We can prove sub-additivity quite easily:

Theorem 13.9

Let $0 \longrightarrow A \longrightarrow B \overset{\pi }{\longrightarrow }C \longrightarrow 0$ be an exact sequence of S-modules. Then,

$$\begin{aligned} \tilde{\mu }(B) \le \tilde{\mu }(A) \oplus \tilde{\mu }(C). \end{aligned}$$

Moreover, $\tilde{\mu }(A) \le \tilde{\mu }(B)$ and $\tilde{\mu }(C) \le \tilde{\mu }(B)$.

Proof

Let ${\overline{B}} = (B_{n})_{n \in \mathbb {N}}$ be a $\lambda$-inert filtering on B. For every $n \in \mathbb {N}$, define

$$\begin{aligned}\begin{aligned} A_{n}&{:=}A \cap B_{n},&C_{n}&{:=}\pi (B_{n});\\ {\overline{A}}&{:=}(A_{n})_{n \in \mathbb {N}},&{\overline{C}}&{:=}(C_{n})_{n \in \mathbb {N}} = {{\,\textrm{Filt}\,}}(C_{0};C). \end{aligned}\end{aligned}$$

It is clear that ${\overline{A}}$, ${\overline{B}}$, and ${\overline{C}}$ are filterings on A, B, C, respectively. $\square$

Claim 10

${\overline{C}}$ and ${\overline{A}}$ are $\lambda$-inert.

In fact, for every $n \in \mathbb {N}$, we have an exact sequence of R-modules

$$\begin{aligned} 0 \rightarrow {\tilde{A}}_{n} \rightarrow {\tilde{B}}_{n} \rightarrow {\tilde{C}}_{n} \rightarrow 0. \end{aligned}$$

Since ${\tilde{B}}_{0}$ is finitely generated and R is Noetherian, both ${\tilde{A}}_{0}$ and ${\tilde{C}}_{0}$ are finitely generated. Since moreover (for n large enough) $\lambda ({\tilde{B}}_{n})$ is finite, both $\lambda ({\tilde{A}}_{n})$ and $\lambda ({\tilde{C}}_{n})$ are finite.

Finally, we have the following exact sequence of S[y]-modules:

$$\begin{aligned} 0 \rightarrow \tilde{{\mathcal {B}}}({\overline{A}}) \rightarrow \tilde{{\mathcal {B}}}({\overline{B}}) \rightarrow \tilde{{\mathcal {B}}}({\overline{C}}) \rightarrow 0; \end{aligned}$$

since $\tilde{{\mathcal {B}}}({\overline{B}})$ is Noetherian, also $\tilde{{\mathcal {B}}}({\overline{A}})$ and $\tilde{{\mathcal {B}}}({\overline{C}})$ are Noetherian.

Notice moreover that, for every $n \in \mathbb {N}$ large enough,

$$\begin{aligned} {\tilde{q}}_{{\overline{A}} }(n) + {\tilde{q}}_{{\overline{C}} }(n) = \lambda ({\tilde{A}}_{n}) + \lambda ({\tilde{C}}_{n}) = \lambda ({\tilde{B}}_{n}) = {\tilde{q}}_{{\overline{B}}}(n). \end{aligned}$$

Thus,

$$\begin{aligned} \tilde{\mu }[{\overline{B}}] = \tilde{\mu }({\overline{A}}) \oplus \tilde{\mu }({\overline{C}}). \end{aligned}$$

Therefore, by Lemma 13.7,

$$\begin{aligned} \tilde{\mu }(B) \le \tilde{\mu }(A) \oplus \tilde{\mu }(C). \end{aligned}$$

Similarly, if ${\overline{A}} = (A_{n})_{n \in \mathbb {N}}$ is a $\lambda$-inert filtering on A, then it is also a $\lambda$-inert filtering on B, and therefore $\tilde{\mu }[{\overline{A}}] \le \tilde{\mu }(B)$; thus; $\tilde{\mu }(A) \le \tilde{\mu }(B)$.

Finally, if ${\overline{C}} = (C_{n})_{n \in \mathbb {N}}$ is a $\lambda$-inert filtering on C, then $\bigl ( \pi ^{-1}(C_{n}) \bigr )_{n \in \mathbb {N}}$ is a $\lambda$-inert filtering on B, and therefore $\tilde{\mu }[{\overline{C}}] \le \tilde{\mu }(B)$; thus; $\tilde{\mu }(C) \le \tilde{\mu }(B)$. $\square$

Let A be an S-module. Let $d \in \mathbb {N}$ be the degree of $\tilde{\mu }(A)$ and $s \in \mathbb {R}$ be its coefficient. We define the intrinsic $\lambda$-dimension of A to be $d+1$ if $\tilde{\mu }(A) \ne 0$, 0 if $\lambda (A) > 0$ and $\tilde{\mu }(A) = 0$, and $-\infty$ if $\lambda (A) =0$. For each $i \le k$, the intrinsic i -dimensional $\lambda$ -entropy of A is

$$\begin{aligned} {\tilde{h}}^{(i)}_{\lambda }(A) {:=}{\left\{ \begin{array}{ll} 0 &{} \text {if } i > d +1;\\ 0 &{}\text {if } i \ge 1 \text { and } \tilde{\mu }(A) = 0;\\ \infty &{} \text {if } i \le d;\\ \frac{s}{(d+1)!} &{} \text {if } i = d+1 \text { and } \tilde{\mu }(A) \ne 0;\\ \lambda (A) &{} \text {if } i = 0. \end{array}\right. } \end{aligned}$$

The intrinsic $\lambda$-entropy is

$$\begin{aligned} {\tilde{h}}_{\lambda }(A) {:=}{\tilde{h}}^{(k)}_{\lambda }(A) \end{aligned}$$

and has been studied already (at least, in the case $R = \mathbb {Z}$ and $k=1$) in [7, 11, 20], and for some non-Noetherian rings in [21]): our definition of $\tilde{\mu }$ is clearly inspired by the intrinsic algebraic entropy (the notation $\widetilde{{{\,\textrm{ent}\,}}}$ is used elsewhere, but we prefer ${\tilde{h}}_{\lambda }$ for consistency).

In general, ${\hat{h}}_{\lambda }$ and ${\tilde{h}}_{\lambda }$ are different.

Example 13.10

Let $R = \mathbb {Z}$, $k = 1$, $\lambda$ be the standard length, and $A = \mathbb {Q}$ seen as S-module via the action $x q {:=}q/2$. Then, ${\tilde{h}}_{\lambda }(A) = \log 2$ (see [7]), while ${\hat{h}}_{\lambda }(A) = 0$ (notice that ${\hat{\mu }}(A) = \infty \cdot t^{0}$).

14 Fine grading

Up to now, we have only considered the case when the degrees are natural numbers. As in the classical case when R is a field, one can consider gradings in any commutative monoid (see e.g. [15]).

14.1 Graded modules

Let $\Gamma$ be a commutative monoid.

Remember that $\Gamma$ has a canonical quasi-ordering, given by $m \le n$ if there exists $p \in \Gamma$ with $m + p = n$. The neutral element 0 is a minimum of $\langle \Gamma , \le \rangle$.

Definition 14.1

We say that ${\bar{\gamma }} \in \Gamma ^{k}$ is good (inside $\Gamma$) if:

for every $\lambda \in \Gamma$ there exist at most finitely many ${\bar{n}} \in \mathbb {N}^{k}$, such that ${\bar{n}} \cdot {\bar{\gamma }} = \lambda$.

We say that ${\bar{\gamma }} \in \Gamma ^{k}$ is very good if:

for every $\lambda \in \Gamma$ there exist at most finitely many ${\bar{n}} \in \mathbb {N}^{k}$, such that ${\bar{n}} \cdot {\bar{\gamma }} \le \lambda$.

For example, ${\bar{\gamma }} \in \mathbb {Z}^{k}$ is good (in $\mathbb {Z}$) if $\gamma _{i} > 0$ for $i = 1, \dotsc , k$. ${\bar{\gamma }} \in \mathbb {N}^{k}$ is very good (in $\mathbb {N}$) iff $\gamma _{i} \ne 0$ for $i = 1, \dotsc , k$. Notice that, in general, if ${\bar{\gamma }}$ is good, then each $\gamma _{i}$ is non-zero (and even non-torsion).

Remark 14.2

Given ${\bar{\gamma }} = \langle \gamma _{1}, \dotsc , \gamma _{k} \rangle \in \Gamma ^{k}$, if ${\bar{\gamma }}$ is good, then the following expression is well defined:

$$\begin{aligned} \frac{1}{\prod _{i=1}^{k}(1 - t^{\gamma _{i}})} \in \mathbb {N}[[t^{\Gamma }]] \end{aligned}$$

Definition 14.3

Fix ${\bar{\gamma }} = \langle \gamma _{1}, \dotsc , \gamma _{k} \rangle \in \Gamma ^{k}$. A $\Gamma$-graded S-module of degree ${\bar{\gamma }}$ is given by an S-module M and a decomposition

$$\begin{aligned} M = \bigoplus _{n\in \Gamma } M_{n}, \end{aligned}$$

where each $M_{n}$ is an R-module, and, for every $i \le k$ and $n \in \Gamma$,

$$\begin{aligned} x_{i} M_{n} \le M_{n+ \gamma _{i}}. \end{aligned}$$

We denote by ${\overline{M}}$ the module M with the given grading (including the tuple ${\bar{\gamma }}:= \langle \gamma _{1}, \dotsc , \gamma _{k} \rangle$).

Theorem 14.4

Let ${\overline{M}}$ be a $\Gamma$-graded S-module of degree ${\bar{\gamma }} \in \Gamma ^{k}$. For every $n \in \mathbb {N}$, let $a_{n}:= \lambda (M_{n})$. Define

$$\begin{aligned} F_{{\overline{M}}}(t):= \sum _{n \in \Gamma } a_{n} t^{n}. \end{aligned}$$

Assume that:

• (1) ${\bar{\gamma }}$ is good;

• (2) $\lambda (M_{n}) < \infty$ for every $n \in \Gamma$;

• (3) M is a Noetherian S-module.

Then, there exists a polynomial $p(t) \in \mathbb {R}[t^{\Gamma }]$ such that

$$\begin{aligned} F_{{\overline{M}}}(t) = \frac{p(t)}{\prod _{i=1}^{k}(1 - t^{\gamma _{i}})}. \end{aligned}$$

Proof

Mutatis mutandis, same proof as Thm. 5.1. $\square$

14.2 Filtered modules

We move now from graded modules to filtered modules.

Definition 14.5

Let ${\bar{\gamma }}:= \langle \gamma _{1}, \dotsc , \gamma _{k} \rangle \in \Gamma ^{k}$ and N be an S-module.

An (increasing) $\Gamma$ -filtering on N with degrees ${\bar{\gamma }}$ is a sequence of R-submodules of N

$$\begin{aligned} (N_{i}: i \in \Gamma ) \end{aligned}$$

such that it is increasing (i.e., if $i \le j$, then $N_{i} \le N_{j}$), $\bigcup _{i \in \Gamma } N_{i} = N$, and $x_{i} N_{j} \le N_{j + \alpha _{i}}$ for every $j \in \Gamma$, $i \le k$. We denote by ${\overline{N}}$ the S-module with the given tuple $\gamma$ and the filtering $(N_{i})_{i \in \Gamma }$.

Definition 14.6

Let ${\bar{\delta }} = \langle \delta _{1}, \delta _{2}, \dots \rangle$ be a tuple of generators of $\Gamma$ (for simplicity, we assume $\Gamma$ countable: later we will be interested only in the case when ${\bar{\delta }}$ is a finite tuple). Let ${\bar{y}}$ be a tuple of variables indexed by ${\bar{\delta }}$ (i.e., there is one variable $y_{j}$ for each chosen generator $\delta _{j}$). The blow-up module associated to ${\overline{N}}$ and the tuple ${\bar{\delta }}$ is the following graded $S[{\bar{y}}]$-module. As an R-module,

$$\begin{aligned} {{\,\mathrm{{\mathcal {B}}}\,}}_{{\bar{\delta }}}({\overline{N}}):= \bigoplus _{n \in \Gamma } N_{n} t^{n}. \end{aligned}$$

The $\Gamma$-grading of ${{\,\mathrm{{\mathcal {B}}}\,}}_{{\bar{\delta }}}({\overline{N}})$ is given by the decomposition ${{\,\mathrm{{\mathcal {B}}}\,}}_{{\bar{\delta }}}({\overline{N}})= \bigoplus _{n \in \Gamma } N_{n} t^{n}$.

The multiplication by $x_{i}$ on ${{\,\mathrm{{\mathcal {B}}}\,}}_{{\bar{\delta }}}({\overline{N}})$ is defined as:

$$\begin{aligned} x_{i}(v t^{n}):= (x_{i}v) t^{n + \gamma _{i}}, \end{aligned}$$

for every $i \le k$, $n \in \Gamma$, $v \in N_{n}$, and then extended by R-linearity on all ${{\,\mathrm{{\mathcal {B}}}\,}}_{{\bar{\delta }}}({\overline{N}})$: notice that the $x_{i}$ has degree $\gamma _{i}$ on ${{\,\mathrm{{\mathcal {B}}}\,}}_{{\bar{\delta }}}({\overline{N}})$. For each $\delta _{j} \in {\bar{\delta }}$, the multiplication by $y_{j}$ on ${{\,\mathrm{{\mathcal {B}}}\,}}_{{\bar{\delta }}}({\overline{N}})$ is defined as:

$$\begin{aligned} y_{j} (v t^{n}):= v t^{n+\delta _{j}}, \end{aligned}$$

for every $n \in \Gamma$, $v \in N_{n}$, and then extended by R-linearity on all ${{\,\mathrm{{\mathcal {B}}}\,}}_{{\bar{\delta }}}({\overline{N}})$: notice that $y_j$ has degree $\delta _{j}$.

Theorem 14.7

Let ${\bar{\mathbb {N}}}$ be a $\Gamma$-filtering on N with degrees ${\bar{\gamma }}$. Let ${\bar{\delta }} = \langle \delta _{1}, \dotsc , \delta _{\ell } \rangle$ be a finite tuple of generators of $\Gamma$, with corresponding variables ${\bar{y}} = \langle y_{1}, \dotsc , y_{\ell } \rangle$.

For every $n \in \mathbb {N}$, let $a_{n}:= \lambda (N_{n})$. Define

$$\begin{aligned} F_{{\overline{N}}}(t):= \sum _{n \in \Gamma } a_{n} t^{n} \in \mathbb {R}[[t^{\Gamma }]] \end{aligned}$$

Then,

$$\begin{aligned} F_{{\overline{N}}} = F_{{{\,\mathrm{{\mathcal {B}}}\,}}_{{\bar{\delta }}}({\overline{N}})}. \end{aligned}$$

Therefore, if we assume that:

• (1) ${\bar{\gamma }} \cup {\bar{\delta }}$ is good;

• (2) for every $n \in \mathbb {N}$, $\lambda (N_{n}) < \infty$;

• (3) ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{N}})$ is Noetherian as $S[{\bar{y}}]$-module.

Then, there exists a polynomial $p(t) \in \mathbb {R}[t^{\Gamma }]$ such that

$$\begin{aligned} F_{{\overline{N}}}(t) = \frac{p(t)}{ \prod _{j = 1}^{\ell }(1 - t^{\delta _{j}}) \prod _{i = 1}^{k} (1 - t^{\gamma _{i}})} \end{aligned}$$

(the $(1 - t^{\delta _{j}})$-factor in the denominator is due to the action of $y_{j}$ on ${{\,\mathrm{{\mathcal {B}}}\,}}_{{\bar{\delta }}}({\overline{N}})$ of degree $\delta _{k}$).

14.3 Growth function

In this subsection we fix a monoid $\Gamma$ with a tuple of generators ${\bar{\delta }} = \langle \delta _{1}, \dotsc , \delta _{\ell } \rangle$.

We also fix a tuple ${\bar{\gamma }} = \langle \gamma _{1}, \dotsc , \gamma _{k} \rangle \in \Gamma ^{k}$. Given a monomial in $S = R[x_1, \dotsc , x_{k}]$ its ${\bar{\gamma }}$-degree $\deg _{{\bar{\gamma }}}$ is defined in the “obvious” way:

$$\begin{aligned} \deg _{{\bar{\gamma }}}(r x_{1}^{n_{1}} \cdots x_{k}^{n_{k}}):= n_{1} \gamma _{1} + \dots + n_{k}\gamma _{k}. \end{aligned}$$

Given a polynomial $p({\bar{x}}) \in S = R[x_1, \dotsc , x_{k}]$, we say that its ${\bar{\gamma }}$-degree is less or equal to $n \in \Gamma$, and write $\deg _{{\bar{\gamma }}}(p) \le n$, if each monomial in p has ${\bar{\gamma }}$-degree less or equal to n (since $\Gamma$ is not linearly ordered in general, it’s not clear how to define the ${\bar{\gamma }}$-degree of a polynomial). For every $n \in \Gamma$, we denote

$$\begin{aligned} S_{n}:= \langle p \in S: \deg _{\gamma }(p) \le n \rangle . \end{aligned}$$

Theorem 14.8

Let N be an S-module. Let $V_{0} \le N$ be an R-submodule. For every $n \in \Gamma$, let $V_{n}:= S_{n} V_{0}$ (notice that $S_{0} =R$, that $V_{0} = S_{0} V_{0}$, and that $S_{n}$ and $V_n$ are R-modules), and $a_{n}:= \lambda (V_{n})$. Define

$$\begin{aligned} G_{V_{0}}(t):= \sum _{n \in \Gamma } a_{n} t^{n} \in \mathbb {R}[[t^{\Gamma }]] \end{aligned}$$

Assume that:

• (1) ${\bar{\gamma }} \cup {\bar{\delta }}$ is very good (inside $\Gamma$);

• (2) $\lambda (V_{0}) < \infty$;

• (3) $V_{0}$ is finitely generated as R-module.

Then, each $a_{n}$ is finite, and there exists a polynomial $p(t) \in \mathbb {R}[t^{\Gamma }]$ such that

$$\begin{aligned} G_{V_{0}}(t) = \frac{p(t)}{\prod _{j = 1}^{\ell } (1 - t^{\delta _{j}}) \prod _{i = 1}^{k} (1 - t^{\gamma _{i}})} \end{aligned}$$

Proof

The fact that $\gamma$ is very good is equivalent to the fact that $S_{n}$ is finitely generated (as R-module) for every $n \in \Gamma$. The above plus the fact that $\lambda (V_{0}) < \infty$ easily implies that $\lambda (V_{n}) < \infty$ for every $n \in \Gamma$. Let ${\overline{V}}:= S V_{0}$ as filtered $S[{\bar{y}}]$-module. Then, $V_{0} t^{0}$ generates ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{V}})$ as $S[{\bar{y}}]$-module, and therefore ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{V}})$ is a Noetherian $S[{\bar{y}}]$-module.

We can conclude as in the proof of Theorem 6.5, using Theorem 14.7. $\square$

Example 14.9

Let ${\bar{x}}:= \langle x_{1}, \dotsc , x_{k} \rangle$, ${\bar{y}}:= \langle y_{1}, \dotsc , y_{\ell } \rangle$, $S:= R[{\bar{x}},{\bar{y}}]$, $\Gamma := \mathbb {N}^{2}$, $\gamma _{i}:= \delta _{1}:= \langle 1,0 \rangle$ for $i = 1, \dotsc , k$, and $\gamma _{i}:= \delta _{2}:= \langle 0,1 \rangle$ for $i:= k+1, \dotsc , k + \ell$. Thus, each $x_{i}$ has degree $\delta _{1}$ and each $y_{j}$ has degree $\delta _{2}$. A monomial in ${\bar{x}}{\bar{y}}$ has therefore a “double degree” $\langle m,n \rangle \in \Gamma$, where m is its total degree in ${\bar{x}}$ and n is its total degree in ${\bar{y}}$. A polynomial in $\mathbb {R}[t^{\Gamma }]$ is the same object as a polynomial in the two variables $t_{1}, t_{2}$. Let N be an S-module and $V_{0}\le N$ be an R-submodule which satisfies (2) and (3). Then, if R is Noetherian, we have a corresponding function

$$\begin{aligned} G_{V_{0}}(t_{1}, t_{2}) = \frac{p(t_{1}, t_{2})}{(1-t_{1})^{k+1} (1 - t_{2})^{\ell +1}} \end{aligned}$$

where $p \in \mathbb {R}[t_{1}, t_{2}]$.

14.4 Multi-variate Hilbert polynomial

Let $P {:=}\langle P_{1}, \dotsc , P_{\ell } \rangle$ be a partition of $\{1, \dotsc , k\}$ into $\ell$ nonempty subsets; for every $j \le \ell$, let $p_{j}$ be the cardinality of $P_{j}$. In the following, we will assume that $P_{1} = \{1, 2, \dotsc , p_{1}\}$, $P_{2} = \{p_{1}+1, p_{1}+2,\dotsc , p_{1} + p_{2}\}$, ..., $P_{\ell } = \{p_{1}+ \dots + p_{\ell -1} + 1, \dotsc , k\}$.

Let $\Gamma := \mathbb {N}^{\ell }$; for every $j \le \ell$, let ${\hat{e}}_{j} \in \Gamma$ be the vector with all coordinates 0 except the j-th which is 1. Let ${\bar{x}}:= \langle x_{1}, \dotsc , x_{k} \rangle$ be a k-tuple of variables; to each variable $x_{i} \in P_{j}$ assign the weight ${\hat{e}}_{j}$, and define

$$\begin{aligned} {\bar{e}} {:=}\langle {\hat{e}}_{1}, {\hat{e}}_{1}, \dotsc , {\hat{e}}_{\ell } \rangle \in \mathbb {N}^{k}, \end{aligned}$$

where each weight ${\hat{e}}_{j}$ is repeated $p_{j}$ times.

As usual, $S {:=}R[x_{1}, \dotsc , x_{k}]$; for every ${\bar{m}} \in \mathbb {N}^{\ell }$, let

$$\begin{aligned} S^{({\bar{e}})}_{{\bar{m}}}:= \{p \in S: \deg _{{\bar{e}}}(p) \le {\bar{m}}\}. \end{aligned}$$

An equivalent way of describing $S_{{\bar{m}}}^{({\bar{e}})}$ is the following. Let ${\bar{t}}:= \langle t_{1}, \dotsc , t_{\ell } \rangle$. Let $\phi : S \rightarrow R[{\bar{t}}]$ be the homomorphism of R-algebrae mapping $x_{i}$ to $t_{j}$ when $i \in P_{j}$. Then, $q \in S_{{\bar{m}}}^{({\bar{e}})}$ iff, for every $j \le \ell$, $\deg _{t_{j}}(\phi (q)) \le m_{j}$.

Let M be a module over S and $V_{0} \le M$ be an R-submodule. For every ${\bar{m}} \in \mathbb {N}^{\ell }$, define $V_{{\bar{m}}}:= S_{{\bar{m}}}^{{\bar{e}}}V_{0}\le M$ and $a_{{\bar{m}}}:= \lambda (V_{{\bar{m}}})$.

Theorem 14.10

In the above setting, assume that $V_{0} \le M$ witnesses that M is $\lambda _{S}$-finite. Then, each $a_{{\bar{m}}}$ is finite. Moreover, there exists a polynomial $q({\bar{t}}) \in \mathbb {R}[{\bar{t}}]$ such that:

• (i) for every ${\bar{m}} \in \mathbb {N}^{\ell }$ large enough,

  $$\begin{aligned} a_{{\bar{m}}} = q({\bar{m}}); \end{aligned}$$

• (ii) for every $j \le \ell$,

  $$\begin{aligned} \deg _{t_{j}}(q) \le p_{j}. \end{aligned}$$

Moreover, the leading homogeneous component of q (see Def. 2.2) is independent from $V_{0}$.

Proof

Choose ${\bar{e}}$ as tuple of generators of $\Gamma$ and apply Theorem 14.8. We obtain that there exists a polynomial $r({\bar{t}}) \in \mathbb {R}[{\bar{t}}]$ such that

$$\begin{aligned} \sum _{{\bar{m}} \in \mathbb {N}^{\ell }} a_{{\bar{m}}} {\bar{t}}^{{\bar{m}}} = \frac{p({\bar{t}})}{\prod _{j = 1}^{\ell } (1 - t_{j})^{p_{j} + 1}} \end{aligned}$$

(the exponents $p_{j} + 1$ in the denominator come from the combination of the $p_{j}$ variables in $P_{j}$, each with degree ${\hat{e}}_{j}$, plus the generator ${\hat{e}}_{j}$). By Proposition 2.1, there exists a polynomial q satisfying (i) and (ii). By Proposition 2.4, the leading homogeneous component of q is independent from $V_{0}$. $\square$

Appendices

Appendix A: Main definitions

For the reader convenience, we collect here the various definitions used up to Sect. 13.

• R is a commutative ring with 1 (most of the time, Noetherian). $S = R[x_{1}, \dotsc , x_{k}]$ for a fixed $1 \le k \in \mathbb {N}$. $S_{n}$ is the set of polynomials of degree at most n, and $S^{(n)}$ is the set of homogeneous polynomials of degree exactly n (plus 0).

1.1 A.1 Lenght

• A length is a function

  $$\begin{aligned} \lambda : {{\,\mathrm{ R\mathrm -mod}\,}}\rightarrow \mathbb {R}_{\ge 0} \cup \{\infty \}\end{aligned}$$

  satisfying the following conditions:

  • (1) $\lambda (0) = 0$;

  • (2) $\lambda (M) = \lambda (M')$ when M and $M'$ are isomorphic;

  • (3) for every exact sequence $0 \rightarrow A \rightarrow B \rightarrow C \rightarrow 0$,

    $$\begin{aligned} \lambda (B) = \lambda (A) + \lambda (C); \end{aligned}$$

  • (4) for every $M \in {{\,\mathrm{ R\mathrm -mod}\,}}$,

    $$\begin{aligned} \lambda (M) = \sup \{\lambda (M'): M' \le M\text { finitely generated { R}-submodule}\}. \end{aligned}$$

Fix a length function $\lambda$ and an R-module N.

• N is locally $\lambda _R$-finite if, for every $N' \le N$ finitely generated, $\lambda (N')$ is finite.

Let T be an R-algebra and A be a T-module.

• A is $\lambda _T$-small if it is locally $\lambda _R$-finite and it is finitely generated as T-module; a witness for it is a finitely generated R-submodule V such that $\lambda (V) < \infty$ and $TV = A$.

1.2 A. 2 Graded modules

Fix ${\bar{\gamma }} = \langle \gamma _{1}, \dotsc , \gamma _{k} \rangle \in \mathbb {N}^{k}$ and an S-module M.

• An $\mathbb {N}$-grading of M of degree ${\bar{\gamma }}$ is given by a decomposition

  $$\begin{aligned} M = \bigoplus _{n \in \mathbb {N}} M_{n}, \end{aligned}$$

  where each $M_{n}$ is an R-module, and, for every $i \le k$ and $n \in \mathbb {N}$,

  $$\begin{aligned} x_{i} M_{n} \le M_{n+ \gamma _{i}}. \end{aligned}$$

• A graded S-module ${\overline{M}}$ is acceptable if $\gamma _{i} = 1$ for $i = 1, \dotsc , k$ and M is finitely generated as S-module.

1.3 A. 3 Filtered module

• An (increasing) filtering ${\overline{M}}$ on M with degrees ${\bar{\gamma }}$ is an increasing sequence of R-submodules of M

  $$\begin{aligned} M_{0} \le M_{1} \le M_{2} \le \cdots \le M \end{aligned}$$

  such that $x_{i} M_{j} \le M_{j + \gamma _{i}}$ for every $j \in \mathbb {N}$, $i \le k$, and it is exhaustive if $\bigcup _{i=0}^\infty M_{i} = M$. (Remember that all filterings we consider are increasing).

Fix a filtering ${\overline{M}}$ on M.

• The blow up of ${\overline{M}}$ is the graded S[y]-module of degree $(\gamma _{1}, \dotsc , \gamma _{k}, 1)$ given by:

  $$\begin{aligned} {{\,\mathrm{{\mathcal {B}}}\,}}(M) = \bigoplus _{n \in \mathbb {N}} M_{n} y^{n}, \end{aligned}$$

  with scalar multiplication defined by

  $$\begin{aligned} x_{i}(v y^{j}):= (x_{i}v) y^{j + \gamma _{i}}, \qquad y (v y^{j}):= v y^{j+1}. \end{aligned}$$

• Given $m \in \mathbb {N}$, define

  $$\begin{aligned} M^{m}:= \bigoplus _{n \le m} M_{n} y^{n} \le {{\,\mathrm{{\mathcal {B}}}\,}}(M). \end{aligned}$$

  We say that $M_{m}$ tightly generates ${\overline{M}}$ if $M^{m}$ generates ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{M}})$.⁶

• Given and R-submodule $V_{0} \le M$, we have the filtering and the graded module

  $$\begin{aligned} {{\,\textrm{Filt}\,}}(V_{0}; M)&{:=}(S_{n }V_{0})_{n \in \mathbb {N}}\\ {{\,\textrm{Gr}\,}}(V_{0}; M)&{:=}{{\,\mathrm{{\mathcal {B}}}\,}}({{\,\textrm{Filt}\,}}(V_{0}; M)) = \bigoplus _{n \in \mathbb {N}} S_{n} V_{0}\, y^{n}. \end{aligned}$$

• ${\overline{M}}$ is acceptable if ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{M}})$ is an acceptable graded S[y]-module: that is, all variables $x_{i}$ and y have degree 1, and ${{\,\mathrm{{\mathcal {B}}}\,}}({\overline{M}})$ is a finitely generated S[y]-module. ${\overline{M}}$ is good if moreover $\forall n \in \mathbb {N}$ $\lambda (M_{n}) < \infty$.

1.4 A. 4 Value monoid

• $\overline{{\mathcal {V}}}$ is the set of monomials of the form $r t^{d}$, with $r \in R_{>0} \cup \{\infty \}$ and $d \in \{1, \dotsc , k\}$ (plus 0).

1.5 A. 5 Hilbert polynomial

Let $V \le M$ be an R-submodule of M.

• The Hilbert polynomial of V is the polynomial $q_{V}(t) \in \mathbb {R}[t]$ (which exists under suitable assumptions) such that, for every n large enough,

  $$\begin{aligned} \lambda (S_{n} V) = q_{V}(n). \end{aligned}$$

• If V witnesses that M is $\lambda _S$-small, the leading term $\mu (V) = \mu _{\lambda }(V) \in {\mathcal {V}}$ of $q_{V}$ does not depend on the choice of V. If $\mu (V) = m t^{d}$, the $\lambda$-dimension of M is $\dim _{\lambda }(M) {:=}d$, the $\lambda$-degree of M is d!m. If M is not $\lambda _{S}$-small,

  $$\begin{aligned} \mu (M):= \sup \{\mu (M'): M' \lambda _S\text { -small submodule of } M\} \in \overline{{\mathcal {V}}}. \end{aligned}$$

• For every $i \le k$, the i-dimensional entropy of M is

  $$\begin{aligned} h^{(i)}_{\lambda }(M) {:=}{\left\{ \begin{array}{ll} \infty &{}\text {if } d > i\\ 0 &{}\text {if } d < i\\ i! \, m &{}\text {if } d = i. \end{array}\right. } \end{aligned}$$

  $h^{(1)}$ is the receptive entropy, $h^{(d)}$ is the algebraic entropy.

1.6 A. 6 Hilbert-Samuel polynomial

Let $I:= (x_{1}, \dotsc , x_{k}) \lhd R$.

• The Hilbert-Samuel polynomial of M is the polynomial ${\bar{q}}(t) \in \mathbb {R}[t]$ (which exists under suitable assumptions) such that, for every n large enough,

  $$\begin{aligned} \lambda (M / I^{n+1} M) = {\bar{q}}(n). \end{aligned}$$

  The leading term of ${\bar{q}}$ is ${\bar{\mu }}(M)$.

1.7 A. 7 Modules over R-algebrae

T is a commutative R-algebra generated by ${\bar{\gamma }} {:=}\langle \gamma _{1}, \dotsc , \gamma _{k} \rangle$. Let $\phi : S \rightarrow T$ be the homomorphism of R-algebrae mapping $x_{i}$ to $\gamma _{i}$. A is a T-module.

• We denote A as an S-module by $\langle A;{\bar{\gamma }} \rangle = \langle A; {\bar{\phi }} \rangle$, and correspondingly $\mu (A; {\bar{\gamma }}) {:=}\mu (\langle A;{\bar{\gamma }} \rangle )$ and $\mu (A; \phi ) {:=}\mu (\langle A;\phi \rangle )$. If A is $\lambda _T$-small the dimension of A (as T-module) is the degree of the monomial $\mu (A; {\bar{\gamma }})$, which does not depend on the choice of ${\bar{\gamma }}$. For $i \le k$, the i-dimensional entropy of A w.r.t. ${\bar{\gamma }}$ is

  $$\begin{aligned} h^{(i,{\bar{\gamma }})} {:=}\sup \{h^{(d)}(A, {\bar{\gamma }}): A' \le A \lambda _T\text { -small } Ts\text { -submodule } \}. \end{aligned}$$

1.8 A. 8 Vámos construction

• An $\lambda _S$-small chain in M of size n is a sequence of S-submodules

  $$\begin{aligned} {\mathfrak {M}}= \bigl ( M_{1} \le M_{2} \le \dots \le M_{2n-1} \le M_{2n} \le M \bigr ), \end{aligned}$$

  such that, for every $i =1, \dotsc , n$, $\lambda ({\hat{M}}_{i}) < \infty$, where ${\hat{M}}_{i} {:=}M_{2 i}/M_{2 i -1}$.

• Let $\theta$ be a suitable function.

  $$\begin{aligned} \theta ({\mathfrak {M}})&{:=}\sum _{i=1}^{n} \theta ({\hat{M}}_{i}),\\ {\hat{\theta }}(A)&{:=}\sup \{\theta ({\mathfrak {A}}): {\mathfrak {M}}\lambda _S\text { -small chain in M }\}. \end{aligned}$$

• The corresponding quantities for $\mu$, $h_{\lambda }^{(i)}$ and $h_{\lambda }^{(i,{\bar{\gamma }})}$ are denoted by ${\hat{\mu }}_{\lambda }$, ${\hat{h}}_{\lambda }^{(i)}$ and ${\hat{h}}_{\lambda }^{(i,{\bar{\gamma }})}$, respectively.

1.9 A. 9 Intrinsic entropy

Let ${\overline{M}}$ be a filtering on M and $V_{0} \le M$.

• $$\begin{aligned}\begin{aligned} {\tilde{M}}_{i}&\,\,{:=}\,\, M_{i+1}/M_{i}\\ \tilde{{\mathcal {B}}}({\overline{M}})&\,\,{:=}\,\, \bigoplus _{i \in \mathbb {N}} {{\tilde{M}}_{i}}\\ \tilde{{{\,\textrm{Gr}\,}}}(V_{0}; M)&\,\,{:=}\,\, \tilde{{\mathcal {B}}}({{\,\textrm{Filt}\,}}(V_{0};M)) = \bigoplus _{n} (S_{n+1}V_{0})/(S_{n} V_{0})\, y^{n}. \end{aligned} \end{aligned}$$

  ${\overline{M}}$ is $\lambda$-inert if $\tilde{{\mathcal {B}}}({\overline{M}})$ is Noetherian and, for every n large enough, $\lambda ({\tilde{M}}_{i}) < \infty$. $V_0$ is $\lambda$-inert if $\lambda ({\tilde{V}}_{0}) < \infty$ and ${\tilde{V}}_{0}$ is finitely generated, where ${\tilde{V}}_{0} {:=}(S_{1} V_{0}) / V_{0}$.

• The intrinsic Hilbert polynomial of the $\lambda$-inert filtering ${\overline{M}}$ is the polynomial $q_{{\overline{M}}}(t) \in \mathbb {R}[t]$ (which exists under suitable assumptions) such that, for every n large enough,

  $$\begin{aligned} \lambda ({\tilde{M}}_{n}) = {\tilde{q}}_{{\overline{M}}}(n); \end{aligned}$$

  $\tilde{\mu }({\overline{M}})$ is the leading term of ${\tilde{q}}_{{\overline{M}}}$.

• ${\tilde{q}}_{V_{0}} {:=}{\tilde{q}}_{\tilde{{{\,\textrm{Gr}\,}}}(M; V_{0}) }$ and $\tilde{\mu }[V_{0}]$ is the leading term of ${\tilde{q}}_{V_{0}}$.

  $$\begin{aligned} \tilde{\mu }(M) {:=}\sup \{ \tilde{\mu }[ V_{0}]:\ V_{0} \le M \text { is } \lambda \text { -inert}\} \end{aligned}$$

  Let d be the degree of $\tilde{\mu }(M)$ and s be its coefficient. The intrinsic $\lambda$-dimension of M is

  $$\begin{aligned} {\left\{ \begin{array}{ll} d+1 &{}\text { if } \tilde{\mu }(M) \ne 0,\\ 0 &{}\text { if } \lambda (M) >0 \text { and } \tilde{\mu }(M) = 0\\ - \infty &{} \text { if } \lambda (A) = 0. \end{array}\right. } \end{aligned}$$

  The intrinsic i-dimensional $\lambda$-entropy of M is

  $$\begin{aligned} {\tilde{h}}^{(i)}_{\lambda }(M) {:=}{\left\{ \begin{array}{ll} 0 &{} \text {if } i > d +1 \text { or } (i = d + 1 \text { and } \tilde{\mu }(M) = 0);\\ \infty &{} \text {if } i \le d;\\ \frac{s}{(d+1)!} &{} \text {if } i = d+1 \text { and } \tilde{\mu }(M) \ne 0;\\ \lambda (M) &{} \text {if } i = 0. \end{array}\right. } \end{aligned}$$

  The intrinsic $\lambda$-entropy is ${\tilde{h}}_{\lambda } {:=}{\tilde{h}}^{(k)}_{\lambda }$.

1.10 A. 10 Polynomials

• Given $p({\bar{t}}) \in \mathbb {R}[{\bar{t}}]$, the homogeneous component of p of degree i is denoted by $p_{i}$. The leading homogeneous component of p is $p_{d}$, where d is the degree of p (or 0 if $p = 0$).

Appendix B. Non-commuative rings

In this appendix, R is no longer assumed to be commuative. Let G be some (associative) monoid, and $T {:=}R[G]$. ${{\,\mathrm{ T\mathrm -mod}\,}}$ is the category of left T-modules (by “modules” we will mean left modules). $\theta$ is some function from ${{\,\mathrm{ T\mathrm -mod}\,}}$ to the family of monomials of the form $r t^{n}$, with $n \in \mathbb {N}$ and $r \in \mathbb {R}_{> 0} \cup \{\infty \}$ (plus the monomial 0). We assume:

• (1) $\theta$ is additive on the category of $\lambda _T$-small T-modules: $\theta (0) = 0$ and, for every exact sequences of $\lambda _T$-small T-modules $0 \rightarrow A \rightarrow B \rightarrow C \rightarrow 0$, $\theta (B) = \theta (A) \oplus \theta (C)$;

• (2) $\theta$ is invariant: if A and B are isomorphic T-modules, then $\theta (A) = \theta (B)$;

• (3) $\theta (A) = \sup \{\theta (B): B \le A \lambda _T\text{-small } \, T\text {-submodule}\}.$

We define

$$\begin{aligned} {\hat{\theta }}(A) {:=}\sup \{\theta ({\mathfrak {A}}): {\mathfrak {A}}\ \lambda _T\text{-small } \text{ chain } \text{ in }\ A\}. \end{aligned}$$

Theorem B.1

Assume that T is (left) Noetherian. Then,

• (a) ${\hat{\theta }}$ is invariant and additive on all ${{\,\mathrm{ T\mathrm -mod}\,}}$;

• (b) if A is locally $\lambda _R$-finite, then ${\hat{\theta }}(A) = \theta (A)$;

• (c) ${\hat{\theta }}(A) = \sup \{{\hat{\theta }}(B): B \le A \text { finitely generated T-submodule}\}$;

• (d) ${\hat{\theta }}\ge \theta$.

Proof

Same as Propositions 12.4 and 12.7. The assumption that $T = S[G]$ is used in the following way: $\square$

Claim 11

Let A be a T-module, generated (as a T-module) by $a_{1}, \dotsc , a_{\ell }$. Assume that $\lambda (Ra_{i})$ is finite, for $i = 1, \dotsc , \ell$. Then, A is locally $\lambda _R$-finite.$\square$

It is unclear if, under the same assumptions as in Thm. B.1, we can conclude that, when A is a finitely generated T-module,

$$\begin{aligned} {\hat{\theta }}(A) = \sup \{{\hat{\theta }}(A/I): I \lhd R \, \,\lambda \text { -cofinite} \,\, \text { ideal}\}. \end{aligned}$$

Example B.2

Let G be an amenable cancellative monoid and $T {:=}R[G]$. Let $\lambda$ be a length on ${{\,\mathrm{ R\mathrm -mod}\,}}$. Let $h_{\lambda }(A)$ be the algebraic entropy of the action of G on A for the length $\lambda$ (see e.g. [6]). Assume that T is Noetherian. Then, $\theta {:=}h_{\lambda }$ satisfies the assumptions of this section. Thus, the function ${\hat{h}}_{\lambda }$ satisfies the conclusion of Theorem B.1, and in particular is a length function on all T-mod.