1 Introduction

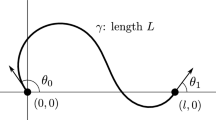
The paper is concerned with the minimization of the bending energy in a certain class of planar open curves subject to clamped boundary conditions and a constraint on the length of the curve. By clamped boundary condition, we mean that the position vector and the tangent vector of the curves are fixed at the boundary points. We will consider two cases: either we look at the classical Euler-Bernoulli elastica problem where one aims to minimize the bending energy

$$\begin{aligned} \mathcal {E}_0(\gamma )=\frac{1}{2} \int _{\gamma } \kappa ^2 \; \mathrm{{d}}s \end{aligned}$$

subject to a given prescribed length. Alternatively, the constraint appears as a penalization leading to the minimization of the modified elastic energy

$$\begin{aligned} \mathcal {E}_\lambda (\gamma ) = \frac{1}{2} \int _{\gamma } \kappa ^2 \; ds + \lambda \int _{\gamma } \, \mathrm{{d}}s, \end{aligned}$$
(1)

where \(\lambda \) is a non-negative constant. The first problem is referred to as the inextensible, the second as the extensible problem. In the above, \(\kappa \) is the curvature of \(\gamma \) and s denotes the arclength parameter. The energy \(\mathcal {E}_{\lambda }\) can be considered as a 1-dimensional version of the Helfrich energy. To see this, recall that for a surface \(\Sigma \subset \mathbb {R}^3\) the Helfrich energy is given by

$$\begin{aligned} \mathcal {H}(\Sigma )= \int _{\Sigma } \left( \frac{1}{2} k_c (H-c_0)^2 + k_{\bar{c}} K\right) \, \mathrm{{d}}A \,, \end{aligned}$$
(2)

where \(k_c,k_{\bar{c}}\) denote the curvature-elastic moduli, \(c_0 \in \mathbb {R}\) is a spontaneous curvature, and H, K denote the mean curvature and Gauss curvature of \(\Sigma \), respectively. Similarly, for curves, one is led to consider the energy

$$\begin{aligned} \int _{\gamma } \frac{1}{2} (\kappa -c_0)^2 \, \mathrm{{d}}s = \int _{\gamma } \frac{1}{2} \kappa ^2 \, \mathrm{{d}}s -c_0 \int _{\gamma } \kappa \, \mathrm{{d}}s + \frac{c_0^2}{2} \int _{\gamma } \, \mathrm{{d}}s . \end{aligned}$$

Since the second integral on the right-hand side is equal to a constant when the tangent vectors are fixed at the boundary (hence, in particular in the case of clamped boundary conditions), we may view \(\mathcal {E}_{\lambda }\) as a 1-dimensional Helfrich energy. It is well-known that both in the extensible and in the inextensible problem, a critical point \(\gamma \) satisfies the Euler-Lagrange equation

$$\begin{aligned} \partial _s^2 \kappa + \frac{1}{2} \kappa ^3 - \lambda \kappa = 0 \quad \text{ on } \gamma , \end{aligned}$$
(3)

where \(\lambda \in \mathbb {R}\) is the Lagrange multiplier associated with the length constraint in the inextensible problem. Solutions to this equation are called elastica and have been studied since Euler by many authors, see, e.g., [11, 14, 20] for an historical overview. By integrating equation (3), Langer and Singer [10] have derived explicit formulae for closed elastica in terms of elliptic integrals. Corresponding formulae have been obtained by Linnér in Linnér [13] for open curves under various boundary conditions both in the extensible and inextensible case. While these formulae give useful insight into the shape of elastica, it is not straightforward and certainly cumbersome to use those in order to solve the minimization problem or (3) subject to clamped boundary conditions. Recently, Miura [16] obtained the existence of a unique global minimizer both in the extensible and inextensible case for \(\lambda \) sufficiently large. By a suitable rescaling argument, he shows in addition that the shape of the solution close to the endpoints can be described with the help of a so–called borderline elastica. The minimization of \(\mathcal {E}_0\) subject to fixed length in the class of curves with prescribed endpoints has been considered by Yoshizawa [21]. In this case, it is possible to explicitly construct all critical points and to select the unique global minimum from these. The gradient flow associated to \(\mathcal {E}_{\lambda }\) has been studied in Lin [12] and Dall’Acqua et al. [5] in the extensible and inextensible problem, respectively. Finally, let us mention that the minimization of the surface energy (2) subject to clamped boundary conditions has been considered in Scholtes [18] and Deckelnick [7] for surfaces of revolution, in Deckelnick et al. [8] for two-dimensional graphs and in Refs. [1, 9] for parametric surfaces.

In this paper, we are interested in establishing existence, uniqueness and properties of minimizers in certain classes of graphs over the unit interval [0, 1]. Note that for a function \(v:[0,1] \rightarrow \mathbb {R}\) we have \(\mathrm{{d}}s = \sqrt{1+v^{\prime }(x)^2} \, \mathrm{{d}}x\) as well as

$$\begin{aligned} \kappa (x)= \frac{v^{\prime \prime }(x)}{(1+v^{\prime }(x)^2)^{\frac{3}{2}}} = \frac{\mathrm{{d}}}{\mathrm{{d}}x} \left( \frac{v^{\prime }(x)}{\sqrt{1+v^{\prime }(x)^2}} \right) . \end{aligned}$$
(4)

The clamped boundary conditions impose that the value of the function and of its derivative is prescribed at 0 and at 1. For \(\beta >0, \ell \ge 1\), we therefore introduce the following sets of admissible functions

$$\begin{aligned} M_{\beta }:= & {} \lbrace v \in H^2(0,1) \cap H^1_0(0,1) \mid v^{\prime }(0) = - v^{\prime }(1) = \beta \rbrace ; \end{aligned}$$
(5)
$$\begin{aligned} M_{\beta ,\ell }:= & {} \lbrace v \in M_{\beta } \mid \int _0^1 \sqrt{1+ v^{\prime }(x)^2} \, \mathrm{{d}}x =\ell \rbrace \end{aligned}$$
(6)

and then consider the problems

$$\begin{aligned} \min _{v \in M_{\beta }} E_\lambda (v) \end{aligned}$$
(7)

as well as

$$\begin{aligned} \min _{v \in M_{\beta ,\ell }} E_0(v) \end{aligned}$$
(8)

with

$$\begin{aligned} E_\lambda (v)= \frac{1}{2} \int _0^1 \frac{v^{\prime \prime }(x)^2}{(1+v^{\prime }(x)^2)^{\frac{5}{2}}} \, \mathrm{{d}}x + \lambda \int _0^1 \sqrt{1+ v^{\prime }(x)^2} \, \mathrm{{d}}x \,, \end{aligned}$$

and \(E_0(v)= \frac{1}{2} \int _0^1 \frac{v^{\prime \prime }(x)^2}{(1+v^{\prime }(x)^2)^{\frac{5}{2}}} \, \mathrm{{d}}x\). Let us emphasize that we consider symmetric boundary conditions but that the functions over which we minimize are not necessarily symmetric. Since the energies do not depend on v but only on its derivative of first and second order it is not a restriction to impose zero boundary values for the function. For the same reason, the case \(\beta <0\) can be considered by simply going from v to \(-v\). The choice \(\beta =0\) is certainly interesting in the inextensible problem but unfortunately our methods do not work in that case.

Even though the functional \(E_{\lambda }\) is highly nonlinear and non-convex, we are able to establish the existence of a unique minimizer both for the extensible and the inextensible problem. More precisely, our first main result reads as follows:

Theorem 1.1

For every \(\beta >0, \lambda \ge 0\), there exists a unique \(u_{\beta ,\lambda } \in M_\beta \) such that

$$\begin{aligned} E_\lambda (u_{\beta ,\lambda })=\min _{v \in M_\beta } E_\lambda (v). \end{aligned}$$

The function \(u_{\beta ,\lambda }\) belongs to \(C^{\infty }([0,1])\), is symmetric with respect to \(x=\frac{1}{2}\) and strictly concave. Furthermore, \(u_{\beta ,\lambda }\) is a solution of the boundary value problem

$$\begin{aligned} \frac{1}{\sqrt{1+u^{\prime }(x)^2}} \frac{\mathrm{{d}}}{\mathrm{{d}}x} \Bigl ( \frac{\kappa ^{\prime }(x)}{\sqrt{1+u^{\prime }(x)^2}} \Bigr ) + \frac{1}{2} \kappa (x)^3 - \lambda \kappa (x)&= 0 \qquad x \in [0,1] \end{aligned}$$
(9)
$$\begin{aligned} u(0)=u(1)=0, u^{\prime }(0)=-u^{\prime }(1)&= \beta . \end{aligned}$$
(10)

This result generalizes Theorem 2 in [6] where the case \(\lambda =0\) was considered and an explicit formula for the solution was derived. We shall prove existence and uniqueness of the minimizers without any restriction on the parameters \(\beta \) and \(\lambda \) and without using explicit formulas. A crucial ingredient of our analysis are Noether identities that will be derived in Sect. 2 from the invariance of \(E_\lambda \) with respect to translations. These identities will play an important role to get insight into the qualitative behaviors of the minimizers, such as curvature bounds, see Lemma 3.4 below.

Even though the problem (9) is of fourth order and hence, in general, no comparison principle is available, we not only have uniqueness of minimizers \(u_{\beta ,\lambda }\), but we can also prove that the solutions are strictly ordered with respect to the parameters \(\beta \) and \(\lambda \).

Theorem 1.2

Let \(u_{\beta ,\lambda } \in M_\beta \) be the unique minimum of \(E_\lambda \) found in Theorem 1.1.

  1. a)

    We have for all \(\lambda \ge 0\) and all \(0< \beta _1< \beta _2\)

    $$\begin{aligned} u_{\beta _1,\lambda }(x)< u_{\beta _2,\lambda }(x), \; x \in (0,1), \quad u_{\beta _1,\lambda }^{\prime }(x) < u_{\beta _2,\lambda }^{\prime }(x), \; x \in [0,\frac{1}{2}). \end{aligned}$$
  2. b)

    We have for all \(\beta >0\) and all \(0 \le \lambda _1<\lambda _2\)

    $$\begin{aligned} u_{\beta ,\lambda _1} (x)> u_{\beta ,\lambda _2}(x), \, x \in (0,1), \quad u_{\beta ,\lambda _1}^{\prime }(x) > u_{\beta ,\lambda _2}^{\prime }(x), \, x \in (0,\frac{1}{2}). \end{aligned}$$

The comparison results will again follow from our Noether identities which allow us to derive a second order equation for the first derivative of the solution, which is then accessible to a comparison argument. The proofs of Theorems 1.1 and 1.2 will be given in Sect. 3. In Sect. 5, we study also the behavior of the minimizers for \((\beta , \lambda ) \rightarrow (+ \infty , 0)\), and for \(\lambda \rightarrow +\infty \). In the second case, we prove straightening and can characterize the limit of the boundary layer as a piece of the so-called borderline elastica.

Our third main result is concerned with the solution of the inextensible problem (8). Here, our idea consists in introducing \(L:[0,\infty ) \rightarrow \mathbb {R}\) by

$$\begin{aligned} L(\lambda ):= \int _0^1 \sqrt{1+u_{\beta ,\lambda }^{\prime }(x)^2} \, \mathrm{{d}}x \end{aligned}$$
(11)

and solving the equation \(L(\lambda )=\ell \). More precisely, we have

Theorem 1.3

Let \(\beta >0\). Then, (8) has a unique solution \(u \in M_{\beta ,\ell }\) for every \(1< \ell \le L_\beta \) where

$$\begin{aligned} L_\beta := \frac{\int _{-\beta }^{\beta } (1+\tau ^2)^{-3/4} \mathrm{{d}} \tau }{\int _{-\beta }^{\beta } (1+\tau ^2)^{-5/4} \mathrm{{d}} \tau } \,. \end{aligned}$$

The function u belongs to \(C^{\infty }([0,1])\), is symmetric and strictly concave on [0, 1]. Furthermore, there exists \(\lambda _{\beta ,\ell } \ge 0\) such that u satisfies (9), (10) with \(\lambda =\lambda _{\beta ,\ell }\).

The proof of Theorem 1.3 is given in Sect. 4.

2 Noether identities and regularity

Let us consider for \(\delta \ge 0\) the functional \(E_{\lambda ,\delta }: M_{\beta } \rightarrow \mathbb {R}\),

$$\begin{aligned} E_{\lambda ,\delta }(v):= E_\lambda (v) + \frac{\delta }{6} \int _0^1 v^{\prime }(x)^6 \mathrm{{d}}x, \end{aligned}$$

where for later purposes, we have included a penalty term.

Lemma 2.1

Let \(\delta \ge 0\) and suppose that \(u \in M_\beta \) is a critical point for \(E_{\lambda ,\delta }\). Then, \(u \in C^{\infty }([0,1])\) and u solves the Euler-Lagrange equation on [0,1], i.e.

$$\begin{aligned} \frac{1}{\sqrt{1+u^{\prime }(x)^2}} \frac{\mathrm {{d}}}{\mathrm {{d}} x} \Bigl ( \frac{\kappa ^{\prime }(x)}{\sqrt{1+u^{\prime }(x)^2}} \Bigr ) + \frac{1}{2} \kappa (x)^3 - \lambda \kappa (x) - 5 \delta u^{\prime }(x)^4 u^{\prime \prime }(x)=0 . \end{aligned}$$
(12)

Proof

Since u is a critical point of \(E_{\lambda ,\delta }\), we have with (4) for every \(v \in H^2_0(0,1)\)

$$\begin{aligned} 0=&{} \langle E_{\lambda ,\delta }^{\prime }(u),v \rangle = \int _0^1 \frac{u''(x) v^{\prime \prime }(x)}{(1+u^{\prime }(x)^2)^{\frac{5}{2}}} \, \mathrm {{d}}x - \frac{5}{2} \int _0^1 \frac{u^{\prime \prime }(x)^2 u^{\prime }(x) v^{\prime }(x)}{(1+ u^{\prime }(x)^2)^{\frac{7}{2}}} \, \mathrm {{d}}x \nonumber \\{}&{} + \lambda \int _0^1 \frac{u^{\prime }(x) v^{\prime }(x)}{\sqrt{1+u^{\prime }(x)^2}} \, \mathrm {{d}}x + \delta \int _0^1 u^{\prime }(x)^5 v^{\prime }(x) \, \mathrm {{d}}x \nonumber \\ =&{} \int _0^1 \kappa (x) \frac{v^{\prime \prime }(x)}{1+u^{\prime }(x)^2} \; \mathrm {{d}}x -\frac{5}{2} \int _0^1 \kappa ^2(x) \frac{u^{\prime }(x)}{\sqrt{1+u^{\prime }(x)^2}} v^{\prime }(x) \; \mathrm {{d}}x \nonumber \\ {}&{} + \lambda \int _0^1 \frac{u^{\prime }(x) v^{\prime }(x)}{\sqrt{1+u^{\prime }(x)^2}} \, \mathrm {{d}}x + \delta \int _0^1 u^{\prime }(x)^5 \, v^{\prime }(x) \mathrm {{d}}x. \end{aligned}$$
(13)

In the same way, as in Proposition 3.2 in Dall’Acqua et al. [4], we can then show that \(u \in C^{\infty }([0,1])\) as well as (12). \(\square \)

In the next result, we show how (12) can be integrated once in two different ways. The relations (14) and (15) in the following corollary can be seen as Noether identities resulting from the invariance of \(E_{\lambda ,\delta }\) with respect to translations and will be crucial for our studies. In the appendix, we explain the construction leading to these identities.

Corollary 2.2

Let \(\delta \ge 0\) and suppose that \(u \in C^4([0,1])\) satisfies (12). Then, there exist \(c_1,c_2 \in \mathbb {R}\) such that

$$\begin{aligned} \frac{\kappa ^{\prime }(x)}{1+u^{\prime }(x)^2} + \frac{1}{2} \frac{u^{\prime }(x) \kappa (x)^2}{\sqrt{1+u^{\prime }(x)^2}} - \lambda \frac{u^{\prime }(x)}{\sqrt{1+u^{\prime }(x)^2}} - \delta u^{\prime }(x)^5= & {} c_1, \quad x \in [0,1]; \end{aligned}$$
(14)
$$\begin{aligned} \frac{u^{\prime }(x) \kappa ^{\prime }(x)}{1+u^{\prime }(x)^2} - \frac{1}{2} \frac{\kappa (x)^2}{\sqrt{1+u^{\prime }(x)^2}} + \lambda \frac{1}{\sqrt{1+u^{\prime }(x)^2}} - \frac{5}{6} \delta u^{\prime }(x)^6= & {} c_2, \quad x \in [0,1]. \end{aligned}$$
(15)

If, in addition \(u(x)=u(1-x)\) for all \(x \in [0,1]\), i.e., u is symmetric, then, \(c_1=0\) and we also have

$$\begin{aligned} \max _{x \in [0,1]} | u^{\prime }(x) | = | u^{\prime }(0) |. \end{aligned}$$
(16)

Proof

We calculate with the help of (12)

$$\begin{aligned} \frac{\mathrm{{d}}}{\mathrm{{d}}x} \left\{ \frac{\kappa ^{\prime }}{1+(u^{\prime })^2} \right\}= & {} \frac{1}{\sqrt{1+(u^{\prime })^2}} \frac{\mathrm{{d}}}{\mathrm{{d}}x} \left\{ \frac{\kappa ^{\prime }}{\sqrt{1+ (u^{\prime })^2}} \right\} - \frac{u^{\prime } \kappa \kappa ^{\prime }}{\sqrt{1+(u^{\prime })^2}}\\= & {} - \frac{1}{2} \kappa ^3 + \lambda \kappa + 5 \delta (u^{\prime })^4 u^{\prime \prime } - \frac{u^{\prime } \kappa \kappa ^{\prime }}{\sqrt{1+(u^{\prime })^2}} \\= & {} - \frac{1}{2} \frac{\mathrm{{d}}}{\mathrm{{d}}x} \left\{ \frac{u^{\prime } \kappa ^2}{\sqrt{1+(u^{\prime })^2}} \right\} + \lambda \frac{\mathrm{{d}}}{\mathrm{{d}}x} \left\{ \frac{u^{\prime }}{\sqrt{1+(u^{\prime })^2}} \right\} + \delta \frac{\mathrm{{d}}}{\mathrm{{d}}x} (u^{\prime })^5, \end{aligned}$$

which yields (14). Since \(u^{\prime } \kappa = - \frac{\mathrm{{d}}}{\mathrm{{d}}x} \bigl ( \frac{1}{\sqrt{1+(u^{\prime })^2}} \bigr )\), we deduce in a similar way that

$$\begin{aligned} \frac{\mathrm{{d}}}{\mathrm{{d}}x} \left\{ \frac{u^{\prime }\kappa ^{\prime }}{1+(u^{\prime })^2} \right\}= & {} \frac{u^{\prime }}{\sqrt{1+(u^{\prime })^2}} \frac{\mathrm{{d}}}{\mathrm{{d}}x} \left\{ \frac{\kappa ^{\prime }}{\sqrt{1+ (u^{\prime })^2}} \right\} + \frac{\mathrm{{d}}}{\mathrm{{d}}x} \left\{ \frac{u^{\prime }}{\sqrt{1+(u^{\prime })^2}} \right\} \frac{\kappa ^{\prime }}{\sqrt{1+(u^{\prime })^2}} \\= & {} - \frac{1}{2} u^{\prime } \kappa ^3 + \lambda u^{\prime } \kappa + 5 \delta (u^{\prime })^5 u^{\prime \prime } + \frac{\kappa \kappa ^{\prime }}{\sqrt{1+(u^{\prime })^2}} \\= & {} \frac{1}{2} \frac{\mathrm{{d}}}{\mathrm{{d}}x} \left\{ \frac{\kappa ^2}{\sqrt{1+(u^{\prime })^2}} \right\} - \lambda \frac{\mathrm{{d}}}{\mathrm{{d}}x} \left\{ \frac{1}{\sqrt{1+(u^{\prime })^2}} \right\} + \frac{5}{6} \delta \frac{\mathrm{{d}}}{\mathrm{{d}}x} (u^{\prime })^6, \end{aligned}$$

so that we obtain (15).

If in addition, u is symmetric with respect to \(x=\frac{1}{2}\), then evaluating (14) for \(x=\frac{1}{2}\) yields \(c_1=0\). In order to prove (16), let us first assume that \(m:= \max _{x \in [0,1]} u^{\prime }(x) > | u^{\prime }(0)|\) and choose \(x_0 \in (0,1)\) such that \(u^{\prime }(x_0)=m\). We then have \(u^{\prime \prime }(x_0)=0\) and \(u^{\prime \prime }(x_0) \le 0\) from which we infer that \(\kappa (x_0)=0\) and \(\kappa ^{\prime }(x_0) \le 0\). Using (14) we obtain

$$\begin{aligned} 0 = \frac{\kappa ^{\prime }(x_0)}{1+u^{\prime }(x_0)^2} - \lambda \frac{u^{\prime }(x_0)}{\sqrt{1+u^{\prime }(x_0)^2}} - \delta u^{\prime }(x_0)^5 \le \frac{\kappa ^{\prime }(x_0)}{1+u^{\prime }(x_0)^2} \le 0 \end{aligned}$$

and hence \(\kappa ^{\prime }(x_0)=0\). By viewing (12) as a second order ODE for \(\kappa \) (since \(u^{\prime \prime }=(1+u^{\prime 2})^{\frac{3}{2}} \kappa \)), we infer that \(\kappa \equiv 0\) and therefore \(u \equiv 0\), a contradiction. In the same way, we can exclude that \(\min _{x \in [0,1]} u^{\prime }(x) < -| u^{\prime }(0)|\). \(\square \)

Thanks to the Noether identities we just derived, we can now generalize some results in Deckelnick et al. [6]. To do so, we introduce the function

$$\begin{aligned} G: \mathbb {R}\rightarrow \left( -\frac{c_0}{2}, \frac{c_0}{2}\right) , \quad G(s):= \int _0^s \frac{1}{(1+\tau ^2)^{\frac{5}{4}}} \; \mathrm{{d}} \tau \,, \end{aligned}$$
(17)

and

$$\begin{aligned} c_0:= \int _{-\infty }^{\infty } \frac{1}{(1+\tau ^2)^{\frac{5}{4}}} \; \mathrm{{d}} \tau = \sqrt{\pi } \frac{\Gamma (3/4)}{\Gamma (5/4)} \simeq 2.396280469....\,. \end{aligned}$$
(18)

A crucial ingredient in Deckelnick et al. [6] (see in particular [6, Lemma 4]) is the observation that u is a solution of (9) with \(\lambda =0\) if and only if \(\frac{d^2}{d x^2} G(u^{\prime }(x)) =0\) for \(x \in [0,1]\). By integrating this equation, twice one then obtains that \(u_{\beta ,0}\) (with the notation used in Theorem 1.1) is explicitly given by

$$\begin{aligned} u_{\beta ,0}(x)=&{} \frac{2}{c \root 4 \of {1+(G^{-1}(c/2-cx))^2}}- \frac{2}{c \root 4 \of {1+(G^{-1}(c/2))^2}}, \; x \in (0,1), \end{aligned}$$
(19)

with \(c=2G(\beta )\). Even though it does not appear possible to derive an explicit formula in the case \(\lambda >0\), the function \(x \mapsto G(u^{\prime }(x))\) plays an important role in our analysis. Indeed, we have

Corollary 2.3

Let \(u \in C^4([0,1])\) be a solution of (12) with \(\delta =0\) and \(\lambda \ge 0\), which is symmetric with respect to \(x=\frac{1}{2}\). Then

$$\begin{aligned} \bigl ( \lambda - \frac{1}{2} \kappa (x)^2 \bigr ) \sqrt{1+ u^{\prime }(x)^2}&= c_2, \quad x \in [0,1]; \end{aligned}$$
(20)
$$\begin{aligned} \kappa ^{\prime }(x) - c_2 u^{\prime }(x)&= 0, \quad x \in [0,1], \end{aligned}$$
(21)

with \(c_2\) the constant in Corollary 2.2, and

$$\begin{aligned} \frac{\mathrm{{d}}^2}{\mathrm{{d}} x^2} G(u^{\prime }(x)) = \lambda u^{\prime }(x) (1+u^{\prime }(x)^2)^{\frac{3}{4}}, \quad x \in [0,1]. \end{aligned}$$

Proof

In view of the symmetry of u, we deduce from Corollary 2.2 that

$$\begin{aligned} \frac{\kappa ^{\prime }(x)}{1+u^{\prime }(x)^2} + \frac{1}{2} \frac{u^{\prime }(x) \kappa (x)^2}{\sqrt{1+u^{\prime }(x)^2}} - \lambda \frac{u^{\prime }(x)}{\sqrt{1+u^{\prime }(x)^2}} = 0, \quad x \in [0,1]. \end{aligned}$$
(22)

By multiplying (22) by \(-u^{\prime }(x)\) and adding the result to (15), we obtain (20). The relation (21) is obtained by inserting (20) into (22).

Clearly,

$$\begin{aligned} \frac{d}{dx} G(u^{\prime }(x)) = \frac{u^{\prime \prime }(x)}{(1+u^{\prime }(x)^2)^{\frac{5}{4}}} = \kappa (x) (1+u^{\prime }(x)^2)^{\frac{1}{4}}, \end{aligned}$$

and hence

$$\begin{aligned} \frac{d^2}{d x^2} G(u^{\prime }(x))= & {} \kappa ^{\prime }(x) (1+u^{\prime }(x)^2)^{\frac{1}{4}} + \frac{1}{2} \kappa (x) u^{\prime }(x) u^{\prime \prime }(x) (1+u^{\prime }(x)^2)^{-\frac{3}{4}} \\= & {} (1+u^{\prime }(x)^2)^{\frac{5}{4}} \left( \frac{\kappa ^{\prime }(x)}{1+u^{\prime }(x)^2} + \frac{1}{2} \frac{u^{\prime }(x) \kappa (x)^2}{\sqrt{1+u^{\prime }(x)^2}} \right) = \lambda u^{\prime }(x)(1+u^{\prime }(x)^2)^{\frac{3}{4}} \end{aligned}$$

in view of (22). \(\square \)

3 Extensible problem

3.1 Existence and uniqueness of minimizers

A direct application of the direct method in the calculus of variations to solve (7) is not straightforward since a bound on \(E_{\lambda }(v)\) does not immediately imply a bound on the \(H^{2}\)-norm of the function v. In particular, it is not clear how to get a bound on \(\Vert v^{\prime }\Vert _{\infty }\). For this reason, we first solve the minimization problem for the penalized functional \(E_{\lambda ,\delta }\). In order to then get rid of the penalization, we work in the class of symmetric functions and make use of (16). Hence, let

$$\begin{aligned} M^{sym}_{\beta }:= \lbrace v \in H^2 \cap H^1_0(0,1) \, | \,&v(x)=v(1-x), x \in [0,1], \ v^{\prime }(0)=-v^{\prime }(1)=\beta \rbrace \, . \end{aligned}$$

Lemma 3.1

For every \(\delta \in (0,1]\), there exists \(u_{\delta } \in M^{sym}_{\beta }\) such that

$$\begin{aligned} E_{\lambda ,\delta }(u_\delta )= \inf _{v \in M^{sym}_{\beta }} E_{\lambda ,\delta }(v). \end{aligned}$$

Moreover, \(u_\delta \in C^\infty ([0,1])\) and \(\max _{x \in [0,1]} | u_{\delta }^{\prime }(x) | =\beta \).

Proof

We proceed similarly to [4, Lemma 3.1, Lemma 2.5]. Let \((u_k)_{k \in \mathbb {N}} \subset M^{sym}_{\beta }\) be a sequence with \(E_{\lambda ,\delta }(u_k) \searrow \inf _{v \in M^{sym}_{\beta }} E_{\lambda ,\delta }(v)\), \(k \rightarrow \infty \). For \(k \in \mathbb {N}\), we find

$$\begin{aligned} \begin{aligned} \int _0^1 | u_k^{\prime \prime }(x) | \mathrm {{d}}x&= \int _0^1 \frac{| u_k^{\prime \prime }(x) |}{(1+ u_k^{\prime }(x)^2)^{\frac{5}{4}}} \, (1+ u_k^{\prime }(x)^2)^{\frac{5}{4}} \mathrm {{d}}x \\ {}&\le {} C(\delta ) \bigl ( E_{\lambda ,\delta }(u_k) +1 \bigr ) \le \tilde{C}(\delta ), \end{aligned} \end{aligned}$$

using the Cauchy-Schwarz inequality and that \(\lambda \ge 0\). Since \(u_k(0)=u_k(1)=0\), there exists \(\xi _k \in (0,1)\) with \(u_k^{\prime }(\xi _k)=0\) and hence

$$\begin{aligned} | u_k^{\prime }(x) | \le \int _0^1 | u_k^{\prime \prime }(y) | \mathrm{{d}}y \le \tilde{C}(\delta ), \quad x \in [0,1], \, k \in \mathbb {N}. \end{aligned}$$

Therefore, the minimizing sequence \((u_k)_{k\in \mathbb {N}}\) is uniformly bounded in \(H^{2}(0,1) \cap H^{1}_0(0,1)\) and hence, there exists \(u_{\delta } \in H^{2}(0,1) \cap H^{1}_0(0,1)\) and a subsequence \((u_{k_j})_{j\in \mathbb {N}}\), such that \( u_{k_j} \rightharpoonup u_{\delta } \text{ in } H^{2}(0,1)\), \( j \rightarrow \infty \) and \(u_{k_j} \rightarrow u_{\delta }\) in \(C^1([0,1])\), \(j \rightarrow \infty \). Clearly, \(u_{\delta } \in M_{\beta }^{sym}\). Moreover,

$$\begin{aligned} E_0(u_{\delta })&= \lim _{j \rightarrow \infty } \int _0^1 u_{k_j}^{\prime \prime } (x)\frac{u_{\delta }^{\prime \prime }(x)}{(1+(u_{\delta }^{\prime }(x))^2)^{\frac{5}{2}}} \; \mathrm {{d}}x \nonumber \\ {}&= \lim _{j \rightarrow \infty } \int _0^1 \frac{u_{k_j}^{\prime \prime }(x)}{(1+(u_{k_j}^{\prime }(x))^2)^{\frac{5}{4}}} \frac{u_{\delta }^{\prime \prime }(x)}{(1+(u_{\delta }^{\prime }(x))^2)^{\frac{5}{4}}} \; \mathrm {{d}} x \nonumber \\ {}&\le \liminf _{j \rightarrow \infty } E_0(u_{k_j})^{\frac{1}{2}} E_0(u_{\delta })^{\frac{1}{2}}, \end{aligned}$$
(23)

from which we infer that \(u_{\delta }\) is a minimum of \(E_{\lambda ,\delta }\) recalling that \(u_{k_j} \rightarrow u_{\delta }\) in \(C^1\). Next, since \(u_\delta \) is a critical point of \(E_{\lambda ,\delta }\) in \(M^{sym}_{\beta }\), we have

$$\begin{aligned} \langle E_{\lambda ,\delta }^{\prime }(u_\delta ),v \rangle = 0 \quad \text{ for } \text{ all } v \in M^{sym}_0. \end{aligned}$$
(24)

By splitting an arbitrary function \(v \in H^2_0(0,1)\) into a symmetric and an antisymmetric part and using the symmetry of \(u_\delta \), we deduce that (13) holds for all \(v \in H^2_0(0,1)\). As in Lemma 2.1 we then have that \(u_\delta \in C^\infty ([0,1])\) and that \(u_\delta \) solves (12). Furthermore, as \(u_\delta \) is symmetric, Corollary 2.2 implies that \(\max _{x \in [0,1]} | u_{\delta }^{\prime }(x)| = |u^{\prime }_\delta (0)| =\beta \). \(\square \)

Lemma 3.2

For every \(\beta >0\) and \(\lambda \ge 0\), there exists \(u \in M^{sym}_{\beta }\) such that

$$\begin{aligned} E_{\lambda }(u)= \inf _{v \in M^{sym}_{\beta }} E_{\lambda }(v). \end{aligned}$$

Moreover, u belongs to \(C^{\infty }([0,1])\) and is a solution of (12) with \(\delta =0\).

Proof

Choose a sequence \((\delta _k)_{k \in \mathbb {N}}\) of positive real numbers with \( \lim _{k \rightarrow \infty }\delta _k=0\). In view of Lemma 3.1, there exists \(u_k \in M^{sym}_{\beta }\) such that \(E_{\lambda ,\delta _k}(u_k)=\inf _{v \in M^{sym}_{\beta }} E_{\lambda ,\delta _k}(v)\) for all \(k \in \mathbb {N}\). Furthermore, \(\max _{x \in [0,1]} | u_k^{\prime }(x)| = \beta \). Since the function \({\bar{u}}(x):= \beta x (1-x)\) belongs to \(M^{sym}_{\beta }\), we obtain

$$\begin{aligned} \begin{aligned} \frac{1}{2} \frac{1}{(1+ \beta ^2)^{\frac{5}{2}}} \Vert u_k^{\prime \prime } \Vert _{L^2}^2&\le \frac{1}{2} \int _0^1 \frac{ u_k^{\prime \prime }(x)^2}{(1+u_k^{\prime }(x)^2)^{\frac{5}{2}}} \mathrm {{d}} x \\ {}&\le E_{\lambda ,\delta _k}(u_k) \le E_{\lambda ,\delta _k}({\bar{u}}) \le c, \qquad k \in \mathbb {N}. \end{aligned} \end{aligned}$$

Since \(u_k(0)=0, k \in \mathbb {N}\), we infer that the sequence \((u_k)_{k \in \mathbb {N}}\) is bounded in \(H^2(0,1)\) so that there exists a subsequence, again denoted by \((u_k)_{k \in \mathbb {N}}\) and \(u \in H^2(0,1)\) such that

$$\begin{aligned} u_k \rightarrow u \; \text{ in } \; C^1([0,1]) \; \; \text{ and } \; \; u_k^{\prime \prime } \rightharpoonup u^{\prime \prime } \; \text{ in } \; L^2(0,1). \end{aligned}$$

Clearly, \(u \in M^{sym}_{\beta }\), and we obtain for every \(v \in M^{sym}_{\beta }\) that

$$\begin{aligned} E_\lambda (u) \le \liminf _{k \rightarrow \infty } E_\lambda (u_k) \le \liminf _{k \rightarrow \infty } E_{\lambda ,\delta _k}(u_k) \le \liminf _{k \rightarrow \infty } E_{\lambda ,\delta _k}(v) = E_\lambda (v), \end{aligned}$$

where the first inequality follows from (23). Hence, \(E_\lambda (u)= \inf _{v \in M^{sym}_{\beta }} E_\lambda (v)\) and similarly as above, we deduce that u belongs to \(C^{\infty }([0,1])\) and is a solution of (12) with \(\delta =0\). \(\square \)

With the help of Corollary 2.3, we now show that the function u obtained in Lemma 3.2 minimizes \(E_\lambda \) even in the larger set \(M_\beta \) and furthermore, is the unique function with this property.

Theorem 3.3

Let \(\beta >0\), \(\lambda \ge 0\) and \(u \in M_{\beta } \cap C^4([0,1])\) be symmetric and a solution of (12) with \(\delta =0\). Then, u is the unique minimum of \(E_\lambda \) in the class \(M_\beta \).

Proof

For every \(v \in M_{\beta }\), we have

$$\begin{aligned} {}&{} E_\lambda (v) - E_\lambda (u) \nonumber \\{}&{} \quad = \frac{1}{2} \int _0^1 \left[ \frac{v^{\prime \prime }(x)^2}{(1+ v^{\prime }(x)^2)^{\frac{5}{2}}} - \frac{u^{\prime \prime }(x)^2}{(1+ u^{\prime }(x)^2)^{\frac{5}{2}}} \right] \, \mathrm {{d}}x \nonumber \\ {}&{}\qquad + \lambda \int _0^1 \bigl ( \sqrt{1+ v^{\prime }(x)^2} - \sqrt{1+u^{\prime }(x)^2} \bigr ) \, \mathrm {{d}}x \nonumber \\{}&{} \quad = \frac{1}{2} \int _0^1 \Big | \frac{v^{\prime \prime }(x)}{(1+ v^{\prime }(x)^2)^{\frac{5}{4}}} - \frac{u^{\prime \prime }(x)}{(1+ u^{\prime }(x)^2)^{\frac{5}{4}}} \Big |^2 \, \mathrm {{d}}x \nonumber \\ {}&{ }\qquad + \lambda \int _0^1 \bigl ( \sqrt{1+ v^{\prime }(x)^2} - \sqrt{1+u^{\prime }(x)^2} \bigr ) \, \mathrm {{d}}x \nonumber \\{}&{} \qquad + \int _0^1 \frac{u^{\prime \prime }(x)}{(1+ u^{\prime }(x)^2)^{\frac{5}{4}}} \Bigl ( \frac{v^{\prime \prime }(x)}{(1+ v^{\prime }(x)^2)^{\frac{5}{4}}} - \frac{u^{\prime \prime }(x)}{(1+ u^{\prime }(x)^2)^{\frac{5}{4}}} \Bigr ) \, \mathrm {{d}}x \nonumber \\{}&{} \quad = \frac{1}{2} \int _0^1 \Big | \frac{v^{\prime \prime }(x)}{(1+ v^{\prime }(x)^2)^{\frac{5}{4}}} - \frac{u^{\prime \prime }(x)}{(1+ u^{\prime }(x)^2)^{\frac{5}{4}}} \Big |^2 \, \mathrm {{d}}x \nonumber \\ {}&{} \qquad + \lambda \int _0^1 \bigl ( \sqrt{1+ v^{\prime }(x)^2} - \sqrt{1+u^{\prime }(x)^2} \bigr ) \, \mathrm {{d}}x \nonumber \\{}&{} \qquad + \int _0^1 \frac{\mathrm {{d}}}{\mathrm {{d}}x} G(u^{\prime }(x)) \frac{d}{dx} \bigl ( G(v^{\prime })-G(u^{\prime }) \bigr )(x) \, \mathrm {{d}}x \equiv I + II + III, \end{aligned}$$
(25)

with G as in (17). Using integration by parts, the fact that \([G(v^{\prime })-G(u^{\prime })](x)=0, x=0,1\) and Corollary 2.3, we obtain

$$\begin{aligned} III= & {} - \int _0^1 \frac{d^2}{d x^2} G(u^{\prime })(x) \bigl ( G(v^{\prime }) - G(u^{\prime }) \bigr )(x) \, \mathrm{{d}}x \\= & {} - \lambda \int _0^1 u^{\prime }(x) (1+ u^{\prime }(x)^2)^{\frac{3}{4}} \bigl ( G(v^{\prime }) - G(u^{\prime }) \bigr )(x) \, \mathrm{{d}}x. \end{aligned}$$

Combining this relation with (25), we have

$$\begin{aligned} \begin{aligned}&{} E_\lambda (v) - E_\lambda (u) = \frac{1}{2} \int _0^1 \Big | \frac{v^{\prime \prime }}{(1+ (v^{\prime })^2)^{\frac{5}{4}}} - \frac{u^{\prime \prime }}{(1+ (u^{\prime })^2)^{\frac{5}{4}}} \Big |^2 \, \mathrm {{d}}x \\{}&\qquad {} + \lambda \int _0^1 \Big [ \sqrt{1+(v^{\prime })^2} - \sqrt{1+(u^{\prime })^2} - u' (1+u'^2)^{\frac{3}{4}} \bigl ( G(v') - G(u') \bigr ) \Big ] \, \mathrm {{d}}x. \\ \end{aligned} \end{aligned}$$
(26)

In order to analyze the second integral, we introduce \(f: \mathbb {R}^2 \rightarrow \mathbb {R}\),

$$\begin{aligned} f(p,q):= \sqrt{1+q^2} - \sqrt{1+p^2} - p (1+p^2)^{\frac{3}{4}} \bigl ( G(q) - G(p) \bigr ). \end{aligned}$$

A straightforward calculation shows that

$$\begin{aligned} \frac{\partial f}{\partial p}(p,q) = - \frac{1+ \frac{5}{2} p^2}{(1+p^2)^{\frac{1}{4}}} \bigl ( G(q) - G(p) \bigr ), \end{aligned}$$

so that

$$\begin{aligned} f(p,q) = f(p,q) - f(q,q) = \frac{\partial f}{\partial p}(\xi ,q)(p-q) = \frac{1+ \frac{5}{2} \xi ^2}{(1+\xi ^2)^{\frac{1}{4}}} \bigl ( G(q) - G(\xi ) \bigr )(q-p) \end{aligned}$$

for some \(\xi \) between p and q. Using the fact that G is strictly increasing, we deduce that \(f(p,q) \ge 0\) for all \((p,q) \in \mathbb {R}^2\), so that we infer from (26) that

$$\begin{aligned} E_\lambda (v) - E_\lambda (u) \ge \frac{1}{2} \int _0^1 \Big | \frac{v^{\prime \prime }(x)}{(1+ v^{\prime }(x)^2)^{\frac{5}{4}}} - \frac{u^{\prime \prime }(x)}{(1+ u^{\prime }(x)^2)^{\frac{5}{4}}} \Big |^2 \, \mathrm{{d}}x \ge 0, \end{aligned}$$
(27)

and u is a minimizer of \(E_\lambda \) in the set \(M_{\beta }\). If \(E_\lambda (v) = E_\lambda (u)\) for some \(v \in M_{\beta }\), then, we have from (27) that

$$\begin{aligned} \frac{d}{dx} G(v^{\prime })(x) = \frac{v^{\prime \prime }(x)}{(1+ v^{\prime }(x)^2)^{\frac{5}{4}}} = \frac{u^{\prime \prime }(x)}{(1+ u^{\prime }(x)^2)^{\frac{5}{4}}} = \frac{\mathrm{{d}}}{\mathrm{{d}}x} G(u^{\prime })(x), \quad x \in [0,1]. \end{aligned}$$

Since \(v^{\prime }(0)=u^{\prime }(0)\), we deduce that \(G(v^{\prime }) \equiv G(u^{\prime })\) and hence \(v^{\prime } \equiv u^{\prime }\) in [0, 1]. This implies that \(v \equiv u\) as \(v(0)=u(0)\), and the proof is complete. \(\square \)

3.2 Qualitative properties of minimizers

In the following, \(u_{\beta ,\lambda } \in M_{\beta }\) denotes the unique minimizer of \(E_{\lambda }\) found in Theorem 3.3. We prove precise bounds on the curvature depending on the relation between \(\beta \) and \(\lambda \), which will in particular imply that \(u_{\beta ,\lambda }\) is strictly concave. In order to formulate the corresponding result, we define

$$\begin{aligned} \beta _0:= \left\{ \begin{array}{cl} \sqrt{\frac{\lambda }{2-\lambda }}, &{} 0 \le \lambda <2; \\ \infty , &{} \lambda \ge 2. \end{array} \right. \end{aligned}$$
(28)

Lemma 3.4

(Concavity) Let \(\lambda \ge 0\) and \(u_{\beta ,\lambda }\) be the minimizer of \(E_{\lambda }\) in \(M_{\beta }\). Then, \(u_{\beta ,\lambda }\) is strictly concave and its curvature \(\kappa \) satisfies:

  1. (i)

    If \(0< \beta < \beta _0\), then \(- \sqrt{2 \lambda }< \kappa <0\) in [0, 1];

  2. (ii)

    If \(\beta =\beta _0\), then \(\kappa \equiv - \sqrt{2 \lambda }\) in [0, 1];

  3. (iii)

    If \(\beta > \beta _0\), then \(\kappa < - \sqrt{2 \lambda }\) in [0, 1].

Proof

In each case, the proof relies on identifying the sign of \(c_2\) in (20). Observing that \(u_{\beta ,\lambda }^{\prime }(0)=-u_{\beta ,\lambda }^{\prime }(1)=\beta \) we have

$$\begin{aligned} - \frac{2 \beta }{\sqrt{1+ \beta ^2}} = \frac{u_{\beta ,\lambda }^{\prime }(1)}{\sqrt{1+ u_{\beta ,\lambda }^{\prime }(1)^2}} - \frac{u_{\beta ,\lambda }^{\prime }(0)}{\sqrt{1+ u_{\beta ,\lambda }^{\prime }(0)^2}} = \int _0^1 \kappa (x) \, {\textrm{d}}x = \kappa (\xi ) \end{aligned}$$

for some \(\xi \in [0,1]\), so that by (20)

$$\begin{aligned} c_2= \bigl ( \lambda - \frac{1}{2} \kappa (\xi )^2 \bigr ) \sqrt{1+ u^{\prime }(\xi )^2} = \bigl ( \lambda - \frac{2 \beta ^2}{1+ \beta ^2} \bigr ) \sqrt{1+ u^{\prime }(\xi )^2} \,. \end{aligned}$$
(29)
  1. (i)

    In this case, we have from (29) and the definition of \(\beta _0\) that \(c_2>0\) and hence (by (20)) \(\lambda > \frac{1}{2} \kappa (x)^2\) for all \(x \in [0,1]\). Let us write (9) in the form

    $$\begin{aligned} -\frac{1}{\sqrt{1+u^{\prime }(x)^2}} \frac{\mathrm{{d}}}{\mathrm{{d}}x} \Bigl ( \frac{\kappa ^{\prime }(x)}{\sqrt{1+u^{\prime }(x)^2}} \Bigr ) + c(x) \kappa (x) =0, \qquad x \in [0,1], \end{aligned}$$
    (30)

    where \(c(x)=\lambda -\frac{1}{2} \kappa (x)^2 >0\) in [0, 1]. Recalling that \(u_{\beta ,\lambda }^{\prime }(x) \le \beta = u_{\beta ,\lambda }^{\prime }(0)\), \(x \in [0,1]\) by (16), we infer that \(u_{\beta ,\lambda }^{\prime \prime }(0),u_{\beta ,\lambda }^{\prime \prime }(1) \le 0\). The maximum principle, applied to (30), then implies that \(\kappa \le 0\) in [0, 1]. If \(\kappa (x_0)=0\) for some \(x_0 \in (0,1)\), then, \(\kappa \equiv 0\) contradicting the fact that \(u_{\beta ,\lambda }(0)=u_{\beta ,\lambda }(1)=0\) and \(\beta >0\). If \(\kappa (0)=0\), then, \(\kappa ^{\prime }(0) \le 0\) contradicting (21). By symmetry, this excludes also the case \(\kappa (1)=0\). Hence, \(\kappa <0\) in [0, 1] and the inequality \(\kappa > - \sqrt{2 \lambda }\) then immediately follows from the estimate \(\lambda > \frac{1}{2} \kappa ^2\).

  2. (ii)

    If \(\beta =\beta _0\), then, we deduce from (29) that \(c_2=0\) and hence \(\kappa \equiv -\sqrt{2 \lambda }\) using again that \(\kappa (0) \le 0\) by (16).

  3. (iii)

    In this case, we infer from (29) that \(c_2<0\) and hence again by (20) that \(\lambda - \frac{1}{2} \kappa (x)^2<0\) for all \(x \in [0,1]\). Thus, \(| \kappa (x) | > \sqrt{2 \lambda }\), \(x \in [0,1]\) which yields that \(\kappa (x) < - \sqrt{2 \lambda }\) for all \(x \in [0,1]\) since \(\kappa (0) \le 0\).

\(\square \)

Proof of Theorem 1.1

All assertions of the theorem except the concavity follow from combining Lemma 3.2 and Theorem 3.3. The strict concavity of the solution is established in Lemma 3.4. \(\square \)

Remark 3.5

By integrating (20) over (0, 1) and recalling the value of \(c_2\) in each of the three cases, we deduce that

$$\begin{aligned} \lambda \int _0^1 \sqrt{1+u_{\beta ,\lambda }^{\prime }(x)^2} {\textrm{d}}x - E_0(u) =c_2 \quad \left\{ \begin{array}{lc}>0, &{}{} 0< \beta< \beta _0, \\ =0, &{}{} \beta = \beta _0, \\ <0, &{}{} \beta > \beta _0. \end{array} \right. \end{aligned}$$

Thus, we obtain a relation between the two parts contributing to the energy \(E_\lambda \). In particular, we have equipartition of energy if the graph of \(u_{\beta ,\lambda }\) is an arc of a circle.

We now prove our assertions about the ordering of the minimizers with respect to the parameters \(\beta \) and \(\lambda \).

Proof of Theorem 1.2 a)

Let \(u_i:=u_{\beta _i,\lambda }\), \(i=1,2\) as well as \(v_i(x):= G(u_i^{\prime }(x))\) with G as in (17). We claim that

$$\begin{aligned} v_1(x) < v_2(x) \quad \text{ for } \text{ all } x \in [0,\frac{1}{2}). \end{aligned}$$
(31)

Let us first consider the case \(\lambda =0\). Corollary 2.3 implies that \(v_i^{\prime \prime }(x)=0\) in [0, 1] and hence \(v_i(x)=G(\beta _i)(1-2x)\), so that (31) immediately follows from the strict monotonicity of G.

Next, let \(\lambda >0\). Since \(v_1(\frac{1}{2})=v_2(\frac{1}{2})=0\), we have that \(\max _{x \in [0,\frac{1}{2}]}(v_1-v_2)(x) \ge 0\). Assume that there exists \(x_0 \in [0,\frac{1}{2})\) such that \((v_1-v_2)(x_0)=\max _{x \in [0,\frac{1}{2}]}(v_1-v_2)(x)\). Since \(v_1(0)-v_2(0)=G(\beta _1)-G(\beta _2)<0\), we must have \(x_0 \in (0,\frac{1}{2})\). Therefore,

$$\begin{aligned} \begin{aligned}{}&{} 0<u_2^{\prime }(x_0)=G^{-1}(v_2(x_0)) \le G^{-1}(v_1(x_0)) = u_1^{\prime }(x_0), \\ {}&{} \text{ and } \;v_1^{\prime }(x_0)=v_2^{\prime }(x_0), \; v_1^{\prime \prime }(x_0) \le v_2^{\prime \prime }(x_0). \end{aligned} \end{aligned}$$

Corollary 2.3 implies

$$\begin{aligned} v_1^{\prime \prime }(x_0) \le v_2^{\prime \prime }(x_0) = \lambda u_2^{\prime }(x_0) (1+ u_2^{\prime }(x_0)^2)^{\frac{3}{4}} \le \lambda u_1^{\prime }(x_0) (1+ u_1^{\prime }(x_0)^2)^{\frac{3}{4}} = v_1^{\prime \prime }(x_0), \end{aligned}$$

and hence \(u_1^{\prime }(x_0)=u_2^{\prime }(x_0)\) since \(\lambda >0\). Furthermore,

$$\begin{aligned} \frac{u_1^{\prime \prime }(x_0)}{(1+ u_1^{\prime }(x_0)^2)^{\frac{5}{4}}} = v_1^{\prime }(x_0)= v_2^{\prime }(x_0)= \frac{u_2^{\prime \prime }(x_0)}{(1+ u_2^{\prime }(x_0)^2)^{\frac{5}{4}}}= \frac{u_2^{\prime \prime }(x_0)}{(1+ u_1^{\prime }(x_0)^2)^{\frac{5}{4}}} \end{aligned}$$

so that \(u_1^{\prime \prime }(x_0) = u_2^{\prime \prime }(x_0)\). By considering \(u_1^{\prime },u_2^{\prime }\) as solutions of the second order ODE (derived from (22))

$$\begin{aligned} w^{\prime \prime } = \frac{5}{2} \frac{w (w^{\prime })^2}{1+w^2} + \lambda w (1+w^2)^2 \end{aligned}$$
(32)

we obtain that \(u_1^{\prime } \equiv u_2^{\prime }\) on [0, 1], a contradiction. Therefore, \(v_1(x)-v_2(x)<0\) for all \(x \in [0,\frac{1}{2})\), i.e., (31). Since G is strictly increasing, we infer that \(u_1^{\prime }(x)<u_2^{\prime }(x)\), \(x \in [0,\frac{1}{2})\). The relation \(u_1(x)< u_2(x), x \in (0,1)\) now follows by integration and taking into account the symmetry of \(u_i\). \(\square \)

Proof of Theorem 1.2 b)

The strategy is similar to a). Let \(u_i:=u_{\beta ,\lambda _i}\), \(i=1,2\) and \(v_i(x):= G(u_i^{\prime }(x))\) with G as in (17). Clearly, \(v_i(x)>0\), \(x \in [0,\frac{1}{2})\), \( v_1(0)=v_2(0)\) and \(v_1(\frac{1}{2})=v_2(\frac{1}{2})\). Assume that there exists \(x_0 \in (0,\frac{1}{2})\) such that \((v_2-v_1)(x_0)=\max _{x \in [0,\frac{1}{2}]}(v_2-v_1)(x) \ge 0\). Then \(0<u_1^{\prime }(x_0)=G^{-1}(v_1(x_0)) \le G^{-1}(v_2(x_0)) = u_2^{\prime }(x_0)\) and \(v_2^{\prime \prime }(x_0) \le v_1^{\prime \prime }(x_0)\). Corollary 2.3 implies

$$\begin{aligned} v_2^{\prime \prime }(x_0) = \lambda _2 u_2^{\prime }(x_0) (1+ u_2^{\prime }(x_0)^2)^{\frac{3}{4}} > \lambda _1 u_1^{\prime }(x_0) (1+ u_1^{\prime }(x_0)^2)^{\frac{3}{4}} = v_1^{\prime \prime }(x_0), \end{aligned}$$

a contradiction. Hence, \(v_2(x)<v_1(x), x \in (0,\frac{1}{2})\) which implies that \(u_2^{\prime }(x)<u_1^{\prime }(x)\), \(x \in (0,\frac{1}{2})\). The relation \(u_2(x)< u_1(x)\), \(x \in (0,1)\) now follows as in a). \(\square \)

4 Existence of minimizers for the inextensible problem

We consider now the minimization problem with prescribed length \(\ell \) and \(\beta >0\). Due to the boundary condition, we see that necessarily \(\ell >1\). Recall that for \(\beta >0\) and \(\lambda \ge 0\), \(u_{\beta ,\lambda }\) denotes the unique minimizer of \(E_{\lambda }\) in \(M_{\beta }\) found in Theorem 1.1.

Our approach is based on the observation that \(u_{\beta ,\lambda }\) is the minimizer of the inextensible problem with length \(\ell \) provided that \(\lambda \) solves the equation \(L(\lambda )=\ell \), with the function L defined in (11). The idea of using the extensible problem in order to study the inextensible problem has previously been used by Miura in [16].

We first study the monotonicity of \(L(\lambda )\) and of the energy.

Lemma 4.1

Let \(\beta >0\) be fixed and \(0\le \lambda _1<\lambda _2\). Then,

  1. (i)

    \(L(\lambda _1)> L(\lambda _2)\);

  2. (ii)

    \(E_0(u_{\beta ,\lambda _1}) < E_0(u_{\beta ,\lambda _2})\);

  3. (iii)

    \(E_{\lambda _1}(u_{\beta ,\lambda _1}) < E_{\lambda _2}(u_{\beta ,\lambda _2})\).

Proof

We define \(u_i:=u_{\beta ,\lambda _i} \in M_\beta \), \(i=1,2\).

  1. (i)

    The claim follows directly since \(u_i\), \(i=1,2\), are symmetric with respect to \(\frac{1}{2}\) and \(u_1^{\prime }(x)> u_2^{\prime }(x)>0\) for \(x \in (0,\frac{1}{2})\) by Theorem 1.2 b).

  2. (ii)

    We have by (i) for \(0<\lambda _1 < \lambda _2\) that

    $$\begin{aligned} \begin{aligned} E_0(u_1)=&{} E_{\lambda _1}(u_1) - \lambda _1 L(\lambda _1) \le E_{\lambda _1}(u_2) - \lambda _1 L(\lambda _1) \\{} =&{} E_0(u_2) + \lambda _1 \bigl ( L(\lambda _2) - L(\lambda _1) \bigr ) < E_0(u_2). \end{aligned} \end{aligned}$$

    If \(\lambda _1=0\), let \(\lambda _3=\frac{1}{2} \lambda _2\) and \(u_3= u_{\lambda _3}\). Then, by minimality of \(u_1\), \(E_0(u_1) \le E_0(u_3)\) whereas by the previous argument, \(E_0(u_3) < E_0(u_2)\). Combining the two inequalities the statement follows also in this case.

  3. (iii)

    Clearly, \(E_{\lambda _1}(u_1) \le E_{\lambda _1}(u_2) = E_{\lambda _2}(u_2) + (\lambda _1 - \lambda _2) L(\lambda _2) < E_{\lambda _2}(u_2)\).

\(\square \)

Lemma 4.2

(Continuous dependence on \(\lambda \)) For \(\beta >0\), the function \(S: [0,\infty ) \mapsto C^1([0,1])\), \(\lambda \mapsto u_{\beta ,\lambda }\) is continuous. In particular, the function \(\lambda \mapsto L(\lambda )\) is continuous.

Proof

Consider \(\lambda _0 \in [0,\infty )\) and a sequence \((\lambda _n)_{n \in \mathbb {N}} \subset [0,\infty )\) such that \(\lambda _ n \rightarrow \lambda _0\). Then, the sequence of minimizers \((u_{\beta ,\lambda _n})_{n \in \mathbb {N}}\) is by (16) uniformly bounded in \(C^1\). As in the proof of Lemma 3.2 considering the function \(\bar{u} \in M_{\beta }\) given by \(\bar{u}(x)=\beta x (1-x)\), we see that the sequence is also uniformly bounded in \(H^2\). Hence, there exists a subsequence \((u_{\beta ,\lambda _{n_j}})_{j \in \mathbb {N}}\) and \(u_* \in H^2\) such that

$$\begin{aligned} u_{\beta ,\lambda _{n_j}} \rightharpoonup u_* \text{ in } H^2 \text{ and } u_{\beta ,\lambda _{n_j}} \rightarrow u_* \text{ in } C^1 . \end{aligned}$$
(33)

We show that \(u_*=u_{\lambda _0}\). For any \(v \in M_{\beta }\), we have

$$\begin{aligned} E_{\lambda _{n_j}}(u_{\beta ,\lambda _{n_j}}) \le E_{\lambda _{n_j}}(v) \,. \end{aligned}$$
(34)

By (33) it follows that \(\lambda _{n_j}L(\lambda _{n_j}) \rightarrow \lambda _{0}\int _0^1 \sqrt{1+(u_{*}^{\prime })^2} \, \mathrm{{d}}x\) as \(j \rightarrow \infty \). Arguing as in (23) taking the limit \(j \rightarrow \infty \) in (34), it follows

$$\begin{aligned} E_{\lambda _0} (u_*) = E_0(u_*)+ \lambda _0 \int _0^1 \sqrt{1+(u_{*}^{\prime })^2} \, dx \le E_{\lambda _0}(v), \quad \text{ for } \text{ any } v \in M_{\beta }, \end{aligned}$$

from which we see that \(u_*\) minimizes \(E_{\lambda _0}\) in \(M_{\beta }\) and hence \(u_*=u_{\beta ,\lambda _0}\) as the minimum is unique. Thus, \(u_{\beta ,\lambda _{n_j}} \rightarrow u_{\beta ,\lambda _0}\) in \(C^1\). A standard argument yields \(u_{\beta ,\lambda _{n}} \rightarrow u_{\beta ,\lambda _0}\) in \(C^1\) and hence the continuity of S. The continuity of \(L(\lambda )\) is then immediate. \(\square \)

Remark 4.3

The Noether identity (20) and the Euler-Lagrange equations allow even to prove that the function \(S: [0,\infty ) \mapsto C^k([0,1])\), \(\lambda \mapsto u_{\beta ,\lambda }\) is continuous for all \(k \in \mathbb {N}\).

We need an auxiliary result describing the behavior of the energy for large \(\lambda \).

Lemma 4.4

Consider \(\beta >0\) and fixed. There exists a constant C which is independent of \(\lambda \) such that for all \(\lambda >4 \beta ^2\)

$$\begin{aligned} \frac{1}{2(1+\beta ^2)^{\frac{5}{2}}}\int _0^1 u_{\beta ,\lambda }^{\prime \prime }(x)^2 \mathrm{{d}}x + \lambda \, (L(\lambda )-1)\le C \sqrt{\lambda }. \end{aligned}$$
(35)

Proof

Let \(\varepsilon >0\) with \(\beta \varepsilon < \frac{1}{2}\) and define

$$\begin{aligned} v_\varepsilon (x):= \left\{ \begin{array}{cl} - \varepsilon + \sqrt{(1+\beta ^2) \varepsilon ^2 - (x-\beta \varepsilon )^2}, &{} 0 \le x \le \beta \varepsilon ; \\ \varepsilon (\sqrt{1+\beta ^2} -1), &{} \beta \varepsilon < x \le \frac{1}{2} \end{array} \right. \end{aligned}$$

and \(v_\varepsilon (x)=v_\varepsilon (1-x)\) for \(\frac{1}{2}< x \le 1\). It is not difficult to verify that \(v_\varepsilon \in M_\beta \) so that

$$\begin{aligned} E_{\lambda } (u_{\beta ,\lambda })&= \frac{1}{2} \int \frac{(u_{\beta ,\lambda }^{\prime \prime })^2}{(1+(u_{\beta ,\lambda }^{\prime })^2)^{\frac{5}{2}}} \, \mathrm{{d}}x + \lambda \int _0^1 \sqrt{1+(u_{\beta ,\lambda }^{\prime })^2} \, \mathrm{{d}}x \\&\le E_{\lambda } (v_\varepsilon ) = \frac{1}{2} \frac{\pi }{\sqrt{1+ \beta ^2}} \frac{1}{\varepsilon } + \lambda \bigl ( \pi \sqrt{1+ \beta ^2} \, \varepsilon + (1 - 2 \beta \varepsilon ) \bigr ). \end{aligned}$$

After rearranging and choosing \(\varepsilon = \lambda ^{-\frac{1}{2}}\), we infer that

$$\begin{aligned} \begin{aligned} \frac{1}{2} \int _0^1 \frac{ u_{\beta ,\lambda }^{\prime \prime }(x)^2}{(1+u_{\beta ,\lambda }^{\prime }(x)^2)^{\frac{5}{2}}} \, {\textrm{d}} x + \lambda \, \int _0^1 \bigl ( \sqrt{1+ u_{\beta ,\lambda }^{\prime }(x)^2} -1 \bigr ) {\textrm{d}} x \le C \sqrt{\lambda } \end{aligned}\end{aligned}$$
(36)

and the result follows from the fact that \(\max _{x \in [0,1]} | u_{\beta ,\lambda }^{\prime }(x) | = \beta \) independently of \(\lambda \). \(\square \)

Proof of Theorem 1.3

Dividing by \(\lambda \) in (35) we see that \(\lim _{\lambda \rightarrow \infty } L(\lambda )=1\). In order to calculate L(0), we apply [6, Lemma 4] which gives \(u_{\beta ,0}^{\prime }(x) = G^{-1}(c/2-cx)\), with \(c=2\,G(\beta )\), see also (19).

Using the substitution \(\displaystyle \tau =G^{-1}(c/2-cx)\) we obtain

$$\begin{aligned} L(0)&= \int _0^1 \sqrt{1+ G^{-1}\left( \frac{c}{2}-cx\right) ^2} \, {\textrm{d}} x = \frac{1}{c} \int _{-G^{-1}\left( \frac{c}{2}\right) }^{G^{-1}\left( \frac{c}{2}\right) } (1+\tau ^2)^{-3/4} \, {\textrm{d}} \tau \nonumber \\ {}&= \frac{1}{2 G(\beta )} \int _{-\beta }^{\beta } (1+ \tau ^2)^{-3/4} \, {\textrm{d}} \tau = \frac{\int _{-\beta }^{\beta } (1+\tau ^2)^{-3/4} {\textrm{d}} \tau }{\int _{-\beta }^{\beta } (1+\tau ^2)^{-5/4} d \tau } = L_\beta . \end{aligned}$$
(37)

By the strict monotonicity of \(\lambda \mapsto L(\lambda )\) (Lemma 4.1) and its continuity (Lemma 4.2), the intermediate value theorem implies that for every \(\ell \in (1, L_{\beta }]\) there exists a unique \(\lambda =\lambda _{\beta ,\ell }\) such that \(L(\lambda _{\beta ,\ell })=\ell \). The unique minimizer \(u_{\lambda _{\beta ,\ell }}\) of \(E_{\lambda _{\beta ,\ell }}\) in \(M_{\beta }\) is then the unique minimizer of \(E_0\) under the constraint of fixed length equal to \(\ell \). By Theorem 1.1, this minimizer is \(C^{\infty }\), symmetric, strictly concave and satisfies (9), (10) with \(\lambda =\lambda _{\beta ,\ell }\ge 0\). \(\square \)

5 Asymptotic behavior

5.1 Analysis of the limit \(\beta \rightarrow \infty \) and \(\lambda \searrow 0\)

We study the limit behavior of the minimizers \(u_{\beta ,\lambda }\) for \(\beta \rightarrow \infty \) and \(\lambda \searrow 0\). Let us introduce \(U_0:[0,1] \rightarrow \mathbb {R}, U_0(x):=\lim _{\beta \rightarrow \infty } u_{\beta ,0}(x)\), with \(u_{\beta ,0}\) as in (19). As this limit corresponds to taking the limit \(c \nearrow c_0\) it is not difficult to check that

$$\begin{aligned} U_0(x)= \frac{2}{c_0 \root 4 \of {1+(G^{-1}(c_0/2-c_0x))^2}}. \end{aligned}$$
(38)

Note that \(U_0\) is smooth in (0, 1), continuous in [0, 1] and symmetric with respect to \(x=\frac{1}{2}\) with \(U_0(0)=U_0(1)=0\). Furthermore, the graph of \(U_0\) has vertical tangent vectors at \(x=0,1\).

Theorem 5.1

For each \(\beta > 0, \, \lambda \ge 0\) we have that \(u_{\beta ,\lambda }(x) \le U_0(x)\) for all \(x \in [0,1]\). Furthermore, \(u_{\beta ,\lambda }\) converges uniformly on [0, 1] to \(U_0\) as \((\beta ,\lambda ) \rightarrow (+\infty ,0)\).

Proof

Using Theorem 1.2 b), (19) and the definition of \(U_0\) we obtain

$$\begin{aligned} u_{\beta ,\lambda }(x) \le u_{\beta ,0}(x) \le U_0(x), \quad x \in [0,1]. \end{aligned}$$

In order to prove the uniform convergence of \(u_{\beta ,\lambda }\), we first consider the sequence \({\tilde{u}}_k:=u_{k,\frac{1}{k}}\). Clearly, \({\tilde{u}}_k \le {\tilde{u}}_{k+1} \le U_0\) by Theorem 1.2 and what we have already shown, so that \({\tilde{u}}(x):= \lim _{k \rightarrow \infty } {\tilde{u}}_k(x)\) exists for every \(x \in [0,1]\) with \({\tilde{u}} \le U_0\) in [0, 1]. On the other hand, we infer from Lemma 4.2 and Theorem 1.2 for \(x \in [0,1]\) and fixed \(\beta >0\) that

$$\begin{aligned} u_{\beta ,0}(x) = \lim _{k \rightarrow \infty } u_{\beta ,\frac{1}{k}}(x) \le \lim _{k \rightarrow \infty } u_{k,\frac{1}{k}}(x) = \lim _{k \rightarrow \infty } {\tilde{u}}_k(x)=\tilde{u}(x) \,. \end{aligned}$$

Taking the limit \(\beta \rightarrow \infty \), we deduce that \(U_0(x)\le \tilde{u}(x), x \in [0,1]\), so that \({\tilde{u}} \equiv U_0\). Since \(U_0\) is continuous, Dini’s theorem implies that \(({\tilde{u}}_k)_{k \in {\mathbb {N}}}\) converges uniformly on [0, 1] to \(U_0\). Thus, given \(\epsilon >0\), there exists \(k_0 \in {\mathbb {N}}\) such that \(\max _{x \in [0,1]} \bigl ( U_0(x) - {\tilde{u}}_{k_0}(x) \bigr ) < \epsilon \). Again by Theorem 1.2, we have for all \(\beta >k_0, 0 \le \lambda < \frac{1}{k_0}\) that \(u_{\beta ,\lambda }(x) \ge u_{k_0,\lambda }(x) \ge u_{k_0,\frac{1}{k_0}}(x)= {\tilde{u}}_{k_0}(x), x \in [0,1]\) and therefore

$$\begin{aligned} \max _{x \in [0,1]} | u_{\beta ,\lambda }(x) - U_0(x) | = \max _{x \in [0,1]} \bigl ( U_0(x) - u_{\beta ,\lambda }(x) \bigr ) \le \max _{x \in [0,1]} \bigl ( U_0(x) - {\tilde{u}}_{k_0}(x) \bigr ) < \epsilon , \end{aligned}$$

for all \(\beta >k_0,0 \le \lambda < \frac{1}{k_0}\). \(\square \)

In Fig. 1, we show plots of the solutions \(u_{\beta ,\lambda }\) for the choices \(\beta =100,\lambda =0.1\) and \(\beta =400,\lambda =0.01\), respectively. The simulations were done with a descent algorithm based on a splitting of the fourth order problem into two second order problems, see [4, Section 6] for a similar approach in the context of the obstacle problem for elastic graphs.

Fig. 1
figure 1

The minimizer \(u_{\beta ,\lambda }\) for \(\beta =100\), \(\lambda =0.1\) and for \(\beta =400\), \(\lambda =0.01\)

Full size image

Remark 5.2

The function \(L_{\beta }\) is strictly increasing in \(\beta \) and

$$\begin{aligned} L_{\infty }:=\lim _{\beta \rightarrow \infty } L_{\beta }&= \frac{\int _{0}^{\infty } (1+\tau ^2)^{-3/4} \mathrm {{d}} \tau }{\int _{0}^{\infty } (1+\tau ^2)^{-5/4} \mathrm {{d}} \tau } = \frac{\int _{0}^{1} x^{-3/4} (1-x)^{-1/2}\mathrm {{d}} x}{\int _{0}^{1} x^{-1/4} (1-x)^{-1/2} \mathrm {{d}}x} \\ {}&= \frac{\mathcal {B}(1/4,1/2)}{\mathcal {B}(3/4,1/2)} = \frac{\Gamma (1/4)\Gamma (5/4)}{(\Gamma (3/4))^2} \sim 2.18844..\, , \end{aligned}$$

with the substitution \(x=1/(1+\tau ^2)\) and \(\mathcal {B}\) the Beta function. Arguing similarly as in (37) one sees that \(L_{\infty }\) is the length of the graph of \(U_0\), see (38).

5.2 Analysis of the singular limit \(\lambda \rightarrow \infty \)

By considering \(\lambda \rightarrow \infty \), we see the elastic energy as a singular perturbation of the length functional. The energy then forces the minimizers to approach a straight line while the boundary conditions induce a non-trivial boundary layer. The shape of this layer turns out to be a borderline elastica, as in [16] where general parameterized curves are considered. Let us also mention that [15] considers a corresponding limit in a graph setting for a functional that contains an additional adhesion term.

In what follows, we fix \(\beta >0\). In order to study the dependence of \(u_{\beta ,\lambda }\) on the parameters \(\beta \) and \(\lambda \), we write \(c_2= c_2(\beta ,\lambda )\), where \(c_2\) is given by (20).

Lemma 5.3

We have \(u_{\beta ,\lambda } \rightarrow 0\) uniformly in [0, 1] and \(u_{\beta ,\lambda } \rightarrow 0\) in \(H^2(a,1-a)\) as \(\lambda \rightarrow \infty \) for every \(0<a<\frac{1}{2}\).

Proof

Let \((\lambda _k)_{k \in \mathbb {N}}\) be an arbitrary sequence such that \(\lambda _k \rightarrow \infty , k \rightarrow \infty \). Abbreviating \(u_k:=u_{\beta ,\lambda _k}\), we find in view of \(\max _{x \in [0,1]} | u_k^{\prime }(x)| =\beta \) and (35) that

$$\begin{aligned} \frac{1}{1+\sqrt{1+\beta ^2}} \int _0^1 u_k^{\prime }(x)^2 \mathrm {{d}}x&\le \int _0^1 \bigl ( \sqrt{1+u_k^{\prime }(x)^2} -1 \bigr ) \mathrm {{d}} x \nonumber \\ {}&\le \frac{C}{\sqrt{\lambda _k}} \rightarrow 0, \quad k \rightarrow \infty . \end{aligned}$$
(39)

Since \(u_k(0)=0\), we deduce from (39)

$$\begin{aligned} \max _{x \in [0,1]} | u_k(x) | \le \Vert u_k^{\prime } \Vert _{L^2(0,1)} \rightarrow 0, \; k \rightarrow \infty , \end{aligned}$$

i.e., the uniform convergence of \((u_{\beta ,\lambda })_{\lambda }\) to zero for \(\lambda \rightarrow \infty \) and that \(u_{\beta , \lambda } \rightarrow 0\) in \(H^1\).

Next, let us fix \(0<a<\frac{1}{2}\). Since \(u_k\) is concave, we have \(0 \le u_k^{\prime }(x) \le u_k^{\prime }(y)\) for all \(0 \le y \le \frac{a}{2}, \frac{a}{2} \le x \le \frac{1}{2}\) and hence

$$\begin{aligned} \max _{\frac{a}{2} \le x \le \frac{1}{2}} u_k^{\prime }(x) \le u_k^{\prime }\left( \frac{a}{2}\right) \le \frac{2}{a} \int _0^{\frac{a}{2}} u_k^{\prime }(y) \mathrm{{d}}y \rightarrow 0, \; k \rightarrow 0 \end{aligned}$$

in view of (39), so that the symmetry of \(u_k\) yields

$$\begin{aligned} \max _{x \in [\frac{a}{2},1-\frac{a}{2}]} | u_k^{\prime }(x) | \rightarrow 0, \quad k \rightarrow \infty . \end{aligned}$$
(40)

Next, recall that \(u_k\) satisfies with \(\kappa _k(x)=\frac{u_k^{\prime \prime }(x)}{(1+ u_k^{\prime }(x)^2)^{\frac{3}{2}}}\)

$$\begin{aligned} \frac{\kappa _k^{\prime }(x)}{1+u_k^{\prime }(x)^2} + \frac{1}{2} \frac{u_k^{\prime }(x) \kappa _k(x)^2}{\sqrt{1+u_k^{\prime }(x)^2}} - \lambda _k \frac{u_k^{\prime }(x)}{\sqrt{1+u_k^{\prime }(x)^2}} = 0, \quad x \in [0,1]. \end{aligned}$$
(41)

Let \(\varphi \in C^1([0,1])\) be a cut-off function such that \({{\text {supp}}}(\varphi ) \subset (\frac{a}{2},1-\frac{a}{2})\) and \(\varphi \equiv 1\) on \([a,1-a]\). If we multiply (41) by \(-\varphi ^2 \, u_k^{\prime }\) and integrate by parts, we obtain

$$\begin{aligned} \begin{aligned}{}&{} \int _0^1 \varphi (x)^2 \, \bigl ( 1 - \frac{5}{2} \, \frac{u_k^{\prime }(x)^2}{1+u_k^{\prime }(x)^2} \bigr ) \frac{ u_k^{\prime \prime }(x)^2}{(1+u_k^{\prime }(x)^2)^{\frac{5}{2}}} \, \mathrm {{d}}x + \lambda _k \int _0^1 \frac{ \varphi (x)^2 u_k^{\prime }(x)^2}{\sqrt{1+u_k^{\prime }(x)^2}} \, \mathrm {{d}}x \\{}&{} \quad \le 2 \int _0^1 | \varphi (x) | \, | \varphi ^{\prime }(x) | \, \frac{| u_k^{\prime }(x)| \, | u_k^{\prime \prime }(x) |}{(1+ u_k^{\prime }(x)^2)^{\frac{5}{2}}} \, \mathrm {{d}}x \\{}&{} \quad \le \frac{1}{2} \int _0^1 \varphi (x)^2 \, \frac{ u_k^{\prime \prime }(x)^2}{(1+u_k^{\prime }(x)^2)^{\frac{5}{2}}} \, \mathrm {{d}}x + 2 \, \bigl ( \max _{x \in [0,1]} | \varphi ^{\prime }(x) | \bigr )^2 \int _0^1 u_k^{\prime }(x)^2 \, \mathrm {{d}}x. \end{aligned} \end{aligned}$$

We deduce from (40) that \(\max _{x \in [\frac{a}{2},1-\frac{a}{2}]} \frac{5}{2} \, \frac{u_k^{\prime }(x)^2}{1+u_k^{\prime }(x)^2} \le \frac{1}{4}\) for \(k \ge k_0\) so that

$$\begin{aligned} \int _{a}^{1-a} u_k^{\prime \prime }(x)^2 \, \mathrm{{d}}x \le C \, \int _0^1 u_k^{\prime }(x)^2 \, \mathrm{{d}}x \rightarrow 0, \; k \rightarrow \infty , \end{aligned}$$
(42)

where we have used again (39) as well as the fact that \((u_k^{\prime })_{k \in \mathbb {N}}\) is uniformly bounded. The claim follows. \(\square \)

Corollary 5.4

We have for \(\beta >0\) that

$$\begin{aligned} \lim _{\lambda \rightarrow \infty } \frac{c_2(\beta ,\lambda )}{\lambda }=1. \end{aligned}$$
(43)

Proof

Integrating the relation (20) over [0, 1], we obtain

$$\begin{aligned} c_2(\beta ,\lambda ) = \lambda \int _0^1 \sqrt{1+u_{\beta ,\lambda }^{\prime }(x)^2} \, \mathrm {{d}} x - \frac{1}{2} \int _0^1 \frac{ u_{\beta ,\lambda }^{\prime \prime }(x)^2}{(1+u_{\beta ,\lambda }^{\prime }(x)^2)^{\frac{5}{2}}} \, \mathrm {{d}}x. \end{aligned}$$

If we divide by \(\lambda \) and rearrange, we infer that

$$\begin{aligned} \frac{c_2(\beta ,\lambda )}{\lambda }-1 = \int _0^1 \bigl ( \sqrt{1+u_{\beta ,\lambda }^{\prime }(x)^2} -1 \bigr ) \, \mathrm {{d}}x - \frac{1}{2} \frac{1}{\lambda } \int _0^1 \frac{ u_{\beta ,\lambda }^{\prime \prime }(x)^2}{(1+u_{\beta ,\lambda }^{\prime }(x)^2)^{\frac{5}{2}}} \,\mathrm {{d}} x \rightarrow 0, \end{aligned}$$

for \(\lambda \rightarrow \infty ,\) in view of (36). \(\square \)

Theorem 5.5

(Boundary layer) Let us define \(v_\lambda : [0,\frac{1}{2} \sqrt{\lambda }] \rightarrow \mathbb {R}\) by \(v_\lambda (y)=\sqrt{\lambda } \, u_{\beta ,\lambda }(\frac{y}{\sqrt{\lambda }} )\) for any fixed \(\beta >0\). Then, \(v_\lambda \rightarrow v\) in \(C^1_{\tiny \text{ loc }}([0,\infty ))\) as \(\lambda \rightarrow \infty \), where \(v:[0,\infty ) \rightarrow \mathbb {R}\) is the unique solution of the initial value problem

$$\begin{aligned} v^{\prime \prime }(y)&= - \sqrt{2} \, \bigl ( 1+v^{\prime }(y)^2 \bigr )^{\frac{3}{2}} \Bigl ( 1- \frac{1}{\sqrt{1+v^{\prime }(y)^2}} \Bigr )^{\frac{1}{2}}, \end{aligned}$$
(44)
$$\begin{aligned} v(0)&= 0, \; v^{\prime }(0)=\beta . \end{aligned}$$
(45)

Proof

Let \((\lambda _k)_{k \in \mathbb {N}}\) be an arbitrary sequence with \(\lambda _k \rightarrow \infty , k \rightarrow \infty \) and abbreviate \(v_k=v_{\lambda _k}\), \(u_k=u_{\beta ,\lambda _k}\). Let us fix \(R>0\). Since \(\max _{0 \le y \le \frac{1}{2} \sqrt{\lambda _k}} | v_k^{\prime }(y) | = \max _{0 \le x \le \frac{1}{2}} | u_k^{\prime }(x) | =\beta \), we easily see that \((v_k)_{k \ge k_R}\) is bounded in \(C^1([0,R])\). Furthermore, (36) implies that

$$\begin{aligned} \begin{aligned} \int _0^R v_k^{\prime \prime }(y)^2 \, \mathrm {{d}} y \le \frac{1}{\sqrt{\lambda _k}} \, \int _0^{\frac{1}{2}} u_k^{\prime \prime }(x)^2 \, \mathrm {{d}} x \le C, \quad k \ge k_R. \end{aligned} \end{aligned}$$

Hence, there exists a subsequence, again denoted by \((v_k)_{k \in \mathbb {N}}\), and \(v_R \in H^2(0,R)\) such that

$$\begin{aligned} v_k \rightharpoonup v_R \text{ in } H^2(0,R), \quad v_k \rightarrow v_R \text{ in } C^1([0,R]). \end{aligned}$$

Using a diagonal argument, we obtain a further subsequence and a function \(v:[0,\infty ) \rightarrow \mathbb {R}\) such that

$$\begin{aligned} v_k \rightharpoonup v \text{ in } H^2(0,R), \quad v_k \rightarrow v \text{ in } C^1([0,R]) \quad \text{ for } \text{ all } R>0. \end{aligned}$$
(46)

In order to identify v, we deduce from (20) that

$$\begin{aligned} \frac{u_k^{\prime \prime }(x)^2}{(1+u_k^{\prime }(x)^2)^3} = 2 \left( \lambda - \frac{c_2(\beta ,\lambda _k)}{\sqrt{1+u_k^{\prime }(x)^2}} \right) , \quad 0 \le x \le \frac{1}{2}. \end{aligned}$$

Since \(u_k^{\prime \prime }(x) \le 0, x \in [0,1]\), we infer that

$$\begin{aligned} \begin{aligned} u_k^{\prime \prime }(x) = - \sqrt{2} \, \bigl ( 1+u_k^{\prime }(x)^2 \bigr )^{\frac{3}{2}} \, \sqrt{\lambda _k} \left( 1- \frac{1}{\lambda _k} \frac{c_2(\beta ,\lambda _k)}{\sqrt{1+u_k^{\prime }(x)^2}} \right) ^{\frac{1}{2}}, \quad 0 \le x \le \frac{1}{2} \end{aligned} \end{aligned}$$

and hence

$$\begin{aligned} v_k^{\prime \prime }(y) = - \sqrt{2} \, \bigl ( 1+v_k^{\prime }(y)^2 \bigr )^{\frac{3}{2}} \left( 1- \frac{c_2(\beta ,\lambda _k)}{\lambda _k} \frac{1}{\sqrt{1+v_k^{\prime }(y)^2}} \right) ^{\frac{1}{2}}, \quad 0 \le y \le \frac{1}{2} \sqrt{\lambda _k}. \end{aligned}$$

Passing to the limit \(k \rightarrow \infty \) using (46) and (43), we obtain (44). Clearly, (45) is satisfied since \(v_k(0)=0, v_k^{\prime }(0)=\beta \) for each \(k \in \mathbb {N}\). \(\square \)

In Fig. 2, we show plots of the solution \(u_{\beta ,\lambda }\) for the choice \(\beta =5\) and \(\lambda =100\) together with the rescaled function \(v_\lambda \) on the interval [0, 3].

Fig. 2
figure 2

The minimizer \(u_{\beta ,\lambda }\) for \(\beta =5\), \(\lambda =100 \) (left) and \(v_{\lambda }\) (near 0) as in Theorem 5.5 (right)

Full size image

Critical points of the elastic energy \(\mathcal {E}_{\lambda }\), called elastica, have been classified in [10] with the help of formulae for the curvature. Using explicit formulae for the curves derived in [17], we are able to show that the function v describing the boundary layer is a piece of a so-called borderline elastica, similar to the findings in Miura [16]. By Müller [17, Proposition B.8] (and changing the orientation), an arclength parametrization of the borderline elastica is

$$\begin{aligned} \tilde{\gamma }(s)= \begin{pmatrix}s- 2 \tanh (s)\\ -2 \textrm{sech}\,(s)\end{pmatrix} \quad \text{ with } \quad \tilde{\gamma }'(s)= \frac{1}{\cosh (s)^2} \begin{pmatrix} \cosh (s)^2-2 \\ 2 \sinh (s) \end{pmatrix} = e^{i \theta (s)}, \end{aligned}$$
(47)

where the angle function \(\theta \) is smooth and strictly decreasing on \([\textrm{arcosh}\,(\sqrt{2}), \infty )\) with values in \((0,\pi /2]\). Hence, for \(\beta >0\), there exists a unique \(s_0 \in (\textrm{arcosh}\,(\sqrt{2}), \infty )\) such that the shifted borderline elastica

$$\begin{aligned} \gamma : \mathbb {R}\rightarrow \mathbb {R}^2, \gamma (s)= \tilde{\gamma }(s+s_0) - \tilde{\gamma }(s_0) \,, \end{aligned}$$

satisfies \(\gamma (0)=(0,0)\) and \(\gamma ^{\prime }(0)= \frac{1}{\sqrt{1+\beta ^2}} \begin{pmatrix}1\\ \beta \end{pmatrix} \). We may describe \(\gamma _{| [0,\infty )}\) as a graph via \(w:[0,\infty ) \rightarrow \mathbb {R}\), where

$$\begin{aligned} w(y):=\gamma ^2(s(y))= -2 \textrm{sech}\,(s(y)+s_0) - \tilde{\gamma }^2(s_0), \end{aligned}$$

with \(s(\cdot )\) the inverse of \(y: [0,\infty ) \rightarrow [0,\infty )\), \(y(s):= \gamma ^1(s)=s+s_0- 2 \tanh (s+s_0)- \tilde{\gamma }^1(s_0).\) The function w satisfies \(w(0)=0\) as well as

$$\begin{aligned} w^{\prime }(y)&= 2 \frac{\sinh (s(y)+s_0)}{(\cosh (s(y)+s_0))^2} s^{\prime }(y) = 2 \frac{\sinh (s(y)+s_0)}{(\cosh (s(y)+s_0))^2-2},\\ w^{\prime \prime }(y)&= - 2 \frac{(\cosh (s(y)+s_0))^5}{((\cosh (s(y)+s_0))^2-2)^3}. \end{aligned}$$

In particular, we have that \(w^{\prime }(0)=2 \frac{\sinh (s_0)}{\cosh (s_0)^2-2}=\beta \) by (47). Furthermore, elementary calculations show that

$$\begin{aligned} w^{\prime \prime }(y) = - \sqrt{2} \, \bigl ( 1+w^{\prime }(y)^2 \bigr )^{\frac{3}{2}} \Bigl ( 1- \frac{1}{\sqrt{1+w^{\prime }(y)^2}} \Bigr )^{\frac{1}{2}}, \quad y \ge 0, \end{aligned}$$

so that w solves (44), (45) and hence coincides with the function v from Theorem 5.5. Summarizing, similarly, as in [16], we have the following

Corollary 5.6

The graph of the solution v of (44), (45) is a piece of a borderline elastica.

Remark 5.7

We may use the above results in order to describe the asymptotic behavior of the minimizer of the inextensible problem for \(\ell \searrow 1\). For \(\beta >0\) and \(\ell \in (1,L_{\beta }]\) denote by \(u_{\ell }\) the unique minimizer of \(E_0\) in \(M_{\beta ,\ell }\). Then, by the proof of Theorem 1.3, there exists a unique \(\lambda _\ell \in [0,\infty )\) such that \(\ell =L(\lambda _\ell )\) and \(u_{\ell }=u_{\beta ,\lambda _\ell }\). We claim that

$$\begin{aligned} \lambda _{\ell } \rightarrow \infty \; \text{ as } \; \ell \searrow 1. \end{aligned}$$
(48)

To see this, consider a sequence \((\ell _j)_{j \in \mathbb {N}} \subset (1,L_{\beta }]\) such that \(\ell _j \rightarrow 1\) and set \(\lambda _j=\lambda _{\ell _{j}}\). If (48) were not true there would exist a bounded and converging subsequence, \(\lambda _{j_k} \rightarrow \bar{\lambda } \in [0,\infty )\) for \(k \rightarrow \infty \). By Lemma 4.2, \(\ell _{j_k}= L(\lambda _{j_k}) \rightarrow L(\bar{\lambda })>1\) as \(k \rightarrow \infty \), a contradiction.

Summarizing, the behavior of the minimizers of the inextensible problem for \(\ell \searrow 1\) corresponds to the behavior for \(\lambda \rightarrow \infty \) of the minimizers of the extensible problem. In particular, we may use Theorems 5.3 and 5.5 and Corollary 5.6 in order to describe the shape of \(u_\ell \) as \(\ell \searrow 1\).