Canonical Witt formal scheme extensions and p-torsion groups

Abstract

We study the nth arithmetic jet space of the p-torsion subgroup attached to a smooth commutative formal group scheme. We show that the nth jet space above fits in the middle of a canonical short exact sequence between a power of the formal scheme of Witt vectors of length n and the p-torsion subgroup we started with. This result generalizes a result of Buium on roots of unity.

1 Introduction

Buium in [8] introduced the theory of arithmetic jet spaces on (formal) abelian schemes over p-adic rings and showed that the jet spaces of an abelian scheme A are naturally affine fibrations over A. Since then, the theory of arithmetic jet spaces has been developed in several articles, such as [1, 6, 7, 9, 12, 15], and has found remarkable applications in diophantine geometry as in [8, 13].

In [7], Borger and Saha construct filtered isocrystals associated with delta characters of a group scheme. For an elliptic curve A defined over $\mathbb {Z}_p$, in [16], Pandit and Saha show that the filtered isocrystal is weakly admissible. In particular, if A does not admit a lift of Frobenius, then the isocrystal is canonically isomorphic to the first crystalline cohomology of A. On the other hand, if A admits a lift of Frobenius, then the isocrystal is isomorphic to the sub-isocrystal of the crystalline cohomology. The result can be viewed as a character theoretic interpretation of the crystalline cohomology.

In this paper, we study the structure of the jet space functors associated with the p-torsion subgroup $G[p^\infty ]$ of a smooth commutative formal group scheme G over a fixed p-adic basis. Here we show that for any n, the nth jet space $J^n(G[p^\infty ])$ is canonically an extension of $G[p^\infty ]$ by a power of the unipotent formal group scheme $\widehat{\mathbb {W}}_{n-1}$, where $\widehat{\mathbb {W}}_{n-1}$ is $\widehat{\mathbb {A}}^n$, the n-dimensional formal affine space endowed with the group scheme structure of the additive Witt vectors of length n. This generalizes results obtained by Buium in [11] for G the multiplicative group scheme. Based on our result, the theory of the isocrystals attached to $G[p^\infty ]$ and its connection with [7, 16] as discussed above, will be developed in a future article.

Before stating our main result in detail, let us introduce some notation. Let K be a finite extension of $\mathbb {Q}_p$ with ramification index e, uniformizer $\pi$ and ring of integers $\mathcal {O}$. We denote by k the residue field of $\mathcal {O}$ and let q be its order. Then, the identity map of $\mathcal {O}$ is a lift of q-Frobenius. Fix a $\pi$-adically complete $\pi$-torsion free $\mathcal {O}$-algebra R with a lifting of Frobenius $\phi$, i.e., an endomorphism of R such that $\phi (r)-r^q\in \pi R$ for all $r\in R$. As an example, consider the ring of restricted power series $\mathcal {O}\langle x \rangle$ with $\phi$ the $\mathcal {O}$-algebra endomorphism given by $\phi (x) = x^q$. Let $W_n$ be the functor of ramified Witt vectors of length $n+1$ (following Borger’s convention, details in § 2.2).

Let $\textbf{Nilp}_R$ be the category of R-algebras on which $\pi$ (or equivalently, p) is nilpotent. Its opposite category is a site with respect to the Zariski topology. Any adic R-algebra A with ideal of definition I containing $\pi$ gives rise to a sheaf (of sets) ${{\,\mathrm{\textrm{Spf}}\,}}(A)$ such that

$$\begin{aligned} {{\,\mathrm{\textrm{Spf}}\,}}(A)(B)=\varinjlim _n {{\,\mathrm{\textrm{Hom}}\,}}_R(A/I^n,B)\, \end{aligned}$$

for any B in $\textbf{Nilp}_R$. By a formal scheme over R, we mean a sheaf on $\textbf{Nilp}_R^{\textrm{op}}$ admitting an open cover by open subfunctors of the type ${{\,\mathrm{\textrm{Spf}}\,}}(A)$ for A as above.

Given a sheaf X on $\textbf{Nilp}_R^{\textrm{op}}$, we define its nth $\pi$-jet by

$$\begin{aligned} J^nX(C)=X(W_n(C)) \end{aligned}$$

(1.1)

for any $C\in \textbf{Nilp}_R$. If X is a formal scheme over R, the same is $J^n X$ and it holds

$$\begin{aligned} {{\,\mathrm{\textrm{Hom}}\,}}_R({{\,\mathrm{\textrm{Spf}}\,}}(C),J^nX)={{\,\mathrm{\textrm{Hom}}\,}}_R({{\,\mathrm{\textrm{Spf}}\,}}(W_n(C)),X) \end{aligned}$$

(1.2)

[2, 4, 7, 8].

For a smooth commutative formal group scheme G over R, there is a short exact sequence of formal group schemes

$$\begin{aligned} 0 \rightarrow N^nG \rightarrow J^nG \rightarrow G \rightarrow 0, \end{aligned}$$

(1.3)

which we call the canonical Witt formal scheme extension of G because of Theorem 3.10. Let $G[p^\nu ]$ be the $p^\nu$-torsion formal subgroup scheme of G, and let $G[p^\infty ]$ denote the sheaf on $\textbf{Nilp}_R^{\textrm{op}}$ such that $G[p^\infty ](C)=\varinjlim _\nu G[p^\nu ](C)$, for any $C\in \textbf{Nilp}_R$. For each $\nu$, the closed immersions $G[p^\nu ] \hookrightarrow G[p^{\nu +1}]$ induce closed immersions of $\pi$-jets $J^n(G[p^\nu ]) \hookrightarrow J^n(G[p^{\nu +1}])$ and

$$\begin{aligned} J^n(G[p^\infty ])= \varinjlim _\nu J^n(G[p^\nu ]) \end{aligned}$$

as sheaves on $\textbf{Nilp}_R^{\textrm{op}}$; see Lemma 4.1.

Consider the natural projection map $u:J^n(G[p^\infty ]) \rightarrow G[p^\infty ]$ and let $N^n(G[p^\infty ])$ denote the kernel of u. Buium in [11, Corollary 1.2] shows that if $e=1$, $p>2$ and G is the formal multiplicative group scheme over R, then the sheaf $N^n(G[p^\infty ])$ is representable by a formal R-scheme and is isomorphic to $\widehat{\mathbb {A}}^n$, the n-dimensional affine space over ${{\,\mathrm{\textrm{Spf}}\,}}(R)$.

In this paper, we will enrich Buium’s result and extend it to any smooth commutative formal R-group scheme G of relative dimension $d\ge 1$. In fact, in Theorem 3.10 we show that if $p\ge e+2$ the kernel $N^n(G[p^\infty ])$ is isomorphic to $(\widehat{\mathbb {W}}_{n-1})^d$ where $\widehat{\mathbb {W}}_{n-1}$ is $\widehat{\mathbb {A}}^n$ endowed with the group structure of Witt vectors of length n. Further, we deduce the following result (see Theorem 4.6).

Main Theorem 1

Assume $p\ge e+2$. Given a smooth commutative formal group scheme G of relative dimension d over R, for any positive integer n the natural morphism $J^nG\rightarrow G$ gives an exact sequence

$$\begin{aligned} 0 \rightarrow (\widehat{\mathbb {W}}_{n-1})^d \rightarrow J^n G[p^\infty ] \rightarrow G[p^\infty ] \rightarrow 0 \end{aligned}$$

of sheaves on $\textbf{Nilp}_R^\textrm{op}$.

We remark that by Lemma 4.1 it is $J^n(G[p^\infty ])=(J^n G)[p^\infty ]$ as sheaves on $\textbf{Nilp}_R^\textrm{op}$; hence, there is no possible ambiguity in the above statement.

1.1 Plan of the paper

In Sect. 2, we recall the definition and properties of $\pi$-jets in the setting of formal schemes, with particular attention to the adjunction between jet algebras and Witt vectors (2.13).

In Sect. 3, we focus on the notion of shifted Witt vectors $W_n^+$, introduced by [7], and show that $W_n^+$ induces an adjoint functor to $N^n$ (Theorem 3.3). This is an important result, analogous to the adjunction formula that involves $W_n$ and $J^n$ (1.2). Then, we show that given a smooth formal R-group scheme G of dimension d, we have

• (i) For all $n>0$, $N^nG \simeq J^{n-1}(N^1G)$; see Theorem 3.7.

• (ii) Assume $p\ge e+2$. Then, there is a natural isomorphism of formal group schemes $N^n G\simeq (\widehat{\mathbb {W}}_{n-1})^d\$; see Theorem 3.10.

The proof of the first fact reduces to a local computation in coordinates, which is detailed in “Appendix” section. Another important ingredient is the notion of lateral Frobenius introduced in [7]. Both results (i) and (ii) are generalized to the case of m-shifted Witt vectors in [16] by the third author.

In Sect. 4, we apply the previous results to the study of the sheaves $J^n(G[p^\infty ])$ and $N^n(G[p^\infty ])$ and deduce a statement similar to Theorem 3.10 where G is replaced by $G[p^\infty ]$, see Theorem 4.6.

In this paper, all rings are assumed to be commutative with unit and ${\textbf{Alg}_{R}}$ denotes the category of R-algebras, i.e., of ring homomorphisms $R\rightarrow B$.

2 Arithmetic jets

2.1 Conventions

Let R be the base ring fixed in the introduction. Given a formal scheme X and a fixed point $x:{{\,\mathrm{\textrm{Spf}}\,}}(R)\rightarrow X$, one can consider the fibre of x under the natural map $J^nX\rightarrow X$, which is the closed formal subscheme $N^nX=(J^nX)_x= J^nX\times _X{{\,\mathrm{\textrm{Spf}}\,}}(R)$. Note that if G is a formal group scheme, then $J^nG$ is naturally a formal group scheme too and we set $N^nG=(J^nG)_\varepsilon =\ker (J^nG\rightarrow G)$ to be the fibre along the unit section $\varepsilon$.

If X is a functor on ${\textbf{Alg}_{R}}$, we will usually denote by ${\widehat{X}}$ the restriction of X to $\textbf{Nilp}_R$. Let $R\langle x_1,...,x_n\rangle$ be the $\pi$-adic completion of the R-polynomial algebra in n variables.

Let $\widehat{\mathbb {G}}_{\textrm{a}}:={{\,\mathrm{\textrm{Spf}}\,}}(R\langle x\rangle )$ be the additive formal group scheme over R. Note that this formal group scheme should not be confused with the (x)-adic formal group $\mathbb {G}_a^{\textrm{for}}={{\,\mathrm{\textrm{Spf}}\,}}(R[[ x]])$, the formal completion of $\mathbb {G}_a$ along the zero section.

If ${\mathcal {F}}\in R[[\textbf{x},\textbf{y}]]$ is a commutative formal group law of dimension g, let ${{\mathcal {F}}} \{n\}$ be the formal group law given by $\pi ^{-n}{\mathcal {F}}(\pi ^n \textbf{x},\pi ^n \textbf{y})$, for any $n\ge 1$. Note that ${{\mathcal {F}}} \{n\}$ endows ${{\,\mathrm{\textrm{Spf}}\,}}(R\langle \textbf{x}\rangle )$ with a structure of formal group scheme over R.

If B is an R-algebra, $\rho =\rho _B:R\rightarrow B$ always denote the corresponding ring homomorphism. If the context is clear, we will write r in place of $\rho (r)\in B$.

2.2 Witt vectors over R

In the following pages, $W_n$ denotes the functor of $\pi$-typical Witt vectors of length $n+1$ on R-algebras. Hence, for any R-algebra B, the ring $W_n(B)$ is always considered with its natural R-algebra structure, which depends on $\phi$. We explain this briefly.

As functor on $\mathcal {O}$-algebras $W_n$ coincides with the so-called functor of ramified Witt vectors of length $n+1$ (see [3, 14]). Let $w:W_n(R) \rightarrow \prod _{i=0}^n R$ be the ghost map. Then for any Witt vector $\textbf{a}=(a_0,\dots , a_n)$, $w(\textbf{a})=(w_0(\textbf{a}), \dots , w_n(\textbf{a}))$ where $w_i$ are the ghost polynomials

$$\begin{aligned} w_i = x_0^{q^i}+ \pi x_1^{q^{i-1}}+ \cdots + \pi ^i x_i. \end{aligned}$$

(2.1)

Since R has a lifting of Frobenius $\phi$, by the universal property of Witt vectors there exists a ring homomorphism of $\mathcal {O}$-algebras $\exp _{\delta }$ making the following diagram commute (see [2, (2.9)])

(2.2)

Let B be an R-algebra. Then $W_n(B)$ is naturally endowed with the R-algebra structure

$$\begin{aligned} R{\mathop {\longrightarrow }\limits ^{\exp _{\delta }}} W_n(R){\mathop {\longrightarrow }\limits ^{W_n(\rho _B)}} W_n(B). \end{aligned}$$

In [7, §3.2], the authors give an equivalent construction of the functor $W_n$. The ghost map w in (2.2) is $\mathcal {O}$-linear, but not R-linear in general, if the ring $\prod _{i=0}^{n} R$ is endowed with the direct product R-module structure. It is then preferable to change the R-module structure on the product ring so that w becomes R-linear. Let ${}^{\phi ^n}\!B$ denote the ring B with the R-algebra structure induced by $\rho _B\circ \phi ^n:R\rightarrow B$, and let

$$\begin{aligned} {\prod }_\phi ^n (B):=\prod _{i=0}^n ({}^{\phi ^i}\!B) \end{aligned}$$

(2.3)

be the direct product algebra. Its underlying ring is $\prod _{i} B$ and there is a commutative diagram of R-algebras

(2.4)

Then, Frobenius and Verschiebung maps can be described in terms of ghost components as in the case of ramified Witt vectors, with caution when considering the R-algebra structure. As for example, the Frobenius ring homomorphism $F:W_n(B)\rightarrow W_{n-1}(B)$ described in terms of ghost components as the left shift is $\phi$-semilinear. We prefer then to write it as the homomorphism of R-algebras

$$\begin{aligned} F:W_n(B)\rightarrow W_{n-1}({}^\phi \!B) \end{aligned}$$

(2.5)

corresponding to the homomorphism of R-algebras

$$\begin{aligned} F_w:{\prod }_\phi ^n\! (B)\rightarrow {\prod }_\phi ^{n{\text {--}}1}\! ({}^\phi \!B), \quad (b_0,\dots , b_n)\mapsto (b_1,\dots ,b_n). \end{aligned}$$

(2.6)

Similarly, the Verschiebung map $V:W_n(B)\rightarrow W_{n+1}(B)$ is described on ghost components as the right shift multiplied by $\pi$. Clearly it is $\mathcal {O}$-linear but not R-linear in general. We prefer then to write it as the homomorphism of R-modules

$$\begin{aligned} V:W_n({}^\phi \!B)\rightarrow W_{n+1}(B) \end{aligned}$$

(2.7)

corresponding to the homomorphism of R-modules

$$\begin{aligned} V_w:{\prod }_\phi ^n\! ({}^\phi \!B)\rightarrow {\prod }_\phi ^{n{\text {+}}1}\! (B), \quad (b_0,\dots , b_n)\mapsto (0,\pi b_0,\dots ,\pi b_n). \end{aligned}$$

(2.8)

Then, FV is multiplication by $\pi$ on $W_n({}^\phi \!B)$.

Since $\phi$ might not be invertible, one cannot write B in place of ${}^\phi \!B$ in (2.5) and (2.7). However, since $\phi$ is the identity on $\mathcal {O}$, the $\mathcal {O}$-module structure on B and ${}^\phi \!B$ are the same.

Remark 2.1

If B is a $\pi$-adic R-algebra (by this we mean $\pi$-adically complete and separated), then the same is $W_n(B)$ for any n. The proof works as in [18, Proposition 3].

2.3 Shifted Witt vectors

We recall the construction of 0-shifted Witt vectors as introduced in [7, 16]. Here we simply refer to them as shifted Witt vectors. The general theory of m-shifted Witt vectors is developed in [16].

Let B be an R-algebra and set-theoretically define

$$\begin{aligned} W^+_n(B):=R \times _B W_n(B) \simeq R \times W_{n-1}(B). \end{aligned}$$

(2.9)

Also define the product ring

$$\begin{aligned} {\prod }^+_n(B):= R \times \prod _{i=1}^n ({}^{\phi ^i}B)= R\times {\prod }_{\phi }^{n-1}({}^{\phi }\!B), \end{aligned}$$

where ${\prod }_\phi ^n(B)$ was introduced in (2.3). Note that there is an isomorphism of R-algebras

$$\begin{aligned} {\prod }^+_nB:= R\times {\prod }_{\phi }^{n-1}({}^{\phi }\!B) \simeq R\times _B {\prod }_{\phi }^{n}(B) \end{aligned}$$

mapping $(r,b_1,\dots ,b_n)$ to the element $\left( r,(\rho (r),b_1,\dots ,b_n)\right)$.

Define the apriori set-theoretic map $w^+:W^+_n(B) \rightarrow {\prod }^+_n(B)$ given by $w^+(r,b_1,\dots , b_n) = (w_0,\dots , w_n)$ where

$$\begin{aligned} w_i = r^{q^i}+\pi b_1^{q^{i-1}} + \dots + \pi ^i b_i, \end{aligned}$$

for all $i=0,\dots , n$. Then, note that $W^+_n(B)$ naturally is endowed with the Witt ring structure of addition and multiplication making $w^+$ a ring homomorphism. Hence, we have the following commutative diagram

(2.10)

where $\textrm{pr}_0$ is the projection onto the 0th component. The R-algebra $W^+_n(B)$ was denoted by ${\tilde{W}}_n(B)$ in [7, §4] and by $W_{0n}(B)$ in [16].

Since the lower horizontal arrows in (2.10) are homomorphisms of R-algebras, the same are the upper horizontal arrows. Hence, the left-hand square in (2.10) is a diagram of R-algebras and, up to the above identifications, it can be illustrated as

(2.11)

where we have written r in place of $\rho (r)$ in B and $w_i$ are the ghost polynomials in (2.1).

2.4 Prolongation sequences

For any formal schemes Y and Z over ${{\,\mathrm{\textrm{Spf}}\,}}(R)$, we say that $(u,\delta ):Z \rightarrow Y$ is a prolongation if $u:Z \rightarrow Y$ is a morphism of formal schemes over ${{\,\mathrm{\textrm{Spf}}\,}}(R)$ and $\delta :\mathcal {O}_Y \rightarrow u_* \mathcal {O}_Z$ is a $\pi$-derivation on the sheaves (cf. Appendix A). Then, a sequence of formal schemes $T^*=\{T^n\}_{n=0}^\infty$ is a prolongation sequence if for each n, $(u_n,\delta _n):T^{n+1} \rightarrow T^n$ is a prolongation of formal group schemes over ${{\,\mathrm{\textrm{Spf}}\,}}(R)$ satisfying $u_{n-1}^* \circ \delta _n = \delta _{n-1} \circ u_n^*$ and making the following diagram commute

A morphism of prolongation sequences $T^*\rightarrow P^*$ is a system of morphisms of formal schemes $f_n:T^n\rightarrow P^n$ that satisfy the expected commutations: $f_n \circ u_{n}= u_{n}\circ f_{n+1}$ and $f_n \circ \delta _{n}= \delta _{n}\circ f_{n+1}$. For each n, let $S^n = {{\,\mathrm{\textrm{Spf}}\,}}(R)$. Then, the fixed $\pi$-derivation $\delta$ on R makes $S^*$ into a prolongation sequence. Let $\mathcal {C}_{S^*}$ denote the category of prolongation sequences defined over $S^*$.

2.5 Jet spaces

Given a formal scheme X over $S^0={{\,\mathrm{\textrm{Spf}}\,}}(R)$, Buium constructs the canonical prolongation sequence $J^*X= \{J^nX \}_{n=0}^\infty$ where $J^0X =X$ and by [9, Proposition 1.1], $J^*X$ satisfies the following universal property: for any $T^*$ in $\mathcal {C}_{S^*}$ it is

$$\begin{aligned} {{\,\mathrm{\textrm{Hom}}\,}}_{S^0} (T^0, X) = {{\,\mathrm{\textrm{Hom}}\,}}_{\mathcal {C}_{S^*}}(T^*,J^*X)\ . \end{aligned}$$

(2.12)

Moreover, by [2, 5] we have the following functorial description:

$$\begin{aligned} J^nX(C) = X(W_n(C)) \end{aligned}$$

for any $C\in \textbf{Nilp}_R$. In particular in the affine case with $X={{\,\mathrm{\textrm{Spf}}\,}}(A)$ and $J^nX={{\,\mathrm{\textrm{Spf}}\,}}(J_nA)$, we have a natural adjunction

$$\begin{aligned} \Theta :{{\,\mathrm{\textrm{Hom}}\,}}_R(J_nA, C) {\mathop {\longrightarrow }\limits ^{\sim }} {{\,\mathrm{\textrm{Hom}}\,}}_R(A,W_n(C)) \end{aligned}$$

(2.13)

such that $w_0\circ \Theta (g)=g\circ \iota$ with $\iota :A\rightarrow J_nA$ the natural morphism.

Here we make the above adjunction explicit when $X = {{\,\mathrm{\textrm{Spf}}\,}}(R\langle x\rangle )$ is the formal affine line over ${{\,\mathrm{\textrm{Spf}}\,}}(R)$. Let $A = R\langle x \rangle$. Then, $J^nX = {{\,\mathrm{\textrm{Spf}}\,}}(J_nA)$ and

$$\begin{aligned} J_nA = R\langle x, x', \dots x^{(n)}\rangle = R\langle \textsf{p}_0,\dots \textsf{p}_n \rangle \end{aligned}$$

(2.14)

where $x,x',\dots , x^{(n)}$ are the Buium–Joyal coordinates and $\textsf{p}_0,\dots \textsf{p}_n$ are the Witt coordinates, and they satisfy $\textsf{p}_0 =x$, $\textsf{p}_1 = x'$, while the general relation between the above two coordinate systems can be found in [2, Proposition 2.10].

If $g \in {{\,\mathrm{\textrm{Hom}}\,}}_R(J_nA,C)$, then $\Theta (g) \in {{\,\mathrm{\textrm{Hom}}\,}}_R(A, W_n(C))$ is determined by

$$\begin{aligned} \Theta (g)(x) = (g(\textsf{p}_0),\dots , g(\textsf{p}_n)). \end{aligned}$$

Note that when $G = \widehat{\mathbb {G}}_{\textrm{a}}$ we have the following isomorphism of formal group schemes

$$\begin{aligned} J^n \widehat{\mathbb {G}}_{\textrm{a}}=\widehat{\mathbb {W}}_n. \end{aligned}$$

(2.15)

where $\widehat{\mathbb {W}}_n$ is $\widehat{\mathbb {A}}^{n+1}$ endowed with the additive group structure of Witt vectors of length $n+1$.

3 The Kernel as a $\pi$-jet space

For any sheaf of groups G on $\textbf{Nilp}_R^{\textrm{op}}$, one defines

$$\begin{aligned} N^nG:=\ker (J^nG{\mathop {\longrightarrow }\limits ^{u}} G) \end{aligned}$$

where u is the natural morphism. Scope of this section is to take a closer look at the kernel $N^nG$ in the case G is representable by a smooth formal scheme. Since the kernel is the fibre at the unit section, we will first consider more general fibres.

Let X be a smooth formal scheme over R with a marked point a and let $u:U\rightarrow \mathbb {A}={{\,\mathrm{\textrm{Spf}}\,}}(R\langle \textbf{x}\rangle )$ be an étale chart around a, where $\textbf{x}$ denotes here a finite family of indeterminates. Hence, U is an open affine formal subscheme of X, u is étale, a factors through u and $u\circ a$ is the zero section 0 of the affine space $\mathbb {A}$. By [10, Proposition 3.13 & Corollary 3.16] (see also [2, Proposition 3.12]), we have $J^nU \simeq J^n\mathbb {A}\times _\mathbb {A}U$ for all n and hence

$$\begin{aligned} N^nX= J^nX\times _{X,a}{{\,\mathrm{\textrm{Spf}}\,}}(R)=J^nU\times _{U,a}{{\,\mathrm{\textrm{Spf}}\,}}(R)=J^n\mathbb {A}\times _{\mathbb {A},0}{{\,\mathrm{\textrm{Spf}}\,}}(R)=N^n\mathbb {A}\; \end{aligned}$$

(3.1)

in particular, $N^nX$ is formal affine and isomorphic to $N^nU$. Up to shrinking U, we may assume $U= {{\,\mathrm{\textrm{Spf}}\,}}(A)$ with A a $\pi$-adically complete separated R-algebra. Then, the point $a:{{\,\mathrm{\textrm{Spf}}\,}}(R)\rightarrow U$ induces an R-algebra morphism $\varepsilon :A \rightarrow R$. Let $J^nU = {{\,\mathrm{\textrm{Spf}}\,}}(J_nA)$. It is immediate to check that

$$\begin{aligned} N^{n}U = {{\,\mathrm{\textrm{Spf}}\,}}(J_{n}A{\hat{\otimes }}_{A,\varepsilon } R). \end{aligned}$$

(3.2)

3.1 Adjunction

Let ${\textbf{Alg}^+_{R}}$ denote the category of augmented (commutative) R-algebras. Its objects are commutative R-algebras A together with an augmentation $\varepsilon$, i.e., an R-algebra morphism $\varepsilon :A\rightarrow R$; morphisms in ${\textbf{Alg}^+_{R}}$ are morphisms of R-algebras $h:A_1\rightarrow A_2$ respecting augmentations, i.e., $\varepsilon _2\circ h=\varepsilon _1$. For any $(A,\varepsilon )$ in ${\textbf{Alg}^+_{R}}$, we define the R-algebra

$$\begin{aligned} N_{n}A:= J_{n}A\otimes _{A,\varepsilon } R. \end{aligned}$$

(3.3)

Note that shifted Witt vectors yield objects in ${\textbf{Alg}^+_{R}}$. Indeed, let B be an R-algebra and let $w_0^+:W_n^+(B)\rightarrow R$ denote the projection onto the first component, i.e., the composition of the upper horizontal arrows in (2.10). Then, $W_n^+(B)$ together with $w_0^+$ is an augmented R-algebra. Hence, the above construction defines a functor

$$\begin{aligned} W_n^+:{\textbf{Alg}_{R}}\longrightarrow {\textbf{Alg}^+_{R}}\, \quad B\mapsto (W_n^+(B),w_0^+) \, \end{aligned}$$

on the category of R-algebras.

We now prove a key result: $N_n$ and $W_n^+$ is a pair of adjoint functors.

Theorem 3.1

For any augmented R-algebra $(A,\varepsilon )$ and any R-algebra B, there is a natural bijection

$$\begin{aligned} \Theta ^+:{{\,\mathrm{\textrm{Hom}}\,}}_R(N_nA,B) {\mathop {\longrightarrow }\limits ^{\sim }}\textrm{Hom}_{{\textbf{Alg}^+_{R}}} (A,W^+_n(B)). \end{aligned}$$

(3.4)

Proof

Let $\iota :A\rightarrow J_nA$ denote the natural morphism. Then,

$$\begin{aligned} {{\,\mathrm{\textrm{Hom}}\,}}_R(N_nA,B)=&\ \{ g \in {{\,\mathrm{\textrm{Hom}}\,}}_R(J_nA,B)\mid g\circ \iota = \rho _B\circ \varepsilon \}\\ =&\ \{f\in {{\,\mathrm{\textrm{Hom}}\,}}_R(A,W_n(B))\mid w_0\circ f=\rho _B\circ \varepsilon \} \\ =&\ \{f^+ \in {{\,\mathrm{\textrm{Hom}}\,}}_R(A,W^+_n(B))\mid w_0^+\circ f^+ =\varepsilon \}\\ =&\ \textrm{Hom}_{{\textbf{Alg}^+_{R}}} (A,W^+_n(B)) \end{aligned}$$

where the first equality follows by (3.3), the second by (2.13) taking $f=\Theta (g)$, the third by definition of $W_n^+(B)$ in (2.9). $\square$

By Remark 2.1, an analogous adjunction holds when working with the category of augmented formal R-algebras ${\textbf{fAlg}^+_{R}}$. We make this fact explicit.

Example 3.2

Let $A=R\langle x\rangle$ and $\varepsilon (x)=0$. By (2.14)

$$\begin{aligned} N_{n}A=J_{n}A{\hat{\otimes }}_{A,\varepsilon } R= R\langle x',\dots , x^{(n)}\rangle =R\langle \textsf{p}_{1}^+,\dots ,\textsf{p}_{n}^+\rangle , \end{aligned}$$

where $\textsf{p}_i^+ \in R[x',\dots , x^{(n)}]$ denotes the polynomial $\textsf{p}_i\in R[x,x',\dots , x^{(n)}]$ evaluated at $x=0$. Then, the formal counterpart of (3.4) works as follow: given $g\in {{\,\mathrm{\textrm{Hom}}\,}}_R(N_nA,B)$, then $\Theta ^+(g)$ maps x to $(0,g(\textsf{p}_1^+),\dots ,g(\textsf{p}_n^+))$.

The higher-dimensional case is analogous. Let $A=R\langle \textbf{x}\rangle$ with $\textbf{x}$ a collection of r indeterminates $\{x_{ 1},\dots ,x_{ r}\}$ and let $\varepsilon$ be the zero section. Then, $J_nA\simeq R\langle \textbf{p}_0,\textbf{p}_1,\dots , \textbf{p}_n\rangle$ where $\textbf{p}_i$ denotes a collection of polynomials $\{\textsf{p}_{i,1},\dots ,\textsf{p}_{i,r}\}$ and $\textsf{p}_{i,j}\in R[x_j,x_j',...,x_j^{(n)}]$ plays the role of $\textsf{p}_i$ in (2.14). Then,

$$\begin{aligned} N_n A \simeq R\langle \textbf{p}_0,\dots \textbf{p}_n\rangle {{\hat{\otimes }}}_{R\langle \textbf{x}\rangle ,\varepsilon } \ R \simeq R\langle \textbf{p}_1^+,\dots , \textbf{p}_n^+\rangle , \end{aligned}$$

(3.5)

where $\textbf{p}_i^+$ denotes the collection of polynomials $\{\textsf{p}_{i,1}^+,\dots ,\textsf{p}_{i,r}^+\}$ with $\textsf{p}_{i,j}^+$ obtained by evaluating $\textsf{p}_{i,j}$ at $x_j=0$. Finally, for a homomorphism $g:N_nA\rightarrow B$, $\Theta ^+(g)$ maps $x_i$ to $(0,g(\textsf{p}_{1,i}^+),\dots ,g(\textsf{p}_{n,i}^+))$.

We can now describe the functor $N^n X$ on R-algebras as done in (1.2) for $J^nX$.

Theorem 3.3

Let X be a smooth formal scheme over R with a marked point x and let B be in $\textbf{Nilp}_R$. Then,

$$\begin{aligned} N^n X(B)={{\,\mathrm{\textrm{Hom}}\,}}_{R\text {-pt}}({{\,\mathrm{\textrm{Spf}}\,}}(W_n^+(B)), X), \end{aligned}$$

where on the right we are considering morphisms of R-pointed formal schemes.

Proof

The result is clearly true if X is affine by Theorem 3.1. For the general case, assume first that X is an R-scheme and consider the following diagram

where $w_0$ is induced by the projection on the first component on algebras, $\rho$ is the structure morphism and u is the natural map. Note that ${{\,\mathrm{\textrm{Spec}}\,}}(W_n^+(B))$ is the push-out of $w,\rho$ in the category of all schemes [17, 07RS]. Then, $N^nX(B)=X(W_n^+(B))$. Indeed,

$$\begin{aligned} N^nX(B)=&\ \{g \in {{\,\mathrm{\textrm{Hom}}\,}}_R ({{\,\mathrm{\textrm{Spec}}\,}}(B),J^nX )\mid u\circ g =x\circ \rho \} \\ =&\ \{f\in {{\,\mathrm{\textrm{Hom}}\,}}_R({{\,\mathrm{\textrm{Spec}}\,}}(W_n(B)), X)\mid f\circ w_0=x\circ \rho \}\\ =&\ \{f^+ \in {{\,\mathrm{\textrm{Hom}}\,}}_R({{\,\mathrm{\textrm{Spec}}\,}}(W_n^+(B)),X)\mid f^+\circ w^+_0 =x\}\\ =&\ {{\,\mathrm{\textrm{Hom}}\,}}_{R\mathrm{-pt}}({{\,\mathrm{\textrm{Spec}}\,}}(W_n^+(B)), X). \end{aligned}$$

If X is a formal scheme, then the above holds for all schemes $X \times {{\,\mathrm{\textrm{Spec}}\,}}R/(\pi ^m)$ and thus one concludes. $\square$

3.2 A special case

Let G be a formal group scheme over R and denote by $G^\textrm{for}$ the formal completion of G along the unit section. Let $\mathcal F\in R[\![x_1,\dots , x_r,y_1,\dots , y_r]\!]$ be the formal group law on $G^\textrm{for}$, ${{\mathcal {F}}}^\phi$ the one obtained by acting on the coefficients of ${\mathcal {F}}$ by $\phi$ and ${{\mathcal {F}}}^\phi \{1\}:=\pi ^{-1}{\mathcal {F}}^\phi (\pi \textbf{x},\pi \textbf{y})$, where $\pi \textbf{x}:=(\pi x_1,\dots , \pi x_r)$. By [8, Lemma 2.2] it is $N^1\,G\simeq {{\mathcal {F}}}^\phi \{1\}$ as formal R-schemes. We give below a direct computation of this fact.

Lemma 3.4

Let the notation be as above. Then, the formal group law on the formal completion of $N^1G$ at the origin is isomorphic to ${{\mathcal {F}}}^\phi \{1\}$.

Proof

As seen in Remark 3.2, we may write $G^\textrm{for}= {{\,\mathrm{\textrm{Spf}}\,}}(R[\![\textbf{x}]\!])$ and $N^1\,G={{\,\mathrm{\textrm{Spf}}\,}}(R\langle \textbf{p}_1^+\rangle )={{\,\mathrm{\textrm{Spf}}\,}}(R\langle \textbf{x}'\rangle )$. Let $\delta :R[\![\textbf{x},\textbf{y}]\!]\rightarrow R[\![\textbf{x},\textbf{y},\textbf{x}',\textbf{y}']\!]$ be the $\pi$-derivation compatible with that of R and such that $\delta (\textbf{x})=\textbf{x}'$, $\delta (\textbf{y})=\textbf{y}'$. If ${\mathcal {F}}(\textbf{x},\textbf{y})$ is the formal group law of G, the formal group law of $N^1G$ is $\delta ({\mathcal {F}}(\textbf{x},\textbf{y}))$ evaluated at $\textbf{x}=\varvec{0},\textbf{y}=\varvec{0}$. Write ${\mathcal {F}}(\textbf{x},\textbf{y})=\sum _{\alpha ,\beta } a_{\alpha ,\beta } \textbf{x}^\alpha \textbf{y}^\beta$ with $\alpha ,\beta$ varying in $\mathbb {N}^r \smallsetminus \{\varvec{0}\}$, $\textbf{x}^\alpha :=x_1^{\alpha _1}x_1^{\alpha _2}\dots x_r^{\alpha _r}$, and the coefficients of the monomials of degree 1 equal to 1. By induction, applying the usual rules of $\pi$-derivations, one checks that

$$\begin{aligned} \delta ({\mathcal {F}}(\textbf{x},\textbf{y}))_{\mid \textbf{x}=\varvec{0}, \textbf{y}=\varvec{0}}= & {} \sum _{\alpha ,\beta } \delta (a_{\alpha ,\beta } \textbf{x}^\alpha \textbf{y}^\beta )_{\mid \textbf{x}=\varvec{0}, \textbf{y}=\varvec{0}}\\ {}= & {} \sum _{\alpha ,\beta } \pi ^{-1}\phi (a_{\alpha ,\beta }) (\pi \textbf{x}')^\alpha (\pi \textbf{y}')^\beta =\pi ^{-1}\mathcal F^\phi (\pi \textbf{x},\pi \textbf{y})={\mathcal {F}}^\phi \{1\}. \end{aligned}$$

$\square$

3.3 Lateral Frobenius

Let X be a formal R-scheme. As n varies, the $\pi$-jet spaces $J^nX$ form an inverse system of formal schemes and, more precisely, a prolongation sequence, whence a lifting of Frobenius $\phi _J$ exists on the limit. Clearly, the transition maps $u=u^{n+1}_n:J^{n+1} X\rightarrow J^nX$ induce homomorphisms $N^{n+1} X\rightarrow N^nX$, but the image of $\phi$ restricted to $N^{n+1}X$ is not necessarily contained in $N^nX$, and hence, $\phi$ does not induce a lifting of Frobenius on the sequence of the kernels. For this reason, the notion of lateral Frobenius was introduced and studied in [7, 16].

On shifted Witt vectors, the lateral Frobenius $F^+$ is defined as the homomorphism of R-algebras making the following diagram

(3.6)

commute, where vertical identifications are meant as sets, and F is the Frobenius on Witt vectors recalled in (2.5). The homomorphism $F^+$ then corresponds to the homomorphism of R-algebras

$$\begin{aligned} F_w^+:R\times {\prod }_\phi ^{n{\text {--}}1}\! ({}^{\phi }\!B)\rightarrow R\times {\prod }_\phi ^{n{\text {--}}2}\! ({}^{\phi ^2}\!B), \quad (r,b_1,\dots , b_n)\mapsto (r,b_2,\dots ,b_n) \end{aligned}$$

(3.7)

via ghost map, i.e., it makes the following diagram

(3.8)

commute. Then, the homomorphism $F^+$ induces via (2.13) a natural morphism

$$\begin{aligned} \mathfrak {f}:N^nX\rightarrow N^{n-1}X \end{aligned}$$

called again lateral Frobenius. It is showed in [7, Theorem 4.3] that $\mathfrak {f}$ is a lift of Frobenius and satisfies

$$\begin{aligned} \phi \circ \phi \circ u=\phi \circ u\circ \mathfrak {f}, \end{aligned}$$

where u denotes the immersion $N^mX\rightarrow J^mX$ and $\phi$ denotes the Frobenius morphism $J^mX\rightarrow J^{m-1}X$ for any m.

Remark 3.5

For later use, note that the element $(0, b_.)=(0,b_1,\dots ,b_n)\in W^+_n(B)$ traces in (3.8) the following images

Hence, $\pi c_1=\pi b_{1}^{q}+ \pi ^{2}b_2$ implies $c_1=b_{1}^{q}+ \pi b_2$ (for B without $\pi$-torsion and hence for any R-algebra B by standard arguments). By recursion, one sees

$$\begin{aligned} (F^+)^i(0,b_{1},\dots ,b_{n})=(0,b_1^{q^i}+\pi b_2^{q^{i-1}}+\dots +\pi ^i b_i, \dots )\in W^+_{n-i}(B) \end{aligned}$$

for any $i<n$.

If G is smooth over R, the same are $J^nG$ and $N^nG$ for all n. As seen in the previous section, $N^nG={{\,\mathrm{\textrm{Spf}}\,}}(N_n A)$ is an affine space over R. In particular, the R-algebras $N_nA$ are $\pi$-torsion free, and therefore, the lateral Frobenius homomorphisms $\mathfrak {f}^* :N_nA \rightarrow N_{n+1}A$ induce a unique $\pi$-derivation $\Delta$ on the prolongation sequence $N_*A:=\{N_nA\}_{n=1}^\infty$.

In order to describe $N^n$ as a jet functor, we need a preparation lemma.

Lemma 3.6

Let $\mathbb {A}= {{\,\mathrm{\textrm{Spf}}\,}}(R\langle \textbf{x}\rangle )$ with $\textbf{x}$ a collection of r indeterminates, and choose the origin as marked point. Let $\mathfrak {f}^i:N^n\mathbb {A}\rightarrow N^{n-i}\mathbb {A}$ denote the ith fold composition of lateral Frobenius for any $i\le n$. Then, $\mathfrak {f}^i$ induces an homomorphism of $\pi$-adic R-algebras

$$\begin{aligned} (\mathfrak {f}^i)^*:R\langle \textbf{p}^+_1,\dots , \textbf{p}^+_{n-i}\rangle \longrightarrow R\langle \textbf{p}^+_1,\dots , \textbf{p}^+_n\rangle \end{aligned}$$

such that

$$\begin{aligned} (\mathfrak {f}^i)^*(\textbf{p}^+_1) = (\textbf{p}^+_1)^{q^{i-1}}+ \pi (\textbf{p}^+_2)^{q^{i-2}} + \cdots + \pi ^{i-1}\textbf{p}^+_i. \end{aligned}$$

Proof

Recall from Example 3.2 that $N^n\mathbb {A}={{\,\mathrm{\textrm{Spf}}\,}}(N_nR\langle \textbf{x}\rangle ) \simeq {{\,\mathrm{\textrm{Spf}}\,}}(R\langle \textbf{p}^+_1,\dots , \textbf{p}^+_n\rangle )$. Then by definition of $\mathfrak {f}$ and (3.4) with $B= N_n R\langle \textbf{x}\rangle$, we have a commutative diagram of rings

By Remark 3.5, the identity map on $R\langle \textbf{p}^+_1,\dots , \textbf{p}^+_{n}\rangle$ traces the following images

The conclusion follows by the explicit description of the map $\Theta ^+$ as in the lines below (3.5) $\square$

We can now prove the main result of this section. This is a particular case of [16, Theorem 1.3] for which we give a shorter proof.

Theorem 3.7

Let G be a smooth formal group scheme over R. Then for all n we have

$$\begin{aligned} N^nG \simeq J^{n-1}(N^1G). \end{aligned}$$

Proof

Let $\mathbb {A}={{\,\mathrm{\textrm{Spf}}\,}}(R\langle \textbf{x}\rangle )$ be an étale coordinate system around the identity section of G. We have seen in (3.1) and Example 3.2 that $N^{n}G = N^{n}\mathbb {A}={{\,\mathrm{\textrm{Spec}}\,}}N_{n}A$ with $N_{n}A \simeq R\langle \textbf{p}^+_1,\dots , \textbf{p}^+_n\rangle$. Now by Lemma 3.6 the lateral Frobenius satisfies

$$\begin{aligned} (\mathfrak {f}^*)^i(\textbf{p}^+_{1}) = (\textbf{p}^+_{1})^{q^{i-1}} + \pi (\textbf{p}^+_{2})^{q^{i-2}} + \cdots + \pi ^{i-1} \textbf{p}^+_{i} \end{aligned}$$

for all $i=0,\dots , n$. Hence, by Theorem 4.9 we have $N_{n}A \simeq J_{n-1}(N_{1}A)$ and we are done. $\square$

Here we discuss examples for $G= \widehat{\mathbb {G}}_{\textrm{a}}$ and $\widehat{\mathbb {G}}_{\textrm{m}}$ in the context of Theorem 3.7

Examples 3.8

• 1. Assume $G=\widehat{\mathbb {G}}_{\textrm{a}}={{\,\mathrm{\textrm{Spf}}\,}}(R\langle x\rangle )$ with the comultiplication mapping x to $x\otimes 1 +1\otimes x$. Then, $J^1\widehat{\mathbb {G}}_{\textrm{a}}={{\,\mathrm{\textrm{Spf}}\,}}(R\langle x,x'\rangle )$ where the group law is described by

  $$\begin{aligned} x&\mapsto x\otimes 1 +1\otimes x\ , \\ x'&\mapsto x'\otimes 1+1\otimes x' +C_\pi (x\otimes 1,1\otimes x) \end{aligned}$$

  with $C_\pi (X,Y) = \frac{X^q + Y^q -(X+Y)^q}{\pi }\in \mathcal {O}[X,Y]$. Hence, $N^1\widehat{\mathbb {G}}_{\textrm{a}}={{\,\mathrm{\textrm{Spf}}\,}}(\langle x'\rangle )= \widehat{\mathbb {G}}_{\textrm{a}}$. By Theorem 3.7 and Eq. (2.15), one concludes $N^n\widehat{\mathbb {G}}_{\textrm{a}}=J^{n-1}(\widehat{\mathbb {G}}_{\textrm{a}})= \widehat{\mathbb {W}}_{n-1}$.

• 2. Assume $G=\widehat{\mathbb {G}}_{\textrm{m}}= {{\,\mathrm{\textrm{Spf}}\,}}(R\langle x,y \rangle /(xy-1 )$ with the comultiplication mapping x to $x\otimes x$. Then, $J^1\widehat{\mathbb {G}}_{\textrm{m}}={{\,\mathrm{\textrm{Spf}}\,}}(R\langle x,y,x',y'\rangle /(xy-1,\delta (xy) ) = {{\,\mathrm{\textrm{Spf}}\,}}(R\langle x,x^{-1},x'\rangle )$ with the group law described by

  $$\begin{aligned} x&\mapsto x\otimes x\ , \\ x'&\mapsto x'\otimes x^q+x^q\otimes x'+\pi x'\otimes x' \ . \end{aligned}$$

  Hence, $N^1\widehat{\mathbb {G}}_{\textrm{m}}={{\,\mathrm{\textrm{Spf}}\,}}\left( R\langle x',y'\rangle / (x'+y'+\pi x'y')\right) = {{\,\mathrm{\textrm{Spf}}\,}}(R\langle x'\rangle )$ and the group law on the latter maps $x'$ to $x'\otimes 1+1\otimes x'+\pi x'\otimes x'$, i.e., $N^1\widehat{\mathbb {G}}_{\textrm{m}}=\mathbb {G}^\textrm{for}_m\{1\}$ as formal group schemes. Now, $\mathbb {G}^\textrm{for}_m\{1\}$, as formal group law, has invariant differential $(1+\pi T)^{-1}dT$ and the corresponding logarithm is

  $$\begin{aligned} \pi ^{-1}\log (1+\pi T)=\sum _{j\ge 1} \frac{(-\pi )^{j-1}}{j}T^j=T+\sum _{j\ge 2} a_jT^j\in K[\![T]\!]. \end{aligned}$$

  Assume $p\ge e+1$. We prove that $\pi ^{-1}\log (1+\pi T)\in \mathcal {O}[\![T]\!]$ and indeed in $\mathcal {O}\langle T\rangle$. It suffices to check that $v_\pi (a_j)\ge 0$ tends to infinity as j tends to infinity. Let $r>0$ and note that $v_\pi (a_{p^r}) = p^r-1-er\ge 0$ since

  $$\begin{aligned} p^r-1=(p-1)(p^{r-1}+\dots +1) \ge er. \end{aligned}$$

  Further $v_\pi (a_{p^r})<v_\pi (a_{p^{r+1}})$ and for $p^r\le j<p^{r+1}$ we have

  $$\begin{aligned} v_\pi (a_{p^r}) = p^r-1-er \le j-1-v_\pi (j)=v_\pi (a_j). \end{aligned}$$

  Hence $\pi ^{-1}\log (1+\pi T)\in \mathcal {O}\langle T\rangle$ and it defines a morphism of formal group schemes $\mathbb {G}^\textrm{for}_m\{1\}\rightarrow \widehat{\mathbb {G}}_{\textrm{a}}$. It is an isomorphism under the stronger hypothesis that $p\ge e+2$. Indeed, the inverse of $\pi ^{-1}\log (1+\pi T)$ is

  $$\begin{aligned} \pi ^{-1}(\exp (\pi T)-1)=\sum _{j\ge 1} \frac{(\pi T)^{j}}{j!}\in K[\![T]\!],\end{aligned}$$

  and the $\pi$-adic valuation of the jth coefficient is

  $$\begin{aligned} v_\pi (\pi ^j/j!)= j-v_\pi (j!)=j-e\cdot \frac{j-s_p(j)}{p-1}= \frac{j(p-1-e)+es_p(j)}{p-1}, \end{aligned}$$

  where $s_p(j)$ denotes the sum of the digits in the base-p expansion of j. Clearly, if $p\ge e+2$ this valuation tends to infinity as j tends to infinity, and hence, $\pi ^{-1}(\exp (\pi T)-1) \in \mathcal {O}\langle T\rangle$. Then, if $p\ge e+2$, one concludes that $N^1 \widehat{\mathbb {G}}_{\textrm{m}}\simeq \widehat{\mathbb {G}}_{\textrm{a}}$ and, with arguments as in Example 3.8(1), that $N^n \widehat{\mathbb {G}}_{\textrm{m}}\simeq \widehat{\mathbb {W}}_{n-1}$.

The next result is an extension of [8, Lemma 2.3].

Lemma 3.9

Let ${\mathcal {F}}$ be a commutative formal group law over R of dimension d. If $n(p-1)\ge e+1$, then ${\mathcal {F}}\{n\}\simeq (\widehat{\mathbb {G}}_{\textrm{a}})^d$ as formal group schemes over R.

Proof

In [8, Lemma 2.3], R is a complete discrete valuation ring with algebraically closed residue field. The proof in our hypothesis works the same. Indeed, Buium applies results in [14] that are valid for any $\mathbb {Z}_{(p)}$-algebra and the key-point is showing that the coefficients of the logarithm and exponential series of ${\mathcal {F}}\{n\}$ over R[1/p] are indeed in $\pi R$. This is done by explicit estimates for the $\pi$-valuation of those coefficients. $\square$

Theorem 3.10

Let G be a smooth commutative formal group scheme of relative dimension d over ${{\,\mathrm{\textrm{Spf}}\,}}(R)$. Assume $p\ge e+2$. Then there is a natural isomorphism of formal group schemes

$$\begin{aligned} N^n G\simeq (\widehat{\mathbb {W}}_{n-1})^d. \end{aligned}$$

Proof

Let $G^\textrm{for}$ be the formal completion of G along the unit section ${{\,\mathrm{\textrm{Spf}}\,}}(R)\rightarrow G$. Let ${\mathcal {F}}\in R[[x_1,\dots , x_d,y_1,\dots , y_d]]$ be the formal group law on $G^\textrm{for}$, ${{\mathcal {F}}}^\phi$ the one obtained by acting the coefficients of ${\mathcal {F}}$ by $\phi$ and ${{\mathcal {F}}}^\phi \{1\}:=\pi ^{-1}\mathcal F^\phi (\pi x_.,\pi y_.)$. By Lemma 3.4 (see also [8, Lemma 2.2]), it is $N^1 G\simeq {{\mathcal {F}}}^\phi \{1\}$ as formal group schemes. Note that since $\phi (\pi )=\pi$ it is ${{\mathcal {F}}}^\phi \{1\}=({{\mathcal {F}}}\{1\})^\phi$. Now by hypothesis and Lemma 3.9, we have ${{\mathcal {F}}}\{1\}\simeq (\widehat{\mathbb {G}}_{\textrm{a}})^d$. Hence, ${{\mathcal {F}}}\{1\}^\phi \simeq ((\widehat{\mathbb {G}}_{\textrm{a}})^d)^\phi =(\widehat{\mathbb {G}}_{\textrm{a}})^d$ and hence $N^1 G\simeq (\widehat{\mathbb {G}}_{\textrm{a}})^d$. By Theorem 3.7 and definition of $J^{n-1}$, it is

$$\begin{aligned} N^n G\simeq J^{n-1}(\widehat{\mathbb {G}}_{\textrm{a}})^d\simeq (J^{n-1}\widehat{\mathbb {G}}_{\textrm{a}})^d \simeq (\widehat{\mathbb {W}}_{n-1})^d. \end{aligned}$$

$\square$

Remark 3.11

Assume $R=\mathcal {O}$, $p>2$ and let G be as in the previous theorem. Then, passing to limit on n, we have a short exact sequence

$$\begin{aligned} 0\rightarrow N^\infty G(k)\rightarrow J^\infty G(k)=G(\mathcal {O}) \rightarrow G(k)\rightarrow 0 \end{aligned}$$

where $G(\mathcal {O}) \rightarrow G(k)$ is the reduction map, and we recover the fact that the kernel of the reduction map is isomorphic to $\mathcal {O}^d=W(k)^d$ as groups.

4 p-power torsion

For any formal commutative R-group scheme G, let $G[p^\nu ]$ denote the kernel of the multiplication by $p^\nu$ on G and let $G[p^\infty ]$ be the sheaf on $\textbf{Nilp}_R^{\textrm{op}}$ such that

$$\begin{aligned} G[p^\infty ](C)=\varinjlim _\nu G[p^\nu ](C) \end{aligned}$$

(4.1)

for any C in $\textbf{Nilp}_R$. Note that $G[p^\infty ]$ is a sheaf since the above colimit commutes with equalizers [17, 04AX]. If G is a formal torus or a formal abelian scheme $G[p^\infty ]$ is p-divisible, but not in general.

For each $\nu >0$ the closed immersions $G[p^\nu ] \hookrightarrow G[p^{\nu +1}]$ induce closed immersions of $\pi$-jets $J^n(G[p^\nu ]) \hookrightarrow J^n(G[p^{\nu +1}])$ [9, Proposition 1.7], [2, Lemma  3.8, Theorem 3.9]. We can naturally pass to limit on $\nu$.

Lemma 4.1

Let the notation be as above. Then

$$\begin{aligned} J^n(G[p^\infty ])= \varinjlim _\nu J^n(G[p^\nu ]) = J^n(G)[p^\infty ] \end{aligned}$$

as sheaves on $\textbf{Nilp}_R^{\textrm{op}}$.

Proof

Recall (1.1) and (4.1). For any C in $\textbf{Nilp}_R$ it is

$$\begin{aligned} J^n(G[p^\infty ])(C)= G[p^\infty ](W_n(C))= \varinjlim _\nu G[p^\nu ](W_n(C)) = \varinjlim _\nu J^n(G[p^\nu ])(C). \end{aligned}$$

Whence the first isomorphism. The second one follows by the fact that $J^n$ is left exact (being a right adjoint) and hence

$$\begin{aligned} \varinjlim _\nu J^n(G[p^\nu ])(C)= \varinjlim _\nu ((J^n G)[p^\nu ])(C)= (J^n(G)[p^\infty ])(C). \end{aligned}$$

$\square$

Recall that $N^nF$ is defined as $\ker (J^nF\rightarrow F)$ for any sheaf of groups on $\textbf{Nilp}_R^{\textrm{op}}$. We then deduce from Lemma 4.1 the following result.

Lemma 4.2

Let notation be as above. Then

$$\begin{aligned} N^n(G[p^\infty ])= \varinjlim _\nu N^n(G[p^\nu ]) = (N^nG)[p^\infty ] \end{aligned}$$

as sheaves on $\textbf{Nilp}_R^{\textrm{op}}$.

Proof

By Theorem 3.3 the functor $N^n$ is left exact; hence $(N^nG)[p^\nu ]=N^n(G[p^\nu ])$ and

$$\begin{aligned} (N^nG)[p^\infty ]:=\varinjlim _\nu (N^nG)[p^\nu ]=\varinjlim _\nu N^n(G[p^\nu ]). \end{aligned}$$

Further, $(N^nG)[p^\infty ]=\ker ((J^nG)[p^\infty ]\rightarrow G[p^\infty ]) = \ker (J^n(G[p^\infty ])\rightarrow G[p^\infty ])=N^n(G[p^\infty ])$. $\square$

We say that a commutative formal R-group scheme is triangular if it admits a finite filtration by formal subgroup schemes whose successive quotients are isomorphic to $\widehat{\mathbb {G}}_{\textrm{a}}$. It is called triangular of level 0 in [8, p. 322]. The formal R-group scheme $\widehat{\mathbb {W}}_n$ is triangular.

Lemma 4.3

If H is a triangular formal R-group scheme, then $H[p^\infty ]=H$ as sheaves on $\textbf{Nilp}_R^{\textrm{op}}$.

Proof

We proceed by induction on the length m of the filtration. The result is clearly true for $H=\widehat{\mathbb {G}}_{\textrm{a}}$ since p is nilpotent in any object C of $\textbf{Nilp}_R$. Assume $m>1$. Then, H is extension of $\widehat{\mathbb {G}}_{\textrm{a}}$ by G where G is a triangular formal group scheme with a filtration of length $m-1$. One concludes by induction hypothesis. $\square$

Moreover, we have the following stronger result.

Theorem 4.4

Assume G is a smooth commutative formal R-group scheme and $p\ge e+2$. Then, $N^n(G[p^\infty ])= N^n G$ as sheaves on $\textbf{Nilp}_R^{\textrm{op}}$.

Proof

By Theorem 3.10, the formal R-group scheme $N^n G$ is triangular. Hence, the result follows by Lemmas 4.2 and 4.3. $\square$

Corollary 4.5

Assume $p\ge e+2$. The exact sequence (1.3) induces an exact sequence of formal groups

$$\begin{aligned} 0 \rightarrow N^n G [p^\infty ] \rightarrow J^n G[p^\infty ] \rightarrow G[p^\infty ]\rightarrow 0, \end{aligned}$$

(4.2)

for any $n\ge 0$.

Proof

Only the right exactness needs to be proved. Let s be a section of G such that $p^ms=0$. It lifts to a section $s'$ of $J^nG$. Now $p^ms'$ comes from a section of $N^nG$ and thus is p-power torsion by the previous theorem. Hence, $s'$ is p-power torsion. $\square$

We are now ready to proof the Main Theorem stated in the introduction.

Theorem 4.6

Assume $p\ge e+2$. Given a smooth commutative formal group scheme G of relative dimension d over R, for any positive integers n the natural morphism $J^nG\rightarrow G$ gives an exact sequence

$$\begin{aligned} 0 \rightarrow (\widehat{\mathbb {W}}_{n-1})^d \rightarrow J^n G[p^\infty ] \rightarrow G[p^\infty ] \rightarrow 0 \end{aligned}$$

as sheaves on $\textbf{Nilp}_R^{\textrm{op}}$.

Proof

This follows directly by applying Theorems 3.10, 4.4 and Corollary 4.5. $\square$

We can now conclude the study of Examples 3.8.

Examples 4.7

• 1. Assume $G=\widehat{\mathbb {G}}_{\textrm{a}}$. We have seen in Example 3.8(1) that $N^1\widehat{\mathbb {G}}_{\textrm{a}}={{\,\mathrm{\textrm{Spf}}\,}}(R\langle x'\rangle )$ is isomorphic to $\widehat{\mathbb {G}}_{\textrm{a}}={{\,\mathrm{\textrm{Spf}}\,}}(R\langle x\rangle )$ as formal group scheme mapping x to $x'$ on algebras. In particular, for any $\nu \ge 1$, it is

  $$\begin{aligned} N^1\widehat{\mathbb {G}}_{\textrm{a}}[p^\nu ]\cong \widehat{\mathbb {G}}_{\textrm{a}}[p^\nu ]. \end{aligned}$$

  This result can be checked directly. Indeed $\widehat{\mathbb {G}}_{\textrm{a}}[p^\nu ]={{\,\mathrm{\textrm{Spf}}\,}}(R\langle x\rangle /(p^\nu x))$ and hence

  $$\begin{aligned} J^1\widehat{\mathbb {G}}_{\textrm{a}}[p^\nu ]={{\,\mathrm{\textrm{Spf}}\,}}\left( \frac{R\langle x,x'\rangle }{(p^\nu x,\delta (p^\nu x))}\right) \,\quad N^1\widehat{\mathbb {G}}_{\textrm{a}}[p^\nu ]={{\,\mathrm{\textrm{Spf}}\,}}\left( \frac{R\langle x'\rangle }{(p^{\nu } x')}\right) , \end{aligned}$$

  since $(p^\nu x)^q+\pi \delta (p^\nu x)=\phi (p^\nu x)=p^\nu \phi (x)=p^\nu (x^q+\pi x')$. Passing to limit on $\nu$ we get an isomorphism $N^1\widehat{\mathbb {G}}_{\textrm{a}}[p^\infty ]\cong \widehat{\mathbb {G}}_{\textrm{a}}[p^\infty ]$.

• 2. Assume $G=\widehat{\mathbb {G}}_{\textrm{m}}$. We have seen in Example 3.8(2) that if $p\ge e+2$ it is $N^1\widehat{\mathbb {G}}_{\textrm{m}}\simeq \widehat{\mathbb {G}}_{\textrm{a}}$. Hence $N^1\widehat{\mathbb {G}}_{\textrm{m}}[p^\infty ]\simeq \widehat{\mathbb {G}}_{\textrm{a}}[p^\infty ]$.

A Prolongation sequences of algebras

Let for this section R be a flat $\mathcal {O}$-algebra with a fixed $\pi$-derivation $\delta$. In particular, it has a lift of Frobenius. Let $u:B\rightarrow C$ be a morphism of R-algebras. Recall that if $u:B\rightarrow C$ is a morphism of $\mathcal {O}$-algebras, a $\pi$-derivation relative to u is a map of sets $\partial :B\rightarrow C$ such that $\partial (0)=0=\partial (1)$ and for any $x,y\in B$

$$\begin{aligned} \partial (x+y)&=\partial (x)+\partial (y)+\frac{ u(x)^q+u(y)^q-u(x+y)^q }{\pi } \end{aligned}$$

(A.1)

$$\begin{aligned} \partial (xy)&= u(x)^q\partial (y)+u(y)^q\partial (x)+\pi \partial (x)\partial (y) . \end{aligned}$$

(A.2)

Associated with $\partial$ there is a lift of Frobenius (relative to u) $\Psi :B \rightarrow C$ given by $\Psi (x)= u(x)^q + \pi \partial (x)$ (see [7, §3.1], [2, §1]).

Fix a positive integer r. Let $B_n = R[\textbf{x}_0,\dots , \textbf{x}_n]$, where for each $i\ge 0$, $\textbf{x}_i$ denotes the r-tuple of variables $x_{i,1},\dots , x_{i,r}$ and denote by $u:B_{n}\rightarrow B_{n+1}$ the natural inclusions. Fix a prolongation sequence

$$\begin{aligned} B=B_0\xrightarrow {u,\partial }B_1 \xrightarrow {u,\partial }B_2\rightarrow ... \end{aligned}$$

(A.3)

i.e., for any n we fix a $\pi$-derivation (relative to u) $\partial :B_n\rightarrow B_{n+1}$ such that

• $\partial$ is compatible with the $\pi$-derivation of R;

• $\partial \circ u=u\circ \partial$ (and thus we avoided using subscripts).

The lift of Frobenius is then the homomorphism

$$\begin{aligned} \Psi :B_n\rightarrow B_{n+1}, \qquad \textbf{x}_i\mapsto \textbf{x}_i^q+\pi \partial \textbf{x}_i, \end{aligned}$$

where we used a compact notation instead of writing $x_{i,j}\mapsto x_{i,j}^q+\pi \partial x_{i,j}$ for all $i\le n$ and $1\le j\le r$. Note that we can handle all $B_n$ together by introducing $B_\infty = R[\textbf{x}_0, \textbf{x}_1,\dots ]=\bigcup _n B_n$ and again denoting by $\partial$ the induced $\pi$-derivation associated with the identity on $B_\infty$ and by $\Psi$ the associated lift of Frobenius.

On the other hand, starting with $B=R[\textbf{x}_0]$ we have a prolongation sequence

$$\begin{aligned} B=B_0\xrightarrow {u,\delta }J_1B_0 \xrightarrow {u,\delta }J_2B_0\rightarrow ... \end{aligned}$$

(A.4)

with $J_nB =R[\textbf{x}_0,\textbf{x}_0',\dots , \textbf{x}_0^{(n)}]$ and $\textbf{x}_0^{(i+1)}=\delta \textbf{x}_0^{(i)}$. Let

$$\begin{aligned} \Phi :J_nB \rightarrow J_{n+1}B,\qquad \textbf{x}_0\mapsto \textbf{x}_0^q+\pi \textbf{x}_0' \end{aligned}$$

be the corresponding lift of Frobenius and define $J_\infty B = \bigcup _n J_nB$.

By [2, (2.9)] the restriction on the first component $W(J_\infty B)\rightarrow J_\infty B$ admits a homomorphic section $\exp$ such that the following diagram

(A.5)

commutes, with w the ghost map of ramified Witt vectors. Let $\exp (\textbf{x}_0)=(\textbf{z}_0,\textbf{z}_1,\textbf{z}_2,\dots )$ so that $\textbf{z}_0=\textbf{x}_0$, $\textbf{z}_1=\ \textbf{x}_0'$ and for $n>1$

$$\begin{aligned} \Phi ^n(\textbf{x}_0) = \Phi ^n(\textbf{z}_0)= \textbf{z}_0^{q^n}+ \pi \textbf{z}_1^{q^{n-1}} + \cdots + \pi ^n \textbf{z}_n. \end{aligned}$$

We will show in Theorem 4.9 that if the indeterminates $\textbf{x}_0,\textbf{x}_1,\dots$ satisfy the analogous property for $\Psi$, i.e.,

$$\begin{aligned} \Psi ^n(\textbf{x}_0) = \textbf{x}_0^{q^n}+ \pi \textbf{x}_1^{q^{n-1}} + \cdots + \pi ^n \textbf{x}_n, \end{aligned}$$

(A.6)

then there is a unique isomorphism between the prolongation sequences (A.3) and (A.4).

We start with a technical result. For brevity, let us define for any $n>1$ the following polynomial in $2n-2$ indeterminates

$$\begin{aligned} H_n(x_0,\dots , x_{n-2};y_0,\dots ,y_{n-2}):=\!\sum _{i=0}^{n-2}\left[ \sum _{j=1}^{q^{n-1-i}}\! \pi ^{i+j} {\left( {\begin{array}{c}q^{n-1-i}\\ j\end{array}}\right) } x_{i}^{ q(q^{n-1-i}-j)}y_{i}^j\right] \end{aligned}$$

Lemma 4.8

Let $B_*$ be the prolongation sequence in (A.3) and assume that it satisfies (A.6) for any n. Then

$$\begin{aligned} \textbf{x}_n= \partial \textbf{x}_{n-1} + H_n(\textbf{x}_0,\dots ,\textbf{x}_{n-2};\partial \textbf{x}_0,\dots , \partial \textbf{x}_{n-2} ) \end{aligned}$$

and hence $\textbf{x}_n-\partial \textbf{x}_{n-1}\in \mathcal {O}[\textbf{x}_0,\dots ,\textbf{x}_{n-2},\partial \textbf{x}_0,\dots , \partial \textbf{x}_{n-2}]$ with trivial constant term. Similarly, in $J_\infty B$ it is

$$\begin{aligned} \textbf{z}_n= \delta \textbf{z}_{n-1} + H_n(\textbf{z}_0,\dots ,\textbf{z}_{n-2};\delta \textbf{z}_0,\dots , \delta \textbf{z}_{n-2} ) \end{aligned}$$

Proof

The second assertion is [2, Proposition 2.10]. The proof of the first one is similar and we write below the main steps:

$$\begin{aligned} \sum _{i=0}^n \pi ^i \textbf{x}_i^{q^{n-i}}= & {} \Psi ^n(\textbf{x}_0)\\= & {} \Psi (\Psi ^{n-1}(\textbf{x}_0)) \\= & {} \Psi \left( \sum _{i=0}^{n-1}\pi ^i \textbf{x}_i^{q^{n-1-i}} \right) \\= & {} \sum _{i=0}^{n-1} \pi ^i \Psi (\textbf{x}_i)^{q^{n_i}}\\= & {} \sum _{i=0}^{n-1} \pi ^i\left( \textbf{x}_i^q + \pi \partial \textbf{x}_i\right) ^{q^{n_i}}\\= & {} \sum _{i=0}^{n-1} \pi ^i \left[ \textbf{x}_i^{q^{n-i}} + \sum _{j=1}^{q^{n_i}} {\left( {\begin{array}{c}q^{n_i}\\ j\end{array}}\right) }\textbf{x}_i^{(q^{n_i}-j)q}\pi ^j(\partial \textbf{x}_i)^j \right] \\= & {} \sum _{i=0}^{n-1}\pi ^i \textbf{x}_i^{q^{n-i}}+ \sum _{i=0}^{n-1} \left[ \sum _{j=1}^{q^{n_i}}\pi ^{i+j} {\left( {\begin{array}{c}q^{n_i}\\ j\end{array}}\right) } \textbf{x}_i^{(q^{n_i}-j)q}(\partial \textbf{x}_i)^j\right] \end{aligned}$$

with $n_i=n-1-i$. Hence cancelling the common terms on both sides of the above equality we get

$$\begin{aligned} \pi ^n\textbf{x}_n = \pi ^n\partial \textbf{x}_{n-1} + \sum _{i=0}^{n-2}\left[ \sum _{j=1}^{q^{n-1-i}} \pi ^{i+j} {\left( {\begin{array}{c}q^{n-1-i}\\ j\end{array}}\right) } \textbf{x}_{i}^{ q(q^{n-1-i}-j)}(\partial \textbf{x}_{i})^j\right] \end{aligned}$$

and one can divide by $\pi ^n$. $\square$

We now prove that prolongation sequences $B_*$ as above satisfying condition (A.6) for all n are unique up to unique isomorphism.

Theorem 4.9

Let $B_*$ be the prolongation sequence in (A.3). Assume that the indeterminates $\textbf{x}_i$ satisfy (A.6) for all n and let $\textbf{z}_i\in J_\infty R[\textbf{x}_0]$ be the elements defined just below (A.5). Then we have

• (i) The inclusion $R[\textbf{z}_0,\dots , \textbf{z}_n]\rightarrow J_n R[\textbf{x}_0]$ is an isomorphism for any n.

• (ii) For any $n\ge 0$ the R-algebra homomorphism $h_n:J_n R[\textbf{x}_0]\rightarrow B_n, \textbf{x}_0^{(i)}\mapsto \partial ^i \textbf{x}_0$ is an isomorphism and the following square

  

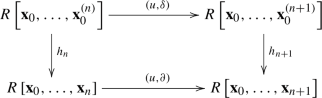
  commutes, where u denotes the inclusion map on both levels.

Proof

The first assertion was proved in [2, Lemma 2.20] with $\textbf{z}_i=P_i(\textbf{x})$. Commutativity of the squares is immediate by definition of $h_n$. We are then left to prove that $h_n$ is an isomorphism. Note hat $J_nR[\textbf{x}_0]=R[\textbf{z}_0,\dots ,\textbf{z}_n]$ by point i) and $B_n=R[\textbf{x}_0,\dots ,\textbf{x}_n]$. If we prove that $h_n(\textbf{z}_i)=\textbf{x}_i$, for all $0\le i\le n$, the result is clear.

We proceed by strong induction on the subset $\{(i,n), 0\le i\le n\}\subset \mathbb {N}^2$ totally ordered as follows:

$$\begin{aligned} (i_1,n_1)<(i_2,n_2) \quad \text { if } \quad i_1+n_1<i_2+n_2 \quad \text { or } \quad i_1+n_1=i_2+n_2 \ \text { and } \ i_1<i_2. \end{aligned}$$

The picture below illustrates the order.

It follows immediately by definition of $h_n$ that $h_n(\textbf{z}_0)=h_n(\textbf{x}_0)=\textbf{x}_0$ and $h_n(\textbf{z}_1)=h_n(\textbf{x}_0')=\partial \textbf{x}_0=\textbf{x}_1$ for all $n\ge 0$. Hence the assertion $h_n(\textbf{z}_i)=\textbf{x}_i$ is clear for $i\le 1$ and any n, in particular for the base step (0, 0). Assume then $i>1$ and that $h_s(\textbf{z}_j)= \textbf{x}_j$ for any $(0,0)\le (j,s)<(i,n)$. By Lemma 4.8, the commutativity of the above square and the induction step, we have

$$\begin{aligned} h_n(\textbf{z}_i)= & {} h_n\left( \delta \textbf{z}_{i-1}+H_i(\textbf{z}_0,\dots ,\textbf{z}_{i-2},\delta \textbf{z}_0,\dots , \delta \textbf{z}_{i-2}) \right) \\= & {} h_n(\delta \textbf{z}_{i-1})+ H_i(h_n(\textbf{z}_0),\dots ,h_n(\textbf{z}_{i-2}),h_n(\delta \textbf{z}_0),\dots , h_n(\delta \textbf{z}_{i-2})) \\= & {} \partial (h_{n-1} (\textbf{z}_{i-1}))+ H_i(\textbf{x}_0,\dots ,\textbf{x}_{i-2},\partial h_{n-1}( \textbf{z}_0),\dots , \partial h_{n-1}( \textbf{z}_{i-2})) \\= & {} \partial \textbf{x}_{i-1}+ H_i(\textbf{x}_0,\dots ,\textbf{x}_{i-2},\partial \textbf{x}_0,\dots , \partial \textbf{x}_{i-2}) \\= & {} \textbf{x}_i. \end{aligned}$$

$\square$