1 Introduction

Tensor methods are prominent tools in a wide range of applications involving high-dimensional data or functions. The exploitation of low-rank structures of tensors is the basis of many approximation or dimension reduction methods, see the surveys [2,3,4, 15, 18, 19] and monograph [11]. Providing a geometrical description of sets of low-rank tensors has many interests. In particular, it allows to devise robust algorithms for optimization [1, 24] or construct reduced order models for dynamical systems [14].

A basic low-rank tensor format is the Tucker format. Given a collection of d vector spaces \(V_\nu \), \(\nu \in D:= \{1,\hdots ,d\}\), and the corresponding algebraic tensor space \({\textbf{V}}_D = V_1 \otimes \hdots \otimes V_d,\) the set of tensors \({\mathfrak {M}}_{{\mathfrak {r}}}({\textbf{V}}_D)\) of tensors in Tucker format with rank \({\mathfrak {r}} = (r_1,\hdots ,r_d)\) is the set of tensors \({\textbf{v}}\) in \({\textbf{V}}_D\) such that \( {\textbf{v}} \in U_1\otimes \hdots \otimes U_d \) for some subspaces \(U_\nu \) in the Grassmann manifold \({\mathbb {G}}_{r_\nu }(V_\nu )\) of \(r_\nu \)-dimensional spaces in \(V_\nu .\) A geometrical description of \({\mathfrak {M}}_{{\mathfrak {r}}}({\textbf{V}}_D)\) has been introduced in [8], providing this set the structure of a \(C^\infty \)-Banach manifold. Tree-based tensor formats [7], also known as tree tensor networks in physics or data science [9, 17, 20, 22], are more general low-rank tensor formats, also based on subspaces. They include the hierarchical format [12] or the tensor-train format [21]. Sets of tensors in tree-based tensor format are the intersection of a collection of sets of tensors in Tucker format associated with a hierarchy of partitions given by a tree. More precisely, given a tree \(T_D\) over D (see Definition 3.2 below for a more precise description), we can define a sequence of partitions \({\mathcal {P}}_1, \hdots , {\mathcal {P}}_L\) of D, with L the depth of the tree, such that each element in \({\mathcal {P}}_k\) is a subset of an element of \( {\mathcal {P}}_{k-1}\) (see example in Fig. 1). For each partition \({{\mathcal {P}}_k}\), a tensor in \({\textbf{V}}_D\) can be identified with a tensor in \({\textbf{V}}_{{\mathcal {P}}_k}:= \bigotimes _{\alpha \in {\mathcal {P}}_k} {\textbf{V}}_{\alpha }\), that allows to define manifolds of tensors in Tucker format \({\mathfrak {M}}_{{\mathfrak {r}}_k}({\textbf{V}}_{{\mathcal {P}}_k})\) with \({\mathfrak {r}}_k \in {\mathbb {N}}^{\# {\mathcal {P}}_k}\). The set \({{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}({\textbf{V}}_D)\) of tensors in \({\textbf{V}}_D\) with tree-based rank \({\mathfrak {r}} = (r_\alpha )_{\alpha \in T_D} \in {\mathbb {N}}^{\#T_D}\) is then given by

$$\begin{aligned} {{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}({\textbf{V}}_D) = \bigcap _{k=1}^L {\mathfrak {M}}_{{\mathfrak {r}}_k}({\textbf{V}}_{{\mathcal {P}}_k}) \end{aligned}$$

where \({\mathfrak {r}}_k = (r_\alpha )_{\alpha \in {\mathcal {P}}_k}\).

In this paper, we provide a new geometrical description of the sets \({{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}({\textbf{V}}_D)\) of tensors with fixed tree-based rank in tensor Banach spaces. This description is compatible with the one of manifolds \( {\mathfrak {M}}_{{\mathfrak {r}}_k}({\textbf{V}}_{{\mathcal {P}}_k})\) introduced in [8]. It is different from the ones from [23] and [13], respectively introduced for hierarchical and tensor train formats in finite-dimensional tensor spaces. It is also different from the one introduced by the authors in [6], that provided a different chart system. The present geometrical description is more natural and we believe that it is more amenable to understand the geometry and topology of the different tensor formats based on subspaces. With the present description, and under similar assumptions on the norms of tensor spaces, Theorem 5.2 and Theorem 5.4 in [8] also hold for tree-based tensor formats, that allows to extend the Dirac–Frenkel variational principle for tree-based tensor formats in tensor Banach spaces.

The outline of this note is as follows. We start in Sect. 2 by recalling results from [8]. Then in Sect. 3 we introduce a description of tree-based tensor formats \({{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}({\textbf{V}}_D)\) as an intersection of Tucker formats. Section 4 is devoted to the geometrical description of manifolds \({\mathfrak {M}}_{{\mathfrak {r}}}({\textbf{V}}_D)\) of tensors in Tucker format with fixed rank. Finally in Sect. 5, we introduce the new geometrical description of the manifold \({{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}({\textbf{V}}_D)\) of tensors in tree-based tensor format with fixed tree-based. We prove that it is an immersed manifold in the ambient tensor Banach space and outline the extension of the Dirac–Frenkel variational principle for tree-based tensor formats in tensor Banach spaces.

2 Preliminary results

Let \(D:=\{1,\ldots ,d\}\) be a finite index set and consider an algebraic tensor space \( {\textbf{V}}_D = \bigotimes _{\alpha \in D} V_{\alpha }\) generated from vector spaces \(V_{\alpha }\), \(\alpha \in D\). Concerning the definition of the algebraic tensor space we refer to Greub [10]. For any partition \({\mathcal {P}}_D\) of D, the algebraic tensor space \( {\textbf{V}}_D \) can be identified with an algebraic tensor space generated from vector spaces \({\textbf{V}}_{\alpha }\), \(\alpha \in {\mathcal {P}}_D\). Indeed, for any partition \({\mathcal {P}}_D\) of D,  the equality

$$\begin{aligned} {\textbf{V}}_D = \left. \bigotimes _{\alpha \in {\mathcal {P}}_D} {\textbf{V}}_{\alpha } \right. \end{aligned}$$

holds, with \({\textbf{V}}_{\alpha }:= \left. \bigotimes _{j \in \alpha } V_j \right. \) if \(\alpha \ne \{j\},\) for some \(j \in D,\) or \({\textbf{V}}_{\alpha }=V_j\) if \(\alpha = \{j\}\) for some \(j \in D.\) Next we identify D with the trivial partition \(\{\{1\},\{2\},\ldots ,\{d\}\}.\)

Remark 2.1

In [8], we considered the tensor space \( {\textbf{V}}_D = \bigotimes _{\alpha \in D} V_{\alpha }\) for a given D. It is not difficult to check that the results from [8] remain true when substituting D by any partition \({\mathcal {P}}_D\), that includes the initial case by identifying D with the trivial partition \(\{\{1\},\{2\},\ldots ,\{d\}\}.\) More precisely, we can substitute with minor changes along the paper “\(\alpha \in D\)” by “\(\alpha \in {\mathcal {P}}_D\)”.

Before restating Theorem 3.17 of [8] in the present framework, we recall some definitions from [8].

Fig. 1
figure 1

A tree over \(D = \{1,2,3,4\}\), with depth \(L=3\), and the associated partitions of D: \({\mathcal {P}}_3 = \{\{1\},\{2\},\{3\},\{4\}\}\), \({\mathcal {P}}_2 = \{\{1\},\{2,3\},\{4\}\}\), \({\mathcal {P}}_1=\{\{1,2,3\},\{4\}\}\)

Full size image

Let X and Y be Banach spaces. We denote by \({\mathcal {L}}(X,Y)\) the space of continuous linear mappings from X into Y. The corresponding operator norm is written as \(\left\| \cdot \right\| _{Y\leftarrow X}.\) It is well known that if Y is a Banach space then \(({\mathcal {L}}(X,Y),\Vert \cdot \Vert _{Y\leftarrow X})\) is also a Banach space.

Let X be a Banach space. We denote by \({\mathbb {G}}(X)\) the Grassmann manifold of closed subspaces in X (see Section 2 in [8]). More precisely, we say that \(U\in {\mathbb {G}}(X)\) holds if and only if U is a closed subspace in X and there exists a closed subspace W in X such that \(X=U\oplus W.\) Every finite-dimensional subspace of X belongs to \({\mathbb {G}}(X),\) and we denote by \({\mathbb {G}}_{n}(X)\) the space of all n-dimensional subspaces of X \((n\ge 0).\) From Proposition 2.11 in [8], the Banach space \({\mathcal {L}}(U,W)\) can be identified with an element of \({\mathbb {G}}({\mathcal {L}}(X,X)).\) Hence it is a closed subspace of \({\mathcal {L}}(X,X).\)

Assume that \({\mathcal {P}}_D\) is a partition of D and \(({\textbf{V}}_{\alpha },\Vert \cdot \Vert _{\alpha })\) is a normed space for each \(\alpha \in {\mathcal {P}}_D.\) Following [5], it is possible to construct for each \(\alpha \in {\mathcal {P}}_D\) a map

$$\begin{aligned} U_{\alpha }^{\min }:{\mathbb {V}}_D \longrightarrow {\mathbb {G}}({\textbf{V}}_{\alpha }), \quad {\textbf{v}} \mapsto U_{\alpha }^{\min }({\textbf{v}}) \end{aligned}$$

which satisfies the following properties:

  1. i)

    \(\dim U_{\alpha }^{\min }({\textbf{v}}) < \infty ,\) for all \({\textbf{v}} \in {\mathbb {V}}_D.\)

  2. ii)

    \({\textbf{v}} \in \left. \bigotimes _{\alpha \in {\mathcal {P}}_D} U_{\alpha }^{\min }({\textbf{v}})\right. \) and if there exist subspaces \({\textbf{U}}_{\alpha } \subset {\textbf{V}}_{\alpha }\) for each \(\alpha \in {\mathcal {P}}_D\) such that \({\textbf{v}} \in \left. \bigotimes _{\alpha \in {\mathcal {P}}_D} {\textbf{U}}_{\alpha }\right. ,\) then \(U_{\alpha }^{\min }({\textbf{v}}) \subset {\textbf{U}}_{\alpha }\) for each \(\alpha \in {\mathcal {P}}_D.\)

The linear subspace \(U_{\alpha }^{\min }({\textbf{v}})\) is called a minimal subspace of \({\textbf{v}}\) in \({\textbf{V}}_D.\) In consequence, given a fixed partition \({\mathcal {P}}_D\) of D,  we can define for each \({\textbf{v}} \in {\textbf{V}}_D\) its \(\alpha \)-rank as \(\dim U_{\alpha }^{\min }({\textbf{v}})\) for \(\alpha \in {\mathcal {P}}_D.\) The \({\mathcal {P}}_D\)-rank for each \({\textbf{v}} \in {\textbf{V}}_D\) is given by the tuple \((\dim U_{\alpha }^{\min }({\textbf{v}}))_{\alpha \in {\mathcal {P}}_D} \in {\mathbb {N}}^{\#{\mathcal {P}}_D}.\)

Given \({\mathfrak {r}}=(r_{\alpha })_{\alpha \in {\mathcal {P}}_D} \in {\mathbb {N}}^{\#{\mathcal {P}}_D},\) we define the set of tensors in \({\textbf{V}}_{D}\) represented in Tucker format with a fixed rank \({\mathfrak {r}}\) as

$$\begin{aligned} {\mathfrak {M}}_{{\mathfrak {r}}}({\textbf{V}}_{D})=\left\{ {\textbf{v}} \in {\textbf{V}}_{D}: \dim U_{\alpha }^{\min }({\textbf{v}}) = r_{\alpha } \text { for each } \alpha \in {\mathcal {P}}_D \right\} . \end{aligned}$$

A tensor \({\textbf{v}} \in {\mathfrak {M}}_{{\mathfrak {r}}}( {\textbf{V}}_{D})\) if and only if for each \(\alpha \in {\mathcal {P}}_D\) there exists a unique subspace \(U_{\alpha }^{\min }({\textbf{v}}) \in {\mathbb {G}}_{r_{\alpha }}({\textbf{V}}_{\alpha })\) such that \({\textbf{v}} \in \left. \bigotimes _{\alpha \in {\mathcal {P}}_D}U_{\alpha }^{\min }({\textbf{v}}) \right. .\) Observe, that

$$\begin{aligned} {\mathfrak {M}}_{{\mathfrak {r}}}\left( \left. \bigotimes _{\alpha \in {\mathcal {P}}_D}U_{\alpha }^{\min }({\textbf{v}}) \right. \right) =\left\{ {\textbf{v}} \in \left. \bigotimes _{\alpha \in {\mathcal {P}}_D}U_{\alpha }^{\min }({\textbf{v}}) \right. : \dim U_{\alpha }^{\min }({\textbf{v}}) = r_{\alpha } \text { for each } \alpha \in {\mathcal {P}}_D \right\} \end{aligned}$$

is the set of full rank tensors in the finite dimensional space \(\left. \bigotimes _{\alpha \in {\mathcal {P}}_D}U_{\alpha }^{\min }({\textbf{v}})\!\!\right. .\) Assume that \(\Vert \cdot \Vert _D\) is a norm on the tensor space \(\textbf{V}_D\) and hence \((\textbf{V}_D,\Vert \cdot \Vert _D)\) is a normed space. Clearly, \(\left. \bigotimes _{\alpha \in {\mathcal {P}}_D}U_{\alpha }^{\min }({\textbf{v}}) \right. \) is also a normed space and it can be shown that \({\mathfrak {M}}_{{\mathfrak {r}}}\left( \left. \bigotimes _{\alpha \in {\mathcal {P}}_D}U_{\alpha }^{\min }({\textbf{v}}) \right. \right) \) is an open set in \(\left. \bigotimes _{\alpha \in {\mathcal {P}}_D}U_{\alpha }^{\min }({\textbf{v}})\right. ,\) and hence a manifold.

Recall that for each fixed \(\alpha \in {\mathcal {P}}_D,\) the finite dimensional vector space \(U_{\alpha }^{\min }({\textbf{v}})\) is linearly isomorphic to the vector space

$$\begin{aligned} {\mathbb {R}}^{\dim U_{\alpha }({\textbf{v}})} = {\mathbb {R}}^{r_{\alpha }} \end{aligned}$$

for all \({\textbf{v}} \in {\mathfrak {M}}_{{\mathfrak {r}}}({\textbf{V}}_{D}).\) Hence the finite dimensional vector space \(\left. \bigotimes _{\alpha \in {\mathcal {P}}_D}U_{\alpha }^{\min }({\textbf{v}})\right. \) is linearly isomorphic to the vector space This fact allows to identify the open set of full rank tensors in denoted by with \({\mathfrak {M}}_{{\mathfrak {r}}}\left( \left. \bigotimes _{\alpha \in {\mathcal {P}}_D}U_{\alpha }^{\min }({\textbf{v}}) \right. \right) .\)

3 The set of tensors in tree-based format with fixed tree-based rank

To introduce the set of tensors in tree-based format with fixed tree-based rank we shall use the minimal subspaces, in particular, Proposition 2.6 in [8] (see also [5] or [11]). Let \({\mathcal {P}}_D\) be a given partition of D. By definition of the minimal subspaces \(U_{\alpha }^{\min }({\textbf{v}}),\) \(\alpha \in {\mathcal {P}}_D\), we have

$$\begin{aligned} {\textbf{v}} \in \left. \bigotimes _{\alpha \in {\mathcal {P}}_D} U_{\alpha }^{\min }({\textbf{v}} )\right. . \end{aligned}$$

For a given \(\alpha \in {\mathcal {P}}_D\) with \(\#\alpha \ge 2\) and any partition \({\mathcal {P}}_{\alpha }\) of \(\alpha \), we also have

$$\begin{aligned} {\textbf{v}} \in \left( \left. \bigotimes _{\beta \in {\mathcal {P}}_{\alpha }} U_{\beta }^{\min }({\textbf{v}}) \right. \right) \otimes \left( \left. \bigotimes _{\delta \in {\mathcal {P}}_D\setminus \{\alpha \}} U_{\delta }^{\min }({\textbf{v}}) \right. \right) . \end{aligned}$$

Given D we will denote its power set (the set of all subsets of D) by \(2^D.\) We recall a useful result on the relation between minimal subspaces (see Section 2 in [5]).

Proposition 3.1

For any \(\alpha \in 2^D\) with \(\#\alpha \ge 2\) and any partition \({\mathcal {P}}_{\alpha }\) of \(\alpha \), it holds

$$\begin{aligned} U_{\alpha }^{\min }({\textbf{v}})\subset \left. \bigotimes _{\beta \in {\mathcal {P}}_{\alpha }}U_{\beta }^{\min }({\textbf{v}})\right. . \end{aligned}$$

In order to define tree-based tensor format we introduce three definitions.

Definition 3.2

(Dimension partition tree) A tree \(T_{D}\) is called a dimension partition tree over D if

  1. (a)

    all vertices \(\alpha \in T_D\) are non-empty subsets of D, 

  2. (b)

    D is the root of \(T_D,\)

  3. (c)

    every vertex \(\alpha \in T_{D}\) with \(\#\alpha \ge 2\) has at least two sons and the set of sons of \(\alpha \), denoted \(S(\alpha )\), is a non-trivial partition of \(\alpha \),

  4. (d)

    every vertex \(\alpha \in T_D\) with \(\#\alpha = 1\) has no son and is called a leaf.

The set of leaves is denoted by \({\mathcal {L}}(T_{D}).\)

A straightforward consequence of Definition  3.2 is that the set of leaves \({\mathcal {L}}(T_{D})\) coincides with the singletons of D,  i.e., \({\mathcal {L}}(T_{D})=\{\{j\}:j\in D\}\).

Definition 3.3

(Levels, depth and partitions) The levels of the vertices of a dimension partition tree \(T_D\), denoted by \(\textrm{level}(\alpha )\), \(\alpha \in T_D\), are integers defined such that \(\textrm{level}(D) = 0\) and for any pair \(\alpha ,\beta \in T_D\) such that \(\beta \in S(\alpha ),\) \(\textrm{level}(\beta ) = \textrm{level}(\alpha )+1\). The depth of the tree \(T_D\) is defined as \(\textrm{depth}(T_D) = \max _{\alpha \in T_D} \textrm{level}(\alpha ).\) Then to each level k of \(T_D\), \(1\le k\le \textrm{depth}(T_D)\), is associated a partition of D : 

$$\begin{aligned} {\mathcal {P}}_k(T_D) = \{\alpha \in T_D: \textrm{level}(\alpha ) = k\} \cup \{\alpha \in {\mathcal {L}}(T_D): \textrm{level}(\alpha )<k\}. \end{aligned}$$

Remark 3.4

Note that for any tree, \({\mathcal {P}}_{1}(T_D) = S(D)\) and \({\mathcal {P}}_{\textrm{depth}(T_D)}(T_D) = {\mathcal {L}}(T_D)\). Also note that some of the leaves of \(T_D\) may be contained in several partitions, and if \(\alpha \in {\mathcal {L}}(T_D)\), then \(\alpha \in {\mathcal {P}}_k(T_D)\) for \(\textrm{level}(\alpha ) \le k \le \textrm{depth}(T_D)\).

For any partition \({\mathcal {P}}_k(T_D)\) of level k, \(1\le k\le \textrm{depth}(T_D)\), we use the identification

$$\begin{aligned} {\textbf{V}}_D = \left. \bigotimes _{\alpha \in {\mathcal {P}}_k(T_D)} {\textbf{V}}_\alpha \right. . \end{aligned}$$

This leads us to the following definition of the representation of the tensor space \({\textbf{V}}_D\) in tree-based format.

Definition 3.5

For a tensor space \({\textbf{V}}_D\) and a dimension partition tree \(T_{D}\), the pair \(({\textbf{V}}_D,T_D)\) is called a representation of the tensor space \({\textbf{V}}_{D}\) in tree-based format, and corresponds to the identification of \({\textbf{V}}_D \) with tensor spaces \( \left. \bigotimes _{\alpha \in {\mathcal {P}}_k(T_D)} {\textbf{V}}_\alpha \right. \) of different levels k, \(1\le k \le \textrm{depth}(T_D). \)

Remark 3.6

By Proposition 3.1, for each \({\textbf{v}} \in {\textbf{V}}_{D},\) it holds that

$$\begin{aligned} {\textbf{v}} \in \left. \bigotimes _{\alpha \in {\mathcal {P}}_1(T_D)}U_{\alpha }^{\min }({\textbf{v}}) \right. \subset \left. \bigotimes _{\alpha \in {\mathcal {P}}_2(T_D)}U_{\alpha }^{\min }({\textbf{v}}) \right. \subset \cdots \subset \left. \bigotimes _{\alpha \in {\mathcal {P}}_{\textrm{depth}(T_D)}(T_D)}U_{\alpha }^{\min }({\textbf{v}}) \right. . \end{aligned}$$

Example 3.7

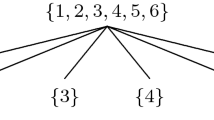
(Tucker format) In Fig. 2, \(D=\{1,2,3,4,5,6\} \) and

$$\begin{aligned} T_D=\{D,\{1\},\{2\},\{3\},\{4\},\{5\},\{6\}\}. \end{aligned}$$

Here \(\textrm{depth}(T_D)=1\) and \({\mathcal {P}}_1(T_D) = {\mathcal {L}}(T_D).\) This tree is related to the basic identification of \({\textbf{V}}_{D}\) with \(\left. \bigotimes _{j=1}^{6}V_{j}\right. .\)

Fig. 2
figure 2

A dimension partition tree with \(\textrm{depth}(T_D)=1\) (Tucker tree)

Full size image

Example 3.8

In Fig. 3, \(D=\{1,2,3,4,5,6\}\) and

$$\begin{aligned} T_D=\{D,\{1,2,3\},\{4,5\},\{2,3\},\{1\},\{2\},\{3\},\{4\},\{5\},\{6\}\}. \end{aligned}$$

Here \(\textrm{depth}(T_D)=3\), \({\mathcal {P}}_1(T_D) = \{\{1,2,3\}, \{4,5\}, \{6\}\}\), \({\mathcal {P}}_2(T_D) = \{\{1\},\{2,3\}, \{4\},\{5\}, \{6\}\}\) and \({\mathcal {P}}_3(T_D) = {\mathcal {L}}(T_D).\) This tree is related to the identification of \({\textbf{V}}_{D}\) with \(\left. \bigotimes _{j=1}^{6}V_{j}\right. \), \({\textbf{V}}_{D} = {V} _{1}\otimes {\textbf{V}} _{23}\otimes {V}_{4}\otimes V_{5}\otimes V_{6} \) and \({\textbf{V}}_{D} = {\textbf{V}} _{123}\otimes {\textbf{V}}_{45}\otimes V_{6} \).

Fig. 3
figure 3

A dimension partition tree with \(\textrm{depth}(T_D)=3\)

Full size image

Let \({\mathbb {N}}_{0}:={\mathbb {N}} \cup \{0\} \) denote the set of non-negative integers. For each \({\textbf{v}} \in {\textbf{V}}_D\), we have that \((\dim {U}_{\alpha }^{\min }({\textbf{v}} ))_{\alpha \in 2^D {\setminus } \{\emptyset \}}\) is in \({\mathbb {N}}_0^{2^{\#D}-1}.\)

Definition 3.9

(Tree-based rank) For a given dimension partition tree \(T_D\) over D, we define the tree-based rank of a tensor \({\textbf{v}}\in {\textbf{V}}_{D}\) by the tuple \(\textrm{rank}_{T_D}( {\textbf{v}} ):= (\dim {U}_{\alpha }^{\min }( {\textbf{v}}))_{\alpha \in T_{D}}\in {\mathbb {N}}_0^{\#T_{D}}.\)

Definition 3.10

(Admissible ranks) A tuple \({\mathfrak {r}}:=(r_{\alpha })_{\alpha \in T_{D}}\in \mathbb {N }^{\#T_{D}}\) is said to be an admissible tuple for \(T_{D}\) if there exists \( {\textbf{v}}\in {\textbf{V}}_{D}\) such that \(\dim U_{\alpha }^{\min }({\textbf{v}})=r_{\alpha }\) for all \(\alpha \in T_{D}.\) The set of admissible ranks for the representation \(({\textbf{V}}_D,T_D)\) of the tensor space \({\textbf{V}}_D\) is denoted by

$$\begin{aligned} {{\mathcal {A}}}{{\mathcal {D}}}({\textbf{V}}_D,T_D):=\{(\dim U_{\alpha }^{\min }({\textbf{v}}))_{\alpha \in T_D}:{\textbf{v}} \in {\textbf{V}}_D\}. \end{aligned}$$

Definition 3.11

Let \(T_{D}\) be a given dimension partition tree and fix some tuple \( {\mathfrak {r}}\in {{\mathcal {A}}}{{\mathcal {D}}}({\textbf{V}}_D,T_D)\). Then the set of tensors of fixed tree-based rank \({\mathfrak {r}}\) is defined by

$$\begin{aligned} {{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}({\textbf{V}}_{D},T_D):=\left\{ {\textbf{v}}\in {\textbf{V}}_{D}:\dim {U}_{\alpha }^{\min }({\textbf{v}} )=r_{\alpha }\text { for all }\alpha \in T_{D}\right\} \end{aligned}$$
(3.1)

and the set of tensors of tree-based rank bounded by \({\mathfrak {r}}\) is defined by

$$\begin{aligned} {{\mathcal {F}}}{{\mathcal {T}}}_{\le {\mathfrak {r}}}({\textbf{V}}_{D},T_D):=\left\{ {\textbf{v}}\in {\textbf{V}}_{D}: \dim {U}_{\alpha }^{\min }({\textbf{v}})\le r_{\alpha }\text { for all }\alpha \in T_{D} \right\} . \end{aligned}$$
(3.2)

For \({\mathfrak {r}},{\mathfrak {s}}\in {\mathbb {N}}_0^{\#T_{D}}\) we write \({\mathfrak {s}}\le {\mathfrak {r}}\) if and only if \( s_{\alpha }\le r_{\alpha }\) for all \(\alpha \in T_{D}.\) Then for a fixed \({\mathfrak {r}} \in {{\mathcal {A}}}{{\mathcal {D}}}({\textbf{V}}_D,T_D)\), we have

$$\begin{aligned} {{\mathcal {F}}}{{\mathcal {T}}}_{\le {\mathfrak {r}}}({\textbf{V}}_{D},T_D):= \bigcup _{\begin{array}{c} {\mathfrak {s}}\le {\mathfrak {r}} \\ {\mathfrak {s}} \in {{\mathcal {A}}}{{\mathcal {D}}}({\textbf{V}}_D,T_D) \end{array}}{{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {s}}}({\textbf{V}} _{D},T_D). \end{aligned}$$
(3.3)

For each partition \({\mathcal {P}}_k(T_D)\) of D, \(1 \le k \le \textrm{depth}(T_D)\), we can introduce a set of tensors in Tucker format with fixed rank \({\mathfrak {r}}_k:=(r_{\alpha })_{\alpha \in {\mathcal {P}}_k(T_D)}\) given by

$$\begin{aligned} {\mathfrak {M}}_{{\mathfrak {r}}_k}({\textbf{V}}_D,{\mathcal {P}}_k(T_D)) =\{ {\textbf{v}} \in {\textbf{V}}_D: \dim U_{\alpha }^{\min }({\textbf{v}})=r_{\alpha } \text { for } \alpha \in {\mathcal {P}}_k(T_D) \}. \end{aligned}$$

Theorem 3.12

For a dimension partition tree \(T_D\) and for \({\mathfrak {r}}=(r_{\alpha })_{\alpha \in T_D} \in {{\mathcal {A}}}{{\mathcal {D}}}({\textbf{V}}_D,T_D),\)

$$\begin{aligned} {{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}({\textbf{V}}_D,T_D) = \bigcap _{k=1}^{\textrm{depth}(T_D)} {\mathfrak {M}}_{{\mathfrak {r}}_k}({\textbf{V}}_D,{\mathcal {P}}_k(T_D)). \end{aligned}$$

Remark 3.13

We point out that in [8] we introduce a representation of \({\textbf{V}}_D\) in Tucker format. Letting \(T_D^{\text {Tucker}}\) be the Tucker dimension partition tree (see example 3.7) and given \({\mathfrak {r}} \in {{\mathcal {A}}}{{\mathcal {D}}}({\textbf{V}}_D,T_D^{\text {Tucker}})\), the set of tensors with fixed Tucker rank \({\mathfrak {r}}\) is defined by

$$\begin{aligned} {\mathfrak {M}}_{{\mathfrak {r}}}({\textbf{V}}_D):= {{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}({\textbf{V}}_{D},T_D^{\text {Tucker}}) = \left\{ {\textbf{v}} \in {\textbf{V}}_D: \dim U_{k}^{\min }({\textbf{v}}) = r_{k}, \, k \in {\mathcal {L}}(T_D^{\text {Tucker}}) \right\} . \end{aligned}$$

This leads to the following representation of \({\textbf{V}}_D\) in Tucker format:

$$\begin{aligned} {\textbf{V}}_D = \bigcup _{{\mathfrak {r}} \in {{\mathcal {A}}}{{\mathcal {D}}}({\textbf{V}}_D,T_D^{\text {Tucker}})}{\mathfrak {M}}_{{\mathfrak {r}}}({\textbf{V}}_D). \end{aligned}$$

Note that for any tree \(T_D\) with \(\textrm{depth}(T_D) = 1\),

$$\begin{aligned} {\mathfrak {M}}_{{\mathfrak {r}}_{\textrm{depth}(T_D)}}({\textbf{V}}_D,{\mathcal {P}}_{\textrm{depth}(T_D)}(T_D))= {\mathfrak {M}}_{{\mathfrak {r}}_{\textrm{depth}(T_D)}}({\textbf{V}}_D). \end{aligned}$$

Finally, we need to take into account the following situation. Let \(T_D\) be the rooted tree given in Fig. 4. For this rooted tree we have \(\textrm{depth}(T_D)=2\) and also

$$\begin{aligned} {\mathcal {P}}_1(T_D)&=\{\{1\},\{2,3,4,5,6\}\}, \\ {\mathcal {P}}_2(T_D)&= \{\{1\},\{2\},\{3\},\{4\},\{5\},\{6\}\}. \end{aligned}$$

From Lemma 2.4 in [5] it can be shown that \(\dim U_{\{1\}}^{\min }({\textbf{v}}) = \dim U_{\{2,3,4,5,6\}}^{\min }({\textbf{v}})\) holds for all \({\textbf{v}} \in {\textbf{V}}_D.\) Hence

$$\begin{aligned} {{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}({\textbf{V}}_D,T_D) = {\mathfrak {M}}_{{\mathfrak {r}}_1}({\textbf{V}}_D,{\mathcal {P}}_1(T_D)) \cap {\mathfrak {M}}_{{\mathfrak {r}}_2}({\textbf{V}}_D,{\mathcal {P}}_2(T_D)) = {\mathfrak {M}}_{{\mathfrak {r}}_2}({\textbf{V}}_D,{\mathcal {P}}_2(T_D)) \end{aligned}$$

holds because

$$\begin{aligned} {\mathfrak {M}}_{{\mathfrak {r}}_1}({\textbf{V}}_D,{\mathcal {P}}_1(T_D))&=\{ {\textbf{v}} \in {\textbf{V}}_D: \dim U_{\{1\}}^{\min }({\textbf{v}}) = r_{\{1\}} = \dim U_{\{2,3,4,5,6\}}^{\min }({\textbf{v}}) \} \end{aligned}$$

contains

$$\begin{aligned} {\mathfrak {M}}_{{\mathfrak {r}}_2}({\textbf{V}}_D,{\mathcal {P}}_2(T_D))&=\{ {\textbf{v}} \in {\textbf{V}}_D: \dim U_{\{i\}}^{\min }({\textbf{v}}) = r_{\{i\}}, \, 1 \le i \le 6 \} . \end{aligned}$$
Fig. 4
figure 4

A dimension partition tree with \(\textrm{depth}(T_D)=2\)

Full size image

Thus in order to avoid this situation we introduce the following definition.

Definition 3.14

For a dimension partition tree \(T_D\) and for \({\mathfrak {r}}=(r_{\alpha })_{\alpha \in T_D} \in {{\mathcal {A}}}{{\mathcal {D}}}({\textbf{V}}_D,T_D),\) we will say that \({{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}({\textbf{V}}_D,T_D)\) is a proper set of tree-based tensors with a fixed tree-based rank \({\mathfrak {r}}\) if

$$\begin{aligned} {{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}({\textbf{V}}_D,T_D) \ne {\mathfrak {M}}_{{\mathfrak {r}}_k}({\textbf{V}}_D,{\mathcal {P}}_k(T_D)) \text { holds for } 1 \le k \le \textrm{depth}(T_D). \end{aligned}$$

4 The manifold of tensors in Tucker format with fixed rank

In this section we start by introducing the geometric structure of the set of tensors in Tucker format with fixed rank in our framework. Next, we give an equivalent result that allows us to provide a manifold structure to a proper set of tree-based tensors with a fixed tree-based rank.

Assume that \({\mathcal {P}}_D\) is a partition of D and \(({\textbf{V}}_{\alpha },\Vert \cdot \Vert _{\alpha })\) is a normed space for each \(\alpha \in {\mathcal {P}}_D.\) We will consider the product space equipped with the product topology induced by the maximum norm \(\Vert ({\textbf{v}}_{\alpha })_{\alpha \in {\mathcal {P}}_D})\Vert _{\times } = \max _{\alpha \in {\mathcal {P}}_D} \Vert {\textbf{v}}_{\alpha }\Vert _{\alpha }.\) Then, from Theorem 3.17 in [8], we have the following result.

Theorem 4.1

Assume that \({\mathcal {P}}_D\) is a partition of D,  \(({\textbf{V}}_{\alpha },\Vert \cdot \Vert _{\alpha })\) is a normed space for each \(\alpha \in {\mathcal {P}}_D\) and that \(\Vert \cdot \Vert _D\) is a norm on the tensor space \({\textbf{V}}_D = \left. \bigotimes _{\alpha \in {\mathcal {P}}_D}{\textbf{V}}_{\alpha }\right. \) such that the tensor product map

(4.1)

is continuous. Then there exists a \({\mathcal {C}}^{\infty }\)-atlas \(\{{\mathcal {U}}({\textbf{v}}),{\widetilde{\xi }}_{{\textbf{v}}}\}_{{\textbf{v}}\in {\mathfrak {M}}_{{\mathfrak {r}}}({\textbf{V}}_{D})}\) for \({\mathfrak {M}}_{{\mathfrak {r}}}( {\textbf{V}}_{D})\) and hence \({\mathfrak {M}}_{{\mathfrak {r}}}( {\textbf{V}}_{D})\) is a \({\mathcal {C}}^{\infty }\)-Banach manifold modelled on a Banach space

Here \({\textbf{U}}_{\alpha } \in {\mathbb {G}}_{r_{\alpha }}({\textbf{V}}_{\alpha })\) and \({\textbf{V}}_{\alpha _{\Vert \cdot \Vert _{\alpha }}} = {\textbf{U}}_{\alpha } \oplus {\textbf{W}}_{\alpha },\) where \({\textbf{V}}_{{\alpha }_{\Vert \cdot \Vert _{\alpha }}}\) is the completion of \({\textbf{V}}_{\alpha }\) for \(\alpha \in {\mathcal {P}}_D.\)

To define a manifold structure (see [16]) we did not require that the vector spaces involved as coordinates are the same or even linearly isomorphic. In our case, we have that \(U_{\alpha }^{\min }({\textbf{v}})\) is linearly isomorphic to \(U_{\alpha }^{\min }({\textbf{w}})\) for all \({\textbf{w}} \in {\mathfrak {M}}_{{\mathfrak {r}}}({\textbf{V}}_{D})\). Thus, we fix one \({\textbf{U}}_{\alpha } = U_{\alpha }^{\min }({\textbf{v}})\) and hence it can be shown that \({\mathcal {L}}({\textbf{U}}_{\alpha },{\textbf{W}}_{\alpha })\) is linearly isomorphic to \({\mathcal {L}}(U_{\alpha }^{\min }({\textbf{w}}),W_{\alpha }^{\min }({\textbf{w}}))\) for all \({\textbf{w}} \in {\mathfrak {M}}_{{\mathfrak {r}}}({\textbf{V}}_{D}),\) where \(W_{\alpha }^{\min }({\textbf{w}})\) is linearly isomorphic to \({\textbf{W}}_{\alpha }\) and satisfies \({\textbf{V}}_{{\alpha }_{\Vert \cdot \Vert _{\alpha }}} = U_{\alpha }^{\min }({\textbf{w}}) \oplus W_{\alpha }^{\min }({\textbf{w}}).\) Moreover, \(\left. \bigotimes _{\alpha \in {\mathcal {P}}_D}{\textbf{U}}_{\alpha } \right. \) is linearly isomorphic to \(\left. \bigotimes _{\alpha \in {\mathcal {P}}_D}U_{\alpha }^{\min }({\textbf{w}}) \right. \) for all \({\textbf{w}} \in {\mathfrak {M}}_{{\mathfrak {r}}}({\textbf{V}}_{D}).\) In consequence, \({\mathfrak {M}}_{{\mathfrak {r}}}({\textbf{V}}_{D})\) has a geometric structure modelled on the Banach space

which is linearly isomorphic to

The atlas \(\{{\mathcal {U}}({\textbf{v}}),{\widetilde{\xi }}_{{\textbf{v}}}\}_{{\textbf{v}}\in {\mathfrak {M}}_{{\mathfrak {r}}}({\textbf{V}}_{D})}\) from Theorem 4.1 is composed by a subset \({\mathcal {U}}({\textbf{v}}) \subset {\mathfrak {M}}_{{\mathfrak {r}}}({\textbf{V}}_{D})\) containing \({\textbf{v}}\) and a bijection \({\widetilde{\xi }}_{{\textbf{v}}}\) from \({\mathcal {U}}({\textbf{v}})\) to the open set

which is contained in the Banach space

From Lemma 3.12 in [8], for \({\textbf{w}} \in {\mathcal {U}}({\textbf{v}}),\) we have \({\widetilde{\xi }}_{{\textbf{v}}}({\textbf{w}}) = ((L_{\alpha })_{\alpha \in {\mathcal {P}}_D},{\textbf{u}})\) if and only if

$$\begin{aligned} {\textbf{w}} ={\widetilde{\xi }}_{{\textbf{v}}}^{-1}((L_{\alpha })_{\alpha \in {\mathcal {P}}_D},{\textbf{u}}) = \left( \bigotimes _{\alpha \in {\mathcal {P}}_D} \exp (L_{\alpha })\right) ({\textbf{u}}). \end{aligned}$$

In particular, we have \({\widetilde{\xi }}_{{\textbf{v}}}({\textbf{v}}) = ((0_{\alpha })_{\alpha \in {\mathcal {P}}_D},{\textbf{v}}),\) where \(0_{\alpha }\) denotes the zero map in \({\mathcal {L}}({\textbf{U}}_{\alpha },{\textbf{W}}_{\alpha }).\)

We recall that \(\overline{{\textbf{V}}_D}^{\Vert \cdot \Vert _D} = {\textbf{V}}_{D_{\Vert \cdot \Vert _D}}\) denotes the tensor Banach space obtained as the completion of the algebraic tensor space \({\textbf{V}}_D\) under the norm \(\Vert \cdot \Vert _D.\) In the case where \({\textbf{V}}_D\) is finite dimensional, \( {\textbf{V}}_{D_{\Vert \cdot \Vert _D}} = {\textbf{V}}_D\). Otherwise, \( {\textbf{V}}_D \subsetneq {\textbf{V}}_{D_{\Vert \cdot \Vert _D}}\). Our next step is, given a fixed partition \({\mathcal {P}}_D\) of D,  to identify the Banach space with a closed subspace of the Banach algebra \({\mathcal {L}}({\textbf{V}}_{D_{\Vert \cdot \Vert _D}},{\textbf{V}}_{D_{\Vert \cdot \Vert _D}}).\) To this end, we need to proceed in the framework of Section 4 in [8]. First, we recall the definition of injective norm (Definition 4.9 in [8]) stated in the present framework.

Definition 4.2

Let \({\textbf{V}}_{\alpha }\) be a Banach space with norm \(\left\| \cdot \right\| _{\alpha }\) for \(\alpha \in {\mathcal {P}}_D.\) Then for \({\textbf{v}}\in {\textbf{V}}=\left. \bigotimes _{\alpha \in {\mathcal {P}}_D}{\textbf{V}}_{\alpha }\right. \) define \(\left\| \cdot \right\| _{\vee (({\textbf{V}}_{\alpha })_{\alpha \in {\mathcal {P}}_D})}\) by

$$\begin{aligned} \left\| {\textbf{v}}\right\| _{\vee (({\textbf{V}}_{\alpha })_{\alpha \in {\mathcal {P}}_D})}:=\sup \left\{ \frac{ \left| \left( \bigotimes _{\alpha \in {\mathcal {P}}_D}\varphi _{\alpha }\right) ({\textbf{v}})\right| }{\prod _{\alpha \in {\mathcal {P}}_D}\Vert \varphi _{\alpha }\Vert _{\alpha }^{*}}:0\ne \varphi _{\alpha }\in {\textbf{V}}_{\alpha }^{*},\alpha \in {\mathcal {P}}_D\right\} , \end{aligned}$$
(4.2)

where \({\textbf{V}}_{\alpha }^{*}\) is the continuous dual of \({\textbf{V}}_{\alpha }\).

Let W and U be closed subspaces of a Banach space X such that \( X=U\oplus W.\) From now on, we will denote by \(P_{_{U\oplus W}}\) the projection onto U along W. Then we have \(P_{_{W\oplus U}}=id_{X}-P_{_{U\oplus W}}.\) The proof of the next result uses Proposition 2.8, Lemma 4.13 and Lemma 4.14 in [8].

Lemma 4.3

Assume that \(({\textbf{V}}_{\alpha },\Vert \cdot \Vert _{\alpha })\) is a normed space for each \(\alpha \in {\mathcal {P}}_D\) and let \(\Vert \cdot \Vert _D\) be a norm on the tensor space \({\textbf{V}}_D = \left. \bigotimes _{\alpha \in {\mathcal {P}}_D}{\textbf{V}}_{\alpha }\right. \) such that

$$\begin{aligned} \left\| \cdot \right\| _{\vee (({\textbf{V}}_{\alpha })_{\alpha \in {\mathcal {P}}_D})}\lesssim \left\| \cdot \right\| _D, \end{aligned}$$
(4.3)

holds. Let \({\textbf{U}}_{\alpha } \in {\mathbb {G}}_{r_{\alpha }}({\textbf{V}}_{\alpha })\) and \({\textbf{V}}_{\alpha _{\Vert \cdot \Vert _{\alpha }}} = {\textbf{U}}_{\alpha } \oplus {\textbf{W}}_{\alpha },\) where \({\textbf{V}}_{{\alpha }_{\Vert \cdot \Vert _{\alpha }}}\) is the completion of \({\textbf{V}}_{\alpha }\) for \(\alpha \in {\mathcal {P}}_D.\) Then for each \(\alpha \in {\mathcal {P}}_D\) we have

$$\begin{aligned} {\mathcal {L}}\left( {\textbf{U}}_{\alpha },{\textbf{W}}_{\alpha } \right) \otimes \textrm{span}\{{{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]}\} \in {\mathbb {G}}\left( {\mathcal {L}}({\textbf{V}}_{D_{\Vert \cdot \Vert _D}},{\textbf{V}}_{D_{\Vert \cdot \Vert _D}})\right) \end{aligned}$$

where \({{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]}:= \bigotimes _{\beta \in {\mathcal {P}}_D {\setminus } \{\alpha \}} id_{{\textbf{V}}_{\beta }}.\) Furthermore,

$$\begin{aligned} \bigoplus _{\alpha \in {\mathcal {P}}_D}{\mathcal {L}}\left( {\textbf{U}}_{\alpha },{\textbf{W}}_{\alpha } \right) \otimes \textrm{span}\{{{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]}\} \in {\mathbb {G}}\left( {\mathcal {L}}({\textbf{V}}_{D_{\Vert \cdot \Vert _D}},{\textbf{V}}_{D_{\Vert \cdot \Vert _D}})\right) . \end{aligned}$$

Proof

To prove the lemma, for a fixed \(\alpha \in {\mathcal {P}}_D,\) note that \(id_{{\textbf{V}}_{\alpha }} = P_{_{{\textbf{U}}_{\alpha } \oplus {\textbf{W}}_{\alpha }}}+ P_{_{{\textbf{W}}_{\alpha }\oplus {\textbf{U}}_{\alpha } }}\) and write

$$\begin{aligned} id_{{\textbf{V}}_{D_{\Vert \cdot \Vert _D}}} = id_{{\textbf{V}}_{\alpha }} \otimes {{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]}. \end{aligned}$$

Since \({\textbf{U}}_{\alpha }\) is a finite dimensional space, \(P_{_{{\textbf{U}}_{\alpha }\oplus {\textbf{W}}_{\alpha } }}\) is a finite rank projection and hence \(P_{_{{\textbf{U}}_{\alpha }\oplus {\textbf{W}}_{\alpha } }} \otimes {{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]} \in {\mathcal {L}}({\textbf{V}}_{D_{\Vert \cdot \Vert _D}},{\textbf{V}}_{D_{\Vert \cdot \Vert _D}}).\) Then by proceeding as in the proof of Lemma 4.13 in [8] we obtain that

$$\begin{aligned} P_{_{{\textbf{W}}_{\alpha }\oplus {\textbf{U}}_{\alpha } }} \otimes {{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]} \in {\mathcal {L}}({\textbf{V}}_{D_{\Vert \cdot \Vert _D}},{\textbf{V}}_{D_{\Vert \cdot \Vert _D}}). \end{aligned}$$

Now, define the linear and bounded map

$$\begin{aligned} {\mathcal {P}}_{\alpha }:{\mathcal {L}}({\textbf{V}}_{D_{\Vert \cdot \Vert _D}},{\textbf{V}}_{D_{\Vert \cdot \Vert _D}}) \longrightarrow {\mathcal {L}}({\textbf{V}}_{D_{\Vert \cdot \Vert _D}},{\textbf{V}}_{D_{\Vert \cdot \Vert _D}}) \end{aligned}$$

as \({\mathcal {P}}_{\alpha }(L) = (P_{_{{\textbf{W}}_{\alpha }\oplus {\textbf{U}}_{\alpha } }} \otimes {{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]}) \circ L \circ (P_{_{{\textbf{U}}_{\alpha }\oplus {\textbf{W}}_{\alpha } }} \otimes {{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]}).\) It satisfies \({\mathcal {P}}_{\alpha } \circ {\mathcal {P}}_{\alpha } = {\mathcal {P}}_{\alpha }\) and

$$\begin{aligned} {\mathcal {P}}_{\alpha }({\mathcal {L}}({\textbf{V}}_{D_{\Vert \cdot \Vert _D}},{\textbf{V}}_{D_{\Vert \cdot \Vert _D}})) = {\mathcal {L}}\left( {\textbf{U}}_{\alpha },{\textbf{W}}_{\alpha } \right) \otimes \textrm{span}\{{{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]}\}. \end{aligned}$$

Proposition 2.8(b) in [8] implies that \({\mathcal {L}}\left( {\textbf{U}}_{\alpha },{\textbf{W}}_{\alpha } \right) \otimes \textrm{span}\{{{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]}\} \in {\mathbb {G}}\left( {\mathcal {L}}({\textbf{V}}_{D_{\Vert \cdot \Vert _D}},{\textbf{V}}_{D_{\Vert \cdot \Vert _D}})\right) .\) Observe that for \(\alpha ,\beta \in {\mathcal {P}}_D\) with \(\alpha \ne \beta \) we have

$$\begin{aligned} ({\mathcal {L}}\left( {\textbf{U}}_{\alpha },{\textbf{W}}_{\alpha } \right) \otimes \textrm{span}\{{{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]}\} ) \cap ({\mathcal {L}}\left( {\textbf{U}}_{\beta },{\textbf{W}}_{\beta } \right) \otimes \textrm{span}\{{{\textbf{i}}}{{\textbf{d}}}_{[\beta ]}\}) = \{{\textbf{0}}\}. \end{aligned}$$

By Lemma 4.14 in [8] we have

$$\begin{aligned} \bigoplus _{\alpha \in {\mathcal {P}}_D}{\mathcal {L}}\left( {\textbf{U}}_{\alpha },{\textbf{W}}_{\alpha } \right) \otimes \textrm{span}\{{{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]}\} \in {\mathbb {G}}\left( {\mathcal {L}}({\textbf{V}}_{D_{\Vert \cdot \Vert _D}},{\textbf{V}}_{D_{\Vert \cdot \Vert _D}})\right) . \end{aligned}$$

This proves the lemma. \(\square \)

Lemma 4.3 allows to introduce the following linear isomorphism:

where \({{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]}:= \bigotimes _{\beta \in {\mathcal {P}}_D {\setminus } \{\alpha \}} id_{{\textbf{V}}_{\beta }}\) for \(\alpha \in {\mathcal {P}}_D.\) The next proposition gives us a useful property of the elements in the image of the map \(\Delta .\)

Proposition 4.4

Assume that \({\mathcal {P}}_D\) is a partition of D,  \(({\textbf{V}}_{\alpha },\Vert \cdot \Vert _{\alpha })\) is a normed space for each \(\alpha \in {\mathcal {P}}_D\) and \(\Vert \cdot \Vert _D\) is a norm on the tensor space \({\textbf{V}}_D = \left. \bigotimes _{\alpha \in {\mathcal {P}}_D} {\textbf{V}}_{\alpha }\right. \) such that (4.3) holds. Then for each it holds that

$$\begin{aligned} \exp (\Delta \left( (L_{\alpha })_{\alpha \in {\mathcal {P}}_D})\right) = \bigotimes _{\alpha \in {\mathcal {P}}_D} \exp (L_{\alpha }). \end{aligned}$$

Proof

Put \(L:=\Delta \left( (L_{\alpha })_{\alpha \in {\mathcal {P}}_D}\right) = \sum _{\alpha \in {\mathcal {P}}_D}L_{\alpha } \otimes {{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]}\) and observe that for each \(\alpha \in {\mathcal {P}}_D\) it holds

$$\begin{aligned} \exp (L_{\alpha } \otimes {{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]}) = \sum _{n=0}^{\infty } \frac{1}{n!} (L_{\alpha } \otimes {{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]})^n = \left( \sum _{n=0}^{\infty } \frac{1}{n!} L_{\alpha }^n\right) \otimes {{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]} = \exp (L_{\alpha })\otimes {{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]}. \end{aligned}$$

Moreover for \(\alpha ,\beta \in {\mathcal {P}}_D\) and \(\alpha \ne \beta \) we have

$$\begin{aligned} (L_{\alpha } \otimes {{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]}) \circ (L_{\beta } \otimes {{\textbf{i}}}{{\textbf{d}}}_{[\beta ]}) = (L_{\beta } \otimes {{\textbf{i}}}{{\textbf{d}}}_{[\beta ]}) \circ (L_{\alpha } \otimes {{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]}) = L_{\alpha } \otimes L_{\beta } \otimes \left( \bigotimes _{\delta \in {\mathcal {P}}_D \setminus \{\alpha , \beta \}} id_{{\textbf{V}}_{\delta }}\right) . \end{aligned}$$

Finally, by seing \({\mathcal {P}}_D\) as an ordered set, and by denoting \( \bigodot _{i=1}^n A_i:= A_1 \circ A_2 \circ \cdots \circ A_n \) is the composition of maps \(A_i\), \(1\le i \le n\), we have

$$\begin{aligned} \exp \left( L \right) = \bigodot _{\alpha \in {\mathcal {P}}_D} \exp (L_{\alpha } \otimes {{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]}) = \bigodot _{\alpha \in {\mathcal {P}}_D} \exp (L_{\alpha })\otimes {{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]} = \bigotimes _{\alpha \in {\mathcal {P}}_D} \exp (L_{\alpha }). \end{aligned}$$

Note that since operators \(\exp (L_{\alpha })\otimes {{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]}\) and \(\exp (L_{\beta })\otimes {{\textbf{i}}}{{\textbf{d}}}_{[\beta ]}\) commute for any \(\alpha ,\beta \in {\mathcal {P}}_D\), the above result is independent of the chosen order on \({\mathcal {P}}_D\). This proves the proposition. \(\square \)

To simplify notation, let

$$\begin{aligned} {\textbf{E}}_{{\mathcal {P}}_D}:= \left( \bigoplus _{\alpha \in {\mathcal {P}}_D}{\mathcal {L}}\left( {\textbf{U}}_{\alpha },{\textbf{W}}_{\alpha } \right) \otimes \textrm{span}\{{{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]}\}\right) . \end{aligned}$$

Recall that \({\widetilde{\xi }}_{{\textbf{v}}}\) is a bijection from \({\mathcal {U}}({\textbf{v}})\) to the open set

Hence the map \(\xi _{{\textbf{v}}}:= (\Delta \times id) \circ {\widetilde{\xi }}_{{\textbf{v}}},\) where \(id: {\mathfrak {M}}_{{\mathfrak {r}}}\left( \left. \bigotimes _{\alpha \in {\mathcal {P}}_D}{\textbf{U}}_{\alpha } \right. \right) \longrightarrow {\mathfrak {M}}_{{\mathfrak {r}}}\left( \left. \bigotimes _{\alpha \in {\mathcal {P}}_D}{\textbf{U}}_{\alpha } \right. \right) \) is the identity map, is a bijection from \({\mathcal {U}}({\textbf{v}})\) to the open set

$$\begin{aligned} {\textbf{E}}_{{\mathcal {P}}_D} \times {\mathfrak {M}}_{{\mathfrak {r}}}\left( \left. \bigotimes _{\alpha \in {\mathcal {P}}_D}{\textbf{U}}_{\alpha } \right. \right) . \end{aligned}$$

For each \({\textbf{w}} \in {\mathcal {U}}({\textbf{v}}),\) we have \( {{\widetilde{\xi }}}_{{\textbf{v}}}({\textbf{w}}) = ((L_{\alpha })_{\alpha \in {\mathcal {P}}_D},{\textbf{u}})\) for some and \({\textbf{u}} \in {\mathfrak {M}}_{{\mathfrak {r}}}\left( \left. \bigotimes _{\alpha \in {\mathcal {P}}_D}{\textbf{U}}_{\alpha } \right. \right) \). Then, letting \(L:= \Delta ((L_{\alpha })_{\alpha \in {\mathcal {P}}_D}),\)

$$\begin{aligned} {\textbf{w}}= & {} \xi _{{\textbf{v}}}^{-1}(L, {\textbf{u}}) = \xi _{{\textbf{v}}}^{-1}(\Delta ((L_{\alpha })_{\alpha \in {\mathcal {P}}_D}), {\textbf{u}})\\ {}= & {} ((\Delta \times id) \circ {\widetilde{\xi }}_{{\textbf{v}}})^{-1}(\Delta ((L_{\alpha })_{\alpha \in {\mathcal {P}}_D}), {\textbf{u}}) = {\widetilde{\xi }}_{{\textbf{v}}}^{-1}((L_{\alpha })_{\alpha \in {\mathcal {P}}_D},{\textbf{u}}). \end{aligned}$$

Thus, thanks to Proposition 4.4, we deduce that the equality

$$\begin{aligned} {\textbf{w}} = \xi _{{\textbf{v}}}^{-1}(\Delta ((L_{\alpha })_{\alpha \in {\mathcal {P}}_D}), {\textbf{u}}) = \left( \bigotimes _{ \alpha \in {\mathcal {P}}_D}\exp (L_{\alpha })\right) ({\textbf{u}}) \end{aligned}$$
(4.4)

is equivalent to

$$\begin{aligned} {\textbf{w}} = \xi _{{\textbf{v}}}^{-1}(L, {\textbf{u}}) = \exp (L)({\textbf{u}}), \end{aligned}$$
(4.5)

where \(L= \sum _{\alpha \in {\mathcal {P}}_D}L_{\alpha } \otimes {{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]}\) is a Laplacian-like map. In consequence, every tensor in Tucker format is locally characterised by a full-rank tensor and a Laplacian-like map. To conclude, we can re-state Theorem 4.1 as follows.

Theorem 4.5

Assume that \({\mathcal {P}}_D\) is a partition of D,  \((V_{\alpha },\Vert \cdot \Vert _{\alpha })\) is a normed space for each \(\alpha \in {\mathcal {P}}_D\) and let \(\Vert \cdot \Vert _D\) be a norm on the tensor space \({\textbf{V}}_D = \left. \bigotimes _{\alpha \in D}{\textbf{V}}_{\alpha }\right. \) such that (4.3) holds. Then there exists a \({\mathcal {C}}^{\infty }\)-atlas \(\{{\mathcal {U}}({\textbf{v}}),\xi _{{\textbf{v}}}\}_{{\textbf{v}}\in {\mathfrak {M}}_{{\mathfrak {r}}}({\textbf{V}}_{D})}\) for \({\mathfrak {M}}_{{\mathfrak {r}}}( {\textbf{V}}_{D})\) and hence \({\mathfrak {M}}_{{\mathfrak {r}}}( {\textbf{V}}_{D})\) is a \({\mathcal {C}}^{\infty }\)-Banach manifold modelled on a Banach space

here \({\textbf{U}}_{\alpha }\in {\mathbb {G}}_{r_{\alpha }}({\textbf{V}}_{\alpha })\) and \({\textbf{V}}_{\alpha _{\Vert \cdot \Vert _{\alpha }}} = {\textbf{U}}_{\alpha } \oplus {\textbf{W}}_{\alpha },\) where \({\textbf{V}}_{{\alpha }_{\Vert \cdot \Vert _{\alpha }}}\) is the completion of \({\textbf{V}}_{\alpha }\) for \(\alpha \in {\mathcal {P}}_D.\)

Observe that for any partition \({\mathcal {P}}_D\) of D,  from Lemma 4.3, the Banach space \({\textbf{E}}_{{\mathcal {P}}_D}\) is a closed linear subspace of the Banach space \({\mathcal {L}}({\textbf{V}}_{D_{\Vert \cdot \Vert _D}},{\textbf{V}}_{D_{\Vert \cdot \Vert _D}}).\)

5 The geometry of tree-based tensor format

For a dimension partition tree \(T_D\) and for \({\mathfrak {r}}=(r_{\alpha })_{\alpha \in T_D} \in {{\mathcal {A}}}{{\mathcal {D}}}({\textbf{V}}_D,T_D),\) assume that \({{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}({\textbf{V}}_D,T_D)\) is a proper set of tree-based tensors with a fixed tree-based rank \({\mathfrak {r}}\) such that

$$\begin{aligned} {{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}({\textbf{V}}_D,T_D) = \bigcap _{k=1}^{\textrm{depth}(T_D)} {\mathfrak {M}}_{{\mathfrak {r}}_k}({\textbf{V}}_D,{\mathcal {P}}_k(T_D)). \end{aligned}$$

Assume that \(({\textbf{V}}_{\alpha },\Vert \cdot \Vert _{\alpha })\) is a normed space for each \(\alpha \in {\mathcal {P}}_{k}(T_D)\) and that \(\Vert \cdot \Vert _D\) is a norm on the tensor space \({\textbf{V}}_D = \left. \bigotimes _{\alpha \in {\mathcal {P}}_{k}(T_D)} {\textbf{V}}_{\alpha }\right. \) such that (4.3) holds for \(1 \le k \le \textrm{depth}(T_D).\)

From Theorem 4.5 we have that for each \(1 \le k \le \textrm{depth}(T_D)\) the collection \({\mathcal {A}}_{k} = \{({\mathcal {U}}^{(k)}({\textbf{v}}),\xi _{{\textbf{v}}}^{(k)})\}_{{\textbf{v}}\in {\mathfrak {M}}_{{\mathfrak {r}}_{k}}({\textbf{V}}_{D},T_D)}\) is a \({\mathcal {C}}^{\infty }\)-atlas for \({\mathfrak {M}}_{{\mathfrak {r}}_{k}}( {\textbf{V}}_{D},T_D)\) and hence \({\mathfrak {M}}_{{\mathfrak {r}}_{{k}}}( {\textbf{V}}_{D},T_D)\) is a \({\mathcal {C}}^{\infty }\)-Banach manifold modelled on

where \( {\textbf{U}}_{\alpha }=U_{\alpha }^{\min }({\textbf{v}})\) is a \(r_{\alpha }\)-dimensional subspace of \({\textbf{V}}_{\alpha }\) for each \(\alpha \in {\mathcal {P}}_k(T_D)\) where \({\textbf{v}} \in \left. \bigotimes _{\alpha \in {\mathcal {P}}_k(T_D)}{\textbf{U}}_{\alpha } \right. \) and \({\textbf{W}}_\alpha \) is a closed subspace of \({\textbf{V}}_{\alpha _{\Vert \cdot \Vert _{\alpha }}}\) such that \({\textbf{V}}_{\alpha _{\Vert \cdot \Vert _{\alpha }}} = {\textbf{U}}_{\alpha } \oplus {\textbf{W}}_{\alpha },\) where \({\textbf{V}}_{{\alpha }_{\Vert \cdot \Vert _{\alpha }}}\) is the completion of \({\textbf{V}}_{\alpha }\) for \(\alpha \in {\mathcal {P}}_{k}(T_D).\)

To simplify notation, here we write

$$\begin{aligned} {\textbf{E}}_k:= \left( \bigoplus _{\alpha \in {\mathcal {P}}_k(T_D)}{\mathcal {L}}\left( {\textbf{U}}_{\alpha },{\textbf{W}}_{\alpha }\right) \otimes \textrm{span}\{{{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]}\}\right) \end{aligned}$$

for \(1 \le k \le \textrm{depth}(T_D).\) Next, we characterise the elements in the product set

$$\begin{aligned} \bigcap _{k=1}^{\textrm{depth}(T_D)}\xi _{{\textbf{v}}}^{(k)}({\mathcal {U}}^{(k)}({\textbf{v}})) = \left( \bigcap _{k=1}^{\textrm{depth}(T_D)}{\textbf{E}}_k \right) \times \left( \bigcap _{k=1}^{\textrm{depth}(T_D)} {\mathfrak {M}}_{{\textbf{r}}_k}\left( \left. \bigotimes _{\alpha \in {\mathcal {P}}_{k}(T_D)} {\textbf{U}}_{\alpha } \right. \right) \right) . \end{aligned}$$

Let \({\mathcal {O}}:=\bigcap _{k=1}^{\textrm{depth}(T_D)} {\mathfrak {M}}_{{\textbf{r}}_k}\left( \left. \bigotimes _{\alpha \in {\mathcal {P}}_{k}(T_D)} {\textbf{U}}_{\alpha } \right. \right) \) and \({\textbf{E}}:= \bigcap _{k=1}^{\textrm{depth}(T_D)}{\textbf{E}}_k.\) Then we have the following result.

Lemma 5.1

Let \(T_D\) be a dimension partition tree with \(\textrm{depth}(T_D) \ge 2,\) and \({\mathfrak {r}}=(r_{\alpha })_{\alpha \in T_D} \in {{\mathcal {A}}}{{\mathcal {D}}}({\textbf{V}}_D,T_D)\) such that \({{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}({\textbf{V}}_D,T_D)\) is a proper set of tree-based tensors with a fixed tree-based rank \({\mathfrak {r}}.\) Assume that \(({\textbf{V}}_{\alpha },\Vert \cdot \Vert _{\alpha })\) is a normed space for each \(\alpha \in T_D \setminus \{D\}\) and that \(\Vert \cdot \Vert _D\) is a norm on the tensor space \({\textbf{V}}_D = \left. \bigotimes _{\alpha \in {\mathcal {P}}_{k}(T_D)} {\textbf{V}}_{\alpha }\right. \) such that (4.3) holds for \(1\le k \le \textrm{depth}(T_D).\) Then for each \({\textbf{v}} \in {{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}({\textbf{V}}_D,T_D)\) we have that

$$\begin{aligned} \bigcap _{k=1}^{\textrm{depth}(T_D)}\xi _{{\textbf{v}}}^{(k)}({\mathcal {U}}^{(k)}({\textbf{v}})) = {\textbf{E}} \times {\mathcal {O}} \end{aligned}$$

is an open set of the Banach space \({\textbf{E}} \times \left. \bigotimes _{\delta \in {\mathcal {P}}_{1}(T_D)} {\textbf{U}}_{\delta } \right. .\)

Proof

First we claim that \({\mathcal {O}}\) is an open set in \(\left. \bigotimes _{\delta \in {\mathcal {P}}_{1}(T_D)} {\textbf{U}}_{\delta } \right. .\) To prove the claim, recall that \({\mathfrak {M}}_{{\textbf{r}}_k}\left( \left. \bigotimes _{\alpha \in {\mathcal {P}}_{k}(T_D)} {\textbf{U}}_{\alpha } \right. \right) \) is an open set in the finite dimensional space \(\left. \bigotimes _{\delta \in {\mathcal {P}}_{k}(T_D)} {\textbf{U}}_{\delta } \right. \) for \(1 \le k \le \textrm{depth}(T_D).\) By using Remark 3.6 we have

$$\begin{aligned} \bigcap _{k=1}^{\textrm{depth}(T_D)} \left. \bigotimes _{\alpha \in {\mathcal {P}}_{k}(T_D)}{\textbf{U}}_{\alpha } \right. = \bigcap _{k=1}^{\textrm{depth}(T_D)} \left. \bigotimes _{\alpha \in {\mathcal {P}}_{k}(T_D)}U_{\alpha }^{\min }({\textbf{v}}) \right. = \left. \bigotimes _{\delta \in {\mathcal {P}}_{1}(T_D)} U_{\delta }^{\min }({\textbf{v}}) \right. = \left. \bigotimes _{\delta \in {\mathcal {P}}_{1}(T_D)} {\textbf{U}}_{\delta } \right. . \end{aligned}$$

Now, put \(\ell = \textrm{depth}(T_D)\) and consider

$$\begin{aligned} {\mathcal {O}}_{\ell ,\ell -1}:= {\mathfrak {M}}_{{\mathfrak {r}}_{\ell }}\left( \left. \bigotimes _{\alpha \in {\mathcal {P}}_{\ell }(T_D)}{\textbf{U}}_{\alpha } \right. \right) \cap {\mathfrak {M}}_{{\mathfrak {r}}_{\ell -1}}\left( \left. \bigotimes _{\alpha \in {\mathcal {P}}_{\ell -1}(T_D)}{\textbf{U}}_{\alpha } \right. \right) \end{aligned}$$

which is equal to

$$\begin{aligned} {\mathcal {O}}_{\ell ,\ell -1} = \left( {\mathfrak {M}}_{{\mathfrak {r}}_{\ell }}\left( \left. \bigotimes _{\alpha \in {\mathcal {P}}_{\ell }(T_D)}{\textbf{U}}_{\alpha } \right. \right) \cap \left. \bigotimes _{\alpha \in {\mathcal {P}}_{\ell -1}(T_D)}{\textbf{U}}_{\alpha } \right. \right) \cap {\mathfrak {M}}_{{\mathfrak {r}}_{\ell -1}}\left( \left. \bigotimes _{\alpha \in {\mathcal {P}}_{\ell -1}(T_D)}{\textbf{U}}_{\alpha } \right. \right) , \end{aligned}$$

where

$$\begin{aligned} {\mathfrak {M}}_{{\mathfrak {r}}_{\ell }}\left( \left. \bigotimes _{\alpha \in {\mathcal {P}}_{\ell }(T_D)}{\textbf{U}}_{\alpha } \right. \right) \cap \left. \bigotimes _{\alpha \in {\mathcal {P}}_{\ell -1}(T_D)}{\textbf{U}}_{\alpha } \right. \end{aligned}$$

is an open set in \(\left. \bigotimes _{\alpha \in {\mathcal {P}}_{\ell -1}(T_D)}{\textbf{U}}_{\alpha } \right. \subset \left. \bigotimes _{\alpha \in {\mathcal {P}}_{\ell }(T_D)}{\textbf{U}}_{\alpha } \right. .\) Next, let

$$\begin{aligned} {\mathcal {O}}_{\ell ,\ell -2}&= {\mathcal {O}}_{\ell ,\ell -1} \cap {\mathfrak {M}}_{{\mathfrak {r}}_{\ell -2}}\left( \left. \bigotimes _{\alpha \in {\mathcal {P}}_{\ell -2}(T_D)}{\textbf{U}}_{\alpha } \right. \right) \\&= \left( {\mathcal {O}}_{\ell ,\ell -1} \cap \left. \bigotimes _{\alpha \in {\mathcal {P}}_{\ell -2}(T_D)}{\textbf{U}}_{\alpha } \right. \right) \cap {\mathfrak {M}}_{{\mathfrak {r}}_{\ell -2}}\left( \left. \bigotimes _{\alpha \in {\mathcal {P}}_{\ell -2}(T_D)}{\textbf{U}}_{\alpha } \right. \right) . \end{aligned}$$

In a similar way as above, \({\mathcal {O}}_{\ell ,\ell -2}\) is an open set in \(\left. \bigotimes _{\alpha \in {\mathcal {P}}_{\ell -2}(T_D)}{\textbf{U}}_{\alpha } \right. .\) By induction, we prove that \({\mathcal {O}}= {\mathcal {O}}_{\ell ,1}\) is an open set in \(\left. \bigotimes _{\delta \in {\mathcal {P}}_{1}(T_D)} U_{\delta }^{\min }({\textbf{v}}) \right. \) and the claim follows. To conclude, from Lemma 4.3, \({\textbf{E}}_k\) is a closed linear space of \({\mathcal {L}}({\textbf{V}}_{D_{\Vert \cdot \Vert _D}},{\textbf{V}}_{D_{\Vert \cdot \Vert _D}})\) for \(1 \le k \le \textrm{depth}(T_D).\) Hence \({\textbf{E}}:= \bigcap _{k=1}^{\textrm{depth}(T_D)}{\textbf{E}}_k\) is a linear closed subspace in the Banach space \({\mathcal {L}}({\textbf{V}}_{D_{\Vert \cdot \Vert _D}},{\textbf{V}}_{D_{\Vert \cdot \Vert _D}}).\) Thus, \({\textbf{E}}\) is also a Banach space. Since \({\textbf{E}} \times {\mathcal {O}}\) is an open set in the Banach space \({\textbf{E}} \times \left. \bigotimes _{\delta \in {\mathcal {P}}_{1}(T_D)} {\textbf{U}}_{\delta } \right. \) the lemma follows. \(\square \)

Given \(L \in {\textbf{E}}\), for each \(1 \le k \le \textrm{depth}(T)\) there exists a unique

such that

$$\begin{aligned} L = \Delta ((L_{\alpha }^{(k)})_{\alpha \in {\mathcal {P}}_{k}(T_D)}) = \sum _{\alpha \in {\mathcal {P}}_{k}(T_D)} L_{\alpha }^{(k)} \otimes {{\textbf{i}}}{{\textbf{d}}}_{[\alpha ]} \end{aligned}$$

holds. From (4.5), each \((L,{\textbf{u}}) \in {\textbf{E}} \times {\mathcal {O}}\) satisfies that

$$\begin{aligned} (\xi _{{\textbf{v}}}^{(k)})^{-1}((L,{\textbf{u}})) = \exp (L)({\textbf{u}}) \in {\mathcal {U}}^{(k)}({\textbf{v}}) \end{aligned}$$

for \(1 \le k \le \textrm{depth}(T_D).\) Hence the image of \((L,{\textbf{u}})\) by \((\xi _{{\textbf{v}}}^{(k)})^{-1}\) is independent on the index k. Thus \((\xi _{{\textbf{v}}}^{(k)})^{-1}\) is a bijection that maps \({\textbf{E}} \times {\mathcal {O}}\) onto a subset \({\mathcal {W}}({\textbf{v}}) \subset \bigcap _{l=1}^{\textrm{depth}(T_D)}{\mathcal {U}}^{(l)}({\textbf{v}})\) containing \({\textbf{v}}\) for each \(1 \le k \le \textrm{depth}(T_D).\) It allows to we define the bijection

$$\begin{aligned} \varvec{\xi }_{{\textbf{v}}}:{\mathcal {W}}({\textbf{v}}) \longrightarrow {\textbf{E}} \times {\mathcal {O}} \end{aligned}$$

by \(\varvec{\xi }_{{\textbf{v}}}({\textbf{w}}) = \xi _{{\textbf{v}}}^{(k)}(\exp (L)({\textbf{u}})) = (L,{\textbf{u}}).\)

Then the following result is straightforward.

Theorem 5.2

Let \(T_D\) be a dimension partition tree with \(\textrm{depth}(T_D) \ge 2,\) and \({\mathfrak {r}}=(r_{\alpha })_{\alpha \in T_D} \in {{\mathcal {A}}}{{\mathcal {D}}}({\textbf{V}}_D,T_D)\) such that \({{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}({\textbf{V}}_D,T_D)\) is a proper set of tree-based tensors with a fixed tree-based rank \({\mathfrak {r}}.\) Assume that \(({\textbf{V}}_{\alpha },\Vert \cdot \Vert _{\alpha })\) is a normed space for each \(\alpha \in T_D \setminus \{D\}\) and that \(\Vert \cdot \Vert _D\) is a norm on the tensor space \({\textbf{V}}_D = \left. \bigotimes _{\alpha \in {\mathcal {P}}_{k}(T_D)} {\textbf{V}}_{\alpha }\right. \) is such that (4.3) holds for \(1\le k \le \textrm{depth}(T_D).\) Then the collection

$$\begin{aligned} {\mathcal {B}} = \{({\mathcal {W}}({\textbf{v}}),\varvec{\xi }_{{\textbf{v}}})\}_{{\textbf{v}} \in {{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}({\textbf{V}}_{D},T_D)} \end{aligned}$$

is a \({\mathcal {C}}^{\infty }\)-atlas for \({{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}( {\textbf{V}}_{D},T_D)\), and hence \({{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}( {\textbf{V}}_{D},T_D)\) is a \({\mathcal {C}}^{\infty }\)-Banach manifold modelled on

Here \( {\textbf{U}}_{\alpha }\) is a \(r_{\alpha }\)-dimensional subspace of \({\textbf{V}}_{\alpha }\) for each \(\alpha \in T_D \setminus \{D\}\) where \({\textbf{v}} \in \left. \bigotimes _{\alpha \in {\mathcal {P}}_k(T_D)}{\textbf{U}}_{\alpha } \right. \) for \(1 \le k \le \textrm{depth}(T_D)\) and \({\textbf{W}}_\alpha \) is a closed subspace of \({\textbf{V}}_{\alpha _{\Vert \cdot \Vert _{\alpha }}}\) such that \({\textbf{V}}_{\alpha _{\Vert \cdot \Vert _{\alpha }}} = {\textbf{U}}_{\alpha } \oplus {\textbf{W}}_{\alpha },\) where \({\textbf{V}}_{{\alpha }_{\Vert \cdot \Vert _{\alpha }}}\) is the completion of \({\textbf{V}}_{\alpha }\) for \(\alpha \in T_D \setminus \{D\}.\)

5.1 \({{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}( {\textbf{V}}_{D},T_D)\) as embedded sub-manifold of \({\mathfrak {M}}_{{\mathfrak {r}}_{{k}}}( {\textbf{V}}_{D},{\mathcal {P}}_k(T_D))\) for \(1 \le k \le \textrm{depth}(T_D)\)

Since \({{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}( {\textbf{V}}_{D},T_D) \subset {\mathfrak {M}}_{{\mathfrak {r}}_{{k}}}( {\textbf{V}}_{D},{\mathcal {P}}_k(T_D)),\) for \(1 \le k \le \textrm{depth}(T_D),\) the natural ambient space of the manifold \({{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}( {\textbf{V}}_{D},T_D)\) is any manifold \({\mathfrak {M}}_{{\mathfrak {r}}_{{k}}}( {\textbf{V}}_{D},{\mathcal {P}}_k(T_D))\) for \(1 \le k \le \textrm{depth}(T_D).\) In order to prove that \({{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}( {\textbf{V}}_{D},T_D)\) is an embedded sub-manifold of \({\mathfrak {M}}_{{\mathfrak {r}}_{{k}}}( {\textbf{V}}_{D},{\mathcal {P}}_k(T_D))\) for \(1 \le k \le \textrm{depth}(T_D)\), we consider the natural inclusion map \({\mathfrak {i}}: {{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}( {\textbf{V}}_{D},T_D)\longrightarrow {\mathfrak {M}}_{{\mathfrak {r}}_{{k}}}( {\textbf{V}}_{D},{\mathcal {P}}_k(T_D))\) given by \({\mathfrak {i}}({\textbf{v}}) = {\textbf{v}}.\) Then, from Theorem 3.5.7 in [16], we only need to check the following two conditions for each \(1 \le k \le \textrm{depth}(T_D):\)

  1. (C1)

    The map \({\mathfrak {i}}\) should be an immersion. From Proposition 4.1 in [8], it is true when the linear map

    $$\begin{aligned} \textrm{T}_{{\textbf{v}}}{\mathfrak {i}} = (\xi _{{\textbf{v}}} \circ {\mathfrak {i}} \circ \varvec{\xi }_{{\textbf{v}}}^{-1})'(\varvec{\xi }_{{\textbf{v}}}({\textbf{v}})):\textrm{T}_{{\textbf{v}}}{{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}( {\textbf{V}}_{D},T_D) \longrightarrow \textrm{T}_{{\textbf{v}}} {\mathfrak {M}}_{\mathfrak { r}_{k}}({\textbf{V}}_{D},{\mathcal {P}}_k(T_D)) \end{aligned}$$

    is injective and \(\textrm{T}_{{\textbf{v}}}{\mathfrak {i}}(\textrm{T}_{{\textbf{v}}}{{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}( {\textbf{V}}_{D},T_D)) \in {\mathbb {G}}\left( \textrm{T}_{{\textbf{v}}} {\mathfrak {M}}_{\mathfrak { r}_{k}}({\textbf{V}}_{D},{\mathcal {P}}_k(T_D))\right) \)

  2. (C2)

    The map

    $$\begin{aligned} {\mathfrak {i}}: {{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}( {\textbf{V}}_{D},T_D) \longrightarrow {\mathfrak {i}}\left( {{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}( {\textbf{V}}_{D},T_D) \right) \end{aligned}$$

    is a topological homeomorphism.

Since \({\mathfrak {i}}:{{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}( {\textbf{V}}_{D},T_D) \longrightarrow {\mathfrak {i}}\left( {{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}( {\textbf{V}}_{D},T_D) \right) \) is the identity map then it is clearly an homeomorphism and (C2) holds. To prove that (C1) is also true, first we claim that the natural inclusion map \({\mathfrak {i}}\) is also written in local coordinates as the natural inclusion map. Indeed, for \({\textbf{v}} \in {{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}( {\textbf{V}}_{D},T_D),\) the open set \({\mathcal {W}}({\textbf{v}}) \subset \bigcap _{\ell =1}^{\textrm{depth}(T_D)} {\mathcal {U}}^{(\ell )}({\textbf{v}}) \subset {{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}( {\textbf{V}}_{D},T_D)\) and hence

$$\begin{aligned} {\mathfrak {i}}:{\mathcal {W}}({\textbf{v}}) \longrightarrow {\mathcal {U}}^{(k)}({\textbf{v}}) \end{aligned}$$

is the identity map on \({\mathcal {W}}({\textbf{v}})\), that is, \({\mathfrak {i}}|_{{\mathcal {W}}({\textbf{v}})}= id_{{\mathcal {W}}({\textbf{v}})}.\) Thus

$$\begin{aligned} (\xi _{{\textbf{v}}}^{(k)} \circ {\mathfrak {i}} \circ \varvec{\xi }^{-1}_{{\textbf{v}}}): {\textbf{E}} \times {\mathcal {O}} \longrightarrow {\textbf{E}}_k \times {\mathfrak {M}}_{{\mathfrak {r}}_{k}}\left( \left. \bigotimes _{\alpha \in {\mathcal {P}}_{k}(T_D)} {\textbf{U}}_{\alpha } \right. \right) \end{aligned}$$

is the natural inclusion map and the claim follows. Hence its derivative

$$\begin{aligned} \textrm{T}_{{\textbf{v}}}{\mathfrak {i}} = (\xi _{{\textbf{v}}} \circ {\mathfrak {i}} \circ \varvec{\xi }_{{\textbf{v}}}^{-1})'(\varvec{\xi }_{{\textbf{v}}}({\textbf{v}})): {\textbf{E}} \times \left( \left. \bigotimes _{\alpha \in {\mathcal {P}}_{1}(T_D)}{\textbf{U}}_{\alpha } \right. \right) \longrightarrow {\textbf{E}}_k \times \left( \left. \bigotimes _{\alpha \in {\mathcal {P}}_{k}(T_D)} {\textbf{U}}_{\alpha } \right. \right) \end{aligned}$$

is also the natural inclusion map which is clearly injective.

In consequence, to obtain (C1) we only need to prove that for each \({\textbf{v}} \in {{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}( {\textbf{V}}_{D},T_D)\) the tangent space

$$\begin{aligned} \textrm{T}_{{\textbf{v}}}{{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}( {\textbf{V}}_{D},T_D) = {\textbf{E}} \times \left. \bigotimes _{\alpha \in {\mathcal {P}}_{1}(T_D)} {\textbf{U}}_{\alpha } \right. \end{aligned}$$

belongs to

$$\begin{aligned} {\mathbb {G}}\left( {\textbf{E}}_k \times \left. \bigotimes _{\alpha \in {\mathcal {P}}_{k}(T_D)} {\textbf{U}}_{\alpha } \right. \right) = {\mathbb {G}}\left( {\textbf{E}}_k\right) \times {\mathbb {G}}\left( \left. \bigotimes _{\alpha \in {\mathcal {P}}_{k}(T_D)} {\textbf{U}}_{\alpha } \right. \right) . \end{aligned}$$

Clearly

$$\begin{aligned} \left. \bigotimes _{\alpha \in {\mathcal {P}}_{1}(T_D)} {\textbf{U}}_{\alpha } \right. \in {\mathbb {G}}\left( \left. \bigotimes _{\alpha \in {\mathcal {P}}_{k}(T_D)} {\textbf{U}}_{\alpha } \right. \right) , \end{aligned}$$

because \(\left. \bigotimes _{\alpha \in {\mathcal {P}}_{k}(T_D)} {\textbf{U}}_{\alpha } \right. \) is a finite dimensional vector space. From Lemma 4.3 we have

$$\begin{aligned} {\textbf{E}}_k \in {\mathbb {G}}\left( {\mathcal {L}}({\textbf{V}}_{D_{\Vert \cdot \Vert _D}},{\textbf{V}}_{D_{\Vert \cdot \Vert _D}}) \right) \end{aligned}$$

for \(1 \le k \le \textrm{depth}(T_D).\) The second statement of Lemma 4.14 in [8] implies

$$\begin{aligned} {\textbf{E}} = \bigcap _{k=1}^{\textrm{depth}(T_D)}{\textbf{E}}_k \in {\mathbb {G}}\left( {\mathcal {L}}({\textbf{V}}_{D_{\Vert \cdot \Vert _D}},{\textbf{V}}_{D_{\Vert \cdot \Vert _D}}) \right) . \end{aligned}$$

Thus we have the following theorem.

Theorem 5.3

Let \(T_{D}\) be a dimension partition tree over D and \({\mathfrak {r}} \in {{\mathcal {A}}}{{\mathcal {D}}}({\textbf{V}}_D,T_D)\) such that \({{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}({\textbf{V}}_D,T_D)\) is a proper set of tree-based tensors with a fixed tree-based rank \({\mathfrak {r}}.\) Assume that \(({\textbf{V}}_{\alpha },\Vert \cdot \Vert _{\alpha })\) is a normed space for each \(\alpha \in T_D \setminus \{D\}\) and let \(\Vert \cdot \Vert _D\) be a norm on the tensor space \({\textbf{V}}_D\) such that (4.3) holds for \(1 \le k \le \textrm{depth}(T_D).\) Then \({{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}( {\textbf{V}}_{D},T_D)\) is an embedded sub-manifold of \({\mathfrak {M}}_{{\mathfrak {r}}_{{k}}}( {\textbf{V}}_{D},{\mathcal {P}}_k(T_D))\) for \(1 \le k \le \textrm{depth}(T_D).\)

Observe that we can also consider the natural inclusion map \({\mathfrak {i}}\) from \({\mathfrak {M}}_{{\mathfrak {r}}_{{k}}}( {\textbf{V}}_{D},{\mathcal {P}}_k(T_D))\) to \({\textbf{V}}_{D_{\Vert \cdot \Vert _D}}.\) Under the assumptions of Theorem 5.3, by using Theorem 4.14 of [8], we have that \({\mathfrak {M}}_{{\mathfrak {r}}_{{k}}}( {\textbf{V}}_{D},{\mathcal {P}}_k(T_D))\) is an immersed sub-manifold of \({\textbf{V}}_{D_{\Vert \cdot \Vert _D}}\) and, for each \({\textbf{v}} \in {\mathfrak {M}}_{{\mathfrak {r}}_{{k}}}( {\textbf{V}}_{D},{\mathcal {P}}_k(T_D)),\) the tangent space

$$\begin{aligned} \textrm{T}_{{\textbf{v}}}{\mathfrak {M}}_{{\mathfrak {r}}_{{k}}}( {\textbf{V}}_{D},{\mathcal {P}}_k(T_D)) = {\textbf{E}}_k \times \left( \left. \bigotimes _{\alpha \in {\mathcal {P}}_k(T_D)}{\textbf{U}}_{\alpha } \right. \right) \end{aligned}$$

is linearly isomorphic to the linear space \( \textrm{T}_{{\textbf{v}}}{\mathfrak {i}}\left( \textrm{T}_{{\textbf{v}}}{\mathfrak {M}}_{{\mathfrak {r}}_{{k}}}( {\textbf{V}}_{D},{\mathcal {P}}_k(T_D)) \right) \in {\mathbb {G}}({\textbf{V}}_{D_{\Vert \cdot \Vert _D}}). \) Moreover,

$$\begin{aligned} \bigcap _{k=1}^{\textrm{depth}(T_D)}\textrm{T}_{{\textbf{v}}}{\mathfrak {M}}_{{\mathfrak {r}}_{{k}}}( {\textbf{V}}_{D},{\mathcal {P}}_k(T_D))&= \bigcap _{k=1}^{\textrm{depth}(T_D)}\left( {\textbf{E}}_k \times \left( \left. \bigotimes _{\alpha \in {\mathcal {P}}_{k}(T_D)} {\textbf{U}}_{\alpha } \right. \right) \right) \\&= \left( \bigcap _{k=1}^{\textrm{depth}(T_D)}{\textbf{E}}_k \right) \times \left( \bigcap _{k=1}^{\textrm{depth}(T_D)} \left. \bigotimes _{\alpha \in {\mathcal {P}}_{k}(T_D)} {\textbf{U}}_{\alpha } \right. \right) \\&= {\textbf{E}} \times \left( \left. \bigotimes _{\alpha \in {\mathcal {P}}_{1}(T_D)} {\textbf{U}}_{\alpha } \right. \right) = \textrm{T}_{{\textbf{v}}}{{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}( {\textbf{V}}_{D},T_D). \end{aligned}$$

Then, by using that \(\textrm{T}_{{\textbf{v}}}{\mathfrak {i}}\) is injective, we obtain

$$\begin{aligned} \textrm{T}_{{\textbf{v}}}{\mathfrak {i}} \left( \textrm{T}_{{\textbf{v}}}{{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}( {\textbf{V}}_{D},T_D) \right)&= \textrm{T}_{{\textbf{v}}}{\mathfrak {i}} \left( \bigcap _{k=1}^{\textrm{depth}(T_D)}\textrm{T}_{{\textbf{v}}}{\mathfrak {M}}_{{\mathfrak {r}}_{{k}}}( {\textbf{V}}_{D},{\mathcal {P}}_k(T_D))\right) \\&= \bigcap _{k=1}^{\textrm{depth}(T_D)} \textrm{T}_{{\textbf{v}}}{\mathfrak {i}} \left( \textrm{T}_{{\textbf{v}}}{\mathfrak {M}}_{{\mathfrak {r}}_{{k}}}( {\textbf{V}}_{D},{\mathcal {P}}_k(T_D))\right) \in {\mathbb {G}}({\textbf{V}}_{D_{\Vert \cdot \Vert _D}}), \end{aligned}$$

also by Lemma 4.14 in [8], and it is linearly isomorphic to \(\textrm{T}_{{\textbf{v}}}{{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}( {\textbf{V}}_{D},T_D).\) Thus, also \({{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}( {\textbf{V}}_{D},T_D)\) is an immersed sub-manifold of \({\textbf{V}}_{D_{\Vert \cdot \Vert _D}}.\) Hence we have the following result.

Corollary 5.4

Let \(T_{D}\) be a dimension partition tree over D and \({\mathfrak {r}} \in {{\mathcal {A}}}{{\mathcal {D}}}({\textbf{V}}_D,T_D)\) such that \({{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}({\textbf{V}}_D,T_D)\) is a proper set of tree-based tensors with a fixed tree-based rank \({\mathfrak {r}}.\) Assume that \(({\textbf{V}}_{\alpha },\Vert \cdot \Vert _{\alpha })\) is a normed space for each \(\alpha \in T_D \setminus \{D\}\) and let \(\Vert \cdot \Vert _D\) be a norm on the tensor space \({\textbf{V}}_D\) such that (4.3) holds for \(1 \le k \le \textrm{depth}(T_D).\) Then \({{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}( {\textbf{V}}_{D},T_D)\) is an immersed sub-manifold of \({\textbf{V}}_{D_{\Vert \cdot \Vert _D}}.\)

5.2 On the Dirac–Frenkel variational principle

To extend Dirac–Frenkel Variational Principle for a proper set of tree-based tensors with a fixed tree-based rank, we consider the abstract ordinary differential equation in a reflexive tensor Banach space \({\textbf{V}}_{D_{\Vert \cdot \Vert _{D}}} = \overline{{\textbf{V}}_D}^{\Vert \cdot \Vert _D},\) given by

$$\begin{aligned} \dot{{\textbf{u}}}(t)&={\textbf{F}}(t,{\textbf{u}}(t)),\text { for }t\ge 0, \end{aligned}$$
(5.1)
$$\begin{aligned} {\textbf{u}}(0)&={\textbf{u}}_{0}, \end{aligned}$$
(5.2)

where we assume \({\textbf{u}}_{0}\ne {\textbf{0}}\) and \({\textbf{F}}:[0,\infty )\times {\textbf{V}}_{D_{\Vert \cdot \Vert _{D}}}\longrightarrow {\textbf{V}} _{D_{\Vert \cdot \Vert _{D}}}\) satisfying the usual conditions to have existence and uniqueness of solutions. Let \(T_{D}\) be a dimension partition tree over D and \({\mathfrak {r}} \in {{\mathcal {A}}}{{\mathcal {D}}}({\textbf{V}}_D,T_D)\) such that \({{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}({\textbf{V}}_D,T_D)\) is a proper set of tree-based tensors with a fixed tree-based rank \({\mathfrak {r}}.\) Assume that \(({\textbf{V}}_{\alpha },\Vert \cdot \Vert _{\alpha })\) is a normed space for each \(\alpha \in T_D \setminus \{D\}\) and let \(\Vert \cdot \Vert _D\) be a norm on the tensor space \({\textbf{V}}_D\) such that (4.3) holds for \(1 \le k \le \textrm{depth}(T_D)\).

We want to approximate \( {\textbf{u}}(t),\) for \(t\in I:=(0,T )\) for some \(T >0,\) by a differentiable curve \(t\mapsto {\textbf{v}}_{r}(t)\) from I to \({{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}({\textbf{V}}_D,T_D),\) where \({\mathfrak {r}}\in {{\mathcal {A}}}{{\mathcal {D}}}({\textbf{V}}_D,T_D)\) \(({\mathfrak {r}} \ne {\textbf{0}}),\) such that \({\textbf{v}}_{r}(0)={\textbf{v}}_{0}\in {{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}({\textbf{V}}_D,T_D)\) is an approximation of \({\textbf{u}}_{0}.\)

To construct a reduced order model of (5.1)–(5.2) over the Banach manifold \({{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}({\textbf{V}}_D,T_D)\) we consider the natural inclusion map

$$\begin{aligned} {\mathfrak {i}}:{{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}( {\textbf{V}}_{D},T_D) \longrightarrow {\textbf{V}}_{D_{\Vert \cdot \Vert _{D}}}. \end{aligned}$$

Since \({{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}( {\textbf{V}}_{D},T_D)\) is an immersed sub-manifold in \({\textbf{V}}_{D_{\Vert \cdot \Vert _D}},\) from Theorem 3.5.7 in [16], we have

$$\begin{aligned} \textrm{T}_{{\textbf{v}}}{\mathfrak {i}} \left( \textrm{T}_{{\textbf{v}}}{{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}( {\textbf{V}}_{D},T_D) \right) \in {\mathbb {G}}({\textbf{V}}_{D_{\Vert \cdot \Vert _D}}). \end{aligned}$$

By using that \({\textbf{F}}(t,{\textbf{v}}_{r}(t))\in {\textbf{V}}_{D_{\Vert \cdot \Vert _{D}}},\) for each \(t\in I,\) together the fact that

$$\begin{aligned} {\textbf{Z}}^{(D)}({\textbf{v}}_{r}(t)):= \textrm{T}_{{\textbf{v}}_{r}(t)}{\mathfrak {i}} \left( \textrm{T}_{{\textbf{v}}_{r}(t)}{{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}({\textbf{V}}_{D},T_D) \right) \end{aligned}$$

is a closed linear subspace in \({\textbf{V}}_{D_{\Vert \cdot \Vert _{D}}},\) we have the existence of a \(\dot{{\textbf{v}}}_{r}(t)\in {\textbf{Z}} ^{(D)}({\textbf{v}}_{r}(t))\) such that

$$\begin{aligned} \Vert \dot{{\textbf{v}}}_{r}(t)-{\textbf{F}}(t,{\textbf{v}}_{r}(t))\Vert _{D}=\min _{\dot{{\textbf{v}}}\in {\textbf{Z}}^{(D)}({\textbf{v}}_{r}(t))}\Vert \dot{{\textbf{v}}}-{\textbf{F}}(t,{\textbf{v}}_{r}(t))\Vert _{D}. \end{aligned}$$
(5.3)

Equation (5.3) extends the variational principle of Dirac–Frenkel to the Banach manifold \({{\mathcal {F}}}{{\mathcal {T}}}_{{\mathfrak {r}}}({\textbf{V}}_{D},T_D).\)