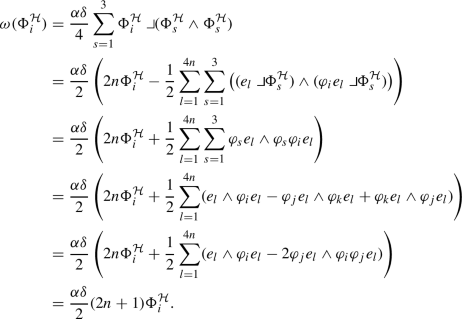Curvature properties of 3-$(\alpha ,\delta )$-Sasaki manifolds

Abstract

We investigate curvature properties of 3-$(\alpha ,\delta )$-Sasaki manifolds, a special class of almost 3-contact metric manifolds generalizing 3-Sasaki manifolds (corresponding to $\alpha =\delta =1$) that admit a canonical metric connection with skew torsion and define a Riemannian submersion over a quaternionic Kähler manifold with vanishing, positive or negative scalar curvature, according to $\delta =0$, $\alpha \delta >0$ or $\alpha \delta <0$. We shall investigate both the Riemannian curvature and the curvature of the canonical connection, with particular focus on their curvature operators, regarded as symmetric endomorphisms of the space of 2-forms. We describe their spectrum, find distinguished eigenforms, and study the conditions of strongly definite curvature in the sense of Thorpe.

1 Preliminaries

1.1 Introduction

The present paper is devoted to the curvature properties of 3-$(\alpha ,\delta )$-Sasaki manifolds, both of the Riemannian connection and the canonical connection and, most importantly, their interaction. We will be particularly concerned with the curvature operators, regarded as symmetric endomorphisms of the space of 2-forms, in order to investigate their spectrum, find distinguished eigenforms, and study the conditions of strongly definite curvature in the sense of Thorpe.

3-$(\alpha ,\delta )$-Sasaki manifolds are a special class of almost 3-contact metric manifolds. They were introduced in [2] as a generalization of 3-Sasaki manifolds (corresponding to $\alpha =\delta =1$), and as a subclass of canonical almost 3-contact metric manifolds, characterized by admitting a canonical metric connection with totally skew-symmetric torsion (skew torsion for brief). The vanishing of the coefficient $\beta :=2(\delta -2\alpha )$ defines parallel 3-$(\alpha ,\delta )$-Sasaki manifolds, for which the canonical connection parallelizes all the structure tensor fields. The geometry of 3-$(\alpha ,\delta )$-Sasaki manifolds has been further investigated in [3], where it was shown that they admit a locally defined Riemannian submersion over a quaternionic Kähler manifold with vanishing, positive or negative scalar curvature, according to $\delta =0$, $\alpha \delta >0$ or $\alpha \delta <0$. These coincide, respectively, with the defining conditions of degenerate, positive and negative 3-$(\alpha ,\delta )$-Sasaki structures, which are all preserved by a special type of deformations, namely $\mathcal {H}$-homothetic deformations. The vertical distribution of the canonical submersion, which turns out to have totally geodesic leaves, coincides with the 3-dimensional distribution spanned by the three Reeb vector fields $\xi _i$, $i=1,2,3$, of the structure. The canonical connection plays a central role in this picture, as it preserves both the vertical and the horizontal distribution, and in fact, when applied to basic vector fields, it projects onto the Levi-Civita connection of the quaternionic Kähler base space. Beyond this introduction, the remaining part of Section 1 will be devoted to a short review of the notions and results needed in this work.

In Sect. 2, we will see how the canonical curvature operator $\mathcal R$ is related to the Riemannian curvature operator $\mathcal R^{g_N}$ of the qK base space of the canonical submersion $\pi :M\rightarrow N$. Introducing a suitable decomposition of $\mathcal R$, we show that if $\mathcal R^{g_N}$ is non-negative, resp. non-positive, then so is the operator $\mathcal R$, provided that $\alpha \beta \ge 0$ for non-negative definiteness (Theorem 2.3). The decomposition of the operator $\mathcal R$ also allows to determine a set of six orthogonal eigenforms of $\mathcal R$, distinguished into two triples: $\Phi _i-\xi _{jk}$, and $\Phi _i+(n+1)\xi _{jk}$, where (ijk) denotes an even permutation of (123), $\Phi _i$ are the fundamental 2-forms of the structure, and $\xi _{jk}:=\xi _j\wedge \xi _k$.

The goal of Sect. 3 is to interpret both triples $\Phi _i-\xi _{jk}$ and $\Phi _i+(n+1)\xi _{jk}$ as eigenforms, not only of $\mathcal R$, but also of the Riemannian curvature operator $\mathcal R^g$ of M. We show that them being eigenforms of $\mathcal R^g$ provides necessary and sufficient conditions for M to be Einstein, which precisely happens when $\delta =\alpha$ or $\delta =(2n+3)\alpha$, with $\dim M=4n+3$ (Theorem 3.1). The result is obtained by taking into account the relation between the operators $\mathcal R$ and $\mathcal R^g$, involving two further symmetric operators $\mathcal G_T$ and $\mathcal S_T$ defined by means of the torsion of the canonical connection.

Section 4 is devoted to the investigation of conditions of strong definiteness for the Riemannian curvature of a 3-$(\alpha ,\delta )$-Sasaki manifold. Recall that a Riemannian manifold (M, g) is said to have strongly positive curvature if for some 4-form $\omega$ the modified symmetric operator $\mathcal R^g+\omega$ is positive definite. On the one hand, this weakens the condition of positive definiteness of the Riemannian curvature operator ($\mathcal {R}^g> 0$), which forces the Riemannian manifold to be diffeomorphic to a space form [9]. On the other hand, this provides a stronger condition than positive sectional curvature as, for any 2-plane $\sigma$, ${\text {sec}}(\sigma )=\langle (\mathcal {R}^g+\omega )(\sigma ),\sigma \rangle$. The method of modifying the curvature operator by a 4-form was originally introduced by Thorpe [16, 17], and then developed by various authors [7, 15, 20]. In the same way, one can introduce a notion of strongly non-negative curvature. Considering a 3-$(\alpha ,\delta )$-Sasaki manifold M with canonical submersion $\pi :M\rightarrow N$, we determine sufficient conditions for strongly non-negative and strongly positive curvature (Theorem 4.1). We require a sufficiently large quotient $\delta /\alpha \gg 0$, together with strongly non-negative or strongly positive curvature for the quaternionic Kähler base space N. Suitable 4-forms modifying the Riemannian curvature operator $\mathcal R^g$ of M are constructed using the pullback $\pi ^*\omega$ of a 4-form $\omega$ which modifies the operator $\mathcal R^{g_N}$, and the 4-form $\sigma _T=\frac{1}{2} dT$, T being the torsion of the canonical connection; this 4-form is known to be a measure of the non-degeneracy of the torsion T, which explains its appearance in this context. We discuss the case of homogeneous 3-$(\alpha ,\delta )$-Sasaki manifolds fibering over symmetric quaternionic Kähler spaces of compact type (Wolf spaces) and their non-compact duals. A construction of these spaces was given in [3], providing a classification in the compact case ($\alpha \delta >0$). In this case, we show that if $\alpha \beta \ge 0$, then the manifold is strongly non-negative. Strong positivity is much more restrictive, as the only spaces admitting a homogeneous structure with strict positive sectional curvature are the 7-dimensional Aloff–Wallach space $W^{1,1}$, the spheres $S^{4n+3}$, and real projective spaces $\mathbb {R}P^{4n+3}$. For these spaces, assuming $\alpha \beta >0$, we provide explicit 4-forms modifying the Riemannian curvature operator to obtain strongly positive curvature (Theorem 4.5). In Sect. 4.3, we show strong positive curvature for a class of inhomogeneous 3-$(\alpha ,\delta )$-Sasaski manifold obtained by 3-Sasaki reduction, compare [11, 13].

1.2 Curvature endomorphisms and strongly positive curvature

We review notations and established properties of connections with skew torsion and their curvature. We refer to [1] for further details.

Let (M, g) be a Riemannian manifold, $\dim M=n$. A metric connection $\nabla$ is said to have skew torsion if the (0, 3)-tensor field T defined by

$$\begin{aligned} T(X,Y,Z)=g(T(X,Y),Z)=g(\nabla _XY-\nabla _YX-[X,Y],Z) \end{aligned}$$

is a 3-form. Then $\nabla$ and the Levi-Civita connection $\nabla ^g$ are related by $\nabla _XY=\nabla ^g_XY+\frac{1}{2}T(X,Y),$ and $\nabla$ has the same geodesics as $\nabla ^g$. Assume further that T is parallel, i.e., $\nabla T=0$. Typical examples of manifolds admitting metric connections with parallel skew torsion include Sasaki, nearly parallel $G_2$, nearly Kähler and several others (see also the recent paper [12]).

The fact that $\nabla T=0$ implies $dT=2\sigma _T$, where $\sigma _T$ is the 4-form defined by

$$\begin{aligned} \sigma _T(X,Y,Z,V)=g(T(X,Y),T(Z,V))+g(T(Y,Z),T(X,V))+g(T(Z,X),T(Y,V)). \end{aligned}$$

Furthermore, the curvature tensor $R(X,Y,Z,V)=g([\nabla _X,\nabla _Y]Z-\nabla _{[X,Y]}Z,V)$ of a connection with parallel skew torsion $\nabla$ satisfies the first Bianchi identity

$$\begin{aligned} {\mathop {\mathfrak {S}}\limits ^{XYZ}}R(X,Y,Z,V)=\sigma _T(X,Y,Z,V)=\frac{1}{2} dT(X,Y,Z,V) \end{aligned}$$

(1.1)

which implies the pair symmetry

$$\begin{aligned} R(X,Y,Z,V)=R(Z,V,X,Y). \end{aligned}$$

(1.2)

These identities trivially apply to the Levi-Civita connection $\nabla ^g$ of (M, g) and its curvature $R^g$. The Riemannian curvature $R^g$ is related to R by

$$\begin{aligned} R^g(X,Y,Z,V)=R(X,Y,Z,V)-\frac{1}{4} g(T(X,Y),T(Z,V))-\frac{1}{4}\sigma _T(X,Y,Z,V). \end{aligned}$$

(1.3)

Recall that, given a Riemannian manifold (M, g), at each point $x\in M$ the space $\Lambda ^p T_xM$ of p-vectors of $T_xM$ can be endowed with the inner product defined by

$$\begin{aligned} \langle u_1\wedge \ldots \wedge u_p,v_1\wedge \ldots \wedge v_p\rangle \ =\ \det [g_x(u_i,v_j)]. \end{aligned}$$

In particular, if $\{e_r, r=1,\ldots ,n\}$ is an orthonormal basis of $T_xM$, then $\{e_{i_1}\wedge \ldots \wedge e_{i_p},1\le i_1<\ldots <i_p\le n\}$ is an orthonormal basis for $\Lambda ^pT_xM$. Furthermore, by means of the inner product, we identify $\Lambda ^pT_xM$ with the space $\Lambda ^pT^*_xM$ of p-forms on $T_xM$.

The curvature tensor R induces by (1.2) a symmetric linear operator

$$\begin{aligned} \mathcal {R}:\Lambda ^2 T_xM\rightarrow \Lambda ^2T_xM\quad \langle \mathcal {R}(X\wedge Y),Z\wedge V\rangle =-g(R(X,Y)Z,V). \end{aligned}$$

The sign − is due to our curvature convention, so that positive curvature operator $\mathcal {R}$ implies positive sectional curvature

$$\begin{aligned} {\text {sec}}(X,Y)=R(X,Y,Y,X). \end{aligned}$$

Indeed, identifying a 2-plane $\sigma \subset T_xM$ with the 2-vector $X\wedge Y\in \Lambda ^2 T_xM$, where X, Y is an orthonormal basis of $T_xM$, the sectional curvature is ${\text {sec}}(\sigma )=\langle \mathcal {R}(\sigma ),\sigma \rangle$.

Any 4-form $\omega$ can be regarded as a symmetric operator

$$\begin{aligned} \omega :\Lambda ^2 T_xM\rightarrow \Lambda ^2T_xM\quad \langle \omega (\alpha ),\beta \rangle =\langle \omega ,\alpha \wedge \beta \rangle . \end{aligned}$$

In fact, the space of all symmetric linear operators splits as $S(\Lambda ^2T_xM) = \ker \mathfrak {b}\oplus \Lambda ^4T_xM$, where $\mathfrak {b}$ denotes the Bianchi map

$$\begin{aligned} \mathfrak {b}(\Omega )(X,Y,Z,V):=\Omega (X,Y,Z,V)+\Omega (Y,Z,X,V)+\Omega (Z,X,Y,V). \end{aligned}$$

Then, $\ker \mathfrak {b}$ is the space of algebraic curvature operators,¹ i.e., operators satisfying the first Bianchi identity (1.1) for vanishing torsion.

Definition 1.1

We will denote by ${\mathcal S}_T:\Lambda ^2M\rightarrow \Lambda ^2M$ the symmetric operator associated to the 4-form $\sigma _T$, i.e.,

$$\begin{aligned} \langle \mathcal S_T(X\wedge Y),Z\wedge V\rangle :=\sigma _T(X,Y,Z,V)=\frac{1}{2} \textrm{d}T(X,Y,Z,V). \end{aligned}$$

(1.4)

We will also consider the (0, 4)-tensor field $G_T$ and the symmetric operator $\mathcal G_T:\Lambda ^2M\rightarrow \Lambda ^2M$ defined by

$$\begin{aligned} \langle {\mathcal G}_T(X\wedge Y),Z\wedge V\rangle =G_T(X,Y,Z,V):=g(T(X,Y),T(Z,V)). \end{aligned}$$

Owing to (1.3), we have

$$\begin{aligned} \mathcal R^g=\mathcal R+\frac{1}{4} \mathcal G_T+\frac{1}{4} \mathcal S_T. \end{aligned}$$

(1.5)

Definition 1.2

A Riemannian manifold (M, g) is said to have strongly positive curvature (resp.  strongly non-negative curvature) if there exists a 4-form $\omega$ such that $\mathcal {R}^g+\omega$ is positive definite (resp. non-negative) at every point $x\in M$ [7, 16, 17].

Such a notion is justified by the fact that for every 2-plane $\sigma$, being $\langle \omega (\sigma ),\sigma \rangle =0$, one has ${\text {sec}}(\sigma )=\langle (\mathcal {R}^g+\omega )(\sigma ),\sigma \rangle$, so that strongly positive curvature implies positive sectional curvature. In fact this is an intermediate notion between positive definiteness of the Riemannian curvature ($\mathcal {R}^g> 0$) and positive sectional curvature.

1.3 Review of 3-$(\alpha ,\delta )$-Sasaki manifolds and their basic properties

We now want to focus on the situation at hand. That is a 3-$(\alpha ,\delta )$-Sasaki manifold and its canonical connection $\nabla$. Let us recall the central definitions and key properties for later reference.

An almost contact metric structure on a $(2n+1)$-dimensional differentiable manifold M is a quadruple $(\varphi ,\xi ,\eta ,g)$, where $\varphi$ is a (1, 1)-tensor field, $\xi$ a vector field, called the characteristic or Reeb vector field, $\eta$ a 1-form, g a Riemannian metric, such that

$$\begin{aligned}{} & {} \varphi ^2=-I+\eta \otimes \xi ,\quad \eta (\xi )=1,\quad \varphi (\xi ) =0,\quad \eta \circ \varphi =0,\\{} & {} g(\varphi X,\varphi Y)=g(X,Y)-\eta (X) \eta (Y)\quad \forall X,Y\in {\mathfrak {X}}(M). \end{aligned}$$

It follows that $\eta =g(\cdot ,\xi )$, and $\varphi$ induces a complex structure on the 2n-dimensional distribution given by $\textrm{Im}(\varphi )=\ker \eta =\langle \xi \rangle ^\perp$. The fundamental 2-form associated to the structure is defined by $\Phi (X,Y)=g(X,\varphi Y)$. The almost contact metric structure is said to be normal if $N_\varphi {:}{=}[\varphi ,\varphi ]+\textrm{d}\eta \otimes \xi$ vanishes, where $[\varphi ,\varphi ]$ is the Nijenhuis torsion of $\varphi$ [8]. An $\alpha$-Sasaki manifold is defined as a normal almost contact metric manifold such that $\textrm{d}\eta \, =\, 2\alpha \Phi$, $\alpha \in \mathbb {R}^*.$ For $\alpha =1$, this is a Sasaki manifold.

An almost 3-contact metric manifold is a differentiable manifold M of dimension $4n+3$ endowed with three almost contact metric structures $(\varphi _i,\xi _i,\eta _i,g)$, $i=1,2,3$, sharing the same Riemannian metric g, and satisfying the following compatibility relations

$$\begin{aligned} \varphi _k=\varphi _i\varphi _j-\eta _j\otimes \xi _i=-\varphi _j\varphi _i+\eta _i\otimes \xi _j,\quad \xi _k\!=\varphi _i\xi _j=-\varphi _j\xi _i, \quad \eta _k=\eta _i\circ \varphi _j=\!-\eta _j\!\circ \varphi _i \end{aligned}$$

for any even permutation (ijk) of (123) [8]. The tangent bundle of M splits into the orthogonal sum $TM=\mathcal {H}\oplus \mathcal {V}$, where $\mathcal {H}$ and $\mathcal {V}$ are, respectively, the horizontal and the vertical distribution, defined by

$$\begin{aligned} \mathcal {H}\, {:}{=}\, \bigcap _{i=1}^{3}\ker \eta _i,\quad \mathcal {V}\, {:}{=}\, \langle \xi _1,\xi _2,\xi _3\rangle . \end{aligned}$$

In particular, $\mathcal {H}$ has rank 4n and the three Reeb vector fields $\xi _1,\xi _2,\xi _3$ are orthonormal. The manifold is said to be hypernormal if each almost contact metric structure $(\varphi _i,\xi _i,\eta _i,g)$ is normal. If the three structures are $\alpha$-Sasaki, M is called a 3-$\alpha$-Sasaki manifold, 3-Sasaki if $\alpha =1$. As a comprehensive introduction to Sasaki and 3-Sasaki geometry, we refer to [10]. We denote an almost 3-contact metric manifold by $(M,\varphi _i,\xi _i,\eta _i, g)$, understanding that the index is running from 1 to 3.

The class of 3-$(\alpha ,\delta )$-Sasaki manifolds was introduced in [2] as a generalization of 3-$\alpha$-Sasaki manifolds, and further investigated in [3].

Definition 1.1

An almost 3-contact metric manifold $(M,\varphi _i,\xi _i,\eta _i,g)$ is called a 3-$(\alpha ,\delta )$-Sasaki manifold if it satisfies

$$\begin{aligned} \textrm{d}\eta _i=2\alpha \Phi _i+2(\alpha - \delta )\eta _j\wedge \eta _k \end{aligned}$$

(1.6)

for every even permutation (ijk) of (123), where $\alpha \ne 0$ and $\delta$ are real constants. A 3-$(\alpha ,\delta )$-Sasaki manifold is called degenerate if $\delta =0$ and non-degenerate otherwise. Non-degenerate 3-$(\alpha ,\delta )$-Sasaki manifolds are called positive or negative, depending on whether $\alpha \delta >0$ or $\alpha \delta <0$.

The distinction into degenerate, positive, and negative 3-$(\alpha ,\delta )$-Sasaki manifolds stems from their behavior under a special type of deformations of the structure, called $\mathcal {H}$-homothetic deformations, which turn out to preserve the three classes [2, Section 2.3].

We recall some basic properties of 3-$(\alpha ,\delta )$-Sasaki manifolds. Any 3-$(\alpha ,\delta )$-Sasaki manifold is hypernormal. Hence, for $\alpha =\delta$ one has a 3-$\alpha$-Sasaki manifold. Each Reeb vector field $\xi _i$ is Killing, and it is an infinitesimal automorphism of the horizontal distribution $\mathcal {H}$, i.e., $\textrm{d}\eta _i(X,\xi _j)=0$ for every $X\in \mathcal {H}$ and $i,j=1,2,3$. The vertical distribution $\mathcal {V}$ is integrable with totally geodesic leaves. In particular, the commutators of the Reeb vector fields are purely vertical and for every even permutation (ijk) of (123) they are given by

$$\begin{aligned} {[}\xi _i,\xi _j]=2\delta \xi _k. \end{aligned}$$

Meanwhile, for any two horizontal vector fields X, Y, the vertical part of commutators is given by

$$\begin{aligned} {[}X,Y]_\mathcal {V}=-2\alpha \sum _{i=1}^3\Phi _i(X,Y)\xi _i. \end{aligned}$$

(1.7)

Any 3-$(\alpha ,\delta )$-Sasaki manifold is a canonical almost 3-contact metric manifold, in the sense of the definition given in [2], which is equivalent to the existence of a canonical connection. The canonical connection of a 3-$(\alpha ,\delta )$-Sasaki manifold $(M,\varphi _i,\xi _i,\eta _i,g)$ is the unique metric connection $\nabla$ with skew torsion such that

$$\begin{aligned} \nabla _X\varphi _i\, =\, \beta (\eta _k(X)\varphi _j -\eta _j(X)\varphi _k) \quad \forall X\in {\mathfrak {X}}(M) \end{aligned}$$

(1.8)

for every even permutation (ijk) of (123), where $\beta =2(\delta -2\alpha )$. The covariant derivatives of the other structure tensor fields are given by

$$\begin{aligned} \nabla _X\xi _i=\beta (\eta _k(X)\xi _j-\eta _j(X)\xi _k),\quad \nabla _X\eta _i=\beta (\eta _k(X)\eta _j-\eta _j(X)\eta _k). \end{aligned}$$

If $\delta =2\alpha$, then $\beta =0$ and the canonical connection parallelizes all the structure tensor fields. Any 3-$(\alpha ,\delta )$-Sasaki manifold with $\delta =2\alpha$, which is a positive 3-$(\alpha ,\delta )$-Sasaki manifold, is called parallel.

The canonical connection plays a central role in the description of the transverse geometry defined by the vertical foliation:

Theorem 1.1

([3, Prop. 2.1.1, Theorem 2.2.1, Theorem 2.2.2]) Every 3-$(\alpha ,\delta )$-Sasaki manifold M gives rise to a locally defined Riemannian submersion $\pi :(M,g)\rightarrow (N,g_N)$ with fibers spanned by $\mathcal {V}$ and

$$\begin{aligned} \nabla ^{g_N}_XY=\pi _*(\nabla _{\overline{X}}\overline{Y}). \end{aligned}$$

The base space N is equipped with a quaternion Kähler structure locally defined by $\check{\varphi }_i=\pi _*\circ \varphi _i\circ s$, $i=1,2,3$, where $s:N\rightarrow M$ is an arbitrary section of $\pi$. The scalar curvature of N is $16n(n+2)\alpha \delta$.

Here and in the following $\overline{X}\in TM$ denotes the horizontal lift of a vector field $X\in TN$ under the Riemannian submersion $\pi :M\rightarrow N$. We further denote the Levi-Civita connection on $(N,g_N)$ by $\nabla ^{g_N}$ and analogously for its associated tensors, e.g., the curvature tensor $R^{g_N}$.

From the above theorem, it follows that any 3-$(\alpha ,\delta )$-Sasaki manifold locally fibers over a quaternionic Kähler manifold of positive or negative scalar curvature if either $\alpha \delta >0$ or $\alpha \delta <0$, respectively, or over a hyper-Kähler manifold in the degenerate case.

The Riemannian Ricci tensor of a 3-$(\alpha ,\delta )$-Sasaki manifold has been computed in [2, Proposition 2.3.3]:

$$\begin{aligned} Ric^g(X,Y)=2\alpha \{2\delta (n+2)-3\alpha \}g(X,Y)+2(\alpha - \delta )\{(2n+3)\alpha - \delta \} \sum _{i=1}^3\eta _i(X)\eta _i(Y)\nonumber \\ \end{aligned}$$

(1.9)

implying that the manifold is Riemannian Einstein if and only if $\delta =\alpha$ or $\delta =\alpha (2n+3)$.

Finally, we recall some properties for the torsion of the canonical connection. The torsion T of the canonical connection of a 3-$(\alpha ,\delta )$-Sasaki manifold is given by

$$\begin{aligned} T\ =\ 2\alpha \sum _{i=1}^3\eta _i\wedge \Phi _i-2(\alpha - \delta )\eta _{123}\ =\ 2\alpha \sum _{i=1}^3\eta _i\wedge \Phi ^{\mathcal H}_i+2(\delta -4 \alpha )\,\eta _{123}, \end{aligned}$$

(1.10)

where $\Phi ^{\mathcal H}_i=\Phi _i+\eta _{jk}\in \Lambda ^2({\mathcal H})$ is the horizontal part of the fundamental 2-form $\Phi _i$. Here we put $\eta _{jk}{:}{=}\eta _j\wedge \eta _k$ and $\eta _{123}{:}{=}\eta _1\wedge \eta _2\wedge \eta _3$. In particular, for every $X,Y\in \mathfrak {X}(M)$,

$$\begin{aligned} T(X,Y)=2\alpha \sum _{i=1}^3\{\eta _i(Y)\varphi _iX-\eta _i(X)\varphi _iY+\Phi _i(X,Y)\xi _i\}-2(\alpha - \delta ) {\mathop {\mathfrak {S}}\limits ^{i,j,k}}\eta _{ij}(X,Y)\xi _k. \end{aligned}$$

(1.11)

The symbol ${\mathop {\mathfrak {S}}\limits ^{i,j,k}}$ means the sum over all even permutations of (123). The torsion of the canonical connection satisfies $\nabla T=0$ and

$$\begin{aligned} \begin{aligned} \textrm{d}T&= 4\alpha ^2\sum _{i=1}^3\Phi _i\wedge \Phi _i + 8\alpha (\delta -\alpha ) {\mathop {\mathfrak {S}}\limits ^{i,j,k}}\Phi _i\wedge \eta _{jk}\\&= 4\alpha ^2\sum _{i=1}^3\Phi ^\mathcal {H}_i\wedge \Phi ^\mathcal {H}_i + 8\alpha (\delta -2 \alpha ) {\mathop {\mathfrak {S}}\limits ^{i,j,k}}\Phi ^\mathcal {H}_i\wedge \eta _{jk}. \end{aligned} \end{aligned}$$

(1.12)

2 The canonical curvature operator

2.1 The canonical curvature and the canonical submersion

The canonical curvature is particularly well behaved on the defining tensors of a 3-$(\alpha ,\delta )$-Sasaki manifold. We will make use of this to compute directly related curvature identities in the following two propositions. These, in turn, allowed us to prove the existence of the canonical submersion in [3].

Proposition 2.1

Let $(M,\varphi _i,\xi _i,\eta _i,g)$ be a 3-$(\alpha ,\delta )$-Sasaki manifold. Let $\nabla$ be the canonical connection and R the curvature tensor of $\nabla$. Then, the following equations hold:

$$\begin{aligned}{} & {} \begin{aligned} R(X,Y)\varphi _iZ-\varphi _i R(X,Y)Z&=2\alpha \beta \{\Phi _k(X,Y)\varphi _jZ-\Phi _j(X,Y)\varphi _kZ\}\\&\quad -2\alpha \beta \{(\eta _i\wedge \eta _j)(X,Y)\varphi _jZ-(\eta _k\wedge \eta _i)(X,Y)\varphi _kZ\}, \end{aligned}\nonumber \\ \end{aligned}$$

(2.1)

$$\begin{aligned}{} & {} \begin{aligned} R(X,Y)\xi _i&=2\alpha \beta \{\Phi _k(X,Y)\xi _j-\Phi _j(X,Y)\xi _k\}\\&\quad -2\alpha \beta \{(\eta _i\wedge \eta _j)(X,Y)\xi _j-(\eta _k\wedge \eta _i)(X,Y)\xi _k\}, \end{aligned} \end{aligned}$$

(2.2)

where $X,Y,Z\in \mathfrak {X}(M)$ and (ijk) is an even permutation of (123).

Proof

Applying the Ricci identity, (1.8) and (1.6), we have

$$\begin{aligned}&R(X,Y)\varphi _iZ-\varphi _i R(X,Y)Z\\&\quad =(\nabla _X(\nabla _Y\varphi _i))Z-(\nabla _Y(\nabla _X\varphi _i))Z-(\nabla _{[X,Y]}\varphi _i)Z\\&\quad =\beta \{X(\eta _k(Y))\varphi _jZ+\eta _k(Y)(\nabla _X\varphi _j)Z-X(\eta _j(Y))\varphi _kZ-\eta _j(Y)(\nabla _X\varphi _k)Z\}\\&\quad \quad -\beta \{Y(\eta _k(X))\varphi _jZ+\eta _k(X)(\nabla _Y\varphi _j)Z-Y(\eta _j(X))\varphi _kZ-\eta _j(X)(\nabla _Y\varphi _k)Z\}\\&\quad \quad -\beta \{\eta _k([X,Y])\varphi _jZ-\eta _j([X,Y])\varphi _kZ\}\\&\quad =\beta \{\textrm{d}\eta _k(X,Y)\varphi _jZ-\textrm{d}\eta _j(X,Y)\varphi _kZ\}\\&\quad \quad +\beta ^2\{\eta _k(Y)(\eta _i(X)\varphi _kZ-\eta _k(X)\varphi _iZ)-\eta _j(Y)(\eta _j(X)\varphi _iZ-\eta _i(X)\varphi _jZ)\}\\&\quad \quad -\beta ^2\{\eta _k(X)(\eta _i(Y)\varphi _kZ-\eta _k(Y)\varphi _iZ)-\eta _j(X)(\eta _j(Y)\varphi _iZ-\eta _i(Y)\varphi _jZ)\}\\&\quad =2\alpha \beta \{\Phi _k(X,Y)\varphi _jZ-\Phi _j(X,Y)\varphi _kZ\}\\&\quad \quad +\{2\beta (\alpha - \delta )+\beta ^2\}\{(\eta _i\wedge \eta _j)(X,Y)\varphi _jZ-(\eta _k\wedge \eta _i)(X,Y)\varphi _kZ\}, \end{aligned}$$

which gives (2.1), since $\beta =2(\delta -2\alpha )$. We obtain (2.2) by setting $Z=\xi _i$ in (2.1) and applying $\varphi _i$ from the left. $\square$

Proposition 2.2

The curvature tensor R of the canonical connection of a 3-$(\alpha ,\delta )$-Sasaki manifold satisfies for any $X,Y,Z\in \mathcal {H}$ and $i,j,k,l=1,2,3$ the identities

$$\begin{aligned} R(X,\xi _i,Y,\xi _j)&=R(X,Y,Z,\xi _i)=R(\xi _i,\xi _j,\xi _k,X)=0, \end{aligned}$$

(2.3)

$$\begin{aligned} R(\xi _i,\xi _j,\xi _k,\xi _l)&=-4\alpha \beta (\delta _{ik}\delta _{jl}-\delta _{il}\delta _{jk}), \end{aligned}$$

(2.4)

and for an even permutation (ijk) of (123)

$$\begin{aligned} R(\xi _i,\xi _j,X,Y)&=2\alpha \beta \Phi _k(X,Y), \end{aligned}$$

(2.5)

$$\begin{aligned} R(X,Y,Z,\varphi _iZ)+R(X,Y,\varphi _jZ,\varphi _kZ)&=2\alpha \beta \Phi _i(X,Y)\Vert Z\Vert ^2. \end{aligned}$$

(2.6)

Proof

Considering the symmetries of R, we immediately obtain the first three expressions from equation (2.2). Using (2.1) for $\varphi _j$ we obtain

$$\begin{aligned} R(X,Y,\varphi _j Z,\varphi _k Z)&= g(\varphi _jR(X,Y)Z,\varphi _kZ)\\&\quad + 2\alpha \beta (\Phi _i(X,Y)g(\varphi _kZ,\varphi _k Z)-\Phi _k(X,Y)g(\varphi _iZ,\varphi _k Z))\\&=-R(X,Y,Z,\varphi _i Z) +2\alpha \beta \Phi _i(X,Y)\Vert Z\Vert ^2. \end{aligned}$$

$\square$

Remark 2.1

The identities (2.3), (2.4), (2.5), (2.6) are used to prove the canonical submersion in [3].

Considering now the canonical submersion $\pi :M\rightarrow N$ defined in Theorem 1.1, in the next theorem we will relate the missing purely horizontal part of the canonical curvature tensor to the curvature of the quaternionic Kähler base space N. We recall a computational lemma from [3].

Lemma 2.1

([3, Lemma 2.2.1]) For any vertical vector field $X\in \mathcal {V}$ and for any basic vector field $Y\in \mathcal {H}$, we have

$$\begin{aligned} (\nabla _{X}Y)_{\mathcal {H}}=-2\alpha \sum _{i=1}^3\eta _i(X)\varphi _i Y. \end{aligned}$$

Theorem 2.1

The canonical curvature on $\Lambda ^2\mathcal {H}\otimes \Lambda ^2\mathcal {H}$ is given by

$$\begin{aligned} R(\overline{X},\overline{Y},\overline{Z},\overline{V})=R^{g_N}(X,Y,Z,V)+4\alpha ^2\sum _{i=1}^3\Phi _i(\overline{X},\overline{Y})\Phi _i(\overline{Z},\overline{V}), \end{aligned}$$

where $X,Y,Z,V\in TN$ with horizontal lifts $\overline{X},\overline{Y},\overline{Z},\overline{V}\in \mathcal {H}$.

Proof

We note that by $\nabla ^{g_N}_XY=\pi _*(\nabla _{\overline{X}}\overline{Y})$ the vector field $\nabla _{\overline{X}}\overline{Y}\in \mathcal {H}$ is $\pi$-related to $\nabla ^{g_N}_XY$ and thus $\nabla _{\overline{X}}\overline{Y}=\overline{\pi _*(\nabla _{\overline{X}}\overline{Y})}$. We obtain

$$\begin{aligned} g_N(\nabla ^{g_N}_X\nabla ^{g_N}_Y Z,V)&=g_N(\nabla ^{g_N}_X\pi _*(\nabla _{\overline{Y}}\overline{Z}),V) =g(\nabla _{\overline{X}}\overline{\pi _*(\nabla _{\overline{Y}}\overline{Z})},\overline{V}) =g(\nabla _{\overline{X}}\nabla _{\overline{Y}}\overline{Z},\overline{V}),\\ g_N(\nabla ^{g_N}_{[X,Y]}Z,V)&=g_N(\pi _*\nabla _{\overline{[X,Y]}}\overline{Z},V)=g(\nabla _{[\overline{X},\overline{Y}]}\overline{Z}-\nabla _{[\overline{X},\overline{Y}]_{\mathcal {V}}}\overline{Z},\overline{V})\\&=g(\nabla _{[\overline{X},\overline{Y}]}\overline{Z},\overline{V})+4\alpha ^2\sum _{i=1}^{3}\Phi _i(\overline{X},\overline{Y})\Phi _i(\overline{Z},\overline{V}) \end{aligned}$$

where we have used (1.7) and Lemma 2.1. Plugging these identities into the curvature, we find

$$\begin{aligned} R^{g_N}(X,Y,Z,V)&=g_N(\nabla ^{g_N}_X\nabla ^{g_N}_YZ-\nabla ^{g_N}_Y\nabla ^{g_N}_XZ-\nabla ^{g_N}_{[X,Y]}Z,V)\\&=g(\nabla _{\overline{X}}\nabla _{\overline{Y}}\overline{Z}-\nabla _{\overline{Y}}\nabla _{\overline{X}}\overline{Z}-\nabla _{[\overline{X},\overline{Y}]}\overline{Z},\overline{V})-4\alpha ^2\sum _{i=1}^{3}\Phi _i(\overline{X},\overline{Y})\Phi _i(\overline{Z},\overline{V})\\&=R(\overline{X},\overline{Y},\overline{Z},\overline{V})-4\alpha ^2\sum _{i=1}^{3}\Phi _i(\overline{X},\overline{Y})\Phi _i(\overline{Z},\overline{V}). \end{aligned}$$

$\square$

2.2 Decomposition of the canonical curvature operator

We now want to look at the canonical curvature as a curvature operator and consider its eigenvalues and definiteness. Recall that the canonical curvature operator $\mathcal R:\Lambda ^2\,M\rightarrow \Lambda ^2\,M$ defines a symmetric operator. Rewriting (2.3) as operator identities we obtain

$$\begin{aligned} \langle \mathcal R(X\wedge \xi _i),Y\wedge \xi _j\rangle =\langle \mathcal R(X\wedge Y),Z\wedge \xi _i\rangle =\langle \mathcal R(\xi _i\wedge \xi _j),\xi _k\wedge X\rangle =0 \end{aligned}$$

showing that the canonical curvature operator vanishes on $\mathcal {V}\wedge \mathcal {H}$. Thus, it can be considered as a symmetric operator $\mathcal R:\Lambda ^2\mathcal {V}\oplus \Lambda ^2\mathcal {H}\rightarrow \Lambda ^2\mathcal {V}\oplus \Lambda ^2\mathcal {H}$. It does not restrict to the individual summands, but we can accomplish a more nuanced decomposition.

Remark 2.2

From here on out, we will freely identify TM and $T^*M$ as well as their exterior products. In particular, we write $\xi _{jk}{:}{=}\xi _j\wedge \xi _k=\eta _{jk}=\eta _j\wedge \eta _k$.

Proposition 2.3

The curvature operator $\mathcal R$ can be decomposed as

$$\begin{aligned} \mathcal R=\alpha \beta \mathcal R_{\perp }+\mathcal {R}_{\textrm{par}}\end{aligned}$$

where $\mathcal {R}_{\perp }$ is defined by

$$\begin{aligned} \mathcal {R}_{\perp }{:}{=}{\mathop {\mathfrak {S}}\limits ^{i,j,k}}(\Phi _i-\xi _{jk})\otimes (\Phi _i-\xi _{jk}) \end{aligned}$$

(2.7)

and $\mathcal {R}_{\textrm{par}}$ is trivial outside of the horizontal part, i.e., $\mathcal {R}_{\textrm{par}}|_{(\Lambda ^2\mathcal {H})^\perp }=0$.

Proof

Equations (2.4) and (2.5) in terms of the curvature operator read

$$\begin{aligned} \langle \mathcal R(\xi _i\wedge \xi _j),\xi _k\wedge \xi _l\rangle&=4\alpha \beta \sum _{\mu =1}^3\Phi _\mu (\xi _i,\xi _j)\Phi _\mu (\xi _k,\xi _l), \end{aligned}$$

(2.8)

$$\begin{aligned} \langle \mathcal R(\xi _i\wedge \xi _j),X\wedge Y\rangle&=2\alpha \beta \sum _{\mu =1}^3\Phi _\mu (\xi _i,\xi _j)\Phi _\mu (X,Y). \end{aligned}$$

(2.9)

We observe that identities (2.8) and (2.9) are of the form $C\sum _{i=1}^3\Phi _i\otimes \Phi _i$, where the coefficient C is $4\alpha \beta$ or $2\alpha \beta$. The comparison with

$$\begin{aligned} \mathcal {R}_{\perp }&{:}{=}{\mathop {\mathfrak {S}}\limits ^{i,j,k}}(\Phi _i-\xi _{jk})\otimes (\Phi _i-\xi _{jk})\\&=\sum _{i=1}^3\big (4(\Phi _i|_{\Lambda ^2\mathcal {V}}\otimes \Phi _i|_{\Lambda ^2\mathcal {V}})+2(\Phi _i|_{\Lambda ^2\mathcal {H}} \otimes \Phi _i|_{\Lambda ^2\mathcal {V}})\\&\quad +2(\Phi _i|_{\Lambda ^2\mathcal {V}}\otimes \Phi _i|_{\Lambda ^2\mathcal {H}})+(\Phi _i|_{\Lambda ^2\mathcal {H}}\otimes \Phi _i|_{\Lambda ^2\mathcal {H}})\big ). \end{aligned}$$

shows that $\mathcal {R}_{\textrm{par}}{:}{=}\mathcal R-\alpha \beta \mathcal {R}_{\perp }$ is trivial outside $\Lambda ^2\mathcal {H}\rightarrow \Lambda ^2\mathcal {H}$. $\square$

The notation $\mathcal {R}_{\textrm{par}}$ is justified by the fact that in the parallel case ($\beta =0$) we have $\mathcal R=\mathcal {R}_{\textrm{par}}$. Taking into account the canonical submersion $\pi :M\rightarrow N$, we may consider the Riemannian curvature operator $\mathcal R^{g_N}$ on the base N as a curvature operator $\Lambda ^2\mathcal {H}\rightarrow \Lambda ^2\mathcal {H}$ via the horizontal lift. From Theorem 2.1, we have

$$\begin{aligned} \mathcal R|_{\Lambda ^2\mathcal {H}\otimes \Lambda ^2\mathcal {H}}=\mathcal R^{g_N}-4\alpha ^2\sum _{\mu =1}^3\Phi ^{\mathcal {H}}_\mu \otimes \Phi ^{\mathcal {H}}_\mu . \end{aligned}$$

Note the sign change due to our convention of sign in $\mathcal R$ compared to R. Comparing with the definition of $\mathcal {R}_{\textrm{par}}$ in Proposition 2.3 and expanding $\beta =2(\delta -2\alpha )$ yields

$$\begin{aligned} \mathcal {R}_{\textrm{par}}=\mathcal R^{g_N}-2\alpha \delta \sum _{\mu =1}^3\Phi ^{\mathcal {H}}_\mu \otimes \Phi ^{\mathcal {H}}_\mu . \end{aligned}$$

(2.10)

Remark 2.3

Recall that the curvature operator of qK spaces is given by $\mathcal {R}^{g_N}=\nu \mathcal {R}_0+\mathcal {R}_1$, where $\nu =4\alpha \delta$ is the reduced scalar curvature, $\mathcal {R}_1$ is a curvature operator of hyper-Kähler type, and

is the curvature operator of $\mathbb {H}P^n$ [4, Tables 1 and 2]. Here denotes the Kulkarni–Nomizu product viewed as an operator. A curvature operator is said to be of hyper-Kähler type if it is Ricci-flat and commutes with the quaternionic structure. Combining this with (2.10), we find

Note that in the degenerate case, the picture simplifies, since then we just have $\mathcal {R}_{\textrm{par}}=\mathcal R_1=\mathcal R^{g_N}$.

We will now show some crucial properties of the spectrum of the introduced operators. Before proving the next lemmas, we remark a few facts on the fundamental 2-forms $\Phi _i$ of a 3-$(\alpha ,\delta )$-Sasaki structure. Each $\Phi _i$ can be expressed as

$$\begin{aligned} \Phi _i=-\frac{1}{2}\sum _{r=1}^{4n+3} e_r\wedge \varphi _i e_r, \end{aligned}$$

(2.11)

where $\{e_r, r=1,\ldots ,4n+3\}$ is a local orthonormal frame. A straightforward computation shows that for every $i,j,k=1,2,3$,

$$\begin{aligned} \langle \Phi _i,\Phi _j\rangle \,=(2n+1)\delta _{ij} \end{aligned}$$

(2.12)

and

$$\begin{aligned} \langle \Phi _i,\xi _{jk}\rangle =-\epsilon _{ijk}, \end{aligned}$$

(2.13)

where $\epsilon _{ijk}$ is the totally skew-symmetric symbol. We will also use adapted bases in the following sense.

Definition 2.1

An adapted basis of a 3-$(\alpha ,\delta )$-Sasaki manifold M is a local orthonormal frame $\{e_1,\dots ,e_{4n+3}\}$ of M such that

$$\begin{aligned} e_{i}=\xi _i, \quad e_{4l+i}=\varphi _ie_{4l} \quad \text { for} \ i=1,2,3,\ l=1,\dots , n. \end{aligned}$$

Therefore, in an adapted basis, the horizontal part $\Phi _i^{\mathcal {H}}=\Phi _i+\xi _{jk}$ is expressed as

$$\begin{aligned} \Phi _i^{\mathcal {H}}=-\frac{1}{4}\sum _{r=4}^{4n+3}e_r\wedge \varphi _i e_r+\varphi _j e_r\wedge \varphi _k e_r. \end{aligned}$$

(2.14)

Lemma 2.2

$\mathcal {R}_{\perp }$ has the only nonzero eigenvalue $2(n+2)$ with eigenspace generated by $\Phi _i-\xi _{jk}$ for $i=1,2, 3$.

Proof

By definition (2.7), $\Phi _i-\xi _{jk}$ are the only eigenvectors with non-vanishing eigenvalue $|\Phi _i-\xi _{jk}|^2$. From (2.12) and (2.13), we obtain the eigenvalue $2(n+2)$. $\square$

Lemma 2.3

The kernel of $\mathcal {R}_{\textrm{par}}$ contains the space generated by $Z\wedge \varphi _iZ+\varphi _jZ\wedge \varphi _kZ$, $Z\in \mathcal {H}$. In particular $\Phi _i^{\mathcal {H}}$, $\Phi _i$, $\Phi _i-\xi _{jk}$, $\Phi _i+(n+1)\xi _{jk}\in \ker \mathcal {R}_{\textrm{par}}$.

Proof

For $X,Y,Z\in \mathcal {H}$, compare (2.6) with (2.7) to obtain

$$\begin{aligned} \langle \mathcal R(X\wedge Y),Z\wedge \varphi _iZ+\varphi _jZ\wedge \varphi _kZ\rangle&=-2\alpha \beta \Phi _i(X,Y)\Vert Z\Vert ^2\\&=\langle \alpha \beta \mathcal {R}_{\perp }(X\wedge Y),Z\wedge \varphi _iZ+\varphi _jZ\wedge \varphi _kZ\rangle \end{aligned}$$

for any even permutation (ijk) of (123). Thus, $Z\wedge \varphi _iZ+\varphi _jZ\wedge \varphi _kZ\in \ker \mathcal {R}_{\textrm{par}}$. The second part of the statement follows immediately from (2.14) and $\mathcal {R}_{\textrm{par}}|_{(\Lambda ^2\mathcal {H})^\perp }=0$. $\square$

As a first consequence, we can obtain a distinguished set of eigenforms of the canonical curvature operator $\mathcal R$, which will have a special role in the characterization of the Einstein condition for a 3-$(\alpha ,\delta )$-Sasaki manifold (see Theorem 3.1).

Theorem 2.2

The curvature operator $\mathcal R$ of the canonical connection of any 3-$(\alpha ,\delta )$-Sasaki manifold $(M,\varphi _i,\xi _i,\eta _i,g)$ admits the following six orthogonal eigenforms:

• $\Phi _i-\xi _{jk}=\Phi _i^{\mathcal {H}}-2\xi _{jk}$, $i=1,2,3$, eigenform with eigenvalue $2\alpha \beta (n+2)$,

• $\Phi _i+(n+1)\xi _{jk}=\Phi _i^{\mathcal {H}}+n\xi _{jk}$, $i=1,2,3$, eigenform with vanishing eigenvalue.

Proof

From Lemma 2.3, all the forms are in the kernel of $\mathcal {R}_{\textrm{par}}$. Therefore, we only have to check that $\Phi _i-\xi _{jk}$ and $\Phi _i+(n+1)\xi _{jk}$ are eigenvectors of $\mathcal {R}_{\perp }$ with the respective eigenvalues. Lemma 2.2 provides just that under the observation $\langle \Phi _i+(n+1)\xi _{jk}, \Phi _i-\xi _{jk}\rangle =0$. $\square$

For later use, we observe that one can immediately obtain:

$$\begin{aligned} \mathcal R(\Phi _i)&=\alpha \beta \mathcal {R}_{\perp }(\Phi _i)=2\alpha \beta (n+1)(\Phi _i-\xi _{jk}), \end{aligned}$$

(2.15)

$$\begin{aligned} \mathcal R(\xi _{jk})&=\alpha \beta \mathcal {R}_{\perp }(\xi _{jk})=-2\alpha \beta (\Phi _i-\xi _{jk}). \end{aligned}$$

(2.16)

Proposition 2.4

The eigenvalues of the canonical curvature operator $\mathcal R$ satisfy

$$\begin{aligned} \textrm{Spec}(\mathcal R)=\textrm{Spec}(\mathcal R_\textrm{par})\cup \{0,2\alpha \beta (n+2)\} \end{aligned}$$

(2.17)

whereas

$$\begin{aligned} \textrm{Spec}(\mathcal R^{g_N})\cup \{0\}=\textrm{Spec}(\mathcal {R}_{\textrm{par}})\cup \{0, 4\alpha \delta n\}. \end{aligned}$$

(2.18)

Proof

Lemmas 2.2 and 2.3 show that $\mathcal R_\textrm{par}$ and $\mathcal {R}_{\perp }$ share eigenspaces. Additionally, the eigenspaces to nonzero eigenvalues of $\mathcal {R}_{\textrm{par}}$ are inside the kernel of $\mathcal {R}_{\perp }$ and vice versa. Thus the eigenvalues of $\mathcal R$ are simply the union

$$\begin{aligned} \textrm{Spec}(\mathcal R)=\textrm{Spec}(\mathcal R_\textrm{par})\cup \{0,2\alpha \beta (n+2)\} \end{aligned}$$

of the eigenvalues of $\mathcal R_\textrm{par}$ and the eigenvalues $\{0,2\alpha \beta (n+2)\}$ of $\alpha \beta \mathcal {R}_{\perp }$. For the second identity, we set $\mathcal {R}_{\perp }^{\mathcal {H}}{:}{=}\sum _{i=1}^3\Phi _i^{\mathcal {H}}\otimes \Phi _i^{\mathcal {H}}$ in analogy to the first identity. Immediately, we find that $\mathcal {R}_{\perp }^{\mathcal {H}}$ has the only nonzero eigenvalue 2n with eigenspace spanned by $\Phi _i^{\mathcal {H}}$, $i=1,2,3$. As before, it follows that the eigenvalues of $\mathcal R^{g_N}$ are the union of those of $\mathcal R_\textrm{par}$ and $2\alpha \delta \mathcal {R}_{\perp }^{\mathcal {H}}$. Thus we have (2.18). Remark that $\textrm{Spec}(\mathcal R)$ certainly contains 0 as $\Phi _i^{\mathcal {H}}+n\xi _{jk}\in \ker \mathcal R$, by Theorem 2.2, while $\textrm{Spec}(\mathcal R^{g_N})$ may or may not contain 0. $\square$

Remark 2.4

The discussion on the curvature operator $\mathcal R^{g_N}$ actually showed that the $\Phi _i$ are eigenvectors of $\mathcal R^{g_N}$ with eigenvalue $4\alpha \delta$. Thus, only now we proved that the canonical submersion of a 7-dimensional 3-$(\alpha ,\delta )$-Sasaki manifold has a quaternionic Kähler base under the stricter definition usually assumed. Compare the discussion ahead of [10, Definition 12.2.12].

The following theorem links the Riemannian curvature of the qK base to the canonical curvature of the total space, thus underlining the intricate relationship of these two connections.

Theorem 2.3

Let M be a 3-$(\alpha ,\delta )$-Sasaki manifold with canonical submersion $\pi :M\rightarrow N$.

• (a) If N has a non-negative Riemannian curvature operator $\mathcal R^{g_N}\ge 0$, then $\mathcal R$ is non-negative if and only if $\alpha \beta \ge 0$.

• (b) If N has a non-positive Riemannian curvature operator $\mathcal R^{g_N}\le 0$, then $\mathcal R$ is non-positive.

Proof

By (2.18), if $\mathcal R^{g_N}$ is either non-negative or non-positive, then so is $\mathcal {R}_{\textrm{par}}$ and the sign of $\alpha \delta$. Using (2.17), we obtain part (a) directly. For part (b), note that if $\alpha \delta \le 0$, then $\alpha \beta =2\alpha \delta -4\alpha ^2<0$. $\square$

3 Curvature eigenforms and the Einstein condition

In [2], the authors computed the Ricci tensor (1.9) implying that a 3-$(\alpha ,\delta )$-Sasaki manifold is Riemannian Einstein if and only if either $\delta =\alpha$ or $\delta =\alpha (2n+3)$. The aim of this section is to provide an additional characterization of the Einstein condition for 3-$(\alpha ,\delta )$-Sasaki manifolds through special eigenforms of the curvature operator $\mathcal R^g$. More precisely, we shall prove:

Theorem 3.1

Let $(M,\varphi _i,\xi _i,\eta _i,g)$ be a 3-$(\alpha ,\delta )$-Sasaki manifold. Then, the following conditions are equivalent:

• (a) each 2-form $\Phi _i-\xi _{jk}$ is an eigenform of $\mathcal R^g$;

• (b) each 2-form $\Phi _i+(n+1)\xi _{jk}$ is an eigenform of $\mathcal R^g$;

• (c) either $\delta =\alpha$ or $\delta =(2n+3)\alpha$;

• (d) (M, g) is Einstein.

If $\delta =\alpha$, that is in the 3-$\alpha$-Sasaki case, the six orthogonal eigenforms $\Phi _i-\xi _{jk}$, $\Phi _i+(n+1)\xi _{jk}$ admit the same eigenvalue $\lambda =\alpha ^2$. If $\delta =\alpha (2n+3)$, then each $\Phi _i-\xi _{jk}$ has eigenvalue $\lambda _1=\alpha ^2(8n^2+16n+9)$, while each $\Phi _i+(n+1)\xi _{jk}$ has eigenvalue $\lambda _2=\alpha ^2(2n+1)^2$.

Remark 3.1

Together with Theorem 2.2, we observe that exclusively in the Einstein case $\Phi _i-\xi _{jk}$ and $\Phi _i+(n+1)\xi _{jk}$ are joint eigenforms of $\mathcal R$, $\mathcal R^g$ and $\mathcal G_T+\mathcal S_T$. Since $\Phi _i+(n+1)\xi _{jk}\in \ker \mathcal R$ we have that the corresponding eigenvalue of $\mathcal G_T+\mathcal S_T$ is $4\lambda$, or $4\lambda _2$, respectively.

In order to prove Theorem 3.1, we will determine throughout the next propositions how $\mathcal {R}^g$ acts on the forms $\Phi _i$ and $\xi _{jk}$. Recall that by (1.5) the curvature operators $\mathcal {R}^g$ and $\mathcal {R}$ are related by the operators $\mathcal S_T$ and ${\mathcal G}_T$ defined in Definition 1.1. They act on the forms $\Phi _i$ and $\xi _{jk}$ as follows.

Proposition 3.1

Let $(M,\varphi _i,\xi _i,\eta _i,g)$ be a 3-$(\alpha ,\delta )$-Sasaki manifold. The torsion T of the canonical connection satisfies the following:

$$\begin{aligned} \mathcal S_T(\xi _{jk})&=2\alpha \beta (\Phi _i+\xi _{jk}), \end{aligned}$$

(3.1)

$$\begin{aligned} \mathcal S_T(\Phi _i)&=\left\{ 4\alpha ^2(2n+1)-2\alpha \beta \right\} \Phi _i+\left\{ 4\alpha ^2(2n+1)+2\alpha \beta (2n-1)\right\} \xi _{jk}. \end{aligned}$$

(3.2)

Proof

First we show that for every vector fields X, Y and for every even permutation (ijk) of (123)

$$\begin{aligned} \textrm{d}T(X,Y,\xi _i,\xi _j)=4\alpha \beta \{\Phi _k(X,Y)+(\eta _i\wedge \eta _j)(X,Y)\}, \end{aligned}$$

(3.3)

which is equivalent to (3.1), taking into account (1.4). Indeed, we compute

$$\begin{aligned}&\sum _{l=1}^3(\Phi _l\wedge \Phi _l)(X,Y,\xi _i,\xi _j)\\&\quad =2\{\Phi _k(X,Y)\Phi _k(\xi _i,\xi _j)+\Phi _k(X,\xi _i)\Phi _k(\xi _j,Y)+\Phi _k(X,\xi _j)\Phi _k(Y,\xi _i)\}\\&\quad =2\{-\Phi _k(X,Y)+\eta _j(X)\eta _i(Y)-\eta _i(X)\eta _j(Y)\}\\&\quad ={}-2\{\Phi _k(X,Y)+(\eta _i\wedge \eta _j)(X,Y)\}. \end{aligned}$$

We can also compute

$$\begin{aligned}&{\mathop {\mathfrak {S}}\limits ^{l,m,n}}(\Phi _l\wedge \eta _m\wedge \eta _n)(X,Y,\xi _i,\xi _j)\\&\quad ={\mathop {\mathfrak {S}}\limits ^{l,m,n}}\{\Phi _l(X,Y)\eta _{mn}(\xi _i,\xi _j)+\Phi _l(X,\xi _i)\eta _{mn}(\xi _j,Y)+\Phi _l(X,\xi _j)\eta _{mn}(Y,\xi _i)\\&\qquad +\Phi _l(\xi _i,\xi _j)\eta _{mn}(X,Y)+\Phi _l(\xi _j,Y)\eta _{mn}(X,\xi _i)+\Phi _l(Y,\xi _i)\eta _{mn}(X,\xi _j)\}\\&\quad =\Phi _k(X,Y)-\Phi _k(X,\xi _i)\eta _i(Y)-\Phi _k(X,\xi _j)\eta _j(Y)\\&\qquad {}-\eta _{ij}(X,Y)-\Phi _k(\xi _j,Y)\eta _j(X)+\Phi _k(Y,\xi _i)\eta _i(X)\\&\quad =\Phi _k(X,Y)-\eta _j(X)\eta _i(Y)+\eta _i(X)\eta _j(Y)-\eta _{ij}(X,Y)-\eta _i(Y)\eta _j(X)+\eta _j(Y)\eta _i(X)\\&\quad =\Phi _k(X,Y)+\eta _{ij}(X,Y). \end{aligned}$$

Therefore, using (1.12) we get (3.3).

In order to prove (3.2), first we show that for every $X,Y\in \Gamma (\mathcal {H})$

$$\begin{aligned} \sum _{r=1}^{4n+3}\textrm{d}T(X,Y,e_r,\varphi _ie_r)=\{-16\alpha ^2(2n+1)+8\alpha \beta \}\Phi _i(X,Y), \end{aligned}$$

(3.4)

where $e_r$, $r=1,\ldots ,4n+3$, is a local orthonormal frame. Indeed, we can compute

$$\begin{aligned}&\sum _{r=1}^{4n+3}\sum _{l=1}^3(\Phi _l\wedge \Phi _l)(X,Y,e_r,\varphi _ie_r)\\&\quad =2\sum _{r}\sum _{l}\{\Phi _l(X,Y)\Phi _l(e_r,\varphi _ie_r)+\Phi _l(X,e_r)\Phi _l(\varphi _ie_r,Y)+\Phi _l(X,\varphi _ie_r)\Phi _l(Y,e_r)\}\\&\quad =2\sum _r\Phi _i(X,Y)\Phi _i(e_r,\varphi _ie_r)+2\sum _lg(\varphi _lX,\varphi _i\varphi _lY)-2\sum _lg(\varphi _i\varphi _lX,\varphi _lY)\\&\quad =-2(4n+2)\Phi _i(X,Y)-2g(\varphi _iX,Y)-4g(X,\varphi _iY)+2g(X,\varphi _iY)+4g(\varphi _iX,Y)\\&\quad =-8(n+1)\Phi _i(X,Y). \end{aligned}$$

We also compute

$$\begin{aligned}&\sum _{r=1}^{4n+3}{\mathop {\mathfrak {S}}\limits ^{l,m,n}}(\Phi _l\wedge \eta _m\wedge \eta _n)(X,Y,e_r,\varphi _ie_r)\\&\quad =\sum _{r}{\mathop {\mathfrak {S}}\limits ^{l,m,n}}\Phi _l(X,Y)(\eta _m\wedge \eta _n)(e_r,\varphi _ie_r)\\&\quad =\Phi _i(X,Y)\{(\eta _j\wedge \eta _k)(\xi _j,\xi _k)+(\eta _j\wedge \eta _k)(\xi _k, -\xi _j)\}\\&\quad =2\Phi _i(X,Y). \end{aligned}$$

Applying (1.12), we can deduce that

$$\begin{aligned} \sum _{r=1}^{4n+3}\textrm{d}T(X,Y,e_r,\varphi _ie_r)=-32\alpha ^2(n+1)\Phi _i(X,Y)-16\alpha (\alpha - \delta )\Phi _i(X,Y), \end{aligned}$$

which gives (3.4), being $\beta =2(\delta -2\alpha )$. Now, from (1.4), (2.11) and (3.4), we have

$$\begin{aligned} \langle \mathcal S_T(\Phi _i),X\wedge Y\rangle&=-\frac{1}{2}\sum _{r=1}^{4n+3}\langle \mathcal S_T(e_r\wedge \varphi _ie_r),X\wedge Y\rangle =-\frac{1}{4}\sum _{r=1}^{4n+3}\textrm{d}T(X,Y,e_r,\varphi _ie_r)\\&=\{4\alpha ^2(2n+1)-2\alpha \beta \}\langle \Phi _i,X\wedge Y\rangle . \end{aligned}$$

From (1.12), one can see that for every $X,Y,Z\in \Gamma (\mathcal {H})$ and $r,s,t=1,2,3$

$$\begin{aligned} \textrm{d}T(X,Y,Z,\xi _r)=0, \quad \textrm{d}T(X,\xi _r,\xi _s,\xi _t)=0, \end{aligned}$$

which imply that

$$\begin{aligned} \langle \mathcal S_T(\Phi _i),X\wedge \xi _s\rangle =-\frac{1}{2} \sum _{r=1}^{4n+3}\langle \mathcal S_T(e_r\wedge \varphi _ie_r),X\wedge \xi _s\rangle =-\frac{1}{4}\sum _{r=1}^{4n+3}\textrm{d}T(e_r,\varphi _ie_r,X,\xi _s)=0. \end{aligned}$$

Finally, using (3.1) and (2.12),

$$\begin{aligned} \langle \mathcal S_T(\Phi _i),\xi _j\wedge \xi _k\rangle&=\langle \mathcal S_T(\xi _j\wedge \xi _k),\Phi _i\rangle =2\alpha \beta \langle \Phi _i+\xi _{jk},\Phi _i\rangle \\&=2\alpha \beta (2n+1+\Phi _i(\xi _j,\xi _k))=4\alpha \beta n \end{aligned}$$

and analogously, $\langle \mathcal S_T(\Phi _i),\xi _i\wedge \xi _j\rangle =\langle \mathcal S_T(\Phi _i),\xi _i\wedge \xi _k\rangle =0$, thus completing the proof of (3.2). $\square$

Proposition 3.2

Let $(M,\varphi _i,\xi _i,\eta _i,g)$ be a 3-$(\alpha ,\delta )$-Sasaki manifold. The torsion T of the canonical connection satisfies the following:

$$\begin{aligned} \mathcal G_T(\xi _{jk})&=(\beta -4\alpha )\left\{ 2\alpha \Phi _i+(\beta -2\alpha )\xi _{jk}\right\} , \end{aligned}$$

(3.5)

$$\begin{aligned} \mathcal G_T(\Phi _i)&=\left\{ 8\alpha ^2(n+1)-2\alpha \beta \right\} \Phi _i+\left\{ -8\alpha ^2(n+1) -\beta ^2+2\alpha \beta (2n+3)\right\} \xi _{jk}. \end{aligned}$$

(3.6)

Proof

By direct computation using (1.10) or (1.11), one easily gets that for all vector fields X, Y and for every even permutation (i, j, k) of (1, 2, 3)

$$\begin{aligned}{} & {} T(X,Y,\xi _i)=2\alpha \Phi _i(X,Y)+2(\delta -3\alpha )(\eta _j\wedge \eta _k)(X,Y),\\{} & {} T(\xi _j,\xi _k)=2(\delta -4\alpha )\xi _i. \end{aligned}$$

Hence,

$$\begin{aligned} \langle \mathcal G_T(\xi _{jk}),X\wedge Y\rangle&=g(T(\xi _j,\xi _k),T(X,Y))=2(\delta -4\alpha )T(X,Y,\xi _i)\\&=2(\delta -4\alpha )\{2\alpha \Phi _i(X,Y)+2(\delta -3\alpha )(\eta _j\wedge \eta _k)(X,Y)\}, \end{aligned}$$

which gives (3.5), since $\beta =2(\delta -2\alpha )$.

In order to prove (3.6), notice that for every $X,Y,Z,V\in \Gamma (\mathcal {H})$, applying (1.11), we have

$$\begin{aligned} G_T(X,Y,Z,V)=4\alpha ^2\sum _{l=1}^3\Phi _l(X,Y)\Phi _l(Z,V). \end{aligned}$$

Then, choosing a local orthonormal frame of type $e_r$, $r=1,\ldots ,4n$, $\xi _i,\xi _j,\xi _k$, and using (2.11), for every $X,Y\in \Gamma (\mathcal {H})$ we have

$$\begin{aligned} \langle \mathcal G_T(\Phi _i),X\wedge Y\rangle&=-\frac{1}{2}\sum _{r=1}^{4n}G_T(e_r,\varphi _ie_r,X,Y)-G_T(\xi _j,\xi _k,X,Y)\\&=-2\alpha ^2\sum _{r=1}^{4n}\sum _{l=1}^3\Phi _l(e_r,\varphi _ie_r)\Phi _l(X,Y)-2\alpha (\beta -4\alpha )\Phi _i(X,Y)\\&=8\alpha ^2n\Phi _i(X,Y)-2\alpha (\beta -4\alpha )\Phi _i(X,Y)\\&=\{8\alpha ^2(n+1)-2\alpha \beta \}\langle \Phi _i,X\wedge Y\rangle . \end{aligned}$$

Now, from (1.11), we also have that for every $X,Y,Z\in \Gamma (\mathcal {H})$ and $r,s,t=1,2,3$,

$$\begin{aligned} G_T(X,Y,Z,\xi _r)=0,\quad G_T(\xi _r,\xi _s,\xi _t,X)=0, \end{aligned}$$

which give

$$\begin{aligned} \langle \mathcal G_T(\Phi _i),X\wedge \xi _s\rangle =-\frac{1}{2}\sum _{r=1}^{4n}G_T(e_r,\varphi _ie_r,X,\xi _s)-G_T(\xi _j,\xi _k,X,\xi _s)=0. \end{aligned}$$

Finally, using (3.5) and (2.12),

$$\begin{aligned} \langle \mathcal G_T(\Phi _i),\xi _{jk}\rangle =\langle \mathcal G_T(\xi _{jk}),\Phi _i\rangle =(\beta -4\alpha )\{2\alpha (2n+1)-\beta +2\alpha \}, \end{aligned}$$

which is coherent with (3.6). Analogously,

$$\begin{aligned} \langle \mathcal G_T(\Phi _i),\xi _{ij}\rangle =\langle \mathcal G_T(\Phi _i),\xi _{ki}\rangle =0, \end{aligned}$$

thus completing the proof of (3.6). $\square$

Proposition 3.3

Let $(M,\varphi _i,\xi _i,\eta _i,g)$ be a 3-$(\alpha ,\delta )$-Sasaki manifold. Then, the Riemannian curvature of M satisfies

$$\begin{aligned} \mathcal R^g(\xi _{jk})&=-\left( 2\alpha ^2+\alpha \beta \right) \Phi _i+\big (2\alpha ^2+\alpha \beta +\frac{1}{4}\beta ^2\big )\xi _{jk}, \end{aligned}$$

(3.7)

$$\begin{aligned} \mathcal R^g(\Phi _i)&=\left\{ \alpha ^2(4n+3)+\alpha \beta (2n+1)\right\} \Phi _i-\big (\alpha +\frac{1}{2}\beta \big )^2\xi _{jk}. \end{aligned}$$

(3.8)

Proof

Since $\mathcal R^g$ and $\mathcal R$ are related by (1.5), the result follows from direct computations using Eqs. (2.16), (3.5), (3.1), and (2.15), (3.6), (3.2). $\square$

Remark 3.2

Being $\beta =2(\delta -2\alpha )$, Eqs. (3.7) and (3.8) can be rephrased as

$$\begin{aligned} \mathcal R^g(\xi _{jk})&=2\alpha (\alpha - \delta )\Phi _i+\{\alpha ^2+(\alpha - \delta )^2\}\xi _{jk}, \end{aligned}$$

(3.9)

$$\begin{aligned} \mathcal R^g(\Phi _i)&=\{\alpha (\delta -\alpha )(4n+1)+\alpha \delta \}\Phi _i-(\alpha - \delta )^2\xi _{jk}. \end{aligned}$$

(3.10)

We have now gathered all necessary results to give a proof of the main theorem.

Proof of Theorem 3.1

The equivalence of (c) and (d) is known, see [2, Proposition 2.3.3]. From (3.9) and (3.10), we have that $\mathcal R^g(\Phi _i-\xi _{jk})=a\Phi _i+b\xi _{jk}$ with

$$\begin{aligned} a=\alpha (\delta -\alpha )(4n+1)+\alpha \delta -2\alpha (\alpha - \delta ),\quad b=-\alpha ^2-2(\alpha - \delta )^2, \end{aligned}$$

which give

$$\begin{aligned} a+b=2(\delta -\alpha )\{\alpha (2n+3)-\delta \}. \end{aligned}$$

Then $\Phi _i-\xi _{jk}$ is an eigenform of $\mathcal R^g$ if and only if $a+b=0$, that is $\delta =\alpha$ or $\delta =(2n+3)\alpha$. In particular, if $\delta =\alpha$, the corresponding eigenvalue is $\lambda =a=\alpha ^2$. If $\delta =\alpha (2n+3)$, the eigenvalue is $\lambda _1=a=\alpha ^2(8n^2+16n+9)$.

Analogously, we can compute $\mathcal R^g(\Phi _i+(n+1)\xi _{jk})=a'\Phi _i+b'\xi _{jk}$ with

$$\begin{aligned}{} & {} a'=\alpha (\delta - \alpha )(4n+1)+\alpha \delta +2\alpha (\alpha - \delta )(n+1),\\{} & {} b'=-(\alpha - \delta )^2+(n+1)\alpha ^2 +(\alpha - \delta )^2(n+1),\end{aligned}$$

from which

$$\begin{aligned} (n+1)a'-b'=n(\delta -\alpha )\{\alpha (2n+3)-\delta \}, \end{aligned}$$

thus proving the equivalence of (b) and (c). If $\delta =\alpha$, then the eigenform $\Phi _i+(n+1)\xi _{jk}$ has eigenvalue $\lambda =a'=\alpha ^2$. If $\delta =\alpha (2n+3)$, the corresponding eigenvalue is $\lambda _2=a'=\alpha ^2(2n+1)^2$. $\square$

4 Definiteness of curvature operators

4.1 Strongly positive curvature

We now investigate strongly non-negative and even strongly positive curvature on (M, g). Recall that, by (1.5), the curvature operators $\mathcal R$ and $\mathcal R^g$ are related by

$$\begin{aligned} \mathcal R^g=\mathcal R+\frac{1}{4} \mathcal G_T+\frac{1}{4} \mathcal S_T. \end{aligned}$$

In particular, (M, g) is strongly non-negative with 4-form $-\frac{1}{4} \sigma _T$ if and only if

$$\begin{aligned} \mathcal R+\frac{1}{4} \mathcal G_T\ge 0. \end{aligned}$$

Observe that $\mathcal G_T$ is non-negative by definition, so we have directly strong non-negativity if $\mathcal R$ is non-negative. Theorem 2.3 thus yields (recall that $\beta := 2 (\delta -2\alpha )$)

Corollary 4.1

Let M be a 3-$(\alpha ,\delta )$-Sasaki manifold with $\alpha \beta \ge 0$ and $\mathcal R^{g_N}\ge 0$. Then (M, g) is strongly non-negative with 4-form $-\frac{1}{4}\sigma _T$.

As we later see, this will be sufficient for homogeneous spaces, but in general the condition $\mathcal R^{g_N}\ge 0$ is too strong. However, we can relax the condition on the base to strong non-negativity, but we need an additional assumption on the 4-form. To do all this, we need some notation.

For $i=1,2,3$, denote the 2-dimensional spaces $N_i:=\textrm{span}\{\Phi _i^{\mathcal {H}},\xi _{jk}\}$. Then decompose the space of 2-forms into orthogonal subbundles

$$\begin{aligned} \Lambda ^2M=\Lambda ^2_1\oplus \Lambda ^2_2\oplus \Lambda ^2_3, \end{aligned}$$

where the $\Lambda _i^2$ are given by

$$\begin{aligned} \Lambda ^2_1=\bigoplus _{i=1}^3N_i,\quad \Lambda ^2_2=\Lambda ^2\mathcal {H}\cap \{\Phi _1^{\mathcal {H}},\Phi _2^{\mathcal {H}},\Phi _3^{\mathcal {H}}\}^\perp ,\quad \Lambda ^2_3=\mathcal {V}\wedge \mathcal {H}. \end{aligned}$$

For a linear map $A:\Lambda ^2M\rightarrow \Lambda ^2M$ we denote $A_1{:}{=}A|_{\Lambda ^2_1}$ and correspondingly for the other spaces.

Let us motivate this decomposition. The obvious $\Lambda ^2(\mathcal {V}\oplus \mathcal {H})=\Lambda ^2\mathcal {V}\oplus \mathcal {V}\wedge \mathcal {H}\oplus \Lambda ^2\mathcal {H}$ motivates $\Lambda ^2_3=\mathcal {V}\wedge \mathcal {H}$, in particular since $\mathcal R|_{\Lambda ^2_3}=0$. However, $\mathcal R$ does not restrict to $\Lambda ^2\mathcal {V}$ and $\Lambda ^2\mathcal {H}$, but to $\Lambda ^2_1$ and $\Lambda ^2_2$. In fact, the characterization $\mathcal R=\alpha \beta \mathcal {R}_{\perp }+\mathcal {R}_{\textrm{par}}$ is with respect to $\Lambda ^2_1$ and $\Lambda _2^2$ as noted in the proof of Theorem 2.2. The space $\Lambda _1^2$ can be seen as controlled by the 3-$(\alpha ,\delta )$-Sasaki structure, while $\Lambda _2^2$ resonates the geometry of the base N. This is emphasized by the fact that the common eigenforms discussed in Sect. 3 all lie in $\Lambda ^2_1$.

Definition 4.1

We call a 4-form $\omega \in \Lambda ^4N$ on a quaternionic Kähler space N adapted with minimal eigenvalue $\nu \in \mathbb {R}$ if for every point $p\in N$ the quaternionic bundle $\mathcal {Q}$ lies in the $\nu _p$-eigenspace of $\omega _p$, considered as an operator $\Lambda ^2T_pN\rightarrow \Lambda ^2T_pN$, where the eigenvalues $\nu _p$ are bounded below by $\nu$.

Given a 3-$(\alpha ,\delta )$-Sasaki manifold with canonical submersion $\pi :M\rightarrow N$ the adaptedness of $\omega \in \Lambda ^4 N$ implies that $\pi ^*\omega$ admits a block diagonal structure $\pi ^*\omega =(\pi ^*\omega )_1\oplus (\pi ^*\omega )_2$. Note that $(\pi ^*\omega )_3$ vanishes trivially as $\pi _*\mathcal {V}=0$. We can now state the result with strong non-negativity on the base. It turns out the proof for strong positivity is almost identical. Hence we formulate the result in the latter case.

Theorem 4.1

Let M be a positive 3-$(\alpha ,\delta )$-Sasaki manifold. Assume that the base N of the canonical submersion is strongly positive with respect to an adapted 4-form $\omega$ with minimal eigenvalue $\nu$. Suppose further that the conditions

$$\begin{aligned} \delta ^2+4n\alpha \delta -6n\alpha ^2+\nu>0,\quad 4n\alpha (\delta -2\alpha )^3+\delta ^2\nu>0,\quad \delta >2\alpha \end{aligned}$$

(4.1)

are satisfied. Then M is strongly positive with 4-form $\pi ^*\omega -(\frac{1}{4}+\varepsilon ) \sigma _T$ for some $\varepsilon >0$ sufficiently small.

Corollary 4.2

If the base N in the situation of Theorem 4.1 is only strongly non-negative and satisfies the non-strict inequalities (4.1) for r, then M is strongly non-negative with 4-form $\pi ^*\omega -\frac{1}{4}\sigma _T$.

The corollary will be proved as a byproduct of Theorem 4.1.

Remark 4.1

Observe that the conditions (4.1) will be fulfilled for $\delta /\alpha \gg 0$ sufficiently big. This can be achieved by $\mathcal {H}$-homothetic deformation, compare [2, Section 2.3]. In fact, the horizontal structure is only changed by global scaling via a parameter a inversely proportional to $\alpha \delta$. However, fixing a we can scale the Reeb orbits by a parameter c implying a quadratic change in $\frac{\delta }{\alpha }$. Therefore, such a $\mathcal {H}$-homothetic deformation does not change the horizontal structure and thereby fixes $\nu$, but it increases the leading term of both polynomial conditions.

To prove these results, we need a more deliberate investigation of how $\mathcal G_T$ acts on the spaces $\Lambda _i^2$. From Eq. (1.11), it follows that the torsion T of the canonical connection satisfies

$$\begin{aligned} X\wedge Y\in \mathcal {V}\wedge \mathcal {H}\ \Rightarrow \ T(X, Y)\in \mathcal {H}\quad \text {and}\quad X\wedge Y\in \Lambda ^2\mathcal {V}\oplus \Lambda ^2\mathcal {H}\ \Rightarrow \ T(X,Y)\in \mathcal {V}. \end{aligned}$$

Thus, $\mathcal G_T$ preserves $\Lambda ^2_3=\mathcal {V}\wedge \mathcal {H}$ and by Proposition 3.2$\Lambda ^2_1$ as well. Therefore $\mathcal G_T$ splits into a direct sum of operators $\mathcal G_1\oplus \mathcal G_2\oplus \mathcal G_3$ on $\Lambda ^2_1\oplus \Lambda ^2_2\oplus \Lambda ^2_3$.

Consider some adapted basis $e_r$, $r=1,\dots , 4n+3$ of M. We may define the quaternionic spaces $\mathcal {H}_l=\textrm{span}\{e_{4l},e_{4l+1},e_{4l+2},e_{4l+3}\}$, $l=1,\dots , n$, and accordingly we have

$$\begin{aligned} \Lambda _2^2=\left( \bigoplus _{l=1}^n\Lambda ^2\mathcal {H}_l\right) \!\cap \!\langle \Phi _i^\mathcal {H}\rangle ^\perp \oplus \bigoplus _{k<l}\mathcal {H}_k\wedge \mathcal {H}_l, \quad \quad \Lambda ^2_3=\bigoplus _{l=1}^n\mathcal {V}\wedge \mathcal {H}_l. \end{aligned}$$

Note that these descriptions depend on the choice of adapted basis unlike the spaces $\Lambda ^2_i$ themselves.

Lemma 4.1

The linear operator $\mathcal G_2$ vanishes. The operator $\mathcal G_3$ has the unique non-vanishing eigenvalue $12\alpha ^2$ with eigenspace generated by $e_l\wedge \xi _1+\varphi _3e_l\wedge \xi _2-\varphi _2e_l\wedge \xi _3$, $l=4,\dots ,4n+3$.

Proof

The space $\left( \bigoplus \Lambda ^2\mathcal {H}_l\right) \cap \langle \Phi _i^\mathcal {H}\rangle ^\perp \subset \Lambda ^2_2$ is spanned by $e_l\wedge \varphi _ie_l-e_r\wedge \varphi _i e_r$, $r,l=4,\dots , 4n+3$, $i=1,2, 3$. $\mathcal G_2$ vanishes on these. Indeed, by expression (1.11) of T

$$\begin{aligned} T(e_l\wedge \varphi _i e_l)=2\alpha \Phi _i(e_l,\varphi _i e_l)\xi _i=-2\alpha \xi _i=T(e_r\wedge \varphi _i e_r) \end{aligned}$$

(4.2)

for any $l=4,\dots , 4n+3$. $\mathcal G_2$ vanishes on $\mathcal {H}_k\wedge \mathcal {H}_l$ as well since $\Phi _i(X,Y)=0$ whenever X and Y are in different quaternionic subspaces.

We observe that $\mathcal G_3$ is the sum of n identical copies $\hat{\mathcal G}_3$ for each space $\mathcal {V}\wedge \mathcal {H}_i$, since $T(X,Y)\in \mathcal {H}_i$ if $X\in \mathcal {H}_i$ and $Y\in \mathcal {V}$. Again using (1.11), we find

$$\begin{aligned} T(e_l\wedge \xi _i)=2\alpha \varphi _ie_l=T(\varphi _k e_l\wedge \xi _j)=-T(\varphi _j e_l\wedge \xi _k). \end{aligned}$$

(4.3)

In particular,

$$\begin{aligned} \mathcal G_T(e_r\wedge \xi _i)=\mathcal G_T(\varphi _k e_r\wedge \xi _j)=\mathcal G_T(-\varphi _j e_r\wedge \xi _k)=4\alpha ^2(e_r\wedge \xi _1+\varphi _3 e_r\wedge \xi _2-\varphi _2 e_r\wedge \xi _3) \end{aligned}$$

for the adapted basis $e_{4l},\dots ,e_{4l+3}$ of $\mathcal {H}_l$. Hence, the vectors $e_r\wedge \xi _1+\varphi _3 e_r\wedge \xi _2-\varphi _2 e_r\wedge \xi _3$ are 4 linearly independent eigenvectors with eigenvalue $12\alpha ^2$. In fact, these are all the eigenvectors with nonzero eigenvalues, since (4.3) shows that

$$\begin{aligned} 4\le \textrm{rk}(\hat{\mathcal G}_3)=\dim T(\mathcal {V}\wedge \mathcal {H}_l)\le \frac{\dim \mathcal {V}\wedge \mathcal {H}_l}{3}=\frac{12}{3}=4. \end{aligned}$$

$\square$

This implies that analogous to $\mathcal {R}_{\perp }$ the sum $\alpha \beta \mathcal {R}_{\perp }+\frac{1}{4} \mathcal G_ T$ is orthogonal to $\mathcal R_\textrm{par}$, i.e., it is trivial on the space $\Lambda ^2_2$ where $\mathcal {R}_{\textrm{par}}$ is non-trivial. It is now time to include the 4-form $\omega$.

Lemma 4.2

The operator $\alpha \beta \mathcal {R}_{\perp }+\frac{1}{4} \mathcal G_1+(\pi ^*\omega )_1$ is positive definite on $N_i$, $i=1,2,3$, if $\alpha$ and $\delta$ satisfy the polynomial conditions in (4.1), i.e., $\delta ^2+4n\alpha \delta -6n\alpha ^2+\nu >0$ and $4n\alpha (\delta -2\alpha )^3+\delta ^2\nu >0$.

Proof

From Proposition 3.2, we obtain

$$\begin{aligned} \mathcal G_T(\Phi _i^\mathcal {H})=\mathcal G_T(\Phi _i+\xi _{jk})&=8\alpha ^2n\Phi _i^\mathcal {H}+8\alpha n(\delta -4\alpha )\xi _{jk},\\ \mathcal G_T(\xi _{jk})&=4\alpha (\delta -4\alpha )\Phi _i^{\mathcal {H}}+4(\delta -4\alpha )^2\xi _{jk}. \end{aligned}$$

By adaptedness of $\omega$ at every point, the two-forms $\Phi _i^\mathcal {H}\in \pi ^*\mathcal {Q}$ lie inside some eigenspace with eigenvalue $\nu _p\ge \nu \in \mathbb {R}$. Thus on $N_i$ with respect to the orthonormal basis $\frac{1}{\sqrt{2n}}\Phi _i^\mathcal {H}$ and $\xi _{jk}$ the sum takes the matrix form

$$\begin{aligned} \alpha \beta \mathcal {R}_{\perp }+\frac{1}{4} \mathcal G_T+(\pi ^*\omega )_1= \begin{pmatrix} 2n\alpha (2\delta -3\alpha )+\nu _p &{} -\sqrt{2n}\alpha (3\delta -4\alpha )\\ -\sqrt{2n}\alpha (3\delta -4\alpha ) &{} \delta ^2 \end{pmatrix}. \end{aligned}$$

Now the restriction to the 2-dimensional space $N_i$ is positive (non-negative) if and only if both the determinant and the trace are. We have

$$\begin{aligned} \textrm{tr}_{N_i}\left( \alpha \beta \mathcal {R}_{\perp }+\frac{1}{4} \mathcal G_T+(\pi ^*\omega )_1\right) =2n\alpha (2\delta -3\alpha )+\delta ^2+\nu _p. \end{aligned}$$

Since the $\nu _p$ are bounded below by $\nu$, the trace is positive if the quadratic polynomial in $\delta$ satisfies $\delta ^2+4n\alpha \delta -6n\alpha ^2+\nu >0$. The determinant is given by

$$\begin{aligned} \det \Bigg (\left( \alpha \beta \mathcal {R}_{\perp }+\frac{1}{4}\mathcal G_T+(\pi ^*\omega )_1\right) \Big |_{N_i}\Bigg )&=4n\alpha \delta ^3-6n\alpha ^2\delta ^2+\nu _p\delta ^2-2n\alpha ^2(3\delta -4\alpha )^2\\&=4n\alpha \delta ^3-24n\alpha ^2\delta ^2+48n\alpha ^3\delta -32n\alpha ^4+\delta ^2\nu _p\\&=4n\alpha (\delta -2\alpha )^3+\delta ^2\nu _p \end{aligned}$$

and, thus, the operator $\alpha \beta \mathcal {R}_{\perp }+\frac{1}{4} \mathcal G_1+(\pi ^*\omega )_1$ is positive if the cubic polynomial $4n\alpha (\delta -2\alpha )^3+\delta ^2\nu$ is positive as well. $\square$

In the unaltered case, or equivalently $\nu =0$, we can quantify the condition more nicely in terms of $\alpha \beta$.

Corollary 4.3

The operator $\alpha \beta \mathcal {R}_{\perp }+\frac{1}{4} \mathcal G_1$ is positive (semi-)definite if and only if $\alpha \beta >0$ ($\alpha \beta \ge 0$).

Proof

In this case, the determinant reads $4n\alpha (\delta -2\alpha )^3=\frac{n}{2}\alpha \beta ^3$ which is positive (non-negative) if and only if $\alpha \beta >0$, ($\alpha \beta \ge 0$). In either case, the trace satisfies

$$\begin{aligned} \delta ^2+4n\alpha \delta -6n\alpha ^2&\ge 4\alpha ^2+8n\alpha ^2-6n\alpha ^2=2\alpha ^2(n+2)>0. \end{aligned}$$

$\square$

Proof of Theorem 4.1

We have seen that under $\mathcal {R}_{\perp }$, $\mathcal R_\textrm{par}$, $\mathcal G_T$ and $\pi ^*\omega$ the spaces $\Lambda ^2_1$, $\Lambda ^2_2$ and $\Lambda ^2_3$ are invariant. Thus, we may decompose

$$\begin{aligned} \mathcal R+\frac{1}{4}\mathcal G_T+\pi ^*\omega =\left( \alpha \beta \mathcal {R}_{\perp }+\frac{1}{4} \mathcal G_1+(\pi ^*\omega )_1\right) \;\oplus \; \left( \mathcal {R}_{\textrm{par}}+(\pi ^*\omega )_2\right) \;\oplus \; \frac{1}{4}\mathcal G_3. \end{aligned}$$

By assumption

$$\begin{aligned} \mathcal {R}_{\textrm{par}}+(\pi ^*\omega )_2=\left( \mathcal R^{g_N}+\omega \right) |_{\mathcal {Q}^\perp } \end{aligned}$$

is positive (non-negative), where we have used the identification $\Lambda ^2_2=\pi ^*\mathcal {Q}^\perp$. The results so far are summarized in Table 1. In fact, in the non-negative case we are done.

In order to prove strong positivity, we need to prove that $-\varepsilon \sigma _T$ provides strict positivity on the kernel of $\mathcal G_3$. For sufficiently small $\varepsilon$, it will do so without destroying positivity where already established. Indeed, Lemma 4.3 shows that $\sigma _T$ is negative definite on the kernel of $\mathcal G_3$. $\square$

Table 1 Positivity on summands of $\Lambda ^2TM$

Lemma 4.3

The operator $\mathcal S_T$ corresponding to $\sigma _T$ is negative definite on the kernel of $\mathcal G_3$ if and only if $\alpha \beta >0$.

Proof

As in the proof of Lemma 4.1, we may split $\mathcal G_3$ into n copies of $\hat{\mathcal G}_3$ on each quaternionic subspace. Let $e_{4l},\ldots ,e_{4l+3}\in \mathcal {H}_l$ be an adapted basis of one such subspace. Then from the same proof we find that $T(e_r\wedge \xi _i)=2\alpha \varphi _ie_l=-T(\varphi _je_r\wedge \xi _k)$. Thus,

$$\begin{aligned} \ker \hat{\mathcal G}_3=\ker T\cap (\mathcal {H}_l\wedge \mathcal {V})=\textrm{span}\{e_r\wedge \xi _i+\varphi _je_r\wedge \xi _k\;\vert \; i=1,2,3;\; r=4l,\dots ,4l+3\}. \end{aligned}$$

By definition of $\mathcal S_T$, we have

$$\begin{aligned} g(\mathcal S_T(e_r\wedge \xi _i),e_s\wedge \xi _a)&=g(T(e_r,\xi _i),T(e_s,\xi _a))+g(T(e_s,e_r),T(\xi _i,\xi _a))\\&\quad -g(T(e_s,\xi _i),T(e_r,\xi _a)). \end{aligned}$$

With $T=2\alpha \sum _{i=1}^n\eta _i\wedge \Phi ^\mathcal {H}_i+2(\delta -4\alpha )\eta _{123}$, we compute each term individually

$$\begin{aligned} g(T(e_r,\xi _i),T(e_s,\xi _a))&={\left\{ \begin{array}{ll}4\alpha ^2, &{} e_s=-\varphi _a\varphi _ie_r\\ 0\end{array}\right. },\\ g(T(e_s,e_r),T(\xi _i,\xi _a))&={\left\{ \begin{array}{ll}2\alpha (\beta -4\alpha ), &{} e_s=\varphi _i\varphi _ae_r\text { and } a\ne i\\ 0\end{array}\right. },\\ g(T(e_s,\xi _i),T(e_r,\xi _a))&={\left\{ \begin{array}{ll}4\alpha ^2, &{} e_s=-\varphi _i\varphi _a e_r\\ 0\end{array}\right. }. \end{aligned}$$

We thus obtain the full expression

$$\begin{aligned} \mathcal S_T(e_r\wedge \xi _i)&=4\alpha ^2\sum _{a=1}^3(-\varphi _a\varphi _ie_r+\varphi _i\varphi _ae_r)\wedge \xi _a+2\alpha (\beta -4\alpha )\sum _{a\ne i}\varphi _i\varphi _ae_r\wedge \xi _a\\&=2\alpha \beta \sum _{a\ne i}\varphi _i\varphi _ae_r\wedge \xi _a\\&=2\alpha \beta (\varphi _ke_r\wedge \xi _j-\varphi _je_r\wedge \xi _k). \end{aligned}$$

Finally we compute $\mathcal S_T$ on $\ker \hat{\mathcal G}_3$ to obtain the result

$$\begin{aligned} \mathcal S_T(e_r\wedge \xi _i+\varphi _je_r\wedge \xi _k)&=2\alpha \beta (\varphi _ke_r\wedge \xi _j-\varphi _je_r\wedge \xi _k+\varphi _j\varphi _je_r\wedge \xi _i-\varphi _i\varphi _je_r\wedge \xi _j)\\&=-2\alpha \beta (e_r\wedge \xi _i+\varphi _je_r\wedge \xi _k). \end{aligned}$$

$\square$

As a word of caution we should state where this theorem might and might not be applicable. By assumption, the quaternionic Kähler orbifold is strongly positive and thereby has positive sectional curvature. M. Berger investigated such manifolds in [5]. As observed in [13], Berger’s argument is purely local. It therefore extends to quaternionic Kähler orbifolds.

Theorem 4.2

([5, 13]) Let $n\ge 2$ and $(M^{4n},g,\mathcal {Q})$ be quaternionic Kähler orbifold of positive sectional curvature. Then $(M^{4n},g,\mathcal {Q})$ is locally isometric to $\mathbb {H}P^n$ with its standard quaternionic Kähler structure.

Thus, the strong positivity result of Theorem 4.1 can only be applicable on 3-$(\alpha ,\delta )$-Sasaki manifolds of dimension 7 or on finite quotients of $S^{4n+3}$. We will see in the next section that indeed both cases appear for homogeneous manifolds.

4.2 The homogeneous case

We would like to apply the positivity discussion to homogeneous 3-$(\alpha ,\delta )$-Sasaki manifolds, more precisely to those that fiber over Wolf spaces and their non-compact duals. We recall their construction from our previous publication [3], extending the similar discussion for homogeneous 3-Sasaki manifolds by [14].

Definition 4.2

A triple $(G,G_0,H)$ is called generalized 3-Sasaki data if $H\subset G_0\subset G$ are connected, real, simple Lie groups with Lie algebras $\mathfrak {h}\subset \mathfrak {g}_0\subset \mathfrak {g}$ such that:

• (i) $\mathfrak {g}_0=\mathfrak {h}\oplus \mathfrak {sp}(1)$ with $\mathfrak {sp}(1)$ and $\mathfrak {h}$ commuting subalgebras,

• (ii) $(\mathfrak {g},\mathfrak {g}_0)$ form a symmetric pair, $\mathfrak {g}=\mathfrak {g}_0\oplus \mathfrak {g}_1$,

• (iii) the complexification $\mathfrak {g}_1^\mathbb {C}=\mathbb {C}^2\otimes _\mathbb {C}W$ for some $\mathfrak h^{\mathbb {C}}$-module of $\dim _\mathbb {C}W=2n$,

• (iv) $\mathfrak {h}^\mathbb {C}, \mathfrak {sp}(1)^\mathbb {C}\subset \mathfrak {g}_0^\mathbb {C}$ act on $\mathfrak {g}_1^\mathbb {C}$ by their respective action on W and $\mathbb {C}^2$.

Theorem 4.3

([3, Theorem 3.1.1]) Consider some generalized 3-Sasaki data $(G,G_0,H)$ and $0\ne \alpha ,\delta \in \mathbb {R}$. Additionally suppose $\alpha \delta >0$ if G is compact and $\alpha \delta <0$ if G is non-compact.

Let $\kappa (X,Y)=\textrm{tr}(\textrm{ad}(X)\circ \textrm{ad}(Y))$ denote the Killing form on $\mathfrak g$. Then define the inner product g on the tangent space $T_pM=T_p(G/H)\cong \mathfrak {m}$ by

$$\begin{aligned} g\vert _{\mathcal {V}}&=\frac{-\kappa }{4\delta ^2(n+2)},\quad g\vert _{\mathcal {H}}=\frac{-\kappa }{8\alpha \delta (n+2)},\quad \mathcal {V}\perp \mathcal {H}. \end{aligned}$$

Let $\xi _i=\delta \sigma _i\in \mathcal {V}=\mathfrak {sp}(1)$, where the $\sigma _i$ are the elements of $\mathfrak {sp}(1)=\mathfrak {su}(2)$ given by

$$\begin{aligned} \sigma _1= \begin{pmatrix} i &{}0\\ 0&{}-i \end{pmatrix},\quad \sigma _2= \begin{pmatrix} 0 &{}-1\\ 1&{}0 \end{pmatrix},\quad \sigma _3= \begin{pmatrix} 0&{}-i\\ -i &{}0 \end{pmatrix}. \end{aligned}$$

Define endomorphisms $\varphi _i\in \textrm{End}_{\mathfrak {h}}(\mathfrak {m})$ for $i=1,2,3$ by

$$\begin{aligned} \varphi _i\vert _{\mathcal {V}}&=\frac{1}{2\delta } \textrm{ad}\,\xi _i,\quad \varphi _i\vert _{\mathcal {H}}=\frac{1}{\delta }\textrm{ad}\,\xi _i. \end{aligned}$$

Together with $\eta _i=g(\xi _i,\cdot )$ the collection $(G/H,\varphi _i,\xi _i,\eta _i,g)$ defines a homogeneous 3-$(\alpha ,\delta )$-Sasaki structure.

Note that the homogeneous 3-$(\alpha ,\delta )$-Sasaki structure on $\mathbb {R}P^{4n+3}$ is not directly obtained by this construction but as the quotient of $S^{4n+3}=\textrm{Sp}(n+1)/\textrm{Sp}(n)$ by $\mathbb {Z}_2$. Here the local structure is the same as for $S^{4n+3}$ given in the theorem. With this exception, we have that all positive homogeneous 3-$(\alpha ,\delta )$-Sasaki manifolds are obtained from the theorem. In the negative case more exist so we will restrict ourselves in the following discussion to those over symmetric base spaces.

Theorem 4.4

Let $M=G/H$ be a homogeneous 3-$(\alpha ,\delta )$-Sasaki manifold.

• (a) If M is a positive 3-$(\alpha ,\delta )$-Sasaki manifold, then the canonical curvature operator $\mathcal R$ is non-negative if and only if $\alpha \beta \ge 0$. In this case, M is strongly non-negative.

• (b) If M is a negative 3-$(\alpha ,\delta )$-Sasaki manifold over a symmetric base, then the canonical curvature operator $\mathcal R$ is non-positive.

Proof

In the positive case, M has to fiber over a symmetric base, compare [3]. In this case, the base is a compact symmetric space; hence, the curvature operator $\mathcal R^{g_N}$ is non-negative. In part (b), the base is a non-compact symmetric space by assumption, hence $\mathcal R^{g_N}\le 0$. Therefore in both cases it fulfills the requirement of Theorem 2.3. In the positive case also, Corollary 4.1 applies. $\square$

We will next focus on strong positivity. This is much more restrictive than strong non-negativity. In particular, strong positivity implies strict positive sectional curvature and homogeneous manifolds with strictly positive sectional curvature have been classified [6, 18, 19]. Out of these only the 7-dimensional Aloff–Wallach space $W^{1,1}$, the spheres $S^{4n+3}$ and real projective spaces $\mathbb {R}P^{4n+3}$ admit homogeneous 3-$(\alpha ,\delta )$-Sasaki structures. We will thus prove

Theorem 4.5

The 3-$(\alpha ,\delta )$-Sasaki manifolds

• (a) $W^{1,1}=\textrm{SU}(3)/S^1$ with 4-form $-(\frac{1}{4}+\varepsilon )\sigma _T$ for small $\varepsilon >0$,

• (b) $S^{4n+3}$, $\mathbb {R}P^{4n+3}$, $n\ge 1$, with 4-form $\frac{\alpha \delta }{4}\pi ^*\Omega _N-(\frac{1}{4}+\varepsilon )\sigma _T$ for small $\varepsilon >0$

where $\pi ^*\Omega _N{:}{=}\sum _{i=1}^3\Phi _i^\mathcal {H}\wedge \Phi _i^H$, i.e., $\Omega _N$ is the fundamental 4-form of the qK base, are strongly positive if and only if $\alpha \beta >0$.

Remark 4.2

The strong positivity of these spaces $W^{1,1}$ and $S^{4n+3}$, $\mathbb {R}P^{4n+3}$, can actually be proven by the Strong Wallach Theorem in [7]. We compare to our case:

• (i) Observe that all positive homogeneous 3-$(\alpha ,\delta )$-Sasaki manifolds are given by a homogeneous fibration

  $$\begin{aligned} \textrm{SO}(3)=G_0/H\rightarrow G/H \rightarrow G/G_0. \end{aligned}$$

  In the case of $S^{4n+3}$, the fiber is $\textrm{Sp}(1)$ instead.

• (ii) In their strong Wallach theorem [7], the authors consider the metrics $g_t=tQ|_{\mathcal {V}}+Q|_\mathcal {H}$ for $0<t<1$, where Q is a negative multiple of the Killing form. If we set $Q=\frac{-\kappa }{8\alpha \delta (n+2)}$ as in the 3-$(\alpha ,\delta )$-Sasaki setting then $t=\frac{2\alpha }{\delta }$ and, thus, the condition $0<t<1$ is equivalent to $\beta >0$.

• (iii) We have $\dim G_0/H=3$ and $G_0/H=\textrm{SO}(3)=\mathbb {R}P^3$, $S^3$ in the case of $S^{4n+3}$, with a scaled standard metric. In particular, the fiber is of positive sectional curvature.

• (iv) They require a strong fatness property for the homogeneous fibration. Adapted to our notation the bundle is strongly fat if there is a 4-form $\tau$ such that $F+\tau :\mathcal {H}\otimes \mathcal {V}\rightarrow \mathcal {H}\otimes \mathcal {V}$ is positive definite, where F is given by

  $$\begin{aligned} g(F(X\wedge \xi _i),Y\wedge \xi _j)&=g([X,\xi _i],[Z,\xi _j])=\delta ^2g(\varphi _iX,\varphi _jY)\\&=\frac{\delta ^2}{4\alpha ^2}g(T(X\wedge \xi _i),T(Y\wedge \xi _j))=\frac{\delta ^2}{4\alpha ^2}g(\mathcal G_T(X\wedge \xi _i),Y\wedge \xi _j). \end{aligned}$$

  Thus by the previous lemma $\tau =-\varepsilon \sigma _T$ accomplishes strong fatness for sufficiently small $\varepsilon$.

• (v) The final condition is for the base to be one of $S^{4n},\mathbb {R}P^{4n},\mathbb {C}P^{2n},\mathbb {H}P^n$. The only homogeneous 3-$(\alpha ,\delta )$-Sasaki manifolds such that this holds are $S^{4n+3}$, $\mathbb {R}P^{4n+3}$ which fiber over $\mathbb {H}P^n$, and $W^{1,1}$ which fibers over $\mathbb {C}P^2$.

Note that (i)–(iv) are valid for all positive homogeneous examples not only for the spheres, real projective spaces and $W^{1,1}$.

Proof of Theorem 4.5

Since our discussion is pointwise we will identify tensors on N with those on $\mathcal {H}$.

• (a) Let $(M,\varphi _i,\xi _i,\eta _i,g)$ be a 7-dimensional 3-$(\alpha ,\delta )$-Sasaki manifold and $\pi :M\rightarrow N$ its canonical submersion. Then N is 4-dimensional and $\Phi _i^\mathcal {H}\wedge \Phi _i^\mathcal {H}=2\textrm{dVol}_N$ for each $i=1,2,3$. By (1.12)

  $$\begin{aligned} \sigma _T\vert _{\Lambda ^4\mathcal {H}}=\frac{1}{2}\textrm{d}T\vert _{\Lambda ^4\mathcal {H}}=2\alpha ^2\sum _{i=1}^3\Phi _i^\mathcal {H}\wedge \Phi _i^\mathcal {H}=12\alpha ^2\textrm{dVol}_N. \end{aligned}$$

  Now the 6-dimensional space $\Lambda ^2 N$ splits as usual into the spaces of self-dual and anti self-dual forms $\Lambda ^2_+$ and $\Lambda ^2_-$. In other words, these are the $\pm 1$-eigenspaces of $\textrm{dVol}_N$ as an operator $\Lambda ^2N\rightarrow \Lambda ^2N$. Checking in an adapted basis, we find that $\textrm{span}\{\Phi _i^\mathcal {H}\}=\Lambda ^2_1\cap \Lambda ^2\mathcal {H}=\Lambda ^2_+$ and $\Lambda ^2_2=\Lambda ^2_-$. Now suppose that N is a compact symmetric space. Then $\mathcal R^{g_N}\ge 0$ and if $\alpha \delta >0$ its restriction $\mathcal R^{g_N}|_{\Lambda ^2_+}>0$ is strictly positive. Indeed, (2.10) shows this, since $\Lambda ^2_1\subset \ker \mathcal {R}_{\textrm{par}}$ (compare Lemma 2.3). Now for sufficiently small $\varepsilon >0$ the operator $\mathcal R^{g_N}-\varepsilon \textrm{dVol}_N>0$. Hence we may apply Theorem 4.1. Note that $\varepsilon$ and therefore the lower bound $\nu$ of eigenvalues of $-\varepsilon \textrm{dVol}_N$ can be chosen arbitrarily small. Since $\alpha \beta >0$ by the proof of Corollary 4.3, we have $\delta ^2+4n\alpha \delta -6n\alpha ^2>0$ and $4n\alpha (\delta -2\alpha )^3>0$, hence also

  $$\begin{aligned} \delta ^2+4n\alpha \delta -6n\alpha ^2+\nu>0\quad \text {and}\quad 4n\alpha (\delta -2\alpha )^3+\delta ^2\nu >0. \end{aligned}$$

  Then Theorem 4.1 finishes the proof.

• (b) Now the 4-form $\omega =\frac{\alpha \delta }{4}\Omega _N$ appears as possible 4-form in the strong positivity of $\mathbb {H}P^n$. In [7], they prove that the 4-form $\mathfrak {b}(\rho )$ suffices where $\rho$ is given as the symmetric product of twice the A-tensor of the submersion $(S^{4n+3},g_0)\rightarrow (\mathbb {H}P^n,g_B)$, $(\mathbb {R}P^{4n+3},g_0)\rightarrow (\mathbb {H}P^n,g_B)$, respectively.² Here the metric $g_0$ denotes up to global scaling by $\frac{1}{8\alpha \delta (n+2)}$ the standard round metric. Adapted to our notation

  $$\begin{aligned} \rho (X\wedge Y,Z\wedge V)=g_0(A_XY,A_ZV){} & {} =\frac{1}{4}g_0([X,Y]_\mathfrak {m},[Z,V]_\mathfrak {m})\nonumber \\ {}{} & {} =\frac{\alpha \delta }{2}\sum _{i=1}^3\Phi _i^\mathcal {H}(X,Y)\Phi _i^\mathcal {H}(Z,V). \end{aligned}$$

  and thus

  $$\begin{aligned} \mathfrak {b}(\rho )=\frac{\alpha \delta }{2}\sum _{i=1}^3\mathfrak {b}(\Phi _i^\mathcal {H}\otimes \Phi _i^\mathcal {H})=\frac{\alpha \delta }{4}\sum _{i=1}^3\Phi _i^\mathcal {H}\wedge \Phi _i^{\mathcal {H}}=\frac{\alpha \delta }{4}\pi ^*\Omega _N. \end{aligned}$$

  Therefore we have $\mathcal R^{g_N}+\frac{\alpha \delta }{4}\Omega _N>0$ on $\Lambda ^2N$. It remains to check that $\mathcal {Q}$ is an eigenspace of $\omega$. We compute for a basis $e_1,\dots ,e_{4n}$ of TN

  

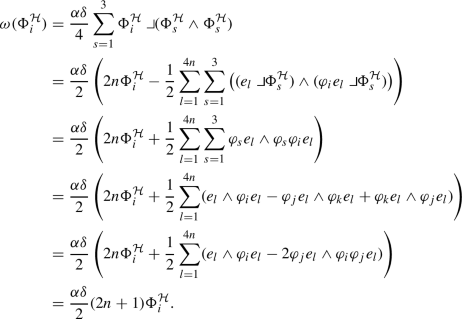
  Since the eigenvalue $\nu >0$ is positive $\alpha \beta \mathcal {R}_{\perp }+\frac{1}{4}\mathcal G_1+(\pi ^*\omega )_1\ge \alpha \beta \mathcal {R}_{\perp }+\frac{1}{4}\mathcal G_1$ and $\alpha \beta >0$ suffices as argued in Corollary 4.3. $\square$

4.3 Some inhomogeneous example

Let us recall 3-Sasaki reduction introduced in [11]. Let $(M,\varphi _i,\xi _i,\eta _i,g)$ be a 3-Sasaki manifold and G a connected compact Lie group acting on M by 3-Sasaki automorphisms. We consider the 3-Sasaki moment map

$$\begin{aligned} \mu :M&\rightarrow \mathfrak {g}^*\otimes \mathbb {R}^3\\ x&\mapsto (X\rightarrow \eta _i(\overline{X}_x))_{i=1,2,3} \end{aligned}$$

where $\overline{X}_x$ is the fundamental vector field of $X\in \mathfrak {g}$ at $x\in M$.

Theorem 4.6

([11]) Assume that 0 is a regular value of $\mu$ and that G acts freely on the preimage $\mu ^{-1}(\{0\})$. Denote the embedding $\iota :\mu ^{-1}(\{0\})\rightarrow M$ and the submersion $\pi :\mu ^{-1}(\{0\})\rightarrow \mu ^{-1}(\{0\})/G$. Then $(\mu ^{-1}(\{0\})/G, \check{\varphi }_i,\check{\xi }_i,\check{\eta }_i,\check{g})_{i=1,2,3}$ is a smooth 3-Sasaki manifold, where the 3-Sasaki structure is uniquely determined by $\iota ^*g=\pi ^*\check{g}$ and $\check{\xi }_i=\pi _*(\xi _i|_{\mu ^{-1}(\{0\})})$.

We will focus on actions of $S^1$ on the 3-Sasaki sphere $S^{11}\subset \mathbb {H}^3$ via

$$\begin{aligned} z\cdot (q_1,q_2,q_3)=(z^{p_1}q_1,z^{p_2}q_2,z^{p_3}q_3). \end{aligned}$$

In [10, Theorem 13.7.6], the authors show that for pairwise coprime, positive integers $p_1,p_2,p_3$ these actions satisfy the assumptions in Theorem 4.6 and, thus, give rise to 3-Sasaki manifolds $\mathcal {S}(p_1,p_2,p_3)$. If $p_1=p_2=p_3=1$, this is exactly the homogeneous 3-Sasaki Aloff–Wallach space $W^{1,1}$. Apart form this, they are shown in [10, Corollary 13.7.13] to be of cohomogeneity 1 or 2.

In [13], the author shows that under the assumption $\sqrt{2}\min p_i> \max p_i$ a certain deformation of the 3-Sasaki metric, corresponding to a $\mathcal {H}$-homothetic deformation in our notation, admits positive sectional curvature. We make use of a key step of his showing that their underlying quaternionic Kähler orbifolds have positive sectional curvature, [13, Theorem 2].

Theorem 4.7

([13]) Let $\mathcal {S}(p_1,p_2,p_3)$ be as before and $\mathcal {O}(p_1,p_2,p_3)$ the underlying quaternionic Kähler orbifold. If $\sqrt{2}\min p_i>\max {p_i}$ then $\mathcal {O}(p_1,p_2,p_3)$ has positive sectional curvature.

In order to make the jump from positive sectional curvature to strongly positive curvature we make use of the fact that $\mathcal {O}(p_1,p_2,p_3)$ is 4-dimensional. In this dimension, Thorpe proves the following [16, Corollary 4.2].

Theorem 4.8

([16, 17]) Let V be a 4-dimensional vector space and R any algebraic curvature operator on V. If $\lambda$ is the minimal sectional curvature of R, then there is a unique $\omega \in \Lambda ^4 V$ such that $\lambda$ is the minimal eigenvalue of $R+\omega$.

We are finally ready to state our main theorem.

Theorem 4.9

Let $p_1,p_2,p_3$ be coprime integers with $\sqrt{2}\min p_i>\max p_i$. Then there is a $\mathcal {H}$-homothetic deformation of $\mathcal {S}(p_1,p_2,p_3)$ that has strongly positive curvature.

Proof

Thorpe’s theorem proves that the orbifold $\mathcal {O}(p_1,p_2,p_3)$ has not only positive sectional curvature but strongly positive curvature. Since we are in dimension 4 the form $\omega$ is necessarily a multiple of the volume form $\omega =\nu _p\textrm{dVol}$. As before the volume form has eigenspaces $\Lambda ^2_\pm$ where $\Lambda ^2_+=\mathcal {Q}$ and $\Lambda ^2_{-}=\mathcal {Q}^\perp$. In particular, $\omega$ is an adapted 4-form with minimal eigenvalue $\nu =\min \nu _p$. The minimum exists since the orbifolds are quotients of compact spaces and, thus, compact themselves. All in all we may apply Theorem 4.1. Note that by Remark 4.1 we obtain a $\mathcal {H}$-homothetic deformation of $\mathcal {S}(p_1,p_2,p_3)$ with $\delta /\alpha \gg 0$ sufficiently big while not changing the metric $g_\mathcal {O}$ on $\mathcal {O}(p_1,p_2,p_3)$. $\square$