Abstract
In this paper we consider semilinear PDEs, with a convex nonlinearity, in a sector-like domain. Using cylindrical coordinates \((r, \theta , z)\), we investigate the shape of possibly sign-changing solutions whose derivative in \(\theta\) vanishes at the boundary. We prove that any solution with Morse index less than two must be either independent of \(\theta\) or strictly monotone with respect to \(\theta\). In the special case of a planar domain, the result holds in a circular sector as well as in an annular one, and it can also be extended to a rectangular domain. The corresponding problem in higher dimensions is also considered, as well as an extension to unbounded domains. The proof is based on a rotating-plane argument: a convenient manifold is introduced in order to avoid overlapping the domain with its reflected image in the case where its opening is larger than \(\pi\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper we consider solutions of semilinear elliptic PDEs in a sector-like domain \(\Omega _{0\beta } \subset {\mathbb {R}}^N\), \(N \ge 2\). To describe the results, for every \(x = (x_1, \ldots , x_N)\in {\mathbb {R}}^N\) we define \(d(x) = \sqrt{x_1^2 + x_2^2 \,}\) and \(z = (x_3, \ldots , x_N) \in {\mathbb {R}}^{N - 2}\), and we denote by \(\Upsilon\) the \((N - 2)\)-dimensional subspace \(\Upsilon :=\{x\in {\mathbb {R}}^N: d(x)=0\}\). Observe that each point \(x\in {\mathbb {R}}^N{\setminus }\Upsilon\) can be represented in cylindrical coordinates as \(i(x) = (r,\theta ,z)\), where \(r = d(x)\), and \(\theta = \theta (x) \in [0,2\pi )\) is uniquely determined by
If \(N = 2\), then \((r,\theta )\) are the polar coordinates of x, the set \(\Upsilon\) contains just the origin, and the symbol z should be ignored. In general, a rotation of \({\mathbb {R}}^N\) about the origin is a linear mapping \(x \mapsto Ax\) associated to an orthogonal matrix A. In the present paper we deal with cylindrical rotations, i.e., the particular rotations whose matrix \(A = A^N_\theta\) is given by
where \(I^{N -2}\) is the \((N - 2)\)-dimensional identity matrix. In the first part of the paper we deal with bounded domains. More precisely, let \(\Omega\) be a bounded, Lipschitz domain which is invariant under cylindrical rotations in the sense that \(x \in \Omega\) if and only if \(A_\theta \, x \in \Omega\) for every \(\theta \in [0,2\pi )\). For \(\theta _1,\theta _2\in [0,2\pi )\) satisfying \(\theta _1<\theta _2\) we introduce the bounded open sector
whose boundary is made of the open, flat surfaces \(\Gamma _{\!\theta _i}:=\{\, x \in \Omega {\setminus } \Upsilon : \theta (x) = \theta _i \,\}\), \(i=1,2\), the torical surface \(\gamma _{\theta _1\theta _2}:= \{\, x \in \partial \Omega {\setminus } \Upsilon : \theta (x) \in [\theta _1,\theta _2] \,\}\) and the (possibly empty) set \(\gamma :={\overline{\Omega }}\cap \Upsilon\). The typical examples of the domain \(\Omega _{\theta _1\theta _2}\) are: a sector of a sphere, a sector of a cylinder, a sector of an annulus, a sector of a torus, a sector of a cone. But also more complicated domains as cylinders (or spheres) with cavities can be considered for \(\Omega\), and even tori with a torical, coaxial tunnel inside. Observe that \(\gamma\) may be empty (which is the case, for instance, when \(\Omega\) is a torus), and can be disconnected as in the case where \(\Omega\) is a cylinder in \({\mathbb {R}}^3\) with a cavity. Now fix \(\beta \in (0,2\pi )\) and consider the boundary-value problem
where \(\Delta\) is the Laplace operator, and f(r, z, u) is locally Hölder continuous on \([0,+\infty ) \times {\mathbb {R}}^{N - 1}\) together with \(f' = \partial f / \partial u\). Observe that \(u_\theta = \frac{\partial u}{\partial \theta }\) is the normal derivative of u on \(\Gamma _{\! 0} \cup \Gamma _{\! \beta }\) while it is the tangential derivative on \(\gamma _{0\beta }\). Let \({\mathcal {X}}\) be the set of all functions \(u \in C^2(\Omega _{0\beta }) \cap C^0({\overline{\Omega }}_{0\beta })\cap H^1(\Omega _{0\beta })\) such that \(u_\theta \in H^1(\Omega _{0\beta })\). We investigate functions \(u \in {\mathcal {X}}\) satisfying (1.1) pointwise. Using [20, Prop. 6.1], it can be proved that the solution u is smooth, namely \(C^2\), in \(\Omega _{0\beta }\cup \Gamma _{\! 0} \cup \Gamma _{\! \beta }\). The assumption that \(u_\theta \in H^1(\Omega _{0\beta })\) is introduced to avoid technicalities and it is satisfied, for instance, if \(u \in W^{2,2}(\Omega _{0\beta })\). Such an assumption is dropped in the last part of the paper, where we use a truncation technique to deal with unbounded domains (see, in particular, (8.1)-(8.2)). The boundary condition \(u_\theta = 0\) on \(\gamma _{0\beta }\) can be interpreted in the sense of traces. However, since u is continuous up to there, the condition implies that the values of u on \(\gamma _{0\beta }\) are constant in \(\theta\). Thus, (1.1) is a shorthand for the following mixed problem of Dirichlet-Neumann type:
where g(r, z) is a continuous function, and \(\nu\) denotes the outward unit normal to \(\partial \Omega _{0\beta }\). If u is a solution to (1.1), we denote by I the identity operator and by
the linearized operator at u. Furthermore,
is the quadratic form associated to \(L_u\) in an open subset \(D \subset \Omega _{0\beta }\). In fact, the operator \(L_u\) and the quadratic form \(Q_D\) are well defined for every \(u \in L^\infty (\Omega _{0\beta })\). If \(\Gamma\) is a sufficiently smooth (possibly disconnected) part of \(\partial D\), we denote by
the Sobolev space of square-summable functions having square-summable weak derivatives and vanishing trace along \(\Gamma\), and, for \(i\ge 1\), we denote by \(\uplambda _i(H^1_\Gamma (D))\) the eigenvalues of the operator \(L_u\) in \(H^1_\Gamma (D)\). We will assume that the solution u to (1.1) satisfies \(\uplambda _2(H^1_{\gamma _{0\beta }}(\Omega _{0\beta }))\ge 0\). Our main result in bounded domains is the following:
Theorem 1.1
Let \(u \in {\mathcal {X}}\) be a solution to (1.1), where f(r, z, u) is convex with respect to u.
-
1.
If \(\uplambda _1(H^1_{\gamma _{0\beta }}(\Omega _{0\beta }))\ge 0\) then u is constant with respect to the angular variable \(\theta\).
-
2.
If \(\uplambda _1(H^1_{\gamma _{0\beta }}(\Omega _{0\beta })) < 0 \le \uplambda _2(H^1_{\gamma _{0\beta }}(\Omega _{0\beta }))\) then u is either independent of \(\theta\) or strictly monotone with respect to \(\theta\) in \(\Omega _{0\beta }\). In the last case, u has a nonvanishing derivative \(u_\theta\), the first Dirichlet eigenvalue \(\uplambda _1(H^1_0(\Omega _{0\beta }))\) equals zero and \(u_\theta\) is a corresponding eigenfunction.
Remark 1.2
In the statement of Theorem 1.1 it is enough to require that f(r, z, s) is convex with respect to s as long as \(s \in (m,M)\), where \(m=\inf \limits _{\Omega _{0\beta }}u(x)\) and \(M=\sup \limits _{\Omega _{0\beta }}u(x)\). This assumption has been introduced in the paper [19] in order to compare the quadratic form \(Q_D\) with the quadratic form associated to the equation satisfied by the difference \(w_\alpha\) of u and its reflection with respect to some \(\Gamma _{\!\alpha }\) (as we also do in Sect. 2).
The proof of Theorem 1.1 is given in Sect. 3 and it is based on the rotating plane method, which was also used in [19, 21] to prove Schwarz symmetry for solutions of low Morse index to the Dirichlet problem in radially symmetric, bounded domains. Indeed, the assumption \(\uplambda _2(H^1_{\gamma _{0\beta }}(\Omega _{0\beta }))\ge 0\) is equivalent to consider solutions of Morse index 1 and it is satisfied by any ground state solution and by any solution of mountain pass type, as well as by local minimizers subject to an integral constraint. Such an assumption is needed to begin with the argument, in place of the positiveness of the solution u which is usually required. Like in the mentioned papers, starting from a bound on the Morse index of the solution we obtain the non-negativity of the first eigenvalue in a half-domain under convenient boundary conditions: this is the purpose of the splitting lemma in Sect. 2. A similar observation is also found in the proof of [10, Lemma 4.2]. Note that the Morse index approach allows to deal with sign-changing solutions. Moreover, a bound on the Morse index usually implies an \(L^\infty\)-bound of the solution as observed in [2] in the case of a Dirichlet problem under some growth condition on the nonlinear term f.
The non-negativity of the first eigenvalue implies a sign-preservation property (Lemma 2.3) for supersolutions of the linearized equation \(L_{u \,} v = 0\), which is applied to the difference of the solution u(x) and its reflection \(u(\sigma _\frac{\beta }{2}(x))\) with respect to \(\Gamma _{\! \frac{\beta }{2}}\). Such a difference, denoted by \(w_\frac{\beta }{2}\), obviously satisfies a Neumann condition on \(\Gamma _{\! 0} \cup \Gamma _{\! \beta }\). However, unlike [19, 21], when the hyperplane \(\theta = \frac{\beta }{2}\) is changed into \(\theta = \alpha \ne \frac{\beta }{2}\) we loose the Neumann condition: hence our problem is in some sense more rigid than theirs. We overcome this difficulty in Sect. 3 using the positivity of the angular derivative \(u_\theta\) in \(\Omega _{0\alpha }\cup \Gamma _{\! \alpha }\), thus completing the proof of Theorem 1.1.
Some comments on the assumption \(u_\theta \in H^1(\Omega _{0\beta })\), which is needed in the proof of Lemma 3.2 and Lemma 3.3, and consequently enters in the theorem. By standard regularity theory, any weak solution \(u \in H^1(\Omega _{0\beta })\) of (1.2) belongs to the smoothness class \(C^2(\Omega _{0\beta }\cup \Gamma _{\! 0} \cup \Gamma _{\! \beta }) \cap C^0({\overline{\Omega }}_{0\beta })\). Furthermore, at least in the case where \(\gamma =\emptyset\), if \(\Omega \in C^{2,\alpha }\) and \(g(d(x),z)\in C^{2,\alpha }\) then \(u\in C^{2,\alpha }({\overline{\Omega }}_{0\beta })\) showing that \(u_\theta \in H^1(\Omega _{0\beta })\). In the particular case of dimension \(N=2\), the domain \(\Omega _{0\beta }\) is a sector of the annulus or a sector of the disc so that \(\gamma _{0\beta }\) is always smooth. In the case of the annulus, the assumption \(u_\theta \in H^1(\Omega _{0\beta })\) is satisfied if g(r) belongs to \(C^{2,\alpha }\). In the case of the disc, instead, we can use the results of [18] and [1], that hold in dimension \(N\ge 2\), to gain the \(W^{2,2}\) regularity of the solution u when the domain is convex.
Previous results on cylindrical symmetry of low Morse index solutions for a mixed problem can be found in [10], where the equation holds in the whole of \(\Omega\) (not only in the sector \(\Omega _{0\beta }\)) and a nonlinear Neumann condition is imposed on a subset of \(\partial \Omega\). If, instead, \(\Omega _{0\beta }\) is a sector of the ball and \(\beta <\pi\), radial symmetry of the positive solution to (1.2) with \(g(d(x),z)=0\) was proved in [5] using an involved version of the rotating plane method. Note that for \(N = 2\) radial symmetry coincides with cylindrical symmetry. Radial symmetry of positive solutions to a mixed problem in a spherical, convex cone with solid angle \(\alpha\) was proved in [17] by using isoperimetric inequalities. A recent extension to anisotropic weighted equations is found in [8]. For further results on convex cones see also [20] and the references therein.
In Sect. 4 we extend Theorem 1.1 to the case where \(\Omega _{0\beta } = (0,\beta )\times \omega\) is a cylindrical domain, which is in some sense the asymptotic shape of a sector-like domain when the opening \(\beta\) is small. In this case we use the standard Cartesian coordinates \((x_1,\dots ,x_N)\), and \(\omega\) denotes a bounded \((N-1)\)-dimensional domain contained in the hyperplane \(x_1=0\). Now the angular variable \(\theta\) is replaced by \(x_1\), and the rotating plane method becomes a sliding plane method that starts from the position \(x_1=\frac{\beta }{2}\). In Theorem 4.1 we obtain, with a different method, some previous results for global and local minimizers of variational problems subject to an integral constraint, for nonlinearities satisfying suitable growth conditions: see Theorem 3.1 and Theorem 3.3 in [6]. The proof of the last theorems relies on a two-point rearrangement and holds not only for Dirichlet boundary conditions on \(\gamma _{0\beta }\) (which is our case), but also for some nonlinear Neumann boundary conditions. However, here we do not require any growth assumption on the nonlinear term f which should only be convex, and we consider solutions of possibly non-variational problems. Furthermore, our assumption on \(\uplambda _2(H^1_{\gamma _{0\beta }}(\Omega _{0\beta }))\) is satisfied when one considers variational solutions with one or without constraints of the type in [6]. Existence and monotonicity with respect to \(x_1\) for global minimizers of some variational problems and for mountain pass solutions were proved in [4] using the monotone increasing rearrangement.
All the occurrences in Theorem 1.1 can happen and we will provide some examples in Sect. 5. In particular we show that if the first Dirichlet eigenvalue \(\uplambda _1(H^1_0(\Omega _{0\beta })) = 0\) then \(u_\theta\) may well vanish identically. We also show that if \(\uplambda _2(H^1_{\gamma _{0\beta }}(\Omega _{0\beta }))< 0\) it can happen that the solution u is neither independent of \(\theta\) nor monotone with respect to \(\theta\).
In the second part of the paper, starting from Sect. 6, we consider problem (1.1) in some unbounded domains. This is more difficult and requires additional ingredients. The main result, Theorem 6.4, follows from three main points: 1. The constraint on the Morse index implies that the subdomain, where the maximum principle may fail, is bounded and keeps away from \(\partial \Omega\). Therefore, it can be enveloped by a suitable torus T; 2. The solution is stable in the complement of T; 3. Even though the complement is unbounded, we show that stability implies a sign-preservation property: this is achieved by cutting off the solution u at infinity like in [14]. We also perform a cut-off near \(\partial \Omega\) to avoid the requirement that \(u_\theta \in H^1(\Omega _{0\beta })\). The use of the torus T and the combination of these ingredients are new.
2 Preliminary results
In order to prove Theorem 1.1 by means of the rotating plane method, we need to introduce the reflection \(\sigma _\alpha\) with respect to \(\Gamma _{\!\alpha }\), where \(\alpha\) is an angular parameter in the given interval \((0,\beta )\). In the special case when \(\alpha \in (0,\pi )\) we may easily define \(\sigma _\alpha :\Omega _{0,2\alpha } \rightarrow \Omega _{0,2\alpha }\) by prescribing that \(i(\sigma _\alpha (x))=(r, \, 2\alpha - \theta , \, z)\) when \(i(x)=(r,\theta ,z)\). However, in order to simplify and generalize the subsequent arguments, it is convenient to extend the definition of \(\sigma _\alpha\) to the general case when \(\alpha \in {\mathbb {R}}\). To this aim we consider the Riemannian manifold \({{\mathcal {M}}} :=\{(r,t,z): r \in (0,+\infty ), t \in {\mathbb {R}}, z \in {\mathbb {R}}^{N-2}\}\) endowed with the flat metric whose first fundamental form is \(ds^2 = dr^2 + r^2 \, dt^2 + dz^2\). Every sector-like domain \(\Omega _{\theta _1\theta _2} \subset {\mathbb {R}}^N\) is isometrically embedded into \({\mathcal {M}}\) by the mapping \(i :\Omega _{\theta _1\theta _2} \rightarrow {\mathcal {M}}\) \(i(x)=(r,\theta ,z)\). We will identify \(\Omega _{\theta _1\theta _2}\) with its image \(i(\Omega _{\theta _1\theta _2})\) and, more generally, we will use the notation \(\Omega _{\theta _1\theta _2}\) to denote the submanifold
for every \(\theta _1,\theta _2 \in {\mathbb {R}}\) with \(\theta _1 < \theta _2\). Now, for any given \(\alpha \in {\mathbb {R}}\), we define the function \(\sigma _\alpha :{{\mathcal {M}}} \rightarrow {{\mathcal {M}}}\) by letting \(\sigma _\alpha (r,t,z) = (r, \, 2\alpha - t, \, z)\). Thus, for instance, if we take \(\alpha \in (\pi ,2\pi )\) and apply \(\sigma _\alpha\) to some point \((r,\theta ,z)\) with \(\theta \in (0,\, 2\alpha -2\pi )\), we obtain \((r, \, 2\alpha - \theta , \, z)\) where \(2\alpha - \theta > 2\pi\). The last point, as an element of \({\mathcal {M}}\), is distinct from the point \((r, \, 2\alpha - \theta - 2\pi , \, z)\). We denote still by x an arbitrary point \((r,t,z) \in {\mathcal {M}}\), for shortness, and we define the function \(d :{{\mathcal {M}}} \rightarrow (0,+\infty )\) by letting \(d(x) = r\). Thus, any function u defined in \(\Omega _{0\beta } \cup \,\Gamma _{\!0} \cup \,\Gamma _{\!\beta }\) can be extended to the submanifold \(\Omega _{-\beta ,2\beta }\) by letting \(u(x) := u(\sigma _0(x))\) for \(x \in \Omega _{-\beta ,0}\) and \(u(x) := u(\sigma _\beta (x))\) for \(x \in \Omega _{\beta ,2\beta }\). If u is a solution to (1.1) and we extend it as above, the extended function (still denoted by u) satisfies \(-\Delta u = f(d(x),z,u)\) not only in \(\Omega _{0\beta }\), but also in \(\Omega _{-\beta ,0}\) and in \(\Omega _{\beta ,2\beta }\). To be precise, here \(\Delta\) denotes the Beltrami-Laplace operator on \({\mathcal {M}}\), which reduces to the standard Laplacian because \({\mathcal {M}}\) is flat. Moreover, since f is Hölder continuous, standard regularity results imply that u is regular through \(\Gamma _{\!0}\) and \(\Gamma _{\!\beta }\), and satisfies the equation in all of \(\Omega _{-\beta ,2\beta }\). Hence for every \(\alpha \in (0,\beta )\), the function \(w_\alpha :\Omega _{0\beta } \rightarrow {\mathbb {R}}\) given by \(w_\alpha (x):=u(\sigma _\alpha (x))-u(x)\) is well defined and satisfies
where
together with
In the sequel, the monotonicity of a solution u of (1.1) will be detected through the sign of \(w_\alpha\): this motivates our interest in the function spaces \(H^1_{\gamma _{0\alpha } \cup \,\Gamma _{\!\alpha }}(\Omega _{0\alpha })\) and \(H^1_{\gamma _{\alpha \beta } \cup \,\Gamma _{\!\alpha }}(\Omega _{\alpha \beta })\). We have:
Lemma 2.1
(Splitting lemma) Let \(u \in L^\infty (\Omega _{0\beta })\). Then for every \(\alpha \in (0,\beta )\) we have
Proof
Let \(\varphi _{0\alpha },\varphi _{\alpha \beta }\) be the eigenfunctions associated to the eigenvalues \(\uplambda _1(H^1_{\gamma _{0\alpha } \cup \,\Gamma _{\!\alpha }}(\Omega _{0\alpha }))\) and \(\uplambda _1(H^1_{\gamma _{\alpha \beta } \cup \,\Gamma _{\!\alpha }}(\Omega _{\alpha \beta }))\), respectively. Without loss of generality we assume \(\Vert \varphi _{0\alpha }\Vert _{\Omega _{0\alpha }} = \Vert \varphi _{\alpha \beta }\Vert _{\Omega _{\alpha \beta }} = 1\), where \(\Vert \cdot \Vert _D\) denotes the norm in \(L^2(D)\). Since \(\varphi _{0\alpha },\varphi _{\alpha \beta }\) satisfy a Dirichlet boundary condition on \(\Gamma _{\!\alpha }\), we may extend them to the whole \(\Omega _{0\beta }\) by letting \(\varphi _{0\alpha } := 0\) in \(\Omega _{\alpha \beta }\) and \(\varphi _{\alpha \beta } := 0\) in \(\Omega _{0\alpha }\). The extended functions are orthogonal in \(H^1_{\gamma _{0\beta }}(\Omega _{0\beta })\) since their supports are disjoint, and we may define the two-dimensional linear subspace \(W_0 = \{\, \phi \in H^1_{\gamma _{0\beta }}(\Omega _{0\beta }) : \phi = a \, \varphi _{0\alpha } + b \, \varphi _{\alpha \beta } \text{ for } a,b \in {\mathbb {R}}\,\}\). Moreover, for every \(\phi = a \, \varphi _{0\alpha } + b \, \varphi _{\alpha \beta } \not \equiv 0\) we have
The variational formulation of the eigenvalues (see [9, Theorem 1.42 (iii)]), sometimes called Poincaré’s minimax characterization, ensures that
and the conclusion follows immediately. \(\square\)
Corollary 2.2
Assume \(\uplambda _2(H^1_{\gamma _{0\beta }}(\Omega _{0\beta }))\ge 0\) for some \(u \in L^\infty (\Omega _{0\beta })\), and let \(\alpha \in (0,\beta )\). Then either \(\uplambda _1(H^1_{\gamma _{0\alpha } \cup \,\Gamma _{\!\alpha }}(\Omega _{0\alpha }))\ge 0\) or \(\uplambda _1(H^1_{\gamma _{\alpha \beta } \cup \,\Gamma _{\!\alpha }}(\Omega _{\alpha \beta }))\ge 0\).
The positivity of the first eigenvalue is a necessary and sufficient condition in order that the weak maximum principle holds: see, for instance, [9, Theorem 1.50]. When the first eigenvalue is allowed to vanish, we have a sign-preservation property for weak supersolutions of the Dirichlet problem associated to the operator \(L_u\), as well as to the corresponding mixed problem. A weak supersolution of the Dirichlet problem for \(L_u\) in \(\Omega _{0\alpha }\) is a function \(v \in H^1(\Omega _{0\alpha })\) such that \(v \ge 0\) almost everywhere on \(\partial \Omega _{0\alpha }\) and the inequality
holds for every nonnegative \(\varphi \in H^1_0(\Omega _{0\alpha })\). Recall, further, that a weak supersolution of the mixed problem for \(L_u\) in \(\Omega _{0\alpha }\), with Neumann condition on \(\Gamma _{\! 0}\), is a function \(v \in H^1(\Omega _{0\alpha })\) such that \(v \ge 0\) a.e. on \(\gamma _{0\alpha } \cup \Gamma _{\! \alpha }\) and the inequality (2.3) holds for every nonnegative \(\varphi \in H^1_{\gamma _{0\alpha } \cup \Gamma _{\! \alpha }}(\Omega _{0\alpha })\) [9, p. 15]. A smooth function v satisfying \(L_u \, v \ge 0\) pointwise in \(\Omega _{0\alpha }\) together with \(v \ge 0\) on \(\gamma _{0\alpha } \cup \Gamma _{\! \alpha }\) and \(\partial v / \partial \nu \ge 0\) on \(\Gamma _{\! 0}\) is also a weak supersolution of the mixed problem.
Lemma 2.3
(Sign preservation) Assume \(\uplambda _1(H^1_{\gamma _{0\alpha } \cup \,\Gamma _{\!\alpha }}(\Omega _{0\alpha })) \ge 0\) for some \(u \in L^\infty (\Omega _{0\beta })\) and \(\alpha \in (0,\beta )\). Let \(v \in C^1(\Omega _{0\alpha } \cup \Gamma _{\! 0}) \cap H^1(\Omega _{0\alpha })\) be either a weak supersolution of the Dirichlet problem associated to the operator \(L_u\) in \(\Omega _{0\alpha }\), or a weak supersolution of the corresponding mixed problem with Neumann condition on \(\Gamma _0\).
-
1.
If v satisfies \(v = 0\) a.e. on \(\Gamma _{\!\alpha }\) without being identically zero in \(\Omega _{0\alpha }\), then either \(v > 0\) in \(\Omega _{0\alpha }\) or \(v < 0\) in \(\Omega _{0\alpha }\).
-
2.
If \(v > 0\) a.e. on \(\Gamma _{\!\alpha }\), then \(v > 0\) in \(\Omega _{0\alpha }\).
Proof
The negative part \(v^-(x) = \min \{\, v(x),0 \,\} \le 0\) satisfies \(v^- = 0\) a.e. on \(\gamma _{0\alpha } \cup \Gamma _{\! \alpha }\). Furthermore, if v is a weak supersolution of the Dirichlet problem, then \(v^- = 0\) on \(\Gamma _{\! 0}\) as well. If v is either a weak supersolution of the Dirichlet problem associated to the operator \(L_u\) in \(\Omega _{0\alpha }\), or a weak supersolution of the corresponding mixed problem with Neumann condition on \(\Gamma _0\), we may take \(\varphi = - v^-\) in (2.3) and get \(Q_{\Omega _{0\alpha }}(v^-) \le 0\). Since
we deduce that either \(v^-\) vanishes identically in \(\Omega _{0\alpha }\), or we may let \(\varphi = v^-\) to minimize the quotient in (2.4). In the last case \(v^-\) is a first eigenfunction of \(L_u\) in \(H^1_{\gamma _{0\alpha } \cup \,\Gamma _{\!\alpha }}(\Omega _{0\alpha })\) and therefore we must have \(v^-<0\) in all of \(\Omega _{0\alpha }\) (see [9, Theorem 1.42 (vi)]). If, instead, \(v^-\) vanishes identically, then \(v \ge 0\) in \(\Omega _{0\alpha }\) and by the strong maximum principle (see [9, Theorem 1.28]) we have either \(v \equiv 0\) or \(v > 0\) in \(\Omega _{0\alpha }\). The two claims follow at once. \(\square\)
The starting point of our rotating plane argument, developed in Sect. 3, is the case when \(\alpha = \frac{\beta }{2}\). The function \(w_\frac{\beta }{2}\), which is odd with respect to \(\Gamma _{\!\frac{\beta }{2}}\), satisfies \(w_\frac{\beta }{2} = 0\) on \(\gamma _{0\beta } \cup \, \Gamma _{\!\frac{\beta }{2}}\). Therefore the following corollary applies:
Corollary 2.4
Assume \(u \in {\mathcal {X}}\) is a solution to (1.1) such that \(\uplambda _2(H^1_{\gamma _{0\beta }}(\Omega _{0\beta }))\ge 0\) and assume f(r, z, u) is convex with respect to u. If \(w_{\frac{\beta }{2}}\) does not vanish identically in \(\Omega _{0\beta }\), then either \(w_{\frac{\beta }{2}} > 0\) in \(\Omega _{0\frac{\beta }{2}}\) or \(w_{\frac{\beta }{2}} > 0\) in \(\Omega _{\frac{\beta }{2}\beta }\).
Proof
By Corollary 2.2 we have that one among \(\uplambda _1(H^1_{\gamma _{0\frac{\beta }{2}} \cup \,\Gamma _{\!\frac{\beta }{2}}}(\Omega _{0\frac{\beta }{2}}))\) and \(\uplambda _1(H^1_{\gamma _{\frac{\beta }{2}\beta } \cup \,\Gamma _{\!\frac{\beta }{2}}}(\Omega _{\frac{\beta }{2}\beta }))\) is nonnegative. Suppose that \(\uplambda _1(H^1_{\gamma _{0\frac{\beta }{2}} \cup \,\Gamma _{\!\frac{\beta }{2}}}(\Omega _{0\frac{\beta }{2}})) \ge 0\), the other case being analogous. By the convexity of f, the function \(v = w_\frac{\beta }{2} \in C^2(\Omega _{0\frac{\beta }{2}} \cup \Gamma _{\! 0} \cup \Gamma _{\! \frac{\beta }{2}}) \cap C^0({\overline{\Omega }}_{0\frac{\beta }{2}}) \cap H^1(\Omega _{0\frac{\beta }{2}})\) satisfies \(L_u \, v \ge 0\) in \(\Omega _{0\frac{\beta }{2}}\). Moreover v vanishes on \(\gamma _{0\frac{\beta }{2}} \cup \Gamma _{\! \frac{\beta }{2}}\) and satisfies \(\frac{\partial v}{\partial \nu } = -\frac{\partial v}{\partial \theta } = 0\) on \(\Gamma _{\! 0}\). Taking into account that \(w_\frac{\beta }{2}\) is odd with respect to \(\Gamma _{\!\frac{\beta }{2}}\), the conclusion follows by letting \(\alpha = \frac{\beta }{2}\) in Claim 1 of Lemma 2.3.\(\square\)
3 Proof of Theorem 1.1
The proof of Theorem 1.1 is based on a fine interplay of the derivative \(u_\theta\) and the function \(w_\alpha\) introduced in Sect. 2. In fact, the strict monotonicity of u with respect to \(\theta\) in \(\Omega _{0\beta }\) holds if and only if \(w_\alpha > 0\) in \(\Omega _{0\alpha }\) for every \(\alpha \in (0,\beta )\). By contrast, symmetry of u with respect to \(\Gamma _{\!\frac{\beta }{2}}\), and constancy with respect to \(\theta\) as a special case, occur when \(w_\frac{\beta }{2}\) vanishes identically. First of all we observe
Proposition 3.1
If \(u \in C^2(\Omega _{0\beta })\) satisfies the equation in (1.1) pointwise, then the derivative \(u_\theta\) still belongs to \(C^2(\Omega _{0\beta })\) and is a classical solution to
Proof
As usual, we call test function any smooth function \(\varphi \in C^\infty (\Omega _{0\beta })\) compactly supported in \(\Omega _{0\beta }\). The set of all test functions is denoted by \(C^\infty _0(\Omega _{0\beta })\). To prove the claim, we differentiate the equality
with respect to \(\theta\). Since \(\varphi _\theta\) is still a test function, the terms containing \(\varphi _\theta\) cancel each other, and we obtain
Hence \(u_\theta\) is a weak solution of \(L_u \, u_\theta = 0\). Since \(f'\) is Hölder continuous by assumption, \(u_\theta\) is a classical solution, as claimed. \(\square\)
To proceed further, observe that by Corollary 2.4 the function \(w_{\frac{\beta }{2}}(x)\) does not change sign in \(\Omega _{0\frac{\beta }{2}}\) nor in \(\Omega _{\frac{\beta }{2}\beta }\). We consider the case when \(w_{\frac{\beta }{2}}(x)\equiv 0\) in \(\Omega _{0\beta }\) first:
Lemma 3.2
Assume \(u \in {\mathcal {X}}\) solves (1.1) and satisfies \(\uplambda _2(H^1_{\gamma _{0\beta }}(\Omega _{0\beta }))\ge 0\). If \(w_{\frac{\beta }{2}}(x)\equiv 0\) in \(\Omega _{0\beta }\) then u is constant with respect to \(\theta\).
Proof
If \(w_{\frac{\beta }{2}}(x)\equiv 0\) then u is symmetric with respect to \(\Gamma _{\!\frac{\beta }{2}}\) and the linearized operator \(L_u\) is invariant under reflections about \(\Gamma _{\!\frac{\beta }{2}}\). In particular, the first eigenfunction \(\varphi _1\) in \(H^1_{\gamma _{0\beta }}(\Omega _{0\beta })\) is symmetric with respect to \(\Gamma _{\!\frac{\beta }{2}}\). Furthermore, since \(u_\theta \in H^1_0(\Omega _{0\beta })\), we may let \(\varphi\) in (3.2) approach \(u_\theta\) in \(H^1(\Omega _{0\beta })\) and deduce \(Q_{\Omega _{0\beta }}(u_\theta ) = 0\). In order to prove the lemma it is enough to show that \(u_\theta\) vanishes identically in \(\Omega _{0\beta }\). The argument is by contradiction. Observe that \(\varphi _1 \perp u_\theta\), i.e., \(\varphi _1\) is orthogonal to \(u_\theta\) in \(L^2(\Omega _{0\beta })\), because \(u_\theta\) is odd with respect to \(\Gamma _{\!\frac{\beta }{2}}\). Furthermore, by assumption we have
If \(u_\theta \not \equiv 0\), we see that the infimum is achieved at \(\varphi = u_\theta\) because \(Q_{\Omega _{0\beta }}(u_\theta ) = 0\). But then \(u_\theta\), being a minimizer of the Rayleigh quotient in \(H^1_{\gamma _{0\beta }}(\Omega _{0\beta })\) under the constraint \(\varphi _1 \perp \varphi\), should satisfy the Neumann conditions \(\partial u_\theta / \partial \nu = 0\) on \(\Gamma _{\!0} \cup \Gamma _{\!\beta }\). If this were the case, we could extend \(u_\theta\) to \(\Omega _{-\beta ,\beta }\) by letting
thus obtaining a function \({\tilde{u}}_\theta \in C^1(\Omega _{-\beta ,\beta })\) that satisfies \(L_u \, {\tilde{u}}_\theta = 0\) in the weak sense in \(\Omega _{-\beta ,\beta }\) and vanishes identically in \(\Omega _{-\beta ,0}\). Since we are assuming that \(u_\theta\) does not vanish identically in \(\Omega _{0\beta }\), this is in contrast with the unique continuation property [22, p. 519], and the lemma follows. \(\square\)
Next we consider the case when \(w_{\frac{\beta }{2}}> 0\) in \(\Omega _{0\frac{\beta }{2}}\). The case when \(w_{\frac{\beta }{2}}>0\) in \(\Omega _{\frac{\beta }{2} \beta }\) is similar. Taking Corollary 2.2 into account, we may assume \(\uplambda _1(H^1_{\gamma _{0\frac{\beta }{2}} \cup \,\Gamma _{\!\frac{\beta }{2}}}(\Omega _{0\frac{\beta }{2}}))\ge 0\) without loss of generality. Let us show that the inequality \(u_\theta > 0\) holds:
Lemma 3.3
Assume \(u \in {\mathcal {X}}\) is a solution to (1.1) such that \(\uplambda _1(H^1_{\gamma _{0\frac{\beta }{2}} \cup \,\Gamma _{\!\frac{\beta }{2}}}(\Omega _{0\frac{\beta }{2}}))\ge 0\). If \(w_{\frac{\beta }{2}}(x)>0\) in \(\Omega _{0\frac{\beta }{2}}\) then
Proof
Arguing as in the proof of Lemma 3.2 we see that the angular derivative \(u_\theta\) (which cannot be odd, now, because u is not symmetric about \(\Gamma _{\!\frac{\beta }{2}}\)) satisfies (3.1) together with the boundary condition \(u_\theta =0\) on \(\gamma _{0\beta }\cup \Gamma _0\cup \Gamma _\beta\). Hence \(u_\theta \in H^1_0(\Omega _{0\beta }) \cap C^1(\Omega _{0\beta } \cup \Gamma _{\! 0} \cup \Gamma _{\! \beta })\). Let us prove that \(u_\theta >0\) on \(\Gamma _{\!\frac{\beta }{2}}\). By (2.1), \(w_\frac{\beta }{2}\) satisfies \(-\Delta w_\frac{\beta }{2}-c_\frac{\beta }{2}(x) \, w_\frac{\beta }{2}=0\) in \(\Omega _{0\frac{\beta }{2}}\). Since \(w_{\frac{\beta }{2}}(x)>0\) in \(\Omega _{0\frac{\beta }{2}}\) by assumption, and \(w=0\) on \(\Gamma _{\!\frac{\beta }{2}}\) by definition, the Hopf boundary lemma [9, Theorem 1.28] implies that \(\frac{\partial w}{\partial \nu }<0\) on \(\Gamma _{\!\frac{\beta }{2}}\). Here \(\nu\) is the outward unit normal to \(\Omega _{0\frac{\beta }{2}}\) at \(\Gamma _{\!\frac{\beta }{2}}\). This means
Hence \(u_\theta > 0\) on \(\Gamma _{\!\frac{\beta }{2}}\), as claimed, and the conclusion follows from Claim 2 of Lemma 2.3. \(\square\)
We are now ready to apply the rotating plane method.
Proof of Theorem 1.1
We assume that \(\uplambda _2(H^1_{\gamma _{0\beta }}(\Omega _{0\beta })) \ge 0\) and prove that either \(u_\theta \equiv 0\) or \(u_\theta\) keeps its sign in \(\Omega _{0\beta }\). In the last case, from (3.1) and the boundary condition it follows immediately that \(u_\theta\) is a first Dirichlet eigenfunction of \(L_u\) in \(\Omega _{0\beta }\) and therefore \(\uplambda _1(H^1_0(\Omega _{0\beta })) = 0\). At the end of the proof, a final observation shows that if \(\uplambda _1(H^1_{\gamma _{0\beta }}(\Omega _{0\beta })) \ge 0\) then u is constant in \(\theta\), which completes the proof of the theorem.
If \(w_{\frac{\beta }{2}}\equiv 0\) in \(\Omega _{0\beta }\) then u is independent of \(\theta\) by Lemma 3.2. Otherwise, by Corollary 2.4, either \(w_\frac{\beta }{2} > 0\) in \(\Omega _{0\frac{\beta }{2}}\) or \(w_\frac{\beta }{2} > 0\) in \(\Omega _{\frac{\beta }{2}\beta }\). By Corollary 2.2 we may assume \(\uplambda _1(H^1_{\gamma _{0\frac{\beta }{2}} \cup \,\Gamma _{\!\frac{\beta }{2}}}(\Omega _{0\frac{\beta }{2}}))\ge 0\) and \(w_{\frac{\beta }{2}} > 0\) in \(\Omega _{0\frac{\beta }{2}}\) without loss of generality (indeed, if \(w_\frac{\beta }{2} < 0\) in \(\Omega _{0\frac{\beta }{2}}\) the argument is similar). Let us prove that \(u_\theta > 0\) in \(\Omega _{0\beta }\). Denote by \(A'\) the set of all \(\alpha ' \in [\frac{\beta }{2},\beta ]\) having the property that for every \(\alpha \in (0,\alpha ')\) the function \(w_{\alpha }\) is positive in \(\Omega _{0\alpha }\).
Part I. The set \(A'\) contains \(\frac{\beta }{2}\) and therefore it is not empty. To see this, we have to prove that \(u(x) < u(\sigma _\alpha (x))\) for every \(\alpha \in (0,\frac{\beta }{2})\) and \(x \in \Omega _{0\alpha }\), which is equivalent to say that \(u(r,\theta _1,z) < u(r,\theta _2,z)\) for \(0< \theta _1 < \theta _2\) such that \(\theta _1 + \theta _2 < \beta\). If \(\theta _2 \le \frac{\beta }{2}\) the conclusion follows from (3.4). Otherwise we must have \(\theta _1< \beta -\theta _2< \frac{\beta }{2} < \theta _2\) and we argue as follows. Let \(x_i\), for \(i = 1,2\), be the point whose cylindrical coordinates are \((r,\theta _i,z)\), and observe that the coordinates of \(\sigma _\frac{\beta }{2}(x_2)\) are \((r, \, \beta - \theta _2, \, z)\). We may write \(u(\sigma _\frac{\beta }{2}(x_2)) < u(x_2)\) because we are considering \(w_\frac{\beta }{2} > 0\) in \(\Omega _{0\frac{\beta }{2}}\) (hence \(w_\frac{\beta }{2} < 0\) in \(\Omega _{\frac{\beta }{2}\beta }\)). Furthermore we have \(u(x_1) < u(\sigma _\frac{\beta }{2}(x_2))\) because of (3.4), and therefore \(\frac{\beta }{2} \in A'\) as claimed. We note for later usage that the preceding argument still holds when \(\theta _1 = 0\), hence
Part II. The set \(A'\) is a closed subinterval of \([\frac{\beta }{2},\beta ]\). Indeed, by the definition of \(A'\) it follows that if \(\alpha ',\alpha ''\) satisfy \(\frac{\beta }{2} \le \alpha ' \le \alpha ''\) and \(\alpha '' \in A'\) then \(\alpha ' \in A'\), hence \(A'\) is an interval. It also follows immediately that \(A'\) is closed, and we may write \(A' = [\frac{\beta }{2},{\tilde{\alpha }}]\) for some \({\tilde{\alpha }} \in [\frac{\beta }{2},\beta ]\).
Part III. The derivative \(u_\theta\) is positive in the sector \(\Omega _{0{\tilde{\alpha }}}\). To check this, we verify that \(u_\theta > 0\) along \(\Gamma _{\!\alpha }\) for each \(\alpha \in (0,{\tilde{\alpha }})\). The argument is the same as in Lemma 3.3: since \(w_\alpha\) is positive in \(\Omega _{0\alpha }\) by the definition of \(A'\), and satisfies (2.1), by the Hopf boundary-point lemma it must also satisfy \(\partial w_\alpha / \partial \nu < 0\) along \(\Gamma _{\!\alpha }\), where \(w_\alpha = 0\). Hence \(u_\theta > 0\) along \(\Gamma _{\!\alpha }\), as claimed.
Part IV. If \({\tilde{\alpha }} < \beta\) then \(w_{{\tilde{\alpha }}} > 0\) in \(\Omega _{0{\tilde{\alpha }}}\). Indeed, by continuity we may write \(w_{{\tilde{\alpha }}} \ge 0\) in \(\Omega _{0{\tilde{\alpha }}}\), and by the convexity of f it follows that \(w_{{\tilde{\alpha }}}\) satisfies the inequality \(L_u \, w_{{\tilde{\alpha }}} \ge 0\). Hence either \(w_{{\tilde{\alpha }}} > 0\) or \(w_{{\tilde{\alpha }}} \equiv 0\) in \(\Omega _{0{\tilde{\alpha }}}\) by the strong maximum principle. Let us exclude the second case. If \(w_{{\tilde{\alpha }}} \equiv 0\) in \(\Omega _{0{\tilde{\alpha }}}\) then \({\tilde{\alpha }} > \frac{\beta }{2}\) because we are assuming \(w_\frac{\beta }{2} > 0\) in \(\Omega _{0\frac{\beta }{2}}\). Furthermore, by differentiating the equality \(u(r, \, 2{\tilde{\alpha }} - \theta , \, z) = u(r,\theta ,z)\) we obtain \(u_\theta (r, \, 2{\tilde{\alpha }} - \theta , \, z) = -u_\theta (r,\theta ,z)\) for \((r,\theta ,z) \in \Omega _{0{\tilde{\alpha }}}\), which yields at \({\tilde{\theta }} = 2{\tilde{\alpha }} - \beta \in (0,{\tilde{\alpha }})\)
contradicting Part III. Hence, we can write the implication \({\tilde{\alpha }} < \beta \implies w_{{\tilde{\alpha }}} > 0\) in \(\Omega _{0{\tilde{\alpha }}}\).
Part V. Recall that for every \(\alpha \in (0,\beta )\) the function \(w_\alpha\) is well defined in \(\Omega _{0\alpha }\) and satisfies (2.1)-(2.2) together with (3.6). To complete the boundary conditions, let us check that
which is equivalent to \(u(r,0,z) < u(r,2\alpha ,z)\). By the definition of the extended function u, we have \(u(r,2\alpha ,z) = u(r, \, 2\beta - 2\alpha , \, z)\). The point \((r, \, 2\beta - 2\alpha , \, z)\) can be rewritten as \(\sigma _{\alpha '}(r,0,z)\) by choosing \(\alpha ' = \beta - \alpha > 0\). If \(\alpha \in (\frac{\beta }{2},\beta )\) then \(\alpha ' < \frac{\beta }{2}\) and the inequality \(u(r,0,z) < u(\sigma _{\alpha '}(r,0,z))\) follows from (3.6). Finally, since \(w_\frac{\beta }{2}\) is positive in \(\Omega _{0\frac{\beta }{2}}\) by assumption and satisfies \(\partial w_\frac{\beta }{2} /\partial \nu = 0\) on \(\Gamma _{\! 0}\), the Hopf boundary point lemma prevents it from vanishing there.
Part VI. The second endpoint \({\tilde{\alpha }} \ge \frac{\beta }{2}\) of the interval \(A'\) is in fact \(\beta\). To prove this, we show that if \({\tilde{\alpha }} < \beta\) then for some \(\varepsilon _0 > 0\) and for every \(\alpha \in [{\tilde{\alpha }}, \, {\tilde{\alpha }} + \varepsilon _0)\) we have \(w_\alpha > 0\) in \(\Omega _{0\alpha }\), which contradicts the definition of \({\tilde{\alpha }}\). In order to reach our goal we need a suitable maximum principle. Observe, to begin with, that the sup-norm \(\Vert c_\alpha \Vert _\infty\) is bounded uniformly with respect to \(\alpha\). Therefore, by the weak maximum principle in small domains [9, Theorem 1.20] there exists \(\delta > 0\) (independent of \(\alpha\)) such that if an open subset \(D \subset \Omega _{0\alpha }\) satisfies \(|D| < \delta\), and if \(w_\alpha \ge 0\) on \(\partial D\), then \(w_\alpha \ge 0\) in all of D. Accordingly, let us fix a (nonempty) compact subset \(K \subset \Omega _{0{\tilde{\alpha }}}\) such that \(|\Omega _{0{\tilde{\alpha }}} {\setminus } K| < \frac{\delta }{2}\) and define
Recall that \(\eta > 0\) by Part IV. Then, for a convenient \(\varepsilon _0 > 0\) we achieve that for all \(\alpha \in [{\tilde{\alpha }}, \, {\tilde{\alpha }} + \varepsilon _0)\) the open set \(D_\alpha = \Omega _{0\alpha } {\setminus } K\) satisfies \(|D_\alpha | < \delta\) and
Taking into account the boundary conditions established in Part V, we may write \(w_\alpha \ge 0\) on \(\partial D_\alpha\) and therefore, by the weak maximum principle in small domains, the inequality \(w_\alpha \ge 0\) holds in \(D_\alpha\), and consequently in all of \(\Omega _{0\alpha }\). More precisely, since \(w_\alpha > 0\) in K, by the strong maximum principle we obtain \(w_\alpha > 0\) in \(\Omega _{0\alpha }\) for every \(\alpha \in [{\tilde{\alpha }}, \, {\tilde{\alpha }} + \varepsilon _0)\). This contradiction proves that \({\tilde{\alpha }} = \beta\), as claimed.
Conclusion. By Part VI, the solution u is strictly increasing with respect to \(\theta\) in \(\Omega _{0\beta }\), and by Part III it satisfies \(u_\theta > 0\). We have thus proved that if \(\uplambda _2(H^1_{\gamma _{0\beta }}(\Omega _{0\beta })) \ge 0\) then either \(u_\theta\) vanishes identically in \(\Omega _{0\beta }\) or it keeps its sign there. In order to complete the proof, it suffices to check that if \(\uplambda _1(H^1_{\gamma _{0\beta }}(\Omega _{0\beta })) \ge 0\) the last case cannot occur, i.e., \(u_\theta\) does not keep its sign in \(\Omega _{0\beta }\). In fact, if this were the case, we would have \(0 \le \uplambda _1(H^1_{\gamma _{0\beta }}(\Omega _{0\beta })) \le \uplambda _1(H^1_0(\Omega _{0\beta })) = 0\) by the comparison of Dirichlet and Neumann eigenvalues (see, for instance, [7, Theorem 1, p. 408] or [15, Example 11.13]). This shows that \(u_\theta\) would also minimize the Rayleigh quotient in \(H^1_{\gamma _{0\beta }}(\Omega _{0\beta })\) and therefore it should satisfy the Neumann boundary condition \(\partial u_\theta / \partial \nu = 0\) on \(\Gamma _{\!0} \cup \Gamma _{\!\beta }\). But then \(u_\theta\) would extend as in (3.3) to a \(C^1\)-eigenfunction in \(\Omega _{-\beta ,\beta }\) vanishing identically in \(\Omega _{-\beta ,0}\), and this is impossible by the unique continuation property. \(\square\)
4 Cylindrical domains
When the opening of a sector-like domain tends to zero, the domain is asymptotic to a cylinder. To manage with this case we have to arrange the notation. Changes are specific to the present section. Here we denote by \(\omega\) a Lipschitz, bounded, \((N - 1)\)-dimensional domain lying in the hyperplane \(x_1 = 0\) and by \(\Omega _{\theta _1\theta _2}\) the cylinder \((\theta _1,\theta _2) \times \omega\), where \(\theta _1,\theta _2 \in {\mathbb {R}}\) satisfy \(\theta _1 < \theta _2\). Given \(\beta \in (0,+\infty )\), we let \({\mathcal {X}}\) be the set of functions \(u\in C^2(\Omega _{0\beta })\cap C^0({\overline{\Omega }}_{0\beta })\cap H^1( \Omega _{0\beta })\) such that \(\frac{\partial u}{\partial x_1}\in H^1(\Omega _{0\beta })\) and we consider functions \(u\in {\mathcal {X}}\) that satisfy, pointwise, the boundary-value problem:
where \(z = (x_2, \ldots , x_N) \in {\mathbb {R}}^{N - 1}\) and f(z, u) is locally Hölder continuous in \({\mathbb {R}}^N\) together with its derivative \(f' = \partial f / \partial u\). Letting \(\Gamma _{\!\alpha } = \{\alpha \} \times \omega\) and \(\gamma _{\theta _1\theta _2} = [\theta _1,\theta _2] \times \partial \omega\), problem (4.1) is equivalent to the following mixed boundary-value problem:
where g is continuous on \(\gamma _{0\beta }\). The preceding results can be extended to such a case. We have:
Theorem 4.1
Let \(u\in {\mathcal {X}}\) be a solution to (4.1), where f(z, u) is convex with respect to u.
-
1.
If \(\uplambda _1(H^1_{\gamma _{0\beta }}(\Omega _{0\beta }))\ge 0\) then u is constant with respect to \(x_1\).
-
2.
If \(\uplambda _1(H^1_{\gamma _{0\beta }}(\Omega _{0\beta })) < 0 \le \uplambda _2(H^1_{\gamma _{0\beta }}(\Omega _{0\beta }))\) then u is either constant with respect to \(x_1\) or strictly monotone with respect to \(x_1\) in \(\Omega _{0\beta }\). In the last case, the derivative \(u_1 = \partial u / \partial x_1\) does not vanish in \(\Omega _{0\beta }\), the first Dirichlet eigenvalue \(\uplambda _1(H^1_0(\Omega _{0\beta }))\) equals zero and \(u_1\) is a corresponding eigenfunction.
The argument is identical to the proof of Theorem 1.1 found in Sect. 3, keeping in mind that in the present case the reflection \(\sigma _\alpha\) is obviously defined as \(\sigma _\alpha (x_1,z) = (2\alpha - x_1, \, z)\), and every occurrence of \(\theta\) has to be replaced with \(x_1\). Since \(\gamma _{0\beta }\) and \(\Gamma _{\alpha }\) intersects orthogonally we can obtain that \(\partial u / \partial x_1\in H^1(\Omega _{0\beta })\) using [20, Proposition 6.1] when \(\omega\) is smooth.
5 Examples
In this section we produce some examples of solutions to (1.1) that are not constant in \(\theta\) and satisfy Claim 2 of Theorem 1.1. In the first examples \(\Omega _{0\beta }\) is a sector of the unit disc \(B_1 \subset {\mathbb {R}}^2\).
Example 5.1
Let \(N = 2\) and \(\Omega =B_1\). We consider the eigenvalue problem
for \(0<\beta <2\pi\). If we neglect to give the eigenvalues an increasing order, the solutions \((\uplambda ,\psi )\) of (5.1) are given by
for \(n=0,1,2,\dots\) and \(k=1,2,\dots\) where \(J_{s_n}\) is the Bessel function of order \(s_n = \frac{n\pi }{\beta }\), and \(j_{s_n,k}\) is the k-th positive zero of \(J_{s_n}\). Each \(\psi _{nk}\) can be considered as a solution of (1.1) or (1.2) where \(f(r,z,u) = \uplambda _{nk} \, u\), and the corresponding linearized operator is \(L_{\psi _{nk}} = -\Delta - \uplambda _{nk} \, I\). Of course, if \(\psi _{nk}\) is the i-th eigenfunction of problem (5.1) for some positive integer i, then the i-th eigenvalue of \(L_{\psi _{nk}}\) in \(H^1_{\gamma _{0\beta }}(\Omega _{0\beta })\) vanishes. The first eigenvalue of problem (5.1) is \(\uplambda _{01}=j^2_{0,1}\) and the first eigenfunction is radial and given by
Thus, we have an instance of problem (1.1) or (1.2) where \(\uplambda _1(H_{\gamma _{0\beta }}(\Omega _{0\beta })) = 0\) and a corresponding solution \(u = \psi _{01}(r,\theta )\) which is radial, as stated in Theorem 1.1, Claim 1. In order to find the second eigenvalue and eigenfunction of (5.1) we have to compare \(j_{0,2}\approx 5.5201\) and \(j_{\frac{\pi }{\beta },1}\) whose value depends on the angle \(\beta\). It can be seen that if \(\beta =\frac{\pi }{2}\) then \(J_\frac{\pi }{\beta }= J_2\) and \(j_{\frac{\pi }{\beta },1}=j_{2,1}\approx 5.1356<j_{0,2}\), while if \(\beta =\frac{\pi }{3}\) then \(J_\frac{\pi }{\beta }= J_3\) and \(j_{\frac{\pi }{\beta },1}=j_{3,1}\approx 6.3802>j_{0,2}\). Next, using that \(j_{s,1}\) is a continuous and strictly increasing function of the variable s (see for instance [11, pp. 67-68]), it follows that there exists a unique angle \({\widehat{\beta }}\in (\frac{\pi }{3},\frac{\pi }{2})\) such that \(j_{\frac{\pi }{{\widehat{\beta }}},1}=j_{0,2}\). Moreover one has \(j_{\frac{\pi }{\beta },1}<j_{0,2}\) for \(\beta > {\widehat{\beta }}\) while \(j_{\frac{\pi }{\beta },1} > j_{0,2}\) for \(0< \beta < {\widehat{\beta }}\). The value of \({\widehat{\beta }}\) can be estimated numerically obtaining \({\widehat{\beta }}\approx 1.3629\). Reassuming, for \(\beta >{\widehat{\beta }}\) the second eigenvalue of (5.1) is \(\uplambda _{11}=j^2_{\frac{\pi }{\beta },1}\), and the second eigenfunction
is nonradial and strictly monotone in the angular variable in \(\Omega _{0\beta }\). Let us observe that the second eigenfunction \(\psi _{11}\) satisfies the assumptions of Theorem 1.1, Claim 2 since the second eigenvalue of the linearized operator \(L_{\psi _{11}} = -\Delta - j^2_{\frac{\pi }{\beta },1} \, I\) in \(H^1_{\gamma _{0 \beta }}(\Omega _{0 \beta })\) vanishes. For \(\beta < {\widehat{\beta }}\) the second eigenvalue of problem (5.1) is \(\uplambda _{02}=j^2_{0,2}\) and the second eigenfunction is radial and given by
while for \(\beta ={\widehat{\beta }}\) the second eigenvalue has multiplicity two and the eigenspace is spanned by \(\psi _{02} = J_0(j_{0,2} \, r)\) and \(\psi _{{\widehat{s}} 1} = J_{{\widehat{s}}}\big (j_{{\widehat{s}},1} \, r\big ) \, \cos \big ({\widehat{s}} \, \theta \big )\), where \({\widehat{s}} = \pi /{\widehat{\beta }}\). Thus, letting \(m = j^2_{0,2} = j^2_{{\widehat{s}},1}\) and \(f(r,z,u) = mu\) we obtain an instance of problem (1.1) or (1.2) where \(\uplambda _2(H^1_{\gamma _{0{\widehat{\beta }}}}(\Omega _{0{\widehat{\beta }}})) = 0\) and there are both a radial solution and a solution strictly monotone in \(\theta\) thus implying that \(\uplambda _1(H^1_0(\Omega _{0{\widehat{\beta }}})=0\). Since we are in the linear case, then \(L_{\psi _{02}}= L_{\psi _{{\widehat{s}} 1}}\) showing that, even if \(\frac{\partial \psi _{02}}{\partial \theta }\equiv 0\), the corresponding Dirichlet eigenvalue \(\uplambda _1(H^1_0(\Omega _{0{\widehat{\beta }}}))\) vanishes (Fig. 1).
Next we want to show that, if we allow the solution u in (1.1) or in (1.2) to have a higher Morse index, namely \(\uplambda _2(H^1_{\gamma _{0\beta }}(\Omega _{0\beta }))<0\), then u can be nonradial without being strictly monotone in \(\theta\) in \(\Omega _{0\beta }\). Indeed if we consider the third eigenvalue and eigenfunction of (5.1) in the case where \(\beta >{\widehat{\beta }}\) we have to compare \(j_{0,2}\approx 5.5201\) and \(j_{\frac{2\pi }{\beta },1}\) (that corresponds to \(n=2\)) and it is easy to see that when \(\beta =\pi\) then \(j_{\frac{2\pi }{\beta },1}=j_{2,1}\approx 5.1356<j_{0,2}\). As before we can say that there exists \({\widetilde{\beta }} >{\widehat{\beta }}\) such that when \(\beta >{\widetilde{\beta }}\) the third eigenvalue of (5.1) is \(\uplambda _{2,1}=j^2_{\frac{2\pi }{\beta },1}\) and the third eigenfunction is
which is symmetric with respect to the bisector of \(\Omega _{0\beta }\), strictly monotone with respect to \(\theta\) in \(\Omega _{0\frac{\beta }{2}}\) and in \(\Omega _{\frac{\beta }{2} \beta }\) and satisfies \(\uplambda _3(H^1_{\gamma _{0\beta }}(\Omega _{0\beta }))=0\).
The extension of Theorem 1.1 to solutions such that \(\uplambda _2(H^1_{\gamma _{0\beta }}(\Omega _{0\beta }))<0\le \uplambda _3(H^1_{\gamma _{0\beta }}(\Omega _{0\beta }))\) should take care of this example of functions symmetric with respect to the bisector and strictly monotone in \(\Omega _{0\frac{\beta }{2}}\). We conjecture that this should be the only new behavior allowed for this type of solutions.
Example 5.2
Next we consider a semilinear equation. Let us recall the Hénon problem
where \(B_1\) is the unit ball in \({\mathbb {R}}^N\), \(\alpha >0\) and \(p>1\). It has been proved in [23] that for any \(p>1\) there exists \(\alpha ^*(p)\) such that for any \(\alpha >\alpha ^*(p)\) the ground state of (5.2) is nonradial. When \(p>2\), ground states have a symmetry axis (that we can assume, up to a rotation, is the \(x_1\)-axis) and they are increasing (or decreasing) in the polar angle from this axis, namely in \(\theta\) (see [3] and [21]). If we call \({\bar{u}}\) the restriction to the half ball \(\Omega _{0\pi } = B_1 \cap \{\, x_2 > 0 \,\}\) of a ground state u to (5.2), we have that \({\bar{u}}\) satisfies
and, when \(\alpha\) is large enough, it is strictly monotone in \(\theta\). Moreover \({\bar{u}}\) satisfies the assumption of Theorem 1.1, namely \(\uplambda _2(H^1_{\gamma _{0\pi }}(\Omega _{0\pi }))\ge 0\). Indeed if \(\uplambda _2(H^1_{\gamma _{0\pi }}(\Omega _{0\pi }))<0\) then the linearized operator has two negative eigenvalues with corresponding eigenfunctions orthogonal in \(L^2(\Omega _{0\pi })\). We can extend the eigenfunctions by symmetry about the hyperplane \(\{\, x_2 = 0 \,\}\) thus obtaining two \(L^2\)-orthogonal eigenfunctions of the linearization to (5.2) associated with negative eigenvalues. This is not possible since the linearized operator associated to a ground state u can have only one negative eigenvalue, hence we must have \(\uplambda _2(H^1_{\gamma _{0\pi }}(\Omega _{0\pi }))\ge 0\). In the special case when \(N = 2\), letting \(v(\rho ,\phi )= c \, {\bar{u}}(r,\theta )\) with \(c=\big (\frac{\pi }{\beta }\big )^\frac{2}{p-1}\) for \(r=\rho ^\frac{\pi }{\beta }\) and \(\theta =\frac{\pi }{\beta }\, \phi\), \(\beta \in (0, 2\pi )\), a straightforward computation shows that v solves
giving an example of monotone solution in a sector of any amplitude \(\beta\). This solution satisfies \(\uplambda _2(H^1_{\gamma _{0\beta }}(\Omega _{0\beta }))\ge 0\). Indeed if \(\varphi _1(\rho ,\phi )\) and \(\varphi _2(\rho ,\phi )\) are two \(L^2(\Omega _{0\beta })\)-orthogonal functions that make negative the quadratic form associated with the linearization to this last equation at the solution v, then the functions \({\bar{\varphi }}_1(r,\theta )=\varphi _1(\rho ,\phi )\) and \({\bar{\varphi }}_2(r,\theta )=\varphi _2(\rho ,\phi )\) are two \(L^2(\Omega _{0\pi })\)-orthogonal functions that make negative the quadratic form associated with the linearization to (5.3) at the solution \({\bar{u}}\) and this is not possible.
Example 5.3
Here we consider the case of an annulus A of \({\mathbb {R}}^2\). In [12, Proposition 1.4] it has been proved that for any \(k=1,2,\dots\), there exists an exponent \(p_k>1\) such that the least energy solution of the Lane-Emden problem
in the space of \(H^1\) functions that are \(\frac{2\pi }{k}\) periodic in \(\theta\) is nonradial when \(p>p_k\). Moreover, by [13], up to a rotation, these solutions are strictly monotone in \(\theta\) in the sector \(\Omega _{0\frac{\pi }{k}}\) and, by symmetry reasons, they satisfy a Neumann boundary condition on \(\Gamma _{\! 0} \cup \Gamma _{\! \frac{\pi }{k}}\). Finally, since they are least energy solutions, they satisfy \(\uplambda _2(H^1_{\gamma _{0\frac{\pi }{k}}}(\Omega _{0\frac{\pi }{k}}))\ge 0\).
6 Symmetry and monotonicity in unbounded domains
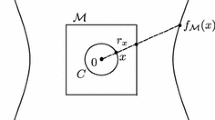
Hereafter we consider the case when \(\Omega _{0\beta }\) is not bounded. To keep the presentation simple and to deal with some difficulties coming from the unboundedness of the domain, we focus on the special case where the domain of the problem is a sector of the N-dimensional Euclidean space with an angular amplitude \(\beta \in (0,2\pi )\). More generally, we also consider the set difference of such a sector and the infinite cylinder \(d(x) \le r_1\), where \(d(x)=\sqrt{x_1^2+x_2^2}\). To be precise, choosing \(r_1 \in [0,+\infty )\) and \(\theta _1,\theta _2 \in [0,2\pi )\), with \(\theta _1 < \theta _2\), we denote by \(\Omega _{\theta _1\theta _2}\) the domain
whose boundary contains the open, flat subsets \(\Gamma _{\!\theta _i} = \{\, x \in {\mathbb {R}}^N : d(x) > r_1,\ \theta (x) = \theta _i \,\}\), \(i =1,2\). Moreover when \(r_1>0\) we may write \(\partial \Omega _{\theta _1\theta _2} =\Gamma _{\! \theta _1}\cup \Gamma _{\! \theta _2} \cup \gamma _{\theta _1\theta _2}\) where \(\gamma _{\theta _1\theta _2}\) is the closed subset
When \(r_1=0\), instead, we have \(\partial \Omega _{\theta _1\theta _2} =\Gamma _{\! \theta _1}\cup \Gamma _{\! \theta _2} \cup \Upsilon\), where \(\Upsilon :=\{x\in {\mathbb {R}}^N: d(x)=0\}\) as before, and \(\gamma _{\theta _1\theta _2} = \emptyset\). In this part of the paper we deal with problem (1.1) where the domain \(\Omega _{0\beta }\) is unbounded and defined as above. The function f(r, z, u) is subject to the same conditions stated in the Introduction. Let \({\mathcal {Y}}\) be the set of all functions \(u \in C^2(\Omega _{0\beta }) \cap C^0({\overline{\Omega }}_{0\beta })\) such that \(u_\theta \in C^0({\overline{\Omega }}_{0\beta }{\setminus } \Upsilon )\) and having a square-summable gradient \(\nabla u \in L^2(\Omega _{0\beta },{\mathbb {R}}^N)\). Here we investigate functions \(u \in {\mathcal {Y}}\) satisfying (1.1) pointwise and having a small Morse index, whose definition is recalled below. By standard regularity theory, any solution \(u \in {\mathcal {Y}}\) belongs to \(C^2(\Omega _{0\beta }\cup \Gamma _{\! 0} \cup \Gamma _{\! \beta })\). As mentioned in the Introduction, problem (1.1) can be rewritten as (1.2). Of course, if \(u \in {\mathcal {Y}}\) then for every \(R > r_1\) we have \(u \in H^1(\Omega _{0\beta } \cap B_R)\), where \(B_R \subset {\mathbb {R}}^N\) denotes the ball with radius R centered at the origin. Now we do not assume that \(u_\theta\) belongs to \(H^1(\Omega _{0\beta } \cap B_R)\), but we require \(u_\theta\) to extend continuously up to the set \(d(x) = r_1\) when \(r_1 > 0\). Roughly speaking, the reason is that in order to derive a conclusion on \(u_\theta\) from a bound on the Morse index (see below) we have to approximate \(u_\theta\) with some compactly supported function: hence \(u_\theta\) must vanish on \(\gamma _{0\beta }\) either in the sense of traces or as a continuous function. In this part of the paper we assume we are in the second case: the assumption is used, for instance, in the proof of (8.9). To proceed further, for any subset \(D \subset {\overline{\Omega }}_{0\beta }\) we denote by \(C^1_0(D)\) the set of functions \(\varphi \in C^1(D)\) having a compact support contained in D.
Definition 6.1
We say that a solution u to (1.1)
-
is stable, and has Morse index \(m(u) = 0\), if \(Q_{\Omega _{0\beta }}(\varphi )\ge 0\) for every \(\varphi \in C^1_{0}(\Omega _{0\beta }\cup \Gamma _{\! 0} \cup \Gamma _{\! \beta })\).
-
has Morse index \(m(u) = M\ge 1\) if M is the maximal dimension of a vector subspace \(X \subset C^1_{0}(\Omega _{0\beta }\cup \Gamma _{\! 0} \cup \Gamma _{\! \beta })\) such that \(Q_{\Omega _{0\beta }}(\varphi )< 0\) for every \(\varphi \in X{\setminus }\{0\}\).
We will investigate solutions with \(m(u) \le 1\). By definition, if \(m(u) = 0\) then the bilinear form
is positive semidefinite in \(C^1_{0}(\Omega _{0\beta }\cup \Gamma _{\! 0} \cup \Gamma _{\! \beta }) \times C^1_{0}( \Omega _{0\beta }\cup \Gamma _{\! 0} \cup \Gamma _{\! \beta })\), and therefore the Cauchy-Schwarz inequality holds:
Since u is locally bounded, so is \(f'(d(x),z,u)\) and the definition of \({\mathcal {B}}(\varphi ,\psi )\) extends to \(H^1_{\gamma _{0\beta } \cup \partial B_R}(D) \times H^1_{\gamma _{0\beta } \cup \partial B_R}(D)\), where \(D = \Omega _{0\beta } \cap B_R\), \(R > r_1\), and \(H^1_{\gamma _{0\beta } \cup \partial B_R}(D)\) denotes the completion of \(C^1_0(\left( \Omega _{0\beta }\cup \Gamma _0\cup \Gamma _\beta \right) \cap B_R)\) in the \(H^1\)-norm. Of course, positive semidefiniteness is preserved under such an extension.
Remark 6.2
The integral in (6.1) makes sense even if we replace \(\varphi\) with some function v having an unbounded support, because the only contribution comes from the bounded set \(\mathrm{supp} \psi\): this will often be done in the sequel in order to prove that \({\mathcal {B}}(v,\psi ) = 0\) for all \(\psi \in C^\infty _0(D)\), i.e., v is locally a weak solution of \(L_u \, v = 0\). In such a case, however, \(Q_{\Omega _{0\beta }}(v)\) is undefined, in general, and (6.2) makes no sense: this difficulty is overcome by means of a truncation technique inspired by [14] (see Sect. 9 for details).
Remark 6.3
If \(m(u) = 1\) then there exists a one-dimensional subspace \(X = \{\, \uplambda \varphi _1 : \uplambda \in {\mathbb {R}} \,\} \subset C^1_{0}(\Omega _{0\beta }\cup \Gamma _{\! 0} \cup \Gamma _{\! \beta })\) such that \(Q_{\Omega _{0\beta }}(\uplambda \varphi _1)< 0\) for every \(\uplambda \ne 0\). In such a case, we have
Indeed, if there were \(\varphi _2 \in C^1_{0}(\Omega _{0\beta }\cup \Gamma _{\! 0} \cup \Gamma _{\! \beta })\) supported in \(\Omega _{0\beta }\cup \Gamma _{\! 0} \cup \Gamma _{\! \beta } {\setminus } \mathrm{supp} \varphi _1\) and such that \(Q_{\Omega _{0\beta }}(\varphi _2) < 0\), we would immediately construct the two dimensional subspace \(W = \{\, a \varphi _1 + b \varphi _2 : a,b \in {\mathbb {R}} \,\} \subset C^1_{0}(\Omega _{0\beta }\cup \Gamma _{\! 0} \cup \Gamma _{\! \beta })\) such that \(Q_{\Omega _{0\beta }}(\varphi ) < 0\) for every \(\varphi \in W {\setminus } \{0\}\), thus contradicting \(m(u) = 1\). The argument extends to the more general case when \(m(u) < +\infty\): see, for instance, [14, Remark 2.7].
The main result in this part of the paper is the extension of Theorem 1.1 to the case of the unbounded domain \(\Omega _{0\beta }\) defined just before. In particular we will prove the following:
Theorem 6.4
Assume \(u \in {\mathcal {Y}}\) is a solution to (1.1) with Morse index \(m(u)\le 1\). Assume further f(r, z, u) is convex with respect to u.
-
1.
If \(m(u) = 0\) then u is constant with respect to the angular variable \(\theta\).
-
2.
If \(m(u) = 1\) then u is either independent of \(\theta\) or strictly monotone with respect to \(\theta\) in \(\Omega _{0\beta }\), in which case u has a nonvanishing derivative \(u_\theta\) and \(\inf _{\psi \in C^1_{0}(\Omega _{0\beta })} Q_{\Omega _{0\beta }}(\psi )= 0\).
The rest of the paper is devoted to prove Theorem 6.4. First, in Sect. 7 we introduce a suitable function space to which the solutions belong and we prove that some sequences of boundary integrals should converge to zero, which is useful to manage the boundary term coming from an integration by parts of the function \(u_\theta\) or the function \(w_\alpha\) over a bounded subset of \(\Omega _{0\beta }\). In Sect. 8 we prove a sign preservation property, in Sect. 9 we extend the splitting lemma and in Sect. 10 we conclude the proof.
We remark that the most difficult point to treat is the extension of Part VI of the proof of Theorem 1.1. Indeed we cannot use the maximum principle in small domains and we need to introduce a suitable torus T, invariant under cylindrical rotations, to overcome this difficulty.
7 A suitable function space
As mentioned before, we consider (possibly unbounded) solutions to (1.1) belonging (in particular) to the set \(E= \{\, v \in C^2(\Omega _{0\beta }) \cap C^1(\Omega _{0\beta } \cup \Gamma _{\! 0} \cup \Gamma _{\! \beta }) \cap C^0({\overline{\Omega }}_{0\beta }) : \nabla v \in L^2(\Omega _{0\beta },{\mathbb {R}}^N) \,\}\). We collect here some properties of the space \(E\) and its subspaces \(E_\alpha\), where for \(\alpha \in (0,\beta ]\), we denote by \(E_\alpha\) the subset of all \(v \in E\) such that \(v = 0\) on \(\Gamma _{\!\alpha }\). Note that the function \(w_\frac{\beta }{2}\) associated to a solution \(u \in E\) obviously belongs to \(E_\frac{\beta }{2}\). For \(\alpha \in (0,\beta ]\) we let \(\Sigma _{\alpha R}\) be the surface \(\Omega _{0\alpha } \cap \partial B_R\), where \(R > r_1\). By Tonelli’s theorem, for every \(v \in E\) and almost every \(R > r_1\) we have
Of course, if \(N = 2\) then \(\Sigma _{\beta R}\) reduces to an arc, \(v \in C^1({\overline{\Sigma }}_{\beta R})\) and the integral above is finite for every \(R > r_1\).
Lemma 7.1
Let \(\alpha \in (0,\beta ]\), \(\Sigma _{\alpha R}=\Omega _{0\alpha } \cap \partial B_R\) and \(\nu\) be the outward normal to the sphere \(\partial B_R\). For every \(v \in E_\alpha\) and almost every \(R > r_1\) the following inequalities hold:
where \(\uplambda _1(r_1,R) > 0\) is given by
and \(\nabla _{\!\tau \,} w\) denotes the intrinsic gradient of w over the surface \(\Sigma _{\alpha R}\).
Proof
By the Cauchy-Schwarz inequality, for almost every \(R > r_1\) we may write
By Poincaré’s inequality, and recalling that \(\nabla v = \nabla _{\!\tau \,} v + \frac{\, \partial v \,}{\, \partial \nu \,} \, \nu\), the first integral in the right-hand side is estimated as follows:
which yields (7.2). Furthermore, we obviously have
and (7.1) follows by multiplying the last two estimates. \(\square\)
Inequalities (7.1)-(7.2) enter in the proof of the following result:
Lemma 7.2
Let the domain \(\Omega _{0\beta }\) and the function spaces \(E\) and \(E_\alpha\) be defined as above.
-
1.
For every \(v \in E_\alpha\) and \(R_0 > r_1\), the iterated integral
$$\begin{aligned} \int _{R_0}^{+\infty } \bigg ( \frac{1}{\, R^2 \,} \int _{ \Sigma _{\alpha R}} v^2 \, d\Sigma \bigg ) dR \end{aligned}$$converges to a finite value, hence it is infinitesimal as \(R_0 \rightarrow +\infty\).
-
2.
For every \(v \in E_\alpha\) there exists a sequence \(R_k \rightarrow +\infty\) such that
$$\begin{aligned} \lim _{k \rightarrow +\infty } \int _{ \Sigma _{\alpha R_k}} v \, \frac{\, \partial v \,}{\partial \nu } \, d\Sigma = 0. \end{aligned}$$(7.4) -
3.
For every \(v \in E\) such that \(v_\theta \in C^1({\overline{\Omega }}_{0\alpha })\) there exists a sequence \(R_k \rightarrow +\infty\) such that the negative part \(v_\theta ^- = \min \{\, 0,v_\theta \,\} \le 0\) satisfies
$$\begin{aligned} \lim _{k \rightarrow +\infty } \int _{ \Sigma _{\alpha R_k}} v_\theta ^- \, \frac{\, \partial v_\theta ^- \,}{\partial \nu } \, d\Sigma = 0. \end{aligned}$$(7.5)
Proof
1. By the scaling property of the eigenvalues we may write
We note in passing that recent advances on spectral asymptotics are found, for instance, in [16] and in the references cited there. From (7.6) it follows that there exists \(\varepsilon _0 > 0\) such that \(\uplambda _1(r_1,R) \ge \varepsilon _0/R^2\) for R large. This and (7.2) imply
Taking into account that the right-hand side is summable by assumption over the interval \((r_1,+\infty )\), Claim 1 follows.
2. If the claim were false, then by (7.1) there would be \(R_0 > r_1\) and \(\varepsilon _0 > 0\) such that for almost every \(R \ge R_0\)
Taking the asymptotics (7.6) into account, for almost every R large enough we may write
Integrating both sides in dR we would get \(\Vert \nabla v \Vert _{L^2(\Omega _{0\alpha })} = +\infty\), which is in contrast with the definition of the function space \(E_\alpha\).
3. Since \(\nabla v \in L^2(\Omega _{0\beta })\), the function
has a finite limit for \(R \rightarrow +\infty\). By differentiation we find
Differentiating once more yields
which may be rewritten as
If the last integral were larger than \(\varepsilon _0 > 0\) for \(R \ge R_0\), then, integrating both sides over the interval \((R_0,R)\), we would get
which implies \(f'(R) \rightarrow +\infty\) as \(R \rightarrow +\infty\). But this is impossible because f(R) converges to a finite limit. A similar contradiction arises if we assume that the integral in (7.5) keeps smaller than \(-\varepsilon _0 < 0\). \(\square\)
We note in passing that (7.4) continues to hold in the special case when \(N = 2\) even though v does not vanish along \(\Gamma _{\!\alpha }\). However, the proof is different:
Proposition 7.3
In the special case when \(N = 2\), for every \(v \in E\) and every \(\alpha \in (0,\beta ]\) there exists a sequence \(R_k \rightarrow +\infty\) such that (7.4) holds.
Proof
By the Cauchy-Schwarz inequality we may still write (7.3), which holds now for every \(R > r_1\) because \(v \in C^1({\overline{\Omega }}_{0\beta } {\setminus } B_R)\). However, the Poincaré inequality fails because of the lack of boundary conditions. Nevertheless, the first integral in the right-hand side is estimated as follows. Fix \(r_0 > r_1\), so that the function \(v(r_0, \theta )\) of the variable \(\theta\) belongs to \(C^1([0,\alpha ])\). By the fundamental theorem of calculus we may write
Recall that the area element in \({\mathbb {R}}^2\) is \(r \, dr \, d\theta\). Therefore, since \(\nabla v \in L^2(\Omega _{0\alpha })\), the last integral converges almost everywhere as \(R \rightarrow +\infty\) to some function \(\psi (\theta ) < +\infty\) which is summable over the interval \((0,\alpha )\). Hence \(v^2(R,\theta ) \le C \, \psi (\theta ) \log R\) for almost every \(\theta\) and for large R, with a convenient constant C. By plugging this estimate into (7.3) we obtain
where we have redefined the constant C. If the claim were false, there would be \(R_0 > r_0\) and \(\varepsilon _0 > 0\) such that for every \(R \ge R_0\)
Integrating both sides over the interval \([R_0,+\infty )\) we would get \(\Vert \nabla v \Vert _{L^2(\Omega _{0\alpha })} = +\infty\), which is in contrast with the definition of the function space \(E\). \(\square\)
Remark 7.4
In general, (7.4) fails for \(v \in E\) and \(N \ge 3\). For instance, we may take \(r_1 > 0\), \(\varepsilon \in (0, \, \frac{N}{2} - 1)\) and
In this example we have \(v \in E\) because \(\varepsilon > 0\). However,
Remark 7.5
A function \(v \in E_\alpha \subset E\) may well be unbounded. To see this, recall that for every \(N \ge 2\) there exists a function \(\varphi \in C^\infty _0(B_1)\) such that \(\Vert \nabla \varphi \Vert _{L^2(B_1)}\) is arbitrarily small and \(\sup |\varphi |\) is arbitrarily large. Then we may take a sequence of centers \(x_k \in \Omega _{0\alpha }\) and a sequence of radii \(r_k > 0\) such that \(|x_k| \rightarrow +\infty\) and the balls \(B_k = B(x_k,r_k) \subset \Omega _{0\alpha }\) are pairwise disjoint. For each k we fix \(\varphi _k \in C^\infty _0(B_k)\) such that \(\Vert \nabla \varphi _k \Vert ^2_{L^2(B_k)} \le 2^{-k}\) and \(\sup |\varphi _k| \ge k\). The series
trivially converges in \(E_\alpha\) because for every x it has at most one nonzero term, and it is apparent that v is unbounded and satisfies
Remark 7.6
If \(N=2\) there exist radial, unbounded functions in the space \(E\). For instance, we may take \(v(x) = \log \log |x|\) for \(|x|>1\): in this case \(\nabla v = (|x| \, \log |x|)^{-1} \, \frac{x}{|x|}\) and therefore \(\nabla v \in L^2(\Omega _{0\beta })\) provided that \(r_1 > 1\). If, instead, \(N \ge 3\), every radial function \(v \in E\) is bounded. To see this, let us write \(v(x) = f(|x|)\). In the special case when \(r_1 = 0\), the surface integral
equals \(\frac{\beta }{2\pi } \, N \omega _N \, \psi (R)\), where \(\psi (R) = R^{N - 1} \, (f'(R))^2\) and \(N \omega _N = |\partial B_1|\) is the Hausdorff measure of the unit spherical surface in \({\mathbb {R}}^N\). Hence, \(\psi (R)\) must be summable over the interval \((0,+\infty )\) because \(\nabla v \in L^2(\Omega _{0\beta })\). By the Cauchy-Schwarz inequality, for every \(R > 1\) we may write
which shows that the right-hand side keeps bounded as \(R \rightarrow +\infty\). In the general case when \(r_1 \ge 0\) the integral I(R) is asymptotic to \(\psi (R)\), and the conclusion follows similarly.
8 Sign preservation in unbounded domains
In this section we prepare two fundamental lemmas which replace Lemma 2.3 in the case where the domain is unbounded. In order to prove the first result, we need to turn the negative part \(v^-\) of a supersolution of the linear equation \(L_u \, v = 0\) into a function with bounded support, thus allowing to use the Cauchy-Schwarz inequality (6.2). Following [14], this is accomplished by a family of cut-off functions \(\xi _R\in C^\infty _0({\mathbb {R}}^N)\), \(R > 0\), such that
Later on we will need a further family of cut-off functions in order to deal with possible singularities at \(d(x) = r_1\), i.e., the case when \(u \not \in W^{2,2}(\Omega _{0\beta } \cap B_R)\), \(R > r_1\). Hence we denote by \(\zeta _\delta (x) \in C^\infty _0({\mathbb {R}}^N)\), \(\delta > 0\), a function depending only on d(x) and such that
Lemma 8.1
(Sign preservation in unbounded domains) Fix \(\alpha \in (0,\beta )\) and let K be a (possibly empty) compact subset of \({\mathbb {R}}^N\). Suppose that the set difference \(D_\alpha = \Omega _{0\alpha } {\setminus } K\) is connected, and let \(v \in E_\alpha\) satisfy \(L_u \, v \ge 0\) in \(D_\alpha\) for some \(u \in L^\infty (\Omega _{0\alpha })\). Define \({\tilde{\Gamma }}_{\! 0} = \partial D_\alpha \cap \Gamma _{\! 0}\), and assume
Assume, further, that \(v \ge 0\) on \(\partial D_\alpha {\setminus } \Gamma _{\! 0}\) together with \(v \ge 0\) or \(\partial v / \partial \nu \ge 0\) on \({\tilde{\Gamma }}_{\! 0}\). If v does not vanish identically in \(D_\alpha\), then either \(v > 0\) in \(D_\alpha\) or \(v < 0\) there.
Proof
Let \(r_K = \max _{x \in K} d(x)\) and define \(R_0 = \max \{\, r_1, r_K \,\}\). By (8.3), for every \(R > R_0\) the bilinear form (6.1) is positive semidefinite in the Cartesian product \(H^1_{\partial D {\setminus } \Gamma _0}(D) \times H^1_{\partial D {\setminus } \Gamma _0}(D)\), where \(D = D_\alpha \cap B_{2R}\), and the Cauchy-Schwarz inequality (6.2) holds. Let us check that the negative part \(v^-(x) = \min \{\ 0, \, v(x) \,\} \le 0\) is a weak solution of
i.e., \({\mathcal {B}}(v^-, \, \psi ) = 0\) for every \(\psi \in C^\infty _0(D_\alpha )\). By making R larger we may achieve that \(\mathrm{supp} \psi \subset B_R\), hence \(\psi \in C^\infty _0(D)\). Letting \(\varphi (x) = \xi _R(x) \, v(x) \in H^1_{\partial D {\setminus } \Gamma _0}(D)\) in (6.2) we obtain
The value of \(Q_{\Omega _{0\alpha }}(\xi _R \, v^-)\) may depend on R: however we claim that it is infinitesimal as \(R \rightarrow +\infty\). Indeed, by differentiation we find
an identity that will be repeatedly used in the sequel, with different choices of \(\varphi\). Taking into account the boundary conditions \(v^- = 0\) on \(\partial D {\setminus } \Gamma _{\! 0}\) and \(v^- \, \frac{\partial v^-}{\partial \nu } \le 0\) on \(\partial D \cap \Gamma _{\! 0}\), multiplication of the inequality \(L_u \, v \ge 0\) by \(\xi _R^2 \, v^-\) and integration over D yields
Letting \(\varphi = v^-\) in (8.6), and using (8.1), this is turned into
where \(\Sigma _{\alpha r} = \Omega _{0\alpha } \cap \partial B_r\). To manage with the last integral, note that
therefore by Claim 1 of Lemma 7.2 the right-hand side of (8.7) is infinitesimal. But then (8.5) implies \({\mathcal {B}}(v^-, \psi ) = 0\). Since \(\psi\) is arbitrary, \(v^-\) is a weak solution of equation (8.4), as claimed. Now the unique continuation property implies that either \(v^- \equiv 0\) or \(v^- < 0\) in \(D_\alpha\). In the last case we obviously have \(v < 0\) in \(D_\alpha\). If, instead, \(v^- \equiv 0\) in \(D_\alpha\), then \(v \ge 0\), and since \(L_u \, v \ge 0\) in \(D_\alpha\), the strong maximum principle implies that either \(v \equiv 0\) or \(v > 0\) in the connected set \(D_\alpha\). \(\square\)
Remark 8.2
If we restrict to the case when \(v \ge 0\) on \(\Gamma _{\! 0}\), we may replace assumption (8.3) with the weaker requirement
In the sequel we will need to apply a similar argument to \(u_\theta\) and \(u^-_\theta\), using a double truncation. Therefore we prepare:
Proposition 8.3
Assume \(u \in {\mathcal {Y}}\) is a solution to (1.1), and define \(u^-_\theta (x) = \min \{\, u_\theta (x), \, 0 \,\}\). Let \(\xi _R, \zeta _\delta\) be the cut-off functions in (8.1)-(8.2). For every \(\varepsilon > 0\) there exist \(\delta > 0\) and \(R > r_1\) such that \(Q_{\Omega _{0\beta }}(\zeta _\delta \, \xi _R \, u_\theta ) \in [0,\varepsilon )\). If, furthermore, \(u^-_\theta = 0\) on \(\Gamma _{\! \frac{\beta }{2}}\) then we may also achieve \(Q_{\Omega _{0\frac{\beta }{2}}}(\zeta _\delta \, \xi _R \, u^-_\theta ) \in [0,\varepsilon )\).
Proof
First of all, we obtain
by taking R large. Indeed, we have
where \(\Sigma _{\beta r}= \Omega _{0\beta } \cap \partial B_r\). Since \(|u_\theta (x)| \le d(x) \, |\nabla u(x)| \le r \, |\nabla u|\) on \(\partial B_r\), we may write
where the right-hand side is infinitesimal as \(R \rightarrow +\infty\). Hence we may choose R so that (8.8) holds. Next we observe that the function \(u_\theta\), which is uniformly continuous in the compact set \({\overline{\Omega }}_{0\beta } \cap {\overline{B}}_{2R}\), converges uniformly to zero when \(d(x) \rightarrow r_1\). Keeping this in mind, and letting \(D_{\delta R} = \{\, x \in \Omega _{0\beta } : \zeta _\delta (x) \, \xi _R(x) > 0 \,\}\), we may check that
To see this, choose \(\mu > 0\) and let \(\delta\) be so small that \(u_\theta ^2 < \mu\) in the set \(S_{\delta R} = \{\, x \in \Omega _{0\beta } \cap B_{2R} : d(x) < r_1 + \delta \,\}\). Since \(\nabla (\zeta _\delta \, \xi _R) = \zeta _\delta \, \nabla \xi _R + \xi _R \, \nabla \zeta _\delta\), we have
and the difference of the two preceding integrals is estimated as follows:
Since R is kept fixed, we have \(|S_{\delta R}| \le C \, \delta ^2\) for some constant C, hence
Finally, since \(\mu\) is arbitrary, (8.9) follows. Recalling (8.8), we conclude that
for convenient R and \(\delta\). Now, multiplying the equation \(L_u \, u_\theta = 0\) (see Proposition 3.1) by \((\zeta _\delta \, \xi _R)^2 \, u_\theta\) and integrating by parts over \(\Omega _{0\beta } \cap B_{2R}\) we obtain
Replacing \(\xi _R\) with \(\zeta _\delta \, \xi _R\) in (8.6) and letting \(\varphi = u_\theta\) (see also (8.7)) this is turned into
Hence \(Q_{\Omega _{0\beta }}(\zeta _\delta \, \xi _R \, u_\theta ) \in [0,\varepsilon )\) for a convenient choice of \(\delta\). To prove the second claim it suffices to multiply the equation \(L_u \, u_\theta = 0\) by \((\zeta _\delta \, \xi _R)^2 \, u_\theta ^-\) and integrate by parts over \(\Omega _{0\frac{\beta }{2}} \cap B_{2R}\). Since \(u^-_\theta = 0\) on \(\Gamma _{\! \frac{\beta }{2}}\) by assumption, we obtain
and therefore (see (8.11))
where \(D'_{\delta R} = \{\, x \in \Omega _{0\frac{\beta }{2}} : \zeta _\delta (x) \, \xi _R(x) > 0 \,\}\). The last integral is made arbitrarily small by a convenient choice of \(\delta\) and R (see (8.10)), and the proof is complete. \(\square\)
9 Preliminaries in the unbounded half-sector
The counterpart of Corollary 2.2 in an unbounded domain is the following
Lemma 9.1
(Splitting lemma for unbounded domains) Assume \(u \in {\mathcal {Y}}\) is a solution to (1.1) with Morse index \(m(u)\le 1\), and let \(\alpha \in (0,\beta )\). Then either
or
Proof
If the thesis is not true there exist two functions \(\varphi _{0\alpha },\varphi _{\alpha \beta }\) supported in \(\Omega _{0\alpha }\cup \Gamma _{\!0}\) and \(\Omega _{\alpha \beta }\cup \Gamma _{\!\beta }\), respectively, such that \(Q_{\Omega _{0\alpha }}(\varphi _{0\alpha }), Q_{\Omega _{\alpha \beta }}(\varphi _{\alpha \beta })<0\). Since they both vanish in a neighborhood of \(\Gamma _{\!\alpha }\) we may extend them to the whole of \(\Omega _{0\beta }\) as in Lemma 2.1. The extended functions belong to \(C^1_{0}(\Omega _{0\beta }\cup \Gamma _{\! 0} \cup \Gamma _{\! \beta })\) and are linearly independent. Then, as in the proof of Lemma 2.1 it is easy to prove that \(Q_{\Omega _{0\beta }}(\phi )<0\) for every \(\phi = a \, \varphi _{0\alpha } + b \, \varphi _{\alpha \beta }\) with \((a,b)\ne (0,0)\) contradicting the fact that the Morse index of u in \(\Omega _{0\beta }\) is at most one. \(\square\)
Next we state a sign preservation property for \(w_\frac{\beta }{2}\) which extends Corollary 2.4 to unbounded domains.
Lemma 9.2
(Sign preservation in the unbounded half-sector) Assume \(u \in {\mathcal {Y}}\) is a solution to (1.1) with Morse index \(m(u)\le 1\). Assume further f(r, z, u) is convex with respect to u. If \(w_{\frac{\beta }{2}}\) does not vanish identically in \(\Omega _{0\frac{\beta }{2}}\), then either \(w_{\frac{\beta }{2}} > 0\) in \(\Omega _{0\frac{\beta }{2}}\) or \(w_{\frac{\beta }{2}} < 0\) there.
Proof
Letting \(\alpha = \frac{\beta }{2}\) in Lemma 9.1, we may suppose
Thus, assumption (8.3) is satisfied, and the claim follows from Lemma 8.1 with \(K = \emptyset\), since, by the convexity of f, \(w_{\frac{\beta }{2}}\) satisfies \(L_u w_{\frac{\beta }{2}}\ge 0\). \(\square\)
We can now prove the following counterpart of Lemma 3.2 for unbounded domains:
Lemma 9.3
Assume \(u \in {\mathcal {Y}}\) is a solution to (1.1) with Morse index \(m(u)\le 1\). If \(w_\frac{\beta }{2}\equiv 0\) in \(\Omega _{0\beta }\) then u is constant with respect to \(\theta\).
Proof
Since \(w_\frac{\beta }{2}\equiv 0\) in \(\Omega _{0\beta }\), the solution u is symmetric about \(\Gamma _{\!\frac{\beta }{2}}\), as well as \(f'(d(x),z,u)\), while the derivative \(u_\theta\) is odd with respect to \(\Gamma _{\!\frac{\beta }{2}}\) in the sense that \(u_\theta (x) = -u_\theta (\sigma _{\frac{\beta }{2}}(x))\) in \(\Omega _{0\beta }\). We already know that \(u_\theta\) satisfies the equation in (3.1) and vanishes on \(\Gamma _{\! 0} \cup \Gamma _{\! \beta }\). Our goal is to prove that \(\partial u_\theta / \partial \nu\) also vanishes there.
Part I. We start by showing that \(Q_{\Omega _{0\beta }}(\varphi _1) \ge 0\) for every \(\varphi _1\) in the vector space \(C^{1,\mathrm odd}_{0}( \Omega _{0\beta } \cup \Gamma _{\! 0} \cup \Gamma _{\! \beta })\) of the odd elements of \(C^1_{0}(\Omega _{0\beta }\cup \Gamma _{\! 0} \cup \Gamma _{\! \beta })\). In fact, if \(\varphi _1\) vanishes identically the claim is obvious. Otherwise we consider the absolute value \(\varphi _2(x) = |\varphi _1(x)|\), which is symmetric about \(\Gamma _{\!\frac{\beta }{2}}\) and therefore
Moreover, we have \(\nabla \varphi _2 = \nabla \varphi _1\) in the set \(\Omega ^+_{0\beta } = \{\, x \in \Omega _{0\beta } : \varphi _1(x) > 0 \,\}\), and \(\nabla \varphi _2 = -\nabla \varphi _1\) in \(\Omega ^-_{0\beta } = \{\, x \in \Omega _{0\beta } : \varphi _1(x) < 0 \,\}\). Since \(\Omega ^-_{0\beta } = \sigma _{\frac{\beta }{2}}(\Omega ^+_{0\beta })\) by the oddity of \(\varphi _1\), we find
Thus, for every \((a,b) \ne (0,0)\) we may compute
Since \(\varphi _1,\varphi _2\) are linearly independent, and since \(m(u) \le 1\) by assumption, we must have \(Q_{\Omega _{0\beta }}(\varphi _1) \ge 0\), as claimed.
Part II. We claim that \({\mathcal {B}}(u_\theta ,\psi ) = 0\) for every \(\psi \in C^{1,\mathrm odd}_{0}( \Omega _{0\beta }\cup \Gamma _{\! 0} \cup \Gamma _{\! \beta })\), which is not obvious because \(\psi\) is allowed to take nonzero values on \(\Gamma _{\! 0} \cup \Gamma _{\! \beta }\). However, by Part I the bilinear form \({\mathcal {B}}\) is positive semidefinite in \(C^{1,\mathrm odd}_{0}( \Omega _{0\beta }\cup \Gamma _{\! 0} \cup \Gamma _{\! \beta }) \times C^{1,\mathrm odd}_{0}( \Omega _{0\beta }\cup \Gamma _{\! 0} \cup \Gamma _{\! \beta })\) and therefore the Cauchy-Schwarz inequality (6.2) holds. Without loss of generality we may assume that the cut-off functions \(\xi _R(x)\) are symmetric with respect to \(\Gamma _{\!\frac{\beta }{2}}\): thus, \(\xi _R(x) \, u_\theta (x)\) is odd and has a compact support. Furthermore, since \(f'(r,z,u)\) is locally Hölder continuous and \(u \in {\mathcal {Y}}\), \(u_\theta\) is in \(C^1(\Omega _{0\beta } \cup \Gamma _{\! 0} \cup \Gamma _{\! \beta }) \cap C^0({\overline{\Omega }}_{0\beta }{\setminus } \Upsilon )\): however, its gradient may fail to belong to \(L^2(\Omega _{0\beta } \cap B_{2R})\), due to the possible singularity at \(d(x) = r_1\). To overcome this difficulty, we use the cut-off functions \(\zeta _\delta (x)\) introduced in (8.2). The doubly truncated function \(\zeta _\delta \, \xi _R \, u_\theta\) is still odd, has a compact support, and belongs to \(C^{1,\mathrm odd}_{0}( \Omega _{0\beta }\cup \Gamma _{\! 0} \cup \Gamma _{\! \beta })\). Thus, we may write
where \(\psi \in C^{1,\mathrm odd}_{0}( \Omega _{0\beta }\cup \Gamma _{\! 0} \cup \Gamma _{\! \beta })\). Keeping \(\psi\) fixed, we take \(\delta\) small and R large to achieve \(\zeta _\delta \, \xi _R = 1\) on the set \(\mathrm{supp} \psi\). Consequently, the preceding inequalities reduce to
By Proposition 8.3, the term \(Q_{\Omega _{0\beta }}(\zeta _\delta \, \xi _R \, u_\theta )\) in the right-hand side becomes arbitrarily small by a convenient choice of R and \(\delta\), which implies \({\mathcal {B}}(u_\theta , \, \psi ) = 0\).
Part III. Let us verify that \(u_\theta\) satisfies the Neumann condition on \(\Gamma _{\! 0}\). Recall that \({\mathcal {B}}(u_\theta , \, \psi ) = 0\) by Part II, and take \(R > r_1\) such that \(\mathrm{supp} \psi \subset B_R\). Multiplying the equation \(L_u \, u_\theta = 0\) by \(\psi \in C^{1,\mathrm odd}_{0}( \Omega _{0\beta }\cup \Gamma _{\! 0} \cup \Gamma _{\! \beta })\) and integrating by parts over \(\Omega _{0\beta } \cap B_R\) we obtain
where the equality holds because \(\psi\) vanishes in a neighborhood of \(\gamma _{0\beta }\) as well as on \(\Omega _{0\beta } \cap \partial B_R\) and \(\psi \, \frac{\, \partial u_\theta \,}{\partial \nu }\) is symmetric with respect to \(\Gamma _{\!\frac{\beta }{2}}\). Since \(\psi\) can take any value on \(\Gamma _{\! 0}\) then \(\frac{\, \partial u_\theta \,}{\partial \nu }=0\) on \(\Gamma _0\) as claimed.
Conclusion. The derivative \(u_\theta\) can be extended to zero in the domain \(\Omega _{-\frac{\beta }{2},0}\) (cf. (3.3)), thus obtaining a \(C^1\) weak solution of \(L_u \, u_\theta = 0\) in \(\Omega _{-\frac{\beta }{2},\frac{\beta }{2}}\). By the unique continuation property, \(u_\theta\) must vanish identically, and therefore u is constant with respect to \(\theta\). \(\square\)
When the domain \(\Omega _{0\beta }\) is unbounded, in place of Lemma 3.3 we have:
Lemma 9.4
Assume \(u \in {\mathcal {Y}}\) is a solution to (1.1) with Morse index \(m(u)\le 1\). Assume further that (9.2) holds. If \(w_{\frac{\beta }{2}}(x)>0\) in \(\Omega _{0\frac{\beta }{2}}\) then
Proof
Let us check that the negative part \(u_\theta ^- = \min \{\, 0,u_\theta \,\} \le 0\) is a weak solution of \(L_u \, u_\theta ^-=0\) in \(\Omega _{0\frac{\beta }{2}}\), i.e., \({\mathcal {B}}(u_\theta ^-,\psi ) = 0\) for all \(\psi \in C^\infty _0(\Omega _{0\frac{\beta }{2}})\). Assumption (9.2) implies that the bilinear form \({\mathcal {B}}\) is positive semidefinite on \(C^1_{0}(\Omega _{0\frac{\beta }{2}}\cup \Gamma _{\! 0}) \times C^1_{0}(\Omega _{0\frac{\beta }{2}}\cup \Gamma _{\! 0})\). Hence we pick \(\psi \in C^\infty _0(\Omega _{0\frac{\beta }{2}})\) and consequently \(R > r_1\) such that \(\mathrm{supp} \psi \subset B_R\), and also \(\delta > 0\) such that
As in the proof of Lemma 3.3, the assumption \(w_\frac{\beta }{2} > 0\) in \(\Omega _{0\frac{\beta }{2}}\) implies \(u_\theta > 0\) on \(\Gamma _{\!\frac{\beta }{2}}\) (see (3.5)), hence \(u_\theta ^- = 0\) on \(\gamma _{0\frac{\beta }{2}} \cup \Gamma _{\!0} \cup \Gamma _{\!\frac{\beta }{2}}\). Furthermore, the doubly truncated function \(\zeta _\delta \, \xi _R \, u_\theta ^-\) has a square-summable gradient and therefore belongs to \(H^1_0(D)\), where \(D = \Omega _{0\frac{\beta }{2}} \cap B_{2R}\). The Cauchy-Schwarz inequality (6.2) yields
By Proposition 8.3, the term \(Q_{\Omega _{0\frac{\beta }{2}}}(\zeta _\delta \, \xi _R \, u_\theta ^-)\) becomes arbitrarily small by a convenient choice of R and \(\delta\), which implies \({\mathcal {B}}(u_\theta ^-,\psi ) = 0\) and therefore \(u_\theta ^-\) is a weak solution of \(L_u \, u_\theta ^- = 0\) in \(\Omega _{0\frac{\beta }{2}}\), as claimed. By the unique continuation property, this implies that either \(u_\theta ^-\equiv 0\) or \(u_\theta ^-<0\) in \(\Omega _{0\frac{\beta }{2}}\). But since \(u_\theta >0\) on \(\Gamma _{\! \frac{\beta }{2}}\), we must have \(u_\theta ^-\equiv 0\) and therefore \(u_\theta \ge 0\) in \(\Omega _{0\frac{\beta }{2}}\). The unique continuation property of \(u_\theta\) proves (9.3). \(\square\)
10 Proof of Theorem 6.4
Proof of Theorem 6.4
If \(w_\frac{\beta }{2} \equiv 0\), then u is independent of \(\theta\) by Lemma 9.3. If, instead, \(w_\frac{\beta }{2}\not \equiv 0\), then Lemma 9.2 implies that either \(w_\frac{\beta }{2}>0\) in \(\Omega _{0\frac{\beta }{2}}\) or \(w_\frac{\beta }{2}>0\) in \(\Omega _{\frac{\beta }{2}\beta }\). By Lemma 9.1 we may assume that (9.1) holds and \(w_\frac{\beta }{2}>0\) in \(\Omega _{0\frac{\beta }{2}}\). We then define the set \(A'\) as in the proof of Theorem 1.1 and, arguing as in Part I with (9.3) instead of (3.4), we get that \(A'\) contains \(\frac{\beta }{2}\). The fact that \(A'\) is a closed subinterval of \(\left[ \frac{\beta }{2},\beta \right]\) follows as in Part II. Next, exactly as in Part III, the Hopf boundary point lemma implies that \(u_\theta >0\) in \(\Omega _{0,{\tilde{\alpha }}}\) if \(A'=\left[ \frac{\beta }{2},{\tilde{\alpha }}\right]\), \({\tilde{\alpha }} < \beta\). In such a case we can repeat exactly Part IV getting that
If the Morse index m(u) is 1, there must be \(\varphi _1 \in C^1_{0}(\Omega _{0\beta }\cup \Gamma _{\! 0} \cup \Gamma _{\! \beta })\) such that \(Q_{\Omega _{0\beta }}(\varphi _1) < 0\) and we may take a torus T containing \(\mathrm{supp} \varphi _1\). By a torus we mean an open subset \(T \subset {\mathbb {R}}^N\), invariant under cylindrical rotations, whose intersection with the hyperplane \(x_1 = 0\) is an \(N-1\) dimensional ball lying in the half-plane \(x_1 = 0\), \(x_2 > r_1 + \varepsilon\) for some \(\varepsilon > 0\). The last condition implies that \(d(x) \ge r_1 + \varepsilon > r_1\) for all \(x \in {\overline{T}}\). In the case where \(m(u) = 0\) we take any torus T as defined above. Note that when \(N = 2\) the tori are just annuli. Since \(w_{{\tilde{\alpha }}}\) and \(u_\theta\) are positive in \(\Omega _{0{\tilde{\alpha }}}\), we obviously have
Part V. By the same argument used to derive (3.6) and (3.7) we see that \(w_\alpha > 0\) on \(\Gamma _{\!0}\) for every \(\alpha \in (0,\beta )\).
Part VI. We claim that \(w_\alpha\) keeps positive in \(G_\alpha = (\Omega _{0\alpha } \cup {\Gamma _{\!0}}) \cap {\overline{T}}\) for every \(\alpha > {\tilde{\alpha }}\) such that the difference \(\alpha - {\tilde{\alpha }}\) is sufficiently small. This can be proved by contradiction: suppose that there exists a sequence \(\alpha _n \searrow {\tilde{\alpha }}\) such that \(w_{\alpha _n}\) becomes negative somewhere in \(G_{\alpha _n}\), and let \(x_n \in {\overline{\Omega }}_{0\alpha _n} \cap {\overline{T}}\) be a point where \(w_{\alpha _n}\) takes its negative minimum. Of course, \(x_n \not \in \Gamma _{\!\alpha _n}\) because \(w_{\alpha _n} = 0\) there, and \(x_n \not \in \Gamma _{\!0}\) by Part V. By compactness there exists a subsequence, still denoted by \((x_n)\), converging to some \(x_0 \in {\overline{\Omega }}_{0\alpha } \cap {\overline{T}}\) with \(w_{{\tilde{\alpha }}}(x_0) = 0\). Since \(w_{{\tilde{\alpha }}} > 0\) on \(\Gamma _{\!0}\) by Part V, and by (10.1), we must have
Furthermore, the gradient \(\nabla w_{\alpha _n}\) vanishes at \(x_n\) in the case where \(x_n \in \Omega _{0\alpha _n} \cap T\), and is directed towards the interior of T if \(x_n \in \Omega _{0\alpha _n} \cap \partial T\). Hence, we may write
Passing to the limit, this property should be inherited by \(\partial w_{{\tilde{\alpha }}} / \partial \theta\) at \(x_0\). However, by (10.2) and by the Hopf boundary point lemma we have \(\partial w_{{\tilde{\alpha }}} / \partial \theta < 0\) at \(x_0\), a contradiction. Hence, \(w_\alpha\) must be positive in \(G_\alpha\) for every \(\alpha > {\tilde{\alpha }}\) such that the difference \(\alpha - {\tilde{\alpha }}\) is sufficiently small, as claimed.
Part VII. For every \(\alpha\) as above, \(w_\alpha\) is in fact positive in all of \(\Omega _{0\alpha }\). To see this, we let \(K = {\overline{T}}\) in Lemma 8.1, hence \(D_\alpha = \Omega _{0\alpha } {\setminus } {\overline{T}}\). The quadratic form \(Q_{\Omega _{0\alpha }}\) is positive semidefinite in \(C^1_{0}(\Omega _{0\alpha } \cup \Gamma _{\! 0} \cup \Gamma _{\! \alpha } {\setminus } {\overline{T}})\) by Remark 6.3, and keeps positive semidefinite in \(H^1_{\gamma _{0\alpha } \cup \partial T \cup \partial B_R}(D_\alpha \cap B_R)\) for \(R > \max _{x \in {\overline{T}}} d(x)\). Taking into account the boundary conditions \(w_\alpha > 0\) on \((\Omega _{0\alpha } \cap \partial T) \cup \Gamma _{\!0}\) and \(w_\alpha = 0\) on \(\gamma _{0\alpha } \cup \Gamma _{\!\alpha }\), by Lemma 8.1 it follows that \(w_\alpha\) is positive in any connected component of \(D_\alpha\) and consequently in \(\Omega _{0\alpha }\).
Conclusion. We have thus seen that if we suppose \({\tilde{\alpha }} < \beta\) we obtain the positivity of \(w_\alpha\) in \(\Omega _{0\alpha }\) for every \(\alpha > {\tilde{\alpha }}\) such that the difference \(\alpha - {\tilde{\alpha }}\) is sufficiently small, contradicting the definition of \({\tilde{\alpha }}\). Hence, under the assumption that \(w_\frac{\beta }{2} > 0\) in \(~\Omega _{0\frac{\beta }{2}}\), we must have \({\tilde{\alpha }} = \beta\) and therefore the solution u is strictly increasing with respect to \(\theta\) in \(\Omega _{0\beta }\). In this case, by Part III we also have \(u_\theta > 0\) in \(\Omega _{0\beta }\) and we can apply Lemma 2.1 in [14] in \(\Omega _{0\beta }\) getting that \(\inf Q_{\Omega _{0\beta }} (\psi )\ge 0\) when \(\psi \in C^1_0(\Omega _{0\beta })\). By Proposition 8.3, the term \(Q_{\Omega _{0\beta }}(\zeta _\delta \, \xi _R \, u_\theta )\) becomes arbitrarily small by a convenient choice of R and \(\delta\) showing that \(\inf _{\psi \in C^1_0(\Omega _{0\beta })} Q_{\Omega _{0\beta }} (\psi )= 0\). In summary, we have shown that if \(m(u) \le 1\) then either \(u_\theta\) vanishes identically in \(\Omega _{0\beta }\) or it keeps its sign there. Now, in order to prove Claim 1 of the statement, it suffices to check that if \(m(u) = 0\) then \(u_\theta\) vanishes identically. To this purpose, take \(\psi \in C^1_{0}( \Omega _{0\beta }\cup \Gamma _{\! 0} \cup \Gamma _{\! \beta })\) and consider the doubly truncated function \(\zeta _\delta \, \xi _R \, u_\theta\) with R such that \(\mathrm{supp} \psi \subset B_R\) and \(\delta\) satisfying (9.4). Since \(Q_{\Omega _{0\beta }}\) is positive semidefinite by assumption, and since \(\zeta _\delta \, \xi _R \, u_\theta\) belongs to \(H^1_{\gamma _{0\beta } \cup \partial B_{2R}}(D)\), where \(D = \Omega _{0\beta } \cap B_{2R}\), the Cauchy-Schwarz inequality yields
By Proposition 8.3, the term \(Q_{\Omega _{0\beta }}(\zeta _\delta \, \xi _R \, u_\theta )\) becomes arbitrarily small by a convenient choice of R and \(\delta\). On the other side, multiplying the equation \(L_u \, u_\theta = 0\) by \(\psi\) and integrating by parts we obtain
hence the integral must vanish. Since \(\psi\) can take any value on \(\Gamma _{\!0} \cup \Gamma _{\!\beta }\), it follows that \(\partial u_\theta / \partial \nu = 0\) there, whence \(u_\theta\) can be extended by zero to \(\Omega _{-\beta ,0}\) as in (3.3), thus obtaining a \(C^1\) weak solution \({\tilde{u}}_\theta\) of \(L_u \, {\tilde{u}}_\theta = 0\) in \(\Omega _{-\beta ,\beta }\). Since \({\tilde{u}}_\theta\) vanishes identically in \(\Omega _{-\beta ,0}\), by the unique continuation property we must have \(u_\theta = 0\) in \(\Omega _{0\beta }\), hence u is independent of \(\theta\), and the proof is complete. \(\square\)
References
Adolfsson, V., Jerison, D.: \(L^p\)-integrability of the second order derivatives for the Neumann problem in convex domains. Indiana Univ. Math. J. 43, 1123–1138 (1994)
Bahri, A., Lions, P.L.: Morse indices of some min-max critical points. I, Application to multiplicity results. Comm. Pure Appl. Math 41, 1027–1037 (1988)
Bartsch, T., Weth, T., Willem, M.: Partial symmetry of least energy nodal solutions to some variational problems. J. Anal. Math. 96, 1–18 (2005)
Berestycki, H., Lachand-Robert, T.: Some properties of the monotone rearrangement with applications to elliptic equations in cylinders. Math. Nachr. 266, 3–19 (2004)
Berestycki, H., Pacella, F.: Symmetry properties for positive solutions of elliptic equations with mixed boundary conditions. J. Funct. Anal. 87(1), 177–211 (1989)
Brock, F.: Symmetry and monotonicity of solutions to some variational problems in cylinders and annuli. Electron. J. Differ. Equ. 108, 20 (2003)
Courant, R., Hilbert, D.: Methods of Mathematical Physics, vol. I. Interscience Publishers (1953)
Dipierro, S., Poggesi, G., Valdinoci, E.: Radial symmetry of solutions to anisotropic and weighted diffusion equations with discontinuous nonlinearities. Calc. Var. Part. Differ. Equ. 61, 31 (2022)
Damascelli, L., Pacella, F.: Morse index of solutions of nonlinear elliptic equations. De Gruyter (2019)
Damascelli, L., Pacella, F.: Morse index and symmetry for elliptic problems with nonlinear mixed boundary conditions. Proc. Roy. Soc. Edinb. Sect. A 149, 305–324 (2019)
Elbert, A.: Some recent results on the zeros of Bessel functions and orthogonal polynomials. J. Comput. Appl. Math. 133, 65–83 (2001)
Gladiali, F.: Separation of branches of \(O(N-1)\)-invariant solutions for a semilinear elliptic equation. J. Math. Anal. Appl. 453, 159–173 (2017)
Gladiali, F.: A monotonicity result under symmetry and Morse index constraints in the plane. Proc. R. Soc. Edinb. Sect. A Math. 151, 885–915 (2021)
Gladiali, F., Pacella, F., Weth, T.: Symmetry and nonexistence of low Morse index solutions in unbounded domains. J. Math. Pures Appl. 93, 536–558 (2010)
Helffer, B.: Spectral Theory and Its Applications. Cambridge University Press (2013)
Jimbo, S.: Eigenvalues of the Laplacian in a domain with a thin tubular hole. J. Elliptic Parabol. Equ. 1, 137–174 (2015)
Kesavan, S., Pacella, F.: Symmetry of positive solutions of a quasilinear elliptic equation via isoperimetric inequalities. Appl. Anal. 54, 27–37 (1994)
Maz’ya, V.: On the boundedness of first derivatives for solutions to the Neumann–Laplace problem in a convex domain. J. Math. Sci. (N.Y.) 159, 104–112 (2009)
Pacella, F.: Symmetry results for solutions of semilinear elliptic equations with convex nonlinearities. J. Funct. Anal. 192, 271–282 (2002)
Pacella, F., Tralli, G.: Overdetermined problems and constant mean curvature surfaces in cones Rev. Mat. Iberoam. 36, 841–867 (2020)
Pacella, F., Weth, T.: Symmetry of solutions to semilinear elliptic equations via Morse index. Proc. Am. Math. Soc. 135, 1753–1762 (2007)
Simon, B.: Schrödinger semigroups. Bull. Am. Math. Soc. New Ser. 7, 447–526 (1982)
Smets, D., Su, J., Willem, M.: Non-radial ground states for the Hénon equation. Commun. Contemp. Math. 4, 467–480 (2002)
Acknowledgements
The authors are members of the Gruppo Nazionale per l’Analisi Matematica, la Probabilità e le loro Applicazioni (GNAMPA) of the Istituto Nazionale di Alta Matematica (INdAM). F. Gladiali is supported by Uniss, fondo di ateneo per la ricerca 2020 and by Fondazione di Sardegna, annualità 2017. A. Greco is partially supported by the research project Evolutive and stationary Partial Differential Equations with a focus on bio-mathematics, funded by Fondazione di Sardegna, annualità 2019. We are grateful to the referee, whose careful review helped us to improve the manuscript. This paper is dedicated to the city of Alghero (Sardinia, Italy) where the authors repeatedly met to carry their work on.
Funding
Open access funding provided by Università degli Studi di Sassari within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gladiali, F., Greco, A. Symmetry and monotonicity results for solutions of semilinear PDEs in sector-like domains. Annali di Matematica 202, 431–461 (2023). https://doi.org/10.1007/s10231-022-01247-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10231-022-01247-1