Eigenvalue problems for slice functions

Abstract

This paper addresses particular eigenvalue problems within the context of two quaternionic function theories. More precisely, we study two concrete classes of quaternionic eigenvalue problems, the first one for the slice derivative operator in the class of quaternionic slice-regular functions and the second one for the Cauchy–Riemann–Fueter operator in the class of axially monogenic functions. The two problems are related to each other by the four-dimensional Laplace operator and Fueter’s Theorem. As an application of a particular case of second order eigenvalue problems, we obtain a representation of axially monogenic solutions for time-harmonic Helmholtz and stationary Klein–Gordon equations.

1 Introduction

Complex function theory represents a powerful toolkit to study eigenvalue problems related to important differential operators arising in harmonic analysis and mathematical physics in two dimensions. Therefore, a strong motivation in mathematical analysis consists in developing higher dimensional analogues in order to tackle similarly corresponding spatial problems. The smallest division algebra that encompasses the three-dimensional space $\mathbb {R}^3$ is the four-dimensional Hamiltonian skew field $\mathbb {H}$ which is not commutative anymore but still associative. It is the first algebra created beyond the complex numbers by applying the well-known Cayley-Dickson duplication process. The concept of holomorphic functions however can be generalized in a number of rather different ways to higher dimensional algebras, even in the simplest context of $\mathbb {H}$. Following the Riemann approach one can consider quaternion-valued functions f that are annihilated either from the left or from the right by the linear Cauchy-Riemann-Fueter operator ${\overline{\partial }}:= \frac{1}{2}\Big (\frac{\partial }{\partial x_0} + i \frac{\partial }{\partial x_1} + j \frac{\partial }{\partial x_2} + k \frac{\partial }{\partial x_3} \Big )$. Here, i, j, k are the quaternionic imaginary units, satisfying $i^2=j^2=k^2=-1$ and $ij=k$, $jk=i$, $ki=j$ as well as $ji=-k$, $kj=-i$, $ik=-j$. Functions in the kernel of this operator are nowadays often called left (resp. right) monogenic functions or also sometimes left (right) Fueter regular functions. They have been studied by a constantly growing community for more than a century. As a classical reference, addressing even more generally the n-dimensional setting, we recommend for example [5]. The function theory presented there is often called Clifford analysis; quaternionic analysis actually is represented specifically in the 4-dimensional setting. The Cauchy-Riemann-Fueter operator is nothing else than the Euclidean Dirac operator in $\mathbb {R}^4$ associated to the Euclidean flat metric and is a first order square root of the Laplacian $\Delta _4$.

An alternative function theory, which actually is even more closely related to classical complex-analytic functions, is the theory of quaternionic slice-regular functions which was basically introduced in 2006-2007 by Gentili and Struppa [12, 13]. This function theory exploits a particular slice-structure of $\mathbb {H}$ which is explained together with its most important definitions and relevant function classes of the so-called slice functions and slice-regular functions in Section 2 including the basic references.

Now the aim of our paper is to investigate some eigenvalue problems for quaternionic slice functions, with particular emphasis on slice-regular functions and on axially monogenic functions.

The right-linear operator that we first consider is the so-called slice derivative operator $\frac{\partial }{\partial x}$ acting on the classes of slice or slice-regular functions defined in Section 2. We study eigenvalue problems of the form $\frac{\partial f}{\partial x}=f\lambda$ on an axially symmetric domain $\Omega$ of the quaternionic space ${\mathbb {H}}$, with $\lambda \in {\mathbb {H}}$. We show in Proposition 3 that in the class of slice functions, the solutions to this problem can be written as slice products of anti-slice-regular functions and a quaternionic exponential function. Slice-regular solutions are obtained when the first factor is a slice-constant function on $\Omega$.

Let ${\mathcal {D}}_\lambda$ be the right-linear operator defined by ${\mathcal {D}}_\lambda f=\frac{\partial f}{\partial x}-f\lambda$. In Propositions 6, 8 and 18 we study the associated non-homogeneous eigenvalue problem ${\mathcal {D}}_\lambda {f}=h$ for a polynomial right-hand side h and for a wide class of entire slice-regular functions. These results in particular permit us to solve (Corollary 11) second-order eigenvalue problems ${\mathcal {D}}_\lambda {\mathcal {D}}_\mu f=0$ for any choice of quaternionic eigenvalues $\lambda ,\mu$. In Corollary 15 we extend this result to the m-th order eigenvalue problem ${\mathcal {D}}_{\lambda _{1}}\cdots {\mathcal {D}}_{\lambda _{m}} f=0$ by means of new generalized exponential functions (see Definition 12) associated with any ordered k-tuple $(\mu _1,\ldots ,\mu _k)\in {\mathbb {H}}^k$.

The second right-linear operator that we consider is the (conjugated) Cauchy-Riemann-Fueter operator $\partial$ acting on the class of quaternionic monogenic (or Fueter-regular) slice functions, i.e., belonging to the kernel of the Cauchy-Riemann-Fueter operator ${\overline{\partial }}$. Using Fueter’s Theorem (see e.g. [7]) as a bridge between the two function theories, we are able to apply the results described above to eigenvalue problems for axially monogenic functions. The crucial fact is the relation $\partial \circ \Delta _4=\Delta _4\circ \frac{\partial }{\partial x}$ on the space of slice-regular functions on $\Omega$, where $\Delta _4$ is the Laplacian of ${\mathbb {R}}^4\simeq {\mathbb {H}}$. Applying the operator $\Delta _4$ to the slice-regular solutions obtained above, we obtain in Proposition 28 the general axially monogenic solution of the eigenvalue problem $\partial f=f\lambda$, with $\lambda \in {\mathbb {H}}$, and more generally (Proposition 32) of the m-th order eigenvalue problem ${\mathcal {L}}_{\lambda _{1}}\cdots {\mathcal {L}}_{\lambda _{m}} f=0$, where $\mathcal {L}_{\lambda }$ is defined by $\mathcal {L}_{\lambda }f=\partial f-f\lambda$. We refer the reader at the beginning of Sect. 4 to references on the study of similar eigenvalue problems in quaternionic and Clifford analysis.

The final section is devoted to applications. We relate the solutions to ${\mathcal {L}}_{\lambda _{1}}{\mathcal {L}}_{\lambda _{2}} f = 0$ to axially monogenic solutions of the three-dimensional time-harmonic Helmholtz and stationary massless Klein-Gordon equation on an axially symmetric domain (Proposition 34).

Let $\Delta _3$ denote the Laplacian operator on ${\mathbb {R}}^3\simeq {\text {Im}}({\mathbb {H}})$. Suppose that $\lambda _1 = I \lambda$ and $\lambda _2 = - I \lambda$, where I is a quaternionic imaginary unit and where $\lambda$ is an arbitrary non-zero real number. Then the solutions to $\mathcal {L}_{I\lambda }\mathcal {L}_{-I\lambda } f = 0$ are axially monogenic solutions to the massless stationary Klein-Gordon equation $(\Delta _3 - \lambda ^2) f = 0$ on $\Omega ^{*} := \Omega \cap \mathbb {R}^3$. If we take $\lambda _1 = \lambda$ and $\lambda _2 =- \lambda$ where again $\lambda$ is supposed to be a non-zero real value, then the solutions to $\mathcal {L}_{\lambda }\mathcal {L}_{-\lambda } f = 0$ are axially monogenic solutions to the time-harmonic Helmholtz equation $(\Delta _3 + \lambda ^2) f = 0$ on $\Omega ^{*}$. Finally, we establish an application (Remark 37) to the non-homogeneous equation associated to the Klein-Gordon equation, i.e., the Yukawa equation $(\Delta _3 -\lambda ^2)f=h$, with $\lambda$ real and h axially monogenic. The paper is structured as follows: In Sect. 2 we recall the basic notions of slice function theory on ${\mathbb {H}}$. Then, in Sect. 3, we present the eigenvalue problems for the slice derivative operator on slice and on slice-regular functions. Here we also introduce the generalized exponential functions $E_\Lambda$. This represents another essential novelty of this paper, and we give some examples to illustrate the method of solution. In Sect. 4 we recall Fueter’s Theorem and present some new results about the Laplacian of a slice-regular function. Then we prove the commutativity relation linking $\Delta$, $\partial$ and $\frac{\partial }{\partial x}$ and obtain the axially monogenic solutions to the eigenvalue problems for $\partial$, in terms of the generalized $\Delta$-exponential functions $E^\Delta _{\Lambda }$. Finally, in Sect. 5, we present applications of the results of Sect. 4 to the Helmholtz, Klein-Gordon and Yukawa equations and round off our paper by presenting some explicit examples.

2 Preliminaries

The theory of quaternionic slice-regular functions was introduced in 2006-2007 by Gentili and Struppa [12, 13]. We refer the reader for instance to [6, 8, 14, 16, 18, 19] and also to the references therein for precise definitions and for more results on this class of functions. Slice function theory is based on the “slice” decomposition of the quaternionic space ${\mathbb {H}}$. For each imaginary unit J in the sphere

$$\begin{aligned}{\mathbb {S}}=\{J\in {\mathbb {H}}\ |\ J^2=-1\}=\{x_1i+x_2j+x_3k\in {\mathbb {H}}\ |\ x_1^2+x_2^2+x_3^2=1\},\end{aligned}$$

we denote by $\mathbb {C}_J=\langle 1,J\rangle \simeq \mathbb {C}$ the subalgebra generated by J. Then it holds

$$\begin{aligned}{\mathbb {H}}=\bigcup _{J\in {\mathbb {S}}}\mathbb {C}_J, \quad \text {with}~ \mathbb {C}_J\cap \mathbb {C}_K=\mathbb {R}~ \text {for every}~{ J,K\in {\mathbb {S}},\ J\ne \pm K.}\end{aligned}$$

A (real) differentiable function $f:\Omega \subseteq {\mathbb {H}}\rightarrow {\mathbb {H}}$ is called (left) slice-regular [13] on the open set $\Omega$ if, for each $J\in {\mathbb {S}}$, the restriction $f_{\,|\Omega \cap \mathbb {C}_J}\, : \, \Omega \cap \mathbb {C}_J\rightarrow {\mathbb {H}}$ is holomorphic with respect to the complex structure defined by left multiplication by J.

2.1 Slice functions

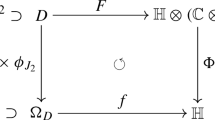
A different approach to slice regularity was introduced in [15, 16], making use of the concept of slice function. These are exactly the quaternionic functions that are compatible with the slice structure of ${\mathbb {H}}$. Given a set $D\subseteq \mathbb {C}$ that is invariant with respect to complex conjugation, a function $F: D\rightarrow {\mathbb {H}}\otimes \mathbb {C}$ that satisfies $F({\overline{z}})=\overline{F(z)}$ for every $z\in D$ is called a stem function on D. Here the conjugation in ${\mathbb {H}}\otimes \mathbb {C}$ is the one induced by complex conjugation of the second factor.

Let D be open and let $\Omega _D=\cup _{J\in {\mathbb {S}}_{\mathbb {H}}}\Phi _J(D)\subset {\mathbb {H}}$, where for any $J\in {\mathbb {S}}$, the map $\Phi _J:\mathbb {C}\rightarrow \mathbb {C}_J$ is the canonical isomorphism defined by $\Phi _J(a+i b):=a+Jb$. Open domains in ${\mathbb {H}}$ of the form $\Omega =\Omega _D$ are called axially symmetric domains. Note that every axially symmetric domain $\Omega$ is either a slice domain if $\Omega \cap \mathbb {R}\ne \emptyset$, or it is a product domain, namely if $\Omega \cap \mathbb {R}=\emptyset$. Moreover, any axially symmetric open set can be represented as a union of a family of domains of these two types.

The stem function $F=F_1+iF_2$ on D (with $F_1$ and $F_2$ ${\mathbb {H}}$-valued functions on D) induces the slice function $f=\mathcal {I}(F):\Omega _D \rightarrow {\mathbb {H}}$ as follows: if $x=\alpha +J\beta =\Phi _J(z)\in \Omega _D\cap \mathbb {C}_J$, then

$$\begin{aligned}f(x):=F_1(z)+JF_2(z).\end{aligned}$$

The tensor product ${\mathbb {H}}\otimes \mathbb {C}$ can be equipped with the complex structure induced by the second factor. The slice function f is then called slice-regular if F is holomorphic. If a domain $\Omega$ in ${\mathbb {H}}$ is axially symmetric and intersects the real axis, then this definition of slice regularity is equivalent to the one proposed by Gentili and Struppa [13]. We will denote by $\mathcal {SR}(\Omega )$ the right quaternionic module of slice-regular functions on $\Omega$. If $f\in \mathcal {SR}({\mathbb {H}})$, then f is called a slice-regular entire function. In particular, every polynomial $f(x)=\sum _{n=0}^dx^na_n\in {\mathbb {H}}[x]$ with right quaternionic coefficients $a_n$, is an entire slice-regular function.

2.2 Operations on slice functions

Let $\Omega =\Omega _D$ be an open axially symmetric domain in ${\mathbb {H}}$. The slice product of two slice functions $f=\mathcal {I}(F)$, $g=\mathcal {I}(G)$ on $\Omega$ is defined by means of the pointwise product of the stem functions F and G:

$$\begin{aligned}f\cdot g=\mathcal {I}(FG).\end{aligned}$$

The function $f=\mathcal {I}(F)$ is called slice-preserving if the ${\mathbb {H}}$-components $F_1$ and $F_2$ of the stem function F are real-valued. This is equivalent to the condition $f(\overline{x})=\overline{f(x)}$ for every $x\in \Omega _D$. If f is slice-preserving, then $f\cdot g$ coincides with the pointwise product of f and g. If f, g are slice-regular on $\Omega$, then also their slice product $f\cdot g$ is slice-regular on $\Omega$. We recall that the slice product has also an interpretation in terms of pointwise quaternionic product:

$$\begin{aligned} (f\cdot g)(x)= {\left\{ \begin{array}{ll}f(x)g(f(x)^{-1}xf(x))&{}\hbox { if } f(x)\ne 0 \hbox {,}\\ 0&{}\text { if } f(x)=0. \end{array}\right. } \end{aligned}$$

For every $f\in \mathcal {S}(\Omega )$, the slice function $f^c=\mathcal {I}(F^c)=\mathcal {I}({\overline{F}}_1+i{\overline{F}}_2)$ is the slice-conjugate of f and $N(f)=f\cdot f^c=f^c\cdot f$ is the normal function of f. If $f\in \mathcal {SR}(\Omega )$, then also $f^c$, N(f) do belong to $\mathcal {SR}(\Omega )$.

Assume that $f\in \mathcal {S}(\Omega )$ is not identically zero on $\Omega$. Then the zero set $V(N(f))=\{x\in \Omega \,|\,N(f)=0\}$ of the normal function does not coincide with the whole set $\Omega$. The slice product permits us to introduce on $\Omega \setminus V(N(f))$ the slice reciprocal $f^{-\bullet }$ of f, as the function $f^{-\bullet }:=N(f)^{-1}\cdot f^c$ (see [18, Prop. 2.4]). Again, if f is slice-regular, then $f^{-\bullet }$ is slice-regular, too.

The slice derivatives $\frac{\partial f}{\partial x},\frac{\partial f\;}{\partial x^c}$ of a slice functions $f=\mathcal {I}(F)$ are defined by means of the Cauchy-Riemann operators applied to the inducing stem function F:

$$\begin{aligned}\frac{\partial f}{\partial x}=\mathcal {I}\left( \frac{\partial F}{\partial z}\right) ,\quad \frac{\partial f\;}{\partial x^c}=\mathcal {I}\left( \frac{\partial F}{\partial {\overline{z}}}\right) .\end{aligned}$$

Note that f is slice-regular on $\Omega$ if and only if $\frac{\partial f\;}{\partial x^c}=0$ and if f is slice-regular on $\Omega$ then also $\frac{\partial f}{\partial x}$ is slice-regular on $\Omega$. Moreover, the slice derivatives satisfy the Leibniz product rule w.r.t. the slice product.

A slice-regular function g is called slice-constant if $\frac{\partial g}{\partial x}=0$ on $\Omega$. We will denote by $\mathcal {SC}(\Omega )$ the right ${\mathbb {H}}$-module of slice-constant functions on $\Omega$. If $\Omega$ is a slice domain, then every $g\in \mathcal {SC}(\Omega )$ is a quaternionic constant. If $\Omega$ is a product domain, then other possibilities arise: for any imaginary unit $I\in {\mathbb {S}}$, a slice-constant function $\mu _I$ on ${\mathbb {H}}\setminus {\mathbb {R}}$ can be defined by setting, such as indicated in [16, Remark 12],

$$\begin{aligned} \mu _I(x):=\frac{1}{2}\left( 1+\frac{{\text {Im}}(x)}{|{\text {Im}}(x)|}I\right) \in \mathcal {SR}({\mathbb {H}}\setminus \mathbb {R}). \end{aligned}$$

(1)

By the representation formula (see [16, Prop. 5] and [2, Prop. 15]), any slice-constant $g\in \mathcal {SC}({\mathbb {H}}\setminus {\mathbb {R}})$ is determined by its values on two arbitrarily chosen half-slices ${\mathbb {C}}_J^+, {\mathbb {C}}_K^+$, with $J\ne K$. If $g_{|{\mathbb {C}}_J^+}=a_1\in {\mathbb {H}}$ and $g_{|{\mathbb {C}}_K^+}=a_2\in {\mathbb {H}}$, then g can be expressed as

$$\begin{aligned} g(x)=2\mu _{J}(x)J(J-K)^{-1}a_2-2\mu _{K}(x)K(J-K)^{-1}a_1. \end{aligned}$$

(2)

3 Eigenvalue problems for slice functions

3.1 Eigenvalue problem for slice-regular functions

Let $\Omega$ be an axially symmetric domain of ${\mathbb {H}}$. Consider the following eigenvalue problem for the slice derivative operator $\frac{\partial }{\partial x}$ in the class of slice-regular functions:

$$\begin{aligned} {\left\{ \begin{array}{ll}\displaystyle \frac{\partial f}{\partial x}=f\lambda \quad \text {on}~{ \Omega },\\ \text {with }f\in \mathcal {SR}(\Omega ),\ \lambda \in {\mathbb {H}}. \end{array}\right. } \end{aligned}$$

(3)

Remark 1

Let $\lambda \in {\mathbb {H}}$ and let $e^{z\lambda }:=\sum _{n=0}^{+\infty } \frac{(z\lambda )^n}{n!}$. Then $e^{z\lambda }$ is a holomorphic stem function on $\mathbb {C}$, that induces the slice-regular entire function

$$\begin{aligned}\exp _\lambda (x):=\mathcal {I}(e^{z\lambda })=\sum _{n=0}^{+\infty }\frac{x^n\lambda ^n}{n!},\end{aligned}$$

cf. also with [3, 8]. Observe that whenever $\lambda$ is not real, then in general $\exp _\lambda (x)\ne e^{x\lambda }:=\sum _{n=0}^{+\infty } \frac{(x\lambda )^n}{n!}$. The exponential function $\exp _\lambda (x)$ is slice-preserving if and only if $\lambda$ is real. In general, if $\lambda \in {\mathbb {C}}_I$, then $\exp _\lambda (x)$ is one-slice-preserving, i.e., it maps the slice ${\mathbb {C}}_I$ into ${\mathbb {C}}_I$.

For any $\lambda \in {\mathbb {H}}$, it holds $\frac{\partial \exp _\lambda (x)}{\partial x}=\exp _\lambda (x)\lambda$, since $\frac{\partial e^{z\lambda }}{\partial z}=e^{z\lambda }\lambda$, i.e., $f(x)=\exp _\lambda (x)$ is a solution of (3) on every $\Omega$.

We consider also a more general eigenvalue problem in which the solutions are searched in the space of slice functions on $\Omega$ which are not necessarily slice-regular.

3.2 Eigenvalue problem for slice functions

Let $\Omega$ be an axially symmetric domain of ${\mathbb {H}}$. Consider the following eigenvalue problem for the slice derivative operator $\frac{\partial }{\partial x}$ in the class $\mathcal {S}^1(\Omega )$ of slice functions induced by stem functions of the class $C^1$ on $\Omega$:

$$\begin{aligned} {\left\{ \begin{array}{ll}\displaystyle \frac{\partial f}{\partial x}=f\lambda \hbox { on}\ \Omega ,\\ \text {with }f\in \mathcal {S}^1(\Omega ),\ \lambda \in {\mathbb {H}}. \end{array}\right. } \end{aligned}$$

(4)

Remark 2

Let $g\in \mathcal {S}^1(\Omega )$. The function $f=g\cdot \exp _\lambda (x)$ obtained by taking the slice product of g and $\exp _\lambda (x)$ is a solution of (4) if and only if

$$\begin{aligned}\frac{\partial f}{\partial x}=\frac{\partial g}{\partial x}\cdot \exp _\lambda (x)+g\cdot \exp _\lambda (x)\lambda =f\lambda \Leftrightarrow \frac{\partial g}{\partial x}\cdot \exp _\lambda (x)=0~\text {on }~\Omega . \end{aligned}$$

Therefore, for any anti-slice-regular function $g\in \mathcal {S}^1(\Omega )$ (i.e., such that $\frac{\partial g}{\partial x}=0$ on $\Omega$), the function $f=g\cdot \exp _\lambda (x)$ is a solution of (4). Moreover, it holds:

• If $\Omega$ is a slice domain (i.e., $\Omega \cap {\mathbb {R}}\ne \emptyset$) and g is constant, then $f=g\cdot \exp _\lambda (x)\in \mathcal {SR}(\Omega )$ is a solution of (3).

• If $\Omega$ is a product domain (i.e., $\Omega \cap {\mathbb {R}}=\emptyset$), then $f=g\cdot \exp _\lambda (x)\in \mathcal {SR}(\Omega )$ is a solution of (3) for every slice-constant function g.

Conversely, if f is a solution of (4), then set $g:=f\cdot (\exp _\lambda (x))^{-\bullet }$. Since the normal function of $\exp _\lambda (x)$ is $N(\exp _\lambda (x))=e^{xt(\lambda )}$, where $t(\lambda )=\lambda +{\overline{\lambda }}$ is the trace of $\lambda$, it holds $V(N(\exp _\lambda (x)))=\emptyset$. More precisely, it holds $(\exp _\lambda (x))^{-\bullet }=\exp _{-\lambda }(x)$, since if $\lambda \in {\mathbb {C}}_J$, then $\exp _\lambda (x)$ is a one-slice preserving function such that $\exp _\lambda (x)\cdot \exp _{-\lambda }(x)=1$ on the slice ${\mathbb {C}}_J$, and therefore, by the representation formula (see [16, Prop. 5]), the equality holds on the whole space ${\mathbb {H}}$. We have

$$\begin{aligned} \frac{\partial g}{\partial x}&=\frac{\partial (f\cdot \exp _{-\lambda }(x))}{\partial x}=\frac{\partial f}{\partial x}\cdot \exp _{-\lambda }(x)+f\cdot (-\exp _{-\lambda }(x)\lambda )\\&= (f\lambda )\cdot \exp _{-\lambda }(x)-f\cdot \exp _{-\lambda }(x)\lambda =0, \end{aligned}$$

and then $f=g\cdot \exp _\lambda (x)$, with $g\in \mathcal {S}^1(\Omega )$ anti-slice-regular.

Denote by $\overline{\mathcal {SR}}(\Omega )$ the right ${\mathbb {H}}$-module of anti-slice-regular functions on $\Omega$. Let $g=\mathcal {I}(G_1+\imath G_2)$. Then $g\in \overline{\mathcal {SR}}(\Omega )$ if and only if the slice function ${\overline{g}}=\mathcal {I}(G_1-\imath G_2)$ is slice-regular, i.e., the stem function $G:=G_1+\imath G_2$ inducing g is anti-holomorphic. We can summarize the previous remarks in the following statement.

Proposition 3

Let $\Omega \subset {\mathbb {H}}$ be an axially symmetric domain. A function $f\in \mathcal {S}^1(\Omega )$ is a solution of (4) if and only if $f=g\cdot \exp _\lambda (x)$, with $g\in {\overline{\mathcal {SR}}}(\Omega )$ anti-slice-regular. The solution f is slice-regular, and then a solution of (3), if and only if $g\in {\overline{\mathcal {SR}}}(\Omega )\cap \mathcal {SR}(\Omega )=\mathcal {SC}(\Omega )$, i.e., g is slice-constant on $\Omega$ (constant if $\Omega$ is a slice domain). $\square$

Let $R_\lambda$ be the operator of right multiplication by $\lambda$ and let ${\mathcal {D}}_\lambda =\frac{\partial }{\partial x}-R_\lambda$ denote the linear operator mapping a slice function $f\in \mathcal {S}^1(\Omega )$ to the continuous slice function

$$\begin{aligned}{\mathcal {D}}_\lambda f=\frac{\partial f}{\partial x}-f\lambda .\end{aligned}$$

Note that ${\mathcal {D}}_\lambda f$ is slice-regular for any slice-regular function f. Another useful property of the operator ${\mathcal {D}}_\lambda$ is the following: for every slice-constant $g\in \mathcal {SC}(\Omega )$ and every $f\in \mathcal {S}^1(\Omega )$, it holds

$$\begin{aligned}{\mathcal {D}}_\lambda (g\cdot f)=g\cdot {\mathcal {D}}_\lambda f. \end{aligned}$$

Remark 4

When $\Omega$ is a slice domain, in view of Proposition 3 it holds

$$\begin{aligned}{\text {Ker}}({\mathcal {D}}_\lambda )\cap \mathcal {SR}(\Omega )=\{c\cdot \exp _\lambda (x)\,|\, c\in {\mathbb {H}}\}. \end{aligned}$$

If $y\in \Omega \cap {\mathbb {R}}$, the solution of (3) is uniquely determined by its value at y, and takes the form $f=c\cdot \exp _\lambda (x)$, with $c=f(y)\exp _{-\lambda }(y)$.

If $\Omega$ is a product domain, then the solutions of (3) have more degrees of freedom (eight real d.o.f. instead of four). If $\mu _I\in \mathcal {SC}({\mathbb {H}}\setminus {\mathbb {R}})$ is the function defined in (1), then formula (2) for $J=-K=I$ implies that $g:=\mu _I a_2+\mu _{-I}a_1$ is the unique slice-constant function on ${\mathbb {H}}\setminus {\mathbb {R}}$ with $g_{|{\mathbb {C}}_I^+}=a_1$, $g_{|{\mathbb {C}}_I^-}=a_2$. We then obtain, for every $I\in {\mathbb {S}}$, the representation

$$\begin{aligned}{\text {Ker}}({\mathcal {D}}_\lambda )\cap \mathcal {SR}(\Omega )=\{(\mu _I a_2)\cdot \exp _\lambda (x)+(\mu _{-I}a_1)\cdot \exp _\lambda (x)\,|\, a_1,a_2\in {\mathbb {H}}\} \end{aligned}$$

for the kernel of the operator ${\mathcal {D}}_\lambda$ on slice-regular functions on $\Omega$. A function $f=g\cdot \exp _\lambda (x)=(\mu _I a_2)\cdot \exp _\lambda (x)+(\mu _{-I}a_1)\cdot \exp _\lambda (x)\in {\text {Ker}}({\mathcal {D}}_\lambda )$ is uniquely determined by its values at two points, for example by I and $-I$. Since $f\cdot \exp _{-\lambda }(x)=g$, a direct computation shows that

$$\begin{aligned} a_1={\left\{ \begin{array}{ll} f(I)\exp _{-\lambda }(f(I)^{-1}If(I))&{}~\text {if }~f(I)\ne 0,\\ 0&{}~\text {if }~f(I)=0, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} a_2= {\left\{ \begin{array}{ll} f(-I)\exp _\lambda (f(-I)^{-1}If(-I))&{}\text {if }~f(-I)\ne 0,\\ 0&{}\text {if }~f(-I)=0, \end{array}\right. } \end{aligned}$$

where we used the fact that $\exp _{-\lambda }(-x)=\exp _\lambda (x)$ for every $x,\lambda \in {\mathbb {H}}$.

The eigenvalue problem (3) is the homogeneous problem associated to the following generalized eigenvalue problem. Given $h\in \mathcal {SR}(\Omega )$ and $\lambda \in {\mathbb {H}}$, find $f\in \mathcal {SR}(\Omega )$ such that

$$\begin{aligned} {\mathcal {D}}_\lambda f=h\hbox { on}\ \Omega . \end{aligned}$$

(5)

Remark 5

Assume that $\lambda \ne 0$. If $h(x)=x c_1+c_0$ is linear ($c_0,c_1\in {\mathbb {H}}$), then $f(x)=-c_1\cdot (\lambda ^{-2}+x\lambda ^{-1})-c_0\lambda ^{-1}$ is a solution of (5), since

$$\begin{aligned} {\mathcal {D}}_\lambda f&=-c_1\cdot \frac{\partial (\lambda ^{-2}+x\lambda ^{-1})}{\partial x}+c_1\cdot (\lambda ^{-2}+x\lambda ^{-1})\lambda +c_0=\\&=-c_1\lambda ^{-1}+c_1\cdot (\lambda ^{-1}+x)+c_0=c_1\cdot x+c_0=xc_1+c_0=h(x).\\ \end{aligned}$$

In view of the linearity of (5), the previous solution is uniquely determined up to solutions of the homogeneous problem (3). From Proposition 3 we can infer that the general solution is

$$\begin{aligned}f(x)=a_0\cdot \exp _\lambda (x)-c_1\cdot (\lambda ^{-2}+x\lambda ^{-1})-c_0\lambda ^{-1}, \end{aligned}$$

for any $a_0\in {\mathbb {H}}$. On product domains the general solutions have similar forms, with any slice-constant function $g\in \mathcal {SC}(\Omega )$ in place of the constant $a_0$. Notice that here and in all that follows the constants $a_0$ and $c_i$ are considered as functions when they appear as one of the objects to be multiplied by means of the product $\cdot$.

The computation in Remark 5 provides a hint for finding solutions of (5) for every polynomial right-hand side $h\in {\mathbb {H}}[x]$ and $\lambda \ne 0$. In this case we can take for $\Omega$ the whole quaternionic space ${\mathbb {H}}$ (a slice domain) or the product domain ${\mathbb {H}}\setminus {\mathbb {R}}$.

Proposition 6

Let $\lambda \ne 0$ and let $h(x)=\sum _{n=0}^dx^nc_n\in {\mathbb {H}}[x]$. For any $n\in {\mathbb {N}}$, let $f_n\in {\mathbb {H}}[x]$ be the slice-regular polynomial

$$\begin{aligned}f_n(x)=-c_n\cdot \left( \sum _{k=0}^n \frac{x^k\lambda ^k}{k!}\right) n!\lambda ^{-n-1}. \end{aligned}$$

Then the polynomial $f_*=\sum _{n=0}^df_n$ is a solution of (5) with right-hand side h. The general solution of (5) on $\Omega$ is $f=f_*+g\cdot \exp _\lambda (x)$, with $g\in \mathcal {SC}(\Omega )$. If $\Omega ={\mathbb {H}}$, a slice domain, and $y\in {\mathbb {R}}$, then the solution of (5) is uniquely determined by its value at y, and takes the form $f=f_*+c\cdot \exp _\lambda (x)$, with $c=(f(y)-f_*(y))\exp _{-\lambda }(y)\in {\mathbb {H}}$. If $\Omega ={\mathbb {H}}\setminus {\mathbb {R}}$, a product domain, then the solution of (5) is uniquely determined by its values at two points.

Proof

We have

$$\begin{aligned} {\mathcal {D}}_\lambda f_n(x)&=-c_n\cdot \frac{\partial }{\partial x}\left( \sum _{k=0}^n \frac{x^k\lambda ^k}{k!}\right) n!\lambda ^{-n-1}+c_n\cdot \left( \sum _{k=0}^n \frac{x^k\lambda ^k}{k!}\right) n!\lambda ^{-n}=\\&=-c_n\cdot \left( \sum _{k=1}^n \frac{x^{k-1}\lambda ^{k-1}}{(k-1)!}\right) n!\lambda ^{-n}+c_n\cdot \left( \sum _{k=0}^n \frac{x^k\lambda ^k}{k!}\right) n!\lambda ^{-n}=c_n\cdot x^n=x^nc_n. \end{aligned}$$

Therefore, ${\mathcal {D}}_\lambda f={\mathcal {D}}_\lambda f_*=h$, if $f=f_*+g\cdot \exp _\lambda (x)$, with $g\in \mathcal {SC}(\Omega )$. The last statement follows immediately from Proposition 3 and from Remark 4. $\square$

The preceding Proposition means that one can define a right inverse of ${\mathcal {D}}_\lambda$ on the space of quaternionic polynomials of degree at most d. It is the operator ${\mathcal {S}}_\lambda :{\mathbb {H}}_d[x]\rightarrow {\mathbb {H}}_d[x]$ defined as follows: if $p(x)=\sum _{n=0}^dx^na_n$, then

$$\begin{aligned} {\mathcal {S}}_\lambda p=-\sum _{n=0}^d a_n\cdot \left( \sum _{k=0}^n\frac{x^k\lambda ^k}{k!}\right) n!\lambda ^{-n-1}=\sum _{k=0}^dx^kb_k, \end{aligned}$$

(6)

with

$$\begin{aligned} b_k=-\sum _{n=k}^d\frac{a_n\lambda ^{k-n-1}n!}{k!}\text {for}~ {k=0,\ldots ,d}. \end{aligned}$$

Now we consider equation (5) with an exponential right-hand side $h(x)=g\cdot \exp _\mu (x)$, with $\mu \in {\mathbb {H}}$ and g slice-constant.

Proposition 7

Let $\lambda ,\mu \in {\mathbb {H}}$, with $0<|\mu |<|\lambda |$. For every $n\in {\mathbb {N}}$, let $f_n^{\mu ,\lambda }\in {\mathbb {H}}[x]$ be the slice-regular polynomial of degree n

$$\begin{aligned}f_n^{\mu ,\lambda }(x):=-\sum _{k=0}^n\frac{x^k\mu ^n\lambda ^k}{k!}\lambda ^{-n-1}. \end{aligned}$$

Then the series of functions $\sum _{n=0}^{+\infty } f_n^{\mu ,\lambda }(x)$ converges uniformly on the compact sets of ${\mathbb {H}}$ to an entire slice-regular function $f^{\mu ,\lambda }\in \mathcal {SR}({\mathbb {H}})$ such that ${\mathcal {D}}_\lambda (f^{\mu ,\lambda })=\exp _\mu (x)$. As a consequence, ${\mathcal {D}}_\lambda (g\cdot f^{\mu ,\lambda })=g\cdot \exp _\mu (x)$ for every slice-constant g on $\Omega$. If $\lambda$ and $\mu$ commute, then the function $f^{\mu ,\lambda }$ has the expected explicit form $f^{\mu ,\lambda }(x)=\exp _\mu (x)(\mu -\lambda )^{-1}$.

Proof

Since $f_n^{\mu ,\lambda }(x):=-\mu ^n\cdot \sum _{k=0}^n\frac{x^k\lambda ^k}{k!}\lambda ^{-n-1}$, as in the proof of Proposition 6 we get that

$$\begin{aligned}{\mathcal {D}}_\lambda (f_n^{\mu ,\lambda })=x^n\frac{\mu ^n}{n!}. \end{aligned}$$

From the estimate

$$\begin{aligned}|f_n^{\mu ,\lambda }(x)|\le \sum _{k=0}^n \frac{|x|^k |\mu |^n|\lambda |^k}{k!}|\lambda |^{-n-1}=\sum _{k=0}^n \frac{|x\lambda |^k}{k!}\frac{|\mu |^n}{|\lambda |^n}|\lambda |^{-1}\le \frac{e^{|x\lambda |}}{|\lambda |} \frac{|\mu |^n}{|\lambda |^n} \end{aligned}$$

follows the uniform convergence of the series on compacts and then the equality ${\mathcal {D}}_\lambda f^{\mu ,\lambda }(x)=\sum _{n=0}^{+\infty } x^n\mu ^n/n!=\exp _\mu (x)$. To prove the last statement, we can assume that $\lambda ,\mu \in {\mathbb {C}}_I$ for a unit $I\in {\mathbb {S}}$ and write

$$\begin{aligned}f^{\mu ,\lambda }(x)=\sum _{n=0}^{+\infty } f_n^{\mu ,\lambda }(x)=\sum _{k=0}^{+\infty } \left( -\sum _{n=k}^{+\infty } \frac{x^k\mu ^n}{k!}\lambda ^{-n-1+k} \right) . \end{aligned}$$

We then compute the sums

$$\begin{aligned}g_k^{\mu ,\lambda }(x):=-\sum _{n=k}^{+\infty } \frac{x^k\mu ^n}{k!}\lambda ^{-n-1+k}= -\frac{x^k}{k!}\lambda ^{-1+k}\sum _{n=k}^{+\infty } (\mu \lambda ^{-1})^n=\frac{x^k}{k!}\mu ^k(\mu -\lambda )^{-1}\end{aligned}$$

and conclude observing that

$$\begin{aligned}f^{\mu ,\lambda }(x)=\sum _{k=0}^{+\infty } g_k^{\mu ,\lambda }(x)=\sum _{k=0}^{+\infty } \frac{x^k}{k!}\mu ^k(\mu -\lambda )^{-1}=\exp _\mu (x)(\mu -\lambda )^{-1}. \end{aligned}$$

$\square$

If $\lambda$ and $\mu$ commute and $\lambda \ne \mu$, then $\exp _\mu (x)(\mu -\lambda )^{-1}$ solves ${\mathcal {D}}_\lambda f=\exp _\mu (x)$ even if $|\mu |\ge |\lambda |$ or if one of the parameters $\lambda ,\mu$ vanishes.

If $\lambda =\mu$, then a solution of the equation ${\mathcal {D}}_\lambda f=\exp _\lambda (x)$ is easily found from the correspondent complex problem. The one-slice-preserving slice-regular function $f(x)= x\exp _\lambda (x)$ satisfies the equation ${\mathcal {D}}_\lambda f=\exp _\lambda (x)$.

In the next Proposition we show how to remove the assumption $0<|\mu |<|\lambda |$ of Proposition 7 and find another slice-regular solution of the equation ${\mathcal {D}}_\lambda f=\exp _\mu (x)$. More precisely, we find the power series expansion around the origin of the unique solution vanishing at 0.

Proposition 8

Let $\lambda ,\mu \in {\mathbb {H}}$. Let $g^{\mu ,\lambda }$ be the sum of the slice-regular power series

$$\begin{aligned}g^{\mu ,\lambda }(x):=\sum _{n=1}^{+\infty }\frac{x^n}{n!}\sum _{k=0}^{n-1}\mu ^k\lambda ^{n-k-1}. \end{aligned}$$

The series converges uniformly on the compact sets of ${\mathbb {H}}$ to an entire slice-regular function such that ${\mathcal {D}}_\lambda (g^{\mu ,\lambda })=\exp _\mu (x)$ and $g^{\mu ,\lambda }(0)=0$. As a consequence, ${\mathcal {D}}_\lambda (h\cdot g^{\mu ,\lambda })=h\cdot \exp _\mu (x)$ for every slice-constant h on $\Omega$. If $\lambda$ and $\mu$ commute and $\lambda \ne \mu$, then the function $g^{\mu ,\lambda }$ has the expected explicit form $g^{\mu ,\lambda }(x)=(\exp _\mu (x)-\exp _\lambda (x))(\mu -\lambda )^{-1}$. If $\lambda =\mu$, then $g^{\lambda ,\lambda }(x)=x\exp _\lambda (x)$.

Proof

Assume for the moment that the series is uniformly convergent. Then

$$\begin{aligned} {\mathcal {D}}_\lambda g^{\mu ,\lambda }&=\frac{\partial }{\partial x}\left( \sum _{n=1}^{+\infty }\frac{x^n}{n!}\sum _{k=0}^{n-1}\mu ^k\lambda ^{n-k-1}\right) -\left( \sum _{n=1}^{+\infty }\frac{x^n}{n!}\sum _{k=0}^{n-1}\mu ^k\lambda ^{n-k-1}\right) \lambda \\&=\sum _{n=1}^{+\infty }\frac{nx^{n-1}}{n!}\sum _{k=0}^{n-1}\mu ^k\lambda ^{n-k-1}-\sum _{n=1}^{+\infty }\frac{x^n}{n!}\sum _{k=0}^{n-1}\mu ^k\lambda ^{n-k}\\&=\sum _{n=0}^{+\infty }\frac{x^{n}}{n!}\sum _{k=0}^{n}\mu ^k\lambda ^{n-k}-\sum _{n=1}^{+\infty }\frac{x^n}{n!}\sum _{k=0}^{n-1}\mu ^k\lambda ^{n-k}\\&=1+\sum _{n=1}^{+\infty }\frac{x^n}{n!}\mu ^n=\exp _\mu (x). \end{aligned}$$

Let

$$\begin{aligned}g_n(x):=\frac{x^n}{n!}\sum _{k=0}^{n-1}\mu ^k\lambda ^{n-k-1}. \end{aligned}$$

If $|\lambda |\ne |\mu |$, then

$$\begin{aligned} |g_n(x)|\le \frac{|x|^n}{n!}\sum _{k=0}^{n-1}|\mu |^k|\lambda |^{n-k-1}= \frac{|x|^n}{n!}\frac{|\lambda |^n-|\mu |^n}{|\lambda |-|\mu |}. \end{aligned}$$

Since the estimate is symmetric in $\lambda$ and $\mu$, we can assume that $|\mu |<|\lambda |$. Then

$$\begin{aligned}|g_n(x)|\le \frac{|2x\lambda |^n}{n!}\frac{2^{-n}}{|\lambda |-|\mu |}\le e^{|2x\lambda |}\frac{2^{-n}}{|\lambda |-|\mu |} \end{aligned}$$

from which follows the uniform convergence of the series $g^{\mu ,\lambda }(x)=\sum _{n\ge 1}g_n(x)$ on the compacts sets of ${\mathbb {H}}$. If $|\lambda |=|\mu |$, then

$$\begin{aligned} |g_n(x)|\le \frac{|x|^n}{n!}\sum _{k=0}^{n-1}|\lambda |^{n-1}= \frac{|x|^n}{(n-1)!}|\lambda |^{n-1}= \frac{|x||2x\lambda |^{n-1}}{(n-1)!}2^{-n+1} \le |x|e^{|2x\lambda |}2^{-n+1} \end{aligned}$$

and the uniform convergence of the series follows also in this case. If $\lambda$ and $\mu$ commute, the following equality holds:

$$\begin{aligned} g^{\mu ,\lambda }(x)=\sum _{n=1}^{+\infty }\frac{x^n}{n!}\sum _{k=0}^{n-1}\mu ^k\lambda ^{n-k-1}=\sum _{n=1}^{+\infty }\frac{x^n}{n!}(\mu ^n-\lambda ^n){(\mu -\lambda )^{-1}}. \end{aligned}$$

The last statement follows immediately from the series expansion

$$\begin{aligned} g^{\lambda ,\lambda }(x)=\sum _{n=1}^{+\infty }\frac{x^n}{n!}n\lambda ^{n-1}=x\sum _{n=0}^{+\infty }\frac{x^n\lambda ^{n}}{n!}=x\exp _\lambda (x). \end{aligned}$$

$\square$

Remark 9

In view of Proposition 3, the solutions $f^{\mu ,\lambda }$ and $g^{\mu ,\lambda }$ of Propositions 7 and 8 of the equation ${\mathcal {D}}_\lambda f=\exp _\mu (x)$, as soon as they are both defined, just differ by a function of the form $h\cdot \exp _\lambda (x)$, with $h\in \mathcal {SC}(\Omega )$. Indeed, it holds $f^{\mu ,\lambda }-g^{\mu ,\lambda }=f^{\mu ,\lambda }(0)\cdot \exp _\lambda (x)$.

Example 10

(1)   Let $\mu =i$, $\lambda =j$. A direct computation shows that the solution $g^{i,j}$ of the equation ${\mathcal {D}}_jf=\exp _i(x)=\cos x+(\sin x) i$ given by Proposition 8 has the explicit expression

$$\begin{aligned} g^{i,j}(x)=\sum _{n=1}^{+\infty }\frac{x^n}{n!}\sum _{k=0}^{n-1}i^k j^{n-k-1}=\frac{1}{2}\left( \sin x+x\cos x+(x\sin x)(i+j)+(\sin x-x\cos x)k\right) . \end{aligned}$$

Observe that the slice-regular functions $\cos x=\mathcal {I}(\cos z)$ and $\sin x=\mathcal {I}(\sin z)$ are exactly the functions defined in [24, Def.11.23] in the more general context of Clifford algebras.

(2)   Let $\mu =i$, $\lambda =2j$. Then the solution $g^{i,2j}$ of the equation ${\mathcal {D}}_{2j}f=\exp _i(x)$ is

$$\begin{aligned} g^{i,2j}(x)=\frac{1}{3}\left( 2\sin (2x)-\sin x+(\cos x-\cos (2x))(i+2j)+(2\sin x-\sin (2x))k\right) . \end{aligned}$$

(3)   Let $\mu =2i$, $\lambda =j$. Then the solution $g^{2i,j}$ of the equation ${\mathcal {D}}_{j}f=\exp _{2i}(x)$ is the function

$$\begin{aligned} g^{2i,j}(x)=\frac{1}{3}\left( 2\sin (2x)-\sin x+(\cos x-\cos (2x))(2i+j)+(2\sin x-\sin (2x))k\right) . \end{aligned}$$

3.3 Eigenvalue problem of the second order for slice-regular functions

Propositions 3 and 8 permit us to study eigenvalue problems of the second order. Given $\lambda ,\mu \in {\mathbb {H}}$, we consider the equation

$$\begin{aligned} {\left\{ \begin{array}{ll}\displaystyle {\mathcal {D}}_\mu {\mathcal {D}}_\lambda f=0\hbox { on}\ \Omega ,\\ \text {with }f\in \mathcal {SR}(\Omega ). \end{array}\right. } \end{aligned}$$

(7)

Notice that two operators ${\mathcal {D}}_\lambda$ and ${\mathcal {D}}_\mu$ commute if and only if $\lambda$ and $\mu$ commute, i.e., they belong to the same complex slice ${\mathbb {C}}_I$, $I\in {\mathbb {S}}$.

Corollary 11

Let $\lambda ,\mu \in {\mathbb {H}}$.

• 1. If $\lambda \ne \mu$, then the function $g^{\mu ,\lambda }$ of Proposition 8 is a solution of (7). Any solution of (7) is of the form $f=h_1\cdot g^{\mu ,\lambda }+h_2\cdot \exp _\lambda (x)$, with $h_1,h_2\in \mathcal {SC}(\Omega )$.

• 2. If $\lambda$ and $\mu$ are distinct and commute, then the solutions of (7) are the functions of the form $f=h_1\cdot \exp _\mu (x)+h_2\cdot \exp _\lambda (x)$, with $h_1,h_2\in \mathcal {SC}(\Omega )$.

• 3. If $\lambda =\mu$, then the solutions of (7), i.e., the functions $f\in \mathcal {SR}(\Omega )$ such that ${\mathcal {D}}_\lambda ^2 f=0$, are the functions of the form $f=h_1\cdot \exp _\lambda (x)+h_2\cdot (x\exp _\lambda (x))$, with $h_1,h_2\in \mathcal {SC}(\Omega )$.

Proof

From Proposition 8 and Proposition 3, ${\mathcal {D}}_\mu {\mathcal {D}}_\lambda (g^{\mu ,\lambda })={\mathcal {D}}_\mu \exp _\mu (x)=0$. Conversely, if f is a solution of (7), then ${\mathcal {D}}_\lambda f$ has the form $h_1\cdot \exp _\mu (x)$, with $h_1\in \mathcal {SC}(\Omega )$, and then $f-h_1\cdot g^{\mu ,\lambda }\in {\text {Ker}}({\mathcal {D}}_\lambda )\cap \mathcal {SR}(\Omega )$. From Proposition 3, we get $f-h_1\cdot g^{\mu ,\lambda }=h_2\cdot \exp _\lambda (x)$, with $h_2\in \mathcal {SC}(\Omega )$.

If $\lambda$ and $\mu$ are distinct but commuting elements, then Proposition 8 gives the solution $g^{\mu ,\lambda }(x)=(\exp _\mu (x)-\exp _\lambda (x))(\mu -\lambda )^{-1}$ of ${\mathcal {D}}_\lambda f=\exp _\mu (x)$. Moreover,

$$\begin{aligned}\exp _\mu (x)(\mu -\lambda )^{-1}=\sum _{k=0}^{+\infty }\frac{x^k\mu ^k}{k!}(\mu -\lambda )^{-1}=\sum _{k=0}^{+\infty }\frac{x^k(\mu -\lambda )^{-1}\mu ^k}{k!}=(\mu -\lambda )^{-1}\cdot \exp _\mu (x) \end{aligned}$$

and similarly for $\exp _\lambda (x)$. Then $h_1\cdot g^{\mu ,\lambda }=(h_1(\mu -\lambda )^{-1})\cdot \exp _\mu (x)-(h_2(\mu -\lambda )^{-1})\cdot \exp _\lambda (x)=h'_1\cdot \exp _\mu (x)+h'_2\cdot \exp _\lambda (x)$, with $h'_1,h'_2\in \mathcal {SC}(\Omega )$. The statement of the third case addressing $\lambda =\mu$ follows from Proposition 8 and Proposition 3. $\square$

3.4 Eigenvalue problem of the mth-order for slice-regular functions

Now we generalize Corollary 11 to eigenvalue problems of any order m. Let $\lambda _1,\ldots ,\lambda _m\in {\mathbb {H}}$ and consider the equation

$$\begin{aligned} {\left\{ \begin{array}{ll}\displaystyle {\mathcal {D}}_{\lambda _{1}}\cdots {\mathcal {D}}_{\lambda _{m}} f=0\hbox { on}\ \Omega ,\\ \text {with }f\in \mathcal {SR}(\Omega ). \end{array}\right. } \end{aligned}$$

(8)

We begin by introducing a family of slice-regular functions which generalize the exponential functions $\exp _\lambda (x)$ of Remark 1.

Definition 12

Let $\lambda _1,\ldots ,\lambda _m\in {\mathbb {H}}$, with $m\ge 1$. The generalized exponential function associated with $\Lambda =(\lambda _1,\ldots ,\lambda _m)$ is the slice-regular entire function $E_\Lambda (x)$ defined by

$$\begin{aligned} E_\Lambda (x):=\sum _{n=m-1}^{+\infty }\frac{x^{n}}{n!}\sum _{|K|=n-m+1}\lambda _1^{k_1}\cdots \lambda _m^{k_m}, \end{aligned}$$

where the sum is extended over the multi-indices $K=(k_1,\ldots ,k_m)$ of non-negative integers such that $|K|=k_1+\cdots +k_m=n-m+1$. In particular, it holds $E_{(\lambda )}=\exp _{\lambda }(x)$ for every $\lambda \in {\mathbb {H}}$.

Proposition 13

The series in the definition of $E_\Lambda (x)$ converges uniformly on the compacts of ${\mathbb {H}}$, i.e., the entire slice-regular function $E_\Lambda$ in the previous definition is well-defined. Moreover, if $\Lambda =(\lambda _1,\ldots ,\lambda _m)=(\lambda ,\ldots ,\lambda )$, then $E_{\Lambda }(x)=\frac{x^{m-1}}{(m-1)!}\exp _\lambda (x)$. It holds $E_\Lambda (0)=1$ if $\Lambda =(\lambda )$, otherwise $E_\Lambda (0)=0$.

Proof

Let m be fixed, $n\ge m-1$ and define

$$\begin{aligned}e_n(x):=\frac{x^n}{n!}\sum _{|K|=n-m+1}\lambda _1^{k_1}\cdots \lambda _m^{k_m}. \end{aligned}$$

Let $a:=\max \{|\lambda _1|,\ldots ,|\lambda _m|\}$. Then we have

$$\begin{aligned} |e_n(x)|&\le \frac{|x|^n}{n!}\sum _{|K|=n-m+1}|\lambda _1|^{k_1}\cdots |\lambda _m|^{k_m} \le \frac{|x|^n}{n!}\sum _{|K|=n-m+1}a^{n-m+1}\\&\le \frac{|x|^n}{n!}\left( {\begin{array}{c}n\\ n-m+1\end{array}}\right) a^{n-m+1} =\frac{|x|^na^{n-m+1}}{(n-m+1)!(m-1)!}\\&=\frac{|2x|^{m-1}}{(m-1)!}\frac{|2ax|^{n-m+1}}{(n-m+1)!}2^{-n} \le \frac{|2x|^{m-1}}{(m-1)!}e^{|2ax|}2^{-n}, \end{aligned}$$

from which follows the uniform convergence of the series $E_\Lambda (x)=\sum _{n\ge m-1}e_n(x)$ on the compacts sets of ${\mathbb {H}}$.

If $\lambda _1=\cdots =\lambda _m=\lambda$, then

$$\begin{aligned} E_{\Lambda }(x)&=\sum _{n=m-1}^{+\infty }\frac{x^{n}}{n!}\sum _{|K|=n-m+1}\lambda ^{n-m+1}= \sum _{n=m-1}^{+\infty }\frac{x^{n}}{n!}\left( {\begin{array}{c}n\\ n-m+1\end{array}}\right) \lambda ^{n-m+1}\\&=x^{m-1}\sum _{n=m-1}^{+\infty }\frac{x^{n-m+1}}{(n-m+1)!(m-1)!}\lambda ^{n-m+1} =\frac{x^{m-1}}{(m-1)!}\exp _\lambda (x). \end{aligned}$$

$\square$

We set $g_1(x):=\exp _{\lambda _1}(x)$ and we define $g_2(x)$ as the solution $g^{\lambda _1,\lambda _2}(x)$ of the equation ${\mathcal {D}}_{\lambda _{2}}g_2=g_1$ obtained in Proposition 8. Then ${\mathcal {D}}_{\lambda _{1}}{\mathcal {D}}_{\lambda _{2}}g_2={\mathcal {D}}_{\lambda _{1}}g_1=0$, as in Corollary 11. Observe that $g_2(x)$ is a generalized exponential function, since $g_2(x)=E_{(\lambda _1,\lambda _2)}(x)$. We now complete the construction of a sequence of entire slice-regular functions $g_1,\ldots g_m$ such that ${\mathcal {D}}_{\lambda _{\ell+1}}g_{\ell +1}=g_\ell$ for every $\ell =1,\ldots ,m-1$. The last element of the sequence, the function $g_m$, is then a solution of equation (8), with the additional property that ${\mathcal {D}}_{\lambda _{2}}\cdots {\mathcal {D}}_{\lambda _{m}} g_m=g_1\ne 0$.

For every $\ell =2,\ldots ,m$, we put

$$\begin{aligned} g_\ell (x):=E_{(\lambda _1,\ldots ,\lambda _\ell )}(x) =\sum _{n=\ell -1}^{+\infty }\frac{x^{n}}{n!}\sum _{|K|=n-\ell +1}\lambda _1^{k_1}\cdots \lambda _\ell ^{k_\ell }. \end{aligned}$$

Proposition 14

It holds ${\mathcal {D}}_{\lambda _{\ell +1}} g_{\ell +1}=g_{\ell }$ for every $\ell =1,\ldots ,m-1$.

Proof

$$\begin{aligned} {\mathcal {D}}_{\lambda _{\ell +1}} g_{\ell +1}&=\frac{\partial }{\partial x}\left( \sum _{n=\ell }^{+\infty }\frac{x^{n}}{n!}\sum _{|K|=n-\ell }\lambda _1^{k_1}\cdots \lambda _{\ell +1}^{k_{\ell +1}}\right) -\left( \sum _{n=\ell }^{+\infty }\frac{x^{n}}{n!}\sum _{|K|=n-\ell }\lambda _1^{k_1}\cdots \lambda _{\ell +1}^{k_{\ell +1}}\right) \lambda _{\ell +1}\\&=\sum _{n=\ell }^{+\infty }\frac{nx^{n-1}}{n!}\sum _{|K|=n-\ell }\lambda _1^{k_1}\cdots \lambda _{\ell +1}^{k_{\ell +1}}-\sum _{n=\ell }^{+\infty }\frac{x^n}{n!}\sum _{|K|=n-\ell }\lambda _1^{k_1}\cdots \lambda _{\ell +1}^{k_{\ell +1}+1}\\&=\sum _{n=\ell -1}^{+\infty }\frac{x^{n}}{n!}\sum _{|K|=n-\ell +1}\lambda _1^{k_1}\cdots \lambda _{\ell +1}^{k_{\ell +1}}-\sum _{n=\ell }^{+\infty }\frac{x^n}{n!}\sum _{|K|=n-\ell }\lambda _1^{k_1}\cdots \lambda _{\ell +1}^{k_{\ell +1}+1}\\&=\frac{x^{\ell -1}}{(\ell -1)!}+\sum _{n=\ell }^{+\infty }\frac{x^{n}}{n!}\sum _{|K|=n-\ell +1}\lambda _1^{k_1}\cdots \lambda _{\ell }^{k_{\ell }}=g_\ell (x). \end{aligned}$$

$\square$

Corollary 15

Let $\lambda _1,\ldots ,\lambda _m\in {\mathbb {H}}$. Let $g_{\lambda _m}(x):=\exp _{\lambda _m}(x)=E_{(\lambda _m)}(x)$. For $m\ge 2$ and $1\le i< m$, let us denote by $g_{\lambda _i,\ldots ,\lambda _m}$ the solution of the equation ${\mathcal {D}}_{\lambda _{m}}g_{\lambda _i,\ldots ,\lambda _m}=g_{\lambda _i,\ldots ,\lambda _{m-1}}$ given by Proposition 14, i.e., $g_{\lambda _i,\ldots ,\lambda _m}=E_{(\lambda _i,\ldots ,\lambda _m)}$. Then the generalized exponential function $g_m=E_{(\lambda _1,\ldots ,\lambda _m)}$ is a solution of (8) and any solution of (8) on $\Omega$ is of the form

$$\begin{aligned} f=\sum _{i=1}^mh_i\cdot E_{(\lambda _i,\ldots ,\lambda _m)} \end{aligned}$$

(9)

with $h_i\in \mathcal {SC}(\Omega )$ for every i.

Proof

From Proposition 14 we infer that ${\mathcal {D}}_{\lambda _{1}}\cdots {\mathcal {D}}_{\lambda _{m}}g_m={\mathcal {D}}_{\lambda _{1}}\cdots {\mathcal {D}}_{\lambda _{m-1}}g_{m-1}=\cdots ={\mathcal {D}}_{\lambda _{1}}g_1=0$. We prove (9) by induction over m. The cases $m=1,2$ have already been considered in Proposition 3 and in Corollary 11. Let $m\ge 3$ and assume that f is a solution of (8). Then ${\mathcal {D}}_{\lambda _{m}}f$ solves the equation ${\mathcal {D}}_{\lambda _{1}}\cdots {\mathcal {D}}_{\lambda _{m-1}}g=0$. By the induction hypothesis, ${\mathcal {D}}_{\lambda _{m}}f$ has the form

$$\begin{aligned} {\mathcal {D}}_{\lambda _{m}}f= \sum _{i=1}^{m-1}h_i\cdot E_{(\lambda _i,\ldots ,\lambda _{m-1})} \end{aligned}$$

with $h_i\in \mathcal {SC}(\Omega )$ for every i. Therefore, $f-\sum _{i=1}^{m-1}h_i\cdot g_{\lambda _i,\ldots ,\lambda _{m}}\in {\text {Ker}}({\mathcal {D}}_{\lambda _{m}})$. From Proposition 3, we get $f-\sum _{i=1}^{m-1}h_i\cdot g_{\lambda _i,\ldots ,\lambda _{m}}=h_m\cdot \exp _{\lambda _m}(x)=h_m\cdot E_{(\lambda _m)}(x)$, with $h_m\in \mathcal {SC}(\Omega )$. This proves (9) for every m. $\square$

Remarks 16

(1)   If $\lambda _1=\cdots =\lambda _m=\lambda$, then the solutions of equation (8), that now takes the form $({\mathcal {D}}_\lambda )^mf=0$, can be deduced directly from the complex case. If $\lambda \in {\mathbb {C}}_I$, the functions $x^k\exp _{\lambda }(x)$ are one-slice preserving slice-regular, and then for any $k=0,\ldots ,m-1$ the complex solutions $x^k\exp _{\lambda }(x)$ for $x\in {\mathbb {C}}_I$ extend slice-regularly in a unique way to $\Omega$, giving the general solution

$$\begin{aligned} f=\sum \limits _{k=0}^{m-1} h_k\cdot (x^{k}\exp _{\lambda }(x)) \end{aligned}$$

on $\Omega$, with $h_k\in \mathcal {SC}(\Omega )$. The same result can be obtained from Corollary 15, since by Proposition 13 it holds $E_{(\lambda _i,\ldots ,\lambda _m)}(x)=\frac{x^{m-i}}{(m-i)!}\exp _{\lambda }(x)$ for every $i=1,\ldots ,m$.

(2)   Given $c_1,\ldots ,c_m\in {\mathbb {H}}$, the combination of generalized exponentials

$$\begin{aligned} f=\sum _{i=1}^mc_i\cdot E_{(\lambda _i,\ldots ,\lambda _m)} =\sum _{i=1}^m\sum _{n=m-i}^{+\infty }\frac{x^{n}c_i}{n!}\sum _{|K|=n-m+i}\lambda _i^{k_i}\cdots \lambda _m^{k_m}. \end{aligned}$$

is the unique entire solution of equation (8) such that

$$\begin{aligned} {\mathcal {D}}_{\lambda _{i+1}}\cdots {\mathcal {D}}_{\lambda _{m}}f(0)=c_i\text { for every }~i=1,\ldots ,m-1,\text { and } f(0)=c_m. \end{aligned}$$

The canonical solution $E_{(\lambda _1,\ldots ,\lambda _m)}\not \in \ker ({\mathcal {D}}_{\lambda _{2}}\cdots {\mathcal {D}}_{\lambda _{m}})$ corresponds to the choice of parameters $c_1=1$, $c_2=\cdots =c_{m}=0$.

(3)   If all the eigenvalues $\lambda _1,\ldots ,\lambda _m$ commute and are distinct, then a simple computation shows that

$$\begin{aligned} f_m(x)=\exp _{\lambda _1}(x)\prod _{j=2}^m(\lambda _1-\lambda _j)^{-1} \end{aligned}$$

satisfies ${\mathcal {D}}_{\lambda _{m}} f_m=f_{m-1}$. Then $f_m$ is another solution of (8). Indeed, using the preceding remark it can be verified that under the commutativity assumption the following equality holds

$$\begin{aligned} f_m(x)= \sum _{i=1}^m\prod _{j=2}^i(\lambda _1-\lambda _j)^{-1}\cdot E_{(\lambda _i,\ldots ,\lambda _m)}(x)=\sum _{i=1}^m E_{(\lambda _i,\ldots ,\lambda _m)}(x)\prod _{j=2}^i(\lambda _1-\lambda _j)^{-1}, \end{aligned}$$

in accordance with formula (9) of Corollary 15. In the preceding formula the product is assumed to be equal to 1 when $i=1$. Since the operators ${\mathcal {D}}_{\lambda _{1}},\ldots ,{\mathcal {D}}_{\lambda _{m}}$ commute, the general form of the solutions of (8) can be written in the form

$$\begin{aligned} f=\sum _{k=1}^m h_k\cdot \exp _{\lambda _k}(x) \end{aligned}$$

with $h_k\in \mathcal {SC}(\Omega )$ for every k. Since $\lambda _1,\ldots ,\lambda _m$ belong to a complex slice ${\mathbb {C}}_I$ (unique is the eigenvalues are not all real), this result can be obtained also from the complex case.

Example 17

(1)   A solution of ${\mathcal {D}}_{1+i}{\mathcal {D}}_{1+j}f=0$ is given by the generalized exponential

$$\begin{aligned} E_{(1+i,1+j)}(x)=\sum _{n=1}^{+\infty }\frac{x^{n}}{n!}\sum _{|K|=n-1}(1+i)^{k_1}(1+j)^{k_2}. \end{aligned}$$

A direct computation shows that

$$\begin{aligned} E_{(1+i,1+j)}(x)=\frac{1}{2} e^x\left( (x\cos x+\sin x) +x\sin x(i+j)+(-x\cos x+\sin x)k\right) . \end{aligned}$$

It holds $E_{(1+i,1+j)}(0)=0$, $\mathcal D_{1+j}E_{(1+i,1+j)}(0)=E_{(1+i)}(0)=\exp _{1+i}(0)=1$.

(2)   The canonical solution of ${\mathcal {D}}_i{\mathcal {D}}_j\mathcal D_kf=0$ is given by the generalized exponential

$$\begin{aligned} E_{(i,j,k)}(x)=\sum _{n=2}^{+\infty }\frac{x^{n}}{n!}\sum _{|K|=n-2}i^{k_1}j^{k_2}k^{k_3}. \end{aligned}$$

A direct computation gives

$$\begin{aligned} E_{(i,j,k)}(x)&=\frac{1}{8}\left( x(x+3)\cos x+(x^2+3x-3)\sin x\right) \\&\quad +\frac{1}{8}\left( -x(x+1)\cos x+(x^2+x+1)\sin x\right) (i+k)\\&\quad +\frac{1}{8}\left( x(x-1)\cos x+(x^2-x+1)\sin x\right) j. \end{aligned}$$

Moreover, it holds

$$\begin{aligned} E_{(i,j,k)}(0)=0,\ {\mathcal {D}}_{k}E_{(i,j,k)}(0)=E_{(i,j)}(0)=0,\ {\mathcal {D}}_{j}{\mathcal {D}}_{k}E_{(i,j,k)}(0)=E_{(i)}(0)=1. \end{aligned}$$

(3)   The generalized exponential functions also solve eigenvalue problems with multiplicities, i.e., with repeated eigenvalues in the sequence $\Lambda =(\lambda _1,\ldots ,\lambda _m)$. For example, the equation ${\mathcal {D}}_i^2{\mathcal {D}}_jf=0$ has the canonical solution

$$\begin{aligned} E_{(i,i,j)}(x)=\sum _{n=2}^{+\infty }\frac{x^{n}}{n!}\sum _{|K|=n-2}i^{k_1+k_2}j^{k_3}. \end{aligned}$$

The sum is the entire function

$$\begin{aligned} E_{(i,i,j)}(x)&=\frac{1}{4}\left( x^2\cos x+x\sin x\right) +\frac{1}{4}\left( -x\cos x+(x^2+1)\sin x \right) i\\&\quad +\frac{1}{4}\left( x\cos x+(x^2-1)\sin x\right) j +\frac{1}{4}\left( -x\cos x+\sin k\right) k. \end{aligned}$$

(4)   In order to illustrate the effect of the non-commutativity of the operators ${\mathcal {D}}_{\lambda _{\ell }}$, we also compute the canonical solution

$$\begin{aligned} E_{(i,j,i)}(x)=\sum _{n=2}^{+\infty }\frac{x^{n}}{n!}\sum _{|K|=n-2}i^{k_1}j^{k_2}i^{k_3} \end{aligned}$$

of the equation ${\mathcal {D}}_i{\mathcal {D}}_j{\mathcal {D}}_if=0$. We get

$$\begin{aligned} E_{(i,j,i)}(x)&=\frac{1}{4}\left( x^2\cos x+x\sin x\right) +\frac{1}{4}\left( -x\cos x+(x^2+1)\sin x \right) i\\&\quad +\frac{1}{2}\left( -x\cos x+\sin x\right) j. \end{aligned}$$

3.5 The non-homogeneous eigenvalue problem

We return to the non-homogeneous eigenvalue equation ${\mathcal {D}}_\lambda f=h$ (5) with a more general right-hand side h. Let

$$\begin{aligned}h(x)=\sum _{n=0}^{+\infty }x^na_n\in \mathcal {SR}({\mathbb {H}})\end{aligned}$$

be an entire function. As suggested by the definition of the generalized exponential $g^{\mu ,\lambda }=E_{(\mu ,\lambda )}$ in Proposition 8, we put

$$\begin{aligned} {\mathcal {E}}_\lambda (h):=\sum _{n=1}^{+\infty }\frac{x^n}{n!}\sum _{k=0}^{n-1}k!a_k\lambda ^{n-k-1}. \end{aligned}$$

(10)

Proposition 18

Let $\lambda \in {\mathbb {H}}$. If $\lambda \ne 0$, assume that there exists a positive real constant C and an integer $d\in {\mathbb {N}}$ such that $n!|a_n|\le C (n+1)^d|\lambda |^n$ for every $n\in {\mathbb {N}}$. Then the series (10) converges uniformly on the compact sets of ${\mathbb {H}}$ to an entire slice-regular function such that ${\mathcal {D}}_\lambda ({\mathcal {E}}_\lambda (h))=h$. As a consequence, ${\mathcal {D}}_\lambda (g\cdot {\mathcal {E}}_\lambda (h))=g\cdot h$ for every slice-constant g on an axially symmetric domain $\Omega$ in ${\mathbb {H}}$.

Proof

We prove that the series (10) is uniformly convergent. The case $\lambda =0$ is immediate from the definition $\mathcal E_0(h)=\sum _{n=1}^{+\infty }x^na_{n-1}/n$. Assume $\lambda \ne 0$ and let

$$\begin{aligned}e_n(x):=\frac{x^n}{n!}\sum _{k=0}^{n-1}k!a_k\lambda ^{n-k-1}. \end{aligned}$$

Let $n\ge 1$. From the estimate

$$\begin{aligned} |e_n(x)|&\le C\frac{|x|^n}{n!}\sum _{k=0}^{n-1}(k+1)^d|\lambda |^{n-1}\le C\frac{|x|^n}{n!}n^{d+1}|\lambda |^{n-1}= C\frac{|x||2x\lambda |^{n-1}}{(n-1)!}\frac{n^d}{2^{n-1}}\\&\le C|x|e^{|2x\lambda |}\frac{n^d}{2^{n-1}} \end{aligned}$$

we directly observe the uniform convergence of the series (10). It holds

$$\begin{aligned} {\mathcal {D}}_\lambda ({\mathcal {E}}_\lambda (h))&=\frac{\partial }{\partial x}\left( \sum _{n=1}^{+\infty }\frac{x^n}{n!}\sum _{k=0}^{n-1}k!a_k\lambda ^{n-k-1}\right) -\left( \sum _{n=1}^{+\infty }\frac{x^n}{n!}\sum _{k=0}^{n-1}k!a_k\lambda ^{n-k-1}\right) \lambda \\&=\sum _{n=1}^{+\infty }\frac{nx^{n-1}}{n!}\sum _{k=0}^{n-1}k!a_k\lambda ^{n-k-1}-\sum _{n=1}^{+\infty }\frac{x^n}{n!}\sum _{k=0}^{n-1}k!a_k\lambda ^{n-k}\\&=\sum _{n=0}^{+\infty }\frac{x^{n}}{n!}\sum _{k=0}^{n}k!a_k\lambda ^{n-k}-\sum _{n=1}^{+\infty }\frac{x^n}{n!}\sum _{k=0}^{n-1}k!a_k\lambda ^{n-k}\\&=a_0+\sum _{n=1}^{+\infty }x^n a_n=h(x). \end{aligned}$$

$\square$

For every $\lambda \in {\mathbb {H}}\setminus \{0\}$, we introduce an ${\mathbb {H}}$-submodule of the right ${\mathbb {H}}$-module of entire slice-regular functions on which it is possible to extend the operator ${\mathcal {E}}_\lambda$. Let ${\mathcal {A}}_\lambda \subset \mathcal {SR}({\mathbb {H}})$ be defined as

$$\begin{aligned} {\mathcal {A}}_\lambda :=\big \{f=\sum _{n=0}^{+\infty }x^na_n\,|\, {\exists C>0, d\in {\mathbb {N}}}~\text { such that}~{ n!|a_n|\le C (n+1)^d|\lambda |^n\ \forall n\in {\mathbb {N}}}\big \}. \end{aligned}$$

Proposition 19

Let $\lambda \in {\mathbb {H}}\setminus \{0\}$. The operators ${\mathcal {D}}_\lambda$ and ${\mathcal {E}}_\lambda$ map ${\mathcal {A}}_\lambda$ into ${\mathcal {A}}_\lambda$. The operator ${\mathcal {E}}_\lambda$ is a right inverse of ${\mathcal {D}}_\lambda$ on ${\mathcal {A}}_\lambda$.

Proof

Let $f=\sum _{n=0}^\infty x^na_n\in {\mathcal {A}}_\lambda$. Then

$$\begin{aligned} {\mathcal {D}}_\lambda f=\sum _{n=1}^\infty x^{n-1}na_n-\sum _{n=0}^\infty x^na_n\lambda =\sum _{n=0}^\infty x^n\left( (n+1)a_{n+1}-a_n\lambda \right) =:\sum _{n=0}^\infty x^nb_n. \end{aligned}$$

There exists a positive real $C'$ such that

$$\begin{aligned} n!|b_n|=|(n+1)!a_{n+1}-n!a_n\lambda |\le C(n+2)^d|\lambda |^{n+1}+C(n+1)^d|\lambda |^{n+1}\le C'(n+1)^d|\lambda |^n \end{aligned}$$

for every $n\in {\mathbb {N}}$, i.e., ${\mathcal {D}}_\lambda f\in {\mathcal {A}}_\lambda$. Now let

$$\begin{aligned} {\mathcal {E}}_\lambda (f)=\sum _{n=1}^{+\infty }\frac{x^n}{n!}\sum _{k=0}^{n-1}k!a_k\lambda ^{n-k-1}=:\sum _{n=1}^{+\infty }x^nc_n. \end{aligned}$$

Then

$$\begin{aligned} n!|c_n|=\left| \sum _{k=0}^{n-1}k!a_k\lambda ^{n-k-1}\right| \le C\sum _{k=0}^{n-1}(k+1)^d|\lambda |^{n-1}\le C|\lambda |^{-1}(n+1)^{d+1}|\lambda |^n, \end{aligned}$$

and this means that also ${\mathcal {E}}_\lambda (f)\in {\mathcal {A}}_\lambda$. The last statement is a consequence of Proposition 18. $\square$

Example 20

Let $h(x)=\sin x$. Then

$$\begin{aligned} \mathcal E_i(h)=\sum _{n=1}^{+\infty }\frac{x^n}{n!}\sum _{h=0}^{\left\lfloor n/2-1\right\rfloor }(-1)^h i^{n-2h-2}=\frac{1}{2} x\sin x+\frac{1}{2}\left( \sin x-x\cos x\right) i \end{aligned}$$

solves ${\mathcal {D}}_if=\sin x$, with ${\mathcal {E}}_i(h)(0)=0$. Since h is slice-preserving (its series coefficients $a_n$ are all real), the solution ${\mathcal {E}}_i(h)$ can also be obtained from the complex solution.

Remark 21

The previous example suggests an alternative method to obtain the entire function ${\mathcal {E}}_\lambda (h)$ for a quaternionic function $h\in {\mathcal {A}}_\lambda$. In view of [17, Lemma 6.1], given a real basis $\{1,\jmath ,\kappa ,\delta \}$ of ${\mathbb {H}}$, every quaternionic slice function h can be written as $h=h_0+h_1\jmath +h_2\kappa +h_3\delta$, with $h_i$ slice-preserving functions for $i=0,1,2,3$. Moreover, h is slice-regular on a domain if and only all the functions $h_i$ are. It is also easy to verify that h belongs to ${\mathcal {A}}_\lambda$ if and only if all the components $h_i\in {\mathcal {A}}_\lambda$. If $\lambda \ne 0$, given any real basis $\{\lambda ,\lambda _1,\lambda _2,\lambda _3\}$ of ${\mathbb {H}}$, also the set $\{1,\lambda _1\lambda ^{-1},\lambda _2\lambda ^{-1},\lambda _3\lambda ^{-1}\}$ is a real basis of ${\mathbb {H}}$. Therefore for any function $h\in {\mathcal {A}}_\lambda$ one can write

$$\begin{aligned} h=h_0+h_1(\lambda _1\lambda ^{-1})+h_2(\lambda _2\lambda ^{-1})+h_3(\lambda _3\lambda ^{-1}) \end{aligned}$$

with slice-preserving functions $h_i$ in ${\mathcal {A}}_\lambda$. If $\lambda \in {\mathbb {C}}_I$, the solution $f_i:={\mathcal {E}}_\lambda (h_i)$ of the equation (5) can be obtained for every $i=0,\ldots ,3$ from the complex solution in ${\mathbb {C}}_I$. Observe that the functions $f_i$ are one-slice preserving, since $f_i({\mathbb {C}}_I)\subseteq {\mathbb {C}}_I$. We then have

$$\begin{aligned} {\mathcal {D}}_\lambda (f_0+\textstyle \sum _{i=1}^3(\lambda _i\lambda ^{-1})\cdot f_i)=h_0+\sum _{i=1}^3(\lambda _i\lambda ^{-1})\cdot h_i= h_0+\sum _{i=1}^3 h_i (\lambda _i\lambda ^{-1})=h. \end{aligned}$$

Here we point out that the second equality holds since the functions $h_i$ are slice-preserving. We then obtain that $f=f_0+\textstyle \sum _{i=1}^3(\lambda _i\lambda ^{-1})\cdot f_i$ is the uniquely determined entire solution ${\mathcal {E}}_\lambda (h)$ of (5) that vanishes at the origin.

4 Eigenvalue problems for axially monogenic functions

Let ${\overline{\partial }}$ denotes the Cauchy-Riemann-Fueter operator

$$\begin{aligned}{\overline{\partial }}=\frac{1}{2}\left( \frac{\partial }{\partial x_0}+i\frac{\partial }{\partial x_1}+j\frac{\partial }{\partial x_2}+k\frac{\partial }{\partial x_3}\right) ,\end{aligned}$$

and let $\partial$ be the conjugated operator

$$\begin{aligned}\partial =\frac{1}{2}\left( \frac{\partial }{\partial x_0}-i\frac{\partial }{\partial x_1}-j\frac{\partial }{\partial x_2}-k\frac{\partial }{\partial x_3}\right) .\end{aligned}$$

Let $\Omega$ be an axially symmetric domain of ${\mathbb {H}}$. Our aim is to apply the results of the previous sections to the following eigenvalue problem for the (conjugated) Cauchy-Riemann-Fueter operator $\partial$ in the class of monogenic slice functions (also called Fueter-regular functions in the present quaternionic case):

$$\begin{aligned} {\left\{ \begin{array}{ll}\displaystyle \partial f=f\lambda \quad \text {on}~{ \Omega }\\ \text {with }~f~ \text {slice function s.t.}~{\overline{\partial }}f=0\text { on }~\Omega ~\text { and}~ {\lambda \in {\mathbb {H}}}. \end{array}\right. } \end{aligned}$$

(11)

Eigenvalue problems of the similar form ${\overline{\partial }}f = \lambda f$ have been studied rather extensively within the very general context where f is some arbitrary function simply belonging to the function space $C^1(\Omega )$ without claiming any further conditions or properties on the considerable f neither on the domain $\Omega$.

The solutions of $({\overline{\partial }}- \lambda )f = 0$ where ${\overline{\partial }}$ is the classical quaternionic Cauchy-Riemann-Fueter operator can be described in the form $e^{\lambda x_0} f$ where f is an element of the kernel of ${\overline{\partial }}$, cf. for example [20], where the most general context of polynomial Cauchy-Riemann equations of general integer order n and general multiplicity of the eigenvalues has been addressed extensively in the Clifford analysis setting, but under the assumption that f is a general function from $C^n(\Omega )$. This general treatment also includes the special case of k-monogenic functions considered more than two decades earlier by F. Brackx in [4].

Notice that above we consider slightly differently its conjugated operator $\partial$ and the action of $\lambda$ from the right hand-side.

F. Sommen and Xu Zhenyuan also studied in [29, 31] the analogous equation in the vector formalism where the Dirac operator is considered instead of the Cauchy-Riemann-Fueter operator exploiting decompositions in terms of axially monogenic functions which have been considered in the preceding work [28]. The particular three-dimensional case has already been treated by K. Gürlebeck in [21]. The conjugated Dirac operator coincides with the Dirac operator up to a minus sign. Also this operator is a first order operator factorizing the Laplacian. The connection to the Helmholtz operator has been explicitly addressed in [21]. See also [25] where this topic has been investigated more extensively. Even more generally, one also considered the case where f belongs to a general Sobolev spaces, for instance to $H^1_p(\Omega )$, cf. [22], however again without considering any further (symmetric) conditions.

In our framework we now address the special situation where f has additionally the property of being a slice function defined over an axially symmetric domain $\Omega$. These analytic and geometric aspects are new. This particular context allows us to use special series representations and the special properties of slice functions which do not hold in the general context in the above mentioned papers, as it will be explained in the sequel.

In order to tackle problem (11), we apply Fueter’s Theorem, which can be seen as a bridge between the classes of slice-regular functions and monogenic functions.

We recall a useful concept introduced in [16]. Given a slice function f on $\Omega$, the function $f'_s:\Omega \setminus \mathbb {R}\rightarrow {\mathbb {H}}$, called spherical derivative of f, is defined as

$$\begin{aligned} f'_s(x):=\tfrac{1}{2} {\text {Im}}(x)^{-1}(f(x)-f({\overline{x}})). \end{aligned}$$

The function $f'_s$ is a slice function, constant on 2-spheres  ${\mathbb {S}}_x=\alpha +{\mathbb {S}}\beta$ for any $x=\alpha +J\beta \in \Omega \setminus \mathbb {R}$. For any slice-regular function f on $\Omega$, ${f}'_s$ extends as the slice derivative $\frac{\partial f}{\partial x}$ on $\Omega \cap \mathbb {R}$. We recall also a result proved in [26, Corollary 3.6.2 and Theorem 3.6.3] about some formulas linking the spherical derivative of slice functions with the Cauchy-Riemann-Fueter operator.

Theorem 22

([26]) Let $\Omega$ be an axially symmetric domain in ${\mathbb {H}}$. Let $f:\Omega \rightarrow {\mathbb {H}}$ be a slice function of class $\mathcal {C}^1(\Omega )$. Then

• 1. f is slice-regular if and only if $\,{\overline{\partial }}f=-f'_s$.

• 2. If $f:\Omega \rightarrow {\mathbb {H}}$ is slice-regular, then it holds:

  • a. The four real components of $f'_s$ are harmonic on $\Omega$.

  • b. The following generalization of Fueter’s Theorem holds:

    $$\begin{aligned}{\overline{\partial }}\Delta f=\Delta {\overline{\partial }}f=-\Delta f'_s=0.\end{aligned}$$

  • c. $\Delta f=-4\,\frac{\partial {f}'_s}{\partial x}$.

In the following we will use also the following result.

Lemma 23

(a)   If $f\in \mathcal {SR}(\Omega )$ and $\Delta f=0$, then f is a quaternionic affine function of the form $xa+b$, with $a,b\in {\mathbb {H}}$.

(b)   The Laplacian of a slice-regular function can be expressed by first order derivatives. If $f\in \mathcal {SR}(\Omega )$, for every $x\in \Omega \setminus {\mathbb {R}}$ it holds

$$\begin{aligned} \Delta f&=-2\frac{{\text {Im}}(x)}{|{\text {Im}}(x)|^2}\left( {f}'_s-\frac{\partial f}{\partial x}\right) =2\frac{{\text {Im}}(x)}{|{\text {Im}}(x)|^2}\left( {\overline{\partial }}f+\frac{\partial f}{\partial x}\right) \end{aligned}$$

(12)

$$\begin{aligned}&=\frac{{\text {Im}}(x)}{|{\text {Im}}(x)|^2}\left( 3\frac{\partial f}{\partial x_0}+i\frac{\partial f}{\partial x_1}+j\frac{\partial f}{\partial x_2}+k\frac{\partial f}{\partial x_3}\right) . \end{aligned}$$

(13)

Proof

Let $f=\mathcal {I}(F_1+iF_2)$, $z=\alpha +i\beta$.

(a)   From Theorem 22(2c), it follows that $\frac{\partial {f}'_s}{\partial x}=0$, i.e., ${f}'_s=\mathcal {I}(\beta ^{-1}F_2(\alpha +i\beta ))$ is anti-slice-regular on $\Omega$. Then the function $\beta ^{-1}F_2(\alpha +i\beta )$ is locally constant, i.e., $F_2=\beta a$ with $a\in {\mathbb {H}}$. Since F is holomorphic, it follows that $F(z)=\alpha a+b+i\beta a=za+b$, and $f=\mathcal {I}(F)=xa+b$, with $b\in {\mathbb {H}}$.

(b)   $\Delta f=-4\frac{\partial {f}'_s}{\partial x}=-4\mathcal {I}\left( \frac{\partial }{\partial z}\left( \frac{F_2}{\beta }\right) \right)$ and

$$\begin{aligned} \frac{\partial }{\partial z}\left( \frac{F_2}{\beta }\right) =\frac{1}{2}(\partial _\alpha -i\partial _\beta )\left( \frac{F_2}{\beta }\right) = \frac{1}{2\beta }(\partial _\alpha -i\partial _\beta )F_2+\frac{i}{2\beta ^2}F_2=-\frac{i}{2\beta }\frac{\partial F}{\partial z}+\frac{i}{2\beta ^2}F_2, \end{aligned}$$

since F is holomorphic. Therefore,

$$\begin{aligned} \frac{\partial {f}'_s}{\partial x}=\mathcal {I}\left( \frac{i}{2\beta }\left( \frac{F_2}{\beta }-\frac{\partial F}{\partial z}\right) \right) = \frac{{\text {Im}}(x)}{2|{\text {Im}}(x)|^2}\left( {f}'_s-\frac{\partial f}{\partial x}\right) \end{aligned}$$

and using Theorem 22(1) we get formula (12). Since f is slice-regular, we have $\frac{\partial f}{\partial x}=\frac{\partial f}{\partial x_0}$ (see e.g. [13]). This equality and (12) give formula (13). $\square$

Let $\mathcal {AM}(\Omega )$ denote the class of axially monogenic functions, i.e., of monogenic slice functions on $\Omega$:

$$\begin{aligned}\mathcal {AM}(\Omega )=\{f\in \mathcal {S}^1(\Omega )\,|\,{\overline{\partial }}f=0\}. \end{aligned}$$

In view of the generalized Fueter’s Theorem, the Laplacian maps the space $\mathcal {SR}(\Omega )$ into $\mathcal {AM}(\Omega )$. It is known that this map is surjective (see e.g. [7]). Now we construct an operator $\mathcal {L}:\mathcal {AM}(\Omega )\rightarrow \mathcal {AM}(\Omega )$ which makes the following diagram

commutative. Chosen a right inverse ${\widetilde{\Delta }}:\mathcal {AM}(\Omega )\rightarrow \mathcal {SR}(\Omega )$ of $\Delta$, we can set $\mathcal {L}:=\Delta \circ \frac{\partial }{\partial x}\circ {\widetilde{\Delta }}$. To define ${\widetilde{\Delta }}$, we start from polynomials. For every $n\in {\mathbb {N}}$, let

$$\begin{aligned} \mathcal {P}_n(x):=-\frac{1}{4}\Delta (x^{n+2})= \frac{\partial }{\partial x}{(x^{n+2})}'_s=\frac{\partial \widetilde{{\mathcal {Z}}}_{n+1}(x)}{\partial x}. \end{aligned}$$

(14)

Here $\widetilde{{\mathcal {Z}}}_{n}(x):={(x^{n+1})}'_s$ is a harmonic homogeneous polynomial of degree n in the four real variables $x_0$, $x_1$, $x_2$, $x_3$. The polynomials $\widetilde{{\mathcal {Z}}}_{n}$ are called zonal harmonic polynomials with pole 1, since they have an axial symmetry with respect to the real axis (see [26, 27]). Observe that the polynomials $\mathcal {P}_n$ are axially monogenic but not zonal.

According to our knowledge, zonal monogenics were introduced in [30]. See also [10] where further basic properties have been studied.

Historical remark: Up to a constant the polynomials $\mathcal {P}_n(x)$ were already mentioned in the early work of R. Fueter [11] on p. 316 (Formula (12)) where he looked at series expansions of $\Delta z^n$. Recently, they have been used specifically in the context of slice regular functions for instance in a series of papers by K. Diki et al, see for example [1, 9].

Proposition 24

The polynomials $\mathcal {P}_n$ are axially monogenic homogeneous polynomial of degree n in $x_0$, $x_1$, $x_2$, $x_3$. They are slice functions on ${\mathbb {H}}$, given by the explicit formula

$$\begin{aligned} \mathcal {P}_n(x)=\sum _{k=1}^{n+1}kx^{k-1}\overline{x}^{n-k+1}=\mathcal {I}(\sum _{k=1}^{n+1}kz^{k-1}{\overline{z}}^{n-k+1}). \end{aligned}$$

(15)

In particular, $\mathcal {P}_n$ is slice-preserving and the restriction of $\mathcal {P}_n$ to the real axis is the monomial $\mathcal {P}_n(x_0)=\left( {\begin{array}{c}n+2\\ 2\end{array}}\right) x_0^n$. The inducing stem functions $p_n(z):=\sum _{k=1}^{n+1}kz^{k-1}{\overline{z}}^{n-k+1}$ satisfy the Vekua equation

$$\begin{aligned} \frac{\partial f}{\partial {\overline{z}}}=\frac{f-{\overline{f}}}{z-{\overline{z}}}\text { for}~{ z\in {\mathbb {C}}\setminus {\mathbb {R}}}. \end{aligned}$$

(16)

Proof

The first statement is a consequence of Fueter’s Theorem. Formula (15) follows from [26, Corollary 6.7], since

$$\begin{aligned} \mathcal {P}_n(x)=\frac{\partial }{\partial x}{(x^{n+2})}'_s=\frac{\partial }{\partial x}(\sum _{k=0}^{n+1}x^{k}\overline{x}^{n-k+1})=\sum _{k=1}^{n+1}kx^{k-1}{\overline{x}}^{n-k+1}. \end{aligned}$$

To prove (16), we observe that

$$\begin{aligned} (z-{\overline{z}})\frac{\partial p_n}{\partial {\overline{z}}}&=(z-{\overline{z}})\sum _{k=1}^{n}k(n-k+1)z^{k-1}{\overline{z}}^{n-k}\\&=\sum _{k=1}^{n}k(n-k+1)z^{k}{\overline{z}}^{n-k}-\sum _{k=1}^{n}k(n-k+1)z^{k-1}{\overline{z}}^{n-k+1}\\&=\sum _{k=1}^{n}k(n-k+1)z^{k}\overline{z}^{n-k}-\sum _{k=0}^{n-1}(k+1)(n-k)z^{k}\overline{z}^{n-k}=\sum _{k=0}^{n}(2k-n)z^{k}{\overline{z}}^{n-k}, \end{aligned}$$

while

$$\begin{aligned} p_n(z)-\overline{p_n(z)}&=\sum _{k=1}^{n+1}kz^{k-1}{\overline{z}}^{n-k+1}-\sum _{k=1}^{n+1}k{\overline{z}}^{k-1} z^{n-k+1}\\&=\sum _{k=1}^{n+1}kz^{k-1}{\overline{z}}^{n-k+1}-\sum _{k=1}^{n+1}(n-k+2) z^{k-1}{\overline{z}}^{n-k+1}\\&=\sum _{k=1}^{n+1}(2k-n-2)z^{k-1}\overline{z}^{n-k+1}=\sum _{k=0}^{n}(2k-n)z^{k}{\overline{z}}^{n-k}. \end{aligned}$$

$\square$

Example 25

The first four axially monogenic polynomials $\mathcal {P}_n$ are

$$\begin{aligned}{\left\{ \begin{array}{ll} \mathcal {P}_0(x)=1,\\ \mathcal {P}_1(x)= 3 x_0+x_1i+x_2j+x_3k,\\ \mathcal {P}_2(x)=6 x_0^2 - 2x_1^2 - 2x_2^2 - 2x_3^2+4x_0(x_1i+x_2j+x_3k),\\ \mathcal {P}_3(x)=10x_0(x_0^2-x_1^2-x_2^2-x_3^2)+2(5x_0^2-x_1^2-x_2^2-x_3^2)(x_1i+x_2j+x_3k). \end{array}\right. } \end{aligned}$$

We define ${\widetilde{\Delta }}:\mathcal {AM}({\mathbb {H}})\cap {\mathbb {H}}[x_0,x_1,x_2,x_3]\rightarrow {\mathbb {H}}[x]$ by extending linearly the mapping that associates the monomial $-\frac{1}{4}x^{n+2}$ to the polynomial $\mathcal {P}_n$

$$\begin{aligned} {\widetilde{\Delta }}\left( \textstyle \sum _{n=0}^d\mathcal {P}_n(x)a_n\right) :=-\tfrac{1}{4}\textstyle \sum _{n=0}^d x^{n+2}a_n. \end{aligned}$$

By applying the definitions, it follows that $\Delta {\widetilde{\Delta }}\mathcal {P}_n=\mathcal {P}_n$ for every $n\in {\mathbb {N}}$, while ${\widetilde{\Delta }}\Delta x^n=x^n$ for every integer $n\ge 2$, and of course ${\widetilde{\Delta }}\Delta x^n=0$ for $n=0,1$.

The mapping ${\widetilde{\Delta }}$ can be extended linearly to convergent series $\sum _{n\in {\mathbb {N}}}\mathcal {P}_n(x)a_n\in \mathcal {AM}(\Omega )$. If $f(x)=\sum _{n\in {\mathbb {N}}}\mathcal {P}_n(x)a_n$, then $f(x_0)=\sum _{n\in {\mathbb {N}}}\left( {\begin{array}{c}n+2\\ 2\end{array}}\right) x_0^na_n$ for real $x_0$. Therefore

$$\begin{aligned}a_n=\frac{2}{(n+2)!}\frac{\partial ^n f}{\partial x_0^n}(0)\hbox { for}\ n\in {\mathbb {N}}\end{aligned}$$

and we can write

$$\begin{aligned} {\widetilde{\Delta }}(f)=-\frac{1}{2}\sum _{n\in {\mathbb {N}}} \frac{x^{n+2}}{(n+2)!}\frac{\partial ^n f}{\partial x_0^n}(0). \end{aligned}$$

Proposition 26

Let $\mathcal {L}=\Delta \circ \frac{\partial }{\partial x}\circ {\widetilde{\Delta }}:\mathcal {AM}(\Omega )\rightarrow \mathcal {AM}(\Omega )$. Then it holds $\mathcal {L}(\mathcal {P}_n)=(n+2)\mathcal {P}_{n-1}$ and $\partial \mathcal {P}_n=(n+2)\mathcal {P}_{n-1}$ for every $n\in {\mathbb {N}},n\ge 1$. As a consequence, $\mathcal {L}$ coincides with the conjugated Cauchy-Riemann-Fueter operator $\partial$ on $\mathcal {AM}(\Omega )$.

Proof

By direct computation, using Theorem 22(2c) and Definition (14), we get

$$\begin{aligned} \Delta \left( \frac{\partial ({\widetilde{\Delta }}\mathcal {P}_n)}{\partial x}\right) =-\frac{1}{4}\Delta \left( \frac{\partial x^{n+2}}{\partial x}\right) = -\frac{1}{4}\Delta \left( (n+2)x^{n+1}\right) =(n+2)\frac{\partial {(x^{n+1})}'_s}{\partial x}, \end{aligned}$$

that is $\mathcal {L}(\mathcal {P}_n)=(n+2)\mathcal {P}_{n-1}$. On the other hand, since $\mathcal {P}_n$ is in the kernel of ${\overline{\partial }}$, it holds

$$\begin{aligned}\partial \mathcal {P}_n=(\partial +{\overline{\partial }})\mathcal {P}_n=\frac{\partial \mathcal {P}_n}{\partial x_0}=-\frac{1}{4}\frac{\partial (\Delta x^{n+2})}{\partial x_0}=-\frac{1}{4}\Delta \left( \frac{\partial x^{n+2}}{\partial x_0}\right) . \end{aligned}$$

Since $x^{n+2}$ is slice-regular, we have $\frac{\partial x^{n+2}}{\partial x_0}=\frac{\partial x^{n+2}}{\partial x}$ (see e.g. [13]) and then as before

$$\begin{aligned} \partial \mathcal {P}_n=-\frac{1}{4}\Delta \left( \frac{\partial x^{n+2}}{\partial x}\right) =(n+2)\mathcal {P}_{n-1} \end{aligned}$$

for every integer $n\ge 1$. $\square$

Remark 27

Definition (14) can be extended to negative indices $n\in {\mathbb {Z}}$. One obtains axially monogenic functions $\mathcal {P}_n\in \mathcal {AM}({\mathbb {H}}\setminus \{0\})$ that satisfy the same relation as in the case $n\ge 0$: $\partial \mathcal {P}_n=(n+2)\mathcal {P}_{n-1}$ for every $n<0$. This property is also known under the term Appell property and has been studied for instance in [23] and in follow-up works, see for instance [1, 9] where the slice-regular setting is addressed. Observe that $\mathcal {P}_{-1}=\mathcal {P}_{-2}=0$. The functions $\mathcal {P}_n$ and $\mathcal {P}_{-n}$ are related through the Kelvin transform of ${\mathbb {R}}^4$ (see [26, Prop.5.1(c)]). It follows that also for negative n the $\mathcal {P}_n$’s are homogeneous of degree n.

Proposition 26 implies that the following diagram

is commutative, since it holds $\mathcal {L}\circ \Delta (x^n)=\partial \circ \Delta (x^n)=\Delta \circ \frac{\partial x^n}{\partial x}$ for every $n\in {\mathbb {N}}$.

Let $\lambda \in {\mathbb {H}}$ and let $\mathcal {L}_\lambda =\mathcal {L}-R_\lambda =\partial -R_\lambda$ denote the linear operator mapping a function $f\in \mathcal {AM}(\Omega )$ to the monogenic slice function

$$\begin{aligned}\mathcal {L}_\lambda f=\partial f -f\lambda .\end{aligned}$$

The solutions of the eigenvalue problem (11) are exactly the elements of the kernel of $\mathcal {L}_\lambda$. Notice that $\mathcal {L}_\lambda =\Delta \circ {\mathcal {D}}_\lambda \circ {\widetilde{\Delta }}$ and that $\mathcal {L}_\lambda \circ \Delta =\Delta \circ {\mathcal {D}}_\lambda$ for every $\lambda \in {\mathbb {H}}$. From this relation and Proposition 3 we can deduce the following characterization of $\ker (\mathcal {L}_\lambda )$.

Proposition 28

The axially monogenic function $\Delta \exp _\lambda (x)\in \mathcal {AM}({\mathbb {H}})$ is a solution of (11) on ${\mathbb {H}}$. If $\lambda \ne 0$ and $\Omega$ is a slice domain, a function $f\in \mathcal {AM}(\Omega )$ is a solution of (11) if and only if $f=c\cdot \Delta \exp _\lambda (x)$, with $c\in {\mathbb {H}}$. If $\lambda =0$, $\ker (\mathcal {L})$ contains only the constants. If $\Omega$ is a product domain and $\lambda \ne 0$, the operator $\mathcal {L}_\lambda$ on $\mathcal {AM}(\Omega )$ has kernel

$$\begin{aligned} \ker (\mathcal {L}_\lambda )=\{\Delta (g\cdot \exp _\lambda (x))\;|\; g\in \mathcal {SC}(\Omega )\}. \end{aligned}$$

If $\lambda =0$, $\ker (\mathcal {L})=\{c+\Delta g\;|\;c\in {\mathbb {H}}, g\in \mathcal {SC}(\Omega )\}$. The function $\Delta \exp _\lambda (x)$ has the following expansion

$$\begin{aligned} \Delta \exp _\lambda (x)=-4\sum _{n=0}^{+\infty }\mathcal {P}_n(x)\frac{\lambda ^{n+2}}{(n+2)!}=-4\sum _{n=0}^{+\infty }\sum _{k=1}^{n+1}kx^{k-1}\overline{x}^{n-k+1}\frac{\lambda ^{n+2}}{(n+2)!}. \end{aligned}$$

Proof

Let $\lambda \ne 0$. The equality ${\mathcal {D}}_\lambda f=0$ implies that $\mathcal {L}_\lambda (\Delta f)=0$. Conversely, if $\mathcal {L}_\lambda (\Delta f)=\Delta ({\mathcal {D}}_\lambda f)=0$, with $f\in \mathcal {SR}(\Omega )$, then the function ${\mathcal {D}}_\lambda f$ is a quaternionic affine function of the form $xa+b$, with $a,b\in {\mathbb {H}}$ (Lemma 23). From Proposition 6 it follows that $f=-a\lambda ^{-2}-b\lambda ^{-1}-x(a\lambda ^{-1})$, up to an element of $\ker ({\mathcal {D}}_\lambda )$. Therefore $\Delta f=\Delta g$, with $g\in \ker ({\mathcal {D}}_\lambda )$. If $\Omega$ is a slice domain, then $\Delta f=\Delta (c\cdot \exp _\lambda (x))=c\cdot \Delta \exp _\lambda (x)$, with $c\in {\mathbb {H}}$. If $\Omega$ is a product domain, then $\Delta f=\Delta (g\cdot \exp _\lambda (x))$, with $g\in \mathcal {SC}(\Omega )$.

If $\lambda =0$ and $\mathcal {L}(\Delta f)=0$, then $\Delta (\frac{\partial f}{\partial x})=0$ and therefore $\frac{\partial f}{\partial x}=xa+b$ is affine. Since $f\in \mathcal {SR}(\Omega )$, it follows that $f=x^2 a/2+bx+c+g$, with $a,b,c\in {\mathbb {H}}$ and $g\in \mathcal {SR}(\Omega )\cap \ker (\frac{\partial }{\partial x})=\mathcal {SC}(\Omega )$. If $\Omega$ is a slice domain, we get that $\Delta f$ is a constant. If $\Omega$ is a product domain, $\Delta f=-2a+\Delta g$, with $g\in \mathcal {SC}(\Omega )$ and then $\ker (\mathcal {L})=\{c+\Delta g\;|\;c\in {\mathbb {H}}, g\in \mathcal {SC}(\Omega )\}$. $\square$

Example 29

Since $\exp _j(x)=\cos x+(\sin x)j$, from Lemma 23 it follows that

$$\begin{aligned} \Delta \exp _j(x) =-2\tfrac{{\text {Im}}(x)}{|{\text {Im}}(x)|^2}\left( {(\cos x)}'_s+{(\sin x)}'_sj+\sin x-(\cos x) j\right) . \end{aligned}$$

A direct computation shows that

$$\begin{aligned} {(\cos x)}'_s=\frac{e^{-\beta }-e^\beta }{2\beta }\sin (x_0),\quad {(\sin x)}'_s=\frac{e^{\beta }-e^{-\beta }}{2\beta }\cos (x_0), \end{aligned}$$

where $\beta =\sqrt{x_1^2+x_2^2+x_3^2}$. The axially monogenic function $\Delta \exp _j(x)$ on ${\mathbb {H}}$ satisfies $\mathcal {L}_j(\Delta \exp _j(x))=0$, i.e., $\partial (\Delta \exp _j(x))=\Delta \exp _j(x)j$.

Remark 30

If $\Omega ={\mathbb {H}}\setminus {\mathbb {R}}$, a product domain, the results of Proposition 28 can be made more explicit. Let $I\in {\mathbb {S}}$ and $\mu _I\in \mathcal {SC}({\mathbb {H}}\setminus {\mathbb {R}})$ as in (1). The equality $\Delta \mu _I=-\frac{{\text {Im}}(x)}{|{\text {Im}}(x)|^3}I$ and formula (2) imply that

$$\begin{aligned}\ker (\mathcal {L})=\ker (\partial )\cap \ker ({\overline{\partial }})=\left\{ a+\tfrac{{\text {Im}}(x)}{|{\text {Im}}(x)|^3}b\;|\;a,b\in {\mathbb {H}}\right\} ,\end{aligned}$$

while for $\lambda \ne 0$ the elements of $\ker (\mathcal {L}_\lambda )$ are ${\mathbb {H}}$-linear combinations of functions of the form

$$\begin{aligned} \Delta (\mu _I\cdot \exp _\lambda (x))=\sum _{n=0}^{+\infty }\Delta (x^n\mu _I(x))\frac{\lambda ^n}{n!}. \end{aligned}$$

Now consider the non-homogeneous equation (5), with $f,h\in \mathcal {SR}(\Omega )$. The equality ${\mathcal {D}}_\lambda f=h$ implies that $\mathcal {L}_\lambda (\Delta f)=\Delta h$. Conversely, if $\mathcal {L}_\lambda (\Delta f)=\Delta h$ for $f,h\in \mathcal {SR}(\Omega )$, then $\Delta ({\mathcal {D}}_\lambda f-h)=0$ and thanks to Lemma 23 the function ${\mathcal {D}}_\lambda f-h$ is a quaternionic affine function of the form $xa+b$, with $a,b\in {\mathbb {H}}$. If $h\in {\mathbb {H}}[x]$ and $\lambda \ne 0$, then Proposition 6 gives $f={\mathcal {S}}_\lambda (h+xa+b)+g={\mathcal {S}}_\lambda (h)+xa'+b'+g$, with $a',b'\in {\mathbb {H}}$ and $g\in \ker ({\mathcal {D}}_\lambda )$. Here ${\mathcal {S}}_\lambda$ is the solution operator defined in (6). Therefore $\Delta f=\Delta {\mathcal {S}}_\lambda (h)+\Delta g$, with $g\in \ker ({\mathcal {D}}_\lambda )$.

4.1 Eigenvalue problem of the mth-order for axially monogenic functions

Now we generalize Proposition 28 to eigenvalue problems of any order m. Let $\lambda _1,\ldots ,\lambda _m\in {\mathbb {H}}$ and consider the equation

$$\begin{aligned} {\left\{ \begin{array}{ll}\displaystyle {\mathcal {L}}_{\lambda _{1}}\cdots {\mathcal {L}}_{\lambda _{m}} f=0\hbox { on}\ \Omega ,\\ \text {with }f\in \mathcal {AM}(\Omega ). \end{array}\right. } \end{aligned}$$

(17)

Definition 31

The generalized $\Delta$-exponential function associated with the n-tuple $\Lambda =(\lambda _1,\ldots ,\lambda _m)\in {\mathbb {H}}^n$ is the axially monogenic function $E^\Delta _\Lambda (x)$ defined on ${\mathbb {H}}$ by

$$\begin{aligned} E^\Delta _\Lambda (x):=\Delta (E_\Lambda (x))=-4\sum _{n=m-1}^{+\infty }\frac{\mathcal {P}_{n-2}(x)}{n!}\sum _{|K|=n-m+1}\lambda _1^{k_1}\cdots \lambda _m^{k_m}, \end{aligned}$$

where the sum is extended over the multi-indices $K=(k_1,\ldots ,k_m)$ of non-negative integers such that $|K|=k_1+\cdots +k_m=n-m+1$. In particular, it holds $E^\Delta _{(\lambda )}=\Delta \exp _{\lambda }(x)$ for every $\lambda \in {\mathbb {H}}$.

In view of formula (15), we have

$$\begin{aligned} E^\Delta _\Lambda (x)=-4\sum _{n=m-1}^{+\infty }\frac{1}{n!}\sum _{k=1}^{n-1}kx^{k-1}\overline{x}^{n-k-1} \sum _{|K|=n-m+1}\lambda _1^{k_1}\cdots \lambda _m^{k_m}. \end{aligned}$$

Observe that for real values $\lambda$, the $\Delta$-exponential $E^\Delta _{(\lambda )}(x)$ coincides up to a multiplicative constant with the function $\text {EXP}_3(\lambda x)$ defined in [24, Ex.11.34] in the context of Clifford algebras:

$$\begin{aligned} E^\Delta _{(\lambda )}(x)=-2e^{\lambda x_0}({\text {sinc}}(\lambda \beta )-I_x(({\text {sinc}}(\lambda \beta ))') \end{aligned}$$

where $I_x=\tfrac{{\text {Im}}(x)}{|{\text {Im}}(x)|}$, $\beta =|{\text {Im}}(x)|$, $\lambda \in {\mathbb {R}}$.

Proposition 32

The axially monogenic function $E^\Delta _\Lambda \in \mathcal {AM}({\mathbb {H}})$ is a solution of (17). In general, every function of the form

$$\begin{aligned} \sum _{i=1}^m \Delta (h_i\cdot E_{(\lambda _i,\ldots ,\lambda _m)}), \end{aligned}$$

(18)

with $h_i\in \mathcal {SC}(\Omega )$, is a solution of (17). If $\lambda _i\ne 0$ for every $i=1,\ldots ,m$, all the solutions of (17) are of the form (18).

Proof

The first two statements follow immediately from Corollary 15:

$$\begin{aligned} {\mathcal {L}}_{\lambda _{1}}\cdots {\mathcal {L}}_{\lambda _{m}}(E^\Delta _\Lambda )={\mathcal {L}}_{\lambda _{1}}\cdots {\mathcal {L}}_{\lambda _{m}}(\Delta (E_\Lambda ))=\Delta ({\mathcal {D}}_{\lambda _{1}}\cdots {\mathcal {D}}_{\lambda _{m}}E_\Lambda )=0. \end{aligned}$$

The same computation holds for every function of the form (18).

Assume that $\lambda _i\ne 0$ for every i and that ${\mathcal {L}}_{\lambda _{1}}\cdots {\mathcal {L}}_{\lambda _{m}}(\Delta g)=0$. Then it holds $\Delta ({\mathcal {D}}_{\lambda _{1}}\cdots {\mathcal {D}}_{\lambda _{m}}g)=0$, which implies by Lemma 23 that ${\mathcal {D}}_{\lambda _{1}}\cdots {\mathcal {D}}_{\lambda _{m}}g$ is a quaternionic affine function of the form $xa+b$, with $a,b\in {\mathbb {H}}$. Therefore we have

$$\begin{aligned} {\mathcal {D}}_{\lambda _{1}}\cdots {\mathcal {D}}_{\lambda _{m}}g=xa+b={\mathcal {D}}_{\lambda _{1}}\cdots {\mathcal {D}}_{\lambda _{m}}\mathcal {S}_{\lambda _m}\cdots \mathcal {S}_{\lambda _1}(xa+b), \end{aligned}$$

where ${\mathcal {S}}_\lambda$ is the right inverse of ${\mathcal {D}}_\lambda$ on polynomials defined for any $\lambda \ne 0$ in (6). By definition, also $\mathcal {S}_{\lambda _m}\cdots \mathcal {S}_{\lambda _1}(xa+b)$ is an affine polynomial $xa'+b'$. Then $g-xa'-b'\in \ker ({\mathcal {D}}_{\lambda _{1}}\cdots {\mathcal {D}}_{\lambda _{m}})$ and thanks to Corollary 15, $f=\Delta g$ is of the form (18). $\square$

Example 33

Let $\lambda _1=i$, $\lambda _2=j$. The solution of $\mathcal D_i{\mathcal {D}}_jg=0$ on ${\mathbb {H}}$ given in Examples 10 is the slice-regular entire function

$$\begin{aligned} E_{(i,j)}(x)=\frac{1}{2}\left( \sin x+x\cos x+(x\sin x)(i+j)+(\sin x-x\cos x)k\right) . \end{aligned}$$

Therefore $f:=\Delta E_{(i,j)}(x)=E^\Delta _{(i,j)}(x)$ is an axially monogenic solution of the equation $\mathcal {L}_i\mathcal {L}_j f=0$, that is

$$\begin{aligned} (\partial -R_i)(\partial -R_j)f = \partial ^2 f-(\partial f)(i+j)-fk=0. \end{aligned}$$

5 Applications

As a very interesting bi-product we can relate the solutions to ${\mathcal {L}}_{\lambda _{1}}{\mathcal {L}}_{\lambda _{2}} f = 0$ to axially monogenic solutions to the 3D and 4D time-harmonic Helmholtz and stationary massless Klein-Gordon equation considered in an axially symmetric domain. In the sequel we abbreviate for convenience the purely quaternionic part of the Cauchy-Riemann-Fueter operator by ${\mathcal {D}}_x := i \frac{\partial }{\partial x_1} + j \frac{\partial }{\partial x_2} + k \frac{\partial }{\partial x_3}$. Actually, ${\mathcal {D}}_x$ is often called the Euclidean Dirac operator and it satisfies ${\mathcal {D}}_x^2 = - \Delta _3$, where $\Delta _3$ is the ordinary Euclidean Laplacian in $\mathbb {R}^3={\text {Im}}({\mathbb {H}})$. Notice that $\overline{\partial } \partial = \frac{1}{4} \Delta _4$, where $\Delta _4$ now represents the Laplacian in $\mathbb {R}^4$, cf. for example [22] and many other classical textbooks on quaternionic and Clifford analysis, such as also [5] and others. In this section we use the symbol $\Delta _4$ instead of $\Delta$ as in the previous section to avoid confusion with $\Delta _3$. As a direct consequence of Proposition 32 we can establish

Proposition 34

Suppose that f is an axially monogenic solution to ${\mathcal {L}}_{\lambda _{1}}{\mathcal {L}}_{\lambda _{2}} f = 0$ on some axially symmetric domain $\Omega \subset \mathbb {H}$.

• (a) Let $I\in {\mathbb {S}}$ be any imaginary unit. In the particular case where we take $\lambda _1 = I \lambda$ and $\lambda _2 = - I \lambda$ where $\lambda$ is a non-zero real number, the solutions to $\mathcal {L}_{I\lambda }\mathcal {L}_{-I\lambda } f = 0$ are axially monogenic solutions to the massless stationary Klein-Gordon equation $(\Delta _3 - \lambda ^2) f = 0$ on $\Omega ^{*} := \Omega \cap \mathbb {R}^3$. For any finite subset A of ${\mathbb {S}}$, the functions of the form

  $$\begin{aligned} f(x)=\sum _{I\in A}\Delta _4(h_I\cdot \exp _{I\lambda }(x)), \end{aligned}$$

  where $h_I\in \mathcal {SC}(\Omega )$, are axially monogenic solutions of the Klein-Gordon equation.

• (b) In the other particular case we take $\lambda _1 = \lambda$ and $\lambda _2 =- \lambda$ where again $\lambda$ is supposed to be a non-zero real value, the solutions to $\mathcal {L}_{\lambda }\mathcal {L}_{-\lambda } f = 0$ are axially monogenic solutions to the time-harmonic Helmholtz equation $(\Delta _3 + \lambda ^2) f = 0$ on $\Omega ^{*} := \Omega \cap \mathbb {R}^3$. For every $h_1,h_2\in \mathcal {SC}(\Omega )$, the function

  $$\begin{aligned} f(x)=\Delta _4(h_1\cdot \exp _{\lambda }(x))+\Delta _4(h_2\cdot \exp _{-\lambda }(x)) \end{aligned}$$

  is an axially monogenic solution of the Helmholtz equation.

Proof

Since f is monogenic and consequently also an element in the kernel of $\Delta _4$, it holds

$$\begin{aligned} \mathcal {D}_xf=-\partial _{x_0}f\quad \text {and}\quad \partial ^2_{x_0}f=-\Delta _3f. \end{aligned}$$

It follows that

$$\begin{aligned} \partial ^2f&=\frac{1}{4}(\partial _{x_0}-{\mathcal {D}}_x)(\partial _{x_0}-{\mathcal {D}}_x)f=\frac{1}{4}(\partial ^2_{x_0}f-\partial _{x_0}{\mathcal {D}}_xf-{\mathcal {D}}_x\partial _{x_0}f+{\mathcal {D}}_x^2 f)\\&=\frac{1}{4}(3\partial ^2_{x_0}f-\Delta _3f)=-\Delta _3f, \end{aligned}$$

and then

$$\begin{aligned} \mathcal {L}_{\lambda _1}\mathcal {L}_{-\lambda _1}f&=(\partial -R_{\lambda _1})(\partial -R_{-\lambda _1})f\\&=\partial ^2f - \underbrace{\partial f( \lambda _1 - \lambda _1)}_{=0} - f\lambda _1^2\\&=-\Delta _3f-f\lambda _1^2. \end{aligned}$$

We first treat the case announced in statement (a): Putting $\lambda _{1,2} = \pm I \lambda$, with $I\in {\mathbb {S}}$, one obtains that

$$\begin{aligned} 0=\mathcal {L}_{I\lambda }\mathcal {L}_{-I\lambda }f=-\Delta _3f+\lambda ^2 f. \end{aligned}$$

Analogously one obtains in the other case the statement (b) by inserting $\lambda _{1,2} = \pm \lambda$, namely

$$\begin{aligned} 0=\mathcal {L}_{\lambda }\mathcal {L}_{-\lambda }f=-\Delta _3f-\lambda ^2 f. \end{aligned}$$

Since we are in the case of commuting eigenvalues, in view of Proposition 32 and Remark 16(3), the general axially monogenic solution of the equation $\mathcal {L}_{\lambda _1}\mathcal {L}_{-\lambda _1}f=0$ is of the form

$$\begin{aligned} g(x)=\Delta _4(h_1\cdot \exp _{\lambda _1}(x))+\Delta _4(h_2\cdot \exp _{-\lambda _1}(x)), \end{aligned}$$

with $h_1$ and $h_2\in \mathcal {SC}(\Omega )$. This implies the last statements of items (a) and (b). $\square$

Example 35

The axially monogenic function $f(x)=\Delta _4\exp _1(x)=\Delta _4e^x$, restricted to ${\text {Im}}({\mathbb {H}})={\mathbb {R}}^3$, satisfies the equation $\Delta _3f+f=0$ on ${\mathbb {R}}^3$, while the function $g(x)=\Delta _4\exp _j(x)$ of Example 29 satisfies the equation $\Delta _3g-g=0$.

Another solution of the Helmholtz equation $\Delta _3f+f=0$ on ${\mathbb {R}}^3\setminus \{0\}={\mathbb {R}}^3\cap ({\mathbb {H}}\setminus {\mathbb {R}})$ is given by the axially monogenic function (see Remark 30)

$$\begin{aligned} f(x)=\Delta _4(\mu _i\cdot \exp _1(x))=\sum _{n=0}^{+\infty }\frac{\Delta _4(x^n\mu _i(x))}{n!}, \end{aligned}$$

while the axially monogenic function

$$\begin{aligned} g(x)=\Delta _4(\mu _i\cdot \exp _j(x))=\sum _{n=0}^{+\infty }\Delta _4(x^n\mu _i(x))\frac{j^n}{n!} \end{aligned}$$

is a solution of the Klein-Gordon equation $\Delta _3g-g=0$ on ${\mathbb {R}}^3\setminus \{0\}$.

Remark 36

The two cases considered in Proposition 34 are included in the more general case $\lambda _1=-\lambda _2=\alpha +\beta I\in {\mathbb {H}}$, with $\alpha ,\beta$ real and $I\in {\mathbb {S}}$. If $f\in \mathcal {AM}(\Omega )$, it holds $\mathcal {L}_{\lambda _1}\mathcal {L}_{-\lambda _1}f=0$ if and only if

$$\begin{aligned} \Delta _3f+(\alpha ^2-\beta ^2)f+(2\alpha \beta )fI=0. \end{aligned}$$

Remark 37

The Klein-Gordon equation is the homogeneous equation associated to the Yukawa equation $\Delta _3 f-\lambda ^2 f=h$, with $\lambda$ real. If g is slice-regular on $\Omega$, $h:=-\Delta _4g$ and $I\in {\mathbb {S}}$, then $h\in \mathcal {AM}(\Omega )$ and every slice-regular solution ${\tilde{f}}$ of the equation ${\mathcal {D}}_{I\lambda }{\mathcal {D}}_{-I\lambda }{\tilde{f}}=g$ gives a solution $f:=\Delta _4{\tilde{f}}$ of the equation $\mathcal {L}_{I\lambda }\mathcal {L}_{-I\lambda } f=\Delta _4 g$, which is the Yukawa equation $\Delta _3f-\lambda ^2 f=h$.

For example, if $h\in {\mathbb {H}}[x_0,x_1,x_2,x_3]$ is an axially monogenic polynomial and $g:=-{\widetilde{\Delta }} h\in {\mathbb {H}}[x]$, where ${\widetilde{\Delta }}$ is the right inverse of $\Delta _4$ defined in the previous section, then ${\tilde{f}}$ can be obtained by means of the right inverses operators ${\mathcal {S}}_{\pm I\lambda }$ of $\mathcal D_{\pm I\lambda }$ introduced in (6): ${\tilde{f}}=\mathcal S_{-I\lambda }{\mathcal {S}}_{I\lambda }(g)$. We then get that

$$\begin{aligned}f:=-\Delta _4{\mathcal {S}}_{-I\lambda }{\mathcal {S}}_{I\lambda }({\widetilde{\Delta }} h) \end{aligned}$$

is an axially monogenic solution of the Yukawa equation with right-hand h.

Example 38

Let $h(x)=\mathcal {P}_3(x)-\mathcal {P}_2(x)(i+j+k)+\mathcal {P}_1(x)(i-j+k)+1$. Then $h(x)=-\frac{1}{4}\Delta _4(x^2(x-i)\cdot (x-j)\cdot (x-k))$. We take $\lambda =1$, $I=i$. A direct computation shows that the solution

$$\begin{aligned} f=\tfrac{1}{4}\Delta _4{\mathcal {S}}_{-i\lambda }\mathcal S_{i\lambda }(x^2(x-i)\cdot (x-j)\cdot (x-k)) \end{aligned}$$

of the Yukawa equation $\Delta _3 f-f=h$ has the form

$$\begin{aligned} f(x)=-\mathcal {P}_3(x)+\mathcal {P}_2(x)(i+j+k)+\mathcal {P}_1(x)(20-i+j-k)-1-12(i+j+k). \end{aligned}$$