Abstract
The convolution of two weighted balls of measures is proved to be contained in a third weighted ball if and only if the supremal convolution of the corresponding two weights is less than or equal to the third weight. Here supremal convolution is introduced as a type of convolution in which integration is replaced with supremum formation. Invoking duality the equivalence implies a characterization of equicontinuity of weight-bounded sets of convolution operators having weighted spaces of continuous functions as domain and range. The overall result is a constructive method to define weighted spaces on which a given set of convolution operators acts as an equicontinuous family of endomorphisms. The result is applied to linear combinations of fractional Weyl integrals and derivatives with orders and coefficients from a given bounded set.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Although necessary and sufficient conditions are known, that make fractional integration a bounded operator between weighted (Lebesgue) spaces, (see [25, 28, 31,32,33] and references therein), applications, extensions and generalizations of weighted convolution inequalities continue to attract widespread interest in potential analysis and its applications to partial differential equations [3, 6, 13,14,15,16,17, 21, 27, 35, 36]. Deviating from the traditional focus on Banach spaces and fractional Riesz integrals, the present article studies weighted convolution algebras of Radon measures and fractional Weyl integrals operating as equicontinuous families of linear endomorphisms on weighted locally convex spaces of continuous functions.
Mathematically, the main objective of this article is to introduce and prove certain weighted norm inequalities for convolution operators given in our Theorems 5 and 6. A known example and special case of Theorem 5 applies to Radon measures from the set \(\mathfrak {M}(w)\) of measures on a locally compact group G with finite norm  , where \(\int ^{\bullet }\) denotes the essential upper integral of w with respect to the absolute value \(|{\mu }|\) of \(\mu \). In [8, Chapter 6] and [10, Section 4], the weighted norm inequality
, where \(\int ^{\bullet }\) denotes the essential upper integral of w with respect to the absolute value \(|{\mu }|\) of \(\mu \). In [8, Chapter 6] and [10, Section 4], the weighted norm inequality

is shown to be equivalent to “submultiplicativity” of the lower semicontinuous weight \(w:G\rightarrow \mathbb {R}^+:=[0,{\infty ^+})\). One calls a weight w submultiplicative, if
holds for all \(x,y\in G\). Recall from [8, 10], that  becomes a Banach convolution algebra of measures, if inequality (1.1) or equivalently (1.2) holds. Extensions and generalizations were obtained in [1, 9, 19] for \(L^p\)-algebras, \(1<p<\infty \), instead of measure algebras.
becomes a Banach convolution algebra of measures, if inequality (1.1) or equivalently (1.2) holds. Extensions and generalizations were obtained in [1, 9, 19] for \(L^p\)-algebras, \(1<p<\infty \), instead of measure algebras.
Define the (multiplicative) supremal convolution of two arbitrary weight functions \(w,v:G\rightarrow \mathbb {R}^{+\infty }\) as

with the convention \(0\cdot \infty =\infty \cdot 0=0\), and let

denote their infimal convolution. Expressing the inequality (1.2) equivalently in terms of infimal convolution

hints at the fundamental role played by supremal and/or infimal convolution for weighted convolution inequalities. In the literature, the additive variant of infimal convolution has been studied as “inf-convolution” or “epi-addition” in the context of convex analysis [24, 30].
Given the equivalence (1.1) \(\Longleftrightarrow \) (1.2) \(\Longleftrightarrow \) (1.5), it is natural to investigate its extension to triples of weights (w, v; u) or triples of sets of weights (W, V; U). Let \(w[\mathfrak {M}]\) denote the subset of measures in \(\mathfrak {M}(w)\) obeying \(\int ^{\bullet }(1/w(x))\,\mathrm {d}|\mu |(x)\le 1\). Our Theorem 5 shows that the inequality  is equivalent to \(w[\mathfrak {M}]*v[\mathfrak {M}]\subseteq u[\mathfrak {M}]\) for locally bounded \(w,v,u:G\rightarrow \mathbb {R}^+\). Regarding existence of \(w[\mathfrak {M}]*v[\mathfrak {M}]\), this is shown to be equivalent to local boundedness of
is equivalent to \(w[\mathfrak {M}]*v[\mathfrak {M}]\subseteq u[\mathfrak {M}]\) for locally bounded \(w,v,u:G\rightarrow \mathbb {R}^+\). Regarding existence of \(w[\mathfrak {M}]*v[\mathfrak {M}]\), this is shown to be equivalent to local boundedness of  . In Theorem 5, the equivalence
. In Theorem 5, the equivalence

is proved, where \(\mathcal {C}_\mathrm {v}[w]\) denotes the space of all continuous functions \({f:G\rightarrow \mathbb {C}}\) with \(w|f|\le 1\) and such that \(w|f|\) vanishes at infinity. Assumptions for (1.6) require that the weights are upper semicontinuous and locally bounded away from zero. More equivalences and inclusions are provided in the precise formulation of Theorem 5.
A preliminary formulation of Theorem 6 highlights the role played by (1.3) for the characterization of convolution as a bounded bilinear operation. Let (W, V; U) be a triple of sets, each consisting of upper semicontinuous functions, that contain all upper semicontinuous functions u such that \(u\le \lambda \max \{w,v\}\) for some \(\lambda \in \mathbb {R}^+\), \(w,v\in W\). Convolution is a well-defined bounded bilinear operation
if and only if

Here \(W(\mathfrak {M})=\bigcup _{w\in W}w[\mathfrak {M}]\) is the space of W-finite measures and \(\mathscr {K}_{W}\) is the bornology consisting of the sets of measures M with \(M\subseteq w[\mathfrak {M}]\) for some \({w\in W}\). The brackets \(\left\lceil \,\cdot \,\right\rceil \) denote upper semicontinuous envelope formation. Assuming \(\chi _K\in W,V,U\) for all compact \(K\subseteq G\), each of (1.7a) and (1.7b) is equivalent to

being a well-defined linear mapping such that bounded sets are mapped to equicontinuous sets of continuous linear operators \(\left( \mathcal {C}_\mathrm {v}(U),\mathscr {T}_{U}\right) \rightarrow \left( \mathcal {C}_\mathrm {v}(V),\mathscr {T}_{V}\right) \). Here \(\mathcal {C}_\mathrm {v}(W)\) denotes the set of continuous functions on G with \(w|f|\) vanishing at infinity for all \(w\in W\) and \(\mathscr {T}_{W}\) is the locally convex topology generated by the weighted supremum norms \(f\mapsto \Vert f\Vert _w:=\sup \{w(x)|f(x)|:x\in G\}\), \(w\in W\). Reflection is denoted by  , \(x\in G\) and \(\chi _K\) is the characteristic function of \(K\subseteq G\).
, \(x\in G\) and \(\chi _K\) is the characteristic function of \(K\subseteq G\).
It is natural to regard (1.7) as a mere consequence of (1.6). But giving a proof of (1.7) requires to drop the positivity assumption on the weights in (1.6). This forces us to deal with convolutes \((\mu *f)(x)\) that can diverge for some or even all \(x\in G\), and in turn, to deal with integrals of \(\mathbb {C}^\infty \)-valued measurable functions that are allowed to diverge. A whole section for notations and results concerning this difficulty has been incorporated to ensure transparency. A byproduct of these preparations is Theorem 2. It guarantees universal measurability of the convolute \(\mu *f\) whenever \(\mu \) is a moderated measure and f a universally measurable \(\mathbb {C}^\infty \)-valued function.
The paper is organized as follows. Basic notations and conventions are summarized in Sect. 2. This includes a discussion of extended arithmetics. Section 3 treats supremal images as preparation for Sect. 4 where basic properties of supremal convolution on locally compact groups are summarized. Section 5 discusses deconvolution. Section 6 provides definitions and results concerning integration of extended \(\mathbb {K}^\infty \)-valued functions that are needed for Theorems 5 and 6. Theorem 5 is stated and proved in Sect. 7, where results on images and tensor products of weighted balls of measures, Theorems 3 and 4, are also included. Theorem 6 is stated and proved in Sect. 8. Section 9 applies the general results to fractional Weyl integrals and derivatives as linear endomorphisms on weighted function spaces.
2 Notations and conventions
Let \(\mathbb {K}\) be \(\mathbb {R}\) or \(\mathbb {C}\) throughout. Define \(\mathbb {K}^\infty :=\mathbb {K}\cup \{\infty \}\), \(\mathbb {R}^+:=[0,{\infty ^+})\) and \(\mathbb {R}^{+\infty }:=\mathbb {R}^+\cup \{{\infty ^+}\}\). The symbol \(\infty \) stands for “divergent,” “undefined” or “infinite” in a generic unsigned sense. The symbol \({\infty ^+}\) stands for “positive divergent.” The extension \(\mathbb {K}^\infty \supseteq \mathbb {K}\) is considered as an Alexandrov compactification, where \(\infty \) is adjoined as the point at infinity. The extension \(\mathbb {R}^{+\infty }\supseteq \mathbb {R}^+\) is understood as an ordering theoretic extension, where \({\infty ^+}\) is adjoined as the greatest element.
Addition, subtraction, multiplication and division are extended to \(\mathbb {K}^\infty \) according to
for all \(x,y\in \mathbb {K}^\infty \) combined with \(-\infty :=\infty \), \(\infty ^{-1}:=0\), and \(0^{-1}:=\infty \). Note that associativity and commutativity hold for addition and multiplication, but the distributive law can fail, because \((1-1)\cdot \infty \ne 1\cdot \infty -1\cdot \infty \). Real and imaginary parts of \(\infty \) are \(\mathfrak {R}\infty :=\infty \) and \(\mathfrak {I}\infty :=\infty \). The absolute value of \(\infty \) is defined as \(|\infty |:={\infty ^+}\). The complex conjugate of \(\infty \) is \(\overline{\infty }:=\infty \).
The operations \(+\), \(\cdot \) and \((\cdot )^{-1}\) are extended to \(\mathbb {R}^{+\infty }\) by replacing \(\infty \) with \({\infty ^+}\) in (2.1) and setting \(({\infty ^+})^{-1}:=0\), and \(0^{-1}:={\infty ^+}\). The extended multiplication is also denoted as  and referred to as supremal multiplication. Subtraction and inverse elements for addition are not defined, but the distributive law holds in \(\mathbb {R}^{+\infty }\).
and referred to as supremal multiplication. Subtraction and inverse elements for addition are not defined, but the distributive law holds in \(\mathbb {R}^{+\infty }\).
For any set S, the set of functions \(S\rightarrow \mathbb {K}\) is denoted by \(\mathcal {F}(S)\). To denote functions with values in \(\mathbb {K}^\infty \), \(\mathbb {R}^+\) or \(\mathbb {R}^{+\infty }\) instead of \(\mathbb {K}\), we replace \(\mathcal {F}\) by \(\mathcal {F}^\infty \), \(\mathcal {F}^+\) or \(\mathcal {F}^{+\infty }\).
Let S be a topological space. The topological space S is called locally compact if every of its points has a compact neighborhood. All locally compact spaces are assumed to be Hausdorff. The set of \(\mathbb {K}\)-valued continuous functions on S is denoted by \(\mathcal {C}(S)\). A function \(f\in \mathcal {F}^{+\infty }(S)\) is called upper (resp. lower) semicontinuous if \(\{f\ge a\}\) (resp. \(\{f\le a\}\)) is closed for every \(a\in \mathbb {R}^{+\infty }\). The sets of \(\mathbb {R}^{+\infty }\)-valued lower, respectively, upper semicontinuous functions are denoted by \(\mathcal {L}^{+\infty }(S)\), respectively, \(\mathcal {U}^{+\infty }(S)\). The upper semicontinuous envelope of \(w\in \mathcal {F}^{+\infty }(S)\) is denoted by
The set \(\mathcal {U}^{+\infty }(S)\) is known to be a closure system [7, Definition 2.33] in \(\mathcal {F}^{+\infty }(S)\), i.e., \(\mathcal {U}^{+\infty }(S)\) is closed with respect to pointwise formation of suprema of arbitrary subsets.
Restrictions to functions that are locally bounded, uniformly bounded, vanishing at infinity or compactly supported, are denoted using a subscript \(\mathcal {F}_{\mathrm {l}\mathrm {b}}\), \(\mathcal {F}_\mathrm {b}\), \(\mathcal {F}_\mathrm {v}\), respectively, \(\mathcal {F}_\mathrm {c}\). A function \(f:S\rightarrow \mathbb {K}^\infty \) is said to “vanish at infinity” if and only if for every \(\varepsilon >0\) there is a compact set \(K_\varepsilon \subset S\) such that \(|f(x)|\le \varepsilon \) for all \(x\in S{\setminus } K_\varepsilon \).
3 Supremal image functions and upper semicontinuity
Let \(\varPhi :S\rightarrow T\) be a mapping between sets and \(w:T\rightarrow \mathbb {R}^{+\infty }\) an arbitrary function. The pullback or inverse image function\({\varPhi }^{-1}w\) of w under \(\varPhi \) can always be defined as \({\varPhi }^{-1}w:=w\circ \varPhi :S\rightarrow \mathbb {R}^{+\infty }\) using the composition of mappings.
Unless \(\varPhi \) is bijective and thus invertible, there is no general or natural notion for a “pushforward” or an “image function” of a function \(w\in \mathcal {F}^{+\infty }(S)\) under \(\varPhi \). However, a useful construction resembling the “pushforward” of a function \(w:S\rightarrow \mathbb {R}^{+\infty }\) under an arbitrary mapping \(\varPhi :S\rightarrow T\) arises from considering \(\mathbb {R}^{+\infty }\) as an ordered set \((\mathbb {R}^{+\infty },\le )\), where \(\le \) is the canonical ordering.
Definition 1
The supremal image function\(\widehat{\varPhi }w\) of w under \(\varPhi \) is defined as
for \(t\in T\). A supremal image function \(\widehat{\varPhi }w\) is called exact if the supremum in (3.1) is a maximum for all \(t\in \varPhi (S)\).
Supremal image formation is analogous to “epi-composition” in [30, Eq. 1(17)]. Note, that \(\widehat{\varPhi }w\) coincides with the pullback under the inverse mapping \(\varPhi ^{-1}\), i.e., \(\widehat{\varPhi }w={(\varPhi ^{-1})}^{-1}w\), whenever \(\varPhi \) is bijective.
Supremal image functions can be characterized in two ways. Firstly, one associates the strict hypograph \(H_w:=\{(s,\alpha )\in S\times (0,{\infty ^+}):\alpha <w(s)\}\subseteq S\times (0,{\infty ^+})\) to a function \(w\in \mathcal {F}^{+\infty }(S)\). The image of the hypograph \(H_w\) under the product mapping \(\varPhi \times \mathrm {i}\mathrm {d}:S\times (0,{\infty ^+})\rightarrow T\times (0,{\infty ^+})\) results in a set \(H_{\varPhi ,w}\subseteq T\times (0,{\infty ^+})\) that is precisely the strict hypograph associated with \(\widehat{\varPhi }w\).
Secondly, the mapping \(\widehat{\varPhi }:\mathcal {F}^{+\infty }(S)\rightarrow \mathcal {F}^{+\infty }(T)\) associated with any mapping \(\varPhi :S\rightarrow T\) by Definition 1 can be seen as the (lower) adjoint to the inverse image operator \({\varPhi }^{-1}:\mathcal {F}^{+\infty }(T)\rightarrow \mathcal {F}^{+\infty }(S)\) in the sense of ordering theory [7, Definition 7.23], where \(\mathcal {F}^{+\infty }(S)\) and \(\mathcal {F}^{+\infty }(T)\) are endowed with the canonical pointwise ordering. This fact is formulated as
Proposition 1
The mappings \(\widehat{\varPhi }:\mathcal {F}^{+\infty }(S)\rightarrow \mathcal {F}^{+\infty }(T)\) and \({\varPhi }^{-1}:\mathcal {F}^{+\infty }(T)\rightarrow \mathcal {F}^{+\infty }(S)\) are isotone. The pair of mappings \((\widehat{\varPhi },{\varPhi }^{-1})\) is a Galois connection (or adjoint pair) in the sense that the two statements
and
hold true.
Proof
Isotony and the statement (3.2a) are proved by pointwise evaluation. This shows that \((\widehat{\varPhi },{\varPhi }^{-1})\) is a Galois connection. The statement (3.2b) is a general property of Galois connections [7, Lemma 7.26, p. 159]. \(\square \)
The following two results on upper semicontinuity and supremal image functions will be useful. For the remainder of the section, \(\varPhi :S\rightarrow T\) is a continuous mapping between topological spaces. The brackets \(\left\lceil \,\cdot \,\right\rceil \) will denote upper semicontinuous envelopes.
Corollary 1
Proposition 1 holds also when \(\mathcal {F}^{+\infty }(T)\) is replaced by \(\mathcal {U}^{+\infty }(T)\) and \(\widehat{\varPhi }\) is replaced by the assignment \(w\mapsto \left\lceil \,\widehat{\varPhi }w\,\right\rceil \).
Proof
Isotony of \(\widehat{\varPhi }\) and \(\left\lceil \,\cdot \,\right\rceil \) imply isotony of \(w\mapsto \left\lceil \,\widehat{\varPhi }w\,\right\rceil \). The equivalence of \(\left\lceil \,\widehat{\varPhi }w\,\right\rceil \le v\) and \(\widehat{\varPhi }w\le v\) for \(w\in \mathcal {F}^{+\infty }(S)\) and \(v\in \mathcal {U}^{+\infty }(T)\) concludes the proof. \(\square \)
Lemma 1
The following relations hold:
Proof
The relations \(\widehat{\varPhi }w\le \widehat{\varPhi }\left\lceil \,w\,\right\rceil \) and \(\left\lceil \,\widehat{\varPhi }w\,\right\rceil \le \left\lceil \,\widehat{\varPhi }\left\lceil \,w\,\right\rceil \,\right\rceil \) follow from the definitions. Further, assume \(\widehat{\varPhi }w\le v\) with \(v\in \mathcal {U}^{+\infty }(T)\). Proposition 1 yields \(w\le {\varPhi }^{-1}v\) and further \(\widehat{\varPhi }w\le \widehat{\varPhi }({\varPhi }^{-1}v)\le v\) where \({\varPhi }^{-1}v\in \mathcal {U}^{+\infty }(S)\). This implies \(\widehat{\varPhi }\left\lceil \,w\,\right\rceil \le \left\lceil \,\widehat{\varPhi }w\,\right\rceil \), and thus, \(\left\lceil \,\widehat{\varPhi }\left\lceil \,w\,\right\rceil \,\right\rceil \le \left\lceil \,\widehat{\varPhi }w\,\right\rceil \) yields the equality. \(\square \)
Proposition 2
Assume that T is locally compact. If \(w:S\rightarrow \mathbb {R}^{+\infty }\) is upper semicontinuous and the restriction of w to the preimage \(\varPhi ^{-1}(C)\) is vanishing at infinity for any compact \(C\subseteq T\), then \(\widehat{\varPhi }w:T\rightarrow \mathbb {R}^{+\infty }\) is upper semicontinuous as well. Further, the supremal image function \(\widehat{\varPhi }w\) is exact.
Proof
The proof is analogous to [30, Proposition 1.32]. \(\square \)
4 Supremal convolution on locally compact groups
Let G be a locally compact group and let \(\varGamma :G\times G\rightarrow G\) be its continuous multiplication written as \(xy=\varGamma (x,y)\) for \(x,y\in G\).
Definition 2
Let \(w,v\in \mathcal {F}^{+\infty }(G)\). The (multiplicative) supremal convolution of w and v, denoted as  , is defined by
, is defined by

Supremal convolutes  are called exact, if the supremum in (4.1) is a maximum for all \(z\in G\).
are called exact, if the supremum in (4.1) is a maximum for all \(z\in G\).
Supremal convolution is an associative binary operation  on \(\mathcal {F}^{+\infty }(G)\) [24, 30] that is analogous to inf-convolution in [30, 1.H.]. The law
on \(\mathcal {F}^{+\infty }(G)\) [24, 30] that is analogous to inf-convolution in [30, 1.H.]. The law  holds for subsets \(A,B\subseteq G\). For \(x\in G\), one has
holds for subsets \(A,B\subseteq G\). For \(x\in G\), one has  and
and  where \(\mathrm {L}_xw(y):=w(x^{-1}y)\) and \(\mathrm {R}_xw(y)=w(yx^{-1})\) denote left and right translation. Supremal convolution respects translation in the sense that
where \(\mathrm {L}_xw(y):=w(x^{-1}y)\) and \(\mathrm {R}_xw(y)=w(yx^{-1})\) denote left and right translation. Supremal convolution respects translation in the sense that  and
and  . Supremal convolution is homogeneous in the sense that
. Supremal convolution is homogeneous in the sense that  for \(\lambda \in \mathbb {R}^{+\infty }\). For infimal multiplication, one obtains only
for \(\lambda \in \mathbb {R}^{+\infty }\). For infimal multiplication, one obtains only  for \(\lambda \in \mathbb {R}^{+\infty }\). Thus, supremal convolution shares many properties with convolution.
for \(\lambda \in \mathbb {R}^{+\infty }\). Thus, supremal convolution shares many properties with convolution.
Supremal convolution can be decomposed as

into the supremal tensor product \(\mathbin {\widehat{\otimes }}\) and the supremal image \(\widehat{\varGamma }\) under the group multiplication \(\varGamma \). The supremal tensor product is defined as

whenever \(s\in S\), \(t\in T\), \(w\in \mathcal {F}^{+\infty }(S)\), \(v\in \mathcal {F}^{+\infty }(T)\) and S, T are sets. It coincides with the usual tensor product \(\otimes \) of functions whenever the functions are finite valued.
The adjective “supremal” refers to the fact that supremal operations (convolution, multiplication or tensor product) are characterized as the unique extensions of the finite-valued case that preserve suprema of arbitrary subsets in each argument. This means that
holds for  . Here \(A,B\subseteq \mathbb {R}^{+\infty }\) or \(A,B\subseteq \mathcal {F}^{+\infty }(G)\) for
. Here \(A,B\subseteq \mathbb {R}^{+\infty }\) or \(A,B\subseteq \mathcal {F}^{+\infty }(G)\) for  , while \(A,B\subseteq \mathcal {F}^{+\infty }(G)\) for
, while \(A,B\subseteq \mathcal {F}^{+\infty }(G)\) for  .
.
Proposition 3
Let \(w,v\in \mathcal {F}^{+\infty }(G)\). If w or v is lower semicontinuous, then  is lower semicontinuous as well.
is lower semicontinuous as well.
Proof
The proposition is an analogue of [24, 4.c. Proposition]. \(\square \)
Proposition 4
Let \(w,v\in \mathcal {U}^+(G)\) such that \(w\otimes v\) is vanishing at infinity on \(\varGamma ^{-1}(C)=\{(x,y)\in G\times G: xy\in C\}\) for all compact \(C\subseteq G\). Then,  is upper semicontinuous and the supremal convolute
is upper semicontinuous and the supremal convolute  is exact.
is exact.
Proof
This follows from Proposition 2 and the fact that tensor products of \(\mathbb {R}^+\)-valued upper semicontinuous functions are upper semicontinuous. \(\square \)
Corollary 2
The following inclusions hold:


Proof
This is merely checking the assumption of Proposition 4. \(\square \)
Remark 1
By means of the exponential transformation \(\mathbb {R}^{\pm \infty }:=[{\infty ^-},{\infty ^+}]\leftrightarrow \mathbb {R}^{+\infty }\) with \(\exp (-x)\leftrightarrow y\), where \({\infty ^-}:=-{\infty ^+}\) and \(-{\infty ^-}:={\infty ^+}\), Proposition 4 is seen to be equivalent to Proposition 1.27 from [30]. Proposition 1.27 from [30] was proved for \(\mathbb {R}^d\), but the proof in [30] extends to locally compact groups without complications. The special case (4.5a) can also be found in [24, Section 4].
Lemma 2
Let S and T be topological spaces. Upper semicontinuous envelopes \(\left\lceil \,\cdot \,\right\rceil \), and tensor products \(\otimes \) are compatible in the following sense:
where \(\mathcal {F}^+_{\mathrm {l}\mathrm {b}}\) denotes locally bounded functions.
Proof
Upper semicontinuous envelopes of locally bounded functions are finite valued, and tensor products of finite-valued upper semicontinuous functions are upper semicontinuous. Therefore, \(\left\lceil \,w\otimes v\,\right\rceil \le \left\lceil \,w\,\right\rceil \otimes \left\lceil \,v\,\right\rceil \in \mathcal {U}^{+\infty }(S\times T)\). On the other hand, if \(w\otimes v\le u\in \mathcal {U}^{+\infty }(S\times T)\), then \(w v(t)=(w\otimes v)(\cdot ,t)\le u(\cdot ,t)\in \mathcal {U}^{+\infty }(S)\) for all \(t\in T\), and thus, \(\left\lceil \,w\,\right\rceil \otimes v\le u\). With the same argument, one obtains \(\left\lceil \,w\,\right\rceil \otimes \left\lceil \,v\,\right\rceil \le u\), and thus, \(\left\lceil \,w\,\right\rceil \otimes \left\lceil \,v\,\right\rceil \le \left\lceil \,w\otimes v\,\right\rceil \). \(\square \)
Proposition 5
Let \(w,v,u\in \mathcal {U}^+(G)\) such that  and
and  are locally bounded. Then, the following associative law holds:
are locally bounded. Then, the following associative law holds:

Proof
Use the definition of  , then the upper semicontinuity of u and then Lemma 2 to get:
, then the upper semicontinuity of u and then Lemma 2 to get:

This, together with Lemma 1 and the definition of  in reverse, gives
in reverse, gives

Now, use the associative law for  and do similar steps in reverse. \(\square \)
and do similar steps in reverse. \(\square \)
Remark 2
Proposition 5 implies that the assignment  defines an associative internal binary operation \(\mathcal {U}^+_\mathrm {b}(G)\times \mathcal {U}^+_\mathrm {b}(G)\rightarrow \mathcal {U}^+_\mathrm {b}(G)\). Setting \(w=\chi _{A}\) and \(v=\chi _{B}\), where \(\chi _{A}\) denotes the characteristic function of a subset \(A\subseteq G\), shows that the assignment \((A,B)\mapsto \overline{AB}\) with \(A,B\subseteq G\) defines an associative internal binary operation on the closed subsets of G. Here \(\overline{A}\) denotes the topological closure of A in G.
defines an associative internal binary operation \(\mathcal {U}^+_\mathrm {b}(G)\times \mathcal {U}^+_\mathrm {b}(G)\rightarrow \mathcal {U}^+_\mathrm {b}(G)\). Setting \(w=\chi _{A}\) and \(v=\chi _{B}\), where \(\chi _{A}\) denotes the characteristic function of a subset \(A\subseteq G\), shows that the assignment \((A,B)\mapsto \overline{AB}\) with \(A,B\subseteq G\) defines an associative internal binary operation on the closed subsets of G. Here \(\overline{A}\) denotes the topological closure of A in G.
5 Supremal deconvolution
Supremal deconvolution is an operation similar to taking the inverse of supremal convolution (see Proposition 6). It is related to infimal convolution , the dual operation to
, the dual operation to  , defined as
, defined as  for \(w,v\in \mathcal {F}^{+\infty }(G)\).
for \(w,v\in \mathcal {F}^{+\infty }(G)\).
Definition 3
Multiplicative supremal left/right deconvolution is defined as


for \(w,v,u\in \mathcal {F}^{+\infty }(G)\). Here “ ” is infimal multiplication defined such that
” is infimal multiplication defined such that  . The definition is analogous to the deconvolution from [22, Introduction].
. The definition is analogous to the deconvolution from [22, Introduction].
Remark 3
Note that  preserves suprema in its left argument and infima in its right argument. Left deconvolution can be written as
preserves suprema in its left argument and infima in its right argument. Left deconvolution can be written as  .
.
Proposition 6
Let \(w,v,u\in \mathcal {F}^{+\infty }(G)\).
-
(a)
The following equivalences hold:
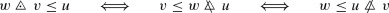 (5.2)
(5.2) -
(b)
The following inequalities hold:
 (5.3a)
(5.3a) (5.3b)
(5.3b) (5.3c)
(5.3c) -
(c)
If u is upper semicontinuous, then
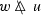 and \(u\mathbin {\,{\triangle /}}v\) are upper semicontinuous as well.
and \(u\mathbin {\,{\triangle /}}v\) are upper semicontinuous as well.
Proof
Part (a) and (b) of Proposition 6 are analogues of Lemma I-1 and Proposition I-4 in [22] carefully extended to the non-commutative case.
Part (c) follows from Proposition 3 by duality. \(\square \)
6 Integration of \(\mathbb {K}^\infty \)-valued measurable functions
This section summarizes notations and results for measures and integration on locally compact spaces [4, 5]. A slight modification of essential integration is introduced [Eq. (6.2) and (6.4)] to allow integration of arbitrary \(\mathbb {K}^\infty \)-valued measurable functions with respect to any \(\mathbb {K}\)-valued Radon measure consistent with the extended arithmetic from Sect. 2. This allows to state and prove that the class of universal measurable \(\mathbb {K}^\infty \)-valued functions on G is preserved under left convolution with moderated Radon measures on G (Theorem 2). The result is derived from Theorem 1 that concerns integration of universally measurable functions with respect to factors of a product measure.
In the remaining text of the article, the “Radon” in Radon measure is dropped, because solely this kind of measure is used.
Let S be a locally compact space. The set of \(\mathbb {K}\)-valued continuous functions with compact support is denoted by \(\mathcal {K}(S)\). The set of \(\mathbb {K}\)-valued measures on S is denoted by \(\mathfrak {M}(S)\), the set of positive measures by \(\mathfrak {M}^+(S)\). The symbols \(\mathfrak {R}\mu \), \(\mathfrak {I}\mu \) and \(|\mu |\) denote the real part, imaginary part and absolute value of \(\mu \in \mathfrak {M}(S)\), respectively. The positive/negative part of a real-valued measure \(\mu \) is denoted by \(\mu ^\pm \) (See [4, Ch. III, §1, Nos. 3, 5, 6]). The upper integral, respectively, the essential upper integral of \(f\in \mathcal {F}^{+\infty }(S)\) with respect to \(\mu \in \mathfrak {M}^+(S)\) is denoted by
(See [4, Ch. IV, §1, No. 1, Def. 1], respectively, [4, Ch. V, §1, No. 1, Def. 1]).
Fix a measure \(\mu \). The following definition of essentially \(\mu \)-integrable \(\mathbb {K}^\infty \)-valued functions is a useful extension of the essentially \(\mu \)-integrable functions from [4, Ch. V, §1, No. 3, Def. 3] to \(\mathbb {K}^\infty \). The set of essentially\(\mu \)-integrable\(\mathbb {K}^\infty \)-valued functions is denoted by \(\mathcal {I}^\infty (\mu )\) and defined as the set of all functions f from \(\mathcal {F}^\infty (S)\) such that \(I_f:=\{s\in S:f(s)=\infty \}\) is a locally \(\mu \)-negligible set and f coincides on \(S{{\setminus }} I_f\) with some \(\mathbb {K}\)-valued\(\mu \)-integrable function\(f^\prime \) [4, Ch. IV, §4, No. 1, Def. 1]. The essential integral of\(f\in \mathcal {I}^\infty (\mu )\)with respect to\(\mu \) is then defined as
where \(\mu (f^\prime )\) is the integral of \(f^\prime \) as defined in [4, Ch. IV, §4, No. 1, Def. 1]. This definition of the essential integral \(\mu (f)\) is analogous to that in [4, Ch. V, §1, No. 3, Def. 3].
The set of \(\mu \)-measurable\(\mathbb {K}^\infty \)-valued functions is denoted as \(\mathcal {M}^\infty (\mu )\) and is defined as in [4, Ch. IV, §5, No. 1, Def. 1] where \(\mathbb {K}^\infty \) is endowed with the topology it obtains when considered as an Alexandroff compactification of \(\mathbb {K}\). The set of universally measurable\(\mathbb {K}^\infty \)-valued functions on S is defined as the intersection of the spaces \(\mathcal {M}^\infty (\mu )\) with \(\mu \) running over all positive measures on S [4, Ch. V, §3, No. 4, Def. 2].
Proposition 7
The sets \(\mathcal {M}^\infty (\mu )\) with \(\mu \in \mathfrak {M}(S)\) and \(\mathcal {M}^\infty (S)\) are closed under the extended addition, multiplication and \(\mathbb {K}^\infty \)-scalar multiplication. Further, they are closed under additive and multiplicative inverses, the formation of real/imaginary parts, positive/negative parts (if \(\mathbb {K}=\mathbb {R}\)) and the absolute value.
Proof
To prove the closedness with respect to extended addition and multiplication, one uses [4, Ch. IV, §5, No. 10, Prop. 16] and the following three observations: 1. The statement of the proposition is known for \(\mathbb {K}\)-valued functions. 2. A \(\mathbb {K}^\infty \)-valued function f is \(\mu \)-measurable if and only if the set \(I_f:=\{s\in S:f(s)=\infty \}\) is \(\mu \)-measurable and the restriction of f to \(F_f:=S{{\setminus }} I_f\) is a \(\mu \)-measurable \(\mathbb {K}\)-valued function on \(F_f\) in the sense of [4, Ch. IV, §5, No.10, Def. 8]. 3. The relations \(I_{f+g}=I_f\cup I_g\) and \(I_{f\cdot g}=(I_f\cap P_g)\cup (P_f\cap I_g)\) hold for arbitrary \(f,g\in \mathcal {F}^\infty (S)\) where \(P_f:=\{s\in S:f(s)\ne 0\}\).
The remaining statements can be proved in a similar vein. \(\square \)
Applying [4, Ch. V, §1, No. 3, Prop. 9] to the definition of the essential \(\mu \)-integral, as defined in (6.2), one obtains the following characterization:
The extended essential\(\mu \)-integral\(\mu (f)\) of \(f\in \mathcal {M}^\infty (\mu )\) with respect to \(\mu \in \mathfrak {M}(S)\) is defined by extending the essential \(\mu \)-integral as follows:
This extension is motivated by the equivalence (6.3). Due to (6.3), one obtains a well-defined mapping \(\mu :\mathcal {M}^\infty (\mu )\rightarrow \mathbb {K}^\infty \).
Proposition 8
The extended essential integral obeys
for \(f,g\in \mathcal {M}^\infty (\mu ),\,\alpha ,\beta \in \mathbb {K},\,\mu \in \mathfrak {M}(S)\) if and only if
Similarly,
holds for \(f\in \mathcal {M}^\infty (\mu )\cap \mathcal {M}^\infty (\nu ),\,\alpha ,\beta \in \mathbb {K},\,\mu ,\nu \in \mathfrak {M}(S)\) if and only if
But,
for \(f\in \mathcal {M}^\infty (\mu )\), \(\mu \in \mathfrak {M}(\mu )\) if and only if
The standard estimate
holds for all \(f\in \mathcal {M}^\infty (\mu ),\,\mu \in \mathfrak {M}(S)\). When \(\infty \) and \({\infty ^+}\) are identified with each other, one has
for all \(f\in \mathcal {M}^{+\infty }(S)\), \(\mu \in \mathfrak {M}^+(S)\).
Proof
One uses that \(\mu :\mathcal {I}^\infty (\mu )\rightarrow \mathbb {K}\) respects extended addition and \(\mathbb {K}\)-scalar multiplication, the equivalence in Eq. (6.3) and distinguishes the different cases that appear according to the definition in Eq. (6.4). \(\square \)
Corollary 3
The following decomposition formula holds:
for all \(f\in \mathcal {M}^\infty (\mu )\) and \(\mu \in \mathfrak {M}(S)\), where \(\mathrm {P}_0:=(\mathfrak {R}\cdot )^+\), \(\mathrm {P}_1:=(\mathfrak {I}\cdot )^+\), \(\mathrm {P}_2:=(\mathfrak {R}\cdot )^-\) and \(\mathrm {P}_3:=(\mathfrak {I}\cdot )^-\).
Proof
The estimates
hold for \(f\in \mathcal {F}^\infty (S)\) and \(\mu \in \mathfrak {M}(S)\) [4, Ch. III, §1, No. 5 & 6]. This yields that
This means that the conditions (6.5b), respectively, (6.6b) can be verified for the linear combinations \(f=\sum ^3_{k=0}\mathrm {i}^k\mathrm {P}_k f\) and \(\mu =\sum ^3_{k=0}\mathrm {i}^k\mathrm {P}_k\mu \). Using (6.5a), (6.6a) and (6.9), one obtains (6.10). \(\square \)
Recall the definition of products of measures: For any two measure \(\mu \in \mathfrak {M}(S)\), \(\nu \in \mathfrak {M}(T)\) and \(f\in \mathcal {K}(S\times T)\), let
Then \(\mu (f)\) and \(\nu (f)\) define continuous functions of compact support. The product measure\(\mu \otimes \nu \) of \(\mu \) and \(\nu \) is defined for \(f\in \mathcal {K}(S\times T)\) by [4, Ch. III, §4, No. 1]:
A \(\mathbb {K}\)-valued measure \(\mu \) on S is called moderated whenever S is a countable union of \(\mu \)-integrable sets [4, Ch. V, §1, No. 2, Def. 2]. In this case, the support \({\text {supp}}\mu \) of \(\mu \) is a countable union of compact subsets of S [2, Lemma 1]. The set of moderated measures on S will be denoted by \(\mathfrak {M}_\sigma (S)\).
Theorem 1
Let \(\mu \in \mathfrak {M}_\sigma (S)\), \(\nu \in \mathfrak {M}_\sigma (T)\) and \(f\in \mathcal {M}^\infty (S\times T)\). Then the functions \(\mu (f)\) and \(\nu (f)\) in (6.11a) are well defined, in a pointwise sense, as extended essential integrals of \(\mathbb {K}^\infty \)-valued measurable functions and they fulfill \(\mu (f)\in \mathcal {M}^\infty (T)\) and \(\nu (f)\in \mathcal {M}^\infty (S)\). In addition, if \(|\mu \otimes \nu |(|f|)<{\infty ^+}\) or \(\mu \), \(\nu \) and f are positive, then the formula (6.11b) holds.
Proof
According to [4, Ch. V, §8, No. 2, Prop. 2], one has \(s^\prime \mapsto f(s^\prime ,t)\in \mathcal {M}^\infty (S)\) and \(t^\prime \mapsto f(s,t^\prime )\in \mathcal {M}^\infty (T)\) whenever \(f\in \mathcal {M}^\infty (S\times T)\), \(t\in T\), \(s\in S\) and this guarantees that \(\mu (f)\) and \(\nu (f)\) are pointwise well defined in the sense of the conventions for extended essential integration from (6.2) and (6.4). Using the decomposition formula (6.10) yields
for all \(t\in T\) and \(s\in S\). According to (6.9) and [4, Ch. V, §8, No. 3, Prop. 7], the functions \((\mathrm {P}_k\mu )(\mathrm {P}_l f)\) and \((\mathrm {P}_k\nu )(\mathrm {P}_l f)\) are universally measurable for all \(k,l\in \{0,1,2,3\}\). From Proposition 7 and Eq. (6.12), one concludes that \(\mu (f)\), respectively, \(\nu (f)\) are from \(\mathcal {M}^\infty (S)\), respectively, \(\mathcal {M}^\infty (T)\).
The additional statements follow from [4, Ch. V, §8, No. 2, Prop. 2] and [4, Ch. V, §8, No. 4, Th. 1]. \(\square \)
Convolution is now defined as the image of a product: For any continuous mapping \(\varPhi :S\rightarrow T\) between locally compact spaces and \(\mu \in \mathfrak {M}(S)\), the image of \(\mu \) under \(\varPhi \) is defined by \((\varPhi \mu )(f):=\mu (f\circ \varPhi )\), \(f\in \mathcal {K}(T)\) whenever it exists, i.e., whenever \(|\mu |(f\circ \varGamma )<{\infty ^+}\) for all \(f\in \mathcal {K}^+(S)\) [4, Ch. V, §6, No. 4, Def. 2]. For two measures \(\mu ,\nu \in \mathfrak {M}(G)\) on a locally compact group G, one defines the convolution
of \(\mu \) and \(\nu \) whenever \(\mu \) and \(\nu \) are convolvable, i.e., whenever the image of \(\mu \otimes \nu \) under \(\varGamma \) exists [4, Ch. VIII, §3, No. 1]. The left convolution of a function \(f\in \mathcal {M}^\infty (G)\) with a measure \(\mu \in \mathfrak {M}(G)\) is defined as
This defines a binary operation \(*:\mathfrak {M}(G)\times \mathcal {M}^\infty (G)\rightarrow \mathcal {F}^\infty (G)\). Linearity holds with restrictions similar to those for the binary operation of extended essential integration \(\mathfrak {M}(G)\times \mathcal {M}^\infty (G)\rightarrow \mathbb {K}^\infty \) as seen in Proposition 8.
Theorem 2
Left convolution (6.14) is well defined as a binary operation
The transposition law
holds for \(f\in \mathcal {M}^\infty (G)\) and \(\mu ,\nu \in \mathfrak {M}_\sigma (G)\) whenever \(\mu \) and \(\nu \) are convolvable and one of the following two expressions is finite:
Proof
Both statements follow from Theorem 1 and the fact that \((x,y)\mapsto f(y^{-1}x)\) defines an element of \(\mathcal {M}^\infty (G\times G)\) whenever \(f\in \mathcal {M}^\infty (G)\). \(\square \)
For a sequence of positive numbers \(x_n\in \mathbb {R}^{+\infty },n\in \mathbb {N}\), their series is declared to be
while for a sequence with \(x_n\in \mathbb {K}^\infty \)
With this definition, linearity \(\sum _{n\in \mathbb {N}}(\alpha x_n+\beta y_n)=\alpha \sum _{n\in \mathbb {N}}x_n+\beta \sum _{n\in \mathbb {N}}y_n\) holds always for positive sequences \((x_n)_{n\in \mathbb {N}}\), \((y_n)_{n\in \mathbb {N}}\) in \(\mathbb {R}^{+\infty }\) and \(\alpha ,\beta \in \mathbb {R}^{+\infty }\). For \(\alpha ,\beta \in \mathbb {K}\) and \((x_n)_{n\in \mathbb {N}}\), \((y_n)_{n\in \mathbb {N}}\) from \(\mathbb {K}^\infty \) linearity holds if and only if \(\sum _{n\in \mathbb {N}}|x_n|<{\infty ^+}\), or \(\sum _{n\in \mathbb {N}}|y_n|<{\infty ^+}\), or \(\sum _{n\in \mathbb {N}}|\alpha x_n+\beta y_n|={\infty ^+}\). The relation \(\sum _{n\in \mathbb {N}}\infty \cdot x_n=\infty \cdot \sum _{n\in \mathbb {N}}x_n\) holds if and only if \(\sum _{n\in \mathbb {N}}x_n\ne 0\), or \(x_n=0\) for all \(n\in \mathbb {N}\). The standard estimate \(|\sum _{n\in \mathbb {N}}x_n|\le \sum _{n\in \mathbb {N}}|x_n|\) holds for all sequences \((x_n)_{n\in \mathbb {N}}\) in \(\mathbb {K}^\infty \).
Remark 4
With these specifications, Theorem 1 can be applied to the situation where \(T=\mathbb {N}\) and \(\nu \in \mathfrak {M}_\sigma (\mathbb {N})=\mathfrak {M}(\mathbb {N})\) is given by the counting measure
for \(g\in \mathcal {M}^\infty (\mathbb {N})=\mathcal {F}^\infty (\mathbb {N})\). The function set \(\mathcal {M}^\infty (S\times \mathbb {N})\) is identified with the set of sequences \((f_n)_{n\in \mathbb {N}}\) with \(f_n\in \mathcal {M}^\infty (S)\). For \(F=(f_n)_{n\in \mathbb {N}}\in \mathcal {M}^\infty (S\times \mathbb {N})\), the pointwise defined function \(s\mapsto \nu (F)(s)\) obeys
7 Operations on weighted balls characterized by weights
This section characterizes the action of image, product and convolution operations on weighted balls of measures and functions in terms of supremal operations on the weight functions. The symbols S and T will denote locally compact spaces, \(\varPhi :S\rightarrow ~T\) is a continuous mapping, and G is a locally compact group with multiplication mapping \(\varGamma :G\times G\rightarrow G\).
Definition 4
For \(w\in \mathcal {F}^{+\infty }(S)\), the w-ball of measures is defined as
The strictw-ball of Dirac measures\(w[\mathfrak {D}_\mathrm {s}]\) is defined as
where \(\delta _s(f):=f(s)\), \(f\in \mathcal {K}(S)\) is the Dirac measure associated with \(s\in S\).
Remark 5
Let \(w,v\in \mathcal {F}^{+\infty }(S)\).
-
(a)
The set \(w[\mathfrak {M}]\) is vaguely bounded iff w is locally bounded.
-
(b)
The set \(w[\mathfrak {M}]\) is vaguely closed iff w is upper semicontinuous.
-
(c)
If w is locally bounded, then the ball \(w[\mathfrak {M}]\) consists of moderated measures (see Lemma 3) and the inequality \(|\mu |^{\bullet }(1/w)\le 1\) in (7.1a) may be replaced by \(|\mu |^{*}(1/w)\le 1\).
-
(d)
The inclusion \(v[\mathfrak {D}_\mathrm {s}]\subseteq w[\mathfrak {M}]\) holds iff \(v\le w\).
Lemma 3
Let \(\mu \) be a measure on S and \(h:S\rightarrow \mathbb {R}^{+\infty }\) a function that is bounded away from zero on each compact subset of S and assume \(|\mu |^{\bullet }(h)\le 1\). Then, there exist measures \(\mu _n\in \mathfrak {M}(S)\) with compact support and numbers \(\alpha _n\in \mathbb {R}^+\), such that \(|\mu _n|^{\bullet }(h)\le 1\), \(n\in \mathbb {N}\), \(\sum ^\infty _{n=1}\alpha _n\le 1\) and \(\mu =\sum ^\infty _{n=1}\alpha _n\mu _n\) in the sense of a vaguely converging series. The following estimate holds:
As a consequence \(\mu \) is moderated.
Proof
The assumptions on h guarantee that the lower semicontinuous envelope \(\lfloor h\rfloor \) of h is strictly positive everywhere. The sets \(H_n:=\{\lfloor h\rfloor >1/n\}\), \(n\in \mathbb {N}\) are \(\mu \)-integrable, because they are open and
Their union is S. Thus, \(\mu \) is moderated. By [2, Lemma 1], its support is the union of a sequence of compact subsets of S. Therefore, there exist functions \(f_n\in \mathcal {K}^+(S)\), \(n\in \mathbb {N}\) such that \(f\cdot \mu =\mu \), where \(f:=\sum _{n=1}^\infty f_n\). Define the measures \(\nu _n:=f_n\cdot \mu \) and the numbers \(\alpha _n:=|\nu _n|^{\bullet }(h)=|\mu |^{\bullet }(f_nh)\in \mathbb {R}^+\). Then, let \(\mu _n:=(1/\alpha _n)\cdot \nu _n\) if \(\alpha _n\ne 0\) and \(\mu _n=0\) otherwise. The numbers \(\alpha _n\) and the measures \(\mu _n\) fulfill the statements in the theorem. Using [4, Ch.V, §1, No.1, Prop.1 d)& e)] and [4, Ch.III, §1, No.4], one estimates
which concludes the proof. \(\square \)
Definition 5
Let \(w\in \mathcal {F}^{+\infty }(S)\). The w-weighted ball of\(\mathbb {K}^\infty \)-valued universally measurable functions is defined as
where the w-supremum norm is
The w-weighted ball ofw-continuous functions is defined as
where the formula for \(\mathcal {C}^{\sim }_\mathrm {v}[w]\) means the closure of \(\mathcal {M}^\infty [w]\cap \mathcal {K}(S)\) in \(\mathcal {M}^\infty [w]\) with respect to the pseudo-metric \((f,g)\mapsto \Vert f-g\Vert _w\) on \(\mathcal {M}^\infty [w]\). Let
denote the strictw-weighted ball of functions supported on a single point.
Remark 6
Let \(w,v\in \mathcal {F}^{+\infty }(S)\).
-
(a)
For any \(f\in \mathcal {K}(S)\), one finds \(\varepsilon >0\) with \(\varepsilon f\in \mathcal {C}^{\sim }_\mathrm {v}[w]\) iff w is locally bounded.
-
(b)
The set \(\mathcal {C}^{\sim }_\mathrm {v}[w]\) consists of \(\mathbb {K}^\infty \)-valued universally measurable functions that are \(\mathbb {K}\)-valued on the set \(\{w>0\}\), such that its restrictions to the sets \(\{w\ge \lambda \}\), \(\lambda >0\) are continuous and w|f| is vanishing at infinity on the subspace \(\{w>0\}\).
-
(c)
The inclusion \(\mathcal {X}_\mathrm {s}[v]\subseteq \mathcal {M}^\infty [w]\) holds iff \(w\le v\).
Lemma 4
The following equations hold:




Proof
The results follow from the definitions by straightforward calculation. \(\square \)
Theorems 3, 4 are now stated and proved in preparation for the main results stated in Theorem 5.
Theorem 3
Let \(w\in \mathcal {F}^+_{\mathrm {l}\mathrm {b}}(S)\), \(v\in \mathcal {F}^+_{\mathrm {l}\mathrm {b}}(T)\). The images \(\varPhi \mu \), \(\mu \in w[\mathfrak {M}]\) exist if and only if \(\widehat{\varPhi }w\) is locally bounded. The following are equivalent:
-
(a)
The inequality \(\widehat{\varPhi }w\le v\) holds.
-
(b)
The inclusion \(\varPhi (w[\mathfrak {M}])\subseteq v[\mathfrak {M}]\) holds.
Proof
Characterization of existence: If \(\widehat{\varPhi }w\) is not locally bounded, then, by local compactness of S, there exists a sequence \((s_n)_{n\in \mathbb {N}}\subseteq S\) and a compact subset \(C\subseteq T\) such that \(2^n\le w(s_n)\) and \(\varPhi (s_n)\in C\) for all \(n\in \mathbb {N}\). Define the positive measure \(\mu \) by \(\mu (f):=\sum ^\infty _{n=1}2^{-n}w(s_n)f(s_n)\) for \(f\in \mathcal {K}(S)\). Because w is locally bounded, \(\{s_n:n\in \mathbb {N}\}\) is necessarily a discrete subset of S. This guarantees that \(\mu \) is a well-defined positive measure, because it renders the sum finite. Then
thus, \(\mu \in w[\mathfrak {M}]\), but
for \(g\in \mathcal {K}^+(T)\). If \(g=1\) on C, then the expression on the right in (7.6) must be infinite. Thus, the image of \(\mu \) under \(\varPhi \) does not exist. The reverse implication follows from the estimate (7.8).
For the converse, assume that \(v:=\widehat{\varPhi }w\) is locally bounded and let \(\mu \in w[\mathfrak {M}]\). Then \(1/(v\circ \varPhi )\le 1/w\) holds by Proposition 1. For \(f\in \mathcal {K}^+(T)\), one finds \(\varepsilon >0\) such that \(\varepsilon f\le 1/v\) because v is locally bounded. Then, one obtains
proving the existence of \(\varPhi \mu \).
“(a) \(\Longleftrightarrow \) (b)”: Let \(\mu \in w[\mathfrak {M}]\) and assume \(\widehat{\varPhi }w\le v\). Using properties of image measures [4, Ch. V, §6, No. 4, (8) & No. 2, Prop. 2] and (3.2a), one obtains
The converse follows from Remark 5(d) and Eq. (7.5a). \(\square \)
Theorem 4
Let \(w\in \mathcal {F}^+_{\mathrm {l}\mathrm {b}}(S)\), \(v\in \mathcal {F}^+_{\mathrm {l}\mathrm {b}}(T)\) and \(u\in \mathcal {F}^+_{\mathrm {l}\mathrm {b}}(S\times T)\). The following are equivalent:
-
(a)
The inequality \(w\otimes v\le u\) holds.
-
(b)
The inclusion \(w[\mathfrak {M}]\otimes v[\mathfrak {M}]\subseteq u[\mathfrak {M}]\) holds.
Proof
If \((\mu ,\nu )\in w[\mathfrak {M}]\times v[\mathfrak {M}]\) and \(w\otimes v\le u\), then, by properties of product measures [4, Ch. III, §4, No. 2, Prop. 3 & Ch. V, §8, No. 3, Prop. 8]:
The converse follows from Remark 5(d) and Eq. (7.5b). \(\square \)
Lemma 5
Let \(w\in \mathcal {U}^+(S)\), \((\alpha _n)_{n\in \mathbb {N}}\) a sequence of numbers \(\alpha _n\in \mathbb {K}\) such that \(\sum ^\infty _{k=1}|\alpha _k|\le 1\) and \((f_n)_{n\in \mathbb {N}}\) a sequence of functions \(f_n\in \mathcal {C}^{\sim }_\mathrm {v}[w]\). Then the function \(f:=\sum _{k=1}^\infty \alpha _k f_k\), that is defined pointwise by this series (in the sense of Sect. 2), fulfills \(f\in \mathcal {C}^{\sim }_\mathrm {v}[w]\).
Proof
First note that \(f\in \mathcal {M}^\infty (S)\) because of Remark 4 and because \(\mathcal {M}^\infty (S)\) is closed under pointwise formation of arbitrary series of sequences. One has
and thus, \(f\in \mathcal {M}^\infty [w]\). For each fixed \(n\in \mathbb {N}\), choose a sequence \(g_{n,m}\in \mathcal {K}(S)\cap \mathcal {M}^\infty [w]\) such that \(g_{n,m}\rightarrow f_n\) with respect to \(\Vert \cdot \Vert _w\) when \(m\rightarrow \infty \). Clearly, \(\sum ^n_{k=1}\alpha _kg_{k,m}\in \mathcal {K}(S)\cap \mathcal {M}^\infty [w]\) for each \(n\in \mathbb {N}\) and the limit for \(m\rightarrow \infty \) coincides with \(\sum ^n_{k=1}\alpha _kf_k\) on each point \(s\in S\) where \(w(s)>0\). (This follows from the fact that \(\alpha _n,f_n(s)\in \mathbb {K}\) for all \(n\in \mathbb {N}\) and \(s\in S\) with \(w(s)>0\).) Therefore, \(\sum ^n_{k=1}\alpha _kf_k\in \mathcal {C}^{\sim }_\mathrm {v}[w]\). As (7.9) implies the convergence of \(\sum ^n_{k=1}\alpha _kf_k \rightarrow f\) in \(\mathcal {M}^\infty [w]\) with respect to \(\Vert \cdot \Vert _w\) for \(n\rightarrow \infty \) and \(\mathcal {C}^{\sim }_\mathrm {v}[w]\) is, by definition, a closed subset of \(\mathcal {M}^\infty [w]\) with respect to \(\Vert \cdot \Vert _w\) one can finally conclude \(f\in \mathcal {C}^{\sim }_\mathrm {v}[w]\). \(\square \)
Theorem 5
Let \(w,v,u\in \mathcal {F}^+_{\mathrm {l}\mathrm {b}}(G)\). All pairs \((\mu ,\nu )\in w[\mathfrak {M}]\times v[\mathfrak {M}]\) are convolvable if and only if  is locally bounded. The following statements are equivalent:
is locally bounded. The following statements are equivalent:
-
(a)
The inequality
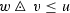 holds.
holds. -
(b)
The inclusion \(w[\mathfrak {M}]*v[\mathfrak {M}]\subseteq u[\mathfrak {M}]\) holds.
-
(c)
The inclusion
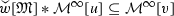 holds.
holds.
In addition, the following statements are equivalent to (a)–(c) if u is upper semicontinuous:
-
(a’)
The inequality
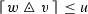 holds.
holds. -
(c’)
The inclusion
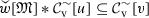 holds.
holds.
Proof
Characterization of existence: Assume that  is not locally bounded. One finds a sequence \((z_n)_{n\in \mathbb {N}}\) in G and a compact subset C of G such that
is not locally bounded. One finds a sequence \((z_n)_{n\in \mathbb {N}}\) in G and a compact subset C of G such that  and such that C is a neighborhood of the set \(\{z_n:n\in \mathbb {N}\}\). One finds sequences \((x_n)_{n\in \mathbb {N}}\) and \((y_n)_{n\in \mathbb {N}}\) in G such that \(w(x_n)v(y_n)\ge 4^n\) and \(x_ny_n=z_n\) for all \(n\in \mathbb {N}\). Passing to a subsequence and using symmetry, if necessary, one may assume that \(w(x_n)\ge 2^n\). Then, the set \(\{x_n:n\in \mathbb {N}\}\) is discrete because w is locally bounded, and therefore, one may assume that the sets \(x_n^{-1}C\), \(n\in \mathbb {N}\) are disjoint (again, by passing to a subsequence if necessary). By construction, \(x_n^{-1}C\) is a neighborhood of \(y_n\) for all \(n\in \mathbb {N}\). Thus, the set \({\{y_n:n\in \mathbb {N}\}}\) is discrete as well. Now the formulas \({\mu (f):=\sum ^\infty _{n=1}2^{-n}w(x_n)f(x_n)}\) and \(\nu (f):=\sum ^\infty _{n=1}2^{-n}v(y_n)f(y_n)\) with \(f\in \mathcal {K}(G)\) define positive measures \(\mu \) and \(\nu \), and one calculates that \(\mu \in w[\mathfrak {M}]\) and \(\nu \in v[\mathfrak {M}]\).
and such that C is a neighborhood of the set \(\{z_n:n\in \mathbb {N}\}\). One finds sequences \((x_n)_{n\in \mathbb {N}}\) and \((y_n)_{n\in \mathbb {N}}\) in G such that \(w(x_n)v(y_n)\ge 4^n\) and \(x_ny_n=z_n\) for all \(n\in \mathbb {N}\). Passing to a subsequence and using symmetry, if necessary, one may assume that \(w(x_n)\ge 2^n\). Then, the set \(\{x_n:n\in \mathbb {N}\}\) is discrete because w is locally bounded, and therefore, one may assume that the sets \(x_n^{-1}C\), \(n\in \mathbb {N}\) are disjoint (again, by passing to a subsequence if necessary). By construction, \(x_n^{-1}C\) is a neighborhood of \(y_n\) for all \(n\in \mathbb {N}\). Thus, the set \({\{y_n:n\in \mathbb {N}\}}\) is discrete as well. Now the formulas \({\mu (f):=\sum ^\infty _{n=1}2^{-n}w(x_n)f(x_n)}\) and \(\nu (f):=\sum ^\infty _{n=1}2^{-n}v(y_n)f(y_n)\) with \(f\in \mathcal {K}(G)\) define positive measures \(\mu \) and \(\nu \), and one calculates that \(\mu \in w[\mathfrak {M}]\) and \(\nu \in v[\mathfrak {M}]\).
On the other hand, the estimate
holds for any \(g\in \mathcal {K}^+(G)\). Choosing \(g=1\) on C, one obtains an infinite expression, and thus, the image of \(\mu \otimes \nu \) under \(\varGamma \) does not exist. The reverse implication follows from Theorems 3 and 4.
“(a) \(\Longleftrightarrow \) (b)”: This follows from Theorems 3 and 4, Remark 5(d) and Eq. (7.5c).
“(a) \(\Rightarrow \) (c)”: From (a), one needs to show

The first statement follows from Remark 5(c) and Theorem 2. For the second statement, let \(y^\prime \in G\) and set \(\nu :=v(y^\prime )\delta _{y^\prime }\in v[\mathfrak {M}]\). One estimates

and this proves (7.11). The standard estimate in the first step is valid because \(f\in \mathcal {M}^\infty (G)\), and therefore, (6.8) can be applied. Resolving the double integral in the second step is justified by Theorem 1 because \(|f|\circ \varGamma \in \mathcal {M}^{+\infty }(G\times G)\) and \(|\mu |\), \(\nu \) are positive and moderated by Remark 5(c). The insertion of “1” in the third step is valid because u is finite valued and the zero set of \(u\circ \varGamma \) is locally \(|\mu |\otimes \nu \)-negligible. This follows because \(|\mu |\otimes \nu \in w[\mathfrak {M}]\otimes v[\mathfrak {M}]\subseteq (w\otimes v)[\mathfrak {M}]\) by Theorem 4 and \(w\otimes v\le u\circ \varGamma \).
“(c) \(\Rightarrow \) (a)”: This follows from (7.5d), Remark 6(c) and Proposition 6.
“(a) \(\Rightarrow \) (c’)”: The estimate (7.11) implies

where \(\mathfrak {M}_\mathrm {c}(G)\) denotes the set of all measures on G with compact support. Equation (7.11) implies that the inclusion in Eq. (7.12) holds also after the right factor on the left-hand side is replaced by its closure in \(\mathcal {M}^\infty (G)\) with respect to \(\Vert \cdot \Vert _u\) and likewise for the term on the right-hand side:

By Lemma 3, every element  can be represented by a vaguely convergent series
can be represented by a vaguely convergent series
where \(\alpha _n\in \mathbb {R}^+\),  for \(n\in \mathbb {N}\) and \(\sum ^\infty _{n=1}\alpha _n=1\). It will be shown in the following paragraph that
for \(n\in \mathbb {N}\) and \(\sum ^\infty _{n=1}\alpha _n=1\). It will be shown in the following paragraph that
Then Eq. (7.13) implies that \(\mu _n*f\in \mathcal {C}^{\sim }_\mathrm {v}[v]\) for all \(n\in \mathbb {N}\). Thus, the inclusion in (c’) follows from Lemma 5.
Finally, to prove (7.14), let \(x\in G\) such that \(v(x)>0\) and \(f\in \mathcal {C}^{\sim }_\mathrm {v}[u]\). Using (6.6) and the premise  reformulated as
reformulated as

one obtains, for \(n\in \mathbb {N}\), that

which proves (7.14) because \(\sum ^\infty _{k=n+1}\alpha _k\rightarrow 0\) for \(n\rightarrow \infty \). The last inequality uses Lemma 3, Eq. (7.2).
“(c’) \(\Rightarrow \) (a)”: Let \(f\in \mathcal {K}^+(G)\) with \(f\le 1/u\) and \(x\in G\). By assumption,

This statement is equivalent to  and, in turn, to \(w(x)\mathrm {L}_xv\le 1/f\). Taking the infimum over f, one obtains \(w(x)\mathrm {L}_xv\le u\) by the upper semicontinuity of u. Taking the supremum over \(x\in G\), one obtains
and, in turn, to \(w(x)\mathrm {L}_xv\le 1/f\). Taking the infimum over f, one obtains \(w(x)\mathrm {L}_xv\le u\) by the upper semicontinuity of u. Taking the supremum over \(x\in G\), one obtains  . \(\square \)
. \(\square \)
8 Convolution as a bounded bilinear operation
With the results of Sect. 7, the main objective of this work can now be achieved. First some notations are introduced, and some basic facts on the weighted spaces of measures or continuous functions are summarized. Throughout the section, S is a locally compact space and G is a locally compact group. The elements of \(\mathcal {U}^+(S)\) will be called weights on S.
Definition 6
Let W be a set of weights on S. The linear space of W-vanishing-at-infinity continuous functions [26, Section 22] is
The space of W-vanishing-at-infinity W-continuous functions is introduced as
where \(\mathcal {M}^\infty (w):=\{f\in \mathcal {M}^\infty (S):\Vert f\Vert _w<{\infty ^+}\}\), \(w\in \mathcal {U}^+(S)\) and the formula for \(\mathcal {C}^{\sim }_\mathrm {v}(w)\) means the closure of \(\mathcal {M}^\infty (w)\cap \mathcal {K}(S)\) in \(\mathcal {M}^\infty (w)\) with respect to the pseudo-metric \((f,g)\mapsto \Vert f-g\Vert _w\) on \(\mathcal {M}^\infty (w)\). The W-weighted topology\(\mathscr {T}_{W}\) on \(\mathcal {C}_\mathrm {v}(W)\) or \(\mathscr {T}^{\sim }_{W}\) on \(\mathcal {C}^{\sim }_\mathrm {v}(W)\) is generated by the pseudo-metric
Introducing the set \(\mathcal {C}^{\sim }_\mathrm {v}(W)\) allows a more elegant formulation of Theorem 6. The relation \(\mathcal {C}_\mathrm {v}(W)=\mathcal {C}^{\sim }_\mathrm {v}(W)\cap \mathcal {C}(S)\) holds. The topology \(\mathscr {T}_{W}\) is the subspace topology induced on \(\mathcal {C}_\mathrm {v}(W)\) by \(\mathscr {T}^{\sim }_{W}\). Remark 6(b) implies that \(\mathcal {C}_\mathrm {v}(W)=\mathcal {C}^{\sim }_\mathrm {v}(W)\) whenever \(\chi _K\in W\) for all compact \(K\subseteq G\). The functions \(\Vert \cdot \Vert _w\), \(w\in W\) are seminorms on \(\mathcal {C}_\mathrm {v}(W)\) making \((\mathcal {C}_\mathrm {v}(W),\mathscr {T}_W)\) a locally convex space. In general, \(\mathcal {C}^{\sim }_\mathrm {v}(W)\) is not even linear, but the natural Hausdorff quotients of \((\mathcal {C}_\mathrm {v}(W),\mathscr {T}_{W})\) and \((\mathcal {C}^{\sim }_\mathrm {v}(W),\mathscr {T}^{\sim }_{W})\) are isomorphic as locally convex spaces.
Definition 7
Those sets W of weights on S such that
for all \(u\in \mathcal {U}^+(S),~w,v\in W,~\lambda \in \mathbb {R}^+\) are called cone ideals of weights on S (or cone ideals on S for short). The cone ideal generated by a set V of weights on S is denoted by \(\langle V\rangle \) and given by
for non-empty V, while \(\langle \emptyset \rangle =\{0\}\).
For any set W of weights on S, the cone ideal \(\langle W\rangle \) is the largest set V of weights on S such that \(\mathscr {T}_{V}=\mathscr {T}_{W}\). It follows that the assignment \(W\mapsto (\mathcal {C}_\mathrm {v}(W),\mathscr {T}_{W})\) defines a bijection between cone ideals W and the locally convex spaces of W-vanishing continuous functions \((\mathcal {C}_\mathrm {v}(W),\mathscr {T}_{W})\). Working with cone ideals instead of general Nachbin families allows a convenient formulation of Theorem 6.
Definition 8
Let W be a cone ideal of weights on S. The linear space of measures withW-finite measure is defined as
The bornology \(\mathscr {K}_{W}\) is defined as
It was shown in [29, p. 152] (see also [34, Theorem 3.1]) that \(W(\mathfrak {M})\) is the topological dual of \((\mathcal {C}_\mathrm {v}(W),\mathscr {T}_{W})\) where the pairing \(\langle \cdot ,\cdot \rangle _W:\mathcal {C}_\mathrm {v}(W)\times W(\mathfrak {M})\rightarrow \mathbb {K}\) is given by the integration
It is immediate from the definitions that \(w[\mathfrak {M}]\) is the polar set of \(\mathcal {C}_\mathrm {v}(W)\cap \mathcal {C}_\mathrm {v}[w]\) whenever \(w\in W\). The latter is the unit ball of \(\Vert \cdot \Vert _w\) in \(\mathcal {C}_\mathrm {v}(W)\). Conversely, \(\mathcal {C}_\mathrm {v}(W)\cap \mathcal {C}_\mathrm {v}[w]\) is the polar set of \(w[\mathfrak {M}]\). Therefore, \(\mathscr {K}_{W}\) is the equicontinuous compactology on \(W(\mathfrak {M})\) associated with \(\mathscr {T}_{W}\) [12, 18] (see also [34, Section 4]). The space \((W(\mathfrak {M}),\mathscr {K}_{W})\) by itself is a linear space with convex vector bornology [12, Def. 1.1].
Theorem 6
Let W, V, U be cone ideals of weights on G. The following statements are equivalent:
-
(a)
The following inclusion holds:
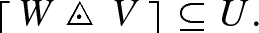 (8.5)
(8.5) -
(b)
The following two conditions hold:
$$\begin{aligned} *:W(\mathfrak {M})\times V(\mathfrak {M})&\rightarrow U(\mathfrak {M})~\text {is well defined}, \end{aligned}$$(8.6a)$$\begin{aligned} \mathscr {K}_{W}*\mathscr {K}_V&\subseteq \mathscr {K}_U. \end{aligned}$$(8.6b) -
(c)
The mapping
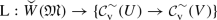 (8.7a)
(8.7a)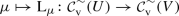 (8.7b)
(8.7b)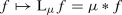 (8.7c)
(8.7c)is well defined. Here \(\mathrm {L}_\mu f=\mu *f\) denotes the left convolution of f with \(\mu \) as given in Eq. (6.14). Images of bounded subsets of
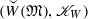 under \(\mathrm {L}\) are equicontinuous sets of continuous mappings $$\begin{aligned} (\mathcal {C}^{\sim }_\mathrm {v}(U),\mathscr {T}^{\sim }_{U})\rightarrow (\mathcal {C}^{\sim }_\mathrm {v}(V),\mathscr {T}^{\sim }_{V}). \end{aligned}$$(8.7d)
under \(\mathrm {L}\) are equicontinuous sets of continuous mappings $$\begin{aligned} (\mathcal {C}^{\sim }_\mathrm {v}(U),\mathscr {T}^{\sim }_{U})\rightarrow (\mathcal {C}^{\sim }_\mathrm {v}(V),\mathscr {T}^{\sim }_{V}). \end{aligned}$$(8.7d)
Proof
Equation (8.5) is equivalent to

Equations (8.6a) and (8.6b) are equivalent to the following statement:
The statement in part (c) means that

and that for all \(\varepsilon >0\),  , \(v\in V\) there exist \(\delta >0\), \(u\in U\) such that for all \(f,g\in \mathcal {C}^{\sim }_\mathrm {v}(U)\) the following implication holds
, \(v\in V\) there exist \(\delta >0\), \(u\in U\) such that for all \(f,g\in \mathcal {C}^{\sim }_\mathrm {v}(U)\) the following implication holds
Whenever the conditions
hold, the distributive law can be applied inside the norm on the right-hand side in (8.8d). [Using Eq. (6.5) in Proposition 8 and \(0\cdot {\infty ^+}=0\).] In this case, Eq. (8.8d) turns into
The condition (8.8e) for this replacement is fulfilled if (8.8c) holds. Statements (8.8c) and (8.8f) in turn are equivalent to the more concise formula

This statement, in turn, implies (8.8c). Thus, the statement in part (c) is equivalent the statement (8.8g).
By Theorem 5 the statements (8.8a), (8.8b) and (8.8g) are equivalent which concludes the proof. \(\square \)
The sets \(\mathcal {C}^{\sim }_\mathrm {v}(U)\) and \(\mathcal {C}^{\sim }_\mathrm {v}(V)\) in statement (c) of Theorem 6 can be replaced by the sets \(\mathcal {C}_\mathrm {v}(U)\) and \(\mathcal {C}_\mathrm {v}(V)\), if the assumption \(\chi _K\in V\) for all compact \(K\subseteq G\) is added. Then the mapping \(\mathrm {L}\) with domain  is a linear mapping with continuous linear operators between locally convex spaces as co-domain.
is a linear mapping with continuous linear operators between locally convex spaces as co-domain.
The implication “(b) \(\Rightarrow \) (a)” in Theorem 6 fails if the condition (8.6b) is dropped. The reason is that the assignment \(W\mapsto \mathscr {K}_{W}\), with W a cone ideal, is injective, but the assignment \(W\mapsto W(\mathfrak {M})\) is not. For example, one obtains \(W(\mathfrak {M})=V(\mathfrak {M})=U(\mathfrak {M})=\mathfrak {M}_\mathrm {f}(G)\) for \(W=V=\mathcal {U}^+_\mathrm {b}(G)\), \(U=\mathcal {U}^+_\mathrm {v}(G)\), but \(W\ne U\) if G is non-compact. This shows that (8.6a) by itself does not imply (8.5), because  contradicts (8.5), but convolution \(*\) is known to be a well-defined internal operation on \(\mathfrak {M}_\mathrm {f}(G)\) in agreement with (8.6a).
contradicts (8.5), but convolution \(*\) is known to be a well-defined internal operation on \(\mathfrak {M}_\mathrm {f}(G)\) in agreement with (8.6a).
9 Application to fractional Weyl integrals
Following [23], the space \(\mathcal {E}:=\left\{ f\in \mathcal {C}^\infty (\mathbb {R})~\Big |~\forall \,{m,n\in \mathbb {N}: t^nf^{(m)}(t)\rightarrow 0 \text { for } t\rightarrow {\infty ^+}}\right\} \) denotes complex valued smooth functions that vanish rapidly at \({\infty ^+}\). Such functions are called “good” in [23]. The generalized fractional Weyl integral of order \(\alpha \in \mathbb {C}\) for a function \(f\in \mathcal {E}\) is defined as [11, 20, 23]
where \(m\in \mathbb {N}_0\) is such that \(\alpha +m\in \mathbb {H}\) with \(\mathbb {H}:=\{z\in \mathbb {C}:\mathfrak {R}z>0\}\). It is known that (9.1) is well defined and the \(\mathrm{I}_{\alpha }\) are linear endomorphisms, even automorphisms, on \(\mathcal {E}\). Further, the index law
holds. An alternative proof for these facts based on Theorem 6 is given below. Using our theorem, continuity of the fractional integrals with respect to a suitable weighted topology is obtained in addition. Furthermore, sets of linear combinations of generalized fractional integrals are seen to be equicontinuous whenever coefficients and orders are bounded.
Let P denote the set of upper semicontinuous functions \(u:\mathbb {R}\rightarrow \mathbb {R}^+\) with the property that \(u(t)\le \lambda (1+|t|^p)\), \(t\in \mathbb {R}\) for some \(\lambda \in \mathbb {R}^+\). Let \(\mathcal {U}^+_+(\mathbb {R})\) denote the set of upper semicontinuous functions \(u:\mathbb {R}\rightarrow \mathbb {R}^+\) such that \({\text {supp}}u\subseteq [t,+\infty )\) for some \(t\in \mathbb {R}\). Then define \(P_+:=P\cap \mathcal {U}^+_+(\mathbb {R})\). The sets \(\mathcal {U}^+_+(\mathbb {R})\), P and \(P_+\) are cone ideals. Define the weights \(w_{+,p}\), \(p\ge 0\) as
It is calculated that

for all \(p,q\ge 0\). The elements of \(P_+\) are characterized as being less or equal than a translate of \(w_{+,p}\) for some \(p\ge 0\) large enough. Together with Proposition 4 and (9.4), this implies that the inclusion

holds and that \(P_+\) is invariant under translations. Observe that \(\mathcal {C}_\mathrm {v}(P_+)\) is a continuous variant for the space \(\mathcal {E}\).
For \(\alpha \in \mathbb {H}\), let \(\mu _\alpha \) denote the measure on \(\mathbb {R}\) with Lebesgue density
and let \(\mu _0=\delta _0\) be the Dirac measure at the origin. Note that
corresponding to the index law for the operators \(\mathrm{I}_{\alpha }\), \(\alpha \in \mathbb {H}\cup \{0\}\). Using \((1+t)^p\ge \max \{1,t^p\}\), the following uniform estimate can be proved
for all \(\alpha \in \mathbb {H}\) with \(\mathfrak {R}\alpha \le \beta \) and \(|\arg \alpha |\le \phi \) where \(\beta <p\), \(\phi <\pi /2\) and \(\varepsilon >0\) are fixed and \(C_{\beta ,\phi ,\varepsilon }<\infty \). This translates to the fact that the set  is contained in a scalar multiple of a translate of the weighted ball
is contained in a scalar multiple of a translate of the weighted ball  for \(p>\beta \).
for \(p>\beta \).
Using Theorem 6 and the above remarks, one arrives at the following conclusion. For \(C<\infty \), \(\phi <\pi /2\) and \(d\in \mathbb {N}\), the set
is an equicontinuous set of continuous linear endomorphisms of \(\mathcal {C}_\mathrm {v}(P_+)\). For \(d=1\), this is referred to as \(\mathrm{I}_{\alpha }\), \(\alpha \in \mathbb {H}\cup \{0\}\) being an equicontinuously parameterized family of continuous linear convolution endomorphisms of \(\mathcal {C}_\mathrm {v}(P_+)\). The result is readily extended to general orders from \(\mathbb {C}\) using the following construction.
For any set of weights W on \(\mathbb {R}\), the space of smooth functions withW-vanishing-at-infinity derivatives is defined as
and endowed with the weighted topology \(\mathscr {T}^\infty _{W}\) that is generated by the seminorms \(f\mapsto \max \{\Vert f^{(k)}\Vert _w:m\ge k\in \mathbb {N}_0\}\) with \(w\in W\), \(m\in \mathbb {N}_0\). Clearly, classical derivatives define continuous linear endomorphisms of \(\mathcal {C}^\infty _\mathrm {v}(W)\).
The linear space \(\mathcal {C}^\infty _\mathrm {v}(P_+)\) coincides with the space \(\mathcal {E}\). Note that \(\mathrm{I}_{\alpha }\), \(\alpha \in \mathbb {C}\) is defined as the composition of a classical derivative of order m, a multiplication with the constant \((-1)^m\) and a convolution with the measure \(\mu _{\alpha +m}\). The index law for \(\alpha ,\beta \in \mathbb {C}\) is obtained from the case \(\alpha ,\beta \in \mathbb {H}\cup \{0\}\) by interchanging derivatives and integration. This is permitted due to the properties of functions in \(\mathcal {E}\). Therefore, the results above carry over to the case \(\alpha \in \mathbb {C}\). For \(C<\infty \) and \(d\in \mathbb {N}\), the set
is an equicontinuous set of continuous linear endomorphisms of \(\mathcal {C}^\infty _\mathrm {v}(P_+)\). Using the index law for \(\beta =-\alpha \in \mathbb {C}\) and the fact that \(\mathrm{I}_{0}\) is the identity operator, it follows that the operators \(\mathrm{I}_{\alpha }\), \(\alpha \in \mathbb {C}\) are also automorphisms.
References
Abtahi, F., Nasr-Isfahani, R., Rejali, A.: Weighted \(L^p\)-Conjecture for Locally Compact Groups. Periodica Mathematica Hungarica 60, 1–11 (2010)
Berberian, S.: On the convolution of a measure and a function. Proceedings of the American Mathematical Society 53, 399–403 (1975)
Biswas, A., Swanson, D.: Navier-Stokes equations and weighted convolution inequalities in groups. Communications in Partial Differential Equations 35, 559–589 (2010)
Bourbaki, N.: Elements of Mathematics: Integration I. Springer, Berlin (2004)
Bourbaki, N.: Elements of Mathematics: Integration II. Springer, Berlin (2004)
Carro, M., Perez, C., Soria, F., Soria, J.: Maximal functions and the control of weighted inequalities for the fractional integral operator. Indiana University Mathematics Journal 54, 627–644 (2005)
Davey, B., Priestley, H.: Introduction to Lattices and Order, 2nd edn. Cambridge University Press, Cambridge (2002)
Edwards, R.: The Stability of Weighted Lebesgue Spaces. Transactions of the American Mathematical Society 93, 369–394 (1959)
El Kinani, A.: On generalized Beurling algebras. Rendiconti del Circolo Matematico di Palermo LVI 369–380, (2007)
Gaudry, G.: Multipliers of weighted Lebesgue and measure spaces. Proc. London Math. Soc. 19, 327–340 (1969)
Hilfer, R.: Applications of Fractional Calculus in Physics. World Scientific Publ. Co., Singapore (2000)
Hogbe-Nlend, H.: Bornologies and Functional Analysis. North-Holland Publ.Co, Amsterdam (1977)
Hoh, W., Jacob, N.: On the Potential Theory of the Kolmogorov Equation. Math. Nachr. 154, 51–66 (1991)
Hoh, W., Jacob, N.: Towards an \(L^p\)-potential theory for sub-Markovian semigroups: variational inequalities and balayage theory. J. Evol. Equ. 4, 297–312 (2004)
Jacob, N.: A Class of Elliptic pseudodifferential operators Generating Symmetric Dirichlet Forms. Potential Analysis 1, 221–232 (1992)
Jacob, N.: Pseudodifferential Operators and Markov Processes II. Imperial College Press, London (2002)
Jacob, N., Schilling, R.: Towards an \(L^p\)-Potential Theory for Sub-Markovian Semigroups: Kernels and Capacities. Acta Mathematica Sinica 22, 1227–1250 (2006)
Jarchow, H.: Locally Convex Spaces. Teubner, Stuttgart (1981)
Kerman, R., Sawyer, E.: Convolution algebras with weighted rearrangement-invariant norm. Studia Mathematica 108, 103–126 (1994)
Kleiner, T.: Lokalkonvexe Funktionenräume und fraktionale Weyl-Ableitungen. Master’s thesis, Universität Stuttgart (2016)
Lacey, M., Moen, K., Perez, C., Torres, R.: Sharp weighted bounds for fractional integral operators. J. Functional Analysis 259, 1073–1097 (2010)
Mazure, M.L.: Équations de convolution et formes quadratiques. Annali di Matematica pura ed applicata CLVIII 75–97, (1991)
Miller, K.: The Weyl fractional calculus. In: Ross, B. (ed.) Fractional Calculus and its Applications, Lecture Notes in Mathematics, vol. 457, pp. 80–89. Springer Verlag, (1975)
Moreau, J.: Fonctionelles convexes. Seminaire Jean Leray 2, 1–108 (1967)
Muckenhoupt, B., Wheeden, R.: Weighted Norm Inequalities for fractional Integrals. Trans. Am. Math. Soc. 192, 261–274 (1974)
Nachbin, L.: Elements of Approximation Theory. Instituto de Matematica Pura e Aplicada de Conselho Nacional de Pesquisas, Rio de Janeiro (1965)
Nursultanov, E., Tikhonov, S.: Weighted Norm Inequalities for Convolution and Riesz Potential. Potential Analysis 42, 435–456 (2015)
Pérez, C.: Two weighted inequalities for potential and fractional type operator. Indiana University Mathematics Journal 43, 663–683 (1994)
Prolla, J.: Weighted Spaces of Vector-Valued Continuous Functions. Annali di Matematica Pura ed Applicata 89, 145–157 (1971)
Rockafellar, H., Wets, R.: Variational Analysis, Grundlehren der mathematischen Wissenschaften, vol. 317. Springer, Berlin (2009)
Sawyer, E.: A Characterization of Two Weight Norm Inequalities for Fractional and Poisson Integrals. Trans. Am. Math. Soc. 308, 533–545 (1988)
Sawyer, E., Wheeden, R.: Weighted Inequalities for Fractional Integrals on Euclidean and Homogeneous Spaces. American Journal of Mathematics 114, 813–874 (1992)
Sawyer, E., Wheeden, R., Zao, S.: Weighted Norm Inequalities for Operators of Potential Type and Fractional Maximal Functions. Potential Analysis 5, 523–580 (1996)
Summers, W.: Dual Spaces of Weighted Spaces. Transactions of the American Mathematical Society 151, 323–333 (1970)
Torchinsky, A.: Weighted Local Estimates for Fractional Type Operators. Potential Analysis 41, 869–885 (2014)
Zähle, M.: Riesz Potentials and Liouville Operators on Fractals. Potential Analysis 21, 193–208 (2004)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kleiner, T., Hilfer, R. Convolution operators on weighted spaces of continuous functions and supremal convolution. Annali di Matematica 199, 1547–1569 (2020). https://doi.org/10.1007/s10231-019-00931-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10231-019-00931-z




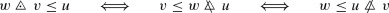



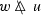 and
and 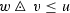 holds.
holds.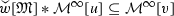 holds.
holds.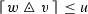 holds.
holds.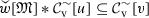 holds.
holds.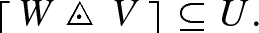
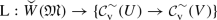
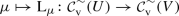
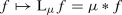
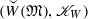 under
under