Finite-Time Singularities of Solutions to Microelectromechanical Systems with General Permittivity

Abstract

Of concern is a study of qualitative properties of solutions to the evolution problem modelling microelectromechanical systems with general permittivity. The system couples a quasilinear parabolic evolution problem for a membrane’s displacement with an elliptic free boundary value problem for the electrostatic potential in the region between the membrane and a rigid ground plate. It is shown that, under a structural condition on the permittivity profile, non-positive solutions develop a singularity in finite time, provided that the applied voltage is large enough and the aspect ratio of the system is small enough.

1 Introduction

The aim of this paper is to describe some qualitative behaviour of the solutions to an evolution problem modelling idealised electrostatically actuated microelectromechanical systems (MEMS). Such MEMS devices consist of a grounded horizontal plate above which an elastic membrane with a general permittivity profile is located. An application of a voltage difference between the ground plate and the membrane leads to the transformation of the electrostatic energy into mechanical energy and causes the upper part of the device to move. The goal of this modelling is to understand the membrane’s displacement and the distribution of the electrostatic potential. We refer the reader to [5] and [8] for a more detailed derivation of the physical model.

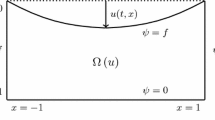
After a suitable scaling, the rigid ground plate is placed at $z=-1$ such that the flat membrane, corresponding to no voltage difference, is located at $z=0$. The horizontal length of the device is given by the interval $I:=(-1,1)$, where we additionally assume homogeneity in transversal horizontal direction. Given $t>0$ and $x\in I$, let $u=u(t,x)$ denote the membrane’s displacement and $f=f(x)$ the permittivity profile of the membrane. The membrane is fixed at the boundary points $x=\pm 1$ to the value 0. A sketch of a simplified MEMS device is offered in Fig. 1.

Fig. 1

Cross section of a MEMS device

Finally, an initial condition $u_*= u_*(x)$ is specified¹ at time $t=0$. The membrane’s displacement is then described by the solution of the quasilinear evolution problem

$$\begin{aligned} u_t -\partial _x\left( \frac{u_x}{\sqrt{1 + \varepsilon ^2 u_x^2}}\right)= & {} -\lambda \left( \varepsilon ^2 \bigl (\psi _x(t,x,u(t,x))\bigr )^2 + \bigl (\psi _z(t,x,u(t,x))\bigr )^2\right) \nonumber \\&+2 \lambda \varepsilon ^2 \psi _x(t,x,u(t,x)) f^{\prime }(x), \quad t > 0,\, x \in I, \end{aligned}$$

(1)

$$\begin{aligned} u(t, \pm 1)= & {} 0, \quad t > 0, \end{aligned}$$

(2)

$$\begin{aligned} u(0,x)= & {} u_{*}(x), \quad x \in I, \end{aligned}$$

(3)

whereas the electrostatic potential $\psi =\psi (t,x,z)$ is given as the solution to the rescaled elliptic free boundary value problem

$$\begin{aligned} \varepsilon ^2 \psi _{xx} + \psi _{zz}= & {} 0, \quad t > 0,\,(x,z) \in \Omega (u(t)), \end{aligned}$$

(4)

$$\begin{aligned} \psi (t,x,z)= & {} \frac{1 + z}{1 + u(t,x)} f(x), \quad t > 0,\,(x,z) \in \partial \Omega (u(t)). \end{aligned}$$

(5)

Here $\varepsilon > 0$ denotes the aspect ratio of the unscaled device and $\lambda > 0$ is proportional to the square of the applied voltage. As the membrane deflects with time, the region

$$\begin{aligned} \Omega (u(t)) = \left\{ (x,z) \in (-1,1) \times (-1,\infty ); -1< z < u(t,x)\right\} \end{aligned}$$

(6)

between the rigid ground plate and the membrane changes with time as well. The dynamic behaviour of the full system is thus prescribed by the pair $(u,\psi )$ of solutions to the quasilinear initial boundary value problem (1)–(3) and the elliptic moving boundary problem (4)–(5). It is worthwhile to mention that the modelling breaks down when the membrane’s deflection u reaches the value $-1$, i.e. when the membrane touches the ground plate. The understanding of this touchdown behaviour is one of the major objectives of the mathematical investigation of MEMS devices. Addressing this topic, the main result of our contribution states that there are finite-time singularities of the form

$$\begin{aligned} \liminf _{t\rightarrow T}\min _{x\in [-1,1]} u(t,x)=-1\quad \text {or} \quad \limsup _{t\rightarrow T}\Vert u(t,\cdot )\Vert _{W^2_q(I)}=\infty , \end{aligned}$$

where $T>0$ denotes the maximal time of existence, provided that

${(A_1)}$ :

$\ u(t,x) \le 0$ for all $(t,x)\in [0,T)\times I$;

${(A_2})$ :

$\ \displaystyle {\max _{x\in [-1,1]}}\,{f(x)} < \sqrt{2}\; \displaystyle {\min _{x\in [-1,1]}}\, {f(x)}\quad$ and $\quad \displaystyle {\min _{x\in [-1,1]}}\, {f(x)}=f(-1)=f(1)$;

${(A_3)}$ :

$\ \varepsilon < \varepsilon _{*}$ and $\lambda > \lambda ^{*} = \lambda ^{*}(\varepsilon _{*})$, where $\varepsilon _{*}$ and $\lambda ^{*}$ are to be determined later.

In order to discuss this result, let $H:=H(\lambda ,\varepsilon ,u)$ denote the right-hand side of (1). Note that the operator H is semilinear in u but also highly nonlocal in u, due to the fact that the solution operator belonging to (4)–(5) is involved (which itself depends on u). Beyond that, it is worthwhile to mention that the left-hand side of (1) represents a quasilinear evolution system.

Note that, given a non-positive initial value $u_{*}$, if the permittivity f is constant, then H is non-positive and thus $(A_1)$ is automatically satisfied. The situation is fairly different for a general permittivity profile. In fact in this case there is numerical evidence that the deflection of the membrane may become positive or yet never becomes negative, even when emerging from the initial datum $u_*\equiv 0$, cf. [2]. There are some properties of the potential $\psi$ and the permittivity profile f which ensure $(A_1)$, cf. [6] and Corollary 2.2. In general, the non-positivity of u cannot be expected. On the other hand, $(A_1)$ is crucial in our approach, cf. the proof of Theorem 3.1.

Assumption $(A_2)$ seems to be of technical nature.² One would expect that also for permittivity profiles with $\max f > \sqrt{2} \min {f}$ finite-time singularities and even more so possible touchdowns should occur. To the best of our knowledge so far no rigorous proof of such a result is available. However, it is worthwhile to note that apart from $(A_2)$ and mild regularity assumptions, no further hypotheses on f, like convexity, concavity, or symmetry, are imposed.

Finally, also assumption $(A_3)$ is physically plausible: for a fairly high voltage value $\lambda$ and a rather small aspect ratio $\varepsilon$, a possible singularity seems likely.

2 Local Well-Posedness and Global Existence

Results on local and global well-posedness of (1)–(5) have recently been established in [4], assuming a constant permittivity profile $f\equiv 1$, and in [7] with a general permittivity profile but with a linearised curvature operator.³ These studies can be fused to derive analogue results for the quasilinear evolution Eq. (1) with general permittivity profiles.

Theorem 2.1

(Local Well-Posedness) Let $q\in (2,\infty )$, $\varepsilon >0$, $\lambda >0$, $f\in C^2([-1,1])$, and an initial value $u_*\in W_q^2(I)$ be given such that $u_{*}(\pm 1)=0$ and $-1 < u_{*}(x)$ for $x\in I$. Then there is a unique $T>0$ and a unique non-extendable solution $(u,\psi )$ to (1)–(5). This means that u is unique in the class

$$\begin{aligned} C^1([0,T),L_q(I))\cap C([0,T), W_q^2(I)). \end{aligned}$$

satisfying (1)–(3) together with

$$\begin{aligned} u(t,x)>-1, \quad (t,x)\in [0,T)\times I, \end{aligned}$$

and that $\psi (t)\in W_2^2(\Omega (u(t))$ uniquely solves (4)–(5) for each $t\in [0,T)$.

Proof

(i) As explained in [4, Remark 3.3], there are two principle differences between the semilinear case

$$\begin{aligned} u_t - u_{xx} = H(\lambda ,\varepsilon ,u) \end{aligned}$$

and its quasilinear counterpart

$$\begin{aligned} u_t - \partial _x\Big (\frac{u_x}{\sqrt{1 + \varepsilon ^2 u_x^2}}\Big ) = H(\lambda ,\varepsilon ,u). \end{aligned}$$

The first difference is that the latter case requires the application of a suitable evolution operator $U_A$, induced by the quasilinear operator $A(v)u = -u_{xx}/(1 + \varepsilon ^2 v_x^2)^{3/2}$. But here we can verbatim use the results derived in [4, Section 3].

(ii) The second difference is related to the mapping properties of the nonlinear operator $H(\lambda ,\varepsilon ,\cdot )$, where $\lambda >0$ and $\varepsilon >0$ are fixed, cf. the proof of (2.8) in [4]. In our case, (2.8) in [4] is satisfied, provided that, given $\xi \in [0,1/2)$ and $\nu \in [0,(1-2\xi )/2)$, there exists a $\kappa \in (0,1)$ and a constant $c = c(\kappa ,\varepsilon )>0$ such that

$$\begin{aligned} \Vert H(\lambda ,\varepsilon ,v)- H(\lambda ,\varepsilon ,w)\Vert _{W^\nu _{2}(I)} \le c \Vert v-w\Vert _{W^{2-\xi }_{q}(I)} \end{aligned}$$

(7)

for all $v,\,w\in \overline{S}_q(\kappa )$, where

$$\begin{aligned} S_q(\kappa ) :=\left\{ v\in W_q^2(I)\,;\, v(\pm 1)=0,\ \Vert v\Vert _{W^2_q(I)}<1/\kappa ,\ -1+\kappa < v(x)\ \text {for}\ x\in I\right\} . \end{aligned}$$

(iii) Analysing the proof of (2.8) in [4] and the structure of $H(\lambda ,\varepsilon ,v)$, it is possible to verify (7) under the mild regularity assumption $f\in C^2([-1,1])$. To establish this, we introduce some further notation. Given $v \in \overline{S}_q(\kappa )$, let

$$\begin{aligned} \Omega (v) := \left\{ (x,z) \in (-1,1) \times (-1,\infty ); -1< z < v(x)\right\} \end{aligned}$$

and let $\psi$ denote the solution to

$$\begin{aligned} \varepsilon ^2 \psi _{xx}(x,z) + \psi _{zz}(x,z)= & {} 0, \quad (x,z) \in \Omega (v), \end{aligned}$$

(8)

$$\begin{aligned} \psi (t,x,z)= & {} \frac{1 + z}{1 + v(x)} f(x), \quad (x,z) \in \partial \Omega (v). \end{aligned}$$

(9)

We further set

$$\begin{aligned} g_\varepsilon (v):= \varepsilon \psi _x^2(\cdot ,v)+\psi _z^2(\cdot ,v), \end{aligned}$$

whence we clearly have

$$\begin{aligned} H(\lambda ,\varepsilon ,v) = -\lambda g_\varepsilon (v)+2\lambda \varepsilon ^2\psi _x(\cdot ,v)f'. \end{aligned}$$

(10)

Note that $\psi$, and therefore also $g_\varepsilon$, depend implicitly on f. Nevertheless, a combination of [7, Theorem 3.3] and [7, Lemma 3.4] with the proof of [4, Proposition 2.1] implies that there is a constant $c_1 > 0$ such that

$$\begin{aligned} \Vert g_\varepsilon (v) - g_\varepsilon (w)\Vert _{W^\nu _{2}(I)} \le c_1 \Vert v-w\Vert _{W^{2-\xi }_{q}(I)} \end{aligned}$$

(11)

for all $v, w\in \overline{S}_q(\kappa )$.

(iv) In order to treat the second summand of H, which involves f or rather $f^{\prime }$ explicitly, we firstly derive the estimate

$$\begin{aligned} \Vert \psi _x(\cdot ,v) - \psi _x(\cdot ,w)\Vert _{W^{\nu }_{2}(I)} \le c_2 \Vert v-w\Vert _{W^{2-\xi }_{q}(I)}, \quad v, w\in \overline{S}_q(\kappa ), \end{aligned}$$

(12)

where $c_2$ is a positive constant. Similarly as in [4] or [7], respectively, we define the rectangle $R := I \times (0,1)$ and denote by

$$\begin{aligned} \phi (v)(x,\eta ):=\psi (x,(1+v(x))\eta - 1), \quad (x,\eta ) \in [-1,1]\times [0,1], \end{aligned}$$

the solution to the transformed elliptic boundary value problem

$$\begin{aligned} \mathcal {L}_v \phi (v)(t,x,\eta )= & {} 0, \quad t > 0,\, (x,\eta ) \in R, \end{aligned}$$

(13)

$$\begin{aligned} \phi (v)(t,x,\eta )= & {} \eta f(x), \quad t > 0, (x,\eta ) \in \partial R, \end{aligned}$$

(14)

with the v-dependent operator

$$\begin{aligned} \mathcal {L}_v \varphi := \varepsilon ^2 \varphi _{xx} - 2 \varepsilon ^2 \eta \frac{v_x}{1+v}\varphi _{x\eta } + \frac{1 + \varepsilon ^2 \eta ^2 v_x^2}{(1+v)^2}\varphi _{\eta \eta } + \varepsilon ^2 \eta \left( 2 \left( \frac{v_x}{1+v}\right) ^2 - \frac{v_{xx}}{1 + v}\right) \varphi _{\eta }, \end{aligned}$$

which is obtained by mapping (8)–(9) via the diffeomorphism

$$\begin{aligned} T_{v}(x,z) := \left( x,\frac{1 + z}{1 + v(x)}\right) , \quad (x,z)\in \Omega (v), \end{aligned}$$

onto R. Note that this implies that

$$\begin{aligned} \psi _x(x,v(x))=f^{\prime }(x) - \frac{v_x(x)}{1+v(x)}\phi _{\eta }(v)(x,1), \quad x\in [-1,1]. \end{aligned}$$

Thus, letting $h(v):=v_x/(1+v)$, we have

$$\begin{aligned} \Vert \psi _x(\cdot ,v) - \psi _x(\cdot ,w)\Vert _{W^{\nu }_{2}(I)}\le & {} \Vert (h(v)-h(w))\phi _{\eta }(v)(\cdot ,1)\Vert _{W^{\nu }_{2}(I)} \nonumber \\&+ \Vert h(w)(\phi _{\eta }(v)(\cdot ,1) - \phi _{\eta }(w)(\cdot ,1))\Vert _{W^{\nu }_{2}(I)}. \end{aligned}$$

(15)

In order to estimate the right-hand side of (15), we introduce the notation

$$\begin{aligned} N_1&:= \Vert (h(v)-h(w))\phi _{\eta }(v)(\cdot ,1)\Vert _{W^{\nu }_{2}(I)}, \\ N_2&:= \Vert h(w)(\phi _{\eta }(v)(\cdot ,1) - \phi _{\eta }(w)(\cdot ,1))\Vert _{W^{\nu }_{2}(I)}, \end{aligned}$$

for the sake of lucidity.

(v) Concerning $N_1$, we recall that pointwise multiplication from $W_q^{1-\xi }(I)\times W^{1/2}_2(I)$ into $W_2^{\nu }(I)$ is continuous, cf. [1, Theorem 4.1]. In the sequel, we use the notation

$$\begin{aligned} W_q^{1-\xi }(I)\cdot W^{1/2}_2(I) \hookrightarrow W_2^{\nu }(I) \end{aligned}$$

(16)

to indicate this property. Now, thanks to (16), we can derive the estimate

$$\begin{aligned} N_1 \le \Vert h(v)-h(w)\Vert _{W^{1-\xi }_{q}(I)}\, \Vert \phi _{\eta }(v)(\cdot ,1)\Vert _{W^{1/2}_{2}(I)}. \end{aligned}$$

(17)

Invoking an adaption of (2.21) in [4] to the case of a non-constant f, there is a constant $c_3 > 0$ such that

$$\begin{aligned} \Vert \phi _{\eta }(v)(\cdot ,1)\Vert _{W^{1/2}_{2}(I)} \le c_3, \quad v\in \overline{S}_q(\kappa ). \end{aligned}$$

(18)

Furthermore, since $W_q^{1-\xi }(I)$ is a multiplication algebra and since v and w belong to $\overline{S}_q(\kappa )$, we get that

$$\begin{aligned} \left\| h(v) - h(w)\right\| _{W^{1-\xi }_{q}(I)}\le & {} \left\| \frac{v_x - w_x}{1+v}\right\| _{W^{1-\xi }_{q}(I)} + \left\| w_x \frac{w-v}{(1 + v)(1 + w)}\right\| _{W^{1-\xi }_{q}(I)}\nonumber \\\le & {} c_4 \left\| v - w\right\| _{W^{2-\xi }_{q}(I)} \end{aligned}$$

(19)

for a suitable constant $c_4$.

(vi) In order to estimate $N_2$, we use the continuity of pointwise multiplication

$$\begin{aligned} W^1_q(I)\cdot W_2^{1/2-\alpha }(I)\hookrightarrow W^{\nu }_2(I), \quad \alpha \in (\xi ,1), \end{aligned}$$

and the analogon of [4, Lemma 2.6] to obtain

$$\begin{aligned} N_2\le & {} \Vert h(w)\Vert _{W^1_q(I)} \Vert \phi _{\eta }(v)(\cdot ,1) - \phi _{\eta }(w)(\cdot ,1)\Vert _{W^{1/2-\alpha }_{2}(I)} \nonumber \\\le & {} \Vert h(w)\Vert _{W^1_q(I)} \Vert v-w\Vert _{W^{2-\xi }_{q}(I)}. \end{aligned}$$

(20)

Also $W^1_q(I)$ is a multiplication algebra, whence we conclude that there is a positive constant $c_5$ such that

$$\begin{aligned} \Vert h(w)\Vert _{W^1_q(I)} \le c_5, \quad w\in \overline{S}_q(\kappa ). \end{aligned}$$

(21)

It remains to combine (10), (11) and (17) – (21) to complete the proof of (12).

(vii) Again by [1, Theorem 4.1], we find that $W^1_\infty (I)\cdot W^{\nu }_2(I)\hookrightarrow W^\nu _2(I)$, whence we end up with

$$\begin{aligned} \Vert f'(\psi _x(\cdot ,v)-\psi _x(\cdot ,w))\Vert _{W^\nu _2(I)} \le \Vert f\Vert _{W^2_\infty (I)} \Vert \psi _x(\cdot ,v)-\psi _x(\cdot ,w)\Vert _{W^{\nu }_2(I)}. \end{aligned}$$

The assertion eventually follows from (12). $\square$

Having the local existence and uniqueness of the solution $(u,\psi )$ to (1)–(5) at hand, we now consider the sign of u in detail. As already mentioned in the introduction, the non-positivity of u is crucial in order to verify the existence of finite-time singularities. In the sequel, the necessary conditions established in [6] for the semilinear counterpart of (1) are applied to the present setting.

Given

$$\begin{aligned} w\in C^1([0,T),L_q(I))\cap C([0,T), W_q^2(I)), \end{aligned}$$

let $U_{A(w)}$ denote the evolution operator generated by the family $\{A(w(t))\,; t\in [0,T)\}$, where

$$\begin{aligned} A(w(t))v := -\frac{v_{xx}}{(1 + \varepsilon ^2 w_x^2(t))^{3/2}}, \quad v\in W^2_q(I). \end{aligned}$$

Then, given $0\le s\le t<T$, it follows from [4, Proposition 3.2] that the operator $U_{A(w)}(t,s)$ is positive in the sense that it leaves the cone of pointwise non-negative elements of $L_q(I)$ invariant. Furthermore, the solution u of (1)–(3) may be represented by the variation-of-constant formula

$$\begin{aligned} u(t) = U_{A(u)}(t,0)u_*+ \int _0^tU_{A(u)}(t,s)H(\lambda ,\varepsilon ,u(s))\,ds, \quad t\in [0,T). \end{aligned}$$

(22)

Let now $v\in S_q(\kappa )$ with $v(x)\le 0$, $x\in I$, be given and assume that the corresponding potential $\psi$ satisfies

$$\begin{aligned} \psi _{zz}(x,-1) \ge 0 \quad \text {and} \quad \psi _{zz}(x,v(x))\ge 0, \quad x\in I. \end{aligned}$$

(23)

Then, it is shown in the proof of [6, Theorem 4.2] that $H(\lambda ,\varepsilon ,v)(x)\le 0$ for all $x\in I$, provided that

$$\begin{aligned} 0<\varepsilon \le \min _{x\in [-1,1]}\frac{f(x)}{{\sqrt{2}\vert f'(x)\vert }}. \end{aligned}$$

(24)

Thus, in view of (22), we get the following result:

Corollary 2.2

(Non-positivity of u; [6, Theorem 4.2]) Let $f\in C^2([-1,1])$ be positive and assume that the solution $\psi$ of (4)–(5) satisfies (23). Then, if $\varepsilon >0$ satisfies (24) and $u_*(x)\le 0$ for $x\in I$, the solution u to (1)–(3) is non-positive, i.e. $u(t,x)\le 0$ for all $(t,x)\in [0,T)\times [-1,1]$.

Remark 2.3

Let us emphasise that (23) is an a-priori condition to be satisfied by the electrostatic potential $\psi$ as a part of the solution. In the regime of the small aspect ratio model, (23) holds true as $\psi$ is then affine in the z-variable. Hitherto no such results are available for the coupled system – not even for constant permittivity profiles (although in this situation the system provides inherently only non-positive deflections).

Finally, we mention that it is possible to prove the existence of temporally global solutions, i.e. $T=\infty$, provided that the applied voltage $\lambda$ and the initial condition $u_*$ are small enough. The proof of this result essentially relies on the exponential decay of the evolution operator for small values of $\lambda$, cf. [4, Proposition 3.2]. Since this result is independent of our study—but enriches the general picture—we state it here but omit the proof.

Theorem 2.4

(Global Existence) Let $q\in (2,\infty )$, $\varepsilon >0$ and $f\in C^2([-1,1])$ be given and choose an initial condition as in Theorem 2.1. Given $\kappa >0$, there are $\lambda _*(\kappa )>$ and $c(\kappa )>0$ such that, if $\lambda \in (0,\lambda _*(\kappa ))$ and $\Vert u_*\Vert _{W^2_q(I)}\le c(\kappa )$, the solution $(u,\psi )$ to (1)–(5) exists forever and $u(t,x)>-1+\kappa$ for $(t,x)\in [0,\infty )\times I$.

It is worthwhile to mention that the solutions considered in Theorem 2.4 cannot touch the ground plate – not even in infinite time.

3 Finite-Time Singularity

We shall see in this section that under certain conditions on the permittivity profile f, there is a critical voltage value $\lambda ^{*} > 0$ such that for $\lambda > \lambda ^{*}$ non-positive solutions u to the evolution problem cease to exist after a finite time T, provided that the aspect ratio $\varepsilon > 0$ is small enough.

The main challenge in the proof of this result is the derivation of an appropriate differential inequality for a certain energy functional. Integration of this differential inequality with respect to time then yields an upper bound for the maximal time T of existence. This approach has recently been used in [3] for the case of constant permittivity.

According to this concept, in the sequel some auxiliary technical results are presented whose combination in the end supplies us with the desired differential inequality.

An important identity which is used several times in the following calculations may be derived from the boundary condition (5) for $\psi$ and reads

$$\begin{aligned} \psi _x(t,x,u(t,x)) = f^{\prime }(x) - \psi _z(t,x,u(t,x)) u_x(t,x), \quad (t,x) \in (0,T)\times I. \end{aligned}$$

(25)

Furthermore, $\psi _x$ vanishes on the lower boundary, i.e.

$$\begin{aligned} \psi _x(t,x,-1) = 0, \quad (t,x) \in (0,T)\times I. \end{aligned}$$

(26)

In order to lighten the notation, we finally make the following general assumptions:

• In the lemmas below the time $t \in (0,T)$ appears as a parameter and is thus omitted in the notation;

• for $t > 0$ we write $\Omega = \Omega (u(t))$;

• $u \in C([0,T),W^2_q(I)),\, q \in (2,\infty )$, denotes the solution to (1)–(3), satisfying $-1 < u(t,x) \le 0$ for all $(t,x) \in [0,T)\times I$;

• $\psi \in W^2_2(\Omega (u(t))) = W^2_2(\Omega )$ is the solution to (4)–(5).

Introducing the notation

$$\begin{aligned} m := \min _{x \in [-1,1]} f(x) \quad \text {and} \quad M := \max _{x \in [-1,1]} f(x) \end{aligned}$$

for the minimum and the maximum of f on $[-1,1]$, respectively, we prove the following result.

Theorem 3.1

(Finite-Time Singularity) Let $q \in (2,\infty ), \varepsilon > 0, \lambda > 0$, and let $f \in C^1(I)$ be positive with $m=f(-1) = f(1)$. Given an initial value $u_{*} \in W^2_{q}(I)$, satisfying $-1 < u_{*}(x) \le 0$ for all $x \in I$ and $u_*(\pm 1)=0$, we denote by $(u,\psi )$ the solution to (1)–(5). In addition, assume that

$$\begin{aligned} u(t,x) \le 0, \quad (t,x) \in [0,T)\times I. \end{aligned}$$

Then, if $M^2 < 2 m^2$, there exist $\varepsilon _{*} > 0$ and $\lambda ^{*} = \lambda ^{*}(\varepsilon _{*}) > 0$ such that $T < \infty$, provided that $\varepsilon \in (0,\varepsilon _{*})$ and $\lambda > \lambda ^{*}$.

The proof of this result requires various technical steps, whence— for the sake of better readability—it is presented in terms of separate lemmas. The first result contains an integral identity based on the elliptic Eq. (4) for the electrostatic potential.

Lemma 3.2

Given $f \in C^1(I)$, there holds

$$\begin{aligned}&\frac{1}{2} \int _I (1 + \varepsilon ^2 u_x^2) (\psi _z(x,u))^2\, dx \\&\quad = \int _I (1 + \varepsilon ^2 u_x^2) \psi _z(x,u) f\, dx + \frac{1}{2} \int _I (\psi _z(x,-1))^2 - 2 \psi _z(x,-1) f\, dx \\&\qquad - \varepsilon ^2 \int _I f f^{\prime } u_x\, dx + \frac{\varepsilon ^2}{2} \int _I (f^{\prime })^2\, dx - \varepsilon ^2 \int _{\Omega } \psi _x f^{\prime }\, d(x,z). \end{aligned}$$

Proof

Thanks to Fubini’s theorem and Eqs. (25) and (26) we can calculate

$$\begin{aligned} - \varepsilon ^2 \int _{\Omega } \psi _x (\psi _{zx} - f^{\prime })\, d(x,z)= & {} -\frac{\varepsilon ^2}{2} \int _{\Omega } (\psi _x^2)_z\, d(x, z)+ \varepsilon ^2 \int _{\Omega } \psi _x f^{\prime }\, d(x,z) \nonumber \\= & {} - \frac{\varepsilon ^2}{2} \int _I (\psi _x(x,u))^2\, dx + \varepsilon ^2 \int _{\Omega } \psi _x f^{\prime }\, d(x,z) \nonumber \\= & {} - \frac{\varepsilon ^2}{2} \int _I (f^{\prime } - \psi _z(x,u) u_x)^2\, dx + \varepsilon ^2 \int _{\Omega } \psi _x f^{\prime }\, d(x,z) \nonumber \\= & {} - \frac{\varepsilon ^2}{2} \int _I (f^{\prime })^2\, dx + \varepsilon ^2 \int _I \psi _z(x,u) u_x f^{\prime }\, dx \nonumber \\&- \frac{\varepsilon ^2}{2} \int _I (\psi _z(x,u))^2 u_x^2\, dx + \varepsilon ^2 \int _{\Omega } \psi _x f^{\prime }\, d(x,z). \end{aligned}$$

(27)

Moreover, invoking the Green–Riemann integration formula⁴ as well as the boundary conditions (5) and (25) we obtain

$$\begin{aligned}&\varepsilon ^2 \int _{\Omega } \psi _{xx} (\psi _z - f)\, d(x,z) \nonumber \\&\quad =\varepsilon ^2 \int _{\Omega } (\psi _{x} (\psi _z - f))_x\, d(x,z) -\varepsilon ^2 \int _{\Omega } \psi _{x} (\psi _{zx} - f^{\prime })\, d(x,z) \nonumber \\&\quad =\varepsilon ^2 \int _{\partial \Omega } \psi _{x} (\psi _z - f)\, dz - \varepsilon ^2 \int _{\Omega } \psi _{x} (\psi _{zx} - f^{\prime })\, d(x,z) \nonumber \\&\quad =\varepsilon ^2 \int _I (\psi _z(x,u))^2 u_x^2\, dx - \varepsilon ^2 \int _I \psi _z(x,u) u_x^2 f\, dx \nonumber \\&\qquad - \varepsilon ^2 \int _I \psi _z(x,u) u_x f^{\prime }\, dx + \varepsilon ^2 \int _I u_x f f^{\prime }\, dx \nonumber \\&\qquad -\varepsilon ^2 \int _{\Omega } \psi _{x} (\psi _{zx} - f^{\prime })\, d(x,z). \end{aligned}$$

(28)

Fusing (27) and (28) then yields

$$\begin{aligned}&\varepsilon ^2 \int _{\Omega } \psi _{xx} (\psi _z - f)\, d(x,z) = \varepsilon ^2 \int _{\Omega } \psi _x f^{\prime }\, d(x,z) \nonumber \\&\quad +\frac{\varepsilon ^2}{2} \int _I (\psi _z(x,u))^2 u_x^2 - (f^{\prime })^2\, dx - \varepsilon ^2 \int _I \psi _z(x,u) u_x^2 f -u_x f f^{\prime }\, dx. \end{aligned}$$

(29)

Again due to Fubini’s theorem, we can derive the identity

$$\begin{aligned}&\int _{\Omega } \psi _{zz} (\psi _z - f)\, d(x,z) \nonumber \\&\quad =- \int _{\Omega } \psi _{zz} f\, d(x,z) + \frac{1}{2} \int _I (\psi _z(x,u))^2 - (\psi _z(x,-1))^2\, dx \nonumber \\&\quad =\int _I (\psi _z(x,-1) - \psi _z(x,u)) f\, dx + \frac{1}{2} \int _I (\psi _z(x,u))^2 - (\psi _z(x,-1))^2\, dx. \end{aligned}$$

(30)

We now multiply Eq. (4) by $(\psi _z - f)$, integrate over $\Omega$ and use the above Eqs. (29) and (30). This leads to

$$\begin{aligned} 0= & {} \int _{\Omega } (\varepsilon ^2 \psi _{xx} + \psi _{zz}) (\psi _z - f)\, d(x,z) \\= & {} \varepsilon ^2 \int _{\Omega } \psi _x f^{\prime }\, d(x,z) + \frac{\varepsilon ^2}{2} \int _I (\psi _z(x,u))^2 u_x^2 - (f^{\prime })^2\, dx -\varepsilon ^2 \int _I \psi _z(x,u) u_x^2 f - f f^{\prime } u_x\, dx. \\&+ \int _I (\psi _z(x,-1) - \psi _z(x,u)) f\, dx + \frac{1}{2} \int _I (\psi _z(x,u))^2 - (\psi _z(x,-1))^2\, dx. \\= & {} \varepsilon ^2 \int _{\Omega } \psi _x f^{\prime }\, d(x,z) +\frac{1}{2} \int _{I} (1 + \varepsilon ^2 u_x^2) (\psi _z(x,u))^2\, dx -\int _{I} (1 + \varepsilon ^2 u_x^2) \psi _z(x,u) f\, dx \\&- \frac{1}{2} \int _I (\psi _z(x,-1))^2 - 2 \psi _z(x,-1) f\, dx + \varepsilon ^2 \int _I f f^{\prime } u_x\, dx - \frac{\varepsilon ^2}{2} \int _I (f^{\prime })^2\, dx. \end{aligned}$$

Finally, we find that the last equation is equivalent to

$$\begin{aligned}&\frac{1}{2} \int _I (1 + \varepsilon ^2 u_x^2) (\psi _z(x,u))^2\, dx \\&\quad =\int _I (1 + \varepsilon ^2 u_x^2) \psi _z(x,u) f\, dx + \frac{1}{2} \int _I (\psi _z(x,-1))^2 - 2 \psi _z(x,-1) f\, dx \\&\qquad - \varepsilon ^2 \int _I f f^{\prime } u_x\, dx + \frac{\varepsilon ^2}{2} \int _I (f^{\prime })^2\, dx - \varepsilon ^2 \int _{\Omega } \psi _x f^{\prime }\, d(x,z), \end{aligned}$$

whence the proof is complete. $\square$

We continue by further manipulating the first term on the right-hand side of the identity in Lemma 3.2.

Lemma 3.3

Given $f \in C^1(I)$, the following identity holds true:

$$\begin{aligned}&\int _I (1 + \varepsilon ^2 u_x^2) \psi _z(x,u) f\, dx \\&\quad = \int _{\Omega } \varepsilon ^2 \psi _x^2 + \psi _z^2\, d(x,z) + \varepsilon ^2 \int _I f f^{\prime } u_x \, dx \\&\qquad - \varepsilon ^2 f(1) \int _{-1}^{0} (1 + z) \psi _x(1,z)\, dz + \varepsilon ^2 f(-1) \int _{-1}^{0} (1 + z) \psi _x(-1,z)\, dz. \end{aligned}$$

Proof

From the boundary condition (5) for $\psi$, it follows that

$$\begin{aligned} \int _{\partial \Omega } \psi _z \psi \, dx = - \int _I \psi _z(x,u) f\, dx. \end{aligned}$$

(31)

By the same argument and additionally using the identity (25), we find that

$$\begin{aligned} \int _{\partial \Omega } \psi _x \psi \, dz= & {} -\int _I \psi _x(x,u) f u_x\, dx \nonumber \\&+ f(1) \int _{-1}^0 \psi _x(1,z) (1 + z)\, dz - f(-1) \int _{-1}^0 \psi _x(-1,z) (1 + z)\, dz \nonumber \\= & {} -\int _I (f^{\prime } - \psi _z(x,u) u_x) f u_x\, dx \nonumber \\&+ f(1) \int _{-1}^0 \psi _x(1,z) (1 + z)\, dz - f(-1) \int _{-1}^0 \psi _x(-1,z) (1 + z)\, dz \nonumber \\= & {} \int _I \psi _z(x,u) f u_x^2\, dx - \int _I f f^{\prime } u_x\, dx \nonumber \\&+ f(1) \int _{-1}^0 \psi _x(1,z) (1 + z)\, dz - f(-1) \int _{-1}^0 \psi _x(-1,z) (1 + z)\, dz.\qquad \end{aligned}$$

(32)

We now multiply Eq. (4) by $\psi$ and integrate over $\Omega$ to obtain

$$\begin{aligned} 0= & {} \int _{\Omega } (\varepsilon ^2 \psi _{xx} + \psi _{zz}) \psi \, d(x,z) \\= & {} - \int _{\Omega } \varepsilon ^2 \psi _x^2 + \psi _z^2\, d(x,z) +\int _{\Omega } \varepsilon ^2 (\psi _x \psi )_x + (\psi _z \psi )_z\, d(x,z). \end{aligned}$$

Thanks to the Green–Riemann integration formula, by using (31) and (32), we see that

$$\begin{aligned} 0= & {} - \int _{\Omega } \varepsilon ^2 \psi _x^2 + \psi _z^2\, d(x,z) + \varepsilon ^2 \int _{\partial \Omega } \psi _x \psi \, dz - \int _{\partial \Omega } \psi _z \psi \, dx \\= & {} - \int _{\Omega } \varepsilon ^2 \psi _x^2 + \psi _z^2\, d(x,z) + \varepsilon ^2 \int _I \psi _z(x,u) f u_x^2\, dx - \varepsilon ^2 \int _I f f^{\prime } u_x\, dx \\&+ \varepsilon ^2 f(1) \int _{-1}^0 \psi _x(1,z) (1 + z)\, dz - \varepsilon ^2 f(-1) \int _{-1}^0 \psi _x(-1,z) (1 + z)\, dz \\&+\int _I \psi _z(x,u) f\, dx \\= & {} - \int _{\Omega } \varepsilon ^2 \psi _x^2 + \psi _z^2\, d(x,z) + \int _I (1 + \varepsilon ^2 u_x^2) \psi _z(x,u) f\, dx - \varepsilon ^2 \int _I f f^{\prime } u_x\, dx \\&+ \varepsilon ^2 f(1) \int _{-1}^0 \psi _x(1,z) (1 + z)\, dz - \varepsilon ^2 f(-1) \int _{-1}^0 \psi _x(-1,z) (1 + z)\, dz. \end{aligned}$$

This is equivalent to

$$\begin{aligned}&\int _I (1 + \varepsilon ^2 u_x^2) \psi _z(x,u) f\, dx \\&\quad = \int _{\Omega } \varepsilon ^2 \psi _x^2 + \psi _z^2\, d(x,z) + \varepsilon ^2 \int _I f f^{\prime } u_x\, dx \\&\qquad - \varepsilon ^2 f(1) \int _{-1}^{0} (1 + z) \psi _x(1,z)\, dz + \varepsilon ^2 f(-1) \int _{-1}^{0} (1 + z) \psi _x(-1,z)\, dz, \end{aligned}$$

whence the proof is complete. $\square$

The next lemma provides a useful subsolution to the elliptic boundary value problem (4)–(5).

Lemma 3.4

Given a positive $f \in C(I)$, the function $\eta$, defined ⁵ by $\eta (x,z) := (1 + z) m$, is a subsolution to (4)–(5). That is, we have

$$\begin{aligned} \eta (x,z) \le \psi (x,z), \quad (x,z) \in \overline{\Omega }. \end{aligned}$$

Proof

By definition of $\eta$, it is clear that $\eta$ satisfies the Eq. (4), i.e.

$$\begin{aligned} \varepsilon ^2 \eta _{xx} + \eta _{zz} = 0 = \varepsilon ^2 \psi _{xx} + \psi _{zz}, \quad (x,z) \in \Omega . \end{aligned}$$

Moreover, on the lateral boundary it holds that

$$\begin{aligned} \eta (-1,z) = (1 + z) m \le (1 + z) f(-1) = \psi (-1,z), \quad z \in (-1,0), \end{aligned}$$

and

$$\begin{aligned} \eta (1,z) = (1 + z) m \le (1 + z) f(1) = \psi (1,z), \quad z \in (-1,0). \end{aligned}$$

Finally, we have

$$\begin{aligned} \eta (x,-1) = 0 = \psi (-1,z), \quad x \in I, \end{aligned}$$

on the ground plate, as well as

$$\begin{aligned} \eta (x,u) = (1 + u) m \le (1 + u) f(x) \le f(x) = \psi (x,u), \quad x \in I, \end{aligned}$$

on the membrane.⁶ An application of the elliptic maximum principle yields the assertion. $\square$

By means of this subsolution, we obtain the following result for $\psi _x$ on the lateral boundary, which is in some sense reminiscent of Hopf’s maximum principle.

Lemma 3.5

Given a positive $f \in C(I)$ with $m=f(-1)=f(1)$, the potential $\psi$ satisfies

$$\begin{aligned} \pm \psi _x(\pm 1,z) \le 0, \quad z \in (-1,0). \end{aligned}$$

Proof

The statement readily follows by an application of Lemma 3.4:

$$\begin{aligned} \psi _x(1,z)= & {} \lim _{h \searrow 0} \frac{\psi (1 - h,z) - \psi (1,z)}{-h} \\= & {} \lim _{h \searrow 0} \frac{\psi (1 - h,z) - (1 + z) f(1)}{-h} \\\le & {} \lim _{h \searrow 0} \frac{\eta (1-h,z) - (1 + z) f(1)}{-h} \\= & {} \lim _{h \searrow 0} \frac{(1 + z) m - (1 + z) f(1)}{-h} \\= & {} 0. \end{aligned}$$

A similar calculation gives $\psi _x(-1,z)\ge 0$ for all $z\in (-1,0)$. $\square$

As mentioned above, the proof of Theorem 3.1 relies on an estimate of a certain energy functional. To this end, we combine the above lemmas and derive the following inequality.

Corollary 3.6

Let $f \in C^1(I)$ be positive with $m=f(-1)=f(1)$. Then there holds

$$\begin{aligned} \int _I (1 + \varepsilon ^2 u_x^2) \psi _z(x,u) f\, dx \ge \int _{\Omega } \varepsilon ^2 \psi _x^2 + \psi _z^2\, d(x,z) + \varepsilon ^2 \int _I f f^{\prime } u_x \, dx. \end{aligned}$$

Proof

Since f is positive, we conclude from Lemma 3.5 that

$$\begin{aligned} -f(1)\psi _x(1,z)\ge 0\quad {\text {and}}\quad f(-1)\psi _x(-1,z)\ge 0\quad {\text {for all}}\ z\in (-1,0). \end{aligned}$$

Thus, the assertion follows from Lemma 3.3. $\square$

In the sequel, another two technical results are stated.

Lemma 3.7

Given $f \in C(I)$, the following estimate holds true:

$$\begin{aligned} \int _I (\psi _z(x,-1))^2 - 2 \psi _z(x,-1) f\, dx \ge - \int _I f^2\, dx. \end{aligned}$$

Proof

We readily obtain

$$\begin{aligned} (\psi _z(x,-1))^2 - 2 \psi _z(x,-1) f + f^2 = (\psi _z(x,-1) - f)^2 \ge 0, \end{aligned}$$

whence

$$\begin{aligned} (\psi _z(x,-1))^2 - 2 \psi _z(x,-1) f \ge - f^2, \end{aligned}$$

and an integration over I with respect to x yields the assertion. $\square$

Lemma 3.8

Let $f \in C^1(I)$ be given, and assume that $u(t,x) \le 0$ for all $(t,x) \in [0,T)\times I$. Then we have

$$\begin{aligned} - \varepsilon ^2 \int _{\Omega } \psi _x f^{\prime }\, d(x,z) \ge -\frac{\varepsilon ^2}{4} \int _{\Omega } \psi _x^2\, d(x,z) - \varepsilon ^2 \int _I (f^{\prime })^2 dx. \end{aligned}$$

Proof

One may readily see that

$$\begin{aligned} 0 \le \left( \frac{1}{2} \psi _x - f^{\prime }\right) ^2 = \frac{1}{4} \psi _x^2 - \psi _x f^{\prime } + (f^{\prime })^2, \end{aligned}$$

whence

$$\begin{aligned} - \psi _x f^{\prime } \ge -\frac{1}{4} \psi _x^2 - (f^{\prime })^2. \end{aligned}$$

Multiplication of this inequality by $\varepsilon ^2$ and integration over $\Omega$ yields

$$\begin{aligned} - \varepsilon ^2 \int _{\Omega } \psi _x f^{\prime }\, d(x,z) \ge -\frac{\varepsilon ^2}{4} \int _{\Omega } \psi _x^2\, d(x,z) - \varepsilon ^2 \int _{\Omega } (f^{\prime })^2 d(x,z). \end{aligned}$$

Using the non-positivity of u, Fubini’s theorem leads to

$$\begin{aligned} - \varepsilon ^2 \int _{\Omega } \psi _x f^{\prime }\, d(x,z)&\ge -\frac{\varepsilon ^2}{4} \int _{\Omega } \psi _x^2\, d(x,z) - \varepsilon ^2 \int _I (f^{\prime })^2 (u + 1)\, dx \\&\ge -\frac{\varepsilon ^2}{4} \int _{\Omega } \psi _x^2\, d(x,z) - \varepsilon ^2 \int _I (f^{\prime })^2 dx \end{aligned}$$

and the proof is complete. $\square$

The next result contains a lower bound for the Dirichlet integral related to (4) in terms of a weighted $L_2$-norm of the permittivity profile.

Lemma 3.9

Given $f \in C(I)$, there holds

$$\begin{aligned} \int _{\Omega } \frac{3}{4} \varepsilon ^2 \psi _x^2 + \psi _z^2\, d(x,z) \ge \int _I \frac{f^2}{1 + u}\, dx. \end{aligned}$$

Proof

We deduce from the boundary condition (5) for $\psi$ and a trivial application of Cauchy–Schwarz’s inequality that

$$\begin{aligned} \frac{f^2}{1 + u} = \frac{(\psi (x,u) - \psi (x,-1))^2}{1 + u} = \frac{1}{1 + u} \left( \int _{-1}^{u} \psi _z\, dz\right) ^2 \le \int _{-1}^{u} \psi _z^2\, dz. \end{aligned}$$

Integrating this inequality with respect to x and using Fubini’s theorem yields

$$\begin{aligned} \int _I \frac{f^2}{1 + u}\, dx \le \int _{\Omega } \psi _z^2\, d(x,z) \le \int _{\Omega } \frac{3}{4} \varepsilon ^2 \psi _x^2 + \psi _z^2\, d(x,z), \end{aligned}$$

which is the statement of the lemma. $\square$

Given $t \in [0,T)$, we now introduce the functional

$$\begin{aligned} \Phi _{\lambda }(t) := \frac{\lambda }{2} \int _I \varepsilon ^2 (\psi _x(x,u))^2 + (\psi _z(x,u))^2\, dx \end{aligned}$$

(33)

and fuse the above auxiliary results to obtain the estimate presented in the next lemma.

Lemma 3.10

Let $f \in C^1(I)$ be positive with $m=f(-1) = f(1)$. Then the functional $\Phi _{\lambda }(t)$, introduced in (33), complies with the inequality

$$\begin{aligned} \Phi _{\lambda }(t) \ge \lambda \left( m^2 \int _I \frac{1}{1 + u}\, dx - M^2 - \varepsilon ^2 \int _I \psi _z(x,u) f^{\prime } u_x\, dx\right) . \end{aligned}$$

Proof

In a first step we manipulate $\Phi _{\lambda }$ by means of the relation (25) to find that

$$\begin{aligned} \Phi _{\lambda }(t)= & {} \frac{\lambda }{2} \int _I \varepsilon ^2 (\psi _x(x,u))^2 + (\psi _z(x,u))^2\, dx \\= & {} \frac{\lambda }{2} \int _I (1 + \varepsilon ^2 u_x^2) (\psi _z(x,u))^2\, dx +\frac{\lambda \varepsilon ^2}{2} \int _I (f^{\prime })^2\, dx \\&- \lambda \varepsilon ^2 \int _I \psi _z(x,u) f^{\prime } u_x\, dx. \end{aligned}$$

Using Lemma 3.2 and Corollary 3.6 we obtain

$$\begin{aligned} \Phi _{\lambda }(t)= & {} \lambda \int _I (1 + \varepsilon ^2 u_x^2) \psi _z(x,u) f\, dx +\frac{\lambda }{2} \int _I (\psi _z(x,-1))^2 - 2 \psi _z(x,-1) f\, dx \\&- \lambda \varepsilon ^2 \int _I f f^{\prime } u_x\, dx + \lambda \varepsilon ^2 \int _I (f^{\prime })^2\, dx - \lambda \varepsilon ^2 \int _I \psi _z(x,u) f^{\prime } u_x\, dx \\&-\lambda \varepsilon ^2 \int _{\Omega } \psi _x f^{\prime }\, d(x,z) \\\ge & {} \lambda \int _{\Omega } \varepsilon ^2 \psi _x^2 + \psi _z^2\, d(x,z) - \lambda \varepsilon ^2 \int _{\Omega } \psi _x f^{\prime }\, d(x,z) + \lambda \varepsilon ^2 \int _I (f^{\prime })^2\, dx\\&+ \frac{\lambda }{2} \int _I (\psi _z(x,-1))^2 - 2 \psi _z(x,-1) f\, dx - \lambda \varepsilon ^2 \int _I \psi _z(x,u) f^{\prime } u_x\, dx. \end{aligned}$$

Hence, thanks to Lemma 3.7 and Lemma 3.8 we obtain the estimate

$$\begin{aligned} \Phi _{\lambda }(t) \ge \lambda \int _{\Omega } \frac{3}{4} \varepsilon ^2 \psi _x^2 + \psi _z^2\, d(x,z) - \frac{\lambda }{2} \int _I f^2\, dx - \lambda \varepsilon ^2 \int _I \psi _z(x,u) f^{\prime } u_x\, dx. \end{aligned}$$

Using Lemma 3.9 and recalling the definition of

$$\begin{aligned} m = \min _{x \in [-1,1]} f(x) \quad \text {and} \quad M = \max _{x \in [-1,1]} f(x), \end{aligned}$$

we finally end up with

$$\begin{aligned} \Phi _{\lambda }(t)&\ge \lambda \int _I \frac{f^2}{1 + u}\, dx - \frac{\lambda }{2} \int _I f^2\, dx - \lambda \varepsilon ^2 \int _I \psi _z(x,u) f^{\prime } u_x\, dx \\&\ge \lambda m^2 \int _I \frac{1}{1 + u}\, dx - \lambda M^2 - \lambda \varepsilon ^2 \int _I \psi _z(x,u) f^{\prime } u_x\, dx, \end{aligned}$$

which completes the proof. $\square$

Having the results from the above lemmas at hand, we are now able to prove Theorem 3.1. From now on, we explicitly mention the time variable t when it is requested from the context.

Proof of Theorem 3.1

Given $t \in [0,T)$, we introduce the functional

$$\begin{aligned} E(t) := -\frac{1}{2} \int _I u(t,x)\, dx. \end{aligned}$$

Since $-1 < u(t,x) \le 0$ for all $(t,x) \in [0,T)\times I$ by assumption, it follows that

$$\begin{aligned} 0 \le E(t) < 1, \quad t \in [0,T). \end{aligned}$$

The use of the evolution Eq. (1) and the definition of $\Phi _{\lambda }(t)$ yields

$$\begin{aligned} \frac{dE}{dt}(t)= & {} -\frac{1}{2} \left[ \frac{u_x}{\sqrt{1 + \varepsilon ^2 u_x^2}}\right] _{x = -1}^{x = 1} + \frac{\lambda }{2} \int _I \varepsilon ^2 (\psi _x(x,u))^2 + (\psi _z(x,u))^2\, dx \nonumber \\&- \lambda \varepsilon ^2 \int _I \psi _x(x,u) f^{\prime }\, dx \nonumber \\\ge & {} - \frac{1}{\varepsilon } + \Phi _{\lambda }(t) - \lambda \varepsilon ^2 \int _I \psi _x(x,u) f^{\prime }\, dx. \end{aligned}$$

(34)

Fusing this inequality with the estimate

$$\begin{aligned} \Phi _{\lambda }(t) \ge \lambda \left( m^2 \int _I \frac{1}{1 + u}\, dx - M^2 - \varepsilon ^2 \int _I \psi _z(x,u) f^{\prime } u_x\, dx\right) \end{aligned}$$

from Lemma 3.10 and applying Jensen’s inequality to the convex function $[r \mapsto 1/(1 + r)]$ and the probability measure dx / 2, we obtain

$$\begin{aligned} \frac{dE}{dt}(t)\ge & {} - \frac{1}{\varepsilon } + \lambda \left( m^2 \int _I \frac{1}{1 + u}\, dx - M^2 - \varepsilon ^2 \int _I \psi _z(x,u) f^{\prime } u_x\, dx\right) \\&-\lambda \varepsilon ^2 \int _I \psi _z(x,u) f^{\prime } u_x \, dx \\\ge & {} - \frac{1}{\varepsilon } + \lambda \left( \frac{2 m^2}{1 - E(t)} - M^2 -\varepsilon ^2 \int _I \psi _z(x,u) f^{\prime } u_x\, dx\right) \\&-\lambda \varepsilon ^2 \int _I \psi _z(x,u) f^{\prime } u_x \, dx. \end{aligned}$$

Applying the identity (25) then leads to

$$\begin{aligned} \frac{dE}{dt}(t) \ge - \frac{1}{\varepsilon } + \lambda \left( m^2 \int _I \frac{1}{1 + u}\, dx - M^2 - \varepsilon ^2 \int _I (f^{\prime })^2 dx\right) , \end{aligned}$$

and finally, introducing the constant

$$\begin{aligned} c_f := \int _I (f^{\prime })^2\, dx, \end{aligned}$$

we end up with the differential inequality

$$\begin{aligned} \frac{dE}{dt}(t) \ge - \frac{1}{\varepsilon } + \lambda \left( \frac{2 m^2}{1 - E(t)} - M^2 - \varepsilon ^2 c_f\right) := F_{\lambda }(E). \end{aligned}$$

Observe that $F_{\lambda }$ is strictly increasing in $E \in [0,1)$ which implies that

$$\begin{aligned} \frac{dE}{dt}(t) \ge F_{\lambda }(E) \ge F_{\lambda }(0). \end{aligned}$$

(35)

Furthermore, evaluating $F_{\lambda }$ in $E \equiv 0$ yields

$$\begin{aligned} F_{\lambda }(0) = - \frac{1}{\varepsilon } + \lambda \left( 2 m^2 - M^2 - \varepsilon ^2 c_f\right) , \end{aligned}$$

whence, because of $M^2 < 2 m^2$, there exists an $\varepsilon _{*} > 0$ such that

$$\begin{aligned} 2 m^2 - M^2 - \varepsilon ^2 c_f > 0 \end{aligned}$$

(36)

for all $\varepsilon \in (0,\varepsilon _{*})$. In this case, $F_{\lambda }(0)$ is strictly increasing in $\lambda$ and there exists a critical value $\lambda ^{*} = \lambda ^{*}(\varepsilon _{*}) > 0$ such that $F_{\lambda ^{*}}(0) = 0$. Integrating inequality (35) with respect to t then implies that $1 \ge E(0) + F_{\lambda }(0) T$ and eventually

$$\begin{aligned} T < \frac{1}{F_{\lambda }(0)} < \infty , \end{aligned}$$

provided that $\varepsilon \in (0,\varepsilon _{*})$ and $\lambda > \lambda ^{*}$. This completes the proof. $\square$