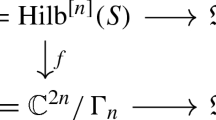Semistable reduction of a normal crossing $\mathbb {Q}$-divisor

Abstract

In a previous work, we have introduced the notion of embedded $\mathbb {Q}$-resolution, which allows the final ambient space to contain abelian quotient singularities, and A’Campo’s formula was calculated in this setting. Here, we study the semistable reduction associated with an embedded $\mathbb {Q}$-resolution and compute the mixed Hodge structure on the cohomology of the Milnor fiber in the isolated case using a generalization of Steenbrink’s spectral sequence. Examples of Yomdin-Lê surface singularities are presented as an application.

1 Introduction

One of the main invariants of a given hypersurface singularity is the mixed Hodge structure (MHS) on the cohomology of the Milnor fiber. In the isolated case, Steenbrink [24] gave a method for computing this Hodge structure using a spectral sequence that is constructed from the divisors associated with the semistable reduction of an embedded resolution, cf. [27, 28].

However, in practice, the combinatorics of the exceptional divisor of the resolution is often so complicated that the study of the spectral sequence becomes very hard, see e.g., [4] where an embedded resolution and its associated semistable reduction for superisolated surface singularities is computed using blow-ups at points and rational curves.

After the semistable reduction process, the new ambient space contains normal singularities which are obtained as the quotient of a ball in $\mathbb {C}^n$ by the linear action of a finite group. Spaces admitting only such singularities are called V-manifolds. They were introduced in [20] and have the same homological properties over $\mathbb {Q}$ as manifolds, e.g., they admit a Poincaré duality if they are compact and carry a pure Hodge structure if they are compact and Kähler [7]. Moreover, a natural notion of normal crossing divisor can be defined on V-manifolds [24].

Motivated by this fact and in order to simplify the combinatorics of the exceptional divisor mentioned above, we introduced the notion of embedded $\mathbb {Q}$-resolution [16]. The idea is as follows. Classically an embedded resolution of $\{f=0\} \subset \mathbb {C}^{n+1}$ is a proper map $\pi : X \rightarrow (\mathbb {C}^{n+1},0)$ from a smooth variety X satisfying, among other conditions, that $\pi ^{*}(\{f=0\})$ is a normal crossing divisor. To weaken the condition on the preimage of the singularity, we allow the new ambient space X to contain abelian quotient singularities and the divisor $\pi ^{*}(\{f=0\})$ to have normal crossings on X.

Hence, the motivation for using embedded $\mathbb {Q}$-resolutions rather than standard ones is twofold. On the one hand, they are a natural generalization of the usual embedded resolutions, for which the invariants above are expected to be calculated effectively. On the other hand, the combinatorial and computational complexity of embedded $\mathbb {Q}$-resolutions is much simpler, and they also keep as much information as needed for the understanding of the topology of the singularity.

For instance, the behavior of the Lefschetz numbers and the zeta function of the monodromy in this setting was treated in [17] providing the corresponding A’Campo’s formula [1]. Also, for plane curves, the local $\delta$-invariant and explicit formulas for the self-intersections numbers of the exceptional divisors were calculated in [8] and [6] respectively.

In this paper, we continue our study about embedded $\mathbb {Q}$-resolutions. In particular, the semistable reduction of a normal crossing $\mathbb {Q}$-divisor on an abelian quotient singularity is investigated. The main idea behind this construction, as mentioned above, is that in the classical case after the semistable reduction the ambient space already contains quotient singularities. Our main result, Theorem 3.7, says that the same is true for embedded $\mathbb {Q}$-resolutions, and hence Steenbrink’s arguments can be adapted to construct a spectral sequence converging to the cohomology of the Milnor fiber thus providing a MHS on $H^q(F,\mathbb {C})$, see Theorem 5.4. Since the embedded $\mathbb {Q}$-resolution can be chosen so that “almost every” exceptional divisor contributes to the complex monodromy, our spectral sequence is finer in the sense that fewer divisors appear in the semistable reduction and thus the combinatorics of the spectral sequence will be simpler.

As a by-product we show that the Jordan blocks of maximal size in the monodromy are easily calculated by just looking at the dual complex associated with the semistable reduction of a $\mathbb {Q}$-resolution, see Proposition 5.12.

Note that the tools developed in [14] for the monodromy zeta function cannot be generalized for computing more involved invariants as the MHS of the Milnor fiber.

This work in combination with [18] can be considered as the first steps in the computation of MHS and the monodromy action [19] of the so-called Yomdin-Lê surface singularities (YLS) [29]. Results on YLS have already been studied in [25] and [22], which contain similar examples as the ones presented here with different approach. A more recent work [26] uses toric methods to attack this kind of examples.

Note that, following the ideas of [4], the generalized Steenbrink’s spectral sequence presented here can be used to find two YLS having the same characteristic polynomials, the same abstract topologies, but different embedded topologies (it is enough to take a Zariski pairs in the tangent cones).

This paper is organized as follows. In Sect. 2, some well-known preliminaries about weighted blow-ups and embedded $\mathbb {Q}$-resolutions are presented. The main result, namely Theorem 3.7 is proven in Sect. 3. After recalling the monodromy filtration in Sect. 4, the generalized Steenbrink’s spectral sequence converging to $H^q(F,\mathbb {C})$ is described in Sect. 5. Finally, as an application, the use of all the results of this work are illustrated in Sect. 6 with several examples including a plane curve and a YLS.

2 Preliminaries

Let us sketch some definitions and properties about V-manifolds, weighted projective spaces, and weighted blow-ups, see [5, 6, 16] for a more detailed exposition.

Definition 2.1

Let $H=\{f=0\}\subset \mathbb {C}^{n+1}$. An embedded $\mathbb {Q}$-resolution of $(H,0) \subset (\mathbb {C}^{n+1},0)$ is a proper analytic map $\pi : X \rightarrow (\mathbb {C}^{n+1},0)$ such that:

• 1. X is a V-manifold with abelian quotient singularities.

• 2. $\pi$ is an isomorphism over $X\setminus \pi ^{-1}({{\mathrm{Sing}}}(H))$.

• 3. $\pi ^{*}(H)$ is a hypersurface with $\mathbb {Q}$-normal crossings on X.

To deal with these resolutions, some notation needs to be introduced. Let $G := \mu _{d_0} \times \cdots \times \mu _{d_r}$ be an arbitrary finite abelian group written as a product of finite cyclic groups, that is, $\mu _{d_i}$ is the cyclic group of $d_i$-th roots of unity. Consider a matrix of weight vectors

$$\begin{aligned} A := (a_{ij})_{i,j} = [\mathbf{a}_0 \, | \, \ldots \, | \, \mathbf{a}_n ] \in \hbox {Mat} ((r+1) \times (n+1), \mathbb {Z}) \end{aligned}$$

and the action

$$\begin{aligned} \begin{array}{c} ( \mu _{d_0} \times \cdots \times \mu _{d_r} ) \times \mathbb {C}^{n+1} \longrightarrow \mathbb {C}^{n+1}, \\ \big ( \varvec{\xi }_{\mathbf {d}} , \mathbf{x} \big ) \mapsto (\xi _{d_0}^{a_{00}} \ldots \xi _{d_r}^{a_{r0}}\, x_0,\, \ldots \, , \xi _{d_0}^{a_{0n}} \ldots \xi _{d_r}^{a_{rn}}\, x_n ). \end{array} \end{aligned}$$

The set of all orbits $\mathbb {C}^{n+1} / G$ is called (cyclic) quotient space of type $(\mathbf{d};A)$ and it is denoted by

$$\begin{aligned} X(\mathbf{d}; A) := X \left( \begin{array}{c|ccc} d_0 &{} a_{00} &{} \cdots &{}\quad a_{0n}\\ \vdots &{} \vdots &{}\quad \ddots &{} \vdots \\ d_r &{} a_{r0} &{} \cdots &{}\quad a_{rn} \end{array} \right) . \end{aligned}$$

The orbit of an element $(x_0,\ldots ,x_n)$ under this action is denoted by $[(x_0,\ldots ,x_n)]$. Condition 3 of the previous definition means the total transform $\pi ^{-1}(H) = (f\circ \pi )^{-1}(0)$ is locally given by a function of the form $x_0^{m_0} \ldots x_k^{m_k} : X(\mathbf{d};A) \rightarrow \mathbb {C}$, see [24]. The previous numbers $m_{i}$’s have no intrinsic meaning unless $\mu _{\mathbf{d}}$ induces a small action on $GL(n+1,\mathbb {C})$. This motivates the following.

Definition 2.2

The type $(\mathbf{d}; A)$ is said to be normalized if the action is free on $(\mathbb {C}^{*})^{n+1}$ and $\mu _\mathbf{d}$ is identified with a small subgroup of $GL(n+1,\mathbb {C})$.

As a tool for finding embedded $\mathbb {Q}$-resolutions one uses weighted blow-ups with smooth center. Special attention is paid to the case of dimension 2 and 3 and blow-ups at points.

Example 2.3

Assume (d; a, b) is normalized and $\gcd (\omega ) =1, \omega := (p,q)$ with $p,q \in \mathbb {N}^{*}$. The total space of the $\omega$-blow-up at the origin of X(d; a, b),

$$\begin{aligned} \pi _{(d;a,b),\omega }: \widehat{X(d;a,b)}_{\omega } \longrightarrow X(d;a,b), \end{aligned}$$

(1)

can be written as

$$\begin{aligned} \widehat{U}_1 \cup \widehat{U}_2 = X \left( \frac{pd}{e}; 1, \frac{-q+\beta p b}{e} \right) \cup X \left( \frac{qd}{e}; \frac{-p+\mu qa}{e}, 1 \right) \end{aligned}$$

and the charts are given by

Above, $e=\gcd (d,pb-qa)$ and $\beta a \equiv \mu b \equiv 1 (\text {mod }d)$. Observe that the origins of the two charts are cyclic quotient singularities; they are located at the exceptional divisor E which is isomorphic to $\mathbb {P}^1_{\omega } \cong \mathbb {P}^1$.

Example 2.4

Let $\pi _{\omega }: \widehat{\mathbb {C}}^3_{\omega } \rightarrow \mathbb {C}^3$ be the $\omega$-weighted blow-up at the origin with $\omega =(p,q,r), \gcd (\omega )=1$, and $p,q,r \in \mathbb {N}^{*}$. The new space is covered by three open sets

$$\begin{aligned} \widehat{\mathbb {C}}^3_{\omega } = U_1 \cup U_2 \cup U_3 = X(p;-1,q,r) \cup X(q;p,-1,r) \cup X(r;p,q,-1), \end{aligned}$$

and the charts are given by

$$\begin{aligned} \begin{array}{cc} X(p;-1,q,r) \longrightarrow U_1: &{} [(x,y,z)] \mapsto ((x^p, x^q y, x^r z),[1:y:z]_{\omega }), \\ X(q;p,-1,r) \longrightarrow U_2: &{} [(x,y,z)] \mapsto ((x y^p,y^q,y^r z),[x:1:z]_{\omega }), \\ X(r;p,q,-1) \longrightarrow U_3: &{} [(x,y,z)] \mapsto ((x z^p, y z^q, z^r),[x:y:1]_{\omega }). \end{array} \end{aligned}$$

(2)

In general $\widehat{\mathbb {C}}^3_{\omega }$ has three lines of (cyclic quotient) singular points located at the three axes of the exceptional divisor $\pi ^{-1}_{\omega }(0) \simeq \mathbb {P}^2_{\omega }$. For instance, a generic point in $x=0$ is a cyclic point of type $\mathbb {C}\times X(\gcd (q,r);p,-1)$. Note that although the quotient spaces are represented by normalized types, the exceptional divisor can still be simplified:

$$\begin{aligned} \begin{array}{rcl} \mathbb {P}^2(p,q,r) &{} \longrightarrow &{} \mathbb {P}^2 \displaystyle \left( \frac{p}{(p,r)\cdot (p,q)},\frac{q}{(q,p)\cdot (q,r)}, \frac{r}{(r,p)\cdot (r,q)}\right) ,\\ \displaystyle \,[x:y:z] &{} \mapsto &{} \left[ x^{\gcd (q,r)}:y^{\gcd (p,r)}:z^{\gcd (p,q)}\right] . \end{array} \end{aligned}$$

(3)

However, this simplification may be not useful when working with the whole ambient space because its charts are not compatible with $\widehat{\mathbb {C}}^3_{\omega }$. Thus the natural covering of the exceptional divisor is

$$\begin{aligned} \mathbb {P}^2_{\omega } = V_1 \cup V_2 \cup V_3 = X(p;q,r) \cup X(q;p,r) \cup X(r;p,q), \end{aligned}$$

and the charts are given by the restrictions of the maps in (2) to $x=0, y=0$, and $z=0$ respectively.

Example 2.5

Assume (d; a, b, c) is normalized and $\omega := (p,q,r)$ with $\gcd (\omega ) =1$ and $p,q,r \in \mathbb {N}^{*}$. The total space of the $\omega$-blow-up at the origin of $X(d;a,b,c), \pi = \pi _{(d;a,b,c),\omega }:\, \widehat{X(d;a,b,c)}_{\omega } \longrightarrow X(d;a,b,c),$ can be covered by three open sets as

$$\begin{aligned} \widehat{X(d;a,b,c)}_{\omega } = \frac{\widehat{\mathbb {C}}^3_{\omega }}{\mu _d} = \frac{U_1 \cup U_2 \cup U_3}{\mu _d} = \widehat{U}_1 \cup \widehat{U}_2 \cup \widehat{U}_3, \end{aligned}$$

where

$$\begin{aligned} \begin{array}{ccc} \displaystyle \widehat{U}_1 = \frac{U_1}{\mu _d} = \frac{X(p;-1,q,r)}{\mu _d} = X \left( \begin{array}{c|ccc} p &{} -1 &{} q &{} r \\ pd &{} a &{} pb-qa &{} pc-ra \end{array}\right) , \\ \displaystyle \widehat{U}_2 = \frac{U_2}{\mu _d} = \frac{X(q;p,-1,r)}{\mu _d} = X \left( \begin{array}{c|ccc} q &{} p &{} -1 &{} r \\ qd &{} qa-pb &{} b &{} qc-rb \end{array}\right) , \\ \displaystyle \widehat{U}_3 = \frac{U_3}{\mu _d} = \frac{X(r;p,q,-1)}{\mu _d} = X \left( \begin{array}{c|ccc} r &{} p &{} q &{} -1 \\ rd &{} ra-pc &{} rb-qc &{} c \end{array}\right) . \end{array} \end{aligned}$$

The charts are given by the induced maps on the corresponding quotient spaces, see Eq. (2). The exceptional divisor $E = \pi ^{-1}_{(d;a,b,c),\omega }(0)$ is identified with the quotient

$$\begin{aligned} \mathbb {P}^2_{\omega }(d;a,b,c) := \frac{\mathbb {P}^2_{\omega }}{\mu _d}. \end{aligned}$$

There are three lines of quotient singular points in E and outside E the map $\pi _{(d;a,b,c),\omega }$ is an isomorphism.

The expression of the quotient spaces can be modified as follows. Let $\alpha$ and $\beta$ be two integers such that $\alpha d + \beta a = \gcd (d,a)$, then one has that the space $X\left( {\begin{matrix} p ; &{} -1 &{} q &{} r \\ pd ; &{} a &{} pb-qa &{} pc-ar \end{matrix}} \right)$ equals

$$\begin{aligned} X\left( \begin{array}{c|ccc} pd &{} (d,a) &{}\quad -q\, (d,a) + \beta pb &{}\quad -r (d,a) + \beta pc \\ (d,a) &{} 0 &{} b &{} c \end{array}\right) . \end{aligned}$$

Note that in general the previous space is not represented by a normalized type. To obtain its normalized one, follow the processes described in (I.1.3) and (I.1.9) of [16].

3 The semistable reduction

This tool was introduced by Mumford in [15, pp. 53–108] and roughly speaking the mission of the semistable reduction is to get a reduced divisor that provides a model of the Milnor fibration. The spectral sequence converging to the cohomology of the Milnor fiber will be defined in terms of this reduced divisor, see Sect. 5. Here, we present a more general approach than the needed for the Milnor fibration.

Notation 3.1

Let X be a complex analytic variety and let $g:X \rightarrow D_\eta ^2$ be a non-constant analytic function. Assume X only has abelian quotient singularities and $g^{-1}(0)$ is a $\mathbb {Q}$-normal crossing divisor, that is, g is locally given by a function of the form $x_0^{m_0} \ldots x_k^{m_k}: X(\mathbf {d};A) \rightarrow \mathbb {C}$. Let e be any common multiple of all possible multiplicities appearing in the divisor $g^{-1}(0)$ and consider $\sigma : D^2_{\eta ^{1/e}} \rightarrow D^2_{\eta }$ the branched covering defined by $\sigma (t) = t^e$.

Denote by $(X_1, g_1, \sigma _1)$, the pull-back of g and $\sigma$.

The map $\sigma _1$ is a cyclic covering of e sheets ramified over $g^{-1}(0)$. If F denotes the Milnor fiber of $g:X \rightarrow \mathbb {C}$, then $\sigma _1^{-1}(F)$ has e connected components which are projected diffeomorphically onto F.

We have not yet completed the construction of the semistable reduction because $X_1$ is not normal. Indeed, given $P\in g^{-1}(0)$ there exist integers $k \ge 0$ and $m_0,\ldots ,m_k \ge 1$ such that

$$\begin{aligned} g(x_0,\ldots ,x_n) = x_0^{m_0}\ldots x_k^{m_k}: B^{2n+2}/\mu _\mathbf {d}\longrightarrow \mathbb {C}, \end{aligned}$$

where $B^{2n+2}$ is an open ball of $\mathbb {C}^{n+1}$ and the group $\mu _\mathbf {d}$ acts diagonally as in $(\mathbf {d};A)$. Denote by $P_1$ the unique point in $\sigma _1^{-1}(P)$. Then, $X_1$ in a neighborhood of $P_1$ is of the form

$$\begin{aligned} \Big \{ \big ( \big [(x_0,\ldots ,x_n)\big ], t \big ) \in X(\mathbf {d};A) \times \mathbb {C}\quad \big | \quad t^e = x_0^{m_0} \ldots x_k^{m_k} \Big \}, \end{aligned}$$

(4)

and hence the space $X_1$ is not necessarily normal.

Let $\nu : \widetilde{X} \rightarrow X_1$ be the normalization and denote by $\widetilde{g} := g_1\circ \nu$ and $\varrho := \sigma _1 \circ \nu$ the natural maps. The normalization process has essentially two steps when the corresponding ring is a unique factorization domain (UFD). First, separate the irreducible components and then find the normalization of each component. In the latter case, the ring in question is a domain and the following result applies.

Lemma 3.2

Let $A \subset B$ be an integral extension of commutative rings. Suppose that B is an integrally closed domain such that Q(B)|Q(A) is a Galois extension. Then, the normalization of the ring A is $\overline{A} = B^{{{\mathrm{Gal}}}(Q(B)|Q(A))}$.

Proof

Since B is normal and the extension $A\subset B$ is integral, then $\overline{A} = B \cap Q(A)$. Now the statement follows from the Galois condition. $\square$

Example 3.3

The algebraic ring of functions of X(2; 1, 1) is isomorphic to $\mathbb {C}[x^2, xy, y^2]$ as an algebraic variety. In this ring, the polynomial xy is irreducible but not prime. To compute the normalization of the quotient ring $\mathbb {C}[x^2,xy,y^2]/\langle xy \rangle$, one cannot proceed in the same way as in a UFD. This happens because $\mu _2$ does not define an action on the factors of the polynomial xy.

Although the ring of functions of the previous space (4) is not a UFD, see Example 3.3 above, to compute the normalization of $X_1$ one can proceed in the same spirit because of the special form of the polynomial $t^e - x_0^{m_0} \ldots x_k^{m_k}$, see proof of Theorem 3.7. Before that we need to introduce some notations.

Definition 3.4

Let X be a complex analytic space having only abelian quotient singularities and consider E a $\mathbb {Q}$-normal crossing divisor on X. Assume $P\in |E|$ is a point such that the local equation of E at P is given by the function

$$\begin{aligned} x_0^{m_0} \ldots x_k^{m_k} :\, X(\mathbf {d}; A) := \mathbb {C}^{n+1}/\mu _\mathbf {d}\longrightarrow \mathbb {C}, \quad (0 \le k \le n) \end{aligned}$$

where $x_0, \ldots , x_n$ are local coordinates of X at $P, \mathbf {d}=(d_0,\ldots ,d_r)$, and $A = (a_{ij})_{i,j} \in {{\mathrm{Mat}}}((r+1)\times (n+1),\mathbb {Z})$.

The multiplicity of E at P, denoted by m(E, P) or simply m(P) if the divisor is clear from de context, is defined by

$$\begin{aligned} m(E,P):= \gcd \bigg ( m_0, \ldots , m_k, \frac{\sum _{j=0}^k a_{0j} m_j}{d_0}, \ldots , \frac{\sum _{j=0}^k a_{rj} m_j}{d_r} \bigg ). \end{aligned}$$

If there exists $T\subset |E|$ such that the function $P\in T \mapsto m(E,P)$ is constant, then we use the notation $m(T) := m(E,P_0)$, where $P_0$ is an arbitrary point in T.

Remark 3.5

Using the general fact ${{\mathrm{lcm}}}(\frac{m}{b_0}, \ldots , \frac{m}{b_r}) = \frac{m}{\gcd (b_0,\ldots ,b_r)}$, one can easily check that this definition coincides with the one of [17, Def. 2.6] for $k=0$, cf. (5), that is,

$$\begin{aligned} m(E,P):= \frac{m}{L}, \qquad L = {{\mathrm{lcm}}}\left( \frac{d_0}{\gcd (d_0,a_{00})},\ldots ,\frac{d_r}{\gcd (d_r,a_{r0})} \right) , \end{aligned}$$

where E is a $\mathbb {Q}$-divisor on X locally given at the point P by the well-defined function $x_0^m: X(\mathbf {d};A) \rightarrow \mathbb {C}$.

In the situation of 3.1, the multiplicity $m(g^{*}(0),P)$ with $P\in g^{-1}(0)$ can be interpreted geometrically as follows.

Lemma 3.6

The number of prime (or irreducible) factors of the polynomial $t^e - x_{0}^{m_0} \ldots x_k^{m_k}$ regarded as an element in $\mathbb {C}[x_0,\ldots ,x_n]^{\mu _\mathbf {d}} \otimes _{\mathbb {C}} \mathbb {C}[t]$ is $m(g^{*}(0),P)$. Hence, this number also coincides with the cardinality of the fiber over P of the covering $\varrho : \widetilde{X} \rightarrow X$.

Proof

Let us denote $\ell = \gcd (m_0,\ldots ,m_k)$ and $C_i = \sum _{j=0}^k a_{ij} m_j$ for $i=0,\ldots ,r$. The polynomial $t^e - x_0^{m_0} \cdots x_k^{m_k} \in \mathbb {C}[x_0, \ldots , x_n, t]$ factorizes into $\ell$ different components as

$$\begin{aligned} t^e - x_0^{m_0} \ldots x_k^{m_k} = \prod _{i=0}^{\ell -1} \Big ( t^{\frac{e}{\ell }} - \zeta ^i_\ell \, x_0^{\frac{m_0}{\ell }} \ldots x_k^{\frac{m_k}{\ell }} \Big ), \end{aligned}$$

where $\zeta _\ell$ is a primitive $\ell$-th root of unity. However, this factors are not invariant under the group $\mu _\mathbf {d}$, since they are mapped to

$$\begin{aligned} t^{\frac{e}{\ell }} - \zeta ^i_\ell \, x_0^{\frac{m_0}{\ell }} \ldots x_k^{\frac{m_k}{\ell }} \quad \longmapsto \quad t^{\frac{e}{\ell }} - \xi _{d_0}^{\frac{C_0}{\ell }} \ldots \xi _{d_r}^{\frac{C_r}{\ell }} \ldots \zeta ^i_\ell \, x_0^{\frac{m_0}{\ell }} \ldots x_k^{\frac{m_k}{\ell }}, \end{aligned}$$

by the action of $(\xi _{d_0}, \ldots , \xi _{d_r}) \in \mu _\mathbf {d}$. Recall that $\mathbb {C}^{n+1}/\mu _\mathbf {d}= X(\mathbf {d}; A)$.

Let $H_i$ be the cyclic group defined by $H_i:= \{ \xi _{d_i}^{C_i/\ell } \mid \xi _{d_i} \in \mu _{d_i} \}$, for $i=0,\ldots ,r$, and consider $H = H_0 \ldots H_r$. Since $t^e - x_0^{m_0} \ldots x_k^{m_k}$ defines a function over $X(\mathbf {d}; A)\times \mathbb {C}$, then $d_i$ must divide $C_i$ and, consequently, all the previous groups are (normal) subgroups of $\mu _{\ell }$. The order of $\mu _{\ell } / H$ is exactly the number of prime (or irreducible) components of the preceding polynomial regarded as an element in $\mathbb {C}[x_0,\ldots ,x_n]^{\mu _\mathbf {d}} \otimes _{\mathbb {C}} \mathbb {C}[t]$.

The order of $H_i$ is $|H_i| = \frac{d_i}{\gcd ( d_i,\, C_i/\ell )} = \frac{\ell }{\gcd ( \ell ,\, C_i/d_i )}$. Then, one has

$$\begin{aligned} \begin{aligned} |H|&= | H_0 \ldots H_r | = {{\mathrm{lcm}}}\big ( |H_0|, \ldots , |H_r| \big ) \\&= \frac{\ell }{ \gcd \left( \ell , \frac{C_0}{d_0}, \ldots , \frac{C_r}{d_r} \right) } = \frac{\ell }{m(P)}. \end{aligned} \end{aligned}$$

(5)

In the expression above, a general property about greatest common divisor and least common multiple already mentioned in 3.5 was used.

Assume that $g^{-1}(0) = E_0 \cup \ldots \cup E_s$ and let us denote $D_i = \varrho ^{-1}(E_i)$ for $i=0,\ldots ,s$ and $D = \bigcup _{i=0}^s D_i$. This commutative diagram illustrates the whole process of the semistable reduction.

(6)

Consider the stratification of X associated with the normal crossing divisor $g^{-1}(0) \subset X$. That is, given a possibly empty set $I\subseteq \{0,1,\ldots ,s\}$, consider

$$\begin{aligned} E_{I}^\circ := \Big ( \cap _{i \in I} E_i \Big ) \setminus \Big ( \cup _{i\notin I} E_i \Big ). \end{aligned}$$

Also, let $X = \bigsqcup _{j\in J} Q_j$ be a finite stratification of X given by its quotient singularities so that the local equation of g at $P \in E_I^{\circ } \cap Q_j$ is of the form

$$\begin{aligned} x_1^{m_1} \ldots x_k^{m_k}:\, B/G \longrightarrow \mathbb {C}, \end{aligned}$$

where B is an open ball around P, and G is an abelian group acting diagonally as in $(\mathbf {d};A)$. The multiplicities $m_i$’s and the action G are the same along each stratum $E_I^{\circ } \cap Q_j$, i.e., they do not depend on the chosen point $P \in E_I^{\circ } \cap Q_j$. Denote $m_{I,j} := m(E_I^{\circ } \cap Q_j)$. Finally, assume that $E^\circ _I \cap Q_j$ is connected.

Theorem 3.7

The variety $\widetilde{X}$ only has abelian quotient singularities located at $\widetilde{g}^{-1}(0) = D$ which is a reduced divisor with normal crossings on $\widetilde{X}$. Also, $\varrho : \widetilde{X} \rightarrow X$ is a cyclic branched covering of e sheets unramified over $X\setminus g^{-1}(0)$. Moreover, for $\emptyset \ne I \subseteq S:= \{0,1,\ldots ,s\}$ and $j \in J$, the following properties hold.

• 1. The restriction $\varrho \,|: \varrho ^{-1}(\overline{E^\circ _I\cap Q_j}) \rightarrow \overline{E_I^\circ \cap Q_j}$ is a cyclic branched covering of $m_{I,j}$ sheets unramified over $E^\circ _I \cap Q_j$.

• 2. The variety $\varrho ^{-1}(\overline{E^\circ _I\cap Q_j})$ is a V-manifold with abelian quotient singularities with $\gcd ( \{ m(P) \mid P\in \overline{E^\circ _I\cap Q_j} \} )$ connected components.

• 3. Let $\varphi : \widetilde{X} \rightarrow \widetilde{X}$ be the canonical generator of the monodromy of the covering $\varrho$. Then, its restriction to $\varrho ^{-1}(\overline{E^\circ _I\cap Q_j})$ is a generator of the monodromy of $\varrho \,|: \varrho ^{-1}(\overline{E^\circ _I\cap Q_j}) \rightarrow \overline{E_I^\circ \cap Q_j}$.

• 4. The Euler characteristic of each connected component of $D_i$ is

  $$\begin{aligned} \qquad \displaystyle {\mathop {\mathop {\sum }\limits _{\{ i \} \subset I\subset \{ 0,1,\ldots ,s \}}}\limits _{j \, \in \, J}} m_{I,j} \cdot \chi (E_I^\circ \cap Q_j) \bigg / \gcd ( \{ m(P) \mid P\in E_i \} ). \end{aligned}$$

Proof

First note that the morphism $\varrho : \widetilde{X} \rightarrow X$ is a cyclic branched covering unramified over $X\setminus g^{-1}(0)$, since so is $\sigma _1: X_1 \rightarrow X$ and the normalization $\nu : \widetilde{X} \rightarrow X_1$ does not change the normal points.

Let $P \in g^{-1}(0)$ and choose coordinates $x_0, \ldots , x_n$ as in 3.1 so that $X_1 \subset X(\mathbf {d};A) \times \mathbb {C}$ is locally given by the polynomial $t^{e} - x_0^{m_0} \ldots x_k^{m_k}$. Let us denote for $i = 0, \ldots , k$,

$$\begin{aligned} m(P) = m(g^{*}(0),P), \qquad e' = e/m(P), \qquad m'_i = m_i/m(P). \end{aligned}$$

Consider the ring

$$\begin{aligned} A = \frac{\mathbb {C}[x_0,\ldots ,x_n, t]}{\langle t^{e} - x_0^{m_0} \ldots x_k^{m_k} \rangle }. \end{aligned}$$

The action given by $X(\mathbf {d};A)$ is extended to A so that the variable t is invariant. Then, by Lemma 3.6, the normalization $\overline{A^{\mu _\mathbf {d}}}$ of the ring $A^{\mu _\mathbf {d}}$ is isomorphic to the direct sum of m(P) isomorphic copies of the normalization of

$$\begin{aligned} \frac{\mathbb {C}[x_0,\ldots ,x_n]^{{\mu _\mathbf {d}}} \otimes _{\mathbb {C}} \mathbb {C}[t]}{ \big \langle t^{e'} - x_0^{m'_0} \cdots x_k^{m'_k} \big \rangle } = \Bigg ( \frac{\mathbb {C}[x_0,\ldots ,x_n,t]}{ \big \langle t^{e'} - x_0^{m'_0} \cdots x_k^{m'_k} \big \rangle } \Bigg )^{{\mu _\mathbf {d}}}. \end{aligned}$$

Therefore to compute it we only need to consider the case $m(P) = 1$, for which the ring $A^{\mu _\mathbf {d}}$ is an integral domain. Now we plan to apply Lemma 3.2 to a ring extension $A^{\mu _\mathbf {d}} \subset B$, where B is a polynomial algebra.

Let $c_i = e/m_i$ for $i=0,\ldots ,k$. Denote $B = \mathbb {C}[y_0,\ldots ,y_n]$ and consider $A^{\mu _\mathbf {d}}$ as subring of B by putting

$$\begin{aligned} {\left\{ \begin{array}{ll} x_i = y_i^{c_i} &{} \text {if} \quad 0 \le i \le k, \\ x_i = y_i &{} \text {for} \quad i > k, \\ t = y_0 \cdots y_k \end{array}\right. } \end{aligned}$$

Note that A cannot be embedded in B because it is not even a domain. Since $\mu _\mathbf {d}$ acts diagonally on $\mathbb {C}^{n+2}$, there exists $N \gg 0$ such that

$$\begin{aligned} y_0^{c_0 N}, \ldots , y_k^{c_k N},\ y_{k+1}^N, \ldots , y_n^N \ \in \ A^{\mu _\mathbf {d}}. \end{aligned}$$

This implies that the extension $A^{\mu _\mathbf {d}} \subset B$ is integral. Also, B is a normal domain. It remains to prove that $Q(B)|Q(A^{\mu _\mathbf {d}})$ is a Galois field extension. One has

$$\begin{aligned} \mathbb {C}\left( y_0^{c_0 N}, \ldots , y_k^{c_k N}, y_{k+1}^N, \ldots , y_n^N\right) \subset Q(A^{\mu _\mathbf {d}}) \subset Q(B) = \mathbb {C}(y_0,\ldots ,y_n). \end{aligned}$$

Note that the largest extension is clearly Galois. Its Galois group is abelian, and it is isomorphic to

$$\begin{aligned} \mu _{c_0 N} \times \cdots \times \mu _{c_k N} \times \mu _{N} \times \mathop {\cdots }\limits ^{n-k} \times \mu _{N}. \end{aligned}$$

Thus $\overline{A^{\mu _\mathbf {d}}} = B^{{{\mathrm{Gal}}}(Q(B)|Q(A^{\mu _\mathbf {d}}))}$.

This shows that ${{\mathrm{Spec}}}(\overline{A^{\mu _\mathbf {d}}})$ and hence $\widetilde{X}$ are V-manifolds. Locally D is the quotient under the group ${{\mathrm{Gal}}}(Q(B)|Q(A^{\mu _\mathbf {d}}))$ of the reduced divisor $y_0 \ldots y_k = 0$. The rest of the statement follows from the fact that the branched coverings involved are cyclic. For the last part, use the classical Riemann–Hurwitz formula.

Remark 3.8

Assume $\mathbb {C}[x_0,\ldots ,x_n]^{\mu _\mathbf {d}} = \mathbb {C}[\{ x_0^{\alpha _0} \ldots x_n^{\alpha _n} \}_{\alpha \in \Lambda }]$. Then $A^{\mu _\mathbf {d}}$ is identified with the subring

$$\begin{aligned} \mathbb {C}\left[ \left\{ y_0^{\alpha _0 c_0} \ldots y_k^{\alpha _k c_k} \ldots y_{k+1}^{\alpha _{k+1}} \ldots y_n^{\alpha _n} \right\} _{\alpha \in \Lambda },\, y_0 \ldots y_k \right] \subset \mathbb {C}[y_0,\ldots ,y_n]. \end{aligned}$$

Hence the Galois extension

$$\begin{aligned} {{\mathrm{Gal}}}(Q(B)|Q(A^{\mu _\mathbf {d}})) \subset \mu _{c_0 N} \times \cdots \times \mu _{c_k N} \times \mu _{N} \times \mathop {\ldots }\limits ^{(n-k)} \times \mu _{N} \end{aligned}$$

is given by the elements $(\xi _0, \ldots , \xi _k, \eta _{k+1}, \ldots , \eta _n)$ such that

$$\begin{aligned} \forall \alpha \in \Lambda , \quad \left\{ \begin{array}{l} \xi _0^{\alpha _0 c_0} \ldots \xi _k^{\alpha _k c_k} \ldots \eta _{k+1}^{\alpha _{k+1}} \ldots \eta _n^{\alpha _n} = 1,\\ \xi _0 \ldots \xi _k = 1. \end{array}\right. \end{aligned}$$

In general, this group is not a small subgroup of $GL(n+1,\mathbb {C})$, that is, there may exist elements of the group having 1 as an eigenvalue of multiplicity precisely n.

Remark 3.9

Note that $\varrho \,|:\varrho ^{-1} ( \overline{E^\circ _i \cap Q_j} ) \rightarrow \overline{E^\circ _i \cap Q_j}$ is an isomorphism when $I = \{ i \}$ and the multiplicity of $E_{i}$ (at the smooth points) is equal to one.

In what follows this construction is applied to $g = f \circ \pi$, where the map $f:(M,0) \rightarrow (\mathbb {C},0)$ is the germ of a non-constant analytic function and $\pi : X \rightarrow (M,0)$ is an embedded $\mathbb {Q}$-resolution of $\{ f=0 \} \subset (M,0)$ with $M = X(\mathbf {d};A)$, cf. Sect. 5. Let us see an example.

Example 3.10

Consider the plane curve defined by $f = x^p + y^q$ in $\mathbb {C}^2$. Recall that after the $(q_1,p_1)$-weighted blow-up at the origin, one obtains an embedded $\mathbb {Q}$-resolution with only one exceptional divisor $\mathcal {E}$ of multiplicity ${{\mathrm{lcm}}}(p,q)$, where $p=p_1 \gcd (p,q)$ and $q=q_1 \gcd (p,q)$, see e.g., [17, Ex. 3.3].

Following Theorem 3.7, $D = \varrho ^{-1}(\mathcal {E})$ is irreducible and the restriction $\varrho : D \rightarrow \mathcal {E}$ is a branched covering of ${{\mathrm{lcm}}}(p,q)$ sheets. Also, the singular point of type $(q_1; -1, p_1)$ (resp. $(p_1; q_1, -1)$) is converted into p (resp. q) smooth points in the semistable reduction (Fig. 1). Finally, $\varrho \,|: \varrho ^{-1}(\mathbf{\widehat{C}}) \rightarrow \mathbf{\widehat{C}}$ is an isomorphism. This implies that the Euler characteristic of D is

$$\begin{aligned} \chi (D) = p + q + \gcd (p,q) - pq = \gcd (p,q) + 1 - \mu . \end{aligned}$$

Fig. 1

Semistable reduction of $x^p + y^q$

The p points in D which are lift over the point of type $(q_1;-1,p_1)$ are smooth. Of course, the same happens for the point of type $(p_1;q_1,-1)$. Also, the intersection of the strict transform with D gives rise to $\gcd (p,q)$ smooth points. As we shall see the smoothness is not relevant for providing a MHS on the cohomology of the Milnor fiber.

4 Monodromy filtration

This exposition is extracted from [4], which is in turn based on the book [2].

Let H be a $\mathbb {C}$-vector space of finite dimension. Consider a nilpotent endomorphism $N: H \rightarrow H$, i.e. there exists $k \in \mathbb {N}$ such that $N^k = 0$. Its Jordan canonical form is determined by the sequence of integers formed by the size of the Jordan blocks.

There is an alternative way to encode the Jordan form giving instead an increasing filtration on H. Let us fix $k \in \mathbb {Z}$; it will be called the central index of the filtration. Consider a basis of H such that the matrix of N in this basis is the Jordan matrix.

Each Jordan block determines a subfamily $\{ v_1,\ldots ,v_r \}$ of the basis such that $N(v_1) = 0$ and $N(v_i) = v_{i-1}$ for $i=2,\ldots ,r$. Let us denote by $l(v_i)$ the unique integer determined by the following two conditions:

• 1. $l(v_i) = l(v_{i-1}) + 2, \forall i=2,\ldots ,r$.

• 2. $\{ l(v_1), \ldots , l(v_r) \}$ is symmetric with respect to k.

In fact, this integer is $l(v_i) = k-r+2i-1, \forall i=1,\ldots ,r$, as one can check directly.

Applying this construction to all the Jordan blocks, one defines $W_l$ as the vector subspace of H generated by $\{ v \mid v \text {in the basis},\ l(v) \le l \}$. This gives rise to an increasing filtration $\{ W_l \}_{l \in \mathbb {Z}}$ on H. Its graded part is denoted by ${{\mathrm{Gr}}}_l^W (H) := W_l / W_{l-1}$ for $l \in \mathbb {Z}$.

Also, denote by $J_l(N)$ the number of Jordan blocks in N of size l. Then, it is satisfied that

$$\begin{aligned} J_l(N) = \dim \left( {{\mathrm{Gr}}}_{k-l+1}^W (H) ) - \dim ( {{\mathrm{Gr}}}_{k-l-1}^W (H) \right) . \end{aligned}$$

Proposition 4.1

([21]) There exists a unique increasing filtration $\{ W_l \}_{l \in \mathbb {Z}}$ such that:

• 1. $N(W_l) \subset W_{l-2}$.

• 2. $N^{l}: {{\mathrm{Gr}}}_{k+l}^W (H) \rightarrow {{\mathrm{Gr}}}_{k-l}^W (H)$ is an isomorphism.

This filtration is called the weight filtration of N with central index k. One checks that the filtration $\{ W_l \}_{l\in \mathbb {Z}}$ defined above satisfies these two properties. In particular, the description of $\{ W_l \}_{l\in \mathbb {Z}}$ does not depend on the chosen basis.

Using this construction, the Jordan form of an arbitrary automorphism $M: H \rightarrow H$ can be described too. Let $M = M_u M_s$ be the decomposition of M into its unipotent and semisimple components. It is known that $M_u M_s = M_s M_u$ and that the decomposition is unique, see [23]. Recall that the semisimple part contains the information about the eigenvalues and the unipotent one, the information about the size of the Jordan blocks. Note that the endomorphism $N:=\log (M_u)$ is nilpotent and the number of Jordan blocks of size l is $J_l (N) = J_l(M_u) = J_l(M)$.

For a given $k \in \mathbb {Z}$, consider the weight filtration associated with N with central index k. Due to the properties of the decomposition, the subspaces $W_l$ are invariant by the action of $M_s$, and thus by the action of M. The endomorphism induced by $M_u$ on each graded part ${{\mathrm{Gr}}}_l^W (H)$ is semisimple and, since $M_u$ is unipotent, it is indeed the identity. Hence the actions of M and $M_s$ on ${{\mathrm{Gr}}}_l^W (H)$ coincide.

The conclusion is that the Jordan form of M is determined by the filtration $\{ W_l \}_{l \in \mathbb {Z}}$ and the action of M over ${{\mathrm{Gr}}}_l^W (H)$ for $l\in \mathbb {Z}$.

Let $(V,0) \subset (\mathbb {C}^{n+1},0)$ be a germ of an isolated hypersurface singularity at the origin. Denote by $\varphi : H^n(F,\mathbb {C}) \rightarrow H^n(F,\mathbb {C})$ its complex monodromy.

Consider the decomposition of $H^n(F,\mathbb {C})$ as a direct sum of two subspaces invariant under $\varphi , H^{\ne 1}$ and $H^{1}$, such that $Id-\varphi$ is invertible over $H^{\ne 1}$ and nilpotent over $H^{1}$.

Let $W^{\ne 1}$ be the weight filtration of $\varphi |_{H^{\ne 1}}$ with central index n. Analogously, denote by $W^{1}$ the weight filtration of $\varphi |_{H^{1}}$ with central index $n+1$. These filtrations satisfy $W^{\ne 1}_{-1} = W^{1}_1 = 0, W^1_{2n} = H^1$, and $W^{\ne 1}_{2n} = H^{\ne 1}$.

Definition 4.2

The monodromy filtration of the cohomology of the Milnor fiber is $W:= W^{1} \oplus W^{\ne 1}$.

Note that the Jordan form of the complex monodromy is completely determined by the action of $\varphi$ over the graded parts of the monodromy filtration W. Let us fix the notation for the characteristic polynomials of $\varphi$ acting on the following vector spaces:

Vector space	Characteristic polynomial
$H := H^n(F,\mathbb {C})$	$\Delta (t)$
${{\mathrm{Gr}}}_{n-l}^{W^{\ne 1}} ( H )$	$\Delta _{l}^{\ne 1}(t)$
${{\mathrm{Gr}}}_{n-l+1}^{W^1} (H)$	$\Delta _{l}^{1}(t)$
${{\mathrm{Gr}}}_{n-l}^{W^{\ne 1}} (H) \oplus {{\mathrm{Gr}}}_{n-l+1}^{W^1} (H)$	$\Delta _l(t)$

Observe that the Jordan blocks of size l are given by the polynomial $\frac{\Delta _{l-1}(t)}{\Delta _{l+1}(t)}$. More precisely, the multiplicity of $\zeta \in \mathbb {C}$ as root is this polynomial equals the number of Jordan blocks of size l for the eigenvalue $\zeta$.

5 Steenbrink’s spectral sequence

The Jordan form of the complex monodromy is closely related to the theory of MHS, first introduced in [9–11]. By different methods, Steenbrink and Varčenko proved that the cohomology of the Milnor fiber admits a MHS compatible with the monodromy, see [24] and [27, 28].

Definition 5.1

A Hodge structure of weight n is a pair $(H_{\mathbb {Z}},F)$ consisting of a finitely generated abelian group $H_{\mathbb {Z}}$ and a decreasing filtration $F = \{ F^p \}_{p \in \mathbb {Z}}$ on $H_{\mathbb {C}} := H_{\mathbb {Z}} \otimes _{\mathbb {Z}} \mathbb {C}$ satisfying $H_\mathbb {C}= F^p \oplus \overline{F^{n-p+1}}$ for all $p \in \mathbb {Z}$. One calls F the Hodge filtration.

An equivalent definition is obtained replacing the Hodge filtration by a decomposition of $H_\mathbb {C}$ into a direct sum of complex subspaces $H^{p,q}$, where $p+q=n$, with the property that $\overline{H^{p,q}} = H^{q,p}$. The relation between these two descriptions is given by

$$\begin{aligned} H_{\mathbb {C}} = \bigoplus _{p+q = n} H^{p,q}, \qquad F^p = \bigoplus _{i\ge p} H^{i,n-i}, \qquad H^{p,q} = F^p \cap \overline{F^q}. \end{aligned}$$

The typical example of a pure Hodge structure of weight n is the cohomology $H^n(X,\mathbb {Z})$ where X is a compact Kähler manifold. In the sequel, we will use the fact that, for compact Kähler V-manifold, $H^n(X,\mathbb {Z})$ can also be endowed with a pure Hodge structure of weight n. Deligne proved that the same is true for smooth compact algebraic varieties, see [10].

Above, one may replace $\mathbb {Z}$ by any ring A contained in $\mathbb {R}$ such that $A \otimes _{\mathbb {Z}} \mathbb {Q}$ is a field and obtain A-Hodge structures. In particular, one uses $A = \mathbb {Q}$ or $\mathbb {R}$. In this way, the primitive cohomology groups of a compact Kähler manifold are $\mathbb {R}$-Hodge structures.

Definition 5.2

A mixed Hodge structure is a triple $(H_\mathbb {Z},W,F)$ where $H_\mathbb {Z}$ is a finitely generated abelian group, $W=\{W_n\}_{n\in \mathbb {Z}}$ is an increasing filtration on $H_{\mathbb {Q}}:= H_{\mathbb {Z}} \otimes _{\mathbb {Z}} \mathbb {Q}$, and $F=\{F^p\}_{p\in \mathbb {Z}}$ is a decreasing filtration on $H_{\mathbb {C}} := H_{\mathbb {Z}} \otimes _{\mathbb {Z}} \mathbb {C}$, such that F induces a $\mathbb {Q}$-Hodge structure of weight n on each graded part ${{\mathrm{Gr}}}_n^W (H_{\mathbb {Q}}), \forall n \in \mathbb {Z}$. One calls F the Hodge filtration and W the weight filtration.

Let us denote again by the same letter the filtration induced by W on the complexification $H_{\mathbb {C}}$, i.e. $W_n(H_{\mathbb {C}}) = W_n \otimes \mathbb {C}$. Then, the filtration induced by F on ${{\mathrm{Gr}}}_n^{W} (H_\mathbb {C})$ is defined by

$$\begin{aligned} F^p \left( {{\mathrm{Gr}}}_n^W (H_\mathbb {C}) \right) = \frac{F^p \cap (W_n \otimes \mathbb {C}) + W_{n-1} \otimes \mathbb {C}}{W_{n-1} \otimes \mathbb {C}}. \end{aligned}$$

Thus the condition above on the weight and Hodge filtrations can be stated as, $\forall n,p \in \mathbb {Z}, F^p \left( {{\mathrm{Gr}}}_n^W (H_\mathbb {C}) \right) \oplus \overline{F^{n-p+1} \left( {{\mathrm{Gr}}}_n^W (H_\mathbb {C}) \right) } = {{\mathrm{Gr}}}^W_n ( H_\mathbb {C})$.

Example 5.3

Let D be a divisor with normal crossings whose irreducible components are smooth and Kähler. Then, $H^{*}(D,\mathbb {Z})$ admits a functorial MHS, see [12]. This results is extended to V-manifolds with $\mathbb {Q}$-normal crossings whose irreducible components are Kähler. Also, in [10], it is proven that if X is the complement in a compact Kähler manifold of a normal crossing divisor, then $H^{*}(X,\mathbb {Z})$ has a functorial MHS which does not depend on the ambient variety as far as one remains in the same bimeromorphic equivalence class.

Let $M = X(\mathbf {d};A) = \mathbb {C}^{n+1}/\mu _{\mathbf {d}}$ be an abelian quotient space and consider a non-constant analytic function germ $f:(M,0) \rightarrow (\mathbb {C},0)$. Let us fix an embedded $\mathbb {Q}$-resolution $\pi : X \rightarrow (M,0)$ of the hypersurface $\{ f=0 \}$. Hence the construction of Sect. 3 is applied to $g = f \circ \pi : X \rightarrow \mathbb {C}$.

The following result can be proven as in [24] repeating exactly the same arguments. The main reason is that, starting with an embedded $\mathbb {Q}$-resolution, the total space produced after the semistable reduction is again a V-manifold with abelian quotient singularities, see Theorem 3.7.

Theorem 5.4

There exists a spectral sequence $\{ E_{n}^{p,q} \}$ constructed from the embedded $\mathbb {Q}$-resolution $\pi$ that verifies:

• 1. It converges to the cohomology of the Milnor fiber and degenerates at $E_2$.

• 2. The spaces $E_{1}^{p,q}$ has a pure Hodge structure of weight p respected by the differentials. In particular, $E_{2}^{p,q} = E_{\infty }^{p,q}$ also has a pure Hodge structure of weight p.

• 3. There exists a Hodge filtration on the cohomology of the Milnor fiber which induces a Hodge filtration on $E_{\infty }^{p,q}$. One constructs a weight filtration using the filtration with respect to the first index:

  $$\begin{aligned} \qquad {{\mathrm{Gr}}}_l^W (H^k (F,\mathbb {C})) \cong E_{\infty }^{l,k-l} \cong E_{2}^{l,k-l}. \end{aligned}$$

Therefore, these two filtrations provide a MHS on the cohomology of the Milnor fibration. This structure is an invariant of the singularity which only depends on the resolution $\pi$.

In [28], there is another construction of the MHS on the cohomology of the Milnor fiber, using asymptotic integration. The weight filtration of both MHS coincide. Although both Hodge filtrations do not coincide, they induce the same pure Hodge structure on the graded part of the weight filtration.

Theorem 5.5

The complexification of the weight filtration of the MHS of the cohomology of the Milnor fiber is exactly the monodromy filtration.

Moreover, the complex monodromy $\varphi$ acts over the first term $E_1$ of the spectral sequence and commutes with the differentials. The action induced on the complexification of $E_2 = E_\infty$ coincides with the action induced on the graded parts of the monodromy filtration.

We finish this section with the explicit description of Steenbrink’s spectral sequence. As we shall see, it is constructed from the divisors associated with the semistable reduction of $g := f \circ \pi : X \rightarrow \mathbb {C}$.

Consider the divisor D associated with the semistable reduction of the embedded $\mathbb {Q}$-resolution $\pi$. Let us decompose $D = D_0 \cup D_1 \cup \ldots \cup D_s$ so that $D_0$ corresponds to the strict transform of the singularity and the divisor $D_{+} := D_1 \cup \cdots \cup D_s$ corresponds to the exceptional components. Let us introduce some notation.

• Let $I = (i_0, \cdots , i_k)$ with $0 \le i_0 < \cdots < i_k \le s$.

  $$\begin{aligned} D_I = D_{i_0,\ldots ,i_k}&:= D_{i_0} \cap \ldots \cap D_{i_k}, \\ \check{D}_I = \check{D}_{i_0,\ldots ,i_k}&:= D_I \setminus \bigcup _{j \ne i_0,\ldots , i_k} ( D_j \cap D_I ). \end{aligned}$$

  The first one is a projective V-manifold of dimension $n-k$. The second one is a smooth complex variety of the same dimension.

• Let $0 \le i_0 < \cdots < i_k \le s, i_j < i'_j < i_{j+1}$ with $-1 \le j \le k$. Denote by

  $$\begin{aligned} \kappa _{i_0, \ldots , i_j, i_{j+1}, \ldots , i_k}^{i'_j}\, :\, D_{i_0,\ldots ,i_j,i'_j,i_{j+1},\ldots ,i_k} \hookrightarrow D_{i_0,\ldots ,i_j,i_{j+1},\ldots ,i_k}, \end{aligned}$$

  the natural inclusion.

• Let $D^{[k]}:= \displaystyle \bigsqcup _{0 \le i_0 < \cdots < i_k \le s} D_{i_0,\ldots ,i_k}, \qquad D_{+}^{[k]}:= \displaystyle \bigsqcup _{1 \le i_0 < \cdots < i_k \le s} D_{i_0,\ldots ,i_k}$.

Definition 5.6

Let $k \in \mathbb {Z}$ with $0 \le k \le n$ and let $i,j \in \mathbb {Z}$ with $i,j \ge 0$.

$$\begin{aligned} \text {}^{k} E_{1}^{i,k-j} := {\left\{ \begin{array}{ll} H^{i} ( D_{+}^{[k]}, \mathbb {Q} ) &{} \text {if} \quad j=0, \\ H^{i-2j} ( D^{[k+j]}, \mathbb {Q} ) &{} \text {if} \quad j>0. \end{array}\right. } \end{aligned}$$

Note that for $j=0$ the divisor $D_{+}$ is used, while for $j>0$ the divisor D is taken. All the spaces whose cohomology is considered are compact. These spaces give rise to the first term $E_1$ of our spectral sequence $E = \{ E^{p,q}_n \}$:

where $^{k} E_{1}^{p,q} = 0$ if it is not defined previously.

Note that the space $^{p} E_1^{i,k-j}$ possesses a natural pure Hodge structure of weight $i-2j$, since it is defined as the cohomology of degree $i-2j$ of a compact Kähler V-manifold. Performing an index shifting $\widetilde{H}^{p+j,q+j}:= H^{p,q}, ^{p} E_1^{i,k-j}$ also has a pure Hodge structure of weight i, cf. Theorem 5.4.

It still remains to define the differentials. In the first term $E_1$, the differentials are of type (0, 1), i.e. upward vertical arrows.

Let us resume the notation above. Let

$$\begin{aligned} \Big ( \kappa _{i_0, \ldots , i_k}^{i'_j} \Big )_{*}\, :\, H_{*} \Big ( D_{i_0,\ldots ,i_j,i'_j,i_{j+1},\ldots ,i_k}, \mathbb {Q} \Big ) \longrightarrow H_{*} \Big ( D_{i_0,\ldots ,i_j,i_{j+1},\ldots ,i_k}, \mathbb {Q} \Big ) \end{aligned}$$

be the homomorphism induced by the inclusion on the homology groups. Using Poincaré duality for compact V-manifolds, one has the following Gysin-type maps:

These arrows are only possible if the spaces are compact. It is always the case except for $k=0$ and $i_0=0$, where the corresponding map is defined as zero. By abuse of notation, the morphism associated with the dashed arrow which completes the previous diagram is again denoted by $\big ( \kappa _{i_0, \ldots , i_k}^{i'_j} \big )_{*}$.

Definition 5.7

The differentials on $^{k} E_1, \text {}^{k} \delta : \text {}^{k} E_1^{i,k-j-1} \rightarrow \text {}^k E_1^{i,k-j}$ are defined by

$$\begin{aligned} \text {}^{k} \delta \, |_{H^{i-2(j+1)}(D_{i_0,\ldots ,i_{k+j+1}},\mathbb {Q})} := \sum _{l=0}^{k+j+1} (-1)^l \Big ( \kappa _{i_0,\ldots ,\widehat{i_l},\ldots ,i_{k+j+1}}^{i_l} \Big )_{*}. \end{aligned}$$

Remark 5.8

The pair $(\text {}^k E_1, \text {}^k \delta )$ is the term $E_1$ of the spectral sequence that provides the MHS of

$$\begin{aligned} \bigsqcup _{0 \le i_0 < \cdots < i_k \le s} \check{D}_{i_0,\ldots ,i_k}, \end{aligned}$$

which is the complement of a divisor with normal crossings on a projective variety.

To finish with the description of the differentials, the interactions between different $\text {}^{k} E_1$ have to be taken into account. These differentials are of Mayer-Viétoris type. Denote by $\big ( \kappa _{i_0,\ldots ,i_{k+j}}^{i_l} \big )^{*}$ the corresponding homomorphism on the cohomology groups.

Definition 5.9

The morphisms $\text {}^{k,k+1} \delta : \text {}^{k} E_1^{i,k-j} \rightarrow \text {}^{k+1} E_1^{i,k-j+1}$ are defined as

$$\begin{aligned} \text {}^{k,k+1} \delta \, |_{H^{i-2j} (D_{i_0,\ldots ,i_{k+j}},\mathbb {Q})} := \sum _{\ell \ne i_0,\ldots ,i_{k+j}} (-1)^{e(l;\, i_0,\ldots ,i_{k+j})} \Big ( \kappa _{i_0,\ldots ,i_{k+j}}^{i_l} \Big )^{*}, \end{aligned}$$

where $e(l;\, i_0,\ldots ,i_{k+j})$ is the number of coefficients $i_0,\ldots ,i_{k+j}$ less than l.

Remark 5.10

The pair $(\text {}^k E_1^{i,k}, \text {}^{k,k+1} \delta )$ is exactly the term $E_1$ of the spectral sequence providing the MHS of the divisor with normal crossings $D_{+}$ which appears in [10]. Observe that the first two columns of this spectral sequence for $k=0$ coincides with the first two columns of the term $E_1$ of $\{ E^{p,q}_{n} \}$ (Fig. 2).

Definition 5.11

The direct sum of the differentials $\text {}^k \delta$ and $\text {}^{k,k+1} \delta$ is the differential $\delta$ of the term $E_1$.

Fig. 2

Decomposition of $E = \{ E^{p,q}_n \}$ for $n=1,2$

As a consequence of this spectral sequence, the standard result about the maximal size of the Jordan blocks holds for embedded $\mathbb {Q}$-resolutions too.

Proposition 5.12

Let $\widetilde{K}$ be the dual complex associated with $D_{+}$ and let $\varphi : H^n(F,\mathbb {C}) \rightarrow H^n(F,\mathbb {C})$ be the monodromy of $\{ f = 0 \} \subset X(\mathbf {d};A)$. Then the Jordan blocks of size $n+1$ is determined by the characteristic polynomial of $\varphi$ acting on $H^n (\widetilde{K},\mathbb {C})$.

Proof

Recall that $E_1^{0,q} = H^{0}(D_{+}^{[q]},\mathbb {C})$. Hence the first column of the spectral sequence $(E_1^{0,\bullet },\delta )$ is isomorphic to the cochain complex $C^{\bullet } (\widetilde{K}) \otimes \mathbb {C}$. Consequently $H^n (\widetilde{K},\mathbb {C}) \cong H^n(E_1^{0,\bullet })$; besides the action of $\varphi$ on both complexes commutes with this isomorphism. On the other hand, since W coincides with the monodromy filtration, the Jordan blocks of size $n+1$ are determined by the action of $\varphi$ on ${{\mathrm{Gr}}}^W_0 ( H^n (F,\mathbb {C}) )$ which is by Theorem 5.4 isomorphic to $E_{\infty }^{0,n} = E_2^{0,n} = H^n (E_1^{0,\bullet })$. The latter isomorphism is again compatible with the action of $\varphi$. This concludes the result. $\square$

Remark 5.13

Analogously, one shows that $H^q(\widetilde{K},\mathbb {C}) \cong {{\mathrm{Gr}}}^W_0 ( H^q(F,\mathbb {C}) )$ and thus $H^0(\widetilde{K},\mathbb {C}) = \mathbb {C}$ and $H^q(\widetilde{K},\mathbb {C}) = 0$ for $q \ne 0,n$.

This section ends with the explicit description of the spectral sequence $\{ E^{p,q}_n \} \otimes _{\mathbb {Q}} \mathbb {C}$ for the cases $n=1,2$. For $n=1$, let us denote with a triangle the terms belonging to $\text {}^1 E_1$ and with a circle the ones belonging to $\text {}^{0} E_1$.

For surfaces, that is $n=2$, denote with a square the terms belonging to $\text {}^2 E_1$, with a triangle the ones belonging to $\text {}^1 E_1$, and finally with a circle those coming from $\text {}^{0} E_1$.

6 Examples

As an application, we illustrate the use of all the preceding results presented in this work with several examples including a plane curve and a YLS. In particular, we provide infinite pairs of irreducible YLS having the same complex monodromy with different topological type.

6.1 Plane curves

Assume $\gcd (p,q) = \gcd (r,s) = 1$ and $\frac{p}{q} < \frac{r}{s}$. Let $f = (x^p + y^q) (x^r + y^s)$ and consider $\mathbf{C}_1 = \{ x^p + y^q = 0 \}$ and $\mathbf{C}_2 = \{ x^r + y^s = 0 \}$. An embedded $\mathbb {Q}$-resolution of $\{ f = 0 \} \subset \mathbb {C}^2$ is calculated in [6, Ex. 4.8] from a (q, p)-blow-up at the origin of $\mathbb {C}^2$, followed by the $(s,qr-ps)$-blow-up at a point of type $(q;-1,p)$. The final situation is shown in Fig. 3.

Fig. 3

Embedded $\mathbb {Q}$-resolution of $f=(x^p+y^q)(x^r+y^s)$

The self-intersection numbers are calculated using [6, Prop. 7.3] and the intersection matrix is $A = \frac{1}{rq-ps} \left( {\begin{matrix} -r/p &{} 1 \\ 1 &{} -q/s \end{matrix}}\right)$. By [17, Th. 2.8], the characteristic polynomial is

$$\begin{aligned} \Delta (t) = \frac{\big ( t-1 \big ) \big ( t^{p(q+s)}-1 \big ) \big ( t^{s(p+r)}-1 \big )}{\big ( t^{q+s}-1 \big ) \big ( t^{p+r}-1 \big )}. \end{aligned}$$

The semistable reduction is studied using Theorem 3.7. The main relevant data to compute are m(E, Q) and the genera $g_1$ and $g_2$ of the new exceptional divisors $D_1$ and $D_2$ in the semistable reduction. As explained in [6], the equation of the total transform at Q is $x^{p(q+s)} y^{s(p+r)}$ in the quotient space of Fig. 4. By Lemma 3.6,

$$\begin{aligned} m(E,Q) = \gcd \Big ( p(q+s), s(p+r), A, B \Big ), \end{aligned}$$

where $A = \frac{p(q+s) \cdot s + s(p+r) \cdot (-q)}{rq-ps} = - s$ and $B = \frac{p(q+s) \cdot (-r) + s(p+r) \cdot p}{rq-ps} = - p$. Consequently, $m(E,Q) = \gcd (p,s)$.

The restriction $\varrho \,|: D_1 \rightarrow \mathcal {E}_1$ is a branched covering of $p(q+s)$ sheets ramifying over three points, where the number of preimages is $\gcd (p,s), 1$, and $q+s$. Analogous situation holds for $D_2$. Hence, by virtue of the Riemann–Hurwitz formula, the genera are

$$\begin{aligned} g_1=\displaystyle \frac{(p-1)(q+s)-\gcd (p,s)+1}{2}, \quad g_2=\displaystyle \frac{(s-1)(p+r)-\gcd (p,s)+1}{2}. \end{aligned}$$

The dual graph of the new normal crossing divisor after the semistable reduction process is shown in Fig. 4.

Fig. 4

Dual graph of the semistable reduction

The MHS on the cohomology of the Milnor fiber $H^1(F,\mathbb {C})$ is obtained from Steenbrink’s spectral sequence:

$$\begin{aligned} H^1 (F, \mathbb {C}) = \underbrace{H^{0,0}}_{{{\mathrm{Gr}}}^W_0 H^1 (F,\mathbb {C})} \oplus \quad \underbrace{H^{0,1} \oplus H^{1,0}}_{{{\mathrm{Gr}}}^W_1 H^1 (F,\mathbb {C})} \quad \oplus \underbrace{H^{1,1}}_{{{\mathrm{Gr}}}^W_2 H^1 (F,\mathbb {C})}, \end{aligned}$$

where $H^{0,0} = \mathbb {C}^{\gcd (p,s)-1}, H^{0,1} = \mathbb {C}^{g_1+g_2} = \overline{H^{1,0}}$, and $H^{1,1} = \mathbb {C}^{\gcd (p,s)}$.

The action of the monodromy on ${{\mathrm{Gr}}}^W_0 H^1 (F, \mathbb {C})$ is given by the polynomial $\frac{t^{\gcd (p,s)}-1}{t-1}$. Note that this provides the eigenvalues of the monodromy with Jordan blocks of size 2. This has to do with the fact that the dual graph possesses $\gcd (p,s)-1$ cycles, see Proposition 5.12, cf. [16, Ch. V.4] for a more detailed exposition. Also, note that this example has already been treated in [13] for the cases $(p,q,r,s) = (21,44,14,11), (33,28,22,7)$; they both have the same monodromy but different topological type as one can easily check.

Remark 6.1

The previous example is generalized to several branches with no significant changes. Let $f = ( x^{p_1} + y^{q_1} ) \cdots ( x^{p_k} + y^{q_k} ), k \ge 1, \frac{p_1}{q_1} < \cdots < \frac{p_k}{q_k}$, and $p_i, q_i \ge 1$ no necessarily coprime, $d_i = \gcd (p_i,q_i)$.

Fig. 5

Dual graph of the semistable reduction of f

Denote $e_i = \gcd ( p_1 + \cdots + p_i, q_{i+1} + \cdots + q_k ), i=1,\ldots ,k-1$. Then the Jordan blocks of size 2 is given by the polynomial $\prod _{i=1}^{k-1} (t^{e_i}-1) / (t-1)$. The dual graph of the semistable reduction is shown in Fig. 5.

6.2 Yomdin-Lê surface singularities

Let (V, 0) be the singularity defined by $f = f_m(x,y,z) + z^{m+k}$. Assume that $\mathbf{C} = \{f_m = 0\} \subset \mathbb {P}^2$ has only one singular point $P = [0:0:1]$, which is locally isomorphic to the cusp $x^q+y^p, \gcd (p,q)=1$. Consider the weight vector $\omega = (\frac{k p}{k_1 k_2}, \frac{k q}{k_1 k_2}, \frac{p q}{k_1 k_2})$, where $k_1= \gcd (k,p)$ and $k_2 = \gcd (k,q)$.

An embedded $\mathbb {Q}$-resolution of $\{ f = 0 \} \subset \mathbb {C}^3$ is calculated in [18]. It is required to perform first the standard blow-up at the origin of $\mathbb {C}^3$ and then the $\omega$-blow-up at the point $P=[0:0:1] \in \mathbf {C} \cap E_1$, where the total transform is not a normal crossing divisor. Denote by $E_1 := \widehat{E}_1$ and by $E_2$ the second exceptional divisor. The final situation is shown in Fig. 6.

Fig. 6

Intersection of $E_0$ and $E_1$ with the rest of components

Applying the generalized A’Campo’s formula [17, Th. 2.8], the characteristic polynomial of (V, 0) is

$$\begin{aligned} \Delta _{(V,0)}(t) = \frac{\big (t^m-1\big )^{\chi (\mathbb {P}^2\setminus \mathbf{C})}}{t-1} \cdot \frac{\big (t^{m+k}-1 \big ) \big ( t^{\frac{p q}{k_1 k_2}(m+k)}-1 \big )^{k_1 k_2}}{\big ( t^{\frac{p}{k_1}(m+k)}-1 \big )^{k_1} \big ( t^{\frac{q}{k_2}(m+k)}-1 \big )^{k_2}}. \end{aligned}$$

The semistable reduction is studied using Theorem 3.7. We only discuss the action of the monodromy on ${{\mathrm{Gr}}}^W_1 H$ and ${{\mathrm{Gr}}}^W_4 H$, being $H:=H^2(F,\mathbb {C})$, which encode the 2 and 3-Jordan blocks. The preimages of $\widehat{V}, E_0, E_1$ under $\varrho$ are denoted by $\widehat{V}, D_0, D_1$; they are all irreducible varieties.

The fifth column of the generalized Steenbrink’s spectral sequence gives rise the following exact sequence of vector spaces

$$\begin{aligned} 0 \longrightarrow {{\mathrm{Gr}}}^W_4H \longrightarrow H^0(D^{[2]}) \longrightarrow H^2 (D^{[1]}) \longrightarrow H^4(D^{[0]}_{+}) \longrightarrow 0. \end{aligned}$$

Note that $D_0, D_1, \widehat{V} \cap D_0, \widehat{V} \cap D_1, D_0 \cap D_1$, and $\widehat{V} \cap D_0 \cap D_1$ are all irreducible varieties because they intersect $\widehat{V}$. Thus $h^4(D^{[0]}_{+}) = h^0(D^{[0]}_{+}) = 2, h^2(D^{[1]}) = h^0(D^{[1]}) =3$, and $h^0(D^{[2]}) = 1$. Therefore ${{\mathrm{Gr}}}^W_4H$ is trivial and then there are neither 2-Jordan blocks for $\lambda =1$ nor 3-Jordan blocks ($\lambda \ne 1$).

From the second column of the spectral sequence,

$$\begin{aligned} 0 \longrightarrow H^1(D^{[0]}_{+}) \longrightarrow H^1(D^{[1]}_{+}) \longrightarrow {{\mathrm{Gr}}}^W_1 H \longrightarrow 0. \end{aligned}$$

The restriction $\varrho \,|:D_1 \rightarrow E_1 \cong \mathbb {P}^2_{\omega }$ is a branched covering of $(m+k)\frac{pq}{k_1k_2}$ sheets ramifying over the axes and the curve $\widehat{V} \cap E_1 = \{ x^q + y^p + z^k = 0 \}$. The composition of the previous map with $E_1 \rightarrow \mathbb {P}^2, [x:y:z]_{\omega } \mapsto [x^q:y^p:z^k]$ is an abelian covering ramifying over 4 lines in general position. This implies $H^1(D_1) = 0$. On the other hand, note that the cohomology $H^1(D_0)$ is determined by the pair $(\mathbb {P}^2,\mathbf {C})$ and hence so is $H^1(D^{[0]}_{+}) = H^1(D_0)$.

Finally, the first cohomology of the Riemann surface $D^{[1]}_{+} = D_0 \cap D_1$ is studied. Using Lemma 3.6, one checks that, $m(\widehat{V} \cap E_0 \cap E_1) = 1, m(``\text {generic point of }E_0\cap E_1'') = \gcd (m,pq)$, and

$$\begin{aligned} m\left( E,\left( \frac{kq}{k_1k_2}\right) \right) = \gcd (m,p), \quad m\left( E,\left( \frac{kp}{k_1k_2}\right) \right) = \gcd (m,q). \end{aligned}$$

This means that $\varrho \,|:D_0 \cap D_1 \rightarrow E_0 \cap E_1$ is a branched covering of $\gcd (m,pq)$ sheets ramifying over three points where the number of preimages are $\gcd (m,p), 1$, and $\gcd (m,q)$. It follows that

$$\begin{aligned} \Delta _{{{\mathrm{Gr}}}^W_1 H} (t) = \frac{1}{\Delta _{H^1(D_0)}(t)} \cdot \frac{\left( t-1 \right) \left( t^{\gcd (m,pq)}-1 \right) }{\left( t^{\gcd (m,p)}-1 \right) \left( t^{\gcd (m,q)}-1 \right) }. \end{aligned}$$

Remark 6.2

The singularity of the tangent cone in the previous example is so simple that the Jordan blocks of size 2 and 3 (for $\lambda \ne 1$ or $\lambda =1$) do not depend on k. However, this is not true in general, see below.

Let V be the YLS defined by $f = f_m(x,y,z) + z^{m+k}$ where $\mathbf{C} = \{f_m = 0\} \subset \mathbb {P}^2$ has only one singular point $P = [0:0:1]$, which is locally isomorphic to $(x^p+y^q)(x^r+y^s)$ with $\gcd (p,q)=\gcd (r,s)=1$ and $\frac{p}{q} < \frac{r}{s}$, cf. Sect. 6.1. Using the techniques presented in this paper and the $\mathbb {Q}$-resolution calculated in [18], we were able to compute the following:

$$\begin{aligned} \Delta _{{{\mathrm{Gr}}}^W_1 H}(t)= & {} \frac{\displaystyle \frac{\big ( t^{(m,p(q+s))}-1 \big ) \big (t^{(m,s(p+r))}-1\big )}{\big (t^{(m,q+s)}-1\big )\big (t^{(m,p+r)}-1\big )} \cdot \frac{\big (t^{(m+k)\frac{(p,s)}{(k,p,s)}}-1\big )^{(k,p,s)}}{(t^{m+k}-1) (t-1)^{(k,p,s)-1}}}{\displaystyle \Delta _{H^1(D_0)}(t) \cdot \Bigg ( \frac{t^{(m,p,s)}-1}{t-1} \Bigg )^{3}},\nonumber \\ \Delta _{{{\mathrm{Gr}}}^W_4 H}(t)= & {} \frac{t^{(m,p,s)}-1}{t-1} \cdot (t-1)^{(k,p,s)}, \end{aligned}$$

where for simplicity (a, b) denotes $\gcd (a,b)$. Note that the cohomology $H^1(D_0)$ is determined by the pair $(\mathbb {P}^2,\mathbf {C})$, the first factor of the numerator has to do with the characteristic polynomial of the tangent cone at [0 : 0 : 1], and the second factor of both the numerator and denominator is related to the 2-Jordan blocks of the tangent cone, see Example in Sect. 6.1.

In particular, considering $(p,q,r,s) = (21,44,14,11), (33,28,22,7)$ and m generic so that $\Delta _{H^1(D_0)}(t)=1$, one obtains infinite pairs of irreducible YLS having the same complex monodromy and different topological type. Examples of this kind have already been found, for instance, in [3] studying the associated Seifert form, which determines the integral monodromy. We ignore whether our preceding example has the same integral monodromy or the same Seifert form.