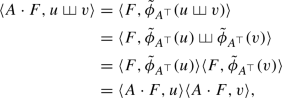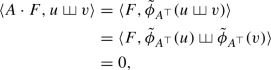Abstract
Geometric, robust-to-noise features of curves in Euclidean space are of great interest for various applications such as machine learning and image analysis. We apply Fels–Olver’s moving-frame method (for geometric features) paired with the log-signature transform (for robust features) to construct a set of integral invariants under rigid motions for curves in \({\mathbb {R}}^d\) from the iterated-integrals signature. In particular, we show that one can algorithmically construct a set of invariants that characterize the equivalence class of the truncated iterated-integrals signature under orthogonal transformations, which yields a characterization of a curve in \({\mathbb {R}}^d\) under rigid motions (and tree-like extensions) and an explicit method to compare curves up to these transformations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A central problem in image science is constructing geometrically relevant features of curves that are robust to noise. In this sense, rigid motions of space make up a natural group of “nuisance” transformations of the data. For this reason, rotation- and translation-invariant features are often desired, for instance, in human activity recognition [39, Section 6] or in matching contours [52]. Classically, differential invariants such as curvature have been used for this purpose [25], and more recently, integral invariants of curves have been of interest [13, 16]. In this work, we construct a rigid motion-invariant representation of a curve through its iterated-integrals signature by applying the Fels–Olver moving-frame method. We show that this yields sets of integral invariants that characterize the truncated iterated integral signature up to rigid motions.
Iterated integrals, a subject of study introduced by Chen in the 50s [6, 8], will be properly reviewed in Sect. 2.2. In a nutshell, they are descriptive features of continuous curves that moreover possess desirable stability properties. Regarding their use for invariant theory, we consider two concrete examples, reproduced from [13]. Given a smooth curve \(X = (X^{(1)}, X^{(2)}): [0,1] \rightarrow {\mathbb {R}}^2\), starting at \(X_0 = 0\), the norm squared of total displacement is clearly invariant to the orthogonal group \({\text {O}}_2({\mathbb {R}})\) acting on the ambient space. Using the fundamental theorem of analysis, we can write this invariant as
where we introduced the shorthand \(dX^{(i)}_t := \dot{X}^{(i)}_t \mathrm{d}t\). We have expressed this invariant as the linear combination of iterated integrals. A less trivial invariant is given by the squareFootnote 1 of the signed areaFootnote 2 enclosed by the curve (for simplicity assume that the curve is closed, i.e., \(X_1 = 0\)). By Green’s theorem (see [48, Theorem 10.33] and [36, Proposition 1]), the signed area can be expressed in terms of iterated integrals, namely as
These examples illustrate that simple, and geometrically relevant, invariants can be found in the collection of iterated integrals.
The Fels–Olver moving-frame method, introduced in [15], is a modern generalization of the classical moving-frame method formulated by Cartan [3]. In the general setting of a Lie group G acting on a manifold M, a moving frame is defined as a G-equivariant map from M to G. A moving frame is determined by a choice of cross-section to the orbits of G and hence a unique “canonical form” for elements of M under G. Thus, the moving-frame method provides a framework for algorithmically constructing G-invariants on M that characterize orbits and for determining equivalence of submanifolds of M under G.
The moving-frame method has been used to construct differential invariants of smooth planar and spatial curves under Euclidean, affine, and projective transformations, and, in certain cases, these differential invariants lead to a differential signature, which can be used to classify curves under these transformation groups [2]. The differential signature has been applied in a variety of image science applications from automatic jigsaw puzzle assembly [26] to medical imaging [22]. Also in the realm of image science, the moving-frame method has been used to construct invariants of grayscale images [1, 51].
We consider the induced action of the orthogonal group of rotations on the log-signature of a curve, which provides a compressed representation of a curve obtained by applying the log transform to the iterated-integrals signature, and provide an explicit cross-section for this action. We show that for most curves and any truncation of the curve’s log-signature, the orbit is characterized by the value on this cross-section. As a consequence, a curve is completely determined up to rigid motions and tree-like extensions by the invariantization of its iterated-integrals signature induced by this cross-section.
This yields a constructive method to compare curves up to rigid motions and to evaluate invariants that characterize the iterated-integrals signature under rotations. These invariants are constructed from integrals on the curve and hence are likely to be more noise-resistant than their differential counterparts such as curvature. One can easily set up an artificial example where this is visible. Consider, for instance, the circle of radius \(n^{-3/2}\) given by the parameterization \(\gamma : [0,1] \rightarrow {\mathbb {R}}^2\) where
which as \(n\rightarrow \infty \) converges to the constant curve (at the origin). Now the curvature of this curve does not converge (in fact, it blows up). In contrast, the iterated integrals do all converge (to zero) since \(\gamma \) converges in variation norm. Then, the invariants built out of the iterated integrals (Sect. 5.1) also converge to their value on the zero curve. On this toy example, these integral invariants are hence more “stable”. More precisely, iterated integrals are continuous in p-variation norm, for \(p < 2\), [20, Proposition 6.11], thus even covering paths that are not even differentiable. Curvature is continuous only in the (much) stronger \(C^2\)-norm.
Additionally, in contrast to the methods in [13], the resulting set of integral invariants is shown to uniquely characterize the curve under rotations, and moreover, does so in a minimal fashion. Since the iterated-integrals signature of a curve is automatically invariant to translations, this provides rigid motion-invariant features of a curve, which can be used for applications such as machine learning or shape analysis.
This work is structured as follows: In Sect. 2, we provide background on the iterated-integrals signature and the moving-frame method, as well as some facts about algebraic groups and invariants. In Sect. 3, we construct the moving-frame map for paths in \({\mathbb {R}}^2\) and \({\mathbb {R}}^3\) motivating the construction of the moving-frame map for \({\mathbb {R}}^d\). We also provide explicit sets of invariants at these lower dimensions, which might be useful for applications. In Sect. 4, we consider the orthogonal action on the second-order truncation of the log-signature over the complex numbers. Using tools from algebraic invariant theory, we construct the linear space, which will form the basis for the cross-section in the following section. We also provide an explicit set of polynomial invariants that characterize the second-order truncation of the log-signature under the orthogonal group. In Sect. 5.1, we construct a general moving frame for paths in \({\mathbb {R}}^d\), and in Sect. 5.2 we introduce sufficient conditions for the resulting moving-frame invariants to be polynomial, showing these conditions are satisfied for some values of d. Finally, in Sect. 6 we discuss some of the interesting questions that arise as a result of our work.
2 Preliminaries
2.1 The Tensor Algebra
Let \(d \ge 1\) be an integer. A word, or multi-index, over the alphabet \(\{{\mathtt {1}},\dotsc ,{\mathtt {d}}\}\) is a tuple \(w=({\mathtt {w}}_1,\dotsc ,{\mathtt {w}}_n)\in \{{\mathtt {1}},\dotsc ,{\mathtt {d}}\}^n\) for some integer \(n\ge 0\), called its length, which is denoted by |w|. As is usual in the literature, we use the short-hand notation \(w={\mathtt {w}}_1\cdots {\mathtt {w}}_n\), where the \({\mathtt {w}}_i\), words of length one, are called letters. The concatenation of two words v, w is the word \(vw{:}{=}{\mathtt {v}}_1\cdots {\mathtt {v}}_n{\mathtt {w}}_1\cdots {\mathtt {w}}_m\) of length \(|vw|=n+m\). Observe that this product is associative and non-commutative. There is a unique element of length zero, called the empty word and denoted by \({\textsf {e}}\). It satisfies \(w{\textsf {e}}={\textsf {e}}w=w\) for all words w. If we denote by \(T({\mathbb {R}}^d)\) the real vector space spanned by words, the bilinear extension of the concatenation product endows it with the structure of an associative (and non-commutative) algebra. We also note that \(T({\mathbb {R}}^d)\) admits the direct sum decomposition
In \(d=4\), typical element of \(T({\mathbb {R}}^d)\) might look like
We note that when writing elements of \(T({\mathbb {R}}^d)\), our notation distinguishes the letter \({\mathtt {3}}\) from the real coefficient \(3\) in the second term.
There is a commutative product on \(T({\mathbb {R}}^d)\), known as the shuffle product, recursively defined by  and
and

where \(v{\mathtt {i}}\) denotes the concatenation of the word v and the letter \({\mathtt {i}}\), and analogously for \(w{\mathtt {j}}\).
Example 2.1
Suppose \(d=2\). The first few non-trivial shuffle products are

The commutator bracket \([u,v]{:}{=}uv-vu\) endows \(T({\mathbb {R}}^d)\) with the structure of a Lie algebra. The free Lie algebra over \({\mathbb {R}}^d\), denoted by \({{\mathfrak {g}}}({\mathbb {R}}^d)\), can be realized as the following subspace of \(T({\mathbb {R}}^d)\),
where \(W_1{:}{=}{\text {span}}_{\mathbb {R}}\{{\mathtt {1}},\dotsc ,{\mathtt {d}}\} \cong {\mathbb {R}}^d\) and
There are multiple choices of bases for \({{\mathfrak {g}}}({\mathbb {R}}^d)\), but we choose to work with the Lyndon basis (see [45] for further details). A Lyndon word is a word \(h\) such that whenever \(h=uv\), with \(u,v\ne {\textsf {e}}\), then \(u<v\) for the lexicographical order. We denote the set of Lyndon words over the alphabet \(\{{\mathtt {1}},\dotsc ,{\mathtt {d}}\}\) by \({\mathscr {L}}_{d}\). In particular, \(h\) with \(|h|\ge 2\) is Lyndon if and only if there exist non-empty Lyndon words \(u\) and \(v\) such that \(u<v\) and \(h=uv\). Although there might be multiple choices for this factorization, the one with \(v\) as long as possible is called the standard factorization of \(h\). The Lyndon basis \(b_{{\mathtt {h}}}\) is recursively defined by setting \(b_{{\mathtt {i}}}={\mathtt {i}}\) and \(b_{h}=[b_u,b_v]\) for all Lyndon words \(h\) with \(|h|\ge 2\), where \(h=uv\) is the standard factorization.
Example 2.2
Suppose \(d=2\). The Lyndon words up to length 4, their standard factorizations and the associated basis elements are shown in Table 1.
Elements of the dual space \(T(\!({\mathbb {R}}^d)\!){:}{=}T({\mathbb {R}}^d)^*\) can be identified with formal word series. For \(F\in T(\!({\mathbb {R}}^d)\!)\), we write
In particular, we have no growth requirement for the coefficients \(\langle F,w\rangle \in {\mathbb {R}}\). The above expression is meant only as a notation for treating the values of \(F\) on words as a single object. This space can be endowed with a multiplication given, for \(F,G\in T(\!({\mathbb {R}}^d)\!)\), by
Observe that since there is a finite number of pairs of words \(u,v\) such that \(uv=w\), the coefficients of \(FG\) are well defined for all \(w\), so the above formula is an honest element of \(T(\!({\mathbb {R}}^d)\!)\). It turns out that this product is dual to the deconcatenation coproduct \(\varDelta :T({\mathbb {R}}^d)\rightarrow T({\mathbb {R}}^d)\otimes T({\mathbb {R}}^d)\) given by
in the sense that
for all words. This formula is nothing but Eq. (2) componentwise. In this sense, one can say that \(\varDelta \) is the transposition of the concatenation product.
More explicitly, if \(w={\mathtt {w}}_1\cdots {\mathtt {w}}_n\) then
One can then think of the coefficient \(\langle FG,w\rangle \) as the coefficient in front of the word \(w\) in the product \(FG\), when the latter is computed by concatenation of words and then re-expanded in the word basis.
Example 2.3
Suppose \(d=2\), and let
be two elements in \(T(\!({\mathbb {R}}^d)\!)\). Then, their product is given by:
Remark 2.4
It is well known (see, for example, [37]) that \(T({\mathbb {R}}^d)\) with the product  , the coproduct \(\varDelta \) and canonical unit, counit and antipode, forms a Hopf algebra.
, the coproduct \(\varDelta \) and canonical unit, counit and antipode, forms a Hopf algebra.
There are two distinct subsets of \(T(\!({\mathbb {R}}^d)\!)\) that will be important in what follows. The first one is the subspace \({{\mathfrak {g}}}(\!({\mathbb {R}}^d)\!)\) of infinitesimal characters, formed by linear maps \(F\) such that  whenever \(u\) and \(v\) are non-empty words, and such that \(\langle F,{\textsf {e}}\rangle =0\). It can be identified with the dual space
whenever \(u\) and \(v\) are non-empty words, and such that \(\langle F,{\textsf {e}}\rangle =0\). It can be identified with the dual space
It is a Lie algebra under the commutator bracket \([F,G]=FG-GF\). The second one is the set \({{\mathscr {G}}}(\!({\mathbb {R}}^d)\!)\) of characters, i.e., linear maps \(F\) such that  for all \(u,v\in T({\mathbb {R}}^d)\).
for all \(u,v\in T({\mathbb {R}}^d)\).
We may define an exponential map \(\exp :{{\mathfrak {g}}}(\!({\mathbb {R}}^d)\!)\rightarrow {{\mathscr {G}}}(\!({\mathbb {R}}^d)\!)\) by its power series
On a single word, the map is given by
and since \(F\) vanishes on the empty word, all terms with \(n>|w|\) also vanish, so that the sum is always finite. Therefore, \(\exp (F)\) is a well-defined element of \(T(\!({\mathbb {R}}^d)\!)\).
Example 2.5
Suppose that \(d=2\) and consider
First, we determine conditions on \(\alpha ,\beta ,\gamma ,\delta \in {\mathbb {R}}\) so that \({{\mathfrak {g}}}(\!({\mathbb {R}}^2)\!)\). Since the coefficient \(\langle F,w\rangle \) vanishes for \(|w|>2\), the only non-trivial shuffle product to check is of the form  for \({\mathtt {i}},{\mathtt {j}}\in \{1,2\}\). In particular, this means that there are no restrictions on \(\alpha ,\beta \), and
for \({\mathtt {i}},{\mathtt {j}}\in \{1,2\}\). In particular, this means that there are no restrictions on \(\alpha ,\beta \), and

so we must have \(\eta =\lambda =0\) and \(\gamma +\delta =0\). Therefore,
Note that \(F\) is expressed in the Lyndon basis (see Example 2.2).
Now, using Eq. (4) (or equivalently Eq. (5)) we may compute
The reader can check that \(\exp (F)\in {{\mathscr {G}}}(\!({\mathbb {R}}^d)\!)\).
It can be shown that the image of \(\exp \) is equal to \({{\mathscr {G}}}(\!({\mathbb {R}}^d)\!)\) and that it is a bijection onto its image [38], with inverse \(\log :{{\mathscr {G}}}(\!({\mathbb {R}}^d)\!)\rightarrow {{\mathfrak {g}}}(\!({\mathbb {R}}^d)\!)\) defined by
where \(\varepsilon \) is the unique linear map such that \(\langle \varepsilon ,{\textsf {e}}\rangle =1\) and zero otherwise.
Finally, we remark some freeness properties of the tensor algebra and its subspaces. Below,
denotes the reduced tensor algebra over \({\mathbb {R}}^d\). The following result can be found in [18, Corollary 2.1].
Proposition 2.6
Let \(\phi :T^+({\mathbb {R}}^d)\rightarrow {\mathbb {R}}^e\) be a linear map. There exists a unique extension \({\tilde{\phi }}:T({\mathbb {R}}^d)\rightarrow T({\mathbb {R}}^e)\) such that
and \(\pi \circ \tilde{\phi }=\phi \), where \(\pi :T({\mathbb {R}}^e)\rightarrow {\mathbb {R}}^e\) denotes the projection of \(T({\mathbb {R}}^e)\) onto \({\mathbb {R}}^e\), orthogonal to \({\mathbb {R}}{\textsf {e}}\) and \(\bigoplus _{n>2}{\text {span}}_{\mathbb {R}}\{w:|w|=n\}\), and \(\varDelta \) denotes the deconcatenation product (3). Moreover, the extension is explicitly given by
By transposition, we obtain a unique map \(\varPhi :T(\!({\mathbb {R}}^e)\!)\rightarrow T(\!({\mathbb {R}}^d)\!)\) such that \(\langle \varPhi (F),w\rangle {:}{=}\langle F,{\tilde{\phi }}(w)\rangle \), i.e.,
In particular, we have that
for all \(F,G\in T(\!({\mathbb {R}}^e)\!)\). Morever, by Eq. (6),
2.2 The Iterated-Integrals Signature
The iterated-integrals signature of (smooth enough) paths was introduced by Chen for homological considerations on loop space [7]. It played a vital role in the rough path analysis of Lyons, a pathwise approach to stochastic analysis [35]. Recently, it has found applications in statistics and machine learning (see, e.g., [9] and references therein), where it serves as a method of feature extraction for possibly non-smooth time-dependent data, as well as in shape analysis [5, 33].
Let \(Z= (Z^{\mathtt {1}}, \dots , Z^{\mathtt {d}}) :[0,1]\rightarrow {\mathbb {R}}^d\) be an absolutely continuous path.Footnote 3 Given a word \(w={\mathtt {w}}_1\cdots {\mathtt {w}}_n\), define
This definition has a unique linear extension to \(T({\mathbb {R}}^d)\). We obtain thus an element \({{\,\mathrm{IIS}\,}}(Z) \in T(\!({\mathbb {R}}^d)\!)\), called the iterated-integrals signature (IIS) of \(Z\).
It was shown by Ree [47] that the coefficients of \({{\,\mathrm{IIS}\,}}(Z)\) satisfy the so-called shuffle relations:

In other words, \({{\,\mathrm{IIS}\,}}(Z)\in {{\mathscr {G}}}(\!({\mathbb {R}}^d)\!)\).
As a consequence of the shuffle relation, one obtains that the log-signature \(\log ({{\,\mathrm{IIS}\,}}(Z))\) is a Lie series, i.e., an element of \({{\mathfrak {g}}}(\!({\mathbb {R}}^d)\!)\). Moreover, the identity \({{\,\mathrm{IIS}\,}}(Z) = \exp \left( \log ( {{\,\mathrm{IIS}\,}}(Z) ) \right) \) holds. The log-signature therefore contains the same amount of information as the signature itself; it in fact is a minimal (linear) depiction of it: there are no functional relations between the coefficients of an general log-signature.Footnote 4
The entire iterated-integrals signature \({{\,\mathrm{IIS}\,}}(Z)\) is an infinite-dimensional object and hence can never actually be numerically computed. We now provide more detail on the truncated, finite-dimensional setting.
For each integer \(N\ge 1\), the subspace \(I_n\subset T(\!({\mathbb {R}}^d)\!)\) generated by formal series such that \(\langle F,w\rangle =0\) for all words with \(|w|\le N\) is a two-sided ideal, that is, the inclusion
holds. Therefore, the quotient space \(T_{\le n}(\!({\mathbb {R}}^d)\!){:}{=}T(\!({\mathbb {R}}^d)\!)/I_n\) inherits an algebra structure from \(T(\!({\mathbb {R}}^d)\!)\). Moreover, it can be identified with the direct sum
We denote by \({\text {proj}}_{\le n}:T(\!({\mathbb {R}}^d)\!)\rightarrow T_{\le n}(\!({\mathbb {R}}^d)\!)\) the canonical projection.
Denote with \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!)\) the free step-\(N\) nilpotent Lie algebra (over \({\mathbb {R}}^d\)). It can be realized as the following subspace of \(T_{\le n}(\!({\mathbb {R}}^d)\!)\), see [20, Section 7.3],
where, as before \(W_1{:}{=}{\text {span}}_{\mathbb {R}}\{ {\mathtt {i}} : i =1 ,\dots , d\} \cong {\mathbb {R}}^d\) and \(W_{n+1}{:}{=}[W_1,W_n]\). In the case of \(N=2\), this reduces to
where we denote with \(\mathfrak {so}(d,{\mathbb {R}})\) the space of skew-symmetric \(d\times d\) matrices. Indeed, an isomorphism is given by:
We remark that the coefficients \(c_{i}\) and \(c_{ij}\) are the coordinatesFootnote 5 with respect to the Lyndon basis (see Example 2.2).
The linear space \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!)\) is in bijection to its image under the exponential map. This image, denoted \({{\mathscr {G}}}_{\le n}({\mathbb {R}}^d){:}{=}\exp {\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!)\), is the free step-\(N\) nilpotent group (over \({\mathbb {R}}^d\)). It is exactly the set of all points in \(T_{\le n}({\mathbb {R}}^d)\) that can be reached by the truncated signature map, that is (see [20, Theorem 7.28])
(Equivalently, the truncated log-signature completely fills out the truncated Lie algebra \({{\mathfrak {g}}}_{\le n}(\!({\mathbb {R}}^d)\!)\).
We have
where \(c_{h}(Z)=\langle {{\,\mathrm{ISS}\,}}(Z),\zeta _h\rangle \) for uniquely determined \(\zeta _h\in T({\mathbb {R}}^d)\). This inspires us to also denote the coordinates of an arbitrary \({{\textbf {c}}}_{\le n}\in {\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!)\) by \(c_{h}\), were analogously
Example 2.7
(Moment curve)
We consider the moment curve in dimension 3, which is the curve \(Z: [0,1] \rightarrow {\mathbb {R}}^3\) given as
It traces out part of the twisted cubic [23, Example 1.10], see also [29, Sect. 15].
We calculate, as an example,

The entire step-2 truncated signature is:

and the step-2 truncated log-signature is:

where

is seen to be skew-symmetric, as expected from (9).
2.3 Invariants
In this section, let G be a subgroup of the general linear group acting linearly on \({\mathbb {R}}^d\). In this work, we are interested in functions on paths in \({\mathbb {R}}^d\) that factor through the signature and that are invariant under this action on the path’s ambient space. While we mostly focus on \(G = {\text {O}}_d({\mathbb {R}})\), the results in this section apply to any subgroup of the general linear group acting linearly. The action of \(A\in G\) on an \({\mathbb {R}}^d\)-valued path \(Z\) is given by \(AZ:[0,1]\rightarrow {\mathbb {R}}^d\), \(t\mapsto AZ_t\).
Using Proposition 2.6, we can extend the action of G on \({\mathbb {R}}^d\) to a diagonal action on words. The matrix \(A^\top \) acts on single letters by
and we set \(\phi _{A^{\top }}(w)=0\) whenever \(|w|\ge 2\). By Proposition 2.6, this induces an endomorphism \({\tilde{\phi }}_{A^\top }:T({\mathbb {R}}^d)\rightarrow T({\mathbb {R}}^d)\), satisfying
In particular, \({\tilde{\phi }}_{A^\top }(u{\mathtt {i}})={\tilde{\phi }}_{A^\top }(u){\tilde{\phi }}_{A^\top }({\mathtt {i}})\) for all words \(u\) and letters \({\mathtt {i}}\in \{{\mathtt {1}},\dotsc ,{\mathtt {d}}\}\). In order to be consistent with the notation in [13], we will denote its transpose map (\(\varPhi _A\) in Proposition 2.6) just by \(A:T(\!({\mathbb {R}}^d)\!)\rightarrow T(\!({\mathbb {R}}^d)\!)\).
Lemma 2.8
The map \({\tilde{\phi }}_{A^\top }:T({\mathbb {R}}^d)\rightarrow T({\mathbb {R}}^d)\) is a shuffle morphism, that is,

for all words \(u,v\).
Proof
We proceed by induction on \(|u|+|v|\ge 0\). If \(|u|+|v|=0\), then necessarily \(u=v={\textsf {e}}\), and the identity becomes

which is true by definition. Now, suppose that the identity is true for all words \(u',v'\) with \(|u'|+|v'|<n\). If \(|u|+|v|=n\) we suppose, without loss of generality, that \(u=u'{\mathtt {i}}, v=v'{\mathtt {j}}\) for some (possibly empty) words \(u',v'\) with \(|u'|+|v'|<n\). Then,

\(\square \)
Remark 2.9
Lemma 2.8 is a special case of [10, Theorem 1.2].
Corollary 2.10
Let \(A \in G\).
-
(i)
The character group is invariant under \(A\), that is, \(A\cdot {{\mathscr {G}}}(\!({\mathbb {R}}^d)\!)\subset {{\mathscr {G}}}(\!({\mathbb {R}}^d)\!)\).
-
(ii)
The restriction of \(A\) to \({{\mathfrak {g}}}(\!({\mathbb {R}}^d)\!)\) is a Lie endomorphism. In particular, the free Lie algebra is invariant under \(A\), that is, \(A\cdot {{\mathfrak {g}}}(\!({\mathbb {R}}^d)\!)\subset {{\mathfrak {g}}}(\!({\mathbb {R}}^d)\!)\).
-
(iii)
\(\log : {{\mathscr {G}}}(\!({\mathbb {R}}^d)\!)\rightarrow {{\mathfrak {g}}}(\!({\mathbb {R}}^d)\!)\) is an equivariant map.
Proof
-
i.
Let \(F\in {{\mathscr {G}}}(\!({\mathbb {R}}^d)\!)\), and \(u,v\) be words. Then
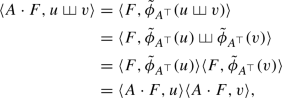
that is, \(A\cdot F\in {{\mathscr {G}}}(\!({\mathbb {R}}^d)\!)\).
-
ii.
Since \(A\cdot (FG)=(A\cdot F)(A\cdot G)\), \(A\) is automatically a Lie morphism. Now we check that \(A\cdot F\in {\mathfrak {g}}(\!({\mathbb {R}}^d)\!)\) whenever \(F\in \mathfrak g(\!({\mathbb {R}}^d)\!)\). It is clear that \(\langle A\cdot F,{\textsf {e}}\rangle =\langle F,{\textsf {e}}\rangle =0\). Now, if \(u,v\) are non-empty words, then
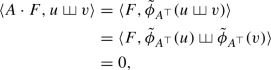
i.e. \(A\cdot F\in {\mathfrak {g}}(\!({\mathbb {R}}^d)\!)\).
-
iii.
Let \(G\in {{\mathscr {G}}}(\!({\mathbb {R}}^d)\!)\). Then, since \(A\cdot \varepsilon =\varepsilon \) we get
$$\begin{aligned} \log ( A \cdot G )&= \sum _{n=1}^\infty \frac{(-1)^{n-1}}{n}(A \cdot G-\varepsilon )^n \\&= A \cdot \sum _{n=1}^\infty \frac{(-1)^{n-1}}{n}(G-\varepsilon )^n \\&= A \cdot \log (G). \end{aligned}$$
\(\square \)
In particular, we easily see that (see also [13, Lemma 3.3])
The same is true for the truncated versions, and we note that, in the special case of \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{d})\!)\), under the isomorphism in Eq. (10), the action has the simple form
where the operations on the right-hand side are matrix-vector resp. matrix–matrix multiplication. Indeed, for the first level we have that
In the same vein, we have that
It follows from Corollary 2.10 and (12) that \(\log ( {{\,\mathrm{IIS}\,}}(A Z) ) = A\cdot \log ( {{\,\mathrm{IIS}\,}}(Z) )\). As already remarked, \(\log \) is a bijection (with inverse \(\exp \)). To obtain invariant expressions in terms of \({{\,\mathrm{IIS}\,}}(Z)\), it is hence enough to obtain invariant expressions in terms of \(\log ({{\,\mathrm{IIS}\,}}(Z))\). Going this route has the benefit of working on a linear object. To be more specific, \({{\,\mathrm{IIS}\,}}(Z)\) is, owing to the shuffle relation, highly redundant. As an example in \(d=2\),
Now, both of these expressions are invariant to \({\text {O}}_2({\mathbb {R}})\). The left-hand side is a nonlinear expressions in the signature, whereas the right-hand side is a linear one. To not have to deal with this kind of redundancy, we work with the log-signature. We note that in [13] the linear invariants of the signature itself are presented. Owing to the shuffle relation, this automatically yields (all) polynomial invariants. But, as just mentioned, it also yields a lot of redundant information.
Example 2.11
We continue with Example 2.7. The rotation
results in the curve
Its step-2 truncated signature is
The step-2 truncated log-signature is
In the present work, we consider general, nonlinear expressions of the log-signature. That way, we use the economical form of the log-signature, while still providing a complete—in a precise sense—set of nonlinear invariants.
2.4 Moving-Frame Method
We now provide a brief introduction to the Fels–Olver moving-frame method introduced in [15], a modern generalization of the classical moving-frame method formulated by Cartan [4]. For a comprehensive overview of the method and survey of many of its applications, see [14, 43]. We will assume in this subsection that G is a finite-dimensional Lie group acting smoothlyFootnote 6 on an m-dimensional manifold M.
Definition 2.12
A moving frame for the action of G on M is a smooth map \(\rho :M \rightarrow G\) such that \(\rho (g\cdot z) = \rho (z) \cdot g^{-1}\).
In general, one can define a moving frame as a smooth G-equivariant map \(\rho :M\rightarrow G\). For simplicity, we assume G acts on itself by right multiplication; this is often referred to as a right moving frame. A moving frame can be constructed through the use of a cross-section to the orbits of the action of G on M.
Definition 2.13
A cross-section for the action of G on M is a submanifold \({\mathcal {K}}\subset M\) such that \({\mathcal {K}}\) intersects each orbit transversally at a unique point.
Definition 2.14
The action of G is free if the stabilizer \(G_z\) of any point \(z\in M\) is trivial, i.e.,
where \({\text {id}}\in G\) denotes the identity transformation.
The following result appears in much of the previous literature on moving frames (see, for instance, [42, Thm. 2.4]).
Theorem 2.15
Let G be an action on M and assume that
- (\(*\)):
-
The action is free, and around each point \(z\in M\) there exists arbitrarily small neighborhoods whose intersection with each orbit is pathwise-connected.
If \({\mathcal {K}}\) is a cross-section, then the map \(\rho : M\rightarrow G\) defined by sending z to the unique group element \(g\in G\) such that \(g\cdot z\in {\mathcal {K}}\) is a moving frame.
Remark 2.16
The equivariance of the map \(\rho :M\rightarrow G\) such that \(\rho (z)\cdot z\in {\mathcal {K}}\) can be seen from the fact that \(\rho (z) \cdot z = \rho (g\cdot z) \cdot (g\cdot z)\) for any \(g\in G\). Since G is free, this implies that \( \rho (z)= \rho (g\cdot z) \cdot g\), and hence, \(\rho \) satisfies Definition 2.12.
Similarly, in this setting, a moving frame \(\rho \) specifies a cross-section defined by \({\mathcal {K}}= \{\rho (z)\cdot z \in M \}\). This construction can be interpreted as a way to assign a “canonical form” to points \(z\in M\) under the action of G, thus producing invariant functions on M under G.
Definition 2.17
Let \(\rho : M\rightarrow G\) be a moving frame. The invariantization of a function \(F:M\rightarrow {\mathbb {R}}\) with respect to \(\rho \) is the invariant function \(\iota (F)\) defined by
Given a moving frame \(\rho \) and local coordinates \(z=(z_1,\ldots ,z_m)\) on M, the invariantization of the coordinate functions \(\iota (z_1),\ldots , \iota (z_m)\) is the fundamental invariants associated with \(\rho \). In particular, we can compute \(\iota (F)\) by
Since \(\iota (I)(z)=I(z)\) for any invariant function I, the fundamental invariants provide a functionally generating set of invariants for the action of G on M. In general, we will call a set of invariants \({\mathfrak {I}}=\{J_1,\ldots ,J_m\}\) fundamental if it functionally generates all invariants, i.e., for any invariant I there is a function \(I'\) such that
Now, suppose further that G is an r-dimensional Lie group and that \(\rho \) is the moving frame associated with a coordinate cross-section \({\mathcal {K}}\) defined by equations
for some constants \(c_1,\ldots , c_r\). Then the first r fundamental invariants are the phantom invariants \(c_1,\ldots , c_r\), while the remaining \(m-r\) invariants \(\{I_1,\ldots , I_{m-r}\}\) form a functionally independent generating set. In this case, we can see that two points \(z_1,z_2\in M\) lie in the same orbit if and only if
Example 2.18
Consider the canonical action of \({\text {SO}}_2({\mathbb {R}})\) on \({\mathbb {R}}^2\setminus \{(0,0)\}\). This action satisfies the assumptions of Theorem 2.15, and a cross-section to the orbits is given by
The unique group element taking a point to the intersection of its orbit with \({\mathcal {K}}\) is the rotation (see Fig. 1)
The fundamental invariants associated with the moving frame \(\rho :{\mathbb {R}}^2\backslash \{(0,0)\}\rightarrow {\text {SO}}_2({\mathbb {R}})\) are given by
Thus, any invariant function for this action can be written as a function of \(\iota (y)\), the Euclidean norm. One can check that indeed for an invariant I(x, y), one has \(I(x,y)=I(0,\sqrt{x^2+y^2})\). This additionally implies that two points are related by a rotation if and only if they have the same Euclidean norm.
In practice, it is difficult, or impossible, to find a global cross-section, and thus a global moving frame, to the orbits of G on M. For instance in the above example, the origin was removed from \({\mathbb {R}}^2\) to ensure freeness of the action. If the action of G on M satisfies condition (\(*\)) from Theorem 2.15, then the existence of a local moving frame around each point \(z\in M\) is guaranteed by [15, Thm. 4.4]. In this case, the moving frame is a map \(\rho : U\rightarrow V\) from a neighborhood \(z\in U\) of M to a neighborhood of the identity in \(V\subset G\). The fundamental set of invariants produced are also local in nature and thus only guaranteed to be invariant on U for elements \(g\in V\).
The condition (\(*\)) in Theorem 2.15 can be relaxed in certain cases. In [28, Sec. 1], the authors outline a method to construct a fundamental set of local invariants for actions of G that are only semi-regular, meaning that all orbits have the same dimension. In particular, Theorem 1.6 in [28] states that for a semi-regular action of G on M, there exists a local coordinate cross-section about every point \(z\in M\). In a neighborhood U containing z, such a linear space intersects transversally the connected component containing \({\overline{z}}\) of the orbit \(G\cdot {\overline{z}}\) at a unique point for each \({\overline{z}}\in U\) and is of complementary dimension to the orbits of the action.
Remark 2.19
The algebraic actions that we define in the next section are automatically semi-regular on a Zariski-open subset of the target space (Proposition 2.20(c)), and hence, a local cross-section exists around any point in this subset. Since orbits are algebraic subsets, a local coordinate cross-section is a submanifold of complementary dimension (to the dimension of orbits) intersecting each orbit about z transversally and hence in finitely-many points. If every sufficiently small neighborhood about z does not have pathwise-connected intersection with each orbit, a local cross-section about z necessarily intersects some orbit at infinitely-many points, and hence, a free algebraic group action necessarily satisfies condition (\(*\)) from Theorem 2.15.
2.5 Algebraic Groups and Invariants
In this work, we will be in the setting of an algebraic group G acting rationally on a variety X. In other words, G is an algebraic variety equipped with a group structure, and the action of G on X is given by a rational map \(\varPhi : G\times X \rightarrow X\). Here we outline some key facts and results about algebraic group actions and the invariants of such actions, following [46] for much of our exposition. Unless specified otherwise, both G and X are both varieties over the algebraically closed field \({\mathbb {C}}\).
The orbit \(G \cdot p\) of a point \(p\in X\) under G is the image of \(G\times \{p\}\) under the rational map \(\varPhi \) defining the action, and hence is open in its closure \(\overline{G\cdot p}\) under the Zariski topology.Footnote 7
The following proposition summarizes a few basic results on orbits of algebraic groups that can be found in [46, Section 1.3].
Proposition 2.20
For any point \(p\in X\), the stabilizer \(G_p\) is an algebraic subgroup of G and \(G\cdot p\) satisfies the following:
-
(a)
The orbit \(G\cdot p\) is a smooth, Zariski-open subset of \(\overline{G\cdot p}\).
-
(b)
The dimension of \(G\cdot p\) satisfies \(\dim G\cdot p = \dim G - \dim G_p,\) where \(\dim G_p=\dim T_p (G\cdot p)\).
-
(c)
The dimension of \(G\cdot p\) is maximal on a non-empty Zariski-open subset of X.
For an arbitrary field k, we denote the ring of polynomial functions on the variety X as k[X], i.e., if \({\mathcal {I}}(X)\) is the ideal generated by the polynomials defining the variety \(X\subset {\mathbb {C}}^d\), then \(k[X] = k[x_1,x_2,\dotsc ,x_d]/{\mathcal {I}}(X)\). If X is irreducible, then the field k(X) of rational functions on X is defined similarly. The polynomial invariants (for the action of G on the variety X) form a subring of k[X] defined by
and the rational invariants form a subfield of k(X) given by
respectively. Constructing invariant functions and finding generatingFootnote 8 sets for \({\mathbb {C}}[X]^G\) is the subject of classical invariant theory [34, 41, 50]. In [24], Hilbert proved his finiteness theorem, showing that for linearly reductive groups acting on a vector space V the polynomial ring \({\mathbb {C}}[V]^G\) is finitely generated leading him to conjecture in his fourteenth problem that \({\mathbb {C}}[X]^G\) is always finitely generated. In [40], Nagata constructed a counter-example to this conjecture. For \({\mathbb {C}}(X)^G\), however, a finite generating set always exists and can be explicitly constructed (see, for instance, [11, 27]). Furthermore, a set of rational invariants is generating if and only if it is also separating.
Definition 2.21
A set of rational invariants \({{\mathfrak {I}}}\subset {\mathbb {C}}(X)^G\) separates orbits on a subset \(U\subset X\) if two points \(p,q\in U\) lie in the same orbit if and only if \(K(p)=K(q)\) for all \(K\in {{\mathfrak {I}}}\). If there exists a non-empty, Zariski-open subset X where \({{\mathfrak {I}}}\) separates orbits then we say \({{\mathfrak {I}}}\) is separating.
Proposition 2.22
For the action of G on X, the field \({\mathbb {C}}(X)^G\) is finitely generated over \({\mathbb {C}}\). Moreover, a subset \({{\mathfrak {I}}}\subset {\mathbb {C}}(X)^G\) is generating if and only if it is separating.
Proof
The backward direction holds by [46, Lem. 2.1]. By [46, Thm. 2.4], there always exists a finite set of separating invariants in \({\mathbb {C}}(X)^G\) and hence a finite generating set. Additionally, this finite set can be rewritten in terms of any generating set, and hence, any generating set is also separating. \(\square \)
Under certain conditions, the polynomial ring \({\mathbb {C}}[X]^G\) is also separating, as the following proposition from [46, Prop. 3.4] shows.
Proposition 2.23
Suppose the variety X is irreducible. There exists a finite, separating set of invariants \({{\mathfrak {I}}}\subset {\mathbb {C}}[X]^G\) if and only if \({\mathbb {C}}(X)^G=Q{\mathbb {C}}[X]^G\) where \(Q{\mathbb {C}}[X]^G=\left. \left\{ \frac{f}{g}\, \right| \, f,g\in {\mathbb {C}}[X]^G\right\} \).
One way to understand the structure of invariant rings is by considering subsets of X that intersect a general orbit.
Definition 2.24
Let \(N \subset G\) be a subgroup. A subvariety S of X is a relative N-section for the action of G on X if the following hold:
-
There exists a non-empty, G-invariant, and Zariski-open subset \(U\subset X\), such that S intersects each orbit that is contained in U. In other words, we have that \(\overline{\varPhi (G\times S)} = X\), where closure is taken in the Zariski topology.
-
One has \(N = \{ n\in G\, |\, nS=S\}\).
We call the subgroup N the normalizer subgroup of S with respect to G. The following proposition summarizes a discussion in [46, Sec. 2.8].
Example 2.25
For the action of \({\text {SO}}_2({\mathbb {C}})\) on the Zariski-open subset of \({\mathbb {C}}^2\) defined by \(x^2+y^2\ne 0\), the variety S defined by \(x=0\) is a relative N-section for the action where N is the 2-element subgroup generated by a rotation of 180 degrees. Then, S intersects each orbit of the action in precisely two points.
Proposition 2.26
Let S be a relative N-section for the action of G on X. Then, the restriction map
restricts to a field isomorphism between \({\mathbb {C}}(X)^G\) and \({\mathbb {C}}(S)^N\).
Corollary 2.27
Let S be a relative N-section for the action of G on X and \({{\mathfrak {I}}}\subset {\mathbb {C}}(X)^G\) a set such that \({\textsf {R}}_{X\rightarrow S}({{\mathfrak {I}}})\) generates \({\mathbb {C}}(S)^N\) where \({\textsf {R}}_{X\rightarrow S}\) is the restriction map from Proposition 2.26. Then, \({{\mathfrak {I}}}\) is a generating set for \({\mathbb {C}}(X)^G\).
Relative sections can be used to construct generating sets of rational invariants for algebraic actions as in [21], which the authors refer to as the slice method. Similar in spirit to the approach in [28], considerations can be restricted to an algebraic subset of X. When the intersection of S with each orbit is zero-dimensional, a relative N-section can be thought of as the algebraic analog to a local cross-section for an action.
We end the section by considering algebraic actions on varieties defined over \({\mathbb {R}}\), where the issue is more delicate. For instance, in this setting Proposition 2.22 no longer holds meaning that generating sets of invariants are not necessarily separating and vice versa (see [32, Rem. 2.7]). Suppose that \(X({\mathbb {R}})\) and \(G({\mathbb {R}})\) are real varieties with action given by \(\varPhi : G({\mathbb {R}}) \times X({\mathbb {R}}) \rightarrow X({\mathbb {R}})\) and that X and G are the associated complex varieties. Then, \(\varPhi \) defines an action of G on X.
Proposition 2.28
\({\mathbb {R}}(X({\mathbb {R}}))^{G({\mathbb {R}})}\) is a subfield of \({\mathbb {C}}(X)^G\).
Proof
If \(f\in {\mathbb {R}}(X({\mathbb {R}}))^{G({\mathbb {R}})}\), then the rational function \(f(g\cdot p) - f(p)\) is identically zero on \(G({\mathbb {R}})\times X({\mathbb {R}})\) and hence is identically zero on \(G\times X\). Thus, \(f\in {\mathbb {C}}(X)^G\).
\(\square \)
Corollary 2.29
If \({{\mathfrak {I}}}=\{I_1,\ldots ,I_s\}\subset {\mathbb {R}}(X({\mathbb {R}}))^{G({\mathbb {R}})}\) generates \({\mathbb {C}}(X)^G\) then \({{\mathfrak {I}}}\) generates \({\mathbb {R}}(X({\mathbb {R}}))^{G({\mathbb {R}})}\).
Proof
Suppose that \({{\mathfrak {I}}}\) generates \({\mathbb {C}}(X)^G\) and that \(f\in {\mathbb {R}}(X({\mathbb {R}}))^{G({\mathbb {R}})}\). Then, there exists a rational function \(g\in {\mathbb {C}}(y_1,\ldots ,y_s)\) such that \(f = g(I_1,\ldots ,I_s)\). We can decompose g as \(g= \text {Re}(g)+i\cdot \text {Im}(g)\) where \(\text {Re}(g), \cdot \text {Im}(g)\in {\mathbb {R}}(y_1,\ldots ,y_s)\). Since f is a real rational function
Thus, g must lie in \({\mathbb {R}}(y_1,\ldots ,y_s)\) proving the result. \(\square \)
Proposition 2.30
Suppose that \({\mathbb {R}}(X({\mathbb {R}}))^{G({\mathbb {R}})}\) separates orbits for the action of \(G({\mathbb {R}})\) on \(X({\mathbb {R}})\). Then so does any generating set for \({\mathbb {R}}(X({\mathbb {R}}))^{G({\mathbb {R}})}\).
Proof
Suppose that \({{\mathfrak {I}}}=\{I_1,I_2,\ldots \}\) generates \({\mathbb {R}}(X({\mathbb {R}}))^{G({\mathbb {R}})}\) and that \({\mathbb {R}}(X({\mathbb {R}}))^{G({\mathbb {R}})}\) separates orbits. Then, for any two points \(p_1, p_2\in X({\mathbb {R}})\) if
for all invariants in \({{\mathfrak {I}}}\), then we also have \(I(p_1)=I(p_2)\) for any invariant \(I\in {\mathbb {R}}(X({\mathbb {R}}))^{G({\mathbb {R}})}\) as \({{\mathfrak {I}}}\) generates \({\mathbb {R}}(X({\mathbb {R}}))^{G({\mathbb {R}})}\). Thus, \(p_1\) and \(p_2\) lie in the same orbit under \(G({\mathbb {R}})\). \(\square \)
3 Rigid-Motion Invariant Iterated-Integrals Signature in Low Dimensions
Here we showcase the moving-frame method and some results about invariantizing the iterated-integrals signature in \({\mathbb {R}}^2\) and \({\mathbb {R}}^3\). We later generalize these results to arbitrary \({\mathbb {R}}^d\) in Sect. 5.1. However, we feel that these low-dimensional cases are useful for understanding how the method works in higher dimension and that these cases are the most useful for applications involving spatial data.
3.1 Planar Curves
In this section, we construct a moving-frame map for the action of \({\text {O}}_2({\mathbb {R}})\) on \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{2})\!)\) and show how this can be used to construct \({\text {O}}_2({\mathbb {R}})\)-invariants in \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{2})\!)\) and hence in the coefficients of the iterated-integrals signature of a curve \(Z\).
First consider the action on \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{2})\!) = {\mathbb {R}}^2\oplus [{\mathbb {R}}^2,{\mathbb {R}}^2]\) (recall the notation from Sect. 2, in particular (1)). We can denote any element of \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{2})\!)\) as \({{\textbf {c}}}_{\le 2}\) with coordinates \(c_{1}, c_{2}, \) and \(c_{12}\). Through the isomorphism in (10), we can consider \({{\textbf {c}}}_{\le 2}\) as an element of \({\mathbb {R}}^2\oplus \mathfrak {so}(2,{\mathbb {R}})\),
and with action as in (13). We will now show that \({\text {O}}_2({\mathbb {R}})\) is free on \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{2})\!)\) and the following submanifold
is a cross-section for the action. Similarly to Example 2.18, we start by defining the group element
which is defined outside of \(\{c_{1}=c_{2}=0\}\). For any such element \({{\textbf {c}}}_{\le 2}\in {\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{2})\!)\), we have that
Unlike in Example 2.18, the action is not free on \({\mathbb {R}}^2\), the submanifold defined by \(c_{1}=0, c_{2} >0\) is not a cross-section, and \(A({{\textbf {c}}}_{\le 2})\) does not define a moving-frame map. This is due to the fact that a reflection about the y-axis will fix v, but change the sign of M. Thus to define a moving-frame map, we must consider the diagonal action of \({\text {O}}_2({\mathbb {R}})\) on all of \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{2})\!)\), not just the action on \({\mathfrak {g}}_{\le 1}(\!({\mathbb {R}}^{2})\!)={\mathbb {R}}^2\). The map \({\tilde{\rho }}_2: {\mathcal {U}}_{2;\le 2} \rightarrow {\text {O}}_2({\mathbb {R}})\) given by
defines the group element \({\tilde{\rho }}_2({{\textbf {c}}}_{\le 2})\) such that \({\tilde{\rho }}_2({{\textbf {c}}}_{\le 2})\cdot {{\textbf {c}}}_{\le 2}\in {\mathcal {K}}\) where
The (unique) intersection point of the orbit \({\text {O}}_2({\mathbb {R}})\cdot {{\textbf {c}}}_{\le 2}\) with \({\mathcal {K}}_{2; \le 2}\) is given by \({\tilde{\rho }}_2({{\textbf {c}}}_{\le 2})\cdot {{\textbf {c}}}_{\le 2}\). We later show that this action is free on \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{2})\!)\) (Corollary 4.13), and hence, the map \({\tilde{\rho }}_2\) defines a moving frame with cross-section \({\mathcal {K}}\). This immediately implies that the coordinates of \({\tilde{\rho }}_2({{\textbf {c}}}_{\le 2})\cdot {{\textbf {c}}}_{\le 2}\) are invariants for the action of \({\text {O}}_2({\mathbb {R}})\) on \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{2})\!)\)Footnote 9:
Furthermore, any two elements \({{\textbf {c}}}_{\le 2}, \tilde{{{\textbf {c}}}}_{\le 2} \in {\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{2})\!)\) are related by an element of \({\text {O}}_2({\mathbb {R}})\) if and only if
For any path \(Z\) in \({\mathbb {R}}^2\), let \({{\textbf {c}}}_{\le 2}(Z)\) denote the element of \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{2})\!)\) given by \({\text {proj}}_{\le 2}(\log ({{\,\mathrm{IIS}\,}}(Z)))\). Then, we can define the “invariantized” path \(Y:={\tilde{\rho }}_2({{\textbf {c}}}_{\le 2}(Z)) \cdot Z\). The above statement implies that for any two paths \(Z, {Z}'\), we have that \({{\textbf {c}}}_{\le 2}(Y) = {{\textbf {c}}}_{\le 2}({Y}')\) if and only if there exists some \(g\in {\text {O}}_2({\mathbb {R}})\) such that
In particular, since the \(\log \) map is an equivariant bijection, the same holds true for the \({{\,\mathrm{IIS}\,}}\) of a path under the projection \({\text {proj}}_{\le 2}\).
Given a path \(Z\) starting at the origin, the values of \(c_{1}(Z), c_{2}(Z)\) correspond to x and y values of \(Z(1)\). Similarly, the value of \(c_{12}(Z)\) corresponds to the so-called Lévy area traced by \(Z\) (see [13, Section 3.2] in the context of classical invariant theory). Thus, the moving-frame map applied to such a path \(Z\) rotates the end point \(Z(1)\) to the y-axis (and reflects about the y-axis if the Lévy area is negative).
The resulting invariants on \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{2})\!)\) are perhaps unsurprising, but the above method also yields \({\text {O}}_2({\mathbb {R}})\)-invariants on \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{2})\!)\) for an arbitrary truncation order n, as we now show. We define a map \(\rho _2:{\mathcal {U}}_{2;\le n}\subset {\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{2})\!) \rightarrow {\text {O}}_2({\mathbb {R}})\) by
for any \({{\textbf {c}}}_{\le n}\in {{\mathcal {U}}}_{2;\le n}\) where
with \({\text {proj}}_{\le n\rightarrow \le 2}\) denoting the canonical projection from \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{2})\!)\) onto \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{2})\!)\). Since \({\text {O}}_2({\mathbb {R}})\) acts diagonally on the whole of \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{2})\!)\), \(\rho _2\) is a moving-frame map on \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{2})\!)\) with cross-section \({{\mathcal {K}}}_{2;\le n}\) where
Then, the resulting coordinate functions of \(\rho _2({{\textbf {c}}}_{\le n})\cdot {{\textbf {c}}}_{\le n}\in {\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{2})\!)\) are \({\text {O}}_2({\mathbb {R}})\) invariants for the action on \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{2})\!)\) (see Sect. 3.1 for a more detailed investigation of these invariants) and hence \({\text {O}}_2({\mathbb {R}})\) invariants for paths in \({\mathbb {R}}^2\). Furthermore, for any truncation order n and paths \(Z,{Z}'\in {\mathbb {R}}^2\), we have that \({{\textbf {c}}}_{\le n}(Y) = {{\textbf {c}}}_{\le n}({Y}')\) if and only if there exists some element of \({\text {O}}_2({\mathbb {R}})\) such that \(g\cdot {{\textbf {c}}}_{\le n}(Z) ={{\textbf {c}}}_{\le n}({Z}').\)
Proposition 3.1
Let \(Z, {Z}'\) be paths in \({\mathbb {R}}^2\) such that
are elements of \({\mathcal {U}}_{2;\le 2}\). Define
Then there exists \(g\in {\text {O}}_2({\mathbb {R}})\) such that \({{\,\mathrm{IIS}\,}}(g\cdot Z) = {{\,\mathrm{IIS}\,}}({Z}')\) if and only if \({{\,\mathrm{IIS}\,}}(Y) = {{\,\mathrm{IIS}\,}}({Y}')\) if and only if \({{\textbf {c}}}_{\le n}(Y)={{\textbf {c}}}_{\le n}({Y}')\) for all \(n\in {\mathbb {N}}\).
Proof
The result holds by the moving-frame property of \({\tilde{\rho }}_2\) and the fact that the \(\log \) map is a bijection. For details, see the Proof of Theorem 5.5. \(\square \)
Therefore, two paths, starting at the origin, are equivalent up to tree-like extensions and action of \({\text {O}}_2({\mathbb {R}})\) if and only if \({{\,\mathrm{IIS}\,}}(Y) = {{\,\mathrm{IIS}\,}}({Y}')\). In this sense, the moving-frame map \({\tilde{\rho }}_2\) yields a method to invariantize a path \(Z\) (Fig. 2).
We end this section with a look at the invariants produced by the construction for truncation order 4, i.e., \({\text {O}}_2({\mathbb {R}})\)-invariants on \({\mathfrak {g}}_{\le 4}(\!({\mathbb {R}}^{2})\!)\). A (Lyndon) basis for \({\mathfrak {g}}_{\le 4}(\!({\mathbb {R}}^{2})\!)\) corresponds to the coordinates (see Example 2.2)
With Y as defined in Proposition 3.1, we have that
and that the coordinate functions of \(\log ({{\,\mathrm{IIS}\,}}(Y))\), in terms of the coordinates of \(\log ({{\,\mathrm{IIS}\,}}(Z))\), are \({\text {O}}_2({\mathbb {R}})\)-invariants. Using the action as defined in Sect. 2.3, one can compute
As implied by Proposition 3.1, for any two paths \(Z\) and \(\tilde{Z}\) starting at the origin, we have that \({{\textbf {c}}}_{\le 4}(Z)\) is related to \({{\textbf {c}}}_{\le 4}(\tilde{Z})\) under \({\text {O}}_2({\mathbb {R}})\) if and only if \({{\textbf {c}}}_{\le 4}(Y) ={{\textbf {c}}}_{\le 4}({\tilde{Y}})\). By inspection, we see that a simpler set of polynomial invariants also determine the equivalence class of the image of a path \(Z\) in \({\mathfrak {g}}_{\le 4}(\!({\mathbb {R}}^{2})\!)\).
The value of \(Z\) on the above invariant set determines the value of \({{\textbf {c}}}_{\le 4}(Y)\). Thus, they provide a simpler invariant representation for \({{\textbf {c}}}_{\le 4}(Z) = {\text {proj}}_{\le 4}(\log ({{\,\mathrm{IIS}\,}}(Z)))\).
Remark 3.2
It is an interesting fact that by adding the invariants \(c_{1112}(Y)\) and \(c_{1222}(Y)\), we get the much simpler invariant
In the polynomial invariant set, one can likewise replace either \(p_5\) or \(p_{7}\) by
3.2 Spatial Curves
Here we replicate the results of the previous section, but instead for curves lying in \({\mathbb {R}}^3\). We believe this case is worth a detailed look for two reasons: (1) rigid-motion invariants of spatial curves is likely of interest for applications, (2) the method of constructing a moving frame in this space more closely the general procedure we outline later in Sect. 5.1. We will show that the subset of \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{3})\!)\) defined by
is a cross-section for action of \({\text {O}}_3({\mathbb {R}})\) on a Zariski-open subset of \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{3})\!)\). In this section, we will denote \({{\textbf {c}}}_{\le 2}\) as an element of \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{3})\!)\cong {\mathbb {R}}^2\oplus \mathfrak {so}(2,{\mathbb {R}})\) (see (10) for the explicit isomorphism) where
The action of \({\text {O}}_3({\mathbb {R}})\) acts as in (13). As is common in constructing a moving frame, we will proceed iteratively. At each stage, we bring an arbitrary element to a successively smaller linear spaces containing the desired cross-section and then restrict our attention to elements of this linear space for the next stage. To start, we choose a transformation in \({\text {O}}_3({\mathbb {R}})\) to bring an arbitrary element to the subset
(We will later refer to this as \(L^{(1)}_3({\mathbb {R}})\subset {L_{3}^{(1)}}\), see (18)) Assuming that v is not the zero vector, we can accomplish this with the group element
with the further assumption that \(c_1^2+c_2^2\ne 0\) (we will see later that this assumption can be dropped). The resulting element is of the form
where
which we denote \({{\textbf {c}}}_{\le 2}^{(1)}\). We can now restrict our attention to elements of \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{3})\!)\) of the form
where \(c^{(1)}_{12}\ne 0, c_{3}^{(1)}>0\). We can omit the formulas for the coordinates of \({{\textbf {c}}}_{\le 2}^{(1)}\) in terms of \({{\textbf {c}}}_{\le 2}\) to simplify the computation for the following step. We still have one degree of freedom left, as the subgroup of matrices of the form
with \(B\in {\text {O}}_2({\mathbb {R}})\), preserves the conditions that \(c_{1}^{(1)}=c_{2}^{(1)}=0, c_{3}^{(1)}>0\). Consider such a matrix \(A^2\), one can show that
Thus, we can choose
where
assuming that \(\left( c_{13}^{(1)}\right) ^2+\left( c_{23}^{(1)}\right) ^2\ne 0\). Thus, we can see the iterative procedure to bring a point of \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{3})\!)\) to \({\mathcal {K}}_{3;\le 2}\). At this point, we can put this together to obtain the group element
where
and
Similarly by substituting in the coordinate functions of \({{\textbf {c}}}_{\le 2}^{(1)}\) in terms of the coordinates of \({{\textbf {c}}}_{\le 2}\), we have that
As the only element of \({\text {O}}_3({\mathbb {R}})\) that brings an element of \({\mathcal {K}}_{3;\le 2}\) to \({\mathcal {K}}_{3;\le 2}\) is the identity, this is the unique intersection point of \({\mathcal {K}}_{3;\le 2}\) with the orbit of an arbitrary \({{\textbf {c}}}_{\le 2}\) in the open subset defined by
and since this action is free (see Corollary 4.13), \({\mathcal {K}}_{3;\le 2}\) is a cross-section. As in the previous section, we can thus define a map \(\rho _3:{\mathcal {U}}_{3;\le n}\subset {\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{3})\!)\rightarrow {\text {O}}_3({\mathbb {R}})\) by
for any \({{\textbf {c}}}_{\le n}\in {\mathcal {U}}_{3;\le n}\) where
which defines a moving-frame map on \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{3})\!)\) with cross-section \({\mathcal {K}}_{3;\le n}\) where
All together this implies the following analogue of Proposition 3.1.
Proposition 3.3
Let \(Z, {Z}'\) be paths in \({\mathbb {R}}^3\) such that
are elements of \({\mathcal {U}}_{3;\le 2}\). Define
Then, there exists \(g\in {\text {O}}_3({\mathbb {R}})\) such that \({{\,\mathrm{IIS}\,}}(g\cdot Z) = {{\,\mathrm{IIS}\,}}({Z}')\) if and only if \({{\,\mathrm{IIS}\,}}(Y) = {{\,\mathrm{IIS}\,}}({Y}')\) if and only if \({{\textbf {c}}}_{\le n}(Y)={{\textbf {c}}}_{\le n}({Y}')\) for all \(n\in {\mathbb {N}}\).
Propositions 3.1 and 3.3 are both special cases of Theorem 5.2, proven later for general paths in \({\mathbb {R}}^d\). We end this section by looking at the invariants produced by this cross-section and an example of how we can use this procedure to invariantize the moment curve in \({\mathbb {R}}^3\).
For a curve Z in \({\mathbb {R}}^3\), the nonzero coordinate functions of \({\text {proj}}_{ \le 2}(\log ({{\,\mathrm{IIS}\,}}(Y)))\), where Y is defined in Proposition 3.3, are given byFootnote 10
where
From this, we can conclude that the polynomial invariants \(p_1(Z), p_2(Z)^2,\) and \(p_3(Z)\) characterize the equivalence class of \({{\textbf {c}}}_{\le 2}(Z)\) under \({\text {O}}_3({\mathbb {R}})\).
Remark 3.4
Note that \(p_3(Z)\ge 0\) for any path \(Z\) in \({\mathbb {R}}^3\). There are two ways to see this: First by the Cauchy–Bunyakovsky–Schwarz inequality via
where \(v=(c_{1}(Z),c_{2}(Z),c_{3}(Z))^{\top }\), \(u=(c_{23}(Z),-c_{13}(Z),c_{12}(Z))^{\top }\). On the other hand, it can also be written as a sum of squares,
revealing that it is nothing but \(Mv\cdot Mv\) in the later Example 4.19, while \(p_1(Z)\) is \(v\cdot v\).
Example 3.5
Continuing with our running example, the moment curve, we have already seen (Example 2.7) that
The matrix
is such that
Note that \(A_1\) can be obtained via the equation in (15). Finally, the matrix
is such that
This invariantization of \({\text {proj}}_{\le 2}\log {{\,\mathrm{IIS}\,}}(Z))\) can either be obtained via this iterative method, or by directly using (16). The advantage of this iterative method is that one does not need to know the invariant functions a priori to invariantize the curve. While we are able to succinctly provide the explicit moving-frame map for an arbitrary curve in \({\mathbb {R}}^3\), this will not always be practical in higher dimensions. Figure 3 shows the effects of these transformations on the path itself.
Geometrically this process corresponds to first rotating the curve so that the end point lies on the z-axis. We then choose a rotation about this axis to force \({{\textbf {c}}}_{\le 2}(Z)=0\), which corresponds to forcing the Lévy area of the projection of \({\hat{Z}}:={\tilde{\rho }}_3({{\textbf {c}}}_2(Z))\cdot Z\) onto the \( (x,z)\) plane to be zero. Figure 4 shows this project; one can check that the total area under the curve vanishes.
Area between the coordinates 1 and 3 of the invariantized curve in Example 3.5
Example 3.6
To get a sense of the robustness of these invariants, we run the following experiment: we perturb a curve, compute the resulting invariants, then repeat this 1,000,000 times, and compute the mean and standard deviation of the resulting values. We consider the smooth curve defined by \(t\mapsto (\cos (t),\sin (t),t)\) for \(t\in [0,2\pi ]\), and we perturb it by adding a standard 3-dimensional Brownian motion, scaled down by a parameter \(\varepsilon >0\), so that our curve looks like
where \(B^{(1)}\), \(B^{(2)}\) and \(B^{(3)}\) are independent Brownian motions on the same interval (see Fig. 5 for some samples of the perturbed curve). The jagged nature of each perturbed curve would make using differential invariants more difficult. In practice, one must often apply appropriate smoothing to the curve before using differential methods, such as the differential signature [2].
In our case, the resulting invariantsFootnote 11 are quite stable as shown by Table 2, even for relatively large values of \(\varepsilon \), although not all three are equally stable.
4 Orthogonal Invariants on \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{d})\!)\)
In this section, we take a closer look at the action of \({\text {O}}_d({\mathbb {R}})\) on \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{d})\!) \cong {\mathbb {R}}^d\oplus \mathfrak {so}_{d}({\mathbb {R}})\). In particular, we construct an explicit linear space, of complementary dimension to the orbits, intersecting each orbit in a large open subset of this space. To achieve this, we consider the associated action of the complex group \({\text {O}}_d({\mathbb {C}})\) on the space \({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}})\) where
As described in Sect. 2.5, we can consider \({\text {O}}_d({\mathbb {R}})\) and \({\mathbb {R}}^d\oplus \mathfrak {so}_{d}({\mathbb {R}})\) as the real points of the varieties \({\text {O}}_d({\mathbb {C}})\) and \({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}})\).
Remark 4.1
The real Lie group
can be considered as a subgroup of the Lie group
We note that we consider \({\text {O}}_d({\mathbb {C}})\) here as a complex Lie group, in contradistinction to the Lie group of unitary matrices
where \(A^*\) is the conjugate transpose of A. Even though \({\text {U}}_d\) contains matrices with complex entries, it can only be considered as real Lie group.
By investigating the associated complex action, we can utilize tools such as the relative sections described in Definition 2.24 and then pass these results down to the real points. As before in (13), the action of \({\text {O}}_d({\mathbb {C}})\) on \({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}})\) is given by
We denote the entries as
to make explicit the connection to Sect. 5.1.
Proposition 4.2
For any \(v\in {\mathbb {C}}^d\) such that \(c_1^2+\cdots +c_d^2\ne 0\), there exists \(A\in {\text {O}}_d({\mathbb {C}})\) such that \({\tilde{v}}=Av\) satisfies \(\tilde{c}_{1}=\cdots =\tilde{c}_{ d-1}=0\) and \(\tilde{c}_{d}\ne 0\).
Proof
The function \((d-1)(c_{1}^2+\cdots +c_{d}^2)\) can be written as the sum of all pairwise sum of squares, i.e.,
Suppose that \(c_{1}^2+\cdots +c_{d}^2\ne 0\) and that there exists some \(c_{i}\ne 0\) where \(1\le i\le d-1\). (Otherwise we are done by choosing A as the identity.) By the above equation, there exists a pair of coordinates \(c_{i}\) and \(c_{j}\) such that \(c_{i}^2+c_{j}^2\ne 0\) for some \(1\le i < j\le d\).
Choose the matrix \(A \in {\text {O}}_d({\mathbb {C}})\) defined by
where w is an element of \({\mathbb {C}}\) that satisfies \(w^2 = c_i^2+c_j^2\). The transformation A is the complex analogue to a Givens Rotation which only rotates two coordinates. Then for \(Av = {\tilde{v}}\) we have that \(\tilde{c}_k=c_k\) for \(k\not \in \{ i,j \}\), \(\tilde{c}_i = 0\), and \(\tilde{c}_j = w \ne 0\). This process can be repeated until \({\tilde{v}}\) is of the desired form. \(\square \)
We define a sequence of linear subspaces of \({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}})\) as
In particular, the subspace \({L_{d}^{(d-1)}}\) is given by pairs (v, M) of the form
Example 4.3
For \(d=4\), elements in \({L_{4}^{(1)}}\) are of the form
elements in \({L_{4}^{(2)}}\) are of the form
and elements in \({L_{4}^{(3)}}\) are of the form
Note again that all \(\mathfrak {so}_{d}({\mathbb {C}})\) matrices are skew-symmetric and thus have zero diagonal.
We will show that \({L_{d}^{(1)}}, {L_{d}^{(2)}}, ..\) form a sequence of relative sections for the action of \({\text {O}}_d({\mathbb {C}})\) on \({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}})\) (see Definition 2.24). For this aim, we need to identify the normalizer subgroup for each \({L_{d}^{(i)}}\), which will be achieved in Proposition 4.5.
The group \({\text {O}}_i({\mathbb {C}})\), for \(1\le i < d\), appears as a subgroup of \({\text {O}}_d({\mathbb {C}})\) in several natural ways, in particular the subgroup obtained by considering elements that rotate some fixed subset of i coordinates and fix the remaining coordinates. For \(B\in {\text {O}}_i({\mathbb {C}})\), denote
a matrix rotating the first i coordinates and fixing the last \(d-i\). The set of such E(B) forms a subgroup of \({\text {O}}_d({\mathbb {C}})\) isomorphic to \({\text {O}}_i({\mathbb {C}})\), which we will denote
Note that \({\text {O}}^i_d({\mathbb {C}})\subset {\text {O}}^{i+1}_d({\mathbb {C}})\).
Proposition 4.4
Let \(1\le i < d\) and \(B \in {\text {O}}_i({\mathbb {C}})\). The image of the coordinates \(c_{1(i+1)}, c_{2(i+1)},\ldots , c_{i(i+1)}\) under the action of \(E(B) \in {\text {O}}^i_d({\mathbb {C}})\) on \((v,M) \in {\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}})\) is given by
the standard action of \({\text {O}}_i({\mathbb {C}})\) on a vector in \({\mathbb {C}}^i\).
Proof
This follows from (17). \(\square \)
Consider the subgroup
The action of an element of \({W_d({\mathbb {C}})}\) changes the sign of various coordinates of \({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}})\). We define the subgroup \({N_{d}^{i}({\mathbb {C}})}\) of \({\text {O}}^i_d({\mathbb {C}})\) as
Note that \({N_{d}^{i}({\mathbb {C}})}\) exactly contains matrices of the form
with \(B \in {\text {O}}^i_d({\mathbb {C}})\).
Proposition 4.5
For \(1\le i < d\), the normalizer of \({L_{d}^{(i)}}\) is equal to \({N_{d}^{d-i}({\mathbb {C}})}\).
Proof
It is immediate that \({N_{d}^{d-1}({\mathbb {C}})}\) leaves the space \({L_{d}^{(1)}}\) invariant.
Considering
we see that for \(g \in {\text {O}}_d({\mathbb {C}})\) to have
we must have \(g_{j d} = g_{d j} = 0\), \(j=1,\dots ,d-1\). This proves the claim for \(i=1\).
Let the statement be true for some \(1\le i \le d-2\). First, the normalizer of \({L_{d}^{(i+1)}}\) is contained in \({L_{d}^{(i)}}\). Diagonal entries of \(\pm 1\) leave every \({L_{d}^{(j)}}\) invariant, so it remains to investigate the matrix B in (21). Now by Proposition 4.4B acts by standard matrix multiplication on the vector \((c_{1(i+1)}, \dots , c_{i(i+1)})^\top \). We can hence apply the argument of the case \({L_{d}^{(1)}}\) to deduce that \({N_{d}^{d-(i+1)}({\mathbb {C}})}\) is the normalizer of \({L_{d}^{(i+1)}}\).
\(\square \)
We now show that \({L_{d}^{(d-1)}}\) is a relative \({W_d({\mathbb {C}})}\)-section, by constructing a sequence of relative sections for the action, drawing inspiration from recursive moving-frame algorithms (see [31] for instance).
Proposition 4.6
The linear space \({L_{d}^{(d-1)}}\) is a relative \({W_d({\mathbb {C}})}\)-section for the action of \({\text {O}}_d({\mathbb {C}})\) on \({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}})\). More precisely, there exists a set of rational invariants
such that if we define the invariant, non-empty, Zariski-open subset
we have that \({L_{d}^{(d-1)}}\) intersects each orbit that is contained in \({U_d({\mathbb {C}})}\). Furthermore, we can restrict each invariant to obtain
-
\(f_1 = c_1^2+\cdots +c_d^2\),
-
\(f_i|_{{L_{d}^{(i-1)}}} = c_{1(d-i+2)}^2+\cdots +c_{(d-i+1)(d-i+2)}^2\) for \(2\le i <d\).
-
\(f_d|_{{L_{d}^{(d-1)}}} = c_{12}^2\).
Proof
By Proposition 4.2, outside of \(f_1= ||v||^2=0\), there exists a rotation \(A_1\in {\text {O}}_d({\mathbb {C}})\) such that \(A_1\cdot (v,M)\in {L_{d}^{(1)}}\). Thus, by Proposition 4.5, \({L_{d}^{(1)}}\) is a relative \({N_{d}^{d-1}({\mathbb {C}})}\)-section. We also have that \(f_1|_{{L_{d}^{(1)}}} = c_d^2\). We proceed by induction. Suppose that for each point in \(U_i = \{ \prod _{k=1}^{i} f_k(p) \ne 0\}\) there exists a rotation \(B_{i}\in {\text {O}}_d({\mathbb {C}})\) such that \(B_{i}\cdot (v,M) \in {L_{d}^{(i)}}\).
By Proposition 4.5, the linear space \({L_{d}^{(i)}}\) is a relative \({N_{d}^{d-i}({\mathbb {C}})}\)-section and, by Proposition 2.26, there exists a field isomorphism \(\sigma _i : {\mathbb {C}}({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}}))^{{\text {O}}_d({\mathbb {C}})} \rightarrow {\mathbb {C}}({L_{d}^{(i)}})^{{N_{d}^{d-i}({\mathbb {C}})}}\). Using Proposition 4.4, one can show that on \({L_{d}^{(i)}}\) the polynomial \(c_{1(d-i+2)}^2+\cdots +c_{(d-i+1)(d-i+2)}^2\) lies in \({\mathbb {C}}({L_{d}^{(i)}})^{{N_{d}^{d-i}({\mathbb {C}})}}\). Let \(f_{i+1}\) be the unique element in \({\mathbb {C}}({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}}))^{{\text {O}}_d({\mathbb {C}})}\) such that \(f_{i+1}= \sigma _i^{-1}( c_{1(d-i+2)}^2+\cdots +c_{(d-i+1)(d-i+2)}^2)\).
By Proposition 4.2, for any \((v,M)\in {L_{d}^{(i)}}\) outside of \(\{f_{i+1}(v,M)=0\}\), there exists a rotation \(A_{i+1}\in {N_{d}^{d-i}({\mathbb {C}})}\) such that \(A_{i+1}\cdot (v,M) \in {L_{d}^{(i+1)}}\). Thus, for any (v, M) in \(U_{i+1} = \{ \prod _{k=1}^{i+1} f_k(v,M) \ne 0\}\) there exists a rotation \(B_{i+1}=A_{i+1}B_i\in {\text {O}}_d({\mathbb {C}})\) such that \(B_{i+1}\cdot (v,M) \in {L_{d}^{(i+1)}}\). Using Proposition 4.5, again, we see that \({L_{d}^{(i+1)}}\) is a relative \({N_{d}^{d-i-1}({\mathbb {C}})}\)-section.
We can continue this induction until we have \(f_{d-1}\) where \(f_{d-1}|_{{L_{d}^{(d-2)}}} = c_{13}^2+c_{23}^2\). Finally, note that the polynomial \(c_{12}^2\) lies in \( {\mathbb {C}}({L_{d}^{(d-1)}})^{W_d({\mathbb {C}})}\). Since \({L_{d}^{(d-1)}}\) is a \({W_d({\mathbb {C}})}\)-section (since \({W_d({\mathbb {C}})}= {N_{d}^{1}({\mathbb {C}})}\)), there exists \(f_d\in {\mathbb {C}}({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}}))^{{\text {O}}_d({\mathbb {C}})}\) such that \(f_d|_{{L_{d}^{(d-1)}}} = c_{12}^2\). \(\square \)
Remark 4.7
Denoting \(\varsigma _1:=\sigma _1,\,\varsigma _{i+1}:=\sigma _{i+1}\circ \sigma _i^{-1}\), we have the following chain of \(O_d({\mathbb {R}})\) transformations \(A_i\) and field isomorphisms \(\varsigma _i\):

Note though that while the \(\varsigma _i\) are uniquely determined, the \(A_i\) are not. The composition \(A_{d-1}A_{d-2}\cdots A_{2}A_{1}\), however, is unique up to a multiplication of a \({W_d({\mathbb {C}})}\) matrix from the left.
In particular, the above proposition implies that \({L_{d}^{(d-1)}}\) is a relative \({W_d({\mathbb {C}})}\)-section for the action of \({\text {O}}_d({\mathbb {C}})\) on \({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}})\), and hence, the function fields \({\mathbb {C}}({L_{d}^{(d-1)}})^{W_d({\mathbb {C}})}\) and \({\mathbb {C}}({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}}))^{{\text {O}}_d({\mathbb {C}})}\) are isomorphic. By examining the action of \({W_d({\mathbb {C}})}\) on \({L_{d}^{(d-1)}}\) and the structure of \({\mathbb {C}}({L_{d}^{(d-1)}})^{W_d({\mathbb {C}})}\), we can therefore glean information about the action of \({\text {O}}_d({\mathbb {C}})\) on \({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}})\). Consider a diagonal matrix \(D\in {W_d({\mathbb {C}})}\) given by
where \(w_i \in \{-1,1\}\) for \(1\le i\le d \). Then, the image of a point in \(L_d^{(d-1)}\) is \(D\cdot (v, M)=({\overline{v}}, {\overline{M}})\) where
Proposition 4.8
The action of \({W_d({\mathbb {C}})}\) on \({L_{d}^{(d-1)}}\cap {U_d({\mathbb {C}})}\) is free.
Proof
Suppose that the action is not free. Then, there exists \(D\in {W_d({\mathbb {C}})}\) such that \(D\cdot (v,M) = (v,M)\) and D is not the identity. Necessarily we have that for some \(1\le i\le d-1\), \(w_i=-1\). Since \(w_iw_{i+1}c_{i(i+1)} = c_{i(i+1)}\) and \(c_{i(i+1)}\ne 0\), then \(w_{i+1}=-1\). Using a similar argument, \(w_{i+2}=-1\) and so forth. However, \(w_dc_d=c_d\), where \(c_d\ne 0\), implying that \(w_d=1\) which is a contradiction. \(\square \)
Corollary 4.9
The action of \({\text {O}}_d({\mathbb {C}})\) on \({U_d({\mathbb {C}})}\subset {\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}})\) is free.
Proof
By Proposition 4.6, each orbit on \({U_d({\mathbb {C}})}\) meets the linear subspace \({L_{d}^{(d-1)}}\). We show that the stabilizer of a point in \({L_{d}^{(d-1)}}\cap {U_d({\mathbb {C}})}\) contains only the identity. This is sufficient to prove the result, as any two points in the same orbit have isomorphic stabilizer groups.
Let \((v,M)\in {L_{d}^{(d-1)}}\) and consider \(g\in G\) such that \(g\cdot (v,M)=(v,M)\). By the proof of Proposition 4.5g must lie in \({W_d({\mathbb {C}})}\). However, by Proposition 4.8, the only element of \({W_d({\mathbb {C}})}\) fixing a point in \({L_{d}^{(d-1)}}\cap {U_d({\mathbb {C}})}\) is the identity. \(\square \)
Since we have that \(w_i^2=1\) for any \(1\le i \le d\), clearly
is a set of invariant functions on \({L_{d}^{(d-1)}}\).
Proposition 4.10
The set \({{\mathfrak {I}}}_{W_d({\mathbb {C}})}\) separates orbits and is a generating set for \({\mathbb {C}}({L_{d}^{(d-1)}})^{W_d({\mathbb {C}})}\).
Proof
Consider the map \(F: {L_{d}^{(d-1)}}\cap {U_d({\mathbb {C}})}\rightarrow {\mathbb {C}}^d\) defined by evaluating the invariants in \({{\mathfrak {I}}}_{W_d({\mathbb {C}})}\) on \({L_{d}^{(d-1)}}\cap {U_d({\mathbb {C}})}\), a non-empty, Zariski-open subset of \({L_{d}^{(d-1)}}\). We show that every fiber of this map is exactly an orbit of \({W_d({\mathbb {C}})}\). Consider any \((v,M)\in {L_{d}^{(d-1)}}\cap {U_d({\mathbb {C}})}\); then, set of points in the fiber of its image is given by
We can individually change the sign for any coordinate of (v, M). To change the sign of only \(c_d\), one can act by the matrix \(D\in {W_d({\mathbb {C}})}\) such that \(w_i=-1\) for all \(1\le i \le d\). Similarly for \(c_{i(i+1)}\), we can act by the matrix \(D\in {W_d({\mathbb {C}})}\) such that \(w_k = -1\) for \(1\le k \le i\) and \(w_k =1 \) otherwise. This implies that the above set is exactly the orbit of (v, M) under \({W_d({\mathbb {C}})}\), and hence, \({{\mathfrak {I}}}_{W_d({\mathbb {C}})}\) is separating on \({L_{d}^{(d-1)}}\cap {U_d({\mathbb {C}})}\). Then by Proposition 2.22, \({{\mathfrak {I}}}_{W_d({\mathbb {C}})}\) generates \({\mathbb {C}}({L_{d}^{(d-1)}})^W\). \(\square \)
Corollary 4.11
The set \({{\mathfrak {I}}}_d\) in (22) is a minimal-generating set of rational invariant functions for \({\mathbb {C}}({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}}))^{{\text {O}}_d({\mathbb {C}})}\) and separates orbits.
Proof
By Proposition 4.6, \({L_{d}^{(d-1)}}\) is a relative \({W_d({\mathbb {C}})}\)-section for the action of \({\text {O}}_d({\mathbb {C}})\) on \({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}})\), and \({{\mathfrak {I}}}_d\) restricts to the set of invariants \({{\mathfrak {I}}}_{W_d({\mathbb {C}})}\) in (25) for the action of \({W_d({\mathbb {C}})}\) on \({L_{d}^{(d-1)}}\). This means \({{\mathfrak {I}}}_{W_d({\mathbb {C}})}=\sigma _{d-1}({{\mathfrak {I}}}_d)\), where \(\sigma _{d-1}\) is the isomorphism from Proof of Proposition 4.6. By Proposition 4.10, the set \({{\mathfrak {I}}}_{W_d({\mathbb {C}})}\) is a generating set for \({\mathbb {C}}({L_{d}^{(d-1)}})^{W_d({\mathbb {C}})}\), and hence, by Corollary 2.27, \({{\mathfrak {I}}}_d\) is a generating set for \({\mathbb {C}}({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}}))^{{\text {O}}_d({\mathbb {C}})}\). By Proposition 2.22, \({{\mathfrak {I}}}_d\) also separates orbits.
By Corollary 4.9, the action of \({\text {O}}_d({\mathbb {C}})\) is free on a non-empty, Zariski-open subset of \({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}})\). Thus, the maximum dimension of an orbit on \({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}})\) is \(\dim ({\text {O}}_d({\mathbb {C}}))=\frac{d(d-1)}{2}\). By [46, Corollary, Section 2.3], the transcendence degreeFootnote 12 of \({\mathbb {C}}({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}}))^{{\text {O}}_d({\mathbb {C}})}\) is \(\frac{d(d+1)}{2} - \frac{d(d-1)}{2} =d\), and hence, any generating set must be at least of size d, implying that \({{\mathfrak {I}}}_d\) is minimal. \(\square \)
The above results for the action of \({\text {O}}_d({\mathbb {C}})\) on \({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}})\) help uncover the structure of the action of \({\text {O}}_d({\mathbb {R}})\) on \({\mathbb {R}}^d\oplus \mathfrak {so}_{d}({\mathbb {R}})\). First we show that the intersection of the set \({U_d({\mathbb {C}})}\) defined in (23) with \({\mathbb {R}}^d\oplus \mathfrak {so}_{d}({\mathbb {R}})\) is a non-empty and well-defined Zariski open subset of \({\mathbb {R}}^d\oplus \mathfrak {so}_{d}({\mathbb {R}})\).
Proposition 4.12
The set \({{\mathfrak {I}}}_d\) in (22) is a subset of \({\mathbb {R}}({\mathbb {R}}^d\oplus \mathfrak {so}_{d}({\mathbb {R}}))^{{\text {O}}_d({\mathbb {R}})}\). In particular,
is a well-defined, \({\text {O}}_d({\mathbb {R}})\)-invariant, and non-empty Zariski open subset of \({\mathbb {R}}^d\oplus \mathfrak {so}_{d}({\mathbb {R}})\), and
intersects each orbit (under \({\text {O}}_d({\mathbb {R}})\)) contained in \({U_{d}({\mathbb {R}})}\).
Proof
In the proof of Proposition 4.6, each function \(f_i\) is obtaining by taking the inverse image of a real invariant function under the field isomorphism \(\sigma _i : {\mathbb {C}}({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}}))^{{\text {O}}_d({\mathbb {C}})} \rightarrow {\mathbb {C}}({L_{d}^{(i)}})^{{N_{d}^{d-i}({\mathbb {C}})}}\). The function \(f_i\) can be decomposed \(f_i = h_1 + \sqrt{-1}\cdot h_2\), where \(h_1\) and \(h_2\) are elements of \({\mathbb {R}}({\mathbb {R}}^d\oplus \mathfrak {so}_{d}({\mathbb {R}}))^{{\text {O}}_d({\mathbb {R}})}\), and hence by Proposition 2.28, are elements of \({\mathbb {C}}({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}}))^{{\text {O}}_d({\mathbb {C}})}\). Thus, \(h_1|_{{L_{d}^{(i)}}}= f_i|_{{L_{d}^{(i)}}}\). Since \(\sigma _i\) is a field isomorphism, \(f_i\) must define the same rational function as \(h_1\) and hence is an element of \({\mathbb {R}}({\mathbb {R}}^d\oplus \mathfrak {so}_{d}({\mathbb {R}}))^{{\text {O}}_d({\mathbb {R}})}\).
Note that Proposition 4.2 also holds for any \(v\in {\mathbb {R}}^d\), i.e., by applying Gram–Schmidt to a linearly independent set of d vectors \(\{v,v_1,\ldots ,v_{d-1}\}\) in \({\mathbb {R}}^d\). Thus if \(f_1(v,M)\ne 0\), there exists a rotation \(A\in {\text {O}}_d({\mathbb {R}})\) such that \(A\cdot (v,M)\in {L_{d}^{(1)}}\cap {\mathbb {R}}^d\oplus \mathfrak {so}_{d}({\mathbb {R}})\). Similarly as in the proof of Proposition 4.6, we can proceed by induction. Suppose \((v,M)\in {L_{d}^{(i)}}\cap {\mathbb {R}}^d\oplus \mathfrak {so}_{d}({\mathbb {R}})\) and \(f_{i+1}(v,M)\ne 0\). Then we have that
By Proposition 4.4, we can find a rotation \(A\in {N_{d}^{d-i}({\mathbb {C}})}\) such that \(A\cdot (v,M)\in {L_{d}^{(i+1)}}\). Therefore, if \((v,M)\in {U_{d}({\mathbb {R}})}\), there exists a rotation \(A\in {\text {O}}_d({\mathbb {R}})\) such that \(A\cdot (v,M)\in {L_{d}^{(d-1)}}\). \(\square \)
The following follows directly from Proposition 4.9.
Corollary 4.13
The action of \({\text {O}}_d({\mathbb {R}})\) on \({U_{d}({\mathbb {R}})}\subset {\mathbb {R}}^d\oplus \mathfrak {so}_{d}({\mathbb {R}})\) is free.
Proposition 4.14
The set \({{\mathfrak {I}}}_d\) generates the invariant function field \({\mathbb {R}}({\mathbb {R}}^d\oplus \mathfrak {so}_{d}({\mathbb {R}}))^{{\text {O}}_d({\mathbb {R}})}\) and separates orbits on \({U_{d}({\mathbb {R}})}\).
Proof
The fact that \({{\mathfrak {I}}}_d\) generates \({\mathbb {R}}({\mathbb {R}}^d\oplus \mathfrak {so}_{d}({\mathbb {R}}))^{{\text {O}}_d({\mathbb {R}})}\) follows from Propositions 4.6, 4.12 and Corollary 2.29. Using a similar argument as in Proposition 4.10, we can see that \({{\mathfrak {I}}}_{W_d({\mathbb {C}})}\) in (25) separates orbits for the action of \({W_d({\mathbb {C}})}\) on \(L_d^{(d-1);{\mathbb {R}}}\cap {U_{d}({\mathbb {R}})}\). By Proposition 4.12, any orbit on \({U_{d}({\mathbb {R}})}\) meets \(L_d^{(d-1);{\mathbb {R}}}\), and the \({{\mathfrak {I}}}_d\) restricts to \({{\mathfrak {I}}}_{W_d({\mathbb {C}})}\) on \(L_d^{(d-1);{\mathbb {R}}}\). Thus, \({{\mathfrak {I}}}_d\) is separating on \({U_{d}({\mathbb {R}})}\). \(\square \)
We finish the section by constructing an explicit set of invariant polynomial functions that generate \({\mathbb {C}}({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}}))^{{\text {O}}_d({\mathbb {C}})}\). Consider the map
Then, for the action of \(A\cdot (v,M)\) we have that
Thus, the polynomial obtained by the dot-product of \(\phi _k\) with itself is an invariant function on \( {\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}})\) under \({\text {O}}_d({\mathbb {C}})\). We will show that the set of polynomial invariants (defining \(a\cdot b := \sum _i a_i b_i\))
generate the field \({\mathbb {C}}({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}}))^{{\text {O}}_d({\mathbb {C}})}\) by restricting them to \({L_{d}^{(d-1)}}\).
Lemma 4.15
Consider a matrix M of the form as in (19), i.e. such that \((v,M)\in {L_{d}^{(d-1)}}\). Then, for \(1\le k< d\), \(M^k\) satisfies
-
(a)
\(\displaystyle M^k(d-k,d) = \prod _{i=1}^k c_{(d-i)(d-i+1)}\),
-
(b)
\(M^k(i,d) = 0\) for \(i < d-k\),
-
(c)
\(M^k(i,d) \in {\mathbb {Q}}[c_{(d-j)(d-j+1)}\, |\, 1\le j < k]\) for \(i > d-k\).
Proof
We proceed by induction. For \(k=1\), \(M^1=M\). Then \(M^1\) satisfies (a)–(c), since \(M(d-1,d)=c_{(d-1)(d)}\) and \(M(i,d)=0\) for \(i<d-1\). Now suppose that (a)–(c) hold for \(M^{k-1}\). We have that for \(M^k=MM^{k-1}\),
where \(1<i<d-1\). Note that \(M^k(i,d)\) is linear combination of \(M^{k-1}(i-1,d)\) and \(M^{k-1}(i+1,d)\). By the induction hypothesis, we know that \(M^{k-1}(i,d)=0\) if \(i < d-k+1\), and hence, \(M^k (i,d)=0\) when \(i+1 < d-k+1\), or equivalently when \(i<d-k\). This proves (b).
Suppose that \(i > d-k\). Then, \(M^k(i,d)\) is linear in the terms
where \(c_{i-1,i}\) and \(c_{i,i+1}\) are of the form \(c_{(d-j)(d-j+1)}\) for \(1\le j< k\). By the induction hypothesis, the latter two terms are polynomials in \(c_{(d-j)(d-j+1)}\) where \(1 \le j < k-1\), proving (c).
Finally suppose that \(i=d-k\). We have that
By the induction hypothesis, we know that
which proves (a). \(\square \)
Lemma 4.16
The polynomials obtained from restricting the functions in \({{\mathfrak {I}}}_M\) to \({L_{d}^{(d-1)}}\) generate the invariant rational function field \({\mathbb {C}}({L_{d}^{(d-1)}})^{W_d({\mathbb {C}})}\).
Proof
First note that to restrict the polynomials in \({{\mathfrak {I}}}_M\) to \({L_{d}^{(d-1)}}\), we can assume that (v, M) are of the form in (19) and then compute the inner product. Then, we can easily see that
This implies that \(c_d^2\) and \(c_{(d-1)d}^2\) are rational functions of \(v\cdot v|_{{L_{d}^{(d-1)}}}\) and \( Mv\cdot Mv|_{{L_{d}^{(d-1)}}}\). We proceed by induction on i: suppose that \(c_{(d-i)(d-i+1)}^2\) is a rational function of \( v\cdot v|_{L_{d}^{(d-1)}}, Mv\cdot Mv|_{L_{d}^{(d-1)}},\ldots , M^iv\cdot M^iv|_{L_{d}^{(d-1)}}\) for all \(1\le i < k\). By Lemma 4.15, we know that
Since \( M^k\cdot M^kv|_{L_{d}^{(d-1)}}\) is an invariant function, as well as \(c_d^2\) and \(c_{(d-i)(d-i+1)}^2\) for \(1\le i < d\), the function I lies in \({\mathbb {C}}({W_d({\mathbb {C}})})^{L_{d}^{(d-1)}}\). By the induction hypothesis and Proposition 4.10, I is a rational function of
Thus, we can rewrite the above equality to
By the induction hypothesis, each \(c_{(d-i)(d-i+1)}^2\) for \(1\le i<k\) is a rational function of
This implies that \(c_{(d-k)(d-k+1)}^2\) is a rational function of
Therefore, each element of \({{\mathfrak {I}}}_{W_d({\mathbb {C}})}\) can be written as a rational function of polynomials in \({{\mathfrak {I}}}_M\) restricted to \({L_{d}^{(d-1)}}\). By Proposition 4.10, \({{\mathfrak {I}}}_M\) restricted to \({L_{d}^{(d-1)}}\) is a generating set for \({\mathbb {C}}({L_{d}^{(d-1)}})^{W_d({\mathbb {C}})}\). \(\square \)
Proposition 4.17
The set of polynomial invariants \({{\mathfrak {I}}}_M\) in (26) generates both \({\mathbb {C}}({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}}))^{{\text {O}}_d({\mathbb {C}})}\) and \({\mathbb {R}}({\mathbb {R}}^d\oplus \mathfrak {so}_{d}({\mathbb {R}}))^{{\text {O}}_d({\mathbb {R}})}\) and also separates orbits on \({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}})\) and \({\mathbb {R}}^d\oplus \mathfrak {so}_{d}({\mathbb {R}})\).
Proof
By Proposition 4.6\({L_{d}^{(d-1)}}\) is a relative \({W_d({\mathbb {C}})}\)-section for the action of \({\text {O}}_d({\mathbb {C}})\) on \({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}})\), and by Proposition 4.10\({{\mathfrak {I}}}_{W_d({\mathbb {C}})}\) is a generating set for \({\mathbb {C}}({L_{d}^{(d-1)}})^{W_d({\mathbb {C}})}\). Thus, by Lemma 4.16 and Corollary 2.27, \({{\mathfrak {I}}}_M\) generates \({\mathbb {C}}({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}}))^{{\text {O}}_d({\mathbb {C}})}\). By Corollary 2.29\({{\mathfrak {I}}}_M\) generates \({\mathbb {R}}({\mathbb {R}}^d\oplus \mathfrak {so}_{d}({\mathbb {R}}))^{{\text {O}}_d({\mathbb {R}})}\).
By Proposition 2.22, \({{\mathfrak {I}}}_M\) separates orbits on \({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}})\). By Proposition 4.14, there exists a separating set of invariants in \({\mathbb {R}}({\mathbb {R}}^d\oplus \mathfrak {so}_{d}({\mathbb {R}}))^{{\text {O}}_d({\mathbb {R}})}\), and hence, \({\mathbb {R}}({\mathbb {R}}^d\oplus \mathfrak {so}_{d}({\mathbb {R}}))^{{\text {O}}_d({\mathbb {R}})}\) separates orbits. Therefore, by Proposition 2.30, \({{\mathfrak {I}}}_M\) separates orbits on \({\mathbb {R}}^d\oplus \mathfrak {so}_{d}({\mathbb {R}})\). \(\square \)
Remark 4.18
As a consequence, we in particular have that all \(M^k v\cdot M^kv\) for \(k\ge d\) can be expressed as rational functions with variables in \({{\mathfrak {I}}}_M\).
Example 4.19
By Proposition 4.17, the field of invariants \({\mathbb {R}}({\mathbb {R}}^3 \times \mathfrak {so}_{3}({\mathbb {R}}))^{{\text {O}}_3({\mathbb {R}})}\) is generated by:
As we saw in Sect. 3.2\(v\cdot v, Mv\cdot Mv\) are equivalent to \(p_1(Z), p_3(Z)\), respectively.
5 \({\text {O}}_d({\mathbb {R}})\)-Invariant Iterated-Integrals Signature
5.1 Moving Frame on \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!)\)
As for \({\text {O}}_2({\mathbb {R}})\) on \({\mathbb {R}}^2\), the action of \({\text {O}}_d({\mathbb {R}})\) on paths in \({\mathbb {R}}^d\) induces an action on its (truncated) signature that coincides with the diagonal action on the ambient space \(T_{\le n}({\mathbb {R}}^d)\). The induced action on the log-signature coincides with this diagonal action as well, when considering \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!)\) as a subspace of \(T_{\le n}({\mathbb {R}}^d)\).
Let \({{\textbf {c}}}_{\le n}\) be an element of \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!)\) with coordinates given by \(c_{i_1i_2\cdots i_m}\) for \(m\le n\). We define the following submanifold of \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!)\):
Let \({\text {proj}}_{\le 2} : {\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!) \rightarrow {\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{d})\!)\) be the projection onto the first two levels (Sect. 2.2). The projection of this submanifold onto \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{d})\!)\), \({\text {proj}}_{\le 2}({{\mathcal {K}}_{d;\le n}})\) is equal (up to the identification \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{d})\!) \cong {\mathbb {R}}^d\oplus \mathfrak {so}_{d}({\mathbb {R}})\)) to the real, positive points of \({L_{d}^{(d-1)}}\) in (19) where
Similarly we can define the analogue to \({U_d({\mathbb {C}})}\) in (23). Consider the rational functions on \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!)\) given by
for \(1\le i\le d\) where \(f_i(v,M)\) is given in Proposition 4.6. By Proposition 4.12, the functions \(F_i\) are rational functions on \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{d})\!)\) with real coefficients. Then the following is a Zariski-open subset of \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!)\),
where \({\text {proj}}_{\le 2}({\mathcal {U}}_{d;\le n})= {U_d({\mathbb {C}})}\) if we identify \({{\textbf {c}}}_{\le 2}\) with (v, M) as above. In particular, both \({\mathcal {U}}_{d;\le n}\) and \({{\mathcal {K}}_{d;\le n}}\) are completely characterized by \({\text {proj}}_{\le 2}({{\textbf {c}}}_{\le n})\), i.e.,
with \({\text {proj}}_{\le n\rightarrow \le 2}\) denoting the canonical projection from \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!)\) onto \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{d})\!)\). Note that \({\mathcal {K}}_{d;\le 2}\) is a subset of \(L^{(1);{\mathbb {R}}}_d\) and \({\mathcal {U}}_{d;\le 2}\) is equal to \({U_{d}({\mathbb {R}})}\), both defined in Proposition 4.12.
We now show that on the subset \({\mathcal {U}}_{d;\le n}\subset {\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!)\) the submanifold \({{\mathcal {K}}_{d;\le n}}\) is a cross-section, which induces a moving frame.
Lemma 5.1
For any point \({{\textbf {c}}}_{\le 2}\in {\mathcal {K}}_{d;\le 2} \cap U_{d;\le 2}\), the orbit \({\text {O}}_d({\mathbb {R}})\cdot {{\textbf {c}}}_{\le 2}\) and \({\mathcal {K}}_{d; \le 2}\) intersect transversally.
Proof
First, we recall that, by definition, \({\text {O}}_d({\mathbb {R}})\cdot {{\textbf {c}}}_{\le 2}\) and \({\mathcal {K}}_{d;\le 2}\) intersect transversally if and only if, at every point \(q\) in the intersection, the tangent spaces \(T_q({\text {O}}_d({\mathbb {R}})\cdot {{\textbf {c}}}_{\le 2})\) and \(T_q{\mathcal {K}}_{d;\le 2}\) generate the whole ambient space \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{d})\!)\), that is
Now, at a point \(q=A\cdot {{\textbf {c}}}_{\le 2}=(Av,AMA^{\top })\) in the orbit, the tangent space has the form
Indeed, recall that for a manifold \(M\), its tangent space at a point \(q\) is the linear space \(T_qM{:}{=}\{\gamma '(0):\gamma \text { curve s.t. }\gamma (0) = q\}\). A curve \(\gamma \) on \({\text {O}}_d({\mathbb {R}})\cdot {{\textbf {c}}}_{\le 2}\) such that \(\gamma (0)=q\) has the form \(\gamma (t)=(L(t)A)\cdot {{\textbf {c}}}_{\le 2}\) for some curve \(t\mapsto L(t)\) in \({\text {O}}_d({\mathbb {R}})\) such that \(L(0)=I\). Hence,
The tangent space to the cross-section is
We note that
where the second equality since the action of \({\text {O}}_d({\mathbb {R}})\) is free on \( U_{d;\le 2}\) by Corollary 4.13. Thus, we have that \(\dim T_q{\mathcal {K}}_{d;\le 2}+\dim T_q\Big ({\text {O}}_d({\mathbb {R}})\cdot {{\textbf {c}}}_{\le 2}\Big )=\dim {\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{d})\!)\). Therefore, we only need to show that \(T_q{\mathcal {K}}_{d;\le 2}\cap T_q\Big ({\text {O}}_d({\mathbb {R}})\cdot {{\textbf {c}}}_{\le 2}\Big )=\{0\}\) for all \(q\in {\mathcal {K}}_{d;\le 2}\cap \left( {\text {O}}_d({\mathbb {R}})\cdot {{\textbf {c}}}_{\le 2}\right) \).
Let \((\varGamma _{i,j}:1\le i<j\le d)\) be the standard basis of \(\mathfrak {so}_{d}({\mathbb {R}})\), that is, \((\varGamma _{i,j})_{k,l}=\delta _{i,k}\delta _{j,l}-\delta _{j,k}\delta _{i,l}\). It is not hard to show that the commutation relations
hold for all \(1\le k<d\) and \(1\le i<j\le d\). By Eq. (28), a generic element \(p\in T_q\Big ({\text {O}}_d({\mathbb {R}})\cdot {{\textbf {c}}}_{\le 2}\Big )\) has the form \(p=(HAv,[H,AMA^{\top }])\) with
But since \(q=(Av,AMA^{\top })\in {\mathcal {K}}_{d;\le 2}\),
with \(\alpha >0\), and \(\beta _k>0\) for all \(k\in \{1,\dotsc ,d-1\}\). If \(p\) also belongs to \(T_q{\mathcal {K}}_{d;\le 2}\), then we have in particular that
for some \(\alpha '\in {\mathbb {R}}\), thus \(h_{i,d}=0\) for all \(i\in \{1,\dotsc ,d-1\}\). Now we show that \(h_{i,j}=0\) for all \(1\le i<j\le d-1\) by induction on \(r{:}{=}d-1-j\). By Eq. (29), we see that
so that
for \(i\in \{1,\dotsc ,d-2\}\). Therefore, \(h_{i,d-1}=0\) for all \(i\in \{1,\dotsc ,d-2\}\), and the claim is proven when \(r=0\). Suppose it is true for all \(r'<r\). Then
for \(i\in \{1,\dotsc ,d-2-r\}\), hence \(h_{i,d-1-r}=0\) for all \(i\in \{1,\dotsc ,d-2-r\}\). Finally, we have \(H=0\) thus \(p=(HAv,[H,AMA^\top ])=0\).
We have shown that if \(q\in {\text {O}}_d({\mathbb {R}})\cdot {{\textbf {c}}}_{\le 2}\cap {\mathcal {K}}_{d;\le 2}\) then \(\dim T_q\Big ({\text {O}}_d({\mathbb {R}})\cdot {{\textbf {c}}}_{\le 2}\Big )+\dim T_q{\mathcal {K}}_{d;\le 2}=\dim {\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{d})\!)\) and \(T_q\Big ({\text {O}}_d({\mathbb {R}})\cdot {{\textbf {c}}}_{\le 2}\Big )\cap T_q{\mathcal {K}}_{d;\le 2}\) is trivial. It follows that if \(q\in \left( {\text {O}}_d({\mathbb {R}})\cdot {{\textbf {c}}}_{\le 2}\right) \cap {\mathcal {K}}_{d;\le 2}\), then
and in particular \({\text {O}}_d({\mathbb {R}})\cdot {{\textbf {c}}}_{\le 2}\) and \({\mathcal {K}}_{d;\le 2}\) intersect transversally. \(\square \)
Theorem 5.2
The submanifold \({{\mathcal {K}}_{d;\le n}}\) in (27) is a cross-section for the action of \({\text {O}}_d({\mathbb {R}})\) on \({\mathcal {U}}_{d;\le n}\subset {\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!)\). In particular, \({{\mathcal {K}}_{d;\le n}}\) induces a moving-frame map \(\rho _d: {\mathcal {U}}_{d;\le n}\rightarrow {\text {O}}_d({\mathbb {R}})\).
Proof
We first claim that \({{\mathcal {K}}_{d;\le n}}\) intersects each orbit in \({\mathcal {U}}_{d;\le n}\) at a unique point. Denote the linear span of \({{\mathcal {K}}_{d;\le n}}\) as
Note that the action on \({\text {proj}}_{\le 2} {\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!) = {\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{d})\!)\) is isomorphic to the action on \({\mathbb {R}}^d\oplus \mathfrak {so}_{d}({\mathbb {R}})\) given in (13). Thus, for any \({{\textbf {c}}}_{\le n}\in {\mathcal {U}}_{d;\le n}\), by Proposition 4.12 and the diagonality of the action (see Sect. 2.3), there exists an element of \(g\in {\text {O}}_d({\mathbb {R}})\) such that \(g\cdot {{\textbf {c}}}_{\le n}= \tilde{{{\textbf {c}}}}_{\le n} \in K\).
Consider the subgroup \(W_{\mathbb {R}}\subset {\text {O}}_d({\mathbb {R}})\) of diagonal matrices w with diagonal entries \(w_{jj}\in \{-1,1\}\), \(1\le j\le d\). By Proposition 4.5, any element of \(W_{\mathbb {R}}\) sends a point in K to K. For any \(\tilde{{{\textbf {c}}}}_{\le n} \in K\), the action of \(W_{\mathbb {R}}\) on the coordinates \({\text {proj}}_{\le 2}({{\textbf {c}}}_{\le n})={{\textbf {c}}}_{\le 2}\) is given by the following (see (24)):
The element \(w\in W_{\mathbb {R}}\) such that \(w_{jj}= -1\) for \(1\le j \le d\) changes only the sign on \(c_{d}\). The element \(w\in W_{\mathbb {R}}\) where \(w_{jj} = -1\) for \(1\le j \le i\) and \(w_{jj} = 1\) for \(i < j \le d\) changes only the sign of \(c_{i(i+1)}\). Thus, there exists \(g\in W_{\mathbb {R}}\) such that \(g\cdot \tilde{{{\textbf {c}}}}_{\le n} \in {{\mathcal {K}}_{d;\le n}}\), implying \({{\mathcal {K}}_{d;\le n}}\) intersects each orbit in \({\mathcal {U}}_{d;\le n}\).
Now suppose that for some \({{\textbf {c}}}_{\le n}\in {{\mathcal {K}}_{d;\le n}}\), \(g\in {\text {O}}_d({\mathbb {R}})\) we have \(g\cdot {{\textbf {c}}}_{\le n}\in {{\mathcal {K}}_{d;\le n}}\). We show that this implies \(g = {\text {id}}\). Since the action of \({\text {O}}_d({\mathbb {R}})\) on \(T_1({\mathbb {R}}^d)\) is isomorphic to the canonical action on \({\mathbb {R}}^d\), \(g\in {\text {O}}^{d-1}_d({\mathbb {R}})\) (recall the notation after (20)). By Proposition 4.4, the action of \({\text {O}}^{d-1}_d({\mathbb {R}})\) on the coordinates \(c_{1d}, c_{2,d},\ldots , c_{(d-1)d}\) of \({{\textbf {c}}}_{\le n}\) is isomorphic to the canonical action on \({\mathbb {R}}^{d-1}\). Thus, we deduce that g must be in \({\text {O}}^{d-2}_d({\mathbb {R}})\). Iterating, we obtain that g must be the identity, as claimed, implying that \({{\mathcal {K}}_{d;\le n}}\) intersects each orbit in \({\mathcal {U}}_{d;\le n}\) exactly once.
We now show that the intersection with each orbit is transverse. By Corollary 4.13, the action is free on \(U_{d;\le 2}\), and thus on \({\mathcal {U}}_{d;\le n}\). Since the action is free on \({\mathcal {U}}_{d;\le n}\), each orbit \({\text {O}}_d({\mathbb {R}})\cdot {{\textbf {c}}}_{\le n}\) is smooth and of dimension \(n(n-1)/2\) (see Proposition 2.20). Let \({{\textbf {c}}}_{\le n}\) be a point in \({{\mathcal {K}}_{d;\le n}}\). Since \({{\mathcal {K}}_{d;\le n}}\) is on open subset of the linear space K, we have \(T_{{{\textbf {c}}}_{\le n}}{{\mathcal {K}}_{d;\le n}}=K\). Since \({{\mathcal {K}}_{d;\le n}}\) and \({\text {O}}_d({\mathbb {R}})\cdot {{\textbf {c}}}_{\le n}\) are of complementary dimension, \({{\mathcal {K}}_{d;\le n}}\) intersects \({\text {O}}_d({\mathbb {R}})\cdot {{\textbf {c}}}_{\le n}\) transversally if and only if the dimension of the span of their tangent spaces is equal to the dimension of \({\mathcal {U}}_{d;\le n}\).
Since \({\text {O}}_d({\mathbb {R}})\) acts diagonally, we have that
where \(V + W\) denotes the span of two subspaces V, W. Then by Lemma 5.1
Since for any vector \(v \in T_{{\text {proj}}_{\le 2}({{\textbf {c}}}_{\le n})} {\text {proj}}_{\le 2}({{\mathcal {K}}_{d;\le n}})\), \(\langle v \rangle \oplus {\mathfrak {g}}_{\le 3}(\!({\mathbb {R}}^{d})\!)\) is a subspace of \(T_{{{\textbf {c}}}_{\le n}}{{\mathcal {K}}_{d;\le n}}\), we have that \(T_{{{\textbf {c}}}_{\le n}}{{\mathcal {K}}_{d;\le n}}+ T_{{{\textbf {c}}}_{\le n}} ({\text {O}}_d({\mathbb {R}})\cdot {{\textbf {c}}}_{\le n})={\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!)\). Thus, \({{\mathcal {K}}_{d;\le n}}\) and \({\text {O}}_d({\mathbb {R}})\cdot {{\textbf {c}}}_{\le n}\) intersect transversally.
Therefore, \({{\mathcal {K}}_{d;\le n}}\) intersects transversally each orbit of \({\mathcal {U}}_{d;\le n}\) at a unique point and hence by definition is a cross-section for this action. The free and algebraic action of \({\text {O}}_d({\mathbb {R}})\) on \({\mathcal {U}}_{d;\le n}\) satisfies the hypothesis of Theorem 2.15 (see Remark 2.19), and hence, there exists a moving-frame map \(\rho _d: {\mathcal {U}}_{d;\le n}\rightarrow {\text {O}}_d({\mathbb {R}})\) taking each element of \({\mathcal {U}}_{d;\le n}\) to the unique intersection point of its orbit and \({{\mathcal {K}}_{d;\le n}}\). \(\square \)
The Proof of Proposition 4.6 provides a road map for explicitly finding the element of \({\text {O}}_d({\mathbb {R}})\) taking any point \({{\textbf {c}}}_{\le n}\in {\mathcal {U}}_{d;\le n}\) to \({{\mathcal {K}}_{d;\le n}}\) and hence \(\rho _d({{\textbf {c}}}_{\le n})\cdot {{\textbf {c}}}_{\le n}\). By successively applying rotations, one can bring \({{\textbf {c}}}_{\le n}\) to the cross-section \({{\mathcal {K}}_{d;\le n}}\).
Remark 5.3
For an example of doing this in practice, see Example 3.5. The two-step process in this example is similar to the iterative process outlined in the Proof of Proposition 4.6 of bringing an element of \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{d})\!)\) to successively smaller linear spaces. The transformation \(A_1\) brings \({{\textbf {c}}}_{\le 2}(Z)\) to \({L_{3}^{(1)}}({\mathbb {R}})\subset {L_{3}^{(1)}}\), then finally to \({\mathcal {K}}_{3;\le 2}\subsetneq {L_{3}^{(2)}}({\mathbb {R}})\subset {L_{3}^{(2)}}\) by a transformation \(A_2\). In principle, given a procedure to rotate an element of \({\mathbb {R}}^d\) to a particular axis, this iterative process is quite easy to perform to bring any \({{\textbf {c}}}_{\le 2}(Z)\) for any path \(Z\) to \({{\mathcal {K}}_{d;\le n}}\), and hence invariantize any path.
An important consequence of Theorem 5.2 is the following corollary.
Corollary 5.4
Two elements \({{\textbf {c}}}_{\le n},\tilde{{{\textbf {c}}}}_{\le n} \in {\mathcal {U}}_{d;\le n}\) lie in the same orbit if and only if they take the same value on the cross-section \({{\mathcal {K}}_{d;\le n}}\), i.e., if and only if \(\rho _d({{\textbf {c}}}_{\le n}) \cdot {{\textbf {c}}}_{\le n}= \rho _d(\tilde{{{\textbf {c}}}}_\le {n}) \cdot \tilde{{{\textbf {c}}}}_{\le n}\).
Thus, to find a unique representative of the orbit of \({{\textbf {c}}}_{\le n}\in {\mathcal {U}}_{d;\le n}\) we can “invariantize” \({{\textbf {c}}}_{\le n}\) by computing \(\rho _d({{\textbf {c}}}_{\le n}) \cdot {{\textbf {c}}}_{\le n}\), and the smooth functions defining the nonzero coordinates of \({{\mathcal {K}}_{d;\le n}}\cap {\text {O}}_d({\mathbb {R}})\cdot {{\textbf {c}}}_{\le n}\) are invariant functions which characterize the orbit. Note that the cross-section \({{\mathcal {K}}_{d;\le n}}\) and the moving frame only depend on the \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{d})\!)\) coordinates. In particular, we have that for any path \(Z\) such that \({{\textbf {c}}}_{\le n}(Z)={\text {proj}}_{\le n}(\log ({{\,\mathrm{IIS}\,}}(Z)))\in U^d_n\)
which implies that the “invariantization” of a path \(Y:= {\tilde{\rho }}_d({{\textbf {c}}}_{\le 2}(Z))\cdot Z\) is well-defined. This is due to the diagonal nature of the action of \({\text {O}}_d({\mathbb {R}})\) on \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!)\), and the fact that \(\dim ({\text {O}}_d({\mathbb {R}})) < \dim ({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{d})\!))\). Since the action of the coordinates on \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{d})\!)\) is not affected by the higher-level coordinates, we can define a cross-section on \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{d})\!)\) that extends naturally to \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!)\). For higher-dimensional groups, one may have to consider a cross-section on \({\mathfrak {g}}_{\le 3}(\!({\mathbb {R}}^{d})\!)\) or higher.
As a consequence, the infinite log signature (and thus the iterated-integrals signature) of a path \(Z\) under the action of \({\text {O}}_d({\mathbb {R}})\) is characterized by its value on the cross-section.
Theorem 5.5
For any two paths \(Z, \tilde{Z}\) in \({\mathbb {R}}^d\) such that \({{\textbf {c}}}_{\le 2}(Z){:}{=}{\text {proj}}_{\le 2}(\log ({{\,\mathrm{IIS}\,}}(Z)))\), \({{\textbf {c}}}_{\le 2}(\tilde{Z}){:}{=}{\text {proj}}_{\le 2}(\log ({{\,\mathrm{IIS}\,}}(\tilde{Z})))\) are elements of \({\mathcal {U}}_{d;\le 2}\), define
Then, there exists \(g\in {\text {O}}_d({\mathbb {R}})\) such that \({{\,\mathrm{IIS}\,}}(g\cdot Z) = {{\,\mathrm{IIS}\,}}({Z}')\) if and only if \({{\,\mathrm{IIS}\,}}(Y) = {{\,\mathrm{IIS}\,}}({Y}')\) if and only if \({{\textbf {c}}}_{\le n}(Y)={{\textbf {c}}}_{\le n}({Y}')\) for all \(n\in {\mathbb {N}}\).
Proof
We first note that \({{\textbf {c}}}_{\le n}(Y)={{\textbf {c}}}_{\le n}({\tilde{Y}})\) for all \(n\in {\mathbb {N}}\) is equivalent to \({{\,\mathrm{ISS}\,}}(Y)={{\,\mathrm{ISS}\,}}({\tilde{Y}})\), and that for any \(g\in {\text {O}}_d({\mathbb {R}})\), \({{\,\mathrm{ISS}\,}}(g\cdot Z)={{\,\mathrm{ISS}\,}}(\tilde{Z})\) is equivalent to \({{\textbf {c}}}_{\le n}(g\cdot Z)={{\textbf {c}}}_{\le n}(\tilde{Z})\) for all \(n\in {\mathbb {N}}\). Indeed, \({{\textbf {c}}}_{\le n}(Y) ={\text {proj}}_{\le n}\log {{\,\mathrm{ISS}\,}}(Y)\), and \(\log {{\,\mathrm{ISS}\,}}(Y)=\sum _{h\in {\mathscr {L}}_{d}}c_h(Y)b_h\) is given by the family \(({{\textbf {c}}}_{\le n}(Y))_n\) through taking each coordinate \(c_h(Y)\) from \({{\textbf {c}}}_{\le |h|}(Y)\) (note that by definition \({{\textbf {c}}}_{\le n}(Y)={\text {proj}}_{\le n}{{\textbf {c}}}_{\le m}(Y)\)), where \(\log \) is bijective. The same argument is used for \({\tilde{Y}},Z, \tilde{Z}\).
Now \({{\textbf {c}}}_{\le n}(Y)={{\textbf {c}}}_{\le n}({\tilde{Y}})\) for all n implies
for all n, with \({\tilde{\rho }}_d({{\textbf {c}}}_{\le 2}(\tilde{Z}))^\top {\tilde{\rho }}_d({{\textbf {c}}}_{\le 2}(Z))\in {\text {O}}_d({\mathbb {R}})\) independent of n.
On the other hand, if there is some \(g\in {\text {O}}_d({\mathbb {R}})\) with \({{\textbf {c}}}_{\le n}(g\cdot Z)={{\textbf {c}}}_{\le n}(\tilde{Z})\) for all n, then
where we have used the moving-frame property \({\tilde{\rho }}_d(g\cdot {{\textbf {c}}}_{\le 2}(Z)) ={\tilde{\rho }}_d({{\textbf {c}}}_{\le 2}(Z))g^\top \). \(\square \)
5.2 Toward a Fundamental Set of Polynomial Invariants
The non-constant-zero coordinates of \(\rho _d({{\textbf {c}}}_{\le n})\cdot {{\textbf {c}}}_{\le n}\) form a fundamental set of invariants for the action of \({\text {O}}_d({\mathbb {R}})\) on \({\mathcal {U}}_{d;\le n}\), since for any \({\text {O}}_d({\mathbb {R}})\) invariant function \(I:\,{\mathcal {U}}_{d;\le n}\rightarrow {\mathbb {R}}\) we have \(I({{\textbf {c}}}_{\le n})=I(\rho _d({{\textbf {c}}}_{\le n})\cdot {{\textbf {c}}}_{\le n})\). The coordinate functions of \(\rho _d({{\textbf {c}}}_{\le n})\cdot {{\textbf {c}}}_{\le n}\) are, however, in general not rational. However, polynomial invariants of the iterated-integrals signature have a rich structure and are often desired (see [13]), and hence, it is of strong interest to obtaining a minimal set of polynomial invariants separating orbits.
In fact, for subgroups G of \({\text {SL}}^{\pm }_d({\mathbb {R}})\) there is even the following conjecture [13, Conjecture 7.2] that polynomial invariants separate orbits of paths up to tree-like equivalence.
Conjecture 5.6
(Diehl-Reizenstein) Let \(Z,Z':\,[0,T]\rightarrow {\mathbb {R}}^d\) be two curves such that
for any \(\varphi \in T({\mathbb {R}}^d)\) such that \(\tilde{\phi }_{A^\top }(\varphi )=\varphi \) for any \(A\in G\). Then, there is \(A\in G\) and a curve \({\bar{Z}}\) which is tree-like equivalent to \(Z\) such that
While a proof of this conjecture for any compact group G is finished and part of work in progress by J.D., Terry Lyons, Hao Ni and R.P., we are here interested in a ’constructive’ proof which leads to an algorithm for the computation of a minimal set of polynomial-separating orbits. The following definition and proposition now provide a sufficient condition for a moving frame to lead to a fundamental set of invariants consisting only of polynomial invariants.
Definition 5.7
A moving frame \(\varrho :\,U\rightarrow G\) for the action of G on U, where U is a non-empty, G-invariant, semialgebraic subset of \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!)\), is called almost-polynomial, if there are maps \(\lambda :\,U\rightarrow {\text {GL}}_d({\mathbb {R}})\) and \(\kappa :\,{\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!)\rightarrow {\text {GL}}_d({\mathbb {R}})\), where \(\lambda \) is G-invariant, such that \(\lambda ({{\textbf {c}}}_{\le n})\) is diagonal for all \({{\textbf {c}}}_{\le n}\in U\), such that \(\lambda _{ii}\varrho _{ij}\in {\mathbb {R}}[{\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!)]\) for all \(i,j=1,\dots ,d\) and
for all \({{\textbf {c}}}_{\le n}\in U\).
Remark 5.8
Equation (30) may seem odd as an asumption at first sight; however, it is necessary for the coordinates of \(\lambda ({{\textbf {c}}}_{\le n})\varrho ({{\textbf {c}}}_{\le n})\cdot {{\textbf {c}}}_{\le n}\) to form a fundamental set of invariants: Since we assume \(\lambda \) to be an invariant function, it must functionally depend on any fundamental set of invariants.
Example 5.9
Looking at the map \(\rho _d\) defined in (14), we introduce
We can see that \(\lambda _2\) is invariant under \({\text {O}}_2({\mathbb {R}})\). Then,
whose entries are polynomial functions. In particular, the nonzero coordinates of \(\lambda _2({{\textbf {c}}}_{\le n})\rho _2({{\textbf {c}}}_{\le n})\cdot {{\textbf {c}}}_{\le n}\) are given by
We finally obtain \(\lambda _2({{\textbf {c}}}_{\le n})=\kappa _2(\lambda _2({{\textbf {c}}}_{\le n})\varrho ({{\textbf {c}}}_{\le n})\cdot {{\textbf {c}}}_{\le n})\) via
showing that \(\rho _2\) is an almost-polynomial moving frame.
Proposition 5.10
If \(\varrho :\,U\rightarrow G\) is an almost-polynomial moving frame for the action of G on U, then the nonzero components of \(\lambda ({{\textbf {c}}}_{\le n})\varrho ({{\textbf {c}}}_{\le n})\cdot {{\textbf {c}}}_{\le n}\) form a fundamental set of invariants consisting only of polynomial invariants.
Proof
Obviously \({{\textbf {c}}}_{\le n}\mapsto \lambda ({{\textbf {c}}}_{\le n})\varrho ({{\textbf {c}}}_{\le n})\cdot {{\textbf {c}}}_{\le n}\) is a polynomial map on U since \(\lambda _{ii}\mu _{ij}\) is polynomial. The components of \(\varrho ({{\textbf {c}}}_{\le n})\cdot {{\textbf {c}}}_{\le n}\) form a fundamental set of invariants since \(\varrho \) is a moving frame which implies that \(I({{\textbf {c}}}_{\le n})=I(\varrho ({{\textbf {c}}}_{\le n})\cdot {{\textbf {c}}}_{\le n})\) for any invariant function \(I:\,U\rightarrow {\mathbb {R}}\). Since \(\lambda \) is G invariant by assumption, we have that the components of \(\lambda ({{\textbf {c}}}_{\le n})\varrho ({{\textbf {c}}}_{\le n})\cdot {{\textbf {c}}}_{\le n}\) are invariants. Furthermore,
implies that the nonzero components of \(\lambda ({{\textbf {c}}}_{\le n})\varrho ({{\textbf {c}}}_{\le n})\cdot {{\textbf {c}}}_{\le n}\) form a fundamental set of invariants, too. \(\square \)
Returning to the specific setting of planar curves, we can in fact explicitly show that the following stronger statement with a slightly different construction on the level of the individual coordinates of the first kind \(c_{h}\) holds.
Theorem 5.11
There exists a set of polynomials \(q_h\) and a polynomial map \(r:\,{\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{2})\!)\rightarrow {\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{2})\!)\) which is bijective when restricted to \({\mathcal {U}}_{2;\le n}\) such that
Thus, the \(q_h({{\textbf {c}}}_{\le n})\) form a set of polynomial invariants determining the equivalence class of a path \(Z\) in \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{2})\!)\).
This theorem is stronger in the sense that the map q relating the two invariant sets is also shown to be polynomial, contrasted with Theorem 5.10 where did not assume the form of the map
Proof
Let \(n({\mathtt {i}},w)\) denote the number of times the letter \({\mathtt {i}}\) appears in the word w. Since \(c_h(Z)=\langle {{\,\mathrm{IIS}\,}}(Z),\zeta _h\rangle \) for unique \(\zeta _h\in T({\mathbb {R}}^d)\), where each \(\zeta _h\) is a linear combination of permutations of the word h, and since B is diagonal, we have

Let \(m(w)=0\) if \(n({\mathtt {1}},w)\) is even and \(m(w)=1\) if \(n({\mathtt {1}},w)\) is odd. Then, on \(U^2_n\),

and

Thus, since \(c_h(C(Z)Z)\) is polynomial in \({{\textbf {c}}}_n(Z)\), also
is polynomial in \({{\textbf {c}}}_n(Z)\) and also polynomial in \((c_h(\rho _2({{\textbf {c}}}_{\le n}(Z))\cdot Z))_h\). Finally, all \(c_h(\rho _2({{\textbf {c}}}_{\le n}(Z))\cdot Z)\) can be retrieved from \((q_h({{\textbf {c}}}_{\le n}(Z)))_h\) via
\(\square \)
We can see here how the resulting invariants differ when obtained using the procedures of Proposition 5.10 and of Theorem 5.11. For the nonzero coordinates of \(\lambda ({{\textbf {c}}}_{\le 3})\rho _2({{\textbf {c}}}_{\le 3}\cdot {{\textbf {c}}}_{\le 3})\), we get
while
Thus up to level 4, they only differ in the 112 coordinate, which is a bit “simpler” than the resulting invariant using the procedure of Theorem 5.11. Looking at the previous \(p_i\)s we listed, we see how this polynomial set can be further simplified. However, we lack a general algorithm for a “full” simplification of the set of polynomial invariants. This would be achieved if they form a minimal algebra generating set for \({\mathbb {R}}[{\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{2})\!)]^{{\text {O}}_2({\mathbb {R}})}\). This is an interesting investigation for future research.
Let us now have a look again on the spatial moving-frame map from Sect. 3.2. In this special case, we can determine the global form of the associated polynomials \(f_i\) from Proposition 4.6:
where \({\hat{c}}_{3}\), \({\hat{c}}_{12}\), \({\hat{c}}_{{23}}\) denote the nonzero components of \({\tilde{\rho }}_3({{\textbf {c}}}_{\le 2})\cdot {{\textbf {c}}}_{\le 2}\) and \(p_i({{\textbf {c}}}_{\le 2})=p_i(Z)\) for \({{\textbf {c}}}_{\le 2}={{\textbf {c}}}_{\le 2}(Z)\). From this, we can show that the moving frame is almost-polynomial. Toward this, let \(\lambda ({{\textbf {c}}}_{\le n})\) be the diagonal matrix with entries
The function \(\lambda _3\) is \({\text {O}}_3({\mathbb {R}})\)-invariant since \(p_1\), \(p_2^2\) and \(p_3\) are invariant. Furthermore, \(\lambda _3({{\textbf {c}}}_{\le n})\mu _3({{\textbf {c}}}_{\le n})\) is diagonal with entries
and hence \(\lambda _3({{\textbf {c}}}_{\le n})\rho _3({{\textbf {c}}}_{\le n})=\lambda _3({{\textbf {c}}}_{\le n})\mu _3({{\textbf {c}}}_{\le n})\nu _3({{\textbf {c}}}_{\le n})\) is also polynomial in \({{\textbf {c}}}_{\le n}\). The nonzero coordinates of \(\lambda _3({{\textbf {c}}}_{\le n})\rho _3({{\textbf {c}}}_{\le n})\cdot {{\textbf {c}}}_{\le 2}\) are then given by
Thus, we have \(\lambda _3({{\textbf {c}}}_{\le n})=\kappa _3(\lambda _3({{\textbf {c}}}_{\le n})\rho _3({{\textbf {c}}}_{\le n})\cdot {{\textbf {c}}}_{\le n})\) with \(\kappa _3(\hat{{{\textbf {c}}}}_{\le n})\) as the diagonal matrix with entries
Hence, \(\rho _3\) is an almost-polynomial moving frame, leading to a fundamental set of polynomial invariants.
Thus, we have shown that \(\rho _d\) is almost-polynomial for \(d=2, 3\). As \(d=3\) is emblematic of the procedure for higher dimensions, it is possible that this property is true for higher dimensions. We end with the following conjecture for the moving frame for which a proof or counter-example would be interesting.
Conjecture 5.12
For any \(d\ge 2\), the moving frame \(\rho _d:\,{\mathcal {U}}_{d;\le n}\rightarrow {\text {O}}_d({\mathbb {R}})\) is almost-polynomial.
We will see in the next section that this conjecture at least also holds true for \(d=3\); however, the conjecture remains open for \(d>3\). This in particular means that we have our ’constructive’ proof for Conjecture 5.6 restricted to paths \(Z\) such that \({{\textbf {c}}}_{\le n}(Z)\in {\mathcal {U}}_{d;\le n}\) in the special case of \({\text {O}}_d({\mathbb {R}})\) for \(d=2,3\). We hope to extend this result to all dimensions, all paths and to further compact groups in future work.
6 Discussion and Open Problems
We conclude with a discussion of some interesting questions arising from this work. We presented a method to construct \({\text {O}}_d({\mathbb {R}})\) invariants for a path \(Z\) from the coordinates of the log signature (of the iterated-integrals signature) in a way that completely characterizes the orbit of \({\text {proj}}_n(\log ({{\,\mathrm{IIS}\,}}(Z))\) (or \({\text {proj}}_n({{\,\mathrm{IIS}\,}}(Z))\)) under \({\text {O}}_d({\mathbb {R}})\). This procedure also furnishes a quick method to compare equivalence classes of paths under \({\text {O}}_d({\mathbb {R}})\) without computing the full set of invariants (see Example 3.5).
In particular, Theorem 5.5 is similar in spirit to [13, Conjecture 7.2], where the authors characterize all linear \({\text {SO}}_d({\mathbb {R}})\)-invariants in the coordinates of \({{\,\mathrm{IIS}\,}}(Z)\) and ask if these determine a path up to \({\text {SO}}_d({\mathbb {R}})\) and tree-like extensions. The invariant sets we construct are smooth functions in the coordinates of \(\log ({{\,\mathrm{IIS}\,}}(Z))\), though in many cases we can, by inspection, find an equivalently generating polynomial set (see Sect. 3.1). Polynomials in coordinates of \(\log ({{\,\mathrm{IIS}\,}}(Z))\) correspond to polynomial invariants in the coordinates of \({{\,\mathrm{IIS}\,}}(Z)\), which yield linear \({\text {O}}_d({\mathbb {R}})\)-invariants by the shuffle relations. Thus, the conjecture remains open, and more broadly, the connection between the two sets of invariants should be explored.
In Sect. 4, we investigate sets of separating sets of rational and polynomial invariants for the action of \({\text {O}}_d({\mathbb {R}})\) on \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{d})\!)\). An open question is whether the polynomial invariants we construct, generates the ring of polynomial invariants for this action. In even more generality questions remain about the relationship between the polynomial invariants we construct and the ring of polynomial invariants for the action of \({\text {O}}_d({\mathbb {R}})\) on \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!)\).
Additionally we only consider \({\text {O}}_d({\mathbb {R}})\)-invariants (and to a lesser extent \({\text {SO}}_d({\mathbb {R}})\)) in this work. The dimension of \({\text {O}}_d({\mathbb {R}})\) implies that to construct a cross-section for the action, one only has to consider the action on \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{d})\!)\). For larger groups like \({\text {GL}}_d({\mathbb {R}})\), one may have to construct a cross-section using coordinates on \({\mathfrak {g}}_{\le 3}(\!({\mathbb {R}}^{d})\!)\).
The cross-section \({\mathcal {K}}\) in Sect. 5.1 can also be used as a starting point for groups containing \({\text {O}}_d({\mathbb {R}})\), since any element of \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{d})\!)\) can be brought to \({\mathcal {K}}\) by an element of \({\text {O}}_d({\mathbb {R}})\). For instance, if one considers scaling transformations in addition to orthogonal transformations, changing the conditions of \(c_{d}, c_{i(i+1)} >0\) on \({\mathcal {K}}\) to \(c_{d}=c_{i(i+1)}=0\), for \(1\le i < d\), likely yields a cross-section.
In Sect. 5.2, we introduce Conjecture 5.12, which we prove holds for \(d=2\) in Theorem 5.11 and for \(d=3\) in Sect. 3.2. In general, the invariants produced by the moving-frame method are only guaranteed to be smooth, and hence, proving this conjecture for \(d>3\) is of interest. In particular, polynomial-invariant functions of iterated-integrals values are desired because they can be expressed as elements of \(T({\mathbb {R}}^d)\), they provide the simplest and most structured (graded) way of looking at invariants, with an immediate connection to polynomial algebraic geometry, and it is widely assumed and partially proven that they are sufficient for characterization of orbits, see the discussion of the Diehl–Reizenstein conjecture in Sect. 5.2.
As mentioned in the introduction, there are many applications of the iterated-integrals signature of paths where finding \({\text {O}}_d({\mathbb {R}})\)-invariant features could be advantageous. It would be interesting to see if the sets of integral invariants constructed, or “invariantization” procedure outlined can be useful for such applications. For example, in [17], the author explores using the features generated from the iterated-integrals signature for different tasks using various machine learning algorithms and demonstrates results that are competitive with state of the art. Two of these tasks include drawing recognition (where a drawing is represented by a time series of 2D points, and the task is to classify the drawing) and human action recognition (where different points on the human body are tracked to construct multiple concurrent time series of 3D points, and the task is to classify the action). In both of these tasks, the data is spatial in nature, and it is possible that using an invariantized iterated-integrals signature or adding invariant features could improve the accuracy of common machine learning algorithms.
Notes
The signed area is an \(\mathrm {SO}_2({\mathbb {R}})\) invariant; however, only its square (resp. its absolute value) is an \({\text {O}}_2({\mathbb {R}})\) invariant.
For more on the specific relevance of signed area in the study of the iterated-integrals signature, see [12].
One can get away with much less regularity, see [35]. Since our considerations are purely algebraic, there is no loss in restricting to ’smooth’ paths.
This follows from Chow’s theorem, [20, Theorem 7.28].
Here actly smoothly means that the map defining the group action is a \(C^\infty \) map. For our purposes, there is no loss in taking ’smooth’ to mean ’\(C^\infty \)’..
The Zariski topology on an affine space \(k^d\) is the topology where closed sets are given by subsets of the form \(V(f_1,\ldots ,f_s) = \{ (x_1,\ldots ,x_d)\in k^d\,| \, f_1(x_1,\ldots ,x_d)=\cdots =f_s(x_1,\ldots ,x_d)=0\}\) for some collection of polynomials \(f_1,\ldots ,f_s\in k[x_1,\ldots ,x_d]\).
By a generating set for \(k[X]^G\), we refer to a subset of \(k[X]^G\) that generates \(k[X]^G\) as a polynomial ring. Similarly, a generating set of \(k(X)^G\) is a subset that generates \(k(X)^G\) as a field.
The constant functions are referred to as the phantom invariants.
Note that Brownian motions technically fall out of the scope of this paper, as we assumed the curves to be studied to be of bounded variation, whereas Brownian motion almost surely has infinite variation. However, any bounded variation curve perturbed by Brownian motion can be reintegrated into the setup of this paper by applying the theory of Stratonovich integration instead of Riemann–Stieltjes integration. For our numerical studies, this technicality is of no effect as we effectively only calculate with piecewise-linear interpolations of Brownian motion, which are of bounded variation again of course. The fact that makes everything fit together is then the well-known result that the signature of piecewise-linearly interpolated Brownian motion converges almost surely to the Stratonovich signature, see [19, Proposition 3.6] (they only prove convergence of the level 2 signature uniformly over any time interval, but this implies convergence of the full signature in a suitable topology). Also compare [20, Proposition 13.18] (which is not enough for what we argue here though).
The transcendence degree of \({\mathbb {C}}(X)^G\) is given by the cardinality of the largest set \(\{f_1,\ldots ,f_n\}\in {\mathbb {C}}(X)^G\) such that there does not exist a rational function F where \(F(f_1,\ldots ,f_n)\equiv 0\in {\mathbb {C}}(X)^G\).
Abbreviations
- \(c_{h}\) :
-
The coordinate of \({{\textbf {c}}}_{\le n}\in {\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!)\) corresponding to the Hall basis element \(b_h\)
- \({{\textbf {c}}}_{\le n}\) :
-
An element of \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!)\) with coordinates given by \(c_{i_1i_2\cdots i_m}\) for \(m\le n\)
- \(G({\mathbb {R}})\) :
-
A real variety with associated complex variety G, of which it is also a subgroup
- \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!)\) :
-
The free step-n nilpotent Lie algebra over \({\mathbb {R}}^d\)
- \(G_z\) :
-
The stabilizer of a point z, the largest subgroup of G that keeps z invariant
- \({{\mathfrak {I}}}_d\) :
-
The set of rational invariants defining \({U_d({\mathbb {C}})}\)
- \({{\,\mathrm{IIS}\,}}(Z)\) :
-
The iterated-integrals signature of the curve \(Z\)
- \({{\mathfrak {I}}}_M\) :
-
The set of polynomial invariants generating \({\mathbb {C}}({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}}))^{{\text {O}}_d({\mathbb {C}})}\) given by \(\phi _k\cdot \phi _k\), \(1\le k<d\)
- \({{\mathfrak {I}}}_{W_d({\mathbb {C}})}\) :
-
The generating set for \({\mathbb {C}}({L_{d}^{(d-1)}})^{W_d({\mathbb {C}})}\) given by \(\sigma _{d-1}({{\mathfrak {I}}}_d)\)
- k(X):
-
The field of rational functions on the variety X with coefficients in k
- \(k(X)^G\) :
-
The subfield of k(X) of rational invariants for the action of G on X
- \({\mathcal {K}}_{2,\le 2}\) :
-
The cross-section for the action of \({\text {O}}_2({\mathbb {R}})\) on \({\mathcal {U}}_{2;\le 2}\)
- \({{\mathcal {K}}_{d;\le n}}\) :
-
The cross-section for the action of \({\text {O}}_d({\mathbb {R}})\) on \({\mathcal {U}}_{d;\le n}\)
- k[X]:
-
The ring of polynomial functions on the variety X with coefficients in k
- \(k[X]^G\) :
-
The subring of k[X] of polynomial invariants for the action of G on X
- \({L_{d}^{(d-1)}}\) :
-
The relative \({W_d({\mathbb {C}})}\)-section for the action of \({\text {O}}_d({\mathbb {C}})\) on \({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}})\)
- \({\mathscr {L}}_{d}\) :
-
The Lyndon words over the alphabet \(\{{\mathtt {1}},\ldots ,{\mathtt {d}}\}\)
- \(L_d^{(d-1);{\mathbb {R}}}\) :
-
The intersection of \({L_{d}^{(d-1)}}\) and \({\mathbb {R}}^d\oplus \mathfrak {so}_{d}({\mathbb {R}})\)
- \({L_{d}^{(i)}}\) :
-
The relative \({N_{d}^{d-i}({\mathbb {C}})}\)-section for the action of \({\text {O}}_d({\mathbb {C}})\) on \({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}})\)
- \(\log ({{\,\mathrm{IIS}\,}}(Z))\) :
-
The log-signature of the curve \(Z\)
- \({N_{d}^{i}({\mathbb {C}})}\) :
-
The product of the groups \({\text {O}}^i_d({\mathbb {C}})\) and \({W_d({\mathbb {C}})}\); the normalizer of \({L_{d}^{(d-i)}}\)
- \({\text {O}}^i_d({\mathbb {C}})\) :
-
The subgroup of \({\text {O}}_d({\mathbb {C}})\) isomorphic to \({\text {O}}_i({\mathbb {C}})\) which leaves the last \(d-i\) components of a \({\mathbb {C}}^d\) vector invariant
- \(\phi _k\) :
-
The map \(\phi _k :{\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}})\rightarrow {\mathbb {C}}^d,\,(v,M) \mapsto M^kv\)
- \({\text {proj}}_{\le n}\) :
-
The canonical projection \({\text {proj}}_{\le n}:T(\!({\mathbb {R}}^d)\!)\rightarrow T_{\le n}(\!({\mathbb {R}}^d)\!)\)
- \({\text {proj}}_{\le n\rightarrow \le 2}\) :
-
The canonical projection \({\text {proj}}_{\le n\rightarrow \le 2}:\,{\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!)\rightarrow {\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{d})\!)\)
- \({\tilde{\rho }}_2\) :
-
The moving-frame map \({\tilde{\rho }}_2:\,{\mathcal {U}}_{2;\le 2} \rightarrow {\text {O}}_2({\mathbb {R}})\) for the action of \({\text {O}}_2({\mathbb {R}})\) on \({\mathcal {U}}_{2;\le 2}\)
- \(\rho _2\) :
-
The moving-frame map for the action of \({\text {O}}_2({\mathbb {R}})\) on \({\mathcal {U}}_{2;\le n}\), where \(\rho _2({{\textbf {c}}}_{\le n})={\tilde{\rho }}_2({\text {proj}}_{\le 2}{{\textbf {c}}}_{\le n})\)
- \({\tilde{\rho }}_d\) :
-
The moving-frame map for the action of \({\text {O}}_d({\mathbb {R}})\) on \({\mathcal {U}}_{d;\le 2}\)
- \(\rho _d\) :
-
The moving-frame map for the action of \({\text {O}}_d({\mathbb {R}})\) on \({\mathcal {U}}_{d;\le n}\), where \(\rho _d({{\textbf {c}}}_{\le n})={\tilde{\rho }}_d({\text {proj}}_{\le 2}{{\textbf {c}}}_{\le n})\)
- \(\sigma _i\) :
-
The field isomorphism \(\sigma _i : {\mathbb {C}}({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}}))^{{\text {O}}_d({\mathbb {C}})} {\rightarrow } {\mathbb {C}}({L_{d}^{(i)}})^{{N_{d}^{d-i}({\mathbb {C}})}}\)
- \(\mathfrak {so}(d,{\mathbb {R}})\) :
-
The space of skew-symmetric \({\mathbb {R}}^{d\times d}\) matrices
- \({\mathcal {U}}_{2;\le 2}\) :
-
The domain of the moving-frame \({\tilde{\rho }}_2\), a Zariski-open subset of \({\mathfrak {g}}_{\le 2}(\!({\mathbb {R}}^{2})\!)\)
- \({\mathcal {U}}_{d;\le n}\) :
-
The domain of the moving frame \(\rho _d\), a Zariski-open subset of \({\mathfrak {g}}_{\le n}(\!({\mathbb {R}}^{d})\!)\)
- \({U_d({\mathbb {C}})}\) :
-
The Zariski-open subset of \({\mathbb {C}}^d\oplus \mathfrak {so}_{d}({\mathbb {C}})\) where none of the invariants in \({{\mathfrak {I}}}_d\) vanishes
- \({U_{d}({\mathbb {R}})}\) :
-
The intersection of \({U_d({\mathbb {C}})}\) and \({\mathbb {R}}^d\oplus \mathfrak {so}_{d}({\mathbb {R}})\), a Zariski open subset of \({\mathbb {R}}^d\oplus \mathfrak {so}_{d}({\mathbb {R}})\)
- \({W_d({\mathbb {C}})}\) :
-
The group of diagonal matrices with diagonal entries in \(\{-1,1\}\); the normalizer of \({L_{d}^{(d-1)}}\)
- \(X({\mathbb {R}})\) :
-
A real variety with associated complex variety X
References
Boutin, M.: The pascal triangle of a discrete image: Definition, properties and application to shape analysis. Symmetry, Integrability and Geometry: Methods and Applications (2013). https://doi.org/10.3842/sigma.2013.031
Calabi, E., Olver, P.J., Shakiban, C., Tannenbaum, A., Haker, S.: Differential and numerically invariant signatures curves applied to object recognition. Int. J. Computer vision 26, Paper 107,135 (1998)
Cartan, E.: La méthode du repère mobile, la théorie des groupes continus, et les espaces généralisés, Exposés de Géométrie, vol. 5. Hermann, Paris (1935)
Cartan, E.: La théorie des groupes finis et continus et la géométrie différentielle, traitées par la méthode du repere mobile. leçons professées à la sorbonne. tgfc (1951)
Celledoni, E., Lystad, P.l.E., Tapia, N.: Signatures in shape analysis: an efficient approach to motion identification. In: Geometric science of information, Lecture Notes in Comput. Sci., vol. 11712, pp. 21–30. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26980-7_3
Chen, K.T.: Iterated integrals and exponential homomorphisms. Proceedings of the London Mathematical Society s3-4(1), 502–512 (1954). https://doi.org/10.1112/plms/s3-4.1.502
Chen, K.T.: Iterated integrals and exponential homomorphisms. Proc. London Math. Soc. s3-4(1), 502–512 (1954). https://doi.org/10.1112/plms/s3-4.1.502
Chen, K.T.: Integration of paths—a faithful representation of paths by non-commutative formal power series. Trans. Amer. Math. Soc. 89, 395–407 (1958). https://doi.org/10.2307/1993193
Chevyrev, I., Kormilitzin, A.: A primer on the signature method in machine learning (2016)
Colmenarejo, L., Preiß, R.: Signatures of paths transformed by polynomial maps. Beitr. Algebra Geom. 61(4), 695–717 (2020). https://doi.org/10.1007/s13366-020-00493-9
Derksen, H., Kemper, G.: Computational invariant theory. Springer (2015)
Diehl, J., Lyons, T., Preiß, R., Reizenstein, J.: Areas of areas generate the shuffle algebra (2021)
Diehl, J., Reizenstein, J.: Invariants of Multidimensional Time Series Based on Their Iterated-Integral Signature. Acta Appl. Math. 164, 83–122 (2019). https://doi.org/10.1007/s10440-018-00227-z
Fels, M., Olver, P.J.: Moving coframes: I. a practical algorithm. Acta Applicandae Mathematica 51(2), 161–213 (1998)
Fels, M., Olver, P.J.: Moving Coframes. II. Regularization and Theoretical Foundations. Acta Appl. Math. 55, 127–208 (1999)
Feng, S., Kogan, I., Krim, H.: Classification of curves in 2d and 3d via affine integral signatures. Acta Applicandae Mathematicae 109(3), 903–937 (2008). https://doi.org/10.1007/s10440-008-9353-9
Fermanian, A.: Embedding and learning with signatures. Computational Statistics & Data Analysis 157, 107148 (2021). https://doi.org/10.1016/j.csda.2020.107148
Foissy, L., Patras, F., Thibon, J.Y.: Deformations of shuffles and quasi-shuffles. Ann. Inst. Fourier (Grenoble) 66(1), 209–237 (2016)
Friz, P.K., Hairer, M.: A Course on Rough Paths: With an Introduction to Regularity Structures, second edn. Universitext. Springer Nature Switzerland (2020). https://doi.org/10.1007/978-3-030-41556-3
Friz, P.K., Victoir, N.B.: Multidimensional stochastic processes as rough paths: theory and applications, vol. 120. Cambridge University Press (2010)
Görlach, P., Hubert, E., Papadopoulo, T.: Rational invariants of even ternary forms under the orthogonal group. Foundations of Computational Mathematics 19(6), 1315–1361 (2018). https://doi.org/10.1007/s10208-018-9404-1
Grim, A., Shakiban, C.: Applications of signature curves to characterize melanomas and moles. In: Applications of computer algebra, Springer Proc. Math. Stat., vol. 198, pp. 171–189. Springer, Cham (2017)
Harris, J.: Algebraic geometry: a first course, vol. 133. Springer Science & Business Media (2013)
Hilbert, D.: Ueber die theorie der algebraischen formen. Mathematische Annalen 36(4), 473–534 (1890). https://doi.org/10.1007/bf01208503
Hoff, D.J., Olver, P.J.: Extensions of invariant signatures for object recognition. J. Math. Imaging Vision 45(2), 176–185 (2013). https://doi.org/10.1007/s10851-012-0358-7
Hoff, D.J., Olver, P.J.: Automatic solution of jigsaw puzzles. J. Math. Imaging Vision 49(1), 234–250 (2014)
Hubert, E., Kogan, I.A.: Rational invariants of a group action. construction and rewriting. Journal of Symbolic Computation 42(1-2), 203–217 (2007).
Hubert, E., Kogan, I.A.: Smooth and algebraic invariants of a group action: local and global constructions. Found. Comput. Math. 7(4), 455–493 (2007)
Karlin, S., Shapley, L.S.: Geometry of moment spaces. 12. American Mathematical Soc. (1953)
Kawski, M.: Chronological calculus in systems and control theory. Mathematics of Complexity and Dynamical Systems p. 88 (2011)
Kogan, I.A.: Two algorithms for a moving frame construction. Canadian Journal of Mathematics 55(2), 266–291 (2003)
Kogan, I.A., Ruddy, M., Vinzant, C.: Differential signatures of algebraic curves. SIAM Journal on Applied Algebra and Geometry 4(1), 185–226 (2020). https://doi.org/10.1137/19m1242859
Lee, D., Ghrist, R.: Path signatures on lie groups (2020)
Littlewood, D.E., Gurevich, G.B., Radok, J.R.M., Spencer, A.J.M.: Foundation of the theory of algebraic invariants. The Mathematical Gazette 49(369), 346 (1965). https://doi.org/10.2307/3612914
Lyons, T.J.: Differential equations driven by rough signals. Revista Matemática Iberoamericana 14(2), 215–310 (1998)
Lyons, T.J., Yam, P.S.: On gauss–green theorem and boundaries of a class of hölder domains. Journal de mathématiques pures et appliquées 85(1), 38–53 (2006)
Manchon, D.: Hopf algebras in renormalisation. Handbook of algebra 5, 365–427 (2008)
Manchon, D.: Hopf algebras in renormalisation. In: Handbook of algebra. Vol. 5, Handb. Algebr., vol. 5, pp. 365–427. Elsevier/North-Holland, Amsterdam (2008). https://doi.org/10.1016/S1570-7954(07)05007-3
Morales, J., Akopian, D.: Physical activity recognition by smartphones, a survey. Biocybernetics and Biomedical Engineering 37(3), 388–400 (2017)
Nagata, M.: On the 14-th problem of hilbert. American Journal of Mathematics 81(3), 766 (1959). https://doi.org/10.2307/2372927
Olver, P.J.: Classical Invariant Theory. Cambridge University Press (1999). https://doi.org/10.1017/cbo9780511623660
Olver, P.J.: Joint invariant signatures. Foundations of Computational Mathematics 1(1), 3–68 (2001). https://doi.org/10.1007/s10208001001
Olver, P.J.: Lectures on Moving Frames (2018)
Owren, B., Marthinsen, A.: Integration methods based on canonical coordinates of the second kind. Numerische Mathematik 87(4), 763–790 (2001)
Perrin, D.: Factorizations of free monoids. In: M. Lothaire (ed.) Combinatorics on Words, 2nd edn. Cambridge University Press (2011)
Popov, V.L., Vinberg, E.B.: Invariant theory. In: Algebraic geometry IV, pp. 123–278. Springer (1994)
Ree, R.: Lie elements and an algebra associated with shuffles. Ann. Math. (2) 68(2), 210–220 (1958). https://doi.org/10.2307/1970243
Rudin, W., et al.: Principles of mathematical analysis, vol. 3. McGraw-hill New York (1964)
Salvi, C.: Rough paths, kernels, differential equations and an algebra of functions on streams. Ph.D. thesis, University of Oxford (2021)
Sturmfels, B.: Algorithms in invariant theory. Springer Science & Business Media (2008)
Tuznik, S.L., Olver, P.J., Tannenbaum, A.: Equi-affine differential invariants for invariant feature point detection. European Journal of Applied Mathematics 31(2), 277–296 (2019). https://doi.org/10.1017/s0956792519000020
Zhang, Y., Li, K., Chen, X., Zhang, S., Geng, G.: A multi feature fusion method for reassembly of 3d cultural heritage artifacts. Journal of Cultural Heritage 33, 191–200 (2018)
Acknowledgements
R.P. is supported by the European Research Council through CoG-683164, M.R. was supported in part by the Max Planck Institute for Mathematics in the Sciences and the Data Institute at University of San Francisco, N.T. is supported by the DFG MATH\(^+\) Excellence Cluster.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Communicated by Teresa Krick.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Diehl, J., Preiß, R., Ruddy, M. et al. The Moving-Frame Method for the Iterated-Integrals Signature: Orthogonal Invariants. Found Comput Math 23, 1273–1333 (2023). https://doi.org/10.1007/s10208-022-09569-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10208-022-09569-5
Keywords
- Geometric invariants
- Orthogonal group
- Shuffle product
- Log-signature
- Coordinates of the first kind
- Polynomial invariants
- Integral invariants
- Signed volume
- Signed area
- Almost-polynomial moving-frame