Abstract
This paper introduces a new notion of a Fenchel conjugate, which generalizes the classical Fenchel conjugation to functions defined on Riemannian manifolds. We investigate its properties, e.g., the Fenchel–Young inequality and the characterization of the convex subdifferential using the analogue of the Fenchel–Moreau Theorem. These properties of the Fenchel conjugate are employed to derive a Riemannian primal-dual optimization algorithm and to prove its convergence for the case of Hadamard manifolds under appropriate assumptions. Numerical results illustrate the performance of the algorithm, which competes with the recently derived Douglas–Rachford algorithm on manifolds of nonpositive curvature. Furthermore, we show numerically that our novel algorithm may even converge on manifolds of positive curvature.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Convex analysis plays an important role in optimization, and an elaborate theory on convex analysis and conjugate duality is available on locally convex vector spaces. Among the vast references on this topic, we mention [4] for convex analysis and monotone operator techniques, [31] for convex analysis and the perturbation approach to duality, or [50] for an in-depth development of convex analysis on Euclidean spaces. Further, conjugate duality on Euclidean spaces is considered in [51], conjugate duality on locally convex vector spaces in [16, 60], and some particular applications of conjugate duality in economics in [44].
We wish to emphasize in particular the role of convex analysis in the analysis and numerical solution of regularized ill-posed problems. Consider for instance the total variation (TV) functional, which was introduced for imaging applications in the famous Rudin–Osher–Fatemi (ROF) model, see [52], and which is known for its ability to preserve sharp edges. We refer the reader to [24] for further details about total variation for image analysis. Further applications and regularizers can be found in [23, 25, 27, 55, 58]. In addition, higher-order differences or differentials can be taken into account, see for example [28, 45] or most prominently the total generalized variation (TGV) [20]. These models use the idea of the pre-dual formulation of the energy functional and Fenchel duality to derive efficient algorithms. Within the image processing community, the resulting algorithms of primal-dual hybrid gradient type are often referred to as the Chambolle–Pock algorithm, see [26].
In recent years, optimization on Riemannian manifolds has gained a lot of interest. Starting in the 1970s, optimization on Riemannian manifolds and corresponding algorithms have been investigated; see for instance [56] and the references therein. In particular, we point out the work by Rapcsák with regard to geodesic convexity in optimization on manifolds; see for instance [47, 48] and [49, Ch. 6]. The latter reference also serves as a source for optimization problems on manifolds obtained by rephrasing equality constrained problems in vector spaces as unconstrained problems on certain manifolds. For a comprehensive textbook on optimization on matrix manifolds, see [1] and the recent [17].
With the emergence of manifold-valued imaging, for example in InSAR imaging [21], data consisting of orientations for example in electron backscattered diffraction (EBSD) [2, 38], dextrous hand grasping [29], or for diffusion tensors in magnetic resonance imaging (DT-MRI), for example discussed in [46], the development of optimization techniques and/or algorithms on manifolds (especially for non-smooth functionals) has gained a lot of attention. Within these applications, the same tasks as in classical Euclidean imaging appear, such as denoising, inpainting, or segmentation. The total variation was introduced as a prior in a variational model for manifold-valued images in [43] as well as [59]. While the first extends a lifting approach previously introduced for cyclic data in [54] to Riemannian manifolds, the latter introduces a cyclic proximal point algorithm (CPPA) to compute a minimizer of the variational model. Such an algorithm was previously introduced by [5] on \({\text {CAT}}(0)\) spaces based on the proximal point algorithm introduced by [34] on Riemannian manifolds. Based on these models and algorithms, higher-order models have been derived [7, 10, 12, 19]. Using a relaxation, the half-quadratic minimization [9], also known as iteratively reweighted least squares (IRLS) [36], has been generalized to manifold-valued image processing tasks and employs a quasi-Newton method. Finally, the parallel Douglas–Rachford algorithm (PDRA) was introduced on Hadamard manifolds [13] and its convergence proof is, to the best of our knowledge, limited to manifolds with constant nonpositive curvature. Numerically, the PDRA still performs well on arbitrary Hadamard manifolds. However, for the classical Euclidean case the Douglas–Rachford algorithm is equivalent to applying the alternating directions method of multipliers (ADMM) [35] on the dual problem and hence is also equivalent to the algorithm of [26].
In this paper, we introduce a new notion of Fenchel duality for Riemannian manifolds, which allows us to derive a conjugate duality theory for convex optimization problems posed on such manifolds. Our theory allows new algorithmic approaches to be devised for optimization problems on manifolds. In the absence of a global concept of convexity on general Riemannian manifolds, our approach is local in nature. On so-called Hadamard manifolds, however, there is a global notion of convexity and our approach also yields a global method.
The work closest to ours is [3], who introduce a Fenchel conjugacy-like concept on Hadamard metric spaces, using a quasilinearization map in terms of distances as the duality product. In contrast, our work makes use of intrinsic tools from differential geometry such as geodesics, tangent and cotangent vectors to establish a conjugation scheme which extends the theory from locally convex vector spaces to Riemannian manifolds. We investigate the application of the correspondence of a primal problem

to a suitably defined dual and derive a primal-dual algorithm on Riemannian manifolds. In the absence of a concept of linear operators between manifolds, we follow the approach of [57] and state an exact and a linearized variant of our newly established Riemannian Chambolle–Pock algorithm (RCPA). We then study convergence of the latter on Hadamard manifolds. Our analysis relies on a careful investigation of the convexity properties of the functions F and G. We distinguish between geodesic convexity and convexity of a function composed with the exponential map on the tangent space. Both types of convexity coincide on Euclidean spaces. This renders the proposed RCPA a direct generalization of the Chambolle–Pock algorithm to Riemannian manifolds.
As an example for a problem of type (1.1), we detail our algorithm for the anisotropic and isotropic total variation with squared distance data term, i.e., the variants of the ROF model on Riemannian manifolds. After illustrating the correspondence to the Euclidean (classical) Chambolle–Pock algorithm, we compare the numerical performance of the RCPA to the CPPA and the PDRA. While the latter has only been shown to converge on Hadamard manifolds of constant curvature, it performs quite well on Hadamard manifolds in general. On the other hand, the CPPA is known to possibly converge arbitrarily slowly, even in the Euclidean case. We illustrate that our linearized algorithm competes with the PDRA, and it even performs favorably on manifolds with nonnegative curvature, like the sphere.
The remainder of the paper is organized as follows. In Sect. 2, we recall a number of classical results from convex analysis in Hilbert spaces. In an effort to make the paper self-contained, we also briefly state the required concepts from differential geometry. Section 3 is devoted to the development of a complete notion of Fenchel conjugation for functions defined on manifolds. To this end, we extend some classical results from convex analysis and locally convex vector spaces to manifolds, like the Fenchel–Moreau Theorem (also known as the Biconjugation Theorem) and useful characterizations of the subdifferential in terms of the conjugate function. In Sect. 4, we formulate the primal-dual hybrid gradient method (also referred to as the Riemannian Chambolle–Pock algorithm, RCPA) for general optimization problems on manifolds involving nonlinear operators. We present an exact and a linearized formulation of this novel method and prove, under suitable assumptions, convergence for the linearized variant to a minimizer of a linearized problem on arbitrary Hadamard manifolds. As an application of our theory, Sect. 5 focuses on the analysis of several total variation models on manifolds. In Sect. 6, we carry out numerical experiments to illustrate the performance of our novel primal-dual algorithm. Finally, we give some conclusions and further remarks on future research in Sect. 7.
2 Preliminaries on Convex Analysis and Differential Geometry
In this section, we review some well-known results from convex analysis in Hilbert spaces as well as necessary concepts from differential geometry. We also revisit the intersection of both topics, convex analysis on Riemannian manifolds, including its subdifferential calculus.
2.1 Convex Analysis
In this subsection, let  , where
, where  denotes the extended real line and
denotes the extended real line and  is a Hilbert space with inner product
is a Hilbert space with inner product  and duality pairing
and duality pairing  , respectively. Here,
, respectively. Here,  denotes the dual space of
denotes the dual space of  . When the space
. When the space  and its dual
and its dual  are clear from the context, we omit the space and just write
are clear from the context, we omit the space and just write  and
and  , respectively. For standard definitions like closedness, properness, lower semicontinuity (lsc) and convexity of f we refer the reader,
, respectively. For standard definitions like closedness, properness, lower semicontinuity (lsc) and convexity of f we refer the reader,  , to the textbooks [4, 50].
, to the textbooks [4, 50].
Definition 2.1
The Fenchel conjugate of a function  is defined as the function
is defined as the function  such that
such that

We recall some properties of the classical Fenchel conjugate function in the following lemma.
Lemma 2.2
[4, Ch. 13] Let  be proper functions,
be proper functions,  ,
,  and
and  . Then the following statements hold.
. Then the following statements hold.
-
(i)
\(f^*\) is convex and lsc.
-
(ii)
If \(f(x)\le g(x)\) for all
 , then \(f^*(x^*)\ge g^*(x^*)\) for all
, then \(f^*(x^*)\ge g^*(x^*)\) for all  .
. -
(iii)
If \(g(x)=f(x)+\alpha \) for all
 , then \(g^*(x^*) = f^*(x^*) - \alpha \) for all
, then \(g^*(x^*) = f^*(x^*) - \alpha \) for all  .
. -
(iv)
If \(g(x) = \lambda f(x)\) for all
 , then \(g^*(x^*)=\lambda f^*(x^*/\lambda )\) for all
, then \(g^*(x^*)=\lambda f^*(x^*/\lambda )\) for all 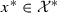 .
. -
(v)
If \(g(x) = f(x+b)\) for all
 , then
, then  for all
for all  .
. -
(vi)
The Fenchel–Young inequality holds,
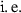 , for all
, for all  we have
we have  (2.2)
(2.2)
The Fenchel conjugate of a function  can be interpreted as a maximum seeking problem on the epigraph
can be interpreted as a maximum seeking problem on the epigraph  . For the case \(d=1\) and some fixed \(x^*\), the conjugate maximizes the (signed) distance
. For the case \(d=1\) and some fixed \(x^*\), the conjugate maximizes the (signed) distance  of the line of slope \(x^*\) to f. For instance, let us focus on the case \(x^*=-4\) highlighted in Fig. 1a. For the linear functional
of the line of slope \(x^*\) to f. For instance, let us focus on the case \(x^*=-4\) highlighted in Fig. 1a. For the linear functional  (dashed), the maximal distance is attained at \({\hat{x}}\). We can find the same value by considering the shifted functional \(h_{x^*}(x) = g_{x^*}(x) - f^*(x^*)\) (dotted line) and its negative value at the origin,
(dashed), the maximal distance is attained at \({\hat{x}}\). We can find the same value by considering the shifted functional \(h_{x^*}(x) = g_{x^*}(x) - f^*(x^*)\) (dotted line) and its negative value at the origin,  , \(-h_{x^*}(0) = f^*(x^*)\). Furthermore, \(h_{x^*}\) is actually tangent to f at the aforementioned maximizer \({\hat{x}}\). The function \(h_{x^*}\) also illustrates the shifting property from Lemma 2.2 (v) and its linear offset
, \(-h_{x^*}(0) = f^*(x^*)\). Furthermore, \(h_{x^*}\) is actually tangent to f at the aforementioned maximizer \({\hat{x}}\). The function \(h_{x^*}\) also illustrates the shifting property from Lemma 2.2 (v) and its linear offset  . The overall plot of the Fenchel conjugate \(f^*\) over an interval of values \(x^*\) is shown in Fig. 1b.
. The overall plot of the Fenchel conjugate \(f^*\) over an interval of values \(x^*\) is shown in Fig. 1b.
We now recall some results related to the definition of the subdifferential of a proper function.
Definition 2.3
[4, Def. 16.1] Let  be a proper function. Its subdifferential is defined as
be a proper function. Its subdifferential is defined as

Theorem 2.4
[4, Prop. 16.9] Let  be a proper function and
be a proper function and  . Then \(x^{*}\in \partial f(x)\) holds if and only if
. Then \(x^{*}\in \partial f(x)\) holds if and only if

Corollary 2.5
[4, Thm. 16.23] Let be a lsc, proper, and convex function and  . Then \(x \in \partial f^*(x^*)\) holds if and only if \(x^* \in \partial f(x)\).
. Then \(x \in \partial f^*(x^*)\) holds if and only if \(x^* \in \partial f(x)\).
The Fenchel biconjugate  of a function
of a function  is given by
is given by

Finally, we conclude this section with the following result known as the Fenchel–Moreau or Biconjugation Theorem.
Theorem 2.6
[4, Thm. 13.32] Given a proper function  , the equality \(f^{**}(x) = f(x)\) holds for all
, the equality \(f^{**}(x) = f(x)\) holds for all  if and only if f is lsc and convex. In this case \(f^*\) is proper as well.
if and only if f is lsc and convex. In this case \(f^*\) is proper as well.
2.2 Differential Geometry
This section is devoted to the collection of necessary concepts from differential geometry. For details concerning the subsequent definitions, the reader may wish to consult [22, 37, 41].
Suppose that \({\mathcal {M}}\) is a d-dimensional connected, smooth manifold. The tangent space at \(p \in {\mathcal {M}}\) is a vector space of dimension d and it is denoted by \({\mathcal {T}}_{p}\). Elements of \({\mathcal {T}}_{p}\),  , tangent vectors, will be denoted by \(X_p\) and \(Y_p\), etc., or simply X and Y when the base point is clear from the context. The disjoint union of all tangent spaces,
, tangent vectors, will be denoted by \(X_p\) and \(Y_p\), etc., or simply X and Y when the base point is clear from the context. The disjoint union of all tangent spaces,  ,
,

is called the tangent bundle of \({\mathcal {M}}\). It is a smooth manifold of dimension 2d.
The dual space of \({\mathcal {T}}_{p}\) is denoted by  and it is called the cotangent space to \({\mathcal {M}}\) at p. The disjoint union
and it is called the cotangent space to \({\mathcal {M}}\) at p. The disjoint union

is known as the cotangent bundle. Elements of  are called cotangent vectors to \({\mathcal {M}}\) at p, and they will be denoted by \(\xi _p\) and \(\eta _p\) or simply \(\xi \) and \(\eta \). The natural duality product between \(X \in {\mathcal {T}}_{p}\) and
are called cotangent vectors to \({\mathcal {M}}\) at p, and they will be denoted by \(\xi _p\) and \(\eta _p\) or simply \(\xi \) and \(\eta \). The natural duality product between \(X \in {\mathcal {T}}_{p}\) and  is denoted by
is denoted by  .
.
We suppose that \({\mathcal {M}}\) is equipped with a Riemannian metric,  , a smoothly varying family of inner products on the tangent spaces \({\mathcal {T}}_{p}\). The metric at \(p \in {\mathcal {M}}\) is denoted by
, a smoothly varying family of inner products on the tangent spaces \({\mathcal {T}}_{p}\). The metric at \(p \in {\mathcal {M}}\) is denoted by  . The induced norm on \({\mathcal {T}}_{p}\) is denoted by
. The induced norm on \({\mathcal {T}}_{p}\) is denoted by  . The Riemannian metric furnishes a linear bijective correspondence between the tangent and cotangent spaces via the Riesz map and its inverse, the so-called musical isomorphisms; see [41, Ch. 8]. They are defined as
. The Riemannian metric furnishes a linear bijective correspondence between the tangent and cotangent spaces via the Riesz map and its inverse, the so-called musical isomorphisms; see [41, Ch. 8]. They are defined as

satisfying

and its inverse,

satisfying

The \(\sharp \)-isomorphism further introduces an inner product and an associated norm on the cotangent space  , which we will also denote by
, which we will also denote by  and
and  , since it is clear which inner product or norm we refer to based on the respective arguments.
, since it is clear which inner product or norm we refer to based on the respective arguments.
The tangent vector of a curve \(c :I \rightarrow {\mathcal {M}}\) defined on some open interval I is denoted by \(\dot{c}(t)\). A curve is said to be geodesic if the directional (covariant) derivative of its tangent in the direction of the tangent vanishes,  , if \(\nabla _{\dot{c}(t)} \dot{c}(t) = 0\) holds for all \(t \in I\), where \(\nabla \) denotes the Levi–Civita connection, cf. [22, Ch. 2] or [42, Thm. 4.24]. As a consequence, geodesic curves have constant speed.
, if \(\nabla _{\dot{c}(t)} \dot{c}(t) = 0\) holds for all \(t \in I\), where \(\nabla \) denotes the Levi–Civita connection, cf. [22, Ch. 2] or [42, Thm. 4.24]. As a consequence, geodesic curves have constant speed.
We say that a geodesic connects p to q if \(c(0)=p\) and \(c(1)=q\) holds. Notice that a geodesic connecting p to q need not always exist, and if it exists, it need not be unique. If a geodesic connecting p to q exists, there also exists a shortest geodesic among them, which may in turn not be unique. If it is, we denote the unique shortest geodesic connecting p and q by  .
.
Using the length of piecewise smooth curves, one can introduce a notion of metric (also known as Riemannian distance)  on \({\mathcal {M}}\); see for instance [42, Ch. 2, pp.33–39]. As usual, we denote by
on \({\mathcal {M}}\); see for instance [42, Ch. 2, pp.33–39]. As usual, we denote by

the open metric ball of radius \(r > 0\) with center \(p \in {\mathcal {M}}\). Moreover, we define \(\mathcal {B}_\infty (p) = \bigcup _{r > 0} \mathcal {B}_r(p)\).
We denote by  , with \(I\subset \mathbb {R}\) being an open interval containing 0, a geodesic starting at p with \({\dot{\gamma }}_{p,X}(0) = X\) for some \(X\in {\mathcal {T}}_{p}\). We denote the subset of \({\mathcal {T}}_{p}\) for which these geodesics are well defined until \(t=1\) by \(\mathcal {G}_p\). A Riemannian manifold \({\mathcal {M}}\) is said to be complete if \(\mathcal {G}_p = {\mathcal {T}}_{p}\) holds for some, and equivalently for all \(p \in {\mathcal {M}}\).
, with \(I\subset \mathbb {R}\) being an open interval containing 0, a geodesic starting at p with \({\dot{\gamma }}_{p,X}(0) = X\) for some \(X\in {\mathcal {T}}_{p}\). We denote the subset of \({\mathcal {T}}_{p}\) for which these geodesics are well defined until \(t=1\) by \(\mathcal {G}_p\). A Riemannian manifold \({\mathcal {M}}\) is said to be complete if \(\mathcal {G}_p = {\mathcal {T}}_{p}\) holds for some, and equivalently for all \(p \in {\mathcal {M}}\).
The exponential map is defined as the function  with
with  . Note that
. Note that  holds for every \(t\in [0,1]\). We further introduce the set \(\mathcal {G}'_p\subset {\mathcal {T}}_{p}\) as some open ball of radius \(0 < r \le \infty \) about the origin such that
holds for every \(t\in [0,1]\). We further introduce the set \(\mathcal {G}'_p\subset {\mathcal {T}}_{p}\) as some open ball of radius \(0 < r \le \infty \) about the origin such that  is a diffeomorphism. The logarithmic map is defined as the inverse of the exponential map,
is a diffeomorphism. The logarithmic map is defined as the inverse of the exponential map,  ,
,  .
.
In the particular case where the sectional curvature of the manifold is nonpositive everywhere, all geodesics connecting any two distinct points are unique. If furthermore the manifold is simply connected and complete, the manifold is called a Hadamard manifold, see [6, p.10]. Then the exponential and logarithmic maps are defined globally.
Given \(p,q\in {\mathcal {M}}\) and \(X\in {\mathcal {T}}_{p}\), we denote by  the so-called parallel transport of X along a unique shortest geodesic
the so-called parallel transport of X along a unique shortest geodesic  . Using the musical isomorphisms presented above, we also have a parallel transport of cotangent vectors along geodesics according to
. Using the musical isomorphisms presented above, we also have a parallel transport of cotangent vectors along geodesics according to

Finally, by a Euclidean space we mean \(\mathbb {R}^d\) (where \({\mathcal {T}}_{p}[\mathbb {R}^d] = \mathbb {R}^d\) holds), equipped with the Riemannian metric given by the Euclidean inner product. In this case,  and
and  hold.
hold.
2.3 Convex Analysis on Riemannian Manifolds
Throughout this subsection, \({\mathcal {M}}\) is assumed to be a complete and connected Riemannian manifold, and we are going to recall the basic concepts of convex analysis on \({\mathcal {M}}\). The central idea is to replace straight lines in the definition of convex sets in Euclidean vector spaces by geodesics.
Definition 2.7
[53, Def. IV.5.1] A subset \(\mathcal {C}\subset {\mathcal {M}}\) of a Riemannian manifold \({\mathcal {M}}\) is said to be strongly convex if for any two points \(p, q \in \mathcal {C}\), there exists a unique shortest geodesic of \({\mathcal {M}}\) connecting p to q, and that geodesic, denoted by  , lies completely in \(\mathcal {C}\).
, lies completely in \(\mathcal {C}\).
On non-Hadamard manifolds, the notion of strongly convex subsets can be quite restrictive. For instance, on the round sphere \(\mathbb {S}^{n}\) with \(n \ge 1\), a metric ball \(\mathcal {B}_r(p)\) is strongly convex if and only if \(r < \pi /2\).
Definition 2.8
Let \(\mathcal {C}\subset {\mathcal {M}}\) and \(p\in \mathcal {C}\). We introduce the tangent subset  as
as

a localized variant of the pre-image of the exponential map.
Note that if \(\mathcal {C}\) is strongly convex, the exponential and logarithmic maps introduce bijections between \(\mathcal {C}\) and  for any \(p\in \mathcal {C}\). In particular, on a Hadamard manifold \({\mathcal {M}}\), we have
for any \(p\in \mathcal {C}\). In particular, on a Hadamard manifold \({\mathcal {M}}\), we have  .
.
The following definition states the important concept of convex functions on Riemannian manifolds.
Definition 2.9
[53, Def. IV.5.9]
-
(i)
A function \(F:{\mathcal {M}}\rightarrow \overline{\mathbb {R}}\) is proper if
 and \(F(p)>-\infty \) holds for all \(p\in {\mathcal {M}}\).
and \(F(p)>-\infty \) holds for all \(p\in {\mathcal {M}}\). -
(ii)
Suppose that \(\mathcal {C}\subset {\mathcal {M}}\) is strongly convex. A function \(F:{\mathcal {M}}\rightarrow \overline{\mathbb {R}}\) is called geodesically convex on \(\mathcal {C}\subset {\mathcal {M}}\) if, for all \(p,q\in \mathcal {C}\), the composition
 is a convex function on [0, 1] in the classical sense. Similarly, F is called strictly or strongly convex if
is a convex function on [0, 1] in the classical sense. Similarly, F is called strictly or strongly convex if  fulfills these properties.
fulfills these properties. -
(iii)
Suppose that \(A \subset {\mathcal {M}}\). The epigraph of a function \(F :A \rightarrow \overline{\mathbb {R}}\) is defined as
 (2.14)
(2.14) -
(iv)
Suppose that \(A \subset {\mathcal {M}}\). A proper function \(F:A\rightarrow \overline{\mathbb {R}}\) is called lower semicontinuous (lsc) if \({{\,\mathrm{epi}\,}}F\) is closed.
Suppose that \(\mathcal {C}\subset {\mathcal {M}}\) is strongly convex and \(F :\mathcal {C}\rightarrow \overline{\mathbb {R}}\), then an equivalent way to describe its lower semicontinuity (iv) is to require that the composition

is lsc for an arbitrary \(m \in \mathcal {C}\) in the classical sense, where  is defined in Definition 2.8.
is defined in Definition 2.8.
We now recall the notion of the subdifferential of a geodesically convex function defined on a Riemannian manifold.
Definition 2.10
[33, 56, Def. 3.4.4] Suppose that \(\mathcal {C}\subset {\mathcal {M}}\) is strongly convex. The subdifferential \(\partial _{\mathcal {M}}F\) on \(\mathcal {C}\) at a point \(p\in \mathcal {C}\) of a proper, geodesically convex function \(F:\mathcal {C}\rightarrow \overline{\mathbb {R}}\), is given by

In the above notation, the index \({\mathcal {M}}\) refers to the fact that it is the Riemannian subdifferential; the set \(\mathcal {C}\) should always be clear from the context.
We further recall the definition of the proximal map, which was generalized to Hadamard manifolds in [34].
Definition 2.11
Let \({\mathcal {M}}\) be a Riemannian manifold, \(F:{\mathcal {M}}\rightarrow \overline{\mathbb {R}}\) be proper, and \(\lambda > 0\). The proximal map of F is defined as

Note that on Hadamard manifolds, the proximal map is single-valued for proper geodesically convex functions; see [6, Ch. 2.2] or [34, Lem. 4.2] for details. The following lemma is used later on to characterize the proximal map using the subdifferential on Hadamard manifolds.
Lemma 2.12
[34, Lem. 4.2] Let \(F :{\mathcal {M}}\rightarrow \overline{\mathbb {R}}\) be a proper, geodesically convex function on the Hadamard manifold \({\mathcal {M}}\). Then the equality  is equivalent to
is equivalent to

3 Fenchel Conjugation Scheme on Manifolds
In this section, we present a novel Fenchel conjugation scheme for extended real-valued functions defined on manifolds. We generalize ideas from [15], who defined local conjugation on manifolds embedded in \(\mathbb {R}^d\) specified by nonlinear equality constraints.
Throughout this section, suppose that \({\mathcal {M}}\) is a Riemannian manifold and \(\mathcal {C}\subset {\mathcal {M}}\) is strongly convex. The definition of the Fenchel conjugate of F is motivated by [50, Thm. 12.1].
Definition 3.1
Suppose that \(F:\mathcal {C}\rightarrow \overline{\mathbb {R}}\), where \(\mathcal {C}\subset {\mathcal {M}}\) is strongly convex, and \(m \in \mathcal {C}\). The m-Fenchel conjugate of F is defined as the function  such that
such that

Remark 3.2
Note that the Fenchel conjugate \(F_m^*\) depends on both the strongly convex set \(\mathcal {C}\) and on the base point m. Observe as well that when \({\mathcal {M}}\) is a Hadamard manifold, it is possible to have \(\mathcal {C}= {\mathcal {M}}\). In the particular case of the Euclidean space \(\mathcal {C}= {\mathcal {M}}= \mathbb {R}^d\), Definition 3.1 becomes

for \(\xi \in \mathbb {R}^d\). Hence, taking m to be the zero vector we recover the classical (Euclidean) conjugate \(F^*\) from Definition 2.1 with  .
.
Example 3.3
Let \({\mathcal {M}}\) be a Hadamard manifold, \(m\in {\mathcal {M}}\) and \(F:{\mathcal {M}}\rightarrow \mathbb {R}\) defined as  . Due to the fact that
. Due to the fact that

we obtain from Definition 3.1 the following representation of the m-conjugate of F:

Notice that the conjugate w.r.t. base points other than m does not have a similarly simple expression. In the Euclidean setting with \({\mathcal {M}}= \mathbb {R}^d\) and  , it is well known that
, it is well known that

holds, and thus, by Remark 3.2,

holds in accordance with the expression obtained above.
We now establish a result regarding the properness of the m-conjugate function, generalizing a result from [4, Prop. 13.9].
Lemma 3.4
Suppose that \(F:\mathcal {C}\rightarrow \overline{\mathbb {R}}\) and \(m \in \mathcal {C}\) where \(\mathcal {C}\) is strongly convex. If \(F_m^*\) is proper, then F is also proper.
Proof
Since \(F_m^*\) is proper we can pick some \(\xi _m\in {{\,\mathrm{dom}\,}}F_m^*\). Hence, applying Definition 3.1 we get

so there must exist at least one  such that
such that  . This shows that \(F \not \equiv + \infty \). On the other hand, let \(p \in \mathcal {C}\) and take
. This shows that \(F \not \equiv + \infty \). On the other hand, let \(p \in \mathcal {C}\) and take  . If F(p) were equal to \(- \infty \), then \(F_m^* (\xi _m) = +\infty \) for any
. If F(p) were equal to \(- \infty \), then \(F_m^* (\xi _m) = +\infty \) for any  , which would contradict the properness of \(F_m^*\). Consequently, F is proper. \(\square \)
, which would contradict the properness of \(F_m^*\). Consequently, F is proper. \(\square \)
Definition 3.5
Suppose that \(F:\mathcal {C}\rightarrow \overline{\mathbb {R}}\), where \(\mathcal {C}\) is strongly convex, and \(m,m' \in \mathcal {C}\). Then the (\(mm^\prime \))-Fenchel biconjugate function \(F_{mm'}^{**} :\mathcal {C}\rightarrow \mathbb {R}\) is defined as

Note that \(F_{mm'}^{**}\) is again a function defined on the Riemannian manifold. The relation between \(F_{mm}^{**}\) and F is discussed further below, as well as properties of higher order conjugates.
Lemma 3.6
Suppose that \(F:\mathcal {C}\rightarrow \overline{\mathbb {R}}\) and \(m \in \mathcal {C}\). Then \(F_{m m}^{**}(p) \le F(p)\) holds for all \(p\in \mathcal {C}\).
Proof
Applying (3.2), we have

which finishes the proof. \(\square \)
The following lemma proves that our definition of the Fenchel conjugate enjoys properties (ii)–(iv) stated in Lemma 2.2 for the classical definition of the conjugate on a Hilbert space. Results parallel to properties (i) and (vi) in Lemma 2.2 will be given in Lemma 3.12 and Proposition 3.9, respectively. Observe that an analogue of property (v) in Lemma 2.2 cannot be expected for \(F:{\mathcal {M}}\rightarrow \mathbb {R}\) due to the lack of a concept of linearity on manifolds.
Lemma 3.7
Suppose that \(\mathcal {C}\subset {\mathcal {M}}\) is strongly convex. Let \(F, G :\mathcal {C}\rightarrow \overline{\mathbb {R}}\) be proper functions, \(m \in \mathcal {C}\), \(\alpha \in \mathbb {R}\) and \(\lambda > 0\). Then the following statements hold.
-
(i)
If \(F(p)\le G(p)\) for all \(p\in \mathcal {C}\), then \(F_m^*(\xi _m) \ge G_m^*(\xi _m)\) for all
 .
. -
(ii)
If \(G(p) = F(p)+\alpha \) for all \(p\in \mathcal {C}\), then \(G_m^*(\xi _m) = F_m^*(\xi _m)-\alpha \) for all
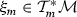 .
. -
(iii)
If \(G(p) = \lambda \, F(p)\) for all \(p\in \mathcal {C}\), then
 for all
for all  .
.
Proof
If \(F(p) \le G(p)\) for all \(p\in \mathcal {C}\), then it also holds  for every
for every  . Then we have for any
. Then we have for any  that
that

This shows (i). Similarly, we prove (ii): let us suppose that \(G(p) = F(p)+\alpha \) for all \(p\in \mathcal {C}\). Then  for every
for every  . Hence, for any
. Hence, for any  we obtain
we obtain

Let us now prove (iii) and suppose that \(\lambda >0\) and  for all
for all  . Then we have for any
. Then we have for any  that
that

\(\square \)
Suppose that \(F:\mathcal {C}\rightarrow \overline{\mathbb {R}}\), where \(\mathcal {C}\) is strongly convex, and \(m,m',m'' \in \mathcal {C}\). The following proposition addresses the triconjugate  of F, which we define as
of F, which we define as
Proposition 3.8
Suppose that \({\mathcal {M}}\) is a Hadamard manifold, \(m \in {\mathcal {M}}\) and \(F :{\mathcal {M}}\rightarrow \overline{\mathbb {R}}\). Then the following holds:

Proof
Using Definitions 2.1, 3.1 and 3.5, it is easy to see that

holds for all p in \({\mathcal {M}}\). Now (3.3), Definition 3.1, and the bijectivity of  and
and  imply that
imply that

holds for all  . We now set
. We now set  and use Definitions 2.1 and 3.1 to infer that
and use Definitions 2.1 and 3.1 to infer that

holds for all  . Consequently, we obtain
. Consequently, we obtain

According to [4, Prop. 13.14 (iii)], we have \(f_m^{***} = f_m^*\). Collecting all equalities confirms (3.4). \(\square \)
The following is the analogue of (vi) in Lemma 2.2.
Proposition 3.9
(Fenchel–Young inequality) Suppose that \(\mathcal {C}\subset {\mathcal {M}}\) is strongly convex. Let \(F:\mathcal {C}\rightarrow \overline{\mathbb {R}}\) be proper and \(m \in \mathcal {C}\). Then

holds for all \(p\in \mathcal {C}\) and  .
.
Proof
If \(F(p) = \infty \) the inequality trivially holds, since F is proper and hence \(F^*\) is nowhere \(-\infty \). It remains to consider \(F(p) <\infty \). Suppose that  , \(p \in \mathcal {C}\) and set
, \(p \in \mathcal {C}\) and set  . From Definition 3.1, we obtain
. From Definition 3.1, we obtain

which is equivalent to (3.5). \(\square \)
We continue by introducing the manifold counterpart of the Fenchel–Moreau Theorem, compare Theorem 2.6. Given a set \(\mathcal {C}\subset {\mathcal {M}}\), \(m \in \mathcal {C}\) and a function \(F :\mathcal {C}\rightarrow \overline{\mathbb {R}}\), we define \(f_m:{\mathcal {T}}_{m} \rightarrow \overline{\mathbb {R}}\) by

Throughout this section, the convexity of the function \(f_m :{\mathcal {T}}_{m} \rightarrow \overline{\mathbb {R}}\) is the usual convexity on the vector space \({\mathcal {T}}_{m}\),  , for all \(X,Y\in {\mathcal {T}}_{m}\) and \(\lambda \in [0,1]\) it holds
, for all \(X,Y\in {\mathcal {T}}_{m}\) and \(\lambda \in [0,1]\) it holds

We present two examples of functions \(F :{\mathcal {M}}\rightarrow \mathbb {R}\) defined on Hadamard manifolds such that \(f_m\) is convex. In the first example, F depends on an arbitrary fixed point \(m'\in {\mathcal {M}}\). In this case, we can guarantee that \(f_m\) is convex only when \(m = m'\). In the second example, F is defined on a particular Hadamard manifold and \(f_m\) is convex for any base point \(m \in {\mathcal {M}}\). It is worth emphasizing that the functions in the following examples are geodesically convex as well but in general, the convexity of F and \(f_m\) are unrelated and all four cases can occur.
Example 3.10
Let \({\mathcal {M}}\) be any Hadamard manifold and \(m'\in {\mathcal {M}}\) arbitrary. Consider the function \(f_{m'}\) defined in (3.6) with \(F:{{\mathcal {M}}} \rightarrow \mathbb {R}\) given by  for all \(p\in {\mathcal {M}}\). Note that
for all \(p\in {\mathcal {M}}\). Note that

Hence, it is easy to see that \(f_{m'}\) satisfies (3.7) and, consequently, it is convex on \({\mathcal {T}}_{m'}\).
Our second example is slightly more involved. A problem involving the special case \(a = 0\) and \(b = 1\) appears in the dextrous hand grasping problem in [29, Sect. 3.4].
Example 3.11
Denote by \(\mathcal {P}(n)\) the set of symmetric matrices of size \(n\times n\) for some \(n \in \mathbb {N}\), and by \({\mathcal {M}}= \mathcal {P}_+(n)\) the cone of symmetric positive definite matrices. The latter is endowed with the affine invariant Riemannian metric, given by

The tangent space \({\mathcal {T}}_{p}[{\mathcal {M}}]\) can be identified with \(\mathcal {P}(n)\). \({\mathcal {M}}\) is a Hadamard manifold, see for example [39, Thm. 1.2, p. 325]. The exponential map  is given by
is given by

Consider the function \(F :{\mathcal {M}}\rightarrow \mathbb {R}\), defined by
where \(a \ge 0\) and \(b \in \mathbb {R}\) are constants. Using (3.9) and properties of \(\det :\mathcal {P}(n) \rightarrow \mathbb {R}\), we have

for any \(m\in {\mathcal {M}}\). Hence, considering  , we obtain
, we obtain
for any \(m\in {\mathcal {M}}\). The Euclidean gradient and Hessian of \(f_m\) are given by
respectively, for all \(X,Y \in \mathcal {P}(n)\). Hence \(f_m''(X)(Y,Y) = 2a {{\,\mathrm{trace}\,}}^2(m^{-1}Y) \ge 0\) holds. Thus, the function \(f_m\) is convex for any \(m \in {\mathcal {M}}\). From [32, Ex. 4.4] we can conclude that (3.10) is also geodesically convex.
Since  is a Hilbert space, the function \(f_m\) defined in (3.6) establishes a relationship between the results of this section and the results of Sect. 2.1. We will exploit this relationship in the demonstration of the following results.
is a Hilbert space, the function \(f_m\) defined in (3.6) establishes a relationship between the results of this section and the results of Sect. 2.1. We will exploit this relationship in the demonstration of the following results.
Lemma 3.12
Suppose that \(\mathcal {C}\subset {\mathcal {M}}\) is strongly convex and \(m \in \mathcal {C}\). Suppose that \(F :\mathcal {C}\rightarrow \overline{\mathbb {R}}\). Then the following statements hold:
-
(i)
F is proper if and only if \(f_m\) is proper.
-
(ii)
\(F_m^*(\xi ) = f_m^*(\xi )\) for all
 .
. -
(iii)
The function \(F_m^*\) is convex and lsc on
 .
. -
(iv)
 for all \(p \in \mathcal {C}\).
for all \(p \in \mathcal {C}\).
Proof
Since \(\mathcal {C}\subset {\mathcal {M}}\) is strongly convex, (i) follows directly from (3.6) and the fact that the map  is bijective. As for (ii), Definition 3.1 and the definition of \(f_m\) in (3.6) imply
is bijective. As for (ii), Definition 3.1 and the definition of \(f_m\) in (3.6) imply

for all  . (iii) follows immediately from [4, Prop. 13.11] and (ii). For (iv), take \(p \in \mathcal {C}\) arbitrary. Using Definition 3.5 and (ii) we have
. (iii) follows immediately from [4, Prop. 13.11] and (ii). For (iv), take \(p \in \mathcal {C}\) arbitrary. Using Definition 3.5 and (ii) we have

which concludes the proof. \(\square \)
In the following theorem, we obtain a version of the Fenchel–Moreau Theorem 2.6 for functions defined on Riemannian manifolds. To this end, it is worth noting that if \(\mathcal {C}\) is strongly convex then
Equality (3.11) is an immediate consequence of (3.6) and will be used in the proof of the following two theorems.
Theorem 3.13
Suppose that \(\mathcal {C}\subset {\mathcal {M}}\) is strongly convex and \(m \in \mathcal {C}\). Let \(F :\mathcal {C}\rightarrow \overline{\mathbb {R}}\) be proper. If \(f_m\) is lsc and convex on \({\mathcal {T}}_{m}\), then \(F = F_{m m}^{**}\). In this case, \(F^*_m\) is proper as well.
Proof
First note that due to Lemma 3.12 (i), the function \(f_m\) is also proper. Taking into account Theorem 2.6, it follows that \(f_m = f_m^{**}\). Thus, considering (3.11), we have \(F(p) = f_m^{**}(\log _mp) \) for all \(p \in \mathcal {C}\). Using Lemma 3.12 (iv) we can conclude that \(F = F_{m m}^{**}\). Furthermore by Lemma 3.12 (i), \(f_m\) is proper. Hence by Theorem 2.6, we obtain that \(f_m^*\) is proper and by Lemma 3.12 (ii), \(F_m^*\) is proper as well. \(\square \)
Theorem 3.14
Suppose that \({\mathcal {M}}\) is a Hadamard manifold and \(m \in {\mathcal {M}}\). Suppose that \(F :{\mathcal {M}}\rightarrow \overline{\mathbb {R}}\) is a proper function. Then \(f_m\) is lsc and convex on \({\mathcal {T}}_{m}\) if and only if \(F=F_{m m}^{**}\).
In this case, \(F_m^*\) is proper as well.
Proof
Observe that due to Lemma 3.12 (i), the function \(f_m\) is proper. Taking into account Theorem 2.6, it follows that \(f_m\) is lsc and convex on \({\mathcal {T}}_{m}\) if and only if \(f_m = f_m^{**}\). Considering (3.11) and Lemma 3.12 (iv), both with \(\mathcal {C}={{\mathcal {M}}}\), we can say that \(f_m = f_m^{**}\) is equivalent to \(F = F_{m m}^{**}\). Properness of \(F_m^*\) follows by the same arguments as in Theorem 3.13. This completes the proof. \(\square \)
We now address the manifold counterpart of Theorem 2.4, whose proof is a minor extension compared to the proof for Theorem 2.4 and therefore omitted.
Theorem 3.15
Suppose that \(\mathcal {C}\subset {\mathcal {M}}\) is strongly convex and \(m, p \in \mathcal {C}\). Let \(F :\mathcal {C}\rightarrow \overline{\mathbb {R}}\) be a proper function. Suppose that \(f_m\) defined in (3.6) is convex on \({\mathcal {T}}_{m}\). Then  if and only if
if and only if

Given \(F :\mathcal {C}\rightarrow \overline{\mathbb {R}}\) and \(m\in \mathcal {C}\), we can state the subdifferential from Definition 2.10 for the Fenchel m-conjugate function  . Note that \(F_m^*\) is convex by Lemma 3.12 (iii) and defined on the cotangent space
. Note that \(F_m^*\) is convex by Lemma 3.12 (iii) and defined on the cotangent space  , so the following equation is a classical subdifferential written in terms of tangent vectors, since the dual space of
, so the following equation is a classical subdifferential written in terms of tangent vectors, since the dual space of  can be canonically identified with \({\mathcal {T}}_{m}\). The subdifferential definition reads as follows:
can be canonically identified with \({\mathcal {T}}_{m}\). The subdifferential definition reads as follows:

Before providing the manifold counterpart of Corollary 2.5, let us show how Theorem 3.15 reads for \(F_m^*\).
Corollary 3.16
Suppose that \(\mathcal {C}\subset {\mathcal {M}}\) is strongly convex and \(m, p \in \mathcal {C}\). Let \(F:\mathcal {C}\rightarrow \overline{\mathbb {R}}\) be a proper function and let \(f_m\) be the function defined in (3.6). Then

holds for all  .
.
Proof
The proof follows directly from the fact that \(F_m^*\) is defined on the vector space  and that \(F_m^*\) is convex due to Lemma 3.12 (iii). \(\square \)
and that \(F_m^*\) is convex due to Lemma 3.12 (iii). \(\square \)
To conclude this section, we state the following result, which generalizes Corollary 2.5 and shows the symmetric relation between the conjugate function and the subdifferential when the function involved is proper, convex and lsc.
Corollary 3.17
Let \(F:\mathcal {C}\rightarrow \overline{\mathbb {R}}\) be a proper function and \(m,p\in \mathcal {C}\). If the function \(f_m\) defined in (3.6) is convex and lsc on \({\mathcal {T}}_{m}\), then

Proof
The proof is a straightforward combination of Theorems 3.15 and 3.13 and taking as a particular cotangent vector  in Corollary 3.16. \(\square \)
in Corollary 3.16. \(\square \)
4 Optimization on Manifolds
In this section, we derive a primal-dual optimization algorithm to solve minimization problems on Riemannian manifolds of the form

Here \(\mathcal {C}\subset {\mathcal {M}}\) and \(\mathcal {D}\subset \mathcal {N}\) are strongly convex sets, \(F:\mathcal {C}\rightarrow \overline{\mathbb {R}}\) and  are proper functions, and \(\varLambda :{\mathcal {M}}\rightarrow \mathcal {N}\) is a general differentiable map such that \(\varLambda (\mathcal {C}) \subset \mathcal {D}\). Furthermore, we assume that \(F:\mathcal {C}\rightarrow \overline{\mathbb {R}}\) is geodesically convex and that
are proper functions, and \(\varLambda :{\mathcal {M}}\rightarrow \mathcal {N}\) is a general differentiable map such that \(\varLambda (\mathcal {C}) \subset \mathcal {D}\). Furthermore, we assume that \(F:\mathcal {C}\rightarrow \overline{\mathbb {R}}\) is geodesically convex and that

is proper, convex and lsc on \({\mathcal {T}}_{n}[\mathcal {N}]\) for some \(n \in \mathcal {D}\). One model that fits these requirements is the dextrous hand grasping problem from [29, Sect. 3.4]. There \({\mathcal {M}}= \mathcal {N}= \mathcal {P}_+(n)\) is the Hadamard manifold of symmetric positive matrices, \(F(p) = {{\,\mathrm{trace}\,}}(wp)\) holds with some \(w \in {\mathcal {M}}\), and \(G(p) = -\log \det (p)\), cf. Example 3.11. Another model verifying the assumptions will be presented in Sect. 5.
Our algorithm requires a choice of a pair of base points \(m \in \mathcal {C}\) and \(n \in \mathcal {D}\). The role of m is to serve as a possible linearization point for \(\varLambda \), while n is the base point of the Fenchel conjugate for G. More generally, the points can be allowed to change during the iterations. We emphasize this possibility by writing \(m^{(k)}\) and \(n^{(k)}\) when appropriate.
Under the standing assumptions, the following saddle-point formulation is equivalent to (4.1):

The proof of equivalence uses Theorem 3.13 applied to G and the details are left to the reader.
From now on, we will consider problem (4.3), whose solution by primal-dual optimization algorithms is challenging due to the lack of a vector space structure, which implies in particular the absence of a concept of linearity of \(\varLambda \). This is also the reason why we cannot derive a dual problem associated with (4.1) following the same reasoning as in vector spaces. Therefore, we concentrate on the saddle-point problem (4.3). Following along the lines of [57, Sect. 2], where a system of optimality conditions for the Hilbert space counterpart of the saddle-point problem (4.3) is stated, we conjecture that if  solves (4.3), then it satisfies the system
solves (4.3), then it satisfies the system

Motivated by [57, Sect. 2.2], we propose to replace \(\widehat{p}\) by m, the point where we linearize the operator \(\varLambda \), which suggests to consider the system

for the unknowns \((p,\xi _n)\).
Remark 4.1
In the specific case that  and \(\mathcal {Y}=\mathcal {N}\) are Hilbert spaces,
and \(\mathcal {Y}=\mathcal {N}\) are Hilbert spaces,  is continuously differentiable,
is continuously differentiable,  is a linear operator, \(m=n=0\), and either \(D\varLambda (m)^*\) has empty null space or \({{\,\mathrm{dom}\,}}G = \mathcal {Y}\), we observe (similar to [57]) that the conditions (4.5) simplify to
is a linear operator, \(m=n=0\), and either \(D\varLambda (m)^*\) has empty null space or \({{\,\mathrm{dom}\,}}G = \mathcal {Y}\), we observe (similar to [57]) that the conditions (4.5) simplify to
where  and
and  .
.
4.1 Exact Riemannian Chambolle–Pock

In this subsection, we develop the exact Riemannian Chambolle–Pock algorithm summarized in Algorithm 1. The name “exact”, introduced by [57], refers to the fact that the operator \(\varLambda \) in the dual step is used in its exact form and only the primal step employs a linearization in order to obtain the adjoint \(D\varLambda (m)^*\). Indeed, our Algorithm 1 can be interpreted as generalization of [57, Alg. 2.1].
Let us motivate the formulation of Algorithm 1. We start from the second inclusion in (4.5) and obtain, for any \(\tau > 0\), the equivalent condition

Similarly we obtain that the first inclusion in (4.5) is equivalent to

for any \(\sigma >0\). Lemma 2.12 now suggests the following alternating algorithmic scheme:

where



Through \(\theta \) we perform an over-relaxation of the primal variable. This basic form of the algorithm can be combined with an acceleration by step size selection as described in [26, Sec. 5]. This yields Algorithm 1.
4.2 Linearized Riemannian Chambolle–Pock
The main obstacle in deriving a complete duality theory for problem (4.3) is the lack of a concept of linearity of operators \(\varLambda \) between manifolds. In the previous section, we chose to linearize \(\varLambda \) in the primal update step only, in order to have an adjoint. By contrast, we now replace \(\varLambda \) by its first order approximation

everywhere throughout this section. Here \(D\varLambda (m):{\mathcal {T}}_{m}\rightarrow {\mathcal {T}}_{\varLambda (m)}[\mathcal {N}]\) denotes the derivative (push-forward) of \(\varLambda \) at m. Since  is a linear operator between tangent bundles, we can utilize the adjoint operator
is a linear operator between tangent bundles, we can utilize the adjoint operator  . We further point out that we can work algorithmically with cotangent vectors
. We further point out that we can work algorithmically with cotangent vectors  with a fixed base point n since, at least locally, we can obtain a cotangent vector
with a fixed base point n since, at least locally, we can obtain a cotangent vector  from it by parallel transport using
from it by parallel transport using  . The duality pairing reads as follows:
. The duality pairing reads as follows:

for every \(p\in \mathcal {C}\) and  .
.
We substitute the approximation (4.10) into (4.1), which yields the linearized primal problem

For simplicity, we assume \(\varLambda (m)=n\) for the remainder of this subection. Hence, the analogue of the saddle-point problem (4.3) reads as follows:

We refer to it as the linearized saddle-point problem. Similar as for (4.1) and (4.3), problems (4.12) and (4.13) are equivalent by Theorem 3.13. In addition, in contrast to (4.1), we are now able to also derive a Fenchel dual problem associated with (4.12).
Theorem 4.2
The dual problem of (4.12) is given by

Weak duality holds,  ,
,

Proof
The proof of (4.14) and (4.15) follows from the application of [60, eq.(2.80)] and Definition 3.1 in (4.13). \(\square \)
Notice that the analogue of (4.5) is

In the situation described in Remark 4.1, (4.16) agrees with (4.6). Motivated by the statement of the linearized primal-dual pair (4.12), (4.14) and saddle-point system (4.13), a further development of duality theory and an investigation of the linearization error is left for future research.
Both the exact and the linearized variants of our Riemannian Chambolle–Pock algorithm (RCPA) can be stated in two variants, which over-relax either the primal variable as in Algorithm 1, or the dual variable as in Algorithm 2. In total this yields four possibilities—exact vs. linearized, and primal vs. dual over-relaxation. This generalizes the analogous cases discussed in [57] for the Hilbert space setting. In each of the four cases, it is possible to allow changes in the base points, and moreover, \(n^{(k)}\) may be equal or different from \(\varLambda (m^{(k)})\). Letting \(m^{(k)}\) depend on k changes the linearization point of the operator while allowing \(n^{(k)}\) to change introduces different \(n^{(k)}\)-Fenchel conjugates  , and it also incurs a parallel transport on the dual variable. These possibilities are reflected in the statement of Algorithm 2.
, and it also incurs a parallel transport on the dual variable. These possibilities are reflected in the statement of Algorithm 2.
Reasonable choices for the base points include, e.g., to set both \(m^{(k)}=m\) and \(n^{(k)}=\varLambda (m)\), for \(k\ge 0\) and some \(m\in {\mathcal {M}}\). This choice eliminates the parallel transport in the dual update step as well as the innermost parallel transport of the primal update step. Another choice is to fix just n and set \(m^{(k)} = p^{(k)}\), which eliminates the parallel transport in the primal update step. It further eliminates both parallel transports of the dual variable in steps 6 and 7 of Algorithm 2.

4.3 Relation to the Chambolle–Pock Algorithm in Hilbert Spaces
In this subsection, we confirm that both Algorithm 1 and Algorithm 2 boil down to the classical Chambolle–Pock method in Hilbert spaces; see [26, Alg. 1]. To this end, suppose in this subsection that  and \(\mathcal {N}= \mathcal {Y}\) are finite-dimensional Hilbert spaces with inner products
and \(\mathcal {N}= \mathcal {Y}\) are finite-dimensional Hilbert spaces with inner products  and
and  , respectively, and that
, respectively, and that  is a linear operator. In Hilbert spaces, geodesics are straight lines in the usual sense. Moreover,
is a linear operator. In Hilbert spaces, geodesics are straight lines in the usual sense. Moreover,  and \(\mathcal {Y}\) can be identified with their tangent spaces at arbitrary points, the exponential map equals addition, and the logarithmic map equals subtraction. In addition, all parallel transports are identity maps.
and \(\mathcal {Y}\) can be identified with their tangent spaces at arbitrary points, the exponential map equals addition, and the logarithmic map equals subtraction. In addition, all parallel transports are identity maps.
We are now showing that Algorithm 1 reduces to the classical Chambolle–Pock method when \(n = 0 \in \mathcal {Y}\) is chosen. The same then holds true for Algorithm 2 as well since \(\varLambda \) is already linear. Notice that the iterates \(p^{(k)}\) belong to  while the iterates \(\xi ^{(k)}\) belong to \(\mathcal {Y}^*\). We can drop the fixed base point \(n = 0\) from their notation. Also notice that \(G_0^*\) agrees with the classical Fenchel conjugate and it will be denoted by \(G^* :\mathcal {Y}\rightarrow \overline{\mathbb {R}}\).
while the iterates \(\xi ^{(k)}\) belong to \(\mathcal {Y}^*\). We can drop the fixed base point \(n = 0\) from their notation. Also notice that \(G_0^*\) agrees with the classical Fenchel conjugate and it will be denoted by \(G^* :\mathcal {Y}\rightarrow \overline{\mathbb {R}}\).
We only need to consider steps 3, 4 and 6 in Algorithm 1. The dual update step becomes

Here \(\flat :\mathcal {Y}\rightarrow \mathcal {Y}^*\) denotes the Riesz isomorphism for the space \(\mathcal {Y}\). Next we address the primal update step, which reads

Here  denotes the inverse Riesz isomorphism for the space
denotes the inverse Riesz isomorphism for the space  . Finally, the (primal) extrapolation step becomes
. Finally, the (primal) extrapolation step becomes

The steps above agree with [26, Alg. 1] (with the roles of F and G reversed).
4.4 Convergence of the Linearized Chambolle–Pock Algorithm
In the following, we adapt the proof of [26] to solve the linearized saddle-point problem (4.13). We restrict the discussion to the case where \({\mathcal {M}}\) and \(\mathcal {N}\) are Hadamard manifolds and \(\mathcal {C}= {\mathcal {M}}\) and \(\mathcal {D}= \mathcal {N}\). Recall that in this case we have  so
so  holds everywhere on \({\mathcal {T}}_{n}[\mathcal {N}]\). Moreover, we fix \(m \in {\mathcal {M}}\) and \(n :=\varLambda (m) \in \mathcal {N}\) during the iteration and set the acceleration parameter \(\gamma \) to zero and choose the over-relaxation parameter \(\theta _k \equiv 1\) in Algorithm 2.
holds everywhere on \({\mathcal {T}}_{n}[\mathcal {N}]\). Moreover, we fix \(m \in {\mathcal {M}}\) and \(n :=\varLambda (m) \in \mathcal {N}\) during the iteration and set the acceleration parameter \(\gamma \) to zero and choose the over-relaxation parameter \(\theta _k \equiv 1\) in Algorithm 2.
Before presenting the main result of this section and motivated by the condition introduced after [57, eq.(2.4)], we introduce the following constant

 , the operator norm of \(D\varLambda (m) :{\mathcal {T}}_{m}[{\mathcal {M}}] \rightarrow {\mathcal {T}}_{n}[\mathcal {N}]\).
, the operator norm of \(D\varLambda (m) :{\mathcal {T}}_{m}[{\mathcal {M}}] \rightarrow {\mathcal {T}}_{n}[\mathcal {N}]\).
Theorem 4.3
Suppose that \({\mathcal {M}}\) and \(\mathcal {N}\) are two Hadamard manifolds. Let \(F:{\mathcal {M}}\rightarrow \overline{\mathbb {R}}\),  be proper and lsc functions, and let \(\varLambda :{\mathcal {M}}\rightarrow \mathcal {N}\) be differentiable. Fix \(m \in {\mathcal {M}}\) and \(n :=\varLambda (m) \in \mathcal {N}\). Assume that F is geodesically convex and that \(g_n = G \circ \exp _n\) is convex on \({\mathcal {T}}_{n}[\mathcal {N}]\). Suppose that the linearized saddle-point problem (4.13) has a saddle-point
be proper and lsc functions, and let \(\varLambda :{\mathcal {M}}\rightarrow \mathcal {N}\) be differentiable. Fix \(m \in {\mathcal {M}}\) and \(n :=\varLambda (m) \in \mathcal {N}\). Assume that F is geodesically convex and that \(g_n = G \circ \exp _n\) is convex on \({\mathcal {T}}_{n}[\mathcal {N}]\). Suppose that the linearized saddle-point problem (4.13) has a saddle-point  . Choose \(\sigma \), \(\tau \) such that \(\sigma \tau L^2<1\), with L defined in (4.17), and let the iterates
. Choose \(\sigma \), \(\tau \) such that \(\sigma \tau L^2<1\), with L defined in (4.17), and let the iterates  be given by Algorithm 2. Suppose that there exists \(K \in \mathbb {N}\) such that for all \(k \ge K\), the following holds:
be given by Algorithm 2. Suppose that there exists \(K \in \mathbb {N}\) such that for all \(k \ge K\), the following holds:

where

and

holds with \({\bar{\xi }}_n^{(k)} = 2\xi _n^{(k)}-\xi _n^{(k-1)}\). Then the following statements are true.
-
(i)
The sequence
 remains bounded,
remains bounded,  ,
,  (4.19)
(4.19) -
(ii)
There exists a saddle-point \((p^*,\xi _n^*)\) such that \(p^{(k)}\rightarrow p^*\) and \(\xi ^{(k)}_n \rightarrow \xi _n^*\).
Remark 4.4
A main difference of Theorem 4.3 to the Hilbert space case is the condition on C(k). Restricting this theorem to the setting of Sect. 4.3, the parallel transport and the logarithmic map simplify to the identity and subtraction, respectively. Then

holds and hence C(k) simplifies to

for any \({\bar{\xi }}_n^{(k)}\), so condition (4.18) is satisfied for all \(k\in \mathbb {N}\).
Proof of Theorem 4.3
Recall that we assume \(\varLambda (m)=n\). Following the lines of [26, Thm. 1], we first write a generic iteration of Algorithm 2 for notational convenience in a general form

We are going to insert \({\bar{p}} = p^{(k+1)}\) and \({\bar{\xi }}_n = 2 \xi ^{(k)}_n - \xi _n^{(k-1)}\) later on, which ensure the iterations agree with Algorithm 2. Applying Lemma 2.12, we get

Due to Definition 2.3 and Definition 2.10, we obtain for every  and \(p\in {\mathcal {M}}\) the inequalities
and \(p\in {\mathcal {M}}\) the inequalities

A concrete choice for p and \(\xi _n\) will be made below. Now we consider the geodesic triangle  . Applying the law of cosines in Hadamard manifolds [34, Thm. 2.2], we obtain
. Applying the law of cosines in Hadamard manifolds [34, Thm. 2.2], we obtain

Rearranging the law of cosines for the triangle  yields
yields

We rephrase the last term as

We insert the estimates above into the first inequality in (4.22) to obtain

Considering now the geodesic triangle  , we get
, we get

and, noticing that

holds, we write

Adding this inequality with the second inequality from (4.22), we get

Recalling now the choice \({\bar{p}} = p^{(k+1)}\), the term (4.23c) vanishes. We also insert \({\bar{\xi }}_n = 2 \xi ^{(k)}_n - \xi _n^{(k-1)}\) and estimate (4.23d) according to

Using that \(2ab\le \alpha a^2+b^2/\alpha \) holds for every \(a,b \ge 0\) and \(\alpha >0\), and choosing \(\alpha = \frac{\sqrt{\tau }}{\sqrt{\sigma }}\), we get

where L is the constant defined in (4.17).
We now make the choice \(p = {\widehat{p}}\) and notice that the sum of (4.23a), (4.23b) and (4.23e) corresponds to C(k). We also notice that the first two lines on the right hand side of (4.24) are the primal-dual gap, denoted in the following by \({\text {PDG}}(k)\). Moreover, we set \(\xi _n = {\widehat{\xi }}_n\). With these substitutions in (4.23a)–(4.23e), we arrive at the estimate

We continue to sum (4.25) from 0 to \(N-1\), where we set \(\xi _n^{(-1)} :=\xi _n ^{(0)}\) in coherence with the initial choice \({\bar{\xi }}_n^{(0)} = \xi _n^{(0)}\). We obtain

We further develop the last term in (4.26) and get

Choosing \(\alpha = 1/(\tau L)\), we conclude

Hence (4.26) becomes

Since  is a saddle-point, the primal-dual gap \({\text {PDG}}(k)\) is non-negative. Moreover, assumption (4.18) and the inequality \(\sigma \tau L^2 < 1\) imply that the sequence
is a saddle-point, the primal-dual gap \({\text {PDG}}(k)\) is non-negative. Moreover, assumption (4.18) and the inequality \(\sigma \tau L^2 < 1\) imply that the sequence  is bounded, which is the statement (i).
is bounded, which is the statement (i).
Part (ii) follows completely analogously to the steps of [26, Thm. 1(c)] adapted to (4.25). \(\square \)
5 ROF Models on Manifolds
A starting point of the work of [26] is the ROF \(\ell ^2\)-TV denoising model [52], which was generalized to manifolds in [43] for the so-called isotropic and anisotropic cases. This class of \(\ell ^2\)-TV models can be formulated in the discrete setting as follows: let \(F = (f_{i,j})_{i,j}\in {\mathcal {M}}^{d_1\times d_2}\), \(d_1,d_2\in \mathbb {N}\) be a manifold-valued image,  , each pixel \(f_{i,j}\) takes values on a manifold \({\mathcal {M}}\). Then the manifold-valued \(\ell ^2\)-TV energy functional reads as follows:
, each pixel \(f_{i,j}\) takes values on a manifold \({\mathcal {M}}\). Then the manifold-valued \(\ell ^2\)-TV energy functional reads as follows:

where \(q \in \{1,2\}\). The parameter \(\alpha > 0\) balances the relative influence of the data fidelity and the total variation terms in (5.1). Moreover,  denotes the generalization of the one-sided finite difference operator, which is defined as
denotes the generalization of the one-sided finite difference operator, which is defined as

The corresponding norm in (5.1) is then given by

For simplicity of notation, we do not explicitly state the base point in the Riemannian metric but denote the norm on  by
by  . Depending on the value of \(q\in \{1,2\}\), we call the energy functional (5.1) isotropic when \(q=2\) and anisotropic for \(q=1\). Note that previous algorithms like CPPA from [59] or Douglas–Rachford (DR) from [13] are only able to tackle the anisotropic case \(q=1\) due to a missing closed form of the proximal map for the isotropic TV summands. A relaxed version of the isotropic case can be computed using the half-quadratic minimization from [9]. Looking at the optimality conditions of the isotropic or anisotropic energy functional, the authors in [14] derived and solved the corresponding q-Laplace equation. This can be generalized even to all cases \(q > 0\).
. Depending on the value of \(q\in \{1,2\}\), we call the energy functional (5.1) isotropic when \(q=2\) and anisotropic for \(q=1\). Note that previous algorithms like CPPA from [59] or Douglas–Rachford (DR) from [13] are only able to tackle the anisotropic case \(q=1\) due to a missing closed form of the proximal map for the isotropic TV summands. A relaxed version of the isotropic case can be computed using the half-quadratic minimization from [9]. Looking at the optimality conditions of the isotropic or anisotropic energy functional, the authors in [14] derived and solved the corresponding q-Laplace equation. This can be generalized even to all cases \(q > 0\).
The minimization of (5.1) fits into the setting of the model problem (4.1). Indeed, \({\mathcal {M}}\) is replaced by \({\mathcal {M}}^{d_1\times d_2}\),  , \(F\) is given by the first term in (5.1), and we set \(\varLambda = \nabla \) and
, \(F\) is given by the first term in (5.1), and we set \(\varLambda = \nabla \) and  . The data fidelity term F clearly fulfills the assumptions stated in the beginning of Sect. 4, since the squared Riemannian distance function is geodesically convex on any strongly convex set \(\mathcal {C}\subset {\mathcal {M}}\). In particular, when \({\mathcal {M}}\) is a Hadamard manifold, then F is geodesically convex on all of \({\mathcal {M}}\).
. The data fidelity term F clearly fulfills the assumptions stated in the beginning of Sect. 4, since the squared Riemannian distance function is geodesically convex on any strongly convex set \(\mathcal {C}\subset {\mathcal {M}}\). In particular, when \({\mathcal {M}}\) is a Hadamard manifold, then F is geodesically convex on all of \({\mathcal {M}}\).
While the properness and continuity of the pullback  are obvious, its convexity is investigated in the following.
are obvious, its convexity is investigated in the following.
Proposition 5.1
Suppose that \({\mathcal {M}}\) is a Hadamard manifold and \(d_1, d_2 \in \mathbb {N}\). Consider \({\mathcal {M}}^{d_1\times d_2}\) and  and
and  with \(q \in [1,\infty )\). For arbitrary \(n \in \mathcal {N}\), define the pullback \(g_{n}:{\mathcal {T}}_{n}[\mathcal {N}] \rightarrow \mathbb {R}\) by \(g_n(Y) = G(\exp _nY)\). Then \(g_n\) is a convex function on \({\mathcal {T}}_{n}[\mathcal {N}]\).
with \(q \in [1,\infty )\). For arbitrary \(n \in \mathcal {N}\), define the pullback \(g_{n}:{\mathcal {T}}_{n}[\mathcal {N}] \rightarrow \mathbb {R}\) by \(g_n(Y) = G(\exp _nY)\). Then \(g_n\) is a convex function on \({\mathcal {T}}_{n}[\mathcal {N}]\).
Proof
Notice first that, since \({\mathcal {M}}\) is Hadamard, \({\mathcal {M}}^{d_1\times d_2}\) and \(\mathcal {N}\) are Hadamard as well. Consequently, \(g_n\) is defined on all of \({\mathcal {T}}_{n}[\mathcal {N}]\). We are using the index \(\cdot _p\) to denote points in \({\mathcal {M}}^{d_1\times d_2}\) and the index \(\cdot _X\) to denote tangent vectors. In particular, we denote the base point as \(n=(n_p,n_X)\in \mathcal {N}\). Let \(Y=(Y_p,Y_X), Z=(Z_p,Z_X)\in {\mathcal {T}}_{n}[\mathcal {N}]\) and \(t \in [0,1]\). Finally, we set  . Notice that in view of the properties of the double tangent bundle as a Riemannian manifold, we have
. Notice that in view of the properties of the double tangent bundle as a Riemannian manifold, we have

Therefore, we obtain

Exploiting that parallel transport is an isometry, we transport the term inside the first norm to  and the term inside the second norm to
and the term inside the second norm to  to obtain
to obtain

\(\square \)
We apply Algorithm 2 to solve the linearized saddle-point problem (4.13). This procedure will yield an approximate minimizer of (5.1). To this end, we require both the Fenchel conjugate and the proximal map of  . Its Fenchel dual can be stated using the dual norms,
. Its Fenchel dual can be stated using the dual norms,  ,
,  similar to Thm. 2 of [30], where \(q^*\in \mathbb {R}\) is the dual exponent of q. Let
similar to Thm. 2 of [30], where \(q^*\in \mathbb {R}\) is the dual exponent of q. Let

denote the 1-norm ball of the dual norm and
the indicator function of the set B. Then the Fenchel dual functions in the two cases of our main interest (\(q = 1\) and \(q = 2\)) are

The corresponding proximal maps read as follows:

Finally, to derive the adjoint of \(D\varLambda (m)\), let \(P\in {\mathcal {M}}^{d_1\times d_2}\) and \(X \in {\mathcal {T}}_{P}^{d_1\times d_2}\). Applying the chain rule, it is not difficult to prove that

with the obvious modifications at the boundary. In the above formula, \(e_k\) represents either the vector (0, 1) or (1, 0) used to reach either the neighbor to the right (\(k = 1\)) or below (\(k = 2\)). The symbols \(D_1\) and \(D_2\) represent the differentiation of the logarithmic map w.r.t. the base point and its argument, respectively. We notice that  and
and  can be computed by an application of Jacobi fields; see for example [10, Lem. 4.1 (ii) and (iii)].
can be computed by an application of Jacobi fields; see for example [10, Lem. 4.1 (ii) and (iii)].
With  given by Jacobi fields, its adjoint can be computed using the so-called adjoint Jacobi fields, see e.g., [11, Sect. 4.2]. Defining \(N_{i,j}\) to be the set of neighbors of the pixel \(p_{i,j}\), for every \(X\in {\mathcal {T}}_{P}^{d_1\times d_2}\) and
given by Jacobi fields, its adjoint can be computed using the so-called adjoint Jacobi fields, see e.g., [11, Sect. 4.2]. Defining \(N_{i,j}\) to be the set of neighbors of the pixel \(p_{i,j}\), for every \(X\in {\mathcal {T}}_{P}^{d_1\times d_2}\) and  we have
we have

which leads to the component-wise entries in the linearized adjoint

We mention that  and
and  can also be found in [10, Sect. 4].
can also be found in [10, Sect. 4].
6 Numerical Experiments
The numerical experiments are implemented in the toolbox Manopt.jlFootnote 1 ([8]) in Julia.Footnote 2 They were run on a MacBook Pro, 2.5 Ghz Intel Core i7, 16 GB RAM, with Julia 1.1. All our examples are based on the linearized saddle-point formulation (4.13) for \(\ell ^2\)-TV, solved with Algorithm 2.
6.1 A Signal with Known Minimizer
The first example uses signal data \({\mathcal {M}}^{d_1}\) instead of an image, where the data space is \({\mathcal {M}}= \mathbb {S}^2\), the two-dimensional sphere with the round sphere Riemannian metric. This gives us the opportunity to consider the same problem also on the embedding manifold \({(\mathbb {R}^3)}^{d_1}\) in order to illustrate the difference between the manifold-valued and Euclidean settings. We construct the data \({(f_i)}_i\) such that the unique minimizer of (5.1) is known in closed form. Therefore, a second purpose of this problem is to compare the numerical solution obtained by Algorithm 2,  , an approximate saddle-point of the linearized problem (4.13), to the solution of the original saddle-point problem (4.3). Third, we wish to explore how the value C(k) from (4.18) behaves numerically.
, an approximate saddle-point of the linearized problem (4.13), to the solution of the original saddle-point problem (4.3). Third, we wish to explore how the value C(k) from (4.18) behaves numerically.
The piecewise constant signal is given by
for two values \(p_1,p_2\in {\mathcal {M}}\) specified below.
Further, since \(d_2 = 1\), the isotropic and anisotropic models (5.1) coincide. The exact minimizer \({\widehat{p}}\) of (5.1) is piecewise constant with the same structure as the data f. Its values are  and
and  where
where  . Notice that the notion of geodesics are different for both manifolds under consideration, and thus, the exact minimizers \(\widehat{p}_{\mathbb {R}^3}\) and \({\widehat{p}}_{\mathbb {S}^2}\) are different.
. Notice that the notion of geodesics are different for both manifolds under consideration, and thus, the exact minimizers \(\widehat{p}_{\mathbb {R}^3}\) and \({\widehat{p}}_{\mathbb {S}^2}\) are different.
In the following, we use \(\alpha = 5\) and \(p_1 = \frac{1}{{\sqrt{2}}}(1,1,0)^{\mathrm{T}}\) and \(p_2 = \frac{1}{{\sqrt{2}}}(1,-1,0)^{\mathrm{T}}\). The data f is shown in Fig. 2a.
Computing the minimizer of the manifold-valued \(\ell ^2\)-TV model for a signal of unit vectors shown in (a) with respect to both manifolds \(\mathbb {R}^3\) and \(\mathbb {S}^2\) with \(\alpha =5\): (b) on \((\mathbb {S}^2)^{30}\) and (c) on \((\mathbb {R}^3)^{30}\). The known effect, loss of contrast is different for both cases, since on \(\mathbb {S}^2\) the vector remain of unit length. The same effect can be seen for a signal of spd matrices,  , \(\mathcal {P}_+(3)\); see (d) and (e)
, \(\mathcal {P}_+(3)\); see (d) and (e)
We applied the linearized Riemannian Chambolle–Pock Algorithm 2 with relaxation parameter \(\theta = 1\) on the dual variable as well as \(\sigma = \tau = \frac{1}{2}\), and \(\gamma = 0\),  , without acceleration, as well as initial guesses \(p^{(0)} = f\) and \(\xi ^{(0)}_n\) as the zero vector. The stopping criterion was set to 500 iterations to compare run times on different manifolds. As linearization point m, we use the mean of the data, which is just
, without acceleration, as well as initial guesses \(p^{(0)} = f\) and \(\xi ^{(0)}_n\) as the zero vector. The stopping criterion was set to 500 iterations to compare run times on different manifolds. As linearization point m, we use the mean of the data, which is just  . We further set \(n = \varLambda (m)\) for the base point of the Fenchel dual of G. For the Euclidean case \({\mathcal {M}}= \mathbb {R}^3\), we obtain a shifted version of the original Chambolle–Pock algorithm, since \(m \ne 0\).
. We further set \(n = \varLambda (m)\) for the base point of the Fenchel dual of G. For the Euclidean case \({\mathcal {M}}= \mathbb {R}^3\), we obtain a shifted version of the original Chambolle–Pock algorithm, since \(m \ne 0\).
While the algorithm on \({\mathcal {M}}= \mathbb {S}^2\) takes about 0.85 seconds, the Euclidean algorithm takes about 0.44 seconds for the same number of iterations, which is most likely due to the exponential and logarithmic maps as well as the parallel transport on \(\mathbb {S}^2\), which involve sines and cosines. The results obtained by the Euclidean algorithm are \(2.18\cdot 10^{-12}\) away in terms of the Euclidean norm from the analytical minimizer \({\widehat{p}}_{\mathbb {R}^3}\). Notice that the convergence of the Euclidean algorithm is covered by the theory in [26]. Moreover, notice that in this setting, \(\varLambda \) is a linear map between vector spaces. During the iterations, we confirmed that the value of C(k) is numerically zero (within \(\pm 5.55\cdot 10^{-17}\)), as expected from Remark 4.4.
Although Algorithm 2 on \({\mathcal {M}}= \mathbb {S}^2\) is based on the linearized saddle-point problem (4.13) instead of (4.3), we observed that it converges to the exact minimizer \(\widehat{p}_{\mathbb {S}^2}\) of (5.1). Therefore it is meaningful to plug in \({\widehat{p}}_{\mathbb {S}^2}\) into the formula (4.18) to evaluate C(k) numerically. The numerical values observed throughout the 500 iterations are in the interval \([-4.0\cdot 10^{-13}, 4.0\cdot 10^{-9}]\). We interpret this as confirmation that C(k) is non-negative in this case. However, even with this observation the convergence of Algorithm 2 is not covered by Theorem 4.3 since \(\mathbb {S}^2\) is not a Hadamard manifold. Quite to the contrary, it has constant positive sectional curvature.
The results are shown in Fig. 2b and c, respectively. They illustrate the capability for preservation of edges, yet also a loss of contrast and reduction of jump heights well known for \(\ell ^2\)-TV problems. This leads to shorter vectors in \({\widehat{p}}_{\mathbb {R}^3}\), while, of course, their unit length is preserved in \({\widehat{p}}_{\mathbb {S}^2}\).
We also constructed a similar signal on \({\mathcal {M}}= \mathcal {P}_+(3)\), the manifold of symmetric positive definite (SPD) matrices with affine-invariant metric; see [46]. This is a Hadamard manifold with non-constant curvature. Let \(I\in \mathbb {R}^{3\times 3}\) denote the unit matrix and

In this case, the run time is 5.94 seconds, which is due to matrix exponentials and logarithms as well as singular value decompositions that need to be computed. Here, C(k) turns out to be numerically zero (within \(\pm 8\cdot 10^{-15}\)) and the distance to the analytical minimizer \({\widehat{p}}_{\mathcal {P}_+(3)}\) is \(1.08\cdot 10^{-12}\). The original data f and the result \({\widehat{p}}_{\mathcal {P}_+(3)}\) (again with a loss of contrast as expected) are shown in Fig. 2d and e, respectively.
6.2 A Comparison of Algorithms
As a second example, we compare Algorithm 2 to the cyclic proximal point algorithm (CPPA) from [5], which was first applied to \(\ell ^2\)-TV problems in [59]. It is known to be a robust but generally slow method. We also compare the proposed method with the parallel Douglas–Rachford algorithm (PDRA), which was introduced in [13].
As an example, we use the anisotropic \(\ell ^2\)-TV model,  , (5.1) with \(q = 1\), on images of size \(32 \times 32\) with values in the manifold of \(3 \times 3\) SPD matrices \(\mathcal {P}_+(3)\) as in the previous subsection. The original data are shown in Fig. 3a. No exact solution is known for this example. We use a regularization parameter of \(\alpha = 6\). To generate a reference solution, we allowed the CPPA with step size \(\lambda _k = \frac{4}{k}\) to run for 4000 iterations. This required 1235.18 seconds, and it yields a value of the objective function (5.1) of approximately 38.7370, see the bottom gray line in Fig. 3c. The result is shown in Fig 3b.
, (5.1) with \(q = 1\), on images of size \(32 \times 32\) with values in the manifold of \(3 \times 3\) SPD matrices \(\mathcal {P}_+(3)\) as in the previous subsection. The original data are shown in Fig. 3a. No exact solution is known for this example. We use a regularization parameter of \(\alpha = 6\). To generate a reference solution, we allowed the CPPA with step size \(\lambda _k = \frac{4}{k}\) to run for 4000 iterations. This required 1235.18 seconds, and it yields a value of the objective function (5.1) of approximately 38.7370, see the bottom gray line in Fig. 3c. The result is shown in Fig 3b.
We compare CPPA to PDRA as well as to our Algorithm 2, using the value of the cost function and the run time as criteria. The PDRA was run with parameters \(\eta = 0.58\), \(\lambda = 0.93\), which where used by [13] for a similar example. It took 379.7 seconds to perform 122 iterations in order to reach the same value of the cost function as obtained by CPPA. The main bottleneck is the approximate evaluation of the involved mean, which has to be computed in every iteration. Here we performed 20 gradient descent steps for this purpose.
For Algorithm 2, we set \(\sigma = \tau = 0.4\) and \(\gamma = 0.2\). We choose the base point \(m\in \mathcal {P}_+(3)^{32\times 32}\) to be the constant image of unit matrices so that \(n=\varLambda (m)\) consists of zero matrices. We initialize the algorithm with \(p^{(0)} = f\) and \(\xi ^{(0)}_n\) as the zero vector. Our algorithm stops after 113 iterations, which take 96.20 seconds, when the value of (5.1) was below the value obtained by the CPPA. While the CPPA requires about half a second per iteration, our method requires a little less than a second per iteration, but it also requires only a fraction of the iteration count of CPPA. The behavior of the cost function is shown in Fig. 3, where the horizontal axis (iteration number) is shown in log scale, since the “tail” of CPPA is quite long.
Development of the three algorithms cyclic proximal point (CPPA), parallel Douglas–Rachford (PDRA) as well as the linearized Riemannian Chambolle–Pock algorithm 2 (lRCPA) starting all from the original data in (a) reaching the final value (image) in (b) is shown in (c), where the iterations on the x axis are in log-scale
6.3 Dependence on the Point of Linearization
We mentioned previously that Algorithm 2 depends on the base points m and n, and it cannot, in general, be expected to converge to a saddle point of (4.3) since it is based on the linearized saddle-point problem (4.13). In this experiment, we illustrate the dependence of the limit of the sequence of primal iterates on the base point m.
As data f we use the S2Whirl image designed by Johannes Persch in [40], adapted to Manopt.jl, see Fig. 4a. We set \(\alpha =1.5\) in the manifold-valued anisotropic \(\ell ^2\)-TV model,  , (5.1) with \(q = 1\). We ran Algorithm 2 with \(\sigma = \tau = 0.35\) and \(\gamma = 0.2\) for 300 iterations. The initial iterate is \(p^{(0)}=f\) and \(\xi ^{(0)}_n\) as the zero vector.
, (5.1) with \(q = 1\). We ran Algorithm 2 with \(\sigma = \tau = 0.35\) and \(\gamma = 0.2\) for 300 iterations. The initial iterate is \(p^{(0)}=f\) and \(\xi ^{(0)}_n\) as the zero vector.
We compare two different base points m. The first base point is the constant image whose value is the mean of all data pixels. The second base point is the constant image whose value is \(p=(1,0,0)^{\mathrm {T}}\) (“west”). The final iterates are shown in Fig. 4b and c, respectively. The evolution of the cost function value during the iterations is given in Fig. 4d. Both runs yield piecewise constant solutions, but since their linearizations of \(\varLambda \) are using different base points, they yield different linearized models. The resulting values of the cost function (5.1) differ, but both show a similar convergence behavior.
7 Conclusions
This paper introduces a novel concept of Fenchel duality for manifolds. We investigate properties of this novel duality concept and study corresponding primal-dual formulations of non-smooth optimization problems on manifolds. This leads to a novel primal-dual algorithm on manifolds, which comes in two variants, termed the exact and linearized Riemannian Chambolle–Pock algorithm. The convergence proof for the linearized version is given on arbitrary Hadamard manifolds under a suitable assumption. It is an open question whether condition (4.18) can be removed. The convergence analysis accompanies an earlier proof of convergence for a comparable method, namely the Douglas–Rachford algorithm, where the proof is restricted to Hadamard manifolds of constant curvature. Numerical results illustrate not only that the linearized Riemannian Chambolle–Pock algorithm performs as well as state-of-the-art methods on Hadamard manifolds, but it also performs similarly well on manifolds with positive sectional curvature. Note that here it also has to deal with the absence of a global convexity concept of the functional.
A more thorough investigation as well as a convergence proof for the exact variant are topics for future research. Another point of future research is an investigation of the choice of the base points \(m\in {\mathcal {M}}\) and \(n\in \mathcal {N}\) on the convergence, especially when the base points vary during the iterations.
Starting from the proper statement of the primal and dual problem for the linearization approach of Sect. 4.2, further aspects are open to investigation, for instance, regularity conditions ensuring strong duality. Well-known closedness-type conditions are then available, opening in this way a new line of rich research topics for optimization on manifolds.
Another point of potential future research is the measurement of the linearization error introduced by the model from Sect. 4.2. The analysis of the discrepancy term, as well as its behavior in the convergence of the linearized algorithm Algorithm 2, are closely related to the choice of the base points during the iteration and should be considered in future research.
Furthermore, our novel concept of duality permits a definition of infimal convolution and thus offers a direct possibility to introduce the total generalized variation. In what way, these novel priors correspond to existing ones, which is another issue of ongoing research. Furthermore, the investigation of both a convergence rate as well as properties on manifolds with nonnegative curvature is also open.
Notes
Available at http://www.manoptjl.org, following the same philosophy as the matlabversion available at https://manopt.org, see also [18].
References
Absil, P.A., Mahony, R., Sepulchre, R.: Optimization Algorithms on Matrix Manifolds. Princeton University Press (2008). https://doi.org/10.1515/9781400830244
Adams, B.L., Wright, S.I., Kunze, K.: Orientation imaging: the emergence of a new microscopy. Journal Metallurgical and Materials Transactions A 24, 819–831 (1993). https://doi.org/10.1007/BF02656503
Ahmadi Kakavandi, B., Amini, M.: Duality and subdifferential for convex functions on complete metric spaces. Nonlinear Analysis: Theory, Methods & Applications 73(10), 3450–3455 (2010). https://doi.org/10.1016/j.na.2010.07.033
Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces. CMS Books in Mathematics/Ouvrages de Mathématiques de la SMC. Springer, New York (2011). https://doi.org/10.1007/978-1-4419-9467-7. With a foreword by Hédy Attouch
Bačák, M.: Computing medians and means in Hadamard spaces. SIAM Journal on Optimization 24(3), 1542–1566 (2014). https://doi.org/10.1137/140953393
Bačák, M.: Convex Analysis and Optimization in Hadamard Spaces, De Gruyter Series in Nonlinear Analysis and Applications, vol. 22. De Gruyter, Berlin (2014). https://doi.org/10.1515/9783110361629
Bačák, M., Bergmann, R., Steidl, G., Weinmann, A.: A second order non-smooth variational model for restoring manifold-valued images. SIAM Journal on Scientific Computing 38(1), A567–A597 (2016). https://doi.org/10.1137/15M101988X
Bergmann, R.: Manopt.jl. Optimization on manifolds in Julia (2019). https://manoptjl.org/
Bergmann, R., Chan, R.H., Hielscher, R., Persch, J., Steidl, G.: Restoration of manifold-valued images by half-quadratic minimization. Inverse Problems in Imaging 10(2), 281–304 (2016). https://doi.org/10.3934/ipi.2016001
Bergmann, R., Fitschen, J.H., Persch, J., Steidl, G.: Priors with coupled first and second order differences for manifold-valued image processing. Journal of Mathematical Imaging and Vision 60(9), 1459–1481 (2018). https://doi.org/10.1007/s10851-018-0840-y
Bergmann, R., Gousenbourger, P.Y.: A variational model for data fitting on manifolds by minimizing the acceleration of a Bézier curve. Frontiers in Applied Mathematics and Statistics (2018). https://doi.org/10.3389/fams.2018.00059. arxiv:1807.10090
Bergmann, R., Laus, F., Steidl, G., Weinmann, A.: Second order differences of cyclic data and applications in variational denoising. SIAM Journal on Imaging Sciences 7(4), 2916–2953 (2014). https://doi.org/10.1137/140969993
Bergmann, R., Persch, J., Steidl, G.: A parallel Douglas Rachford algorithm for minimizing ROF-like functionals on images with values in symmetric Hadamard manifolds. SIAM Journal on Imaging Sciences 9(4), 901–937 (2016). https://doi.org/10.1137/15M1052858
Bergmann, R., Tenbrinck, D.: A graph framework for manifold-valued data. SIAM Journal on Imaging Sciences 11(1), 325–360 (2018). https://doi.org/10.1137/17M1118567
Bertsekas, D.P.: Local convex conjugacy and Fenchel duality. Preprints of Seventh World Congress of IFAC 2, 1079–1084 (1978). https://doi.org/10.1016/s1474-6670(17)66057-9
Boţ, R.I.: Conjugate Duality in Convex Optimization, Lecture Notes in Economics and Mathematical Systems, vol. 637. Springer-Verlag, Berlin (2010). https://doi.org/10.1007/978-3-642-04900-2
Boumal, N.: An Introduction to Optimization on Smooth Manifolds (2020). http://www.nicolasboumal.net/book
Boumal, N., Mishra, B., Absil, P.A., Sepulchre, R.: Manopt, a Matlab toolbox for optimization on manifolds. Journal of Machine Learning Research 15, 1455–1459 (2014)
Bredies, K., Holler, M., Storath, M., Weinmann, A.: Total generalized variation for manifold-valued data. SIAM Journal on Imaging Sciences 11(3), 1785–1848 (2018). https://doi.org/10.1137/17M1147597
Bredies, K., Kunisch, K., Pock, T.: Total generalized variation. SIAM Journal on Imaging Sciences 3(3), 492–526 (2010). https://doi.org/10.1137/090769521
Bürgmann, R., Rosen, P.A., Fielding, E.J.: Synthetic aperture radar interferometry to measure earth’s surface topography and its deformation. Annual Reviews Earth and Planetary Science 28(1), 169–209 (2000). https://doi.org/10.1146/annurev.earth.28.1.169
do Carmo, M.P.a.: Riemannian Geometry. Mathematics: Theory & Applications. Birkhäuser Boston, Inc., Boston, MA (1992)
Chambolle, A.: An algorithm for total variation minimization and applications. Journal of Mathematical Imaging and Vision 20(1-2), 89–97 (2004). https://doi.org/10.1023/B:JMIV.0000011325.36760.1e. Special issue on mathematics and image analysis
Chambolle, A., Caselles, V., Cremers, D., Novaga, M., Pock, T.: An introduction to total variation for image analysis. In: Theoretical Foundations and Numerical Methods for Sparse Recovery, Radon Series on Computational and Applied Mathematics, vol. 9, pp. 263–340. Walter de Gruyter, Berlin (2010). https://doi.org/10.1515/9783110226157.263
Chambolle, A., Lions, P.L.: Image recovery via total variation minimization and related problems. Numerische Mathematik 76(2), 167–188 (1997). https://doi.org/10.1007/s002110050258
Chambolle, A., Pock, T.: A first-order primal-dual algorithm for convex problems with applications to imaging. Journal of Mathematical Imaging and Vision 40(1), 120–145 (2011). https://doi.org/10.1007/s10851-010-0251-1
Chan, T., Esedoglu, S., Park, F., Yip, A.: Total variation image restoration: overview and recent developments. In: Handbook of Mathematical Models in Computer Vision, pp. 17–31. Springer, New York (2006). https://doi.org/10.1007/0-387-28831-7_2
Chan, T., Marquina, A., Mulet, P.: High-order total variation-based image restoration. SIAM Journal on Scientific Computing 22(2), 503–516 (2000). https://doi.org/10.1137/S1064827598344169
Dirr, G., Helmke, U., Lageman, C.: Nonsmooth Riemannian optimization with applications to sphere packing and grasping. In: Lagrangian and Hamiltonian Methods for Nonlinear Control 2006, Lect. Notes Control Inf. Sci., vol. 366, pp. 29–45. Springer, Berlin (2007). https://doi.org/10.1007/978-3-540-73890-9_2
Duran, J., Moeller, M., Sbert, C., Cremers, D.: Collaborative total variation: a general framework for vectorial TV models. SIAM Journal on Imaging Sciences 9(1), 116–151 (2016). https://doi.org/10.1137/15M102873X
Ekeland, I., Temam, R.: Convex Analysis and Variational Problems, Classics in Applied Mathematics, vol. 28. SIAM, Philadelphia (1999)
Ferreira, O.P., Louzeiro, M.S., Prudente, L.F.: Gradient method for optimization on Riemannian manifolds with lower bounded curvature. SIAM Journal on Optimization 29(4), 2517–2541 (2019). https://doi.org/10.1137/18M1180633
Ferreira, O.P., Oliveira, P.R.: Subgradient algorithm on Riemannian manifolds. Journal of Optimization Theory and Applications 97(1), 93–104 (1998). https://doi.org/10.1023/A:1022675100677
Ferreira, O.P., Oliveira, P.R.: Proximal point algorithm on Riemannian manifolds. Optimization. A Journal of Mathematical Programming and Operations Research 51(2), 257–270 (2002). https://doi.org/10.1080/02331930290019413
Gabay, D., Mercier, B.: A dual algorithm for the solution of nonlinear variational problems via finite element approximations. Computer and Mathematics with Applications 2, 17–40 (1976). https://doi.org/10.1016/0898-1221(76)90003-1
Grohs, P., Sprecher, M.: Total variation regularization on Riemannian manifolds by iteratively reweighted minimization. Information and Inference: A Journal of the IMA 5(4), 353–378 (2016). https://doi.org/10.1093/imaiai/iaw011
Jost, J.: Riemannian Geometry and Geometric Analysis, 7 edn. Universitext. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-61860-9
Kunze, K., Wright, S.I., Adams, B.L., Dingley, D.J.: Advances in automatic EBSP single orientation measurements. Textures and Microstructures 20, 41–54 (1993). https://doi.org/10.1155/TSM.20.41
Lang, S.: Fundamentals of Differential Geometry. Springer New York (1999). https://doi.org/10.1007/978-1-4612-0541-8
Laus, F., Nikolova, M., Persch, J., Steidl, G.: A nonlocal denoising algorithm for manifold-valued images using second order statistics. SIAM Journal on Imaging Sciences 10(1), 416–448 (2017). https://doi.org/10.1137/16M1087114
Lee, J.M.: Introduction to Smooth Manifolds, Graduate Texts in Mathematics, vol. 218. Springer-Verlag, New York (2003). https://doi.org/10.1007/978-0-387-21752-9
Lee, J.M.: Introduction to Riemannian Manifolds. Springer International Publishing (2018). https://doi.org/10.1007/978-3-319-91755-9
Lellmann, J., Strekalovskiy, E., Koetter, S., Cremers, D.: Total variation regularization for functions with values in a manifold. In: IEEE ICCV 2013, pp. 2944–2951 (2013). https://doi.org/10.1109/ICCV.2013.366
Martínez-Legaz, J.E.: Generalized convex duality and its economic applications. In: Handbook of Generalized Convexity and Generalized Monotonicity, Nonconvex Optimization and its Applications, vol. 76, pp. 237–292. Springer, New York (2005). https://doi.org/10.1007/0-387-23393-8_6
Papafitsoros, K., Schönlieb, C.B.: A combined first and second order variational approach for image reconstruction. Journal of Mathematical Imaging and Vision 48(2), 308–338 (2014). https://doi.org/10.1007/s10851-013-0445-4
Pennec, X., Fillard, P., Ayache, N.: A Riemannian framework for tensor computing. International Journal of Computer Vision 66, 41–66 (2006). https://doi.org/10.1007/s11263-005-3222-z
Rapcsák, T.: Convex programming on Riemannian manifolds. In: System Modelling and Optimization, pp. 733–740. Springer-Verlag (1986). https://doi.org/10.1007/bfb0043899
Rapcsák, T.: Geodesic convexity in nonlinear optimization. Journal of Optimization Theory and Applications 69(1), 169–183 (1991). https://doi.org/10.1007/bf00940467
Rapcsák, T.: Smooth Nonlinear Optimization in \({R}^n\). Springer US (1997). https://doi.org/10.1007/978-1-4615-6357-0
Rockafellar, R.T.: Convex Analysis. Princeton Mathematical Series, No. 28. Princeton University Press, Princeton, N.J. (1970)
Rockafellar, R.T.: Conjugate Duality and Optimization. Society for Industrial and Applied Mathematics (1974). Lectures given at the Johns Hopkins University, Baltimore, Md., June, 1973, Conference Board of the Mathematical Sciences Regional Conference Series in Applied Mathematics, No. 16
Rudin, L.I., Osher, S., Fatemi, E.: Nonlinear total variation based noise removal algorithms. Physica D 60(1–4), 259–268 (1992). https://doi.org/10.1016/0167-2789(92)90242-F
Sakai, T.: Riemannian Geometry, Translations of Mathematical Monographs, vol. 149. American Mathematical Society, Providence, RI (1996). Translated from the 1992 Japanese original by the author
Strekalovskiy, E., Cremers, D.: Total variation for cyclic structures: convex relaxation and efficient minimization. In: IEEE Conference on Computer Vision and Pattern Recognition, pp. 1905–1911 (2011). https://doi.org/10.1109/CVPR.2011.5995573
Strong, D., Chan, T.: Edge-preserving and scale-dependent properties of total variation regularization. Inverse Problems. An International Journal on the Theory and Practice of Inverse Problems, Inverse Methods and Computerized Inversion of Data 19(6), S165–S187 (2003). https://doi.org/10.1088/0266-5611/19/6/059. Special section on imaging
Udrişte, C.: Convex Functions and Optimization Methods on Riemannian Manifolds, Mathematics and its Applications, vol. 297. Kluwer Academic Publishers Group, Dordrecht (1994). https://doi.org/10.1007/978-94-015-8390-9
Valkonen, T.: A primal–dual hybrid gradient method for nonlinear operators with applications to MRI. Inverse Problems 30(5), 055012 (2014). https://doi.org/10.1088/0266-5611/30/5/055012
Wang, Y., Yang, J., Yin, W., Zhang, Y.: A new alternating minimization algorithm for total variation image reconstruction. SIAM Journal on Imaging Sciences 1(3), 248–272 (2008). https://doi.org/10.1137/080724265
Weinmann, A., Demaret, L., Storath, M.: Total variation regularization for manifold-valued data. SIAM Journal on Imaging Sciences 7(4), 2226–2257 (2014). https://doi.org/10.1137/130951075
Zălinescu, C.: Convex Analysis in General Vector Spaces. World Scientific Publishing Co., Inc., River Edge, NJ (2002). https://doi.org/10.1142/9789812777096
Acknowledgements
The authors would like to thank two anonymous reviewers for their insightful comments which helped to improve the manuscript significantly. RB would like to thank Fjedor Gaede and Leon Bungert for fruitful discussions concerning the Chambolle–Pock algorithm in \(\mathbb {R}^n\), especially concerning the choice of parameters as well as DT for hospitality in Münster and Erlangen. The authors would further like to thank Tuomo Valkonen for discussions on Hadamard manifolds and a three-point inequality remark, as well as Nicolas Boumal, Sebastian Neumayer, Gabriele Steidl for discussions and suggestions on preliminary versions of this manuscript. RB would like to acknowledge funding by the DFG Project BE 5888/2. DT would like to acknowledge support within the EU Grant No. 777826, the NoMADs project. RH and JVN would like to acknowledge the Priority Program SPP 1962 (Non-smooth and Complementarity-based Distributed Parameter Systems: Simulation and Hierarchical Optimization), which supported this work through the DFG grant HE 6077/10–1. MSL is supported by a measure which is co-financed by tax revenue based on the budget approved by the members of the Saxon state parliament. Financial support is gratefully acknowledged.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Communicated by Michael Overton.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bergmann, R., Herzog, R., Silva Louzeiro, M. et al. Fenchel Duality Theory and a Primal-Dual Algorithm on Riemannian Manifolds. Found Comput Math 21, 1465–1504 (2021). https://doi.org/10.1007/s10208-020-09486-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10208-020-09486-5
Keywords
- Convex analysis
- Fenchel conjugate function
- Riemannian manifold
- Hadamard manifold
- Primal-dual algorithm
- Chambolle–Pock algorithm
- Total variation



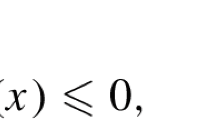

 , then
, then  .
. , then
, then  .
. , then
, then 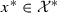 .
. , then
, then  for all
for all  .
.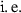 , for all
, for all  we have
we have 

 and
and  is a convex function on [0, 1] in the classical sense. Similarly, F is called strictly or strongly convex if
is a convex function on [0, 1] in the classical sense. Similarly, F is called strictly or strongly convex if  fulfills these properties.
fulfills these properties.
 .
.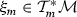 .
. for all
for all  .
. .
. .
. for all
for all  remains bounded,
remains bounded,  ,
, 


