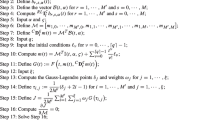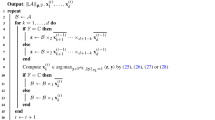Numerical Performance of Optimized Frolov Lattices in Tensor Product Reproducing Kernel Sobolev Spaces

Abstract

In this paper, we deal with several aspects of the universal Frolov cubature method, which is known to achieve optimal asymptotic convergence rates in a broad range of function spaces. Even though every admissible lattice has this favorable asymptotic behavior, there are significant differences concerning the precise numerical behavior of the worst-case error. To this end, we propose new generating polynomials that promise a significant reduction in the integration error compared to the classical polynomials. Moreover, we develop a new algorithm to enumerate the Frolov points from non-orthogonal lattices for numerical cubature in the d-dimensional unit cube $[0,1]^d$. Finally, we study Sobolev spaces with anisotropic mixed smoothness and compact support in $[0,1]^d$ and derive explicit formulas for their reproducing kernels. This allows for the simulation of exact worst-case errors which numerically validate our theoretical results.

1 Introduction

Many scientific approaches that are related to the treatment of real-world phenomena rely on the computation of integrals on high-dimensional domains which often cannot be treated analytically. Examples include physics [4], computational finance [18], econometrics [21] and machine learning [2, 7, 35]. In this paper, we aim for efficient and stable numerical methods to approximately compute the integral

$$\begin{aligned} I_d(f) \,:=\, \int _{[0,1]^d} f({\varvec{x}}) \,\mathrm {d}{\varvec{x}}\end{aligned}$$

and give reliable error guarantees for a class $F_d$ of d-variate functions. In fact, we are particularly interested in the worst-case error

$$\begin{aligned} e(n,F_d) := \sup \limits _{\Vert f\Vert _{F_d} \le 1} |I_d(f) - Q_n^d(f)|, \end{aligned}$$

(1.1)

for special cubature formulas of type

$$\begin{aligned} Q^d_n(f) \,=\, \frac{1}{n}\sum _{{\varvec{k}}\in {\mathbb {Z}}^d}\, f({\varvec{A}}_n{\varvec{k}}), \end{aligned}$$

(1.2)

where ${\varvec{A}}_n:=n^{-1/d} {\varvec{A}}$ is a suitable $d\times d$-matrix with $\det ({\varvec{A}})=1$. This type of cubature rule has a long history going back to the 1970s; see Frolov [15]. In (1.2), the function f is assumed to be supported on a bounded domain ${\varOmega }$ such that only finitely many summands contribute to the sum. Frolov noticed that the property

$$\begin{aligned} \mathrm {Nm}({\varvec{A}}) :=\inf _{{\varvec{k}}\in {\mathbb {Z}}^d\setminus \{0\}} \Big |\prod _{i=1}^d ({\varvec{Ak}})_i\Big | > 0 \end{aligned}$$

(1.3)

guarantees an optimal asymptotic worst-case behavior of (1.1) with respect to functions with $L_p$-bounded mixed derivative of order $r \in {\mathbb {N}}$ supported in $[0,1]^d$. In this context, optimality means that the worst-case error (1.1) cannot be improved in the order sense by any other cubature formula using the same number of points. Note that in case $|\det {\varvec{A}}| = 1$ it can be shown that

$$\begin{aligned} n^{-1}\left| {\{{\varvec{k}}:{\varvec{A}}_n{\varvec{k}}\in {\varOmega }\}}\right| \rightarrow 1 \end{aligned}$$

(1.4)

for every set ${\varOmega }$ with (Lebesgue) volume 1 [37].

Frolov showed that the set of matrices satisfying (1.3) is not empty. Moreover, he gave a rather sophisticated number-theoretic construction with a lot of potential for numerical analysis, as we will see in this paper. Starting with the irreducible (over ${\mathbb {Q}}$) polynomial

$$\begin{aligned} P_d(x) = \prod _{j=1}^d (x-2j+1)-1 = \prod _{i=1}^d (x-\xi _i) \end{aligned}$$

(1.5)

he defined the Vandermonde matrix

$$\begin{aligned} {\varvec{V}} = \left( \begin{array}{cccc} 1 &{}\quad \xi _1 &{}\quad \cdots &{}\quad \xi _1^{d-1}\\ 1 &{}\quad \xi _2 &{}\quad \cdots &{}\quad \xi _2^{d-1}\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ 1 &{}\quad \xi _{d} &{}\quad \cdots &{}\quad \xi _d^{d-1} \end{array}\right) \,\in {\hbox {GL}}_d({\mathbb {R}}). \end{aligned}$$

(1.6)

One reason for the increasing interest in Frolov’s cubature rule is certainly the fact that once a good matrix (1.3) is fixed the integration nodes are simply given as the rescaled image of the integer lattice points ${\mathbb {Z}}^d$ under the matrix ${\varvec{V}}$. The method is therefore comparably simple, at least from a theoretical point of view. Another striking aspect is a certain universality property.

It has been shown, e.g., in [13, 14, 41, 45] that (1.2) provides optimal rates of convergence with respect to various Fourier analytic function spaces (Besov–Sobolev–Triebel–Lizorkin) with zero boundary condition. In other words, and as the proofs show, we do not need to incorporate any a priori knowledge about the integrand (e.g., mixed or isotropic regularity, etc.). However, the efficiency of (1.2) depends on global smoothness properties of the function extended by zero to the whole ${\mathbb {R}}^d$, which is why we impose homogeneous boundary conditions for the function and its partial derivatives. In order to tailor the rule (1.2) to functions with non-homogeneous boundary, one may combine (1.2) with a change of variable or a point-wise multiplication technique (as described in [31, 41]). To some extent, this gives universal methods also for this setting. In this paper, we will restrict to the homogeneous boundary setting.

In Sect. 7, we will observe this property in our numerical experiments by computing the exact worst-case errors of the same method for different function classes.

Note that universality seems to be a rare property. We are only aware of another universal method for the spaces considered here in dimension two: the celebrated Fibonacci cubature and variants; see [9, 42, 48]. For $d>2$, there seems to be no similar universal point construction based on other commonly used quasi-Monte Carlo methods, like digital nets and integration lattices. In fact, several authors optimize their point constructions with respect to the source space or the constructions are just not capable to achieve optimal results; see, e.g., [12, 19, 20] or the thorough study [10].

As we are interested in an efficient implementation and the numerical performance of different Frolov-type cubature methods for functions on $[0,1]^d$, we clearly need to efficiently enumerate Frolov lattice points in axis parallel boxes. It turned out that this is a highly non-trivial task which has been already considered by several authors [26, 27, 39] including three of the present ones. With a naive approach, one may need to touch much more integer lattice points ${\varvec{k}}\in {\mathbb {Z}}^d$ (overhead) to check whether ${\varvec{A}}{\varvec{k}}\in [0,1]^d$. This increases the runtime of an enumeration algorithm drastically in high dimensions. Here, the chosen irreducible polynomial for (1.6) has a significant effect. In [27], the authors observed that for $d=2^m$ Chebyshev polynomials lead to an orthogonal lattice and an equivalent (orthogonal) lattice representation matrix with entries smaller than two in modulus. By exploiting rotational symmetry properties, the mentioned overhead can be reduced and the enumeration procedure is less costly.

This observation already indicated that the choice of the polynomials in (1.6) is crucial. Unfortunately, Chebyshev polynomials and corresponding Vandermonde matrices (1.6) only provide (1.3) if $d = 2^m$. This has been shown, for instance, in Temlyakov [41]. The question remains how to fill the gaps. The classical Frolov polynomials are inappropriate in two respects. First, its roots spread in the range $[-d,d]$ such that (1.6) gets highly ill-conditioned. And secondly, although the lattice satisfies (1.3), the points are not really “spaces filling,” meaning that the points accumulate around a lower-dimensional manifold. This has a severe numerical impact for the worst-case error. In fact, the asymptotic rate of convergence is optimal, but the preasymptotic behavior is useless for any practical issues.

One of the main contributions of the paper is the list of new improved generating polynomials given in Sect. 3. We give polynomials which are optimized according to the mentioned issues in dimensions $d=1,\ldots ,10$, especially with a narrow distribution of its roots. As already mentioned above, Chebyshev polynomials itself are not irreducible if d is not a power of two. However, they may provide admissible factors. This is the main idea of the construction and works if $d \in \{2,3,4,5,6,8,9,10\}$. As for the case $d=7$, a brute-force search led to a polynomial with roots in $(-2.25,1.75)$.

Due to the mentioned universality of Frolov’s cubature rule, it is enough to fix the matrix and the corresponding lattice once and for all. In fact, the point construction does not depend on the respective framework. Therefore, it makes sense to generate the lattice points in a preprocessing step and make them available for practitioners. Our enumeration algorithm is similar to the one in [27] and extends to non-orthogonal lattices by exploiting a QR-factorization; see Sect. 4. Based on the above list of polynomials, we generated a database of Frolov lattice nodes for dimensions up to $d=10$ and $N \approx 10^6$ points. The points are available for download and direct use on the website

https://ins.uni-bonn.de/content/software-frolov.

Having generated the cubature points, we are now able to test the performance of various Frolov methods for functions with bounded mixed (weak) derivative, i.e.,

$$\begin{aligned} \langle f^{({\varvec{r}})}, f^{({\varvec{r}})}\rangle _{L_2} = \Vert f^{({\varvec{r}})}\Vert _2^2 < \infty , \end{aligned}$$

(1.7)

where ${\varvec{r}}= (r_1,\ldots ,r_d) \in {\mathbb {N}}^d$ is a smoothness vector with integer components satisfying

$$\begin{aligned} r=r_1 = \cdots =r_\nu < r_{\nu +1} \le r_{\nu +2} \le \cdots \le r_d. \end{aligned}$$

(1.8)

A natural assumption, see (1.2), is the restriction to functions f supported inside the unit cube ${\varOmega }= [0,1]^d$ satisfying (1.7). In this case, the semi-norm (1.7) becomes a norm and the corresponding space a Hilbert space which will be denoted with $\mathring{H}^{{\mathbf {r}}}_{\text {mix}}$.

Nowadays, the well-known worst-case error

$$\begin{aligned} e(n,\mathring{H}^{{\mathbf {r}}}_{\text {mix}}) \asymp n^{-r}(\log n)^{\frac{\nu -1}{2}}, \end{aligned}$$

(1.9)

has been established in many classical papers [13,14,15, 41]; see also the more recent papers [43, 45]. Note that we encounter another aspect of the universality property for this particular framework of anisotropic mixed smoothness. When using, for instance, a sparse grid approach (see, e.g., “Appendix A”) for the numerical integration one has to know which direction is “rough” in the above sense to adapt the sparse grid accordingly. In fact, one samples more points in rough directions and less points in smoother direction. Frolov’s method does not need this a priori information and behaves according to the optimal rate of convergence given in (1.9). Moreover, using some random perturbation of the point construction described above, one can define a Monte Carlo method that has the same universality properties, see [28], and has a randomized worst-case error of the order $n^{-r-1/2}$; see [44]. Note that this order is independent of the dimension and therefore clearly optimal, as it is the same order as in the univariate case. We presently do not know any other randomized method with this property. Numerical testing of this method is left for future research.

In Sect. 6, we will provide a streamlined and self-contained proof of (1.9) pointing explicitly on the dependence of the constants on the dimension d, since the rate of convergence given by (1.9) completely hides this dependence. In fact, in case of one minimal smoothness component in (1.8) even the logarithm disappears completely and we have a pure polynomial rate as in the univariate setting. In Theorem 2, we give a worst-case error bound which shows the influence of the dimension d. In addition, the result illustrates how the lattice invariants, like the polynomial discriminant $D_P$ and the $\ell _\infty$-diameter of the smallest fundamental cell, enter the error estimates.

Since $\mathring{H}^{{\mathbf {r}}}_{\text {mix}}$ is embedded into the space of continuous functions, a reproducing kernel exists [1]. We use the approach of Wahba [47] as a starting point to derive its reproducing kernel. Together with a standard correction procedure, cf. [3, Lem. 3 & Thm. 11], we derive an explicit formula given in Theorem 1 and (5.15). The reproducing kernel is then being used to simulate the exact worst-case errors which represent the norm of the error functional, i.e., its Riesz representer, which can be computed exactly. This approach allows to gain insights into the true behavior of the constants that are involved in the bounds for the integration error and usually only are estimated. Let us emphasize once again that we simulate the worst-case error with respect to a whole function class rather than testing the algorithm on a single prototype test function.

Finally, in Sect. 7 we show the results of several numerical experiments. In the first part of the experiment section, we compare different well-known methods for numerical integration in the reproducing kernel Hilbert space framework which we established in Sects. 5 and 6. In particular, we compare Frolov lattices based on different generating polynomials, the classical Frolov polynomials and the improved polynomials from Sect. 3. As one would expect, the numerical behavior of the respective worst-case errors differs significantly for small $n$. Where the improved polynomials lead to a rather satisfactory error decay, the classical method is numerically completely useless if the dimension increases. Interestingly, in case $d=2$ Frolov lattices according to the golden ratio polynomial compete with the Fibonacci lattice rule. We also compare Frolov lattices and sparse grids with respect to the numerical performance. Note that the sparse grid cubature method represents a further method which is able to benefit from higher (mixed) smoothness. However, it is well known [9] that sparse grids show a worse behavior in the logarithm compared to Frolov lattices. Our experiments validate this theoretical fact. Among the considered methods (sparse grids, quasi-Monte Carlo), Frolov lattices behave best in our setting. In addition, Frolov lattices do not have to be adapted to the present anisotropy when considering anisotropic mixed smoothness. When considering one minimal smoothness component (1.8), we observe the same pure polynomial rate in different dimensions, only the constant differs. Note that this effect would also be present for sparse grids adapted to the smoothness vector, which one has to know in advance.

Notation As usual ${\mathbb {N}}$ denotes the natural numbers, ${\mathbb {Z}}$ denotes the integers and ${\mathbb {R}}$ the real numbers . The letter d is always reserved for the underlying dimension in ${\mathbb {R}}^d, {\mathbb {Z}}^d$, etc. We denote with ${\varvec{x}}\cdot {\varvec{y}}$ the usual Euclidean inner product in ${\mathbb {R}}^d$. For $0<p\le \infty$, we denote with $|\cdot |_p$ and $\Vert \cdot \Vert _p$ the (d-dimensional) discrete $\ell _p$-norm and the continuous $L_p$-norm on ${\mathbb {R}}$, respectively, where $B_p^d$ denotes the respective unit ball in ${\mathbb {R}}^d$. The function $(\cdot )_+$ is given by $\max \{\cdot ,0\}$. With ${\mathcal {F}}$, we denote the Fourier transform given by ${\mathcal {F}} f(\varvec{\xi }):=\int _{{\mathbb {R}}^d} f(x)\exp (-2\pi i {\varvec{x}}\cdot \varvec{\xi })\,\mathrm {d}{\varvec{x}}$ for a function $f\in L_1({\mathbb {R}}^d)$ and $\varvec{\xi } \in {\mathbb {R}}^d$. For two sequences of real numbers $a_n$ and $b_n$, we will write $a_n \lesssim b_n$ if there exists a constant $c>0$ such that $a_n \le c\,b_n$ for all n. We will write $a_n \asymp b_n$ if $a_n \lesssim b_n$ and $b_n \lesssim a_n$. With $\mathrm {GL}_d:=\mathrm {GL}_d({\mathbb {R}})$, we denote the group of invertible matrices over ${\mathbb {R}}$, whereas $\mathrm {SO}_d:=\mathrm {SO}_d({\mathbb {R}})$ denotes the group of orthogonal matrices over ${\mathbb {R}}$ with unit determinant. With $\mathrm {SL}_d({\mathbb {Z}})$, we denote the group of invertible matrices over ${\mathbb {Z}}$ with unit determinant. The notation $D:=\text{ diag }(x_1,\ldots ,x_d)$ with ${\varvec{x}}= (x_1,\ldots ,x_d) \in {\mathbb {R}}^d$ refers to the diagonal matrix $D \in {\mathbb {R}}^{d\times d}$ with ${\varvec{x}}$ at the diagonal. With $\mathrm {gcd}(a,b)$, we denote the greatest common divisor of two positive integers a, b. And finally, by ${\mathbb {Z}}[x]$ we denote the ring of polynomials with integer coefficients. Although we consider different generating matrices for admissible lattices in the forthcoming, we do not specify the matrix in the denotation $Q^d_n$. This is, because we will fix, for every dimension d under consideration, a matrix that is optimal in a sense that will be explained later. To be precise, for a given dimension d, the matrix A will be a multiple of the Vandermonde matrix as defined in Theorem 1 with the specific polynomials (and roots) as given in Table 1.

2 Admissible Lattices and Their Representation

For a matrix ${\varvec{T}}\in {\hbox {GL}}_d({\mathbb {R}})$, we call $\{{\varvec{Tk}}:{\varvec{k}}\in {\mathbb {Z}}^d\} = {\varvec{T}}({\mathbb {Z}}^d)$ a (full-rank) lattice with lattice representation matrix ${\varvec{T}}$.

For a matrix ${\varvec{U}}\in {\hbox {SL}}_d({\mathbb {Z}})$, the matrices ${\varvec{T}}$ and ${\varvec{TU}}$ generate the same lattice, and it can easily be shown that all possible lattice representations of ${\varvec{T}}({\mathbb {Z}}^d)$ are given this way. Therefore, it makes sense to define the determinant of a lattice ${\varvec{T}}({\mathbb {Z}}^d)$ as $|\det {\varvec{T}}|$. We want to mention that for a given lattice, it is often preferred to have a lattice representation matrix ${\varvec{T}} = ({\varvec{t}}_1|\cdots |{\varvec{t}}_d) \in {\hbox {GL}}_d({\mathbb {R}})$ with column vectors ${\varvec{t}}_1,\ldots ,{\varvec{t}}_d\in {\mathbb {R}}^d$ that are small with respect to some norm, cf. Fig. 1.

Fig. 1

Equivalent lattice representations within the unit cube ${\varOmega }=\left[ -1/2, 1/2\right] ^2$. The highlighted lattice elements are the column vectors of the corresponding lattice representation matrix

Crucial for the performance of the Frolov cubature formula (1.2) will be the notion of admissibility which is settled in the following definition.

Definition 1

(Admissible lattice) A lattice ${\varvec{T}}({\mathbb {Z}}^d)$ is called admissible if

$$\begin{aligned} \mathrm {Nm}({\varvec{T}}) :=\inf _{{\varvec{k}}\in {\mathbb {Z}}^d\setminus \{0\}} \Big |\prod _{i=1}^d ({\varvec{Tk}})_i\Big | > 0 \end{aligned}$$

(2.1)

holds true.

Figure 2 illustrates this property. In fact, lattice points different from 0 lie outside of a hyperbolic cross with ’radius’ $\mathrm {Nm}({\varvec{T}})$. Our construction of choice for admissible lattices is given by the following procedure.

Fig. 2

Admissible lattice and hyperbolic cross

Proposition 1

Let P(x) be a polynomial of degree d satisfying

• P has integer coefficients,

• P has leading coefficient 1,

• P is irreducible over ${\mathbb {Q}}$,

• P has d different real roots $\xi _1, \ldots , \xi _d$.

The Vandermonde matrix

$$\begin{aligned} {\varvec{V}} = \left( \begin{array}{cccc} 1 &{}\quad \xi _1 &{} \cdots &{}\quad \xi _1^{d-1}\\ 1 &{}\quad \xi _2 &{} \cdots &{}\quad \xi _2^{d-1}\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ 1 &{}\quad \xi _{d} &{}\quad \cdots &{}\quad \xi _d^{d-1} \end{array}\right) \,\in {\hbox {GL}}_d({\mathbb {R}})\end{aligned}$$

(2.2)

generates an admissible lattice ${\varvec{V}}({\mathbb {Z}}^d)$ with $\mathrm {Nm}({\varvec{V}}) = 1$. Its determinant equals the polynomial discriminant $D_P$ of P:

$$\begin{aligned} |\det {\varvec{V}}| = \prod _{k<l}|\xi _k-\xi _l| = D_P. \end{aligned}$$

(2.3)

Moreover, it holds

$$\begin{aligned} \mathrm {Nm}({\varvec{V}}^{-\top }) = |\det {\varvec{V}}|^{-2} = D_P^{-2}. \end{aligned}$$

(2.4)

The necessary prerequisites of P can be reformulated with concepts of algebraic number theory: P is the minimal polynomial of an algebraic integer of order d. For the proof of this statement, we refer to [26] or [22] and [30] for a thorough introduction into the theory of algebraic integers. The quantity (2.4) has a direct impact on the convergence behavior of the Frolov cubature formula, and we therefore are interested in polynomials which maximize this quantity for a fixed d, i.e., have a small (or the smallest) polynomial discriminant $D_P$, cf. Fig. 3.

Fig. 3

Lattices corresponding to different polynomials for $d=2$. A small discriminant correlates with a good distribution of lattice points

Using Proposition 1, we obtain the lattice ${\varvec{V}}({\mathbb {Z}}^d)$ represented by a Vandermonde matrix ${\varvec{V}}$. There are two problems with such matrices from the numerical point of view: First, they have large column vectors and therefore a large condition number, and second, its entries are of the form ${\varvec{V}}_{ij} = \xi _i^{j-1}$ for which the calculation gets unstable for increasing j. However, we can bypass this problem using special polynomials, which will be discussed in the next section.

Lemma 1

Let P be a polynomial which satisfies the prerequisites in Proposition 1, and has roots $\xi _1,\ldots ,\xi _d$ which lie in $(-2, 2)$. Furthermore, let $\omega _1,\ldots ,\omega _d\in (-1,1)$ be defined via the equation

$$\begin{aligned} 2\cos (\pi \omega _k) = \xi _k,\quad k=1,\ldots ,d. \end{aligned}$$

The lattice ${\varvec{V}}({\mathbb {Z}}^d)$ generated by the associated Vandermonde matrix

$$\begin{aligned} {\varvec{V}} = \left( \begin{array}{cccc} 1 &{}\quad \xi _1 &{}\quad \cdots &{}\quad \xi _1^{d-1}\\ 1 &{}\quad \xi _2 &{}\quad \cdots &{}\quad \xi _2^{d-1}\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ 1 &{}\quad \xi _{d} &{}\quad \cdots &{}\quad \xi _d^{d-1} \end{array}\right) \,\in {\hbox {GL}}_d({\mathbb {R}})\end{aligned}$$

is also generated by the matrix ${\varvec{T}}$ with

$$\begin{aligned} {\varvec{T}}_{kl} = {\left\{ \begin{array}{ll} 1&{}\quad l=1,\\ 2\cos \left( \pi (l-1)\omega _k\right) &{}\quad l=2,\dots , d. \end{array}\right. } \end{aligned}$$

The resulting matrix ${\varvec{T}}$ has entries in $(-2,2)$ that can be calculated in a numerically stable way, which is optimal for our purposes. The proof is a straightforward application of Euler’s identity and can be found in [26, 27].

Finally, we specify our choice of the matrices ${\varvec{A}}$ and ${\varvec{A}}_n$ used in Frolov’s cubature formula (1.2) as

$$\begin{aligned} {\varvec{A}} = |\det {\varvec{T}}|^{-1/d}{\varvec{T}}, \quad {\varvec{A}}_n= n^{-1/d}{\varvec{A}} \end{aligned}$$

(2.5)

with ${\varvec{T}}$ as in Lemma 1.

3 Improved Generating Polynomials

In this section, we consider polynomials which can be used to create admissible lattices. We will call such polynomials admissible, i.e., a dth-order polynomial P is admissible if it satisfies the prerequisites of Proposition 1. At the end of this section, we provide a list of admissible polynomials with small discriminant for $d=2,\ldots ,10$.

The study of Chebyshev polynomials of the first and second kinds provides us with a wide range of admissible polynomials. The most important features are their real and pair-wise different roots, as well as the narrow distribution thereof. It is also quite fortunate to us that the decomposition into irreducible factors is well understood and can be stated explicitly; see [36].

Definition 2

The Chebyshev polynomials of the first kind $T_d(x)$ are defined recursively via

$$\begin{aligned} T_0(x)= & {} 1,\\ T_1(x)= & {} x,\\ T_d(x)= & {} 2xT_{d-1}(x) - T_{d-2}(x),\quad d\ge 2. \end{aligned}$$

The Chebyshev polynomials of the second kind $U_d(x)$ are defined recursively via

$$\begin{aligned} U_0(x)= & {} 1,\\ U_1(x)= & {} 2x,\\ U_d(x)= & {} 2xU_{d-1}(x) - U_{d-2}(x),\quad d\ge 2. \end{aligned}$$

Lemma 2

The Chebyshev polynomial $T_d(x)$ has the roots

$$\begin{aligned} \cos \left( \frac{\pi (2k-1)}{2d}\right) ,\quad k=1,\dots , d. \end{aligned}$$

The Chebyshev polynomial $U_d(x)$ has the roots

$$\begin{aligned} \cos \left( \frac{\pi k}{d+1}\right) ,\quad k=1,\dots , d. \end{aligned}$$

The polynomials $T_d(x)$ and $U_d(x)$ are not admissible since they do not have leading coefficient 1. But they can be scaled appropriately to achieve this.

Lemma 3

The scaled Chebyshev polynomials ${{\widetilde{T}}}_d(x) = 2T_d(x/2)$ and ${\widetilde{U}}_d(x) = U_d(x/2)$ have leading coefficient 1 and belong to ${\mathbb {Z}}[x]$. The scaled Chebyshev polynomial ${\widetilde{T}}_d(x)$ has the roots

$$\begin{aligned} t_{d,k} = 2\cos \left( \frac{\pi (2k-1)}{2d}\right) ,\quad k=1,\dots , d. \end{aligned}$$

The scaled Chebyshev polynomial ${\widetilde{U}}_d(x)$ has the roots

$$\begin{aligned} u_{d,k} = 2\cos \left( \frac{\pi k}{d+1}\right) ,\quad k=1,\dots , d. \end{aligned}$$

From this lemma, it follows directly that irreducible factors of ${\widetilde{T}}_d(x)$ and ${\widetilde{U}}_d(x)$ are admissible and have roots that lie in $(-2,2)$. As already stated above, [36] lists the complete decomposition of Chebyshev polynomials into irreducible factors, which we reformulate for the scaled versions in the next lemma.

Lemma 4

For a fixed $d>1$, we have

$$\begin{aligned} {\widetilde{T}}_d(x) = \prod _h D_{d,h}(x), \end{aligned}$$

where $h\le d$ runs through all odd positive divisors of d and

$$\begin{aligned} D_{d,h}(x) = \prod _{\begin{array}{c} k=1 \\ \gcd (2k-1,d)=h \end{array}}^d(x-t_{d,k}) \end{aligned}$$

are all irreducible. It also holds

$$\begin{aligned} {\widetilde{U}}_d(x) = \prod _h E_{d,h}(x), \end{aligned}$$

where $h\le d$ runs through all positive divisors of $2d+2$ and

$$\begin{aligned} E_{d,h}(x) = \prod _{\begin{array}{c} k=1\\ \gcd (k,2d+2)=h \end{array}}^d(x-u_{d,k}) \end{aligned}$$

are all irreducible.

It has been shown in [41] that ${\widetilde{T}}_d(x)$ is irreducible for $d=2^m, m\in {\mathbb {N}}$, and that the corresponding lattice is orthogonal [27]. However, in this paper we are more interested in the irreducible factors of ${\widetilde{U}}_d(x)$, mainly for two reasons. First, it can be easily seen that the irreducible factors of ${\widetilde{T}}_d(x)$ have paired roots, i.e.,

$$\begin{aligned} D_{d,h}(t_{d,k}) = 0 \Rightarrow D_{d,h}(t_{d,d-k+1}) = 0. \end{aligned}$$

This means that either $D_{d,h}(x) = x$ or $D_{d,h}(x)$ is a polynomial of even degree, limiting the usefulness to our purposes. Second, it appears to be the case that the discriminant of ${\widetilde{U}}_d(x)$ is smaller than the discriminant of ${\widetilde{T}}_d(x)$, which makes the factors of ${\widetilde{U}}_d(x)$ more attractive. The following lemma is a consequence of Lemma 4.

Table 1 Admissible polynomials with small discriminants for $d=2,\ldots , 10$

Lemma 5

Let $d>1$. If $p=2d+1$ is a prime, the dth-order polynomial

$$\begin{aligned} E_{2d,2}(x) = \prod _{k=1}^d (x-u_{2d,2k}) \end{aligned}$$

is admissible.

Proof

Consider the factorization of ${\widetilde{U}}_{2d}(x)$. We have $2(2d)+2=4d+2=2p$; therefore, we have for $1\le k\le 2d$

$$\begin{aligned} \gcd (k,2(2d)+2) = {\left\{ \begin{array}{ll} 1 &{}\quad k\text { odd} \\ 2 &{}\quad k\text { even} . \end{array}\right. } \end{aligned}$$

This implies that ${\widetilde{U}}_{2d}(x)=E_{2d,1}(x)E_{2d,2}(x)$, which both are of order d. $\square$

This simple rule covers the cases $d\in \{2,3,5,6,8,9\}$. For the cases $d=4$ and $d=10$, we also did find good factors.

Lemma 6

The polynomial $E_{14,2}(x)$ is of order 4 and admissible, and the polynomial $E_{24,2}(x)$ is of order 10 and admissible.

Proof

Both polynomials are admissible by definition; it remains to compute their order. We first consider $E_{14,2}(x)$. Here, $2\cdot 14 +2 = 30$, and for $1\le k \le 14$, one has $\gcd (k, 30) = 2$ if and only if $k\in \{2,4,8,14\}$. Therefore, $E_{14,2}(x)$ is a polynomial of order 4. Now consider $E_{24,2}(x)$. We have $2\cdot 24 + 2 = 50$, and for $1\le k \le 24$, one has $\gcd (k,50) = 2$ if and only if $k\in \{2,4,6,8,12,14,16,18,22,24\}$. Therefore, $E_{24,2}(x)$ is a polynomial of order 10. $\square$

Unfortunately, the case $d=7$ is not covered by the factorization of all ${\widetilde{U}}_d(x)$ and ${\widetilde{T}}_d(x)$. However, using a numerical brute-force approach, we found the following polynomial.

Lemma 7

The polynomial

$$\begin{aligned} P_7(x) = x^7 + x^6 - 6x^5 - 4x^4 + 10x^3 + 4x^2 - 4x - 1 \end{aligned}$$

is of order 7 and admissible.

Proof

We have to prove that $P_7(x)$ is irreducible over ${\mathbb {Q}}$. It has leading coefficient 1 and coefficients in ${\mathbb {Z}}$; therefore, it is irreducible over ${\mathbb {Q}}$ if and only if it is irreducible over ${\mathbb {Z}}$. Here, we consider irreducibility over ${\mathbb {F}}_2$, which is a sufficient condition for irreducibility over ${\mathbb {Z}}$. In ${\mathbb {F}}_2$, one has

$$\begin{aligned} P_7(x) \equiv x^7 + x^6 + 1. \end{aligned}$$

Assume that this polynomial is reducible. Because it has no roots in ${\mathbb {F}}_2$, it would have to contain a factor of degree less then 4 which also has no root in ${\mathbb {F}}_2$. The possible candidates are therefore $x^2+x+1$, $x^3+x+1$ and $x^3+x^2+1$. Doing a polynomial division with these three polynomials, one finds that

$$\begin{aligned} x^7+ x^6 + 1&\equiv (x^2+x+1)(x^5+x^3+x^2+1)&+ x \\&\equiv (x^3+x+1)(x^4+x^3+x^2)&+ x^2 + 1 \\&\equiv (x^3+x^2+1)(x^4+x+1)&+ x^2 + x \end{aligned}$$

and we have a contradiction. Therefore, $P_7(x)$ is irreducible over ${\mathbb {F}}_2$ and subsequently also over ${\mathbb {Q}}$. $\square$

Even though Lemma 1 is not applicable for this polynomial because its roots lie in $(-2.25, 1.75)$, they still lie close to each other, which results in a good polynomial discriminant. Regarding the lattice representation issue in the $d=7$ case, one has to compute the Vandermonde matrix ${\varvec{V}}$ explicitly (using an arbitrary precision data type to avoid stability issues) and find a good lattice representation matrix ${\varvec{T}}$ by means of a lattice reduction algorithm; see, for instance, [29].

This completes our list of polynomials used for the dimensions $2\le d\le 10$; see Table 1. We do not claim that these polynomials are optimal with respect to numerical integration. In fact, the discriminant of admissible polynomials is an extensively studied quantity in the context of geometry of numbers and totally real number fields; see, for instance, [22]. In [46], a complete list of totally real number fields and corresponding admissible polynomials up to dimension $d=9$ is given; however, the optimal ones do not always have roots in $(-2,2)$. For the sake of practicability, we favor Chebyshev factors; in our opinion, the discriminants are reasonably close to the optimum.

4 Efficient Enumeration of Frolov Lattices in d-Cubes

In this section, we present an enumeration algorithm to determine the set of integration points for the Frolov cubature formula. The approach is similar to the one in [27] for orthogonal lattices. Here, we generalize the method for arbitrary lattices.

4.1 Enumeration of Non-orthogonal Frolov Lattices

We fix the integration domain ${\varOmega }= [-1/2, 1/2]^d$ and a lattice ${\varvec{T}}({\mathbb {Z}}^d)$ with lattice representation matrix ${\varvec{T}}$. We are interested in the discrete set

$$\begin{aligned} {\mathcal {N}} = {\varOmega }\cap {\varvec{T}}({\mathbb {Z}}^d) = \{{\varvec{Tk}}\in {\varOmega }\,:\, {\varvec{k}}\in {\mathbb {Z}}^d\}. \end{aligned}$$

Our strategy is to consider a slightly larger set ${\mathcal {B}} \supset {\mathcal {N}}$ which allows for explicit enumeration in a straightforward way. We choose

$$\begin{aligned} {\mathcal {B}} = B_{\sqrt{d}/2}(0)\cap {\varvec{T}}({\mathbb {Z}}^d) = \left\{ {\varvec{Tk}} \,:\, \Vert {\varvec{Tk}}\Vert _2^2\le \frac{d}{4}, {\varvec{k}}\in {\mathbb {Z}}^d\right\} . \end{aligned}$$

Using the matrix decomposition

$$\begin{aligned} {\varvec{T}} = {\varvec{QR}}, \end{aligned}$$

where ${\varvec{Q}}$ is an orthogonal matrix and ${\varvec{R}}$ is an upper triangular matrix, we can rewrite this set as

$$\begin{aligned} {\mathcal {B}} = \left\{ {\varvec{Tk}} \,:\, \Vert {\varvec{Rk}}\Vert _2^2\le \frac{d}{4}, {\varvec{k}}\in {\mathbb {Z}}^d\right\} . \end{aligned}$$

The function $\Vert {\varvec{R}}\cdot \Vert _2^2$ can be split up into additive parts

$$\begin{aligned} \Vert {\varvec{Rk}}\Vert _2^2= & {} \sum _{i=1}^d g_i({\varvec{k}})\\ g_i({\varvec{k}})= & {} ({\varvec{Rk}})_i^2,\quad i=1,\ldots ,d, \end{aligned}$$

and from the upper triangular structure of ${\varvec{R}}$, it follows that $g_j({\varvec{k}})$ only depends on the components $k_j,\ldots ,k_d$. For an integer vector ${\varvec{k}}$, we therefore have

$$\begin{aligned} \Vert {\varvec{Rk}}\Vert _2^2 \le \frac{d}{4} \Longleftrightarrow g_j({\varvec{k}}) \le \frac{d}{4} - \sum _{i=j+1}^d g_i({\varvec{k}}),\quad j=1,\ldots ,d. \end{aligned}$$

(4.1)

Fixing the coordinates $k_{j+1},\ldots ,k_d$ results in explicitly solvable inequalities for $k_j$, since the right-hand side is constant and the left-hand side is a quadratic function in $k_j$. Therefore, the set ${\mathcal {N}}$ can be assembled with Algorithm 1.

This algorithm iterates over all elements of ${\mathcal {B}}$, which determines the complexity that is of order

$$\begin{aligned} \mathrm {vol}_d\left( B_{\sqrt{d}/2}(0)\right) /|\det {\varvec{T}}| \asymp 2^d \cdot |{\mathcal {N}}|. \end{aligned}$$

(4.2)

This is certainly true if the sets $K_j$ appearing in the algorithm are all non-empty, and this should be the case for a lattice with a small determinant and a good choice of its representation matrix.

The exponential dependence on d and linear dependence on $|{\mathcal {N}}|$ in Eq. (4.2) is further discussed in the following subsection.

4.2 Numerical Results

In Table 2, the running times for the enumeration of the Frolov lattice points in $[0,1]^d$ with Algorithm 1 are provided for dimensionalities $d \in \{2,3, \ldots , 9\}$. Firstly, we observe that the number of points N converges to the scaling factor n, as n becomes large, cf. (1.4).

Moreover, one can observe the linear runtime of the algorithm in terms of the number of points N: If the number of points N is quadrupled, then also the required time to assemble these 4N points is approximately quadrupled. However, comparing the runtimes for small d and large d, it is apparent that a dimension-dependent constant is involved. This is analogous to the orthogonal setting for $d = 2^k, k \in {\mathbb {N}}$, as it was treated in [27]. For moderate dimensionalities up to 8, this does not seem to be a hindrance in practical applications, due to the small rate of the exponential dependence on d. Moreover, it is possible to precompute the points and reuse them for numerical integration. For, e.g., $N=10^6$ points, the required storage space as binary double-precision floating point is about $d \cdot 8$ MB. The resulting point sets for dimension $d \in \{2,3,\ldots , 10\}$ are available for download.¹

Table 2 Running times for the assemblation of Frolov cubature points in $[0,1]^d$

5 Compactly Supported Functions with Bounded Mixed Derivative in $L_2$

5.1 Characterization of the Space

We denote with $S({\mathbb {R}}^d)$ the usual Schwartz space. Let ${\mathbf {r}} = (r_1,\ldots ,r_d) \in {\mathbb {N}}^d$ be a smoothness vector with integer components. Then we define the semi-norm

$$\begin{aligned} \Vert \varphi \Vert ^2_{H^{{\mathbf {r}}}_{\text {mix}}} := \sum \limits _{e \subset [d]} \Big \Vert \Big (\prod \limits _{i\in e} \frac{\partial ^{r_i}}{\partial x_i^{r_i}}\Big )\varphi \Big \Vert ^2_2 , \end{aligned}$$

where $\Vert \cdot \Vert _2$ denotes the $L_2({\mathbb {R}}^d)$-norm. Clearly this norm is induced by an inner product. By Plancherel’s theorem together with well-known properties of the Fourier transform, see (6.2), we may rewrite

$$\begin{aligned} \begin{aligned} \Vert \varphi \Vert _{H^{{\mathbf {r}}}_{\text {mix}}}&= \Big \Vert {\mathcal {F}}^{-1}\Big [ \Big (\prod \limits _{i=1}^d (1+|2\pi \xi _i|^{2r_i})\Big )^{1/2} {\mathcal {F}} \varphi (\varvec{\xi })\Big ]\Big \Vert _2\\&= \Big \Vert \Big (\prod \limits _{i=1}^d (1+|2\pi \xi _i|^{2r_i})\Big )^{1/2}{\mathcal {F}}\varphi (\varvec{\xi })\Big \Vert _2 = \Vert v_{{\varvec{r}}}(\varvec{\xi }){\mathcal {F}}\varphi \Vert _2, \end{aligned} \end{aligned}$$

(5.1)

where we define

$$\begin{aligned} v_{{\mathbf {r}}}(\varvec{\xi }):= \Big (\prod \limits _{i=1}^d (1+|2\pi \xi _i|^{2r_i})\Big )^{1/2},\quad \varvec{\xi } \in {\mathbb {R}}^d. \end{aligned}$$

(5.2)

Let now ${\varOmega }$ be a bounded domain in ${\mathbb {R}}^d$. We denote with $C^{\infty }_0({\varOmega })$ the space of all infinitely many times differentiable (real-valued) functions $\varphi :{\mathbb {R}}^d \rightarrow {\mathbb {R}}$ with ${\text {supp}}\varphi \subset {\varOmega }$. Finally, we define the space

$$\begin{aligned} \mathring{H}^{{\mathbf {r}}}_{\text {mix}}({\overline{{\varOmega }}}) := \overline{C_0^{\infty }({\varOmega })}^{\Vert \cdot \Vert _{H^{{\mathbf {r}}}_{\text {mix}}}} \end{aligned}$$

(5.3)

by completion with respect to the norm $\Vert \cdot \Vert _{H^{{\mathbf {r}}}_{\text {mix}}}$. As a consequence, we get that $\mathring{H}^{{\mathbf {r}}}_{\text {mix}}({\overline{{\varOmega }}})$ is a Hilbert space which consists of $r_i-1$ times continuously differentiable functions (mixed in each component) on ${\mathbb {R}}^d$ which vanish on ${\mathbb {R}}^d\setminus {\varOmega }$.

We will now consider a more specific situation. Let ${\varOmega }= (0,1)^d$. Then it holds

$$\begin{aligned} \mathring{H}^{{\mathbf {r}}}_{\text {mix}}:=\mathring{H}^{{\mathbf {r}}}_{\text {mix}}([0,1]^d) = \mathring{H}^{r_1}([0,1]) \otimes \cdots \otimes \mathring{H}^{r_d}([0,1]) \end{aligned}$$

(5.4)

in the sense of tensor products of Hilbert spaces, where $\mathring{H}^{r} = \mathring{H}^{r_i}([0,1])$ is the univariate version of the above-defined spaces. Functions in this class satisfy a left and a right boundary condition, namely $f^{(j)}(0) = f^{(j)}(1) = 0$ for $j=0,\ldots ,r-1$.

The first assertion in the following lemma is a direct consequence of Taylor’s theorem and the homogeneous boundary condition of the function and all its derivatives. The second one follows from (i) together with Hölder’s inequality.

Lemma 8

Let ${\varvec{r}}\in {\mathbb {N}}^d$. (i) Every function $\varphi \in C_0^{\infty }((0,1)^d)$ admits the following representation

$$\begin{aligned} \varphi (x_1,\ldots ,x_d) = \int _0^1 \cdots \int _0^1 \varphi ^{({\varvec{r}})}(t_1,\ldots ,t_d)\prod \limits _{i=1}^d \frac{(x_i-t_i)^{r_i-1}_+}{(r_i-1)!}\,\mathrm{d}t_1\ldots \mathrm{d}t_d. \end{aligned}$$

(ii) Let $e \subset [d]$. Then

$$\begin{aligned} \Big \Vert \Big (\prod \limits _{i\in e} \frac{\partial ^{r_i}}{\partial x_i^{r_i}}\Big )\varphi \Big \Vert ^2_2 \le \Vert \varphi ^{({\varvec{r}})}\Vert ^2_2\prod \limits _{i\in [d]\setminus e} \frac{1}{[(r_i-1)!]^2(2r_i-1)2r_i}, \end{aligned}$$

and therefore,

$$\begin{aligned} \Vert \varphi \Vert ^2_{H^{{\varvec{r}}}_{\text {mix}}} \le \Vert \varphi ^{({\varvec{r}})}\Vert ^2_2\sum \limits _{e \subset [d]} \prod \limits _{i\in e} \frac{1}{[(r_i-1)!]^2(2r_i-1)2r_i} . \end{aligned}$$

Remark 1

(a) Note that the assertions in Lemma 8 hold true for any function $\varphi \in S({\mathbb {R}}^d)$ with ${\text {supp}}\varphi \subset {\mathbb {R}}_+^d$. We only need zero boundary values at 0.

(b) The previous lemma shows that the semi-norm $\Vert \cdot \Vert _{\mathring{H}^{{\varvec{r}}}_{\text {mix}}}$ induced by the bilinear form

$$\begin{aligned} \langle \varphi , \psi \rangle _{\mathring{H}^{{\varvec{r}}}_{\text {mix}}}:= \int _{[0,1]^d} \varphi ^{({\varvec{r}})}({\varvec{x}})\psi ^{({\varvec{r}})}({\varvec{x}})\,\mathrm{d}{\varvec{x}}\end{aligned}$$

(5.5)

is actually a norm on $C^{\infty }_0((0,1)^d)$ since the bilinear form is positive definite as a consequence of (ii). Hence, we could have also used this semi-norm for the completion in (5.3). As it turns out, Lemma 8 and (5.5) are actually the key to derive the reproducing kernel for the space $\mathring{H}^{{\varvec{r}}}_{\text {mix}}$.

(c) We have an explicit upper bound for the norm equivalence constant in (ii). Suppose that we have a constant smoothness vector ${\varvec{r}}= (r,\ldots ,r)$ with $r \in {\mathbb {N}}$. Then it holds

$$\begin{aligned} \begin{aligned} \sum \limits _{e \subset [d]} \prod \limits _{i\in e} \frac{1}{[(r_i-1)!]^2(2r_i-1)2r_i}&= \sum \limits _{i=0}^d \left( {\begin{array}{c}d\\ i\end{array}}\right) \Big (\frac{1}{[(r-1)!]^2(2r-1)2r}\Big )^i\\&= \Big (1+\frac{1}{[(r-1)!]^2(2r-1)2r}\Big )^d. \end{aligned} \end{aligned}$$

(5.6)

Hence, if $r=1$ the constant is bounded by $(3/2)^d$, in case $r=2$ we have $(13/12)^d$ and in case $r=3$ already $(61/60)^d$.

5.2 The Reproducing Kernel of $\mathring{H}^{{\mathbf {r}}}_\mathrm {mix}$

In the sequel, we will identify the space $\mathring{H}^{{\mathbf {r}}}_{\text {mix}}$ as a reproducing kernel Hilbert space. We are looking for a kernel function $\mathring{K}^{{\varvec{r}}}_d({\varvec{x}},{\varvec{y}})$ such that for every $f\in \mathring{H}^{{\mathbf {r}}}_{\text {mix}}$

$$\begin{aligned} \langle f(\cdot ), \mathring{K}^{{\varvec{r}}}_d({\varvec{x}},\cdot )\rangle _{\mathring{H}^{{\varvec{r}}}_{\text {mix}}} = f({\varvec{x}}),\quad {\varvec{x}}\in [0,1]^d. \end{aligned}$$

To this end, we may derive the reproducing kernels of the univariate spaces $\mathring{H}^{r_i}$. The reproducing kernel of the tensor product space (5.4) is then given by the point-wise product of the univariate kernels

$$\begin{aligned} \mathring{K}^{{\varvec{r}}}_{d}({\varvec{x}}, {\varvec{y}}) = \prod _{\ell =1}^d \mathring{K}^r_{1}(x_\ell , y_\ell ) . \end{aligned}$$

(5.7)

Therefore, the problem of computing $\mathring{K}_{d}^{\varvec{r}}({\varvec{x}}, {\varvec{y}})$ is reduced to the construction of $\mathring{K}^r_{1}: [0,1] \times [0,1] \rightarrow {\mathbb {R}}$.

Let us first recall a general fact for Hilbert spaces and orthogonal sums. To this end, let $U:=\mathrm {span}\{u_0,\ldots ,u_{r-1}\} \subset {\mathcal {H}}$ be an r-dimensional subspace of a Hilbert space ${\mathcal {H}}$. Using Gram–Schmidt orthogonalization, the orthogonal projection $P_U: {\mathcal {H}}\rightarrow U$ is given by

$$\begin{aligned} P_U(f)(x) = \sum _{j=0}^{r-1} \left( \sum _{k=0}^{r-1} G^{-1}_{j,k} \cdot \langle f,u_k\rangle _{{\mathcal {H}}} \right) u_j , \end{aligned}$$

(5.8)

where the Gramian matrix ${\mathbf {G}} = \left( \langle u_j, u_k \rangle _{{\mathcal {H}}} \right) _{j,k=0}^{r-1} \in {\mathbb {R}}^{r \times r}$. Moreover, the projection onto the orthogonal complement $U^\perp = {\mathcal {H}}\ominus U$ is $P_{U^\perp }f = (\mathrm {Id} - P_U)f$.

The next lemma provides the necessary utilities to compute the reproducing kernel of closed subspaces that are defined via homogeneous boundary conditions.

Lemma 9

Let ${\mathcal {H}}_K$ be a RKHS with kernel $K: [0,1] \times [0,1] \rightarrow {\mathbb {R}}$. Assuming that $K(x,\cdot )$ is r times weakly differentiable, let $u_{j} := K^{(0,j)}(\cdot , 1) := \frac{\partial ^j}{\partial y^j} K(\cdot , y)_{|y=1}$ for $j=0,\ldots ,r-1$ and $U = \mathrm {span}\{u_0,\ldots , u_{r-1}\}$. Then it holds that

• (i) For $j=0,\ldots ,r-1$, the Riesz representer of the functional $f \mapsto f^{(j)}(1)$ in ${\mathcal {H}}_K$ is given by $u_{j}$, i.e.,

  $$\begin{aligned} \langle f, u_{j} \rangle _{{\mathcal {H}}_K} = f^{(j)}(1) \quad \text { for all } f \in {\mathcal {H}}_K . \end{aligned}$$

• (ii) The reproducing kernel $K_{U^\perp }$ of $U^\perp \subset {\mathcal {H}}_K$, i.e., the orthogonal complement of U in ${\mathcal {H}}_K$, is given by

  $$\begin{aligned} K_{U^\perp }(x,y) = P_{U^\perp } K(\cdot , y)(x) = K(x,y) - \sum _{j=0}^{r-1} \sum _{k=0}^{r-1} G^{-1}_{j,k} u_j(x) u_k(y) . \end{aligned}$$

  (5.9)

• (iii) It holds that

  $$\begin{aligned} U^\perp = \{f \in {\mathcal {H}}_K: f^{(j)}(1)=0, j=0,\ldots ,r-1 \} . \end{aligned}$$

Proof

(i) is [3, Lem. 10] for the linear functional $f \mapsto f^{(j)}(1)$ and (ii) follows by applying [3, Thm. 11] to (5.8). Finally, regarding (iii) we note that it holds for all $f \in U^\perp$ that

$$\begin{aligned} \langle f, u_j \rangle _{{\mathcal {H}}_K} = \langle f, K^{(0,j)}(\cdot , 1) \rangle _{{\mathcal {H}}_K} = f^{(j)}(1) = 0 . \end{aligned}$$

$\square$

We want to apply this machinery to $\mathring{H}^r$ with $r\in {\mathbb {N}}$. The observation in Lemma 8 together with (5.5) gives rise to use the approach of Wahba [47, 1.2] as a starting point. Let us define the kernel function

$$\begin{aligned} K^r_1(x,y) := \int _0^1 \frac{(x-t)^{r-1}_+}{(r-1)!}\cdot \frac{(y-t)^{r-1}_+}{(r-1)!}\,\mathrm{d}t,\quad x,y\in [0,1]. \end{aligned}$$

(5.10)

Then it is immediately clear from Lemma 8,(i) (and a straightforward density argument) that

$$\begin{aligned} f(x) = \langle f(\cdot ), K_1^r(x,\cdot ) \rangle _{\mathring{H}^{r}}, \quad x\in [0,1]. \end{aligned}$$

Indeed, recall that the inner product $\langle \cdot ,\cdot \rangle _{\mathring{H}^r}$ stems from (5.5) and that

$$\begin{aligned} (K^r_1)^{(0,r)}(x,y) = \frac{(x-y)^{r-1}_+}{(r-1)!}. \end{aligned}$$

It is possible to give an explicit formula for (5.10) by using that

$$\begin{aligned} K^r_1(x,y) := \int _0^{\min \{x,y\}} \frac{(x-t)^{r-1}_+}{(r-1)!}\cdot \frac{(y-t)^{r-1}_+}{(r-1)!}\,\mathrm{d}t. \end{aligned}$$

(5.11)

Interpreting this as a Taylor remainder term, we find

$$\begin{aligned} K^r_1(x,y) = \frac{(-1)^r}{(2r-1)!}\Big [\sum \limits _{k=r}^{2r-1}\left( {\begin{array}{c}2r-1\\ k\end{array}}\right) (-\min \{x,y\})^k\max \{x,y\}^{2r-1-k}\Big ]. \end{aligned}$$

(5.12)

However, $\mathring{H}^r$ is only a closed subspace of ${\mathcal {H}}_{K_1^r}$ since the functions $f \in {\mathcal {H}}_{K_1^r}$ may lack the right boundary condition which is $f^{(j)}(1) = 0$ if $j=0,\ldots ,r-1$, whereas the left boundary condition $f^{(j)}(0) = 0$ if $j=0,\ldots ,r-1$ is for free due to the construction. Let us now apply the construction from Lemma 9 to $K^r_1$ to construct a reproducing kernel $\mathring{K}^r_1$ for the closed subspace $\mathring{H}^r$.

Fig. 4

Plots of the kernel $\mathring{K}^r_1: [0,1] \times [0,1] \rightarrow {\mathbb {R}}$ with smoothness $r=1$ (left) and smoothness $r=2$ (right)

First we compute the functions $u_j(\cdot ) = (K_1^r)^{(0,j)}(\cdot ,1)$ for $j = 0,\ldots ,r-1$ explicitly. Using again the formula (5.10), we find

$$\begin{aligned} \begin{aligned} u_j(x)&= \Big (\frac{\mathrm{d}}{\mathrm{d}y}\Big )^j\int _0^{\min \{x,y\}} \frac{(x-t)^{r-1}_+}{(r-1)!}\cdot \frac{(y-t)^{r-1}_+}{(r-1)!}\,\mathrm{d}t{\bigg \vert }_{y=1}\\&=\int _0^x \frac{(x-t)^{r-1}_+}{(r-1)!}\cdot \frac{(1-t)^{r-1-j}}{(r-1-j)!}\,\mathrm{d}t, \end{aligned} \end{aligned}$$

(5.13)

where we used the well-known formula for the differentiation of integrals. Similar as above in (5.11), we interpret this as a Taylor’s remainder term for a specific polynomial. It is not hard to verify that this polynomial is given by

$$\begin{aligned}&u_j(x) = \frac{(-1)^r}{(2r-1-j)!} \Big [\sum \limits _{k=r}^{2r-1-j} \left( {\begin{array}{c}2r-1-j\\ k\end{array}}\right) (-x)^k\Big ], \nonumber \\&\qquad j=0,\ldots ,r-1. \end{aligned}$$

(5.14)

Looking at the functions $u_j$ for $j=0,\ldots ,r-1$, we see immediately that $\{x^r,\ldots ,x^{2r-1}\}$ is a basis of their span. Hence, we may use the system ${\tilde{u}}_j(x) = x^{j+r}/(j+r)!$ in (5.9). This gives the following representation for the kernel $\mathring{K}^r_{1}(x,y)$, namely

$$\begin{aligned} \mathring{K}^r_{1}(x,y) = K_1^r(x,y) - \sum _{j=0}^{r-1} \sum _{k=0}^{r-1} \frac{G^{-1}_{j,k}}{(j+r)!(k+r)!} x^{j+r} y^{k+r}, \end{aligned}$$

(5.15)

where $K_1^r(x,y)$ is given by (5.12) and

$$\begin{aligned} {\mathbf {G}} = \Big (\frac{1}{j! k!(j+k+1)}\Big )_{\begin{array}{c} j=0,\ldots ,r-1\\ k=0,\ldots ,r-1 \end{array}}. \end{aligned}$$

Let us give two examples. Putting $r=1$ in (5.15), we have

$$\begin{aligned} \mathring{K}^1_1(x,y) = \min \{x,y\} - xy,\quad x,y \in [0,1]. \end{aligned}$$

Furthermore, in case $r=2$ we obtain

$$\begin{aligned} \mathring{K}^2_1(x,y) = K^2_1(x,y) - x^2y^2+x^2y^3/2+x^3y^2/2-x^3y^3/3, \end{aligned}$$

where

$$\begin{aligned} K^2_1(x,y) = \frac{1}{2}\min \{x,y\}^2\max \{x,y\}-\frac{1}{6}\min \{x,y\}^3, \end{aligned}$$

For $r=1,2,3$, we obtain the associated Gramian matrices

$$\begin{aligned} ({\mathbf {G}}^1)^{-1} = \left( \begin{matrix} 1 \end{matrix}\right) ,\quad ({\mathbf {G}}^2)^{-1} = \left( \begin{matrix} 4 &{} -6\\ -6 &{} 12 \end{matrix}\right) ,\quad ({\mathbf {G}}^3)^{-1} = \left( \begin{matrix} 9&{} -36 &{} 60\\ -36 &{} 192 &{} -360\\ 60 &{} -360 &{} 720 \end{matrix}\right) . \end{aligned}$$

In the case $d=1$, the kernels for $r=1$ and $r=2$ are depicted in Fig. 4. The smoothness can be observed along the diagonal $x = y$, where the kernel for $r=1$ exhibits a kink.

Regarding the multivariate kernel, we have arrived at the following result.

Theorem 1

Given a smoothness vector ${\mathbf {r}} = (r_1, r_2,\ldots ,r_d) \in {\mathbb {N}}^d$, the reproducing kernel of the tensor product space $\mathring{H}^{{\mathbf {r}}}_\mathrm {mix}= \mathring{H}^{r_1} \otimes \cdots \otimes \mathring{H}^{r_d}$ is given by

$$\begin{aligned} \mathring{K}_{d}^{{\mathbf {r}}}({\varvec{x}}, {\varvec{y}})&= \prod _{\ell =1}^d \mathring{K}_{1}^{r_\ell }(x_\ell , y_\ell ) \end{aligned}$$

(5.16)

$$\begin{aligned}&= \prod _{\ell =1}^d \Big (K_{1}^{r_\ell }(x_\ell , y_\ell ) - \sum _{j=0}^{r_\ell -1} \sum _{k=0}^{r_\ell -1} ({\mathbf {G}}^{r_\ell })^{-1}_{j,k} (K_{1}^{r_\ell })^{(0,j)}(x_\ell ,1) \, (K_{1}^{r_\ell })^{(0,k)}(y_\ell ,1) \Big ), \end{aligned}$$

(5.17)

where $u_j (x_\ell ) = (K_{1}^{r_\ell })^{(0,j)}(x_\ell ,1)$ are given in (5.14) and $({\mathbf {G}}^{r_\ell })^{-1}$ are given in (5.5).

The explicit expression for the reproducing kernel of $\mathring{H}^{{\mathbf {r}}}_\mathrm {mix}$ allows to compute the norms of arbitrary bounded linear functionals $L \in (\mathring{H}^{{\mathbf {r}}}_\mathrm {mix})^\star$, since it holds

$$\begin{aligned} \Vert L\Vert _{(\mathring{H}^{{\mathbf {r}}}_\mathrm {mix})^\star } = \sup _{\Vert f\Vert _{ \mathring{H}^{{\mathbf {r}}}_\mathrm {mix}} \le 1} |L(f)| = \sqrt{ L^{({\varvec{x}})} L^{({\varvec{y}})} \mathring{K}_{d}^{{\mathbf {r}}}({\varvec{x}}, {\varvec{y}}) }. \end{aligned}$$

(5.18)

The right-hand side involves the application of the functional L to both components of the kernel. We will use this in Sect. 7 for the simulation of worst-case integration errors which can be rewritten as norms of certain functionals (7.1) involving the integration functional $L(f) = I_d(f) = \int _{[0,1]^d} f({\varvec{x}}) \, \,\mathrm {d}{\varvec{x}}$. In the sequel, we will compute the norm and its Riesz representer. We have

$$\begin{aligned} \Vert I_d\Vert ^2_{(\mathring{H}^{{\mathbf {r}}}_\mathrm {mix})^\star } = \sup _{\Vert f\Vert _{ \mathring{H}^{{\mathbf {r}}}_\mathrm {mix}} \le 1} |I_d(f)|^2 = \prod _{\ell =1}^d \left( \int _0^1 \int _0^1 \mathring{K}_{1}^{r_\ell }(x_\ell , y_\ell ) \, \,\mathrm {d}x_\ell \,\mathrm {d}y_\ell \right) , \end{aligned}$$

(5.19)

where

$$\begin{aligned}&\int _0^1 \int _0^1 \mathring{K}_{1}^{r}(x, y) \, \,\mathrm {d}x \,\mathrm {d}y \\&\quad = \int _0^1 \int _0^1 K_1^r(x,y) - \sum _{j=0}^{r-1} \sum _{k=0}^{r-1} \frac{G^{-1}_{j,k}}{(j+r)!(k+r)!} x^{j+r} y^{k+r} \, \,\mathrm {d}x \,\mathrm {d}y \\&\quad = \int _0^1 \int _0^1 K_1^r(x,y) \, \,\mathrm {d}x \,\mathrm {d}y - \sum _{j=0}^{r-1} \sum _{k=0}^{r-1} \frac{G^{-1}_{j,k}}{(j+r + 1)!(k+r + 1)!} \\&\quad = \frac{1}{ (r!)^2 (2r+1)} - \sum _{j=0}^{r-1} \sum _{k=0}^{r-1} \frac{G^{-1}_{j,k}}{(j+r + 1)!(k+r + 1)!}. \end{aligned}$$

The last identity follows from the representation (5.11) and

$$\begin{aligned} \int _0^1 \int _0^1 K_1^r(x,y) \, \,\mathrm {d}x \,\mathrm {d}y&= \int _0^1 \left( \int _0^1 \int _0^1 \frac{(x-t)^{r-1}_+}{(r-1)!} \frac{(y-t)^{r-1}_+}{(r-1)!} \, \,\mathrm {d}x \,\mathrm {d}y \right) \,\mathrm {d}t \\&= \int _0^1 \left( \int _t^1 \frac{(x-t)^{r-1}}{(r-1)!} \int _t^1 \frac{(y-t)^{r-1}}{(r-1)!} \, \,\mathrm {d}x \,\mathrm {d}y \right) \,\mathrm {d}t \\&= \int _0^1 \left( \frac{(1-t)^r}{r!} \frac{(1-t)^r}{r!} \right) \,\mathrm {d}t = \int _0^1 \frac{(1-t)^{2r}}{(r!)^2} \ \,\mathrm {d}t \\&= \frac{1}{(2r)! (2r+1) } . \end{aligned}$$

For the Riesz representer of $f \mapsto \int _{[0,1]^d} f({\varvec{x}}) \,\mathrm {d}{\varvec{x}}= \langle f, R_{I_d} \rangle _{\mathring{H}^{{\varvec{r}}}_{\text {mix}}}$, it holds

$$\begin{aligned} R_{I_d}({\varvec{y}}) = \int _{[0,1]^d} \mathring{K}_{d}^{{\mathbf {r}}}({\varvec{x}}, {\varvec{y}})\,\,\mathrm {d}{\varvec{x}}= \prod _{\ell =1}^d \left( \int _0^1 \mathring{K}_{1}^{r_\ell }(x_\ell , y_\ell ) \, \,\mathrm {d}x_\ell \right) \end{aligned}$$

for ${\varvec{y}}= (y_1,\ldots ,y_d)$. Clearly, we have

$$\begin{aligned} \int _0^1 \mathring{K}_{1}^{r_\ell }(x, y) \, \,\mathrm {d}x = \int _0^1 K_{1}^{r_\ell }(x, y) - \sum _{j=0}^{r-1} \sum _{k=0}^{r-1} \frac{G^{-1}_{j,k}}{(j+r)!(k+r)!} x^{j+r} y^{k+r} \, \,\mathrm {d}x. \end{aligned}$$

A similar computation as above together with the identity

$$\begin{aligned} \int _0^1 \frac{(y-t)^{r-1}_+}{(r-1)!}\frac{(1-t)^r}{r!}\,\mathrm {d}t = \frac{(-1)^r}{(2r)!}\sum \limits _{k=r}^{2r} \left( {\begin{array}{c}2r\\ k\end{array}}\right) (-y)^k \end{aligned}$$

(see the computation after (5.13)) leads to the following explicit formula

$$\begin{aligned} \int _0^1 \mathring{K}_{1}^{r_\ell }(x, y) \, \,\mathrm {d}x= & {} \frac{(-1)^r}{(2r)!}\sum \limits _{k=r}^{2r} \left( {\begin{array}{c}2r\\ k\end{array}}\right) (-y)^k \nonumber \\&- \sum _{j=0}^{r-1} \sum _{k=0}^{r-1} \frac{G^{-1}_{j,k}}{(j+r+1)!(k+r)!}y^{k+r}. \end{aligned}$$

(5.20)

6 Worst-Case Error Estimates with Respect to $\mathring{H}^{{\mathbf {r}}}_{\text {mix}}$

In this section, we are interested in the behavior of the worst-case error

$$\begin{aligned} e(n,d,{\varvec{r}}) \,:=\, \sup _{\Vert f\Vert _{\mathring{H}^{{\varvec{r}}}_{\text {mix}} \le 1}}\, \left| {Q_n^d(f)-I_d(f)}\right| \end{aligned}$$

(6.1)

of Frolov’s cubature rule $Q_n^d$ with respect to the unit ball in the norm $\Vert \cdot \Vert _{\mathring{H}^{\varvec{r}}_{\text {mix}}}$; see (5.5). Recall that

$$\begin{aligned} Q_n^d(f) \,=\, \frac{1}{n}\sum _{{\varvec{k}}\in {\mathbb {Z}}^d}\, f({\varvec{A}}_n{\varvec{k}}), \end{aligned}$$

where ${\varvec{A}}_n=n^{-1/d}{\varvec{A}}$ and ${\varvec{A}}=\bigl (\det ({\varvec{V}})\bigr )^{-1/d}{\varvec{V}}$ with ${\varvec{V}}$ from Theorem 1. Let further ${\varvec{B}}_n= ({\varvec{A}}_n)^{-\top }$.

The main tool for analyzing (6.1) is Poisson’s summation formula. Let $\varphi \in S({\mathbb {R}}^d)$ be a multivariate Schwartz function. With ${\mathcal {F}}\varphi$, we denote the Fourier transform

$$\begin{aligned} {\mathcal {F}}\varphi (\varvec{\xi }) = \int _{{\mathbb {R}}^d} \varphi ({\varvec{x}})\exp (-2\pi i{\varvec{x}}\cdot \varvec{\xi })\,\mathrm{d}{\varvec{x}},\qquad \varvec{\xi }\in {\mathbb {R}}^d. \end{aligned}$$

(6.2)

Then it holds

$$\begin{aligned} \sum \limits _{{\varvec{m}}\in {\mathbb {Z}}^d} \varphi (x+{\varvec{m}}) = \sum \limits _{{\varvec{k}}\in {\mathbb {Z}}^d} {\mathcal {F}}\varphi ({\varvec{k}})\exp (2\pi i{\varvec{k}}\cdot {\varvec{x}}) \end{aligned}$$

with absolute convergence on both sides. The following consequence is of particular importance. Let ${\varvec{A}}:{\mathbb {R}}^d \rightarrow {\mathbb {R}}^d$ be a regular matrix with $\det {\varvec{A}} \ne 0$. Let further ${\varvec{B}}={\varvec{A}}^{-\top }$. Then we have

$$\begin{aligned} \det {\varvec{A}} \sum \limits _{{\varvec{m}}\in {\mathbb {Z}}^d} \varphi ({\varvec{A}}({\varvec{x}}+{\varvec{m}})) = \sum \limits _{{\varvec{k}}\in {\mathbb {Z}}^d} {\mathcal {F}} \varphi ({\varvec{B}}{\varvec{k}})\exp (2\pi i{\varvec{k}}\cdot {\varvec{x}}). \end{aligned}$$

(6.3)

Let us finally mention the following special case by putting ${\varvec{x}}= 0$

$$\begin{aligned} \det {\varvec{A}} \sum \limits _{{\varvec{m}}\in {\mathbb {Z}}^d} \varphi ({\varvec{A}}{\varvec{m}}) = \sum \limits _{{\varvec{k}}\in {\mathbb {Z}}^d} {\mathcal {F}}\varphi ({\varvec{B}}{\varvec{k}}). \end{aligned}$$

(6.4)

A more general variant (with respect to the regularity of the participating functions) can be found in [45, Thm. 3.1, Cor. 3.2].

In this section, we show the by now well-known upper bounds on the worst-case error of Frolov’s cubature formula for the Sobolev spaces $\mathring{H}^{{\mathbf {r}}}_{\text {mix}}$. We give relatively short proofs here with special emphasis on the constants. In particular, we will see how the invariants of the used lattice will affect the error estimates.

We will see that only two invariants will play a role in the upper bounds, which we want to discuss shortly. For this, note that the lattices under consideration are generated by a multiple of a Vandermonde matrix ${\varvec{V}}$, which is defined via a generating polynomial P as in Theorem 1. The first invariant is the determinant or in other words the discriminant of the generating polynomial

$$\begin{aligned} D_P \,=\, \det ({\varvec{V}}). \end{aligned}$$

For example, we know from Theorem 1 that $\mathrm {Nm}({\varvec{V}}^{-\top }) =1/D_P^{2}$.

The second invariant is

$$\begin{aligned} B_P \,:=\, \min _{{\varvec{U}}} \Vert {\varvec{V}}{\varvec{U}}\Vert _\infty , \end{aligned}$$

(6.5)

where the minimum is over all ${\varvec{U}}\in {\hbox {SL}}_d({\mathbb {Z}})$. This constant is an upper bound for the diameter (in $\ell _\infty$) of the “smallest” fundamental cell of the lattice. To see this, note that every fundamental cell, i.e., a parallelepiped with corners on the lattice with no lattice point in the interior, is of the form $T([0,1]^d)$, where $T\in {\mathbb {R}}^{d\times d}$ is a generating matrix for the lattice. Moreover, it is well known that every generating matrix of the lattice that is generated by ${\varvec{V}}$ is of the form ${\varvec{V}}{\varvec{U}}$ for some unimodular, integer-valued matrix ${\varvec{U}}$. We will see that both, $D_P$ and $B_P$, should be small to obtain a small upper bound on the errors. This justifies the choice of the generating polynomials in the previous section. Here is the main result of this section.

Theorem 2

Let ${\varvec{r}}=(r_1,\dots ,r_d) \in {\mathbb {N}}^d$ be a smoothness vector with $r=r_1 = \cdots =r_\eta < r_{\eta +1} \le r_{\eta +2} \le \cdots \le r_d$ and $\eta :=\#\{j:r_j=r\}$. Then we have for any $f\in \mathring{H}^{\varvec{r}}_{\mathrm {mix}}$

$$\begin{aligned} \begin{aligned}&\left| {Q_n^d(f)-I_d(f)}\right| \\&\quad \le \; C \cdot \max \left\{ D_P, \frac{(2 B_P)^d}{n}\right\} ^{1/2} \left( \frac{D_P}{n}\right) ^{r}\, \Bigl (2+\log \left( n/D_P\right) \Bigr )^{(\eta -1)/2} \,\left\| {f}\right\| _{\mathring{H}^{{\varvec{r}}}_{\text {mix}}}, \end{aligned} \end{aligned}$$

(6.6)

where $C=C(d,\eta ,{\varvec{r}})$ is given by

$$\begin{aligned} \begin{aligned} C(d,\eta ,{\varvec{r}}) \,&:=\, 2^{d+1}\, \left( 1-2^{-2(r'-r)}\right) ^{-(d-\eta )/2}\, \left( 1-2^{(1-2r)}\right) ^{-\eta /2} \\&\quad \cdot \,\left( \sum \limits _{e \subset [d]} \cdot \prod \limits _{i\in e} \frac{1}{[(r_i-1)!]^2(2r_i-1)2r_i}\right) ^{1/2} \end{aligned} \end{aligned}$$

with $r':=\min _j\{r_j:r_j\ne r\}$.

Let us prove the following estimate first.

Proposition 2

Let $\varphi \in C_0^{\infty }((0,1)^d)$. Then

$$\begin{aligned} \left| {Q_n^d(\varphi )-I_d(\varphi )}\right| \le \sqrt{\frac{M({\varvec{A}}_n)}{\det {\varvec{B}}_n}}\Big (\sum \limits _{{\varvec{k}}\in {\mathbb {Z}}^d\setminus \{{\mathbf {0}}\}} |v_{{\varvec{r}}}( {\varvec{B}}_n{\varvec{k}})|^{-2}\Big )^{1/2} \Vert \varphi \Vert _{H^{{\varvec{r}}}_\text {mix}}, \end{aligned}$$

(6.7)

where

$$\begin{aligned} M({\varvec{A}}_n) \,:=\, \min _{{\varvec{U}}\in {\hbox {SL}}_d({\mathbb {Z}})}\#\Bigl \{{\varvec{m}}\in {\mathbb {Z}}^d:{\varvec{UA}}_n\bigl ({\varvec{m}}+(0,1)^d\bigr )\cap [0,1]^d\ne \emptyset \Bigr \} \end{aligned}$$

(6.8)

is the minimal number of fundamental cells of the integration lattice necessary to cover the unit cube.

Proof

The above special case of Poisson’s summation formula (6.4) gives

$$\begin{aligned} \left| {Q_n^d(\varphi )-I_d(\varphi )}\right|= & {} \Big |\sum \limits _{{\varvec{k}}\in {\mathbb {Z}}^d\setminus \{{\mathbf {0}}\}} {\mathcal {F}}\varphi ({\varvec{B}}_n{\varvec{k}})\Big |\nonumber \\\le & {} \Big (\sum \limits _{{\varvec{k}}\in {\mathbb {Z}}^d\setminus \{{\mathbf {0}}\}}v_{{\mathbf {r}}}({\varvec{B}}_n{\varvec{k}})^{-2}\Big )^{1/2} \Big (\sum \limits _{{\varvec{k}}\in {\mathbb {Z}}^d} |v_{{\mathbf {r}}}({\varvec{B}}_n{\varvec{k}}) {\mathcal {F}}\varphi ({\varvec{B}}_n{\varvec{k}})|^2\Big )^{1/2}.\nonumber \\ \end{aligned}$$

(6.9)

By the definition of $v_{{\varvec{r}}}$, we may rewrite

$$\begin{aligned} |v_{{\mathbf {r}}}({\varvec{B}}_n{\varvec{k}}) {\mathcal {F}}\varphi ({\varvec{B}}_n{\varvec{k}})|^2= \sum \limits _{e \subset [d]}\Big |{\mathcal {F}}\Big [\Big (\prod \limits _{i\in e} \frac{\partial ^{r_i}}{\partial x_i^{r_i}}\Big )\varphi \Big ]({\varvec{B}}_n{\varvec{k}})\Big |^2. \end{aligned}$$

Using this for the second factor in (6.9), we find

$$\begin{aligned} \begin{aligned}&\sum \limits _{{\varvec{k}}\in {\mathbb {Z}}^d} |v_{{\mathbf {r}}}({\varvec{B}}_n{\varvec{k}}) {\mathcal {F}}\varphi ({\varvec{B}}_n{\varvec{k}})|^2\\&\quad =\sum \limits _{e \subset [d]}\int \limits _{[0,1]^d} \Big |\sum \limits _{{\varvec{k}}\in {\mathbb {Z}}^d}{\mathcal {F}}\Big [\Big (\prod \limits _{i\in e} \frac{\partial ^{r_i}}{\partial x_i^{r_i}}\Big )\varphi \Big ]({\varvec{B}}_n{\varvec{k}})\exp (2\pi i{\varvec{k}}\cdot {\varvec{x}})\Big |^2\,d{\varvec{x}}. \end{aligned} \end{aligned}$$

Now we apply Poisson’s summation formula in the form (6.3) to the integrand and find

$$\begin{aligned} \begin{aligned}&\sum \limits _{{\varvec{k}}\in {\mathbb {Z}}^d} |v_{{\mathbf {r}}}({\varvec{B}}_n{\varvec{k}}) {\mathcal {F}}\varphi ({\varvec{B}}_n{\varvec{k}})|^2\\&\quad =(\det {\varvec{A}}_n)^2\sum \limits _{e \subset [d]}\int \limits _{[0,1]^d} \Big |\sum \limits _{{\varvec{m}}\in {\mathbb {Z}}^d}\Big [\Big (\prod \limits _{i\in e} \frac{\partial ^{r_i}}{\partial x_i^{r_i}}\Big ) \varphi \Big ]({\varvec{A}}_n({\varvec{x}}+{\varvec{m}}))\Big |^2\,d{\varvec{x}}\\&\quad \le (\det {\varvec{A}}_n)^2M({\varvec{A}}_n)\sum \limits _{e \subset [d]}\sum \limits _{{\varvec{m}}\in {\mathbb {Z}}^d} \int \limits _{[0,1]^d}\Big |\Big [\Big (\prod \limits _{i\in e} \frac{\partial ^{r_i}}{\partial x_i^{r_i}}\Big )\varphi \Big ] ({\varvec{A}}_n({\varvec{x}}+{\varvec{m}}))\Big |^2\,d{\varvec{x}}\\&\quad =(\det {\varvec{A}}_n)M({\varvec{A}}_n)\sum \limits _{e \subset [d]} \int _{{\mathbb {R}}^d}\Big |\Big [\Big (\prod \limits _{i\in e} \frac{\partial ^{r_i}}{\partial x_i^{r_i}}\Big )\varphi \Big ]({\varvec{y}})\Big |^2\,d{\varvec{y}}\\&\quad = \frac{M({\varvec{A}}_n)}{\det {\varvec{B}}_n}\Vert \varphi \Vert ^2_{H^{{\varvec{r}}}_{\text {mix}}}, \end{aligned} \end{aligned}$$

(6.10)

where we used Hölder’s inequality and the fact that $\varphi$ and all its partial derivatives have compact support in $(0,1)^d$ together with (6.8). $\square$

Remark 2

Let us comment on the number $M({\varvec{A}}_n)$. Clearly, all the fundamental cells are contained in $[-L(n,P),1+L(n,P)]^d$ with $L(n,P):=(D_P n)^{-1/d} B_P$ and $B_P$ from (6.5). Here, we used that ${\varvec{A}}_n=(D_P n)^{-1/d}{\varvec{V}}$. Therefore, $M({\varvec{A}}_n)$ is bounded by the number of lattice points ${\varvec{A}}_n({\mathbb {Z}}^d)$ in this set. This number can be controlled by (6.11), which will be also of some importance later. For a proof, see, e.g., [44, Lem. 5]. In fact, for every axis-parallel box ${\varOmega }\subset {\mathbb {R}}^d$ and every $T\in {\mathbb {R}}^{d\times d}$ we have

$$\begin{aligned} \#\left( {\varvec{T}}({\mathbb {Z}}^d)\cap {\varOmega }\right) \,\le \, \frac{\mathrm {vol}_d({\varOmega })}{\mathrm {Nm}({\varvec{T}})} +1. \end{aligned}$$

(6.11)

With all the definitions from above and $\mathrm {Nm}({\varvec{V}})=1$, we obtain that

$$\begin{aligned} M({\varvec{A}}_n) \,\le \, n\, D_P\,\left( 1+\frac{2 B_P}{(D_P n)^{1/d}}\right) ^d + 1 \,\le \, n\,2^d\, \max \left\{ D_P,\, \frac{(2 B_P)^d}{n}\right\} . \end{aligned}$$

(6.12)

We see that the bound of the second factor of the above error bound depends asymptotically only on $\sqrt{D_P}$ (and the norm of f). However, for preasymptotic bounds also the term $B_P^{d/2}/\sqrt{n}$ plays an important role.

Proof

To finish the proof of Theorem 2, it remains to estimate the middle factor in (6.7). From that, we obtain the bound for $\varphi \in C_0^{\infty }((0,1)^d)$. In order to extend it to the class $\mathring{H}^{\varvec{r}}_{\mathrm {mix}}$, we apply a straightforward density argument recalling (5.3).

If ${\varvec{r}}=(r,\dots ,r)$ where $r\in {\mathbb {N}}_0$ is a constant smoothness vector, the following proof can be found in several articles; see, e.g., [41] or [43, p. 580]. Note that it also works for fractional $r>1/2$, which is essentially shown in [45]. Although the optimal order of convergence is known also in the non-constant case, we were not able to find a proof with explicit constants. Therefore, we give it here. We assume without restriction that $r_1=\dots = r_\eta <r_{\eta +1}\le \dots \le r_d$ for some $\eta \in \{1,\dots ,d\}$.

First, for ${\varvec{m}}=(m_1,\dots ,m_d)\in {\mathbb {N}}_0^d$, we define the sets

$$\begin{aligned} \rho ({\varvec{m}}) \,:=\, \{{\varvec{x}}\in {\mathbb {R}}^d:\lfloor 2^{m_j-1}\rfloor \le |x_j|<2^{m_j} \text { for } j=1,\dots ,d\}. \end{aligned}$$

Note that $\prod _{j=1}^d|x_j|<2^{\Vert {\varvec{m}}\Vert _1}$ for all $x\in \rho ({\varvec{m}})$. Because of $B_n=n^{1/d}B=(D_p n)^{1/d}\, {\varvec{V}}^{-\top }$, we have

$$\begin{aligned} \mathrm {Nm}(B_n) \,=\, \inf _{{\varvec{k}}\in {\mathbb {Z}}^d\setminus \{0\}}\prod _{j=1}^d (B_n{\varvec{k}})_j \,=\, \frac{n}{D_p}. \end{aligned}$$

This shows that $|(B_n({\mathbb {Z}}^d)\setminus 0)\cap \rho ({\varvec{m}})|=0$ for all ${\varvec{m}}\in {\mathbb {N}}_0^d$ with $\Vert {\varvec{m}}\Vert _1< R_n$, where

$$\begin{aligned} R_n\,:=\, \left\lceil \log _2\bigl (n/D_p\bigr ) \right\rceil . \end{aligned}$$

Moreover, for $B_n{\varvec{k}}\in \rho ({\varvec{m}})$, we have

$$\begin{aligned} \nu _{{\varvec{r}}}(B_n{\varvec{k}}) \,\ge \, \prod _{j=1}^d\max \{1,2\pi \lfloor 2^{m_j-1}\rfloor \}^{r_j} \,\ge \, 2^{r_1 m_1+\dots +r_d m_d}. \end{aligned}$$

Since $\rho ({\varvec{m}})$ is a union of $2^d$ axis-parallel boxes each with volume less than $2^{\Vert {\varvec{m}}\Vert _1}$, (6.11) implies $\left| {B_n({\mathbb {Z}}^d)\cap \rho ({\varvec{m}})}\right| \le 2^d(D_p 2^{\Vert {\varvec{m}}\Vert _1}/n+1) \le 2^{d+2} 2^{\Vert {\varvec{m}}\Vert _1-R_n}$ if $\Vert {\varvec{m}}\Vert _1\ge R_n$. Additionally, note that $\left| {\{{\varvec{m}}\in {\mathbb {N}}_0^\eta :\Vert {\varvec{m}}\Vert _1=\ell \}}\right| =\left( {\begin{array}{c}\eta -1+\ell \\ \eta -1\end{array}}\right)$. With $r:=r_1$ and $r':=r_{\eta +1}$, we obtain

$$\begin{aligned} \begin{aligned}&\sum _{{\varvec{k}}\in {\mathbb {Z}}^d\setminus \{0\}} |\nu _{{\varvec{r}}}(B_n{\varvec{k}})|^{-2} \\&\quad \le \sum _{m: \Vert m\Vert _1\ge R_n} \left| {B_n({\mathbb {Z}}^d)\cap \rho (m)}\right| 2^{-2r_1 m_1-\cdots -2r_d m_d}\\&\quad \le 2^{d+2} \sum _{m: \Vert m\Vert _1\ge R_n} 2^{\Vert m\Vert _1-R_n} 2^{-2r (m_1+\cdots +m_\eta )-2r'(m_{\eta +1}+\cdots +m_d)} \\&\quad = 2^{d+2} \sum _{\ell =R_n}^\infty \sum _{m: \Vert m\Vert _1=\ell } 2^{\Vert m\Vert _1-R_n} 2^{-2r (m_1+\cdots +m_\eta )-2r'(m_{\eta +1}+\cdots +m_d)} \\&\quad = 2^{d+2} \sum _{\ell =R_n}^\infty \sum _{\ell '=0}^\ell \; \sum _{\begin{array}{c} m_1,\dots ,m_\eta :\\ \sum _{j=1}^\eta m_j=\ell -\ell ' \end{array}} \; \sum _{\begin{array}{c} m_{\eta +1},\dots ,m_d:\\ \sum _{j=\eta +1}^d m_j=\ell ' \end{array}} 2^{\ell -R_n} 2^{-2r (\ell -\ell ' )-2r'\ell '} \\&\quad = 2^{d+2} \sum _{\ell =R_n}^\infty \sum _{\ell '=0}^\ell \left( {\begin{array}{c}\eta -1+\ell -\ell '\\ \eta -1\end{array}}\right) \left( {\begin{array}{c}d-\eta -1+\ell '\\ d-\eta -1\end{array}}\right) 2^{\ell -R_n-2r \ell -2(r'-r)\ell '} \\&\quad \le 2^{d+2} \sum _{\ell =R_n}^\infty \left( {\begin{array}{c}\eta -1+\ell \\ \eta -1\end{array}}\right) 2^{\ell -R_n-2r \ell }\; \sum _{\ell '=0}^\ell \left( {\begin{array}{c}d-\eta -1+\ell '\\ d-\eta -1\end{array}}\right) 2^{-2(r'-r)\ell '}. \end{aligned} \end{aligned}$$

In the last estimate, we used that $\left( {\begin{array}{c}k+\ell \\ k\end{array}}\right) \le \left( {\begin{array}{c}k+\ell +1\\ k\end{array}}\right)$ for every $k,\ell \in {\mathbb {N}}$. To bound the above two sums, we use the well-known binomial identity

$$\begin{aligned} \sum _{\ell =0}^\infty \left( {\begin{array}{c}D+\ell \\ D\end{array}}\right) \, x^\ell \,=\, \frac{1}{(1-x)^{D+1}} \end{aligned}$$

as well as the bound

$$\begin{aligned} \left( {\begin{array}{c}D+\ell +R\\ D\end{array}}\right) \,\le \, \left( {\begin{array}{c}D+\ell \\ D\end{array}}\right) \,(1+R)^D \end{aligned}$$

for $D,\ell ,R\in {\mathbb {N}}$ and $x\in {\mathbb {C}}$ with $|x|<1$. We obtain for the second sum that

$$\begin{aligned} \sum _{\ell '=0}^\ell \left( {\begin{array}{c}d-\eta -1+\ell '\\ d-\eta -1\end{array}}\right) \, 2^{-2(r'-r)\ell '} \,\le \, \left( 1-2^{-2(r'-r)}\right) ^{-(d-\eta )} \end{aligned}$$

and for the first sum that

$$\begin{aligned} \begin{aligned} \sum _{\ell =R_n}^\infty \, \left( {\begin{array}{c}\eta -1+\ell \\ \eta -1\end{array}}\right) \, 2^{\ell -R_n-2r \ell } \,&=\, \sum _{\ell =0}^\infty \, \left( {\begin{array}{c}\eta -1+\ell +R_n\\ \eta -1\end{array}}\right) \, 2^{\ell -2r(\ell +R_n) } \\ \,&\le \, 2^{-2r R_n}\,(1+R_n)^{\eta -1}\,\sum _{\ell =0}^\infty \, \left( {\begin{array}{c}\eta -1+\ell \\ \eta -1\end{array}}\right) \, 2^{(1-2r)\ell } \\ \,&=\, 2^{-2r R_n}\,(1+R_n)^{\eta -1}\, \left( 1-2^{(1-2r)}\right) ^{-\eta } \end{aligned} \end{aligned}$$

for $r>1/2$. If we use $\log _2\bigl (n/D_p\bigr ) \le R_n\le 1+\log _2\bigl (n/D_p\bigr )$, we finally obtain Theorem 2.$\square$

7 Numerical Results: Exact Worst-Case Errors in $\mathring{H}^{{\mathbf {r}}}_\mathrm {mix}$

In Sect. 6, it has been shown that the Frolov method achieves the optimal rate of convergence in Sobolev spaces with both, uniform and anisotropic mixed smoothness. However, as we have seen in Sect. 3, there are different ways to choose the polynomials, which significantly influence the numerical performance. Therefore, even though the asymptotic convergence rate of all (admissible) Frolov cubature rules have the optimal order ${\mathcal {O}} (N^{-r} (\log N)^{(d-1)/2})$ for uniform smoothness f, there might be huge constants involved. In order to investigate the influence of different Frolov polynomials on the preasymptotic behavior of the integration error, we use a well-known technique for reproducing kernel Hilbert spaces to compute the worst-case error explicitly. This supplements the theoretical bounds from Sect. 6. Moreover, we compare the worst-case errors of Frolov cubature, the sparse grid method and quasi-Monte Carlo methods in $\mathring{H}^r_\mathrm {mix}$.

7.1 Exact Worst-Case Errors via Reproducing Kernels

The worst-case error of any linear cubature rule $Q_N(f) = \sum _{i=1}^N w_i f({\varvec{x}}_i)$ with prescribed weights and nodes can be computed exactly via the norm of the error functional $R_N(f) := I_d(f) - Q_N(f)$, cf. Eq. (5.18). Applying $R_N$ to both components of the kernel $\mathring{K}_{d}^{\varvec{r}}({\varvec{x}}, {\varvec{y}})$, the well-known formula for the (absolute) worst-case error is obtained, i.e.,

$$\begin{aligned} \begin{aligned} \sup _{\Vert f\Vert _{\mathring{H}^{\varvec{r}}_\mathrm {mix}} \le 1} |R_N(f)|^2&= \int _{[0,1]^d} \int _{[0,1]^d} \mathring{K}_{d}^{\varvec{r}}({\varvec{x}}, {\varvec{y}}) \, \,\mathrm {d}{\varvec{x}}\,\mathrm {d}{\varvec{y}}- 2 \sum _{i=1}^N w_i \int _{[0,1]^d} \mathring{K}_{d}^{\varvec{r}}({\varvec{x}}_i, {\varvec{y}}) \, \,\mathrm {d}{\varvec{y}}\\&\quad + \sum _{i=1}^N \sum _{j=1}^N w_i w_j \mathring{K}_{d}^{\varvec{r}}({\varvec{x}}_i, {\varvec{x}}_j) . \end{aligned} \end{aligned}$$

(7.1)

Often, (7.1) is normalized with respect to norm of $I_d$ in the dual space $(\mathring{H}^{\varvec{r}}_\mathrm {mix})^\star$, i.e., (7.1) is divided by $\Vert I_d\Vert _{(\mathring{H}^{\varvec{r}}_\mathrm {mix})^\star } = (\int _{[0,1]^d}\int _{[0,1]^d} \mathring{K}_{d}^{\varvec{r}}({\varvec{x}}, {\varvec{y}}) \, \,\mathrm {d}{\varvec{x}}\,\mathrm {d}{\varvec{y}})^{1/2}$, cf. (5.19). The resulting quantity is called normalized worst-case error.

In order to evaluate (7.1) for an arbitrary given cubature rule, we use the closed-form representation of the kernel $\mathring{K}^{{\varvec{r}}}_{d}$ from Theorem 1 as well as the closed-form representation of the Riesz representer (5.20).

Besides Frolov cubature rules, we will consider the sparse grid construction, which goes back to Smolyak [38], and also higher-order quasi-Monte Carlo integration [25]. Examples for the different point constructions are given in Fig. 5. Their properties will be discussed below.

The Frolov points are generated using our newly developed Algorithm 1. The resulting points obtained by the improved polynomial construction can also be downloaded from https://ins.uni-bonn.de/content/software-frolov.

Fig. 5

A Frolov lattice (left), an order 2 digital net (middle) and a zero boundary sparse grid (right)

7.2 Uniform Mixed Smoothness

As a first step, we compare worst-case errors for cubature formulas that are known to work well in periodic Sobolev spaces, of which $\mathring{H}^r_\mathrm {mix}$ is a subset. These are different Frolov cubature rules that are based on different choices of the generating polynomial. In the following, “classical Frolov” will refer to the classical generating polynomial in (1.5), while “improved Frolov” will refer to the lattices that are generated by the improved polynomials from Sect. 3. Moreover, we consider the sparse grid method that is based on the trapezoidal rule; see “Appendix A.” Due to the zero boundary condition in $\mathring{H}^r$, all points with one component equal to zero are left out, cf. Fig. 5.² It achieves a convergence rate of order ${\mathcal {O}}(N^{-r} (\log N)^{(d-1)(r+1/2)})$ in $\mathring{H}^r_\mathrm {mix}$, which is best possible for a sparse grid method, cf. Theorem 3. As an example for a higher-order quasi-Monte Carlo method, we use a digital net of order 2 that is obtained by interlacing the digits of a (2d)-dimensional Niederreiter–Xing net. This is obtained by using the implementation of Pirsic [34] of Xing–Niederreiter sequences [32] for rational places in dimension $2d-1$. These are known to yield smaller t-values than, e.g., Sobol or classical Niederreiter sequences [11]. Then, a 2d-dimensional digital net is obtained by employing the sequence-to-net propagation rule, cf. [25, 33] for more details. It is known that order 2 nets yield the optimal rate of convergence in periodic Sobolev spaces with bounded mixed derivatives of order $r < 2$, see [23] and also [19], since $\mathring{H}^r_\mathrm {mix}\subset H^r_\mathrm {mix}({\mathbb {T}}^d)$.

Moreover, in the bivariate setting we also consider the Fibonacci lattice, which is not just known to be an order-optimal cubature rule for periodic Sobolev spaces with dominating mixed smoothness [8], but also represents the best possible point set for quasi-Monte Carlo integration in this space, at least for small point numbers [24].

Fig. 6

Worst-case errors for different cubature rules for uniform mixed smoothness $r=2$ in dimension $d=2$ (left) and dimension $d=4$ (right)

In the left-hand side picture of Fig. 6, the worst-case errors for smoothness $r=2$ are computed in dimension $d=2$. Clearly, the Frolov lattice based on the improved polynomial performs best in $\mathring{H}^r_\mathrm {mix}$. Of similar quality is the Fibonacci lattice and the classical Frolov lattice is slightly worse. The sparse grid also achieves the optimal main rate of $N^{-r}$, but it is known that the exponent of its logarithm is smoothness dependent. This is also apparent in Fig. 6, where the sparse grid has an asymptotic behavior that is inferior to all the other considered methods. On the right-hand side of Fig. 6, the worst-case errors for smoothness $r=2$ are computed in dimension $d=4$. Here, the Fibonacci lattice is not considered. However, for all the other methods we note that the picture does not change much, compared to the case $d=2$. As before, the improved Frolov method performs best and the classical Frolov obtains the same optimal asymptotic convergence rate, but a substantially worse constant. This effect is now much stronger than in the bivariate setting, i.e., the classical Frolov lattice has a worst-case error that is about two magnitudes larger than the one of the improved Frolov lattices. Moreover, the order 2 digital net seems to be competitive too, albeit with a substantially larger constant and longer preasymptotic regime. Again, the worse logarithmic exponent of the sparse grid method can be clearly observed (Fig. 7).

In Figs. 8, 9 and 10, the influence of the dimensionality and the smoothness onto the performance of the Frolov cubature method is considered in more detail. As an example for a cubature method with a less than optimal complexity, the sparse grid method is also included. In particular, the classical construction suffers from a strong growth of the constant as the dimensionality increases. Also, the preasymptotic regime seems to last longer. This effect can so far not be thoroughly explained by the existing theory. In dimension $d=7$, the classical Frolov construction needs more than $10^6$ points to achieve the error level of the zero algorithm, i.e., normalized worst-case error 1. Note at this point that all given errors are normalized worst-case errors, which can, for non-optimally weighted cubature rules, be substantially larger than 1. It is apparent that the classical Frolov method is practically useless in dimension $d \ge 5$, due to its unfavorable preasymptotic behavior. Our new approach, however, shows a much better dependence onto the dimensionality and certainly allows the treatment of moderate-dimensional integrals from Sobolev spaces with dominating mixed smoothness of uniform type.

Moreover, we observe the aforementioned universality property of Frolov’s method within the scale of spaces $\mathring{H}^r_\mathrm {mix}$. This means, without adaption to the respective parameters, it achieves the best possible rate of convergence in every $\mathring{H}^r_\mathrm {mix}$, $r \in \{1,2,3\}$.

Fig. 7

Worst-case errors for uniform mixed smoothness in various dimensions. Left-hand side: $r_1=1$ and $r_2 = \cdots = r_d = 2$. Left-hand side: $r_1=2$ and $r_2 = \cdots = r_d = 3$

Fig. 8

Normalized worst-case errors for uniform smoothness parameter $r=1$ in dimension $d \in \{2,3,4,5,6,7\}$ for different Frolov constructions and sparse grids

Fig. 9

Normalized worst-case errors for uniform smoothness parameter $r=2$ in dimension $d \in \{2,3,4,5,6,7\}$ for different Frolov constructions and sparse grids

Fig. 10

Normalized worst-case errors for uniform smoothness parameter $r=3$ in dimension $d \in \{2,3,4,5,6,7\}$ for different Frolov constructions and sparse grids

7.3 Anisotropic Mixed Smoothness

It has been shown in Theorem 2 that in Sobolev spaces with dominating mixed smoothness of different orders in each direction, only the lowest smoothness and associated dimension enter the error estimate. In order to make this phenomenon visible from a numerical perspective, we compute explicit worst-case errors in

$$\begin{aligned} \mathring{H}^{\varvec{r}}_\mathrm {mix}= \mathring{H}^{r_1} \otimes \cdots \otimes \mathring{H}^{r_d} , \end{aligned}$$

where $r_1 = r$ and $r_2 = r_3 = \cdots = r_d = r+1$. Then, Theorem 2 predicts that the worst-case error asymptotically behaves like in the univariate setting, i.e., decays at a rate of ${\mathcal {O}}(N^{-r})$. The question that is investigated in Fig. 7 is how long it takes to overcome the preasymptotic regime until this favorable convergence rate becomes visible.

On the left-hand side of Fig. 7, i.e., for $r=1$, already with less than 3000 points the Frolov method follows the asymptotic regime of $N^{-1}$ in all the considered cases $d \in \{2,3,\ldots , 7\}$.

In contrast, on the right-hand side of Fig. 7, i.e., for $r=2$, the dimension seems to have a much larger impact onto the length of the suboptimal preasymptotic regime. For example, in $d=7$ the $N^{-2}$-rate becomes visible only when the number of points N is larger than $\approx 10^5$.

We remark that the sparse grid method is also able to deal with anisotropic mixed smoothness vectors ${\varvec{r}}= (r_1,\ldots , r_d)$. Then, however, the construction needs to be adjusted to the smoothness vector which has to be known in advance; see [40, pp. 32,36,72], the recent survey [8, Sect. 10.1] and the references therein. The resulting sparse grid construction therefore is not a universal cubature formula.³

However, both plots in Fig. 7 were computed with the exact same set of Frolov points, which automatically benefit from the anisotropic smoothness that is present in a given integration problem, i.e., in this case $r=1$ or $r=2$. Therefore, it is not necessary to estimate the smoothness of the integrand and tune the method appropriately.

Appendix: Sparse Grid Cubature in \(H^r_\mathrm {mix}({\mathbb {T}}^d)\)

Let

$$\begin{aligned} Q_N(f) := \sum _{j=0}^{N-1}\frac{1}{N} f\Big ( \frac{j}{N} \Big ) \end{aligned}$$

(A.1)

denote the uniformly weighted N-point trapezoidal rule. It is known that it achieves the optimal rate of convergence $N^{-r}$ in the periodic Sobolev space $H^r({\mathbb {T}}), r \in {\mathbb {N}}$ (our proof below also works for the univariate case). In order to obtain a multivariate integration method, we define the hierarchical quadrature rules

$$\begin{aligned} {\varDelta }_k := {\varDelta }_k(Q) := Q_{2^{k}} - Q_{2^{k-1}} \quad \text { for all } k = 1, 2, \ldots \end{aligned}$$

(A.2)

and ${\varDelta }_0 = Q_1$. Their tensor product is denoted by ${\varDelta }_{{\varvec{k}}} := \bigotimes _{j=1}^d {\varDelta }_{k_j}$, ${\varvec{k}}\in {\mathbb {N}}_0^d$. The sparse grid cubature rule of level $L\in {\mathbb {N}}$ is then given by

$$\begin{aligned} Q^{sg}_L := \sum _{|{\varvec{k}}|_1 \le L} {\varDelta }_{{\varvec{k}}} , \end{aligned}$$

(A.3)

with multi-indices ${\varvec{k}}= (k_1,\ldots ,k_d) \in {\mathbb {N}}_0^d$. The cubature rule $Q^{sg}_L$ uses

$$\begin{aligned} N_L = \sum _{|{\varvec{k}}|_1 \le L} \prod _{j=1}^d 2^{k_j-1} = {\mathcal {O}}(2^L \cdot L^{d-1}) \end{aligned}$$

(A.4)

function values combined with non-equal weights. The following theorem gives the well-known error bound in $H^r_{\mathrm {mix}}({\mathbb {T}}^d)$. For the convenience of the reader, we will also give a proof.

Theorem 3

Consider the sparse grid cubature rule $Q^{sg}_L$ as it is defined in (A.2) and (A.3) based on the univariate trapezoidal rule (A.1). The worst-case integration error of $Q^{sg}_L$ in $H^r_{\mathrm {mix}}({\mathbb {T}}^d)$ can be bounded by

$$\begin{aligned} \sup _{\Vert f\Vert _{H^r_\mathrm {mix}} \le 1} \left| \int _{[0,1]^d}f({\varvec{x}})\,\mathrm {d}{\varvec{x}}- Q^{sg}_L(f) \right| \asymp N^{-r} (\log N)^{(d-1)(r+1/2)} , \end{aligned}$$

(A.5)

where $N = N_L$ denotes the number of points used by $Q^{sg}_L$.

Proof

The lower bound follows from [9, Thm. 5.2]. Note that the lower bound also holds true for the smaller space $\mathring{H}^r_{\mathrm {mix}}({\mathbb {T}}^d)$ since the constructed fooling functions also belong to this space. For the upper bound, we use the detour to sampling recovery. In the recent paper [6, Thm. 4.7, 4.8, 5.13, 5.14], it has been observed that nested trigonometric interpolation operators

$$\begin{aligned} I_{2^k}[f](x) = \frac{1}{2^k}\sum \limits _{u=0}^{2^{k}-1} f\Big (\frac{u}{2^k}\Big ) {\mathcal {D}}_{2^k}^1\Big (x-\frac{u}{2^k}\Big ) ,\quad k=0,1,2,\ldots , \end{aligned}$$

(A.6)

based upon the modified (nested) Dirichlet kernel ${\mathcal {D}}_{2^k}^1(x) := {\mathcal {D}}_{2^{k-1}}(x) - e^{2\pi i2^{k-1}x}$ may be used to characterize $H^r_{\mathrm {mix}}({\mathbb {T}}^d)$. In fact, the tensor products ${\varDelta }_{{\varvec{k}}}(I)$, ${\varvec{k}}\in {\mathbb {N}}_0^d$, are defined analogously to (A.2) using this time (A.6) (note that ${\mathcal {D}}_{1}^1(x) \equiv 1$). Then we have

$$\begin{aligned} \Vert f\Vert _{H^r_{\mathrm {mix}}}^2 \asymp \sum \limits _{{\varvec{k}}\in {\mathbb {N}}_0^d} 2^{2r|{\varvec{k}}|_1}\Vert {\varDelta }_{{\varvec{k}}}(I)[f]\Vert ^2_2. \end{aligned}$$

(A.7)

See also [5, Prop. 3.3] for the classical (non-nested) trigonometric interpolation. The associated sparse grid interpolation operator $I^{sg}_L$ is defined in the same way as above in (A.3). Now we argue similar as in [5, Thm. 5.4]. Indeed, Hölder’s inequality together with (A.7) gives

$$\begin{aligned} \begin{aligned} \Vert f-I^{sg}_L[f]\Vert _2&\le \Big (\sum \limits _{|{\varvec{k}}|_1>L} 2^{-2|{\varvec{k}}|_1 r}\Big )^{1/2}\cdot \Big (\sum \limits _{|{\varvec{k}}|_1>L} 2^{2r|{\varvec{k}}|_1}\Vert {\varDelta }_{{\varvec{k}}}(I)[f]\Vert ^2_2\Big )^{1/2}\\&\le 2^{-rL}L^{(d-1)/2}\Vert f\Vert _{H^r_{\mathrm {mix}}}. \end{aligned} \end{aligned}$$

(A.8)

Noting further that

$$\begin{aligned} Q_L^{sg}(f) = \int _{[0,1]^d} I^{sg}_L[f]({\varvec{x}})\,\mathrm {d}{\varvec{x}}, \end{aligned}$$

we have by Hölder’s inequality and (A.8)

$$\begin{aligned} \Big |\int _{[0,1]^d}f({\varvec{x}})\,\mathrm {d}{\varvec{x}}- Q^{sg}_L(f)\Big | \le \Vert f-I^{sg}_L[f]\Vert _2 \le 2^{-rL}L^{(d-1)/2}\Vert f\Vert _{H^r_{\mathrm {mix}}}; \end{aligned}$$

see also [8, Rem. 8.9]. Finally, the bound (A.5) follows from (A.4). $\square$

Remark 3

The above multivariate cubature rule on the sparse grid uses a number of nodes on the boundary of $[0,1]^d$ which are not needed when dealing with functions from $\mathring{H}^r_{\mathrm {mix}} \subset H^r_{\mathrm {mix}}({\mathbb {T}}^d)$. However, as already mentioned in the proof of Theorem 3, with respect to the asymptotic rate of convergence we cannot do essentially better. However, to do a fair cost comparison for the different methods considered in Sect. 7 we only counted the interior nodes (see the above diagrams, e.g., Fig. 6).