Abstract
Considering a continuous self-map and the induced endomorphism on homology, we study the eigenvalues and eigenspaces of the latter. Taking a filtration of representations, we define the persistence of the eigenspaces, effectively introducing a hierarchical organization of the map. The algorithm that computes this information for a finite sample is proved to be stable, and to give the correct answer for a sufficiently dense sample. Results computed with an implementation of the algorithm provide evidence of its practical utility.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In recent years, the theory of persistent homology [11, 23] has become a useful tool in several areas, including shape analysis [12], scientific visualization [13], high-dimensional data analysis [3], but also in mathematics itself [21]. The specific aim of this paper is an approach to the persistence of endomorphisms induced in homology by continuous self-maps. The long-term goal is to embed persistence in the computational analysis of dynamical systems, as pursued in [14] and the related literature.
In the case of finitely generated homology with field coefficients, the homomorphism induced by a continuous map between topological spaces is a linear map between finite-dimensional vector spaces. Such a map \(\varphi : Y \rightarrow X\) is characterized up to conjugacy by its rank. This is in contrast to a linear self-map, \(\phi : X \rightarrow X\), which in the case of an algebraically closed fieldFootnote 1 is characterized up to conjugacy by its Jordan form. A weaker piece of information is the eigenvectors, which in our setting captures the homology classes that are invariant under the self-map. Therefore, it is natural to study the persistence of eigenvalues and eigenspaces as a first step to the full understanding of the persistence of the map. We define it in terms of the persistence of vector spaces, a concept that has been around for some time. Specifically, it has been presented as the general idea of zigzag persistence [2], which is based on the theory of quivers [9]. Since we need an algorithm that provides not only the persistence intervals but also a special basis, we give an independent presentation of the concept. We believe this presentation is elementary and in the spirit of the theory of persistent homology. We also note that its generalization to zigzag persistence is straightforward. Beyond describing the algorithm for the persistence of eigenvalues and eigenspaces, we analyze its performance, proving that the persistence diagram it produces is stable under perturbations of the input, and the algorithm converges to the homology of the studied map, reaching the correct ranks for a sufficiently fine sample. In addition, we exhibit results obtained with a software implementation, which suggest that the persistent homology of eigenspaces picks up the important dynamics already from a relatively small sample.
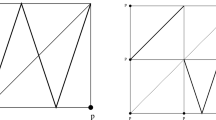
We motivate the technical work in this paper with a small toy example, designed to highlight one of the main difficulties we encounter. Writing \({{\mathbb S}}^1\) for the circle in the complex plane, we consider the map defined by \(f(z) := z^2\), which doubles the angle of the input point. Sampling \({{\mathbb S}}^1\) at eight equally spaced locations, \(x_j := \cos \frac{j \pi }{4} + \mathbf{i}\sin \frac{j \pi }{4}\), we can check that \(f(x_j) = x_{2j}\), where indices are taken modulo \(8\). Assuming the space and the map are unknown, other than at the sampled points and their images, we consider the filtration \(K_1 \subseteq K_2 \subseteq K_3 \subseteq K_4 \subseteq K_5\) shown in the top row of Fig. 1. Each complex \(K_i\) consists of all simplices spanned by the eight points whose smallest enclosing circles have radii that do not exceed a given threshold, and this threshold increases from left to right. The most persistent homology classes in this filtration are the component that appears in \(K_1\) and lasts to \(K_5\) and the loop that appears in \(K_2\) and lasts to \(K_4\).
We would hope that \(f\) extends to simplicial maps on these complexes, but this is unfortunately not the case in general. For instance, \(f\) maps the endpoints of the edge \(x_1 x_7\) in \(K_3\) to the points \(x_2\) and \(x_6\), but they are not endpoints of a common edge in \(K_3\). The reason for this situation is the expanding character of \(f\). To still make sense of the map, we construct the maximal partial simplicial maps, \(\kappa _i: K_i {\nrightarrow }K_i\) consistent with \(f\). Figure 1 shows the domains of these maps in the bottom row, and for \(i = 3, 4\), we can see how \(\kappa _i\) wraps the convex octagon twice around the hole in \(K_i\) shown right above. This reflects the fundamental feature of \(f\), namely that its image wraps around the circle twice. To see this more formally, we compare the homology classes in the domains with their images. For \(i = 1, 3, 5\), the inclusion of the domain of \(\kappa _i\) in \(K_i\) induces an isomorphism in homology. The comparison therefore reduces to the study of eigenvectors of an endomorphism. The lack of isomorphism for \(i = 2, 4\) may be overcome by the study of eigenvectors of pairs of linear maps. In this particular case, we are able to conclude that the eigenspace for eigenvalue \(t = 2\) appears in \(K_3\) and lasts to \(K_4\), thus reconstructing the essential character of \(f\) from a very small sample.
To summarize, there are differences between the partial simplicial maps and the underlying continuous map; see in particular the reorganization that takes place at \(i = 2\) and \(i = 4\). The hope to recover the properties of the latter from the former is based on the ability of persistence to provide a measure that transcends fluctuations and identifies what stays the same when things change.
Outline Section 2 introduces the categories of partial functions, matchings, and linear maps. Section 3 discusses towers within these categories and introduces the concept of persistence. Section 4 describes the algorithm that computes the persistent homology of an endomorphism from a hierarchical representation of the underlying self-map. Section 5 proves that the algorithm converges and produces stable persistence diagrams. Section 6 presents results obtained with our implementation of the algorithm. Section 7 concludes the paper.
2 Categories
We find the language of category theory convenient to talk about persistent homology; see MacLane [16] for a standard reference. Most importantly, we introduce the category of finite sets and matchings, which will lead to an elementary exposition of persistence.
2.1 Partial Functions
We recall that a category consists of objects and (directed) arrows between objects. Importantly, there is the identity arrow from every object to itself, and arrows compose associatively. An arrow, \(\theta : K \rightarrow L\), is invertible if it has an inverse, \(\theta ^{-1}: L \rightarrow K\), such that \(\theta ^{-1} \theta \) and \(\theta \theta ^{-1}\) are the identity arrows for \(K\) and \(L\). If there is an invertible arrow from \(K\) to \(L\), then the two objects are isomorphic. Every category in this paper contains a zero object, which is characterized by having exactly one arrow to and one arrow from every other object. It is unique up to isomorphisms. Two arrows \(\kappa : K \rightarrow K'\) and \(\lambda : L \rightarrow L'\) are conjugate if there are invertible arrows \(\theta : K \rightarrow L\) and \(\theta ' : K' \rightarrow L'\) that commute with \(\kappa \) and \(\lambda \); that is, \(\theta ' \kappa = \lambda \theta \). A functor is an arrow between categories, assigning to each object and each arrow of the first category an object and an arrow of the second category in such a way that the identity arrows are mapped to identity arrows and the functor commutes with the composition of the arrows.
We use a category whose arrows generalize functions between sets as the basis of other categories. Specifically, a partial function is a relation \(\xi \subseteq X \times Y\) such that every \(x \in X\) is either not paired or paired with exactly one element in \(Y\) [15]. We denote it by \(\xi : X {\nrightarrow }Y\), observing that there is a largest subset \(X' \subseteq X\) such that the restriction \(\xi : X' \rightarrow Y\) is a function. We call \(\mathsf{dom\,}{\xi } := X'\) the domain and \(\mathsf{ker\,}{\xi } := X - X'\) the kernel of \(\xi \). For each \(x \in X'\), we write \(\xi (x)\) for the unique element \(y \in Y\) paired with \(x\), as usual. Similarly, we write \(\xi (A)\) for the set of elements \(\xi (x)\) with \(x \in A {\; \cap \;}X'\). The image of \(\xi \) is of course the entire reachable set, \(\mathsf{im\,}{\xi } := \xi (X)\). If \(\xi : X {\nrightarrow }Y\) and \(\eta : Y {\nrightarrow }Z\) are partial functions, then their composition is the partial function \(\eta \xi : X {\nrightarrow }Z\) consisting of all pairs \((x,z) \in X \times Z\) for which there exists \(y \in Y\) such that \(y = \xi (x)\) and \(z = \eta (y)\). Thus, we have a category of sets and partial functions, which we denote as \({\mathbf{Part}}\). The zero object in this category is the empty set, which is connected to all other sets by empty partial functions. It will be convenient to limit the objects in this category to finite sets.
2.2 Matchings
We call an injective partial function \(\alpha : A {\nrightarrow }B\) a matching. Its restriction to the domain and the image is a bijection, hence the name. Bijections have inverses and so do matchings, namely \(\alpha ^{-1} : B {\nrightarrow }A\) with \((b,a) \in \alpha ^{-1} \hbox { iff } (a,b) \in \alpha \).Footnote 2 Clearly, the composition of two matchings is again a matching. We therefore have a category, and we write \({\mathbf{Mch}}\) for this subcategory of \({\mathbf{Part}}\): its objects are finite sets and its arrows are matchings. Writing \([k] := \{1,2,\ldots ,k\}\), we may assume that \(A = [p]\) and \(B = [q]\), in which \(p\) and \(q\) are the cardinalities of \(A\) and \(B\). Representing the matching by its matrix, \(M = (M_{ij})\), we thus get
for \(j \in [p]\) and \(i \in [q]\). Matrices of matchings are characterized by having at most one non-zero entry in each row and in each column. It follows that there are equally many non-zero rows (the cardinality of the image) as there are non-zero columns (the cardinality of the domain). The rank of the matching is this common cardinality, \(\mathsf{rank\,}{\alpha } := {\#{\mathsf{dom\,}{\alpha }}} = {\#{\mathsf{im\,}{\alpha }}}\). The simple structure of matchings makes it easy to compute the ranks of compositions. Letting \(\beta : B {\nrightarrow }C\) be another matching, the rank of \(\beta \alpha : A {\nrightarrow }C\) is the cardinality of \(\mathsf{im\,}{\alpha } {\; \cap \;}\mathsf{dom\,}{\beta }\); see Fig. 2.
We can rewrite this as
It will be useful to extend this relation to the composition of three matchings, adding \(\gamma : C {\nrightarrow }D\) to the two we already have. The number of elements in the domain of \(\beta \) that are neither in the image of \(\alpha \) nor map to the domain of \(\gamma \) is
To see the second line, we construct a set \(\Omega \), first by taking the disjoint union of the sets \(A, B, C\), and \(D\), and second by identifying two elements if they occur in a common pair, which may be in \(\alpha , \beta \), or \(\gamma \). After identification, each matching is a subset of \(\Omega \), namely \(\alpha = A {\; \cap \;}B, \beta \alpha = A {\; \cap \;}B {\; \cap \;}C\), etc. Using the identification, the left-hand side of (2) may be rewritten as the cardinality of the set
By elementary inclusion–exclusion, its cardinality is the right-hand side of (2).
2.3 Linear Maps
Assuming a fixed field, we now consider the category \({\mathbf{Vect}}\), whose objects are the finite-dimensional vector spaces over this field, and whose arrows are the linear maps between these vector spaces. The dimension of a vector space, \(U\), is of course the cardinality of its basis, which we denote as \(\mathrm{dim\,}{U}\). Letting \(\upsilon : U \rightarrow V\) be a linear map, we write \(\mathsf{ker\,}{\upsilon } := \upsilon ^{-1} (0)\) for the kernel, \(\mathsf{im\,}{\upsilon } := \upsilon (U)\) for the image, and \(\mathsf{rank\,}{\upsilon } := \mathrm{dim\,}{\upsilon }(U)\) for the rank of \(\upsilon \).
Given bases \(A\) of \(U\) and \(B\) of \(V\), we construct the matrix \(M = (M_{ij})\) of \(\upsilon \) in these bases. In particular, \(M_{ij}\) is the coefficient of the \(i\)th basis vector of \(B\) in the representation of the image of the \(j\)th basis vector of \(A\). It is generally not the matrix of a matching because \(\upsilon \) does generally not map \(A\) to \(B\). However, if \(M\) is the matrix of a matching, then the partial function \(\alpha : A {\nrightarrow }B\), consisting of all pairs \((a,b) \in A \times B\) with \(\upsilon (a) = b\), is a matching that satisfies \(\mathsf{ker\,}{\alpha } = \mathsf{ker\,}{\upsilon } {\; \cap \;}A, \mathsf{im\,}{\alpha } = \mathsf{im\,}{\upsilon } {\; \cap \;}B\), and, most importantly,
A matching with this property exists, and we can compute it by reducing \(M\) to Smith normal form. However, it is not necessarily unique. On the other hand, any two matchings \(\alpha : A {\nrightarrow }B\) and \(\alpha ': A' {\nrightarrow }B'\) that satisfy (4)—albeit possibly for different bases \(A, A'\) of \(U\) and \(B, B'\) of \(V\)— are conjugate in \({\mathbf{Mch}}\). Indeed, we have \({\#{A}} = {\#{A'}}, {\#{B}} = {\#{B'}}\), and \(\mathsf{rank\,}{\alpha } = \mathsf{rank\,}{\alpha '}\) from (4), which suffices for the existence of bijections that imply the conjugacy of \(\alpha \) and \(\alpha '\).
We have a functor \(\mathrm{Lin }:{\mathbf{Mch}}\rightarrow {\mathbf{Vect}}\) which sends a finite set \(A\) to the linear space spanned by \(A\) and a matching \(\alpha :A\rightarrow B\) to the linear map defined on a basis vector \(a\in A\) as \(\alpha (a)\) if \(a\) is in the domain of \(\alpha \) and as zero otherwise. It follows from the discussion of the preceding paragraph that for every linear map \(\upsilon \) in \({\mathbf{Vect}}\), there exists a matching \(\alpha \) in \({\mathbf{Mch}}\) such that \(\upsilon =\mathrm{Lin }(\alpha )\) and any two matchings with this property are conjugate.
2.4 Eigenvalues and Eigenspaces
Still assuming the same field, we consider a vector space, \(U\), and a linear self-map, \(\phi : U \rightarrow U\). Letting \(t\) be an element in the field, we set
If \(E_t (\phi ) \ne 0\), then \(t\) is an eigenvalue of \(\phi \), and \(E_t (\phi )\) is the corresponding eigenspace. As usual, the non-zero elements of \(E_t (\phi )\) are referred to as the eigenvectors of \(\phi \) and \(t\). It should be clear that \(E_t (\phi )\) is a subspace of \(U\) and thus a vector space itself. We find it convenient to formalize the transition from the linear self-map to its eigenspaces. To this end, we consider another endomorphism, \(\phi ': U' \rightarrow U'\), and a linear map \(\upsilon : U \rightarrow U'\) such that

commutes. We can think of this diagram as an arrow in a new category \(\mathbf{Endo}({\mathbf{Vect}})\); see e.g. [19]. In particular, the objects in \(\mathbf{Endo}({\mathbf{Vect}})\) are the endomorphisms in \({\mathbf{Vect}}\), and the arrows are the linear maps that commute with the endomorphisms. Fixing \(t\), we now map \(\phi \) to \(E_t (\phi )\) and \(\phi '\) to \(E_t (\phi ')\), which are objects in \({\mathbf{Vect}}\). Since (6) commutes, the image of an eigenvector in \(E_t (\phi )\) belongs to \(E_t (\phi ')\). This motivates us to define the restriction of \(\upsilon \) to \(E_t (\phi )\) and \(E_t (\phi ')\) as the image of \(\upsilon \) under \(E_t\), thus completing the definition of \(E_t\) as the eigenspace functor from \(\mathbf{Endo}({\mathbf{Vect}})\) to \({\mathbf{Vect}}\).
2.5 Eigenspace Functor for Pairs
The situation in this paper is more general, and we need an extension from endomorphisms to pairs of linear maps. Let \(\varphi , \psi : U \rightarrow V\) be such a pair, and define \(\bar{E}_t (\varphi , \psi ) := \{u \in U \mid \varphi (u) = t \psi (u)\}\). This is a subspace of \(U\), but it contains the entire intersection of the two kernels, which we remove by taking the quotient:
Assuming \(E_t (\varphi , \psi ) \ne 0\), we call \(t\) an eigenvalue of the pair, and \(E_t (\varphi , \psi )\) the corresponding eigenspace. The non-zero elements of \(E_t (\varphi , \psi )\) are the eigenvectors of \(\varphi , \psi \), and \(t\). Similar to the case of endomorphisms, \(E_t (\varphi , \psi )\) is a vector space, although its elements are not the original vectors but equivalence classes of such. To formalize the transition, we consider a second pair \(\varphi ', \psi ' : U' \rightarrow V'\) and linear maps \(\upsilon \) and \(\nu \) such that

commutes. We can think of this diagram as an arrow in a new category as follows. The objects in \(\mathbf{Pairs}({\mathbf{Vect}})\) are the horizontal pairs of linear maps, and the arrows are the vertical pairs of linear maps that form commutative diagrams, as in (8). Fixing \(t\), we can now map \(\varphi , \psi \) to \(E_t (\varphi , \psi )\) and \(\varphi ', \psi '\) to \(E_t (\varphi ', \psi ')\), which are objects in \({\mathbf{Vect}}\). Since (8) commutes, the images of the vectors in a class \([u] \in E_t (\varphi , \psi )\) form an equivalence class \([\upsilon (u)] \in E_t (\varphi ', \psi ')\). We thus define the arrow that maps \([u]\) to \([\upsilon (u)]\) as the image of \(\upsilon , \nu \) under \(E_t\). This completes the definition of \(E_t\) as the eigenspace functor from \(\mathbf{Pairs}({\mathbf{Vect}})\) to \({\mathbf{Vect}}\).
It is easy to see that if the vertical maps in (8) are isomorphisms, then \(E_t (\varphi , \psi )\) and \(E_t (\varphi ', \psi ')\) are isomorphic. Starting with (8), suppose now that \(V = V' = U'\) and that \(\nu \) and \(\varphi '\) are identities, and redraw the diagram in triangular form:

If \(\varphi \) is an isomorphism, then so is \(\upsilon \), which implies that \(E_t (\varphi , \psi )\) and \(E_t (\psi ')\) are isomorphic. This little fact will be useful in Sect. 5, when we analyze our algorithm by comparing eigenspaces obtained from the homology endomorphism induced by a continuous self-map \(f:{{\mathbb X}}\rightarrow {{\mathbb X}}\) and from pairs of linear maps induced in homology by projections from the graph of \(f\) (comp. diagram (29)).
3 Towers and Persistence
In this section, we study what can persist along paths in a category, similarly to the very recent, independently obtained results [1]. We show that parallel paths in \({\mathbf{Vect}}\) and \({\mathbf{Mch}}\) will naturally lead to the concept of persistent homology, now within a more general framework than in the traditional literature. We note that the concept of tower introduced in the sequel corresponds to persistence module in [23]. We prefer to speak about towers to avoid phrases like ‘persistent module of persistence modules’.
3.1 Paths and Categories of Paths in a Category
A tower is a path with finitely many non-zero objects in a category. More formally, it consists of objects \(X_i\) and arrows \(\xi _i : X_i \rightarrow X_{i+1}\), for all \(i \in {{\mathbb Z}}\), in which all but a finite number of the \(X_i\) are the zero object. We denote this tower as \({{\mathcal X}}= (X_i, \xi _i)\). In later discussions, we will refer to compositions of the arrows, so we write \(\xi _i^i\) for the identity arrow of \(X_i\) and define
for \(i < j\).
Suppose \({{\mathcal Y}}= (Y_i, \eta _i)\) is a second tower in the same category, and there is a vector of arrows \(\varphi = (\varphi _i)\), with \(\varphi _i: X_i \rightarrow Y_i\), such that \(\eta _i \varphi _i = \varphi _{i+1} \xi _i\) for all \(i\). Referring to this vector of arrows as a morphism, we denote this by \(\varphi : {{\mathcal X}}\rightarrow {{\mathcal Y}}\). To verify that the towers and morphisms form a new category, we note that the identity morphism is the vector of identity arrows, and that morphisms compose naturally. The zero object is the tower consisting solely of zero objects. Finally, an isomorphism is an invertible morphism; it consists of invertible arrows between objects that commute with the arrows of the towers. We remark that arrows and morphisms are alternative terms for the same notion in category theory. We find it convenient to use both so we can emphasize different levels of the construction.
3.2 Persistence in a Tower of Matchings
As a first concrete case, we consider a tower \({{\mathcal A}}= (A_i, \alpha _i)\) of matchings. Recall that \(\mathsf{rank\,}{\alpha _i^j}\) is the number of pairs in \(\alpha _i^j\). We formalize this notion by introducing the rank function \(\mathsf{a}: {{\mathbb Z}}\times {{\mathbb N}}_0 \rightarrow {{\mathbb Z}}\) defined by \(\mathsf{a}_i^j := \mathsf{a}(i,j-i) := \mathsf{rank\,}{\alpha _i^j}\), where \({{\mathbb N}}_0\) is the set of non-negative integers. It can alternatively be understood by counting intervals, as we now explain. Letting \(A\) be the disjoint union of the \(A_i\), we call a non-empty partial function \(a: {{\mathbb Z}}{\nrightarrow }A\) an string in \({{\mathcal A}}\) if the domain of \(a\) is an interval \([k,\ell ]\) in \({{\mathbb Z}}, a_i = a(i)\) belongs to \(A_i\) for every \(k \le i \le \ell \), and \(a_{i+1} = \alpha _i (a_i)\) whenever \(k \le i < \ell \); see Fig. 3. The string is maximal if it cannot be extended at either end. Specifically, \(a\) is maximal iff \(a_k \not \in \mathsf{im\,}{\alpha _{k-1}}\) and \(a_\ell \in \mathsf{ker\,}{\alpha _\ell }\). Finally, by a persistence interval Footnote 3, we mean the domain of a maximal string in \({{\mathcal A}}\).
It should be clear that \(\mathsf{a}_k^\ell \) is the number of strings in \({{\mathcal A}}\) with domain \([k,\ell ]\). Equivalently, it is the number of maximal strings with domains that contain \([k,\ell ]\). We can also reverse the relationship and compute the number of persistence intervals from the rank function. Letting \(\#_{[i,j]} = \#_{[i,j]} ({{\mathcal A}})\) denote the number of maximal strings with domain \([i,j]\), we have
To see this, we consider again \(A\) and identify elements if they belong to a common pair in any of the \(\alpha _i\). After identification, every point \(a\) in \(A\) corresponds to a maximal string. The domain of this maximal string is \([i,j]\) iff \(a\) belongs to the domain of \(\alpha _i^{j}\) but not to the image of \(\alpha _{i-1}\) and not to the domain of \(\alpha _i^{j+1}\). The relation (11) now follows from (2) is applied to \(\alpha = \alpha _{i-1}, \beta = \alpha _i^{j}, \gamma = \alpha _j\).
This relationship motivates us to introduce the persistence diagram of \({{\mathcal A}}\) as the multiset of persistence intervals, which we denote as \(\mathrm{Dgm}({{\mathcal A}})\). Note that \(\#_{[i,j]}\) is the multiplicity of \([i,j]\). The number of intervals in the persistence diagram, counted with multiplicities, is therefore \(\# \mathrm{Dgm}({{\mathcal A}}) = \sum _{i \le j} \#_{[i,j]}\). It is important to observe that the persistence diagram characterizes the tower up to isomorphisms.
Equivalence Theorem A
Letting \({{\mathcal A}}\) and \({{\mathcal B}}\) be towers in \({\mathbf{Mch}}\), the following conditions are equivalent:
-
(i)
\({{\mathcal A}}\) and \({{\mathcal B}}\) are isomorphic;
-
(ii)
the rank functions of \({{\mathcal A}}\) and \({{\mathcal B}}\) coincide;
-
(iii)
the persistence diagrams of \({{\mathcal A}}\) and \({{\mathcal B}}\) are the same.
Proof
(i) \(\Rightarrow \) (ii). Since \({{\mathcal A}}\) and \({{\mathcal B}}\) are isomorphic, we have invertible arrows \(\theta _i: A_i \rightarrow B_i\) that commute with the arrows in \({{\mathcal A}}\) and \({{\mathcal B}}\). It follows that \(\mathsf{rank\,}{\alpha _i^j} = \mathsf{rank\,}{\beta _i^j}\), for all \(i \le j\).
(ii) \(\Rightarrow \) (iii). The rank function determines the multiplicities of the intervals in the persistence diagram by (11).
(iii) \(\Rightarrow \) (i). To construct the required isomorphism, we first match up the intervals, and using the matching, we match up the underlying points. \(\square \)
3.3 Persistence in a Tower of Linear Maps
We return to assuming a fixed field, and consider a tower \({{\mathcal U}}= (U_i, \upsilon _i)\) in the category of vector spaces over this field.Footnote 4 For each \(i\), let \(A_i\) be a basis of \(U_i\). Restricting \(\upsilon _i\) to \(A_i\) and \(A_{i+1}\), we get a partial function \(\alpha _i: A_i {\nrightarrow }A_{i+1}\), again for every \(i\).
Definition
We call the tower of partial functions \({{\mathcal A}}= (A_i, \alpha _i)\) a basis of the tower \({{\mathcal U}}\) if \(\alpha _i\) is a matching and \(\mathsf{rank\,}{\alpha _i} = \mathsf{rank\,}{\upsilon _i}\), for every \(i\).
We have seen in Sect. 2 that for each \(\upsilon _i: U_i \rightarrow U_{i+1}\), there are bases \(A_i\) and \(A_{i+1}\) of the two vector spaces such that the implied partial function \(\alpha _i: A_i {\nrightarrow }A_{i+1}\) is a matching that satisfies \(\mathsf{rank\,}{\alpha _i} = \mathsf{rank\,}{\upsilon _i}\); see (4). We will show shortly that such bases exist for all vector spaces in the tower simultaneously; see the Basis Lemma below. For now, we assume that \({{\mathcal A}}= (A_i, \alpha _i)\) is such a basis, deferring the proof to later. Considering compositions \(\alpha _i^j\), we note that \(\mathsf{rank\,}{\alpha _i^j} = \mathsf{rank\,}{\upsilon _i^j}\). Consequently, the rank functions of \({{\mathcal A}}\) and \({{\mathcal U}}\) are the same. The basis of \({{\mathcal U}}\) is not necessarily unique, but the rank function does not depend on the choice. Thus, we can define the persistence diagram of \({{\mathcal U}}\) as the persistence diagram of a basis, \(\mathrm{Dgm}({{\mathcal U}}) := \mathrm{Dgm}({{\mathcal A}})\). We also write \(\#_{[i,j]} ({{\mathcal U}}) := \#_{[i,j]} ({{\mathcal A}})\) for the multiplicity of the interval \([i,j]\) in the persistence diagram of \({{\mathcal U}}\). Writing \(\mathsf{u}_i^j\) for the rank of \(\upsilon _i^j\), we thus get
from (11). Similarly, we can generalize the Equivalence Theorem A to the case of linear maps between finite-dimensional vector spaces.
Equivalence Theorem B
Letting \({{\mathcal U}}\) and \({{\mathcal V}}\) be towers in \({\mathbf{Vect}}\), the following conditions are equivalent:
-
(i)
\({{\mathcal U}}\) and \({{\mathcal V}}\) are isomorphic;
-
(ii)
the rank functions of \({{\mathcal U}}\) and \({{\mathcal V}}\) coincide;
-
(iii)
the persistence diagrams of \({{\mathcal U}}\) and \({{\mathcal V}}\) are the same.
Proof
Implications (i) \(\Rightarrow \) (ii) and (ii) \(\Rightarrow \) (iii) are trivial. To see that (iii) \(\Rightarrow \) (i) select bases \({{\mathcal A}}\) and \({{\mathcal B}}\), respectively, in \({{\mathcal U}}\) and \({{\mathcal V}}\) by the Basis Lemma below. Then \(\mathrm{Dgm}({{\mathcal A}}) = \mathrm{Dgm}({{\mathcal B}})\). Thus, Equivalence Theorem A implies that \({{\mathcal A}}\) and \({{\mathcal B}}\) are isomorphic, and the bijections between the bases \({{\mathcal A}}\) and \({{\mathcal B}}\) define the requested isomorphisms between \({{\mathcal U}}\) and \({{\mathcal V}}\). \(\square \)
3.4 Tower Bases
We now prove the technical result assumed above to get Equivalence Theorem B. It is not new and can be found in different words and with a less elementary proof in [2, 23].
Basis Lemma
Every tower in \({\mathbf{Vect}}\) has a basis.
Proof
We construct the basis in two phases of an algorithm, as sketched in Fig. 4. Let \({{\mathcal U}}= (U_i, \upsilon _i)\) be a tower in \({\mathbf{Vect}}\), and for each \(i\), let \(M_i\) be the matrix that represents the map \(\upsilon _i\) in terms of the given bases of \(U_i\) and \(U_{i+1}\).
In Phase 1, we use column operations to turn \(M_i\) into column echelon form, as sketched in Fig. 4 in the middle. We get a strictly descending staircase of non-zero entries, with zeros and non-zeros below and zeros above the staircase. Here, we call the collection of topmost non-zero entries in the columns the staircase, and we multiply with inverses so that all entries in the staircase are equal to \(1\). By definition, each column contains at most one element of the staircase, and by construction, each row contains at most one element of the staircase. The reduction to echelon form is done from right to left in the sequence of matrices; that is, in the order of decreasing index \(i\). Indeed, every column operation in \(M_i\) changes the basis of \(U_i\), so we need to follow up with the corresponding row operation in \(M_{i-1}\). Since \(M_{i-1}\) has not yet been transformed to echelon form, there is nothing else to do.
In Phase 2, we use row operations to turn the column echelon into the normal form, as sketched in Fig. 4 on the right. Equivalently, we preserve the staircase and turn all non-zero entries below it into zeros. To do this for a single column, we add multiples of the row of its staircase element to lower rows. Processing the columns from left to right, this requires no backtracking. The reduction to normal form is done from left to right in the sequence of matrices; that is, in the order of increasing index \(i\). Each row operation in \(M_i\) changes the basis of \(U_{i+1}\), so we need to follow up with the corresponding column operation in \(M_{i+1}\). This operation is a right-to-left column addition, which preserves the echelon form. Since \(M_{i+1}\) has not yet been transformed to normal form, there is nothing else to do.
In summary, we have an algorithm that turns each matrix \(M_i\) into a matrix in which every row and every column contain at most one non-zero element, which is \(1\). This is the matrix of a matching. Since we use only row and column operations, the ranks of the matrices are the same as at the beginning. Each column operation in \(M_i\) has a corresponding operation on the basis of \(U_i\). Similarly, each row operation in \(M_i\) has a corresponding operation on the basis of \(U_{i+1}\). By performing these operations on the bases of the vector spaces, we arrive at a basis of the tower.\(\square \)
3.5 Persistent Homology and Derivations
Persistent homology as introduced in [11, 23] may be viewed as a special case of the persistence of towers of vector spaces. To see this, let \({{\mathcal C}}= (C_i, \gamma _i)\) be a tower of chain complexes, with \(\gamma _i\) the inclusion of \(C_i\) in \(C_{i+1}\), and obtain \({{\mathcal H}}= (H_i, \eta _i)\) by applying the homology functor. Assuming coefficients in a field, the latter is a tower of vector spaces. The persistent homology groups are the images of the \(\eta _i^j\). A version of persistent homology, recently introduced in [2], studies a sequence of vector spaces \(U_i\) and linear maps, some of which go forward, from \(U_i\) to \(U_{i+1}\), while others go backward, from \(U_{i+1}\) to \(U_i\). This is a zigzag module if we have exactly one map between any two contiguous vector spaces. It turns out that the theory of persistence generalizes to this setting. In view of our approach based on matchings, this is not surprising. Indeed, the inverse of a matching is again a matching, so that there is no difference at all in the category of matchings. To achieve the same in the category of vector spaces, we only need to adapt the above algorithm to obtain the zigzag generalization of the Basis Lemma. The adaptation is also straightforward, running the algorithm on a sequence of matrices that are the original matrices for the forward maps and the transposed matrices for the backward maps.
There are several ways one can derive towers from towers, and we discuss some of them. Letting \({{\mathcal U}}= (U_i, \upsilon _i)\) and \({{\mathcal V}}= (V_i, \nu _i)\) be towers in \({\mathbf{Vect}}\), we call \({{\mathcal V}}\) a subtower of \({{\mathcal U}}\) if \(V_i \subseteq U_i\) and \(\nu _i\) is the restriction of \(\upsilon _i\) to \(V_i\) and \(V_{i+1}\), for each \(i\). Given \({{\mathcal U}}\) and a subtower \({{\mathcal V}}\), we can take quotients and define the quotient tower, \({{\mathcal U}}/ {{\mathcal V}}= (U_i / V_i, \varrho _i)\), where \(\varrho _i\) is the induced map from \(U_i/V_i\) to \(U_{i+1}/V_{i+1}\). Similarly, we can construct towers from a morphism \(\varphi : {{\mathcal U}}\rightarrow {{\mathcal V}}\), where we no longer assume that \({{\mathcal V}}\) is a subtower of \({{\mathcal U}}\). Taking kernels and images, we get the tower of kernels, which is a subtower of \({{\mathcal U}}\), and the tower of images, which is a subtower of \({{\mathcal V}}\). Taking the quotients, \(U_i / \mathsf{ker\,}{\varphi _i}\) and \(V_i / \mathsf{im\,}{\varphi _i}\), we furthermore define the towers of coimages and of cokernels. In [7], towers of kernels are used in the analysis of sampled stratified spaces and introduced along with the towers of images and cokernels. The benefit of the general framework presented in this section is that persistence is now defined for all these towers, without the need to prove or define anything else.
Suppose now that \({{\mathcal V}}= {{\mathcal U}}\), and let \(\phi : {{\mathcal U}}\rightarrow {{\mathcal U}}\) be an endomorphism. We can iterate \(\phi \) and thus obtain a sequence of endomorphisms. The generalized kernel of the component \(\phi _i : U_i \rightarrow U_i\) is the union of the kernels of its iterated compositions. Similarly, the generalized image is the intersection of the images of the iterated compositions:
where \(\phi _i^{\circ k}\) is the \(k\)-fold composition of \(\phi _i\) with itself. Similar to before, we define two subtowers of \({{\mathcal U}}\): the tower of generalized kernels, denoted as \(\mathsf{gker\,}{\phi }\), and the tower of generalized images, denoted as \(\mathsf{gim\,}{\phi }\). By assumption, \(U_i\) has finite dimension, which implies that both the generalized kernel and the generalized image are already defined by finite compositions of \(\phi _i\). Furthermore, the ranks of \(\mathsf{gker\,}{\phi _i}\) and \(\mathsf{gim\,}{\phi _i}\) add up to the rank of \(U_i\). A trivial example of an element in the generalized image is an eigenvector of \(\phi _i\), but \(\mathsf{gim\,}{\phi _i}\) also contains the eigenvectors of the iterated compositions of \(\phi _i\) and the spaces they span.
Of particular interest are the quotient towers, \({{\mathcal U}}/\mathsf{gker\,}{\phi }\) and \({{\mathcal U}}/\mathsf{gim\,}{\phi }\), because of their relation to the Leray functor [18] and Conley index theory [8, 17]. They may be of interest in the future study of the persistence of the Conley index applied to sampled dynamical systems.
3.6 Tower of Eigenspaces
Of particular interest to this paper is the tower of eigenspaces. When studying the eigenvectors of the endomorphisms, we do this for each eigenvalue in turn. To begin, we note that \(\phi : {{\mathcal U}}\rightarrow {{\mathcal U}}\) is a tower in the category \(\mathbf{Endo}({\mathbf{Vect}})\). Indeed, each \(\phi _i: U_i \rightarrow U_i\) is an object, and \(\upsilon _i: U_i \rightarrow U_{i+1}\) commutes with \(\phi _i\) and \(\phi _{i+1}\). Applying the eigenspace functor, \(E_t\), we get the tower \({{\mathcal E}}_t (\phi ) = (E_t (\phi _i), \delta _{t,i})\) in \({\mathbf{Vect}}\). Its objects are the eigenspaces, \(E_t (\phi _i)\), and its arrows are the restrictions, \(\delta _{t,i}\), of the \(\upsilon _i\) to \(E_t (\phi _i)\) and \(E_t (\phi _{i+1})\). We refer to it as the eigenspace tower of \(\phi \) for eigenvalue \(t\).
Much of the technical challenge we face in this paper derives from the difficulty in constructing linear self-maps from sampled self-maps. This motivates us to extend the above construction to a pair of morphisms. Let \({{\mathcal V}}= (V_i, \nu _i)\) be a second tower in \({\mathbf{Vect}}\), let \(\varphi , \psi : {{\mathcal U}}\rightarrow {{\mathcal V}}\) be morphisms between the two towers, and recall that this gives a tower in \(\mathbf{Pairs}({\mathbf{Vect}})\). Its objects are the pairs \(\varphi _i, \psi _i : U_i \rightarrow V_i\), and its arrows are the commutative diagrams with vertical maps \(\upsilon _i\) and \(\nu _i\), as in (8). Similar to the single-map case, we apply the eigenspace functor, \(E_t\), now from \(\mathbf{Pairs}({\mathbf{Vect}})\) to \({\mathbf{Vect}}\). This gives the tower \({{\mathcal E}}_t (\varphi , \psi ) = (E_t (\varphi _i, \psi _i), \epsilon _{t,i})\) in \({\mathbf{Vect}}\). Its objects are the eigenspaces, and its arrows are the linear maps that map \([u] \in E_t (\varphi _i, \psi _i)\) to \([\upsilon _i (u)] \in E_t (\varphi _{i+1}, \psi _{i+1})\). We refer to it as the eigenspace tower of the pair \((\varphi , \psi )\) for the eigenvalue \(t\). This is the main new tool in our study of self-maps. Of particular interest will be the persistence module of this tower.
4 Algorithm
Assuming a hierarchical representation of an endomorphism, we explain how to compute the persistent homology of its eigenspaces in three steps. The general setting consists of a filtration and an increasing sequence of self-maps. In Step 1, we compute the bases of the two towers obtained by applying the homology functor to the filtrations of spaces and domains. In Step 2, we construct matrix representations of the linear maps in the morphism between the two towers. In Step 3, we compute the eigenvalues and the corresponding eigenspaces as well as their persistence.
4.1 Hierarchical Representation
The algorithm does its computations on a simplicial complex, \(K\), and a partial simplicial map, \(\kappa : K {\nrightarrow }K\). More precisely, \(\kappa \) is a partial map on the underlying space of \(K\), but we will ignore this difference. In addition, we assume a filtration of the complex, \(\emptyset = K_0 \subseteq K_1 \subseteq \ldots \subseteq K_n = K\), and of the domain,
with \(\kappa _i: K_i {\nrightarrow }K_i\) being the two-sided restriction of \(\kappa \) to \(K_i\). Writing \(\mathbf{Simp}\) for the category of simplicial complexes and simplicial maps, we use the two filtrations to form a tower in \(\mathbf{Pairs}(\mathbf{Simp})\). Its objects are the pairs \(\iota _i, \kappa _i': \mathsf{dom\,}{\kappa _i} \rightarrow K_i\), in which \(\iota _i\) is the inclusion and \(\kappa _i'\) is the further restriction of \(\kappa _i\) to the domain. Its arrows are the commuting diagrams connecting contiguous objects by inclusions. Applying the homology functor, we get a tower in \(\mathbf{Pairs}({\mathbf{Vect}})\), and applying the eigenspace functor, we get a tower in \({\mathbf{Vect}}\). The algorithm in this section computes the persistence diagram of the latter tower.
In principle, it is irrelevant how \(K\) and \(\kappa \) are obtained. In the context of sampling an unknown map, we may construct both from a finite sample of that map. We explain this in detail. Write \({\mathrm{Vert\,}{K}}\) for the vertex set of \(K\), and let \(g: {\mathrm{Vert\,}{K}} {\nrightarrow }{\mathrm{Vert\,}{K}}\) be a partial function from the vertex set to itself. If the vertices of a simplex \({\sigma }\in K\) map to the vertices of a simplex \({\tau }\in K\), then we extend the vertex map linearly to \({\sigma }\) as follows. Letting \(x_0, x_1, \ldots , x_p\) be the vertices, and \(x = \sum _{i=0}^p \lambda _i x_i\) a point of \({\sigma }\), where \(\sum _{i=0}^p \lambda _i = 1\) and \(\lambda _i \ge 0\) for all \(i\), we define
which is a point of \({\tau }\). Doing this for all such simplices \({\sigma }\), we get a partial simplicial map, \(\kappa : K {\nrightarrow }K\). Its domain consists of all simplices whose vertices map to the vertices of a simplex in \(K\). Having constructed \(\kappa \), it is now easy to construct the partial simplicial maps on the subcomplexes of \(K\). Letting \(g_i: {\mathrm{Vert\,}{K_i}} {\nrightarrow }{\mathrm{Vert\,}{K_i}}\) be the restriction of \(g\) to the vertex set of \(K_i\), we get \(\kappa _i: K_i {\nrightarrow }K_i\) by linear extension as before; it is also the restriction of \(\kappa \) to \(K_i\), as mentioned earlier. We observe that the image is not necessarily the same as the domain. This difference is the reason we construct the tower in \(\mathbf{Pairs}(\mathbf{Simp})\) and not in \(\mathbf{Endo}(\mathbf{Simp})\), as explained above. Finally, we note that the domains of the \(\kappa _i\) form the filtration (15), as required. Indeed, if the vertices of a simplex \({\sigma }\) in \(K_i\) map to the vertices of a simplex \({\tau }\) in \(K_i\), then \({\sigma }\in \mathsf{dom\,}{\kappa _j}\) for all \(i \le j \le n\).
Assuming the above hierarchical representation of the sampled map, we explain now how to compute the persistent homology of its eigenspaces in three steps. In Step 1, we compute the bases of the two towers obtained by applying the homology functor to the filtrations of spaces and domains. In Step 2, we construct matrix representations of the linear maps in the morphism between the two towers. In Step 3, we compute the eigenvalues and the corresponding eigenspaces as well as their persistence.
Step 1: Spaces Applying the homology functor, we get the tower \({{\mathcal X}}= (X_i, \xi _i)\) from the filtration of domains \(\mathsf{dom\,}{\kappa _i}\), and the tower \({{\mathcal Y}}= (Y_i, \eta _i)\) from the filtration of complexes \(K_i\). In this step, we compute the bases of these towers, which we explain for \({{\mathcal X}}\). Importantly, we represent all domains and maps in a single data structure, and we compute the basis in a single step that considers all maps at once.
Call \(\mathsf{dom\,}{\kappa _i} - \mathsf{dom\,}{\kappa _{i-1}}\) the \(i\) -th block of simplices, and sort \(\mathsf{dom\,}{\kappa }\) as \({\sigma }_1, {\sigma }_2, \ldots , {\sigma }_m\) such that each simplex succeeds its faces, and the \(i\)th block succeeds the \((i-1)\)-st block, for every \(1 \le i \le n\). Let \(D\) be the ordered boundary matrix of \(\mathsf{dom\,}{\kappa }\); that is, \(D [k,\ell ]\) is non-zero if \({\sigma }_k\) is a codimension-\(1\) face of \({\sigma }_\ell \), and \(D [k,\ell ] = 0\), otherwise. The ordering implies that the submatrix consisting of the first \(i\) blocks of rows and the first \(i\) blocks of columns is the boundary matrix of \(\mathsf{dom\,}{\kappa _i}\), for each \(i\). We use the original persistence algorithm [10, Chap. VII.1] to construct the basis. Similar to the echelon form, it creates a collection of distinguished non-zero entries, at most one per column and row, but to preserve the order, it does not arrange them in a staircase. Specifically, the algorithm uses left-to-right column additions to get \(D\) into reduced form, which is a matrix \(R\) so that the lowest non-zero entries of the columns belong to distinct rows.
Suppose \(R[k,\ell +1]\) is the lowest non-zero entry in column \(\ell +1\), as in Fig. 5. Then \(R[.,k] = 0\) and \(b_{\ell +1} := R[.,\ell +1]\) is the boundary of a chain that contains \({\sigma }_{\ell +1}\). We note that \(b_{\ell +1}\) existed as early as \(X_k\) but not earlier, and that it changed to a boundary in \(X_{\ell +1}\) but not earlier. In other words, \(b_{\ell +1} \not \in \mathsf{im\,}{\xi _{k-1}}\) and \(b_{\ell +1} \in \mathsf{ker\,}{\xi _\ell }\), as required for a maximal string. Assuming \({\sigma }_k\) belongs to the \(i\)th block of simplices, and \({\sigma }_{\ell +1}\) belongs to the \((j+1)\)-st block, the corresponding persistence interval is \([i,j]\). It is empty if \(i = j+1\). In the persistence literature, the above situation is expressed by saying that \(b_\ell \) is born at \(X_i\) and dies entering \(X_{j+1}\). It is also possible that a cycle is born but never dies, in which case we do not have a corresponding lowest non-zero entry in the matrix. But this case can easily be avoided, for example by adding the cone over the entire complex as a last block of simplices to the filtration.
The rows and columns of the reduced matrix are decomposed into \(n\) blocks each. The \(k\)th column is zero, and the lowest non-zero entry in the \((\ell +1)\)st column belongs to the \(k\)th row. Since the \(k\)th and \((\ell + 1)\)st columns belong to the first and the second blocks, the corresponding persistence interval is \([1,1]\)
Given an index \(1 \le i \le n\), we identify the persistence intervals that contain \(i\) and get a basis of \(X_i\) by gathering the vectors in the corresponding columns of \(R\). The collection of these bases forms a basis of \({{\mathcal X}}\); see Sect. 3. Running the same algorithm on the filtration of \(K\), we get a basis of \({{\mathcal Y}}\).
Step 2: Maps Let \(\varphi _i, \psi _i: {{\mathcal X}}\rightarrow {{\mathcal Y}}\) be the morphisms such that \(\varphi _i\) is induced by \(\iota _i : \mathsf{dom\,}{\kappa _i} \rightarrow K_i\) and \(\psi _i\) is induced by \(\kappa _i' : \mathsf{dom\,}{\kappa _i} \rightarrow K_i\). In the second step of the algorithm, we construct matrix representations of the two morphisms. Both matrices, \(\Phi \) for \(\varphi \) and \(\Psi \) for \(\psi \), have their columns indexed by the non-zero columns of the reduced matrix of \({{\mathcal X}}\) and their rows indexed by the non-zero columns of the reduced matrix of \({{\mathcal Y}}\). We explain the computations for \(\Psi \).
Letting \(R[.,\ell +1]\) be a non-zero column in the reduced matrix of \({{\mathcal X}}\), we recall that \(b_{\ell +1} = R[.,\ell +1]\) is a cycle in \(\mathsf{dom\,}{\kappa }\). First, we compute its image, \(c_{\ell +1} := \kappa (b_{\ell +1})\), which either collapses to zero or is a cycle of the same dimension in \(\mathsf{im\,}{\kappa }\). Second, we write the homology class of \(c_{\ell +1}\) as a linear combination of the basis vectors of \(Y_j\), assuming \({\sigma }_\ell \) belongs to the \(j\)th block of simplices, as before. Most effectively, this is done as part of the reduction of the boundary matrix of \(K\). Indeed, we can insert the images of the columns into the boundary matrix so that their representation as linear combinations of basis vectors of \({{\mathcal Y}}\) falls out as a by-product of the reduction. Running the same algorithm for \(\varphi \), we get the matrix \(\Phi \).
The two computed matrices represent the morphisms, \(\varphi \) and \(\psi \), from which the matrices \(\Phi _i\) and \(\Psi _i\) representing the arrows, \(\varphi _i\) and \(\psi _i\), can be extracted. To do so, we first find all persistence intervals that contain \(i\), as before. Second, we collect the intersections of all corresponding rows and columns, as illustrated in Fig. 6.
Step 3: Eigenspaces We recall that Step 2 provides presentations of \(\varphi \) and \(\psi \) in terms of the same bases, namely those of \({{\mathcal X}}\) and of \({{\mathcal Y}}\) as computed in Step 1. In this step, we compute the filtration of eigenspaces and their persistence, separately for each eigenvalue \(t \ne 0\). Fixing the eigenvalue, we compute the eigenspaces of \(\varphi _i\) and \(\psi _i\) and we take the quotient relative to the intersection of kernels:
It might be interesting to do the computations incrementally, as in Steps 1 and 2, but here we have to add as well as remove rows and columns, which makes the update operation complicated. Besides, the matrices at this stage tend to be small (see Table 1), so we decide to do the computations for each index \(i\) from scratch. At the same time, we extract the kernels of \(\varphi _i\) and \(\psi _i\) from \(\Phi _i\) and \(\Psi _i\), and we use standard methods from linear algebra to compute the quotient. Next, we compute the maps \(\xi _i: \mathsf{dom\,}{\kappa _i} \rightarrow \mathsf{dom\,}{\kappa _{i+1}}\) and their restrictions \(\epsilon _{t,i}: E_t (\varphi _i, \psi _i) \rightarrow E_t (\varphi _{i+1}, \psi _{i+1})\), thus completing the construction of the eigenspace tower defined by \(\varphi \) and \(\psi \). Finally, we compute the persistence of this tower as explained in Sect. 3.
5 Analysis
Given a finite set of sample points and their images, we apply the algorithm of Sect. 4 to compute information about the otherwise unknown map acting on an unknown space. In this section, we prove that under mild assumptions—about the space, the map, and the sample—this information includes the correct dimension of the eigenspaces. We also show that the persistence diagrams of the eigenspace towers are stable under perturbations of the input.
5.1 Graphs and Distances
Let \(f: {{\mathbb X}}\rightarrow {{\mathbb X}}\) be a continuous map acting on a topological space. For convenience, we assume that \({{\mathbb X}}\) is a subset of \({{\mathbb R}}^\ell \), with topology induced by the Euclidean metric.Footnote 5 While we are interested in exploring \(f\), we assume that all we know about it is a finite set, \(S \subseteq {{\mathbb X}}\), and the image, \(f(s)\), for every point \(s \in S\). Assuming that the image of every point is again in \(S\), we write \(g: S \rightarrow S\) for the restriction of \(f\).Footnote 6 The goal is to show that under reasonable conditions, \(f\) and \(g\) are similar so that we can learn about the former by studying the latter. To achieve this, we need some way to measure distance between two functions whose domains need not be the same. To this end, we consider the graphs of the functions,
which are both subsets of \({{\mathbb R}}^\ell \times {{\mathbb R}}^\ell \). Using the product metric, the distance between \((x, x')\) and \((y, y')\) in the product space is the larger of the two Euclidean distances, \({\Vert {x}-{y}\Vert }\) and \({\Vert {x'}-{y'}\Vert }\). We compare two maps using the Hausdorff distance between their graphs. Recall that the Hausdorff distance between two sets is the infimum radius, \(r\), such that every point of either set has a point at distance at most \(r\) in the other set. We note that the Hausdorff distance between the domains of the two functions is bounded from above by the Hausdorff distance between their graphs:
simply because the distance between two points in \({{\mathbb R}}^\ell \times {{\mathbb R}}^\ell \) is at least the distance between their projections to the first factor. The Hausdorff distance between two sets is related to the difference between the distance functions they define. To explain this, let \(d_{{\mathbb X}}, d_S : {{\mathbb R}}^\ell \rightarrow {{\mathbb R}}\) be the functions that map each point \(y\) to the infimum distance to a point in \({{\mathbb X}}\) and \(S\), respectively. Similarly, let \(d_{{G{f}}}, d_{{G{g}}}: {{\mathbb R}}^\ell \times {{\mathbb R}}^\ell \rightarrow {{\mathbb R}}\) be the corresponding distance functions in the product space. Then we have
The conditions under which we can infer properties of \(f\) from \(g\) include that for small distance thresholds, the sublevel sets of \(d_{{\mathbb X}}\) have the same homology as \({{\mathbb X}}\). To quantify this notion, we assume that \(d_{{\mathbb X}}\) is tame, by which we mean that every sublevel set has finite-dimensional homology groups, and there are only finitely many homological critical values that are the values at which the homology of the sublevel set changes non-isomorphically. Following [6], we define the homological feature size of \({{\mathbb X}}\) as the smallest positive homological critical value of \(d_{{\mathbb X}}\), denoting it as \({\mathrm{hfs}{({{{\mathbb X}}})}}\). Similarly, we assume that \(d_{{G{f}}}\) is tame, and we define \({\mathrm{hfs}{({{G{f}}})}}\).
We note that there are functions \(f\) for which \({\mathrm{hfs}{({{{\mathbb X}}})}} < {\mathrm{hfs}{({{G{f}}})}}\), but there are also functions for which the relation is reversed. For example, the graph of the function that wraps the unit circle in \({{\mathbb R}}^2\) \(k\) times around itself is a curve on a torus in \({{\mathbb R}}^4\). For large values of \(k\), thickening this curve by a small radius suffices to get the same homotopy type as the torus, while thickening the circle by the same radius does not change its homotopy type.
5.2 Sublevel Sets
If \(f\) and \(g\) are similar, then the sublevel sets of their distance functions are similar. To make this more precise, we write \(A_r := d_A^{-1} [0,r]\), where \(A\) may be \({{\mathbb X}}, S, {G{f}}, {G{g}}\), or some other sets. Then
provided \({\varepsilon }\ge {\mathrm{Hdf}{({{G{f}}},{{G{g}}})}}\), which we recall is at least the Hausdorff distance between \({{\mathbb X}}\) and \(S\). This suggests that we compare \(f\) and \(g\) based on the sublevel sets of the four distance functions, which is the program we follow.
To apply the algorithms in Sect. 4, we use an indirect approach that encodes the sublevel sets in computationally more amenable simplicial complexes. To explain this connection, we construct a complex by drawing a ball of radius \(r\) around each point of \(S\), and let \(K_r = K_r (S)\) be the nerve of this collection. It is sometimes referred to as the Čech complex of \(S\) and \(r\); see [10, Chap. III]. Similarly, we let \(L_r = L_r ({G{g}})\) be the Čech complex of \({G{g}}\) and \(r\).Footnote 7 While the complexes are abstract, they are constructed over geometric points, which we use to form maps. Specifically, we write \(p_r: L_r \rightarrow K_r\) for the simplicial map we get by projecting \({{\mathbb R}}^\ell \times {{\mathbb R}}^\ell \) to the first factor, and we write \(q_r: L_r \rightarrow K_r\) if we project to the second factor. Both are simplicial maps because for every simplex in \(L_r\), its projections to the two factors both belong to \(K_r\). Note that \(p_r\) is injective, which implies that its inverse is a partial simplicial map, \(p_r^{-1}: K_r {\nrightarrow }L_r\), and its restriction to the domain is a simplicial isomorphism. Composing it with \(q_r\), we get the partial simplicial map \(q_r p_r^{-1}: K_r {\nrightarrow }K_r\).
We are now ready to relate this construction with the setup we use for our algorithm in Sect. 4. There, we begin with a partial simplicial map, \(\kappa : K {\nrightarrow }K\), and a filtration of \(K\). The filtration is furnished by the sequence of Čech complexes of \(S\), which ends with the complete simplicial complex \(K\) over the points in \(S\), and \(\kappa \) is the partial simplicial map defined by \(g: S \rightarrow S\). In this case, \(\kappa \) happens to be a simplicial map because \(K\) is complete. For each radius, \(r\), we have defined \(\kappa _r: K_r {\nrightarrow }K_r\) as the restriction of \(\kappa \), which is a partial simplicial map. It is not difficult to prove that \(\kappa _r\) is equal to the map we have obtained by composing \(p_r^{-1}\) and \(q_r\) before. We state this result and its consequence for towers of eigenvalues without proof.
Projection Lemma
Let \(\kappa _r: K_r {\nrightarrow }K_r\) be the partial simplicial map obtained by restricting \(\kappa \) to \(K_r\), and let \(p_r, q_r : L_r \rightarrow K_r\) be the simplicial maps induced by projecting to the two factors. Then \(\kappa _r = q_r p_r^{-1}\), for every \(r \ge 0\).
Recall that \(\kappa _r'\) is the restriction of \(\kappa _r\) to the domain, and \(\iota _r: \mathsf{dom\,}{\kappa _r} \rightarrow K_r\) is the inclusion map. In view of the Projection Lemma, we can freely move between the tower of eigenspaces we get for \((\iota , \kappa ')\) and \((p,q)\), which we do in the sequel.
5.3 Interleaving
We prepare the main results of this section with a technical lemma about interleaving arrows between eigenspaces. Let \({{\mathbb U}}, {{\mathbb V}}\subseteq {{\mathbb R}}^\ell \), let \(h: {{\mathbb U}}\rightarrow {{\mathbb U}}\) and \(k: {{\mathbb V}}\rightarrow {{\mathbb V}}\) be self-maps, and set \({\varepsilon }:= {\mathrm{Hdf}{({{G{h}}},{{G{k}}})}}\). Projecting a sublevel set of the distance function of the graph to those of the two factors, we get an object in \(\mathbf{Pairs}(\mathbf{Top})\) for \(h\), and another such object for \(k\). Choosing the distance thresholds so they satisfy \(r + {\varepsilon }\le r'\), we have inclusions and therefore an arrow in \(\mathbf{Pairs}(\mathbf{Top})\):

Applying now the homology functor, we get an arrow in \(\mathbf{Pairs}({\mathbf{Vect}})\), where we write \(\varphi _r, \psi _r\) and \(\upsilon _{r'}, \nu _{r'}\) for the maps induced in homology. Next applying the eigenspace functor, we get the arrow \(E_t(\varphi _r, \psi _r) \rightarrow E_t(\upsilon _{r'}, \nu _{r'})\) in \({\mathbf{Vect}}\). The technical lemma states two kinds of interleaving patterns, (27) and (28), with the main difference being the reversed direction on the right.
Interleaving Lemma
Let \({{\mathbb U}}, {{\mathbb V}}\subseteq {{\mathbb R}}^\ell \), and \(h: {{\mathbb U}}\rightarrow {{\mathbb U}}, k: {{\mathbb V}}\rightarrow {{\mathbb V}}\) be such that the associated distance functions are tame. Set \({\varepsilon }:= {\mathrm{Hdf}{({{G{h}}},{{G{k}}})}}\). If \(a+{\varepsilon }\le b \le c \le d-{\varepsilon }\), then

commutes. If \(a + {\varepsilon }\le b \le c\) and \(a \le d \le c - {\varepsilon }\), then the following diagram commutes:

Proof
We prove (27) using the commutative diagram of inclusions and projections in Fig. 7. Within each disk, we have an object of \(\mathbf{Pairs}(\mathbf{Top})\), and for every pair of adjacent disks, we have an arrow of \(\mathbf{Pairs}(\mathbf{Top})\).
The vertical arrows are replicas of (26), which are justified by \(a+{\varepsilon }\le b\) and \(c \le d-{\varepsilon }\). Each horizontal arrow connects objects in \(\mathbf{Pairs}(\mathbf{Top})\) induced by the same self-map, so we only need \(a \le d\) and \(b \le c\), which we get from the assumptions. Applying the homology functor, we get the same diagram, with spaces and maps replaced by the corresponding vector spaces and linear maps. Indeed, the horizontal maps are clear, and the vertical maps are induced by the inclusions that exist because of the assumed relations between \(a, b, c, d\), and \({\varepsilon }\). Applying now the eigenspace functor, we get the diagram in (27), which is easily seen to commute. The proof for the diagram in (28) is similar and omitted. \(\square \)
5.4 Small Thickenings
To further prepare our first main result, we recall that the projections from the graph of a continuous map commute with the map itself, a fact best expressed using a commutative diagram:

Here, we write \(Y\) for the homology group of \({G{f}}, \mu : Y \rightarrow X\) for the map induced on homology by \(p: {G{f}} \rightarrow {{\mathbb X}}\), etc. The restriction of \(p\) to \({G{f}}\) and \({{\mathbb X}}\) is a homeomorphism. We can therefore apply the result stated at the end of Sect. 2, which implies that \(E_t (\mu , \nu )\) and \(E_t (\phi )\) are isomorphic, for every eigenvalue \(t\). This property persists for small thickenings of \({{\mathbb X}}\) and \({G{f}}\) assuming the two spaces are compact absolute neighborhood retracts; see [20, p. 290, Thm. 10]. While the name is intimidating, the requirements for a space to be called an absolute neighborhood retract are mild. Since \({{\mathbb X}}\) and \({G{f}}\) are homeomorphic, the graph is a compact absolute neighborhood retract whenever \({{\mathbb X}}\) is one. The result about thickening such spaces will be useful in the proof of our first main result, so we state this observation more formally, but without proof.
ANR Lemma
Let \({{\mathbb X}}\subseteq {{\mathbb R}}^\ell \) be a compact absolute neighborhood retract, let \(f: {{\mathbb X}}\rightarrow {{\mathbb X}}\) be such that the associated distance functions are tame, and let \(r\) be positive but smaller than \(\min \{ {\mathrm{hfs}{({{{\mathbb X}}})}}, {\mathrm{hfs}{({{G{f}}})}} \}\). Writing \(\mu _r, \nu _r\) for the maps induced in homology by the restrictions of \(p, q\) to \(Gf_r\) and \({{\mathbb X}}_r\), the eigenspace \(E_t (\mu _r, \nu _r)\) is isomorphic to \(E_t (\phi )\), for every eigenvalue \(t\).
5.5 Convergence
We are now ready to formulate our first main result. As before, we consider a continuous self-map \(f: {{\mathbb X}}\rightarrow {{\mathbb X}}\), and write \(\phi : X \rightarrow X\) for the endomorphism induced in homology. Let \(S \subseteq {{\mathbb X}}\) be a finite sample of \({{\mathbb X}}\), and let \(g: S \rightarrow S\) another map, perhaps the restriction of \(f\) to \(S\). As before, we consider the projections from a thickened version of \({G{g}}\) to the two components. Letting \(\varphi _r\) and \(\psi _r\) be the corresponding maps induced in homology, we write
for the map between the eigenspaces. In a nutshell, our result is a relationship between the dimension of \(E_t (\phi )\) and the rank of \(\epsilon _{t,r}^{r'}\), for special values of \(r\) and \(r'\).
Inference Theorem
Let \({{\mathbb X}}\subseteq {{\mathbb R}}^\ell \) be a compact absolute neighborhood retract, \(S \subseteq {{\mathbb X}}\), and let \(f: {{\mathbb X}}\rightarrow {{\mathbb X}}\), be a map such that the distance functions for \({{\mathbb X}}\) and \({G{f}}\) are tame. Then any map \(g: S \rightarrow S\) satisfies
for all \({\mathrm{Hdf}{({{G{f}}},{{G{g}}})}} < {\varepsilon }< \frac{1}{4} \min \{ {\mathrm{hfs}{({{{\mathbb X}}})}}, {\mathrm{hfs}{({{G{f}}})}} \}\).
Proof
Recall that \(p_r and q_r\) are the projections of \({G{f}}_r\) to the two components, and \(\mu _r and \nu _r\) are the maps induced in homology. For \(r \le r'\), we write \(\delta _{t,r}^{r'}: E_t (\mu _r, \nu _r) \rightarrow E_t (\mu _{r'}, \nu _{r'})\) for the induced map on eigenspaces. In view of the ANR Lemma, it suffices to prove
for \(r < \min \{ {\mathrm{hfs}{({{{\mathbb X}}})}}, {\mathrm{hfs}{({{G{f}}})}}\). To prove (32), set \(h = f\) and \(k = g\) in the diagram in Fig. 7. Applying the eigenspace functor now gives

The rest of the argument does the accounting for particular choices of the parameters. Let \(e > {\mathrm{Hdf}{({{G{f}}},{{G{g}}})}}\), assume \(b \le c\), and set \(a = b-e\) and \(d = c+e\). Consider the image of \(E_t (\mu _a,\nu _a)\) in \(E_t (\mu _d,\nu _d)\). We can either follow the horizontal arrow from left to right, or the down-right-up path, and because of commutativity, we get the same image either way. Dropping the arrows at the end and the beginning of the path does not decrease the dimension of the image. We therefore get inequalities between the dimensions of the images of the horizontal maps, which we now decorate with their parameters:
where we get the second inequality by symmetry, switching the assignments to \(h = g\) and \(k = f\) in Fig. 7. Next, choose a positive \(\eta < {\varepsilon }\) small enough such that the Hausdorff distance between the graphs of \(f\) and \(g\) is less than \({\varepsilon }- \eta \). By assumption, the homological feature sizes of \({{\mathbb X}}\) and \({G{f}}\) are both larger than \(4 {\varepsilon }\) and therefore larger than \(4 ({\varepsilon }-\eta )\). Substituting \(b = {\varepsilon }, c = 3 {\varepsilon }, e = {\varepsilon }-\eta \) in (34), and \(b = 2{\varepsilon }-\eta , c = 2{\varepsilon }+\eta , e = {\varepsilon }-\eta \) in (35), we obtain
By definition of \({\varepsilon }\) and \(\eta \), there are no homological critical values of \(d_{{\mathbb X}}\) and \(d_{{G{f}}}\) in \([\eta , 4{\varepsilon }-\eta ]\). It follows that the dimensions of the images of \(\delta _{t,\eta }^\eta , \delta _{t,\eta }^{4{\varepsilon }-\eta }\), and \(\delta _{t,2{\varepsilon }-\eta }^{2{\varepsilon }+\eta }\) are all the same. Hence,
Since \(\mathsf{rank\,}{\delta _{t,\eta }^{\eta }}=\mathrm{dim\,}{E_t (\mu _\eta ,\nu _\eta )}\), we see that (32) is satisfied for \(r=\eta \). \(\square \)
The Inference Theorem may be interpreted as a statement of convergence of our algorithm: if the sampling is fine enough, then we are guaranteed to get the dimensions of the eigenspaces as dimensions of persistent homology groups.
5.6 Stability
Next, we strengthen the convergence result and prove the stability of the persistence diagrams of the eigenspace towers under perturbations of the input. This is interesting because we may sample the same self-map twice and wonder what we can say about the relationship between the two results. Most of the work that allows us to give a meaningful answer to this question has already been done. To set the stage, we consider two self-maps, \(h: {{\mathbb U}}\rightarrow {{\mathbb U}}\) and \(k: {{\mathbb V}}\rightarrow {{\mathbb V}}\), in which both \({{\mathbb U}}\) and \({{\mathbb V}}\) are embedded in \({{\mathbb R}}^\ell \). As before, we assume that the distance functions, \(d_{{\mathbb U}}, d_{{\mathbb V}}, d_{{G{h}}}, and d_{{G{k}}}\) are tame. We can now form towers in \(\mathbf{Pairs}(\mathbf{Top})\) consisting of projections from the sublevel sets of \(d_{{G{h}}}\) and \(d_{{G{k}}}\) to the sublevel sets of \(d_{{\mathbb U}}\) and \(d_{{\mathbb V}}\); see Fig. 7. To formalize the result, we define the bottleneck distance between two persistence diagrams as the maximum distance between pairs in an optimal bijection:
Here, \(P = [a_\mathrm{b}, a_\mathrm{d})\) is a persistence interval in \(\mathsf{E}\), now using the original convention in which \(a_\mathrm{b}\) and \(a_\mathrm{d}\) are the birth- and death-values. If \(Q = [c_\mathrm{b}, c_\mathrm{d})\) is another persistence interval, then we compute \({\Vert {P}-{Q}\Vert _\infty } = \max \{ |a_\mathrm{b} - c_\mathrm{b} |, |a_\mathrm{d} - c_\mathrm{d} | \}\), as for points in the plane.Footnote 8 Letting \({{\mathcal E}}_t\) and \({{\mathcal F}}_t\) be the towers of eigenspaces in \({\mathbf{Vect}}\) we get for \(h\) and \(k\), we write \(\mathrm{Dgm}({{\mathcal E}}_t)\) and \(\mathrm{Dgm}({{\mathcal F}}_t)\) for their persistence diagrams.
Stability Theorem
Let \({{\mathbb U}}, {{\mathbb V}}\subseteq {{\mathbb R}}^\ell \), and \(h: {{\mathbb U}}\rightarrow {{\mathbb U}}\) \(k: {{\mathbb V}}\rightarrow {{\mathbb V}}\) such that the associated distance functions are tame. Then
Proof
According to [4, Thm. 4.9], we only need to verify the \({\varepsilon }\)-strong interleaving of the two towers for \({\varepsilon }\) equal to the Hausdorff distance between \({G{h}}\) and \({G{k}}\), but this is guaranteed by the Interleaving Lemma. \(\square \)
Letting \(h\) and \(k\) be finite samples of \(f: {{\mathbb X}}\rightarrow {{\mathbb X}}\), the Stability Theorem implies that the information they convey about the given function cannot be arbitrarily different. Setting \(h = f\) and \(k = g\), the theorem quantifies the extent to which the persistence diagram for the sampled points can deviate from that of the original self-map.
6 Experiments
In this section, we present the results of a small number of computational experiments based on the implementation of the algorithm described in Sect. 4. We begin with a brief review of the algorithm and a discussion of the design decisions used in writing the software.
6.1 Implementation
We implement the three steps of the algorithm using the C++ language and methods from its STL library. As mentioned before, we use Vietoris–Rips complexes as the basis of persistence computations, as opposed to the theoretically more satisfying but computationally more expensive Čech complexes. With each simplex, we store the vertices so that their images can be easily computed. Conversely, we use a map in STL to find the simplex for a given set of vertices. In addition, we compute the kernels and the quotients in Step 3 using methods from the CAPD library [24] and the CAPD::RedHom library [25].
- Step 1 :
-
compute the bases of the towers \({{\mathcal X}}= (X_i, \xi _i)\) and \({{\mathcal Y}}= (Y_i, \eta _i)\) defined by the filtrations of the domains and complexes. We use the original persistence algorithm with a sparse-matrix representation in which the non-zero elements of each column are stored in a data structure referred to as a vector in C++.
- Step 2 :
-
compute the matrix representations of the morphisms \(\varphi , \psi : {{\mathcal X}}\rightarrow {{\mathcal Y}}\). Similar to Step 1, the algorithm works by incremental reduction of two matrices. The result is a compact representation of the maps \(\epsilon _{t,i}\) in the eigenspace tower.
- Step 3 :
-
construct the sequence of eigenspaces and compute the corresponding persistence diagram. Since the matrices representing the maps \(\epsilon _{t,i}\) tend to be small and dense, we use their full representations and the algorithm in the proof of the Basis Lemma.
All experiments are conducted with an Intel Core2 Quad 2.66 GHz processor with 8 GB RAM, but using only one core. To convey a feeling for the performance of the software, Table 1 states the time needed to process datasets of size between 40 and 140 points, giving complexes between 10,000 and 460,000 simplices.
We mention that the running time can be further improved. In particular, the current implementation is generic, working for any field of coefficients, and the code implementing Step 1 has not yet been optimized. Note the dramatic drop in the running time from Step 1 to Step 2. The reason is the surprisingly small numbers of generators needed in the construction of the matrices \(\Phi \) and \(\Psi \). In the first set of experiments, we get between \(3\) and \(21\) generators for the filtration of \(\mathsf{dom\,}{\kappa }\) and between \(5\) and \(24\) generators for the filtration of \(K\). Compare this with the 10,700 to 457,450 simplices in the \(2\)-skeleta of the Vietoris–Rips complex which have to be processed in Step 1. The code for Step 3 takes more time than for Step 2 because it executes computationally demanding procedures in linear algebra.
6.2 Expansion
In our first set of computational experiments, we consider the unit circle in the complex plane, and the function \(f: {{\mathbb S}}^1 \rightarrow {{\mathbb S}}^1\) defined by \(f(z) := z^2\). It maps each point on the circle to the point with twice the angle. The \(1\)-dimensional homology of the circle has rank \(1\), with the circle itself being a generator. Under \(f\), the image of this generator is the circle that wraps around \({{\mathbb S}}^1\) twice. We see that the map expands the space, doubling the angle between any two points. Our main interest is to see whether the methods of this paper can detect this simple fact.
We chose values for three parameters to generate the datasets on which we run our software: the order of the cyclic field, \({{\mathbb Z}}_k\) with \(k = 1009\), the number of points, \(m = 100\), and the width of the Gaussian noise, \(\sigma \in [0.00, 0.30]\). The finite field is used because we lack a general algorithm for eigenvalues; instead, we try out all possible values. The sample of the function \(f\) is computed by picking points \(z_j := \cos (\frac{2 j \pi }{m}) + \mathbf{i}\sin (\frac{2 j \pi }{m})\), for \(0 \le i < m\), where \(\mathbf{i}\) is the imaginary unit. Next, we let \(x_j\) be a point randomly chosen from the isotropic Gaussian kernel with center \(z_j\) and width \(\sigma \). Let \(S\) be the set of points \(x_j\). Finally, we set the image of \(x_j\) to the point in \(S\) that is closest to \(x_j^2\) under the Euclidean metric in the plane. For an example, see Fig. 8. The \(m\) points define \(n \le {m \atopwithdelims ()2}\) different distances and therefore \(n+1\) different Vietoris–Rips complexes. We are only interested in the \(1\)-dimensional homology, so we can limit ourselves to the \(2\)-skeleta of these complexes. To construct them, we use the algorithm in [22] to compute the complete \(2\)-complex over \(S\). Sorting the edges by length, we get the filtration \(K_0 \subseteq K_1 \subseteq \ldots \subseteq K_n\). Figure 9 shows the \(1\)-dimensional persistence diagrams thus obtained for four different values of the width \(\sigma \).
The representation of the function \(f(z) := z^2\) using \(m = 100\) points with Gaussian noise \(\sigma = 0.18\). The dots mark the points in \(S\) and the crosses mark their squares. The solid polygon generates the \(1\)-cycle visible in the persistence diagram of the eigenspace tower for eigenvalue \(t = 2\); its image is drawn in blue dashed lines and wraps twice around the origin, as expected (Color figure online)
As expected, the persistence of the interval decreases as the noise increases. For \(\sigma = 0.30\), we get a low-persistence interval for every value of \(t\). While we do not observe this all the time, this is a generic phenomenon, and we will shed light on it shortly. For now we just mention that the occurrence of every field value as eigenvalue indicates that we do not have sufficient data to see the features of the map.
6.3 Reflection
In our second set of computational experiments, we let \(f: {{\mathbb S}}^1 \rightarrow {{\mathbb S}}^1\) be defined by \(f(z) := \bar{z}\), where \(\bar{z} = a - \mathbf{i}b\) if \(z = a + \mathbf{i}b\). Going around the circle once, in a counterclockwise order, the image under \(f\) goes around the circle once in a clockwise order. Again we are interested whether the methods in this paper can detect this fact. The points and their images are chosen in the same way as before, except that the image of \(x_j\) is chosen to be the closest point to \(\bar{x}_j\). Figure 10 shows the result for \(\sigma = 0.27\).
The representation of the function \(f(z) := \bar{z}\) using \(m = 100\) points with Gaussian noise \(\sigma = 0.27\). The solid polygon generates the \(1\)-cycle visible in the persistence diagram of the eigenspace tower for eigenvalue \(t = -1\); its image is drawn in blue dashed lines. The dotted polygon generates a second (spurious) \(1\)-cycle in the same diagram. Correspondingly, there are two persistence intervals, drawn as crosses in Fig. 11 (Color figure online)
Instead of showing the individual \(1\)-dimensional persistence diagrams, we superimpose them into one diagram. To further facilitate the comparison with the first set of experiments, we draw the superimposed diagrams side by side in Fig. 11. In both cases, the Gaussian noise varies between \(0.00\) and \(0.30\). We limit the comparison to the eigenvalues \(t = 2\) for the expansion, and \(t = -1\) (the inverse of \(1\) in the used finite field) for the reflection. The diagrams clearly show that the persistence interval shrinks with increasing noise. Indeed, the birth-coordinate grows and the death-coordinate shrinks, so that the sum stays approximately constant, with a faint tendency to shrink. We also see that for the larger noise levels, there are sometimes spurious persistence intervals.
6.4 Abundance of Eigenvalues
We wish to shed light on the phenomenon that for some datasets and some complexes in the filtration, every field value is an eigenvalue of the pair of linear maps. While it might be surprising at first, there is an elementary explanation that has to do with computing the eigenvalues for a pair instead of a single map.
Here is an illustrative example. Let \(Y_r\) be generated by two loops, \(A\) and \(B\), and let \(X_r\) be generated by a single loop, \(C\). Suppose also that \(\varphi _r\) maps both \(A\) and \(B\) to \(C\), while \(\psi _r\) maps \(A\) to \(C\) and \(B\) to \(2 C\). Setting \(y = i A + j B\), we have \(\varphi _r (y) = (i+j) C\) and \(\psi _r (y) = (i + 2 j) C\). Elementary number theoretic considerations show that for every \(t \in {{\mathbb Z}}_k\), there are \(i\) and \(j\) such that \(t = \frac{i+j}{i+2j}\). In other words, we can find \(i\) and \(j\) such that \(\varphi _r (y)\) is the \(t\)-fold multiple of \(\psi _r (y)\). Intersecting the two kernels, we get \(i+j = i+2j = 0\) and therefore \(i = j = 0\). Hence, taking the quotient has no effect, implying that \(E_t (\varphi _r, \psi _r)\) has non-zero rank for every \(t\). Indeed, because the two loops in \(Y_r\) map to different multiples of the same loop in \(X_r\), we have enough flexibility to form combinations whose images under the two maps are arbitrary multiples of each other. This can also happen for an endomorphism \(\phi _r: Y_r \rightarrow Y_r\), for example by setting \(C = B\), but in this case we do not have a second map to compare and therefore get \(t = 2\) as the only non-zero eigenvalue.
The superposition of the \(1\)-dimensional persistence diagrams for \(f(z) := z^2\) and \(t = 2\) on the left and for \(f(z) := \bar{z}\) and \(t = -1\) on the right. The crosses are labeled by the level of the Gaussian noise used to generate the datasets. The dots are labeled similarly, but they alert us of the fact that these persistence intervals occur for all values of \(t\)
Let us now look at the linear algebra of the situation. In Step 2, we compute matrices \(\Phi _r\) and \(\Psi _r\) representing \(\varphi _r, \psi _r: Y_r \rightarrow X_r\), and in Step 3, we compute the nullspace of \(\Phi _r - t \Psi _r\). The entries of this matrix are degree-\(1\) polynomials in \(t\). Let \(t_0\) be a value at which the matrix reaches its maximum rank, which we denote as \(k_0\). Clearly, \(k_0 \le \min \{ \#\mathrm{rows}, \#\mathrm{columns} \}\). Note that \(\Phi _r - t_0 \Psi _r\) has a full-rank minor of size \(k_0\) times \(k_0\). Let \(\Delta (t)\) be the determinant of that minor, but now for arbitrary values \(t\). It is a polynomial of degree \(k_0\), and because \(\Delta (t_0) \ne 0\), it is not identically zero and therefore has at most \(k_0\) roots. By choice of \(t_0\), this implies that the matrix has maximum rank for all but at most \(k_0\) values of \(t\). Correspondingly, the nullspace has minimum dimension, \(\#\mathrm{columns} - k_0\), for all but at most \(k_0\) values of \(t\). This is the dimension of \(\bar{E}_t (\varphi _r, \psi _r)\). We still take the quotient by dividing with \(\mathsf{ker\,}{\varphi _r} {\; \cap \;}\mathsf{ker\,}{\psi _r}\), which amounts to reduce the dimension by the dimension of that intersection, which we denote as \(k_1\). The resulting dimension of the nullspace is the same for all but at most \(k_0\) values of \(t\), namely \(\#\mathrm{columns} - k_0 - k_1\). If \(k_1 < \#\mathrm{columns} - k_0\), then \(E_t (\varphi _r, \psi _r)\) has positive rank for every value of \(t\). This is what happens for the expanding datasets generated with width \(\sigma = 0.15, 0.24, and 0.30\) and for the persistence intervals represented by the dots in the left diagram in Fig. 11. In all other cases, we have \(k_1 = \#\mathrm{columns} - k_0\).
In conclusion, we mention that the extension of the eigenvalue problem to pairs of linear maps for not necessarily square matrices is not well understood. A relevant unpublished manuscript is [5], in which properties of the solution are discussed and a reduction algorithm is given.
6.5 Torus Maps
We test the method to see if it can distinguish between some torus maps. We identify \({{\mathbb S}}^1\) with the quotient space \({{\mathbb R}}/{{\mathbb Z}}\) and consider the torus \({{\mathbb T}}:= {{\mathbb S}}^1 \times {{\mathbb S}}^1 \cong {{\mathbb R}}^2/{{\mathbb Z}}^2\), equipped with the metric induced by the Euclidean distance in the plane. Each \(2\)-by-\(2\) matrix with integer entries induces a self-map on the torus. Using the cycles \({{\mathbb S}}^1 \times 0\) and \(0 \times {{\mathbb S}}^1\) as a basis, the same matrix represents the map induced on first homology. We consider the following three matrices,
Note that \(A_1\) is diagonal with non-trivial eigenspace for the eigenvalue \(2\), which is spanned by two eigenvectors. Matrix \(A_2\) is non-diagonal with diagonal Jordan form. It has one-dimensional eigenspaces for the eigenvalues \(1\) and \(-1\). Matrix \(A_3\) has non-diagonal Jordan form and has only one non-trivial, one-dimensional eigenspace.
We denote the corresponding self-maps by \(f_1, f_2\), and \(f_3\). Selecting a set of \(200\) points uniformly at random on the torus, we compute approximations of the \(f_i\). The persistence diagrams of the eigenspaces of the maps induced in first homology are shown in Fig. 12. In each case, the expected eigenvectors clearly separate from the rest of the diagram, facilitating the easy distinction between the three maps.
7 Discussion
The main concept introduced in this paper is the eigenspace tower of a filtered self-map. Together with its persistence diagram, it forms a powerful tool in the study of discretely sampled dynamical systems. Besides the mathematical development, which is based on a category theory approach to persistence, we give an algorithm for computing persistence diagrams of eigenspace towers, and we provide evidence of its efficacy by presenting results obtained with a software implementation. The work reported in this paper raises a number of yet unanswered questions.
-
Can the persistence of the eigenspace towers of a pair of morphisms be computed directly, for all eigenvalues simultaneously? To answer this question, we may have to study the persistence of generalized eigenspaces and Jordan form representations of endomorphisms.
-
The category approach to persistence opens the door to a number of derived towers, including generalized kernels and generalized images. How can we use their persistence to enhance our understanding of discretely sampled dynamical systems?
We remark that the traditional notion of a discrete dynamical system discretizes time but not space. In contrast, discretizations of space are needed for rigorous numerics of dynamical systems; see e.g. [14, Sect. 10.6]. There, the space is divided into boxes and estimates of the images of the boxes are used as input for the algorithm that computes topological invariants. This is different from the more radical discretization suggested by the work in this paper where we sample the dynamical system only in a finite collection of points. Such an approach may be useful when the dynamical system is available only via experiments. It may also be used to replace rigor in high-dimensional problems where reasonable rigorous estimates are not possible. We believe that it is interesting to continue the program started here and embed persistence more comprehensively in discrete approaches to dynamical systems.
Notes
A field is algebraically closed if every non-constant polynomial over the field has a root.
To be more precise, we should call it a weak inverse, because \(\alpha ^{-1}\alpha \) and \(\alpha \alpha ^{-1}\) are identities on the domain and image of \(\alpha \) and not necessarily on \(A\) and \(B\). We simplify language by ignoring this subtlety.
We note a difference in convention to most of the related literature, in which persistence intervals are defined half-open. In particular, \([k,\ell ]\) in our notation corresponds to \([k,\ell +1)\) in [10]. Reading them as intervals in \({{\mathbb Z}}\), they are the same.
Part of the theory in this section can be developed for the more general case of finitely generated modules over a principal ideal domain. For reasons of simplicity, and because the crucial connection to matchings relies on stronger algebraic properties, we limit this discussion to vector spaces over a field right from the start.
With occasionally more elaborate formalism, everything we say can be generalized to \({{\mathbb X}}\) embedded in a general metric space.
In cases in which the image of a point is not in \(S\), we can snap the image to the nearest point in \(S\), which usually implies only a small perturbation of the map. Similarly, we can relax the assumption that \(g\) be a restriction of \(f\) to allow for errors due to noise, for imprecision of measurement, and for approximations in computation.
A practically more convenient alternative is the Vietoris–Rips complex that consists of all simplices spanned by the data points whose diameters do not exceed \(2r\). We will use it for the computations discussed in Sect. 6, but for now we stay with the Čech complex, which has the theoretical advantage that its homotopy type agrees with that of the sublevel set for the same \(r\).
Following [6], we assume that each persistence diagram contains copies of all empty intervals—points of the form \((a,a)\)—which are used to complete a bijection or decrease the maximum distance.
References
P. Bubenik and J.A. Scott. Categorification of persistent homology. Discrete Comput. Geom. 51 (2014), 600–627.
G. Carlsson and V. de Silva. Zigzag persistence. Found. Comput. Math. 10 (2010), 367–405.
G. Carlsson, T. Ishkanov, V. de Silva and A. Zomorodian. On the local behavior of spaces of natural images. Internat. J. Comput. Vision 76 (2008), 1–12.
F. Chazal, D. Cohen-Steiner, M. Glisse, L. J. Guibas and S. Y. Oudot. Proximity of persistence modules and their diagrams. In “Proc. 25th Sympos. Comput. Geom., 2009”, 237–246.
S. Cohen and C. Tomasi. Systems of bilinear equations. Techn. Rept., Dept. Comput. Sci., Stanford Univ., California, 1997.
D. Cohen-Steiner, H. Edelsbrunner and J. Harer. Stability of persistence diagrams. Discrete Comput. Geom. 37 (2007), 103–120.
D. Cohen-Steiner, H. Edelsbrunner, J. Harer and D. Morozov. Persistent homology for kernels, images, and cokernels. In “Proc. 20th Ann. ACM-SIAM Sympos. Discrete Alg., 2009”, 1011–1020.
C. Conley. Isolated Invariant Sets and the Morse Index. Amer. Math. Soc., CBMS Regional Conf. Series Math. 38, 1978.
H. Derksen and J. Weyman. Quiver representations. Notices Amer. Math. Soc. 52 (2005), 200–206.
H. Edelsbrunner and J. L. Harer. Computational Topology. An Introduction. Amer. Math. Soc., Providence, Rhode Island, 2010.
H. Edelsbrunner, D. Letscher and A. Zomorodian. Topological persistence and simplification. Discrete Comput. Geom. 28 (2002), 511–533.
J. Gamble and G. Heo. Exploring uses of persistent homology for statistical analysis of landmark-based shape data. J. Multivar. Analysis 101 (2010), 2184–2199.
A. Gyulassi, V. Natarajan, V. Pascucci, P.-T. Bremer and B. Hamann. A topological approach to simplification of three-dimensional scalar fields. IEEE Trans. Visual. Comput. Graphics (2006), 474–484.
T. Kaczynski, K. Mischaikow and M. Mrozek. Computational Homology. Springer-Verlag, New York, New York, 2004.
S. Kleene. Introduction to Meta-Mathematics. North Holland, Amsterdam, the Netherlands, 1952.
S. MacLane. Categories for the Working Mathematician. Springer-Verlag, New York, New York, 1971.
K. Mischaikow, M. Mrozek (2002) The Conley index theory. In: B. Fiedler, G. Iooss, N. Kopell (eds) Handbook of Dynamical Systems III: Towards Applications. Elsevier, Singapore 393–460
M. Mrozek. Leray functor and the cohomological Conley index for discrete time dynamical systems. Trans. AMS 318 (1990), 149–178.
M. Mrozek. Normal functors and retractors in categories of endomorphisms. Univ. Jagiell. Acta. Math. 29 (1992), 181–198.
E. Spanier. Algebraic Topology. McGraw-Hill or Springer-Verlag, New York, 1966.
S. Weinberger. What is ... persistent homology? Notices Amer. Math. Soc. 58 (2011), 36–39.
A. Zomorodian. Fast construction of the Vietoris-Rips complex. Computer and Graphics 34 (2010), 263–271.
A. Zomorodian and G. Carlsson. Computing persistent homology. Discrete Comput. Geom. 33 (2005), 249–274.
CAPD: computer assisted proofs in dynamics. http://www.capd.ii.uj.edu.pl.
CAPD::RedHom: reduction algorithms for homology computation. http://www.redhom.ii.uj.edu.pl.
Acknowledgments
This research is partially supported by the Toposys project FP7-ICT-318493-STREP, by ESF under the ACAT Research Network Programme, by the Russian Government under mega project 11.G34.31.0053, and by the Polish National Science Center under Grant No. N201 419639.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Konstantin Mischaikow.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Edelsbrunner, H., Jabłoński, G. & Mrozek, M. The Persistent Homology of a Self-Map. Found Comput Math 15, 1213–1244 (2015). https://doi.org/10.1007/s10208-014-9223-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10208-014-9223-y
Keywords
- Discrete dynamical systems
- Computational topology
- Persistent homology
- Category theory
- Algebraic algorithms
- Convergence
- Stability
- Computational experiments