1 Introduction

Recent developments in information technology, coupled with the ongoing digitization process (including big data, internet of things, digital platforms, blockchain, cloud computing, etc.), are catalysing a significant industrial reorganization. Processes are now frequently executed without the need for physical interaction. Within the insurance industry, this shift is driving the creation of new digital platforms and the enhancement of existing ones, all aimed at boosting the efficiency of the insurance process. This, in turn, leads to a reduction in cost structures and subsequently, insurance premiums. A notable example is InsurePal, a Switzerland-based decentralized insurance platform founded in 2015, which has gained widespread global popularity (see, for instance, (Sun et al. 2020) for more details). InsurePal facilitates policyholders in directing claims towards a reliable network. It represents a new generation of peer-to-peer (P2P) insurance, complementing traditional insurance companies and banks.

The P2P model is a re-imagining of the concept of mutuality that gave rise to insurance: a group of peers chooses to collectively insure themselves against risks by allocating premiums. Upon the policy’s expiration, these funds are redistributed, minus the costs associated with processing claims. This model has been enhanced with new technologies, facilitating easier connections among policyholders and employing analytics to offer more sophisticated customer experiences.

P2P insurance offers several advantages, such as mitigating information asymmetries between the insured party and the company, thereby minimizing the risk of fraud. However, entities that have adopted this model encounter challenges, particularly in recruiting a sufficient number of subscribers to adequately fund claims. The P2P model has seen recent growth due to insurtech incorporating concepts from the sharing economy into the insurance sector, similar to what happened with crowdsourcing or P2P lending in the financial industry. This approach involves creating communities and sharing services, which has now extended to insurance management. This model includes mechanisms that incentivize virtuous behaviour: customers who belong to the same group, sharing the same risk, can reduce their policy premiums through lower claims. In essence, the lower the peer’s claims rate, the higher the premium return or discount applied to the renewal premium for each participant.

These groups are established and managed through a social platform, allowing individuals to invite friends (who are reasonably virtuous individuals) to join their group and, over the year, assess their behaviour. This active involvement and participation in evaluating accidents and the general conduct of peers foster customer trust, thereby promoting retention. Additionally, there is a risk profile benefit: since a low accident rate leads to greater benefits for the group, the group itself will exclude those with incorrect or risky behaviour.

A fundamental point currently under fervent discussion pertains to the nature of this activity: whether this risk-sharing mechanism can be deemed a genuine insurance activity, which would necessitate compliance with sector-specific regulations. In this context, EIOPA (2019) has examined three types of P2P models and suggested the application of the principle of proportionality. This principle considers the P2P risk-sharing scheme as an insurance activity contingent on factors such as the extent of the activity’s implementation and the presence or absence of an intermediary.

The first type of P2P insurance involves a purely self-governing model centred around a community of peers who autonomously manage all insurance functions (for further details, see, e.g., Denuit and Robert (2021b)). The second and most diffused type is the broker model (Rego and Carvalho 2017), where an insurance broker manages a group of peers through a digital platform, participants pay an entry price partly into a common fund and the remaining part to an insurance company. In this way, the peers share the first layer of the realized loss, while the higher level is transferred through a mechanism similar to that of reinsurance. At the end of the year, if there is some remaining fund, it is distributed to the peers as cashback; in the opposite case, if the common fund is insufficient to cover the claims, the insurer has to intervene.

The insurance activity is even more predominant in the third case, the carrier model, where the broker model takes the form of an actual insurance scheme entirely managed through a digital platform.

The literature about P2P risk sharing and allocation framework is spreading, especially in recent years. A first line of contributions concerns the definition of transparent and intuitive risk allocation rules in the pure self-organizing model. In this case, the peers do not pay an initial premium, but an ex-post contribution sufficient to cover the realized loss. Denuit and Dhaene (2012) introduce the Conditional Mean Risk (CMR) allocation rule, according to which each peer has to pay at the end of the year a contribution calculated according to the conditional expectation of the individual loss brought to the pool, given the total loss of the pool. Denuit (2019) and Denuit and Robert (2020) discuss the advantages of the CMR rule. Denuit and Dhaene (2012) prove that it is Pareto-optimal for all risk-averse utility maximizers under the hypothesis of co-monotonic structural losses. Levantesi and Piscopo (2022) modify the CMR rule with an ex-ante contribution, which considers a safety loading to cover the possible fluctuations of total losses. A multivariate extension of the ex-post contribution rule is proposed by Abdikerimova and Feng (2022). Denuit et al. (2022) offer a systematic comparison of different risk allocation rules. Feng et al. (2023) develop an optimal risk allocation mechanism based on the Pareto optimality and actuarial fair.

Unlike the ex-post contributions typical of pure schemes, in the broker model, peers are required to pay an initial premium to participate. Denuit and Robert (2021a) consider an entry fee for participation in a P2P model, similar to the classical insurance premium principle, dependent on the expected single loss rather than the total loss. Feng et al. (2022) compare various risk-sharing schemes within decentralized insurance, while Charpentier et al. (2021) describe a P2P insurance system based on networks and study optimal designs for non-linear contracts.

A more recent line of research focuses on the surplus distribution, net of realized and covered losses. Clemente et al. (2023) focus on the distribution of cashback and propose an optimal distribution rule in the contest of cooperative games exploiting the tool of Shapley Value. Following this contribution, in this paper we extend the cooperative game framework in the broker model by introducing a safety loading in the entry premium calculation, inspired by the literature devoted to premium calculation principles and risk measures. We propose calculating the safety loading as a function of the Shapley Value and defining an optimal rule to distribute the cashback. The Shapley value in the insurance context has been exploited also by Galeotti and Rabitti (2023), to define the pricing of a reinsurance contract in the peer to peer scheme, in the case the community of peers agree to share just the first losses occurred.

The rest of the paper is organized as follows. In Sect. 2 we describe the general framework of our model, giving details on the Shapley contribution rule, which is based on the Shapley value, and the cashback distribution. Section 3 provides numerical examples using a portfolio of motor third-party liability coverages. The last section relates to the concluding remarks.

2 The model

2.1 The actuarial formulation

Let n be the number of participants to the P2P scheme. Each participant i faces a loss represented by a non negative random variable \(L_i\), such that: \(L_i\sim F_{L_i|\Lambda _{i}}(l)\), with \(F_{L_i|\Lambda _{i}}(l)\) cumulative distribution function (c.d.f.), \(E(L_i)=\Lambda _i\) with \(0< E(L_i)<\infty \), and \(Var(L_i)<\infty \) \(\forall i\).

Let X be the random variable that represents the total loss of the network, defined as follows:

$$\begin{aligned} X= \sum _{i=1}^n L_i \end{aligned}$$

It is distributed as \(X \sim F_{X|\varvec{\Lambda }}(x)\) with \(\varvec{\Lambda }=[\Lambda _1, \Lambda _2,..., \Lambda _n]\) vector of the average individual losses. Notice that we consider a general definition of the random variables X and \(L_i\). These definitions are easily applicable to well-known models used in non-life insurance (see, e.g., Daykin et al. (1994) and Kaas et al. (2008)).

Participants define a fair and transparent rule according to which each of them have to contribute to cover the loss of the scheme with a monetary amount \(h_i(X)>0\). When members enter in a pure self-organizing P2P scheme they do not pay any initial commission and contribute ex-post to the total losses realized according to a cooperative risk-sharing mechanism defined a priori. One of this is the Conditional Mean Rule (CMR) proposed by Denuit (2019), according which each participant i must contribute a posteriori to the expected value of the risk brought to the pool, given the total loss realized \(X=x\):

$$\begin{aligned} h_i^{CMR}({x})=E(L_i|X{=x}). \end{aligned}$$
(1)

So that once the loss is realized, we have:

$$\begin{aligned} \sum _{i}h_i^{CMR}({x})=\sum _{i}E[L_i|X{=x}]=x \end{aligned}$$
(2)

and then the sum of contributions exactly hedges the realized loss x without forming any residual capital. Since \(E[E(L_i|X)]=E(L_i)\), the sum of contributions is fair.

In a P2P broker model, the participants pay an initial contribution defined on a cooperative rule. In line with the classical actuarial literature, we propose to calculate this ex-ante contribution adding a safety loading to the fair premium \(E(L_i)\). In this case, however, the sum of the contributions does not necessarily cover exactly the final loss with the consequent formation of capital to be distributed or further losses to be covered. Consequently, the problem to be faced becomes twofold: the ex ante definition of the risk allocation among the participants with an appropriate definition of the contribution \(h_i\) and the ex post distribution of the residual risk with the distribution of the excess capital or loss. The originality of our proposal lies in calculating the amount of safety loading required to each participant as a function of the Shapley value \(\phi _i\):

$$\begin{aligned} h_i(X)=E(L_i) + \alpha \cdot \phi _i \end{aligned}$$
(3)

In the actuarial literature, Mango (1998) exploited the concept of Shapley value from game theory and proposed the first application of the marginal contribution in risk allocation of property catastrophic risk. Afterwards, Chen et al. (2017) described a risk sharing problem in a cooperative game framework where agents pool their random costs together, and an allocation rule redistributes the risk back to them.

2.2 The Shapley value

The Shapley value (Shapley 1953) is a concept of cooperative game theory developed to allocate the output of a game among the participants. Let N be the set of a cooperative game with n players, S with \(S\subseteq N\) be a coalition of players and s with \(s\le n\) the total number of players in the coalition and \(N\setminus \lbrace i\rbrace \) be the set of all possible coalitions excluding player i. Given the characteristic function of the game \(\mu (S)\), the Shapley value is the amount of risk player i confers to N

$$\begin{aligned} \phi _i(\mu ) = \sum _{S\subseteq N\setminus \lbrace i\rbrace } \frac{s!(n-s-1)!}{n!} \left[ \mu (S\cup \lbrace i\rbrace )-\mu (S)\right] . \end{aligned}$$
(4)

The quantity \([\mu (S\cup \lbrace i\rbrace )-\mu (S)]\) is the average marginal contribution of player i where the average is calculated over the permutations of players in which the coalition can be created:

$$\begin{aligned} \phi _i(\mu ) = \frac{1}{n!} \sum _{\psi \in {{P}}(N)} \left[ \mu (P^\psi (i)\cup \lbrace i\rbrace )-\mu (P^\psi (i))\right] \end{aligned}$$
(5)

where P(N) is the set of all permutations of N, \(\psi \) is a permutation of players in N, \(P^\psi (i)\) is the coalition made of all predecessors of player i in the order determined by permutation \(\psi \). More formally, \(P^\psi (i)=\lbrace i \in \psi : \psi (j)<\psi (i)\rbrace \). The sum in Eq. 5 is then divided by n!, which is the number of possible orderings of all the agents.

In a cooperative game where the players contribute in different ways to the achievement of the final result but collaborate to achieve a pay-off much or more as they would obtain from playing independently, The Shapley value permits to distribute the total gain to the players (Roth 1988). Shapley (1953) demonstrated that the rule in Eq. 4 (or Eq. 5) is the unique optimal risk assignment satisfying the axiomatic properties of efficiency, symmetry, additivity and the axiom of dummy players.

2.3 The Shapley contribution rule

In order to define the contribution according to Eq. 3, it is necessary to identify an appropriate risk measure \(\mu \), with respect to which the contribution of each member becomes equal. At first and to identify closed formulas, we set

$$\begin{aligned} \mu (X)=Var\left[ \sum _i L_i \right] =Var(X) \end{aligned}$$
(6)

where Var is the variance of the total loss distribution. In this case, it is proved (Colini-Baldeschi et al. 2018) that:

$$\begin{aligned} \phi _i(\mu )=Cov(L_i,X) \end{aligned}$$
(7)

from which

$$\begin{aligned} h_i(X)=E(L_i) + \alpha \cdot Cov(L_i,X) \end{aligned}$$
(8)

More advanced risk measures such as those related to loss distribution percentiles, Expected Shortfall, and so on can subsequently be introduced into the model.

2.4 The cashback distribution

The collected contributions are used to face the total loss experienced by the group. Once the loss is realized, if any amount remains, it is distributed to the members as a cashback according to a specific rule; if the initial contributions are not sufficient, the members are required to pay an additional sum according to the same distribution mechanism.

In this setting, let K be the residual amount after the payment for loss, which can take both positive or negative values. If positive, it represents a cashback, while if negative, it is an additional sum to be paid to cover losses above the initial contributions. Note that K is a random variable depending on the realizations of total loss x and is not fixed ex-ante as in the classical insurance framework dealing with capital distribution. We defined the amount K as:

$$\begin{aligned} K=\sum _{i=1}^n h_i(X)-x \end{aligned}$$
(9)

Substituting Eq. 3 in the previous one, we obtain:

$$\begin{aligned} K=\sum _{i=1}^n \left[ E(L_i) +\alpha \cdot \phi _i \right] - x \end{aligned}$$
(10)

Using Eq. 7 and reminding that \(\sum _{i=1}^n Cov(L_i,X)=Var(X)\), we rewrite the previous equation as:

$$\begin{aligned} K=\sum _{i=1}^n E(L_i) +\alpha \cdot Var(X) - x \end{aligned}$$
(11)

Let \(\varvec{\kappa }=[K_1,K_2,...,K_n]\) be a vector whose generic element \(K_i\) is the amount of capital distributed to the \(i^{th}\) participant, such that \(\sum _{i=1}^n {K}_i=K\).

We set constant the difference between the ex-ante contribution \(h_i(X)\) of each participant i to the risk brought to the pool, and the ex-post amount of capital distributed to participant i, denoted as \(K_i\). This is expressed as \(h_i(X)-K_i=c\), with c constant value. This approach establishes an optimal allocation rule to ensure that each participant contributes equally to covering realized losses. Specifically, those participants who contribute the most to the pool’s risk will bear a proportionate share of the realized losses or, conversely, will be entitled to a higher distribution of the cashback. This mechanism guarantees that the marginal contribution of each participant to profits and losses remains identical, regardless of the realization of the random variable X. Therefore, setting \(K_i = k_i \cdot K\), we can formulate the following optimization problem:

$$\begin{aligned} \left\{ \begin{array}{l} h_i(X)-k_i \cdot K=c\\ \sum _{i=1}^n k_i=1 \end{array} \right. \end{aligned}$$
(12)

The optimal solution is the following:

$$\begin{aligned} c=\frac{x}{n} \end{aligned}$$
(13)

Proof. From Eq. 12, we express the condition \(\sum _{i=1}^n k_i=1\) as: \( \sum _{i=1}^n \frac{h_i(X)-c}{K}=1\). After some algebra we obtain \(\sum _{i=1}^n h_i(X)-n \cdot c = K\). Deriving from Eq. 9 that \(\sum _{i=1}^n h_i(X)-K=x\), we obtain the solution \(c=\frac{x}{n}\).

As a consequence, from Eq. 12, considering Eqs. 13 and Eq. 9, we obtain the following optimal value of \(k_i\):

$$\begin{aligned} k^{*}_i = \frac{h_i(X)-\frac{x}{n}}{\sum _{i=1}^{n} h_i(X) - x} \end{aligned}$$
(14)

The solution (14) offers the optimal share, denoted as \(k^{*}\), to allocate the residual amount (ex-post profit or losses). It is noteworthy that it is equivalent to the ratio between the additional profit or loss associated with policyholder and the total profit or loss at portfolio level.

3 Numerical example

We implement the suggested methodology on a motor third-party liability insurance portfolio. We examine an actual portfolio comprising 1000 policyholders (i.e., \(n=1000\)) and assume that the portfolio is managed using a system that combines upfront contributions and subsequent cashback. We model individual losses separately based on the following frequency-severity model

$$\begin{aligned} L_{i}= \sum _{h=1}^{NC_{i}} Z_{i,h} \end{aligned}$$
(15)

with \(L_{i}=0\) if \(NC_{i}=0\). Where \(NC_{i}\) is the random variable number of claims of policyholder i and \(Z_{i,h}\) is the average cost of claim of the policyholder. We consider classical assumptions of independence between \(NC_{i}\) and \(Z_{i,h}\) and that the random variables \(Z_{i,h}\) are independent and identically distributed. Dependence between policyholders is also considered.

To model the random variable \(L_{i}\) for each policyholder, we make the following assumptions:

  • As is commonly provided in the literature (see, for example, Daykin et al. (1994)), the distribution of the number of claims is described by the Poisson law (\(NC_{i} \sim Poi(f_i\cdot Q)\)), with an expected frequency \(f_i\) subject to a parameter uncertainty modelled by a structural variable Q.

  • Q serves as a mixing variable (or contagion parameter) and represents the parameter uncertainty associated with the number of claims. It is assumed that \(E(Q)=1\) and that the random variable is defined only for positive values. Following a common approach, we assume that Q follows a Gamma distribution, resulting in \(NC_{i}\) being distributed as a Negative Binomial.

  • Random variables \(Z_{i,h}\) using LogNormal distributions with a mean \(m_{i}\) and coefficient of variation \(CV_{Z_{i}}\).

We consider an initial scenario characterized by the following parameters. Table 1 displays the minimum, maximum, and average values observed among the policyholders in the portfolio. Notably, we initially assume that the only difference between policyholders is represented by the frequency \(f_{i}\).

Table 1 Minimum, maximum and average values of the parameters of the model used for each policyholder i
Full size table
Fig. 1
figure 1

Distributions of pure premiums \(h_{i}\) in case of independence (left hand-side) and correlation (right hand-side) equal to 0.5 between policyholders

Full size image

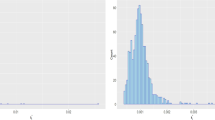
In Fig. 1, we present a comparison between fair premiums \(E(L_{i})\) and pure premiums \(h_{i}\) calculated using Eq. 3. On the right side of the figure, we incorporate a dependency structure among policyholders, modelled using a Gaussian copula with a linear correlation of 0.5 between each pair of policyholders. In Eq. 3, the parameter \(\alpha \) has been calibrated to allocate an overall safety loading of 0.05 to the entire premiums under the P2P scheme.Footnote 1 Notably, there is an increase in the upfront premiums charged to policyholders, reflecting their respective contributions to the risk.

On the left side, we maintain the same value of \(\alpha \), but we assume independence between policyholders. Due to the lower estimated risk for the portfolio, we observe smaller differences between fair and pure premiums.

Fig. 2
figure 2

Distributions of optimal shares \(k_{i}^{*}\) in case of independence (left hand-side) and correlation (right hand-side) equal to 0.5 between policyholders

Full size image

In Fig. 2, we report the distributions of \(k_{i}^{*}\) obtained by means of Eq. 14, assuming independence and correlation between the policyholders. In both scenarios, we have derived the values of \(k_{i}^{*}\) under the assumption that the observed aggregate claim amount is lower than the expected value, potentially due to the positive influence of trust and a more proactive risk management approach among the peers. In this case, the positive surplus, represented by the safety loading and the difference between fair premium and the observed claims, will be redistributed to the participants as a cashback.

On average, the optimal shares \(k_{i}^{*}\) tend to be around \(\frac{1}{n}\), but the distribution displays positive skewness. This means there are more policyholders contributing less to the risk and subsequently receiving a lower cashback. This pattern is driven by the portfolio’s characteristics, where a smaller segment has a higher frequency (approximately 10%) and therefore contributes more to the overall risk.

Taking into account positive correlations among policyholders, which we modelled using a Gaussian copula with a correlation coefficient of 0.5, we note that the optimal shares \(k_{i}^{*}\) continue to gravitate towards \(\frac{1}{n}\). However, there is a reduced level of variability among policyholders, as illustrated in Fig. 2 on the right-hand side. This observation arises from the fact that the disparities in risk contributions are partly offset by the decreased level of diversification within the portfolio. In essence, the positive correlations among policyholders create a more cohesive risk profile, resulting in a narrower range of optimal contribution shares. This effect is particularly pronounced due to the lower degree of diversification present in this specific portfolio, further influencing the allocation of shares.

We then examine the impact on portfolio outcomes when the policyholders’ frequencies exhibit narrower differences. Specifically, the results presented in Figs. 3 and 4 are derived using the same parameters outlined in Table 1, but with a frequency range of \(\left[ 5\%,7\%\right] \). While the average pure premiums and the average values of \(k_{i}^{*}\) remain consistent with the previous example, the impact of reduced variability among policyholders is evident. Specifically, a higher level of uniformity is observed within the pool, resulting in comparable premiums and similar cashback distributions. This analysis underscores the significance of carefully selecting pool members. It becomes apparent that a greater uniformity among policyholders enables a more even-handed approach in terms of safety loading and cashback, helping to mitigate potential anti-selection behaviours.

Fig. 3
figure 3

Distributions of pure premiums \(h_{i}\) in case of independence (left hand-side) and correlation (right hand-side) equal to 0.5 between policyholders, when a lower variability of the frequency is considered (between 5 and 7%)

Full size image
Fig. 4
figure 4

Distributions of optimal shares \(k_{i}^{*}\) in case of independence (left hand-side) and correlation (right hand-side) equal to 0.5 between policyholders, when a lower variability of the frequency is considered (between 5 and 7%)

Full size image

Lastly, we examine a third portfolio consisting of policyholders all exhibiting the same frequency (set at 6%), but with varying levels of severity variability. Specifically, we posit that \(CV_{Z_i}\) ranges from 2 to 6. All other parameters remain consistent with those of the previous portfolios (refer to Table 1). In this scenario, we observe (see Figs. 5 and 6) a reduced level of variability compared to the initial example. This finding underscores the significant influence of frequency on the variability of the aggregate claim amount in contrast to the severity characteristics. This phenomenon is primarily attributed to the diversification effect within the portfolio.

Fig. 5
figure 5

Distributions of pure premiums \(h_{i}\) in case of independence (left hand-side) and correlation (right hand-side) equal to 0.5 between policyholders. In this case, we assume a portfolio where all the policyholders have the same frequency, but with a \(CV_{Z_i}\) that varies between 2 and 6

Full size image
Fig. 6
figure 6

Distributions of optimal shares \(k_{i}^{*}\) in case of independence (left hand-side) and correlation (right hand-side) equal to 0.5 between policyholders. In this case, we assume a portfolio where all the policyholders have the same frequency, but with a \(CV_{Z_i}\) that varies between 2 and 6

Full size image

4 Concluding remarks

The advancement of technology, particularly the development of blockchain, has propelled the P2P insurance industry as a viable alternative to traditional insurance. In this paper, we have combined the actuarial approach with cooperative games to present a valuation model for P2P insurance within the broker scheme.

When well-designed and managed with the appropriate expertise and resources, P2P insurance can bring significant benefits to consumers, including lower insurance premiums and the return of excess funds as cashback, thereby providing incentives for responsible claims reporting. Indeed, P2P insurance models strive to promote responsible behaviour among members through transparency, social emulation, and economic incentives. Members typically have knowledge of the group composition, claim filings, and pool finances. By uniting small groups with shared interests and redistributing unused funds at year-end, P2P insurance aims to alleviate potential conflicts between shareholders in a traditional insurer and policyholders.

While there are numerous positive aspects of P2P insurance, it is essential to consider potential risks. If not managed appropriately, these models could expose consumers to sudden loss of coverage, unforeseen additional costs, or failures in claim payments.

Another critical consideration is the current regulatory ambiguity surrounding this type of insurance, both at national and international levels (see, e.g., Clemente and Marano (2012)). This begins with the question of whether a license for insurance activities is compulsory. EIOPA contributes to this discourse by proposing a principle of proportionality, suggesting that only pure, self-managed P2P models might be exempt from regulatory application, while broker schemes may not. In this context, our proposed model, which factors in the entry premium with a suitable safety loading and outlines the distribution of final cashback, underscores that the broker scheme should be treated similarly to mutual insurance. This prompts a reflection on the need for a clear and precise regulatory framework.