Variance of entropy for testing time-varying regimes with an application to meme stocks

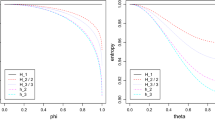
Abstract

Shannon entropy is the most common metric for assessing the degree of randomness of time series in many fields, ranging from physics and finance to medicine and biology. Real-world systems are typically non-stationary, leading to entropy values fluctuating over time. This paper proposes a hypothesis testing procedure to test the null hypothesis of constant Shannon entropy in time series data. The alternative hypothesis is a significant variation in entropy between successive periods. To this end, we derive an unbiased sample entropy variance, accurate up to the order $O(n^{-4})$ with n the sample size. To characterize the variance of the sample entropy, we first provide explicit formulas for the central moments of both binomial and multinomial distributions describing the distribution of the sample entropy. Second, we identify the optimal rolling window length to estimate time-varying Shannon entropy. We optimize this choice using a novel self-consistent criterion based on counting significant entropy variations over time. We corroborate our findings using the novel methodology to assess time-varying regimes of entropy for stock price dynamics by presenting a comparative analysis between meme and IT stocks in 2020 and 2021. We show that low entropy values correspond to periods when profitable trading strategies can be devised starting from the symbolic dynamics used for entropy computation, namely periods of market inefficiency.

1 Introduction

The Shannon entropy is a widely used measure of randomness in many fields, such as finance, physics, medicine, and biology (Pincus et al. 1991; Pincus and Kalman 2004; Dong et al. 2019; Pandey and Sarkar 2015; Strait and Dewey 1996; Bezerianos et al. 2003). One of the main applications of entropy estimation in finance is to measure the randomness of price returns. When the price incorporates all relevant information, the market is called efficient, and the price dynamics is a martingale (Samuelson 1965; Fama 1970). As such, any sequence of symbols built upon the price dynamics does not display predictable patterns, but it is maximally random. Consequently, the Shannon entropy computed for such a sequence is expected to take the maximum value. Significant drops in entropy values signal some predictability of the price dynamics (considering only historical observations as the information set). When this happens, profitable trading strategies can be devised by exploiting such predictable patterns, and the market is said to be inefficient, see, e.g., (Barnett and Serletis 2000) for a review.

The drivers of market dynamics are the result of the complex process of matching the supply and demand of a large number of investors. It is easy to imagine that the market does not necessarily reflect all relevant information at certain times because of the complex nature of the price formation mechanism. Moreover, feedback loops, irrational agents, market panic and speculation, or coordination of retail investors driven by non-economic reasons (like with GameStop, whose price increased significantly in January 2021 (Mancini et al. 2022)) are just a few examples of mechanisms that can potentially create booms and busts (Agliari et al. 2018; Chan and Santi 2021). In such cases, the price dynamics may display some level of predictability, and, as such, the market is inefficient. A significantly low value of Shannon entropy can capture this.

In various research works, the market efficiency hypothesis is relaxed to account for the possibility of periods of inefficiency. To capture this effect, Shannon entropy is employed as a time-varying metric. It is calculated using a rolling window approach, see, e.g., (Molgedey and Ebeling 2000; Risso 2008; Mensi et al. 2012; Olbrys and Majewska 2022). It is important to note that many patterns of price dynamics may jeopardize the estimate of entropy. For example, long memory of volatility can arise from regime-switching behavior (Susmel 2000; Lobo and Tufte 1998; Malik et al. 2005), thereby affecting the estimation of other dynamic patterns. For this reason, it is important to filter out any known pattern of market regularity, such as heteroscedasticity or seasonality, when we aim to use Shannon entropy as a measure signaling the presence of predictability patterns in price dynamics. Interestingly, even after applying such filters to empirical data, price dynamics often exhibit such patterns, as indicated by low sample entropy values. This suggests that the market is inefficient at times (Calcagnile et al. 2020; Shternshis et al. 2022). To show this more rigorously, it is possible to devise trading strategies that are associated with a positive return statistically larger than the one expected in normal periods of high entropy (excluding transaction costs). Consequently, low entropy values can be interpreted as a measure of market inefficiency.

A crucial question is whether a drop in sample entropy at some period is statistically significant or only a fluctuation consistent with the null hypothesis of market efficiency.

This paper proposes a rigorous methodology to identify significant changes in the value of the Shannon entropy. Then, in the case of high-frequency financial data, we show that drops in entropy values are associated with patterns of price predictability (which can be exploited to profit) and, as such, can be interpreted as market inefficiencies. We define a rigorous procedure to test the hypothesis that entropy values associated with two different sequences (based on the symbolization of the price dynamics with the same finite alphabet) are statistically equivalent. To achieve this goal, we address two key problems. The first problem is to find the variance of the sample entropy obtained by the empirical frequencies method (Marton and Shields 1994). The second problem involves identifying the optimal length for a rolling window used to estimate the time-varying entropy of a time series. Finally, we corroborate the results by showing that sequences of symbols that are not consistent with the null hypothesis of market efficiency (i.e., randomness) can be used to define (new) statistical arbitrage strategies based on Shannon entropy as an indicator, in a similar way of mean-reversion or momentum. In this sense, we interpret a low entropy value as a measure of market inefficiency.

The variance of the Shannon entropy is the key quantity to use to determine if two sample entropies associated with two different sequences are statistically equivalent. The variance determines the standard deviation of sample entropy consistent with the constant value of entropy. In fact, it is possible to define a z-score given the sample entropy variance to test the equality of two entropy estimates with a given level of confidence.

Basharin (1959) obtained the first-order approximation of the variance of the sample entropy ${\hat{H}}$ calculated using the empirical frequencies method,

$$\begin{aligned} D_1({\hat{H}})=\frac{1}{n}\left( \sum _j p_j\ln ^2{p_j}-H^2\right) \end{aligned}$$

(1)

where $\{p_j\}_j$ defines the set of probabilities for the possible events and n is the length of the sequence of events. The same result has been later obtained by Dávalos (2019). However, Eq. 1 holds in the asymptotic regime, that is, when the length of the sequence becomes arbitrarily large, i.e., $n\rightarrow \infty$. Here, we aim to estimate a time-varying entropy for finite samples, i.e., using a finite length n of the sequence. Moreover, Eq. 1 is not a consistent estimator of the variance in the case of equal probabilities. When all probabilities $p_j$ are equal, $D_1({\hat{H}})=0$. Thus, a more accurate approximation for the variance is needed.¹

Here, we derive a formula for the variance of the sample entropy as a sum of central moments of binomial and multinomial distributions. These central moments are computed using a novel recursive approach. This approach allows us to approximate the variance with a high level of accuracy, up to an order of $O(n^{-4})$.²

Interestingly, Ricci et al. (2021) have found that the naive estimation of the variance approximation $D_1({\hat{H}})$ in Eq. 1 has a bias term of order $O(n^{-2})$. On the contrary, we show that our proposed sample entropy variance is unbiased. Finally, by leveraging the explicit formulation of the sample entropy variance, we can define a statistical test for entropy variation. In Matilla-García (2007), the author suggests a statistical test for independence of symbolic dynamics by considering a test statistic related to permutation entropy. In our research, we are not restricted to the case when the benchmark value of the entropy is its maximum. A rejection of the null hypothesis signals statistically significant variation between any two possible entropy values.

The second problem relies on finding the optimal time window length when testing for entropy variation between two subsequent time series. We set a window length to detect the largest significant change in the entropy value. Here, the variance of sample entropy is crucial for determining what deviations of sample entropy are consistent with the estimation errors. Finding the optimal length is a problem of bias-variance trade-off: reducing the length of the window allows one to obtain a timely estimate of entropy, i.e., small bias, at the expense of increasing the variance of the estimation, and vice versa.

We present a novel self-consistent criterion to select (in-sample) the optimal window length w. Given a sample of size T, we first define a counting function of the percentage of entropy variations for non-overlapping time series of length w within such sample. Under the assumption of a finite number of true entropy variations, the percentage of estimated variations becomes negligible when w is close to the minimum ($w=1$), while it is zero by definition when w attains its maximum ($w=T$). Then, we show by simulations that the maximum of such a counting function corresponds to the optimal window length.

We use the novel methodology to find significant changes in entropy on simulated and real data. We investigate changes in the efficiency of the New York Stock Exchange with a particular focus on meme stocks. The lower the entropy of the price return time series, the higher the price predictability. In particular, we narrow down the analysis to those particular predictability patterns associated with drops in the entropy value and show that trading that way leads to positive returns statistically larger than average market returns. A specific focus is finally given to the GameStop case, whose price increased significantly in January 2021.

1.1 The GameStop case

The GameStop case captivated global attention in early 2021, showcasing the power of online communities and retail investors in challenging established financial norms. Fueled by Reddit’s WallStreetBets subreddit, a group of individual investors rallied behind GameStop’s stock, driving its value to astronomical heights and causing significant losses for prominent hedge funds that had bet against the company. This unprecedented situation raised questions about market manipulation, the democratization of finance, and the potential for social media to disrupt traditional Wall Street dynamics.

The performance of GameStop, a video game retailer, declined because of the shift of video game sales to online platforms. In 2020, the share price fell below one dollar. In the same year, however, an upward movement of prices of a group of stocks, including GameStop, was driven by the long trades of many individual investors, who fomented a coordinated action on the Reddit social platform. When the prices were hitting their all-time highs, the attention of everyone was focused on such shares, which became known as “meme stocks.” Then, as the end of January 2021 approached, several retail broker-dealers temporarily limited certain operations in some of these stocks and options. Consequently, the trend started to revert, even if such a turbulent period had permanently impacted meme stocks. The stocks have maintained a higher price level with respect to the period before and have been characterized by higher volatility. For a precise description of the GameStop case, see the report by the staff of the US Securities and Exchange Commission (Staff 2021). GameStop’s price began to increase noticeably on January 13, when the closing price rose to $31.40 from $19.95. By January 27, GameStop stock closed at a high of $347.51 per share. The following day, stock prices jumped further to an intraday high of $483.00.

Two crucial aspects have led to the sharp increase in meme stock prices. First, the aggregation of the orders sent to broker-dealers via online trading platforms, such as Robinhood, in the hands of a few off-exchange market makers permitted them to negotiate good agreements. Such a Fintech innovation has resulted in incentives or no fees for the end customers. The absence of trading frictions has positively affected retail trading in long positions. The second and more critical aspect is the coverage of the short positions by professional investors when the prices increased, which has further amplified such a movement.

The meme stock phenomenon marked a period of exceptional market behavior characterized by significant inefficiencies. This scenario provides a perfect opportunity to validate our methodology, demonstrating two key points: Firstly, our entropy change test accurately identifies shifts in efficiency levels. Secondly, our utilization of sample entropy, especially in discerning sequences of symbols that emerge during inefficient periods, offers a practical framework for defining trading strategies that statistically yield positive returns. This approach is akin to the definition of statistical arbitrage strategies and holds potential for successful application.

For the sake of comparison, we also investigate three IT company stocks. We aim to analyze entropy changes for more liquid stocks and point out differences, if any, from the point of view of market efficiency.

1.2 Structure of the paper

Section 2 introduces the statistical procedure for testing the null hypothesis of equal entropy between two subsequent intervals and a method for selecting the length of such interval in an optimal way. In Sect. 2.2, we establish an analytical expression for the variance of sample entropy, approximated up to order $O(n^{-4})$ with n the length of the interval. We propose a method for selecting the length of such interval in Sect. 2.4. We study both the size and power of the statistical testing procedure by using simulations in Sect. 3. Finally, an empirical application to meme and IT stocks is presented in Sect. 4. Appendix Sections A, B, and C contain the proofs of propositions and theorems. Section 5 draws some conclusions.

2 Methodology and dataset

First, we discuss the empirical frequencies method for the computation of sample entropy. Second, we establish an analytical formula for the variance of the sample entropy. Finally, we use this formula to devise a hypothesis testing for equal values of entropy between time intervals.

2.1 Shannon entropy

The Shannon entropy is defined as the average amount of information that a process transmits with each symbol (Shannon 1948).

Definition 1

Let $X = \lbrace X_1, X_2, \ldots \rbrace$ be a stationary random process with a finite alphabet A and a measure p. A k-th-order entropy of X is

$$\begin{aligned} H_k(X)=-\sum _{x^k \in A^k}p(x^k)\ln {p(x^k)} \end{aligned}$$

where $x^k$ are all sequences of length k with the convention $0\ln {0}=0$. A process entropy of X is

$$\begin{aligned} h(X)=\lim _{k\rightarrow \infty } \frac{H_k(p)}{k}. \end{aligned}$$

We use the empirical frequencies method (Marton and Shields 1994) to estimate k-th-order entropy from the sequence $x^n$. For each $a^k \in A^k$ empirical frequencies are defined as

$$\begin{aligned} f(a^k\vert x^n)=\#\{i \in [1, n-k+1]: x_i^{i+k-1}=a^k \}, \end{aligned}$$

where $x_i^{i+k-1}=x_i\ldots x_{i+k-1}$. Sample entropy, namely the estimate of the k-th-order entropy, is defined as

$$\begin{aligned} {\hat{H}}_k(x^n)=-\sum _{a^k}{\hat{p}}_k(a^k\vert x^n)\ln {({\hat{p}}_k(a^k\vert x^n))}, \end{aligned}$$

(2)

with

$$\begin{aligned} {\hat{p}}_k(a^k\vert x^n)=\frac{f(a^k\vert x^n)}{n-k+1} \end{aligned}$$

where $\ln$ is the natural logarithm.

Finally, the process entropy can be estimated as $\frac{{\hat{H}}_k}{k}$.

2.2 Variance of the sample entropy

Let us assume that there are M events which can appear with probabilities $p_0, p_1,\ldots ,p_{M-1}$, $\sum _{j=0}^{M-1}p_j=1$. We assume that all $p_j$ are positive since a zero probability is interpreted as the absence of that particular event, resulting in a restriction of the sample space, without affecting the entropy value $H=-\sum _{j=0}^{M-1}p_j\ln {p_j}$ because of the convention $0\ln 0=0$. If events appear independently n times, the frequencies of events $f_0, f_1, f_{M-1}$ follow a multinomial distribution. Each frequency is distributed as Binomial $B(p_j,n)$. The estimates of probabilities $p_j$ are ${\hat{p}}_j=\frac{f_j}{n}$. This section aims to find the variance of the random variable ${\hat{H}}=-\sum _{j=0}^{M-1}{\hat{p}}_j\ln {{\hat{p}}_j}$. The variable ${\hat{H}}$ is a k-th-order entropy from Eq. 2 based on the assumption that the blocks $a^k\in A^k$ are independent random variables. If all blocks have a nonzero probability of appearing, then it is $M=\vert A \vert ^{k}$ with $\vert A\vert$ the size of the alphabet A.

Theorem 1

(Estimation of variance) Let be $f_j$, $j=0,\ldots , M-1$, multinomial random variables with probability distribution $f^M(p_0,\ldots ,p_{M-1},n)$. Let be ${\hat{H}}=-\sum _{j=0}^{M-1}\frac{f_j}{n}\ln {\frac{f_j}{n}}$ the sample entropy and $Var({\hat{H}})$ the variance of ${\hat{H}}$. Let us assume that all events appear at least once. Then, $E({\hat{Var}})=Var({\hat{H}})+O(n^{-4})$, where

$$\begin{aligned} \begin{aligned} {\hat{\textrm{Var}}}&=\frac{1}{n}\left( \sum _j {\hat{p}}_j\ln ^2{{\hat{p}}_j}-{\hat{H}}^2\right) +\frac{1}{n^2}\left[ \sum _j {\hat{p}}_j\ln ^2{{\hat{p}}_j}-{\hat{H}}^2-M{\hat{H}}\right. \\&\left. \quad -\sum _j{\ln {{\hat{p}}}}-\frac{M}{2}+\frac{1}{2}\right] +\frac{1}{n^3}\left[ \sum _j {\hat{p}}_j\ln ^2{{\hat{p}}_j}-{\hat{H}}^2-M{\hat{H}}\right. \\&\left. -\sum _j{\ln {{\hat{p}}_j}}-\frac{{\hat{H}}}{3}\sum _j{\frac{1}{{\hat{p}}_j}}-\frac{1}{3}\sum _j{\frac{\ln {{\hat{p}}_j}}{{\hat{p}}_j}}-\frac{1}{12}\sum _j{\frac{1}{{\hat{p}}_j}}-\frac{M^2}{4}-\frac{M}{2}+\frac{5}{6}\right] . \end{aligned}\nonumber \\ \end{aligned}$$

(3)

The proof of Theorem 1 is in Appendix C. The proof is based on Lemma 1 for the variance of the sample entropy $Var({\hat{H}})$ given in Appendix B. All propositions used to prove Lemma 1 are in Appendix A. In brief, we use a recursive formula for the central moments of the multinomial distribution of $({\hat{p}}_1,{\hat{p}}_2)$ in Proposition 1. We find an explicit expression for the expectation of ${\hat{p}}^2\ln ^2({\hat{p}})$ that appears in ${\hat{H}}^2$ using the Taylor expansion in Proposition 4. Using the explicit formulas for the central moments of both binomial and multinomial distributions, we provide a formula to compute $Var({\hat{H}})=E({\hat{H}}^2)-E({\hat{H}})^2$.

In Theorem 1, we assume that all the events appear in the sequence at least once. Under this assumption, M is defined as the number of all different events. We discuss this assumption in the remark below.

Remark 1

The number of different events appearing at least once is defined as ${\hat{M}}=M-\sum _{j=0}^{M-1} I\{{\hat{p}}_j=0\}$, where I is the indicator function. It is

$$\begin{aligned} E[{\hat{M}}]=M-\sum _{j=0}^{M-1} (1-{p_j)^{n}}. \end{aligned}$$

The error term $\sum _{j=0}^{M-1} (1-{p_j)^{n}}$ attains its minimum when all $p_j=\frac{1}{M}$. The error grows as the probability $p_i$ approaches 0. However, such an event with $p_i\approx 0$ does not greatly affect the entropy value, since $p\ln {p}\rightarrow 0$ as $p\rightarrow 0$. We can fix the minimum expected value of the error attained when all probabilities have equal values. To this aim, we introduce the following rule. The sequence length is taken such that the minimum error is less than 0.01. With this choice, one event with probability $\frac{1}{M}$ does not appear in 1 case out of 100. In such a way, we fix the minimum length of the sequence. Later in the application part, we show that the optimal length of the interval is greater than its minimum possible value so that all events may appear in the sequence with a high probability. In formulas,

$$\begin{aligned} \begin{aligned}&\sum _{j=0}^{M-1} (1-{p_j)^{n}}<0.01\\&M\left( 1-\frac{1}{M}\right) ^{n}<0.01\\&n>\frac{\ln {\frac{0.01}{M}}}{\ln {\frac{M-1}{M}}}\\&n_\textrm{min}=\lceil {\frac{\ln {\frac{0.01}{M}}}{\ln {\frac{M-1}{M}}}}\rceil . \end{aligned} \end{aligned}$$

2.3 Hypothesis testing

Using sample entropy, we want to introduce a procedure to test if two estimates are statistically different or not. To this end, consider two sequences with entropy values $H_1$ and $H_2$. Let be ${\hat{H}}_1$ and ${\hat{H}}_2$ the corresponding sample entropy estimates. The variance of sample entropy estimates is $\textrm{Var}_1$ and $\textrm{Var}_2$, respectively, as given in Theorem 1. We can define both the null and the alternative hypotheses as follows.

$$\begin{aligned} \begin{aligned} {\mathcal {H}}_0: H_1=H_2\\ {\mathcal {H}}_a: H_1\ne H_2 \end{aligned} \end{aligned}$$

Under the null hypothesis, the z-score

$$\begin{aligned} z=\frac{{\hat{H}}_2-{\hat{H}}_1}{\sqrt{{\hat{\textrm{Var}}}_2+{\hat{\textrm{Var}}}_1}} \end{aligned}$$

(4)

is distributed with zero mean and variance equal to 1.

We reject ${\mathcal {H}}_0$ if $\vert z\vert$ is larger than the quantile associated with some confidence level, here set equal to $99\%$ of confidence. The quantile is then defined empirically as in Sect. 3.1.

2.4 Determining window length

In testing for entropy changes, we assume that there exist regimes in time series described by different values of the Shannon entropy. We consider a piecewise constant function as representing the regime-switching process for the Shannon entropy. A few examples of such a piecewise constant function are in Fig. 1. Such processes with step functions for entropy have been studied in Reif and Storer (2001) with the goal of introducing an optimal encoding for non-stationary sources. When we do not know a priori the regime length, we must devise a method to optimize the window length w, i.e., the length of the rolling window for time-varying entropy estimation. Here, the window length is optimized based on a bias-variance trade-off. The intuition is simple: (i) Inside a regime of constant entropy, we can increase the window length to improve the estimation of the entropy value by reducing the variance of the error; (ii) however, when the window length is larger than the regime itself, the estimation error increases because of the bias effect associated with a change in the entropy value. This impacts also the genuine detection of entropy changes based on the proposed testing procedure.

Fig. 1

Illustration of piecewise constant entropy

In practice, we apply the test to all adjacent non-overlapping intervals. Then, we choose a window length that allows the detection of the maximum z-score. More precisely, we maximize the following objective function f(w)³

$$\begin{aligned} f(w)={\left\{ \begin{array}{ll} \max (\vert z(w)\vert ), \text {if }\%\{\vert z(w)\vert>q_{99}\}>1\%\\ -\frac{1}{w}, \text {otherwise} \end{array}\right. } \end{aligned}$$

(5)

where $q_{99}$ is a $99\%$ quantile for the empirical distribution of z.

A key part of the objective function f(w) is the maximization of the absolute value of the z-score, $\max (\vert z(w)\vert )$. This emphasis on maximizing the z-score for testing non-overlapping intervals can be interpreted in terms of the bias-variance trade-off. When using a rolling window with a large length, it may encompass regimes with different entropy values. Consequently, sample entropy becomes biased because it is computed by estimating empirical frequencies from several stationary processes simultaneously. Therefore, large values of w may not be able to catch the largest change in entropy value reflected by the magnitude of z-score.

Small values of w give small values of the z-score since sample entropy variance increases with the decrease in the window length. Indeed, taking a short window length w implies a large variance of sample entropy. Consequently, it may become challenging to distinguish a genuine change in entropy from estimation errors when w is small, potentially failing to detect significant changes in entropy values. On the other hand, if the process at some period is stationary, we aim to take w as large as possible to improve the accuracy of the sample entropy.⁴ Thus, we find an optimal parameter w maintaining a balance between the bias and the variance of the sample entropy.

The second line of the objective function in Eq. 5 is introduced to determine the window length in the case of a stationary process with no regimes of entropy. In terms of the bias-variance trade-off, if the rolling window covers a period of constant entropy, the error from a bias is eliminated, and the variance decreases with the growth of the window length. If we can not reject the null hypothesis, we want to choose w as large as possible. Thus, we maximize a monotonically increasing function, $-\frac{1}{w}$. Since we are interested in detecting changes in entropy, $\max (\vert z \vert )$ is always nonnegative, and $-\frac{1}{w}$ is always negative. Some plots of different objective functions for various values of w are in Figs. 3 and 5.

In applications, the proposed method for determining the optimal window length is applied to a training set to fix the optimal length to be used in the testing set. We set the upper bound for the window length as $n_\textrm{max}=\lfloor \frac{n}{2}\rfloor$, where n is the total length of the sequence. When the optimal window length is not the maximum, we interpret this as the presence of a regime-switching process for the Shannon entropy. As a result, we consider rolling window estimates of the Shannon entropy to find the changing points with the statistical procedure introduced above. Notice that the entropy estimator, which is based on the assumption of stationarity of the data-generating process, remains consistent within regimes. Such an approach is typical for regime-switching models, see, e.g., (James et al. 1987; Yao and Au 1989).

2.5 Dataset

We consider three meme stocks that became popular in late 2020 and 2021: GameStop (GME), Bed Bath & Beyond (BBBY), and AMC Entertainment Holdings (AMC).⁵ In addition, we consider three well-known IT companies: Apple (AAPL), Salesforce (CRM), and Microsoft (MSFT). The dataset reports the stock price $P_t$ at a one-minute frequency for each trading day from 9:00 to 15:59, covering the period from 1.1.2019 to 20.07.2021. Once a return time series is built by defining ${\tilde{r}}_t=\ln P_t/P_{t-1}$, we define a 4-symbol alphabet as:

$$\begin{aligned} \begin{aligned} s_t= {\left\{ \begin{array}{ll} 0, r_t\le Q_1, \\ 1, Q_1<r_t\le Q_2,\\ 2, Q_2<r_t\le Q_3,\\ 3, Q_3<r_t, \end{array}\right. } \end{aligned} \end{aligned}$$

(6)

where $Q_1$, $Q_2$, $Q_3$ are the quartiles of the empirical distribution of returns $\{r_t\}$. Here, $\{r_t\}$ are the price returns after filtering out data regularities from $\{{\tilde{r}}_t\}$: intraday volatility pattern, heteroskedasticity, price staleness, and microstructure noise, see Shternshis et al. (2022) for a precise description of the filtering process. Data regularities (see, e.g., Cont 2001) are empirical properties of the price returns associated with some stylized facts that can jeopardize the measure of the Shannon entropy (because of some spurious effects for the symbolization) with no implications to market efficiency. For instance, the intraday volatility pattern relates to intraday returns exhibiting high volatility at the market’s opening and closing, lowering during the middle of the day (Wood et al. 1985). This heterogeneous pattern would significantly impact the time series of symbols in Eq. 6, which are defined considering the quartiles of the unconditional distribution of returns over some training period. Similar issues also arise when considering other data regularity patterns. We refer to Shternshis et al. (2022) for a complete description of the phenomenon.

3 Simulation study

3.1 Empirical quantile

In this section, we provide a method to find the quantiles of the z-score distribution in Eq. 4. The larger the M (the number of different events), the closer the sample entropy (as a sum of random variables) is to a normal distribution. (Basharin 1959) proved the asymptotic normality for the distribution of sample entropy. However, if all probabilities are equal, the distribution of re-scaled sample entropy converges to a $\chi ^2$-distribution, see Zubkov (1974). Consequently, quantiles from a normal distribution are appropriate when the entropy value is not close to its maximum. (In other words, all probabilities for the events are almost equal.) As such, when the entropy is close to the maximum (like in the case of financial data), using the normal distribution to define the confidence bound of the test lowers the performance.⁶ To show this, we set large values for both the length of a sequence and the length of blocks.

We perform $N=2\times 10^4$ Monte Carlo simulations. We simulate two sequences with length $n=2\times 10^5$ of 4 symbols with equal probabilities. We set $k=7$ so that $M=4^7=16384$. When probabilities are equal, the expression for the variance (Eq. B6) becomes

$$\begin{aligned} \textrm{Var}({\hat{H}}_\textrm{max})=\frac{M-1}{2(n-k+1)^2}+\frac{M^2-1}{6(n-k+1)^3} \end{aligned}$$

(7)

We use this value as given instead of estimating the variance from the sequence. We can see that the ratio between two terms of Eq. 7 is $\frac{3(n-k+1)}{M+1}$ that can be controlled by the choice of k and M, respectively. Then, for two sequences we find the value of $\Delta {\hat{H}}=\hat{H_2}-\hat{H_1}$. Since $\Delta {\hat{H}}$ is the difference between two independent variables, the variance of the difference is $2\textrm{Var}({\hat{H}}_\textrm{max})$. The empirical $99\%$ ($95\%$) quantile of the empirical distribution of $\vert z \vert$ is 3.30722 (2.54542). Thus, even if both the length of the sequence and the number of blocks are quite large, the tails of the empirical distribution are thicker than those of a normal distribution. For this reason, we use the empirical quantiles obtained with Monte Carlo simulations in the analysis below. If the absolute value of the z-score is larger than such a quantile, we consider the difference between the two entropy values as statistically significant and reject the null hypothesis of equal entropy values.

Below, we fix $k=4$. Thus, the maximum of the sample entropy is $k\ln {\vert A\vert }=4\ln {4}$, $M=256$. Now, we test the empirical quantiles found in this section for shorter sequences. Here, we keep $N=2\times 10^4$ and set $n=2\times 10^3$. Using the quantiles obtained above, the false-positive rate is $1.025\%$ ($4.86\%$) for the level of significance $\alpha =0.01$ ($\alpha =0.05$).⁷ We consider these results as acceptable for retaining the computed values of quantiles for the rest of the paper. Thus, we take $q_{99}$ from Eq. 5 as 3.30722.

3.2 Power and size of the test

In this section, we control for power and size of the proposed testing procedure. We consider a 4-symbol process defined as follows. The probability of repeating a symbol is $\tau$. All other probabilities are equal, that is, the probability of observing 0 after 1 is $\frac{1-\tau }{3}$. To compute the 2-th-order entropy, $H_2(\tau )$, $2^4=16$ probabilities $p_{x_1x_2}$, $x_1,x_2\in A$ are used. Four of them, when $x_1=x_2$, are equal to $\frac{\tau }{4}$. The other twelve probabilities are $\frac{1-\tau }{12}$. Therefore, the value of the 2-th-order entropy is

$$\begin{aligned} H_2(\tau )=-\left( \tau \ln {\frac{\tau }{4}}+(1-\tau )\ln {\frac{1-\tau }{12}}\right) \end{aligned}$$

(8)

and the sample entropy computed with $k=4$ is $H(\tau )=2H_2(\tau )$ since the dependency between symbols is completely described by blocks of length 2.

The larger $\tau$ (considering $\tau >\frac{1}{4}$), the lower the entropy. $\tau =\frac{1}{4}$ corresponds to equiprobable symbols. In this case, the entropy value is maximum. In order to assess both the power and the size of the test, we build two sequences with $H(\frac{1}{4})$ and length $n=10,000$. We compute the sample entropy variance using Eq. 3 and perform the hypothesis testing using Eq. 4. The size, namely the false-positive rate, is $0.86\%$. This value has been obtained by generating two sequences (as described above) $2\times 10^{4}$ times. Now, to measure the power of the test, we simulate one sequence with $H(\frac{1}{4})=4\ln {4}\approx 5.54518$ and a second one with a different entropy value. The results are in Table 1.

Table 1 The power of the hypothesis testing with different $\tau$

3.3 Process with constant entropy

In this section, we consider a rolling window approach for a time-varying estimation of entropy combined with the statistical test for equal entropy values between two subsequent intervals. First, we consider the case of a stationary process having a constant entropy value for the whole period. We perform a test for equal entropies using the empirical quantile values obtained in Sect. 3.1. We simulate a time series containing four equiprobable symbols with a length $N=2\times 10^7$. We divide the time series into overlapping intervals of length $n=2\times 10^3$, and then, we compute the entropy value for each interval. Finally, we examine all differences in entropy values with a gap equal to n, ensuring that there are no overlapping blocks between two intervals. The false-positive rate, based on the $99\%$ ($95\%$) empirical quantile, is found to be $0.9976\%$ ($4.4608\%$), which closely aligns with the significance level.

3.4 Piecewise constant process

Now, we consider a process defined for a 4-symbol alphabet as follows. The length of a sequence is $N=30,000$. We set $k=4$, $M=256$. For this sequence, $n_\textrm{min}=\lceil {\ln {\frac{0.01}{M}}}/{\ln {\frac{M-1}{M}}}\rceil =2594$ and $n_\textrm{max}=\lfloor \frac{N-k+1}{2}\rfloor =14998$. We divide the sequence into three parts as shown in Fig. 1a. The first part is of length 10, 000. The first and the last parts display the maximum entropy value characterized by $\tau _0=\frac{1}{4}$ and four equiprobable symbols. The middle part is of length l and entropy $H(\tau )$ as in Eq. 8.

Time series as a concatenation of sequences with constant entropy values were considered in Reif and Storer (2001) and defined as “sequences with stationary ergodic sources.” In the paper, the authors show that the estimated entropy over the whole period is a linear combination of the entropy values of each stationary source. This result has been obtained using a method for asymptotically optimal compression of the sequence. The method is a modification of the LZ77 algorithm (Ziv and Lempel 1977). Apart from Eq. 2, one way to define the entropy of a stationary process is by using compression methods and optimal encoding (Ziv 1978).

In this case, the variance of the sample entropy is time-varying. As a consequence, we estimate the variance by Eq. 3. We apply the method for determining the optimal window length, $w_\textrm{opt}$, as described in Sect. 2.4. First, we fix $\tau =0.5$. By varying l in the interval $\{n_\textrm{min}, 10,000\}$ with an increment of 100, we estimate the optimal window length and plot it in Fig. 2. The figure shows that the optimal window length is a consistent estimation of the length of the interval. Therefore, the optimal length of the rolling window allows us to estimate the entropy value in the middle interval in the most accurate way because of the bias-variance trade-off explained above.

Fig. 2

Optimal window length for different values of l. The mean and standard deviation (std) are calculated over 100 iterations

Figure 3 shows the plot of the objective function (Eq. 5) for 3 random iterations with different values of l. All plots have one global maximum. The larger l, the larger the argument of the maxima corresponding to $w_\textrm{opt}$. When $l=10,000$ and w is close to $n_\textrm{max}$, the percent of statistically significant changes in entropy is less than 1%, and thus, f(w) becomes negative. We also show in Fig. 4 how sample entropy estimates are obtained by rolling a window of length l. We obtain a time-varying sample entropy because of the interval with a low entropy value in the middle of the sequence. Sample entropy attains its minimum after $t=10,000$ steps when the rolling window coincides with the interval in the middle. The first and the last values of sample entropy are calculated on the sequences with the constant entropy at the maximum. When the rolling window covers two intervals with different entropy values, sample entropy is between the maximum and minimum, showing a monotonic decrease or increase. The lowest entropy value corresponding to the interval in the middle is estimated once the sample entropy attains its minimum. We follow the same intuition in the empirical analysis below in defining the entropy value within an interval between two changing points.

Fig. 3

Realizations of the objective function for different values of l in 3-step process

Fig. 4

Realizations of the sample entropy for different values of l in 3-step process

When the data-generating process is stationary displaying a constant entropy, the range of the objective function may be negative. The objective function of one realization of the stationary process ($\tau =\tau _0$) is given in Fig. 5. Since the function is monotonically increasing, the maximum is attained at $n_\textrm{max}$.

Additionally, we maintain a fixed value of $l=10,000$ and vary $\tau$ from 0.25 to 0.5 with the increment of 0.01 for the process with 3 steps from Fig. 1a. For each $\tau$ within this range, we compute the optimal window length, see Fig. 6. When $\tau =0.25$, the data-generating process is stationary, and w is close to the maximum. This aligns with our intuition in defining the optimality criterion for the window length: A larger window leads to a more accurate entropy estimation because of a reduced variance of the estimation error in the case of a stationary process. However, the deviation of $w_\textrm{opt}$ when $\tau =0.25$ is high because of the first type error for the hypothesis testing. Even if the process is stationary, ${\mathcal {H}}_0$ may be rejected more than in $1\%$ of cases, resulting in a positive value for f(w). Such a significant deviation can be reduced using Bonferroni or Šidák corrections (Šidák 1967) if the distribution of the z-score is known. When the entropy in the middle slightly differs from the maximum ($\tau =0.26$), the method may fail to detect a change in the entropy value, and $w_\textrm{opt}$ is close to the maximum. As $\tau$ increases, $w_\textrm{opt}$ becomes closer to the length of the interval in the middle, and the standard deviation of $w_\textrm{opt}$ decreases accordingly.

Fig. 5

Objective function for one realization of the stationary process

Fig. 6

Optimal window length for different values of $\tau$ in 3-step process. The mean and standard deviation (std) are calculated over 400 iterations

Finally, we consider the case of a process with piecewise constant entropy values as in Fig. 1b. We fix the length of the first interval as 10, 000 and vary the length of the second interval l from $n_\textrm{min}$ to 10, 000, with $\tau _1=0.5$. The last two intervals have equal lengths $l_2=10000-l/2$. We consider $\tau _2=0.4$ and $\tau _3=0.3$. The optimal window lengths are shown in Fig. 7a, b.

Fig. 7

Optimal window length for 4-step process. The mean and standard deviation (std) are calculated over 100 iterations

When $(\tau _2,\tau _3)=(0.4,0.3)$, the optimal length is close to $w_\textrm{opt}=10000$, corresponding to the length of the first interval. A local maximum of objective function explains a slight downward bias close to $w_\textrm{opt}=l=7000$. We accomplished a systematic study of the objective function when $l=7000$ in Fig. 8a obtained for three representative simulations (over a total of 100 simulations, all of them qualitatively equivalent). When $(\tau _2,\tau _3)=(0.3,0.4)$, the optimal window length is close to l, when $\tau _1$ for $l>4000$. For small values of l, the large deviation results from two peaks of objective functions at l and $l_2$. We plot examples of objective functions when $l=3000$ and $l_2=8500$ in Fig. 8b. The global maximum occurs at $w=3000$; however, local extrema are observed at $w=8500$.

Fig. 8

Realizations of objective function for different values of l and $\tau$ for 4-step process

4 Empirical application: the case of meme stocks

4.1 Market efficiency

A market in which prices always fully reflect all available information is said efficient (Fama 1970). We assume the weak form of the efficient market hypothesis, for which the information set is obtained by considering historical observations only. That is, if a market is efficient in the weak form, then historical prices cannot be used to predict future price realizations more accurately than the current price value, namely the martingale hypothesis. For efficient markets (in the weak form), all information about past prices is already incorporated into the current price. Therefore, the next realization is going to contain all new information that was not available one time step before. As noted by Billingsley (1965) for symbolic dynamics, the amount of information received with a new symbol (the discretized price in our case) is the same as the amount of uncertainty before obtaining that symbol. In other words, larger uncertainty about the upcoming symbol corresponds to getting more information at the moment of its occurrence. In practice, the maximum value of entropy must reflect the market efficiency hypothesis. This principle has been considered in a range of research works, see, e.g., (Gulko 1999; Molgedey and Ebeling 2000; Risso 2008). As stated in (Eom et al. 2008), the lower the degree of efficiency, the more predictable the price. The authors have concluded that the predictability of prices correlates with the Hurst exponent, which is another measure of market efficiency (Cajueiro and Tabak 2005; Morales et al. 2012; Sensoy 2013).

Any deviations of the entropy estimate from the maximum can be considered a signal of market inefficiency. However, not all variations can be interpreted as market inefficiency because of the estimation errors, e.g., downward estimation bias (Schürmann and Grassberger 1996). To test if sample entropy differs significantly from the maximum, confidence bounds can be defined by using numerical methods (Calcagnile et al. 2020; Shternshis et al. 2022) or introducing statistical testing procedures (Brouty and Garcin 2023). In this context, our primary interest is identifying changes in the degree of market efficiency. Therefore, we focus on testing the difference between entropy values of two adjacent non-overlapping time intervals. If a market is efficient and the entropy of the price returns is always at the maximum, the hypothesis ${\mathcal {H}}_0$ cannot be rejected. Rejection of ${\mathcal {H}}_0$ for two non-overlapping intervals implies that the entropy value drops significantly below the maximum. Low entropy values thus indicate a significant degree of inefficiency in the sense of price predictability that can be used for devising (statistical) arbitrage strategies. In fact, we validate this interpretation by showing how to devise profitable trading strategies based on Shannon entropy as an indicator, namely considering sequences of symbols that are the most likely to appear and trading by exploiting them.

In other words, we estimate entropy as a measure of efficiency/no predictability. If the sample entropy is consistent with the maximum, the sequence is considered fully random. In order to measure Shannon entropy for financial time series, we discretize price returns as in Eq. 6. It is worth noting that we distinguish predictability stemming from market inefficiency and due to the stylized facts of price returns. Such patterns make prices more regular but do not imply genuine patterns of price predictability. That is, no trading strategy based on them is profitable. At the same time, a signal of market inefficiency indicates the presence of arbitrage opportunities, net of transaction costs. If the market is inefficient, there are opportunities to profit from predictability patterns. To ensure that we focus on such predictability patterns for potential profit, we apply a method to filter out data regularities from price returns before discretizing them, as discussed in Sect. 2.5.

The deviation from market efficiency implies that past prices provide useful information in predicting the next price value. That is, market inefficiency implies a violation of a martingale model for the price and the existence of (statistical) arbitrage opportunity. We test time-varying regimes of entropy for meme and IT stocks in Sects. 4.2 and 4.3, respectively. Additionally, we explore a straightforward trading strategy based on sample entropy and compare the average profits obtained during regimes with high and low entropy values in Sect. 4.4.

4.2 Meme stocks

Here, we focus on three stocks: GME, BBBY, and AMC. We consider data from the year 2019 as a training set, while the period from 01.01.2020 to 20.07.2021 is used as a testing set. First, we filter out data regularities. We define an intraday volatility pattern, fit an autoregressive moving average (ARMA) model, and find an optimal window length, $w_\textrm{opt}$, using the training set. Volatility and the degree of price staleness are defined minute by minute. The ARMA model helps in removing microstructure noise, while volatility estimation addresses heteroskedasticity. Quartiles $Q_1$, $Q_2$, and $Q_3$ used for discretization in Eq. 6 are defined using the return time series of the training set after filtering out the data regularities. All the details about the filtering process can be found in Shternshis et al. (2022).

We compute the Shannon entropy of the discretized sequence $s_t$ of the testing set using a rolling window of length $w_\textrm{opt}$. When comparing the entropy estimates for two adjacent intervals, we can observe three possible outcomes: (i) entropy decreases, (ii) entropy increases, and (iii) entropy does not change significantly. We present results for each stock in Table 2. Each test has a level of confidence equal to 0.99. We plot the sample entropy, price, and trading volumes in Fig. 9 for the stock GME. Plots of BBBY and AMC stocks are in Appendix D. In each plot, we have highlighted points where significant changes in entropy occur. Specifically, (i) red dots indicate statistically significant decreases in the entropy value, (ii) green dots indicate statistically significant increases in the entropy value, and (iii) blue dots indicate no statistical changes.

Table 2 Optimal window length and hypothesis testing for meme and IT stocks $f(w_\textrm{opt})$ are calculated on the training set

Fig. 9

Entropy, price, volume of the GME stock. Dots correspond to statistically significant changes in entropy: red for drops in the entropy value, and green for rises (color figure online)

Similar colors are used also for the dynamics of both the price and the trading volume. These visual representations help us for a better understanding of the relationship between entropy, price, and trading volumes. For GME, there are two series of significant drops in the entropy value. They start from the intervals [17.07.20 15:46 to 14.09.20 15:34] and [7.12.20 15:38 to 19.01.21 09:42] where sample entropies are calculated. For BBBY, there are three series of decreases. They start from the intervals [06.03.20 13:50 to 05.05.20 09:54], [10.12.20 11:47 to 28.01.21 10:59], and [06.05.21 15:16 to 21.06.21 14:45]. For AMC, there are four series of decreases starting at [05.03.20 15:13 to 17.04.20 12:47], [10.08.20 13:08 to 08.09.20 11:27], [08.03.21 14:09 to 30.03.21 10:26], and [05.05.21 14:46 to 27.05.21 15:10]. The time intervals highlighted in bold correspond to sharp increases in price values. These observations help us in identifying critical moments in the market, shedding light on the dynamics of the stocks.

Based on the simulation analysis presented in Fig. 4, we interpret the time-varying pattern of the entropy estimates as a piecewise constant pattern for the entropy value.⁸ As such, the piecewise constant sample entropy between two changing points takes a value equal to the maximum or minimum of the time-varying estimates within the regime. For example, the dynamics of the sample entropy for GME is characterized by two periods of low entropy and three periods of high entropy, resulting in 6 different regimes as shown in Fig. 10.

Fig. 10

Sample entropy for GME and corresponding piecewise constant entropy

4.3 IT stocks

For the sake of comparison, we repeat a similar analysis for the three IT stocks: Apple, Salesforce, and Microsoft. The entropy estimates are shown in Fig. 11. The optimal window lengths are in Table 2.

Fig. 11

Entropy of IT Stocks. Dots correspond to statistically significant changes in entropy: red for drops in the entropy value, and green for rises (color figure online)

The sample entropy of price returns for these stocks displays time-varying behavior. This indicates that the level of unpredictability in price movements changes over time. Notably, the entropy for these stocks does not exhibit such a steep decline as observed in the case of meme stocks. This implies that the meme stocks may have experienced more substantial changes in their price predictability compared to the IT stocks. For the stock CRM in 2019, the entropy of price returns time series is considered constant, as indicated by a negative value of the objective function $f(w_\textrm{opt})$.

4.4 Predictability of price returns

In this section, we compare the levels of price predictability based on low and high entropy values. We employ empirical frequencies to devise a simple trading strategy. We assume no transaction costs and high liquidity. We compare the return distributions for the strategy obtained in intervals with low and high entropy values. Through this comparison, we show that a low degree of market efficiency corresponding to a significantly low entropy value is associated with a profit larger than the average return of the same strategy in efficient periods. This analysis underscores the relationship between market efficiency, price predictability, and potential profitability of statistical arbitrage strategies, highlighting that highly efficient markets tend to exhibit less price predictability and, consequently, yield lower average trading profits.

Fig. 12

Histograms with 25 bins for profits from the simple trading strategy after filtering out data regularities. Green and red (blue in the case of CRM) bins correspond to significantly high and low entropy, respectively (color figure online)

Fig. 13

Histograms with 25 bins for profits from the simple trading strategy before filtering out data regularities. Green and red bins correspond to significantly high and low entropy, respectively (color figure online)

Here, we consider only intervals with significant changes in the entropy value (e.g., red and green periods in Fig. 9). We split each interval into two equal parts: The first half is used for estimating the empirical probabilities of blocks of four symbols, while the second half is for implementing the trading strategy.

We use the following criterion to classify each block in the first half: (i) If the empirical probability of obtaining 2 or 3 (i.e., the price goes up) for the fourth symbol given the sequence of the first three symbols is larger than $\frac{1}{2}$, the sequence (of three symbols) is defined as B(uy); if the empirical probability of obtaining 0 or 1 (i.e., the price goes down) for the fourth symbol given the sequence of the first three symbols is larger than $\frac{1}{2}$, the sequence (of the three symbols) is defined as S(ell). Then, in the second half of the interval, we implement the following trading strategy: Given three symbols, (i) we buy the stock if such a sequence is B, then we sell it one minute later; (ii) we short the stock if the such a sequence is S, then we close the position one minute later. The net of the two trades defines the strategy’s profit or return. The strategy is implemented after filtering out data regularities in the time series of returns. We plot the distributions of the strategy’s returns for all six stocks under investigation, distinguishing intervals of high and low entropy, in Fig. 12. We also show the distributions of the strategy’s returns computed for the true price dynamics (without filtering out data regularities) in Fig. 13. We then average such returns by distinguishing between high and low entropy values. The average profit is shown in Table 3.

In the first instance, the empirical probabilities used for estimating sample entropy are computed after removing heteroscedasticity and linear effects described by the ARMA model. Assuming that the price returns are normal, i.e., $r\sim N(0, 1)$, the maximum profit obtained by perfect forecasting of price direction is $\sqrt{\frac{2}{\pi }}\approx 0.798$. For all stocks except BBBY, the profits obtained for intervals with relatively low entropy values are statistically higher than the ones obtained for the other intervals. In particular, the difference between averaged profits obtained during intervals with low and high entropy values is significant using Welch’s t test (Welch 1947), with a significance level of 0.01.

For the stock CRM, we compare intervals shifted back in time by the length of the rolling window $w_\textrm{opt}$ with intervals having high entropy values. For the stock BBBY, the difference in profits for two types of intervals is visible from the tails of distributions around values of 0.15 and 0.22 in Fig. 12. Moreover, we observe a substantial profit disparity between meme and IT stocks during predictable intervals. This observation aligns with the fact that the entropy values for meme stocks are much lower than the minimum entropy value observed for IT stocks. Higher returns for meme stocks are also expected ex post because of the turbulent period experienced by the market due to the coordination of many retail investors in taking long positions and the consequent reaction of professional investors covering their short positions, a combination that drives the prices of meme stocks to their all-time highs.

From the point of view of market efficiency, we can conclude, however, that meme and IT stocks behave similarly: Higher profit from the statistical arbitrage strategy driven by the Shannon entropy measure corresponds to time intervals when the entropy value is significantly low. Based on the obtained results, we show how the entropy measures are associated with the degree of market efficiency; in particular, a measured violation of the market efficiency hypothesis in the weak form is related to the existence of statistical arbitrage opportunities.

We show a similar analysis for the price returns without filtering out data regularities. Low entropy for price returns without filtering out data regularities may be driven by heteroscedasticity or bid-ask spread. However, for four of the six stocks, the average profit is significantly higher during periods with low entropy than during periods with high entropy. P values of Welch’s t test are equal to $1.63 \times 10^{-13}$ or smaller, thus indicating a significant difference between the two averages for the profits with low and high entropy. We show the results in Table 3. The histograms with the distribution of the strategy return are in Fig. 13.

Table 3 Profits for the simple trading strategy applied to price returns. Window length is obtained by using the testing set

4.5 Quarterly training sets

A possible explanation for higher predictability associated with a drop in the entropy value may be related to some non-stationarity patterns, for example, a change in the structure of data regularities. For instance, the growing popularity of meme stocks could lead to shifts in the intraday volatility pattern from 2019 to 2021. If the behavior of traders has evolved during this period, the intraday volatility pattern estimated in the training set may no longer effectively filter out the data regularity present in the testing set. To address this issue and to filter out data regularities more accurately, we update our estimation of the intraday volatility pattern and fit an ARMA model using quarterly intervals. The prices from the first quarter of 2019 are also used to filter price return time series during both the first and the second quarters of 2019. We determine the optimal window length using data from the year 2019. The results of this approach are shown in Table 4, and the corresponding figures are in Appendix E.

Table 4 Optimal window length and hypothesis testing for stocks using quarterly training sets

In all six cases, entropy still exhibits time-varying behavior. Compared to the previous setting where the training set covers one year, there is an increase in the number of statistically significant changes in entropy for the stocks GME and AAPL. Additionally, in all cases, the maximum value of the objective function, which indicates the extent to which the entropy values of two adjacent intervals differ, also increases.

There are two sequences of statistically significant decreases in entropy value for the stock GME. They start from entropies calculated at the intervals [03.08.20 12:31 to 22.09.20 13:50] and [29.12.20 11:23 to 27.01.21 13:15]. For the stock AMC,⁹ there are three series of low entropy values. They starts from the intervals [25.03.20 12:31 to 13.05.20 14:17], [30.09.20 14:21 to 13.11.20 13:31], and [05.05.21 11:58 to 04.06.21 14:51]. For both stocks, the last interval corresponds to a sharp increase in the prices. For the stock BBBY, the entropy becomes statistically low starting from [07.08.20 11:10 to 18.11.20 11:16]. As a consequence, entropy was low at the time of the rapid growth in the price and trading volumes, as we can expect.

Similar conclusions can be drawn also in this case, in particular when we compare meme and IT stocks. We can conclude that the findings of the previous sections are robust to possible non-stationarity patterns of data regularities.

5 Conclusions and discussion

We introduce a novel procedure of hypothesis testing to determine if two sequences defined for the same alphabet of symbols display statistically different entropy values. In time series analysis, the assumption of stationarity of the data-generating process is required to ensure the consistency of any Shannon entropy estimator. However, signals of time-varying entropy are observed in many applications. We combine the two by studying a piecewise constant process for the Shannon entropy that satisfies the assumption of stationarity within each regime of the entropy value, including the possibility of a regime-switching characterized by a statistically significant change for the entropy value (measured by the proposed hypothesis testing procedure).

The contribution of the paper is threefold. First, we find an analytical approximation for the variance of the sample entropy that is used in hypothesis testing up to order $O(n^{-4})$ with n the sample size, that is, one order more precise in n when compared with previous results by Basharin (1959), Harris (1975). Second, we introduce an unbiased sample entropy variance estimator for the computation of the variance of entropy of a sequence. Finally, we propose a novel method to optimize the optimal window length for entropy estimation in the context of piecewise constant processes. The three contributions are then combined to define a rigorous statistical testing procedure for entropy changes in time series. We show that this method is suitable for determining how to split a sample into subsamples characterized by statistically different estimates of the Shannon entropy.

We apply the novel method to the return time series of meme stocks GME, BBBY, AMC. We find intervals when the estimated entropy value is statistically lower than other periods, thus signaling a higher price predictability. In particular, we focus on three meme stocks and compare them with three standard IT companies, namely AAPL, CRM, and MSFT. Our findings reveal that entropy changes occur for all six stocks during a period spanning from January 2020 to July 2021. Additionally, we observe that entropy exhibits time-varying behavior in the year 2019 for all stocks except CRM. The low entropy values identified for each stock indicate a higher degree of predictability in their return time series, signaling market inefficiency. We corroborate such an interpretation by showing that a drop in the entropy value is associated with a statistical arbitrage opportunity driven by the Shannon entropy as an indicator. In particular, it is possible to devise a trading strategy based on the empirical probabilities of the discretized price for statistical arbitrage, net of transaction costs. Moreover, since the method is based on a preliminary filtering of data regularities in financial time series, we also show that the results are unchanged when we use different filtering approaches. In conclusion, our findings support the violation of the market efficiency hypothesis in the weak form for the US stock market, similarly to other research works, e.g., (Alvarez-Ramirez and Rodriguez 2021; Giglio et al. 2008; Molgedey and Ebeling 2000).

Studying the time-varying patterns of entropy values, it emerges that drops in the entropy value for the meme stocks are more significant than the corresponding ones for IT stocks, thus indicating the existence of periods of much higher predictability. This is, in fact, consistent with the turmoil observed in the market during the so-called GameStop case. Interestingly, for the GME stock, a low level of entropy has been identified for the discretized price dynamics. Additionally, the drop in entropy seems to correlate with the observed increase in the trading volume. Interestingly, such a drop occurred before the boom observed in January 2021. That is some regularity pattern in the price dynamics that appeared before all the news spread to the market leads to a statistically significant signal of market inefficiency. Given the observed timing, such a signal could also be interpreted as an early warning of a turmoil period for the GME stock. Similar conclusions can be drawn also for the other meme stocks.

Today, financial markets are inherently high dimensional due to the plethora of instruments composing the portfolios of investors. At the same time, they are highly challenging to monitor, displaying more and more complex cycles, booms and bursts of prices, economic bubbles, and so on, all of them representing severe risk factors for portfolios. In this high-dimensional and complex context, the existence of indicators of market inefficiency is key. In fact, such signals allow one to anticipate periods of turmoil, thus covering or, at least, mitigating the portfolio risk associated with such events, with potential stabilizing effects for the whole market.

Appendices

Appendix A List of propositions

Proposition 1

Central moments of empirical probabilities ($\frac{f_1}{n}$,$\frac{f_2}{n}$) where ($f_1$, $f_2$) have multinomial distribution $f^M(p_1,p_2,n)$ are defined recursively using the formulas below.

$$\begin{aligned}{} & {} \mu _{0,0}=1, \mu _{1,0}=\mu _{0,1}=0, \mu _{1,1}=-\frac{p_1p_2}{n}\nonumber \\{} & {} \mu _{m+1,k}=\frac{p_1}{n}\left[ (1-p_1)\frac{\partial }{\partial p_1}\mu _{m,k}-p_2\frac{\partial }{\partial p_2}\mu _{m,k}+(1-p_1)m\mu _{m-1,k}-p_2k\mu _{m,k-1}\right] \nonumber \\ \end{aligned}$$

(A1)

where $m>0,k>0$.

Proof:

$$\begin{aligned} \begin{aligned}&\mu ^M_{m,k}(p_1,p_2,n)=\\&=\sum _{x_1\ge 0,x_2\ge 0, x_1+x_2\le n}(x_1-np_1)^m (x_2-np_2)^k \frac{n!}{x_1!x_2!(n-x_1-x_2)!}p_1^{x_1}p_2^{x_2}q^{n-x_1-x_2} \end{aligned} \end{aligned}$$

where $\mu ^M_{m,k}$ is the (m, k)-central moment of the multinomial distribution and $q=1-p_1-p_2$. We can show that

$$\begin{aligned} \begin{aligned} \frac{\partial }{\partial p_1}\mu ^M_{m,k}&=-nm\mu ^M_{m-1,k}+\frac{1-p_2}{p_1q}\mu ^M_{m+1,k}+\frac{1}{q}\mu ^M_{m,k+1}\\ \frac{\partial }{\partial p_2}\mu ^M_{m,k}&=-nk\mu ^M_{m,k-1}+\frac{1-p_1}{p_2q}\mu ^M_{m,k+1}+\frac{1}{q}\mu ^M_{m+1,k} \end{aligned} \end{aligned}$$

Solving the system for $\mu ^M_{m+1,k}$, we get that

$$\begin{aligned} \mu ^M_{m+1,k}=p_1\left[ (1-p_1)\frac{\partial }{\partial p_1}\mu ^M_{m,k}-p_2\frac{\partial }{\partial p_2}\mu ^M_{m,k}+(1-p_1)mn\mu ^M_{m-1,k}-p_2kn\mu ^M_{m,k-1}\right] \end{aligned}$$

Taking into account that $\mu ^M_{m,k}=n^{m+k}\mu _{m,k}$, we obtain the result

$$\begin{aligned} \mu _{m+1,k}=\frac{p_1}{n}\left[ (1-p_1)\frac{\partial }{\partial p_1}\mu _{m,k}-p_2\frac{\partial }{\partial p_2}\mu _{m,k}+(1-p_1)m\mu _{m-1,k}-p_2k\mu _{m,k-1}\right] \end{aligned}$$

and by symmetry

$$\begin{aligned} \mu _{m,k+1}=\frac{p_2}{n}\left[ (1-p_2)\frac{\partial }{\partial p_2}\mu _{m,k}-p_1\frac{\partial }{\partial p_1}\mu _{m,k}+(1-p_2)k\mu _{m,k-1}-p_1m\mu _{m-1,k}\right] \end{aligned}$$

Proposition 2

Central moments of the empirical probability $\frac{f}{n}$, where f has binomial distribution B(p, n), are defined recursively using the formulas below.

$$\begin{aligned} \begin{aligned} \mu _0&=1, \mu _1=0\\ \mu _{m+1}&=\frac{p(1-p)}{n}\left[ m\mu _{m-1}+\frac{\partial }{\partial p}\mu _{m}\right] , m>0 \end{aligned} \end{aligned}$$

(A2)

This is a special case of the previous proposition where $p_2=k=0$. It is known as the Renovsky formula (Riordan 1937).

Proposition 3

$$\begin{aligned} E({\hat{p}}\ln {{\hat{p}}})=p\ln {p}+\sum _{m=2}^{\infty }\frac{(-1)^{m}}{m(m-1)p^{m-1}}\mu _m \end{aligned}$$

(A3)

where $f\sim B(p,n), {\hat{p}}=\frac{f}{n}$ and $\mu _m$ is its central m-moment.

The result of Proposition 3 was obtained in (Basharin 1959). It is derived by using the Taylor expansion around p.

$$\begin{aligned} \begin{aligned} {\hat{p}}\ln {{\hat{p}}}=p\ln {p}+(1+\ln {p})({\hat{p}}-p)+\sum _{m=2}^{\infty }\frac{(-1)^{m}}{m(m-1)p^{m-1}}({\hat{p}}-p)^{m} \end{aligned} \end{aligned}$$

Therefore,

$$\begin{aligned} E[{\hat{p}}\ln {{\hat{p}}}]=p\ln {p}+\sum _{m=2}^{\infty }\frac{(-1)^{m}}{m(m-1)p^{m-1}}\mu _m. \end{aligned}$$

Empirical probability $\frac{f}{n}$, where f has Binomial distribution B(p, n), has the mean p and the variance $\frac{p(1-p)}{n}$.

Proposition 4

Let ${\hat{p}}=\frac{f}{n}, f\sim B(p,n)$. Then,

$$\begin{aligned} \begin{aligned}&E\left( {\hat{p}}^2\ln ^2({\hat{p}})\right) =p^2\ln ^2(p)+(\ln ^2{p}+3\ln {p}+1)\mu _2\\&+4\sum _{m=1}^{\infty }(-1)^{m+1}\left[ \ln {p}-S_{m-1}+\frac{3}{2}\right] \frac{\mu _{m+2}}{{m(m+1)(m+2)p^{m}}} \end{aligned} \end{aligned}$$

(A4)

where $S_m=\sum _{k=1}^m\frac{1}{k}$.

Proof: We consider the Taylor expansion of ${\hat{p}}^2\ln ^2({\hat{p}})$.

$$\begin{aligned} \begin{aligned} {\hat{p}}^2\ln ^2({\hat{p}})&=p^2\ln ^2(p)+2p\ln {p}(\ln {p}+1)({\hat{p}}-p)+(\ln ^2{p}+3\ln {p}+1)({\hat{p}}-p)^2\\&\quad +4\sum _{m=1}^{\infty }(-1)^{m+1}\left[ \ln {p}-S_{m-1}+\frac{3}{2}\right] \frac{({\hat{p}}-p)^{m+2}}{{m(m+1)(m+2)p^{m}}} \end{aligned} \end{aligned}$$

This expression can be obtained by noticing that derivatives of $p^2\ln ^2{(p)}$ starting from the third take the form

$$\begin{aligned} \frac{a_m\ln {p}+b_m}{p^m}, \end{aligned}$$

where $a_{m+1}=-ma_{m}$; $mb_m+b_{m+1}=a_m$ with $a_1=4$; $b_1=6$. The solution of the system is $a_m=4(-1)^{m+1}(m-1)!$ and $b_m=4(-1)^m(m-1)!(S_{m-1}-\frac{3}{2})$. The solution is unique because of the uniqueness of the Taylor series. Taking the expected value, we get the result.

Proposition 5

Let $(f_1, f_2)\sim f^M(p_1,p_2,n)$ and $({\hat{p}}_1,{\hat{p}}_2)=(f_1/n, f_2/n)$. Then,

$$\begin{aligned} \begin{aligned}&E\left( ({\hat{p}}_1\ln {{\hat{p}}_1})({\hat{p}}_2\ln {{\hat{p}}_2})\right) =(p_1\ln {p_1})(p_2\ln {p_2})+(\ln {p_1}+1)(\ln {p_2}+1)\mu _{1,1}\\&+\sum _{m=2}^{\infty }\frac{(-1)^{m}}{m(m-1)}\left[ p_1\ln {p_1}\frac{1}{p_2^{m-1}}\mu _{0,m}+p_2\ln {p_2}\frac{1}{p_1^{m-1}}\mu _{m,0}\right] \\&+\sum _{m=2}^{\infty }\frac{(-1)^{m}}{m(m-1)}\left[ (\ln {p_1}+1)\frac{1}{p_2^{m-1}}\mu _{1,m}+(\ln {p_2}+1)\frac{1}{p_1^{m-1}}\mu _{m,1}\right] \\&+\sum _{m=2}^{\infty }\sum _{k=2}^{\infty }\frac{(-1)^{m+k}}{m(m-1)k(k-1)p_1^{m-1}p_2^{k-1}}\mu _{m,k} \end{aligned} \end{aligned}$$

(A5)

where $\mu _{m,k}$ are (m, k)-central moments associated with empirical probabilities $({\hat{p}}_1,{\hat{p}}_2)$.

Proof:

$$\begin{aligned}{} & {} ({\hat{p}}_1\ln {{\hat{p}}_1})({\hat{p}}_2\ln {{\hat{p}}_2})\\{} & {} \quad =\sum _{m=0}^{\infty }\frac{({\hat{p}}_1-p_1)^m}{m!}\frac{d^m}{dp_1^m}{(p_1\ln {p_1})}\sum _{k=0}^{\infty }\frac{({\hat{p}}_2-p_2)^k}{k!}\frac{d^k}{dp_2^k}{(p_2\ln {p_2})}\\{} & {} \quad =(p_1\ln {p_1})(p_2\ln {p_2})+p_1\ln {p_1}(\ln {p_2}+1)({\hat{p}}_2-p_2)+p_2\ln {p_2}(\ln {p_1}+1)({\hat{p}}_1-p_1)\\{} & {} \quad \quad +p_1\ln {p_1}\sum _{k=2}^{\infty }\frac{(-1)^{k}}{k(k-1)p_2^{k-1}}({\hat{p}}_2-p_2)^{k}+p_2\ln {p_2}\sum _{m=2}^{\infty }\frac{(-1)^{m}}{m(m-1)p_1^{m-1}}({\hat{p}}_1-p_1)^{m}\\{} & {} \quad \quad +(\ln {p_1}+1)({\hat{p}}_1-p_1)\sum _{k=2}^{\infty }\frac{(-1)^{k}}{k(k-1)p_2^{k-1}}({\hat{p}}_2-p_2)^{k}\\{} & {} \quad \quad +(\ln {p_2}+1)({\hat{p}}_2-p_2)\sum _{m=2}^{\infty }\frac{(-1)^{m}}{m(m-1)p_1^{m-1}}({\hat{p}}_1-p_1)^{m}\\{} & {} \quad \quad +(\ln {p_1}+1)(\ln {p_2}+1)({\hat{p}}_1-p_1)({\hat{p}}_2-p_2)\\{} & {} \quad \quad +\sum _{m=2}^{\infty }\sum _{k=2}^{\infty }\frac{(-1)^{m+k}}{m(m-1)k(k-1)p_1^{m-1}p_2^{k-1}}({\hat{p}}_1-p_1)^{m}({\hat{p}}_2-p_2)^{k} \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{aligned}&E\left( ({\hat{p}}_1\ln {{\hat{p}}_1})({\hat{p}}_2\ln {{\hat{p}}_2)}\right) \\&\quad =(p_1\ln {p_1})(p_2\ln {p_2})+p_1\ln {p_1}\sum _{k=2}^{\infty }\frac{(-1)^{k}}{k(k-1)p_2^{k-1}}\mu _{0,k}\\&\quad \quad +p_2\ln {p_2}\sum _{m=2}^{\infty }\frac{(-1)^{m}}{m(m-1)p_1^{m-1}}\mu _{m,0}+(\ln {p_1}+1)\sum _{k=2}^{\infty }\frac{(-1)^{k}}{k(k-1)p_2^{k-1}}\mu _{1,k}\\&\quad \quad +(\ln {p_2}+1)\sum _{m=2}^{\infty }\frac{(-1)^{m}}{m(m-1)p_1^{m-1}}\mu _{m,1}+(\ln {p_1}+1)(\ln {p_2}+1)\mu _{1,1}\\&\quad \quad +\sum _{m=2}^{\infty }\sum _{k=2}^{\infty }\frac{(-1)^{m+k}}{m(m-1)k(k-1)p_1^{m-1}p_2^{k-1}}\mu _{m,k} \end{aligned} \end{aligned}$$

Appendix B Variance of sample entropy

Lemma 1

(Variance of sample entropy) Let us assume that $f_j$, $j=0\ldots M-1$, are distributed as multinomial variables $f^M(p_0,\ldots ,p_{M-1},n)$ and ${\hat{H}}=-\sum _{j=0}^{M-1}\frac{f_j}{n}\ln {\frac{f_j}{n}}$. Then,

$$\begin{aligned} \begin{aligned} \textrm{Var}({\hat{H}})&=\frac{1}{n}\left[ -H^2+\sum _j p_j\ln ^2(p_j)\right] +\frac{1}{n^2}\left[ \frac{M}{2}-\frac{1}{2}\right] \\&+\frac{1}{6n^3}\left[ (1-H)\sum _j\frac{1}{p_j}-\sum _j{\frac{\ln {p_j}}{p_j}}-1\right] +O(n^{-4}) \end{aligned} \end{aligned}$$

(B6)

where $H=-\sum _{j=0}^{M-1}p_j\ln {p_j}$.

Proof:

$$\begin{aligned} \begin{aligned} \textrm{Var}({\hat{H}})&=E({\hat{H}}^2)-E({\hat{H}})^2\\&=\sum _{j=0}^{M-1}E({{\hat{p}}_j^2\ln ^2{{\hat{p}}_j}})+\sum _{j=0}^{M-1}\sum _{i=0, i\ne j}^{M-1}E({{\hat{p}}_j\ln {{\hat{p}}_j}\hat{p_i}\ln {{\hat{p}}_i}})-E({\hat{H}})^2 \end{aligned} \end{aligned}$$

For calculations, we need all moments of orders $n^{-1}$, $n^{-2}$, $n^{-3}$ obtained using Eqs. A1 and A2.

$$\begin{aligned}{} & {} \begin{aligned} \mu _2&=\frac{p(1-p)}{n}\\ \mu _3&=\frac{p(1-p)(1-2p)}{n^2}\\ \mu _{4}&=\frac{3p^2(1-p)^2}{n^2}+\frac{p(1-p)-6p^2(1-p)^2}{n^3}\\ \mu _{5}&=\frac{10p^2(1-p)^2(1-2p)}{n^3}+O(n^{-4})\\ \mu _{6}&=\frac{15p^3(1-p)^3}{n^3}+O(n^{-4}) \end{aligned} \\{} & {} \begin{aligned} \mu _{2,1}&=-\frac{p_1p_2(1-2p_1)}{n^2}\\ \mu _{3,1}&=-\frac{3p_1^2(1-p_1)p_2}{n^2}+\frac{6p_1^2(1-p_1)p_2-p_1p_2}{n^3}\\ \mu _{4,1}&=-\frac{10p_1^2(1-p_1)(1-2p_1)p_2}{n^3}+O(n^{-4})\\ \mu _{5,1}&=-\frac{15p_1^3(1-p_1)^2p_2}{n^3}+O(n^{-4}) \end{aligned} \\{} & {} \begin{aligned} \mu _{2,2}&=\frac{p_1p_2(1-p_1)(1-p_2)+2p_1^2p_2^2}{n^2}\\&\quad +\frac{p_1p_2-2p_1p_2(1-p_1)(1-p_2)-4p_1^2p_2^2}{n^3}\\ \mu _{3,2}&=\frac{10p_1^2p_2^2(1-2p_1)+p_1p_2(1-p_1-p_2)(1-5p_1)}{n^3}\\ \mu _{3,3}&=-\frac{9p_1^2p_2^2(1-p_1)(1-p_2)+6p_1^3p_2^3}{n^3}+O(n^{-4})\\ \mu _{4,2}&=\frac{3p_1^2(1-p_1)p_2((1-p_1)(1-p_2)+4p_1p_2)}{n^3}+O(n^{-4}) \end{aligned} \end{aligned}$$

Moments with $m+k\le 4$ coincide with results obtained in Harris (1975), Ouimet (2021). After summing up $E[\hat{p_j}\ln {\hat{p_j}}]$ in Eq. A3 for all j, the expression becomes

$$\begin{aligned} \begin{aligned} E({\hat{H}})&=-E(\sum _j{\hat{p}}_j\ln ({\hat{p}}_j))=H-\frac{M-1}{2n}+\frac{1}{12n^2}\left( 1-\sum _{j=0}^{M-1}\frac{1}{p_j}\right) \\&\quad +\frac{1}{12n^3}\sum _{j=0}^{M-1}\left( \frac{1}{p_j}-\frac{1}{p_j^2}\right) +O(n^{-4}) \end{aligned} \end{aligned}$$

(B7)

where $H=-\sum _jp_j\ln (p_j)$, $\mu _2,\mu _3,\mu _4,\mu _5,\mu _6$ are used. Similar estimates of the bias of sample entropy were obtained in other works, see, e.g., (Harris 1975; Schürmann and Grassberger 1996; Victor 2000).

$$\begin{aligned} \begin{aligned} E({\hat{H}})^2&=H^2+\frac{1}{n}\left[ -(M-1)H\right] +\frac{1}{n^2}\left[ \frac{M^2}{4}-\frac{M}{2}+\frac{1}{4}+\frac{H}{6}\left( 1-\sum _{j=0}^{M-1}\frac{1}{p_j}\right) \right] \\&\quad +\frac{1}{n^3}\left[ \frac{H}{6}\sum _{j=0}^{M-1}\left( \frac{1}{p_j}-\frac{1}{p_j^2}\right) -\frac{M-1}{12}\left( 1-\sum _{j=0}^{M-1}\frac{1}{p_j}\right) \right] \end{aligned} \end{aligned}$$

The approximation of the second moment of ${\hat{p}}\ln ({\hat{p}})$ from Eq. A4 is

$$\begin{aligned} \begin{aligned} E({\hat{p}}^2\ln ^2({\hat{p}}))&=p^2\ln ^2(p)+\frac{1}{n}\left( \ln ^2{p}+3\ln {p}+1\right) p(1-p)\\&\quad +\frac{1}{n^2}\left[ \left( \frac{5}{6}p^2-p+\frac{1}{6}\right) \ln {p}+\frac{7}{4}p^2-\frac{5}{2}p+\frac{3}{4}\right] \\&\quad +\frac{1}{n^3}\left[ \frac{1}{6}\left( p^2-p\right) \ln {p}+\frac{p^2}{3}-\frac{p}{2}+\frac{1}{12}+\frac{1}{12p}\right] +O(n^{-4}) \end{aligned} \end{aligned}$$

The approximation of the covariances from Eq. A5 is

$$\begin{aligned} \begin{aligned}&E\left( ({\hat{p}}_1\ln {{\hat{p}}_1})({\hat{p}}_2\ln {{\hat{p}}_2})\right) \\&\quad =(p_1\ln {p_1})(p_2\ln {p_2})+\frac{1}{n}\left[ -(\ln {p_1}+1)(\ln {p_2}+1)p_1p_2\right. \\&\qquad \left. +\frac{1}{2}\left( p_1\ln {p_1}(1-p_2)+p_2\ln {p_2}(1-p_1)\right) \right] +\frac{1}{n^2}\left[ \frac{5}{12}p_1p_2(\ln {p_1}+\ln {p_2})\right. \\&\qquad \left. +\frac{1}{12}\left( \frac{p_1}{p_2}\ln {p_1}+\frac{p_2}{p_1}\ln {p_2}\right) +\frac{1}{4}(1+7p_1p_2-p_1-p_2)\right] \\&\qquad +\frac{1}{n^3}\left[ \frac{1}{12}p_1\ln {p_1}\left( p_2+\frac{1}{p_2^2}\right) +\frac{1}{12}p_2\ln {p_2}\left( p_1+\frac{1}{p_1^2}\right) \right. \\&\qquad \left. +\frac{1}{3}p_1p_2+\frac{1}{24}\left( \frac{p_1}{p_2}+\frac{p_2}{p_1}+\frac{1}{p_1}+\frac{1}{p_2}-p_1-p_2\right) \right] +O(n^{-4}) \end{aligned} \end{aligned}$$

Summing up for all indexes j, i of the second moments and covariances, we get that

$$\begin{aligned} E({\hat{H}}^2)= & {} H^2+\frac{1}{n}\left[ -H^2+\sum _j p_j\ln ^2(p_j)-(M-1)H\right] \\ {}{} & {} +\frac{1}{n^2}\left[ \frac{H}{6}\left( 1-\sum _j\frac{1}{p_j}\right) +\frac{1}{4}M^2-\frac{1}{4}\right] \\{} & {} +\frac{1}{n^3}\left[ \frac{M}{12}\sum _j\frac{1}{p_j}+\frac{1}{12}\sum _j\frac{1}{p_j}-\frac{1}{12}-\frac{M}{12}-\frac{1}{6}H\sum _j\frac{1}{p_j^2}-\frac{1}{6}\sum _j\frac{\ln {p_j}}{p_j}\right] \\{} & {} +O(n^{-4}) \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{aligned} \textrm{Var}({\hat{H}})&=\frac{1}{n}\left[ -H^2+\sum _j p_j\ln ^2(p_j)\right] +\frac{1}{n^2}\left[ \frac{M}{2}-\frac{1}{2}\right] \\&\quad +\frac{1}{6n^3}\left[ (1-H)\sum _j\frac{1}{p_j}-\sum _j{\frac{\ln {p_j}}{p_j}}-1\right] \\&\quad +O(n^{-4}) \end{aligned} \end{aligned}$$

Appendix C Proof of Theorem 1

We introduce a random variable ${\hat{Var}}$.

$$\begin{aligned} \begin{aligned} {\hat{\textrm{Var}}}&=\frac{1}{n}(\sum _j {\hat{p}}_j\ln ^2{{\hat{p}}_j}-{\hat{H}}^2)+\frac{1}{n^2}\left[ \sum _j {\hat{p}}_j\ln ^2{{\hat{p}}_j}-{\hat{H}}^2-M{\hat{H}}-\sum _j{\ln {{\hat{p}}}}-\frac{M}{2}+\frac{1}{2}\right] \\&\quad +\frac{1}{n^3}\left[ \sum _j {\hat{p}}_j\ln ^2{{\hat{p}}_j}-{\hat{H}}^2-M{\hat{H}}-\sum _j{\ln {{\hat{p}}_j}}-\right. \\&\quad \left. -\frac{{\hat{H}}}{3}\sum _j{\frac{1}{{\hat{p}}_j}}-\frac{1}{3}\sum _j{\frac{\ln {{\hat{p}}_j}}{{\hat{p}}_j}}-\frac{1}{12}\sum _j{\frac{1}{{\hat{p}}_j}}-\frac{M^2}{4}-\frac{M}{2}+\frac{5}{6}\right] \end{aligned} \end{aligned}$$

From the proof of Lemma 1, we know that

$$\begin{aligned} \begin{aligned} E({\hat{H}}^2)&=H^2+\frac{1}{n}\left[ -H^2+\sum _j p_j\ln ^2(p_j)-MH+H\right] + \\ {}&\quad +\frac{1}{n^2}\left[ \frac{H}{6}-\frac{H}{6}\sum _j\frac{1}{p_j}+\frac{1}{4}M^2-\frac{1}{4}\right] +O(n^{-3}) \end{aligned} \end{aligned}$$

and

$$\begin{aligned} E(M{\hat{H}})=MH+\frac{M-M^2}{2n}+O(n^{-2}). \end{aligned}$$

We can show using Taylor series and moments $\mu _2, \mu _3, \mu _4$ that

$$\begin{aligned} \begin{aligned}&E\left( \sum _j{\hat{p}}_j\ln ^2{\hat{p}}_j\right) =\sum _j p_j\ln ^2{p_j}+\frac{1}{n}\left( \sum _j\ln {p_j}+H+M-1\right) \\&\quad +\frac{1}{n^2}\left( \frac{1}{6}\sum _j\frac{\ln {p_j}}{p_j}+\frac{M}{2}-\frac{1}{4}\sum _j\frac{1}{p_j}+\frac{H}{6}-\frac{1}{4}\right) +O(n^{-3}) \end{aligned} \end{aligned}$$

and

$$\begin{aligned} E\left( \sum _j\ln {{\hat{p}}_j}\right) =\sum _j\ln {p_j}+\frac{1}{n}\left( \frac{M}{2}-\frac{1}{2}\sum _j\frac{1}{p_j}\right) +O(n^{-2}). \end{aligned}$$

We get the result by using the equation

$$\begin{aligned} \begin{aligned}&E\left( -\frac{{\hat{H}}}{3}\sum _j{\frac{1}{{\hat{p}}_j}}-\frac{1}{3}\sum _j{\frac{\ln {{\hat{p}}_j}}{{\hat{p}}_j}}-\frac{1}{12}\sum _j{\frac{1}{{\hat{p}}_j}}\right) \\&=-\frac{H}{3}\sum _j{\frac{1}{p_j}}-\frac{1}{3}\sum _j{\frac{\ln {p_j}}{p_j}}-\frac{1}{12}\sum _j{\frac{1}{p_j}}+O(n^{-1}) \end{aligned} \end{aligned}$$

and substituting all equations in the formula for $E({\hat{\textrm{Var}}})$.

$$\begin{aligned} \begin{aligned} E({\hat{\textrm{Var}}})&=\frac{1}{n}\left[ -H^2+\sum _j p_j\ln ^2(p_j)\right] +\frac{1}{n^2}\left[ \frac{M}{2}-\frac{1}{2}\right] \\&\quad +\frac{1}{6n^3}\left[ (1-H)\sum _j\frac{1}{p_j}-\sum _j{\frac{\ln {p_j}}{p_j}}-1\right] +O(n^{-4}) \end{aligned} \end{aligned}$$

Appendix D Entropies, prices, volumes of BBBY and AMC stocks

Figures 14 and 15 show sample entropies, prices, and trading volumes for the stocks BBBY and AMC, respectively.

Fig. 14

Entropy, price, volume of the BBBY stock. Dots correspond to statistically significant changes in entropy: red for drops in the entropy value, and green for rises (color figure online)

Fig. 15

Entropy, price, volume of the AMC stock. Dots correspond to statistically significant changes in entropy: red for drops in the entropy value, and green for rises (color figure online)

Appendix E: Entropy of Stocks with quarters

Figures 16 and 17 show the sample entropy of stocks obtained after filtering out data regularities using quarterly sets.

Fig. 16

Entropy of meme stocks with quarterly training sets. Dots correspond to statistically significant changes in entropy: red for drops in the entropy value, and green for rises (color figure online)

Fig. 17

Entropy of IT Stocks with quarterly training sets. Dots correspond to statistically significant changes in entropy: red for drops in the entropy value, and green for rises (color figure online)