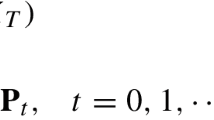Amortization plans in simple, compound and hybrid framework: a unifying approach

Abstract

In this paper, five different types of amortization plans with constant instalments are analyzed with a unified approach: a pair of plans in simple interest regime, a pair of plans in compound interest regime and a plan in a hybrid context. In the two pairs there are a main plan and an auxiliary one. Here we give a comprehensive discussion of all the rules governing these plans, showing similarities and differences. Furthermore, the pair of plans in simple interest regime is at the origin of the hybrid plan, which surprisingly turns out to be a (main) plan in compound regime with variable instalments.

1 Introduction

This paper focuses on mortgage amortization plans and their formulation in the regime of simple and compound interest. We keep as a starting point two papers by Mari-Aretusi (henceforth MA) (Mari and Aretusi 2018; 2019) in order to propose a connection between their approach and a unifying vision, despite relevant differences, of some other types of amortization plans. We deal here only with the case of amortization plans with constant annual instalments. However, we point out that it is quite easy to generalize the approach to the case of non-constant and/or infra-annual instalments.

We consider five types of plans, with the same set of contractual parameters ($D_0$, initial loan balance; N, duration (measured in years) of the contract; i, contractual interest rate on an annual basis¹):

• Two plans characterized by a condition of “financial equivalence” (between lender and borrower payments) under compound capitalization regime (shortly compound regime),

• Two by a condition of “financial equilibrium at the initial date” under the simple interest regime,

• One hybrid that, starting from the simple interest regime, produces a financial equivalence in the compound regime.

These conditions play the role of “feasibility conditions” of the instalment sequence. It obviously follows that two different values of constant instalments correspond to each regime, while in the hybrid plan, the instalments are no longer constant.

It is well known that a mortgage amortization plan is classically described by a numerical table with 4 columns: $\textbf{R}$, instalments; $\textbf{C}$, principal repayments; $\textbf{I}$, interest quotas, and $\textbf{D}$, residual debt. We refer to this as the “main” plan.

In their article MA propose, under the simple interest regime, to “enlarge” the main plan adding three new columns, thus generating the plan called “Extended”. According to the authors, these three additional sequences play only an instrumental role; this would suggest to call them “Auxiliary” sequences.

Here we propose a much more pervasive approach. We consider these additional sequences as the auxiliary counterparts of the classic triplet of repayment quotas (symbol $\varvec{\varGamma }$), interest quotas (symbol $\varvec{\varPhi }$) and residual debt (symbol $\varvec{\varDelta }$). This way an (autonomous) Auxiliary amortization Plan (henceforth AuxP) is provided. Said another way, the Extended Plan in the simple interest regime is the union of two simple interest regime plans: one is the “main” plan with the four classical sequences $(\textbf{R}, \textbf{C}, \textbf{I}, \textbf{D})$ and the other one is the AuxP with sequences $(\textbf{R}, \varvec{\varGamma }, \varvec{\varPhi }, \varvec{\varDelta })$. They have in common the instalment sequence satisfying the feasibility condition of the simple interest regime. The financial meaning of the auxiliary variables has been suggested in the seminal paper by MA.

Our contribution here is to follow an analogous path to understand the financial meaning of the auxiliary sequences under the compound interest regime. We then explore the possibility to produce a cross-plan or “Hybrid” Plan generated by a proper combinations of different sequences coming from a main and an auxiliary plan. This way we are able to provide a formal straightforward definition of such a hybrid plan.

The plan of the paper is as follows. In Sect. 2 we shortly discuss the idea of an Amortization Plan as an input–output algorithm. In Sect. 3, the rules behind the Standardized Traditional Amortization Plans (shortly STAPs) are quickly recalled and commented. Section 4 gives a resume of the approach of Mari-Aretusi to build an Amortization Plan under simple capitalization regime (shortly MAAP). In Sect. 5, taking advantage of MA’s idea to add three new sequences to complete the picture of their plan in a Simple interest regime, we introduce an Auxiliary Plan in the same regime considering these new sequences together with the instalments one (shortly AuxPS). Section 6 is devoted to apply the same approach to generate an Auxiliary Plan in Compound regime starting from the STAP (shortly AuxPC). Finally, in Sect. 7 we propose and discuss the somehow surprising properties of the Hybrid Plan (shortly HP) coming from a proper mixture of the two plans in simple interest regime. Conclusions follow in Sect. 8.

2 The amortization plan as an input–output algorithm

A premise: what is an amortization plan? Something which involves not merely mathematics but also economics, law and accounting. In a narrow sense, it is a set of four sequences (in algebraic terminology, vectors) which describe the plan. The sequences are: instalment payments, reimbursement payments, interest payments and outstanding debt. These sequences should be consistent with the rules, applied to the contractual parameters, which govern the plan. Rules are given as a set of algebraic relationships between those entities.

More technically, an amortization plan is described by an algorithm which transforms, under proper rules, an input $\textbf{X}$ into an output $\textbf{Y}$. Precisely, the input $\textbf{X}$ consists of two elements: the set of contractual parameters $\textbf{x}$ and a trigger sequence which may be either principal quotas $\textbf{C}$ or instalments $\textbf{R}$. In particular, the elements of $\textbf{x}:=(D_0,k,N,{}_{k}i)$ are:

• $D_0$, principal amount at time $t_0$;

• k, frequency of instalments per year;

• $N=T\cdot k$, total number of instalments, given the loan term T (years);

• ${}_{k}i$ effective interest rate referred to the frequency k; it is the concrete interest rate that enters the computations.

Here we concentrate on plans with annual instalments and constant periodic interest rate; thus $k=1$, ${}_{k}i={}_{1}i=i=j$, with j nominal interest rate stated in the loan and, the time interval between two consecutive payments $(t_{h}-t_{h-1})=1$, so that $t_h=h$ for any $h=1, \ldots ,N$.² Henceforth, $\textbf{x}=:(D_0,N,i)$ is our set of contractual parameters.

As for the output $\textbf{Y}$, it may be expressed as a table with four $N-$dimensional vectors which describe the fundamental quantities’ evolution of an amortization plan according to proper rules: $\textbf{C}$, principal reimbursements; $\textbf{I}$, interest quotas; $\textbf{R}$, instalments; $\textbf{D}$, outstanding debts. Table 1 represents the output $\textbf{Y}:(\textbf{C},\textbf{I},\textbf{R},\textbf{D})$ :

Table 1 The amortization plan as a table of four vectors

Let us underline that the vector $\textbf{C}$, or alternatively the vector $\textbf{R}$, are at the same time input (trigger) and output of the plan.

In the next sections we precise their characteristics and discuss different types of plans which, based on the same input $\textbf{x}$, produce different outputs depending on the rules applied for each of them.

In what follows we use the input $\textbf{x}:=(D_0=1000.00,N=4,i=0.10)$ for our examples.

3 The logic of the STAP

In this section we briefly recall the procedure to build the so-called Standardized Traditional Amortization Plans, henceforth STAPs.³

STAPs are surely plans in which the label/name of the four sequences is consistent with the rules that back the plan itself. More specifically, for any $h=1,\ldots , N$, the rules are:

$$\begin{aligned} R_h&=C_h+I_h \end{aligned}$$

(1)

$$\begin{aligned} D_h&=D_0-\sum \limits _{n=1}^{h}C_n=D_{h-1}-C_h \end{aligned}$$

(2)

$$\begin{aligned} I_h&= i\cdot D_{h-1} \end{aligned}$$

(3)

The rule (1) says that the instalment $R_h$, which is the amount of money payable at time h, is the sum of a reimbursement quota $C_h$ and of an interest quota $I_h$ both payable at that time.

The rule (2) defines the outstanding debt $D_h$ at time h, as the initial debt $D_0$ (lender payment at time 0), minus all the reimbursement $C_1+C_2+\ldots +C_h$ payable by the borrower until that time.

The rule (3) specifies how to compute the interest payable at time h. It is coincident with the interest accrued in the $h-$th period. The accrued interest in a period is, in turn, computed as the product of the effective interest rate of the period times the outstanding debt at the beginning of the period.

That’s enough to build a plan characterized by such simple and intuitive rules. No financial sophistication is required to build it, once the triplet of contractual parameters $(D_0, N, i)$, in the simplest case of annual instalments, and the trigger sequence $\textbf{C}$ of agreed reimbursement quotas have been chosen. These quotas, of course, have to satisfy the intuitive feasibility condition that the sum of the reimbursements matches the value of the initial debt; formally:

$$\begin{aligned} \sum _{h=1}^{N}C_h=D_0 \end{aligned}$$

(4)

which, with the further conditions $C_h\ge 0$ for any $h=1,\ldots ,N-1$ (in order to prevent increasing outstanding balances) and $C_N>0$ (concrete duration of the loan not shorter of the contractual one), states that the principal is exactly repaid at the final date. This implies that the so-called closure condition holds:

$$\begin{aligned} D_N=0 \end{aligned}$$

(5)

It may be also checked that the sequence of instalments $\textbf{R}$, obtained in output applying these rules on the input $\textbf{X}:=(\textbf{x},\textbf{C})$, in turn satisfies a more sophisticated financial feasibility condition: the loan amount is equal to the sum of the discounted values, at time 0, of the sequence of instalments; more formally:

$$\begin{aligned} \sum _{h=1}^{N}R_h\,\cdot v(0,h)=D_0 \end{aligned}$$

(6)

where $v(0,h)=\frac{1}{(1+i)^{h}}$ is the discount factor of the interval (0, h) in compound regime.⁴ The further required condition, similar to the one on $\textbf{C}$, is that for each $h=1,\ldots ,N-1$, both $R_h\ge I_h$ and $R_N>I_N$, in order to avoid the possibility of negative reimbursement quotas and, this way, also increasing residual debts.⁵

In this approach, let us rewrite the rule (1) while preserving the others (and, in particular, the one which defines the amount of the interest payable at the end of each period equal to the one accrued in the period). This gives the reimbursement quotas payable at each instalment date as the difference between the instalment trigger $R_h$ and the interest $I_h$ payable at that date. Formally:

$$\begin{aligned} C_h=R_h-I_h \end{aligned}$$

(7)

Now, the following result holds:

Result 1

If in a plan the chosen input of the feasible sequence of instalments $\textbf{R}$ coincides with the sequence of instalments obtained as output in a plan with a given trigger $\textbf{C}$, then the two plans coincide: STAPR and STAPC are called twins.

As a consequence, if the rules of the plan are not trigger-specific, a STAP does not really involve any financial sophistication. Yet, the introduction of such sophistication may be useful, as we shall see, for a better understanding of things.

It turns out that the application of rules (1)-(2)-(3) (and conditions (4) and (6) to their respective feasible input $\textbf{X}=(\textbf{x},\textbf{C})$ and $\textbf{X}=(\textbf{x},\textbf{R})$) produces the following relations for the output $\textbf{Y}$, represented in Table 2:

Table 2 Output relations in a STAP as a function of the input sequence. $v(0,h)=\frac{1}{(1+i)^{h}}$ and $u(0,h)=(1+i)^{h}$

In particular, it is well known that the trigger $\textbf{C}$ needed to obtain constant annual instalments must satisfy the recursive relation $C_{h+1}=C_h\,(1+i)$ with i interest rate stated in the agreement, i.e., the reimbursement quotas are geometrically increasing at the common ratio $(1+i)$ with initial trigger value given by:

$$\begin{aligned} C_1=\frac{D_0\,i}{(1+i)^{N}-1} \end{aligned}$$

(8)

Conversely, the trigger $\textbf{R}$ is given by the well-known solution of Eq. (6):

$$\begin{aligned} R=\frac{D_0\,i}{1-(1+i)^{-N}} \end{aligned}$$

(9)

Table 3 represents an example of a STAP with constant annual instalment $\textbf{R}$.

Table 3 STAP with constant instalment $R=315.47$ and $\textbf{x}:=(D_0=1000.00,N=4,i=10\%)$

Example

With our $\textbf{x}:=(D_0=1000.00,N=4,i=10\%)$ with trigger $\textbf{C}$ geometrically increasing at common ratio $(1+10\%)$ and $C_1$ solution of Eq. (8), or alternatively, with trigger $\textbf{R}$ solution of Eq. (9) according to Result 1, it is:

4 The logic of the MAAP

Here, we recall the approach of Mari-Aretusi (MA) to build a plan under simple capitalization regime, which we label MAAP, MA Amortization Plan.

The MAAP is based on three rules, applied on the same set $\textbf{x}$ of contractual parameters, which still provide the four vectors of a plan $\textbf{Y}:(\textbf{C},\textbf{I},\textbf{R},\textbf{D})$. Formally, the rules of a MAAP are, for any $h=1,\ldots ,N$:

$$\begin{aligned} R_h= & {} C_{h}+I_{h} \end{aligned}$$

(10)

$$\begin{aligned} D_{h}= & {} D_{h-1}-C_h \end{aligned}$$

(11)

$$\begin{aligned} I_h= & {} i\cdot D_{h-1}\cdot v(0,h-1) \end{aligned}$$

(12)

where $v(0,h-1)=\frac{1}{1+i\cdot (h-1)}$ is the discount factor, in the interval $(0,h-1)$, under the simple capitalization regime. The associate capitalization factor is then $u(0,h-1)=1+i\cdot (h-1)$.

It is immediately noted that, with respect to STAP, the only rule that formally changes⁶ is that of the interest quota computation (cf. (3) and (12)). Let us now deepen the meaning of the whole set of rules in the MAAP context and analyze the connection between the latter and the sequences’ labels.

The meaning of the instalment $R_h$ in (10) is clear: it is the amount payable at date h. What is the exact meaning of this rule? If we intend $C_h$ as the reimbursement quota payable at time h, coming from Rule (11) (which defines the outstanding debt), then the meaning of $I_h$ is necessarily an interest quota payment at time h. The rule (12) defines such payment in our interpretation of the MAAP: the interest payable⁷ is not the product of the annual interest rate times the outstanding at the beginning of the period, but the product of the interest rate times a discounted (according to simple interest regime) outstanding.

In the approach of MA, the trigger is the instalments sequence $\textbf{R}$ satisfying the “classical” feasibility condition, but now in the simple interest regime (which is formally the same feasibility condition in STAP, cf. formula (6)):

$$\begin{aligned} \sum \limits _{h=1}^{N}R_h\, v(0,h)=D_0 \end{aligned}$$

(13)

Note that the following interesting properties of the MAAP hold.

Result 2

Given the trigger sequence $\textbf{R}$ (which satisfies the feasibility condition), the output $\textbf{C}$ satisfies, in turn, its corresponding feasibility condition⁸:

$$\begin{aligned} \sum \limits _{h=1}^{N}C_h=D_0 \end{aligned}$$

(14)

Conversely, if we use this sequence $\textbf{C}$ as the trigger of a MAAP, we get the same MAAP as output and, in particular the same $\textbf{R}$ as instalment output.

This confirms that MAAP can be considered the counterpart, under simple interest regime, of STAP under compound regime (so, Result 2 is the analogue of Result 1 in compound regime).

Thus, a MAAP is univocally determined by applying these rules to a feasible input $\textbf{C}$ or, alternatively $\textbf{R}$.⁹ In this framework, the following relations for the output $\textbf{Y}$ of a MAAP are represented in Table 4:

Table 4 Output relations in a MAAP as a function of the input sequence. $v(0,h)=\frac{1}{1+i\cdot h}$ and $u(0,h)=1+i\cdot h$

Let us now consider the case of constant annual instalments, according to the feasibility condition (13) and provide an example of a MAAP.

Example

With our $\textbf{x}$ and $R_h=R$ solution of Eq. (13):

$$\begin{aligned} R=\frac{1000.00}{\sum \limits _{h=1}^{4}(1+0.10\cdot h)^{-1}}=309.99 \end{aligned}$$

by applying the rules, we get the following MAAP:

Table 5 MAAP with constant instalment $R=309.99$ and $\textbf{x}:=(D_0=1000.00,N=4,i=10\%)$

In order to support their approach, the authors introduced three new vectors, which they consider just instrumental or auxiliary for their purpose.¹⁰ and not as a part of a true plan. Nevertheless, these three new vectors have been inserted by the authors in an “extended” plan for a better explanation of the logic of their “main” plan.

In the next section we recall the structure of these vectors and propose to use them, jointly with the instalment one, to build another type of amortization plan, which we name AuxPS, Auxiliary Plan in Simple capitalization regime.

5 Auxiliary plan in simple interest regime

In addition to the instalments sequence $\textbf{R}$, the AuxPS involves three new columns. We name them as $\varvec{\varDelta }$, $\varvec{\varGamma }$, and $\varvec{\varPhi }$.¹¹ Their evolution is now described by the following rules, for any $h=1,\ldots ,N$:

$$\begin{aligned} R_h&=\varGamma _h+\varPhi _h \end{aligned}$$

(15)

$$\begin{aligned} {\varDelta }_h&=\varDelta _{h-1}-\varGamma _h \end{aligned}$$

(16)

$$\begin{aligned} {\varPhi }_h&=\varGamma _h\cdot i\cdot h \end{aligned}$$

(17)

In our interpretation,¹² the structure of these rules is substantially the same of those in the main MAAP; in particular, the instalment (rule (15)) is the sum of an (auxiliary) reimbursement $\varGamma _h$ and of an (auxiliary) interest quota $\varPhi _h$, payable at time h; the (auxiliary) outstanding debt $\varDelta _h$ (rule (16)) is decreasing by the payment of the (auxiliary) reimbursement; the rule (17), with a new formulation, still describes the computation of the (auxiliary) interest payable at time h. This is the accrued interest generated from the (auxiliary) reimbursement quota over the whole interval (0, h) in the simple interest regime.

The comparison between the rules of the main MAAP and those of the AuxPS suggests that each sequence of one plan can be considered a counterpart of the corresponding one in the other plan.

As the sequence $\textbf{R}$ is the same as in MAAP, the feasibility condition to be satisfied in this plan (by the sequence $\textbf{R}$) is still given by (13) and coherently, for the correspondence between $\textbf{D}$ and $\varvec{\varDelta }$, also given by:

$$\begin{aligned} \sum _{h=1}^{N}R_h\,\cdot v(0,h)=\varDelta _0 \end{aligned}$$

(18)

so as $D_0=\varDelta _0$ with $v(0,h)=(1+i\,h)^{-1}$.

Indeed, according to rules (15) and (17), it is, for any h:

$$\begin{aligned} R_h=\varGamma _h+\varPhi _h=\varGamma _h\cdot (1+i\cdot h)=\varGamma _h\, u(0,h) \end{aligned}$$

(19)

and, conversely:

$$\begin{aligned} \varGamma _h=R_h\, v(0,h) \end{aligned}$$

(20)

and according to (18):

$$\begin{aligned} \sum _{h=1}^{N}\varGamma _h=\sum _{h=1}^{N}R_h\,v(0,h)=\varDelta _0=D_0 \end{aligned}$$

(21)

In case of constant instalments, exploiting $\varGamma _{h}+\varPhi _h=\varGamma _{h+1}+\varPhi _{h+1}$, the sequence $\varvec{\varGamma }$ satisfies the following recursive condition:

$$\begin{aligned} \varGamma _{h+1}=\varGamma _{h}\,\frac{u(0,h)}{u(0,h+1)} \end{aligned}$$

(22)

Then, it may be easily shown that:

$$\begin{aligned} \varGamma _h=\varGamma _1\,\frac{u(0,1)}{u(0,h)} \end{aligned}$$

(23)

and

$$\begin{aligned} \sum _{h=1}^{N}\varGamma _h=\varGamma _1\,u(0,1)\,\sum _{h=1}^{N}v(0,h)=\varDelta _0=D_0 \end{aligned}$$

(24)

so that:

$$\begin{aligned} \varGamma _1=\frac{D_0\,v(0,1)}{\sum _{h=1}^{N}v(0,h)} \end{aligned}$$

(25)

Now, starting from (25) and by applying (22), the whole sequence of (auxiliary) reimbursement quotas of the plan with constant instalments trigger is obtained.

Finally, it is easy to check that $\varDelta _h= D_h\, v(0,h)$ for any $h=1,\ldots ,N$ which connects the outstanding sequences of the main and of the auxiliary plan in simple interest regime.

Remark 1

This relation makes clear that the auxiliary outstanding sequence is obtained discounting the outstanding sequence of the main plan and makes clear the connection between the two different rules to compute the sequences of the payable interest in the main and in the auxiliary plan.

Remark 2

We may use the auxiliary reimbursement sequence $\varvec{\varGamma }$ as trigger of the auxiliary plan to obtain the instalment sequence $\textbf{R}$ of the auxiliary plan as an output.

Example

Then, by applying the rules on the usual set of parameters $\textbf{x}$, we get Table 6 describing an AuxPS:

Table 6 AuxP in simple interest regime with constant instalment $R=309.99$ and $\textbf{x}:=(D_0=1000.00,N=4,i=10\%)$

Table 7 Extended MAAP with constant instalment $R=309.99$ and $\textbf{x}:=(D_0=1000.00,N=4,i=10\%)$

Remark 3

A quick comparison between Tables 5 and 6 shows how the sum of the respective interest rate columns is the same, although the composition of the instalments is different in the two plans.

For the sake of completeness, we resume the “extended” MAAP in the Table 7.

Remark 4

We may check that as a consequence of relations (10) and (15), it is $C_h+I_h=R_h=\varGamma _h+\varPhi _h$ for any h.

6 Auxiliary plan in compound regime

Here, starting from a STAP with a given constant instalment sequence $\textbf{R}$, we extend the idea of Auxiliary Plan to the Compound regime (labeled AuxPC) looking for the meaning of the triplet $(\varvec{\varGamma }, \varvec{\varPhi }, \varvec{\varDelta })$, counterpart of $(\textbf{C}, \textbf{I}, \textbf{D})$ triplet.

We use the same rules behind the AuxPS, but in a compound frame. This way we obtain, for any $h=1,\ldots ,N$:

$$\begin{aligned} R_h&=\varGamma _h+\varPhi _h \end{aligned}$$

(26)

$$\begin{aligned} {\varDelta }_h&=\varDelta _{h-1}-\varGamma _h \end{aligned}$$

(27)

$$\begin{aligned} \varPhi _h&=\varGamma _h\, [(1+i)^{h} -1] \end{aligned}$$

(28)

In particular, relation (28) gives the (auxiliary) interest payable at the date h. The interest is produced by the (auxiliary) reimbursement quota $\varGamma _h$ in the period (0, h) in the compound regime. Of course, also the feasibility condition follows the same rule (cf. (18)) but according now to the compound regime.

Then, we use:

$$\begin{aligned} R_h =\varGamma _h+\varPhi _h=\varGamma _h\,[1+(1+i)^{h}-1]=\varGamma _h\, (1+i)^{h} \end{aligned}$$

(29)

which in turn gives:

$$\begin{aligned} \varGamma _h=R_h\, (1+i)^{-h} \end{aligned}$$

(30)

At the end, exploiting still relations (25) and (22), we get the whole sequence of (auxiliary) reimbursement quotas of the plan with constant instalments trigger and, $\varDelta _h=D_h\,v(0,h)$ in compound framework.

Remark 5

The auxiliary reimbursement sequence $\varvec{\varGamma }$ may be use as the trigger of the auxiliary plan to obtain the instalment sequence $\textbf{R}$ of the auxiliary plan as an output.

Example

By applying the rules on the usual set of parameters $\textbf{x}$, we get the following Table 8 table describing an AuxPC:

Table 8 AuxP in compound regime with constant instalment $R=315.47$ and $\textbf{x}:=(D_0=1000.00,N=4,i=10\%)$

Once more the sum of the payable reimbursements and interest quotas of the STAP and of the AuxPC coincide. Moreover, an interesting property emerges:

Remark 6

Both the couple of sequences ($\textbf{C}, \varvec{\varGamma }$), and ($\textbf{I},\varvec{\varPhi }$) are perfectly inverted (cf. Tables 3 and 8).

Just to have an immediate evidence we propose here what could be seen as an “extended” plan in compound regime in Table 9.

7 Hybrid plan

The starting point is a couple of main MAAP and corresponding AuxPS (with constant instalments and $\textbf{x}$, set of contractual parameters).

Now we define Hybrid Plan (HP) the plan whose instalment sequence is:

$$\begin{aligned} R_h^{H}=\varGamma _h+I_h \end{aligned}$$

(31)

where $\varGamma _h$ is the reimbursement quota of AuxPS and $I_h$ is the interest quota of main MAAP.

Table 9 “Extended” STAP with constant instalment $R=315.47$ and $\textbf{x}:=(D_0=1000.00,N=4,i=10\%)$

It turns out that:

Result 3

The sequence $\textbf{R}^{H}$ satisfies the instalment feasibility condition:

$$\begin{aligned} \sum _{h=1}^{N}R_h^{H}\,v(0,h)=D_0 \end{aligned}$$

(32)

but, maybe surprisingly, with v(0, h) of the compound regime.

Now, the following result holds for the HP:

Result 4

Vectors $(\textbf{R}^{H},\textbf{C}^{H}=\varvec{\varGamma })$ are the couple of twin triggers of a STAP.

This means that $\textbf{R}^{H}$ is the trigger instalments of the STAP whose output is $\textbf{Y}^{H}:=(\textbf{C}^{H}=\varvec{\varGamma },\textbf{I}^{H}=\textbf{I}, \textbf{D}^{H}=\varvec{\varDelta }, \textbf{R}^{H}=\textbf{R}^{H})$. Symmetrically, $\textbf{C}^{H}$ is the trigger reimbursement quota of the same STAP.

Remark 7

The $\textbf{R}^{H}$ sequence is not a constant instalment one.

Remark 8

The Hybrid label reflects two facts. The first is that the two components of $\textbf{R}^{H}$ come from two different plans: the main (interest quota, $\textbf{I}$) and the auxiliary (reimbursement quotas, $\varvec{\varGamma }$). The second is that, starting from two components in the simple interest regime, an instalment is obtained in the compound regime: shortly, we go from a simple to a compound world.

Example

Let us represent a HP example in Table 10.

Table 10 HP with reimbursement quota $\varvec{\varGamma }$ of MAAP and interest quota $\textbf{I}$ of AuxPS; $\textbf{x}:=(D_0=1000.00,N=4,i=10\%)$

As it may be checked, the sum of each discounted instalment under compound regime is equal to the initial debt:

$$ \frac{381.81}{(1.1)^1}+\frac{330.14}{(1.1)^2}+\frac{284.44}{(1.1)^3}+\frac{243.56}{(1.1)^4}=1000.00 $$

so respecting the corresponding feasibility condition (32) in Result 3.

So far we have formally introduced five plans: two in simple interest regime, two in compound regime and one hybrid. To the best of our knowledge, these plans have somehow been already proposed in the literature. Without claiming to be exhaustive, here we mention among others (besides STAP universally known): for the main MAAP, see Mari and Aretusi (2018, 2019); for AuxPS, see Fersini and Olivieri (2015), Tabs. (12)-(13), p. 148 and Marcelli (2019), Tab. 1a, p. 64; for AuxPC, see Fersini and Olivieri (2015), eq. (14), p. 140 and Marcelli (2019), Tab. 3b, p. 44; for HP, see Fersini and Olivieri (2015), Tabs. 10-11, pp. 146–147. However, these proposals do not provide a unified approach capable of fully clarify the connections, similarities and differences between them. This is actually our main contribution with this article.

8 Conclusions

We keep as a starting point a couple of relevant papers by Mari e Aretusi. They concern a critique to the classical amortization plans as driven by a compound regime and an alternative proposal of a plan in simple interest regime (main MAAP), which in turn implies the introduction of a triplet of new auxiliary sequences. On this basis, we suggest here to consider such sequences not merely as auxiliary ones, but as sequences which, jointly with the instalment sequence of the main plan, define an auxiliary plan in simple interest regime. This way, the extended plan is the union of two real plans: one main, the MAAP and one auxiliary. The two plans share the same feasibility conditions on the trigger instalment sequence and the same rules, except for the computation of the payable interest sequences.

After that, we suggest to apply the distinction between a main and an auxiliary plan also to the framework of compound regime so as to define an auxiliary version of the (main) well-known STAP (Standardized Traditional Amortization Plan).

Among other things, this approach allows us to shed light on many amortization plans that have often been proposed in recent literature as adhockeries and a source of misunderstandings. In addition, we clearly recognize that one of these plans reveals to have an amphibious or hybrid character. It is a plan whose instalment sequence is obtained by adding the sequence of reimbursement payable in the auxiliary plan and the sequence of interest payable in the main plan, both in simple interest regime. It turns out that this plan coincides with the STAP in compound regime with trigger the sequence of reimbursement of the auxiliary plan in simple interest regime. Apart from the differences all plans discussed satisfy the fundamental connection of input–output changeability of the couple of twin triggers: the sequence of instalments and the sequence of reimbursements.